
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1111, August 2014 --- Screen Reader
Version*
The Domestic and International Effects of Interstate U.S. Banking
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper studies the domestic and international effects of national bank market integration in a two-country, dynamic, stochastic, general equilibrium model with endogenous producer entry. Integration of banking across localities reduces the degree of local monopoly power of financial intermediaries. The economy that implements this form of deregulation experiences increased producer entry, real exchange rate appreciation, and a current account deficit. The foreign economy experiences a long-run increase in GDP and consumption. Less monopoly power in financial intermediation results in less volatile business creation, reduced markup countercyclicality, and weaker substitution effects in labor supply in response to productivity shocks. Bank market integration thus contributes to moderation of firm-level and aggregate output volatility. In turn, trade and financial ties allow also the foreign economy to enjoy lower GDP volatility in most scenarios we consider. These results are consistent with features of U.S. and international fluctuations after the United States began its transition to interstate banking in the late 1970s.
Keywords: Business cycle volatility, current account, deregulation, interstate banking, producer entry, real exchange rate
JEL classification: E32, F32, F41, G21
1 Introduction
The U.S. banking system was highly segmented within and across states until the late 1970s. For decades, a myriad of state and federal laws limited where banks could operate. States effectively barred banks from other states, so the country had fifty banking systems instead of one national banking system (Morgan, Rime, and Strahan, 2004). Moreover, most states also prohibited cross-county branching within the state, so the country effectively had as many banking systems as counties. Starting in the late 1970s, successive waves of state-level deregulation lifted restrictions on bank expansion both within and across states. By the early 1990s, almost all states had removed such restrictions. The transition to interstate banking was completed with passage of federal legislation in the mid 1990s.1
What are the domestic and international consequences of this type of financial market reform? This paper addresses this question in a two-country, dynamic, stochastic, general equilibrium (DSGE) model with endogenous producer entry and a role for financial intermediation. We argue that the removal of banking segmentation may have contributed to U.S. and international macroeconomic dynamics between the beginning of the 1980s and the mid-2000s.
A growing literature emphasizes the role of producer entry as a mechanism for propagation of domestic and international fluctuations.2 With the exceptions of Notz (2012) and Stebunovs (2008), the models in this literature assume that entrants finance their entry costs by raising capital in a perfectly competitive stock market. However, bank finance is a more realistic assumption for small firms, which represent a large portion of the U.S. economy.3 The structure of the banking system is thus likely to affect entry decisions and the propagation of fluctuations, and changes in the banking system itself can trigger macroeconomic dynamics through their impact on business creation.
In fact, there is substantial empirical evidence of the connection between producer entry and the structure of banking in the United States. This evidence emphasizes that potential entrants in product markets face greater difficulty gaining access to credit in localities where banking is concentrated and subject to tighter restrictions on geographical expansion than in localities where banking is more competitive (Black and Strahan, 2002, Cetorelli and Strahan, 2006, and Kerr and Nanda, 2007). These and other studies emphasize that the transition to interstate banking in the U.S.--a form of financial market deregulation--reduced the local monopoly power of commercial banks, facilitating access to finance for new entrants in product markets and resulting in an increased number of operating non-financial establishments.4
We study the domestic and international effects of such easier access to entry finance. Our model builds on Ghironi and Melitz (2005) and Bilbiie, Ghironi, and Melitz (2012) by assuming that investment in the economy takes the form of the creation of new production lines (for convenience, identified with firms). Sunk costs and a time-to-build lag induce the number of firms to respond slowly to shocks, consistent with the notion that the number of productive units is fixed in the short run. Following Stebunovs (2008), we assume that new entrants must obtain funds from financial intermediaries (henceforth, banks) to cover entry costs. Bank markets are initially segmented across different locations within each country in our model, and local market power induces banks to erect a financial barrier to firm entry to protect the profitability of lending. This reduces average entry relative to the competitive benchmark, as in the evidence documented by Black and Strahan (2002), Cetorelli and Strahan (2006), and Kerr and Nanda (2007).5 We take bank concentration as exogenous, and we study the consequences of the removal of within-country banking segmentation, resulting in a decrease in the local monopoly power of banks, in one of the countries in our model.
We show that the economy that implements this deregulation experiences increased producer entry, real exchange rate appreciation, and a current account deficit. Reduced local monopoly power of banks makes the economy that deregulates a relatively more attractive environment for potential entrants, and the number of firms that operate in the economy increases, consistent with the findings of the empirical finance literature. Average firm size decreases, as documented by Cetorelli and Strahan (2006) and Kerr and Nanda (2007). As in Ghironi and Melitz (2005), entry in the economy that deregulates pushes relative labor costs upward, inducing real appreciation. (Non-traded goods and trade costs cause deviations from purchasing power parity--PPP--in the model.) Moreover, when we allow for international borrowing and lending, domestic bank market integration induces the economy that deregulates to run a current account deficit to finance increased firm entry. The foreign economy experiences higher GDP and consumption in the long run.
Comparing business cycle fluctuations around the pre- and post-deregulation steady states, we also show that less monopoly power in financial intermediation results in less volatile business creation, reduced markup countercyclicality, and weaker substitution effects in labor supply in response to productivity shocks--the source of business cycles in our model. Removal of banking segmentation thus contributes to moderation of firm-level and aggregate output volatility.6 In turn, trade and financial ties between the two countries allow also the foreign economy to enjoy lower GDP volatility in most scenarios we consider. Welfare rises in both countries.
Interpreting the economy that removes banking segmentation in our exercise as the United States, the predictions of our model are qualitatively consistent with features of U.S. and international macroeconomic dynamics following the waves of U.S. banking integration that started at the end of the 1970s: The U.S. experienced real appreciation and significant external borrowing in the first half of the 1980s and after the mid-1990s--periods that followed the first wave of deregulation and the completion of the transition to interstate banking, respectively. The decades after the early 1980s--and before the crisis that begun in 2007--were also marked by a reduction of macroeconomic volatility. Thus, our paper offers a new explanation of developments in the U.S. and international business cycle that complements those already present in the literature.7
The conventional explanation for the contemporaneous occurrence of U.S. exchange rate appreciation and external borrowing in the 1980s relies on the traditional Mundell-Fleming analysis of the consequences of expansion in government spending and the monetary policy contraction implemented by Paul Volcker's Federal Reserve. But the tight association between federal budget and external balance has been challenged by more recent literature. For instance, Erceg, Guerrieri, and Gust (2005) find that a fiscal deficit has a relatively small effect on the U.S. trade balance, irrespective of whether the source is a spending increase or a tax cut. With respect to U.S. trade balance and real exchange rate dynamics in the second half of the 1990s, Hunt and Rebucci (2005) conclude that accelerating productivity growth in the U.S. contributed only partly to appreciation and trade balance deterioration.
Recent contributions highlight the role of financial market characteristics and business cycle volatility as a source of external imbalances. Caballero, Farhi, and Gourinchas (2008) rationalize the burgeoning U.S. deficits since the mid-1990s as the outcome of heterogeneity in countries' ability to generate financial assets and cross-country growth rate differentials. Mendoza, Quadrini, and Ríos-Rull (2009) argue that imbalances can be the outcome of international financial integration when countries differ in financial market development (interpreted as the enforcement of financial contracts) and show that countries with more advanced financial markets accumulate foreign liabilities in a gradual, long-lasting process. Finally, Fogli and Perri (2006) argue that imbalances are a consequence of business cycle moderation in the U.S. In their model, if a country experiences a fall in volatility greater than that of its partners, its relative incentive to accumulate precautionary savings weakens, and this causes a deterioration of its external balance.8 The moderation of business cycle volatility between the 1980s and the crisis that began in 2007--often referred to as the Great Moderation--has been the subject of extensive literature that attributes it partly to favorable changes in the shocks to the economy and partly to improved policy.9
Our paper complements this literature by highlighting the effects of increased competition in U.S. banking relative to the rest of the world.10 We emphasize that our results hinge on lower bank monopoly power at the local level. Even if bank consolidation was a documented phenomenon in the U.S. since the 1980s, it is well established by the empirical finance literature referenced above that interstate banking reduced the degree of bank monopoly power at the level of local borrowers--put differently, while the total number of U.S. banks may have declined as a result of consolidation, the number of those represented at any given location tended to increase, generating the effects that we capture. In our model, a differential in the competitiveness of the banking system induces real appreciation of the dollar and U.S. external borrowing by making the U.S. a more attractive environment for business creation. As in Caballero, Farhi, and Gourinchas (2008), Mendoza, Quadrini, and Rí os-Rull (2009), and Fogli and Perri (2006), current account deficit and the accumulation of a persistent (although not permanent) net foreign debt position arise as an equilibrium phenomenon. While Caballero, Fahri, and Gourinchas do not link business cycle moderation with global imbalances, and Fogli and Perri take moderation as exogenous, our model implies that both external borrowing and eventual business cycle moderation occur endogenously.11 An element of similarity between our approach and those of Caballero, Fahri, and Gourinchas and Mendoza, Quadrini, and Rí os-Rull is that net foreign asset imbalances arise as a consequence of capital mobility across asymmetric financial systems: In Caballero, Fahri, and Gourinchas, there is asymmetric ability to generate financial assets; in Mendoza, Quadrini, and Ríos-Rull, there is asymmetric enforcement of financial contracts; in our model, the removal of within-country bank market segmentation results in an asymmetric degree of banking competition across countries.12
The remainder of the paper is organized as follows. Section 2 presents the model under a balanced trade assumption. Section 3 discusses real exchange rate determination and the mechanism for appreciation following banking deregulation. Section 4 presents a numerical exercise that substantiates the results and intuitions of Section 3. Section 5 introduces international capital flows to show the emergence of external borrowing in response to deregulation. Section 6 incorporates countercyclical firm markups and elastic labor supply to highlight the mechanism for the moderation of business cycle volatility. Section 7 concludes. The online Appendix--henceforth referred to simply as the Appendix--contains additional material and technical details.
2 The Model
We begin by developing the model under financial autarky. This allows us to focus on its most innovative features.
The world consists of two countries, home and foreign. We denote foreign variables with an asterisk. Each country is populated by a unit mass of atomistic, identical households, a discrete number of banks, and a continuum of firms. In each country, there are several exogenously given locations with a discrete number of banks and a local continuum of firms in each of them. Monopolistically competitive firms in the traded sector must borrow from banks to finance sunk entry costs, and they have no collateral to pledge except a stream of future profits.13 Each traded-sector firm produces a firm-specific consumption good for sale in the domestic and export markets. Firm entry reduces the stream of future profits of both incumbents and entrants--and thus the amount pledgeable for entry loan repayments--by reducing the share of aggregate demand allocated to each firm.
Before deregulation, firms are restricted to borrow from local banks. These use their monopoly power on the loans they issue to extract all the future profits from the prospective entrants they finance. Each bank holds a portfolio of outstanding loans and decides on the number of new loans to be issued (that is, on the number of entrants to be financed) in each period.14 Each bank trades the increase in revenue from expanding its portfolio of firms (portfolio expansion effect) against the decrease in revenue from all firms in its portfolio due to reduced market share per firm (profit destruction effect). The profit destruction effect induces credit rationing at the extensive margin: Less prospective entrants receive funding than with perfectly competitive financial markets. Each bank supplies one-period deposits to domestic households in a perfectly competitive deposit market. The bank then uses the deposits to fund firm entry. Thus, the cost that each bank faces is the deposit interest rate. Bank deregulation lifts the restriction on borrowing from banks at a different location within the country. The number of banks to which a borrower has access increases, hence reducing bank monopoly power.15
For expositional simplicity, we present the model economy
normalizing the number of banking locations in each country to
1. (This normalization is without loss of
generality because we assume that locations are completely
symmetric ex ante and ex post, and within-country
banking integration implies no net asset flows across locations.)
We denote the number of banks represented at this location with
![]() (
(![]() in the
foreign country). If the number of locations were
in the
foreign country). If the number of locations were ![]() , following integration of the home banking market, the
product
, following integration of the home banking market, the
product ![]() would replace
would replace ![]() in the
equations where this appears below: Before deregulation,
prospective entrants can borrow only from the
in the
equations where this appears below: Before deregulation,
prospective entrants can borrow only from the ![]() banks represented at their location; after deregulation, they can
borrow from
banks represented at their location; after deregulation, they can
borrow from ![]() banks. Having normalized the number of
locations to one, this is isomorphic to an increase in the number
banks. Having normalized the number of
locations to one, this is isomorphic to an increase in the number
![]() of banks represented at this
location.16
of banks represented at this
location.16![]() 17
17
All contracts and prices in the world economy are written in nominal terms. Prices are flexible. Thus, we only solve for the real variables in the model. However, as the composition of consumption baskets in the two countries changes over time (affecting the definitions of the consumption-based price indexes), we introduce money as a convenient unit of account for contracts. Money plays no other role. For this reason, we do not model the demand for cash currency, and we resort to a cashless economy as in Woodford (2003).
We focus on the home economy in presenting the structure of the model and relegate equations for the foreign country to Table 1.
Households
The representative home household supplies ![]() units of labor inelastically in each period at the nominal wage
rate
units of labor inelastically in each period at the nominal wage
rate ![]() , denominated in units of home currency.
The household maximizes expected intertemporal utility from
consumption
, denominated in units of home currency.
The household maximizes expected intertemporal utility from
consumption ![]() ,
,
![]() , where
, where
![]() is the subjective discount
factor and
is the subjective discount
factor and ![]() is the inverse of the
intertemporal elasticity of substitution, subject to the budget
constraint specified below. At time
is the inverse of the
intertemporal elasticity of substitution, subject to the budget
constraint specified below. At time ![]() , the
household consumes the basket of goods
, the
household consumes the basket of goods
![]() , where
, where![]() is a basket of home and foreign
tradable goods,
is a basket of home and foreign
tradable goods, ![]() is a non-tradable good, and
is a non-tradable good, and
![]() is the weight of the
tradable basket in consumption.18 The consumption-based price index
is
is the weight of the
tradable basket in consumption.18 The consumption-based price index
is
![]() , where
, where ![]() is the price index of the tradable
basket, and
is the price index of the tradable
basket, and ![]() is the price of the non-tradable
good. The basket of tradable goods is
is the price of the non-tradable
good. The basket of tradable goods is
 , where
, where ![]() is the symmetric elasticity of
substitution. At any given time
is the symmetric elasticity of
substitution. At any given time ![]() , only a subset of
goods
, only a subset of
goods
![]() is actually
available for consumption at home and abroad. Let
is actually
available for consumption at home and abroad. Let
![]() denote the home currency price
of traded good
denote the home currency price
of traded good
![]() . Then,
. Then,
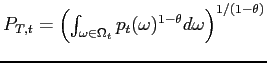 . The household's demand for each individual traded good
. The household's demand for each individual traded good
![]() is
is
![]() . The household's demand for the non-tradable good is
. The household's demand for the non-tradable good is
![]() .
.
The foreign household is modeled similarly. Importantly, the
subset of tradable goods available for consumption in the foreign
economy during period ![]() coincides with the subset of
tradable goods that are available in the home economy (
coincides with the subset of
tradable goods that are available in the home economy (
![]() ).
).
Households in each country hold two types of assets: one-period
deposits supplied by domestic banks and shares in a mutual fund of
domestic banks.19![]() 20 We
assume that deposits pay risk-free, consumption-based real returns.
(Nominal returns are indexed to consumer price inflation, so that
deposits provide a risk-free, real return in units of the
consumption basket.) Let
20 We
assume that deposits pay risk-free, consumption-based real returns.
(Nominal returns are indexed to consumer price inflation, so that
deposits provide a risk-free, real return in units of the
consumption basket.) Let ![]() be the share in the
mutual fund of
be the share in the
mutual fund of ![]() home banks held by the
representative home household entering period
home banks held by the
representative home household entering period ![]() .
The mutual fund pays a total profit in each period (in units of
currency) equal to the total profit of all home banks,
.
The mutual fund pays a total profit in each period (in units of
currency) equal to the total profit of all home banks,
![]() , where
, where
![]() denotes the profit of home bank
denotes the profit of home bank
![]() . During period
. During period ![]() , the
household buys
, the
household buys ![]() shares in the mutual fund.
The date
shares in the mutual fund.
The date ![]() price (in units of currency) of a claim to
the future profit stream of the mutual fund is equal to the nominal
price of claims to future profits of home banks,
price (in units of currency) of a claim to
the future profit stream of the mutual fund is equal to the nominal
price of claims to future profits of home banks,
![]() , where
, where ![]() is the price of claims to future profits of bank
is the price of claims to future profits of bank
![]() . In addition to mutual fund share holdings
. In addition to mutual fund share holdings
![]() , the household enters period
, the household enters period
![]() with deposits
with deposits ![]() in units
of consumption. It receives gross interest income on deposits,
dividend income on mutual fund share holdings, the value of selling
its initial share position, and labor income. The household
allocates these resources between consumption and purchases of
deposits and shares to be carried into next period. The period
budget constraint (in units of consumption) is
in units
of consumption. It receives gross interest income on deposits,
dividend income on mutual fund share holdings, the value of selling
its initial share position, and labor income. The household
allocates these resources between consumption and purchases of
deposits and shares to be carried into next period. The period
budget constraint (in units of consumption) is
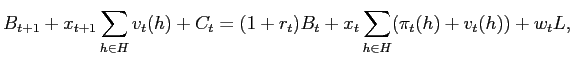 |
(1) |
where ![]() is the consumption-based interest rate
on holdings of deposits between
is the consumption-based interest rate
on holdings of deposits between ![]() and
and ![]() (known with certainty at
(known with certainty at ![]() ), and
), and
![]() is the real wage. The home
household maximizes its expected intertemporal utility subject to
(1).
is the real wage. The home
household maximizes its expected intertemporal utility subject to
(1).
The Euler equations for deposits and share holdings are:
![]() and
and
![]() where
where
![]() and
and
![]() .
We omit the transversality conditions for deposits and shares.
Forward iteration of the Euler equation for share holdings and
absence of speculative bubbles yield the value of the mutual fund,
.
We omit the transversality conditions for deposits and shares.
Forward iteration of the Euler equation for share holdings and
absence of speculative bubbles yield the value of the mutual fund,
![]() , as expected present discounted value
of the stream of bank profits,
, as expected present discounted value
of the stream of bank profits,
![]() . Similar Euler
equations, transversality conditions, and expression for
. Similar Euler
equations, transversality conditions, and expression for
![]() hold abroad.
hold abroad.
Firms
Traded Goods Producers
There is a continuum traded-sector of firms in each country,
each producing a different traded variety
![]() . Aggregate labor
productivity is indexed by
. Aggregate labor
productivity is indexed by ![]() , which
represents the effectiveness of one unit of home labor. Production
requires only one factor, labor: The output of firm
, which
represents the effectiveness of one unit of home labor. Production
requires only one factor, labor: The output of firm ![]() is
is
![]() , where
, where
![]() is the amount of labor
employed by the firm. The unit production cost, measured in units
of consumption, is
is the amount of labor
employed by the firm. The unit production cost, measured in units
of consumption, is
![]() . Traded goods producers serve
both their domestic and export markets. Exporting is costly, and it
involves a melting-iceberg trade cost
. Traded goods producers serve
both their domestic and export markets. Exporting is costly, and it
involves a melting-iceberg trade cost ![]() .
Foreign traded-sector firms are modeled similarly.
.
Foreign traded-sector firms are modeled similarly.
All traded goods producers face a residual demand curve with
constant elasticity ![]() in both markets, and
they set flexible prices that reflect the same proportional markup
in both markets, and
they set flexible prices that reflect the same proportional markup
![]() over marginal
cost. Let
over marginal
cost. Let
![]() and
and
![]() denote the nominal domestic
and export prices of a home firm (in the currency of the
destination market). Define the relative prices
denote the nominal domestic
and export prices of a home firm (in the currency of the
destination market). Define the relative prices
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
Then,
.
Then,
![]() and
and
![]() where
where
![]() is
the consumption-based real exchange rate (units of home consumption
per unit of foreign consumption), and
is
the consumption-based real exchange rate (units of home consumption
per unit of foreign consumption), and
![]() is the nominal exchange rate
(units of home currency per unit of foreign). Total profits of firm
is the nominal exchange rate
(units of home currency per unit of foreign). Total profits of firm
![]() in period
in period ![]() are given by
are given by
![]() , where
, where
![]() denotes profits from domestic sales and
denotes profits from domestic sales and
![]() denotes profits from exports. Since all firms behave identically
in equilibrium, we drop the index
denotes profits from exports. Since all firms behave identically
in equilibrium, we drop the index ![]() below.
21
below.
21
Non-Traded Good Producers
There is a constant mass of firms in each country producing the
homogeneous non-traded good. These firms are perfectly competitive
and possess the same technology as the firms producing traded
goods.22Labor is perfectly mobile across
sectors in each country. Hence, the price of the non-traded good,
in real terms relative to the domestic price index, is given by
![]() .
Foreign non-traded good producers behave similarly.
.
Foreign non-traded good producers behave similarly.
Banks and Firm Entry
In every period there is an unbounded number of prospective
entrants in both countries' traded sectors. Prior to entry, firms
face a sunk entry cost of one effective labor unit, equal to
![]() units of consumption in the home
country (
units of consumption in the home
country (
![]() units of foreign
consumption abroad). Since there are no fixed production costs, all
firms produce in every period, until they are hit with an exogenous
exit shock, which occurs with probability
units of foreign
consumption abroad). Since there are no fixed production costs, all
firms produce in every period, until they are hit with an exogenous
exit shock, which occurs with probability
![]() in every period. Entrants
are forward looking, and correctly anticipate their future expected
profits
in every period. Entrants
are forward looking, and correctly anticipate their future expected
profits ![]() in every period as well as the
probability
in every period as well as the
probability ![]() (in every period) of incurring
the exit-inducing shock. Unspecified financial frictions force
entrants to borrow the amount necessary to cover the sunk entry
cost from a local bank in the firm's domestic market. Since the
bank has all the bargaining power, it sets the entry loan repayment
in each period at
(in every period) of incurring
the exit-inducing shock. Unspecified financial frictions force
entrants to borrow the amount necessary to cover the sunk entry
cost from a local bank in the firm's domestic market. Since the
bank has all the bargaining power, it sets the entry loan repayment
in each period at ![]() to extract all the firm
profit.23
to extract all the firm
profit.23
There is a number ![]() of forward looking banks in
the home country, which compete in Cournot fashion over the number
of loans issued. Each bank takes the decisions of its competitors
as given. Bank
of forward looking banks in
the home country, which compete in Cournot fashion over the number
of loans issued. Each bank takes the decisions of its competitors
as given. Bank ![]() has
has ![]() producing firms in its portfolio and decides simultaneously with
other banks on the number of entrants to fund,
producing firms in its portfolio and decides simultaneously with
other banks on the number of entrants to fund,
![]() taking into account the
post-entry firm profit maximization as each firm sets optimal
prices for its product.24
taking into account the
post-entry firm profit maximization as each firm sets optimal
prices for its product.24
We assume that entrants at time ![]() only start
producing at time
only start
producing at time ![]() , which introduces a
one-period time-to-build lag in the model. The exogenous exit shock
occurs at the very end of the time period (after production and
entry). A proportion of new entrants will therefore never produce.
The bank does not know which firms will be hit by the exogenous
exit shock
, which introduces a
one-period time-to-build lag in the model. The exogenous exit shock
occurs at the very end of the time period (after production and
entry). A proportion of new entrants will therefore never produce.
The bank does not know which firms will be hit by the exogenous
exit shock ![]() at the very end of period
at the very end of period
![]() The timing of entry and production
implies that the number of firms in bank
The timing of entry and production
implies that the number of firms in bank ![]() 's
portfolio during period
's
portfolio during period ![]() is given by
is given by
![]() . Then, the number of producing home firms in period
. Then, the number of producing home firms in period ![]() is
is
![]() , where
, where
![]() , and
the number of home entrants is
, and
the number of home entrants is
![]() . As
in Bilbiie, Ghironi, and Melitz (2012) and Ghironi and Melitz
(2005), the number of producing firms in period
. As
in Bilbiie, Ghironi, and Melitz (2012) and Ghironi and Melitz
(2005), the number of producing firms in period ![]() is an endogenous state variable that behaves like physical capital
in standard real business cycle models.
is an endogenous state variable that behaves like physical capital
in standard real business cycle models.
The Euler equation for household holdings of shares in the bank
fund implies that the objective function for bank ![]() is
is
![]() , which the bank maximizes with respect to
, which the bank maximizes with respect to
![]() and
and
![]() . Bank
. Bank
![]() 's profit is
's profit is
![]() , where
, where
![]() is the revenue from bank
is the revenue from bank
![]() 's portfolio of
's portfolio of ![]() outstanding loans (or producing firms),
outstanding loans (or producing firms),
![]() denotes household deposits into
bank
denotes household deposits into
bank ![]() entering period
entering period ![]() (so
that
(so
that
![]() ),
),
![]() is the amount lent
to
is the amount lent
to
![]() entrants, and
entrants, and
![]() is the
principal and interest on the previous period's deposits. We assume
that banks accrue revenues after firm entry has been funded and
then rebate profits to the mutual fund owned by households. Hence,
bank
is the
principal and interest on the previous period's deposits. We assume
that banks accrue revenues after firm entry has been funded and
then rebate profits to the mutual fund owned by households. Hence,
bank ![]() 's balance sheet constraint is
's balance sheet constraint is
![]() . In
solving its optimization problem, bank
. In
solving its optimization problem, bank ![]() takes
aggregate consumption, wages, and the interest rate as given.
takes
aggregate consumption, wages, and the interest rate as given.
The first-order condition with respect to
![]() yields the Euler equation for the
value of a firm producing in period
yields the Euler equation for the
value of a firm producing in period ![]() to bank
to bank
![]() ,
, ![]() which
involves a term capturing the bank's internalization of the profit
destruction externality (PDE) generated by firm entry:
which
involves a term capturing the bank's internalization of the profit
destruction externality (PDE) generated by firm entry:
![$\displaystyle q_{t}(h)=\beta E_{t}\left\{ \left( \frac{C_{t+1}}{C_{t}}\right) ^{-\gamma } \left[ d_{t+1}+\underset{\text{Internalization of PDE}}{\underbrace{ N_{t+1}(h)\frac{\partial d_{t+1}}{\partial N_{t+1}}\frac{\partial N_{t+1}}{ \partial N_{t+1}(h)}}}+(1-\delta )q_{t+1}(h)\right] \right\} .$](img146.gif) |
The bank internalizes the effect of entry on firm profits through
the effect of entry on the domestic and export relative prices
![]() and
and
![]() . Firm entry reduces firm size
and profits, and hence decreases the repayments to the bank. The
bank internalizes only the effects of the entry it funds. Hence,
. Firm entry reduces firm size
and profits, and hence decreases the repayments to the bank. The
bank internalizes only the effects of the entry it funds. Hence,
![]() multiplies the profit destruction
externality,
multiplies the profit destruction
externality,
![]() . (See the Appendix for details.)
. (See the Appendix for details.)
The first-order condition with respect to
![]() defines a firm entry condition,
which holds with equality as long as the number of entrants,
defines a firm entry condition,
which holds with equality as long as the number of entrants,
![]() , is positive. We verified that
this is the case in every period in all our exercises. Entry occurs
until the value of an additional producer to the bank,
, is positive. We verified that
this is the case in every period in all our exercises. Entry occurs
until the value of an additional producer to the bank, ![]() , is equalized with the expected, discounted entry
cost, given by the deposit principal and the interest to be paid
back at
, is equalized with the expected, discounted entry
cost, given by the deposit principal and the interest to be paid
back at ![]() :
:
 |
(2) |
where the second equality follows from the household's Euler
equation for deposits. The cost of creating a firm to be repaid at
![]() is known with certainty as of period
is known with certainty as of period
![]() . As there is no difference between the
bank's valuation of a marginal new entrant and its valuation of an
incumbent, firm entry reduces not only the value of entering firms,
but also the value of incumbents until the value of all firms is
equalized with the sunk entry cost (adjusted by a premium for the
risk of firm exit).25
. As there is no difference between the
bank's valuation of a marginal new entrant and its valuation of an
incumbent, firm entry reduces not only the value of entering firms,
but also the value of incumbents until the value of all firms is
equalized with the sunk entry cost (adjusted by a premium for the
risk of firm exit).25
Since all banks are identical, we impose symmetry to obtain the
Nash equilibrium. The equation for firm value, ![]() , becomes:
, becomes:
![$\displaystyle q_{t}=\beta E_{t}\left\{ \left( \frac{C_{t+1}}{C_{t}}\right) ^{-\gamma } \left[ \left( 1-\frac{1}{H}\right) d_{t+1}+(1-\delta )q_{t+1}\right] \right\} .$](img163.gif) |
(3) |
The parameter ![]() plays the same role in the banking
market that
plays the same role in the banking
market that ![]() plays in the goods market. At
one extreme,
plays in the goods market. At
one extreme, ![]() or absolute bank monopoly, equation
(3) implies that there is no entry as the
marginal (and average) return from funding an entrant is zero: The
portfolio expansion effect is totally offset by profit
destruction.26The economy is starved of firm
entry--and thus, eventually, of any activity.27 Bank market
power decreases as
or absolute bank monopoly, equation
(3) implies that there is no entry as the
marginal (and average) return from funding an entrant is zero: The
portfolio expansion effect is totally offset by profit
destruction.26The economy is starved of firm
entry--and thus, eventually, of any activity.27 Bank market
power decreases as ![]() increases. At the other
extreme,
increases. At the other
extreme,
![]() , equation (3) simplifies to the usual asset pricing equation
of a perfectly competitive market.
, equation (3) simplifies to the usual asset pricing equation
of a perfectly competitive market.
Equation (3) allows us to relate our results on the effects of bank monopoly power on firm creation to Hayashi's (1982) results on the consequences of firm monopoly power for capital accumulation. Solving (3) forward yields:
 |
where
![]() corresponds to the average
corresponds to the average ![]() of Hayashi (1982):
of Hayashi (1982):
![]() would be the valuation of an
additional firm (or unit of capital) producing at time
would be the valuation of an
additional firm (or unit of capital) producing at time ![]() generated by a perfectly competitive financial market
(for instance, by a competitive market for shares in firms). As
demonstrated by Hayashi, the existence of monopoly power induces a
discrepancy between average
generated by a perfectly competitive financial market
(for instance, by a competitive market for shares in firms). As
demonstrated by Hayashi, the existence of monopoly power induces a
discrepancy between average ![]() and marginal
and marginal
![]() --the measure of
--the measure of ![]() that
determines decisions. In our model, monopoly power in banking
results in a proportional mark-down (
that
determines decisions. In our model, monopoly power in banking
results in a proportional mark-down (
![]() ) of the value of firms
to the bank relative to the competitive valuation (much as monopoly
power in production of goods results in a proportional markup
) of the value of firms
to the bank relative to the competitive valuation (much as monopoly
power in production of goods results in a proportional markup
![]() relative to
competitive pricing and would induce marginal
relative to
competitive pricing and would induce marginal ![]() to be lower than average
to be lower than average ![]() if firms accumulated
capital). As in Hayashi's capital accumulation model, the
discrepancy between average and marginal
if firms accumulated
capital). As in Hayashi's capital accumulation model, the
discrepancy between average and marginal ![]() disappears as the economy approaches the competitive benchmark (
disappears as the economy approaches the competitive benchmark (
![]() ). Monopoly power causes
marginal
). Monopoly power causes
marginal ![]() to be below average
to be below average ![]() because additional firm creation (or capital accumulation)
conflicts with a monopolist's incentive to reduce supply relative
to the competitive benchmark in order to generate higher profit.
The results of our model thus parallel those of traditional theory
of capital accumulation.
because additional firm creation (or capital accumulation)
conflicts with a monopolist's incentive to reduce supply relative
to the competitive benchmark in order to generate higher profit.
The results of our model thus parallel those of traditional theory
of capital accumulation.
Although the model does not feature an explicit bank markup, we
can define a measure of ex post bank markup as
![]() . The ratio
. The ratio
![]() measures the
relative return from funding a marginal (and average) firm. Similar
equations and bank markup definition hold abroad.28
measures the
relative return from funding a marginal (and average) firm. Similar
equations and bank markup definition hold abroad.28
Aggregate Accounting and Balanced Trade
Aggregating the budget constraint (1) across
home households and imposing the equilibrium conditions
![]() and
and
![]() yields the
aggregate accounting equation
yields the
aggregate accounting equation
![]() . Consumption
in each period must equal labor income plus investment income net
of the cost of investing in new firms. Since this cost,
. Consumption
in each period must equal labor income plus investment income net
of the cost of investing in new firms. Since this cost,
![]() , is the value
of home investment in new firms, aggregate accounting also states
the familiar equality of spending (consumption plus investment) and
income (labor plus dividend). The right-hand side of the aggregate
accounting equation defines GDP from the income side of the
economy; the left-hand side defines GDP from the spending side. We
denote GDP with
, is the value
of home investment in new firms, aggregate accounting also states
the familiar equality of spending (consumption plus investment) and
income (labor plus dividend). The right-hand side of the aggregate
accounting equation defines GDP from the income side of the
economy; the left-hand side defines GDP from the spending side. We
denote GDP with ![]() below.
below.
To close the model, observe that financial autarky implies
balanced trade: The value of home exports must equal the value of
foreign exports. Hence,
![]() . As in Ghironi and Melitz (2005), balanced trade under financial
autarky implies labor market clearing: Aggregate labor supply must
be equal to the total amount of labor employed in production of
goods and creation of new firms:
. As in Ghironi and Melitz (2005), balanced trade under financial
autarky implies labor market clearing: Aggregate labor supply must
be equal to the total amount of labor employed in production of
goods and creation of new firms:
![]() . Fluctuations result in reallocation of labor between production
of existing goods and creation of new ones.
. Fluctuations result in reallocation of labor between production
of existing goods and creation of new ones.
Model Summary
Table 1 summarizes the main equilibrium conditions of the model.
The equations in the table constitute a system of 29 equations in 29 variables endogenously determined at
time ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() . The
model features two exogenous variables: the aggregate
productivities
. The
model features two exogenous variables: the aggregate
productivities ![]() and
and
![]() . We model domestic bank market
integration as a one-time, permanent increase in the number of home
banks,
. We model domestic bank market
integration as a one-time, permanent increase in the number of home
banks, ![]() . Since this is the only change we allow in
the number of banks, we do not denote the latter with a time
subscript to economize on notation.
. Since this is the only change we allow in
the number of banks, we do not denote the latter with a time
subscript to economize on notation.
3 Interstate Banking and the Real Exchange Rate
This section discusses real exchange rate determination in our model and the mechanism for appreciation following banking deregulation. A property of our model with exogenously non-traded goods is that we do not need to differentiate between welfare-consistent and data-consistent real exchange rates. As discussed in Ghironi and Melitz (2005), welfare-consistent price indexes in this class of models must be adjusted by removing pure variety effects in order to obtain price indexes that correspond to the data. In Ghironi and Melitz's model with endogenously non-traded goods, this implies a difference between welfare- and data-consistent real exchange rates. By contrast, in our model, consumers have access to the same set of tradable (and traded) goods in the two countries, and they attach identical weights to non-tradable consumption. This implies that welfare- and data-consistent real exchange rates coincide. (See the Appendix for details. This property no longer holds in the model with home bias, as we show in the Appendix.)
Using the price index equations, we obtain:
![$\displaystyle Q_{t}=\left( TOL_{t}\right) ^{1-\alpha }\left[ \frac{\frac{N_{t}^{\ast }}{ N_{t}}\left( TOL_{t}\right) ^{1-\theta }+\tau ^{1-\theta }}{1+\frac{ N_{t}^{\ast }}{N_{t}}\left( \tau ^{\ast }TOL_{t}\right) ^{1-\theta }}\right] ^{\frac{\alpha }{1-\theta }},$](img246.gif) |
(4) |
where, following Ghironi and Melitz (2005), we defined the terms of
labor
![]() The terms of labor measure the relative cost of effective labor
across countries. A decrease in
The terms of labor measure the relative cost of effective labor
across countries. A decrease in ![]() indicates an
appreciation of home effective labor relative to foreign. Note
that, absent trade costs (
indicates an
appreciation of home effective labor relative to foreign. Note
that, absent trade costs (
![]() ), the real exchange
rate reduces to
), the real exchange
rate reduces to
![]() ,
reflecting the presence of non-traded goods with weight
,
reflecting the presence of non-traded goods with weight ![]() in consumption. PPP holds if there are no trade
costs and
in consumption. PPP holds if there are no trade
costs and ![]() .
.
Dropping time subscripts to denote a variable's level in steady
state, we assume
![]() . Assume further that the
number of banks is equal in the two countries in the initial steady
state (
. Assume further that the
number of banks is equal in the two countries in the initial steady
state (
![]() ) and that
) and that
![]() and
and
![]() . The model then features a
unique, symmetric steady state with
. The model then features a
unique, symmetric steady state with ![]() . (The
solution for the steady-state levels of selected variables is in
the Appendix.) Log-linearizing equation (4)
around the steady state yields:
. (The
solution for the steady-state levels of selected variables is in
the Appendix.) Log-linearizing equation (4)
around the steady state yields:
 |
(5) |
where we use sans serif fonts to denote percentage deviations from
the steady state. It is possible to verify that the coefficients of
![]() and
and
![]() in
this equation are strictly positive (as long as
in
this equation are strictly positive (as long as ![]() ). An appreciation of home effective labor relative
to foreign induces real exchange rate appreciation. In the absence
of trade costs, this is motivated by an increase in the relative
price of the non-traded good. Trade costs strengthen the effect of
the terms of labor on the real exchange rate (since
). An appreciation of home effective labor relative
to foreign induces real exchange rate appreciation. In the absence
of trade costs, this is motivated by an increase in the relative
price of the non-traded good. Trade costs strengthen the effect of
the terms of labor on the real exchange rate (since
![]() )
by causing the appreciation of the former to induce an increase
also in the relative price of home traded goods. In contrast, an
increase in the number of home traded goods relative to foreign
induces the real exchange rate to depreciate. The reason is that
the number of varieties on which home households are not paying
trade costs rises, with a positive welfare effect. (The portion
)
by causing the appreciation of the former to induce an increase
also in the relative price of home traded goods. In contrast, an
increase in the number of home traded goods relative to foreign
induces the real exchange rate to depreciate. The reason is that
the number of varieties on which home households are not paying
trade costs rises, with a positive welfare effect. (The portion
![]() of the
coefficient of
of the
coefficient of
![]() reflects the welfare benefit of additional traded goods.) The
empirically plausible restriction
reflects the welfare benefit of additional traded goods.) The
empirically plausible restriction
![]() is sufficient for the
coefficient of
is sufficient for the
coefficient of
![]() to be strictly larger than
the coefficient of
to be strictly larger than
the coefficient of
![]() in
equation (5).
in
equation (5).
Consider now a permanent increase in the number of home banks
![]() (holding the number of foreign banks
constant). Reduced monopoly power induces home banks to finance a
larger number of entrants. This amounts to a decrease in effective
entry costs facing firms.29 From the perspective of prospective
entrants, relative to the old steady state, the decrease in
monopoly power of home banks makes the home economy a more
attractive location. Absent any change in the relative cost of
effective labor (
(holding the number of foreign banks
constant). Reduced monopoly power induces home banks to finance a
larger number of entrants. This amounts to a decrease in effective
entry costs facing firms.29 From the perspective of prospective
entrants, relative to the old steady state, the decrease in
monopoly power of home banks makes the home economy a more
attractive location. Absent any change in the relative cost of
effective labor (![]() ), all new firms would only
enter the home economy (there would be no new entrants into
foreign). Thus, in the new long-run equilibrium, home effective
labor must appreciate (
), all new firms would only
enter the home economy (there would be no new entrants into
foreign). Thus, in the new long-run equilibrium, home effective
labor must appreciate (![]() must decrease) in
order to keep the foreign traded sector from disappearing.30 It
is precisely the entry of a larger number of firms into home that
puts pressure on home labor demand and induces the terms of labor
to appreciate. In turn, this causes real exchange rate appreciation
as described above. As we show below, for plausible parameter
values, the terms of labor effect prevails on the variety term in
equation (5), implying that an economy with
permanently more competitive banking (relative to its trading
partners) has a permanently appreciated real exchange rate.31
must decrease) in
order to keep the foreign traded sector from disappearing.30 It
is precisely the entry of a larger number of firms into home that
puts pressure on home labor demand and induces the terms of labor
to appreciate. In turn, this causes real exchange rate appreciation
as described above. As we show below, for plausible parameter
values, the terms of labor effect prevails on the variety term in
equation (5), implying that an economy with
permanently more competitive banking (relative to its trading
partners) has a permanently appreciated real exchange rate.31
To conclude this section, we note that the results and intuitions we discussed do not depend on the assumption of financial autarky. Equations (4)-(5) hold also when households can hold deposits abroad (or under any other assumption on international asset markets), and terms of labor and variety remain the fundamental determinants of real exchange rate dynamics.
4 Interstate Banking and Macroeconomic Dynamics Under Financial Autarky
In this section, we substantiate the results and intuitions of Section 3 by means of a numerical example, which allows us to characterize the full response path of the home and foreign economies to home banking deregulation from the impact period of the shock to the new long run. For consistency with the discussion in Section 3, we log-linearize the system in Table 1 around the initial, symmetric steady state under assumptions of log-normality and homoskedasticity. We verified that a global, Newton-type solution algorithm yields similar results.
Calibration
We interpret periods as quarters and set
![]() and
and ![]() ,
both standard choices for quarterly business cycle models. (The
choice of log utility from consumption is motivated by consistency
with the elastic labor supply case below, where we restrict utility
to the log case for the properties of separable preferences
discussed by King, Plosser, and Rebelo, 1988.) We follow Ghironi
and Melitz (2005) for the calibration of most remaining parameters.
We set the size of the exogenous firm exit shock
,
both standard choices for quarterly business cycle models. (The
choice of log utility from consumption is motivated by consistency
with the elastic labor supply case below, where we restrict utility
to the log case for the properties of separable preferences
discussed by King, Plosser, and Rebelo, 1988.) We follow Ghironi
and Melitz (2005) for the calibration of most remaining parameters.
We set the size of the exogenous firm exit shock
![]() to match the U. S. empirical
level of 10 percent job destruction per year.32 We
posit
to match the U. S. empirical
level of 10 percent job destruction per year.32 We
posit
![]() , which fits U.S. plant and macro
trade data as shown by Bernard, Eaton, Jensen, and Kortum
(2003).33 We postulate that
, which fits U.S. plant and macro
trade data as shown by Bernard, Eaton, Jensen, and Kortum
(2003).33 We postulate that
![]() , which is in line
with Anderson and van Wincoop (2004) and Obstfeld and Rogoff
(2001). Given the trade cost, we calibrate the share of tradable
goods in consumption to match the average 12
percent U.S. import share of GDP. (The steady-state import share of
GDP is
, which is in line
with Anderson and van Wincoop (2004) and Obstfeld and Rogoff
(2001). Given the trade cost, we calibrate the share of tradable
goods in consumption to match the average 12
percent U.S. import share of GDP. (The steady-state import share of
GDP is
![]() .) This results in
.) This results in
![]() . As noted above, we set labor
effort,
. As noted above, we set labor
effort,
![]() , and steady-state productivity,
, and steady-state productivity,
![]() , equal to 1
without loss of generality. These parameters determine the size of
economy but leave dynamics unaffected.
, equal to 1
without loss of generality. These parameters determine the size of
economy but leave dynamics unaffected.
With respect to banking, we set the initial steady-state number
of banks
![]() such that it implies a bank
markup of about 10 percentage points. To determine
the size of the banking deregulation shock, we calculate the change
in
such that it implies a bank
markup of about 10 percentage points. To determine
the size of the banking deregulation shock, we calculate the change
in ![]() that induces a 12 percent
long-run increase in the number of firms in the home country. This
choice is based on the evidence from the empirical finance
literature: Using the new business incorporations series compiled
by Dun and Bradstreet Corporation, Black and Strahan (2002) find
that the number of new incorporations per capita rose by
3.8 percent following the removal of
restrictions on intrastate branching; the number of new
incorporations per capita rose by another 7.9
percent following the removal of restrictions on interstate
banking. Hence, the move from pervasive segmentation (no branching
or interstate banking) to integrated banking (branching and
interstate banking) increased the number of non-financial
establishments by 11.7 percentage points. Using
the County Business Patterns series compiled by the Census Bureau,
Cetorelli and Strahan (2006) find that the transition to interstate
banking and the associated increase in banking competition
increased the number of non-financial establishments by 11.6 percent and reduced establishment size by 12.3 percent in the external-finance-dependent sectors
relative to non-dependent sectors.34 Importantly, the size
of the change in
that induces a 12 percent
long-run increase in the number of firms in the home country. This
choice is based on the evidence from the empirical finance
literature: Using the new business incorporations series compiled
by Dun and Bradstreet Corporation, Black and Strahan (2002) find
that the number of new incorporations per capita rose by
3.8 percent following the removal of
restrictions on intrastate branching; the number of new
incorporations per capita rose by another 7.9
percent following the removal of restrictions on interstate
banking. Hence, the move from pervasive segmentation (no branching
or interstate banking) to integrated banking (branching and
interstate banking) increased the number of non-financial
establishments by 11.7 percentage points. Using
the County Business Patterns series compiled by the Census Bureau,
Cetorelli and Strahan (2006) find that the transition to interstate
banking and the associated increase in banking competition
increased the number of non-financial establishments by 11.6 percent and reduced establishment size by 12.3 percent in the external-finance-dependent sectors
relative to non-dependent sectors.34 Importantly, the size
of the change in ![]() that we consider does not affect
qualitative results.
that we consider does not affect
qualitative results.
Impulse Responses
Figure 1 shows selected responses (percent deviations from steady state) to a permanent banking deregulation in the home economy. The number of quarters after the shock is on the horizontal axis. In plot titles, H refers to home and F to foreign.
Consider first the long-run effects in the new steady state.
These substantiate the discussion in Section 3. With the fall in
bank monopoly power, the home economy draws a permanently higher
number of entrants: Profits per firm, ![]() , are
permanently lower, as firms are now smaller. This results in a
lower valuation of firms under perfectly competitive finance,
, are
permanently lower, as firms are now smaller. This results in a
lower valuation of firms under perfectly competitive finance,
![]() (not shown). However, this is more
than offset by the smaller mark-down of
(not shown). However, this is more
than offset by the smaller mark-down of ![]() implied by a larger number of banks,
implied by a larger number of banks, ![]() . This
implies that the value of firms to banks,
. This
implies that the value of firms to banks, ![]() ,
rises, eliciting more entry. Lower bank monopoly power also
translates in a lower bank markup,
,
rises, eliciting more entry. Lower bank monopoly power also
translates in a lower bank markup,
![]() , profits,
, profits, ![]() ,
and prices of bank shares,
,
and prices of bank shares, ![]() . The return
on bank shares is pinned down by the discount factor
. The return
on bank shares is pinned down by the discount factor ![]() in steady state, so there is no long-run effect of the
banking deregulation on this variable. Increased financing of entry
translates into a permanently higher number of producers and
generates higher labor demand and upward pressure on wages. This
induces the terms of labor,
in steady state, so there is no long-run effect of the
banking deregulation on this variable. Increased financing of entry
translates into a permanently higher number of producers and
generates higher labor demand and upward pressure on wages. This
induces the terms of labor, ![]() , to
appreciate, causing appreciation of the real exchange rate,
, to
appreciate, causing appreciation of the real exchange rate,
![]() . The less regulated economy exhibits
higher prices relative to its trading partner.35 Consumption
increases at home and abroad, due to higher income and the access
to a larger range of (home) tradable goods. Notice that the number
of foreign firms is essentially unaffected: While foreign firm
profits are higher as a consequence of higher consumption demand,
and
. The less regulated economy exhibits
higher prices relative to its trading partner.35 Consumption
increases at home and abroad, due to higher income and the access
to a larger range of (home) tradable goods. Notice that the number
of foreign firms is essentially unaffected: While foreign firm
profits are higher as a consequence of higher consumption demand,
and
![]() rises, there is no noticeable
adjustment in foreign entry. This mirrors Ghironi and Melitz's
(2005) result that home product market deregulation causes
increased domestic entry but has a very small effect on foreign
entry.36
rises, there is no noticeable
adjustment in foreign entry. This mirrors Ghironi and Melitz's
(2005) result that home product market deregulation causes
increased domestic entry but has a very small effect on foreign
entry.36
We next describe the transitional dynamics in response to the
permanent deregulation. Absent sunk entry costs, and the associated
time-to-build lag before production, the number of producing firms,
![]() , would immediately adjust to its new
steady-state level. Sunk costs and time-to-build transform
, would immediately adjust to its new
steady-state level. Sunk costs and time-to-build transform
![]() into a state variable that behaves
very much like a capital stock: The number of entrants,
into a state variable that behaves
very much like a capital stock: The number of entrants, ![]() , represents home investment, which translates into
increases in the stock
, represents home investment, which translates into
increases in the stock ![]() over time. (The figures
plot the end-of-period response of the number of firms.) The terms
of labor steadily appreciate with the increase in home labor demand
generated by entry. The gradual increase in
over time. (The figures
plot the end-of-period response of the number of firms.) The terms
of labor steadily appreciate with the increase in home labor demand
generated by entry. The gradual increase in ![]() and
domestic labor costs is associated with gradually declining firm
profits,
and
domestic labor costs is associated with gradually declining firm
profits, ![]() , after the initial fall. The paths of
firm profits and consumption at home combine to produce an impact
decline in
, after the initial fall. The paths of
firm profits and consumption at home combine to produce an impact
decline in ![]() that overshoots the new
long-run level before increasing toward it. As a consequence,
that overshoots the new
long-run level before increasing toward it. As a consequence,
![]() (a re-scaling of
(a re-scaling of ![]() ) rises on impact and during the transition. While
the bank markup,
) rises on impact and during the transition. While
the bank markup,
![]() , declines monotonically, bank
profits,
, declines monotonically, bank
profits, ![]() , fall in the short term by more
than in the long run and converge toward the new long-run level
from below, reflecting the gradual expansion in the portfolio of
loans. This is mirrored in the behavior of bank share prices,
, fall in the short term by more
than in the long run and converge toward the new long-run level
from below, reflecting the gradual expansion in the portfolio of
loans. This is mirrored in the behavior of bank share prices,
![]() . The return from holding bank shares
rises on impact and returns to the steady state monotonically. As
we shall note in more detail below, the countercyclical response of
bank markups to shocks in our model is consistent with the
empirical evidence.
. The return from holding bank shares
rises on impact and returns to the steady state monotonically. As
we shall note in more detail below, the countercyclical response of
bank markups to shocks in our model is consistent with the
empirical evidence.
The dynamics of several foreign variables are qualitatively
similar to those at home. Perhaps the most significant difference
is that foreign firm profits fall initially, but rise above the
initial steady state quickly. This causes
![]() ,
,
![]() , and the price of shares in
foreign banks to rise above the initial level shortly after an
impact decline. Home consumption decreases in the short run, as
households save to finance the entry of new firms with increased
deposits into banks. Foreign consumption also falls in the short
run, as foreign real depreciation increases the cost of purchasing
home goods. We note that the real exchange rate change unfolds
slowly. Reaching the new long-run level takes over seven years.
Finally, GDP initially declines in both countries before rising
above the initial level. As shown in the Appendix, the responses to
banking deregulation are qualitatively similar when the model
features home bias in preferences for tradables rather than
non-traded goods.
, and the price of shares in
foreign banks to rise above the initial level shortly after an
impact decline. Home consumption decreases in the short run, as
households save to finance the entry of new firms with increased
deposits into banks. Foreign consumption also falls in the short
run, as foreign real depreciation increases the cost of purchasing
home goods. We note that the real exchange rate change unfolds
slowly. Reaching the new long-run level takes over seven years.
Finally, GDP initially declines in both countries before rising
above the initial level. As shown in the Appendix, the responses to
banking deregulation are qualitatively similar when the model
features home bias in preferences for tradables rather than
non-traded goods.
To conclude this section, we quantify the direct welfare effects
of banking deregulation (abstracting from its implications for the
business cycle) by computing the percentage increase ![]() in consumption that would leave the representative
household in each country indifferent between alternative banking
regulation regimes. Denote with
in consumption that would leave the representative
household in each country indifferent between alternative banking
regulation regimes. Denote with ![]() the
(symmetric) steady-state level of consumption when bank markets are
segmented across different locations within each country, and let
the
(symmetric) steady-state level of consumption when bank markets are
segmented across different locations within each country, and let
![]() and
and
![]() be the consumption levels
in the two countries following banking deregulation at home. Time
subscripts in
be the consumption levels
in the two countries following banking deregulation at home. Time
subscripts in ![]() and
and
![]() capture the presence of
transition dynamics following deregulation, which we assume to be
implemented at time
capture the presence of
transition dynamics following deregulation, which we assume to be
implemented at time ![]() . The consumption
equivalent
. The consumption
equivalent ![]() is obtained by solving the
following equation:
is obtained by solving the
following equation:
![$\displaystyle \sum_{t=0}^{\infty }\beta ^{t}u(C_{t}^{D})=\frac{u\left[ \left( 1+\frac{ \Delta }{100}\right) C^{SBM})\right] }{1-\beta },$](img338.gif) |
and similarly abroad. As shown in Table 3, home banking deregulation improves welfare in both countries. Quantitatively, welfare gains are significantly larger at home (1.15 percent of pre-deregulation steady-state consumption, approximately ten times as abroad). We obtain a similar result in the model with home bias (see the Appendix).
5 International Deposits
We now extend the model of the previous section to allow households to hold deposits abroad.37 We study how international deposits affect the results we have previously described and how microeconomic dynamics affect the current account in our model. Since the extension to international deposits does not involve especially innovative features relative to the financial autarky setup, we limit ourselves to describing its main ingredients in words here and present the relevant model equations in the Appendix.
We assume that banks can supply deposits domestically and
internationally. Home deposits, issued to home and foreign
households, are denominated in home currency. Foreign deposits,
issued to home and foreign households, are denominated in foreign
currency. We maintain the assumption that nominal returns are
indexed to inflation in each country, so that deposits issued by
each country provide a risk-free return measured in units of that
country's consumption basket. International asset markets are
incomplete, as only risk-free deposits are traded across countries.
We assume that agents must pay quadratic transaction fees to banks
when adjusting their deposits abroad. Banks then rebate the
revenues from deposit adjustment fees to households. These fees pin
down a unique deterministic steady-state allocation of deposits
with zero net foreign assets and ensure stationary responses of the
model to non-permanent shocks. Since agents pay fees only when they
adjust their deposits abroad, the steady state of the model with
international deposits coincides with the steady state of the model
under financial autarky. In particular,
![]() ,
,
![]() , and
, and
![]() , where
, where ![]() (
(
![]() ) is home (foreign)
holdings of home (foreign) deposits,
) is home (foreign)
holdings of home (foreign) deposits, ![]() (
(![]() ) is home (foreign) holdings of
foreign (home) deposits, and we assumed
) is home (foreign) holdings of
foreign (home) deposits, and we assumed
![]() . Realistic parameter values
imply that the cost of adjusting deposits has a very small impact
on model dynamics, other than pinning down the deterministic steady
state and ensuring mean reversion in the long run when shocks are
transitory.38
. Realistic parameter values
imply that the cost of adjusting deposits has a very small impact
on model dynamics, other than pinning down the deterministic steady
state and ensuring mean reversion in the long run when shocks are
transitory.38
In equilibrium, the markets for home and foreign deposits clear,
and each country's net foreign assets entering period ![]() depend on interest income from deposit holdings entering
period
depend on interest income from deposit holdings entering
period ![]() , labor income, net investment income, and
consumption during period
, labor income, net investment income, and
consumption during period ![]() . The change in net
foreign deposit holdings between
. The change in net
foreign deposit holdings between ![]() and
and ![]() is the country's current account. Home and foreign
current accounts add to zero when expressed in units of the same
consumption basket. There are now three Euler equations in each
country: the Euler equation for share holdings, which is unchanged,
and Euler equations for holdings of domestic and foreign deposits.
Euler equations for deposits in each country imply a no-arbitrage
condition between domestic and foreign deposits. The balanced trade
condition closed the model under financial autarky. Since trade is
no longer balanced with international deposits, we must explicitly
impose labor market clearing conditions in both countries. These
conditions state that the amount of labor used in production and to
cover entry costs in each country must equal labor supply in that
country in each period.
is the country's current account. Home and foreign
current accounts add to zero when expressed in units of the same
consumption basket. There are now three Euler equations in each
country: the Euler equation for share holdings, which is unchanged,
and Euler equations for holdings of domestic and foreign deposits.
Euler equations for deposits in each country imply a no-arbitrage
condition between domestic and foreign deposits. The balanced trade
condition closed the model under financial autarky. Since trade is
no longer balanced with international deposits, we must explicitly
impose labor market clearing conditions in both countries. These
conditions state that the amount of labor used in production and to
cover entry costs in each country must equal labor supply in that
country in each period.
As before, we analyze the response path of the real exchange
rate and other key variables to a permanent banking deregulation.
We set the scale parameter for the deposit adjustment cost,
![]() , to 0.0025--sufficient
to generate stationarity in response to transitory shocks (such as
the productivity shocks we will consider below), but small enough
to avoid overstating the role of this friction in determining the
dynamics of our model.
, to 0.0025--sufficient
to generate stationarity in response to transitory shocks (such as
the productivity shocks we will consider below), but small enough
to avoid overstating the role of this friction in determining the
dynamics of our model.
Interstate Banking and Macroeconomic Dynamics under Incomplete Markets
As under financial autarky, we consider the responses to a
deregulation of home banking (a permanent increase in the number of
home banks, ![]() ) such that the number of home
producers increases by 12 percent in the long-run.
Figure 2 shows the results. To save space, we do not discuss the
behavior of bank markups, profits, share prices, and the value of
firms to the bank in this scenario. Most responses are
qualitatively similar to Figure 1.
) such that the number of home
producers increases by 12 percent in the long-run.
Figure 2 shows the results. To save space, we do not discuss the
behavior of bank markups, profits, share prices, and the value of
firms to the bank in this scenario. Most responses are
qualitatively similar to Figure 1.
Initially, households in both countries reduce consumption to
finance increased producer entry in the deregulated home economy.
Home runs current account deficits for approximately two years in
response to the shock, resulting in the accumulation of a
persistent net foreign debt position. Home households borrow from
abroad to finance higher initial investment (relative to financial
autarky) in new home firms. The home household's incentive to
front-load producer entry is mirrored by the foreign household's
desire to invest in the more attractive economy. Although home
consumption declines initially, it is permanently higher in the
long run. Foreign consumption moves by more than in Figure 1 as
foreign households initially save in the form of foreign lending
and then receive income from their positive asset position.
Although foreign households cannot hold shares in the mutual fund
of home banks (since deposits are the only international financial
asset), the return on deposit holdings is tied to the return on
holdings of shares in home banks by no-arbitrage between deposits
and shares within the home economy. Therefore, foreign households
share the benefits of expansion in the home economy via
international deposit holdings. As in the case of financial
autarky, ![]() must decrease in the long run (home
effective labor must relatively appreciate); otherwise, all new
entrants would choose to locate in the home economy. The
accelerated entry of new home firms financed by external borrowing
induces an immediate relative increase in home labor demand, and
must decrease in the long run (home
effective labor must relatively appreciate); otherwise, all new
entrants would choose to locate in the home economy. The
accelerated entry of new home firms financed by external borrowing
induces an immediate relative increase in home labor demand, and
![]() immediately appreciates (as opposed
to a gradual appreciation under financial autarky). Thus, the real
exchange rate
immediately appreciates (as opposed
to a gradual appreciation under financial autarky). Thus, the real
exchange rate ![]() also immediately
appreciates.39 The opening of the economy to
international deposits does not qualitatively change the mechanism
that leads to real exchange rate appreciation following banking
deregulation in our model. Foreign consumption and GDP increase in
the long run, even though the number of foreign producers is
reduced by the relocation of business creation to the home country.
Higher income and the permanent expansion in the number of home
producers more than compensates the loss in the number of foreign
firms to determine the increase in long-run foreign consumption.
Finally, as under financial autarky, banking deregulation in one
country improves welfare in both countries (see Table 3 ).
also immediately
appreciates.39 The opening of the economy to
international deposits does not qualitatively change the mechanism
that leads to real exchange rate appreciation following banking
deregulation in our model. Foreign consumption and GDP increase in
the long run, even though the number of foreign producers is
reduced by the relocation of business creation to the home country.
Higher income and the permanent expansion in the number of home
producers more than compensates the loss in the number of foreign
firms to determine the increase in long-run foreign consumption.
Finally, as under financial autarky, banking deregulation in one
country improves welfare in both countries (see Table 3 ).
The Role of Market Incompleteness
Before turning to two model extensions that deliver more persistent current account deficits, we briefly discuss the role of market incompleteness for our results. We present selected figures in the Appendix.
Market incompleteness interacts with substitutability between domestic and foreign products to determine the extent of international borrowing and lending. High substitutability and internationally complete asset markets strengthen the incentive and ability to shift resources toward the home economy to finance the investment expansion in new products triggered by bank deregulation. With complete markets, this transfer of resources is not encoded in history dependence of the equilibrium allocation, and net foreign assets are determined residually. With incomplete markets, the equilibrium allocation depends on the net foreign assets position at the beginning of each period. Under both scenarios, external borrowing--the transfer of resources in response to deregulation--increases with the share of tradables in consumption or, in the model with home bias, with the extent to which preferences are biased toward domestic goods. In both cases, the stronger incentive of home households to invest in creation of new domestic products drives the result. The effects of tradable share and home bias are consistent with the analysis in Corsetti, Dedola, and Leduc (2008).40
With respect to international relative prices, expansion in the number of producers results in appreciation of the terms of labor, improvement of the terms of trade, and appreciation of the data-consistent real exchange rate in response to banking deregulation under both complete and incomplete markets. (The welfare-consistent real exchange rate depreciates in the long run in the model with home bias.) A larger tradable share or home bias parameter amplifies the appreciation of the data-consistent real exchange rate by inducing larger expansion in home product creation.
Persistent Current Account Deficits
Figure 2 shows that the home country runs current account deficits for two years following the banking deregulation. U.S. current account deficits have been longer lasting in the 1980s and 1990s. However, it is easy to extend our model to generate more persistent deficits while preserving the other key results. For instance, the current account deficit is significantly more persistent if the banking deregulation is treated as an anticipated, rather than unanticipated, event. This is a plausible scenario, considering the legislative process required by the deregulation. Figure 3 presents the results when the deregulation is expected to happen two years in the future. As the figure shows, the home country starts borrowing immediately, to finance increased business creation in anticipation of the coming deregulation, and the current account deficit lasts for three years.
Another way to increase current account persistence is to assume
that the entry cost depends on the number of existing firms as in
Grossman and Helpman (1991). Suppose that creating a new firm
requires
![]() units of
effective labor. When
units of
effective labor. When
![]() , there is a positive
externality from the number of existing firms to entry costs. The
intuition is that product creation is easier in an environment
where there has been much creation in the past.41 Figure 4 presents
the responses to (unanticipated) banking deregulation in this
scenario, with
, there is a positive
externality from the number of existing firms to entry costs. The
intuition is that product creation is easier in an environment
where there has been much creation in the past.41 Figure 4 presents
the responses to (unanticipated) banking deregulation in this
scenario, with
![]() for illustrative purposes.
This version of the model results in a significantly more
persistent deficit, lasting approximately eight years. Since
current entry reduces future entry costs, the incentive to borrow
to finance firm creation is strengthened, and this propagates the
deficit over time.
for illustrative purposes.
This version of the model results in a significantly more
persistent deficit, lasting approximately eight years. Since
current entry reduces future entry costs, the incentive to borrow
to finance firm creation is strengthened, and this propagates the
deficit over time.
We have thus established two consequences of lower local monopoly power of banks: real exchange rate appreciation and external borrowing to finance increased business creation. Next, we turn to a more quantitative version of our model to study the consequences of interstate banking for macroeconomic volatility.
Interstate Banking and International Business Cycles
We now extend the model with international deposits to incorporate countercyclical firm markups and elastic labor supply. Assuming that fluctuations in home and foreign productivity are the sources of international business cycles, this allows us to illustrate the mechanism behind the moderation of business cycle volatility generated by interstate banking in our model. This extension exploits the implications of endogenous variety by allowing for endogenous demand elasticity and countercyclical firm markups.
The representative home household now supplies ![]() units of labor endogenously in each period. The
household maximizes expected intertemporal utility from consumption
and labor effort subject to the same budget constraint as in the
previous section. Expected intertemporal utility is
units of labor endogenously in each period. The
household maximizes expected intertemporal utility from consumption
and labor effort subject to the same budget constraint as in the
previous section. Expected intertemporal utility is
![$ E_{t}\sum_{s=t}^{\infty }\beta ^{s-t}\left[ \log C_{s}-\chi \left( L_{s}\right) ^{1+1/\varphi }/\left( 1+1/\varphi \right) \right] $](img367.gif) , where
, where ![]() is the weight of disutility of
labor effort, and
is the weight of disutility of
labor effort, and
![]() is the Frisch elasticity of
labor supply to wages. The household's intertemporal optimality
conditions remain the same. The only additional optimality
condition is the intratemporal optimality condition for labor
supply. Elastic labor supply implies that households have an extra
margin of adjustment to shocks. This enhances the propagation
mechanism of the model by amplifying the responses of endogenous
variables with respect to the benchmark model.
is the Frisch elasticity of
labor supply to wages. The household's intertemporal optimality
conditions remain the same. The only additional optimality
condition is the intratemporal optimality condition for labor
supply. Elastic labor supply implies that households have an extra
margin of adjustment to shocks. This enhances the propagation
mechanism of the model by amplifying the responses of endogenous
variables with respect to the benchmark model.
To generate endogenously fluctuating markups, we now define the
baskets of goods over discrete numbers of home and foreign
varieties.42 The basket of tradable goods now is
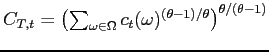 ; hence,
; hence,
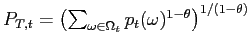 . Each producer no longer ignores the effects of its nominal
domestic price,
. Each producer no longer ignores the effects of its nominal
domestic price,
![]() , on the home tradable price
index,
, on the home tradable price
index, ![]() , and the effect of its nominal
export price,
, and the effect of its nominal
export price,
![]() , on the foreign tradable
price index,
, on the foreign tradable
price index,
![]() .43 Home demand elasticity
is then
.43 Home demand elasticity
is then
![$ \theta _{D,t}(\omega )\equiv \theta \left[ 1-\left( p_{D,t}(\omega )/P_{T,t}\right) ^{1-\theta }\right] $](img376.gif) and foreign demand elasticity is
and foreign demand elasticity is
![$ \theta _{X,t}(\omega )\equiv \theta \left[ 1-\left( p_{X,t}(\omega )/P_{T,t}^{\ast }\right) ^{1-\theta }\right] $](img377.gif) . Note that taking into account this indirect price effect
decreases the demand elasticities for firm
. Note that taking into account this indirect price effect
decreases the demand elasticities for firm ![]() :
:
![]() and
and
![]() ; hence, it
increases its monopoly power in both markets. The implied markup is
; hence, it
increases its monopoly power in both markets. The implied markup is
![]() in the domestic market and
in the domestic market and
![]() in the foreign market. Firms set flexible prices that reflect
these different markups over marginal cost in the different markets
where they sell their output.44 As before, define the relative
prices
in the foreign market. Firms set flexible prices that reflect
these different markups over marginal cost in the different markets
where they sell their output.44 As before, define the relative
prices
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
Then,
.
Then,
![]() and
and
![]() . Profits generated by domestic sales are
. Profits generated by domestic sales are
![]() , and profits generated by exports are
, and profits generated by exports are
![]() . Since all firms are identical in equilibrium, we drop the index
. Since all firms are identical in equilibrium, we drop the index
![]() below.
below.
In this version of the model, banks internalize the effect of
entry on firm profits through the effect of entry on the nominal
domestic price, ![]() , and then on the home
tradable price index,
, and then on the home
tradable price index, ![]() , and the effect of
entry on the nominal export price,
, and the effect of
entry on the nominal export price, ![]() , and
then on the foreign tradable price index,
, and
then on the foreign tradable price index,
![]() . The equation for firm
value,
. The equation for firm
value, ![]() , becomes:
, becomes:
![$\displaystyle q_{t}=\beta E_{t}\left\{ \left( \frac{C_{t+1}}{C_{t}}\right) ^{-1}\left[ \left( 1-\frac{1}{H}\frac{\theta }{\theta _{D,t+1}}\right) d_{D,t+1}+\left( 1-\frac{1}{H}\frac{\theta }{\theta _{X,t+1}}\right) d_{X,t+1}+(1-\delta )q_{t+1}\right] \right\} .$](img397.gif) |
(6) |
(Derivation details are in the Appendix. A similar equation holds
abroad. This equation holds also in the model with home bias.) As
in the benchmark model, equation (6) implies that there is no entry at the
extreme ![]() of absolute bank monopoly: The return
from funding an entrant is negative in this case, as the portfolio
expansion effect is dominated by profit destruction (recall that
of absolute bank monopoly: The return
from funding an entrant is negative in this case, as the portfolio
expansion effect is dominated by profit destruction (recall that
![]() and
and
![]() ). Bank monopoly
power decreases as
). Bank monopoly
power decreases as ![]() increases, and equation
(6) simplifies to the familiar
asset pricing equation with perfectly competitive asset pricing at
the other extreme,
increases, and equation
(6) simplifies to the familiar
asset pricing equation with perfectly competitive asset pricing at
the other extreme, ![]() . Over the business
cycle generated by an increase in productivity, as the number of
firms increases, the demand elasticities
. Over the business
cycle generated by an increase in productivity, as the number of
firms increases, the demand elasticities
![]() and
and
![]() increase, and markups fall. On
the one hand, the fact that the ratios
increase, and markups fall. On
the one hand, the fact that the ratios
![]() and
and
![]() are larger than one
reduces bank incentives to invest in new firms. On the other hand,
since firm profits are procyclical and banks own claims to these
profits, the importance of the profit destruction externality falls
as
are larger than one
reduces bank incentives to invest in new firms. On the other hand,
since firm profits are procyclical and banks own claims to these
profits, the importance of the profit destruction externality falls
as
![]() and
and
![]() decrease,
strengthening bank incentives to invest.
decrease,
strengthening bank incentives to invest.
Table 2 summarizes the main equilibrium conditions of this
version of the model (showing only the equations pertaining to home
variables and net foreign assets).45 We study the model
predictions with Frisch elasticity
![]() .46We set the weight of
the disutility of labor,
.46We set the weight of
the disutility of labor, ![]() , to 1.
In this and the following section, we set the share of tradable
goods in the consumption basket,
, to 1.
In this and the following section, we set the share of tradable
goods in the consumption basket, ![]() , to
0.5, while iceberg trade costs are kept at
, to
0.5, while iceberg trade costs are kept at
![]() . The choice of
. The choice of
![]() is dictated by difficulties in
computing the model's steady state, and it implies a steady-state
import share of about 18 percent.47 The
other preference parameters, and the size of the exogenous exit
probability
is dictated by difficulties in
computing the model's steady state, and it implies a steady-state
import share of about 18 percent.47 The
other preference parameters, and the size of the exogenous exit
probability ![]() , remain the same as in the
benchmark model. The calibration strategy for
, remain the same as in the
benchmark model. The calibration strategy for ![]() is the same as before. We set the pre-deregulation
is the same as before. We set the pre-deregulation ![]() to imply a 10 percent bank markup. Then, a
12 percent long-run increase in the number
of domestic firms pins down the size of the increase in
to imply a 10 percent bank markup. Then, a
12 percent long-run increase in the number
of domestic firms pins down the size of the increase in ![]() that captures banking deregulation. We keep the
steady-state home and foreign productivity levels,
that captures banking deregulation. We keep the
steady-state home and foreign productivity levels, ![]() and
and ![]() , at 1. Note that,
in this version of the model, this choice not only determines the
number of firms (the size of the economy ) in steady state, and
hence the steady-state firm markups, but it also matters for the
cyclical properties of markups. The lower steady-state
productivity, the lower the number of firms, and the higher
steady-state firm markups. In turn, this implies more
countercyclical markups over the business cycle. The intuition is
simple: When the steady-state number of firms is low (so that each
of them is operating on a larger share of the market), banks have
an incentive to finance more entry (as a percentage of the initial
steady state) following a favorable productivity shock than when
the steady-state number of firms is large. As a consequence, the
markup falls by more (in percent of the initial steady state) when
expansions happen around a steady state with a smaller number of
firms. This effect is mirrored by household labor supply decisions.
By adjusting steady-state productivity, we can affect the interplay
of wealth and substitution effects in labor supply. As lower
steady-state productivity leads to more countercyclical markups,
and hence more procyclical wages, it generates stronger
substitution effects and weaker wealth effects in labor supply in
the impact response to temporary productivity shocks. For
persistent enough shocks, the representative household then is
willing to take advantage of temporarily high productivity by
supplying more labor to increase substantially the available number
of products, lower firm monopoly power, and experience
significantly higher consumption in the later portion of the
transition.
, at 1. Note that,
in this version of the model, this choice not only determines the
number of firms (the size of the economy ) in steady state, and
hence the steady-state firm markups, but it also matters for the
cyclical properties of markups. The lower steady-state
productivity, the lower the number of firms, and the higher
steady-state firm markups. In turn, this implies more
countercyclical markups over the business cycle. The intuition is
simple: When the steady-state number of firms is low (so that each
of them is operating on a larger share of the market), banks have
an incentive to finance more entry (as a percentage of the initial
steady state) following a favorable productivity shock than when
the steady-state number of firms is large. As a consequence, the
markup falls by more (in percent of the initial steady state) when
expansions happen around a steady state with a smaller number of
firms. This effect is mirrored by household labor supply decisions.
By adjusting steady-state productivity, we can affect the interplay
of wealth and substitution effects in labor supply. As lower
steady-state productivity leads to more countercyclical markups,
and hence more procyclical wages, it generates stronger
substitution effects and weaker wealth effects in labor supply in
the impact response to temporary productivity shocks. For
persistent enough shocks, the representative household then is
willing to take advantage of temporarily high productivity by
supplying more labor to increase substantially the available number
of products, lower firm monopoly power, and experience
significantly higher consumption in the later portion of the
transition.
The Responses to Banking Deregulation
Figure 5 shows the responses to home banking deregulation. Time varying firm markups and elastic labor supply result in amplified responses of endogenous variables. Consistent with a reduction in monopoly power in the economy, home labor supply is permanently higher. Since households can now respond to the shock also by expanding their labor effort, and firm markups decline, home consumption no longer falls on impact. Similarly, the response of foreign labor allows the foreign economy to enjoy increased business creation and GDP. As in the model with inelastic labor and constant firm markups, the terms of labor appreciate, leading to real exchange rate appreciation, and the home economy borrows to finance increased business creation.48
Productivity Shocks and Macroeconomic Dynamics
Figure 6 illustrates the business cycle propagation properties of our model by showing the impulse responses to a transitory increase in home productivity. We assume a 1 percent innovation to home productivity with persistence 0.9. The solid lines are the impulse responses around the pre-deregulation steady state, while dashes denote impulse responses around the post-deregulation steady state. As the figure shows, the shock has no permanent effect since all endogenous variables are stationary in response to stationary exogenous shocks. However, the responses also clearly highlight the substantial persistence of key endogenous variables--well beyond the exogenous persistence of the productivity shock. For example, it takes over ten years for the real exchange rate to return to the steady-state level.
Note the initial appreciation of the terms of labor, again motivated by the effect of increased entry of new firms into the home economy on home labor costs. Since shock persistence is relatively low (by real business cycle standards), lending abroad to smooth the consequences of a temporary, favorable shock on consumption is the main determinant of net foreign asset dynamics, and the home economy runs a current account surplus for most of the first four years, accumulating net foreign assets above the steady state.49
While the value of additional firms to the bank rises as the economy expands, positive productivity shocks are associated with lower domestic bank markups and (for some quarters) declining bank profits.50 Even if individual firm profits fall below the steady state quickly, expansion of the loan portfolio causes bank profits to recover and remain above the steady state for a substantial portion of the transition. As a consequence, share prices in home banks rise above the steady state for approximately five years. The return to home bank share holdings also rises on impact.
As for the responses to banking deregulation, increased producer entry causes the terms of labor to appreciate. This results in an impact, small appreciation of the real exchange rate. However, this is quickly reversed: The number of home tradable producers increases enough relative to foreign that the second term in equation (5) becomes the key driver of exchange rate dynamics, as home households save on trade costs (for some time) over an increasing portion of their consumption basket.
Importantly, lower bank monopoly power implies a smaller percent deviation of firm entry from the steady state, less countercyclical firm markups, and weaker substitution effects in labor supply. As a consequence of deregulation, the responses of firm entry, labor supply, consumption, investment in new products, and aggregate output are muted in the home economy. Given the trade and financial ties with home, banking deregulation at home results in dampened fluctuations also abroad.
The intuition is straightforward, and related to the discussion of the consequences of changes in steady-state productivity above. Post-deregulation, the economy is populated by a larger steady-state number of firms, which are operating on a smaller share of the market and charging lower markups due to higher elasticity of demand. As a consequence, when a favorable productivity shock happens, the banks' incentive to let additional firms into the economy is weakened, and we observe less business creation as a percentage of the steady-state number of firms than around the pre-deregulation steady state. In turn, this dampens markup fluctuations around the post-deregulation steady state, and it is accompanied by weaker substitution effects in labor supply and muted responses of home and foreign endogenous variables to the productivity shock.51
Deregulation and Moderation
The model includes only one source of fluctuations at business
cycle frequency, the shocks to aggregate productivity ![]() and
and
![]() . Our interest is not in
whether the model has the ability to replicate a wide range of data
moments, but in studying the consequences of the transition to
interstate U.S. banking for macroeconomic volatility through the
channel discussed above. For this purpose, we assume that the
percentage deviations of
. Our interest is not in
whether the model has the ability to replicate a wide range of data
moments, but in studying the consequences of the transition to
interstate U.S. banking for macroeconomic volatility through the
channel discussed above. For this purpose, we assume that the
percentage deviations of ![]() and
and
![]() from the steady state follow a
bivariate process with persistence parameters
from the steady state follow a
bivariate process with persistence parameters ![]() and
and
![]() , non-negative spillover
parameters
, non-negative spillover
parameters
![]() and
and
![]() , and normally
distributed, zero-mean innovations.
, and normally
distributed, zero-mean innovations.
We consider two alternative calibrations for the productivity
process. First, we use the symmetrized estimate of the bivariate
productivity process for the United States and an aggregate of
European economies in Backus, Kehoe, and Kydland (1992) and set
![]() and
and
![]() .
The latter value implies a small, positive productivity spillover
across countries, such that, if home productivity rises during
period
.
The latter value implies a small, positive productivity spillover
across countries, such that, if home productivity rises during
period ![]() , foreign productivity will also increase
at
, foreign productivity will also increase
at ![]() . We set the standard deviation of the
productivity innovations to 0.00852 (a
0.73 percent variance) and the correlation
to 0.258 (corresponding to a 0.19 percent covariance) as estimated by Backus, Kehoe, and
Kydland (1992). In the second parameterization, we follow Baxter
(1995) and Baxter and Farr (2005), who argue for increased
persistence and absence of spillovers, and we set the spillover
parameters
. We set the standard deviation of the
productivity innovations to 0.00852 (a
0.73 percent variance) and the correlation
to 0.258 (corresponding to a 0.19 percent covariance) as estimated by Backus, Kehoe, and
Kydland (1992). In the second parameterization, we follow Baxter
(1995) and Baxter and Farr (2005), who argue for increased
persistence and absence of spillovers, and we set the spillover
parameters
![]() and
persistence
and
persistence
![]() , leaving
the variance-covariance matrix of innovations unchanged. We
calculate the implied values of theoretical second moments of
Hodrick-Prescott (HP)-filtered endogenous variables (percent
deviations from steady state). As customary, we set the HP filter
parameter
, leaving
the variance-covariance matrix of innovations unchanged. We
calculate the implied values of theoretical second moments of
Hodrick-Prescott (HP)-filtered endogenous variables (percent
deviations from steady state). As customary, we set the HP filter
parameter
![]() .
.
We present second moments of data-consistent real variables
computed by deflating nominal ones with data-consistent price
indexes. These are obtained by removing pure variety effects from
the welfare-consistent price indexes as described in the Appendix.
Denoting the data-consistent price index at home with
![]() , data-consistent, real
variables are obtained as
, data-consistent, real
variables are obtained as
![]() ,
where
,
where ![]() is any variable in units of the
consumption basket.52 As we previously discussed, creation
of new firms is the form taken by capital accumulation in our
model, and the stock of firms represents the capital stock of the
economy. The measure of investment in our model is therefore
is any variable in units of the
consumption basket.52 As we previously discussed, creation
of new firms is the form taken by capital accumulation in our
model, and the stock of firms represents the capital stock of the
economy. The measure of investment in our model is therefore
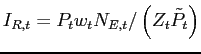 and
and
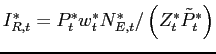 .
.
Table 4 presents model-generated standard deviations for key macroeconomic aggregates and the real exchange rate for both calibrations of the productivity process. (The Appendix presents the corresponding table for the model with home bias. Most results are similar.) Focus on the Backus-Kehoe-Kydland parameterization first. The model generates less volatile consumption and labor effort than GDP.53 Clearly, there is excess volatility of investment--a standard finding absent an adjustment cost of the type usually introduced in business cycle models. Eliminating productivity spillovers and increasing the persistence of shocks as in the Baxter parameterization reduces the volatility across all variables. Both parameterizations show that lower local monopoly power of banks reduces the volatility of home GDP (more so under the Backus-Kehoe-Kydland parameterization).54Firm-level output fluctuations (not reported) are also less volatile following banking deregulation, consistent with the evidence in Correa and Suarez (2007). As suggested by Figure 6, banking deregulation moderates the cycle across all relevant macroeconomic aggregates in the home country.55 Foreign GDP volatility also declines, while foreign consumption becomes somewhat more volatile.
To conclude our analysis, we quantify the welfare effects of
banking deregulation due to the change in business cycle dynamics.
Specifically, for a given level of bank monopoly power in financial
intermediation (segmented banking, denoted with ![]() , or integrated banking, denoted with
, or integrated banking, denoted with ![]() ), we compute the percentage
), we compute the percentage ![]() of
steady-state consumption that would make households indifferent
between living in a world with uncertainty and living in a
deterministic world:
of
steady-state consumption that would make households indifferent
between living in a world with uncertainty and living in a
deterministic world:
![$\displaystyle E_{0}\sum_{t=0}^{\infty }\beta ^{t}u(C_{t}^{reg},L_{t}^{reg})=\frac{u\left[ \left( 1+\frac{\Delta }{100}\right) C^{SB},L^{SB})\right] }{1-\beta },$](img473.gif) |
and similarly abroad, where ![]() denotes the
level of bank market integration at home (
denotes the
level of bank market integration at home (![]() or
or
![]() ).
).
We compute welfare by using a second-order approximation to the policy functions. As shown in Table 3, moderation of fluctuations around the post-deregulation steady state results in smaller welfare costs of business cycles in both countries. Notice, however, that the welfare gain through the business cycle effect is small compared to the direct gains discussed above. This result is not surprising since welfare costs of business cycles in our model are already small when local monopoly power of banks is high.
7 Conclusion
We developed a two-country model of the domestic and external effects of removing national bank market segmentation that predicts real appreciation, external borrowing, and moderation of domestic and international business cycles as joint equilibrium consequences of increased local banking competition. The key channel through which this occurs is increased business creation in the deregulating economy relative to the rest of the world, as potential entrants in product markets have easier access to bank finance in the less segmented market. The model provides an explanation of features of U.S. and international macroeconomic dynamics following the transition to interstate U.S. banking that started in the late 1970s. This explanation complements those already studied in the literature. By focusing on the structure of banking, the reduction in the local monopoly power of banks implied by deregulation, and the incentives for producer entry, the model is consistent with a large body of evidence from the empirical finance literature.
The mechanism we highlight is very robust. We focused on the effects of the removal of geographical segmentation of bank markets, but any form of financial market deregulation that facilitates access to finance by product market entrants would lead to real appreciation, external borrowing, and eventual business cycle moderation through the channels we discussed. In this respect, our model provides a lens through which one can look at the consequences of financial deregulation more broadly defined as any action that facilitates access to finance. Of course, one would want to extend the model to incorporate heterogeneous borrower quality, asymmetric information, risk of default, and other forms of market regulation (or deregulation) to capture the crisis that began in 2007.56 Incorporation of within-country, idiosyncratic risk would also make it possible to confront the model with the empirical results of another strand of literature in finance, which documents that U.S. banking deregulation improved risk sharing across U.S. states by facilitating access to finance for small business owners (Demyanyk, Ø stergaard, and Sørensen, 2007). We leave these extensions for future work, along with an exploration of optimal regulation policy and endogenous financial market development.
Acknowledgments
This paper was circulated previously under the title "The Domestic and International Effects of Financial Deregulation." First draft: July 21, 2007. For helpful comments, we thank Giancarlo Corsetti, two anonymous referees, Alessandro Barattieri, Rucha Bhate, Claudia Buch, Silvio Contessi, Mathias Hoffmann, Michael Koetter, Guay Lim, Federico Mandelman, Alan Sutherland, Cédric Tille, and conference and seminar participants at Atlanta Fed, Boston Fed (seminar and Dynare Conference 2008), Bundesbank Spring Conference 2010 (International Risk Sharing and Global Imbalances), ECB Financial Markets and Macroeconomic Stability Conference, Econometric Society NASM 2008, EEA 2008, ESEM 2009, Federal Reserve Board, HEC Montréal, IMF, Kansas City Fed (System Conference on Macroeconomics 2008), LACEA 2008, MIT, NBER IFM Spring 2008, Pacific Rim Conference 2013, Reserve Bank of Australia 2007 Research Workshop on Monetary Policy in Open Economies, SED 2008, University of Connecticut, University of Houston, University of Maryland, University of Wisconsin-Madison, and Vanderbilt University. We are grateful to Alessandro Barattieri and Rucha Bhate for outstanding research assistance. All remaining errors are ours. Ghironi thanks the NSF for financial support through a grant to the NBER. Work on this paper was done while Ghironi was a Visiting Scholar at the Federal Reserve Bank of Boston. The support of this institution is also acknowledged with gratitude. The views presented in this paper are solely of the authors and do not necessarily represent the views or policy of the CEPR, the Federal Reserve Bank of Boston, the Federal Reserve Board, or the NBER.
References
Aliaga-Díaz, Roger, and María Pía Olivero. 2010. "Is There a Financial Accelerator in U.S. Banking? Evidence from the Cyclicality of Banks' Price-Cost Margins," Economics Letters 108: 167-171.
Aliaga-Díaz, Roger, and María Pía Olivero. 2011. "The Cyclicality of Price-Cost Margins in Banking: An Empirical Analysis of Its Determinants," Economic Inquiry 49: 26-46.
Anderson, James, and Eric van Wincoop. 2004. "Trade Costs," Journal of Economic Literature 42(3): 691-751.
Baxter, Marianne. 1995. "International Trade and Business Cycles," Handbook of International Economics, vol. 3, ed. Grossman, G. M., and K. Rogoff, 1801-1864. Amsterdam: Elsevier.
Baxter, Marianne, and Dorsey D. Farr. 2005. "Variable Factor Utilization and International Business Cycles," Journal of International Economics 65(2): 335-347.
Berger, Allen N., Rebecca S. Demsetz, and Philip E. Strahan. 1999. "The Consolidation of the Financial Services Industry: Causes, Consequences, and Implications for the Future," Journal of Banking and Finance 23(2-4): 135-194.
Bernanke, Ben S. 2005. "The Global Saving Glut and the U.S. Current Account Deficit," Sandridge Lecture, Virginia Association of Economics, Richmond, Virginia.
Bernard, Andrew B., J. Eaton, Jonathan, Bradford Jensen, and Samuel Kortum. 2003. "Plants and Productivity in International Trade," American Economic Review 93 (4): 1268-1290.
Bertrand, Marianne, Antoinette Schoar, and David Thesmar. 2007. "Banking Deregulation and Industry Structure: Evidence from the French Banking Reforms of 1985," Journal of Finance 62(2): 597-628.
Bilbiie, Florin O., Fabio Ghironi, and Marc J. Melitz. 2012. "Endogenous Entry, Product Variety, and Business Cycles," Journal of Political Economy 120: 304-345.
Black, Sandra E., and Philip. E. Strahan. 2002. "Entrepreneurship and Bank Credit Availability," Journal of Finance 57(6): 2801-2833.
Bremus, Franziska, Claudia M. Buch, Katheryn N. Russ, and Monika Schnitzer. 2013. "Big Banks and Macroeconomic Outcomes: Theory and Cross-Country Evidence of Granularity," NBER WP 19093.
Caballero, Ricardo J., Emmanuel Fahri, and Pierre-Olivier Gourinchas. 2008. "An Equilibrium Model of `Global Imbalances' and Low Interest Rates," American Economic Review 98(1): 358-393.
Cacciatore, Matteo, Giuseppe Fiori, and Fabio Ghironi. 2013. "Market Deregulation and Optimal Monetary Policy in a Monetary Union," NBER WP 19025.
Cestone, Giacinta, and Lucy White. 2003. "Anticompetitive Financial Contracting: The Design of Financial Claims," Journal of Finance 58 (5): 2109-2142.
Cetorelli, Nicola, and Philip E. Strahan. 2006. "Finance as a Barrier to Entry: Bank Competition and Industry Structure in Local U.S. Markets," Journal of Finance 61(1): 437-461.
Cogley, Timothy, and Thomas J. Sargent. 2005. "Drifts and Volatilities: Monetary Policies and Outcomes in the Post WWII U.S.," Review of Economic Dynamics 8(2): 262-302.
Corbae, Dean, and Pablo D'Erasmo. 2011. "A Quantitative Model of Banking Industry Dynamics," manuscript, University of Wisconsin, Madison, and University of Maryland.
Correa, Ricardo, and Gustavo A. Suarez. 2007. "Firm Volatility and Banks: Evidence from U.S. Banking Deregulation," manuscript, Board of Governors of the Federal Reserve System.
Corsetti, Giancarlo, Luca Dedola, and Sylvain Leduc. 2008. "International Risk Sharing and the Transmission of Productivity Shocks," Review of Economic Studies 75: 443-473.
Corsetti, Giancarlo, Philippe Martin, and Paolo Pesenti. 2007. "Productivity, Terms of Trade, and the `Home Market Effect'," Journal of International Economics 73(1): 99-127.
Corsetti, Giancarlo, Philippe Martin, and Paolo Pesenti. 2013. "Varieties and the Transfer Problem," Journal of International Economics 89(1): 1-12.
D'Aspremont, Claude, Rodolphe D. S. Ferreira, and Louis-Andre Gerard-Varet. 1996. "On the Dixit-Stiglitz Model of Monopolistic Competition," American Economic Review 86(3): 623-629.
De Bandt, Olivier, and E. Philip Davis. 2000. "Competition, Contestability and Market Structure in European Banking Sectors on the Eve of EMU" Journal of Banking and Finance 24(6): 1045-1066.
de Blas, Beatriz, and Katheryn N. Russ. 2013. "All Banks Great, Small, and Global: Loan Pricing and Foreign Competition," International Review of Economics & Finance 26 (April): 4-24.
Demyanyk, Yuliya, Charlotte Østergaard, and Bent E. Sørensen. 2007. "U.S. Banking Deregulation, Small Businesses, and Interstate Insurance of Personal Income," Journal of Finance 62: 2763-2801.
Devereux, Marcel B., and Alan Sutherland. 2010. "Country Portfolios in Open Economy Macro Models," Journal of the European Economic Association, forthcoming.
Dick, Astrid A. 2006. "Nationwide Branching and Its Impact on Market Structure, Quality, and Bank Performance," Journal of Business 79(2): 567-592.
Erceg, Christopher J., Luca Guerrieri, and Christopher J. Gust. 2005. "Expansionary Fiscal Shocks and the Trade Deficit," International Finance 8(3): 363-397.
Ferrero, Andrea. 2007. "The Long-Run Determinants of U.S. External Imbalances," Federal Reserve Bank of New York Staff Report 295.
Fogli, Alessandra, and Fabrizio Perri. 2006. "The `Great Moderation' and the U.S. External Imbalance," NBER WP 12708.
Gertler, Mark, and Peter Karadi. 2011. "A Model of Unconventional Monetary Policy," Journal of Monetary Economics 58(1): 17-34.
Ghironi, Fabio, and Marc J. Melitz. 2005. "International Trade and Macroeconomic Dynamics with Heterogeneous Firms," Quarterly Journal of Economics 120(3): 865-915.
Giannone, Domenico, Michele Lenza, and Lucrezia Reichlin. 2008. "Explaining the Great Moderation: It Is Not the Shocks," Journal of the European Economic Association Papers and Proceedings 6(2-3): 621-633.
González-Maestre, Miguel, and Luis M. Granero. 2003. "Industrial Loans and Market Structure," European Economic Review 47(5): 841-855.
Gourinchas, Pierre-Olivier, and Helen Rey. 2007. "International Financial Adjustment," Journal of Political Economy 115(4): 665-703.
Grossman, Gene M., and Elhanan Helpman .1991. Innovation and Growth in the Global Economy, MIT Press, Cambridge, MA.
Hamano Masashige. 2014. "International Equity and Bond Positions in a DSGE Model with Variety Risk in Consumption," manuscript, Sophia University.
Hayashi, Fumio. 1982. "Tobin's Marginal q and Average q: A Neoclassical Interpretation," Econometrica 50(1): 213-224.
Hunt, Benjamin, and A. Rebucci. 2005. "The U.S. Dollar and the Trade Deficit: What Accounts for the Late 1990s?" International Finance 8(3): 399-434.
Jayaratne, Jith, and Philip E. Strahan. 1998. "Entry Restrictions, Industry Evolution and Dynamic Efficiency: Evidence from Commercial Banking," Journal of Law and Economics 41(1): 239-274.
Justiniano, Alejandro, and Giorgio E. Primiceri. 2008. "The Time-Varying Volatility of Macroeconomic Fluctuations," American Economic Review 98(3): 604-641.
Kerr, William, and Ramana Nanda. 2007. "Democratizing Entry: Banking Deregulations, Financing Constraints, and Entrepreneurship," Harvard Business School WP 07-033.
King, Robert G., Charles I. Plosser, and Sergio T. Rebelo. 1988. "Production, Growth, and Business Cycles: I. The Basic Neoclassical Model," Journal of Monetary Economics 21(2-3): 195-232.
Kiyotaki, Nobuhiro, and John Moore. 1997. "Credit Cycles," Journal of Political Economy 105(2): 211-248.
Lewis, Vivien. 2006. "Macroeconomic Fluctuations and Firm Entry: Theory and Evidence," manuscript, Catholic University Leuven.
Mandelman, Federico S. 2010. "Business Cycles and Monetary Regimes in Emerging Economies: A Role for a Monopolistic Banking Sector," Journal of International Economics 81(1): 122-138.
Mandelman, Federico S. 2011. "Business Cycles and the Role of Imperfect Competition in the Banking System," International Finance 14: 103-133.
Méjean, Isabelle. 2008. "Can Firms' Location Decisions Counteract the Balassa-Samuelson Effect?" Journal of International Economics 76(2): 139-154.
Mendoza, Enrique G., Vincenzo Quadrini, and Jose'-Victor Rí os-Rull. 2009. "Financial Integration, Financial Development, and Global Imbalances," Journal of Political Economy 117(3): 371-416.
Morgan, Donald P., Bertrand Rime, and Philip E. Strahan. 2004. "Bank Integration and State Business Cycles," Quarterly Journal of Economics 129(4): 1555-1585.
Niepmann, Friederike. 2012. "Banking across Borders," Federal Reserve Bank of New York Staff Report 576.
Niepmann, Friederike. 2013. "Banking across Borders with Heterogeneous Banks," Federal Reserve Bank of New York Staff Report 609.
Notz, Stefan. 2012. "Macroeconomic Implications of U.S. Banking Liberalisation," manuscript, University of Zurich.
Obstfeld, Maurice, and Kenneth S. Rogoff. 2001. "The Six Major Puzzles in International Macroeconomics: Is There a Common Cause?" in NBER Macroeconomics Annual 2000, ed. Ben S. Bernanke and Kenneth S. Rogoff, 339-390. Cambridge, MA: The MIT Press.
Petersen, Mitchell A., and Raghuram G. Rajan. 2002. "Does Distance Still Matter? The Information Revolution in Small Business Lending," Journal of Finance 57(6): 2533-2570.
Sims, Christopher A., and Tao Zha. 2006. "Were There Regime Switches in U.S. Monetary Policy?" American Economic Review 96(1): 54-81.
Stebunovs, Viktors. 2008. "Finance as a Barrier to Entry: U.S. Bank Deregulation and Business Cycle," manuscript, Board of Governors of the Federal Reserve System.
Stock, James H., and Mark W. Watson. 2003. "Has the Business Cycle Changed and Why?" in Gertler, M., and K. S. Rogoff, eds., NBER Macroeconomics Annual 2002, MIT Press, Cambridge, MA, pp. 159-218.
Tille, Cedric and Eric van Wincoop. 2010. "International Capital Flows," Journal of International Economics, 80(2): 157-175.
Woodford, Michael. 2003. Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton University Press, Princeton, NJ.
Yang, Xiaokai, and Ben J. Heijdra. 1993. "Monopolistic Competition and Optimum Product Diversity: Comment" American Economic Review 83(1): 295-301.
Table 1. Benchmark Model, Summary
| Consumption price indexes |
|
|---|---|
| Tradable price indexes |
|
| Good prices, domestic market |
|
| Good prices, export market |
|
| Good prices, non-tradable |
|
| Firm profits |
|
| Bank profits |
|
| Firm entry |
|
| Firm value |
|
| Number of firms |
|
| Euler equation, deposits |
|
| Euler equation, shares |
|
| Depoist market clearing |
|
| Aggregate accounting |
|
| Balanced trade |
Table 2. Quantitative Model, Summary
| Consumption price index | |
|---|---|
| Tradable price index | |
| Demand elasticity, home market | |
| Good prices, home market | |
| Demand elasticity, export market | |
| Good prices, export market | |
| Good prices, non-tradable | |
| Firm profits, home market | |
| Firm profits, export market | |
| Bank profits | |
| Firm entry | |
| Firm value | ![\begin{displaymath}q_{t}=\beta E_{t}\left\{ \left( \frac{C_{t+1}}{C_{t}}\right) ^{-1}\left[ \begin{array}[c]{c} \left( 1-\frac{1}{H}\frac{\theta}{\theta_{D,t+1}}\right) d_{D,t+1}\ +\left( 1-\frac{1}{H}\frac{\theta}{\theta_{X,t+1}}\right) d_{X,t+1}\ +(1-\delta)q_{t+1} \end{array}\right] \right\} \end{displaymath}](img41a.gif) |
| Number of firms | |
| Euler equation, domestic deposits | |
| Euler equation, deposits abroad | |
| Euler equation (shares) | |
| Deposit market clearing | |
| Labor supply | |
| Labor market clearing | |
| Net foreign assets |
Table 3a. Welfare Effects of Deregulation: Direct Effect1
| Home | Foreign | |
|---|---|---|
| ΔW: Financial Autarky | 1.15% | 0.09% |
| ΔW: International Deposits, Inelastic Labor, and Fixed Markups | 1.17% | 0.07% |
| ΔW: International Deposits, Elastic Labor, and Fixed Markups | 1.23% | 0.10% |
| ΔW: International Deposits, Elastic Labor, and Time-Varying Markups | 2.46% | 0.29% |
Table 3b. Welfare Effects of Deregulation: Business Cycle Effect2
| Home | Foreign | |
|---|---|---|
| ΔW: Backus-Kehoe-Kydland Calibration | 0.003% | 0.001% |
| ΔW: Baxter Calibration | 0.003% | 0.001% |
1Welfare calculations inclue transition dynamics.
2We report results only for the model with international deposits, elastic labor, and time-varying markups. A positive welfare change denotes a reduction in the welfare costs of business cycle following deregulation.
Table 4a. Standard Deviations Before and After Deregulation: Backus-Keohe-Kydland Calibration
| Before | After | % Change | |
|---|---|---|---|
| YR | 6.4767 | 5.7779 | -10.79 |
| YR* | 6.4767 | 5.9629 | -7.93 |
| CR | 1.1890 | 1.0479 | -11.87 |
| CR* | 1.1890 | 1.2201 | 2.62 |
| IR | 126.62 | 104.31 | -17.62 |
| IR* | 126.62 | 116.63 | -7.89 |
| L | 5.1940 | 4.7461 | -8.62 |
| L* | 5.1940 | 4.7827 | -7.92 |
Table 4b. Standard Deviations Before and After Deregulation: Baxter Calibration
| Before | After | % Change | |
|---|---|---|---|
| YR | 1.9105 | 1.7984 | -5.87 |
| YR* | 1.9105 | 1.8135 | -5.08 |
| CR | 1.1673 | 1.1047 | -5.36 |
| CR* | 1.1673 | 1.1859 | 1.59 |
| IR | 24.826 | 19.9587 | -19.61 |
| IR* | 24.826 | 23.0943 | -6.98 |
| L | 0.8625 | 0.8013 | -7.10 |
| L* | 0.8625 | 0.7558 | -12.37 |
Figure 1. Banking Deregulation Under Financial Autarky
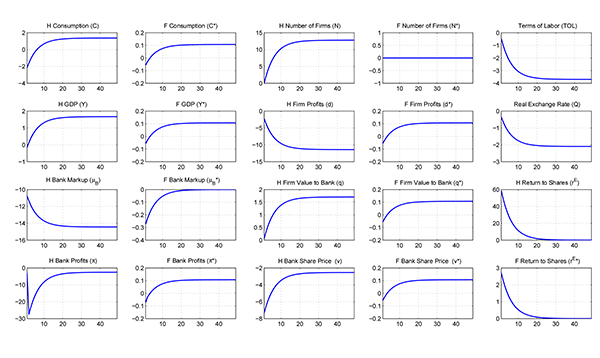
Figure 2. Banking Deregulation With International Deposits
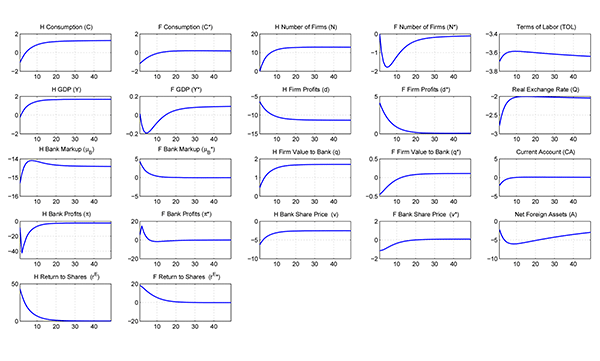
Figure 3. Anticipated Banking Deregulation With International Deposits
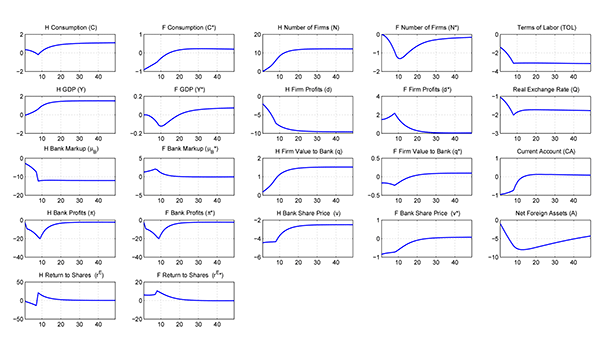
Figure 4. Banking Deregulation With International Deposits, Grossman-Helpman Entry Cost
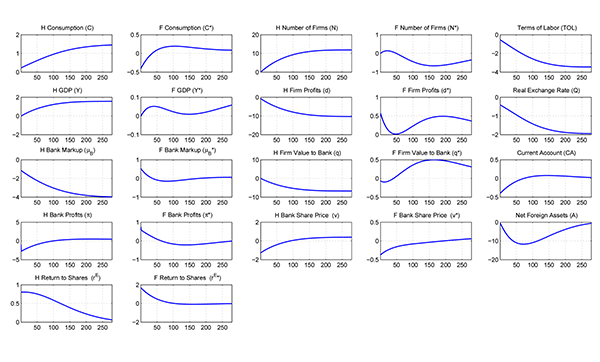
Figure 5. Banking Deregulation With Elastic Labor and Endogenous Firm Markups

Figure 6. Business Cycles, Pre-And Post-Deregulation
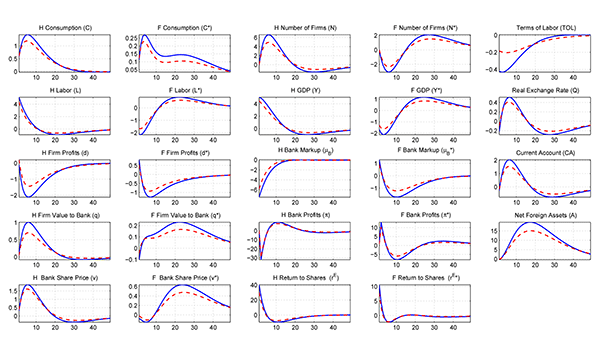
Footnotes
† HEC Montréal, Institute of Applied Economics 3000, chemin de la Côte-Sainte-Catherine, Montréal, Quebec, Canada; matteo.cacciatore@hec.ca. URL: http://www.hec.ca/in/profs/matteo.cacciatore. Return to text
†† Department of Economics, University of Washington, Savery Hall, Box 353330, Seattle, Washington, WA 98195, U.S.A.; ghiro@uw.edu. URL: http://faculty.washington.edu/ghiro. Return to text
††† Board of Governors of the Federal Reserve System, Division of International Finance, 20th Street and Constitution Avenue, NW, Washington, DC 20551, U.S.A.; viktors.stebunovs@frb.gov. URL: http://www.federalreserve.gov/econresdata/viktors-stebunovs.htm. Return to text
1. We provide a more detailed account of the removal of geographical restrictions to U.S. bank expansion in a separate online Appendix available at http://faculty.washington.edu/ghiro. Return to text
2. See, for instance, Bilbiie, Ghironi, and Melitz (2012), Corsetti, Martin, and Pesenti (2007, 2013), Ghironi and Melitz (2005), Lewis (2006), Mé jean (2008), Notz (2012), and Stebunovs (2008). Return to text
3. According to the U.S. Small Business Administration, small firms (with fewer than 500 employees) represent 99.7 percent of all firms, employ half of all private sector employees, and produce half of non-farm private GDP. Return to text
4. Jayaratne and Strahan (1998) and Dick (2006) find that loan prices and net interest rate margins declined with the integration of U.S. bank markets. Berger, Demsetz, and Strahan (1999) document that the deregulation caused reduced concentration in local banking. See Stebunovs (2008) for a more detailed discussion. Return to text
5. See also Bertrand, Schoar, and Thesmar (2007). Our model incorporates Cestone and White's (2003) insight that entry deterrence takes place through financial rather than product markets. Return to text
6. The reduction in firm-level volatility is consistent with evidence in Correa and Suarez (2007), who find a causal link between banking deregulation and lower firm-level volatility in the U.S. Return to text
7. Since our model predicts permanent real appreciation following permanent banking deregulation, the model does not explain the return of the U.S. effective real exchange rate to pre-appreciation levels after the appreciation phases in the 1980s and 1990s. This can be attributed to the reversal of other forces that contributed to observed exchange rate dynamics. If one views integrated national banking as a characteristic of more developed countries, the prediction of persistently higher average prices is consistent with the evidence of higher prices in high-income countries. Return to text
8. In contrast to Fogli and Perri (2006), our model and solution approach imply that precautionary savings play no role in the current account and real exchange rate dynamics caused by banking deregulation in our exercise. Other explanations of the recent dynamics of the U.S. external position emphasize demographics (Ferrero, 2007), a "global saving glut" (Bernanke, 2005), and valuation effects (Gourinchas and Rey, 2007). Return to text
9. See Stock and Watson (2003) and references therein. An incomplete list of more recent contributions includes Cogley and Sargent (2005), Giannone, Lenza, and Reichlin (2008), Justiniano and Primiceri (2008), and Sims and Zha (2006). Return to text
10. Our analysis can of course be applied also to the intra-European and international consequences of bank market integration within the European Union (EU) since the signing of the Single European Act in 1986. However, the process of EU banking integration has been lagging behind the implementation of interstate banking in the U.S. See the online Appendix for historical details. De Bandt and Davis (2000) provide evidence that the behavior of large banks in Europe was not as competitive as that of U.S. counterparts over the period 1992-1996. Regarding small banks, the level of competition in Europe was even lower. Return to text
11. Of course, our model does not explain (and does not aim to explain) the period of financial market turmoil that began in 2007 and its business cycle implications. Extending the model to capture these phenomena is beyond the scope of this paper. Return to text
12. See also Niepmann (2012, 2013) on the role of differences in the characteristics of the banking sector for international capital flows. Return to text
13. Financial frictions that we leave unspecified force prospective entrants to borrow the amount necessary to cover sunk entry costs from banks rather than raising funds in equity markets. Our model does not incorporate a theory of why banks exist or a role for banks in screening/monitoring in the presence of asymmetric information. We simply assume that bank intermediation is necessary, and we focus on the consequences of changes in bank monopoly power. The key qualitative results of our exercise would be unaffected in a richer model with a screening/monitoring role for banks that still captures the documented increase in non-financial-sector entry generated by less bank monopoly power. For alternative models of banking with market power, see Bremus, Buch, Russ, and Schnitzer (2013), de Blas and Russ (2013), and Mandelman (2010, 2011). Return to text
14. Banks compete in the number of entrants in Cournot fashion as in the static, partial equilibrium model of González-Maestre and Granero (2003). Since banks extract all firm profits through loan repayments, banks de facto hold portfolios of firms in the economy. Financial intermediaries are equity holders also in Gertler and Karadi (2011). Return to text
15. Since the completion of deregulation in the U.S. in 1994, it is increasingly less plausible to view banking markets as local (Cetorelli and Strahan, 2006). The ability of banks to expand across local markets and new technologies that allow banks to lend to distant borrowers act to limit the incumbent banks' local monopoly power (Petersen and Rajan, 2002). Return to text
16. We remark that while the normalization
![]() implies that
implies that ![]() becomes the
total number of home banks, our results do not hinge on
deregulation resulting in an increase in the total number of home
banks (in reality or in the model without normalization). In fact,
consolidation lowered the total number of banks in the U.S. But
this is not inconsistent with an increase in the number of banks
represented in each location and a decline in their local monopoly
power, which is what our model captures. Return to text
becomes the
total number of home banks, our results do not hinge on
deregulation resulting in an increase in the total number of home
banks (in reality or in the model without normalization). In fact,
consolidation lowered the total number of banks in the U.S. But
this is not inconsistent with an increase in the number of banks
represented in each location and a decline in their local monopoly
power, which is what our model captures. Return to text
17. We abstract from endogenous entry into banking as function of economic conditions (for given regulatory environment). While there is evidence of cyclical variation of entry in goods markets (see Bilbiie, Ghironi, and Melitz, 2012, and references therein), the evidence of bank creation at business cycle frequency is less pervasive. Return to text
18. Differently from Ghironi and Melitz (2005), we do not model the endogenous determination of the subset of traded goods within a tradable set, since this is not central to the analysis in this paper. All tradable goods that are produced in equilibrium are also traded, and there is an exogenously non-tradable good in each country. We present in the Appendix an alternative version of the model in which there is no non-tradable good, and home bias in consumption preferences for tradable goods is the source of PPP deviations. Return to text
19. Because of the assumption that banks de facto own domestic firms, this implies that households are the ultimate owners of the firms. However, as we show below, bank monopoly power in lending distorts the allocation of funds from the competitive deposit market to firms. Return to text
20. The assumption that banks lend locally but collect deposits in a country-wide deposit market substitutes a scenario in which deposits are collected locally but there is country-wide interbank lending. The latter scenario would require to study the determination of the interbank lending rate in an environment with non-atomistic banks. Return to text
21. Symmetry across traded goods producers within each country implies that our framework will not capture the reallocation effects of banking deregulation across firms highlighted by Bertrand, Schoar, and Thesmar (2007) and Kerr and Nanda (2007). Return to text
22. For simplicity, we assume identical labor productivity across traded and non-traded sectors (and across production of existing goods and creation of new products in the traded sector--see below). Productivity differences between traded and non-traded sectors would not alter our main results. Return to text
23. The assumption that banks have all the bargaining power and are able to extract all the profit simplifies the model solution substantially. Relative to a debt contract, it is not necessary to keep track of outstanding loan amounts for each cohort of firms, making it possible to treat firms of different vintages equally. Notz (2012) extends Stebunovs (2008) to incorporate financial intermediation as in Kiyotaki and Moore (1997). Notz's results suggest that the key mechanisms of our model would still operate--and the main results would not be affected--as long as the debt contract (or other contracts between banks and firms) does not alter the fact that deregulation facilitates access to finance. Return to text
24. As will become clear later, this is not exactly the static Cournot model as not only the value of entrants, but also the value of incumbents depends on the number of entrants. Return to text
25. The first-order condition with
respect to the number of entrants in period ![]() recognizes that some of these entrants will be hit by the exit
shock and will not produce and repay the loan at
recognizes that some of these entrants will be hit by the exit
shock and will not produce and repay the loan at ![]() . To compensate the bank for the risk of entrant death,
the entry condition requires that
. To compensate the bank for the risk of entrant death,
the entry condition requires that
![]() be higher than the
entry cost by the factor
be higher than the
entry cost by the factor
![]() . Return to text
. Return to text
26. When ![]() , equation
(3) becomes
, equation
(3) becomes
![]() This is a contraction mapping because of discounting, and by
forward iteration under the assumption
This is a contraction mapping because of discounting, and by
forward iteration under the assumption
![]() (the value of firms is zero when reaching the terminal period),
the only stable solution is
(the value of firms is zero when reaching the terminal period),
the only stable solution is ![]() , which
implies
, which
implies ![]() . Return
to text
. Return
to text
27. ![]() falls to 0
over time if the economy had started with higher
falls to 0
over time if the economy had started with higher ![]() and a positive number of firms. This starvation of the economy
would not happen if we assumed that the single monopolist bank
takes into account its influence on aggregate consumption. This
would be reminiscent of the "Ford effect" described in
D'Aspremont, Ferreira, and Gerard-Varet (1996). Return to text
and a positive number of firms. This starvation of the economy
would not happen if we assumed that the single monopolist bank
takes into account its influence on aggregate consumption. This
would be reminiscent of the "Ford effect" described in
D'Aspremont, Ferreira, and Gerard-Varet (1996). Return to text
28. An alternative definition of bank
markup is
![]() . In this definition,
. In this definition, ![]() is the
is the ![]() value to the bank of an additional firm producing at
value to the bank of an additional firm producing at
![]() (whose entry was funded at
(whose entry was funded at ![]() ),
), ![]() is the realized return that this
same firm generates. The benchmark definition compares the return
from firms that were funded in period
is the realized return that this
same firm generates. The benchmark definition compares the return
from firms that were funded in period ![]() (and
earlier) to the value of firms producing at
(and
earlier) to the value of firms producing at ![]() and
funded in period
and
funded in period ![]() , i.e., there is a discrepancy in
the timing of entry funding at numerator and denominator of
, i.e., there is a discrepancy in
the timing of entry funding at numerator and denominator of
![]() . By focusing on "the same firm," the alternative definition provides a more
accurate measure of the return from funding an entrant. However,
the benchmark definition is closer to empirical measures of bank
interest margins. Importantly, both definitions imply
countercyclical responses of the bank markup to shocks. Moreover,
the definitions are identical in steady state. Since we use only
the steady-state markup for calibration, the difference between
definitions is immaterial for our results. Return to text
. By focusing on "the same firm," the alternative definition provides a more
accurate measure of the return from funding an entrant. However,
the benchmark definition is closer to empirical measures of bank
interest margins. Importantly, both definitions imply
countercyclical responses of the bank markup to shocks. Moreover,
the definitions are identical in steady state. Since we use only
the steady-state markup for calibration, the difference between
definitions is immaterial for our results. Return to text
29. Relative to the deregulation scenarios studied in Ghironi and Melitz (2005) and Cacciatore, Fiori, and Ghironi (2013), in which deregulation is modeled as an exogenous reduction in sunk entry cost, here--as in Stebunovs (2008)--banking deregulation lowers the financial barrier to entry erected by banks for given size of exogenous sunk costs by narrowing the gap between the marginal value of an additional firm to a monopolistic bank and its perfectly competitive counterpart. The effects on firm behavior are intuitively similar. Return to text
30. Absent entry into the foreign country, the number of foreign traded-sector firms would steadily decrease with the exit shock. Return to text
31. Terms of labor dynamics are also the
key determinant of the terms of trade in our model. The terms of
trade are given by
![]() . Hence, appreciation of the terms of labor implies an improvement
in the terms of trade. Return to
text
. Hence, appreciation of the terms of labor implies an improvement
in the terms of trade. Return to
text
32. Empirically, job destruction is induced by both firm exit and contraction. We include the latter portion of job destruction in the exit shock in our model, consistent with interpreting productive units also as production lines within potentially multi-product firms. The fraction of firm closures and bankruptcies over the total number of firms reported by the U.S. Small Business Administration--consistently around 10 percent per year over the recent years--yields the same calibration. Return to text
33. The main qualitative features of our
results are not affected if we set ![]() . Return to text
. Return to text
34. Using the Longitudinal Business Database compiled by the Census Bureau, Kerr and Nanda (2006) find that interstate banking increased the entry of startups by 11 percent relative to facility expansions by existing firms. Further, they find that interstate deregulation increased the entry of small startups, with 20 or fewer employees, by 15 to 22 percent relative to facility expansions by existing firms. Return to text
35. As noted above, if banking integration is associated with economic development, this is consistent with the Harrod-Balassa-Samuelson evidence that more developed economies exhibit appreciated real exchange rates relative to their trading partners. Return to text
36. The entry condition (2) can be rewritten as
![]() , and a similar condition holds in foreign. When
, and a similar condition holds in foreign. When ![]() rises, other things given, the value of productive units in home is
above the entry cost. Entry occurs to the point that restores
equality through the implied effects on
rises, other things given, the value of productive units in home is
above the entry cost. Entry occurs to the point that restores
equality through the implied effects on ![]() and
and
![]() . There is no need for such entry in
foreign, as the deregulation shock has no impact on the entry
condition there that requires adjustment on the entry margin. This
intuition does not apply to the transition dynamics with
international borrowing and lending below. In that case, resource
shifting across countries implies an effect of the deregulation
shock on foreign wages that requires reduced entry--and therefore a
lower number of foreign tradable producers--for some time to
restore equality to the entry condition during the transition.
Consistent with the intuition, the shock has no long-run effect on
foreign entry. In Ghironi and Melitz (2005), endogenous tradedness
is responsible for a small adjustment in the number of foreign
producers under financial autarky. Return to text
. There is no need for such entry in
foreign, as the deregulation shock has no impact on the entry
condition there that requires adjustment on the entry margin. This
intuition does not apply to the transition dynamics with
international borrowing and lending below. In that case, resource
shifting across countries implies an effect of the deregulation
shock on foreign wages that requires reduced entry--and therefore a
lower number of foreign tradable producers--for some time to
restore equality to the entry condition during the transition.
Consistent with the intuition, the shock has no long-run effect on
foreign entry. In Ghironi and Melitz (2005), endogenous tradedness
is responsible for a small adjustment in the number of foreign
producers under financial autarky. Return to text
37. For simplicity, we continue to assume that banks are owned only domestically. International trade in bank equity would enhance international risk sharing in the model, as total dividend payments to households would become contingent on productivity abroad. The same would happen if we allowed for cross-country bank lending. The assumption that entrants must borrow from domestic banks is quite plausible for small firms (as we noted above, a large portion of U.S. GDP). This assumption implies that, even if international deposits give borrowers (indirect) access to foreign savings, the number of domestic banks represented in each locality remains the relevant measure of bank monopoly power. To evaluate the consequences of enhanced international risk sharing, we discuss some properties of the complete markets allocation below. de Blas and Russ (2013), Mandelman (2010), and Niepmann (2012, 2013) study the consequences of richer forms of cross-border banking. Return to text
38. Devereux and Sutherland (2010) and Tille and van Wincoop (2010) develop an alternative technique for pinning down steady-state international asset portfolios. We use a convenient specification of adjustment costs to pin down the steady-state allocation of deposits and ensure stationarity since our interest is in the dynamics of overall net foreign assets rather than the composition of portfolios. Moreover, we are interested in evaluating how international deposits affect dynamics around the same steady state as under financial autarky, while the Devereux-Sutherland/Tille-van Wincoop technique would imply a different steady state. See Hamano (2014) for an application of this technique to a model with extensive margin dynamics. Return to text
39. The terms of labor and the real exchange rate overshoot their new long-run appreciated levels on impact, reflecting the effect on home labor costs of the spike in labor demand from increased business creation on impact. Return to text
40. Substitutability between home and foreign goods is constrained to be strictly larger than 1 in our model, in which we do not differentiate between cross-country and within-country substitutability. This prevents us from analyzing the low substitutability scenarios studied by Corsetti, Dedola, and Leduc (2008). Return to text
41. This is the case on which Grossman and Helpman (1991) focus in their analysis of endogenous growth. Return to text
42. An alternative way to generate endogenously fluctuating markups would be to use translog preferences with a continuum of producers as in Bilbiie, Ghironi, and Melitz (2012). Since both specifications result in countercyclical markups, we conjecture that results would be similar for our purposes. Return to text
43. See Yang and Heijdra (1993) for an analysis of Dixit-Stiglitz monopolistic competition with a discrete number of producers. Return to text
44. We implicitly assume that firms have the ability to segment markets, so that consumers cannot arbitrage away deviations from the law of one price in excess of those implied by trade costs. Since firm entry is procyclical in our model, markups are countercyclical, and their movements amplify fluctuations in firm output. Return to text
45. Note that
![]() , and hence a foreign firm earns export profits
, and hence a foreign firm earns export profits
![]() . Return to text
. Return to text
46. The case in which
![]() corresponds to
linear disutility of effort and is often studied in the business
cycle literature. Return to text
corresponds to
linear disutility of effort and is often studied in the business
cycle literature. Return to text
47. The lowest steady-state import share
we obtained with
![]() was 16
percent with
was 16
percent with ![]() approximately 0.35. Return to text
approximately 0.35. Return to text
48. As in the model with inelastic labor supply and constant firm markups, assuming that the transition to interstate banking is anticipated or introducing an externality in entry costs increases the persistence of the current account deficit. Figures for these cases are available on request. Return to text
49. When the shock is more persistent, financing increased firm entry in the more productive economy becomes the main determinant of the current account, and the home economy runs a deficit in response to higher productivity. The procyclicality of entry that characterizes our model is strongly supported empirically. The NBER Working Paper version of Bilbiie, Ghironi, and Melitz (2012) documents a contemporaneous correlation between U.S. GDP and net entry (measured as the difference between new incorporations and failures) equal to 0.4. See Bilbiie, Ghironi, and Melitz (2012) and references therein for additional discussion of the evidence of strong procyclicality of entry (and relative acyclicality of exit) at plant and product levels. Our model yields a contemporaneous correlation between GDP and entry equal to 0.72 for the benchmark calibration. If our goal were to match the correlation above, it would be easy to accomplish that by introducing adjustment costs that delay entry in the model without altering our main conclusions. Return to text
50. The literature on bank dynamics convincingly documents the countercyclicality of various measures of bank margins (often measured by net interest margins) and markups. See, for instance, Aliaga-Díaz and Olivero (2010, 2011), Corbae and D'Erasmo (2011), and Mandelman (2011). Aliaga-Díaz and Olivero report numbers approximately between -0.20 and -0.35 for the contemporaneous correlation of U.S. bank margins with GDP (per capita) at quarterly frequency. Corbae and D'Erasmo find a correlation of approximately -0.50 between bank markups and GDP at annual frequency. Our model and benchmark calibration generate a correlation of bank markup with GDP at -0.83 for the benchmark markup measure (-0.90 for the alternative) both before and after the deregulation. Although, the model overstates the countercyclicality of the bank markup, we view the qualitative result as a success. Return to text
51. We discuss the role of market incompleteness for the transmission of productivity shocks in the Appendix. Return to text
52. While the distinction between welfare- and data-consistent variables does not matter for the real exchange rate in our model with non-traded goods, it matters for variables that are not defined as cross-country ratios. Return to text
53. King and Rebelo (1999) document that the ratios of standard volatilities of consumption, labor effort, and investment to GDP in U.S. data are 0.74, 0.99, and 2.93, respectively, over the sample they consider. Return to text
54. The volatility of U.S. GDP declined by approximately 30 percent during the Great Moderation. Our model explains between one-fourth and one-third of this reduction depending on the calibration of the productivity process. Return to text
55. Bank markup volatility also declines. Return to text
56. Note that one can view the decision to purchase a house as an entry decision (into home ownership) requiring a sunk investment of resources that must (for the most part) be borrowed from banks. Deregulation that makes access to this finance easier for households will result in more entry into home ownership and external borrowing. Household heterogeneity, asymmetric information, and debt default would then be necessary additional ingredients for a model of the recent international financial crisis that preserves the key logic of our model. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text