Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-06 Screen Reader version ^♣

A Closer Look at the Sensitivity Puzzle:
The Sensitivity of Expected Future Short Rates
and Term Premia to Macroeconomic News

Meredith Beechey¹

December 26, 2006

Keywords: forward rates, sensitivity puzzle, affine term structure model, risk premia

Abstract:

Nominal forward rates are sensitive at surprisingly long horizons to macroeconomic news and monetary-policy surprises. This paper takes advantage of affine term-structure modelling to demonstrate that movements in term premia, not expected future short rates, account for most of the reaction of forward rates at long horizons. Specifically, term premia account for about three quarters of the reaction of nominal forward rates 10 to 15 years hence to the surprise component of numerous macroeconomic news announcements. This has strong implications for the interpretation of interest-rate sensitivity. Contrary to some recent conjectures, long-horizon expectations of the level of inflation and real rates appear reasonably well anchored in the United States, but the associated term premia are quite variable.

1 Introduction

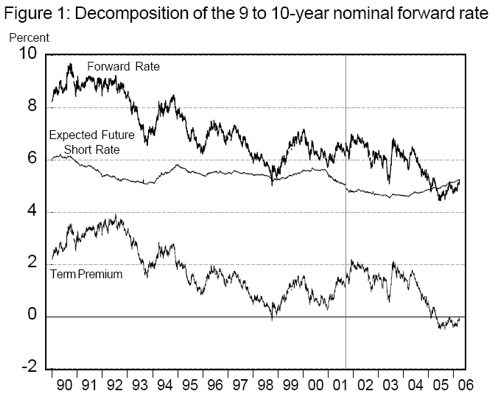
The purpose of this paper is to separate the reaction of U.S. Treasury forward rates to macroeconomic news into components attributable to term premia and expected future short rates. The analysis employs the decomposition of forward rates into expected future short rates and term premia made possible by a standard affine, no-arbitrage, three-factor model of the term structure. Such modelling permits a closer look at the nature of interest rate sensitivity than recent research whose scope has been confined to nominal forward rates. I confirm that distant-horizon nominal forward rates are sensitive to current economic news and monetary policy surprises but show that movements in term premia, not expected future short rates, account for most of the reaction.

Specifically, movements in term premia account for about three quarters of the reaction of nominal forward rates 10 to 15 years hence in response to a range of important macroeconomic surprises. This has strong implications for the interpretation of interest-rate sensitivity, namely, that long-horizon expectations of inflation and real rates are reasonably well anchored in the United States, contrary to recent conjecture by Gürkaynak, Sack, and Swanson (2005) (GSS). Why term premia exhibit such sensitivity to economic news and monetary policy surprises is not clear-cut. It may represent changing uncertainty (a change in the quantity of risk), a change in the price of risk, or a behavioral overreaction to new information.

These findings are relevant to what is meant by "well-anchored expectations". Are interest-rate expectations well anchored when expectations of future nominal policy rates mean revert at reasonable horizons following the release of new information? Or must uncertainty about long-run interest rate expectations also be fairly insensitive to current macroeconomic surprises? The results shown in this paper suggest that the second condition is not met in U.S. Treasury markets. The paper is structured as follows. Section 2 gives a brief overview of the affine term-structure model used to generate the decompositions, describes the data and presents the estimation strategy. Section 3 presents and discusses the results and considers an alternative estimate of the term premium and Section 4 concludes.

2 Model and Estimation Strategy

2.1 Term-structure Model

The model of the nominal term structure is the implementation by Kim and Orphanides (2005) of a model proposed by Duffie (2002) using three underlying latent factors to describe the time-series behavior of the U.S. yield curve. As is standard in affine term-structure models, the model hinges on the fundamental asset pricing condition

$\displaystyle E_{t}(M_{t+1}R_{t+1})=1$

where $R_{t+1}$ is the gross nominal return on a zero-coupon bond at time

and $M_{t+1}$ is a stochastic discount factor derived from a standard utility maximization problem of a representative investor. The simple nature of zero-coupon bonds allows the price of an

period bond to be expressed recursively as

$\displaystyle P_{n,t}=E_{t}(\Pi_{j=1}^{n}M_{t+j}).%$

(1)

The model assumes that the pricing relationship (1) holds for all bonds and in this sense the framework imposes the no-arbitrage restriction. For the model generating the financial data for this paper, the stochastic discount factor, $M_{t+1}$ , is specified as an affine function of a $3\times1$ vector of latent factors, $X_{t}$ . It is assumed to be conditionally lognormal, as in the following discrete-time specification:

$\displaystyle \log(M_{t+1})=-y_{1,t}-\lambda_{t}^{\prime}\varepsilon_{t+1}-0.5\lambda _{t}^{\prime}\lambda_{t}%$

where $y_{1,t}$ is the one-period yield, $\lambda_{t}$ is a $3\times1$ vector, and $y_{1,t}$ and $\lambda_{t}$ are affine functions of the factors,

$\displaystyle y_{1,t}$	$\displaystyle =\delta_{0}+\delta_{1}^{\prime}X_{t}$
$\displaystyle \lambda_{t}$	$\displaystyle =v_{0}+v_{1}^{\prime}X_{t}.$

The coefficient $\delta_{0}$ is a scalar, $\delta_{1}$ and $v_{0}$ are $3\times1$ vectors, $v_{1}$ is a $3\times3$ matrix and the vector of latent factors evolve as a VAR(1),²

$\displaystyle X_{t}=\Phi X_{t-1}+\Sigma\varepsilon_{t}%$

with the shock $\varepsilon_{t}$ i.i.d. normal with mean zero and identity variance-covariance matrix and $\Sigma=diag(\sigma_{1},\sigma_{2},\sigma_{3}% )$ . The vector $\lambda_{t}$ can be interpreted as the market price of risk, and the model permits a time-varying price of risk, as well as tractable and nonnegative bond prices. Yields, forward rates, expected future short rates and term premia are affine functions of the latent factors. Specifically, yields can be calculated as follows:

$\displaystyle y_{n,t}=a_{n}+b_{n}X_{t}%$

where $a_{n}$ and $b_{n}$ are functions of the parameters of the model ( $\delta_{0},$ $\delta_{1},v_{0},v_{1},\Phi$ and $\left\{ \sigma_{j}% ^{2}\right\} _{j=1}^{3}$ ). The parameters of the model are estimated by maximum likelihood using monthly nominal zero-coupon yield data from 1961 and the latent factors, forward rates and term premia are constructed at a daily frequency. Rather than employ both yield-curve and macroeconomic factors for forecasting in the model, as in Diebold, Rudebusch, and Aruoba (2006) and Rudebusch and Wu (2004), this paper considers whether affine functions of purely latent yield-curve factors exhibit systematic responses to new macroeconomic information not included in the term-structure model. Figure 1 plots the forward rate nine-to-ten years hence, as well as the model's decomposition into the expected future short rate and term premium.

2.2 Data

The financial data for the analysis consist of zero-coupon yields and forward rates from an estimated nominal Svensson yield curve for U.S. Treasuries. The zero-coupon yields are used to estimate the parameters of the affine factor model described above, and once estimated, the model provides decompositions of forward rates into expected future nominal short rates and term premia. Daily changes in the one-year forward rates and their components are then employed as dependent variables in announcement regressions.

The macroeconomic data consist of the surprise elements of thirteen major U.S. data releases and a monetary-policy target surprise. The macroeconomic surprises are nearly identical to those of GSS (2005) but the sample end-date has been extended from December 2002 to October 2005 and missing observations replaced.³ Following GSS, the surprise component of a macroeconomic data release is measured as the released value less the market expectation reported the prior Friday by Money Market Services (MMS, provided by Action Economics), and each surprise series is divided by its standard error. To facilitate comparison with earlier results, the macroeconomic variables included in the regressions are the subset of releases deemed by GSS to be significant determinants of the one-year forward rate ending one year hence; namely, capacity utilization, consumer confidence, core CPI, civilian employees' employment cost index, advance GDP, initial jobless claims, index of leading indicators, ISM PMI index (NAPM), new home sales, change in nonfarm payrolls, core PPI, retail sales and the unemployment rate.⁴ The monetary policy surprise is measured as the daily change in the current or next month's futures contract around an FOMC announcement, as recommended by Kuttner (2001).

2.3 Estimation Strategy

Daily changes in forward rates, expected nominal short rates and term premia from the affine factor model are regressed at various horizons on the surprise components of macroeconomic data releases. The equations to be estimated take a simple form:

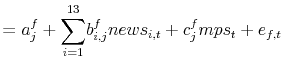$\displaystyle \Delta f_{j,t}$	$\displaystyle =a_{j}^{f}+% {\displaystyle\sum\limits_{i=1}^{13}} b_{i,j}^{f}news_{i,t}+c_{j}^{f}mps_{t}+e_{f,t}$	(2)
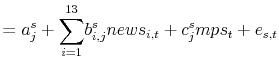$\displaystyle \Delta s_{j,t}$	$\displaystyle =a_{j}^{s}+% {\displaystyle\sum\limits_{i=1}^{13}} b_{i,j}^{s}news_{i,t}+c_{j}^{s}mps_{t}+e_{s,t}$	(3)
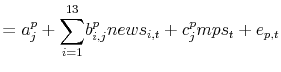$\displaystyle \Delta p_{j,t}$	$\displaystyle =a_{j}^{p}+% {\displaystyle\sum\limits_{i=1}^{13}} b_{i,j}^{p}news_{i,t}+c_{j}^{p}mps_{t}+e_{p,t}%$	(4)

where $f_{j,t}$ denotes the one-year ahead forward rate ending

years hence at time

, and $s_{j,t}$ and $p_{j,t}$ denote the expected short rate and term premium at horizon

and the difference operator indicates daily changes.⁵ The variable $news_{i,t}%$ indexes the

macro data releases and $mps_{t}$ is the monetary policy surprise at date

. Newey-West standard errors are estimated to take into account any heteroskedasticity and serial correlation.

Two points are worth making here. First, the fit of the factor model is sufficiently good that coefficient estimates from regressions using the fitted forward rates are indistinguishable from those using the Svensson-curve forward rates. Second, while there may be measurement error present in $s_{j,t}$ and $p_{j,t}$ , as long as this measurement error is uncorrelated with the surprise components of the data releases, it will not bias the coefficient estimates but just sacrifice precision.

3 Estimation results

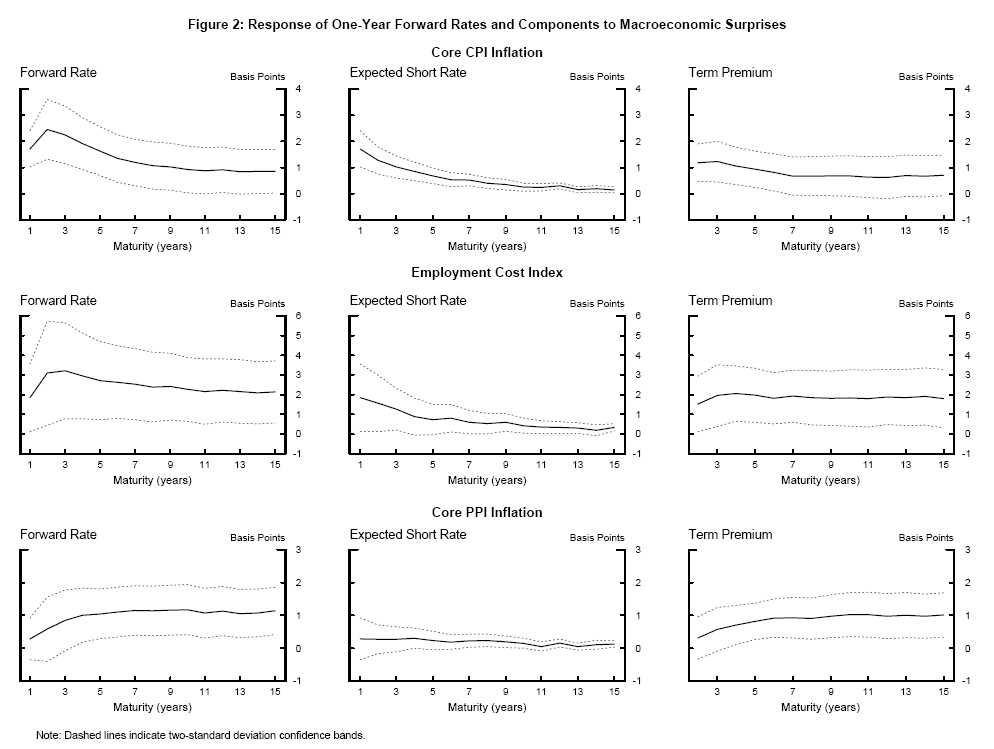
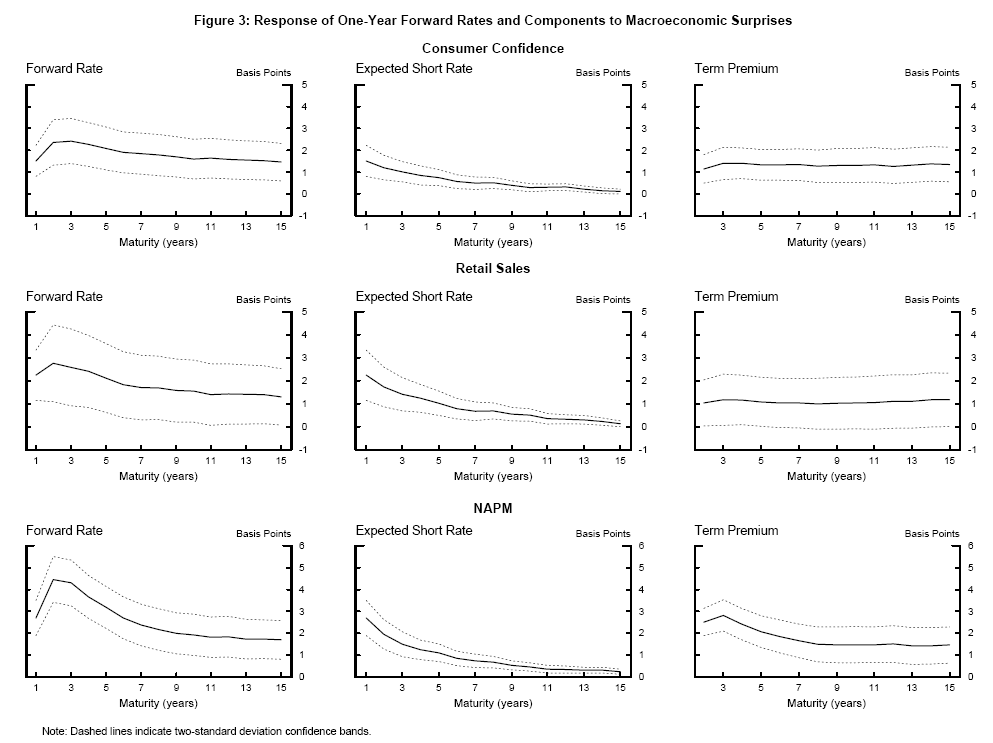
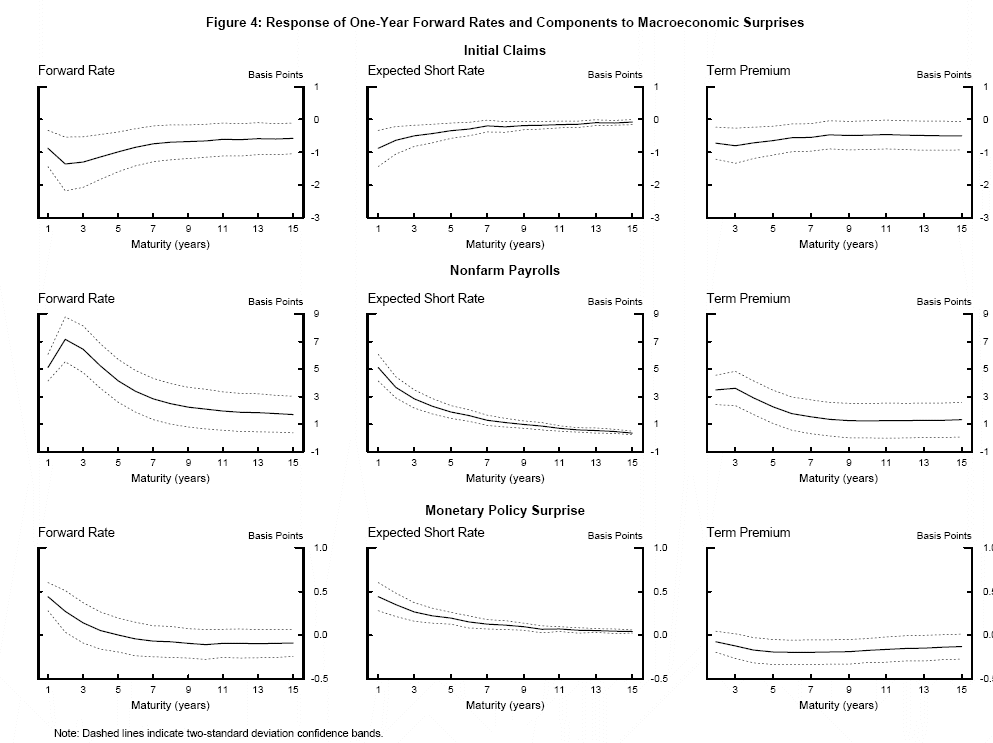
Table 1 presents the estimated coefficients from equation (2) from regressing daily changes in Svensson forward rates and the fitted factor-model forward rates on economic news variables for the sample January 1990 to December 2002. The columns marked GSS report the results published in GSS (2005). The coefficients estimated from fitted forward rates are very similar to the Svensson forward rates and the standard errors remain small, testimony to the good fit of the three-factor model. Only the coefficient on advance GDP differs noticeably, with the replacement of missing data points lowering the estimated response by one third. Table 2 presents the same regressions updated to include data to end-October 2005, also plotted as the solid black line in Figures 2 to 4 (95 percent confidence intervals are shown as dashed lines). Extending the sample has little effect on the coefficients or standard errors.

Table 3 presents the results of equations (3) and (4) for expected future short rates and term premia. The coefficient estimates are summarized in Figures 2 to 4 along with 95 percent confidence intervals. Several points are worth making. First, as expected, the estimated coefficients on the expected short rate and term premium sum to the coefficient on the nominal forward rate at each maturity. Second, it is immediately clear that the majority of the sensitivity of long-horizon forward rates is due to the response of term premia to macroeconomic surprises. Between 70 and 80 percent of the total response at 10 years can be attributed to movement in term premia. Expected nominal short rates respond strongly to macroeconomic shocks in the near term but the response then declines smoothly over the forecast horizon to a small (but precisely estimated) response 10 years hence. The minimal response of expected future nominal short rates at long horizons suggests that the sum of long-run inflation expectations and the perceived equilibrium real rate is reasonably well anchored in the United States.

3.1 Reaction to macroeconomic news

The term premia response at long horizons dominates the expected short-rate response for all economic news variables used as regressors. Positive inflation surprises and real-side surprises cause expected future short rates to rise in the near term, while term premia dominate in the longer run. Notably, nonfarm payrolls surprises seem to elicit a larger response of expected nominal short rates than other variables, suggesting that this important release prompts the most revision to long-run expectations. Weaker-than-expected inflation and real-side news are associated with lower term premia. One possible reason for this is that investors may demand less compensation for inflation risk when news indicates that inflation outcomes are likely to be lower, consistent with the positive correlation between the level and volatility of inflation discussed by Svensson (1997) and Mishkin and Westelius (2006), among others.

3.2 Reaction to monetary-policy surprises

The reaction of forward rates to a monetary-policy surprise--defined as the unexpected target surprise of an FOMC decision--is particularly interesting. Positive policy surprises elicit a small rise in nominal short-rate expectations in the near to medium term, but short rates are then projected to revert slowly to their pre-shock level within a decade. In contrast, a positive policy surprise is associated with a decline in the term premium at all horizons, sufficient to offset the rise in nominal short rate expectations. The connection between tighter monetary policy with a lower market price of risk, or a larger market appetite for assets, could be consistent with monetary-policy tightening lowering market uncertainty, especially the compensation that investors demand for inflation risk.

3.3 An alternative estimate of the term premium

Cochrane and Piazzesi (2005) estimate bond term premiums by regressing excess bond returns on the term structure of forward rates, where excess bond returns are measured as the return on holding an -year bond over the return on holding a one-year bond for a holding period of one year. Their resulting forecasting factor shares a high correlation (0.71) with the term premium on a one-year forward rate 5-years hence estimated by the three-factor model. Thus it comes as no surprise that estimating equation (3) on daily changes in the return forecasting factor reveals significant reactions to the same news surprises that move term premia (see Table 4). And because excess returns at different horizons are proportional to the return forecasting factor, this implies that the response does not diminish with maturity, the same property seen clearly in Figures 2, 3 and 4 for the affine factor model's term premia.

3.4 Discussion

An important question to ask at this point is whether the results are an artifact of the construction of the three-factor model. The factors of the arbitrage-free model are estimated as unobservable, latent factors without macroeconomic data input, and as such the regressions presented here do not exploit pre-constructed relationships between expected interest rates, term premia and economic news. Therefore, the assumption that any measurement error in the term premium and expected future short-term rates estimated by the three-factor model should be uncorrelated with the MMS surprises seems reasonable. Similar results to those presented here are obtained using the forward-rate decomposition from a three-factor model augmented with Blue Chip survey inflation expectations (Kim and Orphanides, 2005). These survey expectations presumably incorporate information about macroeconomic surprises comparable to that in MMS expectations used to derive the surprise regressors and, accordingly, the results differ little.

The affine term-structure model also has the characteristic that its latent factors are stationary. However, the half life of the most persistent factor is over 10 years, so gradual that fitted term premia and expected short rates can be far from their means for very long periods. The coefficients, and thus the decomposition of the sensitivity puzzle, are quite insensitive to increasing the persistence of the most persistent factor as done by Wright (2006). It is also important to remember that term premiums and expected short rates are fitted jointly in the model and as such, both are functions of the same three factors. Freely estimated coefficients determine the affine combination of factors that represent the best fit of the data.

4 Conclusion

This paper has shown that expectations of the central bank's policy rate account for only a small fraction of the response of long-horizon forward rates to news. The finding casts doubt upon explanations of long forward-rate sensitivity that posit that data surprises prompt changes in perceptions of the central bank's inflation target, or perceptions of equilibrium real interest rates. Such explanations overlook the role of adjustment of risk premia in response to new information, which appear to dominate the response at long horizons.

Term premia at all maturities rise in response to stronger-than-expected real and inflation news, and in response to surprise policy easings. This is true of both the term premia estimated by the affine factor model and Cochrane and Piazzesi's (2005) return forecasting factor. This procyclicality contrasts with the common finding that term premia are somewhat countercyclical. The two are not necessarily at odds, however, as countercyclicality is found at the business-cycle frequency and need not reflect the high-frequency reaction of term premia in short windows around macroeconomic news announcements.

Indeed, the nature of the term-premium response to news-declining with weaker-than-expected macroeconomic data and tighter monetary policy-is suggestive of a role for inflation risk premia. Paired with the findings of Gürkaynak, Levin, and Swanson (2005), that long-horizon inflation compensation (comprising expected future inflation and an inflation risk premium) also responds to macroeconomic news, it seems likely that inflation risk premia are variable in the United States. However, to accurately parse out the effect of news announcements on inflation risk premia and real risk premia requires term-structure models that can identify both quantities and is the subject of ongoing research.

Bibliography

COCHRANE, J., AND M. PIAZZESI (2005):

"Bond Risk Premia," American Economic Review, 95, 138-160.

DIEBOLD, F., G. RUDEBUSCH, AND S. B. ARUOBA (2006):

"The Macroeconomy and the Yield Curve: A Dynamic Latent Factor Approach," Journal of Econometrics, 131(1-2), 309-338.

DUFFIE, G. (2002):

"Term Premia and Interest Rate Forecasts in Affine Models," Journal of Finance, 57, 405-443.

GÜRKAYNAK, R., A. LEVIN, AND E. SWANSON (2005):

"Inflation Targeting and the Anchoring of Long-Run Inflation Expectations: International Evidence from Daily Bond Yield Data," Unpublished manuscript.

GÜRKAYNAK, R., B. SACK, AND E. SWANSON (2005):

"The Excess Sensitivity of Long Term Interest Rates: Evidence and Implications for Macroeconomic Models," American Economic Review, 95, 425-436.

KIM, D., AND A. ORPHANIDES (2005):

"Term Structure estimation with survey data on interest rate forecasts," FEDS Working Paper Series No. 2005-48, Board of Governors of the Federal Reserve.

KIM, D., AND J. WRIGHT (2005):

"An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates," FEDS Working Paper Series No. 2005-33, Board of Governors of the Federal Reserve.

KUTTNER, K. (2001):

"Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market," Journal of Monetary Economics, 47(3), 523-544.

MISHKIN, F., AND N. WESTELIUS (2006):

"Inflation Band Targeting and Optimal Inflation Contracts," NBER Working Paper 12384.

RUDEBUSCH, G., AND T. WU (2004):

"A Macro-Finance Model of the Term Structure, Monetary Policy and the Economy," FRBSF Working Paper 2003-17.

SVENSSON, L. E. O. (1997):

"Optimal Inflation Targets, "Conservative" Central Banks, and Linear Inflation Contracts," American Economic Review, 87, 98-114.

WRIGHT, J. (2006):

"Stationarity, Nonstationarity and Near-nonstationarity in Don Kim's model," unpublished manuscript, Board of Governors of the Federal Reserve, April 2006.

Figure 1: Decomposition of the 9 to 10-year nominal forward rate. The figure plots three variables from January 1990 to May 2006: the one-year nominal forward rate nine-years hence fitted by affine factor model described in the paper, and the expected future short rate and term premium component of the forward rate. The nominal forward rate has drifted down from a high around nine percent in the early 1990s to values between four and six percent in 2005 and 2006. The expected short rate has moved in a smaller range, between six and four percent over the whole sample and exhibits much less cyclical and day-to-day variation than the forward rate. The term premium is the lowest of the three series, but varies in a wider range than the expected short rate. Specifically, it oscillates between four and minus one half percent and exhibits most of the cyclical and day-to-day movement in the forward rate.

Figure 2: Response of One-Year Forward Rates and Components to Macroeconomic Suprises. The figure shows the response of one-year forward rates, expected short rates and term premia to inflation news. The figure is comprised of three rows, and each row consists of three panels corresponding to equations 2, 3 and 4 in the text respectively. Moving from left to right, the left panel plots the response of the nominal forward rate in basis points to a data surprise at one-year intervals from one to fifteen years. The middle panel plots the response of the expected short rate in basis points to a data surprise at one-year intervals from one to fifteen years. The right panel plots the response of the term premium in basis points to a data surprise at one-year intervals from one to fifteen years. The first row plots coefficients pertaining to core CPI inflation surprises, the second row plots coefficients pertaining to surprises in the Employment Cost Index and the third row plots coefficients pertaining to core PPI inflation surprises. Each row exhibits approximately the same dynamics. The nominal forward rate reacts to inflation news by one to two basis points at all horizons between one and fifteen years. The expected short rate reacts strongly to the news at horizons of one to three years but the reaction dies out over the following ten years. At fifteen years, the reaction is very small, but statistically significantly above zero. The term premium reacts strongly and significantly at all horizons to the news and does not die out with maturity horizon.

Figure 3: Response of One-Year Forward Rates and Components to Macroeconomic Suprises. The figure shows the response of one-year forward rates, expected short rates and term premia to real-sector news. The figure is comprised of three rows, and each row consists of three panels corresponding to equations 2, 3 and 4 in the text respectively. Moving from left to right, the left panel plots the response of the nominal forward rate in basis points to a data surprise at one-year intervals from one to fifteen years. The middle panel plots the response of the expected short rate in basis points to a data surprise at one-year intervals from one to fifteen years. The right panel plots the response of the term premium in basis points to a data surprise at one-year intervals from one to fifteen years. The first row plots coefficients pertaining to consumer confidence surprises, the second row plots coefficients pertaining to surprises in retail sales and the third row plots coefficients pertaining to surprises in the National Association of Purchasing Managers (NAPM) index. Each row exhibits approximately the same dynamics. The nominal forward rate reacts to the news by one to four basis points at all horizons between one and fifteen years. The expected short rate reacts strongly to the news at horizons of one to three years but the reaction dies out over the following ten years. At fifteen years, the reaction is very small, but statistically significantly above zero. The term premium reacts strongly and significantly at all horizons to the news and does not die out with maturity horizon.

Figure 4: Response of One-Year Forward Rates and Components to Macroeconomic Suprises. The figure shows the response of one-year forward rates, expected short rates and term premia to labor-sector news and monetary policy surprises. The figure is comprised of three rows, and each row consists of three panels corresponding to equations 2, 3 and 4 in the text respectively. Moving from left to right, the left panel plots the response of the nominal forward rate in basis points to a data surprise at one-year intervals from one to fifteen years. The middle panel plots the response of the expected short rate in basis points to a data surprise at one-year intervals from one to fifteen years. The right panel plots the response of the term premium in basis points to a data surprise at one-year intervals from one to fifteen years. The first row plots coefficients pertaining to initial claims surprises, the second row plots coefficients pertaining to nonfarm payrolls surprises and the third row plots coefficients pertaining to monetary-policy surprises as defined in the text. In the first row, the nominal forward rate declines to one to a half basis points at all horizons between one and fifteen years. The expected short rate reacts strongly to the news at horizons of one to three years but the reaction dies out over the following ten years. At fifteen years, the reaction is very small, but statistically significantly below zero. The term premium reacts strongly and significantly at all horizons to the news and does not die out with maturity horizon. In the second row, the nominal forward rate increases strongly, by five to seven basis points, at horizons of one to three years in response to a non-farm payrolls surprise. The expected short rate also reacts strongly to the news at horizons of one to three years but the reaction dies out over the following ten years. At fifteen years, the reaction is very small, but statistically significantly above zero. The term premium reacts strongly and significantly at all horizons to the news and does not die out with maturity horizon. The third row plots the response of interest rates to a monetary policy surprise. The nominal forward rate increases significantly by a half to a quarter percentage point at horizons of one to three years in response to a positive monetary policy surprise. The expected short rate also exhibits a small but significantly positive reaction to the surprises between one and five years but the reaction dies out over the following ten years. At fifteen years, the reaction is very small, but statistically significantly above zero. In contrast, the term premium declines in response to the policy surprise and the reaction does not die out with maturity horizon. The reaction is small (less than one quarter percentage point) but significantly less than zero.

Table 1: Responses of Nominal Forward Rates to Economic News, Jan 1990 to Dec 2002
Macroeconomic data releases and Monetary Policy Surprises	Ending 1 year ahead - GSS	Ending 1 year ahead - Three-factor model	Ending 5 years ahead - GSS	Ending 5 years ahead - Three-factor model	Ending 10 years ahead - GSS	Ending 10 years ahead - Three-factor model
Capacity utilisation	1.36*** ($1.33)	1.42*** ($1.32)	1.26** ($1.57)	1.33** ($1.57)	0.80 ($1.61)	0.46 ($1.61)
Consumer confidence	2.11*** ($1.40)	2.02*** ($1.40)	2.88*** ($1.56)	2.75*** ($1.52)	1.97*** ($1.54)	2.08*** ($1.51)
CPI (core)	1.67*** ($1.42)	1.67*** ($1.40)	1.81*** ($1.60)	1.68*** ($1.54)	1.09* ($1.66)	1.10** ($1.52)
Employment cost index	3.43*** ($1.89)	3.65*** ($1.86)	4.42*** ($1.13)	4.46*** ($1.98)	3.73*** ($1.93)	3.65*** ($1.87)
GDP (advance)	4.39*** ($1.42)	2.69** ($1.24)	4.12* ($1.19)	2.17 ($1.62)	3.76** ($1.82)	1.36 ($1.43)
Initial Claims	-0.83*** ($1.24)	-0.95** ($1.41)	-0.79*** ($1.29)	-0.93** ($1.41)	-0.59** ($1.27)	-0.65** ($1.33)
Leading Indicators	0.95*** ($1.34)	0.95*** ($1.33)	0.61 ($1.57)	0.56 ($1.53)	0.55 ($1.58)	0.57 ($1.55)
NAPM	3.00*** ($1.51)	2.91*** ($1.49)	3.29*** ($1.54)	2.98*** ($1.53)	1.53** ($1.63)	1.76*** ($1.54)
New home sales	1.08*** ($1.39)	1.10*** ($1.42)	1.65*** ($1.54)	1.55*** ($1.56)	0.92* ($1.51)	1.31*** ($1.51)
Non-farm payrolls	5.10*** ($1.57)	4.91*** ($1.56)	3.48*** ($1.91)	3.33*** ($1.90)	1.88* ($1.97)	1.64* ($1.87)
PPI (core)	0.39 ($1.45)	0.42 ($1.43)	1.22** ($1.56)	1.29** ($1.51)	1.46*** ($1.50)	1.32*** ($1.51)
Retail sales	2.97*** ($1.72)	3.05*** ($1.68)	2.62** ($1.03)	2.46*** ($1.90)	1.93** ($1.92)	1.83** ($1.87)
Unemployment Rate	-1.76*** ($1.51)	-1.58*** ($1.47)	-0.77 ($1.73)	-0.62 ($1.66)	0.14 ($1.66)	0.03 ($1.63)
Monetary Policy Surprises	0.47*** ($1.10)	0.44*** ($1.08)	-0.04 ($1.14)	-0.03 ($1.10)	-0.16** ($1.07)	-0.13 ($1.09)

Notes: Newey-West standard errors. *** indicates significance at the 1-percent level, ** at the 5-percent level and * at the 10-percent level. Coefficients in columns labelled 'GSS' are values reported in GSS
(2005). The estimated coefficients represent the basis-point repsonse of the one-year forward rate per standard deviation of the macroeconomic release surprise and per basis-point surprise in monetary policy announcements. Constant terms not shown.

Table 2: Responses of Nominal Forward Rates to Economic News, 1990 to 2002 and 1990 to 2005
Macroeconomic data releases and Monetary Policy Surprises	Ending 1 year ahead: Jan 1990 - Dec 2002	Ending 1 year ahead: Jan 1990 - Oct 2005	Ending 5 years ahead: Jan 1990 - Dec 2002	Ending 5 years ahead: Jan 1990 - Oct 2005	Ending 10 years ahead: Jan 1990 - Dec 2002	Ending 10 years ahead: Jan 1990 - Oct 2005
Capacity utilisation	1.42*** ($1.32)	1.17*** ($1.29)	1.33** ($1.57)	1.04** ($1.48)	0.46 ($1.61)	0.45 ($1.52)
Consumer confidence	2.02*** ($1.40)	1.48*** ($1.37)	2.75*** ($1.52)	2.03*** ($1.51)	2.08*** ($1.51)	1.56*** ($1.48)
CPI (core)	1.67*** ($1.40)	1.73*** ($1.36)	1.68*** ($1.54)	1.63*** ($1.48)	1.10** ($1.52)	0.93** ($1.46)
Employment cost index	3.65*** ($1.86)	1.91** ($1.89)	4.46*** ($1.98)	2.73*** ($1.03)	3.65*** ($1.87)	2.26*** ($1.83)
GDP (advance)	2.69** ($1.24)	2.50** ($1.98)	2.17 ($1.62)	2.99** ($1.30)	1.36 ($1.43)	2.08 ($1.16)
Initial Claims	-0.95** ($1.41)	-0.91*** ($1.30)	-0.93** ($1.41)	-1.00*** ($1.32)	-0.65** ($1.33)	-0.66** ($1.27)
Leading Indicators	0.95*** ($1.33)	0.65* ($1.34)	0.56 ($1.53)	0.59 ($1.48)	0.57 ($1.55)	0.72 ($1.50)
NAPM	2.91*** ($1.49)	2.72*** ($1.42)	2.98*** ($1.53)	3.22*** ($1.50)	1.76*** ($1.54)	1.97*** ($1.49)
New home sales	1.10*** ($1.42)	0.80*** ($1.31)	1.55*** ($1.56)	1.15*** ($1.43)	1.31*** ($1.51)	1.04*** ($1.39)
Non-farm payrolls	4.91*** ($1.56)	5.20*** ($1.50)	3.33*** ($1.90)	4.19*** ($1.81)	1.64* ($1.87)	2.11* ($1.75)
PPI (core)	0.42 ($1.43)	0.27 ($1.34)	1.29** ($1.51)	1.00** ($1.39)	1.32*** ($1.51)	1.14*** ($1.40)
Retail sales	3.05*** ($1.68)	2.33*** ($1.59)	2.46*** ($1.90)	2.13*** ($1.82)	1.83** ($1.87)	1.58** ($1.73)
Unemployment Rate	-1.58*** ($1.47)	-1.30*** ($1.45)	-0.62 ($1.66)	-0.04 ($1.65)	0.03 ($1.63)	0.36 ($1.61)
Monetary Policy Surprises	0.44*** ($1.08)	0.45*** ($1.08)	-0.03 ($1.10)	-0.02 ($1.10)	-0.13 ($1.09)	-0.13 ($1.09)

Notes: Newey-West standard errors. *** indicates significance at the 1-percent level, ** at the 5-percent level and * at the 10-percent level. The estimated coefficient indicates the basis-point repsonse of the one-year forward rate per standard deviation of the macroeconomic release surprise and per basis-point surprise in monetary policy announcements. Constant terms not shown.

Table 3: Responses of Expected Short Rates and Term Premia to Economic News
Macroeconomic data releases and Monetary Policy Surprises	Ending 1 year ahead: Short rate	Ending 1 year ahead: Term premium	Ending 5 years ahead: Short rate	Ending 5 years ahead: Term premium	Ending 10 years ahead: Short rate	Ending 10 years ahead: Term premium
Capacity utilisation	1.17*** ($1.29)	--	0.34* ($1.18)	0.70** ($1.35)	0.20** ($1.10)	0.24 ($1.44)
Consumer confidence	1.48*** ($1.37)	--	0.73*** ($1.19)	1.31*** ($1.37)	0.27*** ($1.09)	1.29*** ($1.41)
CPI (core)	1.73*** ($1.36)	--	0.69*** ($1.15)	0.94*** ($1.36)	0.25*** ($1.08)	0.68* ($1.40)
Employment cost index	1.91*** ($1.89)	--	0.76* ($1.40)	1.98*** ($1.71)	0.44** ($1.20)	1.82** ($1.73)
GDP (advance)	2.50** ($1.98)	--	0.99** ($1.41)	2.00* ($1.05)	0.60*** ($1.23)	1.48 ($1.03)
Initial Claims	-0.91** ($1.30)	--	-0.35*** ($1.13)	-0.65*** ($1.23)	-0.18*** ($1.06)	-0.49** ($1.24)
Leading Indicators	0.65*** ($1.34)	--	0.37** ($1.16)	0.22 ($1.38)	0.18** ($1.07)	0.54 ($1.46)
NAPM	2.72*** ($1.42)	--	1.12*** ($1.21)	2.10*** ($1.38)	0.46*** ($1.10)	1.51*** ($1.43)
New home sales	0.80*** ($1.31)	--	0.42*** ($1.14)	0.73** ($1.33)	0.21*** ($1.07)	0.83** ($1.35)
Non-farm payrolls	5.20*** ($1.50)	--	1.93*** ($1.24)	2.26*** ($1.63)	0.87*** ($1.14)	1.23* ($1.65)
PPI (core)	0.27 ($1.34)	--	0.23 ($1.15)	0.78*** ($1.29)	0.14** ($1.07)	1.00*** ($1.35)
Retail sales	2.33*** ($1.59)	--	1.07*** ($1.28)	1.06** ($1.58)	0.55*** ($1.15)	1.04* ($1.62)
Unemployment Rate	-1.29*** ($1.45)	--	-0.50** ($1.22)	0.46 ($1.50)	-0.19** ($1.11)	0.55** ($1.54)
Monetary Policy Surprises	0.45*** ($1.08)	--	0.20*** ($1.03)	-0.21*** ($1.07)	0.07*** ($1.02)	-0.20*** ($1.07)

Table 4: Response of Bond Excess Return Forecasting Factor to Economic News
Macroeconomic data releases and Monetary Policy Surprises	Response
Capacity utilisation	3.32*** ($1.08)
Consumer confidence	3.41*** ($1.08)
CPI (core)	3.48*** ($1.11)
Employment cost index	5.91** ($1.43)
GDP (advance)	2.93 ($1.69)
Initial Claims	-1.26* ($1.66)
Leading Indicators	-0.21 ($1.02)
NAPM	7.78*** ($1.30)
New home sales	1.26 ($1.06)
Non-farm payrolls	10.1*** ($1.82)
PPI (core)	0.52 ($1.99)
Retail sales	3.39* ($1.79)
Unemployment Rate	0.20 ($1.27)
Monetary Policy Surprises	-0.29 ($1.23)

Notes: Newey-West standard errors. *** indicates significance at the 1-percent level, ** at the 5-percent level and * at the 10-percent level. The estimated coefficient indicates the repsonse of Cochrane and Piazzesi's return forecasting factor per one standard-deviation macroeconomic release surprise and per basis-point surprise in monetary policy announcements. Constant terms not shown.

Footnotes

1. Division of Monetary Affairs, Board of Governors of the Federal Reserve System, Washington DC 20551. Email: [email protected]. I am grateful to Andrew Levin, Jonathan Wright and workshop participants at the ECB and the Reserve Bank of Australia for helpful discussions and to Brian Bunker and Katherine Femia for research assistance. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to Text

2. In the continuous-time specification of the model, the vector of latent factors actually evolve as a continuous-time analogue of the vector autoregression, a multivariate Ornstein-Uhlenbeck process, see Kim and Wright (2005). Return to Text

3. Extending the sample to October 2005 has little material effect on the nominal forward rate sensitivity coefficients. However, sixteen observations of advance GDP releases have been added to the data set by replacing missing observations and extending the sample used by GSS, who relied on only twelve data points for advance GDP surprises. Other special features of the data set, such as removing FOMC announcements that conflict with employment reports early in the sample and excluding the week around September 11, 2001, have been retained. Return to Text

4. These variables continue to be the significant for the longer sample used in this paper. Return to Text

5. An attractive extension is to estimate responses over narrower windows, but this would also require forecasting intraday results from the three-factor model. Return to Text

A Closer Look at the Sensitivity Puzzle: The Sensitivity of Expected Future Short Rates and Term Premia to Macroeconomic News

A Closer Look at the Sensitivity Puzzle:
The Sensitivity of Expected Future Short Rates
and Term Premia to Macroeconomic News