
Corporate Asset Purchases and Sales:
Theory and Evidence
Missaka Warusawitharana*Board of Governors of the Federal Reserve
June 18, 2007
1 Introduction
Firms regularly trade product lines, operations in a specific locale, subsidiaries and other business units. Approximately $100 billion worth of assets were transacted between firms in 2004. From 1985 onwards, these transactions lead to a net gain of $162 billion for shareholders in participating firms.1 This suggests that asset transactions improve the allocative efficiency of capital in the economy.
The paper argues that firms' investment needs drive their decisions to grow organically or inorganically. Firms that wish to grow rapidly do so through acquisitions and firms aiming for slower growth do so through internal investments. Further, firms downsize when they find themselves with surplus assets. Essentially, acquisitions and asset sales are driven by choices over the scale of the firm. Alternative theories that argue these decisions are driven by decisions over the scope of the firm include the transactions cost economics approach (see Williamson (1975); and Klein, Crawford, and Alchian (1978)), and the property rights approach (see Grossman and Hart (1986); and Hart and Moore (1990)).
This study presents and tests a model in which asset purchases and sales enable the transfer of capital from less productive to more productive firms. These transactions occur as part of the overall investment decisions of value-maximizing firms. The theoretical development produces an endogenous selection model that links asset purchases and sales to fundamentals of the firm. The empirical analysis builds on the theoretical results and employs logit regressions and selection models to test the predictions of the model. The key findings are: (a) return on assets and size strongly influence the choice of a firm to purchase or sell existing assets, and (b) conditional on the decision to engage in a transaction, firms with high growth opportunities buy more assets.
The model builds on the Q-theoretic framework for investment (see Lucas (1967); Hayashi (1982); and Abel (1983)). The model economy consists of a large number of firms with heterogeneous profitability. Decreasing returns to scale lead managers to vary the size of the firm as profitability varies exogenously. The key economic idea is that firms engage in asset purchases and sales in order to move the firm towards its optimal size, which varies with profitability.
Transaction costs keep firms from buying existing assets until desired investment exceeds a threshold. However, when a firm elects to purchase (sell) existing assets, the marginal value of capital inside the firm must equal the marginal cost (payoff) of the transaction. This yields a selection model where the quantity of assets traded depends on marginal Q, while the choice of purchasing or selling assets depends on firm characteristics. The model identifies profitability and firm size as the key determinants of the choice of firms to buy and sell existing assets. Given size, optimal investment rises with profitability, and highly profitable firms will engage in asset purchases. Conversely, less profitable firms find it optimal to downsize and sell existing assets.
This paper focuses on the productivity driven decision of firms to seek organic growth, acquisitions or asset sales.2 As such, it is closely related to the work of Jovanovic and Rousseau (2002), who argue that mergers can be viewed as acquisitions of unproductive assets by firms with high productivity. At a more disaggregated level, Maksimovic and Phillips (2001) study plant sales between firms and find that transactions improve the allocation of resources. Eisfeldt and Rampini (2006a) use a productivity based approach to study asset sales and acquisitions at the macro level. A recent paper by Yang (2006) demonstrates that a neo-classical model of asset transactions can explain return characteristics and pro-cyclical transaction volumes. Other papers which use an investment based approach to study aspects of corporate finance include Gomes and Livdan (2004), Hennessy and Whited (2005) and Hennessy, Levy, and Whited (2006).
The empirical analysis employs a comprehensive set of asset purchases and sales obtained from the SDC Platinum mergers and acquisitions database.3 This database contains information on asset purchases and sales by public firms, their subsidiaries and private firms. The data set provides extensive coverage on these transactions in the United States, recording more than 10,000 completed asset transactions involving public firms or their subsidiaries over the past 20 years. Prior studies on asset sales by Lang, Poulson, and Stulz (1995) and Bates (2005) analyze much smaller samples.
Logit regressions identify the primary determinants of the choice of firms to engage in asset purchases and sales. Consistent with the model, return on assets strongly predicts the likelihood of a firm engaging in an asset purchase or sale. A unit standard deviation increase in return on assets increases the probability of an asset purchase by 29%. Similarly, a unit standard deviation decrease in return on assets increases the probability of an asset sale by 34%. The analysis reveals that large firms engage in asset purchases and sales much more than small firms. The selection models incorporate information from the logit regressions and test the first-order conditions for asset transactions. Two-step estimation of the investment regressions demonstrate that transaction size covaries with Tobin's Q for asset purchases. Conditional on the firm electing to buy assets, transaction size increases as growth opportunities increase.
Limiting the analysis to large asset purchases (those with value greater than 50% of capital expenditures) by firms during periods of rapid growth generates similar findings. Within this sample, firms with higher profitability seek external growth through asset purchases. Conditional on a large asset purchase, firms with higher values of Tobin's Q acquire more assets. Thus, the above results extend to an economically more meaningful subset of asset purchases.
The results on asset purchases and sales contrasts with the findings of value losses in mergers (see Loughran and Vijh (1997); and Moeller, Schlingemann, and Stulz (2005)). Asset purchases lead to positive abnormal returns for buyers while mergers lead to negative or zero abnormal returns (see Andrade, Mitchell, and Stafford (2001)). The empirical analysis also finds that firms with higher cash holdings or free cash flow do not engage in more asset purchases, thereby rejecting alternative agency-based explanations of asset purchases. Taken together, these findings suggest that asset purchases and sales are more likely to be purely driven by efficient investment considerations. This is perhaps not surprising since these transactions lack the corporate control issues that often arise in mergers.
There have been relatively few empirical studies on asset purchases and sales and these mainly focus on the effects of these transactions on firm value (see Alexander, Bensen, and Kampmeyer (1984); Jain (1985); Hite, Owers, and Rogers (1987); Slovin, Sushka, and Poloncheck (2005) and Ray and Warusawitharana (2007)). Lang, Poulson, and Stulz (1995) and Bates (2005) study the use of proceeds generated from asset sales. John and Ofek (1995) and Schoar (2002), respectively, examine the operating performance of firms and manufacturing plants after asset sales. There is much less work on what determines asset purchases and sales. These studies include Maksimovic and Phillips (2002), who formulate and test a model of conglomerate investment on manufacturing plants; Schlingemann, Stulz, and Walkling (2002); and Eisfeldt and Rampini (2006a). The novel approach in this study captures the purchase, as well as the sale, of operating assets by firms and demonstrates that, in contrast to mergers, asset purchases and sales are consistent with efficient investment decisions.
The remainder of the paper is organized as follows. Section 2 presents the model and derives testable implications. Section 3 tests the model predictions on a simulated data set. Section 4 discusses the actual data and documents some initial findings. Section 5 presents the empirical evidence using the actual data set and Section 6 concludes.
2 Investment Model
The model adapts the Q-theory of investment to study asset transactions. The partial equilibrium analysis focuses on the behavior of firms, and assumes exogenous wages and constant expected returns. Decreasing returns to scale lead firms to grow and shrink as their profitability changes. Firms disinvest by selling their operating units to other firms. In response to improved profitability, firms have the option of growing internally through new investment or externally through asset purchases. Firms with low profitability can improve their average productivity of capital via asset sales. This leads to asset purchases and sales between firms.
The model economy consists of a large number of firms. Each firm produces an identical good, which can be used for consumption or new investment. The market for this good is perfectly competitive and its price is normalized to 1. Firms fund projects with equity, and there are no external costs to raising funds or paying dividends. Managers maximize the discounted present value of dividends. Each firm optimally selects investment and dividends. The investment can be in new assets or
existing assets, which must be purchased from another firm. A unit of new capital costs 1, while a unit of existing capital trades at price ![]() . Once installed, both types of assets are equally productive. Firms disinvest by selling assets to other firms at the price
. Once installed, both types of assets are equally productive. Firms disinvest by selling assets to other firms at the price ![]() .4 Hennessy and Whited (2005) assume a discount on the resale value of capital only in the event of financial
distress. Firms face two costs of changing the capital stock: a convex constant returns to scale adjustment cost applying to all investment, and a concave transaction cost of purchasing existing assets. This leads to non-convexity in the total cost of changing the capital stock. In contrast to
Eisfeldt and Rampini (2006b), purchased capital does not require additional maintenance costs in the future.
.4 Hennessy and Whited (2005) assume a discount on the resale value of capital only in the event of financial
distress. Firms face two costs of changing the capital stock: a convex constant returns to scale adjustment cost applying to all investment, and a concave transaction cost of purchasing existing assets. This leads to non-convexity in the total cost of changing the capital stock. In contrast to
Eisfeldt and Rampini (2006b), purchased capital does not require additional maintenance costs in the future.
The timeline of events is as follows. At the beginning of the period, each firm draws its random productivity shock from the conditional distribution. Firms produce and sell their output using their current capital stock. At the end of the period, each firm decides how much to invest. Firms grow through investment in new capital or purchases of existing assets, and shrink through asset sales. Each firm returns the cash remaining after investment activity to shareholders as a dividend.5 A firm may also elect to sell all its assets to other firms and exit.
Value maximizing decisions drive both asset purchases and sales. Decreasing returns to scale result in a one-to-one relationship between profitability and the optimal size of the firm. Firms that grew rapidly when profitability was high may find themselves with too many assets when their profitability declines. These firms respond by shrinking their size towards the optimal through asset sales. The buyers benefit by obtaining assets at a relative discount. These transactions create value by reallocating assets from less profitable firms to more profitable firms. The participants split the surplus generated by the transaction.
A Output and Profits
Each firm uses capital and labor as inputs, with a decreasing returns to scale production function given by
where
where
where
B Firm Growth
Firms may invest in new or existing capital. Though implicit, changes in capital lead to changes in the labor inputs of the firm. Once acquired, both new and acquired capital are equally productive, with their profitability level determined by ![]() . Denote the quantity of new investment and existing capital traded by
. Denote the quantity of new investment and existing capital traded by ![]() and
and ![]() , respectively. The current capital stock depreciates linearly at the rate
, respectively. The current capital stock depreciates linearly at the rate ![]() . The law of motion for capital can be written
as
. The law of motion for capital can be written
as
The relative price of existing capital
where
A key assumption is that there are concave transaction costs, ![]() , of purchasing capital from other firms. A firm that seeks to expand through an asset purchase would need to spend
considerable time and effort looking for a suitable target. This can be thought of as a search cost. In some cases, managers earn a bonus for completing an acquisition. Alternatively, an investment banker could help find suitable assets to purchase. Typically, an investment bank charges a
percentage of the deal value as fees, with the percentage declining with deal value. There would be legal and administrative costs of buying assets as well as possible restructuring costs associated with adapting the purchased units with the firm.
, of purchasing capital from other firms. A firm that seeks to expand through an asset purchase would need to spend
considerable time and effort looking for a suitable target. This can be thought of as a search cost. In some cases, managers earn a bonus for completing an acquisition. Alternatively, an investment banker could help find suitable assets to purchase. Typically, an investment bank charges a
percentage of the deal value as fees, with the percentage declining with deal value. There would be legal and administrative costs of buying assets as well as possible restructuring costs associated with adapting the purchased units with the firm. ![]() captures these costs and allows for larger transactions to have a lower average cost than smaller transactions. An alternative model with fixed and variable transaction cost components would imply similar investment behavior.
Yang (2006) analyzes a model with a fixed cost of purchasing and selling assets. The transaction costs involved in an asset purchase lead to lumpy investment in the existing assets market, with firms seeking to buy existing capital only when their total investment exceeds a
threshold.
captures these costs and allows for larger transactions to have a lower average cost than smaller transactions. An alternative model with fixed and variable transaction cost components would imply similar investment behavior.
Yang (2006) analyzes a model with a fixed cost of purchasing and selling assets. The transaction costs involved in an asset purchase lead to lumpy investment in the existing assets market, with firms seeking to buy existing capital only when their total investment exceeds a
threshold.
C Value of the Firm
The firm pays out the cash remaining after investment as a dividend:
The discounted present value of future dividends yields the value of the firm:
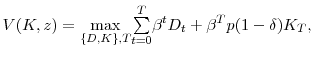
| (A.7) | ||
| s.t. |
The analysis can be simplified by separating the problem into a dynamic and static component. This enables the characterization of the optimal investment policy of the firm. Conditional on a desired level of total investment, the allocation decision between new and existing capital becomes a static problem. Given the optimal allocation decision, the dynamic programming problem can be solved in terms of total investment:
where
| (A.9) | ||
| s.t. |
||
The following proposition presents the solution to the allocation decision given a desired level of total investment.
![\tilde{I} = \left[ \frac{a}{1-p}\right] ^{1/(1-\theta)}](img70.gif) below which all investment consists of new investment and above which all investment consists of purchased existing capital
below which all investment consists of new investment and above which all investment consists of purchased existing capital
Corollary #.:
The concave transaction cost of purchasing existing capital and the relative price of existing assets impact the optimal allocation choice. For low levels of investment, all investment consists of new capital. Beyond the threshold ![]() , the cost saving from purchasing existing assets exceeds the transaction cost
, the cost saving from purchasing existing assets exceeds the transaction cost ![]() . Therefore, firms that grow more than
. Therefore, firms that grow more than ![]() will do so by purchasing existing assets from another firm. Substitution of the optimal allocation choices to the total cost of investment
will do so by purchasing existing assets from another firm. Substitution of the optimal allocation choices to the total cost of investment ![]() yields the minimum cash outflow for that level of investment
yields the minimum cash outflow for that level of investment
![]() . This enables the Bellman equation to be written solely in terms of total investment and future capital. This formulation reduces the dimensionality of the problem, and
simplifies the analysis. The following proposition establishes the uniqueness and monotonicity of the solution to the dynamic programming problem (8).
. This enables the Bellman equation to be written solely in terms of total investment and future capital. This formulation reduces the dimensionality of the problem, and
simplifies the analysis. The following proposition establishes the uniqueness and monotonicity of the solution to the dynamic programming problem (8).
The derivation of the comparative statics of the model requires the solution ![]() to be differentiable. As the investment cost function
to be differentiable. As the investment cost function
![]() contains kinks at
contains kinks at ![]() and
and
![]() , the value function may not be differentiable everywhere. The following proposition establishes differentiability for points in the interior of the regions where the firm
purchases existing assets, invests in new assets or sells assets.
, the value function may not be differentiable everywhere. The following proposition establishes differentiability for points in the interior of the regions where the firm
purchases existing assets, invests in new assets or sells assets.
D Empirical Predictions on Asset Purchases and Sales
This section establishes some characteristics of firms that engage in asset purchases and sales, and derives testable implications for the subsequent empirical analysis. The optimal total investment varies with the current size ![]() and profitability
and profitability ![]() of the firm. The following first-order condition solves for the optimal
of the firm. The following first-order condition solves for the optimal ![]() except when
except when ![]() or
or
![]() :
:
Given a level of total investment, the solution to the allocation problem given in proposition 1 determines whether the firm acquires existing assets, invests in new capital or sells assets. Firms will buy existing assets when desired investment
The first-order conditions for investment can be simplified by adding more structure to the adjustment cost of investment. Assume a standard quadratic adjustment cost function for
![]() . Denote the marginal value of capital inside the firm by
. Denote the marginal value of capital inside the firm by
![]() . Simplification of (10) implies that for firms that purchase
existing assets,
. Simplification of (10) implies that for firms that purchase
existing assets,
As the above condition holds when
A firm elects to engage in an asset purchase or sale depending on the state variables ![]() and
and ![]() . The following proposition links profitability to asset purchase and sale activity.
. The following proposition links profitability to asset purchase and sale activity.
The persistence in profitability ![]() and decreasing marginal productivity of capital results in a monotone relationship between the optimal size of the firm and
and decreasing marginal productivity of capital results in a monotone relationship between the optimal size of the firm and ![]() . An increase in profitability leads to an increase in the optimal size of the firm. For a firm of given size
. An increase in profitability leads to an increase in the optimal size of the firm. For a firm of given size ![]() ,
investment increases (decreases) as
,
investment increases (decreases) as ![]() increases (decreases). As firms acquire existing assets when
increases (decreases). As firms acquire existing assets when
![]() , the most profitable firms will engage in asset purchases. Similar reasoning implies that the least profitable firms will downsize through an asset sale.
, the most profitable firms will engage in asset purchases. Similar reasoning implies that the least profitable firms will downsize through an asset sale.
Figure 1 plots the optimal investment of a firm with fixed size ![]() as a function of profitability
as a function of profitability ![]() . The figure demonstrates the monotonic increase of investment with profitability. The minimum cost function for investment
. The figure demonstrates the monotonic increase of investment with profitability. The minimum cost function for investment
![]() contains a kink at
contains a kink at ![]() . This kink influences investment
activity by introducing a discontinuity in the first-order condition (10). The jump in the marginal investment cost function at
. This kink influences investment
activity by introducing a discontinuity in the first-order condition (10). The jump in the marginal investment cost function at ![]() leads to a jump in the policy
function. Therefore, firms that engage in asset purchases grow much more than firms that do not. The wedge between the purchase cost of new assets and the resale value of capital leads to an inactivity region for investment as demonstrated by Abel and Eberly (1994).
leads to a jump in the policy
function. Therefore, firms that engage in asset purchases grow much more than firms that do not. The wedge between the purchase cost of new assets and the resale value of capital leads to an inactivity region for investment as demonstrated by Abel and Eberly (1994).
Size, in addition to profitability, determines the likelihood of a firm engaging in an asset purchase or sale. The following proposition demonstrates that larger firms are more likely to sell assets.
As the optimal size of the firm decreases when profitability decreases, some firms that suffer a negative profitability shock will find themselves with more assets than optimal. These firms will sell assets to reach the optimal size. The asset sale improves the average productivity of the remaining assets of the firm. Large firms will be more likely to find themselves with too many assets than optimal, and therefore will be more likely to engage in asset sales.
For most parameter values, the probability of an asset purchase will increase with firm size.10 For a given level of investment ![]() , the constant returns to scale adjustment cost of investment lowers the investment cost as the size of the firm increases. This captures the intuition that larger firms integrate new assets more easily
than smaller firms. As size decreases, the cost of investing more than
, the constant returns to scale adjustment cost of investment lowers the investment cost as the size of the firm increases. This captures the intuition that larger firms integrate new assets more easily
than smaller firms. As size decreases, the cost of investing more than ![]() increases, thereby lowering the likelihood of an asset purchase.
increases, thereby lowering the likelihood of an asset purchase.
The determinants of firm's decisions to engage in an asset purchase or sale can be tested using limited dependent variable regressions. Define ![]() as a variable that takes values of
-1, 0 or 1 depending on whether the
as a variable that takes values of
-1, 0 or 1 depending on whether the
![]() firm sells existing assets, neither buys nor sells assets or buys existing assets from another firm during the
firm sells existing assets, neither buys nor sells assets or buys existing assets from another firm during the ![]() fiscal year.
fiscal year.
| (A.13) |
where
3 Calibration and Simulation
The study of simulated data sets follows a burgeoning literature.11 This approach is particularly beneficial when issues such as endogeneity, multi-collinearity and measurement errors cause problems for statistical analysis. This section presents the results of testing the model predictions on a simulated data set; Section 5 replicates this analysis on the actual data.
A Calibration
The calibration exercise fits the model parameters to their empirical counterparts at an annual frequency. The calibration focuses on generating a plausible panel of firm characteristics. The discount factor in the simulated economy
![]() . The decreasing returns to scale parameter
. The decreasing returns to scale parameter
![]() follows Gomes (2001) and maps to capital and labor elasticities in the economy of 2/3 and 30% respectively. The depreciation rate of 12% corresponds to the
rate of new investment in the economy. The study parameterizes the adjustment costs as
follows Gomes (2001) and maps to capital and labor elasticities in the economy of 2/3 and 30% respectively. The depreciation rate of 12% corresponds to the
rate of new investment in the economy. The study parameterizes the adjustment costs as
![]() . Whited (1992) estimates structural investment models and obtains values for the adjustment cost parameter
. Whited (1992) estimates structural investment models and obtains values for the adjustment cost parameter ![]() of .5 to 2. Hall (2004) uses industry level data and obtains an estimate for
of .5 to 2. Hall (2004) uses industry level data and obtains an estimate for ![]() close to 0. The study uses a
value of
close to 0. The study uses a
value of
![]() . The parameters of the transition equation,
. The parameters of the transition equation,
![]() and
and![]() , determine the cross-sectional and time series properties of profitability. The
calibrated parameters imply an autocorrelation coefficient of .85 and an unconditional standard deviation of 30% for profitability.
, determine the cross-sectional and time series properties of profitability. The
calibrated parameters imply an autocorrelation coefficient of .85 and an unconditional standard deviation of 30% for profitability.
The calibration of the transaction cost of asset purchases selects a value to match the observed frequency of asset transactions in the sample. The chosen values of ![]() and
and
![]() represent approximately 8% of the annual profits of the median firm. The relative price of purchased capital
represent approximately 8% of the annual profits of the median firm. The relative price of purchased capital ![]() is set such that aggregate asset purchases equal aggregate asset sales. This corresponds to the price that clears the market for corporate assets in the stationary state of the economy. The calibrated value of
is set such that aggregate asset purchases equal aggregate asset sales. This corresponds to the price that clears the market for corporate assets in the stationary state of the economy. The calibrated value of ![]() equals 0.98. Empirically, this measures the discount at which firms transact operating units. Pulvino (1998) provides an empirical counterpart to this value. He studies the discount on used airplane sales, and
finds no discount in good times, and a mean discount of 14% in bad times. Cooper and Haltiwanger (2006) structurally estimate an investment model with a discount on the resale value and obtain values of
equals 0.98. Empirically, this measures the discount at which firms transact operating units. Pulvino (1998) provides an empirical counterpart to this value. He studies the discount on used airplane sales, and
finds no discount in good times, and a mean discount of 14% in bad times. Cooper and Haltiwanger (2006) structurally estimate an investment model with a discount on the resale value and obtain values of ![]() ranging from 0.80 to 0.98 in their most general specification. A higher value for
ranging from 0.80 to 0.98 in their most general specification. A higher value for ![]() would imply a lower value for
would imply a lower value for ![]() and fewer transactions. A lower value of
and fewer transactions. A lower value of ![]() does not significantly impact the results of the logit regression and the
investment regression for buyers and sellers.
does not significantly impact the results of the logit regression and the
investment regression for buyers and sellers.
Appendix B provides details on the numerical solution of the value function and the characterization of the optimal investment policies. Figure 2 plots the regions in which the firm buys and sells assets. As the model predicts, highly profitable firms engage in asset purchases, and firms with low profitability sell assets. The profitability level below which the firm sells assets increases with size. As firms become larger, the likelihood that their size is greater than is optimal for a given profitability level increases, leading to an increased likelihood of an asset sale.
B Simulation Results
The model sheds light on firms' decisions to grow internally, grow through acquisitions or sell assets. The empirical analysis focuses on testing the first-order conditions given in (11) and (12), conditional on the selection criteria identified in propositions 4 and 5. Logit regressions on the choice of firms to buy and sell assets identify the primary determinants of these decisions. The selection models study the relationship between (dis)investment and Tobin's Q, conditional on a firm engaging in an asset purchase or sale. These regressions test the model's predictions that changes in profitability and investment opportunities drive asset purchases and sales.
The empirical analysis tests approximations to the optimal investment policies of the firm. The logistic regressions linearize investment as a function of the state variables and the selection models use average Q as a proxy for marginal Q. Performing these regressions on the simulated data set tests the validity of these approximations, and provides a basis for the subsequent empirical analysis. Additionally, this approach helps quantify the impact of measurement error on these regressions.
Appendix C details the construction of the simulated data set. Panel A of Table 1 reports the results of an ordered logit regression on asset purchases and sales for the full sample, and asset purchases by rapidly growing firms. This regression tests
the prediction of proposition 4. As predicted by the model, there exists a clear ordering between profitability and asset purchases and sales. Limiting the sample to firms with investment to capital greater than ![]() (rapid growth firms) leads to similar results. Conditioning on a firm entering a period of high growth, those with higher profitability seek external growth. Columns 2 and 3 of panel A demonstrate that the addition of noise leads to lower
coefficients and pseudo
(rapid growth firms) leads to similar results. Conditioning on a firm entering a period of high growth, those with higher profitability seek external growth. Columns 2 and 3 of panel A demonstrate that the addition of noise leads to lower
coefficients and pseudo ![]() values. The noise was added by interchanging 10% and 20% of firms that engaged in asset purchases and sales with a matching number of firms that grew
organically. The statistical significance of the coefficient on return on assets remains robust to mixing 20% of the buyers and sellers.
values. The noise was added by interchanging 10% and 20% of firms that engaged in asset purchases and sales with a matching number of firms that grew
organically. The statistical significance of the coefficient on return on assets remains robust to mixing 20% of the buyers and sellers.
Panel B reports the results of the multinomial regression for the full sample. The signs of the coefficients on return on assets and size match those predicted by propositions 4 and 5. The addition of noise by mixing the participants drives the
coefficients towards zero and lowers the pseudo ![]() values. However, the coefficients retain their sign and statistical significance. This indicates that even in the presence of random
mixing, one would find a robust relationship between profitability, size and asset purchases and sales.
values. However, the coefficients retain their sign and statistical significance. This indicates that even in the presence of random
mixing, one would find a robust relationship between profitability, size and asset purchases and sales.
Panel C reports the results of testing the investment regression for asset purchases and sales on the full sample as well as for asset purchases by rapidly growing firms. The strongly significant coefficient on Tobin's Q demonstrates that average Q functions as a good proxy for marginal Q in the
simulated data. This finding extends to limiting the sample to firms with capital expenditures above 25%.12 The positive coefficient on cash flow supports
the argument of Cooper and Ejarque (2003) that market power, as captured by decreasing returns to scale in profitability, leads to a positive coefficient on cash flow for investment regressions. However, adding cash flow has almost no impact on the ![]() value for both the asset purchase regressions. The next section presents the actual data used to test the model.
value for both the asset purchase regressions. The next section presents the actual data used to test the model.
4 Data
The data on asset purchases and sales is obtained from the SDC Platinum mergers and acquisitions database. Thomson Financial Services Ltd. maintains the data set, which contains detailed information on purchases and sales of operating units by firms. The data categorizes each transaction as a merger, an acquisition, an asset acquisition or an acquisition of certain assets. The sample of asset purchases and sales in the study consists of transactions listed in the last two categories. The value of the transaction is available for about half of the sample. The selected sample consists of all buyers and sellers from 1985 to the end of 2005, who are either publicly listed firms or subsidiaries of listed companies.13 The sample includes transactions where one of the parties is a private firm. The selection scheme yields a comprehensive list of firms who have elected to grow or shrink via asset purchases and sales.
The Compustat annual files and the CRSP monthly stock files provide information on the operating performance and market valuation of firms. These are linked to the SDC sample via the CUSIP numbers of the participants, or for transactions by subsidiaries, the CUSIP numbers of their listed parents. The sample is categorized according to the Fama-French 48 industry groups and excludes all financial firms and regulated utilities. This yields a panel of firms that can be used to study the determinants of firms' decisions to buy or sell business units. The median transaction size in the sample is $14.6 million. The study constructs the following independent variables at the end of each fiscal year: return on assets (RoA) equals earnings before interest, depreciation and taxes scaled by book assets at the beginning of the period; size is the log of the book value of assets; finance Q is the ratio of market value of assets14 to the book value of assets; market-to-book is the ratio of market value of equity to the book value of equity; leverage is the book value of debt divided by book value of debt plus equity; sales growth measures the growth in net sales over the previous year; plant, property, and equipment (PPE) growth measures the change in net plant, property and equipment over the previous fiscal year; stock return measures the return over the fiscal year; and cash is the value of cash and short-term instruments scaled by book assets. Sales growth and PPE growth are adjusted for inflation using the deflator for gross private investment. Additionally, an asset purchase wave dummy variable is constructed following the method employed by Harford (2005). A wave dummy value of 1 corresponds to a heightened period of activity for each industry over a two year time period. The wave dummy variable takes a value of 1, if in the two year period with the maximum number of transactions, that number is greater than the 95th percentile obtained by simulating draws from an uniform distribution. The study also reports results using industry means of market-to-book, leverage, sales growth, PPE growth, stock return and cash to mitigate endogeneity concerns.
Measurement error in average Q affects statistical inference on both the Q coefficient as well as other coefficients. The finance Q measure, popular in the corporate finance literature, focuses on the market to book value of all assets employed by the firm. Erickson and Whited (2006) demonstrates that macro Q measures have less measurement error than finance Q measures. Macro Q equals the ratio of the market value of the capital stock to its replacement value. This study computes the replacement value of capital using the perpetual inventory method of Salinger and Summers (1983). The market value of capital equals common equity + preferred equity + debt - inventories - cash.15 The macro Q regressions drop observations with Q values less than 0 or greater than 20.
Potential errors in the SDC database can impact the results of the empirical analysis.16 The study relies on SDC to identify the participants, the transaction value and the fiscal year. A detailed search using Factiva on 498 asset purchases yielded information on 388 transactions. Of these, 343 (88% of the sample) had deal values within 5% of the value reported in the SDC. There were 8 transactions whose reported values differed by 50% or more. SDC reported the buyer as the seller and vice versa for 8 transactions. The SDC dates were accurate within a business day for 92% of the sample. These findings indicate that data errors in the SDC sample on asset transactions are relatively small and would not materially impact statistical inference.
A Summary Statistics
Table 2 reports sample statistics for all firms listed on Compustat from 1984 to 2004, and for the subsample of buyers and sellers of existing assets in the year prior to the transaction. On average, 12% of all listed firms will buy assets from another firm, and 5% of firms will sell. As the model predicts, buyers tend to have a higher return on assets than other firms. This suggests that managers of firms with high profitability elect to grow through an asset purchase. Sellers have a higher mean and lower median return on assets than other firms. Both buyers and sellers are larger than the average firm. Large firms will be more likely to have exhausted their internal growth opportunities and may seek to expand through an acquisition. A large firm will also find it easier to integrate an acquired unit. On the other hand, a troubled large firm can improve profitability by selling an underperforming unit to another firm.
The market values buyers more and sellers less than average firms when market-to-book ratios and finance and macro Q values are used as metrics. Acquiring firms may exercise their growth options through the purchase of relatively inefficient units of other firms. Acquiring firms have been growing rapidly in the year prior to the transaction. They exhibit significantly higher sales growth, and net plant, property and equipment growth than the average firm. Sellers, on the other hand, demonstrate anemic growth prior to the transaction.
Selling firms demonstrate some evidence of financial distress. Both buyers and sellers have less cash than average firms, but this is more pronounced for sellers. Some selling firms may face liquidity problems, and sell units to raise cash. This would be consistent with the arguments of Lang, Poulson, and Stulz (1995). Sellers also have higher leverage than average firms, increasing the potential costs of obtaining new funds in the bond market. The next section test the predictions of the model using this data set and compares the findings to those obtained with the simulated data set.
5 Evidence on Asset Purchases and Sales
The empirical implementation tests two hypotheses derived from the above model. Hypothesis 1 states that large firms with high profitability grow by acquiring assets and that large firms with low profitability sell assets. An alternative hypothesis, based on agency arguments, states that large firms with high free cash flow acquire existing assets whereas firms with lower free cash flow grow organically. Hypothesis 2 states that, conditional on a firm buying or selling assets, the quantity of assets transacted covaries with Tobin's Q.
Discrete choice models provide a natural method for determining the characteristics of buyers and sellers. Hypothesis 1 predicts a monotone ordering between profitability and the choice of a firm to sell assets, invest in new capital or buy existing assets. The next subsection tests this prediction using an ordered logit model.
A Ordered Logit Regressions
The ordered logit model estimates the limited dependent variable system given in (13). The logit regression imposes the additional distributional assumption that the cumulative distribution function of the error term
![]() follows a logistic distribution:
follows a logistic distribution:
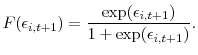
Table 3 reports the results from estimation of the above ordered logit model. The full sample results from Panel A in Table 1 provide the simulation counterpart. Standard errors are reported in parentheses. The regressors includes year and industry dummies. The standard error computation clusters by firms to adjust for within-firm serial correlation and is robust to heteroskedasticity across firms. The study evaluates statistical significance using bootstrapped finite-sample critical values for the t-statistics.17 The table also reports the odds ratios corresponding to the given parameter estimates. The odds ratios represent the relative increase in the odds in favor of an asset purchase relative to not purchasing assets for a unit standard deviation increase in the independent variable. The latter half of the table reports the results obtained by replacing the control variables of market-to-book, leverage, cash, stock return, sales growth and PPE growth with their industry means. The industry values help mitigate endogeneity concerns. The Value columns report results where the dependent variable takes values of -1 and 1 only when SDC reports a deal value for the asset sale or purchase. This focuses the analysis on larger and presumably more important transactions.
The regression coefficients of all covariates except cash do not vary much across either of the two specifications for the dependent variable when using firm level controls. RoA strongly predicts the decision of the firm to buy or sell assets. A unit standard deviation increase in RoA increases
the odds in favor of an asset purchase, and decreases the odds in favor of a sale by 26%. This supports the prediction of the model that high ![]() firms would buy existing assets and low
firms would buy existing assets and low
![]() firms would sell assets. The impact of RoA remains strong when the firm level controls are replaced by industry counterparts. Adjusting for industry characteristics, a unit standard
deviation increase in RoA increases the odds in favor of an asset purchase by 20%. While RoA has the strongest impact on the relative odds of a transaction, the control variables also influence the decision to engage in an asset purchase or sale. The positive and significant coefficient on realized
stock return accords with the model intuition that positive shocks to profitability lead to asset purchases. Similarly, the coefficients on sales growth and PPE growth demonstrate that buyers have had strong growth while sellers have had weak growth.
firms would sell assets. The impact of RoA remains strong when the firm level controls are replaced by industry counterparts. Adjusting for industry characteristics, a unit standard
deviation increase in RoA increases the odds in favor of an asset purchase by 20%. While RoA has the strongest impact on the relative odds of a transaction, the control variables also influence the decision to engage in an asset purchase or sale. The positive and significant coefficient on realized
stock return accords with the model intuition that positive shocks to profitability lead to asset purchases. Similarly, the coefficients on sales growth and PPE growth demonstrate that buyers have had strong growth while sellers have had weak growth.
The significant coefficients on cash and leverage demonstrate that the model does not capture all the determinants of the choice of a firm to engage in an asset purchase or sale. Purchasers have lower leverage and sellers higher leverage than other firms, indicating that high leverage can deter asset purchases through reduced managerial flexibility. Endogenous leverage models, such as Hennessy and Whited (2005), generate a similar result. In these models a high leverage firm would be less willing to invest heavily following a positive shock as this would typically require them to increase leverage, thereby driving the firm away from its optimum. The leverage effect in the data extends to the industry measures. The positive coefficient on the stock of liquid assets demonstrates that financing considerations influence asset purchase or sale decisions. The ordered logit regressions implicitly assume that the independent variables have the same impact on the asset purchase and sale decisions. This restriction leads to a low pseudo R-square value for the regression. The next section reports the results of multinomial regressions on the same data set. This specification allows the covariates to have a different impact on the purchase and sale decisions, and provides a more thorough test of hypothesis 1.
B Multinomial Logit Regressions
The multinomial regressions model the choice of a firm purchasing existing assets versus investing in new capital conditional on not selling assets as following a standard logit model. The probability model specifies that
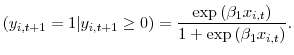
Table 4 reports the results from estimation of the above multinomial logit model for asset purchases and sales. Standard errors are reported in parentheses. The analysis includes year and industry dummies. The standard error computation clusters by firms to adjust for within-firm serial correlation and is robust to heteroskedasticity across firms. Statistical significance is evaluated using bootstrapped critical values for the t-statistics. The table also reports the odds ratios corresponding to the given parameter estimates. The first half of the table reports the coefficients for asset purchases, while the latter half reports the results for asset sales. The Firm and Industry columns report results using firm and industry level measures for the control variables. The simultaneous estimation of the probability models for asset purchases and sales yields the reported coefficients.
The results for the purchase decision support hypothesis 1 and match the findings from the simulated data set reported in Panel B of Table 1. RoA and size positively predict the likelihood of a firm engaging in an asset purchase, and they have a much larger impact on the decision than the control variables. A unit standard deviation increase in RoA increases the odds in favor of a purchase by 29%. The profitability and size of the firm has a strong impact on the asset purchase decision when other firm characteristics are replaced by their industry counterparts. As in the ordered regressions, buyers display strong returns and robust growth prior to the transaction. This accords with the intuition of the model. The significant and negative coefficient on leverage indicates that highly levered firms buy existing assets less frequently than firms with low leverage. The leverage result strengthens when firm measures are replaced by industry averages. The negative and significant coefficient on cash rejects the empire-building hypothesis that firms use surplus cash to grow by asset purchases. These results support the contention of hypothesis 1 that profitability and firm size determine asset purchases and sales.
The results for the sale of existing assets also support the model predictions. RoA enters the predictive equation with a significant and negative coefficient indicating that low profitability induces firms to sell assets. A unit standard deviation increase in profitability decreases the odds in favor of an asset sale by 34% and 23%, respectively when firm and industry control variables are used. Size also has a strong impact on the choice of a firm to sell assets, with large firms selling assets more frequently than small firms. In contrast to buyers, firms that sell assets demonstrate low realized returns, and poor sales and PPE growth prior to the asset sale. The level of liquid assets strongly impacts the choice of a firm to sell assets. A unit standard deviation increase in cash stocks decreases the odds in favor of an asset sale by 32%. This confirms the findings of Lang, Poulson, and Stulz (1995) that firms in financial distress sell assets to raise funds. Evidence of financial distress does not imply that agency considerations lead to asset sales, as financing difficulties may coexist with efficient investment. The positive coefficient on leverage provides further evidence in support of financial difficulties leading to asset sales. At the industry level, none of the control variables have a significant impact on predicting asset sales.
The logit regressions identify the primary determinant of the choice of a firm to buy or sell existing assets and provide strong support for hypothesis 1. However, one would reject the stronger hypothesis that profitability and size solely determine asset purchases and sales. Given an asset purchase or sale, the model also links the size of the transaction to the marginal value of capital inside the firm. The next section employs selection models to test hypothesis 2.
C Selection Models
Conditional on a firm engaging in an asset purchase, the first-order conditions given in (11) link transaction size to the marginal Q of the firm. The empirical implementation proxies for marginal Q with average Q. Assuming that the transaction cost of asset purchases is approximately linear in the relevant region, the first order condition for asset purchases can be written as
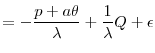 |
||
| if |
Linearization of the selection equation provides a selection model, which can be estimated using the two-step estimator developed in Heckman (1974). The two-step approach first estimates the selection equation and then estimates the investment equation with the inverse Mill's ratio from the selection model as an additional covariate. The empirical implementation of the selection model focuses only on the transactions for which SDC reports a deal value. The value of the transaction proxies for
Table 5 reports the results from estimation of the investment models for the purchase and sale of existing assets.18 The asset purchase and sales results from Panel C of Table 1 provide the simulation counterpart. Standard errors are reported in parentheses. The statistical inference employs bootstrapped critical values for the t-statistics. The specification for the selection and investment equations include industry and year dummies. The variables are scaled by book assets for the finance Q regression and replacement value of capital for the macro Q regression. Following the investment literature, the regressors also include cash flow. The coefficients for the selection equations, once adjusted for a scaling factor to account for the use of a probit model, closely match the results of the multinomial regressions.
The positive and significant coefficient on Tobin's Q for asset purchases supports hypothesis 2: the transaction size covaries positively with the firm's Q. Conditional on engaging in an asset purchase, a firm with a higher Q will purchase more assets. This indicates that firms engage in asset purchases in response to changes in the productivity of capital employed by the firm. Macro Q leads to higher point estimates than finance Q, which would be consistent with reduced measurement error in macro Q. The asset sales regression leads to mixed findings. Using finance Q with firm controls leads to a significantly positive point estimate, as with the simulated data. The point estimate is insignificant for the other specifications. This may be due to the influence of financial distress on asset sales. Alternatively, a different adjustment cost structure may break the link between Q and the quantity of assets sold.
Typical of investment regressions, cash flow has a positive and statistically significant coefficient. Following Fazzari, Hubbard, and Petersen (1988), this has been interpreted as evidence of financial constraints of firms. However, recent work by Erickson and Whited (2000) and Hennessy, Levy, and Whited (2006) have argued that this is driven by measurement error and model misspecification. Cooper and Ejarque (2003) demonstrate that when firms have market power, investment regressions will lead to significant and positive coefficients on cash flow. In the context of asset purchases, a financial constraints explanation would be less plausible, as firms that buy assets tend to have had strong profitability and growth.
The statistically significant coefficient on the inverse Mill's Ratio for both asset purchases and sales demonstrates the importance of accounting for endogeneity in this regression. A regression of transaction size on Q would lead to biased estimates in the absence of the selection term.
D Large Asset Purchases by Rapidly Growing Firms
This section examines large asset purchases by firms during periods of rapid growth.19 Such an analysis provides a more focused test on the model's predictions regarding firms' decisions to seek external growth versus organic investment.
The study defines periods of rapid growth as those in which the ratio of capital expenditure to replacement value of capital was greater than ![]() or greater than twice the firm's median
value.20 The following approaches lead to similar results: defining rapid growth with respect to industry medians; defining investment as the change in the
replacement value of capital; and defining investment as the change in book assets scaled by book assets. Using higher thresholds for rapid growth lead to weaker results, possibly due to the drop in sample size. The analysis focuses on firms with assets purchases greater than 50% of the value of
capital expenditures.
or greater than twice the firm's median
value.20 The following approaches lead to similar results: defining rapid growth with respect to industry medians; defining investment as the change in the
replacement value of capital; and defining investment as the change in book assets scaled by book assets. Using higher thresholds for rapid growth lead to weaker results, possibly due to the drop in sample size. The analysis focuses on firms with assets purchases greater than 50% of the value of
capital expenditures.
Table 6 presents the results of a logit regression on firms' engaging in large asset purchases during periods of rapid growth. The rapid growth columns in Panel A of Table 1 present the results of a similar analysis on the simulated data set. The standard errors in parentheses adjust for heteroskedasticity and clustering at the firm level. Statistical significance is inferred using bootstrapped critical values for the t-statistics. As with the simulated data, firms with higher RoA engage in large asset purchases during periods of rapid growth. The odds ratios indicate an economically meaningful impact of RoA on the asset purchase decision. While most of the control variables have little impact, low industry leverage values encourage asset purchases. These findings support the model's prediction that firms with higher profitability seek external growth.
Hypothesis 2 links the level of asset purchases to the firm's investment opportunities. Table 7 presents the results of testing this relationship for firms with large asset purchases, conditional on a period of rapid growth. The rapid growth columns in Panel C of Table 1 report the simulation counterpart to this analysis. The selection equation uses the same controls as in the logit regressions. Statistical significance is inferred using bootstrapped critical values for the t-statistics.
The results demonstrate that, as predicted by the model, transaction size covaries with the firm's Q for large asset purchases. The macro Q regressions yield consistently higher point estimates and lower p-values than finance Q regressions. Further, cash flow is not significant in any of these specifications. Whereas the inverse Mill's ratio is not significant using the bootstrapped critical values, it is asymptotically significant in many of the regressions. Thus, conditional on a decision to engage in a large asset purchase, the transaction size increases with the firm's growth opportunities.
E Robustness
The panel nature of the sample provides some challenges to the statistical analysis. A fixed-effects logit regression estimates a binary logit model for asset purchases only on the subsample of firms that either purchased or sold assets in at least one year. This allows for a firm-level fixed effect in the estimation. The estimation of fixed-effects logit models for asset purchases and sales generate similar results for RoA and size to those reported in the multinomial regressions. Replicating the multinomial regressions for transactions with only deal values lead to similar results for RoA and size as those reported in table 4.
The correlation pattern in the error terms may significantly influence the estimated standard errors (see Petersen (2006)). The study reports standard errors obtained by clustering the data at the firm level. This allows for a constant serial correlation term for the observations of the same firm across different years. An alternative approach using the Fama and MacBeth (1973) procedure yields similar results for the ordered and multinomial logit regressions. Such an approach would generate standard errors robust to cross correlation across firms in a given year. The study reports heteroskedasticity robust clustered estimates, as firm-level factors would be more likely to influence asset purchase and sale decisions than macro variables.
Measurement error in Q can lead to unwarranted conclusions in investment regressions (see Erickson and Whited (2000); and Gomes (2001)). The testable predictions of the model relate to the coefficient on Q. Measurement error in a given regressor will bias that coefficient down towards zero, making it harder to find statistical significance. Therefore, it is unlikely that the significant coefficients on Q for the asset purchase regressions in tables 5 and 7 are driven by measurement errors in Q. In the absence of measurement error, the true point estimates would be greater than those reported in the above tables.
Measurement error in Q also affects inference on the cash flow coefficient. The proxy quality threshold method of Erickson and Whited (2005) computes the minimum correlation between observed and true Q required to infer positivity of another coefficient under various assumptions on the measurement error structure. A high threshold value implies that the observed Q must be a very good proxy for the true Q in order for the coefficient sign of interest to be robust to measurement error. The reverse regression of Q on investment, cash flow and the inverse Mill's ratio for asset purchases yields positive cash flow coefficients with the finance Q and negative coefficients with the macro Q. This indicates that, using the finance Q as the proxy for true Q, the cash flow coefficient is positive under the classical errors-in-variables model and when the measurement error is correlated with one or more of the regressors but not the disturbance. Proxy quality computation using macro Q leads to thresholds around 0.20 under the above assumptions. Under the assumption that the measurement error correlates with the disturbance but not the regressors the threshold increases to 0.50 for the macro Q. This implies that the correlation between macro Q and the true incentive to invest must be greater than 0.50 in order for the positive cash flow coefficient to be robust to measurement error. Whereas the positive cash flow coefficients in Table 5 match the simulation results, these computations demonstrate that inference on the cash flow coefficients is sensitive to measurement error in Q (see Erickson and Whited (2000)).
The significant and positive coefficient on RoA can be interpreted in favor of an alternative hypothesis based on agency conflicts. The agency hypothesis argues that managers derive benefits from increased size, and use free cash flow to grow via asset purchases. High return on assets indicates increased cash flow to the firm, and managers with misaligned incentives use the excess cash to grow the firm and increase their private benefits. Proposition 4 demonstrates that value-maximizing managers respond to increased profitability by engaging in asset purchases. The replication of the above logit regressions with a free cash flow measure provides a test of the alternative hypothesis. The free cash flow variable measures net operating cash flow minus cash flow for investing activities, divided by book assets at the beginning of the fiscal year.21
Table 8 presents the results of estimating the multinomial logit regression using free cash flow in place of RoA. The coefficient on free cash flow itself is statistically insignificant as a predictor of asset purchases, and significantly negative as a predictor of asset sales. This provides evidence that high free cash flow does not lead to asset purchases, and indicates that the impact of RoA on asset purchases does not capture a free cash flow effect. These findings demonstrate that one can reject the alternative hypothesis on asset purchases based on agency arguments. Overall, the empirical evidence supports the two efficiency based hypotheses on asset purchases and sales.
6 Conclusion
This study argues that decisions over the optimal scale of the firm drive organic investment, acquisitions and asset sales. The paper analyzes these transactions in the context of an efficiency based model: asset purchases and sales help firms move towards their optimal size after heterogenous productivity shocks. Conditional on a firm buying or selling existing assets, the model links purchases and sales of existing assets to the marginal value of capital inside the firm. The profitability and size of the firm determines whether the firm chooses to buy or sell existing assets.
The paper tests the implications of the model using a data set of asset purchases and sales from the SDC Platinum database. The estimation of the selection models for investment demonstrates a positive link between the quantity of assets purchased and the investment opportunities of the firm. Return on assets and size strongly predict the likelihood of a firm engaging in an asset purchase or sale. A unit standard deviation increase in RoA increases the probability of an asset purchase by 29%, while a corresponding decrease in RoA increases the likelihood of an asset sale by 34%. Focusing the analysis on large asset purchases by firms during periods of rapid growth yields similar results. The empirical analysis also finds that financing considerations influence the decision of firms to sell assets, with lower levels of liquid assets leading to more asset sales. On the other hand, increased cash stocks do not lead to increased asset purchases, indicating that empire-building tendencies do not influence asset purchases.
The findings on asset purchases contrast with the evidence linking agency problems and misvaluations to mergers. Further research on the sources and effects of the differences between mergers and asset purchases may prove fruitful, given that the fundamental action of both transactions is to shift ownership of some productive assets from one firm to another.
A Proofs
![\tilde{I} = \left[ \frac{a}{1-p}\right] ^{1/(1-\theta)}](img70.gif) below which all investment consists of new investment and above which all investment consists of purchased existing capital
below which all investment consists of new investment and above which all investment consists of purchased existing capital
| (A.1) | ||
Corollary #.:
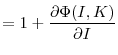 |
||
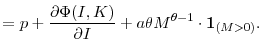 |
There does not exist an interior solution to the problem. The boundary conditions imply that
![\tilde{I} = \left[ \frac{a}{1-p}\right] ^{1/(1-\theta)}](img70.gif) . As asset purchases have a lower marginal cost of investment for
. As asset purchases have a lower marginal cost of investment for
The following equation yields the minimum cost of an investment of ![]() at current capital
at current capital ![]() :
:
Substitution of the optimal allocation to asset purchases, new investment and asset sales to the investment cash flow equation given in (5) yields the investment cost function (A.2). The continuity of
In the interior points, the partial derivative of the investment cost function is the following:
First consider two firms that buy assets, with profitability levels
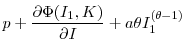 |
![\displaystyle = \beta E\left[ \frac{\partial{V(K(1-\delta) + I_{1} ,z^{\prime})}}% {\partial{I}}\vert z_{1}\right]](img152.gif) |
|
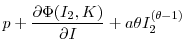 |
![\displaystyle = \beta E\left[ \frac{\partial{V(K(1-\delta) + I_{2} ,z^{\prime})}}% {\partial{I}}\vert z_{2}\right] .](img154.gif) |
Monotonocity of the transition function for
![\displaystyle E\left[ \frac{\partial{V(K(1-\delta) + I_{2} ,z^{\prime})}}{\partial{I}}% \vert z_{2}\right] > E\left[ \frac{\partial{V(K(1-\delta) + I_{2} ,z^{\prime})}% }{\partial{I}}\vert z_{1}\right] .](img155.gif)
A proof by contradiction establishes that
![\displaystyle E\left[ \frac{\partial{V(K(1-\delta) + I_{1} ,z^{\prime})}}{\partial{I}% }\vert z_{1}\right] - \frac{\partial{\Phi(I_{1},K)}}{\partial{I}} - a\theta I_{1}^{\theta-1} \le](img160.gif) |
||
![\displaystyle \hspace{2cm} E\left[ \frac{\partial{V(K(1-\delta) + I_{2} ,z^{\prime})}% }{\partial{I}}\vert z_{1}\right] - \frac{\partial{\Phi(I_{2},K)}}{\partial{I}} - a\theta I_{2}^{\theta-1}.](img161.gif) |
This contradicts (A.6). Therefore
A similar proof establishes that for two firms both of which either sell assets or invest in new capital, the firm with higher profitability will invest more
![]() . Investment increases monotonically with
. Investment increases monotonically with ![]() , and a firm buys assets if
, and a firm buys assets if
![]() and sells assets when
and sells assets when ![]() . This establishes the proposition.
. This establishes the proposition.
![]()
The constant returns to scale assumption implies that
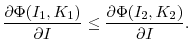
![\displaystyle E\left[ \frac{\partial{V(K_{1}(1-\delta) + I_{1} ,z^{\prime})}}{\partial{I}% }\vert z\right] \le E\left[ \frac{\partial{V(K_{2}(1-\delta) + I_{2} ,z^{\prime}% )}}{\partial{I}}\vert z\right] .](img177.gif)
Therefore
B Numerical Solution
The numerical solution employs value function iteration over a grid of values for current capital, investment and profitability. The capital grid consists of 500 equally spaced points, while the investment grid contains 5000 points. The Tauchen and Hussey (1991)
approximation for AR(1) processes yields the grid of values for profitability. This grid contains 10 points. The solution uses the optimal allocation choices derived as the solution to (9). The solution yields an optimal policy for new investment, asset purchases and asset
sales. For a given level of capital, the transaction costs of asset purchases lead to an upper and lower bound for profitability beyond which the firm buys and sells assets, respectively. These bounds follow a smooth function as ![]() varies. The acquisition boundary for a given capital level is approximated by the interpolated value of
varies. The acquisition boundary for a given capital level is approximated by the interpolated value of ![]() , which yields an optimal total investment of
, which yields an optimal total investment of
![]() . The mid-point of the profitability levels over which the firm begins to disinvest yields the approximate sale threshold. These values act as inputs to a polynomial approximation of
the acquire and sell thresholds as a function of log
. The mid-point of the profitability levels over which the firm begins to disinvest yields the approximate sale threshold. These values act as inputs to a polynomial approximation of
the acquire and sell thresholds as a function of log![]() . The solution uses a second-order approximation with Hermite polynomials. Within each action region, linear interpolation provides the
investment decisions and firm values.
. The solution uses a second-order approximation with Hermite polynomials. Within each action region, linear interpolation provides the
investment decisions and firm values.
C Simulations
The simulations apply the policy functions derived above to a panel of firms. The simulated sample consists of 1000 firms over 100 time periods. The simulation employs the boundaries for asset purchases and sales obtained in the numerical solution. The initial 20 periods function as a burn-in
sample. The sequence of solutions to the value function and simulation iterates until the equilibrium value of ![]() at which total demand for asset purchases equals total asset sales is
obtained. This corresponds to the steady state of the economy, where the inter-firm assets market clears. Hopenhayn (1992) provides the theoretical foundation for this approach.
at which total demand for asset purchases equals total asset sales is
obtained. This corresponds to the steady state of the economy, where the inter-firm assets market clears. Hopenhayn (1992) provides the theoretical foundation for this approach.
Bibliography
Table 1: Logit Regressions and Investment Regressions on Simulated Data
The table presents the results obtained by estimating the logit regressions on asset purchases and sales, and the investment regressions on transaction size using the simulated data set. Section 3 details the construction of simulated data set. Panel A presents the results of the ordered logit for all firms and those with investment to capital(rapid growth firms). Panel B presents the results of the multinomial logit for all firms. In each case, the noise columns demonstrate the impact of adding random noise to the sample. The noise is added by mixing 10% and 20% of the purchase and sale firms with the firms that invest in new capital. Panel C reports the results of using selection models to estimate the first order conditions for asset purchases and sales by all firms, and asset purchases by rapid growth firms. In each table, standard errors are reported in parentheses.
| All firms Sample |
All firms 10% Noise |
All firms 20% Noise |
Rapid growth Sample |
Rapid growth 10% Noise |
Rapid growth 20% Noise |
|
|---|---|---|---|---|---|---|
| Return on Assets | 4.46 | 3.77 | 3.20 | 12.23 | 7.64 | 5.63 |
| Return on Assets S.E. | (0.07) | (0.07) | (0.07) | (0.34) | (0.21) | (0.17) |
| Observations | 80000 | 80000 | 80000 | 16245 | 16245 | 16245 |
| Pseudo R-square | 0.15 | 0.11 | 0.08 | 0.66 | 0.47 | 0.34 |
| Purchases Sample |
Purchases 10% Noise |
Purchases 20% Noise |
Sales Sample |
Sales 10% Noise |
Sales 20% Noise |
|
|---|---|---|---|---|---|---|
| Return on Assets | 14.40 | 8.57 | 6.62 | -2.78 | -1.59 | -1.04 |
| Return on Assets S.E. | (0.32) | (0.16) | (0.12) | (0.13) | (0.11) | (0.09) |
| Size | 2.52 | 1.57 | 1.08 | 2.34 | 1.62 | 1.20 |
| Size S.E. | (0.03) | (0.02) | (0.02) | (0.03) | (0.02) | (0.02) |
| Observations | 80000 | 80000 | 80000 | 80000 | 80000 | 80000 |
| Pseudo R-square | 0.49 | 0.36 | 0.26 | 0.49 | 0.36 | 0.26 |
| Purchases (1) |
Purchases (2) |
Sales (1) |
Sales (2) |
Rapid growth (1) |
Rapid growth (2) |
|
|---|---|---|---|---|---|---|
| Tobin's Q | 0.358 | 0.348 | 0.149 | 0.228 | 0.355 | 0.370 |
| Tobin's Q S.E. | (0.001) | (0.003) | (0.003) | (0.002) | (0.001) | (0.002) |
| Cash Flow | 0.107 | 2.288 | -0.108 | |||
| Cash Flow S.E. | (0.023) | (0.018) | (0.013) | |||
| Inverse Mill's Ratio | 0.012 | 0.033 | -0.037 | 0.002 | -0.025 | -0.044 |
| Inverse Mill's Ratio S.E. | (0.003) | (0.005) | (0.002) | (0.001) | (0.003) | (0.003) |
| Observations | 1550 | 1550 | 6591 | 6591 | 1508 | 1508 |
| Adj. R-square | 0.98 | 0.98 | 0.60 | 0.88 | 0.99 | 0.99 |
Table 2: Characteristics of Buyers and Sellers of Existing Assets
The table reports end of fiscal year summary statistics for firms that purchase and sell operating assets during the next fiscal year. The list of acquirers and sellers is obtained from the SDC Platinum database, and the targets may be public, private or subsidiaries of firms. These are linked to Compustat and CRSP using CUSIP numbers. The sample consists of all firms listed on Compustat from 1984 to 2004 that contain information on the independent variables. Return on assets is the operating income before depreciation scaled by book assets at the beginning of the fiscal year. Size measures the log book value of assets in millions of dollars. Stock return is computed over the fiscal year. Finance Q is computed as the ratio between the market value of assets and the book value of assets. Macro Q equals the market value of the capital stock scaled by its replacement value. Market to book is the ratio of market value of equity to the book value of equity. Cash denotes cash and short-term investments scaled by the book value of assets. Leverage denotes book value of debt scaled by book value of debt plus equity. Sales growth and PPE growth measure growth in net sales and net plant, property and equipment over the previous fiscal year. RoA, finance Q, market to book, sales growth and PPE growth are Winsorized at the 1st and 99th percentiles. The deal value reports the value of the asset purchase or sale in millions of dollars, as reported by SDC Platinum. The sample size is reported in thousands.
| Firm Characteristic | All N(000) |
All Mean |
All Median |
All Std. |
Buyers N(000) |
Buyers Mean |
Buyers Median |
Sellers N(000) |
Sellers Mean |
Sellers Median |
|---|---|---|---|---|---|---|---|---|---|---|
| Return on Assets | 107 | 0.05 | 0.11 | 0.33 | 13 | 0.13 | 0.16 | 5 | 0.06 | 0.10 |
| Size | 109 | 4.62 | 4.48 | 2.21 | 13 | 5.54 | 5.46 | 5 | 6.43 | 6.43 |
| Stock Return | 110 | 0.14 | 0.10 | 0.66 | 12 | 0.23 | 0.18 | 5 | 0.07 | 0.09 |
| Finance Q | 101 | 1.96 | 1.33 | 1.85 | 12 | 2.04 | 1.49 | 5 | 1.54 | 1.20 |
| Macro Q | 80 | 3.73 | 2.05 | 4.18 | 10 | 4.47 | 2.88 | 4 | 3.04 | 1.76 |
| Market to Book | 104 | 3.17 | 1.82 | 4.60 | 12 | 3.30 | 2.15 | 5 | 2.79 | 1.73 |
| Cash | 109 | 0.18 | 0.08 | 0.22 | 13 | 0.16 | 0.08 | 5 | 0.10 | 0.04 |
| Leverage | 104 | 0.25 | 0.18 | 0.25 | 12 | 0.26 | 0.22 | 5 | 0.35 | 0.34 |
| Sales Growth | 101 | 0.29 | 0.09 | 0.95 | 12 | 0.38 | 0.14 | 5 | 0.13 | 0.04 |
| PPE Growth | 103 | 0.30 | 0.04 | 1.04 | 12 | 0.42 | 0.10 | 5 | 0.14 | 0.01 |
| Deal Value | 6 | 70.3 | 14.6 | 3 | 111.2 | 23.0 |
Table 3: Ordered Logit Regression for Purchase and Sale of Existing Assets
The table represents the results from an ordered logit regression of the choice of a firm to purchase or sell existing assets:
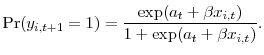 |
The dependent variableequals one if the firm or a subsidiary acquired some operations, minus one if the firm or a subsidiary sold assets, and zero otherwise. The list of purchasers and sellers is obtained from the SDC Platinum database, and the participants may be public firms or subsidiaries of public firms. The sample consists of all firms listed on Compustat from 1984 to 2004 that contain information on the independent variables. The independent variables are all measured at the end of the previous fiscal year. Table 2 details the variable construction. Columns 4 and 5 report results replacing the control variables with their industry means. The `Value' columns focuses only on transactions for which SDC reports a deal value. The regressions include year and industry dummies. Standard errors are robust to heteroskedasticity and adjust for clustering at the firm level. The odds ratios report the increase in the relative odds of a purchase for a firm whose independent variable increases by 1 standard deviation. * and ** signify statistical significance at the 5% and 1% levels using bootstrapped critical values for the t-statistics.
| Firm Control All Deals Coef. |
Firm Control All Deals Odds |
Firm Control Value Coef. |
Firm Control Value Odds |
Industry Controls All Deals Coef. |
Industry Controls All Deals Odds |
Industry Controls Value Coef. |
Industry Controls Value Odds |
|
|---|---|---|---|---|---|---|---|---|
| Return on Assets | 0.90** | 1.26 | 0.96** | 1.28 | 0.55** | 1.20 | 0.56** | 1.21 |
| Return on Assets S.E. | (0.04) | (0.05) | (0.03) | (0.04) | ||||
| Size | 0.03** | 1.06 | -0.002 | 1.00 | 0.01 | 1.02 | -0.02 | 0.96 |
| Size S.E. | (0.01) | (0.01) | (0.01) | (0.01) | ||||
| Wave Dummy | 0.13** | 1.05 | 0.11** | 1.05 | 0.15** | 1.06 | 0.14** | 1.06 |
| Wave Dummy S.E. | (0.03) | (0.04) | (0.03) | (0.04) | ||||
| Stock Return | 0.10** | 1.07 | 0.10** | 1.06 | -0.05 | 0.99 | -0.12 | 0.98 |
| Stock Return S.E. | (0.01) | (0.02) | (0.06) | (0.08) | ||||
| Market to Book | 0.01** | 1.06 | 0.01** | 1.06 | 0.04* | 1.05 | 0.05* | 1.06 |
| Market to Book S.E. | (0.002) | (0.003) | (0.015) | (0.019) | ||||
| Leverage | -0.36** | 0.92 | -0.25** | 0.94 | -1.81** | 0.84 | -1.78** | 0.84 |
| Leverage S.E. | (0.05) | (0.06) | (0.40) | (0.49) | ||||
| Cash | 0.18** | 1.04 | 0.47** | 1.10 | -0.16 | 0.98 | 0.43 | 1.05 |
| Cash S.E. | (0.05) | (0.07) | (0.36) | (0.43) | ||||
| Sales Growth | 0.09** | 1.08 | 0.10** | 1.09 | 0.09 | 1.02 | 0.19 | 1.04 |
| Sales Growth S.E. | (0.01) | (0.01) | (0.09) | (0.11) | ||||
| PPE Growth | 0.07** | 1.06 | 0.08** | 1.07 | 0.11 | 1.02 | 0.09 | 1.02 |
| PPE Growth S.E. | (0.01) | (0.01) | (0.07) | (0.09) | ||||
| Observations | 86397 | 86397 | 102387 | 102387 | ||||
| Pseudo R-square | 0.02 | 0.02 | 0.02 | 0.01 |
Table 4: Multinomial Logit Regression for Purchase and Sale of Existing Assets
The table represents the results from a multinomial logit regression of the choice of a firm to purchase or sell existing assets:
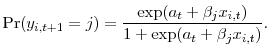 |
The dependent variabletakes three values depending on whether the firm or a subsidiary bought existing assets, sold existing assets or did neither. The table reports the coefficients for purchasing or selling assets compared to doing neither. The list of purchasers and sellers is obtained from the SDC Platinum database, and the participants may be public firms or subsidiaries of public firms. The sample consists of all firms listed on Compustat from 1984 to 2004 that contain information on the independent variables. The independent variables are all measured at the end of the previous fiscal year. Table 2 details the variable construction. Columns 3 and 5 report results replacing the control variables with their industry means. The regressions include year and industry dummies. Standard errors are robust to heteroskedasticity and adjust for clustering at the firm level. The odds ratios report the change in the relative odds of a purchase or a sale for a firm whose independent variable increases by 1 standard deviation. * and ** signify statistical significance at the 5% and 1% levels using bootstrapped critical values for the t-statistics.
| Purchases Firm Coef. |
Purchases Firm Odds |
Purchases Industry Coef. |
Purchases Industry Odds |
Sales Firm Coef. |
Sales Firm Odds |
Sales Industry Coef. |
Sales Industry Odds |
|
|---|---|---|---|---|---|---|---|---|
| Return on Assets | 1.00** | 1.29 | 0.70** | 1.27 | -1.64** | 0.66 | -0.78** | 0.77 |
| Return on Assets S.E. | (0.08) | (0.07) | (0.07) | (0.04) | ||||
| Size | 0.25** | 1.73 | 0.23** | 1.66 | 0.44** | 2.57 | 0.44** | 2.66 |
| Size S.E. | (0.01) | (0.01) | (0.01) | (0.01) | ||||
| Wave Dummy | 0.12** | 1.05 | 0.14** | 1.06 | -0.04 | 0.99 | -0.07 | 0.97 |
| Wave Dummy S.E. | (0.03) | (0.03) | (0.05) | (0.05) | ||||
| Stock Return | 0.11** | 1.08 | 0.04 | 1.01 | -0.11** | 0.93 | 0.18 | 1.04 |
| Stock Return S.E. | (0.02) | (0.08) | (0.03) | (0.11) | ||||
| Market to Book | 0.02** | 1.08 | 0.06** | 1.08 | 0.01 | 1.04 | 0.04 | 1.06 |
| Market to Book S.E. | (0.003) | (0.018) | (0.004) | (0.025) | ||||
| Leverage | -0.26** | 0.94 | -2.19** | 0.81 | 0.43** | 1.11 | -0.51 | 0.95 |
| Leverage S.E. | (0.07) | (0.48) | (0.10) | (0.64) | ||||
| Cash | -0.25** | 0.95 | -0.14 | 0.98 | -1.87** | 0.68 | -1.20 | 0.88 |
| Cash S.E. | (0.09) | (0.50) | (0.16) | (0.68) | ||||
| Sales Growth | 0.11** | 1.10 | 0.04 | 1.01 | -0.19** | 0.85 | -0.13 | 0.97 |
| Sales Growth S.E. | (0.01) | (0.12) | (0.04) | (0.17) | ||||
| PPE Growth | 0.05** | 1.05 | 0.11 | 1.02 | -0.12** | 0.90 | -0.14 | 0.97 |
| PPE Growth S.E. | (0.01) | (0.09) | (0.04) | (0.13) | ||||
| Observations | 86397 | 102387 | 86397 | 102387 | ||||
| Pseudo R-square | 0.09 | 0.08 | 0.09 | 0.08 |
Table 5: Investment Regression for Asset Purchases and Sales
The table reports the results from estimating the following equation:
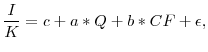 |
conditional on the firm either purchasing or selling existing assets, wheredenotes the value of the assets purchased or sold,
measures either finance Q or macro Q, and CF equals cash flow. The scaling variable
equals book assets for the finance Q regression and the replacement value of capital for the macro Q regression. The resulting model is estimated using a Heckman two-step estimator. The selection equation includes size, return on assets, market to book, wave dummy, stock return, leverage, cash, sales growth and PPE growth as independent variables. Columns 3 and 5 present results with the control variables for the selection equation replaced by their industry means. The selection equation and the investment equation include year and industry dummies. The sample of asset purchases and sales is obtained from SDC Platinum and consists of all asset transactions from 1985 to the end of 2005. Panel A reports the results obtained for the purchase of assets and Panel B reports the results for the sale of assets. The tables report the number of uncensored observations. * and ** signify statistical significance at the 5% and 1% levels using bootstrapped critical values for the t-statistics.
| Finance Q Firm |
Finance Q Industry |
Macro Q Firm |
Macro Q Industry |
|
|---|---|---|---|---|
| Tobin's Q | 0.019** | 0.011** | 0.029** | 0.027** |
| Tobin's Q S.E. | (0.002) | (0.001) | (0.002) | (0.002) |
| Cash Flow | 0.116** | 0.113** | 0.078** | 0.085** |
| Cash Flow S.E. | (0.017) | (0.016) | (0.011) | (0.010) |
| Inverse Mill's Ratio | 0.302** | 0.340** | 0.855** | 0.891** |
| Inverse Mill's Ratio S.E. | (0.016) | (0.017) | (0.048) | (0.049) |
| Observations | 5652 | 6363 | 4344 | 4864 |
| Adj. R-square | 0.11 | 0.12 | 0.16 | 0.16 |
| Finance Q Firm |
Finance Q Industry |
Macro Q Firm |
Macro Q Industry |
|
|---|---|---|---|---|
| Tobin's Q | 0.0054* | 0.0008 | 0.0002 | -0.0015 |
| Tobin's Q S.E. | (0.0021) | (0.0020) | (0.0010) | (0.0010) |
| Cash Flow | 0.075** | 0.030** | 0.009 | 0.009 |
| Cash Flow S.E. | (0.010) | (0.010) | (0.005) | (0.004) |
| Inverse Mill's Ratio | -0.109** | -0.133** | -0.108** | -0.115** |
| Inverse Mill's Ratio S.E. | (0.006) | (0.007) | (0.007) | (0.007) |
| Observations | 2474 | 2626 | 1722 | 1919 |
| Adj. R-square | 0.19 | 0.22 | 0.19 | 0.20 |
Table 6: Logit Regression for Large Asset Purchases by Rapidly Growing Firms
The table represents the results from a logit regression of the choice of a firm to purchase existing assets:
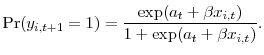 |
The dependent variableequals 1 if the value of asset purchases by the firm during a year was greater than
of capital expenditures. The samples includes either firms with values of capital expenditures to replacement value of capital greater than
or, in the latter columns, greater than 2 times the firm's median. The list of purchasers is obtained from the SDC Platinum database, and the participants may be public firms or subsidiaries of public firms. The independent variables are all measured at the end of the previous fiscal year. Table 2 details the variable construction. The regressions include year and industry dummies. Standard errors are robust to heteroskedasticity and adjust for clustering at the firm level. The odds ratios report the change in the relative odds of a purchase or a sale for a firm whose independent variable increases by 1 standard deviation.
, * and ** signify statistical significance at the 10%, 5% and 1% levels using bootstrapped critical values for the t-statistics.
| Capex Firm Coef. |
Capex Firm Odds |
Capex Industry Coef. |
Capex Industry Odds |
Capex
Firm Coef. |
Capex
Firm Odds |
Capex
Industry Coef. |
Capex
Industry Odds |
|
|---|---|---|---|---|---|---|---|---|
| Return on Assets | 0.56** | 1.20 | 0.25** | 1.12 | 0.64** | 1.24 | 0.21 |
1.11 |
| Return on Assets S.E. | (0.13) | (0.08) | (0.19) | (0.11) | ||||
| Size | 0.01 | 1.03 | 0.04* | 1.08 | 0.10** | 1.20 | 0.12** | 1.24 |
| Size S.E. | (0.02) | (0.02) | (0.03) | (0.02) | ||||
| Wave Dummy | 0.13 |
1.06 | 0.19* | 1.08 | 0.21 | 1.09 | 0.10 | 1.05 |
| Wave Dummy S.E. | (0.08) | (0.07) | (0.13) | (0.12) | ||||
| Stock Return | 0.07 | 1.05 | -0.13 | 0.98 | 0.00 | 1.00 | 0.04 | 1.01 |
| Stock Return S.E. | (0.04) | (0.22) | (0.06) | (0.37) | ||||
| Market to Book | -0.00 | 0.98 | 0.07 | 1.10 | 0.01 | 1.03 | 0.18* | 1.29 |
| Market to Book S.E. | (0.01) | (0.05) | (0.01) | (0.08) | ||||
| Leverage | 0.53** | 1.13 | -2.93* | 0.76 | 0.36 | 1.09 | -4.17* | 0.68 |
| Leverage S.E. | (0.16) | (1.37) | (0.24) | (2.06) | ||||
| Cash | 0.27 | 1.06 | 0.69 | 1.08 | 0.45 |
1.11 | -3.30 |
0.68 |
| Cash S.E. | (0.17) | (1.28) | (0.26) | (1.87) | ||||
| Sales Growth | 0.04 | 1.05 | -0.09 | 0.98 | 0.06 | 1.07 | 0.65 | 1.15 |
| Sales Growth S.E. | (0.03) | (0.30) | (0.04) | (0.47) | ||||
| PPE Growth | 0.03 | 1.04 | -0.26 | 0.94 | 0.02 | 1.02 | -0.44 | 0.91 |
| PPE Growth S.E. | (0.02) | (0.24) | (0.03) | (0.34) | ||||
| Observations | 18166 | 22352 | 8416 | 10636 | ||||
| Pseudo R-square | 0.05 | 0.05 | 0.06 | 0.06 |
Table 7: Investment Regression for Large Asset Purchases by Rapidly Growing Firms
The table reports the results from estimating the following equation:
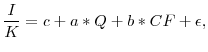 |
conditional on the firm purchasing existing assets worth greater thanof capital expenditures, where
denotes the value of the assets purchased,
measures either finance Q or macro Q, and CF equals cash flow. The scaling variable
equals book assets for the finance Q regression and the replacement value of capital for the macro Q regression. The samples includes either firms with values of capital expenditures to replacement value of capital greater than
or, in Panel B, greater than 2 times the firm's median. The resulting model is estimated using a Heckman two-step estimator. The selection equation includes size, return on assets, market to book, wave dummy, stock return, leverage, cash, sales growth and PPE growth as independent variables. Columns 3 and 5 present results with the control variables for the selection equation replaced by their industry means. The selection equation and the investment equation include year and industry dummies. The sample of asset purchases is obtained from SDC Platinum and ranges from 1985 to the end of 2005. The tables report the number of uncensored observations. * and ** signify statistical significance at the 5% and 1% levels using bootstrapped critical values for the t-statistics.
| Finance Q Firm |
Finance Q Industry |
Macro Q Firm |
Macro Q Industry |
|
|---|---|---|---|---|
| Tobin's Q | 0.009* | 0.008* | 0.013* | 0.015** |
| Tobin's Q S.E. | (0.003) | (0.003) | (0.005) | (0.005) |
| Cash Flow | 0.051 | 0.036 | 0.020 | 0.023 |
| Cash Flow S.E. | (0.030) | (0.023) | (0.034) | (0.033) |
| Inverse Mill's Ratio | 0.298 | 0.445 | 0.567 | 0.729 |
| Inverse Mill's Ratio S.E. | (0.093) | (0.108) | (0.276) | (0.261) |
| Observations | 1198 | 1475 | 720 | 836 |
| Adj. R-square | 0.06 | 0.06 | 0.02 | 0.03 |
| Finance Q Firm |
Finance Q Industry |
Macro Q Firm |
Macro Q Industry |
|
|---|---|---|---|---|
| Tobin's Q | 0.012* | 0.011* | 0.035** | 0.027** |
| Tobin's Q S.E. | (0.005) | (0.004) | (0.009) | (0.008) |
| Cash Flow | 0.083 | 0.018 | 0.050 | 0.029 |
| Cash Flow S.E. | (0.046) | (0.027) | (0.062) | (0.053) |
| Inverse Mill's Ratio | 0.241 | 0.138 | 0.663 | 0.502 |
| Inverse Mill's Ratio S.E. | (0.099) | (0.082) | (0.328) | (0.285) |
| Observations | 468 | 573 | 298 | 344 |
| Adj. R-square | 0.12 | 0.11 | 0.04 | 0.03 |
Table 8: Multinomial Logit Regression for Asset Transactions with Free Cash Flow
The table represents the results from a multinomial logit regression of the choice of a firm to purchase or sell existing assets:
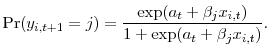 |
The dependent variabletakes three values depending on whether the firm or a subsidiary bought existing assets, sold existing assets or did neither. The table reports the coefficients for purchasing or selling assets compared to doing neither. The list of purchasers and sellers is obtained from the SDC Platinum database, and the participants may be public firms or subsidiaries of public firms. The sample consists of all firms listed on Compustat from 1984 to 2004 that contain information on the independent variables. The independent variables are all measured at the end of the previous fiscal year. Free cash flow equals operating cash flow net of investment activity and is obtained from the statement of cash flows. Table 2 details the construction of other variables. The regressions include year and industry dummies. Standard errors are robust to heteroskedasticity and adjust for clustering at the firm level. The odds ratios report the change in the relative odds of a purchase or a sale for a firm whose independent variable increases by 1 standard deviation. * and ** signify statistical significance at the 5% and 1% levels using bootstrapped critical values for the t-statistics.
| Purchase Coefficients |
Purchase Odds Ratio |
Sale Coefficient |
Sale Odds Ratio |
|
|---|---|---|---|---|
| Free Cash Flow | -0.05 | 0.98 | -0.28** | 0.89 |
| Free Cash Flow S.E. | (0.03) | (0.07) | ||
| Size | 0.26** | 1.75 | 0.38** | 2.27 |
| Size S.E. | (0.01) | (0.01) | ||
| Wave Dummy | 0.11** | 1.05 | -0.05 | 0.98 |
| Wave Dummy S.E. | (0.03) | (0.05) | ||
| Stock Return | 0.14** | 1.10 | -0.20** | 0.88 |
| Stock Return S.E. | (0.02) | (0.04) | ||
| Market to Book | 0.02** | 1.08 | 0.02** | 1.07 |
| Market to Book S.E. | (0.003) | (0.004) | ||
| Leverage | -0.35** | 0.92 | 0.51** | 1.14 |
| Leverage S.E. | (0.07) | (0.10) | ||
| Cash | -0.48** | 0.91 | -1.32** | 0.76 |
| Cash S.E. | (0.09) | (0.16) | ||
| Sales Growth | 0.09** | 1.08 | -0.18** | 0.86 |
| Sales Growth S.E. | (0.01) | (0.06) | ||
| PPE Growth | 0.06** | 1.05 | -0.18** | 0.86 |
| PPE Growth S.E. | (0.01) | (0.06) | ||
| Observations | 74227 | 74227 | ||
| Pseudo R-square | 0.07 | 0.07 |
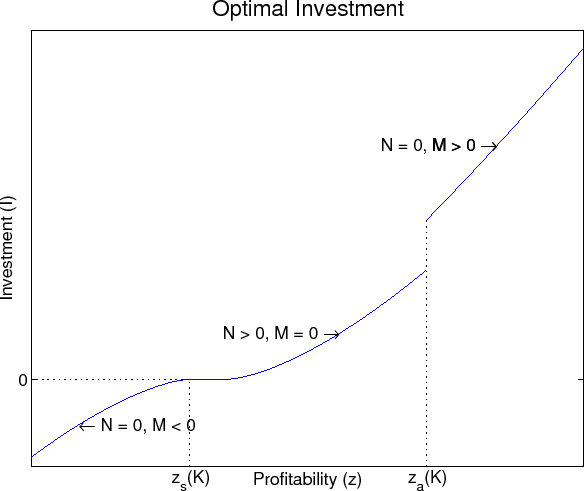 |
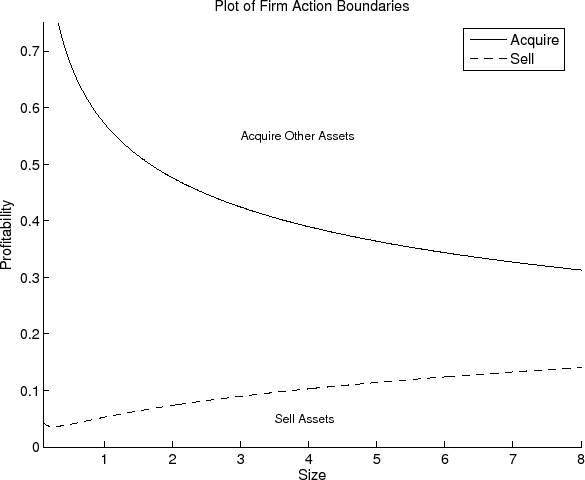 |
Footnotes
![L_{t} = \left[ \frac{e^{x_{i,t}}\alpha_{L} K_{t}^{\alpha_{K}}}{w}\right] ^{1/(1-\alpha_{L})}%](img18.gif) . Return to Text
. Return to Text![\displaystyle \frac{\partial C^{\ast}(I,K)}{\partial I} = \frac{\partial}{\partial K^{\prime}}\left( \beta E\left[ V(K^{\prime},z^{\prime})\vert z\right] \right) .%](img83.gif)
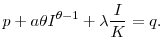
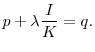
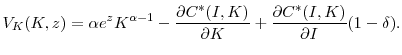
![\displaystyle \frac{\partial{C^{\ast}(I,K)}}{\partial{I}} = \beta E\left[ \frac {\partial{V(K(1-\delta)+I,z^{\prime})}}{\partial{I}}\vert z\right] .%](img144.gif)
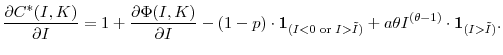
![\displaystyle E\left[ \frac{\partial{V(K(1-\delta) + I_{1} ,z^{\prime})}}{\partial{I}% }\vert z_{1}\right] - \frac{\partial{\Phi(I_{1},K)}}{\partial{I}} - a\theta I_{1}^{\theta-1} >](img156.gif)
![\displaystyle \hspace{2cm} E\left[ \frac{\partial{V(K(1-\delta) + I_{2} ,z^{\prime})}% }{\partial{I}}\vert z_{1}\right] - \frac{\partial{\Phi(I_{2},K)}}{\partial{I}} - a\theta I_{2}^{\theta-1}.%](img157.gif)
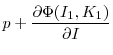
![\displaystyle = \beta E\left[ \frac{\partial{V(K_{1}(1-\delta) + I_{1} ,z^{\prime})}}{\partial{I}}\vert z\right]](img169.gif)
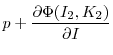
![\displaystyle \le \beta E\left[ \frac{\partial{V(K_{2}(1-\delta) + I_{2} ,z^{\prime})}}{\partial{I}}\vert z\right] .](img171.gif)