Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-45 Screen Reader version

Does Health Affect Portfolio Choice?

David A. Love*

Paul A. Smith*

Keywords: Household portfolios, Health, Risk

Abstract:

Previous studies find a strong and positive empirical connection between health status and the share of risky assets held in household portfolios. But is this relationship truly causal, in the sense that households respond to changes in health by altering their portfolio allocation, or does it simply reflect unobserved differences across households? We find that most of the variation by health is on the extensive margin of stock ownership (rather than the marginal allocation conditional on ownership), which more plausibly points to non-causal explanations. Moreover, we find that any link between health and risky assets depends crucially on the econometric treatment of unobserved heterogeneity. Once we account adequately for unobserved household differences, there is no longer a statistically significant relationship between any of our health measures and household portfolio decisions.

JEL classification: G11; I10

1 Introduction

Health considerations are often paramount in the decision-making of older households. A sudden stroke or a cancer diagnosis can upset a household's expectations about the future, including longevity, the pursuit of leisure, and the likelihood of needing assisted care. Translating these into the language of the life cycle model, health shocks in retirement can alter horizon length, utility, and resource constraints, and thus may affect a wide range of household economic decisions. Our study focuses on the effect of health on one key decision: how to allocate financial wealth between risky and safe assets. As discussed below, the theoretical sign of the effect of health on portfolio choice is ambiguous, depending on the relative sizes of potentially offsetting effects. Nonetheless, a number of recent papers find an empirical relationship between health status and portfolio choice, with poor health associated with a safer allocation. It is difficult to say, however, whether this relationship is causal. Both health status and financial decisions are driven by characteristics such as risk preference and impatience that are unobserved by the researcher, and such unobservables, if inadequately accounted for, can induce severe bias in the estimates of asset demand equations. Our contribution is to investigate whether the connection between health and portfolio choice is causal, or rather an artifact of unobserved heterogeneity. We conclude that when unobserved heterogeneity is adequately accounted for, health itself does not significantly affect portfolio choice.

Why might we expect health to affect household portfolios? Within the framework of the life cycle model, health shocks could affect portfolios through several channels. First, and most directly, health shocks could alter the marginal utility of consumption, and thus households' valuation of risk. As pointed out by Edwards (forthcoming,2006,2007), however, health shocks could either increase or decrease the marginal utility of consumption. A positive cross partial implies that health and consumption are complements, while a negative one implies they are substitutes. Health and consumption could be complements if improved health allows individuals to take advantage of costly leisure activities, such as going out to the movies, taking a trip, or going out to eat. They could be substitutes if worsening health places a premium on spending that eases painful activities such as walking, cleaning, or making trips to the store. Depending on whether health and consumption are complements or substitutes, changes in health status could lead to either safer or riskier portfolios.

Second, health could affect portfolio choice through a longevity channel. While the canonical life cycle model finds that horizon length should not affect asset allocation, Bodie, Merton, and Samuelson (1992) show that it can, particularly when there is a sizable stream of future income (e.g., Social Security or pension income) that can substitute for bonds in a household's total wealth portfolio. Intuitively, when expected annuity income is large relative to financial wealth, fluctuations in asset returns have a comparatively smaller effect on the marginal utility of consumption and therefore the valuation of risk in a given portfolio. Shorter horizons reduce the present value of these income streams and therefore tend to push households toward safer portfolio decisions.

Finally, health shocks can affect out-of-pocket medical expenses, which can in turn have a large impact on economic decisions. French and Jones (2004) estimate a dynamic programming model with uncertain medical expenses and find that both medical expense shocks and the uncertainty surrounding future expenses can have a substantial effect on consumption and saving decisions. Love and Perozek (2007) incorporate uncertain medical expenses into a life cycle model of portfolio choice, and find that medical expense shocks can influence optimal portfolio decisions as well: as the probability of relatively large medical expenses goes up, households reallocate toward safer portfolios.

To summarize, there are several theoretical channels through which health could affect portfolio allocation, but the sign of the effect depends on whether health and consumption are complements or substitutes. If they are substitutes, a negative health shock should lead to safer portfolios. But if they are complements, the direction depends on the relative sizes of offsetting effects, and the theoretical prediction is ambiguous. One implication of these considerations is that the theoretical effect of health on portfolios is more plausible on the intensive margin--i.e., the share of financial assets held as stocks among households that own stocks--rather than the extensive margin of stock ownership itself. For example, it seems less likely that a negative health shock would lead to a household's divestment of all of its stock holdings than just a partial re-adjustment, unless the household happened to be close to the extensive margin prior to the health shock. Even harder to imagine is that an older household would choose to buy stocks for the first time after an improvement in a health condition. As a result, one must carefully consider the role of other factors, including unobservable factors affecting the perceived costs and benefits of stock ownership, when explaining variation across the extensive margin of stock holding.^a

A number of recent empirical studies have examined the relationship between health status and portfolio choice on the extensive and intensive margins. Rosen and Wu (2004), using the first four waves of the Health and Retirement Study (HRS), estimate that being in poor health is associated with a reduction in the probability of owning any stocks or mutual funds of about 1.7 percentage points. Incorporating the intensive margin via a random-effects Tobit estimator, they find an overall negative effect of health on stock shares of about two percentage points, suggesting that much of the effect is occurring on the extensive margin. Using a Heckman-type selection model, Christelis, Jappelli, and Padula (2005) find small negative and statistically significant correlations between poor health and both stock ownership and stock shares in a cross-sectional data-set covering ten major European countries. Edwards (forthcoming) employs a Tobit model similar to Rosen and Wu (2004) and finds a negative effect of poor health on the stock share of assets in the first two waves of the Aging and Health Dynamics (AHEAD) survey.

These papers establish a correlation between poor health and lower stock holding, but they do not fully resolve whether the relationship is due to causality or unobserved heterogeneity. That is, does poor health directly cause a reduction in stock holding, or are unobserved factors correlated with poor health also correlated with lower stock holding? A standard random effects probit or Tobit model (as in Rosen and Wu, 2004) does not adequately account for unobserved factors if the unobserved random effect is correlated with observed variables--a situation that is likely to obtain in this case (in which unobserved effects include preference parameters such as attitudes toward risk).

A few recent papers have shed some light on the difference between causal effects and unobserved heterogeneity. Berkowitz and Qiu (2006), using the first six waves of the HRS, find that the effect of health on portfolio allocation operates through its effect on financial wealth, and that no further effect is evident after conditioning on differences in financial wealth. Using the first six waves of the HRS to perform "event studies" of health changes, Coile and Milligan (2006) find a small but statistically significant negative effect of a chronic health shock on the probability of holding IRAs or stocks, though no effect on the marginal share.

Our goal in this paper is to try to distinguish between a causal effect of health on portfolios and mere correlation attributable to unobserved individual effects. We begin by looking at the effects of health changes on portfolio changes in a descriptive setting. The broad patterns indicate that poor health is associated with lower rates of stock ownership but little difference in stock allocations conditional on stock ownership. The next step in our analysis replicates previous studies by performing random effect probit regressions on stock ownership and Tobit regressions on asset allocation. In line with previous findings, these estimates indicate a negative relationship between poor health and stock holding. The magnitudes and statistical significance of these results are similar to those in Rosen and Wu (2004), and as such provide a reasonable baseline for our regressions that account more carefully for unobserved heterogeneity.

We address unobserved effects using two different specifications: a correlated random effects approach and a fixed effects estimator. The correlated random effects approach allows unobserved effects to be linearly related to the covariates in the regression. Explicitly including this relationship in a random effects regression allows us to account for potential correlations between unobserved factors and observed characteristics. The fixed effects approach allows us to difference out time-invariant sources of individual heterogeneity, making it possible to focus on the effect of health changes on portfolio changes--an effect that is more likely to suggest a causal relationship.

Each of these techniques has drawbacks, which we discuss below, but both generate the same result: the link between portfolio choice and health is no longer evident once we account adequately for unobserved factors. When we examine coefficient estimates from the correlated random effects models of stock participation and allocation, for instance, we no longer see a statistically significant impact of health on portfolio choice. We do, however, find ample evidence of at least a linear relationship between the unobserved effects and our independent variables. In the fixed effects specifications, we again find no evidence that changes in health status induce households to either adjust their portfolios or enter or exit the stock market. We interpret these results as suggesting that current sources of data do not provide evidence of a strong causal relationship between health and asset allocation.

The rest of the paper proceeds as follows: Section 2 discusses the data, Section 3 provides some descriptive analysis of the relationship between health shocks and portfolios, Section 4 lays out our estimation strategy, Section 5 presents the estimation results, and Section 6 concludes.

2 Data

We use the 1998 through 2004 waves of the Health and Retirement Study (HRS). While several previous papers have followed the initial 1992 cohort of the HRS (see Coile and Milligan, 2006; Berkowitz and Qiu, 2006; Rosen and Wu, 2004), we begin with the 1998 wave because it is the first to represent all cohorts aged 51 and over, rather than just the initial HRS cohort of households aged 51-61 in 1992. Our sample is therefore older, on average, and more representative of aged households than samples drawn from the initial 1992 cohort. We restrict our analysis to households aged 65 or older in 1998, in order to focus our attention on households generally in the retirement phase of their lifetimes.^b

Including younger households in our sample would introduce either sample selection bias or measurement error. If we conditioned on retirement status, but included the 50- to 60-year-olds, sample selection bias would arise to the extent that poor health motivated earlier retirements. In that case, our sample of younger retirees would tend to be less healthy than the general population. We could, of course, handle the sample selection issue by including both workers and retirees, but this would exacerbate measurement error for at least two reasons. The first involves the accuracy of self-reported wealth variables. Since our data contain self-reported measures for Social Security and pension income, measurement error is likely to be more of a problem for pre-retirement households who have yet to receive regular payments from these sources. Second, including younger households also requires making strong assumptions about the timing of retirement and the amount of future labor earnings, assumptions which would tend to amplify the amount of measurement error. In the end, we preferred to work with an older sample because it controls for the present value of wages, allows for better measurement of Social Security and pensions, and avoids the potential endogeneity of the retirement decision.

Our data set supplements the RAND HRS mainfile, a longitudinal file of commonly-used HRS variables, with variables taken from the RAND "fat files," which contain nearly all of the unrestricted variables in the original survey. In addition to linking the households to construct a longitudinal file, the mainfile also provides consistent imputations of missing variables. Where possible, we pursue a similar imputation strategy for variables taken from the fat files. We supplement the RAND HRS data with our own calculations of the actuarial present value of expected flows from Social Security, defined-benefit pensions, annuities, life insurance, and transfer payments such as veterans' benefits, Food Stamps, and Supplemental Security Income. These calculations provide measures of annuitized wealth that are often excluded from empirical analyses of portfolio and saving behavior.^c

Table 1 provides a few demographic statistics for our sample. About three-quarters of single households are women (often widowed), with an average age of about 77 years.^d Couples are about five years younger than singles, on average. Singles are also more likely to be nonwhite and to have an additional household member present.

Table 2 shows that couples report substantially greater wealth than singles in all categories. In this table, we pool all observations across the four waves, and report the totals in 2004 dollars. Net financial wealth, including checking, saving and money-market accounts, CDs, stocks, bonds, mutual funds, and trusts, net of non-mortgage debts, averages about $100,000 for singles and about $167,000 for couples. The average value of retirement accounts, including IRAs and defined-contribution pension plans, are more than three times larger for couples than singles, a disparity which probably reflects a combination of cohort effects (such accounts are more prevalent among younger households) and the tendency for couples to have more of all types of wealth. The table shows that couples have about twice as much nonfinancial wealth, which consists mostly housing but also includes the value of businesses and vehicles. Couples also have substantially more annuitized wealth, which does not include Social Security in our analysis. We treat Social Security as a separate variable because, unlike other forms of annuitized wealth, it is a direct function of lifetime earnings and thus provides a measure of permanent income that is of interest apart from its value as an annuity.^e Our measure of comprehensive wealth, which is the total of the categories listed above, averages about $435,000 for single households and about $923,000 for couples.

2.1 Stock Share of Financial Assets

To simplify and focus our analysis of portfolio allocation, we choose a single dependent variable of interest, which is the share of total financial assets allocated to stocks. To construct this, we sum up the value of directly held stocks and stocks held in mutual funds, trusts, and retirement accounts, and divide by the total of financial assets and retirement accounts.^f

The HRS asks respondents directly about the value of stock shares held by themselves, in mutual funds, and in trusts, but it does not ask directly for the value of stocks held in retirement accounts. Rather, for both IRAs and DC plans, the survey asks "Is the money in this account invested mostly in stocks, mostly in interest-earning assets, is it about evenly split between these, or what?"^g We coded these responses as follows: if a household reported "mostly or all stocks," we allocated the entire account to stocks. If a household reported "mostly or all interest-earning," we allocated all of the account to non-stock investments. For all other responses, we divided the account evenly between stocks and non-stock investments. We chose these "extreme value" rules to allow for corner solutions. For example, we know that some households hold zero stocks in their retirement accounts, and an alternative rule allocating, say 10% of "mostly or all interest-earning" accounts to stocks would imply that all retirement-account holders were automatically stockholders.^h

The lower part of Table 2 provides information on the portfolio allocations of our sample households, using the rules described above. Nearly all households hold some safe assets (defined here as any non-stock financial asset). About 29% of singles and 43% of couples own some shares of stock either directly or through mutual funds or trusts. About 29% of singles and 57% of couples own retirement accounts (though not all of these hold any stocks). All told, about 45% of singles and 69% of couples hold any stocks. The average stock share of total financial assets is about 21% for singles and 32% for couples.

2.2 Health Measures

We use three measures to capture respondents' current health status: self-reported health status, the number of diagnosed conditions, and out-of-pocket medical expenses. While obviously related, we include these measures separately to account for three different dimensions of health: a subjective measure of how individuals perceive their own health, an objective measure of actual illnesses diagnosed by a doctor, and the financial impact of health status. Medical expenses are different from the other two measures in that they are more endogenous--they are likely to reflect a household's propensity to spend on discretionary medical care as well as underlying health status. We include them because they are an important theoretical channel of causal health effects, but their potential endogeneity highlights the importance of accounting adequately for unobserved preference and attitudinal differences across households.

Medical expenses can also induce a "mechanical" effect of health shocks on portfolios--if a health shock results in a non-discretionary medical expense, the way the expense is financed could affect the portfolio even in the absence of behavioral adjustments. For example, if the expense is financed out of liquid assets, stock shares might rise mechanically, while if the expense is financed by selling stock, stock shares could fall. Theoretically, households would finance non-discretionary expenses in a way that would maintain their optimal portfolio shares, but short-term liquidity or adjustment costs might result in mechanical effects. Such effects would add to the theoretical ambiguity of the effect of health shocks on portfolios.

Respondents can describe their current health status as "excellent," "very good," "good," "fair" or "poor." To simplify the analysis, we collapse these into three categories: a "best" category of excellent or very good, a "medium" category of good, and a "worst" category of fair or poor. As shown in Table 3, singles are roughly evenly distributed across these three categories, while couples are about 8 percentage points more likely to report themselves in the best health category and 7 percentage less likely to be in the worst health category.ⁱ

The number of diagnosed conditions reports how many of the following serious illnesses have been diagnosed by a doctor: high blood pressure, diabetes, cancer, lung disease, heart problems, stroke, psychiatric problems, and arthritis. Thus, the number of diagnoses can range between zero and eight. As shown in Table 3, about a third of singles report no diagnosed conditions, nearly half report one to three, and about 18% report four or more. Again, couples (who are five years younger, on average) appear healthier: they are about 5 to 8 percentage points more likely to report no conditions, and about 5 percentage points less likely to report four or more.^j

Out of pocket (OOP) medical expenses include uninsured costs over the previous two years related to the following: doctor visits, outpatient surgery, hospital and nursing home stays, prescription drugs, home health care, and special medical facilities or services. As is well-known, the cross-sectional distribution of medical expenses is characterized by a very long upper tail (see e.g., French and Jones, 2004). We therefore report percentiles of OOP expenses rather than means. The importance of considering the entire distribution can be seen in Table 3, which shows that while median OOP expenses are about $1,300 over a two-year period, the 90th percentile is about $7,300 and the 99th percentile is about $38,000 for singles. In our regression specifications, we group respondents into three categories defined by the 33rd and 67th percentiles of the distribution of OOP expenses (calculated separately for single and married households).

2.3 Controls

In our empirical analysis, we regress stock holding and asset allocation on our health measures and other covariates. Our controls include wealth, age, sex, education, race, and other household demographics. We control separately for financial wealth, nonfinancial wealth, Social Security wealth, and other annuitized wealth.^k We also allow for an interaction between health status and financial wealth, to test whether health status has differential effects on portfolio allocation for high-wealth vs. low-wealth households.

Finally, we condition on two expectation measures that could affect portfolio allocation. The first is a subjective probability that the household will leave a bequest of at least $100,000 to heirs. We divide respondents into three bins: a "low probability" group that indicates a subjective probability of less than 20%, a "medium probability" group that indicates a 20%-80% chance, and a "high probability" group that corresponds to responses greater than 80%. Table 4 shows that about 54% of singles report a low probability of leaving a bequest, 15% report a medium probability and 31% report a high probability. Couples are more likely to report a good chance of a bequest, with about a third reporting a low probability and just under half reporting a high probability.

The second expectation measure is the subjective probability of living about ten more years.^l Rather than use this response directly, we take the ratio of the self-reported probability to the probability implied by that year's life table for a person of the respondent's age and sex. This ratio provides a measure of whether the respondent is more optimistic, less optimistic, or about in line with the life table. We arbitrarily define a ratio of between 75% and 125% of the life table to be "in line" with the life table, and responses outside that band to be either more or less optimistic. Table 4 shows that about 27% of singles are more pessimistic than the life table about their survival probabilities, while a quarter are in line with the life table and just under a half are more optimistic. Couples are slightly more likely to be in line with the life table and slightly less likely to be more optimistic.

3 Descriptive Analysis

The left-hand columns of Table 5 show average portfolio allocations by our various health measures. There is clearly a positive correlation between health and stock allocation. Singles in the top self-rated health group have about 10% more of their financial portfolios allocated to stock, on average, than singles in the bottom health group, while for couples, the difference is about 13 percentage points. A similar result holds when looking at diagnosed conditions. When we move to out-of-pocket expenses, however, we see a different pattern: households in the middle third allocate about 6 or 7 percentage points more to stock than the lower group, and there is little difference between the middle and upper OOP groups. The difference between the OOP pattern and the other health measures suggests that OOP may measure something quite different from health status: perhaps the ability or willingness to pay for medical care, or a preference for a greater amount or higher quality care. Alternatively, as discussed above, it could represent a mechanical effect in which high expenses are financed out of liquid (non-stock) assets, driving up the portfolio shares.

One question that arises from these results is whether the difference in portfolio allocation by health is coming from the extensive or intensive margins (or both)--that is, whether sicker households are less likely to own any stocks, and/or less likely to hold smaller stock shares conditional on owning any. The right-hand columns of the table show that there is a large difference on the extensive margin: households in the lowest self-rated health group are about 20 percentage points less likely to hold any stocks than those in the highest group. On the other hand, there is little variation on the intensive margin: conditional on owning any stocks, the average share allocated to equities is between 45% and 50% for all health groups and marital status groups (not shown for brevity). This result suggests that the association between health and portfolio allocation could have more to do with factors that explain why some households don't hold any stock than factors that influence the amount of stock held on the margin.

This observation leads us to the central question of our paper: is the difference in portfolio allocation by health status causal or explained by other correlated (and potentially unobserved) factors? In the next section, we will address this question econometrically. But first, we can gain some insight by examining the simple correlation between health changes and portfolio changes. If the relationship between health and stock allocation is truly causal, then one would expect changes in health status to be accompanied, or followed, by changes in portfolio allocation.

Table 6 shows that, among singles, there does appear to be a small negative correlation between worsening health and changes in stock allocation, on the order of about three percentage points. However, this effect is not at all precisely estimated: the standard errors are on the order of 0.25 to 0.3 for all table entries. In addition, the same pattern is not evident among married couples. Finally, this exercise does not control for age: if stock allocations decline with age and households with worsening health are older than those with stable health, the negative correlation could be an age effect rather than a health effect.

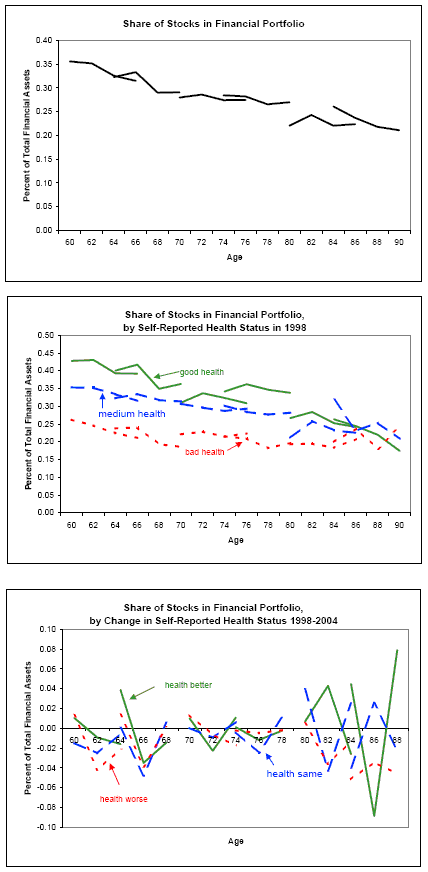
Figure 1 explores the role played by age by plotting age profiles of stock allocation. These profiles are estimated by tracing out the average stock allocation held by various cohorts over the length of the panel. Each cohort's segment has four points, representing the four waves of the panel. Connecting the segments combines the cross-sectional and longitudinal variation to form a long pseudo-panel that traces out a "life-cycle" from age 60 to age 90. The upper panel of the figure, which plots the age profile for all households in the sample, shows a slight negative tilt to the age profile, suggesting that households reduce their stock exposure as they age. However, our method of constructing the profile cannot distinguish between a true age effect and a cohort effect. Consistent with Table 5, the middle panel shows that healthier households have significantly higher stock allocations, at least until later ages. However, the bottom panel shows that there is no obvious relationship between health changes and portfolio changes, conditional on age.

4 Estimation Strategy

4.1 Econometric Models

Next, we estimate equations for stock ownership and stock share of assets using three different methods: a standard random effects specification, a Chamberlain-type correlated random effects approach, and a fixed effects estimator. We begin with a specification very similar to those used in earlier studies, and then apply different techniques for accounting for unobserved heterogeneity to test the robustness of the relationship between health and portfolio choice.^m

As discussed above, poor health might affect the demand for risky assets through two channels: ownership, or the decision whether to hold any amount of risky assets, and allocation, or the marginal holding of risky assets conditional on ownership. Previous studies suggest that health operates on the extensive margin, and may also operate on the intensive margin. But the question remains: is the link causal or coincidental?

Earlier studies use cross-sectional regressions, pooled regressions, or random effects probit/Tobit specifications. These techniques break down in the presence of unobserved household differences that may be correlated with observed characteristics. For example, suppose that key determinants of stock ownership include financial sophistication and attitudes toward risk. These factors are unobserved, though likely to be correlated with observed characteristics such as age, education and financial wealth, as well as health status. Depending on the sign of the correlation, a cross-sectional or pooled regression would either exaggerate or attenuate the effect of the observable on stock ownership. Even the random effects regression would have this problem, because the consistency of the standard random effects estimator requires that the random effect be uncorrelated with observables.

Examples of unobserved factors that might be correlated with both portfolio choice and our health measures include risk aversion, expected longevity, impatience, information networks, and family values regarding health and finances. We include proxies for some of these variables in our analysis, but this provides, at best, an imperfect characterization of the unobserved effects. Without properly accounting for unobserved heterogeneity, our estimates will be inconsistent, and it is nearly impossible to say whether worsening health causes a decline in the share of risky assets or is merely correlated through unobserved factors.

Our empirical approach exploits the panel nature of the data to account for unobserved household effects that might influence both portfolio choice as well as some of our explanatory variables. Following earlier studies, we first estimate binary response models (probits and logits) to identify the effect of health on the extensive margin, i.e., the decision to hold any risky assets. We then estimate censored regression models to uncover the link between health and the marginal stock allocation.

4.1.1 Random Effects Probits and Tobits

We begin by following the literature and estimating a standard random effects probit model for stock ownership and random effects Tobit model for marginal allocation. Underlying all of the specifications is a latent variable model of the form:

$\displaystyle y^{*}_{it}=\mathbf{x}_{it}\mathbf{\beta}+c_i+u_{it},$

(1)

where $\mathbf{x}_{it}$ is a vector of exogenous explanatory variables,

is an unobserved, time-invariant, individual-specific effect, and $u_{it}$ is an idiosyncratic error. In the participation equations, the dependent variable $y_{it}$ is an indicator for holding positive amounts of risky assets, such that $y_{it}=1$ if $y^{*}_{it}0$ . In the stock-share regressions, $y^{*}_{it}$ represents the desired portfolio share, but the observed risky asset shares lie between 0 and 1, so that $y_{it}=\max\{0,\min\{y^{*}_{it},1\}\}$ .

It can be seen from the specification above that failing to account for unobserved effects will generally lead to biased coefficient estimates unless the omitted variables are perfectly uncorrelated with any of the independent variables in the regression. The bias comes from a violation of the orthogonality assumption applied to the composite error in the latent variable model above. In a pooled regression, $E(\mathbf{x'}_{it}\vert(c_i+u_{it}))$ will generally be nonzero if the unobserved factor is correlated with the observables $\mathbf{x'}_{it}$ . The standard random effects models obtain coefficient estimates by integrating the unobserved factor out of the likelihood function. However, consistency requires that $E(c_i\mid\mathbf{x}_{i1},...,\mathbf{x}_{iT})=E(c_i)=0$ , which is violated whenever there is correlation between and any of the $\mathbf{x}_{it}$ 's. That is, the random effects estimator is only consistent in the special case that the unobserved effect is uncorrelated with the observables--unlikely in this context, because some of the key parameters in the life cycle model, such as risk preference, impatience, and longevity are unobserved and likely to be correlated with education, wealth, and other observables. To some extent, we can control for these factors by including proxy variables, such as subjective survival probabilities, but these are at best imperfectly measured, and the omitted variables problem remains. A more promising approach would be to attempt to account for the correlation between the unobserved random effect and the observables, or better yet, to difference out the individual effects via a fixed-effects strategy.

4.1.2 Correlated Random Effects Probits and Tobits

Next we attempt to account for the correlation between unobserved and observed variables. If we are willing to impose an additional assumption that the unobserved effects are linearly related to the independent variables, we can estimate a correlated random effects regression in the spirit of Chamberlain (1984).ⁿ The correlated random effects approach assumes that the individual effect can be written a linear function of the explanatory variables:

$\displaystyle c_i=\Psi+\mathbf{\bar{x}}_{i}\mathbf{\lambda}+a_i,$ $\displaystyle a_i\mid \mathbf{x_i} \sim N(0,\sigma_a^2),$

where the vector $\mathbf{\bar{x}}_{i}$ contains the means of the time-varying regressors, $\Psi$ is a constant, and

is the independent portion of the individual effect.^o The idiosyncratic error term $u_{it}$ in equation (1) is assumed to be normally distributed, conditional on $x_{i}$ and

This approach accounts for the correlation between unobserved and observed variables, reducing the omitted variable problem. In our context, if health is correlated with stock ownership in the correlated random effects specification, then we have a bit more evidence that the correlation is indicative of a causal effect rather than spurious correlation. However, this approach assumes a linear relationship between unobservables and observables, as well as normally distributed errors. If these conditions do not hold, our omitted variable problem remains. Thus, our final specification attempts to difference out individual effects altogether using a fixed effect approach.

4.1.3 Conditional Fixed Effect Logit and Censoring Models

In general, fixed effect differencing cannot be applied to nonlinear models such as ours, because differencing would not remove the individual effect. However, Chamberlain (1980) showed that, in the binary choice case, a logit specification in which the likelihood function is conditioned on the number of observations with $y_{it}=1$ can be constructed in a way that effectively removes unobserved heterogeneity from the choice probabilities. This estimator, called the conditional fixed effect logit estimator, can be used to obtain fixed effect estimates from longitudinal binary choice data, such as stock ownership.

In the continuous case, until recently, there was no estimator that could handle a fixed effect specification in the presence of two-sided censoring. However, a new semi-parametric estimator developed by Honor and Leth-Petersen (2006),which generalizes the one-sided least absolute deviation estimator in Honoré (1992) to handle the case of two-sided censoring, allows us to apply a fixed effects estimator to the marginal allocation problem.^p Relative to the correlated random effects Tobit, Honoré's method imposes minimal structure on the error process while still accounting for correlated, unobserved heterogeneity. The estimator assumes that the error terms are identically, but not necessarily symmetrically, distributed.^q

The main strength of the resulting estimator is that it produces consistent estimates of a fixed effect Tobit-type model, and it does so with minimal restrictions on the distribution of the error term (e.g., it need not be normal). A disadvantage of this technique, however, is that it cannot be used to compute the marginal effects in the censored regressions. The marginal effects typically depend on both the estimated parameters as well as the unobserved fixed effects, but the semi-parametric estimator strips these away and estimates the coefficients using only time variation in the regressors. Thus, we estimate our model using the semi-parametric fixed effects specification as a test of the robustness of the relationship between health and portfolio allocation.^r

4.2 Specifications

In addition to accounting for unobserved heterogeneity, we want to allow for the possibility that health influences both the intensive and extensive margins of stock allocation. We consider ownership separately because many of the households in our sample hold no stock, and hence a significant share of the sample is censored at zero.^s A popular method for dealing with censored data is to use a Tobit specification, which models both the probability of limit observations and the value of non-limit observations in the same log-likelihood function. The method imposes, however, some particularly strong assumptions, the most restrictive of which is that the probability of selection (e.g., stock ownership) depends on the same variables, and in the same way, as the non-limit outcomes (e.g., marginal stock allocation).^t

Because the effects of health on participation and allocation could very well be different, our analysis proceeds in two steps. In the first, we examine stock ownership independently of allocation, modeling the ownership decision as a binary outcome (while still accounting for unobserved heterogeneity). Following the discussion above, we begin with a standard random effect probit, then move to a correlated random effect probit specification, and then finally the conditional fixed effect logit model. In the second section, we consider the joint determination of allocation and participation, beginning with a standard random effects Tobit model, then moving to correlated random effects Tobit specifications, and finally Honor's fixed effects censored regression model.^u

In the ownership regressions, the dependent variable is an indicator for holding any stock, whether directly or indirectly through mutual funds, trust, or retirement accounts. In the marginal allocation regressions, the dependent variable is the share of risky assets measured as the fraction of stocks held both inside and outside retirement accounts over total financial assets (see Section 2.1 for details). All of our regressions are unweighted, and the sample is restricted to individuals 65 or older with financial assets between $0 and $3 million. The regressions include indicator variables for health status, diagnosed medical conditions, out-of-pocket medical costs, subjective life expectancy and expected bequests, in addition to interactions between health and financial wealth.

We report two models for each case, one using a single measure of health (the self-reported health status, as used in previous studies), and one using the full set of health measures, including diagnosed conditions and OOP expenses. We report these models separately because the various health measures are likely to be correlated (particularly the self-report and the number of conditions), and we do not want our conclusions to be driven by the resulting reduction in the precision of the estimates. Many of our covariates, such as financial wealth, non-financial wealth, age, race, education, and family size, are standard following Rosen and Wu (2004) and others, but we also include some unique measures of the lifetime resources and value of annuitized income. In particular, we include the present discounted value of Social Security income, which should be highly correlated with lifetime earnings up to a limit, and the present discounted value of defined benefit pensions and other annuity income, which also acts as a bond-like safe asset in the total household portfolio.^v

5 Estimation Results

5.1 Stock Ownership

5.1.1 Random Effects Probit

As a baseline of comparison with previous studies, we begin by presenting estimates from a random effects probit regression of stock ownership on health and other household characteristics. The left-hand panel of Table 7 reports the random effects estimates for single households in our sample.^w Financial wealth, social security wealth and education are all strongly and positively associated with stock ownership, consistent with financial and/or informational barriers to entry in asset markets. We observe a declining age profile in stock ownership, which could be picking up either a cohort effect or a life-cycle effect. Households expecting to leave a bequest are much more likely to own stock. We find a negative relationship between expected longevity (relative to the life tables) and stock participation--evidence, perhaps, that the most optimistic respondents may be less informed or sophisticated than those whose expectations are in line with the life tables.

The results from both specifications--that with just self-reported health and that with the full set of health variables--suggest that bad health is strongly and significantly related to stock ownership. We estimate the marginal effect of bad self-reported health to be about negative 12.5 percentage points, relative to the omitted category of "excellent or very good" health.^x Results for the number of health conditions are similar. Higher out-of-pocket medical expenses, on the other hand, are associated with higher probabilities of stock ownership--consistent with our descriptive evidence that suggested OOP expenses might have discretionary or "luxury good" aspects. The effect of being in "medium" health is not statistically significant in the long regression (though it is in the short regression), but the interaction term with financial wealth shows that higher-financial-wealth households have a stronger negative effect of being in "medium" (relative to the best category of "excellent or very good") health than lower-financial-wealth households. The interaction term between bad health and financial wealth is not statistically significant.

The random effects probit estimates suggest a strong link between health and stock ownership, as in Rosen and Wu (2004).^y The question, though, is whether this finding represents a true causal relationship, or rather bias due to unobserved heterogeneity. One reason to suspect that it is not necessarily causal is given by Rosen and Wu's explanation for their empirical findings. Building on the logic in Bodie, Merton, and Samuelson (1992), they argue that sick households are less able to absorb low asset returns by adjusting labor supply and therefore tend to shift toward safer portfolio allocations. But this cannot be the entire story, because we find very similar results for a sample of retired households who can no longer avail themselves of a labor supply channel. Either another channel is at work, or the empirical findings are picking up the effects of omitted variables. One way to get at this question is to assume that the unobserved effects are linearly related to the regressors and estimate a correlated random effects probit.

5.1.2 Correlated Random Effects Probit

The middle panel of Table 7 reports the results for the correlated random effects specification for singles. The upper set of results displays the slope coefficients on the regressors--the $\beta$ coefficients. The lower set of results--the $\lambda$ coefficients--shows the correlations between the unobservables and our independent variables. The estimates confirm the importance of accounting adequately for unobserved effects. Health variables that were previously important in both magnitude and significance now have a statistically insignificant effect on the probability of stock ownership. Estimates of self-reported health, out-of-pocket expenses, and the number of health conditions are all insignificant with marginal effects close to zero.

While health appears insignificant in the $\beta$ coefficient estimates, the estimates of the $\lambda$ coefficients suggest that it is strongly related to the unobserved variables. Since the $\lambda$ coefficients are essentially identified off of differences in characteristics across household units, we can interpret the significance of the $\lambda$ coefficients, and in particular, the $\lambda$ coefficients on the health variables, as evidence that differences in stock ownership and health can be explained by unobserved variables, such as risk and time preference. After all, the decision to take an active part in the stock market could in many ways resemble the decision to regularly visit a doctor, get a colonoscopy, and so forth. Some people, perhaps, do these things as a matter of course, while others require stronger incentives. The $\lambda$ coefficients may therefore indicate a violation of one of the key assumptions in the standard random effects specification--the independence of and the $\textbf{x}_{it}$ 's.

Another interpretation of the $\lambda$ coefficients is that health matters for portfolio choice, but that the effect is not contemporaneous with the change in health status. Suppose, for example, that bad health is predictable and that households adjust their portfolio allocations the moment they learn something new about their expected health status. In this case, even though an expected change in health may not occur for several years in the future, the household adjusts its portfolio immediately. Health and portfolio choice may therefore be linked across households, even though we do not observe a relationship between changes in these variables within households. The correlation across households occurs because individuals currently in poor (or good) health may have adjusted their portfolios the moment--potentially years in the past--that they learned of their expected health outcomes. This gap in timing between expectations of health and realized health shocks then explains why we do not observe a correlation between changes in health and changes in portfolios; the realization of a health shock may actually be old news to which the household has already responded.

5.1.3 Conditional Fixed Effects Logit

The right-hand panel of Table 7 shows the results from the conditional fixed effects logit specification. None of the health variables in these regressions are statistically significant at the 10 percent level, and several of them actually flip signs. As with all fixed effects estimators, the panel version of the logit has the disadvantage that it only includes explanatory variables that vary within a household over time. A direct implication of this is that we are unable to estimate the slope coefficients of potentially interesting variables such as education, race, and gender. Another drawback associated with the fixed effects estimator is its tendency to exacerbate the effects of measurement error, particular if there is comparatively limited "within" variation (Bound, Brown, and Mathiowetz, 2001). In our case, the effect of health on ownership is identified by changes in health and stock ownership over our 8-year sample period. If a large fraction of the changes in ownership status simply reflects measurement error, the coefficient estimates may be noisily measured indeed. Because the imprecision of our estimates may be due to measurement error, we interpret our results as evidence against evidence: we do not find any effect of health on risky asset ownership within households.^z

A weak connection between stock ownership and health is not that surprising. What, after all, explains why a person, falling ill, would decide to exit the stock market? Or even more difficult to imagine is an older individual in improved health finally choosing to purchase stocks. With the exception of households very close to the participation margin (i.e., households that would like to hold slightly short position in stocks or just want a sliver of their portfolio in risky assets), we simply cannot come up with a convincing theoretical explanation for why health would drive ownership. In that sense, our "negative" result actually accords with intuition.

Unlike the case of participation, however, there are good theoretical reasons to expect a relationship between health and portfolio choice. Changes in health status and out-of-pocket medical costs represent substantial background risks that should, according to theory, diminish the demand for risky assets. We need to be careful here, however, to distinguish between background risk (i.e., variance) and the impact of particular realizations from the distribution of risks. Theoretical models of portfolio choice (see, e.g., Kimball and Elmendorf, 2000) predict that an increase in background risk per se should reduce the optimal portfolio share of stocks. What happens when these risks are actually realized depends on the degree of auto-correlation in the time-series process for health or medical expenses. With these qualifications in mind, we now turn to our results from the allocation equations.

5.2 Stock Allocation

5.2.1 Random Effects Tobit

Again, for the sake of comparison with previous studies, we begin with the standard random effects specification. The left-hand panel of Table 9 reports the results for single households. The focus of our analysis is on health, but first we comment briefly on variables that play a central role in the life cycle model of saving: education, Social Security wealth, and expected bequests.

Education is of interest because of its presumed correlation with lifetime earnings and financial sophistication. The results in the tables indicate that more educated households tend to hold a larger fraction of risky assets, and the effect is large and precisely measured. Relative to individuals without a high school diploma, for instance, college graduates hold about 15 percentage points more of their financial wealth in the form of stocks, and the figure for high school graduates is around 8 percentage points.

Social Security, as an annuitized stream of payments, represents a safe, bond-like asset that provides a counterweight to stocks in a household's portfolio. Since households care about their total exposure to risk, a larger bond-like asset should increase a household's desired holding of stocks. But Social Security also depends positively on lifetime earnings, and lifetime earnings are in turn likely to be correlated with unobserved variables such as risk aversion, exposure to financial markets, and financial sophistication. Under this interpretation, higher Social Security might be correlated with the stock share even if there is no direct connection between the two variables.

In all of our random effects regressions, the expected present value of Social Security is a strong predictor of portfolio choice, with higher present values associated with a larger share in stocks. The results in Table 9 show that even after controlling for age, education, and financial wealth, a $100,000 increase in the present value of Social Security corresponds to about a 1.8 percentage point rise in the stock share for couples and to about a 1.7 percentage point rise for singles.¹

The estimates in the tables for both singles and couples indicate that the probability of leaving a bequest is strongly and positively related to the share of risky assets. Relative to households whose respondents report a low probability of leaving a bequest, households with probabilities in the middle and upper range tend to hold stock shares that are between 4 and 6 percentage points higher.²

Turning to the health variables, the results indicate a clear and striking relationship between health status and portfolio allocation: a lower health status is correlated with a significantly smaller share of assets in stocks. Having poor self-reported health, for instance, is associated with about a 3.5 percentage point reduction in the share of stocks for singles relative to the omitted category of good health. It does not seem to matter whether it is the respondent or the spouse who suffers poor health; the estimates are very similar. As was the case in the probit specifications, our estimates suggest that the number of health conditions has a smaller and less significant impact on portfolio decisions, perhaps because it is highly collinear with self-reported health status.

We find a positive relationship between OOP expenses and the stock share. Again, the mechanical explanation for this relationship is that some households may be reluctant to finance out-of-pocket expenses out of stocks and choose instead to pay for them out of safe assets. In this case, the share of stock could rise even if the total value of stocks remains unchanged. Another potential explanation for the relationship involves the discretionary nature of some medical costs. Since households can choose different levels of medical care, high out-of-pocket medical expenses might be correlated with unobserved shocks to future income and non-medical expenses. Under this interpretation, the positive relationship is accounted for by the correlation between stocks, medical expenses, and some third unobserved variable. To explore this possibility, we move on to the results of our alternative empirical specifications.

5.2.2 Correlated Random Effects Tobit

The middle panel of Table 9 shows that in the correlated random effects specification, financial wealth remains an important determinant of portfolio allocation, with higher values of wealth associated with a portfolio movement toward stocks. Almost all of the other time-varying regressors, however appear to be unimportant in both magnitude and statistical significance. In particular, the effects of health status and medical expenses appear substantially weaker when we move to the correlated random effects model. Almost none of the coefficients are statistically significant, and some, such as those on health conditions and medical expenses, actually flip signs. An interpretation of these results is that while health may be useful for explaining differences across individuals and households, it exerts no obvious influence on portfolio decisions for a given person or household over time. Another possibility, however, is that expectations about health status, rather than realized health states, are really what matters for portfolio decisions. Under this interpretation, we might expect that observed, but predictable, changes in health status would produce relatively little variation in people's portfolios.

Further, if we look at the coefficient estimates for the $\lambda$ variables, we can get a sense of the extent to which the simple random effects Tobit estimates are driven by unobserved heterogeneity. Most of the $\lambda$ coefficient estimates share the same sign, magnitude, and significance as their counterparts in the random effects model. Thus, one explanation for the finding in previous studies of a strong relationship between health and portfolio choice could simply be that households differ along some unobservable dimensions, and these differences are what really drive portfolio selection and health. A caveat here, as with the correlated random effects probit specification, is that unobservable heterogeneity is modeled to be linearly dependent on the included regressors. To see whether our findings are sensitive to this assumption, we end by discussing our results from the semi-parametric fixed effects regressions.

5.2.3 Fixed Effect Censored Regression Model

The right-hand panel of Table 9 reports the results for the semi-parametric fixed effects specification. The estimates for financial wealth and the present values of Social Security and other annuitized income are generally consistent with the results from our other regressions. The estimated coefficients on stocks and safe assets suggest that households increase their holding of stocks as financial wealth rises, but at a diminishing rate and that the present value of other annuitized wealth has no significant impact on either of the non-retirement shares. Interestingly, the estimate on nonfinancial wealth, which was generally insignificant in all of our other regressions, is now mildly significant and negative.

Turning to the effect of the health and bequest variables, we see that the fixed effects attenuate both the magnitude and statistical significance of the coefficient estimates. In the random effects Tobit estimates, health status and the number of health conditions were both negatively related to the share of stocks, and the impact of out-of-pocket medical expenses was weakly positive. The estimates in the fixed effects specification, however, are either statistically insignificant or have reversed signs. For example, while the random effects estimates for singles indicate a strongly negative relationship between health status and the share of stocks, the fixed effects estimates show exactly the opposite. Similarly, the positive association between out-of-pocket medical expenses and the share of risky assets found in the random effects estimates disappears almost completely when we account for unobserved heterogeneity through fixed effects. The loss of significance may be driven partly by the tendency for measurement error in the explanatory variables to blow up the noise-to-signal ratio in a fixed effect regression. But even if this is the case, the estimates suggest that the relationship between health and portfolio choice may be considerably more complicated than findings in previous studies suggest.

6 Conclusion

This paper tests whether the relationship between health and portfolio choice persists even after accounting adequately for the effects of unobserved heterogeneity. Our results suggest that it does not. We find no evidence that health operates on either the extensive margin of stock ownership or on the intensive margin of asset allocation. Once we account for unobserved effects through a correlated random effects model or a fixed effects estimator, the estimates on almost all of our health variables become small and statistically insignificant. One explanation, of course, is that health and portfolio choice are unrelated. However, there are other possible explanations, including measurement error, the role of expectations, and heterogeneity across similar households in the relationship between health and portfolios.

Attenuation bias due to measurement error is typically exacerbated in the fixed effects framework. Because the fixed effects estimator only uses information about changes in variables within observations, it tends to decrease the signal-to-noise ratio and therefore the reliability associated with each coefficient estimate. In a sense, noisier and attenuated coefficient estimates can be seen as the cost of controlling for a potentially more severe source of bias due to unobserved heterogeneity. Nevertheless, we cannot rule out the possibility that measurement error is behind the small and insignificant coefficient estimates on our health variables.

Another possibility is that health affects portfolio choice, but that the effect operates through the role of expectations. To some extent, changes in health status are predictable. Individuals who smoke, are overweight, or drink heavily presumably understand that these activities expose them to greater risks of cancer, diabetes, and liver problems. If these individuals adjust their financial portfolios in light of this risk assessment, there might be a link between health expectations and asset allocation, even though no such link is apparent when we consider changes in health status.

Finally, it could just be that our results are reflecting the ambiguous relationship between health and portfolio choice. As we argued in the introduction, the effect of health on allocation decisions depends on the cross-partial derivative between consumption and health in the marginal utility function. Since this derivative can plausibly take either a positive or a negative sign, the net effect of health could be ambiguous. Some households might respond to worsening health by increasing their stock share, while others might move toward safer assets. Or, if the opposing forces of health on desired consumption affect each household's utility in the same way, our finding could reflect genuine ambivalence on the part of the household.

No matter what the interpretation, though, our findings indicate that the empirical relationship between health and portfolio choice is far less clear than previous studies suggest. If such a relationship exists, we expect that it will emerge empirically only after a careful treatment of unobservable heterogeneity, measurement error, and expectations.

Bibliography

ALAN, S., AND S.LETH-PETERSEN (2006):

"Tax Incentives and Household Portfolios: A Panel Data Analysis," CAM Working Paper 2006-13.

BAKIJA, J. (2004):

"The Effect of Taxes on Portfolio Choice: Evidence from Panel Data Spanning the Tax Reform Act of 1986," Manuscript.

BERKOWITZ, M. K., AND J. QIU (2006):

"A Further Look at Household Portfolio Choice and Health Status," The Journal of Banking and Finance, 30, 1201-1217.

BODIE, Z., R. C. MERTON, AND W. F. SAMUELSON (1992):

"Labor Flexibility and Porfolio Choice in a Life Cycle Model," Journal of Economic Dynamics and Control, 16, 427-449.

BOUND, J., C. BROWN, AND N. MATHIOWETZ (2001):

"Measurement Error in Survey Data," in Handbook of Econometrics, ed. by J. Heckman, and E. Leamer, pp. 3705-3843. North-Holland, Amsterdam.

BROWN, J. R., Z. IVKOVIC, P. A. SMITH, AND S. WEISBENNER (forthcoming):

"Neighbors Matter: Causal Community Effects and Stock Market Participation," forthcoming in Journal of Finance.

CHAMBERLAIN, G. (1980):

"Analysis of Covariance with Qualitative Data," Review of Economic Studies, 47, 225-238.

CHAMBERLAIN, G. (1984):

"Panel Data," in Handbook of Econometrics, ed. by Z. Griliches, and M. Intrilligator, chap. Panel Data, pp. 1247-1318. North-Holland, Amsterdam.

CHRISTELIS, D., T. JAPPELLI, AND M. PADULA (2005):

"The Portfolio Choice of European Elderly Households," Manuscript.

COILE, C., AND K. MILLIGAN (2006):

"How Household Portfolios Evolve After Retirement: The Effect of Aging and Health Shocks," NBER Working Paper No. 12391.

EDWARDS, R. D. (2006):

"Health Shocks and Consumption Among Elderly U.S. Households," Manuscript.

-------- (2007):

"Optimal Portfolio Choice Under State-Dependent Utility," Manuscript.

-------- (forthcoming):

"Health Risk and Portfolio Choice," forthcoming in Journal of Business and Economic Statistics.

FRENCH, E., AND J. B. JONES (2004):

"On the Distribution and Dynamics of Health Care Costs," Journal of Applied Econometrics, 19, 705-721.

HECKMAN, J. J. (1979):

"Sample Selection Bias as a Specification Error," Econometrica, 47(1), 153-161.

HOCHGUERTEL, S. (2003):

"Precautionary Motives and Portfolio Decisions," Journal of Applied Econometrics, 18, 61-77.

HONG, H., J. D. KUBIK, AND J. C. STEIN (2004):

"Social interaction and stock-market participation," Journal of Finance, 59, 137-163.

HONOR´E, B. E. (1992):

"Trimmed LAD and Least Squares Estimation of Truncated and Censored Regression Models with Fixed Effects," Econometrica, 60(3), 533-565.

HONOR´E, B. E., AND S. LETH-PETERSEN (2006):

"Estimation of Panel Data Models with Two-sided Censoring," Manuscript.

KIMBALL, M. S., AND D. W. ELMENDORF (2000):

"Taxation of Labor Income and the Demand for Risky Assets," International Economic Review, 41, 801-832.

KYRIAZIDOU, E. (1997):

"Estimation of a Panel Data Sample Selection Model," Econometrica, 65(6), 1335-1364.

LOVE, D. A., AND M. G. PEROZEK (2007):

"Should the Old Play it Safe? Portfolio Choice with Uncertain Medical Expenses," manuscript.

LOVE, D. A., P. A. SMITH, AND L. C. MCNAIR (2007):

"Do Households Have Enough Wealth for Retirement?," Federal Reserve Board Finance and Economics Discussion Series 2007-17.

ROSEN, H. S., AND S. WU (2004):

"Portfolio Choice and Health Status," Journal of Financial Economics, 72, 457-484.

VAN SOEST, A., AND A. KAPETYN (2006):

"Savings, Portfolio Choice, and Retirement Expectations," University of Michigan Retirement Research Center WP 2006-119.

VISSING-JORGENSEN, A. (2002):

"Towards an Explanation of Household Portfolio Choice Heterogeneity: Nonfinancial Income and Participation Cost Structures," NBER Working Paper No. 8884.

WOOLDRIDGE, J. (2002):

Econometric Analysis of Cross Section and Panel Data. MIT Press.

Tables and Figures

Table 1: Demographics
Variable	Singles	Respondent	Spouse
Female	.768	.369	.631
Age	76.9	73.1	70.8
Education	11.9	12.8	12.4
Nonwhite	.101	.061	.064
Hispanic	.033	.033	.034
Number of Children*	3.0	3.5	3.5
Additional Household Member*	.277	.151	.151
Sample Size*	14,061	11,709	11,709

Sample pools household observations from 1998 to 2004.