Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-46 Screen Reader version

Cracking the Conundrum^*

David K. Backus^†

and

Jonathan H. Wright^‡

Keywords: Yield curve, forward rates, volatility, term premium, affine models, monetary policy

Abstract:

From 2004 to 2006, the FOMC raised the target federal funds rate by 4.25 percentage points, yet long-maturity yields and forward rates fell. We consider several possible explanations for this " conundrum." The most likely, in our view, is a fall in the term premium, probably associated with some combination of diminished macroeconomic uncertainty and financial market volatility, more predictable monetary policy, and the state of the business cycle.

1 The conundrum

Between June 29, 2004 and February 2, 2005, the Federal Open Market Committee increased the target federal funds rate by 150 bps (basis points) or 1.5 percentage points. Over the same period, the long end of the yield curve fell, with the ten-year yield declining by 70 bps and the ten-year (instantaneous) forward rate by more than 100 bps. This pronounced rotation in the yield and forward rate curves caught many by surprise. Alan Greenspan, in his February 2005 testimony to Congress (Greenspan, 2005), noted:

This development contrasts with most experience, which suggests that ... increasing short-term interest rates are normally accompanied by a rise in longer-term yields. Historically, even ... distant forward rates have tended to rise in association with monetary policy tightening. ... For the moment, the broadly unanticipated behavior of world bond markets remains a conundrum.

Market participants were similarly puzzled. Bill Gross, PIMCO's legendary bond investor advised clients in February 2004 to reduce duration, only to see long bonds rally. Thirteen months later, he confessed confusion over what had occurred (Gross, 2005):

Who would have thought that the bond market could have [done so well]? Not yours truly, ... How then to explain it? ... I must tell you that we at PIMCO have been talking about this topic for months. We, too, have been befuddled.

Subsequently, the Fed continued raising the fed funds target, but the ten-year forward rate continued to fall. Overall, the ten-year forward rate fell 170 basis points between June 2004 and June 2005, and has rebounded only about 50 bps since then.

If the word "conundrum" from a respected central banker covered red faces in the investment community, it did little to explain what had happened. Observers had no shortage of ideas: a decline in long-run growth or inflation expectations; an increase in the global supply of savings; an improvement in the ability of global capital markets to allocate risk efficiently; massive purchases of U.S. Treasuries by Asian central banks and petroleum exporters; increased demand for long bonds by pension funds; reduced supply of long-maturity instruments following the Treasury's 2001 decision (later rescinded) to discontinue auctions of the thirty-year bond; or a global decline in macroeconomic and financial market uncertainty, perhaps the result of improved procedures for monetary policy or the state of the business cycle.

So what happened? We look at a number of possible explanations, holding each up to a broad array of evidence. Section 2 is devoted to facts. Like Sherlock Holmes, we believe it's helpful to know the facts before speculating about their resolution. Over the conundrum period, real rates fell along with nominal rates, long-term survey expectations of inflation, growth, and interest rates were roughly flat, volatilities and risk spreads fell across a wide range of assets, and distant-horizon forward rates fell on British and German government bonds. In Section 3, we consider interpretations of the facts based on affine bond-pricing models, which allow us to decompose forward rates into term premiums and expected future short rates, and then to further parse each into real and inflation components. The models suggest that term premiums declined considerably over the period of interest. In Section 4 we consider changes in the macroeconomic environment that might help explain such changes in term premiums, including a discussion of the explanations mentioned earlier.

2 Facts

We collect a number of related facts -- figures, really -- to provide a context for later discussion. We organize them around a series of topics.

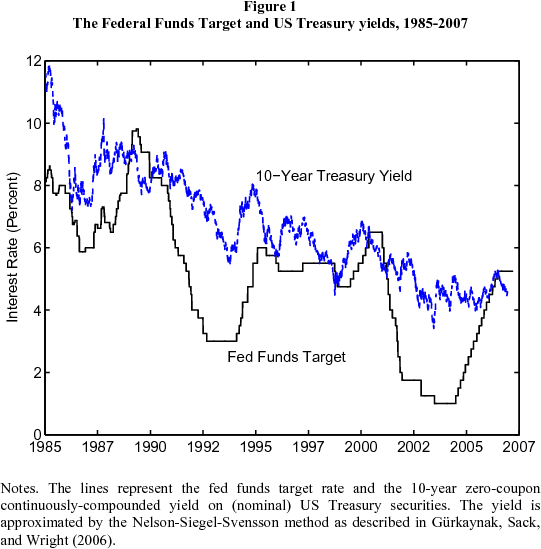
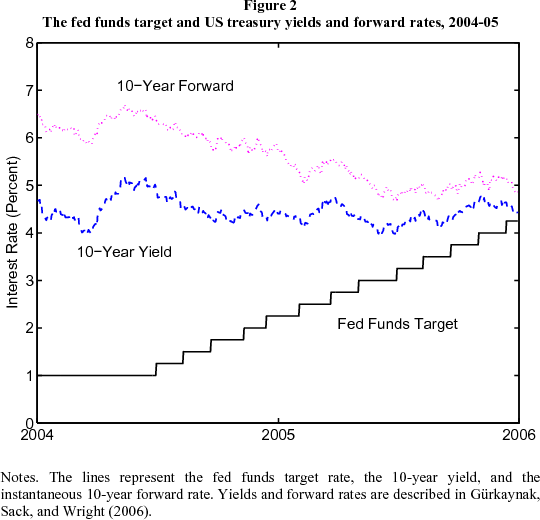
Cyclical behavior of interest rates. The essence of the conundrum is evident in Figure 1. During the three preceding episodes of monetary policy tightening, starting in 1986, 1994, and 1999, the ten-year yield on US Treasuries increased sharply along with the fed funds target. However, during the first year of the most recent period of tightening, ten-year yields declined. We see in Figure 2 that the ten-year forward rate fell 170 bps from June 2004 to June 2005, reaching its lowest point in 30 years in the summer of 2005. The more modest decline in the ten-year yield is essentially an average of the sharp decline in long forward rates and the concurrent increase in short rates. We focus much of our analysis on forward rates, since they capture the behavior of interest rates in a particularly clean way. Here and below, yields and forward rates are derived from prices of Treasury securities by the Nelson-Siegel-Svensson method, as described in Grkaynak, Sack, and Wright (2006). Data sources and descriptions are given in Appendix A.

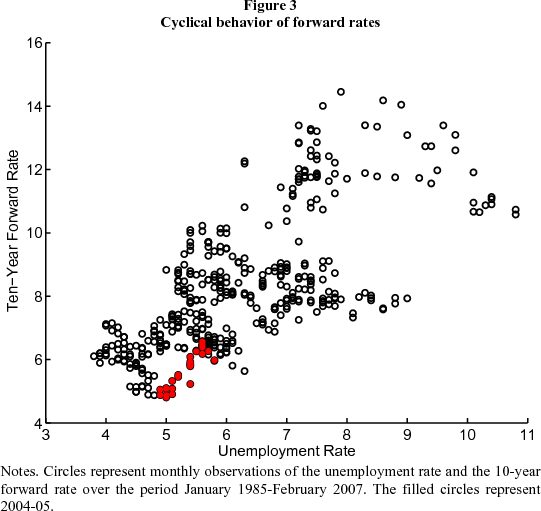
The recent behavior of forward rates is clearly different from the three preceding tightening episodes, but what can we say about the cyclical behavior of forward rates more generally? Figure 3 is a scatter-plot of the ten-year forward rate against the unemployment rate, a convenient indicator of the state of the business cycle. [Lehman Brothers (2006, Figure 6) includes a similar figure.] There's a clear association between the two variables, with forward rates and unemployment being quite strongly positively correlated (the correlation is 0.64), indicating that long forward rates have been countercyclical. The recent past (the solid circles) is not very different from the general pattern, though recent forward rates have been a bit on the low end.

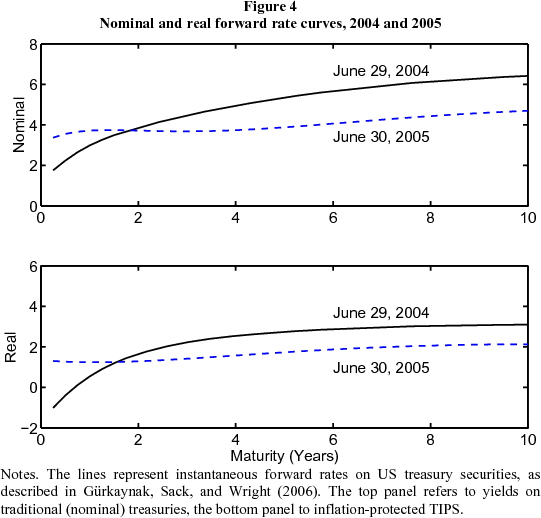
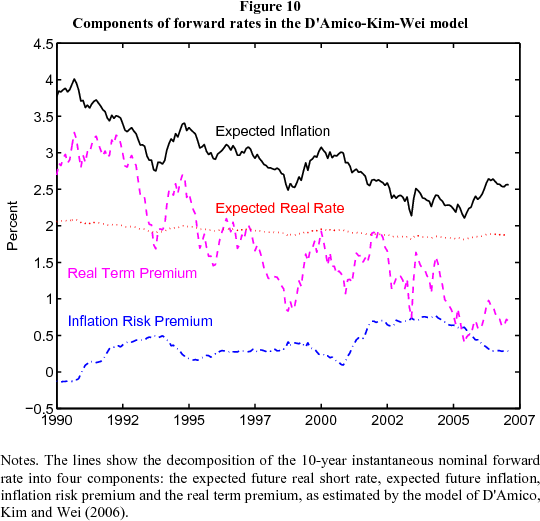
Real and nominal interest rates. In Figure 4, we compare the change in the nominal forward rate curve between June 2004 and June 2005 with the analogous change in the inflation-protected TIPS curve. Evidently the nominal and real forward rate curves experienced similar shifts, although the nominal curve shifted by a larger amount. If we compare ten-year forward rates, the nominal curve dropped by 172 bps and the real curve by 96 bps, a little more than half. The difference between the two curves reflects compensation for inflation. It is often used as a measure of inflation expectations, but it also includes an inflation risk premium and a TIPS liquidity premium. We'll return to this later.

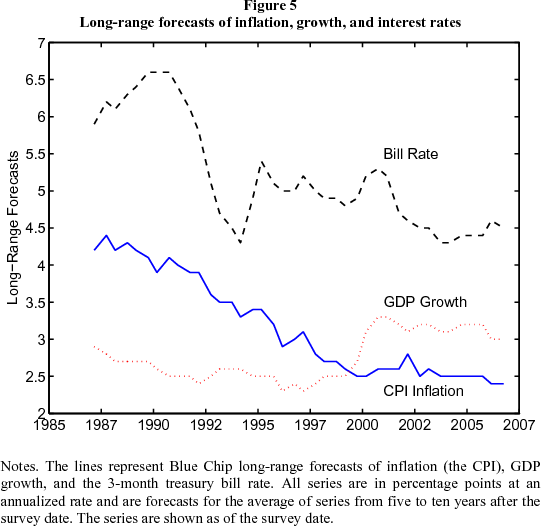
Expectations of inflation and growth. If we look directly at what forecasters tell us about future inflation, GDP growth, and short-term interest rates, there is no apparent change in 2004-05 that might account for the drop in long forward rates. The data summarized in Figure 5 are 5-10-year "long-range forecasts" produced by Blue Chip Economic Indicators and consist of averages over a large number of professional forecasters. The steady drop in the forecast of long-term expected inflation over the 1990s coincides with a similar drop in the ten-year yield (see Figure 1), but there is little or no movement in expected inflation or GDP growth during 2004-05. The inflation forecast in the figure is for the CPI; the analogous series for the GDP deflator is lower throughout, but has similar movements through time. The long-range growth forecast increases dramatically in 2000, which you might expect to be associated with an increase in long forward rates, but has moved little since then. Similarly, the long-range forecast of the 3-month Treasury bill rate has been flat over the last three years. Given this evidence, it's hard to argue convincingly that the recent decline in long yields reflects expectations of lower inflation, slower growth, or lower short-term interest rates.

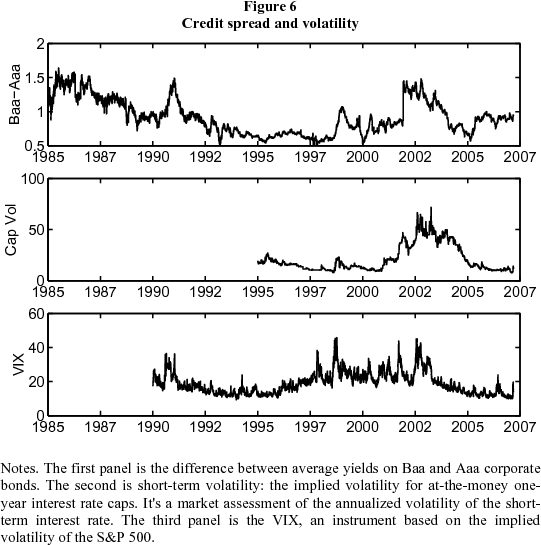
Credit spreads and volatility. One striking feature of the recent past has been the unusually low spreads on risky instruments. The spread between Baa and Aaa corporate debt, for example, is an indication of how much the market discounts lower-rated bonds. It reflects a combination of the risk inherent in these bonds and the price applied to such risk. In the first panel of Figure 6, we see that the spread declined sharply between 2000 and early 2005. The second panel reflects interest rate risk: the implied volatility of one-year interest rate caps, market-based measure of short-term volatility on a short-term interest rate (6-month LIBOR). It, too, fell sharply over the period of interest. Moreover, realized volatility -- in this case, the standard deviation of daily changes in forward rates -- also fell, as Berner and Miles (2006) note. The annual standard deviation of one-day changes in the ten-year instantaneous forward rate dropped from 6.8 basis points in 2003 to 4.1 basis points in 2006. Over the conundrum period, investors not only expected less interest rate volatility, there was less volatility. The third panel in the figure is the CBOE volatility index or VIX, whose price is tied to the short-term (30-day) volatility of S&P 500 stock index options. The figure shows that the VIX also declined between 2002 and 2005. We think the evidence indicates that financial market risk and risk premiums across a range of assets were substantially lower in 2005 than they had been a year or two earlier.

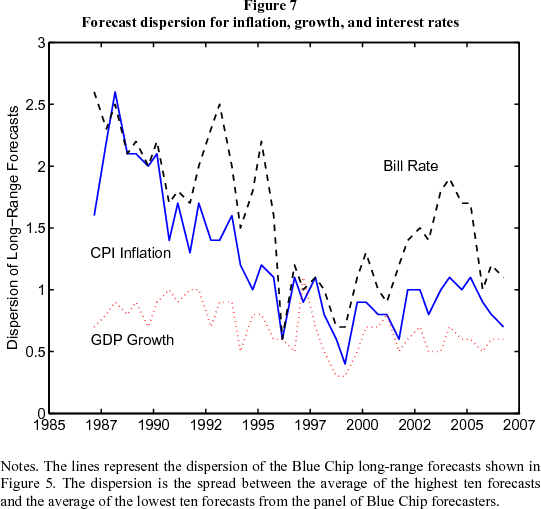
Macroeconomic uncertainty. The underlying source of the decline in asset market volatility remains unclear. Federal Reserve communications have, in the last few years, given markets more forward-looking guidance on the path of monetary policy, making it more predictable. This might account for a fall in near-term interest rate uncertainty, but its broader impact on asset market volatility is less evident. Macroeconomic uncertainty is inherently difficult to measure, particularly when we are concerned with uncertainty at long horizons, but the dispersion of long-horizon survey predictions serves as a crude proxy. The Blue Chip surveys report a simple dispersion measure for their long-horizon survey questions: the difference between the averages of the ten highest and ten lowest responses. Figure 7 shows a time series of the dispersion of expectations for inflation (CPI), real GDP growth, and 3-month Treasury bill yields for 5-10 years hence. Although somewhat noisy, they have all been trending noticeably lower. Note, too, that this period of reduced macroeconomic volatility comes well after the start of the Great Moderation, the decline in macroeconomic volatility that researchers typically date to the early 1980s. Most of the decline in Blue Chip dispersion measures comes in the early 1990s, but there has been further decline in the dispersion of interest rate and inflation expectations over the last few years. Perhaps investors believe that macroeconomic uncertainty has declined further, or perhaps they only lately became convinced of the Great Moderation.

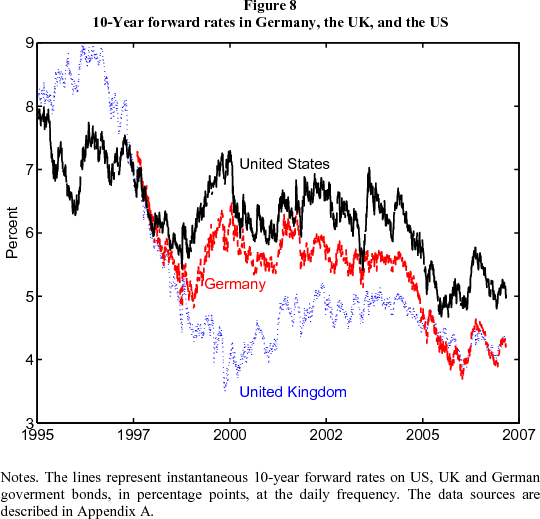
Forward rates in Germany and the UK. The fall in forward rates since mid-2004 was not unique to the US. In Figure 8, we plot ten-year forward rates for the US, Germany, and the UK. The conundrum is evident in all three, even though they are at different stages of the business cycle. Indeed, forward rates in these countries have been unusually highly correlated over the last two or three years. Kroszner (2006) observes that long rates have declined even in such middle-income countries as Brazil, Chile, Colombia, Indonesia, Mexico, Russia, and Thailand. In several, countries now issue local-currency debt at modest yields at maturities that didn't exist a decade ago.

3 Affine interpretations of forward rates

The recent decline in long forward rates, a similar decline in many measures of volatility, and the apparent absence of any change in expected inflation and Treasury bill rates suggest to us that smaller term premiums played a role in the conundrum. We wouldn't call the evidence definitive, but it's suggestive. A complementary source of information comes from estimates of affine bond pricing models. There are lots of examples in the literature, not all of them the same, but a collection of models estimated by researchers at the Federal Reserve illustrates their potential to shed light on the behavior of long forward rates.

Our starting point is a common decomposition of long forward rates into expected future short rates and term premiums:

$\displaystyle f_{t}^{(n)}$

$\displaystyle = E_{t} r_{t+n} +$ tp $\displaystyle _{t}^{(n)} .%$

(1)

Here $f_{t}^{(n)}$ is the

-period-ahead forward rate at date

, $r_{t+n} \equiv f_{t+n}^{(0)}$ is the short rate

periods in the future, and tp $^{n}_{t}$ is a term premium. Equation (1) is essentially a definition of the term premium; it has content only if we have a way to identify the components.

We face two hurdles in turning equation (1) into a useable decomposition. The first is the time series variability of long forward rates. Stationary ergodic models imply that the variance of forward rates converges to zero as the maturity increases. Shiller (1979) made this point in a setting with constant term premiums, but it applies more generally. It applies, for example, to most affine models. One way or another, a realistic model must incorporate a high degree of persistence somewhere, so that convergence works slowly enough that forward rates with maturities of (say) ten years still have significant volatility. A related issue is the impact of news on long-maturity forward rates. It is not uncommon for a single macroeconomic news announcement to cause large changes in forward rates with maturities of ten years or more; see, for example, Beechey (2007), Gürkaynak, Sack, and Swanson (2005), and Lu and Wu (2005). Whether this reflects changes in expectations of distant short rates or term premiums remains to be seen, but it's clear we need persistence in one or the other.

The second hurdle is identifying the two components of (1). An older line of research used the expectations hypothesis, which in this context amounts to the assumption that term premiums are constant: they can vary with but not with . In this case, all of the movement in long forward rates is associated with changes in expected short rates. This not only assumes the answer to the decomposition (1), it conflicts with an enormous body of work documenting the empirical weaknesses of the expectations hypothesis. See, among many others, the survey and synthesis in Dai and Singleton (2002). One issue is the predictability of long yields. Under the expectations hypothesis, a steep yield curve implies that short-term interest rates are expected to increase, so long-term yields should rise. In US data we find the opposite, as Macaulay (1938) noted years ago:

The yields on [long-maturity] bonds should fall during a period in which short-term rates are higher than the yields of the bonds and rise during a period in which short-term rates are lower. Now experience is more nearly the opposite.

Similarly, excess returns on long bonds can be predicted from the term structure of interest rates, which contradicts the expectations hypothesis. All of this evidence implies that term premiums vary with time, and therefore that the expectations hypothesis is a poor guide to interest rate dynamics.

Financial models use this predictability to estimate term premiums from observed bond yields and perhaps other data. They have the potential to distinguish between changes in term premiums and expected short rates, and therefore to point to the source of the conundrum. The most popular of these models are affine: they generate yields and forward rates that are linear functions of a vector of state variables, which in turn follows a linear autoregressive process. We describe below some of the properties of estimated versions of Duffee's (2002) "essentially affine" model, an example of the more general class of affine models characterized by Duffie and Kan (1996). We describe a one-factor version in Appendix B.

The Kim-Orphanides model

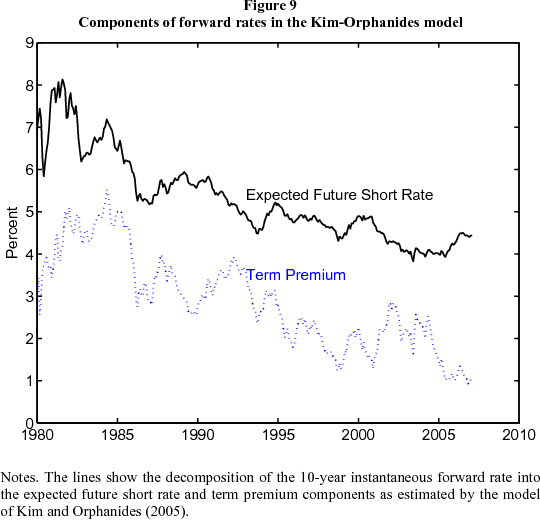
Most estimated essentially affine models identify the two components of forward rates from the predictability of yields or returns alone, as described in the previous paragraph. Kim and Orphanides (2005) add direct information about the dynamics of interest rates to a three-factor model. They use professional forecasts of Treasury bill rates to help identify the expected future short rate component of the forward rate, which allows relatively precise estimation of the term premium through (1). The estimated model is stationary but very persistent: the half-life of the most persistent factor is 13 years, which allows it to generate substantial movement in long-maturity forward rates.

The results are apparent in Figure 9, where we plot the ten-year forward rate and the decomposition implied by the model. This decomposition suggests that the decline in ten-year ahead forward rates from June 2004 to June 2005 is nearly fully explained by a declining term premium. Expected future short rates edged lower over this period, but the forward term premium declined from 2-1/2 percentage points to 1. Since June 2005, forward rates have risen a little, but the term premium has remained at around 1 percent. One can likewise decompose long yields into components. The term premium component of the ten-year yield is estimated to have fallen from 1-1/4 percentage points in June 2004 to a scant 30 bps in June 2005.

Real and nominal term premiums

We can look further into the role of inflation in these developments by incorporating inflation and TIPS rates into the analysis. If one adds the dynamics of inflation to the model, then it becomes possible also to price synthetic real bonds and to decompose real forward rates into a real term premium and the expected future real short-term interest rate. Such an exercise does not require TIPS: it is a real term structure model constructed from inflation and nominal interest rate data alone. Kim (2004) and Ang, Bekaert and Wei (2007) are two such models. Both allow for a four-way decomposition of nominal forward rates into expected future real short-term interest rates, expected future inflation, the real term premium and the inflation risk premium. The expected nominal rate is the sum of the expected future real short-term interest rate and expected future inflation; the nominal term premium is the sum of the real term premium and the inflation risk premium.

It seems a pity however completely to ignore the information in TIPS. TIPS have only been trading since 1997, and evidently had large liquidity premiums in the early years of trading. Meanwhile, the synthetic real bond that we would wish to price is one with liquidity that is comparable to a nominal Treasury bond. But, the liquidity of TIPS has improved, and the inflation compensation implied by TIPS is a widely-used barometer of inflation expectations even though inflation compensation is not the same thing as expected inflation. Motivated by these considerations, D'Amico, Kim, and Wei (2006) augment a real term structure model with TIPS. The model is estimated over the period since 1990. TIPS are treated as missing data before 1999, which is straightforward to handle via the Kalman filter. Also, the yields on TIPS are assumed to equal the sum of yields on the synthetic liquid real bonds and a TIPS liquidity premium. We refer the reader to that paper for more details on the specification. Its properties are illustrated in Figure 10, a plot of the ten-year forward rate and four components. The estimates suggest that the real term premium has fallen sharply since June 2004, and the inflation risk premium has fallen by a lesser amount. On the other hand, expected future real short-term interest rates have been flat and expected future inflation has actually risen modestly.

Accounting

All in all, given the time-variation in term premiums, the facts about risk spreads and volatilities (Figure 6), survey expectations (Figure 5), and the Kim-Orphanides estimates of affine model (Figure 9), we think that a decline in term premiums is likely to be the principal explanation for the decline in long-horizon forward rates from June 2004 to June 2005. But we cannot be sure of this. What we can be sure of is the arithmetic identity that forward rates are the sum of expected future rates and term premiums. If term premiums did not decline, then the long-run expectation of the federal funds rate must have fallen by about 1.7 percentage points. Indeed, there are economic forces that may have pushed expected equilibrium real interest rates down. For example, an increase in the global supply of savings could represent a permanent leftward shift in the IS curve, resulting in lower expected future real short-term interest rates. Or, investors may have scaled back their expectations for future productivity growth amid weak business investment. Still, economic growth was robust, inflation was drifting up and a 1.7 percentage point decline in expected future short-term interest rates would seem surprising. But arithmetically, this is the only alternative explanation to a fall in the term premium. In a similar calculation, on average over the last 20 years, the spread between the federal funds rate and ten-year forward rates is 2 percentage points, which is an estimate of the average term premium over this period. The ten-year forward rate now stands around 5 percent. This means that either the expected federal funds rate ten years' hence is close to 3 percent, or that the term premium is below its average over the past 20 years.

4 Integrating macroeconomics and finance

Affine models suggest that term premiums fell in the recent past, but the absence of macroeconomic structure in these models makes it difficult to say why. Did Federal Reserve policy change? Did macroeconomic risk fall? Are any of the ideas mentioned at the start persuasive? We fill the gap with a combination of speculation and casual empiricism.

The first issue is the cyclical behavior of the term premium. There's a wide range of evidence on asset returns that suggests that risk premiums in general are countercyclical: smaller in booms than recessions. Cochrane and Piazzesi (2005, 2006) and Ludvigson and Ng (2006) are good examples for bond returns. Since the recent period has been an expansion, we would indeed expect term premiums to have declined. And this helps explain the otherwise-puzzling correlation between unemployment and distant-horizon forward rate shown in Figure 3.

There may also have been a secular decline in asset price volatility, which could account for lower risk premiums in general, and lower term premiums in particular, as discussed by Rudebusch, Swanson, and Wu (2006). That in turn begs the question of why asset price volatility fell. But as shown in Figure 7, judging from surveys, the dispersion of agents' long-run macroeconomic expectations and especially their long-run inflation expectations has fallen, which is at least suggestive of a decline in uncertainty about long-run inflation rates. This could in turn owe to more credible and transparent monetary policy, in which future interest rates moves are indicated well in advance. The last decade has seen a global trend towards central banks becoming more independent of political influences, providing more explicit information to the public about their decisions including publishing forecasts, and many adopting some form of inflation targeting. Also, more integrated financial markets may reduce the potential short-term gain from any one country adopting more inflationary policies, which in turn makes a commitment to a low and stable level of inflation more credible. All this might help account for a global decline in inflation uncertainty and hence in inflation risk premiums. Some evidence for this interpretation is given by the especially sharp decline in forward rates in the United Kingdom around the time that the Bank of England was granted operational independence, as can be seen in Figure 8. Arguably, in the last few years, investors in the United States and abroad have become convinced that inflation has been conquered forever -- or at least for the relevant time horizon -- and so no longer demand large inflation risk premiums. In the United States, the Volcker disinflation took place a long time ago, and it is indeed a little hard to see why the last three years should be the time that investors suddenly became confident that inflation would remain contained indefinitely. Still, reduced inflation uncertainty amid changes in central bank policy seems to be high on the list of plausible explanations for the global decline in distant horizon forward rates. Growth uncertainty might also have declined, for a variety of reasons: monetary policy, financial innovation, or inventory management.

Some analysts have suggested that a fall in term premiums may owe to increased demand for longer-duration securities stemming from the prospect of corporate pension reform that might encourage pension funds better to match the duration of their assets and liabilities. This seems a plausible story in the United Kingdom, where pension funds must satisfy strict duration-matching requirements. The real yield on fifty-year indexed government bonds in the United Kingdom fell below 50 basis points in January 2006, which is consistent with special demand from pension funds for this unusually long-duration security. Still, the explanation does not make as much sense in the United States, where corporate pension reform has proceeded more slowly.

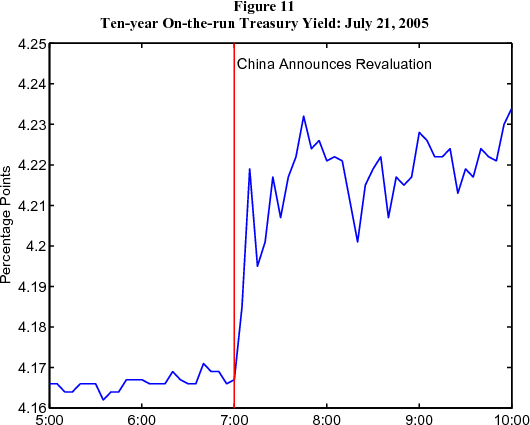
Another explanation is that Asian central banks may be buying up Treasury securities, driving the term premium down; see Bernanke, Reinhart, and Sack (2004) and Warnock and Warnock (2004). This does not seem satisfying as a complete explanation for the "conundrum" because, as shown earlier, foreign forward rates exhibited similar swings to those in the United States. But US and foreign government bonds may be close substitutes, and as such, purchases of Treasuries may drive foreign term premiums down. One "natural experiment" suggests that Asian central bank purchases could be part of the story. On July 21, 2005, the Peoples' Bank of China announced that it was modestly revaluing the renminbi and adopting a new exchange rate regime. The announcement came out at 7 a.m. Eastern time, and was immediately understood by market participants as implying that China would not need to buy as many Treasuries to hold the value of the renmibni down as had previously been thought. At the time of the announcement, the yield of the on-the-run ten-year Treasury note jumped up about 7 bps, as shown in Figure 11. The timing of the jump in Treasury yields clearly indicates that it owes to the announcement from the Peoples' Bank of China. To be sure, 7 basis points represents a tiny share of the "conundrum", but the revaluation of the renminbi was not big, and so the episode suggests that foreign central bank purchases of Treasury securities have at least played some role. Capital flows from petroleum exporting countries could have a similar effect.

Finally, some analysts have pointed to demographics as an explanation for falling term premiums, as substantial cohorts of the populations of industrialized economies near retirement. In this explanation, aging populations in industrialized countries are expected to shift their holdings away from risky assets such as equities and towards bonds and other assets that are perceived to be relatively safe, and these shifts may place some downward pressure on term premiums (and upward pressure on equity risk premiums). However, demographics are slow-moving and predictable, and it can hardly be claimed that there has been a substantial or unexpected shift in demographics since June 2004.

Finally, term premiums do not have to owe to any fundamental explanation and could instead be a consequence of irrational behavior of investors. Arguably, the choppy behavior of ten-year forward rates is hard to make sense of either in terms of expected short term interest rates or of risk compensation from any rational equilibrium asset pricing model.

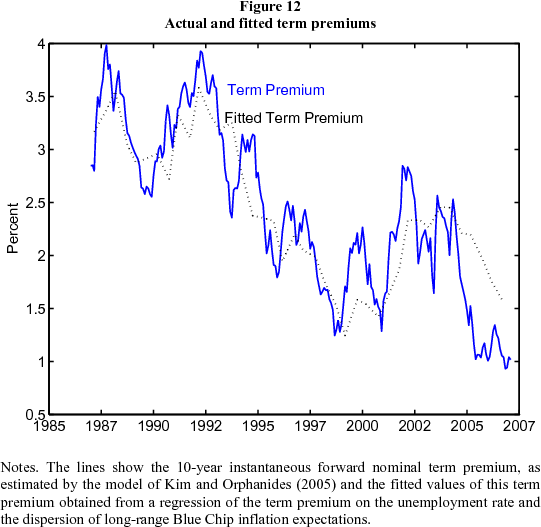
A regression model

The affine term structure models introduced in the previous section use a set of latent factors as the state vector. This has the advantage of fitting the data well, but the disadvantage of lacking a direct economic interpretation. To get some sense of the ability of some of the economic explanations discussed above to account for the conundrum, we regressed the ten-year forward nominal term premiums as estimated by the model of Kim and Orphanides (2005) on the unemployment rate (to represent the cyclical patterns in term premiums) and the dispersion of Blue-Chip long-horizon survey measures of inflation (to proxy the impact of inflation uncertainty on term premiums). The regression was run at the same frequency as the Blue Chip long-horizon survey. The results are shown in Table 1. Higher interest rate implied volatility, greater dispersion of inflation expectations and higher unemployment are all associated with larger term premiums and the coefficients are all statistically significant. The actual and fitted term premiums from this regression are plotted in Figure 12. The model is able to explain a good bit of the decline in term premiums since 1990, and even some of the fall in the last three years, as the dispersion of inflation expectations has fallen while the economy has been going through an expansionary period. Only some of the decline in term premiums since June 2004 can be explained by this model, but it suggests that these factors may be at least part of the explanation.

5 Conclusion

We think the evidence points to a declining term premium as the primary source of the recent fall in long forward rates. This interpretation is broadly consistent with observed changes in risk spreads, interest rate and stock market volatility, the dispersion in long-range forecasts, and estimates of (some) affine bond-pricing models. In contrast, long-range forecasts of inflation, growth, and short-term interest rates provide little reason to believe that they might account for the same decline in long forward rates. In this sense, we follow a long line of work in suggesting that expectations-hypothesis intuition, based on constant term premiums, is likely to be misleading not only in this case but more generally.

The next step, in our view, should be to develop models in which macroeconomic policy and behavior can be tied more directly to the properties of interest rates. We might want to know, for example, whether changes in the volatility of output or in the nature or communication of monetary policy had an impact on the behavior of long rates in the recent past. Neither of this is possible with existing models. Ang and Piazzesi (2003) show how macroeconomic variables influence the behavior of bond yields, but this and related work has little in the way of macroeconomic structure. Bekaert, Cho, and Moreno (2005) and Gallmeyer, Hollifield, and Zin (2005) have made progress on setting up affine term structure models in which the short-term interest rate is related to inflation and output growth by a monetary policy rule, while inflation and output growth are in turn determined within a structural new-Keynesian model. Perhaps this will lead to further advances that allow the next attack on this issue to bring the macroeconomic contributions in line with the financial contributions, to the benefit of both.

A. Data sources and definitions

US interest rates in this paper are estimated from quoted prices of Treasury securities. Estimates of nominal yields and forward rates are constructed from a smooth Nelson-Siegel-Svensson curve as described by Grkaynak, Sack, and Wright (2006). The data are available on the Federal Reserve website. A similar curve (estimated by Federal Reserve staff) is used to estimate yields and forward rates from (inflation-protected) TIPS. Throughout, yields are understood to be continuously-compounded rates on zero-coupon bonds. Forward rates are instantaneous.

UK and German forward rate data were provided by the Bank of England and the Deutsche Bundesbank, respectively, and are available on their public websites. In the case of the German data, forward rates are constructed from Nelson-Siegel-Svensson parameters provided by the Bundesbank.

Other macroeconomic and financial data are taken from Datastream.

Term premium estimates were calculated by Federal Reserve staff using the models of Kim and Orphanides (2005) and D'Amico, Kim and Wei (2006). The former are posted quarterly at

http://federalreserve.gov/pubs/feds/2005/200533/feds200533.xlshttp://federalreserve.gov/pubs/feds/2005/200533/feds200533.xls.

B. Affine models

Modern asset pricing theory works like this: in an arbitrage-free setting, there exists a pricing kernel $m_{t+1}$ that reconciles the market price $v_{t}$ at date with its cash flows $c_{t+1}$ at :

$\displaystyle v_{t}$

$\displaystyle = E_{t} \left( m_{t+1} c_{t+1} \right) .$

Bond pricing is a particularly elegant application. If $b^{(n)}_{t}$ is the price at date

of one (dollar, say) paid at

, the bond prices can be computed recursively from

$\displaystyle b^{(n+1)}_{t}$

$\displaystyle = E_{t} \left( m_{t+1} b^{(n)}_{t+1} \right) ,%$

(2)

starting with $b^{(0)}_{t} = 1$ .

Affine models put enough structure on the pricing kernel that prices are log-linear functions of a state-vector :

$\displaystyle - \log b^{(n)}_{t}$

$\displaystyle = A_{n} + B_{n}^{\top}z_{t}%$

(3)

for some parameters $\{A_{n}, B_{n}\}$ . In essentially affine models, the link between forward rates and the dynamics of

is particularly transparent. Consider a one-dimensional example:

$\displaystyle - \log m_{t+1}$	$\displaystyle = \lambda(z_{t})^{2}/2 + z_{t} + \lambda(z_{t}) \varepsilon_{t+1}$
$\displaystyle \lambda(z_{t})$	$\displaystyle = \lambda_{0} + \lambda_{1} z_{t}$
$\displaystyle z_{t+1}$	$\displaystyle = (1-\varphi) \theta+ \varphi z_{t} + \sigma\varepsilon_{t+1} ,$

where

is a (scalar) state variable, $\varepsilon$ is an iid normal random variable with zero mean and unit variance, $\sigma> 0$ , and $0 < \varphi< 1$ . The last equation describes the dynamic behavior of the state variable: it follows a linear process with autoregressive parameter $\varphi$ . The "price of risk" $\lambda(z)$ governs risk premiums; in particular, $\lambda_{1}$ controls the sensitivity of the term premium to movements in

The key to the solution is that the model is linear in the right places. Equation (2) and our guess (3) imply that the coefficients satisfy

$\displaystyle A_{n+1}$	$\displaystyle = A_{n} + B_{n} (1-\varphi)\theta+ B_{n} \sigma\lambda_{0} - (B_{n} \sigma)^{2}/2$
$\displaystyle B_{n+1}$	$\displaystyle = 1 + (\varphi+\sigma\lambda_{1}) B_{n}%$

starting with $A_{0} = B_{0} = 0$ . If we set $\varphi^{*} \equiv\varphi+ \sigma\lambda_{1}$ , the second can be solved directly:

$\displaystyle B_{n}$

$\displaystyle = (1-\varphi^{*n})/(1-\varphi^{*}) .$

The first we compute recursively.

The beauty of this solution lies in the difference between $\varphi$ and $\varphi^{*}$ . The former represents the dynamics of the state variable, the latter the "risk-neutral" (or risk-adjusted) dynamics that are built into long forward rates and term premiums. If $\lambda_{1} = 0$ , the two are the same and we are back in the world of the expectations hypothesis: term premiums are constant and all the variation in forward rates comes from expected future short rates. In general, however, they are different, and their difference is what generates time-varying term premiums. To be specific, let us define one-period (as opposed to instantaneous) forward rates by

$\displaystyle \log\left( b^{(n)}_{t} / b^{(n+1)}_{t} \right)$

$\displaystyle = f^{(n)}_{t} .$

Then

$\displaystyle f^{(n)}_{t}$

$\displaystyle = (A_{n+1}-A_{n}) + (B_{n+1} - B_{n}) z_{t} \;=\; (A_{n+1}-A_{n}) + \varphi^{*n} z_{t}%$

and $r_{t} \equiv f^{(0)}_{t} = z_{t}$ (the short rate is

). In words: the sensitivity of forward rates comes from the risk-neutral dynamics. The expected future short rate, in contrast, follows from the true dynamics, represented here by $\varphi$ :

$\displaystyle E_{t} r_{t+n}$

$\displaystyle = (1-\varphi^{n}) \theta+ \varphi^{n} z_{t} .$

The term premium is therefore

$\displaystyle tp^{(n)}_{t}$

$\displaystyle =$ constant $\displaystyle + (\varphi^{*n} - \varphi^{n}) z_{t} ,$

which evidently depends on the difference between the two kinds of dynamics. The term premium component is more sensitive to movements in

(hence more variable) if

$\displaystyle (\varphi^{*n} - \varphi^{n})$

$\displaystyle > \varphi^{n} .$

This holds for large

if $\varphi^{*} > \varphi$ .

References

Ang, Andrew, and Monika Piazzesi, 2003,

"A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables," Journal of Monetary Economics 50, 745-787.

Ang, Andrew, Geert Bekaert and Min Wei, 2007,

"The term structure of real rates and expected inflation," Journal of Finance, forthcoming.

Beechey, Meredith, 2007,

"A closer look at the sensitivity puzzle: the sensitivity of expected future short rates and term premiums to macroeconomic news," Finance and Economics Discussion Series, Board of Governors of the Federal Reserve System, 2007-6.

Bekaert, Geert, Seonghoon Cho, and Antonio Moreno, 2005,

"New-Keynesian macroeconomics and the term structure," NBER Working Paper 11340, May.

Bernanke, Ben, Vincent Reinhart, and Brian Sack, 2004,

"Monetary Policy Alternatives at the Zero Bound: An Empirical Assessment," Brookings Papers on Economic Activity 2, 2004, 1-78.

Berner, Richard, and David Miles, 2006,

"The term-premium case for higher yields," Morgan Stanley Equity Research, January 20.

Cochrane, John H., and Monika Piazzesi, 2005,

"Bond Risk Premia," American Economic Review 95, 138-160.

Cochrane, John H., and Monika Piazzesi, 2006,

"Decomposing the yield curve," manuscript.

Dai, Qiang, and Kenneth J. Singleton, 2002,

"Expectation puzzles, time-varying risk premia, and affine models of the term structure," Journal of Financial Economics 63, 415-441.

D'Amico, Stefania, Don H. Kim, and Min Wei, 2006,

"TIPS from TIPS," manuscript.

Duffee, Gregory R., 2002,

"Term premia and interest rate forecasts in affine models," Journal of Finance 57, 405-443.

Duffie, Darrell, and Rui Kan, 1996,

"A yield-factor model of interest rates," Mathematical Finance 6, 379-406.

Gallmeyer, Michael F., Burton Hollifield, and Stanley E. Zin, 2005,

"Taylor rules, McCallum rules and the term structure of interest rates," Journal of Monetary Economics 52, 921-950.

Greenspan, Alan, 2005,

"Semiannual Monetary Policy Report to the Congress," February 16.

Gross, Bill, 2005,

"I've got to admit it's getting better, getting better all the time," Investment Outlook, PIMCO, March.

Grkaynak, Refet, Brian Sack, and Eric T. Swanson, 2005,

"The sensitivity of long-term interest rates to economic news: evidence and implications for macroeconomic models," American Economic Review 95, 425-436.

Gürkaynak, Refet, Brian Sack, and Jonathan H. Wright, 2007,

"The US Treasury Yield Curve: 1961 to the Present," Journal of Monetary Economics, forthcoming.

Kim, D.H., 2004,

"Inflation and the Real Term Structure," manuscript.

Kim, D.H. and A. Orphanides, 2005,

"Term Structure Estimation with Survey Data on Interest Rate Forecasts," Finance and Economics Discussion Paper 2005-48, Board of Governors of the Federal Reserve System.

Kroszner, Randall S., 2006,

"Why are yield curves so flat and long rates so low globally?," remarks presented at the Institute of International Bankers, June 16.

Lehman Brothers, 2006,

Outlook 2007: The Conundrum Runs its Course, December.

Lu, Biao, and Liuren Wu, 2005,

"Systematic movements in macroeconomic releases and the term structure of interest rates, manuscript.

Ludvigson, Sydney C., and Serena Ng, 2006,

"Macro factors in bond risk premiums," manuscript, August.

Macaulay, Frederick R., 1938,

"The Movement of Interest Rates, Bond yields and Stock prices in the United States since 1856," National Bureau of Economic Research.

Rudebusch, Glenn D., Eric T. Swanson, and Tao Wu, 2006,

"The bond yield `conundrum' from a macro-finance perspective," Monetary and Economic Studies, December.

Shiller, Robert J., 1979,

"The volatility of long-term interest rates and expectations models of the term structure," Journal of Political Economy 87, 1190-1219.

Warnock, Frank and Veronica Warnock, 2006,

"International capital flows and US interest rates," manuscript, September.

Table 1 Regression of Ten-Year Forward Term Premium Estimates on Selected Macro Variables

Constant	-0.83
Unemployment	0.42 $^{^{\ast\ast\ast}}$
BC long-term Inflation Dispersion	0.76 $^{^{\ast\ast\ast}}$

Notes: This reports the results of a regression of estimated nominal ten-year forward term premiums from the model of Kim and Orphanides (2005) (month average) on the unemployment rate and the dispersion of long-term Blue Chip survey expectations of CPI inflation. Only months for which there was such a survey are included in the regression. This survey comes out twice a year, for a total of 40 observations spanning March 1987 to October 2006. Newey-West standard errors were used. $^{^{\ast\ast\ast}% }\$ denotes significance at the 1 percent significance level.

Figure 1: The Federal Funds Target and US Treasury yields, 1985-2007. Figure 1 is a line chart, showing the time series of the fed funds target rate (the black line) and the 10-year zero-coupon continuously-compounded yield (the dashed blue line) on nominal US Treasury securities since 1985. The yield is approximated by the Nelson-Siegel-Svensson method as described in Gürkaynak, Sack, and Wright (2006). During the three preceding episodes of monetary policy tightening, starting in 1986, 1994, and 1999, the ten-year yield on US Treasuries increased sharply along with the fed funds target. However, during the first year of the most recent period of tightening, ten-year yields declined.

Figure 2: The fed funds target and US treasury yields and forward rates, 2004-05. Figure 2 is a line chart showing the fed funds target rate (black solid line), the 10-year zero coupon yield (blue dashed line), and the instantaneous 10-year forward rate (magenta dots) since the start of 2004. Yields and forward rates are described in Gürkaynak, Sack, and Wright (2006). Over this time, the target federal funds rate was being raised. But the ten-year forward rate fell 170 bps from June 2004 to June 2005, reaching its lowest point in 30 years in the summer of 2005. The more modest decline in the ten-year yield is essentially an average of the sharp decline in long forward rates and the concurrent increase in short rates.

Figure 3: Cyclical behavior of forward rates. Figure 3 is a scatter-plot of the ten-year forward rate against the unemployment rate, a convenient indicator of the state of the business cycle over the period January 1985-February 2007. The filled circles represent 2004-05. There's a clear association between the two variables, with forward rates and unemployment being quite strongly positively correlated (the correlation is 0.64), indicating that long forward rates have been countercyclical. The recent past (the solid circles) is not very different from the general pattern, though recent forward rates have been a bit on the low end.

Figure 4: Nominal and real forward rate curves, 2004 and 2005. Figure 4 has two panels. The top panel is a line chart showing the instantaneous forward rates on US Treasury securities, as described in Gürkaynak, Sack, and Wright (2006) out to ten years on June 29, 2004 (the black solid line) and June 30, 2005 (the blue dashed line). The bottom panel is identical, except that it shows the corresponding real forward rates from Treasury Inflation Protected Securities (TIPS). Evidently the nominal and real forward rate curves experienced similar shifts, although the nominal curve shifted by a larger amount. If we compare ten-year forward rates, the nominal curve dropped by 172 bps and the real curve by 96 bps, a little more than half. The difference between the two curves reflects compensation for inflation. It is often used as a measure of inflation expectations, but it also includes an inflation risk premium and a TIPS liquidity premium.

Figure 5: Long-range forecasts of inflation, growth, and interest rates. Figure 5 is a line chart showing twice-yearly Blue Chip long-range forecasts of inflation (the CPI), GDP growth, and the 3-month Treasury bill rate as the blue solid line, the red dotted line and the black dashed line, respectively since 1987. All series are in percentage points at an annualized rate and are forecasts for the average of series from five to ten years after the survey date. The series are shown as of the survey date. The steady drop in the forecast of long-term expected inflation over the 1990s coincides with a similar drop in the ten-year yield (see Figure 1), but there is little or no movement in expected inflation or GDP growth during 2004-05. The inflation forecast in the figure is for the CPI; the analogous series for the GDP deflator is lower throughout, but has similar movements through time. The long-range growth forecast increases dramatically in 2000, which you might expect to be associated with an increase in long forward rates, but has moved little since then. Similarly, the long-range forecast of the 3-month Treasury bill rate has been flat over the last three years.

Figure 6: Credit spread and volatility. Figure 6 has three panels. The first panel is a line chart that shows the spread between yields on Baa and Aaa corporate bonds since 1985. It was at about 1.5 percentage points in the late 1980s, trended down to about 50 basis points in the late 1990s and rose again in the last recession. However, over the period from the middle of 2004 to 2005 it fell back and reached levels comparable to those of the late 1990s. The second panel is a line chart showing short-term interest rate volatility: the implied volatility for at-the-money one-year interest rate caps back to 1995. This is a market assessment of the annualized volatility of the short-term interest rate. It rose sharply during the last recession, but fell back subsequently and reached very low levels in 2005. The third panel is a line chart showing the VIX -- the implied volatility of the S&P 500 from equity options back to 1990. Similarly to the two panels above, it reached low levels in the late 1990s, rose in the last recession but fell back to those low levels again over 2004 and 2005. Overall these panels indicate that financial market risk and risk premiums across a range of assets were substantially lower in 2005 than they had been a year or two earlier.

Figure 7: Forecast dispersion for inflation, growth, and interest rates. Figure 7 is a line chart showing the dispersion of the twice-yearly Blue Chip long-range forecasts of inflation (the CPI), GDP growth, and the 3-month Treasury bill rate as the blue solid line, the red dotted line and the black dashed line, respectively since 1987. The dispersion is the spread between the average of the highest ten forecasts and the average of the lowest ten forecasts from the panel of Blue Chip forecasters. All series are in percentage points at an annualized rate and are forecasts for the average of series from five to ten years after the survey date. The series are shown as of the survey date. Although somewhat noisy, these dispersion measures have all been trending noticeably lower. Most of the decline in Blue Chip dispersion measures comes in the early 1990s, but there has been further decline in the dispersion of interest rate and inflation expectations over the last few years.

Figure 8: 10-Year forward rates in Germany, the UK, and the US. Figure 8 is a line chart showing the ten-year instantaneous forward rate on US, UK and German government bonds as the black solid line, the blue dotted line and the red dashed line, respectively. The data extend back to 1995 for the US and the UK and to 1997 for Germany. The decline in forward rates in 2004-2005 is evident in all three, even though they are at different stages of the business cycle. Indeed, forward rates in these countries have been unusually highly correlated over the last two or three years. These forward rates declined in the US and Germany from 1996 to 1998, but then rebounded in 1999 and 2000. The forward rates in the UK declined by more and continued falling until about 2000.

Figure 9: Components of forward rates in the Kim-Orphanides model. Figure 9 is a line chart showing the decomposition of the 10-year instantaneous forward rate into the expected future short rate (solid black line) and term premium (dashed blue line) components as estimated by the model of Kim and Orphanides (2005) back to 1980. The term premium rose in the early 1980s before trending lower over the late 1980s and 1990s. Meanwhile expected future short rates trended lower for the 1980s and 1990s. The decomposition in this figure suggests that the decline in ten-year ahead forward rates from June 2004 to June 2005 is nearly fully explained by a declining term premium. Expected future short rates edged lower over this period, but the forward term premium declined from 2-1/2 percentage points to 1. Since June 2005, forward rates have risen a little, but the term premium has remained at around 1 percent. One can likewise decompose long yields into components. The term premium component of the ten-year yield is estimated to have fallen from 1-1/4 percentage points in June 2004 to a scant 30 bps in June 2005.

Figure 10: Components of forward rates in the D'Amico-Kim-Wei model. Figure 10 is a line chart showing the decomposition of the 10-year instantaneous forward rate into the following four components: Expected future inflation (solid black line), the expected future real rate (red dotted line), the inflation risk premium (blue dashed and dotted line) and the real term premium (magenta dashed line) as estimated by the model of D'Amico, Kim and Wei (2006) back to 1990. The estimates suggest that the real term premium has fallen sharply since June 2004, and the inflation risk premium has fallen by a lesser amount. On the other hand, expected future real short-term interest rates have been flat and expected future inflation has actually risen modestly.

Figure 11: Ten-year On-the-run Treasury Yield: July 21, 2005. Figure 11 is a line chart showing intradaily quotes on ten-year on-the-run Treasury yields from 5 a.m. to 10 a.m. on July 21, 2005, the day on which the People's Bank of China announced the revaluation of the renminbi. A vertical red line, at 7 a.m., denotes the time at which the announcement came out. Yields jumped upwards from about 4.16 percentage points to about 4.23 percentage points quickly after the announcement.

Figure 12: Actual and fitted term premiums. Figure 12 is a line chart showing the 10-year instantaneous forward nominal term premium, as estimated by the model of Kim and Orphanides (2005) (the blue solid line) and the fitted values of this term premium obtained from a regression of the term premium on the unemployment rate and the dispersion of long-range Blue Chip inflation expectations (the black dotted line). The model is able to explain a good bit of the decline in term premiums since 1990, and even some of the fall in the last three years, as the dispersion of inflation expectations has fallen while the economy has been going through an expansionary period. Only some of the decline in term premiums since June 2004 can be explained by this model, but it suggests that these factors may be at least part of the explanation.

Footnotes

* We thank Bill Brainard, John Cochrane, Frank Diebold, Don Kim, George Perry, Monika Piazzesi, Dick Sylla, and Stan Zin for comments and advice. The views expressed are the sole responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other employees of the Federal Reserve System. Return to Text

† Stern School of Business, New York University, and NBER; [email protected] Return to Text

‡ Board of Governors of the Federal Reserve System; [email protected]. Return to Text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text