
Two Pitfalls of Linearization Methods*
Keywords: Linearization, linear-quadratic method, second-order approximation, welfare.
Abstract:
JEL Classification: C6.
1 Introduction
The economics profession has long been using linear models due to their simplicity, and linear modeling has been applied to forward-looking models as well as backward-looking ones. A related phenomenon is a wide usage of a linear quadratic (LQ) framework in analyzing optimal policy problems, since the combination of a quadratic criterion function with a linear constraint is well known to yield a linear behavior for the optimal solution. However, this attractiveness of linear models has sometimes misled the profession to adopt certain kinds of linearization methods that can deliver spurious results.
In this paper, we present two types of pitfalls that arise when linearization methods are improperly applied in the dynamic macroeconomics literature. Our paper is not the first to point out such pitfalls; rather, this paper is intended to illustrate these two pitfalls in a succinct way and to distinguish between the two types of pitfalls.1 In solving an optimal policy problem whose criterion function and constraints are nonlinear, some researchers have linearized the constraint--as well as quadratically approximating the criterion function--before deriving the optimality conditions.2 The resulting optimality conditions from this procedure are not a correct linear representation of the original nonlinear optimality conditions. A simple two-agent model will show that this pitfall leads to an implication that risk sharing can reduce the welfare level of the economy.
While the first pitfall originates from the improperly derived optimality conditions, the second pitfall happens even after the optimality conditions are properly derived. In this case, since the nonlinear optimality conditions are a correct representation of the original model, a linear approximation of derived optimality conditions would yield a correct linear representation of the original model. However, when applied to calculate welfare levels, this linear approximation can generate incorrect welfare implications. Using the same two agent model as in the first pitfall, we demonstrate that linearization can yield a spurious result that the welfare level of the complete markets economy can be lower than that of the autarky. This pitfall can occur in welfare evaluation of any equilibrium models, regardless of whether the optimality conditions are derived from optimization problems or given by ad hoc assumptions.
The remainder of this paper proceeds as follows. Section 2 presents a model economy, which is used as an example for the discussion of two types of pitfalls. Section 3 illustrates the first pitfall, and Section 4, the second pitfall. Some additional examples are included in the Appendix.
2 The Model
For both types of pitfalls, we use a simple two-agent endowment economy model with complete asset markets.3 Assuming symmetry, the competitive equilibrium of this economy is equivalent to a social planner problem maximizing the average of two agents' utilities,
subject to the aggregate resource constraint
We assume that utility is a power function of consumption where the degree of risk aversion is
Note that the second order approximation of this power utility function with respect to
where the constant term,
Two endowment levels, denoted as ![]() and
and ![]() , are independent and lognormally
distributed,
, are independent and lognormally
distributed,
where the superscript `exa' represents an exact solution for the complete markets economy. The (log-)linear approximation of this solution is
where the superscript `lin' represents the linear approximation of the exact solution and the bar variables represent steady state values.
Throughout the paper, we use the second order approximation of the utility function (4)--instead of the original utility function (3)--for welfare evaluation due to its simplicity and convenience for welfare comparison purposes. Substituting (4) into the social planner's objective function (1), we have the following quadratic welfare criterion for the social planner:
3 The First Pitfall: Linearizing the Constraint
We first show how the first pitfall arises and then discuss ways to avoid this pitfall.5 Suppose we start by approximating the constraint (2) to the first order in logs before deriving optimality conditions:
where
Due to the symmetry, the necessary condition for optimality is
![]() . In the case of
. In the case of ![]() the objective function is concave with
respect to log consumption so this condition is also sufficient. Therefore, the solution of this maximization problem would be the same as (6), a correct loglinear approximation of the exact solution. However, when
the objective function is concave with
respect to log consumption so this condition is also sufficient. Therefore, the solution of this maximization problem would be the same as (6), a correct loglinear approximation of the exact solution. However, when ![]() the sufficient condition for concavity is not satisfied, and
the sufficient condition for concavity is not satisfied, and
![]() does not correspond to an optimum.6 In
fact, optimality comes under a corner solution. That is, risk sharing reduces the level of welfare.7 The solution from this LQ problem--maximizing the
quadratic objective function subject to a linearized budget constraint--can be different from a correct linear representation of the exact solution. This improper LQ setup is referred to as a "naive" LQ problem by Benigno and Woodford (2006).
does not correspond to an optimum.6 In
fact, optimality comes under a corner solution. That is, risk sharing reduces the level of welfare.7 The solution from this LQ problem--maximizing the
quadratic objective function subject to a linearized budget constraint--can be different from a correct linear representation of the exact solution. This improper LQ setup is referred to as a "naive" LQ problem by Benigno and Woodford (2006).
3.1 Ways to avoid the first pitfall
An evident way to avoid the first pitfall is to derive the optimality conditions based on the original nonlinear constraints and then to linearize the optimality conditions as well as the constraints. This method is widely used in dynamic macroeconomics. Recently, Benigno and Woodford (2004, 2005) provided another way to avoid this pitfall while keeping the linear quadratic framework in solving a general class of nonlinear optimization problems.
Their critical step is to approximate the constraint (2) quadratically rather than linearly:
This quadratic constraint (9) can now be used to substitute out the linear terms in the objective function (7), which is then transformed into the following quadratic form (without any linear terms for endogenous variables):
![\begin{displaymath} \frac{\bar{C}^{1-\gamma}}{2}\left[ \begin{array}[c]{c}% -\frac{\gamma}{2}\left( \log\frac{C_{1}}{\bar{C}}\right) ^{2}-\frac{\gamma }{2}\left( \log\frac{C_{2}}{\bar{C}}\right) ^{2}\ +\log\frac{Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}+\frac{1}{2}\left[ \left( \log\frac{Y_{1}}{\bar{Y}}\right) ^{2}+\left( \log\frac{Y_{2}}% {\bar{Y}}\right) ^{2}\right] \end{array}\right] . \end{displaymath}](img24.gif)
Now we maximize this transformed quadratic objective function (10) subject to the linear constraint (8). The solution of this problem is (6) implying full risk sharing, and it is the correct loglinear approximation of the exact solution: avoiding the first pitfall. This "revised" LQ approach can be applied to dynamic models, including models with backward-looking constraints such as stochastic growth models and ones with forward-looking constraints such as optimal monetary policy.8
4 The Second Pitfall: Linearizing the Model
From now on, we assume that one is equipped with a correct linear representation of the optimality conditions. The second pitfall takes place when this set of linear equations (or its solution that expresses endogenous variables in terms of exogenous and predetermined variables) is used for welfare evaluations. Our illustration of how the second pitfall arises is based on the same model as was used for the case of the first pitfall.
Linear representation of the correctly derived optimality conditions produces the loglinear solution (6). By plugging this equation into the quadratic welfare criterion function (7), we can calculate the welfare level of the complete markets economy based on the loglinear approximation of the optimality conditions:
In contrast, the level of welfare under autarky is
Comparison of these two welfare levels reveals that, when ![]() , the welfare level of autarky is higher than that of the complete markets economy. This result is clearly spurious,
given that it violates the first welfare theorem. In general, this second pitfall yields incorrect welfare implications.
, the welfare level of autarky is higher than that of the complete markets economy. This result is clearly spurious,
given that it violates the first welfare theorem. In general, this second pitfall yields incorrect welfare implications.
4.1 Ways to avoid the second pitfall
The revised LQ approach in the previous section, proposed by Benigno and Woodford, avoids the second pitfall as well. Suppose that we plug the loglinear solution (6) into the purely quadratic objective function (10). Then, this criterion yields the following level of welfare under the complete markets economy:
![\displaystyle =-\frac{\gamma\bar{C}^{1-\gamma}}{4}\left[ \frac{1}{2}\left( \log\frac{Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}\right) ^{2}\right]](img34.gif) |
||
 |
This value is higher than the level of welfare under autarky evaluated with the purely quadratic objective function (10),
![\displaystyle =-\frac{\gamma \bar{C}^{1-\gamma}}{4}\left[ \left( \log\frac{Y_{1}}{\bar{Y}}\right) ^{2}+\left( \log\frac{Y_{2}}{\bar{Y}}\right) ^{2}\right]](img37.gif) |
||
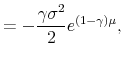 |
and we have avoided the second pitfall. This approach can also be applied to evaluate the welfare implications of any sub-optimal economies.
Another way to avoid the second pitfall, employed in Kim and Kim (2003), is the second order approximation of the economy--including the optimality conditions as well as the constraints.9 That is, the solution need be of second order with respect to the exogenous and predetermined variables--as well as the standard deviation of shocks in a stochastic case. In the complete markets economy, the solution based on the second order approximation becomes
where the superscript `quad' denotes a quadratic approximation.10 Plugging this consumption solution into the quadratic welfare criterion function (7), we can derive the welfare level of the complete markets economy based on the second order solution of the model,
The welfare level is always greater than that under autarky as in (12) for any positive values for the risk aversion parameter (
Appendices
A. Growth Model
This example shows how to apply the revised LQ approach to a simple deterministic growth model:
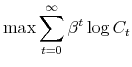
where
To convert the linear terms of the utility function into a purely quadratic form, we need the following relationship among the steady-state values,
Multiplying the former equation by
Using this relationship, we transform the linear terms in the criterion function as follows:
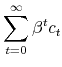 |
||
![\displaystyle =\bar{\eta}\sum_{t=0}^{\infty}\beta^{t}\left[ \beta^{-1}\exp\left( \log\bar{K}\right) k_{t}+\exp\left( \log\bar{C}\right) c_{t}-\Theta k_{t}\right]](img64.gif) |
||
The parenthesized term in the last expression (i.e.
B. Optimal Monetary Policy
This example illustrates an application of the revised LQ approach to an optimal policy problem with a nonlinear forward looking constraint.11 The policy problem is to
![\displaystyle \max-.5E_{t}\left[ \left( 1-\tilde{\beta}\right) \sum_{i=0}^{\infty}% \tilde{\beta}^{i}\left( \alpha\left( x_{t+i}-\kappa\right) ^{2}+\pi _{t+i}^{2}\right) \right]](img69.gif)
![\displaystyle \pi_{t}=\lambda x_{t}+\frac{\zeta}{2}x_{t}^{2}+\beta E_{t}\left[ \pi _{t+1}\right] +u_{t}.](img70.gif)
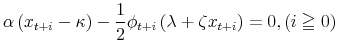
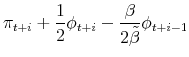 |
||
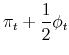 |
where
Rewriting this constraint forward, we have
![\displaystyle =\lambda x_{t}+\frac{\zeta}{2}x_{t}^{2}+\beta E_{t}\left[ \pi_{t+1}\right] +u_{t}](img78.gif) |
||
![\displaystyle =\sum_{i=0}^{\infty}\beta^{i}E_{t}\left[ \lambda x_{t+i}+\frac{\zeta}% {2}x_{t+i}^{2}+u_{t+i}\right] .](img79.gif) |
That is,
![\displaystyle \lambda\sum_{i=0}^{\infty}\beta^{i}E_{t}\left[ x_{t+i}\right] =\pi_{t}% -\sum_{i=0}^{\infty}\beta^{i}E_{t}\left[ \frac{\zeta}{2}x_{t+i}^{2}% +u_{t+i}\right] .](img80.gif)
![\displaystyle -.5E_{t}\left[ \left( 1-\tilde{\beta}\right) \sum_{i=0}^{\infty}% \tilde{\beta}^{i}\left( \alpha\left( x_{t+i}-\kappa\right) ^{2}+\pi _{t+i}^{2}\right) \right]](img81.gif) |
||
![\displaystyle =-.5E_{t}\left[ \left( 1-\tilde{\beta}\right) \sum_{i=0}^{\infty}% \tilde{\beta}^{i}\left( \alpha x_{t+i}^{2}-2\alpha\kappa x_{t+i}+\alpha \kappa^{2}+\pi_{t+i}^{2}\right) \right] \mid_{_{\left( \tilde{\beta}% =\beta\right) }}](img82.gif) |
||
![\displaystyle =-.5E_{t}\left[ \left( 1-\beta\right) \sum_{i=0}^{\infty}\beta^{i}\left( \alpha x_{t+i}^{2}+\pi_{t+i}^{2}\right) \right] +.5\alpha\kappa^{2}](img83.gif) |
||
![\displaystyle +\left( 1-\beta\right) \frac{\alpha\kappa}{\lambda}\left( \pi_{t}% -\sum_{i=0}^{\infty}\beta^{i}E_{t}\left[ \frac{\zeta}{2}x_{t+i}^{2}% +u_{t+i}\right] \right)](img84.gif) |
||
![\displaystyle =\left( 1-\beta\right) \frac{\alpha\kappa}{\lambda}\pi_{t}-.5E_{t}\left[ \left( 1-\beta\right) \sum_{i=0}^{\infty}\beta^{i}\left[ \left( \alpha+\frac{\alpha\kappa}{\lambda}\zeta\right) x_{t+i}^{2}+\pi_{t+i}% ^{2}\right] \right] +t.i.p.](img85.gif) |
The first term of the last expression reflects the inflation gain in the first period, which would disappear under the timeless perspective.
The optimality conditions corresponding to the transformed criterion function are
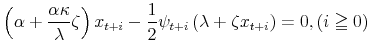
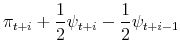 |
||
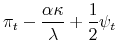 |
where
C. Third-Order Properties of Utility and Constraint
Suppose that the criterion function of the social planner is
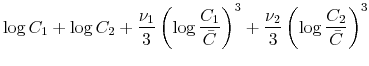
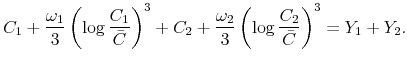
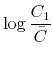 |
![\displaystyle =\frac{1}{2}\left( \log\frac{Y_{1}}{\bar{Y}% }+\log\frac{Y_{2}}{\bar{Y}}\right) +\frac{1}{8}\left[ \begin{array}[c]{c}% \left( \log\frac{Y_{1}}{\bar{Y}}-\log\frac{Y_{2}}{\bar{Y}}\right) ^{2}\\ -\left( \nu_{1}-\nu_{2}-\omega_{1}+\omega_{2}\right) \left( \log\frac {Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}\right) ^{2}% \end{array} \right] ,](img93.gif)
|
|
 |
![\displaystyle =\frac{1}{2}\left( \log\frac{Y_{1}}{\bar{Y}% }+\log\frac{Y_{2}}{\bar{Y}}\right) +\frac{1}{8}\left[ \begin{array}[c]{c}% \left( \log\frac{Y_{1}}{\bar{Y}}-\log\frac{Y_{2}}{\bar{Y}}\right) ^{2}\\ +\left( \nu_{1}-\nu_{2}-\omega_{1}+\omega_{2}\right) \left( \log\frac {Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}\right) ^{2}% \end{array} \right] .](img95.gif)
|
That is, four third-order parameters do in fact affect the quadratic solution without affecting the level of welfare based on its quadratic approximation--a criterion of the revised LQ approach as well the quadratic perturbation approach.
Intuition for this property comes from the reason why the revised LQ approach works in the first place. The reason why this approach works is that, though (10) is not any kind of approximation of (7) in general, the two expressions are equivalent up to the second order for all outcomes that are consistent with the constraint. In the same vein, modification of the criterion function and the constraint would not affect (10)--hence no influence on the level of welfare up to the second order.

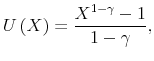
![\displaystyle U^{\left( 2\right) }\left( X\right) =\bar{X}^{1-\gamma}\left[ \left( \log\frac{X}{\bar{X}}\right) +\frac{1-\gamma}{2}\left( \log\frac{X}{\bar{X}% }\right) ^{2}\right] ,%](img7.gif)
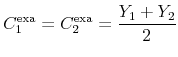
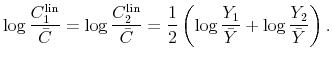
![\displaystyle \frac{\bar{C}^{1-\gamma}}{2}\left[ \left( \log\frac{C_{1}}{\bar{C}}\right) +\left( \log\frac{C_{2}}{\bar{C}}\right) +\frac{1-\gamma}{2}\left( \log\frac{C_{1}}{\bar{C}}\right) ^{2}+\frac{1-\gamma}{2}\left( \log \frac{C_{2}}{\bar{C}}\right) ^{2}\right] .%](img16.gif)
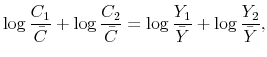
![\displaystyle \log\frac{C_{1}}{\bar{C}}+\log\frac{C_{2}}{\bar{C}}+\frac{1}{2}\left[ \left( \log\frac{C_{1}}{\bar{C}}\right) ^{2}+\left( \log\frac{C_{2}}% {\bar{C}}\right) ^{2}\right]](img22.gif)
![\displaystyle =\log\frac{Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}+\frac{1}{2}\left[ \left( \log\frac{Y_{1}}{\bar{Y}}\right) ^{2}+\left( \log\frac{Y_{2}}% {\bar{Y}}\right) ^{2}\right] .%](img23.gif)
![\displaystyle V\left( C_{1},C_{2}\right) =-\frac{\gamma\bar{C}^{1-\gamma}}{4}\left[ \left( \log\frac{C_{1}}{\bar{C}}\right) ^{2}+\left( \log\frac{C_{2}}% {\bar{C}}\right) ^{2}\right]%](img25.gif)
![\displaystyle =\bar{C}% ^{1-\gamma}\left[ \frac{1}{2}\left( \log\frac{Y_{1}}{\bar{Y}}+\log \frac{Y_{2}}{\bar{Y}}\right) +\frac{1-\gamma}{8}\left( \log\frac{Y_{1}}% {\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}\right) ^{2}\right]](img27.gif)

![\displaystyle =\bar{C}% ^{1-\gamma}\left[ \log\frac{Y_{i}}{\bar{Y}}+\frac{1-\gamma}{2}\left( \log\frac{Y_{i}}{\bar{Y}}\right) ^{2}\right]](img30.gif)
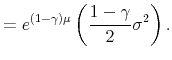

![\displaystyle =\bar {C}^{1-\gamma}\left[ \begin{array}[c]{c}% \frac{1}{2}\left( \log\frac{Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}}\right) +\frac{1}{8}\left( \log\frac{Y_{1}}{\bar{Y}}-\log\frac{Y_{2}}{\bar{Y}% }\right) ^{2}\\ +\frac{1-\gamma}{8}\left( \log\frac{Y_{1}}{\bar{Y}}+\log\frac{Y_{2}}{\bar{Y}% }\right) ^{2}% \end{array} \right]](img41.gif)
