Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-66 Screen Reader version ^♣

Stability of Risk Preference

Claudia R. Sahm*

Keywords: Risk tolerance, risk aversion, correlated random effects, interval regression

Abstract:

Stability of preferences is central to how economists study behavior. This paper uses panel data on hypothetical gambles over lifetime income in the Health and Retirement Study to quantify changes in risk tolerance over time and differences across individuals. The maximum-likelihood estimation of a correlated random effects model utilizes information from 12,000 respondents in the 1992-2002 HRS. The results support constant relative risk aversion and career selection on preferences. While risk tolerance changes with age and macroeconomic conditions, persistent differences across individuals account for 73% of the systematic variation. The measure of risk tolerance also relates to actual stock ownership.

1 INTRODUCTION

"One does not argue over tastes for the same reason that one does not argue over the Rocky Mountains -- both are there, will be there next year, too, and are the same to all men." Stigler and Becker (1977)

This paper approaches the fundamental debate on preference stability as an empirical question. Hypothetical gambles asked repeatedly to the same individuals over ten years provide a unique lever for this direct study of changes in risk tolerance. The gambles pose a well-defined risky choice that is comparable both across individuals and over time. The odds of the gambles are explicit, the stakes over lifetime income are large, albeit hypothetical, and most importantly for this study, the substance of the gambles does not change over time. As a result, the panel of gamble responses provides a clearer picture of long-term preference stability than standard behavioral data in surveys or experiments.

To quantify the stability of risk preference, I use gamble responses across the 1992 to 2002 waves of the Health and Retirement Study (HRS).¹The placement of the gambles in the HRS with its rich individual and household information is also crucial for measuring the systematic changes in risk preference. To interpret the gamble responses, I adapt the framework from Barsky et al. (1997) and Kimball et al. (Forthcoming) that maps the gambles to the coefficient of relative risk tolerance. Yet my paper is distinct from other work with HRS gambles. I provide the first direct test of whether risk preferences are stable, and in particular whether individuals exhibit constant relative risk aversion.² My analysis of the gamble responses also incorporates the detailed information on individuals over the panel period. This allows me to investigate the drivers of preference change and the degree of selection on preference type. I model risk tolerance with a time-varying component and a time-constant component and use the panel to separate within-person and across-person variation in preferences. Specifically, I estimate a correlated random effects model of risk tolerance with 18,625 gamble responses from 12,003 individuals between ages 45 and 70.

The results present a nuanced view of the stability in risk preference. There is a modest decline in risk tolerance with age, and an improvement in macroeconomic conditions is associated with an increase in risk tolerance. But changes in income and wealth do not measurably alter an individual's willingness to take risk. In addition, major life events of a job displacement and the diagnosis of a serious health condition that likely reduce expected lifetime income have little impact on measured risk tolerance. The invariance of risk tolerance to within-person changes in income -- the explicit stake of the gamble -- provides support for the specification of utility with constant relative risk aversion. While the gamble responses reveal few sources of systematic change in risk preference, there is substantial evidence of large persistent differences in preferences across individuals. Demographics, including gender, race, education, and marital status are all associated with significant differences in the time-constant component of risk tolerance. The panel also points to the past selection of risky careers and high debt levels based on the individual's risk tolerance type. Altogether, the time-varying attributes account for 27% of the systematic variation in risk tolerance. There are also large persistent differences across individuals in their willingness to take risk in the hypothetical gambles that are not explained by any of the observables. The time-constant variance of preferences from the gambles that is unrelated to observables is twice as large as the systematic variance of preferences.

One potential concern is the credibility of results from hypothetical gambles. There are three main justifications for using this data to study changes in preferences. First, I estimate the systematic changes with a risky choice that is consistently defined over time. Extraneous details in the gambles, such as the sequence of the risks, may affect the responses and bias the estimated level of risk tolerance. However, I focus on the changes in risk preferences which are unaffected by constant question effects. Unlike panels of actual risky behavior, such as Brunnermeier and Nagel's (Forthcoming) analysis of household asset allocation, I can cleanly identify preference changes, as opposed to a mix of preference, expectations, and institutional changes.³ Second, the stakes of the gambles over lifetime income are large, as Rabin (2000) argues is necessary for measuring risk preference. This limits the question to a hypothetical situation, but the most likely cost is an increase in the noise. In a review of several experiments, Camerer and Hogarth (1999) find that financial incentives generally reduce the unexplained variability in behavior but do not affect the average behavior. Accordingly, my statistical model of risk tolerance removes the random variation in the gamble responses and the results focus on systematic changes in preferences. Third, individuals' responses to hypothetical gambles are correlated with their actual, incentivized risky behavior. In the last section, I show that more risk tolerant individuals (according to the gambles) are more likely to own stocks and increases in an individual's risk tolerance raise the probability of stock ownership. This is consistent with Barsky et al. (1997) who find a positive correlation between the level of measured risk tolerance and numerous actual risky behaviors. In addition, the experimental validation by Dohmen et al. (2006) of a hypothetical lottery question supports the use of hypothetical choice data. Altogether the gamble responses in the HRS offer valuable information on the stability of risk preferences.

The plan of the paper is as follows. Section 2 discusses the hypothetical gambles in the HRS. Section 3 uses expected utility theory to map the gamble responses to the coefficient of relative risk tolerance. The section then develops a statistical model of risk tolerance based on the gamble responses. Section 4 presents the results from maximum-likelihood estimation of the model. Section 5 uses the estimates of risk tolerance to study the household's actual decision to own stocks. The final section offers conclusions.

2 GAMBLES OVER LIFETIME INCOME

The Health and Retirement Study uses hypothetical gambles over lifetime income to elicit risk attitudes. In a short series of questions, individuals choose between two jobs; one job guarantees current lifetime income and the other job offers an unpredictable, but on average higher lifetime income. In the 1992 HRS, individuals consider the following scenario:

Suppose that you are the only income earner in the family, and you have a good job guaranteed to give you your current (family) income every year for life.

You are given the opportunity to take a new and equally good job, with a 50-50 chance it will double your (family) income and a 50-50 chance that it will cut your (family) income by a third. Would you take the new job?

Individuals who accept the first risky job then consider a job with a larger downside risk of one-half. Those who reject the first risky job are asked about a job with a smaller downside risk of one-fifth. Starting with the 1994 HRS, individuals who reject their first two risky jobs consider a third job that could cut their lifetime income by one-tenth. Likewise individuals who accept their first two risky jobs consider a third job that could cut their lifetime income by three-quarters. I use these responses to order individuals in a small number of categories. Table 1 relates the gamble response category to the downside risks that the individual accepts and rejects. The category numbers are increasing in an individual's willingness to accept income risk, so the gamble responses provide a coarse ranking of individuals by their risk preference.

Barsky et al. (1997) designed the gambles and analyzed the responses on the first two waves of the HRS. They acknowledge the potential for a status qua bias in the gamble responses due to the question wording, since individuals may have an aversion to a new job unrelated to its income risk. The 1998 HRS revised the hypothetical scenario so that individuals now choose between two new jobs:

Suppose that you are the only income earner in the family. Your doctor recommends that you move because of allergies, and you have to choose between two possible jobs.

The first would guarantee your current total family income for life. The second is possibly better paying, but the income is also less certain. There is a 50-50 chance the second job would double your total lifetime income and a 50-50 chance that it would cut it by a third. Which job would you take -- the first job or the second job?

The objective attributes of the two jobs are identical in the original and revised versions of the question. Furthermore the 1998, 2000, and 2002 HRS use the same sequence of downside risks for the second job as the 1994 HRS uses for the new job. Over 30% of the individuals respond to both versions of the question which allows me to estimate the size of the status quo bias in the original question.

In this paper, I analyze 18,625 gamble responses on the 1992, 1994, 1998, 2000, and 2002 waves of the HRS from 12,003 individuals in the 1931 to 1947 birth cohorts.⁴ The panel is unbalanced due to survey attrition, expansion of the survey in 1998, and targeted delivery of the gamble questions in the survey. In particular, the survey usually asks the gambles to new respondents and a random sub-sample of returning respondents. Nonetheless 45% of the individuals answer the battery of income gambles in multiple waves and 8% answer the gambles in three or more waves.

The distribution of gamble responses in Table 2 shows that most individuals are unwilling to take income risks even when the expected value of the gamble is substantially larger than their current lifetime income. In 1992, more than two-thirds of individuals reject the risky job that offers a 50-50 chance to double lifetime income or cut it by one-fifth. The expected value of the income from this risky job is 140% of current lifetime income. And less than 13% of individuals accept the risky job with a downside risk of one-half which has an expected value of 125% of current lifetime income. The distribution of the gamble response categories is fairly stable across waves, though individuals in 1998 are willing to accept somewhat more income risk.

The placement of these gambles on a large panel study provides an ideal opportunity to study systematic changes in risk tolerance, and the decade in which the gambles are fielded coincides with many significant changes in individual circumstances and macroeconomic conditions. Table 3 summarizes the primary set of individual attributes and events that I use to quantify systematic changes in risk tolerance. First the considerable diversity in the sample of gamble respondents in the HRS is worth noting. Of the 18,625 gamble responses, 43% are from men, 15% are from blacks, and 8% are from Hispanics.⁵ About one-fifth of the responses are from individuals with less than twelve years of education versus one-fifth from individuals with sixteen or more years of education.

Over the panel, several individuals have experiences that plausibly alter their expected lifetime income. I focus particularly on job displacements and serious health conditions. While an individual's past behavior may influence the occurrence of these events, they are not perfectly predictable and should represent some shock to an individual. Prior to their gamble response, 25% of the respondents had experienced a job displacement, that is, a job ending with a firm closure or layoff, and 22% had received a diagnosis of heart disease, a stroke, cancer, or lung disease. Most importantly, 13% of the gamble responses were followed later in the survey by a first job displacement for the individual and 17% by a first diagnosis of a serious health condition. This within-person variation is what allows me to identify the direct effect of these events on an individual's risk tolerance. Table 3 also shows that there are meaningful changes in income and wealth during the panel period.⁶ On average, the household income and wealth of the respondents at the time of their gamble response is below the average levels of their total income and wealth across the 1992 to 2002 survey waves. But there is substantial variation across respondents in both the average level and changes in income and wealth.

The gamble responses also coincide with significant changes in the macroeconomy. Performance of the U.S. stock market particularly defined the survey period of April 1992 to February 2003. Figure 1 depicts the large increase and then sharp decline in the annual real returns on the S&P 500 Index. The shaded areas on the figure denote months in which the HRS asked the income gamble questions. The gambles appear on five waves of the HRS and each wave spans 8 to 15 months. This yields meaningful variation both across and within survey waves. Figure 1 also highlights positive association between consumer sentiment and stock market returns. I use the Index of Consumer Sentiment (ICS) in the month of an individual's interview to measure the general economic condition at the time of a gamble response.⁷ There is considerable variation in general economic outlook both across and within survey waves. From October 1992 to February 2000 the index rose sharply from 70.3 to 111.3 and over the course of the 2002 HRS the index dropped sharply from 96.9 in May 2002 to 79.9 in February 2003.

3 MODEL OF RISK TOLERANCE

In this section, I discuss how I use the gamble responses on the HRS to quantify changes in an individual's risk tolerance over time, as well as differences across individuals at a point in time. I adopt the expected utility interpretation of the gambles and the general estimation strategy developed by Barsky et al. (1997) and later used in Kimball et al. (Forthcoming). I use a rich set of covariates to investigate systematic changes in risk tolerance. My model incorporates the potential correlation between the time-constant component of risk tolerance and other time-varying attributes. The estimates from a panel of gamble responses and attributes allow me to determine whether a change in individual circumstances leads to a change in risk tolerance or simply signals an individual's risk tolerance type.

3.1 Mapping Gambles to Preferences

Expected utility theory offers a translation of an individual's gamble responses to a standard metric of risk preference -- the coefficient of relative risk tolerance. Specifically, choices in the gambles establish a range for an individual's risk tolerance. Consider a general utility function and a level of permanent consumption . Offered a 50-50 chance of doubling lifetime income or cutting it by a fraction $\pi$ , an individual accepts a risky job when its expected utility exceeds the utility from the certain job, that is, if

$\displaystyle 0.5 U(2c) + 0.5U((1-\pi)c)$

$\displaystyle \ge U(c)$ . $\displaystyle %$

(1)

The greater the curvature of

, the smaller the downside risk $\pi$ an individual accepts. This interpretation of the gamble responses links lifetime income to permanent consumption and ignores the potential effect of wealth.⁸ To quantify risk preference, I assume that relative risk aversion (and its reciprocal relative risk tolerance) are constant in the range of the gambles, such that

$\displaystyle U(c)$

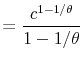$\displaystyle = \frac{c^{1-1/\theta}}{1-1/\theta}%$

(2)

The coefficient of relative risk tolerance, $\theta= -U^{\prime}% /cU^{\prime\prime}$ (Pratt, 1964), in this specification of utility may differ across individuals. It is assumed to be constant for all values of permanent consumption for a given individual. The estimated model of risk tolerance in Section 4, which includes measures of income and wealth, is consistent with this assumption of constant relative risk aversion utility.

In this framework, the gamble responses define a range for an individual's risk tolerance $\theta$ . Consider an individual, in gamble response category 3, who accepts the job with a one-fifth downside risk and rejects the job with a one-third downside risk. These choices imply a coefficient of relative risk tolerance between 0.27 and 0.50, since

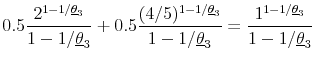$\displaystyle 0.5 \frac{2^{1-1/\underline{\theta}_{3}}}{1-1/\underline{\theta}_{3}} + 0.5\frac{(4/5)^{1-1/\underline{\theta}_{3}}}{1-1/\underline{\theta}_{3}} = \frac{1^{1-1/\underline{\theta}_{3}}}{1-1/\underline{\theta}_{3}}$	$\displaystyle \rightarrow\underline{\theta}_{3} = 0.27$	(3)
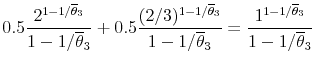$\displaystyle 0.5 \frac{2^{1-1/\overline{\theta}_{3}}}{1-1/\overline{\theta}_{3}} + 0.5\frac{(2/3)^{1-1/\overline{\theta}_{3}}}{1-1/\overline{\theta}_{3}}= \frac{1^{1-1/\overline{\theta}_{3}}}{1-1/\overline{\theta}_{3}}$	$\displaystyle \rightarrow\overline{\theta}_{3} = 0.50$ . $\displaystyle %$	(4)

The highest downside risk accepted and the smallest risk rejected establish the upper and lower bounds on risk tolerance. The last two columns of Table 1 provides the range of risk tolerance for each of the gamble response categories.

3.2 Model of Measured Log Risk Tolerance

The statistical model of risk tolerance $\theta_{it}$ encompasses systematic changes in preferences and a persistent attitude toward risk, such that,

$\displaystyle \log\theta_{it}$

$\displaystyle = x_{it}\beta+ a_{i}%$

(5)

where $x_{it}\beta$ is the time-varying component and $a_{i}$ is the time-constant component of the logarithm of risk tolerance. The logarithmic specification of risk tolerance captures the fact that most individuals exhibit a low tolerance of risks in the gambles, but some individuals are willing to take large income risks. The parameter $\beta$ measures the percent change in risk tolerance associated with a change in the attributes $x_{it}$ .

The time-constant component of risk tolerance $a_{i}$ may be correlated with the individual circumstances $x_{it}$ that can change risk tolerance. For example, the experience of a job displacement may reduce an individual's willingness to take further risks, that is, $\beta< 0$ . Or the event could primarily reveal an individual's risk tolerance type if more risk tolerant individuals tend to select career paths with a higher risk of displacement. To accommodate such selection effects, I model a relationship between the time-constant component $a_{i}$ and observable attributes as

$\displaystyle a_{i} = \overline{x}_{i}\lambda+ u_{i}%$

(6)

where $\overline{x}_{i}$ is the panel average of $x_{i1},...,x_{iT}$ for individual

and the type effect $\lambda$ measures the persistent systematic differences across individuals in risk tolerance.⁹ The term $u_{i}$ captures the portion of constant risk tolerance $a_{i}$ that is unrelated to the attributes in $\overline{x}_{i}$ , a vector that includes a constant. This mean-zero residual is constant for a given individual over time and is independently distributed across individuals conditional on observables, such that, $u_{i} \vert \overline{x}_{i} \sim$ N $(0,\sigma_{u}^{2})$ . The model of the correlated random effects in equation (6) follows from Mundlak (1978). Chamberlain (1984) summarizes this modeling strategy and presents a more general specification of the type effects.¹⁰

The estimation strategy also recognizes the limitations of using a small set of hypothetical gamble responses to infer individual preferences. First, the gamble responses establish an interval, not a point estimate, for risk tolerance, so I do not have the data to simply estimate the linear model. Second, the income gamble questions likely generate substantial survey response error as is common with hypothetical and cognitively difficult questions. Nearly half of the individuals switch their gamble responses across waves -- one sign of random noise. Comments made by individuals during the survey also highlight difficulties respondents had in answering the hypothetical income gamble questions.¹¹ Survey response errors can arise on the gambles when individuals misinterpret the hypothetical scenario or make computational mistakes in their comparison of the jobs.

To incorporate these additional features of the data, I model the latent signal $\xi _{it}$ from the individual's gamble responses as a combination of risk tolerance $\theta_{it}$ and a survey response error $\epsilon_{it}$ , such that

$\displaystyle \xi_{it}$	$\displaystyle = \log\theta_{it} + \epsilon_{it}$	(7)
$\displaystyle c_{it}$	$\displaystyle = j$ , if $\displaystyle \hspace{.3cm} \log\underline {\theta}_{j} < \xi_{it} < \log\overline{\theta}_{j} \hspace{.5cm} (i=1,...,N; t=1,...T)$	(8)

where $c_{it}$ is the gamble response category that is observed in the data. An individual in response category

has a noisy signal of risk tolerance that lies in the interval $(\log\underline{\theta}_{j},\log\overline{\theta }_{j})$ , where the cutoffs are the logarithm of the values in Table 1. The odds and outcomes are explicit in the gamble questions, so with the assumption of constant relative risk aversion utility, the intervals of risk tolerance are known values and do not vary across individuals or across waves. The model of the latent signal incorporates two sources of variation in the gamble responses over time: systematic changes in risk tolerance and survey response error. Earlier studies of the income gambles by Barsky et al. (1997) and Kimball et al. (Forthcoming) on the HRS also model the time variation in gamble responses due to response error. My analysis is the first to investigate changes in risk tolerance that are both systematically associated with observed changes in circumstances and due to the random variation from response errors. For identification, I assign all the changes in the latent signal that are unrelated to these covariates to the survey response error. This assumption likely understates any high frequency shifts in risk tolerance. My focus on the time-constant and systematic variation in preferences is consistent a well-defined measure of risk preference that would apply to other risky decisions made by the individual.

In modeling the survey response error, I also investigate the question framing effects and heteroscedasticity in the response error. The survey response error $\epsilon_{it}$ has the form

$\displaystyle \epsilon_{it}$

$\displaystyle = q_{it}\delta+ e_{it}%$

(9)

where $q_{it}$ is an indicator for a gamble response to the original ("new job") version of the question, so $\delta$ measures the degree of status quo bias in responses to the gamble question on the 1992 and 1994 HRS.¹² The term $e_{it}$ is a survey response error that is unrelated to both the question type and other observables. It is independently distributed N $(0,\sigma_{e it}^{2})$ across individuals and over time. I allow the observed attributes in the model of risk tolerance and the question type to also affect the dispersion of the response error. Specifically, the dispersion in response errors is $\sigma_{eit}=\exp [(x_{it},\overline{x}_{i},q_{it})\sigma_{e}]$ , where $\sigma_{e}$ is a parameter vector that relates individual attributes to the variation in response errors. Thus individuals with a particular attribute, such as less education, do not systematically understate (or overstate) their risk tolerance in their gamble responses. The response errors in this group, however, may be larger in absolute value than the response errors from individuals with more education. The term $e_{it}$ soaks up changes in an individual's gamble responses that are not associated with the observed attributes, as well as the unsystematic transitory variation in the gamble responses across individuals. The heteroscedastic variance of $e_{it}$ permits the precision in the gamble responses -- or the degree of wave-to-wave switches -- to vary with individual attributes and question type. The gambles are complicated hypothetical questions on a lengthy survey and answers to the gambles have no real consequences, so a careful treatment of the survey response error is essential to infer risk tolerance from the gamble responses.¹³

Combining the models of risk tolerance and survey response error yields a reduced-form description of the latent signal in the gamble responses:

$\displaystyle \xi_{it}$	$\displaystyle = x_{it}\beta+ a_{i} + q_{it}\delta+ e_{it}$	(10)
	$\displaystyle = x_{it}\beta+ \overline{x}_{i}\lambda+ q_{it}\delta+ u_{i} + e_{it} %$	(11)

A restatement of the model draws particular attention to the variation in the preference signal within and between individuals. Specifically,

$\displaystyle \xi_{it}$

$\displaystyle = (x_{it}-\overline{x}_{i})\beta+ \overline{x}_{i}(\lambda+\beta) + q_{it}\delta+ u_{i} + e_{it}%$

(12)

where the first term $(x_{it}-\overline{x}_{i})\beta$ captures a change in risk tolerance for a given individual and the second term $\overline{x}% _{i}(\lambda+\beta)$ captures the differences in risk tolerance across individuals that are associated with observed attributes. The separate identification of the direct effect $\beta$ and the type effect $\lambda$ depends crucially on variation in $x_{it}$ over the panel period and variation in $\overline{x}_{i}$ across the individuals. For time-constant attributes, such as gender and race, or choices made before the survey period, such as years of education, I can only identify the composite term of $(\beta+ \lambda)$ , not the direct effect $\beta$ . In contrast, the type effect $\lambda$ of a covariate is not identified when its panel average $\overline{x}_{i}$ is the same for all individuals. For example, the gamble respondents all experienced the same macroeconomy of the 1990s, so any association between the average economic outlook in the panel and the persistent component of risk tolerance is absorbed in the estimate of the constant.

3.3 Log-Likelihood of Gamble Responses

I use maximum-likelihood methods to estimate the parameters $(\beta ,\lambda,\delta,\sigma_{u},\sigma_{e})$ of the reduced-form model in equation (11) with the panel of income gamble responses and covariates. I compute the probability of observing an individual's set of gamble responses over the survey period with a truncated normal distribution function, where the order of the function corresponds to the number of waves (up to five) in which an individual answers the income gambles. Consider, for example, an individual who answers the gambles in only one wave of the HRS, but participates in multiple waves of the survey. The attributes $x_{it}$ that are observed with a response to version $q_{it}$ of the income gambles and the average of these attributes across the entire panel $\overline{x}_{i}$ yield the following likelihood that the individual is in gamble response category at time :

P $\displaystyle (c_{it}=j\vert x_{it},\overline{{x}}_{i},q_{it})$	$\displaystyle =$ P $\displaystyle % (\log\underline{\theta}_{j} < \xi_{it}< \log\overline{\theta}_{j} \vert x_{it},\overline{{x}}_{i},q_{it})$
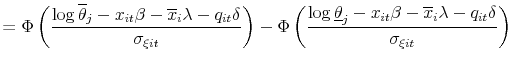	$\displaystyle = {\Phi}\left( \frac{\log\overline{\theta}_{j}-x_{it}\beta-\overline {x}_{i}\lambda-q_{it}\delta}{\sigma_{\xi it}}\right) - {\Phi}\left( \frac{\log\underline{\theta}_{j}-x_{it}\beta-\overline{x}_{i}\lambda -q_{it}\delta}{\sigma_{\xi it}}\right)$	(13)

where $\sigma^{2}_{\xi it} =$ Var $(\xi_{it}\vert x_{it},\overline{{x}}% _{i},q_{it})=\sigma_{u}^{2} + \sigma_{e it}^{2}$ and ${\Phi}(\cdot)$ is the univariate normal cumulative distribution function. I adjust the likelihood function accordingly for the individuals who answer the gamble questions in multiple survey waves.¹⁴ Since the lower bound $\log\underline {\theta}$ and upper bound $\log\overline{\theta}$ for the latent signal in each response category are known, the mean effects of $\beta$ , $\lambda$ , and $\delta$ are identified separately from the variance terms and are interpretable as if the latent signal $\xi _{it}$ were directly observed.¹⁵ Given the model of preferences, the estimate of $\beta$ is the percent change in risk tolerance for a given individual due to a change in $x_{it}$ and $\lambda$ is the percent difference in risk tolerance across individuals due to a difference in $\overline{x}_{i}$ .

The maximum-likelihood estimator finds the values of the parameters that maximize the conditional log-likelihood $\mathcal{L}$ of the sample:

$\displaystyle \mathcal{L}(\beta,\lambda,\delta,\sigma_{u},\sigma_{e}\vert c_{i}, x_{it}% ,\overline{{x}}_{i},q_{it})$

$\displaystyle = \sum_{i \in N} \sum_{j \in J} 1[c_{i}=j] \log$ P $\displaystyle (c_{i}=j\vert x_{it},\overline{{x}}_{i},q_{it})$

(14)

where $c_{i}=(c_{i1},...c_{iT})$ is the set of an individual's gamble responses on the HRS and

contains all possible sets of response categories. For the estimator, I use the modified method of scoring, a Newton-Raphson algorithm in which the sample average of the outer product from the score function approximates the information matrix.¹⁶The estimates of the asymptotic standard errors are also derived from this estimator of the information matrix.

4 ESTIMATES OF RISK TOLERANCE

The results from the maximum-likelihood estimation reveal a low degree of risk tolerance on average, although there is considerable preference heterogeneity across individuals. The mean of relative risk aversion in the sample is 9.6 and its standard deviation is also 9.6.¹⁷ This implies that an average respondent would be willing to pay 28% of lifetime income to avoid a gamble with the 50-50 chance of doubling lifetime income or cutting it by one-third. It is possible that some feature in the framing, fielding, or modeling of the gambles may bias the estimated level of risk preference. Yet even with a persistent misstatement in the gamble responses, this panel of answers to the same question over a decade still provides valid information on the stability of individuals' preferences.

In this sample of older individuals, the gamble responses reveal few sources of systematic and long-lasting shifts in risk tolerance. I find a moderate decline in risk tolerance with age and a co-movement of individual risk tolerance and the macroeconomic conditions. But changes in the individual's total household income or wealth do not significantly alter an individual's willingness to take risk. In addition, a job displacement and diagnosis of a serious health condition, two personal events that plausibly reduce expected lifetime income, have little impact on risk tolerance. These results support the standard utility specification of constant relative risk aversion for within-person changes in consumption. I also find large stable differences across individuals in risk tolerance type that relate to commonly observed attributes. The estimated effects of time-constant observed attributes, such as gender and race, broadly conform to the results in earlier cross-sectional studies of risk attitudes. The panel structure of the HRS also reveals a relationship between individuals' earlier decisions, such as career choice, and their risk tolerance type. The rest of this section discusses the results from the maximum-likelihood estimation. The full model has 55 parameters, including direct effects, type effects, and error variance effects related to 20 observed attributes, so I have chosen to present the results in pieces. Appendix Table 9 contains the full set of covariates and estimates.

4.1 Household Income and Wealth

The outcomes in the hypothetical gambles are defined as fractions of "your current family income every year for life," so the changes in income that individuals experience over the panel of gamble responses provide the power to test the utility specification of constant relative risk aversion. The gamble responses reveal no discernible change in risk tolerance when an individual's current income or wealth deviates from its average level in the panel.¹⁸ The first column of Table 4 shows that a 10% increase in current income relative to the individual's average income is associated with only a 0.3% increase in risk tolerance. With a standard error of 0.3% the direct effect of a within-person change in income on risk tolerance is a precisely estimated zero effect. Likewise changes in an individual's current wealth have no discernible effect on risk tolerance. These results suggest that the assumption of constant relative risk aversion as consumption changes for a particular individual is justifiable.¹⁹

The gamble responses, however, do not imply that risk aversion is constant across individuals with different levels of consumption. There are modest and statistically significant differences in risk tolerance across individuals related to their level of average income and average wealth in the panel. A 10% higher level of average income is associated with a 0.9% higher relative risk tolerance - a pattern consistent with more risk tolerant individuals selecting higher risk, higher return sources of income. This effect is modest in size but is statistically different from zero at the 5% level. Similarly, individuals with greater indebtedness reveal a higher level of risk tolerance in their gamble responses, with a 10% more negative average wealth associated with a 0.5% higher relative risk tolerance. There is no discernible pattern in risk tolerance across individuals with different, positive levels of average wealth. This could result from a cancelling of two effects: less risk tolerant individuals accumulate precautionary saving and more risk tolerant individuals select riskier, higher return assets.

These results from the HRS are comparable to previous cross-sectional studies of hypothetical choice data that find an association between the willingness to take risk and the level of income and wealth, including Donkers et al. (2001) and Dohmen et al. (2006). With different survey questions and modelling approaches in their cross-section studies, their point estimates are not directly comparable to my results. In general, the association between risk preferences and income or wealth in all of these studies is consistently small relative to demographics, such as gender and age.²⁰

The second column of Table 4 investigates the robustness of the baseline estimates of income and wealth effects. The question frame of a hypothetical job choice may impede non-workers from revealing their true preferences and obscure an effect of income or wealth on risk tolerance. This issue could be particularly severe in the HRS where one-third of the individuals are not working at the time of their gamble response and over 40% experience a change in their work status during the panel. The estimates in the second column of Table 4 demonstrate that the risk tolerance of working household heads is no more sensitive to changes in income or wealth than the risk tolerance of all respondents. The direct effects of income and wealth in this sub-sample are not substantially altered and remain statistically indistinguishable from zero at the 5% level. The positive association between the logarithm of average income and risk tolerance does increases to 0.14 from 0.09. The type effect of negative wealth decreases to 0.01 from 0.05 and is no longer distinguishable from zero.

4.2 Job Displacement and Health Condition

I also examine the association between risk tolerance and two major life events, a job displacement and a serious health condition, that likely affect an individual's expected lifetime income.²¹ The gambles on the HRS are defined over current lifetime income, so a shift in this reference point could alter an individual's attitude toward risk. For example, individuals may accept more income risk after a negative personal shock if that gamble could restore their original level of lifetime income. Or individuals who have received one draw of bad luck may simply be less willing to "spin the wheel" again.²² Rather than a change in risk tolerance, these events -- which do not occur purely at random -- could also signal an individual's risk tolerance type. For example, high risk tolerant types may have selected riskier career paths with a higher chance of displacement, so they comprise a large fraction of the workers who actually experience displacements. Or more risk tolerant individuals may have forgone preventative health care, and thus accepted a higher risk of a serious health condition. A panel of gamble responses and events is essential for separating these mechanisms.

In Table 5 both a job displacement and the onset of a health condition are associated with a decline in risk tolerance of 6% and 9% respectively. These direct effects are imprecisely estimated and not statistically different from zero at the 5% level.²³ More striking is the evidence of selection into risky careers based on individual preferences. Among individuals with no prior job displacement at the time of their gamble response, those who will experience a displacement later in the panel are 19% more risk tolerant than those who will never experience a displacement. The estimate of the type effect is both economically and statistically significant, as it suggests that high risk tolerance types have systematically chosen riskier careers with a higher chance of displacement. The positive correlation between risk tolerance and income risk underscores the need for a direct measure of individual preferences. For example, studies of household wealth accumulation that do not address this systematic variation in preferences would underestimate the amount of precautionary savings.²⁴ The estimated type effect of a serious health condition is only 2% and is not statistically different from zero at the 5% level.

I use the gamble responses that individuals provide before and after major life events to identify the impact of these events on risk tolerance. In an unbalanced panel, attrition could be systematically related to these events and thus to changes in risk tolerance. The second column of Table 5 presents the results from the model estimated with individuals who respond in all six waves of the HRS.²⁵ The balanced panel produces similar estimates of the type effects, but different estimates of the direct effects. The estimated direct effects imply a larger declines in risk tolerance of 11% after a job displacement and of 15% after the onset of a health condition. The direct effect of a health condition is now statistically significant. The bottom panel of Table 5 shows that the estimated type effects in the unbalanced and balanced panels are similar. In the balanced panel, individuals who will experience a job displacement later in the panel are 20% more risk tolerant and those who will experience the onset of a health condition are 6% more risk tolerant than individuals who will not experience the event before the end of the panel. As in the unbalanced panel, the across-person difference in risk tolerance that is revealed by a job displacement is statistically significant.

4.3 Age, Cohort, and Time

The ten-year panel of gamble responses also provides a unique opportunity to examine systematic changes in risk tolerance with age and with changes in the macroeconomic conditions. Yet, even with multiple observations from the same individuals, I face the standard challenge of separating the effects of age, birth cohort and time.²⁶ I model the time effects with a measure of macroeconomic conditions at the time of the gamble response. I use a linear specification for the age effects and indicator variables that span five to six birth years for the cohort effects. The first column of Table 6 presents the estimates of the model. I find that each year of age is associated with a 1.7% decline in an individual's risk tolerance. This implies almost a 20% decrease in risk tolerance over the survey period associated with aging.²⁷ Individuals in the 1937-41 birth cohorts are also 16% more risk tolerant than individuals in the 1931-1936 cohorts. The effects of birth cohort are suggestive of individuals closer to the Great Depression being less willing to take risk. Finally there is a strong positive relationship between risk tolerance and macroeconomic conditions, as measured by the Index of Consumer Sentiment (ICS) in the month of the gamble response. A ten-point increase in the sentiment index is associated with a 9% increase in an risk tolerance. During the panel period, there are substantial movements in this measure of economic conditions which imply quantitatively important changes in average risk tolerance. For example, risk tolerance increased steadily by 36% from October 1992 to February 2000 and then decreased sharply by 15% from May 2002 to February 2003. The movements in risk tolerance over the business cycle are substantial in magnitude; however, they do not signal a permanent shift in an individual's risk tolerance. To explore the duration of the macroeconomic effects, the second column of Table 6 adds a measure of consumer sentiment at six months and one year prior to the gamble response. The strongest association of 0.006 (t-statistic of 2.2) is between current macroeconomic conditions and risk tolerance. The estimated effect declines to 0.004 (t-statistic of 1.6)and -0.001 (t-statistic of -0.4) for macroeconomic conditions at six months and one year prior to the gamble response respectively. These results suggest the effect of changes in the macroeconomic conditions on risk tolerance is short-lived.

The last two columns of Table 6 use an alternate specification of the year effects that includes indicator variables for the survey wave. In the third column, the model controls for the survey wave of a gamble response, but not for consumer sentiment.²⁸ All of the year effects are economically and statistically significant. This alternate specification has only a modest impact on the point estimate for age and birth cohort. In the last column, the model includes both the indicators of the survey wave and the measure of consumer sentiment. Here the effect of macroeconomic conditions is identified entirely from within-wave variation. Nonetheless the estimate of 0.007 is only 17% lower than the estimate of 0.009 in the baseline model and is still statistically different from zero at the 5% level. In addition, the Index of Consumer Sentiment soaks up much the wave-to-wave differences in gamble responses. Only in the 1994 HRS do the gamble respondents remain significantly more risk tolerant than the gamble respondents in the 1992 HRS.²⁹ Again the estimated effects of age and birth cohort are not altered by different specification of the time effects. The comparison of the results in Table 6 demonstrates that my parsimonious model of age, cohort, and time in the first column captures the systematic change in individuals' risk tolerance with age and macroeconomic conditions.

4.4 Individual Attributes

While there are modest changes in risk tolerance, 73% of the systematic variation in preferences is driven by the time-constant differences across individuals. The estimates in the first column of Table 7 reveal substantial differences in risk tolerance by gender, race, and years of education. The relative risk tolerance of men is 14% higher than of women -- a finding consistent with a vast literature on gender differences in risk taking; see Byrnes et al. (1999) for a meta-analysis of the studies in psychology. There is an even larger disparity in the willingness to take risk by race with blacks 28% less risk tolerant than whites. The income gambles on the HRS also reveal a strong positive association between education and risk tolerance, such that those with more than post-graduate education are 32% more risk tolerant than high school graduates. Other work that analyzes hypothetical risky choices and qualitative measures of risk taking on large-scale surveys, such as Dohmen et al. (2006) and Donkers et al. (2001), has found similar patterns for all three variables. My analysis is one of the few attempts to quantify these differences in terms of the coefficient of relative risk tolerance.³⁰

Table 7 also provides the estimated effects of marital status on risk tolerance. Entering a marriage is associated with an 11% increase in risk tolerance, though the estimate is not statistically different from zero at the 5% level. Yet less risk tolerant individuals are more likely to be consistently married in the panel. All else equal, an individual who is married at each survey is 16% less risk tolerant than an individual who is never married and the selection effect is statistically significant.³¹ Again this pattern is consistent with a stable attitude toward risk that influences actual behavior.

Finally there is a strong relationship between the measures of risk tolerance and probabilistic thinking skills in the HRS. Individuals who provide more precise answers to the subjective probability questions in the survey are also willing to take more risk on the hypothetical income gambles and exhibit less random variation in their gamble responses across survey waves. In my model of risk tolerance, I use the measure of probability precision developed by Lillard and Willis (2001), that is, the fraction of the subjective probability questions to which the individual provides an exact answer (not 0, 50, 100). There are roughly 20 such questions in each survey wave that cover future personal and general events. On average respondents only give exact answers to about 40% of the probability questions. Lillard and Willis (2001) use a model of uncertainty aversion to argue that individuals with less precise probability beliefs should be less willing to take risk.³² The results in Table 7 are consistent with their hypothesis, such that a one-standard deviation higher average FEP is associated with a 20% higher level of risk tolerance.³³ An increase in current FEP relative to the individual's panel average FEP is also associated with a substantial increase in risk tolerance.

This paper focuses on within-person changes and across-person differences in risk tolerance that are systematically related to other observed attributes. Yet, the gamble responses also imply a large amount of residual variation. The model of risk tolerance allows for an individual-specific, time-constant component of risk tolerance that is uncorrelated with the observables. In Table 7 the estimated standard deviation of this random individual effect is 0.72 which is large both in absolute terms and relative to the other estimated mean effects. As a comparison, the standard deviation of log risk tolerance that is systematically associated with the rich set of covariates is 0.41. There is even more transitory variation in the gamble responses that is unrelated to the observables. The estimated standard deviation of the response errors is 1.55 and is more than twice the standard deviation of the individual effect. The magnitude of these residuals highlights the scope for further investigation of time-constant survey response errors and transitory preference shocks.

As the first two columns of Table 7 reveal, the modelling of the response error variance affects the estimates of risk tolerance. The baseline model in the first column allows the estimated standard deviation of the transitory response errors to vary with the model covariates. The model in the second column instead imposes homoscedasticity. While the qualitative patterns in risk tolerance are largely the same, in many cases, the point estimates on the direct and type effects differ substantial across the two models of response error variance. For example, the standard deviation of men's response error is 12% larger than women's response error, so in the homoscedastic model, the estimated difference in risk tolerance by gender increases to 22% from 14% in the heteroscedastic model.³⁴ These shifts in the point estimates also reflect the nonlinearity of the maximum-likelihood model.

4.5 Measure of Individual Risk Tolerance

The model estimates can also be used to form a proxy for an individual's risk tolerance at a particular point in time. Specifically, I calculate the expected value of log risk tolerance conditional on the individual's observed attributes $x_{it}$ and $\overline{x}_{i}$ and gamble responses $c_{i}$ in the panel, such that,

E $\displaystyle (\log\theta_{it}\vert x_{it},\overline{x}_{i},c_{i} )$

$\displaystyle = x_{it}{\beta} + \overline{x}_{i}{\lambda} +$ E $\displaystyle (u_{i}\vert x_{it},\overline{x}_{i}% ,c_{it},...c_{iT})$ . $\displaystyle %$

(15)

The mean of the random effect $u_{i}$ conditional on attributes $\overline{x}_{i}$ is zero, yet an individual's set of gamble responses $c_{i}% =(c_{it},...c_{iT})$ does provide some information on the expected level of this component.³⁵

The decomposition of the preference measure into permanent and transitory components is again useful with

E $\displaystyle (\log\theta_{it}\vert x_{it},\overline{x}_{i},c_{i} )$

$\displaystyle = (x_{it}% -\overline{x}_{i}){\beta} + \overline{x}_{i}({\beta} + {\lambda}) +$ E $\displaystyle (u_{i}\vert x_{it},\overline{x}_{i},c_{i} )$

(16)

where the first term on the right is a transitory component related to changes in the observed attributes of an individual, the second term is a permanent component related to differences across individuals in their observed attributes, and the third term is a permanent component related only to the difference across individuals in their gamble responses. The variance of the systematic within-person changes in risk tolerance (the first term) accounts for only 11% of the total variance in the individual measure of risk tolerance, whereas the variance of the systematic across-person differences (the second term) accounts for 45% of the total variance. Both changes in risk tolerance over time and differences in risk tolerance across individuals contribute to the systematic heterogeneity in measured preferences, though the stable differences across individuals are empirically more important. A substantial portion of the between-person variation in the risk tolerance proxy is not related to the observables in the model.

5 STOCK OWNERSHIP

The primary reason to study preferences is to better understand behavior, so in this section I use the individual measure of risk tolerance from the gamble responses to analyze the considerable differences in stock ownership across households over the 1990s. As economic theory predicts, there is a strong positive association between the measure of risk tolerance and the holding of risky financial assets. A transitory increase in risk tolerance, as well as a persistently higher level of risk tolerance both raise the marginal probability of actual stock ownership. The measure of risk tolerance also refines the common inference on other determinants of stock ownership, including the effects of gender, education, and wealth. Finally this analysis of stock ownership highlights the usefulness and validity of the risk tolerance proxy.

To study stock ownership, I follow the financial respondents from the original HRS households over the first six waves from 1992 to 2002. The financial respondent is the individual who is most knowledgeable about the finances of the household and who reports on the income and wealth in the survey. In my analysis of stock ownership, I exclude financial respondents who are in households with no financial assets, negative net worth, or no income at any of the six survey waves. This yields a balanced panel of 2,464 financial respondents with 14,784 household-wave observations.³⁶ In the pooled sample, 46% of the financial respondents own stocks directly.³⁷ The cross-sectional rate of stock ownership varies in the panel period. Stock ownership increases from 41% of households in the 1992 HRS to 47% of households in the 2000 HRS and then decreases slightly to 45% in the 2002 HRS. Following the same respondents over the panel, 28% never hold stocks, 20% always hold stocks, and 52% change ownership status at least once.

The first column of Table 8 presents the estimated marginal effects on the probability of owning stocks for a subset of the model covariates.³⁸ The results in the first column are similar to the results in numerous studies of household portfolios, for examples, see Guiso et al. (2002). Men are 3 percentage points more likely to own stocks than women, though the effect is not precisely estimated. Higher levels of education and wealth are particularly strong predictors of stock ownership. College graduates are 19 percentage points more likely to own stocks than high school graduates. A 10% higher average wealth across individuals is associated with a 2.9 percentage point higher probability of stock ownership, and a 10% increase in wealth for a particular individual increases the probability of stock ownership by 1.4 percentage points.

The results in the second column of Table 8 show how a direct measure of risk tolerance refines the inferences on stock ownership. This model adds two measures of individual's risk tolerance: the average of log risk tolerance across the six survey waves and the deviation between current log risk tolerance and the panel average level. As economic theory predicts, both measures of risk tolerance are positively associated with stock ownership.³⁹ A 10% higher level of average risk tolerance across individuals is associated with a 1.0 percentage point higher probability of stock ownership. And a 10% increase in an individual's risk tolerance raises the probability of stock ownership by 0.9 percentage points. Both of these effects are statistically and economically significant.⁴⁰The model of risk tolerance estimated in Section 4 reveals considerable heterogeneity, so a one-standard difference in risk tolerance corresponds to a 8.2 percentage point difference in the predicted probability of stock ownership -- almost one-fifth of the actual ownership rate.

The measure of risk tolerance also refines the association between stock ownership and the other covariates. For example, the variation in risk tolerance absorbs much of the higher probability of stock ownership among men that is estimated in the first model. Likewise the effect of education on stock ownership is partially reduced when the model includes a measure of risk tolerance. Specifically, the estimated marginal effects of a college education and post-graduate education drop by 17% and 35% respectively. These results suggest that differences in risk preference can account for some of the commonly observed association between education and stock ownership. In contrast, Table 8 shows that the marginal effect of wealth on stock ownership is unrelated to differences in risk preference. Alternate explanations, such as transaction costs, are needed to explain the strong association between wealth and stock ownership, since there is no evidence of decreasing relative risk aversion. A direct measure of risk tolerance provides an opportunity to explore the mechanisms behind the large differences in stock ownership across households and over time. The strong association between the measure of risk tolerance and actual stock ownership also demonstrates that the hypothetical gambles capture meaningful differences in preferences.

6 CONCLUSION

Risk tolerance differs systematically both across individuals and over time. Most of these differences stem from characteristics, such as gender and ethnicity, that are constant over time for a particular individual; however, there are some sources of systematic change in an individual's risk tolerance, such as aging and changes in macroeconomic conditions. Other changes in individual circumstances, including the loss of a job or the end of a marriage, reveal information about individuals' risk tolerance type, not a change in their willingness to take risk.

The fact that risk tolerance differs greatly across individuals but is relatively stable for a particular individual has important consequences for studying risky behavior. The large differences in risk preference across individuals underscore the need for a direct measure of these differences. The relative stability of preferences and the correspondence between this survey measure of risk tolerance and actual risky behavior support our ability to measure risk preference at the individual level. Yet, the apparent noisiness of the hypothetical gamble responses needs to be further explored with higher frequency data and other survey questions, since the "survey response error" may be absorbing short-lived, but behaviorally important preference shocks. In addition, the gamble responses from individuals ages 45 to 70 in the HRS provide little insight on the formation of preferences, in particular on the direction of causality in the positive association between education and risk tolerance. The estimation techniques in this paper could be applied directly to this interesting question if the gambles were asked to the same individuals at different points in their education. Among individuals in their formative years, the systematic time-variation in risk preference is likely to be larger than among the older individuals in the HRS. Nonetheless, the results of this paper make clear that economic studies of behavior need to take into account the stable component of risk preference that differs systematically across individuals.

Bibliography

Barsky, R. B., Juster, F. T., Kimball, M. S. & Shapiro, M. D. (1997).

Preference parameters and behavioral heterogeneity: An experimental approach in the health and retirement study, Quarterly Journal of Economics 112(2): 537 - 579.

Brunnermeier, M. K. & Nagel, S. ( Forthcoming).

Do wealth fluctuations generate time-varying risk aversion? micro-evidence on individuals' asset allocation, American Economic Review.

Byrnes, J. P., Miller, D. C. & Schafer, W. D. ( 1999).

Gender differences in risk taking: A meta-analysis, Psychological Bulletin 125(3): 367-383.

Camerer, C. F. & Hogarth, R. M. ( 1999).

The effects of financial incentives in experiments: A review and capital-labor production framework, Journal of Risk and Uncertainty 19(1): 7-42.

Cameron, C. A. & Trivedi, P. K. ( 2005).

Microeconometrics: Methods and Applications, Cambridge University Press, New York.

Chamberlain, G. (1984).

Panel data, in Z. Griliches & M. Intriligator (eds), Handbook of Econometrics, Elsevier Science Publishers BV, Amsterdam, pp. 1248-1318.

Dohmen, T., Falk, A., Huffman, D. & Sunde, U. ( 2006).

The intergenerational transmission of risk and trust attitudes. IZA DP No. 2380.

Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J. & Wagner, G. G. (2006).

Individual risk attitudes: New evidence from a large, representative, experimentally-validated survey. CEPR DP No. 5517.

Donkers, B., Melenberg, B. & Van Soest, A. ( 2001).

Estimating risk attitudes using lotteries: A large sample approach, Journal of Risk and Uncertainty 22(2): 165-195.

Fuchs-Schuendeln, N. & Schuendeln, M. ( 2005).

Precautionary savings and self-selection: Evidence from the german reunification experiment, Quarterly Journal of Economics 120(3): 1085-1120.

Guiso, Luigi, M. H. & Jappelli, T. ( 2002).

Household Portfolios, MIT Press, Cambridge, Massachusetts.

Hall, Brownwyn H., J. M. & Turner, L. ( 2005).

Identifying age, cohort and period effects in scientific research productivity: Discussion and illustration using simulated and actual data on french physicists. Working Paper.

Holt, C. A. & Laury, S. K. (2002).

Risk aversion and incentive effects, The American Economic Review 92(5): 1644-1655.

Howrey, E. P. (2001).

The predictive power of the index of consumer sentiment, Brookings Papers on Economic Activity 2001(1): 175-207.

Kézdi, G. & Willis, R. J. ( 2006).

Who becomes a stockholder? expectations, subjective uncertainty, and asset allocation. Working Paper.

Kimball, M. S., Shapiro, M. D. & Sahm, C. R. ( Forthcoming).

Imputing risk tolerance from survey responses, Jornal of the American Statistical Association.

Lillard, L. & Willis, R. (2001).

Cognition and wealth: The importance of probabilistic thinking. Michigan Retirement Research Center Working Paper 2001-007.

Miranda, M. J. & Fackler, P. L. ( 2002).

Applied Computational Economics and Finance, The MIT Press.

Mundlak, Y. (1978).

On the pooling of time series and cross section data, Econometrica 46(1): 69-85.

Pratt, J. W. (1964).

Risk aversion in the small and in the large, Econometrica 32(1/2): 122-136.

Rabin, M. (2000).

Risk aversion and expected-utility theory: A calibration theorem, Econometrica 68(5): 1281-1292.

Ruhm, C. (1991).

Are workers permanently scarred by job displacements?, American Economic Review 81(1): 319-324.

Smith, J. P. (2003).

Consequences and predictors of new health events. NBER Working Paper No. 10063.

Stephens, M. (2001).

The long-run consumption effects of earnings shocks, Review of Economics and Statistics 83(1): 28-36.

Stigler, G. J. & Becker, G. S. ( 1977).

De gustibus non est disputandum, American Economic Review 67(2): 76-90.

Table 1: Risk Tolerance Response Categories
Response Category	Downside Risk of Risky Job: Accepted	Downside Risk of Risky Job: Rejected	Bounds on Risk Tolerance: Lower	Bounds on Risk Tolerance: Upper
1	None	1/10	0	0.13
2	1/10	1/5	0.13	0.27
3	1/5	1/3	0.27	0.50
4	1/3	1/2	0.50	1.00
5	1/2	3/4	1.00	3.27
6	3/4	None	3.27	$\infty$

NOTE: In a series of questions, respondents choose between a job with a certain income and a job with risky income. With equal chances, the risky job will double lifetime income or cut lifetime income by a specific fraction (downside risk). The largest risk accepted and the smallest risk rejected across gambles define a response category. In 1992 there are four categories 1-2, 3, 4, and 5-6. In 1994 and later surveys, the response categories range from 1 to 6. At the lower bound of risk tolerance for a category, an individual with CRRA utility is indifferent between the certain job and a risky job with the largest downside risk accepted. The upper bound similarly follows from the smallest downside risk rejected.

Table 2: Responses to Lifetime Income Gambles (% by HRS Survey Wave)
Response	1992	1994	1998	2000	2002
1	64.7	44.4	39.5	45.0	43.2
2	64.7	17.2	18.7	19.4	18.8
3	11.9	13.8	16.2	14.6	15.6
4	10.9	15.0	9.4	8.6	9.9
5	12.5	5.9	9.1	6.8	6.5
6	12.5	3.7	7.1	5.6	6.0
Responses	9,647	594	2,502	943	4,939

NOTE: Author's unweighted tabulations from HRS public access data files. The sample includes 12,003 individuals in the 1931 to 1947 birth cohorts. See the text for details on the sample selection. See Table 1 for the definition of the response category.

Table 3: Attributes at Gamble Response 1992 - 2002
Percent	1992-2002
Male	42.9
Black	14.7
Hispanic	7.5
High School Drop Out	22.0
H.S. Grad / Some College	57.2
College / Post Graduate	20.8
Job Displacement: Prior to Response	24.7
Job Displacement: After Response	12.9
Health Condition: Prior to Response	22.0
Health Condition: After Response	16.8
Married: Current Status	78.9
Married: Change in Panel	13.5
Age (Mean)	56.9
Age (Std. Dev.)	(4.5)
Fraction Exact Probability: Individual Panel Average	0.41
Fraction Exact Probability: Individual Panel (Std. Dev.)	(0.18)
Fraction Exact Probability: Current - Panel Average	0.04
Fraction Exact Probability: Current - Panel (Std. Dev.)	(0.16)
Log of Income: Individual Panel Average	10.9
Log of Income: Individual Panel (Std. Dev.)	(0.8)
Log of Income: Current - Panel Average	-0.04
Log of Income: Current - Panel (Std. Dev.)	(0.47)
Log of Wealth (Positive): Individual Panel Average	11.5
Log of Wealth (Positive): Individual Panel (Std. Dev.)	(2.5)
Log of Wealth (Positive): Current - Panel Average	-0.15
Log of Wealth (Positive): Current - Panel (Std. Dev.)	(0.75)
Responses	18,625

NOTE: Author's unweighted tabulations are from HRS public access data files and Rand HRS (Version F) data set. The sample includes 12,003 individuals. A job displacement is a job ending with a firm closure or layoff. A health condition includes heart disease, stroke, cancer, and lung disease. Fraction exact probability is the fraction of subjective probability questions to which the respondent gave a non-focal answer (not 0, 50, or 100). Wealth is the total household net worth and income is the total income of the respondent and spouse. Both variables are from the RAND HRS data and include imputations.

Table 4: Household Income and Wealth (Latent Variable: Log of Risk Tolerance)
Parameter	All Gamble Respondents	Working Household Heads
Direct Effect: $\beta$ , Log of Current Income	0.03	0.03
Direct Effect: $\beta$ , Log of Current Income (Std. Dev.)	(0.03)	(0.06)
Direct Effect: $\beta$ , Log of Positive Current Wealth	0.01	-0.03
Direct Effect: $\beta$ , Log of Positive Current Wealth (Std. Dev.)	(0.02)	(0.03)
Direct Effect: $\beta$ , Log of $\vert$ Negative Current Wealth $\vert$	0.03	0.01
Direct Effect: $\beta$ , Log of $\vert$ Negative Current Wealth $\vert$ (Std. Dev.)	(0.02)	(0.03)
Direct and Type Effects: $\beta+\lambda$ , Log of Average Income	0.09	0.14
Direct and Type Effects: $\beta+\lambda$ , Log of Average Income (Std. Dev.)	(0.03)	(0.06)
Direct and Type Effects: $\beta+\lambda$ , Log of Positive Average Wealth	0.003	-0.02
Direct and Type Effects: $\beta+\lambda$ , Log of Positive Average Wealth (Std. Dev.)	(0.014)	(0.02)
Direct and Type Effects: $\beta+\lambda$ , Log of $\vert$ Negative Average Wealth $\vert$	0.05	0.01
Direct and Type Effects: $\beta+\lambda$ , Log of $\vert$ Negative Average Wealth $\vert$ (Std. Dev.)	(0.03)	(0.04)
Log-likelihood	-23573.5	-10022.8
Number of Respondents	12,003	5,692

NOTE: Asymptotic standard errors are in parentheses. Estimates in bold are statistically significant at the 5% level. Income is total earnings, pensions, government transfers, and capital income received by the respondent and spouse in the household. Wealth is total household wealth (including housing, vehicles, businesses, and IRAs) minus all debts. The model in the first column is estimated with all the gamble responses. Appendix Table 9 provides the full set of covariates and estimates. The second column only includes gamble responses from household heads who are working.

Table 5: Job Displacements and Health Conditions (Latent Variable: Log of Risk Tolerance)
Parameter	All Gamble Respondents	Balanced Panel of HRS
Direct Effect: $\beta$ , Previous Job Displacement	-0.06	-0.11
Direct Effect: $\beta$ , Previous Job Displacement (Std. Dev.)	(0.07)	(0.08)
Direct Effect: $\beta$ , Previous Health Condition	-0.09	-0.15
Direct Effect: $\beta$ , Previous Health Condition (Std. Dev.)	(0.06)	(0.07)
Type Effect: $\lambda$ , Ever Job Displacement	0.19	0.20
Type Effect: $\lambda$ , Ever Job Displacement (Std. Dev.)	(0.06)	(0.07)
Type Effect: $\lambda$ , Ever Health Condition	0.02	0.06
Type Effect: $\lambda$ , Ever Health Condition (Std. Dev.)	(0.06)	(0.07)
Log-likelihood	-23573.5	-13426.4
Number of Respondents	12,003	6,591

NOTE: Asymptotic standard errors are in parentheses. Estimates in bold are statistically significant at the 5% level. A job displacement is a job ending with a firm closure or layoff. A health condition is heart disease, stroke, cancer, or lung disease. The model in the first column is estimated with all the gamble respondents. Appendix Table 9 provides the full set of covariates and estimates. The model in the second column only uses the gamble responses of the individuals who respond to all six HRS waves 1992-2002.

Table 6: Age, Cohort, and Time (Latent Variable: Log of Risk Tolerance)
Parameter	Alternate Specification of Time Effect (1)	Alternate Specification of Time Effect (2)	Alternate Specification of Time Effect (3)	Alternate Specification of Time Effect (4)
Age	-0.017	-0.16	-0.021	-0.021
Age (standard error)	0.008	(0.09)	0.010	0.010
Age (standard error) continued		(0.00)
1937-1941 Cohorts	0.16	0.17	0.14	0.14
1937-1941 Cohorts (standard error)	(0.06)	(0.07)	(0.07)	(0.07)
1942-1947 Cohorts (standard error) continued	0.16	0.16	0.10	0.10
1942-1947 Cohort	(0.10)	(0.11)	(0.12)	(0.12)
1942-1947 Cohort (standard error)		(0.00)
Consumer Sentiment	0.009	0.006		0.007
Consumer Sentiment(standard error)	(0.002)	(0.003)		(0.004)
ICS Six Months Ago		0.004
ICS Six Months Ago (standard error)		(0.003)
ICS One Year Ago		-0.001
ICS One Year Ago (standard error)		(0.003)
1994 HRS			0.27	0.19
1994 HRS (standard error)			(0.08)	(0.09)
1998 HRS			0.37	0.19
1998 HRS (standard error)			(0.08)	(0.11)
2000 HRS			0.32	0.12
2000 HRS (standard error)			(0.11)	(0.14)
2002 HRS			0.24	0.17
2002 HRS (standard error)			(0.11)	(0.11)
2002 HRS (standard error) continued
1992/1994 Version	-0.08	-0.05
1992/1994 Version (standard error)	(0.09)	(0.12)
Log-likelihood	-23573.5	-23571.5	-23571.2	-23569.0
Parameters	55	59	59	61

NOTE: Asymptotic standard errors are in parentheses. Estimates in bold are statistically significant at the 5% level. The sample includes 12,003 individuals. The first column is the baseline specification of the model, see Appendix Table 9 for the full set of covariates and estimates. The 1931-1936 birth cohort is the omitted cohort group. Consumer Sentiment is the value of the University of Michigan Index of Consumer Sentiment (ICS) in the month of an individual's gamble response. Over the months with HRS gamble responses, the ICS from the Survey of Consumers ranges from a low of 73.3 in October 1992 to high of 111.3 in February 2000. A gamble response on the 1992 HRS survey is the omitted wave control. The "new job" version of the income gamble question is asked in the 1992 and 1994 waves of the HRS.

Table 7: Individual Attributes (Latent Variable: Log of Risk Tolerance)
Parameter	Model Allows for Heteroscedastic Errors: Yes	Model Allows for Heteroscedastic Errors: No
Direct and Type Effects: $\beta+\lambda$ , Male	0.14	0.22
Direct and Type Effects: $\beta+\lambda$ , Male (standard error)	(0.04)	(0.03)
Direct and Type Effects: $\beta+\lambda$ , Black	-0.28	-0.12
Direct and Type Effects: $\beta+\lambda$ , Black (standard error)	(0.06)	(0.05)
Direct and Type Effects: $\beta+\lambda$ , Hispanic	-0.03	0.05
Direct and Type Effects: $\beta+\lambda$ , Hispanic (standard error)	(0.08)	(0.06)
Direct and Type Effects: $\beta+\lambda$ , High School Drop Out	0.02	0.09
Direct and Type Effects: $\beta+\lambda$ , High School Drop Out (standard error)	(0.06)	(0.04)
Direct and Type Effects: $\beta+\lambda$ , Some College	0.17	0.19
Direct and Type Effects: $\beta+\lambda$ , Some College (standard error)	(0.05)	(0.04)
Direct and Type Effects: $\beta+\lambda$ , College Graduate	0.22	0.25
Direct and Type Effects: $\beta+\lambda$ , College Graduate (standard error)	(0.06)	(0.06)
Direct and Type Effects: $\beta+\lambda$ , Post Graduate	0.32	0.40
Direct and Type Effects: $\beta+\lambda$ , Post Graduate (standard error)	(0.06)	(0.06)
Direct Effect: $\beta$ , Currently Married	0.11	0.10
Direct Effect: $\beta$ , Currently Married (standard error)	(0.09)	(0.08)
Direct Effect: $\beta$ , Fraction Exact Probability	0.82	0.52
Direct Effect: $\beta$ , Fraction Exact Probability (standard error)	(0.10)	(0.09)
Type Effect: $\lambda$ , Proportion of Years Married	-0.27	-0.23
Type Effect: $\lambda$ , Proportion of Years Married (standard error)	(0.10)	(0.09)
Type Effect: $\lambda$ , Average FEP Across Waves	0.27	-0.05
Type Effect: $\lambda$ , Average FEP Across Waves (standard error)	(0.14)	(0.12)
Std. Dev. of Individual Effect : $\sigma_{u}$ ,	0.72	0.77
Std. Dev. of Individual Effect : $\sigma_{u}$ (standard error)	(0.03)	(0.03)
Std. Dev. of Response Error: $\sigma_{e}$ ,	1.55	1.50
Std. Dev. of Response Error: $\sigma_{e}$ (standard error)	(0.01)	(0.02)
Log-likelihood	-23573.5	-23801.3
Parameters	55	29

NOTE: Asymptotic standard errors are in parentheses. Estimates in bold are statistically significant at the 5% level. The sample includes 12,003 individuals. See Appendix Table 9 for the full set of covariates and estimates. The model in the second column imposes homoscedasticity on the response errors. Fraction exact probability (FEP) is the fraction of the subjection probability questions in the survey to which an individual gives a non-focal response (not 0, 50, or 100). Covariates under the type effects are for an individual over the panel period.

Table 8: Decision to Own Stocks (Dependent Variable: Indicator of Stock Ownership)
Parameter	Marginal Effect on Probability (1)	Marginal Effect on Probability (2)
Log Risk Tolerance Individual Panel Average		0.10
Log Risk Tolerance: Individual Panel Average (standard error)		(0.03)
Log Risk Tolerance: Current - Panel Average		0.09
Log Risk Tolerance: Current - Panel Averag (standard error)		(0.04)
Male	0.03	0.01
Male (standard error)	(0.03)	(0.03)
High School Drop Out	-0.15	-0.15
High School Drop Out (standard error)	(0.03)	(0.03)
Some College	0.06	0.04
Some College (standard error)	(0.03)	(0.03)
College Graduate	0.19	0.16
College Graduate (standard error)	(0.04)	(0.04)
Post Graduate	0.11	0.07
Post Graduate (standard error)	(0.04)	(0.04)
Log of Current Wealth	0.14	0.15
Log of Current Wealth (standard error)	(0.01)	(0.01)
Log of Average Wealth	0.15	0.16
Log of Average Wealth (standard error)	(0.02)	(0.02)
Predicted Probability	0.31	0.34
Log-Likelihood	-6904.94	-6897.3

NOTE: Asymptotic standard errors are in parentheses. Estimates in bold are statistically significant at the 5% level. The correlated random effects probit is estimated on a balanced panel with 2,464 financial respondents and 14,784 total observations from the 1992 to 2002 HRS. The model of stock ownership includes all the covariates from the model of risk tolerance (see Appendix Table 9) except for the fraction of exact probability responses, job displacements and health conditions. The stock ownership model adds indicator variables for the survey waves. The marginal effect of a variable on the probability to own stocks is computed at the median values of the variables with the random effect equal to 0.

Table 9: Appendix Table: Maximum-Likelihood Estimates of Log Risk Tolerance (Latent Variable: Log of Noisy Risk Tolerance: $\xi _{it}$ )
Variable	Mean Effect: Direct	Mean Effect: Type	Mean Effect: Composite	Std. Dev.: Effect
Constant			-3.30	1.46
Constant (standard error)			(0.74)	(0.49)
Male			0.14	0.12
Male (standard error)			(0.04)	(0.02)
Black			-0.28	0.18
Black (standard error)			(0.06)	(0.03)
Hispanic			-0.03	0.10
Hispanic (standard error)			-(0.03)	(0.05)
1937-1941 Cohorts			0.16	0.003
1937-1941 Cohorts (standard error)			(0.06)	(0.04)
1942-1947 Cohorts			0.16	0.03
1942-1947 Cohorts (standard error)			(0.10)	(0.07)
High School Drop Out			0.02	0.09
High School Drop Out (standard error)			(0.06)	(0.03)
Some College			0.17	0.03
Some College (standard error)			(0.05)	(0.03)
College Graduate			0.22	-0.01
College Graduate (standard error)			(0.06)	(0.04)
Post Graduate			0.32	0.03
Post Graduate (standard error)			(0.06)	(0.04)
Index Consumer Sentiment / 10	0.09			-0.04
Index Consumer Sentiment / 10 (standard error)	(0.02)			(0.02)
Current Age / 10	-0.17			0.02
Current Age / 10 (standard error)	(0.08)			(0.05)
Currently Married	0.11			-0.07
Currently Married (standard error)	(0.09)			(0.06)
Fraction Exact Probability	0.82			-0.42
Fraction Exact Probability (standard error)	(0.10)			(0.07)
Previous Job Displacement	-0.06			0.01
Previous Job Displacement (standard error)	(0.07)			(0.05)
Previous Health Condition	-0.09			-0.05
Previous Health Condition (standard error)	(0.06)			(0.05)
Log (Current Income) / 10	0.29			0.14
Log (Current Income) / 10 (standard error)	(0.34)			(0.25)
Log (Current Wealth) / 10	0.10			-0.22
Log (Current Wealth) / 10 (standard error)	(0.17)			(0.11)
Log ( $\vert$ Current - Wealth $\vert$ ) / 10	0.35			-0.10
Log ( $\vert$ Current - Wealth $\vert$ ) / 10 (standard error)	(0.21)			(0.13)
Proportion of Years Married		-0.27		-0.05
Proportion of Years Married (standard error)		(0.10)		(0.07)
Panel Average FEP		0.27		-0.57
Panel Average FEP (standard error)		(0.14)		(0.09)
Ever Job Displacement		0.19		0.02
Ever Job Displacement (standard error)		(0.06)		(0.05)
Ever Health Condition		0.02		0.02
Ever Health Condition (standard error)		(0.06)		(0.04)
Log (Average Income) / 10		0.60		0.68
Log (Average Income) / 10 (standard error)		(0.45)		(0.30)
Log (Average Wealth) / 10		-0.07		0.31
Log (Average Wealth) / 10 (standard error)		(0.22)		(0.14)
Log ( $\vert$ Average - Wealth $\vert$ ) / 10		0.15		0.51
Log ( $\vert$ Average - Wealth $\vert$ ) / 10 (standard error)		(0.30)		(0.18)
"New Job" Version			-0.08	-0.07
"New Job" Version (standard error)			(0.09)	(0.06)

NOTE: Standard errors are in parentheses. Estimates in bold are statistically significant at the 5% level. The log-likelihood is -23573.5. The sample includes 12,003 individuals. The estimated standard deviation of the unpredictable persistent component of risk tolerance is 0.72. The standard deviation of the transitory component is $\sigma_{eit}=\exp[(x_{it}% ,\overline{x}_{i},q_{it})\sigma_{e}]$ where $\sigma_{e}$ is the parameter vector of the standard deviation effects. The gambles in the 1992 and 1994 HRS ask about a new job, whereas the wording in the later waves removes the status quo bias. See the notes on Table 4-7 and text for details on the variables.

Figure 1: Stock Market Returns and Consumer Sentiment, 1992 - 2004
NOTE: The solid line is the total annual return from the S&P 500 Total Return Index (including dividends) over the previous 12 months. The monthly value of the S&P 500 Index is the closing value on the last business day of the month. The index from Global Financial Data is adjusted for dividends and splits. The CPI-U removes general price inflation from the return. The dashed line is the current monthly value of the Index of Consumer Sentiment from the University of Michigan Survey of Consumers. The shaded areas denote months in which the HRS fielded the income gambles. These interview months for the five waves are 4/1992 to 3/1993, 5/1994 to 12/1994, 1/1998 to 3/1999, 2/2000 to 11/2000, and 4/2002 to 2/2003.

Footnotes

* Claudia R. Sahm is an Economist at the Federal Reserve Board, Washington, DC 20551 (Email: [email protected]). The author thanks Matthew Shapiro, Miles Kimball, Gary Solon, Tyler Shumway, Bob Willis, Dan Benjamin, Chris House, David Laibson, Matthew Rabin, Richard Thaler, and seminar participants at University of Michigan, University of Illinois, Rice, Ohio State University, Wharton, Michigan State University, University of Wisconsin-La Crosse, and the Federal Reserve Bank of Dallas and Board of Governors for helpful discussions. The author gratefully acknowledges the support of a National Institute on Aging Pre-Doctoral Training Fellowship and an Innovation in Social Research Award from the University of Michigan Institute for Social Research. This paper subsumes the draft previously circulated with the title "Does Risk Tolerance Change?" The views presented in the paper are those of the author and are not necessarily those of the Federal Reserve Board or its staff. Return to Text

1. The Health and Retirement Study began in 1992 as a large biennial panel survey of Americans over the age of 50 and their spouses. Further information on the survey and the data are available at http://hrsonline.isr.umich.edu. Return to Text

2. Barsky et al. (1997) and Kimball et al. (Forthcoming) both assume that any changes in an individual's gamble responses over time are noise and that constant relative risk aversion is a good approximation for utility. Furthermore these papers focus on the level of individual risk tolerance that is based only on the gamble responses. Return to Text

3. Nonetheless, Brunnermeier and Nagel's (Forthcoming) finding that transitory increases in wealth do not alter the share of risky assets held in stocks is consistent with my results. These two papers with very different types of data both support the utility specification of constant relative risk aversion. Return to Text

4. In 1992 the HRS has a representative sample of individuals age 51 to 61, that is, the 1931 to 1941 birth cohorts, plus their spouses. The spouses are not necessarily representative of their birth cohort. The HRS periodically updates its sample to maintain a snapshot of Americans over age 50. Starting in 1998, the HRS has a representative sample of individuals in the 1942 to 1947 birth cohorts that includes some of the spouses surveyed in earlier waves of the HRS. I use all of the survey responses from individuals in the 1931 to 1947 cohorts across the first six waves. I exclude the gamble responses of spouses outside these birth cohorts, as well as the representative sample of individuals in the 1921 to 1929 cohorts, since they are mostly retired at their initial survey and some express difficulty with the job-related gambles. To insure that the gamble is defined over non-trivial amounts of income, I also exclude individuals with total income less than $6,500 in 2002 dollars (or roughly the fifth percentile of income) at the time of their gamble responses or as an average across the six survey waves. The sample selection criteria have qualitatively little effect on the results. Return to Text

5. The HRS over-samples blacks, Hispanics, and residents of Florida. The tabulations and estimation in the paper place equal weight on each gamble respondent and do not reflect the distribution of attributes in the population. Return to Text

6. Wealth is the total household net worth including housing wealth and excluding pension and Social Security wealth. Income is the total income of a respondent and spouse from all earnings, transfers, and other sources of income. Wealth and income are from the RAND HRS data set and include imputed values. Return to Text

7. A description of the index is available at the Survey of Consumers (http://www.sca.isr.umich.edu). Howrey (2001) demonstrates that the index has predictive power for economic recessions. Other indicators of the macroeconomic conditions, such as the unemployment rate or real return on the S&P 500 provide qualitatively similar results. Return to Text

8. As a sensitivity check, I model wealth explicitly in the argument of the utility function, such that $c \propto y +\phi w$ , where

is the current total household income and

is 5% of total household net worth (or an approximate annuity income value of wealth). The estimated weight on wealth $\phi$ is 0.019 and is not statistically different from zero at the 5% level. Annuitization based on a life table and the respondent's age has no qualitative effect on the estimated weight. Thus the simplifying assumption of approximating consumption with income is appropriate when interpreting the gamble responses. Return to Text

9. The panel is unbalanced, so the average is $\overline{x}_{i} =(1/T_{i}\sum _{j=1}^{T} w_{it} x_{it})$ , where $T_{i}$ is the number of survey waves for individual

and $w_{it}$ is an indicator for participation in wave

. I include information on an individual's circumstances from the first six waves of the HRS, not just the waves in which an individual answers the income gambles. To make the estimated effects of an event easier to interpret, I define $x_{it}$ as an event prior to time

and $\overline{x}_{i}$ as an event before the end of the panel. Return to Text

10. Specifically, Chamberlain controls for the full set of an individual's covariates $x_{i1},...,x_{iT}$ , not just the panel average, which yields estimates of the type effects that can vary over time or $\lambda_{t}$ . One limitation of the general specification is the need for a balanced panel of the observables $x_{it}$ . This restriction would have reduced my sample of gamble respondents by 46%, so I use the more parsimonious form of the correlated random effects with the panel average of observables. Return to Text

11. Examples from the 1998 HRS interviewer records include: "I'd take the one with more money," "It's too hard for me over the phone," and "I don't have experience. Anything without experience I can't answer." The interviewer records comments made by the respondent at each question. In the 1998 HRS, there were comments to the gambles from less than 8% of individuals and many entries only noted a repetition of the question. This para-data is restricted access and its availability varies across waves. For further information contact [email protected]. Return to Text

12. Features of the gamble delivery, such as a face-to-face or a telephone interview, or differences in respondent's survey behavior, such as time to complete the interview and frequency of item non-response, could also be included in $q_{it}$ . For covariates that systematically affect both preferences and response errors, it would not be possible to separately estimate $\beta$ and $\delta$ . Return to Text

13. Previous research also finds that the use of hypothetical questions leads to more variance in responses -- not a systematic bias in the responses. In their survey of experimental studies, Camerer and Hogarth (1999) find that the size of financial incentives does not affect the average performance on judgment tasks. But smaller financial incentives are associated with greater variance or noise in the responses. Similarly Dohmen et al. (2006) establish a strong but imperfect correlation between the responses to hypothetical gambles on a large survey and gambles in an experiment with actual payoffs. Return to Text

14. The individual-specific random effect $u_{i}$ is constant over time, such that the Cov $(\xi_{is},\xi_{it}% \vert x_{is},x_{it},\overline{{x}}_{i},q_{is},q_{it})=\sigma_{u}^{2}$ for $s \ne t$ . To simplify the computation of the higher order probabilities, I integrate the product of the univariate densities conditional on $u_{i}$ over the distribution of $u_{i}$ . See Cameron and Trivedi (2005) for a further discussion of this standard method. For the integration, I use Matlab codes for Gaussian quadrature from Miranda and Fackler (2002). I use correlated random effects for the probit model of gamble responses, since there is no consistent fixed-effects estimator, see Chamberlain (1984) for a discussion. Return to Text

15. In contrast, a standard ordered probit model also estimates the cutoffs, so only the ratio of the mean effects to the unobserved standard deviation is identified. Even with known cutoffs, the identification of $\sigma_{u}$ and $\sigma_{e}$ requires that at least some individuals respond to the gambles in more than one wave. Return to Text

16. I calculate the score with numerical differentiation code from Miranda and Fackler (2002) and implement the maximum-likelihood estimator in Matlab. Return to Text

17. See Kimball et al. (Forthcoming) for more details on the distribution of risk preference estimated with a similar sample of HRS gamble responses. Return to Text

18. The net value of total household wealth is the sum of all wealth minus all debts. Wealth components include value of primary residence, net value of other real estate, net value of vehicles, net value of businesses, and net value of financial assets (IRAs, stocks, CDs, bonds, cash, and other assets). Debts include value of all mortgages, value of other home loans, and value of other debts. Total household income includes earnings, employer pensions, Supplemental Security Income, Social Security disability and retirement, unemployment and workers compensation, and other government transfers for the husband and wife plus household capital income and other income. This analysis uses RAND HRS (Version F) data and imputations for wealth and income. Return to Text

19. The absence of an effect from changes in wealth could either signal a non-integration of wealth in the evaluation of the income gamble or provide support for CRRA. The hypothetical nature of the question may also play a role in the results. In an experimental study with actual and hypothetical stakes, Holt and Laury (2002) find that changes in the magnitude of the stakes lead to changes in an individual risk aversion only when the stakes are real, but not when they are hypothetical. The largest possible payoff to a single gamble in their experiment is $346.50 and the largest change is the payoffs across their treatments is $342.65. In contrast, the stakes in the HRS gambles are defined over lifetime income where the median level of current income is $54,176 and the median deviation in current income from average income is $2,167. The large difference in the scale of the risks between their study and mine complicates a direct comparison of the results. Return to Text

20. In their index of risk aversion, Donkers et al. (2001) find that being 10 years younger has the same marginal effect as having 81% more income. On a qualitative general risk question and a hypothetical lottery question, Dohmen et al. (2006) find even smaller marginal effects, such that a one year difference in age is equivalent to more than a 75% difference in income or wealth. By my estimates, the decline in risk tolerance from a one year increase in age is equivalent to the decline in risk tolerance from current income 59% below average income or current wealth 49% below average wealth. Return to Text

21. Several studies find that a job displacement lowers current and future earnings (Ruhm, 1991), as well as reduces long-run consumption (Stephens, 2001). Likewise Smith (2003) finds that a severe health event affects household income and wealth. Return to Text

22. Alternatively, a decrease in an individual's risk tolerance following a negative income shock could also follow from a model of internal habit formation. Return to Text

23. I define a job displacement as a job ending with a business closure or a layoff. The HRS provides information on up to two jobs prior to the initial interview, the job at each interview, and jobs between interviews. I define a serious health condition as heart disease, stroke, cancer, or lung disease. The HRS asks separately about these and other conditions. Return to Text

24. In a comparison of savings in the former East and West Germany after reunification, Fuchs-Schündeln and Schündeln (2005) also find evidence of job selection due to risk preferences. They also show that ignoring this selection would underestimate precautionary wealth by 40% among German households. Return to Text

25. Note that this is a balanced panel of information on job displacements, health conditions, and other demographics, but not on the income gambles. The income gambles are only asked in five of the six survey waves and not to all respondents. Return to Text

26. Age, birth cohort, and time form a perfect relationship, that is, age

year - birth year, so the separation of the effects requires further assumptions. See Hall et al. (2005) for a discussion of various identification strategies and other references. Sample attrition that is related to an individual's risk tolerance, such as engaging in risky health behaviors that raise the chance of death, could also bias the estimates. Return to Text

27. In comments during the gamble sequences, some individuals explicitly recognize the effect of aging on risk tolerance: "Depends on how old you are. If you are 25, you gamble, but not now." and "If I were younger, I would take a chance." Other studies, including Barsky et al. (1997), Donkers et al. (2001), and Dohmen et al. (2006), also find that older individuals are less willing to take risks. But my analysis is the first to use within person variation in gamble responses to identify the effect of aging. Even though this analysis uses a rich set of covariates, there are several events that are correlated with aging and are not included in this model of risk tolerance. The current results show an negative association, but not a causal link, between aging and risk tolerance. Return to Text

28. In addition, I cannot control separately for the question version, since all the gamble respondents in the 1992 HRS and 1994 HRS answer the "new job" version of the question. Return to Text

29. The gambles on the 1994 HRS are asked in a module at the end of the survey. In the four other waves, the gambles appear near the end of the Cognition or Expectations Section of the core survey. This section is generally in the middle-end of the survey. Individuals are randomly selected to participate in the module in 1994, and they are explicitly given an opportunity to skip this extra section. The group of gamble respondents -- and the environment of the question collection -- in 1994 may not be entirely comparable to gamble responses on other waves. Return to Text

30. In their study of the income gambles on the HRS, Barsky et al. (1997) compare their measure of an individual's risk tolerance -- estimated from only the gamble responses -- across several groups. Their findings are qualitatively similar to mine. In contrast to their univariate comparisons, my analysis of risk tolerance uses a multivariate maximum-likelihood model and a richer set of covariates. Return to Text

31. This calculation adds the estimated direct effect of 11% with the type effect of -27%. The comment data also provide evidence of how a family mitigates the desire to take risks, such as "If just I, gamble, but for family go with the first." Return to Text

32. A common survey response strategy on subjective questions could provide an alternate source of covariation between an individual's gamble and probability responses. To minimize survey time and effort, some individuals may choose the "easy" answer to both questions, that is, 0-50-100 on the probabilities and reject the risky (and computationally intensive) job on the gambles. Return to Text

33. K $\acute{e}$ zdi and Willis (2006) also establish a positive association between actual stock ownership and more precise probability beliefs. The statistical model of risk tolerance that I estimate is observationally equivalent to uncertainty aversion model of Lillard and Willis (2001), but I do not explicitly test their mechanism. Return to Text

34. The estimated effects of age and income, not reported here, are also greatly affected by the error variance assumptions. The homoscedastic model estimates a 47% smaller decrease in risk tolerance with age than the baseline model (a direct effect of -1.2% under versus -1.7%). The difference in risk tolerance associated with differences in average income is 50% smaller (0.06% versus 0.09%) and no longer statistically different from zero. Return to Text

35. The variance of the conditional expectation of $\log\theta_{it}$ is much smaller than its unconditional variance. See Kimball et al. (Forthcoming) for a further discussion of how this diminished variability impacts the use of a proxy based on the conditional expectation. Return to Text

36. I follow a financial respondent even if his or her original household dissolves. This structure to the data reflects the fact that I measure risk tolerance at the individual level, but assets are typically held jointly in the household. At any wave, there is only one member of each household in my sample. Return to Text

37. The definition of stocks includes financial assets in corporate stocks, mutual funds, or investment funds and excludes stocks held indirectly in IRAs or DC-pensions. Return to Text

38. The correlated random effects probit of stock ownership estimated in Stata includes all the covariates from the model of risk tolerance (see Appendix Table 9), except for the fraction of exact probability responses, job displacements and health conditions, and adds indicator variables for the survey waves. The key exclusion restriction is that FEP does not affect stockholding directly. Its effect on stock ownership is mediated through risk tolerance. The marginal effects are computed at the sample median of the variables with the random effect set to zero. Return to Text

39. Other measures of stock ownership, such as the dollar value of stock holding and the share of financial assets held in stocks, produce qualitatively similar results. My results in the panel are consistent with the results of Barsky et al. (1997) in the cross-section. Return to Text

40. The asymptotic standard errors in the second column Table 8 do not account for the sampling variation in the risk tolerance measures which are generated from the first-step maximum-likelihood estimates. Bootstrap replications on a related, but computationally less intensive model in Kimball et al. (Forthcoming) yield only modest increases in the standard errors. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text