
Continuous Time Extraction of a Nonstationary Signal with Illustrations in Continuous Low-pass and Band-pass Filtering
Keywords: Continuous Time Processes, Cycles, Hodrick-Prescott Filter, Linear Filtering, Signal Extraction, Turning points
Abstract:
Disclaimer:
Disclaimer: This report is released to inform interested parties of research and to encourage discussion. The views expressed on statistical issues are those of the authors and not necessarily those of the U.S. Census Bureau or of the Federal Reserve Board.
1 Introduction
This paper concentrates on signal extraction in continuous-time. The goal is to set the stage for the development of coherent discrete filters in various applications. Thus, we start by setting up a fundamental signal extraction problem and by investigating the properties of the optimal continuous-lag filters . This part of the frequency and time domain analysis is done independently of sampling type and interval and so may be seen as fundamental to the dynamics of the problem.
A key result of the paper is a proof of the signal extraction formula for nonstationary models; this is crucial for many applications in economics. In discrete-time, methods for nonstationary series rely on theoretical foundations, as set out in Bell (1984). In continuous-time, Whittle (1983) sketches an argument for stationary models; a satisfactory proof of the signal extraction formula in this case is provided by Kailath, Sayed, and Hassibi (2000). Whittle (1983) also provides results for the nonstationary case, but omits proof, and in particular, fails to consider the initial value assumptions that are central to the problem.
In this paper, we extend the proof to the case of a nonstationary signal, that is, integrated of order ![]() , where
, where ![]() is an integer. We also treat the case of a white noise irregular, which is frequently used in standard models in continuous-time econometrics. Since continuous-time white noise is essentially the first derivative of Brownian motion (which is nowhere
differential), this requires a careful mathematical treatment to ensure that the signal extraction problem is well-defined.
is an integer. We also treat the case of a white noise irregular, which is frequently used in standard models in continuous-time econometrics. Since continuous-time white noise is essentially the first derivative of Brownian motion (which is nowhere
differential), this requires a careful mathematical treatment to ensure that the signal extraction problem is well-defined.
A second result is the development of a class of continuous-lag Butterworth filters for economic data. In particular, we introduce low-pass and band-pass filters in continuous-time that are analogous to the filters derived by Harvey and Trimbur (2003) for the corresponding discrete-time models, and their properties are illustrated through plots of the continuous-time gain functions. One special case of interest is the derivation of a continuous-lag filter from the smooth trend model; this gives a continuous-time extension of the popular Hodrick-Prescott (HP) filter (Hodrick and Prescott, 1997). At the root of the model-based band-pass is a class of higher order cycles in continuous-time. This class generalizes the stochastic differential equation (SDE) model for a stochastic cycle developed in Harvey (1989) and Harvey and Stock (1993).
The study of business cycles has remained of interest to researchers and policymakers for some time. Some of the early work in continuous-time econometrics was geared toward this application; Kalecki (1935) and James and Belz (1936) used a model in the form of a differential-difference equation (DDE) to describe business cycle movements. The DDE form gives an alternative to the SDE form that is of some theoretical interest; see Chambers and McGarry (2002). Its usefulness for methodology seems, however, limited since the DDE admits no convenient representation in either the time or frequency domain. The SDE form, in contrast, has an intuitive structure. In introducing the class of higher order models, we derive analytical expressions for the spectral density; this gives a clear summary of the cyclical properties of the model.
Our formulation remains general so that, for instance, it includes the Continuous-Time Autoregressive Integrated Moving Average (CARIMA) processes of Brockwell and Marquardt (2005). These follow the SDE form and so can be handled analytically. Throughout the paper, examples are given to help explain the methodology.
In focussing on continuous-time foundations in this paper, we also note the clear practical motivations for this strategy. A continuous-time approach gives flexibility in a number of directions: in the treatment of stock and flow variables in economics, in working with missing data and with irregularly spaced data, and in handling a general frequency of observation. This last point is immediately practical; even when considering just a single economic variable, with different sampling frequencies (for instance, quarterly and annual), to preserve consistency in discrete trend estimates requires a unified basis for filter design. See Bergstrom (1988, 1990) for further discussions of the advantages of continuous-time analysis.
The practical application of the continuous-time strategy is sketched at the end of this paper, and is set out in greater detail in a companion paper (McElroy and Trimbur, 2007); therein we examine how the optimal continuous-lag filter may be discretized to yield expressions for the discrete-time weights appropriate for data sampled under various conditions. The method is illustrated with a number of examples, including the continuous-time HP filter. In recent work, Ravn and Uhlig (2002), Maravall and del Rio (2001), and Harvey and Trimbur (2007) have investigated how to adapt the HP filter to monthly and annual series, given that the filter was originally designed for quarterly US GDP. We show how the continuous-time analogue of the HP filter is discretized to yield a set of consistent discrete filters, thereby solving the problem of adapting the filter.
Most previous methods rely on the discretization of the underlying continuous-time model, so that the analysis is done in discrete-time. Our approach instead uses the continuous-time formulation of filtering more directly. Thus, the method centers on the use of the underlying continuous-lag filters, on their properties, and on the transformations needed for discrete datasets.
The theoretical results derived here set the foundation for broader applications. For instance, a new class of low-pass and band-pass filters are presented in Section 4 of this paper. Further, in considering the signal extraction problem in continuous-time, we derive filters to measure velocity and acceleration of a time series, which could be useful for the analysis of turning points.
The rest of the paper is organized as follows. Section 2 reviews continuous-time filtering, based on material from Priestley (1981), Hannan (1970), and Koopmans (1974). Section 3 sets out the signal extraction framework. In section 4, examples are given for economic series; an extension of the standard HP filter is derived from the smooth trend model, and a general class of band-pass filters is presented. Extensions to methodology are then described, specifically, the conversion of continuous-lag filters to estimate growth rates and other characteristics of an underlying component. Section 5 discusses the application of the method to real series, and Section 6 concludes. Proofs are given in the Appendix.
2 Continuous-Time Processes and Filters
This section sets out the theoretical framework for the analysis of continuous-time signal processing and filtering. Much of the treatment follows Hannan (1970); also see Priestley (1981) and Koopmans (1974). Let ![]() for
for
![]() , the set of real numbers, denote a real-valued time series that is measurable and square-integrable at each time. The process is weakly stationary by definition if it has
constant mean - set to zero for simplicity - and autocovariance function
, the set of real numbers, denote a real-valued time series that is measurable and square-integrable at each time. The process is weakly stationary by definition if it has
constant mean - set to zero for simplicity - and autocovariance function ![]() given by
given by
Note that the autocovariances are defined for the continuous range of lags
where
As an example, Brockwell's (2001) Continuous-time Autoregressive Moving Average (![]() ) models can be written as
) models can be written as
Next, we define the continuous-time lag operator ![]() via the equation
via the equation
for any
The effect of the filter on a process
The requirement of integrability for the function
This development parallels the discussion in Priestley (1981), where the filter is written as
![\displaystyle \mathcal{L} [\psi] (D) = \int_{-\infty}^{\infty} \psi(x) e^{- D x} \, dx,](img47.gif)
2.1 Continuous-lag filters in the Frequency Domain
In analogy with the discrete-time case, the frequency response function is obtained by replacing ![]() by the argument
by the argument
![]() :
:
Denoting the continuous-time Fourier Transform by
Example 1
Consider a Gaussian kernel
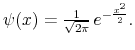 In this example, the inclusion of the normalizing constant means that the function integrates to one; since applying the filter tends
to preserve the level of the process, it could be used as a simple trend estimator. The frequency response has the same form as the weighting kernel and is given by
In this example, the inclusion of the normalizing constant means that the function integrates to one; since applying the filter tends
to preserve the level of the process, it could be used as a simple trend estimator. The frequency response has the same form as the weighting kernel and is given by
=e^{-\frac{\lambda^{2}}{2}}](img55.gif) .
.
The power spectrum of a continuous time process ![]() is the Fourier Transform of its autocovariance function
is the Fourier Transform of its autocovariance function ![]() :
:
The gain function of a filter
As in discrete time series signal processing, passing an input (stationary) process through the filter
This expression is well-defined for any integrable
Example 2
Weighting kernels that decay exponentially on either side of the observation point have often been applied in smoothing trends; this pattern arises frequently in discrete model-based frameworks, e.g., Harvey and Trimbur (2003). Similarly, in the continuous time setting, a simple example of a
trend estimator is the double exponential weighting pattern
![]() ,
,
![]() In this case, one can show using integral calculus that
In this case, one can show using integral calculus that
![]() , as a formal expression. The Fourier transform has the same form as a Cauchy probability density function, namely
, as a formal expression. The Fourier transform has the same form as a Cauchy probability density function, namely
![]() . This means that the gain of the low-pass filter
. This means that the gain of the low-pass filter ![]() decays slowly as
decays slowly as
![]()
2.2 The Derivative Filter and Nonstationary Processes
In (3), the extension of the lag operator ![]() to the continuous-time framework is made explicit. In building models, we can treat
to the continuous-time framework is made explicit. In building models, we can treat ![]() as an algebraic quantity as in the discrete-time framework. The extension of the differencing operator,
as an algebraic quantity as in the discrete-time framework. The extension of the differencing operator,
![]() , used to define nonstationary models, is discussed in Hannan (1970, p. 55) and Koopmans (1974).
, used to define nonstationary models, is discussed in Hannan (1970, p. 55) and Koopmans (1974).
To define the mean-square differentiation operator ![]() , consider the limit of measuring the displacement of a continuous-time process, per unit of time, over an arbitrarily small interval
, consider the limit of measuring the displacement of a continuous-time process, per unit of time, over an arbitrarily small interval
![]() :
:
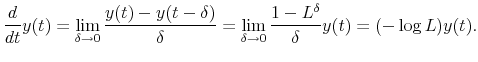
Standard discrete-time ![]() processes are written as difference equations, built on white noise disturbances. In analogy, continuous time processes can be written as differential
equations, built on an extension of white noise to continuous-time. Thus a natural class of models is the Integrated Filtered Noise processes, which are given by
processes are written as difference equations, built on white noise disturbances. In analogy, continuous time processes can be written as differential
equations, built on an extension of white noise to continuous-time. Thus a natural class of models is the Integrated Filtered Noise processes, which are given by
for some integrable
Thus, applying the derivative filter
| (A.12) |
Using the definition of
Example 3: Higher order stochastic cycles
We consider a general class of continuous-time stochastic cycles. These are indexed by a positive integer ![]() that denotes the order of the model.
that denotes the order of the model. ![]()
Denote the cyclical process by
![]() , and let
, and let
![]() represent an auxiliary process used in the construction of the model. Define
represent an auxiliary process used in the construction of the model. Define
![]()
![]() . An
. An ![]() th order stochastic cycle in continuous-time
is given by
th order stochastic cycle in continuous-time
is given by
where
![\begin{displaymath} \mathbf{A}=\left[ \begin{array}[c]{cc}% \log\rho & \lambda_{c}\ -\lambda_{c} & \log\rho \end{array}\right] \end{displaymath}](img110.gif)
Since the parameter
![]() corresponds roughly to a peak in the spectrum, it indicates a central frequency of the cycle, and 2
corresponds roughly to a peak in the spectrum, it indicates a central frequency of the cycle, and 2
![]() is an average period of oscillation. As
is an average period of oscillation. As
![]() is a frequency in continuous-time, it can be any positive real number, though for macroeconomic data, business cycle theory will usually suggest a value in some intermediate
range.
is a frequency in continuous-time, it can be any positive real number, though for macroeconomic data, business cycle theory will usually suggest a value in some intermediate
range.
To construct a Gaussian cyclical process, the increment ![]() can be derived from Brownian motion
can be derived from Brownian motion
![]() , that is,
, that is,
![]() .
.
In analyzing cyclical behavior, it is natural to consider the frequency domain properties. To derive the spectra for various ![]() , start by rewriting (13) as a
recursive formula:
, start by rewriting (13) as a
recursive formula:
![\begin{displaymath} \left[ \begin{array}[c]{ll}% D-\log\rho & -\lambda_{c}\ \lambda_{c} & D-\log\rho \end{array}\right] \left[ \begin{array}[c]{l}% \psi_{i}(t)\ \psi_{i}^{\ast}(t) \end{array}\right] =\left[ \begin{array}[c]{l}% \psi_{i-1}(t)\ 0 \end{array}\right] ,\text{ \ \ }i=1,...,n \end{displaymath}](img119.gif)
One advantage of working with the cycle in continuous-time is the possibility of analyzing turning points instantaneously. The expected incremental change in the cycle for ![]() is
is
For
Based on the smoothness of estimated cycles, the higher order models are likely to give more reliable indication of turning points.
Expression (16) is similar to the one in Harvey (1989, p. 487). There is, however, a slight difference because the form in (13) is analogous to the `Butterworth form' used in Harvey and Trimbur (2003). The alternative form in Harvey (1989) and in Harvey and Stock (1985) is analogous to the `balanced form' also considered in Harvey and Trimbur (2003). The key advantage of the Butterworth form, as used here, is its convenience for the analysis of spectra and gain functions.
We have shown that the class of models in (13) are equivalent to ![]() processes whose parameters satisfy the conditions needed for periodic behavior. As an
alternative, an openly specified model can be used to describe a general pattern of serial correlation; thus, a
processes whose parameters satisfy the conditions needed for periodic behavior. As an
alternative, an openly specified model can be used to describe a general pattern of serial correlation; thus, a ![]() could be used to capture first-order autocorrelation in the noise
component, for instance, due to temporary effects of weather. When there is clear indication of cyclical dynamics, however, the models in (13) give a more direct analysis that is easier to interpret.
could be used to capture first-order autocorrelation in the noise
component, for instance, due to temporary effects of weather. When there is clear indication of cyclical dynamics, however, the models in (13) give a more direct analysis that is easier to interpret.
The properties of a class of stochastic cycles1 are set out in Trimbur (2006) for the discrete-time case. The properties of the continuous-time models give a similar flexibility in describing periodic behavior.
Figure 1 shows the spectrum for parameter values
![]() . In particular, the function
. In particular, the function
![]() is plotted, where the normalizing constant includes the unconditional variance
is plotted, where the normalizing constant includes the unconditional variance
![]() of the cycle; this is computed in Mathematica by numerical integration of the power spectrum for given values of
of the cycle; this is computed in Mathematica by numerical integration of the power spectrum for given values of ![]() and
and ![]() . For
. For ![]() , the
damping factor is set to
, the
damping factor is set to ![]() , and for
, and for ![]() , it is set to
, it is set to ![]() . Lower values of
. Lower values of ![]() are appropriate for the higher order models because of
their resonance property. Thus, the cyclical shocks reinforce the periodicity in
are appropriate for the higher order models because of
their resonance property. Thus, the cyclical shocks reinforce the periodicity in
![]() , making the oscillations more persistent for given
, making the oscillations more persistent for given ![]() . The
difference in spectra in figure 1 indicates that the periodicity is more clearly defined for the second order cycle.
. The
difference in spectra in figure 1 indicates that the periodicity is more clearly defined for the second order cycle.
The spectrum peaks at a period around
![]() for moderate values of
for moderate values of
![]() , say
, say
![]()
![]() which is the standard business cycle range. The
maximum does not occur exactly at
which is the standard business cycle range. The
maximum does not occur exactly at
![]() , however, except as
, however, except as ![]() tends to unity. The case
tends to unity. The case
![]() gives a nonstationary cycle, where one could, in theory, forecast out to unlimited horizons. Thus, in economic modeling, attention is usually restricted to stationary models where
gives a nonstationary cycle, where one could, in theory, forecast out to unlimited horizons. Thus, in economic modeling, attention is usually restricted to stationary models where
![]() .
.
3 Signal Extraction in Continuous Time
This section develops the signal extraction problem in continuous time. A new result with proof is given for estimating a nonstationary signal from stationary noise. Whittle (1983) shows a similar result for nonstationary processes, but omits the proof and in particular, fails to recognize the
importance of initial conditions. Kailath, Sayed, and Hassibi (2000, p. 221 - 227) prove the formula for the special case of a stationary signal. We extend the treatment of Whittle (1983) by providing proofs, at the same time illustrating the importance of initial value assumptions to the result.
Further, the cases where the differentiated signal or noise process or both are ![]() are treated rigorously.
are treated rigorously.
3.1 Nonstationary signal and initial conditions
Consider the following model for a continuous time process ![]() :
:
where
In general, ![]() is any non-negative integer; the special case
is any non-negative integer; the special case ![]() reduces to
stationary
reduces to
stationary ![]() . In many applications of interest, we have
. In many applications of interest, we have ![]() , so that the
, so that the
![]() th derivative of
th derivative of ![]() denoted by
denoted by ![]() , is stationary. It is assumed that
, is stationary. It is assumed that ![]() and
and ![]() are mean zero and uncorrelated with one another. In the standard case, both autocovariance functions,
are mean zero and uncorrelated with one another. In the standard case, both autocovariance functions, ![]() and
and ![]() , are integrable. An extension could also be considered where
, are integrable. An extension could also be considered where ![]() or
or ![]() or both are represented by a multiple of the Dirac delta function, which gives rise to tempered distributions (see Folland, 1995); the associated spectral densities are flat, indicating a corresponding
or both are represented by a multiple of the Dirac delta function, which gives rise to tempered distributions (see Folland, 1995); the associated spectral densities are flat, indicating a corresponding ![]() process.
process.
The process ![]() satisfies the stochastic differential equation
satisfies the stochastic differential equation
From Section 2.2, the spectral density of
From Hannan (1970, p. 81), the nonstationary process ![]() can be written in terms of some initial values plus a
can be written in terms of some initial values plus a ![]() -fold integral of the stationary
-fold integral of the stationary ![]() . For example, when
. For example, when ![]() ,
,
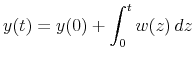
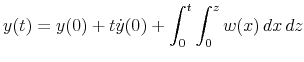
with the
For an ![]() process, let
process, let
![]() denote the collection of
denote the collection of ![]() values and higher order derivatives at time
values and higher order derivatives at time ![]() . It is assumed that
. It is assumed that
![]() is uncorrelated with both
is uncorrelated with both ![]() and
and
![]() for all
for all ![]() . This assumption is analogous to Assumption A in Bell (1984),
except that now higher order derivatives are involved.
. This assumption is analogous to Assumption A in Bell (1984),
except that now higher order derivatives are involved.
3.2 Formula for the optimal filter
Consider the theoretical signal extraction problem for a bi-infinite series ![]() that follows (17). The optimal linear estimator
of the signal
that follows (17). The optimal linear estimator
of the signal ![]() gives the minimum mean square error. Thus, the goal is to minimize
gives the minimum mean square error. Thus, the goal is to minimize
![]() such that
such that
![]() for some weighting kernel
for some weighting kernel ![]() . The
notation
. The
notation ![]() for a continuous-lag filter was introduced earlier. The problem is to determine the optimal choice of
for a continuous-lag filter was introduced earlier. The problem is to determine the optimal choice of ![]() for general nonstationary models of the form (17). The following theorem shows the main result.
for general nonstationary models of the form (17). The following theorem shows the main result.
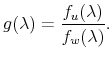
The function
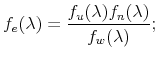
If ![]() is Gaussian, then
is Gaussian, then
![]() is optimal among all estimators. The filter
is optimal among all estimators. The filter ![]() will be referred to
as a continuous-lag Wiener-Kolmogorov (
will be referred to
as a continuous-lag Wiener-Kolmogorov (![]() ) filter. This distinguishes
) filter. This distinguishes ![]() from
discrete-time model-based filters, which are only defined over a discrete set of lags. In contrast, here we focus on the model-based filters derived in continuous-time.
from
discrete-time model-based filters, which are only defined over a discrete set of lags. In contrast, here we focus on the model-based filters derived in continuous-time.
One of the important properties of the ![]() filters is that they pass, or preserve, polynomials, in analogy to discrete-lag filters constructed to have this property in discrete-time. In
particular,
filters is that they pass, or preserve, polynomials, in analogy to discrete-lag filters constructed to have this property in discrete-time. In
particular,
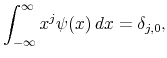
Note that the noise and differentiated signal can be either ![]() or can have integrable autocovariance functions. The signal extraction problem for different cases determines different
classes of weighting kernels. We can now define continuous-lag filters that reflect the nonstationary component of a time series.
or can have integrable autocovariance functions. The signal extraction problem for different cases determines different
classes of weighting kernels. We can now define continuous-lag filters that reflect the nonstationary component of a time series.
In particular, the nonstationarity means that the signal includes a stochastic trend and so is represented by an integrated process. First, we show a simple example of the case ![]() ; this
reduces to stationarity, so the only requirement on
; this
reduces to stationarity, so the only requirement on ![]() is continuity.
is continuity.
Example 4
For ![]() , let
, let ![]() have autocovariance function
have autocovariance function ![]() denoted by
denoted by
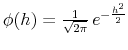 . Suppose further that
. Suppose further that ![]() has autocovariance function
has autocovariance function
![]() . Then
. Then ![]() is characterized by
is characterized by
![]() , and the associated spectral densities are
, and the associated spectral densities are
Example 5
Consider now the case ![]() , and suppose that the spectral density of the differentiated signal is
, and suppose that the spectral density of the differentiated signal is
![]() where
where ![]() has the form of the standard normal
density function, and that
has the form of the standard normal
density function, and that
![]() for some constant
for some constant ![]() . The signal extraction
filter has a continuous-time frequency response given by
. The signal extraction
filter has a continuous-time frequency response given by
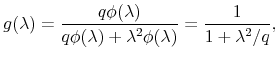
4 Illustrations of Continuous-Lag Filtering
In this section, examples of continuous-lag ![]() filters are given for economic time series. The filters are based on the class of
filters are given for economic time series. The filters are based on the class of ![]() models; this class is particularly convenient for computing
models; this class is particularly convenient for computing ![]() weighting kernels and offers flexibility for a range of
applications. The spectral densities
weighting kernels and offers flexibility for a range of
applications. The spectral densities ![]() and
and ![]() that enter the formula for
the gain are both rational functions in
that enter the formula for
the gain are both rational functions in
![]() . Taking their ratio yields another rational function in
. Taking their ratio yields another rational function in
![]() for
for
![]() As these analytical expressions summarize the comprehensive effects of the filter, they can be studied and used in filter design in different contexts.
As these analytical expressions summarize the comprehensive effects of the filter, they can be studied and used in filter design in different contexts.
We focus on examples where ![]() models are set up within different signal extraction problems. The specifications are guided by applications of interest in economics; their solutions
rely on the theorem given in the last Section for handling nonstationary series. In the first example, we start with the simplest case, the local level model. The second example considers an extension of the well-known HP filter, which has been widely used in macroeconomics as a detrending method.
We show that the expression for the continuous-lag HP filter is relatively simple, and this gives a basis for detrending data with different sampling conditions.
models are set up within different signal extraction problems. The specifications are guided by applications of interest in economics; their solutions
rely on the theorem given in the last Section for handling nonstationary series. In the first example, we start with the simplest case, the local level model. The second example considers an extension of the well-known HP filter, which has been widely used in macroeconomics as a detrending method.
We show that the expression for the continuous-lag HP filter is relatively simple, and this gives a basis for detrending data with different sampling conditions.
The third example extends the treatment with a derivation of continuous-lag low-pass and band-pass Butterworth filters. This class of filters represents the analogue of the discrete-time filters introduced in Harvey and Trimbur (2003). The band-pass filters arise naturally as cycle estimators in
a well-defined model that jointly describes trend, cyclical, and noisy movements. The general cyclical processes in continuous-time are defined in an analogous way to the discrete-time models studied in Trimbur (2006). Note that the cyclical components are equivalent to certain ![]() models. In the analysis of periodic behavior, it is more direct to work with the structural form; the frequency parameter, for instance, reflects the average, or central, periodicity.
models. In the analysis of periodic behavior, it is more direct to work with the structural form; the frequency parameter, for instance, reflects the average, or central, periodicity.
The low-pass and band-pass filters we present have the property of mutual consistency. That is, they may be applied simultaneously. Other procedures, in contrast, do not preserve this property when the two filters are designed separately, or when they are based on different source models.
It is generally straightforward to investigate the weighting kernels of the ![]() filters. This involves calculating the residues of rational functions, a standard problem for which well-known
procedures are available. Still, the computations can become burdensome in particular cases, so in presenting illustrations, we restrict attention to some standard filters. In these cases, the derivation of analytical results is feasible, with the expressions simple enough to provide a clear
interpretation.
filters. This involves calculating the residues of rational functions, a standard problem for which well-known
procedures are available. Still, the computations can become burdensome in particular cases, so in presenting illustrations, we restrict attention to some standard filters. In these cases, the derivation of analytical results is feasible, with the expressions simple enough to provide a clear
interpretation.
In the framework of ![]() filters, source models can be formulated to adapt to different situations. For instance, some series of Industrial Output are subject to weather effects that induce
short-lived serial correlation. In estimating the trend, the base model can be set up with a low-order CAR or CARMA component.
filters, source models can be formulated to adapt to different situations. For instance, some series of Industrial Output are subject to weather effects that induce
short-lived serial correlation. In estimating the trend, the base model can be set up with a low-order CAR or CARMA component.
The approach to filter design can also be adapted to focus on certain properties of the signal, such as rate of change. Thus, in a more general framework, our target of estimation becomes a functional of the signal. This opens the door to a number of potential applications, such as turning point analysis, where the interest centers on some aspect of the signal's evolution over an interval. After describing the basic principle, in a fourth example, we examine an application to measuring velocity and acceleration of signal.
Illustration 1: Local Level Model
The trend plus noise model is written as
![]() where
where ![]() denotes the stochastic level, and
denotes the stochastic level, and
![]() is continuous-time white noise with variance parameter
is continuous-time white noise with variance parameter
![]() , denoted by
, denoted by
![]() . See Harvey (1989) for discussion. An interpretation of the variance
. See Harvey (1989) for discussion. An interpretation of the variance
![]() is that
is that
![]() has autocovariance function
has autocovariance function
![]() for any (integrable) auxiliary weighting kernel
for any (integrable) auxiliary weighting kernel ![]() .
.
The local level model assumes
![]() , where
, where
![]() . The signal-noise ratio in the continuous-time framework is defined as
. The signal-noise ratio in the continuous-time framework is defined as
![]() . So the observed process
. So the observed process ![]() requires
one derivative for stationarity, and we write
requires
one derivative for stationarity, and we write
![]() . The spectral densities of the differentiated trend and observed process are
. The spectral densities of the differentiated trend and observed process are
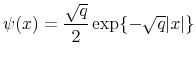
Illustration 2: Smooth Trend Model
The local linear trend model (Harvey 1989, p. 485) has the following specification:
where
Recall that the discrete-time smooth trend model underpins the well-known HP filter for estimating trends in discrete time series; see Hodrick and Prescott (1997), as well as Harvey and Trimbur (2003). Here we develop an analogous ![]() filter for the continuous-time smooth trend model. We may write the model as
filter for the continuous-time smooth trend model. We may write the model as
The spectral densities of the appropriately differentiated trend and series are
This gives the continuous-time extension of the HP filter. From the discussion following Theorem 1, the kernel in (22) passes cubics.
Figure 2 shows the weighting function for three different values of ![]() . As the signal-noise ratio increases, the trend becomes more variable relative to noise, so
the resulting kernel places more emphasis on nearby observations. Similarly, as
. As the signal-noise ratio increases, the trend becomes more variable relative to noise, so
the resulting kernel places more emphasis on nearby observations. Similarly, as ![]() decreases, the filter adapts by smoothing over a wider range. The negative side-lobes, apparent in the figure
for
decreases, the filter adapts by smoothing over a wider range. The negative side-lobes, apparent in the figure
for ![]() enable the filter to pass quadratics.
enable the filter to pass quadratics.
Illustration 3: Continuous-Lag Band-Pass
Consider again the class of stochastic cycles in Example 3. A simple (nonseasonal) model for a continuous-time process in macroeconomics is given by
In formulating the estimation of
![]() as a signal extraction problem, we set the nonstationary signal to
as a signal extraction problem, we set the nonstationary signal to
![]() and the `noise' to
and the `noise' to
![]() . This is done just to map the estimation problem to the framework developed in the last Section; it is not intended to suggest any special importance of `signal' as a target of
extraction. Actually in this case, the `noise' part will usually be of greatest interest in a business cycle analysis. Thus, the optimal filter
. This is done just to map the estimation problem to the framework developed in the last Section; it is not intended to suggest any special importance of `signal' as a target of
extraction. Actually in this case, the `noise' part will usually be of greatest interest in a business cycle analysis. Thus, the optimal filter ![]() is constructed for
is constructed for
![]() , and the complement of this filter, (
, and the complement of this filter, (![]() yields
the band-pass. Similarly, to formulate the estimation of
yields
the band-pass. Similarly, to formulate the estimation of
![]() , take
, take
![]() and
and
![]() .
.
Thus, the class of continuous-lag Butterworth filters are given by
![\displaystyle LP_{m,n}(\lambda)=\frac{\sigma_{\zeta}^{2}/\lambda^{2m}}{\frac{\sigma_{\zeta }^{2}}{\lambda^{2m}}+\sigma_{\kappa}^{2}\left[ \frac{\lambda^{2}+\log^{2}% \rho}{\left( \log^{2}\rho+{(\lambda-\lambda_{c})}^{2}\right) \left( \log^{2}\rho+{(\lambda+\lambda_{c})}^{2}\right) }\right] ^{n}+\sigma _{\varepsilon}^{2}},](img255.gif)
![\displaystyle BP_{m,n}(\lambda)=\frac{\sigma_{\kappa}^{2}\left[ \frac{\lambda^{2}+\log ^{2}\rho}{\left( \log^{2}\rho+{(\lambda-\lambda_{c})}^{2}\right) \left( \log^{2}\rho+{(\lambda+\lambda_{c})}^{2}\right) }\right] ^{n}}{\frac {\sigma_{\zeta}^{2}}{\lambda^{2m}}+\sigma_{\kappa}^{2}\left[ \frac {\lambda^{2}+\log^{2}\rho}{\left( \log^{2}\rho+{(\lambda-\lambda_{c})}% ^{2}\right) \left( \log^{2}\rho+{(\lambda+\lambda_{c})}^{2}\right) }\right] ^{n}+\sigma_{\varepsilon}^{2}},](img256.gif)
Here the order
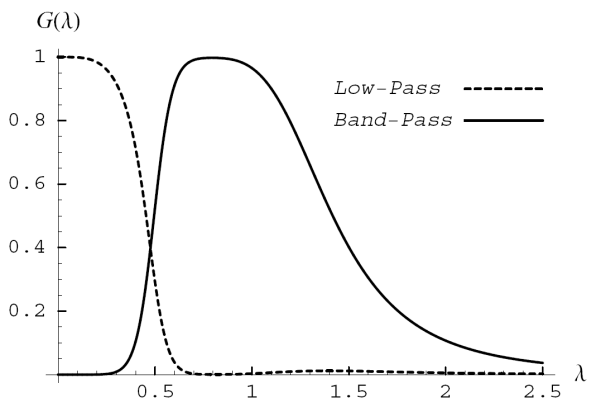 |
Figure 3 illustrates the low-pass and band-pass gain functions for trend order ![]() and cycle orders
and cycle orders ![]() The low-pass dips at intermediate frequencies to accommodate the presence of the cycle in the model. Figure 4 shows a comparison of the band-pass filter for
The low-pass dips at intermediate frequencies to accommodate the presence of the cycle in the model. Figure 4 shows a comparison of the band-pass filter for ![]() and 4. The other parameters are the same as in the previous figure. Note the increased sharpness produced by the higher order model.
and 4. The other parameters are the same as in the previous figure. Note the increased sharpness produced by the higher order model.
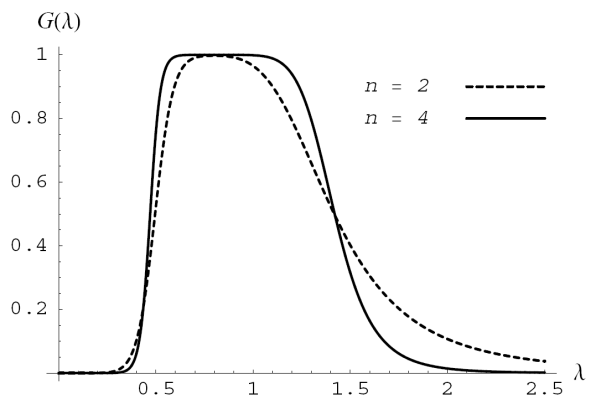 |
Illustration 4: Smooth Trend Velocity and Acceleration
In some applications, interest centers on some property of the signal, such as its growth rate, rather than on the value of the signal itself. In particular, consider the linear operator ![]() . The conditional expectation of
. The conditional expectation of ![]() is equal to
is equal to ![]() applied to the conditional expectation of
applied to the conditional expectation of ![]() , since
, since ![]() is linear. So for
Gaussian processes, assuming that
is linear. So for
Gaussian processes, assuming that
![]() is integrable - where
is integrable - where ![]() is the frequency response of the
original
is the frequency response of the
original ![]() filter - the weighting kernel for estimating
filter - the weighting kernel for estimating
![]() is given by the
is given by the ![]() th derivative of
th derivative of ![]() , that is,
, that is,
![]() . The first derivative of the signal indicates a velocity, or growth rate. The second derivative indicates acceleration, or variation in growth rate.
. The first derivative of the signal indicates a velocity, or growth rate. The second derivative indicates acceleration, or variation in growth rate.
More generally, we can consider signals ![]() with
with ![]() a linear operator. To
compute the mean squared error of
a linear operator. To
compute the mean squared error of
![]() as an estimate of the target
as an estimate of the target ![]() , multiply the error spectrum
from Theorem 1 by the squared magnitude of
, multiply the error spectrum
from Theorem 1 by the squared magnitude of
![]() . This results in the spectrum of the new error, whose integral equals the mean squared error. If, for example,
. This results in the spectrum of the new error, whose integral equals the mean squared error. If, for example, ![]() then the error spectrum is multiplied by by
then the error spectrum is multiplied by by
![]() , and the result is then integrated over (
, and the result is then integrated over (
![]() .
.
Velocity and acceleration estimates can be computed for the HP filtered signal. The filters are constructed directly from the Smooth Trend model. In Newtonian mechanics, a local maximum in a particle's trajectory is indicated by zero velocity together with a negative acceleration; similarly, velocity and acceleration indicators may be used to discern a downturn or recession in a macroeconomic series.
Since
![]() is integrable, both derivatives of
is integrable, both derivatives of ![]() are
well-defined. Direct calculation yields
are
well-defined. Direct calculation yields
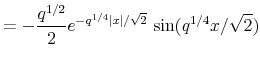 |
||
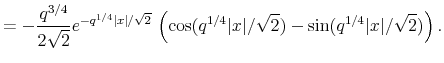 |
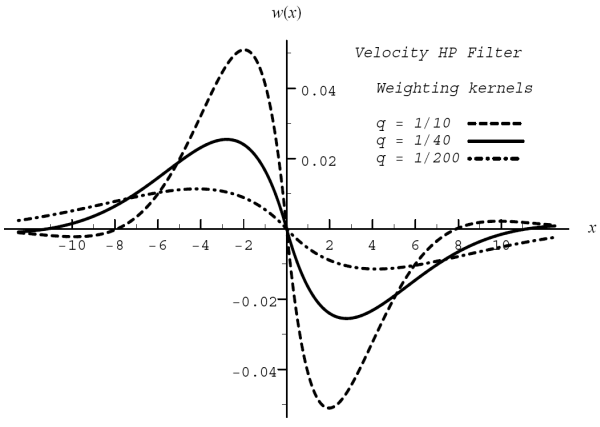
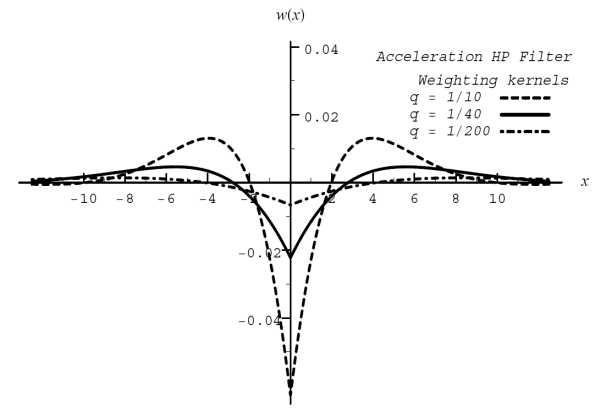
The velocity filter, or first derivative with respect to time, has the interpretation of a growth rate for the trend. The weighting kernel in Figure 5 shows how the growth in the signal is assessed by comparing forward-looking displacements with recent displacements. Likewise, the acceleration indicates the second derivative, or curvature. The weighting kernel in Figure 6 has a characteristic sharp decline around the origin, so that contemporaneous and nearby values are subtracted in estimating changes in growth.
5 Application: unequally sampled data
In this Section, we outline a procedure for the practical application of the method. The discussion of discretization is kept concise, as this material is set out in detail in McElroy and Trimbur (2007).
Starting with a base model incontinuous-time, the classification into stock and flow is reflected in the measurement of observations. Denote the underlying process by ![]() . Given the
sampling interval
. Given the
sampling interval ![]() , a stock observation at the
, a stock observation at the ![]() th time point is
defined as
th time point is
defined as
The times of observations correspond to
![]() for integer
for integer ![]() . The discrete stock time series is then the
sequence of values {
. The discrete stock time series is then the
sequence of values {
![]() .
.
A series of flow observations has the form
where
For a finite sample, let
![]() be the column vector of observations. Then for a Gaussian process
be the column vector of observations. Then for a Gaussian process ![]() , the law of iterated conditional expectations yields
, the law of iterated conditional expectations yields
That is, our best estimate of the signal at any time
- Determine
 from a fitted continuous-time model.
from a fitted continuous-time model. - Compute
![\mathbb{E}[y(z)\vert\mathbf{y}]](img293.gif) for a set of
for a set of  values on a fine mesh.
values on a fine mesh. - Compute a numerical approximation to the integral in (27) and in this way approximate the signal estimate.
Explicit worked examples are beyond the scope of this paper, but the above suggests how the continuous-lag filter could be directly applied for a general problem. Another approach, which we prefer, is to first discretize ![]() and then apply the appropriate discrete filter to the observed data
and then apply the appropriate discrete filter to the observed data
![]() , and this approach is set out in detail in McElroy and Trimbur (2007). For now, it should be emphasized that our approach, based on a continuous-lag kernel, can handle signal
estimation in a rather general context, that is, with an unequally spaced series of stock or flow data, and a with a signal time point lying in between observation times. This generality of the signal extraction problem cannot be achieved in a purely discrete-time setting and could only possibly be
achieved, with great difficulty, in an approach requiring full model discretization.
, and this approach is set out in detail in McElroy and Trimbur (2007). For now, it should be emphasized that our approach, based on a continuous-lag kernel, can handle signal
estimation in a rather general context, that is, with an unequally spaced series of stock or flow data, and a with a signal time point lying in between observation times. This generality of the signal extraction problem cannot be achieved in a purely discrete-time setting and could only possibly be
achieved, with great difficulty, in an approach requiring full model discretization.
6 Conclusion
This paper has solved the problem of establishing a theoretical foundation for continuous-time signal extraction with nonstationary models. Economic series commonly show some kind of stochastic trend. The rigorous treatment of nonstationarity given in this paper thus paves the way for the design of filters appropriate in economics. As examples we have presented a new class of low-pass and band-pass filters for time series.
In further work (see McElroy and Trimbur, 2007), we show how such continuous-lag filters may be discretized for application to real data. One special case of interest is how to adapt the HP filter to changing observation interval and to different modes of measurement, such as stock and flow
sampling. More generally, a broad range of filters may be used as the basis for analysis. In addition to model flexibility, there is also flexibility how the ![]() filters may be adapted to the
target of estimation. This has been illustrated with velocity and acceleration filters that could be used in applications where turning point indicators are of interest.
filters may be adapted to the
target of estimation. This has been illustrated with velocity and acceleration filters that could be used in applications where turning point indicators are of interest.
A key aspect of our approach is the rigor and generality of the treatment. A continuous-lag filter gives the basis for estimating a flexible target signal when the sample has various properties, such as unequal spacing, stock or flow sampling, missing data, and mixed frequency data.
Acknowledgements.
The authors thank David Findley for helpful comments and discussion.
Appendix: Proofs
Proof of Theorem 1. Throughout, we shall assume that ![]() , since the
, since the ![]() case is essentially handled in Kailath et al. (2000). In order to prove the theorem, it suffices to show that the error process
case is essentially handled in Kailath et al. (2000). In order to prove the theorem, it suffices to show that the error process
![]() is orthogonal to the underlying process
is orthogonal to the underlying process ![]() . By (20), it suffices to show that
. By (20), it suffices to show that ![]() is orthogonal to
is orthogonal to ![]() and the initial values
and the initial values ![]() . So we begin by analyzing the error process produced by the proposed weighting kernel
. So we begin by analyzing the error process produced by the proposed weighting kernel
![]() . We first note the following interesting property of
. We first note the following interesting property of ![]() . The moments of
. The moments of ![]()
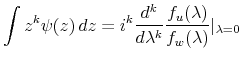
![\displaystyle \epsilon (t) = \int (\psi (x) - \Delta_0 (x)) [I^d u] (t-x)\, dx + \int \psi (x) n(t-x) \, dx,](img310.gif)
which uses the fact that
If
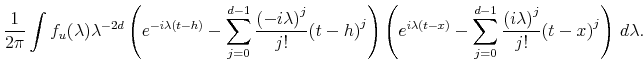
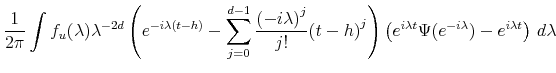 |
||
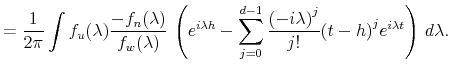 |
This uses
![\displaystyle \int \psi(x) \mathbb{E}[ n(t-x) n(t-h)] \, dx = \int \psi (x) R_n (x-h)\, dx = \frac{1}{2 \pi} \int f_n (\lambda) e^{i \lambda h } \Psi (e^{-i \lambda}) \, d\lambda.](img331.gif)
![\displaystyle \mathbb{E}[ n (t-x) n^{(j)} (0) ] = \frac{ \partial^j}{ \partial z^j} \mathbb{E}[ n(t-x) n(z) ] \vert_{z=0} = \frac{ \partial^j}{ \partial z^j} R_n (t - x - z) \vert_{z=0} = \frac{ \partial^j}{ \partial x^j} R_n (t - x )](img333.gif)
![\displaystyle \int \psi(x) \mathbb{E}[ n (t-x) n^{(j)} (0) ] \, dx = {(-1)}^j \int \psi^{(j)} (x) R_n (t-x) \, dx.](img334.gif)
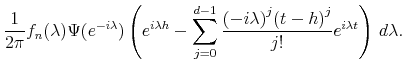
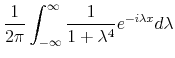
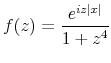
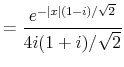 |
||
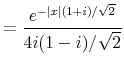 |
respectively. Summing these and multiplying by
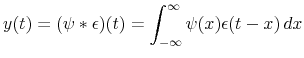
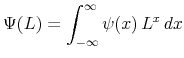
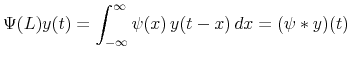
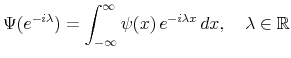
=\frac{1}{2\pi}\int_{-\infty}^{\infty}g(\lambda )e^{i\lambda x}\,dx,\quad x\in\mathbb{R}%](img60.gif)
![\displaystyle =\mathbf{A}\boldsymbol{\psi}_{i}(t)dt+\left[ \begin{array}[c]{l}% \psi_{i-1}(t)\\ 0 \end{array} \right] dt,](img102.gif)
![\displaystyle =\mathbf{A}\boldsymbol{\psi}_{1}(t)dt+\left[ \begin{array}[c]{l}% \kappa(t)\\ 0 \end{array} \right] dt,](img105.gif)
![\displaystyle \gamma_{\psi_{n}}(\lambda)=\sigma_{\kappa}^{2}\left[ \frac{\lambda^{2}% +\log^{2}\rho}{\left( \log^{2}\rho+{(\lambda-\lambda_{c})}^{2}\right) \left( \log^{2}\rho+{(\lambda+\lambda_{c})}^{2}\right) }\right] ^{n} %](img123.gif)
 %](img160.gif)
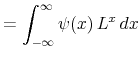
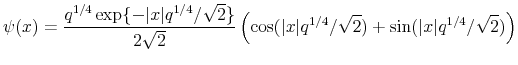
![\displaystyle LP_{m,n}(\lambda;q_{\zeta},q_{\kappa})=\frac{q_{\zeta}}{q_{\zeta}+q_{\kappa }\lambda^{2m}\left[ \frac{\lambda^{2}+\log^{2}\rho}{\left( \log^{2}% \rho+{(\lambda-\lambda_{c})}^{2}\right) \left( \log^{2}\rho+{(\lambda +\lambda_{c})}^{2}\right) }\right] ^{n}+\lambda^{2m}},%](img262.gif)
![\displaystyle BP_{m,n}(\lambda;q_{\zeta},q_{\kappa})=\frac{q_{\kappa}\lambda^{2m}\left[ \frac{\lambda^{2}+\log^{2}\rho}{\left( \log^{2}\rho+{(\lambda-\lambda_{c}% )}^{2}\right) \left( \log^{2}\rho+{(\lambda+\lambda_{c})}^{2}\right) }\right] ^{n}}{q_{\zeta}+\sigma_{\kappa}^{2}\left[ \frac{\lambda^{2}% +\log^{2}\rho}{\left( \log^{2}\rho+{(\lambda-\lambda_{c})}^{2}\right) \left( \log^{2}\rho+{(\lambda+\lambda_{c})}^{2}\right) }\right] ^{n}+\lambda^{2m}},%](img263.gif)
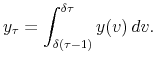
![\displaystyle \mathbb{E}[s(t)\vert\mathbf{y}]=\mathbb{E}\left[ (\psi\ast y)(t)\vert\mathbf{y}% \right] =\int\psi(t-z)\mathbb{E}[y(z)\vert\mathbf{y}]\,dz.%](img291.gif)
![\displaystyle = \int (\psi (x) - \Delta_0 (x)) \mathbb{E}\left( [I^d u] (t-x) [I^d u] (t+h) \right)\, dx](img313.gif)
![\displaystyle + \int \psi (x) \mathbb{E}\left[ n(t-x) \left(n (t-h) - \sum_{j=0}^{d-1} \frac{ {(t+h)}^j}{j!} n^{(j)} (0) \right) \right] \, dx,](img314.gif)
![\displaystyle \mathbb{E}\left[ [I^d u] (t-x) [I^d u] (t+h) \right] = \int_0^{t-x} \int_0^{t+h} \frac{ {(t-x-r)}^{d-1} {(t+h-z)}^{d-1} }{ {(d-1)!}^2 } R_u (r-z) \, dz \, dr.](img316.gif)