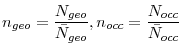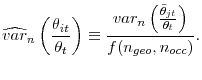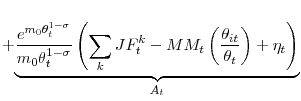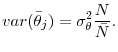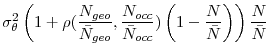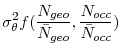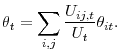What Drives Matching Efficiency?
A Tale of Composition and Dispersion*
Keywords: Matching function, matching efficiency, composition effect, mismatch.
Abstract:
JEL classifications: J6, E24, E32
1 Introduction
The unemployment rate is a major indicator of economic activity. Understanding its movements is useful in assessing the causes of economic fluctuations and their impact on welfare, as well as assessing inflationary pressures in the economy. An important determinant of the unemployment rate is the ability of the labor market to match unemployed workers to jobs. If aggregate matching efficiency declines, i.e. if fewer job matches are formed each period conditional on unemployment and vacancies, the unemployment rate increases with adverse effects on welfare and possibly inflation. Further, the effects of a decline in matching efficiency on the economy will depend on the forces behind this decline. A larger share of long-term unemployed, a larger fraction of permanent layoffs, geographic mismatch, skill mismatch, or more generous unemployment benefits can all lower aggregate matching efficiency but with differing degrees of persistence.
In this paper, we study the determinants of aggregate matching efficiency fluctuations over the last four decades.
As a first pass towards capturing changes in aggregate matching efficiency, we estimate an aggregate matching function tying levels of vacancies and unemployment to the job finding rate. While the matching function appears relatively stable over time, a testimony of the success of the matching
function, the regression residual, or aggregate matching efficiency, displays a cyclical pattern, increasing in the later stages of expansions, and declining in the early stages of recoveries. In the 2008-2009 recession however, the decline in aggregate matching efficiency started before the
recession and was a lot more pronounced, adding an estimated
![]() percentage points to the unemployment rate (Barnichon and Figura, 2010).
percentage points to the unemployment rate (Barnichon and Figura, 2010).
The first contribution of this paper is to present an empirical framework to study movements in aggregate matching efficiency. Under fairly general assumptions, we link movements in aggregate matching efficiency to two measurable factors: (i) composition of the unemployment pool, and (ii) dispersion in labor market conditions. First, if composition changes, and a group with a lower than average job finding probability (such as workers on permanent layoff) becomes over-represented among the unemployed, the average job finding probability will decline more than what a matching function would imply. Second, changes in the location and nature (e.g., skill requirements) of new jobs can lead to a misallocation of jobs and workers across labor markets and generate dispersion in labor market conditions as tight labor markets coexist with slack labor markets. Because of the concavity of the matching function, an increase in dispersion in labor market conditions will lower matching efficiency. Moreover, the effect of higher dispersion on matching efficiency may be exaggerated if workers can find a job outside of their local labor market (Abraham, 1991). To address this little studied issue, we introduce the concept of "permeability" between labor market segments. With higher permeability, workers are more likely to cross local labor market barriers and find a job in a different labor market segment, and dispersion has a weaker effect on matching efficiency.
The second contribution of this paper is to use matched CPS micro data on unemployment-employment transitions over four decades to estimate a model of job finding probability and to empirically relate aggregate matching efficiency to composition and dispersion. In addition, because the effect of misallocation on matching efficiency is a function of dispersion in labor market conditions across segments, it is crucial to observe segments at a high level of disaggregation in order to correctly assess the extent of dispersion. We thus separately consider shorter datasets that allow us to probe dispersion across more refined labor market segments. In particular, we present a new dataset on labor market tightness by occupation and geographic location covering a total of 564 segments, a 55-fold improvement over publicly available data such as the Job Openings and Labor Turnover Survey (JOLTS). Further, because 564 segments may still be well below the true number of segments in the US, we propose a method using UK data to scale up our measure of dispersion over 564 segments to a more realistic number of labor market segments.
Our main findings can be summarized as follows: (1) Changes in composition are important and generate non-trivial cyclical movements in matching efficiency. Because cyclical movements in composition are positively correlated with aggregate labor market tightness, regressions that do not control for composition estimate the matching function elasticity with an upward bias. (2) Movements in composition are mostly due to two factors: (i) an increase in the fraction of long-term unemployed during recessions, and (ii) a larger fraction of unemployed workers on permanent (rather than temporary) layoff during recessions. (3) Until 2006, changes in composition are responsible for most of the cyclical movements in matching efficiency, while dispersion appears to have played a modest role. (4) Since 2006, composition explains only 40 percent of a dramatic decline in matching efficiency. Instead, the unexplained decline coincides with an increase in dispersion in labor market conditions. Quantitatively, dispersion may account for a quarter, and perhaps more, of the unexplained decline in matching efficiency. (5) Extended unemployment benefits, reduced worker mobility caused by a distressed housing market or industry specific shocks do not seem to have significantly lowered matching efficiency.
This paper builds on a large literature studying the matching function (see Petrongolo and Pissarides (2001) for a review) and extends Bleakley and Fuhrer (1997) to identify changes in matching efficiency. While that latter study focuses on aggregate labor market tightness as the main explanatory variable of the aggregate job finding rate, we emphasize that the aggregate job finding probability is an average of probabilities across heterogeneous workers working in different segments of the labor market. Baker (1992) studies the role played by composition in explaining the counter-cyclicality of average unemployment duration. This paper extends Baker (1992) by presenting a model of job finding probability based on the concept of a matching function that takes into account individual characteristics as well as local labor market characteristics. Finally, the literature on mismatch has typically relied on a variety of dispersion measures (Padoa Schioppa, 1991, Layard, Nickell and Jackman, 2005) to capture the extent of misallocation of jobs and workers, and absent a unifying framework, there was no consensus on the most appropriate measure. This paper fills the gap by providing a dispersion measure, the variance of labor market tightness across labor market segments, that can be analytically related to matching efficiency and to the equilibrium unemployment rate.1
The next section takes a first pass at capturing changes in matching efficiency with an aggregate matching function regression. Section 3 presents a more refined empirical framework to identify the driving forces of matching efficiency, and Section 4 uses micro data to estimate that framework and discuss the results. Section 5 estimates the extent of dispersion across labor market conditions at a high disaggregation level and evaluates the effect on matching efficiency. Section 6 concludes.
2 A first look at changes in matching efficiency
The matching function relates the flow of new hires to the stocks of vacancies and unemployment. Like the production function, the matching function is a convenient device that partially captures a complex reality with workers looking for the right job and firms looking for the right worker. In a continuous time framework, the flow of hires can be modeled with a standard Cobb-Douglas matching function with constant returns to scale, and we can write
| (1) |
with
Since the job finding rate ![]() is the ratio of new hires to the stock of unemployed, we have
is the ratio of new hires to the stock of unemployed, we have
![]() so that
so that
![]() with
with ![]() =
=
![]() the aggregate labor market tightness,
the aggregate labor market tightness, ![]() =
=![]() ,
, ![]() =
=![]() and
and ![]() the labor force. To identify
the labor force. To identify ![]() , a simple approach is
thus to estimate an aggregate matching function and interpret movements in the residual as movements in matching efficiency. Specifically, we regress
, a simple approach is
thus to estimate an aggregate matching function and interpret movements in the residual as movements in matching efficiency. Specifically, we regress
with E
| (3) |
We measure the job finding rate ![]() from unemployment-employment transitions from the Current Population Survey (CPS), and we use the composite help-wanted index presented in Barnichon
(2010) as a proxy for vacancy posting.3 We use non-detrended quarterly data, allow for first-order serial correlation in the residual and estimate (2) over 1976-2007. Table 1 presents the results. The elasticity is estimated at 0.67. Using lagged values of
from unemployment-employment transitions from the Current Population Survey (CPS), and we use the composite help-wanted index presented in Barnichon
(2010) as a proxy for vacancy posting.3 We use non-detrended quarterly data, allow for first-order serial correlation in the residual and estimate (2) over 1976-2007. Table 1 presents the results. The elasticity is estimated at 0.67. Using lagged values of ![]() and
and ![]() as instruments gives similar results, and the elasticity is little changed at 0.66.
as instruments gives similar results, and the elasticity is little changed at 0.66.
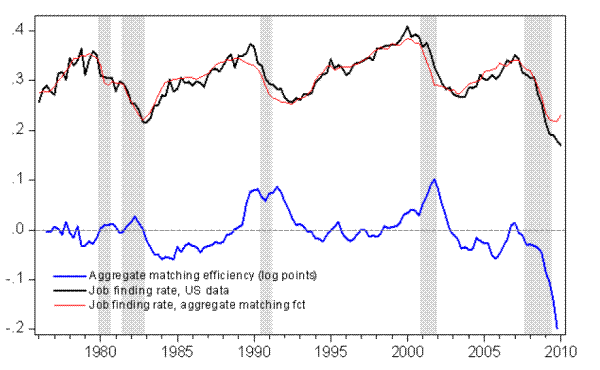
Figure 1 plots the empirical job finding rate, its fitted value, and the residual of equation (2), i.e., ![]() the movements in aggregate matching efficiency.
A first observation is that the matching function appears relatively stable over time, a corollary of the success of the matching function. However, aggregate matching efficiency displays a clear cyclical pattern, and typically lags the business cycle, increasing in the later stages of expansions,
peaking in the late stages of recessions or the early stages of recoveries, and declining thereafter. In the 2008-2009 recession however, the decline in matching efficiency occurred earlier than in previous recessions and was a lot more pronounced. In the fourth quarter of 2009, the residual
reached an all time low of four standard-deviations. 4 The expansion period preceding the 2008-2009 recession also appears peculiar, because the increase in
matching efficiency that typically occurs before recessions was a lot more muted.
the movements in aggregate matching efficiency.
A first observation is that the matching function appears relatively stable over time, a corollary of the success of the matching function. However, aggregate matching efficiency displays a clear cyclical pattern, and typically lags the business cycle, increasing in the later stages of expansions,
peaking in the late stages of recessions or the early stages of recoveries, and declining thereafter. In the 2008-2009 recession however, the decline in matching efficiency occurred earlier than in previous recessions and was a lot more pronounced. In the fourth quarter of 2009, the residual
reached an all time low of four standard-deviations. 4 The expansion period preceding the 2008-2009 recession also appears peculiar, because the increase in
matching efficiency that typically occurs before recessions was a lot more muted.
3 A framework to study movements in matching efficiency
In this section, we present a general framework to investigate the factors responsible for movements in aggregate matching efficiency. In particular, we identify two observable factors that affect aggregate matching efficiency: the composition of the unemployment pool, and the amount of dispersion in labor market conditions. The former arises if the characteristics of the unemployed change throughout the cycle, making job finding more or less likely, while the latter is caused by the concavity of the matching function and arises if tight labor markets coexist with slack labor markets.
3.1 Composition and dispersion
Denote ![]() the job finding probability of an individual of type
the job finding probability of an individual of type ![]() in labor
market segment
in labor
market segment ![]() .5 A labor market segment can be
defined by its geographic location, industry group or occupation group. The labor market segment
.5 A labor market segment can be
defined by its geographic location, industry group or occupation group. The labor market segment ![]() of individual type
of individual type ![]() can then be thought of as the labor market in which individual
can then be thought of as the labor market in which individual ![]() is most likely to look for work and to find a job. Typically, this will be proxied by his
location and past employment history. Individual type
is most likely to look for work and to find a job. Typically, this will be proxied by his
location and past employment history. Individual type ![]() is defined by a vector of
is defined by a vector of ![]() characteristics
characteristics
![]() , and labor market segment
, and labor market segment ![]() is characterized by its
labor market tightness (or vacancy-unemployment ratio)
is characterized by its
labor market tightness (or vacancy-unemployment ratio)
![]() . Because an unemployed worker may also look outside of his labor market segment, his job finding probability may also depend on the aggregate labor market tightness
. Because an unemployed worker may also look outside of his labor market segment, his job finding probability may also depend on the aggregate labor market tightness
![]() .6
.6
Thus, we postulate that the job finding probability of individual type ![]() in labor market i can be written
in labor market i can be written
| (4) |
so that the average job finding rate is given by
To highlight the effects of composition and dispersion on the average job finding probability, we take a second-order Taylor of expansion of ![]() with respect to
with respect to
![]() around
around
![]() and
and ![]() around
around
 with
with
![]() and
and
![]() the
the ![]() th observable characteristics of individual
th observable characteristics of individual ![]() , and we get7
, and we get7
The first term in (6),
3.1.0.1 Composition:
The second term in (6),
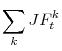 , captures the total composition effect with
, captures the total composition effect with
![]() , the contribution of a given characteristic
, the contribution of a given characteristic ![]() to the average job finding
probability8
to the average job finding
probability8
The composition effect arises because of worker heterogeneity. If the share
![]() of a demographic group (e.g. job losers) with a lower than average job finding probability (i.e.,
of a demographic group (e.g. job losers) with a lower than average job finding probability (i.e.,
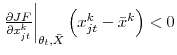 ) increases in recessions, then the average job finding probability will decline without any change in individuals' job finding probabilities.
) increases in recessions, then the average job finding probability will decline without any change in individuals' job finding probabilities.
3.1.0.2 Dispersion:
The third term in (6) captures the effect of dispersion in labor market conditions on the average job finding probability with
and
3.2 Postulating a functional form for 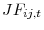
To bring our framework to the data, we need to posit a functional form for the job finding probability ![]() . We adopt a logistic functional form
. We adopt a logistic functional form
with
This specification has a number of advantages:
First, a logistic functional form is consistent with the fact that the job finding probability falls between 0 and 1.
Second, in the absence of worker heterogeneity (
![]() ) and labor market dispersion (
) and labor market dispersion (
![]() ), (9) reduces to
), (9) reduces to
![]() , the reduced-form aggregate specification (2) with
, the reduced-form aggregate specification (2) with
![]() .
.
Third, to relate
![]() and
and
![]() to the job finding probability of individual type
to the job finding probability of individual type ![]() , we assume that the
job finding probability is a geometric average of local labor market tightness
, we assume that the
job finding probability is a geometric average of local labor market tightness
![]() and the aggregate labor market tightness
and the aggregate labor market tightness
![]() . Put differently, we allow for the possibility that a worker crosses barriers between labor market segments, so that his job finding probability is not solely a function of
tightness in his local labor market. To get some intuition, consider the simpler case without worker heterogeneity. The job finding rate of a worker in segment
. Put differently, we allow for the possibility that a worker crosses barriers between labor market segments, so that his job finding probability is not solely a function of
tightness in his local labor market. To get some intuition, consider the simpler case without worker heterogeneity. The job finding rate of a worker in segment ![]() becomes
becomes
![]() , i.e. a weighted (geometric) average of the segment labor market tightness and
the aggregate labor market tightness. The weight
, i.e. a weighted (geometric) average of the segment labor market tightness and
the aggregate labor market tightness. The weight
![]() captures the impermeability of the local labor market. If
captures the impermeability of the local labor market. If ![]() , labor market segments are impossible to cross, and aggregate labor market tightness has no impact on the local job finding rate. In contrast, if there are no barriers between labor markets,
, labor market segments are impossible to cross, and aggregate labor market tightness has no impact on the local job finding rate. In contrast, if there are no barriers between labor markets, ![]() , a worker's job finding rate only depends on the aggregate labor market tightness.
, a worker's job finding rate only depends on the aggregate labor market tightness.
3.3 A decomposition of aggregate matching efficiency
Thanks to our decomposition (6), we can now link movements in aggregate matching efficiency to the composition of the unemployment pool and the amount of dispersion in labor market conditions. After some manipulation of (6) left for the Appendix,
![]() E
E
![]() , the deviations of aggregate matching efficiency from its average value, can be written
, the deviations of aggregate matching efficiency from its average value, can be written
with
and
Aggregate matching efficiency ![]() is a function of the distribution of individual characteristics and labor market segments' tightness. Movements in aggregate matching efficiency can be
decomposed into a composition effect, the first term on the right-hand side of (10), a dispersion (or misallocation) effect, the second term, and an unexplained component (that includes the approximation error), the last term.
is a function of the distribution of individual characteristics and labor market segments' tightness. Movements in aggregate matching efficiency can be
decomposed into a composition effect, the first term on the right-hand side of (10), a dispersion (or misallocation) effect, the second term, and an unexplained component (that includes the approximation error), the last term.
Expression (11) describes the effect of misallocation (also called mismatch) on aggregate matching efficiency. Three observations are worth noting. First, the effect of misallocation is roughly proportional to the variance of labor market tightness, so that one can
readily estimate the effect of misallocation by looking at the dispersion in labor market conditions.10 The literature on mismatch has used various
measures to quantify the effect of misallocation on the unemployment rate. For example, some use
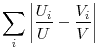 (e.g., Jackman and Roper 1987, Franz 1991, Brunello 1991), others unemployment rate dispersion measures
(e.g., Jackman and Roper 1987, Franz 1991, Brunello 1991), others unemployment rate dispersion measures
![]() or
or
 (e.g., Jackman, Layard and Savouri (1991), Attanasio and Padoa Schioppa (1991)), others
(e.g., Jackman, Layard and Savouri (1991), Attanasio and Padoa Schioppa (1991)), others
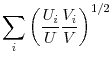 (Bean and Pissarides, 1991), and others
(Bean and Pissarides, 1991), and others
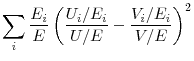 (Layard, Nickell and Jackman, 1991) with
(Layard, Nickell and Jackman, 1991) with ![]() the number of employed workers in segment
the number of employed workers in segment ![]() and
and ![]() the total number of employed workers. Some measures were constructed using employment or labor force weights (but surprisingly, rarely unemployment weights), but other measures did not weight observations. While all these measures capture the extent
of dispersion across labor markets, absent a unifying framework, there was no consensus on the most appropriate measure. The measure we propose has an important advantage over these other measures: It can be directly related to aggregate matching efficiency and thus to the equilibrium unemployment
rate (Barnichon and Figura, 2010).11
the total number of employed workers. Some measures were constructed using employment or labor force weights (but surprisingly, rarely unemployment weights), but other measures did not weight observations. While all these measures capture the extent
of dispersion across labor markets, absent a unifying framework, there was no consensus on the most appropriate measure. The measure we propose has an important advantage over these other measures: It can be directly related to aggregate matching efficiency and thus to the equilibrium unemployment
rate (Barnichon and Figura, 2010).11
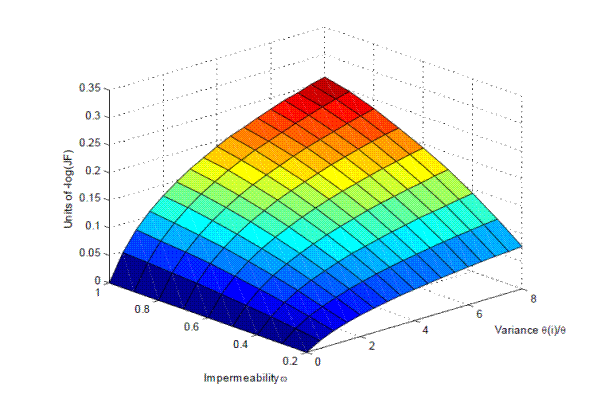
Second, while the mismatch literature imposes tight labor market segments boundaries, our framework allows for some permeability between labor market segments. The effect of dispersion on the average job finding rate and matching efficiency depends on ![]() . For the range of plausible values for
. For the range of plausible values for ![]() and
and
![]() , the effect of dispersion increases with barriers between labor market segments (i.e. when
, the effect of dispersion increases with barriers between labor market segments (i.e. when ![]() increases) and is strongest when labor market segments' barriers are infinite. Conversely, with higher permeability, workers are more likely to cross local labor market barriers and find a job in a different labor market, and this possibility weakens
the effect of dispersion on aggregate matching efficiency.
increases) and is strongest when labor market segments' barriers are infinite. Conversely, with higher permeability, workers are more likely to cross local labor market barriers and find a job in a different labor market, and this possibility weakens
the effect of dispersion on aggregate matching efficiency.
Finally, because average dispersion is positive (
![]() ,
, ![]() ), the effect
of misallocation on aggregate matching efficiency movements
), the effect
of misallocation on aggregate matching efficiency movements ![]() is not given by
is not given by ![]() , the level of dispersion, but by
, the level of dispersion, but by
![]() , the deviations of dispersion from its average level.
, the deviations of dispersion from its average level.
4.1 Estimation
We use matched data from the Current Population Survey (CPS) covering January 1976 to December 2007 to estimate the Unemployment-Employment (UE) transition probability for an individual ![]() in labor market market segment
in labor market market segment ![]() . We restrict the estimation to pre-2008 data so that any changes in matching efficiency post 2007 do not affect our coefficient estimates. In 1994, a major
redesign of the CPS survey was implemented and introduced breaks in many important variables, such as reason for unemployment and duration of unemployment.12 To control for these breaks, we estimate separate coefficients for the pre and post redesign periods. Our whole sample contains about 1.2 million observations.
. We restrict the estimation to pre-2008 data so that any changes in matching efficiency post 2007 do not affect our coefficient estimates. In 1994, a major
redesign of the CPS survey was implemented and introduced breaks in many important variables, such as reason for unemployment and duration of unemployment.12 To control for these breaks, we estimate separate coefficients for the pre and post redesign periods. Our whole sample contains about 1.2 million observations.
In this section, we present the individual characteristics that influence the job finding probability, discuss our method for measuring labor market tightness by segment, and present results.
4.1.0.1 1. Controlling for individual characteristics
The CPS data provides information allowing us to control for changes in the characteristics of the unemployed. We use three main types of information: demographic, reason for unemployment and duration of unemployment, and we include a set of monthly dummies to control for seasonality in job finding probabilities.13
Demographic information includes the age and sex of the unemployed individual. We model the effect of age on the job finding probability using a quadratic in age. The CPS distinguishes between 5 main reasons for unemployment: permanent layoff, temporary layoff, new labor force entrant, reentering the labor force, and quit job. We use dummy variables for each reason. The CPS records the duration (in weeks) of individuals' current spells of unemployment, which we allow to linearly affect the probability of exit.
Prior research suggests that the job finding probability declines with duration, and two reasons are often cited. First, prolonged unemployment may lower individuals' skills relative to other job seekers, making them less desirable to employers, or it may reduce their contacts in job-finding networks, making it harder to find employment. Henceforth, we describe this effect as scarring. Second, prolonged unemployment may signal that the individuals have unobserved characteristics that make it difficult to find employment. Prolonged unemployment may also capture unobserved circumstances. For instance, an individual may be looking for work in a too narrow (relative to data availabilities), and hence unobservable, labor market segment with a very low vacancy-to-unemployment ratio. As such workers remain in the unemployment pool longer, the unobserved circumstances will be correlated with unemployment duration. Thus, unobserved characteristics or circumstances may be responsible for duration's ability to predict the job finding probability.
Average unemployment duration is also likely affected by aggregate labor market conditions. When labor demand is low, it typically takes unemployed individuals longer to find jobs, and durations rise. Thus, the signal about job finding prospects from an individual's unemployment duration may be weaker when average durations are higher. To allow the signal from an individual's unemployment duration to change as aggregate conditions change, we interact an individual's duration with the average duration, which is highly countercyclical. In effect, this specification allows the slope of the relationship between job finding and duration to change as aggregate conditions change.
4.1.0.2 2. Measuring labor market tightness by segment
To estimate the effect of dispersion in
![]() on aggregate matching efficiency, we need vacancy posting data by industry and region going back to 1976. Moreover, since the effect of misallocation arises out of the concavity
of the matching function, it is important to reach a good level of disaggregation as dispersion increases with the number of observed segments. Unfortunately, the two data sources with vacancy posting data, the JOLTS and the Help-Wanted Indexes (HWI) from the Conference Board do not satisfy these
criteria. JOLTS is only available since December 2000, and while the JOLTS measure of job openings can be disaggregated into 10 industry groups, the survey's sample size is too small to allow for a disaggregation by regions and industries.14 The HWI can be disaggregated by regions (the nine US Census divisions), but not by industry.
on aggregate matching efficiency, we need vacancy posting data by industry and region going back to 1976. Moreover, since the effect of misallocation arises out of the concavity
of the matching function, it is important to reach a good level of disaggregation as dispersion increases with the number of observed segments. Unfortunately, the two data sources with vacancy posting data, the JOLTS and the Help-Wanted Indexes (HWI) from the Conference Board do not satisfy these
criteria. JOLTS is only available since December 2000, and while the JOLTS measure of job openings can be disaggregated into 10 industry groups, the survey's sample size is too small to allow for a disaggregation by regions and industries.14 The HWI can be disaggregated by regions (the nine US Census divisions), but not by industry.
Instead, we use the unemployment rate to proxy for the labor market tightness in a particular segment. Regional and industry data on vacancy posting from the JOLTS over 2000-2010 show that vacancies and unemployment rates are highly negatively correlated across regions or industries, and that
![]() is a very good proxy for
is a very good proxy for
![]() with no apparent break over 2008-2009. 15 We use the CPS micro data to estimate unemployment rates for each segment. Since new entrants to the labor force cannot be easily classified in a particular industry, we use the average unemployment rate in their state of residence. While the CPS sample is large (about
60,000 households) and allows for a higher level of disaggregation over 1976-2009 than available vacancy data, we nonetheless face some limitations regarding the degree of disaggregation we can achieve. We define 150 segments based on the cross product of 50 states and three broad industry
groups.16 Our three broad industry groups roughly correspond to goods producing, business/health care/educational services, and other services.17
with no apparent break over 2008-2009. 15 We use the CPS micro data to estimate unemployment rates for each segment. Since new entrants to the labor force cannot be easily classified in a particular industry, we use the average unemployment rate in their state of residence. While the CPS sample is large (about
60,000 households) and allows for a higher level of disaggregation over 1976-2009 than available vacancy data, we nonetheless face some limitations regarding the degree of disaggregation we can achieve. We define 150 segments based on the cross product of 50 states and three broad industry
groups.16 Our three broad industry groups roughly correspond to goods producing, business/health care/educational services, and other services.17
Accordingly, we estimate the slightly modified form of equation (9)
by maximum likelihood with
4.2.1 Coefficient estimates
Table 2 reports our coefficient estimates. The coefficient on the aggregate vacancy-unemployment ratio is highly significant but is lower than the coefficient estimated in Section 2 using only aggregate labor market tightness. This suggests that characteristics and/or dispersion are on average procyclical, and that failing to control for those parameters biases estimates of the aggregate matching function elasticity upward.
The impermeability coefficient of labor market segments is significantly smaller than one (
![]() ). While barriers between labor market segments appear to be non trivial, they are also not insurmountable. As a result, the effect of labor market
tightness on exit hazards within a segment (
). While barriers between labor market segments appear to be non trivial, they are also not insurmountable. As a result, the effect of labor market
tightness on exit hazards within a segment (
![]() ) is not as great as the effect of aggregate labor market tightness (
) is not as great as the effect of aggregate labor market tightness (
![]() .
.
Turning to individual characteristics, JF is decreasing in unemployment duration. Using (6) and (7), the coefficient on unemployment duration implies that having a spell of unemployment lasting 6 months is associated with a decrease in an
individual's job finding probability of about 1-
![]() percentage point. However, the coefficient on the interaction of individual and aggregate duration implies that this effect is mitigated if the average unemployment duration is
also high. In other words, the slope of the relationship between job finding and unemployment duration becomes flatter in downturns. As a result, increases in duration in a cyclical downswing do not send as strong a signal about reduced job finding probabilities as in other periods because these
increases reflect, in part, changes in aggregate conditions, which we have already controlled for.
percentage point. However, the coefficient on the interaction of individual and aggregate duration implies that this effect is mitigated if the average unemployment duration is
also high. In other words, the slope of the relationship between job finding and unemployment duration becomes flatter in downturns. As a result, increases in duration in a cyclical downswing do not send as strong a signal about reduced job finding probabilities as in other periods because these
increases reflect, in part, changes in aggregate conditions, which we have already controlled for.
The estimates of the effect of the reason for unemployment on the job finding probability are relative to that of a job leaver. The estimates reveal that it is particularly difficult for permanent job losers and new entrants to the labor force to find employment. Unsurprisingly, workers on temporary layoff have an easier time becoming reemployed. As expected, the CPS redesign, by restricting temporary layoffs to individuals expecting to be recalled within 6 months, increased the difference in exit hazards for permanently and temporarily laid off workers.
Turning to demographics, the coefficient on the male dummy indicates that males are more likely to find jobs than females. However, a comparison of the pre and post redesign coefficients shows that this relative advantage has lessened over time. The estimated coefficients on the age variables indicate that the probability of job finding initially increases and then decreases with age. In the pre redesign period, the age with the highest job finding probability is around 30. In the post redesign period, it is close to 17.
4.2.2 The effect of individual characteristics and dispersion on the job finding probability
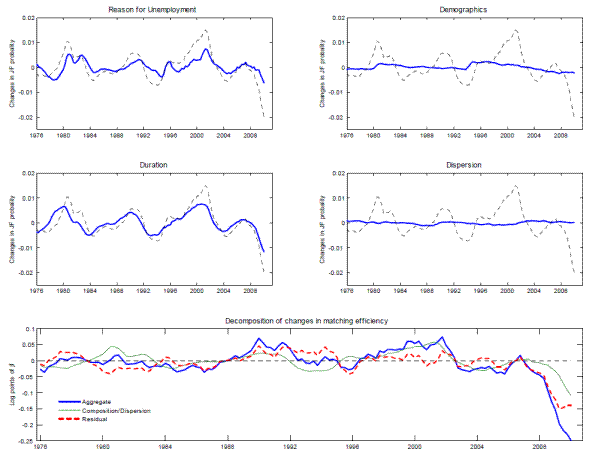
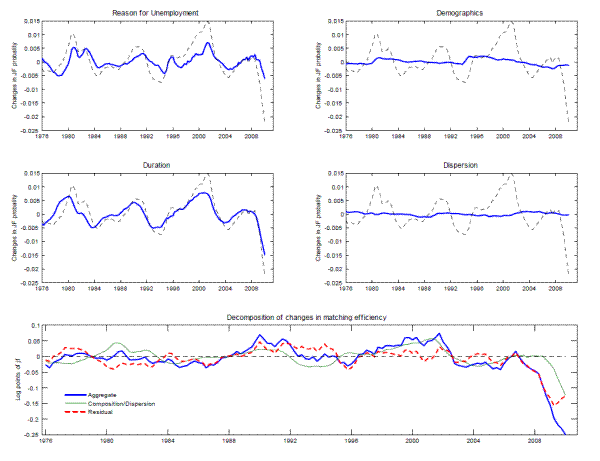
Next, we use our decomposition (6) to estimate the effect of individual characteristics and labor market dispersion on the average job finding probability over 1976-2009. Figure 2 graphs
![]() , the contributions of characteristics -reason for unemployment, unemployment duration, demographics-, and
, the contributions of characteristics -reason for unemployment, unemployment duration, demographics-, and ![]() , the contribution of dispersion in labor market tightness, to
, the contribution of dispersion in labor market tightness, to ![]() .
.
The contribution of reason for unemployment is procyclical, falling in recessions and rising in recoveries. This pattern owes, in part, to an increasing share of permanent job losers and a declining share of temporary job losers during recessions. The contribution of duration is also procyclical. Although the coefficient on the interaction term suggests that the effect of duration on job finding probabilities is reduced in recessions, longer duration always implies a lower job finding probability. This indicates that some of the increase in individual durations during cyclically weak periods reflects scarring or unfavorable unobserved circumstances.
Demographics generate a downward trend in the average job finding probability over the sample period, as the labor force ages and women's share of the labor force increases, before leveling out at the end of the sample, as the share of men in the unemployment pool increases. Consistent with Baker (1992), demographic characteristics have little influence on the cyclical behavior of the job finding probability. Finally, the effect of dispersion on the job finding probability, given by (8), is very small because the cross-sectional variance of relative labor market tightness is too small, at least for the segments we observe, for misallocation to have a noticeable effect on aggregate matching efficiency.
4.2.3 Movements in aggregate matching efficiency
Using decomposition (10), the lower panel of Figure 2 presents movements in aggregate matching efficiency, in a similar fashion to Figure 1 , but allowing for a
richer specification than the reduced-form approach ( 2) from Section 2. The plain thick line is analogous to the residual of Figure 1 and shows ![]() , the total
movements in aggregate matching efficiency, given by (10). The plain thin line plots
, the total
movements in aggregate matching efficiency, given by (10). The plain thin line plots
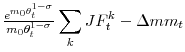 , the effect of composition and dispersion on
, the effect of composition and dispersion on ![]() . Finally, the dotted line plots the difference between the two other lines, i.e.
. Finally, the dotted line plots the difference between the two other lines, i.e.
![]() , the changes in aggregate matching efficiency that cannot be accounted for by composition or dispersion.
, the changes in aggregate matching efficiency that cannot be accounted for by composition or dispersion.
Up until 2006, composition accounted for most of the cyclical movements in aggregate matching efficiency. Changes in composition make aggregate matching efficiency procyclical because, as noted above, (i) the fraction of long-term unemployed increases during recessions, and (ii) a larger fraction of unemployed workers is on permanent layoff during recessions. Interestingly, the muted increase in aggregate matching efficiency in the run-up to the 2008-2009 recession can also be explained by composition, with both (i) and (ii) playing a role and demographics contributing to a downward trend in matching efficiency. Prior to 1994, the ability of composition to account for matching efficiency movements is not as good, and this is probably due to the quality of the data and the loose distinction between temporary and permanent layoff before 1994.19
Since 2007, a large fraction of the decline in aggregate matching function efficiency has been due to unobserved factors. Initially, the deterioration in late 2007 and 2008 owed almost entirely to unobservable factors, as observable components were relatively constant. Thereafter, observable factors, especially unemployment duration and reason for unemployment, began to contribute to the deterioration, and this contribution has grown steadily, while the unexplained component has been relatively constant. As a result, as of 2009Q4, observable factors account for about 40 percent of the decline in aggregate matching efficiency since 2007, while unobserved factors account for the remainder.
After controlling for dispersion and observed characteristics, the unexplained decline in matching efficiency amounts to about 0.15 log points in end 2009, compared to 0.20 log points (Figure 1) using a reduced-form regression (2) that only conditioned on aggregate labor market tightness. It is perhaps surprising that the difference between these two numbers is not larger given that changes in the composition of the unemployed have led to a deterioration in matching efficiency and are responsible for 40 percent of the total decline. The reason is that the deterioration in matching efficiency caused by changes in observed characteristics is in line with what one would have predicted conditioning on aggregate labor market tightness. As a result, these effects were already captured (in a reduced form sense) by the aggregate matching function regression. As mentioned above, the coefficient in the aggregate regression is larger than in a regression using micro data, because it reflects the correlation between aggregate labor market tightness and the characteristics of the unemployed.
4.2.4 Digging further: matching efficiency in the 2008-2009 recession
To try to understand the unexplained portion of the recent decline in aggregate matching efficiency, we explore several other estimation specifications.
4.2.4.1 Allowing for a break after 2007
First, we estimate (12) over 1976-2009 and allow for breaks in the coefficients on the right-hand-side variables after 2007. Specifically, each right-hand-side variable is interacted with a dummy variable equal to 1 after 2007. If the deterioration in matching efficiency is related to a larger contribution of permanent job losers or older workers, for example, then the post-2007 coefficients on permanent job loss or age should change to reflect this fact. If, however, the deterioration is not related to the observed characteristics of the unemployed, then it will be reflected by changes in the coefficients of the aggregate matching function.
Table 3 shows our estimation results, while Figure 3 shows the contributions of the right-hand-side variables after allowing for a break in the post 2007 coefficients. The deterioration in matching efficiency appears mostly as a higher aggregate elasticity (from 0.28 to 0.36) and as a larger effect of unemployment duration. As shown in Figure 3, the increase in unemployment duration has been associated with a large decrease in matching efficiency. The coefficient on the interaction between average duration and individual duration has decreased significantly post 2007. Whereas in previous recessions, the contribution of individual duration to a reduction in job finding was attenuated (because it likely reflected aggregate labor market conditions, already controlled for, rather than individual circumstances) in the most recent recession, this was not the case and the effect of duration on matching efficiency was stronger. Changes in other characteristics have had little effect.
The lower panel of Figure 3 repeats the lower panel of Figure 2, which shows the explained and unexplained components of the deterioration in matching efficiency, except that Figure 3 includes in the explained component the part explained by a break in post-2007 coefficients. The explained component now accounts for somewhat more (50 versus 40 percent) of the deterioration in matching efficiency. Moreover, the fraction of explained variation seems to grow overtime, due largely to the duration component. This pattern suggests that duration is capturing the effect of unobserved circumstances, rather than scarring, on the job finding probability. Indeed, if unobserved circumstances lowered the job finding probability of some individuals, the contribution of the unexplained component to lower matching efficiency would be large initially. But with time, it would fade as the (increasing) unemployment duration of the affected individuals began to capture the effect of the unobserved circumstances. This pattern is not what one would expect, however, if scarring were the explanation for the explanatory power of duration.
4.2.4.2 The effect of extended emergency unemployment benefits
Next, we study whether the increases in the maximum length of eligibility for unemployment insurance, which went into effect at the onset of the recession, have had any effect on worker's search intensity and thus on matching efficiency. To identify the effect of extended and emergency unemployment benefits (EEB) on job finding probabilities, we follow a strategy used by Kuang and Valletta (2010) who note that job losers are predominantly eligible for unemployment insurance (UI) benefits while job leavers and new labor force entrants are not. While Kuang and Valletta (2010) study the effect of EEB on unemployment durations, we identify the effect of EEB on the job finding probability by interacting a job loser dummy with a post-2008 dummy (the period when EEB was in full effect) in our regression (12). We find that EEB has little effect on job finding probabilities.20 The coefficient on the interaction between the job loser dummy and the post 2008 dummy is nearly identical to that on the interaction between the other unemployed dummy and the 2008 dummy.
4.2.4.3 Is the deterioration in matching efficiency concentrated by sector or region?
Next, we look at whether the deterioration in matching efficiency has been concentrated by industry or by location.21 To do so, we estimate two separate specifications of (12), where we interact a post-2007 dummy with, respectively, dummies for an individual's last industry of employment, and dummies for an individual's current state of residence. If the deterioration in matching efficiency is concentrated, then there will be significant differences in the interaction coefficients across industries or states. One can think of these interaction terms as shifts in local labor market or industry Beveridge curves.
Turning first to concentration by industry, we find that there is no significant difference across our three broad industry categories. The coefficients on the post-2007 interaction terms are almost identical, and the decline in matching efficiency appears to be present in all industry groups.
In contrast, there are statistically significant differences in the deterioration in matching efficiency across states. However, there is no apparent pattern to the differences. The top 5 states (in terms of deterioration) are (in order) Florida, South Carolina, New Hampshire, Minnesota, and Missouri. The presence of Florida is perhaps unsurprising as that state has suffered a large drop in home prices and a large number of foreclosures. The drop in home prices may have increased the number of homeowners who are underwater on their mortgages and therefore less mobile than other households. At the same time, large numbers of foreclosures may signal the presence of many homeowners with scarce financial resources and little ability to borrow, which might also impede mobility. Still, three other states often mentioned with Florida as states with particularly bad housing markets, Nevada, Arizona and California, are not in the top 10 (Nevada is 14th, Arizona 18th and California 28th), and the remaining states in the top 5 have no apparent similarities.22
4.2.4.4 Discussion
From these results we take away two main conclusions. First, many of the popular explanations for the deterioration in aggregate matching efficiency find little support in the data. For example, some observers have speculated that job finding difficulties of unemployed workers from the construction industry, which was particularly hard hit in the last recession, were behind the deterioration in matching efficiency. We find the deterioration in matching efficiency to be widespread across industries, consistent with Barnichon, Elsby, Hobijn and Sahin's (2010) findings based on JOLTS data that the decline in the vacancy yield is relatively broad-based across industries. Other observers suggested that underwater mortgages and their detrimental effect on mobility were responsible for the deterioration in match efficiency. Although Florida, a state with particularly hard hit real estate markets, did appear to suffer particularly large deteriorations in matching efficiency, three other states with problem real estate markets--Nevada, Arizona and California--did not. More generally, the geographic distribution of match efficiency did not suggest real estate, or any other factor, as a single cause. Finally, the advent of EEB does not appear responsible for the deterioration in matching efficiency, although it does appear to have dissuaded some individuals from dropping out of the labor force.
Second, much of the deterioration in aggregate matching efficiency seems to be associated with long-duration spells of unemployment. Moreover, the timing pattern of the decline in efficiency, in which the fraction of the decline that is unexplained has rapidly decreased over time, suggests that unobserved characteristics, rather than scarring, explain the correlation between duration and deterioration in matching efficiency. These unobserved characteristics could be related to a mismatch between workers' skills and location and the skills/location required by available jobs. Although we have found little evidence of misallocation, our dispersion measure has been highly aggregated, and dispersion may be occurring at a much more disaggregated level. We explore this possibility in the next section.
5 More evidence on dispersion
Our empirical exercise has so far relied on the unemployment rate by state and industry to proxy for labor market tightness and capture the extent of dispersion across labor market segments. In this section, we instead use direct measures of vacancy posting, and, using three different datasets, we consider three measures of dispersion: (i) dispersion by industry, (ii) dispersion by region, and (iii) dispersion by occupation and geographic location.
Available dispersion measures are confronted with two limitations. First, not all hires occur with the formal posting of a vacancy, and the fraction of informal hiring is not necessarily identical across occupation, industry or geographic location. As a result, dispersion in labor market tightness need not solely capture misallocation of jobs and workers but also the fact that some segments have a higher level of informal hiring than others. Second, the level of disaggregation allowed by direct measures of labor market tightness is probably too coarse to capture the full extent of dispersion. To address these two measurement issues, we rely on a simpler framework which abstracts from worker heterogeneity and allows us to (i) estimate the fraction of informal hiring by segment, and (ii) use UK data to infer the extent of dispersion at a very fine level of disaggregation.
5.1 A simpler empirical framework
To explore whether dispersion can account for the 0.15 log points decline in matching efficiency not accounted for by composition, we simplify our empirical framework by considering the case without worker heterogeneity but using the elasticity estimated after controlling for composition, i.e.,
![]() =0.72. Without worker heterogeneity, the job finding rate in segment
=0.72. Without worker heterogeneity, the job finding rate in segment ![]() absent worker heterogeneity is given by
absent worker heterogeneity is given by
and the effect of dispersion on aggregate matching efficiency movements is given by
5.2 Data on labor market tightness by segment
We consider three datasets. First, the JOLTS measure of job openings can be disaggregated into 10 industry groups over 2000-2010.23 Second, the Conference Board Help-Wanted Index originally proxied for the number of help-wanted advertisements in 51 major newspapers. While the print index is not disaggregated by industries, the index can be disaggregated by region, and an index of newspaper help-wanted advertising for the nine US census divisions is available. These newspaper indexes have become increasingly unrepresentative with the advent of online advertising, and the Conference Board began collecting data on online job posting in 2005.24 By splicing the regional print help-wanted indexes with online job openings by regions as in Barnichon (2010), we build composite indexes of print and online vacancy posting for the nine US census divisions over 2000-2010.
Third, since November 2006, the Conference Board has published the number of help-wanted online ads by state and occupation, as well as the number of ads by metropolitan statistical areas (MSA) and occupation.
The coverage of these two datasets is unique as it allows us to build a direct counterpart of
![]() at a high level of disaggregation. To the best of our knowledge, these datasets are the first ones to contain information on vacancy posting in the US by occupation
and geographic location. Moreover, we expand the coverage of each dataset by combining the state-level information with the MSA-level information to produce series of vacancy posting by occupation and geographic areas across the US. With 50 states and 52 MSAs, we get a
total of 94 geographic areas. 25 The Conference Board reports online ads for six occupation groups.26 After combining these vacancy series with the number of unemployed by geographic area and occupation estimated from the CPS, we can survey the extent of dispersion over
at a high level of disaggregation. To the best of our knowledge, these datasets are the first ones to contain information on vacancy posting in the US by occupation
and geographic location. Moreover, we expand the coverage of each dataset by combining the state-level information with the MSA-level information to produce series of vacancy posting by occupation and geographic areas across the US. With 50 states and 52 MSAs, we get a
total of 94 geographic areas. 25 The Conference Board reports online ads for six occupation groups.26 After combining these vacancy series with the number of unemployed by geographic area and occupation estimated from the CPS, we can survey the extent of dispersion over
![]() labor market segments during the 2008-2009 recession.
labor market segments during the 2008-2009 recession.
One concern about using vacancy data by segment is that some segments may have a higher share of informal hiring. For example, it is likely that a lot of hiring in construction occurs without the formal posting of a vacancy. While the aggregate vacancy-unemployment ratio from Conference Board data averaged 1.1 in 2006, the vacancy-unemployment ratio averaged 0.5 in construction and maintenance but about 4 in management and business/financial. Similarly, because a broad industry group may contain industries with different levels of informal hiring, the levels of job openings may not be comparable across regions with different industry specializations. For example, labor market tightness in services is on average three times higher in Denver than in New York. Similarly, rural areas and urban areas need not display the same fraction of informal hiring.
Because of such differences in informal hiring, dispersion in observed labor market tightness need not solely capture misallocation of jobs and workers but also the fact that some segments have a higher level of informal hiring than others. Formally, informal hiring is akin to measurement error
in vacancy posting, as we do not measure
![]() but
but
![]() with
with
![]() and
and
![]() the share of formal hiring.27 With
the share of formal hiring.27 With
![]() , we then get
, we then get
![]() with
with
![]() . According to (14), the effect of dispersion on matching efficiency is thus a function of
. According to (14), the effect of dispersion on matching efficiency is thus a function of
![]() .
.
To estimate
![]() for each dataset, we use data on the job finding rate by segment. Taking the log of
for each dataset, we use data on the job finding rate by segment. Taking the log of
![]() for segment
for segment ![]() and an arbitrarily chosen segment 1, we can back-out
and an arbitrarily chosen segment 1, we can back-out
![]() from the regression
from the regression
where we take the log-difference between two segments to remove the non-observable parameter
5.3 Dispersion measures
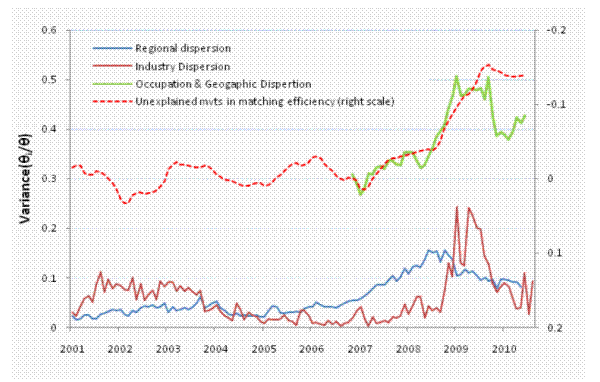
Figure 4 plots the dispersions in labor market tightness over 2000-2010 using our three data sources. JOLTS data indicate that dispersion across ten industry groups increased in the 2008-2009 recession by about twice as much as during the 2001 recession, but that it receded in 2009. Dispersion across the 9 census divisions also rose in the 2008-2009 recession, but the increase started in late 2006, earlier than for sectoral dispersion. In comparison, the increases in regional dispersion in the 2001 recession were small.
Dispersion by geography and occupation shows a clear increase in the 2008-2009 recession, and Figure 4 shows that the behavior of the series matches very well with the behavior of the unexplained component of Figure 2 . In fact, the correlation between the two series is high at 0.82. Over 2007-2008, the increase in dispersion coincides with the decline in match efficiency, while composition was flat (Figure 2). In 2009, both dispersion and the unexplained component of matching efficiency peaked before declining slightly.
Geography/occupation dispersion was constant in 2009 while both dispersion across regions and dispersion across industry groups declined. These different results highlight the importance of looking simultaneously at geography and occupation or industry when studying the effect of dispersion. Thus in the rest of the paper, we will concentrate on dispersion by geography and occupation, which we think provides the most accurate description of dispersion in labor market conditions.
5.4 Inferring the true amount of dispersion from UK data
Because the effect of dispersion arises out of the concavity of the matching function, it is crucial to reach a good level of disaggregation. Our highest level of disaggregation covers only 564 labor market segments, probably a small amount compared to the true number of segments in the US. As Shimer (2007) emphasized, the Occupational Employment Statistics (OES) counts about 800 occupations, and there are 362 metropolitan statistical areas and 560 micropolitan statistical areas, so a total of about 740,000 labor market segments.29
Thus, we now present a method using UK data to scale up our measure of dispersion over 564 segments to a more realistic number of labor market segments. Define an elementary labor market segment as the smallest segment in which the matching function is still well described by (13). We will refer to an elementary segment as a unit. The effect of misallocation on matching efficiency is thus given by the dispersion in labor market conditions across such units. We cannot observe labor market tightness at the unit level. Instead, we observe
![]() , the average value of the
, the average value of the
![]() s over segment
s over segment ![]() , consisting of m
, consisting of m
![]() units indexed by
units indexed by
![]() with
with ![]() the total number
of units and
the total number
of units and ![]() the number of observed (larger) segments. Thus, we cannot measure
the number of observed (larger) segments. Thus, we cannot measure
![]() , the dispersion over the
, the dispersion over the ![]() units, but we can measure
units, but we can measure
![]() , the variance in labor market tightness over
, the variance in labor market tightness over ![]() larger segments with n
larger segments with n
![]() .30
.30
To relate these two quantities and get an estimate of
![]() from
from
![]() , we turn to UK data. Unlike the US, the UK public employment office collects vacancies by occupation and geography at very
different levels of disaggregation, from low levels of disaggregation to very high levels of disaggregation (as high as 80,000 segments). These numbers can in turn be matched to the number of job seekers' allowance claimants to construct measures of labor market tightness across various occupation
and geographic segments.31 With these data, we can then establish an empirical "scaling law"that captures how
, we turn to UK data. Unlike the US, the UK public employment office collects vacancies by occupation and geography at very
different levels of disaggregation, from low levels of disaggregation to very high levels of disaggregation (as high as 80,000 segments). These numbers can in turn be matched to the number of job seekers' allowance claimants to construct measures of labor market tightness across various occupation
and geographic segments.31 With these data, we can then establish an empirical "scaling law"that captures how
![]() increases when we raise the number of observations
increases when we raise the number of observations ![]() and consider smaller labor market segments.
and consider smaller labor market segments.
The UK data by occupation are available at the one- to four- digits SOC levels, consisting of respectively 9, 25, 81 and 353 groups, and we use data by geographic region at three disaggregation levels; government office regions (11 segments), Job Center plus Districts (48 segments), and Travel
to Work Areas (232 segments). Thanks to these different levels of disaggregation, we can probe how
![]() varies as we increase the precision of observations from
varies as we increase the precision of observations from
![]() segments to
segments to
![]() segments. To increase the sample size, we took averages of unemployment and vacancy data over the whole sample period July 2006-July 2010.32
segments. To increase the sample size, we took averages of unemployment and vacancy data over the whole sample period July 2006-July 2010.32
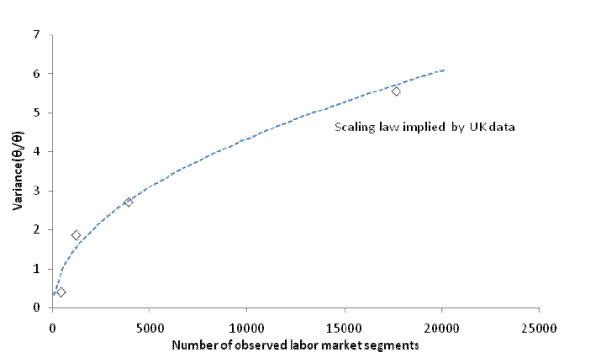
A simple theoretical framework left for the Appendix shows that we could expect a relation of the form
with
Empirically, a power law
![]() fits the UK data extremely well with an
fits the UK data extremely well with an ![]() of 0.98 (Table 4).33 This encouragingly suggests that one need not probe the data at a very
high level of disaggregation to estimate the effect of dispersion on matching efficiency, but can instead use
of 0.98 (Table 4).33 This encouragingly suggests that one need not probe the data at a very
high level of disaggregation to estimate the effect of dispersion on matching efficiency, but can instead use
![]() to scale up our estimate
to scale up our estimate
![]() . To illustrate the empirical relation, Figure 5 plots the relationship between the total number of observed segments and
. To illustrate the empirical relation, Figure 5 plots the relationship between the total number of observed segments and
![]() as we increase the number of occupation categories from 9 (comparable with the 6 occupations observed using Conference Board data)
to 353, and holding the number of geographic areas constant at 48 (comparable with the 94 areas observed using Conference Board data).
as we increase the number of occupation categories from 9 (comparable with the 6 occupations observed using Conference Board data)
to 353, and holding the number of geographic areas constant at 48 (comparable with the 94 areas observed using Conference Board data).
Assuming that ![]() is similar in the UK and in the US (i.e. that the scaling law parameters
is similar in the UK and in the US (i.e. that the scaling law parameters ![]() and
and ![]() are not country specific) 34 and given an estimate of the number of labor market units
are not country specific) 34 and given an estimate of the number of labor market units
![]() and
and
![]() , we can use the UK scaling law to build an estimator of
, we can use the UK scaling law to build an estimator of
![]()
Assuming that there are 353 distinct occupations in the US and 232 geographic segments, probably a conservative estimate given Shimer's (2007) aforementioned observation and the fact that the US is, geography-wise, much larger than the UK, we get that
5.5 Effects of dispersion on matching efficiency
To translate our estimated increase in dispersion into lower matching efficiency, we need to address one final issue. The previous section suggests that the increase in dispersion in labor market conditions lead to a high value of
![]() at about 10 in 2009. With such high dispersion, the Taylor expansion (14) need not provide a good approximation of
the effect of dispersion on matching efficiency.
at about 10 in 2009. With such high dispersion, the Taylor expansion (14) need not provide a good approximation of
the effect of dispersion on matching efficiency.
Instead, we resort to numerical simulations to calculate the exact effect of dispersion on matching efficiency. If the job finding rate in segment ![]() is described by (13),
is described by (13), ![]() , the effect of dispersion on matching efficiency is given by the difference in the average job finding rate when
, the effect of dispersion on matching efficiency is given by the difference in the average job finding rate when
![]() always equals 1 and when
always equals 1 and when
![]() is distributed with variance
is distributed with variance
![]() . Specifically,
. Specifically,
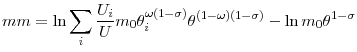 |
(19) |
and we calculate
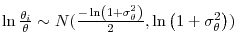 , so that E
, so that E
With the variance of
![]() increasing from about 5 in November 2006 to about 10 in December 2009, misallocation can explain 26 percent (0.04 log-points out of the 0.15 unexplained
log-decline in
increasing from about 5 in November 2006 to about 10 in December 2009, misallocation can explain 26 percent (0.04 log-points out of the 0.15 unexplained
log-decline in ![]() , cf. Figure 2) of the decline in matching efficiency when
, cf. Figure 2) of the decline in matching efficiency when
![]() , about 36 percent (.055 log points) when
, about 36 percent (.055 log points) when
![]() , and about 20 percent (.03 log-points) when
, and about 20 percent (.03 log-points) when
![]() 35 As a very conservative
estimate, we can take the increase in dispersion from online HWI at face value (an increase from 0.25 to 0.5) and not use the UK scaling law. In that case, dispersion accounts for about 10 percent (0.015 log-points) of the unexplained decline in matching efficiency (using
35 As a very conservative
estimate, we can take the increase in dispersion from online HWI at face value (an increase from 0.25 to 0.5) and not use the UK scaling law. In that case, dispersion accounts for about 10 percent (0.015 log-points) of the unexplained decline in matching efficiency (using
![]() ).
).
Thus, we conclude that an increase in labor market dispersion likely led to a noticeable decline in matching efficiency, though a significant fraction of the overall decline remains unexplained.36
5.6 Taking stock
It is difficult to estimate the effect of dispersion on matching efficiency because data on vacancies and unemployment at high levels of disaggregation are not available. However, with some assumptions, one can use the available data to estimate the effect of dispersion at high levels of
disaggregation. These assumptions are: (1) most of the differences in matching efficiency across segments are due to different fractions of informal hiring, (2) the UK scaling relationship linking
![]() , the actual dispersion in labor market conditions, to
, the actual dispersion in labor market conditions, to
![]() , the dispersion measured over a number of larger segments, is time invariant and can be applied to the US. Given these
assumptions, it is likely that greater dispersion has accounted for a substantial portion -about a quarter but possibly more- of the unexplained drop in matching efficiency over the past three years.
, the dispersion measured over a number of larger segments, is time invariant and can be applied to the US. Given these
assumptions, it is likely that greater dispersion has accounted for a substantial portion -about a quarter but possibly more- of the unexplained drop in matching efficiency over the past three years.
6 Conclusion
In this paper, we study the determinants of aggregate matching efficiency fluctuations over the last four decades.
Under fairly general assumptions, we link movements in aggregate matching efficiency to two measurable factors: (i) composition of the unemployment pool, and (ii) dispersion in labor market conditions. We also show that the effect of misallocation on aggregate matching efficiency is a function of the dispersion in conditions across labor markets segment and of the segments' permeability. While a number of dispersion measures have been proposed in the literature, our framework provides a dispersion measure -the variance of labor market tightness- that can be analytically related to matching efficiency and to the equilibrium unemployment rate.
Using CPS micro data over 1976-2009, we find that changes in composition of the unemployment pool generate non-trivial procyclical movements in matching efficiency, implying that estimates of the aggregate matching function elasticity are biased upwards. Until 2006, the composition of the unemployment pool (mostly the share of job losers on permanent layoffs and the share of long-term unemployed) is responsible for most of the cyclical movements in matching efficiency, while dispersion in labor market conditions appears to have played a modest role. Since 2006, composition explains only 40 percent of a dramatic decline in matching efficiency. Instead, the behavior of the unexplained decline is highly (negatively) correlated with dispersion in labor market conditions. Quantitatively, misallocation of workers and jobs may account for a quarter, and perhaps more, of the unexplained decline. We also test a number of popular explanations but find no evidence that matching efficiency was affected by the extension of unemployment coverage, by a " house-lock"or by industry specific shocks.
A remaining question is what accounted for the remaining unexplained decline in matching efficiency. An obvious possibility, given the difficulty to assess dispersion at high levels of disaggregation, is that our UK scaling law lead us to understate the extent of the increase in dispersion and hence the effect of dispersion on matching efficiency. Another possibility, not tested in this paper, is that part of the decline in matching efficiency was caused by a compositional change in vacancy posting. For example, because the construction sector has a high fraction of informal hiring (and hence an apparently high matching efficiency), a decline in the fraction of construction ads among vacancies will lower matching efficiency. However, Barnichon, Elsby, Hobijn and Sahin (2010) do not find that vacancy composition significantly contributed to the decline in the vacancy yield. A related hypothesis raised by Davis, Faberman and Haltiwanger (2010) is that firms vary recruiting intensity during recessions. Despite the fact that our empirical framework does not allow for varying recruiting intensity, it can successfully capture job finding probability movements over 1976-2006. This suggests that aggregate labor market tightness (or sectoral tightness) can proxy for varying recruiting intensity over that period. Thus, if the recent unexplained decline in matching efficiency was caused by lower recruiting intensity, this would imply that recruiting intensity was exceptionally low in the current recession. Assessing this hypothesis would be an interesting goal for future research.
A second-order Taylor expansion of the job finding probability
Rewriting (9), the individual job finding probability is given by
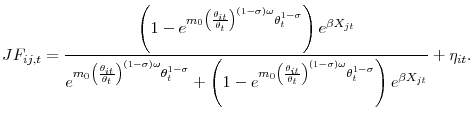
|
Expanding with respect to
 |
with
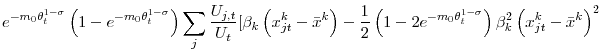
|
|||
![\displaystyle +\frac{1}{2}\displaystyle\sum\limits_{l\neq k}\left( 1-2e^{-m_{0}\theta _{t}^{1-\sigma }}\right) \beta _{k}\left( x_{jt}^{k}-\bar{x}^{k}\right) \beta _{l}\left( x_{jt}^{l}-\bar{x}^{l}\right) ]](img191.gif) |
the (second-order) composition effect from characteristic
 |
the term capturing the effect of dispersion on the average job finding rate with
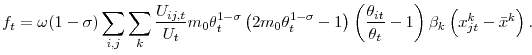 |
capturing the interaction of composition and dispersion.37
Decomposing movements in aggregate matching efficiency
To establish a link between aggregate movements in matching efficiency and changes in composition and dispersion, we write the job finding rate ![]() as a function of the job finding
probability
as a function of the job finding
probability ![]() , and use (6) to get
, and use (6) to get
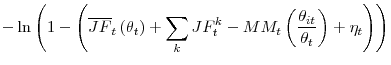 |
|||
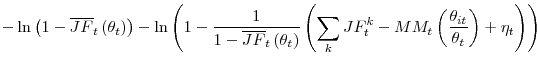 |
|||
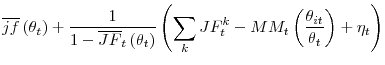 |
with
Using the functional form (9), we have
![]() , and taking the log of the previous expression gives us
, and taking the log of the previous expression gives us
where for the last expression, we used the fact that
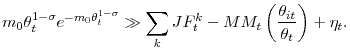 Expression
(19) has the same form as our aggregate regression (2).
Expression
(19) has the same form as our aggregate regression (2).
Thus, the deviations of aggregate matching efficiency from its average level can be written
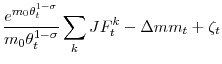 |
with
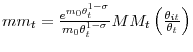 and
and
![\displaystyle \Delta mm_{t}\simeq \frac{1}{2}\omega (1-\sigma )\left[ (1-\omega (1-\sigma )\left( 1-m_{0}\theta _{t}^{1-\sigma }\right) \right] \left[ var\left( \frac{ \theta _{it}}{\theta _{t}}\right) -\text{E}_{T}var\left( \frac{\theta _{it}}{ \theta _{t}}\right) \right] .](img218.gif) |
A theoretical link between actual labor market dispersion and observed dispersion
Assume that the
![]() are independently distributed across
are independently distributed across ![]() elementary labor market
segments of equal size (i.e., with the same number of unemployed). For clarity of exposition, we will refer to the elementary segments as units. Denote
elementary labor market
segments of equal size (i.e., with the same number of unemployed). For clarity of exposition, we will refer to the elementary segments as units. Denote ![]() the distribution of
the distribution of
![]() across units so that
across units so that
![]() (mean
(mean ![]() and variance
and variance
![]() ) with
) with
![]() . We cannot observe the value of
. We cannot observe the value of
![]() for the
for the ![]() units, but we do observe the average value of
units, but we do observe the average value of
![]() over many units. Specifically, for
over many units. Specifically, for ![]() segments that consist of
segments that consist of
![]() units, we observe
units, we observe
![]() , the average value of the
, the average value of the
![]() s over segment
s over segment ![]() indexed by
indexed by
![]() , a segment consisting of
, a segment consisting of
![]() observations of
observations of
![]() To estimate the true amount of dispersion in the labor market, we want to recover
To estimate the true amount of dispersion in the labor market, we want to recover
![]() from the observed variance across larger segments, i.e.,
from the observed variance across larger segments, i.e.,
![]()
If the observed segments were random samples of the
![]() s (i.e., if the
s (i.e., if the
![]() s were independently distributed across units in each observed segment), we would have a linear relation linking the true dispersion to the observed variance
s were independently distributed across units in each observed segment), we would have a linear relation linking the true dispersion to the observed variance
which converges to
In fact, however, the segments that we observe are not random samples of the
![]() s. Instead, because the segments that we observe correspond to an occupation group or/and a geographic location, the labor market units inside those segments are likely to be
correlated. Denote
s. Instead, because the segments that we observe correspond to an occupation group or/and a geographic location, the labor market units inside those segments are likely to be
correlated. Denote ![]() the average correlation between labor market units within a segment. Specifically,
the average correlation between labor market units within a segment. Specifically,
![]() , and, for simplicity, we assume that the average correlation
, and, for simplicity, we assume that the average correlation ![]() is the same for all observed segments.
is the same for all observed segments. ![]() is likely to increase as we refine our definition of a segment. For example, the
average correlation between labor markets across the large US Census region "West" is certainly lower than the average correlation between labor markets across the city of Los Angeles. Denoting
is likely to increase as we refine our definition of a segment. For example, the
average correlation between labor markets across the large US Census region "West" is certainly lower than the average correlation between labor markets across the city of Los Angeles. Denoting ![]() the number of observed geographic locations and
the number of observed geographic locations and ![]() the number of observed occupations, we have
the number of observed occupations, we have
![]() , and we assume that
, and we assume that
![]() with
with
![]() ,
,
![]() and
and
![]() when
when
![]() . A little bit of algebra gives us
. A little bit of algebra gives us
which also converges to
Thus, we can build an estimator of
![]()
This theoretical framework is useful to clarify what kind of assumptions are necessary to use the UK scaling law and the estimator
Finally, we do not observe
![]() but the sample variance
but the sample variance
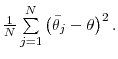 As a result, we can only use (22) if
As a result, we can only use (22) if ![]() is large enough to ensure
is large enough to ensure
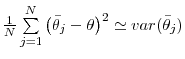 . For low values of
. For low values of ![]() (as would be the case with JOLTS data with only 10 industry groups and 1 area), the sample variance may not be a good approximation of the actual variance, and the scaling law could give misguided results.
(as would be the case with JOLTS data with only 10 industry groups and 1 area), the sample variance may not be a good approximation of the actual variance, and the scaling law could give misguided results.
Figure 1
Figure 1: Empirical (log) job finding rate, model job finding rate and residual, 1967-2009. This figure plots the residual of equation (3) estimated over 1967-2009. While the matching function appears relatively stable over time, a testimony of the success of the matching function, the residual can become large. In the third quarter of 2009, the residual reached an all time low of three standard-deviations.Figure 2
Figure 2: The regression is estimated over 1976-2007. The upper panel plots the decomposition of composition effect/mismatch due to reason for unemployment, demographics, unemployment duration and mismatch. The contribution of reason for unemployment is procyclical, falling in recessions and rising in recoveries. The contribution of duration is also procyclical. The contribution of demographics declines gradually over the sample period. The effect of dispersion on the job finding probability is very small. The lower panel plots a decomposition of changes in matching efficiency into composition effect/mismatch and an unexplained aggregate effect. Up until 2006, composition accounted for most of the cyclical movements in matching efficiency movements. Since 2007, most of the decline in matching function efficiency has been due to unobserved factors.Figure 3
Figure 3: The regression is estimated over 1976-2009, allowing for a break in the coefficients in 2008. The upper panel shows the decomposition of composition effect/mismatch due to reason for unemployment, demographics, unemployment duration and mismatch. The lower panel shows the decomposition of changes in matching efficiency into composition effect/mismatch and an unexplained aggregate effect. The deterioration in matching efficiency appears mostly as a higher aggregate elasticity, and except for unemployment duration, seems little related to observed characteristics.Figure 4
Figure 4: It plots the dispersions in labor market tightness over 2000-2010 using our three data sources. JOLTS data indicate that dispersion across ten industry groups increased in the 2008-2009 recession by about twice as much as during the 2001 recession, but that it receded in 2009. Dispersion in geography/occupation labor market tightness shows a clear increase in the 2008-2009 recession, and the timing matches that of the unexplained component of Figure 2.Figure 5
Figure 5: It shows a decomposition of the geography/occupation dispersion measure by plotting geographic dispersion for each occupation group. Geographic dispersion in construction initially contributed to the increase in dispersion, but subsided after mid-2007. Thereafter, geographic dispersion in services, professional and management are responsible for the increase in dispersion.Figure 6
Figure 6: Dispersion in labor market tightness across 9 regions, measuring vacancy posting from Conference Board Help-Wanted Indexes or proxying it with the unemployment rate. Mismatch across the 9 census divisions rose in the 2008-2009 recession, but the increase started in late 2006, earlier than for sectoral mismatch.Table 1: Estimating a Cobb-Douglas matching function
| Dependent variable: | ||
|---|---|---|
| Sample (quarterly frequency) | 1976-2007 | 1976-2007 |
| Regression | (1) | (2) |
| Estimation | OLS | GMM |
| 1- |
0.33*** | 0.34*** |
| 1- |
(0.01) | (0.01) |
| R2 | 0.87 | -- |
Note: Standard-errors are reported in parentheses. In equation (2), we use 3 lags of v and u as instruments. We allow for first-order serial correlation in the residual.
Table 2 Estimated Coefficients for Job Finding probability regression, 1976-2007
| Explanatory Variable | Pre-redesign 1976-1993 | Post-redesign 1994-2007 | |
|---|---|---|---|
| Matching Function parameter: Aggregate elasticity: 1- |
0.28 | ||
| Matching Function parameter: Aggregate elasticity: 1- |
(0.01) | ||
| Matching Function parameter: Constant: ln(m |
-1.43 | ||
| Matching Function parameter: Constant: ln(m |
(0.003) | ||
| Matching Function parameter: Local elasticity: |
0.16 | ||
| Matching Function parameter: Local elasticity: |
(0.01) | ||
| Other parameters: Age | 0.0026 | 0.0004 | |
| Other parameters: Age standard error | (0.001) | (0.001) | |
| Other parameters: Age squared | -0.0002 | -0.0002 | |
| Other parameters: Age squared standard error | (0.00002) | (0.00002) | |
| Other parameters: Male dummy | 0.2 | 0.12 | |
| Other parameters: Male dummy standard error | (0.01) | (0.01) | |
| Other parameters: Permanent layoff dummy | -0.27 | -0.27 | |
| Other parameters: Permanent layoff dummy standard error | (0.01) | (0.01) | |
| Other parameters: Temporary layoff dummy | 0.38 | 0.67 | |
| Other parameters: Temporary layoff dummy standard error | (0.001) | (0.01) | |
| Other parameters: Reentrant dummy | -0.26 | -0.32 | |
| Other parameters: Reentrant dummy standard error | (0.01) | (0.01) | |
| Other parameters: New Entrant dummy | -0.58 | -0.88 | |
| Other parameters: New Entrant dummy standard error | (0.01) | (0.02) | |
| Other parameters: Unemployment duration | -0.025 | -0.021 | |
| Other parameters: Unemployment duration standard error | (0.001) | (0.002) | |
| Other parameters: Duration interacted with average duration | 0.0006 | 0.0003 | |
| Other parameters: Duration interacted with average duration standard error | (0.0001) | (0.0001) | |
| Pseudo R |
0.0455 |
Note. Explanatory variables also include monthly dummies. All variables, except age after 1993, are significant at conventional levels. Standard errors are in parentheses.
Table 3 (part 1) Estimated Coefficients for Job Finding probability regression, 1976-2009
| Explanatory Variable: Matching Function parameter | 1976-2007 | Post 2007 |
|---|---|---|
| Aggregate elasticity: 1- |
0.28 | 0.36 |
| Aggregate elasticity: 1- |
(0.01) | (0.23) |
| Constant: ln(m |
-1.43 | -1.54 |
| Constant: ln(m |
(0.002) | (0.002) |
| Local elasticity: |
0.16 | 0.19 |
| Local elasticity: |
(0.01) | (0.02) |
Table 3 (part 2) Estimated Coefficients for Job Finding probability regression, 1976-2009
| Explanatory Variable: Other parameters | 1994-2007 | |
|---|---|---|
| Age | 0.0004 | 0.0036 |
| Age standard error | (0.001) | (0.002) |
| Age squared | -0.0002 | -0.0002 |
| Age squared standard error | (0.00002) | (0.000) |
| Male dummy | 0.12 | 0.059 |
| Male dummy standard error | (0.01) | (0.02) |
| Permanent layoff dummy | -0.28 | -0.26 |
| Permanent layoff dummy standard error | (0.01 | (0.03) |
| Temporary layoff dummy | 0.68 | 0.93 |
| Temporary layoff standard error | (0.01) | (0.04) |
| Reentrant dummy | -0.32 | -0.25 |
| Reentrant dummy standard error | (0.01) | (0.04) |
| New Entrant dummy | -0.88 | -0.8 |
| New Entrant dummy standard error | (0.02) | (0.05) |
| Unemployment duration | -0.021 | -0.019 |
| Unemployment duration standard error | (0.002) | (0.003) |
| Duration interacted with average duration | 0.0003 | 0.0001 |
| Duration interacted with average duration standard error | (0.0001) | (0.0001) |
| Pseudo R |
0.0457 |
Note. Explanatory variables also include monthly dummies. All variables, except duration interacted with average duration after 2007 and age, are significant at conventional levels. Standard errors are in parentheses.
Table 4: Estimating a functional form for the UK scaling law
| Dependent variable: | |
|---|---|
| a |
5.08 |
| a |
(0.5) |
| a |
0.67 |
| a |
(0.03) |
| a |
0.13 |
| a |
(0.04) |
| R |
0.98 |
Appendix
Not for publication
Table A1: Proxying
![]() with
with
![]()
| Dependent variable: |
|
|
|
|
| Sample (quarterly frequency) Data source | 2000-2010 JOLTS Industry groups | 2000-2009 JOLTS US Census Regions | 2006-2010 Conference Board Occupations | 2006-2010 Conference Board State/MSA regions |
|---|---|---|---|---|
| -1.34*** | -1.32*** | -1.71*** | -1.29*** | |
| (0.03) | (0.11) | (0.08) | (0.02) | |
| Number of observations | 1170 | 444 | 234 | 3510 |
| R |
0.76 | 0.73 | 0.89 | 0.83 |
Note: Standard-errors are reported in parentheses. All panel regressions include industry or region fixed effects. The first two regressions include a quadratic trend. The first two columns use vacancy measures from the JOLT, and the last two columns use data on online advertising from the Conference Board.
Table A2: Effects of EEB on UE and UN transition probabilities in the 2008-2009 recession
| UE probability | UN probability | |
|---|---|---|
| Job loser | -0.12 | -0.22 |
| Job loser standard error | (0.02) | (0.02) |
| Non job loser | -0.16 | -0.05 |
| Non job loser standard error | (0.02) | (0.02) |
Note: The two rows report the coefficients on the interaction term between a post-2008 dummy and, respectively, a job loser and non-job loser dummy. In the first column, the dependent variable is the UE transition probability, and in the second column, the dependent variable is the UN transition probability.
Table A3: Coefficients on post-2007 last industry of employment dummy
| Industry | Coefficients |
|---|---|
| Goods production | -0.11 |
| Goods production standard error | (0.02) |
| Professional services | -0.13 |
| Professional services standard error | (0.02) |
| Sales and other services | -0.12 |
| Sales and other services standard error | (0.02) |
| No industry (new entrant) | -0.15 |
| No industry (new entrant) standard error | (0.04) |
Note: Except for the industry dummy, the regression is identical to Table 3. Other coefficients are little changed and are available upon request.
Table A4: Coefficients on post-2007 state of residence dummy
| State of residence | Coefficients | State of residence | Coefficients |
|---|---|---|---|
| FL | -0.41 | KS | -0.16 |
| SC | -0.37 | CA | -0.15 |
| NE | -0.3 | IL | -0.15 |
| MN | -0.29 | HI | -0.15 |
| MO | -0.28 | IA | -0.15 |
| UT | -0.28 | KY | -0.15 |
| AL | -0.27 | TN | -0.12 |
| NH | -0.27 | VA | -0.11 |
| IN | -0.26 | RI | -0.11 |
| OR | -0.25 | WY | -0.09 |
| AR | -0.25 | SD | -0.08 |
| OH | -0.25 | PA | -0.08 |
| MI | -0.24 | MS | -0.07 |
| NV | -0.22 | VT | -0.07 |
| GA | -0.22 | CT | -0.07 |
| MA | -0.21 | ND | -0.01 |
| OK | -0.21 | NY | -0.01 |
| AZ | -0.2 | ID | 0 |
| DE | -0.2 | TX | 0 |
| ME | -0.19 | NJ | 0.01 |
| MD | -0.18 | DC | 0.02 |
| NC | -0.16 | LA | 0.06 |
| CO | -0.16 | AK | 0.06 |
| WI | -0.16 | WV | 0.06 |
| WA | -0.16 | NM | 0.14 |
| MT | -0.16 |
Note: Except for the state of residence dummy, the regression is identical to Table 3. Other coefficients are little changed and are available upon request.
Table A5: List of geographic areas
| AK | FL | LA | WA | SD |
| Other, AK | Jacksonville, FL | New Orleans, LA | Other, WA | Other, SD |
| AL | Miami, FL | Other, LA | Seattle-Tacoma, WA | TN |
| Birmingham, AL | Orlando, FL | MA/RI | WI | Memphis, TN |
| Other, AL | Other, FL | Boston, MA | Milwaukee, WI | Nashville, TN |
| AR | Tampa, FL | Other, MA/RI | Other, WI | TD |
| Other, AR | GA | Providence, RI | WV | Other, TD |
| AZ | Atlanta, GA | MD | Other, WV | TX |
| Other, AZ | Other, GA | Baltimore, MD | WY | Austin, TX |
| Phoenix, AZ | HI | Other, MD | Other, WY | Dallas, TX |
| Tucson, AZ | Honolulu, HI | ME | NH | Houston, TX |
| CA | Other, HI | Other, ME | Other, NH | Other, TX |
| Los Angeles, CA | IA | MI | NM | San Antonio, TX |
| Other, CA | Other, IA | Detroit, MI | Other, NM | UT |
| Riverside, CA | ID | Other, MI | NV | Other, UT |
| Sacramento, CA | Other, ID | MN | Las Vegas, NV | Salt Lake City, UT |
| San Diego, CA | IN/IL/KS/MO | Minneapolis-St. Paul, MN | Other, NV | VA |
| San Francisco, CA | Chicago, IL | Other, MN | OK | Other, VA |
| San Jose, CA | Indianapolis, IN | MS | Oklahoma City, OK | Richmond, VA |
| CO | Kansas City, MO | Other, MS | Other, OK | Virginia Beach, VA |
| Denver, CO | Other, IN/IL/KS/MO | MT | OR | VT |
| Other, CO | St. Louis, MO | Other, MT | Other, OR | Other, VT |
| CT | KY/OH | NC/SC | Portland, OR | |
| Hartford, CT | Cincinnati, OH | Charlotte, NC | PA/NJ/NY | |
| Other, CT | Cleveland, OH | Other, NC/SC | Buffalo, NY | |
| DC | Columbus, OH | ND | New York, NY | |
| Washington, DC | Louisville, KY | Other, ND | Other, PA/NJ/NY | |
| DE | Other, KY/OH | NE | Philadelphia, PA | |
| Other, DE | Other, NE | Pittsburgh, PA | ||
| Rochester, NY |
Footnotes
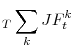 is small, which is empirically the case since the second-order approximation of
is small, which is empirically the case since the second-order approximation of
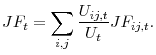
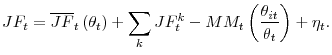
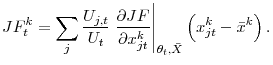

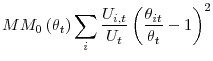
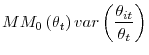


![\displaystyle mm_{t}=\frac{1}{2}\omega (1-\sigma )\left[ (1-\omega (1-\sigma )\left( 1-m_{0}\theta _{t}^{1-\sigma }\right) \right] var\left( \frac{\theta _{it}}{ \theta _{t}}\right)](img76.gif)
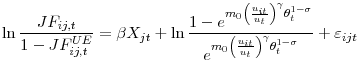
![\displaystyle \Delta mm_{t}\simeq \frac{1}{2}\omega (1-\sigma )(1-\omega (1-\sigma ))\left[ var\left( \frac{\theta _{it}}{\theta _{t}}\right) -\text{E}_{T}var\left( \frac{\theta _{it}}{\theta _{t}}\right) \right] .](img113.gif)
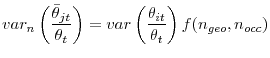 with
with