The Information Content of Forward and Futures Prices: Market Expectations and the Price of Risk

Sergey V. Chernenko, Krista B. Schwarz and Jonathan H. Wright $^{\ast}$ ¹

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Forward and futures rates are frequently used as measures of market expectations. In this paper we apply standard forecast efficiency tests, and some newer exact sign and rank tests, to a wide range of forward and futures rates, and in this way test whether these are in fact rational expectations of future actual prices. The forward and futures rates that we study under a common methodology include foreign exchange forward rates, U.S. and foreign interest rate futures and forward rates, oil futures, and natural gas futures. For most, but not all, of these instruments, we find that we can reject the hypothesis that the forward or futures rates are rational expectations of actual future prices. It is well known that foreign exchange forward rates give less accurate forecasts than a random walk, but we show that this is also true for some interest rate futures and forward rates. We conclude that forward and futures prices are not generally pure measures of market expectations. They are also heavily affected by the market price of risk.

Keywords: forward contracts, futures, forecast evaluation, risk premia, random walk.

JEL Classification: C22, E17, G12

1 Introduction

Analysts and policymakers frequently use forward and futures prices in financial markets to gauge market expectations. The idea that these prices are necessarily pure measures of market expectations is seductive. But it is often very misleading. These financial market prices embody not just the rational expectations of agents, but also the market price of risk.

This paper is an empirical study of the usefulness of a wide variety of forward and futures rates as objective measures of market expectations. Our methodology is a simple one. If forward and futures rates are rational or efficient forecasts of future outcomes, then the forecast errors must have mean zero and must be uncorrelated with any variable in the information set at the time that the forecast was made. We test whether the forecast errors are in fact predictable. In principle, there are a number of ways in which forecast errors might be found to be predictable:

1. Under standard equilibrium asset pricing theory forward and futures rates are the sum of an expectations component and a risk premium component. Thus, rejection of forecast efficiency could simply mean that the risk premium component is important. Forward and futures rates are not market expectations in this case.

2. Systematic forecast errors we find in a short sample could be due to rational learning on the part of market participants. Many authors have considered predictability in returns ascribed to rational learning behavior (e.g. Lewis (1989), Timmerman (1993)). Forward and futures rates are market expectations in this case. But there are stringent limits to how long we can observe systematic forecast errors and still attribute this to rational learning. Rational agents using least squares learning cannot continue to make systematic mistakes after enough of the sample has gone by for them to be able to reject forecast efficiency.

3. Market expectations may simply not be rational expectations at all. Forward and futures rates could be market expectations in this case, even if the forecast errors are systematic. Departing from the conventional asset pricing paradigm, recent ideas in behavioral finance admit the possibility that market participants may have expectations that are not rational.

4. The tests could be falsely rejecting the efficiency hypothesis because of Type 1 hypothesis testing error. Forward and futures rates are market expectations in this case. We attempt to minimize the risk of false rejection due to size distortions by augmenting results of standard tests with some alternative exact tests.

5. The test could be falsely rejecting the efficiency hypothesis because of a ``peso problem''. That is, there could be some low probability potential outcome (such as a currency crisis) that did not actually occur in a short sample, but might have. The possibility would nevertheless have been priced into forward and futures rates, and so it could incorrectly appear to the econometrician that the forecast errors are predictable. Forward and futures rates are market expectations in this case. We attempt to minimize the risk of false rejections due to ``peso problems'' by using long samples of data.

Where we find that forward and futures rates are far from being efficient forecasts, it is our judgement that the existence of a risk premium, as in (1), is the most natural explanation. We are skeptical of accounting for large systematic predictability in forecast errors solely in terms of explanations (2)-(5), as we discuss above, but agree that it is possible to make a case that these might be part of the story. We interpret our tests for forecast efficiency as tests for risk premia (constant or time-varying) in forward and futures rates. Risk premia mean that these rates are not market expectations. If we can adequately model these risk premia, we can of course adjust these rates to convert them into market expectations.

The motivation of the present paper is to provide a compendium of results on the accuracy of a wide range of forward and futures rates, as predictors of future actual prices, under a common methodology. Its goal is simply to serve as a reference material for those who are interested in looking up the historical properties of different financial market prices that one might wisely or unwisely interpret as market expectations. The statistical evaluation of the forecasting properties of forward and futures rates is by no means new. An enormous literature has shown how forward exchange rates provide inefficient forecasts of future spot exchange rates. The expectations hypothesis of the term structure has been consistently and decisively rejected, for the United States at least, and so we should not expect to find that forward interest rates and interest rate futures are efficient forecasts of future interest rates. The literature on these and other cases in which the forecasting properties of forward and futures prices are considered is vast, and we make no attempt to review it.

We shall consider S&P500 futures, 3-month eurodollar, euroyen, euribor, sterling libor and Canadian bankers acceptance futures, Federal Funds futures, oil price and natural gas futures, forward currency rates, forward one-year U.S. Treasury rates and forward one-year U.K. Treasury rates. We analyze each of these under a common methodology, using data going back to 1991 and earlier.

The plan for the remainder of this paper is as follows. The data we use are described in section 2, including brief descriptions of the different forward and futures markets. Our methodology is described in section 3. Section 4 contains the empirical results. Section 5 concludes.

2 Forward and Futures Markets and our Data

In this section, we briefly describe the different forward and futures prices that we consider in this paper, and the data that we have obtained on each of these. We use forward prices for currency rates and forward one-year U.S. Treasury rates, but futures prices in other cases.² Forward and futures prices are very close to being equivalent. However, a futures contract has to be marked-to-market daily, as it is exchange-traded, whereas an over-the-counter forward contract does not have to be marked-to-market. If the overnight funding rate is correlated with the futures price (very likely in the case of interest rate futures) this implies a small convexity adjustment (Burghardt (2003)). An investor may prefer to bet on lower rates than on higher rates because it is cheaper to mark losses to market in the former case. In principle, this convexity adjustment could be a reason why futures rates can give systematically biased estimates of the future actual price. In practice, numerical calibrations of the size of the convexity adjustment indicate that this is a small effect (Hull (1996)).³

2.1 3-month interest rate futures

Eurodollar contracts trade on the Chicago Mercantile Exchange (CME). There is a contract for settlement in March, June, September and December of each year. These contracts are cash settled. The settlement price for each contract is simply the 3-month eurodollar deposit rate on the settlement day. In the middle of each month⁴, we linearly interpolate the prices between these contracts to get implied predictions of the 3-month interest rate in 90 days, 180 days and 360 days time. We can similarly obtain 90, 180 and 360 day ahead forecasts of 3-month euro area, UK, Japanese and Canadian interest rates from analogous foreign interest rate futures markets. These are euribor and sterling libor futures contracts that trade on the London International Financial Futures Exchange (LIFFE), euroyen futures that trade on the Tokyo International Financial Futures Exchange (TIFFE) and Canadian Bankers' Acceptance futures that trade on the Montreal Exchange.

2.2 Federal Funds futures

Federal funds futures trade on the Chicago Board of Trade (CBOT). There is a contract for every month. Contracts trade for several months out, but only the first few contracts have been liquid for a long period of time. These contracts are cash settled, and the settlement price for each contract is the average effective Fed Funds rate for that month. We take the prices of these futures in the middle of each month as forecasts of the average effective Fed Funds rate in each of the next 3 months.

2.3 S&P500 futures

S&P500 futures trade on the Chicago Mercantile Exchange (CME). There is a contract for settlement in March, June, September and December of each year. These contracts are cash settled. The settlement price for each contract is simply the level of the S&P500 index on the settlement day. In the middle of each month, we linearly interpolate the prices between these contracts to get implied predictions of the S&P500 index 90 days later.

2.4 Oil Price and Natural Gas futures

Oil price and natural gas futures trade on the New York Mercantile Exchange (NYMEX). Light sweet crude oil futures trade for settlement in each month. The oil contract provides for the physical delivery of 1,000 barrels of oil in Cushing, Oklahoma at any point during the settlement month. The contract provides for the delivery of any one of several different types of crude oil, but West Texas Intermediate is usually delivered. Natural gas futures similarly provide for the physical delivery of 10,000 million British thermal units of natural gas at the Henry Hub in Louisiana. In the middle of each month, we take the prices on 3-month, 6-month, and 1-year ahead oil and natural gas futures and take these as forecasts of the future monthly average spot prices of West Texas Intermediate crude oil and Henry Hub natural gas⁵ respectively.

2.5 Foreign Exchange Forward Rates

We obtained 3-month, 6-month and 1-year forward rates for the dollar vis-à-vis the yen, the euro, the pound, and the Canadian dollar in the middle of each month. We treated these as predictors of the corresponding spot rates 3 months, 6 months and 1 year hence.

2.6 Forward U.S. Interest Rates.

We used the 1-year forward rates, 1-5 years hence, as computed by Federal Reserve staff. We took these forward rates in the middle of each month and treated these as predictors of the future 1-year interest rates in 1-5 years time.

2.7 Forward U.K. Interest Rates.

We used the 1-year forward rates, 1-5 years hence, as computed from U.K. Gilt prices by the Bank of England. We took these forward rates in the middle of each month and treated these as predictors of the future 1-year interest rates in 1-5 years time.

Table 1 recapitulates all the forecasts that we have obtained from forward and futures rates. It also gives the dates for which we have the required data. As is the usual convention, we work with the log of foreign exchange rates, stock prices and the prices of oil and natural gas, but with the level of interest rates.

For comparability, all of the forecasts considered are at horizons 90, 180 and 360 days (3-months, 6 months and 1 year), except for Fed Funds futures which are liquid only at short horizons, S&P500 futures for which a long history is only available at short horizons, and the one-year forward rates.

3 Methodology

Using the data we have described in the previous section, we have many forward and futures rates, each of which we are treating as a forecast of the future settlement price. For example, we have a 90-day ahead eurodollar futures rate (interpolated), which we are treating as a forecast of the actual spot eurodollar interest rate in 90 days time.

Let $f_{t,h}$ denote some futures or forward rate at time for time in the future, and let $y_{t+h}$ denote the corresponding actual realized value. Neglecting marking-to-market considerations, a long position has no initial cost and a random payoff of $y_{t+h} -f_{t,h}$ . Standard no-arbitrage reasoning then implies that

$\displaystyle E_{t} [m_{t+h} (y_{t+h} -f_{t,h} )]=0$

where $m_{t+h}$ is the stochastic pricing kernel where

subscripts throughout denote conditioning on the information set at time

. Rearranging gives

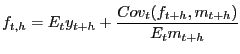
$\displaystyle f_{t,h} =E_{t} y_{t+h} +\frac{Cov_{t} (f_{t+h} ,m_{t+h} )}{E_{t} m_{t+h} }$

which says that $f_{t,h}$ is the expectation for the future realized value (the first term) plus the risk premium (the second term). This does not of course tell us what the pricing kernel is.

Our approach in this paper is a purely statistical one, using the standard tools of forecast evaluation. If forward and futures rates are rational expectations of future prices, then the forecast errors must have mean zero and must be uncorrelated with any variable in the information set at the time that the forecast was made. By testing these hypotheses, we can test for the existence of risk premia, estimate the average magnitude of any risk premia, and test for time variation in risk premia.

We first estimate the mean of the ex-post forecast errors, i.e. the average of $y_{t+h} -f_{t,h}$ , and test whether this is significantly different from zero. If so, we conclude that there is a significant average risk premium.

Next, we consider the standard forecast efficiency regression,

$\displaystyle y_{t+h} -y_{t} =\alpha+\beta(f_{t,h} -y_{t} )+\varepsilon_{t}$

(1)

and test the hypothesis that the slope coefficient $\beta$ is equal to 1, and the joint hypothesis that $\alpha=0$ and $\beta=1$ . This is often known as the Mincer-Zarnowitz regression (Mincer and Zarnowitz (1969)). If the slope coefficient $\beta$ is significantly different from 1, we conclude that the risk premium is time-varying.

Lastly, we consider the relative root mean square error of two predictions for $y_{t+h}$ : the futures rate, $f_{t,h}$ , and the current level, $y_{t}$ . In other words, this is the ratio of the root mean square error of the futures-based forecast to the root mean square error of the random walk forecast. If the futures rate gives a less accurate prediction than the random walk benchmark, we again conclude that the futures rate is not a rational expectation of the future actual price, and so that the futures rate must embody some risk premium.

4 Results

We now turn to the results, contained in Table 2. This Table shows the average ex-post forecast error, along with the associated standard error.⁶ The Table also shows the coefficient estimate of $\beta$ in equation (1), along with the associated standard error and t statistic testing the hypothesis that $\beta=1$ . The second column from the right of the Table gives the p-value in an F-test of the hypothesis that $\alpha=0$ and $\beta=1$ in equation (1). The final column of the Table gives the root mean square error of the futures-based prediction relative to that of the random walk prediction, a naive time series benchmark. A number greater than one means that the random walk gives a more accurate forecast.

In this Table, any forecast for which we reject the hypothesis that $\beta=1$ in equation (1), or the joint hypothesis that $\alpha=0$ and $\beta=1$ , at the 10% level, or any forecast which is less accurate than a random walk, is shown in bold. The forecasts for which the hypothesis that $\beta=1$ is rejected are shown in bold italics.

For interest rate futures or forward interest rates we can refer to the risk premium as a term premium, and will henceforth use both of these terms interchangeably.

Here is a summary of the broad patterns of the results:

1. Forward currency rates do less well than the random walk in terms of root mean square prediction error. This repeats the famous result of Meese and Rogoff (1983). Equation (1) for forward currency rates is of course just the uncovered interest parity (UIP) regression of Fama (1984) and others for testing the UIP hypothesis that the forward currency rate is an efficient forecast of the future spot rate. Our evidence against the UIP hypothesis is strong, but a little less overwhelming than other researchers have obtained with earlier data. For example, we fail to reject the hypothesis that the slope coefficient is equal to one for the pound, but still find that the UIP forecast has larger mean square error than the random walk forecast. Flood and Rose (2002) find that rejections of UIP are less overwhelming in the 1990s than in earlier sample periods.

The failure of UIP means that investors fail to exploit a carry-trade strategy that, although risky, has positive expected value.⁷ Understanding the UIP risk premium remains a central challenge in international finance.

2. Fed Funds futures are useful predictors of the future Fed Funds rate. We find a modest but statistically significant average risk premium of about 4 basis points for one month, that increases in the forecast horizon to about 16 basis points for three months. We find no evidence of time-varying risk premia. This is consistent with existing research, including Gurkaynak, Sack and Swanson (2002) who find that Fed Funds futures are the best available indicators of market monetary policy expectations at horizons of up to a few months, but that even these are slightly biased predictors.

3. Many 3-month interest rate futures have large and statistically significant average risk premia, which are increasing in the horizon. The slope of the futures curve will typically be much too steep relative to expectations. This is especially true for eurodollar futures. The estimated average term premium in eurodollar futures is about 9 basis points per month. But, the risk premium in eurodollar futures is significantly time-varying, so no constant adjustment can correct for it. Large and time-varying risk premia in eurodollar futures rates have been noted in extant work, including Piazzesi and Swanson (2004). Eurodollar futures rates are indeed less good predictors of future eurodollar spot interest rates than a random walk, in terms of root mean square prediction error, at the horizons we consider.

It is worth emphasizing that the historical bias in eurodollar futures rates is not the artifact of one or two special episodes. Similar results exist if we shorten our sample to include just data since 1990. Over our full sample, the actual 3-month interest rate turned out to be lower than what the eurodollar futures market had predicted 1 year in 77% of observations. The eurodollar futures rate over-predicted the interest rate by 12 basis points or more 74% of the time, and by 24 basis points or more 71% of the time.

The average estimated risk premium in Bankers' Acceptance rates is similarly large. Euribor and sterling libor futures rates, however, show a substantially smaller estimated average risk premium.

4. Treasury one-year forward rates have large and statistically significant average risk premia, just like eurodollar 3-month futures rates. There is significant time-variation in these risk premia, at horizons of 3 years and longer⁸. Forward rates are less accurate predictors of future one-year rates than a random walk at all horizons. The average risk premium is not estimated to be linear in the forecast horizon, and is instead concave. This concavity is noteworthy because a term premium of basis points per month in forward and futures rates, combined with an assumption of linearity, would imply approximately a basis point term premium in a ten-year zero-coupon rate. This might in turn deter us from thinking that the term premium in near-term forward and futures rates could be large, because it might imply an implausibly large term premium in ten-year yields. But this argument relies on the assumption of linearity. If the risk premium is in fact concave, there a large per-month term premium in near term forward and futures rates does not have to imply such a large term premium in ten year rates.

5. U.K. one-year forward rates also have statistically significant average risk premia, but these are smaller than for the U.S. forward rates. U.K. forward rates are about as accurate predictors of future U.K. one-year rates as a random walk. Though, for U.K. forward rates, the hypothesis that $\beta=1$ is not rejected at horizons longer than 2 years.

6. There is less evidence of risk premia associated with oil and natural gas futures, though even here the results are still somewhat mixed.

4.1 Discussion

Forward exchange rates should not be taken as expectations of future spot exchange rates. Likewise, U.S. forward interest rates and interest rate futures should not be taken as expectations of future U.S. interest rates, with the exception of near-term Federal Funds futures. While it is well known that foreign exchange forward rates give less accurate forecasts than a random walk, we show that this is also true for eurodollar interest rate futures at horizons as short as 3 months, and for Treasury forward interest rates. The evidence against the expectations hypothesis of the term structure is weaker in the U.K. and the euro area than in the United States. This is consistent with earlier findings of Hardouvelis (1994) and others. Nevertheless, forward interest rates and interest rate futures should not generally be taken as pure expectations in the euro area or the U.K. either.

Hedging demand is a factor in U.S. interest rate markets that may generate large and time-varying risk premia. Dupont and Sack (1999) and Sack and Elsasser (2004) discuss the role of hedging demand in the Treasury market. Perli and Sack (2003) find that mortgage hedging amplifies movements in long-term U.S. interest rates. Also, on average over time, the marginal investor in U.S. interest rate markets appears to be willing to pay a big premium to hedge against rises in interest rates. Discussions with market participants indicate that the eurodollar futures market is typically dominated by agents with fixed rate assets but floating rate liabilities which implies a large demand for hedging against increasing interest rates. Speculators who might see this as an arbitrage opportunity, such as hedge funds, are perhaps outweighed by the scale of this hedging activity. These factors do not seem to lead to such large distortions in U.K. and euro area interest rate markets.

We believe that the predictability of forecast errors in U.S. forward interest rates and U.S. interest rate futures is evidence of a large and time-varying risk premium. But an important caveat is that it is however quite possible that rational learning explains part of the systematic forecast errors in our sample, as discussed in point (2) of the introduction. Our sample is a period over which agents arguably learned about a break in the trend growth rate of U.S. productivity that in turn implies lower-than-expected inflation and lower-than-expected interest rates. As such, the shocks in our sample period may be ``special'', not a good guide to those we should expect in the future, and not representative of any market pricing of risk. This could mean that we are overestimating the average bias.

We nevertheless believe that there are large and time-varying risk premia in eurodollar futures rates. Strong evidence for this comes from comparing one-year-ahead eurodollar futures rates with one-year-ahead survey expectations for future 3-month interest rates from Consensus forecasts. The futures rate is on average significantly above the survey rate, and the spread between these two has significant predictive power for the futures-based forecast error. If the eurodollar futures rates were genuine market expectations, but happened to be wrong because of learning, then the same errors should have shown up in Consensus forecasts too. On the other hand, a risk premium would lead to a divergence between futures rates and survey expectations, as we find.

There is much less evidence for risk premia in oil and natural gas futures. Discussions with market participants indicate that speculative hedge funds are large participants in oil and natural gas futures markets and that they are willing and able to take aggressive positions if any expected profit opportunity arises.

One caveat about the relatively favorable results for oil price and natural gas futures is that while it is possible to find that forward and futures rates yield forecasts with errors that are predictable, it is never possible to conclude that these errors are not predictable. We have only checked for correlation between the forecast error and a constant and the forecast itself. But any variable in the information set at the time that the forecast is made could potentially have significant predictive power for the forecast error and we cannot check all variables in this information set.

4.2 Exact Sign and Rank Tests

It is possible that the forecast efficiency test in equation (1) may be affected by size distortions (e.g. Maynard and Phillips (2001)).

One rejoinder to this concern is to test forecast efficiency using tests that are exact. Exact tests may or may not have good power properties, but they cannot suffer from size distortions under the assumptions used to derive their exact distributions. Campbell and Dufour (1995) propose various nonparametric sign and rank tests of the hypothesis that $\alpha=0$ and $\beta=1$ in regression (1), that have exact null distributions under very mild conditions, given in their paper. These conditions allow for the regressors to have unit roots, or near unit roots, or to be fractionally integrated, though require the errors to be serially uncorrelated. Authors using such tests to test for forecast efficiency include Campbell and Ghysels (1995) and Maynard (2001). For one-step ahead forecasts (, the test statistics are

$\displaystyle S=\Sigma_{t} u(x_{t} e_{t} )$

$\displaystyle SR=\Sigma_{t} u(x_{t} e_{t} )r(\vert x_{t} e_{t} \vert)$

and

$\displaystyle W=\Sigma_{t} u(x_{t} e_{t} )r(\vert e_{t} \vert)$

where $x_{t} =f_{t,h} -y_{t}$ , $e_{t} =(y_{t+h} -y_{t} )-(f_{t,h} -y_{t} )$ ,

denotes the sample size,

is the indicator function that the argument is nonnegative and $r(Z_{t} )$ is the rank of $Z_{t}$ among $\{Z_{t} \}$ in ascending order. If

, the errors in equation (1) are overlapping which would violate the requirement of no serial correlation in the errors. We deal with this by the simple device of keeping only one in every

observations, ensuring that the errors are nonoverlapping. Specifically, the test statistics for general

are

$\displaystyle S=\Sigma_{j} u(x_{hj-h+1} e_{hj-h+1} )$

$\displaystyle SR=\Sigma_{j} u(x_{hj-h+1} e_{hj-h+1} )r(\vert x_{hj-h+1} e_{hj-h+1} \vert)$

and

$\displaystyle W=\Sigma_{j} u(x_{hj-h+1} e_{hj-h+1} )r(\vert e_{hj-h+1} \vert)$

Table 3 presents the exact p-values associated with each of these tests, for all of the forward and futures based forecasts that we consider in this paper. Especially at longer horizons, these tests discard a lot of data because of the device that we have adopted to deal with overlapping forecasts. Thus, especially at longer horizons, the tests should not be expected to be very powerful⁹.

Nevertheless, despite the possibly low power of these tests, we are still able to reject the null that $\alpha=0$ and $\beta=1$ in several cases. The third test, using the statistic , rejects the null at the 10% level or better for the eurodollar rate (at 3-month, 6-month and 1-year horizons), for Treasury forward rates (at horizons up to 5 years), for several currency forward rates, and indeed for oil and natural gas futures at the 3-month horizon.

4.3 Adjusting Forward and Futures Rates

We believe that most forward and futures rates are far from being expectations. That leaves open the possibility that we can extract information about expectations from these rates, if we can first purge the effect of risk premia. To that end, this paper puts forth a baseline for the size, changes with forecast horizon, and time variation in risk premia across a range of assets. Purging the effect of risk premia is however easier said than done. Economists have not had much luck in extracting information about future exchange rates from forward exchange rates. Recent work by Cochrane and Piazzesi (2002) and Piazzesi and Swanson (2004) has proposed promising methods for estimating time-varying risk premia in U.S. forward rates and in U.S. interest rate futures.

5 Conclusion

We have applied a set of standard forecast evaluation tests to a wide range of futures and forward rates from financial markets and found that there is evidence in most cases that these are not pure expectations. They are also affected by risk premia, that are often time-varying. We should not interpret these forward and futures rates as the rational expectations of market participants, unless we are willing to assume that the historical time series are unrepresentative of what we should expect in the future.

We find some exceptions to the proposition that forward and futures rates are not useful as measures of expectations. The risk premia we find in Fed Funds futures are modest and do not vary significantly over time, though appear to increase with the forecast horizon. Also, there is little evidence for risk premia in oil and natural gas futures.

We do not adequately understand the underlying nature of risk premia in futures and forward rates. Our goal in this paper has been to document the empirical existence of these risk premia, not to provide economic explanations for them, though we have discussed some potentially relevant factors especially in the context of interest rate futures. Clearly, we should not refuse to believe the evidence that these risk premia exist just because we do not adequately understand their origin. Yet, as recently as 1999, the Bank of England persisted in using forward currency rates as predictors of future spot rates despite all the evidence to the contrary, appealing to the reasoning:

``Some Committee Members were inclined towards UIP, in part because they could see no compelling reasons relating to risk to assume that the exchange rate will depreciate at a slower rate than implied by interest differentials.'' (Bank of England (1999)).

Table 1: Data Availability

Instrument	Horizon	Sample Period
Fed Funds Futures	1-3 Months	2/1989-12/2003
Canadian Dollar Forwards	3 Months, 6 Months, 1 Year	12/1984-12/2003
Pound Forwards	3 Months, 6 Months, 1 Year	12/1984-12/2003
DM/Euro Forwards	3 Months, 6 Months, 1 Year	12/1984-12/2003
Yen Forwards	3 Months, 6 Months, 1 Year	12/1984-12/2003
Natural Gas Futures	3 Months, 6 Months, 1 Year	11/1990-12/2003
Oil Futures	3 Months, 6 Months, 1 Year	4/1989-12/2003
Eurodollar Futures	3 Months, 6 Months, 1 Year *	1/1984-12/2003
Sterling Libor Futures	3 Months, 6 Months, 1 Year *	11/1984-12/2003
Bankers Acceptance Futures	3 Months, 6 Months, 1 Year *	10/1988-12/2003
Euromark/Euribor Futures	3 Months, 6 Months, 1 Year *	1/1990-12/2003
Euroyen Futures	3 Months, 6 Months, 1 Year *	4/1991-12/2003
S&P 500 Futures	3 months*	1/1984-12/2003
US 1 Year Forwards**	1-5 Years	12/1987-12/2003
UK 1 Year Forwards***	1-5 Years	1/1979-12/2003

**:One year Treasury forward rates obtained by the Svensson method, as calculated by the Monetary Affairs Division.

Note that the sample period is the same over all horizons for any one instrument.

Table 2: Predictability of Forward and Futures Based Forecast Errors

* Average ex-post forecast error (in basis points) with the associated standard error in the next column.

** Estimated slope coefficient beta in equation (1), with the associated standard error in the next column.

† t-statistic p-value from test of the hypothesis that beta=1 in equation (1).

§ F-statistic p-value from test of the joint hypothesis that alpha=0 and beta=1 in equation (1).

*** Root Mean Square Prediction Error from Futures/Forwards Based Forecast, relative to the random walk naive time series benchmark.

Forward/Futures Based Horizon	Horizon	Mean Forecast Error*	standard error	Slope Coefficient**	standard error	t-stat†	F-stat (p-val)§	Relative RMSPE***
Fed Funds	1 month	4.3	1.1	0.89	0.09	-1.22	0.00	0.75
Fed Funds	2 months	9.5	2.1	1.09	0.10	0.90	0.00	0.70
Fed Funds	3 months	16.0	3.7	1.15	0.13	1.15	0.00	0.72
Canadian Dollar	3 months	27.3	25.0	-0.89	0.38	-4.97	0.00	1.05
Canadian Dollar	6 months	53.2	52.9	-0.95	0.38	-5.13	0.00	1.09
Canadian Dollar	1 year	81.4	117.6	-0.81	0.55	-3.29	0.00	1.10
Pound	3 months	-116.1	52.7	-1.00	1.32	-1.52	0.08	1.03
Pound	6 months	-210.0	99.4	-0.31	1.39	-0.94	0.09	1.04
Pound	1 year	-346.6	177.7	-0.02	1.24	-0.82	0.13	1.07
DM/Euro	3 months	75.2	58.0	-0.03	0.88	-1.17	0.21	1.00
DM/Euro	6 months	139.1	120.2	-0.08	0.89	-1.21	0.15	1.01
DM/Euro	1 year	219.9	268.9	0.03	1.00	-0.97	0.19	1.00
Yen	3 months	41.9	67.2	-3.04	1.04	-3.88	0.00	1.01
Yen	6 months	71.2	134.8	-3.11	0.97	-4.24	0.00	1.02
Yen	1 year	96.8	300.4	-3.10	0.89	-4.61	0.00	1.04
Natural Gas	3 months	-75.3	307.6	0.62	0.16	-2.38	0.05	0.96
Natural Gas	6 months	-360.5	522.0	0.77	0.16	-1.44	0.17	0.90
Natural Gas	1 year	-1024.9	789.0	1.40	0.30	1.33	0.09	0.84
Oil	3 months	-250.1	175.6	0.75	0.43	-0.58	0.17	0.99
Oil	6 months	-502.2	315.1	0.74	0.46	-0.57	0.16	0.99
Oil	1 year	-832.4	565.1	1.01	0.36	0.03	0.31	0.96
Eurodollar	3 months	27.0	6.3	0.77	0.23	-1.00	0.00	1.01
Eurodollar	6 months	57.8	14.0	0.42	0.30	-1.93	0.00	1.13
Eurodollar	1 year	127.3	32.6	0.25	0.37	-2.03	0.00	1.26
Euromark/Euribor	3 months	8.9	3.5	0.85	0.12	-1.25	0.04	0.78
Euromark/Euribor	6 months	17.6	8.4	0.78	0.11	-2.00	0.07	0.78
Euromark/Euribor	1 year	52.8	22.1	0.67	0.21	-1.57	0.04	0.92
Euroyen	3 months	17.7	3.1	0.96	0.14	-0.29	0.00	0.84
Euroyen	6 months	34.3	7.3	1.02	0.23	0.09	0.00	0.86
Euroyen	1 year	80.5	17.5	0.84	0.53	-0.30	0.00	1.08
Bankers' Accept	3 months	19.8	9.0	0.71	0.20	-1.45	0.04	0.95
Bankers' Accept	6 months	44.7	17.3	0.64	0.26	-1.38	0.00	0.98
Bankers' Accept	1 year	111.1	35.5	0.81	0.36	-0.53	0.00	1.01
Sterling Libor	3 months	-1.3	8.6	0.68	0.16	-2.00	0.12	0.95
Sterling Libor	6 months	6.8	16.2	0.67	0.17	-1.94	0.16	0.92
Sterling Libor	1 year	28.1	34.9	0.73	0.24	-1.13	0.27	0.89
S&P 500	3 months	-155.7	68.4	0.41	1.00	-0.59	0.07	0.97
US Forwards	1 year	103.6	31.5	0.51	0.49	-1.00	0.00	1.18
US Forwards	2 years	182.3	52.9	1.12	0.45	0.27	0.00	1.13
US Forwards	3 years	244.5	60.0	1.64	0.25	2.56	0.00	1.08
US Forwards	4 years	286.9	60.0	1.49	0.17	2.88	0.00	1.18
US Forwards	5 years	314.2	46.9	1.22	0.09	2.44	0.00	1.30
UK Forwards	1 year	47.9	28.2	0.41	0.27	-2.19	0.00	1.06
UK Forwards	2 years	101.6	46.9	0.60	0.22	-1.82	0.00	1.01
UK Forwards	3 years	151.7	55.2	0.91	0.28	-0.32	0.00	0.96
UK Forwards	4 years	197.9	56.3	1.07	0.34	0.21	0.00	0.95
UK Forwards	5 years	239.4	48.9	0.91	0.25	-0.36	0.00	1.02

All forecasts for which (i) the hypothesis that beta=1, or (ii) the hypothesis that alpha=0 and beta=1 are rejected, or (iii) for which the root mean square prediction error is greater than that of the random walk benchmark, are shown in bold. Those forecasts for which the hypothesis that beta=1 is rejected are shown in bold italics. All significance tests were conducted at the 10% level.

Table 3: P-values from exact sign/rank tests for unpredictable forecast errors

This table gives the p-values for the exact nonparametric tests S, SR and W described in the text.

References

Bank of England (1999): Monetary Policy Report, November 1999, Bank of England, London.

Burghardt, G. (2003): The Eurodollar Futures and Options Handbook, McGraw Hill, New York.

Campbell, B. and J-M Dufour (1995): Exact Nonparametric Orthogonality and Random Walk Tests, Review of Economics and Statistics, 77, pp.1-16.

Campbell, B. and E. Ghysels (1995): Federal Budget Projections: A Nonparametric Assessment of Bias and Efficiency, Review of Economics and Statistics, 77, pp.17-31.

Cochrane, J.H. and M. Piazzesi (2002): Bond Risk Premia, NBER Working Paper 9178.

Dupont, D. and B. Sack (1999): The Treasury Securities Market: Overview and Recent Developments, Federal Reserve Bulletin, 85, pp.785-806.

Elliott, G. and T. Ito (1999): Heterogenous Expectations and Tests of Efficiency in the Yen/Dollar Forward Foreign Exchange Rate Market, Journal of Monetary Economics, 43, pp.435-456.

Fama, E. (1984): Forward and Spot Exchange Rates, Journal of Monetary Economics, 14, pp.319-338.

Flood, R.P. and A.K. Rose (2002): Uncovered Interest Parity in Crisis, IMF Staff Papers, 49, pp.252-266.

Gurkaynak, R.S., B. Sack and E.T. Swanson (2002): Market-Based Measures of Monetary Policy Expectations, Finance and Economics Discussion Series, 40.

Hardouvelis, G.A. (1994): The Term Structure Spread and Future Changes in Long and Short Rates in the G7 Countries: Is There A Puzzle?, Journal of Monetary Economics, 33, pp.255-283.

Hull, J.C. (1996): Options, Futures and Other Derivatives, Third Edition, Prentice Hall, New York.

Lewis, K. (1989): Changing Beliefs and Systematic Rational Forecast Errors with Evidence from Foreign Exchange, American Economic Review, 79, pp.621-636.

Maynard, A. (2001): Persistence, bias, and the forward premium anomaly: How bad is it?, mimeo, University of Toronto.

Maynard, A. and P.C.B. Phillips (2001): Rethinking an Old Empirical Puzzle: Econometric Evidence on the Forward Discount Anomaly, Journal of Applied Econometrics, 16, pp.671-708.

Meese, R.A. and K. Rogoff (1983): Empirical Exchange Rate Models of the Seventies: Do They Fit Out of Sample?, International Economic Review, 14, pp.3-24.

Mincer, J. and V. Zarnowitz (1969): The Evaluation of Economic Forecasts in J. Mincer (ed.), ``Economic Forecasts and Expectations'', NBER, New York.

Perli, R. and B. Sack (2003): Does Mortgage-Hedging Amplify Movements in Long-Term Interest Rates, Finance and Economics Discussion Series, 49.

Phillips, K.L. and K. Snow (1998): The Forward Bias: Is it a Money Tree?, Economics Letters, 61, pp.373-379.

Piazessi, Monika, and Eric Swanson (2004). Futures Prices as Risk-Adjusted Forecasts of Monetary Policy, mimeo, University of Chicago and Federal Reserve Board.

Sack, Brian, and Robert Elsasser (2004). Treasury Inflation-Indexed Debt: A Review of the U.S. Experience, Federal Reserve Bank of New York Economic Policy Review, 10, pp.47-63.

Timmermann, A. (1993): How Learning in Financial Markets Generates Excess Volatility and Predictability in Stock Prices, Quarterly Journal of Economics, 108, pp.1135-1145.

Footnotes

1. $^{\ast}$ International Finance Division, Board of Governors of the Federal Reserve System, Washington DC 20551(Chernenko and Wright) and Markets Group, Federal Reserve Bank of New York, 33 Liberty Street, New York NY 10045 (Schwarz). We are grateful to Jon Faust and Dale Henderson for helpful comments. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any person associated with the Federal Reserve System. Return to text

2. The liquidity in foreign exchange forward contracts is much greater than in foreign exchange futures contracts, though the latter exist as well (on the Chicago Mercantile Exchange). Return to text

3. Unless the maturity date of the futures contract is several years into the future, but we will not be considering any such futures in this paper. Return to text

4. Specifically, on the 15th day of each month, or the next business day. Return to text

5. The spot price of West Texas Intermediate oil is a price for delivery next month and so is very similar to a front month futures price. In the natural gas market, the Henry Hub spot price is for next day delivery. Return to text

6. Newey-West heteroskedasticity and autocorrelation robust standard errors with lag truncation parameter set equal to the number of overlapping observations. Return to text

7. Authors such as Phillips and Snow (1998) and Elliott and Ito (1999) find that the carry-trade strategy is typically profitable but that the risk-return tradeoff is not especially favorable. Return to text

8. The Newey-West standard errors have lag truncation parameters set equal to the number of overlapping observations, which is about one third of the sample size in the case of 5-year-ahead forecasts. This is a very large truncation parameter relative to the sample size, so these standard errors and the associated test statistics should be interpreted with special caution. Return to text

9. One might suppose that nonparametric rank and sign tests necessarily waste a lot of power even without the issue of reducing the dataset to avoid overlapping forecasts. Actually, as discussed by Campbell and Dufour (1995), these tests do not generally waste much power. Indeed, they can even be more powerful than conventional F-tests if the errors have fat tails. Return to text