
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 810, July 2004--Screen Reader Version*
The Delayed Response To A Technology Shock.
A Flexible Price Explanation
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
I present empirical evidence of how the U.S. economy, including per-capita hours worked, responds to a technology shock. In particular, I present results based on permanent changes to a constructed direct measure of technological change for U.S. manufacturing industries.
Based on empirical evidence, some claim that hours worked declines and never recovers in response to a positive technology shock. This paper's empirical evidence suggests that emphasizing the drop in hours worked is misdirected. Because the sharp drop in hours is not present here, the emphasis rather should be on the small (perhaps negative) initial response followed by a subsequent large positive response. Investment, consumption, and output have similar dynamic responses.
In response to a positive technology shock, a standard flexible price model would have an immediate increase in hours worked. Therefore, such a model is inconsistent with the empirical dynamic responses. I show, however, that a flexible price model with habit persistence in consumption and certain kinds of capital adjustment costs can better match the empirical responses.
Some recent papers have critiqued the use of long run VARs to identify the dynamic responses to a technology shock. In particular they report that, when long run VARs are applied to data simulated from particular economic models, the point estimates of the impulse responses may be imprecisely estimated. However, based on additional simulation evidence, I find that, although the impact response may be imprecisely estimated, a finding of a delayed response is much more likely when the true model response also has a delayed response.
Keywords: macroeconomic models, vector autoregressions, impulse responses, weak instruments, long-run identification assumption
JEL Classifications: D24 E24 E32 O47
1 Introduction
Recent papers by Galí (1999), Basu, Fernald, and Kimball (2004), and Francis and Ramey (2003) have claimed that in response to an unexpected improvement in technology, hours spent working declines. This finding challenges the standard macroeconomic flexible-price model because that model predicts a strong positive correlation between employment and technology.
This paper's empirical evidence suggests that emphasizing the drop in hours worked is misdirected. Because the sharp drop in hours is not present in several of the data series examined here, the emphasis rather should be on the small (perhaps negative) initial response followed by a subsequent large positive responses. The paper also presents a flexible-price model that is broadly consistent with the empirical dynamic responses. The empirical evidence describes how the economy responds to shocks to a productivity measure that has been corrected for utilization and reallocation. For the quantities considered here (output, consumption, investment, and hours worked), a consistent pattern emerges. When the technology shock occurs, the variables respond only slightly. Over time, the variables' dynamic responses gain strength.
To be consistent with the empirical responses, the standard quantitative dynamic flexible-price model must be modified. The modifications pursued here are to make utility depend on past consumption (habit persistence) and to have capital adjustment costs.
Galí (1999) and Francis and Ramey (2003) measure productivity using aggregate labor productivity. Aggregate labor productivity, however, is a poor measure of technology because it can change for many reasons besides technological growth. In particular, in response to changes in the economy, workers sometimes vary their effort and, hence, output. Because this variation in the utilization of inputs is unobservable, changes in the utilization rate will appear as changes in productivity. To obtain an accurate measure of how technology increases productivity, one must control for these changes in utilization. In addition, reallocation of labor from an industry with low labor productivity to an industry with high labor productivity will also show up as in improvement in aggregate labor productivity that may not be due to increases in technology.
Combining the methods of Burnside, Eichenbaum, and Rebelo (1996) and Basu, Fernald, and Kimball (2004), the current paper constructs a quarterly measure of productivity that has been corrected for variations in utilization and also for reallocation between industries. In spite of the steps taken to remove endogenous influences, this productivity measure still might be influenced by other economic variables. To control for this endogeneity, I use the long-run approach of Galí (1999) to consider how the economy responds to exogenous shocks to the productivity series. The empirical results support the view that the immediate response to a technology shock is either negative or small. Although the initial responses are small, this paper shows that, within six quarters, the responses are positive and large.
The empirical work is presented with an emphasis on robustness. The paper considers responses to a technology shock identified under different identification assumptions. In addition, the paper reports confidence intervals for the impact response of a technology shock that are valid under the assumption of weak instruments. Although the resulting confidence intervals are wide, compared to the possible range associated with an unidentified shock, the identification scheme does restrict the possible responses.
Having documented how the economy responds to a technology shock, the challenge is to construct a model that has the same dynamic responses. The empirical responses are incompatible with a standard quantitative dynamic flexible-price model; because, in the standard model, the period of the technology shock is when the variables respond most. The model needs to be modified to generate a more realistic delayed dynamic response. Galí (1999) and Basu, Fernald, and Kimball (2004) propose to resolve the model's problem by including sticky prices. Basu (1998) presents a sticky price model that successfully matches the immediate small empirical responses to a technology shock but fails to match the medium-term empirical responses. With both sticky prices and wages, Altig, Christiano, Eichenbaum and Linde (2004) better match these responses. The current paper does not use sticky prices. Rather it uses a flexible-price model with modifications to both preferences and technology. Preferences are modified such that today's utility depends on the previous level of consumption, habit persistence. Habit persistence implies that consumption responds more slowly to an increase in technology. Just habit persistence, however, is not enough to match the data. The technology to transform investment into capital must be modified to dampen the responses by investment and output. The paper presents two specifications for the investment technology: time-to-plan and convex capital adjustment costs. When the capital adjustment costs depend on the ratio of new investment to capital, the model can match the initial period's responses but fails to match the subsequent increases. Having the adjustment costs depend on the growth rate of investment results in a better match to the long-run response. A time-to-plan model also matches but, with only one kind of investment good, its responses are somewhat too jagged. These last two specifications work better because although they constrain the initial response by investment they allow the subsequent responses to be strong.
Although these models can match the consumption, investment and hours worked responses, the models presented here have a difficult time matching the response of the real interest rate. Although there is some uncertainty with respect to the true real interest rate response, the empirical impulse responses, in general, indicate that the real interest rate increases in response to a positive technology shock. Chiefly because of habit persistence, in the reported economic models, the real interest rate instead falls in response to a positive technology shock. I show that a model with consumption adjustment costs can better match the real interest rate response. Even this model, however, does not completely capture the empirical response by the real interest rate.
Recent papers by Erceg, Guerrieri and Gust (2004) and Chari Kehoe and McGrattan (2004) have critiqued the use of long-run VARs to construct impulse responses. Using simulated data from particular economic models, they show that, for these particular models, the point estimates of long run VARs are imprecisely estimated. However, when I adopt their approach of simulating data from a benchmark model, I find further evidence in favor of studying the shape of the impulse responses. Although the impact response may be imprecisely estimated, a finding of a delayed response is much more likely when the true model response also has a delayed response.
2 Empirical Work
This paper's empirical work combines the two approaches taken in the literature to study productivity shocks. As in Basu Fernald and Kimball (2004), industry-level data is used to construct a utilization-corrected aggregate technology series. This series is then used as a variable in a vector autoregression, where, as in Galí (1998), exogenous technology shocks are identified under the assumption that only exogenous technology shocks affect the permanent level of productivity. In the first subsection, I describe how to use fluctuations in electricity usage (as in Burnside, Eichenbaum and Rebelo (1996)) and fluctuations in average hours (as in Basu Fernald and Kimball (2004)) to construct a quarterly utilization-corrected technology series. In the second subsection, I then use the same vector autoregression approach that Galí (1999) and Francis and Ramey (2003) used for labor productivity to calculate impulse responses to a permanent shock to my constructed technology series. The main findings are that the response by per capita hours worked is initially small but ,within two years, hours worked experiences a large increase.
2.1 Accounting For Utilization and Reallocation
Forces besides technological progress affect labor productivity. In particular, the effort expended by workers and machines can vary endogenously over time. One cannot always observe this time-varying utilization of inputs, which can be a serious issue in measuring technology growth because a change in utilization can be mistaken for a change in technology.
This section uses methods proposed by Basu, Fernald, and Kimball (2004) [BFK] and Burnside Eichenbaum and Rebelo (1996) [BER] to approximate the changes in utilization with changes in observable variables. BFK approximate changes in utilization by using changes in average hours worked. The intuition for this approximation is that a firm would choose to vary both workers' hours and utilization until the costs and the benefits are the same.3 BER approximate changes in capital services by changes in electricity usage. In addition, because reallocation can increase aggregate productivity without requiring an increase in technology, one should also control for reallocation between industries. As is done in BFK, the aggregate productivity series is constructed by aggregating industry-level productivity series.
To calculate the productivity series at the quarterly frequency requires a few strong assumptions. Because the industry-level capital stock is unobservable at the quarterly frequencies, changes in electricity usage are used to approximate the changes in capital services. Because data on material usage is unavailable at the quarterly frequency, one must assume that there is very limited substitutability between materials and a mix of capital services and labor. BFK have been critical of estimating productivity without data on materials usage. In trying to measure quarterly productivity growth, it, however, is likely better to implement partially their methods than not use them at all.
Industry-Level Data
The productivity equation is estimated using quarterly data at the industry level between 1972 to 2001. As in BFK, these industry-level productivity series are then aggregated to generate an economy-wide productivity series.4 The industries used here are the eighteen two-digit SIC manufacturing industries. Their names and SIC codes are reported in Table 1.
Applying the methods of BER and BFK results in the following
equation whose residual is a measure of productivity growth. Output
and all the inputs are expressed in logged first differences of
quarterly data. For each industry ![]() , the growth rate at quarter
, the growth rate at quarter ![]() of the productivity series
of the productivity series
![]() will be
the residual from the following estimated equation5:
will be
the residual from the following estimated equation5:
| (1) |
This output data ![]() will be measured by the Federal Reserve's measures of industrial
production. The capital services variable
will be measured by the Federal Reserve's measures of industrial
production. The capital services variable ![]() will be approximated by data
on electricity usage.6 The
average hours
will be approximated by data
on electricity usage.6 The
average hours ![]() and
employment data
and
employment data ![]() are taken from the corresponding BLS measure. The capital
are taken from the corresponding BLS measure. The capital
![]() and labor
shares
and labor
shares ![]() are
calculated as the average value-added shares from the BLS KLEMS
database.7The values
of
are
calculated as the average value-added shares from the BLS KLEMS
database.7The values
of ![]() and
and ![]() are estimated. The values of
are estimated. The values of
![]() and
and ![]() are constrained to be the same for
all durable good sectors and the same for all nondurable good
sectors.
are constrained to be the same for
all durable good sectors and the same for all nondurable good
sectors.
In aggregating these industry level estimates, the aggregation equation is the same as in BFK.8 Aggregate productivity is calculated as
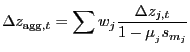
|
(2) |
The weight ![]() is the
share of value added by industry
is the
share of value added by industry ![]() . The share of materials
. The share of materials ![]() is calculated using the
materials share of gross-output reported in the KLEMS dataset.
is calculated using the
materials share of gross-output reported in the KLEMS dataset.
The parameters are estimated using two-step GMM under the
assumption that the values of
![]() and
and
![]() are
correlated but that there is no serial correlation. I use the three
instruments that are commonly used in estimating this kind of
production function. One of the instruments is the previous
quarter's value of the Federal Funds shock resulting from the
monetary VAR estimated in Christiano, Eichenbaum, and Evans (2001).
The second instrument is the current and previous quarters' values
of the difference between the aggregate GDP price deflator and the
growth rate of the price of oil.9 The
third instrument is the current and previous quarters' growth rate
in real defense spending.10
are
correlated but that there is no serial correlation. I use the three
instruments that are commonly used in estimating this kind of
production function. One of the instruments is the previous
quarter's value of the Federal Funds shock resulting from the
monetary VAR estimated in Christiano, Eichenbaum, and Evans (2001).
The second instrument is the current and previous quarters' values
of the difference between the aggregate GDP price deflator and the
growth rate of the price of oil.9 The
third instrument is the current and previous quarters' growth rate
in real defense spending.10
The GMM estimator requires an estimate of the variance-covariance matrix. Because, the estimation exercise is a system of equations for eighteen industries, the unconstrained version of the variance-covariance matrix requires a large (171) number of parameters. To reduce this number, one could place structure on the correlation between sectors. Conley and Dupor (2003) assume that the industries that use similar inputs have similar patterns of productivity. Given my interest in aggregated quantities, this correction has only a small effect on the aggregated results. 11
2.1.1 Results
The coefficient estimates are reported in Table 2. For the
nondurable goods producing sectors, the estimate of the mark-up
parameter ![]() is less
than one. The difference between the estimate and constant returns,
however, is not statistically significant. Some of the estimates
reported in BFK were also less than one. They argue (p.29) that one
possible explanation for these low estimates of
is less
than one. The difference between the estimate and constant returns,
however, is not statistically significant. Some of the estimates
reported in BFK were also less than one. They argue (p.29) that one
possible explanation for these low estimates of ![]() is the omitted variable bias that
would result from not including an estimate of reallocation
effects.
is the omitted variable bias that
would result from not including an estimate of reallocation
effects.
The estimates of ![]() are
positive and significantly different from zero. Positive
coefficients imply that when utilization growth and, therefore,
average hours growth are high, the growth in the
utilization-corrected measure of productivity is less than the
growth in the measure of uncorrected productivity.
are
positive and significantly different from zero. Positive
coefficients imply that when utilization growth and, therefore,
average hours growth are high, the growth in the
utilization-corrected measure of productivity is less than the
growth in the measure of uncorrected productivity.
Although the work here has tried to construct a technology series that corrects for utilization and reallocation, one may be concerned that the series is still affected by measurement error. A such, this estimated technology series will be combined with a long-run identification assumption to identify the part of this series that seems to have a long-run affect on the level of technology. The next section describes how to implement such a long-run identification assumption.
2.2 Estimating A Vector Autoregression with A Long Run Identification Assumption
Here, as in Galí (1999), a technology shock will be
identified as a permanent shock to productivity.12 These shocks and resulting impulse
responses are computed in the following manner. Consider the
following structural vector autoregression (VAR) for a vector of
variables ![]()
![$\displaystyle A_{0}y_{t}=A(L)y_{t-1}+\left( \begin{array}[c]{c} \varepsilon_{t}^{z}\\ v_{t} \end{array} \right)$](img20.gif)
|
(3) |
The vector
![$\displaystyle y_{t}=\left( \begin{array}[c]{c} \Delta z_{t}\\ x_{t} \end{array} \right)$](img25.gif)
|
(4) |
The shocks
![]() and
and
![]() (where
(where
![]() has
has ![]() elements) are assumed to be
independent. Galí identifies the technology shock by
assuming that only the technology shock
elements) are assumed to be
independent. Galí identifies the technology shock by
assuming that only the technology shock
![]() can
have a permanent effect on the level of productivity
can
have a permanent effect on the level of productivity ![]() . All other shocks are assumed to
have no long-run effect. To impose this restriction is to impose a
restriction on the moving average representation of the data.
Denote the moving average representation by:
. All other shocks are assumed to
have no long-run effect. To impose this restriction is to impose a
restriction on the moving average representation of the data.
Denote the moving average representation by:
![$\displaystyle \ \left( \begin{array}[c]{c} \Delta z_{t}\\ x_{t} \end{array} \ri... ...ght) \left( \begin{array}[c]{c} \varepsilon_{t}^{z}\\ v_{t} \end{array} \right)$](img29.gif)
|
(5) |
the restriction that the long run impact on
To actually estimate the structural VAR with this long-run restriction requires a restriction on the structural VAR coefficients. To make the notation clear, I rewrite the structural VAR as
![$\displaystyle \left( \begin{array}[c]{cc} a_{0,11}-A_{11}(L) & \left[ a_{0,1j}\... ...ht) =\left( \begin{array}[c]{c} \varepsilon_{t}^{z}\\ v_{t} \end{array} \right)$](img32.gif)
|
(6) |
Because
| (7) |
To implement this restriction we estimate the equation14
![$\displaystyle \left( \begin{array}[c]{cc} a_{0,11}-A_{11}(L) & \tilde{A}(L)(1-L... ...egin{array}[c]{c} \Delta z_{t}\\ x_{t} \end{array} \right) =\varepsilon_{t}^{z}$](img39.gif)
|
(8) |
To estimate this equation, one has to instrument for
Estimating this equation results in a time series of the
technology shocks. To calculate the impulse responses requires the
moving average representation of ![]() in terms of
in terms of
![]() and
and
![]() . One approach to
calculate this moving average representations starts with the
reduced form VAR16
. One approach to
calculate this moving average representations starts with the
reduced form VAR16
| (9) |
where
| (10) |
To summarize, the impulse responses can be calculated using the following four steps.
![$\displaystyle \left( \begin{array}[c]{cc} a_{0,11}-A_{11}(L) & \tilde{A}(L)(1-L... ...ay} \right) \left( \begin{array}[c]{c} \Delta z_{t}\\ x_{t} \end{array} \right)$](img58.gif)
|
(11) | |
2.3 Impulse Responses
The next section reports the dynamic responses to an exogenous shock to productivity. The measure of productivity is the result of using Equation 2 to aggregate the industry-level estimates calculated using Equation 1.
Two sets of results are reported. The first results correspond exactly to the methods used by Galí (1999) and Francis and Ramey (2003) except that I replace their use of labor productivity with my productivity measure. Compared to the initial response by hours when using labor-productivity, the initial response here is much more positive. Either hours declines less or it does not decline at all. The result reported here do not overturn earlier critiques of the standard quantitative dynamic flexible-price model. Hours still do not respond positively to the shock for the first year.
The second set of results report the dynamic responses by investment, output, and consumption as well as hours. These results are useful because they provide the basis upon which to characterize the ability of the macroeconomic model to match the data. These variables do not respond much in the period of the shock. In subsequent periods, the variables start to increase in response to the technology shock.
2.3.1 Bivariate VAR with Hours Worked
As in Galí (1999) and Francis and Ramey (2003), the impulse response are from a two-variable VAR on the growth rates of a productivity series and the growth rates of hours worked. Productivity is measured using two different time series: labor productivity and my constructed aggregate productivity series. In addition, impulse responses are calculated from a VAR of the constructed productivity series and the levels of per-capita hours worked. Christiano, Eichenbaum and Vigfusson (2003) argue that estimating the long-run VAR with hours in first differences is mis-specified relative to estimating a VAR with per-capita hours in levels. This section, however, reports both sets of results to maximize comparability with the earlier literature. Confidence intervals around the estimate are calculated using a bootstrapped approach. Sampling from the residuals with replacement, the estimated VAR is used as a data generating process to simulate time series. Using the simulated data, the VAR is estimated and the responses to a permanent positive increase in technology are calculated. After simulating the data 500 times, the variance of each period's impulse response is calculated. The resulting confidence interval is the estimated response plus or minus 1.96 times the standard deviation.17
Figure 1 reports the response of the three different VARs. The three different specifications have similar responses. Nothing much happens on impact. Subsequently, hours worked begins to increase. For all three VARs, the response on impact is much greater than that reported in Galí or in Francis and Ramey. These results, however, are not large enough to overturn the conclusions of previous work. Hours still do not respond much initially to a positive productivity shock. Therefore, the evidence is still against models that predict a large initial response to increases in productivity.
2.3.2 VAR with Hours Worked and Other Variables
To compare the model to the data, one needs to know how other
variables in the economy respond to a technology shock. This
section describes how other variables (output ![]() , consumption
, consumption![]() , investment
, investment ![]() , and the real interest rate
, and the real interest rate
![]() )18respond to a technology shock. The
approach taken here is to estimate the set of equations described
in Section 2.2 . The
vector of other variables is constructed as follows
)18respond to a technology shock. The
approach taken here is to estimate the set of equations described
in Section 2.2 . The
vector of other variables is constructed as follows
![$\displaystyle x_{t}=\left( \begin{array}[c]{c} h_{t}\\ r_{t}\\ \Delta y_{t}\\ i_{t}-y_{t}\\ c_{t}-y_{t} \end{array} \right)$](img69.gif)
|
(12) |
Cointegrating relationships are defined between investment and output, and consumption and output. There is no assumption of a cointegrating relationship between per-capita output and the technology series, in order to allow for other shocks to have a permanent effect on per-capita output. Besides this baseline VAR, I also report impulse responses for two other VARs. One uses the same reduced form VAR but identifies the technology shock not with a long-run identifying assumption but rather uses a standard recursiveness assumption with technology ordered first. In other words I estimate the same reduced form VAR but identify my technology shock
Figure 2 reports the data used in the VAR. The log of per-capita hours worked increases over this time period. This increase in hours worked is the result of two opposite trends. An increase in the labor force participation rate (from 60 to 67 percent over this time period) offsets the decline in average hours worked, (for production workers, the average work week has declined from 36 hours to 34 hours).
Figure 3 reports the implications for the technology growth series by applying the long-run identification assumption. The constructed technology series is presented along with the technology series implied by the VAR and allowing only permanent shocks to technology. In order to emphasize the role of the long run identification assumption, both series are presented with mean zero. Perhaps not surprising the series that results from the long run identification series is much less volatile than the original series.
Impulse responses for the baseline long-run VAR are reported in Figure 4. In general, quantities take time to respond to the technology shock. Hours worked responds only slightly in the impact period of the shock. It takes several quarters before hours worked has a strong response. Consumption only responds gradually over time. In the impact period, the response is only about half of what it will be 10 quarters later. In percentage terms, the investment response is stronger on impact but the strongest investment response is about four quarters later. The real interest rate, however, has a very different response. The real rate jumps 80 basis points on impact. It then steadily declines but it does take six years before the real rate returns to normal.
The results for the two other VARs are similar. Identify technology shocks with a short-run recursiveness assumption produces a few small differences. The largest difference is that the real interest rate response is much weaker. Also, the consumption response is not as strong but the investment response is of greater size and duration. For this dataset, identifying a technology shock as a permanent shock to labor productivity again produces a very similar set of responses.
2.3.3 The Shape of the Impulse Responses
I have claimed that the delayed response to a positive technology shock is a robust feature of the data. The following section characterizes this robustness. Using the baseline VAR as the DGP process, Figure 5 reports that in the majority of cases the response by hours six quarters after a shock is greater than the response on impact.
Table 3 reports that for the majority of simulations, the impact period response for consumption, investment, or hours worked is much smaller than responses several periods later.
2.4 Weak Instruments And the Delay in the Hours Response
To identify a permanent change in technology requires estimating an instrumental variables regression. One may be concerned about whether the above conclusions concerning the shape of the impulse responses are robust to weak instruments. Although the actual instrumental variables regression may have problems with weak instruments, the evidence is that the conclusions concerning shape are more robust.20
When instruments are only weakly correlated with the explanatory
variables, confidence intervals can often be much wider than those
calculated using standard methods. In the equation estimated here,
the lagged level of hours worked is used to instrument for the
growth rate of hours worked. If hours worked has either a unit root
or else approaches a unit root asymptotically, then hour worked
would be a weak instrument.21 Valid
confidence intervals for estimation using weak instruments,
however, were established by Anderson and Rubin (1949). In the
present context, their method can be implemented as follows. Begin
with the IV regression where any dependence on lagged values has
been removed by a linear projection. All that is left is to
estimate ![]() , in the
following equation,
, in the
following equation,
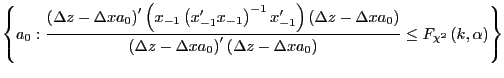
These confidence intervals are constructed holding as fixed the
values of the reduced form VAR coefficients. Hence if we combine
these estimates of the possible values of ![]() with the reduced form VAR, the
resulting hours response six quarters later is between 0.05 and
0.27.
with the reduced form VAR, the
resulting hours response six quarters later is between 0.05 and
0.27.
Similar calculations can be done for the six variable system. A
grid search on all the possible values of ![]() would be particularly laborious
for the larger system. For example, a five dimensional space with
100 grid points per dimension would be ten billion points. However,
one can approximate the grid search by instead sampling over the
parameter space. A random sample of the same space should be
sufficiently informative.23 Table 4
reports confidence intervals for
would be particularly laborious
for the larger system. For example, a five dimensional space with
100 grid points per dimension would be ten billion points. However,
one can approximate the grid search by instead sampling over the
parameter space. A random sample of the same space should be
sufficiently informative.23 Table 4
reports confidence intervals for
![]() that result
from those values of
that result
from those values of ![]() that belong to the AR confidence interval. Going from the bivariate
autoregression to the multivariate regression seems to have both
tightened and shifted upwards the confidence intervals on the hours
worked response.
that belong to the AR confidence interval. Going from the bivariate
autoregression to the multivariate regression seems to have both
tightened and shifted upwards the confidence intervals on the hours
worked response.
There appears to be a great deal of uncertainty of investment's response on impact. This uncertainty does not seem to be reflected in the standard bootstrap confidence intervals reported above. Perhaps the most surprising thing is the improvement of identification that results from using the constructed technology series.
The emphasis on the shape of the hours worked response can also
be studied in the context of weak instruments. Consider Figure 7,
which shows the connection between the response by hours on impact
combined with its response six quarters later. The oval indicates
all observed responses, holding the reduced form VAR coefficients
![]() fixed. The grey
area indicates those values that are associated with a value of the
Anderson Rubin statistic less than the 95 percent critical value of
9.488. Although this oval does not take into account the sampling
uncertainty of
fixed. The grey
area indicates those values that are associated with a value of the
Anderson Rubin statistic less than the 95 percent critical value of
9.488. Although this oval does not take into account the sampling
uncertainty of ![]() ,
the figure is supportive of placing a greater emphasis on the shape
of responses.
,
the figure is supportive of placing a greater emphasis on the shape
of responses.
The evidence from the weak instruments reinforces the view that the robust finding is that the hours response is initially small but grows over time. Models therefore should be constructed to attempt to match this finding.
2.5 Sensitivity of Results
The following sections report on the sensitivity to using different data and also to using different sample periods.
2.5.1 Ex ante Real Interest Rate
To check for data sensitivity, the empirical VAR is estimated using an ex ante measure of the real interest rate in place of the ex post measure. The ex ante real interest rate is based on the difference between the three month treasury rate and the forecasted inflation in the GDP deflator for the next quarter. The forecasted inflation is the median forecast from the Survey of Professional Forecasters. The results are presented in Figure 8. On impact, the ex ante real interest rate only increase 50 basis points rather than the ex post real interest rate increase of 100 basis points. However, all of the quantities experience responses that are similar to those reported in the baseline VAR.
2.5.2 Shorter Sample, Starting in 1983
One might wonder if the strong-interest rate response is stable
over time. In particular, Galí, López-Salido and
Vallés (2003) argue that monetary policy changed in the
United States with Paul Volker and that therefore the responses to
a technology shock look very different after 1983 than they did
earlier. There are two ways to test the stability. The first is to
calculate ![]() from a
regression of just a subsample of the identified technology series
on the reduced form residuals, estimated from the full-sample VAR.
This method holds the VAR fixed but sees whether a particular
episode drove the estimation results. These results, although not
reported, are almost identical to the results in Figure 8.
Therefore, we have evidence against any particular technology shock
episode driving the results.
from a
regression of just a subsample of the identified technology series
on the reduced form residuals, estimated from the full-sample VAR.
This method holds the VAR fixed but sees whether a particular
episode drove the estimation results. These results, although not
reported, are almost identical to the results in Figure 8.
Therefore, we have evidence against any particular technology shock
episode driving the results.
The second approach, which was used by Galí López-Salido and Vallés, is to re-estimate the entire VAR but begin in 1983. The impulse responses from this VAR are reported in Figure 8. For the first year after impact, these responses are quite different from the responses in the baseline VAR. For the shorter sample VAR, the variables are less responsive on impact. After two years, the responses by quantities are quite similar. These results emphasizes the robustness of describing the response to a technology shock as being a delayed response. One important difference between the two sets of results is that, with the shorter sample, the real interest rate does not respond to the technology shock.
The shocks identified using the post-1982 VAR are very different from the same shocks identified using the full sample of data. The full sample shocks are much more volatile. In addition, they are not closely related to the post-1982 shocks. The post-1982 shocks are the same sign as the full sample shocks only about 50 percent of the time.
The question is whether the full sample or the truncated sample correctly identifies the true technology shocks. Determining which is the correct set of responses is a difficult question. A simple likelihood ratio test would support using the truncated sample. However, to exclude three of the four recessions in the covered time period throws away a lot of information. As such, the analysis here will continue to use the benchmark responses, but with the caveat that other responses are possible.
3 Models
Having described the empirical responses, the next step is to develop a model that can match the data. The model presented here has two features that are different from a standard quantitative dynamic flexible-price model. The first is that the economic agent has habit persistence in the utility function. Thus, the previous period's level of consumption affects current utility. Habit persistence results in a slower response by consumption. (In order to match the real interest rate response, a model with consumption adjustment costs is also presented.) The second feature and the focus of the paper is how investment is transformed into capital. I consider two different specifications of this transformation: time-to-build and capital-adjustment-cost models. Both specifications have the property of preventing capital from adjusting quickly.24 The time-to-build model has a lag between the decision to increase the capital stock and the actual increase in the capital stock. Likewise in the capital adjustment model, increasing investment is expensive and therefore an economic agent will have an incentive to smooth out investment.
All of these features have been used previously to explain other economic phenomena. In particular, Christiano and Todd (1995) and Christiano and Vigfusson (2003) document the properties of a particular parameterization of the time-to-build model, the time-to-plan model, where investment cannot respond much in the first period of a shock. Christiano and Vigfusson show that this model is much better than a standard quantitative dynamic flexible-price model in matching the output growth dynamics and the lead-lag relationship between output and business investment.25 Models with capital adjustment costs that depend on the ratio of investment to capital have been used extensively in the Tobin's Q literature. (See Chirinko (1993) for a survey.) Boldrin, Christiano, and Fisher (2000) and Beaudry and Guay: (1996) document how adding capital adjustment costs and habit persistence allows a macroeconomic model to explain both business cycle facts and asset pricing issues. Topel and Rosen (1988) make capital adjustment costs depend on the growth rate of investment to explain housing investment. Christiano, Eichenbaum, and Evans (2001) use a similar specification to generate improved dynamics in a sticky price model. Francis and Ramey (2003) also consider a capital adjustment model to explain the low correlations between productivity and employment. In their model, capital adjustment costs depend on the ratio of investment to capital.
3.1 The Utility Function
The model has a representative agent who chooses consumption
![]() and the fraction of
time spent working
and the fraction of
time spent working ![]() to
maximize utility, where utility is defined as
to
maximize utility, where utility is defined as
| (13) |
The coefficient
| (14) |
The amount of output produced depends on the amount of labor
As an alternative to habit persistence, I also consider a model that features consumption adjustment costs. In this model, the habit persistence coefficient is set to zero and the resource constraint is the following.
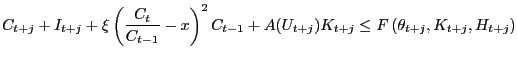
|
(15) |
As will be discussed in the section on the real interest rate, consumption adjustment costs
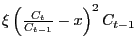 are a useful alternative to habit persistence. This feature results
in the same dampened consumption response without driving down the
response of the real interest rate.
are a useful alternative to habit persistence. This feature results
in the same dampened consumption response without driving down the
response of the real interest rate.
Two different production functions are considered here. As is common in the macroeconomic literature, I use a Cobb Douglas technology function.
![$\displaystyle F\left( \theta_{t+j},K_{t+j},H_{t+j}\right) =\left[ \alpha^{1-\ps... ...+\theta_{t+j}\left( 1-\alpha\right) ^{1-\psi} (H_{t+j}^{\psi}\right] ^{1/\psi} $](img104.gif)
The second constraint specifies how investment is transformed into capital and will be described in Section 3.3 .
One difference between this model and Francis and Ramey is the specification of the utility for leisure. They used an indivisible labor model; whereas, here, the model has the standard divisible labor utility function. The two specifications imply very different values for the labor supply elasticity. The labor supply elasticity is much greater for the indivisible labor model, where the labor supply is infinitely elastic. With divisible labor, the labor supply would have an elasticity of about three.28 Therefore, the labor supply will be less responsive in the specification studied here.
3.2 The Technology Shocks
In order to match the data, the model should have growth and
therefore the level of technology should be nonstationary. The
level of technology
![]() has the
following functional form
has the
following functional form
| (16) |
where
| (17) |
where
3.3 Transforming Investment into Capital
This section describes how investment is transformed into capital. Three different specifications are considered. The first is the time-to-build model of Kydland and Prescott (1982). In this model, several quarters pass before a desired increase in the capital stock is realized. The second is the convex capital adjustment costs where the costs are a function of the ratio of investment to capital. The third has adjustment costs that depend on the growth rate of investment.29
3.3.1 Time-to-Build
In the time-to-build model (Kydland and Prescott 1982), the
investment technology has two features. The first is that the time
between the decision to increase the capital stock and the actual
increase is greater than a quarter. In the current application,
four quarters pass between making a decision to increase the
capital stock and the actual increase. The second feature is that
the increase in the capital stock is paid for over time. In other
words, a project ![]() initiated at quarter
initiated at quarter ![]() results
in an increase in the capital stock
results
in an increase in the capital stock
![]() four quarter later. The
total cost of the project
four quarter later. The
total cost of the project ![]() equals the increase
equals the increase
![]() , but the project is paid for
in installments. Thus, investment consists of several different
projects that are at various stages of completion. In particular,
period
, but the project is paid for
in installments. Thus, investment consists of several different
projects that are at various stages of completion. In particular,
period ![]() investment equals:
investment equals:
| (18) |
where
3.3.2 Capital Adjustment Costs
Two versions of capital adjustment costs are described here. The first, (which I will refer to as CIK), is the more common version where the cost of capital adjustment is a function of the ratio of current investment to capital
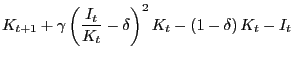
|
(19) |
The second (which I will refer to as CII) is less common but it allows the adjustment costs to depend on the ratio of current investment to the previous period's investment.
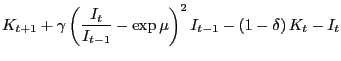
|
(20) |
For the specifications given here, adjustment costs parameterized by
3.4 Model Parameterization
At calibrated values, the standard RBC model fails to match the main facts discussed in the empirical section. In particular, all the variables respond to a positive technology shock most strongly on impact. Therefore, they completely miss the delayed response observed in the data.
Recent model estimation has often tried to match impulse responses by using a GMM weighting function. However, the goal of this paper is to show the flexibility of these macroeconomic models to match estimated technology impulse responses. As such, rather than attempting to match any particular set of responses, I will present a comparative analysis that will clarify how the flexible-price models are compatible with the responses observed both in this paper and in many of the other papers in the literature.
Figure 9 reports results for just the response of hours on
impact and how the different models are able to capture the
response of hours to a positive technology shock. For each of the
different models, some of the model's coefficients were fixed and
others were allowed to vary. The coefficients that were allowed to
vary were the ones that characterize the newer features of the
model. In particular, results are reported for different values of
both the degree of habit persistence and the coefficients related
to how investment is translated into capital, (i.e. the degree of
investment adjustment costs ![]() or time-to-build weights
or time-to-build weights ![]() .). The other coefficients were
held constant.31The
models were log-linearized and solved using the undetermined
coefficients method of Christiano (2001).32
.). The other coefficients were
held constant.31The
models were log-linearized and solved using the undetermined
coefficients method of Christiano (2001).32
In Figure 9, there are several things to note. First, all three models have parameterization that are consistent with hours worked falling in response to a positive technology shock. Many, including Galí and Basu, Fernald, and Kimball, have argued that the earlier empirical claims of negative hours responses to a technology shock is evidence against flexible-price models. Clearly, the flexible-price models reported here can imply that hours fall on impact of a positive technology shock. Therefore, these previous criticism of flexible-price models, although valid for the standard RBC model, do not apply to these models. Furthermore, for all three models, different combinations of investment adjustment costs and habit persistence can generate a given hours response. Habit persistence and investment adjustment costs actually work against each other. Investment adjustment costs decrease the investment response and increase the consumption response, and habit persistence increases the investment response and decreases the consumption response.
Figure 10 illustrates these trade offs for the CII model and how consumption and investment impact responses depend on the degree of habit persistence and investment adjustment costs. The shaded areas indicate the bootstrap confidence intervals around the empirical impact effect. For investment, the width of the area suggest that the investment response is not very informative about the best values of habit persistence and the investment adjustment cost.
3.5 Dynamic Responses
Figure 11 reports on the ability of all three models to capture the dynamic response of hours worked, consumption, and investment. The benchmark empirical results from Figure 2 are reproduced here.
The first panel reports responses for a model with habit persistence and investment adjustment costs that depend on the growth rate of investment, the CII model. As seen in Figure 10, it is fairly easy to find model parameterization that match the consumption response. The investment response is somewhat more difficult with the response being too strong compared to the empirical response. The hours worked response is delayed. However, hours actually do not respond enough on impact and then responds too strongly afterwards. The differences in responses, however, are within the standard bootstrapped confidence intervals, indicated by the shaded regions.
The second panel reports results from the time-to-build and CIK models. The CIK model can match the initial responses. However the CIK model can not match the increases in responses because the ratio of investment to capital does not quickly change. Without a change in the ratio of investment to capital, the investment adjustment costs remain high. The time-to-build model does better at creating responses that are small initially but then increase. The main problem with the time-to-build model is that the responses are too jagged. The jaggedness results from there being only one kind of capital with only a four period building period. A time-to-build model with much smoother responses can be found in Edge (2000) where there are many different kinds of capital goods, with each kind of capital requiring a different number of periods to build.33
3.6 Real Interest Rate Response
Although both the investment growth rate model and the time-to-plan model have done well in fitting the responses of consumption, investment and hours worked, this section makes clear that the models have a much harder time matching the strong interest rate response observed in the benchmark results. Figure 12 reports the real interest rate results from the empirical VAR and from the economic models. Given that consumption only slowly increases in both the CII and time-to-build models, it may seem puzzling that the real interest rate actually falls on impact. The explanation, however, involves the definition of marginal utility with habit persistence. First, the real interest rate can be expressed in terms of a ratio of marginal utilities. In particular, ignoring uncertainty, the real interest rate can be written as
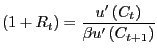
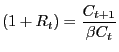
For further intuition, consider the real interest rate in a model of internal habit which drops the forward looking part of the external habit specification used here.34
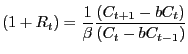
Modeling the production function as a CES production function, rather than Cobb-Douglas, does strengthen the growth rates of investment. However, this feature does not overcome the negative interest rate response generated by the habit persistence. Another option would be to have habit persistence depend on the difference between current consumption and a habit stock that only slowly evolved with current consumption. In other words, the new utility function is
Although adding a habit stock ameliorates the decline in the real interest rate, the real interest rate still falls in response to a positive technology shock.
One partial remedy to the falling real rate is to replace habit persistence with consumption adjustment costs. With consumption adjustment costs, one continues to delay the consumption response but, unlike habit persistence, consumption adjustment costs do not introduce the growth rate of consumption into marginal utility. As such, the real interest rate increases on impact. However, as seen in Figure 12, the rise is not as much or as persistent as the empirical point estimates.
Consumption adjustment costs may seem particularly ad-hoc. However, like investment adjustment costs, they help macroeconomic models match the empirical impulse response functions. Future work will be required to find a more structural mechanism to reduce how quickly both the level and the marginal utility of consumption increases in response to a positive technology.
Another possible solution would be to have serially correlated
technology shocks. Although serially correlated shocks can result
in a model with a stronger real interest rate response. Figure 13
reports results with the assumption that the autoregressive
coefficient on the growth rate of technology ![]() equals 0.7. As shown in
Figure 13, in models with investment adjustment costs, the real
interest rate increases almost 50 basis points on impact. 35 However, this real interest rate
response is less than the estimated response. In addition, the
responses of the other variables particularly investment and hours
worked are now too weak compared to the estimated responses. So any
gain in better real interest rate fit is lost in worse fit of hours
worked and the real interest rate.
equals 0.7. As shown in
Figure 13, in models with investment adjustment costs, the real
interest rate increases almost 50 basis points on impact. 35 However, this real interest rate
response is less than the estimated response. In addition, the
responses of the other variables particularly investment and hours
worked are now too weak compared to the estimated responses. So any
gain in better real interest rate fit is lost in worse fit of hours
worked and the real interest rate.
The real interest rate response is a problem for these models. As mentioned in the empirical section, the interest rate response is somewhat uncertain with both a wide confidence interval and being sensitive to the sample period. Therefore, some may question the seriousness of a failure to match this response. In fact, many researchers have felt that a fall in real interest rates followed by a positive increase in output is a desirable characteristic in a technology driven model.
4 Criticisms of Long Run VARs
Recent papers by Erceg, Guerrieri and Gust (2004) and Chari Kehoe and McGrattan (2004) have criticized the use of long-run VARs to construct impulse response. Both papers have shown that, for particular model parameterizations, the point estimates of the impulse responses may be estimated imprecisely. This section provides some additional simulation evidence concerning the responses. I show for a particular set of models that, although, these authors do have a valid concern about the possible imprecision of the point estimates, the impulse responses are informative about the shape of the responses. Of specific relevance to the current paper, simulation evidence shows that these impulse responses can distinguish between a model where hours responds most on impact and a model where hours have a delayed (hump shaped) response. However, sign restrictions are not as informative. For the models considered here, the finding of a positive response is unlikely to allow us to discriminate between a model that has a positive hours response on impact and a model that has a negative hours response on impact.
The simulation evidence presented here comes from three models:
a standard quantitative dynamic flexible-price model (where hours
responds positively and with the largest response being immediate),
a model with CII investment adjustment costs (where hours responds
positively and with a delayed response), and a model with CII
investment adjustment costs and habit persistence. In order to
estimate a non-trivial bivariate VAR, each model has an additional
shock
![]() that affects the labor preference parameter
that affects the labor preference parameter ![]() . Hence the utility function
becomes
. Hence the utility function
becomes
| (21) |
and the shock
Given these estimates, I then used each model to generate 500 data sets of 200 observations each on labor productivity and hours worked. For each simulated data set, I then estimated a long run VAR on the growth rate of labor productivity and the log level of hours worked. Figure 14 reports the theoretical model response for hours worked and also the average response estimated from the simulated data. For all models, the average responses are biased upwards, but the average responses are reasonably close. However, an interval that contains 90 percent of the simulated responses is very large. Figure 14 plots such an interval for the CII model. Given these wide intervals, one may be concerned that one could not distinguish between the models.
Some measures but not others are able to distinguish between the models. Figure 15 reports the probability of observing two results in each model. The top panel reports the probability of observing a positive impact response. Because of the wide confidence intervals and the upward bias in the hours response, all three models, including the model where the true response is negative, have a high probability of observing a positive value. Therefore, a finding of a positive response is not very informative about the true data generating model. As can be seen in the bottom panel of Figure 15, the shape results are much more informative. In the standard RBC model, the downward trend in the hours response is apparent in the small fraction of responses that are greater than the impact response. Likewise, in the model with investment adjustment costs, the hump-shaped response is readily apparent by the large fraction of responses that are greater than the impact response.
One way to quantify the difference between models would be with
a posterior odds ratio. In particular given the observed data
![]() , one would calculate
the odds of model one
, one would calculate
the odds of model one ![]() being preferred over model two
being preferred over model two ![]() as follows.
as follows.
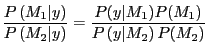
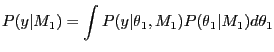
These calculations should be taken as only a guideline. Other models with more features or other shocks might give different results for both the identification of point estimates and response shapes. However, at least for these simple models where the criticisms of EGG and CKM are valid, studying the shape of the responses seems to be a valid way to use long-run VARS to learn about the economy.38
5 Conclusions
The main empirical conclusion of this paper is that, for the U.S. economy, the response by per-capita hours worked to a technology shock is initially small but subsequently increases. The small initial response is evidence against any model, including the standard quantitative dynamic flexible-price model, that predicts a large immediate response by employment to a technology shock. These results do not, however, completely invalidate the use of real technology shocks to explain business cycles since variables do respond in the medium term to these shocks. Therefore, the task is to develop models that can explain both the short-term and long-term responses to technology shocks.
The current paper presents quantitative dynamic flexible-price models that can be reconciled with the observed responses by quantities to a technology shock. Of course, this reconciliation is not a rejection of other possible explanations. These other possible explanations might include the examples provided by Basu, Fernald, and Kimball (2004): sticky-price models, multi-sector reallocation models, and cleansing models of recessions. All of these explanations should be scrutinized further to determine their relative merits.
The current paper has done three things. First, it has presented new empirical dynamic responses for models to match. Second, it has shown that the estimated shape of these dynamic responses may be more informative than the sign of the impact response. Third, it has put forward flexible-price models that better explain these delayed responses. In effect, it has raised the standard for criticisms of the flexible-price model. It was easy to show that the small initial response by hours worked was inconsistent with the standard flexible-price model. With the additional features discussed here, a flexible-price model can be made consistent with these observations concerning hours worked. The new challenge will be to build upon the improved fits described here.
A A Summary of Model Estimation by Maximum Likelihood in the Frequency Domain
In order to make the paper somewhat more self-contained, this appendix summarizes how to estimate a model by maximum likelihood in the frequency domain. For more details and application,. see Christiano and Vigfusson (2003).
Begin with a time series of data,
![]() where
where ![]() is a
finite-dimensional column vector with zero mean. In this paper's
analysis, the vector
is a
finite-dimensional column vector with zero mean. In this paper's
analysis, the vector ![]() is
defined as
is
defined as
![$\displaystyle y_{t}=\left[ \begin{array}[c]{c} \Delta\log(Y_{t}/H_{t})\\ \log(H_{t}) \end{array} \right] ,$](img164.gif)
|
(22) |
where
It is well known (Harvey, 1989, p. 193) that for ![]() large, the Gaussian likelihood for
such a time series of data is well approximated by:
large, the Gaussian likelihood for
such a time series of data is well approximated by:
![$\displaystyle L(y,\Phi)=-\frac{1}{2}\sum_{j=0}^{T-1}\left\{ 2\log2\pi+\log\left... ...\right) \right] +tr\left( F(\omega_{j} ;\Phi)^{-1}I(\omega_{j})\right) \right\}$](img168.gif)
|
(23) |
where
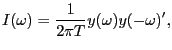
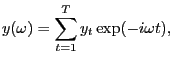 |
(24) |
and
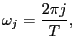
To estimate a model by frequency domain maximum likelihood, one
needs the mapping from the model's parameters, ![]() to the spectral density matrix
of the data,
to the spectral density matrix
of the data,
![]() .
The following describes this mapping.
.
The following describes this mapping.
The first step is to solve a linearized version of the
macroeconomic model. One can then use the linearized solution to
write a linear approximation of the ![]() process
process
| (25) |
In the two-shock model, ![]() is defined in (22),
is defined in (22),
![]() is
is
![]() matrix
polynomial in
matrix
polynomial in ![]() and
and
![\begin{displaymath} \varepsilon_{t}=\left( \begin{array}[c]{c} \eta_{t}\ u_{t}... ...igma_{\eta}^{2} & 0\ 0 & \sigma_{u}^{2} \end{array}\right] . \end{displaymath}](img189.gif)
In all cases, I restrict ![]() so that
so that
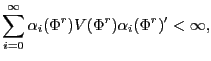
The spectral density of ![]() at frequency
at frequency ![]() is
is
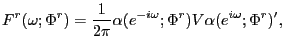
References
Altig, David, Lawrence J. Christiano, Martin Eichenbaum and Jesper Linde, 2004, `` An Estimated Dynamic, General Equilibrium Model for Monetary Policy Analysis,'' Manuscript.
Anderson, T.W. and H. Rubin 1949 `` Estimation of the Parameters of A Single Equation in A Complete System of Stochastic Equations'', Annals of Mathematical Statistics, 20, pp. 46-63
Basu Susanto 1998 `` Technology and Business Cycles: How Well Do Standard Models Explain the Facts?'' Beyond Shocks: What Causes Business Cycles? Federal Reserve Bank of Boston, Conference Series No. 42
Basu Susanto John G. Fernald 2000 `` Why is Productivity Procyclical? Why do we care?'' NBER Working Paper 7940
Basu Susanto, John G. Fernald, and Miles S. Kimball. 2004. `` Are Technology Improvements Contractionary'' NBER Working Paper 10592
Basu Susanto John G. Fernald and Matthew D. Shapiro 2001 `` Productivity Growth in the 1990s Technology Utilization or Adjustment'' NBER Working Paper 8359
Beaudry Paul, Alain Guay. 1996 `` What Do Interest Rates Reveal about the Functioning of Real Business Cycle Models?'', Journal of Economic Dynamics and Control, 20,.1661-1682
Boldrin, Michele, Lawrence J. Christiano and Jonas D.M. Fisher, 2001 `` Habit Persistence, Asset Returns and the Business Cycle'' American Economic Review 91 149-166.
Burnside Craig 1996 `` Production Function Regressions, Returns to Scale and Externalities,'' Journal of Monetary Economics, 37, 177-201.
Burnside Craig, Martin Eichenbaum and Sergio Rebelo, 1996 `` Sectoral Solow Residuals,'' European Economic Review, 40, 861-869.
Carroll Christopher D. , Jody Overland, and David N. Weil 2000 `` Saving and Growth with Habit Formation'' American Economic Review, 90(3), 341-355
Chari, V.V., Patrick Kehoe, and Ellen McGrattan 2004 `` An Economic Test of Structural VARs'' Federal Reserve Bank of Minneapolis Research Department Working Paper Number 631
Chirinko Robert S. 1993 `` Business Fixed Investment Spending'' Journal of Economic Literature 31 1875-1911.
Christiano, Lawrence J., 2001, `` Solving Dynamic Equilibrium Models by a Method of Undetermined Coefficients'', forthcoming. See also, NBER Technical Working paper 225.
Christiano Lawrence J. Martin Eichenbaum and Charles Evans 2001 `` Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy'' manuscript Northwestern University
Christiano, Lawrence J. and Martin Eichenbaum, 1992, `` Current Real-Business-Cycle Theories and Aggregate Labor-Market Fluctuations'', American Economic Review, 82(3), June, 430-50.
Christiano Lawrence J. and Jonas D. M. Fisher 1998 `` Stock Market and Investment Good Prices: Implications for Macroeconomics,'' Federal Reserve Bank of Chicago Working Paper
Christiano, Lawrence J. and Richard M. Todd, 1996, `Time to Plan and Aggregate Fluctuations', Federal Reserve Bank of Minneapolis Quarterly Review, Winter, 14-27.
Christiano,Lawrence J. and Robert J. Vigfusson Maximum likelihood in the frequency domain: the importance of time-to-plan Journal of Monetary Economics 50(4),789-815
Conley Timothy G. William D. Dupor 2003 `` A Spatial Analysis of Sectoral Complementarity'' Journal of Political Economy 111(2) p 311-52
Cooper, Russell W. and John C. Haltiwanger 2000 `` On the Nature of Capital Adjustment Costs'' manuscript
DeJong David N., Beth F. Ingram, and Charles H. Whiteman, 2000 `` Keynesian Impulses versus Solow Residuals: Identifying Sources of Business Cycle Fluctuations'', Journal of Applied Econometrics, 15(3), pp. 275-287.
Edge, Rochelle M. 2000 `` Time-to-build, time-to-plan, habit-persistence, and the liquidity effect,'' Board of Governors International Finance Discussion Paper 673
Erceg,Christopher, Luca Guerrieri and Christopher Gust. 2004 `` Can Long-Run Restrictions Identify Technology Shocks?'', Federal Reserve Board of Governors International Finance Discussion Paper 792
Faust, Jon and Eric Leeper 1997 `` When Do Long-Run Identifying Restrictions Give Reliable Results?'' Journal of Business and Economic Statistics 15(3) 345-53
Francis, Neville and Valerie A. Ramey 2003 `` Is the Technology-Driven Real Business Cycle Hypothesis Dead? Shocks and Aggregate Fluctuations Revisited'' manuscript October
Fuhrer, Jeffrey C. 2000 `` Habit Formation in Consumption and Its Implications for Monetary-Policy Models'' American Economic Review 90(3) 371-390
Galí, Jordi, 1999 `` Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations,'' American Economic Review, 89 249-271.
Galí, Jord, J. David López-Salido and Javier Vallés 2003 `` Technology shocks and monetary policy: assessing the Fed's performance'' Journal of Monetary Economics, 50(4), 723-743
Harvey, Andrew, 1989, Forecasting Structural Time Series Models and the Kalman Filter, Cambridge University Press.
Jermann, Urban J., 1998 `` Asset Pricing in Production Economies,'' Journal of Monetary Economics 41 257-276.
King, Robert G., Charles. I. Plosser, James H. Stock, and Mark W. Watson. 1991. `` Stochastic Trends and Economic Fluctuations.'' American Economic Review. 81(4) 819-840.
King Robert G. and Mark W. Watson 1997 `` Testing long-run neutrality'' Federal Reserve Bank of Richmond Economic Quarterly 69-101
Koeva, Petya 2000 `` The Facts About Time-to-Build'' IMF Working Paper August
Kydland, Finn E. and Edward C. Prescott, 1982, `` Time to Build and Aggregate Fluctuations', Econometrica, 50, November, 1345-70.
Lum Sherlene K.S. and Brian C. Moyer 1998 `` Gross Product by Industry 1995-97'' Survey of Current Business November
Pesavento, Elena and Barbara Rossi 2003 `` Do Technology Shocks Drive Hours Up or Down? A Little Evidence From an Agnostic Procedure'' Duke University manuscript
Shleifer, Andrei 1986 `` Implementation Cycles'',Journal of Political Economy, 94(6) 1163-90
Topel, Robert and Sherwin Rosen 1988 `` Housing Investment in the United States'', Journal of Political Economy 96:4 718-740.
Vigfusson, Robert J. 2003 `` How Does the Border Affect Productivity? Evidence from American and Canadian Manufacturing Industries '', Federal Reserve Board of Governors, International Finance Discussion Papers 788
Whelan, Karl 2000 `` A Guide to the Use of Chain Aggregated NIPA Data'' Federal Reserve Board of Governors Finance and Economics Discussion Series 2000-35 (June)
Wright, Jonathan H. 2002 `` Testing the Null of Identification in GMM'', Federal Reserve Board of Governors, International Finance Discussion Papers 732
A Tables
Table 1: Manufacturing Industries
| Durable Good Producers | SIC Code | Nondurable Good Producers | SIC Code |
|---|---|---|---|
| Lumber | 24 | Food | 20 |
| Furniture | 25 | Textiles | 22 |
| Glass Stone & Clay | 32 | Apparel | 23 |
| Primary Metals | 33 | Paper | 26 |
| Fabricated Metals | 34 | Printing | 27 |
| Industrial Machinery | 35 | Chemicals | 28 |
| Electrical Machinery | 36 | Petroleum | 29 |
| Transportation | 37 | Rubber and Plastics | 30 |
| Instruments | 38 | ||
| Miscellaneous | 39 |
Table 2: Coefficient Estimates
Coef NonDurable |
T-stat NonDurable |
Coef Durable |
T-stat Durable |
|
|---|---|---|---|---|
| 0.82 | -1.13 | 1.04 | 0.28 | |
| 0.31 | 2.45 | 0.17 | 1.65 |
Results: 18 Manufacturing
Industries 1972-2001
GMM Estimation with Asymptotic
Standard Errors
T-stat for ![]() is test of
is test of ![]() equal to one.
equal to one.
T-stat for ![]() is test of
is test of ![]() equal to zero.
equal to zero.
Degrees of Freedom Equal to
167
Table 3: Percent of Simulations where the response
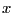 periods after the shock is greater than the response
on impact
periods after the shock is greater than the response
on impact
| H | C | I | |
|---|---|---|---|
| 1 | 90.1 | 77.4 | 94.1 |
| 2 | 90.7 | 68.0 | 92.0 |
| 3 | 91.4 | 77.0 | 93.4 |
| 4 | 87.8 | 74.4 | 88.4 |
| 5 | 88.5 | 79.4 | 88.2 |
| 6 | 90.3 | 84.7 | 87.6 |
| 7 | 89.7 | 83.8 | 86.3 |
| 8 | 89.0 | 85.6 | 85.1 |
| 9 | 88.6 | 86.0 | 83.1 |
Table 4: Estimated Confidence Intervals and Theoretical Bounds on Impact Response to A Technology Shock
Estimate Confidence Intervals Technology |
Estimate Confidence Intervals Labor Productivity |
Theoretical Bounds Technology VAR |
Theoretical Bounds Labor Productivity VAR |
|
|---|---|---|---|---|
| Labor Productivity | (-0.06, 0.38) | (-0.22, 0.36) | ||
| Hours Worked | (-0.007, 0.084) | (-0.09, 0.11) | ||
| Real Interest Rate | (28, 98) | (-38, 100) | ||
| Output | (-0.05, 0.42) | (-0.31, 0.45) | ||
| Consumption | (0.07, 0.32) | (-0.03, 0.20) | ||
| Investment | (-0.69, 1.08) | (-1.09, 1.30) |
Notes: Confidence Intervals Constructed using 95 percent critical value
of 11.07 for tech and 9.488 for labor
productivity
B Figures
Figure 1: Hours Response
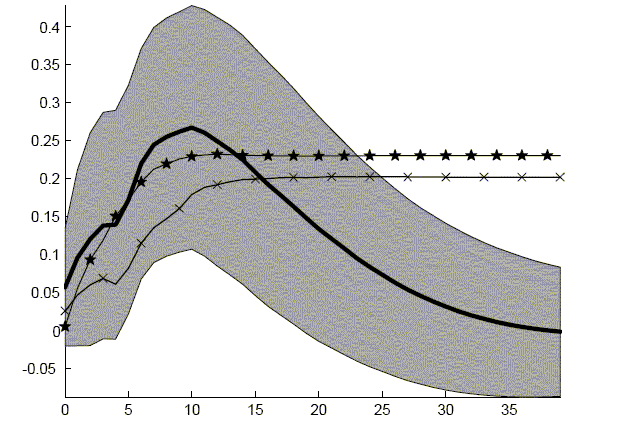
Thick Line VAR with Constructed Productivity Series and Hours In Levels
'X's: VAR with Constructed Productivity Series and Hours In Difference
Stars VAR with Labor Productivity and Hours in Differences
Grey Area: 95 Percent Bootstrapped Confidence Interval Centered Around VAR with Constructed Productivity Series and Hours In Levels
Description of Figure 1
Figure 1 is titled ``Hours Response''.The x-axis represents time after the shock and ranges from zero to forty in increments of five.
The y-axis ranges from 0 to 0.45 in increments of 0.05.
Figure 1 reports the response of three different VARs.
- The first response is from the VAR with constructed
productivity series and hours in levels. In period 0, it begins
with value 0.05 and increases to 0.25 when time t equals ten. This
is its maximum point. Afterwards, it slowly decreases until it
reaches zero at period 40.
- A gray area surrounds this line corresponding to the 95 percent bootstrapped confidence interval. The interval is roughly the same above and below the line, about 0.15. The interval is roughly the same for all periods.
- The second response was constructed from the VAR with constructed productivity series and hours in difference. This line begins at zero and increases to 0.22 in period 10. For the remaining periods, the line remains at this value.
- The third response was constructed from the VAR with labor productivity and hours in differences. The line begins at 0.02 and increase to 0.18 in period 12. For the remaining periods, the line remains at this value.
Figure 2: Data Used In the VAR Analysis
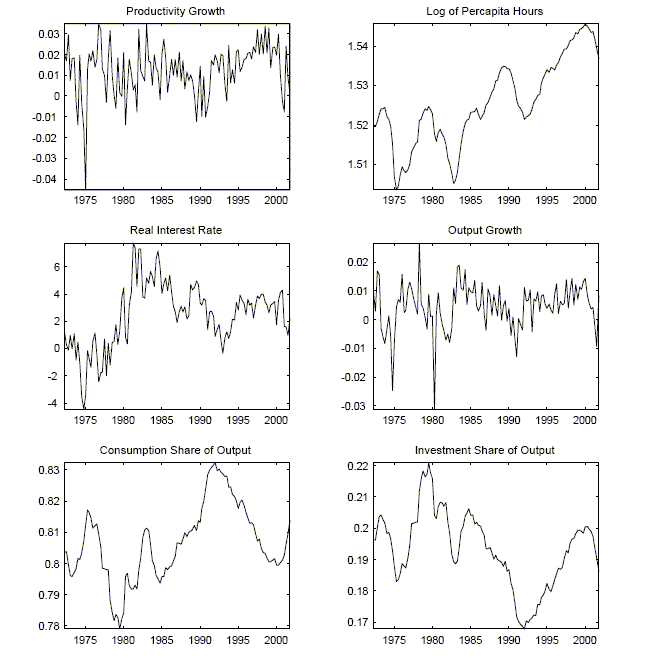
Description of Figure 2
Figure 2 is titled ``Data Used in the VAR Analysis''. It consists of six graphs presented in a three-by-two matrix.
The values on the x-axis are years ranging from 1972 to 2001.
The upper left graph is titled ``Productivity Growth''.
The y-axis ranges from -0.045 to 0.035.
The line appears as jagged oscillations around 0.01.
The upper right graph is titled ``Log of Per capita Hours''.
The y-axis ranges from 1.505 to 1.545 in increments of 0.05
The line begins at 1.52. By 1975, it has decreased to about 1.505. It gradually increases to about 1.525 in 1980. It decreases to 1.505 in 1983. Afterwards, it increases fairly quickly and achieves a value of 1.535 in 1987. It then begins to drop, and has a value of 1.52 in 1992. Afterwards, it increases sharply to 1.545 in 2000. In the remaining year of the graph, it decreases slightly and ends with a value of 1.535 in 2001.
The middle left graph is titled ``Real Interest Rate''.
The y-axis ranges from -4 to 8 in increments of 2.
The real interest appears to follow a general trend. The actual values appear to oscillate around this trend. The trend remains close to -1 from 1973 to 1980. Afterwards, it increases to about 6 by 1983. From there, the trend appears to decreases to about 2 in 1993. Afterwards, it increases slightly to 3 in 1995 and remains roughly there for the remaining periods.
The middle right graph is titled ``Output Growth''.
The y-axis ranges from -0.03 to 0.025 in increments of 0.01.
The line appears as jagged oscillations around 0.005. There are three noticeable spikes in this time frame. In 1975, output growth feel to about -0.025. In 1978, output growth grew at about 0.025. In 1981, output growth fell to about -0.03.
The lower left graph is titled ``The Consumption Share of Output''.
The y-axis ranges from 0.78 to 0.83 in increments of 0.01.
The line begins at 0.805. It increases to 0.815 in 1975. It then decreases to 0.78 in 1980. From there it increases to 0.81 in 1983 before falling down again to 0.795 in 1984. Afterwards, it trends upwards to about 0.83 in 1992. From there, it trends downwards to 0.80 in 1999. Afterwards, it increases up to 0.815 in 2001.
The lower right graph is titled ``Investment Share of Output''.
The y-axis ranges from 0.17 to 0.22 in increments of 0.01.
The line begins at 0.195. It decreases to about 0.185 in 1975. From there it trends upwards to 0.22 in 1978. It decreases to 0.185 in 1983. From there it increases slightly until 0.205 in 1985 before falling to 0.170 in 1992. It trends upwards from there and has a value of 0.20 in 199. It decreases until it has a value of 0.185 in 2001.
Figure 3: The Result of Applying The Long Run Identification Assumption
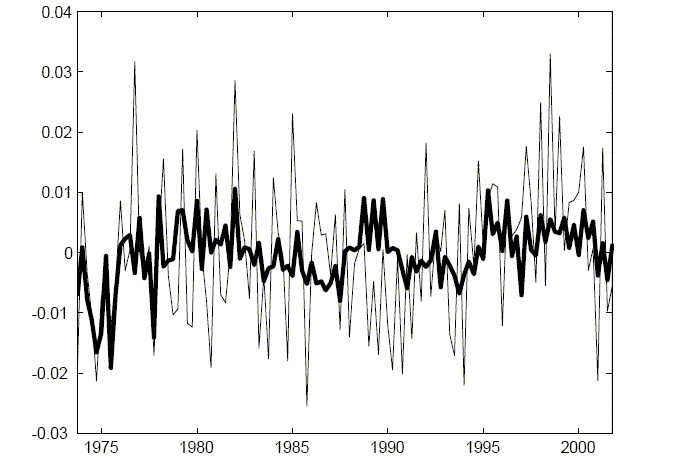
Thin Line Constructed Technology Growth Rate Series (Demeanded)
Thick Line: Technology Growth Rate Series (Demeanded) implied by the Long Run Identification Assumption
Description of Figure 3
Figure 3 is titled ``The Result of Applying the Long-Run Identification Assumption''.
The x-axis ranges from 1972 to 2001.
The y-axis ranges from -0.03 to 0.04.
The graph consists of two lines.
- The first line is the constructed technology growth rate series. The line appears like white noise around zero, with values ranging from -0.02 to 0.01.
- The second line is the technology growth rate series implied by the Long Run Identification Assumption. Like the first line, this second line appears like white noise except it has more extreme values. It ranges from -0.028 to 0.03.
Figure 4: Responses to Productivity Shock
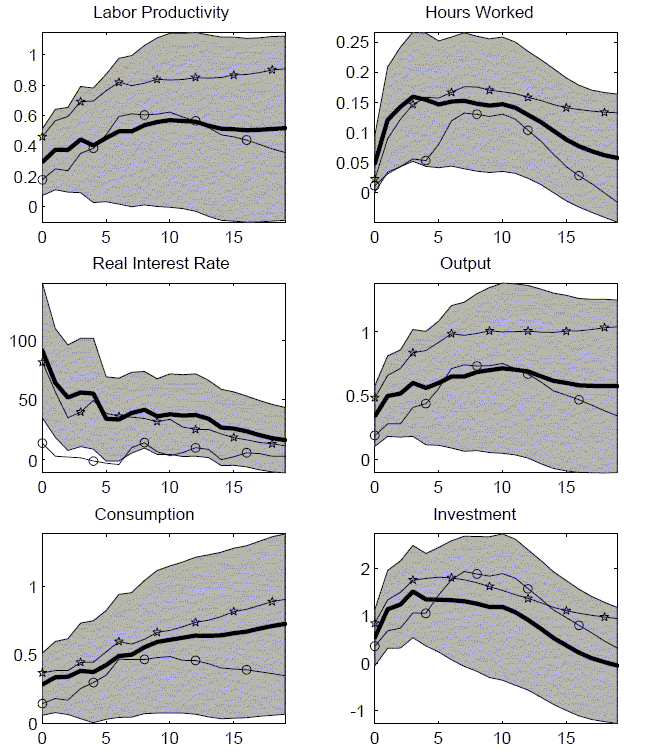
Thick Line VAR with Constructed Productivity Series and Hours In Levels, with Long Run Identification Assumption
Grey Area: 95 Percent Bootstrapped Confidence Interval Centered Around VAR with Constructed Productivity Series and Hours In Levels
Circles VAR with Constructed Productivity Series and Hours In Levels, with Short Run Identification Assumption
'Stars's VAR with Labor Productivity and Hours in Differences with Long Run Identification Assumption
Description of Figure 4
Figure 4 consists of six graphs presented in a three-by-two matrix.
In each of these six graphs, the x-axis ranges from zero to 20 in increments of five.
Each of the six graphs reports the response of three different VARs.
The first response was from the VAR with constructed productivity series and hours in levels.
A gray area surrounds this line corresponding to the 95 percent bootstrapped confidence interval.
The second response was constructed from the VAR with constructed productivity series and hours in levels, with short-run identification assumption.
The third response was constructed from the VAR with labor productivity and hours in differences, with long-run identification assumptions.
The upper left graph shows ``Labor productivity''. The y-axis ranges from -0.2 to 1.2.
- The first response begins at 0.3 and gradually increases to 0.5
at in period 10. It then holds at this value for the remaining 10
periods.
- A 95 percent bootstrapped confidence interval is centered on this response. In the beginning, it is about 0.1 above and below the response. This interval gradually increases and by period 20, the interval is about 0.6 above and below the response.
- The second response begins at 0.2. It increases to about 0.5 in period 6. It remains fairly consistent there until time t equals nine. Afterwards, it steadily decreases to about 0.4 in period 20.
- The third response begins at 0.5. It increases to 0.8 at period 5. Afterwards, it continues to increase but more slowly. At the end, it has a value of 0.9.
The upper right graph shows ``Hours Worked''. The y-axis ranges from -0.05 to 0.25.
- The first response begins at 0.05 and quickly increases to 0.17
in period 3. It remains around this level until period 10.
Afterwards, it slowly decreases to about 0.07 at the end.
- A 95 percent boostrapped confidence interval is centered on this response. In the beginning, it is about 0.05 above and below the response. This interval increases and by period 20, the interval is about 1 above and below the response.
- The second response begins at zero. It increases to 0.12 in period 7. It stays at this value until period 10 and decreases to zero by period 20.
- The third response begins at zero. It quickly increases to 0.17 in period 7. It decreases slightly from there and ends at 0.15 in period 20.
The middle left graph shows ``Real Interest Rate''.
- The first response begins at 80. It quickly declines to about
40 in period 5. It decreases slowly from there to about 25 in
period 20.
- A 95 percent bootstrapped confidence interval is centered on this response. Throughout the graph, it is about 0.35 above and below the response.
- The second response begins at 15. It decreases to zero in period 6. It then increases to 0.15 and remains roughly there.
- The third response begins at 0.80. It quickly decreases to 45 in period 3. From there is slowly decreases to about 0.15 by the end.
The middle right graph shows ``Output''.
- The first response begins at about 0.4. It steadily increases
to 0.7 in period 10. Afterwards, it slowly declines until 0.6 in
period 20.
- A 95 percent bootstrapped confidence interval is centered on this response. At the beginning of this graph, it is about 0.20 above and below the line. This interval increases and by period 20, the interval is about 0.6 above and below the line.
- The second line begins at 0.2 and increases to 0.7 in period 6. It remains at around this value until period 10. Afterwards, it decreases to 0.35 at the end.
- The third line begins at 0.7 and increases to 1 in period 5. It then remains steady at this value.
The lower left graph shows ``Consumption''.
- The first response begins about 0.3. It increases almost
linearly to 0.6 in period 20.
- A 95 percent bootstrapped confidence interval is centered on this response. At the beginning of this graph, it is about 0.20 above and below the line. This interval increases and by period 20, the interval is about 0.6 above and below the line.
- The second response begins at about 0.2. It increases to 0.5 in period 6. It declines almost linearly until it has the value 0.3 in period 20.
- The third response begins at about 0.35. It increases almost linearly to 0.8 at the end.
The lower right graph shows ``Investment''.
- The first response begins at 0.5. It increases to about 1.3
when time t equals 4. There, it holds steady until period 10.
Afterwards, it slowly declines to zero.
- A 95 percent bootstrapped confidence interval is centered on this response. At the beginning of the graph, it is about 0.5 above and below the line. This interval increases to about 1.25 in period 20.
- The second response begins at about 0.25 and increases to 2 in period 6. It stays at roughly this value until period 10. Afterwards, it decreases to about 0.5 by the time t equals 20.
- The third response begins at about 0.75 and increases to about 1.75 in period 3. From there, it slowly declines to 1.25 by period 20.
Figure 5: Shape of The Response of Hours
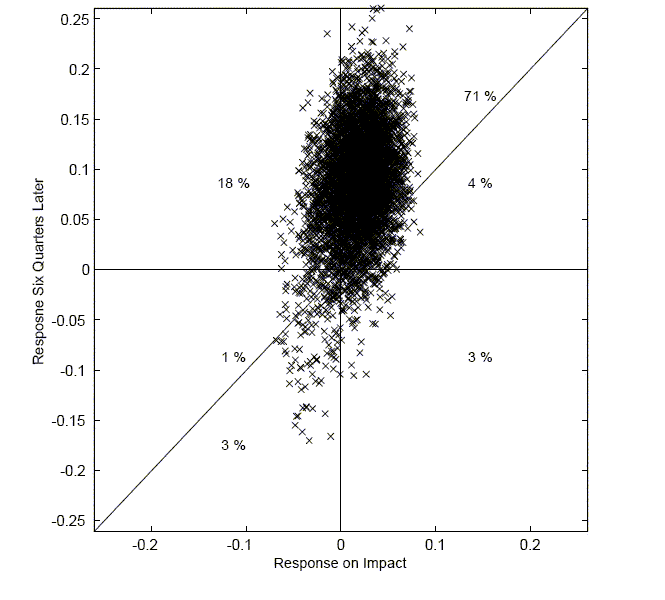
Description of Figure 5
Figure 5 is titled ``Shape of the Response of Hours''.
The x-axis is labeled ``Response on Impact'' and ranges from -0.25 to 0.25; a vertical line ranges through zero.
The y-axis is labeled ``Response Six Quarters later'' and ranges from -0.25 to 0.25; a horizontal line ranges through zero.
A diagonal line runs through the points where y equals x.
Thus, there are four quadrants. In the upper right quadrant and the lower left quadrant, a diagonal line runs from the bottom left point to the upper right point.
The upper left quadrant contains the label ``18 percent''.
The top left half of the upper right quadrant contains the label ``71 percent''.
The bottom right half of the upper right quadrant contains the label ``4%''.
The top left half of the bottom left quadrant contains the label ``1 percent''.
The bottom right half of the bottom left quadrant contains the label ``3%''.
The bottom right quadrant contains the label ``3%''.
The graph's points are densely located in an oval region where the x-value is between -0.02 to 0.08, and the y-value is between -0.02 and 0.17. Points outside this region do exist, but they are less densely packed.
Figure 6: Confidence Intervals
for 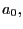 Impact Response
on Hours, and the Response Six Periods Later
Impact Response
on Hours, and the Response Six Periods Later
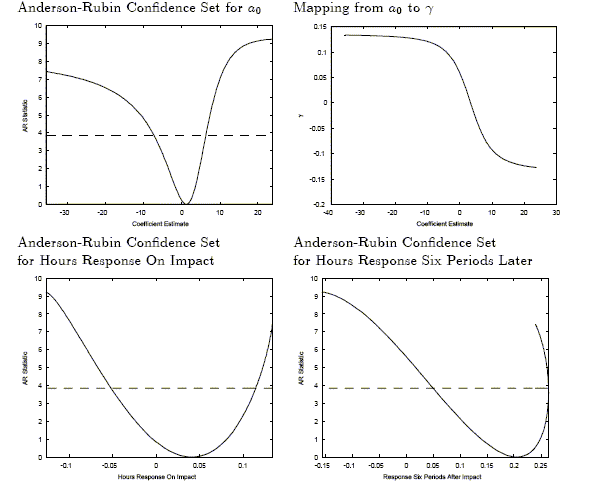
Description of Figure 6
Figure 6 is titled ``Confidence Intervals for a0, Impact Response on Hours, and the Response Six Periods Later''. It consists of four graphs presented in a two-by-two matrix.
The upper left graph titled ``Anderson-Rubin Confidence Set for a0''.
The x-axis is labeled ``Coefficient Estimate'' and ranges from -35 to 25.
The y-axis is labeled ``AR Statistic'' and ranges from 0 to 10.
A dashed line exists where the AR statistic is about 3.9.
The line begins at 7.5. It slowly decreases to 5 when the coefficient estimate is -10. It then quickly decreases to 0 when the coefficient estimate is 2. From there it quickly increases to 8.5 when the coefficient estimate is 12. It finally ends at 9.2 when the coefficient estimate is 25.
The upper right graph is titled ``Mapping from a0 to Gamma''.
The x-axis is labeled ``Coefficient Estimate'' and ranges form -40 to 30.
The y-axis is labeled ``Gamma'' and ranges from -0.2 to 0.15.
The line has a negative logistic shape. It begins at 0.12 and slowly decreases to 0.1 when the coefficient estimate is -5. It then quickly decrease to -0.12 when the coefficient estimate is 8. From there, it slowly decreases to -0.12 when the coefficient estimate is 22.
The lower left graph is titled ``Anderson-Rubin Confidence Set for Hours Response on Impact''.
The x-axis is labeled ``Hours Response on Impact'' and ranges from -0.125 to 0.125.
The y-axis is labeled ``AR Statistic'' and goes from 0 to 10.
A dashed line exists where the AR statistic is about 3.9.
The line has a parabolic shape. It begins at 9.2 when the response on hours is about -0.125. It decreases to 0 when the hours response on impact is 0.04. Afterwards, it increases to 7.5 when hours response on impact is 0.125.
The lower right graph is titled ``Anderson-Rubin Confidence Set for Hours Response Six Periods Later''.
The x-axis is labeled ``Response Six Periods after Impact'' and goes from -0.15 to 0.25.
The y-axis is labeled ``AR Statistic'' and goes from 0 to 10.
A dashed line exists where the AR statistic is about 3.9.
The line begins at 9.2. It decreases to 0 when the x-value is 0.2. It then increases to 3.9 when the x-value is 0.25. Afterwards, the line continues to increase and arch leftwards. It ends at 8 when the x-value is 0.22.
Figure 7: Anderson-Rubin Confidence Set
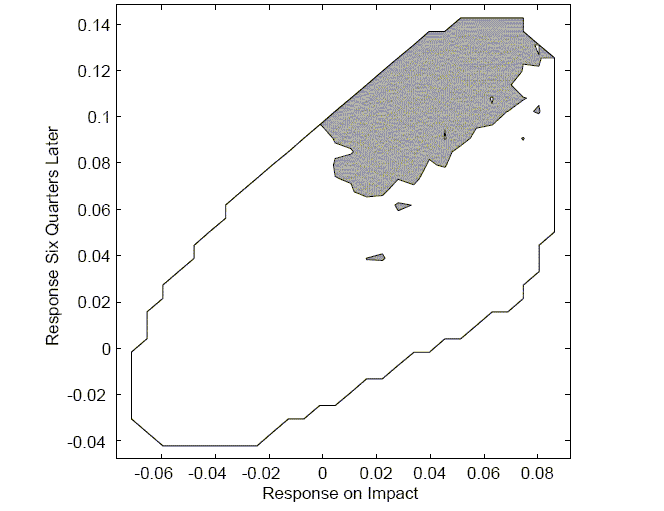
Description of Figure 7
Figure 7 is titled ``Anderson-Rubin Confidence Set.
The x-axis is labeled ``Response on Impact'' and ranges from -0.8 to 0.10.
The y-axis is labeled ``response six Quarters Later. It ranges from -0.04 to 0.14.
The chart contains an oval-shaped figure whose ends extend from the lower-left region of the graph to the upper right region. These lines of this oval-like figure indicated all possible combinations of gamma sub zero with H superscript and gamma sub six with H superscript.
The area of this oval where the x-values are between 0 and 0.06, and where the y-values are between 0.06 and 0.14 are shaded in a gray color.
The gray area indicates those combinations with an Anderson-Rubin statistics less than the 95 percent critical value.
Figure 8: Robustness of Impulse Responses to Different Subsamples.
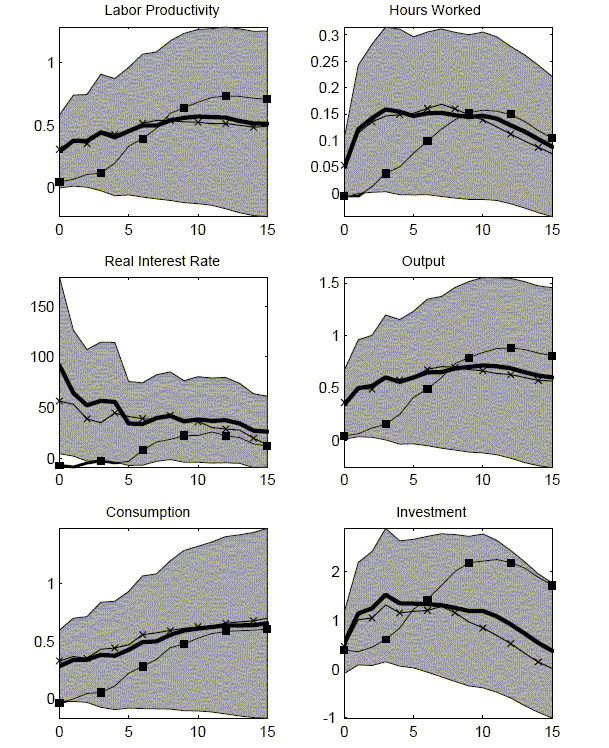
Thick Line VAR and Grey Area: Baseline Results replicated from Figure 4
'X's VAR with exante Real Interest Rate, full sample 1973-2001.
Squares VAR with exante Real Interest Rate, short sample 1983-2001.Description of Figure 8
Figure 8 is titled ``Robustness of Impulse Responses to Different Subsamples''.
It consists of six graphs presented in a three-by-two matrix.
In each of these graphs, the x-axis is labeled from 0 to 15 in increments of 5.
The graphs each contain the results from three responses.
The first line represents the baseline results replicated from figure 4
The second line is from the VAR with ex ante Real Interest Rate, full sample 1973 to 2001.
The third line is from the VAR with ex ante Real Interest Rate, short sample 1983 to 2001.
The upper left graph is titled ``Labor Productivity''.
- The first line begins at about 0.25 and steadily increases to
about 0.5 by period 10. It remains roughly at this value for the
remaining periods.
- This line is surrounded by a confidence interval. At the beginning of the graph, the line is about 0.3 above and below the line. By the end of the graph, the interval extends 0.7 above and below the line.
- The second line begins at 0.25. It remains roughly equal to the first line for the beginning seven periods. For the remaining periods, it remains near the first line but slightly below it.
- The third line follows a logistic shape. It begins at about 0 and slightly increases to 0.1 by age 3. It then increases more quickly until period 8 where it has a value of 0.6. Afterwards, it continues to increase albeit more slowly. It finishes with a value of 0.65.
The upper right graph is titled ``Hours Worked''.
- The first line begins at 0.05. It increases to 0.15 by the
third period. It remains at this value until period 11. Afterwards,
it decreases slightly to 0.10.
- A confidence interval surrounds this first line. In the beginning, it is about 0.05 above and below the line. By the third period, it is 0.15 above and below the line. For the remaining periods, it remains this wide.
- The second line begins at 0.25. It remains roughly equal to the first line for the beginning seven periods. For the remaining periods, it remains near the first line but slightly below it.
- The third line begins at zero. It increases to 0.15 by period 10, then decreases to 0.10 in period 15.
The middle left graph is titled ``Real Interest Rate''.
- The first line begins at 90. It decreases to 40 by period five.
It remains roughly at this level for the remaining periods.
- A confidence interval surrounds this first line. In the beginning it is about 80 above and below the first line. This interval decreases to about 50 by the end of the line.
- The second line begins at 50. It follows a decline and end at 0.25 in period 15.
- The third line begins at 0. It increases to 0.25 by period 9 and remains at roughly this value.
The middle right graph is titled ``Output''.
- The first line begins at 0.4 and slowly increases to 0.6 by
period 10. It remains roughly there for the remaining periods.
- A confidence interval surrounds this first line. In the beginning it is about 0.4 above and below the line. This interval increases to about 0.9 above and below the line.
- The second line begins at 0.4. It remains roughly equal to the first line for the beginning seven periods. For the remaining periods, it remains near the first line but slightly below it.
- The third line follows a logistic shape. It begins at 0 and increases slightly to 0.1 by period 3. It increases to 0.8 by period 8. It remains at roughly this value for the remaining periods.
The lower left graph is titled ``Consumption''.
- The first line begins at 0.3 and increases to 0.6 by period 10.
It remains at roughly this value.
- A confidence interval surrounds this first line. In the beginning, it is about 0.3 above and below the line. This interval increases to 0.8 above and below the line
- The second line begins at 0.3. It is roughly slightly above the first graph for the first second periods. For the remaining periods, it is roughly equal to the first line.
- The third line zero. It increases to 0.5 by period 11, and remains at roughly this value for the remaining periods.
The lower right graph is titled ``Investment''.
- The first line begins at 0.5. It increases to about 1.25 by the
first period. It remains at roughly this value until period 10. It
slowly decreases back to 0.5 by the end of the line.
- A confidence interval surrounds this first line. In the beginning, it is about 0.6 above and below the line. This interval increases to 1.5 above and below the line.
- The second line begins at 0.5. It increases to 1 by the first period. It remains at this value until period 7. It then slowly decreases until reaching 0 in the end of the line.
- The third follows a logistic shape. It begins at 0.5 and increase to 0.75 by the third period. Afterwards, it increases to 2.25 by the eighth period. It remains at roughly this value for two periods, and then decreases to about 1.9 by the end.
Figure 9: How Hours Responds on Impact
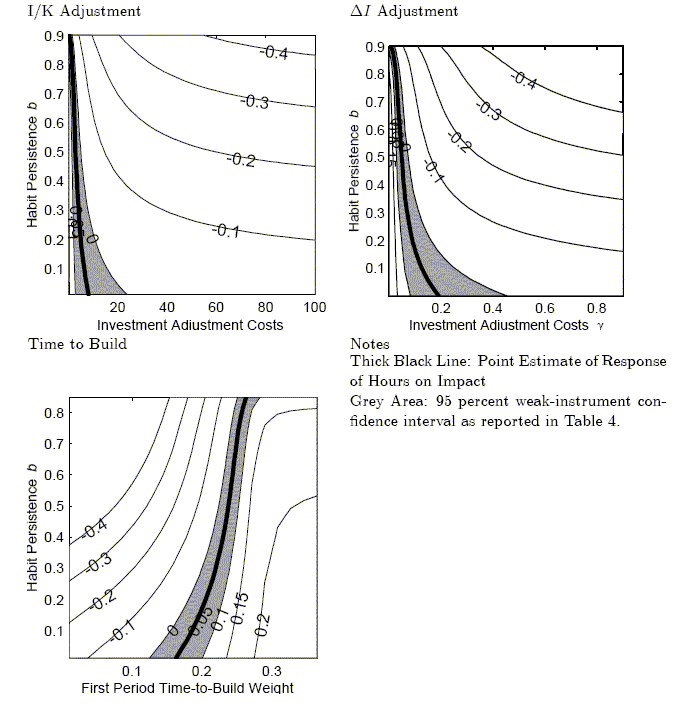
Notes
Thick Black Line: Point Estimate of Response of Hours on Impact
Grey Area: 95 percent weak-instrument confidence interval as reported in Table 4.
Description of Figure 9
Figure 9 is titled ``How Hours Responds on Impact''.
It consists of three contour plots presented in a two-by-two matrix with the lower right graph deleted.
The upper left graph is titled ``Investment-divided-by-Capital Adjustment''.
The x-axis is labeled ``Investment Adjustment Costs, gamma'', and ranges from 0 to 100 in increments of 20.
The y-axis is labeled ``Habit persistence b'', and ranges from 0 to 0.9 in increments of 0.1.
The plot shows the combinations of investment adjustment costs and habit persistence which produce no change in the response of hours. A line runs from investment adjustment costs of 0 and a habit persistence of 0.9 to the point where investment adjustment costs are about 5 and habit persistence is 0. A confidence region surrounds this line.
The plot also shows that as investment adjustment costs increase and habit persistence increase, there is a more negative effect on how hours respond.
The upper right graph is titled ``Change in Investment Adjustment''.
The x-axis is labeled ``Investment Adjustment Costs, gamma'', and ranges from 0 to 1 in increments of 0.2.
The y-axis is labeled ``Habit Persistence b'' and ranges from 0 to 0.9.
The plot shows the combinations of investment adjustment costs and habit persistence which produce no change in the response of hours. A line runs from investment adjustment costs of 0 and a habit persistence of 0.9 to the point where the investment adjustment costs are 0.2 and habit persistence is 0. A confidence interval surrounds this line.
The plot also shows that as investment adjustment costs increase and habit persistence increase, there is a more negative effect on how hours respond.
The lower left graph is titled ``Time to Build''.
The x-axis is labeled ``fire period time-to-build weight'', and ranges from 0 to 0.4 in increments of 0.1.
The y-axis is labeled ``Habit persistence b'', and ranges from 0 to 0.9 in increments of 0.01.
The plot shows the combinations of first period time-to-build weight and habit persistence which produce no change in the response of hours. A line runs from first period time-to-build weight of 0.15 and habit persistence of 0 to the point where the first period time-to-build weight of 0.25 and habit persistence of 0.9. A confidence interval surrounds this line.
The plot also shows that as habit persistence increases and first period time-to-build weight decreases, there is a more negative effect on how hours respond.
Figure 10: The Trade-off Between Investment Adjustment Costs and Habit Persistence
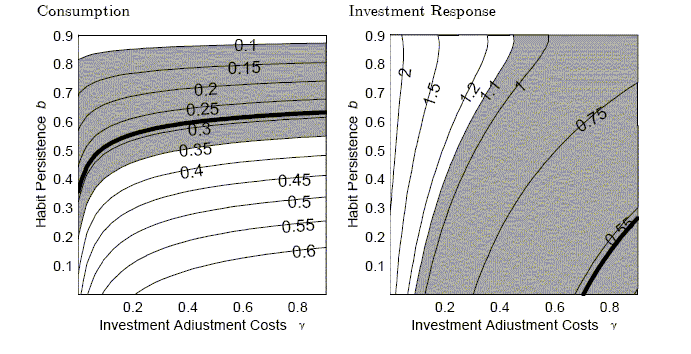
Description of Figure 10
Figure 10 is titled ``The Trade-off between Investment Adjustment Costs and Habit Persistence''.
It consists of two contour graphs, side-by-side.
The left graph is titled ``Consumption''.
The x-axis is labeled ``Investment Adjustment Costs, gamma''. It ranges from 0 to 1 in increments of 0.2.
The y-axis is labeled ``Habit Persistence, rho''. It ranges from 0 to 0.9 in increments of 0.1.
As habit persistence increases, there is a smaller effect on consumption.
The right graph is titled ``Investment Response''.
The x-axis is labeled ``Investment Adjustment Costs, gamma''. It ranges from 0 to 1 in increments of 0.2.
The y-axis is labeled ``Habit Persistence, rho''. It ranges from 0 to 0.9 in increments of 0.1.
As investment adjustment costs decrease and habit persistence increase, there is a larger effect on the Investment Response.
Figure 11: Dynamic Responses Comparing Models and Data Investment Adjustment Costs as Function of Investment Growth
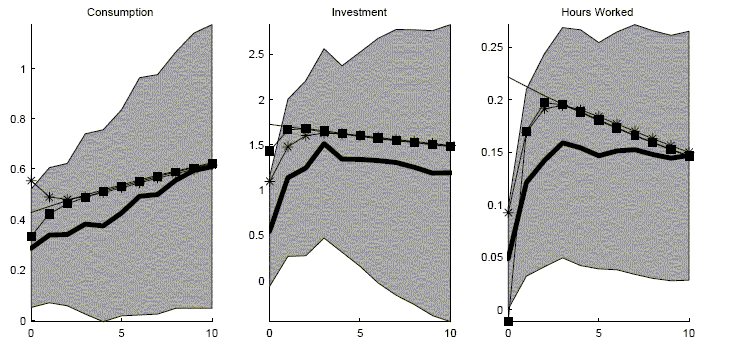
Notes on first row of figures in Figure 11:
Thick Solid Line: Empirical Response, Thin Line, Standard flexible-price model
![]()
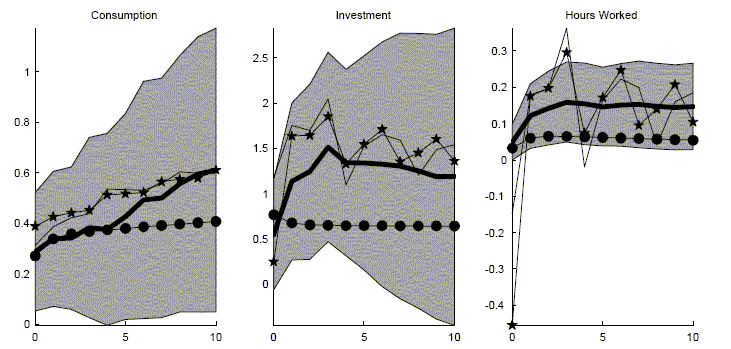
Notes on second row of figures in Figure 11:
Description of Figure 11
Figure 11 is titled ``Dynamic Responses Comparing Models and Data Investment Adjustment Costs as Function of Investment Growth''. It consists of six graphs presented in a two-by-three matrix.
The two graphs on the left are titled ``Consumption''.
The two middle graphs are titled ``Investment''.
The two graphs on the right are titled ``Hours Worked''.
The x-axis of each of the three graphs ranges from zero to ten in increments of five.
In the top three graphs, each contains four lines.
The first line is the empirical response.
The second line is the response from the standard flexible-price model with b and phi are zero.
The third line is the response from the model with habit persistence and investment adjustment costs where b equals 0.4 and phi equals 0.09.
The fourth line is the response from the model with investment adjustment costs where b equals 0 and phi equals 0.09.
Recall that the upper left graph is labeled ``Consumption''.
- The first line begins at 0.3 and it steady increases throughout
the ten periods. It reaches a value of 0.6 by period 10.
- A confidence interval surrounds this line. In the beginning, it is about 0.25 above and below the line. The interval increases and by the end, it is about 0.6 above and below the line.
- The second line begins at about 0.42 and increases linearly until period 10, where its value is 0.6.
- The third line begins at 0.3. It increases slightly, and y the third period, it has converged to the second line. For the remaining periods, it is equal to the second line.
- The fourth line begins at about 0.58. It decreases slightly and by the third period, it has converged to the second line. For the remaining periods, it is equal to the second line.
Recall that the upper middle graph is labeled ``Investment''.
- The first line begins at 0.5. By the third period, it reaches a
value of 1.5. From there, it slowly decreases to about 1.25 by
period 10.
- A confidence interval surrounds this line. In the beginning, the confidence interval is about 0.5 above and below the line. The interval increases and by the end, it is above 1.25 above and below the line.
- The second line begins at about 1.75 and decreases linearly to 1.5 by period 10.
- The third line begins at 1.45. It increases slightly and by the third period, it has converged to the second line. For the remaining periods, it is equal to the second line.
- The fourth line begins at 1. It increases and by the third period, it has converged to the second line. For the remaining periods, it is equal to the second line.
Recall that the upper right graph is labeled ``Hours Worked''.
- The first line begins at 0.05. By period 3, it increases to
0.15. It remains at roughly this level for the remaining periods.
- A confidence interval surrounds this line. In the beginning, the confidence interval is about 0.5 above and below the line. The interval increases and by the end, it is 0.13 above and below the line.
- The second line begins at about 0.22. It decreases linearly to 0.15 by period 10.
- The third line begins at 0. It increases quickly to 0.2 by period 2. By period 3, it has converged to the second line. For the remaining periods, it is equal to the second line.
- The fourth line begins at 0.1. It increases to 0.18 by period 2. By period 3, it has converged to the second line. For the remaining periods, it is equal to the second line.
In the bottom three graphs, each graph contains four lines.
The first line is the empirical response.
The second line is the model with habit persistence and time to plan where b equals 0.5 and phi equals 0.05.
The third line is the response from the model with habit persistence and time to build where b equals 0.5 and phi equals 0.20.
The fourth line is the response from the C-I-K model with habit persistence where b equals 0.28 and phi equals 5.
Recall that the lower left graphs is labeled ``Consumption''.
- The first line begins at 0.3. It increases to 0.4 by period 5.
It then increases even more quickly to 0.6 by period 10.
- A confidence interval surrounds this line. In the beginning it is 0.2 above and below the line. The interval increase and by period 10, it is a
- The second line begins at 0.4. It steadily increases to 0.6 by period 10.
- The third line begins at 0.3. It increases to 0.5 by period 5. It then increases more slowly and has a value of 0.6 by period 10.
- The fourth line begins at 0.3. By period2, it has a value of 0.35. It steadily increases; by period 10, its value is 0.4.
Recall that the lower middle graph is labeled ``Investment''.
- The first line begins at 0.5. By the third period, it reaches a
value of 1.5. From there, it slowly decreases to about 1.25 by
period 10.
- A confidence interval surrounds this line. In the beginning, the confidence interval is about 0.5 above and below the line. The interval increases and by the end, it is above 1.25 above and below the line.
- The second line begins at 0.25. In period 1, it jumps to 1.6. For the remaining periods, it oscillates around 0.5 in values ranging between 1.25 and 1.75.
- The third line begins at 1.25. It oscillates around 0.5 in values ranging between 1.25 and 1.75 for the remaining periods.
- The fourth line begins at 0.80. It appears to decrease only slight and converges to 0.75 by period 2. It remains there for the remaining periods.
Recall that the lower right graph is labeled ``Hours Worked''.
- The first line begins at 0.5. It increases slightly to 0.13 by
period 3 and remains roughly there for there for the remaining
periods.
- A confidence interval surrounds this line. In the beginning, it is about 0.5 above and below the line. By period 10, it is about 0.12 above and below the line.
- The second line begins at -0.45. By period 1, it quickly jumps to 0.2. The line oscillates around 0.2 in values ranging between 0 .1 and 0.3.
- The third line begins at -0.15. By period 1, it quickly jumps to 0.2. The line oscillates around 0.2 in values ranging between 0.1 and 0.3.
- The fourth line begins at 0.25. In period 1, it has a value of 0.5. It remains there for the remaining periods.
Figure 12: Real Interest Rate Response
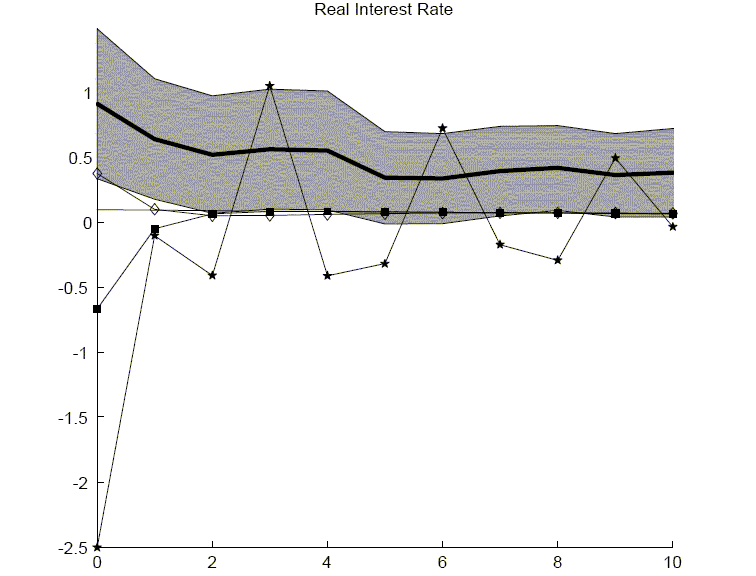
Thick Solid Line: Empirical
Response, Thin Line, Standard flexible-price model
![]()
Squares: Model with habit
persistence and investment adjustment Costs
![]()
Stars: Model with habit
persistence and Time to Plan
![]()
Diamonds: Model with
consumption adjustment costs and investment adjustment
costs.
![]()
Description of Figure 12
Figure 12 is titled ``Real Interest Rate Response''.
The x-axis ranges from zero to ten in increments of two.
The y-axis ranges from -2.5 to 1.5 in increment of 0.5.
The graph contains five lines.
The first line shows the empirical response.
The second line shows the response of the standard flexible-price model when b and phi equals 0.
The third line shows the response of the model with habit persistence and investment adjustment costs when b equals 0.4 and phi equals 0.09.
The fourth line shows the response from the model with habit persistence and Time to Plan when b equals 0.5 and phi equals 0.05.
The fifth line shows the response of the model with consumption adjustment costs and investment adjustment costs when b equals 0.4 and phi equals 0.2.
- The first line begins at 1. It decreases to about 0.5 by period
2, and decreases further to 0.3 by period 5. It remains at roughly
this level.
- A confidence interval surrounds this line. It is about 0.6 above and below the line.
- The second line is a horizontal line at about 0.1.
- The third line has a logarithmic shape. It starts at -0.7, and converges to zero by the second period.
- The fourth line follows an erratic pattern. It would be easier to describe each point. Period 0 has a value of -2.5. Period 1 is -0.1. Period 2 is -0.4. Period 3 is 1. Period 4 is -0.4. Period 5 is -0.3. Period 6 is 0.75. Period 7 is -0.25. Period 8 is -0.3. Period 9 is 0.6. Period 10 is 0.
- The fifth line starts at about 0.4. It converges to zero by stage 2, and remains there.
Figure 13: Model Responses with Correlated Shocks
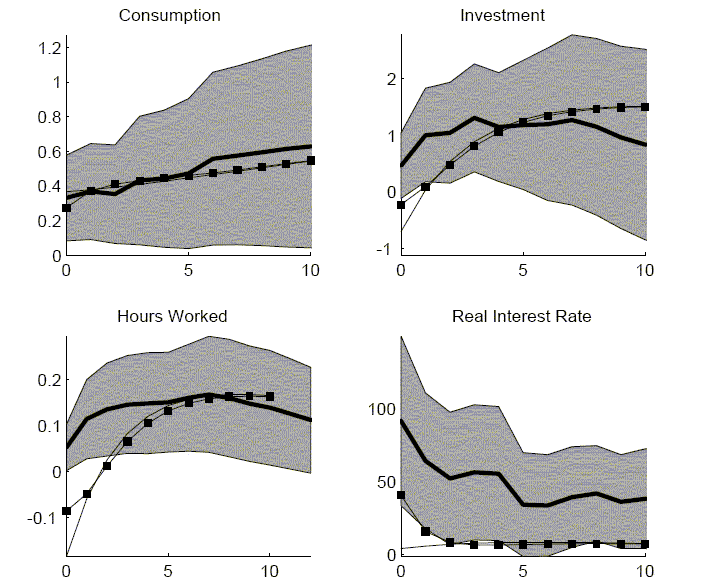
Thick Solid Line: Empirical
Response, Thin Line, Standard flexible-price model
![]() with
with
![]()
Squares: Model with habit
persistence and investment adjustment Costs
![]() with
with
![]()
Description of Figure 13
Figure 13 is titled ``Model Responses with Correlated Shocks''.
It presents four graphs, presented in a two-by-two matrix.
Each graph contains three lines.
The first line is the empirical response.
The second line is the response from the standard flexible-price model when b and phi equal zero and rho sub z equals 0.7.
The third line is the response of the model with habit persistence and investment adjustment costs where b equals 0.4, phi equals 0.09, and rho sub z equals 0.7.
The upper left graph is titled ``Consumption''.
The x-axis ranges from zero to ten in increments of five.
The y-axis ranges from 0 to 1.2.
- The first line begins at 0.3. It increases to 0.5 by period 6.
Afterwards, it increases linearly to 0.6 by the tenth period.
- A confidence interval surrounds this line. In the beginning, it is about 0.3 above and below the line. By the end, it is 0.5 above and below the line.
- The second line begins at 0.4. It increases almost linearly and achieves a value of 0.5 by the end.
- The third line begins at 0.3. It increases to 0.4 by the third period. Afterwards, it increases almost linearly and achieves a value of 0.5 by the end.
The upper right graph is titled ``Investment''.
The x-axis ranges from zero to ten in increments of five.
The y-axis ranges from -1 to 3.
- The first line begins at 0.5. It increases to 1 in the first
period. It remains at roughly this value until period 7.
Afterwards, it decreases lightly to 0.8 by the tenth period.
- A confidence interval surrounds this line. In the beginning it is about 0.5 above and below the line. By the end, it is 1.8 above and below the line.
- The second line follows the shape of a logarithmic shape. It begins at -0.5. At period 5, it has a value of 1. It increases slowly afterwards, and finishes with a value of 1.25 by the tenth period.
- The third line follows the shape of a logarithmic shape. It begins at about 0. At period 5, it has a value of 1. It increases slowly afterwards and finishes with a value of 1.25 by the tenth period.
The lower left graph is titled ``Hours Worked''.
The x-axis ranges from zero to twelve in increments of five.
The y-axis ranges from -0.2 to 0.3.
- The first line begins at 0.05. It increases to 0.1 by the first
period and slightly increases to 0.15 by the seventh period.
Afterwards, it decreases back to 0.1 by the twelfth period.
- A confidence interval surrounds this first line. In the beginning, it is about 0.05 above and below the line. This interval increases; by the end of the line, it is about .12 above and below the line.
- The second line follows a logarithmic shape. It begins at -0.2. It increases to 0.1 by the fifth period. Afterwards it slightly increases until reaching a value of about 0.12 in the tenth period.
- The third line follows a logarithmic shape. It begins at -0.1. It increases to 0.1 by the fifth period. Afterwards, it slightly increases until reaching a value of about 0.12 in the tenth period.
The lower right graph is titled ``Real Interest Rate''.
The x-axis ranges from 0 to 10 in increments of 10.
The y-axis ranges from 0 to 150 in increments of 50.
- The first line begins at 90. It decreases to 40 by the fifth
period and holds steady roughly there.
- A confidence interval surrounds this first line. In the beginning, it is about 0. 60 above and below the line. This interval decreases; by the end of the line, it is about 30 above and below the line.
- The second line begins at roughly 10. It remains roughly flat at that level.
- The third line begins 40. It decreases to about 10 and remains there for the remaining periods.
Figure 14: Hours Response to A Technology Shock
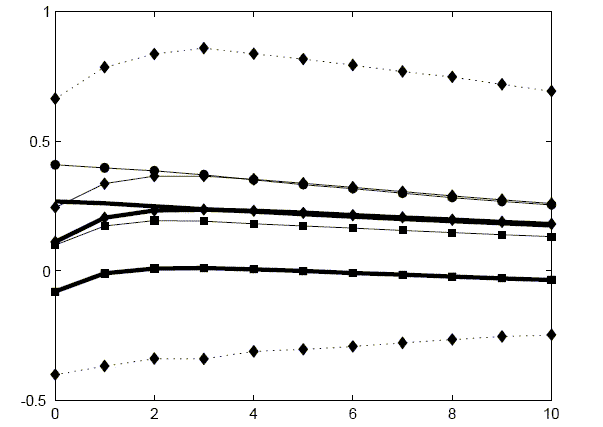
Thick Lines, Model Responses, Plain Standard RBC, Diamonds CII Adjustment Cost, Squares,
CII Adjustment and Habit
Thin Lines, Average Estimated Response, Plain Standard RBC, Diamonds CII Adjustment Cost,
Squares, CII Adjustment and Habit
Dashed Lines, 90 Percent of all estimated responses for the CII Model are contained within dashed lines
Description of Figure 14
Figure 14 is titled ``Hours Response to a Technology Shock''.
The x-axis ranges from 0 to 10 in increments of 2.
The y-axis ranges from -0.5 to 1 in increments of 0.5.
It graph contains six lines.
The three lines correspond to model responses.
The first line is the response from the standard RBC.
The second line is the response from the C-I-I Adjustment Cost.
The third line is C-I-I Adjustment and Habit.
The last three lines correspond to the average estimate response.
The fourth line is the response from the standard RBC.
The fifth line is the response from the C-I-I Adjustment Cost.
The sixth line is from the C-I-I Adjustment and Habit.
The seventh and eight lines show the 90 percent interval of all estimated responses for the C-I-I Model.
- The first line begins at about 0.30 and converges to about 0.25 by period 3. It remains there for the remaining periods.
- The second line begins at about 0.125 and converges to 0.25 by period 3. It remains there for the remaining periods.
- The third line begins at -0.1 and converges to 0 by period 3. It remains there for the remaining periods.
- The fourth line begins at 0.4. It decreases almost linearly and has a value of about 0.25 by period 10.
- The fifth line begins at about 0.25. It increases to 0.3 by period 2. Afterwards, it decreases almost linearly to 0.25 by period 10.
- The sixth line begins at about -0.1. It converges to 0 by period 2, and remains there for the remaining periods.
- Recall that the seventh and eighth lines show the 90 percent
interval of all estimate response for the C-I-I Model.
- The lower part of the interval begins at -0.4. It increases roughly linearly to -0.25 by period 10.
- The upper part of the interval begins at 0.67. It increases to about 0.84 by period 3. Afterwards it decrease slightly and has a value of 0.75 by period 10.
Figure 15: Simulations Results
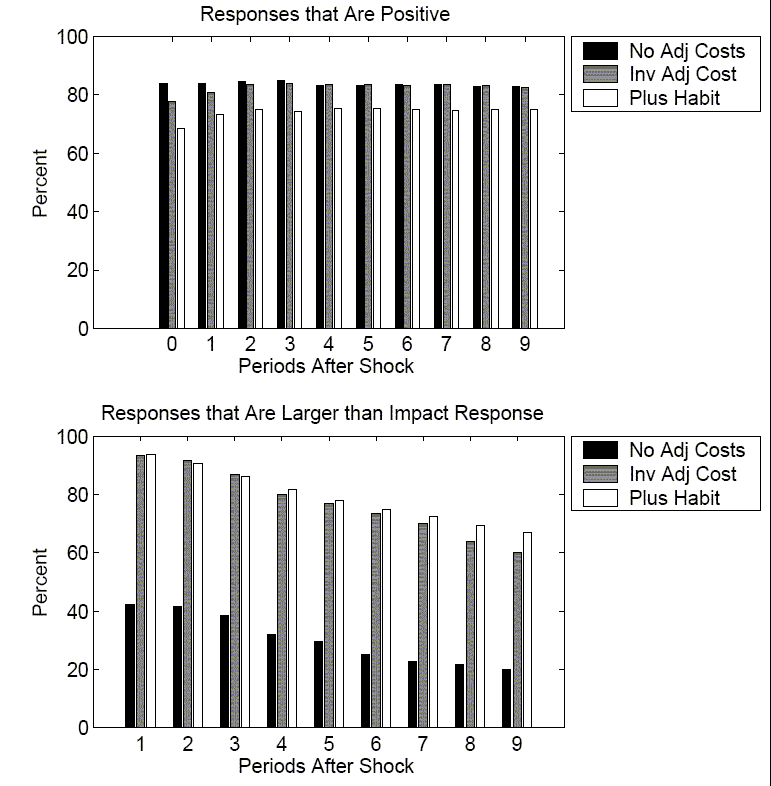
No Adj Costs: Standard flexible-price model with no investment adjustment costs or habit persistence.
Inv Adj Costs: flexible-price model with CII-type investment adjustment costs (
![]()
Description of Figure 15
Figure 15 is titled ``Simulations Results''.
It contains two bar graphs presented in a two-by-one matrix.
In both graphs, the x-axis is labeled ``Periods after Shock'' and ranges from zero to nine, and
The y-axis is labeled ``Percent'' and ranges from 0 to 100 in increments of 20.
At each time period, there exist three bars corresponding to three different scenarios.
The first bar is labeled ``No adjustment costs'' and comes from the standard flexible-price model with no investment adjustment costs or habit persistence.
The second bar is labeled ``Investment Adjustment Costs'' and comes from the flexible-price model with C-I-I-type investment adjustment costs (gamma equals 0.01).
The third bar is labeled ``Plus Habit'' and comes from the flexible-price model with C-I-I type investment adjustment costs (gamma equals 0.01) and with habit persistence coefficient (b equals 0.6).
The top bar graph is titled ``Responses that are Positive''.
For the bars corresponding to ``No adjustment costs'', the value remains at roughly 83 percent for all the periods.
For the bars corresponding to ``investment adjustment costs'', the bars begin at 78 percent and increases to 83 percent by period 3. It remains there for the remaining periods.
For the bars corresponding to ``Plus Habit'', the bars begin at about 67 percent and increase to 74 percent by period 2. It remains there for the remaining periods.
The bottom bar graph is titled ``Responses that are larger than Impact Response''.
For the bars corresponding to ``No adjustment costs'', the bars begin at 40 percent. They gradually decrease to about 25 by period 7 and stay there for the remaining periods.
For the bars corresponding to ``investment adjustment costs'', the bars begin at 90 percent. They decrease almost linearly until period 9, where the value is about 60.
For the bars corresponding to ``plus habit'', the bars begin at 90 percent. They decrease almost linearly until period 9, where the value is about 67.
Footnotes
1. Board of Governors of the Federal Reserve System. (Email [email protected]) Return to text
2. Thanks to Martin Eichenbaum, Larry Christiano, Tim Conley, and John Fernald for helpful comments in early drafts of this paper. Additional thanks for comments from Rochelle Edge, Chris Erceg, Chris Gust, William McCausland, and seminar participants at the Bank of Canada, the Bank of England, Northwestern University, the University of Alberta, UQAM, the Université de Montréal, and the Board of Governors of the Federal Reserve. An earlier draft of this paper was circulated as The negative response to a positive technology shock, a neoclassical explanation. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any person associated with the Federal Reserve System. Return to text
3. In more formal terms, using hours to approximate for utilization implies an assumption that, at least for empirically relevant values, the output expansion path is an upward sloping line. The assumption would be satisfied if output were produced, for example, by a homothetic production function (such as Cobb-Douglas) using hours and utilization with constant costs of increasing either input. Return to text
4. A lack of data requires the use of this manufacturing-based technology measure to approximate the economy-wide fluctuations in technology. Return to text
5. This equation is similar to that
estimated in Burnside Eichenbaum and Rebelo (1996) and in Conley
and Dupor (2003) except for two differences. First, these authors
don't use the average hours correction, represented in Equation 2
by
![]() . Second, the
value of
. Second, the
value of ![]() is
estimated as the sum of the shares of capital services and labor
which are estimated separately. In other words, they don't use the
information on KLEMS shares but rather just estimate the shares.
Impulse responses generated using this approach were similar to the
ones reported in the paper. Return to
text
is
estimated as the sum of the shares of capital services and labor
which are estimated separately. In other words, they don't use the
information on KLEMS shares but rather just estimate the shares.
Impulse responses generated using this approach were similar to the
ones reported in the paper. Return to
text
6. Some might be concerned that electricity usage might be overly sensitive to weather fluctuations. Because the electricity usage data is on a national basis, geographic diversification should limit any dependence on weather. Return to text
7. The KLEMS dataset is used to measure multi-factor productivity as the annual frequency. It and the Canadian equivalent are featured in Vigfusson (2003). Return to text
8. This aggregation equation calculates the increase in aggregate technology resulting from industry-level technology growth holding the distribution of inputs among industries fixed. Return to text
9. The results reported here use the IMF world price of oil, an average of international well-head prices. Other researchers including Basu, Fernald, and Shapiro (2001) have used the Producer Price Index for crude oil as an instrument. The Producer Price Index, however, only measures the price paid for domestic but not foreign oil. Not including foreign oil results in a very misleading price series because, between the summer of 1973 and January 1981, American produced oil was under government-imposed price controls. Because of these price controls, the PPI does not measure the true cost of oil. In particular, it does not capture the dramatic effect of the oil shocks of 1973 and 1979 that are observable in other series such as the IMF oil series or the Department of Energy's series, Refiner Acquisition Nominal Cost of Imported Crude Oil. Return to text
10. To specify these variables as instruments requires an assumption that these variables are uncorrelated with the technology shocks. There are models in which this assumption would be violated. For example, if implementation cycles models (Shleifer 1986) were empirically relevant, then these variables may be correlated. In such a model, reductions in oil prices could result in an economic expansion that would cause people to implement their ideas increasing productivity. Return to text
11. The aggregation, however, does obscure the important role played by industry-specific productivity growth that is found in US industrial production data in Conley and Dupor (2003) and again in KLEMS data for both Canada and the United States in Vigfusson (2003). Return to text
12. Several recent papers have identified a technology shock using a long-run restriction. These papers include Gali (1999); Francis and Ramey (2003); Altig, Christiano, Eichenbaum, and Linde (2004); and Fisher (2002). Although these methods have proven popular, some researches have critiqued these methods. In particular, Faust and Leeper (1997) describe problems associated with constructing confidence intervals (see footnote 15 for more discussion), and the perils of excluding variables from the VAR. Erceg, Guerrieri,and Gust (2004) present model-based Monte Carlo evidence on the long-run identification assumption. Their work will be discussed in section 4. Return to text
13. The equivalency can be seen by examination of the co-factor formula for the inverse of a matrix. Return to text
14. This specification is the `` double difference'' approach described in King and Watson (1997). Return to text
15. If the VAR is correctly
specified, lagged
![]() 's cannot
be used as instruments for
's cannot
be used as instruments for
![]() For a VAR
with
For a VAR
with ![]() lags, the first
lags, the first
![]() values of
values of
![]()
![]() will also be in the equation. Hence, they cannot serve as
instruments. Other values
will also be in the equation. Hence, they cannot serve as
instruments. Other values
![]() are
not valid instruments by the definition of the VAR being correctly
specified. Being correctly specified implies that these values
cannot contain any information about
are
not valid instruments by the definition of the VAR being correctly
specified. Being correctly specified implies that these values
cannot contain any information about
![]() beyond
that contained in
beyond
that contained in
![]() .
Return to text
.
Return to text
16. Because there are no other
restriction on the equation, the results calculated using the
reduced form VAR are identical to results calculated using the
structural VAR with coefficients ![]() and
and ![]() . Imposing additional restrictions on
. Imposing additional restrictions on ![]() such as also identifying a
monetary policy shock, as in Altig, Christiano, Eichenbaum, and
Linde (2003), would require using the structural VAR to calculate
impulse responses. Return to
text
such as also identifying a
monetary policy shock, as in Altig, Christiano, Eichenbaum, and
Linde (2003), would require using the structural VAR to calculate
impulse responses. Return to
text
17. Faust and Leeper (1997) note that the standard confidence intervals for impulse responses are not valid unless restrictive assumptions are made concerning the data generating process. For the bootstrapped confidence intervals considere here, the implicit assumption is the true data generating process actually is a six lag bivariate vector autoregression. Under such a restrictive assumption, the confidence intervals reported here would be valid. Return to text
18. All variables are expressed in logs. The variables span the second quarter of 1972 to the end of 2001 and are taken from the DRI BASIC Economics (nee Citibase) database. The series with their mnemonics are as follows: real consumption (the sum of consumption of services GCS, nondurables GCN and government consumption divided by the gross output price deflator GDPD and consumption of durables GCD), real investment (gross private investment (GPI) and government investment divided by the output price deflator GDPD), output (nominal consumption and investment divided by GDPD), real interest rate (3 month Treasury Bill rate minus the growth rate of the GDP price deflator), and hours worked (nonfarm business hours LBMNU). All quantities are expressed in per-capita term by dividing by the population over 16. Deflating consumption and investment by the same price measure rather than using the separate published deflators for investment and consumption is deliberate. See Whelan (2000) for a discussion of using chain-weighted data. Return to text
19. The labor productivity output series considers total output divided by business hours. As such, this definition of labor productivity is more like the work by Gali (1999) than the definition used in Francis and Ramey and Christiano, Eichenbaum, and Vigfusson (2003). As in CEV, I could have defined labor productivity as the ratio of business output to business hours worked. This has the advantage of avoiding the problem of increases in government spending being misconstrued as a technology shock. However, it comes at the cost of being less transparent concerning the imposed cointegration results. Return to text
20. Complementary to this work is a paper by Pesavento and Rossi (2003) where they calculate confidence intervals for impulse responses at long horizons. Return to text
21. Addition detail is provided in Christiano, Eichenbaum and Vigfusson for the weak instruments problem that occurs when hours has a unit root. Return to text
22. The proof of this claim is
straightforward. By definition the part of ![]() that does not depend on lagged
that does not depend on lagged
![]() is
is ![]() Given the previously described
identity,
Given the previously described
identity,
23. The following table is based on 20,000 samples over the parameter space. These results were then checked by making an additional 30,000 simulations. In no case did these additional samples change the results reported here. Return to text
24. Models with capital adjustment costs do have a similarity with models of marginal efficiency shocks (Dejong Ingram and Whiteman 2000). In both models, the amount of output required to produce a unit of capital (the marginal efficiency of investment) varies over time. The models differ in how they determine the marginal efficiency. In models with capital adjustment costs, the marginal efficiency varies endogenously as agents vary how much they invest. In Dejong Ingram and Whiteman (2000), the marginal efficiency is an exogenous random variable. Return to text
25. Additional support for time-to-build models comes from Kovea (2000), which presents firm-level evidence of time-to-build being a feature of investment in structures. Based on reports from newspapers and trade journals on 106 randomly chosen firms, she estimates an average time-to-build for structures of about two years. Furthermore, she reports that very few of the projects that she examines were cancelled. Return to text
26. The specification of habit
persistence used here is standard in the literature. One drawback
of this specification is that it requires that the level of
consumption ![]() must
always be greater than the habit stock
must
always be greater than the habit stock ![]() to avoid marginal utility being
infinite. Carroll, Overland, and Weil (2000) discuss a different
specification, where what matters is the ratio of current
consumption to the lagged habit stock. Using the ratio avoids the
problems of infinite marginal utility as long as consumption is
positive. Return to text
to avoid marginal utility being
infinite. Carroll, Overland, and Weil (2000) discuss a different
specification, where what matters is the ratio of current
consumption to the lagged habit stock. Using the ratio avoids the
problems of infinite marginal utility as long as consumption is
positive. Return to text
27. For the CES production function, technology is labor augmenting. This assumption is important for the normalization required when technology is a random walk. Return to text
28. Microeconomic evidence suggests that the labor supply elasticities are much smaller. The labor literature reports labor supply elasticities near zero for males and about 1 for females. Most macroeconomic models, however, require these larger estimates in order to match the data. Return to text
29. The emphasis in this paper is on convex adjustment costs. Cooper and Haltiwanger (2000) emphasize that including firm-level non-convex costs (such as fixed costs) also matters for aggregate investment. Including such non-convexities is a goal for future work. Return to text
30. The difference in the two
specifications can be seen by examining the cost of the investment
adjustments costs when investment is
![]() times greater than the steady state value. For the investment to
capital ratio case, the adjustment costs would equal
times greater than the steady state value. For the investment to
capital ratio case, the adjustment costs would equal
![]() For the investment
growth rate case, the adjustment costs would equal
For the investment
growth rate case, the adjustment costs would equal
![]() . Hence, the values
of
. Hence, the values
of ![]() must be
different for the two specifications. Return to text
must be
different for the two specifications. Return to text
31. The value of ![]() is 1.5.The following
coefficients were taken from Christiano and Eichenbaum (1992). The
vector
is 1.5.The following
coefficients were taken from Christiano and Eichenbaum (1992). The
vector
![]() equals
equals
![]() . Return to text
. Return to text
32. Because the model is assumed to
have a unit root in the technology, in calculating a solution, the
variables will be normalized by dividing through by the level of
technology. Hence the model will be solved for {
![]() where
where
![]() equals
equals
![]() .
Return to text
.
Return to text
33. As is evident in Christiano and Vigfusson (2003), this jaggedness is not a problem when examining the spectrum implied by the time-to-plan model. Return to text
34. With external habit, the real interest rate is a somewhat less tractable
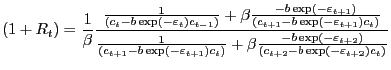
35. With serially correlated shocks,the standard flexible price model has a delayed response to the onset of a technology shock. The response on impact however seem to be too negative with both investment and hours worked falling sharply. Return to text
36. Appendix A describes briefly the estimation procedure. Return to text
37. These values were calculated for the version of the flexible price model without any adjustment costs. As such, a richer structure might result in different parameter estimates. However, the goal of this section is to provide some evidence on the usefulness of long run VARs to discriminate between models, not a full maximum likelihood estimation. Return to text
38. In the above results, I did not consider the effect of using the growth rate of hours in the long-run VAR. In these models, hours worked is stationary. As is discussed in CEV (2003), estimating a VAR after first differencing a stationary variable is a form of specification error. Hence using the first difference VAR on model-simulated data would be using a misspecficied VAR. As was found in CEV and CKM, I also found that applying the first difference VARs would result in a very high probability of a negative response by hours on impact. Return to text
39. Let
![]() for integer values
of
for integer values
of ![]() Then,
Then,
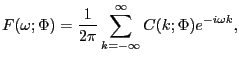
This version is optimized for use by screen readers. A printable pdf version is available.