Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1018, June 2011 --- Screen Reader Version*

Quantitative Easing and Bank Lending: Evidence from Japan

David Bowman, Fang Cai, Sally Davies, and Steven Kamin^**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Prior to the recent financial crisis, one of the most prominent examples of unconventional monetary stimulus was Japan's "quantitative easing policy" (QEP). Most analysts agree that QEP did not succeed in stimulating aggregate demand sufficiently to overcome persistent deflation. However, it remains unclear whether QEP simply provided little stimulus, or whether its positive effects were overwhelmed by the contractionary forces in Japan's post-bubble economy. In the spirit of Kashyap and Stein (2000) and Hosono (2006), this paper uses bank-level data from 2000 to 2009 to examine the effectiveness in promoting bank lending of a key element of QEP, the Bank of Japan's injections of liquidity into the interbank market. We identify a robust, positive, and statistically significant effect of bank liquidity positions on lending, suggesting that the expansion of reserves associated with QEP likely boosted the flow of credit. However, the overall size of that boost was probably quite small. First, the estimated response of lending to liquidity positions in our regressions is small. Second, much of the effect of the BOJ's reserve injections on bank liquidity was offset as banks reduced their lending to each other. Finally, the effect of liquidity on lending appears to have held only during the initial years of QEP, when the banking system was at its weakest; by 2005, even before QEP was abandoned, the relationship between liquidity and lending had evaporated.

Keywords: Quantitative easing, Japan, bank lending, unconventional monetary policy, central bank, credit

JEL classification: E44, E52, E58, G21

I.  Introduction

During the recent global financial crisis, the Federal Reserve and a number of foreign central banks initiated unconventional monetary policies to provide stimulus to aggregate demand. These policies, which involved the substantial expansion of central bank assets and liabilities, were intended to address dysfunctions in the financial system, reduce interest rates along the term structure, and promote the flow of credit to households and businesses. However, there was little historical precedent to provide guidance regarding the effects of expanding central bank balance sheets on financial and economic performance.

This paper describes research to assess the effects on macroeconomic performance--in particular, bank lending--of the most prominent previous example of unconventional monetary stimulus, Japan's "quantitative easing policy," or QEP. In the aftermath of the bursting of Japan's bubble economy in the 1990s, economic activity languished and consumer price deflation set in. The Bank of Japan's (BOJ) reduction of its policy rate to zero by 1999 failed to reverse the process. In March 2001, declining consumer prices, a weak banking system, and the prospect of renewed recession following the collapse of the global IT bubble prompted the BOJ to launch QEP.

The QEP consisted of three key elements: (1) The BOJ changed its main operating target from the uncollateralized overnight call rate to the outstanding current account balances (CABs) held by financial institutions at the BOJ (i.e., bank reserves), and ultimately boosted the CAB well in excess of required reserves.¹ (2) The BOJ boosted its purchases of government bonds, including long-term JGBs, and some other assets, in order to help achieve the targeted increases in CABs. (3) The BOJ committed to maintain the QEP until the core CPI (which in Japan is defined to exclude perishables but not energy) stopped declining.

As shown in Figure 1, the QEP started in March 2001 with a CAB target of ¥5 trillion, higher than required reserves of ¥4 trillion. The BOJ progressively raised its target range to ¥30-35 trillion, or 6 to 7 percent of GDP, by January 2004 and maintained it there for several years. This was well in excess of required reserves and also well beyond the amount needed to keep overnight rates at zero. As indicated in Figure 2, both the uncollateralized call rate and the 3-month Treasury bill rate fell nearly to zero during the duration of QEP, while bank loan rates steadily declined and 10-year JGB yields fell during the first couple of years. The BOJ formally ended QEP in March 2006, returning to the overnight call rate as its policy target. However, it did not actually raise the call rate until July 2006, as it first allowed current account balances to be drained.

Most analysts agree that QEP was not very successful in achieving its goal of stimulating aggregate demand sufficiently to eliminate persistent deflation. As shown in Figure 3, following a shallow recession in late 2001 and early 2002, Japanese GDP growth put in a solid but uninspiring performance that was not sufficient to pull inflation out of negative territory. Moreover, in spite of extremely low interest rates and the enormous level of excess reserves, bank loans continued to decline through most of the QEP period (Figure 4).

The fact that QEP failed to achieve its ultimate objective of eliminating deflation, however, does not mean that it provided no stimulus to the Japanese economy. It is possible that QEP exerted positive effects, but that these were simply overwhelmed by the drag on aggregate spending coming from severe weakness in the banking sector and balance sheet problems among households and firms.

There are a number of means by which QEP might have stimulated spending. First, the BOJ's outright purchases of JGBs probably helped to lower longer-term interest rates, although previous analysis does not point to very large effects (Oda and Ueda, 2005), perhaps because these purchases were not large enough. Second, by committing to keep interest rates low until deflation ended, QEP might have reduced expected future interest rates, thus lowering nominal longer-term rates, while increasing expected inflation, thus lowering real interest rates. Studies such as Baba et.al. (2005) and Okina and Shiratsuka (2004) find, again, that these effects were probably relatively small.

Finally, QEP might have operated through the so-called "credit channel" of monetary policy, increasing the liquidity of banks so that they expanded their supply of loans and thus making credit more available to bank-dependent borrowers (Bernanke and Blinder, 1992, Kashyap and Stein, 2000). There is some reason to believe Japanese banks may have desired additional liquidity. Shirakawa (2002) noted that while demand for excess reserves fell soon after the September 2001 terrorist attack in most developed countries, demand stayed high in Japan due to concerns over corporate bankruptcies and falling equity prices. Kimura et al. (2003) also argue that easing liquidity could have a stabilizing impact on financial markets and perhaps induce a portfolio shift resulting in credit extension.

Concrete evidence on the effectiveness of QEP through this channel is scant. Certainly, QEP failed to reverse the decline in bank lending over the period, and neither Ugai (2007) nor Kimura (2003) find much effect from the large expansion of Japan's monetary base. But it is difficult, using aggregate macroeconomic data over just a number of years, to evaluate the counterfactual hypothesis that in the absence of QEP, bank lending might have fallen even further.

Our paper uses a novel approach to evaluate the effect of QEP on bank lending, using data on individual banks. If QEP helped promote lending by increasing the reserves and thus the liquidity of Japanese banks, then it must have been the case that some of those banks must have been liquidity-constrained and, all else equal, those banks with stronger liquidity positions should have lent more than those banks with less liquidity. Kashyap and Stein (2000) find such a relationship to hold among U.S. banks that were most likely to be liquidity-constrained, and Hosono (2006) finds evidence of that relationship for Japanese banks in the years prior to QEP. However, Kobayashi, Spiegel, and Yamori (2006) find that the increases in CAB appeared to benefit weaker banks with higher bad loan ratio, but do not find a significant relationship between bank stock returns and liquidity position.

Accordingly, in our research, we estimate panel data regressions, using semiannual data for 137 banks over the period of March 2000 to March 2009, that explain each bank's change in loans using the lagged liquidity position of the bank as well as an array of control variables, including the bank's total assets, equity ratio, non-performing loan ratio, and the bank type. We take a positive and significant relationship between banks' liquidity positions and their lending growth to suggest that QEP, by boosting reserves and thus liquidity in the banking system, helped boost lending as well.

To summarize our key findings, we identify a robust, positive and statistically significant effect of bank liquidity positions on lending, suggesting that the expansion of reserves associated with QEP likely boosted the flow of credit to the economy. However, for a number of reasons, the overall size of that boost was probably quite small. First, the estimated coefficient on liquidity positions in the panel data regressions is quite small. Second, we found that much of the effect of the BOJ's reserve injections on bank liquidity was offset as banks reduced their lending to each other--thus, banks' overall liquidity rose by less than their current account balances with the BOJ. Finally, the effect of liquidity on lending appears to have held only during the initial years of QEP, when the banking system was at its weakest and thus QEP was most likely to have been helpful; by 2005, even before QEP was abandoned, the relationship between liquidity and lending had evaporated.

The remainder of the paper is structured as follows. Section II discusses trends in bank liquidity and reserves during QEP. Section III describes our econometric methodology and estimation results. Section IV concludes.

II.  Trends in Liquidity and Bank Reserves During QEP

Before describing our econometric methodology and results, we first review salient developments in the evolution of Japanese banks' liquidity and current account balances with the BOJ during QEP. We define a bank's liquid assets as the sum of vault cash, deposits at the BOJ and at other banks, and call loans (short-term loans) to other banks.

To the extent that QEP was intended to inject liquidity into the banking system by boosting banks' current account balances, we would expect it to increase banks' holdings of liquid assets. However, as shown in Figure 5, domestic banks' total liquid assets went up by only 14 trillion yen between March 2001 and their peak in March 2003, less than the 25 trillion yen increase in banks' current account balances (CAB) at the BOJ during the same period.² This result suggests that even as banks increased their holdings of deposits at the BOJ, they reduced their holdings of other liquid assets. This suggestion is supported by data from Japan's flow of funds accounts, as presented in Figure 6.

Figure 6 indicates why the BOJ's injections of bank reserves led to less than proportionate increases in liquidity: even as domestic banks increased their deposits at the BOJ, they simultaneously decreased deposits held at other domestic banks. There are several reasons why banks may have preferred holding deposits at the BOJ to holding deposits with each other. First, there may have been some perceived risk to holding deposits with other banks, even though they were short-term. And second, banks may have been reluctant to deposit with each other at near-zero interest rates because BIS regulations require 20 percent of deposits with other banks be included in risk assets. Therefore, banks need to hold capital against their deposits with other banks while they do not need to do so with their deposits at the BOJ.

We conclude from this finding that the impact of the BOJ's reserve injections was substantially offset by banks' reductions of deposits with each other. Nonetheless, it is possible that in the absence of QEP, the liquidity position of banks might have weakened considerably further. Moreover, this chart suggests that QEP did succeed in increasing bank's holdings of liquid assets to some extent. Accordingly, we next turn to an examination as to whether this may have had a positive impact on bank lending.

III.  Econometric Methodology and Estimation Results

1.  Baseline Regression

Our bank-level data are available from September 2000 to March 2009 and are taken from semi-annual balance sheet reports obtained from the Japanese Bankers Association (See Appendix 2 for more details.). Using panel data for 138 banks over the nine-year period, we study the relationship between loan growth and the liquidity ratio, which we define as the ratio of liquid assets to total bank assets.³ Our baseline regression is:

$$\Delta Loan_{i,t}=\alpha+\beta LR_{i,t-1}+\delta^{^{\prime}}X_{i,t-1} +\varepsilon_{i,t}$$ (1)

where $$\par$$ denotes the natural log of loans made by bank i at time t, ${Loan}_{i,t}$ denotes the liquidity ratio for bank i at time t, and ${LR}_{i,t}$ is a vector of control variables. We control for measures of bank health and other bank characteristics that may be related to a bank's prospects for lending, including: bank size (measured by total assets); the equity ratio, measured by net assets as a percentage of total assets; the bad loan ratio, measured as the ratio of the notional value of non-performing loans, as defined by the Japanese Banking Law, to net assets; lags of deposit growth, and lags of loan growth. We also include semi-annual time dummies as well as dummy variables for varying bank types. The bank types and variable definitions are discussed in Appendices 1 and 2 respectively, while Figure 7 presents the median total assets, equity ratio, liquidity ratio, bad loan ratio, loan growth and deposit growth for each bank type.

One may note that there is a potential endogeneity problem in our panel regression, since banks intending to lend more may acquire additional liquidity beforehand. In our baseline regression, we use lagged terms of these variables to mitigate this endogeneity problem, although they may not fully resolve it. We revisit this issue below.

The first column of Table 1 reports the results of our baseline panel regressions, estimated by ordinary least squares (OLS), for the QEP period. The coefficients related to the dummy variables are not shown in the results for the sake of brevity. Our main finding is that, controlling for other factors, the lagged liquidity ratio appears to have exerted a positive and significant impact on bank loan growth during the QEP period. The economic significance of this impact is, however, small. If the liquidity ratio increases 1 percentage point, loan growth increases 0.11 percentage points in the next six months, or 0.22 percent points annually, other things equal. Given that the aggregate liquidity ratio increased 1.6 percentage points, from 5.2 percent in March 2001 to 6.8 percent in March 2004, the addition to loan growth resulting from the higher liquidity is estimated to have been about 0.35 percentage points annually. This evidence suggests that, in the absence of the BOJ's injection of liquidity, the amount of bank credit would have fallen at only a slightly more rapid pace. In addition, we find that lagged bad loan ratio is negatively correlated with loan growth over the entire sample period, suggesting that weaker banks had lower loan growth. The coefficients on bank size and equity ratio are not statistically significant.

To correct for potential biases related to endogeneity, we also estimate the baseline model using a system GMM procedure implemented as instrumental variables, following Arrellano and Bover (1995) and Blundell and Bond (1998).⁴ This technique is often used to control for endogeneity problems in panel data with small T and large N, as well as endogenous and predetermined regressors. The estimator is implemented using t-2 lags of the untransformed variables as instruments in the difference equation, and the same lags of differenced variables in the levels equation. We include lagged loan growth and lagged liquidity ratio as instruments in the regressions.⁵

As shown in the second column of Table 1, the liquidity effect is robust, and is actually stronger in the GMM regression, suggesting that the potential endogeneity issue, if any, appears to bias our previous results downward.⁶ Moreover, the signs and magnitudes of the coefficients related to our control variables are fairly similar to those estimated using OLS; although the coefficient on the lagged equity ratio changes sign depending on the method of estimation, it is not statistically significant in either case. We interpret these results as indicating that endogeneity bias is not driving our finding of a positive relation between the liquidity ratio and loan growth. For the rest of the results reported in this paper, we will therefore show only estimates using OLS.

In the first column of Table 2, we expand the time period to the full sample period from March 2000 to March 2009, in order to examine if the liquidity channel was more or less effective during the QEP period than during the non-QEP period. We use two time dummies D_{_QEP} (September 2001 to March 2006) and D_{_NONQEP} (March 2000 to March 2001 and September 2006 to March 2009) for the corresponding policy periods. These dummies are interacted with lagged liquidity ratio to examine whether the relationship between liquidity and loan growth differed across the QEP and the non-QEP periods. For the QEP period, the results are qualitatively similar to those in Table 1. After the QEP period, however, the relationship between liquidity ratio and loan growth becomes negative and insignificant. The sharp difference in the impact of liquidity on bank lending during the two periods reinforces our view that banks were liquidity constrained during the QEP, and the quantitative easing helped to relieve banks from their liquidity constraints. In our view, which is supported by the results in the second column, the differing effects of liquidity on lending did not reflect the QEP itself. Rather, the QEP happened to be implemented during the period when the banking sector was most stressed, and that is when liquidity mattered the most. Once stresses started to alleviate and the economy started to recovery, liquidity appeared to become a less important factor in lending and--at the same time--the QEP was ended.

The second column of Table 2 allows the relationship between the liquidity ratio and loan growth to vary across the QEP period. Instead of interacting D_{_QEP} and D_{_NONQEP}with lagged liquidity ratio, we interact each semi-annual time dummy during the QEP with lagged liquidity ratio. We find that liquidity is not significantly correlated with loan growth beginning in March 2005 through the end of the QEP a year later. This suggests that the BOJ's rapid unwinding of CABs after March 2006 likely had little impact on lending, because banks were no longer liquidity constrained by that time. A significant factor in the easing of liquidity constraints by March 2005 was the special inspections by the Financial Services Agency and the banks' subsequent resolution of NPLs, which helped reduce uncertainty and restore confidence in the banking sector.

2.  Cross-Sectional Differences

Some existing studies such as Kashyap and Stein (2000), Hosono (2006) and Kobayashi, Spiegel, and Yamori (2006) suggest that the impact of monetary policy could vary across banks depending on bank characteristics. In particular, Kashyap and Stein (2000) find that lending by larger banks are less sensitive to changes in liquidity, which they interpret as suggesting that larger banks face fewer financing constraints. Hosono (2006) suggests that the effect of monetary policy on lending is stronger for banks that are smaller, less liquid, and more abundant with capital. To test whether various bank characteristics affected the sensitivity of bank credit supply to central bank liquidity provision during the QEP period, we add interaction terms between the liquidity ratio and total bank assets, equity ratio and bad loan ratio, respectively. The specification is as follows:

$$\Delta Loan_{i,t}=\alpha+\beta LR_{i,t-1}+\delta^{^{\prime}}X_{i,t-1} +\gamma^{^{\prime}}(LR_{i,t-1}\cdot X_{i,t-1})+\varepsilon_{i,t}$$ (2)

The results are shown in Table 3. We find that bank size has a negative, albeit not significant, influence on the impact of liquidity on lending for Japanese banks during the QEP, in line with the finding of Kashyap and Stein for U.S. banks. Moreover, the equity ratio appears to affect the impact of liquidity on lending negatively and significantly during the QEP period, suggesting that weaker banks benefited more from the QEP than banks with stronger equity positions. The bad loan ratio does not appear to have any significant influence on banks' response to the increased liquidity.

To check how the sensitivity of banks' credit supply to increased liquidity vary across banks, we also run the baseline regression with the sample split into terciles by total assets, equity ratio and bad loan ratio, respectively, and shown the results in Table 4. Consistent with Table 3, it seems that banks with low equity ratio exhibited a greater impact of liquidity on lending than those with high equity ratio. In contrast to Table 3, which found no significant impact between bad loans and the liquidity impact, Table 4 finds some evidence that banks with higher bad loan ratios were associated with higher effect of liquidity on loan growth than those with low bad loan ratio. On the other hand, bank size does not seem to have a significant impact on the sensitivity of bank loan growth to liquidity in either specification. In sum, Tables 3 and 4 suggest some evidence of cross-sectional responses to the QEP being greater among financially weak banks; however the results on bank size and bad loan ratio are not always consistent.

3.  Robustness Checks

As a robustness check, we replaced the bank type dummies in our baseline model with individual bank fixed effects. These fixed effects help to control for macroeconomic or financial developments that might affect loan demand across time and across banks. The results, shown in Table 5, are qualitatively similar to the results reported above.

We also use two alternative variable definitions in the regressions shown in Table 1-4. One alternative measured bad loans less loan-loss reserves, to control for the fact that bad loans against which there are already loan-loss reserves are not as likely to hold back lending. Another alternative adjusted loan growth to control for write-offs, so that reductions in lending do not include write-offs on bad loans. The results (not shown) are qualitatively similar to those in Table 2.

In summary, the liquidity effect on bank lending is strongly significant, albeit small, across all model specifications. There is also evidence of some cross-sectional differences in banks sensitivity to quantitative easing, in the sense that weaker banks seem to respond more to the BOJ's liquidity injection.

VI.  Conclusion

This paper is the first to test the liquidity channel of monetary policy by investigating the policy impact of QEP on bank lending in Japan. Our key findings are as follows. First, the effect of the Bank of Japan's liquidity injections on bank lending was muted by the substitution of central bank liquidity for interbank liquidity. Second, despite the dampening of the stimulus from the liquidity injections due to this substitution, we find a positive and significant effect of liquidity on bank lending. This suggests some scope for quantitative easing to affect the supply of credit, particularly during periods of financial stress. However, the overall effect was measured to be quite small, so that eye-popping amounts of liquidity would have been needed to achieve noticeable effects. Third, we find some evidence that weak banks benefited more from QEP than stronger banks. Finally, our analysis suggests that the rapid unwinding of liquidity infusions observed at the conclusion of QEP had little impact on lending growth once bank health and confidence in the banking system had been restored.

Appendix 1:  The Structure of the Japanese Banking System

In Japan, commercial banks are traditionally broken down into four types: city banks, regional banks and member banks of the Second Association of Regional Banks (also called Tier II regional banks), long-term credit banks, trust banks and other. City banks are major banks that offer banking services nationwide to large corporate customers. There are a total of 11 city banks in our sample. Regional banks and Tier II regional banks are usually banks that focus their business mainly on retail banking. There are 64 regional banks in total. The majority of their loan customers are local small and medium-sized companies and consumers. The number of regional banks increased significantly in 1989 when 66 sogo, or mutual savings and loan institutions, were converted into second tier regional banks. There are 57 Tier II regional banks in our sample. Regional banks are significantly smaller in size than city banks. Trust banks, long-term credit banks, and various specialized financial institutions. Trust banks were authorized to conduct retail and trust banking and often combined the work of commercial and long-term credit banks. Trust banks not only managed portfolios but also raised funds through the sale of negotiable loan trust certificates. Long-term credit banks were created to provide long-term loans to private industry. There are 17 banks in this category.

Table A1 shows the number of banks, total loans, liquid assets, and total assets by bank type as of March 2001. City banks account for about 50 percent of total assets in the banking sector.

As shown in Figure 7, city banks have by far the largest total assets and high liquidity ratios but their equity ratios are the lowest. Trust banks and others have the highest equity ratios and the lowest bad loan ratios, indicating their relative balance sheet strength. Regional banks seem to have higher loan growth than other types of banks during most of the QEP period.

Table A1.  Total Loans and Bank Assets in Japan by Bank Type

Bank Type	Total number	Loans and bills discounted	Total assets
City banks	8	207.84	378.70
Regional Banks	64	136.00	205.83
Tier II Regional Banks	56	45.96	62.90
Long-term credit banks, trust banks and other	10	65.30	126.57

Source: Japanese Bankers Association. Amounts outstanding are in trillions of yen as of March 2001.

Appendix 2:  Japanese Bankers Association Data

Our bank-level balance sheet data are obtained from the Japanese Bankers Association (JBA) website: http://www.zenginkyo.or.jp/en/stats/year2_01/index.html.

The liquid assets variable used in our analysis is constructed as the sum of "cash and due from banks" and "call loans" under "Assets" on banks' balance sheets. Due from banks include both banks' reserves at the BOJ and banks' deposits with other banks. The JBA data does not distinguish between deposits held at the BOJ and deposits held with other banks. Other variables in our regression analysis include:

Δlog(Loan_i,t): log loan growth from time t-1 to t. Bank loan is listed as "Loans and bills discounted" under "Assets";

log(TA_i,t-1): log total assets at time t-1;

LR_i,t-1: liquidity ratio at time t-1, constructed as liquid assets divided by total assets;

ER_i,t-1: equity ratio at time t-1, constructed as bank equity divided by total assets;

BLR_i,t-1: bad loan ratio at time t-1, constructed as bad loans divided by bank equity. Bad loans are constructed as the sum of "Loans to borrowers in legal bankruptcy", "Past due loans in arrears by 6 months or more", "Loans in arrears by 3 months or more and less than 6 months", and "Restructured loans";

Δlog(Deposit_i,t-1): log deposit growth from time t-2 to t-1;

Δlog(Deposit_i,t-2): log deposit growth from time t-3 to t-2;

Δlog(Loan_i,t-1): log loan growth from time t-2 to t-1;

Δlog(Deposit_i,t-2): log loan growth from time t-3 to t-2;

D_Regional: dummy variable that equals to 1 if the bank is a regional bank and 0 otherwise;

D_RegionalII: dummy variable that equals to 1 if the bank is a Tiere II regional bank and 0 otherwise;

D_Trust: dummy variable that equals to 1 if the bank is a trust bank or others and 0 otherwise;

D_{_QEP}: dummy variable that equals to 1 if the time period is with the QEP period and 0 othewise;

D_{_NONQEP}: dummy variable that equals to 1 if the time period is not within the QEP period and 0 otherwise.

mar02, sep02, etc: time dummy variable that equals to 1 if the time period is March 2002, September 2002, etc., and 0 otherwise.

References

Arellano, Manuel, and Stephen R. Bond, 1991, Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations, Review of Economic Studies 58, 277-297.

Arellano, Manuel, and Olympia Bover, 1995, Another Look at the Instrumental-variable Estimation of Error Components Models, Journal of Econometrics 68, 29-51.

Baba, Naohiko, Shinichi Nishioka, Nobuyuki Oda, Masaaki Shirakawa, Kazuo Ueda, and Hiroshi Ugai, 2005, Japan's Deflation, Problems in the Financial System and Monetary Policy, Monetary and Economic Studies, 23 (1), Institute for Monetary and Economic Studies, Bank of Japan, 47-111.

Bernanke, Ben S. and Alan S. Blinder, 1992, The Federal Funds Rate and the Channels of Monetary Transmission, American Economic Review, September 1992, 82(4), 901-921.

Blundell, Richard W., and Stephen R. Bond, 1998, Initial Conditions and Moment Restrictions in Dynamic Panel Data Models, Journal of Econometrics 87, 115-143.

Hansen, Lars Peter, 1982, Large Sample Properties of Generalized Method of Moments Estimators, Econometrica 50, 1029-1054.

Hosono, Kaoru, 2006, The Transmission Mechanism of Monetary Policy in Japan: Evidence from Banks' Balance Sheets, Journal of Japanese International Economics 20, 380-405.

International Monetary Fund (IMF), 2003, Japan: Financial Stability Assessment and Supplementary Information. Country report No. 03/287, IMF.

Kashyap, Anil K., and Jeremy C. Stein, 2000, What Do a Million Observations on Banks Say about the Transmission of Monetary Policy? American Economic Review 90(3), 407-428.

Kimura, T., H. Kobayashi, J. Muranaga, and H. Ugai, 2003, The Effect of the Increase in the Monetary Base on Japan's Economy at Zero Interest Rates: An Empirical Analysis, in Monetary Policy in a Changing Environment, Bank for International Settlements Conference Series, 19, 276-312.

Kobayashi, Takeshi, Mark M. Spiegel, and Nobuyoshi Yamori, 2006, Quantitative Easing and Japanese Bank Equity Values, Journal of Japanese International Economics 20, 699-721.

Oda, Nobuyuki, and Kazuo Ueda, 2005, The Effect of the Bank of Japan's Zero Interest Rate Commitment and Quantitative Monetary Easing on the Yield Curve: A Macro-Finance Approach, Bank of Japan, Working Paper No. 05-E-6 (Tokyo: Bank of Japan).

Okina, K., and S. Shiratsuka, 2004, Policy Commitment and Expectation Formation: Japan's Experience under Zero Interest Rates, North American Journal of Economics and Finance, 15 (1), 75-100.

Roodman, David, 2006, How to do xtabond2: An Introduction to "Difference" and "System" GMM in Stata, Center for Global Development Working Paper 103.

Shirakawa Masaaki, 2002, One Year under 'Quantitative Easing', IMES Discussion Paper Series, Bank of Japan, No. 2002-E-3.

Ugai, Hiroshi, 2007, Effects of the Quantitative Easing Policy: A Survey of Empirical Analyses," Monetary and Economic Studies, 25(1), Institute for Monetary and Economic Studies, Bank of Japan, 1-47.

Windmeijer, Frank, 2005, A Finite Sample Correction for the Variance of Linear Efficient Two-step GMM Estimators, Journal of Econometrics 126, 25-51.

Figure 1. Current Account Balance and Required Reserves

Figure 2. Interest Rates

Figure 3. Macroeconomic Conditions

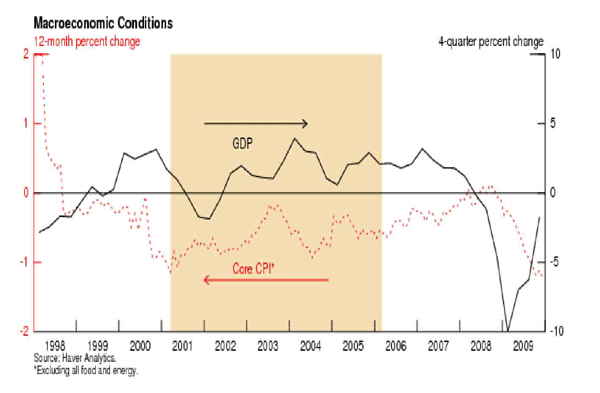
Figure 4. Loans

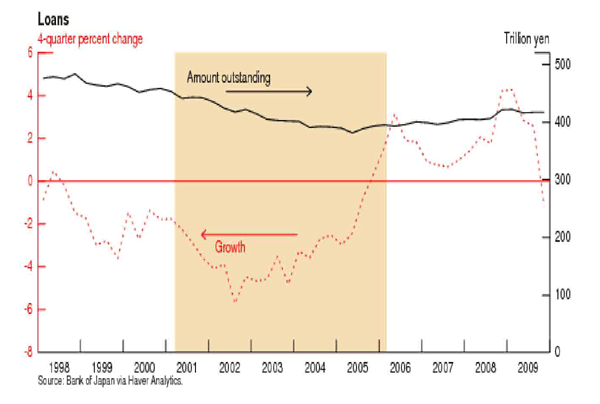
Figure 5. Current Account Balances and Liquid Assets

Figure 6. Banks' Deposits with Banks*

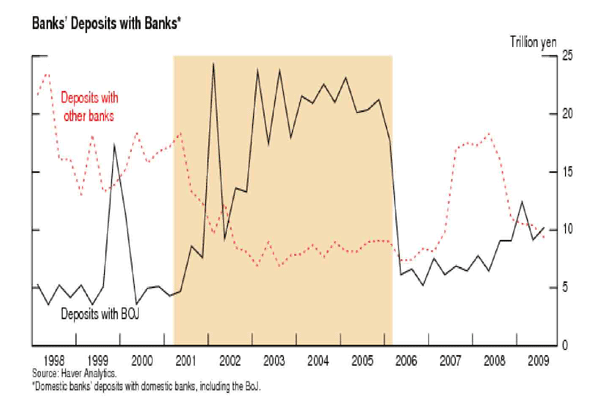
Figure 7. Bank Characteristics by Bank Type

Table 1. Loan Growth and Liquidity (QEP period)

The results are from the panel regression (1) for the QEP period (March 2001 to March 2006). A bank's log loan growth (ΔLoan_i,t) is regressed on its lagged liquidity ratio(LR_i,t-1), controlling for lagged values of bank size (log(TA_i,t-1)), equity ratio (ER_i,t-1), bad loan ratio (BLR_i,t-1) as well as two lags of banks' loan growth and deposit growth (Δlog(Loan_i,t-1), Δlog(Loan_i,t-2)). We also include semiannual time dummies and bank type dummies (not shown). See Appendix 2 for variable definitions. System GMM is estimated following Arellano and Bover (1995) and Blundell and Bond (1998). Lags 1 and 2 of loan growth variable and liquidity ratio are used as instruments. Hansen test is the p-value of the J-statistic for over-identifying restrictions (distributed chi-square). Statistical significance of estimates is calculated using Windmeijer (2005) corrected standard errors. ***, **, * denote significance at 1, 5, and 10 percent significance levels respectively.

	OLS	GMM
LRi,t-1	0.11***	0.33***
log(TAi,t-1)	-0.00*	-0.01
ERi,t-1	-0.06	0.13
BLRi,t-1	-0.01***	-0.01
Δlog(Depositi,t-1)	0.15***	0.28**
Δlog(Depositi,t-2)	0.04*	0.04
Δlog(Loani,t-1)	-0.02	-0.08
Δlog(Loani,t-2)	0.02	0.04
Observations	1230	1230
R-square	0.24	--
Hansen test	--	0.19
2nd-order serial correl.	--	0.30

Table 2. Loan Growth and Liquidity Over Time

The results are from a variation of panel regression (1) for the full period. A bank's log loan growth (Δlog(Loan_i,t)) is regressed on its lagged liquidity ratio(LR_i,t-1), lagged values of bank size (log(TA_i,t-1)), equity ratio (ER_i,t-1), bad loan ratio (BLR_i,t-1), two lags of banks' loan growth and deposit growth (Δlog(Loan_i,t-1), Δlog(Loan_i,t-2)), as well as interaction terms between LR_i,t-1 and either dummies for the QEP and non-QEP periods (D_{_QEP} and D_{_NONQEP}) or semi-annual time dummies (mar02, sep02, etc.) during the QEP period. We also include bank type dummies (not shown). See Appendix 2 for variable definitions. ***, **, * denote significance at 1, 5, and 10 percent significance levels respectively.

	w/ QEP Interaction Terms	w/ Semi-Annual Interaction Terms
D_QEP*LRi,t-1	0.13***	--
D_NONQEP*LRi,t-1	-0.03	--
LRi,t-1	--	-0.02
mar02*LRi,t-1	--	0.17*
sep02*LRi,t-1	--	0.23**
mar03*LRi,t-1	--	0.19*
sep03*LRi,t-1	--	0.42***
mar04*LRi,t-1	--	0.19**
sep04*LRi,t-1	--	0.21***
mar05*LRi,t-1	--	0.01
sep05*LRi,t-1	--	0.04
mar06*LRi,t-1	--	-0.08
log(TAi,t-1)	0.00	0.00
ERi,t-1	0.03	0.03
BLRi,t-1	-0.01***	-0.01***
Δlog(Depositi,t-1)	0.16***	0.15***
Δlog(Depositi,t-2)	0.02	0.01
Δlog(Loani,t-1)	0.01	0.01
Δlog(Loani,t-2)	0.05***	0.06***
Observations	1950	1950
R-square	0.24	0.25

Table 3. Loan Growth and Liquidity With Interaction Terms

The results are from the panel regression (2) for the QEP period (March 2001 to March 2006). A bank's log loan growth (Δlog(Loan_i,t)) is regressed on its lagged liquidity ratio(LR_i,t-1), lagged values of bank size (log(TA_i,t-1)), equity ratio (ER_i,t-1), bad loan ratio (BLR_i,t-1), two lags of banks' loan growth and deposit growth (Δlog(Loan_i,t-1), Δlog(Loan_i,t-2)), as well as the interaction terms between bank characteristics (log(TA_i,t-1), ER_i,t-1, and BLR_i,t-1) and LR_i,t-1. We also include semiannual time dummies and bank type dummies (not shown). See Appendix 2 for variable definitions. ***, **, * denote significance at 1, 5, and 10 percent significance levels respectively.

LRi,t-1	0.93**
LRi,t-1*log(TAi,t-1)	-0.04
LRi,t-1*ERi,t-1	-6.79***
LRi,t-1*BLRi,t-1	-0.01
log(TAi,t-1)	0.00
ERi,t-1	0.33**
BLRi,t-1	-0.01**
Δlog(Depositi,t-1)	0.17***
Δlog(Depositi,t-2)	0.03
Δlog(Loani,t-1)	-0.04
Δlog(Loani,t-2)	0.03
Observations	1230
R-square	0.25

Table 4. Baseline Regression With Sample Split for the QEP Period

The panel regression (1) for the QEP period (March 2001 to March 2006) is modified with the sample split into terciles based on bank size, equity ratio and bad loan ratio, respectively. A bank's log loan growth (Δlog(Loan_i,t)) is regressed on its lagged liquidity ratio(LR_i,t-1), controlling for lagged values of other bank characteristics as well as two lags of banks' loan growth and deposit growth (Δlog(Loan_i,t-1), Δlog(Loan_i,t-2)). We also include semiannual time dummies (not shown), to control for macroeconomic developments that might affect loan demand across time as well as bank type dummies (coefficients not shown). See Appendix 2 for variable definitions. ***, **, * denote significance at 1, 5, and 10 percent significance levels respectively.

	Top Third Assets	Bottom Third Assets	Top Third Equity Ratio	Bottom Third Equity Ratio	Top Third Bad Loan Ratio	Bottom Third Bad Loan Ratio
LRi,t-1	0.14**	0.13**	0.09	0.13**	0.11*	0.06
log(TAi,t-1)			0.00	0.00	0.00	0.00
ERi,t-1	-0.23**	0.16			-0.06	0.39***
BLRi,t-1	-0.01***	-0.00***	-0.02***	-0.00***
Δlog(Depositi,t-1)	0.10**	0.25***	0.12***	0.16***	0.08**	-0.02
Δlog(Depositi,t-2)	0.06	0.16***	0.14***	-0.02	0.00 0	0.09
Δlog(Loani,t-1)	0.01	-0.14***	0.03	-0.05	0.07	-0.02
Δlog(Loani,t-2)	-0.01	-0.03	0.19***	0.07	0.04	0.00 0
Observations	397	411	385	423	494	354
R-square	0.28	0.37	0.43	0.18	0.20	0.34

Table 5. Baseline Regression with Individual Bank Dummies

The results are from a variation of panel regression (1) for the QEP period (March 2001 to March 2006). A bank's log loan growth (Δlog(Loan_i,t)) is regressed on its lagged liquidity ratio(LR_i,t-1), controlling for lagged values of bank size (log(TA_i,t-1)), equity ratio (ER_i,t-1), bad loan ratio (BLR_i,t-1) as well as two lags of banks' loan growth and deposit growth (Δlog(Loan_i,t-1), ?log(Loan_i,t-2)). We also include individual bank dummies and semiannual time dummies (not shown). See Appendix 2 for variable definitions. ***, **, * denote significance at 1, 5, and 10 percent significance levels respectively.

LRi,t-1	0.21***
log(TAi,t-1)	0.00
ERi,t-1	-0.08***
BLRi,t-1	0.16
Δlog(Depositi,t-1)	0.00
Δlog(Depositi,t-2)	0.15***
Δlog(Loani,t-1)	0.08***
Δlog(Loani,t-2)	-0.13***
Observations	1230
R-square	0.40

Footnotes

**  The authors are staff economists in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. We are grateful to Mark Carey, Neil Ericsson, Takeo Hoshi, Anil Kashyap, Takeshi Kobayashi, Mark M. Spiegel, Chikara Toyokura, Nobuyoshi Yamori, Akira Yokoya, and participants in the IF workshop for helpful discussions. We thank Michael Gulick and Daniel Silver for excellent research assistance. Corresponding author: Fang Cai, [email protected], or (202) 452-3540. Return to text

1.   Current account balances are reserves held by financial institutions at the BOJ. The BOJ targeted current account balances, which are equal to the monetary base excluding cash in circulation, rather than the monetary base itself, because it believed that it would be difficult to control short-run movements of cash in circulation. Return to text

2.   The CAB in Figure 5 is much lower than the CAB in Figure 1 because the CAB in Figure 1 includes bank reserves of foreign banks and other institutions subject to the reserve requirement as well as other institutions (i.e. not subject to the reserve requirement) that are not included in Figure 5. Return to text

3.   To control for outliers, we deleted any observations in which a bank had experienced a merger, acquisition or a public capital injection, and we deleted banks with less than two records of loans outstanding or liquidity assets. Return to text

4.   Arellano and Bond (1991) develop a Generalized Method of Moments (GMM) estimator that instruments the differenced variables that are not strictly exogenous with all their available lags in levels. Arellano and Bover (1995) describe how, if the original equation in levels is added to the system, additional instruments can be brought to bear to increase efficiency. In this equation, variables in levels are instrumented with suitable lags of their own first differences. The assumption needed is that these differences are uncorrelated with the unobserved bank effects.  Return to text

5.   This estimator was proposed by Arellano and Bover (1995) and Blundell and Bond (1998). We implement it using the command xtabond2 in Stata, see Roodman (2006). Return to text

6.   We report second stage coefficients and standard errors using Windmeijer's (2005) small-sample correction method. We conduct two tests to assess the validity of the instruments used in the empirical estimations. The first test, developed by Arellano and Bond (1991), evaluates if there is no first-order autocorrelation in the idiosyncratic disturbances ( $\varepsilon$_it). This test determines if lags of the explanatory variables are valid instruments, as they are not endogenous to lagged values of $\varepsilon$_it. We report the test of second-order autocorrelation on first-differences of the idiosyncratic disturbances, which is the most relevant for our purposes, as it is equivalent to a test of first-order autocorrelation for levels of $\varepsilon$_it. The second test, called the J-statistic, was proposed by Hansen (1982) and evaluates the joint validity of the instruments, i.e., uncorrelated with the error term. Under the null hypothesis, it is distributed as χ²with degrees of freedom equal to the number of overidentifying restrictions.  Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: June 13, 2011