
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1026, August 2011 --- Screen Reader
Version*
The Revealed Competitiveness of U.S. Exports1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The U.S. share of world merchandise exports has declined sharply over the last decade. Using data at the level of detailed industries, this paper analyzes the decline in U.S. share against the backdrop of alternative measures of the competitiveness of the U.S. economy. We document the following facts: (i) only a few industries contributed to the decline in any meaningful way, (ii) a large part of the drop was driven by the changing size of U.S. export industries and not the size of U.S. sales within those industries, (iii) in a gravity framework, the majority of the decline in the U.S. export share within industries was due to the declining U.S. share of world income, and (iv) in a computed structural measure of firm productivity, average U.S. export productivity has generally maintained its high level versus other countries over time. Overall, our analysis suggests that the dismal performance of the U.S. market share is not a sufficient statistic for competitiveness.
Keywords: Trade competitiveness, gravity model, firm productivity
JEL classification: F14, F17
1 Introduction
The U.S. share of world merchandise exports has declined sharply over the last decade. Using data at the level of detailed industries, this paper analyzes the decline in U.S. share against the backdrop of alternative measures of the competitiveness of the U.S. economy.
Usual suspects for a given country's decline in export share might include: unfavorable relative price movements, crowding out from the proliferation of low-cost exporters from developing countries, uneven reductions in trade costs and barriers around the world, or possibly the deterioriating productivity of exporting firms compared to foreign rivals. Disentangling these factors presents several complications. First, relative prices are only weakly (unconditionally) correlated with U.S. market share, and are thus not very helpful in explaining its recent dynamics. This is evidenced by the accelerating drop in share during the 2000's amidst a decline in the value of the broad real dollar. Second, in many instances, and particularly for international comparisons, trade costs and firm productivity are difficult to measure directly.2 And third, export shares may additionally reflect the idiosyncratic composition of the U.S. export bundle, which may have little to do with the ability of U.S. exporters within a given industry to compete.
To tackle these issues, Section 2 begins by decomposing the decline in share into detailed industry groups. We find that only a handful of industries contributed to the decline in any meaningful way. Moreover, a large part of the drop was driven by the changing size of U.S. export industries rather than the size of U.S. sales within those industries. This means that U.S. exporters happened to be specialized in industries that grew slowly as a share of world trade. Together, these observations offer our first suggestion that the fall in aggregate U.S. share has little to do with the underlying productivity of U.S. exporting firms.
We then present two measures of trade competitiveness which, insofar as they are inferred from actual trade flows, we refer to as revealed competitiveness. The first measure, in Section 3, is derived as a residual from a standard gravity equation. The objective of the exercise is to purge bilateral trade flows of the effect of national income and geography, wherein the residual contains information about the relative productivity and unmeasured trade costs of exporters. We find that the majority of the decline in the U.S. export share is in fact due to the declining share of U.S. income in the world. The residual, which we view as a 'purer' measure of competitiveness, is declining but not as dramatically.
Our second approach, in Section 4, is derived from a structural model and builds on the multi-country, multi-sector version of Melitz-Ottaviano (2008).3 In that framework, the overall competitiveness of a country in a given sector is the outcome of a process of firm selection driven by: (1) the degree of 'accessibility' (i.e. trade costs) of the country and the size of its domestic market, as well as (2) the exogenous ability of the country to generate low cost firms, which depends on structural and technological factors. We extend previous empirical applications of that model by using richer product level detail, and additionally employ an innovative approach by Novy (2009) to compute competitiveness indicators which are comparable over time. Consistent with our gravity residual exercise we find that, notwithstanding significant heterogeneity across sectors, U.S. export productivity has generally maintained its high level versus other countries over time. Overall, our analysis suggests that the dismal performance of the U.S. market share is not a sufficient statistic for competitiveness.
2 The State of U.S. Export Share
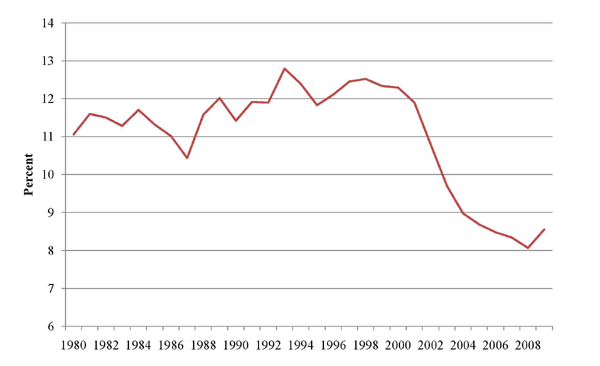
From 1980 to 2009 the U.S. share of world exports fell by almost one third, declining from about 11 percent to just over 8 percent of world exports. In this section we examine the decline in the U.S. share using NBER-UN bilateral trade data from Feenstra, Lipsey, Deng, Ma and Mo (2005).
As shown in Figure 1, the U.S. share of world merchandise
exports rose slightly from 1986 to 1999, increasing from about 10
![]() to 12
to 12
![]() percent of world exports, before
falling 4 percentage points between 1999 and 2009. The bilateral
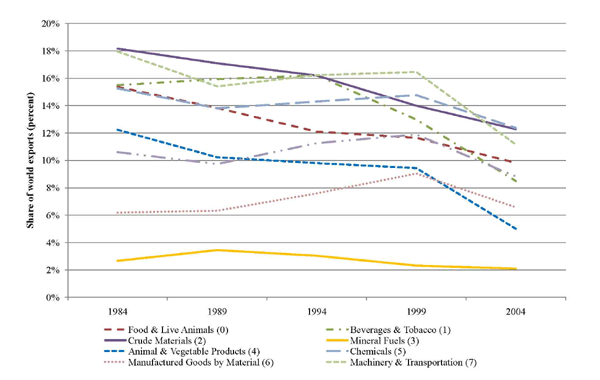
trade data run through 2004 and, in Figure 2, we observe that every
industry group at SITC 1-digit aggregation registered a decrease
over the period from 1984 to 2004, with many of the larger changes
occuring in the early 2000's. The largest declines in share were
recorded among the basic materials categories (SITC 0 through 4),
which account for approximately 25 percent of U.S. exports, and in
machinery and transportation equipment (SITC 7), which account for
almost half of U.S. export sales. It is interesting to note that
the timing of the decline in U.S. share differs over SITC
categories. The fall in basic material shares is gradual and
persistent, while decline in machinery & transportation
equipment is abrupt, primarily occurring after 1999.
percent of world exports, before
falling 4 percentage points between 1999 and 2009. The bilateral
trade data run through 2004 and, in Figure 2, we observe that every
industry group at SITC 1-digit aggregation registered a decrease
over the period from 1984 to 2004, with many of the larger changes
occuring in the early 2000's. The largest declines in share were
recorded among the basic materials categories (SITC 0 through 4),
which account for approximately 25 percent of U.S. exports, and in
machinery and transportation equipment (SITC 7), which account for
almost half of U.S. export sales. It is interesting to note that
the timing of the decline in U.S. share differs over SITC
categories. The fall in basic material shares is gradual and
persistent, while decline in machinery & transportation
equipment is abrupt, primarily occurring after 1999.
The decline in market share is machinery and transportation equipment is particularly notable given the importance of the sector in overall U.S. exports. The fall in the U.S. share of machinery and transportation equipment is examined further in Table 1, which breaks the category into SITC 2-digit subcategories. Although the decline in U.S. share is apparent across most 2-digit machinery categories, the fall in the U.S. share of office machine and computer exports is particularly striking, with U.S. share of world exports falling from a third of the total to just under one tenth. As with overall exports, there is some dispersion in the timing of the decline in shares across subcategories. Whereas the fall in computers is steep and steady over the entire period, in most other categories of machinery the U.S. was able to maintain or expand export share through 1999 before shares plummeted sharply.
A more meaningful way of decomposing the decline in the
aggregate export share is to compute the appropriately weighted
contribution from disaggregate categories of goods. The change in
aggregate export share can be expressed as the sum of changes
across product categories (![]() ) as a ratio of the
change in world exports:
) as a ratio of the
change in world exports:
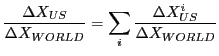
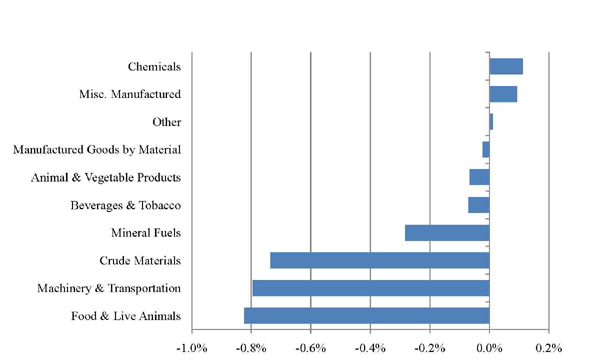
Figure 3 depicts the contributions to the change in aggregate export share for each 1-digit SITC code over the period from 1984 to 2004. Food & live animals provided the largest contribution to the decline in share, accounting for almost one fourth of the aggregate decline. Almost as large were the contributions of machinery & transportation and crude materials, also each contributing about one fourth to the overall decline in share. The importance of raw materials for the decline in U.S. share raises a note of caution in interpreting aggregate export share statistics. Commodity prices fell over most the period under consideration, and since the exports of the United States are relatively commodity intensive, so did the U.S. share of world exports.
The importance of commodities is further illustrated in Figure 4, which depicts the top 10 contributors to the aggregate decline among 4-digit SITC codes. Corn and soybeans contribute a combined one sixth of the overall decline. However, the 4-digit data also reveals that a number of categories of manufactured goods also contributed to the decline, including motor vehicle parts and digital processing units (computers). The take away message is that a true measure of developments in U.S. competitiveness is more likely to be found by looking at U.S. export performance within relatively narrowly defined categories.
The importance of foods for the explaining the overall decline in U.S. share is somewhat surprising given foods relatively small share in U.S. exports and, as shown in Figure 2, the lack of an abnormally large fall in the U.S. share of food specific exports. However, it is important to note that the contribution of each individual category to the fall in the U.S. aggregate share occurs along both an intensive and an extensive margin. The decline in the U.S. aggregate share reflects both an intensive decline in market share within each category, as well as an extensive decline stemming from changes in the size of each category in world exports. For instance, corn (SITC 0440) contributes to the decline in U.S. aggregate share both as the U.S. captures a smaller proportion of the corn-specific export market and also as corn's share of overall world exports declines.
One established method of assessing the importance of composition for changes in trade shares is constant market share analysis (see ECB (2005) for a detailed description).4 Constant market share analysis separates changes in aggregate market share into two components, a commodity effect and competitiveness effect defined as follows:5
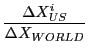 |
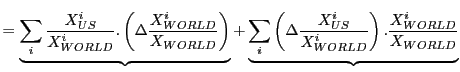 |
|
Commodity Effect |
Competitiveness
Effect |
|
The commodity effect measures the effect of composition on the change in the aggregate export share, by weighting the change in the composition of world exports by the initial composition of the U.S. export bundle. The competitiveness effect measures the portion of the change in the aggregate share that is due to changes in the within category share of U.S. exports.
Figure 5 decomposes the contribution of each 1-digit SITC export category to the change in the aggregate export share (the blue bars) into components due to commodity (the green bars) and competitiveness (the red bars) effects over the 1984 to 2006 period. The large negative contributions of food and live animals and crude materials largely reflect the declining importance of these goods in world exports (signified by negative commodity effects), although U.S. exports also suffered a negative competitiveness effect in each case. In contrast the negative contribution to the aggregate recorded by the machinery and transportation sector is completely due to a decline in U.S. competitiveness, as the sector has greatly increased its weight in the world exports over the time frame under consideration.
In summary, interpreting the decline in the U.S. export share is complicated by compositional effects. The primary drivers of the decline in aggregate U.S. share were raw commodities, with negative contributions that largely derived from their declining weight in the world export basket. That said, the U.S. did experience a large decline in the share in the machinery and transportation sector, which was not reflected in the composition of U.S. exports but rather declines within detailed sub-categories. Here the evidence of a fall in U.S. competitiveness is more compelling. Against this background, the following sections focus on U.S. export performance within industries and attmept to identify its drivers. We suggest two alternative empirical methodologies to parse out a narrower definition of competitiveness: exporter productivity purged of geographical and relative market size considerations. This strategy is termed, "revealed competitiveness," which derives from the fact that it is inferred from observable trade flows.
3 Reduced Form Revealed Competitiveness
One possible explanation for the decline in U.S. export share is simply that the U.S. now accounts for a smaller share of global output. As China and other emerging economies expand rapidly and become more integrated into the global economy, it is natural that the U.S. share of world exports would fall without necessarily indicating any decline in the productivity of U.S. exporters. As shown in Figure 6, the fall in the U.S. share of global exports of about 4 percentage points over the past decade corresponds to a decrease in the U.S. share of global output of about 3 1/2 percentage points on a PPP basis. The relatively tight correlation between export share and income holds true for many other countries as well. Across the G7, France, Italy, and Japan have experienced declines in export share that broadly match their declining share of world output. On the other hand, Germany has more less maintained export share even as its share of world income has declined, while Canada and the UK have suffered much steeper falloffs in exports than income. In percentage terms, the export share growth of China has outpaced its income share, and the same holds for India.
Figure 6 strongly suggests that changes in market share may be conflating competitiveness effects with income dynamics. Specifically, country characteristics such as size may be influencing market share but have little to do with the underlying ability of a country's exporters to compete. To control for such characteristics, our first approach is to non-parametrically estimate trade flows minus the contribution of country size, geography and certain trade costs. A derivative of the gravity equation is a natural candidate to do so. Previous studies such as Baier and Bergstrand (2001), and more recently Whalley and Xin (2009) and Novy (2009), use gravity to decompose the levels of bilateral trade flows into contributions from income, trade costs or otherwise. Each finds that exporter and importer income plays a substantial, even dominant, role in explaining trade. Our approach extends this logic to the case of relative trade performance, where the gravity equation is 'folded' by dividing through by a reference exporter. In the particular case where the reference country is the entire world, the gravity equation converts neatly into an expression for market share in terms of relative exporter size, relative geographic characteristics and relative productivity.
Our approach to 'decomposing' the share into factors that have to do with competitiveness and those that don't involves simply looking at the time variation in the residual of a panel gravity estimation. The intuition is that if a country is increasingly outperforming the average exporter's performance (i.e., a country exports more relative to its own size and more to distant countries over time) then its residual will grow over time. We posit that this residual contains information about changes in the underlying productivity of exporters. In this section, we do not apply a structural interpretation to that productivity, it is merely contained in the residual. In the section that follows, we apply a structure that allows for more specific interpretation of the residual and, moreover, is consistent with the reduced form gravity equation herein.
To be concrete, define
![]() as country
as country ![]() 's
exports to country
's
exports to country ![]() in sector
in sector ![]() in a given period
in a given period ![]() :
:
| (1) |
Equation (1) corresponds to a
generic gravity model, where bilateral trade is a function of
country size (![]() ), latent country-specific multilateral
resistance (
), latent country-specific multilateral
resistance (![]() ), geographic characteristics
(
), geographic characteristics
(![]() ) and global shocks (
) and global shocks (![]() ). Exploiting the multiplicative form of the equation, we
cancel out importer-specific terms by dividing through by total
exports to country
). Exploiting the multiplicative form of the equation, we
cancel out importer-specific terms by dividing through by total
exports to country ![]() in industry
in industry ![]() .
.
 |
(2) |
The intuition for this reduced form is that the change in a given
importer's income or multilateral resistance will affect the level
of that country's imports but not how the new imports are allocated
across exporters. Moreover, a global shock affecting all exporters
will not affect their relative performance and hence the
![]() terms cancel out as well. The method of
taking ratios of the gravity equation has three ostensible
benefits. First, for our purpose of relating the share of U.S.
exports to underlying productivity measures, equation (2) is expressed in the correct units of
share owing to income, trade costs and productivity. Second, the
size of the data matrix used in the estimation is reduced by
folding in the importer-specific terms. Third, multilateral
resistance terms (as defined in Anderson and van Wincoop (2003))
associated with importers cancel out, sparing the need to
approximate them using fixed effects.6
terms cancel out as well. The method of
taking ratios of the gravity equation has three ostensible
benefits. First, for our purpose of relating the share of U.S.
exports to underlying productivity measures, equation (2) is expressed in the correct units of
share owing to income, trade costs and productivity. Second, the
size of the data matrix used in the estimation is reduced by
folding in the importer-specific terms. Third, multilateral
resistance terms (as defined in Anderson and van Wincoop (2003))
associated with importers cancel out, sparing the need to
approximate them using fixed effects.6
Denoting the geometric mean of a given variable by
![]() ,
taking logs, and allowing for a mean-zero perturbation (
,
taking logs, and allowing for a mean-zero perturbation (
![]() ), we can rewrite the above
expression as:7
), we can rewrite the above
expression as:7
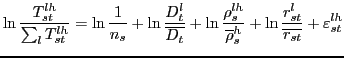 |
(3) |
The log of country ![]() 's market share in
destination market
's market share in
destination market ![]() is a positive function of
its relative income, its geographic proximity and its relative
productivity. Again, this specification is isomorphic to a standard
gravity model, though specified in relative terms. With the
additional assumptions that
is a positive function of
its relative income, its geographic proximity and its relative
productivity. Again, this specification is isomorphic to a standard
gravity model, though specified in relative terms. With the
additional assumptions that ![]() and
and ![]() are constant over time, variation in exporter multilateral
resistance and productivity is identified as the residual of a
model with exporter relative income and country-pair fixed effects
on the right-hand side. That is, the actual market share changes
over time relative to the changes in the gravity model prediction
contains information about the evolution of relative exporter
productivity. This is what we will refer to as the share-to-model
ratio, or simply the growth in the model residual by exporting
country, averaged across industries:
are constant over time, variation in exporter multilateral
resistance and productivity is identified as the residual of a
model with exporter relative income and country-pair fixed effects
on the right-hand side. That is, the actual market share changes
over time relative to the changes in the gravity model prediction
contains information about the evolution of relative exporter
productivity. This is what we will refer to as the share-to-model
ratio, or simply the growth in the model residual by exporting
country, averaged across industries:
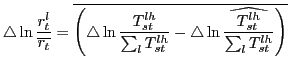 |
(4) |
The assumption of a time-invariant ![]() is similar
to standard gravity approaches using variables such as distance,
common border and common language that don't tend to change much.
The implication of this assumption, however, is that decreases in
trade costs due to changing trade policy will also be captured in
the residual term. In our implementation we add dummies for
significant shifts in policy (e.g., NAFTA, EMU) as well as over the
course of our sample to try to control for changing trade costs,
but nonetheless the residual likely captures elements of falling
trade costs in addition to relative productivity. As such, in this
section we jointly estimate relative performance due to these
factors, both of which fit into a reasonable, if broad, definition
of export competitiveness; in the following section we use a
structural model to parse the residual more finely.
is similar
to standard gravity approaches using variables such as distance,
common border and common language that don't tend to change much.
The implication of this assumption, however, is that decreases in
trade costs due to changing trade policy will also be captured in
the residual term. In our implementation we add dummies for
significant shifts in policy (e.g., NAFTA, EMU) as well as over the
course of our sample to try to control for changing trade costs,
but nonetheless the residual likely captures elements of falling
trade costs in addition to relative productivity. As such, in this
section we jointly estimate relative performance due to these
factors, both of which fit into a reasonable, if broad, definition
of export competitiveness; in the following section we use a
structural model to parse the residual more finely.
The assumption of a constant number of trading partners per
importer (![]() ) may be less benign. Due to the seminal
work of Feenstra (1994), there has been much study of the increase
in product variety within even narrowly defined product categories.
We address this empirically in two ways. First, every specification
below contains time fixed effects which would soak up a secular
trend in varieties. Secondly, most specifications contain
country-pair fixed effects or exporter-time fixed effects which
would pick up at least a portion of the level differences in
) may be less benign. Due to the seminal
work of Feenstra (1994), there has been much study of the increase
in product variety within even narrowly defined product categories.
We address this empirically in two ways. First, every specification
below contains time fixed effects which would soak up a secular
trend in varieties. Secondly, most specifications contain
country-pair fixed effects or exporter-time fixed effects which
would pick up at least a portion of the level differences in
![]() by country. We note that a disproportionate
rise in relative product variety to certain countries over time
would decrease the term
by country. We note that a disproportionate
rise in relative product variety to certain countries over time
would decrease the term ![]() and hence work against
the finding of rising productivity in the residual. For the most
prolific traders in terms of their number of trading partners,
which includes the U.S., we thus take our estimates of the rising
residual as an underestimate of the true change in productivity and
trade costs.
and hence work against
the finding of rising productivity in the residual. For the most
prolific traders in terms of their number of trading partners,
which includes the U.S., we thus take our estimates of the rising
residual as an underestimate of the true change in productivity and
trade costs.
3.1 Reduced Form Revealed Competitiveness: Data & Specification
The data used in the estimation are bilateral trade flows as described in the previous section, nominal GDP data from the Penn World Table which are converted into international dollars at PPP exchange rates, dummy variables for NAFTA, EU and EMI trade flows, the distance between capital cities, as well as common border and common language dummies. We follow previous studies by truncating the data at $10,000 per annual bilateral flow to avoid potential distortions from errors of units in the data and implausibly small trade values. We run each gravity regression at the SITC 4-digit level and constrain ourselves to products with over 1,000 exporter-importer-year observations. The amount of data lost due to concordance issues for income and distance data will vary by specification since the use of fixed effects often obviates the use of those variables, but the most punitive cut of the data still accounts for over 83 percent of global trade value between 1980 and 2004.
Our estimator is OLS on the log-linear specification of
(3). Cognizant of the fact that
there are many different ways to take that equation to data, we try
an array of five different panel specifications with varying
degrees of control for multilateral resistance terms. Again, our
objective is to compute various indexes of the change in the
residual (4) which will be informative
of the portion of U.S. share decline not explained by gravity
controls such as income and geography. The differences among these
five regressions are the treatment of the ![]() terms
(which in some cases are country-pair fixed effects and in others
are the standard distance, border and language controls), the
measure of country-specific variables
terms
(which in some cases are country-pair fixed effects and in others
are the standard distance, border and language controls), the
measure of country-specific variables ![]() , as well as
the subset of data used for the estimation.
, as well as
the subset of data used for the estimation.
The specifications are described in Table 2. In specification
(i), we regress the exporter's share of global sales in each SITC
product on the exporter's relative nominal income (recall that the
importer-specific terms cancel by dividing by a reference
exporter), exporter-importer fixed effects, year fixed effects, and
dummies for NAFTA and EMU. An actual measure of income is used to
control for the trends described in the previous section. The
exporter-importer FE is a static measure of trade costs which wipes
out variation in border, distance and language, and arguably
includes many more unmeasured (and unchanging) barriers to trade.
To control for some large policy changes during our sample which we
do not view as endogenous to competitiveness, dummies for
post-NAFTA and post Euro years are included for the appropriate
countries. Finally, year fixed effects soak up secular trends in
![]() .
.
Specification (ii) uses the same regressors as (i), but on a subset of the data that has observations for at least 20 of the 25 years in the sample (i.e., within each exporter-importer-SITC cell). It is informative to constrain ourselves to the subset of bilateral trade flows that are balanced over the course of the sample for at least two reasons. First, the average results statistics reported across products may be skewed by compositional changes over time in the unbalanced panel. Secondly, our linear-in-logs specification potentially introduces selection bias by dropping the observations with zero trade flows. One possible way to assess the sensitivity of the results to loosening the data truncation at zero would be to tighten it further; that is, any selection bias caused by dropping zero values would be enhanced by dropping sporadic ones.
Specification (iii) uses exporter-year fixed effects in the place of GDP. Since these fixed effects also approximate changes to the multilateral resistance terms of the exporter, they may in fact be soaking up some of the information on competitiveness intended to be measured. As such, the robustness of the result consists of a similar profile of residual changes in specifications (i) through (iii), due to the following trade-off: in the first two there is likely some omitted variable bias since implicit indexes of multilateral resistance (as defined in Anderson and van Wincoop (2003)) are themselves a function of geographic variables included in the regression. On the other hand, the appropriate control for multilateral resistance removes from the residual at least some information on the relative performance of exporters. Specifications (iv) and (v) check the robustness of the results to more standard gravity specifications, by unfolding (3) into levels and incorporating conventional measures of static trade costs. Specification (vi) uses a an alternative data source on bilateral international trade flows aggregated into broader ISIC 2-digit sectors.8
3.2 Reduced Form Revealed Competitiveness: Results
After controlling for model factors in several alternative formulations of the gravity model, we find that the U.S. export share is only in slight decline. In our benchmark specification (i), the majority of the roughly 20 percent decline in aggregate U.S. export share is explained by the model with about a 6 percent decline in the residual.9
Table 3 shows the estimates of control variables for (3) estimated across all products.10 As expected, exporter GDP share is positively related to export share, with a 1 percent decrease in relative income decreasing export share by roughly 0.4-0.6 percent. These magnitudes are similar to the coefficients on GDP in the level regressions and slightly lower than those using the ISIC data. The effect of NAFTA and the introduction of the euro are both positive and significant, with coefficients ranging from 0.4-1.5 and 0.1-0.5, respectively. Measures of distance, language and border have the expected sign.
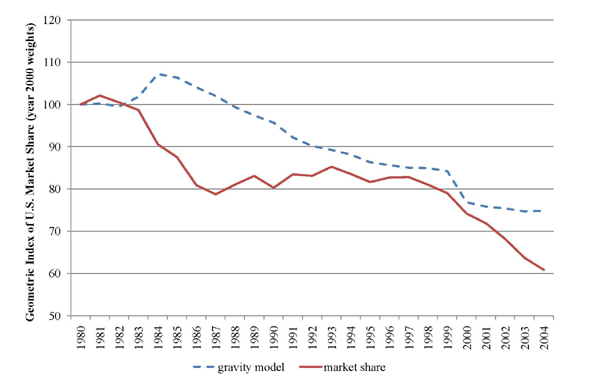
An index of market share changes for the U.S., along with an index of model predicted values, are shown in Figure 7. The index in each year is a geometric mean of share changes across U.S. destination countries and products, where each change in share is weighted by the SITC-importer value in the year 2000.11 Despite a widening of the gap between the two indices in the early period, the model prediction broadly follows the share trend. Since there are not many time-varying regressors in our gravity estimation, this result is closely related to the observation in Figure 6 that U.S. income share and trade share have similar dynamics.
To construct a statistic for the overall percent change in market share due to the gravity residual, the ratio of actual to predicted share is averaged across time periods in the early part of the sample (1980-1992) and the latter part (1993-2004) and the log-difference of these two ratios is taken for each exporter-importer-SITC group. The average of those statistics across destinations and 4-digit product groups is shown in Figure 8 for the G20 plus Singapore, Taiwan and Hong Kong.12 Across all products, the U.S. is in the middle of the pack with decreases in its residual of 6 percent. This can be interpreted as a decrease in U.S. export market share of 6 percent that is not accounted for by the dynamics of income, and is notably smaller than the overall share decline of approximately 20 percent over that period. This suggests that U.S. relative productivity competitiveness, albeit in slight decline by this measure, did not decline by nearly as much as its fall in share might suggest. This result is consistent across product categories, shown in Table 4, even for SITC 7 (machinery and transportation) where U.S. share performance was particularly grave, as well as for other specifications shown in Appendix B. For other exporters, clear winners and losers emerge. Indonesia, China, India and Mexico had among the highest increases in their gravity residual by a large margin, as their export growth far outpaced the increase in their income shares. On the other hand, certain large Asian exporters had dramatic falls in their residuals presumably due to the rise of China and large increases in Mexican exports to the U.S. over the sample period. European countries and Canada had more moderate changes in their export performance and, with a few exceptions, tended to lag behind the rest of the world.
In summary, this reduced form exercise strongly supports the story that exporter income shares are an important determinant of trade shares. Beyond that, however, it is difficult to know whether the gravity residual reflects the actual evolution in the underlying productivity of exporters rather than other factors, such as evolving trade costs. In the following section we take a different approach to identifying relative cost competitiveness across countries by modelling the micro-foundations of trade shares explicitly.
4 Structural Revealed Competitiveness
In this section we build on a multi-country multi-sector version of the Melitz-Ottaviano (2008) model to obtain a (computable) structural equation for the relative competitiveness of a country. A full description of the reference model is reported in Corcos et al. (FEEM, 2010), although its main properties are summarized in Appendix A.
The model yields the following expression for aggregate
bilateral trade from country ![]() to country
to country
![]() in a given sector
in a given sector ![]() 13:
13:
| (5) |
where
![]() is the shape parameter of the
(Pareto) marginal cost distribution in sector
is the shape parameter of the
(Pareto) marginal cost distribution in sector ![]() ;
;
![]() is a bundling sectoral parameter playing no role in subsequent
analysis;
is a bundling sectoral parameter playing no role in subsequent
analysis; ![]() is the number of entrants in
country
is the number of entrants in
country ![]() - sector
- sector ![]() ;
;
![]() is the upper bound of the
exogenous marginal cost distribution in country
is the upper bound of the
exogenous marginal cost distribution in country ![]() -
sector
-
sector ![]() (exogenous cost cutoff);
(exogenous cost cutoff);
![]() is a measure of trade
freeness between country
is a measure of trade
freeness between country ![]() and country
and country ![]() in sector
in sector ![]() ;
; ![]() is country size
(i.e population and, by extension, GDP);
is country size
(i.e population and, by extension, GDP);
![]() is the endogenous maximum possible
marginal cost for a generic domestic firm producing and selling in
country
is the endogenous maximum possible
marginal cost for a generic domestic firm producing and selling in
country ![]() - sector
- sector ![]() (endogenous cost
cutoff).
(endogenous cost
cutoff).
Equation (5) expresses exports
from ![]() to
to ![]() in a given sector
as a function of bilateral trade freeness [
in a given sector
as a function of bilateral trade freeness [
![]() ] and a set of country
characteristics specific to the exporting [
] and a set of country
characteristics specific to the exporting [
![]() ,
, ![]() ] or
the importing [
] or
the importing [![]() ,
,
![]() ] country.14
] country.14
It is worth noting how, bearing in mind equations (13) and (14), the vector
of inverse endogenous cutoffs
![]() (with generic element
(with generic element
![]() ) can be interpreted, once
ordered, as a country ranking in terms of actual competitiveness.
On the other hand, the vector of inverse exogenous cutoffs
) can be interpreted, once
ordered, as a country ranking in terms of actual competitiveness.
On the other hand, the vector of inverse exogenous cutoffs
![]() , with generic element
, with generic element
![]() , can be thought of, once ordered, as a country ranking in terms of
the exogenous ability to generate low cost firms. Given
, can be thought of, once ordered, as a country ranking in terms of
the exogenous ability to generate low cost firms. Given
![]() , a country's position in
, a country's position in
![]() is an inverse function of
home market size (
is an inverse function of
home market size (![]() ) and trade freeness (
) and trade freeness (
![]() ). As explained in Appendix A, to stress this relationship between
). As explained in Appendix A, to stress this relationship between
![]() and
and
![]() , we refer to the former as the
Producer (Marginal Cost) Competitiveness of country
, we refer to the former as the
Producer (Marginal Cost) Competitiveness of country
![]() and to the latter as its Overall
(Marginal Cost) Competitiveness (henceforth OC and PC
respectively).
and to the latter as its Overall
(Marginal Cost) Competitiveness (henceforth OC and PC
respectively).
Equation (5) provides us with
the chance to derive an analytical expression that can be used to
infer the vector
![]() of the OC of the countries
from observed bilateral trade flows. To this aim, we start by
noting that only
of the OC of the countries
from observed bilateral trade flows. To this aim, we start by
noting that only
![]() and
and ![]() are
observable. Thus we first of all need to purge (5) of the unobservable terms. However,
consider that the terms in (5) are
specific to both the origin and the destination country [i.e.
are
observable. Thus we first of all need to purge (5) of the unobservable terms. However,
consider that the terms in (5) are
specific to both the origin and the destination country [i.e.
![]() ], or either to the former
(i.e.
], or either to the former
(i.e.
![]() ) or
the latter (i.e.
) or
the latter (i.e.
![]() ) only. To
isolate OC, we can therefore use country
) only. To
isolate OC, we can therefore use country ![]() 's exports to
a reference country
's exports to
a reference country ![]() (UK in the application), to
transform equation (5) into a
prediction of relative (instead of absolute) trade flows:
(UK in the application), to
transform equation (5) into a
prediction of relative (instead of absolute) trade flows:
![$\displaystyle \frac{T_{s}^{lh}/D^{h}}{T_{s}^{lf}/D^{f}}=\frac{\rho_{s}^{lh}}{\rho_{s}^{lf} }\left[ \frac{m_{s}^{hh}}{m_{s}^{ff}}\right] ^{\gamma_{s}+2}$](img96.gif) |
(6) |
This expression, in which measurable terms are grouped on the left hand side, expresses measurable (relative) trade flows as a function of trade freeness and OC, both in relative terms.
Using a tilde to indicate that a variable is expressed in
relative terms (
![]() ;
;
![]() ;
;
![]() ),
relative average marginal costs in a given country-sector can be
written as
),
relative average marginal costs in a given country-sector can be
written as
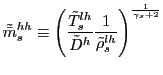 |
(7) |
where we also used the fact that, under the Pareto assumption,
![]() , and thus
, and thus
![]() .
.
Bilateral trade costs - or more precisely the degree of trade
freeness
![]() - are however unknown.
To deal with this issue, we derive - as suggested by Novy (2009) -
a very simple form for bilateral trade freeness, which exploits the
structure of the reference model without the need to estimate a
gravity equation. From (6),
bilateral trade freeness between country
- are however unknown.
To deal with this issue, we derive - as suggested by Novy (2009) -
a very simple form for bilateral trade freeness, which exploits the
structure of the reference model without the need to estimate a
gravity equation. From (6),
bilateral trade freeness between country ![]() and country
and country
![]() can be in fact expressed as
can be in fact expressed as
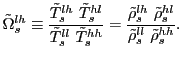 |
(8) |
The intuition behind (8) is (Novy, 2009)
straightforward. If bilateral trade flows between two countries
increase relative to domestic trade flows, it must have become
relatively easier for the two countries to trade with each other.
This is captured by an increase in
![]() , and vice
versa.
, and vice
versa.
Assuming
![]() ,
(8) can be plugged into (7) in order to obtain the following
measure of Revealed Overall Competitiveness (henceforth
ROC)15:
,
(8) can be plugged into (7) in order to obtain the following
measure of Revealed Overall Competitiveness (henceforth
ROC)15:
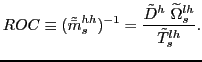 |
(9) |
Equation (9) does not require
econometrics. The advantage over gravity estimates16 is
that
![]() can be
calculated not only for cross-sectional data but also for time
series and panel data. Thus, the evolution of the resulting country
rankings can in this case be trusted. Note also that, although
can be
calculated not only for cross-sectional data but also for time
series and panel data. Thus, the evolution of the resulting country
rankings can in this case be trusted. Note also that, although
![]() ,
,
![]() normally differs from
normally differs from
![]() . Thus, what equation
(9) suggests is that the difference in
. Thus, what equation
(9) suggests is that the difference in
![]() respect to
respect to
![]() has to be traced back to
differences in relative costs (
has to be traced back to
differences in relative costs (
![]() ) and market
size (
) and market
size (
![]() ).
).
Finally, it is worth noting that the idea of "revealed"
competitiveness associated with (7) is more general than more conventional
measures of aggregate total factor productivity (![]() ). To see this, consider equation (12): our measure of "overall competitiveness" is a
composition of "inverse
). To see this, consider equation (12): our measure of "overall competitiveness" is a
composition of "inverse ![]() " (
" (![]() ) and
input costs (
) and
input costs (
![]() ), as well as input shares (
), as well as input shares (
![]() ). Although a country could
have high
). Although a country could
have high ![]() (i.e. low
(i.e. low ![]() ) in
sector
) in
sector ![]() , that may not be sufficient to be
competitive in international markets. It could be that
international differences in input costs (such as capital, labour
and intermediates) are a disadvantage to that country.
, that may not be sufficient to be
competitive in international markets. It could be that
international differences in input costs (such as capital, labour
and intermediates) are a disadvantage to that country.
Moreover, a country's domestic value added (DVA) content of
exports might be low, which would dampen the link between a
country's ![]() and its export performance. The
importance of
and its export performance. The
importance of ![]() in determining the international
competitiveness of a country decreases with the degree of
international fragmentation of the production process in the
country. By definition,
in determining the international
competitiveness of a country decreases with the degree of
international fragmentation of the production process in the
country. By definition, ![]() is meant to measure the
output differences which are not explained by different input
choices and occurs, instead, through marginal product increases.
Due to this physical nature, firms'
is meant to measure the
output differences which are not explained by different input
choices and occurs, instead, through marginal product increases.
Due to this physical nature, firms' ![]() (and
thus a country's
(and
thus a country's ![]() ) is invariant to different
choices concerning whether to outsource phases of the production
process and whether to buy intermediates domestically or abroad.
Whilst
) is invariant to different
choices concerning whether to outsource phases of the production
process and whether to buy intermediates domestically or abroad.
Whilst ![]() is not affected by these choices,
marginal costs are. For given quantities of intermediate inputs
used in production, the possibility to import them from abroad
offers a chance to reduce marginal costs (see equation (12)). In the aggregate, this results in an
improved capacity to target the international consumers of the
final good
is not affected by these choices,
marginal costs are. For given quantities of intermediate inputs
used in production, the possibility to import them from abroad
offers a chance to reduce marginal costs (see equation (12)). In the aggregate, this results in an
improved capacity to target the international consumers of the
final good ![]() at relatively low prices. Since it is
expressed in units of marginal costs, ROC is a measure of
competitiveness which is "naturally" linked to the concept of
DVA.
at relatively low prices. Since it is
expressed in units of marginal costs, ROC is a measure of
competitiveness which is "naturally" linked to the concept of
DVA.
Moreover, since the international structure of ROC (vector
![]() ) results from a combination of forces
(such as trade costs and market size) affecting the degree of
international competition for final goods, ROC is informative of a
given country's ability to sell good
) results from a combination of forces
(such as trade costs and market size) affecting the degree of
international competition for final goods, ROC is informative of a
given country's ability to sell good ![]() at low
prices to the international market; in contrast,
at low
prices to the international market; in contrast, ![]() is informative of that country's ability to sell good
is informative of that country's ability to sell good
![]() at low prices domestically.
at low prices domestically.
4.2 Structural Revealed Competitiveness: Data & Specification
As equation
(9) derives country ![]() 's ROC from its bilateral trade flows with a given country
's ROC from its bilateral trade flows with a given country
![]() , for each country
, for each country ![]() (and
industry
(and
industry ![]() ) we compute
) we compute
![]() as many times as
the number of its commercial partners. In other words, our reported
ROCs are obtained considering, for each country, all the country
pairs for which bilateral trade flows are available. A single value
for
as many times as
the number of its commercial partners. In other words, our reported
ROCs are obtained considering, for each country, all the country
pairs for which bilateral trade flows are available. A single value
for
![]() is then obtained
as a weighted average in which each country is assigned its share
on country
is then obtained
as a weighted average in which each country is assigned its share
on country ![]() 's total imports as weight.17
's total imports as weight.17
As in section 3, we focus on two periods (1980-1991 and 1992-2004). Data on bilateral flows are obtained from the CEPII TradeProd database. The choice is driven by the fact that, in contrast to the bilateral trade data used above, TradeProd reports reliable internal trade flows. Trade flows are provided in nominal dollars at the 3-digit level of the ISIC Rev.2 classification. Again, we truncate the data at $10,000 per annual bilateral flow; this has no remarkable effects on the results. As above, data on country GDP from the Penn World Tables are converted into international dollars at PPP exchange rates. We use United Kingdom as our reference country since it has the highest number of observations as importer or exporter. Consistent with the reducted form exercise, results are presented for the G20 country group with the exception of Saudi Arabia, for which information on internal trade flows is unavailable.
4.2 Structural Revealed Competitiveness: Results
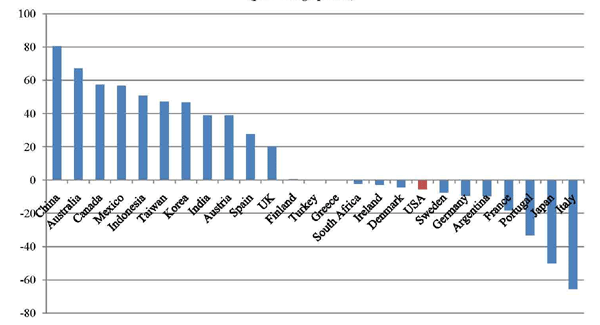
In this section we focus on average percentage changes in ROC from the early to the late period. Our main results are synthesized in Figure 9, though readers are directed to Appendix B for additional detail on countries and industries.
Figure 9 reports the average ROC percentage change for those G20 countries for which ROC is available for at least 23 out of our 28 sectors. For each country, the sectors are weighted using the product's average share in the country's export bundle during the late period. Standardization is by sector and with respect to the whole G20. A slight decline (-5.58%) characterizes the evolution of the average ROC variation in the U.S. Overall, Figure 9 confirms the exceptional competitiveness growth of certain emerging market competitors such as China and Mexico but also that of other, more traditional, competitors such as Canada and Australia. Among EU countries, only UK, Spain and Austria show a positive variation in ROC. In particular, Italy is the worst performing G20 country, followed by Portugal and traditional U.S. competitors like France and Germany.
Throughout the paper we have interpreted the gravity residual and structural cost estimates as largely reflecting latent exporter productivity. However, other factors likely contribute to export performance in excess of what might be predicted by these frameworks. As mentioned in the model description, the structure of production within certain regions of the global economy could be playing an important role. For example, regions that are relatively intensive in cross-border production sharing would record higher exports for a given unit of output independent of exporter productivity. Indeed, this may be behind some of the high measures of performance that we estimate for China and Mexico over the sample period. In principle, though, the dynamic trade cost measure in the structural analysis (which compares international to intranational trade flows) captures some of the increasing incidence of production sharing. The fact that East Asian countries, excluding China, had competitiveness losses in the reduced form estimates and competitiveness gains in the structural estimates is consistent with the reality of large flows of goods passing through China for final assembly.
5 Conclusion
The U.S. share of global exports has fallen by roughly 20 percent over the last decade. This paper aims to deconstruct the drivers of the decline in share. First, we document that the distribution of the decline is quite uneven, with a minority of categories contributing disproportionately. Second, when controlling for the relative decline in the U.S. share of global output, driven by a large extent by rapid growth in emerging market economies, the fall in share is far less pronounced. We formalize this notion within a gravity framework and assess changes in competitiveness through the evolution of the estimation residuals in an array of empirical specifications. We find that, accounting for income share and other controls, the decline in U.S. export share is largely explained by model factors.
We then take a more structural approach to examining the evolution of U.S. competitiveness, deriving an expression for U.S. export share from a heterogeneous firms model in the style of Melitz-Ottaviano (2005). This approach confirms the outcome of our gravity model exercise, that the U.S. has generally maintained its level of competitiveness within detailed product categories, despite the fall in the overall share. All together this analysis points to the inadequacy of the aggregate export share as an indicator of country export competitiveness.
Bibliography
Anderson, J.E. and E. van Wincoop (2003), "Gravity with Gravitas: A Solution to the Border Puzzle", American Economic Review, 93(1), 170-92.
Baier, S.L. and J.H. Bergstrand (2001), "The growth of world trade: tariffs, transport costs and income similarity", Journal of International Economics, 53, 1-27.
Chen N. and Novy D. (2009) "International Trade Integration: A Disaggregated Approach", CEPR dp, 7103.
Corcos G., Del Gatto M., G. Mion and G.I.P. Ottaviano (2009), "Productivity and Firm-Selection: Quantifying the "New" Gains from Trade", FEEM wp, 115.
Del Gatto M., di Mauro F., Forster K. (2010), "Re-establishing competitiveness in the EURO area: insights from a computable partial equilibrium trade model with heterogeneous firms". mimeo.
Del Gatto M., G. Mion and G.I.P. Ottaviano (2006), "Trade Integration, Firm Selection and the Costs of Non-Europe", CEPR Discussion Paper, 5730.
European Central Bank (2005), "Competitiveness and the Export Performance of the Euro Area", Occasional Paper Series, 30.
Fadinger H. and Fleiss P. (2008) "Trade and Sectoral Productivity". MPRA wp, 6938.
Finicelli A., Pagano P. Sbracia M. (2009) "Trade-revealed TFP". Banca d'Italia wp, 729.
Jacks D. Meissner C., and Novy D. (2008) "Trade Costs, 1870-2000". American Economic Review, Papers & Proceedings, 98(2), 529-534.
Head, K. and T. Mayer (2000), "Non-Europe: the Magnitude and Causes of the Market Fragmentation in the EU", Weltwirtschaftliches Archiv, 136(2), 285-314.
Head, K., T. Mayer and J. Reis (2010), "The erosion of colonial trade linkages after indepenence", Journal of International Economics, 81, 1-14.
Martin, P., T. Mayer and M. Thoenig (2008), "Make trade not war?" Review of Economic Studies, 75(3), 865-900.
Melitz M. and Ottaviano G. (2008), "Market Size, Trade, and Productivity", Review of Economic Studies, 75, 295-316.
Novy D. (2009) "Gravity Redux: Measuring International Trade Costs with Panel Data". mimeo.
Ottaviano G.I.P., Taglioni D. and di Mauro F. (2009). "The euro and the competitiveness of European firms". Economic Policy, 24(01).
Richardson J. D. (1971), "Constant-Market-Shares Analysis of Export Growth", Journal of International Economics, 227-239.
Waugh M.E. (2009) "International trade and income differences". Federal Reserve Bank of Minneapolis, Staff Report, 435.
Whalley, J. and X. Xin (2009), "Regionalization, changes in home bias, and the growth of world trade", Journal of Policy Modeling, forthcoming.
Figure 1. U.S. Share of World Merchandise Exports
Data for Figure 1
| Year | USA Export Share |
|---|---|
| 1980 | 11.05 |
| 1981 | 11.60 |
| 1982 | 11.50 |
| 1983 | 11.28 |
| 1984 | 11.71 |
| 1985 | 11.32 |
| 1986 | 11.02 |
| 1987 | 10.44 |
| 1988 | 11.58 |
| 1989 | 12.02 |
| 1990 | 11.42 |
| 1991 | 11.92 |
| 1992 | 11.90 |
| 1993 | 12.79 |
| 1994 | 12.39 |
| 1995 | 11.83 |
| 1996 | 12.11 |
| 1997 | 12.46 |
| 1998 | 12.52 |
| 1999 | 12.34 |
| 2000 | 12.29 |
| 2001 | 11.90 |
| 2002 | 10.80 |
| 2003 | 9.71 |
| 2004 | 8.98 |
| 2005 | 8.68 |
| 2006 | 8.48 |
| 2007 | 8.34 |
| 2008 | 8.07 |
| 2009 | 8.55 |
Figure 2. U.S. Share of World Merchanside Exports, by SITC 1-Digit Sector
Data for Figure 2
| Sitc Code | United States: 1984 | United States: 1989 | United States: 1994 | United States: 1999 | United States: 2004 | United States: SITC | United States: dshare |
|---|---|---|---|---|---|---|---|
| Food & Live Animals (0) | 0.153675 | 0.138257 | 0.120957 | 0.116474 | 0.09821 | 0 | -0.05546 |
| Beverages & Tobacco (1) | 0.154872 | 0.159389 | 0.162049 | 0.129804 | 0.084888 | 1 | -0.06998 |
| Crude Materials (2) | 0.181614 | 0.170907 | 0.161918 | 0.139926 | 0.122751 | 2 | -0.05886 |
| Mineral Fuels (3) | 0.026624 | 0.034469 | 0.030325 | 0.023139 | 0.020947 | 3 | -0.00568 |
| Animal & Vegetable Products (4) | 0.122311 | 0.102278 | 0.097983 | 0.094349 | 0.050053 | 4 | -0.07226 |
| Chemicals (5) | 0.152535 | 0.138034 | 0.142977 | 0.147651 | 0.123687 | 5 | -0.02885 |
| Manufactured Goods by Material (6) | 0.061844 | 0.063232 | 0.075922 | 0.090383 | 0.065723 | 6 | 0.00388 |
| Machinery & Transportation (7) | 0.17944 | 0.154052 | 0.162266 | 0.164544 | 0.111591 | 7 | -0.06785 |
| Misc. Manufactured (8) | 0.106005 | 0.097303 | 0.112581 | 0.118921 | 0.088217 | 8 | -0.01779 |
| Other (9) | 0.103736 | 0.144919 | 0.14905 | 0.088294 | 0.096906 | 9 | -0.00683 |
Figure 3. SITC 1-Digit Contributions to the Aggregate Share Decline (Percentage Points)
Data for Figure 3
| Corn | -0.00322 |
|---|---|
| Motor vehicle parts and accessories | -0.00253 |
| Soybeans | -0.00218 |
| Lignite | -0.00198 |
| Digital processing units | -0.00176 |
| Oscilloscopes & spectrum analyzers | -0.00116 |
| Office and data processing machines | -0.00107 |
| Aircraft parts | -0.00105 |
| Cotton, not carded or combed | -0.0009 |
| Fuel oils | -0.0009 |
Figure 4. Top 10 4-Digit Contributions to the Aggregate Share Decline (Percentage Points)
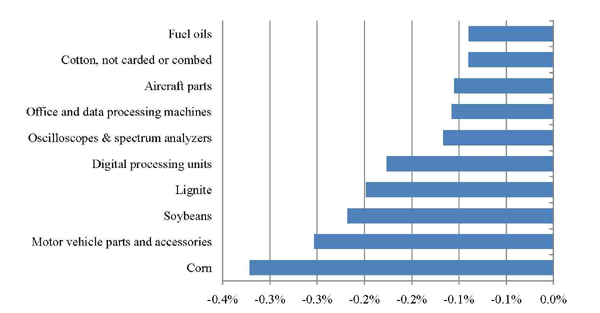
Figure 5. Commodity and Competitiveness Contributions to the Aggregate Share Decline (Percentage Points)
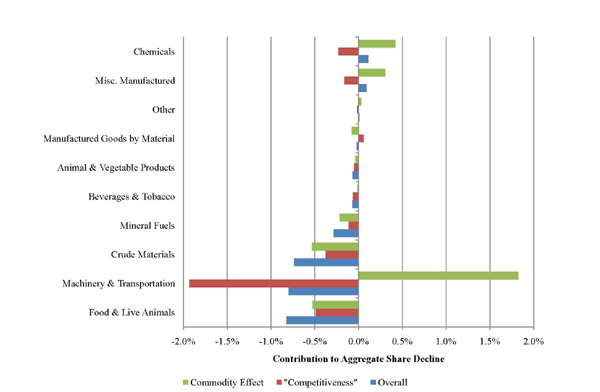
Figure 6a. Export and GDP Shares
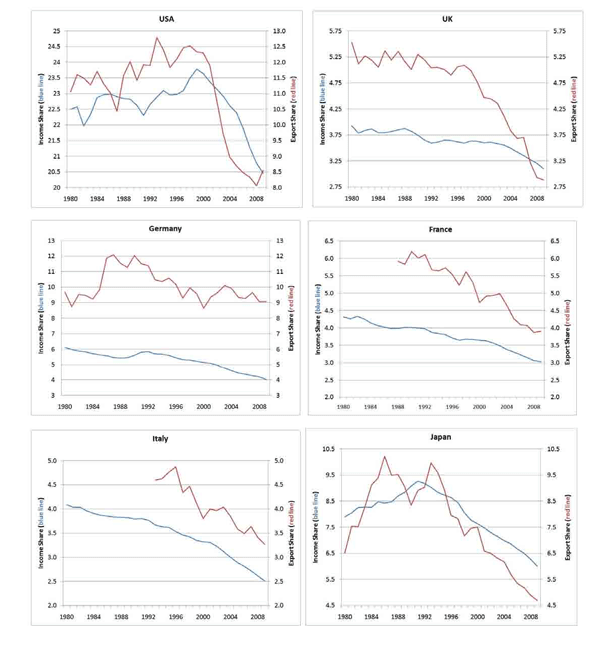
Figure 6b. Export and GDP Shares (cont'd)
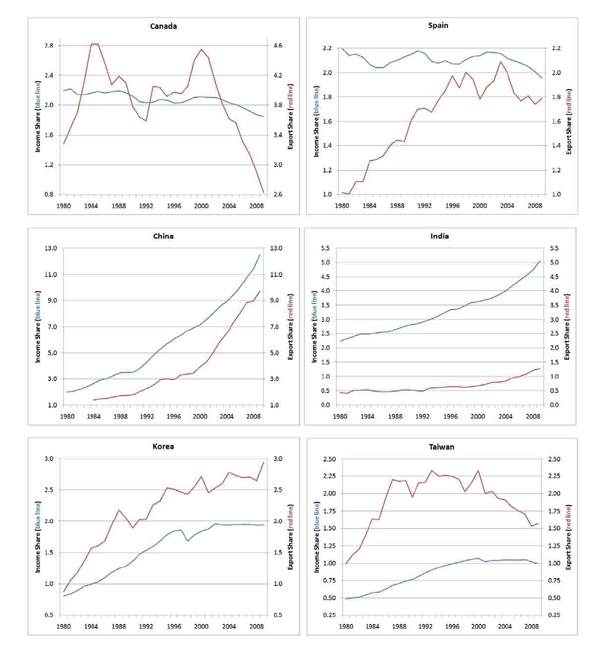
Figure 7. Predicted adn Actual Market Share Indices
Data for Figure 7
| year | gravity model | market share |
|---|---|---|
| 1980 | 100 | 100 |
| 1981 | 100.21722 | 102.10952 |
| 1982 | 99.51950771 | 100.4635452 |
| 1983 | 101.7977182 | 98.66312793 |
| 1984 | 107.1954404 | 90.57168588 |
| 1985 | 106.3671627 | 87.49859763 |
| 1986 | 104.0471353 | 80.88658236 |
| 1987 | 102.022222 | 78.71434892 |
| 1988 | 99.37482698 | 81.02090762 |
| 1989 | 97.39483324 | 83.07720205 |
| 1990 | 95.70273437 | 80.27475048 |
| 1991 | 92.19158288 | 83.45226593 |
| 1992 | 90.1492443 | 83.09862861 |
| 1993 | 89.23541043 | 85.25630943 |
| 1994 | 88.12575025 | 83.54162601 |
| 1995 | 86.33296405 | 81.61488043 |
| 1996 | 85.61549396 | 82.69111953 |
| 1997 | 85.02316316 | 82.80315773 |
| 1998 | 84.92405166 | 80.99820622 |
| 1999 | 84.22009072 | 79.00458927 |
| 2000 | 76.83763549 | 74.17610529 |
| 2001 | 75.82161144 | 71.86184047 |
| 2002 | 75.39027745 | 68.15747039 |
| 2003 | 74.67860831 | 63.70143721 |
| 2004 | 74.83270015 | 60.84569541 |
Figure 8. Reduced Form Measure of Competitiveness, Change Between Early and Late Sample (Percentage Points)

Data for Figure 8
| UN Comtrade (SITC) | Chelem (ISIC) | |
|---|---|---|
| Indonesia | 0.50498653 | 0.71561738 |
| China | 0.4647502 | 0.68373595 |
| India | 0.39043716 | 0.56362496 |
| Turkey | 0.3676972 | 0.6390655 |
| Mexico | 0.36051769 | 0.72107074 |
| Saudi Arabia | 0.30919203 | 0.19683399 |
| Spain | 0.18772961 | 0.01071516 |
| Italy | 0.14607755 | 0.0618769 |
| South Africa | 0.13659886 | 0.86433848 |
| Rest of World | 0.07967903 | 0.00450146 |
| Australia | 0.04503912 | 0.05880159 |
| France | 0.02608082 | -0.17244206 |
| All | 0.0214243 | -0.02268058 |
| Other EU | 0.01706058 | -0.13606494 |
| Germany | 0.01055769 | -0.16091488 |
| Brazil | -0.05609352 | -0.12218161 |
| USA | -0.06091851 | -0.02762394 |
| Canada | -0.10314775 | -0.1176693 |
| Korea | -0.115841 | -0.46735922 |
| UK | -0.12033621 | -0.36014848 |
| Argentina | -0.1203525 | -0.13767552 |
| Singapore | -0.29100903 | -0.50380707 |
| Japan | -0.29132421 | -0.55357127 |
| Taiwan | -0.2922583 | -0.49385896 |
| Hong Kong | -0.40803643 | -0.23891996 |
Figure 9. Structural Measure of Competitiveness, Change Between Early and Late Sample (Index)
Data for Figure 9
| country | avg |
|---|---|
| China | 80.55 |
| Australia | 67.09 |
| Canada | 57.44 |
| Mexico | 56.55 |
| Indonesia | 50.61 |
| Taiwan | 47.24 |
| Korea | 46.75 |
| India | 38.86 |
| Austria | 38.77 |
| Spain | 27.72 |
| UK | 20.05 |
| Finland | 0.48 |
| Turkey | 0.43 |
| Greece | -0.03 |
| South Africa | -2.25 |
| Ireland | -2.69 |
| Denmark | -4.47 |
| USA | -5.58 |
| Sweden | -7.64 |
| Germany | -9.54 |
| Argentina | -9.6 |
| France | -18.32 |
| Portugal | -33.16 |
| Japan | -50.16 |
| Italy | -65.52 |
Table 1. U.S. Export Share in Machinery and Equipment Categories
| SITC | Description | U.S. Export Share: 1984 | U.S. Export Share: 1989 | U.S. Export Share: 1994 | U.S. Export Share: 1999 | U.S. Export Share: 2004 |
|---|---|---|---|---|---|---|
| 71 | POWER GENERATING MACHINERY AND EQUIPMENT | 0.25 | 0.23 | 0.23 | 0.26 | 0.20 |
| 72 | MACHINERY SPECIALIZED FOR PARTICULAR INDUSTRIES | 0.16 | 0.12 | 0.14 | 0.16 | 0.13 |
| 73 | METALWORKING MACHINERY | 0.10 | 0.10 | 0.13 | 0.14 | 0.12 |
| 74 | GENERAL INDUSTRIAL MACHINERY AND MACHINE PARTS | 0.17 | 0.15 | 0.17 | 0.18 | 0.12 |
| 75 | OFFICE MACHINES AND AUTOMATIC DATA PROCESSING MACHINES | 0.33 | 0.24 | 0.20 | 0.14 | 0.09 |
| 76 | TELECOMMUNICATIONS AND SOUND EQUIPMENT | 0.08 | 0.08 | 0.11 | 0.13 | 0.06 |
| 77 | ELECTRICAL MACHINERY AND ELECTRICAL PARTS THEREOF | 0.20 | 0.16 | 0.17 | 0.18 | 0.12 |
| 78 | ROAD VEHICLES | 0.14 | 0.10 | 0.11 | 0.10 | 0.08 |
| 79 | TRANSPORT EQUIPMENT | 0.21 | 0.30 | 0.29 | 0.32 | 0.24 |
Table 2. Gravity Regression Specifications
| Dependent | (i): Export share | (ii): Export share | (iii): Export share | (iv): Export sales | (v): Export sales | (vi): Export share |
|---|---|---|---|---|---|---|
| D | Exporter GDP share | Exporter GDP share | Exporter-year FE | Exporter GDP, Importer GDP | Exporter GDP, Importer GDP | Exporter GDP share |
| ρ | Country-pair FE, NAFTA, EMU | Country-pair FE, NAFTA, EMU | Country-pair FE, NAFTA, EMU | Country-pair FE, NAFTA, EMU | Distance, language, border, NAFTA, EMU | Country-pair FE, NAFTA, EMU |
| n | Year FE | Year FE | Year FE | Year FE | Year FE | Year FE |
| Sample | Full | Balanced | Full | Full | Full | Full |
| Data | SITC-4 | SITC-4 | SITC-4 | SITC-4 | SITC-4 | ISIC-2 |
Table 3. Estimates of Control Variables in the Gravity Regression
| Dependent var. ---> | Export Share (i) | Export Share (ii) | Export Share (iii) | Export Volume (iv) | Export Volume (v) | Memo: ISIC Industries |
|---|---|---|---|---|---|---|
| Exporter GDP share | 0.430** (0.001) | 0.644** (0.005) | 0.890** 0.008 | |||
| Exporter GDP | 0.682** (0.005) | 0.345** (0.001) | ||||
| Importer GDP | 0.522** (0.004) | 0.478** (0.001) | ||||
| NAFTA | 0.484** (0.011) | 0.424** (0.011) | 1.486** (0.010) | 0.922** (0.012) | 1.281** (0.009) | 1.192** 0.055 |
| EMU | 0.417** (0.004) | 0.305** (0.005) | 0.074** (0.005) | 0.332** (0.005) | 0.461** (0.004) | 0.191** 0.011 |
| Distance | -0.263** (0.001) | |||||
| Common Language | 0.142** (0.002) | |||||
| Common Border | 0.409** (0.002) | |||||
| Exporter-Importer FE | Yes | Yes | No | Yes | No | Yes |
| Exporter-Year FE | No | No | Yes | No | No | No |
| Year-FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Balanced panel | No | Yes | No | No | No | No |
| N | 11,638,401 | 4,526,163 | 12,672,551 | 11,253,727 | 10,101,064 | 2,998,339 |
| R-squared | 0.40 | 0.44 | 0.20 | 0.25 | 0.20 | 0.60 |
| RMSE | 1.65 | 1.37 | 1.89 | 1.67 | 1.74 | 1.69 |
Table 4. Evolution of the Gravity Residual (Earlyl Sample to Late Sample)
| All SITC | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Indonesia | 50% | 29% | 9% | 17% | 36% | 71% | 36% | 57% | 91% | 48% |
| China | 46% | 26% | 5% | 27% | 7% | 9% | 21% | 45% | 65% | 64% |
| India | 39% | 33% | 18% | 16% | 41% | 49% | 66% | 49% | 9% | 44% |
| Turkey | 37% | 7% | 10% | 7% | -19% | 5% | -4% | 57% | 48% | 56% |
| Mexico | 36% | 22% | 62% | 6% | -17% | 0% | 24% | 37% | 53% | 47% |
| Saudi Arabia | 31% | 54% | 29% | 5% | 5% | 30% | 46% | 66% | -16% | 13% |
| Spain | 19% | 13% | 6% | 22% | 17% | 31% | 20% | 15% | 21% | 24% |
| Italy | 15% | 5% | 10% | 13% | -21% | 19% | 10% | 22% | 12% | 17% |
| South Africa | 14% | 3% | 40% | 8% | 50% | 4% | 11% | 8% | 31% | 11% |
| Rest of World | 8% | -2% | 6% | 4% | 22% | 2% | 4% | 11% | 11% | 11% |
| Australia | 5% | 5% | 27% | 3% | 2% | -7% | 3% | 2% | 4% | 10% |
| France | 3% | 2% | -10% | 2% | 15% | 3% | 2% | -2% | 7% | 2% |
| Other EU | 2% | 0% | 3% | 5% | 1% | 7% | 4% | -4% | 5% | 2% |
| Germany | 1% | 6% | 6% | 17% | -1% | -1% | -8% | -2% | 7% | -4% |
| Brazil | -6% | -7% | -6% | 18% | -40% | -20% | -5% | -3% | -9% | -13% |
| USA | -6% | -9% | -6% | -4% | -16% | 2% | -2% | -9% | -6% | -4% |
| Canada | -10% | -12% | 2% | -4% | -4% | 7% | -23% | -19% | -9% | 5% |
| Korea | -12% | -27% | -23% | -2% | 50% | -35% | 17% | -18% | 13% | -58% |
| UK | -12% | -8% | -1% | -1% | -19% | 17% | -21% | -13% | -11% | -11% |
| Argentina | -12% | 1% | 27% | -7% | 16% | 11% | 8% | -17% | -48% | -20% |
| Singapore | -29% | -37% | -3% | -42% | -33% | -47% | -6% | -42% | -22% | -34% |
| Japan | -29% | -49% | -23% | -31% | -10% | -53% | -9% | -44% | -20% | -42% |
| Taiwan | -29% | -100% | -15% | -25% | -32% | -29% | -10% | -23% | -14% | -57% |
| Hong Kong | -41% | -52% | -26% | -63% | -19% | -61% | -46% | -42% | -28% | -46% |
Appendix A: Short Description of the Reference Model
The theoretical background is the framework developed by Del Gatto et al. (2006), also used in Ottaviano et al. (2009). While the reader is redirected to those papers, and in particular to Corcos-DelGatto-Mion-Ottaviano (FEEM, 2010)18 for an extensive exposition, here we report a short description of the logic behind the model and the key equations for the application.
The model is a multi-country multi-sector version of Melitz and
Ottaviano (2008) encompassing S industries (with no inter-industry
linkages)19 active in ![]() countries, indexed
countries, indexed
![]() . Each country-industry is
endowed with given amounts of labor
. Each country-industry is
endowed with given amounts of labor ![]() and
capital
and
capital ![]() (factors are geographically immobile)
and the output of each industry is horizontally differentiated in a
large set of varieties.
(factors are geographically immobile)
and the output of each industry is horizontally differentiated in a
large set of varieties.
Consumers maximize a quasi-linear utility function with
quadratic sub-utility, as in Ottaviano et al. (2002). Under this
hypothesis, the demand of a generic variety in a given country is
positive only provided that its selling price is lower than a
certain (cutoff) level
![]() . This level is higher when:
consumers like the differentiated good a lot, varieties are very
differentiated, the average price is high, the number of competing
varieties is small.
. This level is higher when:
consumers like the differentiated good a lot, varieties are very
differentiated, the average price is high, the number of competing
varieties is small.
Firms compete in a monopolistic market and each variety is supplied by one and only one firm. Each firm is negligible to the market and does not compete directly with the other firms. However, given the demand structure, firms interact indirectly through an aggregate demand effect, as the total output of the industry has an influence on firms' profit.
Firms in a given sector share the same (Cobb-Douglas) technology
but are heterogeneous in terms of Unit Input Requirement (UIR)
![]() , defined as inverse 'total factor
productivity' (tfp) (i.e.
, defined as inverse 'total factor
productivity' (tfp) (i.e.
![]() ).
). ![]() is used
to identify the firm. Accordingly, the marginal cost faced by a
generic firm
is used
to identify the firm. Accordingly, the marginal cost faced by a
generic firm ![]() active in country
active in country ![]() and sector
and sector ![]() is:
is:
| (12) |
where
![]() , with
, with
![]() and
and
![]() denoting input
denoting input ![]() 's cost and share (in country
's cost and share (in country ![]() - sector
- sector
![]() ) respectively, and
) respectively, and
![]() (i.e. capital,
labour, and intermediates) and
(i.e. capital,
labour, and intermediates) and
![]() .
. ![]() is the bundle of parameters associated with the
Cobb-Douglas.20
is the bundle of parameters associated with the
Cobb-Douglas.20
National markets are segmented but firms can export and, as
production faces constant returns to scale, they independently
maximize the profits earned in different destination countries.
Exporting firms incur a per-unit trade cost, encompassing not only
carriage in a strict sense, but all those "impediments to trade"
whose amount is related to the quantity exported. For each
delivered unit from country ![]() to country
to country
![]() ,
,
![]() units have to be shipped.
Moreover, we also allow for costly trade within a country with
units have to be shipped.
Moreover, we also allow for costly trade within a country with
![]() .
.
Firm heterogeneity is modeled as follows. In order to enter the
market, each firm has to make an irreversible investment in terms
of labor and capital. This "sunk cost of entry" amounts to
![]() . Only once this
cost has been payed, and production started, a firm is allowed to
observe its own marginal cost
. Only once this
cost has been payed, and production started, a firm is allowed to
observe its own marginal cost ![]() . This is
modeled as the outcome of a draw from a common and known Pareto
distribution
. This is
modeled as the outcome of a draw from a common and known Pareto
distribution
![]() ,
with support
,
with support
![]() varying across
countries.21
varying across
countries.21
Only those firms whose cost draw is good enough to enable them
to sell to market ![]() at a price below the price
cutoff
at a price below the price
cutoff
![]() earn non-negative profits and
can afford to serve that market. Let
earn non-negative profits and
can afford to serve that market. Let
![]() denote the marginal cost
inclusive of trade frictions faced by a producer in country
denote the marginal cost
inclusive of trade frictions faced by a producer in country
![]() -industry
-industry ![]() that is just
indifferent between serving its local market or not. Then, by
definition
that is just
indifferent between serving its local market or not. Then, by
definition
![]() . A firm, wherever
located, can serve market
. A firm, wherever
located, can serve market ![]() only provided that
its delivered cost does not exceed
only provided that
its delivered cost does not exceed
![]() . In other words: firm
. In other words: firm ![]() producing in country
producing in country ![]() is able to target
market
is able to target
market ![]() when
when
![]() , it is
not able to target market
, it is
not able to target market ![]() when
when
![]() , it is
indifferent between serving or not market
, it is
indifferent between serving or not market ![]() when
when
![]() . Thus,
. Thus,
![]() measures the 'cutoff cost' in
country
measures the 'cutoff cost' in
country ![]() -industry
-industry ![]() .
.
The analytical solution in terms of the
![]() equilibrium cost cutoffs is:
equilibrium cost cutoffs is:
 |
(13) |
where:
-
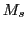 is the
is the 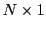 vector of the equilibrium cost cutoffs in industry
vector of the equilibrium cost cutoffs in industry 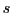 ,
whose
,
whose 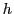 -th element
-th element
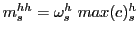 denotes the maximum possible marginal cost for a generic (domestic)
firm active in industry
denotes the maximum possible marginal cost for a generic (domestic)
firm active in industry 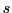 , producing and selling in
country
, producing and selling in
country 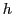 ;
; -
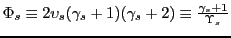 is a (scalar) positive bundling parameter22;
is a (scalar) positive bundling parameter22; -
 is a
is a
 'trade freeness matrix' whose
element in row
'trade freeness matrix' whose
element in row  and column
and column 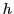 is
is
![$ \rho_{s}^{lh}\equiv\left( \tau_{s}^{lh}\right) ^{-\gamma_{s} }\in(0,1]$](img226.gif) .
.
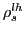 denotes the degree of trade
freeness between country
denotes the degree of trade
freeness between country 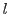 and country
and country 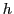 ,
;
,
; - D is a
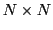 diagonal matrix with population
along its diagonal and zero elsewhere. In a wide sense, population
can be thought of as a measure for the size of the domestic
market;
diagonal matrix with population
along its diagonal and zero elsewhere. In a wide sense, population
can be thought of as a measure for the size of the domestic
market; -
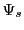 is a
is a 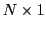 vector with
vector with 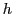 -th generic element
-th generic element
 , where
, where 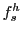 and
and
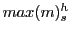 denote respectively the fixed
cost of entry and the upper bound of the (exogenous) marginal cost
distribution in country
denote respectively the fixed
cost of entry and the upper bound of the (exogenous) marginal cost
distribution in country 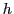 -industry
-industry 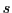 (exogenous cost cutoff). As presently discussed,
(exogenous cost cutoff). As presently discussed,
 is an inverse measure for the
'exogenous competitiveness' of country
is an inverse measure for the
'exogenous competitiveness' of country 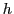 in a given
industry
in a given
industry 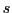 ;
; -
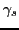 is the shape parameter of the
marginal cost distribution in sector
is the shape parameter of the
marginal cost distribution in sector 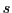 , with higher
values denoting a distribution which is more skewed towards high
cost (less productive) firms.
, with higher
values denoting a distribution which is more skewed towards high
cost (less productive) firms.
Each row of (13) states, for each country
in a given sector, the marginal cost above which a firm is not
productive enough to serve the domestic market from therein and,
since
![]() ,
from anywhere.23
,
from anywhere.23
Overall (
![]() ) and producer (
) and producer (
![]() ) competitiveness. By Cramer's rule, the
) competitiveness. By Cramer's rule, the ![]() -th generic element (i.e.
the cutoff level in country
-th generic element (i.e.
the cutoff level in country ![]() -industry
-industry
![]() ) of
) of
![]() can be expressed as
can be expressed as
![$\displaystyle m_{s}^{hh}=\left[ \frac{\Phi_{s}}{D^{h}} \frac{\sum_{l=1}^{M}\left\vert R_{s}^{lh}\right\vert \psi_{s}^{l}} {\left\vert \bm{P_{s}} \right\vert }\right] ^{\frac{1}{\gamma_{s} +2}}$](img251.gif) |
(14) |
where
![]() is the
determinant of the trade freeness matrix in sector
is the
determinant of the trade freeness matrix in sector ![]() and
and
![]() is the
corresponding cofactor.
is the
corresponding cofactor.
Equation (14) entails a
relationship between
![]() and
and
![]() , basically two measures for the
"competitiveness" of a country. In this relationship:
, basically two measures for the
"competitiveness" of a country. In this relationship:
-
 is endogenously determined
by a selection process in which the degree of 'remoteness', through
the term
is endogenously determined
by a selection process in which the degree of 'remoteness', through
the term
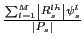 , and the size of the domestic market, through
, and the size of the domestic market, through 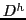 , play a key role.
, play a key role. -
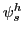 captures the exogenous
ability of country
captures the exogenous
ability of country 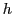 to generate low cost firms
in industry
to generate low cost firms
in industry 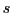 , abstracting from its market size and
the degree of remoteness in that sector: low entry costs (low
, abstracting from its market size and
the degree of remoteness in that sector: low entry costs (low
 ), low factor prices [low
), low factor prices [low
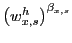 ],
and low probability of inefficient draws by entrants [i.e. low
],
and low probability of inefficient draws by entrants [i.e. low
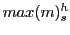 ] foster the creation of low
cost firms.
] foster the creation of low
cost firms.
From a practical point of view, (14) can be used to see how much of the actual
competitiveness of a country, measured in terms of marginal costs
(i.e.
![]() ), can be traced back to its
exogenous competitiveness, expressed in terms of a mixture of
"traditional" competitive advantages (i.e. factor prices and
technology) and entry costs. To highlight this relationship, we
refer, for each sector
), can be traced back to its
exogenous competitiveness, expressed in terms of a mixture of
"traditional" competitive advantages (i.e. factor prices and
technology) and entry costs. To highlight this relationship, we
refer, for each sector ![]() , to
, to
![]() and
and
![]() as respectively
"overall" and "producer" competitiveness of country
as respectively
"overall" and "producer" competitiveness of country
![]() (OC and PC respectively), with
(OC and PC respectively), with
![]() and
and
![]() denoting (once ordered)
the corresponding country-rankings.
denoting (once ordered)
the corresponding country-rankings.
Appendix B. Alternative Gravity Specifications
Table B1. Percent Change of the Gravity Regression Residual From the Early Period (1980-1992) to the Late Period (1993-2004) - Specification (ii)
| All SITC | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Change in Residual: China | 45% | 24% | 6% | 19% | -30% | -5% | 10% | 41% | 68% | 83% |
| # of Observations: China | 4,803 | 502 | 43 | 294 | 44 | 18 | 752 | 1,457 | 529 | 1,160 |
| Change in Residual: India | 39% | 31% | 35% | 11% | 3% | 76% | 48% | 42% | 12% | 61% |
| # of Observations: India | 2,335 | 321 | 17 | 194 | 2 | 7 | 219 | 754 | 293 | 523 |
| Change in Residual: Turkey | 38% | 12% | 37% | -13% | -10% | -7% | 17% | 51% | 68% | 78% |
| # of Observations: Turkey | 1,228 | 337 | 25 | 121 | 2 | 8 | 68 | 330 | 70 | 265 |
| Change in Residual: Indonesia | 38% | 11% | 16% | 9% | -7% | 69% | 23% | 51% | 29% | 77% |
| # of Observations: Indonesia | 1,010 | 227 | 23 | 141 | 18 | 34 | 76 | 246 | 21 | 221 |
| Change in Residual: Mexico | 32% | 12% | 63% | 6% | -45% | -30% | 21% | 31% | 66% | 34% |
| # of Observations: Mexico | 1,227 | 144 | 32 | 106 | 15 | 6 | 232 | 252 | 265 | 173 |
| Change in Residual: Spain | 27% | 20% | 2% | 26% | 5% | 11% | 34% | 30% | 27% | 24% |
| # of Observations: Spain | 7,007 | 596 | 104 | 317 | 62 | 57 | 1,073 | 2,186 | 1,597 | 1,006 |
| Change in Residual: Italy | 17% | 4% | 19% | 6% | -15% | 32% | 14% | 25% | 16% | 16% |
| # of Observations: Italy | 15,316 | 798 | 125 | 472 | 107 | 57 | 2,073 | 4,520 | 4,602 | 2,546 |
| Change in Residual: Australia | 6% | 3% | 25% | 10% | 2% | -7% | -1% | 1% | 12% | 12% |
| # of Observations: Australia | 3,180 | 656 | 55 | 336 | 49 | 32 | 331 | 692 | 623 | 393 |
| Change in Residual: South Africa | 4% | -7% | 91% | -4% | 47% | -52% | -20% | -11% | 57% | 43% |
| # of Observations: South Africa | 1,166 | 204 | 15 | 231 | 25 | 3 | 108 | 358 | 123 | 98 |
| Change in Residual: Other EU | 4% | 0% | -2% | 2% | -3% | 5% | 8% | 0% | 6% | 8% |
| # of Observations: Other EU | 45,610 | 3,920 | 557 | 2,156 | 457 | 330 | 6,939 | 12,450 | 12,059 | 6,677 |
| Change in Residual: Saudi Arabia | 4% | 53% | 92% | -16% | -23% | . | 27% | 74% | -27% | 8% |
| # of Observations: Saudi Arabia | 179 | 7 | 2 | 23 | 41 | 0 | 47 | 12 | 31 | 15 |
| Change in Residual: Rest of World | 3% | -6% | 0% | -2% | 11% | 1% | -3% | 8% | 8% | 9% |
| # of Observations: Rest of World | 29,912 | 5,154 | 417 | 2,612 | 371 | 211 | 3,512 | 6,783 | 5,018 | 5,730 |
| Change in Residual: France | 3% | 7% | -16% | -3% | 20% | 1% | 4% | 0% | 6% | 3% |
| # of Observations: France | 17,937 | 1,476 | 303 | 709 | 152 | 101 | 2,878 | 4,755 | 4,762 | 2,791 |
| Change in Residual: Canada | 2% | -2% | -5% | 3% | 34% | 11% | -10% | -9% | 5% | 27% |
| # of Observations: Canada | 3,773 | 448 | 37 | 420 | 34 | 18 | 433 | 840 | 1,044 | 480 |
| Change in Residual: Brazil | 1% | -8% | -17% | 23% | -30% | -7% | 2% | 2% | 4% | -11% |
| # of Observations: Brazil | 3,467 | 415 | 58 | 241 | 17 | 45 | 459 | 1,138 | 767 | 320 |
| Change in Residual: Argentina | -5% | -1% | 46% | -13% | 48% | 6% | 11% | -13% | -34% | -23% |
| # of Observations: Argentina | 1,155 | 320 | 27 | 107 | 17 | 37 | 198 | 236 | 128 | 82 |
| Change in Residual: USA | -6% | -4% | 3% | -8% | -5% | -5% | -3% | -7% | -11% | 0% |
| # of Observations: USA | 20,678 | 1,709 | 238 | 1,192 | 256 | 166 | 3,212 | 4,663 | 6,239 | 2,906 |
| Change in Residual: Germany | -7% | 0% | 0% | 8% | -5% | -10% | -16% | -7% | -4% | -8% |
| # of Observations: Germany | 21,815 | 1,277 | 175 | 947 | 232 | 187 | 4,004 | 5,808 | 6,169 | 3,000 |
| Change in Residual: UK | -9% | -5% | 2% | 3% | -25% | 28% | -17% | -9% | -10% | -6% |
| # of Observations: UK | 18,277 | 1,187 | 291 | 675 | 207 | 76 | 3,045 | 4,828 | 5,113 | 2,834 |
| Change in Residual: Japan | -25% | -37% | -5% | -28% | 6% | -33% | 3% | -38% | -20% | -36% |
| # of Observations: Japan | 13,711 | 306 | 55 | 358 | 79 | 36 | 1,849 | 3,601 | 5,205 | 2,192 |
| Change in Residual: Singapore | -27% | -28% | -18% | -42% | -2% | -54% | -12% | -42% | -19% | -31% |
| # of Observations: Singapore | 3,950 | 330 | 42 | 204 | 56 | 69 | 466 | 807 | 1,232 | 720 |
| Change in Residual: Korea | -28% | -39% | 30% | -17% | 55% | -144% | 18% | -25% | -4% | -75% |
| # of Observations: Korea | 4,047 | 121 | 10 | 91 | 10 | 1 | 415 | 1,460 | 947 | 988 |
| Change in Residual: Taiwan | -38% | -95% | -14% | -20% | -2% | -3% | -22% | -30% | -22% | -65% |
| # of Observations: Taiwan | 4,961 | 193 | 13 | 137 | 10 | 4 | 409 | 1,521 | 1,466 | 1,204 |
| Change in Residual: Hong Kong | -41% | -44% | -34% | -57% | 15% | -105% | -47% | -46% | -22% | -47% |
| # of Observations: Hong Kong | 3,595 | 160 | 14 | 67 | 7 | 8 | 165 | 881 | 825 | 1,460 |
Table B2. Percent Change of the Gravity Regression Residual From the Early Period (1980-1992) to the Late Period (1993-2004) - Specification (iii)
| All SITC | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Change in Residual: South Africa | 14% | 12% | 14% | 8% | 18% | 13% | 18% | 16% | 15% | 8% |
| # of Observations: South Africa | 7,179 | 903 | 130 | 768 | 117 | 38 | 981 | 2,193 | 1,262 | 737 |
| Change in Residual: Indonesia | 9% | 3% | 8% | 8% | 19% | 5% | 7% | 12% | 19% | 4% |
| # of Observations: Indonesia | 6,688 | 717 | 72 | 535 | 90 | 155 | 683 | 2,116 | 768 | 1,499 |
| Change in Residual: Mexico | 9% | 3% | 15% | 5% | 3% | 12% | 11% | 8% | 11% | 7% |
| # of Observations: Mexico | 6,748 | 492 | 109 | 461 | 93 | 29 | 1,367 | 1,618 | 1,597 | 948 |
| Change in Residual: Saudi Arabia | 8% | -8% | -28% | 12% | -1% | 22% | 17% | 12% | 1% | 7% |
| # of Observations: Saudi Arabia | 2,156 | 194 | 11 | 161 | 165 | 18 | 527 | 520 | 329 | 205 |
| Change in Residual: Turkey | 6% | -3% | 1% | 10% | 11% | -6% | 11% | 8% | 15% | -2% |
| # of Observations: Turkey | 7,665 | 1,113 | 103 | 547 | 55 | 62 | 729 | 2,531 | 1,277 | 1,211 |
| Change in Residual: Rest of World | 6% | 3% | 9% | 6% | 7% | 8% | 7% | 5% | 10% | 5% |
| # of Observations: Rest of World | 181,193 | 21,917 | 2,353 | 13,804 | 3,044 | 1,485 | 22,931 | 44,440 | 38,135 | 31,393 |
| Change in Residual: Hong Kong | 6% | 1% | 19% | 5% | 16% | 10% | 11% | 6% | 8% | 2% |
| # of Observations: Hong Kong | 11,992 | 557 | 64 | 396 | 42 | 41 | 1,023 | 3,273 | 2,982 | 3,537 |
| Change in Residual: India | 6% | 3% | 7% | 5% | 10% | 4% | 8% | 5% | 12% | -2% |
| # of Observations: India | 11,476 | 1,018 | 110 | 739 | 36 | 82 | 1,597 | 3,679 | 2,255 | 1,885 |
| Change in Residual: Singapore | 5% | -4% | 16% | 8% | -6% | -1% | 5% | 3% | 8% | 6% |
| # of Observations: Singapore | 14,478 | 1,156 | 135 | 659 | 244 | 350 | 1,691 | 3,096 | 4,598 | 2,424 |
| Change in Residual: Argentina | 4% | 1% | 6% | 7% | -22% | 1% | 4% | 3% | 6% | 7% |
| # of Observations: Argentina | 5,515 | 1,081 | 108 | 455 | 90 | 186 | 827 | 1,228 | 970 | 529 |
| Change in Residual: Korea | 4% | 3% | -15% | 5% | -5% | 31% | -2% | -1% | 8% | 8% |
| # of Observations: Korea | 15,442 | 506 | 72 | 420 | 113 | 22 | 1,739 | 5,110 | 4,579 | 2,841 |
| Change in Residual: Australia | 3% | -1% | -6% | 1% | 1% | -4% | 5% | 3% | 5% | 3% |
| # of Observations: Australia | 11,242 | 1,764 | 147 | 1,024 | 199 | 100 | 1,213 | 2,510 | 2,729 | 1,441 |
| Change in Residual: All | 2% | -1% | 4% | 3% | 2% | 4% | 2% | 1% | 4% | 0% |
| # of Observations: All | 690,889 | 63,144 | 8,143 | 40,081 | 8,996 | 6,156 | 93,134 | 180,759 | 177,818 | 107,995 |
| Change in Residual: Other EU | 1% | -2% | 1% | 2% | 2% | 2% | 1% | -1% | 3% | -1% |
| # of Observations: Other EU | 127,706 | 10,737 | 1,550 | 6,073 | 1,520 | 1,282 | 18,771 | 33,177 | 36,519 | 17,294 |
| Change in Residual: Brazil | 0% | 0% | 3% | -2% | -3% | 4% | 0% | -1% | 2% | 3% |
| # of Observations: Brazil | 13,557 | 1,312 | 206 | 833 | 109 | 204 | 1,865 | 4,160 | 3,361 | 1,442 |
| Change in Residual: Taiwan | 0% | -6% | 6% | 2% | -8% | 1% | 1% | -1% | 1% | 1% |
| # of Observations: Taiwan | 14,543 | 590 | 35 | 554 | 87 | 48 | 1,598 | 4,347 | 4,253 | 2,983 |
| Change in Residual: All | 0% | -2% | 1% | 0% | -1% | 0% | 0% | 0% | 0% | 0% |
| # of Observations: All | 230,339 | 20,808 | 2,678 | 12,151 | 2,270 | 1,511 | 32,963 | 60,578 | 59,128 | 37,784 |
| Change in Residual: Japan | 0% | -4% | -10% | 1% | -8% | 7% | -5% | -1% | 2% | 1% |
| # of Observations: Japan | 29,191 | 887 | 130 | 990 | 245 | 133 | 3,913 | 7,772 | 10,635 | 4,320 |
| Change in Residual: USA | -1% | -3% | 3% | 3% | 1% | 6% | -2% | -1% | 0% | -4% |
| # of Observations: USA | 45,837 | 4,353 | 646 | 3,059 | 678 | 586 | 6,281 | 10,739 | 13,016 | 6,173 |
| Change in Residual: UK | -1% | -6% | -3% | -1% | -4% | 2% | 0% | -2% | 1% | -2% |
| # of Observations: UK | 40,583 | 2,850 | 621 | 1,887 | 530 | 337 | 6,332 | 10,534 | 11,376 | 5,902 |
| Canada | -1% | -5% | -2% | -4% | -11% | 4% | 1% | 0% | 0% | -7% |
| # of Observations: Canada | 15,341 | 1,624 | 127 | 1,158 | 146 | 104 | 1,764 | 3,564 | 4,673 | 2,026 |
| Change in Residual: France | -3% | -9% | 0% | 2% | -4% | 1% | -1% | -4% | -1% | -3% |
| # of Observations: France | 41,510 | 3,709 | 605 | 1,890 | 464 | 360 | 6,027 | 10,585 | 11,538 | 6,137 |
| Change in Residual: China | -3% | 3% | 0% | 3% | 18% | 9% | 4% | -3% | -1% | -14% |
| # of Observations: China | 20,356 | 1,469 | 153 | 1,100 | 242 | 97 | 2,697 | 6,126 | 4,377 | 4,030 |
| Change in Residual: Italy | -4% | -6% | -3% | 2% | -10% | -6% | -3% | -6% | -4% | -5% |
| # of Observations: Italy | 37,678 | 2,292 | 366 | 1,522 | 396 | 241 | 5,139 | 10,702 | 11,002 | 5,851 |
| Change in Residual: Spain | -4% | -10% | 1% | -1% | 5% | 6% | -6% | -9% | 1% | -1% |
| # of Observations: Spain | 22,813 | 1,903 | 290 | 1,046 | 291 | 196 | 3,439 | 6,739 | 5,587 | 3,187 |
Table B3. Percent Change of the Gravity Regression Residual From the Early Period (1980-1992) to the Late Period (1993-2004) - Specification (iv)
| All SITC | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Change in Residual: China | 48% | 31% | 7% | 17% | 18% | 1% | 26% | 49% | 58% | 69% |
| # of Observations: China | 16,841 | 1,228 | 127 | 925 | 187 | 92 | 2,107 | 5,204 | 3,531 | 3,384 |
| Change in Residual: Mexico | 31% | 26% | 53% | 7% | -24% | -21% | 15% | 30% | 48% | 43% |
| # of Observations: Mexico | 6,872 | 500 | 106 | 463 | 91 | 27 | 1,363 | 1,694 | 1,609 | 984 |
| Change in Residual: Spain | 18% | 21% | 16% | 16% | 1% | 12% | 18% | 14% | 18% | 27% |
| # of Observations: Spain | 23,001 | 1,881 | 287 | 1,057 | 275 | 190 | 3,384 | 6,888 | 5,621 | 3,284 |
| Change in Residual: Italy | 17% | 10% | 29% | 12% | -17% | -9% | 8% | 27% | 12% | 25% |
| # of Observations: Italy | 36,339 | 2,214 | 344 | 1,553 | 380 | 257 | 4,893 | 10,444 | 10,443 | 5,643 |
| Change in Residual: Belgium | 12% | 9% | 38% | 16% | 2% | 7% | 21% | 2% | 15% | 21% |
| # of Observations: Belgium | 25,062 | 1,949 | 243 | 1,229 | 377 | 265 | 4,331 | 7,180 | 6,337 | 2,950 |
| Change in Residual: France | 3% | 1% | -4% | 0% | 0% | -9% | 2% | 1% | 7% | 3% |
| # of Observations: France | 39,142 | 3,408 | 525 | 1,912 | 442 | 357 | 5,651 | 10,183 | 10,626 | 5,845 |
| Change in Residual: Rest of World | 3% | -1% | -2% | 5% | 12% | 11% | 0% | 6% | 2% | 2% |
| # of Observations: Rest of World | 214,349 | 27,861 | 2,895 | 16,466 | 3,047 | 2,071 | 23,715 | 56,116 | 43,358 | 36,870 |
| Change in Residual: USA | 2% | -4% | -12% | -3% | -7% | 4% | 1% | -3% | 9% | 5% |
| # of Observations: USA | 41,024 | 3,859 | 592 | 2,771 | 571 | 585 | 5,456 | 9,836 | 11,444 | 5,658 |
| Change in Residual: All | 0% | -3% | 0% | 1% | 1% | 0% | -1% | -1% | 2% | -2% |
| # of Observations: All | 622,628 | 56,551 | 7,112 | 36,199 | 7,559 | 5,704 | 80,308 | 166,556 | 158,213 | 100,215 |
| Change in Residual: Netherlands | -1% | 2% | 0% | 7% | -28% | -5% | -10% | -7% | 6% | 6% |
| # of Observations: Netherlands | 29,022 | 3,179 | 466 | 1,559 | 482 | 597 | 4,976 | 6,914 | 7,260 | 3,438 |
| Change in Residual: Sweden | -3% | 8% | 5% | -11% | 28% | 28% | 0% | -9% | -5% | 4% |
| # of Observations: Sweden | 17,535 | 732 | 101 | 793 | 154 | 116 | 1,931 | 4,938 | 6,293 | 2,374 |
| Change in Residual: Austria | -11% | -10% | 15% | -11% | 4% | 23% | -21% | -15% | -1% | -18% |
| # of Observations: Austrai | 15,782 | 739 | 128 | 617 | 89 | 32 | 1,823 | 4,822 | 4,860 | 2,589 |
| Change in Residual: Korea | -11% | -28% | -48% | 3% | 59% | -35% | 16% | -15% | 12% | -57% |
| # of Observations: Korea | 14,841 | 478 | 64 | 436 | 107 | 22 | 1,634 | 4,947 | 4,320 | 2,798 |
| Change in Residual: Switzerland | -11% | -26% | -11% | -14% | 9% | -43% | -19% | -16% | -3% | -6% |
| # of Observations: Switzerland | 19,748 | 964 | 213 | 639 | 123 | 50 | 3,578 | 4,872 | 5,971 | 3,245 |
| Change in Residual: UK | -13% | -10% | -3% | -6% | -15% | 5% | -21% | -14% | -11% | -12% |
| # of Observations: UK | 39,904 | 2,817 | 564 | 2,006 | 530 | 391 | 6,107 | 10,533 | 10,857 | 5,871 |
| Change in Residual: Canada | -19% | -14% | -16% | -8% | -4% | -5% | -36% | -32% | -14% | -10% |
| # of Observations: Canada | 15,718 | 1,569 | 125 | 1,131 | 148 | 103 | 1,772 | 3,773 | 4,782 | 2,169 |
| Change in Residual: Japan | -20% | -40% | -17% | -11% | 0% | -29% | 4% | -32% | -16% | -34% |
| # of Observations: Japan | 27,744 | 884 | 117 | 1,013 | 233 | 145 | 3,663 | 7,494 | 9,772 | 4,274 |
| Change in Residual: Singapore | -26% | -29% | -11% | -21% | -39% | -45% | -3% | -40% | -16% | -36% |
| # of Observations: Singapore | 12,794 | 1,059 | 120 | 620 | 196 | 314 | 1,336 | 2,826 | 3,980 | 2,240 |
| Change in Residual: Hong Kong | -35% | -48% | -27% | -55% | -8% | -26% | -52% | -34% | -24% | -35% |
| # of Observations: Hong Kong | 12,270 | 605 | 61 | 419 | 42 | 39 | 1,011 | 3,458 | 2,993 | 3,565 |
| Change in Residual: Taiwan | -37% | -95% | -49% | -26% | -20% | -10% | -21% | -31% | -24% | -62% |
| # of Observations: Taiwan | 14,640 | 625 | 34 | 590 | 85 | 51 | 1,577 | 4,434 | 4,156 | 3,034 |
Table B4. Percent Change of the Gravity Regression Residual From the Early Period (1980-1992) to the Late Period (1993-2004) - Specification (v)
| All SITC | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Change in Residual: China | 61% | 48% | 17% | 11% | 12% | 6% | 26% | 63% | 74% | 93% |
| # of Observations: China | 18,461 | 1,313 | 133 | 1,055 | 217 | 98 | 2,428 | 5,594 | 3,989 | 3,566 |
| Change in Residual: Mexico | 21% | 31% | 72% | -20% | -47% | -40% | 15% | 19% | 28% | 36% |
| # of Observations: Mexico | 6,751 | 504 | 107 | 459 | 88 | 25 | 1,324 | 1,644 | 1,592 | 972 |
| Change in Residual: Spain | 6% | 30% | 43% | 2% | -12% | 57% | 4% | 5% | -5% | 16% |
| # of Observations: Spain | 22,178 | 1,805 | 275 | 1,039 | 267 | 183 | 3,270 | 6,629 | 5,439 | 3,140 |
| Change in Residual: Rest of World | 1% | 12% | 26% | -6% | 4% | 26% | 4% | 4% | -8% | -3% |
| # of Observations: Rest of World | 207,430 | 26,969 | 2,697 | 16,052 | 2,880 | 2,037 | 23,261 | 54,220 | 42,659 | 34,740 |
| Change in Residual: Italy | 1% | 23% | 52% | -2% | -30% | 22% | -4% | 12% | -15% | 8% |
| # of Observations: Italy | 34,256 | 2,042 | 330 | 1,470 | 343 | 226 | 4,631 | 9,830 | 9,947 | 5,277 |
| Change in Residual: Belgium | -2% | 19% | 58% | 0% | -15% | 7% | 9% | -11% | -9% | 4% |
| # of Observations: Belgium | 24,799 | 1,909 | 243 | 1,226 | 385 | 264 | 4,286 | 7,123 | 6,279 | 2,889 |
| Change in Residual: All | -5% | 11% | 29% | -9% | -11% | 15% | -4% | -5% | -13% | -7% |
| # of Observations: All | 613,553 | 55,439 | 6,848 | 36,080 | 7,449 | 5,659 | 79,968 | 164,164 | 156,967 | 96,809 |
| Change in Residual: USA | -6% | 9% | 14% | -13% | -28% | 16% | -2% | -8% | -12% | -1% |
| # of Observations: USA | 43,270 | 4,084 | 591 | 3,060 | 645 | 618 | 5,909 | 10,462 | 11,924 | 5,717 |
| Change in Residual: Korea | -6% | -10% | -21% | -6% | 48% | -16% | 16% | -8% | 18% | -53% |
| # of Observations: Korea | 14,608 | 470 | 69 | 434 | 108 | 22 | 1,613 | 4,855 | 4,270 | 2,730 |
| Change in Residual: Sweden | -8% | 36% | 44% | -18% | 25% | 43% | 1% | -11% | -19% | -2% |
| # of Observations: Sweden | 17,348 | 731 | 103 | 799 | 154 | 116 | 1,941 | 4,860 | 6,235 | 2,306 |
| Change in Residual: France | -10% | 13% | 27% | -11% | -14% | 1% | -7% | -13% | -17% | -13% |
| # of Observations: France | 38,088 | 3,307 | 507 | 1,894 | 438 | 355 | 5,498 | 9,950 | 10,316 | 5,633 |
| Change in Residual: Netherlands | -11% | 12% | 29% | -2% | -39% | 3% | -19% | -17% | -15% | -8% |
| # of Observations: Netherlands | 28,499 | 3,105 | 453 | 1,533 | 480 | 595 | 4,867 | 6,802 | 7,168 | 3,349 |
| Change in Residual: Switzerland | -16% | 8% | 33% | -21% | 12% | -28% | -18% | -19% | -20% | -14% |
| # of Observations: Switzerland | 19,667 | 954 | 209 | 643 | 122 | 51 | 3,649 | 4,865 | 5,904 | 3,170 |
| Change in Residual: Singapore | -19% | -10% | 23% | -30% | -61% | -24% | 8% | -29% | -12% | -34% |
| # of Observations: Singapore | 12,981 | 1,052 | 111 | 632 | 193 | 304 | 1,448 | 2,872 | 4,054 | 2,218 |
| Change in Residual: UK | -20% | 13% | 32% | -10% | -28% | 23% | -29% | -19% | -31% | -20% |
| # of Observations: UK | 39,476 | 2,810 | 561 | 2,005 | 518 | 396 | 6,028 | 10,482 | 10,742 | 5,703 |
| Change in Residual: Austria | -24% | -2% | 54% | -23% | -10% | 10% | -26% | -26% | -24% | -34% |
| # of Observations: Austria | 15,024 | 678 | 121 | 589 | 81 | 26 | 1,719 | 4,616 | 4,651 | 2,459 |
| Change in Residual: Canada | -26% | -1% | 19% | -24% | -28% | -14% | -29% | -33% | -33% | -17% |
| # of Observations: Canada | 15,643 | 1,550 | 123 | 1,130 | 153 | 103 | 1,771 | 3,767 | 4,780 | 2,125 |
| Change in Residual: Taiwan | -28% | -74% | -18% | -34% | -42% | -3% | -17% | -18% | -20% | -50% |
| # of Observations: Taiwan | 15,017 | 636 | 36 | 601 | 91 | 54 | 1,619 | 4,575 | 4,280 | 3,071 |
| Change in Residual: Japan | -32% | -20% | 13% | -18% | -8% | -19% | -1% | -41% | -36% | -45% |
| # of Observations: Japan | 27,598 | 909 | 122 | 1,017 | 239 | 146 | 3,654 | 7,496 | 9,689 | 4,180 |
| Change in Residual: Hong Kong | -34% | -28% | 6% | -68% | -34% | -41% | -48% | -30% | -31% | -35% |
| # of Observations: Hong Kong | 12,459 | 611 | 57 | 442 | 47 | 40 | 1,052 | 3,522 | 3,049 | 3,564 |
Table B5a. Structural Estimates of Revealed Overall Competitiveness, Change From Early to Late Period
| COUNTRY | All Sectors | Food | Beverages | Tobacco | Textiles | Apparel | Leather | Footwear | Wood | Furniture | Paper | Printing | Industrial Chemicals | Other Chemicals | Petroleum |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| China | 80.6 | 95.6 | 23.4 | 77.1 | 45.0 | 84.3 | 40.6 | - | 147.0 | 185.8 | 106.8 | 152.6 | 70.1 | 128.5 | 123.6 |
| Australia | 67.1 | 21.4 | 50.2 | 6.0 | 34.8 | 0.4 | 46.5 | -9.7 | -73.5 | -56.8 | -23.9 | 11.1 | 189.6 | 63.5 | 15.3 |
| Canada | 57.4 | 27.0 | 37.8 | -3.9 | 17.5 | 19.7 | -70.3 | -6.9 | 114.6 | -32.6 | 66.5 | 34.6 | 64.9 | 0.3 | 30.4 |
| Mexico | 56.6 | -33.7 | -33.0 | -334.3 | 38.7 | 93.9 | 62.3 | 9.2 | 87.9 | 214.6 | -152.2 | -16.4 | -68.8 | -58.2 | 160.3 |
| Indonesia | 50.6 | 44.8 | -86.7 | - | 31.4 | 9.7 | -75.5 | 8.3 | 86.9 | 161.9 | 125.1 | -132.3 | 43.9 | 5.5 | - |
| Taiwan | 47.2 | 56.0 | 13.4 | 126.7 | 61.2 | 61.0 | - | -34.1 | 32.3 | 55.6 | 62.0 | 131.2 | 99.2 | 36.9 | 49.1 |
| Korea | 46.8 | 70.2 | -26.0 | 52.2 | 36.0 | -158.5 | 36.1 | -438.6 | 88.7 | 55.4 | 99.1 | 113.3 | 82.0 | 53.5 | 94.7 |
| India | 38.9 | 24.1 | -215.7 | 25.6 | 29.0 | 95.2 | 129.0 | 42.3 | 44.2 | 13.4 | 19.2 | -42.2 | 14.5 | 28.8 | -66.4 |
| Austria | 38.8 | 20.6 | -78.9 | -7.0 | 12.6 | 66.1 | 87.2 | 59.6 | -58.1 | -31.0 | 25.8 | 19.7 | -3.2 | 78.0 | 26.8 |
| Spain | 27.7 | 25.1 | 55.9 | 2.5 | 11.9 | 14.4 | -12.9 | 20.1 | 49.6 | 1.0 | 17.5 | 44.3 | 14.1 | 11.0 | 29.7 |
| UK | 20.1 | 9.6 | 53.3 | 13.0 | 2.5 | 15.8 | 20.2 | 43.0 | 38.4 | -15.1 | 0.1 | 33.2 | 16.2 | 24.8 | 10.0 |
| Finland | 0.5 | -6.2 | -19.4 | 126.7 | 16.6 | -249.0 | 87.2 | 0.4 | 45.8 | -112.3 | -29.5 | -12.1 | 0.7 | 12.5 | -18.3 |
| Turkey | 0.4 | -15.1 | 55.7 | 108.1 | 17.0 | 34.5 | -67.2 | 14.2 | 16.3 | -180.4 | -38.4 | -240.1 | -54.0 | -44.5 | -175.0 |
| Greece | 0.0 | -0.4 | -44.3 | 45.1 | 18.8 | - | -81.5 | 14.3 | 47.3 | -65.8 | -44.2 | -115.1 | -142.8 | -10.7 | -21.7 |
| South Africa | -2.3 | -74.2 | -157.8 | -154.5 | -494.7 | 21.2 | 14.2 | -56.3 | -221.6 | -44.6 | -105.0 | -289.3 | 89.2 | -150.8 | -7.5 |
| Ireland | -2.7 | 86.4 | 118.4 | 24.3 | 44.8 | 40.1 | 106.7 | 82.2 | -206.2 | -59.0 | -66.9 | 82.6 | - | 140.8 | - |
| Denmark | -4.5 | 24.2 | 31.9 | -13.9 | 29.4 | - | - | 65.3 | -7.6 | 203.2 | -2.0 | 14.1 | -106.5 | 78.9 | -19.8 |
| USA | -5.6 | 21.2 | 45.7 | 37.2 | 2.1 | 8.9 | -8.6 | 42.4 | 50.0 | 1.5 | 5.7 | 51.2 | -46.9 | -13.4 | 42.1 |
| Sweden | -7.6 | 2.5 | -28.2 | -3.7 | 25.0 | 84.0 | -324.3 | 73.8 | 48.5 | 162.2 | -32.3 | -4.5 | -30.5 | 82.4 | 99.3 |
| Germany | -9.5 | 10.4 | 33.1 | 28.0 | 38.2 | 27.1 | 102.1 | 41.0 | 43.5 | -27.6 | 23.5 | 12.4 | -168.6 | 26.1 | 21.0 |
| Argentina | -9.6 | 12.0 | -12.6 | - | 37.4 | -24.8 | 55.4 | 8.0 | -203.6 | -38.5 | -53.5 | -99.7 | -52.4 | -65.7 | 42.1 |
| France | -18.3 | 1.2 | 17.9 | 21.9 | 2.9 | 12.6 | 79.2 | 27.8 | 30.4 | -21.0 | -5.9 | 19.0 | -57.2 | -21.6 | 11.6 |
| Portugal | -33.2 | 13.4 | -103.7 | -19.1 | 7.1 | -328.7 | -39.4 | -40.5 | -18.6 | -101.1 | 48.8 | -42.8 | 6.3 | -9.5 | 79.2 |
| Japan | -50.2 | -10.7 | 14.6 | 10.0 | -12.8 | -13.6 | -69.9 | 25.1 | 21.3 | -33.8 | -47.7 | 15.4 | -82.3 | -53.5 | 17.3 |
| Italy | -65.5 | -8.1 | 5.8 | -29.0 | -11.9 | -14.4 | -117.2 | -72.5 | 10.1 | -113.5 | -24.4 | 9.5 | -24.1 | -37.3 | -18.0 |
| Belgium | - | 42.4 | 54.7 | 36.0 | 31.3 | 47.3 | - | 81.8 | -67.8 | -0.8 | 118.1 | 13.1 | 172.2 | - | -34.5 |
| Brazil | - | -281.3 | -214.3 | -224.7 | -66.7 | -23.1 | - | - | -205.0 | 27.2 | -356.9 | -46.5 | -204.4 | - | - |
| Hong Kong | - | 172.3 | 288.0 | - | - | 76.0 | - | - | - | - | - | 93.7 | - | - | - |
| Netherlands | - | 24.4 | 120.8 | 49.8 | -5.2 | - | - | - | 59.1 | -62.5 | 88.0 | 39.7 | 179.0 | 80.7 | -156.9 |
| Singapore | - | -375.0 | - | - | - | - | - | - | - | -85.4 | 176.5 | 150.6 | - | -387.1 | -334.4 |
Table B5b. Structural Estimates of Revealed Overall Competitiveness, Change From Early to Late Period (cont'd)
| COUNTRY | All Sectors | Fuels | Rubber | Plastic | Pottery | Glass | Non-metal Minerals | Iron & Steel | Other Metal | Fabricated Metal | Other Machinery | Electric Machinery | Transport | Scientific Equipment | Other Mnfg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| China | 80.6 | - | 107.2 | 125.9 | 77.0 | 84.1 | 106.7 | 94.1 | 33.9 | 185.9 | 108.8 | 59.7 | 11.8 | 63.1 | 41.1 |
| Australia | 67.1 | 25.4 | -33.6 | -226.9 | -10.6 | -120.2 | 28.0 | 145.4 | 183.2 | 11.8 | 34.8 | -27.5 | -99.3 | 55.7 | 10.2 |
| Canada | 57.4 | 46.6 | 19.7 | -63.3 | 27.1 | 32.1 | -17.8 | -13.6 | 133.8 | 20.1 | 49.2 | 30.9 | 55.8 | 42.6 | 30.1 |
| Mexico | 56.6 | 35.2 | -24.3 | -4.5 | 93.1 | 31.6 | -40.9 | -18.8 | 78.1 | 266.2 | 149.9 | - | 84.8 | - | - |
| Indonesia | 50.6 | - | 33.1 | 6.1 | -26.0 | 90.6 | -34.9 | -208.3 | - | -96.6 | 147.5 | 103.4 | -131.1 | 56.8 | 41.7 |
| Taiwan | 47.2 | 3.3 | 111.2 | 51.5 | -478.4 | 68.2 | 40.5 | 76.2 | 5.7 | 148.5 | - | 60.6 | 13.8 | 69.6 | 40.9 |
| Korea | 46.8 | 56.1 | 122.2 | 107.1 | -11.7 | 55.5 | 81.1 | 48.0 | 92.5 | 76.5 | 48.1 | 55.9 | 44.7 | 51.9 | 31.4 |
| India | 38.9 | -294.6 | 40.3 | 49.1 | -11.3 | -65.3 | 67.4 | 7.6 | -28.8 | 107.6 | 23.5 | -15.6 | 25.3 | 42.2 | - |
| Austria | 38.8 | 32.2 | 68.2 | 47.9 | 15.0 | 41.9 | -3.2 | 36.6 | -13.9 | 1.3 | 92.7 | -21.1 | 121.0 | -0.9 | - |
| Spain | 27.7 | 42.1 | 67.9 | 61.1 | 25.9 | 28.4 | 29.3 | -2.3 | -24.7 | -9.7 | -9.2 | 14.5 | 59.1 | 26.0 | 32.2 |
| UK | 20.1 | 85.7 | 3.6 | 37.5 | 24.2 | 9.3 | 15.9 | 11.9 | 0.6 | -32.7 | 22.9 | 66.2 | 12.2 | -55.8 | 37.1 |
| Finland | 0.5 | -188.5 | 93.4 | -37.7 | 9.5 | 4.5 | -2.8 | 51.7 | 17.7 | -35.3 | -10.8 | 13.0 | 38.1 | 26.1 | 30.8 |
| Turkey | 0.4 | 64.5 | -85.1 | 3.6 | 6.7 | 35.0 | 16.1 | -20.3 | -20.2 | -128.0 | 16.1 | 10.2 | -0.6 | -25.7 | 38.1 |
| Greece | 0.0 | - | -223.6 | 33.2 | -72.5 | 22.9 | 166.0 | -118.6 | 152.7 | -22.6 | 36.3 | -35.8 | -19.2 | 61.9 | 36.7 |
| South Africa | -2.3 | -175.4 | -133.9 | -357.8 | -13.4 | -449.5 | -441.1 | 114.8 | 78.9 | -200.0 | 12.2 | -176.9 | -46.9 | 37.4 | 12.9 |
| Ireland | -2.7 | - | 136.3 | 91.3 | 47.4 | 27.1 | 47.8 | -205.9 | - | 74.2 | -273.2 | 152.9 | 98.4 | -22.7 | - |
| Denmark | -4.5 | 66.6 | 33.5 | -113.0 | 54.9 | -27.3 | 3.7 | 150.5 | - | -31.6 | -74.8 | 56.2 | 57.7 | -425.1 | 23.2 |
| USA | -5.6 | 49.3 | -10.8 | 55.8 | 16.1 | 25.6 | 24.0 | -18.2 | -50.4 | 0.1 | -9.4 | -19.9 | -1.9 | 34.6 | 29.9 |
| Sweden | -7.6 | 33.2 | 68.7 | 6.6 | 77.5 | 12.6 | 12.8 | 23.2 | 41.3 | -43.8 | -55.9 | 13.9 | -28.6 | -7.7 | -378.9 |
| Germany | -9.5 | 31.4 | 45.7 | 38.0 | 17.9 | 24.1 | -0.2 | 12.9 | -12.3 | -28.0 | 5.8 | -4.3 | -6.5 | 30.8 | 39.6 |
| Argentina | -9.6 | - | -93.5 | -138.8 | 10.0 | -19.9 | -61.5 | -104.8 | -58.3 | -54.3 | -29.0 | -238.5 | 14.5 | 32.0 | 24.1 |
| France | -18.3 | 40.8 | -66.0 | 30.2 | - | 0.9 | -4.3 | 3.5 | -48.6 | -59.0 | -3.8 | -26.0 | -33.2 | -0.1 | 30.7 |
| Portugal | -33.2 | -91.5 | 59.5 | 38.9 | 29.2 | 25.6 | 19.4 | 9.8 | -81.9 | 10.4 | -75.7 | 53.4 | 66.9 | -149.7 | 16.5 |
| Japan | -50.2 | 41.8 | -62.2 | 21.3 | -2.8 | 6.8 | -7.0 | -64.4 | -82.6 | -64.9 | -49.9 | -88.7 | -32.7 | 29.0 | 25.6 |
| Italy | -65.5 | - | -21.4 | 9.6 | 47.5 | -1.4 | -58.4 | -16.4 | -102.4 | -160.6 | -149.5 | -64.3 | -0.3 | 22.2 | -193.8 |
| Belgium | - | 51.8 | - | 52.0 | 4.7 | -17.3 | -97.6 | - | -294.3 | -6.7 | 172.1 | 126.7 | - | - | - |
| Brazil | - | - | -256.2 | -5.6 | -14.4 | - | - | -176.8 | - | - | -178.6 | -247.8 | -413.5 | 5.7 | - |
| Hong Kong | - | - | - | - | - | - | 27.5 | - | - | - | - | - | - | - | - |
| Netherlands | - | 44.0 | - | 31.5 | 8.3 | 74.1 | -2.3 | 182.4 | - | -26.2 | - | 148.8 | 124.5 | - | - |
| Singapore | - | - | - | 49.4 | 48.8 | - | 86.0 | - | - | 97.2 | - | - | -14.5 | - | - |
Figure B1. Comparison of Gravity Residual Changes Using UN-NBER and CEPII Data
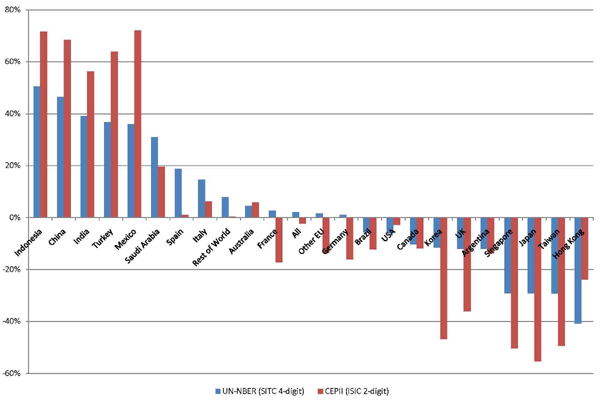
Data for Figure B1
| UN-NBER (SITC 4-digit) | CEPII (ISIC 2-digit) | |
|---|---|---|
| Indonesia | 0.50498653 | 0.71561738 |
| China | 0.4647502 | 0.68373595 |
| India | 0.39043716 | 0.56362496 |
| Turkey | 0.3676972 | 0.6390655 |
| Mexico | 0.36051769 | 0.72107074 |
| Saudi Arabia | 0.30919203 | 0.19683399 |
| Spain | 0.18772961 | 0.01071516 |
| Italy | 0.14607755 | 0.0618769 |
| Rest of World | 0.07967903 | 0.00450146 |
| Australia | 0.04503912 | 0.05880159 |
| France | 0.02608082 | -0.17244206 |
| All | 0.0214243 | -0.02268058 |
| Other EU | 0.01706058 | -0.13606494 |
| Germany | 0.01055769 | -0.16091488 |
| Brazil | -0.05609352 | -0.12218161 |
| USA | -0.06091851 | -0.02762394 |
| Canada | -0.10314775 | -0.1176693 |
| Korea | -0.115841 | -0.46735922 |
| UK | -0.12033621 | -0.36014848 |
| Argentina | -0.1203525 | -0.13767552 |
| Singapore | -0.29100903 | -0.50380707 |
| Japan | -0.29132421 | -0.55357127 |
| Taiwan | -0.2922583 | -0.49385896 |
| Hong Kong | -0.40803643 | -0.23891996 |
Footnotes
1. The authors thank Brian Andrew for excellent research assistance. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, any other person associated with the Federal Reserve System, or the European Central Bank. Return to text
a. G.d'Annunzio University and CRENoS Return to text
b. European Central Bank Return to text
c. Federal Reserve Board Return to text
2. Measures of aggregate ![]() ,
comparable across countries, are usually obtained as the residual
component of GDP growth that cannot be explained by the growth of
production inputs. One of the drawbacks of the growth accounting
approach is that the role of the sectoral composition of output is
ruled out by assumption. By assuming that GDP is produced by a
single sector, one cannot disentangle
,
comparable across countries, are usually obtained as the residual
component of GDP growth that cannot be explained by the growth of
production inputs. One of the drawbacks of the growth accounting
approach is that the role of the sectoral composition of output is
ruled out by assumption. By assuming that GDP is produced by a
single sector, one cannot disentangle ![]() differences
(across countries) due to sectoral specialization from
differences
(across countries) due to sectoral specialization from ![]() differences due to other factors. Return to text
differences due to other factors. Return to text
3. That model was first brought to the data by Del Gatto, Mion and Ottaviano (2006) and further developed by Ottaviano, Taglioni and di Mauro (2009). Return to text
4. Constant market share analysis is beset by a number of well documented theoretical problems (see Richardson (1971) for an overview). However, the approach remains illustrative and simple to implement even if interpretation is complicated by relative price changes and other issues. Return to text
5. The constant market share approach often includes an additional ''market effect'' related to the geographical pattern of trade. For ease of exposition we have focused only on the commodity effect, in a sense wrapping the market effect into our measurement of the competitiveness effect. With declining trade costs it is likely that the market effect has become a less pronounced determinate of aggregate share in any case. Return to text
6. Other examples of cancelling out the importer fixed effects in a gravity framework include: Head and Mayer (2000), Martin, Mayer and Thoenig (2008) and Head, Mayer and Ries (2010). Return to text
7. Expression (3) imposes separability across right-hand
side ratios with the assumption that
![]() . In practice, this may
have the effect of overestimating the share of each exporter (i.e.,
since the shares as decomposed on the right-hand side will add up
to more than 1), but little impact on the relative size of the
shares. Return to text
. In practice, this may
have the effect of overestimating the share of each exporter (i.e.,
since the shares as decomposed on the right-hand side will add up
to more than 1), but little impact on the relative size of the
shares. Return to text
8. Specification (vi) confirms the consistency of the reduced form results with the empirical exercise in the following section. While the reduced form regressions use the Feentra et al. (2005) data described above, the methodology in the next section additionally requires data on sectoral intra-national trade, which necessitates using an alternative data set. Those data are described below. Return to text
9. Results for the remaining five specifications can be found in Appendix B. Return to text
10. As mentioned, the gravity residuals are estimated at the SITC 4-digit level for specifications (i)-(v) and at the ISIC 2-digit level for specification (vi). In the table, due to computational constraints on such a large dataset, we present aggregate control variables estimated without product fixed effects. As such, the coefficients can be interpreted as simple averages across SITC products, or in the case of specification (vi), ISIC products. Return to text
11. For the sake of comparability, the predicted and actual market share changes are aggregated over exactly the same SITC-destination pairs. The index of share change does not exactly match that in Figure 1, since: (a) it is a geometric index, whereas simply adding up share across products as in Figure 1 is analogous to an arithmetic mean, and (ii) because the index is matched in each period (i.e., the trade flow had to occur in both time t and t-1 for it to be included), the composition of items in the Figure 2 index will be a subset of those in Figure 1. Overall, the magnitude of the drop of the geometric index seems reasonably close to the aggregate drop and the dynamics of contractions in the early 1980's and 2000's parallel one another. Return to text
12. This list corresponds well with the top twenty exporters by size in 1980. In the table, the category 'Other EU' includes: Austria, Belguim, Denmark, Finland, Ireland, Netherlands, Portugal and Sweden. Return to text
13. The number of exporters from
![]() to
to ![]() amounts to
amounts to
![]() . Each exporter from
. Each exporter from ![]() to
to ![]() generates f.o.b. export sales equal to
generates f.o.b. export sales equal to
![]() . Aggregating over all
exporters yields equation (5). Return to
text
. Aggregating over all
exporters yields equation (5). Return to
text
14. Note that the adjustment of
![]() takes place along both the
'extensive margin' (number of exporters) and the 'intensive margin'
(per capita exports). Return to
text
takes place along both the
'extensive margin' (number of exporters) and the 'intensive margin'
(per capita exports). Return to
text
15. Since the exponent
![]() plays no role in
determining the country rankings, as it only entails a re-scaling
by sector, it will be omitted hereinafter. Return to text
plays no role in
determining the country rankings, as it only entails a re-scaling
by sector, it will be omitted hereinafter. Return to text
16. Equation (6) could be interpreted as a gravity equation and estimated as
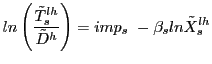 |
(10) |
where vector
![]() includes bilateral
distances, as well as a number of dummies controlling for the
presence of border effects (contiguity, language indicators, etc.),
and
includes bilateral
distances, as well as a number of dummies controlling for the
presence of border effects (contiguity, language indicators, etc.),
and ![]() is a (destination) country-sector
dummy capturing the ROC. Estimation of (10) provides us with information on trade
costs, through
is a (destination) country-sector
dummy capturing the ROC. Estimation of (10) provides us with information on trade
costs, through
![]() , and, at the same time, with
information on ROC. More precisely, the fixed effects in (10) can be estimated (see Fadinger and
Fleiss, 2008) as
, and, at the same time, with
information on ROC. More precisely, the fixed effects in (10) can be estimated (see Fadinger and
Fleiss, 2008) as
![$\displaystyle \tilde{\bar{m}}_{s}^{hh}=exp\left[ ln\left( \frac{\tilde{T}_{s}^{lh}} {\tilde{D}^{h}}\right) -\hat{\beta}_{s}ln\bar{\tilde{X}}_{s}^{lh}\right]$](img115.gif) |
(11) |
where the bar refers to the mean across exporting countries. Return to text
17. With this specification,
zeros-missings in bilateral trade do not translate one-to-one into
zeros in
![]() . The latter can
instead be due to missing information on GDP and/or internal trade
in country
. The latter can
instead be due to missing information on GDP and/or internal trade
in country ![]() . Return to
text
. Return to
text
18. The paper is downloadable at http://www.feem.it/userfiles/attach/2009121116814115-09.pdf. Return to text
19. As inter-industry linkages are ruled
out, the ![]() index could be omitted and the model
presented as an "industry-model", with all the equations referring
to a generic industry. However, the
index could be omitted and the model
presented as an "industry-model", with all the equations referring
to a generic industry. However, the ![]() index will
reveal useful in subsequent analysis, as country, industry, and
country-industry specific variables (parameters) coexist in the
model. Return to text
index will
reveal useful in subsequent analysis, as country, industry, and
country-industry specific variables (parameters) coexist in the
model. Return to text
20. Equation (12) expresses the marginal cost associated with a standard Cobb-Douglas production function
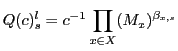
21. In a strict sense, the Pareto
assumption refers to ![]() (i.e. the UIR). However, as
evident from (12),
(i.e. the UIR). However, as
evident from (12),
![]() for
for
![]() . Thus, there
is no loss of generality in thinking (and solving) the model in
terms of marginal costs. Return to
text
. Thus, there
is no loss of generality in thinking (and solving) the model in
terms of marginal costs. Return to
text
22. Parameter
![]() comes from the utility function
and measures the degree of product differentiation between
different varieties of good
comes from the utility function
and measures the degree of product differentiation between
different varieties of good ![]() . When
. When
![]() , consumers only care about
their total consumption level over the varieties of good
, consumers only care about
their total consumption level over the varieties of good
![]() . Return to
text
. Return to
text
23. Since there are no inter-industry linkages, rows in (13) are independent one another. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text