
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1031, October 2011 --- Screen Reader
Version*
Oil Efficiency, Demand, and Prices: A Tale of Ups and Downs**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The macroeconomic implications of oil price fluctuations vary according to their sources. Our estimated two-country DSGE model distinguishes between country-specific oil supply shocks, various domestic and foreign activity shocks, and oil efficiency shocks. Changes in foreign oil efficiency, modeled as factor-augmenting technology, were the key driver of fluctuations in oil prices between 1984 and 2008, but have modest effects on U.S. activity. A pickup in foreign activity played an important role in the 2003-2008 oil price runup. Beyond quantifying the responses of oil prices and economic activity, our model informs about the propagation mechanisms. We find evidence that nonoil trade linkages are an important transmission channel for shocks that affect oil prices. Conversely, nominal rigidities and monetary policy are not.
Keywords: Oil shocks, DSGE models, maximum likelihood
JEL classification: F32, F41
1. Introduction
Not all oil price fluctuations have the same macroeconomic repercussions. If oil demand and oil prices rise because of strong foreign aggregate demand, worldwide activity expands rather than contracting, as it would for price increases stemming from foreign oil supply disruptions. Similarly, U.S. activity reacts differently to oil price movements that originate in the U.S. rather than abroad. Disagreement persists regarding the relative importance of oil supply and demand factors in determining oil prices. For instance, Hamilton (1983, 2003, 2009) emphasizes oil supply disruptions in explaining major runups in oil prices, while Killian (2009) argues that shocks to oil demand have driven oil prices historically.
In addition to the challenges of identifying empirically the sources of fluctuations - domestic or foreign, demand or supply - studying the macroeconomic effects of oil price movements is further complicated by the response of monetary policy. Monetary authorities are often seen as contributing to the slowdown in economic activity associated with oil price increases by raising policy interest rates. Perhaps most prominently, Bernanke, Gertler, and Watson (1997) argued that the output decline that coincided with the oil price hikes of the 1970s and early 1980s could have been largely reduced by an alternative policy response.1
The international dimension of oil trade matters beyond distinguishing whether oil price fluctuations originate at home or abroad. Due to intertemporal consumption smoothing, an oil-importing country, such as the United States, offsets oil deficits associated with oil price increases by expanding nonoil trade. The expansion of nonoil net exports buffers the response of gross domestic product and is accompanied by a depreciation of the dollar that affects import prices and inflation.
To disentangle domestic and foreign sources of oil price fluctuations, to evaluate their repercussions on economic activity and inflation, and to assess the role of monetary policy in an internally consistent framework, we estimate a dynamic stochastic general equilibrium model (DSGE) using full information maximum likelihood. In the model, oil is both a factor of production and a direct input in consumption. Building on the work of Backus and Crucini (1998), the model allows for trade in oil and nonoil goods and encompasses U.S. and foreign trade blocs. Drawing on the monetary policy literature, the model incorporates nominal wage and price rigidities, as well as real rigidities. Following Smets and Wouters (2007), cyclical fluctuations are linked to a rich stochastic structure. Previous estimates of the sources of oil price fluctuations and their macroeconomic effects have disregarded the nature of oil as a globally traded commodity, or have taken econometric approaches that do not allow explaining the transmission channels and the role of monetary policy, or both.2
Our analysis distinguishes between country-specific shocks associated with oil supply and demand. On the demand side, we allow for numerous sources of variation that influence oil demand indirectly through economic activity. The indirect demand sources reflect the dependence of oil demand on broader macroeconomic events, such as shifts in productivity, changes in government spending, or, possibly, the conduct of monetary policy. Our results assign a relatively modest role to these factors in explaining oil prices in dollar terms for the period between 1984 and 2003. However, a pickup in economic activity in the foreign bloc of the model plays an important role in explaining the increase in oil demand and prices between 2003 and 2008.
In our model, oil demand is also influenced directly by changes in oil efficiency, modeled as a factor-augmenting technology. Movements in oil efficiency may capture changes in consumption patterns or production processes. Examples include a shift towards motorization in emerging Asia, continuing industrialization of China, or energy-efficient cars becoming more popular in the United States.
We find that movements in foreign oil efficiency are of principal importance in the determination of oil demand and prices over the period 1984 to 2008 both at business-cycle and longer frequencies. Between 1984 and the late 1990s the real dollar price of oil (measured by the U.S. refiners' acquisition costs for imported crude deflated by the U.S. GDP deflator) dropped by 140% as oil efficiency sharply improved in the industrialized countries and around the globe. Since the late 1990s, improvements in oil efficiency have slowed down and oil prices have been catching up to levels that would have prevailed absent the earlier gains.
Going beyond the focus on an aggregate foreign bloc of our DSGE model, we construct measures of oil efficiency for individual foreign countries using the approach of growth-accounting studies in the style of Solow (1957) and Griliches and Jorgenson (1966). Starting from the oil demand equations in our model, we show that the growth rate of oil efficiency can be expressed in terms of directly observable quantities and parameters, such as the rate of trend growth in efficiency and the oil price elasticity of demand. To construct country-by-country measures of oil efficiency consistent with the foreign aggregate included in the DSGE model, we use disaggregate data in conjunction with the parameter estimates obtained for the entire foreign bloc of the model. Our results imply that the inverted U-shaped pattern for the evolution of foreign oil efficiency over the sample is not merely a consequence of aggregation. On the contrary, that pattern is shared by all the foreign industrialized economies and by many developing countries.
While our results highlight the importance of shocks that affect oil demand, oil supply shocks are estimated to play a small role in driving oil price fluctuations. Disentangling oil demand and supply sources of fluctuations based solely on observed equilibrium quantities is no easy task. In our case, this task is facilitated by the rich stochastic structure of the model and by the information provided by an equally rich set of observed variables. Over our sample, global oil supply displays relatively little volatility. For oil supply sources to account for a large share of the volatility in oil prices, oil demand would have to be price insensitive. We estimate the oil price elasticity of demand to be -0.41. In our model, a more inelastic oil demand would imply a larger role not only for oil supply shocks, but also for many other sources of fluctuations. In that case, the volatility in oil prices implied by the model would be counterfactually high relative to the volatility in oil prices in the observed data.
One of the transmission channels scrutinized by the literature on the macroeconomic effects of oil shocks is the response of monetary policy.3 For the period between 1984 and 2008, our analysis finds no evidence that monetary policy played a quantitatively important role in shaping the response of economic activity to oil price fluctuations. We assess the role of monetary policy through the lens of a potential economy with flexible prices and wages and show that output levels in the actual and potential economy differ only slightly when conditioning on the smoothed estimates of oil supply and oil efficiency shocks. Even after ascribing most of the variation in oil prices to foreign sources, there remains the possibility that U.S. monetary policy may have raised the volatility of oil prices. We also dispel this argument as the price of oil in our model with nominal rigidities and a role for monetary policy evolves similarly to its counterpart in the potential economy.
Jones, Leiby, and Paik (2004), Hamilton (2008), Kilian (2008) surveyed the broad literature on the macroeconomic impact of oil price fluctuations. Ramey and Vine (2011) gave an overview of the transmission channels typically embedded in DSGE models with a closed-economy focus. The review in Bodenstein, Erceg, and Guerrieri (2011) placed a greater emphasis on work that captured the international nature of oil trade.
2 Model Description
Like the model in Backus and Crucini (1998), our model encompasses international trade in oil and nonoil goods. We extend the model in Backus and Crucini (1998) by incorporating the nominal and real rigidities that Smets and Wouters (2007) and Christiano, Eichenbaum, and Evans (2005) have found to be empirically relevant in closed economy models. As in Bodenstein, Erceg, and Guerrieri (2011), the assumption of incomplete asset markets across countries is a key ingredient in generating country-specific wealth effects in reaction to shocks that affect the price of oil.
There are two countries, country 1, the home country, and country 2, the foreign country. We estimate the model using U.S. data for the home country and aggregate data for the principal trading partners of the United States for the foreign bloc. Because the structure of the country blocs is symmetric, we focus on the home country in describing the model. Country specific values for the parameters allow for differences in population size, oil shares in production and consumption, oil endowments, expenditures shares and in nonoil and oil trade flows.
In each country, a continuum of firms produces differentiated varieties of an intermediate good under monopolistic competition. These firms use capital, labor, and oil as factor inputs. Goods prices are determined by Calvo-Yun staggered contracts. Trade occurs at the level of intermediate goods and within each country the varieties are aggregated into a (nonoil) consumption and an investment good. Households consume oil, the nonoil consumption good, save and invest, and supply differentiated labor services under monopolistic competition. Wages are determined by Calvo-Yun staggered contracts. While asset markets are complete at the country level, asset markets are incomplete internationally. The two country-blocs are endowed with a nonstorable supply of oil each period. Finally, to allow for a balanced growth path, the oil efficiency must grow over time to bridge the gap between the growth rates of labor augmenting technology and oil supply.
2.1 Households and Firms
The preferences of the representative household are given by:
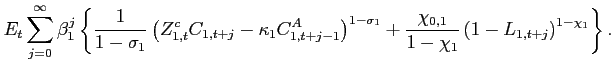 |
(1) |
![]() denotes the expectations conditional on
information available at time
denotes the expectations conditional on
information available at time ![]() . The variables
. The variables
![]() and
and ![]() represent
consumption and hours worked, respectively. The parameter
represent
consumption and hours worked, respectively. The parameter
![]() is used for determining the
intertemporal elasticity of substitution,
is used for determining the
intertemporal elasticity of substitution, ![]() for
the Frisch elasticity of labor supply, and
for
the Frisch elasticity of labor supply, and ![]() for the number of hours worked along the balanced growth path. The
term
for the number of hours worked along the balanced growth path. The
term ![]() models a preference shock to
consumption. In addition, a household's utility from consumption is
affected by the presence of external consumption habits,
parameterized by
models a preference shock to
consumption. In addition, a household's utility from consumption is
affected by the presence of external consumption habits,
parameterized by ![]() .
. ![]() is
the per capita aggregate consumption level.
is
the per capita aggregate consumption level.
The time ![]() budget constraint of the household
states that the combined expenditures on goods and the net
accumulation of financial assets must equal disposable
income:
budget constraint of the household
states that the combined expenditures on goods and the net
accumulation of financial assets must equal disposable
income:
 |
|
| (2) |
Final consumption and investment goods, ![]() and
and
![]() , are purchased at the prices
, are purchased at the prices
![]() and
and ![]() ,
respectively. The household earns labor income
,
respectively. The household earns labor income
![]() and capital income
and capital income
![]() . The household also
receives an aliquot share
. The household also
receives an aliquot share ![]() of firm
and union profits, a share of the country's (unrefined) oil
endowment
of firm
and union profits, a share of the country's (unrefined) oil
endowment
![]() , and net transfers of
, and net transfers of
![]() .
.
Households accumulate financial assets by purchasing
state-contingent domestic bonds, and a non state-contingent foreign
bond. The state contingent domestic bonds are denoted by
![]() . The term
. The term ![]() in the budget constraint represents the quantity of the non
state-contingent bond purchased by a typical household that pays
one unit of foreign currency in the subsequent period,
in the budget constraint represents the quantity of the non
state-contingent bond purchased by a typical household that pays
one unit of foreign currency in the subsequent period, ![]() is the foreign currency price of the bond, and
is the foreign currency price of the bond, and
![]() is the exchange rate expressed in
units of home currency per unit of foreign currency.
is the exchange rate expressed in
units of home currency per unit of foreign currency.
![]() captures intermediation costs
incurred to purchase the foreign bond and render the dynamics of
captures intermediation costs
incurred to purchase the foreign bond and render the dynamics of
![]() stationary.4
stationary.4
The evolution of the capital stock follows:
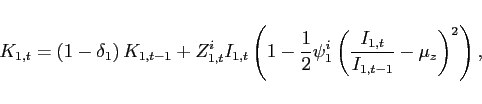 |
(3) |
where ![]() is the depreciation rate of
capital. For
is the depreciation rate of
capital. For
![]() , changing the level of
gross investment from the previous period is costly, so that the
acceleration in the capital stock is penalized. The term
, changing the level of
gross investment from the previous period is costly, so that the
acceleration in the capital stock is penalized. The term
![]() captures an investment-specific
technology shock.
captures an investment-specific
technology shock. ![]() is the deterministic
growth rate of labor augmenting technological change discussed
below.
is the deterministic
growth rate of labor augmenting technological change discussed
below.
In every period ![]() , household
, household ![]() maximizes the utility functional (1) with respect to
consumption, labor supply, investment, end-of-period capital stock,
and holdings of domestic and foreign bonds, subject the budget
constraint (2), and the
transition equation for capital (3). In doing so,
prices, wages, and net transfers are taken as given.
maximizes the utility functional (1) with respect to
consumption, labor supply, investment, end-of-period capital stock,
and holdings of domestic and foreign bonds, subject the budget
constraint (2), and the
transition equation for capital (3). In doing so,
prices, wages, and net transfers are taken as given.
Labor Bundling
As in Smets and Wouters (2007), households supply their homogenous labor to
intermediate labor unions. These unions introduce distinguishing
characteristics on the labor services and resell them to
intermediate labor bundlers. The unions use Calvo contracts to set
the wages charged to the intermediate bundlers. In turn, firms
purchase a labor bundle ![]() from the labor
bundlers.
from the labor
bundlers.
The labor bundle demanded by firms takes the from:
![\begin{displaymath} L^d_{1,t}=\left[ \int_{0}^{1}L_{1,t}(h)^{\frac{1}{1+\theta^{w} _{1,t}}}dh\right] ^{1+\theta^{w} _{1,t}}, \end{displaymath}](img42.gif) |
(4) |
where
![]() is time-varying reflecting
shocks to the wage markup.
is time-varying reflecting
shocks to the wage markup.
The labor bundlers buy the labor services ![]() from unions, combine them to obtain
from unions, combine them to obtain ![]() , and resell them to the intermediate goods producers
at wage
, and resell them to the intermediate goods producers
at wage ![]() . In a perfectly competitive
environment, profit maximization by the bundlers implies:
. In a perfectly competitive
environment, profit maximization by the bundlers implies:
![\begin{displaymath} L_{1,t}(h)=\left[ \frac{W_{1,t}(h)}{W_{1,t}}\right] ^{-\frac{1+\theta^{w} _{1,t}}{ \theta^{w} _{1,t}}}L^d_{1,t}, \end{displaymath}](img47.gif) |
(5) |
and the zero-profit condition yields:
![\begin{displaymath} W_{1,t}=\left[ \int_{0}^{1}W_{1,t}(h)^{-\frac{1}{\theta^{w} _{1,t}}}dh\right] ^{-\theta^{w} _{1,t}}. \end{displaymath}](img48.gif) |
(6) |
Labor bundlers purchase labor from the unions that intermediate
between the households and the labor bundlers. The unions allocate
and differentiate the labor services from the households and have
market power, i.e., they choose a wage subject to the labor demand
equation. We denote the real wage desired by the household
![]() which reflects the
marginal rate of substitution between leisure and consumption.
which reflects the
marginal rate of substitution between leisure and consumption.
Labor unions take
![]() as the cost of labor
services in their negotiations with the labor bundlers. The markup
above the marginal disutility is distributed to the households.
However, unions are subject to nominal rigidities as in Calvo. A
union can readjust a wage with probability
as the cost of labor
services in their negotiations with the labor bundlers. The markup
above the marginal disutility is distributed to the households.
However, unions are subject to nominal rigidities as in Calvo. A
union can readjust a wage with probability
![]() in each period. For those
unions which cannot adjust wages in a given period, wages grow by a
geometric average of last period's nominal wage inflation and the
wage inflation rate along the balanced growth path. The problem of
a union
in each period. For those
unions which cannot adjust wages in a given period, wages grow by a
geometric average of last period's nominal wage inflation and the
wage inflation rate along the balanced growth path. The problem of
a union ![]() is given by:
is given by:
![$\displaystyle \max_{W_{t}(h)}E_{t}\sum_{j=0}^{\infty }(\xi^{w}_{1})^{j}\psi _{t,t+j} \left[ (1+\tau^{w} _{1})\omega _{t,j}^{l}W_{t}(h)L_{t+j}(h)-W_{t+j}^{f}L_{t+j}(h) \right]$](img53.gif) |
(7) |
![$\displaystyle L_{1,t}(h)=\left[ \frac{W_{1,t}(h)}{W_{1,t}}\right] ^{-\frac{1+\theta^{w} _{1,t}}{ \theta^{w} _{1,t}}}L^d_{1,t},$](img55.gif) |
(8) |
| (9) |
The subsidy ![]() guarantees the efficient
level of labor supply along the balanced growth path.
guarantees the efficient
level of labor supply along the balanced growth path.
Bundlers of Varieties
A continuum of representative bundlers combines differentiated
intermediate products (whose production is described below) into a
composite home-produced good ![]() according
to:
according
to:
![\begin{displaymath} Y^d_{1,t}=\left[ \int_{0}^{1}Y_{1,t}\left( i\right) ^{\frac{1}{1+\theta^{p}_{1,t}}}di \right] ^{1+\theta^{p}_{1,t}}, \end{displaymath}](img59.gif) |
(10) |
where ![]() is used as the domestic input in
producing all final use goods, including exports. The term
is used as the domestic input in
producing all final use goods, including exports. The term
![]() represents a domestic mark-up
shock. The optimal bundle of intermediate goods minimizes the cost
of producing
represents a domestic mark-up
shock. The optimal bundle of intermediate goods minimizes the cost
of producing ![]() taking the price of each
intermediate good as given. One unit of the sectoral output index
sells at the price:
taking the price of each
intermediate good as given. One unit of the sectoral output index
sells at the price:
![\begin{displaymath} P^d_{1,t}=\left[ \int_{0}^{1}P^d_{1,t}\left( i\right) ^{\frac{-1\,\,}{\theta^{p} _{1,t} }}di\right] ^{-\theta^{p} _{1,t}} . \end{displaymath}](img63.gif) |
(11) |
Under producer currency pricing, the exports sell at the foreign
price
![]() .
.
Production of Domestic Intermediate Goods
There is a continuum of differentiated intermediate goods indexed
by ![]() , each of which is produced by a
single monopolistically competitive firm.
, each of which is produced by a
single monopolistically competitive firm.
Firm ![]() faces a demand function that varies
inversely with its output price
faces a demand function that varies
inversely with its output price ![]() and
directly with aggregate demand
and
directly with aggregate demand ![]() for country
1's products:
for country
1's products:
![\begin{displaymath} Y_{1,t}(i)=\left[ \frac{P_{1,t}(i)}{P^d_{1,t}}\right] ^{-\frac{1+\theta^{p}_{1,t}}{\theta^{p}_{1,t}}}Y^d_{1,t}, \end{displaymath}](img69.gif) |
(12) |
where
![]() is time-varying in order
to allow for price mark-up shocks.
is time-varying in order
to allow for price mark-up shocks.
Each firm utilizes capital, labor, and oil and acts in perfectly
competitive factor markets. The production technology is given by a
nested constant-elasticity of substitution specification. Since
capital is owned by households and rented out to firms, the cost
minimization problem of firm ![]() that intends to
produce overall output
that intends to
produce overall output ![]() can be written
as:
can be written
as:
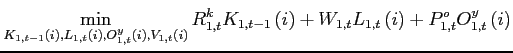 |
(13) |
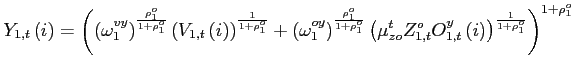 |
(14) |
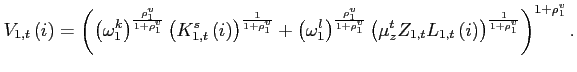 |
(15) |
Utilizing capital ![]() and labor services
and labor services
![]() , the firm produces a
"value-added" input
, the firm produces a
"value-added" input ![]() , which is
then combined with oil
, which is
then combined with oil
![]() to produce the domestic nonoil
variety
to produce the domestic nonoil
variety ![]() . In equilibrium, aggregating over
firms, overall demand for the various factor inputs needs to clear
the quantities of each input available for rent from households and
unions.
. In equilibrium, aggregating over
firms, overall demand for the various factor inputs needs to clear
the quantities of each input available for rent from households and
unions.
The quasi-share parameter
![]() determines the importance of
oil purchases in the firm's output, and the parameter
determines the importance of
oil purchases in the firm's output, and the parameter ![]() determines the price elasticity of demand for
oil. The substitutability between capital and labor is measured by
determines the price elasticity of demand for
oil. The substitutability between capital and labor is measured by
![]() . The term
. The term ![]() represents a stochastic process for the evolution of
technology while
represents a stochastic process for the evolution of
technology while ![]() denotes constant labor
augmenting technological progress. Oil efficiency is also modeled
as a factor-augmenting technology. The term
denotes constant labor
augmenting technological progress. Oil efficiency is also modeled
as a factor-augmenting technology. The term ![]() represents a stochastic process that influences the oil efficiency
in production while
represents a stochastic process that influences the oil efficiency
in production while ![]() denotes a
constant rate of oil efficiency gains.
denotes a
constant rate of oil efficiency gains.
The prices of intermediate goods ![]() are
determined by Calvo-style staggered contracts, see Calvo (1983) and
Yun (1996). Each period, a firm faces a constant probability,
are
determined by Calvo-style staggered contracts, see Calvo (1983) and
Yun (1996). Each period, a firm faces a constant probability,
![]() , to reoptimize its price
, to reoptimize its price
![]() , that is common across destinations
under producer currency pricing without pricing-to-market. These
probabilities are independent across firms, time, and countries.
Firms that do not reoptimize their price partially index it to the
inflation rate in the aggregate price
, that is common across destinations
under producer currency pricing without pricing-to-market. These
probabilities are independent across firms, time, and countries.
Firms that do not reoptimize their price partially index it to the
inflation rate in the aggregate price ![]() . The
indexation scheme for prices is analogous to that for wages in
Equation (9). For prices,
the indexation weight is denoted by
. The
indexation scheme for prices is analogous to that for wages in
Equation (9). For prices,
the indexation weight is denoted by ![]() .
.
Production of Consumption Goods
The consumption basket ![]() that enters the
household's budget constraint is produced by perfectly competitive
consumption distributors whose production function mirrors the
preferences of households over home and foreign nonoil goods and
oil. For convenience, we suppress firm-specific indices as all the
distributors behave identically in equilibrium. The cost
minimization problem of a representative distributor that produces
that enters the
household's budget constraint is produced by perfectly competitive
consumption distributors whose production function mirrors the
preferences of households over home and foreign nonoil goods and
oil. For convenience, we suppress firm-specific indices as all the
distributors behave identically in equilibrium. The cost
minimization problem of a representative distributor that produces
![]() can be written as:
can be written as:
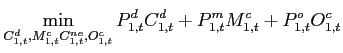 |
(16) |
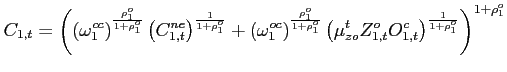 |
(17) |
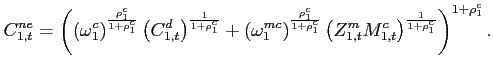 |
(18) |
Each distribution firm produces a nonoil aggregate ![]() from the home and foreign intermediate
consumption aggregates
from the home and foreign intermediate
consumption aggregates ![]() and
and ![]() , which is then combined with oil
, which is then combined with oil ![]() to produce the final consumption good in the home
country
to produce the final consumption good in the home
country ![]() and sold under perfect competition.
and sold under perfect competition.
The parameter
![]() determines the ratio of oil
purchases to the output of the firm. The price elasticity of oil
demand
determines the ratio of oil
purchases to the output of the firm. The price elasticity of oil
demand ![]() in the consumption aggregate
(17)
coincides with the one in the production function (14). The same shock
in the consumption aggregate
(17)
coincides with the one in the production function (14). The same shock
![]() that affects oil efficiency in
production also affects the oil efficiency of consumption.
that affects oil efficiency in
production also affects the oil efficiency of consumption.
![]() denotes a constant rate of oil
efficiency gains. The quasi-share
denotes a constant rate of oil
efficiency gains. The quasi-share
![]() determines the importance of
nonoil imports in the nonoil aggregate. The elasticity of
substitution between the home and foreign intermediate good is
denoted by
determines the importance of
nonoil imports in the nonoil aggregate. The elasticity of
substitution between the home and foreign intermediate good is
denoted by ![]() . The term
. The term ![]() captures an import preference shock. In our
estimation, this shock accounts for the volatility of nonoil goods
trade that is not explained by the remaining shocks.
captures an import preference shock. In our
estimation, this shock accounts for the volatility of nonoil goods
trade that is not explained by the remaining shocks.
The price of the consumption aggregate ![]() coincides with the Lagrange multiplier on Equation
(17) in
the cost minimization problem of a distributor. The price of the
nonoil consumption good
coincides with the Lagrange multiplier on Equation
(17) in
the cost minimization problem of a distributor. The price of the
nonoil consumption good ![]() is referred to as
the "core" price level
is referred to as
the "core" price level ![]() .
.
Production of Investment Goods
The investment good is also produced by perfectly competitive distributors. In contrast to the consumption distributors, however, the production of the investment aggregate does not require oil as input. The cost minimization of a representative investment distributor is:
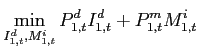 |
(19) |
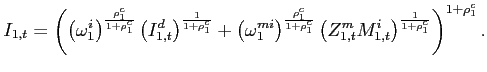 |
(20) |
The quasi-share parameter
![]() determines the importance of
nonoil imports in the investment aggregate. The same import
preference shock
determines the importance of
nonoil imports in the investment aggregate. The same import
preference shock ![]() also affects investment
imports. The Lagrangian from the problem of investment distributors
determines the price of new investment goods
also affects investment
imports. The Lagrangian from the problem of investment distributors
determines the price of new investment goods ![]() , that appears in the household's budget
constraint.
, that appears in the household's budget
constraint.
2.2 The Oil Market
Each period the home and foreign countries are endowed with
exogenous supplies of oil ![]() and
and
![]() , respectively. The two endowments
are governed by distinct stochastic processes. With both domestic
and foreign oil supply determined exogenously, the oil price
, respectively. The two endowments
are governed by distinct stochastic processes. With both domestic
and foreign oil supply determined exogenously, the oil price
![]() adjusts endogenously to clear the
world oil market:
adjusts endogenously to clear the
world oil market:
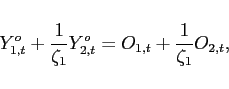 |
(21) |
where
![]() . To clear the
oil market, the sum of home and foreign oil production must equal
the sum of home and foreign oil consumption by firms and
households. Because all variables are expressed in per capita
terms, foreign variables are scaled by the relative population size
of the home country
. To clear the
oil market, the sum of home and foreign oil production must equal
the sum of home and foreign oil consumption by firms and
households. Because all variables are expressed in per capita
terms, foreign variables are scaled by the relative population size
of the home country
![]() .
.
2.3 Fiscal Policy
The government purchases some of the domestic nonoil good
![]() but the import content of
government purchases is zero. Government purchases have no direct
effect on household utility and are given by:
but the import content of
government purchases is zero. Government purchases have no direct
effect on household utility and are given by:
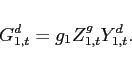 |
(22) |
The share of government spending in value added along the balanced
growth path is denoted by ![]() . The stochastic
component to this autonomous spending is
. The stochastic
component to this autonomous spending is ![]() .
.
Given the Ricardian structure of our model, net lump-sum
transfers ![]() are assumed to adjust each period
to balance the government receipts and revenues, so that:
are assumed to adjust each period
to balance the government receipts and revenues, so that:
| (23) |
2.4 Monetary Policy
Monetary policy follows a modified version of the interest rate reaction function suggested by Taylor (1993):
![\begin{displaymath} i_{1,t}= \bar{i}_{1} + \gamma^{i}_{1} (i_{1,t-1} - \bar{i}_{1}) +(1-\gamma^{i}_{1})\left[(\pi_{1,t}^{core}-\bar{\pi}^{core}_{1})+ \gamma^{\pi }_{1}(\pi^{core} _{1,t}-\bar{\pi}^{core}_{1}-\bar{\pi}^{core}_{1,t})+\gamma^{y}_{1} y_{1,t}^{gap}\right]. \end{displaymath}](img133.gif) |
(24) |
The terms ![]() and
and
![]() are the steady state
values for the nominal interest rate and inflation, respectively.
The inflation rate
are the steady state
values for the nominal interest rate and inflation, respectively.
The inflation rate
![]() is expressed as the
logarithmic percentage change of the core price level, i.e.,
inflation in nonoil consumer prices
is expressed as the
logarithmic percentage change of the core price level, i.e.,
inflation in nonoil consumer prices
![]() . The term
. The term
![]() denotes the log deviation of
gross output from the value of gross output in a model that
excludes nominal rigidities, but is otherwise identical to the one
described.5 The parameter
denotes the log deviation of
gross output from the value of gross output in a model that
excludes nominal rigidities, but is otherwise identical to the one
described.5 The parameter ![]() allows for interest rate smoothing. The term
allows for interest rate smoothing. The term
![]() reflects a time
varying inflation target.
reflects a time
varying inflation target.
2.5 Resource Constraints for Nonoil Goods and Net Foreign Assets
The resource constraint for the nonoil goods sector of the home economy can be written as:
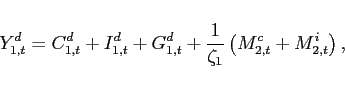 |
(25) |
where
![]() denotes the
per capita imports of the foreign country, which accounts for the
population scaling factor
denotes the
per capita imports of the foreign country, which accounts for the
population scaling factor
![]() .
.
The evolution of net foreign assets can be expressed as:
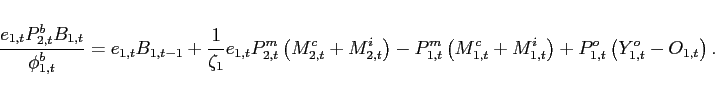 |
(26) |
This expression can be derived by combining the budget constraint
for households, the government budget constraint, and the
definition of firm profits. Market clearing for the
non-state-contingent bond requires
![]() .
.
2.6 Balanced Growth Path
Our model is consistent with a balanced steady state growth path
driven by a labor-augmenting technological progress, increases in
oil supply, and increases in oil efficiency. All growth rates are
common across countries. The growth rate of labor productivity is
denoted by ![]() while oil supply grows at the
rate
while oil supply grows at the
rate ![]() . To allow for a balanced growth path,
oil efficiency must improve over time to bridge the gap between
labor augmenting technological progress and oil supply growth at
the rate
. To allow for a balanced growth path,
oil efficiency must improve over time to bridge the gap between
labor augmenting technological progress and oil supply growth at
the rate
![]() .
Consequently, the price of oil is expected to grow at the rate
.
Consequently, the price of oil is expected to grow at the rate
![]() unconditionally.6
unconditionally.6
3 Model Solution and Estimation Strategy
The model is linearized around its balanced growth path and solved using the algorithm of Anderson and Moore (1985). The estimation by the method of maximum likelihood uses fifteen observed series: the log of U.S. and foreign GDP, U.S. and foreign oil production, the U.S. dollar price of oil (deflated by the U.S. GDP deflator), U.S. hours worked per capita, and the real dollar trade-weighted exchange rate; the GDP share of U.S. private consumption expenditures, the GDP share of U.S. oil imports, the GDP share of U.S. nonoil goods imports, the GDP share of U.S. goods exports, the GDP share of U.S. fixed investment; the level of U.S. core PCE inflation, U.S. wage inflation (demeaned), and the U.S. federal funds rate (demeaned). An appendix provides further details on data sources. The data are quarterly and run between 1984 and 2008. A presample that starts in 1974 trains the Kalman filter used to form the likelihood. The sample stops in the fall of 2008 to avoid a break in U.S. monetary policy associated with the zero bound on nominal interest rates.7
The model is just identified, as it also contains fifteen
exogenous shock processes: U.S. and foreign productivity
(![]() and
and ![]() ), U.S.
and foreign oil supply (
), U.S.
and foreign oil supply (![]() and
and ![]() ), U.S. and foreign oil efficiency (
), U.S. and foreign oil efficiency (![]() and
and ![]() ), U.S. autonomous
spending (
), U.S. autonomous
spending (![]() ), U.S. and foreign consumption
preferences (
), U.S. and foreign consumption
preferences (![]() and
and ![]() ),
U.S. and foreign import preferences (
),
U.S. and foreign import preferences (![]() and
and
![]() ), U.S. investment specific
technology (
), U.S. investment specific
technology (![]() ), U.S. price markup (
), U.S. price markup (
![]() ), U.S. labor supply (
), U.S. labor supply (
![]() ), and U.S. inflation target (
), and U.S. inflation target (
![]() ). Our first estimation
attempt involved specifying all shock processes as auto-regressive
of order one. However, the estimates of the parameters governing
some of the shock processes chafed against the upper bound of the
unit circle, imposed to ensure stationarity. To avoid constraining
the shock processes arbitrarily, we introduced AR(2) processes for
the following shocks: domestic and foreign productivity, domestic
and foreign oil supply, domestic and foreign oil efficiency,
domestic and foreign import preferences. While allowing for
distinct estimates of the size of the standard deviation of the
innovation to the shock process, we constrained the autoregressive
parameters for the home and foreign shocks to be the same in the
case of the shocks to: productivity, oil efficiency, consumption
preferences, and import preferences. Table 1 summarizes
the stochastic processes of the shocks and the data.
). Our first estimation
attempt involved specifying all shock processes as auto-regressive
of order one. However, the estimates of the parameters governing
some of the shock processes chafed against the upper bound of the
unit circle, imposed to ensure stationarity. To avoid constraining
the shock processes arbitrarily, we introduced AR(2) processes for
the following shocks: domestic and foreign productivity, domestic
and foreign oil supply, domestic and foreign oil efficiency,
domestic and foreign import preferences. While allowing for
distinct estimates of the size of the standard deviation of the
innovation to the shock process, we constrained the autoregressive
parameters for the home and foreign shocks to be the same in the
case of the shocks to: productivity, oil efficiency, consumption
preferences, and import preferences. Table 1 summarizes
the stochastic processes of the shocks and the data.
In the case of the home economy, we have adhered closely to the choice of observed series of closed-economy estimation exercises such as Smets and Wouters (2007) and Justiniano and Primiceri (2008). The asymmetry between the observed series for the home and foreign economies is dictated by data limitations. However, with regard to the home economy, the open-economy nature of our model avoids shortcuts taken by papers with a narrower one-sector, closed-economy focus. For instance, Smets and Wouters (2007) include investment and consumption measures not deflated by their own NIPA deflators, but rather by the overall GDP deflator - a sensible choice given that their model only implies one relative price. We prefer to observe consumption and investment as a share of GDP because our model has multiple relative prices, i.e., oil and import prices. A similar parallel to the closed-economy literature inspired our choice of stochastic processes. However, in our model the shock to autonomous spending has a different interpretation. As observations on trade data inform the likelihood, autonomous spending captures movements in the components of GDP not directly observed, specifically, government spending and inventory investment. By contrast, in closed-economy models, Chari, Kehoe, and McGrattan (2009) noticed that the shock to autonomous spending would also have to capture the bulk of fluctuations in the trade balance.
We estimate all the parameters governing the shock processes
listed in Table 1. We also
estimate all behavioral parameters in the model with the exception
of: the depreciation rate of capital, ![]() ,
fixed at 0.025; the intertemporal elasticity for consumption
,
fixed at 0.025; the intertemporal elasticity for consumption
![]() , fixed at 1; the curvature of the
intermediation cost for foreign bonds,
, fixed at 1; the curvature of the
intermediation cost for foreign bonds, ![]() ,
fixed at 0.0001; and the discount factor
,
fixed at 0.0001; and the discount factor ![]() ,
fixed so that taking into account the estimate for trend
productivity growth, the real interest rate along the balanced
growth path is 4% per year. Following Ireland (2004), this
calibration of
,
fixed so that taking into account the estimate for trend
productivity growth, the real interest rate along the balanced
growth path is 4% per year. Following Ireland (2004), this
calibration of ![]() avoids the systematic
over-prediction of the historical returns on U.S. Treasury bills in
representative agent models to that Weil (1989) calls "the risk
free rate puzzle." The foreign parameters take on the same values
as for the home country.
avoids the systematic
over-prediction of the historical returns on U.S. Treasury bills in
representative agent models to that Weil (1989) calls "the risk
free rate puzzle." The foreign parameters take on the same values
as for the home country.
Table 2 summarizes
parameters and the values for ratios (along the balanced growth
path) that enter the linearized conditions for our model. Values
for government spending ![]() , and
, and
![]() are consistent with data from
the National Income and Product Accounts (NIPA). The parmeter
are consistent with data from
the National Income and Product Accounts (NIPA). The parmeter
![]() implies that nonoil production in
the home country is half the size of nonoil production in the
foreign country.
implies that nonoil production in
the home country is half the size of nonoil production in the
foreign country.
Values for
![]() and
and
![]() are determined by the overall
oil share of output, and the ratios of the quantity of oil used as
an intermediate input in production relative to the quantity used
as a final input in consumption. Based on data from the Energy
Information Administration of the U.S. Department of Energy for
2008, the overall oil share of the domestic economy is set to 4.2
percent of GDP. The relative size of oil use in consumption and
production is sized using the U.S. Input-Output Use tables. Over
the period 2002-2008, for which the tables are available annually,
the Use tables point to a low in 2002 of 0.30 and a peak in 2008 of
0.39. We settle on a calibration equal to the average over the last
ten years in the sample of 0.35, which implies that
are determined by the overall
oil share of output, and the ratios of the quantity of oil used as
an intermediate input in production relative to the quantity used
as a final input in consumption. Based on data from the Energy
Information Administration of the U.S. Department of Energy for
2008, the overall oil share of the domestic economy is set to 4.2
percent of GDP. The relative size of oil use in consumption and
production is sized using the U.S. Input-Output Use tables. Over
the period 2002-2008, for which the tables are available annually,
the Use tables point to a low in 2002 of 0.30 and a peak in 2008 of
0.39. We settle on a calibration equal to the average over the last
ten years in the sample of 0.35, which implies that
![]() and
and
![]() are equal to 0.026 and 0.021,
respectively.
are equal to 0.026 and 0.021,
respectively.
The oil imports of the home country are set to 70 percent of
total demand in the steady state, implying that 30 percent of oil
demand is satisfied by domestic production. This estimate is based
on 2008 NIPA data. In the foreign bloc, the overall oil share is
set to 8.2 percent. The oil endowment abroad is 9.5 percent of
foreign GDP, based on oil supply data from the Energy Information
Administration. The common trend growth rate for oil supply
![]() is fixed at 1.0026,
implying 0.26 percent growth per quarter, the average growth rate
of world oil supply over the sample period.
is fixed at 1.0026,
implying 0.26 percent growth per quarter, the average growth rate
of world oil supply over the sample period.
Turning to the parameters determining trade flows, the parameter
![]() and
and
![]() are chosen to reflect NIPA
data for nonoil imports while equalizing the nonoil
import-intensity of consumption and investment. This calibration
implies a ratio of nonoil goods imports relative to GDP for the
home country of about 12 percent and values of for both
are chosen to reflect NIPA
data for nonoil imports while equalizing the nonoil
import-intensity of consumption and investment. This calibration
implies a ratio of nonoil goods imports relative to GDP for the
home country of about 12 percent and values of for both
![]() and
and
![]() equal to 0.15. Given that
trade is balanced in along the balanced growth path, and that the
oil import share for the home country is 3 percent of GDP, the
goods export share is 15 percent of GDP.
equal to 0.15. Given that
trade is balanced in along the balanced growth path, and that the
oil import share for the home country is 3 percent of GDP, the
goods export share is 15 percent of GDP.
3.1 Parameter Estimates and Empirical Fit
Table 3 reports
estimates of the main behavioral parameters and confidence
intervals.8 Starting from the trends, the growth
rate of productivity for the home and foreign economies,
![]() , is estimated at 0.6 percent per
quarter, or 2.4 percent per year, lower than the 2.9 average U.S.
GDP growth over the sample and the 3.5 average foreign GDP growth.
As world oil supply expands at the quarterly rate of 0.26 percent,
oil efficiency improves at the quarterly rate of 0.32 percent along
the balanced growth path given the relationship
, is estimated at 0.6 percent per
quarter, or 2.4 percent per year, lower than the 2.9 average U.S.
GDP growth over the sample and the 3.5 average foreign GDP growth.
As world oil supply expands at the quarterly rate of 0.26 percent,
oil efficiency improves at the quarterly rate of 0.32 percent along
the balanced growth path given the relationship
![]() . Consequently,
the trend growth in the real price of oil is also 0.32 percent per
quarter, or roughly 1.3 percent per year. The U.S. steady state
inflation rate,
. Consequently,
the trend growth in the real price of oil is also 0.32 percent per
quarter, or roughly 1.3 percent per year. The U.S. steady state
inflation rate,
![]() , is estimated at 1.1 percent
per quarter, which is a close match to the 3.84 average for U.S.
core PCE inflation over the sample.
, is estimated at 1.1 percent
per quarter, which is a close match to the 3.84 average for U.S.
core PCE inflation over the sample.
Turning to substitution elasticities, we estimate the oil
substitution elasticity,
![]() , to be 0.42.
Notice that, in our model, substitution elasticities map one for
one into price elasticities of demand. Perhaps the closest results
to ours are those of Kilian and Murphy (2010), who gauge the price
elasticity of oil demand as the ratio of the impact response of oil
production to the impact response of the real price of oil
conditional on an oil supply shock. The absolute value of their
posterior median estimate is 0.44. From the same type of
calculation, Baumeister and Peersman (2009) estimate the price elasticity at
0.38. In our model such a ratio is influenced not only by the price
elasticity of oil demand, but also by the contemporaneous response
of consumption and gross output (the activity variables driving oil
demand). However, since the response of consumption and gross
output to a foreign oil supply shock is of a different order of
magnitude relative to the response of the real dollar price of oil,
and given the theoretical restriction that the activity elasticity
is 1, the ratio of oil supply to the the price of oil on impact is
0.40 in our model.
, to be 0.42.
Notice that, in our model, substitution elasticities map one for
one into price elasticities of demand. Perhaps the closest results
to ours are those of Kilian and Murphy (2010), who gauge the price
elasticity of oil demand as the ratio of the impact response of oil
production to the impact response of the real price of oil
conditional on an oil supply shock. The absolute value of their
posterior median estimate is 0.44. From the same type of
calculation, Baumeister and Peersman (2009) estimate the price elasticity at
0.38. In our model such a ratio is influenced not only by the price
elasticity of oil demand, but also by the contemporaneous response
of consumption and gross output (the activity variables driving oil
demand). However, since the response of consumption and gross
output to a foreign oil supply shock is of a different order of
magnitude relative to the response of the real dollar price of oil,
and given the theoretical restriction that the activity elasticity
is 1, the ratio of oil supply to the the price of oil on impact is
0.40 in our model.
On the nonoil goods trade side, the estimate of the elasticity of substitution between domestic and foreign goods, at 1.8 is also close to other estimates based on aggregate data. For instance, Hooper, Johnson, and Marquez (2000) estimated trade price elasticities using data for G-7 countries and reported an export price elasticity of 1.5 for the United States.
The model has two parameters governing real rigidities. The
parameter for consumption habits, ![]() , is
estimated at 0.65. This estimate is in line with values typically
reported by studies with a closed economy focus such as
Smets and Wouters (2007), who show a posterior distribution with a mean and a
mode of 0.71. Our estimate for the adjustment costs of investment
, is
estimated at 0.65. This estimate is in line with values typically
reported by studies with a closed economy focus such as
Smets and Wouters (2007), who show a posterior distribution with a mean and a
mode of 0.71. Our estimate for the adjustment costs of investment
![]() , at 3.5, is also in line with other
authors' estimates of this parameter in DSGE models. For
comparison, Christiano, Eichenbaum, and Evans (2005) report an estimate of the
curvature of the adjustment cost function equal to 4, well within
the 95% confidence interval for our estimate.
, at 3.5, is also in line with other
authors' estimates of this parameter in DSGE models. For
comparison, Christiano, Eichenbaum, and Evans (2005) report an estimate of the
curvature of the adjustment cost function equal to 4, well within
the 95% confidence interval for our estimate.
The estimates of parameters in the monetary policy rule indicate
a stronger weight on inflation than the output gap. The weight on
inflation is
![]() , the estimated weight on
the output gap is
, the estimated weight on
the output gap is
![]() .9 We find evidence for
substantial interest rate smoothing, as our estimate of the
smoothing parameter is
.9 We find evidence for
substantial interest rate smoothing, as our estimate of the
smoothing parameter is
![]() .
.
Moving to the wage- and price-setting equations, the Calvo
parameter for wages, ![]() , is estimated at
0.89. The Calvo parameter for prices,
, is estimated at
0.89. The Calvo parameter for prices, ![]() , is
estimated at 0.81. We find little evidence in favor of lagged
indexation for either prices or wages. Following
Eichenbaum and Fisher (2007) and Guerrieri, Gust, and Lopéz-Salido (2010) one could reinterpret
the estimate of the slope of marginal cost in the Phillips curve,
determined by the parameters
, is
estimated at 0.81. We find little evidence in favor of lagged
indexation for either prices or wages. Following
Eichenbaum and Fisher (2007) and Guerrieri, Gust, and Lopéz-Salido (2010) one could reinterpret
the estimate of the slope of marginal cost in the Phillips curve,
determined by the parameters ![]() and
and
![]() in our model, through the lens of a
more general aggregator for intermediate goods such as the one
suggested by Kimball (1995). That aggregator allows for the
possibility that the elasticity of demand for the product of an
intermediate firm is increasing in its price. The results in
Guerrieri, Gust, and Lopéz-Salido (2010) for the curvature of the elasticity with
respect to price suggest that our estimate of
in our model, through the lens of a
more general aggregator for intermediate goods such as the one
suggested by Kimball (1995). That aggregator allows for the
possibility that the elasticity of demand for the product of an
intermediate firm is increasing in its price. The results in
Guerrieri, Gust, and Lopéz-Salido (2010) for the curvature of the elasticity with
respect to price suggest that our estimate of ![]() implies an average contract duration below 2
quarters, in line with the micro evidence in Klenow and Krytsov (2008).
implies an average contract duration below 2
quarters, in line with the micro evidence in Klenow and Krytsov (2008).
While Table 3 reports estimates of the parameters governing all the shock processes, to interpret these estimates, we prefer to focus on Table 4. The latter table shows a break-down by shock of the population variance of key variables. The table focuses on decomposing population variances over the business cycle, obtained by isolating oscillations with a periodicity between 6 and 36 quarters.10
Focusing on the price of oil, domestic shocks play a negligible role. The bulk of the population variance, 88%, is explained by foreign oil efficiency shocks, with foreign oil supply shocks playing a non-negligible role. Despite the finding that most of the variance of oil shocks is explained by oil efficiency shocks, the price of oil is not the only channel for the transmission of those shocks. For instance, foreign oil efficiency shocks, account for 19% of the population variance of the real dollar exchange rate. This finding underscores the importance of general equilibrium effects for the transmission of shocks that are specific to the oil market and is in line with previous results in Bodenstein, Erceg, and Guerrieri (2011).
Moving to U.S. nonoil gross output and its components, shocks that are directly related to the oil market, play a negligible role in explaining population variances. Altogether, those shocks account for only 3% of the population variance of U.S. output. They play a slightly larger role for consumption and the trade balance, respectively, 6% and 10% in total. Not surprisingly, oil shocks have a larger effect on foreign output. The data imply that oil is a proportionately more substantial input in foreign production and consumption, and is a sizable source of exports. Accordingly, foreign oil efficiency shocks account for about 33% of the population variance of foreign nonoil gross output.
Comparing the sources of fluctuation for domestic and foreign output in Table 4 underscores a substantial asymmetry. Economy-wide productivity shocks account for the prevalent share of the population movements for foreign output, about 60%. By contrast, in the home economy, economy-wide and investment-specific productivity shocks account for about 30% of output fluctuations and are less important than labor supply shocks. It is hard to gauge to what extent the differences on the determinants of domestic and foreign business cycles are extant or artificially driven by the exclusion of foreign labor supply shocks in the model. Without series for foreign hours worked - and to our knowledge, only few countries maintain statistics on hours worked - it is infeasible to separately identify labor supply and productivity shocks for the foreign bloc. However, when we excluded U.S. hours worked from the observations in the likelihood (and removed the labor supply shock from the U.S. bloc of the model), the asymmetries on the role of technology shocks in the domestic and foreign blocs were practically eliminated.
It is not straight-forward to relate some of our estimates to those in exercises with a closed economy focus on U.S. data. Our model implies additional channels that influence the variability of wages deflated by consumption prices. Closed economy models miss variation stemming from import prices and oil prices. Given these additional sources of variation for real wages, it may not be surprising that our estimate for the Frisch elasticity of labor supply is already deemed unlikely by the prior used in Smets and Wouters (2007). Their Normal prior with a mean of 2 is more than two prior standard deviations away from our estimate.
3.2 Cyclical Properties
Our estimated model captures the business cycle properties of key variables. For those variables that are directly observed in the estimation, Table 5 reports the 2.5th percentile, 97.5th percentile, and the median of the standard deviations and autocorrelations implied by the model, along with their sample estimates in the data.11 In most cases, the statistic derived from the observed data lies between the 2.5th and the 97.5th percentile of the model implied distribution. In a similar fashion, the table also reports contemporaneous correlations of the price of oil with other observed variables.12 We conclude that the model is consistent with a remarkable array of sample moments.
3.3 Interpreting Oil Efficiency Shocks
While oil efficiency shocks are meant to capture fundamental changes in the demand for oil - such as a shift towards motorization in emerging Asia, continuing industrialization of China, or energy-efficient cars becoming more popular in the United States - we would like to exclude the possibility that the efficiency shocks are nothing but a catchall for all unmodeled disturbances that can affect oil demand.
Accordingly, we conduct a simple exogeneity test for our
estimated oil efficiency innovations
![]() and
and
![]() following the exercise
in Evans (1992) for technology shocks. Let
following the exercise
in Evans (1992) for technology shocks. Let
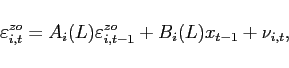 |
(27) |
where ![]() is a mean zero, i.i.d random
variable,
is a mean zero, i.i.d random
variable, ![]() and
and ![]() are
polynomials in the lag operator
are
polynomials in the lag operator ![]() ,
, ![]() is a vector that includes potential explanatory variables for oil
demand. Ideally, none of the variables included in
is a vector that includes potential explanatory variables for oil
demand. Ideally, none of the variables included in ![]() should Granger cause the innovations
should Granger cause the innovations
![]() and
and
![]() .
.
Unmodeled determinants of oil demand that we would like to see assessed as unimportant for our measure of oil efficiency are: (i) log-changes in oil inventories (OECD and U.S. inventory data), (ii) log-changes of the price of oil substitutes in energy generation (price of coal), (iii) financial market activities (log-changes in oil futures, real stock market returns), (iv) changes in and the level of activity-driven demand for all commodities (index proposed in Killian (2009)) as these should already be captured by our GDP measures.13
When including each of the variables separately with up to three
lags, the null hypothesis of exogeneity, ![]() ,
was never rejected for the foreign oil efficiency shocks at the 5
significance level.14 For the U.S. oil efficiency shock,
the null hypothesis was rejected at the 5% level of significance
for log-changes in OECD oil inventories and changes in Kilian's
shipping index. Yet, the adjusted
,
was never rejected for the foreign oil efficiency shocks at the 5
significance level.14 For the U.S. oil efficiency shock,
the null hypothesis was rejected at the 5% level of significance
for log-changes in OECD oil inventories and changes in Kilian's
shipping index. Yet, the adjusted ![]() never
exceeds 11%. With up to three lags in the VAR, no
combination of variables ever implied a rejection of the null
hypothesis at conventional significance levels for the foreign oil
efficiency shock (up to 10%). Moreover, the adjusted
never
exceeds 11%. With up to three lags in the VAR, no
combination of variables ever implied a rejection of the null
hypothesis at conventional significance levels for the foreign oil
efficiency shock (up to 10%). Moreover, the adjusted
![]() never exceeds 12%. For the
U.S. oil efficiency shock, the most challenging combination of
variables is given by the set of changes in Kilian's activity
measure, and log-changes in OECD and U.S. oil inventories. In this
case, the null hypothesis of block exogeneity is rejected at the 1%
significance level for each lag-length up to three lags. However,
with adjusted
never exceeds 12%. For the
U.S. oil efficiency shock, the most challenging combination of
variables is given by the set of changes in Kilian's activity
measure, and log-changes in OECD and U.S. oil inventories. In this
case, the null hypothesis of block exogeneity is rejected at the 1%
significance level for each lag-length up to three lags. However,
with adjusted ![]() values not exceeding 15%, the combined explanatory power of these variables is
low. We conclude that none of the combinations we tested poses an
important challenge to our interpretation of the oil efficiency
shocks.15
values not exceeding 15%, the combined explanatory power of these variables is
low. We conclude that none of the combinations we tested poses an
important challenge to our interpretation of the oil efficiency
shocks.15
4 Foreign Oil Efficiency Shocks
Based on the decompositions of the population variance, foreign oil efficiency shocks are the key determinant of movements in oil prices. The effects of an innovation to the shock that governs foreign oil efficiency highlight the propagation mechanisms in the model. The reaction of domestic production cannot be understood without considering the general equilibrium repercussions through trade channels, as well as the reaction of inflation and the systematic role of monetary policy. However important, efficiency shocks are not the only determinant of movements in the price of oil or even oil demand. Comparing the implications of the shocks in the model, it emerges that there is no such a thing as a typical oil price shock and that the impact of the oil price fluctuations remarkably varies depending on the underlying source.
4.1 The Effects of an Oil Efficiency Shock
Figure 1 illustrates the
effects of a two-standard deviation shock that reduces foreign oil
efficiency, ![]() . As foreign oil demand expands,
the price of oil increases. Initially, the price rises 30%. The
half life of the response is close to 5 years. Home oil demand
contracts as both households and firms substitute away from the
more expensive oil input. Since the oil price elasticity of demand
is estimated close to 1/3, the decline in demand is also
approximately 1/3 of the price increase.
. As foreign oil demand expands,
the price of oil increases. Initially, the price rises 30%. The
half life of the response is close to 5 years. Home oil demand
contracts as both households and firms substitute away from the
more expensive oil input. Since the oil price elasticity of demand
is estimated close to 1/3, the decline in demand is also
approximately 1/3 of the price increase.
Eventually, the decline in oil use has effects on gross nonoil output, the expenditure components, and the real interest rate that resemble those of a highly persistent decline in productivity. Lower oil use leads to a fall in the current and future marginal product of capital, causing investment, consumption, and gross output to fall. However, in the short run, the shock does not unequivocally lead to a fall in output. Real rigidities prevent both consumption and investment from adjusting immediately, as can be evinced from the response of domestic absorption. Furthermore, the response of net nonoil exports, as well as the role of nominal rigidities and monetary policy need to be taken into account.
Focusing on trade, for an oil importer with a low oil price elasticity, an oil price increase results in a marked deterioration of the oil balance. With incomplete international financial markets, the deterioration in the oil balance is linked to substantial differences in wealth effects across countries. As the negative wealth effect is relatively larger for the oil importer, the home nonoil terms of trade worsen and induce an expansion in nonoil net exports.16
Apart from net exports, nominal rigidities, and monetary policy also play an important role in shaping the short-term response. In Figure 1, realized output expands whereas potential output contracts. The differences in the responses of the realized real interest rate and the potential real interest rate are stark. In the presence of pronounced real rigidities that make the economy relative insensitive to movements in the real interest rate in the short run, very large swings in the real interest rate occur in the potential economy in order to curb domestic absorption. Consequently, potential absorption drops more substantially than realized absorption. By contrast, the smoothing component of the estimated historical monetary policy rule generates a gradual increase in real rates that ends up overshooting the increase in potential rates after a couple of quarters. The relative movements of realized and potential output mirror those of the interest rate movements. After a couple of quarters, as potential real rates fall more sharply than realized rates, potential output recovers more quickly and "leapfrogs" realized output. The figure also reveals that the initial expansion in realized output is associated with an expansion in hours worked. By contrast, the demand for oil and capital falls uniformly.
Core inflation rises above domestic inflation, as the terms of trade worsen and import prices rise. The rise in domestic inflation is related to the rise in marginal cost. In turn the rise in marginal cost is mostly linked to the gap between the marginal product of labor and the real wage. As firms shift away from using more expensive oil, they push up the relative demand for other factor inputs. The labor input is the only factor that can be adjusted immediately, so hours worked increase and the marginal product of labor falls below the real wage. Sticky nominal wages ward off a large immediate rise in the rental rate for labor, but they also hinder subsequent downward adjustment towards the marginal product. The resulting persistent gap between the real wage and the marginal product of labor is the key contributor to the rise in marginal cost and domestic price inflation. Eventually, as oil prices come down, the effects on inflation are reversed and inflation turns negative. However, the core and domestic price levels remain persistently elevated.
4.2 Output Responses
Figure 2 showcases the richness of our model by highlighting how the broad array of shocks influences the price of oil. All the shocks considered are sized at two standard deviations and their sign is chosen to induce an increase in the price of oil. The figure paints stark differences regarding the magnitude and dynamic response of oil prices depending on whether the sources of fluctuations are domestic or foreign. Furthermore, it shows that drastically different results obtain depending on the specific source of activity shocks.
The explicit open economy nature of our model distinguishes between domestic and foreign sources of fluctuations. Apart from size differences, the response of the oil price to domestic and foreign efficiency shocks appear similar. However, the impact on gross output is quite different. Abstracting from short-lived impact differences, the price responses differ by about a factor of 10, while the output responses only differ by a factor of about 2.5. This asymmetry occurs because, a fall in oil efficiency at home pushes up home oil demand despite an increase in oil prices. Consequently, conditioning on the same price increase, the associated negative wealth effect is larger for the home country. Aggregation of sources of fluctuation does lead to an loss in important details.
Moving to oil supply shocks, we can also distinguish between domestic and foreign sources. We estimate markedly different processes for domestic and foreign shocks that translate into quite different price paths for oil. In particular, the domestic shock is much closer to resembling a unit root process and almost leads to one-time shift in oil prices.17 Accordingly, gross output contracts almost permanently in response to the domestic shock.
The right panels of Figure 2 focus on shocks that affect oil prices through broader movements in activity. Aside from disentangling the domestic or foreign source, we illustrate a wide array of distinct activity shocks. Apart from differences in magnitudes and rates of decay, striking differences in sign are apparent. All of the shocks shown are sized to induce an increase in the price of oil, but these shocks do not all induce an expansion in activity. For example, a negative domestic consumption preference shock contracts home activity, reduces overall oil demand, yet a depreciation of the dollar raises the price of oil in dollar terms. Similar effects obtain for a contraction in foreign activity because of offsetting changes in exchange rates. By contrast, a domestic technology shock increases domestic activity and pushes up the demand for oil. The resulting increase in the price of oil is reinforced by the depreciation of the domestic currency.
Thus, explicit modeling of oil as an internationally traded commodity leads to complications in the formulation of sign restrictions that can identify supply and demand shocks. In particular, the increase in the price of oil (in dollar terms) is associated with a decrease in oil demand and contradicts the typical sign restrictions applied to disentangle demand and supply movements implemented in Lippi and Nobili (2010), or in Kilian and Murphy (2009).
5 Historical Decompositions
The estimates in this section alternatively apportion movements in the observed series to a rotating cast of shocks. The goal is to learn which types of shocks are good candidates to explain the behavior of oil prices and U.S. oil demand over the sample. Since the model is linear in the size of shocks, isolating the role of any arbitrary subset of shocks in explaining the observed data comes without loss of information and the contributions to the observed series associated with different groups of shocks are additive.
Use of the Kalman filter ensures that the smoothed estimates of the shocks, together with trends and estimated initial conditions yield an exact match for the series observed. As we choose to ignore trend and initial conditions, the series produced when all shocks are turned on can be interpreted as a detrended measure of the series observed.
5.1 What Moves Oil Prices and Oil Demand?
The top panel in the first column of Figure 3 parses out the role of oil shocks and nonoil shocks in determining the observed movements in the detrended real price of oil, i.e. the observed dollar price deflated by the U.S. GDP deflator. The term "oil shocks" refers to oil supply and efficiency shocks both at home and abroad combined. All other shocks are grouped in the category "nonoil shocks." The dashed line, shows the path of oil conditional on nonoil shocks only. Mostly because productivity growth in the foreign bloc is on average above trend over the sample, nonoil shocks have tended to push oil prices above the estimated oil trend.
By contrast, oil shocks have tended to depress oil prices, on average. The dash-dotted line reports the path of the oil price conditional on the occurrence of oil shocks only. The cumulative effects of persistent shocks can generate protracted deviations from the balanced growth path. Since the path of oil that obtains with oil shocks follows the detrended observed price closely (the solid line), oil shocks are the major determinant of fluctuations in the price of oil over the sample period. Nonetheless, nonoil shocks play a non-negligible role. For instance, between 2003 and 2008, when the detrended real price of oil in log terms rose about 120%, if only nonoil shocks had occurred, the oil price would have risen 40%.18
The bottom panel in the first column of Figure 3 de-constructs the oil price further. In focusing on two subsets of the oil shocks. The dotted dashed line shows the path of the oil price that would obtain with home and foreign oil supply shocks only. The dashed line shows the price of oil conditional on home and foreign oil efficiency shocks only. For ease of comparison, the solid line shows the path of oil conditional on both demand and supply shocks (and matches the "oil shocks" line in the top left panel). The proximity of the dashed and solid lines indicates that among oil shocks, oil efficiency shocks play a pivotal role. This result is the sample counterpart of our finding that oil efficiency shocks are the single largest source of variation in population.
The rich structure of our model allows us to decompose the sources of fluctuations in oil prices further. The second column in Figure 3 shows the price of oil conditional on domestic and foreign determinants. As the path of oil price conditional on shocks of foreign origin hugs the observed price closely in the top panel, the bulk of fluctuations in oil prices is explained by foreign shocks. The panel below shows that among foreign shocks, foreign activity shocks have played a relatively minor role on average. However, over particular episodes, they made a non-negligible contribution. Focusing again on the 2003-2008 oil price runup, of the 120% increase in the log of detrended real oil prices, a 35% increase was due to foreign activity shocks.
The remaining columns of Figure 3 shift the focus away from prices, and onto the demand for oil. The solid lines in the third column of the figure show U.S. oil demand. The solid lines in the fourth column show foreign demand. It is immediately apparent that detrended oil demand is less volatile than detrended oil prices (notice the different scales). This observation gives an intuitive justification for our estimate of a price elasticity of demand below unity. In the right columns oil demand is decomposed alternatively into contributions of domestic and foreign shocks (the top panels) and into contributions of efficiency shocks and other shocks (the bottom panels). From the top panels, one can see that foreign shocks play a pivotal role in shaping both U.S. and foreign oil demand, just as for the oil price.
Moving to the bottom panels, the component that isolates oil efficiency shocks hugs the detrended demand closely for both country blocs. While remaining important, the role of efficiency shocks is not preponderant for the period between 2003 and 2008. Of the 20% increase in detrended foreign oil demand in that period, roughly half the increase is accounted for by declines in efficiency and half by other shocks. A finer decomposition of the other shocks reveals an important role for technology shocks. Faster productivity growth in the foreign bloc brought up foreign oil demand over that period. Interestingly, the effects of the foreign productivity increases on the detrended price of oil in dollar terms were offset by the effects on the dollar exchange rate, as in isolation, those shocks tend to appreciate the U.S. dollar.
5.2 Monetary Policy
One of the fundamental themes that has beguiled the literature on the macroeconomic effects of oil shocks is the role of monetary policy in influencing the relationship between U.S. activity and oil prices.19 Figure 4 considers the effects on realized and potential output of all the shocks specific to the oil market retrieved from our estimation, which include oil efficiency and oil supply shocks both in the United States and abroad. The solid line in the top panel shows the movements in U.S. gross output conditional on the smoothed estimates of oil demand and supply shocks both at home and abroad. The bottom panel isolates the oil price movements associated with the same shocks. In both panels, the dotted lines denote the responses in the potential economy without nominal rigidities. The price responses in the realized and potential economies appear indistinguishable. We interpret this finding as evidence that U.S. monetary policy plays no role in shaping the evolution of oil prices.
However, monetary policy does have consequences for the transmission of oil shocks to the macroeconomy. The "leapfrogging" of potential and realized output highlighted in the discussion of Figure 1 is a feature that comes through for the full set of the oil shocks throughout the sample. This feature is associated with the response to lagged interest rates in the estimated monetary policy rule. The interest rate smoothing is so strong that monetary policy first cushions the effects of oil shocks on output. However, when monetary policy does respond, it responds in a fashion that is too protracted. Nonetheless, the gaps between potential and realized output appear modest in magnitude, relative to the overall effects on potential output. Accordingly, we conclude that monetary policy and nominal rigidities did not have a quantitatively important role in magnifying the effects of oil demand and supply shocks for U.S. economic activity through the estimation sample.
5.3 A Look Beyond the Model
As shown in Figure 3, the detrended
real oil price fell 140% over the first part of the estimation
sample, from 1984 to 1998. However, over the second half of the
sample, the oil price moved back up and by 2008 it had surpassed
its 1984 level. One of the main results to emerge from the
estimation of our DSGE model is that foreign oil efficiency is the
major driver of the price of oil at business-cycle and longer
frequencies. The top left panel of Figure 5 shows that
the cumulative growth in foreign oil efficiency outpaced its trend
![]() over the first half of the sample
when oil prices declined.20 Since the late 1990s, improvements
in oil efficiency have slowed down and oil prices have been
catching up to levels that would have prevailed absent the earlier
gains in oil efficiency.
over the first half of the sample
when oil prices declined.20 Since the late 1990s, improvements
in oil efficiency have slowed down and oil prices have been
catching up to levels that would have prevailed absent the earlier
gains in oil efficiency.
While our estimation restricted attention to an aggregate foreign bloc, we can construct measures of oil efficiency for individual foreign countries using the approach of growth-accounting studies in the style of Solow (1957) and Griliches and Jorgenson (1966). Starting from the oil demand equations, we show that the growth rate of oil efficiency can be expressed in terms of directly observable quantities. However, our theoretically-founded concept of efficiency, also depends on parameters, such as the rate of trend growth in efficiency and the oil price elasticity of demand. To construct country-by-country measures of oil efficiency consistent with the foreign aggregate included in the DSGE model, we use disaggregate data in conjunction with the parameter estimates obtained for the entire foreign bloc of the model.
Using the first order conditions for oil use by foreign firms
![]() and households
and households ![]() derived from problems (13) and (16),
respectively, foreign oil efficiency growth can be written
as:
derived from problems (13) and (16),
respectively, foreign oil efficiency growth can be written
as:
 |
||
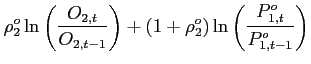 |
||
 |
(28) |
Along the balanced growth path, oil efficiency grows at the
constant rate ![]() . Growth in efficiency relative
to the balanced growth path is measured by the term
. Growth in efficiency relative
to the balanced growth path is measured by the term
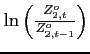 . In
summary, oil efficiency is measured by those changes in oil demand
that cannot be explained by movements in the oil price or movements
in a broad measure of economic activity. Finally, the term
. In
summary, oil efficiency is measured by those changes in oil demand
that cannot be explained by movements in the oil price or movements
in a broad measure of economic activity. Finally, the term
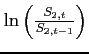 corrects for changes in the composition of aggregate oil
demand.21
corrects for changes in the composition of aggregate oil
demand.21
Some intuitive measures of oil efficiency emerge as special
cases of our approach. Abstracting from composition effects
captured by the term
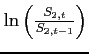 ,
if the elasticity of substitution between oil and other factor
inputs were zero, oil efficiency would collapse to the ratio of
real oil demand to real GDP. With a unitary price elasticity, our
measure would coincide with the nominal oil share in GDP.22
Ultimately, we do not find these alternative intuitive measures
compelling, since reconciling them with economic theory relies on
assumptions regarding the price elasticity of oil demand that are
refuted empirically.
,
if the elasticity of substitution between oil and other factor
inputs were zero, oil efficiency would collapse to the ratio of
real oil demand to real GDP. With a unitary price elasticity, our
measure would coincide with the nominal oil share in GDP.22
Ultimately, we do not find these alternative intuitive measures
compelling, since reconciling them with economic theory relies on
assumptions regarding the price elasticity of oil demand that are
refuted empirically.
We use annual data for oil consumption from the BP Statistical Review of World Energy 2011 and the refiners' acquisition costs for imported crude from the U.S. Energy Information Administration. Data for nominal (in U.S. dollars) and real GDP and consumption are taken from the World Bank's World Development Indicators (WDI) database. We construct gross output measures based on GDP and oil shares. As we use annual data, we simplify the analysis by abstracting from nominal rigidities and taking real marginal costs to be constant.
Figure 5 plots the
cumulative change in oil efficiency net of its balanced growth path
rate ![]() for various foreign countries
starting in 1984. For each country, the log-level of oil efficiency
is normalized to zero at the beginning of the sample. Foreign
industrialized economies across the board showed strong
improvements in oil efficiency between 1984 and 1998. Among the
emerging economies, Brazil, Korea, and India stand out for not
having experienced the pronounced increases in efficiency in the
first part of the sample, or having registered almost monotonic
declines through the sample relative to trend. In Mexico and China,
however, as in the foreign industrialized countries, oil efficiency
showed significant faster growth than
for various foreign countries
starting in 1984. For each country, the log-level of oil efficiency
is normalized to zero at the beginning of the sample. Foreign
industrialized economies across the board showed strong
improvements in oil efficiency between 1984 and 1998. Among the
emerging economies, Brazil, Korea, and India stand out for not
having experienced the pronounced increases in efficiency in the
first part of the sample, or having registered almost monotonic
declines through the sample relative to trend. In Mexico and China,
however, as in the foreign industrialized countries, oil efficiency
showed significant faster growth than ![]() in the
first half of the sample. After the late 1990s, foreign efficiency
improvements slowed down and the gap between actual oil efficiency
and cumulative trend growth in oil efficiency narrowed. Hence, the
inverted U-shaped pattern for the evolution of foreign oil
efficiency over the sample is shared by many countries and is not
merely a consequence of aggregation.
in the
first half of the sample. After the late 1990s, foreign efficiency
improvements slowed down and the gap between actual oil efficiency
and cumulative trend growth in oil efficiency narrowed. Hence, the
inverted U-shaped pattern for the evolution of foreign oil
efficiency over the sample is shared by many countries and is not
merely a consequence of aggregation.
The bottom panels of the figure show a decomposition of the
growth rate of world oil efficiency by region and the shares of oil
consumption by region. The decomposition apportions the average
annual growth in world oil efficiency relative to trend to regional
contributions based on regional consumption shares and regional
growth rates of efficiency.23 For ease of presentation, we show
results for groups of aggregates: the OECD countries (excluding
South Korea), Emerging Asia (including South Korea), and the rest
of the world bloc. Consistent with the country-specific evidence
and our estimation results, between 1984 and 1998, oil efficiency
grew faster than predicted by the balanced growth rate both in the
aggregate and in each bloc. Afterwards, actual oil efficiency
growth fell below the balanced growth rate ![]() .
.
The industrialized countries accounted for the bulk of the improvements in world oil efficiency.24 Due to its relatively low share in world oil consumption, Emerging Asia played a modest role in driving oil efficiency at the beginning of the sample. However, as oil demand expanded faster there than elsewhere, this group's share in world oil consumption has climbed from less than 10% between 1984-1988 to more than 20%. Accordingly, Emerging Asia has made a larger contribution to the slowdown in oil efficiency growth between 2004 and 2008.
6 Conclusion
We broadened the study of changes in crude oil prices to consider their global macroeconomic sources. Using an estimated two-country DSGE model, we used observations from 15 aggregate time series to decompose fluctuations in the price of oil into components driven by country-specific oil supply shocks, oil efficiency shocks, and various domestic and foreign shocks that affect the price of oil indirectly through activity. Foreign oil efficiency shocks were the key driver of fluctuations in oil prices between 1984 and 2008. Our analysis shows that oil efficiency grew above trend around the globe from 1984 to the mid-nineties and oil prices fell below trend. When oil efficiency growth slowed down, oil prices caught up to levels that would have prevailed absent the earlier gains.
Our economic model has the distinct advantage of being explicit on the transmission channels of all the shocks considered. We find evidence that shocks that affect oil demand or supply do not only transmit through oil prices, but also through nonoil trade and related exchange rate movements. For instance, shocks that led to a pick up in foreign activity played an important role in boosting foreign oil demand between 2003 and 2008. However, their effects on the price of oil in dollar terms were not proportional to the increase in global demand since they also had the partial effect of appreciating the dollar exchange rate.
Previous estimates have disregarded the nature of oil as a globally traded commodity, or have taken an econometric approach that does not allow to explain the transmission channels, or both. The conduct of monetary policy has often been indicated as a likely candidate for the amplification of the macroeconomic effects of shocks that affect the price of oil. We found no evidence that monetary policy had an important effect in magnifying the macroeconomic spillovers of oil efficiency and oil supply shocks for the United States. Furthermore, we found no evidence that U.S. monetary policy had a quantitatively important influence on the evolution of oil prices.
References
Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247-52.
Backus, D. and M. Crucini (1998). Oil Prices and the Terms of Trade. Journal of International Economics 50, 185-213.
Balke, N., S. P. A. Brown, and M. K. Yucel (2010). Oil Price Shocks and U.S. Economic Activity: An International Perspective. Mimeo, Federal Reserve Bank of Dallas.
Baumeister, C. and G. Peersman (2009). Sources of the Volatility Puzzle in the Crude Oil Market. Mimeo, Ghent University.
Bernanke, B., M. Gertler, and M. Watson (1997). Systematic Monetary Policy and the Effects of Oil Price Shocks. Brookings Papers on Economics Activity (1), 91-142.
Bodenstein, M. (2011). Closing Large Open Economy Models. Journal of International Economics 84 (2), 160-177.
Bodenstein, M., C. Erceg, and L. Guerrieri (2011). Oil Shocks and External Adjustment. Journal of International Economics 83 (1), 168-184.
Chari, V. V., P. J. Kehoe, and E. R. McGrattan (2009). New Keynesian Models: Not Yet Useful for Policy Analysis. American Economic Journal: Macroeconomics 1 (1), 242-266.
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal Rigidities and the Dynamic E®ects of a Shock to Monetary Policy. Journal of Political Economy 113 (1), 1-45.
Eichenbaum, M. and J. D. M. Fisher (2007). Estimating the frequency of price reoptimization in Calvo-style Models. Journal of Monetary Economics, 2032-2047.
Evans, C. L. (1992). Productivity Shocks and Real Business Cycles. Journal of Monetary Economics 29, 191-208.
Griliches, Z. and D. W. Jorgenson (1966). Sources of Measured Productivity Change: Capital Input. The American Economic Review 56 (1/2), 50-61.
Guerrieri, L., C. Gust, and J. D. Lopéz-Salido (2010). International Competition and Inflation: A New Keynesian Perspective. American Economic Journal: Macroeconomics 2 (4), 247-80.
Hamilton, J. (1983). Oil and the Macroeconomy since World War II. Journal of Political Economy 91 (2), 228-48.
Hamilton, J. (1994). Time Series Analysis. Princeton, NJ: Princeton University Press.
Hamilton, J. (2003). What Is an Oil Shock. Journal of Econometrics 113, 363-98.
Hamilton, J. (2008). The New Palgrave Dictionary of Economics, Chapter Oil and the Macroeconomy. Palgrave Macmillan Ltd.
Hamilton, J. (2009). Causes and Consequences of the Oil Shock of 2007-08. Brookings Papers on Economic Activity (1), 215-84.
Hamilton, J. and C. Herrera (2004). Oil Shocks and Aggregate Macroeconomic Behavior: The Role of Monetary Policy: Comment. Journal of Money, Credit, Banking 36 (2), 265-86.
Hooper, P., K. Johnson, and J. Marquez (2000). Trade Elasticities for the G-7 Countries. Princeton Studies in International Economics.
Ireland, P. N. (2004). Technology Shocks in the New Keynesian Model. The Review of Economics and Statistics 86 (4), 923-936.
Jones, D. W., P. Leiby, and I. K. Paik (2004). Oil Price Shocks and the Macroeconomy: What Has Been Learned Since 1996. Energy Journal 25 (2), page 1-32.
Justiniano, A. and G. Primiceri (2008). The Time Varying Volatility of Macroeconomic Fluctuations. American Economic Review 98 (3), 604-641.
Kilian, L. (2008). The Economic Effects of Energy Price Shocks. Journal of Economic Literature 46 (4), 871-909.
Kilian, L. (2009). Not All Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market. American Economic Review 99 (3), 1053-69.
Kilian, L. and L. Lewis (2010). Does the Fed Respond to Oil Price Shocks? Forthcoming in The Economic Journal.
Kilian, L. and D. Murphy (2009). Why Agnostic Sign Restrictions Are Not Enough: Understanding the Dynamics of Oil Market VAR Models. Forthcoming in the Journal of the European Economic Association.
Kilian, L. and D. Murphy (2010). The Role of Inventories and Speculative Trading in the Global Market for Crude Oil. Mimeo, University of Michigan.
Kimball, M. (1995). The quantitative analytics of the basic neomonetarist model. Journal of Money, Credit, and Banking 27 (4), 1241-1277.
Klenow, P. and O. Krytsov (2008). State-Dependent or Time-Dependent Pricing: Does it Matter for Recent U.S. Inflation. Quarterly Journal of Economics 123 (3).
Leduc, S. and K. Sill (2004). A Quantitative Analysis of Oil-Price Shocks, Systematic Monetary Policy, and Economic Downturns. Journal of Monetary Economics 51, 781-808.
Lippi, F. and A. Nobili (2010). Oil and the macroeconomy: A quantitative structural analysis. EIEF Working Papers Series 1009, Einaudi Institute for Economic and Finance (EIEF).
Nakov, A. and A. Pescatori (2010). Oil and the Great Moderation. Economic Journal 120 (543), 131-156.
Ramey, V. A. and D. J. Vine (2011). Oil, Automobiles, and the U.S. Economy: How Much Have Things Really Changed? In NBER Macroconomics Annual 2010, Volume 25, pp. 333-367. National Bureau of Economic Research, Inc.
Smets, F. and R. Wouters (2007). Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach. American Economic Review 97 (3), 586-606.
Solow, R. (1957). Technical change and the aggregate production function. Review of Economics and Statistics 39 (3), 312-320.
Stefanski, R. (2011). Structural Transformation and the Oil Price. Oxford University, Ox-Carre Research Paper 48.
Taylor, J. B. (1993). Discretion versus Policy Rules in Practice. Carnegie-Rochester Conference Series on Public Policy 39, 195-214.
Weil, P. (1989). The equity premium puzzle and the risk-free rate puzzle. Journal of Monetary Economics 24 (3), 401-421.
Table 1. Shocks and Data
| Shock | Stochastic Process | Data Series |
|---|---|---|
| Home Shocks: neutral technology | | U.S. GDP |
| Home Shocks: investment | | U.S. fixed invest. (GDP share) |
| Home Shocks: consumption | | U.S. consumption (GDP share) |
| Home Shocks: spending | | U.S. hours worked |
| Home Shocks: price markup | | U.S. core inflation |
| Home Shocks: wage markup | | U.S. wage inflation |
| Home Shocks: monetary policy | | U.S. federal funds |
| Oil Shocks: home oil supply | | U.S. oil production |
| Oil Shocks: foreign oil supply | | for. oil production |
| Oil Shocks: home oil efficiency | | U.S. oil imports (GDP share) |
| Oil Shocks: for. oil efficiency | | real oil price |
| Other Open-Economy Shocks: for. neutral tech. | | for. trade-weighted GDP |
| Other Open-Economy Shocks: home import | | U.S. imports (share GDP) |
| Other Open-Economy Shocks: foreign import | | U.S. exports (share GDP) |
| Other Open-Economy Shocks: foreign consumption | | exch. rate (real, t.w.) |
For shock-types that occur in both countries, we impose that the autoregressive coefficients are identical except for the case of oil supply shocks.
Table 2. Steady State Retios and Calibrated Parameters
| Parameter | Used to Determine | Parameter | Used to Determine |
|---|---|---|---|
| Parameters common across countries: | discount factor | intertemporal consumption elasticity | |
| Parameters common across countries: | depreciation rate of capital | K-L sub. elasticity (0.5) | |
| Parameters common across countries: | steady state gov. cons. share of GDP | steady state labor share to fix | |
| Parameters common across countries: | trend growth in oil supply | ||
| Parameters not common across countries: | parameter on K in value added (home) | | parameter on K in value added (foreign) |
| Parameters not common across countries: | weight on oil in production (home) | | weight on oil in production (foreign) |
| Parameters not common across countries: | weight on oil in consumption (home) | | weight on oil in consumption (foreign) |
| Parameters not common across countries: | weight on imports in consumption (home) | | weight on imports in consumption (foreign) |
| Parameters not common across countries: | weight on imports in investment (home) | | weight on imports in investment (foreign) |
| Parameters specific to home country: | relative size of home country | 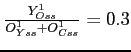 | steady state ratio oil prod. to cons. (home) |
| Parameters specific to home country: | curvature of bond intermed. cost |
Table 3. Estimation Results
| Parameter | Estimate | Conf. Interval |
|---|---|---|
| | 0.2163 | 0.1736-0.3001 |
| | 0.0001 | 0.0001-0.0214 |
| | 0.0066 | 0.0058-0.0121 |
| | 0.0108 | 0.0096-0.0140 |
| | 0.9059 | 0.8000-0.9931 |
| | 0.0269 | 0.0231-0.0599 |
| | 0.9980 | 0.9591-0.9989 |
| | 0.0246 | 0.0213-0.0288 |
| | 0.1236 | 0.0650-0.2070 |
| | 0.0001 | 0.0001-0.0414 |
| | 0.0253 | 0.0222-0.0299 |
| | 0.0001 | 0.0001-0.0689 |
| | 0.0378 | 0.0005-0.0308 |
| | 0.0181 | 0.0163-0.0234 |
| | 0.0001 | 0.0001-0.0565 |
| | 0.0145 | 0.0061-0.0461 |
| | 0.0470 | 0.0411-0.0586 |
| | 0.1269 | 0.1087-0.1514 |
| | 0.9188 | 0.8882-0.9512 |
| | 0.6484 | 0.5931-0.7894 |
| | 0.7174 | 0.6827-0.8838 |
| | 0.0001 | 0.0001-0.0476 |
| | 0.0019 | 0.0003-0.0082 |
| | 0.0263 | 0.0224-0.0311 |
| | 0.0412 | 0.0354-0.0483 |
| | 0.9768 | 0.9481-0.9943 |
| | 3.6988 | 3.1693-3.9912 |
| | 0.7401 | 0.6206-0.8153 |
| | 0.4774 | 0.04292-0.6043 |
| | 0.4026 | 0.3338-0.4739 |
| | 0.0217 | 0.0180-0.0409 |
| | 0.4225 | 0.4009-0.4540 |
| | 1.7570 | 1.6755-1.8567 |
| 1.0058 | 1.0000-1.0070 | |
| | 0.6512 | 0.5965-0.6915 |
| | 0.6553 | 0.6314-0.6920 |
| | 0.1907 | 0.1444-0.2371 |
| | 0.0000 | 0.0000-0.0574 |
| | 0.8140 | 0.7804--0.8434 |
| | 0.8900 | 0.8743-0.9300 |
| | 0.0000 | 0.0000-0.0748 |
| | 0.0000 | 0.0000-0.0617 |
| | 1.0114 | 0.9993-1.0125 |
| | 3.5154 | 3.1631-4.4161 |
| 59.5402 | 49.7207-64.1135 |
The lower bound for the coefficient on the level error correction components is 0.0001. The 95% confidence interval reported in the table is obtained by repeating the maximum likelihood estimation exercise on 1000 bootstrap samples of length equal to that of the observed estimation sample.
Table 4. Decomposition of Population Variance at Business-Cycle Frequencies
| Oil Price (Real) | Dollar Exch. Rate (Real) | Output (Real) | Consumption (GDP Share) | Investment (GDP Share) | Core Inflation | Output Foreign (Real) | Overall Goods Bal. (GDP Share) | |
|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.01 | 0.02 | 0.08 | 0.00 | 0.00 | 0.00 | 0.01 | |
| 0.00 | 0.01 | 0.27 | 0.10 | 0.10 | 0.01 | 0.00 | 0.02 | |
| 0.00 | 0.02 | 0.02 | 0.06 | 0.63 | 0.21 | 0.00 | 0.14 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.01 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.03 | |
| 0.00 | 0.03 | 0.03 | 0.38 | 0.03 | 0.15 | 0.00 | 0.29 | |
| 0.00 | 0.00 | 0.00 | 0.09 | 0.01 | 0.12 | 0.00 | 0.02 | |
| 0.01 | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 | 0.59 | 0.04 | |
| 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | |
| 0.88 | 0.03 | 0.03 | 0.05 | 0.01 | 0.03 | 0.33 | 0.06 | |
| 0.01 | 0.01 | 0.01 | 0.07 | 0.02 | 0.10 | 0.06 | 0.30 | |
| 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.06 | 0.00 | 0.02 | |
| 0.00 | 0.13 | 0.13 | 0.02 | 0.04 | 0.15 | 0.00 | 0.02 | |
| 0.00 | 0.37 | 0.37 | 0.08 | 0.14 | 0.01 | 0.00 | 0.02 | |
| 0.00 | 0.09 | 0.09 | 0.02 | 0.01 | 0.14 | 0.00 | 0.02 |
Table 5a. Key Moments at Business Cycle Frequencies: Data Observations and Model Implications: Standard Deviations
| Standard Deviations | 2.5% | 97.5% | Median | Data |
|---|---|---|---|---|
| U.S. GDP | 0.95 | 1.81 | 1.32 | 1.26 |
| Foreign GDP | 0.98 | 1.94 | 1.39 | 0.70 |
| U.S. Oil Production | 2.23 | 4.20 | 3.10 | 1.97 |
| Foreign Oil Production | 1.47 | 2.70 | 1.99 | 2.23 |
| U.S. Oil Imports (GDP Share) | 0.18 | 0.33 | 0.24 | 0.16 |
| Real Oil Price | 12.28 | 22.13 | 16.55 | 15.65 |
| U.S. Nonoil Goods Imports (GDP Share) | 0.23 | 0.44 | 0.32 | 0.32 |
| U.S. Goods Exports (GDP Share) | 0.35 | 0.68 | 0.49 | 0.32 |
| U.S. Real Exchange Rate | 1.96 | 3.59 | 2.68 | 2.80 |
| U.S. Private Consumption (GDP Share) | 0.55 | 1.15 | 0.80 | 0.37 |
| U.S. Fixed Investment (GDP Share) | 0.44 | 1.01 | 0.68 | 0.55 |
| U.S. Core Inflation (qr) | 0.33 | 0.55 | 0.43 | 0.15 |
| U.S. Federal Funds Rate (qr) | 0.24 | 0.45 | 0.33 | 0.31 |
| U.S. Wage Inflation (qr) | 0.84 | 1.38 | 1.09 | 0.33 |
| U.S. Hours Worked (PC) | 1.02 | 1.87 | 1.40 | 1.52 |
| U.S. Overall Goods Balance (GDP Share) | 0.40 | 0.80 | 0.57 | 0.36 |
| U.S. Nonoil Goods Balance (GDP Share) | 0.40 | 0.78 | 0.56 | 0.38 |
Table 5b. Key Moments at Business Cycle Frequencies: Data Observations and Model Implications: Autocorrelations
| Autocorrelations | 2.5% | 97.5% | Median | Data |
|---|---|---|---|---|
| U.S. GDP | 0.86 | 0.94 | 0.90 | 0.93 |
| Foreign GDP | 0.87 | 0.95 | 0.92 | 0.89 |
| U.S. Oil Production | 0.84 | 0.94 | 0.90 | 0.90 |
| Foreign Oil Production | 0.84 | 0.93 | 0.89 | 0.90 |
| U.S. Oil Imports (GDP Share) | 0.83 | 0.93 | 0.89 | 0.88 |
| Real Oil Price | 0.83 | 0.93 | 0.89 | 0.88 |
| U.S. Nonoil Goods Imports (GDP Share) | 0.85 | 0.94 | 0.90 | 0.89 |
| U.S. Goods Exports (GDP Share) | 0.85 | 0.94 | 0.91 | 0.92 |
| U.S. Real Exchange Rate | 0.84 | 0.93 | 0.89 | 0.91 |
| U.S. Private Consumption (GDP Share) | 0.87 | 0.95 | 0.92 | 0.88 |
| U.S. Fixed Investment (GDP Share) | 0.90 | 0.96 | 0.94 | 0.94 |
| U.S. Core Inflation (qr) | 0.79 | 0.90 | 0.85 | 0.87 |
| U.S. Federal Funds Rate (qr) | 0.85 | 0.93 | 0.90 | 0.89 |
| U.S. Wage Inflation (qr) | 0.80 | 0.90 | 0.86 | 0.81 |
| U.S. Hours Worked (PC) | 0.85 | 0.93 | 0.90 | 0.92 |
| U.S. Overall Goods Balance (GDP Share) | 0.87 | 0.95 | 0.92 | 0.92 |
| U.S. Nonoil Goods Balance (GDP Share) | 0.86 | 0.94 | 0.91 | 0.94 |
Table 5c. Key Moments at Business Cycle Frequencies: Data Observations and Model Implications: Correlation with Oil Price
| Correlation with Oil Price | 2.5% | 97.5% | Median | Data |
|---|---|---|---|---|
| U.S. GDP | -0.30 | 0.52 | 0.13 | 0.04 |
| Foreign GDP | -0.70 | 0.00 | -0.40 | 0.51 |
| U.S. Real Exchange Rate | 0.16 | 0.77 | 0.54 | 0.11 |
| U.S. Core Inflation (qr) | -0.33 | 0.40 | 0.05 | 0.24 |
| U.S. Federal Funds Rate (qr) | -0.34 | 0.47 | 0.09 | 0.37 |
| U.S. Overall Goods Balance (GDP Share) | -0.54 | 0.31 | -0.14 | -0.02 |
| U.S. Nonoil Goods Balance (GDP Share) | -0.22 | 0.60 | 0.23 | 0.32 |
Figure 1. The Effects of a Two-Standard Deviation Decrease in Foreign Oil Efficiency: Deviations from the Balanced Growth Path
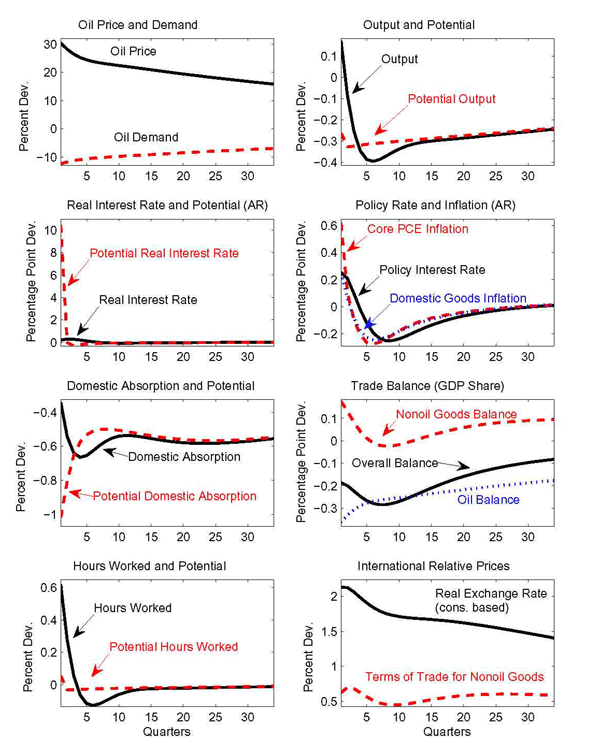
Figure 2. The Effects of the Price of Oil and Home Output of Oil Supplyl, Oil Efficiency, and Activity Shocks (Deviations from the Balanced Growth Path)

Figure 3. Contributions to Movements in Oil Prices and Oil Demand*
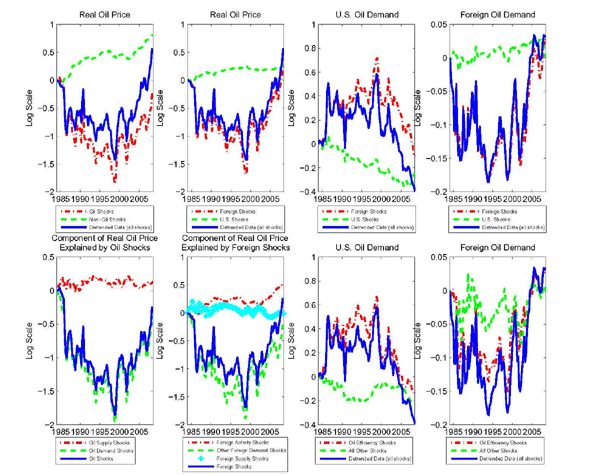
*The figure shows the contribution to the price of oil of the smoothed estimates of various groups of shocks, ignoring trends and initial conditions. As the model is linear in the shocks, the contributions are additive. The solid lines in the top left panels show the cumulative effect of all shocks, amounting to a detrended measure of the price of oil. The bottom left panels decompose further one of the components shown in the top panels. Each solid line in the bottom two panels reproduces the dash-dotted line in the respective top panel.
Figure 4. Contributions of Oil Demand and Supply Shocks (Both at Home and Abroad) to Movements in Gross Output*
*"Oil Shocks" include oil supply and oil efficiency shocks both at home and abroad. The label "Potential" refers to outcomes in the model without nominal rigidities (but otherwise identical). "Detrended" refers to the exclusion of the estimated trends in productivity, oil supply, and oil prices as detailed in Section 2.
Figure 5. Oil Efficiency Across Foreign Countries*
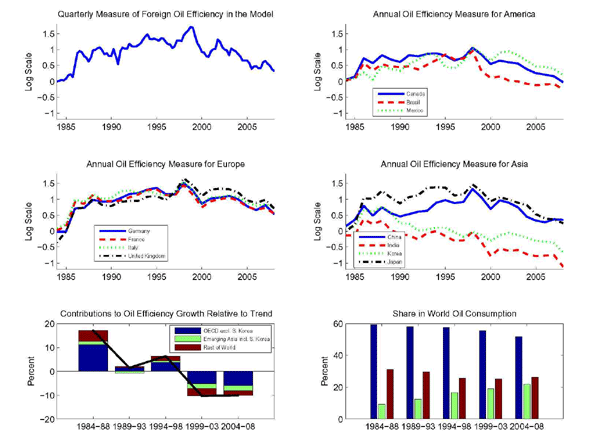
The figure plots the changes in oil efficiency net of the balanced growth path rate. The aggregate measure derived from the model is the smoothed estimate of foreign oil efficiency; country measures are derived using annual data in combination with the model's oil demand equation. When plotting cumulative growth rates, the log-level of oil efficiency is normalized to zero in 1984. When aggregating across country regions, country-specific oil efficiency growth rates were weighted by a country's share in world oil consumption.
Footnotes
** We thank Mario Crucini, James Hamilton, Matteo Iacoviello, Lutz Kilian, Sylvain Leduc, David López-Salido, John Rogers, Rob Vigfusson, and seminar participants at the Federal Reserve Bank of Atlanta, Federal Reserve Board, Federal Reserve Bank of San Francisco, and University of Michigan. This draft replaces a previous version of this paper circulated under the title:"On the Sources of Oil Price Fluctuations." The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
*** Contact Information: Telephone (202) 452 2550. E-mail Luca.Guerrieri@frb.gov. Return to text
1. The approach and conclusions in Bernanke, Gertler, and Watson (1997) have subsequently been challenged by Hamilton and Herrera (2004), Leduc and Sill (2004), and Kilian and Lewis (2010). Return to text
2. Others have estimated DSGE models that include oil inputs. Nakov and Pescatori (2010) abstracted from the open economy links and restricted key parameters such as the oil price elasticity of demand. Balke, Brown, and Yucel (2010) focused on the open economy dimension, but excluded a role for monetary policy. Return to text
3. An overview is offered in Kilian and Lewis (2010). Return to text
4. See Bodenstein (2011) for a detailed discussion of stationarity inducing devices in linearized models with incomplete asset markets. Return to text
5. Notice that the capital stock in the parallel model with flexible prices and wages is not imposed to be identical to the capital stock in the model with nominal rigidities. Return to text
6. Focusing exclusively on trend growth in real oil prices, recent work by Stefanski (2011) investigates the link between oil prices and structural change in Asia in a multi-sector model. Return to text
7. To maximize the likelihood, we employ a combination of optimization algorithms. We rely on simulated annealing to identify a candidate global maximum and refine the estimates through Nelder-Meade and Newton-Raphson algorithms. The candidate global maximum needs to then survive repeated calls to the simulated annealing algorithm with a high initial temperature and slow cooling process. Return to text
8. The 95 confidence interval reported in the table is obtained by repeating the maximum likelihood estimation exercise on 1000 bootstrap samples of length equal to that of the observed estimation sample. The bootstrap samples were generated taking the point estimates in Table 3 as pseudo-true values for the parameters in the model. Return to text
9. Notice that the Taylor principle is satisfied given the form of the interest rate rule in Equation 24. Return to text
10. Given that the model is stationary, we used its numerical solution to form the correlogram and could then construct a bandbass filter by integrating the spectrum analytically. Return to text
11. The statistics are computed from 10000 simulated series each of length 138, the same length as the observed data. The business cycle component of each simulated series is extracted using the bandpass filter, retaining only oscillations with amplitude between 6 and 32 quarters. Return to text
12. Others have compared the fit of the model with that of a vector auto-regression. Given the large number of observed variables and relatively small sample, we would have to restrict the lag length of the VAR to such an extent that the comparison would not be informative. Return to text
13. The
variables in ![]() in Equation (27) enter either as
a return or in growth rates. The data sources are as follows. Oil
inventory: U.S. Energy Information Administration; given the lack
of data on crude oil inventories for countries other than the
United States, we construct OECD crude oil inventories by scaling
OECD petroleum stocks over U.S. petroleum stocks for each period as
suggested in Hamilton (2009), and Kilian and Murphy (2010). Price of
coal: Australian Coal, World Bank Commodity Price Data (Pink
Sheet). Oil futures: three months NYMAX contract, U.S. Energy
Information Administration. Stock market index: S&P 500, FRED database St. Louis Fed. World commodity
demand: index of global real economic activity in industrial
commodity markets, available at
http://www-personal.umich.edu/ lkilian/reaupdate.txt.
Return to text
in Equation (27) enter either as
a return or in growth rates. The data sources are as follows. Oil
inventory: U.S. Energy Information Administration; given the lack
of data on crude oil inventories for countries other than the
United States, we construct OECD crude oil inventories by scaling
OECD petroleum stocks over U.S. petroleum stocks for each period as
suggested in Hamilton (2009), and Kilian and Murphy (2010). Price of
coal: Australian Coal, World Bank Commodity Price Data (Pink
Sheet). Oil futures: three months NYMAX contract, U.S. Energy
Information Administration. Stock market index: S&P 500, FRED database St. Louis Fed. World commodity
demand: index of global real economic activity in industrial
commodity markets, available at
http://www-personal.umich.edu/ lkilian/reaupdate.txt.
Return to text
14. A
detailed description of Granger causality tests in a multivariate
context is given in Hamilton (1994), chapter 11. Let
![]() be the estimate of
the variance of the innovations,
be the estimate of
the variance of the innovations,
![]() under the null hypothesis and
under the null hypothesis and
![]() be the unrestricted
estimate. The test statistic
be the unrestricted
estimate. The test statistic
![]() follows a
follows a ![]() distribution with the degrees of
freedom, df, given by the product of the number of lags and the
number of variables included in
distribution with the degrees of
freedom, df, given by the product of the number of lags and the
number of variables included in ![]() . If the test
statistic exceeds the
. If the test
statistic exceeds the ![]() critical value for
critical value for
![]() , the block exogeneity assumption
is rejected at the
, the block exogeneity assumption
is rejected at the ![]() level of
significance. Return to
text
level of
significance. Return to
text
15. Further increases in the lag-length not only did not overturn our overall assessment, but reinforced it, instead. Return to text
16. As shown in Bodenstein, Erceg, and Guerrieri (2011), these effects occur regardless of the presence of nominal rigidities. Return to text
17. The processes are literally stationary, but return to the balanced growth path at horizons beyond the one shown in the figure. Return to text
18. By construction, the relationship between the lines shown in the panel is such that the the broken lines, denoting contributions of particular groups of shocks, sum to the solid line, denoting the observed data excluding contributions of the trends and initial conditions. Return to text
19. For instance, see Bernanke, Gertler, and Watson (1997), Leduc and Sill (2004). Return to text
20. To facilitate comparison across panels, foreign oil efficiency is plotted relative to its value in 1984. Return to text
21. The
level term
![]() is given
by
is given
by
![$\displaystyle \frac{O_{2,0}^{y\ast }}{O_{2,0}^{\ast }} \left[ \ln \left( \frac{Y_{2,t}}{ GDP_{2,t}}\right) -\left( 1+\rho _{2}^{o}\right) \ln \left( \frac{P_{2,t}^{d}Y_{2,t}}{P_{2,t}^{gdp}GDP_{2,t}} \right)-\left( 1+\rho _{2}^{o}\right) \ln \left( \frac{MC_{2,t}}{ P_{2,t}^{d}}\right) \right]$](img245.gif) |
|||
![$\displaystyle +\left(1-\frac{O_{2,0}^{y\ast }}{O_{2,0}^{\ast }}\right)\left[ \ln \left( \frac{C_{2,t}}{ GDP_{2,t}}\right)-\left( 1+\rho _{2}^{o}\right) \ln \left( \frac{P_{2,t}^{c}C_{2,t}}{P_{2,t}^{gdp}GDP_{2,t}} \right) \right].$](img246.gif) |
(29) |
Return to text
22. Eurostat and the U.S. Energy Information Administration compute energy efficiency by dividing total primary energy consumption in British thermal units through real GDP. Stefanski (2011) refers to the nominal oil share in GDP as a measure oil efficiency/intensity. Return to text
23. We used data for Australia, Canada, France, Germany, Italy, Japan, South Korea, the United Kingdom, the United States, an aggregate of the remaining OECD members (see WDI category OEC); China, India, Indonesia, Malaysia, the Philippines, Thailand, an aggregate of the remaining countries in Emerging Asia (see WDI category EAS (East Asia)); Brazil, Mexico; an aggregate of the rest of the world. Oil efficiency growth rates by country are weighted by a country's share in world oil consumption when computing country bloc contributions to world oil efficiency growth. Return to text
24. Further investigation of the large contribution from the rest of the world bloc between 1983-1988 reveals that those gains in efficiency occurred in the Soviet Union and its satellite countries. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text