
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1032, October 2011 --- Screen Reader
Version*
Housing and Debt Over the Life Cycle and Over the Business Cycle**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We study housing and debt in a quantitative general equilibrium model. In the cross-section, the model matches the wealth distribution, the age profiles of homeownership and mortgage debt, and the frequency of housing adjustment. In the time-series, the model matches the procyclicality and volatility of housing investment, and the procyclicality of mortgage debt. We use the model to conduct two experiments. First, we investigate the consequences of higher individual income risk and lower downpayments, and find that these two changes can explain, in the model and in the data, the reduced volatility of housing investment, the reduced procyclicality of mortgage debt, and a small fraction of the reduced volatility of GDP. Second, we use the model to look at the behavior of housing investment and mortgage debt in an experiment that mimics the Great Recession: we find that countercyclical financial conditions can account for large drops in housing activity and mortgage debt when the economy is hit by large negative shocks.
Keywords: Housing, housing investment, mortgage debt, life-cycle models, income risk, homeownership, precautionary savings, borrowing constraints
JEL classification: E22, E32, E44, E51, D92, R21
1. Introduction
This paper studies the business cycle and the life-cycle properties of housing investment and household mortgage debt in a quantitative general equilibrium model. To this end, we modify a life-cycle model with uninsurable individual income risk to allow for aggregate uncertainty and for an explicit treatment of housing. We introduce housing by modeling its role as collateral, its lumpiness, and the choice of renting versus owning; these features have, to a large extent, eluded existing business cycle models of housing.
At the cross-sectional level, our model accurately reproduces the U.S. wealth distribution, and replicates the life-cycle profiles of housing and nonhousing wealth. The young, the old and the poor are renters and hold few assets; the middle-aged and the wealth-rich are homeowners. For a typical household, the asset portfolio consists of a house and a large mortgage. The model also reproduces frequency and size of individual housing adjustment: because of nonconvex adjustment costs, homeowners change house size infrequently but in large amounts when they do so; renters change house size often, but in smaller amounts. Over the business cycle, the model replicates two empirical characteristics of housing investment: its procyclicality and its high volatility. In addition, the model matches the procyclical behavior of household mortgage debt. To our knowledge, no previous model with rigorous micro-foundations for housing demand has reproduced these regularities in general equilibrium.
We use the model to look at the role of the housing market in two events of the recent U.S. macroeconomic history: the Great Moderation and the Great Recession.
Debt and Housing in the Great Moderation. We study how higher household income risk and lower downpayments affect the sensitivity of debt and housing to macroeconomic shocks. Higher risk and the reduction in downpayments occurred around the 1980s, around the beginning of the Great Moderation,1 and are potentially important determinants of housing demand and housing tenure: higher risk should make individuals reluctant to buy large items that are costly to sell in bad times; lower downpayments should encourage and smooth housing demand. Their role could be relevant given two observations on the post-1980s period (see Figure 1 and Table 1). First, the volatility of housing investment has fallen more than proportionally relative to GDP; second, the correlations between mortgage debt and GDP and mortgage debt and aggregate consumption have roughly halved, from 0.78 to 0.43 and from 0.72 to 0.37 respectively.2 In line with the data, we find that lower downpayments and larger idiosyncratic risk reduce the volatility of housing investment, and reduce the correlation between mortgage debt and economic activity. Lower downpayments provide a cushion to smooth housing demand; increase homeownership rates, raising the number of people who do not change their housing consumption over the cycle (relative to an economy with a large number of renters who can become first-time buyers); lead to higher debt, creating a mechanism that weakens the correlation between output and hours. Higher idiosyncratic risk makes wealth-poor individuals more cautious: these individuals adjust consumption, hours, and housing by smaller amounts in response to aggregate shocks. This mechanism is pronounced for housing purchases, since a house is a large item that is costly to purchase and sell; and is reinforced by low downpayments, since low downpayments allow people to borrow more, increasing the utility cost of buying and selling when net worth is lower. Together, lower downpayments and higher risk can explain about 15 percent of the reduction in the variance of GDP, 60 percent of the reduction in the variance of housing investment, and the decline in the correlation between debt and GDP.
Debt and Housing in the Great Recession. During the 2007-2009 period, changes in financial conditions are likely to have made the recession worse. In particular, the housing market appears to have been held back - more than other sectors - by tighter credit conditions and higher borrowing costs. In hindsight, it looks like housing did not stabilize the economy during the recession. We use the model to determine the extent to which housing can smooth regular business cycle shocks but amplify extremely negative ones, by defining "Normal Recessions" as periods of low aggregate productivity, and "Great Recessions" periods of low aggregate productivity coupled with tight credit conditions. When we do so, we find an interesting nonlinearity: higher risk and lower downpayments can make housing and debt more stable in response to small positive and negative shocks (as in the Great Moderation), but can make it more fragile in response to large negative shocks (as in the Great Recession).
Previous Literature. Two strands of literature study the role of housing in the macroeconomy. On the one hand, business cycle models with housing - Greenwood and Hercowitz (1991), Gomme, Kydland and Rupert (2001), Davis and Heathcote (2005), Fisher (2007) and Iacoviello and Neri (2010) - match housing investment well, but abstract from a detailed modeling of the microfoundations of housing demand; these models feature no wealth heterogeneity, no distinction between owning and renting, and unrealistic transaction costs. On the other hand, incomplete markets models with housing - Gervais (2002), Fernandez-Villaverde and Krueger (2004), Chambers, Garriga and Schlagenhauf (2009), and Díaz and Luengo-Prado (2010) - have a rich treatment of the microfoundations of housing demand, but ignore aggregate shocks: however, because these papers model individual heterogeneity, they are better suited to study issues such as debt, risk, and wealth distribution.
Our model combines both strands of literature. Others have also done so, albeit with a different focus. Silos (2007) studies the link between aggregate shocks and housing choice, but does not model the own/rent decision and assumes convex costs for housing adjustment.3 Fisher and Gervais (2007) find that the decline in housing investment volatility is driven by a change in the demographics of the population together with an increase in the cross-sectional variance of earnings. Their approach sidesteps general equilibrium considerations. Kiyotaki, Michaelides and Nikolov (2011) use a stylized life-cycle model of housing tenure to study the interaction between borrowing constraints, housing prices, and economic activity. Favilukis, Ludvigson and Van Nieuwerburgh (2009) use a two-sector RBC model with housing that also considers the interaction between borrowing constraints and aggregate activity, but address a different set of questions than we do. Finally, Campbell and Hercowitz (2005) study the impact of financial innovation on macroeconomic volatility in a model with two household types. In their model, looser collateral constraints weaken the connection between constrained households' housing investment, debt accumulation and labor supply through a mechanism that shares some features with ours; however, their model does not study the interaction between life cycle, risk and housing demand, which are important elements of our story.
2. The Model
Our economy is a version of the stochastic growth model with
overlapping generations of heterogeneous households, extended to
allow for housing investment, collateralized debt and a housing
rental market. Aggregate uncertainty is introduced in the form of a
shock to total factor productivity. Individuals live at most
![]() periods and work until age
periods and work until age
![]() Their labor endowment
depends on a deterministic age-specific productivity and a
stochastic component. After retirement, people receive a pension.
Each period, the probability of surviving from age
Their labor endowment
depends on a deterministic age-specific productivity and a
stochastic component. After retirement, people receive a pension.
Each period, the probability of surviving from age ![]() to
to ![]() is
is
![]() . Each period a generation is born
of the same measure of dead agents, so that the total population,
which we normalize to 1, is constant. When an agent
dies, he is replaced by a descendant who inherits his assets.
. Each period a generation is born
of the same measure of dead agents, so that the total population,
which we normalize to 1, is constant. When an agent
dies, he is replaced by a descendant who inherits his assets.
At each point in time, agents differ by their age and productivity; moreover, we assume that agents differ in their degree of impatience. We do so for two reasons: first, a large literature (see Guvenen, 2011) suggests that preference heterogeneity may be an important source of wealth inequality. For example, Venti and Wise (2001) study wealth inequality at the onset of retirement among households with similar lifetime earnings and conclude that the dispersion must be attributed to differences in the amount that households choose to save.4 Second, we want a model that generates average debt and wealth dispersion as in the data, and a model with discount factor heterogeneity works remarkably well in this regard (our robustness analysis discusses the properties of the model with a single discount factor).
Household Preferences and Endowments. Households receive utility from consumption ![]() ,
leisure
,
leisure
![]() (where
(where
![]() is the time endowment), and
service flows
is the time endowment), and
service flows ![]() from housing, which are proportional to
the housing stock owned or rented. The momentary utility function
is:
from housing, which are proportional to
the housing stock owned or rented. The momentary utility function
is:
| (1) |
Above, ![]() if
if ![]() (the
individual owns), while
(the
individual owns), while ![]() if
if ![]() (the individual rents). The assumption for
(the individual rents). The assumption for ![]() implies that a household experiences a utility gain when
transitioning from renting to owning, as in Rosen (1985) and
Poterba (1992). We also assume that homeowners need to hold a
minimum size house
implies that a household experiences a utility gain when
transitioning from renting to owning, as in Rosen (1985) and
Poterba (1992). We also assume that homeowners need to hold a
minimum size house ![]() , and that rental units
may come in smaller sizes than houses, allowing renters to consume
a smaller amount of housing services, as in Gervais (2002). The log
specification over consumption and housing services follows Davis
and Ortalo-Magné (2011) who find that, over time and across
cities, the expenditure share on housing is constant.
, and that rental units
may come in smaller sizes than houses, allowing renters to consume
a smaller amount of housing services, as in Gervais (2002). The log
specification over consumption and housing services follows Davis
and Ortalo-Magné (2011) who find that, over time and across
cities, the expenditure share on housing is constant.
Time supplied in the labor market is paid at the wage
![]() . The productivity endowment of an agent
at age
. The productivity endowment of an agent
at age ![]() is given by
is given by
![]() where
where ![]() is a
deterministic age-specific component and
is a
deterministic age-specific component and ![]() is a
shock to the efficiency units of labor,
is a
shock to the efficiency units of labor,
![]() .
The shock follows a Markov process with transition matrix
.
The shock follows a Markov process with transition matrix
![]() and stationary distribution
and stationary distribution
![]() . The total
amount of labor efficiency units
. The total
amount of labor efficiency units
![]() and of age-specific productivity values
and of age-specific productivity values
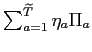 are constant and normalized to one. From
are constant and normalized to one. From
![]() onwards labor efficiency is
zero (
onwards labor efficiency is
zero (![]() ) and agents live off their pension
) and agents live off their pension
![]() and their accumulated wealth. Pensions are
fully financed through the government's revenues from a lump-sum
tax
and their accumulated wealth. Pensions are
fully financed through the government's revenues from a lump-sum
tax ![]() paid by workers.5 Total net income
at age
paid by workers.5 Total net income
at age ![]() in period
in period ![]() is denoted by
is denoted by
![]() . Then:
. Then:
| (2) |
Households start their life with endowments ![]() and
and ![]() the accidental bequests left
by a dead agent. They can trade a one-period bond
the accidental bequests left
by a dead agent. They can trade a one-period bond ![]() which pays a gross interest rate of
which pays a gross interest rate of ![]() . Positive
amounts of this bond denote a debt position.6 Households cannot
borrow more than a fraction
. Positive
amounts of this bond denote a debt position.6 Households cannot
borrow more than a fraction ![]() of their
housing stock and a fraction
of their
housing stock and a fraction ![]() of their
expected earnings:
of their
expected earnings:
| (3) |
Above,
![]() approximates the present discounted value of lifetime labor
earnings and pension.7 The motivation for this borrowing
constraint is realism: we want to study mortgage debt and we want
to have a constraint which prevents the elderly from borrowing too
much late in life (when the present discounted value of earnings is
low), as in the data. The constraint is also consistent with
typical lending criteria in the mortgage market that take into
account minimum downpayments, ratios of debt payments to income,
current and expected future employment conditions.8
Finally, we assume that an owner incurs a transaction cost whenever
he adjusts the housing stock:
approximates the present discounted value of lifetime labor
earnings and pension.7 The motivation for this borrowing
constraint is realism: we want to study mortgage debt and we want
to have a constraint which prevents the elderly from borrowing too
much late in life (when the present discounted value of earnings is
low), as in the data. The constraint is also consistent with
typical lending criteria in the mortgage market that take into
account minimum downpayments, ratios of debt payments to income,
current and expected future employment conditions.8
Finally, we assume that an owner incurs a transaction cost whenever
he adjusts the housing stock:
![]() if
if
![]() .
This assumption captures common practices in the housing market
that require, for instance, fees paid to realtors to be equal to a
fraction of the value of the house being sold. Summing up,
households maximize expected lifetime utility:
.
This assumption captures common practices in the housing market
that require, for instance, fees paid to realtors to be equal to a
fraction of the value of the house being sold. Summing up,
households maximize expected lifetime utility:
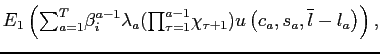 |
(4) |
where ![]() denotes expectations at age
denotes expectations at age ![]() ,
,
![]() is a deterministic preference
shifter that mimics changes in household size, and
is a deterministic preference
shifter that mimics changes in household size, and ![]() is a household-specific discount factor. In the
calibration, we assume that households are born either impatient
(low
is a household-specific discount factor. In the
calibration, we assume that households are born either impatient
(low ![]() ) or patient (high
) or patient (high ![]() ).
).
Financial Sector and Housing Rental Market. A competitive financial sector collects deposits from households
who save, lends to firms and households who borrow, and buys
capital to be rented in the same period to tenants. The financial
sector can convert the final good into housing and capital at no
cost. This assumption ensures that the consumption prices of
housing and capital are constant. Let ![]() be the
price of one unit of rental services. Then a no-arbitrage condition
holds such that the net revenue from lending one unit of financial
capital must equal the net revenue from renting one unit of housing
capital,
be the
price of one unit of rental services. Then a no-arbitrage condition
holds such that the net revenue from lending one unit of financial
capital must equal the net revenue from renting one unit of housing
capital,
| (5) |
at any ![]() where
where
![]() is the depreciation rate of the
housing stock.9
is the depreciation rate of the
housing stock.9
Production. The goods market is competitive and characterized by constant returns to scale, so that we consider a single representative firm. Output is produced according to
| (6) |
where ![]() and
and ![]() are total capital
and labor input;
are total capital
and labor input; ![]() is the capital share, and
is the capital share, and
![]() is a shock to total factor productivity. This shock follows a
Markov process with transition matrix
is a shock to total factor productivity. This shock follows a
Markov process with transition matrix
![]() . The aggregate feasibility constraint requires that production of
the good
. The aggregate feasibility constraint requires that production of
the good ![]() equals the sum of aggregate consumption
equals the sum of aggregate consumption
![]() investment in the stock of aggregate
capital
investment in the stock of aggregate
capital ![]() investment in the stock of aggregate
housing
investment in the stock of aggregate
housing
![]() and total
transaction costs incurred by homeowners for changing housing
stock, denoted by
and total
transaction costs incurred by homeowners for changing housing
stock, denoted by
![]() :
:
| (7) |
with
![]() and
and
![]() denoting the depreciation rates of
housing and capital, respectively.
denoting the depreciation rates of
housing and capital, respectively.
The Household Problem and Equilibrium. Denote with
![]() the distribution of households over earnings shocks, asset
holdings, housing wealth, discount factors and ages in period
the distribution of households over earnings shocks, asset
holdings, housing wealth, discount factors and ages in period
![]() Without aggregate uncertainty, the economy
would be in a stationary equilibrium, with an invariant
distribution
Without aggregate uncertainty, the economy
would be in a stationary equilibrium, with an invariant
distribution ![]() and constant prices. Given aggregate
volatility, this distribution will change over time. When solving
their dynamic optimization problem, agents need to predict future
wages and interest rates. Both variables depend on future
productivity and aggregate capital-labor ratio, which in turn are
determined by the overall distribution of individual states. As a
consequence, the distribution
and constant prices. Given aggregate
volatility, this distribution will change over time. When solving
their dynamic optimization problem, agents need to predict future
wages and interest rates. Both variables depend on future
productivity and aggregate capital-labor ratio, which in turn are
determined by the overall distribution of individual states. As a
consequence, the distribution ![]() - and its
law of motion - is one of the aggregate state variables that agents
need to know in order to make their decisions (together with total
factor productivity). This distribution is an infinite-dimensional
object, and its law of motion maps an infinite-dimensional space
onto itself, which imposes a crucial complication for the solution
of the model economy. To circumvent this problem, we adopt the
strategy of Krusell and Smith (1998) and let agents use one moment
of the distribution
- and its
law of motion - is one of the aggregate state variables that agents
need to know in order to make their decisions (together with total
factor productivity). This distribution is an infinite-dimensional
object, and its law of motion maps an infinite-dimensional space
onto itself, which imposes a crucial complication for the solution
of the model economy. To circumvent this problem, we adopt the
strategy of Krusell and Smith (1998) and let agents use one moment
of the distribution ![]() - the aggregate capital
stock
- the aggregate capital
stock ![]() - in order to forecast future prices. As
documented in Appendix A, using one moment only allows us to obtain
a fairly precise forecast, as measured by the
- in order to forecast future prices. As
documented in Appendix A, using one moment only allows us to obtain
a fairly precise forecast, as measured by the ![]() of the forecasting equations, which are between
0.99 and 1.10
of the forecasting equations, which are between
0.99 and 1.10
We write the household optimization problem recursively. The
individual states are productivity ![]() debt
debt
![]() and housing wealth
and housing wealth ![]() . We assume that agents observe beginning of period
capital
. We assume that agents observe beginning of period
capital ![]() and approximate the evolution of
aggregate capital and labor with linear functions that depend on
the aggregate shock
and approximate the evolution of
aggregate capital and labor with linear functions that depend on
the aggregate shock ![]() Denote
Denote
![]() the vector of individual and aggregate states. The dynamic problem
of an age
the vector of individual and aggregate states. The dynamic problem
of an age ![]() household is:
household is:
| (8) |
where ![]() and
and ![]() are
the value functions if the agent owns and rents, respectively, and
are
the value functions if the agent owns and rents, respectively, and
![]() corresponds to the decision to own.
The value of being a homeowner solves:
corresponds to the decision to own.
The value of being a homeowner solves:
| (9) | |
| s.t. |
|
Here
![]() and
and
![]() are linear functions in
are linear functions in
![]() whose parameters depend on the
whose parameters depend on the
![]() . They denote the law of motion of the
aggregate state, which agents take as given.
. They denote the law of motion of the
aggregate state, which agents take as given.
The value of renting a house is determined by solving the problem:
| (10) | |
| s.t. |
|
At the agent's last age,
![]() for
any
for
any
![]() .
.
We are now ready to define the equilibrium for this economy.
A recursive competitive equilibrium consists of value functions
![]() policy functions
policy functions
![]() for each
for each ![]() age and period
age and period ![]() ,
prices
,
prices ![]() ,
, ![]() and
and
![]() aggregate quantities
aggregate quantities
![]() and
and ![]() for each
for each ![]() taxes
taxes ![]() and pensions
and pensions ![]() and laws of
motion
and laws of
motion
![]() and
and
![]() such that at any
such that at any ![]() :
:
Agents optimize: Given ![]() ,
, ![]()
![]() and the laws of motion
and the laws of motion
![]() and
and
![]() , the value functions solve the
individual's problem, with the corresponding policy functions.
, the value functions solve the
individual's problem, with the corresponding policy functions.
Factor prices and rental prices satisfy:
| (11) | |
| (12) | |
| (13) |
Markets clear:
| (14) | |
| (15) |
where ![]() and
and
![]() are defined as:
are defined as:
| (16) | |
| (17) |
The government budget is balanced:
 . . |
(18) |
The laws of motion for the aggregate capital and aggregate labor are given by
| (19) |
Appendix A provides the details on our computational strategy.
3. Calibration
Our calibration is summarized in Table 2. One
period is a year. Agents enter the model at age 21, retire at age 65, and die no later than age
90. The survival probabilities correspond to
the survival probabilities for men aged 21-90 from the U.S.
Decennial Life Tables for 1989-1991. Each period, the measure of
those who are born is equal to the measure of those who die. The
age polynomial
![]() , which captures the effect of
demographic variables in the utility function, is taken from
Cagetti (2003) and approximated using a fourth-order polynomial
(see Figure 2). After normalizing the household size to 1 at age 21, the household size peaks at
2.5 at age 40, and
declines thereafter.
, which captures the effect of
demographic variables in the utility function, is taken from
Cagetti (2003) and approximated using a fourth-order polynomial
(see Figure 2). After normalizing the household size to 1 at age 21, the household size peaks at
2.5 at age 40, and
declines thereafter.
We take the deterministic profile of efficiency units of labor for males aged 21-65 from Hansen (1993) and approximate it using a quadratic polynomial (see Figure 2). Upon retirement, an agent receives a pension equal to 40 percent of the average labor income.11 The idiosyncratic shock to labor productivity is specified as:
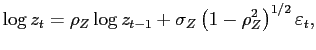 |
(20) |
which we approximate with a three-state Markov process following
Tauchen (1986). There is a vast literature on the nature and
specification of a parsimonious yet empirically plausible income
process: the bulk of the studies (see Guvenen, 2011) look at
earnings (rather than wages) and estimate persistence coefficients
ranging from 0.7 to 0.95.
Exception are Floden and Lindé (2001), who use PSID data to
estimate an AR(1) process for wages similar to ours and find an
autocorrelation coefficient of 0.91; and Card
(1991), who finds an AR(1) coefficient of 0.89.
Based on this evidence, we set
![]() and conduct robustness
analysis in Section 8, based on evidence from other studies that we
review in Appendix B. The standard deviation of the labor
productivity process is set at
and conduct robustness
analysis in Section 8, based on evidence from other studies that we
review in Appendix B. The standard deviation of the labor
productivity process is set at
![]() (see Appendix B). Later, we
increase
(see Appendix B). Later, we
increase
![]() to 0.45 to
capture the increased earnings volatility of the 1990s, and to
study the consequences for macroeconomic aggregates of increased
risk at the household level, as emphasized by Moffitt and
Gottschalk (2008) and Dynan, Elmendorf and Sichel (2007).
to 0.45 to
capture the increased earnings volatility of the 1990s, and to
study the consequences for macroeconomic aggregates of increased
risk at the household level, as emphasized by Moffitt and
Gottschalk (2008) and Dynan, Elmendorf and Sichel (2007).
We assume that there are two classes of households, a "patient" group with a discount factor of 0.999
(one third of the population) and an "impatient" group with a
discount factor of 0.941 (two thirds of the
population). The high discount factor pins the average real
interest rate down to 3 percent. The low discount
factor is in the range of estimates in the literature (see, for
instance, Hendricks, 2007). The gap between discount rates and the
relative population shares deliver a Gini coefficient for wealth
around 0.75, close to the data. In Section 8 we
discuss the properties of the model when we assume that all people
have identical discount rates. We set ![]() and
the endowment of time
and
the endowment of time
![]() ; these parameters imply
that time spent working is 40 percent of the
agents' time.
; these parameters imply
that time spent working is 40 percent of the
agents' time.
We set the weight on housing in utility at ![]() and the depreciation rate for housing
and the depreciation rate for housing
![]() . These parameters yield
average housing investment to private output ratios around
7 percent, and a ratio of the housing stock
to output 1.4. These values are in accordance with
the National Income and Product Accounts and the Fixed Assets
Tables.12 Finally, the housing transaction
cost is set at
. These parameters yield
average housing investment to private output ratios around
7 percent, and a ratio of the housing stock
to output 1.4. These values are in accordance with
the National Income and Product Accounts and the Fixed Assets
Tables.12 Finally, the housing transaction
cost is set at ![]() based on estimates from the
National Association of Realtors (2005).13 Section 8 conducts
robustness analysis for alternative values of
based on estimates from the
National Association of Realtors (2005).13 Section 8 conducts
robustness analysis for alternative values of ![]() and
and
![]() .
.
We set
![]() and
and
![]() These values yield an
average capital to output ratios around 2.2 and
average business investment to output ratios around 20
percent. The aggregate shock is calibrated to match the standard
deviation of output in the data for the period 1952-1982. We use a
Markov-chain specification with seven states to match the following
first-order autoregression for the log of total factor
productivity:
These values yield an
average capital to output ratios around 2.2 and
average business investment to output ratios around 20
percent. The aggregate shock is calibrated to match the standard
deviation of output in the data for the period 1952-1982. We use a
Markov-chain specification with seven states to match the following
first-order autoregression for the log of total factor
productivity:
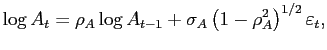 |
(21) |
We set
![]() and
and
![]() . After rounding, the first
number mimics a quarterly autocorrelation rate of productivity of
0.979, as in King and Rebelo (1999). The
second number is chosen to match the standard deviation of model
output to its data counterpart.
. After rounding, the first
number mimics a quarterly autocorrelation rate of productivity of
0.979, as in King and Rebelo (1999). The
second number is chosen to match the standard deviation of model
output to its data counterpart.
Our baseline calibration sets the maximum loan-to-value ratio
![]() at 0.75 We increase
at 0.75 We increase
![]() to 0.85 in the
calibration for the late period. The value of
to 0.85 in the
calibration for the late period. The value of ![]() is set at 0.25 in the baseline and
raised to 0.5 in the late period: with these
numbers, the income constraint only binds late in life, preventing
old homeowners from borrowing. Aside from this, our choice for
is set at 0.25 in the baseline and
raised to 0.5 in the late period: with these
numbers, the income constraint only binds late in life, preventing
old homeowners from borrowing. Aside from this, our choice for
![]() is of small importance for the model
dynamics. Lastly, the minimum-size house available for purchase
(
is of small importance for the model
dynamics. Lastly, the minimum-size house available for purchase
(![]() )
)![]() costs 1.5 times the average annual pre-tax household
income.14 Together with the minimum house
size, the parameter that has a large impact on homeownership is the
utility penalty for renting
costs 1.5 times the average annual pre-tax household
income.14 Together with the minimum house
size, the parameter that has a large impact on homeownership is the
utility penalty for renting
![]() . We set
. We set
![]() to obtain a homeownership rate
of 64 percent, as in the data for the period
1952-1982.
to obtain a homeownership rate
of 64 percent, as in the data for the period
1952-1982.
4. Steady-State Results
Household Behavior. At each stage in the life, the household chooses consumption, saving, hours, and housing investment by taking into account current and expected income, and liquid assets and housing position at the beginning of the period. Here, we mostly focus on housing decisions, since other features of the model are in line with existing models of life-cycle consumption and saving behavior. We defer illustrating labor supply behavior to the next section, when we discuss the model dynamics in response to aggregate shocks.
It is simple to characterize the behavior of agents depending on
whether they start the period as renters or homeowners. For
renters, the housing choice is as follows: given the initial state,
there is a threshold amount of liquid assets (![]() in our notation) such that, if assets exceed the threshold, renters
become homeowners. Also, the larger initial liquid assets are, the
less likely a household is to borrow to finance its housing
purchase.
in our notation) such that, if assets exceed the threshold, renters
become homeowners. Also, the larger initial liquid assets are, the
less likely a household is to borrow to finance its housing
purchase.
Homeowners can stay put, increase house size, downsize or switch
to renting. Figure 3 plots optimal housing
choice as a function of initial house size and liquid
wealth.15 The downward sloping line plots the
borrowing constraint that restricts debt from exceeding a fraction
![]() of its housing stock. As the figure
illustrates, larger liquid assets trigger larger housing. In
addition, buying and selling costs create a region of inaction
where the household keeps its housing constant. If liquid wealth
falls, the household either downsizes or switches to renting. One
feature of the model is that, for a household with very small
liquid assets, the housing tenure decision is non-monotonic in the
initial level of housing wealth. Consider, for instance, a
homeowner with liquid assets equal to about one. If the initial
house size is small, the homeowner does not change house size,
since, given the small amount of assets, the house size is closer
to its optimal choice. If the initial house is medium-sized, the
homeowner pays the adjustment cost and, because of his low liquid
assets, switches to renting. If the initial house size is large, it
is optimal to downsize, and to buy a smaller house.
of its housing stock. As the figure
illustrates, larger liquid assets trigger larger housing. In
addition, buying and selling costs create a region of inaction
where the household keeps its housing constant. If liquid wealth
falls, the household either downsizes or switches to renting. One
feature of the model is that, for a household with very small
liquid assets, the housing tenure decision is non-monotonic in the
initial level of housing wealth. Consider, for instance, a
homeowner with liquid assets equal to about one. If the initial
house size is small, the homeowner does not change house size,
since, given the small amount of assets, the house size is closer
to its optimal choice. If the initial house is medium-sized, the
homeowner pays the adjustment cost and, because of his low liquid
assets, switches to renting. If the initial house size is large, it
is optimal to downsize, and to buy a smaller house.
Life-Cycle Profiles. Figure 4 plots a typical individual life-cycle profile in our model. We choose an agent with a low discount factor since the behavior of an agent with low assets and often close to the borrowing constraint best illustrates the main workings of the model. The agent starts life as a renter, with little assets and low income. At the age of 22, he is hit by a positive income shock, saves in order to afford the downpayment and buys a house a year after. Prior to buying a house, the individual works more: the positive income shock raises the incentive to work; and such incentive is reinforced by need to set resources aside for the downpayment. Following a series of above average income shocks beginning at the age of 32, the agent buys a larger house at the age of 39. This time, in order to afford the larger house, the individual is much closer to his borrowing limit. In particular, while he owns and is close to the borrowing limit, hours move in the opposite direction to wage shocks, rising in bad times (age 42), falling in good times (age 45): such mechanism is explained in detail in the next Section. As retirement approaches, the agent pays back part of the mortgage, and works more. After retirement, at the age of 70, he switches to a small rental unit, before dying at the age of 90.
One dimension where it is illustrative to compare the model with the data is the frequency of housing adjustment for homeowners.16 Using the 1993 Survey of Income and Program Participation, Hansen (1998) reports that the median homeowner stays in the same house for about 8 years. Anily, Hornik, and Israeli (1999) estimate that the average homeowner lives in the same residence for 13 years. The corresponding number for our model is 15 years.17
Figure 5 compares the age profiles of housing, debt and homeownership with their empirical counterparts. Like the data, the model is able to capture the hump-shaped profiles of these variables. There are two discrepancies: as for mortgage debt, the model slightly underpredicts debt early in life, and overpredicts debt later in life. The model also underpredicts homeownership later in life: we believe that, late in life, the absence of any bequest motive and the need to finance consumption expenditure by selling the house more than offset the adjustment costs, thus generating a sharp decline in homeownership.
The Wealth Distribution. Our model reproduces the U.S. wealth distribution quite well. The Lorenz curves for the U.S. economy and for our model economy are reported in figure 6. The Gini coefficient for wealth in the model is 0.73, and is about the same as in the data (equal to 0.79). Our model still underpredicts wealth inequality at the very top of the distribution, both for housing and for total wealth. However, the model does well at matching the fraction of wealth (both housing wealth and overall wealth) held by the poorest 40 percent of the U.S. population, which has essentially no assets and no debt. Instead, a model without preference heterogeneity would do much worse: in Section 8 we show that the Gini coefficient for wealth in the model with a single discount factor is 0.53, much lower than in the data.
In the same vein, the model predicts a mortgage debt to GDP ratio that is roughly in line with the data (0.31 vs. 0.34) and a fraction of liquidity constrained agents that is consistent with the available empirical estimates. Following Hall (2011), we take a model agent to be liquidity-constrained if the holdings of net liquid assets are less than two months (16.67% on an annual basis) of income.18 Using this definition, 45% of households are liquidity constrained.19 Jappelli (1990) estimates the share of liquidity constrained individuals to be 20%. Studies that have combined self-reported measures of credit constraints from the Survey of Consumer Finances with indirect inference from other datasets (such as the PSID), have typically found that 20 percent is more likely to be a lower bound. For instance, using evidence on the response of spending to changes in credit card limits, Gross and Souleles (2002) argue that the overall fraction of potentially constrained households is over two thirds.
5. Business Cycle Results
We now illustrate the propagation mechanism of aggregate shocks. There are two aspects of heterogeneity that matter for aggregate dynamics: one is exogenous, and reflects the assumption that individuals have different abilities, planning horizons, and utility weights. Because other papers have studied these features in life-cycle models with aggregate shocks, we do not explore them in detail here.20 Instead, we focus on the endogenous component of heterogeneity, which reflects the fact that individuals with different ages and income histories accumulate different amounts of wealth over time; in turn, heterogeneity in wealth implies different individual responses to the same shock.
Workings of the Model. We focus on the response of aggregate hours to a technology
shock, since movements in hours are the key element of the
propagation mechanism in models that rely on technology shocks as
sources of aggregate fluctuations. In particular, we study how the
wealth distribution and its composition shape agents' responses to
shocks. To fix ideas, consider a stripped-down version of the
budget constraint of a working individual that keeps wealth
constant between two periods:
![]() and
and
![]() .21 Abstracting from
taxes and pensions, this implies the following budget
constraint:
.21 Abstracting from
taxes and pensions, this implies the following budget
constraint:
| (22) |
where
![]() measures the resources besides wages that can be used to finance
consumption:22 the term
measures the resources besides wages that can be used to finance
consumption:22 the term
![]() is net interest income;
the term
is net interest income;
the term
![]() is the maintenance cost required
to keep housing unchanged. Different values of
is the maintenance cost required
to keep housing unchanged. Different values of ![]() map into different positions of the agents along the
wealth distribution. For a wealthy homeowner (negative
map into different positions of the agents along the
wealth distribution. For a wealthy homeowner (negative ![]() ),
), ![]() is positive and large, and wage
income is a small fraction of consumption
is positive and large, and wage
income is a small fraction of consumption ![]() . For a
renter,
. For a
renter, ![]() ; in addition, assuming that the renter
is not saving,
; in addition, assuming that the renter
is not saving, ![]() , so that
, so that ![]() too. For a homeowner with a mortgage (positive
too. For a homeowner with a mortgage (positive ![]() ),
), ![]() is negative. Normalize
is negative. Normalize
![]() and set aside idiosyncratic
shocks, so that
and set aside idiosyncratic
shocks, so that ![]() at all times. Assuming that
at all times. Assuming that
![]() stays constant, the log-linearized
budget constaint becomes, denoting with
stays constant, the log-linearized
budget constaint becomes, denoting with
![]() where
where
![]() is the steady-state value of a variable:
is the steady-state value of a variable:
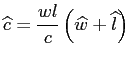 . . |
(23) |
This constraint can be interpreted as an equation dictating how
much the household needs to work to finance a given consumption
stream, given the wage. The larger the desired consumption
![]() the larger the required hours
the larger the required hours
![]() needed to finance the
consumption stream, with an elasticity of hours to consumption
given by consumption-wage income ratio
needed to finance the
consumption stream, with an elasticity of hours to consumption
given by consumption-wage income ratio
![]() . For a
wealthy individual,
. For a
wealthy individual, ![]() is high and larger than
one, since labor income is a small share of total earnings; for a
renter without assets,
is high and larger than
one, since labor income is a small share of total earnings; for a
renter without assets, ![]() ; for an indebted
homeowner,
; for an indebted
homeowner, ![]() , reflecting the need to use
part of the earnings to finance maintenance costs and to service
the mortgage. In other words, a wealthy person needs to increase
hours by more than 1 percent to finance a
1 percent rise in consumption, since labor
income is less than consumption; an indebted homeowner needs to
increase hours by less than 1 percent to finance
a 1 percent rise in consumption, because of
the leverage effect; a renter without assets needs to increase
hours 1 for 1 with
consumption.
, reflecting the need to use
part of the earnings to finance maintenance costs and to service
the mortgage. In other words, a wealthy person needs to increase
hours by more than 1 percent to finance a
1 percent rise in consumption, since labor
income is less than consumption; an indebted homeowner needs to
increase hours by less than 1 percent to finance
a 1 percent rise in consumption, because of
the leverage effect; a renter without assets needs to increase
hours 1 for 1 with
consumption.
The other key equation determining hours is the standard labor
supply schedule. Letting ![]() denote the steady-state
Frisch labor supply elasticity, this curve reads as
denote the steady-state
Frisch labor supply elasticity, this curve reads as
| (24) |
Combining equations 23 and 24 yields:
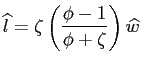 . . |
(25) |
Take the wage as the exogenous driving force of the model, since an
exogenous rise in productivity exerts a direct effect on the wage.
Whether the rise in the wage leads to an increase in hours depends
on whether the consumption-wage income ratio, ![]() is smaller or larger than one. In other words, all else
equal, borrowers (
is smaller or larger than one. In other words, all else
equal, borrowers (![]() ) are more likely to
reduce hours following a positive wage shock, whereas savers
(
) are more likely to
reduce hours following a positive wage shock, whereas savers
(![]() ) are more likely to increase them.
) are more likely to increase them.
For the economy as a whole, the response of total hours to a wage change will be an average of the labor supply responses of all households. If individual labor schedules were linear in net wealth, the aggregate labor supply response would be linear in average wealth, and wealth distribution would not affect labor supply. There are, however, two main forces that undo the linearity. First, retirees do not work, so any transfer of wealth to and from them could affect how the workers respond to wage shocks. Second, the interaction between borrowing constraints and housing purchases creates an interesting nonlinearity. Above, we have assumed that households do not change wealth in response to a shock in the wage. However, if households switch from renting to owning (or if they increase their house size) in good times, they typically need to save for the downpayment. This increases the incentive to work: intuitively, if the individual wants to keep consumption constant when he buys the house, he needs to work more hours. This effect creates comovement between hours and housing purchases.23 In particular, it reinforces the correlation between hours and housing demand in periods when a large fraction of the population has, all else equal, low net worth.
Business Cycle Statistics. In HP-filtered U.S. data, the variability of housing investment is large, with a standard deviation that is between three and four times that of GDP (in the period 1952-1982). Also, housing investment is procyclical, with a correlation with GDP around 0.9. Together, these two facts imply that the growth contribution of housing investment to the business cycle is larger than its share of GDP. Household mortgage debt is strongly procyclical from 1952 to 1982, but it becomes less procyclical after, with a correlation with GDP that drops from 0.78 to 0.43. Table 3 compares the benchmark model with the data. Overall, our baseline model does a good job in reproducing the relative volatility of each component of aggregate demand. In particular, it can account for about three quarters of the variance of housing investment. On the contrary, the model overpredicts the volatility of aggregate consumption. The volatility of business investment is only slightly lower than in the data. As in many RBC models without an extensive margin of work and without direct shocks to the labor supply, our model underpredicts the volatility of hours (0.33 percent in the model, 1.6 percent in the data).
Turning to debt, the model does well in reproducing its cyclical behavior.24 The key to this result is that the bulk of the debt holders (mostly impatients) upgrades housing in good times by taking out a (larger) mortgage. At the same time, the model overpredicts the volatility of debt itself: the standard deviation of the model variable is about four times larger than in the data. We suspect that the reason for the higher volatility of debt in the model has to do with the simplifying assumption that only one financial asset is available, whereas in the data some households (especially the wealthy) own simultaneously a mortgage and other financial assets. If debt of low-wealth households is more volatile than debt of high-wealth households, our model variable can exhibit more volatility than its data counterpart.
One dimension where it is useful to compare the model with the data pertains to home sales. In our model, we count a sale as every instance in which a household pays the transaction cost to change its housing: this involves own-to-own, rent-to-own and own-to-rent transitions. By this metric, the average turnover rate in the model (the ratio of sales to total houses) is 4 percent, a number that matches the 3.9 percent in the data.25 Moreover, the model correlation between turnover rate and GDP is 0.39, and the standard deviation is 0.29. The corresponding numbers from the data are 0.69 and 0.54. The positive correlation between sales and economic activity that the model captures reflects the presence of liquidity constraints: when the economy is in recession and household balance sheets have deteriorated, the potential movers in the model find their liquidity so impaired, whether they are owners or renters, that they are better off staying in their old house rather than attempting to move and paying the transaction cost.
6. Effects of Lower Downpayments and Higher Risk
Having shown above that the model roughly captures postwar U.S.
business cycles, we now consider the implications of two
experiments. In the first, we lower the downpayment from
25 to 15 percent. In the
second, we increase the idiosyncratic risk faced by households,
changing the unconditional standard deviation of income
![]() from 0.30 to
0.45. Our experiment is intended to mirror
two of the main changes that have occurred in the U.S. economy
since the mid 1980s. The model results are in Table 4.
from 0.30 to
0.45. Our experiment is intended to mirror
two of the main changes that have occurred in the U.S. economy
since the mid 1980s. The model results are in Table 4.
A Decline in Downpayments. Lower downpayments (column 2 in Table 4) lead to an increase in
the homeownership rate (from 64 to 76 percent) and to a higher level of debt (from 31 to 50 percent of GDP). Smaller downpayments
allow more housing ownership among the portion of the population
with very little net worth. While debt is higher, the increase in
homeownership works to keep total wealth inequality unchanged:
financial wealth inequality is higher, but housing wealth
inequality is lower. Turning to business cycles, the rise in
![]() tends to reduce the volatility of
housing investment, from 6.42 to 5.94 percent, for two reasons. The first reason has to do
with adjustment costs: on average, because of adjustment costs,
homeowners modify their housing little over time relative to
renters. The second motive operates through the interaction of
labor supply and housing purchases. As we explained above, indebted
homeowners are more likely, compared to renters, to reduce hours in
response to positive technology shocks, so their presence dampens
aggregate shocks. Therefore, the higher homeownership rate induced
by looser borrowing constraints reduces aggregate
volatility.26
tends to reduce the volatility of
housing investment, from 6.42 to 5.94 percent, for two reasons. The first reason has to do
with adjustment costs: on average, because of adjustment costs,
homeowners modify their housing little over time relative to
renters. The second motive operates through the interaction of
labor supply and housing purchases. As we explained above, indebted
homeowners are more likely, compared to renters, to reduce hours in
response to positive technology shocks, so their presence dampens
aggregate shocks. Therefore, the higher homeownership rate induced
by looser borrowing constraints reduces aggregate
volatility.26
An Increase in Individual Earnings
Volatility. Column 3 in Table 4 shows that, following a rise in
![]() , the homeownership rate falls
from 64 to 59 percent: higher
risk makes individuals more reluctant to buy an asset that is
costly to change. All else equal, the lower homeownership rate
would tend to increase the volatility of housing investment, since
renters change housing consumption more often. However, this effect
is more than offset by the behavior of those who remain homeowners:
these people are now more reluctant to change their housing
consumption (relative to a world with less individual risk). This
occurs because modifying housing, in the presence of transaction
costs, depletes holdings of liquid assets and increases the utility
cost of a negative idiosyncratic shock, thus increasing the option
value of not adjusting the stock for given changes in net worth.
Quantitatively, the higher earnings volatility reduces the standard
deviation of housing investment from 6.42 to
5.52 percent. Moreover, higher income
volatility also reduces the sensitivity of debt to aggregate
shocks, since debt is used to finance housing purchases, and
housing purchases respond less to shocks.
, the homeownership rate falls
from 64 to 59 percent: higher
risk makes individuals more reluctant to buy an asset that is
costly to change. All else equal, the lower homeownership rate
would tend to increase the volatility of housing investment, since
renters change housing consumption more often. However, this effect
is more than offset by the behavior of those who remain homeowners:
these people are now more reluctant to change their housing
consumption (relative to a world with less individual risk). This
occurs because modifying housing, in the presence of transaction
costs, depletes holdings of liquid assets and increases the utility
cost of a negative idiosyncratic shock, thus increasing the option
value of not adjusting the stock for given changes in net worth.
Quantitatively, the higher earnings volatility reduces the standard
deviation of housing investment from 6.42 to
5.52 percent. Moreover, higher income
volatility also reduces the sensitivity of debt to aggregate
shocks, since debt is used to finance housing purchases, and
housing purchases respond less to shocks.
Combining Lower Downpayments and Higher Volatility. The last column of Table 4 shows the effects of combining lower downpayments and higher volatility. The two forces together predict an increase in homeownership rates from 64 to 67 percent. The data counterpart is a two percentage points rise, from 64 to 66 percent. Moreover, the joint effect of these two forces makes debt less procyclical, as in the data. The correlation between debt and output falls from 0.71 to 0.39, a change that is remarkably similar to the data (from 0.78 to 0.43, see Table 1).27 Together, lower downpayments and high idiosyncratic volatility reduce the standard deviation of GDP from 2.09 to 2.03 percent, and the standard deviation of housing investment from 6.42 to 5.04. percent. When these numbers are compared to the data, the two changes combined can account for 13 percent of the variance reduction in GDP and about 60 percent of the variance reduction in housing investment.
Our interpretation of these results is as follows: in response to lower downpayments and higher income volatility, leveraged households become more cautious in response to aggregate shocks, thus changing less borrowing and housing demand when aggregate productivity changes.28 This is especially true for housing, relative to other categories of expenditure, since housing is a highly durable good and is subject to adjustment costs. Because individuals are reluctant to adjust their housing consumption during uncertain times, the sensitivity of hours to aggregate shocks falls too. As a consequence, even if the volatilities of consumption and business investment are not changing, total output is less volatile.
In Figure 7, each panel shows average debt, hours and housing positions by age in the lowest and the highest aggregate state. The top panel plots the calibration with high downpayments and low idiosyncratic risk (the period 1952-1982): changes in the aggregate state generate large differences in debt, housing and hours. The bottom panel plots the case with low downpayments and high idiosyncratic risk (the period 1983-2010): changes in the aggregate state generate smaller differences in debt, housing, and hours, thus illustrating how these variables become less volatile and less procyclical.
Figure 8 plots the model dynamics when technology switches from its average value to a higher value (about 1 percent rise) in period 1. The responses are larger in the earlier period. On impact, housing falls before rising strongly in period 1. This result is well known in the household production literature (see, for instance, Greenwood and Hercowitz 1991 and Fisher 2007). In models with housing and business capital, business capital is useful for producing more types of goods than housing capital. Hence, after a positive productivity shock, the rise in the marginal product of capital implies that there is a strong incentive to move resources out of the housing to build up business capital, and only later is housing accumulated. The key aspect to note here is that higher idiosyncratic risk and lower downpayment requirements dampen the incentive to adjust housing capital, so that housing investment becomes less volatile.
Our result that higher individual uncertainty reduces the
volatility of aggregate housing investment echoes the results of
papers that study how durable purchases respond to changes in
income uncertainty in
![]() models resulting from
transaction costs. Eberly (1994), using data from the Survey of
Consumer Finances, considers automobile purchases in presence of
transaction costs: she finds that higher income variability
broadens the range of inaction, and that the effect is larger for
households that are liquidity constrained. Foote, Hurst and Leahy
(2000) find a similar result using data on car holdings from the
Consumer Expenditure Survey, and offer an explanation that involves
the presence of liquidity constraints and precautionary saving:
adjusting the capital stock for people with low levels of net worth
depletes holdings of liquid assets and increases the utility cost
of a negative idiosyncratic shock, thus increasing the option value
of not adjusting the stock for given changes in net worth.
models resulting from
transaction costs. Eberly (1994), using data from the Survey of
Consumer Finances, considers automobile purchases in presence of
transaction costs: she finds that higher income variability
broadens the range of inaction, and that the effect is larger for
households that are liquidity constrained. Foote, Hurst and Leahy
(2000) find a similar result using data on car holdings from the
Consumer Expenditure Survey, and offer an explanation that involves
the presence of liquidity constraints and precautionary saving:
adjusting the capital stock for people with low levels of net worth
depletes holdings of liquid assets and increases the utility cost
of a negative idiosyncratic shock, thus increasing the option value
of not adjusting the stock for given changes in net worth.
7. Debt and Housing in a Great Recession Experiment
The finding that housing and debt are less sensitive to
aggregate shocks when downpayments are low and idiosyncratic risk
is high can account for part of the Great Moderation, but is at
odds with the events of the 2007-2009 financial crisis, when both
housing and debt fell substantially. Explaining the crisis is
beyond the scope of this paper, but in this section we show that
our model expanded to take into account the "credit crunch" can
generate, at least qualitatively, the observed response of housing
and debt in the Great Recession. We extend the stochastic structure
of the model so that, when the worst technology shocks hit, credit
standards get tighter too, in the form of lower loan-to-value
ratios and higher costs of financial intermediation (higher
borrowing interest rates). In other words, consistent with the
post-2007 evidence,29 recessions are now a combination of
negative financial and negative technology shocks occurring
simultaneously. We implement this scenario by assuming that the
maximum loan-to-value ratio ![]() changes over
time as a function of total factor productivity,
changes over
time as a function of total factor productivity, ![]() : formally,
: formally,
![]() Moreover,
we also introduce an additional cost of financial intermediation in
the form of an interest rate premium
Moreover,
we also introduce an additional cost of financial intermediation in
the form of an interest rate premium
![]()
![]() to be paid by debtors. The
budget constraint for a home buyer become respectively:
to be paid by debtors. The
budget constraint for a home buyer become respectively:
| (26) |
with
| |
(27) |
where
![]() is the indicator
function equal to 1 if the household is a net
debtor, 0 otherwise. The state vector
is the indicator
function equal to 1 if the household is a net
debtor, 0 otherwise. The state vector ![]() remains
unchanged with respect to the benchmark model, and so does the
equilibrium definition. In the calibration, we let
remains
unchanged with respect to the benchmark model, and so does the
equilibrium definition. In the calibration, we let ![]() drop by 6 percentage points in
correspondence of the two lowest values of
drop by 6 percentage points in
correspondence of the two lowest values of ![]() ,
and leave it constant for all other values of
,
and leave it constant for all other values of ![]() .30 We set the values of the interest
rate premium at 0.75% for the two lowest aggregate
productivity realizations, in both periods (
.30 We set the values of the interest
rate premium at 0.75% for the two lowest aggregate
productivity realizations, in both periods (![]() is
equal to zero for all other values of
is
equal to zero for all other values of ![]() ).
).
We find that this simple modification of the model can qualitatively account for the behavior of housing and debt in the most recent events. Figure 9 shows the impulse responses to positive and negative productivity shocks, comparing the early period with the late period (defined as in the baseline exercise). In the late period, debt, housing and GDP respond less to positive shocks, so that one finds evidence of the Great Moderation so long as the economy is lucky enough not to be hit by (too negative) negative shocks. When the worst recessionary shocks hit, however, the decline in debt and in housing purchases are considerably larger in the late period than in the early period. In other words, when leverage is high, the housing sector can better absorb "small" business-cycle shocks, but becomes more vulnerable to large negative shocks that result in a credit crunch: these shocks cause highly-leveraged households to sharply reduce their debt and housing purchases.31
8. Sensitivity Analysis
We discuss in this section four alternative versions of the model where we modify the calibration used in our benchmark.
Discount Factor. To analyze the model with homogeneous discounting, we modify the
calibration for the discount factor (
![]() ) and for the relative utility
from renting (
) and for the relative utility
from renting (
![]() ) in order to achieve the same
homeownership rate and interest rate as in our baseline. As shown
in Table 5, the volatilities of housing investment
and output are now slightly higher than in the baseline
calibration, but the correlations of housing investment and of
hours with output fall: this result occurs because fewer people are
close to the borrowing limit (only 15 percent of households are
liquidity-constrained) and in need of increasing hours to finance
the downpayment in good times. In addition, with a single discount
factor, very few people hold debt in equilibrium, and the
distribution of wealth is more egalitarian than in the data: the
Gini coefficient for wealth is 0.53, lower than in
the data and in the benchmark model. The model predicts, unlike the
data, a negative correlation between turnover and GDP: with a
single discount rate, more housing capital reallocation occurs in
bad times.
) in order to achieve the same
homeownership rate and interest rate as in our baseline. As shown
in Table 5, the volatilities of housing investment
and output are now slightly higher than in the baseline
calibration, but the correlations of housing investment and of
hours with output fall: this result occurs because fewer people are
close to the borrowing limit (only 15 percent of households are
liquidity-constrained) and in need of increasing hours to finance
the downpayment in good times. In addition, with a single discount
factor, very few people hold debt in equilibrium, and the
distribution of wealth is more egalitarian than in the data: the
Gini coefficient for wealth is 0.53, lower than in
the data and in the benchmark model. The model predicts, unlike the
data, a negative correlation between turnover and GDP: with a
single discount rate, more housing capital reallocation occurs in
bad times.
Persistence of the Income Process One key parameter is the persistence of income shocks. Our
benchmark sets
![]() . The robustness analysis in
Table 5 shows that, holding total income risk constant, some of the
model properties are a non-monotonic function of
. The robustness analysis in
Table 5 shows that, holding total income risk constant, some of the
model properties are a non-monotonic function of ![]() . When the shocks are not very persistent (
. When the shocks are not very persistent (
![]() ), the equilibrium level of
debt is relatively low, fewer people are at the liquidity
constraint, and debt and housing investment are less volatile and
slightly less cyclical. Conversely, when income shocks are highly
persistent (
), the equilibrium level of
debt is relatively low, fewer people are at the liquidity
constraint, and debt and housing investment are less volatile and
slightly less cyclical. Conversely, when income shocks are highly
persistent (
![]() ), more people are liquidity
constrained, but more people are lucky for a spell long enough to
afford the downpayment for a house and to keep housing and debt
relatively unchanged in response to shocks.32 In other
experiments not reported in the Table, we have found that only for
intermediate values of the persistence coefficient (between
0.85 and 0.92), can the model
account for both the high volatility of housing investment and the
high correlation of debt with economic activity. Moreover, for
values of
), more people are liquidity
constrained, but more people are lucky for a spell long enough to
afford the downpayment for a house and to keep housing and debt
relatively unchanged in response to shocks.32 In other
experiments not reported in the Table, we have found that only for
intermediate values of the persistence coefficient (between
0.85 and 0.92), can the model
account for both the high volatility of housing investment and the
high correlation of debt with economic activity. Moreover, for
values of ![]() above 0.95
housing turnover is negatively correlated with GDP, and housing is
negatively correlated with business investment.
above 0.95
housing turnover is negatively correlated with GDP, and housing is
negatively correlated with business investment.
Housing Transaction Costs. We consider two polar cases, zero and high transaction costs. With no transaction costs, the standard deviation of housing investment, which is 6.42 percent in the baseline, rises to 10.42 percent (see Table 5).33 Because houses are less risky, homeownership rises, from 64 to 68 percent. Aggregate volatility falls: housing and nonhousing capital become closer substitutes as means of saving, and the higher volatility of housing investment is offset by the reduced covariance between housing and nonhousing investment. The correlation between housing and non-housing investment, which is 0.18 in the baseline (0.36 in the data), becomes -0.40 in absence of transaction costs. It is interesting to relate this result to the household production literature, which models adjustment costs either as convex or using a time-to-build specification.34 Fisher (2007) argues that the household production model predicts that housing and business investment are negatively correlated, unless one assumes that household capital is complementary to business capital and labor in market production. Here, we note that our baseline model with nonconvex housing adjustment costs reproduces (unlike the model with no transaction costs) the positive correlation between housing and business investment that one finds in the data: sooner or later these costs must be paid in order to consume more housing, and it is better to pay them in good times, when the marginal utility of consumption is low. Moreover, impatient renters cannot wait to become homeowners, thus effectively buying houses and borrowing (i.e. selling claims on capital) after a positive productivity shock.
Table 5 also reports the results for the high
adjustment cost case (![]() ). The high
). The high
![]() model predicts low housing turnover
(2.1 percent) relative to the data
(4 percent), and an acyclical behavior of
housing sales (sales are procyclical both in the data and in the
benchmark model). Such model severely underpredicts the volatility
of housing investment. We conjecture that moving shocks (when
combined with income shocks) could restore the level of housing
turnover that is observed in the data even in the presence of high
transaction costs. It is not clear, however, whether moving shocks
could make turnover procyclical, unless they are more likely to
happen in good times.
model predicts low housing turnover
(2.1 percent) relative to the data
(4 percent), and an acyclical behavior of
housing sales (sales are procyclical both in the data and in the
benchmark model). Such model severely underpredicts the volatility
of housing investment. We conjecture that moving shocks (when
combined with income shocks) could restore the level of housing
turnover that is observed in the data even in the presence of high
transaction costs. It is not clear, however, whether moving shocks
could make turnover procyclical, unless they are more likely to
happen in good times.
Housing Depreciation. The last column of Table 5 reports the results when the housing depreciation rate is lowered from 5 to 3 percent. The performance of some of the model's second moments worsens considerably. Housing investment becomes too volatile, the cyclicality of housing investment is much lower than in the data, and the model fails to match the comovement of housing with business investment.
9. Conclusions
In this paper, we develop an equilibrium business cycle model where houses can be used as collateral, purchased or rented, and adjusted at a large cost. The resulting dynamics of housing investment and household debt are realistic not only at the macroeconomic level, but also at the level of individual household behavior: even if agents only infrequently adjust their housing choice, housing investment is the most volatile component of aggregate demand in our model, a result that is mirrored in the data. Our model accounts for the procyclicality and volatility of housing investment, as well as for the procyclicality of household debt. The model can also explain why housing investment has become relatively less volatile, and household debt less procyclical, as a consequence of increased household-level risk and lower downpayment requirements, two structural changes that have occurred in the U.S. economy around the mid-1980s. We further extend the model to account for a "Great Recession" episode characterized by negative technology shocks coupled with tighter credit conditions. This simple modification generates an interesting nonlinearity which is consistent with recent events: when leverage is high, housing, debt and output respond less to positive shocks (as in the Great Moderation) but are relatively more vulnerable to negative shocks, making a recession worse (as in the Great Recession).
Despite its complexity, the model precludes an examination of certain aspects of housing behavior that may be relevant for understanding business cycle fluctuations. One limitation is that we have not endogenized house prices.35 There are two main reasons for our choice. First, allowing for variable house prices would require specifying a two-sector model with housing and nonhousing goods that are produced using different technologies, or a model with different price stickiness in housing and nonhousing goods; and would probably require a rich array of shocks in addition to productivity shocks, since we know from existing studies that technology shocks alone cannot quantitatively explain observed movements in house prices: all of this would considerably increase computational costs. Second, although movements in house prices are economically important, cyclical fluctuations in the price of housing are smaller than the corresponding fluctuations in its quantity, which are the focus of our paper: for example, over the period 1970-2008, the standard deviation of year-on-year growth in real housing investment is 14 percent, while the corresponding number for real house prices is 3.7 percent.36
A second aspect of our model is that it does not explicitly consider mortgage default. Under the assumption that all debt is collateralized, and given that no shock is large enough to cause agents to owe on their house more than they are worth, agents would not find it optimal to default on their debts, even if they had this option. However, default is an important device against risk in an economy where housing values decline in recessions. In Appendix C,37 we sketch an extension of our model that dispenses from aggregate productivity shocks and features large housing depreciation shocks as the main source of business cycles. The model allows debtors to default on their mortgage, at the cost of losing their house and being excluded from the mortgage market. We assume that lenders cannot observe individual borrowers' characteristics, but can charge a higher interest rate on all loans in states of the world where default rates are higher to satisfy a zero profit condition. In this setup, indebted households will weigh the utility premium benefit of being homeowners against the cost of servicing their debt in states where they have negative equity. When a depreciation shock destroys part of the housing capital, borrowing rates rise, and highly leveraged individuals find themselves underwater, and decide to default on their debt, becoming renters. The model can be used to study how shocks to housing values interact with the mortgage default rate, interest rates, debt and the housing stock. For plausibly calibrated values, a shock that destroys 20 percent of the existing housing stock leads to a rise in defaults (from 0 to 10 percent), a rise in borrowing premia (from 0 to 1.5 percent), and a sharp decline in debt, output and housing investment.
References
Anily, Shoshana, Jacob Hornik, and Miron Israeli (1999) 'Inferring the distribution of households duration of residence from data on current residence time.' Journal of Business & Economic Statistics 17(3), 373-81
Cagetti, Marco (2003) 'Wealth accumulation over the life cycle and precautionary savings.' Journal of Business & Economic Statistics 21(3), 339-53
Campbell, Jeffrey R., and Zvi Hercowitz (2005) 'The role of collateralized household debt in macroeconomic stabilization.' NBER Working Papers 11330, National Bureau of Economic Research, Inc, May
Card, David (1991) 'Intertemporal labor supply: An assessment.' NBER Working Papers 3602, National Bureau of Economic Research, Inc, January
Carroll, Christopher, and Wendy Dunn (1997) 'Unemployment expectations, jumping (s,s) triggers, and household balance sheets.' In 'NBER Macroeconomics Annual 1997, Volume 12' (MIT Press)
Chambers, Matthew, Carlos Garriga, and Don E. Schlagenhauf (2009) 'Housing policy and the progressivity of income taxation.' Journal of Monetary Economics 56(8), 1116-1134
Davis, Morris A., and Francois Ortalo-Magne (2011) 'Household expenditures,wages, rents.' Review of Economic Dynamics 14(2), 248-261
Davis, Morris A., and Jonathan Heathcote (2005) 'Housing and the business cycle.' International Economic Review 46(3), 751-784
Díaz, Antonia, and María José Luengo-Prado (2010) 'The wealth distribution with durable goods.' International Economic Review 51(1), 143-170
Dynan, Karen E., Douglas W. Elmendorf, and Daniel E. Sichel (2007) 'The evolution of household income volatility.' Finance and Economics Discussion Series 2007-61, Board of Governors of the Federal Reserve System (U.S.)
Eberly, Janice C (1994) 'Adjustment of consumers' durables stocks: Evidence from automobile purchases.' Journal of Political Economy 102(3), 403-36
Favilukis, Jack, Sydney Ludvigson, and Stijn Van Nieuwerburgh (2009)'Macroeconomic implications of housing wealth, housing finance, and limited risk-sharing in general equilibrium.' Unpublished Manuscript
Fernandez-Villaverde, Jesus, and Dirk Krueger (2004) 'Consumption and saving over the life cycle: How important are consumer durables?' 2004 Meeting Papers 357b, Society for Economic Dynamics
Fisher, Jonas D. M. (2007) 'Why does household investment lead business investment over the business cycle?' Journal of Political Economy 115, 141-168
Fisher, Jonas D. M., and Martin Gervais (2007) 'First-time home buyers and residential investment volatility.' Working Paper Series WP-07-15, Federal Reserve Bank of Chicago
Floden, Martin, and Jesper Lindé (2001) 'Idiosyncratic risk in the united states and sweden: Is there a role for government insurance?' Review of Economic Dynamics 4(2), 406-437
Foote, Christopher, Erik Hurst, and John Leahy (2000) 'Testing the (s,s) model.' American Economic Review 90(2), 116-119
Francis, Neville, and Valerie A. Ramey (2009) 'Measures of per capita hours and their implications for the technology-hours debate.' Journal of Money, Credit and Banking 41(6), 1071-1097
Fraumeni, Barbara (1997) 'The measurement of depreciation in the U.S. national income and product accounts.' Survey of Current Business pp. 7-23
Gerardi, Kristopher S., Harvey S. Rosen, and Paul S. Willen (2010) 'The impact of deregulation and financial innovation on consumers: The case of the mortgage market.' Journal of Finance 65(1), 333-360
Gervais, Martin (2002) 'Housing taxation and capital accumulation.' Journal of Monetary Economics 49(7), 1461-1489
Gomme, Paul, Finn E. Kydland, and Peter Rupert (2001) 'Home production meets time to build.' Journal of Political Economy 109(5), 1115-1131
Gomme, Paul, Richard Rogerson, Peter Rupert, and Randall Wright (2004) 'The business cycle and the life cycle.' In 'NBER Macroeconomics Annual 2004, Volume 19' (MIT Press)
Greenwood, Jeremy, and Zvi Hercowitz (1991) 'The allocation of capital and timeover the business cycle.' Journal of Political Economy 99(6), 1188-214
Gross, David B., and Nicholas S. Souleles (2002) 'Do liquidity constraints and interest rates matter for consumer behavior? evidence from credit card data.' The Quarterly Journal of Economics 117(1), 149-185
Guvenen, Fatih (2011) 'Macroeconomics with heterogeneity: A practical guide.' Unpublished Manuscript
Haider, Steven J (2001) 'Earnings instability and earnings inequality of malesin the united states: 1967-1991.' Journal of Labor Economics 19(4), 799-836
Hall, Robert E. (2011) 'The long slump.' The American Economic Review 101(2), 431-469
Hansen, Gary D (1993) 'The cyclical and secular behaviour of the labour input: Comparing efficiency units and hours worked.' Journal of Applied Econometrics 8(1), 71-80
Hansen, Kristin A. (1998) 'Seasonality of moves and duration of residence.' Current Population Reports, Household Economic Studies, P70-66 (October), U.S. Census Bureau
Heathcote, Jonathan, Kjetil Storesletten, and Giovanni L. Violante (2010) 'The macroeconomic implications of rising wage inequality in the united states.' Journal of Political Economy 118(4), 681-722
Hendricks, Lutz (2007) 'How important is discount rate heterogeneity for wealth in equality?' Journal of Economic Dynamics and Control 31(9), 3042-3068
Iacoviello, Matteo, and Stefano Neri (2010) 'Housing market spillovers: Evidence from an estimated dsge model.' American Economic Journal: Macroeconomics 2(2), 125-64
Jappelli, Tullio (1990) 'Who is credit constrained in the U.S. economy?' The Quarterly Journal of Economics 105(1), 219-34
Jermann, Urban, and Vincenzo Quadrini (forthcoming) 'Macroeconomic effects of financial shocks.' The American Economic Review
Kennickell, Arthur, and Janice Shack-Marquez (1992) 'Changes in family finances from 1983 to 1989: evidence from the survey of consumer finances.' Federal Reserve Bulletin pp. 1-18
King, Robert G., and Sergio T. Rebelo (1999) 'Resuscitating real business cycles.' In Handbook of Macroeconomics, ed. J. B. Taylor and M. Woodford, 1 ed., vol. 1 (Elsevier) chapter 14, pp. 927-1007
Kiyotaki, Nobuhiro, Alexander Michaelides, and Kalin Nikolov (2011) 'Winners and losers in housing markets.' Journal of Money, Credit and Banking 43, 255-296
Krueger, Dirk, and Fabrizio Perri (2006) 'Does income inequality lead to consumption inequality? evidence and theory.' Review of Economic Studies 73(1), 163-193
Krusell, Per, and Anthony A. Smith (1998) 'Income and wealth heterogeneity in the macroeconomy.' Journal of Political Economy 106(5), 867-896
Moffitt, Robert, and Peter Gottschalk (2008) 'Trends in the transitory variance of male earnings in the u.s., 1970-2004.' Boston College Working Papers in Economics 697, Boston College Department of Economics, December
National Association of Realtors (2005) 'Structure, conduct, and performance of the real estate brokerage industry.' Technical Report
Peek, Joe, and James A. Wilcox (1991) 'The measurement and determinants of single-family house prices.' Real Estate Economics 19(3), 353-382
Poterba, James M. (1992) 'Taxation and housing markets.' In 'Canada-U.S. Tax Comparisons' (University of Chicago Press)
Queisser, Monika, and Edward Whitehouse (2005) 'Pensions at a glance: public policies across oecd countries.' MPRA Paper 10907, University Library of Munich, Germany, May
Ríos-Rull, José-Víctor (1996) 'Life-cycle economies and aggregate fluctuations.' Review of Economic Studies 63(3), 465-89
Ríos-Rull, José-Víctor, and Virginia Sánchez-Marcos (2008) 'An aggregate economy with different size houses.' Journal of the European Economic Association 6(2-3), 705-714
Rosen, Harvey S. (1985) 'Housing subsidies: Effects on housing decisions, efficiency, and equity.' In Handbook of Public Economics, ed. A. J. Auerbach and M. Feldstein, vol. Handbook of Public Economics (North Holland)
Scholz, John Karl, Ananth Seshadri, and Surachai Khitatrakun (2006) 'Are americans saving "optimally" for retirement?' Journal of Political Economy 114(4), 607-643
Silos, Pedro (2007) 'Housing, portfolio choice and the macroeconomy.' Journal of Economic Dynamics and Control 31(8), 2774-2801
Tauchen, George (1986) 'Finite state markov-chain approximations to univariateand vector autoregressions.' Economics Letters 20(2), 177-181
Thomas, Julia K. (2002) 'Is lumpy investment relevant for the business cycle?' Journal of Political Economy 110(3), 508-534
Venti, Steven F., and David A. Wise (2001) 'Choice, chance, and wealth dispersion at retirement.' In 'Aging Issues in the United States and Japan' (University of Chicago Press)
Young, Eric R. (2010) 'Solving the incomplete markets model with aggregate uncertainty using the krusell-smith algorithm and non-stochastic simulations.' Journal of Economic Dynamics and Control 34(1), 36-41
Appendix A: Computational Details
We solve for the model equilibrium using a computational method similar to the one used in Krusell and Smith (1998). The value and policy functions are computed on grids of points for the state variables, and then approximated with linear interpolation at points not on the grids (with the exception of the policy functions for housing, that are defined only on points on the grid). The algorithm consists of the following steps:
- Specify grids for the state space of individual and aggregate
state variables.
The number of grid points was chosen as follows: 7 points for the aggregate shock, 3 values for the idiosyncratic shock, 25 points for the housing stock, and 500 points for the financial asset.38 For aggregate capital, we choose a grid of 15 equally spaced points in the initial range
![$ \left[ 0.8K^{\ast },1.2K^{\ast}\right] ,$](img423.gif) where
where  denotes the average value of this
variable in the simulations. The range is then updated at each
iteration consistently with the simulated
denotes the average value of this
variable in the simulations. The range is then updated at each
iteration consistently with the simulated  ,
assigning as its boundaries the minimum and the maximum simulated
values.
,
assigning as its boundaries the minimum and the maximum simulated
values. - Guess initial coefficients
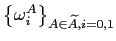 for the linear functions that approximate the laws of motion of
capital and labor:
for the linear functions that approximate the laws of motion of
capital and labor:
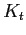

(28) 
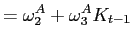 .
.(29) Because factor prices (wages and interest rates) only depend on aggregate capital and labor in equilibrium, this approach is equivalent to assuming that individuals forecast these factor prices using a function of
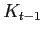 for each
value of the aggregate state
for each
value of the aggregate state 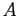 .
. - Starting from age
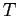 backward, compute optimal
policies as a function of the individual and aggregate states,
solving first the homeowner's and renter's problems
separately.39 Notice that the intra-temporal
optimal value for labor hours as a function of consumption and
productivity shock for ages
backward, compute optimal
policies as a function of the individual and aggregate states,
solving first the homeowner's and renter's problems
separately.39 Notice that the intra-temporal
optimal value for labor hours as a function of consumption and
productivity shock for ages
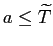 is the
following:40
is the
following:40
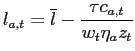
(30) which allows one to derive consumption before age
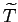 directly from the budget
constraint. For the homeowner:
directly from the budget
constraint. For the homeowner:
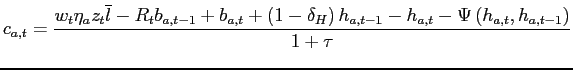
(31) so that the per-period utility function for
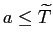 can be transformed as
follows:
can be transformed as
follows:
(32)
For the tenant, taking into consideration the intra-temporal condition for optimal house services to rent:
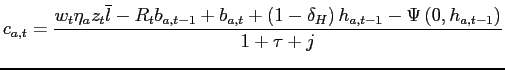
(33)
so that the per-period utility function for
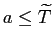 can be transformed as
follows:
can be transformed as
follows: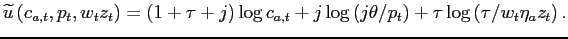
(34)
As a consequence, the homeowner's dynamic optimization problem entails solving for policy functions for
 and
and
 only, while the renter's one consists in
solving for
only, while the renter's one consists in
solving for  only. The problems of the retired
people (
only. The problems of the retired
people (
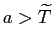 ) are similar to the
above, where we set
) are similar to the
above, where we set 
- Draw a series of aggregate and idiosyncratic shocks according
to the related stochastic processes. Draw a series of "death"
shocks according to the survival probabilities. Use the
(approximated) policy functions and the predicted aggregate
variables to simulate the optimal decisions of a large number of
agents for many periods. In the simulations, we perform linear
interpolation between grid points for
 but we restrict the choices of
but we restrict the choices of
 to lie on the grid. We simulate
90,000 individuals for 5,000 periods, discarding the first 200
periods.41 Compute the aggregate variables
to lie on the grid. We simulate
90,000 individuals for 5,000 periods, discarding the first 200
periods.41 Compute the aggregate variables
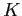 and
and 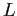 at each
at each
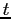 .
.
- Run a regression of the simulated aggregate capital and the
simulated aggregate labor on lagged aggregate capital, retrieving
the new coefficients
 for the
laws of motion for
for the
laws of motion for 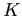 and
and 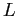 . We
repeat steps 3 and 4 until convergence over the coefficients of the
regressions. We measure goodness of fit using the
. We
repeat steps 3 and 4 until convergence over the coefficients of the
regressions. We measure goodness of fit using the 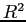 of the regressions: they are always equal to
0.997 or higher at convergence for
of the regressions: they are always equal to
0.997 or higher at convergence for
 and around 0.95 for
and around 0.95 for
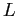 ; the corresponding wage rate and interest
rate functions are also very accurate: the
; the corresponding wage rate and interest
rate functions are also very accurate: the  of
the regression of the wage rate on aggregate
of
the regression of the wage rate on aggregate 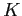 is 0.999, the
is 0.999, the 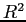 of the
regression of the interest rate on aggregate
of the
regression of the interest rate on aggregate 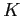 is 0.992.
is 0.992.
Appendix B: Calibrating the Income Process
The Persistence of Wage Shocks
The (parsimonious) process for individual income productivity that we specify in the model is:
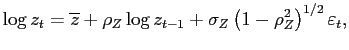 |
(35) |
We want to pick values for ![]() and
and
![]() that are in line with
evidence.
that are in line with
evidence.
- Floden and Lindé (2001) estimate an AR(1) process for
wages of the form in (35) and estimate (using
PSID data covering the 1988-1992 period), after controlling for
observable characteristics and measurement error, values of
 (and
(and
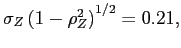 thus
implying
thus
implying
 ).
). - Heathcote, Storesletten and Violante (2010) estimate an ARMA(1,1) process for wages using PSID data. Their estimate of the autoregressive component is 0.97.
- Scholz, Seshadri, and Khitatrakun (2006) specify and estimate a
model of household log labor earnings (not wages) that controls for
fixed effects, a polynomial in age, and autocorrelation in
earnings. Their sample is the social security earnings records.
Their estimates for married, no college, two-earners are
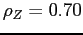 (and
(and
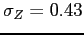 ).
).
The Change in Volatility
Several studies document the increase in the cross-sectional dispersion of earnings in the United States between the 1970s and the 1990s. This increase is often decomposed into a rise in permanent inequality (attributable to education, experience, sex, etc.) and a rise of the persistent or transitory shocks volatility. Despite some disagreement on the relative importance of these two components, the literature finds that both play a role in explaining the increase in income dispersion.
- Moffitt and Gottschalk (2008) study changes in the variance of permanent and transitory component of income volatility using data from the PSID from 1970 to 2004. They find that the non-permanent component (transitory) variance of earnings (for male workers) increased substantially in the 1980s and then remained at this new higher level through 2004. They report (see Figure 7 in their paper) that the variance of the transitory component rose from around 0.10 to 0.22 between the 1970s and the 1980s-1990s. This corresponds to a rise in the standard deviation from 0.32 to 0.47. Their estimate of the autocorrelation of the transitory shocks is 0.85.
- Using PSID data, Heathcote, Storesletten, and Violante (2010) decompose the evolution of the cross-sectional variance of individual earnings over the period 1967-2000 into the variances of fixed effects, persistent shocks, and transitory shocks. They find that the variance of persistent shocks roughly doubles during the 1975-1985 decade.
- Haider (2001) finds that increases in earnings instability over
the 1970s and increases in lifetime earnings inequality in the
1980s account in equal parts for the increase of inequality in the
data. To measure the magnitude of earnings instability in year
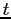 , he uses the cross-sectional variance of
the idiosyncratic deviations in year
, he uses the cross-sectional variance of
the idiosyncratic deviations in year 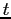 . His
estimate of
. His
estimate of 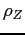 is 0.64. He finds
that the unconditional standard deviation of the instability
component rises from around 0.23-0.24 to about
0.35-0.37 during the 1980s.
is 0.64. He finds
that the unconditional standard deviation of the instability
component rises from around 0.23-0.24 to about
0.35-0.37 during the 1980s. - Krueger and Perri (2006) model log income as an ARMA process of
the kind
where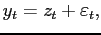
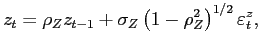

(36)  and
and
 are
are
 . They allow the
innovation variances
. They allow the
innovation variances
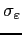 and
and
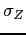 to vary by year. They find that
the values of
to vary by year. They find that
the values of
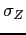 and
and
 are respectively
0.42 and 0.28 in 1980, and
0.52 and 0.36 in 2003. Given
these numbers, the standard deviation of log income
are respectively
0.42 and 0.28 in 1980, and
0.52 and 0.36 in 2003. Given
these numbers, the standard deviation of log income 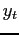 rises by 0.13, from
rises by 0.13, from
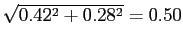 to
to
 .
.
From this brief review, we conclude that a plausible value for the persistence of the productivity shock is around 0.9. We set the standard deviation of income to be equal to 0.3 in the early part of the sample, which is the lower bound of the estimates reported above. We set the standard deviation to 0.45 in the second part of the sample: a change of 0.15 is in the range of estimates reported by Moffitt and Gottschalk (2008).
Tables
Table 1: U.S. Economy. Cyclical Statistics and Housing Market Facts
| Early Period 1952.I -1982.IV | Late Period 1983.I -2010.IV | Whole Sample 1952.I -2010.IV | |
|---|---|---|---|
| Standard Dev: GDP | 2.09 | 1.62 | 1.88 |
| Standard Dev: C | 0.93 | 0.83 | 0.88 |
| Standard Dev: IH | 7.12 | 4.45 | 6.00 |
| Standard Dev: IK | 4.90 | 5.36 | 5.11 |
| Standard Dev: Debt | 2.23 | 2.20 | 2.21 |
| Standard Dev: Hours | 1.60 | 1.37 | 1.49 |
| Standard Dev: Housing Turnover | 0.54 (68.I-82.IV) | 0.29 | 0.40 |
| Correlations: IH,GDP | 0.89 | 0.75 | 0.84 |
| Correlations: Debt,GDP | 0.78 | 0.43 | 0.63 |
| Correlations: Hours,GDP | 0.82 | 0.86 | 0.83 |
| Correlations: Turnover,GDP | 0.69 | 0.10 | 0.46 |
| Correlations: IH,IK | 0.36 | 0.40 | 0.36 |
| Correlations: Debt,C | 0.72 | 0.37 | 0.56 |
| Averages: Homeownership | 64% | 66% | 65% |
| Averages: Debt to GDP | 34% | 59% | 46% |
| Averages: Housing Turnover | 3.9% | 4.3% | 3.2% |
| Averages: Gini wealth | 0.79 | 0.83 | 0.81 |
| Averages: Gini labor income | 0.40 | 0.46 | 0.83 |
| Averages: Gini consumption | 0.23 | 0.26 | 0.25 |
Notes: C, IH and IK are consumption, residential fixed investment and business fixed investment respectively, divided by the GDP deflator (sources: BEA). GDP is the sum of the three series. Durables expenditures are included in IH. Debt is the stock of Home mortgages held by households and nonprofit organizations (source: Flow of Funds Accounts), divided by the GDP deflator. Hours are total hours worked for the entire economy from Francis and Ramey (2009). Cyclical statistics (standard deviations and correlations) for all series refer to the series logged and detrended with HP-filter (smoothing parameter 1,600). Data on inequality are from Wolff, 2010 (wealth); http://www.census.gov/hhes/www/income/data/ (income); and from Krueger and Perri, 2006 (consumption). Housing Turnover is the ratio of total home sales divided by the existing housing stock (see text for the source).
Table 2: Parameter Values for the Benchmark Model Economy
| Parameter | Value | Target/Source | |
|---|---|---|---|
| Preferences: Discount factor, patients | 0.999 | ||
| Preferences: Discount factor, impatients | 0.941 | Hendricks (2007) | |
| Preferences: Fraction of impatient agents | - | 2/3 | Gini coefficient of Wealth: 0.73 |
| Preferences: Weight on leisure in utility | 1.65 | - | |
| Preferences: Productive time | | 2.65 | Time worked: 40% |
| Preferences: Weight on housing in utility | 0.15 | ||
| Preferences: Utility, renting vs. owning | 0.838 | Home ownership rate = 64% | |
| Preferences: Utility weights (family size) | | see text | Cagetti (2003) |
| Life, Retirement: Survival probabilities | see text | Decennial Life Tables | |
| Life, Retirement: Retirement period | | 46 | Retirement age 65 years |
| Life, Retirement: Pension | 0.4xinc. | 40% average income | |
| Technology: Capital share | 0.26 | ||
| Technology: Capital depreciation rate | | 0.09 | |
| Technology: Housing depreciation rate | | 0.05 | |
| Technology: Autocorrelation, technology shock | 0.925 | King and Rebelo (1999) | |
| Technology: Standard dev., technology shock | | 0.0148 | |
| Technology: Housing transaction cost | 0.05 | National Association Realtors (2005) | |
| Technology: Minimum House Size | | 1.5xinc. | See text |
| Borrowing: Max debt, fraction lifetime wage | 0.25 | See text | |
| Borrowing: Maximum debt, fraction of house | 0.75 | See text | |
| Individual Income Process: Autocorrelation, earnings shock | 0.90 | Floden and Linde (2001) | |
| Individual Income Process: Standard deviation, earnings shock | | 0.30 | See appendix B |
| Individual Income Process: Age-dependent earnings ability | see text | Hansen (1993) |
Table 3: U.S. Economy and Baseline Model. Comparison for the Early Period
| 1952.I -1982.IV (Early Period) | Model | |
|---|---|---|
| Standard Dev: GDP | 2.09 | 2.09 |
| Standard Dev: C | 0.93 | 1.63 |
| Standard Dev: IH | 7.12 | 6.42 |
| Standard Dev: IK | 4.90 | 4.16 |
| Standard Dev: Debt | 2.23 | 8.34 |
| Standard Dev: Hours | 1.60 | 0.33 |
| Standard Dev: Housing Turnover | 0.54 (68.1-82.IV) | 0.29 |
| Correlations: IH,GDP | 0.89 | 0.66 |
| Correlations: Debt,GDP | 0.78 | 0.71 |
| Correlations: Hours,GDP | 0.82 | 0.65 |
| Correlations: Turnover,GDP | 0.69 | 0.39 |
| Correlations: IH,IK | 0.36 | 0.18 |
| Correlations: Debt,C | 0.72 | 0.85 |
| Averages: Homeownership | 64% | 64% |
| Averages: Debt to GDP | 34% | 31% |
| Averages: Housing Turnover | 3.9% | 4.0% |
| Averages: Gini wealth | 0.79 | 0.73 |
| Averages: Gini labor income | 0.40 | 0.41 |
| Averages: Gini consumption | 0.23 | 0.26 |
| Averages: Liquidity constrained | NA | 0.45 |
Notes: The model moments are based on statistics from a simulation of 5,000 periods. Liquidity constrained agents in the model are those who own liquid assets less than 16.67 percent (two months in a year) of annual income.
Table 4: Model Predictions, Changing Downpayment Requirements and Income Volatility
| (1) Baseline Early Period | (2) | (3) | (4) Late Period | |
|---|---|---|---|---|
| Standard Deviation: GDP | 2.09 | 2.08 | 2.05 | 2.03 |
| Standard Deviation: C | 1.63 | 1.63 | 1.66 | 1.68 |
| Standard Deviation: IH | 6.42 | 5.94 | 5.52 | 5.04 |
| Standard Deviation: IK | 4.16 | 4.05 | 4.21 | 4.16 |
| Standard Deviation: Debt | 8.34 | 3.04 | 2.61 | 1.44 |
| Standard Deviation: Hours | 0.33 | 0.32 | 0.31 | 0.31 |
| Standard Deviation: Housing Turnover | 0.29 | 0.44 | 0.21 | 0.21 |
| Correlations: IH, GDP | 0.66 | 0.69 | 0.55 | 0.54 |
| Correlations: Debt, GDP | 0.71 | 0.63 | 0.50 | 0.39 |
| Correlations: Hours, GDP | 0.65 | 0.64 | 0.47 | 0.42 |
| Correlations: Turnover, GDP | 0.39 | 0.77 | 0.42 | 0.28 |
| Correlations: IH, IK | 0.18 | 0.24 | 0.08 | 0.09 |
| Correlations: Debt, C | 0.85 | 0.77 | 0.68 | 0.58 |
| Averages: Homeownership | 64% | 76% | 59% | 67% |
| Averages: Debt to GDP | 31% | 50% | 23% | 35% |
| Averages: Housing Turnover | 4.0% | 3.0% | 5.1% | 5.6% |
| Averages: Gini wealth | 0.73 | 0.73 | 0.73 | 0.73 |
| Averages: Gini labor income | 0.41 | 0.41 | 0.48 | 0.48 |
| Averages: Gini consumption | 0.26 | 0.26 | 0.31 | 0.31 |
| Averages: Liquidity constrained | 0.45 | 0.45 | 0.39 | 0.38 |
Notes: Baseline calibration and sensitivity analysis. (1) is the baseline calibration that is targeted to the U.S. data for the period 1952-1982. In (2), we increase the loan-to-value ratio from 0.75 to 0.85. In (3), we increase earnings volatility from 0.3 to 0.45. In (4), we increase both loan-to-value ratio and earnings volatility so to calibrate the U.S. economy for the period 1983-2010.
Table 5: Robustness Analysis
| Data | Model | One- |
Persistence |
Transaction cost |
Low |
|||
|---|---|---|---|---|---|---|---|---|
| Standard Dev: GDP | 2.09 | 2.09 | 2.16 | 2.08 | 2.02 | 2.05 | 2.01 | 2.05 |
| Standard Dev: C | 0.93 | 1.63 | 1.69 | 1.69 | 1.69 | 1.69 | 1.72 | 1.68 |
| Standard Dev: IH | 7.12 | 6.42 | 6.72 | 4.99 | 4.73 | 10.42 | 3.45 | 11.33 |
| Standard Dev: IK | 4.90 | 4.16 | 4.83 | 4.24 | 4.12 | 4.99 | 3.95 | 5.17 |
| Standard Dev: Debt | 2.23 | 8.34 | 14.78 | 2.68 | 2.11 | 1.68 | 2.11 | 0.68 |
| Standard Dev: Hours | 1.60 | 0.33 | 0.39 | 0.32 | 0.27 | 0.36 | 0.27 | 0.30 |
| Standard Dev: Housing Turnover | 0.54 | 0.29 | 0.40 | 0.16 | 0.22 | 2.14 | 0.13 | 0.16 |
| Correlations: IH,GDP | 0.89 | 0.66 | 0.58 | 0.61 | 0.49 | 0.34 | 0.54 | 0.30 |
| Correlations: Debt,GDP | 0.78 | 0.71 | 0.72 | 0.60 | 0.58 | 0.69 | 0.39 | 0.11 |
| Correlations: Hours,GDP | 0.82 | 0.65 | 0.60 | 0.50 | 0.43 | 0.45 | 0.34 | 0.45 |
| Correlations: Turnover,GDP | 0.69 | 0.39 | -0.32 | 0.18 | -0.15 | 0.67 | -0.08 | 0.10 |
| Correlations: IH,IK | 0.36 | 0.18 | 0.08 | 0.19 | 0.03 | -0.40 | 0.19 | -0.44 |
| Correlations: Debt,C | 0.72 | 0.85 | 0.83 | 0.78 | 0.72 | 0.82 | 0.54 | 0.24 |
| Averages: Homeownership | 64% | 64% | 64% | 66% | 71% | 68% | 74% | 70% |
| Averages: Debt to GDP | 34% | 31% | 9% | 17% | 42% | 40% | 37% | 46% |
| Averages: Housing Turnover | 3.9% | 4.0% | 3.3% | 4.7% | 2.9% | 42.0% | 2.1% | 3.8% |
| Averages: Gini wealth | 0.79 | 0.73 | 0.53 | 0.68 | 0.73 | 0.73 | 0.72 | 0.72 |
| Averages: Gini labor income | 0.40 | 0.41 | 0.42 | 0.45 | 0.39 | 0.41 | 0.41 | 0.42 |
| Averages: Gini consumption | 0.23 | 0.26 | 0.24 | 0.23 | 0.26 | 0.26 | 0.26 | 0.26 |
| Averages: Liquidity constrained | NA | 0.45 | 0.15 | 0.30 | 0.49 | 0.47 | 0.45 | 0.45 |
Notes: In the one-![]() model, we
recalibrate
model, we
recalibrate ![]() and the average
and the average ![]() so that the homeownership rate is 64% and the interest
rate is 3%, as in the baseline model. No parameter changes are made
in the other models, except those noted in row 2 of the Table.
so that the homeownership rate is 64% and the interest
rate is 3%, as in the baseline model. No parameter changes are made
in the other models, except those noted in row 2 of the Table.
Figures
Figure 1: Mortgage Debt, Housing Investment and GDP
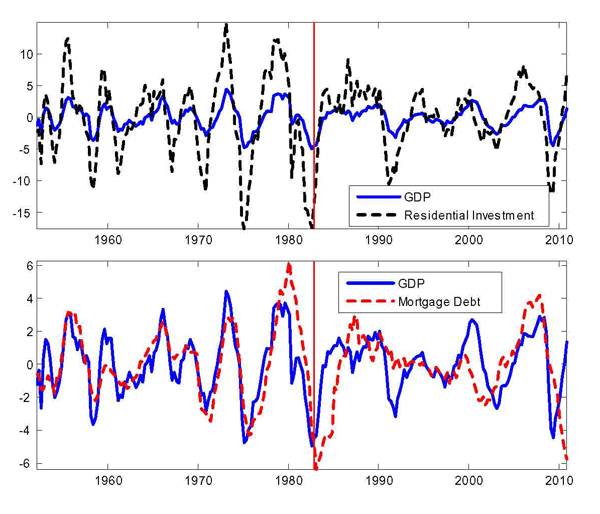
Note: Variables are inflation-adjusted, HP-filtered (
![]() ) and expressed in percent
deviation from their trend.
) and expressed in percent
deviation from their trend.
Figure 2: Efficiency and Preference Profiles
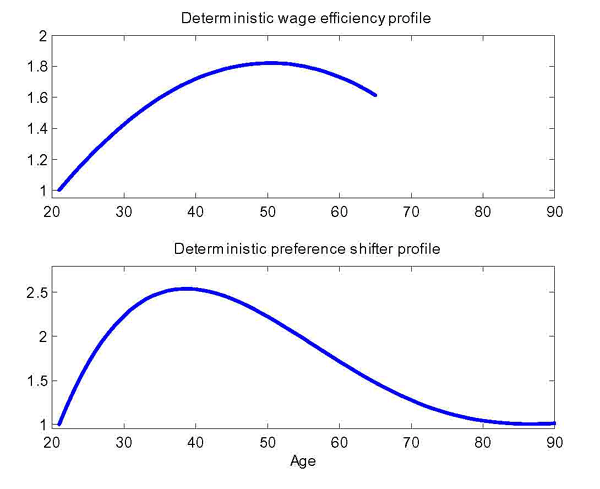
Figure 3: Homeowner's Housing Investment Decision as a Function of Initial House Size and Liquid Assets
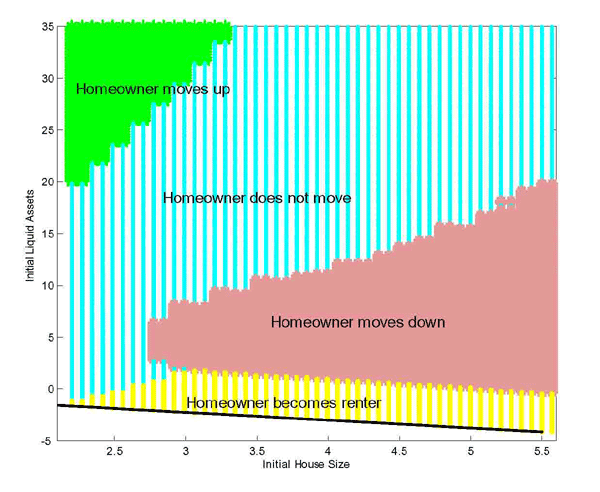
Note: The figure illustrates, for each combination of initial house and liquid assets, the homeowner's housing decision for next period. It is plotted for a patient agent who is 65 years old, when aggregate productivity and the average capital labor ratio are equal to their average value.
Figure 4: A Typical Life-Cycle Profile
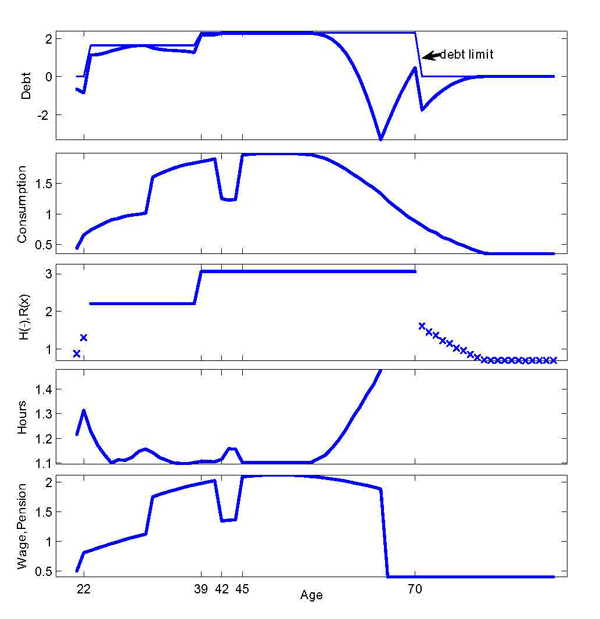
Note: This figure plots life-cycle choices of a randomly chosen impatient agent from birth (age 21) to death (age 90). In panel 1, the thin line denotes the maximum debt limit given the housing choice. In panel 3, the "x" symbol denotes the amount rented when the individual is renting, whereas the solid line denotes the amount owned when the individual owns a house.
Figure 5: Comparison Between Model (Baseline Calibration) and Data
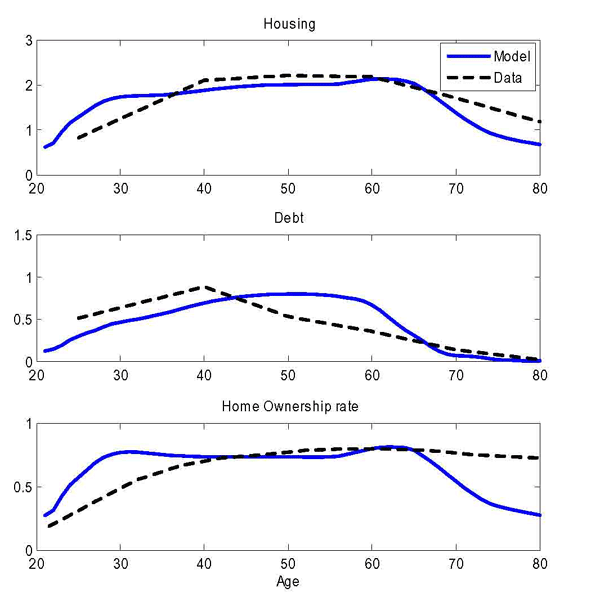
Note: The data come from the summary statistics of the 1983 Survey of Consumer Finances, as reported in Kennickell and Shack-Marquez (1992). For each age, the model variable is the product of the fraction of households in that age holding housing or debt, times the median holding of housing or debt. The data variable is constructed in the same way.
Figure 6: Lorenz Curves for Total Wealth and Housing Wealth
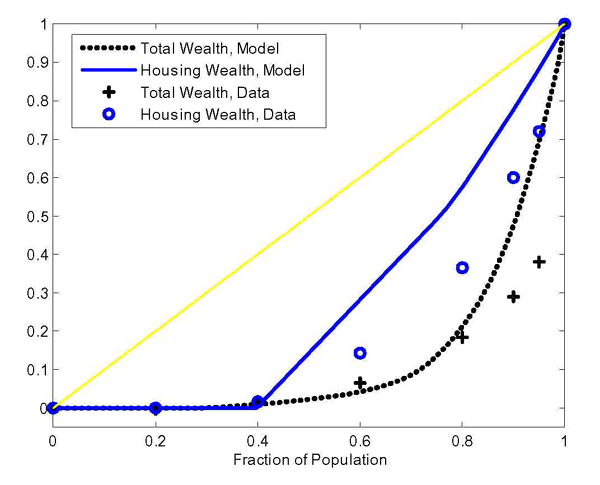
Note: The Lorenz curves for total wealth and housing wealth in the data are from Díaz and Luengo-Prado (2010) using data from 1998 Survey of Consumer Finances.
Figure 7: Comparison between Early and Late Period: Debt, Hours and Housing by Age
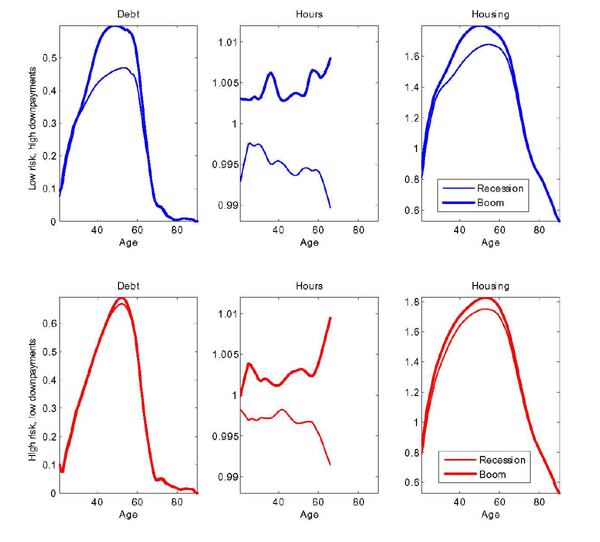
Note: The top panel plots model variables in the baseline
calibration (low individual risk and high downpayment
requirements), where housing, debt and hours worked are relatively
more volatile (the difference between a boom and a recession is
larger). The bottom panel plots the calibration with high
individual risk and low downpayment requirements.
The thin/thick line shows the reading of each variable by age
when the economy is in the lowest/highest aggregate state
(recession/boom). Housing and Debt are expressed as a ratio of
average GDP. Hours are normalized in each age by their age
average.
Figure 8: Impulse Responses to a Positive Technology Shock: Early and Late Period Calibration
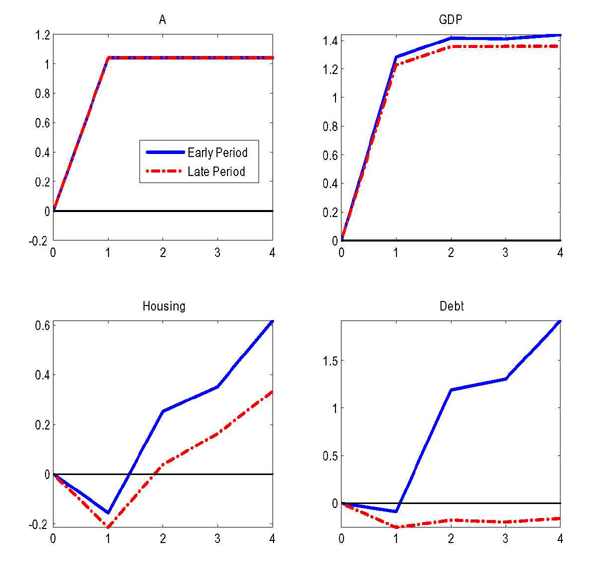
Note: Model dynamics following an exogenous switch in
aggregate productivity ![]() (in period zero) from the
median state to next higher value (a 1 percent increase) lasting
four periods. Each variable is displayed in percent deviation from
the unshocked path.
(in period zero) from the
median state to next higher value (a 1 percent increase) lasting
four periods. Each variable is displayed in percent deviation from
the unshocked path.
Figure 9: Impulse Responses to Positive and Negative Technology Shocks: Comparison between the Early and Late Period Calibration, Model with Cyclical Loan-to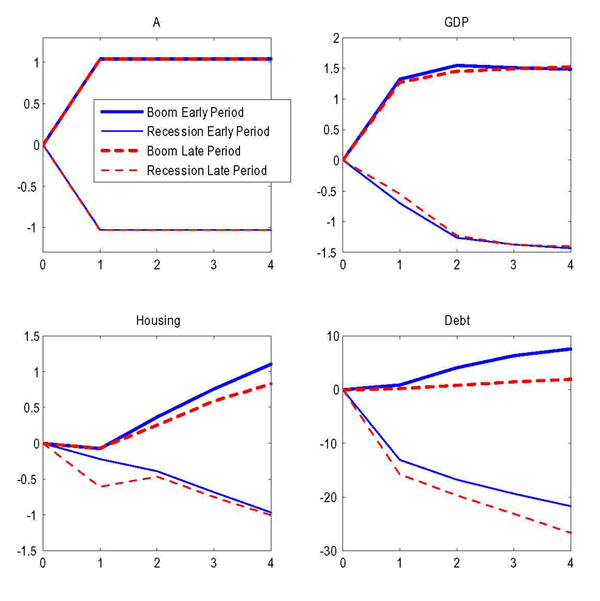 -Value Ratios and Interest Rate Premia
-Value Ratios and Interest Rate Premia
Note: Model dynamics following an exogenous switch in
productivity ![]() in period zero. The thick lines plot a
1 percent increase in productivity that does not change financial
conditions in the early (solid lines) and late (dashed lines)
period calibration. The thin lines plot a 1 percent decrease in
productivity together with a worsening in financial conditions.
Each variable is displayed in percentage deviation from the
unshocked path.
in period zero. The thick lines plot a
1 percent increase in productivity that does not change financial
conditions in the early (solid lines) and late (dashed lines)
period calibration. The thin lines plot a 1 percent decrease in
productivity together with a worsening in financial conditions.
Each variable is displayed in percentage deviation from the
unshocked path.
Footnotes
** We thank Massimo Giovannini and Joachim Goeschel for their invaluable research assistance. We thank Chris Carroll, Kalin Nikolov, Dirk Krueger, Makoto Nakajima, as well as various seminar and conference participants for helpful comments on various drafts of this paper. Pavan aknowledges financial support from the Spanish Ministry of Education (Programa de Movilidad de Jovenes Doctores Extranjeros). Supplementary material is available at the website https://www2.bc.edu/~ iacoviel/. Return to text
+ Matteo Iacoviello, Division of International Finance, Federal Reserve Board, 20th and C St. NW, Washington, DC 20551. Email: matteo.iacoviello@frb.gov. Return to text
++ Marina Pavan, Universitat Jaume I & LEE, Castellón, Spain. E-mail: pavan@eco.uji.es. Return to text
1. Campbell and Hercowitz (2005) and Gerardi, Rosen and Willen (2010) discuss the role of financial reforms, and Dynan, Elmendorf and Sichel (2007) discuss the evolution of household income volatility. Return to text
2. If one excludes the 2008-2010 period from the time-series, the decline in the volatility of housing investment and the decline in the correlation between debt and GDP are slightly larger. Return to text
3. Under
convex costs, housing adjustment takes the form of a series of
small adjustments over a number of periods. Under our
specification, the homeowner's housing stock follows an
![]() rule, remaining unchanged
over a long period and ultimately changing by a potentially large
amount. See Carroll and Dunn (1997) for an early partial
equilibrium model with
rule, remaining unchanged
over a long period and ultimately changing by a potentially large
amount. See Carroll and Dunn (1997) for an early partial
equilibrium model with
![]() behavior for
housing. Return to text
behavior for
housing. Return to text
4. Krusell and Smith (1998) explore a heterogeneous-agents setting with discount rate heterogeneity which replicates key features of the data on the distribution of wealth. Return to text
5. We crudely assume that the pension is the same for everyone. Allowing pensions to mimic something that looks like the actual Social Security system in the U.S. would make our model computationally intractable, since it would enlarge the state variables in the household problem to encompass their entire income history. Return to text
6. We refer
to ![]() as financial liabilities, and to
as financial liabilities, and to
![]() as financial assets. Because bonds are
claims on aggregate capital, their return varies with the aggregate
state. Return to text
as financial assets. Because bonds are
claims on aggregate capital, their return varies with the aggregate
state. Return to text
7. To
compute ![]() , we fix interest and wages at current
values. To compute
, we fix interest and wages at current
values. To compute
![]() we assume
we assume
![]() for
for
![]() . Return to text
. Return to text
8. In the United States, lending institutions typically send a "Verification of Employment" (VOE) form to the borrower's employer to determine start date of employment, current and previous salary, and the probability of continued employment among other things. Return to text
9. One can
interpret the marginal cost of one house to be 1
for the financial sector, since loanable funds can be converted
into housing costlessly; and the marginal benefit to be the sum of
the current rental income, ![]() , plus expected
return next period,
, plus expected
return next period,
![]() ,
where
,
where ![]() is the opportunity cost of funds for
the financial sector. Equating costs and benefits yields equation
(5)
.
Return to text
is the opportunity cost of funds for
the financial sector. Equating costs and benefits yields equation
(5)
.
Return to text
10. We have
examined the robustness of our results by letting agents use both
the aggregate capital stock ![]() and the housing
stock
and the housing
stock ![]() in forecasting future prices, with nearly
identical results, but at a higher computational cost. It is
possible that higher moments of the wealth distribution could be
both relevant in predicting future prices and yield different
aggregate dynamics, so that our decision rules would describe a
bounded rationality equilibrium, rather than a good approximation
to the rational expectations equilibrium. Yet the evidence that
adding
in forecasting future prices, with nearly
identical results, but at a higher computational cost. It is
possible that higher moments of the wealth distribution could be
both relevant in predicting future prices and yield different
aggregate dynamics, so that our decision rules would describe a
bounded rationality equilibrium, rather than a good approximation
to the rational expectations equilibrium. Yet the evidence that
adding ![]() to the set of the state variables does not
change aggregate dynamics leads us to be skeptical of this
interpretation. See Young (2010) for an insightful discussion of
these issues. Return to
text
to the set of the state variables does not
change aggregate dynamics leads us to be skeptical of this
interpretation. See Young (2010) for an insightful discussion of
these issues. Return to
text
11. Queisser and Whitehouse (2005) report that average pensions for males in the United States are 40 percent of the economy-wide average earnings. Return to text
12. The NIPA Fixed Asset Tables indicate depreciation rates for housing ranging from 1.2 to 4.5 percent, depending on the type of structure and its use (see Fraumeni, 1997). We choose a slightly higher value because we want to account for unmeasured labor time that is used to repair, renovate, or maintain or improve the quality of housing at a given location (Peek and Wilcox, 1991); because higher values are typically considered in the existing literature, especially when housing is broadly interpreted to include consumer durables (Chambers, Garriga and Schlagenhauf, 2009, Gervais 2002, and Díaz and José Luengo-Prado, 2010); and because a higher depreciation rate (5 percent instead of 2 percent, say) reduces the extent to which aggregate housing tends to decrease on impact following a positive aggregate technology shock in a model with two capital goods. Return to text
13. The National Association of Realtors estimates that average commission rates (excluding houses sold without brokers, which account for about 10 to 25 percent of existing home sales, according to media reports, reports of the National Association of Realtors, and academic studies) range from 4.3 to 5.4 percent, based on 2004 data documenting a $65 billion brokerage industry and an existing home sales volume of $1.35 trillion. Return to text
14. According to the 2009 American Housing Survey, only 20 percent of total owner-occupied units have a ratio to current income less than 1.5. Return to text
15. The figure is plotted for a patient agent who is entering retirement (65 years old), when aggregate productivity and the capital-labor ratio are equal to their average value. Return to text
16. In the model, renters change their housing position every period, since they face no cost in doing so. This assumption is in line with the data, that show that on average renters move about every two years. Return to text
17. We are aware, of course, of the difficulty in comparing the model with the data along this dimension: in the data, 15 percent of the moves are associated with a move to a different state, and 35 percent of the moves are associated with a move to a different county. Most of these moves are probably "moving shocks" rather than movements along the housing ladder. Return to text
18. Liquid
assets are defined as
![]() According to this definition, an owner
According to this definition, an owner
![]() is not liquidity
constrained so long as it saves sufficiently more (borrows less)
than the minimum downpayment in the house (
is not liquidity
constrained so long as it saves sufficiently more (borrows less)
than the minimum downpayment in the house (
![]() ); a renter (
); a renter (
![]() ) is not constrained if
financial assets are sufficiently large (
) is not constrained if
financial assets are sufficiently large (
![]() ). Return to text
). Return to text
19. The baseline model predicts that 70 percent of renters and 31 percent of homeowners are liquidity constrained; and that 67 percent of impatient agents and 2 percent of patient agents are liquidity constrained. Return to text
20. See for instance the work of Ríos-Rull (1996) and Gomme et al. (2004). Return to text
21. Obviously, the optimal decisions involve the joint choice of (1) consumption, (2) housing, (3) debt and (4) hours worked. By assuming that housing and debt remain constant across two subperiods, we can study the joint determination of consumption and hours by focusing on the budget constraint and the Euler equation for labor supply only. This is a reasonable assumption for small shocks (such as aggregate shocks). Return to text
22. Renters
have constant shares of housing and nonhousing consumption, so that
![]() where
where ![]() is the ratio of housing expenditure to
nondurable consumption. With minor modifications, the arguments in
the text carry over to this case, since
is the ratio of housing expenditure to
nondurable consumption. With minor modifications, the arguments in
the text carry over to this case, since ![]() cannot be
negative for renters
cannot be
negative for renters![]() Return to text
Return to text
23. The limiting case of zero forced savings would be the case in which no downpayment is needed to buy a house. In that case the individual can keep consumption constant at the time of the purchase without increasing hours worked if transaction costs are zero. If the individual has to pay the transaction cost, this provides an incentive to work more at the time of the purchase. Campbell and Hercowitz (2005) propose a similar argument to discuss the relationship between hours and durable purchases. Return to text
24. We
define household debt as
![]() (that is, the average of the household
liabilities). Return to
text
(that is, the average of the household
liabilities). Return to
text
25. The turnover rate in the data is constructed as the sum of sales of existing single-family homes (source: National Association of Realtors) plus new single-family homes sold (from Census Bureau), divided by the total housing stock (from Census Bureau). The series starts in 1968. Return to text
26. A similar intuition has been proposed in Campbell and Hercowitz (2005), who show that financial innovation alone can explain more than half of the reduction in aggregate volatility in a model with borrowers and lenders and downpayment constraints. Aside from modeling differences (our model considers the owning/renting margin and addresses issues related to life cycle, lumpiness and risk that are absent in their setup), the intuition they offer for their result carries over to our model, but we find that the effect of lower downpayment requirements is quantitatively smaller. We conjecture that the differences depend on one modeling assumption: in our setup, indebted homeowners mitigate aggregate volatility, but this effect is partly offset by the wealthier homeowners (the creditors) who tend to increase aggregate volatility by working relatively more in response to positive aggregate shocks; instead, Campbell and Hercowitz assume that labor supply of wealthy homeowners is constant, thus killing this offsetting mechanism. Return to text
27. Likewise, the correlation between debt and consumption falls in the model from 0.85 to 0.58, a decline similar to the data (from 0.72 to 0.37). Return to text
28. Higher uncertainty in itself reduces the willingness to borrow, whereas lower downpayments lead to an increase in debt. In our baseline calibration, the second effect dominates - as shown in table 4, the ratio of debt to GDP rises from 0.31 to 0.35 when both changes are present. As a consequence, in the late period individuals are more cautious, even if they hold more debt. For this reason, the fraction of liquidity constrained households in the model falls from 45 to 38 percent. Return to text
29. Jermann and Quadrini (forthcoming) document that credit shocks have played an important role in capturing U.S. output during the last decades. Return to text
30. Total
factor productivity is discretized using a 7-state Markov chain
(see Appendix). For the lowest two aggregate productivity levels:
in the period 1952-1982,
![]() , and in the period 1983-2010,
, and in the period 1983-2010,
![]() . Return to text
. Return to text
31. Incidentally, we note that the volatility of GDP is still smaller in the late than in the early period calibration. Return to text
32. To keep our experiments simple and easier to interpret, we do not attempt here at recalibrating some of the other parameters in order to match the same targets as in the benchmark model. Return to text
33. Thomas (2002) argues that lumpiness of fixed investment at the level of a single production unit bears no implications for the behavior of aggregate quantities in an otherwise standard RBC model. Her argument rests on the representative household's desire to smooth consumption over time, a desire that undoes any lumpiness at the level of the individual firm. Our sensitivity analysis shows that there are differences between the models with and without adjustment cost. Adjustment costs imply smaller housing adjustment at the aggregate level, but larger housing adjustments (when they occur) at the individual level. Return to text
34. See for instance Gomme, Kydland and Rupert (2001). Return to text
35. The recent papers by Kiyotaki, Michaelides and Nikolov (2011), Favilukis, Ludvigson and Van Nieuwerburgh (2009), and Ríos-Rull and Sánchez-Marcos (2008) are steps in this direction. Return to text
36. For house prices, we use the Conventional Mortgage Home Price Index (adjusted for inflation). Return to text
37. Appendix C is available at https://www2.bc.edu/~iacoviel/. Return to text
38. The upper bound for the housing grid and the lower bound for debt are chosen wide enough so that they never bind in the simulations. Return to text
39. In computation, we exploit the strict concavity of the value function in the choice for assets as well as the monotonicity of the policy function in assets (for the homeowner problem, the monotonocity is for any given choice of the housing stock). Return to text
40. We prevent individuals from choosing negative hours. Return to text
41. We enforce the law of large numbers by making sure that the simulated fractions of ages and of labor productivity shocks correspond to the theoretical ones, by randomly adjusting the values of the shocks. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text