The Federal Reserve Board eagle logo links to home page

How Do Laffer Curves Differ Across Countries?

Mathias Trabandt and Harald Uhlig

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We seek to understand how Laffer curves differ across countries in the US and the EU-14, thereby providing insights into fiscal limits for government spending and the service of sovereign debt. As an application, we analyze the consequences for the permanent sustainability of current debt levels, when interest rates are permanently increased e.g. due to default fears. We build on the analysis in Trabandt and Uhlig (2011) and extend it in several ways. To obtain a better fit to the data, we allow for monopolistic competition as well as partial taxation of pure profit income. We update the sample to 2010, thereby including recent increases in government spending and their fiscal consequences. We provide new tax rate data. We conduct an analysis for the pessimistic case that the recent fiscal shifts are permanent. We include a cross-country analysis on consumption taxes as well as a more detailed investigation of the inclusion of human capital considerations for labor taxation.

Keywords: Laffer curve, taxation, cross country comparison, debt sustainability, fiscal limits, quantitative endogenous growth, human capital and labor taxation

JEL classification: E0, E13, E2, E3, E62, H0, H2, H3, H6


1.  Introduction

We seek to understand how Laffer curves differ across countries in the US and the EU-14. This provides insight into the limits of taxation. As an application, we analyze the consequences of recent increases in government spending and their fiscal consequences as well as the consequences for the permanent sustainability of current debt levels, when interest rates are permanently high e.g. due to default fears.

We build on the analysis in Trabandt and Uhlig (2011). There, we have characterized Laffer curves for labor and capital taxation for the U.S., the EU-14, and individual European countries. In the analysis, a neoclassical growth model featuring "constant Frisch elasticity" (CFE) preferences are introduced and analyzed: we use the same preferences here. The results there suggest that the U.S. could increase tax revenues considerably more than the EU-14, and that conversely the degree of self-financing of tax cuts is much larger in the EU-14 than in the U.S. While we have calculated results for individual European countries, the focus there was directed towards a comparison of the U.S. and the aggregate EU-14 economy.

This paper provides a more in-depth analysis of the cross-country comparison. Furthermore, we modify the analysis in two important dimensions. The model in Trabandt and Uhlig (2011) overstates total tax revenues to GDP compared to the data: in particular, labor tax revenues to GDP are too high. We introduce monopolistic competition to solve this: capital income now consists out of rental rates to capital as well as pure profits, decreasing the share of labor income in the economy. With this change alone, the model now overpredicts the capital income tax revenue. We therefore furthermore assume that only a fraction of pure profit income is actually reported to the tax authorities and therefore taxed. With these two changes, the fit to the data improves compared to the original version, see figure 2. In terms of the Laffer curves, this moves countries somewhat closer to the peak of the labor tax Laffer curve and somewhat farther away from the peak of the capital tax Laffer curve. For the cross-country comparison, we assume that all structural parameters for technologies and preferences are the same across countries. The differences between the Laffer curves therefore arise solely due to differences in fiscal policy i.e. the mix of distortionary taxes, government spending and government debt. We find that labor income and consumption taxes are important for accounting for most of the cross-country differences.

We refine the methodology of Mendoza et al. (1994) to calculate effective tax rates on labor and capital income. Broadly, we expand the measured labor tax base by including supplements to wages as well as a fraction of entrepreneurial income of households. As a result, the refinements imply a more reasonable labor share in line with the literature. More importantly, the average 1995-2010 labor income taxes turn out to be lower while capital income taxes are somewhat higher as previously calculated in Trabandt and Uhlig (2011).

We update our analysis in Trabandt and Uhlig (2011) by including the additional years 2008-2010. This is particularly interesting, as it allows us to examine the implications of the recent substantial tax and revenue shocks. While recent fiscal policy changes were intended to be temporary, we examine the pessimistic scenario that they are permanent. To do so, we calibrate the model to the Laffer curves implied by the strained fiscal situation of 2010, and compare them to the Laffer curves of the average extended sample 1995-2010. We find that the 2010 calibration moves almost all countries closer to the peak of the labor tax Laffer curve, with the scope for additional labor tax increases cut by a third for most countries and by up to one half for some countries. It is important, however, to keep the general equilibrium repercussions of raising taxes in mind: even though tax revenues may be increased by some limited amount, tax bases and thereby output fall when moving to the peak of the Laffer curve due to the negative incentive effects of higher taxes.

We then use these results to examine the scope for long-term sustainability of current debt levels, when interest rates are permanently higher due to, say, default fears. This helps to understand the more complex situation of an extended period with substantially increased interest rates due to, say, default fears. More precisely, we answer the following question: what is the maximum steady state interest rate on outstanding government debt that the government could afford without cutting government spending, based on a calibration to the fiscal situation in 2010? To do so, we calculate the implied peak of the Laffer curve and compute the maximum interest rate on outstanding government debt in 2010 that would still balance the government budget constraint in steady state. The results of our baseline model are in table 7: the most interesting column there may be the second one. We find that the USA can afford the highest interest rate if labor taxes are moved to the peak of the Laffer curve: depending on the debt measure used, a real interest rate of of 12% to 15.5% is sustainable. Interestingly, Ireland can also afford the high rate of 11.2%, when moving labor taxes only. By contrast, Austria, Belgium, Denmark, Finland, France, Greece and Italy can only afford permanent real rates in the range of 4.4% to 7.1%, when financing the additional interest payments with higher labor tax rates alone, while, say, Germany, Portugal and Spain can all afford an interest rate somewhere above 9%. The picture improves somewhat, but not much, when labor taxes and capital taxes can both be adjusted: notably, Belgium, Denmark, Finland, France and Italy cannot permanently afford real interest rates above 6.5%. Below we also examine the implications of human capital accumulation and show that the maximum interest rates may be even lower than suggested by our baseline model. It is worth emphasizing that we have not included the possibility of cutting government spending and/or transfers and that our analysis has focussed on the most pessimistic scenario of a permanent shift.

In the baseline model, physical capital is the production factor that gets accumulated. It may be important, however, to allow for and consider human capital accumulation, when examining the consequences of changing labor taxation. We build on the quantitative endogenous growth models introduced in Trabandt and Uhlig (2011), and provide a more detailed cross-country comparison. We find that the capital tax Laffer curve is affected only rather little across countries when human capital is introduced into the model. By contrast, the introduction of human capital has important effects for the labor income tax Laffer curve. Several countries are pushed on the slippery slope sides of their labor tax Laffer curves once human capital is accounted for. Intuitively, higher labor taxes lead to a faster reduction of the labor tax base since households work less and aquire less human capital which in turn leads to lower labor income. We recalculate the implied maximum interest rates on government debt in 2010 when human capital accumulation is allowed for in the model. Table 9 contains the results: the US may only afford a real interest rate between 5.8% to 6.6% in this case. Most of the European countries cluster between 4% and 4.9% except for Denmark, Finland and Ireland who can afford real interest rates between 5.9% and 9.5%.

We add a cross-country analysis on consumption taxes. In Trabandt and Uhlig (2011), we have shown that the consumption tax Laffer curve has no peak. Essentially, the difference between the labor tax Laffer curve and the consumption tax Laffer curve arises due to "accounting" reasons: the additional revenues are provided as transfers, and are used for consumption purchases, to be taxed at the consumption tax rate. In Trabandt and Uhlig (2011), we only provided the analysis for the U.S. and the aggregate EU-14 economy. Here, we extend the consumption tax analysis to individual countries. The range of maximum additional tax revenues (in percent of GDP) in the baseline model is roughly 40-100 percent while it shrinks to roughly 10-30 percent in the model with added human capital. Higher consumption taxes affect equilibrium labor via the labor wedge, similar to labor taxes. As above, human capital amplifies the reduction of the labor tax base triggered by the change in the labor wedge. Overall, maximum possible tax revenues due to consumption taxes are reduced massively, although at fairly high consumption tax rates.

The paper is organized as follows. Section 2 provides the model. The calibration and parameterization of the model can be found in section 3. Section 4 provides and discusses the results. Section 5 discusses the extension of the model with human capital as well as the results for consumption taxation. Finally, section 6 concludes.


2.  Model

We employ the baseline model in Trabandt and Uhlig (2011) and extend it by allowing for intermediate inputs, supplied by monopolistically competitive firms. Time is discrete, $ t=0,1,\ldots,\infty$. Households maximize

$\displaystyle max_{c_{t},n_{t},k_{t},x_{t},b_t} \quad E_{0}\sum_{t=0}^\infty\beta^{t}\left[u(c_t,n_t)+v(g_t)\right]$    

subject to

$\displaystyle (1+\tau^c_t)c_{t}+x_{t}+b_t$ $\displaystyle =$ $\displaystyle (1-\tau_{t}^n)w_{t}n_{t}+(1-\tau_t^k)[(d_{t}-\delta)k_{t-1}+\phi\Pi_t]$  
    $\displaystyle +\delta k_{t-1}+R^b_{t}b_{t-1}+s_{t}+(1-\phi)\Pi_t + m_t \nonumber$  
$\displaystyle k_{t}$ $\displaystyle =$ $\displaystyle (1-\delta)k_{t-1}+x_{t}$ (1)

where $ c_t$, $ n_{t}$, $ k_{t}$, $ x_{t}$, $ b_t$, $ m_t$ denote consumption, hours worked, capital, investment, government bonds and an exogenous stream of payments. The household takes government consumption $ g_t$, which provides utility, as given. Further, the household receives wages $ w_t$, dividends $ d_t$, profits $ \Pi_t$ from firms and asset payments $ m_t$. The payments $ m_t$ are a stand-in for net imports, modelled here as exogenously given income from a "tree", see Trabandt and Uhlig (2011) for further discussion. The household obtains interest earnings $ R^b_{t}$ and lump-sum transfers $ s_t$ from the government. It has to pay consumption taxes $ \tau_t^c$, labor income taxes $ \tau_t^n$ and capital income taxes $ \tau_t^k$ on dividends and on a share $ \phi$ of profits.1

As introduced and extensively discussed in Trabandt and Uhlig (2011), but also used in Hall (2009), Shimer (2009) and King and Rebelo (1999), we work with constant Frisch elasticity preferences (CFE), given by

$\displaystyle u(c,n) = \log(c) - \kappa n^{1 + \frac{1}{\varphi}}$ (2)

if $ \eta = 1$, and by

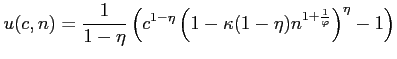
$\displaystyle u(c,n) = \frac{1}{1-\eta} \left( c^{1-\eta} \left( 1 - \kappa (1 - \eta ) n^{1+\frac{1}{\varphi}} \right)^\eta - 1 \right)$ (3)

if $ \eta > 0, \eta \neq 1$, where $ \kappa > 0$. These preferences are consistent with balanced growth and feature a constant Frisch elasticity of labor supply, given by $ \varphi$, without constraining the intertemporal elasticity of substitution.

Competitive final good firms maximize profits

$\displaystyle max_{k_{t-1}, z_{t}} \quad y_{t}-d_{t}k_{t-1}-p_{t}z_{t}$ (4)

subject to the Cobb-Douglas production technology, $ y_{t}=\xi^t k_{t-1}^{\theta} z_{t}^{1-\theta}$, where $ \xi^t$ denotes the trend of total factor productivity. $ p_{t}$ denotes the price of an homogenous input, $ z_{t}$, which in turn is produced by competitive firms who maximize profits

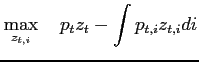
$\displaystyle \max_{z_{t,i}} \quad p_{t}z_{t}-\int p_{t,i}z_{t,i}di$ (5)

subject to 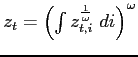$ z_{t}=\left( \int z_{t,i}^{\frac{1}{\omega }}\text{ }di\right) ^{\omega }$ with $ \omega >1$. Intermediate inputs, $ z_{t,i}$, are produced by monopolistically competitive firms which maximize profits

$\displaystyle \max_{p_{t,i}} \quad p_{t,i}z_{t,i}-w_{t}n_{t,i}$    

subject to their demand functions and production technologies:

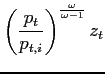
$\displaystyle z_{t,i}$ $\displaystyle =$ $\displaystyle \left( \frac{p_{t}}{p_{t,i}}\right) ^{\frac{\omega }{\omega -1}}z_{t}$  
$\displaystyle z_{t,i}$ $\displaystyle =$ $\displaystyle n_{t,i}$  

In equilibrium, all firms set the same price which is a markup over marginal costs. Formally, $ p_{t,i}=p_{t}=\omega w_{t}$. Aggregate equilibrium profits are given by $ \Pi _{t}=\left( \omega -1\right) w_{t}n_{t}$.

The government faces the budget constraint,

$\displaystyle g_{t}+s_{t}+R_{t}^b b_{t-1}=b_t+T_t$ (6)

where government tax revenues are given by

$\displaystyle T_t=\tau_t^c c_t+\tau_t^n w_t n_t+\tau_t^k[(d_{t}-\delta)k_{t-1}+\phi\Pi_t]$ (7)

It is the goal to analyze how the equilibrium shifts, as tax rates are shifted. More generally, the tax rates may be interpreted as wedges as in Chari et al. (2007), and some of the results in this paper carry over to that more general interpretation. What is special to the tax rate interpretation and crucial to the analysis in this paper, however, is the link between tax receipts and transfers (or government spending) via the government budget constraint.

The paper focuses on the comparison of balanced growth paths. We assume that government debt, government spending as well as net imports do not deviate from their balanced growth paths, i.e. we assume that $ b_{t-1}=\psi^t \bar b$, $ g_{t}=\psi^t \bar g$ as well as $ m_t = \psi^t \bar{m}$ where $ \psi$ is the growth factor of aggregate output. We consider exogenously imposed shifts in tax rates or in returns on government debt. We assume that government transfers adjust according to the government budget constraint (6), rewritten as $ s_t=\psi^t\bar b(\psi-R^b_{t})+T_t-\psi^t \bar g$.

2.1  Equilibrium

In equilibrium the household chooses plans to maximize its utility, the firm solves its maximization problem and the government sets policies that satisfy its budget constraint. In what follows, key balanced growth relationships of the model that are necessary for computing Laffer curves are summarized. Except for hours worked, interest rates and taxes all other variables grow at a constant rate $ \psi=\xi^{\frac{1}{1-\theta}}$. For CFE preferences, the balanced growth after-tax return on any asset is $ \bar{R} = \psi^{ \eta}/\beta $. It is assumed throughout that $ \xi \geq 1$ and that parameters are such that $ \bar{R} > 1$, but $ \beta$ is not necessarily restricted to be less than one. Let $ \overline{k/y}$ denote the balanced growth path value of the capital-output ratio $ k_{t-1}/y_t$. In the model, it is given by

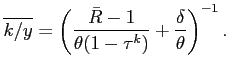
$\displaystyle \overline{k/y} = \left( \frac{ \bar{R} - 1}{ \theta (1 - \tau^k ) } + \frac{ \delta }{\theta} \right)^{-1}.$ (8)

Labor productivity and the before-tax wage level are given by,

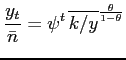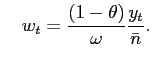
$\displaystyle \frac{ y_t}{ \bar{n}} = \psi^{t} \, \overline{k/y}^{ \frac{\theta}{1 - \theta} }$    and$\displaystyle \quad w_t = \frac{(1 - \theta)}{\omega}\frac{y_t}{\bar{n}}.$      

It remains to solve for the level of equilibrium labor. Let $ \overline{c/y}$ denote the balanced growth path ratio $ c_t/y_t$. With the CFE preference specification and along the balanced growth path, the first-order conditions of the household and the firm imply

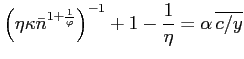
$\displaystyle \left( \eta \kappa {\bar{n}}^{1 + \frac{1}{\varphi}} \right)^{-1} + 1 - \frac{1}{\eta} = \alpha \, \overline{c/y}$ (9)

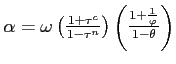where $ \alpha = \omega \left( \frac{ 1 + \tau^c}{ 1 - \tau^n } \right) \left( \frac{1 + \frac{1}{\varphi}}{ 1 - \theta } \right)$ depends on tax rates, the labor share, the Frisch elasticity of labor supply and the markup.

In this paper, we shall concentrate on the case when transfers $ \bar{s}$ are varied and government spending $ \bar{g}$ is fixed. Then, the feasibility constraint implies

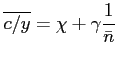
$\displaystyle \overline{c/y} = \chi + \gamma \frac{1}{{\bar{n}}}$ (10)

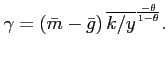where $ \chi = 1 - (\psi - 1 + \delta) \, \overline{k/y}$ and $ \gamma = \left( \bar{m} - \bar{g} \right) \overline{k/y}^{ \frac{- \theta}{1 - \theta} }.$ Substituting equation (10) into (9) therefore yields a one-dimensional nonlinear equation in $ {\bar{n}}$, which can be solved numerically, given values for preference parameters, production parameters, tax rates and the levels of $ \bar{b}$, $ \bar{g}$ and $ \bar{m}$.After some straightforward algebra, total tax revenues along a balanced growth path can be calculated as

$\displaystyle \overline{T}=\left[\tau ^{c}\overline{c/y}+\tau ^{n}\frac{(1-\theta )}{\omega } +\tau ^{k}\left(\theta -\delta \overline{k/y}+\phi (1-\theta) \frac{\omega -1}{\omega}\right)\right]\overline{y}$ (11)

and equilibrium transfers are given by,

$\displaystyle \overline{s}=\left( \psi -R^{b}\right) \overline{b}-\overline{g}+\overline{T}.$ (12)

3.  Data, Calibration and Parameterization

The model is calibrated to annual post-war data of the USA, the aggregate EU-14 economy and individual European countries. An overview of the calibration is in tables 1 and 2.

We refine the methodology of Mendoza at al. (1994) to calculate effective tax rates on labor and capital income. Broadly, we expand the measured labor tax base by including supplements to wages as well as a fraction of entrepreneurial income of households. As a result, the refinements imply a more reasonable labor share in line with the empirical literature. More importantly, the average 1995-2010 labor income taxes turn out to be lower while capital income taxes are higher as previously calculated in Trabandt and Uhlig (2011). Appendix A provides the new tax rates across countries over time and Appendix B contains the details on the calculations with further discussion of the implications for e.g. the Laffer curves.

There are two new key parameters, compared to Trabandt and Uhlig (2011). The first parameter is $ \omega$, the gross markup, due to monopolistic competition. We set $ \omega = 1.1$, which appears to be a reasonable number, given the literature. The second parameter is $ \phi$, the share of monopolistic-competition profits which are subject to capital taxes. We set this parameter equal to the capital share, i.e. to 0.36. While we could have explored specific evidence to help us pin down this parameter, we have chosen this value rather arbitrarily and with an eye towards the fit of the model to the data instead.

The sample covered in Trabandt and Uhlig (2011) is 1995-2007. Here we extend the sample to 2010 using the same data sources. We update all data up to 2010, except for taxes and tax revenues which we can update only to 2009 due to data availability reasons. For most of the analysis in this paper, we assume that the 2010 observation for taxes and revenues are the same as in 2009. We also pursue an alternative approach for tax rates for the year 2010, see subsection 3.2 below for the details.

We also refine the calculation of transfers in the data compared to Trabandt and Uhlig (2011). In the data, there is a non-neglible difference between government tax revenues and government revenues. This difference is mostly due to "other government revenue" and "government sales". We substract these two items from the measure of transfers defined in Trabandt and Uhlig (2011).

US and aggregate EU-14 tax rates, government expenditures and government debt are set according to the upper part of table 1. We also calibrate the model to individual EU-14 country data for tax rates, government spending and government debt as provided in table 2. Although we allow fiscal policy to be different across countries, we restrict the analysis to identical parameters across countries for preferences and technology, see the lower part of table 1 for the details.2

Finally, the empirical measure of government debt for the US as well as the EU-14 area provided by the AMECO database is nominal general government consolidated gross debt (excessive deficit procedure, based on ESA 1995) which is divided by nominal GDP. For the US the gross debt to GDP ratio is 66.2% in the sample. For checking purposes, we also examine the implications if we use an alternative measure of US government debt: debt held by the public. See tables 1 and 2 for the differences. However, given that to our knowledge data on "debt held by the public" is not available for European countries, we shall proceed by using gross debt as a benchmark if not otherwise noted. Where appropriate, we shall perform a sensitivity analysis with respect to the measure of US government debt.

3.1  Model Fit and Sensitivity

The structual parameters are set such that model implied steady states are close to the data. In particular, figure 1 provides a comparison of the data vs. model fit for key great ratios, hours as well as transfers and tax revenues.3 Overall, the fit is remarkable given the relatively simple model in which country differences are entirely due to fiscal policy.4

Most of the structual parameter values in the lower part of table 1 are standard and perhaps uncontroversial, see e.g. Cooley and Prescott (1995), Prescott (2002, 2004, 2006) and Kimball and Shapiro (2008).

The new parameters here compared to Trabandt and Uhlig (2011) are the gross markup, $ \omega=1.1$ and the share of monopolistic-competition profits subject to capital taxation, $ \phi=\theta=0.36$. Figure 2 contains a sensitivity analysis for $ \omega$ and $ \phi$. When $ \omega\rightarrow1$, the model overstates labor tax revenues and understates capital tax revenues, see the black crosses in figure 2.5. In the adapted model with intermediate inputs, a gross markup $ \omega>1$ reduces the labor tax base. At the same time, profits increase the capital tax base, but too much if profits are fully subject to capital taxation, i.e. $ \phi=1$, see the red triangles in figure 2. Overall, the fit improves considerably if we set the share of profits subject to capital taxes, $ \phi=\theta=0.36$. The fit is not sensitive to $ \phi$: all values in $ \phi \in [0.3, 0.4]$ work practically just as well in terms of the fit, for example.

3.2  The Year 2010

At the end of our sample, government spending and government debt have risen substantially as a fallout of the financial crisis, see table 2. We are particularly interested in characterizing Laffer curves for the year 2010. While there is no tax rate data for the year 2010 at the time of writing this paper, we do have data for government spending and debt in 2010. We wish to consider the pessimistic scenario of a steady state, in which these changes are permanent. We therefore use the government budget constraint of the model to infer the labor tax rate, i.e. we calculate the implied labor tax given government debt and government consumption in 2010 as well as average (1995-2010) model implied government transfers.

Table 2 contains the resulting labor tax rates across countries. According to the model, in the US and EU-14 labor taxes need to be 5-8 percentage points higher to balance the government budget in 2010 compared to the sample average. There is substantial country specific variation. While e.g. labor taxes in Germany and Italy remain unchanged, those in the United Kingdom, Ireland, Spain and the Netherlands increase by 10 or more percentage points.


4.  Results

4.1.  Sources of Differences of Laffer Curves

What accounts for the differences between the USA Laffer curves and (individual) EU-14 Laffer curves? To answer this question, we proceed as follows. As before, we calibrate the model to country specific averages of 1995-2010, see table 2, keeping structural parameters as in table 1. Next, we compute Laffer curves.

Results are in the "Baseline" column of tables 3 and 4. All other columns report results if in the USA calibration, fiscal instruments are set to European country specific values, one at a time. It appears that labor income and consumption taxes are most important for accounting for cross-country differences.

Imposing country specific debt to GDP ratios has no effect in our calculations, due to Ricardian equivalence: a different debt to GDP ratio, holding taxes and government consumption fixed, results in different transfers along the equilibrium path.

Finally, note that compared to Trabandt and Uhlig (2011), intermediate inputs and profit taxation in the present paper move countries somewhat closer to the peak of the labor tax Laffer curve and somewhat farther away from the peak of the capital tax Laffer curve.

4.2  Laffer Curves: Average 1995-2010 vs. 2010

To compute Laffer curves, we trace out tax revenues across balanced growth paths, as we change either labor tax rates or capital tax rates, and computing the resulting changes in transfers. When changing both tax rates, we obtain a "Laffer hill". We compute Laffer curves and the Laffer hill for a 1995-2010 vs. 2010 calibration, i.e., when the model is calibrated in terms of fiscal policy either to the average of 1995-2010 or to the year 2010, see table 2. Structural parameters are set as in table 1.

Figure 3 shows the resulting Laffer curves for all countries for the average 1995-2010 calibration. Figure 4 provides a comparison of Laffer curves for the 1995-2010 vs. 2010 calibration for the USA and aggregate EU-14 economy. Further cross-country results in this respect are available in table 5 and in figure 5. The latter figure shows how far each country is from its peak, given its own tax rate: perhaps not surprisingly, the points line up pretty well. In the figure, we compare it to the benchmark of performing the same calculation for the US, given by the dash-dotted line: there, we change, say, the labor tax rate, and, for each new labor tax rate, recalculate $ \kappa$ as well as $ \bar{g}, \bar{m}$ and $ \bar{b}$ to obtain the same $ \bar{n}$ and $ \overline{g/y}$, $ \overline{b/y}$ and $ \overline{m/y}$ as in table 1. We then recalculate $ \bar{s}$ and $ \overline{s/y}$ to balance the government budget and calculate the distance to the peak of the Laffer curve. One would expect this exercise to result in a line with a slope close to -1, and indeed, this is what the figure shows. The points for the individual countries line up close to this line, though not perfectly: in particular, for the capital tax rate, the distance can be considerable, and is largely explained by the cross-country variation in labor taxes and consumption taxes.

According to the results, the vast majority of countries have moved closer to the peaks of their labor and capital income tax Laffer curves and Laffer hills respectively. The movements to the peaks are sizeable for some countries such as e.g. the United Kingdom, the Netherlands and Ireland for labor taxes. As above and for the average 1995-2010 sample, it does not matter whether "gross US debt or "US debt held by the public" is used. For the year 2010, however, small differences arise since transfers are kept at the model average for 1995-2010.

Finally, table 6 provides the output losses associated with moving to the peak of the Laffer curve. According to the model, US and EU-14 output falls by about 27 respectively 14 percent when labor taxes are moved to the peak of the Laffer curve. The magnitudes for the case of capital taxes are similar. There is considerable country specific variation among European countries: Denmark looses 4 percent while Ireland looses 24 percent of output at the labor tax Laffer curve peak. Clearly, if a country is already close to its Laffer curve peak in terms of tax rates, the output losses associated with increasing taxes a little more to attain the peak are more muted than in a country that has more scope to increase tax revenues. Nevertheless, the table highlights the general equilibrium repercussions of raising taxes: even though tax revenues may be increased by some limited amount, tax bases and thereby output fall when moving to the peak of the Laffer curve due to the negative incentive effects of higher taxes.

4.3  Laffer Curve and Interest Rates

What is the maximum interest rate on outstanding government debt that the government could afford without cutting government spending? Put differently, how high can interest rates on government debt be due to, say, default fears (and not due to generally higher discounting by households), so that fiscal sustainability is still preserved if countries move to the peak of their Laffer curves?

To answer this question we pursue the following experiment. We calibrate the model in terms of fiscal policy to the year 2010, see table 2. Structual parameters are set as in table 1. We calculate Laffer curves for labor and capital taxation as well as the Laffer hill for joint variations of capital and labor taxes. Keeping model implied government transfers and government consumption to GDP ratios at their 2010 levels, we calcuate the interest rate that balances the government budget at maximal tax revenues.

For the calcuations, we focus on balanced growth relationships ignoring transition issues for simplicity. Consider the scaled government budget constraint along the balanced growth path:

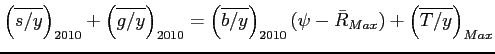
$\displaystyle \left(\overline{s/y}\right)_{2010}+\left(\overline{g/y}\right)_{2010}=\left(\overline{b/y}\right)_{2010}(\psi-\bar R_{Max})+\left(\overline{T/y}\right)_{Max}$ (13)

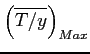where $ \left(\overline{T/y}\right)_{Max}$ denotes the maximum additional tax revenues (expressed in % of baseline GDP) that results from moving from the 2010 status quo to the peak of the Laffer curve. We solve for $ \bar R_{Max}=1+\bar r_{Max}$ that balances the above government budget constraint.

Table 7 contains the baseline model results. For each of the three tax experiments (adjusting only labor taxes, adjusting only capital taxes, adjusting both), the table lists the maximal additional obtainable revenue as a share of GDP as well as the maximal sustainable interest rate that can be sustained with these revenues. For comparison, the last two columns of the table also contain real long-term interest rates for 2010 downloaded from the European Commission AMECO database. These are nominal 10 years government bond interest rates minus inflation - either using the GDP deflator (ILRV, first column) or the consumption deflator (ILRC, second column). The value for the aggregate EU-14 is the real GDP weighted average of individual European countries.

The most interesting column in table 7 may be the second one. We find that the USA can afford the highest interest rate if labor taxes are moved to the peak of the Laffer curve: depending on the debt measure used, a real interest rate of of 12% to 15.5% is sustainable. Interestingly, Ireland can also afford the high rate of 11.2%, when moving labor taxes only. By contrast, Austria, Belgium, Denmark, Finland, France, Greece and Italy can only afford permanent real rates in the range of 4.4% to 7.1%, when financing the additional interest payments with higher labor tax rates alone, while, say, Germany, Portugal and Spain can all afford an interest rate somewhere above 9%. The picture improves somewhat, but not much, when labor taxes and capital taxes can both be adjusted: notably, Belgium, Denmark, Finland, France and Italy cannot permanently afford real interest rates above 6.5%.

Note that now, the comparison of "US gross government debt" vs. "US debt held by the public" matters for the results since government spending is kept constant. Indeed, the US could affort higher interest rates if "US debt held by the public" is considered.

Interestingly, in the next section, we also examine the implications of human capital accumulation and show that the maximum interest rates may be even lower than suggested by our baseline model.

For the above analysis, some caveats should be kept in mind. The interest rate on outstanding government debt deviates from the one on private capital but does not crowd out private investment. In other words, it is implicitly assumed that the interest rate payments due to the higher interest rate are paid lump-sum to the households and thereby do not affect household consumption, hours or investment, and that it does not affect the rate at which firms can borrow privately.6

Note that the steady state safe real interest rate is calibrated to equal 4 percent and represents therefore the lower bound for $ \bar r_{Max}$: our analysis on sustainable rates may therefore be too optimistic, keeping in mind that the interest rates are real interest rates, not nominal interest rates. It is worth emphasizing that we have not included the possibility of cutting government spending and/or transfers and that our analysis has focussed on the most pessimistic scenario of a permanent shift.


5.  Extensions: Human Capital, Consumption Taxes

5.1.  Baseline Model vs. Human Capital Accumulation

We compare the distance to the peak of Laffer curves for the above baseline model and the above baseline model with added human capital accumulation. More specifically, we assume that human capital is accumulated following the second generation case considered in Trabandt and Uhlig (2011).7

In particular, we assume that human capital can be accumulated by both learning-by-doing as well as schooling. The agent splits total non-leisure time $ n_t$ into work-place labor $ q_t n_t$ and schooling time $ (1-q_t) n_t$, where $ 0 \leq q_t \leq 1$. Agents accumulate human capital according to

$\displaystyle h_{t}$ $\displaystyle =$ $\displaystyle \left(A q_t n_t + B (1 - q_t) n_{t} \right)^\nu h_{t-1}^{1-\nu} + (1 -\delta_h) h_{t-1}$ (14)

where $ A \geq 0 $ and $ B > A$ parameterize the effectiveness of learning-by-doing and schooling respectively and where $ 0 < \delta_h \leq 1$ is the depreciation rate of human capital. Wages are paid per unit of labor and human capital so that the after-tax labor income is given by $ (1-\tau^n_t) w_t h_{t-1} q_t n_t.$ Given this, the adaptions of the model on the parts of firms is straightforward so that we shall leave them out here.

The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1. Parameters for human capital accumulation are set as in Trabandt and Uhlig (2011). More precisely, the same calibration strategy for the initial steady state is applied as before, except assuming now $ \bar{q} \bar{n} _{US}=0.25$. Further, $ \nu =0.5$ and $ \delta _{h}=\delta $ are set for simplicity. $ A$ is set such that initial $ \bar{q}_{US}=0.8$. Moreover, $ B$ is set to have $ h_{US}=1$ initially.

Figure 6 shows the comparison for the US and EU-14. Further cross-country results are contained in figure 7. Interestingly, the capital tax Laffer curve is affected only very little across countries when human capital is introduced. By contrast, the introduction of human capital has important effects for the labor income tax Laffer curve. Several countries are pushed on the slippery slope sides of their labor tax Laffer curves. This result is due to two effects. First, human capital turns labor into a stock variable rather than a flow variable as in the baseline model. Higher labor taxes induce households to work less and to aquire less human capital which in turn leads to lower labor income. Consequently, the labor tax base shrinks much more quickly when labor taxes are raised. Second, the introduction of intermediate inputs moves countries closer to the peaks of their labor tax Laffer curves already in the baseline model compared to Trabandt and Uhlig (2011). This effect is reinforced when human capital is introduced.

Finally, we recalculate the implied maximum interest rates on government debt in 2010 when human capital accumulation is allowed for in the model. Table 9 contains the results: the US may only afford a real interest rate between 5.8% to 6.6% in this case. Most of the European countries cluster between 4% and 4.9% except for Denmark, Finland and Ireland who can afford real interest rates between 5.9% and 9.5%.

5.2.  Consumption Taxes

We compute maximum additional tax revenues that are possible from increasing consumption taxes. We do this in the above baseline model and in the model with added human capital accumulation as in the previous subsection. The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1. Parameters for human capital accumulation are set as in the previous subsection.

The upper panel of figure 8 shows the comparison for the US and EU-14. Further cross-country results are shown in the lower panel of the same figure. As documented and examined in Trabandt and Uhlig (2011), the consumption tax Laffer curve has no peak. However, the introduction of human capital has important quantitative effects across countries. The range of maximum additional tax revenues (in percent of GDP) in the above baseline model is roughly 40-100 percent while it shrinks to roughly 10-30 percent in the model with added human capital. Higher consumption taxes affect equilibrium labor via the labor wedge, similar to labor taxes. Human capital amplifies the reduction of the labor tax base triggered by the change in the labor wedge by the same argument as in the previous subsection. Overall, maximum possible tax revenues due to consumption taxes are reduced massively, although at fairly high consumption tax rates.


6.  Conclusion

We have studied how Laffer curves differ across countries in the US and the EU-14. This provides insight into the limits of taxation. To that end, we extended the analysis in Trabandt and Uhlig (2011) to include monopolistic competition as well as partial taxation of the monopolistic-competition profits: we have shown that this improves the fit to the data considerably. We have also provided refined data for effective labor and capital income taxes across countries. For the cross-country comparison, we assume that all structural parameters for technologies and preferences are the same across countries. The differences between the Laffer curves therefore arise solely due to differences in fiscal policy i.e. the mix of distortionary taxes, government spending and government debt. We find that labor income and consumption taxes are important for accounting for most of the cross-country differences.

To examine recent developments, we calibrate the steady state of the model to the Laffer curves implied by the strained fiscal situation of 2010, and compare them to the Laffer curves of the average extended sample 1995-2010. We find that the 2010 calibration moves all countries considerably closer to the peak of the labor tax Laffer curve, with the scope for additional labor tax increases cut by a third for most countries and by up to one half for some countries. In this context, we show that it is important to keep the general equilibrium repercussions of raising taxes in mind: even though tax revenues may be increased by some limited amount, tax bases and thereby output fall when moving to the peak of the Laffer curve due to the negative incentive effects of higher taxes.

We calculate the implications for the long-term sustainability of current debt levels, by calculating the maximal permanently sustainable interest rate. We calculated that the USA can afford the highest interest rate if only labor taxes are adjusted to service the additional debt burden: depending on the debt measure used, a real interest rate of of 12% to 15.5% is sustainable. Interestingly, Ireland can also afford the high rate of 11.2%, when moving labor taxes only. By contrast, Austria, Belgium, Denmark, Finland, France, Greece and Italy can only afford permanent real rates in the range of 4.4% to 7.1%, when financing the additional interest payments with higher labor tax rates alone, while, say, Germany, Portugal and Spain can all afford an interest rate somewhere above 9%. The picture improves somewhat, but not much, when labor taxes and capital taxes can both be adjusted: notably, Belgium, Denmark, Finland, France and Italy cannot permanently afford real interest rates above 6.5%.

We have shown that the introduction of human capital has important effects for the labor income tax Laffer curve across countries. Several countries are pushed on the slippery slope sides of their labor tax Laffer curves once human capital is accounted for. We recalculated the implied maximum interest rates on government debt in 2010 when human capital accumulation is allowed for in the model. In this case, the US may only afford a real interest rate between 5.8% to 6.6%. Most of the European countries cluster between 4% and 4.9% except for Denmark, Finland and Ireland who can afford real interest rates between 5.9% and 9.5%.

We have performed a cross-country analysis on consumption taxes. We document that the range of maximum additional tax revenues (in percent of GDP) in the baseline model is roughly 40-100 percent while it shrinks to roughly 10-30 percent in the model with added human capital, although the underlying consumption taxes are fairly high in both cases.


References

Acemoglu, D., 2008. Introduction to Modern Economic Growth, 1st Edition. Princeton University Press, Princeton.

Alesina, A., Glaeser, E., Sacerdote, B., 2006. Work and leisure in the US and Europe: Why so different? NBER Macroeconomic Annual 2005, Vol. 20, MIT Press, Cambridge, pp. 1-100.

Barro, R. J., i Martin, X. S., 2003. Economic Growth, 2nd Edition. MIT Press, Cambridge.

Bi, H., 2010. Sovereign default risk premia, fiscal limits, and fiscal policy. Unpublished Manuscript.

Bi, H., Leeper, E. M., Leith, C., 2010. Stabilization versus sustainability: Macroeconomic policy tradeoffs. Unpublished Manuscript.

Blanchard, O., 2004. The economic future of europe. Journal Of Economic Perspectives 18(4), 3-26.

Chari, V. V., Kehoe, P. J., Mcgrattan, E. R., 2007. Business cycle accounting. Econometrica 75(3), 781-836.

Cooley, T. F., Prescott, E., 1995. Economic growth and business cycles. In: T. F. Cooley (Ed.), Frontiers Of Business Cycle Research, Princeton University Press, Princeton, pp. 1-38.

Green, J., Kotlikoff, L. J., 2009. On the general relativity of fiscal language. Key Issues in Public Finance - A Conference in Memory of David Bradford, Eds. Alan J. Auerbach And Daniel Shaviro, Harvard University Press.

Hall, R. E., 2009. Reconciling cyclical movements in the marginal value of time and the marginal product of labor. Journal of Political Economy 117(2), 281-323.

Jones, C. I., 2001. Introduction to Economic Growth, 2nd Edition. Norton, New York.

Kimball, M. S., Shapiro, M. D., 2008. Labor supply: Are the income and substitution effects both large or both small? NBER Working Paper 14208, NBER.

King, R. S., Rebelo, S. T., 1999. Resuscitating real business cycles. In: J. B. Taylor And M. Woodford (Eds.), Handbook Of Macroeconomics, Amsterdam: Elsevier 1B, pp. 927-1007.

Levine, R., Renelt, D., 1992. A sensitivity analysis of cross-country growth regressions. American Economic Review 82(4), 942-63.

Ljungqvist, L., Sargent, T. J., 2007. Do taxes explain european employment? Indivisible labor, human capital, lotteries, and savings. NBER Macroeconomics Annual 2006, Vol. 21, MIT Press, Cambridge, pp. 181-246.

Lucas, R. E., 1988. On the mechanics of economic development. Journal of Monetary Economics 22, 3-42.

Mendoza, E. G., Razin, A., Tesar, L. L., 1994. Effective tax rates in macroeconomics: Cross-country estimates of tax rates on factor incomes and consumption. Journal Of Monetary Economics 34, 297-323.

Pissarides, C., Ngai, L. R., 2009. Welfare policy and the sectoral distribution of employment. Center for Structual Econometrics Discussion Paper No. 09/04, London School of Economics.

Prescott, E. C., 2002. Prosperity and depression. American Economic Review 92, 1-15.

Prescott, E. C., 2004. Why do americans work so much more than europeans? Quarterly Review, Federal Reserve Bank Of Minneapolis 28, 2-13.

Prescott, E. C., 2006. Nobel lecture: The transformation of macroeconomic policy and research. Journal Of Political Economy 114(2), 203-235.

Rogerson, R., 2007. Taxation and market work: is Scandinavia an outlier? Economic Theory 32 (1), 59-85.

Shimer, R., 2009. Convergence in macroeconomics: The labor wedge. American Economic Journal: Macroeconomics 1(1), 280-297.

Trabandt, M., Uhlig, H., May 2011. The Laffer curve revisited. Journal of Monetary Economics 58 (4), 305-327.

Uzawa, H., 1965. Optimum technical change in an aggregative model of economic growth. International Economic Review 6, 18-31.


7.  Tables and Figures

Table 1a: Baseline Calibration and Parameterization (Fiscal Policy)

VariableUSEU-14DescriptionRestriction
$ \tau^n$22.134.2Labor tax rateData
$ \tau^k$41.136.8Capital tax rateData
$ \tau^c$4.616.7Consumption tax rateData
$ \overline{g/y}$18.023.1Gov. consumption+invest. to GDPData

Table 1: Baseline calibration and parameterization for the US and EU-14 benchmark model. Numbers expressed in percent where applicable. Sample: 1995-2010. IES denotes intertemporal elasticity of substitution. CFE refers to constant Frisch elasticity preferences. $ \bar{n}_{us}$ denotes balanced growth labor in the US which is set to 25 percent of total time.

Table 1b: Baseline Calibration and Parameterization (Gross Government Debt)

VariableUSEU-14DescriptionRestriction
$ \overline{b/y}$66.267.3Government gross debt to GDPData
$ \overline{s/y}$4.311.1Government transfers to GDPImplied

Table 1: Baseline calibration and parameterization for the US and EU-14 benchmark model. Numbers expressed in percent where applicable. Sample: 1995-2010. IES denotes intertemporal elasticity of substitution. CFE refers to constant Frisch elasticity preferences. $ \bar{n}_{us}$ denotes balanced growth labor in the US which is set to 25 percent of total time.

Table 1c: Baseline Calibration and Parameterization (Sensitivity: Government Debt Held By The Public)

VariableUSEU-14DescriptionRestriction
$ \overline{b/y}$42.4-Government debt held by public to GDPData
$ \overline{s/y}$4.9-Government transfers to GDPImplied

Table 1: Baseline calibration and parameterization for the US and EU-14 benchmark model. Numbers expressed in percent where applicable. Sample: 1995-2010. IES denotes intertemporal elasticity of substitution. CFE refers to constant Frisch elasticity preferences. $ \bar{n}_{us}$ denotes balanced growth labor in the US which is set to 25 percent of total time.

Table 1d: Baseline Calibration and Parameterization (Trade)

VariableUSEU-14DescriptionRestriction
$ \overline{m/y}$3.6-1.2Net imports to GDPData

Table 1: Baseline calibration and parameterization for the US and EU-14 benchmark model. Numbers expressed in percent where applicable. Sample: 1995-2010. IES denotes intertemporal elasticity of substitution. CFE refers to constant Frisch elasticity preferences. $ \bar{n}_{us}$ denotes balanced growth labor in the US which is set to 25 percent of total time.

Table 1e: Baseline Calibration and Parameterization (Technology)

VariableUSEU-14DescriptionRestriction
$ \psi$1.51.5Annual balanced growth rateData
$ \theta$0.360.36Capital share in productionData
$ \delta$0.070.07Annual depreciation rate of capitalData
$ \bar R-1$44Annual real interest rateData
$ \omega$1.11.1Gross markupData
$ \phi$0.360.36Share of profits subject to capital taxesData

Table 1: Baseline calibration and parameterization for the US and EU-14 benchmark model. Numbers expressed in percent where applicable. Sample: 1995-2010. IES denotes intertemporal elasticity of substitution. CFE refers to constant Frisch elasticity preferences. $ \bar{n}_{us}$ denotes balanced growth labor in the US which is set to 25 percent of total time.

Table 1f: Baseline Calibration and Parameterization (CFE Preferences)

VariableUSEU-14DescriptionRestriction
$ \eta$22Inverse of IESData
$ \varphi$11Frisch labor supply elasticityData
$ \kappa$3.303.30Weight of labor $ \bar{n}_{us}=0.25$

Table 1: Baseline calibration and parameterization for the US and EU-14 benchmark model. Numbers expressed in percent where applicable. Sample: 1995-2010. IES denotes intertemporal elasticity of substitution. CFE refers to constant Frisch elasticity preferences. $ \bar{n}_{us}$ denotes balanced growth labor in the US which is set to 25 percent of total time.

Table 2: Calibration of the Model to Individual Countries

  $ \bar \tau^n$: $ \varnothing$$ \bar \tau^n$: $ 2010^a $$ \bar \tau^n$: $ 2010^b$ $ \bar \tau^c$: $ \varnothing$$ \bar \tau^c$: $ 2010$ $ \bar \tau^k$: $ \varnothing$$ \bar \tau^k$: 2010 $ \overline{b/y}$: $ \varnothing$$ \overline{b/y}$: 2010 $ \overline{m/y} $: $ \varnothing$$ \overline{m/y} $: 2010 $ \overline{g/y}$: $ \varnothing$$ \overline{g/y}$: 2010 $ \overline{s/y}$: $ \varnothing$$ \overline{s/y}$: 2010
USA222028544138669244182044
USA$ ^*$222028544138426444182055
EU-14343540171537366783-1-123251111
GER343535161725276483-3-521211010
FRA393943181643436382-0227281212
ITA36393914134145111119-1222231313
GBR2425361513525048802322261111
AUT434345202026246672-3-521211818
BEL3938431717515010497-4-324261616
DNK434450343149564944-5-628322222
FIN444151262331304548-6-325271717
GRE29283515131917105143108212166
IRL252440241917164896-13-19192377
NET363850191932235863-7-8273266
PRT22243019163234619397232477
ESP30304214103124546032222488
SWE504643262640525440-7-630311616

Table 2: Individual country calibration of the benchmark model for the average ( $ \varnothing$) sample 1995-2010 and for the year 2010. Country codes: Germany (GER), France (FRA), Italy (ITA), United Kingdom (GBR), Austria (AUT), Belgium (BEL), Denmark (DNK), Finland (FIN), Greece (GRE), Ireland (IRL), Netherlands (NET), Portugal (PRT), Spain (ESP) and Sweden (SWE). See table 1 for abbreviations of variables. All numbers are expressed in percent. $ a$ - due to data availability reasons, the year 2009 value for tax rates has been assumed to remain in 2010 for most of the analysis in this paper. $ b$ - we deviate from $ a$ in subsection 3.2 by letting labor taxes in 2010 adjust to balance the 2010 government budget. More precisely, we calculate the 2010 labor tax given government debt and consumption in 2010 as well as average (1995-2010) model implied transfers. $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database.

Table 3: Max. Add. Tax Revenues (In % of Baseline GDP)

 Baseline Start with U.S. and impose country calibration for: $ \bar \tau^n$ Start with U.S. and impose country calibration for: $ \bar \tau^k$ Start with U.S. and impose country calibration for: $ \bar \tau^c$ Start with U.S. and impose country calibration for: $ \overline{b/y}$ Start with U.S. and impose country calibration for: $ \overline{g/y}$ Start with U.S. and impose country calibration for: $ \overline{m/y}$
USA9.09.09.09.09.09.09.0
USA$ ^*$9.09.09.09.09.09.09.0
EU-144.34.99.36.69.09.69.6
GER5.04.810.26.79.09.39.9
FRA2.93.68.86.39.010.29.5
ITA3.64.39.07.09.09.49.6
GBR6.08.48.06.89.09.59.2
AUT2.12.510.15.99.09.39.8
BEL2.43.48.26.49.09.810.0
DNK0.72.48.33.79.010.410.1
FIN1.82.29.74.99.09.910.4
GRE5.66.510.66.99.09.38.3
IRL9.07.910.75.39.09.211.8
NET5.24.39.76.19.010.310.4
PRT6.78.99.76.19.09.68.4
ESP5.76.29.77.19.09.59.1
SWE0.91.09.15.09.010.710.5

Table 3: Labor tax Laffer curve: sources of differences across countries. The table provides maximal additional tax revenues (in percent of baseline GDP) if labor taxes are varied. "Baseline" refers to the results when the model is calibrated to country specific averages of 1995-2010, see table 2. Parameters for technology and preferences are set as in table 1. All other columns report results if in the US calibration, fiscal instruments are set to country specific values (each at a time). * - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database.

Table 4: Max. Add. Tax Revenues (In % of Baseline GDP)

 Baseline Start with U.S. and impose country calibration for: $ \bar \tau^n$ Start with U.S. and impose country calibration for: $ \bar \tau^k$ Start with U.S. and impose country calibration for: $ \bar \tau^c$ Start with U.S. and impose country calibration for: $ \overline{b/y}$ Start with U.S. and impose country calibration for: $ \overline{g/y}$ Start with U.S. and impose country calibration for: $ \overline{m/y}$
USA2.62.62.62.62.62.62.6
USA$ ^*$2.62.62.62.62.62.62.6
EU-141.21.23.11.42.62.82.8
GER2.21.24.51.52.62.73.0
FRA0.40.92.31.32.63.12.8
ITA0.81.12.51.62.62.82.8
GBR0.62.41.31.52.62.82.7
AUT1.10.64.41.12.62.72.9
BEL0.10.81.51.42.62.93.0
DNK0.00.61.60.42.63.23.0
FIN0.70.53.70.82.63.03.2
GRE2.71.75.11.52.62.72.3
IRL4.12.25.30.92.62.63.7
NET1.91.13.71.22.63.13.2
PRT2.02.63.71.22.62.82.4
ESP2.01.73.71.62.62.82.6
SWE0.20.22.70.82.63.33.2

Table 4: Capital tax Laffer curve: sources of differences across countries. The table provides maximal additional tax revenues (in percent of baseline GDP) if capital taxes are varied. "Baseline refers" to the results when the model is calibrated to country specific averages of 1995-2010, see table 2. Parameters for technology and preferences are set as in table 1. All other columns report results if in the US calibration, fiscal instruments are set to country specific values (each at a time). $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database.

Table 5: Max. Additonal Tax Revenues (In %): Average 1995-2010 vs. Year 2010

  Vary Labor Taxes, $ \bar \tau^n$; $ \Delta\overline{T}_{Max}$: $ \varnothing$Vary Labor Taxes, $ \bar \tau^n$; $ \Delta\overline{T}_{Max}$: 2010 Vary Capital Taxes, $ \bar \tau^k$; $ \Delta\overline{T}_{Max}$: $ \varnothing$Vary Capital Taxes, $ \bar \tau^k$; $ \Delta\overline{T}_{Max}$: 2010 Vary $ \bar \tau^n$ and $ \bar \tau^k$ jointly; $ \Delta\overline{T}_{Max}$: $ \varnothing$Vary $ \bar \tau^n$ and $ \bar \tau^k$ jointly; $ \Delta\overline{T}_{Max}$: 2010
USA37.627.910.78.837.628.1
USA$ ^*$37.628.210.78.937.628.4
EU-1411.97.93.22.512.18.2
GER15.414.96.86.116.415.7
FRA7.14.61.10.77.14.6
ITA9.87.32.11.19.97.3
GBR17.58.61.70.717.98.8
AUT5.24.72.62.85.85.5
BEL5.74.00.30.15.94.1
DNK1.30.30.00.41.61.0
FIN4.11.61.61.04.41.9
GRE18.914.28.97.819.915.6
IRL32.721.514.912.235.425.9
NET14.76.65.34.615.68.6
PRT21.615.46.64.621.815.6
ESP18.510.36.55.419.011.4
SWE2.03.30.50.02.13.5

Table 5: Laffer curves and Laffer hill for 1995-2010 vs. 2010 calibration. The model is either calibrated to the average of 1995-2010 or to the 2010, see table 2. Parameters are set as in table 1. $ \Delta\overline{T}_{Max}$ denotes the maximum additional tax revenues (in %) that results from moving from to the peak of the Laffer curve. $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database.

Table 6: Output Losses (In %) From Moving to the Laffer Curve Peak

  Vary Labor Taxes, $ \bar \tau^n$ $ \Delta\overline{y}$ at $ \Delta\overline{T}_{Max}$ Vary Capital Taxes, $ \bar \tau^k$ $ \Delta\overline{y}$ at $ \Delta\overline{T}_{Max}$ Vary $ \bar \tau^n$ and $ \bar \tau^k$ jointly $ \Delta\overline{y}$ at $ \Delta\overline{T}_{Max}$
USA-27.2-21.1-29.6
USA$ ^*$-27.3-21.1-29.7
EU-14-17.5-12.8-20.1
GER-22.0-17.7-26.5
FRA-14.2-7.5-14.3
ITA-17.6-8.8-16.7
GBR-18.5-7.3-15.8
AUT-14.6-13.0-18.9
BEL-13.6-3.8-11.2
DNK-3.96.02.2
FIN-9.0-8.3-12.5
GRE-22.3-20.3-27.5
IRL-23.6-23.6-34.6
NET-15.9-16.1-23.7
PRT-22.6-16.5-24.5
ESP-19.3-17.7-24.8
SWE-12.3-1.0-8.5

Table 6: Output losses in perent from moving to the peak of Laffer curves. The model is calibrated to the year 2010, see table 2. Parameters are set as in table 1. $ \Delta\overline{y}$ is the reduction of balanced growth output in the model from moving from the status quo equilibrium to the peak of the Laffer curve. $ \Delta\overline{T}_{Max}$ denotes the maximum additional tax revenues (in %) that results from moving from to the peak of the Laffer curve. $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database

Table 7: Baseline Model: Maximum Real Interest Rates on Government Debt (In %)

 Vary Labor Taxes, $ \bar \tau^n$ $ \Delta\overline{T/y}_{Max}$Vary Labor Taxes, $ \bar \tau^n$ $ \bar r_{Max}$Vary Capital Taxes, $ \bar \tau^k$ $ \Delta\overline{T/y}_{Max}$Vary Capital Taxes, $ \bar \tau^k$ $ \bar r_{Max}$Vary $ \bar \tau^n$ and $ \bar \tau^k$ jointly $ \Delta\overline{T/y}_{Max}$Vary $ \bar \tau^n$ and $ \bar \tau^k$ jointly $ \bar r_{Max}$Data: long-term interest rates$ ^\dagger$Data: long-term interest rates$ ^\dagger$
USA7.312.02.36.57.412.02.01.4
USA$ ^*$7.415.52.37.77.415.62.01.4
EU-143.07.60.95.13.17.72.41.5
GER5.010.02.06.45.210.32.10.8
FRA1.96.40.34.41.96.42.31.9
ITA2.86.40.44.32.86.43.72.5
GBR3.48.20.34.33.48.30.5-0.4
AUT1.96.61.15.62.27.11.41.1
BEL1.85.80.14.11.85.91.61.6
DNK0.24.40.24.50.65.3-0.50.4
FIN0.75.50.55.00.95.82.61.1
GRE4.47.12.45.74.87.47.34.4
IRL6.911.23.98.18.312.78.48.0
NET2.68.21.86.93.49.41.71.5
PRT5.19.51.55.65.29.54.33.7
ESP3.59.81.87.03.910.53.81.8
SWE1.68.00.04.01.78.21.61.6

Table 7: Maximum additional tax revenue and interest rates for the labor and capital tax Laffer curve respectively Laffer hill. The model is calibrated to the year 2010, see table 2. Parameters are set as in table 1. $ \Delta\overline{T/y}_{Max}$ denotes the maximum additional tax revenues (expressed in % of baseline GDP) that results from moving from the 2010 status quo to the peak of the Laffer curve. $ \bar r_{Max}$ is the maximum net real interest rate that the government could afford on outstanding debt in the year 2010 if all additonal tax revenue is spent on interest rate payments. $ ^\dagger$ - real long-term interest rates for 2010 downloaded from the European Commission AMECO database. These are nominal 10 years government bond interest rates minus inflation - either using the GDP deflator (ILRV, first column) or the consumption deflator (ILRC, second column). EU-14 value is the real GDP weighted average of European countries. $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database. All numbers in the table in percent.

Table 8: Distance to Peak in Terms of Tax Rates (In %)

 Vary Labor Taxes, $ \bar \tau^n$ BaselineVary Labor Taxes, $ \bar \tau^n$ Human CapitalVary Capital Taxes, $ \bar \tau^k$ BaselineVary Capital Taxes, $ \bar \tau^k$ Human Capital
USA39.920.929.927.9
USA$ ^*$39.920.929.927.9
EU-1426.87.823.222.2
GER28.511.536.136.1
FRA21.41.413.612.6
ITA23.83.817.715.7
GBR33.211.212.99.9
AUT17.2-3.826.322.3
BEL19.7-1.36.54.5
DNK10.7-15.3-2.4-5.4
FIN17.0-4.020.520.5
GRE29.97.941.034.0
IRL42.834.850.756.7
NET30.917.932.336.3
PRT34.812.830.326.3
ESP31.012.031.928.9
SWE12.2-8.812.213.2

Table 8: Distance to the peak of Laffer curves for baseline model and baseline model with added human capital accumulation (second generation, see the main text and Trabandt and Uhlig (2011) for details). Distance is measured in terms of tax rates. All numbers are expressed in percent. The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1. Parameters for human capital accumulation are set as in the main text and Trabandt and Uhlig (2011). $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database. All numbers in the table in percent.

Table 9: Model with Human Capital: Max. Real Interest Rates on Government Debt (In %)

  Vary Labor Taxes, $ \bar \tau^n$ $ \Delta\overline{T/y}_{Max}$ Vary Labor Taxes, $ \bar \tau^n$ $ \bar r_{Max}$ Vary Capital Taxes, $ \bar \tau^k$ $ \Delta\overline{T/y}_{Max}$ Vary Capital Taxes, $ \bar \tau^k$ $ \bar r_{Max}$Data: long-term interest rates$ ^\dagger$Data: long-term interest rates$ ^\dagger$
USA1.75.81.75.82.01.4
USA$ ^*$1.76.61.76.62.01.4
EU-140.04.00.64.82.41.5
GER0.84.91.76.02.10.8
FRA0.14.10.14.22.31.9
ITA0.04.00.24.13.72.5
GBR0.04.00.14.10.5-0.4
AUT0.14.10.75.01.41.1
BEL0.14.10.04.01.61.6
DNK2.49.50.24.5-0.50.4
FIN0.95.90.34.62.61.1
GRE0.24.11.34.97.34.4
IRL4.08.14.89.08.48.0
NET0.34.52.27.51.71.5
PRT0.44.40.94.94.33.7
ESP0.14.21.36.13.81.8
SWE0.14.30.04.01.61.6

Table 9: Model with human capital: maximum additional tax revenue and interest rates for the labor and capital tax Laffer curves. Second generation model with human capital accumulation, see the main text and Trabandt and Uhlig (2011) for details. The model is calibrated to the year 2010, see table 2. Parameters are set as in table 1. For human capital accumulation parameters see the main text and Trabandt and Uhlig (2011). $ \Delta\overline{T/y}_{Max}$ denotes the maximum additional tax revenues (expressed in % of baseline GDP) that results from moving from the 2010 status quo to the peak of the Laffer curve. $ \bar r_{Max}$ is the maximum net real interest rate that the government could afford on outstanding debt in the year 2010 if all additonal tax revenue is spent on interest rate payments. $ ^\dagger$ - real long-term interest rates for 2010 downloaded from the European Commission AMECO database. These are nominal 10 years government bond interest rates minus inflation - either using the GDP deflator (ILRV, first column) or the consumption deflator (ILRC, second column). EU-14 value is the real GDP weighted average of European countries. $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database. All numbers in the table in percent.

Table 10: Vary Consumption Taxes: Distance to Peak in Terms of Tax Revenues (In % of GDP)

 BaselineHuman Capital
USA         90.727.2
USA$ ^*$         90.727.2
EU-14         63.919.9
GER         61.720.2
FRA         58.717.9
ITA         67.820.0
GBR         79.723.5
AUT         62.618.5
BEL         58.217.3
DNK         48.914.4
FIN         47.015.2
GRE         97.827.3
IRL         44.218.1
NET         42.315.8
PRT         91.226.8
ESP         76.023.2
SWE         37.812.5

Table 10: Maximum additional tax revenues due to consumption taxes. Baseline model versus baseline model with added human capital accumulation (second generation human capital accumulation growth model, see the main text and Trabandt and Uhlig (2011) for details). Additional tax revenues are measured in percent of baseline GDP. The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1. Parameters for human capital accumulation are set as in the main text and Trabandt and Uhlig (2011). $ ^*$ - results when "debt held by the public" is used for the USA rather than the harmonized cross-country measure of gross government debt provided by the AMECO database. All numbers in the table in percent.

Figure 1: Comparison of "Actual" vs. "Predicted" Variables

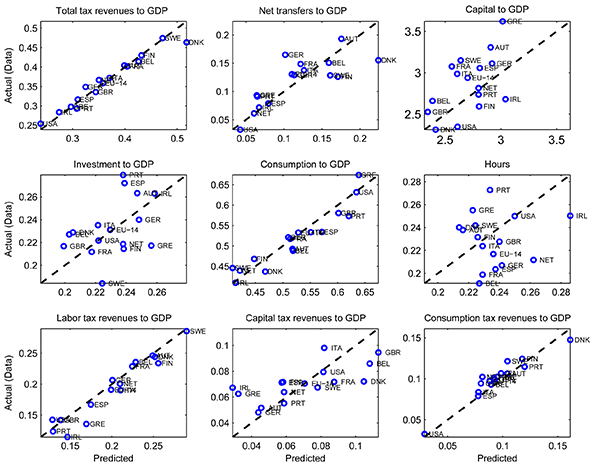
Figure 1: Comparison of actual vs. predicted variables. Actual refers to data sample averages for 1995-2010. Predicted refers to model implied steady state (balanced growth path) variables when the model is calibrated as in table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross debt).

Figure 1: Comparison of "actual" vs. "predicted" variables. "Actual" refers to data sample averages for 1995-2010. "Predicted" refers to model implied steady state (balanced growth path) variables when the model is calibrated as in table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross debt).

Figure 2: Sensitivity of "Actual" vs. "Predicted" Tax Revenues and Government Transfers

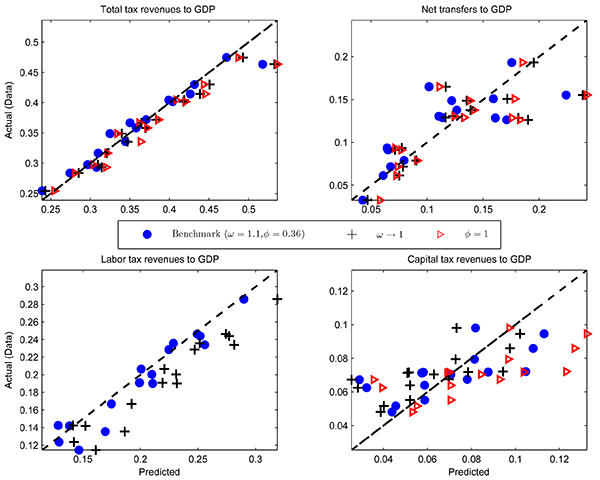
Figure 2: Sensitivity of actual vs. predicted tax revenues and government transfers. Actual refers to data sample averages for 1995-2010. Predicted refers to model implied steady state (balanced growth path). Three cases are examined. The benchmark case is the model used in the paper, and as in figure 1. The case omega --> 1 obtains, when there is no market power by intermediate goods producers: this is our previously used model in Trabandt and Uhlig (2011). Finally, there is the intermediate case with monopolistic competition, but where profits are fully subject to capital taxation, phi = 1. Note that all other variables plotted in figure 1 are unaffected by the sensitivity analysis, except for hours. However, the impact on hours is small and therefore omitted here. All other parameters and steady states are as in tables 1 and 2 (gross US debt).

Figure 2: Sensitivity of "actual" vs. "predicted" tax revenues and government transfers. "Actual" refers to data sample averages for 1995-2010. "Predicted" refers to model implied steady state (balanced growth path). Three cases are examined. The benchmark case is the model used in the paper, and as in figure 1. The case ω → 1 obtains, when there is no market power by intermediate goods producers: this is our previously used model in Trabandt and Uhlig (2011). Finally, there is the intermediate case with monopolistic competition, but where profits are fully subject to capital taxation, ϕ = 1. Note that all other variables plotted in figure 1 are unaffected by the sensitivity analysis, except for hours. However, the impact on hours is small and therefore omitted here. All other parameters and steady states are as in tables 1 and 2 (gross US debt).

Figure 3: Labor Tax Laffer Curves Across Countries

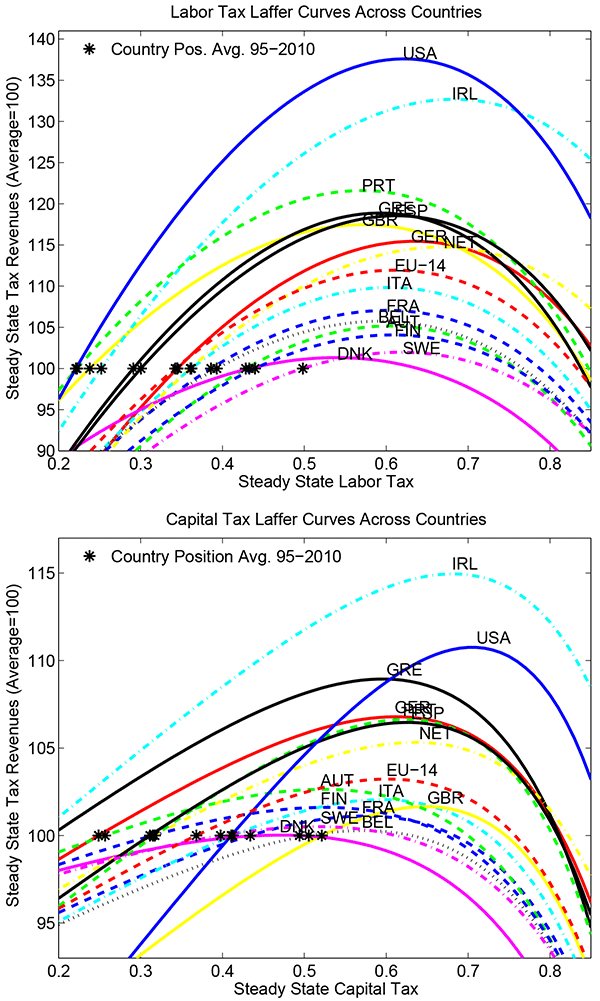
Figure 3: Labor and capital tax Laffer curves across all countries. The model is calibrated to the average of 1995-2010, see table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross US debt). Shown are steady state (balanced growth path) total tax revenues when labor taxes (upper panel) or capital taxes (lower panel) are varied between 0 and 100 percent. All other taxes and parameters are held constant. Total tax revenues at the average 1995-2010 tax rates are normalized to 100. Stars indicate positions of respective countries on their Laffer curves. Note that the first letter of each country name indicates the peak of the respective Laffer curve.

Figure 3: Labor and capital tax Laffer curves across all countries. The model is calibrated to the average of 1995-2010, see table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross US debt). Shown are steady state (balanced growth path) total tax revenues when labor taxes (upper panel) or capital taxes (lower panel) are varied between 0 and 100 percent. All other taxes and parameters are held constant. Total tax revenues at the average 1995-2010 tax rates are normalized to 100. Stars indicate positions of respective countries on their Laffer curves. Note that the first letter of each country name indicates the peak of the respective Laffer curve.

Figure 4: Labor Tax Laffer Curves for USA and EU-14

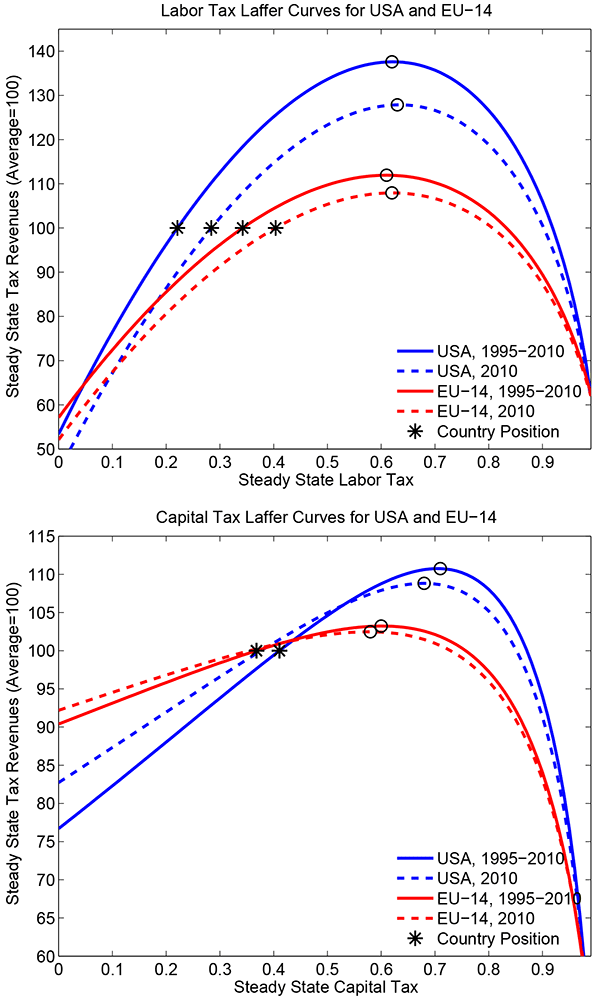
Figure 4: Comparing the US and the EU-14 labor and capital tax Laffer curve. The model is either calibrated to the average of 1995-2010 or to the 2010, see table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross US debt). Shown are steady state (balanced growth path) total tax revenues when labor taxes (upper panel) or capital taxes (lower panel) are varied between 0 and 100 percent. All other taxes and parameters are held constant. Total tax revenues at the average 1995-2010 or at the year 2010 tax rates are normalized to 100. Stars indicate positions of respective countries on their Laffer curves.

Figure 4: Comparing the US and the EU-14 labor and capital tax Laffer curve. The model is either calibrated to the average of 1995-2010 or to the 2010, see table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross US debt). Shown are steady state (balanced growth path) total tax revenues when labor taxes (upper panel) or capital taxes (lower panel) are varied between 0 and 100 percent. All other taxes and parameters are held constant. Total tax revenues at the average 1995-2010 or at the year 2010 tax rates are normalized to 100. Stars indicate positions of respective countries on their Laffer curves.

Figure 5: Changes of Distance to the Peak of the Labor Tax Laffer Curve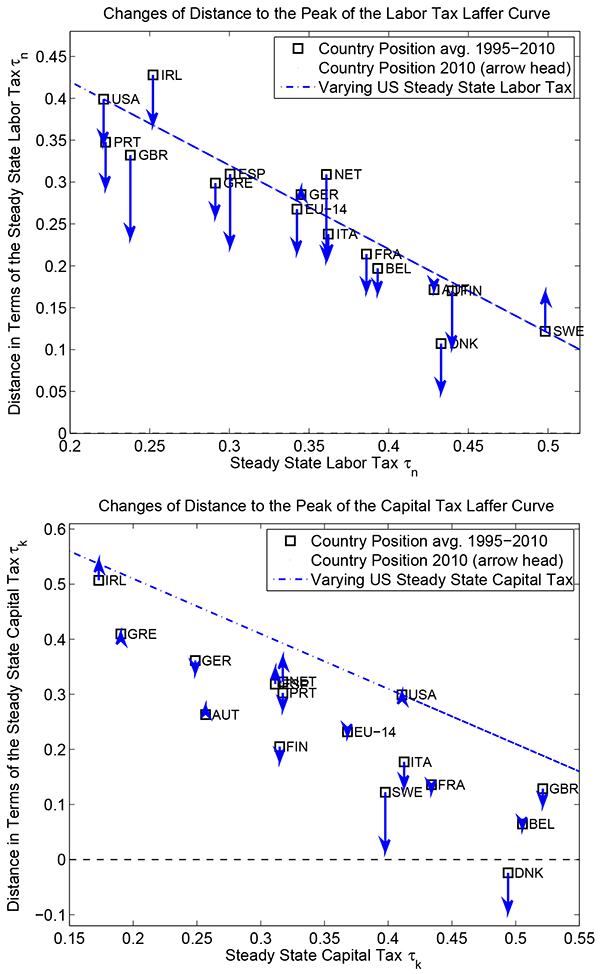Figure 5: Distance to the peak of Laffer curves for average 1995-2010 vs. 2010 calibration. The model is either calibrated to the average of 1995-2010 or to the 2010, see table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross US debt). Horizontal axis shows calibrated tax rates. Vertial axis shows distance to the peak in terms of tax rates. The dashed-dotted line shows the distance to the peak for the US when the initial steady state tax is varied and the model is re-calibrated for each assumed tax rate.

Figure 5: Distance to the peak of Laffer curves for average 1995-2010 vs. 2010 calibration. The model is either calibrated to the average of 1995-2010 or to the 2010, see table 2 (gross US debt). Parameters for technology and preferences are set as in table 1 (gross US debt). Horizontal axis shows calibrated tax rates. Vertial axis shows distance to the peak in terms of tax rates. The dashed-dotted line shows the distance to the peak for the US when the initial steady state tax is varied and the model is re-calibrated for each assumed tax rate.

Figure 6: Labor Tax Laffer Curves for USA and EU-14

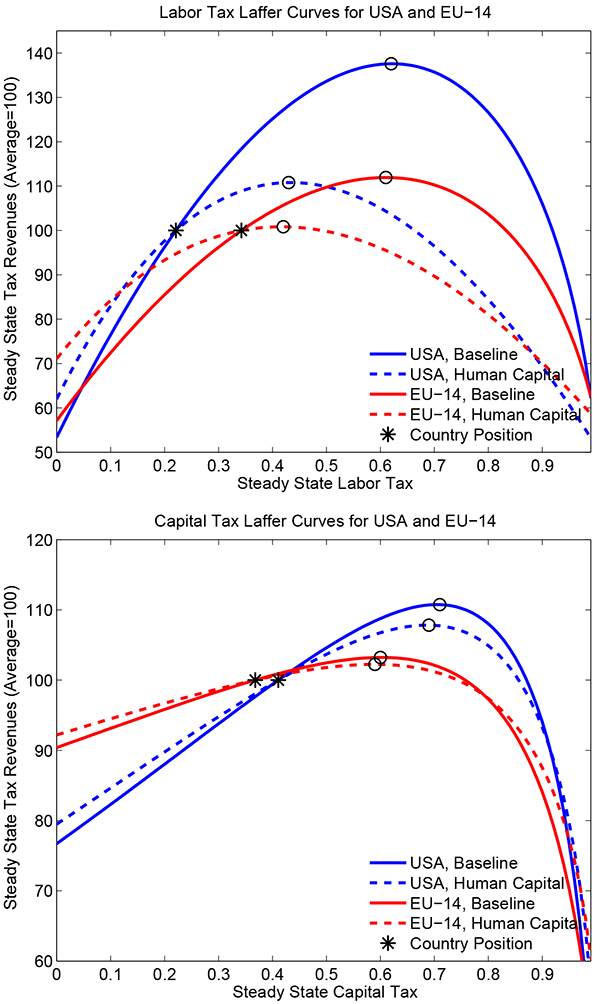
Figure 6: Labor and capital tax Laffer curves: the impact of endogenous human capital accumulation. Shown are steady state (balanced growth path) total tax revenues when labor taxes are varied between 0 and 100 percent in the USA and EU-14. All other taxes and parameters are held constant. Total tax revenues at the average tax rates are normalized to 100. Two cases are examined. First, the benchmark model with exogenous growth. Second, the benchmark model with a second generation version of endogenous human capital accumulation (see the main text and Trabandt and Uhlig (2011) for details). The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1 (gross US debt). Parameters for human capital accumulation are set as in the main text Trabandt and Uhlig (2011).

Figure 6: Labor and capital tax Laffer curves: the impact of endogenous human capital accumulation. Shown are steady state (balanced growth path) total tax revenues when labor taxes are varied between 0 and 100 percent in the USA and EU-14. All other taxes and parameters are held constant. Total tax revenues at the average tax rates are normalized to 100. Two cases are examined. First, the benchmark model with exogenous growth. Second, the benchmark model with a second generation version of endogenous human capital accumulation (see the main text and Trabandt and Uhlig (2011) for details). The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1 (gross US debt). Parameters for human capital accumulation are set as in the main text Trabandt and Uhlig (2011).

Figure 7: Changes of Distance to the Peak of the Labor Tax Laffer Curve

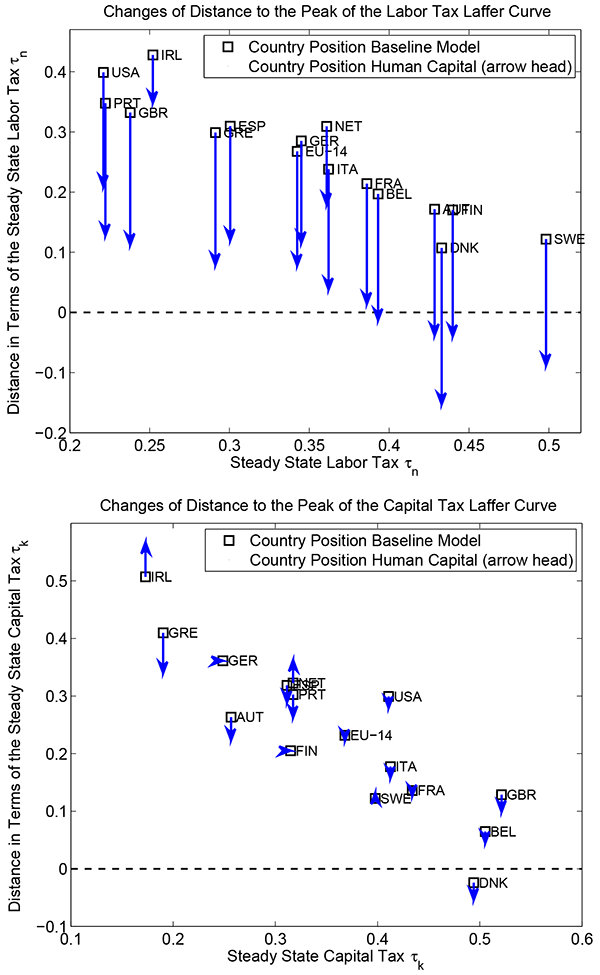
Figure 7: Distance to the peak of Laffer curves for baseline model and baseline model with added human capital accumulation (second generation, see the main text and Trabandt and Uhlig (2011) for details). The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1 (gross US debt). Parameters for human capital accumulation are set as in the main text and Trabandt and Uhlig (2011). Horizontal axis shows calibrated tax rates. Vertial axis shows distance to the peak in terms of tax rates.

Figure 7: Distance to the peak of Laffer curves for baseline model and baseline model with added human capital accumulation (second generation, see the main text and Trabandt and Uhlig (2011) for details). The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1 (gross US debt). Parameters for human capital accumulation are set as in the main text and Trabandt and Uhlig (2011). Horizontal axis shows calibrated tax rates. Vertial axis shows distance to the peak in terms of tax rates.

Figure 8: Consumption Tax Laffer Curves for USA and EU-14

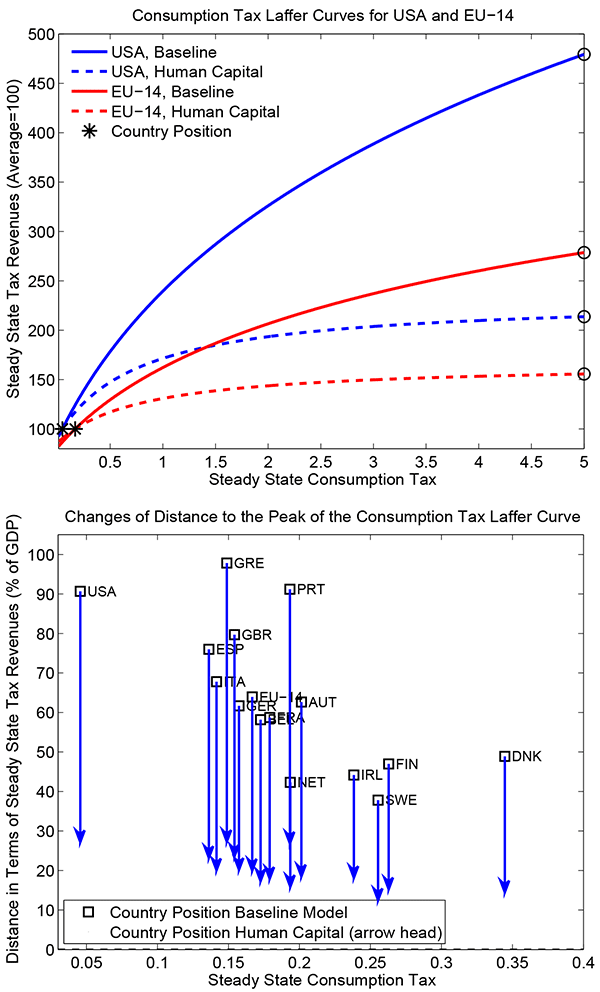
Figure 8: Upper panel: Consumption tax Laffer curve in the USA and EU-14: the impact of endogenous human capital accumulation. Shown are steady state (balanced growth path) total tax revenues when consumption taxes are varied between 0 and 500 percent. All other taxes and parameters are held constant. Total tax revenues at the average consumption tax rate are normalized to 100. Two cases are examined. First, the benchmark model with exogenous growth. Second, the benchmark model with a second generation version of endogenous human capital accumulation (see the main text and Trabandt and Uhlig (2011) for details). The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1 (gross US debt). Parameters for human capital accumulation are set as in the main text and Trabandt and Uhlig (2011). Lower panel: Distance to the peak of Laffer curves for baseline model and baseline model with added human capital accumulation. Horizontal axis shows calibrated tax rates. Vertial axis shows distance to the peak in terms of tax revenues (in percent of GDP).

Figure 8: Upper panel: Consumption tax Laffer curve in the USA and EU-14: the impact of endogenous human capital accumulation. Shown are steady state (balanced growth path) total tax revenues when consumption taxes are varied between 0 and 500 percent. All other taxes and parameters are held constant. Total tax revenues at the average consumption tax rate are normalized to 100. Two cases are examined. First, the benchmark model with exogenous growth. Second, the benchmark model with a second generation version of endogenous human capital accumulation (see the main text and Trabandt and Uhlig (2011) for details). The model is calibrated to the average of 1995-2010 for fiscal variables. Standard parameters for technology and preferences are set as in table 1 (gross US debt). Parameters for human capital accumulation are set as in the main text and Trabandt and Uhlig (2011). Lower panel: Distance to the peak of Laffer curves for baseline model and baseline model with added human capital accumulation. Horizontal axis shows calibrated tax rates. Vertial axis shows distance to the peak in terms of tax revenues (in percent of GDP).


Appendix A. Tax Rate Tables

 1995199619971998199920002001200220032004200520062007200820092010$ ^*$
USA22.222.823.323.523.824.123.821.720.720.621.621.922.321.420.020.0
EU-1434.935.034.934.334.733.833.633.233.533.433.734.134.334.834.834.8
GER35.234.434.635.035.134.935.234.434.033.533.233.734.134.335.235.2
FRA38.739.239.238.338.938.537.937.738.338.039.139.138.738.738.638.6
ITA33.736.337.634.835.434.934.835.035.535.735.836.037.438.439.039.0
GBR22.721.921.622.623.223.623.623.123.324.224.625.225.725.824.824.8
AUT40.841.842.843.042.942.443.843.843.743.442.642.442.343.043.443.4
BEL39.039.039.639.739.539.239.140.040.340.639.738.838.638.838.538.5
DNK42.042.343.042.244.744.944.243.343.342.442.442.143.443.344.444.4
FIN47.448.246.045.744.744.944.444.042.741.842.743.242.842.341.441.4
GRENaNNaNNaNNaNNaN26.828.329.730.529.729.529.229.330.328.528.5
IRLNaNNaNNaNNaNNaNNaNNaN23.824.425.825.927.026.724.324.424.4
NET40.738.038.334.235.535.632.933.133.233.534.236.936.638.438.138.1
PRT20.921.121.321.221.221.722.422.422.722.022.122.723.423.423.623.6
ESPNaNNaNNaNNaNNaN28.929.529.729.829.830.230.731.330.630.030.0
SWE48.550.052.053.655.351.549.848.449.850.250.250.248.247.645.945.9

Table A.11: Labor income taxes in percent across countries and time. Country codes: Germany (GER), France (FRA), Italy (ITA), United Kingdom (GBR), Austria (AUT), Belgium (BEL), Denmark (DNK), Finland (FIN), Greece (GRE), Ireland (IRL), Netherlands (NET), Portugal (PRT), Spain (ESP) and Sweden (SWE). * - due to data availability reasons, 2010 tax rates are assumed to be the same as in 2009. For an alternative, see subsection 3.2 in the main text.

 1995199619971998199920002001200220032004200520062007200820092010$ ^*$
USA44.042.641.742.641.943.239.937.438.738.740.942.145.642.637.637.6
EU-1433.435.637.738.240.339.837.935.334.134.636.739.038.337.135.535.5
GER22.923.623.825.127.829.420.921.723.522.924.225.925.726.327.127.1
FRA34.638.540.742.044.844.045.944.141.944.544.448.646.548.442.842.8
ITA41.143.045.839.141.937.039.038.035.836.037.644.146.146.144.844.8
GBR47.346.250.354.755.661.662.752.448.048.052.154.950.149.750.250.2
AUT22.026.027.927.626.225.932.125.325.425.324.523.524.626.424.124.1
BEL44.848.550.054.254.653.256.652.447.945.149.050.548.652.450.450.4
DNK40.041.441.750.944.042.846.747.448.549.455.158.757.156.055.555.5
FIN26.130.832.033.834.140.632.031.730.130.430.830.130.430.730.130.1
GRENaNNaNNaNNaNNaN27.320.620.317.917.519.017.218.617.316.816.8
IRLNaNNaNNaNNaNNaNNaNNaN15.216.417.718.120.418.817.615.715.7
NET31.635.735.936.937.335.436.533.429.830.533.129.128.827.423.323.3
PRT25.027.127.526.930.733.730.132.131.330.233.734.837.040.333.833.8
ESPNaNNaNNaNNaNNaN28.727.129.029.732.537.340.141.328.124.424.4
SWE27.334.236.436.638.048.344.437.634.835.840.138.039.940.252.552.5

Table A.12: Capital income taxes in percent across countries and time. Country codes: Germany (GER), France (FRA), Italy (ITA), United Kingdom (GBR), Austria (AUT), Belgium (BEL), Denmark (DNK), Finland (FIN), Greece (GRE), Ireland (IRL), Netherlands (NET), Portugal (PRT), Spain (ESP) and Sweden (SWE). * - due to data availability reasons, 2010 tax rates are assumed to be the same as in 2009.

 1995199619971998199920002001200220032004200520062007200820092010$ ^*$
USA5.15.15.05.04.94.74.64.54.44.44.54.54.34.14.04.0
EU-1417.017.117.117.317.617.416.916.816.716.616.516.616.716.115.215.2
GER15.415.315.015.216.016.015.615.515.715.315.115.316.716.616.716.7
FRA18.619.419.619.619.818.818.118.017.517.617.517.417.116.515.615.6
ITA15.414.414.215.114.715.614.914.614.113.713.714.214.013.112.512.5
GBR16.716.916.716.716.716.315.715.515.615.615.014.814.714.113.013.0
AUT19.320.021.021.021.620.520.220.720.220.220.019.219.619.619.519.5
BEL16.516.817.117.018.017.916.817.217.017.818.218.317.816.816.516.5
DNK32.433.934.235.436.435.735.835.735.034.835.636.035.333.131.031.0
FIN26.526.428.928.528.928.126.826.727.226.226.125.824.823.922.922.9
GRE15.715.816.315.615.815.115.715.614.914.514.214.414.814.112.812.8
IRL24.124.424.826.026.525.422.323.523.325.026.025.924.521.119.319.3
NET17.918.418.518.719.519.319.919.119.219.820.720.520.520.218.718.7
PRT19.219.819.520.620.619.419.520.220.019.720.520.719.618.415.915.9
ESP12.813.113.514.315.014.714.214.314.714.714.914.914.312.410.210.2
SWE26.825.425.225.525.024.725.125.125.125.325.725.826.126.325.825.8

Table A.13: Consumption taxes in percent across countries and time. Country codes: Germany (GER), France (FRA), Italy (ITA), United Kingdom (GBR), Austria (AUT), Belgium (BEL), Denmark (DNK), Finland (FIN), Greece (GRE), Ireland (IRL), Netherlands (NET), Portugal (PRT), Spain (ESP) and Sweden (SWE). * - due to data availability reasons, 2010 tax rates are assumed to be the same as in 2009.


Appendix B. Calculation of Tax Rates

We use the same data sources as in Trabandt and Uhlig (2011), i.e. the AMECO database of the European Commission, the OECD revenue statistics database and the NIPA database of the BEA.

In this paper, we refine the methodology of Mendoza et al. (1994) to calculate effective tax rates on labor and capital income. Broadly, we expand the measured labor tax base by including supplements to wages as well as a fraction of entrepreneurial income of households. Supplements to wages beyond employers social security contributions account for about 7 percent of e.g. U.S. GDP. Also, entrepreneurial income of households is sizable as a fraction of GDP but entirely accounted as capital income in Mendoza et al. (1994). We argue that at least a fraction, say $ \alpha$, of this income ought to be attributed to labor income. As a result, the refinements imply in a more reasonable labor share in line with the empirical literature. More importantly, the average 1995-2010 labor income taxes turn out to be lower while capital income taxes are higher as previously calculated in Trabandt and Uhlig (2011). Table B.14 provides an overview of the refinements.8

Table B.14: Calculations of Effective Tax Rates: Mendoza Et Al. (1994) as Used in Trabandt and Uhlig (2011) vs. This Paper

Income Tax Mendoza et al. (1994) This paper
Personal: $ \tau^h=\frac{1100}{OSPUE+PEI+W}$ $ \tau^h=\frac{1100}{(1-\alpha+\alpha)(OSPUE+PEI)+W+W^{suppl}}$
Labor: $ \tau^n=\frac{\tau^h W+2000+3000}{W+2200}$ $ \tau^n=\frac{\tau^h [W+W^{suppl}+\alpha(OSPUE+PEI)]+2000+3000}{W+W^{suppl}+\alpha(OSPUE+PEI)+2200}$
Capital: $ \tau^k=\frac{\tau^h (OSPUE+PEI)+1200+4100+4400}{OS}$ $ \tau^k=\frac{\tau^h (1-\alpha)(OSPUE+PEI)+1200+4100+4400}{OS-\alpha(OSPUE+PEI)}$

Table B.14: Calculations of e ective tax rates: Mendoza et al. (1994) as used in Trabandt and Uhlig (2011) vs. this paper.

where
1100: Income, profit and capital gains taxes of individuals, revenue statistics (OECD).
1200: Income, profit and capital gains taxes of corporations, revenue statistics (OECD).
2000: Social security contributions, revenue statistics (OECD).
2200: Social security contributions of employers, revenue statistics (OECD).
3000: Payroll taxes, revenue statistics (OECD).
4000: Property taxes, revenue statistics (OECD).
4100: Recurrent taxes on immovable property, revenue statistics (OECD).
4400: Taxes on financial and capital transactions, revenue statistics (OECD).
OS: Net operating surplus: total economy (AMECO, NIPA).
W: Gross wages and salaries: households and NPISH (AMECO, NIPA).
OSPUE+PEI: Gross operating surplus minus consumption of fixed capital plus mixed income plus net property income: households and NPISH (AMECO).
W$ ^{suppl}$: Supplements to wages: households and NPISH. Calculated as the residual of compensation of employees minus wages and salaries minus social security contributions of employers.

We select a value for $ \alpha$ such that the average 1995-2010 labor share, i.e. $ W+W^{suppl}+\alpha(OSPUE+PEI)+2200)/GDP$ equals 64 percent in the U.S. It turns out that we need to set $ \alpha=0.35$. We keep the same value for $ \alpha$ for all other countries.

Table B. 15 shows the resulting effective tax rates across countries and compares them to those when the standard Mendoza et al. (1994) methodology is applied as used e.g. in Trabandt and Uhlig (2011). It turns out, that due to the broader labor tax base, effective labor taxes are somewhat smaller while effective capital taxes are higher.

Finally, table B.16 provides maximum additional tax revenues that result from moving from the peak of the Laffer curve when either the standard Mendoza et al. (1994) tax rates or the refined version proposed in this paper are used. Further, the table also shows the implications of imperfect vs. perfect competition. The introduction of imperfect competition reduces the effective labor tax base and thus less additional tax revenues are attainable when varying labor taxes. By contrast, profits arising from market power increase maximum additional tax revenues when capital taxes are varied. The fourth column shows the results when the standard Mendoza tax rates are used in the analysis and are essentially those obtained by Trabandt and Uhlig (2011). In this case, higher effective labor taxes at the status quo equlibrium reduce the scope for more tax revenues when labor and capital taxes are varied.

Table B.15: Comparison of Effective Tax Rates

 Labor Taxes, $ \bar \tau^n$ TU (2011)Labor Taxes, $ \bar \tau^n$ This paperCapital Taxes, $ \bar \tau^k$ TU (2011)Capital Taxes, $ \bar \tau^k$ This paperLabor Share TU (2011)Labor Share This paper
USA0.270.220.350.410.500.64
EU-140.410.340.320.370.480.58
GER0.410.340.220.250.490.60
FRA0.450.390.350.430.500.59
ITA0.470.360.340.410.380.52
GBR0.280.240.440.520.500.60
AUT0.500.430.240.260.480.57
BEL0.480.390.430.510.480.60
DNK0.480.430.500.490.500.56
FIN0.480.440.320.310.480.53
GRE0.410.290.170.190.320.46
IRL0.270.250.170.170.420.45
NET0.440.360.280.320.450.55
PRT0.280.220.270.320.440.56
ESP0.350.300.270.310.460.55
SWE0.560.500.390.400.510.57

Table B.15: Comparison of effective tax rates. TU (2011) abbreviates Trabandt and Uhlig (2011) who use the methodology proposed by Mendoza et al. (1994). The table shows the implications of the refined calculations of effective tax rates as well as the implied labor share. See Appendix B for details.

Table B.16: Laffer Curves for the 1995-2010 Calibration

  Vary Labor Taxes, $ \bar \tau^n$ $ \Delta\overline{T}_{Max}$ This Paper $ \omega=1.1$ Vary Labor Taxes, $ \bar \tau^n$ $ \Delta\overline{T}_{Max}$ This Paper $ \omega\rightarrow1$ Vary Labor Taxes, $ \bar \tau^n$ $ \Delta\overline{T}_{Max}$ TU (2011) $ \omega\rightarrow1$ Vary Capital Taxes, $ \bar \tau^k$ $ \Delta\overline{T}_{Max}$ This Paper $ \omega=1.1$ Vary Capital Taxes, $ \bar \tau^k$ $ \Delta\overline{T}_{Max}$ This Paper $ \omega\rightarrow1$ Vary Capital Taxes, $ \bar \tau^k$ $ \Delta\overline{T}_{Max}$ TU (2011) $ \omega\rightarrow1$
USA37.642.533.310.78.27.3
EU-1411.913.98.43.21.61.0
GER15.417.310.16.83.92.3
FRA7.18.64.91.10.30.3
ITA9.811.64.22.10.90.3
GBR17.521.018.71.70.91.6
AUT5.26.12.02.61.00.3
BEL5.77.23.00.30.00.0
DNK1.32.10.60.00.40.9
FIN4.15.12.91.60.40.2
GRE18.921.08.28.95.62.1
IRL32.736.332.314.910.79.4
NET14.716.98.75.33.01.6
PRT21.625.118.66.64.53.6
ESP18.521.015.06.54.03.1
SWE2.02.70.70.50.00.0

Table B.16: Laffer curves for the 1995-2010 calibration. $ \Delta\overline{T}_{Max}$ denotes the maximum additional tax revenues (in %) that results from moving from to the peak of the Laffer curve. Results are shown for the standard Mendoza et al. (1994) taxes used in Trabandt and Uhlig (2011), "TU", as well as for the refined tax rate calculations discussed in Appendix B. Further, the case of imperfect competition with a gross markup $ \omega=1.1$ is compared to the case of perfect competition, i.e. $ \omega\rightarrow1$.


Footnotes

1.  We allow for partial profit taxation due to the various deductions and exemptions that are available for firms and households in this regard. Further, note that capital income taxes are levied on dividends net-of-depreciation as in Prescott (2002, 2004) and in line with Mendoza et al. (1994). Return to text

2.  See Trabandt and Uhlig (2011) for the differences with respect to Laffer curves when parameters for technology and preferences are assumed to be identical or country specific. Return to text

3.  We assume a mapping of data and model in the literal sense, i.e. the one based on the definitions of the national income and product accounts and the revenues statistics. For work that takes an alternative perspective and emphasizes the general relativity of fiscal language, see Green and Kotlikoff (2009).  Return to text

4.  The present paper, and in particular the comparison of data vs. model hours is closely related to Prescott (2002, 2004) and subsequent contributions by e.g. Blanchard (2004), Alesina et al. (200), Ljungqvvist and Sargent (2006), Rogerson (2007) and Pissarides Ngai (2009).  Return to text

5.  Note that in this case, the value of $ \phi$ becomes immaterial since equilibrium profits are zero. Return to text

6.  For related work, see e.g. Bi (2010) and Bi et al. (2010). Return to text

7.  See e.g. Jones (2001), Barro and i Martin (2003) or Acemoglu (2008) for textbook treatments of models with endogenous growth and human capital accumulation. Below we consider a specification incorporating learning-by-doing as well as schooling, following Lucas (1988) and Uzawa (1965). While first-generation endogenous growth models have stressed the endogeneity of the overall long-run growth rate, second-generation growth models have stressed potentially large level effects, without affecting the long-run growth rate. We shall focus on the second generation case here since little evidence has been found that taxation impacts on the long-run growth rate, see e.g. Levine and Renelt (1992).  Return to text

8.  Note that we retain the assumption in Mendoza et al. (1994) that, implicitly, income from capital and labor is taxed at the same rate. In future research, it would be interesting to take differences in the taxation of labor and capital income explicitly into account when calculating tax rates. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: June 5, 2013