
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1051, August 2012 --- Screen Reader
Version*
U.S. Real Interest Rates and Default Risk in Emerging Economies
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper empirically investigates the impact of changes in U.S. real interest rates on sovereign default risk in emerging economies using the method of identification through heteroskedasticity. Policy-induced increases in U.S. interest rates starkly raise default risk in emerging market economies. However, the overall correlation between U.S. real interest rates and the risk of default is negative, demonstrating that the effects of other variables dominate the anterior relationship.
Keywords: Real interest rates, default risk, sovereign debt, identification through heteroskedasticity
JEL classification: F34, G15
1 Introduction
The theoretical economic effect of changes in U.S. real interest rates on default risk in emerging economies has been studied by, amongst others, Guimaraes (2011) and the channel is often cited as a non-domestic driver of country risk premia (Neumeyer and Perri 2005). The mechanism runs that when U.S. real interest rates rise, the opportunity costs to those who buy emerging economies' debt increase, which raises interest rates in emerging economies. This direct effect increases the debt burden on emerging economies, raising the risk that they will default on their debt and requiring emerging economies to offer even higher interest rates in compensation. Anecdotal evidence from the Latin American debt crisis of the 1980's and the Mexican crisis in 1994, both of which were preceded by sharp interest rate hikes in the U.S., suggests that this theoretical channel might be an important empirical one.
Empirically identifying this theoretical relationship is not trivial, however, owing to the usual problems of reverse causality and common omitted variables. The latter is especially problematic because U.S. real interest rates and default risk in emerging economies are both affected by variables that cannot be easily measured, such as global market factors, risk appetite, and expectations about economic performance and the political scenario.
This paper identifies the effects of changes in U.S. real interest rates on default risk in emerging economies using the method of identification through heteroskedasticity as set out by Rigobon and Rigobon and Sack (2004). As discussed in detail in Section 2, we take data on U.S. real interest rates from inflation-indexed Treasury bonds, and proxy default risk using J.P. Morgan's Emerging Markets Bond Index Plus (EMBI+) premia in emerging economies over the period between 1998 and 2008. The idea behind the identification method is that there is a greater variance of changes in real interest rates on dates when the Federal Open Market Committee (FOMC) meets. The meetings of the FOMC can be seen as an extra shock to U.S. interest rates, which have an impact on the EMBI+ premia.
The key identifying assumption is that the timing of FOMC meetings does not affect the EMBI+ premia through any channel other than the changes in real interest rates. Other shocks that directly affect the EMBI+ premia are assumed to be uncorrelated with the timing of FOMC meetings. This assumption resembles the desired characteristics of an instrument in IV regressions. However, the timing of FOMC meetings affects the variance, not the level of shocks, so a usual IV strategy cannot be employed. The methodology of identification through heteroskedasticity yields a synthetic instrument based on differences in the covariance matrices of our data between dates when the FOMC does and does not meet.
Our findings are presented in Section 3, where we show that unexpected policy-induced increases in interest rates lead to greater EMBI+ premia and, by implication, default risk in emerging economies. A 1 basis-point increase in 10-year U.S. real interest rates raises EMBI+ premia by around 1 basis point, which means that the cost of borrowing in emerging economies rises substantially more than in the U.S. This confirms the hypothesised theoretical relationship between changes in U.S. real interest rates and the risk of default and suggests that more attention ought to be paid to this relationship in the literature on default risk.
A positive correlation between default risk and U.S. real interest rates would imply that emerging economies should issue debt contingent on U.S. real interest rates because such a contingency would negate the increased default risk not associated with fundamental changes in emerging economies. Note, however, that this policy prescription depends not on the causal relationship between U.S. real interest rates and the EMBI+ premium, but on the correlation between both. Omitted variables that significantly affect this correlation would also affect the performance of debt contracts contingent on U.S. real interest rates.
In actuality, on dates when the FOMC does not meet, we observe a significant correlation with the opposite sign: changes in real interest rates are negatively related to changes in EMBI+ premia. Moreover, the overall correlation between real interest rates and the EMBI+ premium is negative: a 2 bp increase in the 10-year U.S. real rate is on average related to a 1 bp decrease in the EMBI+. The results suggest that high real interest rates reflect favourable external conditions for emerging markets, which reduce the risk of default. This finding resonates with that of Longstaff et al. (2011), where global risk factors (proxied by U.S. markets) are shown to be the major determinant of sovereign credit risk premia. Regardless of the precise reason for the negative correlation, the policy implication is clear: emerging economies should not issue debt contingent on U.S. real interest rates.
Previous academic work has attempted to establish the nature of the relationship between U.S. real interest rates and sovereign default risk by applying different methods to deal with the aforementioned endogeneity problems. Some of this work has relied on structural assumptions in vector autoregressions to identify the relationship (e.g., Uribe and Yue 2006). For our purposes, high-frequency data on financial prices can provide more information and allow for a cleaner identification strategy.1
An alternative to structural assumptions are 'traditional' instruments in IV strategies, such as in Zettelmeyer (2004), where changes in the policy rate are employed as instruments for longer-term real interest rates. This methodology also needs to assume that changes in the instrument do not affect EMBI+ premia through alternative channels. Moreover, the instruments themselves must be exogenous, which is a stronger, and therefore less desirable, assumption than that employed in this paper.
Additional studies investigate the direct effect of changes in the U.S. federal funds target rate on emerging market spreads (Arora and Cerisola 2001). However, the theoretical relationship of interest is between default risk and the longer-term real interest rate, not the short-term nominal rate, which cannot be assumed to be endogenous. Moreover, even changes in the target rate might not be truly exogenous (see Rigobon and Sack 2004). In a more closely related exercise, Robitaille and Roush (2006) employ an event study approach using Brazilian data and find similar results to those of our paper.
2 Data and Empirical Methodology
Our measure of the interest rate, ![]() , is from 10-year inflation-indexed Treasury bonds.2 To
quantify the risk of default,
, is from 10-year inflation-indexed Treasury bonds.2 To
quantify the risk of default, ![]() , we use J.P.
Morgan's Emerging Markets Bond Index Plus (EMBI+), which is
comprised of medium-term debt of more than one year to
maturity.3 All data are obtained from the Global
Financial Database (www.globalfinancialdata.com).
, we use J.P.
Morgan's Emerging Markets Bond Index Plus (EMBI+), which is
comprised of medium-term debt of more than one year to
maturity.3 All data are obtained from the Global
Financial Database (www.globalfinancialdata.com).
We want to obtain long data series with
minimal concern for events that might obfuscate a potential
relationship. For this reason we select emerging economies that
have not defaulted, and use daily data running from January 1998 to
December 2008. We are interested in how a change in the interest
rate affects the EMBI+ premia, so our sample consists of values of
![]() and
and
![]() and is divided in
two: the sub-sample
and is divided in
two: the sub-sample ![]() corresponds to the dates of
monetary policy shocks, and the sub-sample
corresponds to the dates of
monetary policy shocks, and the sub-sample ![]() corresponds to dates with no shocks.4
corresponds to dates with no shocks.4![]() 5
5
There are two endogeneity concerns that
mean a simple ordinary least squares regression will not identify
the effect of changes in U.S. real interest rates on the risk of
default (EMBI+ premia). First, changes in the EMBI+ premia can
cause changes in the interest rate, for example, when default risk
falls and in response investors switch demand from safe Treasury
assets to emerging market debt. Second, and more importantly, the
interest rate and the exchange rate are influenced by other common
omitted variables. The following system of equations is a simple
representation of both endogeneity issues6:
| (1) | |||
| (2) |
Where
![]() is the change in U.S. real
interest rate;
is the change in U.S. real
interest rate;
![]() the change in the EMBI+ premium;
the change in the EMBI+ premium;
![]() a vector of omitted variables
including, for example, external market conditions;
a vector of omitted variables
including, for example, external market conditions;
![]() a monetary policy shock; and
a monetary policy shock; and
![]() a shock to EMBI+.
a shock to EMBI+.
The objective is to identify ![]() in Equation 1. Our
identification strategy is borrowed from Rigobon and Sack (2004), who show that the impact of monetary
policy shocks on asset prices can be identified because the
variance of shocks is substantially larger on the days in
sub-sample
in Equation 1. Our
identification strategy is borrowed from Rigobon and Sack (2004), who show that the impact of monetary
policy shocks on asset prices can be identified because the
variance of shocks is substantially larger on the days in
sub-sample ![]() . Their paper used the identification
strategy to establish a significant response of 10-year Treasury
yields to monetary policy shocks.
. Their paper used the identification
strategy to establish a significant response of 10-year Treasury
yields to monetary policy shocks.
That monetary policy shocks can influence
10-year real interest rates means that the variance of changes in
these rates is significantly larger on the days in sub-sample
![]() . This effect is not large, but is large
enough to significantly affect the variance of
. This effect is not large, but is large
enough to significantly affect the variance of
![]() . We exploit this effect by
combining it with the assumption that the policy shock to real
interest rates neither affects EMBI+ through
. We exploit this effect by
combining it with the assumption that the policy shock to real
interest rates neither affects EMBI+ through ![]() nor
nor ![]() , but only through its effect
on
, but only through its effect
on ![]() .
.
In sum, we assume that the variance of
interest rate shocks (
![]() ) in sub-sample
) in sub-sample ![]() is higher than the variance in sub-sample
is higher than the variance in sub-sample ![]() ;
whilst the variances of
;
whilst the variances of ![]() and
and ![]() are the same across both sub-samples. As is usual in
other identification strategies for our underlying system of
equations, we assume
are the same across both sub-samples. As is usual in
other identification strategies for our underlying system of
equations, we assume ![]() ,
,
![]() and
and ![]() have no serial correlation and are uncorrelated with each other.
Our assumptions can be written in terms of the second moments of
the shocks in the two sub-samples
have no serial correlation and are uncorrelated with each other.
Our assumptions can be written in terms of the second moments of
the shocks in the two sub-samples ![]() and
and
![]() in the following way:
in the following way:
To help justify the underlying assumptions,
Table 1 shows the
increase in the variation in the U.S. real interest rate and the
change in covariance between the real interest rate and EMBI+
premia over the sub-samples. The fact that the standard deviations
of EMBI+ premia appear to decrease from sub-sample ![]() to sub-sample
to sub-sample ![]() , when we expect mild increases,
suggests that we require a more accurate statistical test of
whether our assumptions on the variance of shocks over the two
sub-samples are valid.7 Applying the test set out in Levene (1960), reported in Table 2, we established
that the standard deviation of the real interest rate increases
significantly in sub-sample
, when we expect mild increases,
suggests that we require a more accurate statistical test of
whether our assumptions on the variance of shocks over the two
sub-samples are valid.7 Applying the test set out in Levene (1960), reported in Table 2, we established
that the standard deviation of the real interest rate increases
significantly in sub-sample ![]() , while the variance
of EMBI+ does not significantly change because the effect of the
variance increase in Equation 2 only weakly
effects the variance of EMBI+ through the interest rate.8
, while the variance
of EMBI+ does not significantly change because the effect of the
variance increase in Equation 2 only weakly
effects the variance of EMBI+ through the interest rate.8
Table 1: Data Descriptives
| Standard Deviation: Sub-sample C | Standard Deviation: Sub-sample N | Covariance With U.S. Real Rate: Sub-sample C | Covariance With U.S. Real Rate: Sub-sample N | |
|---|---|---|---|---|
| U.S. real rate | 0.093 | 0.063 | . | . |
| Emerging Market | 24.491 | 29.020 | 0.198 | -0.211 |
| Latin America | 25.017 | 32.317 | 0.278 | -0.253 |
| Brazil | 30.249 | 48.318 | 0.357 | -0.278 |
| Bulgaria | 24.476 | 27.181 | 0.175 | -0.117 |
| Mexico | 19.221 | 21.876 | 0.066 | -0.214 |
| Panama | 12.486 | 14.849 | 0.028 | -0.208 |
| Peru | 20.892 | 20.939 | 0.128 | -0.185 |
| Venezuela | 43.545 | 50.526 | 0.852 | -0.263 |
Note: 131 observations in sub-sample C, 2,604 days in sub-sample N.
We are not assuming that the FOMC ignores factors that affect emerging market default risk, nor are we supposing that FOMC decisions have no impact on emerging market prices - that is actually the effect we are estimating. We are precisely assuming that FOMC decisions do not directly reveal important information about emerging markets that might otherwise affect EMBI+ premia, they are only affecting EMBI+ premia through changes in U.S. real interest rates. The underlying view is that the Committee might have private information about how it will react to movements in emerging markets and how it plans to conduct monetary policies in general but does not know more than the market about emerging economies.
Table 2: Levene (1960) Test of Equal Variance
| Test Statistic Based on Mean | p-value | |
|---|---|---|
| U.S. real rate | 12.371 | 0.000 |
| Emerging Market | 0.215 | 0.643 |
| Latin America | 0.458 | 0.499 |
| Brazil | 2.273 | 0.132 |
| Bulgaria | 0.000 | 0.977 |
| Mexico | 0.031 | 0.860 |
| Panama | 0.021 | 0.884 |
| Peru | 0.908 | 0.341 |
| Venezuela | 0.635 | 0.801 |
Note: Null hypothesis is equal variance
Now, consider the following variables:
![$\displaystyle \left[ \frac{\Delta i_{C}^{\prime }~}{\sqrt{T_{C}}},~\frac{ \Delta i_{N}^{\prime }}{\sqrt{T_{N}}}\right] ^{\prime }$](img51.gif) |
![$\displaystyle \left[ \frac{\Delta e_{C}^{\prime }}{\sqrt{T_{C}}}~,~\frac{ \Delta e_{N}^{\prime }}{\sqrt{T_{N}}}\right] ^{\prime }$](img54.gif) |
![$\displaystyle \left[ \frac{\Delta i_{C}^{\prime }~}{\sqrt{T_{C}}},~\frac{ -\Delta i_{N}^{\prime }}{\sqrt{T_{N}}}\right] ^{\prime }$](img57.gif) |
A major result in Rigobon and Sack (2004) is that ![]() can be
consistently estimated by a standard instrumental variables
approach with the novel instrument,
can be
consistently estimated by a standard instrumental variables
approach with the novel instrument, ![]() , which is
correlated with the dependent variable,
, which is
correlated with the dependent variable, ![]() , but
is neither correlated with
, but
is neither correlated with ![]() nor
nor ![]() . It is correlated with
. It is correlated with ![]() be
be![]() cause the greater variance in sub-sample
cause the greater variance in sub-sample ![]() implies
the positive correlation between
and
implies
the positive correlation between
and
![]() more than
outweighs the negative correlation between
more than
outweighs the negative correlation between
![]() and
and
![]() . It is
neither correlated with
. It is
neither correlated with ![]() nor
nor ![]() because the positive and negative correlation of
each part of the vector cancel each other out.
because the positive and negative correlation of
each part of the vector cancel each other out.
The usual assumption in IV regressions is
that the instrument affects the dependent variable only through the
regressor. The key difference here is that instead of having a
variable assumed to be correlated with
![]() and uncorrelated with any of the
other variables, we assume that the variance of
and uncorrelated with any of the
other variables, we assume that the variance of
![]() is larger on the days in
sub-sample C and the variances of other variables are the same in
both sub-samples.
is larger on the days in
sub-sample C and the variances of other variables are the same in
both sub-samples.
3 Results
Table 3 presents the results from implementing our identification strategy, which reveals that policy shocks to real interest rates are positively correlated with emerging economies' EMBI+. This coincides with our original intuition that when the U.S. tightens monetary policy, it is harder for emerging economies to borrow, and the risk of default proxied by EMBI+ increases.
Table 3: The Response of EMBI+ Premia to Interest Rate Shocks
| Co-eff | Std Err | T-stat | |
|---|---|---|---|
| Emerging Market | 0.868 | 0.179 | 4.840 |
| Latin America | 1.115 | 0.195 | 5.717 |
| Brazil | 1.334 | 0.269 | 4.969 |
| Bulgaria | 0.649 | 0.170 | 3.808 |
| Mexico | 0.607 | 0.138 | 4.394 |
| Panama | 0.496 | 0.094 | 5.264 |
| Peru | 0.659 | 0.140 | 4.697 |
| Venezuela | 2.279 | 0.318 | 7.162 |
Note: Each estimation uses 2,735 observations.
The magnitude of the response is large: an unexpected increase in the 10-year real interest rate of one basis point leads to an increase in the EMBI+ premium of a similar order of magnitude.
Table 4 shows the
results from analysis of the relationship between U.S. real interest
rates and EMBI+ premia in each separate sub-sample (the results
across both samples are in Table 5). Crucially, the
'normal' correlation between ![]() and
and
![]() is actually negative (and smaller in
absolute value) in sub-sample
is actually negative (and smaller in
absolute value) in sub-sample ![]() . Our interpretation
is that increases in U.S. real interest rates are correlated with
other things that are good for emerging markets and thus decrease
their cost of borrowing. Future research ought to investigate which
aspects of international financial markets, correlated with U.S. real
interest rates, are most important to the risk of emerging market
default.
. Our interpretation
is that increases in U.S. real interest rates are correlated with
other things that are good for emerging markets and thus decrease
their cost of borrowing. Future research ought to investigate which
aspects of international financial markets, correlated with U.S. real
interest rates, are most important to the risk of emerging market
default.
The results in Table 3 are substantially different from the OLS estimates using only the sub-sample C presented in Table 4. While the former shows a strong positive relation, the latter shows a mild and insignificant effect. Rosa (2011) as noted that, in some applications, the results from employing the identification through heteroskedasticity methodology are not much different from a simple OLS using the subsample where the FOMC meets. That is not the case here since we are using the long-term interest rates, where endogeneity is likely to be much more important than when the policy rate is used, and the correlation between variables in the N sample is different from the causal effect.
Table 4: Separate Analysis of Sub-Samples
| Sub-Sample C: Coeff | Sub-Sample C: Std Err | Sub-Sample C: T-Stat | Sub-Sample N: Coeff | Sub-Sample N: Std Err | Sub-Sample N: T-stat | |
|---|---|---|---|---|---|---|
| Emerging Market | 0.230 | 0.224 | 1.029 | -0.494 | 0.087 | -5.700 |
| Latin America | 0.317 | 0.228 | 1.390 | -0.591 | 0.096 | -6.131 |
| Brazil | 0.406 | 0.275 | 1.474 | -0.649 | 0.145 | -4.492 |
| Bulgaria | 0.217 | 0.226 | 0.960 | -0.274 | 0.081 | -3.363 |
| Mexico | 0.089 | 0.177 | 0.503 | -0.500 | 0.065 | -7.692 |
| Panama | 0.036 | 0.114 | 0.311 | -0.487 | 0.044 | -11.186 |
| Peru | 0.146 | 0.191 | 0.766 | -0.430 | 0.062 | -6.937 |
| Venezuela | 0.924 | 0.389 | 2.371 | -0.617 | 0.151 | -4.076 |
Note: 131 observations in sub-sample C, 2,604 days in sub-sample N.
Table 5: Full Sample Analysis
| Co-eff | Std Err | T-stat | |
|---|---|---|---|
| Emerging Market | -0.423 | 0.082 | -5.174 |
| Latin America | -0.503 | 0.091 | -5.535 |
| Brazil | -0.547 | 0.135 | -4.038 |
| Bulgaria | -0.226 | 0.077 | -2.934 |
| Mexico | -0.443 | 0.062 | -7.194 |
| Panama | -0.437 | 0.041 | -10.586 |
| Peru | -0.375 | 0.059 | -6.347 |
| Venezuela | -0.467 | 0.143 | -3.266 |
Note: Each estimation uses 2,735 observations.
4 Concluding Remarks
The strong and positive relation between exogenous changes in U.S. real interest rates and the EMBI+ premium highlights the importance of U.S. interest rate shocks. The fact that the overall correlation between U.S. rates and the EMBI+ premium is negative highlights the importance of other aspects of international financial markets, such as favourable external conditions to emerging economy borrowing. From a policy perspective, our result has implications for proposals to issue debt that is contingent on exogenous factors that affect the ability to repay. One of these ideas is that a higher U.S. real interest rate makes it more difficult for emerging market economies to repay, so reducing emerging market debt payments when U.S. interest rates increase would be welfare improving. Our finding that the overall correlation is negative implies that making emerging market sovereign debt contingent on U.S. real interest rates would have an opposite result from the desired effect. Research on sovereign default should note that shocks affecting foreign real interest rates might have very different effects on emerging market default risk.
References
Arora, V. and Cerisola, M. (2001). How Does U.S. Monetary Policy Influence Sovereign Spreads in Emerging Markets?, IMF Staff Papers 48: 474-498.
Guimaraes, B. (2011). Sovereign default: which shocks matter?, Review of Economic Dynamics 14(4): 553-576.
Levene, H. (1960). Robust tests for equality of variances, in I. O. et al. (ed.), In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling, Stanford University Press, pp. 278-292.
Longstaff, F. A., Pan, J., Pedersen, L. H. and Singleton, K. J. (2011). How sovereign is sovereign credit risk?, American Economic Journal: Macroeconomics 3(2): 75-103.
Neumeyer, P. and Perri, F. (2005). Business cycles in emerging economies: the role of interest rates, Journal of Monetary Economics 52(2): 345-380.
Rigobon, R. (2003). Identification through heteroskedasticity, Review of Economics and Statistics 85(4): 777-792.
Rigobon, R. and Sack, B. (2004). The impact of monetary policy on asset prices, Journal of Monetary Economics 51(8): 1553-1575.
Robitaille, P. and Roush, J. (2006). How Do FOMC Actions and U.S. Macroeconomic Data Announcements Move Brazilian Sovereign Yield Spreads and Stock Prices?, Board of Governors of the Federal Reserve System, International Finance Discussion Paper No. 868.
Rosa, C. (2011). The validity of the Event-Study Approach: Evidence from the Impact of the Fed's Monetary Policy on U.S. and Foreign Asset Prices, Economica (311): 429-439.
Uribe, M. and Yue, V. (2006). Country spreads and emerging countries: Who drives whom?, Journal of International Economics 69(1): 6-36.
Zettelmeyer, J. (2004). The impact of monetary policy on exchange rates: evidence from three small open economies, Journal of Monetary Economics 51(3): 635-652.
A Appendix - Alternative U.S. Interest Rates
In this appendix we prepare four alternative estimates of U.S. real interest rates which are then used in place of the real rates reported in the main text as a robustness exercise.
We obtain two nominal interest rate series and two inflation measures from the Global Financial Database (www.globalfinancialdata.com). Both interest rate series are constant maturity, consistent with the data in the main text. We use a 3 month T-Bill rate consistent with existing quantitative studies in the literature, and a 10 year Treasury Bond rate consistent with the data in the main text because we maintain that long term rates are a more appropriate measure of the opportunity cost to investors in emerging market sovereign debt.
The first measure of inflation is based on the Bureau of Labor Statistics monthly Consumer Price Index. We obtain the annual inflation rate in the year prior to each month, and average over the previous three months' annual inflation rates to obtain a monthly estimate of future inflation. The second measure is the University of Michigan survey of annual CPI inflation expectations, which are also reported monthly. Both monthly series are assigned to the last working day of the month and subsequently cubic splined to obtain interpolated daily series of annual expected inflation.
Each gross interest rate is divided by both gross expected inflation measures and netted. Figure 1 below shows the comparison of rates over time, and Table 6 shows the cross-correlations between the series.
Tables 7 - 16 show the results from repeating the analysis described in the main text with the full sample, individual sub-samples (FOMC and non-FOMC meeting days) and applying the method of identification through heteroscedasticity for the four alternative measures of real interest rates.
When using T-Bill rates, the standard errors are generally lower but the coefficients are much smaller. There are fewer significant coefficients and the magnitudes appear to be lower (no statistical tests of differences were run). Running the analysis separately on the sub-samples shows that the coefficients on the days when the FOMC meet are again insignificant, but those days when the FOMC do not meet appear to be of smaller magnitude although they remain significantly negative.
When using T-Bond rates, the coefficients are generally of comparable magnitudes but the standard errors are much larger resulting in fewer significant positive coefficients. This is probably reflecting the fact that our measures of expected inflation are noisy when applied to daily data. All coefficients that are significant are positive.
Figure 1: U.S. Real Interest Rates
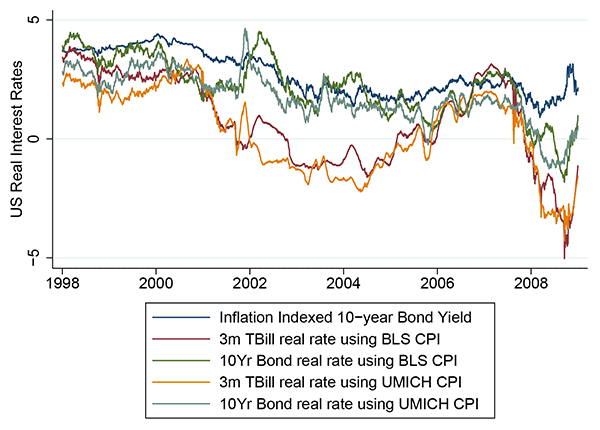
Table 6: Correlation Between Real Interest Rate Measures
| TIPS Yield | T-Bill & BLS CPI | T-Bill & UMICH CPI | T-Bond & BLS CPI | |
|---|---|---|---|---|
| T-Bill & BLS CPI | 0.753 | . | ||
| T-Bill & UMICH CPI | 0.766 | 0.936 | . | |
| T-Bond & BLS CPI | 0.763 | 0.769 | 0.620 | . |
| T-Bond & UMICH CPI | 0.846 | 0.710 | 0.745 | 0.862 |
A.1 T-Bill Rates and Univ. of Michigan CPI Inflation Expectations
Table 7: Full Sample Analysis (T-Bill & BLS CPI)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | -0.301 | 0.060 | -4.986 |
| Latin America | -0.332 | 0.067 | -4.950 |
| Brazil | -0.325 | 0.100 | -3.248 |
| Bulgaria | -0.147 | 0.058 | -2.552 |
| Mexico | -0.211 | 0.045 | -4.688 |
| Panama | -0.207 | 0.031 | -6.678 |
| Peru | -0.237 | 0.044 | -5.419 |
| Venezuela | -0.479 | 0.106 | -4.539 |
Table 8: The Response of EMBI+ Premia to Interest Rate Changes (T-Bill & BLS CPI)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | 0.227 | 0.107 | 2.122 |
| Latin America | 0.165 | 0.115 | 1.443 |
| Brazil | 0.199 | 0.160 | 1.244 |
| Bulgaria | 0.211 | 0.105 | 2.014 |
| Mexico | 0.177 | 0.081 | 2.174 |
| Panama | 0.114 | 0.055 | 2.078 |
| Peru | 0.224 | 0.084 | 2.677 |
| Venezuela | 0.137 | 0.189 | 0.726 |
Table 9: Separate analysis of FOMC and non-FOMC meeting days (T-Bill & BLS CPI)
| Sub-Sample C: Co-eff | Sub-Sample C: StdErr | Sub-Sample C: T-stat | Sub-Sample N: Co-eff | Sub-Sample N: StdErr | Sub-Sample N: T-stat | |
|---|---|---|---|---|---|---|
| Emerging Market | -0.007 | 0.146 | -0.045 | -0.339 | 0.065 | -5.247 |
| Latin America | -0.055 | 0.148 | -0.369 | -0.368 | 0.072 | -5.105 |
| Brazil | -0.033 | 0.178 | -0.184 | -0.364 | 0.108 | -3.358 |
| Bulgaria | 0.053 | 0.152 | 0.347 | -0.173 | 0.062 | -2.812 |
| Mexico | 0.005 | 0.115 | 0.047 | -0.239 | 0.048 | -4.970 |
| Panama | -0.028 | 0.074 | -0.373 | -0.230 | 0.033 | -6.934 |
| Peru | 0.019 | 0.125 | 0.154 | -0.271 | 0.047 | -5.809 |
| Venezuela | -0.135 | 0.269 | -0.502 | -0.524 | 0.113 | -4.639 |
A.2 T-Bill Rates and Univ. of Michigan CPI Inflation Expectations
Table 10: Full Sample Analysis (T-Bill & UMICH CPI exp.)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | -0.241 | 0.059 | -4.117 |
| Latin America | -0.248 | 0.065 | -3.810 |
| Brazil | -0.301 | 0.097 | -3.098 |
| Bulgaria | -0.146 | 0.056 | -2.617 |
| Mexico | -0.203 | 0.044 | -4.661 |
| Panama | -0.191 | 0.030 | -6.343 |
| Peru | -0.238 | 0.043 | -5.595 |
| Venezuela | -0.476 | 0.102 | -4.651 |
Table 11: The Response of EMBI+ Premia to Interest Rate Changes (T-Bill & UMICH CPI exp.)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | 0.282 | 0.112 | 2.513 |
| Latin America | 0.186 | 0.120 | 1.553 |
| Brazil | 0.238 | 0.168 | 1.416 |
| Bulgaria | 0.280 | 0.110 | 2.541 |
| Mexico | 0.235 | 0.086 | 2.747 |
| Panama | 0.153 | 0.058 | 2.646 |
| Peru | 0.281 | 0.088 | 3.203 |
| Venezuela | 0.224 | 0.199 | 1.126 |
Table 12: Separate Analysis of FOMC and Non-FOMC Meeting Days (T-Bill & UMICH CPI exp.)
| Sub-Sample C: Co-eff | Sub-Sample C: StdErr | Sub-Sample C: T-stat | Sub-Sample N: Co-eff | Sub-Sample N: StdErr | Sub-Sample N: T-stat | |
|---|---|---|---|---|---|---|
| Emerging Market | 0.038 | 0.145 | 0.263 | -0.276 | 0.063 | -4.405 |
| Latin America | -0.016 | 0.147 | -0.109 | -0.277 | 0.070 | -3.964 |
| Brazil | -0.013 | 0.177 | -0.074 | -0.336 | 0.105 | -3.214 |
| Bulgaria | 0.081 | 0.151 | 0.539 | -0.174 | 0.059 | -2.929 |
| Mexico | 0.031 | 0.115 | 0.271 | -0.232 | 0.046 | -4.994 |
| Panama | -0.007 | 0.074 | -0.094 | -0.213 | 0.032 | -6.642 |
| Peru | 0.040 | 0.124 | 0.318 | -0.272 | 0.045 | -6.033 |
| Venezuela | -0.102 | 0.268 | -0.380 | -0.522 | 0.109 | -4.783 |
A.3 10Yr Bond Rates and BLS CPI Inflation Expectations
Table 13: Full Sample Analysis (T-Bond & BLS CPI)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | -0.865 | 0.064 | -13.484 |
| Latin America | -0.962 | 0.071 | -13.497 |
| Brazil | -0.975 | 0.108 | -8.997 |
| Bulgaria | -0.377 | 0.063 | -6.014 |
| Mexico | -0.873 | 0.046 | -18.825 |
| Panama | -0.577 | 0.032 | -17.893 |
| Peru | -0.576 | 0.047 | -12.267 |
| Venezuela | -1.027 | 0.114 | -8.986 |
Table 14: The Response of EMBI+ Premia to Interest Rate Changes (T-Bond & BLS CPI)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | 1.316 | 0.509 | 2.586 |
| Latin America | 1.909 | 0.591 | 3.233 |
| Brazil | 2.944 | 0.825 | 3.570 |
| Bulgaria | 1.317 | 0.478 | 2.755 |
| Mexico | 0.686 | 0.373 | 1.840 |
| Panama | 0.679 | 0.268 | 2.533 |
| Peru | 0.684 | 0.372 | 1.837 |
| Venezuela | 2.682 | 0.905 | 2.963 |
Table 15: Separate Analysis of FOMC and Non-FOMC Meeting Days (T-Bond & BLS CPI)
| Sub-Sample C: Co-eff | Sub-Sample C: StdErr | Sub-Sample C: T-stat | Sub-Sample N: Co-eff | Sub-Sample N: StdErr | Sub-Sample N: T-stat | |
|---|---|---|---|---|---|---|
| Emerging Market | -0.378 | 0.210 | -1.801 | -0.899 | 0.067 | -13.453 |
| Latin America | -0.322 | 0.213 | -1.511 | -1.007 | 0.074 | -13.521 |
| Brazil | -0.101 | 0.259 | -0.389 | -1.036 | 0.114 | -9.101 |
| Bulgaria | 0.000 | 0.221 | 0.002 | -0.404 | 0.065 | -6.194 |
| Mexico | -0.526 | 0.161 | -3.259 | -0.898 | 0.048 | -18.615 |
| Panama | -0.297 | 0.105 | -2.828 | -0.597 | 0.034 | -17.758 |
| Peru | -0.298 | 0.180 | -1.657 | -0.595 | 0.049 | -12.251 |
| Venezuela | -0.200 | 0.392 | -0.510 | -1.085 | 0.119 | -9.128 |
A.4 10Yr Bond Rates and Univ. of Michigan CPI Inflation Expectations
Table 16: The Response of EMBI+ Premia to Interest Rate Changes (T-Bond & UMICH CPI exp.)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | -0.761 | 0.063 | -12.149 |
| Latin America | -0.824 | 0.070 | -11.813 |
| Brazil | -0.910 | 0.105 | -8.643 |
| Bulgaria | -0.364 | 0.061 | -5.976 |
| Mexico | -0.830 | 0.045 | -18.373 |
| Panama | -0.537 | 0.031 | -17.056 |
| Peru | -0.559 | 0.046 | -12.244 |
| Venezuela | -0.994 | 0.111 | -8.960 |
Table 17: The Response of EMBI+ Premia to Interest Rate Changes (T-Bond & UMICH CPI exp.)
| Co-eff | StdErr | T-stat | |
|---|---|---|---|
| Emerging Market | 2.144 | 0.807 | 2.656 |
| Latin America | 2.722 | 0.928 | 2.934 |
| Brazil | 4.267 | 1.332 | 3.203 |
| Bulgaria | 2.227 | 0.767 | 2.904 |
| Mexico | 1.334 | 0.599 | 2.227 |
| Panama | 1.180 | 0.441 | 2.677 |
| Peru | 1.294 | 0.579 | 2.237 |
| Venezuela | 4.266 | 1.458 | 2.925 |
Table 18: Separate Analysis of FOMC and Non-FOMC Meeting Days (T-Bond & UMICH CPI exp.)
| Sub-Sample C: Co-eff | Sub-Sample C: StdErr | Sub-Sample C: T-stat | Sub-Sample N: Co-eff | Sub-Sample N: StdErr | Sub-Sample N: T-stat | |
|---|---|---|---|---|---|---|
| Emerging Market | -0.282 | 0.213 | -1.327 | -0.793 | 0.065 | -12.166 |
| Latin America | -0.240 | 0.216 | -1.114 | -0.862 | 0.073 | -11.852 |
| Brazil | -0.056 | 0.261 | -0.215 | -0.966 | 0.110 | -8.747 |
| Bulgaria | 0.063 | 0.222 | 0.284 | -0.392 | 0.063 | -6.206 |
| Mexico | -0.473 | 0.164 | -2.890 | -0.853 | 0.047 | -18.217 |
| Panama | -0.254 | 0.107 | -2.380 | -0.555 | 0.033 | -16.975 |
| Peru | -0.254 | 0.181 | -1.399 | -0.579 | 0.047 | -12.279 |
| Venezuela | -0.127 | 0.395 | -0.321 | -1.051 | 0.115 | -9.127 |
B Appendix - Estimation in Levels
The analysis presented in this appendix is intended to justify time-differencing the data in the paper. We show that (i) there is no significant increase in the variance of the levels of the U.S. real interest rate on the dates the FOMC meets, which is inconsistent with the fundamental assumption underpinning the methodology of identification through heteroskedasticity; and (ii) the data we use are highly persistent over time, and as a result the usual tests cannot reject a unit root. An analysis in levels would be subject to the critique that any results were spurious.
The fundamental assumption underpinning the methodology of identification is not directly testable because we cannot identify the shocks. But the best available evidence we have suggests that it is appropriate to apply the methodology in differences, but not in levels. Table 19 shows the descriptive statistics for our variables in levels using data defined to capture the level of each variable on the day after the FOMC meeting dates. The analysis is repeated in Table 20 using the level of variables on the same day as the FOMC meeting. In both cases, and similar to Table 1, there is no significant difference in the standard deviation of EMBI+ variables on the days when the FOMC meets from the days when it does not. In Table 1 there is a (weakly) significant reduction in the standard deviation of the U.S. real interest rate on the days when the FOMC meets, and in Table 19 there is no significant change. This is not consistent with the assumption that the variance of the interest rate would significantly increase on FOMC meeting days.
Table 21 shows the results from tests of stationarity on the variables in levels and first differences. Both tests include a constant but no trend term; the Phillips-Perron specification includes seven Newey-West lags.
The variables in levels are all non-stationary. Identical specifications for the differenced time-series employed in the paper show they are stationary. We conclude that it is more appropriate to specify the model in terms of differences than in levels.
Table 19: Data Descriptives (Levels)
| Standard Deviation: FOMC | Standard Deviation: No FOMC | Covariance With U.S. Real Rate: FOMC | Covariance With U.S. Real Rate: No FOMC | Levene (1960) Test of Equal Variance: Mean Test | Levene (1960) Test of Equal Variance: p-Value | |
|---|---|---|---|---|---|---|
| U.S. real rate | 0.885 | 0.898 | . | . | 2.717 | 0.066 |
| Emerging Market | 314.595 | 319.333 | 194.756 | 202.617 | 0.103 | 0.749 |
| Latin America | 296.342 | 295.865 | 124.524 | 127.392 | 0.037 | 0.847 |
| Brazil | 421.413 | 418.673 | 153.673 | 156.705 | 0.078 | 0.780 |
| Bulgaria | 302.345 | 313.245 | 223.860 | 238.411 | 0.449 | 0.503 |
| Mexico | 180.834 | 184.149 | 114.845 | 120.151 | 0.183 | 0.668 |
| Panama | 119.021 | 120.635 | 61.070 | 63.281 | 0.009 | 0.924 |
| Peru | 217.518 | 213.622 | 124.616 | 123.782 | 0.032 | 0.858 |
| Venezuela | 381.318 | 386.208 | 130.639 | 152.410 | 0.008 | 0.927 |
Notes: Levene (1960) test statistic based on mean; null hypothesis is equal variance
FOMC means the set of days immediately after FOMC meetings
Table 20: Data Descriptives (Levels)
| Standard Deviation: FOMC | Standard Deviation: No FOMC | Covariance With U.S. Real Rate: FOMC | Covariance With U.S. Real Rate: No FOMC | Levene (1960) Test of Equal Variance: Mean Test | Levene (1960) Test of Equal Variance: p-Value | |
|---|---|---|---|---|---|---|
| U.S. Real Rate | 0.883 | 0.898 | . | . | 0.668 | 0.414 |
| Emerging Market | 314.952 | 319.314 | 194.621 | 202.629 | 0.070 | 0.792 |
| Latin America | 298.070 | 295.774 | 123.374 | 127.455 | 0.054 | 0.816 |
| Brazil | 426.906 | 418.392 | 151.228 | 156.836 | 0.091 | 0.764 |
| Bulgaria | 309.204 | 312.911 | 227.779 | 238.222 | 0.096 | 0.757 |
| Mexico | 182.428 | 184.070 | 115.595 | 120.116 | 0.147 | 0.702 |
| Panama | 120.181 | 120.577 | 61.350 | 63.272 | 0.018 | 0.893 |
| Peru | 216.637 | 213.664 | 123.413 | 123.843 | 0.018 | 0.894 |
| Venezuela | 379.584 | 386.308 | 130.098 | 152.424 | 0.003 | 0.953 |
Notes: Levene (1960) test statistic based on mean; null hypothesis is equal variance
FOMC means the set of days on which FOMC meetings are held
Table 21: Stationarity Test Statistics
| Levels: Phillips-Perron | Levels: Dickey-Fuller | First Differences: Phillips-Perron | First Differences: Dickey-Fuller | |
|---|---|---|---|---|
| U.S. real rate | -1.32 | -1.28 | -24.36 | -25.14 |
| Emerging Market | -1.11 | -1.03 | -22.70 | -23.83 |
| Latin America | -1.49 | -1.46 | -23.32 | -24.66 |
| Brazil | -2.84 | -2.80 | -22.36 | -23.47 |
| Bulgaria | -1.60 | -1.59 | -25.08 | -25.26 |
| Mexico | -1.51 | -1.50 | -23.05 | -24.31 |
| Panama | -0.88 | -0.59 | -24.74 | -25.27 |
| Peru | -1.95 | -1.92 | -25.21 | -25.58 |
| Venezuela | -0.44 | -0.29 | -25.50 | -26.43 |
Notes: Null hypothesis is stationarity in all unit root tests
Phillips-Perron specifications use seven Newey-West lags
Critical values are -3.43 (1%); -2.86 (5%); -2.57 (10%)
C Appendix - Dynamic Model
This appendix reports the results from a
dynamic specification of the model, as an investigation of dynamic
effects, for example overshooting, in the reaction of the EMBI+
spread to changes in U.S. real interest rates9. We maintain the
definition of the variables as in the main text, i.e.
![]() , but
re-specify the model as follows:
, but
re-specify the model as follows:
| Table 22: | 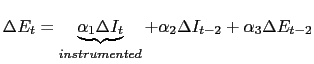
|
||
| Table 23: |
The Tables below should be compared with
Tables 3 and 5 in the main text. Following the notation in the main
text, the instruments employed in the 2SLS estimates of dynamic
model in Table 22 are
![]() and
and
![]() .
.
We find that in general the coefficients on the lags in both specifications were statistically insignificant and conclude that there is no systematic evidence of dynamic effects present in the data.
Table 22: Identification Via Heteroscedasticity Dynamic Analysis
| Co-Efficients: US RR | Co-Efficients: L.US RR | Co-Efficients: L.DV | Standard Error: US RR | Standard Error: L.US RR | Standard Error: L.DV | T-Statistic: US RR | T-Statistic: L.US RR | T-Statistic: L.DV | |
|---|---|---|---|---|---|---|---|---|---|
| E. Market | 0.96 | 0.00 | 7.34 | 0.17 | 0.00 | 6.50 | 5.57 | 2.56 | 1.13 |
| L Am. | 1.23 | 0.00 | 4.26 | 0.19 | 0.00 | 7.08 | 6.52 | 0.37 | 0.60 |
| Brazil | 1.48 | 0.00 | 2.49 | 0.26 | 0.00 | 9.81 | 5.69 | 0.17 | 0.25 |
| Bulgaria | 0.69 | 0.00 | 8.56 | 0.16 | 0.00 | 6.21 | 4.17 | 0.48 | 1.38 |
| Mexico | 0.68 | 0.00 | 6.18 | 0.13 | 0.00 | 4.99 | 5.15 | 1.55 | 1.24 |
| Panama | 0.54 | -0.00 | 2.57 | 0.09 | 0.00 | 3.46 | 5.91 | -0.01 | 0.74 |
| Peru | 0.73 | 0.00 | 5.22 | 0.13 | 0.00 | 5.05 | 5.43 | 1.66 | 1.04 |
| Venezuela | 2.28 | 0.00 | -1.24 | 0.31 | 0.00 | 11.76 | 7.33 | 4.82 | -0.11 |
Notes: DV - dependent variable - EMBI+ premium.
US RR - U.S. real interest rate.
Each estimation uses 2,611 observations.
Table 23: Full Sample Dynamic Analysis
| Co-Efficients: US RR | Co-Efficients: L.US RR | Co-Efficients: L.DV | Standard Error: US RR | Standard Error: L.US RR | Standard Error: L.DV | T-Statistic: US RR | T-Statistic: L.US RR | T-Statistic: L.DV | |
|---|---|---|---|---|---|---|---|---|---|
| E. Market | -0.39 | -0.02 | 0.04 | 0.08 | 0.08 | 0.02 | -4.64 | -0.25 | 2.00 |
| L. Am. | -0.47 | -0.06 | 0.00 | 0.09 | 0.09 | 0.02 | -5.00 | -0.68 | 0.06 |
| Brazil | -0.49 | -0.16 | 0.00 | 0.14 | 0.14 | 0.02 | -3.53 | -1.11 | 0.13 |
| Bulgaria | -0.20 | 0.17 | -0.03 | 0.08 | 0.08 | 0.02 | -2.49 | 2.12 | -1.65 |
| Mexico | -0.41 | -0.03 | 0.00 | 0.06 | 0.06 | 0.02 | -6.63 | -0.47 | 0.19 |
| Panama | -0.42 | -0.06 | 0.01 | 0.04 | 0.04 | 0.02 | -9.91 | -1.39 | 0.75 |
| Peru | -0.36 | 0.03 | 0.07 | 0.06 | 0.06 | 0.02 | -6.02 | 0.51 | 3.67 |
| Venezuela | -0.47 | -0.13 | 0.03 | 0.15 | 0.15 | 0.02 | -3.18 | -0.88 | 1.27 |
Notes: DV - dependent variable - EMBI+ premium.
US RR - U.S. real interest rate.
Each estimation uses 2,611 observations.
D Appendix - Tests of Variance
The increase in the variation in the U.S. real
interest rate and the change in covariance between the real
interest rate and EMBI+ premia over the sub-samples are apparent
from Table 1 in the main text, but the fact that the standard
deviations of EMBI+ premia appear to decrease from sub-sample
![]() to sub-sample
to sub-sample ![]() , when we
expect mild increases, suggests we require a more accurate
statistical test of whether our assumptions on the variance of
shocks over the two sub-samples are valid.
, when we
expect mild increases, suggests we require a more accurate
statistical test of whether our assumptions on the variance of
shocks over the two sub-samples are valid.
Importantly, however, we cannot apply standard tests of variance equality, because they require that the underlying data be normally distributed. As the plots of each variables' quantiles against those of the normal distribution in Figure 2 demonstrate, and the empirical tests of skewness and kurtosis confirm in Table 24, none of our series are normally distributed.
Levene (1960) provides a test where the null is equal variance when samples are drawn from a distribution that is not Gaussian normal. The results from this test are presented in Table 25, and show that the variance of the U.S. real interest rate significantly increases, but the variance of all EMBI+ premia does not change significantly.10
On the basis of these results, we conclude that the standard deviation of the real interest rate increases significantly on the days when the variance of interest rate movements is greater. We cannot reject the null that the variance of EMBI+ is the same in both sub-samples. According to our assumptions, the policy shocks should yield only small increases in the variance of EMBI+, as the unexpected policy shocks to U.S. real interest rates are only a small part of the variation of emerging market default risk, so the results of the tests on variances in both sub-samples, albeit not conclusive, are not at odds with the identifying assumptions.
Figure 2: Q-Q Plots of Each Variable Quantiles Against Normal Distribution Quantiles
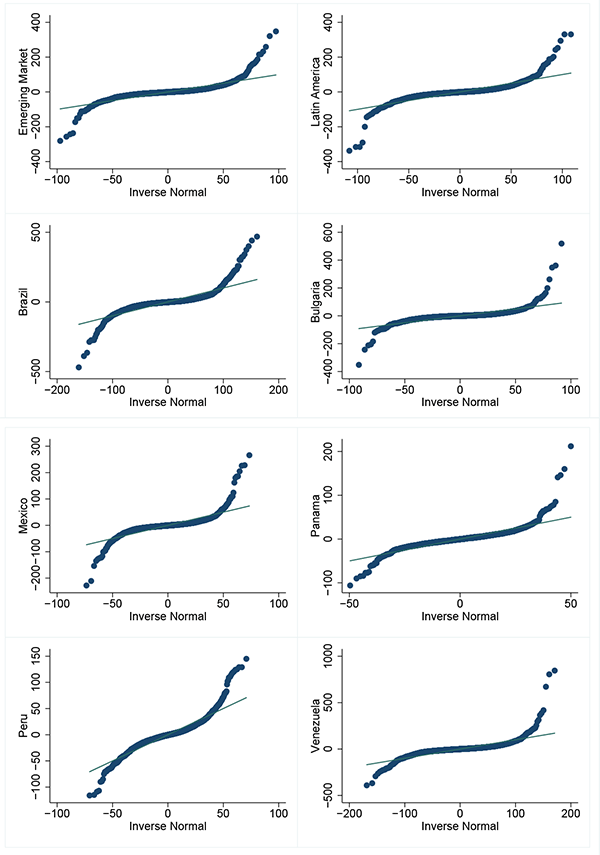
Table 24: Test of Skewness and Kurtosis
| Skewness p-value | Kurtosis p-value | |
|---|---|---|
| U.S. real rate | 0.000 | 0.000 |
| Emerging Market | 0.000 | 0.000 |
| Latin America | 0.000 | 0.000 |
| Brazil | 0.000 | 0.000 |
| Bulgaria | 0.000 | 0.000 |
| Mexico | 0.000 | 0.000 |
| Panama | 0.000 | 0.000 |
| Peru | 0.000 | 0.000 |
| Venezuela | 0.000 | 0.000 |
Note: Null hypothesis is equal variance
Table 25: Levene (1960) Test of Equal Variance
| Test Statistic Based on Mean | p-value | |
|---|---|---|
| U.S. real rate | 12.371 | 0.000 |
| Emerging Market | 0.215 | 0.643 |
| Latin America | 0.458 | 0.499 |
| Brazil | 2.273 | 0.132 |
| Bulgaria | 0.000 | 0.977 |
| Mexico | 0.031 | 0.860 |
| Panama | 0.021 | 0.884 |
| Peru | 0.908 | 0.341 |
| Venezuela | 0.635 | 0.801 |
Note: Null hypothesis is equal variance
Footnotes
1. Uribe and Yue (2006) also study the effect of interest rates and the EMBI+ premium on variables like output, and in that case our methodology cannot be applied. Return to text
2. Our analysis is robust to the use of alternative measures of the real interest rate based on inflation-adjusted nominal Treasury rates of 3 months and 10 years. See Appendix A. Return to text
3. EMBI+ tracks total returns for traded U.S. dollar- and other external currency-denominated Brady bonds, loans, Eurobonds and local market instruments. Return to text
4. For additional justification for using data in differences rather than levels, see Appendix B. Return to text
5. Sub-sample C contains the dates of scheduled and unscheduled FOMC meetings and the Federal Reserve Chairman's semi-annual monetary policy testimony to Congress. For a full list of these dates, see http://www.federalreserve.gov/monetarypolicy/fomccalendars.htm Return to text
6. We show in Appendix C that allowing for a richer lag structure does not materially affect the results. Return to text
7. We cannot apply standard tests of variance equality, because they require that the underlying data be normally distributed. As is reported in Appendix D, demonstrated through plots of each variables' quantiles against those of the normal distribution and empirical tests of skewness and kurtosis, none of our series are normally distributed. Return to text
8. Although the test results are presented using the sample mean of the data, similar results are obtained when using the 50th percentile or 10% trimmed mean. Return to text
9. We gratefully acknowledge this follows the suggestion of an anonymous referee. Return to text
10. The results are presented using the sample mean of the data, similar results are obtained when using the 50th percentile or 10% trimmed mean. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text