
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1052, August 2012 --- Screen Reader
Version*
Individual Price Adjustment Along the Extensive Margin**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Firms employ a rich variety of pricing strategies whose implications for aggregate price dynamics often diverge. This situation poses a challenge for macroeconomists interested in bridging micro and macro price stickiness. In responding to this challenge, we note that differences in macro price stickiness across pricing mechanisms can often be traced back to price changes that are either triggered or cancelled by shocks. We exploit observed micro price behavior to quantify the importance of this margin of adjustment for the response of inflation to shocks. Across a range of empirical exercises, we find strong evidence that changes in the timing of price adjustments contribute significantly to the flexibility of the aggregate price level.
Keywords: Inflation, intensive margin, extensive margin
JEL classification: E31
1 Introduction
Over the past decade, economists have devoted substantial efforts to documenting basic facts about consumer micro price behavior, an endeavor made possible by the increased availability of large datasets.1 A salient finding is that firms employ a rich variety of pricing strategies. In some sectors, such as energy, air travel, or fresh produce, firms adjust prices frequently, whereas in others, such as newspapers, health services, or maintenance activities, firms adjust prices infrequently. Even at the level of universal product codes (UPC), researchers have found variation across firms in the magnitude and frequency of price adjustments. And while sales and promotions are a defining feature of the way items are marketed to consumers in retail trade, temporary price discounts are uncommon in several other sectors.
Many macroeconomists had hoped that the new micro evidence would shorten the list of pricing mechanisms used in macroeconomic applications by revealing which mechanisms have empirical support and which ones do not. The variety of new micro facts has instead stimulated researchers to introduce several new mechanisms and to refine existing ones.2 In retrospect, this outcome was probably unavoidable. As has long been recognized in the field of industrial organization (e.g., Carlton [1989]), product markets differ along several dimensions that influence pricing strategies. These dimensions include the number of buyers and sellers, the degree of product homogeneity, the durability of items, the presence of long-term relationships between buyers and sellers, the role of advertisement and information, the firm's price discrimination motives, and the ability to hold inventories. This heterogeneity would be immaterial to macroeconomists if all pricing mechanisms implied similar effects of aggregate shocks on inflation and output. Unfortunately, the choice of a particular mechanism is often consequential in macroeconomic applications. For instance, models matching the same average frequency and size of price changes can vary greatly in the speed of aggregate shock pass-through (see Golosov and Lucas [2007] for an illustration). The variety of facts and pricing mechanisms thus underscores the importance of identifying key features of micro price behavior that are important for aggregate adjustment and that macro models should aim to reproduce.
In this paper, we seek to connect micro and macro price stickiness by distinguishing between price adjustments that are determined ahead of shocks and those that are either triggered or cancelled by shocks. This distinction offers a natural way of contrasting popular time-dependent models, for which the timing of all price changes is predetermined, and state-dependent models, for which the timing of price changes can respond to shocks. In practice, asserting whether a price adjustment is predetermined or not, or should have occurred when it did not, is a challenging task. However, we argue that one can go a long way in deriving the aggregate implications of micro price stickiness by focusing on the initial response to aggregate shocks and by studying the determinants of individual price adjustments. The key finding of our empirical implementation is that some shocks alter the timing of individual price changes in ways that contribute significantly to the flexibility of the aggregate price level. One immediate implication is that pricing models abstracting from variation in the timing of price changes are missing an important channel of macroeconomic adjustment.
We formalize the distinction between predetermined price
adjustments and those triggered or cancelled by shocks using the
generalized ![]() model developed by Caballero and Engel
(1993a, 1993b, and 1999). The model is consistent with lumpy and
infrequent price adjustments, a key empirical feature that we seek
to reproduce, and has the added benefit of encompassing several
pricing mechanisms commonly used in macroeconomic applications.
Following Caballero and Engel (2007, henceforth "CE"), we then
decompose the initialinflation response to an aggregate shock as
the sum of an intensive margin and an extensive margin. The
intensive margin captures the contribution of predetermined
price adjustments and is connected to the observed frequency of
price changes. The extensive margin captures the
contribution of price adjustments that are triggered or cancelled
by the shock. It is at the heart of many debates about how
item-level price stickiness translates into aggregate price
stickiness, and is the key statistic that our paper aims to
quantify.
model developed by Caballero and Engel
(1993a, 1993b, and 1999). The model is consistent with lumpy and
infrequent price adjustments, a key empirical feature that we seek
to reproduce, and has the added benefit of encompassing several
pricing mechanisms commonly used in macroeconomic applications.
Following Caballero and Engel (2007, henceforth "CE"), we then
decompose the initialinflation response to an aggregate shock as
the sum of an intensive margin and an extensive margin. The
intensive margin captures the contribution of predetermined
price adjustments and is connected to the observed frequency of
price changes. The extensive margin captures the
contribution of price adjustments that are triggered or cancelled
by the shock. It is at the heart of many debates about how
item-level price stickiness translates into aggregate price
stickiness, and is the key statistic that our paper aims to
quantify.
The extensive margin depends on what we call the individual reset price; that is, the posted price that a firm would set if granted a one-time opportunity to adjust it for free, with all constraints otherwise remaining in place (including the possibility that the posted price will not change for some time). If individual reset prices were observed, one could assess the role of the extensive margin by studying how deviations of posted prices from individual reset prices are distributed and how these deviations influence price adjustment decisions. However, partial identification is possible by noting that, in a broad class of models, firms reveal their individual reset price whenever they adjust their posted price. The history of price adjustments can therefore provide a benchmark for the path of individual reset prices. Individual price changes can also reveal the amount of price pressure having accumulated between adjustment periods, making the distribution of price changes an informative object about underlying inflation.
We next show how one can use variation in the shape of the distribution of nonzero price changes to derive lower bounds on the importance of adjustment along the extensive margin. If the timing of all price changes was predetermined, then an inflationary shock would simply create additional price pressure on items. As a result, the distribution of individual price changes would shift laterally by an amount equivalent to the extra pressure. Our procedure compares the observed distribution to an estimate of the distribution that would have prevailed in the absence of the shock. Any evidence that the two distributions differ by more than a translation is attributed to the extensive margin. We apply our procedure to the study of three macroeconomic shocks whose timing and size are rather well identified: the sudden devaluation of the Mexican peso in late 1994 and the hikes in the Mexican value-added tax (VAT) in April 1995 and January 2010. Our results point to substantial price level flexibility that was due primarily to changes in the timing of price adjustments.
The extensive margin can be especially important in the presence of a selection effect by which items having accumulated much price pressure are especially likely to have the timing of their adjustment altered by shocks. Such a selection effect was highlighted in the work of Caplin and Spulber (1987) and Golosov and Lucas (2007), and later clarified in CE, as the root of the lack of intrinsic persistence in standard menu-cost models. In the absence of a selection effect, the accumulation of aggregate price pressure should lead to a rise in the average size of individual price changes. To check whether this is the case empirically, we use the massive repricing of items created by the Mexican VAT hike in April 1995 to compute the distribution of consumer price changes in an environment dominated by aggregate reset price inflation. We find no drift in the average price change even as large amounts of aggregate reset price inflation accumulate, consistent with strong selectivity.
We find more direct support for a selection effect by studying how price adjustment decisions relate to deviations from the price of local competitors, which we use as a proxy for the individual reset price. We undertake this task using the IRI Marketing database, a very large (and relatively new to macroeconomists) dataset of weekly scanner prices from grocery stores and drugstores across the United States. The exceptional sample coverage makes it possible to track prices of identical items across multiple competing outlets. We follow Campbell and Eden (2010) in calculating the deviation from the average price of local competitors at the UPC-market level. After accounting for permanent differences across stores, we find somewhat limited dispersion in the level of prices within local markets. Some of that dispersion is due to firms choosing prices away from those of their local competitors, which cautions against interpreting all forms of price dispersion as evidence of resource misallocations. We also find support for an adjustment probability that increases in our proxy of the (absolute) deviation. Like the limited price dispersion, this finding is consistent with a selection effect. Finally, we use our estimates of the distribution of deviations and of the probability of a price change conditional on the deviation to compute the extensive margin directly from the micro data. This exercise again points to an economically important role of changes in the timing of price adjustments for price level flexibility.
The paper is organized as follows. Section 2 presents our conceptual framework, highlights the importance of price adjustments triggered or cancelled by shocks in connecting micro and macro price stickiness, and discusses their identification. Section 3 proposes a method for bounding the importance of the extensive margin and applies it to the study of three macroeconomic shocks. Section 4 uncovers evidence of a selection effect in micro price adjustment by first analyzing the distribution of price changes as price pressure builds up, and then by estimating the adjustment hazard. Section 5 offers some concluding remarks.
2 Conceptual Framework
We use a variant of the generalized ![]() model
developed in a series of papers by Caballero and Engel (1993a,
1993b, and 1999) to formalize the link between changes in the
timing of individual price adjustments and macro price flexibility.
The main appeal of this sticky-price framework is that it
encompasses several pricing mechanisms commonly used in
macroeconomic applications and can incorporate real rigidities.
model
developed in a series of papers by Caballero and Engel (1993a,
1993b, and 1999) to formalize the link between changes in the
timing of individual price adjustments and macro price flexibility.
The main appeal of this sticky-price framework is that it
encompasses several pricing mechanisms commonly used in
macroeconomic applications and can incorporate real rigidities.
2.1 Economic Environment
We assume that time is discrete and that the length of the time
intervals match that of price collection. The economy is populated
by a continuum of firms indexed by
![]() . Each firm produces a
single item sold directly to consumers. Due to the presence of
nominal rigidities, the posted price,
. Each firm produces a
single item sold directly to consumers. Due to the presence of
nominal rigidities, the posted price, ![]() , may deviate from the target price,
, may deviate from the target price,
![]() , between price adjustment
periods (all prices are in natural logs). The object
, between price adjustment
periods (all prices are in natural logs). The object
![]() corresponds to the posted price
chosen by a firm granted a one-time opportunity to adjust it
freely, with all constraints otherwise remaining in place,
including the possibility that the new price may be sticky in
subsequent periods. In choosing
corresponds to the posted price
chosen by a firm granted a one-time opportunity to adjust it
freely, with all constraints otherwise remaining in place,
including the possibility that the new price may be sticky in
subsequent periods. In choosing
![]() , the firm takes into account
how today's posted price impacts profitability in the current and
future periods; therefore, it generally differs from the price that
maximizes current-period profits.3We will refer to
, the firm takes into account
how today's posted price impacts profitability in the current and
future periods; therefore, it generally differs from the price that
maximizes current-period profits.3We will refer to
![]() as the firm's individual
reset price. Our terminology highlights the connection between
as the firm's individual
reset price. Our terminology highlights the connection between
![]() and the posted price chosen by
the firm when resetting it. It also ties in with the idea of
aggregate reset price inflation studied by Bils, Klenow, and
Malin (forthcoming), who recover the component of innovations to
individual reset prices that is common across items under specific
pricing assumptions.
and the posted price chosen by
the firm when resetting it. It also ties in with the idea of
aggregate reset price inflation studied by Bils, Klenow, and
Malin (forthcoming), who recover the component of innovations to
individual reset prices that is common across items under specific
pricing assumptions.
Because the individual reset price is a forward-looking object,
it can be a complicated function of how the economy is expected to
evolve over time, and how that evolution impacts future price
adjustment decisions. In our benchmark specification, we assume
that innovations to
![]() are described by
are described by
| (1) |
where
![]() is aggregate reset price
inflation and
is aggregate reset price
inflation and ![]() is a mean-zero idiosyncratic
component that is
is a mean-zero idiosyncratic
component that is ![]() across firms and over
time. Our specification of
across firms and over
time. Our specification of ![]() introduces
a random-walk element in individual reset prices. We make no
particular assumption regarding the process describing the
aggregate component of individual reset prices, except that its
innovations,
introduces
a random-walk element in individual reset prices. We make no
particular assumption regarding the process describing the
aggregate component of individual reset prices, except that its
innovations,
![]() , are common across items. For
consistency, we also impose that firms share the same price-setting
mechanism, to be described shortly. These simplifying assumptions
are unlikely to hold in reality. For instance, differences in price
stickiness, real rigidities, or item durability can lead to
heterogenous responses to aggregate shocks.4 We partially
address this concern in our empirical implementation by considering
relatively homogenous groups of products.
, are common across items. For
consistency, we also impose that firms share the same price-setting
mechanism, to be described shortly. These simplifying assumptions
are unlikely to hold in reality. For instance, differences in price
stickiness, real rigidities, or item durability can lead to
heterogenous responses to aggregate shocks.4 We partially
address this concern in our empirical implementation by considering
relatively homogenous groups of products.
The decision to change the posted price is made after observing
the shocks and aggregate variables in the period. We define the
deviation from the individual reset price as
![]() , where
, where
![]() is the firm's posted price
inherited from the previous period. Following CE, we postulate that
the probability of observing a price change is a time-invariant
smooth function of the deviation from the individual reset price,
is the firm's posted price
inherited from the previous period. Following CE, we postulate that
the probability of observing a price change is a time-invariant
smooth function of the deviation from the individual reset price,
![]() , called the "adjustment hazard function." The model gives rise to infrequent
and lumpy price adjustments, which is a central feature of consumer
price data that we seek to reproduce.5
, called the "adjustment hazard function." The model gives rise to infrequent
and lumpy price adjustments, which is a central feature of consumer
price data that we seek to reproduce.5
One appealing aspect of postulating a smooth adjustment hazard
function is that forecasting individual price adjustments is
typically a difficult task, as periods marked by frequent price
changes are sometimes followed by long spells of inaction (and
vice-versa) with no apparent change in economic conditions. The
adjustment hazard captures this randomness by leaving some
uncertainty regarding the timing of adjustments. Its dependence on
![]() allows for the possibility that large
deviations, which are suboptimal from the point of view of profit
maximization, are more likely than small ones to trigger price
adjustments. The function can also embed asymmetries in the
response to positive and negative deviations that some authors
argue could play a role in explaining apparent differences in the
response of aggregate inflation to positive and negative shocks
(e.g., Caballero and Engel [1993b]). In what follows, we treat the
adjustment hazard as a function of
allows for the possibility that large
deviations, which are suboptimal from the point of view of profit
maximization, are more likely than small ones to trigger price
adjustments. The function can also embed asymmetries in the
response to positive and negative deviations that some authors
argue could play a role in explaining apparent differences in the
response of aggregate inflation to positive and negative shocks
(e.g., Caballero and Engel [1993b]). In what follows, we treat the
adjustment hazard as a function of ![]() alone.
All results carry through if we instead consider
alone.
All results carry through if we instead consider
![]() ,
where
,
where
![]() is a vector of idiosyncratic
states that influence the adjustment probability but otherwise have
no impact on how a firm's individual reset price responds to an
aggregate shock (e.g., month-specific and duration-specific dummies
capturing seasonal patterns and duration dependence,
respectively).6
is a vector of idiosyncratic
states that influence the adjustment probability but otherwise have
no impact on how a firm's individual reset price responds to an
aggregate shock (e.g., month-specific and duration-specific dummies
capturing seasonal patterns and duration dependence,
respectively).6
2.2 Price Adjustment Along the Intensive and the Extensive Margins
Given the above assumptions, consumer price inflation can be expressed as
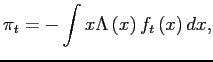
|
(2) |
where
![]() is the density of
deviations from individual reset prices prevailing at the beginning
of period
is the density of
deviations from individual reset prices prevailing at the beginning
of period ![]() . Consider the impact on inflation of an
aggregate shock to
. Consider the impact on inflation of an
aggregate shock to
![]() taking place immediately
before price adjustment decisions. For now, we assume that the
shock,
taking place immediately
before price adjustment decisions. For now, we assume that the
shock, ![]() , is fully passed through to
individual reset prices, thus ruling out real rigidities. We shall
return to the implications of real rigidities shortly. The shock
shifts the distribution of deviations from individual reset prices
by
, is fully passed through to
individual reset prices, thus ruling out real rigidities. We shall
return to the implications of real rigidities shortly. The shock
shifts the distribution of deviations from individual reset prices
by ![]() , resulting in observed inflation
, resulting in observed inflation
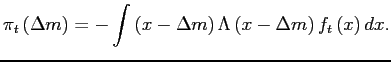
|
(3) |
Taking a first-order Taylor series expansion of
![]() around
around
![]() , rearranging terms, and taking the
limit as
, rearranging terms, and taking the
limit as
![]() , one obtains
, one obtains
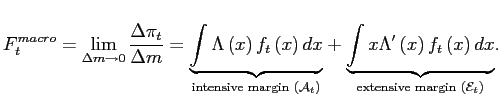
|
(4) |
The above statistic captures the share of an (infinitesimal)
aggregate shock to individual reset prices passed-through to posted
prices upon impact. CE refer to this object as the index of
macroeconomic flexibility, which they denote
![]() . This index has two components.
The intensive margin,
. This index has two components.
The intensive margin,
![]() , captures the contribution of
items whose posted price would have been adjusted absent the
shock. These items respond to the shock by altering the size of
their price adjustment. The extensive margin,
, captures the contribution of
items whose posted price would have been adjusted absent the
shock. These items respond to the shock by altering the size of
their price adjustment. The extensive margin,
![]() , captures the inflation
contribution of items whose price adjustment is either triggered
or cancelled by the occurrence of the shock, as hinted by the
presence of
, captures the inflation
contribution of items whose price adjustment is either triggered
or cancelled by the occurrence of the shock, as hinted by the
presence of
![]() .7
.7
We note several aspects of equation (4) that are useful in understanding the nature of the two margins and in assessing their empirical importance. First, the intensive and the extensive margins are functions of deviations from individual reset prices, which are typically unobserved. Under the assumptions made thus far, however, firms reveal their individual reset price whenever they adjust their posted price. Moreover, the size of price changes corresponds to the amount of price pressure that has cumulated since the last price adjustment. We call these two implications of our framework the revelation principle. This principle will play a central role in our empirical strategy, which is laid out in section 3.
Second, the intensive margin has a strong connection to
observables. To see this, notice that integrating the adjustment
hazard over the distribution of deviations gives the observed
frequency of price changes. In low-inflation environments, the
fraction of adjusting prices typically does not vary much due to
offsetting movements in the number of price increases and price
decreases (see Klenow and Kryvtsov [2008] and Gagnon [2009]). For
these environments, the average frequency of price changes,
![]() , offers a reasonable
approximation of the intensive margin,
, offers a reasonable
approximation of the intensive margin,
![]() . Appendix B provides
estimates of the average frequency of price changes for the U.S.
CPI and IRI Marketing scanner database. The extensive margin is
more difficult to relate to observables because disentangling items
whose price adjustment is either triggered or cancelled by the
shock from items whose price adjustment is predetermined is a
challenging task. That said, in section 3, we will
show how one can use changes in the shape of the
distribution of price changes to bound its macroeconomic
importance.
. Appendix B provides
estimates of the average frequency of price changes for the U.S.
CPI and IRI Marketing scanner database. The extensive margin is
more difficult to relate to observables because disentangling items
whose price adjustment is either triggered or cancelled by the
shock from items whose price adjustment is predetermined is a
challenging task. That said, in section 3, we will
show how one can use changes in the shape of the
distribution of price changes to bound its macroeconomic
importance.
Third, the decomposition offers an intuitive way of
distinguishing between popular time-dependent models, for which the
timing of all price changes is predetermined, and state-dependent
models, for which the timing of price changes can be impacted by
shocks. In time-dependent models such as the popular Calvo (1983)
model and fixed-duration contracts (Taylor 1980), by construction
![]() . More generally, the
frequency of price changes is a lower bound on the index of
macroeconomic flexibility because the extensive margin is typically
positive.
. More generally, the
frequency of price changes is a lower bound on the index of
macroeconomic flexibility because the extensive margin is typically
positive.
Fourth, there need not be many price changes triggered or
cancelled by a shock for the extensive margin to be a major
contributor to the inflation response. In the presence of a
selection effect by which items with much price pressure are
especially likely to have their adjustment either triggered or
cancelled by the shock, a small number of items revising the timing
of their price adjustment can have a large impact on inflation. For
example, if a 1-percent shock to
![]() induces a firm to raise its
price by 10 percent rather than keep it constant (thus
releasing pressure accumulated from a variety of sources since its
last price adjustment), then the impact of that single price change
on inflation will be as large as that of 10
predetermined price changes increasing their size by an extra
percentage point. Caplin and Spulber (1987) and Golosov and Lucas
(2007) trace the lack of intrinsic persistence in standard
menu-cost models to this selection effect.
induces a firm to raise its
price by 10 percent rather than keep it constant (thus
releasing pressure accumulated from a variety of sources since its
last price adjustment), then the impact of that single price change
on inflation will be as large as that of 10
predetermined price changes increasing their size by an extra
percentage point. Caplin and Spulber (1987) and Golosov and Lucas
(2007) trace the lack of intrinsic persistence in standard
menu-cost models to this selection effect.
Fifth, the shape of the distribution of deviations, ![]() , also affects the magnitude of the selection effect.
If
, also affects the magnitude of the selection effect.
If
![]() is large in regions
where
is large in regions
where
![]() is large and the
adjustment hazard is steep, then the extensive margin will be
important. That said, identifying the distribution of deviations
over time can be challenging due to its dependence on the history
of shocks, especially in periods of elevated macroeconomic
instability. To circumvent this difficulty, our analysis refrains
from characterizing the full dynamic process of inflation, focusing
instead on the initial response to shocks for which a reasonable
estimate of
is large and the
adjustment hazard is steep, then the extensive margin will be
important. That said, identifying the distribution of deviations
over time can be challenging due to its dependence on the history
of shocks, especially in periods of elevated macroeconomic
instability. To circumvent this difficulty, our analysis refrains
from characterizing the full dynamic process of inflation, focusing
instead on the initial response to shocks for which a reasonable
estimate of ![]() can be computed.
can be computed.
Finally, equation (4) was derived for an
infinitesimal shock ![]() . In the data, large
shocks are not only the easiest to identify but also the most
likely to alter the timing of price changes. Inference about the
relative importance for shock pass-through of price changes that
are predetermined versus those that are triggered or cancelled may
thus depend on the magnitude of the shock. One can decompose the
initial pass-through to a shock of arbitrary size as
. In the data, large
shocks are not only the easiest to identify but also the most
likely to alter the timing of price changes. Inference about the
relative importance for shock pass-through of price changes that
are predetermined versus those that are triggered or cancelled may
thus depend on the magnitude of the shock. One can decompose the
initial pass-through to a shock of arbitrary size as
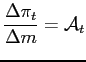 |
(5) |
where
![]() is the sum, scaled by
is the sum, scaled by ![]() , of all terms of
order two or higher in the Taylor-series expansion of
, of all terms of
order two or higher in the Taylor-series expansion of
![]() around
around
![]() . The terms
. The terms
![]() and
and
![]() are as
defined in equation (4). In particular, the
intensive margin is the frequency of price changes that would have
been observed in the absence of the shock. The term
are as
defined in equation (4). In particular, the
intensive margin is the frequency of price changes that would have
been observed in the absence of the shock. The term
![]() converges to zero as
converges to zero as
![]() . Importantly, it equals
zero whenever all price adjustments are predetermined. For this
reason, our empirical implementation of equation (5) using observed shocks, which
is presented in section 3.1, lumps together
. Importantly, it equals
zero whenever all price adjustments are predetermined. For this
reason, our empirical implementation of equation (5) using observed shocks, which
is presented in section 3.1, lumps together
![]() and
and
![]() .
We will refer to any price movement that contributes to
.
We will refer to any price movement that contributes to
![]() or
or
![]() as an adjustment along the extensive margin.
as an adjustment along the extensive margin.
2.3 The Revelation Principle and the Distribution of Price Changes
Under the revelation principle, individual reset prices are
observed whenever posted prices are adjusted. For example, Bils and
Klenow (2004) report an average frequency of price changes of
26 percent in the U.S. CPI in the mid-1990s.
Applying the principle to these data implies that
![]() is observed about a quarter of
the time. The revelation principle also leads to new
interpretations of the distribution of price changes. For items
experiencing a price adjustment, we have
is observed about a quarter of
the time. The revelation principle also leads to new
interpretations of the distribution of price changes. For items
experiencing a price adjustment, we have
![]() . The distribution of
price changes thus maps into the distribution of deviations from
individual reset prices that prevailed for price adjusters.
. The distribution of
price changes thus maps into the distribution of deviations from
individual reset prices that prevailed for price adjusters.
Alternatively,
![]() equals the cumulative change
in the individual reset price since the last nominal adjustment.
Hence, for a firm changing its posted price after keeping it
constant for
equals the cumulative change
in the individual reset price since the last nominal adjustment.
Hence, for a firm changing its posted price after keeping it
constant for ![]() periods,
periods,
![]() . As such,
the distribution of price changes can be used to extract
information on how price pressure builds over time at the item
level. For instance, one can condition this distribution on the
number of periods since the last price adjustment (we use this
approach in section 4). These observations
suggest that the distribution of price changes is a richly
informative object and that replicating it in macro models is a key
step towards ensuring consistency with microeconomic facts.8
. As such,
the distribution of price changes can be used to extract
information on how price pressure builds over time at the item
level. For instance, one can condition this distribution on the
number of periods since the last price adjustment (we use this
approach in section 4). These observations
suggest that the distribution of price changes is a richly
informative object and that replicating it in macro models is a key
step towards ensuring consistency with microeconomic facts.8
These interpretations come with some qualifications. First, Chevalier and Kashyap (2011) present empirical evidence that the price of competing brands may be jointly determined by retailers, so that it may be difficult to analyze individual price decisions separately from those of their close substitutes. Second, there could be environments in which both the timing and size of price adjustments are predetermined; for example, if firms followed price plans or pre-announced price changes. Price adjustments that do not coincide with a reoptimization obscure the inference about the set of firms adjusting their posted prices in response to shocks. That said, there is limited support for widespread use of pre-announcements, at least at the retail level, and of price plans by firms. Fabiani et al. (2006) report that price reviews are more common than price changes among European firms. Alvarez, Lippi, and Paciello (2011) argue that adjusting prices without reoptimizing them is a suboptimal strategy in low-inflation environments. Finally, the individual reset price may not be unique; for instance, when firms follow mixed pricing strategies.9For all situations described above, the revelation principle does not hold with the consequence that individual price changes need not equal the amount of price pressure having accrued since the last adjustment.
2.4 Real Rigidities
We have so far abstracted from real rigidities, which dampen the response of individual reset prices to nominal shocks. Several authors have argued that real rigidities are essential for sticky-price models to generate the observed inertia in aggregate inflation and output.10 Attempts to infer their importance from micro price data have yielded mixed results.11 We will not seek to reconcile the micro and macro evidence on real rigidities, but simply stress that key properties of equation (4) extend to environments where they are present. To this end, we follow CE in assuming that aggregate reset price inflation is described as
| (6) |
The parameter ![]() controls the extent to which firms
trade-off raising their price in line with the price of their
competitors versus matching the rate of money growth,
controls the extent to which firms
trade-off raising their price in line with the price of their
competitors versus matching the rate of money growth,
![]() . This money growth term should
be interpreted as standing for a host of nominal shocks impacting
. This money growth term should
be interpreted as standing for a host of nominal shocks impacting
![]() , such as nominal wages or the
nominal exchange rate. The elasticity
, such as nominal wages or the
nominal exchange rate. The elasticity ![]() is an index
of real rigidities; the smaller is
is an index
of real rigidities; the smaller is ![]() , the faster
the response of individual reset prices to the aggregate shock. The
process described by equation (6) should not be seen as a
general description of
, the faster
the response of individual reset prices to the aggregate shock. The
process described by equation (6) should not be seen as a
general description of
![]() but as a local approximation
taken at a particular point in time.12
but as a local approximation
taken at a particular point in time.12
As stated in CE, the presence of real rigidities makes the index of macroeconomic flexibility a nonlinear function of the intensive and extensive margins,
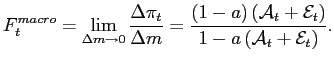
|
(7) |
This function is strictly increasing in
![]() , is
bounded between 0 and
, is
bounded between 0 and ![]() whenever
whenever
![]() , and is decreasing in the extent of real rigidities (i.e.,
, and is decreasing in the extent of real rigidities (i.e.,
![]() ).13 Hence, the main implication of real
rigidities is that they dampen the transmission of the shock to
individual reset prices. The initial shift in the distribution of
deviations from individual reset prices that accompanies a shock
).13 Hence, the main implication of real
rigidities is that they dampen the transmission of the shock to
individual reset prices. The initial shift in the distribution of
deviations from individual reset prices that accompanies a shock
![]() is now
is now
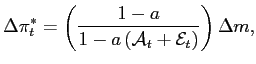
which is less than ![]() whenever
whenever
![]() is less than
is less than ![]() . Importantly for our empirical
analysis, the revelation principle continues to hold: Individual
reset prices are revealed through price adjustments and the size of
price changes corresponds to the price pressure accumulated since
the previous adjustment. Moreover, as was the case in our baseline
framework without real rigidities, the extensive margin may add
substantially to the flexibility of the price level.
. Importantly for our empirical
analysis, the revelation principle continues to hold: Individual
reset prices are revealed through price adjustments and the size of
price changes corresponds to the price pressure accumulated since
the previous adjustment. Moreover, as was the case in our baseline
framework without real rigidities, the extensive margin may add
substantially to the flexibility of the price level.
3 Extensive Margin Adjustment to Large Shocks
Our first strategy to assess the importance of adjustment along
the extensive margin stems from the following observation: If the
timing of all price changes was predetermined, then the initial
impact of a shock to
![]() would be to shift the
distribution of individual price changes laterally by the size of
the shock. Aside from this translation, the shape of the
distribution would be preserved. One can thus measure the
importance of adjustment along the extensive margin by comparing
the observed distribution of price changes to an estimate of the
distribution that would have been observed in the absence ofthe
shock (the "counterfactual distribution"). Although this
counterfactual distribution is not observed, one can often infer
its shape by considering the distribution that prevailed prior to
the shock. This section formalizes these ideas and then applies
them to the study of the Mexican peso collapse in late 1994 and to
the Mexican VAT hikes of April 1995 and January 2010.
would be to shift the
distribution of individual price changes laterally by the size of
the shock. Aside from this translation, the shape of the
distribution would be preserved. One can thus measure the
importance of adjustment along the extensive margin by comparing
the observed distribution of price changes to an estimate of the
distribution that would have been observed in the absence ofthe
shock (the "counterfactual distribution"). Although this
counterfactual distribution is not observed, one can often infer
its shape by considering the distribution that prevailed prior to
the shock. This section formalizes these ideas and then applies
them to the study of the Mexican peso collapse in late 1994 and to
the Mexican VAT hikes of April 1995 and January 2010.
3.1 Inference from the Distribution of Price Changes
Let
![]() and
and
![]() be
measures representing the observed and counterfactual distributions
of price changes, respectively. These measures have a mass point at
0 corresponding to the fraction of items whose price is unchanged.
They are otherwise equal to the density of individual price
changes. Suppose that an observable shock
be
measures representing the observed and counterfactual distributions
of price changes, respectively. These measures have a mass point at
0 corresponding to the fraction of items whose price is unchanged.
They are otherwise equal to the density of individual price
changes. Suppose that an observable shock ![]() raises all individual reset prices by
raises all individual reset prices by
![]() upon impact. We can
rewrite observed inflation from equation (3) as
upon impact. We can
rewrite observed inflation from equation (3) as
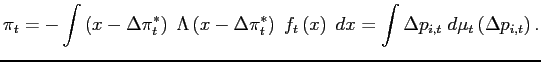
The above equality uses the revelation principle to connect deviations from individual reset prices to observed price adjustments. Absent the shock, inflation would have been
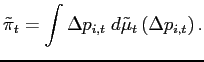
The difference between ![]() and
and
![]() is the initial boost to
inflation attributable to the shock,
is the initial boost to
inflation attributable to the shock,
![]() . Adding and subtracting the
inflation contribution of predetermined price changes,
. Adding and subtracting the
inflation contribution of predetermined price changes,
![]() , performing a change of variable, and reorganizing terms, we get
, performing a change of variable, and reorganizing terms, we get
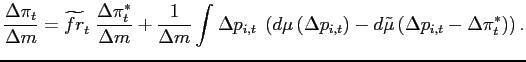
|
(8) |
The first and second terms on the right-hand side capture the
contribution to the index of macroeconomic flexibility of
adjustment along the intensive and the extensive margin,
respectively. The shock initially shifts the distribution of
predetermined price changes by
![]() , resulting in a boost
to inflation of
, resulting in a boost
to inflation of
![]() .
The shock may also trigger or cancel price adjustments, in which
case the observed distribution of price changes will differ from
the counterfactual distribution shifted by
.
The shock may also trigger or cancel price adjustments, in which
case the observed distribution of price changes will differ from
the counterfactual distribution shifted by
![]() . Our decomposition
attributes any such difference to an adjustment along the extensive
margin.
. Our decomposition
attributes any such difference to an adjustment along the extensive
margin.
If we knew
![]() , then computing the
contribution of adjustment along each margin would be
straightforward given an estimate of the counterfactual
distribution. Absent knowledge of
, then computing the
contribution of adjustment along each margin would be
straightforward given an estimate of the counterfactual
distribution. Absent knowledge of
![]() , we can nevertheless compute
bounds on the importance of adjustment along the extensive margin.
We pursue two strategies to achieve this objective.
, we can nevertheless compute
bounds on the importance of adjustment along the extensive margin.
We pursue two strategies to achieve this objective.
First, in our "full-pass-through" approach, we assume full
immediate pass-through of the shock to individual reset prices (
![]() ), thus
ruling out real rigidities. With estimates of
), thus
ruling out real rigidities. With estimates of
![]() and
and
![]() in hand, we then compute
the contribution of adjustment along the extensive margin in
equation (8) as
a residual. To see how this approach provides a lower bound, note
that given
in hand, we then compute
the contribution of adjustment along the extensive margin in
equation (8) as
a residual. To see how this approach provides a lower bound, note
that given
![]() and
and
![]() , the larger is
, the larger is
![]() , the larger
will be the importance of adjustment along the intensive margin.
Assuming full immediate pass-through to
, the larger
will be the importance of adjustment along the intensive margin.
Assuming full immediate pass-through to
![]() of the shock thus minimizes
the importance of adjustment along the extensive margin.
of the shock thus minimizes
the importance of adjustment along the extensive margin.
In our second approach, we assume that price adjustments
triggered or cancelled by the shock are not subject to a selection
effect. In such a case, the initial impact of the shock is to shift
the counterfactual distribution of price changes by
![]() and to scale it by a
factor
and to scale it by a
factor
![]() . This situation is
similar to what would happen in a Calvo model in which the
probability of price adjustment, while exogenous to the firm,
varies with the state of the economy. For this reason, and to
highlight the model-dependence of this computation, we refer to
this approach as "Calvo+." In the absence of the shock,
inflation would be given by
. This situation is
similar to what would happen in a Calvo model in which the
probability of price adjustment, while exogenous to the firm,
varies with the state of the economy. For this reason, and to
highlight the model-dependence of this computation, we refer to
this approach as "Calvo+." In the absence of the shock,
inflation would be given by
![]() ,
where
,
where
![]() is the average size of
nonzero price changes. Following a shock
is the average size of
nonzero price changes. Following a shock ![]() ,
and absent real rigidities, the average nonzero price change would
increase by
,
and absent real rigidities, the average nonzero price change would
increase by ![]() and the frequency of price
changes would rise to
and the frequency of price
changes would rise to ![]() , so that inflation
would equal
, so that inflation
would equal
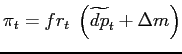 .
The boost to inflation due to the shock can be written as
.
The boost to inflation due to the shock can be written as
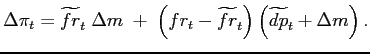
|
(9) |
Given the observed and the counterfactual distribution of price
changes (i.e., with knowledge of ![]() ,
,
![]() ,
,
![]() , and
, and
![]() ), one can recover
), one can recover ![]() and the respective contributions to
and the respective contributions to
![]() of adjustment along
the intensive and the extensive margins.
of adjustment along
the intensive and the extensive margins.
The approaches described above to recover the importance of adjustment along the extensive margin are applicable to the study of the initial response to well-identified aggregate shocks. More generally, one may wonder whether observed price behavior can be used to recover a time series of aggregate reset price inflation and of the importance of adjustment along the extensive margin. In appendix C, we illustrate the challenges of doing so using a related method proposed by Bils, Klenow, and Malin (forthcoming).
3.2 The Late-1994 Peso Devaluation
Prior to the collapse of the peso in late 1994, Mexico was operating under a crawling peg system in which the exchange rate acted as the economy's de facto nominal anchor. Facing escalating pressure on its foreign exchange reserves, the government announced a 15-percent devaluation of the currency on December 19, 1994. The measure proved insufficient and was abandoned three days later in favor of a free-floating system. A week after the initial devaluation, the exchange rate had lost about 40 percent of its value vis-à-vis the U.S. dollar. Annualized inflation, which had hovered around 7 percent in 1994, jumped to more than 40 percent in early 1995. The devaluation is a particularly interesting shock because it was broadly unexpected and its timing is clear. Moreover, its occurrence late in December means that the price of most items in the CPI had already been collected for that month.
The upper panel of figure 1 shows the distribution of monthly price changes observed in January 1995 along with the distribution that prevailed 12 months earlier, which we use as our counterfactual distribution.14 We do not depict the mass points at zero because they do not contribute to inflation. The fraction of nonzero price changes doubled from 24.9 percent in January 1994 to 50.7 percent in January 1995, pointing to a major role of the extensive margin in the adjustment to the macro shock. The actual distribution lost some of its mass of negative price changes relative to the counterfactual, especially in the -10 percent to 0 percent range, while gaining significantly more mass on the positive side. The jump in the frequency of price changes was observed across all major groups of products and is perhaps clearest among product categories whose frequencies were initially low to moderate. Processed food and nonenergy industrial goods witnessed increases in the frequency of price changes of 30 percentage points or more. The distribution for unprocessed food, with its pre-shock frequency of price changes around 40 percent, already featured an important role for the intensive margin as a large number of price changes were predetermined. The arrival of the shock pushed the frequency up to about 55 percent.
We compute our two sets of lower bounds to gauge the importance
of adjustment along the extensive margin. The first bound posits
full immediate pass-through of the nominal exchange rate
devaluation, ![]() , to the price of imported final
consumption items and imported intermediate inputs going into the
production of final consumption items. If there are no real
rigidities, the change in the optimal reset prices is
, to the price of imported final
consumption items and imported intermediate inputs going into the
production of final consumption items. If there are no real
rigidities, the change in the optimal reset prices is
![]() , where
, where
![]() measures the importance of imports in
the consumption basket. Based on input-output tables, Burstein,
Eichenbaum, and Rebelo (2005) estimate the total import content of
Mexican consumption expenditures around that period to be 10.9 percent (and a direct import content
only half as large), a figure reflecting Mexico's low openness at
the time. Setting
measures the importance of imports in
the consumption basket. Based on input-output tables, Burstein,
Eichenbaum, and Rebelo (2005) estimate the total import content of
Mexican consumption expenditures around that period to be 10.9 percent (and a direct import content
only half as large), a figure reflecting Mexico's low openness at
the time. Setting ![]() and
and
![]() (roughly the peso depreciation
in the month that followed its collapse), we get that individual
reset prices should have jumped 5 percentage points under full pass
through. The second bound is based on equation (9).
(roughly the peso depreciation
in the month that followed its collapse), we get that individual
reset prices should have jumped 5 percentage points under full pass
through. The second bound is based on equation (9).
As seen in table 2,
both approaches suggest that adjustment along the extensive margin
was the dominant channel. Under the full-pass-through method, the
extensive margin accounts for over two thirds of the initial price
level response. The Calvo+ method provides a similar lower bound
(63 percent). Table 2 also provides estimates by
special groups of product using the same value of ![]() . With the exception of unprocessed food, all special
groups of items suggest contributions of the extensive margin in
excess of 75 percent. The relatively small share
for unprocessed food likely reflects the initially high frequency
of price changes (38.4 percent) which, all else
equal, tends to boost the role of the intensive margin. In
addition, the import content of unprocessed food items may have
been higher than 10.9 percent, which would tend to
raise the lower bound on the extensive margin. Finally, we note
that the shape of the actual distributions of price changes
displayed in figure 1 appears inconsistent with the random selection of items whose price
change is triggered by the shock. In particular, the positive
skewness increased following the shock, which is suggestive of a
role for the selection effect in the extensive margin, contrary to
the assumption behind the Calvo+ method.
. With the exception of unprocessed food, all special
groups of items suggest contributions of the extensive margin in
excess of 75 percent. The relatively small share
for unprocessed food likely reflects the initially high frequency
of price changes (38.4 percent) which, all else
equal, tends to boost the role of the intensive margin. In
addition, the import content of unprocessed food items may have
been higher than 10.9 percent, which would tend to
raise the lower bound on the extensive margin. Finally, we note
that the shape of the actual distributions of price changes
displayed in figure 1 appears inconsistent with the random selection of items whose price
change is triggered by the shock. In particular, the positive
skewness increased following the shock, which is suggestive of a
role for the selection effect in the extensive margin, contrary to
the assumption behind the Calvo+ method.
Our full-pass-through method assumed that the devaluation was the only shock to individual reset prices in late 1994. However, the rise in the price level in 1995 was much larger than implied by the devaluation alone, hinting that other factors also pushed up individual reset prices. Some of these factors arguably had limited impact initially. Notably, monetary policy was tight in early 1995 as the central bank pushed up overnight rates to contain the outflow of capital. In addition, labor costs did not accelerate until late 1995. Also consistent with a somewhat moderate initial response of individual reset prices is the change in inflation expectations. According to a survey of private forecasters conducted by the Bank of Mexico (reported by Capistrán and López-Moctezuma [2010]), respondents surveyed in January and February 1995 expected consumer prices to rise 25 percent over the course of the year, roughly half the observed increase that year but significantly more than the 7 percent rise experienced in the twelve months to December 1994. As an alternative gauge of the amount of price pressure, we recomputed our bounds assuming that the initial shock to reset prices was 18 percentage points. This alternative scenario, also reported in table 2, implies that almost a third of the shock was passed-through to prices upon impact, with the extensive margin making a significant contribution in most groups of products.
To put our bound estimates into perspective, recall that the extensive margin is zero whenever the timing of all price adjustments is predetermined. The working paper version of CE further shows that, as a rule of thumb, the extensive margin approximately accounts for two-third of the index of macroeconomic flexibility in models featuring a smooth adjustment hazard that is increasing in the (absolute) size of deviations and is zero if no price pressure is present. Our bound estimates derived from the revision to inflation forecasts are an intermediate case between these two benchmarks, whereas our bounds obtained under full exchange rate pass-through are aligned with CE's rule of thumb.
On a related note, micro price studies have documented the presence of seasonal patterns in the timing of consumer price adjustments for many product categories. Several authors (e.g., Dhyne et al. [2005]) have associated such patterns to features of time-dependent pricing models and to fixed-duration contracts in particular. However, a preference for implementing price changes at particular times of the year needs not imply that the timing of price changes is exogenous to the firm. The behavior of services prices in the wake of the peso crisis illustrates this point. From 1995 to 2000, a quarter of these prices were adjusted every January, a figure almost twice as large as in other months of the year (13 percent). As the inflationary consequences of the peso crisis drew to an end, the January frequency of price changes stepped down to below 15 percent in 2001 and stayed near that level thereafter. This step down offers further evidence that the number of firms adjusting their price is responsive to aggregate conditions, consistent with an economically important role of adjustment along the extensive margin.
3.3 Hikes in the Mexican Value-Added Tax
Changes in VAT are relatively simple to study because their
timing and size are observed by economic agents. Mexican firms must
include the VAT and mandated duties in their posted prices. Changes
in VAT affect effective mark-ups over costs, creating an incentive
for price adjustments. About a third of items in the Mexican CPI
excluding housing rents are subject to either the VAT or special
duties. Exempt items include most education services, food at home
excluding beverages, patented drugs, and books and periodicals.
Items subject to special duties include gasoline, phone lines,
tobacco products, and alcoholic beverages. The most recent VAT hike
occurred on January 1, 2010, when the rate rose by one percentage
point throughout Mexico. This shock was much smaller than the
devaluation and thus less likely to present strong nonlinear
effects (i.e.,
![]() in equation (5) is
likely small). Firms had a few price collection periods to prepare
for its implementation. The VAT hike also coincided with a rise in
special duties on a few products. A more substantial 5-percentage
point hike took place amid the peso crisis on April 1, 1995, when
the Mexican government, faced with an urgent need for revenues,
increased the rate from 10 to 15 percent. Its large size aside, two
features make the 1995 hike particularly interesting. First, it was
decreed on March 18, giving retailers little notice before its
enactment. Second, firms located in the touristic regions of Baja
California and Quintana Roo, and within a narrow corridor along the
country's southern and northern international borders, were exempt
from the hike. We will use these regions as a control group to
analyze the impact of the hike.
in equation (5) is
likely small). Firms had a few price collection periods to prepare
for its implementation. The VAT hike also coincided with a rise in
special duties on a few products. A more substantial 5-percentage
point hike took place amid the peso crisis on April 1, 1995, when
the Mexican government, faced with an urgent need for revenues,
increased the rate from 10 to 15 percent. Its large size aside, two
features make the 1995 hike particularly interesting. First, it was
decreed on March 18, giving retailers little notice before its
enactment. Second, firms located in the touristic regions of Baja
California and Quintana Roo, and within a narrow corridor along the
country's southern and northern international borders, were exempt
from the hike. We will use these regions as a control group to
analyze the impact of the hike.
Figures 2 and 3 show the observed distributions of price changes associated with the January 2010 and April 1995 VAT hikes, respectively. For the 2010 hike, our counterfactual distribution is the average density of price changes in the month of January during the years 2003 to 2007. For the 1995 hike, our counterfactual distribution is the one that prevailed that month in regions not subject to the increase. This regional difference approach helps control for macroeconomic shocks other than the VAT hike that likely influenced pricing decisions at the time, notably the sharp contraction in economic activity.
For both hikes, we find strong responses of the frequency of price changes. Price changes among taxable items were twice as frequent in January 2010 (38.5 percent) than in January of 2003 to 2007 (average of 17.9 percent). In April 1995, 75.6 percent of taxable items in regions subject to the hike experienced a price adjustment, compared to 48.0 percent in regions exempt from the hike. As is apparent from figures 2 and 3, a large proportion of price changes clustered around 1 percent in 2010 and 5 percent in 1995. Many firms also seized the opportunity to raise prices by more than the hike, providing evidence that price pressure from other sources was being released in the process. Note that these relatively large price adjustments triggered by the shock are especially important contributors to the initial pass-through. For items exempted from the VAT hikes, such as food products, the observed and counterfactual distributions of price changes had similar shape during both VAT hike episodes.
Under the assumption of full immediate pass-through of the VAT hike, the price of taxable items should have risen 0.90 percent in 2010 and 4.45 percent in 1995. As reported in table 3, the observed rate of inflation for taxable items in 2010 was 0.65 percentage point higher than the counterfactual rate, consistent with an index of macroeconomic flexibility of about 75 percent. The initial pass-through rate was especially high for taxable nonenergy industrial goods (83.6 percent) but only about a third for taxable services. The difference in inflation for taxable items in April 1995 between regions subject to and exempt from the hike is consistent with a somewhat lower index of62.8 percent. However, this estimate likely understates the initial pass-through rate in April 1995. Inflation was running higher in exempt regions in early 1995, consistent with border regions experiencing greater price pressure from the devaluation. If we add the inflation differential for non-taxable items observed in April 1995 to the inflation response of taxable items, then we obtain an initial pass-through rate closer to 80 percent.
Table 3 also reports
lower bounds on the relative importance of adjustment along the
extensive margin. For the 2010 hike, the full-pass-through method
suggests that at least three quarters of the observed jump in
![]() was attributable to adjustment
along the extensive margin, a finding that holds for both goods and
services. The corresponding lower bounds for 1995 are noticeably
smaller at about a quarter or less. This result is unsurprising in
light of the high frequency of price changes under the
counterfactual scenario, which implies that the timing of a large
number of price adjustments was determined ahead of the tax hike.
These results offer an interesting contrast between the sources of
adjustment to the two VAT hikes. While both episodes shared similar
degrees of initial pass-through, price adjustment in the
low-inflation environment of 2010 operated to a greater extent via
the extensive margin--despite a smaller shock--than in the
high-inflation environment of 1995.15
was attributable to adjustment
along the extensive margin, a finding that holds for both goods and
services. The corresponding lower bounds for 1995 are noticeably
smaller at about a quarter or less. This result is unsurprising in
light of the high frequency of price changes under the
counterfactual scenario, which implies that the timing of a large
number of price adjustments was determined ahead of the tax hike.
These results offer an interesting contrast between the sources of
adjustment to the two VAT hikes. While both episodes shared similar
degrees of initial pass-through, price adjustment in the
low-inflation environment of 2010 operated to a greater extent via
the extensive margin--despite a smaller shock--than in the
high-inflation environment of 1995.15
We also note that several implications of the Calvo+ lower bound
method are counterintuitive. Absent a selection effect, ![]() is revealed by the difference between the observed
and counterfactual average (nonzero) price change. This difference
was negative for some groups of products, notably services,
following the VAT hikes, leading to the unappealing implication
that the shock was deflationary. And for categories with positive
estimates of
is revealed by the difference between the observed
and counterfactual average (nonzero) price change. This difference
was negative for some groups of products, notably services,
following the VAT hikes, leading to the unappealing implication
that the shock was deflationary. And for categories with positive
estimates of ![]() , we sometimes find that the
index of macroeconomic flexibility is greater than one. Such an
overshooting is at odds with the data because we find no evidence
of inflation payback (or, for that matter, continued pass-through)
in the months that followed the hikes. We interpret these
counterintuitive implications as the data rejecting the absence of
selection effects in the response to the VAT hike, as posited by
the Calvo+ approach.
, we sometimes find that the
index of macroeconomic flexibility is greater than one. Such an
overshooting is at odds with the data because we find no evidence
of inflation payback (or, for that matter, continued pass-through)
in the months that followed the hikes. We interpret these
counterintuitive implications as the data rejecting the absence of
selection effects in the response to the VAT hike, as posited by
the Calvo+ approach.
4 Some Evidence of a Selection Effect
Adjustment along the extensive margin could be especially relevant for macro price stickiness if items with large deviations from their individual reset price are more likely than others to have the timing of their price adjustment altered by shocks. This section first documents indirect manifestations of such a selection effect on the observed distribution of price changes, and then attempts a more direct assessment by studying how a firm's pricing decisions relate to those of its local competitors.
4.1 Price Pressure and the Distribution of Price Changes
One consequence of the presence of a selection effect is that the distribution of deviations should remain relatively compact. This observation has testable implications for the shape of the distribution of nonzero price changes. Absent a selection effect, the size of (nonzero) individual price changes should equal, on average, the amount of aggregate reset price inflation having accrued since the last adjustment. Also, absent a selection effect, the dispersion of individual price changes should rise as idiosyncratic shocks pile up. The data provide little empirical support for either phenomenon.
We use the massive repricing of items associated with the April 1995 Mexican VAT hike to look for a drift in the mean price change conditional on the number of periods since the last adjustment (a statistic called the "duration" or the "age of the price" in the literature). Although we do not observe aggregate reset price inflation directly, we know that it was substantial at the time because price adjustments were frequent and the CPI rose 40 percent in the 12 months that followed the hike. We consider only items that experienced a price change in April 1995, so that any pressure on individual reset prices stemming from the VAT hike and other sources should have been released that month. We then look at the first price adjustment that followed the hike conditional on the duration of the price. For example, the 3-month-duration distribution uses only items that experienced a price change in April 1995 and had their next price change in July 1995. Such a conditioning ensures that items have similar degrees of cumulated aggregate reset price inflation given the timing of their first price adjustment following the VAT hike.
As figure 4 shows, the distributions of price changes are remarkably similar across durations. For all special groups of products considered, we find no apparent rise in the mean nonzero price change in the first six months following the hike. For instance, the average price change among nonenergy industrial goods was roughly 10 percent whether items had their first adjustment one month, three months, or six months after the VAT hike. The rise in the price index of nonenergy industrial goods differed much over these horizons, however, at 7 percent after one month and at almost 20 percent after six months. Our findings are similar for other groups of products. A related observation is that the average price change taking place shortly after the VAT hike is larger than the amount of cumulated inflation, whereas the average price change taking place several periods after the VAT hike is smaller than the amount of cumulated inflation. This behavior is consistent with early price changers having initially more price pressure to release than others in the sample due to idiosyncratic factors, and late price changers initially benefiting from an offsetting of aggregate reset price inflation by idiosyncratic shocks, thus limiting the extent of the deviation from their individual reset price.
To gauge the degree of similarity across the distributions at various durations, we compute Kolmogorov-Smirnov statistics to test the hypothesis that the samples of nonzero price changes used to compute the distributions at various durations are drawn from the same population. In the vast majority of cases, we cannot reject at the 5-percent significance level that pairs of the distributions shown in figure 4 are statistically different.16 One may suspect that the absence of rejection is due to the low power of the Kolmogorov-Smirnov test, especially given that the number of usable observations declines rapidly with the duration considered. However, the test would have easily rejected the null of no difference in nearly all cases if the mean of the distributions had drifted by the amount of cumulated inflation.
Low-inflation environments arguably provide better conditions to identify any drift in the dispersion of nonzero price changes as idiosyncratic shocks accumulate. Figure 5 presents the distributions in the U.S. consumer prices for four special groups of products. We find no obvious increase in the dispersion of price changes as a function of duration, consistent with a selection effect limiting the size of price adjustments as idiosyncratic shocks accumulate. If anything, some groups of products display a small decrease in the dispersion of price changes conditional on the duration. Arguably, our distributions do not control for heterogeneity in price-setting practices, which could imply, for example, that items with relatively elevated idiosyncratic noise choose to reprice more often than those facing less volatility. Nevertheless, the findings are consistent with that reported by Campbell and Eden (2010) and Klenow and Kryvtsov (2008), who control for such heterogeneity.
4.2 Local Competition and the Adjustment Hazard
We next investigate how an item's price adjustment probability relates to the deviation from its individual reset price. An immediate difficulty in pursuing this objective is that the deviation is typically not observed unless there is a price adjustment. There are two approaches in the literature for dealing with this hurdle. The first approach is to parametrize the shape of the adjustment hazard to target moments of some aggregate variables of interest (e.g., Caballero and Engel [1993a and 1993b]). It has the benefit of not requiring the identification of individual reset prices but comes at the cost of ignoring rich micro data information. The second approach, which we follow below, is to proxy the deviation using information from observables. This approach has notably been employed to study car purchase decisions by Eberly (1994) and Attanasio (2000), and hiring decisions by Caballero, Engel, and Haltiwanger (1997).
Applications of this latter approach to the study of pricing decisions have been constrained by the lack of micro data that can be used to proxy individual reset prices. We note two exceptions. Using weekly scanner data from a large U.S. retailer, Eichenbaum, Jaimovich, and Rebelo (2011) show that the probability of observing a change in an item's "reference" price (defined as the modal price in the quarter) is increasing in the deviation from the average mark-up over the vendor cost (measured at the UPC-store level). Their estimates imply a potent selection effect: a 5-percentage-point increase in the deviation from the average markup raises the probability of adjusting the reference price during a given week by over 10 percentage points. A related finding is that deviations from the average markup are small, with 90 percent of items having an absolute deviation of 10 percentage points or less.
The other notable exception, which we follow below, is Campbell and Eden (2010), who use weekly scanner data from two small Midwestern cities. They report that the probability of observing a price change is increasing in the deviation between an item's price and the average price of local competitors selling the same UPC. A rationale for their approach is that individual reset prices, when measured at the UPC-market level, may comove strongly due to similarities in costs and the degree of local competition. Indeed, we will provide evidence of limited dispersion in the level of prices across stores. There are also limitations to this approach. Deviations from the average price of local competitors abstract from idiosyncratic factors influencing individual reset prices. And even if firms shared the same individual reset price, the deviation may imperfectly proxy for the actual amount of price pressure because the average price of local competitors only gradually reflects common shocks due to nominal rigidities.
4.2.1 Proxying for the Deviation
We use the SymphonyIRI Marketing dataset to investigate pricing decisions and local competition. As appendix A details, this dataset contains UPC-level information on weekly sales and prices of U.S. grocery stores and drug stores. It allows us to control for the geographic location and to identify stores belonging to the same retail chain. The sample size is unusually large at about 300 billion individual price observations per year. The dataset covers staple food (e.g., carbonated beverages, condiments, and cereals) and personal care products (e.g., toilet paper and laundry detergent). We converted the price series to a monthly frequency, as explained in appendix A.
To construct an estimate of the deviation, we follow Campbell
and Eden (2010) in defining the average price of store ![]() 's local competitors in month
's local competitors in month ![]() ,
,
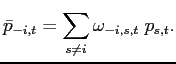
The weight
![]() is the share of total UPC
sales by item
is the share of total UPC
sales by item ![]() 's local competitors that is accounted
for by store
's local competitors that is accounted
for by store ![]() on a yearly basis. We then compute the
deviation from
on a yearly basis. We then compute the
deviation from
![]() prevailing at the beginning
of the period,
prevailing at the beginning
of the period,
![]() .
There could be factors leading to permanent differences in the
level of prices across stores, even conditioning on the UPC and
market. For example, the Chicago-area grocery chain Dominick's
Finer Foods uses a four-tier system to set the level of prices
across its stores in order to account for differences in consumer
price sensitivity and the degree of local competition. For this
reason, we use demeaned time series of the deviation unless
otherwise indicated.
.
There could be factors leading to permanent differences in the
level of prices across stores, even conditioning on the UPC and
market. For example, the Chicago-area grocery chain Dominick's
Finer Foods uses a four-tier system to set the level of prices
across its stores in order to account for differences in consumer
price sensitivity and the degree of local competition. For this
reason, we use demeaned time series of the deviation unless
otherwise indicated.
As section 2.3 mentions, only price adjustments coinciding with a reoptimization should be comprised in the intensive and the extensive margins. Accordingly, in addition to using posted prices, we consider a "regular" price series excluding one-month temporary price drops and a "reference" price series computed as the modal posted price observed during a 13-week period centered around the 15th day of the month. Our objective is not to dismiss sales and nonreference prices as channels for the transmission of shocks. On the contrary, there is mounting evidence that these prices are responsive to aggregate conditions, although the extent of this response remains the subject of ongoing debate.17 Instead, we use these alternative price series to provide statistics under a wider range of assumptions regarding the set of price adjustments coinciding with a reoptimization. Appendix A details the construction of these series.
4.2.2 Local Price Dispersion and the Nonparametric Adjustment Hazard
We first use our estimates
![]() to document the importance of
dispersion in the level of prices across stores at the UPC-market
level.18 We sort
to document the importance of
dispersion in the level of prices across stores at the UPC-market
level.18 We sort
![]() from all UPCs and markets with
sufficient observations into 1-percentage-point bins, pooling
together observations from all months. The distributions weigh
equally all UPC-market combinations. As a first step, observations
for a UPC-market combination are also weighted uniformly to
highlight price dispersion across stores. The upper panel of figure 6 shows the
resulting distributions of deviations for posted, regular, and
reference prices before demeaning
from all UPCs and markets with
sufficient observations into 1-percentage-point bins, pooling
together observations from all months. The distributions weigh
equally all UPC-market combinations. As a first step, observations
for a UPC-market combination are also weighted uniformly to
highlight price dispersion across stores. The upper panel of figure 6 shows the
resulting distributions of deviations for posted, regular, and
reference prices before demeaning
![]() . The distributions are clearly
skewed to the right of zero: About 10 percent of
observations for posted prices and regular prices have
. The distributions are clearly
skewed to the right of zero: About 10 percent of
observations for posted prices and regular prices have
![]() , a proportion that
doubles to 20 percent for reference prices. The
explanation for this skewness is that total UPC sales within local
markets tend to be dominated by a small number of stores with
relatively low prices. The distributions also have a relatively
high density at or near zero due to some UPC-market combinations
displaying little if any dispersion in the level of prices.19 The
lower panel of figure 6 reports the
distributions after demeaning
, a proportion that
doubles to 20 percent for reference prices. The
explanation for this skewness is that total UPC sales within local
markets tend to be dominated by a small number of stores with
relatively low prices. The distributions also have a relatively
high density at or near zero due to some UPC-market combinations
displaying little if any dispersion in the level of prices.19 The
lower panel of figure 6 reports the
distributions after demeaning
![]() by its average over time.
These distributions are relatively tight, which suggests that
fluctuations in the level of prices are somewhat limited once one
accounts for permanent differences across stores.
by its average over time.
These distributions are relatively tight, which suggests that
fluctuations in the level of prices are somewhat limited once one
accounts for permanent differences across stores.
We note at the outset that some of the observed price dispersion
is not due to nominal rigidities hampering price adjustment in
response to shocks, but is rather traced back to firms' own pricing
decisions. The upper panel of figure 7 illustrates
this fact by showing how prices at the edges of the distribution
tend to be relatively young. The average age of posted, regular,
and reference prices peaks near 5 months, 6 months, and 10 months,
respectively, for
![]() near zero. The average age
then falls steadily as we consider increasingly large absolute
deviations from the average price of local competitors. In the case
of posted and regular prices, the average age of items with an
absolute deviation around 20 percent is
roughly 40 percent smaller than that of items with a
deviation near zero. The relative age difference is even larger for
reference prices. These findings are consistent with those of
Campbell and Eden (2010), though obtained with a much larger
sample, and caution against associating all forms of price
dispersion with resource misallocation. Consequently, we will take
this feature of the data into account in our subsequent
analysis.
near zero. The average age
then falls steadily as we consider increasingly large absolute
deviations from the average price of local competitors. In the case
of posted and regular prices, the average age of items with an
absolute deviation around 20 percent is
roughly 40 percent smaller than that of items with a
deviation near zero. The relative age difference is even larger for
reference prices. These findings are consistent with those of
Campbell and Eden (2010), though obtained with a much larger
sample, and caution against associating all forms of price
dispersion with resource misallocation. Consequently, we will take
this feature of the data into account in our subsequent
analysis.
The middle panel of figure 7 plots the
nonparametric adjustment hazard,
![]() ,
obtained by computing the price change frequency for each
1-percentage point bin. Unsurprisingly,
,
obtained by computing the price change frequency for each
1-percentage point bin. Unsurprisingly,
![]() is highest for posted prices, which are relatively flexible, and
lowest for reference prices, which are relatively sticky. More
importantly and consistent with the presence of a selection effect,
is highest for posted prices, which are relatively flexible, and
lowest for reference prices, which are relatively sticky. More
importantly and consistent with the presence of a selection effect,
![]() is
increasing in the absolute deviation from the average price of
local competitors. One may suspect that this phenomenon is driven
by temporary sales and promotions, which can cause posted prices to
be temporarily located on the edges of the distribution of
deviations. However, the V shape is preserved when we exclude sales
and nonreference price changes. For instance, the probability of
observing a reference price change leaps from 7
percent when the item's price equals the average reference price of
its local competitors, to between 20 percent and 30 percent when its (absolute) deviation
reaches 20 percent.
is
increasing in the absolute deviation from the average price of
local competitors. One may suspect that this phenomenon is driven
by temporary sales and promotions, which can cause posted prices to
be temporarily located on the edges of the distribution of
deviations. However, the V shape is preserved when we exclude sales
and nonreference price changes. For instance, the probability of
observing a reference price change leaps from 7
percent when the item's price equals the average reference price of
its local competitors, to between 20 percent and 30 percent when its (absolute) deviation
reaches 20 percent.
The bottom panel of figure 7 shows that
the median firm adjusts its reference price by the full size of its
price gap vis-à-vis local competitors (i.e.,
![]() ). A
similar conclusion holds for posted prices and regular prices (not
shown). That said, there is some heterogeneity in the size of price
changes conditional on
). A
similar conclusion holds for posted prices and regular prices (not
shown). That said, there is some heterogeneity in the size of price
changes conditional on
![]() , as evidenced by the 10th and
90th percentile lines reported in the panel. This variation
suggests that, while
, as evidenced by the 10th and
90th percentile lines reported in the panel. This variation
suggests that, while
![]() is a roughly unbiased estimate
of the actual deviation,
is a roughly unbiased estimate
of the actual deviation, ![]() , it misses other
factors influencing individual reset prices.
, it misses other
factors influencing individual reset prices.
Figures 8 and 9 provide some evidence that
the shape of
![]() is
robust to alterations to our baseline methodology. First, it
retains its V shape when we compute it for narrower product
categories, as illustrated in figure 8 for salty
snacks, carbonated beverages, cold cereal, and frozen dinners.
Second, we allow for the possibility that pricing decisions are
made at the chain level rather than at the store level by excluding
stores belonging to the same chain as retailer
is
robust to alterations to our baseline methodology. First, it
retains its V shape when we compute it for narrower product
categories, as illustrated in figure 8 for salty
snacks, carbonated beverages, cold cereal, and frozen dinners.
Second, we allow for the possibility that pricing decisions are
made at the chain level rather than at the store level by excluding
stores belonging to the same chain as retailer ![]() from the computation of
from the computation of
![]() . The upper panel of figure 9 shows that the
resulting adjustment hazard is only a bit flatter than our
benchmark case for reference prices. The findings are qualitatively
similar for posted prices and regular prices when we control for
chains (not shown). Third, figure 9 also presents the
nonparametric adjustment hazard obtained when the deviation is
constructed using only the average price of the local competitors
that have reset their price over the previous six months. In this
case,
. The upper panel of figure 9 shows that the
resulting adjustment hazard is only a bit flatter than our
benchmark case for reference prices. The findings are qualitatively
similar for posted prices and regular prices when we control for
chains (not shown). Third, figure 9 also presents the
nonparametric adjustment hazard obtained when the deviation is
constructed using only the average price of the local competitors
that have reset their price over the previous six months. In this
case,
![]() is
a bit steeper than in our benchmark case. Finally, the lower panel
of figure 9 reports
is
a bit steeper than in our benchmark case. Finally, the lower panel
of figure 9 reports
![]() conditional on the age of the price. While the V shape is preserved
at all durations considered, the level of the estimated adjustment
hazard declines with the age of the price, consistent with negative
duration dependence in the data.
conditional on the age of the price. While the V shape is preserved
at all durations considered, the level of the estimated adjustment
hazard declines with the age of the price, consistent with negative
duration dependence in the data.
4.2.3 Parametric Estimation of the Adjustment Hazard
The nonparametric nature of our analysis so far has precluded us
from controlling for various factors that could affect the shape of
the adjustment hazard function, such as seasonal repricing and a
selection bias by which items with large deviations are drawn from
UPC-market combinations with relatively flexible prices. To assess
whether these elements impact our findings, in particular the V
shape of the adjustment hazard, we estimate linear probability
models with item fixed effects in the spirit of Campbell and Eden
(2010). We focus on reference prices to further limit the risk that
sales, promotions, and other transitory price movements bias our
estimate of
![]() , and UPC-store fixed
effects are also included. Our specification is
, and UPC-store fixed
effects are also included. Our specification is
where
![]() is an
indicator variable that item
is an
indicator variable that item ![]() 's price has
changed,
's price has
changed,
![]() is
is
![]() whenever
whenever
![]() and zero otherwise,
and zero otherwise,
![]() is
similarly defined for positive deviations, and
is
similarly defined for positive deviations, and ![]() is a vector of control variables that include period
dummies, the age of the price, and a measure of store size (total
yearly revenues).
is a vector of control variables that include period
dummies, the age of the price, and a measure of store size (total
yearly revenues).
![]() and
allow the
adjustment hazard to have different slopes for negative and
positive deviations. We also c
and
allow the
adjustment hazard to have different slopes for negative and
positive deviations. We also c![]() onsidered higher-order terms
but their economic significance was minimal. We cluster the
standard errors at the store level and, given the expansive size of
the IRI Marketing dataset, run the regressions at the product
category-market level. We only include in our sample items from
UPC-market combinations that have at least 10
observations.
onsidered higher-order terms
but their economic significance was minimal. We cluster the
standard errors at the store level and, given the expansive size of
the IRI Marketing dataset, run the regressions at the product
category-market level. We only include in our sample items from
UPC-market combinations that have at least 10
observations.
The first three columns of table 4 display the estimated coefficients for three product category-market combinations: salty snacks in New York City, carbonated beverages in Los Angeles, and frozen dinners in Boston. All slope coefficients are statistically significant and increasing in the (absolute) size of positive and negative deviations. In addition, the slopes are comparable in magnitude to those obtained in our nonparametric exercise. As was the case earlier, the results point to a steeper adjustment hazard for negative deviations than positive ones, suggesting that relatively low prices are especially unlikely to persist for long.20
We also ran regressions with duration-specific dummies to determine whether the shape of the adjustment hazard is driven by young prices. The results reported in table 5 show that this is not the case. The coefficients on the duration-specific dummies are economically small and often not statistically significant, indicating that the age of prices is not an important determinant of the slope of the adjustment hazard function. The lack of any improvement in the goodness of fit relative to the benchmark regressions in table 4 is consistent with this conclusion.
4.2.4 Local Competition and the Index of Macroeconomic Flexibility
Our benchmark nonparametric hazard has proven robust to
controlling for several elements unrelated to the selection effect
that could influence its slope. Consistent with the limited amount
of price dispersion across stores shown in figure 6, we see our
regression results as evidence that the timing of pricing decisions
is sensitive to deviations from individual reset prices, and that
adjustment along the extensive margin may play a role at the
macroeconomic level. If we believe that the deviation from the
price of local competitors (
![]() ) and our estimate
) and our estimate
![]() are good proxies for the deviation from the actual individual reset
price (
are good proxies for the deviation from the actual individual reset
price (![]() ) and adjustment hazard function (
) and adjustment hazard function (
![]() ),
respectively, then we have all the elements needed to estimate the
intensive and the extensive margins in equation 4 directly on the micro data. Specifically, the
intensive margin can be obtained by integrating
),
respectively, then we have all the elements needed to estimate the
intensive and the extensive margins in equation 4 directly on the micro data. Specifically, the
intensive margin can be obtained by integrating
![]() over the distribution of
over the distribution of
![]() , and the extensive margin can
be recovered by integrating the product of
, and the extensive margin can
be recovered by integrating the product of
![]() and the derivative of
and the derivative of
![]() over the distribution of
over the distribution of
![]() .
.
Table 6 shows
our estimates of
![]() and
and
![]() when we
perform such an exercise. We recover the slope of
when we
perform such an exercise. We recover the slope of
![]() separately for positive and negative deviations with linear
regressions using the point estimates for each 1-percentage point
bin in figure 7 as
observations. Absent real rigidities, the index of macroeconomic
flexibility ranges from 0.13 for reference prices to 0.37 for posted prices. About 30 percent of these index values is due to the extensive
margin, making this margin an economically important channel of
price adjustment irrespective of whether one uses posted, regular,
or reference prices. If we instead assume moderate real rigidities
(
separately for positive and negative deviations with linear
regressions using the point estimates for each 1-percentage point
bin in figure 7 as
observations. Absent real rigidities, the index of macroeconomic
flexibility ranges from 0.13 for reference prices to 0.37 for posted prices. About 30 percent of these index values is due to the extensive
margin, making this margin an economically important channel of
price adjustment irrespective of whether one uses posted, regular,
or reference prices. If we instead assume moderate real rigidities
(![]() ) similar to those estimated on retail
data by Burstein and Hellwig (2007), then the estimated indexes of
macroeconomic flexibility roughly halve. Although these results
imply greater macro price stickiness, it does not alter our view
about the importance of the extensive margin to
) similar to those estimated on retail
data by Burstein and Hellwig (2007), then the estimated indexes of
macroeconomic flexibility roughly halve. Although these results
imply greater macro price stickiness, it does not alter our view
about the importance of the extensive margin to ![]() .
.
There is admittedly much uncertainty surrounding these estimates. Importantly, they rely on an imperfect measure of the true deviation from individual reset prices. Whether this measure leads us to underestimate or overestimate the slope of the adjustment hazard is unclear. On the one hand, by omitting idiosyncratic factors, we add noise to the deviation that could bias downward the slope of the adjustment hazard. The importance of the extensive margin in table 6 is also near or below the lower bounds derived in section 3 in the case of adjustment to large shocks. On the other hand, sluggish adjustment of the price of local competitors to shocks could bias upward the slope of the nonparametric adjustment hazard function. For these reasons, we see these estimates as suggestive that the extensive margin is an important channel for macro price adjustment, but more work remains to be done to refine these estimates and broaden the set of products to which they apply.
5 Conclusion
In this paper, we have sought to connect micro price stickiness and macro price stickiness by distinguishing between price changes whose timing is determined ahead of shocks and price changes whose timing is altered by shocks. We have discussed the assumptions under which observed price behavior can be used to infer the importance of each type of price changes for aggregate inflation. We have found compelling evidence that some shocks alter the timing of price changes, contributing significantly to the flexibility of the price level. Using the terminology of Caballero and Engel (2007), this evidence of state-dependent behavior points to an important role for the extensive margin in the initial response of inflation to shocks.
Our findings have several implications for macroeconomic modelling. First, researchers primarily interested in fitting macro facts should be careful when claiming that their models are consistent with micro facts. The current generation of macro models is still a long way from capturing the richness of pricing strategies employed by firms; some simplification is unavoidable. But, as our findings make clear, models featuring no extensive margin abstract from an economically important channel of adjustment and their calibration should take that aspect into account. Our results also suggest that micro-level price stickiness is at most a moderate contributor to the transmission mechanism. Moreover, rapid initial pass-through of the shocks covered in our study seems mostly incompatible with the presence of strong real rigidities, a conclusion echoing that of Bils and Klenow (2004) and Bils et al. (forthcoming) based on the dynamics of sectoral U.S. CPI inflation series.
Obviously, our work leaves several questions unanswered. We have considered only a subset of sectoral and aggregate shocks that share the characteristic of being relatively easy to identify. Micro price adjustment to other types of aggregate shocks --notably monetary shocks-- could be more sluggish. Also, there continues to be a lack of microeconomic data on both costs and local competition, which could help refine estimates of individual reset prices between price adjustment periods. Moreover, micro-level price evidence on the importance of real rigidities, which is important for refining estimates of adjustment along the extensive margin, remains constrained by limited data availability.
References
Alvarez, Fernando, Francesco Lippi, and Luigi Paciello. 2011. "Optimal Price Setting with Observation and Menu Costs." Quarterly Journal of Economics 126, no.4:1909-1960.
Álvarez, Luis J. and Ignacio Hernando. 2004. "Price Setting Behaviour in Spain: Stylised Facts using Consumer Price Micro Data." Working Paper Series 416, European Central Bank.
Attanasio, Orazio P. 2000. "Consumer Durables and Inertial Behaviour: Estimation and Aggregation of (S,s) Rules for Automobile Purchases." Review of Economic Studies 67, no.4:667-96.
Baharad, Eyal and Benjamin Eden. 2004. "Price Rigidity and Price Dispersion: Evidence from Micro Data." Review of Economic Dynamics 7, no.3:613-641.
Ball, Laurence M., and David Romer. 1990. "Real Rigidities and the Non-neutrality of Money." Review of Economic Studies 57, no.2:183-203.
Barsky, Robert B., Christopher L. House, and Miles S. Kimball. 2007. "Sticky-Price Models and Durable Goods." American Economic Review 97, no. 3:984-998.
Barro, Robert J. 1972. "A Theory of Monopolistic Price Adjustment." Review of Economic Studies 39, no.1:17-26.
Berger, David and Joseph Vavra. 2011. "Dynamics of the U.S. Price Distribution." Yale University.
Bils, Mark and Peter J. Klenow. 2004. "Some Evidence on the Importance of Sticky Prices." Journal of Political Economy 112, no.5:947-985.
Bils, Mark, Peter J. Klenow, and Benjamin A. Malin. (forthcoming). "Reset Price Inflation and the Impact of Monetary Policy Shocks," American Economic Review.
Blanchard, Oliver J. and S. Fisher. 1989. Lectures on Macroeconomics. Cambridge: MIT Press.
Bronnenberg, Bart J., Michael W. Kruger, and Carl F. Mela. 2008. "Database paper: The IRI Marketing Data Set." Marketing Science 27, no.4:745-748.
Burstein, Ariel T. 2006. "Inflation and Output Dynamics with State-Dependent Pricing Decisions." Journal of Monetary Economics 53, no.7:1235-1257.
Burstein, Ariel, Martin Eichenbaum, and Sergio Rebelo. 2005. "Large Devaluations and the Real Exchange Rate." Journal of Political Economy 113, no.4:742-784.
Burstein, Ariel and Christian Hellwig. 2007. "Prices and Market Shares in a Menu Cost Model." NBER Working Papers 13455, National Bureau of Economic Research.
Caballero, Ricardo J. and Eduardo M.R.A. Engel. 1993a. "Microeconomic Adjustment Hazards and Aggregate Dynamics." Quarterly Journal of Economics 108, no.2:359-383.
Caballero, Ricardo J. and Eduardo M. R. A. Engel. 1993b. "Microeconomic Rigidities and Aggregate Price Dynamics." European Economic Review 37, no.4:697-711.
Caballero, Ricardo J. and Eduardo M. R. A. Engel. 1999. "Explaining Investment Dynamics in U.S. Manufacturing: A Generalized (S,s) Approach." Econometrica 67, no.4:783-826.
Caballero, Ricardo J. and Eduardo M.R.A. Engel. 2007. "Price Stickiness in Ss Models: New Interpretations of Old Results." Journal of Monetary Economics 54, (Supplement):100-121.
Caballero, Ricardo J., Eduardo M.R.A. Engel, and John Haltiwanger. 1997. "Aggregate Employment Dynamics: Building from Microeconomic Evidence." American Economic Review 87, no.1:115-137.
Calvo, Guillermo A. 1983. "Staggered Prices in a Utility-Maximizing Framework." Journal of Monetary Economics 12, no.3:383-398.
Campbell, Jeffrey R. and Benjamin Eden. 2010. "Rigid Prices: Evidence from U.S. Scanner Data." Working Paper Series WP-05-08, Federal Reserve Bank of Chicago.
Caplin, Andrew S. and Daniel F. Spulber. 1987. "Menu Costs and the Neutrality of Money." Quarterly Journal of Economics 102, no.4:703-25.
Capistrán, Carlos and Gabriel López-Moctezuma. 2010. "Forecast Revisions of Mexican Inflation and GDP Growth." Working Paper 2010-11, Banco de Mèxico.
Carlton, Dennis W. 1986. "The Rigidity of Prices." American Economic Review 76, no.4:637-58.
Carlton, Dennis W. 1989. "The Theory and the Facts of How Markets Clear: Is Industrial Organization Valuable for Understanding Macroeconomics?" Handbook of Industrial Organization, ed. by R. Schmalensee & R. Willig, 1 ch.15:909-946.
Cecchetti, Stephen G. 1986. "The Frequency of Price Adjustment: A Study of the Newsstand Prices of Magazines." Journal of Econometrics 31, no. 3:255-274.
Chevalier, Judith A. and Anil K. Kashyap. 2011. "Best prices." NBER Working Paper 16680.
Christiano, Lawrence J., Martin Eichenbaum, and Charles L. Evans. 2005. "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy." Journal of Political Economy 113, no.1:1-45.
Costain, James and Anton Nakov. 2011. "Distributional Dynamics under Smoothly State-Dependent Pricing." Journal of Monetary Economics 58, no.6-8:646-665.
Dhyne, Emmanuel, Luis J. Álvarez, Hervé Le Bihan, Giovanni Veronese, Daniel Dias, Johannes Hoffmann, Nicole Jonker, Patrick Lünnemann, Fabio Rumler, and Jouko Vilmunen, 2005. "Price Setting in the Euro Area: Some Stylized Facts from Individual Consumer Price Data," Working Paper 524, European Central Bank.
Dotsey, Michael and Robert G. King. 2005. "Implications of State-dependent Pricing for Dynamic Macroeconomic Models." Journal of Monetary Economics 52, no.1:213-242.
Eichenbaum, Martin, Nir Jaimovich, and Sergio Rebelo. 2011. "Reference Prices and Nominal Rigidities." American Economic Review 101, no.1:234-262.
Eberly, Janice C. 1994. "Adjustment of Consumers' Durables Stocks: Evidence from Automobile Purchases." Journal of Political Economy 102, no.1:403-36.
Eden, Benjamin. 1994. "The Adjustment of Prices to Monetary Shocks When Trade Is Uncertain and Sequential." Journal of Political Economy 102, no.3:493-509.
Eden, Benjamin. 2001. "Inflation and Price Adjustment: An Analysis of Microdata." Review of Economic Dynamics 4, no.3:607-636.
Fabiani, Silvia, Martine Druant, Ignacio Hernando, Claudia Kwapil, Bettina Landau, Claire Loupias, Fernando Martins, Thomas Mathä, Roberto Sabbatini, Harald Stahl, and Ad Stokman. 2006. "What Firms' Surveys Tell Us about Price-Setting Behavior in the Euro Area." International Journal of Central Banking, September:3-48.
Gagnon, Etienne. 2009. "Price Setting during Low and High Inflation: Evidence from Mexico." Quarterly Journal of Economics 124, no.4:1221-1263.
Golosov, Mikhail and Robert E. Lucas Jr. 2007. "Menu Costs and Phillips Curves." Journal of Political Economy, 115:171-199.
Gopinath, Gita and Oleg Itskhoki. 2010. "Frequency of Price Adjustment and Pass-Through." Quarterly Journal of Economics 125, no.2:675-727.
Gopinath, Gita and Oleg Itskhoki. 2011. "In Search of Real Rigidities." NBER Chapters, NBER Macroconomics Annual 2010 25:261-309.
Head, Allen, Lucy Qian Liu, Guido Menzio, and Randall Wright. (forthcoming). "Sticky Prices: a New Monetarist Approach." Journal of the European Economic Association.
Kara, Engin. 2011. "Understand and Modelling Reset Price Inflation." Discussion Paper 11.623. University of Bristol.
Karadi, Peter and Adam Reiff. 2010. "Inflation Asymmetry, Menu Costs and Aggregation Bias - A Further Case for State Dependent Pricing." Working Papers 20103, Magyar Nemzeti Bank.
Kashyap, Anil K. 1995. "Sticky Prices: New Evidence from Retail Catalogs." Quarterly Journal of Economics 110, no.1:245-74.
Klenow, Peter J. and Oleksiy Kryvtsov. 2008. "State-Dependent or Time-Dependent Pricing: Does It Matter for Recent U.S. Inflation?" Quarterly Journal of Economics 123, no.3:863-904.
Klenow, Peter J. and Benjamin A. Malin. 2011. "Microeconomic Evidence on Price-Setting." Handbook of Monetary Economics, Volume 3, Chapter 6, in B. M. Friedman and M. Woodford (editors), pages 231-284.
Lach, Saul and Daniel Tsiddon. 1992. "The Behavior of Prices and Inflation: An Empirical Analysis of Disaggregated Price Data." Journal of Political Economy 100, no.2:349-89.
Levy, Daniel, Dongwon Lee, Haipeng Chen, Robert J. Kauffman, and Mark Bergen. 2011. "Price Points and Price Rigidity." Review of Economics and Statistics 93, no.4:1417-1431.
Mackowiak, Bartosz and Frank Smets. 2008. "On Implications of Micro Price Data for Macro Models." Working Paper 960, European Central Bank.
Mankiw, N. Gregory and Ricardo Reis. 2002. "Sticky Information Versus Sticky Prices: A Proposal To Replace The New Keynesian Phillips Curve." Quarterly Journal of Economics 117, no.4:1295-1328.
Midrigan, Virgiliu. 2011. "Menu-Costs, Multi-Product Firms and Aggregate Fluctuations." Econometrica 79, no.4:1139-1180.
Nakamura, Emi and Jón Steinsson. 2008. "Five Facts about Prices: A Reevaluation of Menu Cost Models." The Quarterly Journal of Economics 123, no.4:1415-1464.
Reinsdorf, Marshall. 1994. "New Evidence on the Relation between Inflation and Price Dispersion." American Economic Review 84, no.3:720-731.
Rotemberg, Julio J. 2011. "Fair Pricing." Journal of the European Economic Association 9, no.5:952-981.
Sims, Christopher A. 2003. "Implications of Rational Inattention." Journal of Monetary Economics 50, no.3:665-690.
Sheshinski, Eytan and Yoram Weiss. 1977. "Inflation and Costs of Price Adjustment." Review of Economic Studies 44, no.2:287-303.
Smets, Frank and Rafael Wouters, 2007. "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach," American Economic Review 97, no.3:586-606.
Taylor, John B. 1980. "Aggregate Dynamics and Staggered Contracts." Journal of Political Economy 88, no.1:1-23.
Varian, Hal R. 1980. "A Model of Sales," American Economic Review 70, no.4:651-659.
Woodford, Michael. 2008. "Inattention as a Source of Randomized Discrete Adjustment." mimeo, Columbia University.
Woodford, Michael. 2009. "Information-Constrained State-Dependent Pricing." Journal of Monetary Economics 56, (Supplement):S100-S124.
Wulfsberg, Fredrik. 2009. "Price Adjustments and Inflation - Evidence from Norwegian Consumer Price Data 1975-2004." Working Paper 2009/11, Norges Bank.
Appendix A. Data Description
The datasets used in this paper have been described in earlier work, so we shall concentrate on the features that are most relevant for our analysis.
Mexican CPI Database
Gagnon (2009) constructed the Mexican micro CPI dataset for the period January 1994 to December 2004 using monthly price and item substitution lists published by the Bank of Mexico. We extended his sample period back to July 1993 and forward to December 2010. Price lists were not available electronically for 1993; the observations were manually coded by a data entry firm using scans of the original documents made by Mexico's Archivo General de la Nación.
The dataset excludes product categories whose prices are regulated (e.g., taxi fares, phone services, gasoline, and tuition fees) or reported as a sectoral index (e.g., housing, utilities, and insurance). The sample covers 54 percent of Mexican consumer price expenditures prior to the basket update of July 2002, and about 61 percent thereafter. The number of usable monthly observations ranges from 21,000 in 1993 to 57,000 in 2010. Prices are inclusive of sales as long as these sales are conditional on the purchase of a single item. There is no flag in the dataset indicating that an item is on sale but the application of filters to remove V-shaped price patterns suggests that sales are less prominent than in the U.S. CPI.
U.S. CPI Database
The Bureau of Labor Statistics (BLS) makes available most of the micro data behind the official U.S. CPI on a restricted-access basis through its CPI-Research Database. This database excludes housing rents, whose index is computed separately due to differences in sampling and treatment. With the exceptions of food, energy, and a few additional product categories, item prices are collected every other month in all metropolitan areas but the largest three (New York City, Los Angeles, and Chicago), where price collection takes place monthly for all items. The database starts in January 1988 and we extracted data through December 2009. We restrict the sample to the largest three metropolitan areas, leaving us with between 12,000 and 19,000 observations per month. The individual observations are weighted using the same procedure and product category weights as BKM.21 We classified the product categories according to the United Nations Classification of Individual Consumption According to Purpose (COICOP) in order to compute statistics for special groups of products. For additional details on this dataset, see the BLS Handbook of Methods, Bils and Klenow (2004), Klenow and Kryvtsov (2008), and Nakamura and Steinsson (2008).
SymphonyIRI Group Scanner Database
The IRI Marketing dataset includes scanner data from U.S. grocery stores and drugstores. Its content is detailed in Bronnenberg, Kruger, and Mela (2008). An observation corresponds to a specific item sold by a given store in a particular week. Available information includes total revenue from the sale of the item and the number of units sold. As is customary with scanner data, the unit price is obtained by dividing total revenue by the quantity sold. The number of usable observations in the dataset is enormous at about 300 billion per year.
The dataset has several appealing features. First, observations are collected frequently. Second, the sample covers a relatively long time span, January 2001 to December 2007, that allows us to look at price dynamics. Third, information is available for 31 food and personal care product categories, such as beer, household cleaners, and milk. Fourth, the geographical coverage --50 U.S. markets-- is more extensive than that of other scanner datasets used in the literature, and includes several retailers within each market. To study pricing decisions in competitive environments, we restrict the sample to Boston, Chicago, Houston, Los Angeles, New York, Philadelphia, San Diego, and Washington D.C.. These markets have between 30 and 97 stores. One limitation of the dataset is that it does not contain information about costs.
We applied a number of filters to the data to make them suitable
for our analysis. First, we censored fractional price observations.
For various reasons (use of membership cards, price changes during
the week, etc.), dividing total revenue by the number of units sold
occasionally yields a price with fractional cents (e.g.,
$3.7485). For New York City, fractional
prices represent less than 0.2 percent of
posted prices, and a negligible proportion of reference prices;
censoring fractional prices is thus mostly inconsequential for our
results. Second, in some applications, we filtered out temporary
sales, which we define as a price drop that is offset within two
weeks by a price increase of equal magnitude. Third, we considered
a slight variant of the reference price filter of Eichenbaum et
al. (2011). Specifically, the reference price of a given item
in week ![]() corresponds to the mode of the posted
price over a 13-week centered window. Fourth, we
converted weekly statistics to a monthly frequency by selecting
weekly observations encompassing the 15th day of every month.
Fifth, we require a minimum of 10 observations (stores) in
constructing the average price of local competitors,
corresponds to the mode of the posted
price over a 13-week centered window. Fourth, we
converted weekly statistics to a monthly frequency by selecting
weekly observations encompassing the 15th day of every month.
Fifth, we require a minimum of 10 observations (stores) in
constructing the average price of local competitors,
![]() . Finally, an item must be
present in the sample at least 24 months to be included in the
analysis.
. Finally, an item must be
present in the sample at least 24 months to be included in the
analysis.
Appendix B. Adjustment Along the Intensive Margin
The frequency of price change is approximately equal to the intensive margin and, provided real rigidities are not too strong, offers a lower bound on the index of macroeconomic flexibility. For the revelation principle to apply, only price adjustments coinciding with a reoptimization should be comprised in the intensive margin. For this reason, we report alternative measures of the average frequency that exclude sales and nonreference prices changes. These alternative measures provide a range of estimates for the intensive margin under widely used assumptions regarding the set of price adjustments coinciding with a reoptimization.
The top of table 1 reports the average frequency of price changes in the CPI excluding shelter in the three largest U.S. metropolitan areas. According to Klenow and Kryvtsov (2008), items representing 36.2 percent of consumer expenditures experience a price adjustment every month. This statistic suggests that, absent strong real rigidities, nominal shocks are initially passed through rapidly to individual reset prices even if no adjustment along the extensive margin were to take place. The average frequency of price changes slides to a still-elevated 29.9 percent when one excludes price changes flagged by the BLS as related to sales and promotions. Filtering out nonreference price changes is more consequential. Klenow and Malin (2011) find an average frequency of 14.6 percent when they define the reference price as the modal price over a 13-month window centered on the current month, implying that reference prices are considerably stickier than regular prices. Whether one should ignore all nonreference price changes is debatable, however. Klenow and Malin (2011) show that price changes exhibit considerable novelty: Every month, the price of a quarter of items in the U.S. CPI is adjusted to a level not seen over the previous 12 months. Also, some frequently occurring prices could be chosen because consumers find them more attractive than others (e.g., $9.99 versus $10.47), in which case some of the stickiness in references prices could be due to features of consumer demand rather than rigidity in pricing strategy.22 Finally, Eichenbaum et al. (2011) show that replacement costs also exhibit reference behavior. It is thus plausible that reference price behavior reflects to some degree a similar feature of individual reset prices.
In the bottom of table 1, we present related statistics for the IRI Marketing database. Although its product coverage is restricted to food and personal care product, the frequency statistics are similar to the U.S. CPI. The monthly average frequency is 37.2 percent for posted prices and 25.6 percent after filtering out V-shaped price drops. Monthly reference prices changes, at 13.5 percent, are less frequent but, as was the case with CPI prices, scanner prices exhibit considerable novelty.
Appendix C. The Extensive Margin and Bils-Klenow-Malin Reset Price Inflation
Imputing individual reset prices between adjustment periods is a delicate task. With only price information at hand, one does not know if an item's price change is releasing pressure generated by a single large shock or accumulated gradually from various sources. In a recent paper, Bils, Klenow, and Malin (forthcoming, henceforth "BKM") propose a method that uses the behavior of items changing their price to infer the amount of price pressure building up for other items in the sample. The method works under specific assumptions about the data-generating process that commonly hold in models in which the timing of price changes is exogenous. It is employed to recover a time series for the common component of individual reset price inflation whose behavior is then used to assess the empirical relevance of the initial assumptions. This appendix briefly reviews this method, shows how the identification is informed by the CE decomposition, and then discusses the challenges of applying it to assess the importance of adjustment along the extensive margin.
BKM's Identification Method
BKM estimate item ![]() 's individual reset price in
period
's individual reset price in
period ![]() as follows
as follows
![$\displaystyle p_{i,t}^{\ast BKM}=\left\{ \begin{array}[c]{cc} p_{i,t} & \text{if }p_{i,t}\neq p_{i,t-1}\\ p_{i,t-1}^{\ast}+\pi_{t}^{\ast BKM} & \text{if }p_{i,t}=p_{i,t-1} \end{array} \right. .$](img266.gif)
|
(10) |
The individual reset prices of an item whose posted price is
unchanged is obtained by incrementing the previous-period imputed
value by an estimate of aggregate reset price inflation,
![]() . This estimate
corresponds to the average change in
. This estimate
corresponds to the average change in
![]() of items whose posted
price is adjusted in period
of items whose posted
price is adjusted in period ![]() . A time series for
. A time series for
![]() is constructed by
initializing individual reset prices and then recursively computing
is constructed by
initializing individual reset prices and then recursively computing
![]() . The dependence of
. The dependence of
![]() on the initial conditions
quickly fades as price adjustments occur. Equation (10) can be alternatively written as
on the initial conditions
quickly fades as price adjustments occur. Equation (10) can be alternatively written as
![\begin{displaymath} p_{i,t}^{\ast BKM}=\left\{ \begin{array}[c]{cc} p_{i,t} & \text{if }p_{i,t}\neq p_{i,t-1}\ p_{i,t-\tau}+\sum_{s=0}^{\tau-1}\pi_{t-s}^{\ast BKM} & \text{if } p_{i,t}=p_{i,t-1} \end{array}\right. , \end{displaymath}](img273.gif)
where ![]() is the number of periods since item
is the number of periods since item
![]() 's last price adjustment. This
data-generating process differs from that assumed in equation
(1), which implies that item's
's last price adjustment. This
data-generating process differs from that assumed in equation
(1), which implies that item's ![]() individual reset price evolves according to
individual reset price evolves according to
![$\displaystyle p_{i,t}^{\ast}=\left\{ \begin{array}[c]{cc} p_{i,t} & \text{if }p_{i,t}\neq p_{i,t-1}\\ p_{i,t-\tau}+\sum_{s=0}^{\tau-1}\pi_{t-s}^{\ast}+\sum_{s=0}^{\tau-1}v_{i,t-s} & \text{if }p_{i,t}=p_{i,t-1} \end{array} \right. .$](img277.gif)
|
(11) |
The term
![]() captures the
accumulation of idiosyncratic shocks since the last price
adjustment. Comparing the above two equations, it is apparent that
BKM's method abstracts from the presence of idiosyncratic shocks.
These shocks play no role in aggregate price dynamics for models in
which the timing of adjustments is exogenous to the firms, such as
the popular Calvo (1983) and Taylor (1980) models. As we now
illustrate, abstracting from idiosyncratic shocks can create a
wedge between
captures the
accumulation of idiosyncratic shocks since the last price
adjustment. Comparing the above two equations, it is apparent that
BKM's method abstracts from the presence of idiosyncratic shocks.
These shocks play no role in aggregate price dynamics for models in
which the timing of adjustments is exogenous to the firms, such as
the popular Calvo (1983) and Taylor (1980) models. As we now
illustrate, abstracting from idiosyncratic shocks can create a
wedge between
![]() and
and
![]() when these shocks are present
and firms adjust along the extensive margin.
when these shocks are present
and firms adjust along the extensive margin.
BKM's Identification and the CE Decomposition: an Approximation
For ease of exposition, consider an economy that starts in a
steady state with
![]() and in which actual individual reset prices evolve according to
equation (11). Suppose that
all individual reset prices are perturbed by a small one-time
impulse
and in which actual individual reset prices evolve according to
equation (11). Suppose that
all individual reset prices are perturbed by a small one-time
impulse
![]() prior to price adjustment
decisions in period
prior to price adjustment
decisions in period ![]() . Let
. Let ![]() and
and ![]() denote the initial response
of the average frequency and size of (nonzero) price changes,
respectively. As in section 3.1, we denote the
variables under the counterfactual scenario of no shock using a "
denote the initial response
of the average frequency and size of (nonzero) price changes,
respectively. As in section 3.1, we denote the
variables under the counterfactual scenario of no shock using a "
![]() ". The inflation innovation
attributable to the shock in the initial period can be written as
". The inflation innovation
attributable to the shock in the initial period can be written as
Klenow and Kryvtsov (2008) show that nearly all the variation in
U.S. CPI inflation over the past two decades is attributable to
movements in ![]() while movements in
while movements in ![]() are relatively small and only weakly correlated with
inflation. Using this observation, we approximate
are relatively small and only weakly correlated with
inflation. Using this observation, we approximate ![]() and
and
![]() by the average frequency,
by the average frequency,
![]() , to get
, to get
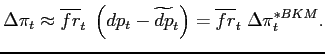
The last equality uses the fact that BKM's procedure imputes any
movement in the average size of nonzero price changes to a movement
in aggregate reset price inflation. Finally, using equation (4) and
![]() , we
obtain
, we
obtain
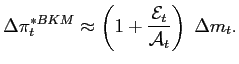
|
(12) |
In short, BKM's method overestimates the innovation to reset price
inflation by a factor that depends on the importance of the
extensive margin relative to the intensive margin. In the absence
of adjustment along the extensive margin (
![]() ),
),
![]() would be an unbiased
estimator of
would be an unbiased
estimator of
![]() . One implication is that
. One implication is that
![]() is overly volatile
relative to
is overly volatile
relative to
![]() whenever
whenever
![]() . Another implication is that the extra
. Another implication is that the extra
![]() wrongly imputed to the individual reset price of nonadjusters in
period
wrongly imputed to the individual reset price of nonadjusters in
period ![]() needs to be offset in subsequent periods
by increments to
needs to be offset in subsequent periods
by increments to
![]() summing up to negative
summing up to negative
![]() . A rapid offsetting can help generate uncorrelated or negatively
persistent measured aggregate reset price inflation, as found by
BKM and Gopinath and Itskhoki (2011). Figure 10 illustrates these
effects in a baseline menu-cost model à la Golosov and Lucas
(2007) in which
. A rapid offsetting can help generate uncorrelated or negatively
persistent measured aggregate reset price inflation, as found by
BKM and Gopinath and Itskhoki (2011). Figure 10 illustrates these
effects in a baseline menu-cost model à la Golosov and Lucas
(2007) in which
![]() is about 2.23 Upon impact of a 1-percent shock to
individual reset prices, the BKM procedure imputes a change in
individual reset prices of nonadjusters of about 3
percent. The procedure quickly corrects this overestimation in
subsequent periods as firms responding to the shock with a delay
release less price pressure than initially imputed.
is about 2.23 Upon impact of a 1-percent shock to
individual reset prices, the BKM procedure imputes a change in
individual reset prices of nonadjusters of about 3
percent. The procedure quickly corrects this overestimation in
subsequent periods as firms responding to the shock with a delay
release less price pressure than initially imputed.
We stress that the bias in BKM's method is not due to the extensive margin in itself but rather to the joint presence of idiosyncratic shocks and the asymmetric effect of the shock on the probability of price change of items with positive and negative deviations.24 A positive aggregate shock triggers the release of price pressure due to idiosyncratic factors through the selection effect, but BKM's procedure is not designed to disentangle that pressure from that accruing to the common component of individual reset prices.
BKM are well aware that their identifying assumptions do not hold for general data-generating processes. Indeed, their objective is precisely to test the empirical relevance of their assumptions by studying the behavior of reset price inflation series calculated on the micro data. In their 2009 NBER working paper, they pursue this objective notably by applying their method to series generated from baseline Calvo and menu-cost models calibrated to match CPI inflation dynamics. They then compare the predicted reset price inflation series to that estimated on CPI micro data. The estimated series is highly volatile and exhibits either no or negative persistence. These features are most closely replicated by their baseline menu-cost model with no strategic complementarities. This model entails a major role for adjustment along the extensive margin in explaining U.S. inflation dynamics, a conclusion that echoes the findings obtained using the alternative approaches in our paper.
However, at least three factors other than the extensive margin
could create spurious volatility and negative persistence in
![]() . As with
. As with
![]() discussed
above, these factors imply that the behavior of price adjusters is
not representative of that of nonadjusters. First, the method is
sensitive to sample size because it leverages the behavior of a
minority of price adjusters to infer the price pressure accruing to
all items. Any sampling uncertainty or coding mistakes in the
subset of adjusters will thus be imputed to nonadjusters. Second,
sectoral shocks may be confused with aggregate shocks. BKM deal
with this issue by estimating separate reset price inflation series
for 64 groups of products, but we see a risk of accentuating biases
due to sample size. Third, the response of individual reset prices
to aggregate shocks may be asymmetric across items in ways that
correlate with the frequency of price changes. For instance,
Gopinath and Itskhoki (2010) show that frequent adjusters
pass-through a larger share of exchange rate movements than
infrequent adjusters in a sample of U.S. trade prices. Kara (2011)
provides a theoretical example in which frequent adjusters are more
responsive to transitory shocks than infrequent adjusters. We
believe that further work on these aspects could help shed further
light on the importance of adjustment along the extensive margin
for U.S. inflation dynamics.
discussed
above, these factors imply that the behavior of price adjusters is
not representative of that of nonadjusters. First, the method is
sensitive to sample size because it leverages the behavior of a
minority of price adjusters to infer the price pressure accruing to
all items. Any sampling uncertainty or coding mistakes in the
subset of adjusters will thus be imputed to nonadjusters. Second,
sectoral shocks may be confused with aggregate shocks. BKM deal
with this issue by estimating separate reset price inflation series
for 64 groups of products, but we see a risk of accentuating biases
due to sample size. Third, the response of individual reset prices
to aggregate shocks may be asymmetric across items in ways that
correlate with the frequency of price changes. For instance,
Gopinath and Itskhoki (2010) show that frequent adjusters
pass-through a larger share of exchange rate movements than
infrequent adjusters in a sample of U.S. trade prices. Kara (2011)
provides a theoretical example in which frequent adjusters are more
responsive to transitory shocks than infrequent adjusters. We
believe that further work on these aspects could help shed further
light on the importance of adjustment along the extensive margin
for U.S. inflation dynamics.
Table 1a: Standard Measures of the Intensive Margin in the U.S. CPI Database
| U.S. CPI Database | Weekly frequency (percent) | Monthly frequency (percent) | Sample period |
|---|---|---|---|
Posted pricesa | n.a. | 36.2 | 1/1988 - 1/2005 |
| Regular pricesa | n.a. | 29.9 | 1/1988 - 1/2005 |
| Reference pricesa 13-month window | n.a. | 14.6 | 1/1988 - 10/2009 |
| Novel pricesa | n.a. | 25.0 | 1/1988 - 10/2009 |
Notes: (a) Source: Klenow and Kryvtsov (2008). Regular prices correspond to posted prices excluding sales and promotions as flagged by the BLS. (b) Source: Klenow and Malin (2011). Novel prices are defined as prices that have not been observed for at least 12 months. An item's reference price is defined as the modal price over a centered 13-month window. (c) Regular prices exclude price drops returning to their original level within 2 weeks. The reference price is defined as the modal price over a centered window.
Table 1b: Standard Measures of the Intensive Margin in the IRI Marketing Database
| IRI Marketing Database | Weekly frequency (percent) | Monthly frequency (percent) | Sample period |
|---|---|---|---|
| Posted prices | 22.6 | 37.2 | 1/2001 - 12/2007 |
| Regular pricesc | 18.1 | 25.6 | 1/2001 - 12/2007 |
| Reference prices 13-week window | 4.0 | 13.5 | 1/2001 - 12/2007 |
| Novel prices | n.a. | 23.8 | 1/2001 - 12/207 |
Notes: (a) Source: Klenow and Kryvtsov (2008). Regular prices correspond to posted prices excluding sales and promotions as flagged by the BLS. (b) Source: Klenow and Malin (2011). Novel prices are defined as prices that have not been observed for at least 12 months. An item's reference price is defined as the modal price over a centered 13-month window. (c) Regular prices exclude price drops returning to their original level within 2 weeks. The reference price is defined as the modal price over a centered window.
Table 2: Lower Bounds on the Share of Initial Pass-Through Attributed to Adjustment Along the Extensive Margin During the Late-1994 Mexican Peso Devaluation
| Bound Method | Initial Pass-Through(Δπ/Δm, percent) | Share Attributed To Extensive Margin (percent) |
|---|---|---|
| Full pass-through (Δe = 50%) - posted prices | 84.7 | 70.5 |
| Full pass-through (Δe = 50%) - posted prices: unprocessed food | 72.9 | 47.4 |
| Full pass-through (Δe = 50%) - posted prices: processed food | 85.4 | 75.2 |
| Full pass-through (Δe = 50%) - posted prices: nonenergy industrial goods | 95.9 | 84.8 |
| Full pass-through (Δe = 50%) - posted prices: services | 57.8 | 84.5 |
| Full pass-through (forecast revision) - posted prices | 30.8 | 18.9 |
| Full pass-through (forecast revision) - posted prices: unprocessed food | 26.5 | -44.9 |
| Full pass-through (forecast revision) - posted prices: processed food | 31.0 | 31.7 |
| Full pass-through (forecast revision) - posted prices: nonenergy industrial goods | 34.9 | 58.1 |
| Full pass-through (forecast revision) - posted prices: services | 21.0 | 57.4 |
| Calvo + - posted prices | 67.5 | 63.0 |
| Calvo + - posted prices: unprocessed food | 60.1 | 36.2 |
| Calvo + - posted prices: processed food | 83.9 | 74.7 |
| Calvo + - posted prices: nonenergy industrial goods | 64.2 | 77.3 |
| Calvo + - posted prices: services | 46.2 | 80.6 |
Notes: The "full pass-through" method first assumes full immediate pass-through of a devaluation to individual reset price based on a total import content of consumption equal to , as estimated by Burstein et al. (2005). It then assumes that individual reset prices rose as much as the revision to the mean inflation forecast for the calendar year 1995 observed in a Bank of Mexico survey at the turn of 1995. The "Calvo+" method assumes no real rigidities and the random selection of items whose price adjustment is triggered by the shock.
Table 3: Lower Bounds on the Share of Initial Pass-Through Attributed to Adjustment Along the Extensive Margin During the January 2001 and April 1995 VAT Hikes
| Initial Pass-Through(Δπ/Δm, percent) | Share Attributed to Extensive Margin (percent) | |
|---|---|---|
| January 2010 hike Full pass-through - posted prices | 72.3 | 75.2 |
| January 2010 hike Full pass-through - posted prices: nonenergy industrial goods | 83.6 | 75.3 |
| January 2010 hike Full pass-through - posted prices: services | 34.8 | 66.2 |
| January 2010 hike Calvo+ - posted prices | 266.9 | 93.3 |
| January 2010 hike Calvo+ - posted prices: nonenergy industrial goods | 104.0 | 80.1 |
| January 2010 hike Calvo+ - posted prices: services | 38.8 | 130.3 |
| April 1995 hike Full pass-through - posted prices | 62.8 | 23.5 |
| April 1995 hike Full pass-through - posted prices: nonenergy industrial goods | 67.8 | 15.0 |
| April 1995 hike Full pass-through - posted prices: services | 41.3 | 24.7 |
| April 1995 hike Calvo+ - posted prices | 249.1 | 119.3 |
| April 1995 hike Calvo+ - posted prices: nonenergy industrial goods | 134.4 | 57.1 |
| April 1995 hike Calvo+ - posted prices: services | 356.1 | 108.7 |
Notes: The "full pass-through" method full immediate pass-through of the VAT hike to individual reset prices of taxable items. The "Calvo+" method assumes no real rigidities and the random selection of items whose price adjustment is triggered by the shock. Only taxable items were used in the computation of the statistics.
Table 4: Probability of Price Adjustment
| New York City Salty Snacks (1) | Los Angeles Carbonated Beverages (2) | Boston Frozen Dinner Entrees (3) | |
|---|---|---|---|
| Regressor | -1.220 | -0.979 | -0.891 |
| Regressor | 0.665 | 0.574 | 0.495 (0.042) |
| R2 | 0.11 | 0.06 | 0.07 |
| N | 1,056,906 | 938,349 | 396,471 |
Notes: Fixed effect (store-UPC) linear probability regression
model for the monthly change in reference prices across different
categories and markets:
![]()
where Ι(Δpi,t≠0) is an indicator variable that a reference price change has occurred, ![]() equals
equals![]() if
if ![]() < 0 and zero otherwise (with
< 0 and zero otherwise (with ![]() similarly defined for positive deviations), and
Ζi,t is a vector of control variables that includes monthly dummies, the age of the price,
and a measure of store size (total yearly revenues). Standard errors (in parentheses) are
corrected for heteroskedasticity and clustered at the store level. N is the number of monthly
observations from January 2001 to December 2007.
similarly defined for positive deviations), and
Ζi,t is a vector of control variables that includes monthly dummies, the age of the price,
and a measure of store size (total yearly revenues). Standard errors (in parentheses) are
corrected for heteroskedasticity and clustered at the store level. N is the number of monthly
observations from January 2001 to December 2007.
Table 5: Probability of a Price Adjustment by Spell Duration
| New York City Salty Snacks (4) | Los Angeles Carbonated Beverages (5) | Boston Frozen Dinner Entrees (6) | |
|---|---|---|---|
| Regressor | -1.263 | −1.084 (0.021) | −0.928 (0.062) |
| Regressor | 0.698 (0.038) | 0.586 (0.019) | 0.576 (0.050) |
| Regressor | 0.217 (0.025) | 0.180 (0.023) | 0.154 (0.092) |
| Regressor | −0.008 (0.018) | −0.031 (0.023) | −0.020 (0.045) |
| Regressor | 0.049 (0.047) | 0.220 (0.022) | 0.112 (0.116) |
| Regressor | -0.014 (0.023) | 0.068 (0.035) | −0.155 (0.067) |
| Regressor | 0.160 (0.024) | 0.337 (0.023) | −0.003 (0.088) |
| Regressor | -0.160 (0.024) | −0.061 (0.024) | −0.203 (0.048) |
| R2 | 0.12 | 0.06 | 0.06 |
| N | 1,056,906 | 938,349 | 396,471 |
Notes: Fixed effect (store-UPC) linear probability regression
model for the monthly change in reference prices across different
categories and markets:
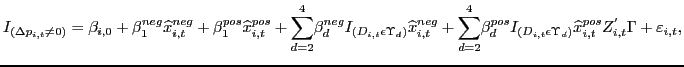
where ![]() ,
, ![]() and
and ![]() have been defined in Table 4.
have been defined in Table 4.
![]() is an indicator variable that the duration of the price spell Di,t
belongs to age group γd, where the age groups considered are 4 to 8 months, 9 to 12 months
and more than 12 months. Ζi,t is a vector of control variables that
includes monthly dummies and a measure of store size (total yearly
revenues). Standard errors (in parentheses) are corrected for
heteroskedasticity and clustered at the store level. is the number
of monthly observations from January 2001 to December 2007.
is an indicator variable that the duration of the price spell Di,t
belongs to age group γd, where the age groups considered are 4 to 8 months, 9 to 12 months
and more than 12 months. Ζi,t is a vector of control variables that
includes monthly dummies and a measure of store size (total yearly
revenues). Standard errors (in parentheses) are corrected for
heteroskedasticity and clustered at the store level. is the number
of monthly observations from January 2001 to December 2007.
Table 6: Index of Macroeconomic Flexibility
| Posted Prices | 0.27 | 0.10 | 0.37 | 0.19 |
|---|---|---|---|---|
| Regular Prices | 0.18 | 0.08 | 0.25 | 0.12 |
| Reference Prices | 0.09 | 0.04 | 0.13 | 0.06 |
Notes: This table reports estimates of the intensive and the extensive margins based on equation 7 for the IRI Marketing dataset. We use deviations from the average price of local competitors to proxy for deviations from individual reset prices and to estimate a nonparametric adjustment hazard function. The index of macroeconomic flexibility is computed given no real rigidities (a = 0) and moderate real rigidities (a = 0.6).
Figure 1: Initial Impact of the Mexican Peso Devaluation on the Distribution of Price Changes
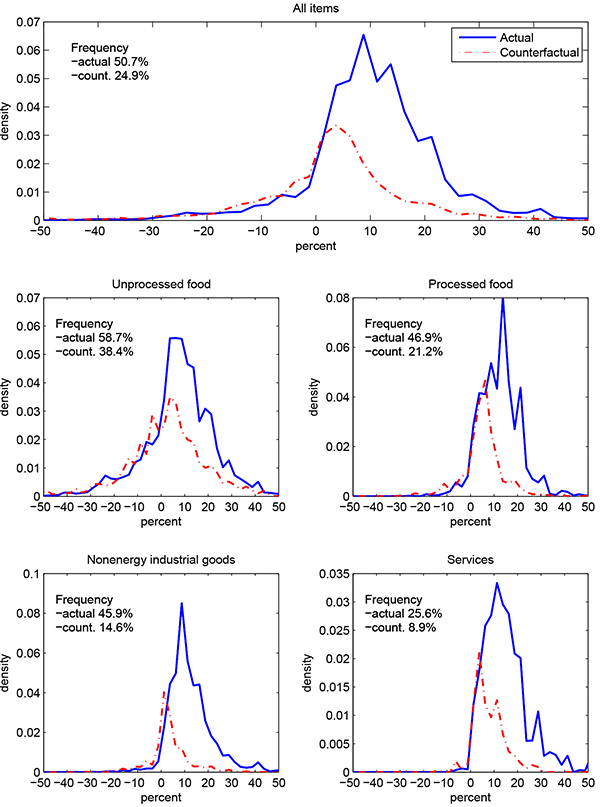
Notes: This figure shows the distribution of nonzero price changes in the Mexican CPI observed in January 1995 (the "actual" distribution) and in January 1994 (the "counterfactual" distribution) for special groups of products. Observations are grouped into bins of 2.5 percentage points and weighted by their relative importance in the CPI. The inserts in the panels report the monthly frequency of price changes.
Data for Figure 1
| Middle of Band | All Items Actual | All Items Count | Unprocessed Food Actual | Unprocessed Food Count | Processed Food Actual | Processed Food Count | Nonenergy Industrial Goods Actual | Nonenergy Industrial Goods Count | Services Actual | Services Count |
|---|---|---|---|---|---|---|---|---|---|---|
| -0.5875 | 0 | 0.000459 | 0 | 0.001294 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.5625 | 0.000168 | 0.000218 | 0.000475 | 0.000616 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.5375 | 0 | 0.000116 | 0 | 0.000327 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.5125 | 4.89E-05 | 0.00047 | 0.000138 | 0.001212 | 0 | 0 | 0 | 0.000115 | 0 | 0 |
| -0.4875 | 7.87E-05 | 0.000708 | 0.000222 | 0.001996 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.4625 | 0.000119 | 0.000264 | 0.000336 | 0.000699 | 0 | 5.59E-05 | 0 | 0 | 0 | 0 |
| -0.4375 | 0.000159 | 0.000342 | 0.000449 | 0.000849 | 0 | 6.44E-05 | 0 | 6.33E-05 | 0 | 0 |
| -0.4125 | 0.00046 | 0.000405 | 0.001298 | 0.001143 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.3875 | 0.000456 | 0.000402 | 0.001287 | 0.001134 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.3625 | 0.000352 | 0.000948 | 0.000901 | 0.002674 | 0 | 0 | 9.23E-05 | 0 | 0 | 0 |
| -0.3375 | 0.000413 | 0.000586 | 0.001164 | 0.001313 | 0 | 6.96E-05 | 0 | 0.000282 | 0 | 0 |
| -0.3125 | 0.000562 | 0.000759 | 0.001493 | 0.001896 | 0.000111 | 0.000103 | 0 | 0.00016 | 0 | 0 |
| -0.2875 | 0.001166 | 0.001557 | 0.003136 | 0.004271 | 0 | 0.000148 | 0.000153 | 0 | 0 | 0.000159 |
| -0.2625 | 0.001685 | 0.001631 | 0.004559 | 0.004329 | 0.000236 | 0.000192 | 0 | 0.000115 | 0 | 0.000159 |
| -0.2375 | 0.002742 | 0.001687 | 0.007315 | 0.003789 | 8.58E-05 | 0.00118 | 0.000348 | 0 | 0 | 0 |
| -0.2125 | 0.002356 | 0.001946 | 0.006209 | 0.004098 | 0 | 0.000952 | 0.000439 | 0.000609 | 0 | 0 |
| -0.1875 | 0.002431 | 0.002438 | 0.006043 | 0.005831 | 0.000868 | 0.00052 | 0.000102 | 0.000619 | 0 | 0 |
| -0.1625 | 0.002888 | 0.004132 | 0.006751 | 0.009071 | 0.000395 | 0.000991 | 0.001071 | 0.001773 | 0 | 0 |
| -0.1375 | 0.003012 | 0.00572 | 0.007584 | 0.013405 | 0.000436 | 0.002016 | 0.000555 | 0.001076 | 0 | 0.000333 |
| -0.1125 | 0.005146 | 0.006483 | 0.011935 | 0.011302 | 0.001119 | 0.005034 | 0.001663 | 0.002851 | 0 | 0 |
| -0.0875 | 0.005599 | 0.008364 | 0.012948 | 0.018855 | 0.001989 | 0.002623 | 0.001213 | 0.002586 | 0 | 0 |
| -0.0625 | 0.00905 | 0.008641 | 0.019148 | 0.014906 | 0.005605 | 0.004627 | 0.001777 | 0.005673 | 0.000384 | 0.001962 |
| -0.0375 | 0.008242 | 0.013939 | 0.018251 | 0.028854 | 0.003895 | 0.008235 | 0.0018 | 0.003704 | 0.000637 | 0.00029 |
| -0.0125 | 0.011834 | 0.015409 | 0.021355 | 0.02343 | 0.00805 | 0.008609 | 0.005418 | 0.012973 | 0.000484 | 0.001463 |
| 0.0125 | 0.028428 | 0.029987 | 0.033852 | 0.024615 | 0.028754 | 0.024068 | 0.022733 | 0.040228 | 0.011935 | 0.011826 |
| 0.0375 | 0.047569 | 0.033587 | 0.055704 | 0.034931 | 0.041543 | 0.038078 | 0.04438 | 0.028551 | 0.017952 | 0.021236 |
| 0.0625 | 0.049358 | 0.029661 | 0.055774 | 0.033072 | 0.041094 | 0.046573 | 0.04973 | 0.012348 | 0.025799 | 0.011876 |
| 0.0875 | 0.065416 | 0.019913 | 0.055486 | 0.022942 | 0.053622 | 0.025964 | 0.085047 | 0.011908 | 0.027609 | 0.009672 |
| 0.1125 | 0.048932 | 0.01338 | 0.046591 | 0.019957 | 0.043379 | 0.015121 | 0.055838 | 0.005368 | 0.033327 | 0.012656 |
| 0.1375 | 0.055036 | 0.00952 | 0.045386 | 0.019047 | 0.080638 | 0.006032 | 0.043651 | 0.002855 | 0.029557 | 0.006698 |
| 0.1625 | 0.038396 | 0.006789 | 0.026376 | 0.01185 | 0.046069 | 0.005301 | 0.044116 | 0.002948 | 0.027868 | 0.00363 |
| 0.1875 | 0.027988 | 0.006198 | 0.030895 | 0.009984 | 0.027053 | 0.006518 | 0.025848 | 0.002146 | 0.020881 | 0.002894 |
| 0.2125 | 0.029445 | 0.005821 | 0.028934 | 0.010764 | 0.043735 | 0.003291 | 0.01821 | 0.002955 | 0.020107 | 0.001591 |
| 0.2375 | 0.014409 | 0.003798 | 0.016821 | 0.008383 | 0.01151 | 0.001648 | 0.014378 | 0.000978 | 0.005506 | 0.000653 |
| 0.2625 | 0.008618 | 0.002024 | 0.010243 | 0.004518 | 0.007011 | 0.000816 | 0.008314 | 0.000521 | 0.005555 | 0.001248 |
| 0.2875 | 0.009162 | 0.002475 | 0.012615 | 0.00518 | 0.005613 | 0.000754 | 0.008623 | 0.001183 | 0.010679 | 0.000889 |
| 0.3125 | 0.006834 | 0.001694 | 0.0074 | 0.003935 | 0.008276 | 0.000519 | 0.005082 | 0.000417 | 0.002871 | 0 |
| 0.3375 | 0.003407 | 0.001043 | 0.006149 | 0.00245 | 0.000989 | 0.000461 | 0.00265 | 0.000113 | 0.003528 | 0 |
| 0.3625 | 0.002634 | 0.001367 | 0.004782 | 0.003455 | 0.0005 | 4.20E-05 | 0.002237 | 0.000366 | 0.003035 | 0 |
| 0.3875 | 0.002698 | 0.000878 | 0.003247 | 0.002013 | 0.002212 | 0.000461 | 0.002548 | 8.52E-05 | 0.001268 | 0 |
| 0.4125 | 0.004072 | 0.000456 | 0.005116 | 0.001075 | 0.001788 | 9.04E-05 | 0.004905 | 0.000138 | 0.002876 | 0 |
| 0.4375 | 0.00116 | 0.000683 | 0.001361 | 0.001892 | 0.000319 | 0 | 0.00165 | 3.60E-05 | 0 | 0 |
| 0.4625 | 0.00081 | 0.000194 | 0.001185 | 0.000549 | 0.000829 | 0 | 0.00042 | 0 | 0.000351 | 0.000187 |
| 0.4875 | 0.000717 | 6.90E-05 | 0.000945 | 0 | 0.000347 | 0.000113 | 0.000791 | 0.000102 | 0.00028 | 0 |
| 0.5125 | 0.000727 | 0.000212 | 0.000761 | 0.000195 | 0.000277 | 0.000231 | 0.001063 | 0.000215 | 0.002787 | 0 |
| 0.5375 | 0.000598 | 0.000241 | 0.000548 | 0.000453 | 0.000129 | 0.000231 | 0.001033 | 3.60E-05 | 0.000524 | 0 |
| 0.5625 | 0.00033 | 9.71E-05 | 0.000645 | 0.000274 | 0.000347 | 0 | 0 | 0 | 0 | 0 |
| 0.5875 | 0.000208 | 0.000159 | 0.000505 | 0.000413 | 4.07E-05 | 4.20E-05 | 4.91E-05 | 0 | 0 | 0 |
Figure 2: Initial Impact of the January 2010 1-Percent Hike in the Mexican VAT on the Distribution of Price Changes
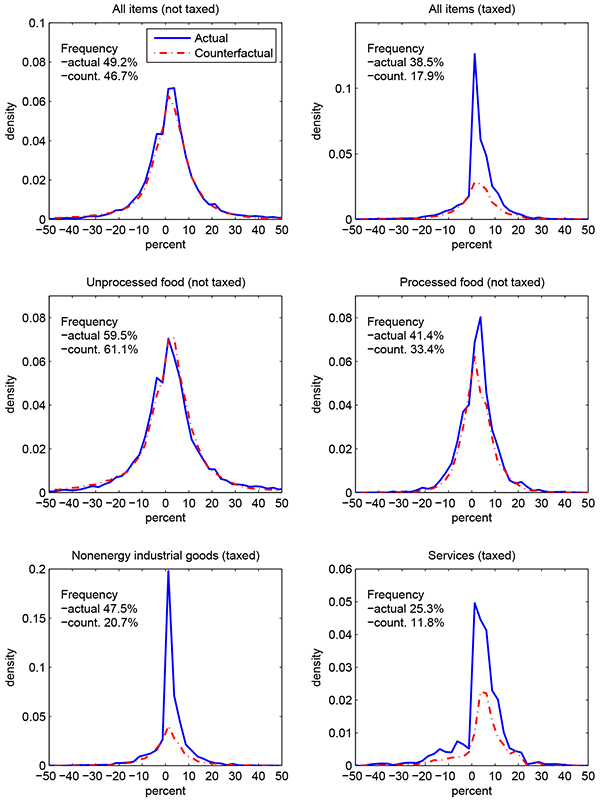
Notes: This figure shows the distribution of nonzero price changes in the Mexican CPI observed in January 2010 (the "actual" distribution) and an average of distributions observed in January from 2003 to 2007 (the "counterfactual" distribution) for special groups of products. Observations are grouped into bins of 2.5 percentage points and weighted by their relative importance in the CPI. Inserts in the panels report the monthly frequency of price changes.
Data for Figure 2
| Middle of Band | All items (not taxed) Actual | All items (not taxed) Count | All items (taxed) Actual | All items (taxed) Count | Unprocessed food (not taxed) Actual | Unprocessed food (not taxed) Count | Processed food (not taxed) Actual | Processed food (not taxed) Count | Nonenergy industrial goods (taxed)Â Actual | Nonenergy industrial goods (taxed)Â Count | Services (taxed) Actual | Services (taxed) Count |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -0.5875 | 1.56E-05 | 0 | 0 | 0 | 2.82E-05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.5625 | 8.91E-05 | 0 | 0 | 0 | 6.56E-05 | 0 | 0.000174 | 0 | 0 | 0 | 0 | 0 |
| -0.5375 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.5125 | 0.000153 | 0 | 0 | 0 | 0.000217 | 0 | 0.000108 | 0 | 0 | 0 | 0 | 0 |
| -0.4875 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.4625 | 0.000168 | 0 | 0 | 0 | 0.000302 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.4375 | 1.56E-05 | 0 | 0 | 0 | 2.82E-05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.4125 | 0.000123 | 0 | 0 | 0 | 0.000222 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.3875 | 0.000198 | 0 | 0 | 0 | 0.000358 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -0.3625 | 0.000313 | 0 | 0 | 0 | 0.000501 | 0 | 0.000115 | 0 | 0 | 0 | 0 | 0 |
| -0.3375 | 0.000448 | 0.000465 | 7.22E-05 | 0 | 0.000688 | 0.000838 | 0.000219 | 0 | 0.000154 | 0 | 0 | 0 |
| -0.3125 | 0.000352 | 0 | 1.20E-05 | 0 | 0.000636 | 0 | 0 | 0 | 2.56E-05 | 0 | 0 | 0 |
| -0.2875 | 0.000589 | 0.000129 | 0 | 0 | 0.001042 | 0.000232 | 3.80E-05 | 0 | 0 | 0 | 0 | 0 |
| -0.2625 | 0.000981 | 0.000875 | 0 | 0 | 0.001674 | 0.001578 | 0.000174 | 0 | 0 | 0 | 0 | 0 |
| -0.2375 | 0.001156 | 0.000233 | 0.000126 | 0 | 0.001621 | 0.00042 | 0.000484 | 0 | 0.000208 | 0 | 0 | 0 |
| -0.2125 | 0.001883 | 0.001255 | 4.54E-05 | 0 | 0.003365 | 0.002265 | 5.86E-05 | 0 | 0 | 0 | 0 | 0 |
| -0.1875 | 0.002518 | 0.001463 | 0.000164 | 0.000343 | 0.004347 | 0.002639 | 0 | 0 | 0 | 0.000732 | 0.000435 | 0 |
| -0.1625 | 0.004366 | 0.005564 | 0.000431 | 0 | 0.007649 | 0.009963 | 0.000418 | 0.000139 | 0.000668 | 0 | 0 | 0 |
| -0.1375 | 0.005553 | 0.003191 | 0.000726 | 0.000448 | 0.009779 | 0.005757 | 0.000437 | 0 | 0.000873 | 0.000955 | 0.000842 | 0 |
| -0.1125 | 0.007803 | 0.008326 | 0.000128 | 0.000895 | 0.013106 | 0.010368 | 0.001547 | 0.008501 | 0.000236 | 0.001612 | 0 | 0 |
| -0.0875 | 0.009986 | 0.00997 | 0.000468 | 0.000861 | 0.016364 | 0.016765 | 0.00205 | 0 | 0.000676 | 0 | 0 | 0.002289 |
| -0.0625 | 0.011543 | 0.007398 | 0.001913 | 0.000358 | 0.019472 | 0.012836 | 0.001958 | 0.000933 | 0.002726 | 0.000764 | 0.000276 | 0 |
| -0.0375 | 0.015655 | 0.022126 | 0.001076 | 0.000985 | 0.025233 | 0.030542 | 0.004863 | 0.017129 | 0.001382 | 0.002101 | 0.000712 | 0 |
| -0.0125 | 0.018575 | 0.016761 | 0.002422 | 0.003007 | 0.027648 | 0.027464 | 0.010181 | 0.00507 | 0.002195 | 0.005259 | 0.002263 | 0 |
| 0.0125 | 0.043589 | 0.040601 | 0.021691 | 0.020476 | 0.049095 | 0.049064 | 0.051826 | 0.041951 | 0.02349 | 0.010754 | 0.022625 | 0.01084 |
| 0.0375 | 0.080617 | 0.068716 | 0.188485 | 0.036923 | 0.072971 | 0.08532 | 0.07758 | 0.064228 | 0.216197 | 0.029824 | 0.181491 | 0.025385 |
| 0.0625 | 0.071635 | 0.069315 | 0.087009 | 0.053511 | 0.063525 | 0.089957 | 0.100606 | 0.060572 | 0.066881 | 0.064024 | 0.108696 | 0.048075 |
| 0.0875 | 0.059127 | 0.081659 | 0.079089 | 0.085991 | 0.052183 | 0.069368 | 0.083948 | 0.124808 | 0.079364 | 0.106639 | 0.070466 | 0.052728 |
| 0.1125 | 0.047032 | 0.065424 | 0.079007 | 0.041359 | 0.044463 | 0.07052 | 0.059045 | 0.086803 | 0.084956 | 0.051932 | 0.067107 | 0.024156 |
| 0.1375 | 0.039286 | 0.028015 | 0.072409 | 0.069856 | 0.031577 | 0.025148 | 0.0482 | 0.031364 | 0.082561 | 0.104044 | 0.057056 | 0.034153 |
| 0.1625 | 0.029948 | 0.038619 | 0.056847 | 0.055387 | 0.02671 | 0.033335 | 0.037317 | 0.065069 | 0.070529 | 0.072962 | 0.030334 | 0.035314 |
| 0.1875 | 0.022994 | 0.019762 | 0.046234 | 0.031752 | 0.017875 | 0.015048 | 0.027626 | 0.034387 | 0.056064 | 0.038433 | 0.024838 | 0.023723 |
| 0.2125 | 0.020669 | 0.02646 | 0.036701 | 0.029198 | 0.015503 | 0.02819 | 0.028981 | 0.030795 | 0.040814 | 0.029688 | 0.020173 | 0.016056 |
| 0.2375 | 0.011684 | 0.009653 | 0.018565 | 0.012788 | 0.006516 | 0.005028 | 0.024246 | 0.02192 | 0.025443 | 0.018533 | 0.003619 | 0.002451 |
| 0.2625 | 0.011726 | 0.016965 | 0.015419 | 0.012904 | 0.009843 | 0.017041 | 0.014628 | 0.024785 | 0.020489 | 0.010074 | 0.006895 | 0.018513 |
| 0.2875 | 0.006101 | 0.014708 | 0.010182 | 0.008003 | 0.003396 | 0.011394 | 0.010176 | 0.022173 | 0.012834 | 0.013589 | 0.004679 | 0.004341 |
| 0.3125 | 0.007186 | 0.010772 | 0.009539 | 0.005572 | 0.006662 | 0.00574 | 0.006111 | 0.017869 | 0.013383 | 0.005096 | 0.002355 | 0.006237 |
| 0.3375 | 0.004438 | 0.002608 | 0.009293 | 0.004602 | 0.003715 | 0.002145 | 0.00716 | 0.003966 | 0.007422 | 0.003713 | 0.007012 | 0.001967 |
| 0.3625 | 0.004518 | 0.002854 | 0.003645 | 0.000817 | 0.003148 | 0.002474 | 0.007438 | 0.004173 | 0.006215 | 0.001743 | 0.001318 | 0 |
| 0.3875 | 0.002563 | 0.004743 | 0.003349 | 0.000258 | 0.002001 | 0.004581 | 0.004057 | 0.005842 | 0.004118 | 0.000551 | 0.00023 | 0 |
| 0.4125 | 0.004254 | 0.001375 | 0.002555 | 0.002318 | 0.002809 | 0 | 0.00327 | 0.002591 | 0.004926 | 0.002061 | 0.000397 | 0.00153 |
| 0.4375 | 0.002124 | 0.001328 | 0.001837 | 0 | 0.002529 | 0.00045 | 0.002014 | 0.001322 | 0.003516 | 0 | 0.000388 | 0 |
| 0.4625 | 0.001491 | 0.000786 | 0.002594 | 0.000127 | 0.00091 | 0 | 0.003251 | 0.002591 | 0.003969 | 0.000271 | 0.001725 | 0 |
| 0.4875 | 0.000719 | 0.001098 | 0.00103 | 9.70E-05 | 0.001161 | 0.001257 | 0.000247 | 0.001322 | 0.002095 | 0.000207 | 0 | 0 |
| 0.5125 | 0.000828 | 0.000564 | 0.001104 | 0.001403 | 0.000561 | 0 | 0.000235 | 0.001858 | 0.001852 | 0.000788 | 0.000435 | 0.002747 |
| 0.5375 | 0.000435 | 0 | 0.000464 | 0 | 0.000773 | 0 | 2.30E-05 | 0 | 0.000755 | 0 | 0.00023 | 0 |
| 0.5625 | 0.000314 | 0.00061 | 0.000373 | 0 | 0.000408 | 0.000807 | 0.000291 | 0.000536 | 0.000706 | 0 | 0 | 0 |
| 0.5875 | 0.000324 | 0 | 0.000815 | 0 | 0.000275 | 0 | 0.000567 | 0 | 0.00136 | 0 | 0.00023 | 0 |
Figure 3: Initial impact of the April 1995 5-percent hike in the Mexican VAT on the distribution of price changes

Notes: This figure shows the distribution of nonzero price changes in the Mexican CPI observed in April 1995 in regions subject to the VAT hike (the "actual" distribution) and in regions not subject to the VAT hike (the "counterfactual" distribution) for special groups of products. Observations are grouped into bins of 2.5 percentage points and weighted by their relative importance in the CPI. Inserts in the panels report the monthly frequency of price changes.
Data for Figure 3
| middle of band | All items (not taxed): Actual | All items (not taxed): Count | All items (taxed): Actual | All items (taxed): Count | Unprocessed food (not taxed): Actual | Unprocessed food (not taxed): Count | Processed food (not taxed): Actual | Processed food (not taxed): Count | Nonenergy industrial goods (taxed): Â Actual | Nonenergy industrial goods (taxed): Â Count | Services (taxed): Actual | Services (taxed): Count |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -0.5875 | 6.26E-05 | 0.000647 | 6.21E-06 | 8.18E-06 | 1.15E-04 | 0.001189 | 0 | 0 | 0 | 1.76E-05 | 1.46E-05 | 0 |
| -0.5625 | 2.83E-04 | 0.000653 | 0 | 4.25E-05 | 5.20E-04 | 0.001199 | 0 | 0 | 0 | 1.89E-05 | 0 | 7.95E-05 |
| -0.5375 | 0.00013 | 0.000677 | 3.71E-05 | 2.91E-05 | 0.000239 | 0.001243 | 0 | 0 | 7.99E-05 | 1.05E-05 | 0 | 4.10E-05 |
| -0.5125 | 0.000387 | 0.000749 | 0.000101 | 2.87E-05 | 0.000711 | 0.001353 | 0 | 3.09E-05 | 1.38E-05 | 5.21E-05 | 0.000224 | 1.06E-05 |
| -0.4875 | 0.000261 | 0.000809 | 7.38E-05 | 5.33E-05 | 0.000479 | 0.001466 | 0 | 2.72E-05 | 0.000159 | 9.64E-05 | 0 | 2.51E-06 |
| -0.4625 | 0.000438 | 0.000683 | 2.15E-05 | 6.12E-05 | 0.000805 | 0.00125 | 0 | 5.38E-06 | 4.63E-05 | 4.31E-05 | 0 | 8.45E-05 |
| -0.4375 | 6.82E-04 | 0.000906 | 0.000162 | 0.000115 | 1.24E-03 | 0.001661 | 2.16E-05 | 3.75E-06 | 0 | 0.000156 | 0.000383 | 8.45E-05 |
| -0.4125 | 0.000676 | 0.001215 | 0.000309 | 0.000136 | 0.001038 | 0.002135 | 4.04E-05 | 0.000114 | 0.00018 | 0.000164 | 0.000532 | 7.44E-05 |
| -0.3875 | 0.000595 | 0.001251 | 0.000514 | 0.000128 | 0.001075 | 0.002215 | 2.43E-05 | 0.000114 | 0.000494 | 0.000139 | 0.000672 | 0.000128 |
| -0.3625 | 0.00079 | 0.0014 | 0.000565 | 0.00028 | 0.00145 | 0.002519 | 0 | 7.24E-05 | 0.000642 | 0.000516 | 0.00063 | 7.87E-05 |
| -0.3375 | 0.001418 | 0.001877 | 4.01E-04 | 0.000337 | 0.002246 | 0.003397 | 0.000499 | 6.91E-05 | 0.000688 | 0.000469 | 0.000191 | 0.000248 |
| -0.3125 | 0.001605 | 0.002017 | 4.70E-04 | 0.000259 | 0.00293 | 0.003523 | 2.56E-05 | 0.000231 | 5.50E-04 | 0.000301 | 0.000506 | 0.00023 |
| -0.2875 | 0.001535 | 0.002187 | 0.000785 | 0.000427 | 0.002485 | 0.003858 | 4.65E-04 | 0.000221 | 0.000741 | 0.00058 | 0.00083 | 0.000279 |
| -0.2625 | 0.00224 | 0.003128 | 0.000915 | 0.000485 | 0.003779 | 0.005322 | 0.000297 | 0.000504 | 0.000916 | 0.000482 | 0.000923 | 0.000487 |
| -0.2375 | 0.002976 | 0.003184 | 0.000775 | 0.000488 | 0.004706 | 0.005628 | 0.001059 | 0.000305 | 0.00077 | 0.000579 | 0.000825 | 0.000311 |
| -0.2125 | 0.004671 | 0.004594 | 1.98E-03 | 0.001192 | 0.006919 | 0.007545 | 2.21E-03 | 0.00121 | 0.002727 | 0.00152 | 0.001479 | 0.001 |
| -0.1875 | 0.004788 | 0.004924 | 0.002535 | 0.001321 | 0.007552 | 0.00817 | 0.001732 | 0.001196 | 0.002703 | 0.001508 | 0.00294 | 0.000972 |
| -0.1625 | 0.00649 | 0.006113 | 0.003055 | 0.002326 | 0.010057 | 0.009597 | 0.002429 | 0.002093 | 0.003223 | 0.002813 | 0.003579 | 0.001696 |
| -0.1375 | 0.009847 | 0.008515 | 0.004351 | 0.002636 | 0.014057 | 0.013043 | 0.005345 | 0.003461 | 0.004055 | 0.003085 | 0.00507 | 0.001517 |
| -0.1125 | 0.013078 | 0.011335 | 0.006384 | 0.004422 | 0.017191 | 0.016408 | 0.009006 | 0.005949 | 0.009262 | 0.006186 | 0.004179 | 0.002006 |
| -0.0875 | 0.019159 | 0.015969 | 0.007493 | 0.005629 | 0.025512 | 0.021812 | 0.013255 | 0.009924 | 0.010826 | 0.007534 | 0.004028 | 0.002457 |
| -0.0625 | 0.029397 | 0.025297 | 0.010563 | 0.008556 | 0.036982 | 0.032952 | 0.023168 | 0.018362 | 0.012574 | 0.012269 | 0.007439 | 0.002592 |
| -0.0375 | 0.043475 | 0.036314 | 0.012286 | 0.012303 | 0.052529 | 0.044669 | 0.036973 | 0.029857 | 0.016131 | 0.017821 | 0.006518 | 0.002715 |
| -0.0125 | 0.043308 | 0.045904 | 0.01779 | 0.018494 | 0.050302 | 0.051425 | 0.040195 | 0.045411 | 0.026727 | 0.025519 | 0.00521 | 0.004151 |
| 0.0125 | 0.066375 | 0.062816 | 0.126207 | 0.028382 | 0.070421 | 0.069791 | 0.068812 | 0.062184 | 0.198087 | 0.040522 | 0.049615 | 0.010135 |
| 0.0375 | 0.066793 | 0.057081 | 0.060955 | 0.027067 | 0.061918 | 0.070794 | 0.080254 | 0.045362 | 0.071037 | 0.028046 | 0.04455 | 0.022534 |
| 0.0625 | 0.046895 | 0.045269 | 0.048487 | 0.022692 | 0.052149 | 0.053367 | 0.045739 | 0.040067 | 0.044439 | 0.020274 | 0.041341 | 0.022097 |
| 0.0875 | 0.031971 | 0.032658 | 0.025404 | 0.013005 | 0.036815 | 0.041411 | 0.028714 | 0.024978 | 0.021412 | 0.010073 | 0.022926 | 0.013673 |
| 0.1125 | 0.02151 | 0.02132 | 0.019905 | 0.009494 | 0.024276 | 0.029216 | 0.020692 | 0.013445 | 0.015423 | 0.008466 | 0.020125 | 0.008536 |
| 0.1375 | 0.015534 | 0.016112 | 0.010716 | 0.005585 | 0.019487 | 0.021514 | 0.011789 | 0.010695 | 0.009289 | 0.004492 | 0.010094 | 0.006324 |
| 0.1625 | 0.010553 | 0.011107 | 0.006704 | 0.003901 | 0.015046 | 0.015352 | 0.005529 | 0.006664 | 0.007079 | 0.003748 | 0.005349 | 0.003575 |
| 0.1875 | 0.007592 | 0.007736 | 0.004808 | 0.003471 | 0.01073 | 0.01097 | 0.004141 | 0.004475 | 0.00432 | 0.002211 | 0.004475 | 0.004445 |
| 0.2125 | 0.007777 | 0.006027 | 0.003626 | 0.002435 | 0.01057 | 0.009025 | 0.004839 | 0.002533 | 0.002684 | 0.002217 | 0.004005 | 0.002564 |
| 0.2375 | 0.004449 | 0.00434 | 0.001602 | 0.000649 | 0.006283 | 0.007041 | 0.002632 | 0.001261 | 0.002364 | 0.000878 | 0.00044 | 0.000179 |
| 0.2625 | 0.003423 | 0.003066 | 0.00073 | 0.00072 | 0.005561 | 0.005053 | 0.000907 | 0.000804 | 0.000693 | 0.000862 | 0.000758 | 0.000617 |
| 0.2875 | 0.002636 | 0.002762 | 0.001452 | 0.000799 | 0.003795 | 0.004378 | 0.00125 | 0.000927 | 0.001839 | 0.00071 | 0.001157 | 0.000899 |
| 0.3125 | 0.002233 | 0.001962 | 0.000645 | 0.000268 | 0.003727 | 0.003164 | 0.000521 | 0.000613 | 0.000605 | 0.000275 | 0.000491 | 0.000162 |
| 0.3375 | 0.001937 | 0.001407 | 0.000292 | 0.000229 | 0.003398 | 0.002481 | 0.000222 | 0.000144 | 0.000215 | 0.000351 | 0.000452 | 0.000139 |
| 0.3625 | 0.001541 | 0.001158 | 0.000443 | 0.000282 | 0.002643 | 0.001953 | 0.000262 | 0.000112 | 0.000487 | 0.000461 | 0.000484 | 7.63E-05 |
| 0.3875 | 0.001716 | 0.000944 | 0.000208 | 4.95E-05 | 0.002899 | 0.001642 | 0.000352 | 9.25E-05 | 0.000142 | 9.20E-05 | 0.000335 | 5.03E-06 |
| 0.4125 | 0.00144 | 0.000817 | 0.000141 | 9.75E-05 | 0.002645 | 0.001485 | 0 | 2.17E-05 | 0.000133 | 0.000117 | 0.000132 | 0.000102 |
| 0.4375 | 0.001016 | 0.000729 | 0.000163 | 7.02E-05 | 0.001803 | 0.001313 | 8.78E-05 | 3.58E-05 | 0.000282 | 0.000147 | 7.58E-05 | 5.03E-06 |
| 0.4625 | 0.001203 | 0.000694 | 7.65E-05 | 6.58E-05 | 0.002209 | 0.001227 | 0 | 6.57E-05 | 0.000165 | 0.000101 | 0 | 4.42E-05 |
| 0.4875 | 0.00077 | 0.000362 | 2.35E-05 | 2.02E-05 | 0.001414 | 0.000658 | 0 | 9.69E-06 | 5.05E-05 | 2.19E-05 | 0 | 7.54E-06 |
| 0.5125 | 0.000957 | 0.000364 | 3.03E-05 | 7.63E-05 | 0.001758 | 0.000656 | 0 | 1.80E-05 | 0 | 0.000124 | 7.15E-05 | 4.47E-05 |
| 0.5375 | 0.000796 | 0.000283 | 3.67E-05 | 1.87E-05 | 0.001462 | 0.00049 | 0.00E+00 | 4.29E-05 | 7.90E-05 | 3.31E-05 | 0 | 7.78E-06 |
| 0.5625 | 0.000736 | 0.000317 | 3.37E-05 | 2.01E-05 | 0.001352 | 0.000575 | 0 | 1.11E-05 | 4.12E-05 | 4.33E-05 | 0 | 0 |
| 0.5875 | 0.000587 | 0.000189 | 1.85E-05 | 1.09E-05 | 0.001078 | 0.000346 | 0 | 0 | 0 | 1.43E-06 | 4.36E-05 | 2.41E-05 |
Figure 4: Distribution of Nonzero Price Changes in the Mexican CPI Conditional on a Price Change in April 1995
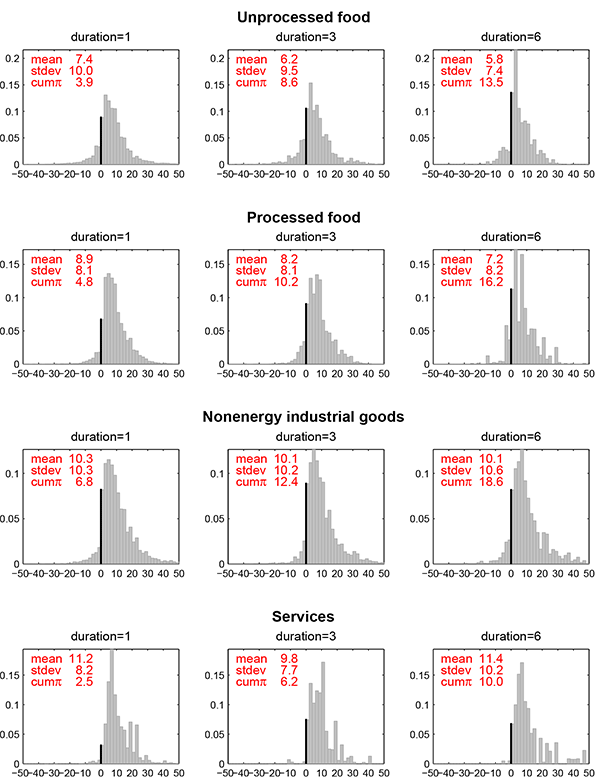
Notes: This figure shows the distributions of first nonzero price changes in the Mexican CPI conditional on a nonzero price change in April 1995 and the duration (in months). The upper-left corner of each panel reports the mean (in percent), its standard deviation (in percentage points), and the cumulated inflation in the special group since April 1995 (in percent).
Data for Figure 4
| Left edge of bin | Unprocessed food: duration=1 | Unprocessed food: duration=3 | Unprocessed food: duration=6 | Processed food: duration=1 | Processed food: duration=3 | Processed food: duration=6 | Nonenergy Industrial Goods: duration=1 | Nonenergy Industrial Goods: duration=3 | Nonenergy Industrial Goods: duration=6 | Services: duration=1 | Services: duration=3 | Services: duration=6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -60 | 4.61E-05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -57.5 | 6.46E-05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.000519 | 0 | 0 |
| -55 | 0.00011 | 4.78E-05 | 0 | 0 | 0 | 0 | 0 | 0.000458 | 0 | 0 | 0 | 0 |
| -52.5 | 9.83E-05 | 0 | 0 | 0 | 0 | 0 | 3.37E-05 | 0 | 0 | 0 | 0 | 0 |
| -50 | 0.000252 | 4.80E-05 | 0 | 7.41E-05 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -47.5 | 0.000183 | 0.000104 | 0 | 3.66E-05 | 0 | 0 | 6.36E-05 | 0 | 0 | 0 | 0 | 0 |
| -45 | 0.000282 | 0.000414 | 0 | 3.66E-05 | 0 | 0 | 5.76E-05 | 0 | 0 | 0 | 0 | 0 |
| -42.5 | 0.000279 | 0 | 0 | 0 | 0 | 0 | 0.000146 | 0 | 0 | 0 | 0 | 0 |
| -40 | 0.000358 | 0.000189 | 0 | 2.29E-05 | 0.000257 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -37.5 | 0.000448 | 0.000353 | 0 | 1.80E-05 | 0 | 0 | 0.000105 | 9.93E-05 | 0 | 0.000519 | 0 | 0 |
| -35 | 0.000488 | 0.000327 | 0 | 6.81E-05 | 5.47E-05 | 0 | 0 | 0.000181 | 0 | 0 | 0 | 0 |
| -32.5 | 0.000764 | 0.000454 | 0 | 1.80E-05 | 0.000115 | 0 | 5.00E-05 | 0 | 0 | 0 | 0 | 0 |
| -30 | 0.000935 | 0.000954 | 0.000613 | 0.000232 | 0 | 0 | 0.000105 | 0 | 0.000732 | 0.000137 | 0 | 0 |
| -27.5 | 0.001187 | 0.001308 | 0 | 0.000337 | 0 | 0.001043 | 0.000557 | 0.000124 | 0 | 0 | 0 | 0 |
| -25 | 0.001879 | 0.000929 | 0 | 9.45E-05 | 0 | 0 | 0.000288 | 0.000298 | 0 | 0 | 0.000662 | 0 |
| -22.5 | 0.002685 | 0.003575 | 0.000681 | 0.000366 | 0.000448 | 0.001443 | 0.000844 | 0.001652 | 0.001457 | 0 | 0 | 0 |
| -20 | 0.002453 | 0.003072 | 0 | 0.00047 | 0.000577 | 0 | 0.000913 | 0.000224 | 0.003024 | 0 | 0 | 0 |
| -17.5 | 0.00432 | 0.006469 | 0.002135 | 0.000871 | 0.001965 | 0.012598 | 0.002788 | 0.002146 | 0.001369 | 0 | 0 | 0 |
| -15 | 0.00484 | 0.003778 | 0.00297 | 0.001414 | 0.001099 | 0.000971 | 0.003512 | 0.000982 | 0.003179 | 4.68E-05 | 0 | 0 |
| -12.5 | 0.007746 | 0.017653 | 0.006136 | 0.003352 | 0.002096 | 0.002542 | 0.004598 | 0.001277 | 0.003675 | 0.000544 | 0.007084 | 0 |
| -10 | 0.011805 | 0.0149 | 0.011679 | 0.005692 | 0.005753 | 0.002988 | 0.004776 | 0.003488 | 0.004022 | 0.000623 | 0.002846 | 0 |
| -7.5 | 0.016997 | 0.018884 | 0.047853 | 0.009403 | 0.011244 | 0.005538 | 0.010094 | 0.009431 | 0.009074 | 0.003321 | 0 | 0 |
| -5 | 0.032572 | 0.048849 | 0.025115 | 0.01703 | 0.031644 | 0.053168 | 0.016571 | 0.015103 | 0.029134 | 0.004974 | 0.00037 | 0.00466 |
| -2.5 | 0.044348 | 0.05651 | 0.033207 | 0.023162 | 0.042027 | 0.042843 | 0.021222 | 0.026966 | 0.03166 | 0.00628 | 0.003496 | 0.004813 |
| 0 | 0.125777 | 0.138042 | 0.189152 | 0.099796 | 0.118338 | 0.154674 | 0.113504 | 0.115913 | 0.118857 | 0.046117 | 0.114391 | 0.102651 |
| 2.5 | 0.160234 | 0.178582 | 0.195449 | 0.173497 | 0.162346 | 0.158127 | 0.146484 | 0.153118 | 0.126149 | 0.107338 | 0.13974 | 0.129367 |
| 5 | 0.137099 | 0.130394 | 0.133356 | 0.160286 | 0.155357 | 0.196244 | 0.134638 | 0.155537 | 0.151604 | 0.265803 | 0.17629 | 0.234874 |
| 7.5 | 0.127315 | 0.112117 | 0.099943 | 0.150693 | 0.150672 | 0.088649 | 0.121175 | 0.112182 | 0.122042 | 0.128596 | 0.125794 | 0.127941 |
| 10 | 0.091503 | 0.056779 | 0.082751 | 0.093799 | 0.078544 | 0.070302 | 0.091802 | 0.102174 | 0.085704 | 0.087836 | 0.173553 | 0.09353 |
| 12.5 | 0.063165 | 0.071659 | 0.033049 | 0.070238 | 0.061656 | 0.044048 | 0.074828 | 0.066859 | 0.065317 | 0.075648 | 0.063397 | 0.051545 |
| 15 | 0.048701 | 0.044302 | 0.061661 | 0.053787 | 0.049418 | 0.059085 | 0.061685 | 0.059555 | 0.056395 | 0.058924 | 0.03106 | 0.059367 |
| 17.5 | 0.030857 | 0.019766 | 0.02735 | 0.045269 | 0.042782 | 0.015616 | 0.04727 | 0.038042 | 0.020063 | 0.075036 | 0.079428 | 0.043103 |
| 20 | 0.019907 | 0.023435 | 0.031613 | 0.032396 | 0.023026 | 0.044032 | 0.038825 | 0.03231 | 0.053406 | 0.078089 | 0.030984 | 0.020438 |
| 22.5 | 0.013662 | 0.002489 | 0.002706 | 0.014613 | 0.016399 | 0.015051 | 0.021514 | 0.01834 | 0.019461 | 0.010711 | 0.009078 | 0.027226 |
| 25 | 0.010954 | 0.007783 | 0.00785 | 0.015684 | 0.0212 | 0.000539 | 0.017881 | 0.014836 | 0.013282 | 0.011824 | 0.010955 | 0.010662 |
| 27.5 | 0.007625 | 0.012175 | 0.003143 | 0.01044 | 0.011808 | 0.025363 | 0.015708 | 0.011834 | 0.022669 | 0.014417 | 0.013307 | 0.035666 |
| 30 | 0.007433 | 0.007386 | 0.000792 | 0.00497 | 0.003232 | 0.002507 | 0.010155 | 0.015518 | 0.00852 | 0.005836 | 0.002526 | 0 |
| 32.5 | 0.004607 | 0.005632 | 0 | 0.004458 | 0.004264 | 0 | 0.00777 | 0.011226 | 0.015187 | 0.002952 | 0 | 0 |
| 35 | 0.002507 | 0.006143 | 0 | 0.002015 | 0.000667 | 0.000971 | 0.00741 | 0.005652 | 0.010551 | 0.002445 | 0.002355 | 0 |
| 37.5 | 0.00293 | 0.000288 | 0.000182 | 0.0009 | 0.001303 | 0.000559 | 0.003128 | 0.007514 | 0.004646 | 0.000826 | 0 | 0.015743 |
| 40 | 0.002572 | 0.001539 | 0 | 0.001621 | 0.000546 | 0 | 0.004998 | 0.004376 | 0.005242 | 0.005394 | 0.012684 | 0.007409 |
| 42.5 | 0.002359 | 0.001263 | 0 | 0.000609 | 9.86E-05 | 0 | 0.003156 | 0.003995 | 0.006798 | 0.002252 | 0 | 0.008334 |
| 45 | 0.001156 | 0.000196 | 0 | 0.00072 | 0.000107 | 0.001102 | 0.004179 | 0.001405 | 0.005404 | 0.000519 | 0 | 0.022672 |
| 47.5 | 0.000898 | 0.000583 | 0.000613 | 0.00044 | 8.49E-05 | 0 | 0.001475 | 0.00181 | 0.0003 | 0.000269 | 0 | 0 |
| 50 | 0.00122 | 7.01E-05 | 0 | 0.000539 | 0.000603 | 0 | 0.002383 | 0.002699 | 0.001076 | 0.002067 | 0 | 0 |
| 52.5 | 0.000678 | 0.000209 | 0 | 0.000372 | 0.00011 | 0 | 0.001602 | 0.000532 | 0 | 0 | 0 | 0 |
| 55 | 0.000979 | 0 | 0 | 6.82E-05 | 0.000107 | 0 | 0.000874 | 0.001128 | 0 | 0.000137 | 0 | 0 |
| 57.5 | 0.000724 | 0.000352 | 0 | 9.01E-05 | 5.03E-05 | 0 | 0.000833 | 0.001018 | 0 | 0 | 0 | 0 |
Figure 5: Distribution of Nonzero Posted Price Changes in the U.S. CPI Conditional on the Duration Since the Last Price Change
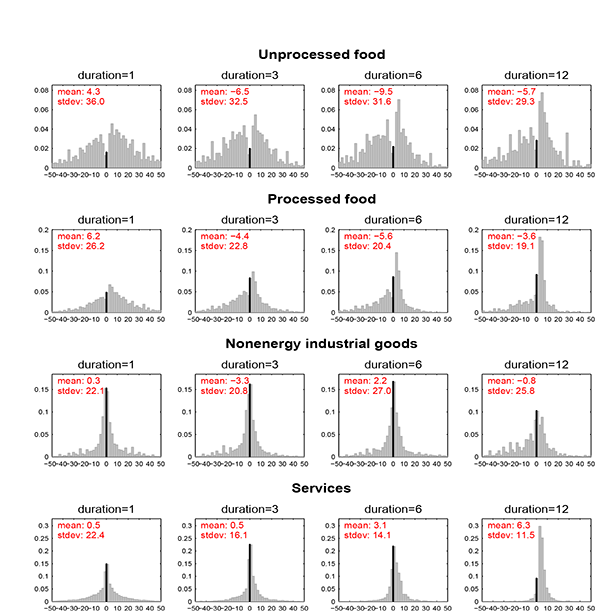
Notes: This figure shows the distribution of nonzero posted price changes in the U.S. CPI conditional on the duration (in months) since the last price change. The sample period is January 1988 to August 2010.
Data for Figure 5
| Left edge of bin | Unprocessed food: duration=1 | Unprocessed food: duration=3 | Unprocessed food: duration=6 | Unprocessed food: duration=12 | Processed food: duration=1 | Processed food: duration=3 | Processed food: duration=6 | Processed food: duration=12 | Nonenergy Industrial Goods: duration=1 | Nonenergy Industrial Goods: duration=3 | Nonenergy Industrial Goods: duration=6 | Nonenergy Industrial Goods: duration=12 | Services: duration=1 | Services: duration=3 | Services: duration=6 | Services: duration=12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -50 | 0.005 | 0.007 | 0.006 | 0.008 | 0.002 | 0.003 | 0.005 | 0.005 | 0.001 | 0.002 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 | 0 |
| -47.9167 | 0.005 | 0.007 | 0.011 | 0.011 | 0.002 | 0.003 | 0.002 | 0.001 | 0.001 | 0.002 | 0.001 | 0.004 | 0.002 | 0.001 | 0 | 0 |
| -45.8333 | 0.005 | 0.005 | 0.004 | 0.004 | 0.002 | 0.004 | 0.006 | 0.001 | 0.001 | 0.002 | 0.001 | 0.004 | 0.003 | 0.002 | 0 | 0 |
| -43.75 | 0.009 | 0.013 | 0.013 | 0.008 | 0.004 | 0.006 | 0.005 | 0.003 | 0.006 | 0.007 | 0.005 | 0.014 | 0.003 | 0.001 | 0.001 | 0.001 |
| -41.6667 | 0.005 | 0.006 | 0.006 | 0.009 | 0.002 | 0.003 | 0.002 | 0.002 | 0.001 | 0.002 | 0.001 | 0.004 | 0.004 | 0.001 | 0.001 | 0 |
| -39.5833 | 0.008 | 0.012 | 0.011 | 0.011 | 0.005 | 0.008 | 0.007 | 0.009 | 0.003 | 0.004 | 0.003 | 0.004 | 0.004 | 0.002 | 0.001 | 0 |
| -37.5 | 0.006 | 0.009 | 0.008 | 0.008 | 0.003 | 0.006 | 0.005 | 0.002 | 0.002 | 0.003 | 0.004 | 0.008 | 0.004 | 0.002 | 0.001 | 0 |
| -35.4167 | 0.019 | 0.027 | 0.025 | 0.021 | 0.01 | 0.016 | 0.016 | 0.009 | 0.009 | 0.01 | 0.008 | 0.014 | 0.006 | 0.002 | 0.002 | 0 |
| -33.3333 | 0.007 | 0.008 | 0.006 | 0.006 | 0.005 | 0.008 | 0.009 | 0.005 | 0.003 | 0.004 | 0.003 | 0.004 | 0.006 | 0.003 | 0.001 | 0 |
| -31.25 | 0.011 | 0.015 | 0.016 | 0.013 | 0.006 | 0.009 | 0.008 | 0.007 | 0.011 | 0.013 | 0.01 | 0.022 | 0.007 | 0.003 | 0.001 | 0 |
| -29.1667 | 0.013 | 0.015 | 0.019 | 0.008 | 0.009 | 0.015 | 0.016 | 0.004 | 0.007 | 0.008 | 0.005 | 0.011 | 0.007 | 0.004 | 0.002 | 0 |
| -27.0833 | 0.009 | 0.012 | 0.015 | 0.015 | 0.007 | 0.009 | 0.008 | 0.007 | 0.005 | 0.007 | 0.004 | 0.009 | 0.008 | 0.005 | 0.002 | 0.001 |
| -25 | 0.021 | 0.031 | 0.035 | 0.034 | 0.014 | 0.022 | 0.02 | 0.019 | 0.019 | 0.026 | 0.018 | 0.033 | 0.01 | 0.005 | 0.002 | 0.002 |
| -22.9167 | 0.019 | 0.025 | 0.028 | 0.018 | 0.012 | 0.018 | 0.014 | 0.015 | 0.007 | 0.009 | 0.009 | 0.016 | 0.012 | 0.008 | 0.004 | 0.001 |
| -20.8333 | 0.015 | 0.02 | 0.024 | 0.018 | 0.011 | 0.017 | 0.015 | 0.017 | 0.005 | 0.006 | 0.005 | 0.01 | 0.013 | 0.006 | 0.004 | 0.003 |
| -18.75 | 0.023 | 0.029 | 0.032 | 0.017 | 0.018 | 0.026 | 0.024 | 0.02 | 0.017 | 0.021 | 0.019 | 0.032 | 0.016 | 0.012 | 0.005 | 0.001 |
| -16.6667 | 0.025 | 0.037 | 0.033 | 0.039 | 0.023 | 0.03 | 0.026 | 0.029 | 0.012 | 0.014 | 0.016 | 0.022 | 0.018 | 0.016 | 0.005 | 0.002 |
| -14.5833 | 0.023 | 0.029 | 0.034 | 0.025 | 0.021 | 0.028 | 0.02 | 0.019 | 0.013 | 0.016 | 0.015 | 0.014 | 0.022 | 0.017 | 0.007 | 0.002 |
| -12.5 | 0.029 | 0.034 | 0.03 | 0.032 | 0.025 | 0.035 | 0.034 | 0.024 | 0.015 | 0.018 | 0.014 | 0.021 | 0.027 | 0.019 | 0.009 | 0.003 |
| -10.4167 | 0.031 | 0.037 | 0.033 | 0.03 | 0.03 | 0.042 | 0.036 | 0.027 | 0.022 | 0.026 | 0.021 | 0.039 | 0.028 | 0.022 | 0.011 | 0.004 |
| -8.33333 | 0.027 | 0.033 | 0.033 | 0.025 | 0.032 | 0.042 | 0.041 | 0.02 | 0.029 | 0.03 | 0.032 | 0.038 | 0.034 | 0.026 | 0.016 | 0.005 |
| -6.25 | 0.034 | 0.044 | 0.05 | 0.042 | 0.036 | 0.051 | 0.055 | 0.032 | 0.051 | 0.052 | 0.047 | 0.052 | 0.045 | 0.038 | 0.03 | 0.011 |
| -4.16667 | 0.025 | 0.031 | 0.027 | 0.033 | 0.037 | 0.049 | 0.049 | 0.027 | 0.09 | 0.104 | 0.069 | 0.035 | 0.053 | 0.051 | 0.059 | 0.013 |
| -2.08333 | 0.013 | 0.014 | 0.015 | 0.018 | 0.032 | 0.041 | 0.036 | 0.042 | 0.153 | 0.139 | 0.11 | 0.083 | 0.119 | 0.167 | 0.128 | 0.03 |
| 5.55E-15 | 0.016 | 0.02 | 0.022 | 0.028 | 0.048 | 0.083 | 0.086 | 0.091 | 0.146 | 0.162 | 0.167 | 0.102 | 0.148 | 0.225 | 0.218 | 0.092 |
| 2.083333 | 0.035 | 0.043 | 0.058 | 0.069 | 0.067 | 0.099 | 0.145 | 0.183 | 0.077 | 0.082 | 0.098 | 0.071 | 0.07 | 0.101 | 0.154 | 0.298 |
| 4.166667 | 0.046 | 0.055 | 0.071 | 0.078 | 0.061 | 0.075 | 0.101 | 0.174 | 0.052 | 0.057 | 0.067 | 0.089 | 0.054 | 0.07 | 0.113 | 0.252 |
| 6.25 | 0.034 | 0.038 | 0.036 | 0.057 | 0.049 | 0.044 | 0.056 | 0.078 | 0.029 | 0.034 | 0.046 | 0.052 | 0.038 | 0.045 | 0.081 | 0.125 |
| 8.333333 | 0.039 | 0.036 | 0.04 | 0.046 | 0.049 | 0.037 | 0.032 | 0.026 | 0.027 | 0.023 | 0.022 | 0.03 | 0.032 | 0.028 | 0.029 | 0.054 |
| 10.41667 | 0.036 | 0.034 | 0.033 | 0.031 | 0.042 | 0.023 | 0.02 | 0.018 | 0.017 | 0.015 | 0.014 | 0.019 | 0.025 | 0.02 | 0.029 | 0.033 |
| 12.5 | 0.03 | 0.026 | 0.023 | 0.028 | 0.034 | 0.021 | 0.015 | 0.015 | 0.016 | 0.012 | 0.012 | 0.016 | 0.021 | 0.014 | 0.019 | 0.016 |
| 14.58333 | 0.033 | 0.029 | 0.026 | 0.021 | 0.037 | 0.021 | 0.013 | 0.018 | 0.013 | 0.009 | 0.011 | 0.02 | 0.018 | 0.014 | 0.01 | 0.013 |
| 16.66667 | 0.03 | 0.02 | 0.015 | 0.018 | 0.031 | 0.015 | 0.011 | 0.007 | 0.02 | 0.01 | 0.01 | 0.012 | 0.017 | 0.008 | 0.008 | 0.006 |
| 18.75 | 0.02 | 0.014 | 0.009 | 0.013 | 0.021 | 0.009 | 0.005 | 0.003 | 0.007 | 0.004 | 0.006 | 0.003 | 0.014 | 0.007 | 0.004 | 0.004 |
| 20.83333 | 0.025 | 0.019 | 0.013 | 0.017 | 0.022 | 0.01 | 0.008 | 0.002 | 0.008 | 0.006 | 0.006 | 0.008 | 0.013 | 0.008 | 0.008 | 0.002 |
| 22.91667 | 0.029 | 0.02 | 0.013 | 0.009 | 0.028 | 0.009 | 0.007 | 0.002 | 0.022 | 0.009 | 0.01 | 0.004 | 0.012 | 0.007 | 0.005 | 0.001 |
| 25 | 0.012 | 0.006 | 0.004 | 0.002 | 0.013 | 0.004 | 0.002 | 0 | 0.005 | 0.003 | 0.005 | 0.007 | 0.009 | 0.004 | 0.002 | 0.001 |
| 27.08333 | 0.017 | 0.009 | 0.007 | 0.036 | 0.017 | 0.007 | 0.004 | 0.004 | 0.006 | 0.003 | 0.005 | 0.002 | 0.008 | 0.004 | 0.004 | 0.003 |
| 29.16667 | 0.016 | 0.007 | 0.006 | 0.002 | 0.012 | 0.004 | 0.002 | 0.001 | 0.011 | 0.004 | 0.007 | 0.003 | 0.007 | 0.005 | 0.003 | 0.002 |
| 31.25 | 0.009 | 0.004 | 0.002 | 0.002 | 0.01 | 0.003 | 0.001 | 0 | 0.003 | 0.001 | 0.003 | 0.003 | 0.005 | 0.003 | 0.002 | 0 |
| 33.33333 | 0.025 | 0.017 | 0.015 | 0.008 | 0.02 | 0.007 | 0.002 | 0.002 | 0.007 | 0.003 | 0.005 | 0.001 | 0.006 | 0.003 | 0.002 | 0.001 |
| 35.41667 | 0.009 | 0.004 | 0.001 | 0.002 | 0.006 | 0.002 | 0 | 0 | 0.003 | 0.001 | 0.004 | 0.003 | 0.005 | 0.002 | 0.001 | 0 |
| 37.5 | 0.012 | 0.005 | 0.002 | 0.008 | 0.011 | 0.003 | 0.001 | 0.003 | 0.003 | 0.001 | 0.003 | 0.002 | 0.005 | 0.002 | 0.001 | 0 |
| 39.58333 | 0.007 | 0.002 | 0.001 | 0.002 | 0.004 | 0.001 | 0 | 0 | 0.002 | 0.001 | 0.002 | 0.001 | 0.004 | 0.001 | 0.001 | 0 |
| 41.66667 | 0.013 | 0.007 | 0.004 | 0.001 | 0.007 | 0.002 | 0.001 | 0 | 0.005 | 0.002 | 0.005 | 0.001 | 0.003 | 0.001 | 0.001 | 0 |
| 43.75 | 0.007 | 0.003 | 0.001 | 0.001 | 0.005 | 0.001 | 0.001 | 0 | 0.002 | 0.001 | 0.002 | 0.004 | 0.002 | 0.002 | 0.001 | 0 |
| 45.83333 | 0.008 | 0.002 | 0.001 | 0.004 | 0.005 | 0.001 | 0 | 0 | 0.001 | 0.001 | 0.003 | 0.001 | 0.002 | 0.001 | 0.002 | 0 |
| 47.91667 | 0.007 | 0.003 | 0.001 | 0.004 | 0.005 | 0.002 | 0 | 0 | 0.001 | 0.001 | 0.002 | 0.003 | 0.002 | 0.001 | 0 | 0 |
Figure 6: Deviation From the Average Posted Price of Competitors and Individual Price Adjustments
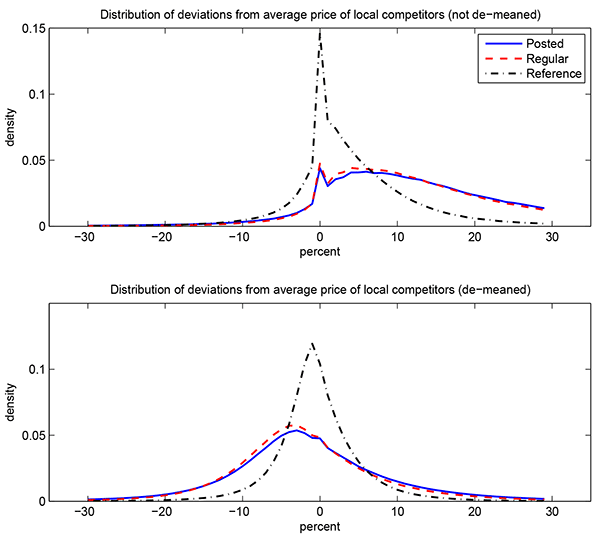
Notes: The upper and lower panels show the distribution of deviations from the average price of local competitors, computed at the UPC-market level in the IRI Marketing dataset, before and after removing item fixed effects to account for permanent differences in the level of prices across stores.
Data for Figure 6
| Left edge of bin | Not de-meaned: Posted | Not de-meaned: Regular | Not de-meaned: Reference | De-meaned: Posted | De-meaned: Regular | De-meaned: Reference |
|---|---|---|---|---|---|---|
| -30 | 0.000498 | 0.00025 | 0.00028 | 0.001401 | 0.000924 | 0.000189 |
| -29 | 0.000526 | 0.000269 | 0.000313 | 0.001555 | 0.001046 | 0.00022 |
| -28 | 0.000586 | 0.000301 | 0.000342 | 0.001721 | 0.001205 | 0.000254 |
| -27 | 0.000621 | 0.00033 | 0.000412 | 0.001963 | 0.0014 | 0.000295 |
| -26 | 0.000683 | 0.00038 | 0.000458 | 0.002186 | 0.001625 | 0.000342 |
| -25 | 0.000738 | 0.000417 | 0.00051 | 0.002493 | 0.001887 | 0.000392 |
| -24 | 0.000797 | 0.000449 | 0.000593 | 0.002851 | 0.002236 | 0.000458 |
| -23 | 0.000977 | 0.00052 | 0.000685 | 0.003232 | 0.002623 | 0.000538 |
| -22 | 0.000976 | 0.000544 | 0.000748 | 0.003777 | 0.003136 | 0.000627 |
| -21 | 0.001044 | 0.000594 | 0.000849 | 0.00437 | 0.003792 | 0.000748 |
| -20 | 0.001137 | 0.000676 | 0.000957 | 0.005133 | 0.00451 | 0.000903 |
| -19 | 0.001245 | 0.000759 | 0.001115 | 0.006 | 0.005416 | 0.001086 |
| -18 | 0.001362 | 0.00085 | 0.001209 | 0.007059 | 0.006552 | 0.001338 |
| -17 | 0.001451 | 0.000909 | 0.001429 | 0.008329 | 0.007979 | 0.001639 |
| -16 | 0.001661 | 0.001043 | 0.00169 | 0.009838 | 0.009679 | 0.001993 |
| -15 | 0.001819 | 0.001165 | 0.001974 | 0.011584 | 0.011733 | 0.00249 |
| -14 | 0.001986 | 0.001312 | 0.002295 | 0.013793 | 0.014113 | 0.003126 |
| -13 | 0.002266 | 0.001553 | 0.002655 | 0.016166 | 0.017104 | 0.003935 |
| -12 | 0.002535 | 0.001746 | 0.003165 | 0.01909 | 0.02052 | 0.005132 |
| -11 | 0.002957 | 0.002095 | 0.003802 | 0.022558 | 0.024555 | 0.00668 |
| -10 | 0.00332 | 0.002466 | 0.004555 | 0.026582 | 0.029185 | 0.00871 |
| -9 | 0.003805 | 0.002941 | 0.005536 | 0.030973 | 0.034494 | 0.011623 |
| -8 | 0.004412 | 0.003443 | 0.006659 | 0.035797 | 0.039888 | 0.015684 |
| -7 | 0.005005 | 0.004052 | 0.00841 | 0.040531 | 0.045101 | 0.021545 |
| -6 | 0.005749 | 0.004785 | 0.010374 | 0.045452 | 0.050293 | 0.030031 |
| -5 | 0.006908 | 0.005995 | 0.01329 | 0.049663 | 0.054378 | 0.041728 |
| -4 | 0.008252 | 0.007261 | 0.017601 | 0.052377 | 0.05723 | 0.058161 |
| -3 | 0.010083 | 0.00943 | 0.023985 | 0.053703 | 0.057523 | 0.080017 |
| -2 | 0.013004 | 0.012453 | 0.033406 | 0.051661 | 0.0546 | 0.103676 |
| -1 | 0.016995 | 0.01716 | 0.04525 | 0.048028 | 0.04992 | 0.119368 |
| 0 | 0.044019 | 0.047488 | 0.146529 | 0.047621 | 0.048378 | 0.104141 |
| 1 | 0.03044 | 0.032282 | 0.079675 | 0.040366 | 0.040578 | 0.080311 |
| 2 | 0.035591 | 0.0396 | 0.074115 | 0.036704 | 0.036281 | 0.063276 |
| 3 | 0.037135 | 0.040848 | 0.065288 | 0.033217 | 0.032306 | 0.04943 |
| 4 | 0.040679 | 0.044132 | 0.057729 | 0.02975 | 0.028494 | 0.038566 |
| 5 | 0.040784 | 0.04365 | 0.050857 | 0.026326 | 0.024983 | 0.029899 |
| 6 | 0.041301 | 0.043387 | 0.044991 | 0.023656 | 0.021998 | 0.023249 |
| 7 | 0.04029 | 0.042603 | 0.039878 | 0.021212 | 0.019247 | 0.01808 |
| 8 | 0.040423 | 0.042372 | 0.034666 | 0.018807 | 0.016922 | 0.01411 |
| 9 | 0.039609 | 0.041663 | 0.030163 | 0.016717 | 0.014879 | 0.011112 |
| 10 | 0.038465 | 0.040247 | 0.026109 | 0.014953 | 0.013023 | 0.008722 |
| 11 | 0.037143 | 0.038357 | 0.022301 | 0.013302 | 0.011406 | 0.006924 |
| 12 | 0.036037 | 0.036858 | 0.019219 | 0.011921 | 0.010147 | 0.005491 |
| 13 | 0.035167 | 0.03551 | 0.016643 | 0.010648 | 0.008938 | 0.004474 |
| 14 | 0.03328 | 0.032987 | 0.014271 | 0.009491 | 0.007796 | 0.003606 |
| 15 | 0.031613 | 0.031726 | 0.012259 | 0.008494 | 0.00686 | 0.002953 |
| 16 | 0.030299 | 0.029791 | 0.010518 | 0.007619 | 0.006035 | 0.002404 |
| 17 | 0.028564 | 0.027947 | 0.009115 | 0.006808 | 0.005346 | 0.001953 |
| 18 | 0.026756 | 0.026229 | 0.007983 | 0.006067 | 0.004752 | 0.001605 |
| 19 | 0.024901 | 0.024392 | 0.006815 | 0.005452 | 0.004217 | 0.001325 |
| 20 | 0.023603 | 0.022983 | 0.005911 | 0.004835 | 0.003727 | 0.001098 |
| 21 | 0.022412 | 0.021345 | 0.005288 | 0.004328 | 0.003283 | 0.000912 |
| 22 | 0.021145 | 0.019838 | 0.00475 | 0.003895 | 0.002907 | 0.000756 |
| 23 | 0.019898 | 0.018628 | 0.00404 | 0.00349 | 0.002577 | 0.000625 |
| 24 | 0.018458 | 0.017274 | 0.003579 | 0.003129 | 0.00229 | 0.000514 |
| 25 | 0.017744 | 0.016477 | 0.003216 | 0.0028 | 0.002029 | 0.000428 |
| 26 | 0.016829 | 0.015259 | 0.002802 | 0.002497 | 0.001787 | 0.000358 |
| 27 | 0.015723 | 0.01425 | 0.002521 | 0.002246 | 0.001557 | 0.000293 |
| 28 | 0.014638 | 0.01333 | 0.002241 | 0.001995 | 0.001381 | 0.000249 |
| 29 | 0.01366 | 0.012399 | 0.001986 | 0.001792 | 0.001235 | 0.00021 |
Figure 7: Deviation From the Average Reference Price of Competitors and Individual Price Adjustments
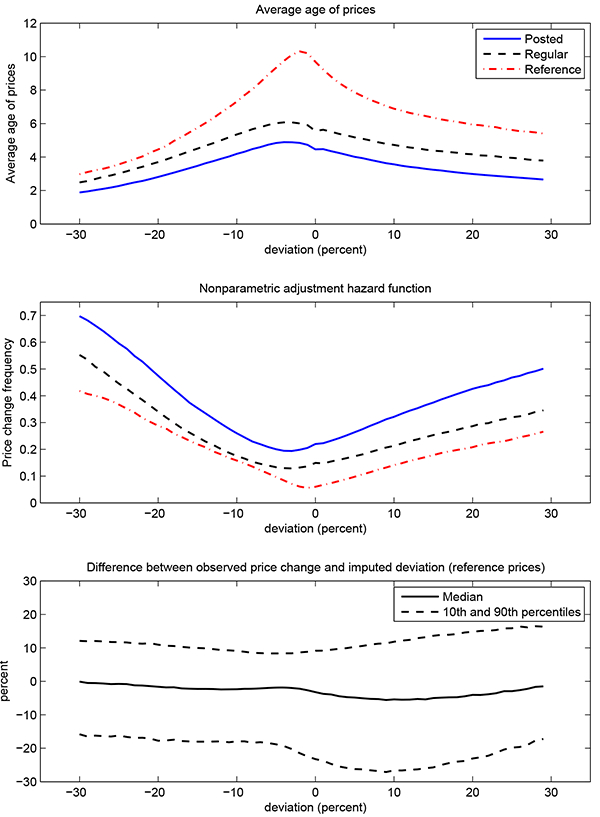
Notes: The upper panel shows the average age of monthly posted, regular, and reference prices in the IRI Marketing dataset conditional on the (demeaned) deviation from the corresponding average price of local competitors. The middle panel shows the fraction of items experiencing a price change during the month conditional on the deviation. The lower panel shows the median difference between the observed price change (ΔPi,t) and the imputed price pressure , along with the 10th and 90th percentiles differences.
Data for Figure 7
| Left edge of bin | Average age: Posted | Average age: Regular | Average age: Reference | Nonparametric adjustment hazard: Posted | Nonparametric adjustment hazard: Regular | Nonparametric adjustment hazard: Reference | Difference between observed and imputed deviation: median | Difference between observed and imputed deviation: 10th percentile | Difference between observed and imputed deviation: 90th percentile |
|---|---|---|---|---|---|---|---|---|---|
| -30 | 1.883369 | 2.482718 | 2.976248 | 0.697495 | 0.552343 | 0.41802 | -0.0939 | -15.8237 | 12.08438 |
| -29 | 1.943599 | 2.567569 | 3.105562 | 0.681442 | 0.534797 | 0.406916 | -0.49805 | -16.4975 | 11.97766 |
| -28 | 2.023565 | 2.685868 | 3.207686 | 0.661939 | 0.508392 | 0.400242 | -0.51207 | -16.2243 | 12.04183 |
| -27 | 2.098498 | 2.813687 | 3.302565 | 0.641558 | 0.491307 | 0.391774 | -0.63812 | -16.3827 | 11.94076 |
| -26 | 2.180329 | 2.901932 | 3.414222 | 0.619135 | 0.467668 | 0.381289 | -0.81654 | -16.4812 | 11.73592 |
| -25 | 2.268165 | 3.024781 | 3.561575 | 0.595381 | 0.445293 | 0.366998 | -0.76518 | -16.2031 | 11.72073 |
| -24 | 2.378429 | 3.146535 | 3.720045 | 0.575936 | 0.426356 | 0.352051 | -0.82723 | -16.6048 | 11.62239 |
| -23 | 2.486768 | 3.296341 | 3.877955 | 0.548075 | 0.40417 | 0.337177 | -1.20145 | -16.9075 | 11.35357 |
| -22 | 2.573798 | 3.415565 | 4.034797 | 0.527554 | 0.384289 | 0.317533 | -1.25482 | -16.8652 | 11.24836 |
| -21 | 2.686829 | 3.565818 | 4.268355 | 0.500558 | 0.362268 | 0.302045 | -1.43625 | -17.1125 | 11.38064 |
| -20 | 2.812087 | 3.698041 | 4.452252 | 0.474767 | 0.340404 | 0.28788 | -1.63415 | -17.7625 | 10.95438 |
| -19 | 2.938416 | 3.84962 | 4.653114 | 0.449132 | 0.319132 | 0.277631 | -1.79903 | -17.6508 | 10.64187 |
| -18 | 3.069289 | 4.015001 | 4.958313 | 0.423613 | 0.29922 | 0.258772 | -1.78282 | -17.4409 | 10.56164 |
| -17 | 3.202572 | 4.179101 | 5.199077 | 0.399 | 0.278921 | 0.245984 | -2.11191 | -17.8372 | 10.30356 |
| -16 | 3.33724 | 4.348517 | 5.477068 | 0.373752 | 0.26226 | 0.232021 | -2.21021 | -17.9569 | 10.09277 |
| -15 | 3.4715 | 4.498884 | 5.744755 | 0.353858 | 0.245831 | 0.218522 | -2.27909 | -18.0162 | 9.96032 |
| -14 | 3.627676 | 4.672035 | 6.028403 | 0.334162 | 0.22924 | 0.207743 | -2.281 | -18.0142 | 9.87796 |
| -13 | 3.754759 | 4.824134 | 6.321256 | 0.315557 | 0.216193 | 0.192043 | -2.3069 | -17.9937 | 9.63279 |
| -12 | 3.894359 | 5.000554 | 6.657076 | 0.296048 | 0.201055 | 0.181159 | -2.42481 | -17.9366 | 9.33705 |
| -11 | 4.030202 | 5.177071 | 6.973313 | 0.276521 | 0.187325 | 0.168074 | -2.40387 | -18.2182 | 9.25984 |
| -10 | 4.186066 | 5.349204 | 7.306823 | 0.260101 | 0.175036 | 0.158214 | -2.35298 | -17.9375 | 9.09892 |
| -9 | 4.318327 | 5.492293 | 7.698063 | 0.244439 | 0.165275 | 0.146974 | -2.24493 | -17.9465 | 8.82885 |
| -8 | 4.474749 | 5.664209 | 8.051177 | 0.228936 | 0.153586 | 0.135643 | -2.25715 | -18.3513 | 8.53616 |
| -7 | 4.592694 | 5.781687 | 8.472473 | 0.21889 | 0.145769 | 0.122016 | -2.09658 | -18.1742 | 8.4194 |
| -6 | 4.7334 | 5.919298 | 8.920522 | 0.208759 | 0.139333 | 0.109864 | -1.94377 | -18.4157 | 8.33247 |
| -5 | 4.837984 | 6.023399 | 9.332672 | 0.200279 | 0.133346 | 0.096392 | -1.89074 | -18.8145 | 8.3491 |
| -4 | 4.887086 | 6.072996 | 9.743611 | 0.194543 | 0.129673 | 0.083617 | -1.86739 | -19.3335 | 8.37006 |
| -3 | 4.880982 | 6.067954 | 10.102 | 0.193918 | 0.128483 | 0.070835 | -2.00799 | -20.2329 | 8.36133 |
| -2 | 4.841825 | 6.007019 | 10.31122 | 0.198147 | 0.132015 | 0.060782 | -2.21661 | -21.4597 | 8.64469 |
| -1 | 4.727597 | 5.905589 | 10.19883 | 0.205332 | 0.136227 | 0.055651 | -2.66432 | -22.4348 | 8.83958 |
| 0 | 4.455693 | 5.561748 | 9.691263 | 0.219968 | 0.149139 | 0.059998 | -3.21122 | -23.2267 | 9.14684 |
| 1 | 4.469487 | 5.62841 | 9.220005 | 0.222741 | 0.147175 | 0.067129 | -3.72693 | -23.7499 | 9.17071 |
| 2 | 4.346498 | 5.511476 | 8.795852 | 0.231906 | 0.154749 | 0.073662 | -3.91081 | -24.691 | 9.43687 |
| 3 | 4.241889 | 5.383336 | 8.429718 | 0.2418 | 0.160912 | 0.081323 | -4.43736 | -25.4475 | 9.72167 |
| 4 | 4.130735 | 5.286088 | 8.128401 | 0.252544 | 0.167408 | 0.089051 | -4.70934 | -25.8902 | 9.94194 |
| 5 | 4.01348 | 5.175508 | 7.858963 | 0.263801 | 0.174299 | 0.097367 | -4.84326 | -26.2094 | 10.29145 |
| 6 | 3.933776 | 5.090686 | 7.630933 | 0.275369 | 0.181137 | 0.10649 | -5.04605 | -26.3195 | 10.58843 |
| 7 | 3.824426 | 4.994815 | 7.413342 | 0.287895 | 0.189726 | 0.114724 | -5.25139 | -26.5665 | 10.96728 |
| 8 | 3.726661 | 4.882583 | 7.233564 | 0.299336 | 0.198378 | 0.124069 | -5.2974 | -26.8219 | 11.25659 |
| 9 | 3.631217 | 4.790666 | 7.047244 | 0.311998 | 0.206773 | 0.132049 | -5.57572 | -27.0928 | 11.35186 |
| 10 | 3.562589 | 4.719513 | 6.88701 | 0.321456 | 0.21293 | 0.140755 | -5.3852 | -26.6245 | 11.84808 |
| 11 | 3.475378 | 4.640049 | 6.767556 | 0.33318 | 0.221773 | 0.148239 | -5.49899 | -26.6353 | 12.15658 |
| 12 | 3.413319 | 4.570573 | 6.634601 | 0.344347 | 0.230876 | 0.156998 | -5.46682 | -26.425 | 12.39407 |
| 13 | 3.363306 | 4.520404 | 6.542209 | 0.353357 | 0.237565 | 0.163923 | -5.265 | -26.3148 | 12.89405 |
| 14 | 3.291563 | 4.440259 | 6.450922 | 0.364961 | 0.245322 | 0.170589 | -5.40641 | -25.9686 | 13.18879 |
| 15 | 3.235964 | 4.378768 | 6.351955 | 0.374508 | 0.252967 | 0.17828 | -5.00931 | -25.7346 | 13.61825 |
| 16 | 3.194911 | 4.349831 | 6.246724 | 0.386266 | 0.260174 | 0.186017 | -4.8705 | -24.9971 | 13.90092 |
| 17 | 3.132445 | 4.29811 | 6.169882 | 0.395914 | 0.26592 | 0.191868 | -4.79458 | -24.4332 | 13.91012 |
| 18 | 3.079221 | 4.255048 | 6.109771 | 0.406557 | 0.272795 | 0.197727 | -4.76722 | -24.014 | 14.12767 |
| 19 | 3.032913 | 4.186554 | 6.022639 | 0.416107 | 0.280356 | 0.202285 | -4.48109 | -23.7774 | 14.59393 |
| 20 | 2.994784 | 4.164708 | 5.933611 | 0.425879 | 0.286656 | 0.207985 | -4.03598 | -23.0646 | 14.81473 |
| 21 | 2.940145 | 4.094966 | 5.898978 | 0.433461 | 0.295305 | 0.216213 | -4.07896 | -22.7254 | 15.05995 |
| 22 | 2.915054 | 4.076072 | 5.831718 | 0.439778 | 0.297633 | 0.222012 | -3.86405 | -22.217 | 15.10091 |
| 23 | 2.871268 | 4.043289 | 5.782063 | 0.450261 | 0.30749 | 0.226724 | -3.54406 | -21.3415 | 15.33584 |
| 24 | 2.834707 | 3.980753 | 5.673446 | 0.457496 | 0.312535 | 0.230214 | -2.93418 | -20.3946 | 15.81176 |
| 25 | 2.79679 | 3.951339 | 5.619708 | 0.468003 | 0.319877 | 0.23717 | -2.95587 | -19.8054 | 15.85423 |
| 26 | 2.767551 | 3.920457 | 5.546409 | 0.474368 | 0.323329 | 0.245137 | -2.62995 | -19.6172 | 16.36386 |
| 27 | 2.732773 | 3.850913 | 5.515856 | 0.484768 | 0.330097 | 0.250944 | -2.22492 | -18.9758 | 16.13649 |
| 28 | 2.695798 | 3.806302 | 5.470025 | 0.491725 | 0.339658 | 0.257988 | -1.66701 | -17.6899 | 16.46892 |
| 29 | 2.656827 | 3.790377 | 5.402389 | 0.501065 | 0.345556 | 0.265762 | -1.50368 | -17.2377 | 16.34346 |
Figure 8: Nonparametric Adjustment Hazard Function for Four Product Categories
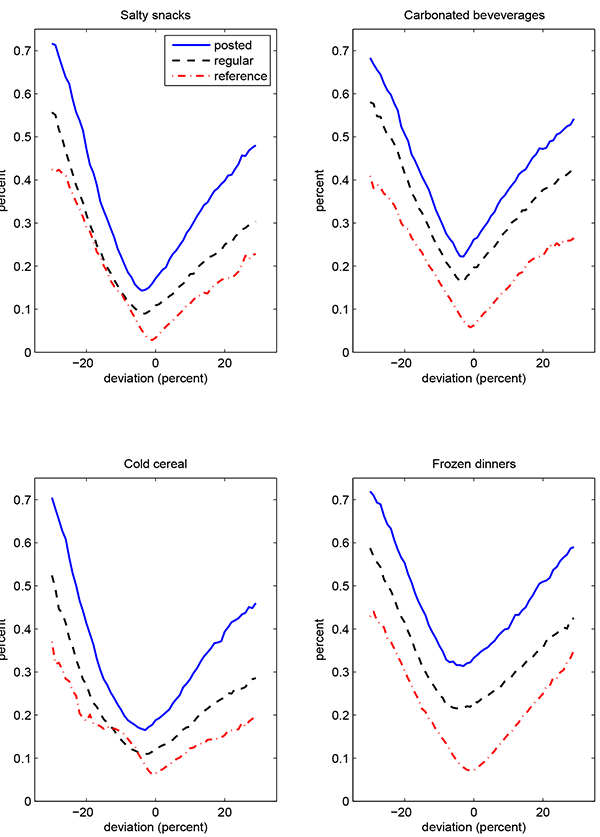
Notes: The figure shows the monthly probability of observing a change in the reference price conditional on the (demeaned) deviation from the average reference price of local competitors for four product categories in the IRI Marketing dataset.
Data for Figure 8
| Left edge of bin | Salty snacks: Posted | Salty snacks: Regular | Salty snacks: Reference | Carbonated beveverages: Posted | Carbonated beveverages: Regular | Carbonated beveverages: Reference | Cold cereal: Posted | Cold cereal: Regular | Cold cereal: Reference | Frozen dinners: Posted | Frozen dinners: Regular | Frozen dinners: Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -30 | 0.716167 | 0.556639 | 0.42445 | 0.68324 | 0.580571 | 0.408948 | 0.704618 | 0.523934 | 0.369841 | 0.719056 | 0.587475 | 0.428585 |
| -29 | 0.712977 | 0.550778 | 0.418335 | 0.668506 | 0.576504 | 0.380817 | 0.678376 | 0.493293 | 0.317935 | 0.709531 | 0.56786 | 0.439834 |
| -28 | 0.686373 | 0.516695 | 0.42372 | 0.655357 | 0.547473 | 0.389371 | 0.653378 | 0.446066 | 0.321366 | 0.692974 | 0.554289 | 0.417943 |
| -27 | 0.661343 | 0.495007 | 0.415332 | 0.644809 | 0.546671 | 0.382107 | 0.62727 | 0.436861 | 0.305503 | 0.689369 | 0.543471 | 0.411399 |
| -26 | 0.637695 | 0.465929 | 0.411853 | 0.624088 | 0.52228 | 0.368137 | 0.607997 | 0.413141 | 0.283864 | 0.662328 | 0.514825 | 0.403707 |
| -25 | 0.623452 | 0.440346 | 0.385073 | 0.607852 | 0.503832 | 0.363052 | 0.565401 | 0.37898 | 0.278654 | 0.642421 | 0.50157 | 0.37819 |
| -24 | 0.586933 | 0.414575 | 0.366822 | 0.597677 | 0.498144 | 0.351633 | 0.528952 | 0.35928 | 0.255823 | 0.632764 | 0.488704 | 0.370291 |
| -23 | 0.557286 | 0.387533 | 0.348492 | 0.577676 | 0.483253 | 0.341284 | 0.500681 | 0.329282 | 0.245148 | 0.605994 | 0.46965 | 0.353714 |
| -22 | 0.538377 | 0.367664 | 0.333067 | 0.561501 | 0.465366 | 0.323738 | 0.465975 | 0.30657 | 0.204083 | 0.583922 | 0.446593 | 0.336676 |
| -21 | 0.514642 | 0.34736 | 0.314017 | 0.524053 | 0.439767 | 0.300152 | 0.441324 | 0.282667 | 0.193793 | 0.565686 | 0.428279 | 0.320961 |
| -20 | 0.471557 | 0.319091 | 0.289332 | 0.506615 | 0.41555 | 0.288704 | 0.412421 | 0.270718 | 0.185725 | 0.553107 | 0.414878 | 0.302129 |
| -19 | 0.435363 | 0.296597 | 0.280135 | 0.490451 | 0.396636 | 0.285322 | 0.388646 | 0.246671 | 0.201093 | 0.526941 | 0.393904 | 0.284651 |
| -18 | 0.41658 | 0.276463 | 0.258464 | 0.459445 | 0.370681 | 0.266065 | 0.364047 | 0.228231 | 0.17972 | 0.50805 | 0.375853 | 0.268972 |
| -17 | 0.388444 | 0.247694 | 0.23285 | 0.444812 | 0.357058 | 0.253538 | 0.330403 | 0.218898 | 0.178243 | 0.48315 | 0.35166 | 0.251369 |
| -16 | 0.349945 | 0.236202 | 0.223109 | 0.426739 | 0.335621 | 0.242022 | 0.304718 | 0.204092 | 0.174152 | 0.463398 | 0.336816 | 0.236503 |
| -15 | 0.32894 | 0.214279 | 0.200983 | 0.40809 | 0.324357 | 0.231982 | 0.283061 | 0.190444 | 0.168026 | 0.447549 | 0.314098 | 0.214791 |
| -14 | 0.309057 | 0.197454 | 0.186984 | 0.393008 | 0.307608 | 0.215233 | 0.270305 | 0.182354 | 0.174467 | 0.43237 | 0.300361 | 0.20814 |
| -13 | 0.287657 | 0.183708 | 0.166251 | 0.377138 | 0.290706 | 0.201501 | 0.252573 | 0.174365 | 0.166194 | 0.408454 | 0.28556 | 0.191115 |
| -12 | 0.267713 | 0.168325 | 0.153283 | 0.35477 | 0.269858 | 0.190681 | 0.239827 | 0.164618 | 0.169253 | 0.392418 | 0.273361 | 0.182962 |
| -11 | 0.240522 | 0.154633 | 0.14241 | 0.330392 | 0.252714 | 0.177992 | 0.2244 | 0.151587 | 0.1654 | 0.378299 | 0.260611 | 0.166804 |
| -10 | 0.222465 | 0.139979 | 0.139519 | 0.312849 | 0.239546 | 0.1633 | 0.212294 | 0.142817 | 0.160886 | 0.361298 | 0.246646 | 0.156743 |
| -9 | 0.20345 | 0.130158 | 0.122193 | 0.294807 | 0.225467 | 0.150074 | 0.19755 | 0.134037 | 0.155303 | 0.34778 | 0.240382 | 0.144791 |
| -8 | 0.185282 | 0.115942 | 0.11077 | 0.275454 | 0.209125 | 0.13718 | 0.187977 | 0.127324 | 0.144526 | 0.328658 | 0.223336 | 0.133587 |
| -7 | 0.17445 | 0.110038 | 0.094007 | 0.263592 | 0.198251 | 0.125929 | 0.182329 | 0.120844 | 0.134474 | 0.322732 | 0.221597 | 0.119473 |
| -6 | 0.15789 | 0.102076 | 0.079777 | 0.253796 | 0.187544 | 0.111921 | 0.177018 | 0.11776 | 0.12766 | 0.324304 | 0.217039 | 0.106622 |
| -5 | 0.149147 | 0.095392 | 0.064439 | 0.236313 | 0.173784 | 0.099469 | 0.171013 | 0.113431 | 0.109633 | 0.315884 | 0.215504 | 0.09529 |
| -4 | 0.143082 | 0.090672 | 0.051243 | 0.223006 | 0.165408 | 0.085754 | 0.167929 | 0.112186 | 0.096873 | 0.315936 | 0.21587 | 0.085044 |
| -3 | 0.14507 | 0.089717 | 0.03909 | 0.222198 | 0.162933 | 0.073578 | 0.165184 | 0.109762 | 0.083009 | 0.313753 | 0.215214 | 0.078599 |
| -2 | 0.149833 | 0.094568 | 0.031433 | 0.23406 | 0.1765 | 0.064132 | 0.172407 | 0.110068 | 0.07065 | 0.320273 | 0.220629 | 0.07315 |
| -1 | 0.159296 | 0.098393 | 0.02855 | 0.246802 | 0.183303 | 0.057797 | 0.177149 | 0.115056 | 0.062223 | 0.322259 | 0.218973 | 0.071264 |
| 0 | 0.171463 | 0.108629 | 0.033442 | 0.261722 | 0.19691 | 0.062364 | 0.188271 | 0.123435 | 0.064087 | 0.332519 | 0.233494 | 0.072021 |
| 1 | 0.181136 | 0.111581 | 0.041917 | 0.266047 | 0.197698 | 0.072636 | 0.192612 | 0.125748 | 0.07085 | 0.339198 | 0.229157 | 0.077885 |
| 2 | 0.191366 | 0.118229 | 0.051033 | 0.279481 | 0.21218 | 0.081226 | 0.199179 | 0.129757 | 0.074141 | 0.346529 | 0.235662 | 0.08451 |
| 3 | 0.197174 | 0.122549 | 0.059457 | 0.290803 | 0.219931 | 0.091572 | 0.206459 | 0.132603 | 0.079877 | 0.352416 | 0.242893 | 0.091157 |
| 4 | 0.215088 | 0.13028 | 0.067005 | 0.3016 | 0.229968 | 0.097359 | 0.213124 | 0.137365 | 0.085137 | 0.356908 | 0.245188 | 0.099534 |
| 5 | 0.228046 | 0.135449 | 0.073556 | 0.316467 | 0.240344 | 0.106442 | 0.227269 | 0.142511 | 0.091396 | 0.365302 | 0.251155 | 0.10771 |
| 6 | 0.236474 | 0.145753 | 0.082433 | 0.325674 | 0.245092 | 0.117458 | 0.237009 | 0.150302 | 0.097622 | 0.372081 | 0.257235 | 0.116657 |
| 7 | 0.248804 | 0.153382 | 0.090372 | 0.343287 | 0.256482 | 0.126565 | 0.246125 | 0.155478 | 0.101473 | 0.383137 | 0.260017 | 0.128258 |
| 8 | 0.259892 | 0.15939 | 0.098366 | 0.356668 | 0.270355 | 0.135843 | 0.26486 | 0.166296 | 0.108485 | 0.391735 | 0.267758 | 0.135137 |
| 9 | 0.277122 | 0.168068 | 0.108902 | 0.364259 | 0.278892 | 0.14284 | 0.272994 | 0.171401 | 0.113328 | 0.399025 | 0.278503 | 0.146236 |
| 10 | 0.287488 | 0.181577 | 0.11307 | 0.37671 | 0.286816 | 0.150657 | 0.283366 | 0.172787 | 0.122869 | 0.400438 | 0.282051 | 0.155349 |
| 11 | 0.301611 | 0.182169 | 0.122124 | 0.387445 | 0.301054 | 0.159486 | 0.297807 | 0.184103 | 0.124455 | 0.416032 | 0.289462 | 0.161825 |
| 12 | 0.316459 | 0.19624 | 0.131125 | 0.397382 | 0.307261 | 0.171797 | 0.308789 | 0.194438 | 0.131043 | 0.432406 | 0.300417 | 0.174312 |
| 13 | 0.328142 | 0.203498 | 0.131761 | 0.412514 | 0.31244 | 0.182393 | 0.323561 | 0.202782 | 0.133726 | 0.432348 | 0.308695 | 0.183106 |
| 14 | 0.341881 | 0.210301 | 0.138323 | 0.41983 | 0.32956 | 0.185696 | 0.336108 | 0.208893 | 0.13351 | 0.443144 | 0.312563 | 0.196702 |
| 15 | 0.347735 | 0.219659 | 0.136387 | 0.424348 | 0.32966 | 0.198908 | 0.345182 | 0.21483 | 0.142512 | 0.449957 | 0.322262 | 0.202143 |
| 16 | 0.36132 | 0.222227 | 0.147867 | 0.438328 | 0.339321 | 0.210023 | 0.354671 | 0.221585 | 0.143287 | 0.465598 | 0.331628 | 0.213143 |
| 17 | 0.374524 | 0.226253 | 0.155395 | 0.451296 | 0.351344 | 0.215634 | 0.36678 | 0.227745 | 0.147074 | 0.476852 | 0.334084 | 0.223429 |
| 18 | 0.38054 | 0.232271 | 0.161837 | 0.459417 | 0.360068 | 0.220352 | 0.368507 | 0.23212 | 0.144286 | 0.491635 | 0.344077 | 0.232204 |
| 19 | 0.390606 | 0.237046 | 0.16769 | 0.473349 | 0.367937 | 0.221992 | 0.371285 | 0.237016 | 0.147898 | 0.505211 | 0.351944 | 0.239962 |
| 20 | 0.397935 | 0.249648 | 0.171736 | 0.471871 | 0.376841 | 0.223063 | 0.393673 | 0.240545 | 0.153353 | 0.509397 | 0.356122 | 0.249619 |
| 21 | 0.410443 | 0.256057 | 0.172575 | 0.474563 | 0.380991 | 0.236415 | 0.403827 | 0.250878 | 0.164124 | 0.512138 | 0.372169 | 0.265635 |
| 22 | 0.411725 | 0.254854 | 0.172867 | 0.489283 | 0.382545 | 0.249837 | 0.415813 | 0.249644 | 0.164644 | 0.518725 | 0.372401 | 0.26767 |
| 23 | 0.425225 | 0.267915 | 0.1792 | 0.491735 | 0.387574 | 0.242929 | 0.419762 | 0.260863 | 0.1645 | 0.537094 | 0.38438 | 0.286947 |
| 24 | 0.436888 | 0.27695 | 0.18741 | 0.505451 | 0.396223 | 0.253412 | 0.424797 | 0.260169 | 0.167307 | 0.543301 | 0.389567 | 0.284734 |
| 25 | 0.456866 | 0.284717 | 0.203355 | 0.50905 | 0.406548 | 0.246691 | 0.433659 | 0.261565 | 0.182134 | 0.557529 | 0.397304 | 0.298822 |
| 26 | 0.455443 | 0.288826 | 0.224289 | 0.517097 | 0.407459 | 0.259476 | 0.437266 | 0.265084 | 0.17375 | 0.566052 | 0.403657 | 0.304614 |
| 27 | 0.467838 | 0.295152 | 0.215364 | 0.524457 | 0.412446 | 0.258819 | 0.450509 | 0.277389 | 0.184742 | 0.572549 | 0.40054 | 0.322478 |
| 28 | 0.474807 | 0.298546 | 0.226362 | 0.528123 | 0.419472 | 0.259487 | 0.448247 | 0.283054 | 0.191428 | 0.586568 | 0.421891 | 0.332536 |
| 29 | 0.480136 | 0.303243 | 0.227984 | 0.542057 | 0.43501 | 0.265043 | 0.459869 | 0.285893 | 0.197752 | 0.589979 | 0.424491 | 0.350538 |
Figure 9: Nonparametric Adjustment Hazard Conditional on Age and Alternative Measures of Local Competitition

Notes: The upper panel shows the probability of a reference price change conditional on alternative measures of the (demeaned) deviation from the prices of local competitors. The measures use either all other stores ("All stores"), stores belonging to competing chains ("Competing chains"), or retailers that have adjusted their price over the current or previous six months ("Recent adjusters"). The lower panel shows the probability of a reference price change as a function of the deviation from the average price of competitors, conditional on the duration since the last price change. The data source is the IRI Marketing dataset.
Data for Figure 9
| Left edge of bin | Alternative measures of local competition: All stores | Alternative measures of local competition: Competing chains | Alternative measures of local competition: Recent Adjusters | Conditional on age: 2 months | Conditional on age: 6 months | Conditional on age: 12 months |
|---|---|---|---|---|---|---|
| -30 | 0.41802 | 0.377611 | 0.477884 | 0.424166 | 0.32215 | 0.247222 |
| -29 | 0.406916 | 0.36883 | 0.47645 | 0.409836 | 0.307652 | 0.245119 |
| -28 | 0.400242 | 0.357877 | 0.459841 | 0.406897 | 0.30903 | 0.289231 |
| -27 | 0.391774 | 0.345963 | 0.457421 | 0.395715 | 0.302901 | 0.232342 |
| -26 | 0.381289 | 0.337327 | 0.440029 | 0.390338 | 0.286071 | 0.266816 |
| -25 | 0.366998 | 0.32307 | 0.423367 | 0.373861 | 0.276739 | 0.240051 |
| -24 | 0.352051 | 0.311414 | 0.409696 | 0.35885 | 0.267392 | 0.234973 |
| -23 | 0.337177 | 0.300574 | 0.397705 | 0.342018 | 0.264659 | 0.219111 |
| -22 | 0.317533 | 0.283535 | 0.381619 | 0.327032 | 0.254197 | 0.19429 |
| -21 | 0.302045 | 0.272904 | 0.36775 | 0.315792 | 0.240845 | 0.193921 |
| -20 | 0.28788 | 0.257615 | 0.353904 | 0.30402 | 0.229396 | 0.184077 |
| -19 | 0.277631 | 0.248096 | 0.33908 | 0.289865 | 0.224844 | 0.15653 |
| -18 | 0.258772 | 0.237502 | 0.32403 | 0.276951 | 0.205348 | 0.168855 |
| -17 | 0.245984 | 0.223691 | 0.306211 | 0.265739 | 0.195791 | 0.175968 |
| -16 | 0.232021 | 0.213301 | 0.296771 | 0.250627 | 0.196607 | 0.153701 |
| -15 | 0.218522 | 0.200192 | 0.283544 | 0.239521 | 0.179095 | 0.146489 |
| -14 | 0.207743 | 0.188104 | 0.267829 | 0.226086 | 0.173967 | 0.155298 |
| -13 | 0.192043 | 0.177844 | 0.247154 | 0.21188 | 0.166227 | 0.139394 |
| -12 | 0.181159 | 0.16759 | 0.229017 | 0.199511 | 0.158978 | 0.140096 |
| -11 | 0.168074 | 0.158019 | 0.213368 | 0.186401 | 0.154556 | 0.135982 |
| -10 | 0.158214 | 0.149611 | 0.197236 | 0.175354 | 0.146751 | 0.132055 |
| -9 | 0.146974 | 0.138837 | 0.180741 | 0.16379 | 0.136623 | 0.122804 |
| -8 | 0.135643 | 0.128832 | 0.165484 | 0.151674 | 0.133428 | 0.118331 |
| -7 | 0.122016 | 0.118676 | 0.150971 | 0.140652 | 0.123895 | 0.110456 |
| -6 | 0.109864 | 0.109579 | 0.136738 | 0.129491 | 0.115407 | 0.099885 |
| -5 | 0.096392 | 0.099066 | 0.122683 | 0.11885 | 0.10475 | 0.090756 |
| -4 | 0.083617 | 0.087935 | 0.110172 | 0.10913 | 0.094754 | 0.080433 |
| -3 | 0.070835 | 0.078013 | 0.096723 | 0.097763 | 0.085043 | 0.068064 |
| -2 | 0.060782 | 0.071531 | 0.083886 | 0.091109 | 0.077876 | 0.058788 |
| -1 | 0.055651 | 0.068078 | 0.071095 | 0.08492 | 0.070179 | 0.053436 |
| 0 | 0.059998 | 0.071789 | 0.065426 | 0.084906 | 0.07332 | 0.05721 |
| 1 | 0.067129 | 0.076458 | 0.072344 | 0.087955 | 0.078724 | 0.062302 |
| 2 | 0.073662 | 0.081298 | 0.078153 | 0.091519 | 0.083421 | 0.064551 |
| 3 | 0.081323 | 0.086969 | 0.085193 | 0.095746 | 0.089034 | 0.072322 |
| 4 | 0.089051 | 0.092742 | 0.093421 | 0.101252 | 0.095975 | 0.078103 |
| 5 | 0.097367 | 0.098782 | 0.104027 | 0.107 | 0.102631 | 0.085404 |
| 6 | 0.10649 | 0.105685 | 0.112129 | 0.113617 | 0.110785 | 0.091443 |
| 7 | 0.114724 | 0.110694 | 0.123841 | 0.11982 | 0.119936 | 0.100707 |
| 8 | 0.124069 | 0.117525 | 0.134588 | 0.127134 | 0.126553 | 0.106872 |
| 9 | 0.132049 | 0.123713 | 0.145134 | 0.134585 | 0.135993 | 0.110951 |
| 10 | 0.140755 | 0.12889 | 0.157196 | 0.140044 | 0.144417 | 0.120505 |
| 11 | 0.148239 | 0.135327 | 0.16894 | 0.14775 | 0.148733 | 0.119843 |
| 12 | 0.156998 | 0.140659 | 0.179268 | 0.153475 | 0.159639 | 0.132179 |
| 13 | 0.163923 | 0.145541 | 0.189173 | 0.159572 | 0.167655 | 0.140903 |
| 14 | 0.170589 | 0.150764 | 0.20015 | 0.16598 | 0.174794 | 0.136331 |
| 15 | 0.17828 | 0.156187 | 0.209413 | 0.173804 | 0.17995 | 0.143255 |
| 16 | 0.186017 | 0.159967 | 0.221139 | 0.178462 | 0.184116 | 0.143808 |
| 17 | 0.191868 | 0.165389 | 0.234039 | 0.183591 | 0.197165 | 0.150571 |
| 18 | 0.197727 | 0.1675 | 0.245976 | 0.190153 | 0.196002 | 0.145223 |
| 19 | 0.202285 | 0.171636 | 0.254099 | 0.19425 | 0.204891 | 0.152802 |
| 20 | 0.207985 | 0.175882 | 0.268561 | 0.191612 | 0.213763 | 0.173397 |
| 21 | 0.216213 | 0.179363 | 0.276278 | 0.203462 | 0.215684 | 0.16141 |
| 22 | 0.222012 | 0.185284 | 0.286541 | 0.207395 | 0.221649 | 0.167706 |
| 23 | 0.226724 | 0.18697 | 0.298534 | 0.215078 | 0.21911 | 0.176132 |
| 24 | 0.230214 | 0.19218 | 0.314181 | 0.213995 | 0.226395 | 0.175638 |
| 25 | 0.23717 | 0.195287 | 0.323052 | 0.217893 | 0.229071 | 0.181948 |
| 26 | 0.245137 | 0.198199 | 0.331808 | 0.220881 | 0.235538 | 0.189304 |
| 27 | 0.250944 | 0.197879 | 0.347612 | 0.227893 | 0.236279 | 0.170806 |
| 28 | 0.257988 | 0.203875 | 0.349504 | 0.240063 | 0.249714 | 0.185567 |
| 29 | 0.265762 | 0.211417 | 0.362755 | 0.238976 | 0.254726 | 0.198417 |
Figure 10: Estimated Aggregate Reset Price Inflation Using BKM's Methodology in Response to a 1-Percent Shock to Actual Aggregate Reset Price Inflation (Menu-Cost Model)

Notes: This figure applies BKM's methodology for identifying aggregate reset price inflation to the study of a 1-percent jump in the level of individual reset prices in a baseline menu-cost model. The model assumes a symmetric band, a process for individual reset prices as in equation (11), and normally distributed idiosyncratic shocks. The model is calibrated to match an average frequency of price changes of 25 percent and an average size of price changes of 10 percent.
Data for Figure 10
| Period | Actual | Estimated |
|---|---|---|
| -3 | 0 | 0.0068 |
| -2 | 0 | -0.0126 |
| -1 | 0 | 0.0009 |
| 0 | 1 | 3.245 |
| 1 | 0 | -1.7287 |
| 2 | 0 | -0.311 |
| 3 | 0 | -0.1198 |
| 4 | 0 | -0.0471 |
| 5 | 0 | -0.0202 |
| 6 | 0 | -0.0078 |
| 7 | 0 | 0.0001 |
| 8 | 0 | -0.011 |
| 9 | 0 | 0.0002 |
| 10 | 0 | -0.0005 |
| 11 | 0 | 0.0058 |
| 12 | 0 | -0.0143 |
Note: Estimated response is the average of 25 simulations.
Footnotes
** This research was conducted in part with restricted access to Bureau of Labor Statistics (BLS) data. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, the BLS, or any other person associated with the Federal Reserve System or the BLS. We thank Ben Malin and Randal Verbrugge for their support with BLS micro data, as well as Mike Woodford, Jeff Campbell, Gita Gopinath, Anil Kashyap, and Ed Nelson for their insightful comments. Christine Garnier and Andrew Giffin provided superb research assistance. Nicolas Vincent acknowledges financial support from the Fonds québécois de la recherche sur la société et la culture. We are grateful to the SymphonyIRI Group for the scanner data. As a condition of use, SymphonyIRI reviews all papers using their data to check that the data are not described in a misleading fashion. However, all analyses in this paper based on SymphonyIRI Group, Inc. data reflect the work and conclusions of the authors, not SymphonyIRI Group, Inc. Comments and suggestions can be directed to etienne.gagnon@frb.gov, david.j.lopez-salido@frb.gov, nicolas.vincent@hec.ca. Return to text
1. Initial empirical work using sectoral data by Carlton (1986), Cecchetti (1986), Lach and Tsiddon (1992), and Kashyap (1995) has been followed by the work on consumer prices of Bils and Klenow (2004), Baharad and Eden (2004) for Israel, and several euro-area national studies summarized in Dhyne et al. (2005). For recent literature surveys, see Mackowiak and Smets (2008) and Klenow and Malin (2011). Return to text
2. The list of pricing strategies and relevant frictions includes menu-cost models (e.g., Barro [1972] and Sheshinski and Weiss [1977]), the Calvo (1983) model, fixed-duration contracts (Taylor [1980]), infrequent information (e.g., Mankiw and Reis [2002]), rational inattention (e.g., Sims [2003]), uncertain and sequential trade (e.g., Eden [1994]), fair pricing (Rotemberg [2011]), price points (e.g., Levy et al. [2011]), search models (e.g., Head et al. [forthcoming]), price plans (Burstein [2006] and Alvarez, Lippi, and Paciello [2011]), reference prices (Eichenbaum, Jaimovich, and Rebelo [2011]), and price discrimination (e.g., Varian [1980]). Return to text
3. The concept of a price that maximizes current-period profits --either in a partial equilibrium or in a frictionless general equilibrium environment-- and the concept of a price that maximizes the present discounted stream of profits at times overlap in the work of Caballero and Engel. In a menu-cost model, these concepts coincide when innovations to the frictionless optimal price follows a random walk with no drift and firms set prices under certainty equivalence. Departure from either of these assumptions breaks the equivalence between the two concepts. Return to text
4. Barsky, House, and Kimball (2007) and Gopinath and Itskhoki (2010) highlight this heterogeneity in the presence of differences in durability and the degree of real rigidities, respectively. Return to text
5. Woodford (2008 and 2009) provides micro-foundations for a smooth adjustment hazard increasing in the absolute size of the deviation. Return to text
6. In theory, the adjustment hazard could
depend on aggregate conditions beyond their influence on
![]() . Most notably, Sheshinski and Weiss
(1977) prove that the width of the
. Most notably, Sheshinski and Weiss
(1977) prove that the width of the ![]() band
increases with steady-state inflation in a menu-cost model without
idiosyncratic shocks. This effect is much weaker in models with
idiosyncratic shocks, however, consistent with the empirical
evidence. Gagnon (2009) reports that the average absolute size of
price adjustments was little impacted by the burst in inflation
that accompanied the Mexican Peso crisis. Similarly, Wulfsberg
(2009) uncovers no apparent change in the absolute size of price
adjustments in Norway as trend inflation fell from around 10
percent in the mid-1970s to 2 percent in the mid-1990s. Both
studies note a rise in the average absolute size since the late
1990s but it is difficult to attribute this rise to changing
aggregate conditions. Return to
text
band
increases with steady-state inflation in a menu-cost model without
idiosyncratic shocks. This effect is much weaker in models with
idiosyncratic shocks, however, consistent with the empirical
evidence. Gagnon (2009) reports that the average absolute size of
price adjustments was little impacted by the burst in inflation
that accompanied the Mexican Peso crisis. Similarly, Wulfsberg
(2009) uncovers no apparent change in the absolute size of price
adjustments in Norway as trend inflation fell from around 10
percent in the mid-1970s to 2 percent in the mid-1990s. Both
studies note a rise in the average absolute size since the late
1990s but it is difficult to attribute this rise to changing
aggregate conditions. Return to
text
7. It should be noted that CE's usage of the terms "intensive" and "extensive" margins differs from that popularized by Klenow and Kryvtsov (2008). The latter define the extensive margin as the frequency of price changes and the intensive margin as the average size of (nonzero) price changes. These definitions are motivated by Klenow and Kryvtsov's investigation of how variation in the number of prices changes contributes to inflation dynamics. In contrast with these authors, who seek to explain the level of inflation, CE are only interested in the boost to inflation due to the aggregate shock. And while the extensive margin in Klenow and Kryvtsov's decomposition is a function of all price changes, the extensive margin in equation (4) depends only on the subset whose timing is altered by the shock. For example, a shock resulting in the simultaneous cancelling of a price decrease and triggering of a price increase would impact inflation solely through the intensive margin under Klenow and Kryvtsov's decomposition because it leaves the number of price adjustments unchanged. The same shock would instead operate entirely through the extensive margin under CE's decomposition. To avoid any confusion, our terminology follows exclusively that of CE. Return to text
8. See Eden (2001) for an early investigation of how the shape of the distribution of consumer price changes differs between low and high inflation. For U.S. evidence on consumer prices, see Klenow and Kryvtsov (2008), Klenow and Malin (2011), and Berger and Vavra (2011). Calibrations to the distribution of price changes have appeared recently in the literature (e.g., Midrigan [2011] and Costain and Nakov [2011]) Return to text
9. A multiplicity of optimal prices can arise when the profit function is very flat because firms trade-off the unit markup and the number of consumer purchases. See Eden's (1994) model of uncertain and sequential trade and the search model of Head et al. (forthcoming). Return to text
10. See Blanchard and Fisher (1989) and Ball and Romer (1990) for early expositions. Christiano, Eichenbaum, and Evans (2005), and Smets and Wouters (2007) argue, as do many others, that the inclusion of real rigidities in DSGE models improves their ability to account for observed aggregate economic dynamics. Return to text
11. Bils, Klenow, and Malin (forthcoming) note that CPI inflation since the turn of the 1990s is too volatile and transient to be explained by standard sticky-price models, even absent real rigidities. Burstein and Hellwig (2007) and Gopinath and Itskhoki (2011) find moderate amount of real rigidities in retail prices and trade prices respectively, but the accompanying macroeconomic effects are limited. Return to text
12. Burstein and Hellwig (2007) provide
microfoundations for the reduced-form parameter ![]() .
In their environment, firms have a CES demand function with
elasticity
.
In their environment, firms have a CES demand function with
elasticity ![]() , use production functions with
decreasing returns in labor of the form
, use production functions with
decreasing returns in labor of the form
![]() , and
face nominal wages determined by
, and
face nominal wages determined by
![]() . Their linearlized solution around the frictionless steady-state
has
. Their linearlized solution around the frictionless steady-state
has
![]() .
Return to text
.
Return to text
13. While intuitive, this latter property
does not hold in all environments. Dotsey and King (2005) present
an example in which an increase in real rigidities raises the
flexibility of the price level. In their menu-cost model, the
negative impact on
![]() of an increase in
of an increase in ![]() is more than offset by the positive impact of a rise in
is more than offset by the positive impact of a rise in
![]() as more firms find it profitable to incur the fixed cost of
adjusting prices. Return to text
as more firms find it profitable to incur the fixed cost of
adjusting prices. Return to text
14. We use the distribution of price changes 12 months earlier as our counterfactual to account for seasonal repricing, which is especially noticeable for services in January. The results are broadly similar when we perform the analysis using the distribution observed in the fourth quarter of 1994 as the counterfactual. Return to text
15. Our Mexican sample does not allow us to explore asymetries in price adjustments to VAT increases and decreases. Karadi and Reiff (2010) report greater pass-through for VAT hikes than for VAT cuts in Hungarian data. Return to text
16. The Kolmogorov-Smirnov test assumes equal weights on the observations used to construct the distributions, whereas our distributions weigh observations according to their relative spending share in the sample. Given that our objective is largely illustrative, we calculate the test statistics as if all observations had the same weight. Return to text
17. See Klenow and Malin (2011) for a recent survey and several new facts, and Chevalier and Kashyap (2011) for evidence that multi-product retailers may adjust the frequency and intensity of sales in response to aggregate shocks. Return to text
18. Consistent with the CE decomposition,
![]() measures the deviation
before an item's price adjustment decision, whereas previous
studies of price dispersion (e.g., Reinsdorf 1994) focus on the
deviation after price adjustments take place. The shape of
the distributions is little changed when we adopt this alternative
timing. Return to text
measures the deviation
before an item's price adjustment decision, whereas previous
studies of price dispersion (e.g., Reinsdorf 1994) focus on the
deviation after price adjustments take place. The shape of
the distributions is little changed when we adopt this alternative
timing. Return to text
19. The spike near zero diminishes when
we increase the minimum number of stores required for a UPC-market
combination to be included in the sample or when exclude stores
belonging to the same chain as store ![]() from the
calculation of
from the
calculation of
![]() . Our central finding of
limited price dispersion remains, however. Return to text
. Our central finding of
limited price dispersion remains, however. Return to text
20. We also ran separate regressions for
price increases and price decreases (not reported). We found that
the magnitude of the negative deviation (
![]() ) has a large impact on
the probability of a price increase, but almost no impact on the
likelihood of price decreases. The reverse is true for positive
deviations. Return to text
) has a large impact on
the probability of a price increase, but almost no impact on the
likelihood of price decreases. The reverse is true for positive
deviations. Return to text
21. We thank them for sharing these weights with us. Return to text
22. See Levy et al. (2011) for evidence that some digits are overrepresented in posted prices. Return to text
23. The model assumes a symmetric
![]() band, a process for individual reset
prices as in equation (11),
and normally distributed idiosyncratic shocks. Aggregate reset
price inflation is set to the average monthly U.S. CPI inflation
excluding shelter from 1988 to 2007. The width of the
band, a process for individual reset
prices as in equation (11),
and normally distributed idiosyncratic shocks. Aggregate reset
price inflation is set to the average monthly U.S. CPI inflation
excluding shelter from 1988 to 2007. The width of the ![]() band and the variance of idiosyncratic innovations are
calibrated to match an average frequency and average absolute
magnitude of nonzero price changes of 25 percent and 10 percent,
respectively. Return to text
band and the variance of idiosyncratic innovations are
calibrated to match an average frequency and average absolute
magnitude of nonzero price changes of 25 percent and 10 percent,
respectively. Return to text
24. In particular, BKM's procedure is consistent when the data are generated from the Caplin and Spulber (1987) model for which all price adjustments occur along the extensive margin through the selection effect. That model has no idiosyncratic shocks, so there is no confusion that price adjustments reflect solely price pressure attributable to aggregate shocks. The method is also consistent when the data are generated from a Calvo model with idiosyncratic shocks for which the exogenous probability of price changes varies in response to aggregate conditions. Although this model has no selection effect, it still has an extensive margin due to variation in the frequency of price changes. In both of these examples, the frequency of price changes is sensitive to the size of the shock. The approximation of the frequency of price changes by a constant used to derive equation (12) would not be appealing in these environments. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text