
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1061, November 2012 --- Screen Reader Version*
Gauging the Effects of Fiscal Stimulus Packages in the Euro Area
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We seek to quantify the impact on euro area GDP of the European Economic Recovery Plan (EERP) enacted in response to the financial crisis of 2008-09. To do so, we estimate an extended version of the ECB's New Area-Wide Model with a richly specified fiscal sector. The estimation results point to the existence of important complementarities between private and government consumption and, to a lesser extent, between private and public capital. We first examine the implied present-value multipliers for seven distinct fiscal instruments and show that the estimated complementarities result in fiscal multipliers larger than one for government consumption and investment. We highlight the importance of monetary accommodation for these findings. We then show that the EERP, if implemented as initially enacted, had a sizeable, although short-lived impact on euro area GDP. Since the EERP comprised both revenue and expenditure-based fiscal stimulus measures, the total multiplier is below unity.
Keywords: Fiscal policy, fiscal multiplier, European Economic Recovery Plan, DSGE modelling, Bayesian inference, euro area
JEL classification: C11, E32, E62
1 Introduction
The launch of large-scale fiscal stimulus packages following the financial crisis of 2008-09 has triggered a lively debate in both academic and policy circles about the effectiveness of fiscal policy. Two such large-scale fiscal packages were the American Recovery and Reinvestment Act (ARRA) in the United States and the European Economic Recovery Plan (EERP) in the European Union. In response to the debate, a growing academic literature has emerged analysing the economic effects of the fiscal stimulus packages. Most of this literature studies the impact of the ARRA. Prominent examples are the studies by Cogan et al. (2010), Drautzburg and Uhlig (2011) and Coenen et al. (2012).1
In this paper, we seek to quantify the impact of the EERP on euro area GDP. To this end, we estimate an extended version of the ECB's New Area-Wide Model (NAWM; see Christoffel et al., 2008) with a rich fiscal sector. Our specification of the fiscal sector aims at balancing the need for a high degree of detail, which is deemed important for conducting a meaningful quantitative analysis of the impact of fiscal policy on GDP, and tractability, which permits identifying the relevant economic mechanisms. Specifically, the extended NAWM features: (i) non-Ricardian households, so that government transfers have real effects; (ii) government consumption, which is valued by households in a non-separable way; (iii) public capital subject to a time-to-build technology, which can be either a complement or a substitute of private capital; (iv) time-varying distortionary tax rates; and (v) fiscal rules governing the endogenous adjustment of fiscal policy.
The estimation of the extended model makes use of 25 quarterly time series, 8 of which are from a newly available database for fiscal revenue and expenditure data as well as government debt. The estimation results point to the existence of important complementarities between private and government consumption and, to a lesser extent, between private and public capital. Employing the estimated model, we first examine the implied present-value multipliers for 7 distinct fiscal instruments. The estimated complementarities result in fiscal multipliers larger than one for government consumption and investment. We highlight the importance of monetary accommodation for these findings. Assuming that its implementation was carried out in line with the initial enactment, we then show that the EERP had a sizeable, although short-lived impact on euro area GDP. Since the EERP consisted of revenue and spending-based fiscal measures, the total EERP multiplier is below unity.
Based on a growth accounting exercise, as detailed in Coenen, Straub and Trabandt (2012), we furthermore study the role of endogenous adjustments of fiscal policy for euro area GDP during the crisis, with findings that hint at the importance of fiscal stabilisation beyond the effects of purely discretionary measures. In a similar vein, we provide evidence that the EERP alone does not account for the total discretionary fiscal stimulus.
Our analysis is related to Cwik and Wieland (2011) who evaluate the spending part of the EERP and conclude that the associated multiplier is below unity. Relative to Cwik and Wieland, our paper emphasises the following dimensions. First, we highlight the importance of possible complementarities between private and government consumption. Second, our analysis provides a more encompassing analysis of the effects of the EERP since we take into account a variety of instruments for government spending and revenue. Third, none of the models used by Cwik and Wieland is estimated using fiscal data, while we use a model that is estimated on lots of fiscal data. Fourth, we emphasise the importance of monetary accommodation for the assessment of the overall efficacy of fiscal stimulus packages.
The remainder of the paper is structured as follows. Section 2 provides an overview of the model, while Section 3 reports on the data and the main estimation results. Section 4 studies the estimated present-value fiscal multipliers and highlights the importance of monetary accommodation. Section 5 presents the results regarding the effectiveness of the EERP in stabilising economic activity in the euro area and provides extensive sensitivity analysis. In Section 6, we contrast the EERP results with an alternative measure of discretionary fiscal policy based on historical decompositions. Finally, Section 7 concludes.
2 The Model
In this section we give a brief overview of the extended version of the ECB's New Area-Wide Model (NAWM) with a detailed specification of the fiscal sector. As the main elements of the model's baseline version are relatively standard, we just provide a non-technical sketch of its basic structure and highlight subsequently those features that are most relevant for understanding the enhanced role of fiscal policy in the extended model.
2.1 The Baseline Model: A Bird's Eye View
The baseline version of the NAWM is an open-economy DSGE model of the euro area designed for use in the (Broad) Macroeconomic Projection Exercises regularly undertaken by ECB/Eurosystem staff and for analysis of topical policy issues; see Christoffel, Coenen and Warne (2008) for a detailed description of the model's structure. Its development has been guided by the principal consideration of covering a comprehensive set of core projection variables, including a small number of foreign variables, which, in the form of exogenous assumptions, play an important role in the projections.
The NAWM features four types of economic agents: households, firms, a fiscal authority and a monetary authority. Households make optimal choices regarding their purchases of consumption and investment goods, the latter determining the economy-wide capital stock. They supply differentiated labour services in monopolistically competitive markets, they set wages as a mark-up over the marginal rate of substitution between consumption and leisure, and they trade in domestic and foreign bonds.
As regards firms, the NAWM distinguishes between domestic producers of tradable intermediate goods and domestic producers of three types of non-tradable final goods: a private consumption good, a private investment good, and a public consumption good. The intermediate-good firms use labour and capital services as inputs to produce differentiated goods, which are sold in monopolistically competitive markets domestically and abroad. Accordingly, they set different prices for domestic and foreign markets as a mark-up over their marginal costs. The final-good firms combine domestic and foreign intermediate goods in different proportions, acting as price takers in fully competitive markets. The foreign intermediate goods are imported from producers abroad, who set their prices in euro in monopolistically competitive markets, allowing for an incomplete exchange-rate pass-through. A foreign retail firm in turn combines the exported domestic intermediate goods, where aggregate export demand depends on total foreign demand.
Both households and firms face nominal and real frictions, which have been identified as important in generating empirically plausible dynamics. Real frictions are introduced via external habit formation in consumption, through generalised adjustment costs in investment, imports and exports, and through fixed costs in intermediate goods production. Nominal frictions arise from staggered price and wage-setting à la Calvo (1983), along with (partial) dynamic indexation of price and wage contracts. In addition, there exist financial frictions in the form of domestic and external risk premia.
The fiscal authority purchases the public consumption good, issues domestic bonds, and levies different types of distortionary taxes, albeit at constant rates. Nevertheless, Ricardian equivalence holds because of the simplifying assumption that the fiscal authority's budget is balanced each period by means of lump-sum taxes. The monetary authority sets the short-term nominal interest rate according to a Taylor (1993)-type interest-rate rule, stabilising inflation in line with the ECB's definition of price stability.
The NAWM is closed by a rest-of-the-world block, which is represented by a structural VAR (SVAR) model determining five foreign variables: foreign demand, foreign prices, the foreign interest rate, foreign competitors' export prices and the price of oil. The SVAR model does not feature spill-overs from the euro area, in line with the treatment of the foreign variables as exogenous assumptions in the projections.
2.2 The Model with an Enhanced Role for Fiscal Policy
In the extended version of the NAWM, we allow fiscal policy to influence the economy through several additional channels. Specifically, the extended model features: (i) non-Ricardian households, so that, inter alia, government transfers have real effects; (ii) government consumption, which is valued by households in a non-separable way; (iii) public capital subject to a time-to-build technology, which can be a complement or a substitute of private capital; (iv) time-varying distortionary tax rates; and (v) fiscal rules that determine the endogenous adjustment of the different fiscal instruments.
2.2.1 Households and Government Consumption
We adapt the baseline model by introducing non-Ricardian households in the form of rule-of-thumb consumers,
following Coenen and Straub (2005) and Galí, López-Salido and Vallés (2007).2 To this end, we assume that there is a continuum of households, indexed by
![]() , which is split
into two groups: (i) Ricardian households, indexed by
, which is split
into two groups: (i) Ricardian households, indexed by
![]() , who accumulate physical capital
and have access to financial markets, and (ii) non-Ricardian households, indexed by
, who accumulate physical capital
and have access to financial markets, and (ii) non-Ricardian households, indexed by
![]() ,
who do not. As a result, the former group of households can smooth consumption intertemporally in response to
shocks, whereas the latter simply consume their after-tax disposable income.3
,
who do not. As a result, the former group of households can smooth consumption intertemporally in response to
shocks, whereas the latter simply consume their after-tax disposable income.3
Furthermore, we adapt the model by allowing for non-separable valuable government consumption similar to Leeper, Walker, and Yang (2009b). This feature has several interesting implications. First, changes in government consumption affect optimal private consumption decisions directly, as opposed to the indirect wealth effect in case of separable government consumption. Second, conditional on the estimated degree of complementarity a co-movement of private and government consumption may be obtained. Examples of public consumption goods that represent complements to private consumption goods are public security provision such as border control or police patrols, basic education, operas and theaters and many more.
Formally, aggregate consumption
![]() of household
of household ![]() is defined as a constant elasticity of
substitution (CES) aggregate:
is defined as a constant elasticity of
substitution (CES) aggregate:
 |
(1) |
where ![]() denotes the household's consumption of private goods, and
denotes the household's consumption of private goods, and ![]() measures government
consumption. Note that
measures government
consumption. Note that ![]() is a share parameter and
is a share parameter and
![]() , where
, where ![]() measures the elasticity of substitution between private consumption and government consumption.
measures the elasticity of substitution between private consumption and government consumption.
![]() implies perfect complementarity,
implies perfect complementarity,
![]() gives perfect
substitutability, and
gives perfect
substitutability, and
![]() yields the Cobb-Douglas (CD) case.
yields the Cobb-Douglas (CD) case.
Ricardian Households
Each Ricardian household ![]() maximises its lifetime utility in a given period
maximises its lifetime utility in a given period ![]() by choosing purchases of
the private consumption good,
by choosing purchases of
the private consumption good, ![]() , purchases of a private investment good,
, purchases of a private investment good, ![]() , which determines
next period's private capital stock,
, which determines
next period's private capital stock, ![]() , and next period's (net) holdings of domestic government
bonds and internationally traded foreign bonds,
, and next period's (net) holdings of domestic government
bonds and internationally traded foreign bonds, ![]() and
and
![]() , respectively. The
household's lifetime utility function is given by:
, respectively. The
household's lifetime utility function is given by:
![\begin{displaymath}
\mbox{E}_{t} \left[ \,\sum_{k=0}^{\infty} \beta^{k} \left( \ln \left( \tilde{C}_{i,t+k}
- \kappa \, \tilde{C}_{t+k-1}
\right)
- \frac{1}{1+\zeta } \, \left(N_{i,t+k}\right)^{1+\zeta} \,
\right) \,
\right],
\end{displaymath}](img27.gif) |
(2) |
where ![]() denotes the discount factor and
denotes the discount factor and ![]() is the inverse of the Frisch elasticity of labour
supply. The parameter
is the inverse of the Frisch elasticity of labour
supply. The parameter ![]() measures the degree of external habit formation in consumption. Thus, the
utility of household
measures the degree of external habit formation in consumption. Thus, the
utility of household ![]() depends positively on the difference between the current household-specific
aggregate consumption bundle,
depends positively on the difference between the current household-specific
aggregate consumption bundle,
![]() , and the lagged economy-wide aggregate consumption
bundle,
, and the lagged economy-wide aggregate consumption
bundle,
![]() , and negatively on labour supply,
, and negatively on labour supply, ![]() .
.
The household faces the following period-by-period budget constraint:
![$\displaystyle \hspace*{-0.5cm}
(1+\tau_{t}^{C}) \, P_{C,t} \, C_{i,t}
+ P_{I,t} \, I_{i,t}
+ \frac{B_{i,t+1}}{\epsilon_{t}^{R\!P} R_{t}}
+ \frac{S_{t}\,B_{i,t+1}^{\ast }}{\left[ 1-\Gamma_{B^{\ast }}(B^{\ast }_{t+1};\epsilon_{t}^{R\!P^{\ast}})\right] \, R_{t}^{\ast}}
+ T_{i,t}$](img35.gif) |
(3) |
where ![]() and
and ![]() are the prices of a unit of the private consumption good
are the prices of a unit of the private consumption good ![]() and the
investment good
and the
investment good ![]() , respectively.
, respectively. ![]() denotes the wage rate for the labour services provided to
firms,
denotes the wage rate for the labour services provided to
firms, ![]() ;
; ![]() indicates the rental rate for the capital services rented to firms,
indicates the rental rate for the capital services rented to firms, ![]() ;
and
;
and ![]() are the dividends paid by the household-owned firms.
are the dividends paid by the household-owned firms. ![]() and
and ![]() denote the
respective risk-less returns on domestic government bonds and internationally traded foreign bonds. The
latter are denominated in foreign currency and, thus, their domestic value depends on the nominal exchange
rate
denote the
respective risk-less returns on domestic government bonds and internationally traded foreign bonds. The
latter are denominated in foreign currency and, thus, their domestic value depends on the nominal exchange
rate ![]() .
.
The fiscal authority absorbs part of the household's gross income to finance its expenditure. ![]() denotes the consumption tax rate that is levied on the household's consumption purchases; and
denotes the consumption tax rate that is levied on the household's consumption purchases; and ![]() ,
,
![]() and
and ![]() are the tax rates levied on the different sources of the household's
income: wage income, capital income and dividend income. We assume that the physical capital depreciation,
are the tax rates levied on the different sources of the household's
income: wage income, capital income and dividend income. We assume that the physical capital depreciation,
![]() , is exempted from taxation.
, is exempted from taxation.
![]() is the additional payroll tax
rate levied on wage income (representing the household's contribution to social security). The terms
is the additional payroll tax
rate levied on wage income (representing the household's contribution to social security). The terms
![]() and
and ![]() denote lump-sum taxes and lump-sum transfers, respectively.
denote lump-sum taxes and lump-sum transfers, respectively.
The effective return on the risk-less domestic bonds depends on a financial intermediation premium,
represented by an exogenous domestic risk premium shock
![]() , which drives a wedge between
the interest rate controlled by the monetary authority and the return required by households. Similarly, when
taking a position in the international bond market, the household encounters an external financial
intermediation premium
, which drives a wedge between
the interest rate controlled by the monetary authority and the return required by households. Similarly, when
taking a position in the international bond market, the household encounters an external financial
intermediation premium
![]() , where
, where
![]() represents an external risk premium shock. This specification implies that, in
the non-stochastic steady state, households have no incentive to hold foreign bonds and the economy's net
foreign asset position is zero. The incurred intermediation premia are rebated in the form of lump-sum
payments,
represents an external risk premium shock. This specification implies that, in
the non-stochastic steady state, households have no incentive to hold foreign bonds and the economy's net
foreign asset position is zero. The incurred intermediation premia are rebated in the form of lump-sum
payments, ![]() and
and
![]() .
.
Finally, the physical capital stock owned by household ![]() evolves according to the following capital
accumulation equation:
evolves according to the following capital
accumulation equation:
| (4) |
where ![]() denotes the depreciation rate of the private capital stock.
denotes the depreciation rate of the private capital stock.
![]() represents a generalised adjustment cost function in investment and
represents a generalised adjustment cost function in investment and
![]() is an
investment-specific technology shock.
is an
investment-specific technology shock.
Non-Ricardian Households
The preferences of non-Ricardian and Ricardian households are identical. However, non-Ricardian households do
not invest in physical capital and have no access to financial markets. Therefore, each non-Ricardian
household ![]() sets nominal consumption expenditure equal to after-tax disposable wage income plus government
transfers. This results in the following period-by-period budget constraint:
sets nominal consumption expenditure equal to after-tax disposable wage income plus government
transfers. This results in the following period-by-period budget constraint:
| (5) |
Note that the approach to introducing non-Ricardian households adopted here implies that lump-sum taxes are
only paid by Ricardian households. Moreover, we allow for a possibly uneven distribution of transfers amongst
Ricardian and non-Ricardian households according to the following rule:
![]() .4
.4
Wage Setting and Labour Supply
As in Coenen and Straub (2005), we assume that both the Ricardian and the non-Ricardian households supply their labour services to firms via unions which act as wage setters in monopolistically competitive markets, taking firms' aggregate demand for labour as given. Furthermore, we assume that the individual union's choice variable is a common nominal wage rate for both types of households. These assumptions imply that the model's aggregate wage Phillips curve is unaffected by the introduction of non-Ricardian households.
Finally, we assume that the unions pool the wage income of all households and then distribute the aggregate
wage income in equal proportions.5 The common wage rate,
![]() , and identical labour demand curves imply that Ricardian
and non-Ricardian households supply the same amount of labour, i.e.
, and identical labour demand curves imply that Ricardian
and non-Ricardian households supply the same amount of labour, i.e.
![]() .6
.6
2.2.2 Intermediate-Good Firms and Public Capital
Public capital is added as an input for domestic intermediate goods production. In particular, each
intermediate-good firm
![]() producing a differentiated intermediate good
producing a differentiated intermediate good ![]() has access
to a Cobb-Douglas technology which takes as inputs labour services
has access
to a Cobb-Douglas technology which takes as inputs labour services ![]() and physical capital
and physical capital
![]() :
:
| (6) |
The variable
![]() represents a serially correlated, but transitory technology shock that affects
total factor productivity, while the variable
represents a serially correlated, but transitory technology shock that affects
total factor productivity, while the variable ![]() denotes a permanent technology shock that introduces a
unit root in the firm's output by augmenting the productivity of labour lastingly. The (gross) rate of
labour-augmenting productivity
denotes a permanent technology shock that introduces a
unit root in the firm's output by augmenting the productivity of labour lastingly. The (gross) rate of
labour-augmenting productivity
![]() follows a serially correlated process and determines
the model's balanced growth path. Similar to Christiano, Eichenbaum and Evans (2005) and Smets and Wouters
(2007), the term
follows a serially correlated process and determines
the model's balanced growth path. Similar to Christiano, Eichenbaum and Evans (2005) and Smets and Wouters
(2007), the term ![]() is the amount of production that is sunk (or lost) each period by the firm.
is the amount of production that is sunk (or lost) each period by the firm.
Physical capital is a CES aggregate of private capital services ![]() and the public capital stock
and the public capital stock
![]() :
:
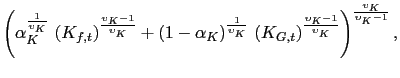 |
(7) |
where ![]() is a share parameter, and the parameter
is a share parameter, and the parameter
![]() denotes the elasticity of
substitution between private capital services and the public capital stock.
denotes the elasticity of
substitution between private capital services and the public capital stock.
![]() implies perfect complements,
implies perfect complements,
![]() gives perfect substitutes, and
gives perfect substitutes, and
![]() yields the CD case. Note that each intermediate-good firm
yields the CD case. Note that each intermediate-good firm ![]() has access to the same public
capital stock and that the latter grows at the same speed as private capital services along the balanced
growth path of the model.
has access to the same public
capital stock and that the latter grows at the same speed as private capital services along the balanced
growth path of the model.
Recently, Leeper, Walker and Yang (2009b) have argued that time-to-build for public capital is important for analysing the ARRA. In fact, government investment is typically subject to longer implementation delays than, for example, government goods purchases. In particular, it takes time until a budgeted government investment project (e.g. infrastructure) is implemented and contributes to the public capital stock. Leeper, Walker and Yang (2009b) model the delays between the authorisation of a government spending plan and completion of an investment project by a time-to-build technology for public capital projects, as in Kydland and Prescott (1982).7
We allow for the possibility of several periods of time-to-build in public capital, adopting a similar
specification. We thus assume that the government initiates investment projects that take ![]() periods until
they become productive and augment the public capital stock. The law of motion for public capital is then
given by:
periods until
they become productive and augment the public capital stock. The law of motion for public capital is then
given by:
| (8) |
where ![]() , denotes the depreciation rate of the public capital stock.
, denotes the depreciation rate of the public capital stock.
![]() is the
authorised budget for government investment in period
is the
authorised budget for government investment in period ![]() . Government investment that is actually
implemented (outlayed) is defined by:
. Government investment that is actually
implemented (outlayed) is defined by:
 |
(9) |
with
![]() , and enters the government budget constraint as well as the economy's
aggregate resource constraint.
, and enters the government budget constraint as well as the economy's
aggregate resource constraint.
In the case of a one-period time-to-build technology (as assumed for private investment), public investment
outlayed in period ![]() becomes productive in period
becomes productive in period ![]() , i.e.
, i.e. ![]() and
and
![]() .
.
2.2.3 Government Budget Constraint and Fiscal Rules
The fiscal authority purchases the public consumption good, ![]() , and the public investment good,
, and the public investment good, ![]() ,
issues bonds to refinance its debt,
,
issues bonds to refinance its debt, ![]() , makes transfer payments,
, makes transfer payments, ![]() , and raises different types of
taxes with details on the latter given above. The fiscal authority's period-by-period budget constraint has
the following form:8
, and raises different types of
taxes with details on the latter given above. The fiscal authority's period-by-period budget constraint has
the following form:8
| (10) | |
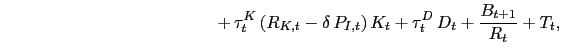 |
where ![]() and
and ![]() are the prices of a unit of the public consumption good and the public
investment good, respectively.
are the prices of a unit of the public consumption good and the public
investment good, respectively.
![]() denotes the rate of firms' contributions to social
security. Note that all quantities are expressed in per-capita terms.9
denotes the rate of firms' contributions to social
security. Note that all quantities are expressed in per-capita terms.9
The fiscal instruments on the expenditure and revenue side are assumed to follow the prescriptions of simple
feedback rules with a uniform specification. Specifically, we assume that all fiscal instruments react to
their own lagged values, to real government debt, ![]() , and to output,
, and to output, ![]() .
.
On the expenditure side, taking government consumption as an example, the log-linear specification of the rule is given by:
| (11) |
where a '^' denotes log-deviations from the values implied by the model's balanced growth path,
or steady state. ![]() is an unanticipated shock to government consumption, representing a
discretionary fiscal impulse. Following Leeper, Walker and Yang (2009a) we allow for pre-announcement
effects, with a weight of
is an unanticipated shock to government consumption, representing a
discretionary fiscal impulse. Following Leeper, Walker and Yang (2009a) we allow for pre-announcement
effects, with a weight of ![]() . In terms of fiscal feedback rules, we allow for the same structure for
government investment and government transfers.
. In terms of fiscal feedback rules, we allow for the same structure for
government investment and government transfers.
Similarly, as an illustration of the fiscal rules on the revenue side, the labour tax rule is given by:
| (12) |
where a '\/' denotes percentage-point deviations from the steady-state tax rate. In terms of rules, we allow for the same structure for employers' and employees' social security contributions as well as for lump-sum taxes. Note that for consumption taxes, we only allow for pre-announcement but not for feedback on debt or output. All other tax instruments are kept constant at their steady-state values.
Below, we shall assume that the parameters governing the lag dependence of the fiscal instruments and the importance of pre-announcement effects fall in the unit interval. Regarding the feedback parameters on government debt and output we shall be agnostic. That is, we shall estimate these parameters using a prior that is centred at zero and has support on the entire real line. This way, we do not restrict ourselves to imposing a priori restrictions that a particular fiscal instrument stabilises government debt or is counter-cyclical with respect to output. In other words, we envisage to let the data "speak" about which fiscal instrument contributes to debt stabilisation and whether it is pro or counter-cyclical with respect to the business cycle.10
3 Bayesian Estimation
We adopt the approach outlined in An and Schorfheide (2007) and Schorfheide (2000) and estimate the extended version of the NAWM employing Bayesian inference methods over the sample period from 1985Q1 to 2010Q2 (using the period 1980Q2 to 1984Q4 as training sample). This involves obtaining the posterior distribution of the model's parameters based on its log-linear state-space representation using the Kalman filter.11
An extensive discussion of the estimation results for the extended NAWM is beyond the scope of this paper. Here we report selectively on the data used in the estimation, on the model's shock processes, on the calibration of important steady-state ratios and on the prior and posterior distributions of key parameters, to the extent that this helps to understand the enhanced role of fiscal policy in our model. For details concerning the estimation of the baseline model structure the reader is referred to Christoffel et al. (2008, Section 3).
3.1 Data and Shock Processes
In estimating the extended version of the NAWM, we use quarterly time series for 17 out of the 18 macroeconomic variables used in the estimation of the baseline model: real GDP, private consumption, government consumption, extra-euro area exports and imports, the GDP deflator, the consumption deflator, the extra-euro area import deflator, total employment, nominal wages per head, the short-term nominal interest rate, the nominal effective exchange rate, foreign demand, foreign prices, the foreign interest rate, competitors' export prices, and the price of oil. The time series for total investment is replaced by the time series for private investment. All time series are taken from an updated version of the AWM database (see Fagan, Henry and Mestre, 2001), except for the extra-euro area trade data and the government consumption data. For further details on the data and their transformation prior to estimation see Christoffel et al. (2008, Section 3.2).
For government consumption and 7 additional fiscal variables, namely government investment, government transfers, indirect taxes, direct taxes, employees' and employers' social security contributions, as well as government debt, we use quarterly time series from a new fiscal database by Paredes, Pedregal and Pérez (2009). This database exploits intra-annual fiscal information for interpolation purposes which allows to capture genuine intra-annual "fiscal" dynamics in the data. This helps to circumvent two important problems that are present in fiscal time series interpolated on the basis of general macroeconomic indicators: (i) the endogenous bias that arises if such interpolated fiscal series were used with macroeconomic variables to assess the impact of fiscal policies; and (ii) the well-known decoupling of tax collection from the evolution of macroeconomic tax bases (revenue windfalls/shortfalls). For further details on the fiscal data see the Appendix.
By using euro area aggregate data for estimating fiscal rules and fiscal multipliers, we follow the approach pursued by Coenen and Straub (2005) and Forni et al. (2009). One disadvantage of using aggregate euro area data is that fiscal policy within the euro area is conducted at the national level. Focusing on the aggregate euro area in our analysis has, however, also some advantages. First, we can rely on a framework that matches the dynamics of the euro area macro aggregates quite well (see Christoffel et al., 2008). Second, we can neglect all the theoretical and empirical problems related to the analysis of a monetary union in a multi-country framework. Finally, the empirical literature finds relatively limited cross-country spillovers from fiscal policy shocks. As a result, country-specific components still contribute to a significant share of the variability of the macroeconomic aggregates (see De Bandt and Mongelli, 2000). In that sense, estimating (a weighted average of) fiscal rules and fiscal multipliers using euro area aggregate data might be appropriate for the analysis of the dynamics of euro area aggregates.
Data on government consumption are available in real terms, while existing nominal data on government investment and on government transfers and government debt are deflated using, respectively, the private investment deflator and the private consumption deflator from the AWM database. Revenue data are constructed as a ratio to consumption expenditure (indirect taxes) or to wage and salary income (direct taxes as well as social security contributions). We remove a linear trend from all fiscal data, except for social security contributions and government debt from which we subtract HP-trends and a broken linear trend, respectively.12 Figure 1 shows the time series of the transformed fiscal variables for our sample period from 1980Q2 to 2010Q2.
Commensurate with the number of time series used in the estimation, the extended NAWM features 20 distinct structural shocks, several of which have been discussed in Section 2, plus the 5 shocks for the foreign variables.13 In particular, we distinguish 7 shocks entering the fiscal feedback rules for government consumption, investment and transfers, for indirect and direct taxes, and for employees' and employers' social security contributions, plus a shock to the lump-sum tax rule which closes the government budget constraint in the model. All shocks are assumed to follow first-order autoregressive processes, except for the shocks to the interest-rate and fiscal feedback rules and the shocks in the autoregressive models for the foreign variables, which are assumed to be serially uncorrelated.14
3.2 Calibration and Prior Selection
Regarding the NAWM's steady state, all real variables are assumed to evolve along a balanced-growth path with
a steady-state growth rate of 2% per annum, which roughly matches average real GDP growth in our estimation
sample. Consistent with the balanced-growth assumption, we then calibrate key steady-state ratios of the
model by matching their empirical counterparts over the sample period. For example, the expenditure shares of
private consumption, private investment, government consumption and government investment are set to,
respectively, 57.5%, 18.3%, 21.5% and 2.8% of nominal GDP, while the export and import shares are set to
16%, ensuring balanced trade in steady state; see Table 1. Conditional on the model's
steady-state growth rate, the discount factor ![]() is chosen to imply an annualised equilibrium real
interest rate of 2.5%, while, on the nominal side, the steady-state inflation rate is set equal to 1.9% per
annum, consistent with the ECB's quantitative definition of price stability.
is chosen to imply an annualised equilibrium real
interest rate of 2.5%, while, on the nominal side, the steady-state inflation rate is set equal to 1.9% per
annum, consistent with the ECB's quantitative definition of price stability.
On the demand side of our model, we set the share of private consumption in the aggregate consumption bundle,
![]() , equal to 0.75. At the prior and posterior modes, this parameter value implies roughly equal
marginal utilities of private (Ricardian) consumption and government consumption. Turning to the model's
supply side, we set the capital share of output,
, equal to 0.75. At the prior and posterior modes, this parameter value implies roughly equal
marginal utilities of private (Ricardian) consumption and government consumption. Turning to the model's
supply side, we set the capital share of output, ![]() , to 30% and the depreciation rate of both private
capital,
, to 30% and the depreciation rate of both private
capital, ![]() , and public capital,
, and public capital, ![]() , to 6% at an annualised rate. Furthermore, we assume
, to 6% at an annualised rate. Furthermore, we assume
![]() with one period time-to-build for public capital and set
with one period time-to-build for public capital and set ![]() . The latter parameter value
implies that the marginal products of private and public capital are roughly equal at the prior and posterior
modes. Finally, similar to e.g. Drautzburg and Uhlig (2011), we allow for a wedge between the return on
capital and government bonds. We assume this wedge to be constant over time and set it to roughly 0.8
percentage points per annum in steady state. The introduction of this wedge permits us to pin down the
(endogenous) capital income tax rate at
. The latter parameter value
implies that the marginal products of private and public capital are roughly equal at the prior and posterior
modes. Finally, similar to e.g. Drautzburg and Uhlig (2011), we allow for a wedge between the return on
capital and government bonds. We assume this wedge to be constant over time and set it to roughly 0.8
percentage points per annum in steady state. The introduction of this wedge permits us to pin down the
(endogenous) capital income tax rate at ![]() in line with Trabandt and Uhlig (2011).15
in line with Trabandt and Uhlig (2011).15
As regards the fiscal sector, the other steady-state tax rates are calibrated so that average tax rates match
the corresponding average revenue-to-tax base ratios in the data. This approach is consistent with our
treatment of distortionary taxes as latent variables by measuring tax revenues in the data. Specifically, we
set the steady-state values of the indirect and direct tax rates, ![]() and
and ![]() , to 22.3% and
11.6%, respectively. Similarly, employees' and employers' social security contributions,
, to 22.3% and
11.6%, respectively. Similarly, employees' and employers' social security contributions,
![]() and
and
![]() , are set to 12.7% and 13.2%, respectively. Because of a lack of data, we set the tax
rate
, are set to 12.7% and 13.2%, respectively. Because of a lack of data, we set the tax
rate ![]() to zero throughout. Regarding government debt, we assume a steady-state debt-to-GDP ratio of
60% per annum consistent with the Stability and Growth Pact, which provides a normative anchor for debt
developments in the euro area over the medium to long term. This value is close to the average share of
government debt to GDP of approximately 65% at the onset of the financial crisis, but significantly below
the levels of debt reached in the aftermath of the crisis.
to zero throughout. Regarding government debt, we assume a steady-state debt-to-GDP ratio of
60% per annum consistent with the Stability and Growth Pact, which provides a normative anchor for debt
developments in the euro area over the medium to long term. This value is close to the average share of
government debt to GDP of approximately 65% at the onset of the financial crisis, but significantly below
the levels of debt reached in the aftermath of the crisis.
Finally, we calibrate a small number of additional parameters that are inherently difficult to identify. This
concerns, for example, the inverse of the labour supply elasticity ![]() , which we set equal to 2 in line
with the range of available estimates in the literature, and the parameter
, which we set equal to 2 in line
with the range of available estimates in the literature, and the parameter ![]() determining the sunk (or
lost) part of production of intermediate-good firms, which we calibrate such that firms' profits are zero in
steady state.
determining the sunk (or
lost) part of production of intermediate-good firms, which we calibrate such that firms' profits are zero in
steady state.
As regards the model parameters that we decided to estimate, we select our priors endogenously using a strategy similar to Christiano, Trabandt and Walentin (2011). Concerning the choice of the initial prior distributions for those parameters that are common to the baseline and the extended version of the NAWM, we use broadly the same priors as Christoffel et al. (2008). So our discussion here focuses on the prior distributions of the parameters characterising the fiscal sector in the extended model.
As detailed in Table 2, for the share of non-Ricardian households ![]() we
choose a beta distribution with a mean of 0.5 and a standard deviation of 0.1. Similarly, for the
distribution parameter
we
choose a beta distribution with a mean of 0.5 and a standard deviation of 0.1. Similarly, for the
distribution parameter ![]() we assume a beta distribution with mean 0.5 and standard deviation 0.2.
Noting that the elasticities
we assume a beta distribution with mean 0.5 and standard deviation 0.2.
Noting that the elasticities ![]() and
and ![]() of the CES aggregates determining aggregate
consumption and the aggregate capital stock are restricted to be positive by theory, we specify a truncated
normal distribution with mean 1 (corresponding to the CD case) and standard deviation 0.5 for these
parameters.
of the CES aggregates determining aggregate
consumption and the aggregate capital stock are restricted to be positive by theory, we specify a truncated
normal distribution with mean 1 (corresponding to the CD case) and standard deviation 0.5 for these
parameters.
Regarding the feedback coefficients on output and debt in the fiscal rules,
![]() and
and
![]() , we adopt normal distributions with mean 0 and standard deviation 2. For the coefficient
on the own lagged value of the fiscal instrument,
, we adopt normal distributions with mean 0 and standard deviation 2. For the coefficient
on the own lagged value of the fiscal instrument, ![]() , we use a beta distribution with mean 0.5
and standard deviation 0.2. In the same vein, for the weights concerning the importance of pre-announcement
effects,
, we use a beta distribution with mean 0.5
and standard deviation 0.2. In the same vein, for the weights concerning the importance of pre-announcement
effects, ![]() , we employ a beta distribution with mean 0.5 and standard deviation 0.2. Finally, for
the standard deviations of the fiscal shocks we use inverse gamma distributions with mode 0.10 and 2 degrees
of freedom, reflecting the fact that there is little a priori information on these parameters.
, we employ a beta distribution with mean 0.5 and standard deviation 0.2. Finally, for
the standard deviations of the fiscal shocks we use inverse gamma distributions with mode 0.10 and 2 degrees
of freedom, reflecting the fact that there is little a priori information on these parameters.
3.3 Posterior Distributions
In Table 2, we present estimation results for selected parameters characterising the fiscal sector in the extended version of the NAWM. The entries in the posterior-mode column refer to the values of the structural parameters that are obtained by maximising the model's posterior distribution. The remaining three columns report the mean as well as the 5% and 95% percentiles of the (marginal) posterior distributions which are computed using a posterior sampling algorithm.
The posterior mode of the share of non-Ricardian households equals ![]() which is similar to, if
not somewhat smaller than the estimates in Coenen and Straub (2005). The estimated share would, in general,
be too low for generating a positive output multiplier of government consumption shocks in a standard
New-Keynesian DSGE model (see e.g. Coenen and Straub, 2005, and Galí et al., 2007). In our model it
nevertheless allows transfer shocks to play a material role via distributional effects. The strength of these
effects depends on the distribution parameter
which is similar to, if
not somewhat smaller than the estimates in Coenen and Straub (2005). The estimated share would, in general,
be too low for generating a positive output multiplier of government consumption shocks in a standard
New-Keynesian DSGE model (see e.g. Coenen and Straub, 2005, and Galí et al., 2007). In our model it
nevertheless allows transfer shocks to play a material role via distributional effects. The strength of these
effects depends on the distribution parameter ![]() .16 As we obtain a posterior mode
estimate of 0.30, the overall impact of transfer shocks is however found to be rather small.
.16 As we obtain a posterior mode
estimate of 0.30, the overall impact of transfer shocks is however found to be rather small.
The posterior mode estimate of the elasticity of substitution between private and government consumption
goods is
![]() , so that the two goods enter the households' utility function as rather strong
complements. Similarly, the posterior mode estimate of the elasticity of substitution between private and
public capital is
, so that the two goods enter the households' utility function as rather strong
complements. Similarly, the posterior mode estimate of the elasticity of substitution between private and
public capital is
![]() , giving rise to moderate complementarities in the composite capital
stock. We have studied the impact of the parameters
, giving rise to moderate complementarities in the composite capital
stock. We have studied the impact of the parameters ![]() and
and ![]() on the marginal likelihood
of our model. Assuming a CD-aggregate in private and government consumption with
on the marginal likelihood
of our model. Assuming a CD-aggregate in private and government consumption with
![]() , the
(Laplace approximation of the) marginal likelihood falls on a log-scale from -3169.6 to 3171.8. The implied
posterior odds ratio of 9:1 suggests that there is substantial support for the existence of complementarities
between private and government consumption. By contrast, assuming a CD-aggregate in private and public
capital with
, the
(Laplace approximation of the) marginal likelihood falls on a log-scale from -3169.6 to 3171.8. The implied
posterior odds ratio of 9:1 suggests that there is substantial support for the existence of complementarities
between private and government consumption. By contrast, assuming a CD-aggregate in private and public
capital with
![]() results in a posterior odds ratio of 1.2:1, providing only weak support for the
existence of complementarities regarding capital.
results in a posterior odds ratio of 1.2:1, providing only weak support for the
existence of complementarities regarding capital.
Interestingly, the model offers two channels for government consumption to co-move with private consumption.
First, via the feature of non-Ricardian households. Second, via the degree of complementarity of private and
government consumption. It appears that the data prefer the second channel. This explains, at least to some
extent, why the estimated share of non-Ricardian households, ![]() , and the transfer distribution
parameter,
, and the transfer distribution
parameter, ![]() , are rather low. The model simply has an alternative channel at its disposal to explain
the possible co-movement between private and government consumption.
, are rather low. The model simply has an alternative channel at its disposal to explain
the possible co-movement between private and government consumption.
Turning to the parameters of the fiscal rules, the feedback coefficients in both the expenditure and revenue
rules seem in general not very well identified by the data. For government investment and transfers, we
estimate relatively sizeable feedback coefficients on government debt with
![]() and
and
![]() , while the reaction of government consumption to debt is estimated to be weaker
with
, while the reaction of government consumption to debt is estimated to be weaker
with
![]() . With the exception of government investment, the expenditure items are estimated
to react less strongly to movements in output, but positively: the posterior mode estimates are
. With the exception of government investment, the expenditure items are estimated
to react less strongly to movements in output, but positively: the posterior mode estimates are
![]() ,
,
![]() , and
, and
![]() , respectively. On the revenue
side, the feedback of lump-sum taxes to government debt and output is estimated at
, respectively. On the revenue
side, the feedback of lump-sum taxes to government debt and output is estimated at
![]() and
and
![]() , respectively. Smaller feedback coefficients are obtained for
employees' social security contributions (
, respectively. Smaller feedback coefficients are obtained for
employees' social security contributions (
![]() and
and
![]() ) and
for employers' social security contributions (
) and
for employers' social security contributions (
![]() and
and
![]() ).
In addition, pre-announcement effects seem to play a role, in particular for government investment
(
).
In addition, pre-announcement effects seem to play a role, in particular for government investment
(
![]() ), transfers (
), transfers (
![]() ), and lump-sum taxes (
), and lump-sum taxes (![]() ).
).
Overall, our estimates of the feedback coefficients suggest that there is only weak evidence of automatic stabilisation of fiscal policy in the euro area. One explanation is that the fiscal variables used in the estimation correspond to rather highly aggregated times series that mask the expected counter-cyclical behaviour of particular fiscal sub-categories. For example, our measure of general transfers to households used in the estimation does not allow to distinguish between unemployment benefits and other transfers, and therefore the high level of aggregation may hide automatic stabilisation effects.17
In Table 3, we compare the posterior mode estimates of selected parameters that are common to the extended and the baseline version of the NAWM. Overall, the posterior mode estimates of the parameters characterising households' preferences, wage and price-setting behaviour, final-good production, adjustment costs and monetary policy are found to be broadly similar across the two model versions. That is, the estimation of the common parameters appears rather robust to the extension of the NAWM's fiscal sector and to the inclusion of the additional 7 fiscal variables in the set of observables.
4 Fiscal Multipliers
In this section, we shall briefly examine the multipliers for different fiscal instruments implied by our estimated model, before turning to the evaluation of the EERP in the next section. We investigate fiscal multipliers in two ways. First, we analyse multipliers based on estimated impulse responses assuming a standard monetary and fiscal policy reaction. Second, we examine multipliers based on standardised fiscal stimuli with a duration of two years and when the monetary and fiscal policies are accommodative, similar to the analysis in Coenen et al. (2012). The latter approach resembles more closely the duration of the actual fiscal stimulus, as well as the policy actions, in response to the financial crisis, and it thereby enables a better understanding of the implied multipliers.
4.1 Multipliers Based on Estimated Impulse Responses
The upper panel in Table 4 contains the values of the present-value multipliers based on impulse responses evaluated at the posterior mode estimates of the model's parameters.18 The initial fiscal impulse is a one standard deviation shock for a particular fiscal instrument. The fiscal instruments with the largest multiplier are government consumption and government investment. The impact multiplier for a government consumption shock equals 1.02, while the long-run present-value multiplier is 0.84. By contrast, the fiscal multiplier following a shock to government investment equals 0.95 on impact, but increases to 1.13 in the long run.
The findings concerning the profile of the government consumption and investment multipliers are of course driven by the estimated degrees of complementarity between private and government consumption as well as private and public capital. The more sluggish rise of the government investment multiplier is mainly due to the slow response of the private capital stock reflecting the existence of investment adjustments costs. In the long run, however, the response of output to government investment shocks is stronger than to shocks to government consumption.19
In contrast, transfers to households have rather modest effects on output, despite the presence of non-Ricardian households and their distributional impact in our model. Similarly, the multipliers on the revenue side are found to be low, notably for employers' social security contributions (SSC). Not surprisingly, reductions in labour income taxes and in employees' social security contributions have a very similar impact on output, as they affect the same margin in the model.
Figure 2 depicts the posterior distributions of the present-value multiplier for selected fiscal instruments. The 10% and 90% percentiles of the posterior distributions suggest that parameter uncertainty matters, especially in the medium to longer run.
4.2 Multipliers Based on Standardised Fiscal Stimulus
In the lower panel of Table 4, we report present-value fiscal multipliers of a 2-year stimulus of 1% of GDP accompanied by 2 years of monetary accommodation, i.e. with an unchanged nominal interest rate. Thereafter, the nominal interest rate adjusts according to a Taylor-type rule, which for the sake of comparability with other studies (see Cogan et al., 2010, Cwik and Wieland, 2011, and Coenen et al., 2012) reacts only to contemporaneous inflation and output growth, with response coefficients of 1.5 and 0.125, respectively. In addition, we assume that the government does not stabilise government debt for the first two years, i.e. the fiscal rules are temporarily switched off.
This approach to computing multipliers is significantly different from the one discussed in the previous subsection. First, changes in fiscal policy are anticipated, and both monetary and fiscal policy are accommodative. Second, the size and duration of fiscal stimulus is standardised compared to the impulse response function approach with e.g. different coefficients on the lagged dependent terms for the alternative fiscal instruments (see Table 2). These features affect the transmission of fiscal policy in our model in important ways.
The results in Table 4 show that under this approach the fiscal instrument with the largest multiplier is government consumption. The impact multiplier equals 1.26, while the long-run present-value multiplier is 1.63. The long-run multiplier is also above one for exogenous increases in government investment.
Note that, except for employers' social security contributions, the maximum and long-run fiscal multipliers are larger across the board compared to the impulse response function approach. The bulk of the differences is explained by the duration of monetary accommodation, similar to the findings in Coenen et al. (2012).
5 Evaluating the European Economic Recovery Plan
5.1 Composition of the EERP
Governments in the euro area have responded to the financial crisis with a range of fiscal stimulus measures within the framework of the European Economic Recovery Plan (EERP). Table 5 provides a breakdown of the different fiscal measures implemented at the euro area level, as estimated by the European Commission (2009). In total, the fiscal stimulus measures amount to 1.1% and 0.8% of GDP in the years 2009 and 2010, respectively. These fiscal measures have been implemented in addition to the stimulus provided through the operation of automatic fiscal stabilisers and do not include other extra budgetary actions such as capital injections, loans and guarantees to the financial sector, as well as investment by public corporations.
Table 5 reveals that under the EERP, support for households' purchasing power accounts for about 40% of the total stimulus in the euro area countries in 2009-10. These fiscal measures have taken the form of a reduction in VAT, direct taxes, social security contributions, as well as direct aid, such as income support for households and support for housing or property markets. Notable stimulus measures have also been adopted to support investment and businesses directly. These categories account for roughly 30% and 20% of the total stimulus, respectively. Support for investment has primarily taken the form of public (infrastructure) investment, while the measures directly targeted at supporting business activity have mainly been targeted at reducing business costs (reduction of taxes and social security contributions, direct aid in the form of earlier payment of VAT returns, subsidies and the stepping up of export promotion). Labour-market measures (wage subsidies and active labour-market policies) account for about 10% of the total stimulus and thus represent the smallest fraction of the total stimulus measures.
We use our model to quantify, by means of simulations, the likely economic effects of the EERP and compare them with the standardised fiscal multipliers of the estimated model. To this end, Table 5 also provides information on how the different fiscal measures implemented under the EERP were allocated to the model's fiscal variables in the simulation exercise. Because of the unavoidably imperfect match between the exact fiscal stimulus measures adopted by the euro area member states and the model's fiscal variables, a certain amount of judgement is needed. For instance, labour-market measures are allocated to government consumption since they represent primarily active labour-market policies, the costs of which are paid for by the government. Nevertheless, keeping the above-mentioned caveat in mind, the simulations should broadly reflect the actual EERP measures.
5.2 Benchmark Results: Effects of the EERP
Table 6 reports the simulation results for the EERP on the basis of the information provided in Table 5. In the simulations, the intra-annual profile of the EERP stimulus measures in 2009 and 2010 is assumed to be flat. The reported output effects of the EERP are average percentage deviations from the model's balanced growth path after a 2-year standardised fiscal stimulus (1.1% in the first year and 0.8% in the second year in terms of baseline GDP) accompanied by 2 years of monetary and fiscal accommodation. For comparison with other studies, we assume no pre-announcement or feedbacks, except for a debt feedback on lump-sum taxes which sets in after 2 years and is needed for ensuring debt sustainability. Furthermore, we set also the coefficients on the own lagged value of the fiscal instruments to zero. Again, the nominal interest rate adjusts according to a static Taylor-type rule after a period of 2 years with unchanged interest rates.
Panel A in Table 6 shows both the EERP fiscal multiplier and the EERP output effects for our benchmark simulation setup. The multiplier in the first two years is positive, amounting to about 0.52 and 0.57, respectively, and converges eventually to a long-run multiplier of around 0.73. Assuming that the fiscal stimulus measures are lifted at the beginning of the third year, the effects on real GDP fade away however rather quickly, as can be clearly seen from the corresponding output effects.
Interestingly, these results are broadly comparable with, if not somewhat larger than, those from model-based analysis provided in policy reports such as European Commission (2009) and ECB (2010). However, the present paper offers much more detail and an in-depth analysis of the various determinants of the EERP fiscal multiplier. For example, below we highlight the importance of e.g. complementarities between private and public consumption and capital. Moreover, our results are based on a model estimated with lots of fiscal data compared to the models used in the above reports. Finally, below we also offer new insights about the relation of the EERP stimulus package and the overall fiscal stimulus in the euro area during the crisis.
5.3 Sensitivity of the EERP Effects
What drives the effects of the EERP in our model? To answer this question, we conduct a sensitivity analysis of our benchmark simulation results. Panel B in Table 6 illustrates the sensitivity of our results to variations of the model specification, as reflected in the assignment of alternative values to key parameters, while panel C focuses on the consequences of alternative assumptions with respect to the implementation of the EERP.
Consider the results in panel B of Table 6 first. Relative to our benchmark results, the fiscal multiplier of the EERP falls when a Cobb-Douglas aggregate in private and public capital is assumed and when government consumption is not valued by households (line 1). However, it turns out that the quantitative impact is relatively small. This does not imply that the complementarities in private and public consumption and capital in our model are quantitatively not important. It is the small overall importance of government consumption and investment which amount to only 35% in the EERP that limits the effectiveness of the complementarity channels. Interestingly, a specification that imposes very strong complementarities between public and private capital and that leads to comovement between private and public investment (see Coenen, Straub and Trabandt, 2012) has virtually identical short-run multipliers but considerably higher long-run multipliers (line 2). The reason is that the large and persistent build-up of public and private capital results in a persistent deviation of output from the model's balanced growth path even beyond the duration of the actual stimulus. When the share of non-Ricardian households is increased to 50%, the EERP multiplier increases markedly (line 3). Non-Ricardian households have a higher propensity to consume out of disposable income. Accordingly, the same aggregate increase in transfers has a larger impact on GDP and thus on the EERP multiplier.
Finally, when the importance of nominal rigidities in the model is reduced such that prices and wages adjust every 6 months on average, the EERP multiplier increases considerably (line 4). Higher government consumption and investment increase demand and induce an increase in actual and expected inflation. When the nominal interest rate is held fixed, as we assume for the first 2 years, higher inflation implies a stronger fall in the real interest rate, inducing a surge in private absorption. Similarly, higher transfers, reduced consumption and labour income taxes as well as lower social security contributions of employees boost disposable income of especially non-Ricardian households and yet again trigger inflationary effects via the aggregate demand channel in the model. This reinforces the fall in the real interest rate.20 In short, more flexible prices and wages induce a stronger increase in actual and expected inflation and, thereby, a more pronounced fall in the real interest rate: a larger multiplier for the EERP results.
Next, inspect the results in panel C of Table 6. When the assumption of monetary accommodation is dropped, the EERP multiplier is noticeably smaller compared to the benchmark multiplier (line 1). In this case, the Taylor principle dictates that the nominal interest rate is increased more than one for one with the rate of inflation. As a result, the real interest rate rises so that economic activity is boosted less: the multiplier falls. In contrast, when using the estimated rule, the implied multiplier is larger (line 2). In our benchmark simulation, monetary policy follows the prescriptions of a static Taylor-type rule, with the nominal interest rate responding to contemporaneous inflation and output growth. Our estimated interest rate rule deviates from the static Taylor-type rule by allowing for (i) interest rate smoothing and (ii) reactions to changes in inflation and output growth. Due to the relatively strong degree of interest rate smoothing in the estimated rule, the interest rate is kept at a lower level than under the static rule once monetary accommodation has ended. As a result, the real interest rate does not rise as much under the estimated rule which induces favourable output effects, i.e. a higher multiplier.
In our benchmark simulation, we assume no feedbacks, except for a small debt feedback on lump-sum taxes which sets in after 2 years and is needed for ensuring debt sustainability. Accordingly, the EERP is initially fully deficit-financed, leading to a very persistent increase in government debt. Modifying the debt feedback on lump-sum taxes (paid by Ricardian households only) does not have a material impact on the output effects of the EERP as Ricardian equivalence applies. By contrast, if a debt feedback on distortionary labour taxes is considered instead, like in Drautzburg and Uhlig (2011), the output effects are dampened because of the corrective future tax increases (line 3), notably in the long. Interestingly, when the estimated fiscal feedback rules are active in the simulations, the implied present-value multiplier turns out to be larger, especially in the medium to long run (line 4). The reason is that the fiscal rules have a debt stabilising effect once they are activated, notably on the expenditure side. In other words, the estimated fiscal rules imply a "spending reversal" of the sort Corsetti et al. (2009) have emphasised. Finally, when the EERP is assumed to be nearly permanent, the multiplier falls sharply (line 5). A strong negative wealth effect is responsible for this result.21
All in all, the multipliers in our benchmark EERP simulation are relatively low, and more importantly so, below one. Since the composition of the EERP consists of many fiscal instruments, the overall EERP multiplier represents an average of the multipliers of the individual instruments. Line 6 in Table 6 shows the maximum possible EERP multiplier in our model. Given our assumptions about the duration and the path of the EERP, that multiplier is identical to the one for government consumption. In other words, had all resources of the EERP been used for government consumption, the EERP impact on GDP would have been 2 to 3 times larger than in the benchmark simulation.
Last but not least, line 7 shows the effects when a one-year implementation delay of the fiscal package is assumed. That is, agents anticipate the EERP one year ahead. Unfavourable anticipation effects similar to those reported in e.g. Cwik and Wieland (2011) result in a noticeably lower EERP multiplier.
5.4 Relation to an Alternative Study of the EERP
Our paper is related to the study by Cwik and Wieland (2011) more generally. The authors of this study calculate the amounts of fiscal stimulus in the euro area for 2009 and 2010 by examining information provided by European national governments. According to the authors, the EU-11 total fiscal stimulus package, as a percentage of GDP, amounts to 1.04% in 2009 and to 0.86% in 2010. These numbers are reasonably close to the European Commission numbers of 1.1% and 0.8% of GDP (see Table 5), which were used in the simulations presented in the previous subsection.
However, Cwik and Wieland (2011) focus almost exclusively on evaluating the part of the total stimulus package that represents government spending for goods and services plus investment. As a percentage of GDP, that part of the total package amounts to 0.48% in 2009 and to 0.2% in 2010. Again, these numbers are reasonably close to the sum of the government consumption and government investment shares in Table 5.
Panel A of Table 7 contains the time profile of the government spending stimulus examined by Cwik and Wieland (2011). In contrast to our analysis in the previous subsection, the time profile is not flat in 2009. Rather, it is assumed that the stimulus builds up gradually and reaches its maximum in 2009Q3-Q4. Further, it is assumed that all government spending takes the form of non-valued government consumption.
The implied output effects reported by Cwik and Wieland (2011) for the case when no monetary accommodation is assumed are shown in panel B of Table 7.22 It turns out that the output effects are smaller than the stimulus itself and, therefore, the fiscal multiplier is smaller than one. When using the same simulation input, our model predicts output effects that exceed those of Cwik and Wieland. In particular, the implied multiplier exceeds 1 from 2009Q3 onwards; see panel D in the table. The gradual build-up of the multiplier is caused by the hump-shaped private consumption response to a government spending shock in our model; see Coenen, Straub and Trabandt (2012) for an illustration.
What accounts for the differences in results? Line 3 in panel B of Table 7 shows the
implications when we assume that government consumption is not valued by the households in our model,
i.e. ![]() . In this case, the differences in results essentially disappear. In other words, our
estimated model highlights a channel that appears important for the conclusions about the effectiveness of
fiscal stimulus. Once valued government consumption, which represents a complement to private consumption in
our model, is taken into account, the implied fiscal multiplier may be easily larger than one.
. In this case, the differences in results essentially disappear. In other words, our
estimated model highlights a channel that appears important for the conclusions about the effectiveness of
fiscal stimulus. Once valued government consumption, which represents a complement to private consumption in
our model, is taken into account, the implied fiscal multiplier may be easily larger than one.
In addition, we also examine the implications of monetary accommodation more closely. Interestingly, when Cwik and Wieland (2011) assume that the central bank keeps the nominal interest unchanged in 2009 and 2010, the output effects exceed the size of the stimulus; see panel C in Table 7. In other words, Cwik and Wieland do obtain a multiplier larger than one once they assume two years of monetary accommodation. Again, our results are essentially identical when we assume non-valued government consumption. By contrast, when complementarities as supported by our estimation results are taken into account, the output effects and, hence, the multiplier are substantially larger.
Overall, relative to Cwik and Wieland (2011), our paper emphasises the following dimensions. First, we highlight the importance of possible complementarities between private and government consumption. Second, our analysis provides a more encompassing analysis of the effects of the EERP since we take into account a variety of instruments for government spending and revenue. Third, none of the models used by Cwik and Wieland is estimated using fiscal data while we use a model that is estimated on lots of fiscal data. Fourth, we emphasise the importance of monetary accommodation for the assessment of the overall efficacy of fiscal stimulus packages.
6 Putting the EERP Effects into Perspective
The estimated model with its rich fiscal sector enables us to cross-check the simulated output effects of the EERP against the findings of an alternative approach to measuring the effects of discretionary fiscal policy: the historical decomposition of observed real GDP growth by means of a growth accounting exercise.
6.1 Fiscal Stimulus Based on Historical Decompositions
In conducting the growth accounting exercise, we decompose the dynamics of euro area real GDP growth over the period 2007-10 into the contributions of the fiscal and non-fiscal shocks that are identified through the lens of our estimated model. The contribution of the fiscal shocks are depicted in Figure 3 and suggest that discretionary fiscal policy pushed up annualised quarter-on-quarter growth rates by up to 1.6 percentage points (in 2009Q2).
In a companion paper (see Coenen, Straub and Trabandt, 2012), we show that our strategy of allowing for a rich fiscal sector and using lots of fiscal data are pivotal for this result. That is, when the baseline version of our model is employed, which only features a very stylised fiscal sector and which is estimated using government consumption as the only observable fiscal variable, the contribution of discretionary fiscal policy to real GDP growth during the crisis is found to be essentially zero. We also show that shocks to government investment, consumption and transfers, as well as consumption and labour income taxes were all important in supporting euro area GDP growth. These findings on the relative importance of the fiscal shocks are broadly in line with the fiscal measures that were actually enacted by national governments under the EERP in response to the crisis; see Table 5.
In the following, we extend the analysis in Coenen, Straub and Trabandt (2012) in two directions. First, we account for parameter uncertainty when calculating the growth contributions of the fiscal shocks. Figure 3 indicates that our result concerning the contribution of discretionary fiscal policy to euro area real GDP growth is fairly unaffected by parameter uncertainty, as revealed by the tightness of the band represented by the 10% and 90% percentiles from the joint posterior distribution of the model parameters. Second, we assess the importance of the fiscal feedback rules in our analysis by performing the following experiment. We set all fiscal feedback parameters to zero (except for the parameter governing the feedback from debt on lump-sum taxes) and conduct another historical decomposition of real GDP growth into fiscal and non-fiscal shocks. Then we compare the contributions of the fiscal shocks in the above benchmark case and in our experiment. The results shown in Figure 4 highlight the importance of endogenous fiscal responses for the analysis. In particular, in a model with no endogenous fiscal policy the cumulated impact of discretionary policy on real GDP would have been much smaller than in a model that explicitly takes into account fiscal feedback. However, this experiment is subject to the caveat that it might overstate the importance of fiscal feedback since all other model parameters are held fixed at their posterior mode estimates.23
6.2 EERP vs. Historical Decomposition
How do the insights from the EERP simulation compare with those from the historical decomposition? To answer this question, the upper panel of Figure 5 depicts the path of actual euro area real GDP growth over the period from 2008Q2 to 2010Q1. In addition, the figure shows the results of two counterfactual scenarios. First, we subtract the contributions of the estimated fiscal shocks to real GDP growth from actual real GDP growth. In other words, we calculate the counterfactual path for real GDP growth had there been no fiscal shocks during the financial crisis, as identified by our model. Second, we calculate another counterfactual path for real GDP growth by subtracting the simulated effects of the EERP as reported in panel A of Table 6.
The upper panel of Figure 5 shows that, absent the fiscal shocks estimated on the basis of our model, real GDP growth in the euro area would have been smaller on average compared to the case when there would have been no EERP. Examining both cases more closely, it appears that there are some noticeable differences. First, the EERP simulation suggests a stronger impact on real GDP growth in 2009Q1, but predicts less pronounced effects during the subsequent recovery. Put differently, the EERP simulation generates a too strong push in terms of real GDP growth compared to the predictions on the basis of the historical decomposition. This result is to a large extent related to our timing assumption regarding the profile of the EERP stimulus measures which we have assumed to be flat during 2009 and 2010. A slow phasing-in of the stimulus measures in 2009 similar to the profile assumed by Cwik and Wieland (2011) would imply a less strong initial growth effect in 2009Q1.
Even though the quarterly profile in 2009Q1 reveals perhaps somewhat controversial implications, the overall effect of the EERP is likely to be smaller than the one implied by the estimated fiscal shocks. The lower panel of Figure 5 provides the cumulated impact of our two measures of fiscal stimulus on euro area real GDP growth. Importantly, the EERP alone does not account for the full estimated discretionary stimulus during the crisis period. Partly, this is due to the nature of the EERP scenario which implicitly assumes that no measures had been enacted prior to 2009Q1. On the other hand, even after 2009Q2, the estimated shocks predict larger effects of discretionary fiscal policy compared to the EERP. Moreover, the historical decomposition points to the existence of fiscal stimulus right from the onset of the crisis in 2008Q3 and therefore before the start of the implementation of the EERP. Hence, these results indicate that the EERP alone is not sufficient to gauge the effects of fiscal stimulus during the crisis. Rather, our results based on the historical decomposition points to the presence of more sizeable fiscal support during the crisis than the EERP alone would suggest.
7 Conclusions
In this paper, we have quantified the impact of the EERP on euro area GDP during the recent financial crisis. To this end, we estimated an open-economy DSGE model for the euro area with a rich fiscal sector. The estimation makes use of 25 quarterly time series, 8 of which are from a newly available database for fiscal revenue and expenditure data as well as government debt. The estimation results point to the existence of important complementarities between private and government consumption and, to a lesser extent, between private and public capital. Employing the estimated model, we examined the implied present-value multipliers for 7 distinct fiscal instruments. Most notably, the estimated complementarities were found to result in fiscal multipliers larger than one for government consumption and investment. We highlighted the importance of monetary accommodation for this result. Regarding the EERP, we provided model-based evidence that, if implemented as initially enacted, it had a sizeable, although short-lived impact on euro area GDP. Since the EERP comprised both revenue and spending-based fiscal measures, the total multiplier is below unity. We also studied the role of endogenous adjustments of fiscal policy for euro area GDP during the crisis and provided evidence that the EERP alone does not account for the total discretionary fiscal stimulus in the euro area.
While our analysis has focused on the quantitative evaluation of the expansionary effects of discretionary fiscal measures during the crisis, the latter has led--partly as a consequence of the implemented measures--to a sizeable increase in government deficits and debt levels. Hence, future research ought to be extended towards examining the effects of fiscal consolidation strategies aimed at curtailing deficits and debt levels over the medium term. In pursuing this research, accounting for the endogenous nature of government bond premia, which have been rising sharply in some countries, will be a fundamental challenge.
References
An, S. and F. Schorfheide, 2007,"Bayesian Analysis of DSGE Models", Econometric Reviews, 26, 113-172.
Calvo, G. A., 1983, "Staggered Prices in a Utility-Maximizing Framework", Journal of Monetary Economics, 12, 383-398.
Campbell, J. Y. and N. G. Mankiw, 1989, "Consumption, Income, and Interest Rates: Reinterpreting the Time Series Evidence", in O. J. Blanchard and S. Fischer (eds), NBER Macroeconomics Annual, 1989, Vol. 4, MIT Press, Cambridge, 185-216.
Christiano, L. J., M. Eichenbaum and S. Rebelo, 2011, "When Is the Government Spending Multiplier Large?", Journal of Political Economy, 119, 78-121.
Christiano, L. J., M. Eichenbaum and C. L. Evans, 2005, "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy", Journal of Political Economy, 113, 1-45.
Christiano, L. J., M. Trabandt and K. Walentin, 2011, "Introducing Financial Frictions and Unemployment into a Small Open Economy Model", Journal of Economic Dynamics and Control, 35, 1999-2041.
Christoffel, K., G. Coenen, and A. Warne, 2008, "The New Area-Wide Model of the Euro Area: A Micro-Founded Open-Economy Model for Forecasting and Policy Analysis", ECB Working Paper No. 944, European Central Bank, October.
Coenen, G., C. J. Erceg, C. Freedman, D. Furceri, M. Kumhof, R. Lalonde, D. Laxton, J. Lindé, A. Mourougane, D. Muir, S. Mursula, C. de Resende, J. Roberts, W. Roeger, S. Snudden, M. Trabandt and J. in't Veld, 2012,"Effects of Fiscal Stimulus in Structural Models", American Economic Journal: Macroeconomics, 4, 22-68.
Coenen, G., P. McAdam and R. Straub, 2008, "Tax Reform and Labour-Market Performance in the Euro Area: A Simulation-Based Analysis Using the New Area-Wide Model", Journal of Economic Dynamics and Control, 32, 2543-2583.
Coenen, G. and R. Straub, 2005, "Does Government Spending Crowd in Private Consumption? Theory and Empirical Evidence for the Euro Area", International Finance, 8, 435-470.
Coenen, G., R. Straub and M. Trabandt 2012, "Fiscal Policy and the Great Recession in the Euro Area", American Economic Review, Papers and Proceedings, 102, 71-76.
Cogan, J. F., T. Cwik, J. B. Taylor and V. Wieland, 2010, "New Keynesian versus Old Keynesian Government Spending Multipliers", Journal of Economic Dynamics and Control, 34, 281-295.
Corsetti, G., A. Meier and G. Müller, 2009, "Fiscal Stimulus with Spending Reversals", IMF Working Paper 09/106, International Monetary Fund.
Cwik, T. and V. Wieland, 2011, "Keynesian Government Spending Multipliers and Spillovers in the Euro Area", Economic Policy, 26, 495-549.
De Bandt, O. and F. P. Mongelli, 2000, "Convergence of Fiscal Policies in the Euro Area", ECB Working Paper No. 20, European Central Bank, May.
Drautzburg, T. and H. Uhlig, 2011, "Fiscal Stimulus and Distortionary Taxation", NBER Working Paper No. 17111.
ECB, 2007, Government Finance Statistics Guide, European Central Bank, January.
ECB, 2010, "The Effectiveness of Euro Area Fiscal Policies", Monthly Bulletin, European Central Bank, July.
Eggertsson, G. B., 2011, "What Fiscal Policy Is Effective at Zero Interest Rates?", in D. Acemoglu and M. Woodford (eds), NBER Macroeconomics Annual 2010, Vol. 25, University of Chicago Press, Chicago, 59-112.
Erceg, C. J. and J. Lindé, 2010, "Is There a Fiscal Free Lunch in a Liquidity Trap?", International Finance Discussion Paper No. 1003, Board of Governors of the Federal Reserve System.
European Commission, 2009, "Public Finances in EMU", European Economy, 5/2009, European Commission.
Fagan, G., J. Henry, and R. Mestre, 2001, "An Area-Wide Model (AWM) for the Euro Area", ECB Working Paper No. 42, European Central Bank, January.
Forni, L., L. Monteforte, and L. Sessa, 2009, "The General Equilibrium Effects of Fiscal Policy: Estimates for the Euro Area", Journal of Public Economics, 93, 559-585.
Galí, J., J. D. López-Salido and J. Vallés, 2007, "Understanding the Effects of Government Spending on Consumption", Journal of the European Economic Association, 5, 227-270.
Kydland, F. E. and E. C. Prescott, 1982, "Time to Build and Aggregate Fluctuations", Econometrica, 50, 1345-1370.
Leeper, E., T. B. Walker and S. C. S. Yang, 2009a, "Fiscal Foresight and Information Flows", NBER Working Paper No. 14630.
Leeper, E., T. B. Walker and S. C. S. Yang, 2009b, "Government Investment and Fiscal Stimulus in the Short and Long Runs", NBER Working Paper No. 15153.
Mankiw, N. G., 2000, "The Savers-Spenders Theory of Fiscal Policy", American Economic Review, 90, 120-125.
Paredes, J., D. J. Pedregal and J. Pérez, 2009, "A Quarterly Fiscal Database for the Euro Area Based on Intra-Annual Fiscal Information", ECB Working Paper No. 1132, European Central Bank, September.
Schorfheide, F., 2000, "Loss-Function-Based Evaluation of DSGE Models", Journal of Applied Econometrics, 15, 645-670.
Sims, C., 2012, "Modeling Fiscal Impacts on Inflation in a DSGE Model", mimeo, Princeton University.
Smets, F. and R. Wouters, 2003, "An Estimated Stochastic Dynamic General Equilibrium Model of the Euro Area", Journal of the European Economic Association, 1, 1123-1175.
Smets, F. and R. Wouters, 2007, "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach", American Economic Review, 97, 586-607.
Taylor, J. B., 1993, "Discretion Versus Policy Rules in Practice", Carnegie-Rochester Conference Series on Public Policy, 39, 195-214.
Trabandt, M. and H. Uhlig, 2011, "The Laffer Curve Revisited", Journal of Monetary Economics, 58, 305-327.
Uhlig, H., 2010, "Some Fiscal Calculus", American Economic Review, 100, 30-34.
Woodford, M., 2011, "Simple Analytics of the Government Expenditure Multiplier", American Economic Journal: Macroeconomics, 3, 1-35.
Table 1: Calibration of Key Steady-State Ratios and Selected Parameters of the Extended Version of the NAWM
| Share/Parameter | Description | Value |
|---|---|---|
| A. Expenditure shares: |
Private consumption | 57.5 |
| A. Expenditure shares: |
Private investment | 18.3 |
| A. Expenditure shares: |
Government consumption | 21.5 |
| A. Expenditure shares: |
Government investment | 2.8 |
| A. Expenditure shares: |
Exports | 16.0 |
| A. Expenditure shares: |
Imports | 16.0 |
| B. Preferences: β | Discount factor | 0.997 |
| B. Preferences: ζ | Inverse Frisch elasticity | 2.0 |
| B. Preferences: αG | Private consumption share in CES | 0.75 |
| C. Technology: δ | Depreciation rate: private capital | 0.015 |
| C. Technology: δK | Depreciation rate: private capital | 0.015 |
| C. Technology: αK | Private capital share in CES | 0.9 |
| C. Technology: b0 | Time-to-build parameter | 1 |
| D. Tax rates: | Consumption tax | 22.3 |
| D. Tax rates: | Labour income tax | 11.6 |
| D. Tax rates: | Employees' social security contribution | 12.7 |
| D. Tax rates: | Employers's social security contribution | 13.2 |
| D. Tax rates: | Capital income tax | 35.0 |
| D. Tax rates: | Profit income tax | 0.0 |
| E. Monetary Policy: | Inflation objective | 1.90 |
| F. Fiscal Policy: BY | Government debt-to-output ratio | 2.40 |
Table 2: Selected Estimates of the Fiscal Parameters in the Extended Version of the NAWM
| Parameter | Prior Distribution | Posterior Distribution: Mode | Posterior Distribution: Mean | Posterior Distribution: 5% | Posterior Distribution: 95% |
|---|---|---|---|---|---|
| A. Share of non-Ricardian households: | B(0.5,0.1) | 0.18 | 0.18 | 0.12 | 0.24 |
| A. Share of non-Ricardian households: | B(0.5,0.2) | 0.30 | 0.32 | 0.11 | 0.52 |
| B. Elasticity of substitution in CES aggregates: | Ntr(1,0.5;0) | 0.29 | 0.37 | 0.00 | 0.61 |
| B. Elasticity of substitution in CES aggregates: | Ntr(1,0.5;0) | 0.84 | 0.98 | 0.17 | 1.69 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | 0.06 | 0.08 | 0.00 | 0.15 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | 0.55 | 0.52 | -0.04 | 1.10 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | 0.10 | 0.11 | -0.27 | 0.50 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | 0.21 | 0.43 | 0.08 | 0.80 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | 0.04 | 0.04 | -0.03 | 0.11 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | -0.05 | -0.05 | -0.08 | -0.02 |
| C. Output feedback coefficients in fiscal rules: | N(0,2) | -0.03 | -0.03 | -0.06 | 0.00 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | -0.02 | -0.02 | -0.06 | 0.02 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | -0.18 | -0.20 | -0.45 | 0.06 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | -0.14 | -0.13 | -0.30 | 0.05 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | 0.07 | 0.15 | 0.04 | 0.27 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | 0.05 | 0.05 | 0.02 | 0.09 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | -0.01 | -0.01 | -0.03 | 0.00 |
| D. Debt feedback coefficients in fiscal rules: | N(0,2) | 0.01 | 0.01 | -0.01 | 0.02 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.77, 0.06 | 0.73, 0.08 | 0.64, 0.02 | 0.82, 0.15 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.70, 0.93 | 0.66, 0.90 | 0.54, 0.83 | 0.79, 0.98 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.72, 0.81 | 0.65, 0.77 | 0.52, 0.65 | 0.79, 0.90 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.91, 0.31 | 0.90, 0.30 | 0.85, 0.25 | 0.94, 0.36 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.68, 0.90 | 0.48, 0.62 | 0.15, 0.09 | 0.80, 0.96 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.81, 0.11 | 0.79, 0.13 | 0.71, 0.05 | 0.87, 0.22 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.74, 0.26 | 0.73, 0.27 | 0.62, 0.19 | 0.84, 0.35 |
| E. Lagged dependent variable and pre-announcement coefficients in fiscal rules: | B(0.5,0.2) | 0.69, 0.77 | 0.66, 0.76 | 0.53, 0.68 | 0.80, 0.84 |
Note: This table provides information on the (marginal) prior and posterior distributions of selected parameters characterising the fiscal sector of the extended version of the NAWM. The posterior distributions are based on two Markov chains with 1,000,000 draws, with 300,000 draws being discarded as burn-in draws. The average acceptance rate is roughly 24%.
Table 3: Selected Estimates of the Parameters Common to the Baseline and the Extended Version of the NAWM
| Parameter | Description | Posterior mode of baseline NAWM | Posterior distribution of extended NAWM: mode | Posterior distribution of extended NAWM: 5% | Posterior distribution of extended NAWM: 95% |
|---|---|---|---|---|---|
| A. Preferences: | Habit formation | 0.59 | 0.57 | 0.53 | 0.66 |
| B. Wage and price setting: | Calvo: wages | 0.78 | 0.85 | 0.81 | 0.90 |
| B. Wage and price setting: | Indexation: wages | 0.54 | 0.53 | 0.36 | 0.69 |
| B. Wage and price setting: | Calvo: domestic prices | 0.93 | 0.92 | 0.88 | 0.93 |
| B. Wage and price setting: | Indexation: domestic prices | 0.38 | 0.82 | 0.63 | 0.89 |
| B. Wage and price setting: | Calvo: export prices | 0.80 | 0.55 | 0.34 | 0.64 |
| B. Wage and price setting: | Indexation: export prices | 0.50 | 0.81 | 0.62 | 0.92 |
| B. Wage and price setting: | Calvo: import prices | 0.50 | 0.07 | 0.05 | 0.10 |
| B. Wage and price setting: | Indexation: import prices | 0.35 | 0.44 | 0.27 | 0.64 |
| C. Final-good production: | Subst. elasticity: consumption | 2.28 | 1.98 | 1.66 | 2.55 |
| C. Final-good production: | Subst. elasticity: investment | 1.69 | 1.75 | 1.39 | 2.31 |
| D. Adjustment costs: | Investment | 5.56 | 6.10 | 5.05 | 7.20 |
| D. Adjustment costs: | Import content: consumption | 5.62 | 4.16 | 2.20 | 5.71 |
| D. Adjustment costs: | Import content: investment | 0.83 | 0.80 | 0.35 | 5.17 |
| D. Adjustment costs: | Export market share | 2.68 | 2.69 | 1.69 | 5.07 |
| E. Interest-rate rule: | Interest-rate smoothing | 0.88 | 0.86 | 0.81 | 0.90 |
| E. Interest-rate rule: | Resp. to inflation | 1.89 | 1.73 | 1.54 | 1.84 |
| E. Interest-rate rule: | Resp. to change in inflation | 0.14 | 0.20 | 0.13 | 0.30 |
| E. Interest-rate rule: | Resp. to output growth | 0.16 | 0.11 | 0.07 | 0.17 |
Note: This table provides information on the (marginal) posterior distributions of selected parameters common to the baseline and the extended version of the NAWM. The posterior distributions for the extended NAWM are based on two Markov chains, each with 1,000,000 draws, with 300,000 draws being discarded as burn-in draws. The average acceptance rate is roughly 24%. Note that the baseline NAWM has been re-estimated using data until 2010.
Table 4: Fiscal Multipliers for Various Fiscal Instruments
| Quarters: 1 | Quarters: 4 | Quarters: 8 | Quarters: 16 | Long Run | Maximum | |
|---|---|---|---|---|---|---|
| A. Fiscal multipliers based on estimated impulse responses: Gov. consumption, G | 1.02 | 1.15 | 1.11 | 0.98 | 0.84 | 1.15 |
| A. Fiscal multipliers based on estimated impulse responses: Gov. investment, IG | 0.95 | 0.85 | 0.77 | 0.74 | 1.13 | 1.13 |
| A. Fiscal multipliers based on estimated impulse responses: Gov. transfers, TR | 0.06 | 0.05 | 0.04 | 0.04 | 0.03 | 0.06 |
| A. Fiscal multipliers based on estimated impulse responses: Consumption taxes, ΤC | 0.25 | 0.28 | 0.26 | 0.21 | 0.13 | 0.28 |
| A. Fiscal multipliers based on estimated impulse responses: Labour income taxes, ΤN | 0.11 | 0.09 | 0.08 | 0.08 | 0.10 | 0.11 |
| A. Fiscal multipliers based on estimated impulse responses: SSC: employees, | 0.12 | 0.10 | 0.09 | 0.09 | 0.10 | 0.12 |
| A. Fiscal multipliers based on estimated impulse responses: SSC: employees, | -0.01 | 0.00 | 0.03 | 0.07 | 0.07 | 0.07 |
| B. Fiscal multipliers based on standardised fiscal stimulus: Gov. consumption, G | 1.26 | 1.55 | 1.62 | 1.67 | 1.63 | 1.69 |
| B. Fiscal multipliers based on standardised fiscal stimulus:Gov. investment, IG | 1.08 | 1.08 | 1.08 | 1.13 | 1.55 | 1.55 |
| B. Fiscal multipliers based on standardised fiscal stimulus: Gov. transfers, TR | 0.06 | 0.07 | 0.06 | 0.06 | 0.06 | 0.07 |
| B. Fiscal multipliers based on standardised fiscal stimulus: Consumption taxes, ΤC | 0.36 | 0.46 | 0.48 | 0.48 | 0.48 | 0.50 |
| B. Fiscal multipliers based on standardised fiscal stimulus: Labour income taxes, ΤN | 0.13 | 0.12 | 0.12 | 0.15 | 0.15 | 0.15 |
| B. Fiscal multipliers based on standardised fiscal stimulus: SSC: employees, | 0.13 | 0.12 | 0.13 | 0.04 | 0.15 | 0.15 |
| B. Fiscal multipliers based on standardised fiscal stimulus: SSC: employees, | -0.04 | -0.04 | -0.00 | 0.05 | 0.04 | 0.05 |
Note: Panel A provides present-value fiscal multipliers based on estimated impulse responses computed at the posterior mode estimates of the model parameters. "SSC" are social security contributions. For comparison with the results in part B, no pre-announcement or feedbacks in the fiscal rules (except for debt on lump-sum taxes) are assumed. See the main text for more details. Panel B shows presentvalue fiscal multipliers of a 2-year stimulus of 1% of GDP accompanied by 2 years of monetary and fiscal accommodation. No pre-announcement, feedbacks (except for debt on lump-sum taxes) and no lagged dependent terms in the fiscal rules are assumed to enable maximum comparability with the results provided in Table 6.
Table 5: Composition of the European Economic Recovery Plan (EERP)
| Stimulus Measures | 2009 | 2010 | Fiscal Instruments |
|---|---|---|---|
| Measures aimed at households | 0.4 | 0.3 | |
| Measures aimed at businesses | 0.2 | 0.2 | |
| Increased public investment | 0.3 | 0.2 | IG |
| Increased spending on labour market | 0.1 | 0.1 | G |
| Total | 1.1 | 0.8 |
Note: Stimulus measures are expressed as a percentage of GDP. The measures aimed at households are evenly distributed across the model’s fiscal instruments.
Table 6: EERP Fiscal Multipliers, Effects on Output, and Sensitivity Analysis
| 2009Q1 | 2009Q4 | 2010Q4 | 2012Q4 | Long Run | |
|---|---|---|---|---|---|
| A. Benchmark results: Impact of EERP: Fiscal multiplier | 0.52 | 0.57 | 0.59 | 0.61 | 0.73 |
| A. Benchmark results: Impact of EERP: Output effects | 0.55 | 0.59 | 0.49 | 0.02 | 0.00 |
| B. Sensitivity of EERP multiplier wrt. model specification: υG = 1, αG = 1 (Cobb-Douglas, non-valued G) | 0.50 | 0.53 | 0.54 | 0.57 | 0.68 |
| B. Sensitivity of EERP multiplier wrt. model specification: αK = 0.85, υK = 0.25 (more complementarity) | 0.50 | 0.55 | 0.59 | 0.70 | 1.36 |
| B. Sensitivity of EERP multiplier wrt. model specification: ω = 0.5 (share of non-Ricardian households) | 0.66 | 0.70 | 0.72 | 0.74 | 0.85 |
| B. Sensitivity of EERP multiplier wrt. model specification: Prices/wages adjust every 6 months | 1.07 | 1.27 | 1.16 | 1.17 | 1.55 |
| C. Sensitivity of EERP multiplier wrt. implementation: No monetary accommodation | 0.42 | 0.43 | 0.44 | 0.44 | 0.55 |
| C. Sensitivity of EERP multiplier wrt. implementation: Estimated nominal interest rate rule | 0.60 | 0.71 | 0.78 | 0.96 | 1.16 |
| C. Sensitivity of EERP multiplier wrt. implementation: Feedb. on lab. taxes (θN,B = 0.025 after 2 years) | 0.52 | 0.57 | 0.59 | 0.60 | 0.48 |
| C. Sensitivity of EERP multiplier wrt. implementation: Estimated fiscal feedback rules (after 2 years) | 0.53 | 0.58 | 0.61 | 0.72 | 1.07 |
| C. Sensitivity of EERP multiplier wrt. implementation: Lagged dependent terms ---> 1 (after 2 years) | 0.29 | 0.23 | 0.23 | 0.36 | 0.73 |
| C. Sensitivity of EERP multiplier wrt. implementation: Full package allocated to G only (upper bound) | 1.26 | 1.55 | 1.62 | 1.67 | 1.63 |
| C. Sensitivity of EERP multiplier wrt. implementation: Package delayed by one year | --- | --- | 0.33 | 0.39 | 0.49 |
Note: The benchmark present-value fiscal multipliers and output effects of the European Economic Recovery Plan (EERP) are computed at the posterior mode estimates of the model parameters. In the simulations, the intra-annual profile of the EERP stimulus measures in 2009 and 2010 is assumed to be flat. The output effects of the EERP are average percentage deviations from the model’s balanced growth path after a 2-year standardised fiscal stimulus (1.1% in the first year, and 0.8% in the second year in terms of baseline GDP, see Table 5) accompanied by 2 years of monetary and fiscal accommodation. Thereafter, the nominal interest rate adjusts according to a static Taylor-type rule which reacts only to contemporaneous inflation and real GDP growth, with response coefficients of 1.5 and 0.125, respectively. We also assume no pre-announcement or feedbacks (except for debt on lump-sum taxes), and no lagged dependent terms in the fiscal rules.
Table 7: Evaluation of EERP Fiscal Stimulus Package Based on Cwik and Wieland (2011)
| 2009 Q1 | 2009 Q2 | 2009 Q3 | 2009 Q4 | 2010 | 2011-12 | Long Run | |
|---|---|---|---|---|---|---|---|
| A. Simulation input: Cwik and Wieland (2011) government spending stimulus: G in % of GDP | 0.24 | 0.48 | 0.60 | 0.60 | 0.20 | 0.00 | 0.00 |
| B. Output effects: no monetary accommodation: Cwik and Wieland (2011) | 0.20 | 0.40 | 0.50 | 0.49 | 0.10 | -0.04 | 0.00 |
| B. Output effects: no monetary accommodation: This paper | 0.18 | 0.49 | 0.71 | 0.79 | 0.28 | -0.03 | 0.00 |
| B. Output effects: no monetary accommodation: This paper, αG=1 | 0.18 | 0.39 | 0.51 | 0.51 | 0.13 | -0.02 | 0.00 |
| C. Output effects: 2 years of monetary accommodation: Cwik and Wieland (2011) | 0.31 | 0.57 | 0.69 | 0.68 | 0.26 | 0.00 | 0.00 |
| C. Output effects: 2 years of monetary accommodation: This paper | 0.31 | 0.68 | 0.93 | 1.00 | 0.41 | 0.01 | 0.00 |
| C. Output effects: 2 years of monetary accommodation: This paper, αG=1 | 0.26 | 0.52 | 0.65 | 0.65 | 0.22 | -0.01 | 0.00 |
| D. Implied present-value fiscal multiplier: no monetary accommodation: This paper | 0.75 | 0.92 | 1.04 | 1.13 | 1.20 | 1.18 | 1.08 |
| D. Implied present-value fiscal multiplier: no monetary accommodation: This paper, αG=1 | 0.76 | 0.80 | 0.82 | 0.83 | 0.79 | 0.73 | 0.68 |
| E. Implied present-value fiscal multiplier: 2 years of monetary accommodation: This paper | 1.28 | 1.37 | 1.45 | 1.52 | 1.66 | 1.71 | 1.66 |
| E. Implied present-value fiscal multiplier: 2 years of monetary accommodation: This paper, αG=1 | 1.10 | 1.09 | 1.09 | 1.09 | 1.09 | 1.08 | 1.06 |
Note: This table evaluates an alternative EERP fiscal stimulus package based on Cwik and Wieland (2011). See the main text for details. The output effects of the EERP are average percentage deviations from the model’s balanced growth path. αG = 1 denotes the share parameter of private consumption (relative to government consumption) in the composite consumption bundle that provides utility to households. In other words, αG = 1 implies that government consumption is not valued by households as opposed to our baseline case.
Figure 1: The Fiscal Data, 1980Q2-2010Q2

Note: This figure shows the time series of the fiscal variables used in the estimation of the extended version of the NAWM. Details on the variable transformations are provided in Section 3.1. "SSC" are social security contributions. Shaded areas are CEPR recession dates and periods of significant growth slowdowns.
Figure 2: Present-Value Fiscal Multipliers
Note: This figure shows the mean of the posterior distribution of the present-value fiscal multipliers for different fiscal instruments, along with the 10% and 90% percentiles.
Figure 3: Historical Decomposition of Euro Area Real GDP Growth with the Extended NAWM, 2007-2010: The Contribution of Fiscal Shocks
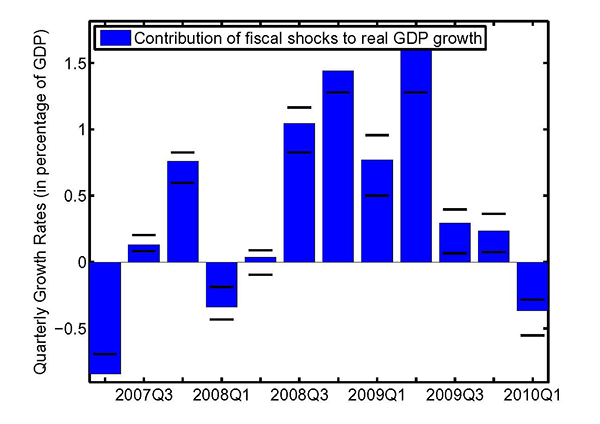
Note: This figure shows the contribution of fiscal shocks to annualised quarterly euro area real GDP growth using the extended NAWM at the estimated posterior mode, along with the 10% and 90% percentiles of the corresponding posterior distribution.
Figure 4: Historical Decomposition: Importance of Fiscal Rules
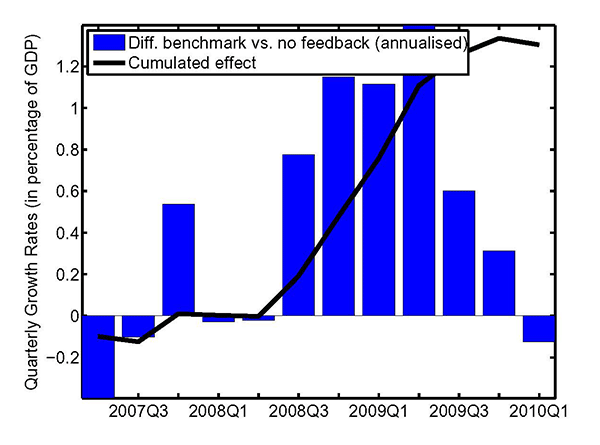
Note: This figure highlights the importance of the fiscal rules for the historical decomposition. The blue bars show the difference, in terms of annualised euro area quarterly GDP growth, between the contribution of fiscal shocks in the estimated benchmark model and a model with no feedback coefficients in the fiscal rules. The black line shows the cumulated impact on quarterly real GDP growth rates.
Figure 5: Euro Area Real GDP Growth and the Effects of Fiscal Stimulus
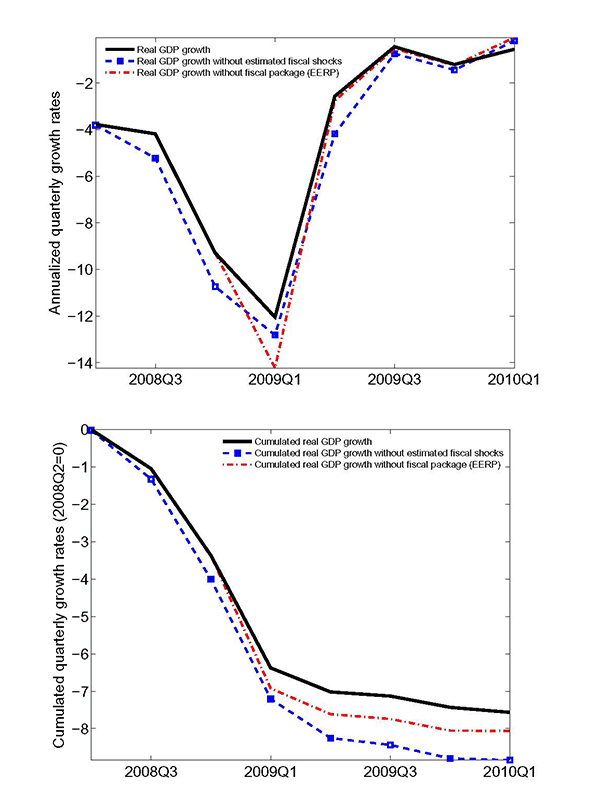
Note: The upper panel of this figure presents the evolution of annualised quarterly real GDP growth under the scenarios of (i) no fiscal shocks as obtained by Bayesian estimation and (ii) no EERP fiscal package as calibrated in Tables 5 and 6. The lower panel of the figure shows the implied cumulated quarterly real GDP growth rates under both scenarios.
Appendix:The Fiscal Data
In the estimation of our model, we use quarterly euro area data on general government expenditures and revenues as well as general government debt from the new fiscal database by Paredes et al. (2009):
- real general government final consumption expenditure (GCR)
- nominal general government gross fixed capital formation (GIN)
- nominal general government transfers to households (THN)
- nominal general government revenues from indirect taxes, total (TIN)
- nominal general government revenues from direct taxes, total (DTX)
- nominal general government revenues from employer social security contributions (SCR)
- nominal general government revenues from employee (and other, self-employed) social security contributions (SCE)
- nominal general government debt (GDN)
with the data abbreviations following the conventions in the Government Finance Statistics Guide (ECB, 2007).
In the Paredes et al. (2009) database social security contributions for employers and employees are only available after 1991Q1. Before that date only total social security contributions are available. We compute the shares of employer and employee social security contributions on total social security contributions from 1991Q1 to 2007Q1. These shares are relatively stable. Therefore we impose the average 1991Q1-2007Q1 shares to total social security contributions prior to 1991Q1 in order to obtain data on employer and employee social security contributions.
The database provides nominal unadjusted data for all fiscal variables, plus real seasonally adjusted data for government consumption. The methodology developed by Paredes et al. (2009) to interpolate annual fiscal data to quarterly frequencies using cash data explicitly models a seasonal component. Hence, the quarterly fiscal database also delivers nominal seasonally adjusted data.24
Footnotes
**Correspondence: Coenen: Directorate General Research, European Central Bank, Kaiserstrasse 29, 60311 Frankfurt am Main, Germany, e-mail: gunter.coenen@ecb.int; Straub: Directorate General International and European Relations, European Central Bank, Kaiserstrasse 29, 60311 Frankfurt am Main, Germany, e-mail: roland.straub@ecb.int; Trabandt: Division of International Finance, Board of Governors of the Federal Reserve System, 20th Street and Constitution Avenue N.W., Washington, DC 20551, USA, e-mail: mathias.trabandt@gmail.com. Return to text
***We are grateful to our discussant Raf Wouters and to participants in the conference on "Fiscal Policy in the Aftermath of the Crisis" held at the European Commission in Brussels on 2-3 March 2012, to seminar participants at the European University Institute, the University of Hohenheim and the annual meeting of the Committee on Macroeconomic Research of the Verein für Socialpolitik, as well as to the editor and two anonymous referees. The opinions expressed in the paper are those of the authors and do not necessarily reflect the views of the European Central Bank, the Board of Governors of the Federal Reserve System or any other person associated with the Eurosystem or the Federal Reserve System. Return to text
1. A more voluminous body of literature has focused on the size and sensitivity of fiscal multipliers, as opposed to the effects of comprehensive fiscal packages. See e.g. Christiano et al. (2011), Coenen et al. (2012), Corsetti et al. (2009), Drautzburg and Uhlig (2011), Eggertsson (2011), Erceg and Lindé (2010), Uhlig (2010) and Woodford (2011). A review of this literature can be found in Coenen et al. (2012). Return to text
2. There is a large literature on rule-of-thumb consumers, with early contributions by Campbell and Mankiw (1989) and Mankiw (2000). Return to text
3. Coenen, McAdam and Straub (2008) consider a generalised framework in which non-Ricardian households can adjust their holdings of money subject to a transaction cost technology, which gives rise to limited consumption smoothing on the part of non-Ricardian households. Return to text
4. In steady state, we compute ![]() and
and ![]() such that
such that
![]() , where
, where ![]() is an estimated parameter which equals roughly 0.8 at the posterior mode. Return to text
is an estimated parameter which equals roughly 0.8 at the posterior mode. Return to text
5. Formally, this can be justified by the existence of state-contingent securities that are traded amongst unions in order to insure households against variations in household-specific wage income associated with Calvo-type wage rigidities. Return to text
6. The alternative assumption that non-Ricardian households set their wage rate equal to the average wage rate of Ricardian households and face identical labour demand would yield the same result that wages and labour supply are identical across both groups. Return to text
7. For an approach in which the government chooses government investment to maximise output net of government investment, see e.g. Drautzburg and Uhlig (2011). Return to text
8. In deriving the budget constraint, we have used the fact that the total wage sum paid by firms to
the households equals
![]() , where
, where ![]() denotes the steady-state wage markup in the model. Return to text
denotes the steady-state wage markup in the model. Return to text
9. The aggregate quantity of a household-specific variable ![]() , expressed in per-capita terms,
is given by
, expressed in per-capita terms,
is given by
![]() . Return to text
. Return to text
10. While government debt in all fiscal feedback rules is pre-determined, output enters contemporaneously. We have also experimented with lagged output instead of contemporaneous output in the fiscal rules. None of our core results changes visibly. Return to text
11. Although we employ linear methods to solve and estimate the model, recent data for euro area nominal interest rates may be subject to a potentially important non-linearity--the zero lower bound (ZLB). To this end, we studied the importance of the ZLB for euro area data. We found that the ZLB does not appear to be of importance for our analysis. For this to be the case, it is key that there is some degree of interest rate smoothing in the interest rate feedback rule embedded in our model. Since the data favour a strong degree of interest rate smoothing, we proceed with using linear methods. Return to text
12. Compared to the earlier part of the sample, government debt grew at a much slower rate after the year 1993, i.e. after the Maastricht treaty became effective. Since political economy considerations are beyond the scope of the model, we choose a breakpoint for the linear trend of government debt in 1993Q4. Further, due to institutional reforms in e.g. Italy data on social security contributions (SSC) show a quantitatively large increase in the mid-1990s for several years before reverting back. A simple linear trend would imply negative deviations of detrended SSC before and after the mid-1990s throughout. As a step forward, we remove HP-trends from these data. For work that emphasises the importance of modelling changing trends explicitly, see e.g. Sims (2012). Return to text
13. In contrast to Christoffel et al. (2008) who use a SVAR(2) to model the foreign variables we assume, because of computational issues, an AR(2) process for foreign output and AR(1) processes for the four remaining foreign variables. This specification works reasonably well compared to the full SVAR specification in terms of one-step-ahead prediction errors. Return to text
14. In addition, see Christoffel et al. (2008), we account for measurement error in extra-euro area trade data as they are prone to sizeable revisions. We also allow for small errors in the measurement of real GDP and the GDP deflator to alleviate discrepancies between the national accounts framework underlying the construction of official GDP data and the model's aggregate resource constraint. Return to text
15. We have also experimented with allowing for exogenous time variation in this wedge to reflect the notion of risk premia in observed corporate bond yields. However, none of our results changed substantially. Return to text
16. In Coenen et al. (2012), it is shown that targeted transfers, corresponding to a distribution
parameter of ![]() , may result in sizeable transfer multipliers. Return to text
, may result in sizeable transfer multipliers. Return to text
17. Another reason is that the aggregation of national fiscal data may cause the counter-cyclical nature of fiscal policy to disappear if national business cycles are not sufficiently synchronised. Return to text
18. In this paper, we compute the present-value multiplier as in Uhlig (2010). More precisely, we compute the government consumption present value multiplier as:
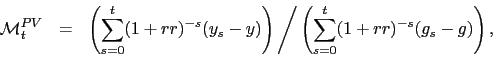
where ![]() denotes the steady-state real interest rate on government debt. The cases for other fiscal
instruments follow accordingly. Return to text
denotes the steady-state real interest rate on government debt. The cases for other fiscal
instruments follow accordingly. Return to text
19. See Coenen, Straub and Trabandt (2012) for an analysis of the effects of government consumption and
investment shocks as functions of the degrees of complementarity, ![]() and
and ![]() . Return to text
. Return to text
20. Lower social security contributions of firms are the only counterbalancing force that triggers a fall of marginal costs and thereby inflation, leading ceteris paribus to an increase in the real rate. However, this effect is clearly dominated by the effects described above. Return to text
21. See e.g. Coenen et al. (2012) for a more extensive comparison of the effects of temporary versus permanent fiscal stimulus. Return to text
22. The numbers are the average of the results shown in Figure 1 of Cwik and Wieland (2011) which are generated by three models used by the authors: the Smets and Wouters (2003) model, the European Commission's Quest model and the small IMF model. We are grateful to Tobias Cwik for providing us with the simulation results. Return to text
23. An alternative approach would be to re-estimate the model without feedback parameters and compare the resulting historical decomposition against the benchmark decomposition. This comparison, however, would suffer from the problem that presumably some parameters, especially those of the exogenous shock processes would take on different values and thereby blur the assessment of the effects of fiscal feedback. Return to text
24. Both series are identical to the corresponding ESA95 quarterly national accounts data, where government consumption is the only item available in real, seasonally adjusted terms. However, Eurostat only provides data from 1991Q1 onwards for real government consumption, and data from 1995Q1 onwards for nominal government consumption. By construction, the government consumption data provided by Paredes et al. (2009) therefore pins down the ESA95 data from 1991Q1 and 1995Q1 onwards. The same holds for the remaining data in nominal unadjusted terms which are available from Eurostat from 1999Q1 onwards. The ESA95 quarterly national accounts series which are available from 1999Q1 onwards only are total direct taxes, total indirect taxes, total social security contributions, government investment, and transfers to households. For the period for which no quarterly national accounts data is available, the annual sums of the fiscal data match annual national accounts data from the European Commission's AMECO database. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text