Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1065r, January 2013 --- Screen Reader Version*

Interest Rates and the Volatility and Correlation of Commodity Prices

Joseph W. Gruber and Robert J. Vigfusson^**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We propose a novel explanation for the observed increase in the correlation of commodity prices over the past decade. In contrast to theories that rely on the increased influence of financial speculators, we show that price correlation can increase as a result of a decline in interest rates. More generally, we examine the effect of interest rates on the volatility and correlation of commodity prices, theoretically through the framework of Deaton and Laroque (1992) and empirically via a panel GARCH model. In theory, we show that lower interest rates decrease the volatility of prices, as lower inventory costs promote the smoothing of transient shocks, and can increase price correlation if common shocks are more persistent than idiosyncratic shocks. Empirically, as predicted by theory, we find that price volatility attributable to transitory shocks declines with interest rates, while, particularly for metals prices, price correlation increases as interest rates decline.

Keywords: Commodity storage, panel GARCH, dynamic factor model

JEL classification: Q00, G12

Introduction

The past decade has been marked by rising commodity prices, with the Dow Jones-UBS index of spot commodity prices increasing over 400 percent from the beginning of 2002 to the end of 2012. At the same time there has been a noticeable increase in both the volatility of commodity prices and the correlation of price changes across commodities.¹

In assessing the rise in commodity prices, low interest rates are frequently listed as a potential causal factor along with a slew of other possibilities, including changing global demand patterns, particularly strong growth in emerging market economies, supply disruptions, movements in the value of the dollar, and the increasing size and changing investor composition of commodity futures markets. The theory linking low interest rates to higher commodity prices is well developed. As outlined in Frankel (2008), all else equal, a decline in the interest rate is a decline in the opportunity cost of holding commodity inventories and as such should boost prices by increasing demand for inventories. Frankel also theorizes that lower interest rates discourage commodity extraction by reducing the value of monetizing undeveloped commodity resources on the part of producers, providing a further upward impetus to prices.²

Less examined, however, has been the role of interest rates in explaining the volatility of commodity prices. We show here that in the standard storable commodity pricing model presented in Deaton and Laroque (1992 and 1996) the level of the interest rate has clear implications for price volatility.³ The model suggests that lower interest rates dampen the volatility of prices in response to transient shocks to commodity supply and demand by decreasing holding costs and encouraging the use of inventories to smooth prices over temporary shocks. In contrast, low interest rates have no effect on the volatility of prices originating from persistent shocks, as long-lasting shocks do not allow inventory smoothing to be profitably undertaken.⁴

Theory suggests that low interest rates are not behind the observed increase in commodity price volatility over the past decade. Rather, the increase in price volatility is likely attributable to changes in the underlying shock processes. Even though the shock processes may have changed, the theory is still testable. By decomposing commodity price movements into transitory and persistent components, we can examine whether the volatility of prices attributable to transitory shocks indeed declines when interest rates are low.

We also develop a two commodity extension of the Deaton and Laroque model to provide a novel explanation for the increase in commodity price correlation witnessed over the past decade. Conditional on the structure of the underlying shocks, we show that the model predicts that a decline in the interest rate will increase the correlation of prices. In particular, if idiosyncratic shocks (such as a mine strike or crop failure) are more transitory than shocks common to all commodity prices (such as growing emerging market demand), then lower interest rates increase commodity price correlation in the model. Low interest rates promote inventory smoothing in response to transitory shocks, reducing idiosyncratic volatility, while leaving the price response to persistent shocks unaffected. Therefore, for each particular commodity, lower interest rates decrease the proportion of variance stemming from idiosyncratic transient shocks and increase the proportion of variance due to common persistent shocks, thus increasing the measured correlation of prices.

That low interest rates might promote commodity price correlation via lower inventory costs contrasts with other popular explanations for the increase in correlation. In particular, Tang and Xiong (2009) point to the increase in correlation as being evidence of the increased financialization of commodity markets. Alternatively, Fattouh, Kilian, and Mahadeva (2012) attribute the increase in price correlation to an increase in the preponderance of common shocks. While it is certainly the case that in our model price correlation would rise with an increase in the number and size of common shocks, such an increase is unnecessary, as lower interest rates increase correlation independent of any change in the time series properties of the shocks.

In the empirical component of the paper we first examine the theoretical model's predictions regarding the effect of interest rates on the volatility of prices. Following Schwartz and Smith (2000), we identify persistent shocks as movements in the year-ahead futures price and temporary shocks as movements in the time spread of the futures curve. Using a GARCH model, we then show that the volatility due to transitory shocks (as identified by movements in the time spread) decreases significantly with the interest rate, particularly for highly storable commodities such as metals and energy products. In contrast, the volatility due to persistent shocks is unaffected by changes in the interest rate.

Looking at the correlation of prices, we first use a dynamic factor model to show that common price shocks are indeed more persistent than idiosyncratic shocks, a necessary condition for our theoretical model to predict an increase in price correlation as the interest rate declines. Estimating a panel GARCH model, we find evidence that an decrease in the interest rate has a significant positive effect on price correlation, particularly among metals prices.

The remainder of the paper is organized as follows. First, referencing the model of Deaton and Laroque, we show that the variance of the price of a storable commodity declines as the interest rate falls, and that under the assumption that common shocks are relatively more persistent than idiosyncratic shocks the correlation of commodity prices increases as the interest rate falls. We conduct a simple numerical simulation to quantify the importance of interest rates for price volatility and covariance. In the subsequent section, we present our empirical results, first looking at the effect of interest rates on volatility and then examining the impact on price correlation.

Model

In this section we use a simple commodity storage model to investigate the effect of interest rates on price volatility and price correlation across commodities. The model is in the style of Routledge, Seppi, and Spatt (2000), which in turn builds off the work of Deaton and Laroque (1992, 1996). Since the literature on commodity storage models is well developed, we keep our exposition to a minimum. We start with a single commodity and single shock and then expand the model to consider two commodities and three shocks.

Single Commodity

We start with a single storable commodity traded in discrete time. Demand for and supply of the commodity are both subject to stochastic shocks; however, we will combine demand and supply and consider shocks to net demand ($a$). In each period, supply of the commodity can be consumed or entered into inventory for future consumption. Likewise, consumption can either come from current supply or out of inventory. Inventories ($Q$) are costly, both physically, through depreciation ($\delta$), and financially, with an opportunity cost determined by the interest rate ($r$). Additionally, inventories are constrained to be non-negative.

Inventories evolve such that $\triangle Q_t=Q_t-(1-\delta )Q_{t-1}$. The price of the commodity can be represented by an inverse demand function: $P_t=f\left(a_t,\ \triangle Q_t\right)$, where $P_t$ is increasing in both net demand $a$, and inventory demand $\Delta$$\ Q$.

Given storability, equilibrium in the model requires that:

$$P_t=\frac{1-\delta }{1+r}E_tP_{t+1}\ if\ Q_t>0$$

$$P_t\ge \frac{1-\delta }{1+r}E_tP_{t+1}\ if\ Q_t=0$$

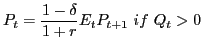
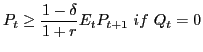
That is to say that, in the presence of positive inventories, the price is expected to remain constant, subject to a discount factor determined by the cost of inventory holding. Abstracting from negative inventory holding costs, perhaps due to a convenience yield or a sufficiently negative real interest rate, the price is never expected to increase. A higher expected price in the future would provoke additional inventory accumulation, driving up the current price until arbitrage was no longer profitable. The possibility of stock outs ($Q_t=0$) allows for expected price declines.

We construct a simple numerical example (again very similar to that in Routledge, Seppi, and Spatt (2000)) to illustrate this point. We assume a linear demand curve, with an inverse demand function,

$$P_t=a_t+\triangle Q_t$$

such that prices respond directly to net demand and changes in inventory. The physical cost of inventories ($\delta$) was set at 0.05. We model $a$ as a two-state Markov process with values a = {0.001,1}. We consider a variety of transition matrices in order to investigate the impact of shock persistence on the model solution, but always impose the condition that the transition probabilities are non-zero such that the Markov process is irreducible.

The solution method involves guessing a policy function, $Q_t=J(a_t,Q_{t-1})$, and then solving for the current price and the expected price:

$${E[P}_{t+1}]={E[a}_{t+1}+\ J\left(a_{t+1},Q_t\right)-(1-\delta )J(a_t,Q_{t-1})]$$

From the initial guess of the policy function, we iterate on the equilibrium pricing conditions of the model until convergence. The model was solved on a grid of 3000 inventory states, bounded from below by zero and with the upper limit set at a level that was non-binding during the subsequent simulations.

Once the policy function has been approximated, a path of inventories and prices was constructed from a simulated Markov process for $a$. The simulations were constructed from an initial inventory state of zero, and then the first 1000 of a total of 10000 periods were thrown out.

Proposition 1: If commodity markets are subject to transient shocks, volatility decreases as the interest rate declines.

Table 1 reports the volatility of the simulated price paths under different assumptions regarding the persistence of net demand shocks. The real interest rate is allowed to vary from negative 3 percent to positive 5 percent, a range roughly consistent with that of the real interest rate series used in the empirical component of this paper over the range from 1992 to mid-2012 (as shown in Figure 1). Figure 2 plots the same data as in Table 1 but for a wider range of real interest rates extending to an upper bound of 10 percent.

As can be seen by comparing the different lines in Figure 2, prices are less volatile when shocks are relatively transitory, regardless of the level of the interest rate, as inventories provide a mechanism to smooth prices across shocks. As shocks become more persistent, the ability of inventories to smooth prices fades, as doing so becomes too costly, and the volatility of prices increases.

Tracing along the lines in Figure 2, increasing the interest rate, and therefore the cost of holding inventories, increases price volatility. The magnitude of the effect of higher interest rates on price volatility is determined by the persistence of the net demand shocks. The price response to transitory shocks is smoothed by inventories; as inventory costs increase, less smoothing occurs and prices become more volatile. In contrast, highly persistent shocks elicit little inventory response regardless of the level of the interest rate, and thus the impact of higher interest rates on price volatility is relatively muted.⁵ As shown in Table 1, when shocks have no persistence, price volatility increases 68 percent as the interest rate moves from negative 3 percent to positive 5 percent. If shocks have a persistence of .99, the same increase in the interest rate only increases price volatility by 9 percent.

Two Commodities

In this section we expand the model to include a second commodity. Each commodity is subject to two shocks, an idiosyncratic shock ($a_i$) unique to an individual commodity i and a common shock ($b$) the affects all commodities equally. The shocks are assumed to be independent. Both shocks are modeled as two-state Markov processes $a$ = $b$ = {0.001,1}. The transition matrices are identical for each of the idiosyncratic shocks, but are allowed to vary over the idiosyncratic and the common shocks.

The model is solved in the same manner as with the single commodity model except the price function for commodity i now defined as:

$$P_{it}=a_{it}+b_t+\triangle Q_{it}$$

The two Markov processes are combined into an irreducible four-state process and the policy function becomes: $Q_{it+1}=J(a_{it},{b_t,Q}_{it})$. The solution to the policy function is identical for both commodities.

To create price and inventory paths for both commodities, three independent Markov processes are simulated. One process was deemed the common shock and entered into the policy function for both commodities, while each of the remaining two shocks were construed as an idiosyncratic shock particular to one of the two commodities.

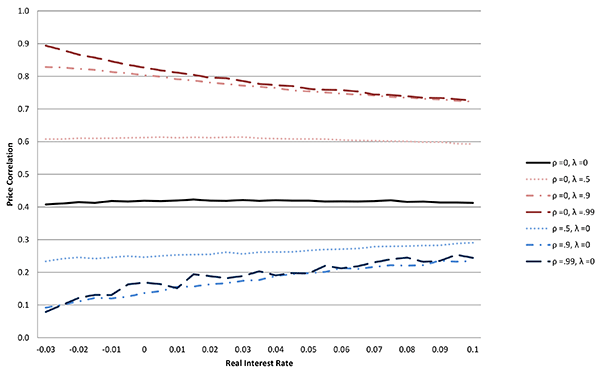
Proposition 2: If idiosyncratic shocks are more transient than common shocks, then commodity correlation increases as the interest rate declines.

Table 2 and Figure 3 examine price correlation as a function of the interest rate under different assumptions regarding the relative persistence of common and idiosyncratic shocks. When the common shock is relatively more persistent, price correlation is decreasing as the interest rate increases (shown by the red dashed line). Conversely, if idiosyncratic shocks are relatively more persistent, the correlation is increasing with the interest rate (the heavy blue dashed line).

The explanation for these results is as follows. As shown with the single commodity model, a fall in the interest rate (and inventory holding costs) decreases the volatility of the price in response to transitory shocks, but has little effect on the volatility due to persistent shocks. If idiosyncratic shocks are less persistent than common shocks, a decline in the interest rate will decrease the response of prices to idiosyncratic shocks, by promoting inventory smoothing through such shocks, while leaving the response to persistent common shocks unchanged. Thus, the decline in the interest rate increases the proportion of variation in the price of each commodity that is attributable to the common persistent shock, increasing the measured correlation of commodity prices.

The final column of Table 2 shows that when the idiosyncratic shock is completely transitory and the common shock is very persistent ( $\rho =0,\lambda =.99$), increasing the interest rate from negative 3 percent to positive 5 percent decreases price correlation by 15 percent. Conversely, when the transitory shock is very persistent and the common shocks is completely transitory ( $\rho =.99,\lambda =0$), the same change in the interest rate increases price correlation by 149 percent.

Empirical Results

In this section we examine the empirical validity of Propositions 1 and 2 using commodity price data over the period from 1985 to mid-2012. We examine prices at a monthly frequency for a diverse range of commodities (listed in the appendix). All prices are deflated by the U.S. headline CPI, such that we consider movements in real prices.

Price Volatility

The volatility of prices for many commodities has increased in the last decade. The first three columns of Table 3 examine the change in the volatility of front month futures prices over a wide sample of commodities. To quantify the change in volatility we first estimate a GARCH(1,1) regression over the entire sample period. The first column in Table 3, computes the average conditional standard deviation from the GARCH(1,1) regression over the eleven years between 1992 and 2002, while the second column reports a similar statistic for the period between 2003 and mid-2012. ⁶ The third column then reports the ratio of the two standard deviations, with a value greater than one signifying an increase in volatility. With the exception of natural gas and live hogs, the front month contract for all commodities recorded an increase in volatility between the two periods, with metals prices showing the most notable jumps.

Seemingly in contradiction to our model and Proposition 1, this apparent increase in volatility occurred against a backdrop of sharply lower real interest rates. As shown in Figure 1, notwithstanding spikes in 2007 and late 2008 / early 2009, the real interest rate was on average lower post-2002 than in the prior decade.⁷

However, notwithstanding the increased volatility of prices over the past decade, Proposition 1 could still hold. For example, the increase in price volatility over the past decade despite lower interest rates could reflect an increase in the volatility of the underlying shocks driving commodity prices or a shift towards persistent shocks away from transitory shocks. However, since the shocks are observed only through movements in the price, it is difficult to disentangle changes in volatility that might be due to changes in the underlying shock process and changes that arise from a decline in interest rates.

One decomposition that can help alleviate the identification problem introduced by possible changes in the distribution of shocks is to separate shocks into persistent and transitory components. The theoretical model predicts that a decrease in interest rates will decrease price volatility emanating from transitory shocks, but have little impact on the volatility associated with persistent shocks. As such, a preferred testing methodology would decompose movements in commodity prices into those due to either persistent or transitory shocks, and then examine the impact of interest rates on the volatility from transitory shocks alone.

Our methodology for identifying transitory versus persistent shocks is similar to that outlined in Schwartz and Smith (2000). We assume that front month commodity prices are affected by transitory and persistent shocks, while year-ahead prices reflect only persistent shocks. Under these assumptions movements in the time spread of the futures curve can be attributed to transitory shocks. Testing our model then relates to examining the volatility of commodity time spreads relative to the level of the interest rate.

Before formally examining the relationship between interest rates and price volatility, we first compare the volatility of persistent and transitory shocks across the 1992 - 2002 and 2003 - mid-2012 subsamples discussed earlier. As shown in Table 3, year-ahead futures prices (columns 4 and 5) are generally less volatile than the front month futures (columns 1 and 2). However, as shown in column 6, there was a large increase in the volatility of year-ahead futures prices post-2003, with the volatility of year-ahead crude oil contracts increasing over 80 percent over 2003 - 2012 relative to 1992 - 2002. In contrast, as shown in column 9, the volatility of the time spread declined in the latter period. Thus, it appears as through for most commodities the increase in the volatility of front-month contracts (shown in column 3) is more than fully explained by an increase in the volatility of persistent shocks, while the volatility of transitory shocks actually declined.

Next we estimate the following GARCH (1,1) model for each commodity,

$$\triangle {\log P_t=\mu \ }{\rm +}{\varepsilon }_t$$

$${\sigma }_t=a+b*{{\varepsilon }_{t-1}}^2+c*{\sigma }_{t-1}+d*r_t$$

where $\mu$ is a constant and $r_t$ is the real interest rate. Testing the theoretical model is equivalent to testing whether d $>$ 0, such that an increase in the interest rate increases the volatility of prices.

Our estimation results are reported in Table 4, with column 1 showing results for the front-month contract, column 3 for the year-ahead contract (persistent shock), and column 5 for the time spread (transitory shock). For the year-ahead contracts, the coefficient on the real interest rate is largely insignificant, such that the interest rate appears to have no effect on the volatility of prices in response to persistent shocks. The coefficients for the front-month contracts are also insignificant, perhaps reflecting the relative importance of persistent shocks in explaining movements in front-month prices. However, for many commodities, the coefficients are significant and positive in regard to the volatility of the time spread (column 5). This pattern of significance and insignificance aligns with the predictions of the model, in that interest rates should impact the response only to transitory (and not to persistent) shocks.

The model tends to work better for energy and metals and not as well for agricultural commodities, where the coefficients in column 5 are insignificant and often of the wrong sign. A potential explanation for this lack of significance is that physical inventory costs tend to be higher for these commodities compared with energy and metals; as such, a given decline in the financial cost of inventories is less meaningful and less likely to have an effect on price dynamics.

Price Correlation

The higher level and increased volatility of commodity prices over the last decade has also been associated with an increase in commodity price correlation. Table 5 reports the difference in pairwise correlations over the 2003 - 2012 period compared to the correlation over the 1992 - 2002. A positive number reports an increase in correlation. Similar to what was reported for volatility, the correlation was calculated as the average conditional correlation derived from a panel GARCH (1,1) model estimated over the entire sample period. As can be seen in the table, the majority (80 percent) of pairwise correlations increased in the latter period.

As discussed in the model component of the paper, the theoretical effect of interest rates on the correlation of commodity prices is dependent on the structure of shocks impacting commodity markets, in particular on the relative persistence of common versus idiosyncratic shocks. It is only when idiosyncratic shocks are relatively less persistent that lower interest rates should increase price correlation.

Are idiosyncratic shocks less persistent than common shocks? We start by addressing a slightly different question: Are persistent shocks more correlated than transitory shocks? Table 6 reports the pairwise correlation of year-ahead futures prices (which reflect persistent shocks) less the correlation of time-spreads (which reflect transitory shocks) computed over the entire 1992 - 2012 sample. A positive number indicates that persistent shocks are more correlated than transitory shocks. As shown in the table, for about 75 percent of commodity pairs, persistent shocks (captured by year-ahead futures prices) were more correlated than transitory shocks (embodied in time spreads).

Dynamic Factor Model

To assess directly whether idiosyncratic shocks are less persistent than common shocks we turn to a dynamic factor model. We estimate the following specification,

$$p_{it}=af_t+f_{it}+u_{it}$$

$$f_t=\rho f_{t-1}+v_t$$

$$f_{i,t}={\rho }_if_{i,t-1}+v_{it}$$

where $f_t$ is a common factor for all commodity prices with persistence $\rho$, and $f_{i,t}$ is a commodity specific factor with persistence ${\rho }_i$.⁸

To assess the relative persistence of the factors, in Table 7 we compare the estimate of $\rho$ to the estimates of ${\rho }_i$. While the persistence of the common factor, estimated to be 0.97, is higher than that of any of the idiosyncratic factors, the idiosyncratic factors are nonetheless quite persistent.⁹

Panel GARCH

Similar to our earlier test for the effect of the interest rate on volatility, we now estimate a panel GARCH model to examine the impact of the interest rate on price correlation. The model is set up as follows:

$$\triangle {\log P_{it}={\mu }_i\ }{\rm +}{\varepsilon }_{it}$$

$${\sigma }_{it}=a_i+b_i*{{\varepsilon }_{it-1}}^2+c_i*{\sigma }_{it-1}+d_i*r_t$$

$${cov}_{ijt}=a_{ij}+b_{ij}*{\varepsilon }_{it-1}*{\varepsilon }_{jt-1}+c_{ij}*{cov}_{it-1}+d_{ij}*r_t$$

In particular we are interested in examining the coefficient on the interest rate in the covariance equations and testing whether $d_{ij}$$<$ 0. A negative and significant coefficient $d_{ij}$ indicates that commodity correlation increases as the interest rate declines.

Estimating the unconstrained model for the entire panel of commodities would require estimating 560 parameters across 3920 observations and proved infeasible in practice. In order to cut down on the number of estimated parameters, we pursued two alternative approaches. First, we estimated the model using the entire panel, but constrained the coefficient on the interest rate in the covariance equations to be identical across all commodity pairs. Second, we estimated separate two-commodity panels for each of the 120 possible commodity pairings, while allowing the coefficient on the interest rate to vary with each regression.

Table 8 reports the coefficient estimates for $d_{ij}$ as well as the associated standard errors from our first approach, with $d_{ij}$ constrained to be equal across all i and j. When the panel consists of all commodities (or only food prices), the coefficient on the interest rate is negative, in line with the theory, though insignificant. However, if we constrain the panel to include only metals prices or metals and oil prices, the coefficient is negative and significant. One interpretation of these results, as with our volatility estimates, is that the relatively low physical storage costs for metals increases the importance of interest rate movements for explaining price dynamics. In contrast, where financial inventory costs may be small relative to physical costs (such as with foods), interest rates appear to be less important.

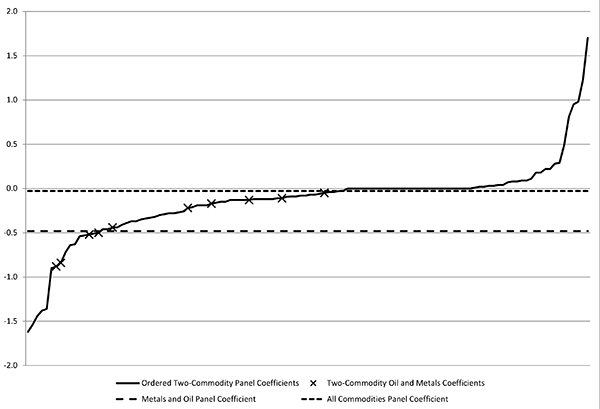
The results of our second approach are reported in Table 9, which shows the coefficients on the interest rate in the covariance equation for each of the separate 120 two-commodity panels. The majority of the coefficients are negative but insignificant, with the lack of significance likely reflecting the low power of the test due to the small size of the samples. The solid black line in Figure 4 presents an ordering (from most negative to most positive) of all 120 coefficients and shows that just over half of the coefficients are negative. In particular, as indicated by the large Xs in Figure 4, all pairings between metals and between oil and metals are negative. Furthermore, from these results, it is apparent that many pairings that do not include metals also have large negative coefficients. The dashed line in Figure 4 is the coefficient estimate from a panel including all metals and oil (as reported in Table 8), and lies at about the average for two-commodity estimates with those same commodities. The dotted line in Figure 4 depicts the coefficient estimate from the panel with all commodities (also reported in Table 8).

Conclusion

We examine the effect of interest rates on the volatility and correlation of commodity prices. An established literature posits that lower interest rates raise the level of commodity prices by lowering inventory carrying costs and increasing inventory demand. Using the framework of Deaton and Laroque (1992), we show that lower interest rates should also decrease the volatility of commodity prices, as lower inventory carrying costs increase incentives to smooth prices in response to transient shocks. Also, we show that lower interest rates can lead to an increase in commodity price correlation under the additional assumption that shocks common to all commodities are more persistent than idiosyncratic shocks. With idiosyncratic shocks that are relatively more transient, lower interest rates decrease the volatility of prices due to idiosyncratic shocks but have little effect on the volatility resulting from (relatively more persistent) common shocks, thereby increasing the measured correlation of prices across commodities.

First, to analyze the impact of interest rates on commodity price volatility, we empirically identify transient shocks via variation in the time spread of the futures curve, under the assumption that persistent shocks affect both front-month and year-ahead futures prices, while transient shocks affect only front-month prices. Using a GARCH model, we show that for a number of commodities the volatility of the time spread falls as the real interest rate declines, in line with the theoretical model. Our results suggest that the observed increase in commodity price volatility over the past decade primarily reflects an increase in the volatility of persistent shocks to commodity markets.

Second, in order to understand the impact on commodity price correlation, we examine a panel of commodity prices, disentangling common versus idiosyncratic shocks via a dynamic factor model. We find that common shocks are more persistent than idiosyncratic shocks. Using a panel GARCH model, we show that as the interest rate increases, correlation decreases, most significantly for the prices of highly storable metals. In this regard, we have provided evidence of a theoretical channel based on physical demand and supply fundamentals to explain the increase in commodity price correlation observed in the past decade, in contrast to theories that rely on financial market factors. Although our results do not rule out the importance of financial market developments in explaining the correlation of prices, they do suggest that the increase in correlation cannot be taken as prima facie evidence in favor of financial factors determining commodity prices. As such, our work increases the demand for a theoretical model relating financial markets to commodity price correlation so that the effect of financial factors can be distinguished from the fundamental channels that we have identified.

Figure 1: One-Year Real Interest Rate

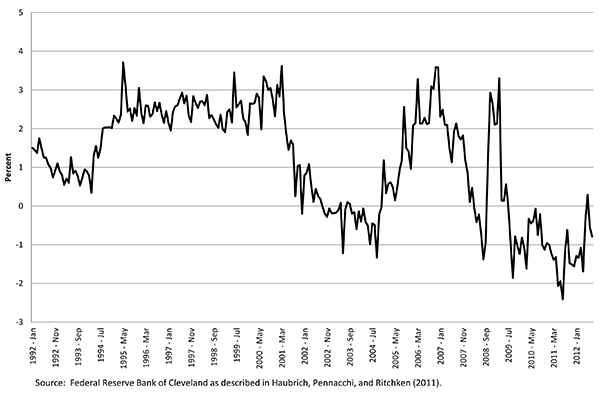
Source: Federal Reserve Bank of Cleveland as described in Haubrich, Pennacchi, and Ritchken (2011).

Data for Figure 1

Date	Real Interest Rate
1982 - Jan	4.34
1982 - Feb	6.71
1982 - Mar	7.67
1982 - Apr	8.17
1982 - May	8.27
1982 - Jun	9.29
1982 - Jul	7.45
1982 - Aug	5.67
1982 - Sep	3.3
1982 - Oct	4.63
1982 - Nov	5.76
1982 - Dec	5.35
1983 - Jan	4.7
1983 - Feb	4.87
1983 - Mar	5.3
1983 - Apr	5.09
1983 - May	5.3
1983 - Jun	5.96
1983 - Jul	4.73
1983 - Aug	5.74
1983 - Sep	5.47
1983 - Oct	4.93
1983 - Nov	4.62
1983 - Dec	4.45
1984 - Jan	5.35
1984 - Feb	5.2
1984 - Mar	5.6
1984 - Apr	5.36
1984 - May	5.37
1984 - Jun	5.38
1984 - Jul	6.29
1984 - Aug	6.07
1984 - Sep	6.43
1984 - Oct	6.86
1984 - Nov	6.38
1984 - Dec	5.75
1985 - Jan	5.14
1985 - Feb	4.79
1985 - Mar	4.54
1985 - Apr	5.72
1985 - May	4.99
1985 - Jun	3.52
1985 - Jul	4.46
1985 - Aug	4.26
1985 - Sep	4.12
1985 - Oct	4.08
1985 - Nov	4.21
1985 - Dec	4.46
1986 - Jan	4.29
1986 - Feb	4.48
1986 - Mar	5.32
1986 - Apr	5.12
1986 - May	4.97
1986 - Jun	4.49
1986 - Jul	3.5
1986 - Aug	3.36
1986 - Sep	3
1986 - Oct	2.77
1986 - Nov	2.69
1986 - Dec	2.42
1987 - Jan	2.48
1987 - Feb	2.29
1987 - Mar	3.29
1987 - Apr	2.5
1987 - May	2.11
1987 - Jun	2.85
1987 - Jul	2.27
1987 - Aug	2.57
1987 - Sep	2.38
1987 - Oct	3.65
1987 - Nov	3.43
1987 - Dec	2.41
1988 - Jan	2.47
1988 - Feb	2.86
1988 - Mar	2.7
1988 - Apr	2.81
1988 - May	2.91
1988 - Jun	3.13
1988 - Jul	2.52
1988 - Aug	3.24
1988 - Sep	3.36
1988 - Oct	3.12
1988 - Nov	3.04
1988 - Dec	3.27
1989 - Jan	3.25
1989 - Feb	3.41
1989 - Mar	3.47
1989 - Apr	4.06
1989 - May	4.51
1989 - Jun	4.45
1989 - Jul	3.9
1989 - Aug	3.73
1989 - Sep	3.97
1989 - Oct	3.94
1989 - Nov	3.86
1989 - Dec	3.92
1990 - Jan	3.82
1990 - Feb	3.37
1990 - Mar	4.43
1990 - Apr	4.53
1990 - May	4.31
1990 - Jun	3.72
1990 - Jul	4.29
1990 - Aug	3.9
1990 - Sep	2.85
1990 - Oct	2.58
1990 - Nov	2.06
1990 - Dec	2.09
1991 - Jan	2.69
1991 - Feb	3.01
1991 - Mar	2.83
1991 - Apr	3.42
1991 - May	3.15
1991 - Jun	2.96
1991 - Jul	2.86
1991 - Aug	2.7
1991 - Sep	2.63
1991 - Oct	2.16
1991 - Nov	2.07
1991 - Dec	1.64
1992 - Jan	1.5
1992 - Feb	1.45
1992 - Mar	1.37
1992 - Apr	1.75
1992 - May	1.49
1992 - Jun	1.25
1992 - Jul	1.25
1992 - Aug	1.07
1992 - Sep	0.98
1992 - Oct	0.74
1992 - Nov	0.91
1992 - Dec	1.1
1993 - Jan	0.9
1993 - Feb	0.8
1993 - Mar	0.55
1993 - Apr	0.71
1993 - May	0.6
1993 - Jun	1.26
1993 - Jul	0.84
1993 - Aug	0.91
1993 - Sep	0.77
1993 - Oct	0.53
1993 - Nov	0.73
1993 - Dec	0.95
1994 - Jan	0.89
1994 - Feb	0.78
1994 - Mar	0.34
1994 - Apr	1.3
1994 - May	1.55
1994 - Jun	1.25
1994 - Jul	1.48
1994 - Aug	2
1994 - Sep	2.03
1994 - Oct	2.03
1994 - Nov	2.04
1994 - Dec	2.01
1995 - Jan	2.33
1995 - Feb	2.26
1995 - Mar	2.16
1995 - Apr	2.36
1995 - May	3.71
1995 - Jun	3.11
1995 - Jul	2.44
1995 - Aug	2.52
1995 - Sep	2.2
1995 - Oct	2.53
1995 - Nov	2.33
1995 - Dec	3.05
1996 - Jan	2.42
1996 - Feb	2.14
1996 - Mar	2.6
1996 - Apr	2.59
1996 - May	2.31
1996 - Jun	2.38
1996 - Jul	2.68
1996 - Aug	2.45
1996 - Sep	2.67
1996 - Oct	2.36
1996 - Nov	2.15
1996 - Dec	2.45
1997 - Jan	2.15
1997 - Feb	1.95
1997 - Mar	2.43
1997 - Apr	2.58
1997 - May	2.6
1997 - Jun	2.77
1997 - Jul	2.93
1997 - Aug	2.65
1997 - Sep	2.85
1997 - Oct	2.33
1997 - Nov	2.17
1997 - Dec	2.84
1998 - Jan	2.66
1998 - Feb	2.53
1998 - Mar	2.7
1998 - Apr	2.71
1998 - May	2.6
1998 - Jun	2.87
1998 - Jul	2.27
1998 - Aug	2.35
1998 - Sep	2.24
1998 - Oct	2.12
1998 - Nov	2.02
1998 - Dec	2.36
1999 - Jan	1.98
1999 - Feb	1.91
1999 - Mar	2.43
1999 - Apr	2.5
1999 - May	2.16
1999 - Jun	3.45
1999 - Jul	2.55
1999 - Aug	2.63
1999 - Sep	2.72
1999 - Oct	2.26
1999 - Nov	2.17
1999 - Dec	1.84
2000 - Jan	2.65
2000 - Feb	2.64
2000 - Mar	2.66
2000 - Apr	2.9
2000 - May	2.79
2000 - Jun	1.98
2000 - Jul	3.35
2000 - Aug	3.24
2000 - Sep	3
2000 - Oct	3.05
2000 - Nov	2.76
2000 - Dec	2.32
2001 - Jan	3.13
2001 - Feb	2.83
2001 - Mar	3.62
2001 - Apr	2.4
2001 - May	1.86
2001 - Jun	1.45
2001 - Jul	1.69
2001 - Aug	1.59
2001 - Sep	0.25
2001 - Oct	1.03
2001 - Nov	1.06
2001 - Dec	-0.2
2002 - Jan	0.79
2002 - Feb	0.86
2002 - Mar	1.08
2002 - Apr	0.53
2002 - May	0.11
2002 - Jun	0.44
2002 - Jul	0.26
2002 - Aug	0.18
2002 - Sep	-0.02
2002 - Oct	-0.2
2002 - Nov	-0.28
2002 - Dec	-0.06
2003 - Jan	-0.19
2003 - Feb	-0.19
2003 - Mar	-0.17
2003 - Apr	-0.11
2003 - May	0.08
2003 - Jun	-1.22
2003 - Jul	-0.09
2003 - Aug	0.1
2003 - Sep	0.06
2003 - Oct	-0.2
2003 - Nov	-0.16
2003 - Dec	-0.6
2004 - Jan	-0.14
2004 - Feb	-0.4
2004 - Mar	-0.06
2004 - Apr	-0.41
2004 - May	-0.51
2004 - Jun	-0.99
2004 - Jul	-0.45
2004 - Aug	-0.49
2004 - Sep	-1.33
2004 - Oct	-0.21
2004 - Nov	-0.04
2004 - Dec	1.18
2005 - Jan	0.33
2005 - Feb	0.57
2005 - Mar	0.61
2005 - Apr	0.49
2005 - May	0.15
2005 - Jun	0.49
2005 - Jul	0.93
2005 - Aug	1.18
2005 - Sep	2.56
2005 - Oct	1.5
2005 - Nov	1.41
2005 - Dec	0.96
2006 - Jan	2.08
2006 - Feb	2.14
2006 - Mar	3.28
2006 - Apr	2.13
2006 - May	2.13
2006 - Jun	2.28
2006 - Jul	2.12
2006 - Aug	2.14
2006 - Sep	3.09
2006 - Oct	3.03
2006 - Nov	3.59
2006 - Dec	3.58
2007 - Jan	2.31
2007 - Feb	2.49
2007 - Mar	2.1
2007 - Apr	2.09
2007 - May	1.52
2007 - Jun	1.13
2007 - Jul	1.92
2007 - Aug	2.13
2007 - Sep	1.81
2007 - Oct	1.72
2007 - Nov	1.82
2007 - Dec	1.18
2008 - Jan	0.86
2008 - Feb	0.1
2008 - Mar	0.47
2008 - Apr	-0.06
2008 - May	-0.42
2008 - Jun	-0.22
2008 - Jul	-0.7
2008 - Aug	-1.38
2008 - Sep	-0.95
2008 - Oct	1.23
2008 - Nov	2.93
2008 - Dec	2.65
2009 - Jan	2.1
2009 - Feb	2.13
2009 - Mar	3.3
2009 - Apr	0.14
2009 - May	0.13
2009 - Jun	0.56
2009 - Jul	-0.04
2009 - Aug	-0.95
2009 - Sep	-1.86
2009 - Oct	-0.79
2009 - Nov	-1.03
2009 - Dec	-1.24
2010 - Jan	-0.82
2010 - Feb	-1.08
2010 - Mar	-1.62
2010 - Apr	-0.33
2010 - May	-0.45
2010 - Jun	-0.39
2010 - Jul	-0.07
2010 - Aug	-0.75
2010 - Sep	-0.21
2010 - Oct	-1.01
2010 - Nov	-1.13
2010 - Dec	-0.96
2011 - Jan	-1
2011 - Feb	-1.23
2011 - Mar	-1.39
2011 - Apr	-1.32
2011 - May	-2.07
2011 - Jun	-1.94
2011 - Jul	-2.41
2011 - Aug	-1.19
2011 - Sep	-0.62
2011 - Oct	-1.48
2011 - Nov	-1.51
2011 - Dec	-1.56
2012 - Jan	-1.29
2012 - Feb	-1.34
2012 - Mar	-1.08
2012 - Apr	-1.69
2012 - May	-0.38
2012 - Jun	0.29
2012 - Jul	-0.55
2012 - Aug	-0.79
2012 - Sep	-2.3

Source: Federal Reserve Bank of Cleveland as described in Haubrich, Pennacchi, and Ritchken (2011).

Figure 2: Price Volatility and the Interest Rate

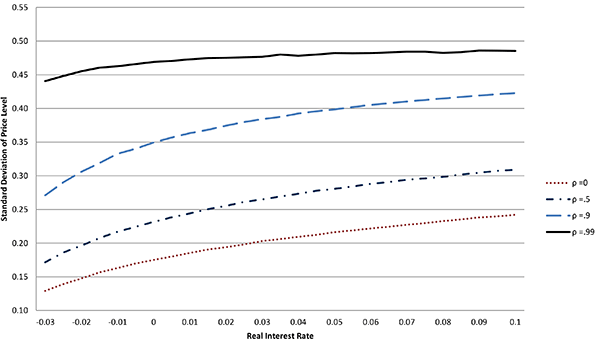
Note: ρ is the persistence of the shock. The average standard deviation over 100 simulated price paths. Each simulation was intialized with zero inventories. Each simulation was ran over 10000 observations of the net demand shock and then the first 1000 observations were discarded.

Data for Figure 2

r	ρ =0	ρ =.5	ρ =.9	ρ =.99
-0.03	0.129	0.172	0.271	0.441
-0.025	0.139	0.186	0.290	0.448
-0.02	0.148	0.196	0.306	0.455
-0.015	0.157	0.207	0.319	0.460
-0.01	0.163	0.217	0.333	0.463
-0.005	0.170	0.224	0.340	0.466
0	0.175	0.232	0.349	0.469
0.005	0.180	0.238	0.357	0.470
0.01	0.185	0.244	0.363	0.473
0.015	0.191	0.250	0.368	0.475
0.02	0.194	0.255	0.374	0.475
0.025	0.198	0.261	0.380	0.476
0.03	0.203	0.265	0.384	0.477
0.035	0.206	0.269	0.387	0.480
0.04	0.209	0.273	0.392	0.478
0.045	0.212	0.278	0.396	0.480
0.05	0.216	0.281	0.399	0.482
0.055	0.219	0.284	0.402	0.482
0.06	0.222	0.288	0.405	0.482
0.065	0.224	0.291	0.408	0.483
0.07	0.227	0.294	0.410	0.484
0.075	0.230	0.296	0.413	0.484
0.08	0.233	0.298	0.415	0.483
0.085	0.235	0.302	0.417	0.484
0.09	0.238	0.305	0.419	0.486
0.095	0.240	0.307	0.421	0.486
0.1	0.242	0.309	0.423	0.485

Note: ρ is the persistence of the shock. The average standard deviation over 100 simulated price paths. Each simulation was intialized with zero inventories. Each simulation was ran over 10000 observations of the net demand shock and then the first 1000 observations were discarded.

Figure 3: Price Correlation and Interest Rates

Note: ρ is the persistence of the idiosyncatic shock. λ is the persistence of the common shock. The average correlation over 100 simulated price paths. Each simulation was intialized with zero inventories. Each simulation was ran over 10000 observations of the net demand shock and then the first 1000 observations were discarded.

Data for Figure 3

r	ρ =0, λ =0	ρ =0, λ =.5	ρ =0, λ =.9	ρ =0, λ =.99	ρ =.5, λ =0	ρ =.9, λ =0	ρ =.99, λ =0
-0.03	0.408	0.608	0.828	0.894	0.234	0.092	0.079
-0.025	0.411	0.608	0.827	0.881	0.241	0.101	0.100
-0.02	0.415	0.611	0.823	0.866	0.246	0.110	0.121
-0.015	0.413	0.610	0.820	0.857	0.242	0.122	0.131
-0.01	0.418	0.611	0.813	0.846	0.246	0.120	0.131
-0.005	0.417	0.612	0.809	0.835	0.250	0.126	0.163
0	0.419	0.612	0.803	0.827	0.246	0.137	0.169
0.005	0.418	0.614	0.799	0.818	0.250	0.143	0.164
0.01	0.420	0.612	0.791	0.811	0.253	0.156	0.152
0.015	0.423	0.613	0.787	0.804	0.254	0.157	0.194
0.02	0.419	0.612	0.781	0.796	0.255	0.163	0.188
0.025	0.419	0.613	0.777	0.794	0.262	0.167	0.182
0.03	0.421	0.614	0.771	0.786	0.256	0.174	0.189
0.035	0.419	0.611	0.768	0.777	0.262	0.177	0.203
0.04	0.421	0.609	0.764	0.773	0.262	0.188	0.191
0.045	0.419	0.608	0.757	0.770	0.263	0.195	0.198
0.05	0.419	0.608	0.754	0.762	0.267	0.198	0.196
0.055	0.417	0.608	0.751	0.758	0.270	0.201	0.220
0.06	0.417	0.605	0.747	0.758	0.271	0.213	0.212
0.065	0.417	0.604	0.744	0.754	0.273	0.210	0.219
0.07	0.418	0.602	0.741	0.744	0.278	0.217	0.230
0.075	0.420	0.602	0.737	0.743	0.280	0.222	0.240
0.08	0.416	0.601	0.735	0.739	0.280	0.220	0.245
0.085	0.416	0.599	0.731	0.734	0.282	0.222	0.232
0.09	0.414	0.599	0.730	0.734	0.283	0.236	0.235
0.095	0.414	0.594	0.725	0.730	0.288	0.232	0.254
0.1	0.412	0.593	0.723	0.725	0.290	0.235	0.244

Note: ρ is the persistence of the idiosyncatic shock. λ is the persistence of the common shock. The average correlation over 100 simulated price paths. Each simulation was intialized with zero inventories. Each simulation was ran over 10000 observations of the net demand shock and then the first 1000 observations were discarded.

Figure 4: Coefficient on the Interest Rate in Covariance Equation

Data for Figure 4

Observation	Ordered Two-Commodity Panel Coefficients	Two-Commodity Oil and Metals Coefficients	Metals and Oil Panel Coefficient	All Commodities Panel Coefficient
1	-1.62		-0.48	-0.03
2	-1.54		-0.48	-0.03
3	-1.44		-0.48	-0.03
4	-1.38		-0.48	-0.03
5	-1.36		-0.48	-0.03
6	-0.90		-0.48	-0.03
7	-0.88	-0.88	-0.48	-0.03
8	-0.84	-0.84	-0.48	-0.03
9	-0.72		-0.48	-0.03
10	-0.64		-0.48	-0.03
11	-0.63		-0.48	-0.03
12	-0.54		-0.48	-0.03
13	-0.53		-0.48	-0.03
14	-0.52	-0.52	-0.48	-0.03
15	-0.51		-0.48	-0.03
16	-0.50	-0.50	-0.48	-0.03
17	-0.46		-0.48	-0.03
18	-0.46		-0.48	-0.03
19	-0.44	-0.44	-0.48	-0.03
20	-0.44		-0.48	-0.03
21	-0.41		-0.48	-0.03
22	-0.39		-0.48	-0.03
23	-0.37		-0.48	-0.03
24	-0.37		-0.48	-0.03
25	-0.35		-0.48	-0.03
26	-0.34		-0.48	-0.03
27	-0.33		-0.48	-0.03
28	-0.32		-0.48	-0.03
29	-0.30		-0.48	-0.03
30	-0.29		-0.48	-0.03
31	-0.28		-0.48	-0.03
32	-0.28		-0.48	-0.03
33	-0.27		-0.48	-0.03
34	-0.26		-0.48	-0.03
35	-0.22	-0.22	-0.48	-0.03
36	-0.21		-0.48	-0.03
37	-0.19		-0.48	-0.03
38	-0.19		-0.48	-0.03
39	-0.19		-0.48	-0.03
40	-0.17	-0.17	-0.48	-0.03
41	-0.16		-0.48	-0.03
42	-0.15		-0.48	-0.03
43	-0.15		-0.48	-0.03
44	-0.13		-0.48	-0.03
45	-0.13		-0.48	-0.03
46	-0.13		-0.48	-0.03
47	-0.13		-0.48	-0.03
48	-0.13	-0.13	-0.48	-0.03
49	-0.12		-0.48	-0.03
50	-0.12		-0.48	-0.03
51	-0.12		-0.48	-0.03
52	-0.12		-0.48	-0.03
53	-0.12		-0.48	-0.03
54	-0.11		-0.48	-0.03
55	-0.11	-0.11	-0.48	-0.03
56	-0.09		-0.48	-0.03
57	-0.09		-0.48	-0.03
58	-0.09		-0.48	-0.03
59	-0.08		-0.48	-0.03
60	-0.08		-0.48	-0.03
61	-0.07		-0.48	-0.03
62	-0.07		-0.48	-0.03
63	-0.06		-0.48	-0.03
64	-0.05	-0.05	-0.48	-0.03
65	-0.04		-0.48	-0.03
66	-0.04		-0.48	-0.03
67	-0.03		-0.48	-0.03
68	-0.03		-0.48	-0.03
69	0.00		-0.48	-0.03
70	0.00		-0.48	-0.03
71	0.00		-0.48	-0.03
72	0.00		-0.48	-0.03
73	0.00		-0.48	-0.03
74	0.00		-0.48	-0.03
75	0.00		-0.48	-0.03
76	0.00		-0.48	-0.03
77	0.00		-0.48	-0.03
78	0.00		-0.48	-0.03
79	0.00		-0.48	-0.03
80	0.00		-0.48	-0.03
81	0.00		-0.48	-0.03
82	0.00		-0.48	-0.03
83	0.00		-0.48	-0.03
84	0.00		-0.48	-0.03
85	0.00		-0.48	-0.03
86	0.00		-0.48	-0.03
87	0.00		-0.48	-0.03
88	0.00		-0.48	-0.03
89	0.00		-0.48	-0.03
90	0.00		-0.48	-0.03
91	0.00		-0.48	-0.03
92	0.00		-0.48	-0.03
93	0.00		-0.48	-0.03
94	0.00		-0.48	-0.03
95	0.00		-0.48	-0.03
96	0.01		-0.48	-0.03
97	0.02		-0.48	-0.03
98	0.02		-0.48	-0.03
99	0.03		-0.48	-0.03
100	0.03		-0.48	-0.03
101	0.04		-0.48	-0.03
102	0.04		-0.48	-0.03
103	0.07		-0.48	-0.03
104	0.08		-0.48	-0.03
105	0.08		-0.48	-0.03
106	0.09		-0.48	-0.03
107	0.09		-0.48	-0.03
108	0.11		-0.48	-0.03
109	0.18		-0.48	-0.03
110	0.18		-0.48	-0.03
111	0.22		-0.48	-0.03
112	0.22		-0.48	-0.03
113	0.28		-0.48	-0.03
114	0.29		-0.48	-0.03
115	0.49		-0.48	-0.03
116	0.81		-0.48	-0.03
117	0.95		-0.48	-0.03
118	0.98		-0.48	-0.03
119	1.23		-0.48	-0.03
120	1.70		-0.48	-0.03

Table 1a: Price Volatility over Interest Rates and Shock Persistence (Single Commodity): Price Volatility

Shock Persistence	Interest Rate: -0.03	Interest Rate: 0	Interest Rate: 0.025	Interest Rate: 0.05
ρ =0	0.13	0.18	0.20	0.22
ρ =.5	0.17	0.23	0.26	0.28
ρ =.9	0.27	0.35	0.38	0.40
ρ =.99	0.44	0.47	0.48	0.48

Table 1b: Price Volatility over Interest Rates and Shock Persistence (Single Commodity): Change in Volatility

Shock Persistence	Percent Change from r = -0.03 to r = 0.05
ρ =0	68
ρ =.5	63
ρ =.9	47
ρ =.99	9

Table 2a: Price Correlation over Interest Rates and Shock Persistence (Two Commodities): Price Correlation

Shock Persistence	Interest Rate: -0.03	Interest Rate: 0	Interest Rate: 0.025	Interest Rate: 0.05
ρ =0, λ =0	0.41	0.42	0.42	0.42
ρ =0, λ =.5	0.61	0.61	0.61	0.61
ρ =0, λ =.9	0.83	0.80	0.78	0.75
ρ =0, λ =.99	0.89	0.83	0.79	0.76
ρ =.5, λ =0	0.23	0.25	0.26	0.27
ρ =.9, λ =0	0.09	0.14	0.17	0.20
ρ =.99, λ =0	0.08	0.17	0.18	0.20

Table 2b: Price Correlation over Interest Rates and Shock Persistence (Two Commodities): Change in Correlation

Shock Persistence	Percent Change from r = -0.03 to r = 0.05
ρ =0, λ =0	3
ρ =0, λ =.5	0
ρ =0, λ =.9	-9
ρ =0, λ =.99	-15
ρ =.5, λ =0	14
ρ =.9, λ =0	115
ρ =.99, λ =0	149

Note:

ρ is the persistence of idiosyncratic shocks

λ is the persistence of common shocks.

Table 3: Commodity Price Volatility: Standard Deviation of Log Changes

	(1) Front Month Price: 1992:1 to 2002:12	(2) Front Month Price: 20003:1 to 2012:7	(3)Front Month Price: Ratio	(4)Year Ahead Futures Price: 1992:1 to 2002:12	(5)Year Ahead Futures Price: 2003:1 to 2012:7	(6)Year Ahead Futures Price: Ratio	(7)Time Spread (Ft/St): 1992:1 to 2002:12	(8)Time Spread (Ft/St): 2003:1 to 2012:7	(9)Time Spread (Ft/St): Ratio
Energy: Crude Oil	0.073	0.082	1.123	0.037	0.068	1.843	0.047	0.041	0.886
Energy: Heating Oil	0.070	0.080	1.147	0.036	0.063	1.761	0.045	0.039	0.851
Energy: Natural Gas	0.089	0.125	1.402	0.057	0.061	1.077	0.089	0.089	1.000
Raw Materials: Cotton	0.066	0.083	1.245	0.039	0.055	1.409	0.040	0.047	1.181
Foods & Beverages: Cocoa	0.064	0.065	1.015	0.054	0.058	1.075	0.019	0.018	0.911
Foods & Beverages: Corn	0.063	0.070	1.124	0.039	0.053	1.361	0.032	0.031	0.958
Foods & Beverages: Live Hogs	0.077	0.071	0.931	0.046	0.044	0.951	0.082	0.074	0.905
Foods & Beverages: Orange Juice	0.067	0.072	1.072	0.052	0.051	0.975	0.029	0.029	0.985
Foods & Beverages: Soybeans	0.053	0.064	1.208	0.045	0.051	1.118	0.028	0.037	1.308
Foods & Beverages: Soybean Meal	0.058	0.073	1.244	0.048	0.055	1.142	0.039	0.045	1.151
Foods & Beverages: Soybean Oil	0.054	0.060	1.110	0.048	0.054	1.126	0.016	0.016	1.002
Foods & Beverages: Wheat	0.062	0.074	1.191	0.042	0.053	1.254	0.037	0.041	1.116
Metals: Aluminum	0.043	0.054	1.264	0.030	0.048	1.617	0.022	0.018	0.835
Metals: Copper	0.062	0.073	1.168	0.047	0.081	1.728	0.030	0.022	0.744
Metals: Nickel	0.070	0.099	1.414	0.061	0.083	1.355	0.021	0.039	1.864
Metals: Zinc	0.054	0.079	1.463	0.030	0.070	2.359	0.036	0.021	0.599

Note: For the Aluminum, Copper, Nickel, and Zinc, year-ahead futures price is the 15-month contract. Computed as the average conditional standard deviation from a GARCH(1,1) model.

Table 4: Price Volatility and the Interest Rate: Coefficent on Real Interest Rate in the Variance Equation in GARCH(1,1) Model

	(1) Front Month Price: Coefficient	(2) Front Month Price: S.E.	(3) Year Ahead Futures Price: Coefficient	(4) Year Ahead Futures Price: S.E.	(5) Time Spread (Ft/St): Coefficient	(6) Time Spread (Ft/St): S.E.
Energy: Crude Oil	-0.46	1.10	-0.30	0.29	1.55	0.58
Energy: Heating Oil	0.23	0.95	-0.31	0.33	0.98	0.33
Energy: Natural Gas	2.42	3.72	-0.46	-0.44	3.03	2.14
Foods & Beverages: Cocoa	-0.83	0.89	-0.78	0.67	-0.75	0.49
Foods & Beverages: Corn	0.46	0.34	0.09	0.21	-0.57	0.28
Foods & Beverages: Live Hogs	0.69	0.52	-0.13	0.71	0.18	2.02
Foods & Beverages: Orange Juice	-2.80	2.69	-0.89	0.80	-0.17	0.34
Foods & Beverages: Soybeans	-0.47	0.43	-0.18	0.35	-0.18	0.10
Foods & Beverages: Soybean Meal	-0.37	0.36	0.00	0.26	-0.20	0.15
Foods & Beverages: Soybean Oil	-1.05	1.16	-0.60	-0.78	0.01	0.01
Foods & Beverages: Wheat	0.18	0.38	-0.08	0.31	-1.07	0.45
Raw Materials: Cotton	-3.63	2.49	-1.78	1.17	-0.60	0.48
Metals: Aluminum	-0.01	0.40	0.34	0.22	0.19	0.09
Metals: Copper	2.18	1.72	-0.34	0.91	0.01	0.02
Metals: Nickel	-0.13	0.88	-0.04	0.66	0.03	0.01
Metals: Zinc	-0.12	0.40	-4.96	0.80	0.15	0.07

Note: For the Aluminum, Copper, Nickel, and Zinc, year-ahead futures price is the 15-month contract.

Red denotes significance at the 1 percent level.

Orange denotes significance at the 5 percent level.

Table 5: Commodity Price Correlation: Correlation of Log Changes 2003:1 to 2012:7 Minus Correlation of Log Changes 1992:1 to 2002:12

	Crude Oil	Heating Oil	Natural Gas	Cotton	Cocoa	Corn	Hogs	Orange Juice	Soybeans	Soybean Meal	Soybean Oil	Wheat	Alum.	Copper	Nickel
Heating Oil	0.15
Natural Gas	-0.02	-0.06
Cotton	0.14	0.18	-0.01
Cocoa	0.17	0.40	0.11	0.13
Corn	0.09	0.19	0.23	0.02	0.15
Hogs	-0.09	-0.13	0.06	-0.04	0.18	0.08
Orange Juice	0.12	0.13	-0.07	0.15	-0.05	0.06	0.17
Soybeans	0.17	0.30	0.07	0.20	0.16	0.23	-0.04	-0.02
Soybean Meal	0.02	0.03	-0.07	0.11	0.22	0.24	-0.04	0.01	0.25
Soybean Oil	0.43	0.36	0.09	0.33	0.18	0.24	0.09	0.03	0.37	0.62
Wheat	0.22	0.06	0.01	0.24	0.08	0.07	-0.04	0.07	0.19	0.27	0.11
Alum.	0.34	0.37	0.16	0.12	0.24	0.36	0.02	0.23	0.19	0.17	0.35	0.20
Copper	0.41	0.24	-0.14	-0.01	0.14	0.32	-0.01	0.28	0.02	0.04	0.22	0.13	-0.13
Nickel	0.19	0.22	0.13	0.02	0.27	0.07	-0.09	0.20	0.12	0.03	0.28	0.05	-0.09	0.21
Zinc	0.23	0.16	-0.02	0.05	0.11	0.29	-0.04	0.25	0.12	-0.04	0.32	0.36	0.16	0.00	-0.13

Note: Front month contracts. Average conditional correlation from panel GARCH(1,1) model.

Table 6: Commodity Price Correlation: Correlation of Year-ahead Futures Prices Minus Correlation of Time Spread (Ft/St)

	Crude Oil	Heating Oil	Natural Gas	Cotton	Cocoa	Corn	Hogs	Orange Juice	Soybeans	Soybean Meal	Soybean Oil	Wheat	Alum.	Copper	Nickel
Heating Oil	0.23
Natural Gas	-0.04	-0.17
Cotton	0.04	0.16	-0.13
Cocoa	0.27	0.25	0.14	0.12
Corn	0.03	-0.05	-0.06	0.12	-0.08
Hogs	0.03	0.04	-0.08	-0.01	-0.03	0.17
Orange Juice	0.01	0.06	0.15	0.10	-0.09	-0.03	0.05
Soybeans	0.21	0.17	-0.01	0.20	-0.07	0.40	-0.02	0.08
Soybean Meal	0.16	0.13	0.02	0.13	-0.10	0.46	0.00	0.07	0.08
Soybean Oil	0.13	0.10	-0.04	0.24	0.04	0.25	0.03	0.07	0.41	0.29
Wheat	0.02	-0.06	-0.05	0.22	0.05	0.16	0.17	0.06	0.41	0.46	0.30
Alum.	0.09	0.08	-0.09	0.25	0.05	0.02	-0.01	0.10	0.04	0.02	0.25	0.06
Copper	0.21	0.19	-0.01	0.29	0.08	-0.03	-0.04	0.14	0.00	0.00	0.12	0.05	0.26
Nickel	0.18	-0.01	-0.23	0.23	-0.04	-0.02	-0.06	-0.01	0.05	0.09	0.16	0.09	0.22	0.35
Zinc	0.22	0.13	-0.01	0.22	0.10	0.04	0.00	-0.01	0.04	0.03	0.15	0.08	0.19	0.35	0.28

Note: Average conditional correlation from panel GARCH(1,1) model for 1992:1 to 2012:7 period.

Table 7: Dynamic Factor Model: Persistence of Global and Idiosyncratic Factors

Global Persistence	0.97
Idiosyncratic Persistence: Crude Oil	0.97
Idiosyncratic Persistence: Heating Oil	0.69
Idiosyncratic Persistence: Natural Gas	0.88
Idiosyncratic Persistence: Corn	0.91
Idiosyncratic Persistence: Cocoa	0.92
Idiosyncratic Persistence: Live Hogs	0.84
Idiosyncratic Persistence: Orange Juice	0.89
Idiosyncratic Persistence: Soybeans	0.80
Idiosyncratic Persistence: Soybean Oil	0.95
Idiosyncratic Persistence: Wheat	0.93
Idiosyncratic Persistence: Cotton	0.96
Idiosyncratic Persistence: Aluminum	0.88
Idiosyncratic Persistence: Copper	0.92
Idiosyncratic Persistence: Nickel	0.92
Idiosyncratic Persistence: Zinc	0.89

Table 8: Price Correlation and the Interest Rate: Coefficient on Interest Rate in Covariance Equation of Panel GARCH model

Metals	-0.40
Metals (s.e.)	0.22
Foods	-0.02
Foods (s.e.)	0.02
Oil and Metals	-0.48
Oil and Metals (s.e.)	0.27
Energy and Metals	-0.41
Energy and Metals (s.e.)	0.27
All Commodities	-0.03
All Commodities (s.e.)	0.08

Note: Coefficients have been multiplied by 10,000.

Red denotes significance at the 5 percent level.

Orange denotes significance at the 10 percent level.

Energy includes oil, heating oil, and natural gas. Foods includes cotton, cocoa, corn, hogs, orange juice, soybeans, soybean meal, soybean oil, wheat Metals includes aluminium, copper, nickel, and zinc

Table 9: Price Correlation and the Interest Rate (Two-Commodity Panels): Coefficient on Interest Rate in Covariance Equation of Panel GARCH model

	Crude Oil	Heating Oil	Natural Gas	Cotton	Cocoa	Corn	Hogs	Orange Juice	Soybeans	Soybean Meal	Soybean Oil	Wheat	Alum.	Copper	Nickel
Heating Oil	-0.03
Heating Oil (s.e.)	0.06
Natural Gas	-0.09	0.98
Natural Gas (s.e.)	0.95	0.99
Cotton	0.00	-0.03	0.81
Cotton (s.e.)	1.03	0.36	0.88
Cocoa	-0.33	-0.34	-1.36	0.00
Cocca (s.e.)	0.97	0.27	1.28	0.73
Corn	-0.32	-0.53	0.95	-0.37	-0.12
Corn (s.e.)	0.52	0.37	0.52	0.25	0.44
Hogs	-0.13	-0.46	-1.62	-0.13	-0.13	0.29
Hogs (s.e.)	0.89	0.51	1.41	0.42	0.25	0.29
Orange Juice	0.00	-0.37	0.11	0.00	0.00	0.09	-0.46
Orange Juice (s.e.)	0.99	0.82	0.95	1.13	0.77	0.62	0.45
Soybeans	0.00	-0.08	0.22	0.00	0.00	0.02	0.08	0.00
Soybeans (s.e.)	0.49	0.34	1.14	0.97	0.34	0.32	0.39	0.56
Soybean Meal	0.00	0.04	0.28	0.00	-0.08	0.03	0.07	0.00	0.00
Soybean Meal (s.e.)	0.70	0.44	1.61	1.34	0.18	0.28	0.39	0.80	0.16
Soybean Oil	-0.13	-0.44	0.22	-0.41	0.00	-0.19	0.18	0.00	-0.12	-0.19
Soybean Oil (s.e.)	0.33	0.26	0.96	0.21	0.38	0.25	0.44	0.53	0.13	0.21
Wheat	0.00	-0.06	0.49	-0.15	0.00	0.18	0.00	0.01	0.03	0.09	0.08
Wheat (s.e.)	0.78	0.35	0.67	0.32	0.44	0.53	0.33	0.75	0.42	0.37	0.50
Alum.	-0.22	-0.21	0.02	-0.04	-0.16	-0.28	-0.30	-0.19	-0.04	0.00	-0.12	-0.12
(s.e.)	0.24	0.23	0.36	0.40	0.15	0.21	0.27	0.87	0.19	0.27	0.18	0.15
Copper	-0.88	-1.44	1.70	-0.35	-0.51	-1.38	1.23	-0.54	-0.90	-0.63	-1.54	-0.72	-0.11
Copper (s.e.)	0.74	0.54	1.62	1.34	0.83	0.49	0.57	1.17	0.57	0.70	0.70	0.69	0.55
Nickel	-0.05	-0.27	0.04	0.00	-0.07	-0.12	-0.11	0.00	0.00	0.00	0.00	-0.07	-0.50	-0.84
Nickel (s.e.)	0.82	0.37	0.87	1.25	0.19	0.38	0.34	0.86	0.35	0.34	0.35	0.53	0.11	0.49
Zinc	-0.44	-0.39	-0.64	0.00	-0.09	-0.28	-0.26	0.00	-0.09	0.00	-0.29	-0.15	-0.13	-0.52	-0.17
Zinc (s.e.)	0.37	0.26	0.54	0.78	0.17	0.19	0.32	0.56	0.22	0.17	0.26	0.19	0.09	0.13	0.14

Note: Coefficients have been multiplied by 10,000.

Red denotes significance at the 5 percent level.

Orange denotes significance at the 10 percent level.

Bibliography

Akram, Q. Farooq, 2009, Commodity Prices, Interest Rates and the Dollar, Energy Economics 31, 838-851.

Arseneau, David M. and Sylvain Leduc, 2012, Commodity Price Movements in a General Equilibrium Model of Storage, International Finance Discussion Paper 1054, Board of Governors of the Federal Reserve.

Deaton, Angus, and Guy Laroque, 1992, On the Behavior of Commodity Prices, The Review of Economic Studies 59, 1-23.

Deaton, Angus, and Guy Laroque, 1996, Competitive Storage and Commodity Price Dynamics, Journal of Political Economy 104, 896-923.

Engel, Charles, and Kenneth D. West, 2005, Exchange Rates and Fundamentals, Journal of Political Economy 113, 485-517.

Fattouh, Bassam, Lutz Kilian, and Lavan Mahadeva, 2012, The Role of Speculation in Oil Markets: What Have We Learned So Far? Working Paper, University of Michigan.

Frankel, Jeffrey, 2008, The Effect of Monetary Policy on Real Commodity Prices, in John Campbell, ed. Asset Prices and Monetary Policy (University of Chicago Press), 291-327.

Haubrich, Joseph G., George Pennacchi, and Peter Ritchken, 2011, Inflation Expectations, Real Rates, and Risk Premia: Evidence from Inflation Swaps, Working paper 11-07, Federal Reserve Bank of Cleveland.

Routledge, Bryan R., Duane J. Seppi, and Chester S. Spatt, 2000, Equilibrium Forward Curves for Commodities, The Journal of Finance 55, 1297-1338.

Schwartz, Eduardo, and James E. Smith, 2000, Short-Term Variations and Long-Term Dynamics in Commodity Prices, Management Science 46, 893-911.

Tang, Ke, and Wei Xiong, 2011, Index Investment and Financialization of Commodities, Working paper, Princeton University.

Vansteenkiste, Isabel, 2009, How Important are Common Factors in Driving Non-Fuel Commodity Prices? A Dynamic Factor Analysis, Working Paper 1072, European Central Bank.

Footnotes

**   Division of International Finance Division, Board of Governors of the Federal Reserve System, Washington, DC 20551 U.S.A. Authors can be reached at [email protected] and [email protected]. Return to text

1.   Tang and Xiong (2011) is one reference documenting the apparent increase in price volatility and correlation. Return to text

2.   The link between the level of commodity prices and interest rates has been subject to a number of empirical tests, often with mixed results. Frankel found evidence of a negative relationship based on data from the 1970s. However, extending his analysis to more recent data can lead to an estimated positive relationship. The endogenity of both interest rates and commodity prices to the business cycle complicates empirical analysis. Akram (2009) estimates a VAR to control for the effect of output and finds strong evidence of a negative relationship between interest rates and commodity prices.  Return to text

3.   Most of the previous literature on storable commodities has held the interest rate constant. One exception is a recent paper by Arseneau and Leduc (2012) that embeds the storable commodity price model within a general equilibrium framework such that the interest rate is endogenous to the model. Return to text

4.   Another implication is that as interest rates fall and transitory shocks are smoothed, movements in commodity prices will increasingly be driven by persistent shocks, such that the level of any particular commodity price should approach approximation as a random walk. This argument is similar to that presented by Engel and West (2005) in the context of financial assets and currencies in particular.  Return to text

5.   As the shock becomes more persistent, price volatility approaches that of a non-inventory model. Without inventories, $P_t=a_t$ , and price volatility should be equal to the long-run mean of our two-state Markov process, or about .5. Return to text

6.   In examining changes in the standard deviation of prices, the conditional standard deviation from a GARCH model may be superior to other methodologies (including breaking the sample or rolling sample statistics) in that it allows for a more precise identification of the timing of changes in volatility as well as maintaining a common mean around which to compute the variance.  Return to text

7.   We use the Federal Reserve Bank of Cleveland's reported measure of the one-year real interest rate as described in Haubrich, Pennacchi, and Ritchken (2011). Alternative calculations of the real interest rate, for example subtracting lagging twelve month inflation from the constant maturity one-year Treasury Bill yield, are not markedly different. Although Figure 1 reports a measure of the real interest rate in the United States, the appropriateness of which may be suspect given the global nature of commodity markets, it seems likely that global real rates followed a similar trajectory.  Return to text

8.   The dynamic factor model is estimated in levels rather than in changes.  Return to text

9.   Vansteenkiste (2009) also examines commodity prices via a dynamic factor model, showing that a common factor can explain a substantial portion of movements in commodities prices. She shows that prices became more correlated with the common factor through the 2000s. The relative persistent of common versus idiosyncratic shocks, the exercise reported here, is not examined in her paper.  Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: December 5, 2013