Portfolio Diversification and the Cross-Sectional Distribution of Foreign Investment

Alexandra Tabova^**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

In this paper I explore the role of portfolio diversification in explaining the distribution of foreign investment across countries. I capture the portfolio diversification motive by a measure of country-specific riskiness, "covariance risk", which I construct as how countries' growth rates covary with the stochastic discount factor of a representative international investor. My key new empirical finding is a strong and significant correlation between this new measure of country riskiness and foreign investment allocations. Less risky countries, i.e. countries whose growth rates are more highly correlated with the investor's stochastic discount factor, receive larger investment shares than more risky countries. I interpret this result as evidence that investors do take into account diversification opportunities, not only for portfolio investment decisions, but also for foreign direct investment decisions. My empirical results confirm the theoretical predictions of standard portfolio allocation models.

Keywords: Foreign direct investment, global risk, international portfolio choice, portfolio diversification

JEL classification: F21, F34, F41, G11

1 Introduction

This paper contributes to the literature on the determinants of foreign investment by considering the role of portfolio diversification. Unlike the literature on portfolio investment, the literature on foreign direct investment (FDI) does not explore the portfolio selection motive behind investors' decisions. The literature on FDI looks at the cross-sectional distribution of investment as the result of investors evaluating countries on their individual merits. Real-world evidence, however, suggests that multinational corporations (MNCs) take diversification opportunities into account when making investment decisions. For example, in the last year the Wall Street Journal documented the experience of several MNCs such as HSBC, Banco Santander and Tesco PLC that benefited from regional diversification, especially in the current economic downturn.

My objective is to explore the role of diversification in the cross-sectional distribution of total foreign investment, which includes FDI as well as portfolio investment. To do so I extend the existing analyses of the determinants of foreign investment by adopting a portfolio allocation approach to risk. I capture the portfolio diversification motive by a measure of country-specific riskiness, which I refer to as "covariance risk". I construct this measure as how countries' growth rates covary with the stochastic discount factor (SDF) of a representative international investor. The idea is to capture the extent to which investments in a foreign economy provide a hedge against the investor's overall risk.

I find evidence that investors do take into account diversification opportunities. My key new finding is that less risky countries, i.e. countries whose growth rates are more highly correlated with the investor's SDF, receive larger investment shares than more risky countries. This result has both statistical as well as strong economic significance. For example, if a country's riskiness declines from the 25th percentile to the 75th percentile, on average the total foreign investment per capita increases by more than 135%.

My approach allows me to study the role of portfolio diversification in the distribution of foreign investment in general and across a large sample of countries that includes low-income countries. First, I look at total foreign investment that includes both FDI and portfolio investment. The role of diversification has been studied for portfolio investment allocations, but not for FDI allocations. It is important to explore FDI allocations because the data shows that FDI is the main component of foreign investment for the majority of countries. Portfolio investment constitutes a significant share of total foreign investment only for high-income countries, while for the majority of low- and middle-income countries FDI is more than 90 percent of total foreign investment. Second, my measure of covariance risk that captures the investors' diversification motive is available for 104 countries. In contrast, the empirical literature on portfolio investment usually uses stock market return correlations, which limits the country coverage to countries with well developed stock markets and reliable stock market data.

I study the role of portfolio diversification in the distribution of foreign investment using both a theoretical and an empirical approach. In the theoretical motivation I show that the share of investment a foreign economy receives is a decreasing function of the covariance of its returns with the returns of the investor's domestic economy. This covariance of returns captures the idea of diversification in the model. I use a standard portfolio allocation model based on Merton (1969, 1971) and incorporate elements that have been used in the literature (see for example Kraay and Ventura (2000); Kraay et al. (2005); Asiedu et al. (2009); Coeurdacier and Guibaud (2010)), but have either been studied separately or have not been thoroughly explored. This allows for a general theoretical framework of allocation of foreign investment that includes both FDI and portfolio investment.

Next, I test whether this theoretical prediction finds support in the data. In my empirical investigation I capture the portfolio diversification motive by a new measure of country-specific riskiness: "covariance risk". This measure is constructed in Burnside and Tabova (2009) as the covariance between countries' growth rates and a measure of global risk that is a proxy for the stochastic discount factor (SDF) of a representative international investor. The approach is analogous to the two-pass regression method used in empirical finance to explain cross-sectional variation in expected returns across portfolios, with country growth rates replacing portfolio returns in the regressions. The first step is to obtain country-specific exposures to global risk factors. The risk factors are: the US real GDP growth, the US real interest rate, the change in the relative prices of oil, metals, and agricultural commodities, and the US stock market excess return. The second step is to obtain the cost of risk by regressing average growth rates on the estimated exposures to the risk factors. Using this approach Burnside and Tabova (2009) construct a measure of global risk that is a proxy for the global investor's SDF. All relevant information about a country's exposure to global risk factors can be summarized in the covariance between its growth rate and this proxy SDF. This single variable is my covariance risk measure. Countries with higher values of this measure are less risky because their growth rates are more highly correlated with the stochastic discount factor.

For the empirical analysis I use two measures of foreign investment: (i) the stock of FDI originating from the US; and (ii) the stock of total FDI and portfolio investment, adjusted for valuation effects (see Lane and Milesi-Ferretti, 2009).

My key empirical finding is a strong and significant correlation between my measure of country riskiness and the foreign investment allocations across countries. Riskier countries receive smaller shares of FDI originating from the US than less risky countries. Riskier countries also attract less total FDI and portfolio investment. The results show that the diversification motive, captured by countries' riskiness, has statistical as well as strong economic significance. In my analysis I control for factors that the existing literature has identified as important determinants of investment allocations, including expropriation risk (see Asiedu et al., 2009; and Blonigen, 2005 for an extensive overview of the empirical literature). The results are also robust when I use an estimation procedure that accounts for the fact that the measure of covariance risk is a generated regressor.

The results of the paper suggest that mitigation of covariance risk has the potential to make countries more attractive for foreign investment. This has important implications especially for developing countries where foreign investment finances development projects and is crucial in bridging the gap between domestic savings and investment needs.

The rest of the paper is organized as follows. Section 2 introduces the theoretical model that links foreign investment to covariance risk. Section 3 describes the data and variables used in the empirical analysis. It provides the details of how the new measure of covariance risk is constructed. Section 4 describes the empirical methodology and presents the main results and robustness checks. Section 5 outlines the policy implications and concludes.

2 A Model of Foreign Investment and Portfolio Diversification

I use a portfolio allocation approach to model the role of portfolio diversification in the distribution of foreign investment. The model is based on Merton (1969, 1971). It relates closely to Kraay and Ventura (2000) and Kraay et al. (2005) who use portfolio selection models to examine classical questions in international economics. In the model a representative investor chooses how to distribute his/her capital stock among the domestic economy, (N-1) foreign economies, and a riskless asset. The representative investor's lifetime utility is:

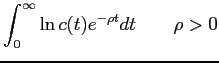
$\displaystyle \int_0^\infty \textrm{ln} \,c(t) e^{-\rho t} dt \qquad \rho>0$

(1)

where is consumption and $\rho$ is the rate of time preference ( $\rho>0$ ). Capital is the only factor of production and there is a single good that can be used for consumption and investment. To simplify the exposition, I assume that capital does not depreciate over time. The production function is linear in the capital stock in all economies. The stochastic rate of return for the domestic and foreign economies is:

$\displaystyle \mathbf{R} \,dt \,+\, \mathbf{\Sigma}^{1/2}\, \mathbf{dz} \,- \, \mathbf{dq}$

$\mathbf{R} = \left[ \begin{array}{c} R_P \ \mathbf{R_F} \end{array} \right] \qquad \textrm{ is the vector of mean returns in the domestic} (R_P) \textrm{and foreign economies} (R_F)$ $\mathbf{\Sigma} = \left[ \begin{array}{cc} \sigma^2_{P} & \omega'\ \omega & \Sigma_{F} \end{array} \right] \qquad \textrm{is the covariance matrix of returns}$

$\sigma^2_{P}$ is the variance of the domestic economy's returns, $\mathbf{\omega}$ is the vector of covariances of the foreign economies' returns with the domestic economy's returns, $\mathbf{\Sigma_F}$ is the covariance matrix of the foreign economies' returns, $\mathbf{dz}$ is the vector of Wiener processes. Since contracts across borders cannot be enforced, the international investor faces the risk that the host country may either expropriate or unilaterally modify the contract governing the investment. The probability of expropriation is captured by the term , which is a Poisson process.¹ In this formulation the threat of expropriation is exogenous from the investor's point of view. This is analogous to the set-up in the theoretical literature on the role of expropriation where although the decision of expropriation is endogenously determined by the recipient country, it is taken as given by the international investor (Eaton and Gersovitz, 1984).² If expropriation occurs the entire output accrues to the host country and the representative investor does not invest in this country in the future. This assumption is standard in the literature.

Denote by the aggregate capital stock. Let $\phi_P$ be the share invested in the domestic economy, $\mathbf{\phi_F}$ : the vector of shares invested in foreign economies. Then the fraction employed in the riskless activity, $\phi_f$ , is:

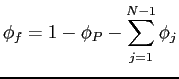
$\displaystyle \phi_f=1-\phi_P -\sum_{j=1}^{N-1} \phi_j$

The investor's budget constraint can be expressed as follows:

$\displaystyle dk\, =\, \Big[ \{ \phi'(R\,-\, r^f \iota) \,+\, r^f \} \,k \,-\, c \Big]\,dt \,+\, k \, \phi'\, \Sigma^{1/2}\,dz - k \, \phi'\, dq$

(2)

where $\mathbf{\phi} \equiv [\phi_P, \mathbf{\phi_F}]$ . The budget constraint illustrates the trade-off between risk and return that underlies investment decisions. To determine the optimal consumption and capital allocation rules the representative investor maximizes his/her lifetime utility subject to the budget constraint. The optimization problem is:

$\displaystyle \rho J$	$\displaystyle =$	$\displaystyle max_{\{c,\mathbf{\phi}\}}\Big\{\, ln(c) \,+\, \frac{\partial J}{\partial k} \, \Big[ \{ \phi'(R\,-\,r^f \mathbf{\iota}) \,+\, r^f \} \,k \,-\, c \Big] + {}$
		$\displaystyle {} + \, \frac{1}{2} \frac{\partial^2 J}{\partial k^2} \, k^2 [\phi'\, \Sigma \, \phi] \,+\, \alpha'[J(k^d)\,- \,{J}(k) \iota] \Big\}$	(3)

where is the capital stock in the event of expropriation, $\mathbf{\alpha}$ is the vector of probabilities of expropriation. Throughout I impose the usual transversality condition and assume that the investor's holdings of capital in all economies are nonnegative.³ In this framework closed form solutions for the portfolio allocations are obtained.⁴ The optimal consumption rule is:

$\displaystyle c \,=\, \rho \, k$

(4)

The optimal investment shares are:

$\displaystyle \phi_P=\sigma_P^{-2}(R_P-r^f)-\sigma_P^{-2}\phi_F'\omega$

(5)

$\displaystyle \phi_F = \Sigma_F^{-1}(R_F - r^f \iota)-\Sigma_F^{-1}\omega \phi_P \, - \mathbf{\Sigma_{F}}^{-1}[\mathbf{I}_{n-1}-\mathbf{D}(\mathbf{\phi_F})]^{-1}\alpha$

(6)

where $D(\phi_F)$ is a diagonal matrix with the capital shares $\mathbf{\phi_F}$ on the diagonal. Equations (4),(5), and (6) show that both the consumption-capital ratio and the fractions of capital employed in the foreign economies are constant. Equation (4) states that consumption depends only on the aggregate stock of capital. For the special case of logarithmic utility that I use here, the consumption decision is independent of the expected return or the variances and covariances of the economies' returns. Equations (5) and (6) state that the international investor behaves as a mean-variance investor. For example, the share of capital invested in each foreign economy equals its expected excess return relative to its variance and covariance and corrected for the risk of expropriation. For constant relative risk aversion utility the investment decision is independent of the consumption decision (Samuelson, 1969 and Merton, 1969).⁵ ⁶

Denote by $\omega_i$ the covariance between foreign economy and the domestic economy, and by $\phi_i$ the share of investment in the foreign country . I interpret $\omega_{i}$ as the measure of country i's covariance risk. Then the role of county i's covariance risk on the share of foreign investment it receives can be expressed as:

$\displaystyle \frac{\partial \, \phi_i}{\partial \, \omega_i}\, = \, \frac{-\, \phi_P \, (\mathbf{\Sigma_F}^{-1})_{ii} \,-\, \frac{\partial \, \phi_P}{\partial \, \omega_i}\, [\mathbf{(\Sigma_F}^{-1})_{i~}\, \omega]}{\mathbf{\alpha_i \, (1-\phi_i)^{-2}\,(\Sigma_F}^{-1})_{ii} + \, 1}$

(7)

where $(\mathbf{\Sigma_F}^{-1})_{ii} \, > \,0$ is the $i^\textrm{th}$ coefficient on the diagonal of matrix $\Sigma_F^{-1}$ ; $(\mathbf{\Sigma_F}^{-1})_{i~}$ is the $i^\textrm{th}$ row of matrix $\Sigma_F^{-1}$ . In the model this derivative captures the role of portfolio diversification in the distribution of foreign investment. The first term of the numerator, i.e. $\phi_P \, (\mathbf{\Sigma_F}^{-1})_{ii}$ , and the denominator are positive, so the sign of the derivative depends on the sensitivity of the share of investment in the domestic economy to its covariance with the foreign economies. To evaluate the sign of the derivative I use two approaches. First, I follow the literature on "home bias" that allows me to analytically sign the derivative. Second, I use numerical evaluation. In both cases I find that the derivative is strictly negative: the share of foreign investment is decreasing in its covariance with the domestic economy.

First, equation (7) shows that the share of foreign investment is decreasing in the covariance, $\frac{\partial \, \phi_i}{\partial \, \omega_i} \, < \, 0$ , if the share of investment in the domestic economy is not sensitive to its covariance with the foreign economies, i.e. when $\frac{\partial \, \phi_P}{\partial \, \omega_i} \, = \, 0$ . The literature on "home bias" provides a reason why this might be the case. I follow this literature and introduce an investment constraint that states that the share of capital invested in the domestic economy must exceed a certain threshold; this restriction is binding (see for example Coeurdacier and Guibaud, 2010):

$\displaystyle \phi_P = \underline{\phi}_P > \phi_P^*$

where $\phi_P^*$ is the optimal share for the unconstrained problem and $\underline{\phi}_P$ is fixed. This type of restriction reflects both regulatory constraints faced by investors as well as risk management practices of MNCs or institutional investors. Since the constraint is binding, the investor is forced to invest more in its economy than it is optimal under the unconstrained problem. The portfolio constraint forces a "home bias": a widely documented and studied phenomenon in the literature on international portfolio allocations. The constraint limits the investor's portfolio choice by fixing the share of investment in the domestic economy. Therefore:

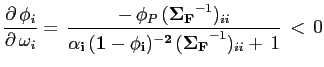
$\displaystyle \frac{\partial \, \phi_i}{\partial \, \omega_i} = \, \frac{-\, \phi_P \, (\mathbf{\Sigma_F}^{-1})_{ii} }{\mathbf{\alpha_i \, (1-\phi_i)^{-2}\,(\Sigma_F}^{-1})_{ii} + \, 1} \, < \, 0$

Second, using a numerical evaluation, I show that even if the share invested in the domestic economy, $\phi_P$ , is sensitive to changes in the covariance, $\omega_i$ , the share invested in the foreign economy i is strictly decreasing in $\omega_i$ . I evaluate the derivative numerically for the case of a single foreign economy i. Figures 1 and 2 show the simulated fractions of capital for a range of plausible values for the covariance and for different magnitudes of the risk of expropriation. I set the range of values for $\omega$ to correspond to the range of values observed in the data for the covariance of the US per capita GDP growth rate with the GDP growth rates of 106 countries. The time period is 1971-2007. I set $\sigma^2_{P}$ equal to the variance of the US per capita GDP growth, which is 0.036; and $(\Sigma_{F})_{ii}$ equal to the median variance of per capita GDP growth for the sample of countries, which is 0.15. The plot does not change much for a broader range of values for $(\Sigma_{F})_{ii}$ and $\sigma^2_{P}$ . Finally, I set and to correspond to the average growth rates in the US, $\bar{g}^{P}$ , and the median of the average growth rates of countries in the sample, $\bar{g}^i$ , such that $\bar{g}^{P}\,-\,\bar{g}^i \, = \, -\, (R_P\,-\,R_i)$ . The plots show the negative relation between the fraction of investment employed in the foreign economy, $\phi_i$ , and its covariance with the domestic economy $\omega_i$ :

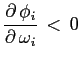
$\displaystyle \frac{\partial \, \phi_i}{\partial \, \omega_i} \, < \, 0$

Figure 1: Investment Shares for a Range of Values for $\omega_{i}$ , $\alpha_i=0.1$

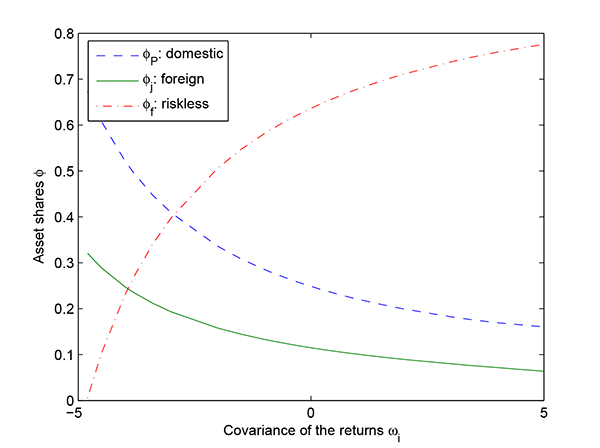
$Figure 1: Figure 1 plots the simulated fractions of investment employed in a foreign economy, Φ_i, using an expropriation parameter, α_i, of 0.1 and a range of plausible values for its covariance with the domestic economy, ω_i. The vertical axis ranges from 0 to positive 0.8 for Φ_i. The horizontal axis ranges from negative 5 to positive 5 for ω_i. The plot shows a negative relation between the fraction of investment employed in the foreign economy, Φ_i, and its covariance with the domestic economy, ω_i.$

Although the focus of this paper is on the role of covariance risk, I also take into account the risk of expropriation. The role of expropriation risk on foreign country i's investment allocation, , can be expressed as follows:

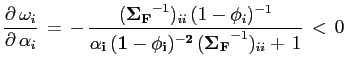
$\displaystyle \frac{\partial \, \omega_i }{\partial \, \alpha_i} \, = \, - \, \frac{(\mathbf{\Sigma_F}^{-1})_{ii}\, (1-\phi_i)^{-1} }{\mathbf{\alpha_i \, (1-\phi_i)^{-2}\,(\Sigma_F}^{-1})_{ii} + \, 1} \, < \, 0$

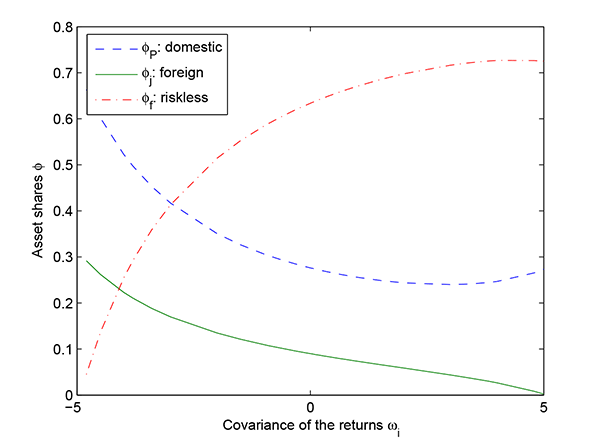
To summarize, the model shows that the covariance of returns does play a role in the decision making process of a representative international investor. The more negatively correlated the return of a foreign economy is with the investor's home economy, the larger the share of capital that the investor is willing to allocate to that economy. This relationship captures the role of diversification in the foreign investment allocations across countries. In what follows, I develop a general empirical specification to study whether this relationship holds in the data.

Figure 2: Investment Shares for a Range of Values for $\omega_{i}$ , $\alpha_i=0.5$

$Figure 2: Figure 2 plots the simulated fractions of investment employed in a foreign economy, Φ_i, using an expropriation parameter, α_i, of 0.5 and a range of plausible values for its covariance with the domestic economy, ω_i. The vertical axis ranges from 0 to positive 0.8 for Φ_i. The horizontal axis ranges from negative 5 to positive 5 for ω_i. The plot shows a negative relation between the fraction of investment employed in the foreign economy, Φ_i, and its covariance with the domestic economy, ω_i.$

3 Measures of Covariance Risk and Foreign Investment

Before proceeding with the empirical analysis, in this Section I first describe the main variables for the analysis: foreign investment and my measure of covariance risk that captures the diversification motive behind investors' allocation decisions.

3.1 Covariance Risk

In my empirical investigation I capture the portfolio diversification motive by a new measure of country-specific riskiness, which I refer to as covariance risk. This new measure is constructed in Burnside and Tabova (2009) as the covariance between countries' growth rates and a measure of global risk that is a proxy for the stochastic discount factor (SDF) of a representative international investor. The approach is analogous to the two-pass regression method used in empirical finance to explain cross-sectional variation in expected returns across portfolios, with country growth rates replacing portfolio returns in the regressions. Ideally one would assess whether risk explains differences in rates of return across countries by gathering data on rates of return to investment, and estimating an explicit model of the international investor's stochastic discount factor. Unfortunately this approach is fraught with difficulty.⁷

The first step is to obtain country-specific exposures to global risk factors. The risk factors are: the US real GDP growth, the US real interest rate, the change in the relative prices of oil, metals, and agricultural commodities, and the US stock market excess return. This involves time series regression of each country's real growth rate, $g_{it}$ , on a vector of six risk factors, $\mathbf{f}_{t}$ :

$\displaystyle g_{it}=a_{i}+\mathbf{f}_{t}^{\prime }\mathbf{\beta }_{i}+\epsilon _{it}\textrm{ ,\quad }t=1,\dots ,T\textrm{, for each }i=1,\dots ,n.$

the time period is 1971-2007 for a total of 104 countries. The choice of the factors is motivated by the notion that to some extent they reflect global demand conditions, global financial conditions, and terms of trade shocks that might be considered important to the small economies in our sample. The betas, $\beta_i$ , measure countries' exposure to the risk factors. There are two important findings from this estimation. First, the results show a considerable spread among the betas, $\beta_i$ , across countries. Second, between roughly 15 and 30 percent of the estimated betas are individually statistically significant at the 5 percent level (see Burnside and Tabova, 2009 for more details).

The second step is to obtain the cost of risk by regressing average growth rates on the estimated exposures to the risk factors using a single cross-sectional regression of average growth rates on the estimated $\beta_i$ from the time series regression:

$\displaystyle g_{i}=\lambda _{0}+\mathbf{\hat{\beta}}_{i}^{\prime }\mathbf{\lambda }+u_{i} \textrm{,\qquad }i=1,\dots ,n$

where $\mathbf{\hat{\beta}}_{i}$ is the OLS estimate of $\mathbf{\beta}_{i}$ obtained in the time series regression, and $u_{i}$ is an error term. The parameter $\lambda$ measures the cost in percentage points of growth, of different exposures to risk. Using this approach Burnside and Tabova (2009) construct a measure of global risk that is a proxy for the global investor's SDF $\hat{m}_{t}$ :

$\displaystyle \hat{m}_{t}=\left( \mathbf{f}_{t}-\mathbf{\bar{f}}\right) ^{\prime }\mathbf{\hat{\Sigma}}_{ \mathbf{f}}^{-1}\mathbf{\hat{\lambda}}$

All relevant information about a country's exposure to global risk factors can be summarized in the covariance (or beta) between its growth rate and this proxy SDF. This single variable is my "covariance risk" measure, $\beta_{mi}$ :

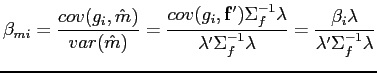
$\displaystyle \beta_{mi}=\frac{cov(g_{i},\hat{m})}{var(\hat{m})}= \frac{cov(g_{i},\mathbf{f}')\Sigma^{-1}_f\lambda}{\lambda'\Sigma^{-1}_f\lambda} = \frac{\beta_{i}\lambda}{\lambda'\Sigma^{-1}_f\lambda}$

Countries with higher values of this measure are less risky because their growth rates are more highly correlated with the stochastic discount factor. The degree of a country's riskiness, $\beta_{mi}$ , depends on the sign and magnitude of its exposure to the specific risk factors, $\beta_i$ . For example, countries with more negative exposures to US interest rates and more positive exposures to changes in oil and metals prices are riskier. Risk exposure is highly correlated with initial income: the highest-income countries tend to have roughly zero $\beta_{mi}$ , while lower income countries tend to have negative $\beta_{mi}$ .

It is useful to establish the explicit link between the empirical measure of covariance risk and the measure $\omega_i$ that I used in the theoretical model. Recall that the empirical measure of covariance risk is: $\beta_{mi}=\textrm{cov}(g_{i},\hat{m})\, / \, var(\hat{m})$ . Since the global stochastic discount factor $\hat{m}$ is the same for all countries, $\textrm{cov}(g_{i},\hat{m})$ identifies the country-specific riskiness. Replacing $g_{i}$ with $R_{i}$ does not change the sign of the covariance: the sign of $\textrm{cov}(R_i,\hat{m})$ will be the same as the sign of $\textrm{cov}(g_{i},\hat{m})$ .⁸ The direct link between the empirical and theoretical measure of covariance risk can be expressed as:

$% latex2html id marker 2152 $\displaystyle \beta_{mi} \, \propto -\, \omega_{i} $$

Therefore, for the data to confirm the theoretical predictions of the role of portfolio diversification, in the empirical investigation we would expect to find a positive correlation between $\beta_{mi}$ and the foreign investment allocations across countries:

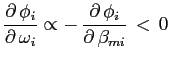
$% latex2html id marker 2156 $\displaystyle \frac{\partial \, \phi_i}{\partial \, \omega_i} \propto - \, \frac{\partial \, \phi_i}{\partial \, \beta_{mi}} \, < \, 0 $$

3.2 Foreign Investment

In the empirical analysis I use two measures of foreign investment: (i) the stock of FDI originating from the US; and (ii) the stock of total FDI and portfolio investment. I do not consider the debt-creating component of capital flows for two main reasons. First, the focus of the paper is on pure investment motives that are not reflected in debt flows. Second, official concessional lending, which is not determined by investment objectives, is the main component of the debt stock for the majority of low-income countries in the sample.

The source of data for FDI originating from the US is the International Economics Accounts reported by the Bureau of Economic Analysis. The data is available for 93 countries. For total FDI and portfolio investment I use a database constructed by Lane and Milesi-Ferretti (2006) where the stock measures are adjusted for valuation effects, such as exchange rate changes, variations in the price of capital goods and changes in the values of stock market indices. The stock data also takes into account unrecorded capital flight and debt reductions that are not captured in "crude" cumulative current account data. The data is available for 145 countries.

Given that most of the variation in the data is across countries, it is appropriate to consider average stock of foreign investment and estimate a single cross-sectional regression. Since capital liberalization plays an important role for the dynamics of foreign inflows, I use average stock for each recipient country for the period 1995-2007.⁹ Before the early 1990s capital movements were still restricted in many economies, and foreign investment was, therefore, less sensitive to the economic and institutional environment (see Lane and Milesi-Ferretti (2003, 2005, 2006), Harms and Lutz (2006)).

4 Empirical Analysis

The theoretical model in Section 2 shows that portfolio diversification does play a role in the decision making process of a representative international investor. The more negatively correlated the return of a foreign economy is with the investor's home economy, the larger the share of capital that the investor is willing to allocate to this foreign economy. Now I develop a general empirical specification to study whether this relationship holds in the data. I first use data on FDI originating from the US. Next, I capture the role of portfolio diversification on total foreign investment by using data on recipient countries' total stock of FDI and portfolio investment. In the empirical analysis I use my measure of covariance risk to capture the portfolio diversification motive behind investors' decisions.

4.1 Portfolio Diversification and FDI Originating From the US

Figure 3 shows that the covariance risk measure, $\beta_{mi}$ , is positively related with the US FDI allocations across countries. This positive relation can be interpreted as initial evidence that the theoretical predictions find support in the data. Note that by construction countries with higher values of $\beta_{mi}$ are less risky since their growth rates are more positively correlated with the investor's stochastic discount factor. In Figure 3 countries are sorted by their stock of FDI scaled either by the total stock of US FDI across all recipient countries or by population and are then grouped into quartiles. The vertical axis shows the average $\beta_{mi}$ .

Figure 3: $\textrm{FDI}^{\textrm{US}}$ Versus Covariance Risk $\beta_{mi}$

Figure 3: In Figure 3 countries are sorted by their stock of FDI from the U.S., scaled either by the total stock of U.S FDI across all recipient countries (top panel) or by population (bottom panel) and are then grouped in quartiles. The top panel plots the average U.S. FDI as a percent of U.S total FDI for the quartiles (horizontal axis) and the average covariance risk measure,β_mi, for the quartiles (vertical axis). The horizontal axis ranges from 0 to 3.84, the vertical axis ranges from negative 0.5 to 0. The panel shows that β_(mi )is positively correlated with the measure of FDI. The bottom panel plots the average U.S. FDI per capita for the quartiles (horizontal axis) and the average covariance risk measure,β_mi, for the quartiles (vertical axis). The horizontal axis ranges from ranges from 0 to positive 9, the vertical axis ranges from negative 0.7 to positive 0.1. The panel shows that β_(mi )is positively correlated with the measure of FDI.

The horizontal axis of each graph shows the average stock of FDI expressed either as a share of the total US FDI across all countries or in per capita terms.

In addition, I use simple bivariate cross-sectional regressions to show that the correlation between covariance risk and foreign investment is strongly statistically significant (see Table 1). The results hold for either measure of FDI. The full sample includes all 92 countries for which I have constructed the new measure of country-specific riskiness (covariance risk) and for which data is available of FDI originating from the US. For a robustness check I also exclude the largest recipients of $FDI^{US}$ . These are Canada (CAN), the Netherlands (NLD), and Great Britain (GBR) in the case of $FDI_i/FDI^{US}$ ; and the financial centers Bahamas (BHS), Bermuda (BMU), Luxembourg (LUX), and Panama (PAN) for the case of FDI per capita.

Table 1: FDI Originating From the US and Covariance Risk (1995-2007)

Dependent variable	Constant	Covariance risk	R²
FDI per capita: (log): Full Sample	4.54*** (0.40)	2.06*** (0.54)	0.127
Excluding LUX, BMU, BHS, PAN	4.21*** (0.40)	1.77*** (0.58)	0.102
FDI as a share of total: $FDI_i/FDI^{US}$ (log): Full Sample	-2.55*** (0.41)	1.71*** (0.62)	0.085
Excluding CAN, NLD, GBR	-2.77*** (0.41)	1.60*** (0.61)

Notes: Heteroscedasticity-consistent standard errors in parentheses.

4.1.1 Holding Companies and Redirection of FDI

US parent companies funnel a share of their direct investments abroad through holding company affiliates.¹⁰ Data from BEA shows that in 2007 30 percent of the US direct investment position abroad is accounted for by holding companies, which may have invested the funds in other countries. To take this into account, I check if the positive relationship between the stock of FDI and $\beta_{mi}$ is preserved for bilateral FDI originating from the countries with the largest share in $\textrm{FDI}^{\textrm{US}}$ and the largest share of holding companies recipients of $\textrm{FDI}^{\textrm{US}}$ : the Netherlands (NL) and the United Kingdom (UK). In 2007 the Netherlands held 14 percent of total $\textrm{FDI}^{\textrm{US}}$ and 68 percent was accounted for by holding companies; the UK held 13 percent of total $\textrm{FDI}^{\textrm{US}}$ and 22 percent was accounted for by holding companies (source: BEA 2008, 2009). The source of data on bilateral FDI stock originating from the Netherlands and the UK is OECD International Direct Investment Statistics, the sample period and methodology are identical to the ones used above for the FDI originating from the US. When I regress the FDI per capita (in logs) on $\beta_{mi}$ , I obtain the following estimates:

$\displaystyle \textrm{FDI}^{\textrm{UK}}_{i}=\underset{(0.36)}{4.24}+\underset{(0.65)}{1.58}\beta_{mi} \qquad R^2=0.07$

(8)

$\displaystyle \textrm{FDI}^{\textrm{NL}}_{i}=\underset{(0.32)}{2.78}+\underset{(0.54)}{1.22}\beta_{mi} \qquad R^2=0.05$

(9)

where heteroskedasticity-consistent standard errors are in parentheses. The results show that for both the Netherlands and the United Kingdom the positive relationship between $\beta_{mi}$ and FDI allocations is preserved. Therefore, even though the final destination of the funds channeled through holding companies is unknown, there is evidence that the countries with the largest share of holding companies in the FDI portfolio of the US follow the logic of portfolio diversification.

4.1.2 Controlling for Traditional Determinants of FDI

Next, I show that my key empirical finding on the role of portfolio diversification, captured by my covariance risk measure, is preserved if I control for country-specific characteristics drawn from the empirical literature on the determinants of FDI.¹¹ In the cross sectional regression I include an expropriation risk rating to capture the risk that host countries might either expropriate the foreign investment or unilaterally modify the contract governing the investment. This is a more traditional measure of risk that has been used in recent empirical studies. The source of data is the International Country Risk Guide database.¹² A high score implies less risk.¹³ The rating is available for 80 of the 93 countries in my sample. I also include GDP growth rates to capture growth opportunities in the host country; the level of GDP as a measure of market size; $(\textrm{Exports}+\textrm{Imports})/\textrm{GDP}$ as a measure of trade openness; the number of phones per 1000 people as a measure of infrastructure availability and the level of development.¹⁴ The data source for these variables is the World Development Indicators (2009). To be consistent with the dependent variable, I average the control variables over the same period. An additional control variable is the distance between the capitals of the originating country and the host country as a proxy for the relative magnitude of transaction costs. Transaction costs of control and potential problems stemming from cultural differences are expected to increase with distance.¹⁵ The descriptive statistics are reported in Appendix A.

Since most of the variation in the data is across countries, reflecting conditions that change slowly, I use cross-sectional regressions. All variables are averages for the period 1995-2007. The model I estimate is:

$\displaystyle Y_i \, = \, \gamma_0 \, +\, \gamma_1 \, \beta_{mi} \, +\, \mathbf{Z_i} \, \mathbf{\Gamma_2} \, + \, \epsilon_i$

(10)

where $\beta_{mi}$ is the measure of covariance risk, $\mathbf{Z}$ is the vector of control variables described above, and $\mathbf{\Gamma_2}$ is the coefficient vector associated with the control variables. I first estimate the model using the shares of countries' FDI, $FDI_i/FDI^{US}$ , as the dependent variable . This estimation provides a direct link to the predictions of the theoretical model where the representative investor solves for optimal investment shares across the foreign economies. I also estimate the model using per capita FDI originating from the US, as the dependent variable.

First, I estimate the model by OLS. The sample includes 78 countries due to data availability of the expropriation risk rating. Columns 1 and 3 in Table 2 presents the results of this estimation. The coefficient on covariance risk, $\beta_{mi}$ , is positive and significant at the 3 percent level. This means that less risky countries from the international investor's perspective, i.e. those with higher values for $\beta_{mi}$ , receive on average a larger share of the total stock of FDI. Less risky countries have also a higher level of FDI per capita.

The results show that the diversification motive, captured by my covariance risk measure, has statistical as well as strong economic significance. The 25th percentile value for the $\beta_{mi}$ in the sample is -0.69, while the 75th is 0.02. The point estimates for the coefficient associated with $\beta_{mi}$ suggest that the cross-sectional regression predicts that if a country's riskiness declines from the 25th percentile to the 75th percentile, on average per capita FDI from the US increases by more than 183 percent. The magnitude is similar for the case when the share of FDI is the dependent variable. This empirical result confirms the theoretical prediction: the stock of FDI in a foreign economy, measured either in per capita terms or as a share of total FDI across all countries, is a decreasing function of the covariance of its return with the return of the investor's home economy.

I now turn my attention to the other explanatory variables. Table 2 shows that consistent with Asiedu et al. (2009) the coefficient on the expropriation risk variable is positive and significant for all specifications. Recall from the data description section that higher values of the expropriation risk rating imply less risk. I find that openness to trade, infrastructure availability, and the size of the domestic market, measured by either level of GDP or population, have a positive and significant effect on FDI. As expected, oil producers attract on average a larger share of FDI; while distance is negatively and significantly correlated with FDI.

Because $\beta_{mi}$ is a generated regressor, it may be the case that the estimate of $\gamma_1$ is biased towards zero because of measurement error.¹⁶ This would only reinforce my finding of a positive relationship between FDI holdings and the measure of covariance risk $\beta_{mi}$ . A related concern in the case of generated regressors is that OLS standard errors understate the true standard errors. To address this issue I use maximum likelihood estimation (MLE). My approach follows Kim (1995) who derives a maximum likelihood estimator that takes into account the measurement error of the generated regressor. Kim (1995) develops the correction for the two-pass estimation methodology of expected returns, but the correction can easily be applied for more general problems. Appendix B contains a detailed description of the MLE methodology. The correction provides a robustness check for the validity of the uncorrected OLS estimates and standard errors.

Columns 2 and 4 in Table 2 present the MLE results along with the OLS coefficients for comparison. Consistent with the theory, the results show that the OLS estimation results in an underestimation of the coefficient associated with $\beta_{mi}$ (the variable measured with error). The correction does not change the main findings and serves as a robustness check for the link between FDI and covariance risk.

Table 2: Impact of Covariance Risk on the Stock of FDI Originating From the US After Controlling for Country-Specific Factors

	Dependent var: FDI_i/FDI^US(log): OLS	Dependent var: FDI_i/FDI^US(log): MLE	Dependent var: FDI per capita (log): OLS	Dependent var: FDI per capita (log): MLE
Covariance risk (β_mi)	0.978** (0.472)	1.533** (0.722)	0.836** (0.419)	1.217** (0.583)
GDP growth	-0.279** (0.137)	-0.270** (0.123)	-0.287** (0.131)	-0.278** (0.110)
In(GDP)	1.326*** (0.152)	1.351*** (0.141)	0.536*** (0.138)	0.544*** (0.124)
Trade/GDP	0.014** (0.003)	0.015*** (0.004)	0.015*** (0.003)	0.016*** (0.003)
ln(1 + Phones)	1.337*** (0.237)	1.263*** (0.206)	0.759** (0.306)	0.702*** (0.245)
ln(Distance)	-0.915*** (0.317)	-0.904** (0.345)	-1.039*** (0.365)	-1.025*** (0.318)
Expropriation risk	2.318* (1.231)	2.349** (1.178)	2.144* (1.193)	2.130** (1.039)
Oil exporter dummy	0.918 (0.729)	1.149* (0.602)	0.606 (0.688)	0.755 (0.525)
Constant	-24.756*** (3.977)	-25.021*** (4.355)	-6.505 (4.071)	-6.564 (4.115)
obs	78	78	78	78
R²	0.776	0.767	0.800	0.795

Notes: Heteroscedasticity-consistent standard errors in parentheses. *(10%), **(5%), ***(1%). Countries with higher values of $\beta_{mi}$ are less risky. Similarly, higher values of the expropriation risk variable imply lower expropriation risk.

4.2 Portfolio Diversification and Total Stock of Foreign Investment

In this section I explore the role of portfolio diversification using (i) the entire stock of FDI in the recipient countries, and (ii) the stock of total foreign investment that includes FDI as well as portfolio investment (PO). The data is adjusted for valuation effects (see Lane and Milesi-Ferretti, 2009).

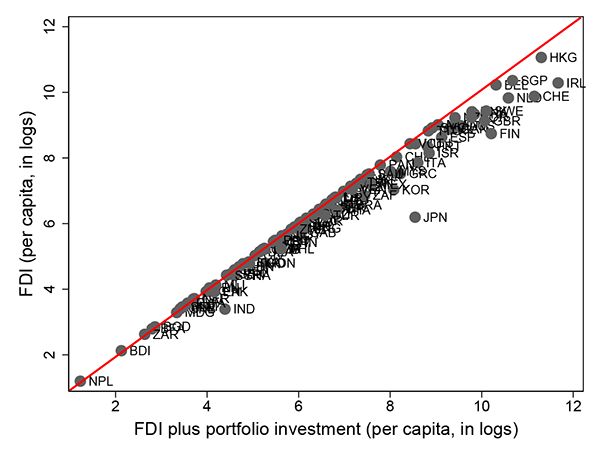
The scatter plot of FDI versus total foreign investment shows that FDI is the main component of total foreign investment for the majority of countries. Portfolio investment constitutes a significant share of total foreign investment only for the high-income countries (see Figure 4). The summary statistics in Table 3 confirm this fact. Therefore, in the cross-section the majority of variation in foreign investment is explained by the variation in FDI rather than portfolio investment.

Figure 4: FDI Versus FDI Plus Portfolio Investment (Average 1995-2007)

Figure 4: Figure 4 is a scatter plot of 96 individual countries' stock of foreign direct investment per capita (in logs) as an average over the period 1995-2007 and the stock of total foreign investment per capita (in logs) as an average over the period 1995-2007. Total foreign investment is defined as foreign direct investment plus portfolio investment. Both axes range from 1 to 12. The Figure also shows a 45 degree line. Overall, the stock of foreign direct investment and the stock of total investment line up closely on the 45 degree line. Only for the high-income countries in the sample the two measures do not line up closely on the 45 degree line as portfolio investment constitutes a significant share of total foreign investment in these countries.

Using this new database I again find evidence that the international investors take into account diversification opportunities in their allocation decisions. Figure 5 shows that foreign investment across countries is positively associated with my covariance risk measure, $\beta_{mi}$ . By construction countries with higher values $\beta_{mi}$ are less risky since their growth rates are more positively correlated with the investor's stochastic discount factor. In the Figure countries are sorted either by the stock of FDI per capita or by the total stock of foreign investment and are then grouped into quartiles. The vertical axis shows the average $\beta_{mi}$ , while the horizontal axis of each graph shows either the average per capita FDI or the average per capita total foreign investment.

In addition, in Table 4 I use simple bivariate cross-sectional regressions to show that the correlation between covariance risk and foreign investment is statistically significant. The relation between $\beta_{mi}$ and foreign investment is preserved if the sample includes only low- and middle-income countries. The results also confirm the evidence from Figure 5 that for low- and middle-income countries the majority of foreign investment is explained by FDI rather than portfolio investment.

Table 3: Share of FDI in Total Foreign Investment: FDI/(FDI+PO) (Mean 1995-2007)

	Obs.	Mean	Median	St.Dev.
Low-income countries	34	0.933	0.989	0.131
Middle-income countries	29	0.864	0.920	0.141
High-income countries	30	0.633	0.611	0.236

Figure 5: Foreign Investment Versus Covariance Risk $\beta_{mi}$

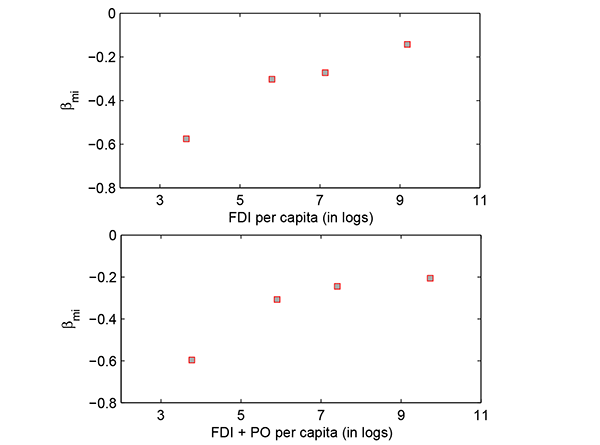
Figure 5: In the top panel of Figure 5 countries are sorted by their stock of FDI per capita (in logs) and are then grouped in quartiles. The panel plots the average stock of FDI per capita (in logs) for the quartiles (horizontal axis) and the average covariance risk measure,β_mi, for the quartiles (vertical axis). The horizontal axis ranges from 0 to positive 11, the vertical axis ranges from negative 0.8 to zero. The plot shows a positive correlation between FDI per capita and the covariance risk measure,β_mi. In the bottom panel of Figure 5 countries are sorted by their stock of total foreign investment per capita (in logs) and are then grouped in quartiles. Total foreign investment is defined as foreign direct investment plus portfolio investment. The panel plots the average stock of total foreign investment per capita (in logs) for the quartiles (horizontal axis) and the average covariance risk measure,β_mi, for the quartiles (vertical axis). The horizontal axis ranges from 0 to positive 11, the vertical axis ranges from negative 0.8 to zero. The plot shows a positive correlation between total foreign investment per capita and the covariance risk measure,β_mi.

Table 4: Impact of Covariance Risk on the Total Stock of Foreign Investment

	Right-hand side variables: Constant	Right-hand side variables: Covariance risk $\beta_{mi}$	R²	obs
A. Full sample: Regressions with FDI	6.96 (0.26)	1.16 (0.30)	0.104	90
A. Full sample: Regressions with FDI + PO	7.24 (0.28)	1.24 (0.32)	0.100	90
B. Low and middle-income countries: Regressions with FDI	5.67 (0.22)	0.61 (0.23)	0.069	61
B. Low and middle-income countries: Regressions with FDI + PO	5.81 (0.23)	0.63 (0.23)	0.071	61

Notes. Dependent variable: in log per capita.
Heteroscedasticity-consistent standard errors in parentheses.

4.2.1 Controlling for Traditional Determinants of Foreign Investment

Next, I show that my key empirical finding on the role of portfolio diversification, captured by my covariance risk measure, is preserved if I control for the country-specific characteristics described in the previous Section. For the regressions where the dependent variable is total foreign investment I include dummies for the high-income countries in the sample to account for the fact that portfolio investment constitutes a significant share of foreign investment only for these countries.

The results show a strong and significant relation between my measure of covariance risk and foreign investment, measured either by per capita FDI or per capita total foreign investment that includes portfolio investment. Countries that are perceived as more risky, i.e. countries with lower values of the covariance risk measure, receive lower levels of per capita foreign investment.

This relationship is not only statistically significant, but has economic significance as well. The 25th percentile value for the $\beta_{mi}$ in the sample is -0.69, while the 75th percentile value is 0.02. The point estimates for the coefficient associated with $\beta_{mi}$ suggest that the cross-sectional regression predicts that if a country's covariance risk declines from the 25th percentile to the 75th percentile, on average total foreign investment per capita increases by more than 165 percent. The estimated increase for FDI per capita is 135 percent. Also, the role of the control variables is preserved: the coefficient on the expropriation risk variable is positive and significant for all specifications, openness to trade, infrastructure availability, and the size of the domestic market, have a positive and significant effect on total foreign investment. The results do not change if the size of the domestic market is measured by the countries' population instead of the level of their GDP.

Table 5: Impact of Covariance Risk on the Total Stock of Foreign Investment After Controlling for Country-Specific Factors

	FDI: OLS	FDI: MLE	FDI + Portfolio investment: OLS	FDI + Portfolio investment: MLE
Covariance risk (β_mi)	0.420** (0.203)	0.461** (0.230)	0.431** (0.204)	0.489** (0.248)
GDP growth	-0.087 (0.047)	-0.067 (0.051)	-0.062 (0.047)	-0.062 (0.057)
ln(GDP)	-0.067 (0.067)	-0.079 (0.065)	0.023 (0.068)	0.023 (0.072)
Trade/GDP	0.010*** (0.003)	0.009*** (0.002)	0.009*** (0.003)	0.009*** (0.002)
ln(1 + Phones)	1.211*** (0.157)	1.234*** (0.122)	0.947*** (0.184)	0.938*** (0.160)
Expropriation risk	1.726*** (0.599)	1.540*** (0.577)	1.469*** (0.577)	1.460*** (0.651)
Oil exporter dummy	0.985*** (0.307)	0.972*** (0.277)	0.826*** (0.275)	0.851*** (0.307)
High-income country dummy			1.242*** (0.297)	1.248*** (0.338)
Constant	1.254 (1.984)	1.941 (1.888)	0.140 (1.901)	0.182 (2.106)
obs	80	80	80	80
R²	0.882	0.893	0.890	0.889

Notes. Dependent variable: in log per capita; *(10%), **(5%), ***(1%).
Heteroscedasticity-consistent standard errors in parentheses.

5 Concluding Remarks

In this paper I explore the role of diversification in the cross-sectional distribution of total foreign investment, which includes FDI as well as portfolio investment. To do so I extend the existing analyses of the determinants of foreign investment by adopting a portfolio allocation approach to risk. I capture the portfolio diversification motive by a measure of country-specific riskiness, which I refer to as "covariance risk". I construct this measure as how countries' growth rates covary with the stochastic discount factor of a representative international investor. I develop a general empirical specification that highlights the role of diversification but allows for host country specific characteristics to also influence portfolio allocations. My key new result is that the diversification motive, captured by my covariance risk measure, has statistical as well as strong economic significance. Therefore, I find empirical evidence that international investors take into account diversification opportunities in their investment allocation decisions, which confirms the predictions of standard portfolio allocation models.

References

Alfaro, L., 2003. Foreign Direct Investment and Growth: Does the Sector Matter? Unpublished. Harvard Business School.

Asiedu, E., 2002. On the Determinants of Foreign Direct Investment to Developing Countries: Is Africa Different? World Development, 30(1), 107-119.

Asiedu E., Jin, Y., and Nandwa, B., 2009. Does foreign aid mitigate the adverse effect of expropriation risk on foreign direct investment? Journal of International Economics.

Benigno, P. and Nisticò, S., 2009. International Portfolio Allocation under Model Uncertainty. NBER Working Paper No. 14734

Blonigen, B., 2005. A Review of the Empirical Literature on FDI Determinants. NBER Working Paper No. 11299.

Borga, M. and R. J. Mataloni, Jr., 2001. Direct Investment Positions for 2000: Country and Industry Detail. Technical Note. Survey of Current Business 81 (July 2001): 23–25.

Brainard, S.L., 1993. A simple theory of multinational corporations and trade within a trade-off between proximity and concentration. NBER Working Paper No. 4269.

Brainard, S.L., 1997. An empirical assessment of the proximity-concentration trade-off between multinational sales and trade. Am. Econ. Rev. 87, 520–544.

Burnside, C. and Tabova, A., 2009. Risk, Volatility, and the Global Cross-Section of Growth Rates. NBER Working Paper 15225.

Carroll, R., Ruppert, D., Stephanski, L. and Crainiceanu, C., 2006. Measurement error in nonlinear models: a modern perspective. Second Edition, Chapman & Hall/CRC.

Coeurdacier, N., 2009. Do trade costs in goods market lead to home bias in equities? Journal of International Economics 77 (2009) 86-100.

Coeurdacier, N. and Guibaud, S., 2008. A Dynamic Equilibrium Model of Imperfectly Integrated Financial Markets. Working Paper, London Business School.

Coeurdacier, N. and Guibaud, S., 2010. International Portfolio Diversification Is Better Than You Think. Journal of International Money and Finance, forthcoming

Coeurdacier, N., Kollmann, R. and Martin, P., 2010. International Portfolios, Capital Accumulation and Foreign Asset Dynamics. Journal Of International Economics 80 (2010) 100-112.

Eaton, J. and Gersovitz, M., 1984. A Theory of Expropriation and Deviations from Perfect Capital Mobility. The Economic Journal 94, 16-40.

Fama, E. and James D. MacBeth, J., 1973. Risk, Return, and Equilibrium: Empirical Tests. Journal of Political Economy 81(3, May-Jun.), 607-36.

Ferri, G., 2004. More analysts, better ratings: do rating agencies invest enough in less developed countries? Journal of Applied Economics 12, 77–98.

Fuller, W. (1987). Measurement error models. John Wiley $\&$ Sons.

Gourinchas, P. and O. Jeanne. Capital Flows to Developing Countries: The Allocation Puzzle. NBER Working Paper 2009.

Harms, P., Lutz, M., 2006. Aid, governance and private foreign investment: some puzzling findings for the 1990s. The Economic Journal 116, 773–790.

Hausmann, R. and Fernandez-Arias, E., 2001. Foreign Direct Investment: Good Cholesterol? In Foreign Direct Investment Versus Other Flows to Latin America. Development Center Seminars, OECD.

Hines, J., 1995. Forbidden payment: Foreign bribery and American business after 1977. NBER Working Paper no. 5266. Cambridge, Mass.: National Bureau of Economic Research, September.

Hnatkovska, V., 2010. Home Bias and High Turnover: Dynamic Portfolio Choice with Incomplete Markets. Journal of International Economics 80 (1), 2010.

Ibarra, M. and Koncz, J., 2008. Direct Investment Positions for 2008: Country and Industry Detail. Survey of Current Business (July 2008), 20-34.

Kaufmann, D., Kraay, A. and Mastruzzi, M., 2009. Governance matters VIII: Aggregate and Individual Governance Indicators, 1996–2008. Policy Research Working Paper 4978, World Bank.

Kim, D. (1995). The errors in the variables problem in the cross-section of expected stock returns. Journal of Finance, 50(5).

Klenow, P. and Andrés Rodríguez-Clare, 1997. The Neoclassical Revival in Growth Economics: Has it Gone too Far? NBER Macroeconomics Annual 1997. Cambridge, MA: MIT Press.

Kraay, A., Loayza, N., Serven, L., Ventura, J. (2005). Country Portfolios. Journal of the European Economic Association. 3 (4): 914-945.

Lane, P.R. and Milesi-Ferretti, G.M., 2000. External Capital Structure: Theory and Evidence. IMF Working Paper 152.

Lane, P.R. and G.M. Milesi-Ferretti (2006). The External Wealth of Nations Mark II: Revised and Extended Estimates of Foreign Assets and Liabilities, 1970-2004. IMF Working Paper, March 2006.

Lane, P.R. and G.M. Milesi-Ferretti (2008). International Investment Patterns. The Review of Economics and Statistics, August 2008, 90(3): 538-549.

Loree, D., Guisinger, S., 1995. Policy and non-Policy Determinants of U.S. Foreign Direct Investment. Journal of International Business Studies 26(2), 281-299.

Lucas, R., 1990. Why Doesn't Capital Flow from Rich to Poor Countries? American Economic Review 80(2), 92-96.

Merton, R. (1969). Lifetime Portfolio Selection under Uncertainty: The Continuous-Time Case. The Review of Economics and Statistics, Vol. 51, No. 3, 247-257.

Merton, R. (1971). Optimum Consumption and Portfolio Rules in a Continuous-Time Model. Journal of Economic Theory 3, 373-413

Merton, R. (1990). Continuous-Time Finance. Basil Blackwell, Cambridge.

Pinheiro-Alves, R., 2008. Behavioural Determinants of Foreign Direct Investment. MPRA Paper No. 10297.

Political Risk Services, 2009. International Country Risk Guide. NY.

Samuelson, P.A., 1969. Lifetime Portfolio Selection by Dynamic Stochastic Programming. Review of Economics and Statistics 51, August: 239-46.

Van Nieuwerburgh, S. and Veldkamp, L., 2007. Information Immobility and the Home Bias Puzzle. Working Paper, New York University.

Wei, S.J., 2000. How taxing is corruption on international investors? Review of Economics and Statistics 82 (1): 1–11.

Woodridge, J.M., 2002. Econometric Analysis of Cross Section and Panel Data. MIT Press, Cambridge, Massachusetts.

World Bank, 2009. World Development Indicators, Washington, D.C.

A Appendix: Control Variables and Country List

Table 6: Descriptive Statistics

Variable	Mean	St.Dev.	Min	Max
ln(FDI^US per capita)	4.08	3.05	-3.44	9.25
ln(FDI per capita)	6.45	2.19	-1.20	10.87
ln((FDI + PO) per capita)	6.72	2.36	-1.20	11.36
Covariance risk	-0.33	0.56	-1.98	1.16
GDP growth (%)	2.27	1.56	-1.68	8.05
ln(GDP)	24.49	1.97	19.90	28.02
ln(Population)	16.55	1.56	12.56	20.96
Trade/GDP (%)	40.85	31.00	10.50	218.7
ln(Phones)	21.95	22.12	0.03	69.27
ln(Distance)	8.90	0.57	6.31	9.69
Expropriation risk	8.09	1.66	4.08	10.64

Table 7: Correlation Matrix of the Independent Variables

	Inv. risk	>Growth	ln(GDP)	Trade/GDP	ln(Phones)	ln(Distance)
Covariance risk	1.000
GDP growth	0.057	1.000
ln(GDP)	0.149	0.344	1.000
Trade/GDP	0.135	0.116	-0.007	1.000
ln(Phones)	0.312	0.189	0.563	0.320	1.000
ln(Distance)	-0.178	0.003	-0.041	0.089	-0.263	1.000<
Expropriation risk	0.326	0.287	0.344	0.374	0.713	-0.251

Institutional Variables

In the empirical analysis I use an expropriation risk variable that specifically measures the risk of expropriation or arbitrary contract modifications. The table below shows that the expropriation risk variable and three empirical indicators (Source: Kaufmann et al., 2009) that capture different dimensions of institutional quality (political stability, rule of law and control of corruption) are very highly correlated. Therefore, expropriation risk can be interpreted more broadly as a measure of public governance, which can include bureaucratic corruption, deviations from rule of law, arbitrary government regulations.

Table 8: Institutional Variables: Correlation Matrix

	Expropriation risk	Political stability	Rule of law	Control of corruption
Expropriation risk	1.00	0.81	0.84	0.85
Political stability	0.81	1.00	0.89	0.85
Rule of law	0.84	0.89	1.00	0.97
Control of corruption	0.85	0.85	0.97	1.00

Country List for Multivariate Regressions:

Algeria, Argentina, Australia, Austria, Belgium, Burkina Faso, Bangladesh, Bahamas*, Brazil, Botswana, Canada, Chile, China, Cote d'Ivoire, Cameroon, Rep. of Congo, Colombia, Costa Rica, Denmark, Dominican Republic, Ecuador, Egypt, Finland, France, Gabon, United Kingdom, Ghana, Gambia, Greece, Guatemala, Hong Kong, Honduras, Hungary, India, Indonesia, Ireland, Iran, Island, Israel, Italy, Jamaica, Kenya, Korea, Luxembourg*, Malaysia, Morocco, Madagascar, Mexico, Mali, Malta, Malawi, Niger, Nigeria, the Netherlands, Norway, New Zealand, Pakistan, Panama*, Peru, Philippines, Papua New Guinea, Portugal, Sudan, Senegal, Sierra Leone, Singapore, South Africa, Spain, Sri Lanka, Sweden, Switzerland, Syria, Togo, Thailand, Trinidad and Tobago, Tunisia, Turkey, Venezuela, Zambia, Zimbabwe.

B Appendix: MLE Estimation With a Generated Regressor

The model I estimate is:

$\displaystyle Y = \gamma_0 + \gamma_1 \, \hat{\beta}_{mi} + \mathbf{Z} \, \mathbf{\Gamma_2} + \epsilon_i$

where $\mathbf{Z}$ is the vector of control variables measured without error, and $\mathbf{\Gamma_2}$ is the coefficient vector associated with the control variables. Let the measurement error of the generated regressor be :

$\displaystyle \hat{\beta}_{mi} \, = \, \beta_{mi} \, + \, u_i$

where the covariance risk variable $\beta_{mi}$ is the true variable, while $\hat{\beta}_{mi}$ is the estimated or observed variable. The idea behind the adjusted estimator is to choose $(\gamma_0,\gamma_1)$ to minimize the quadratic form $\eta'\Omega^{-1}\eta$ where:

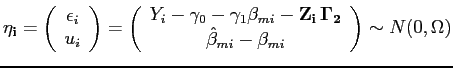
$\displaystyle \mathbf{\eta_i} = \left( \begin{array}{c} \epsilon_i \ u_i \end{array} \right)= \left( \begin{array}{c} Y_i - \gamma_0 - \gamma_1 \beta_{mi} - \mathbf{Z_i} \, \mathbf{\Gamma_2} \ \hat{\beta}_{mi} - \beta_{mi} \end{array} \right) \sim N(0,\Omega)$

$\displaystyle \mathbf{\Omega} = \left[ \begin{array}{cc} \Sigma_{\epsilon} & 0 \ 0 & \Sigma_{u} \end{array} \right]$

where $\Sigma_{\epsilon}$ is the covariance matrix of the residuals from the cross-sectional regression regression; and $\Sigma_{u}$ is the covariance matrix of the measurement error in $\hat{\beta}_{mi}$ .

The MLE is a function of $\delta$ : the relative magnitude of the error variances of Y and $\hat{\beta}_{mi}$ . Without additional information about the error terms, $\epsilon$ and , the MLE of the unknown parameter vector that minimizes the likelihood function does not exist. Fuller (1987) assumes the relative magnitude of the error variances is known, while Kim (1995) derives it for the two-pass estimation of expected returns. Since in my case the relative variance is neither known nor can be easily derived from the model, I get $\Sigma_u$ and $\Sigma_{\epsilon}$ using a bootstrap procedure and set $\delta$ equal to the median of the diagonal of $\Sigma^{-1}_u \Sigma_{\epsilon}$ . In what follows I use the simulated relative variances and apply the correction proposed Kim (1995). The MLE of $\gamma_1$ , $\mathbf{\Gamma_2}$ , and $\gamma_0$ are given by:

$\displaystyle \hat{\gamma}_1 = \frac{S + \Big[S^2 + 4\delta\Big(m_{Y \hat{\beta}_{mi}}-\mathbf{M}'_{\hat{\beta}_{mi}\mathbf{Z}} \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}_{Y\mathbf{Z}}\Big)^2 \Big]^{1/2}}{2\Big(m_{Y \hat{\beta}_{mi}}-\mathbf{M}'_{\hat{\beta}_{mi}\mathbf{Z}} \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}_{Y\mathbf{Z}}\Big)}$

$\displaystyle \mathbf{\hat{\Gamma}_2} = \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}'_{Y\mathbf{Z}} - \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}'_{\hat{\beta}_{mi}\mathbf{Z}}\hat{\gamma}_1$

$\displaystyle \hat{\gamma}_0 = E[Y]-\hat{\gamma}_1 \, E[\hat{\beta}_{mi}] - E[\mathbf{Z}]\, \mathbf{\hat{\Gamma}_2}$

where:

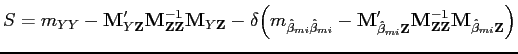
$\displaystyle S = m_{YY}-\mathbf{M}'_{Y\mathbf{Z}} \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}_{Y\mathbf{Z}} - \delta\Big(m_{\hat{\beta}_{mi} \hat{\beta}_{mi}}-\mathbf{M}'_{\hat{\beta}_{mi}\mathbf{Z}} \mathbf{M}^{-1}_{\mathbf{Z}\mathbf{Z}}\mathbf{M}_{\hat{\beta}_{mi}\mathbf{Z}}\Big)$

and $m_{xy}$ and $\mathbf{M}_{xy}$ are the second co-moment between variables and (the boldface represents a vector or a matrix). Let $\mathbf{\hat{\Gamma}}=(\gamma_0,\gamma_1,\mathbf{\Gamma_2})$ , then Kim (1995) shows that the asymptotic distribution of $\mathbf{\hat{\Gamma}}$ is given by:

$\displaystyle \sqrt{N}(\mathbf{\hat{\Gamma}} - \mathbf{\Gamma}) \rightarrow N(\mathbf{0},\mathbf{\Sigma}_{\mathbf{\hat{\Gamma}}})$

$\displaystyle \mathbf{\Sigma}_{\mathbf{\hat{\Gamma}}} = \left[ \begin{array}{ccc} (1+\mathbf{\mu}'_z \Sigma^{-1}_{zz}\mathbf{\mu}_z)\sigma^2_w + \phi^2 \sigma^2_{\hat{\gamma}_1} & -\phi \sigma^2_{\hat{\gamma}_1} & -\sigma^2_w \Sigma^{-1}_{zz}\mathbf{\mu}_z + \phi\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\sigma^2_{\hat{\gamma}_1}\\ [10pt] -\phi \sigma^2_{\hat{\gamma}_1} & \sigma^2_{\hat{\gamma}_1} & - \Sigma'_{\beta_{mi}z} \Sigma^{-1}_{zz}\sigma^2_{\hat{\gamma}_1} \\ [10pt] -\sigma^2_w \Sigma^{-1}_{zz}\mathbf{\mu}_z + \phi\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\sigma^2_{\hat{\gamma}_1} & -\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\sigma^2_{\hat{\gamma}_1} & \sigma^2_w \Sigma^{-1}_{zz} + \Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z}\Sigma'_{\beta_{mi}z}\Sigma^{-1}_{zz} \sigma^2_{\hat{\gamma}_1} \end{array} \right],$

$\displaystyle \sigma^2_{\hat{\gamma}_1}\equiv Var(\hat{\gamma}_1)=(\sigma^2_{\beta_{mi}}-\Sigma'_{\beta_{mi}z}\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z})^{-2}[(\sigma^2_{\beta_{mi}}-\Sigma'_{\beta_{mi}z}\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z})\sigma^2_w +\delta\sigma^2_{u}],$

$\displaystyle \sigma^2_w = (\delta+\gamma^2_1)\sigma^2_{u}, \qquad \phi = \mu_{\beta_{mi}} - \mathbf{\mu}'_z\Sigma^{-1}_{zz}\Sigma_{\beta_{mi}z},$

$\displaystyle \textrm{and} \qquad (\mu_{\beta_{mi}}, \mathbf{\mu}_z) \qquad \textrm{and} \qquad \left[ \begin{array}{cc} \sigma^2_{\beta_{mi}} & \Sigma'_{\beta_{mi}z} \ \Sigma_{\beta_{mi}z} & \Sigma_{zz} \end{array} \right]$

are the mean vector and variance matrix of $\beta_{mi}$ and explanatory variables $\mathbf{Z}$ . The variance matrix, $\Sigma_{\hat{\Gamma}}$ is estimated by replacing the unknown parameters with their sample estimates:

$\displaystyle \hat{\sigma}^2_{\beta_{mi}} = (2\delta)^{-1}\{[S^2 + 4\delta(m_{y \hat{\beta}_{mi}}-\mathbf{M}'_{\hat{\beta}_{mi}z} \mathbf{M}^{-1}_{zz}\mathbf{M}_{yz})^2]^{1/2} - S \}$

$\displaystyle \hat{\sigma}^2_{u} = (2\delta)^{-1}\{ \bar{S} - [S^2 + 4\delta(\mu_{y\hat{\beta}_{mi}} - M'_{\hat{\beta}_{mi}z}M^{-1}_{zz}M_{yz})^2]^{1/2}\}$

where:

$\displaystyle \bar{S} = S + 2\delta( \sigma^2_{\hat{\beta}_{mi}} - M'_{\hat{\beta}_{mi}z}M^{-1}_{zz}M_{yz})$

Footnotes

** Staff economist in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 USA. E-mail: alexandra.m.tabova@frb.gov. This paper is based on a chapter of my PhD dissertation. I thank Craig Burnside for guidance and valuable advice; Barbara Rossi, Pietro Peretto, Gian Maria Milesi-Ferretti, Daniele Terlizzese and participants at Duke University seminars, MOOD 10th Doctoral Workshop in Economic Theory and Econometrics, IMF Research Seminar, Board of Governors IF seminar, and 2011 SEA meetings for helpful comments. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1. The Poisson process is a continuous-time process which allows discrete (i.e. discontinuous) changes in the variables. Return to text

2. In their seminal paper, Eaton and Gersovitz (1984) the decision of expropriation is determined by the binding expropriation constraint that states that the host country's discounted income if expropriation occurs equals the host country's discounted income if no expropriation occurs. Return to text

3. See Merton (1990) for proof and discussion of the role of the form of the value function for the solution of the problem. Return to text

4. For utility functions of the form yielding constant relative risk aversion the problem can be solved explicitly. Return to text

5. I consider only interior optimal solutions. If the problem is formulated in the more general Khun-Tucker form the equalities of (4),(5), and (6) will be replaced with inequalities. Return to text

6. Merton (1990) shows that the sample paths of consumption and capital are identical to those generated in the complete markets case. Return to text

7. One might, for example, assume a Cobb-Douglas production technology and measure the marginal product of capital in each country and at each point in time, using assumptions about model parameters and data on output and capital stocks. It is not trivial to measure capital stocks. See, for example, Klenow and Rodriguez-Clare's (1997) analysis of the neoclassical growth model, in which they measure capital stocks by accumulating investment data in the Penn World Tables. However, if rates of return are inclusive of adjustment costs, further assumptions about functional forms need to be made. Measuring returns to investment in human capital would be even more difficult. Return to text

8. The covariances are time-series statistics. In standard stochastic growth models rates of return and growth rates of GDP are highly correlated in the time series dimension because changes in technology and labor inputs (as opposed to the slow-moving changes in capital inputs) drive the comovements. Improvements in technology and increases in labor inputs due to other shocks increase growth and the marginal product of capital, and, hence, the rate of return to investments in capital. Hence, at a minimum, the sign of $\textrm{cov}(R_{i},\hat{m})$ will be the same as the sign of $\textrm{cov}(g_{i},\hat{m})$ . Return to text

9. It is customary in the empirical literature on FDI to smooth out cyclical fluctuations by averaging the dependent and independent variables. See Harms and Lutz (2006), Asiedu et al. (2009) among others. Return to text

10. A holding company is a company whose primary activity is holding the securities or financial assets of other companies. Return to text

11. Hausmann and Fernandez-Arias (2001); Asiedu et al. (2002, 2009) among others. Return to text

12. See International country risk guide (2007). Return to text

13. The consensus in the empirical literature is that expropriation risk has a negative effect on FDI (see Loree and Guisinger (1995), Asiedu et al. (2009) among others). Return to text

14. Some empirical studies use GDP per capita as a proxy for development. Since the number of phones is highly correlated with GDP per capita (correlation coefficient 0.91) and can be used as a proxy for availability of infrastructure in the host country (see Asiedu et al., 2009), it is an appropriate control variable for this study. Return to text

15. Distance is usually featured in gravity models that are widely used in empirical international economics, most commonly in trade studies. A number of studies, however, have shown that the gravity model also has explanatory power when applied to FDI. Brainard (1993, 1997) provides a theoretical model for gravity-like forces for FDI analyses. Return to text

16. This is in the case of classical attenuation bias (see Wooldridge 2001), assuming that measurement errors are orthogonal to the other variables of interest. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text