A Model of Slow Recoveries from Financial Crises¹

Albert Queralto²

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper documents highly persistent effects of financial crises on output, labor productivity and employment in a sample of emerging economies. To address these facts, it introduces a quantitative macroeconomic model that includes endogenous TFP growth through firm creation. Firm creators obtain funding from a financial intermediation sector which is subject to frictions. These frictions become especially severe in a financial crisis, increasing the cost of credit for firm creators and thereby lowering the growth rate of aggregate TFP. As a consequence, the model produces medium-run dynamics following crises that are in line with the data.

Keywords: Business cycles, financial crises, total factor productivity

JEL classification: E32, E44, F41, O33

1 Introduction

A stylized fact of financial crises, consistent with the recent experience in the advanced economies, is that their aftermath tends to be characterized by a slow recovery. Numerous researchers have documented highly persistent output losses following financial crises using a variety of different approaches.³

In this paper, I first complement the existing evidence by documenting persistent effects of financial crises in a sample of emerging market economies, using a methodology similar to Cerra and Saxena (2008). I also decompose the effects on output into movements in labor productivity and employment. The analysis reveals that losses in output, labor productivity and employment during the crisis are not reversed. Moreover, I find that a substantial portion of the medium-run output decline is due to a fall in labor productivity: of the 11 percent medium-run output loss, labor productivity accounts for over 6 percent of it, with the remaining loss explained by decreases in employment.

The main goal of this paper is then to develop a quantitative model to address the empirical results on the effects of financial crises. Guided by the evidence, I introduce two key modifications to a relatively standard neoclassical economy, the backbone of modern quantitative macroeconomic frameworks. First, I explicitly model the process of firm creation as a source of endogenous medium-run productivity growth. Second, I introduce financial intermediaries (banks, for short) that obtain funds from savers and channel them to entrepreneurs, who are the agents with the ability to create new firms. Because of an agency problem between banks and their creditors, there may be frictions in the process of transferring funds from savers to entrepreneurs. These frictions become especially severe in a financial crisis.⁴

The model features sustained TFP growth that arises due to an endogenously expanding variety of intermediates, as in Romer (1990). There is an unbounded mass of entrepreneurs in the model economy, each with an "idea" for a new firm or variety but lacking the funds to finance the startup costs of their project. To obtain the necessary funds, entrepreneurs borrow from banks. Once an entrepreneur pays the initial entry cost, his project follows a simple life-cycle pattern whereby it can either fail or successfully become a new variety according to an exogenously given probability.

To provide funding to entrepreneurs, banks borrow from both domestic households and international creditors. I assume that banks are efficient at monitoring entrepreneurial projects, so that the relationship between banks and entrepreneurs is frictionless: entrepreneurs can offer the bank perfectly state-contingent equity in exchange for funds. On the other hand, the bank faces frictions in the process of obtaining funds from creditors. As in Gertler and Karadi (2011) and others,⁵ I model these frictions through a simple limited enforcement problem: after borrowing funds, the bank can renege on its debt and divert a certain fraction of resources for its own personal gain, at which point creditors can force it into bankruptcy. The limited enforcement friction effectively introduces an endogenous constraint on the bank's lending that may tighten as economic conditions worsen.

An important determinant of the degree of financial constraints is the state of banks' balance sheets, summarized by their net worth. The primary source of fluctuations in banks' net worth is the movement in the prices of the assets on their balance sheets. These assets consist of claims on fully successful firms (interpretable as mature or old firms) as well as projects that have not yet successfully turned into a new variety (interpretable as young startups or products in development). In the model, the presence of the latter type of assets introduces a source of adverse feedback between the price of the equity issued by entrepreneurs and banks' net worth, which acts as an important amplification mechanism. In particular, a decline in bank net worth forces banks to cut back on project funding. This lowers the price at which new entrepreneurs can sell equity, and at the same time lowers the franchise value of projects that have already been created but have not yet been successful.⁶ Since the asset side of banks' balance sheets includes the latter, a decline in their price leads to further drops in banks' net worth.

I embed these two features, endogenous growth through firm creation and frictional financial intermediation, into a conventional small open economy model that is modified to allow for variable capital utilization, habit formation in consumption and a need for working capital of intermediate goods producers. These modifications are standard in the emerging market business cycles literature. Although not critical for obtaining the main results on the persistent effects of financial crises -which arise due to the novel mechanism linking firm creation with financial frictions- these features help enhance the quantitative properties of the model at little cost of added complexity.

After describing the model, I turn to presenting a quantitative analysis of a financial crisis experiment. The analysis is designed to explore the model's ability to account for the evidence described in Section 2. The crisis is modeled as the simultaneous occurrence of two exogenous shocks: an increase in the country interest rate, to represent a sudden stop in capital inflows, and a direct disruption of domestic capital markets, to capture a corresponding loss of confidence in the domestic banking sector. The main result is that the baseline model is successful at qualitatively and quantitatively capturing the empirical behavior of output, labor productivity and employment. Endogenous TFP growth is critical for the model to generate the high persistence observed in the data: it allows a crisis shock to induce a slowdown in the growth rate of TFP, leading to lasting effects on productivity, employment and output. In addition, I show that financial factors play a crucial role in generating this persistence - in the baseline calibrated model, close to half of the medium run output decline is explained by the financial side of the model. In summary, through the mechanisms described above the model can closely replicate the medium-run movements in output, labor productivity and employment identified in the data.

The modeling approach in this paper combines elements of the literature on endogenous growth through an expanding variety of products, due to Romer (1990), with ideas from the literature on financial factors in macroeconomics, pioneered by Bernanke and Gertler (1989) and Kiyotaki and Moore (1997). A more recent literature has incorporated mechanisms in the spirit of Romer (1990) within quantitative macroeconomic frameworks- notably Comin and Gertler (2006), who propose a model to study medium-term cycles in the U.S.,⁷ or Bilbiie, Ghironi and Melitz (2012), who analyze producer entry over the business cycle. Likewise, financial market frictions were first incorporated within a macroeconomic model by Bernanke, Gertler and Gilchrist (1999). The latest incarnation of this class of models, which this paper follows most closely, focuses on financial intermediaries, as in Gertler and Karadi (2011) and others. This paper puts together ideas from both literatures by studying a quantitative model where financing frictions affect the creation of new firms.

The evidence and the model presented here are related to Aguiar and Gopinath (2007), who argue that a distinctive feature of emerging market business cycles is large movements in trend TFP growth, while developed economies are better characterized by transitory fluctuations around the trend. The evidence in this paper shows that financial crises are an example of such nonstationary behavior. Further, the model in this paper provides a foundation for the type of TFP process that Aguiar and Gopinath (2007) take as exogenous, and connects it explicitly with financial market imperfections.

Finally, this paper is also related to a large and growing literature that proposes quantitative macroeconomic models for emerging market economies, including Uribe and Yue (2006), Neumeyer and Perri (2005) or Mendoza (2010). A related branch of this literature has proposed quantitative frameworks to account for aspects of emerging markets financial crises, like Gertler, Gilchrist and Natalucci (2007) or Mendoza and Yue (2012). Some of these frameworks, as well as several others,⁸offer explanations for the observed decline in TFP during financial crises, including declines in capacity utilization, sectoral reallocation, and disruption in trade of imported inputs. While I view the mechanism in this paper as complementary to theirs, there is a key difference based on my focus on accounting for the medium-run TFP decline and its role in generating a slow recovery.

The rest of the paper is organized as follows. In Section 2, I present the evidence on the effects of financial crises. In Section 3 I describe the model, and present the simulation results in Section 4. Section 5 concludes.

2 Evidence from Systemic Banking Crises

I now turn to describing the empirical exercise. Figure 1 provides some suggestive evidence: it plots (log) output, labor productivity and employment for a group of Asian countries around the financial crisis of 1997.⁹ The first panel suggests a very persistent output loss following the crisis: output does not recover to the pre-crisis trend (green dashed line), but rather remains permanently below trend in the aftermath of the crisis. From the second and third panels, there is a considerable decline in labor productivity, which is also very persistent, and a more modest slowdown in employment. In particular, labor productivity falls by about 10 percent relative to the pre-crisis trend, and it never rebounds.¹⁰

To provide more formal evidence on the behavior of output, labor productivity and employment following financial crises, I employ an approach similar to Cerra and Saxena (2008), who estimate a univariate autoregressive model for output growth, augmented to include current and lagged values of dummies indicating financial crises and other shocks. I start by decomposing (log) output as the sum of employment and labor productivity ( $n_{i,t}$ and $z_{i,t}$ respectively, in logs):

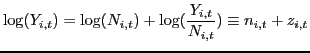
$\displaystyle \log(Y_{i,t}) = \log(N_{i,t}) + \log(\frac{Y_{i,t}}{N_{i,t}}) \equiv n_{i,t} + z_{i,t}$

I then estimate the following bivariate model:

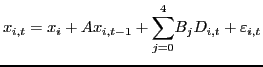$\displaystyle x_{i,t}=x_{i}+Ax_{i,t-1}+ {\displaystyle\sum\limits_{j=0}^{4}} B_{j}D_{i,t}+\varepsilon_{i,t}$

(1)

where $\begin{displaymath}x_{i,t}=\left[ \begin{array}[c]{c} \Delta n_{i,t}\ \Delta z_{i,t} \end{array}\right] \end{displaymath}$ .

The specification is motivated by the assumption that both hours and labor productivity are integrated of order one, so that first-differencing is necessary to achieve stationarity.¹¹ The regressors in (1) include a country fixed effect, one lag of the endogenous vector, and current and lagged values of a dummy variable $D_{i,t}$ indicating the year in which a systemic banking crisis starts in country , year . Lag selection procedures recommend one lag for the endogenous vector. I include four lags for the crisis indicator since coefficients on lags above 4 are insignificant, although results are robust to the inclusion of a larger number of lags of $D_{i,t}$ .

The model in (1) is estimated on a sample of 17 emerging economies. Data for annual real output and employment are obtained from the Total Economy Database. I obtain systemic banking crisis dates from Laeven and Valencia (2012), an updated version of the dates in Caprio and Klingebiel (2003), also used by Cerra and Saxena (2008) among many others.¹²

Figure 2 shows the impulse responses of labor productivity and employment from estimated model (1), as well as the response of output.¹³ For this sample of countries, the response of output is large and highly persistent, consistent with the findings in Cerra and Saxena (2008). Four years after the crisis, the output loss reaches and remains at almost 12 percent. Decomposing output into labor productivity and employment reveals a substantial decline in productivity, which remains at about negative 6 percent after 4 years. From the panel on the right, the drop in employment is slightly more modest in magnitude, and it is also highly persistent. The impulse responses reported in Figure 2 constitute the data moments against which I will evaluate the model presented below.¹⁴

Figure 1: Total output, employment and output per employed worker (logs) for group of 6 South East Asian countries (Indonesia, Malaysia, Phillipines, Korea, Thailand and Hong Kong). Pre-crisis linear trend (green dashed line) computed for the period 1980-1996.

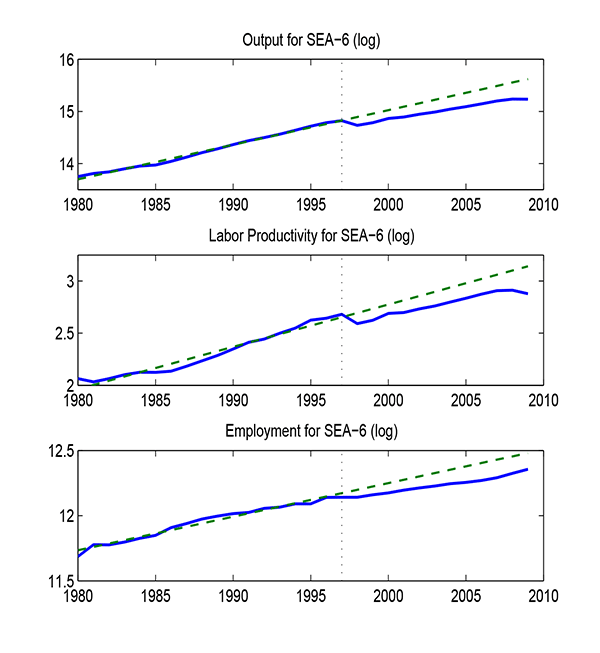
Figure 2: Estimated impulse responses to a banking crisis. The dashed lines indicate 90% confidence bands computed by bootstrapping. Time measured in years. All variables in logs.

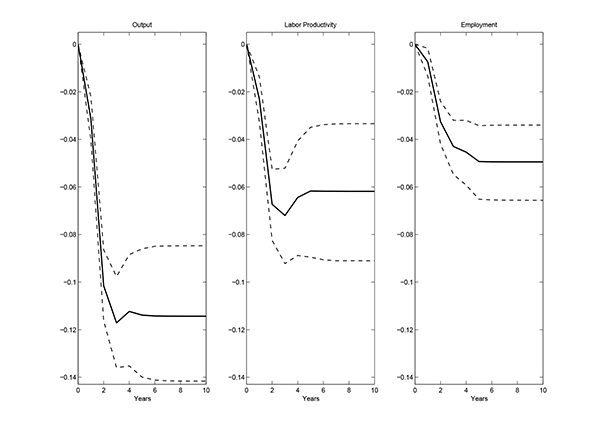
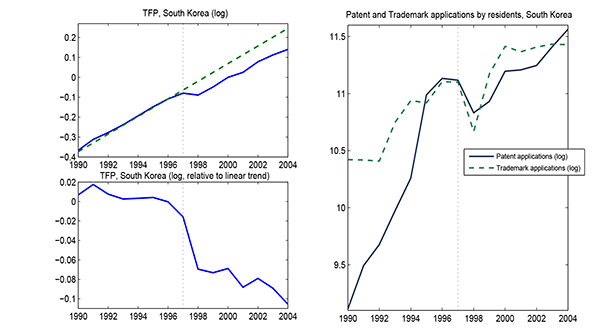
Figure 3 displays time series on TFP and patent and trademark applications by residents in South Korea. As shown in the top left panel, the 1997 financial crisis involved a persistent slowdown in TFP relative to trend. From the bottom left panel, after a moderate slowdown prior to the crisis, in 1997 TFP plunges by about 6% relative to trend. Consistent with the evidence just presented, this decline is never recovered.¹⁵ The right panel shows patent and trademark applications in Korea. After rising for almost two decades practically without interruption, these variables display large declines during the crisis episode - about 25% for patents, and more than 35% in the case of trademarks.

This evidence lends support to the mechanism introduced in this paper, namely that a financial crisis such as the one suffered by South Korea in 1997 may lead to a reduction in the pace at which new firms are created, resulting in a highly persistent effect of the crisis. The mechanism is also supported by empirical studies on the effects of finance on firm creation in the case of the U.S.¹⁶ In turn, the hypothesis that difficult access to external finance hinders innovation and R&D is backed by several firm-level studies.¹⁷ Finally, a number of papers document such effects for developing economies.¹⁸

To summarize, the evidence described above confirms that the large and persistent output declines associated with financial crises in emerging countries is indeed a general phenomenon across episodes and countries. The magnitudes of the declines in productivity uncovered by the exercise are comparable to those found by other studies of emerging market crises.¹⁹ Further, these declines tend to have a very large permanent component. In the following sections I describe and analyze a quantitative model capable of generating drops in TFP, productivity and employment of size and persistence comparable to those in the data.

3 Model

The core framework is a small open economy model with endogenous TFP growth through an expanding variety of intermediates, as in Romer (1990) or Comin and Gertler (2006). The difference with respect to these frameworks is that there is an imperfection in financial markets that impedes the smooth flow of resources from savers (households and international investors) to banks, who finance the introduction of new firms. I introduce three further modifications that have become common in the DSGE literature recently, and that help the model produce a more realistic behavior of macroeconomic aggregates in response to the crisis: variable capital utilization, habit formation in consumption, and a working capital requirement for intermediate goods producers.

Figure 3: TFP, Patents and Trademarks, South Korea (in logs). Trend for TFP computed for the period 1980-1996. Source: TFP from Coe, Helpman and Hoffmaister (2009). Patent and trademark applications from World Development Indicators.

There are six types of agents in the model: households, entrepreneurs, banks, final goods producers, intermediate goods producers and capital producers. Homogeneous output is produced by final output producers using an expanding variety of intermediates. The entrepreneurial sector uses funds borrowed from banks to finance the creation of new firms. In turn, banks obtain financing from domestic households and from foreign capital markets. In what follows, I discuss the behavior of each of these agents in turn, and derive the aggregate relationships that characterize the dynamic path of the economy.

3.2 Households

Suppose there is a representative family with a unit measure of members. Households make decisions on consumption, labor supply, investment in physical capital and saving through a risk-free international bond. There are two types of members within each household: workers and bankers, with measures and respectively. A fraction of the workers are specialized or "skilled" workers, and supply labor inelastically to the entrepreneurial sector. Their role will be clear as I discuss entrepreneurs below. Regular workers supply labor elastically to intermediates producers. Both types of labor return wages to the family. Banks use borrowed funds to make loans to entrepreneurs, and also transfer any earnings from this activity back to the household. There is perfect consumption insurance among family members. As in Gertler and Karadi (2011) and others, this formulation is a simple way of introducing heterogeneity in terms of borrowers and lenders while maintaining the tractability of a representative agent model.

There is random turnover between bankers and workers: a banker becomes a worker with probability $(1-\sigma)$ . At the end of their careers, bankers transfer their net wealth to the family. At the same time, each period a fraction $(1-\sigma)\frac{f}{1-f}$ of workers start a career as bankers, exactly offsetting the number of bankers who exit. As explained below, it is assumed that the family transfers a small amount of resources to bankers who start out so they are able to start operations. Bank exit is introduced as a device to ensure that the financial imperfection will be relevant: otherwise banks might reach a point where internal resources are enough to finance all desired loans to entrepreneurs.

Letting $C_{t}$ denote consumption and $L_{t}$ hours of work in the sector producing intermediates, a households' utility function is

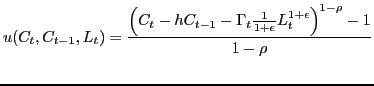$\displaystyle u(C_{t},C_{t-1},L_{t})= \frac{ \left( C_{t} - hC_{t-1} - \Gamma_{t} \frac {1}{1+\epsilon} L_{t}^{1+\epsilon} \right) ^{1-\rho} - 1 }{1-\rho}$

(2)

The preference structure follows Uribe and Yue (2006), Neumeyer and Perri (2005) and much of the emerging market business cycle literature. It abstracts from wealth effects on labor supply, as in Greenwood, Hercowitz and Huffman (GHH, 1988). The term multiplying the disutility of work, $\Gamma_{t}$ , depends on the aggregate technological level, $A_{t}$ , as follows:

$\displaystyle \Gamma_{t} = A_{t}^{\gamma} \Gamma_{t-1}^{1-\gamma}$

(3)

The term $\Gamma_{t}$ , which at the low frequency grows at the same rate as $A_{t}$ , is introduced to ensure the existence of a balanced growth path with stationary hours. In the calibrated version of the model, I will set $\gamma$ to a very small value, so that fluctuations in $A_{t}$ have a negligible impact on the disutility of labor at high and medium frequencies. Under the interpretation of GHH preferences as a reduced form for an economy with home production (Benhabib, Rogerson and Wright (1991) ), a small value of $\gamma$ can be viewed as capturing a process of "slow diffusion" of the varieties used in the final goods sector into the home production sector.

The households' decision problem is to choose stochastic sequences for consumption, labor supply, purchases of the international bond and purchases of following-period physical capital to solve the following problem:

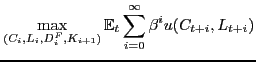
$\displaystyle \max_{(C_{i},L_{i},D^{F}_{i},K_{i+1})} \mathbb{E}_{t} \sum_{i=0}^{\infty} \beta^{i} u(C_{t+i},L_{t+i})$

subject to

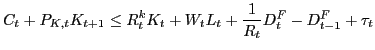
$\displaystyle C_{t} + P_{K,t} K_{t+1} \leq R^{k}_{t} K_{t} + W_{t} L_{t} + \frac{1}{R_{t}} D^{F}_{t} - D^{F}_{t-1} + \tau_{t}$

Above, $P_{K,t}$ is the price of capital and $R^{k}_{t}$ is its rental rate, $W_{t}$ the wage rate and $R_{t}$ is the interest rate on the international bond. $D^{F}_{t}$ denotes the family's choice of foreign debt and $K_{t+1}$ is the choice for physical capital holdings. Finally, $\tau_{t}$ denotes net transfers from firm ownership plus wages earned by skilled workers.

The international interest rate $R_{t}$ depends on aggregate net foreign indebtedness $B_{t}$ and on a random shock $r_{t}$ as follows:

$\displaystyle R_{t} = r + e^{r_{t}} + \psi\left[ e^{\frac{B_{t}-B}{Y_{t}}} -1\right]$

(4)

As is usual in the small open economy literature, the reason for introducing a dependence of the cost of borrowing on net foreign indebtedness is to ensure stationary dynamics. I choose a very small value for $\psi$ so that this feature does not affect the dyamics of the model. A raise in $r_{t}$ , interpretable as a country interest rate shock, is a simple way to model the sudden capital outflows that have accompanied many of the emerging market financial crises analyzed in the previous section. The expression for marginal utility of consumption, $U_{C,t}$ is the following:

$\displaystyle U_{C,t}= u_{C,t} - \beta\gamma\mathbb{E}_{t} \left( u_{C,t+1} \right)$

(5)

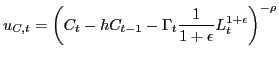$\displaystyle u_{C,t} = \left( C_{t} - hC_{t-1} - \Gamma_{t} \frac{1}{1+\epsilon} L_{t}^{1+\epsilon} \right) ^{-\rho}$

(6)

Define the households' stochastic discount factor between periods and , $\Lambda_{t,t+i}$ as

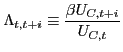$\displaystyle \Lambda_{t,t+i} \equiv\frac{\beta U_{C,t+i}}{U_{C,t}}$

(7)

Then the household's decision on bond and capital holdings are characterized by two conventional Euler equations:

$\displaystyle 1=\mathbb{E}_{t} \left( \Lambda_{t,t+1} \right) R_{t}$

(8)

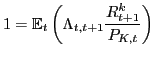$\displaystyle 1=\mathbb{E}_{t} \left( \Lambda_{t,t+1} \frac{R^{k}_{t+1}}{P_{K,t}} \right)$

(9)

Labor supply is given by

$\displaystyle u_{C,t} \Gamma_{t} L_{t}^{\epsilon} = U_{C,t} W_{t}$

(10)

3.2 Entrepreneurs

In every period there is an unbounded mass of prospective entrepreneurs with the ability to introduce new varieties of intermediates, interpretable as "innovations" or new types of products or technologies which may be entirely novel to the small open economy or possibly adaptations of varieties already in use in more advanced countries.²⁰Specifically, each entrepreneur can use resources to create a new "potential" firm, which will then become a successful new variety with a certain (exogenous) probability each period. At the same time, both successful and unsuccessful firms face the risk of an exogenous exit shock. This process is meant to capture in a simple way the life-cycle dynamics of the firm.

Entrepreneurs need to obtain funding from banks to finance entry. Here the idea is that banks are "specialists" with skills in evaluating and monitoring entrepreneurs. Contracts between banks are entrepreneurs are assumed to be frictionless: in exchange for funding, each entrepreneur can offer the bank a security which is perfectly contingent on the success of his or her project. On the other hand, as explained in detail in the following section, banks do face frictions in obtaining funds.

To be more specific, each entrepreneur can produce new potential firms by employing materials and skilled workers as inputs, according to the following production function:

$\displaystyle Z_{N,t} = N_{t}^{\eta} (A_{t} L_{S,t})^{1-\eta}$

(11)

Above, $N_{t}$ is the amount of materials used (in units of final output) and $L_{S,t}$ is the number of skilled workers hired. $A_{t}$ denotes the aggregate technological level of the economy, which as explained below is equal to the total number of firm varieties in operation. As in Romer (1990), (11) incorporates an externality of the aggregate level of knowledge on the efficiency of skilled labor in introducing new types of firms. This assumption is key to generate endogenous growth.

Given constant returns to scale of (11), the entrepreneurial sector can be formulated as consisting of a representative entrepreneur or potential entrant who decides how many new firms to introduce, subject to production function (11). An alternative, perhaps more plausible, interpretation is that there is an unbounded mass of entrepreneurs, each with an "idea" for a project, which can be put into practice by paying a sunk cost $MC_{t}$ given by the marginal cost associated with (11). Denoting the skilled labor wage by $W_{S,t}$ , the expression for this marginal cost is the following:²¹

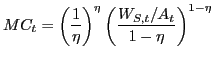$\displaystyle MC_{t} = \left( \frac{1}{\eta} \right) ^{\eta} \left( \frac{ W_{S,t}/A_{t} }{1-\eta} \right) ^{1-\eta}$

(12)

The entrepreneur has no funds to finance the sunk cost $MC_{t}$ . To obtain funds, he or she issues equity to banks. Let $J_{t}$ be the price of a unit of entrepreneur equity. There are no commitment or enforcement frictions between entrepreneurs and banks, so the entrepreneur can commit to pay all the contingent proceeds from the project to the equity holding bank. At the same time, given free entry of entrepreneurs, the price of equity issued by entrepreneurs must equal the sunk cost of introducing a new project:

$\displaystyle J_{t} = MC_{t}$

(13)

Once the entrepreneur has paid the sunk cost, the dynamics of the firm are as follows. A firm that has just entered is still not a successful new business. The firm becomes successful with an exogenous probability $\lambda$ . Here the idea is that an entering entrepreneur cannot grow into a successful business immediately, but rather it takes time to turn his or her idea into a marketable new product. Once the entrepreneur's idea becomes successful, it generates profits $\pi_{t}$ per period (determined below when discussing the problem of intermediates producers). At the same time, both successful and still-unsuccessful businesses face the risk of receiving an exogenous exit shock: the corresponding survival probabilities are denoted $\phi_{A}$ and $\phi_{Z}$ respectively. I assume that $\phi_{A} > \phi_{Z}$ , to capture the fact that small, young firms have higher exit rates than firms that are large and mature.²²

Finally, as explained earlier, the supply of skilled labor is assumed to be inelastic and fixed at $\overline{L}_{S}$ . One can then combine (12), (13) and the first-order condition for $L_{S,t}$ to obtain the following relation between the price of entrepreneur equity $J_{t}$ and the number of new entrants $Z_{N,t}$ :

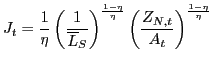$\displaystyle J_{t} =\frac{1}{\eta} \left( \frac{1}{\overline{L}_{S}} \right) ^{\frac{1-\eta}{\eta}} \left( \frac{Z_{N,t}}{A_{t}} \right) ^{\frac{1-\eta}{\eta}}$

(14)

Equation (14) can be interpreted as an aggregate supply curve of new entrant firms, as a function of the price of a unit of entrepreneur equity $J_{t}$ .

3.3 Banks

Banks lend funds obtained in capital markets to entrepreneurs. As in Gertler and Kiyotaki (2011), banks are interpreted as specialists who assist in channeling funds from savers to entrepreneurs. They purchase securities issued by entrepreneurs that are perfectly state-contingent. These claims offer to pay the full value of the entrepreneur's project in the contingency that the project is successful. In addition, banks engage in maturity transformation: they hold long-term assets (claims on entrepreneurial projects) and fund these assets with short-term liabilities (beyond their own equity capital).

The agency friction in financial markets takes the form of a limited enforcement problem between the bank and its creditors: at the end of the period, after borrowing funds, a bank can default on his or her debt and divert an exogenous fraction $\theta_{t}$ of resources, with creditors only being able to recover the remaining part $1-\theta_{t}$ . This imposes a limit on how much debt the bank is able to take on ex-ante, as lenders recognize that excessive debt will lead to default.

I allow the fraction divertable $\theta_{t}$ to be time-varying. An increase in $\theta_{t}$ is interpretable as a reduction in the efficiency of financial markets, as lenders expect to be able to recover a smaller amount from defaulting borrowers.²³

Given these considerations, the bank's sequence problem is the following:

$\displaystyle \max_{ \left\{ s_{t+i-1},d_{t+i-1}\right\} _{i=1}^{\infty} } \left[ \mathbb{E}_{t} \sum_{i=1}^{\infty} \sigma^{i-1} (1-\sigma) \Lambda_{t,t+i} \left\{ \phi_{Z} \left[ \lambda v_{t+i} + (1-\lambda) J_{t+i} \right] s_{t+i-1} - R_{t+i-1} d_{t+i-1} \right\} \right]$

(15)

subject to

$\displaystyle J_{t} s_{t} + R_{t-1} d_{t-1} \leq\phi_{Z} \left[ \lambda v_{t} + (1-\lambda) J_{t} \right] s_{t-1} + d_{t}$

(16)

$\displaystyle \mathbb{E}_{t} \sum_{i=1}^{\infty} \sigma^{i-1} (1-\sigma) \Lambda_{t,t+i} \left\{ \phi_{Z} \left[ \lambda v_{t+i} + (1-\lambda) J_{t+i} \right] s_{t+i-1}-R_{t+i-1} d_{t+i-1} \right\} \geq\theta_{t} J_{t} s_{t}$

(17)

Examining first the budget constraint, equation (16), the bank's use of funds (left hand side) includes the purchase of an amount $s_{t}$ of claims on entrepreneurs, which costs $J_{t} s_{t}$ , as well as debt repayments, $R_{t-1} d_{t-1}$ . The sources of funds are the revenues obtained from previous loans (the first term on the right hand side) as well as new debt issued, $d_{t}$ . Projects financed the previous period, $s_{t-1}$ , have a survival probability $\phi_{Z}$ . If the project survives, it is successful with probability $\lambda$ , in which case the bank receives its full value, denoted $v_{t}$ . If the project is unsuccessful this period, then given the simple Poisson process for the evolution of projects it is exactly equivalent to a security issued by a new entrant entrepreneur, so that its value is $J_{t}$ .

A successful project generates a stream of profits $\left\{ \pi_{t+i} \right\} _{i=0}^{\infty}$ obtained from manufacturing and selling the new variety of intermediate. Therefore, the value of a successful project is given by the expected discounted value of the profit stream, accounting for the survival rate $\phi_{A}$ of successful firms:²⁴

$\displaystyle v_{t} = \mathbb{E}_{t} \left[ \sum_{i=0}^{\infty} \phi_{A}^{i} \Lambda _{t,t+i} \pi_{t+i} \right]$

(18)

As indicated by (15), if a bank alive at exits in period (which happens with probability $\sigma^{i-1} (1-\sigma)$ ) it the accumulated wealth back to the household. The resources accumulated until period are given by the term in curly brackets in (15). The bank thus values payoffs in the period and state at which it exits with the household's stochastic discount factor, $\Lambda_{t,t+i}$ .

Equation (17) is the bank's incentive constraint. At the end of period , after having borrowed in capital markets, the bank may choose to default on its creditors and divert fraction $\theta_{t}$ of available funds, which it then transfers back to its household. Creditors can then force the bank into bankruptcy and recover the remaining fraction $1-\theta_{t}$ of resources, but it is too costly for them to recover the fraction $\theta_{t}$ of funds that the bank diverted. Accordingly, for creditors to be willing to supply funds to the bank, equation (17) must hold: the bank's value if he honors the contract with his creditors must be greater than the value of diverting resources in the amount $\theta_{t} J_{t} s_{t}$ and being shut down.

To simplify the bank's problem, define first the rate of return to one dollar invested in entrepreneurial projects, $R_{Z,t}$ :

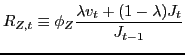
$\displaystyle R_{Z,t} \equiv\phi_{Z} \frac{\lambda v_{t} + (1-\lambda) J_{t}}{J_{t-1}}$

$R_{Z,t}$ depends only on the aggregate state, through prices $v_{t}$ and $J_{t}$ . Times of low realizations of the value of a new intermediate, $v_{t}$ and of the value of entrepreneur equity, $J_{t}$ , will be times of low returns $R_{Z,t}$ . Noting that bank's individual state variables at the beginning of period are $s_{t-1}$ and $d_{t-1}$ , the entrepreneur's problem can be expressed recursively as follows:

$\displaystyle V_{t} (s_{t-1},d_{t-1}) = \max_{s_{t},d_{t}} \hspace{.25cm} (1-\sigma) \mathbb{E}_{t} \left[ \Lambda_{t,t+1} \left( R_{Z,t+1} J_{t} s_{t} - R_{t} d_{t} \right) \right] + \sigma\mathbb{E}_{t} \left[ \Lambda_{t,t+1} V_{t+1} (s_{t}, d_{t}) \right]$

(19)

subject to

$\displaystyle J_{t} s_{t} + R_{t-1} d_{t-1} \leq R_{Z,t} J_{t-1} s_{t-1} + d_{t}$

(20)

$\displaystyle (1-\sigma) \mathbb{E}_{t} \left[ \Lambda_{t,t+1} \left( R_{Z,t+1} J_{t} s_{t} - R_{t} d_{t} \right) \right] + \sigma\mathbb{E}_{t} \left[ \Lambda_{t,t+1} V_{t+1} (s_{t}, d_{t}) \right] \geq\theta_{t} J_{t} s_{t}$

(21)

Above, the time index on the value function reflects aggregate uncertainty. The problem can be simplified further by realizing that the key individual state variable is the bank's net worth $w_{t}$ , defined as the difference between the value of assets and debt:

$\displaystyle w_{t} \equiv J_{t} s_{t} - d_{t}$

(22)

From the budget constraint (20) at equality, the evolution of net worth is

$\displaystyle w_{t} = (R_{Z,t} - R_{t-1})J_{t-1} s_{t-1} + R_{t-1} w_{t-1}$

(23)

Net worth at is given by the gross return to the bank's investments financed during , net of repayments to creditors. Equation (23) shows that net worth at depends on the individual state at $(s_{t-1},w_{t-1})$ together with the realization of the aggregate state at , through the rate of return $R_{Z,t}$ . This suggests making the following guess for the bank's value function:

$\displaystyle V_{t}(s_{t-1},d_{t-1}) = \overline{\Omega}_{t} w_{t}$

(24)

Above, the undetermined coefficient $\overline{\Omega}_{t}$ is conjectured to depend only on the aggregate state, and dependence of $w_{t}$ on $(s_{t-1},d_{t-1})$ through (22) and (23) is understood. Define also the following variables:

$\displaystyle \Omega_{t+1} \equiv1-\sigma+ \sigma\overline{\Omega}_{t+1}$

(25)

$\displaystyle \mu_{t} \equiv\mathbb{E}_{t} \left[ \Lambda_{t,t+1} \Omega_{t+1} \left( R_{Z,t+1} - R_{t} \right) \right]$

(26)

$\displaystyle \nu_{t} \equiv\mathbb{E}_{t} \left( \Lambda_{t,t+1} \Omega_{t+1} \right) R_{t}$

(27)

Variable $\Omega_{t+1}$ is interpretable as the prospective value of a unit of net worth, before the bank finds out whether he will have to exit at the end of the period. From equation (26), $\mu_{t}$ is interpretable to the return for the bank of investing in excess of the cost of funds. Finally, $\nu_{t}$ represents the value of an extra unit of net worth today.

Given the definitions above, the problem of the bank reduces to the following:

$\displaystyle \overline{\Omega}_{t} w_{t} = \max_{s_{t}} \hspace{.3cm} \mu_{t} J_{t} s_{t} + \nu_{t} w_{t}$

(28)

subject to

$\displaystyle \mu_{t} J_{t} s_{t} + \nu_{t} w_{t} \geq\theta_{t} J_{t} s_{t}$

(29)

Here $\mu_{t}$ reflects the value to the bank of funding an additional project (increasing $s_{t}$ ) while holding net worth constant. On the other hand, $\nu_{t}$ is the value of an additional unit of net worth, holding constant $s_{t}$ . With frictionless financial markets banks would be unconstrained, with the implication that $\mu_{t} = 0$ . The agency problem introduces a friction that makes banks potentially constrained, and that may therefore place limits on arbitrage.

Equation (29) is the incentive constraint. Note that as long as $\mu_{t} \geq0$ , it is profitable for the bank to borrow and fund an additional project. Thus, in this instance, and given $w_{t}>0$ , the constraint binds:

$\displaystyle J_{t} s_{t} = \frac{\nu_{t}}{\theta_{t} - \mu_{t}} w_{t}$

(30)

Equation (30) shows that the amount the bank can spend on funding projects, $J_{t} s_{t}$ , is constrained by his net worth $w_{t}$ , through a limit on the amount the bank is allowed to borrow in capital markets.²⁵

Define the banks maximum leverage ratio $\phi_{t}$ as

$\displaystyle \phi_{t} \equiv\frac{\nu_{t}}{\theta_{t} - \mu_{t}}$

(31)

so that when the credit constraint binds,

$\displaystyle J_{t} s_{t} = \phi_{t} w_{t}$

(32)

Then with a binding constraint, solving the undetermined coefficient from (28)-(29) we have that

$\displaystyle \overline{\Omega}_{t} = \mu_{t} \phi_{t} + \nu_{t}$

(33)

The value of a unit of net worth today ( $\overline{\Omega}_{t}$ ) derives from its value holding assets constant ( $\nu_{t}$ ) plus the capacity that it generates to fund additional projects ( $\phi_{t}$ ) multiplied by the value to the bank of those additional projects ( $\mu_{t}$ ).

3.3.1 Aggregation

Aggregation accross banks is simple given the linearity of (32). The aggregate amount of projects funded, $S_{t}$ , is constrained by aggregate net worth of the financial intermediation sector:

$\displaystyle J_{t} S_{t} = \phi_{t} W_{t}$

(34)

At the same time, aggregate net worth at is given by the sum of net worth of surviving banks, which evolves individually according to (23), and the transfer that newborn ones obtain from their family. For simplicity I assume that the transfer is a small fraction $\xi$ of the total value of the projects funded the previous period. Accordingly, the law of motion of aggregate net worth is given by

$\displaystyle W_{t} = \sigma\left[ \left( R_{Z,t} - R_{t-1} \right) J_{t-1}S_{t-1} + R_{t-1} W_{t-1} \right] + (1-\sigma) \xi J_{t-1} S_{t-1}$

(35)

Note that the source of fluctuations in aggregate net worth of the financial intermediation sector are movements in return $R_{Z,t}$ , which as discussed earlier arise from movements in the prices $v_{t}$ and $J_{t}$ .

In what follows I describe the evolution of the aggregate stock of projects for new varieties. At the beginning of period , a total number of potential firms $Z_{t}$ exist in the economy. Each point in $[0,Z_{t}]$ represents a project for a different intermediate. The points between 0 and $A_{t}$ correspond to already successful new intermediates, with $A_{t}<Z_{t}$ . In period , the entrepreneurial sector introduces a measure $Z_{N,t}$ of new potential firms. At the same time, a fraction $1-\phi_{Z}$ of unsuccessful firms exit each period. Thus, the aggregate number of potential firms $Z_{t}$ evolves as follows:

$\displaystyle Z_{t+1} = \phi_{Z} \left( Z_{t} + Z_{N,t} \right)$

(36)

In period the points between $A_{t}$ and $Z_{t} + Z_{N,t}$ correspond to projects "in process", i.e. projects that the entrepreneurial sector is currently attempting to turn into successful firms. Fraction $\lambda$ of these projects will become successful during period . Also, only fraction $\phi_{A}$ of firms operating in period survive into . Therefore, the total number of varieties of intermediates, $A_{t}$ , evolves as follows:

$\displaystyle A_{t+1} = \lambda\left[ \phi_{Z} \left( Z_{t} + Z_{N,t} \right) - A_{t} \right] + \phi_{A} A_{t}$

(37)

where the term in brackets is the measure of potential firms that have not yet been successful, accounting for the fact that only fraction $\phi_{Z}$ of potential firms survive each period.

Recall that $S_{t}$ refers to the aggregate number of projects financed by banks. In equilibrium, we must have

$\displaystyle S_{t} = \phi_{Z} \left( Z_{t} + Z_{N,t} \right) - A_{t}$

(38)

That is, the total number of projects financed by the financial intermediation sector must be equal to the total number of projects that entrepreneurs are currently holding and trying to develop.

These considerations clarify how financial factors may affect the evolution of TFP. When net worth is low, through equation (34) the aggregate number of projects that the intermediation sector can finance, $S_{t}$ , is reduced. This makes demand for new entrants $Z_{N,t}$ lower, as equation (38) suggests. With a smaller number of products being attempted, the growth rate of TFP will decline, as equation (37) indicates.

3.3.2 The Frictionless Benchmark

As emphasized earlier, with frictionless markets there is perfect arbitrage, so that excess returns $\mu_{t}$ must be equal to zero. It follows from (25)-(27) and (33) that $\mathbb{E}_{t} (\Lambda_{t,t+1} R_{Z,t+1}) = \mathbb{E}_{t}(\Lambda_{t,t+1})R_{t} = 1$ , or

$\displaystyle J_{t} = \mathbb{E}_{t} \left\{ \Lambda_{t,t+1} \phi_{Z} \left[ \lambda v_{t+1} + (1-\lambda) J_{t+1} \right] \right\}$

(39)

The value of entrepreneur equity, $J_{t}$ , is given by the option value of obtaining a successful new intermediate the following period, valued $v_{t+1}$ - this happens with probability $\lambda$ . With financial frictions and constrained banks, we will have

$\displaystyle J_{t} < \mathbb{E}_{t} \left\{ \Lambda_{t,t+1} \phi_{Z} \left[ \lambda v_{t+1} + (1-\lambda) J_{t+1} \right] \right\}$

(40)

The gap between the left and right hand side of (40) widens whenever banks' financial constraints are tighter, which happens in times in which the net worth of the intermediation sector is low. This implies that the rate of new firm creation falls below its frictionless level. The imperfection in financial markets also implies that the growth rate of TFP, and therefore of output, along the balanced growth path is below its value in a model without financial frictions.²⁶

3.4 Final Output and Intermediates Producers

The final good is produced in a competitive sector which aggregates a continuum of measure $A_{t}$ of intermediates:

$\displaystyle Y_{t} = \left[ \int_{0}^{A_{t}} Y_{t}(s)^{\frac {\vartheta-1}{\vartheta}} ds \right] ^{\frac{\vartheta}{\vartheta-1}}$

(41)

Given the aggregator above, demand for each intermediate by the final good sector is

$\displaystyle Y_{t}(s) = \left[ \frac{P_{t}(s)}{P_{t}} \right] ^{-\vartheta}Y_{t}$

(42)

where the price level $P_{t}$ is defined as

$\displaystyle P_{t} = \left[ \int_{0}^{A_{t}} P_{t}(s)^{1-\vartheta} ds \right] ^{\frac {1}{1-\vartheta}}$

(43)

Equation (42) gives the demand facing each intermediate good producer . Intermediates are produced using a standard Cobb-Douglas technology with capital services $u_{t}(s) K_{t}(s)$ and labor $L_{t}(s)$ as inputs:

$\displaystyle Y_{t}(s)=\left[ u_{t}(s)K_{t}(s)\right] ^{\alpha}L_{t}(s)^{1-\alpha}$

(44)

Intermediate goods firms face a working capital requirement which forces them to hold an amount of non-interest-bearing assets that is no smaller than a multiple $\theta_{W}$ of the quarterly wage bill:

$\displaystyle \kappa_{t}(s) \geq\theta_{W} W_{t} L_{t}(s) \; \; \; \; \; \; \; \; \theta_{W} \geq0$

where $\kappa_{t}(s)$ denotes the amount of working capital held by firm in period . As shown in Uribe and Yue (2006) and Mendoza and Yue (2012), this formulation implies that the effective cost of labor becomes $\left[ 1 + \theta_{W} \left( \frac{R_{t}-1}{R_{t}} \right) \right] W_{t}$ , and therefore an increase in the interest rate reduces the demand of labor by intermediates firms.

The objective of intermediates producers is to maximize profits, including the value of the remaining part of capital they rent from households. Firms face a replacement price of depreciated capital equal to unity.²⁷Thus, their objective is to solve

$\pi_{t}=\underset{P_{t}(s),Y_{t}(s),u_{t}(s),K_{t}(s),L_{t}(s)}{\max} P_{t}(s)Y_{t}(s)+P_{K,t}K_{t}(s)-\delta(u_{t}(s))K_{t}(s)-\left[ 1+\theta _{W}(\frac{R_{t}-1}{R_{t}})\right] W_{t}L_{t}(s)-R_{t}^{k}K_{t}(s)$

Subject to (42) and (44). Solving the firm's problem yields the following equations:

$\displaystyle \left[ 1 + \theta_{W} \left( \frac{R_{t}-1}{R_{t}} \right) \right] W_{t}=(1-\alpha)\frac{Y_{t}}{L_{t}}$

(45)

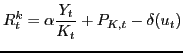$\displaystyle R_{t}^{k}=\alpha\frac{Y_{t}}{K_{t}} + P_{K,t} - \delta(u_{t})$

(46)

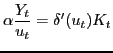$\displaystyle \alpha\frac{Y_{t}}{u_{t}}=\delta^{\prime}(u_{t})K_{t}$

(47)

Each intermediates producer sets its price to a constant markup over marginal cost - the ratio of price to marginal cost equals $\frac{\vartheta} {\vartheta-1}$ . Per period profits of intermediates producers, $\pi_{t}$ , can then be shown to be equal to

$\displaystyle \pi_{t}=\frac{1}{\vartheta} \frac{Y_{t}}{A_{t}}$

(48)

Finally, one can combine (41) with the first-order conditions for intermediates producers and with equilibrium in factor markets to obtain an expression for final output:

$\displaystyle Y_{t}=A_{t}^{\frac{1}{\vartheta-1}} (u_{t}K_{t})^{\alpha }L_{t}^{1-\alpha}$

(49)

3.5 Capital Producers

At the end of period , capital producing firms repair depreciated capital and produce new capital. For simplicity I assume that no financial frictions apply to the production and purchase of capital goods, in order to focus on the role of frictions on the creation of new firms. However, it would be straightforward to extend the model to allow for frictions in investment of existing firms as well, along the lines of Gertler and Karadi (2011) and others.²⁸

As in and Gertler et. al. (2007), repair of old capital is not subject to adjustment costs, but there are stock adjustment costs associated with the production of new capital. Let $I_{t}^{n}$ be net investment, the amount of investment used for construction of new capital goods:

$\displaystyle I_{t}^{n}=I_{t}-\delta(u_{t})K_{t}$

(50)

To produce new capital, capital producers combine final output with existing capital via the constant returns to scale technology $\Phi(I_{t}^{n} /K_{t})K_{t}$ , where $\Phi(\cdot)$ is increasing and concave and satisfies $\Phi(I^{n}/K)=0$ and $\Phi^{\prime n}/K)=1$ , where $I^{n}/K$ is the net investment to capital ratio along the balanced growth path.

The economy-wide capital stock evolves according to²⁹

$\displaystyle K_{t+1}=K_{t}+\Phi\left( \frac{I_{t}^{n}}{K_{t}} \right) K_{t}$

(51)

As in Gertler et. al. (2007), I assume that capital producing firms make production plans one period in advance, with the objective of capturing the delayed response of investment observed in the data. Accordingly, the optimality condition for capital producers is

$\displaystyle \mathbb{E}_{t-1}(P_{K,t}) = \mathbb{E}_{t-1} \left\{ \left[ \Phi^{\prime }\left( \frac{I_{t}^{n}}{K_{t}}\right) \right] ^{-1} \right\}$

(52)

3.6 Market Clearing

The economy uses output and international borrowing to finance consumption, investment in physical capital, and investment in new technology. The resulting market clearing condition is

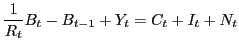$\displaystyle \frac{1}{R_{t}}B_{t} - B_{t-1} + Y_{t} = C_{t} + I_{t} + N_{t}$

(53)

$B_{t}$ is economywide foreign indebtedness, equal to the sum of aggregate family and entrepreneurial debt ( $B_{t}=D_{t}^{F}+D_{t}$ ). Equation (53) can be derived by combining family and entrepreneur budget constraints with equilibrium conditions.

This completes the description of the model.

4 Model Analysis

This section presents numerical results from a dynamic simulation of the model, meant to capture in a rough way the type of crises analyzed empirically in Section 2. The goal is to illustrate how the novel mechanism introduced in the paper, namely financially constrained firm creation, is crucial for the model to be able to produce persistent declines in output, productivity and employment that are quantitatively close to those identified in the data.³⁰

Table 1: Parameter Values

Symbol	Value	Description
Conventional: $\beta$	0.99	Discount factor
Conventional: $\rho$	1	Risk aversion
Conventional: $\epsilon$	1	Inverse Frisch elasticity
Conventional:	0.25	Habits Uribe adn Yue (2006)
Conventional: $\gamma$	0.01	Parameter on labor disutility term
Conventional: $\delta$	0.025	Capital depreciation
Conventional: $\alpha$	1/3	Capital share
Conventional: $\delta^{\prime\prime}/\delta^{\prime}$	0.15	Elasticity of depreciation to utilization Comin et. al. (2009)
Conventional: $\vartheta$	2.5	Demand elasticity for intermediates Comin and Gertler (2006)
Conventional: Φ^"(Iⁿ/K)	0.2	Elasticity of P_k to Iⁿ/K Gertler et. al. (2007)
Conventional: θ_W	0.35	Working capital requirement
Conventional: τ	0.00001	Elasticity of interest rate to foreign debt
Conventional: B/Y	0.2	Foreign debt to output
Entrepreneurs: λ	0.125	Adoption prob. 2 years success lag - Pakes and Schankerman (1984)
Entrepreneurs: 1-φ_A	0.025	Exit rate old Bilbiie et. al (2012)
Entrepreneurs: 1-φ_Z	0.05	Exit rate young Haltiwanger et. al (2012)
Entrepreneurs: η	0.125	Final output in entrepreneurs' prod. fun. 10% o foutput used by entrepreneurs along BGP
Entrepreneurs: $\eta$	0.033	Skilled labor supply 2% TFP growth rate - Young (1995)
Banks: σ	0.98	Survival rate 12 years horizon
Banks: θ	0.45	Fraction divertable 1% annual spread
Banks: ξ	0.0075	Transfer rate leverage = 4

4.1 Parameter Values

Table 1 lists the choice of parameter values. Overall there are twenty-two parameters, fourteen of which relate to preferences and technology. Of the remaining eight, five relate to the entrepreneurial sector: the success probability ( $\lambda$ ), the exit rates ( $1-\phi_{A}$ , $1-\phi_{Z}$ ), the weight of materials in entrepreneurs' production function ( $\eta$ ) and the aggregate supply of skilled labor ( $\bar{L}_{S}$ ). The remaining three parameters relate to financial intermediaries. They include the survival rate of banks ( $\sigma$ ), the steady state divertable fraction of assets ( $\theta$ ), and the transfer rate to new bankers ( $\xi$ ).

I choose relatively conventional values for the preference and technology parameters. The discount factor is set at 0.99, and risk aversion is set at unity. I set the inverse Frisch elasticity of labor supply, $\epsilon$ , equal to one. I set the habits parameter at 0.25, similar to the value estimated by Uribe and Yue (2006). The parameter $\gamma$ governing the impact of the total number of varieties $A_{t}$ on the labor disutility term $\Gamma_{t}$ is set at 0.01, implying that aggregate technology affects the disutility of work only over the very long run. Turning to technology parameters, I set the capital share $\alpha$ to 1/3, and the quarterly depreciation rate of physical capital, $\delta$ , to 2.5 $\%$ . Capital utilization along the balanced growth path is normalized to 1, and the elasticity of marginal depreciation with respect to the utilization rate ( $\delta^{\prime\prime}/\delta^{\prime}$ ), is set at 0.15, as in Jaimovich and Rebelo (2009) and Comin, Gertler and Santacreu (2009). I set the elasticity of the price of capital with respect to the investment-capital ratio at 0.2, as in Gertler et. al. (2007) and Bernanke et. al. (1999). I choose the parameter on the intermediate goods aggregator, $\vartheta$ , so that output is proportional to TFP along the balanced growth path, which by examining equation (49) amounts to imposing $(1-\alpha)(\vartheta-1)=1$ . This restriction makes profits per period, $\pi_{t}$ , a stationary variable, and simplifies somewhat the characterization of the balanced growth path. Given $\alpha=1/3$ , the resulting value for the markup is $\vartheta/(\vartheta-1)=1.66$ , close to the value of 1.6 chosen by Comin and Gertler (2006).

Regarding the working capital constraint, I set $\theta_{W} = 0.35$ , implying that firms need to pay less than a month's worth of the wage bill in advance.³¹ The debt to GDP ratio along the balanced growth path is set at 0.2, and the elasticity of the interest rate with respect to the debt-output ratio equals 0.00001 - the latter ensures that the dynamics of the model are virtually unaffected by the debt-elastic interest rate at high and medium frequencies, while still making the foreign asset position revert to trend over the long run.

Turning to the parameters relating to the entrepreneurial sector, I set the probability of successfully obtaining a new variety, $\lambda$ , to 0.125, implying an average success lag ( $\frac{1}{\lambda}$ ) of 8 quarters or 2 years. This is based on evidence on mean R&D gestation lags reported by Pakes and Schankerman (1984), defined as the average time between the initial outlay of resources and the beginning of the associated revenue stream. The exit rate for mature firms ( $1-\phi_{A}$ ) is set to 10 percent annually, following Bilbiie et. al. (2012), and the corresponding number for young firms ( $1-\phi_{Z}$ ) is set to twice that number, consistent with the evidence in Haltiwanger et. al. (2012) of substantially higher firm exit by younger firms. The weight of final output in entrepreneurs' production function, $\eta$ , is set to 0.125, implying that along the balanced growth path 10 percent of output is used by the entrepreneurial sector. This number represents a rough estimate of expenditures on firm creation as a fraction of GDP.³² Finally, the inelastic supply of skilled labor, $\overline{L}_{S}$ , is set to deliver a growth rate of TFP along the balanced growth path of 2 percent, similar to the numbers reported by Young (1995).

The choice of the financial sector parameters is meant to be suggestive. Similar to Gertler and Kiyotaki (2010), I set the entrepreneur survival rate $\sigma=0.98$ , implying an expected horizon of bankers of about twelve years. To calibrate the fraction of resources that bankers can divert in steady state, $\theta$ , and the transfer to newborn bankers, $\xi$ , I target two features of the balanced growth path of the model economy: a bank leverage ratio (assets to net worth) of four, and an excess return $\mathbb{E} (R_{Z})-R$ equal to one hundred basis points annually. The target for the leverage ratio reflects a relatively conservative attempt to capture an average leverage ratio of the financial intermediation sector. For example, most housing finance is typically intermediated by financial institutions with leverage ratios of at least 10 on average in the case of commercial banks, and substantially higher for investment banks.³³ On the other hand, leverage ratios are clearly smaller in other sectors of the economy. The target for the spread along the balanced growth path is based on evidence on BBB industrial corporate spreads in the US and Europe prior to the crisis. These targets imply setting the divertible fraction $\theta$ to 0.45, and the transfer rate $\xi$ to 0.0075.

4.2 Crisis Experiment

I now turn to the crisis experiment. The initiating disturbance is the combined impact of two shocks: an increase in the country interest rate $R_{t}$ , and an increase in the variable governing the agency friction, $\theta_{t}$ .

I consider a 500 basis point increase in the interest rate that persists as a first-order autoregressive process with a 0.88 coefficient. These magnitudes are close to the evidence for the crisis in South Korea in 1997, as shown by Gertler et. al. (2007).³⁴ At the same time, $\theta_{t}$ rises by fifty percent, and the increase persists as a first order autoregressive process with coefficient 0.95 (the time paths for $R_{t}$ and $\theta_{t}$ are shown in Figure 5). The idea is to capture a situation in which not only there is a capital outflow, as captured by an increase in $R_{t}$ , but also a disruption in domestic financial markets, corresponding in the model to the increase in $\theta_{t}$ . It is best to think of the shock as a rare event.

Figure 4 shows the main result of the paper, by plotting a dynamic simulation for the model economy along with its empirical counterpart. It shows the behavior of output, labor productivity and employment following the shocks to $R_{t}$ and to the agency parameter $\theta_{t}$ , relative to the balanced growth path of the economy. In the baseline model (blue solid line), there is a large permanent component to the decline in output, whose magnitude is close to the data. As an example, six years after the shock output is depressed by about 11 percent relative to the unshocked path of the economy, very close to the empirical value. This is the case even though the exogenous driving forces, $R_{t}$ and $\theta_{t}$ , have almost completely returned to their steady state values. As made clear in the following section, behind this result is the behavior of firm creation following the crisis, which implies that the financial crisis shock has a permanent effect on aggregate TFP. This is the main driving force behind the behavior of labor productivity displayed in the figure. At the same time, as shown in the last panel of Figure 4, the permanent decline in productivity leads to a decline in labor demand by producers of intermediates. As a result, employment also falls persistently relative to the balanced growth path of the economy. Thus, the model is also able to account for the evidence provided in Section 2 that employment remains persistently depressed following financial crises. Overall, the bottomline from Figure 4 is that the mechanisms introduced in the model have potential for quantitatively accounting for the medium-run behavior of output, labor productivity and employment following financial crises.³⁵

Figure 4: Crisis experiment: Responses of output, labor productivity and employment. Time measured in years. All vairables in log deviations from the balanced growth path.

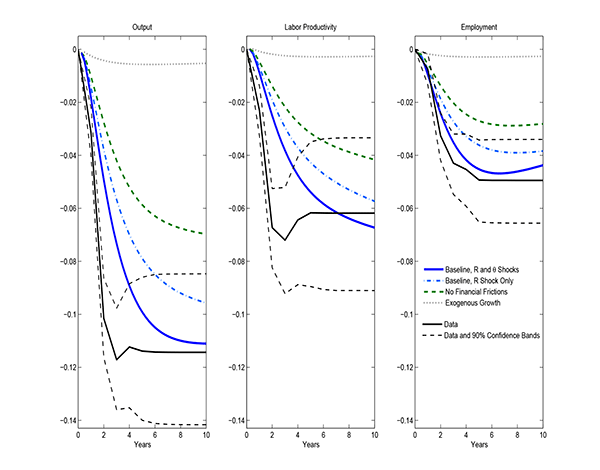
Figure 5: Shock paths for interest rate R (log deviation) and fraction divertable θ (level) in crisis experiment. Time measured in years.

Figure 5: Figure 5 shows the time paths for R sub t and Theta sub t. The idea is to capture a situation in which not only there is a capital outflow, as captured by an increase in R sub t, but also a disruption in domestic financial markets, corresponding in the model to the increase in Theta sub t. It is best to think of the shock as a rare event.

The financial intermediation sector plays an important role in accounting for the model's behavior. Without financial market frictions (green dashed line), the responses of all three variables differ significantly from their empirical counterparts: for example, the decline in output six years after the shock hits is approximately 6 percent in the case without financial frictions, compared to the 11 percent in the baseline case and in the data. The difference is driven to a large extent by the endogenous amplification implied the interaction between the financial intermediation sector and the process of firm creation (described in detail in the following section). This can be seen by comparing the case without financial frictions and the case with financial frictions but without the shock to $\theta_{t}$ (light blue dash-dotted line). The increase in $\theta_{t}$ then contributes an extra decline in all three variables - in the case of output its contribution is about 2 percentage points in the medium run.

Finally, Figure 4 also reports the response in a model in which the endogenous growth channel is inactive (grey dotted line) - what is then left is a relatively standard RBC model of a small open economy, subjected to an interest rate shock. As made clear by the figure, the behavior of the model in this case is very far from the data, due to the absence of endogenous movements in TFP.

How does the model's transmission mechanism operate? Figure 6 documents the behavior of the financial and entrepreneurial side of the model following the crisis shock. The disturbance induces a large decline in the value of a new variety, $v_{t}$ , and in the price of entrepreneur equity, $J_{t}$ (top panels), as the stream of future profits per new intermediate good is discounted more heavily. This has the effect of generating a large drop in the net worth of the intermediation sector, as equation (35) indicates. Notice that the interest rate shock leads the price of entrepreneur equity, $J_{t}$ , to fall substantially more in the baseline model with frictions (light blue dash-dotted line) than in the model without financial frictions (green dashed) - about sixty percent more on impact. This is at the core of the amplification mechanism in the model: as banks' constraints tighten (as reflected in the increase in the multiplier on the incentive constraint), they are forced to cut back on project funding to a larger extent than what would happen with frictionless financial markets. Along the way, there is an "adverse feedback" effect between bank net worth and the value of entrepreneur equity $J_{t}$ : as the former falls, bank' constraints tighten, forcing a decline in the credit available for projects in development. The decrease in demand for new projects leads to further reductions in value $J_{t}$ , starting a new round of declines in bank net worth. The end result is a large decline in the aggregate number of new projects started, $Z_{N,t}$ , as made clear by the last panel.

Figure 6: Crisis experiment: responses of growth and financial intermediation variables. Time measured in years. All variables in log deviations from the balanced growth path except net worth, expressed in level deviation as fraction of value in the balanced growth path.

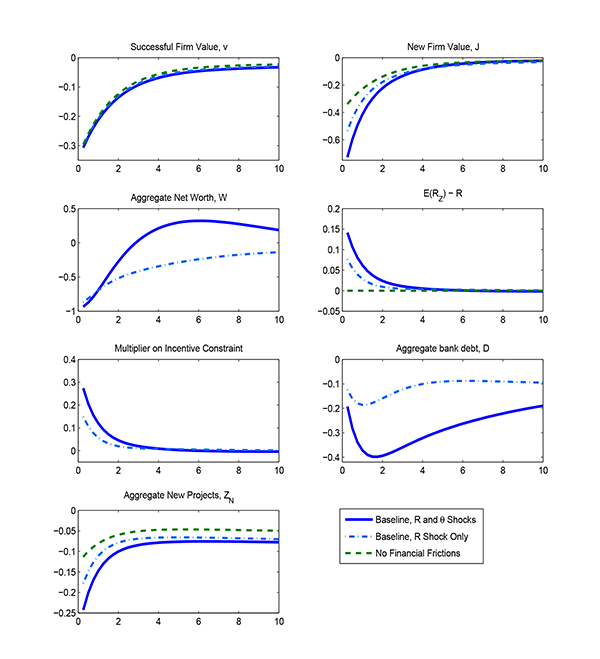
The tightening of financial constraints is also reflected in the rise in excess returns $\mathbb{E}_{t}(R_{Z,t+1})-R_{t}$ , which reflects that profitable opportunities in the entrepreneurial sector go unexploited due to an intensification of financial market frictions. The rise in the spread represents a widening of the departure from perfect arbitrage, as exemplified by equation (40). It is accompanied by a substantial reduction in the flow of credit to banks, as indicated by the right panel in the third row.

The blue solid line shows the effects of the $R_{t}$ and $\theta_{t}$ shocks combined. Relative to the case with the interest rate shock only, the increase in $\theta_{t}$ further restricts the flow of credit to banks (right panel in the third row), as they are able to borrow less per unit of net worth. This initiates another round of cuts in project funding, again amplified by the adverse feedback channel described above.

The decline in the number of projects funded by the entrepreneurial sector directly translates into a decline in the rate of newly successful firms. As shown in Figure 7, it follows that there is a substantial slowdown in the growth rate of TFP, leading to a permanent drop in the level of this variable relative to the balanced growth path. Further, the magnitude of the medium-run decline is substantially larger due to financial factors - in the baseline model, the level of TFP after six years falls more than 6 percent with both shocks and almost 5 percent with only the interest rate shock, compared to only 3.5 percent in the model without financial frictions. Thus, the financial friction plays a quantitatively significant role in helping the model generate a persistent decline in TFP following a crisis. Such movements in TFP are a salient feature of financial crises, as illustrated for example in the case of South Korea reviewed earlier, in which TFP remained persistently depressed relative to trend by about 6%. In a standard RBC economy, of course, TFP growth would be unaffected by the crisis shock.

Figure 7: Crisis experiment: responses of growth rate and level of TFP. Time measured in years. Variables in log deviations from the balanced growth path.

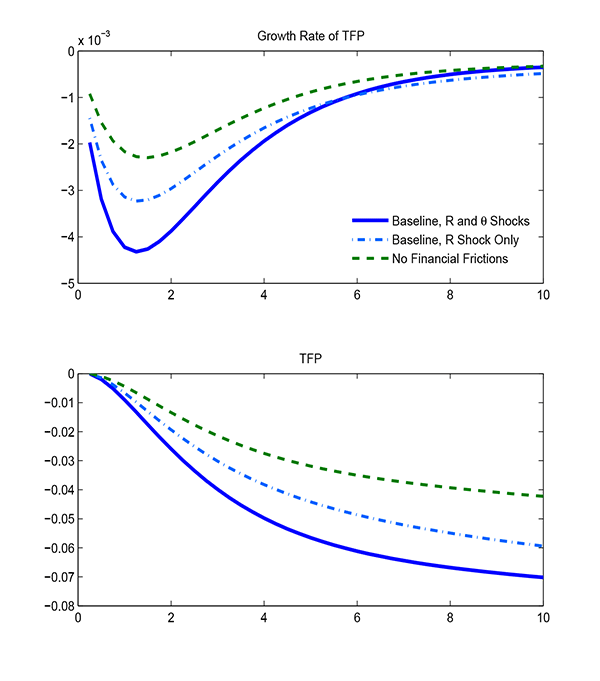
Finally, Figure 8 plots the response of a set of standard macroeconomic variables. Overall, the model does a relatively good job of capturing quantitatively the macroeconomic effects of the typical emerging market financial crisis. In particular, the responses of the variables displayed in Figure 8 are reasonably close to the evidence for the Korean 1997 crisis, as documented for example in Gertler et. al. (2007). The mechanisms introduced in this paper contribute to explaining the persistence of the decline in output and other variables following these episodes. A final point to highlight from Figure 8 is the substantial amplification due to the financial friction of aggregate consumption, a variable which is well known to display higher volatility relative to GDP in emerging markets when compared to more developed economies, and also of the ratio of net exports to GDP.

Figure 8: Crisis experiment: Responses of macroeconomic variables. Time measured in years. All variables in log deviations from the balanced growth path.

5 Conclusion

This paper has sought to explain the highly persistent effects of financial crises. It has argued that the phenomenon of slow recoveries from financial crises can be a natural consequence of an adverse shock in an environment in which productivity growth is endogenous through the creation of new firms. Further, it has shown how domestic financial market disruptions can work to amplify these declines. Thanks to these mechanisms, the model developed here is able to quantitatively reproduce the persistent declines in output, labor productivity and employment following financial crises identified from the data.

The evidence presented in this paper has been based on the experience of emerging market economies, as have been some of the modeling choices made (for example, the interest rate shock used to motivate a crisis, or the small open economy assumption). The reason is that it is in these countries where most financial crises have occurred over the past decades. The recent wave of financial crises in advanced economies, however, also appears to display a substantial degree of persistence, and many have suggested a slowdown in the underlying rate of productivity growth as a possible explanation.³⁶ With minor adaptation, the mechanisms introduced in this paper could be used to address the case of advanced economies as well.

A potentially interesting application of the framework presented in this paper would be an evaluation of the welfare gains of government intervention in mitigating a financial crisis. Gertler and Karadi (2011) and Gertler, Kiyotaki and Queralto (2012), for example, analyze different government financial policies in the context of the recent financial crisis in the US, finding important benefits of government intervention. The endogenous productivity growth mechanism introduced in this paper would likely affect what is at stake when considering intervention during a financial meltdown, and therefore it could have a substantial impact on the welfare gains of government policies directed at ameliorating the impact of a crisis.

Bibliography

Aoki, K., G. Benigno and N. Kiyotaki (2007). "Capital Flows and Asset Prices," NBER International Seminar on Macroeconomics 2007

Aguiar, M. and G. Gopinath (2007). "Emerging Market Business Cycles: The Cycle Is the Trend," Journal of Political Economy 115(1), 69-102

Ayyagari, M., A. Demirgüç-Kunt and V. Maksimovic (2007) "Firm Innovation in Emerging Markets: The Roles of Governance and Finance," World Bank Policy Research Working Paper 4157

Bank of England (2012). Inflation Report, November 2012

Benhabib, J. and M. Spiegel (1994). "The Role of Human Capital in Economic Development: Evidence from Aggregate Cross-Country Data," Journal of Monetary Economics 34(2), 143-173

Benjamin, D. and F. Meza (2009). "Total Factor Productivity and Labor Reallocation: The Case of the Korean 1997 Crisis,"The B.E. Journal of Macroeconomics: Vol. 9: Iss.1 (Advances), Article 31

Benhabib, J., R. Rogerson and R. Wright (1991). "Homework in Macroeconomics: Household Production and Aggregate Fluctuations," Journal of Political Economy 99(6), 1166-1187

Bernanke, B. (2012). "The Economic Recovery and Economic Policy," Speech at the Economic Club of New York, November 2012

Bernanke, B. and M. Gertler (1989). "Agency Costs, Net Worth, and Business Fluctuations," American Economic Review 79(1), 14-31

Bernanke, B., M. Gertler and S. Gilchrist (1999). "The Financial Accelerator in a Quantitative Business Cycle Framework," Handbook of Macroeconomics, North Holland

Bilbiie, F., F. Ghironi and M. Melitz (2012). "Endogenous Entry, Product Variety, and Business Cycles," Journal of Political Economy, 120(2), 304-345

Calvo, G. (1998). "Capital Flows and Capital-Market Crises: The Simple Economics of Sudden Stops," Journal of Applied Economics, I(1), 35-54

Caprio, G. and D. Klingebiel (2003). "Episodes of Systemic and Borderline Financial Crises," mimeo

Cerra, V. and S. C. Saxena (2008). "Growth Dynamics: The Myth of Economic Recovery," American Economic Review 98(1), 439-457

Chari, V. V., Kehoe, P. and E. McGrattan (2008). "Business Cycle Accounting," Econometrica 75(3), 781-836

Coe, D., E. Helpman and A. Hoffmaister (2009). "International R&D Spillovers and Institutions," European Economic Review 53(7), 723-741

Comin, D. and M. Gertler (2006). "Medium-Term Business Cycles," American Economic Review 96(3), 523-551

Comin, D., M. Gertler and A. Santacreu (2009). "Technology Innovation and Diffusion as Sources of Output and Asset Price Fluctuations," mimeo

Comin, D., N. Loayza, F. Pasha and L. Serven (2009). `` Medium-Term Cycles in Developing Countries," mimeo

Del Negro, M., G. Eggertsson, A. Ferrero and N. Kiyotaki (2010)"The Great Escape? A Quantitative Evaluation of the Fed's Non-Standard Policies," mimeo

Galí, J., M. Gertler and D. López-Salido (2007), "Markups, Gaps, and the Welfare Costs of Business Fluctuations," Review of Economics and Statistics 89(1), 44-59

Gertler, M., S. Gilchrist and F. Natalucci (2007). "External Constraints on Monetary Policy and the Financial Accelerator," Journal of Money, Credit and Banking 39(2-3), 295-330

Gertler, M. and P. Karadi (2011). "A Model of ``Unconventional" Monetary Policy," Journal of Monetary Economics 58, 17-34

Gertler, M. and N. Kiyotaki (2010). "Financial Intermediation and Credit Policy in Business Cycle Analysis," Handbook of Monetary Economics Vol.3, 547-599

Gertler, M., N. Kiyotaki and A. Queralto (2012). "Financial Crises, Bank Risk Exposure and Government Financial Policy," Journal of Monetary Economics 59, S17-S34

Gopinath, G. and B. Neiman (2011). "Trade Adjustment and Productivity in Large Crises," American Economic Review, forthcoming

Gorodnichenko, Y. and M. Schnitzer (2010). "Financial Constraints and Innovation: Why Poor Countries Don't Catch Up," Journal of the European Economic Association, forthcoming

Greenwood, J., Z. Hercowitz and G. W. Huffman (1988). `` Investment, Capacity Utilization and the Real Business Cycle," American Economic Review 78, 402-417

Griliches, Z. (1990). "Patent Statistics as Economic Indicators: A Survey," Journal of Economic Literature XXVIII (December 1990), 1661-1707

Hall, R. (1997). "Macroeconomic Fluctuations and the Allocation of Time," Journal of Labor Economics 15(1), S223-50

Hall, B. (2002). "The Financing of Research and Development," Oxford Review of Economic Policy, 18(1): 35-51

Hall, B. and J. Lerner (2009). "The Financing of R $\&$ D and Innovation," NBER Working Paper No. 15325

Howard, G., R. Martin and B. A. Wilson (2011). "Are Recoveries from Banking and Financial Crises Really So Different?," International Finance Discussion Paper Number 1037

International Monetary Fund (2009). World Economic Outlook, October 2009 Edition

Jaimovich, N. and S. Rebelo (2009)."Can News about the Future Drive the Business Cycle?," American Economic Review 99(4), 1097-1118

Jaffe, A. B. and M. Trajtenberg (2002)."Patents, Citations and Innovations: A Window on the Knowledge Economy," Cambridge, MA: MIT Press

Jermann, U. and V. Quadrini (2012)."Macroeconomic Effects of Financial Shocks," American Economic Review 102(1), 238-271(34)

Kalemli-Ozcan, S., B. Sorensen and S. Yesiltas (2012). `` Leverage across firms, banks, and countries" Journal of International Economics 88, 284-289

Kehoe, T. and K. Ruhl (2009)."Sudden stops, sectoral reallocations, and the real exchange rate," Journal of Development Economics 89(2), 235-249

Kerr, W. and R. Nanda (2009). "Democratizing entry: Banking deregulations, financing constraints, and entrepreneurship" Journal of Financial Economics 94, 124-149

Kiyotaki, N. and J. Moore (1997). "Credit Cycles," Journal of Political Economy 105(2), 211-248

Kiyotaki, N. and J. Moore (2012). "Liquidity, Business Cycles and Monetary Policy," mimeo

Kortum, S. and J. Lerner (2000). "Assessing the contribution of venture capital to innovation," RAND Journal of Economics 31(4), 674-692

Krueger, A. and J. Yoo (2001). ``Chaebol Capitalism and the Currency-Financial Crisis in Korea," NBER Conference on Currency Crises Prevention

Laeven, L. and F. Valencia (2012). "Systemic Banking Crises Database: An Update," IMF Working Paper

Levine, R. (1997). "Financial Development and Economic Growth: Views and Agenda," Journal of Economic Literature 35(2), 688-726

Levine, R. (2005). "Finance and Growth: Theory and Evidence," in P. Aghion and S. Durlauf, eds: Handbook of Economic Growth (North-Holland Elsevier Publishers, Amsterdam)

Mansfield, E., M. Schwartz and S. Wagner (1981). "Imitation Costs and Patents: An Empirical Study," The Economic Journal 91, 907-918

McGrattan, E. and E. Prescott (2010). "Technology Capital and the US Current Account," American Economic Review 100(4): 1493-1522

Mendoza, E. (2010). "Sudden Stops, Financial Crises, and Leverage" American Economic Review 100(5): 1941-1966

Mendoza, E. and V. Z. Yue (2012). "A General Equilibrium Model of Sovereign Default and Business Cycles," Quarterly Journal of Economics 127(2): 889-946

Meza, F. and E. Quintin (2007). "Factor Utilization and the Real Impact of Financial Crises," The B.E. Journal of Macroeconomics : Vol. 7: Iss.1 (Advances), Article 33

Neumeyer, P. A. and F. Perri (2005). "Business Cycles in Emerging Economies: The Role of Interest Rates," Journal of Monetary Economics 52, 345-380

Pakes, A. and M. Schankerman (1984). "The Rate of Obsolescence of Knowledge, Research Gestation Lags, and the Private Rate of Return to Research Resources," pp. 73-88 in Z. Griliches (Ed.),Patents, R $\&$ D and Productivity, The University of Chicago Press

Pratap, S. and C. Urrutia (2010). "Financial Frictions and Total Factor Productivity: Accounting for the Real Effects of Financial Crises," Review of Economic Dynamics, 15(3) 336-358

Reinhart, C. M. and V. R. Reinhart (2010) "After the Fall," NBER Working Paper 16334

Reinhart, C. M. and K. S. Rogoff (2009) "This Time is Different: Eight Centuries of Financial Folly," Princeton University Press

Romer, P. (1990). "Endogenous Technological Change," Journal of Political Economy 98(5), 71-102

Uribe, M. and V. Z. Yue (2006). "Country Spreads and Emerging Countries: Who Drives Whom?," Journal of International Economics 69, 6-36

Young, A. (1995). "The Tyranny of Numbers: Confronting the Statistical Realities of the East Asian Growth Experience," Quarterly Journal of Economics 110(3): 641-680

Appendix

A Data

Data on real output and employment (in number of persons) are obtained from the Total Economy Database.³⁷ The data on employment used is broadly consistent with the employment dataset in Neumeyer and Perri (2005) for the set of countries used in that analysis. Systemic banking crisis episode dates are from Laeven and Valencia (2012).

The list of countries and episodes used in the analysis is the following (episode starting date in parenthesis): Indonesia (1997), Malaysia (1997), Korea (1997), Thailand (1983, 1997), Philippines (1983, 1997), Argentina (1980, 1989, 1995, 2001), Brazil (1990, 1994), Chile (1976, 1981), Colombia (1982, 1998), Mexico (1981, 1994), Peru (1983), Israel (1977), Poland (1990), Turkey (1982, 2000), Hungary (1991, 2008), Czech Republic (1996), Slovak Republic (1998).

B Complete Set of Equilibrium Conditions

B.1 Households and Firms

$\displaystyle Y_{t}=A_{t}^{\frac{1}{\vartheta-1}} (u_{t}K_{t})^{\alpha}L_{t}^{1-\alpha}$

(B.1)

$\displaystyle U_{C,t}= u_{C,t} - \beta h \mathbb{E}_{t} \left( u_{C,t+1} \right)$

(B.2)

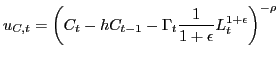$\displaystyle u_{C,t} = \left( C_{t} - hC_{t-1} - \Gamma_{t} \frac{1}{1+\epsilon} L_{t}^{1+\epsilon} \right) ^{-\rho}$

(B.3)

$\displaystyle \frac{u_{C,t} \Gamma_{t} L_{t}^{\epsilon}}{U_{C,t}} = \frac{1}{1 + \theta_{W} \left( \frac{R_{t}-1}{R_{t}} \right) } (1-\alpha) \frac{Y_{t}}{L_{t}}$

(B.4)

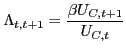$\displaystyle \Lambda_{t,t+1}=\frac{\beta U_{C,t+1}}{U_{C,t}}$

(B.5)

$\displaystyle 1=\mathbb{E}_{t} \left( \Lambda_{t,t+1} \right) R_{t}$

(B.6)

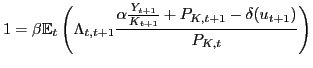$\displaystyle 1=\beta\mathbb{E}_{t} \left( \Lambda_{t,t+1} \frac{\alpha\frac{Y_{t+1} }{K_{t+1}} + P_{K,t+1} - \delta(u_{t+1})}{P_{K,t}} \right)$

(B.7)

$\displaystyle \mathbb{E}_{t-1}(P_{K,t}) = \mathbb{E}_{t-1} \left\{ \left[ \Phi^{\prime }\left( \frac{I_{t}^{n}}{K_{t}}\right) \right] ^{-1} \right\}$

(B.8)

$\displaystyle I_{t}^{n}=I_{t}-\delta(u_{t})K_{t}$

(B.9)

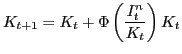$\displaystyle K_{t+1}=K_{t}+\Phi\left( \frac{I_{t}^{n}}{K_{t}} \right) K_{t}$

(B.10)

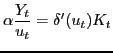$\displaystyle \alpha\frac{Y_{t}}{u_{t}}=\delta^{\prime}(u_{t})K_{t}$

(B.11)

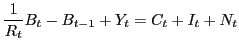$\displaystyle \frac{1}{R_{t}} B_{t} - B_{t-1} + Y_{t} = C_{t} + I_{t} + N_{t}$

(B.12)

$\displaystyle R_{t} = r + e^{r_{t}} + \psi\left[ e^{\frac{B_{t}-B}{Y_{t}}} -1\right]$

(B.13)

B.2 Entrepreneurs and Financial Intermediaries

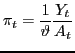$\displaystyle \pi_{t}=\frac{1}{\vartheta} \frac{Y_{t}}{A_{t}}$

(B.14)

$\displaystyle v_{t}=\pi_{t} + \phi_{A} \mathbb{E}_{t} (\Lambda_{t,t+1} v_{t+1})$

(B.15)

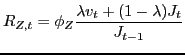$\displaystyle R_{Z,t} = \phi_{Z} \frac{\lambda v_{t} + (1-\lambda) J_{t}}{J_{t-1}}$

(B.16)

$\displaystyle W_{t} = \sigma\left[ \left( R_{Z,t} - R_{t-1} \right) J_{t-1}S_{t-1} + R_{t-1} W_{t-1} \right] + (1-\sigma) \xi J_{t-1} S_{t-1}$

(B.17)

$\displaystyle J_{t} \left[ \phi_{Z} \left( Z_{t} + Z_{N,t} \right) - A_{t} \right] = \phi_{t} W_{t}$

(B.18)

$\displaystyle \Omega_{t} = 1-\sigma+ \sigma\left( \nu_{t} + \phi_{t} \mu_{t} \right)$

(B.19)

$\displaystyle \mu_{t} = \mathbb{E}_{t} \left[ \Lambda_{t,t+1} \Omega_{t+1} \left( R_{Z,t+1} - R_{t} \right) \right]$

(B.20)

$\displaystyle \nu_{t} = \mathbb{E}_{t} \left( \Lambda_{t,t+1} \Omega_{t+1} \right) R_{t}$

(B.21)

$\displaystyle \phi_{t} = \frac{\nu_{t}}{\theta- \mu_{t}}$

(B.22)

$\displaystyle A_{t+1} = \lambda\left[ \phi_{Z} \left( Z_{t} + Z_{N,t} \right) - A_{t} \right] + \phi_{A} A_{t}$

(B.23)

$\displaystyle Z_{t+1} = \phi_{Z} \left( Z_{t} + Z_{N,t} \right)$

(B.24)

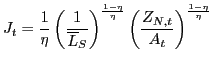$\displaystyle J_{t} = \frac{1}{\eta} \left( \frac{1}{\overline{L}_{S}} \right) ^{\frac{1-\eta}{\eta}} \left( \frac{ Z_{N,t}}{A_{t}} \right) ^{\frac{1-\eta }{\eta}}$

(B.25)

$\displaystyle N_{t}=\eta Z_{N,t} J_{t}$

(B.26)

In the frictionless benchmark, equations (B.17)-(B.21) become irrelevant, and instead perfect arbitrage holds:

$\displaystyle J_{t} = \mathbb{E}_{t} \left\{ \Lambda_{t,t+1} \phi_{Z} \left[ \lambda v_{t+1} + (1-\lambda) J_{t+1} \right] \right\}$

(B.27)

The model is solved by first appropriately detrending the variables that exhibit long-run growth, in order to obtain a stationary system. The steady state of that system characterizes the balanced growth path of the economy. Dynamics are obtained by computing a loglinear approximation around the balanced growth path.

C Effects of Non-financial Shocks

Here I analyze the behavior of the model economy following two types of non-financial shocks that have been highlighted in the literature as important sources of business cycle fluctuations: an exogenous TFP shock, and a wage markup shock. To introduce the former, I modify the production function of intermediate goods firms as follows:

$\displaystyle Y_{t}(s)= \overline{A}_{t} \left[ u_{t}(s)K_{t}(s)\right] ^{\alpha} L_{t}(s)^{1-\alpha}$

(C.1)

Above, $\overline{A}_{t}$ is an exogenous aggregate TFP shock. To introduce the wage markup shock, the labor supply equation is modified according to the following:

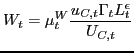$\displaystyle W_{t} = \mu^{W}_{t} \frac{u_{C,t} \Gamma_{t} L_{t}^{\epsilon}}{U_{C,t}}$

(C.2)

$\mu^{W}_{t}$ is a markup of the wage over the household's marginal disutility of work. Several authors have argued that countercyclical movements in the wage markup are an important source of business fluctuations,³⁸ possibly by capturing in a reduced-form way the effects of nominal price and wage rigidities or labor market frictions.

Figures 9 and 10 report the effects of a 5% decline in exogenous TFP and a 5% increase in the wage markup, respectively. Both shocks persist as an AR(1) with a 0.95 coefficient. The key point to note is that both shocks induce only modest declines in the endogenous component of TFP, and that the degree of amplification through the credit market imperfection is also relatively small. The reason is that unlike financial shocks, these two types of shocks induce modest movements in the asset prices $v_{t}$ and $J_{t}$ . As a consequence, both the frictionless effect on firm creation is small (since the movement in $v_{t}$ is relatively small) and also the degree of amplification due to financial frictions is small, since the relatively modest movements in asset prices lead to only mild fluctuations in banks' net worth. Further, in the case of wage markup shocks, labor productivity does not decline - in fact it slightly increases initially due to the sharp drop in employment. As the figures illustrate, these types of disturbances are followed by a recovery, which is driven by the unwinding of the shock. Thus, the bottomline from Figures 9 and 10 is that the model is also consistent with the evidence that especially deep and persistent output losses are a phenomenon especially associated with recessions involving financial crises, as Reinhart and Rogoff (2009) and others have noted.

Figure 9: Responses to exogenous TFP shock. Time measured in years. All variables in log deviations from the balanced growth path.

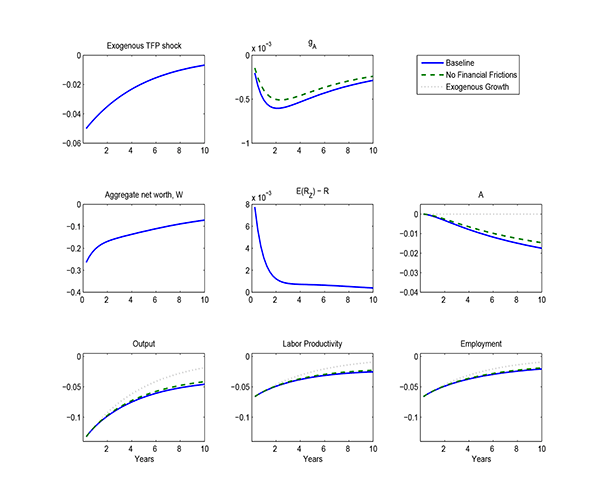
Figure 10: Responses to wage markup shock. Time measured in years. All variables in log deviations from the balanced growth path.

Footnotes

1. I thank Ozge Akinci, Dario Caldara, Diego Comin, Jordi Galí, Matteo Iacoviello, Leyla Karakas, Robert Kollmann, John Leahy, Virgiliu Midrigan, Vivian Yue and seminar participants at various venues for very useful comments and discussions. I am especially indebted to Mark Gertler for his advice and guidance on this project. Financial support from Fundación Rafael del Pino is gratefully acknowledged. The views expressed in this paper are those of the author, and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

2. Division of International Finance, Federal Reserve Board. E-mail: albert.queralto@frb.gov Return to text

3. Cerra and Saxena (2008) document little evidence of output recovery from financial crises in a large cross-section of countries. See also Reinhart and Reinhart (2010), Reinhart and Rogoff (2009) or Chapter 4 in International Monetary Fund (2009) and references therein. Return to text

4. At the end of section 2, I present some evidence suggesting a decline in firm creation during financial crises, by examining the behavior of time series data on patent and trademark applications during the 1997 crisis in South Korea. Return to text

5. See also Gertler and Kiyotaki (2010) or Gertler, Kiyotaki and Queralto (2012). Return to text

6. Since projects become successful through a simple time-invariant Poisson process, at any given date the value of a unit of the equity issued by an entrant entrepreneur must equal the franchise value of an entrepreneur that entered in the past but that has so far not been successful. Return to text

7. See also Comin, Gertler and Santacreu (2009), who estimate a version of the model in Comin and Gertler (2006), or Comin, Loayza, Pasha and Serven (2009) who propose a related framework for developing countries. Return to text

8. For instance, Gopinath and Neiman (2011), Benjamin and Meza (2009), Meza and Quintin (2007), Kehoe and Ruhl (2009), Pratap and Urrutia (2010) or Aoki, Benigno and Kiyotaki (2007). Return to text

9. The countries included are Indonesia, Malaysia, Phillipines, Korea, Thailand and Hong Kong, labelled "SEA-6". Area totals are computed by adding constant dollar, PPP-adjusted GDP for each of the countries. Labor productivity is defined as output per employed worker. See Appendix 1 for details on the data. Return to text

10. This is robust to different choices for the period used to compute the pre-crisis trend. Annualized growth of labor productivity for the period 1980-1996 is 4.06%, which is close to that for the entire pre-crisis sample (1960-1996), equal to 3.69%. Annual productivity growth for the post-crisis period of 1998-2007 is 3.61%, close to the figure for the pre-crisis sample. Return to text

11. That assumption is motivated by the outcome of standard augmented Dickey-Fuller tests, which for virtually all countries do not reject the null of a unit root in the levels of ouput, employment and productivity, but do reject the same null when applied to the first differences (at the 1-percent significance level). Return to text

12. See Appendix 1 for details on the data and the complete list of crises dates. Return to text

13. The latter is obtained by estimating a univariate model for the first difference of log output analogous to (1). This approach is more efficient than computing output as the sum of labor productivity and employment from (1) as it requires estimating a smaller number of parameters. Return to text

14. The results documented here contrast to some extent to those in Howard, Martin and Wilson (2011), who find that the recoveries from recessions associated with banking or financial crises are not unusually weak. The discrepancy is partly because they focus on growth following the recession trough, while the analysis above studies the impulse response to a banking crisis shock. Both sets of findings can be partly reconciled by the observation in Howard, Martin and Wilson (2011) that since banking and financial crises tend to be deep and long, and post-trough growth is about average, the output declines in these episodes are not made up quickly. Return to text

15. See Chapter 4 of International Monetary Fund (2009) for further evidence on persistent declines in TFP following financial crises. Return to text

16. Kortum and Lerner (2000) establish a positive effect on innovation of the availability of venture capital funding, and Kerr and Nanda (2009) show that US financial reforms enhanced the process of small firm entry. Return to text

17. See Hall (2002) and Hall and Lerner (2009) for surveys of work using data from OECD countries. Return to text

18. See Ayyagari et. al. (2007), and particularly Gorodnichenko and Schnitzer (2010), for studies using firm-level survey data from developing economies. Return to text

19. For example Meza and Quintin (2005) or Kehoe and Ruhl (2009). Return to text

20. In the latter case, the assumption is that it is still costly to introduce an innovation that is already in use in a more developed economy. See Mansfield, Schwartz and Wagner (1981) for evidence suggesting that "imitation" costs can indeed be substantial. Return to text

21. The expression for $MC_{t}$ can be obtained by solving the cost minimization problem of an entrepreneur :

$\displaystyle \min_{N_{t}(i),L_{S,t}(i)} N_{t}(i) + W_{S,t} L_{S,t}(i)$

subject to

$\displaystyle N_{t}(i)^{\eta} \left[ A_{t} L_{S,t}(i) \right] ^{1-\eta} \geq1$

The marginal cost $MC_{t}$ is then equal to the multiplier associated with the constraint of the problem above. Return to text

22. See Haltiwanger, Jarmin and Miranda (2012). Return to text

23. Kiyotaki and Moore (2012), Del Negro, Eggertsson, Ferrero and Kiyotaki (2010) and Jermann and Quadrini (2012) use a mechanism in this spirit to motivate a disruption in financial markets. Return to text

24. Here the underlying assumption is that the entrepreneur, when successful, sells the idea to a monopolist producer of intermediates, who then obtains the stream of profits $\left\{ \pi_{t+i} \right\} _{i=0}^{\infty}$ from manufacturing and selling the new variety and therefore is willing to pay $v_{t}$ for the project. Return to text

25. Note that for the incentive constraint to bind we must also have $\mu_{t} < \theta_{t}$ : otherwise, the value of an extra project is greater than the gain from diverting the additional funds, so there is never an incentive to default. In the equilibrium constructed below, for reasonable parameterizations the constraint always binds along the balanced growth path. Return to text

26. See Levine (1997, 2005) for surveys of evidence suggesting that financial development has a positive impact on long-run TFP and output growth. Return to text

27. As made clear below, adjustment costs are on net rather than gross investment, so that replacing worn-out capital does not involve adjustment costs. This formulation makes the capital utilization decision independent of the price of capital. Return to text

28. To elaborate on this, one could follow Gertler and Karadi (2011) and assume that firms need to obtain loans from banks to finance their purchases of physical capital. In this generalized model, banks would then make two types of loans: loans to existing firms to invest, and loans to entrepreneurs to create new firms. One could postulate different intensities of the financial friction for each type of activity, which could be captured by assuming that the fractions divertable are different for each of the two types of banks' assets. Return to text

29. Given the assumptions on $\Phi(\cdot)$ , to a first order the evolution of capital along the balanced growth path is the usual $K_{t+1}=\left[ 1-\delta(u_{t})\right] K_{t} + I_{t}$ . Return to text

30. Appendix C contains some additional model results regarding the effects of non-financial shocks. Return to text

31. While higher values of this parameter are frequently used in the literature, Mendoza and Yue (2012) argue that it is desirable to set this parameter at a relatively low value, since empirical estimates suggest that working capital is a small fraction of GDP. A working capital requirement of 0.35, together with a wage bill of two thirds of GDP, implies a ratio of working capital to GDP of around 23%. Return to text

32. MacGrattan and Prescott (2010), for example, estimate investment in technology capital at about 6 percent of GNP in the US. This is likely a lower bound on total entry costs, as not all firm creation is captured by R&D data. Return to text

33. See Kalemli-Ozcan, Sorensen and Yesiltas (2012) for cross-country evidence on bank leverage ratios. Return to text

34. Unanticipated increases in country interest rates, reflecting sudden stops in capital inflows, are considered an important force behind recent financial crises, and behind emerging market business cycles more generally - see for example Calvo (1998), Neumeyer and Perri (2005) or Uribe and Yue (2006). Return to text

35. As Figure 4 shows, the model understates the short-run declines following the crisis. These are likely related to phenomena like nominal price or wage rigidities which for simplicity have been ignored in the model, focusing instead on the novel aspects regarding persistence. It would be straightforward to extend the model along these dimensions. Return to text

36. See Bernanke (2012) or Section 3 of Bank of England (2012). Return to text

37. http://www.conference-board.org/data/economydatabase/ Return to text

38. See Hall (1997), Galí, Gertler and López-Salido (2007) and Chari, Kehoe and McGrattan (2007). Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

A Model of Slow Recoveries from Financial Crises1

1 Introduction

2 Evidence from Systemic Banking Crises

3 Model

3.2 Households

3.2 Entrepreneurs

3.3 Banks

3.3.1 Aggregation

3.3.2 The Frictionless Benchmark

3.4 Final Output and Intermediates Producers

3.5 Capital Producers

3.6 Market Clearing

4 Model Analysis

4.1 Parameter Values

4.2 Crisis Experiment

5 Conclusion

Bibliography

Appendix

A Data

B Complete Set of Equilibrium Conditions

B.1 Households and Firms

B.2 Entrepreneurs and Financial Intermediaries

C Effects of Non-financial Shocks

Footnotes

A Model of Slow Recoveries from Financial Crises¹