The Federal Reserve Board eagle logo links to home page
Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]
Finance and Economics Discussion Series: 2009-25 Screen Reader version ♣

Whither the Liquidity Effect: The Impact of Federal Reserve Open Market Operations in Recent Years

Ruth Judson*
Elizabeth Klee**

Keywords: Liquidity effect, open market operations, monetary policy implementation

Abstract:

Previous research indicated that the daily liquidity effect, or the change in the federal funds rate associated with an exogenous change in Fed balances, varies with several factors including the day of the maintenance period. In this paper, we examine the data over the recent period of increased Federal Reserve transparency and find that the liquidity effect stabilized across days of the maintenance period. Rather, the liquidity effect may be a function of the uncertainty about banks' end-of-day balances. Moreover, we find that increased transparency led to a larger liquidity effect on the days prior to an FOMC meeting.


1 Introduction

Whether short-term interest rates change in response to a change in the money supply is a perennially debated issue. Identifying this phenomenon, known as the "liquidity effect," is central to understanding the Federal Reserve's ability to implement monetary policy under its current operating regime. Previous literature has discussed two types of liquidity effects, long-range and daily. Evidence of the former has been mixed: over monthly and yearly horizons, some researchers have shown that short-term interest rates respond to a change in the money supply (Bernanke and Mihov, 1998), while others do not find such an effect (Leeper and Gordon (1992)). The differences in the estimated liquidity effects stem from different specifications, sample periods, and measures of the money supply, suggesting that if a long-range liquidity effect does exist, it is not necessarily econometrically robust or stable through time. Indeed, more recently, Carpenter and Demiralp (2008) provide evidence of a liquidity effect at a monthly frequency, using a more relevant measure of the money supply - balances held at the Federal Reserve - for such an exercise. Consistent with this more relevant definition of the money supply, evidence of a daily liquidity effect has been found repeatedly and robustly: on a daily frequency, the effective federal funds rate moves lower in response to unexpected increases in the supply of Fed balances. Research by Hamilton (1997) and Carpenter and Demiralp (2006a) indicates that this daily liquidity effect varies according to the day of the maintenance period, becoming particularly pronounced on settlement Wednesday, the last day on which banks can satisfy their reserve requirements.

Significant changes in the structure of the market for Federal Reserve balances over the past decade may have affected the magnitude and the nature of the daily liquidity effect. Hilton (2005) points to four operations-related changes: the reintroduction of lagged reserve accounting in 1998, ongoing modernization in banking and account monitoring technology, increasingly frequent fine tuning operations, and improved forecasting by the Federal Reserve staff.

In addition, the Federal Reserve has been increasingly transparent in its communication of monetary policy over the past two decades. Starting with indications of the intended policy rate and bias in the late 1980s, continuing with the explicit announcement of changes in the target federal funds rate in 1995 and extended with the release of a statement after every meeting, the Federal Reserve has provided ever-clearer signals of its outlook.1 As a result, market participants have been able to anticipate more precisely changes in the target federal funds rate. There may be implications of this anticipation in the slope of the demand curve leading up to FOMC meetings: Banks may attempt to minimize total funding costs over a maintenance period, thereby reallocating demand across days on either side of the anticipated rate change.

This paper examines the liquidity effect in the current environment and advances the literature in several dimensions. First, we demonstrate that the liquidity effect attenuated considerably in the recent period, and we identify a break following the re-introduction of lagged reserve requirements in 1998. Second, we find that the liquidity effect is systematically stronger on high-payment-flow days, and that these days do not necessarily correspond to the standard set of calendar days typically presumed to be high-payment-flow days. Third, we find that the liquidity effect intensifies well in advance of an FOMC meeting at which an increase in the target federal funds rate is anticipated, particularly when the FOMC meeting falls late in the two-week reserve maintenance period.

Our main results are as follows. In contrast to research using data from earlier periods, we find that the liquidity effect is roughly constant across the days of the maintenance period, except on the last day of the maintenance period. Furthermore, in all cases, the liquidity effect has attenuated markedly through time. We conjecture that improved reserve management and increased transparency in monetary policy likely contributed to the diminished liquidity effect.

These results have a few policy implications. First, the results suggest that the technical innovations in reserves management have allowed banks to better monitor their reserve positions. Similar to previous work, we do find a statistically significant difference on settlement day; however, the magnitude of this difference is quite small compared to that estimated on data from earlier periods. In addition, the results are consistent with the idea that funds market behavior during the period of increased transparency has been better anchored around the target rate and has been associated with fewer large deviations of the funds rate from the target rate. Depository institutions have come to expect funds to trade close to the target rate, and thus do not generally have as dramatic reactions to forecast misses as may have occurred in the earlier period. Moreover, there may be broad expectations that the trading desk ("the Desk") at the Federal Reserve Bank of New York will successfully offset these misses in later days of the maintenance period by adding or draining balances accordingly, diminishing the incentive for institutions to react materially to balance shortfalls or excesses on most days of the maintenance period.

In September 2008, the Federal Reserve implemented several measures to provide liquidity to financial markets. These measures were not completely offset by corresponding reductions in the Federal Reserve's assets and, as a result, excess reserve balances reached very high levels. Under these conditions, the Federal Reserve's approach to monetary policy implementation differed from that described in this paper. The measures taken to provide additional liquidity are currently described as temporary.

The remainder of the paper proceeds as follows. Section 2 reviews the primary features of monetary policy implementation. Section 3 reviews our analytical framework. Section 4 presents our estimation results. Section 5 offers concluding remarks.

2 Background

The Federal Reserve implements monetary policy by conducting open market operations to align the supply of balances held by depository institutions at Reserve Banks with demand for those balances so that federal funds trade around the target rate set by the Federal Open Market Committee (FOMC). Because the Desk adjusts supply in part to address day-to-day changes in demand, there is a classic simultaneity problem when estimating the slope of the demand curve. For this reason, this paper follows the work of Hamilton (1996, 1997) and Carpenter and Demiralp (2006a, 2006b) in using the change in the federal funds rate associated with an unanticipated change in the supply of balances held at the Federal Reserve to trace out the demand curve. In order to provide background for the subsequent analysis, this section reviews the main components of supply and demand for fed balances.

Demand for balances by depository institutions (DIs) at the Federal Reserve is generated by the need to satisfy reserve requirements, to cover clearing needs, and to provide a cushion against unexpected reserve balance or clearing needs. Balances that are held to satisfy reserve requirements not covered by holdings of vault cash are called required reserve balances, and amount to about half of balances held at the Federal Reserve. Service-related balances, or "contractual clearing balances" are balances that DIs agree to hold, primarily to cover payment services related needs. Should a DI satisfy their reserve requirement with vault cash or have what they view as a relatively low required reserve balance requirement, a DI can choose to hold balances at the Federal Reserve to cover payments clearing needs. Currently, these are the only balances for which DIs are compensated; in this case, in the form of credits toward payment for Federal Reserve priced services. Because there are penalties for not meeting either a reserve balance requirement or a clearing balance requirement, some DIs will hold a cushion of balances, called "excess balances", which are held voluntarily by DIs. In aggregate and on average, these balances represent the smallest share of balances held at the Fed.

The demand for balances can vary significantly from day to day. Desk and Board staff estimate the expected demand for balances at the policy target each day taking into account market conditions, including expected payment flows, the day of the two-week maintenance period, and discussions with banks and brokers.

The supply of reserve balances is determined largely by the Federal Reserve's portfolio of securities and repurchase agreements, discount window borrowing, and other items on the Fed's balance sheet, also known as "autonomous factors"2 Board and Desk staff produce forecasts each morning for the major autonomous factors, including the Treasury's balance at the Fed, the change in currency in circulation, and check float. Each day, the Desk decides whether an open market operation is needed to bring the expected supply of balances into alignment with the projected demand for balances at the target rate.

Forecasting is an inexact exercise, and there can be errors in the forecasts of individual autonomous factors. However, from a monetary policy implementation point of view, only the net effect of these errors on the total supply of balances is important. For example, if the actual level of Fed liabilities is higher than the forecasted level (such as the Treasury General Account (TGA) coming in at a higher level than forecast), then there will be a lower level of Fed balances than forecast. As a result, it is likely that the funds rate will rise. But, if at the same time the actual level of Fed assets is also higher than the forecast (such as the level of check float coming in higher than forecast), then the assets miss will offset the liabilities miss and the actual quantity of Fed balances will be closer to the forecast.

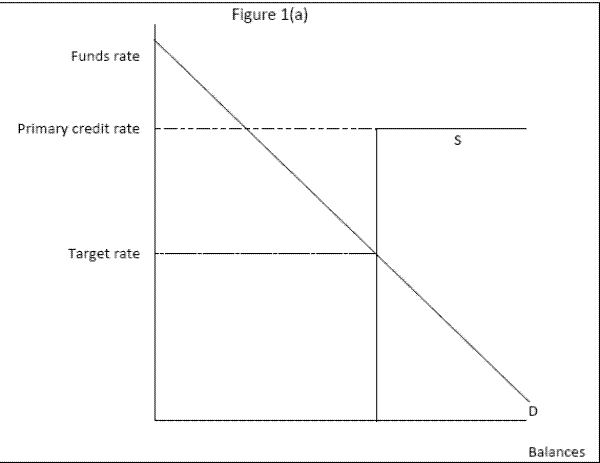
Figure 1 (a) summarizes a stylized supply and demand framework for balances. The (inverse) demand curve for reserve balances slopes down, as demand for balances is assumed to increase with decreases in the federal funds rate. The slope of this curve is the liquidity effect. The supply curve for reserve balances is determined solely by the level of autonomous factors and the open market operation at rates below the primary credit rate. It then extends horizontally at the primary credit rate as the Federal Reserve provides as much balances are demanded at that rate when market conditions are tight, increasing the total supply of fed balances.

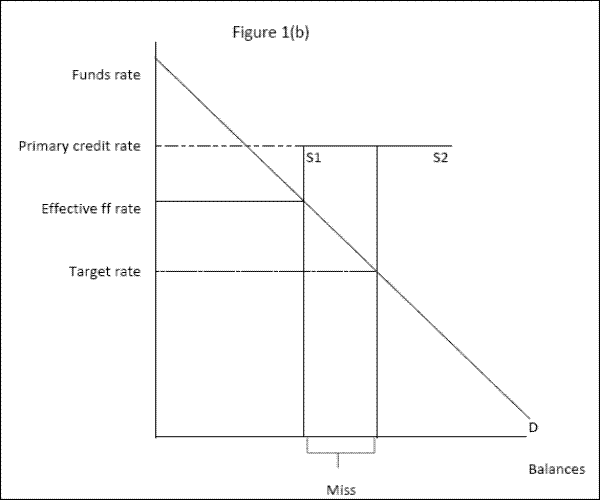
Despite the Desk's efforts, the daily effective federal funds rate occasionally differs significantly from the target rate. Such deviations often occur when large errors in the forecasts of the autonomous factors result in a supply of balances that differs substantially from the projected level used as a basis for the open market operation. This "factors miss" is the unanticipated quantity of balances used to identify the liquidity effect in our analysis and is shown in figure 1 (b). As shown in the case of a draining miss, the supply curve shifts in and the equilibrium funds rate increases. An adding miss would work similarly: The supply curve would shift out and the funds rate would decrease. Because these misses are unanticipated both by the Desk and by market participants, we can use them as an instrument to trace out the slope of the demand curve.

3 Analytical Framework

This next section develops the analytical framework in three parts. The first reviews the baseline analytical framework, the second explores a few extensions, the third presents the empirical specification, and the fourth addresses the specification of the error term, a particularly critical part of the analysis.

3.1 Baseline specification

Our basic analytical framework follows earlier work by Hamilton (1996, 1997), Carpenter and Demiralp (2006a, 2006b), and others. As explained in the background section above, the daily supply of Fed balances depends largely on the level of autonomous factors, f_{t, } and the open market operation, omo_{t}, with the size of the open market operation chosen at a level such that it is expected that the rate where the demand for funds equals the supply for funds is near the target federal funds rate. There are two elements that are unknown at the time of the operation, however. First, the actual level of autonomous factors is unknown at the time of the operation, and as a result the operation is based on a forecast, E_{t-1}f_{t}. Second, the Desk does not know exactly the parameters of the demand curve, although through analysis and experience, it is able to infer implicitly these parameters.

Specifically, we posit that the supply of funds obeys the following relation

\begin{displaymath} s_t =E_{t-1} f_t +miss_t +omo_t \end{displaymath}

and the true demand for funds is
\begin{displaymath} d_t =\beta _0 X_t +\beta _1 ff_t +\varepsilon _t \end{displaymath}

The Desk, however, only knows estimates of the parameters of the demand function, and sets expected supply equal to expected demand at the target federal funds rate, or
\begin{displaymath} E_{t-1} f_t +omo_t =\beta ^\ast _0 X_t +\beta ^\ast _1 fftar_t \end{displaymath}

Note that in expectation, the factors miss is zero. Rearranging a little leads to our initial empirical specification:
\begin{displaymath} (ff_t -fftar_t )=\frac{\left( {\beta ^\ast _0 -\beta _0 } \right)}{\beta _1 }X_t +\frac{\left( {\beta ^\ast _1 -\beta _1 } \right)}{\beta _1 }fftar_t +\frac{1}{\beta _1 }miss_t -\frac{1}{\beta _1 }\varepsilon _t \end{displaymath}

The liquidity effect can be inferred from the coefficient on the miss term.

3.2 Extensions

One of the major contributions of this paper is a discussion of the effect of uncertainty on the liquidity effect. Suppose that banks are not sure what their end-of-day balances will be, and, instead, only have a noisy signal of their true need for funds. In that world, the demand for funds can be written as

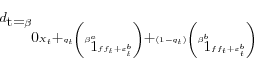
\begin{displaymath} d_\mbox{t} \mbox{=}\beta _\mbox{0} X_t \mbox{+}q_t \left( {\beta ^a_\mbox{1} ff_t +\varepsilon ^b_t } \right)\mbox{+}\left( {1-q_t } \right)\left( {\beta ^b_\mbox{1} ff_t +\varepsilon ^b_t } \right) \end{displaymath}

where q_{t} is the probability that demand is in state a, and (1-q_{t}) is the probability that demand is in state b. Without loss of generality, let \beta ^{l}_{a} \quad <>\beta 1_{b}, which implies that demand is in the high state in date a.

A little rearranging shows that the equilibrium condition now becomes

\begin{displaymath} \begin{array}{c} \left( {ff_t -fftar_t } \right)=\frac{\bet... ...eta ^a_1 +\left( {1-q_t } \right)\beta ^b_1 } \ \end{array}\end{displaymath}

We can glean a few predictions from this setup. First, note that the existence of uncertainty over the demand curve pushes up the liquidity effect on days when demand is usually not very responsive to the quantity of balances. Second, in theory, it should be the case that this uncertainty over the demand curve should cause the liquidity effect to moderate on days when demand is usually quite responsive to balances. However, there is a minor problem with this proposition: Banks face asymmetric penalties for holding too few balances as opposed to too many, making it likely that banks are reluctant to gamble that demand might actually be low that day. Banks may instead operate under the following assumption:
\begin{displaymath} \begin{array}{c} \left( {ff_t -fftar_t } \right)=\frac{\bet... ...eta ^a_1 +\left( {1-q_t } \right)\beta ^b_1 } \ \end{array}\end{displaymath}

where banks react more sharply to shortfalls or surpluses on high demand days, and will also mark up the response on low demand days.

Moreover, at the end of the day, there is likely some resolution of the uncertainty. If there appears to have been too few funds in the market, reserves managers will continue to bid up funds, creating a more pronounced liquidity effect. On the other hand, if it is revealed that enough funds are available in the market, funds managers may quickly act to sell as many funds as possible, thereby compounding the liquidity effect on the downside. As a result, the existence of uncertainty and asymmetric penalties are sufficient in order to increase the magnitude of the liquidity effect. Similarly, the existence of uncertainty about end-of-day balances necessarily pushes up the variance of the error term. If uncertainty changes throughout the sample period, it is unlikely that the variance of the error term would stay constant over time.

3.3 Empirical specification

With this discussion in mind, we now turn to the empirical specification. Our dependent variable is the deviation from the target of the effective federal funds rate. Not all trades in the fed funds market occur at the target federal funds rate. We focus on the daily effective federal funds rate, which is the dollar-weighted average of rates on trades arranged by major brokers. This is the rate reported by the Federal Reserve Bank of New York to the public and is considered the official measure of the actual federal funds rate on a given day. We follow the lead of Carpenter and Demiralp (2006a, 2006b) and posit that the deviation of the effective federal funds rate from the target federal funds rate obeys the following relation:

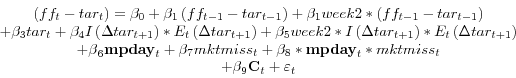
\begin{displaymath} \begin{array}{c} \left( {ff_t -tar_t } \right)=\beta _0 +\b... ...{\bf\beta }}_9 {\rm {\bf C}}_t +\varepsilon _t \ \end{array}\end{displaymath}

where mpday is a vector of dummy variables that equal 1 if it is the particular day of the maintenance period. C is a vector of calendar day indicator variables including the month start, mid-month, end of month, end of year, and first of year. Each day, depository institutions send trillions of dollars over the Fedwire Funds Transfer Service, the large-value payment system owned and operated by the Federal Reserve. Payment flows tend to be elevated at month-start, mid-month, the twenty-fifth of the month, month-end, and on days after holidays, owing in part to corporate tax due dates, principal and interest payments on securities, and pent-up flows after a long weekend. As documented by Furfine (2001) and others, funds tend to trade at rates somewhat above the target on these days.

We also include information on monetary policy actions in our specification. To start, we include the level of the target federal funds rate, in order to test whether the level of the cost of funds has any bearing on the liquidity effect. In addition, we control for changes in the target federal funds rate, denoted by I\left( {\Delta tar} \right). These controls include anticipated changes in the target federal funds rate (allowing for differential effects according to the timing in the maintenance period and denoted by E) and unanticipated changes in the target federal funds rate. Anticipated and unanticipated changes in the target federal funds rate are calculated using fed funds futures rates according to an algorithm developed by Kuttner (2001) and as used in Carpenter and Demiralp (2006b).

Finally, we include variables that are intended to capture the liquidity effect. The variable mktmiss is the factors forecast miss, and mpday*mktmiss is the factors forecast miss interacted with the day of the maintenance period, which allows the liquidity effect to vary with the day of the maintenance period. Mktmiss is constructed using the Board staff factors forecast miss, which is the net autonomous factors forecast miss.3 We also include a term that provides an estimate of the liquidity effect on the day after a federal funds rate target change, as funds will sometimes stray from the target notably on these days and may bias estimates of the overall liquidity effect.

3.4 Error specification

In order to control for changes in volatility of the funds rate over time, and in line with previous research, we use an EGARCH specification for the error term developed by Nelson (1991). This specification allows for persistence in volatility, variation in volatility across observations, and differential effects of positive and negative surprises on volatility. The model we use for the error term is

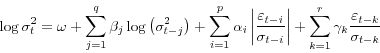
\begin{displaymath} \log \sigma ^2_t =\omega +\sum\limits_{j=1}^q {\beta _j \log \left( {\sigma ^2_{t-j} } \right)+\sum\limits_{i=1}^p {\alpha _i \left\vert {\frac{\varepsilon _{t-i} }{\sigma _{t-i} }} \right\vert+\sum\limits_{k=1}^r {\gamma _k \frac{\varepsilon _{t-k} }{\sigma _{t-k} }} } } \end{displaymath}

The log of the variance is a function of previous variances, plus a constant. Moreover, the \gamma _{k} terms capture possible asymmetry of the effect of shocks on volatility. If the \gamma _{k} terms are positive, then positive shocks to the funds rate are associated with higher volatility; conversely, if the \gamma _{k} terms are negative, then positive shocks are associated with lower volatility. We include one lag for each of these terms.

We also include dummy variables in the error term specification in order to control for types of days with elevated levels of volatility. These include the last three days of the maintenance period, Fridays, the day before and the day after a change in the federal funds target rate, December, and the days before and after holidays.

4 Estimation Results

4.1 Replication and extension to recent period

As a first step, we explore the data for two samples: the 1994 to 2004 sample used by Carpenter and Demiralp (2006a), and a sample beginning in January, 2004, the period during which changes in the target federal funds rate were nearly perfectly anticipated, as illustrated in Figure 2. We use business day data from February 1, 1994 to August 1, 2007, updating the sample used in Carpenter-Demiralp and overlapping with Hamilton.4 We dropped observations from September 11 to September 20, 2001 and from December 27 to 30, 1999.

Table 1 presents summary statistics for the deviation from the target rate and the forecast miss for the three samples. As is shown in the table, the average deviation from the target, both in actual and absolute terms, attenuated considerably in the most recent sample. A simple means test easily rejects the hypothesis that the mean absolute deviation from the target from 2004 to 2007 was the same as that from 1994 to 2004.5

While the daily forecast miss data are confidential, the summary statistics presented in table 1 show the stability of the miss over the different samples. In contrast to the behavior of the funds rate, the factors forecast miss was only slightly lower in the 2004 to 2007 period, and the means of the absolute forecast misses are not statistically different in the two samples. Thus, even before controlling for all factors in our specification, there is some evidence that the behavior of the funds rate may have changed in the recent period.

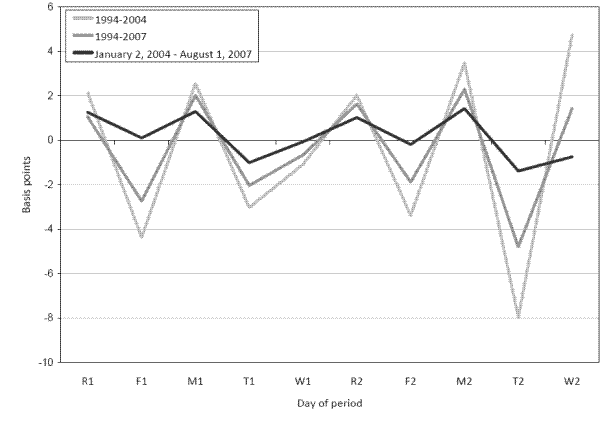
As our first step, we re-estimate the model developed in Hamilton (1996) and extended by Carpenter and Demiralp (2006a) using the samples in those works as well as data for the more recent period. Estimation results from the baseline specification over the two samples are shown in table 2. The first column covers Carpenter and Demiralp's (2006a) 1994 - 2004 sample. The estimated coefficients for the average deviation from the target across the days of the maintenance period are plotted in figure 3. As illustrated by the lighter gray line, funds tend to trade quite soft on the first and second Fridays of the maintenance period, labeled F1 and F2, respectively. This phenomenon likely reflects the fact that funds held on these days count for three days of requirements, and DIs may be reluctant to hold excess reserves and lose the option value of holding more reserves later in the period. Mondays, labeled M1 and M2, tend to be firm, due in part to elevated payment flows.6

Demand on the first Tuesday (T1) and Wednesday (W1) tends to be somewhat slack, as payment flows are generally relatively soft in the middle of the week and DIs still have plenty of days to fulfill their requirements. Finally, in this sample funds tend to trade quite firm on the last day of the maintenance period: the point estimate suggests that on average, funds trade about 5 basis points firm to the target. These systematic deviations are largely the result of demand factors that the Desk does not completely offset in its operations. In terms of figures 1(a) and 1(b), it would be as if the intersection of the demand curve and the supply curve was at a rate different from the target federal funds rate. The liquidity effect, by contrast, is measured by the coefficient on a purely unanticipated shock to balances and thus shifts the supply curve, allowing us to infer the slope of the demand curve.

As previous research suggests (for example, Hamilton (1996) and Furfine (2001)), our results show that there are systematic deviations from the target according to calendar effects. As shown in the second block of rows on Table 2, these calendar days are generally associated with rate firmness, particularly on quarter-end, when payment flows usually hit peaks for the year and rates are about 40 basis points firm to the target.7 Although payment flows are also generally elevated on year-end, in recent years funds have tended to trade quite soft to the target on the year-end itself.8 It is important to note that our empirical specification assumes that the Desk is able to infer the demand curve on average accurately in order to identify the liquidity effect. As a result, we assume that the systematic misses from target are fully captured by these linear shift parameters.

The next block of rows in table 2 displays the coefficients on factors associated with the level of and changes in the federal funds target rate. As evidenced by the positive coefficients on the lagged deviation from the target variables, there is some persistence in deviations from the target from one day to the next: on average, firm days are generally followed by firm days, and soft days are followed by more softness. The persistence is apparently generally more pronounced in the second week of the maintenance period, with the total effect about one-and-a-third times that for the first week of the maintenance period. Should a shortfall in balances occur in the first half of the maintenance period, banks are more able to shift their demand towards later days of the maintenance period and therefore do not need to bid up the price of funds to the same extent as would be necessary in the latter part of the maintenance period, when there are fewer remaining days for DIs to fulfill their requirements. The logic for persistent softness is similar.

The level of the target federal funds rate does not appear to have a statistically significant effect on the deviation from the target over the sample period. This result suggests that the Desk is able to infer the demand for balances accurately at any target federal funds rate and there is no systematic bias in the estimation of the demand for balances due to the level of the target. However, anticipated changes in the target federal funds rate evidently do have an effect. Funds tend to trade in the direction of the anticipated target change on the day before the actual change: on average, for every 2 basis points of anticipated change, funds deviate from the current target about 1 basis point in the anticipated direction of change, in line with the results in Carpenter and Demiralp (2006b).

The final section of the table details the results on the liquidity effect. In addition to the previously discussed systematic deviations in the target across days of the maintenance period, there are systematic differences across days in the magnitude of the liquidity effect. Similar to previous work, we find that the liquidity effect is pronounced on the first Monday of the maintenance period and on the last two days of the maintenance period. On the first Monday of the maintenance period, the liquidity effect is about 3 basis points per $1 billion of unanticipated balances. There are also statistically significant liquidity effects on the last two days of the maintenance period, with settlement day associated with a liquidity effect of about 2 basis points per $1 billion. Evaluating the liquidity effect at the mean absolute value of the miss implies that a typical miss would result in an incremental deviation from the target of about 2 basis points on settlement day.

The coefficients in the EGARCH terms suggest that there exists a positive leverage effect in the funds market; that is, volatility tends to increase with positive deviations from the target. Other factors, such as the last three days of the period and some calendar effects also serve to increase funds market volatility.

The second set of results on the table presents results from the same specification, but extends the sample from where Carpenter and Demiralp (2006a) left off, starting in January 2, 2004 and continuing to August 1, 2007. The results using data from earlier periods are in marked contrast to those obtained using more recent data. First, as shown in figure 3, the magnitude of the day of the maintenance period coefficients is much smaller in the recent period. Second, while the Monday coefficients are still positive and statistically significant, the last day of the maintenance period is associated with softness, not firmness. Theoretical research (Clouse and Dow (2002)) would lead us to expect to find firmness on the last day of the maintenance period: they show that because aggregate shocks to balances can occur after the last operation of the period of the Open Market Desk, and because there are fixed costs to going to the discount window, some banks are willing to pay very high rates for funds in order to avoid a reserves deficiency charge for the maintenance period. Our empirical results suggest that funds trade about 1 basis point soft on the last day of the period on average, suggesting that the Open Market Desk may be systematically providing more balances than strictly necessary in order to prevent just this sort of outcome.

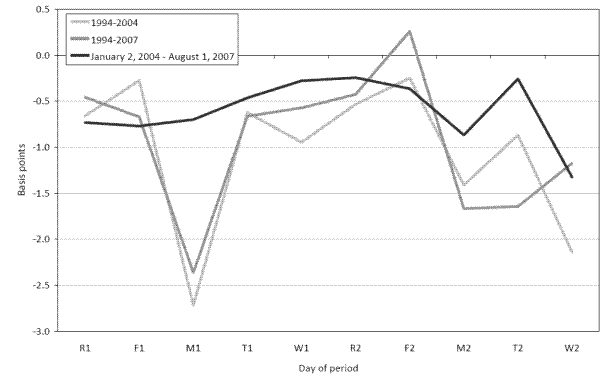
The estimated liquidity effect is also strikingly different in the more recent sample than in the earlier period. Consistent with Carpenter-Demiralp (2006a), we find liquidity effects on more than one day of the maintenance period, but the magnitudes are much more muted. As depicted by the black line in figure 4, we find that the magnitude of this liquidity effect is relatively uniform across days. The exception is settlement day, when the liquidity effect is estimated to be 1.3 basis points. This liquidity effect is about half of the mean absolute deviation from the target for the sample period. As is evident from the figure, estimates of the liquidity effect across all three samples usually fall within a 4 basis point range.

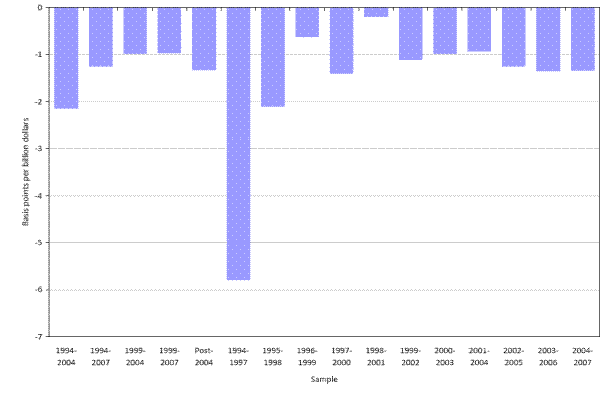
Upon finding these results, our conjecture was that there was a secular trend in the liquidity effect that had not been previously documented. In order to examine this hypothesis, we divided the data into four-year samples starting in 1994 and continuing to August 1, 2007. Figure 5 displays the estimated liquidity effect on settlement day for these periods. The estimated liquidity effect trends down considerably through time - falling from 6 basis points per $1 billion of unanticipated balances in the early part of the period, to a range of 1 \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} to 2 basis points from 1995 through the turn of the century. Since 1999, the settlement day liquidity effect as estimated with this specification fluctuates in a narrow band between 1 and 1 \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} basis points. Notably, lagged reserve requirements were re-introduced in July, 1998. Structural break tests on linear versions of the model strongly reject the null hypothesis that the elasticity coefficients were stable before and after 1998.

4.2 Modifying the specification

One difficulty with the results presented above is that, for the specification used in Carpenter and Demiralp (2006a) the null hypothesis of no serial correlation in the residuals is resoundingly rejected for the period from 2004 through 2007, even though it uses a first order autoregressive process with an EGARCH specification for the variance of the error term that was adequate for the earlier period.9 For this reason, we took a close look at the specification and considered whether there may have been a regime shift in the factors that affect the deviation from the target from the earlier to the more recent period.

4.2.1 Investigating the original specification and the anticipation effect

Table 3 presents results from a specification that includes all of the controls in equation (1), and supplements with some other key variables. In this specification, we target three major weaknesses of the Carpenter and Demiralp (2006a) specification for the more recent period. We first focus on the variables related to the anticipation effect (Carpenter and Demiralp 2006b). The coefficient on the anticipated target change variable in the original specification is practically equal to 1, suggesting perfect anticipation of policy changes the day before a move. Moreover, an inspection of the residuals from the baseline specification suggests that the anticipated policy change variables included in the baseline specification did not sufficiently control for the anticipation effect in the more recent sample, since, as documented in Carpenter and Demiralp (2006b), federal funds market participants systematically bid up federal funds well in advance of policy tightenings, and not just the day before. In order to address these concerns, the new specification allows for anticipation to affect the funds rate up to five days before the anticipated policy tightening.

Next, we address the apparent serial correlation of the errors, as evidenced by the failure of the Q-test (up to 10 lags) and the LM test when the original specification is estimated over the 2004 to August 1, 2007 sample. Instead of the more parsimonious AR(1) model, we include an MA(1) term as well in order to control for persistent correlation.

The third item addressed is the controls used in the error specification. Inspection of the residuals from the baseline specification suggests that the specification could be improved, as there was some change in the nature of the volatility in 2004 to 2007. First, we relaxed the assumption that the volatility coefficients on the last three days of the maintenance period are equal (as assumed in Carpenter and Demiralp (2006a)), and included three separate indicator variables for M2, T2, and W2. We might expect volatility to be different on each of the last three days of the maintenance period than on other days, because these are often the days when large depository institutions hold the greatest amount of excess, and therefore may affect the volatility of the effective federal funds rate. Second, we included a dummy variable for forecast misses above $2.5 billion in absolute value, approximately the 95th percentile over the sample. Finally, we add an indicator variable for year-end.

Results from this specification are presented in the first column of table 3. Similar to the results presented above, the coefficient on the level of the target rate is negative, although not statistically different from zero. The anticipation effect variables are highly statistically significant, implying that funds are bid up several days in advance of a target rate increase. Adding together the effects from the level of the anticipated target change and the indicator variable for anticipated target change, we find that all else equal, on the day before a policy action, funds trade roughly 19 basis points firm to the current target, only 9 basis points below the new target given that each of the policy moves in the sample were 25 basis points. In addition, the moving average term is highly statistically significant, suggesting increased persistence of shocks to the funds rate from 2004 to 2007.10

The coefficients on the M2, T2, and W2 EGARCH terms show very clear evidence that volatility behaves differently on each of these days of the maintenance period, with more pronounced volatility on settlement day than on M2 or T2. In addition, consistent with intuition, days with a large forecast miss are associated with higher funds market volatility. Moreover, diagnostic statistics indicate that this specification provides a much better fit. The Durbin-Watson statistic for this specification suggests that we have adequately controlled for serial correlation in this specification, while the Akaike and Schwarz information criteria (AIC and SIC, respectively) indicate that the addition of the new variables has improved the overall fit of the model, despite the additional terms.

The results in the new specification are striking, but there are still a number of factors included that could be dropped for the 2004-2007 period. The second column removes these insignificant variables from the original specification. Specifically, from the mean equation, we eliminate the target federal funds rate, the anticipation effects constructed using futures quotes, and the indicator variable for December (included in the calendar effects, which are not shown). In addition, we only include the M2, W2, quarter-end and "giant miss" (over $2.5 billion, approximately the top 5 percent of the distribution) terms in the EGARCH specification, eliminating all others that were insignificant in the previous specification.

Comparing the results in column 1 and column 2 shows that dropping these factors improved the specification somewhat: While the AIC rose a little, the SIC fell a bit more. In addition, the point estimates for most of the remaining variables stayed relatively constant. The baseline liquidity effect is estimated to be between 0 and 1 basis point on all days of the maintenance period, with the positive coefficient on F2 not significantly different from zero.

4.2.2 Exploring the interaction between the liquidity effect and the anticipation effect

With some of the extraneous variables removed, we turned to exploring two new hypotheses concerning the interplay of the anticipation effect and the liquidity effect. First, we considered the possibility that the anticipation effect may vary systematically according to the meeting's timing within the maintenance period. For regularly scheduled FOMC meetings, rate decisions are usually announced on Tuesday, Wednesday, or Thursday afternoon, typically around 2: 15 p.m. We conjecture that the anticipation effect may be different if the meeting falls on R1, T1, W1, or R2, as opposed to T2 or W2. In the earlier set of days, there are a minimum of three trading days left in the maintenance period for DIs to satisfy their requirements after the rate decision is announced. In the latter set, there is only one full trading day, or, in the case of a W2 announcement, only the remainder of the current trading day left. It is possible that anticipation effects could differ considerably depending on the number of trading days remaining in the maintenance period.11

In addition, we wanted to investigate the possibility that there could be some interaction between the liquidity effect and the anticipation effect. If market participants expect a rate hike at a meeting within the current maintenance period, they expect funds to be more expensive at the end of the maintenance period than on the current day. Should there be a reserves-draining miss, they might be more willing than they would otherwise to pay up for funds in the market, as they expect funds to be more expensive later in the period. Likewise, during periods when daily balances provided by the Desk are already at generous levels as the Desk attempts to partially offset the anticipation effect, an adding miss might generate a more dramatic softening of rates than on ordinary days. Thus, the liquidity effect should be more pronounced on days leading up to a target change than on other days.

Both of these conjectures are supported in the estimation results. Column 3 presents results from estimating a specification that includes different liquidity effects that depend on the existence of an FOMC meeting. As is shown in the table, the liquidity effect is more pronounced on the days immediately preceding an anticipated rate hike. This liquidity effect is estimate to be roughly 2 basis points per $1 billion in balances for meetings late in the period, more than three times the baseline liquidity effect of 0.5 basis points per $1 billion. Because funds are expected to be more expensive on the day of the FOMC meeting and the days following (as our sample covers a tightening cycle only), DIs react more strongly to a fall in the supply, and accordingly, are willing to pay up due to the anticipation of more expensive funding in the remainder of the period. In results not shown, we found that this liquidity effect was more muted earlier in the period. As there are many trading sessions remaining, DIs may feel as if they have plenty of time to satisfy their requirements, and the savings from buying funds cheaply earlier in the period may be outweighed by the option value of holding funds later in the period, particularly if a day with known calendar effects is in the latter part of the period.

4.2.3 Evaluating the effect of uncertainty of end-of-day balances

Our final exercise focuses on the effect of uncertainty about end-of-day balances on deviations from the target and on the liquidity effect. We proxy for this uncertainty using a dummy variable for high payment flow days, defined as those days in the top quartile by detrended payment volume, measured in dollar value terms.12 These days overlap somewhat, but not completely, with the calendar effects used in the previous specifications. In particular, the data-determined high payment flow days include most month ends, some month starts, nearly all mid-month dates, and a share of the days after holidays. In addition, we find that many of the 25th of the month dates, which is a principal and interest payment date for Fannie Mae, are included in this group. Payment flows are at least 10 percent higher than their long-run trend values on high payment flow days. While the Desk usually leaves higher levels of balances on high payment flow days, reserve managers face considerably more uncertainty about their positions than usual, as balances usually turn over more often on these days.

Our hypothesis is that uncertainty regarding end-of-day positions intensifies the liquidity effect. As noted above, there are asymmetric risks to too-low or too-high balances. Should balances drop below zero, DIs must pay an overdraft fee equal to 400 basis points above the funds rate. However, if a DI holds excess balances, the opportunity cost is equal to the prevailing rate in the market at that time. Although rates occasionally do spike during the day, these occasions are rare and the spikes are usually considerably lower than 400 basis points higher than the target rate.

Under these circumstances, a reserves shortfall will likely cause the funds rate to rise, particularly on settlement day, which has the associated penalty of a reserves deficiency charge should a DI not meet its requirement. By the same token, a reserves-adding miss on the last day of the maintenance period may be met with relatively attenuated demand, as there is no possibility of smoothing reserves demand over other days of the maintenance period and the potential for carryover to the next maintenance period is limited.

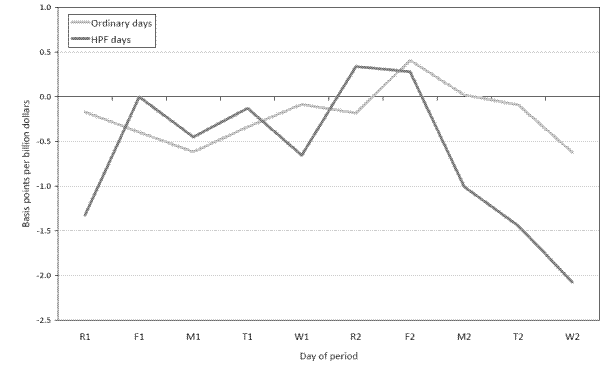
Indeed, evidence of these phenomena is present in the estimation results listed in table 3. As shown in the third set of columns, the liquidity effect is more pronounced on high payment flow days, with the incremental effect estimated to be about \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} of a basis point. In results not shown, we found that the incremental liquidity effect on a high payment flow day is strong on the first day of the maintenance period and the last three days of the maintenance period, ranging from 1 to 1 \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} basis points. There is also a more muted incremental liquidity effect on the first Wednesday of the period. As banks scramble to satisfy requirements towards the end of the maintenance period, uncertainty created by high payment flow days will cause them to react more strongly to a shortfall or surplus than on other days, likely because there is less time left in the maintenance period to hit the desired average level of balances to hold. Moreover, after controlling for the high payment flow effects, a good number of days in the maintenance period have similar liquidity effects of about \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} a basis point, pointing to the fact that sharp moves in the estimated liquidity effects are only evident on the high payment flow-factors miss interaction terms.

As a result of this exploration, the last set of columns displays our final specification, in which we consolidate the liquidity effect increment on high payment flow days into two groups. The first group of days, a "high liquidity" group, includes the first Thursday and the last three days of the period, days on which the incremental liquidity effect is large and statistically significant. The second "low liquidity" group includes the remaining days of the maintenance period.13 14 Overall, we see that the liquidity effect is stronger on these days of heightened uncertainty. Explanations for this phenomenon have been stated above; these days stand in stark contrast to those with relatively lower movements due to payment flows, with a statistically insignificant coefficient on the interaction term.

5 Discussion and conclusion

Our results offer further support for a liquidity effect at a daily frequency. Our hypothesis is that the magnitude of the liquidity effect depends critically on three factors: uncertainty on the part of DIs about their Federal Reserve account balance positions, expectations for the funds rate in the remainder of the maintenance period, and proximity to settlement day. The falloff in the liquidity effect after the implementation of lagged reserve accounting and the differential effects of high payment flow days support our first hypothesis; the FOMC anticipation-liquidity effect supports the second, and the estimated coefficients on all settlement day effects support the third.

Going forward, an important extension of this work is whether there exist different liquidity effects on an institution-level basis. Like other researchers, we have documented liquidity effects in aggregate. However, investigating the response of depository institutions at a micro level will help us better understand this part of monetary policy transmission.

References

Bartolini, Leonardo, Bertola, Giuseppi, and Prati, Alessandro. 2002. "Day-to-Day Monetary Policy and the Volatility of the Federal Funds Interest Rate," Journal of Money, Credit and Banking, vol. 24, p. 137-159.

Bernanke, Ben, and Mihov, Ilian. 1998. "The Liquidity Effect and Long-Run Neutrality," Carnegie-Rochester Conference Series on Public Policy, vol. 49, 149-194.

Carpenter, Seth and Demiralp, Selva. 2006a. "The Liquidity Effect in the Federal Funds Market: Evidence from Daily Open Market Operations", Journal of Money, Credit, and Banking, vol. 38, June, p. 901-920.

Carpenter, Seth, and Demiralp, Selva. 2006b. "Anticipation of Monetary Policy and Open Market Operations," International Journal of Central Banking, vol. 2 (June).

Carpenter, Seth and Demiralp, Selva. 2008. "The Liquidity Effect in the Federal Funds Market: Evidence at the Monthly Frequency", Journal of Money, Credit and Banking, vol. 40.

Clouse, James, and Dow, James P. 2002. "A Computational Model of Banks' Optimal Reserve Management Policy," Journal of Economic Dynamics and Control, vol. 26, p. 1787-1814, September.

Edwards, Cheryl. 1997. "Open Market Operations in the 1990s," Federal Reserve Bulletin, vol. 83, November, p. 859-874.

Federal Reserve Bank of New York. 2008, "Domestic Open Market Operations during 2007", Report prepared for the Open Market Committee, February.

Furfine, Craig. 2001. "Banks Monitoring Other Banks: Evidence from the Federal Funds Market," Journal of Business 74 (2001), p. 33-58.

Hamilton, James. 1996. "The Daily Market for Federal Funds," Journal of Political Economy, vol. 104, no. 1, p. 26-56.

Hamilton, James. 1997. "Measuring the Liquidity Effect," American Economic Review, vol. 87, no. 1, March, p.80-97.

Hamilton, James. 1998. "The Supply and Demand for Federal Reserve Deposits," Carnegie-Rochester Conference Series on Public Policy, vol. 49, 1-44.

Hilton, Spence. 2005. "Trends in Federal Funds Rate Volatility," Current Issues in Economics and Finance, Federal Reserve Bank of New York, vol. 7, no. 11, July.

Kuttner, Kenneth. 2001. "Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market," Journal of Monetary Economics, vol. 47, no. 3, p. 527-44.

Leeper, Eric, and David B. Gordon. 1992. "In Search of the Liquidity Effect," Journal of Monetary Economics, vol. 29, no. 3 (June), pp. 341 - 370.

Leeper, Eric, Walker, Todd, and Yang, Shu-Chun. 2008. "Fiscal Foresight: Analytics and Econometrics," manuscript, Indiana University, May.

Nelson, D. B. (1991). "Conditional heteroskedasticity in asset returns: A new approach," Econometrica 59: 347-370.

Thornton, Daniel. 2001. "Identifying the Liquidity Effect at the Daily Frequency," Federal Reserve Bank of St. Louis Review, July/August, 59-78.


Table 1a: Deviation from target (bp)
 MeanStd. Dev.MedianMin.Max
February 3, 1994 - January 30, 20042180-151255
February 3, 1994 - August 1, 20072160-151255
January 2, 2004 - August 1, 2007160-3927


Table 1b: Absolute value of deviation from target (bp)
 MeanStd. Dev.MedianMin.Max
February 3, 1994 - January 30, 200491650255
May 18, 1989 - August 1, 200781440255
January 2, 2004 - August 1, 2007352s39


Table 1c: Forecast miss ($ millions)
 MeanStd. Dev.MedianMin.Max
February 3, 1994 - January 30, 2004-51131-11-66796586
February 3, 1994 - August 1, 2007-161123-15-76236586
January 2, 2004 - August 1, 2007-441098-20-76235459


Table 1d: Absolute value of forecast miss ($ millions)
 Mean Std. Dev. Median Min. Max
February 3, 1994 - January 30, 200483676165206679
May 18, 1989 - August 1, 200782076763107623
January 2, 2004 - August 1, 200777577957907623


Table 2
 1994-2004 Coeff.1994-2004 T-statJanuary 2, 2004 - August 1, 2007 Coeff.January 2, 2004 - August 1, 2007 T-stat
Day of Maintenance period: First Thursday (R1)2.124.71.255.4
Day of Maintenance period: First Friday (F1)-4.37-9.20.110.5
Day of Maintenance period: First Monday (M1)2.565.11.296.7
Day of Maintenance period: First Tuesday (T1)-3.03-6.4-1.01-4.9
Day of Maintenance period: First Wednesday (W1)-1.08-2.4-0.07-0.4
Day of Maintenance period: Second Thursday (R2)2.024.51.035.8
Day of Maintenance period: Second Friday (F2)-3.38-6.4-0.19-0.8
Day of Maintenance period: Second Monday (M2)3.494.91.435.4
Day of Maintenance period: Second Tuesday (T2)-7.96-7.3-1.38-4.9
Day of Maintenance period: Second Wednesday (W2)4.744.2-0.74-2.4
Day of Maintenance period (Calendar effects): Month start6.055.21.363.3
Day of Maintenance period (Calendar effects): Mid month9.0310.73.5510.8
Day of Maintenance period (Calendar effects): Month end12.869.54.512.4
Day of Maintenance period (Calendar effects): Quarter start4.961.34.74.3
Day of Maintenance period (Calendar effects): Quarter end43.732.211.025.7
Day of Maintenance period (Calendar effects): Year start-17.91-3.85.062
Day of Maintenance period (Calendar effects): Year end-79.4-2.9-37.33-9.5
Day of Maintenance period (Calendar effects): Day before holiday-1.72-1.4-1.05-2
Day of Maintenance period (Calendar effects): Day after holiday15.38.24.598.4
Day of Maintenance period (Calendar effects): December-0.68-1.3-0.43-1
Target variables: Deviation from target (t-1)0.2910.10.175.6
Target variables: Deviation from target(t-1)*Week 20.091.90.111.9
Target variables: Fed funds target-0.09-1.5-0.08-2.5
Target variables: Target change (t+1)*ant. target change0.1620.44.5
Target variables: Target change(t+1)*ant. target change*Week 20.224.40.562.9
Target variables: Target change(t)*unant. target change-0.24-0.7-2.61-10
Liquidity effect: Maintenance period    
Liquidity effect: R1*(Factors miss)-0.66-1.8-0.73-2.3
Liquidity effect: F1*(Factors miss)-0.28-0.5-0.77-3.4
Liquidity effect: M1*(Factors miss)-2.72-4.7-0.7-3
Liquidity effect: T1*(Factors miss)-0.62-1.4-0.46-3.3
Liquidity effect: W1*(Factors miss)-0.95-2.2-0.28-2.6
Liquidity effect: R2*(Factors miss)-0.53-1.6-0.24-1.4
Liquidity effect: F2*(Factors miss)-0.25-0.6-0.36-1
Liquidity effect: M2*(Factors miss)-1.41-1.9-0.87-3.8
Liquidity effect: T2*(Factors miss)-0.87-0.6-0.26-1
Liquidity effect: W2*(Factors miss)-2.14-2.4-1.33-3.8
Monetary policy: Target change (t-1)*(Factors miss)1.350.81.631.8
Variance equation: Constant1.15.6-0.25-1.53
Variance equation: ABS(resid(-1))0.556.91.2311.1
Variance equation: Resid(-1)0.040.70.192.26
Variance equation: Log(GARCH(-1))0.5413.60.547.16
Variance equation: F1-0.42-2.2-0.04-0.29
Variance equation: F20.150.70.010.05
Variance equation: M2+T2+W21.158.50.795.95
Variance equation: Day before holiday0.893-0.23-0.55
Variance equation: Day after holiday1.094.10.10.34
Variance equation: Month end1.264.80.150.61
Variance equation: Quarter end2.335.42.446.85
Variance equation: December0.362.60.361.79
Variance equation: Target change (t-1)-0.07-0.1-0.73-1.95
Variance equation: Target change (t+1)0.6420.350.67
Variance equation: Target change (t)1.194.30.781.95
R-squared0.26 0.41 
Adjusted R20.25 0.37 
S.E. of regression15.42 4.58 
Sum squared residuals579249 17312 
Log likelihood-8960 -2176 
Durbin-Watson stat2.15 1.35 
Mean dependent variable2.18 1.17 
S.D. dependent variable17.78 5.76 
Akaike information criterion7.25 5.07 
Schwarz criterion7.37 5.35 
N2487 879 


Table 3
 Original specification + MA and anticipation: Coeff.Original specification + MA and anticipation: T-statTarget change variables consolidated: Coeff.Target change variables consolidated: T-statFull Set of Inde-pendent Variables: Coeff.Full Set of Inde-pendent Variables: T-statFinal Specifi-cation: Coeff.Final Specifi-cation: T-stat
Day of MP: Constant0.742.35      
Day of MP: First Thursday (R1)  0.331.20.0100.311.3
Day of MP: First Friday (F1)-0.78-3.3-0.34-1.4-0.5-2.3-0.38-1.9
Day of MP: First Monday (M1)0.55214.60.793.80.984.8
Day of MP: First Tuesday (T1)-1.47-4.7-0.99-4.2-0.96-3.9-1.04-4.4
Day of MP: First Wednesday (W1)-0.95-3.2-0.52-2.4-0.61-2.8-0.63-3
Day of MP: Second Thursday (R2)0.270.90.723.80.673.50.663.5
Day of MP: Second Friday (F2)-0.88-2.7-0.43-1.8-0.53-2.4-0.5-2.4
Day of MP: Second Monday (M2)0.391.10.973.10.662.30.612.1
Day of MP: Second Tuesday (T2)-2.28-7-1.71-5.6-1.85-6.5-1.89-6.8
Day of MP: Settlement day (W2)-1.48-5.5-1.31-3.2-1.43-3.5-1.3-3.8
Calendar effects: Month start2.538.72.447.41.394.11.544.6
Calendar effects: Mid month3.3911.43.5211.32.387.42.377.8
Calendar effects: Month end4.4713.14.3912.93.348.83.410
Calendar effects: Quarter start3.33.62.392.12.512.21.451.4
Calendar effects: Quarter end6.394.36.053.86.694.65.644
Calendar effects: Year start-2.5-1.5      
Calendar effects: Year end-33.67-12.3-33.71-13.8-32.06-13.8-32.56-15.7
Calendar effects: Day before holiday-0.84-1.9      
Calendar effects: Day after holiday3.777.73.926.13.415.83.56
Calendar effects: December-1.05-1.6      
Monetary policy effects: Fed funds target-0.06-1.1      
Monetary policy effects: Target change (t+1)*ant. target change1.132.1      
Monetary policy effects: Target change(t+1)*ant. target change*Week 21.262.2      
Monetary policy effects: Target change(t)*Unant. target change-0.33-1.3      
Monetary policy effects: Target change (t)-3.41-7-3.76-6.2-3.59-6.2-3.59-6.6
Monetary policy effects: Anticipated target change (t+1)-9.67-0.716.7318.617.7921.417.7722.4
Monetary policy effects: Anticipated target change (t+2)14.717.813.9717.514.7520.114.5421.6
Monetary policy effects: Anticipated target change (t+3)9.9613.19.4712.69.7713.59.214.5
Monetary policy effects: Anticipated target change (t+4)4.794.44.944.26.45.65.075.2
Monetary policy effects: Anticipated target change (t+5)1.591.21.821.34.414.42.32.2
Monetary policy effects: Target change (t-1)*(Factors miss)1.030.9      
FOMC on days 12-14: Target change (t)*(Factors miss)  5.85.95.364.75.265.6
FOMC on days 12-14: Target change (t+1)*(Factors miss)  -1.82-2.4-1.82-2.4-2.77-3.9
Liquidity effect: Factors miss-0.46-1.9-0.73-2.6    
Liquidity effect: R1*(Factors miss)  -0.61-2.3-0.23-0.8-0.26-1.1
Liquidity effect: F1*(Factors miss)0.050.2-0.21-10.290.8-0.33-1.9
Liquidity effect: M1*(Factors miss)-0.35-1.1-0.75-3.6-0.09-0.3-0.7-3.8
Liquidity effect: T1*(Factors miss)0.120.4-0.34-2.50.170.6-0.2-1.7
Liquidity effect: W1*(Factors miss)0.180.6-0.24-1.40.411.3-0.25-2
Liquidity effect: R2*(Factors miss)0.321-0.1-0.50.661.9-0.08-0.4
Liquidity effect: F2*(Factors miss)0.852.10.3410.972.30.411.4
Liquidity effect: M2*(Factors miss)0.020-0.54-2.30.150.4-0.01-0.1
Liquidity effect: T2*(Factors miss)0.180.5-1.12-2.70.441.1-0.12-0.6
Liquidity effect: W2*(Factors miss)-0.36-1.1-1.07-3.1-0.31-0.9-0.72-2.7
Incremental HPF day effects: HPF75    1.276.2  
Incremental HPF day effects: HPF75*MKTMISS    -0.55-3  
Incremental HPF day effects: HPF75*LOWLIQ      1.185.6
Incremental HPF day effects: HPF75*MKTMISS*LOWLIQ      -0.14-1.1
Incremental HPF day effects: HPF75*HILIQ      1.274.2
Incremental HPF day effects: HPF75*MKTMISS*HILIQ      -1.24-4.3
Incremental HPF day effects: AR(1)  0.376.60.346.20.367.2
Incremental HPF day effects: MA(1)0.071.10.111.80.193.40.173.3
Variance equation: Constant-0.15-1.10.060.5-0.02-0.2-0.15-1.4
Variance equation: ABS(resid(-1))0.910.50.8410.20.8910.40.9811.2
Variance equation: Resid(-1)-0.02-0.300-0.02-0.40-0.1
Variance equation: Log(GARCH(-1))0.498.20.478.80.499.70.5211
Variance equation: M20.72.90.692.90.622.70.693.1
Variance equation: T20.412      
Variance equation: W21.235.81.486.11.375.71.145.2
Variance equation: F10.150.9      
Variance equation: F20.20.9      
Variance equation: Target change (t-1)0.351.4      
Variance equation: Target change (t+1)0.752.40.712.90.732.70.772.9
Variance equation: Target change (t)-0.73-2.2-0.9-2.6-0.87-2.6-0.89-2.6
Variance equation: Day after holiday0.080.3      
Variance equation: Day before holiday0.472.10.522.40.542.40.592.8
Variance equation: Month end0.160.6      
Variance equation: Quarter end2.3972.368.72.338.82.428
Variance equation: December0.351.7      
Variance equation: Year end-0.86-1.8      
Variance equation: Giant miss1.233.71.082.61.082.51.112.8
R-squared0.59 0.6 0.62 0.64 
Adjusted R20.59 0.62 1 0.61 
S.E. of regression3.69 3.55 3.56 3.59 
Sum squared resid11144 10458 10459 10597 
Log likelihood-2047 -2066 -2037 -2026 
Mean dependent variable1.17 1.17 1.17 1.17 
S.D. dependent variable5.76 5.76 5.77 5.77 
Akaike information criterion4.8 4.81 4.76 4.74 
Schwarz information criterion5.13 5.07 5.04 5.03 
Hannan-Quinn4.93 4.91 4.87 4.85 
Durbin-Watson statistic2.01 2.04 2.1 2.09 
N879 879 876 876 


Figure 1, Panel A
The figure has two panels. Each panel is a schematic drawing of demand for reserve balances at different rates. In both panels, the vertical axis represents the federal funds rate and the horizontal axis represents reserve balances. In both panels, the vertical axis has a dot-dashed horizontal line about halfway up to indicate the target federal funds rate and a dotted horizontal line to near the top to indicate the primary credit rate. In both panels, a downward-sloping solid diagonal line indicates the demand curve. In the upper panel (a), the supply curve is indicated by a two-segment line. The first segment of the supply curve is vertical and extends upward from the x axis, through the intersection of the demand curve and the federal funds rate target to the line indicating the primary credit rate. The second segment connects with the first segment and overlays the line indicating the primary credit rate. In the lower panel (b),a third horizontal line, which is light and solid, indicates the federal funds effective rate. In the lower panel, two supply curves are drawn. The curve labeled S2 is indicated by a solid line and is the same as in the upper panel. The curve labeled S1 has two segments indicated by dashed lines. The first segment lies parallel and to the left of S1, extending in a vertical line from the x axis through the intersection of the effective federal funds rate and the demand curve to the line indicating the primary credit rate. The second segment overlays S2 and the horizontal line indicating the primary credit rate.
Figure 1, Panel B
The figure has two panels. Each panel is a schematic drawing of demand for reserve balances at different rates. In both panels, the vertical axis represents the federal funds rate and the horizontal axis represents reserve balances. In both panels, the vertical axis has a dot-dashed horizontal line about halfway up to indicate the target federal funds rate and a dotted horizontal line to near the top to indicate the primary credit rate. In both panels, a downward-sloping solid diagonal line indicates the demand curve. In the upper panel (a), the supply curve is indicated by a two-segment line. The first segment of the supply curve is vertical and extends upward from the x axis, through the intersection of the demand curve and the federal funds rate target to the line indicating the primary credit rate. The second segment connects with the first segment and overlays the line indicating the primary credit rate. In the lower panel (b),a third horizontal line, which is light and solid, indicates the federal funds effective rate. In the lower panel, two supply curves are drawn. The curve labeled S2 is indicated by a solid line and is the same as in the upper panel. The curve labeled S1 has two segments indicated by dashed lines. The first segment lies parallel and to the left of S1, extending in a vertical line from the x axis through the intersection of the effective federal funds rate and the demand curve to the line indicating the primary credit rate. The second segment overlays S2 and the horizontal line indicating the primary credit rate.


Figure 2: Unanticipated Share of Federal Funds Target Changes
Figure 2: Unanticipated Share of Federal Funds Target Changes. Refer to link below for data. Figure 2 Data


Figure 3: Maintenance Period Dummies, Various Sample Periods
Figure 3: Maintenance Period Dummies, Various Sample Periods. Refer to link below for data. Figure 3 Data


Figure 4: Estimated Liquidity Effects, Various Sample Periods, Original Specification
Figure 4: Estimated Liquidity Effects, Various Sample Periods, Original Specification. Refer to link below for data. Figure 4 Data


Figure 5: Day 14 Elasticity Estimates
Figure 5: Day 14 Elasticity Estimates. Refer to link below for data. Figure 5 Data


Figure 6: Estimated Liquidity Effects for High Payment Flow Days and Ordinary Days,2004 through August 1, 2007
Figure 6: Estimated Liquidity Effects for High Payment Flow Days and Ordinary Days,2004 through August 1, 2007. Refer to link below for data. Figure 6 Data


Footnotes

*The views represented here are those of the authors and not of the Board of Governors, other members of its staff, or of the Federal Reserve System.

Ruth A. Judson, Economist, Mail Stop 59, Board of Governors of the Federal Reserve System, 20th and C Streets, NW Washington, DC 20551 Telephone: (202) 736-5612 Fax: (202) 452-2301 Email: [email protected] Return to Text

**Elizabeth Klee, Economist, Mail Stop 59, Board of Governors of the Federal Reserve System, 20th and C Streets, NW Washington, DC 20551 Telephone: (202) 721-4501 Fax: (202) 452-2301 Email: [email protected] Return to Text
1. The FOMC has changed its post-meeting statements over time. For many years, the FOMC did not release any statement after its meetings. After the February 4, 1994 FOMC meeting, the Chairman of the Federal Reserve released a statement that described intended changes in the "degree of pressure on reserve conditions," At the May 1994 FOMC meeting, the statement structure was revised and declared that the "Board approved an increase in the discount rate," included an explicit number for this rate, and, in addition, stated that the rate increase "should be allowed to show through completely into interest rates in reserve markets." This structure remained until July 1995, when an explicit target for the federal funds rate was announced. During that period, no statement was released after meetings without rate changes. Starting in May 1999, a statement was released after each meeting, regardless of whether a rate change occurred. Most recently, starting with the October, 2007, FOMC meeting, economic projections for each of the FOMC participants were released in the minutes for the meeting. Return to Text
2. Overnight overdrafts in DIs' accounts also supply balances; however, due to the stiff penalties (both monetary and otherwise) for doing so, these are not a substantial supply of balances. Return to Text
3. Using the "consensus miss" (which incorporates forecast information from Desk staff as well as Treasury staff) does not change our results materially. Return to Text
4. We end the sample at August 1, 2007, the end of the last full maintenance period before the beginning of the current financial-market turmoil. Return to Text
5. Bartolini et al (2002) offers a theoretical model of this phenomenon in which increased Fed transparency has as a byproduct lower volatility in interest rates. Return to Text
6. Payment flows on Mondays are about three percent higher than on other days of the week, a difference that is statistically significant. In addition, Carpenter and Demiralp (2006a) argue that DIs tend to adjust their positions more actively following the weekend. Return to Text
7. Edwards (1997) discusses the critical role of payment flows in shaping the daily market for federal funds. Return to Text
8. Balance sheet maneuvers in order to avoid tax liabilities have occasionally pushed up rates on year-end. Refer to OMO 1997, Leeper et al (2008). Return to Text
9. The Durbin-Watson test is biased toward 2 in the presence of a lagged dependent variable, resulting in lower power for the test. Even with the reduced power, the test statistic indicates that there is cause for concern about serial correlation, which is borne out by the strong significance of the autoregressive error term introduced later. The table reports Q-statistics for first-order serial correlation. Return to Text
10. Intended federal funds rates are effective on the day of the rate announcement. For a list of dates when the intended federal funds rate changed, refer to http://www.federalreserve.gov/fomc/fundsrate.htm. Return to Text
11. One might conjecture that the anticipation effects and their interaction are asymmetric with respect to the direction of the expected move. Our sample includes only increases in the target, and thus we are only able to examine the effects in that case. Return to Text
12. We choose the top quartile of days because the share of calendar-determined high payment flow days is about one quarter. Return to Text
13. A Wald test indicates that the null hypothesis that the high payment flow liquidity effect coefficients within these two groups are equal to one another cannot be rejected. Return to Text
14. The magnitude of the forecast error, MKTMISS, is not statistically significantly correlated with the HPF75*LOLIQ and HPF75*HILIQ dummies. Return to Text

♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text
Home | Economic Research and Data | Accessibility | Contact us
Last update: June 19, 2009