Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2012-05 Screen Reader version ^♣

Quantifying the Role of Federal and State Taxes in Mitigating Wage Inequality

Daniel H. Cooper*

Byron F. Lutz†

Michael G. Palumbo‡

Keywords: Wage inequality, tax incidence

Abstract:

Wage inequality has risen dramatically in the United States since at least 1980. This paper quantifies the role that the tax policies of the federal and state governments have played in mitigating wage inequality. The analysis, which isolates the contribution of federal taxes and state taxes separately, employs two approaches. First, cross-sectional estimates compare before-tax and after-tax inequality across the 50 states and the District of Columbia. Second, inequality estimates across time are calculated to assess the evolution of the effects of tax policies. The results from the first approach indicate that the tax code reduces wage inequality substantially in all states. On average, taxes reverse approximately the last two decades of growth in wage inequality. Most of this compression of the income distribution is attributable to federal taxes. Nevertheless, there is substantial cross-state variation in the extent to which state tax policies compress the income distribution. Cross-state differences in gasoline taxes have a surprisingly large impact on income compression, as do sales tax exemptions for food and clothing. The results of the second approach indicate that the mitigating influence of tax policy on wage inequality has increased very modestly since the early 1980s. The increase is due to the widening of the pre-tax wage distribution interacting with a progressive tax structure. In contrast, legislated tax changes over this period decreased income compression somewhat.

JEL Classification: H22, H71, J31

1 Introduction

Income inequality has been increasing in the United States since at least 1980 and possibly as far back as 1970 (Karoly, 1993; Gottschalk & Smeeding, 2000). An important component of this increase has been a widening of the wage structure. Wage differentials associated with education, occupation, and experience have risen, and wage dispersion within these broad groups has also increased (Katz & Autor, 1999; Autor et al., 2008). The increase in wage inequality has, in turn, produced increases in consumption inequality (Cutler & Katz, 1992).

The tax policies of the federal and state governments are a potential compensating factor in the rise in wage inequality, particularly as they relate to progressivity or the rate at which taxes rise with income. This paper quantifies the role of taxes in mitigating wage inequality. Our analysis has two components, and considers separately the influence of the federal and state tax systems. While increases in concentration at the very top-end of the income distribution have received significant attention recently, this paper follows much of the literature on wage inequality and examines inequality in the broad middle of the income distribution.

Our first approach is cross-sectional in nature and compares before-tax and after-tax inequality across the 50 states. Overall, we find that the combined federal and state tax codes substantially mitigate wage inequality. Turning to state taxes, the states are ranked by the extent to which their tax codes compress the after-tax distribution of income relative to the before-tax distribution. On average, the compression achieved by state taxes is equal to only around 10 percent of the compression achieved by the federal tax code. This average effect, though, obscures economically meaningful differences across the states. In a few states, such as Minnesota, Oregon, and Wisconsin, state tax compression amounts to one-fourth to one-third of the compression brought about by federal taxes. On the other hand, the tax systems in thirteen states--including some large states such as Florida, Texas, and Illinois--actually widen the distribution of income. We find that the state-levied gasoline tax plays a surprisingly large role in the amount of compression across states. On average, it is estimated to offset roughly 25 percent of the income compression achieved by state income and general sales taxes. Our analysis also shows that exemptions for food and clothing from some states' sales taxes play a quantitatively important role in narrowing the after-tax income distributions of these states.

Our second approach assesses the evolution over time of tax-induced income compression. We find that income compression due to federal and state taxes has risen mildly over the last 25 years. The rapid increase in before-tax labor income inequality documented widely by other researchers has thus been transmitted a bit less than one-for-one into after-tax labor income. Our analysis concludes by decomposing this increase in tax compression into the portion attributable to legislated changes in the tax code and the portion attributable to changes in the pre-tax distribution of earnings. We conclude that the increase in tax compression is more than explained by the latter. Specifically, the substantial increase in pre-tax wage inequality over this period interacted with progressive tax parameters to increase the amount of income compression caused by the tax system. We find that legislated changes to the tax code worked to offset some of this increase. That is, over time the tax code was adjusted to reduce income compression.

This paper is closely related to two distinct and large literatures--the wage inequality literature and the empirical tax incidence literature (which attempts to determine who bears the economic burden of taxation). Recent research on U.S. wage inequality suggests that there was a broad-based surge in inequality from 1979 through 1987 as lower incomes fell and upper incomes rose. Since 1988, the labor market has become "polarized'' as upper-income inequality has continued to rise, while the increase in lower-income inequality has eased or even partially reversed. These stylized facts can be largely reconciled with changes in the supply of and demand for skill and the erosion of labor market institutions, such as the minimum wage and labor unions, which had played an important role in supporting middle and low incomes.¹$^,$²

A very long-running literature documents the incidence of federal taxes by income group (see Gramlich et al., 1993; Musgrave, 1951; Pechman, 1985; Pechman & Okner, 1974; Congressional Budget Office, 2007; Kasten et al., 1994), and a substantially smaller literature considers the same issue for state taxes (see Metcalf, 1994; H. & Pollock, 1988; Berliant & Strauss, 1993). Most relevant for this paper is previous research that explicitly explores the connection between broad income inequality and taxes (Karoly, 1994; Gramlich et al., 1993). These papers, like our own, can be viewed as synthesizing the inequality and tax incidence literatures.

Several aspects of our work distinguish it from existing studies. First, our results are driven primarily by the connection between taxes and wage inequality. Almost all previous tax incidence studies have focused on broader definitions of income inequality. However, the labor market is the primary source of income for most individuals and families, and the distribution of labor income is therefore the chief determinant of the overall distribution of economic well-being (Karoly, 1993). Given the importance of wage inequality and its rapid rise in recent years, it is useful to carefully quantify how the tax system mediates this specific form of income inequality. Furthermore, there are a number of conceptual and methodological advantages to focusing on labor income inequality (see Section 2.4 below). Second, we provide an unusually rich analysis of the influence of state taxes on income inequality over a long period of time. Past studies have tended to focus on a very short time period (such as immediately before and after the Tax Reform Act of 1986) and/or consider the impact of state tax codes as a group, instead of individually. We also capture the three largest state taxes -- the personal income tax, the general sales tax and the gasoline tax -- with the analysis of the final two taxes based on expenditure data. Many previous studies have focused on one of these taxes--not all three--and only very limited attention has been given to state gas taxes and sales tax exemptions. Third, we decompose the evolution of income compression into the portion produced by changes in the tax code versus changes in the distribution of pre-tax income. Finally, we carefully assess the robustness of our results to various tax incidence assumptions, including consideration of lifetime versus static tax incidence.

The remainder of the paper proceeds as follows. Section 2 discusses our methodology and Section 3 presents the data. Section 4 discusses the results. Section 5 concludes.

2 Methodology

2.1 Measuring Income Inequality

Studies of income inequality vary along three primary dimensions--the inequality metric, the unit of analysis and the income metric (Karoly, 1994). We use two complementary measures of inequality-- the 90/10 income differential (the difference between incomes at the $90th$ percentile of the income distribution and the $10th$ percentile, measured in natural logs) and the gini coefficient. The gini coefficient can range from a value of 0 (which would represent a perfectly equal distribution in which every person's income was exactly the same) to a value of 1 (which would represent a perfectly unequal distribution in which one person earned all of the income in the society).³ The gini coefficient tends to be heavily influenced by the middle of the income distribution and generally underweights differences in income in the tails of the distribution. The 90/10 income split, which has been has been widely used in the recent literature on wage inequality, does a relatively better job of capturing differences in the tails of the income distribution and can be viewed as capturing overall inequality. We heavily emphasize this metric in our analysis. We also present a few 90/50 and 50/10 income percentile splits to capture inequality in the upper and lower halves of the income distribution, respectively. REMOVE FOR NTJ SUBMISSION: We do not address the effect of taxes on concentration at the very top of the income distribution - an issue many are focused on currently. As discussed below, our data are ill suited to such an examination.

Our unit of analysis is the federal tax unit--typically a household. We follow Autor et al. (2008) and restrict our attention to tax units headed by full-time, full-year (FTFY) workers aged 16 to 64 years who are not self-employed.⁴ We are forced to use total income as our income metric, as it forms the base for the personal income tax, despite our focus on wage inequality. That said, by focusing on FTFY workers and using either the gini coefficient or the 90/10 income differential as the measures of inequality, our conclusions about income inequality are bound to be driven by wage inequality. In particular, the FTFY age 16-64 restriction excludes most households with government transfer income. Medicare benefits are mostly eliminated, as are most transfers of Supplementary Security Income (SSI), unemployment insurance, most social security payments, etc. Furthermore, our measures are little influenced by capital income. Such income is mostly located at the very upper end of the income distribution and very high incomes do not contribute to the calculation of the 90/10 income differential and have very little influence on the gini coefficient (that is most responsive to the middle of the distribution).⁵ For the median household in our sample, wages account for 100 percent of total income.

As shown in Figure 1, measures of overall total income inequality (blue line) are extremely similar to measures of overall wage inequality (red line) in our sample (Panels A and B). Upper and lower-tail inequality display similar patterns (Panels C and D). Overall, total income inequality appears to correspond very closely to wage inequality in our sample.

2.2 Interpreting the Income Compression Metrics

We quantify the effect of taxes on income inequality by comparing before-tax measures of inequality to the corresponding after-tax measures. The primary income compression metric is the difference between the before and after-tax 90/10 income split:

$$comp_{90/10}=[log(Y_{90})-log(Y_{10})]-[\log (Y_{90}\ast (1-t_{90}))-\log (Y_{10}\ast (1-t_{10}))] \hspace{2mm}$$ (1)

where $Y_{g}$ is income at the $gth$ percentile of the before-tax income distribution and $t_{g}$ is the average tax rate at the $gth$ percentile. The first term in brackets in equation (1) approximates the percentage difference between before-tax incomes at the $90th$ and $10th$ percentiles, while the second term captures this percentage difference for after-tax incomes. A value of 0 indicates that the tax code has no influence on income inequality, while a value greater than 0 indicates that the tax code is compressing the after-tax income distribution relative to the before-tax distribution. The before-tax 90/10 income differential has been widely used in the literature on wage inequality. The difference between this before-tax inequality measure and the corresponding after-tax measure therefore provides a natural and easily interpreted way to quantify how the tax system mitigates wage inequality.

Simplifying the terms in equation (1) reveals that $% comp_{90/10}$ is solely a function of the average tax rates at the different points in the before-tax income distribution

$$comp_{90/10}=\log \left( \frac{1-t_{10}}{1-t_{90}} \right) \hspace{2mm}$$

A system in which taxes are perfectly proportional to income will have a constant average tax rate: $t_{90}=t_{10}$. Such a system would produce no compression of the income distribution because $t_{90}=t_{10}\Longleftrightarrow comp_{90/10}=0$. A progressive tax system has average tax rates that increase with income (Kiefer, 2005; Musgrave & Thin, 1948): $t_{90}>t_{10}$. Such a system therefore produces compression because $t_{90}>t_{10}\Longleftrightarrow comp_{90/10}>0$. Thus, the $comp_{90/10}$ metric can be viewed as a measure of tax progressivity. A positive value indicates a progressive tax, 0 indicates a proportional tax, and a negative value indicates a regressive tax.⁶

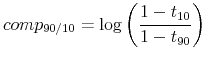
Changes in tax compression occur in two ways. First, holding the before-tax distribution of income fixed, legislated tax changes that alter average tax rates may change tax compression (for example, $% \frac{\partial comp_{90/10}}{\partial t_{90}}>0$). Second, holding the legislated parameters of the tax system fixed, changes in the distribution of before-tax income may cause a change in compression if the tax system is progressive or regressive, but not if the system is proportional. For instance, under a progressive personal income tax, $\frac{\partial t_{90}}{\partial Y_{90}}>0$, as an increase in income for the $90th$ percentile taxpayer will either bump him to a higher marginal tax bracket or will lead him to pay his existing marginal tax rate on a larger fraction of his income. Thus, an increase in $90th$ percentile income will increase compression: $% \frac{\partial comp_{90/10}}{\partial Y_{90}}=\frac{\partial comp_{90/10}}{% \partial t_{90}}\ast \frac{\partial t_{90}}{\partial Y_{90}} > 0$.

Incomes will often change simultaneously at different points in the before-tax income distribution. Under a progressive tax structure, as long as the dollar increase at the $90th$ percentile is equal to or larger than the dollar increase at the $10th$ percentile, compression will increase. In particular, assume that the tax system is "equally" progressive at both the $90th$ and $10th$ percentile of before-tax income such that $\frac{\partial t_{90}}{\partial Y_{90}}=\frac{\partial t_{10}}{\partial Y_{10}}=\alpha$. The change in compression with an increase in $90th$ percentile income is: $% \frac{\partial comp_{90/10}}{\partial Y_{90}}=\frac{\partial comp_{90/10}}{% \partial t_{90}}\ast \frac{\partial t_{90}}{\partial Y_{90}}=\frac{1}{% 1-t_{90}}\ast \alpha$. The corresponding compression change at the $10th$ percentile is $\frac{\partial comp_{90/10}}{\partial Y_{10}}=\frac{\partial comp_{90/10}}{\partial t_{10}}\ast \frac{\partial t_{10}}{\partial Y_{10}}=% \frac{-1}{1-t_{10}}\ast \alpha$. Increasing average tax rates, $t_{90}>t_{10}$, imply that $\frac{% \partial t_{comp_{90/10}}}{\partial Y_{90}}>$ $\left\vert \frac{\partial t_{comp_{90/10}}}{\partial Y_{10}}\right\vert .$

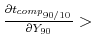
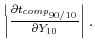
Under the same progressivity assumption, equal percentage increases in income at the $90th$ and $10th$ percentiles--which would hold the before-tax 90/10 income differential constant--result in an increase in compression, as such a change implies a larger dollar increase in $Y_{90}$ than in $Y_{10}$. Similarly, an increase in incomes that widens the before-tax 90/10 differential will yield an increase in compression under a progressive tax system.

Our second measure of tax compression is similar to $comp_{90/10}$, but replaces the 90/10 income differentials with gini coefficients

$$comp_{gini}=gini_{before-tax}-gini_{after-tax} \hspace{2mm}$$

As previously noted, a value greater than 0 indicates compression of the after-tax income distribution relative to the before-tax distribution. A value greater than 0 can also be interpreted as indicating that the tax system causes a shift in income toward equality (as defined by the gini coefficient).⁷

2.3 Tax Incidence Assumptions

The statutory incidence of a tax - i.e. the legal responsibility for paying the tax - may differ sharply from the economic incidence of the tax. We generally follow the previous literature in our incidence assumptions: As in Musgrave (1951), Pechman (1985), Gramlich et al. (1993), and numerous others, we assign the incidence of payroll taxes to workers, the incidence of the personal income tax to the individual receiving the income, and incidence of general sales and excise taxes to those who consume the taxed commodities. These assumptions are necessary in that they make large scale empirical incidence estimates, such as those calculated here, feasible. Furthermore, they are generally quite consistent with recent empirical research.

Starting with the payroll tax, the assumption that the full incidence falls on workers has been "tested and confirmed repeatedly'' (Fullerton & Metcalf, 2005). Although it has been almost universally assumed that the legal and economic incidence of the personal income tax are equal, this assumption has never been tested (see Fullerton & Metcalf, 2005). However, as discussed below in section 2.4, recent research has concluded that individuals in the broad middle of the income distribution - the focus of this study - display little behavioral response to changes in income tax parameters. It is a "fundamental principle'' of incidence analysis that the inelastic agent bears the incidence of a tax (Kotlikoff & Summers, 1987). Thus, the assumption that individuals bear the full incidence of the income tax is quite plausible for our sample.

The assumption that the general sales tax falls on consumers is supported by some recent research (Cole, 2009; Poterba, 1996), although there is also evidence of over-shifting (Besley & Rosen, 1999). Overshifting occurs when prices rise by more than the amount of the tax - a phenomenon consistent with models of tax incidence under imperfect competition.⁸ We test the robustness of our conclusions to overshifting of the sales tax. Turning to the gasoline tax, recent evidence strongly suggests that the tax is fully born by consumers at the state level (Alm et al., 2009; Marion & Muehlegger, 2011; Chouinard & Perloff, 2004). ⁹

The incidence of the corporate income tax depends crucially on the extent of international capital mobility: In a small open economy the tax falls fully on labor, while in a closed economy it falls fully on capital (Fullerton & Metcalf, 2005). Although we do not account for the corporate income tax in our primary results, we provide sensitivity analysis that demonstrates our conclusions are robust to accounting for the tax under varying assumptions about its incidence. Finally, we do not account for the property tax in any of our results because it is primarily a local tax while our focus is on state and federal taxes.¹⁰

We acknowledge that we primarily rely on annual incidence estimates, which can differ substantially from lifetime tax incidence calculations (Metcalf, 1994; Fullerton & Rogers, 1993; Poterba, 1991). Certain individuals, such as students and retirees, may have low annual income, but high permanent (or lifetime) income. Thus, static, point-in-time incidence calculations can differ greatly from dynamic incidence calculations based on a person's lifetime resources. We note, though, that the annual versus lifetime limitation is inherent in much, though not all, of the wage inequality literature. This literature generally lumps together permanent and transitory income inequality, and thus fails to distinguish between "lifetime'' and "annual'' wage inequality. Furthermore, we provide sensitivity analysis that indicates our conclusions are robust to the use of lifetime style incidence calculations.

2.4 Advantages of Focusing on Wage Inequality

The inequality measures used in this study, which mostly capture labor income inequality (see Figure 1), are of great significance given the primary role of labor income in setting the distribution of overall economic well-being. They also provide a clear focus on the growth in wage inequality -- arguably one of the central economic developments of the last 30 years. Moreover, these measures have substantial conceptual and methodological advantages over broader measures of income inequality for at least four reasons.

First, from a policy perspective, it may be useful to consider very low, middle, and very high income inequality separately (Cutler, 1994). Policy aimed at income inequality at the high end of the income distribution must contend with issues, such as substantial business and capital income and greater mobility of resources, that are not as relevant for earners in the middle of the income distribution. Similarly, the problems of the very poor likely go beyond holding low-wage jobs. While we generally refer to `wage inequality' throughout the paper, our inequality measures can alternatively be thought of as capturing the `middle-class' income inequality (which is mostly comprised of labor income).

Second, measuring income in the far tails of the distribution is quite challenging. Properly measuring very high incomes involves a host of difficulties, including thin data, top coding and difficulty measuring capital income.¹¹ Such measurements are best left to studies focusing on the very top earners that are undertaken with income tax filing data (see Saez & Veall, 2005; Piketty & Saez, 2003) or specialized data such as executive compensation records (Frydman & Molloy, 2012; Frydman & Saks, 2010). Turning to the lower end of the distribution, transfer income is a critical component of total income for the poor. Unfortunately, measuring transfer income has become increasingly difficult. Reporting rates for transfer income in the Current Population Survey (CPS)--our source of income data--have fallen to around 50 percent in recent years for programs such as TANF and food stamps (see Meyer et al., 2009). As a result, the examination of transfer income is also likely best left to very focused studies.

Third, taxes may influence the after-tax income distribution both through a direct mechanical effect and through an indirect behavioral response. For instance, if the top marginal rate of the personal income tax is lowered, but other tax brackets are left unchanged, high-earners may increase their supply of labor. This tax change would therefore increase inequality both by increasing before-tax income inequality (a behavioral response operating through labor supply) and by lessening the compression of the after-tax distribution achieved by the tax code (a mechanical response). Our approach primarily captures the direct, mechanical response. Any behavioral responses to taxes are captured in before-tax income inequality.¹² Behavioral responses to taxation, however, are likely of only limited relevance for our measures of middle-income inequality. Recent research has found evidence of substantial behavioral response to income taxes in the tails of the income distribution, but it has generally concluded that there is little evidence of a behavioral response in the broad middle of the distribution.¹³ As a result, our decision to abstract from behavioral responses to taxes likely has only a limited influence on our conclusions.

Finally, our focus on FTFY workers will tend to substantially reduce the difference between our annual estimates of tax incidence and lifetime tax incidence, since our approach eliminates taxpayers who are out of the labor force (students, retirees, the temporarily disabled, etc.) as well as those who are unemployed. We substantiate this claim through the sensitivity analysis in section 4.3.

3 Data

The main data source for this paper is the March Current Population Survey (CPS). The March CPS, which we access through IPUMS at the University of Minnesota, contains detailed information on household earnings.¹⁴ The CPS contains annual income data for U.S. households in all 50 states and the District of Columbia, allowing us to evaluate the impact of state tax policies across every state. There is little direct information, however, on households' income tax liability and other tax payments. Households' federal and state income tax burdens are estimated using the NBER's TAXSIM module, which takes a variety of inputs and returns an estimate of each tax unit's federal and state tax liabilities. The TAXSIM module applies stylized, but reasonably accurate, algorithms to reflect the personal income tax codes at the federal level and for each state. Federal tax estimates include employee and employer contributions to social insurance (Social Security and Medicare).

This paper uses a number of sample selection criteria to clean up the CPS data and to properly implement the TAXSIM module. We follow Autor et al. (2008) and focus our analysis on households headed by full-time, full-year (FTFY) workers who are between 16 and 64 years old with 0 to 39 years of potential experience and whose class of work in their longest held job of the year was private or government wage/salary employment.¹⁵ Our sample runs from 1984 through 2008. Percentile and other distributional analysis is weighted using the CPS household weights to take into account how representative given households are of the overall U.S. population.

A major task is to combine the individual-level CPS data into tax units (single versus married filers), since the TAXSIM procedure uses tax units as the level of observation. Individuals over the age of 18 are defined as their own tax unit even if they are living in the same household as their parents and/or other relatives. Children over the age of 15 who are members of a household in the CPS, but who have positive wages and/or other earnings, are also classified as their own tax unit. Tax units are identified as "joint" filers if the primary tax payer (household head) is married, "single" if the primary tax payer is unmarried, and "head of household" if he or she is unmarried but has dependents. Total earnings are defined as the sum of business, farm, and wage income.¹⁶ When available, spouses' income data are combined with the primary tax payer's income data for all categories.

There is a fairly direct match between the remaining data needed to run TAXSIM and the data available in the CPS, with a few exceptions. In particular, dividend income data are only available as a separate category in the CPS from 1988 onward (TAXSIM #9). Prior to 1988 these data were included in capital income, which falls under the "other income" category in TAXSIM (TAXSIM #10). As a result, the stand-alone dividend income category is set to zero prior to 1988. In addition, the CPS does not have data on households' rent paid, child care expenditures, or unemployment compensations (TAXSIM #s 14, 17, 18). These fields are also set to zero. We impute capital gains, which are not available in the CPS, based on tax return data collected by the Statistics of Income (SOI) section of the IRS. This imputation procedure is based on a tax unit's inflation-adjusted wages and marital status. Finally, we use the same SOI imputation procedure to impute whether or not a tax unit itemizes its deductions and its amount itemized (if applicable).¹⁷

Households' estimated income taxes are added to their estimated sales tax and gas tax burdens to get a measure of their total tax burden. There are no direct data in the CPS on annual sales taxes and motor-fuel taxes paid by households. These data are inferred based on household expenditure data in the Consumer Expenditure Survey (CEX) and separate data on state sales tax rates and state and federal gas tax rates.

The CEX is nationally representative, but it contains a smaller sample than the CPS and the state identifiers for households living in a number of the smaller states in the U.S. are suppressed for confidentiality reasons. As a result, we calculate households' average expenditures on food, clothing, and other taxable goods by age and income groups.¹⁸ Households are divided into 10-year age groups and average expenditures are calculated within age groups by income decile. The appendix discusses the selection criteria for the CEX sample. The CEX expenditure data are translated into the CPS based on the equivalent age and income groupings. The sales tax burden for each CPS tax unit is then obtained by applying the sales tax rate in the tax unit's state of residence to the relevant expenditure data. Our sales tax liability estimates take into account whether food and/or clothing are exempt from sales taxes in a household's given state of residence.^{19 20}

Our approach to calculate households' gas tax burden is slightly different. We estimate a reduced-form demand equation for households' gallons of gasoline consumed in the CEX, making use of our data on the total (tax inclusive) price of gasoline to capture the price elasticity of demand. In particular, we estimate

$$g_{it} = \beta_1 p^s_{t} + \beta_2 Y_{it}*A_{it} + \beta_3D_{t} + \epsilon_{it} ,$$ (2)

where $g_{it}$ is gallons of gas consumed by individual $i$ in year $t$, $p^s_t$ is the state-specific price of gas, $Y_t*A_t$ are a set of income (Y) and age group (A) interaction terms (to capture life-cycle influences on gas consumption), and $D_t$ are year and region dummy variables to capture region and time-specific trends in gasoline consumption.²¹ The $\beta$ parameters from equation (2) are used to impute households' gallons of gasoline consumed in the CPS. A tax unit's gas tax burden is then calculated based on state-specific fuel taxes and their imputed gasoline consumption.²²

Overall, we account for the three largest taxes applied to individuals at the state level -- general sales, personal income and motor fuels. There are other taxes that we do not account for, such as alcohol excise taxes. These taxes are relatively minor and the taxes that are accounted for in this paper capture much of the variation in households' tax burdens across states.

A final data issue worth noting is that the disaggregated income data in the CPS prior to 1996 are top-coded based on censor points that change over time. We adjust the income data to take this top-coding into account. In particular, we assign households with top-coded income in a given category to have earnings equal to 150 percent of the top-coded amount. After 1996, the CPS changed to a procedure in which all income values are assigned and the top-coded values are adjusted so that aggregate income in the CPS matches total reported income in the non-public, uncensored CPS data. The pre-1996 and post-1996 data at the very top of the income distribution are therefore not directly comparable, due to this change in top-coding methodology. The analysis in this paper circumvents this problem by evaluating differences between the $90th$ and $10th$ percentile of the income distribution, as well as gini coefficients.²³ Although our estimated gini coefficients utilize the entire income distribution, variation in the tails of the income distribution have little influence on this measure of inequality.

4 Results

4.1 Cross-Sectional Approach

Figures 2 and 3 examine the variation in tax-based income compression across states. As already mentioned, the underlying data are annual observations from 1984 to 2008. Nominal income data are converted to real income using the personal consumption expenditure (PCE) deflator in the National Income and Product Accounts. In addition, the figures and tables refer to "gross income'' when displaying before-tax income and "net income'' when displaying after-tax income. We will use the terms "gross income'' and before-tax income interchangeably. The same applies to "net income'' and after-tax income.²⁴

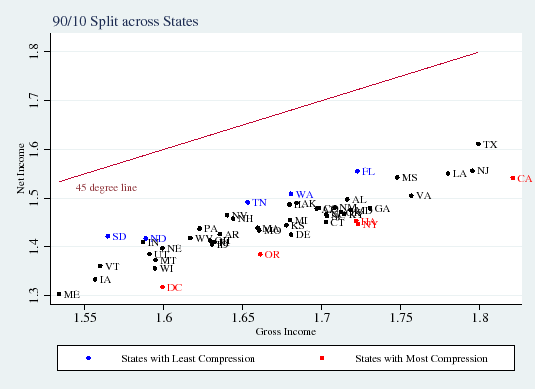
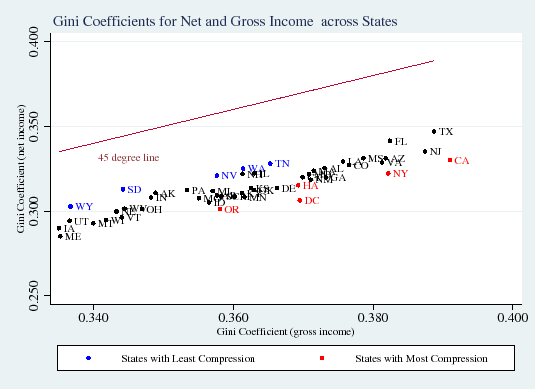
Figure 2 compares gross income (before-tax) inequality to net income (after-tax) inequality across states. The vertical distance between a state and the 45-degree line is equal to the $comp_{90/10}$ metric (Panel A) or the $comp_{gini}$ metric (Panel B). All of the states fall beneath the 45-degree line, indicating they are progressive -- the after-tax distribution of income is compressed relative to the before-tax distribution. States with relatively progressive personal income taxes, such as California, New York, and Oregon, have the highest tax compression, while states without a broad-based income tax, such as Florida, Tennessee, and Washington, are in the group of states with the least overall tax compression.

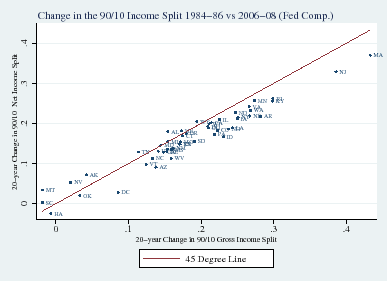
The effect of taxes on reducing labor income inequality across states can be decomposed into the impact of federal versus state tax policies. This breakdown is shown in Figure 3, which distinguishes federal tax compression (compression excluding state taxes) in Panel A from state tax compression (compression excluding federal taxes) in Panel B.²⁵

The results demonstrate that federal taxes are by far the larger contributor to compressing the net income distribution relative to the gross income distribution. Furthermore, despite significant heterogeneity across states in the extent of before-tax inequality, there is almost no variation across states in terms of the amount of federal compression: The states are very tightly bunched around a downward almost parallel shift in the 45-degree line.²⁶

Panels B reveals much greater dispersion in the extent to which state taxes influence inequality compared with federal taxes. States such as Hawaii, Oregon, Minnesota, and New York, along with the District of Columbia, exhibit the greatest reduction in labor income inequality due to state tax programs. In contrast, relatively regressive states such as Texas, Florida, Illinois, South Dakota and Tennessee, have state tax structures that appear to increase inequality and effectively offset some of the progressive nature of the federal tax code.

Tables 1 and 2 provide more detailed analysis. Table 1 shows gross versus net income at the $90th$ percentile of the distribution and at the $10th$ percentile of distribution for each state. Net income in Table 1 incorporates both federal and state taxes. Gross and net income data are shown in levels for clarity (in 1000s of 2000 dollars). The final column of Table 1 displays compression as quantified by the $comp_{90/10}$ metric. (The $comp_{90/10}$ metric is multiplied by 100 for ease of exposition in this and all subsequent tables.) The results show that on average taxes reduce labor income inequality in a state by approximately 22 percentage points (bottom row). To place this figure into perspective, 90/10 before-tax wage inequality rose roughly 1 percentage point per year over our sample period (see Panel B of Figure 1). Thus, taxes undo around 19 years worth of wage inequality growth. The reduction in inequality ranges from nearly 30 percentage points in states such as California and Oregon to about 15 percentage points in less progressive states such as Tennessee, New Hampshire, and Florida.

Table 2 reports the same compression measure separately for federal taxes (column 1) and state taxes (column 2). (A full set of federal and state compression results are shown in the appendix.) The table also compares the relative magnitude of state versus federal compression (column 3). The results show that state taxes reduce labor income inequality by a relatively small amount compared with federal taxes. Specifically, the reduction in inequality due to state tax programs is only about 8 percent, on average, of the reduction achieved by federal tax programs (bottom row). This relatively low average, though, masks significant variation across the states. Tax policies in states such as Wisconsin, Oregon, Maine, and Hawaii achieve a reduction in income inequality that is roughly one-fourth to one-third the size of federal compression within the same state. In contrast, tax policies in a number of other states including Wyoming, Texas, Tennessee, South Dakota, and Illinois undo some of the reduction in inequality achieved by the federal tax system.

A final cross-sectional analysis considers the impact of state gas taxes and sales tax exemptions. Starting with the gas tax, previous studies of overall state tax incidence for the most part have not singled out and analyzed the effect of state gas tax policies. However, as Table 3 shows, there are noticeable differences across states in the role played by gas taxes on income compression. Column (7) repeats the state compression measure from the middle column of Table 2. Column (8) then shows the amount of state income compression assuming the counter-factual that state gas taxes are zero for all states. On average (bottom row), compression is 1.5 percentage points with gas taxes included and 2.1 percentage points when gas taxes are excluded. That is, state gas taxes undo the reduction in labor income inequality achieved by other elements of state tax systems by nearly 30 percent.²⁷

A further examination of Table 3 shows that in some states, such as Georgia and Nevada, gas taxes have very little impact on state income compression. In contrast, gas taxes undo a substantial portion of the reduction in inequality achieved by other state tax policies in states such as New Hampshire, Arizona, North Dakota, and New Mexico. In addition, gas taxes add noticeably to the increase in inequality caused by state tax programs in states such as Mississippi, Nevada, and Illinois. It is also worth noting that state gas taxes in Louisiana cause the impact of that state's tax policies to shift from being slightly progressive to being a touch regressive. Overall, gas taxes play an important role in the extent to which states' tax policies are able to reduce labor income inequality.

Turning to sales tax exemptions, many states exempt clothing and/or food from the sales tax on equity grounds.²⁸ Although these policies have a significant effect on sales tax revenues - the food exemption alone reduces revenue by as much as 20 percent, all else equal (Due & Mikesell, 2005) - there is little evidence on their distributional effect. We provide such evidence. Specifically, we assess the policy's effectiveness at mitigating a specific form of inequality (wage inequality).

Table 4 reveals that these exemptions substantially reduce wage income inequality. On average (bottom row), the 90/10 difference in state compression when the exemptions are included is 1.5 percentage points (column 9), and it falls to 0.9 percentage points under the counterfactual of no exemptions in any state (column 10). That is, sales tax exemptions account for around one-third of state tax compression on average ( $\frac{0.6}{1.5}$, see columns 12)-- an extremely large share given that 18 states had no exemptions over the period of our study, and therefore contributed zeros to the average amount of compression caused by the exemptions. Similarly, if all states had exempted food and clothing over the entire sample period, income compression would have risen to 2.0 percentage points (column 11)--an increase of one-third ( $\frac{-0.5}{1.5}$, see column 13).

4.2 Time-Series Approach

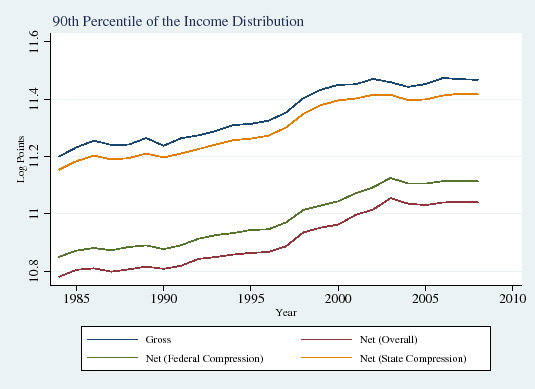
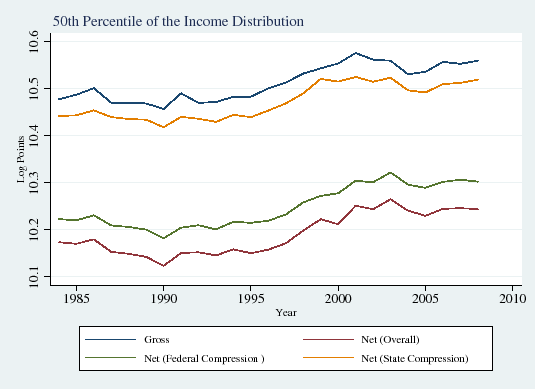
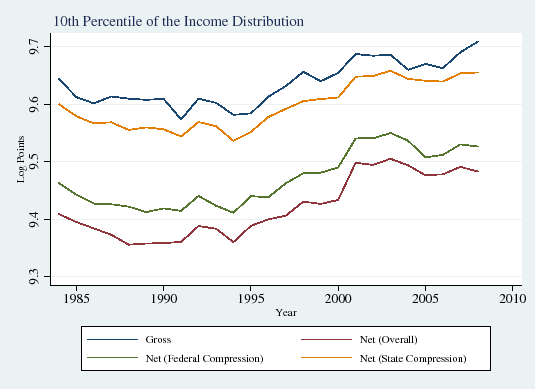
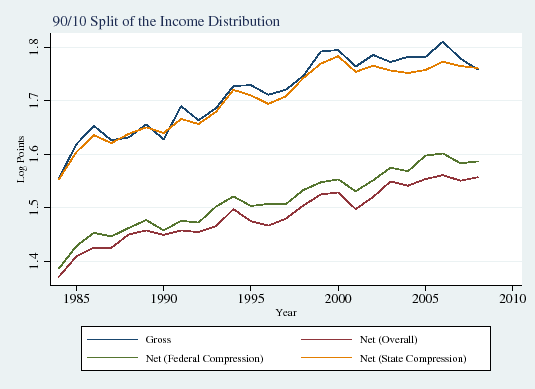
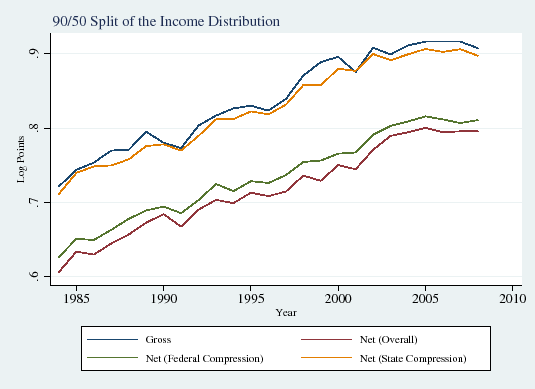
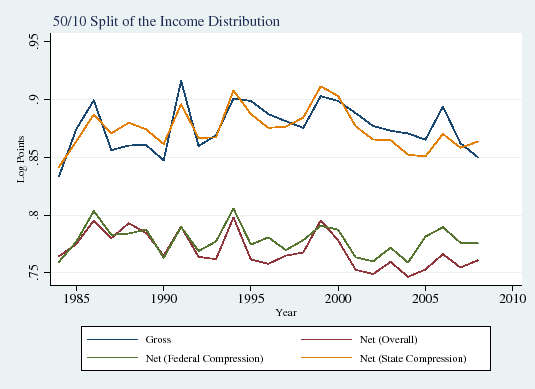
In this subsection we explore how the influence of taxes on income inequality has evolved over time. Figure 1 displays the well-documented increase in overall gross (that is, before-tax) wage inequality over the period of our study, the mid-1980s through the late 2000s (Panels A and B). Consistent with the findings of the recent literature on the polarization of the labor market (see Autor et al., 2008), inequality in the upper half of the income distribution also rose sharply (90/50 differential; Panel C), but lower-half inequality was roughly flat (50/10 differential; Panel D).

Figure 4 displays the evolution of the $90th$, $50th$ and $10th$ percentiles (Panels A, B, and C, respectively) of gross wages (blue line), wages net of federal taxes (green line), wages net of state taxes (yellow line) and wages net of both state and local taxes (red line).²⁹ Although there are considerable changes over time in gross income--for example, persistent increases at the $90th$ percentile and a fall followed by an increase at the $10th$ percentile--the wedge between gross and net income appears to roughly hold constant over time in all three cases. Thus it appears that there have not been dramatic changes over time in tax based compression of income inequality.

Panels D, E and F display pre and post-tax overall inequality (90/10 differential), upper-tail inequality (90/50 differential), and lower-tail inequality (50/10 differential), respectively. Overall tax compression, $comp_{90/10}$, is the difference between gross income inequality (blue line) and net income inequality (red line) in Panel D. This difference widens a bit over time, rising from an average of 0.21 log points in 1988-1995 to an average of 0.24 in 1996-2008. That is, overall tax compression rose a relatively modest 0.03, an increase of about 15 percent. Tax compression of upper and lower tail inequality display similar, modest increases.

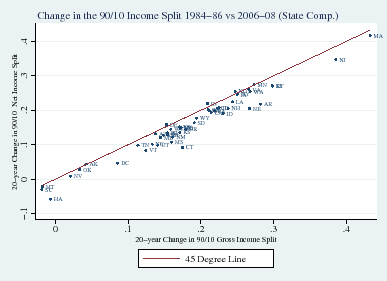
Figure 5 explores changes in the evolution of tax compression on a state-by-state basis. In the top panel, the horizontal axis displays the 20-year change in the gross 90/10 log income differential, and the vertical axis displays the corresponding 20-year change in the net 90/10 split. Small cell sizes for some states cause the 90/10 splits to vary considerably from year to year. We use 3-year windows of 1984-1986 and 2006-2008 to calculate the 20-year changes in order to smooth through this variability. States on the 45-degree line passed the change in before-tax wage inequality one-for-one into after-tax inequality. States below the line mitigated the rise in inequality by passing through less than 100 percent of the before-tax rise in inequality to after-tax inequality. Similarly, states above the line intensified the increase in inequality by passing through more than 100 percent of the before-tax rise in inequality to after-tax inequality.

On average, the states are roughly clustered around a slight, almost parallel, downward shift in the 45-degree line. These results therefore again indicate a small increase in tax compression over the period of study. The second and third panels perform the same exercise for only the federal tax code and only the state tax code, respectively. Both the state and federal codes play a role in the less than full pass through of the rise in pre-tax inequality, with the federal code playing a somewhat larger role.

The above time-series analysis confounds two factors. First, as before-tax income inequality increases, the impact of the tax system on inequality may change even in the absence of any adjustments to the tax code. More specifically, under a progressive tax system in which the function relating income to taxes is stable, an increase in before-tax inequality would be expected to increase compression as quantified by the $comp_{90/10}$ metric (see Section 2.2). Second, the tax code is often adjusted over time, and may even be adjusted in response to changes in pre-tax inequality (e.g. Piketty (1995); Kerr (2011)). ³⁰

Figure 6 displays counterfactual exercises which isolate the contribution of these two factors. Panel A displays two net income counterfactuals: one assuming that the 1988 federal and state tax codes held in all years (the yellow line) and one assuming that the 2008 tax codes held in all years (the green line). By holding the tax code fixed, the effect of the change in pre-tax income inequality on tax compression is isolated. As expected, the increase in gross income inequality produces an increase in $comp_{90/10}$. Holding the tax code fixed at its 1988 level, the rise in pre-tax inequality produces a 0.04 increase in tax compression (as tax compression-the difference between gross income inequality and counterfactual net income inequality-averages 0.192 from 1984-1995 and then rises to 0.235 over 1996-2008). The 2008 tax counterfactual yields a similar increase of 0.05.

Panel B displays two additional net income counterfactuals: one assuming that the 2008 real income distribution held in all years (the green line) and one assuming that the 1988 real income distribution held in all years (the yellow line). By holding the income distribution fixed, the effect of legislated tax changes is isolated. The 2008 counterfactual tax compression measure is calculated as the difference between gross wage inequality in 2008 and counterfactual net wage inequality in 2008. As 2008 gross wage inequality is fixed (i.e. a horizontal line on the graph), movements in the 2008 counterfactual net income inequality map one-for-one into the counterfactual tax compression measure. The 2008 counterfactual is somewhat variable (particularly toward the end of the sample period), but displays an upward trend on average: tax compression is 0.043 lower on average in 1996-2008 as compared to 1984-1995. That is, the changes to the tax code increased post-tax wage inequality relative to pre-tax wage inequality. This effect is lower when income is held at its 1988 distribution. In this case, changes to the tax code reduce $comp_{90/10}$ by only 0.0143. The difference between the 1988 and 2008 counterfactuals reflects the different income distributions. The legislated tax changes have a larger impact on the relatively more disperse 2008 income distribution.

The timing of several major reforms to the federal personal income tax are indicated in Panel B. The effect of any given reform appears to be moderate to small. The one possible exception is the Economic Growth and Tax Relief Reconciliation Act of 2001 as the 2008 counterfactual shows a marked increase, on average, after this change to the tax code. Both the 1988 and 2008 counterfactual increase somewhat around the Tax Reform Act of 1986, although the increases continue through 1998, past the 1987 implementation of the tax changes.

Our final piece of counterfactual analysis focuses on state taxes and is presented in Figure 7. Again, two net income counterfactuals are displayed. The first assumes that the entire sample is subject to the state tax code of California in all years (green line), while the second assumes that the entire sample is subject to the state tax of Tennessee in all years (yellow line). The choice of California and Tennessee reflect the analysis in Table 2 which indicates California is a high compression state whereas Tennessee is a state that widens the income distribution through taxation. Actual net income inequality (red line) is calculated using taxpayers' true state of residence. California net income inequality (green line) is well below actual net income inequality, suggesting that if all states switched to California's tax code, after-tax wage inequality would fall somewhat. On the other hand, a switch by all states to the Tennessee tax code (yellow line) would serve to increase after-tax inequality substantially. The gap between the two state net income counterfactuals, 0.08 log points, is quite large, highlighting the substantial dispersion in state based tax compression across the U.S. states.

Overall, our time-series analysis produces two primary conclusions. First, the influence of taxes on the wedge between pre and post-tax wage inequality has increased by a relatively small amount from the mid-1980s through 2008. Second, this small increase masks offsetting effects: Legislated tax changes have worked to reduce tax compression, while the widening of the pre-tax wage distribution in the presence of a progressive tax system has worked to increase tax compression.

4.3 Tax Incidence Sensitivity Analysis

Table 5 assesses the robustness of our conclusions to differing assumptions about tax incidence. The analysis is presented for mean outcomes across the fifty states plus the District of Columbia. The first row replicates the bottom row of Table 2 in order to provide a baseline. Section 2.3 contains a discussion of the incidence assumptions upon which the sensitivity analysis is based.

Panel A presents results which assume that the sales tax is subject to 100 percent overshifting, consistent with the evidence in Besley & Rosen (1999) as well as some of the older evidence reviewed in Poterba (1996). The sales tax is a relatively regressive component of state tax systems. Correspondingly, increasing its magnitude reduces the amount of compression caused by state taxes. The magnitude of the reduction is large, as state based compression falls from 1.5 to 0.0. Although this result is an important caveat to our conclusions, we are hesitant to place too much weight on it for two reasons. First, a number of recent studies suggest the sales tax is not overshifted (see Cole, 2009; Poterba, 1996). Second, overshifting is a theoretic possibility only when firms have pricing power. We assume in our sensitivity analysis that all retail goods are subject to 100 percent overshifting, but many goods are subject to competitive pressures which limit the ability of firms to set prices. Thus, even if overshifting is prevalent for some goods, the results in Panel A almost certainly overstate its importance.

Panel B presents results which account for the federal corporate income tax.³¹ Consistent with previous studies (see Gramlich et al., 1993), we assign the incidence of the tax based on a household's share of either aggregate labor income or aggregate capital income. Capital income is measured as the sum of interest income, dividend income and realized capital gains. The first row assigns the full incidence of the corporate income tax to capital, consistent with a closed economy, while the second row assigns the full incidence to labor, consistent with a small open economy. The third row assigns the incidence 40 percent to capital and 60 percent to labor, consistent with the beliefs of public finance economists at top-40 U.S. institutions (Fuchs et al., 1998). Under all three assumptions, accounting for the corporate income tax has essentially no effect on the results.

Panel C presents estimates which assess the robustness of our conclusions to use of lifetime inequality calculations, as opposed to the annual calculations used throughout the rest of the paper. Transitory income shocks and mobility within the income distribution may cause annual measures of income inequality to overstate lifetime inequality.

In order to calculate lifetime style estimates we require longitudinal data and therefore turn to the the Panel Study of Income Dynamics (PSID). The PSID is a nationally representative survey of households containing information on labor, capital and other income. Households and their offspring are followed annually through 1997 and biennially thereafter. We utilize the same sample period as previously: 1984 - 2008. We require that a household be observed a minimum of twelve times over this horizon. We then take the annual average of the households' pre-tax and post-tax income data to determine their "lifetime'' tax compression. The twelve observation minimum balances the desire to have as many observations per household as possible in order to approximate "lifetime'' incidence against considerations of sample size (as the higher the minimum, the fewer households are included in the sample). The approach is very similar to the "time-exposure'' approach developed by Slemrod (1992).³²

The bottom row of Panel C replicates our cross-sectional/annual procedure using the PSID data. Federal compression is quite similar across the CPS and PSID samples (19.1 in the CPS versus 16.0 in the PSID). State compression though differs across the samples (1.5 in the CPS versus 0.6 in the PSID). While this represents a large percentage difference--the PSID estimate is roughly $\frac{1}{3}$ the size of the CPS estimate--the results can be viewed as similar in that they are both a relatively small fraction of federal compression. The PSID sample size is only roughly 20 percent of the CPS sample size. Additionally, the CPS contains more detailed and extensive data on income. We therefore have more confidence in the CPS estimates.

Despite our relative preference for the CPS estimates, we view the comparison between the annual PSID and lifetime PSID estimates as extremely useful because it sheds light on the extent to which our annual-based estimates would be expected to differ from lifetime estimates. The results of the exercise suggest they would differ very little, as the PSID cross-section and PSID lifetime estimates are very similar. Our interest in wage inequality and corresponding focus on FTFY year workers makes this result unsurprising. Many of the factors which would mostly likely cause annual and lifetime estimates to differ--time spent as a student, retirement, unemployment, etc.--are absent.

5 Conclusion

This paper documents the role of the federal and state tax codes in compressing the after-tax distribution of income relative to the before-tax distribution. The focus is on the distribution of wage income, given the substantial rise in wage inequality over the past 25 years and the central role of wage income in setting the determining the overall distribution of economic well-being. While federal taxes tend to mitigate income inequality across U.S. households to a substantial extent among all states, we find that state-levied taxes on individuals, on average, mitigate wage inequality by much less. Looking at the average reduction in inequality, though, masks significant heterogeneity across states. A few states' income compression is equal to one-third or more of the compression caused by the federal code in the same state. On the other hand, the tax systems in several states actually widen their distributions of income. We find that the gas tax and sales tax exemptions are important determinants of state tax income compression. High gas taxes tend to substantially reduce compression while sales tax exemptions tend to substantially increase compression.

Over the period of the mid-1980s to the mid-2000s, the mitigating effect of federal and state taxes on wage inequality appears to have strengthened modestly as the rapid rise in wage inequality among households in the before-tax distribution was passed less than one-for-one into the after-tax distribution. This increase reflects the interaction of the rise in pre-tax wage dispersion with the progressive nature of the tax system. Legislated changes to the federal and state tax codes worked in the opposite direction, reducing the propensity of the tax code to reduce wage inequality over time.

Bibliography

Alm, James, Edward Sennoga, and Mark Skidmore (2009).

`Perfect Competition, Urbanicity, and Tax Incidence in the Retail Gasoline Market'. Economic Inquiry 47:118-134.

Auerbach, Alan (1988).

`Capital Gains Taxation in the United States'. Brookings Papers on Economic Activity 2:595-631.

Autor, David H., Lawrence F. Katz, and Melissa S. Kearney (2008).

`Trends in U.S. Wage Inequality'. Review of Economics and Statistics 90:300-323.

Berliant, Marcus C., and Robert P. Strauss (1993).

`State and Federal Tax Equity: Estimates before and after the Tax Reform Act of 1986'. Journal of Policy Analysis and Management 12:9-43.

Besley, T., and H. Rosen (1999).

`Sales Taxes and Prices: An Empirical Analysis'. National Tax Journal 52:157-178.

Blundell, Richard, Luigi Pistaferri, and Ian Preston (2006).

`Imputing Consumption in the PSID Using Food Demand Estimates from the CEX'. mimeo.

Card, David, and John E. DiNardo (2002).

`Skill-Biased Technological Change and RisingWage Inequality: Some Problems and Puzzles'. Journal of Labor Economics 20:733-783.

Chetty, Raj, and Emmanuel Saez (2005).

`Dividend Taxes and Coporate Behavior: Evidence fro the 2003 Dividend Tax Cut'. Quarterly Journal of Economics pp. 791-833.

Chouinard, Hayley, and Jeffrey M. Perloff (2004).

`Incidence of Federal and State Gasoline Taxes'. Economics Letters 83:55-60.

Cole, Adam (2009).

`Christmas in August: Prices and Quantities During Sales Tax Holidays'. University of Michigan.

Congressional Budget Office (2007).

`historical Effective Federal Tax Rates: 1979 to 2005'. Tech. rep., Congresional Budget Office.

Cutler, David (1994).

`Comments on Trends in Income Inequality: The Impact of, and Implications for, Tax Policy'. In J. Slemrod (ed.), Tax Progressivity and Income Inequality. Press Syndicate of Cambridge University Press, New York, NY.

Cutler, David M., and Lawrence F. Katz (1992).

`Rising Inequality? Changes in the Distribution of Income and Consumption in the 1980s'. American Economic Review 82:546-551.

Due, John F., and John L. Mikesell (2005).

`Retail Sales Tax, State and Local'. In R. E. Cordes, Joseph & J. Gravelle (eds.), Encyclopedia of Taxation and Tax Policy. Urban Institute Press, Washington D.C.

Frydman, Carola, and Raven Molloy (2012).

`The Effect of Tax Policy on Executive Compensation: Evidence from Postwar Reforms'. forthcoming in Journal of Public Economics.

Frydman, Carola and Raven Saks (2010).

`Executive Compensation: A New View from a Long-Term Perspective, 1936-2005'. Review of Financial Studies 23:2099-2138.

Fuchs, Victor, Alan Krueger, and James Poterba. (1998).

`Economists' Views about Parameters, Values, and Policies: Survey Results in Labor and Public Economics'. Journal of Economic Literature XXXVI:1387-1425.

Fullerton, Don, and Gilber Metcalf (2005).

`Tax Incidence'. In A. Auerbauch & M. Feldstein (eds.), Handbook of Public Economics, Volume 4.

Fullerton, Don, and Diane Lim Rogers (1993).

Who Bears the Lifetime Tax Burden? The Brookings Institution, Washington D.C.

Gottschalk, Peter and Timothy Smeeding (2000).

`Empirical Evidence on Income Inequality on Industralized Countries'. In A. B. Atkinson & F. Bourguignon (eds.), Handbook of Income Distribution. Elsevier Science, San Diego, CA.

Gramlich, Edward, Richard Kasten, and Frank Sammartino (1993).

`Growing Inequality in the 1980s: The Role of Federal Taxes and Cash Transfers'. In S. Danzinger & P. Gottschalk (eds.), Uneven Tides: Rising Inequality in America. Russell Sage Foundation, New York, NY.

H., Galpher, and S Pollock (1988).

`Models of State Income Tax Reform'. In S. Gold (ed.), The Unfinished Agenda for State Tax Reform. National Conference of State Legislatures, Washington, DC.

Inman, Robert P. (1994).

`Comments on The Lifetime Incidence of State and Local Taxes: Measuring Changes During the 1980s'. In J. Slemrod (ed.), Tax Progressivity and Income Inequality. Press Syndicate of Cambridge University Press, New York, NY.

Karoly, Lynne (1993).

`The Trend in Inequality Among Families, Individuals, and Workers in the United States: A Twenty-Five Year Perspective'. In S. Danzinger & P. Gottschalk (eds.), Uneven Tides: Rising Inequality in America. Russell Sage Foundation, New York, NY.

Karoly, Lynn (1994).

`Trends in Income Inequality: The Impact of, and Implications for, Tax Policy'. In J. Slemrod (ed.), Tax Progressivity and Income Inequality. Press Syndicate of Cambridge University Press, New York, NY.

Kasten, Richard, Frank Sammartino, and Eric Todder (1994).

`Trends in Federal Tax Progressivity, 1980-93'. In J. Slemrod (ed.), Tax Progressivity and Income Inequality. Press Syndicate of Cambridge University Press, New York, NY.

Katz, Lawrence, and David Autor (1999).

`Changes in the Wage Structure and Earnings Inequality'. In O. Ashenfeher & D. Card (eds.), Handbook of Labor Economics. Elsevier Science, San Diego, CA.

Kerr, William (2011).

`Income Inequality and Social Preferences for Redistribution and Compensation Differentials'. Harvard Business School.

Kiefer, Donald (2005).

`Measures of Progressivity'. In R. E. Cordes, Joseph & J. Gravelle (eds.), Encyclopedia of Taxation and Tax Policy. Urban Institute Press, Washington D.C.

Kotlikoff, Lawrence, and Lawrence Summers (1987).

`Tax Incidence'. In A. Auerbauch & M. Feldstein (eds.), Handbook of Public Economics, Volume 2.

Marion, Justin, and Erich Muehlegger (2011).

`Fuel Tax Incidence and Supply Conditions'. Journal of Public Economics 95:1202-1212.

Metcalf, Gilbert (1994).

`The Lifetime Incidence of State and Local Taxes: Measuring Changes During the 1980s'. In J. Slemrod (ed.), Tax Progressivity and Income Inequality. Press Syndicate of Cambridge University Press, New York, NY.

Meyer, Bruce, Wallace K.C. Mok, and James X. Sullivan (2009).

`The Under-Reporting of Transfers in Household Surveys: Its Nature and Consequences'. NBER W.P. #15181.

Musgrave et. al., R.A. (1951).

`Distribution of Tax Payments by Income Groups: a Case Study for 1948'. National Tax Journal pp. 1-54.

Musgrave, Richard, and Tun Thin (1948).

`Income Tax Progression, 1929-48'. Journal of Political Economy 56:298-514.

Pechman, Joseph (1985).

Who Paid the Taxes, 1966-85. Brookings Institution, Washington DC.

Pechman, Joseph, and Benjamin Okner (1974).

Who Bears the Tax Burden. Brookings Institution, Washington DC.

Piketty, Thomas (1995).

`Social Mobility and Redistributive Politics'. Quarterly Journal of Economics CX:551-584.

Piketty, Thomas, and Emmanuel Saez (2003).

`Income Inequality in the United States, 1913-1998'. Quarterly Journal of Economics CXVIII:1-39.

Poterba, James (1991).

`Is the Gasoline Tax Regressive?'. In D. Bradford (ed.), Tax Policy and the Economy, Volume 5. National Bureau of Economic Research, Cambridge, MA.

Poterba, James (1996).

`Retail Price Reactions to Changes in State and Local Taxes'. National Tax Journal 49:165-176.

Reynolds, Morgan, and Eugene Smolensky (1977).

`Post Fisc Distributions of Income in 1950, 1961 and 1970'. Public Finance Quarterly 5:419-438.

Saez, Emmanuel (2004).

`Reported Incomes and Marginal Tax Rate, 1960-2000: Evidence and Policy Implications'. In J. Poterba (ed.), Tax Policy and the Economy (2004). National Bureau of Economic Research, Cambridge, MA.

Saez, Emmanuel (2010).

`Do Taxpayers Bunch at Kink Points?'. American Economic Journal: Economic Policy 2:180-212.

Saez, Emmanuel, Joel Slemrod, and Seth Giertz (2010).

`The Elasticity of Taxable Income with Respect to Marginal Tax Rates: A Critical Review'. forthcoming in Journal of Economic Literature.

Saez, Emmanuel, and Michael Veall (2005).

`The Evolution of High Incomes in Northern America: Lessons from Canadian Evidence'. American Economic Review 95:831-849.

Slemrod, Joel (1992).

`Taxation and Inequality: A Time-Exposure Perspective'. In J. Poterba (ed.), Tax Policy and the Economy, Vol. 6. MIT Press, Cambridge, MA.

Smith, Chris (2011).

`Polarization, immigration, education: What's behind the dramatic decline in youth employment?'. Finance and Economics Discussion Series 2011-41, Federal Reserve Board.

Figure 1: Inequality over Time

Panel A

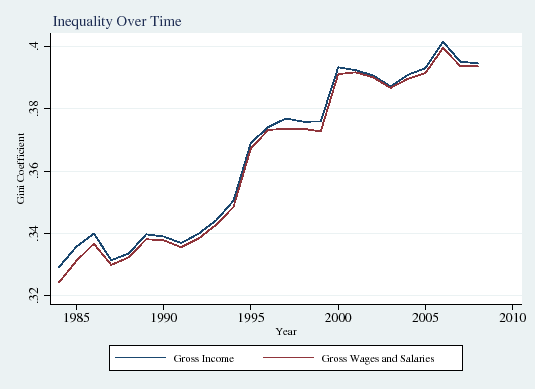Figure 1A Data

Panel B

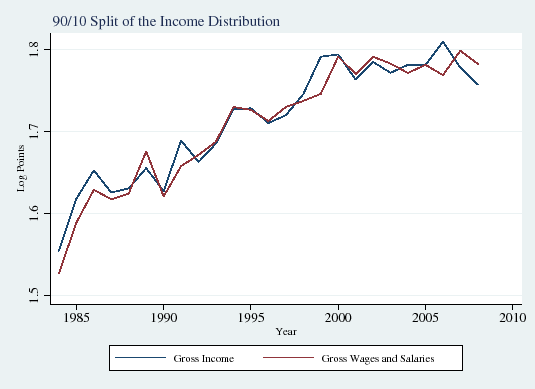Figure 1B Data

Panel C

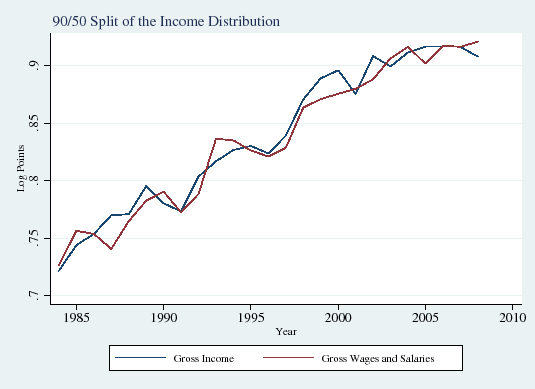Figure 1C Data

Panel D

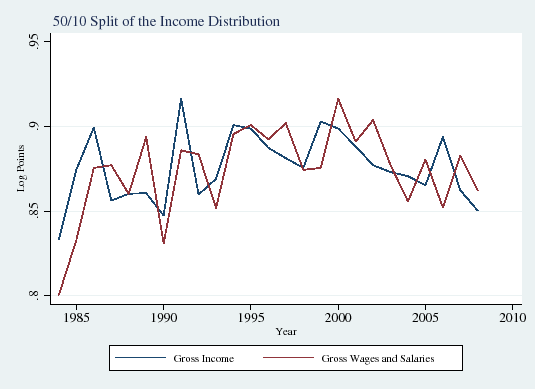Figure 1D Data

Source: Authors' calculations using CPS data.

Figure 2: Across State Differences

Panel A

Figure 2A Data

Panel B

Figure 2B Data

Source: Authors' calculations using CPS data.

Figure 3: Federal and State Compression Across States

Panel A

Figure 3A Data

Panel B

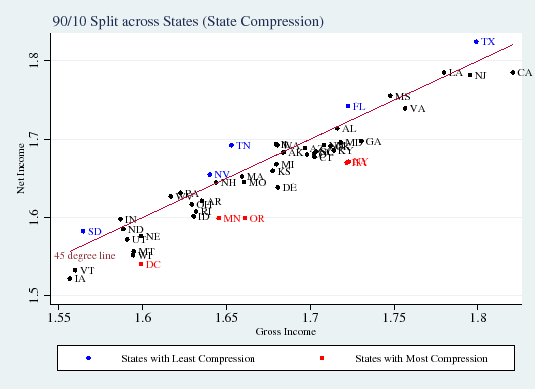Figure 3B Data

Source: Authors' calculations using CPS data.

Figure 4: Inequality over Time

Panel A

Figure 4A Data

Panel B

Figure 4B Data

Panel C

Figure 4C Data

Panel D

Figure 4D Data

Panel E

Figure 4E Data

Panel F

Figure 4F Data

Source: Authors' calculations using CPS data.

Figure 5: Changes in Inequality 1980s to 2000s

Figure 5A Data

Figure 5B Data

Figure 5C Data

Source: Authors' calculations using CPS data.

Figure 6: Counterfactual Tax and Income Distribution

Panel A: Tax Code Held Fixed

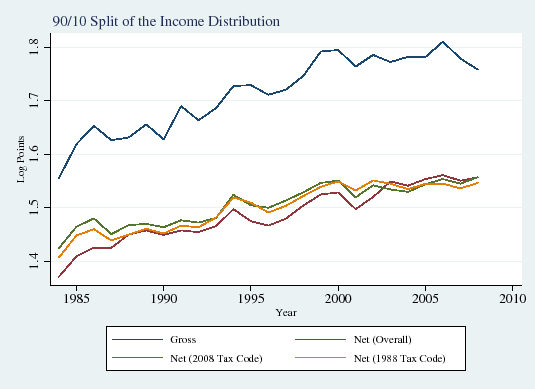Figure 6A Data

Panel B: Income Distribution Held Fixed

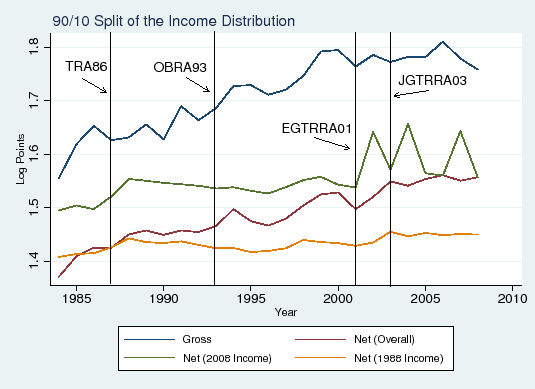Figure 6B Data

Source: Authors' calculations using CPS data. In Panel B, TRA86 refers to Tax Reform Act of 1986, OBRA93 refers to Omnibus Budget Reconciliation Act of 1993, EGTRRA01 refers to Economic Growth and Tax Relief Reconciliation Act of 2001, and JGTRRA03 refers to Jobs and Growth Tax Relief Reconciliation Act of 2003. The line for TRA86 is fixed at the 1987 tax year - the year the act was first implemented.

Figure 7: Counterfactual State Tax Schemes

Figure 7 Data

Source: Authors' calculations using CPS data.

Table 1: Total Compression

	Gross Inc. 90th Percentile	Net Inc. 90th Percentile	Gross Inc. 10th Percentile	Net Inc. 10th Percentile	Gross90/10-Net 90/101
AK	102.7	69.7	19.1	15.7	19.4
AL	77.6	51.0	14.0	11.4	21.9
AR	70.2	46.2	13.7	11.1	20.9
AZ	80.4	52.8	14.7	12.0	21.9
CA	91.6	56.7	14.8	12.1	27.9
CO	89.5	57.1	16.4	13.0	21.8
CT	100.4	62.9	18.3	14.7	25.1
DC	76.6	46.0	15.5	12.3	28.1
DE	84.8	54.3	15.8	13.1	25.5
FL	79.8	54.8	14.3	11.6	16.7
GA	83.3	53.0	14.8	12.1	25.1
HA	87.2	52.9	15.6	12.4	26.8
IA	78.8	50.7	16.6	13.4	22.3
ID	74.8	47.9	14.6	11.8	22.5
IL	87.1	55.9	16.2	12.6	19.2
IN	79.3	52.1	16.2	12.7	17.7
KS	83.1	53.2	15.5	12.5	23.3
KY	78.4	50.4	14.1	11.6	24.7
LA	81.4	53.4	13.7	11.3	22.9
MA	94.8	58.8	18.0	13.9	22.0
MD	95.0	59.0	17.0	13.5	24.2
ME	74.9	48.3	16.2	13.1	23.0
MI	89.7	57.1	16.7	13.3	22.4
MN	90.4	55.4	17.4	13.8	25.6
MO	81.2	52.4	15.4	12.5	22.6
MS	72.7	48.1	12.7	10.3	20.5
MT	71.1	47.5	14.4	12.0	22.1
NC	79.9	50.3	14.6	11.6	23.6
ND	73.9	50.4	15.1	12.2	17.1
NE	78.7	51.2	15.9	12.7	20.2
NH	91.2	62.0	17.6	14.4	18.6
NJ	102.2	64.5	17.0	13.6	23.9
NM	74.5	48.7	13.5	11.1	22.8
NV	80.4	54.8	15.6	12.7	17.5
NY	87.3	54.1	15.6	12.7	27.6
OH	83.5	53.7	16.4	13.1	21.6
OK	79.4	50.5	14.3	11.6	24.1
OR	80.7	50.0	15.3	12.5	27.6
PA	82.7	54.3	16.3	12.9	18.5
RI	85.0	53.9	16.6	13.2	22.2
SC	79.4	50.5	14.5	11.7	23.9
SD	71.9	50.5	15.0	12.2	14.2
TN	76.2	52.2	14.6	11.7	16.2
TX	84.2	57.3	13.9	11.4	18.8
UT	78.9	50.6	16.1	12.7	20.5
VA	91.7	56.6	15.8	12.6	25.2
VT	77.5	50.9	16.3	13.0	19.8
WA	88.8	59.8	16.5	13.2	17.1
WI	81.1	51.1	16.5	13.2	23.8
WV	72.8	47.1	14.5	11.4	19.8
WY	80.3	55.4	15.8	13.0	17.3
Average	82.7	53.5	15.6	12.6	21.9

Source: Authors' calculations using CPS data; all income data values are in $1000s of 2000 dollars (first four columns). ¹ Percentage points.

Table 2: Federal and State Compression

	Gross 90/10-Net 90/10 Federal1	Gross 90/10-Net 90/10 State1	State as % Federal
AK	18.6	0.1	0.5%
AL	19.5	0.2	1.1%
AR	17.9	1.4	7.8%
AZ	19.0	0.8	4.1%
CA	21.9	3.5	16.2%
CO	17.8	1.8	9.9%
CT	20.7	2.5	12.1%
DC	20.1	5.9	29.1%
DE	19.6	4.2	21.6%
FL	19.0	-2.0	-10.5%
GA	20.3	3.3	16.1%
HA	18.8	5.2	27.5%
IA	16.8	3.5	20.6%
ID	18.1	2.9	16.0%
IL	20.4	-1.5	-7.2%
IN	18.1	-1.1	-6.0%
KS	19.1	1.8	9.4%
KY	21.0	2.8	13.4%
LA	22.6	-0.6	-2.5%
MA	20.0	0.7	3.5%
MD	20.0	2.2	11.1%
ME	16.8	4.5	26.5%
MI	20.6	1.2	5.7%
MN	18.1	4.6	25.5%
MO	19.5	1.5	7.7%
MS	20.2	-0.8	-3.9%
MT	16.8	3.8	22.7%
NC	19.0	2.0	10.5%
ND	16.0	0.3	2.1%
NE	16.5	2.3	13.9%
NH	18.7	-0.1	-0.4%
NJ	21.7	1.3	6.1%
NM	20.3	1.5	7.6%
NV	19.2	-1.5	-7.7%
NY	20.9	5.2	24.7%
OH	18.7	1.3	6.7%
OK	19.8	2.1	10.5%
OR	18.8	6.1	32.6%
PA	18.8	-0.9	-4.8%
RI	17.6	2.4	13.8%
SC	19.9	1.9	9.6%
SD	16.1	-1.8	-11.1%
TN	20.2	-3.9	-19.4%
TX	21.3	-2.6	-12.0%
UT	16.9	1.9	11.2%
VA	21.3	1.7	8.0%
VT	15.9	2.7	17.0%
WA	18.5	-1.2	-6.5%
WI	17.5	4.3	24.4%
WV	19.0	-1.0	-5.4%
WY	17.9	-1.5	-8.2%
Average	19.1	1.5	7.9%

Source: Authors' calculations using CPS data. ¹Percentage points.

Table 3: State Compression: Gas Tax Analysis

	90th Percentile Gross Inc. (1)	90th Percentile Net Inc. (2)	Net Inc. x Gas 1(3)	10th Percentile Gross Inc. (4)	10th Percentile Net Inc. (5)	10th Percentile Net Inc. x Gas 1(6)	90/10 Compression 2(7)	90/10 Compression $^1,$ $^2$(8)	[(7)-(8)]2 (9)
AK	102.7	103.0	103.1	19.1	19.1	19.2	0.1	0.2	-0.2
AL	77.6	73.9	74.2	14.0	13.3	13.5	0.2	1.0	-0.8
AR	70.2	65.9	66.2	13.7	13.0	13.2	1.4	2.3	-0.9
AZ	80.4	76.9	77.2	14.7	14.2	14.4	0.8	1.5	-0.7
CA	91.6	85.6	85.9	14.8	14.4	14.5	3.5	4.1	-0.5
CO	89.5	85.0	85.4	16.4	15.8	16.0	1.8	2.5	-0.7
CT	100.4	95.7	96.1	18.3	17.9	18.0	2.5	2.9	-0.4
DC	76.6	69.7	70.0	15.5	14.9	15.1	5.9	6.5	-0.7
DE	84.8	80.2	80.6	15.8	15.6	15.8	4.2	4.9	-0.7
FL	79.8	78.8	79.0	14.3	13.8	13.9	-2.0	-1.4	-0.6
GA	83.3	78.5	78.6	14.8	14.4	14.4	3.3	3.7	-0.4
HA	87.2	79.8	80.1	15.6	15.0	15.1	5.2	5.5	-0.3
IA	78.8	74.0	74.3	16.6	16.2	16.3	3.5	4.1	-0.6
ID	74.8	69.2	69.5	14.6	13.9	14.1	2.9	3.7	-0.8
IL	87.1	83.0	83.3	16.2	15.3	15.4	-1.5	-0.9	-0.6
IN	79.3	75.8	76.1	16.2	15.3	15.5	-1.1	-0.5	-0.6
KS	83.1	78.4	78.7	15.5	14.9	15.1	1.8	2.4	-0.6
KY	78.4	73.6	73.8	14.1	13.6	13.8	2.8	3.6	-0.8
LA	81.4	78.1	78.5	13.7	13.1	13.3	-0.6	0.4	-1.0
MA	94.8	89.2	89.4	18.0	17.1	17.2	0.7	1.0	-0.3
MD	95.0	89.5	89.8	17.0	16.4	16.6	2.2	2.9	-0.7
ME	74.9	70.0	70.2	16.2	15.8	15.9	4.5	4.8	-0.4
MI	89.7	85.0	85.3	16.7	16.0	16.2	1.2	1.7	-0.6
MN	90.4	83.7	84.1	17.4	16.9	17.1	4.6	5.2	-0.6
MO	81.2	76.9	77.1	15.4	14.8	15.0	1.5	2.0	-0.5
MS	72.7	68.6	68.9	12.7	11.9	12.0	-0.8	0.2	-1.0
MT	71.1	67.6	68.0	14.4	14.3	14.5	3.8	4.7	-0.9
NC	79.9	74.2	74.6	14.6	13.8	14.0	2.0	2.9	-0.9
ND	73.9	71.5	71.8	15.1	14.6	14.8	0.3	1.0	-0.6
NE	78.7	74.4	74.8	15.9	15.4	15.6	2.3	3.0	-0.7
NH	91.2	91.0	91.3	17.6	17.6	17.7	-0.1	0.3	-0.4
NJ	102.2	97.8	98.0	17.0	16.5	16.5	1.3	1.6	-0.2
NM	74.5	70.6	70.8	13.5	13.0	13.1	1.5	2.3	-0.8
NV	80.4	79.3	79.6	15.6	15.2	15.3	-1.5	-0.9	-0.6
NY	87.3	81.3	81.6	15.6	15.3	15.4	5.2	5.6	-0.4
OH	83.5	79.2	79.6	16.4	15.7	15.9	1.3	1.9	-0.6
OK	79.4	74.3	74.6	14.3	13.7	13.9	2.1	2.9	-0.8
OR	80.7	74.4	74.8	15.3	15.0	15.2	6.1	6.7	-0.6
PA	82.7	79.4	79.7	16.3	15.5	15.7	-0.9	-0.4	-0.5
RI	85.0	80.2	80.6	16.6	16.1	16.2	2.4	2.9	-0.5
SC	79.4	74.2	74.5	14.5	13.8	13.9	1.9	2.7	-0.8
SD	71.9	70.7	71.0	15.0	14.5	14.7	-1.8	-1.1	-0.7
TN	76.2	74.6	75.0	14.6	13.7	13.9	-3.9	-3.0	-1.0
TX	84.2	83.2	83.5	13.9	13.4	13.6	-2.6	-1.7	-0.9
UT	78.9	73.3	73.6	16.1	15.2	15.4	1.9	2.6	-0.7
VA	91.7	85.9	86.2	15.8	15.1	15.2	1.7	2.4	-0.7
VT	77.5	73.6	73.9	16.3	15.9	16.0	2.7	3.1	-0.4
WA	88.8	87.5	87.9	16.5	16.1	16.3	-1.2	-0.5	-0.7
WI	81.1	75.4	75.7	16.5	16.0	16.2	4.3	4.9	-0.7
WV	72.8	68.0	68.3	14.5	13.4	13.6	-1.0	-0.1	-0.9
WY	80.3	79.4	79.6	15.8	15.4	15.5	-1.5	-1.1	-0.4
Total	82.7	78.6	78.9	15.6	15.0	15.2	1.5	2.1	-0.6

Source: Authors' calculations using CPS data; all income data values are in $1000s of 2000 dollars (first four columns). ¹ Post-tax income excludes state gas taxes; ² Percentage points.

Table 4: State Compression: Sales Tax Exemption Analysis

	90th Percentile Gross Inc. (1)	90th Percentile Net Inc. (2)	90th Percentile Net Inc. no Ex.1 (3)	90th Percentile Net Inc. Full Ex.2(4)	10th Percentile Gross Inc. (5)	10th Percentile Net Inc. (6)	10th Percentile Net Inc. no Ex.1(7)	10th Percentile Net Inc. Full Ex.2(8)	90/10 Compression3 (9)	90/10 Compression No Ex.1,3 (10)	90/10 Compression Full Ex.1,3 (11)	(9)-(10)3 (12)	(9)-(11)3 (13)
AK	102.7	103.0	103.0	103.0	19.1	19.1	19.1	19.1	0.1	0.1	0.1	0.0	0.0
AL	77.6	73.9	73.9	74.3	14.0	13.3	13.3	13.5	0.2	0.2	1.4	0.0	-1.2
AR	70.2	65.9	65.9	66.3	13.7	13.0	13.0	13.3	1.4	1.4	2.8	0.0	-1.4
AZ	80.4	76.9	76.5	77.0	14.7	14.2	14.0	14.3	0.8	-0.2	1.0	1.0	-0.2
CA	91.6	85.6	85.1	85.8	14.8	14.4	14.1	14.4	3.5	2.2	3.9	1.4	-0.3
CO	89.5	85.0	84.8	85.1	16.4	15.8	15.7	15.9	1.8	1.1	1.9	0.6	-0.1
CT	100.4	95.7	95.1	95.7	18.3	17.9	17.6	17.9	2.5	1.5	2.5	1.1	-0.0
DC	76.6	69.7	69.3	69.8	15.5	14.9	14.7	15.0	5.9	4.8	6.1	1.0	-0.2
DE	84.8	80.2	80.2	80.2	15.8	15.6	15.6	15.6	4.2	4.2	4.2	0.0	0.0
FL	79.8	78.8	78.4	78.9	14.3	13.8	13.5	13.9	-2.0	-3.4	-1.7	1.4	-0.3
GA	83.3	78.5	78.3	78.7	14.8	14.4	14.3	14.5	3.3	2.8	3.9	0.5	-0.6
HA	87.2	79.8	79.8	80.2	15.6	15.0	15.0	15.2	5.2	5.2	6.0	0.0	-0.9
IA	78.8	74.0	73.7	74.1	16.6	16.2	16.0	16.2	3.5	2.7	3.6	0.7	-0.1
ID	74.8	69.2	69.2	69.6	14.6	13.9	13.9	14.2	2.9	2.9	4.2	0.0	-1.3
IL	87.1	83.0	82.9	83.5	16.2	15.3	15.2	15.5	-1.5	-1.7	-0.5	0.3	-1.0
IN	79.3	75.8	75.4	75.9	16.2	15.3	15.1	15.4	-1.1	-2.0	-0.9	0.9	-0.2
KS	83.1	78.4	78.4	78.8	15.5	14.9	14.9	15.1	1.8	1.8	2.8	0.0	-1.0
KY	78.4	73.6	73.2	73.7	14.1	13.6	13.4	13.7	2.8	1.6	3.1	1.3	-0.3
LA	81.4	78.1	78.0	78.4	13.7	13.1	13.0	13.3	-0.6	-1.0	0.3	0.4	-0.8
MA	94.8	89.2	88.7	89.2	18.0	17.1	16.8	17.1	0.7	-0.1	0.7	0.8	0.0
MD	95.0	89.5	89.2	89.7	17.0	16.4	16.2	16.5	2.2	1.5	2.5	0.7	-0.3
ME	74.9	70.0	69.6	70.1	16.2	15.8	15.6	15.8	4.5	3.6	4.6	0.9	-0.2
MI	89.7	85.0	84.6	85.1	16.7	16.0	15.8	16.1	1.2	0.4	1.3	0.8	-0.2
MN	90.4	83.7	83.1	83.7	17.4	16.9	16.6	16.9	4.6	3.5	4.6	1.1	0.0
MO	81.2	76.9	76.9	77.3	15.4	14.8	14.8	15.1	1.5	1.5	2.6	0.0	-1.1
MS	72.7	68.6	68.6	69.2	12.7	11.9	11.9	12.2	-0.8	-0.8	1.3	0.0	-2.1
MT	71.1	67.6	67.6	67.6	14.4	14.3	14.3	14.3	3.8	3.8	3.8	0.0	0.0
NC	79.9	74.2	74.2	74.6	14.6	13.8	13.8	14.0	2.0	2.0	3.0	0.0	-1.0
ND	73.9	71.5	71.1	71.6	15.1	14.6	14.4	14.7	0.3	-0.7	0.6	1.1	-0.2
NE	78.7	74.4	74.1	74.5	15.9	15.4	15.2	15.4	2.3	1.4	2.5	0.9	-0.2
NH	91.2	91.0	91.0	91.0	17.6	17.6	17.6	17.6	-0.1	-0.1	-0.1	0.0	0.0
NJ	102.2	97.8	97.2	97.8	17.0	16.5	16.2	16.5	1.3	0.2	1.3	1.1	0.0
NM	74.5	70.6	70.5	70.9	13.5	13.0	13.0	13.2	1.5	1.4	2.8	0.2	-1.2
NV	80.4	79.3	78.9	79.4	15.6	15.2	14.9	15.2	-1.5	-2.7	-1.2	1.2	-0.3
NY	87.3	81.3	81.0	81.4	15.6	15.3	15.1	15.3	5.2	4.4	5.3	0.8	-0.1
OH	83.5	79.2	78.9	79.3	16.4	15.7	15.5	15.8	1.3	0.2	1.4	1.0	-0.2
OK	79.4	74.3	74.3	74.7	14.3	13.7	13.7	13.9	2.1	2.1	3.3	0.0	-1.2
OR	80.7	74.4	74.4	74.4	15.3	15.0	15.0	15.0	6.1	6.1	6.1	0.0	0.0
PA	82.7	79.4	78.9	79.4	16.3	15.5	15.2	15.5	-0.9	-2.2	-0.9	1.3	0.0
RI	85.0	80.2	79.6	80.2	16.6	16.1	15.7	16.1	2.4	1.0	2.4	1.4	0.0
SC	79.4	74.2	74.2	74.6	14.5	13.8	13.8	14.0	1.9	1.8	3.2	0.1	-1.3
SD	71.9	70.7	70.7	71.1	15.0	14.5	14.5	14.8	-1.8	-1.8	-0.7	0.0	-1.1
TN	76.2	74.6	74.6	75.2	14.6	13.7	13.7	14.1	-3.9	-3.9	-2.2	0.0	-1.8
TX	84.2	83.2	82.7	83.3	13.9	13.4	13.2	13.5	-2.6	-4.0	-2.3	1.4	-0.3
UT	78.9	73.3	73.3	73.8	16.1	15.2	15.2	15.5	1.9	1.9	2.9	0.0	-1.0
VA	91.7	85.9	85.9	86.3	15.8	15.1	15.1	15.3	1.7	1.7	2.8	0.0	-1.1
VT	77.5	73.6	73.2	73.7	16.3	15.9	15.7	15.9	2.7	1.9	2.8	0.8	-0.1
WA	88.8	87.5	87.1	87.7	16.5	16.1	15.8	16.2	-1.2	-2.4	-1.0	1.2	-0.2
WI	81.1	75.4	75.0	75.5	16.5	16.0	15.8	16.0	4.3	3.5	4.4	0.8	-0.2
WV	72.8	68.0	67.9	68.4	14.5	13.4	13.3	13.6	-1.0	-1.3	0.4	0.2	-1.4
WY	80.3	79.4	79.3	79.7	15.8	15.4	15.4	15.6	-1.5	-1.5	-0.7	0.1	-0.8
Average	82.7	78.6	78.4	78.8	15.6	15.0	14.9	15.2	1.5	0.9	2.0	0.6	-0.5

Source: Authors' calculations using CPS data; all income data values are in $1000s of 2000 dollars (first eight columns). ¹Post-tax income excludes state sales tax exemptions; ² Post-tax income assume food and clothing are exempt from sales taxes in all states; $^3$ Percentage points.

Table 5: Sensitivity Analysis: Average U.S. Tax Incidence

	Gross 90/10-Net 90/10 Federal1	Gross 90/10-Net 90/10 State1	State as a % Federal
Baseline (Table 2)	19.1	1.5	7.9%
Panel A:100% Sales Tax Over Shift	19.1	0.0	0.3%
Panel B:Corporate Taxes
Panel B:Accrues 100% to Capital1	18.6	1.5	8.0%
Panel B:Accrues 100% to Labor2	20.0	1.5	7.5%
Panel B:Accrues 40% Capital 60% Labor	19.5	1.5	7.7%
Panel C:Lifetime Tax Incidence
Panel C: PSID Lifetime	14.0	0.5	3.5 %
Panel C: PSID Cross Section	16.0	0.6	3.8 %

Source: Authors' calculations using CPS data; ¹ Corporate tax allocated based on a household's share of aggregate capital income; $^2$ Corporate tax allocated based on a household's share of aggregate labor income.

6 Appendix

6.1 CEX Sample Selection

There are two distinct surveys that constitute the CEX: a "Diary" component that surveys consumers' daily spending habits over the course of two weeks, and an "Interview" survey that asks respondents to report their spending habits for the past three months. In the interview survey, households are followed for up to four consecutive quarters.³³ Since the interview survey collects household spending data for a longer horizon than the diary survey, the interview part of CEX is used in this paper and others.

The sample selection for the CEX data follows the standard approach in the literature. The primary criteria are that households must be in the sample for all four interviews, and they must have complete income responses.³⁴ It is necessary for households to be in the survey for all four quarters in order to get an accurate picture of their annual expenditures. The income data are necessary in order to match the CEX expenditures with the CPS data. The CEX tracks the income of husbands and wives separately. These data are combined, where applicable, to get a measure of total income for each household. The earnings categories are chosen to most closely match the earnings data available in the CPS.

In addition, households may begin their quarterly interviews at any month during the year, so it is important to take this timing into account when calculating households' annual expenditures. If a household is interviewed for at least two quarters in a given year $t$, then the reference year for their consumption is $t$, otherwise the reference year for their spending is $t-1$. This timing convention is consistent with the approach in Blundell et al. (2006).

Table A-1: Federal Compression

	90th Percentile Gross Inc.	90th Percentile Net Inc.	10th Percentile Gross Inc.	10th Percentile Net Inc.	Gross 90/10-Net 90/101
AK	102.7	69.9	19.1	15.6	18.6
AL	77.6	55.0	14.0	12.0	19.5
AR	70.2	50.6	13.7	11.8	17.9
AZ	80.4	56.6	14.7	12.5	19.0
CA	91.6	62.7	14.8	12.6	21.9
CO	89.5	61.6	16.4	13.5	17.8
CT	100.4	67.7	18.3	15.2	20.7
DC	76.6	52.8	15.5	13.0	20.1
DE	84.8	58.8	15.8	13.3	19.6
FL	79.8	55.9	14.3	12.1	19.0
GA	83.3	58.0	14.8	12.6	20.3
HA	87.2	60.3	15.6	13.0	18.8
IA	78.8	55.7	16.6	13.9	16.8
ID	74.8	53.6	14.6	12.6	18.1
IL	87.1	59.9	16.2	13.7	20.4
IN	79.3	55.8	16.2	13.7	18.1
KS	83.1	58.3	15.5	13.2	19.1
KY	78.4	55.4	14.1	12.3	21.0
LA	81.4	57.1	13.7	12.1	22.6
MA	94.8	64.4	18.0	15.0	20.0
MD	95.0	64.4	17.0	14.1	20.0
ME	74.9	53.3	16.2	13.6	16.8
MI	89.7	61.9	16.7	14.2	20.6
MN	90.4	62.2	17.4	14.4	18.1
MO	81.2	56.8	15.4	13.1	19.5
MS	72.7	52.2	12.7	11.1	20.2
MT	71.1	51.2	14.4	12.3	16.8
NC	79.9	56.1	14.6	12.4	19.0
ND	73.9	53.0	15.1	12.7	16.0
NE	78.7	55.5	15.9	13.2	16.5
NH	91.2	62.4	17.6	14.5	18.7
NJ	102.2	68.8	17.0	14.2	21.7
NM	74.5	52.8	13.5	11.7	20.3
NV	80.4	56.1	15.6	13.2	19.2
NY	87.3	60.0	15.6	13.2	20.9
OH	83.5	58.1	16.4	13.7	18.7
OK	79.4	55.6	14.3	12.2	19.8
OR	80.7	56.1	15.3	12.9	18.8
PA	82.7	57.6	16.3	13.7	18.8
RI	85.0	58.8	16.6	13.7	17.6
SC	79.4	55.9	14.5	12.4	19.9
SD	71.9	51.7	15.0	12.7	16.1
TN	76.2	53.8	14.6	12.6	20.2
TX	84.2	58.5	13.9	12.0	21.3
UT	78.9	56.1	16.1	13.5	16.9
VA	91.7	62.4	15.8	13.3	21.3
VT	77.5	54.7	16.3	13.5	15.9
WA	88.8	61.1	16.5	13.7	18.5
WI	81.1	56.9	16.5	13.8	17.5
WV	72.8	51.9	14.5	12.5	19.0
WY	80.3	56.4	15.8	13.3	17.9
Average	82.7	57.7	15.6	13.2	19.1

Source: Authors' calculations using CPS data; all income data values are in $1000s of 2000 dollars (first four columns). ¹ Percentage points.

Table A-2: State Compression

	90th Percentile Gross Inc.	90th Percentile Net Inc.	10th Percentile Gross Inc.	10th Percentile Net Inc.	Gross 90/10-Net 90/101
AK	102.7	103.0	19.1	19.1	0.1
AL	77.6	73.9	14.0	13.3	0.2
AR	70.2	65.9	13.7	13.0	1.4
AZ	80.4	76.9	14.7	14.2	0.8
CA	91.6	85.6	14.8	14.4	3.5
CO	89.5	85.0	16.4	15.8	1.8
CT	100.4	95.7	18.3	17.9	2.5
DC	76.6	69.7	15.5	14.9	5.9
DE	84.8	80.2	15.8	15.6	4.2
FL	79.8	78.8	14.3	13.8	-2.0
GA	83.3	78.5	14.8	14.4	3.3
HA	87.2	79.8	15.6	15.0	5.2
IA	78.8	74.0	16.6	16.2	3.5
ID	74.8	69.2	14.6	13.9	2.9
IL	87.1	83.0	16.2	15.3	-1.5
IN	79.3	75.8	16.2	15.3	-1.1
KS	83.1	78.4	15.5	14.9	1.8
KY	78.4	73.6	14.1	13.6	2.8
LA	81.4	78.1	13.7	13.1	-0.6
MA	94.8	89.2	18.0	17.1	0.7
MD	95.0	89.5	17.0	16.4	2.2
ME	74.9	70.0	16.2	15.8	4.5
MI	89.7	85.0	16.7	16.0	1.2
MN	90.4	83.7	17.4	16.9	4.6
MO	81.2	76.9	15.4	14.8	1.5
MS	72.7	68.6	12.7	11.9	-0.8
MT	71.1	67.6	14.4	14.3	3.8
NC	79.9	74.2	14.6	13.8	2.0
ND	73.9	71.5	15.1	14.6	0.3
NE	78.7	74.4	15.9	15.4	2.3
NH	91.2	91.0	17.6	17.6	-0.1
NJ	102.2	97.8	17.0	16.5	1.3
NM	74.5	70.6	13.5	13.0	1.5
NV	80.4	79.3	15.6	15.2	-1.5
NY	87.3	81.3	15.6	15.3	5.2
OH	83.5	79.2	16.4	15.7	1.3
OK	79.4	74.3	14.3	13.7	2.1
OR	80.7	74.4	15.3	15.0	6.1
PA	82.7	79.4	16.3	15.5	-0.9
RI	85.0	80.2	16.6	16.1	2.4
SC	79.4	74.2	14.5	13.8	1.9
SD	71.9	70.7	15.0	14.5	-1.8
TN	76.2	74.6	14.6	13.7	-3.9
TX	84.2	83.2	13.9	13.4	-2.6
UT	78.9	73.3	16.1	15.2	1.9
VA	91.7	85.9	15.8	15.1	1.7
VT	77.5	73.6	16.3	15.9	2.7
WA	88.8	87.5	16.5	16.1	-1.2
WI	81.1	75.4	16.5	16.0	4.3
WV	72.8	68.0	14.5	13.4	-1.0
WY	80.3	79.4	15.8	15.4	-1.5
Average	82.7	78.6	15.6	15.0	1.5

Source: Authors' calculations using CPS data; all income data values are in $1000s of 2000 dollars (first four columns). ¹ Percentage points.

Footnotes

* Contact author: Research Department, Federal Reserve Bank of Boston, [email protected] Return to Text

† Division of Research and Statistics, Federal Reserve Board, [email protected] Return to Text

‡ Division of Research and Statistics, Federal Reserve Board, [email protected]. A preliminary version of this paper was released as Federal Reserve Bank of Boston Public Policy Discussion Paper No. 11-7 (2011). The views expressed herein are those of the authors and do not indicate concurrence by other members of the research staff or principals of the Board of Governors or the Federal Reserve System. We thank David Agrawal for a helpful discussion of this paper and participants at the IIPF Congress for comments. We also thank Jim Sullivan for helpful comments on an earlier draft and thank Carl Nadler, Kevin Todd, Shoshana Schwartz, and Paul Eliason for excellent research assistance. We are also grateful to Adam Looney for providing state sales tax data, Erich Muehlegger for providing us with gas tax data, and to Chris Foote and Rich Ryan for help with STATA graphics. We take responsibility for any errors and omissions. Return to Text

1. This discussion draws heavily from Autor et al. (2008), which contains a review of the literature, recent evidence, and a discussion of the revisionist literature. The revisionist literature posits that the rise in wage inequality was an episodic event confined to the 1980s (see Card & DiNardo, 2002). See Smith (2011) for further evidence on polarization. Return to Text

2. There is also a literature on income inequality more broadly construed, focusing not just on labor income, but also on capital income and government transfer income (see Gottschalk & Smeeding, 2000). However, we largely confine our analysis to labor income. Return to Text

3. The gini coefficient can be interpreted relative to the Lorenz curve, which plots the percentage of total income held by a given percentage of the population. In particular, the gini coefficient equals two times the area between a 45-degree-line (perfect income equality) and the Lorenz curve. Return to Text

4. In most cases the tax unit is the household. Exceptions include children who are FTFY workers who are assumed to file their own tax returns. Return to Text

5. At the $10th$ percentile of the income distribution in our sample of FTFY workers, measured transfer income accounts for a bit more than 1 percent of total income. At the $90th$ percentile, measured capital income accounts for only 2 percent of total income. Return to Text

6. The $comp_{90/10}$ metric is related to the residual income progression measure of Musgrave & Thin (1948), defined as the ratio of the percentage difference in income after tax to the percentage difference in income before tax. The $comp_{90/10}$ metric takes the difference in (approximations of) these percentage changes, as opposed to their ratio. Return to Text

7. The $comp_{gini\text{ }}$index was used by Reynolds & Smolensky (1977) and is closely related to the progressivity index of Pechman & Okner (1974), defined as $\frac{gini_{after-tax}-gini_{before-tax}}{gini_{before-tax}}$. Return to Text

8. Overshifting may arise when firms have market power and engage in strategic behavior. When a tax is shifted onto consumers, demand for the good will fall. In some cases, firms will raise the price of the product by more than the tax in order to replace revenue lost to decreased demand (see Fullerton & Metcalf, 2005). Return to Text

9. The only evidence that we are aware of on the incidence of the federal gas tax suggests that consumers bear half of the tax (Chouinard & Perloff, 2004). Gas tax receipts are a very small fraction of overall federal tax collections, though, and have little effect on our conclusions. Return to Text

10. One view of property tax incidence suggests property taxes are not a tax at all, but instead are a payment for local public goods consumption within a Tiebout-style economy. Inman (1994) uses this logic to argue that the property tax is "irrelevant to matters of economic fairness and hence tax progressivity.'' Under this view, the tax would not properly be included in a study of the distributional consequences of taxation. Other views of the property tax, though, suggest it is a tax on capital. Return to Text

11. Some forms of capital income, such as capital gains, are not measured in most large, representative datasets. Return to Text

12. According to Gramlich et al. (1993), there are at least three ways in which taxes may influence the before-tax distribution of income. The first is supply-side adjustments such as labor supply changes and investment changes. The second is portfolio effects such as the timing of realizing accrued capital gains and shifts in the composition of compensation. The third is general equilibrium effects, which may alter the overall growth of the economy. Return to Text

13. Saez (2004) concludes that the bottom 99 percent of income earners display no evidence of a behavioral response to taxation. Similarly, Saez et al. (2010) note that the economics profession has settled on a value near zero for the compensated labor supply elasticity, suggesting little labor supply response to taxes. Saez (2010) finds no evidence of bunching at kink points in the tax schedule beyond the first income tax bracket, again suggesting no behavioral response to taxes through much of the income distribution. In terms of the tails of the distribution, Saez (2004) finds substantial evidence of behavioral responses for the top 1 percent of earners. Auerbach (1988) documents that capital gains, which accrue mostly to high-income individuals, are quite responsive to changes in marginal tax rates. Chetty & Saez (2005) document that dividend income, which "accrues very disproportionately to wealthy individuals,'' is also quite sensitive to tax changes. Saez (2010) finds evidence of bunching at kinks of the EITC and the first income tax bracket, indicating a behavioral response to taxes in the bottom tail of the income distribution. Finally, we acknowledge the implicit assumption that the non-personal income taxes we examine, such as the general sales tax, do not influence labor supply. Given the consensus in the literature that income taxes, which are directly applied to wage income, do not influence labor supply for our sample, we are comfortable with this assumption. Return to Text

14. The CPS also contains information on households' transfer receipts, including disability benefits, veterans benefits, welfare payments, unemployment compensation, social security, and supplemental security income. We include these data in our income measure, but do not analyze the effect of transfers on income inequality given our focus on wage inequality (see section 2.1). Return to Text

15. Full-time, full-year workers are those who work at least 35 hours a week for 40 or more weeks in a given year. Return to Text

16. Given that we restrict our sample to FTFY workers whose labor income comes from the private or government sector, business and farm income has little influence on our measure of total earnings. Return to Text

17. For the itemization imputation, each household's taxes are calculated twice by TAXSIM - once assuming the household itemizes and once assuming it does not. The personal income tax burden is the weighted average of these two measures with the weight equal to their implied probability of itemization. Return to Text

18. Other taxable items include tobacco, alcohol, personal care items (including grooming services), toys, flowers, paper goods, home furnishings, home appliances, vehicles, vehicle parts, medical supplies, books, recreation (including equipment), and jewelry. Return to Text

19. Data on state sales tax rates and sales tax exemptions come from the yearly State Tax Handbook, published by Commerce Clearing House, Inc. and the yearly Guide to Sales and Use Taxes, published by the Research Institute of America. Return to Text

20. The CEX expenditure data include sales taxes. As a result, the state sales tax rates are applied to the average expenditure data to back out households' before-tax expenditures. A household's sales tax burden is the difference between its total expenditures and its before-tax expenditures. Return to Text

21. Households are divided into five 10-year age groups and 10 income groups. Regional effects are included because households in Wyoming may have different driving needs than those in Rhode Island or Massachusetts. Return to Text

22. Erich Muehlegger kindly provided yearly data on federal and state gas tax rates per gallon as well as data on before-tax fuel costs (per gallon) by state. Return to Text

23. The $90th$ percentile of the income distribution is not subject to top-coding. Return to Text

24. To calculate the $comp_{90/10}$ metric, percentiles of gross and net income for each state are identified separately by year and then averaged. These state averages are used as inputs to calculate $comp_{90/10}$. Return to Text

25. The deductibility of state taxes on federal tax returns, which could reasonably be assigned to either the federal or state tax codes, is assigned to the federal code. Return to Text

26. As demonstrated in section 2.2, holding the parameters of a progressive tax system fixed, greater income inequality will produce greater tax induced income compression. This prediction holds in Panel A as the states with the greatest inequality (shown in red) have the greatest compression, while the states with the least inequality (shown in blue) have the least compression. The difference in compression, though, is quite minor. Return to Text

27. Federal gas taxes undo the progressivity of the tax system by an amount similar to state gas taxes. Since federal taxes are the same across all states, there is much less between-state variation due to these taxes, and we therefore focus on the effect of state gas taxes. Return to Text

28. Some states reduce, but do not eliminate, the sales tax on food and clothing. Our analysis captures these reductions. We do not, however, capture exemptions for items other than food and clothing (for example, books are sometimes exempt). Return to Text

29. The data shown in Figure 4 are in logs. As a result, adding the amount of federal compression and the amount of state compression will not equal total (net) compression (that is, $log(A-B) \neq log(A) - log(B)$). Return to Text

30. The increase in overall tax compression is also a function of the interaction of these two factors. Return to Text

31. We do not consider state corporate income taxes as they usually account for 5 percent or less of annual state tax collections. Return to Text

32. An alternative to the time-exposure approach is to estimate a CGE model (Fullerton & Rogers, 1993); (see Fullerton & Metcalf, 2005, for more discussion). However, Slemrod (1992) argues that the time-exposure approach is a reasonable compromise between annual estimates and computable general equilibrium (CGE) lifetime estimates and that, furthermore, they benefit from not requiring the heroic assumptions needed to operationalize CGE lifetime calculations. Return to Text

33. Data collection starts in the $2^{nd}$ interview and runs though the $5^{th}$ interview. The $1^{st}$ interview is used only to gather background information on the household. Return to Text

34. Income data are collected only in the $2^{nd}$ and $5^{th}$ interviews. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Home | Economic Research and Data | Accessibility | Contact us
Last update: March 12, 2012