The Federal Reserve's Portfolio and its Effects on Mortgage Markets
Keywords: QE1, QE2, Federal Reserve, MBS, mortgage, interest rates, mortgage rate
Abstract:
1 Introduction
On Tuesday, August 10, 2010, the Federal Reserve announced its second round of quantitative easing or QE2. In what would become the first phase of QE2, the Federal Open Market Committee (FOMC) decided to hold constant the Federal Reserve's portfolio holdings of securities by using the principle payments from agency debt and agency mortgage-backed securities holdings to purchase longer-term Treasury securities. The purpose of these asset purchases was to end the de facto tightening of credit that was occurring as the Federal Reserve portfolio was shrinking, thereby helping to offset a surprise slackening of economic growth during an already weak economic recovery.1
The second phase of QE2 began on November 
of the same year, when the FOMC announced it would purchase an additional $600 billion of longer-term Treasury securities by the end of
the second-quarter of 2011. As stated in the announcement, the purpose was: "To promote a stronger pace of recovery and to help ensure that inflation, over time, is at levels consistent with its mandate." QE2 ended on June 20, 2011. By then, the Federal Reserve's portfolio had expanded by $1.25
trillion.2
Over the course of QE2, the Federal Reserve purchased about $770 billion in Treasury securities. Even after the end of additional Treasury purchases, however, the Federal Reserve continued to reinvest MBS prepayments and maturing agency debt into Treasury securities.
QE2 followed QE1, where the Federal Reserve had surprised almost everyone in November 2008 when it announced that it would initiate a program to purchase substantial quantities of mortgage-backed securities (MBS) backed by the housing-related government-sponsored enterprises (GSEs), Fannie Mae and Freddie Mac, and backed by Ginnie Mae. The goal of the QE1 program was to "reduce the cost and increase the availability of credit for the purchase of houses."
QE2 was followed by a monetary action popularly referred to as "Operation Twist." In September, 2011, the FOMC decided to purchase $400 billion in longer maturity Treasury bonds to replace $400 billion in shorter-term Treasury securities.3 In addition, the FOMC decided to maintain the size of the Federal Reserve's MBS portfolio by reinvesting proceeds from the MBS portfolio into purchases of MBS. Both of these actions were designed to lengthen (or, in the case of MBS to maintain) the maturity of the Federal Reserve's portfolio and thereby place downward pressure on longer-term interest rates. Operation Twist was still in place at year-end 2011 (when we end our empirical analysis).
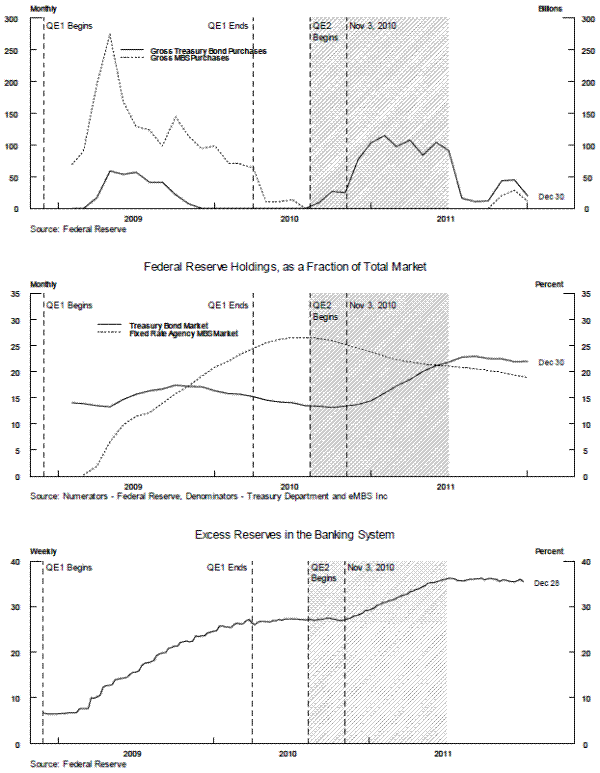
The Federal Reserve's purchases of agency MBS are shown in the top panel of figure 1 (the dotted black line). During QE2 (indicated by shading), these MBS purchases were allowed to runoff and were replaced with longer-term Treasury securities (the solid black line). In addition, after November 3, 2010, additional purchases of long-term Treasury securities were made. As shown by the black line in the top panel of figure 1, Federal Reserve purchases of Treasury bonds ran about $100 billion per month during the height of QE2.
In the middle panel of figure 1, the cumulative stock of Federal Reserve agency MBS purchases (shown by the dotted line) eventually amounted to about one-quarter of all outstanding fixed-rate agency MBS.4 This share of MBS had dropped to less than 20 percent by the year-end 2011. Also, by the end of QE2, Federal Reserve holdings of Treasury bonds also amounted to close to one-quarter of outstanding treasury securities (the solid black line). This share of outstanding Treasury bonds of had been maintained by year-end 2001. These asset purchases resulted in the accumulation of excess reserves in the banking system, which amounted to almost 40 percent of assets at large U.S. domestic banks (shown in the bottom panel).5
This paper is focused on two interrelated questions: "How does quantitative easing such as QE2 work?" and "What was its effect on mortgage rates?" Our earlier work established that QE1, which had been specifically targeted toward mortgages rates, had indeed been effective in mortgage rates.6 But QE2 and "Operation Twist" were not specifically oriented toward the mortgage markets. Moreover, financial market functioning during this time, albeit at times stressed, was not in the complete disarray that characterized such markets in the fall of 2008 Thus, QE2 had to work through normal market channels and did not simply create its effects by ending a financial panic.
Even without targeting mortgage markets, and even during times of normal financial market functioning, we argue that QE2 still had significant effects on such markets and likely resulted in lower mortgage rates. However, the transmission channels through which this effect was realized were quite complicated compared to the implementation and execution of the QE1 program.
Indeed, our work is unusual in that we attempt to directly empirically test various transmission channels of quantitative easing policies. To date, most other researchers have focused on event studies of Federal Reserve longer-term asset purchase policies (see, for example, Gagnon et.al. 2010 and Wright 2011).7 Event studies attempt to isolate the effects of a policy by defining a brief period during which market participants become informed about a Federal Reserve policy action and respond to it. For event studies, it is assumed that market participants can determine the future consequences of the policy action and that these consequences are quickly reflected in the prices for financial assets. In contrast, our approach assumes that information about the effects of new government programs is often, but not always, learned over time and as a consequence asset prices adjust more slowly.8
2 The Traditional Transmission Channels of Quantitative Easing
The Federal Reserve's longer-term asset purchase programs (QE1 and QE2) affected mortgage rates though three transmission channels: (1) improved market functioning in both primary and secondary mortgage markets, (2) clearer government backing for Fannie Mae and Freddie Mac, and (3) anticipation of portfolio rebalancing effects.9 The first channel reflects the signal to market participants that a large and reliable MBS purchaser would be available in the secondary market under all market conditions. The optimal combination of interest rate cuts and asset purchases in response to a financial crisis has been much discussed in the literature; a good analysis and summary is found in Freixas et. al (2011).
The second channel reflects the mitigation of concerns by investors about the effectiveness of the implicit government guarantee against credit risk that was offered by Fannie Mae and Freddie Mac after they were placed into conservatorship in September 2008. Both of these channels were crucial in the period during the announcement of QE1 and through these two channels the Federal Reserve substantially lowered mortgage rates.10
But with financial markets functioning normally, QE2 and "Operation Twist" had to work through a third transmission channel. Federal Reserve purchases of longer-term Treasuries were expected to have a portfolio rebalancing effect (sometimes referred to as a "stock effect"). The portfolio rebalance channel works as follows: (1) when the Federal Reserve purchases an asset, it reduces the amount of the security that the private sector holds, while simultaneously increasing the amount of short-term, risk-free, bank reserves held by the private sector, (2) in order to induce private sector investors to adjust their portfolios (i.e., reduce their holdings), the expected return on the asset must fall (i.e., the Federal Reserve purchases bid up the price of the asset and lower its yield).11 This adjustment by investors has two components: (1) a willingness to take less compensation for hedging the interest rate risks of financial assets or a "duration effect" that applies to both Treasury securities and MBS; and, (2) a willingness to take less compensation for hedging the prepayment and volatility risks associated with holding MBS.12 In designing QE2 and "Operation Twist," the Federal Reserve was quite aware of the duration effect and specifically targeted its purchases of Treasury securities toward those with a maturity of 4 to 7 years, so that it would withdraw more duration from the market.13
The portfolio rebalancing channel is generally described in terms of the pricing of financial assets, particularly in the secondary mortgage market. In the U.S. mortgage markets, however, there is a substantial disparity between rates in secondary mortgage markets (i.e., MBS yields) and rates paid by homeowners to purchase houses in the primary mortgage market. Primary mortgage market pricing is dominated by the top three or four mortgage originators, along with the government-sponsored enterprises, Fannie Mae and Freddie Mac. The complicated interactions among these institutions determine the primary mortgage rates for conventional mortgages (that is, mortgages other than those insured by the Federal Housing Administration (FHA). As a result, the portfolio rebalancing channel for monetary policy in the United States is influenced by institutional mortgage pricing.14
As a result, declines in the yield on MBS brought about by financial market investors rebalancing their portfolios may or may not be "passed-through" to the primary market mortgage rate. Part or all of such declines might be absorbed by the profits of mortgage originators, at least in the short-run. In addition, the distribution of excess reserves across the banking system also becomes important. As will be discussed in Section 3, excess reserves and their influence on banks' pricing of mortgages may have also played an instrumental role in the effect of the Federal Reserve's portfolio on mortgage rates.
The remainder of this paper is structured as follows: Section 3 models how longer-term asset purchases of the Federal Reserve and the excess reserves created in the banking system by these purchases might be an additional transmission channel that influences mortgage rates. Section 4 describes mortgage pricing practices by banks, and their interactions with Fannie Mae and Freddie Mac. Sections 6 and 7 presents our secondary market and primary market mortgage pricing models and our time-series estimates of the effects of the Federal Reserve's quantitative easing programs on mortgage rates. Section 8 describes and estimates our method for determining the relative importance of the monetary policy channels on mortgage rates. Section 9 provides the conclusion.
3 A Fourth Channel: Excess Reserves and Bank Balance Sheets
To understand the excess reserves transmission channel, it is important to understand that the response of a bank to an increase in excess reserves will depend on its capital position, the condition of bank funding markets, and the demand for loans.15 Importantly, injecting more excess reserves into the banking system may not necessarily result in more bank lending, which might potentially lower mortgage rates. Indeed, under most circumstances, the interest rate on a marginal loan is set equal to the marginal cost of funds (which may or may not be higher than the interest rate paid on the reserves) and the quantity of lending is determined independently of the quantity of reserves.16
That said, substantial holdings of excess reserves by the banking system might "crowd out" bank lending if banks are capital constrained. Just like with traditional monetary policy, this crowding out effect is what gives rise to the general impression that bank lending is encouraged by
increasing reserves in the banking system. If the marginal return on loans (
) exceeds the return on excess reserves (
), then each bank has an incentive to eliminate its reserves in favor of making more loans. Moreover, if regulatory capital requirements are binding and the cost of capital is high enough,
additional excess reserves can effectively impose a tax on the banking system because bankers are tying up capital for a low profit, or perhaps unprofitable, use. But while each individual bank may have an incentive to lessen its "tax," the banking system overall cannot avoid taxes.
We summarize these results with the equation:
 |
(1) |
where D denotes deposits and K denotes equity capital.
The marginal interest rate on loans is set equal to the weighted-average marginal cost of funding (where
is the capital risk-weight on the loan), which includes an implicit return to capital, 
, and an explicit deposit interest rate, 
, plus the marginal cost of additional balance-sheet capacity (where marginal cost of balance
sheet capacity is described by the function c). For banks with no capital constraints, c(D+K) should be constant and have little influence on the bank's propensity to hold assets. For banks facing a capital constraint, however, the incentive is to shed low yielding liquid assets and add
higher-yielding illiquid assets. Excess reserves have, in essence, added "too much" liquidity to some banks' balance sheets and these banks can create room on their balance sheets by selling Treasury securities and MBS. In addition, in order to maintain its return on equity, such banks are
motivated to seek out higher yielding loans. In this manner, excess reserves might "crowd out" low-yielding securities, but "crowd in" higher yielding loans. Do more excess reserves result in more lending in aggregate? The answer depends on loan demand and on how c(D+K) varies across banks.
For mortgages in particular, the structure of the marginal cost of balance sheet capacity, c(D+K), is also influenced by several other factors. First, mortgages have the lowest regulatory risk-weight among different types of whole loans to households. And MBS issued by Fannie Mae and Freddie Mac have an even lower risk-weight. Second, there is substantial concentration among mortgage originators and mortgage holders. The four largest U.S. banks generally originate about 60 percent of all mortgage loans and finance almost all conventional mortgages not securitized by the GSEs. The market structure of the U.S. mortgage markets suggests that mortgage origination may have substantial economies of scale or that mortgage rates may be influenced by the pricing practices of the large originators, or both. Finally, mortgage markets provide numerous outlets for hedging the risks associated with holding mortgages. Any comparison of return on excess reserves to returns on holding mortgages or returns on holding MBS has to account for the costs of hedging these risks.
Thus, the overall effect of adding reserves into the banking system on mortgage lending (which may then affect mortgage rates) becomes an empirical question. Capital constraints among banks raise the possibility that excess reserves result in a crowding out of lending. However, in a dynamic setting, the cost of excess reserves may provide a strong incentive to substitute higher yielding loans and securities for low yielding reserves, perhaps even creating pressures on banks to chase poor quality loans or to engage in "excess competition" for loans. Depending on the prevalence of capital constraints and on how excess reserves become distributed (or redistributed) among banking system participants, the effects of the marginal cost of balance sheet capacity, c(D+K), on mortgage rates may be zero, positive, or negative.
4 The Determination of Conventional Mortgage Rates Offered by Banks
We use empirical pricing models for MBS yields in the secondary mortgage market and for mortgage rates paid by homeowners in the primary mortgage market to measure the relative importance of the transmission channels described above. We discussed the first two channels, improved market functioning and clearer government backing, at length in our earlier paper on QE1. There, we estimated that the announcement of the Federal Reserve's MBS purchase program resulted in lower mortgage rates of about 100 basis points for purchasing houses. About half of this decline resulted from the anticipation of portfolio rebalancing. The other half resulted from improved market functioning, and perhaps mainly from investors' perceptions of clearer government backing for Fannie Mae and Freddie Mac.
Here, we focus on QE2 and the third and fourth channels of influence for quantitative easing -- the portfolio rebalancing and bank balance sheet channels described above. Before describing our empirical technique, some background about the institutional structure of the U.S. mortgage market is needed.
Most mortgages in the United States are 30-year, fixed rate mortgages. Banks typically originate and then hold many fixed-rate and non-jumbo mortgages in their portfolios. For example, among all mortgages originated since 2008 and held in banks portfolios, 77 percent were fixed-rate non-jumbo mortgages. Almost all of these fixed-rate mortgages held in bank portfolios could potentially be sold either to Fannie Mae, Freddie Mac or Ginnie Mae for securitization. The remaining mortgages held in bank portfolios were either a jumbo fixed-rate mortgage (5 percent), a jumbo adjustable-rate mortgage (9 percent), or a non-jumbo adjustable-rate mortgage (9 percent).17
Banks also have large holdings of MBS backed by Fannie Mae, Freddie Mac, or Ginnie Mae. At year-end 2011, banks held about $1.1 trillion of such MBS, along with $1.5 trillion in mortgages. As described below, most of these MBS have been acquired by swapping originated (non-jumbo) mortgages for such securities.
Prepayment Options. When a homeowner finances a home with a 30-year fixed-rate conforming mortgage, the borrower receives the option to prepay the mortgage at any time. The option is implicitly paid for with an upward adjustment in the mortgage rate relative to the rate that would be charged on a mortgage without the prepayment option. Therefore, the provider of the mortgage has to estimate how much to increase the mortgage rate over its cost of funds to cover the expected costs associated with this prepay option. The valuation of the prepay option entails estimating how quickly the homeowner is likely to prepay the mortgage.
The US secondary market is primarily focused on the hedging of the risks associated with 30-year fixed rate mortgages that do not allow the lender to charge directly for the option prepay the mortgage early. Suppose a mortgage is incorporated into an agency MBS. The holder of the MBS has no credit risk (because the MBS is guaranteed by Fannie Mae, Freddie Mac or Ginnie Mae), but still must manage interest rate risk and prepayment risk associated with holding MBS. In the event that the homeowner prepays the mortgage, the resulting cash payment is sent to the holders of the agency MBS on a pro-rata basis. Although the holders of the MBS are uncertain about when such a pre-payment will be received, the prepayment is more likely when mortgage rates become lower than the original rate.
Credit and Interest Rate Risks. When a bank (or other type of entity) originates a mortgage that is eligible for GSE securitization, it must decide whether to (1) bear the credit risk of the mortgage itself (i.e., hold the mortgage in its own portfolio) or (2) have a GSE guarantee the mortgage by converting the mortgage into MBS. If a bank converts its mortgage into GSE MBS, it is still funded by the same liability structure as the mortgage, which consists mainly of FDIC insured deposits, Federal Home Loan Bank advances, and an imputed cost to equity. Moreover, since a bank's liabilities have a much shorter expected maturity relative to the expected life of a mortgage loan, a bank, as well as most other MBS investors, almost always incurs significant costs when hedging against the interest rate and prepayment risks associated with mortgages and MBS.
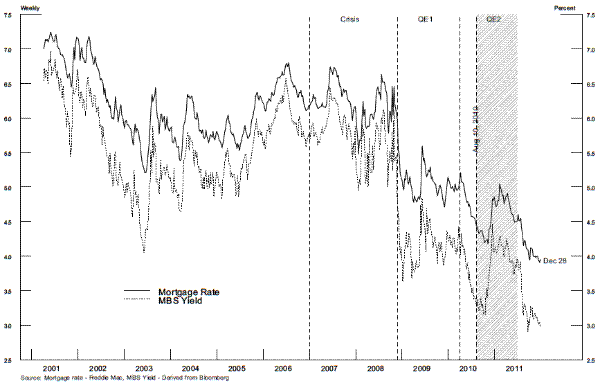
Primary Mortgage Rates. As shown in figure 2, both MBS yields and mortgage rates were pushed down by QE1 and have remained relatively low since then when compared to levels that were observed prior to the financial crisis. To actually influence the primary conforming
mortgage rate directly (the mortgage rate that applies to mortgages eligible for GSE purchase), the Federal Reserve had to change the economic calculations associated with the mortgage originator's two decisions. The first decision faced by a bank, which usually originates the mortgage, is made by
comparing the mortgage rate to the costs outlined above. Expanding on equation (1) and making it specific for a mortgage loan, the marginal profit condition for holding the mortgage on a bank's balance sheet equates the mortgage rate,
to these marginal costs or:
 |
(2) |
Equation (2) equates the marginal revenue of holding a mortgage on the balance sheet to the marginal costs, where 
represents the bank's costs associated
with hedging the interest rate and prepayment risks associated with the mortgage and cr is the credit risk borne by the bank, including the costs of handling delinquencies and foreclosures.
Once the mortgage is originated, the bank's second decision is whether or not to exchange the mortgage for an MBS created by Fannie Mae or Freddie Mac.18
Here, the marginal profitability of holding the MBS on the bank's balance sheet equates the MBS yield, denoted 
, to marginal costs. These marginal costs are similar to those associated
with holding the mortgage directly, or:
 |
(3) |
The marginal profitability of converting the mortgage to a GSE MBS includes 
which is the market's costs of hedging the interest rate risks associated
with the mortgage-backed security, and g, which is the GSE guarantee fee. Note that the amount of equity behind the financing of the mortgage can vary across the two options, depending on regulatory requirements and market practices.
We can derive the primary-secondary market mortgage spread from equations (2) and (3) above:
 |
(4) |
Since the bank is able to fund either the mortgage or the MBS--and banks often hold large amounts of both--the hedging costs and the marginal balance sheet costs are one in the same. We can rewrite equation (4) as:
 |
(5) |
In words, the mortgage rate is modeled as a mark-up over the MBS yield. This mark-up represents an equity risk premium,
multiplied by the difference between mortgage and MBS capital risk-weights,
, and the difference between the bank's marginal costs of managing credit risks (including all the costs associated with origination, servicing and managing the
credits risk of mortgages, along with market concentration effects) and the GSE guarantee fee, which reflects similar costs. This difference is denoted 
. The MBS yield captures the
costs of hedging the interest rate and prepayment risks associated with both the mortgage and the MBS, and thus these costs do not appear independently in this equation..
5 An Empirical Model of MBS Yields and Mortgage Rate Determination
MBS Yields
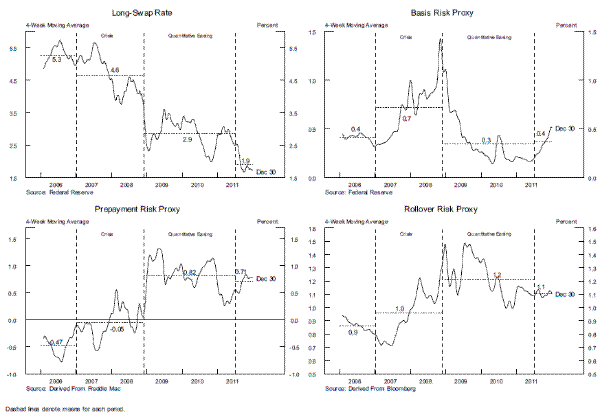
Both mortgage rates and MBS yields must compensate investors for their funding costs, hedging costs, prepayment risks, and other marginal costs. To utilize the marginal profitability conditions outlined above in an empirical analysis, measures of hedging costs and credit risks are needed. For hedging costs, private investors in MBS often purchase an interest rate swap, for which they pay the fixed-portion of the swap and receive the short-term variable payment; almost always a payment based on the three-month Libor rate. This interest rate swap removes the interest rate risk associated with holding MBS if the holder is funded by short-term (three-month) liabilities. We average across the five-year and ten-year swap rates to approximate these average costs of hedging MBS. Durations for MBS are notoriously difficult to calculate, but averaging the five-year and ten-year swap rate is a common industry practice for approximating the relevant swap yield because hedges are usually built using these maturities, which have far greater liquidity than other swaps with different maturities. The time-series history of long-term swap rates is provided in the upper-left panel of figure 3. Strikingly, during the period of the Federal Reserve's long-term asset purchase programs, these swap rates fell to historically low levels.
Using a long-term swap to hedge mortgage interest rate risk would still leave the holder of the MBS with a significant maturity mismatch and some basis risk if their underlying funding structure is not similar to three-month Libor.19 Banks typically have a fairly short maturity of liabilities (e.g., one or two years). Our representative bank is modeled as using a swap to convert its three-month Libor payment for an average yield on one-year and two-year Treasury securities in order to help match the effective maturity of its liabilities. Because the bank would still likely continue to have basis risk (since its liability structure would probably be more sensitive to Treasury rates than to the average swap rates), we also include the spread between the short-term swap rate and the Treasury rate in the regression as a proxy for the cost of this basis risk. As shown in the upper-right figure 3, our proxy for basis risk increased significantly during the crisis, but fell to relatively low levels after the Federal Reserve's intervention in the MBS market and remained low during QE2. During "Operation Twist," our basis risk proxy has shown an upward trend because the Treasury yield curve remained flatt while the the swap yield curve drifted upward.
After engaging in these two swap transactions, the holder of the MBS is left with a portfolio asset that has roughly a one and one-half year Treasury yield over the life of the mortgage. However, this yield may disappear if the homeowner prepays or if swap markets become illiquid. Usually, an estimate of the cost of the prepay option is a model-based estimate of the fair value of selling the option to the homeowner. It reflects the cost to the investor of either being forced into a low-yielding asset during a period of low interest rates, or the risk of carrying unhedged interest rate risk, if interest rates rise and the mortgage is outstanding longer than expected (so-called extension risk).
The valuation of the prepay options of homeowners is difficult and complex even in normal circumstances. Since the financial crisis, prepayment models have become even less reliable. Given that even the best prepayment option models often could not reliably gauge prepayment risk over our estimation periods, we use a simple measure--the difference of the mortgage rate averaged over the past three years and the current mortgage rate. This measure reflects the risk that the stream of MBS payments is terminated either sooner than expected because of a relatively low mortgage rate environment, or later than expected because of a relatively high mortgage rate environment than was expected.
Like more sophisticated models of prepayment risk, this measure indicates that such risks were high during the period of the Federal Reserve's intervention (shown in the lower-left panel of figure 3), even though the actual refinancing rate of mortgages was very low compared to the past. In fact, the level of actual prepayments was low relative to the historical level associated with low mortgage rates because (1) many households had home values that had fallen near (or even below) their outstanding mortgage value (i.e., their mortgages were "under water"), (2) the credit quality of many households had deteriorated, (3) mortgage originators implemented tighter credit standards after the financial crisis, and (4) the costs associated with refinancing a mortgage had become much higher.20
Lastly, we account for the "rollover risk" that is associated with the shorter-term swap in our MBS yield specification. We use the volatility (measured by the 90 percent confidence interval) of the forward swap rates implied by swaptions between two and ten years to proxy for rollover risk during the life of the mortgage that results from financial market disruptions, credit downgrades, and other unanticipated events.21 As shown in lower-right panel of figure 3, this measure of rollover risk follows the expected pattern; falling during the period prior to the financial crisis, rising sharply during the crisis, and then declining somewhat during the course of the Federal Reserve's long-term asset purchases.
Using the hedging strategy described above, we can estimate as:
 |
(6) |
By setting marginal revenues equal to marginal costs, an MBS yield regression can be written as:
 |
 |
|
 |
(7) |
where 
is the residual.
The bank's cost of funds is likely correlated with shorter-term Treasury rates, which is why the bank engages in the hedging strategy described above. Bank liability structures are relatively short and are generally assumed to have around a one-to-two-year maturity. The deposit rate moves very imperfectly with the Treasury rates because of convenience and branch services provided to depositors. Expected equity returns might also move imperfectly with Treasury rate because of a time-varying equity risk premium. Thus, the GSE guarantee fee, the sticky aspect of deposit rates, for residual risks related to balance sheet costs, and slow-moving adjustments of an equity premium reflecting the returns to banking will be subsumed into intercept of an estimated regression based on this equation.
When estimating equation (6), we would also expect the coefficient on the swap rate to be positive and to reflect the hedging strategies undertaken by banks. In contrast, the coefficient on our measure of basis risk, measured by a short-term swap-to-Treasury spread, could have been either positive or negative since it depends on (1) the liability structure of the banks that finance the mortgages, and (2) the supply and demand conditions in both the swap and Treasury markets, which are not possible to measure directly with available data.
Prepayment risks and rollover risks, which were proxied using the uncertainties involved with extending two-year swaps into the future, are both expected to add to the costs of holding MBS and thus would be expected to have positive coefficients. As for the coefficient on the two-year Treasury rate, it reflects a myriad of factors, but also would be expected to be positive as it proxies for financing the bank's assets. The two-year Treasury yield is related to the maturity structure of the financing available (e.g. deposits) to the bank. It also includes the costs of capital for using an uncertain hedging strategy to create a short-term risk-free instrument funded by despoits and other bank liabilities, which is supposedly matched to the .life of the mortgage (but rarely is).
Mortgage Rates
As outlined by equation 5, mortgage rates are determined by the marginal costs of banks when funding and managing the risks associated with the mortgage, which can be written as a mark-up over the MBS yield. Since the bank originates the mortgage and then compares the marginal cost of holding a mortgage to the marginal cost of holding an MBS, it is directly examining the difference between these two marginal profitability conditions.
A key part of this difference is the Fannie Mae and Freddie Mac guarantee fee. The GSEs move their guarantee fees slowly and with long pre-announcement periods. As a result, the bulk of the mark-up over MBS yields reflects bank's credit risks and the costs associated with servicing mortgages.
These credit risks and servicing costs are proxied using the following factors: (1) the level of unemployment, (2) an index of credit-default spreads (REIT CDS) of investment-grade real-estate investment trusts (REITs), which reflects forward-looking expectations about housing markets, including
house prices and equity premiums, (3) the credit rating distribution, or FICO scores, of homebuyers and (4) the MBA refinancing index. We expect that higher unemployment and higher REIT CDS spreads would be associated with higher credit risks. In contrast, higher FICO scores for homebuyers are
expected to be associated with lower credit risks (our measure of tightness for underwriting is the FICO score of mortgage borrowers at the 
percentile of the mortgage borrowers' FICO
distribution). As for the coefficient on the MBS refinancing index, a higher level of mortgage refinancing would raise mortgage origination costs if capacity was limited, putting upward pressure on the mortgage rate. Other factors that influence credit risks, such as inflation and home prices, are
only captured in this model to the extent that they are components of the four factors listed above. Of course, there are strong correlations with these four factors and other macroeconomic variables, but we keep the model parsimonious so the regression results can be more clearly interpreted.
Finally, we assume the return to the additional increment of capital needed to hold a mortgage and manage its credit risk (relative to the alterative of swapping the mortgage for an MBS that is held on a bank's balance sheet) affects the intercept. That is, the intercept in the mortgage rate regression would represent any persistence in the additional equity premium demanded by bank investors in the costs of managing credit risks beyond the GSEs' pricing of such risks (which are embedded in the MBS yield) as well as possibly other factors, such as any persistence in the mark-up in mortgage rates over MBS yields because of market concentration. As mentioned above, note the MBS yield also already reflects the financing and hedging costs of the bank.
Thus, our mortgage rate .regression equation (as derived from equation (5)) can be rewritten as:
 |
(8) |
where the coefficient on the MBS yield would be expected to be close to one, and 
is the residual.22
6 An Empirical Analysis
We employ time series regressions to examine the determinants of MBS yields and mortgage rates, and the possible effect of QE2 on such yields and rates. We estimate our models over the period from July 2000 to July 2007, with the beginning of the period reflecting the availability of data and the end of the period reflecting a time before the financial crisis is underway. The crisis period began with a seizing-up of the intra-bank market in August 2007, which signaled the widespread contagion of the financial crisis (Swagel 2009). The data during the seven-year period prior to the start of the crisis provides the basis for our benchmark regressions.
Both the MBS yield and mortgage rate regressions are cointegrated. We use the fully-modified ordinary least squares (FMOLS) regression technique provided in EViews (2009) with a constant in the cointegrating equation.23 The properties of these estimators are described in Hansen and Phillips (1990) and Phillips (1995). The Phillips-Ouliaris (1990) test is used to establish that the residuals of our regressions are stationary. The strong cointegration of these variables is consistent with our view that the regressions represent pricing relationships used by market participants to determine MBS yields and mortgage rates.
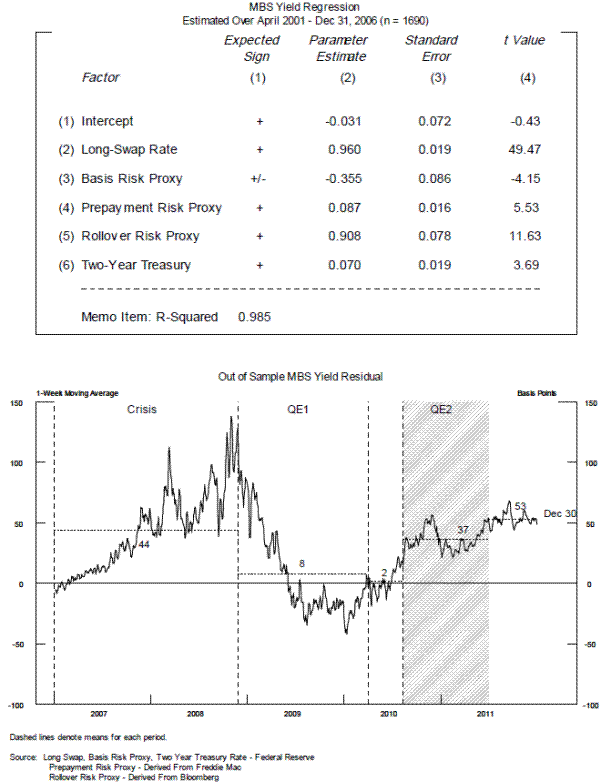
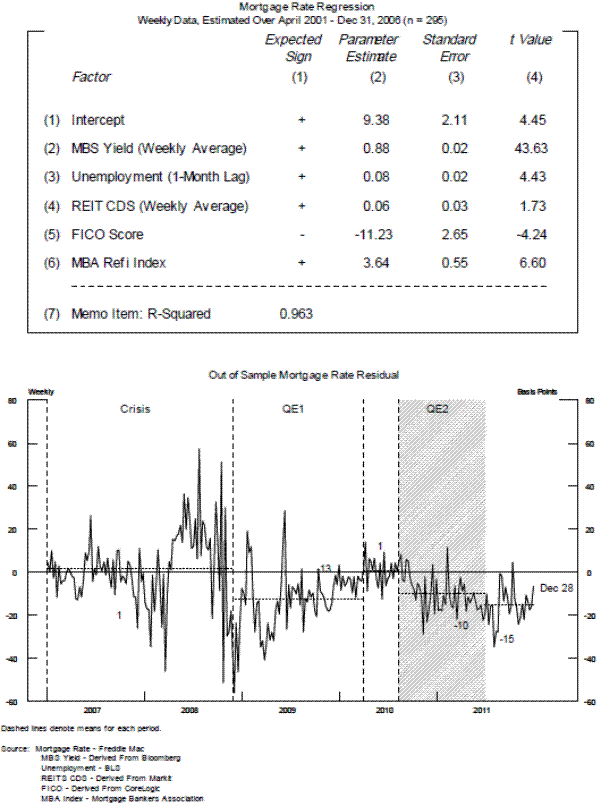
The results for our MBS yield regression are given in the top panel of figure 4. The signs of the coefficient estimates are consistent with the theory outlined above. In particular, note that coefficient on the long swap rate is close to one. MBS yields and swaps rates are very closely linked, because almost all MBS traders and holders use swaps to hedge MBS and because long-term swaps are an alternative, yet similar, investment to MBS.
To consider the effects of the financial crisis and of the Federal Reserve's interventions, we examine the out-of-sample fit of the regressions estimated. As shown in the bottom panel of figure 4, the out-of-sample residuals for the MBS yields suggest that actual yields were higher than expected yields during the crisis, fell significantly lower than expected (i.e. were negative) during QE1,24 and once again averaged higher than expected (i.e., were positive) over the course of QE2 and "Operation Twist."
We follow a similar procedure for the mortgage rate analysis. Our coefficient estimates for the mortgage rate regression are given in the top panel of figure 5. The coefficients have the expected signs, and all but one is significant at the 95 percent confidence interval, although the coefficient on the MBS yield is significantly less than one. On average, mortgage rates were persistently somewhat below expectations during most of the time MBS purchase programs were in place.
7 The Effects of the Federal Reserve's Asset Purchase Programs
The Federal Reserve's MBS purchases are designed to put downward pressure on the MBS yield. As the MBS yield falls, the declines are passed through to the mortgage rate, as described above and estimated in Figure 5. But the Federal Reserve's purchases did not begin until after the onset of the financial crisis, and thus we have to improvise to account for their influence in our MBS yield and mortgage pricing models.
We observe that the residuals from our MBS yield regression can be decomposed into four factors: (1) the effects of withdrawing supply from securities markets, (2) the effects of adding excess reserves to the banking system on balance sheet costs (which may be different for MBS yields than for mortgage rates), (3) shifts in the coefficients of the factors used in the original regressions because of structural changes in mortgage markets such as the reduction in the number of providers, and (4) other factors that were also not present during our estimation period. More formally, we estimate the regression:
 |
(9) |
where 
is a function of the share of particular securities held by the Federal Reserve, J(
) is a function of the marginal cost to the bank from adding additional reserves,
represents the shifts in the coefficients after the financial crisis, 
are other persistent factors that we cannot measure during our benchmark period (such as the potential contagion from the European debt crisis on U.S. financial markets), and 
is the residual.
From the portfolio rebalancing theory described earlier, we would expect that a higher share of Federal Reserve ownership would withdraw supply from the market, causing the security price to rise and the observed yield to fall. For longer-term securities, this story is often told in terms of duration: If the Federal Reserve withdraws duration from the market, the private sector's aggregated need for hedging falls and aggregate interest rate hedging costs that are one important component of longer-term yields fall commensurately.
Also, as described earlier, the marginal cost of adding reserves can be zero, positive or negative. This marginal cost is zero if the bank is not capital constrained; it is positive if the bank is capital constrained and has no higher yielding assets that it can substitute for lower yielding assets; and it is negative if the bank is capital constrained but can successfully shed lower-yielding (generally more liquid) assets for higher yielding (generally less liquid) assets.
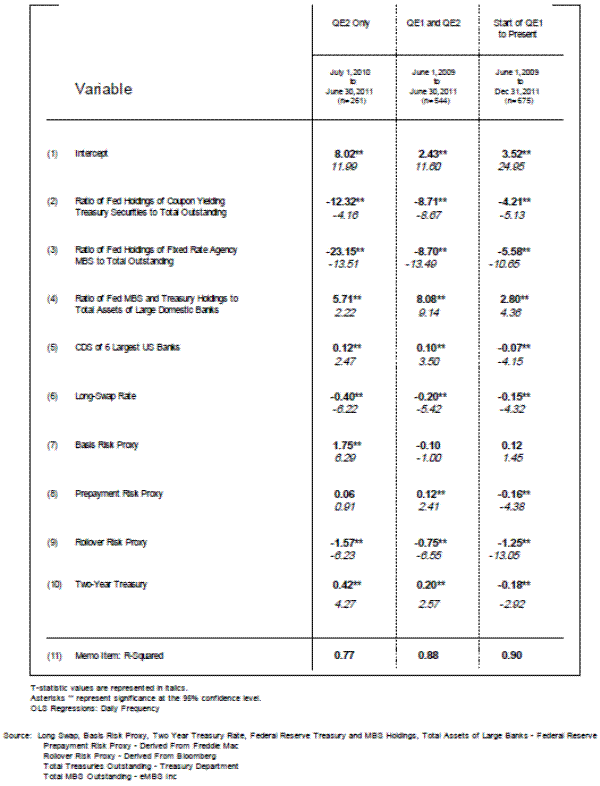
For both the QE2 period by itself and the QE1 and QE2 periods together, we estimate the effects of the Federal Reserve's purchases using our MBS yield regression residuals as the dependent variable.25 As independent variables, we use the Federal Reserve's share of Treasury bonds outstanding, the Federal Reserve's share of MBS outstanding, and the sum of the Federal Reserve's Treasury bonds and MBS holdings divided by the assets held by the largest domestic US banks. The first two independent variables measure the possible effects of withdrawing (or adding) duration to the fixed-income markets, while the third independent variable is a close proxy of the proportion of excess reserves held by the banks that dominate the banking system.
We use OLS to obtain regression estimates since the residuals from the previous MBS yield regression are I(0). The coefficients and t-statistics for three MBS yield residual regression specifications are presented in figure 6. The policy variables--the ratios of Federal Reserve Treasury holdings to the stock of Treasury securities, the ratio of Federal Reserve MBS purchases to the stock of MBS securities, and the proxy for reserve holdings by large banks--are I(2). By design, they embed some serial correlation over these short time periods because the Federal Reserve methodically purchased a roughly similar amount of securities each week while implementing the QE1 and QE2 programs. All the other variables in these regressions are a mix of I(0) and I(1) variables over these short horizons, and the residuals of these residual regressions are I(0),.
Looking at either the QE2 period by itself, or the QE1 and QE2 periods together, an increase in the share of Federal Reserve holdings of Treasury bond and MBS seems to put downward pressure on MBS yields relative to their expected level (figure 6, lines 2 and 3, columns 1 and 2). This finding is consistent with the portfolio rebalancing view. But note that the Federal Reserve's share of MBS was falling during QE2 (figure 1); thus, the effect on MBS yields from increases in Federal Reserve holdings of Treasury bonds was being offset by the decline in MBS holdings. Since the Federal Reserve held a sizeable portfolio of Treasury and MBS securities even after QE2, we also estimate a residual regression over the entire post-crisis period. The results are somewhat the same for all three regressions (compare results in columns 1 or 2 with results in column 3).
Our empirical results also suggest that adding more reserves to the banking system seems to place upward pressure on MBS yields relative to expected levels (figure 6, line 4). This result is consistent with the view that banks were capital constrained and, in response to holding more reserves, sold low yielding assets such as GSE MBS. Taken literally, our results would suggest that this pressure to lend from excess reserves and capital constraints caused the largest banks to sell enough longer-term MBS and Treasury securities to offset some of the effects of the Federal Reserve's buying of Treasury bonds on MBS yields. As mentioned earlier, excess reserves might be, in essence, reshuffled in the banking system so they are held by banks that are not capital constrained or by banks that need liquidity.26 But, of course, if loan demand is weak across the country, then the extent of this reshuffling may be limited.
We include the CDS premiums of the 6 largest U.S. banks in the equation to capture the contagion effects of the ongoing European sovereign debt crisis over these time periods, particularly during QE2. The coefficient on these CDS premiums (line 5) may suggest that there was some slight upward pressure on MBS yields. Finally, note that there seems to have been some shifts in the estimated coefficient values of our MBS yield regression after the crisis, as many of the coefficient estimates are significantly different from zero, indicating that the coefficient estimate has shifted from the earlier period (rows 5 through 10 on figure 6--a significant positive coefficient indicates that the coefficient is much larger than the earlier estimate) Given the short periods of estimation, it is difficult to know if these large shifts represent responses to the financial crisis or to short-run (and complicated) time series dynamics.
To give a sense of the magnitudes of these various effects of Federal Reserve actions on MBS yields, we use the coefficient point estimates from the residual regressions and estimate the effect a Federal Reserve purchase of $100 billion MBS. Using the values of the variables at year-end 2011, such a purchase would have increased the ratio of Federal Reserve holdings to the outstanding stock of MBS by slightly more than two-tenths of one percentage point. For ease of presentation, we assume that the Federal Reserve's ratio of Treasury bond holdings to the outstanding stock of MBS is unchanged
An increase in the Federal Reserve's MBS holdings has two effects. First, the additional Federal Reserve MBS holdings results in a lower the MBS yield because the Federal Reserve's increased demand for MBS pushes up prices. Second, the additional excess reserves in the banking system create some offsetting downward pressure on the MBS prices. We focus on the coefficient estimates for the entire period the Federal Reserve has held substantial amounts of MBS (column 3, figure 6). Employing these estimates, a $100 billion increase in MBS holdings would result in MBS yields falling about 5.6 basis points. Assuming a long-run pass-through rate of 88 percent (from the mortgage rate regression in figure 5), the effect on mortgage rates would be a little smaller, around 5 basis points. Note that any additional effects on Treasury rates, or any indirect effects on long-swap rates, would lead to even higher estimates for decline in the mortgage rate. Also note that our coefficient estimates for only the QE2 period would suggest that the decline would be almost four times larger, perhaps indicating that the effect is bigger over shorter time horizons and while a purchase program is ongoing. Regardless, our findings suggest that it takes a sizeable purchase by the Federal Reserve to move the mortgage rate down by a noticeable amount (unless perhaps financial markets are in disarray, as was the case in November 2008 and as discussed in Hancock and Passmore, 2011).
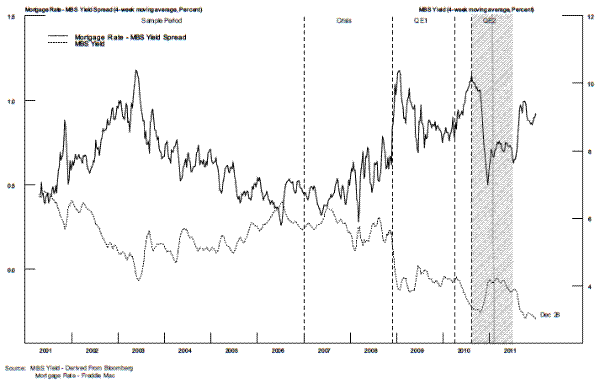
Moreover, the dynamics of mortgage pricing appear to make it more difficult to pass-through changes in MBS yields to mortgage rates during times when mortgage rates are low. As shown in figure 7, the spread between mortgage rates and MBS yields is significantly larger when MBS yields are low. This empirical regularity of the mortgage market suggests that efforts to push down mortgage rates quickly by lowering MBS yields through the portfolio rebalancing channel require even larger MBS purchases when mortgage rates are already low.27
The calculated effects outlined above provide evidence that Federal Reserve MBS purchases do place downward pressure on mortgage rates; however the uncertainty in these calculations is large. Moreover, these calculations assume all other things were held constant. But, of course, during the actual implementation of QE1 and QE2, little was actually held constant, as one might expect during times of financial stress. Indeed, the different size of the effects of Federal Reserve MBS purchases (during QE1) versus the effects of Federal Reserve run-offs of MBS (during QE2) suggests that the effects of changes in Federal Reserve MBS holdings may (1) not be the same during all time periods, (2) be highly dependent on market conditions, and (3) differ substantially over a short-horizon compared with a longer-horizon. Moreover, our results suggest that Federal Reserve Treasury purchases and Federal Reserve MBS purchases may have dramatically different effects. Better data and more research are needed to adequately capture the short-term supply and demand dynamics of the MBS markets and their linkages to primary mortgage rates.
8 Conclusion
We provide an empirical analysis of the effects of the Federal Reserve's asset purchases on MBS yields and mortgage rates during both the second round of quantitative easing, commonly referred to as QE2, as well as during the longer period over which there has been substantial holdings of longer-term securities by the Federal Reserve. Assessing the effects of these portfolio holdings is difficult because they operate through both a "portfolio rebalancing" channel and an "excess reserves" channel, which at times may work in opposite directions. Moreover, QE2 in particular consisted of both an expansion of the Federal Reserve's Treasury bond portfolio and a contraction of its MBS portfolio, which again created effects on MBS yields that offset each other somewhat. Finally, understanding the particulars of the U.S. mortgage markets related to hedging and managing risks, as well as the sometimes loose link between the secondary and primary mortgage markets, are important in estimating how Federal Reserve purchases might have influenced mortgage rates. Overall, we find evidence that the Federal Reserve's MBS purchase program operated through both a "portfolio rebalancing channel" and an "excess reserves" channel. The magnitudes of these effects were very difficult to estimate, but overall the larger Federal Reserve holdings of MBS and Treasury securities seem to have pushed down MBS yields and, as a result, lowered mortgage rates somewhat.
9 References
Bernanke, Ben S., 2009, "The Crisis and the Policy Response," Remarks at the Stamp Lecture, London School of Economics (London, England), January 13 (available at http:/www.federalreserve.go/newsevents/speech/bernanke20090113a.htm).
Bernanke, Ben S. and Vincent R. Reinhart, 2004, "Conducting Monetary Policy at Very Low Short-term Interest Rates," American Economic Review, vol. 94, no. 2, pp. 85-90, May.
Bernanke, Ben S., 2011a, "The Economic Outlook and Macroeconomic Policy," Speech given at the National Press Club, Washington, D.C., February 3.
Bernanke, Ben. S., 2011b, "Semiannual Monetary Policy Report to the Congress," Before the Committee on Banking, Housing, and Urban Affairs, U.S. Senate (Washington, D.C.), March 1
Bernanke, Ben S., 2012, "Housing Markets in Transition," Speech given at the National Association of Homebuilders International Builders Show, Orlando, Florida, February 10.
Berry, Kate, 2012, "Bank of America Says it Can't Process all Refinance Applications," American Banker, February 8.
Benford, J., S. Berry, K. Nikolov, and C. Young, 2009, "Quantitative Easing," Quarterly Bulletin, Bank of England, Q2, pp. 90-100.
Board of Governors of the Federal Reserve System, 2008, Monetary Policy Releases, November 25 (available at http://www.federalreserve.gov/newsevents/press/monetary/20081125b.htm).
Board of Governors of the Federal Reserve, 2010, Monetary Policy Releases, August 10, (available at http://www.federalreserve.gov/newsevents/press/monetary/20100810a.htm).
D'Amico, Stefania and Thomas B. King, 2010, "Flow and Stock Effects of Large-Scale Treasury Purchases," Federal Reserve Board, Finance and Economics Discussion Series (FEDS) working paper, no. 2010-52.
Fuster, Andreas and Paul Willen, 2010, "$1.25 Trillion is Still Real Money: Some Facts about the Effects of the Fed's Mortgage Market Investments," Federal Reserve Bank of Boston Public Policy Discussion Papers, No. 10-4, November 18.
EViews, 2009, User's Guide II, (Irvine CA), Quantitative Micro Software, pp. 219-247.
Freixas, Xavier. Antoine Martin and David Skeie, 2011, "Bank Liquidity, Interbank Markets,and Monetary Policy," Review of Financial Studies, vol. 24, no. 8, pp. 2656-2692,
Gagnon, Joseph, Matthew Raskin, Julie Remache and Brian Sack, 2010, "Large Scale Asset Purchases by the Federal Reserve: Did They Work?" Federal Reserve Bank of New York Staff Reports, no. 441, March.
Hancock, Diana and Wayne Passmore, 2011, "Did the Federal Reserve's MBS Purchase Program Lower Mortgage Rates?" Journal of Monetary Economics, vol. 58, no. 5, pp. 498-514.
Hansen, B. and Phillips, P., 1990, 'Estimation and Inference in Models of Cointegration: A Simulation Study," Co-integration, Spurious Regressions, and Unit Roots pp. 225-248 Advances in Econometrics series, vol. 8
Heuson, Andrea, S.W. Passmore, and Roger Sparks, 2001, "Credit Scoring and Mortgage Securitization: Implications for Mortgage Rates and Credit Availability," Journal of Real Estate Finance and Economics, vol. 23, November, pp. 337-363.
Krishnamurthy, Arvind and Annette Vissing-Jorgensen, 2011, "The Effects of Quantitative Easing on Interest Rates," Northwestern University, Kellogg School of Management working paper, February 10.
Lehnert, A. Passmore S. W. and S. Sherlund, 2008, "Mortgage Rates, and Secondary Market Activities," Journal of Real Estate Finance and Economics, vol. 36, no. 3, 343-63.
Maddaloni, Angela and Jose-Luis Peydro, 2011, "Bank Risk-taking, Securitization, Supervision, and Low Interest Rates: Evidence from Euro-area and U.S. Lending Standards, Review of Financial Studies, vol. 24, no. 6, pp. 2121-2165.
Martin, A., J. McAndrews and D. Skeie, 2011, "A Note of Bank Lending in Times of Large Bank Reserves," Federal Reserve Bank of New York Staff Reports, no. 497, May.
Newton, D. P.; Sharp, N.; Duck, P., 2008, "An Improved Fixed-Rate Mortgage Valuation Methodology With Interacting Prepayment and Default Options," Journal of Real Estate Finance and Economics, vol. 36, 307-342.
Passmore, S. Wayne, Shane Sherlund, and Gillian Burgess, 2005, "The Effect of Housing Government-Sponsored Enterprises on Mortgage Rates," Real Estate Economics, vol. 33, pp. 427-463.
Phillips, Peter C.B., 1995, "Fully-Modified Least Squares and Vector Autoregression," Econometrica, vol. 63 (5), pages 1023-78, September.
Phillips, Peter C.B. and S Ouliaris, 1990, "Asymptotic Equivalence of Residual Based Tests for Cointegration," Econometrica, vol. 58, 165-193.
Stroebel, Johannes and John Taylor, 2010, "Estimated Impact of the Fed's Mortgage-Backed Securities," Stanford University, mimeo, October.
Swagel, Phillip, 2009, "The Financial Crisis: An Inside View," Brookings Papers on Economic Activity, Spring.
Tobin, James, 1958, "Liquidity Preference as Behavior Towards Risk," Review of Economic Studies, 25, pp. 124-131.
Wright, Jonathan H., 2011, "What does Monetary Policy do to Long-Term Interest Rates at the Zero Lower Bound?" Johns Hopkins University Economics DepartmentWorking Paper, June 13, 2011.