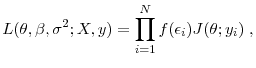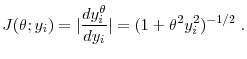The Properties of Income Risk in Privately Held Businesses
Keywords: Business income, privately held businesses, business risk
Abstract:
1 Introduction
The recent macro and finance literature has increasingly focused on questions related to uninsurable idiosyncratic business income risk and its implications for investment and capital accumulation, for entrepreneurial returns, for business entry and exit decisions, for consumption fluctuations and for asset prices. Such questions become even more important when we consider that, even in the United States, privately owned businesses account for almost half of aggregate capital and employment. Moreover, the typical investor has a large undiversified stake in his firm. For example, about 80% of all private equity is owned by agents who are actively involved in the management of their own firm, and for whom such investment constitutes at least half of their total net worth. However, despite this theoretical and empirical relevance of private business income risk, a proper analysis of business income using the time dimension, which is precisely crucial for the dynamic decisions of saving, portfolio allocation, investment and so on, has proven elusive in the literature, due to the lack of available data. As a result, most of the known facts about the variability of business income are derived from cross sectional data.
Our paper is in fact the first study in the literature to empirically document the properties of business income risk, using longitudinal data. We use a new, large and confidential administrative panel of US individual income tax returns for the period 1987-2009, to establish a variety of stylized facts about the nature and properties of business income risk over time. We also compare to labor income risk, in order to give a better idea of the quantitative magnitudes involved.1
Data. Our annual cross sections come from individual income tax returns data from the Internal Revenue Service (IRS) over the period 1987-2009. Over the 23 years, this repeated cross sectional dataset consists of over three million observations for the total number of returns filed. Our data are not subject to top-coding. In addition, they include information on age and gender of the primary filer from matched Social Security Administration (SSA) records. Our business income measure is net income received by the household from pass-through entities, namely from sole proprietorships, partnerships and S corporations, and reported in the corresponding box of Form 1040. For purposes of comparison, we also use the labor income received by the household, namely wages and salaries reported on Form 1040. The main contribution of our paper relies on the use of a business income panel, which is a one-in-5,000 random sample of tax units followed over 1987-2009. Our largest business income panel consists of about 150,000 household-year observations, while our corresponding labor income panel of about 280,000 household-year observations.
Findings. Using our annual cross sections, we document that business income is more concentrated at the top and that this concentration has been increasing faster over time, compared to labor income. Moving to our panel results, our paper makes a methodological contribution in demonstrating that an appropriate treatment of business income risk should carefully deal with zero and negative business income observations. In our work, we interpret the zeros as exit from business endeavors, and the losses as contributing to the business risk, conditional on no exit.
Therefore, starting with a panel of ![]() household-year observations, we begin by characterizing the probability of exiting business endeavors. We find that years immediately before
business exit are a bit more likely than other years to have been preceded by a longer streak of losses and are more likely to be years with losses. However, households do not appear to be realizing big capital gains upon exit, as average capital gains are actually lower in exit years. We also find
that, conditional on not having had business income in the previous year, the probability of having non-zero business income in the current year is 13%. Conditional on having had business income in the previous year, the probability of having business income in the current year is 86%. This latter
probability is also increasing in the length of the most recent unbroken business income spell and/or in total business experience.
household-year observations, we begin by characterizing the probability of exiting business endeavors. We find that years immediately before
business exit are a bit more likely than other years to have been preceded by a longer streak of losses and are more likely to be years with losses. However, households do not appear to be realizing big capital gains upon exit, as average capital gains are actually lower in exit years. We also find
that, conditional on not having had business income in the previous year, the probability of having non-zero business income in the current year is 13%. Conditional on having had business income in the previous year, the probability of having business income in the current year is 86%. This latter
probability is also increasing in the length of the most recent unbroken business income spell and/or in total business experience.
We then focus on a panel of ![]() household-year observations to describe the properties of business income risk conditional on no exit. For comparison, we also use a corresponding panel
for labor income. We consider the panel that conditions on no exit to, if anything, understate the " true" risk of the business income process. Still, dropping the zeros permits the examination of business income risk facing a household from a lifetime perspective, because, conceptually, the
appropriate treatment of business risk should take into account the fact that a household may fail, say, a couple of times, before coming back with a more successful business. We therefore employ a variety of measures to document the risk of business income, conditional on no exit, and we also
compare to labor income risk (conditional on no labor market exit).
household-year observations to describe the properties of business income risk conditional on no exit. For comparison, we also use a corresponding panel
for labor income. We consider the panel that conditions on no exit to, if anything, understate the " true" risk of the business income process. Still, dropping the zeros permits the examination of business income risk facing a household from a lifetime perspective, because, conceptually, the
appropriate treatment of business risk should take into account the fact that a household may fail, say, a couple of times, before coming back with a more successful business. We therefore employ a variety of measures to document the risk of business income, conditional on no exit, and we also
compare to labor income risk (conditional on no labor market exit).
First, using one year transition matrices, we find that business income has lower staying probabilities than labor income. In particular, the immobility ratio is about 0.4 for business income, and about 0.6 for labor income. More importantly, households starting at the lowest decile of the business income distribution face a 12% probability of transitioning to decile 8 or higher, whereas the corresponding probability is essentially zero for labor income. Hence, transitioning from rags to riches within the span of one year is possible for business income, while it is highly unlikely for labor income. Overall, our evidence is consistent with the idea that business people have inherently different risk preferences than wage earners, as they are willingly participating in a process that entails higher risks. They also appear to be participating in this process precisely because of the possibility of achieving extremely high outcomes over short periods of time. This qualitative picture of business vs. labor income risk is also preserved over longer horizons.
Second, we demonstrate that the distribution of percent changes is more dispersed for business than for labor income, where our definition of percent changes is modified to deal with negative income observations. Furthermore, for business income, the size distribution of percent changes has less mass in the middle and more mass in the tails. Specifically, about 12% of all one year business income percent changes were increases smaller than 10% or decreases smaller than 10%, compared to about 22% for labor income. In addition, about 32% of all business income percent changes were increases bigger than 100% or decreases bigger than 100%, compared to about 20% for labor income. Overall, then, business income is characterized by much higher tail risks, both in the positive and in the negative realm, compared to labor income. This qualitative picture is also preserved over longer horizons. In addition, it turns out that richer households are actually more likely than poorer households to receive both the big positive percent changes and the big negative percent changes of business income. In other words, the households to be found at both tails of the business income distribution of percent changes are more likely income-rich households, which is evidence for the presence of income (or wealth) heteroscedasticity in business risk.
Third, we calculate, for each household, the time series standard deviation of its business income, normalized by the household's average total income over time. We then combine those business income "coefficients of variation" into one cross sectional average, both with and without weighting
by the household's presence in the panel. The cross sectional weighted average is 45% for business income. The corresponding number for labor income is 30%. We note that the number of 45% is the closest empirical analog to the theoretical concept of the variance of (uninsurable) idiosyncratic
income risk from privately held businesses showing up in calibrations of certain theoretical models in the macro and finance literature. Traditionally, researchers have used a number like ![]() , motivated by the analysis in Moskowitz and Vissing-Jorgensen (2002), who, however, do not have a panel of privately held businesses. Our number turns out to be very close to 50%, but it is in fact derived from a panel, and therefore appropriately captures risk, as opposed to
heterogeneity.
, motivated by the analysis in Moskowitz and Vissing-Jorgensen (2002), who, however, do not have a panel of privately held businesses. Our number turns out to be very close to 50%, but it is in fact derived from a panel, and therefore appropriately captures risk, as opposed to
heterogeneity.
Fourth, we employ statistical models of income dynamics, proposing an appropriate methodology for inputting business income in statistical models. This includes the choice of an appropriate transformation that takes care of negative observations. We find that a positive one standard deviation model-estimated shock leads to a percentage increase to the level of business income that is about 4-6 times larger than the corresponding increase for labor income. We also show that our results about the comparison between business and labor income risk are preserved even when we consider risk from an individual business perspective, rather than a lifetime perspective, though, as expected, the latter risk is higher than the former.
In sum, the conclusion of our analysis is that business income risk is much higher than labor income risk, not only because of the probability of exiting business endeavors, but also because of more pronounced income fluctuations conditional on no exit. Most importantly, the risk involved in business income appears to be, to a large extent, tail risk, namely risk associated with large positive and/or negative income changes. Furthermore, our evidence suggests that both ends of the tail risk are actually born by rich households. Another way of putting this is to say that the frequently utilized assumption of a constant business income variance, which does not depend on income, does not seem to be entirely supported by the data. Instead, a big part of the large vicissitudes associated with business income occur at the top of the (total) income distribution, where rich households can experience dramatic swings from big profits in one year to big losses in the next. Our findings therefore indicate that the much greater variability of business income, compared to labor income, could be responsible for both the consumption and the investment spending behavior of the rich households.
2 Literature review
In the macro and finance literature, issues of business income risk have usually been examined in conjunction with topics on entrepreneurship. For example, a number of papers study the implications of uninsurable idiosyncratic business income risk for a variety of important questions, such as growth and the business cycle, capital flows and global imbalances, the role of fiscal policy, entrepreneurial effort and entry/exit, income inequality, social status, the distribution of wealth, and asset prices. A non-exhaustive list includes Heaton and Lucas (2000), Bitler, Moskowitz and Vissing-Jorgensen (2005), Angeletos (2007), Angeletos and Calvet (2006), Angeletos and Panousi (2009), Roussanov (2010), Angeletos and Panousi (2011), Panousi (2012), Benhabib and Zhu (2008), Zhu (2009), Parker and Vissing-Jorgensen (2009), Wang, Wang and Yang (2012), and Panousi and Reis (2012). In addition, entrepreneurial models in the Bewley tradition, such as Cagetti and De Nardi (2006), have implications about business income or entrepreneurial returns that can be tested using our data.2
Most of the known facts about the returns of private business endeavors come from cross sectional data, such as the Survey of Consumer Finances (SCF). In papers documenting some of the empirically relevant aspects of entrepreneurship in the cross section, Quadrini (2000), Gentry and Hubbard (2000), Carroll (2001), Cagetti and De Nardi (2006), Moskowitz and Vissing-Jorgensen (2002), and Moore (2004) document the poor portfolio diversification and extreme wealth concentration in the hands of private business owners and entrepreneurs in the United States. Moskowitz and Vissing-Jorgensen (2002) especially are in fact unable to provide a reliable measure for the risk faced by individual investors due to lack of sufficient time series variation in the data. As a result, they end up proposing the approximate number of 50%, namely the standard deviation of the annual return to an individual publicly traded stock. Numbers in that range have subsequently been used in model calibrations by Polkovnichenko (2003), Roussanov (2010), Heaton and Lucas (2004), Bitler, Moskowitz and Vissing-Jorgensen (2005), Angeletos (2007), Angeletos and Panousi (2009, 2011), and Panousi (2012).
Our paper is the first to extensively document the properties of business income risk in a large panel, which is what the aforementioned studies really necessitate. Hamilton (2002) uses a three year panel of the Survey of Income and Program Participation (SIPP), with a total of fewer than 2,000 observations, to show that returns to entrepreneurship are not significantly higher than the expected returns from paid labor. Heaton and Lucas (2000), using a 1979-1990 panel of tax returns, postulate that, as business income covaries with the stock market more than labor income, owners of private businesses will be more likely than wage earners to hold the rest of their portfolios in safe assets. However, their analysis uses a measure of business income that actually includes many other income categories from Form 1040, in addition to "true" business income, and it furthermore excludes negative observations.
Recently, the literature has started exploring comparisons between publicly traded and privately held firms, along any dimensions possible given data availability. Asker, Farre-Mensa and Ljungqvist (2012) examine differences in investment behavior between stock market listed and privately held firms in the U.S. using Sageworks, a recent 2001-2007 panel with accounting information from income statements and balance sheets for privately held businesses.3 Sheen (2009) analyzes hand-collected investment data for about 80 public and 40 private firms in seven commodity chemicals. Gao, Lemmon, and Li (2010) compare CEO compensation in public and private firms in the CapitalIQ database.
Related is also the literature on job creation and firm dynamics, as it studies the growth rate of revenue and the pace of job creation and job destruction for all nonfarm non-government businesses in the US, including privately held businesses. Some examples here include Davis et al. (2009), Jarmin and Miranda (2003), Boden and Nucci (2004), Haltiwanger, Jarmin and Miranda (2009), and in Haltiwanger (2011). As is the case with our paper, the work by Davis et al. (2009) also (partly) relies on business income information from individual income tax returns. Some aspects of entrepreneurship, especially as pertaining to business entry and exit, have also been discussed in the industrial organization literature. See for example Holmes and Schmitz (1990, 1995, 1996), Evans and Leighton (1989), Evans and Jovanovic (1989), and Blanchflower et al. (1994).
A strand of the literature has examined questions of entrepreneurial wealth and mobility. Quadrini (2000) and Basaluzzo (2006a) develop theoretical models of entrepreneurial mobility, while Holtz-Eakins, Rosen, Weathers (2000) use the PSID to examine if entrepreneurship has affected the relative positions in the income distribution of those individuals who have tried it. Along related lines, Terajima (2006), using the SCF studies the big increase in the earnings of college self-employed over other groups, and the much bigger concentration of their wealth over the period 1983-2001. Parker and Vissing-Jorgensen (2009), who do not use a panel, find that high income households are more exposed to consumption fluctuations, due to higher betas of their wage income. Instead, our findings that business income is more variable than labor income and that rich households are likely to bear both the large positive and the large negative business income changes, indicate that business income could be responsible for the consumption and the investment spending behavior of the rich. Kennickell (2009), using SCF data, reports evidence of wealth mobility over relatively short periods of time, when life-cycle related factors cannot be the reason. This suggests that the changes in mobility at the household level might be due to business income. Castaneda, Diaz-Gimenez, and Rios-Rull (2002) match the US earnings and wealth inequality almost exactly by calibrating a four-state Markov process for the uninsured idiosyncratic shocks on households' endowment of efficiency labor units. The highest state, with its lower persistence and large difference in the values of its realizations indicates that business income might help match the thick right tail of the observed income and wealth distributions.
3 Data description
This section describes our cross sections and panels, it presents our definitions of income variables and it discusses some potential data issues and concerns.
3.1 Annual cross sections and panels
Our dataset is constructed from 23 years of individual tax returns data, spanning the period 1987-2009, and produced by the Statistics of Income (SOI) division of the Internal Revenue Service.4 Each year, the IRS draws a stratified sample of tax returns, consisting of two subsamples. The first subsample includes all tax units where the primary filer's social security number ends in one of a set of four-digit combinations. In particular, two four-digit endings were sampled up to 1997, five were sampled from 1998-2005, and ten have been sampled since 2006. The second subsample, known as the high income oversample, consists of returns sampled at progressively higher rates at higher income levels, with the highest income returns selected with certainty. The overall sample has about 120,000-200,000 observations per year, and is weighted so as to be representative of the universe of tax filers (which includes about 140 million returns per year). Over the 23 years, this repeated cross sectional dataset consists of over three million observations for the total number of returns filed. Each cross section contains information from the taxpayers' Form 1040 and from a number of other forms and schedules. In addition, our data include information on age and gender of the primary filer from matched Social Security Administration records.
For the main contribution of our paper, we require a panel dimension. To create this panel, we cut the strictly random subsample of our 1987 cross section to returns for which the primary filer had a social security number (SSN) that ended in one of the two original four-digit combinations mentioned above. Over the following years, we then track tax returns where the primary filer has an SSN ending in those two four-digit combinations. The panel is unbalanced, with some tax units exiting the sample due to death, emigration, or falling below the filing threshold, and other added due to immigration or becoming filers. The resulting panel is thus a one-in-5,000 random sample of tax units followed over 1987-2009.5 In the end, our business income panel, which includes tax units who ever reported business income over 1987-2009, consists of about 150,000 household-year observations, and our labor income panel of about 280,000 household-year observations.
3.2 Definitions and sample selection
Throughout this study, the unit of observation is the tax unit, as our business income variable is not available at the individual level for all sample years. Therefore, our business and labor income variables are at the tax unit level. A tax unit consists of a primary filer if the taxpayer is single (or is married but filing separately or is head of household or widow(er)), and a primary and secondary filer (as well as any dependents) if the taxpayer is married filing jointly. However, as a notational clarification, in this paper we will be using the words "tax unit" and "household" interchangeably. In addition, all our income measures are in real 2005 dollars.
Our measure of business income includes the income reported on Form 1040 of individual income tax returns as stemming from three types of businesses, namely sole proprietorships, partnerships, and S corporations. In particular, this income is the owner's share of the net profit or loss from business operations, after all expenses, costs, and deductions have been subtracted. The IRS defines each of these business types as follows. A sole proprietor is an individual owner of an unincorporated business. Sole proprietorships report income and expenses to the IRS on Schedule C of Form 1040. A partnership consists of more than one person, who jointly form a business in which each person contributes money, property, labor or skill and shares in the profits and losses. The partnership files an information return (Form 1065) with the IRS. In addition, each partner receives a Schedule K-1 from the partnership, which reports that partner's share of the partnership profits or losses. The partner then reports these amounts to the IRS on Schedule E.6 Our measure of net income from partnerships includes income and losses from both passive and active partnerships. Finally, S corporations are corporations that satisfy a number of criteria and elect to pass the income and losses through to their shareholders for federal tax purposes.7 These shareholders then report the income or loss from the S corporation on Schedule E.8 We note that our measure of business income does not include rental income or capital gains.
All three business types are able to carry back or carry forward net operating losses to other tax years, as long as the income and losses are from active owners or partners. Before 1998, losses could be carried back three years and forward 15 years.9 Starting in 1998, these were changed to two and 20, respectively. These net operating loss carrybacks and carryforwards do not affect our measure of business income, since they are claimed on a separate area of the tax form.10
Our measure of labor income comes from the box " Wages, salaries, tips, etc." of Form 1040. In other words, by "labor income" we mean income from wages and salaries or earnings income. This measure does not include the portion of income that the taxpayer's employer has placed in a retirement account or the amount of health insurance premiums paid by the taxpayer and excluded from taxable wages. Using amounts reported on Form 1040, we created a variable termed "Adjusted Total Income" (ATI). This variable comprises the tax unit's total amount of income (including labor, business, capital, and retirement income), after some excludable income items are added back. These items include tax-exempt interest, nontaxable IRA and pension distributions, and nontaxable Social Security benefits.11
For our capital gains variable, we use all capital gains reported on Form 1040, including those reported on Schedule D and those reported on Form 4797. Although the capital gains tax law changed numerous times during the sample period, our data unfortunately do not contain sufficient detail for all years to make this measure more consistent over time.
In our panel data, we track each household over time based on the social security number of its primary filer.12 We restrict our panels to households where the primary filer has either some nonzero labor income or some nonzero business income (or both). We restrict the ages of the primary filer to 30-60, and we drop households where the head is a farmer (filing Schedule F). We restrict ages primarily for purposes of comparison between labor and business income (filers over 60 are likely to have a lower attachment to the labor market and/or may take on a business as a hobby). We exclude farmers because their business income, in contrast to that of non-farmer households, likely includes significant assistance from the government in the form of subsidies.
3.3 Issues
First, when dealing with tax returns data in general, and possibly with business income in particular, income misreporting emerges as a potential problem. We note that, though the literature has not reached a consensus about the distribution of tax non-compliance, either in the cross section or over time, there is nonetheless some evidence of tax evasion, especially among the sole proprietors.13 For example, sole proprietorship underreporting seems to be about 30%, according to the 1992 IRS tax gap study and the work by Feldman and Slemrod (2005). Partnership and S corporation income appears to be more accurately reported. In particular, the IRS estimates that underreporting was about 7-8% in 1992 and 18% in 2001. Other than that, not much is known about the specifics of the distribution of tax evasion. There is some evidence that smaller businesses misreport income more to the IRS, though estimates vary depending on the year, methodology, and type of small business. Andreoni, Erard and Feinstein (1998) argue that misreporting varies by occupation and industry, with lower percentages for finance, real estate, insurance, agriculture, and wholesale trades. In his review of the literature, Slemrod (2007) collects information indicating that the rich tend to evade less than the poor, although this is for income overall, as opposed to business income in particular. In addition, he finds evidence for substantial heterogeneity, even within narrow groupings of people. Plumley (1996) finds that economic variables, such as the unemployment rate, are not a statistically significant determinant of income under-reporting.
Importantly, however, survey data is also plagued by similar business income misreporting issues. For example, Hurst, Li and Pugsley estimate that self-employment income underreporting in household surveys is about 30%. Furthermore, using our large annual cross-sections, we get descriptive statistics about business and other income aggregates that are very close to the numbers reported in the SCF cross sections. These properties of our cross sections are also preserved in our business income panels, thereby providing additional confidence about the quality of our panel data. It is also worth pointing out that the SCF actually uses income data from tax returns for purposes of identifying and oversampling the rich. Kennickell (2009) reports that the process used by SCF to infer wealth from IRS income data comes remarkably close to matching household wealth, for those households who then choose to respond to the SCF's questions. Finally, using our cross sections, we find results similar to those in Moore (2004), who uses the SCF. For example, we find that demographics (such as age, gender and so on) have very low predictive power for business income, contrary to what happens for labor income.
Second, and related to the point above, Knittel et al. (2011) provide evidence that income misreporting, at least for sole proprietors, likely occurs on the expense side, as opposed to on the revenue side. In particular, travel expenses and meal deductions can be manipulated to artificially lower net profits from business operations. In this paper, we use net profits as our measure of business income. However, we note that the time-series correlation between gross receipts and net profits for the sole proprietors in our sample is over 90%.14 We further explore the distinction between gross receipts and net income in DeBacker, Panousi and Ramnath (2012).
Third, as already mentioned, we define business income as the residual or net income accruing to owners after all expenses have been paid, including any wage payments to the owners themselves. In particular, sole proprietorships do not issue W2 forms for the owner, and partnerships do not issue W2 forms for partners. For both of these business types then, our business income measure will also include whatever labor income the individual earned from the business. In other words, for sole proprietors and partners, all returns to labor and capital are included in our measure of business income (net profits/losses), and are subject to self-employment taxes. For S corporations, on the other hand, W2 forms are issued for employees. In fact, if an owner of an S corporation is also an employee of the firm, he is technically supposed to report "reasonable compensation" in the form of wages and salaries. Therefore, his labor income from the firm will not be included in our business income measure. Instead, it will be included in the wages and salaries box of Form 1040, grouped together with other compensation for paid employment. Hence, we have no way of backing it out in order to add it back to our business income measure for consistency with the treatment of sole proprietors and partners. Nonetheless, we note that S corporation owners do have an incentive to take their compensation in forms other than wages, in order to avoid payroll taxes on wage income.15
4 Business income in the cross section
In this section, we document some properties of business income using the data from our annual cross sections. We do so for three reasons. First, to give a better idea about the qualitative and descriptive features of our tax returns data, as our cross sections are even bigger than our panels. Second, to demonstrate the increasing importance of business income for aggregate total income and for filers with high total household income. Third, because the properties of the cross sectional data turn out to be preserved in our panel. This gives us additional confidence about the quality of our panel data, which we then use for estimating the properties of business income risk.
To begin with, we note that the importance of business income in the cross section of tax returns as well as in the composition of aggregate income has been increasing over our sample period. In particular, tax returns claiming income from a business as a fraction of total tax returns filed have
increased from about 16% in 1987 to 25% in 2009.16 Hence, in recent years, about a quarter of all returns filed includes some business income. Furthermore,
business income as fraction of adjusted total income (ATI; our measure of total household income) increased from 4% in 1987 to 10% in 2006, although it has dropped to 8% at the aftermath of the great recession. In addition, in 1987, average business income per business return filed was about
![]() of average labor income per labor return filed, but this ratio increased to over 50% in 2006 and is still higher in 2009 than in 1987, despite a drop from 2006 to 2009. This suggests that
households do indeed receive non-negligible amounts of income from their businesses.
of average labor income per labor return filed, but this ratio increased to over 50% in 2006 and is still higher in 2009 than in 1987, despite a drop from 2006 to 2009. This suggests that
households do indeed receive non-negligible amounts of income from their businesses.
The importance of business income is even more pronounced for those households at the top of the income distribution. As Figures 1 and 2 show, the top ![]() of households based on ATI holds
about
of households based on ATI holds
about ![]() of aggregate business income on average over our sample period, whereas it only holds about
of aggregate business income on average over our sample period, whereas it only holds about ![]() of aggregate labor income. Furthermore, the fraction of business income held at the top 1% of high ATI households has increased much faster than the corresponding fraction of labor income, namely by 80% vs. 30% over our sample period. Similar comparisons hold for the business
vs. labor income holdings of the top 5% and the top 10% of high ATI households.
of aggregate labor income. Furthermore, the fraction of business income held at the top 1% of high ATI households has increased much faster than the corresponding fraction of labor income, namely by 80% vs. 30% over our sample period. Similar comparisons hold for the business
vs. labor income holdings of the top 5% and the top 10% of high ATI households.
The distribution of business income is more skewed and has a thicker right tail than the distribution of labor income. Specifically, the top 1% of the business income distribution holds about 66% of business income on average over the period 1987-2009. By contrast, the top 1% of the labor income
distribution holds only about 11% of labor income. As another example, the p90/p50 percentile ratio, which shows how much more unequal the top of the distribution is compared to the middle, is about 14 for business income, whereas it is about 3 for labor income on average over our period. In
addition, the ratio
![]() is 2.6 for business income and 0.75 for labor income.17
is 2.6 for business income and 0.75 for labor income.17
Table (1) presents the cross sectional business income distribution for 2006. In total, about 18 million households filed business income tax returns. Most of business income profits are reported on returns with business income higher than $10,000 in real 2005 terms. In addition, a significant amount of losses is reported in returns with losses higher than $25,000. We note that in 2006, and on average in all years, about 30% of all business returns filed are returns with losses. This means that the issue of negative business income is an important concern that should be addressed in our technical analysis that follows.
Overall, business income is highly concentrated in the hands of households who file returns with total ATI over $50,000: About 70% of all returns filed with ATI higher than $50,000 include some income from a business. Furthermore, households with ATI higher than $100,000 hold about 70% of aggregate business profits and 35% of all business losses.18 Though it is natural that there is a positive correlation between high profits and high ATI, the point to note here is that ATI-rich households also bear about one third of total business losses. This suggests that such households are rich despite the fact that they also face a substantial amount of business losses. Or, that they become rich precisely because they participate in business endeavors, which at times entail big losses. Along the same lines, we note that, on average, over 80% of returns reporting business losses higher than $100,000 actually have positive ATI. This indicates that households are in a position to sustain substantial business losses within a given year, while still reporting positive total income.
5 Business income risk in the panel: methodology
This section describes our methodology for characterizing the income risk facing private business owners. To that end, we view the overall business income process as consisting of two components. First, a household faces a probability of exiting from the business endeavor in any given year. Second, conditional on participating in business endeavors, a household faces fluctuations to its business-related income. We will begin by characterizing the features of the exit process, and then we will focus on the nature of business risk, conditional on participation in business endeavors.
Specifically, in our 1987-2009 panel, a household may have positive business income (business profits) in some years, negative business income (business losses) in other years, and zero business income in yet other years. Due to IRS coding, a value of zero could indicate either exactly zero
income from a business or that the household did not submit a business return in that year. For the sole proprietors in our data, we can actually tell the two sources of zeros apart. In particular, we find that less than ![]() of the zeros in sole proprietor returns were due to exactly zero profits from an operating business. Hence, in all likelihood, a zero value for the business income variable in any given year indicates that the household did not operate a sole proprietorship in that
year. Although we do not have corresponding data for partnerships and S corporations, we will nonetheless assume in the rest of our analysis that a value of zero for business income represents exit from a business endeavor. We will be referring to this process as " exiting". As long as business
income is non-zero, then we will assume that the household is participating in business endeavors and is making profits or losses from the operation of business(es). We will be referring to this process as "conditional on no exit".19 This is essentially the same panel as the one that allows us to characterize exit, but where we drop the zero income observations. We will be referring to this panel as our benchmark or "drop zeros"
panel.20 Note that dropping the zeros reduces the number of household-year observations from about
of the zeros in sole proprietor returns were due to exactly zero profits from an operating business. Hence, in all likelihood, a zero value for the business income variable in any given year indicates that the household did not operate a sole proprietorship in that
year. Although we do not have corresponding data for partnerships and S corporations, we will nonetheless assume in the rest of our analysis that a value of zero for business income represents exit from a business endeavor. We will be referring to this process as " exiting". As long as business
income is non-zero, then we will assume that the household is participating in business endeavors and is making profits or losses from the operation of business(es). We will be referring to this process as "conditional on no exit".19 This is essentially the same panel as the one that allows us to characterize exit, but where we drop the zero income observations. We will be referring to this panel as our benchmark or "drop zeros"
panel.20 Note that dropping the zeros reduces the number of household-year observations from about ![]() to about
to about ![]() and that therefore the number of zeros is non-negligible and needs to be addressed in the analysis.
and that therefore the number of zeros is non-negligible and needs to be addressed in the analysis.
Note that, because our data is at the tax unit level, we do not know which business the household's income is coming from over time. Specifically, we do not know if a household, say, owns two sole proprietorships, both surviving over the years, or one surviving and the other not. As a result, we use the terminology "conditional on no exit" rather than "conditional on survival" and we also talk about participation in business endeavors or having business income, rather than having a particular business.
Taken in isolation, dropping the zeros likely underestimates the risk involved in business endeavors, as it abstracts from the possibility of exit, which is a fundamental part of the risk of business endeavors.21 Nonetheless, dropping the zeros still has the advantage of permitting the examination of business income risk facing a household from a life-time perspective. In other words, our view is that, conceptually, the appropriate treatment of business risk should take into account the fact that a household may fail a couple of times in its business endeavors, before coming back with a more successful business. Or, it could be that business households keep trying, despite never making it big, because their risk preferences or tolerance are inherently different than those of other households. In any case, moving in and out of the business endeavor, with a different business each time, is an inherent part of business risk for a household over time, hence our choice about the benchmark panel that drops zeros.
Having said that, we will also perform some robustness tests with alternative treatments of zeros. For example, in section 7.11, we will also report results from transition matrices on panels that do not drop the zeros. In addition, in section 7.4.3, we will present results from panels where we focus on the risk involved in each separate business endeavor, as opposed to in all the business endeavors a household undertakes over the entire period. One such instance will be to single out the longest continuous streak of non-zero business income for each household, and repeat our analysis in that sample.
6 Business income risk in the panel: characterizing exit
We start by presenting a characterization of the exit process, namely of the possibility that a household may stop participating in business endeavors and may have zero business income for one or more years as a result. To that end, we use a panel of households that ever reported a non-zero
amount of business income over the period 1987-2009, and we keep those households in the panel for all the years they show up, even in years when they have zero business income. The rest of our sample restrictions are reported in section 3.2. This panel consists of ![]() household-year observations.
household-year observations.
To begin with, we note that, conditional on ever reporting non-zero business income, a household shows up in the panel for 13 years, and it has non-zero business income for about seven of them. Conditional on non-zero business income, the (pooled) average continuous streak of business losses is two years. Conditional on zero/exit following the last year of a continuous non-zero business income spell, the average streak of losses before exit is 2.5 years. In years immediately before exit, the probability of losses is higher than in other years (31% vs. 27%), and average business income is lower ($10,000 vs. $26,000). However, average capital gains are lower in exit years, compared to other years ($5,000 vs. $14,000). Therefore, it appears that years immediately before exit are more likely to have been preceded by a longer streak of losses and are more likely to be years with losses. However, we do not see evidence for the view that households participating in business endeavors draw no income from their business, in order to eventually realize big capital gains, as capital gains are actually lower in end-of-business years.22
Next, we document some properties of the exit (or zero business income) probability. The unconditional probability of having non-zero business income in any given year is 46%. Conditional on not having had business income in the previous year, i.e. conditional on zero business income in the previous year, the probability of having (non-zero) business income in the current year is 13%. Conditional on having had business income in the previous year, the probability of having business income in the current year is 86%.
We also examine how the probability of no exit or of continuing to have business income varies with the length of the most recent unbroken streak of non-zero business income. If we knew for certain that this income was coming from the same business, then this variable could be interpreted as (current) business age or tenure. We estimate the probabilities of continuing to participate in the business endeavor using a random effects model that controls for age and year effects, as well as for marital status of the primary filer. The results indicate that, conditional on having had business income in the previous period, the probability of having business income in the current period, on average across all sample years, increases with the length of the most recent unbroken streak of non-zero business income, from 75% when the spell is 1 year to 95% when the spell is 10 years.23 Therefore, the probability of having business income in the current year, conditional on having had business income in the previous year, is higher if the household has recently been participating longer in business endeavors.
The exercise above, however, does not control separately for total or general business experience. Nonetheless, it could be the case that what matters for business success/survival is not simply the experience acquired while running the current business, but rather the cumulative experience acquired by the household through all its business endeavors over time, even if this experience was obtained through operating different or eventually unsuccessful businesses. Hence, we next estimate the probabilities of continuing to have non-zero business income as a function of the most recent unbroken streak of non-zero business income, but also controlling for general business experience. The results from a similar random effects model indicate that, for a household with total business experience of 5 years, the probability of having business income in the current period, conditional on having had business income in the previous period, increases with the length of the most recent unbroken streak of non-zero business income, from 78% when the spell is 1 year, to 83% when the spell is 5 years.24
We also repeat the analysis above by calendar year, in order to examine the cyclical properties of business exit. Overall, we do not find any striking or economically significant cyclical patterns in our data. Thus, it appears that the probability of having business income does not vary much with the cycle. For example, households do not appear to be exiting more in recessions. Of course, our data here is on business income at the household level, and we cannot tell how much of total household business income is coming from which specific business, and how the composition of business ownership for a household changes over time. Therefore, one should be careful about the interpretation of our cyclicality results. Having said that, Panousi, DeBacker and Ramnath (2012) focus on sole proprietors, who are more likely to own just one business at any given time. They also examine whether the potential cyclicality of business risk is reflected in investment expenditures.25
7 Business income risk in the panel: conditional on no exit
In this section, we present various ways of characterizing the time-series properties of business income risk, conditional on the household not exiting or continuing to participate in business endeavors. This panel, which includes households who have at some point in 1987-2009 reported non-zero
business income, and keeps them in the sample only in years when they have non-zero business income, consists of ![]() household-year observations. Basically, this is the panel in section
6 after dropping all the zero business income observations. We call this our benchmark or "drop zeros" panel.
household-year observations. Basically, this is the panel in section
6 after dropping all the zero business income observations. We call this our benchmark or "drop zeros" panel.
Additionally, in order to provide a better idea of the quantitative magnitude of business income risk, we contrast its properties to those of labor income risk. This is because the dynamic properties of labor or earnings income (risk) have been extensively examined in the literature and are much
better understood than those of business income. We therefore construct a panel for labor income, where we include all households who ever reported non-zero labor income in 1987-2009, for all the years they show up with non-zero labor income. This panel consists of ![]() household-year observations. The rest of our sample restrictions are reported in section 3.2. Tables (2) and (3) present some descriptives statistics for our "drop zeros" business and labor income panels, respectively.
household-year observations. The rest of our sample restrictions are reported in section 3.2. Tables (2) and (3) present some descriptives statistics for our "drop zeros" business and labor income panels, respectively.
The main issue that will have to be addressed in the context of our analysis conditional on no exit are the negative business income observations. As already mentioned, returns with losses account for about 30% of total business returns in every year. Furthermore, losses are also an inherent part of the riskiness of the business income process, and one of the main features that differentiate this process from that of labor income. Therefore, an appropriate analysis of business income risk will have to find ways to take the losses into account.
7.1 Transition matrices
To begin our characterization of business income risk, conditional on no exit, we use our benchmark "drop zeros" business income panel to construct a one year transition matrix for business income, shown in Table (4). In particular, each year, we split the business income distribution (in real 2005 dollars) into deciles. The rows show the decile a household starts at in any given year and the columns show the decile the household reaches at the end of the transition period. The numbers in the table denote probabilities, and are calculated as the number of household-year observations for which there is a transition from decile x to decile y over the period, divided by the number of household-year observations of any transition over that same period. The calculations include households that are in the panel at both ends of the transition. Averaging across time, the " blurred" bounds for the business income deciles 1 through 10, respectively, are: lower than -6,000, [-6,000; -1,300], [-1,300; 0], [0; 1,000], [1,000; 4,000], [4,000; 8,000], [8,000; 13,000], [13,000; 24,000], [24,000; 51,000], higher than 51,000.26 For purposes of comparison, we also construct the corresponding one year transition matrix for labor income, shown in Table (5). The time averages for the " blurred" labor income deciles are: [0; 10,000], [10,000; 18,000], [18,000; 25,000], [25,000; 33,000], [33,000; 41,000], [41,000; 50,000], [50,000; 61,000], [61,000; 77,000], [77,000; 103,000], higher than 103,000.
The most notable points emerging from the comparison of the transition matrices are as follows. First, business income has lower staying probabilities (lower probabilities on the main diagonal) than labor income, and therefore exhibits lower persistence. This information can be summarized in the immobility ratio, which is essentially the average of the diagonal elements of a transition matrix. The immobility ratio for business income is 0.43, whereas for labor income it is 0.57. However, at the top decile of the business income distribution, the staying probability is 75%, noticeably higher than the staying probabilities in the rest of the business income distribution. Second, conditional on leaving the starting business income decile, a household faces a 52% probability of moving to either of the two immediately adjacent deciles, whereas the corresponding probability is 71% for labor income. Therefore, movement in the business distribution is more likely to occur between deciles that are far apart, which demonstrates the higher risk of the business endeavor. Third, households starting at the lowest decile of the business income distribution face a 12% probability of transitioning to decile 8 or higher, whereas the corresponding probability is essentially zero for labor income. Hence, transitioning from rags to riches within the span of one year is possible for business income, while it is highly unlikely for labor income. This indicates that business income is characterized by "superstar" stories of households who achieve great success in their business endeavors, whereas labor income is less likely to exhibit extreme upward mobility. Overall, our evidence is consistent with the idea that business people have inherently different risk preferences than wage earners, as they are willingly participating in a process that entails higher risks. Furthermore, they could be participating in this process because of the possibility of achieving extremely high outcomes.
7.1.1 Robustness tests
In order to examine the robustness of these results, we perform the following tests.
First, to remove income variation that is due to observables and therefore cannot be termed risk, we conduct the analysis using residuals of income from a "first stage" regression of income on demographics. In particular, it has been shown that predictable variation in income over the lifecycle matters a lot for labor income. We therefore regress each type of income (business and labor), separately for each year, on a full set of age dummies for the primary filer, the number of children in the household (up to ten), as well as the gender and the marital status of the primary filer. In other words, our first-stage regression is:
where
We then take the resulting income residuals and we split them into deciles, separately for each year, so as to proceed with the construction of the one year transition matrix following the steps detailed above. The resulting matrices present the same qualitative picture for the comparison of business and labor income risk as do Tables (4) and (5).
Second, in order to address the issue of potential changes in household composition, and though this issue was also partially addressed by the first robustness test above, we restrict our samples to continuously married households and repeat the transition matrix analysis. The results about the qualitative comparison of business and labor income riskiness are again unchanged.
Third, we examine whether the higher riskiness of business income is preserved over longer horizons. To that end, we also construct three year business and labor income transition matrices, following a similar procedure to that outlined in section 7.1. Here, both business and labor income exhibit higher mobility than in their corresponding one year matrices, but the comparison between business and labor income is again qualitatively preserved, in that business income has a lower immobility ratio (lower persistence), higher probabilities of transitioning to deciles far apart, and higher probabilities of transitioning from the bottom to the top of the distribution.
Fourth, we also construct transition matrices using fixed income bins, so as to fix the starting points across distributions. In particular, we first de-trend each income measure, and we then run the residuals through fixed income bins. For example, the first bin includes (residuals of) income more negative than -$25,000, the second bin goes from -$25,000 to zero, and so on until the last bin, which includes income residuals higher than $1 million. The qualitative comparison between business and labor income is again similar to that in Tables (4) and (5). In particular, it is important to note that business income exhibits higher probabilities of transitioning from the bottom to the top of the distribution, even when the starting position is the same across business and labor income.
Fifth, in order to capture the risk associated with business exit, we construct transition matrices for our business income panel without dropping zero income observations. Specifically, we keep the zeros in a separate bin each year, then we split the non-zero business income distribution in deciles, and then we proceed with our transition matrix as before. The results are overall similar to those in Table (4), with the addition now of the zero state, which is also a likely state for business income. The probability of exiting or dropping to zero is smaller as the income in the starting decile increases, and it is about 4% for those starting at the top decile of the distribution.
Sixth, to examine whether our results are different when we focus on households who have had more business experience, as captured by more non-zero business income years, we construct transition matrices for business income in a panel that drops households who have had (non-zero) business income for less than 8 years. The results are overall similar to those in Table (4), indicating that business income is riskier than labor income, even among more " experienced" business households.
Finally, we construct income residuals from a modified version of (1). In particular, for each type of income, we run a pooled regression with time and household fixed effects, plus our other controls. We then run those residuals through our transition matrices and proceed as before. The results about the qualitative comparison between business and labor income continue to hold.
7.2 Distribution of percent changes in income
In this section, we use our benchmark "drop zeros" business income panel to study the distribution of percent changes in income, which can be interpreted as a measure of income riskiness, conditional on no exit. Let ![]() denote income, whether business or labor. Then, we define the one year percent change in income,
denote income, whether business or labor. Then, we define the one year percent change in income, ![]() , between year
, between year ![]() and year
and year ![]() , as follows:
, as follows:
where
Because we are here using percent changes as a measure of risk, it would also make sense to remove the part of the income changes that is due to observables, and therefore does not represent risk. As already explained in section 7.1.1, a regression of income on our available demographics has
essentially no predictive power for business income, whereas it has an ![]() of about 0.3 for labor income. Hence, for business income, it does not much matter whether the analysis is conducted
in terms of levels or residuals.28 However, this distinction may matter for labor income, and therefore we proceed to purge income from the effect of
observables using our first stage regression in (1). We then use formula (2) to construct percent changes, where now
of about 0.3 for labor income. Hence, for business income, it does not much matter whether the analysis is conducted
in terms of levels or residuals.28 However, this distinction may matter for labor income, and therefore we proceed to purge income from the effect of
observables using our first stage regression in (1). We then use formula (2) to construct percent changes, where now ![]() represents residuals from the first stage regression. However, note
that all our results carry through qualitatively if we use levels of income instead.
represents residuals from the first stage regression. However, note
that all our results carry through qualitatively if we use levels of income instead.
As a first pass at comparing business and labor income risk, we calculate the percentiles of the business and the labor income distribution of percent changes. The results are presented in Table (6), which shows the ratio of each percentile of the distribution of percent changes for business income, over the corresponding percentile of the distribution of percent changes for labor income. For both business and labor income, the 50th percentile (median) of percent changes is round zero. However, all other percentiles are 1.5-2 times more dispersed for business income, compared to the corresponding percentiles for labor income. For example, on average over our sample, the ratio of the 5th percentile of business income percent changes to the 5th percentile of labor income percent changes is 1.6, the ratio of the 40th percentiles is 2.3, the ratio of the 60th percentiles is 1.8, and the ratio of the 95th percentiles is 1.8. This clearly shows that the distribution of percent changes is more dispersed for business than for labor income, and it demonstrates in an intuitive fashion the higher riskiness of the business income process.
Second, we present the (pooled) distribution of the one year percent changes in income residuals, by size of the corresponding percent change. The results are presented in Figure 3. The horizontal axis shows the size of the percent changes. For example, the bin termed " 20% to 30%" indicates that residual income increased between 20% and 30% over the period, while the bin termed "-20% to -30%" indicates that residual income fell between 20% and 30% over the period. All bins have a size of 10 percentage points, except the last bin on the right and the last bin on the left. The last bin on the right groups together all observations for which residual income increased by more than 100%, while the last bin on the left groups together all observations for which residual income decreased by more than 100%.29 The blue bars indicate business income and the red bars indicate labor income. The vertical axis shows, for each type of income, the fraction of all percent change observations in each size-bin.
The overall picture that emerges is very striking and shows the following. First, the distribution of percent changes for business income has less mass in the middle. In other words, business income is characterized by fewer small increases or small declines, compared to labor income. For example, about 13% of all business income percent changes were increases smaller than 10% or decreases smaller than 10%, compared to about 23% for labor income. Second, the distribution of percent changes for business income has thicker tails than the one for labor income. This is demonstrated by the fact that, away from the origin, the blue bars are taller than the red bars, and they also decline more slowly. For example, about 30% of all business income percent changes were increases bigger than 100% or decreases bigger than 100%, compared to about 20% for labor income. This picture is consistent with the results emerging from our transition matrices, which clearly showed the potential for big transitions across the business income distribution. Overall, then, business income is characterized by much higher tail risks, both in the positive and in the negative realm, compared to labor income. Furthermore, as the robustness tests in the next section will demonstrate, this higher tail risk of business income is not due to the influence of income observations around zero or, in other words, to the swing from small levels of profits to small levels of losses.
In addition, it turns out that richer households are actually more likely than poorer households to receive both the big positive percent changes and the big negative percent changes of business income. In other words, the households to be found at both tails of the business income distribution
of percent changes are more likely high ATI households. In order to demonstrate this, we run a probit using the percent changes we derived from our first stage regressions as follows.30 The dependent variable in year ![]() takes the value 1 when a percent change is bigger than
takes the value 1 when a percent change is bigger than ![]() or bigger (in absolute value) than
or bigger (in absolute value) than ![]() . Hence, the dependent variable captures " big" positive or " big" negative business income percent
changes. The independent variable is average total income or average ATI in
. Hence, the dependent variable captures " big" positive or " big" negative business income percent
changes. The independent variable is average total income or average ATI in ![]() , where the average is taken over the periods
, where the average is taken over the periods ![]() to
to ![]() . As we do not have asset or net worth information in our data, average ATI is our best proxy for wealth. We have experimented with
splitting average lagged ATI in either 5 or 10 equal-sized bins, and the results are of a similar flavor regardless. In particular, the probability of having big positive/negative business income percent changes increases by about 6 percentage points in the highest ATI bin, compared to the lowest
ATI bin. Furthermore, the null that the coefficients on lagged ATI are equal between the highest and the lowest bin is in fact rejected. The quantification of this result cannot be very precise in our framework, due to lack of wealth data. However, the result also emerges very starkly in the
2007-2009 SCF panel that was recently made publicly available. In particular, Panousi and Barnett (2012) find that 5% of households with net worth below the median experienced business income declines bigger than
. As we do not have asset or net worth information in our data, average ATI is our best proxy for wealth. We have experimented with
splitting average lagged ATI in either 5 or 10 equal-sized bins, and the results are of a similar flavor regardless. In particular, the probability of having big positive/negative business income percent changes increases by about 6 percentage points in the highest ATI bin, compared to the lowest
ATI bin. Furthermore, the null that the coefficients on lagged ATI are equal between the highest and the lowest bin is in fact rejected. The quantification of this result cannot be very precise in our framework, due to lack of wealth data. However, the result also emerges very starkly in the
2007-2009 SCF panel that was recently made publicly available. In particular, Panousi and Barnett (2012) find that 5% of households with net worth below the median experienced business income declines bigger than ![]() , whereas that fraction was
, whereas that fraction was ![]() for households at the top 1% of the net worth distribution.
for households at the top 1% of the net worth distribution.
Altogether, we interpret these results as indicating that business income risk is possibly heteroskedastic, with richer households more likely to experience not only the big positive but also the big negative business income percent changes. This might also imply that the rich households can endogenously undertake more risk, because of decreasing absolute risk aversion. In this sense, the rich households become rich precisely because they are willing to participate in risky business endeavors, which do occasionally necessitate income declines, but they also hold the promise of big income increases when things go well.
7.2.1 Robustness tests
In order to examine the robustness of our results, we have performed the following tests.
First, we have conducted the analysis using levels of income, as opposed to residuals from a first stage regression. The results are qualitatively very similar to those in section 7.2.
Second, we have experimented with alternative definitions of percent changes. In particular, we have used in the denominator of 2 either
![]() or
or
![]() . We use the average in order to smooth out some of the most extreme fluctuations in business income. We use the absolute value of the sum in order to capture the
idea that a business making +$15,000 in one year and -$5,000 in the next year is a business of size +$10,000. We use the sum of the absolute values to address the problem that the previous definition would encounter when the business makes +$5,000 in one year and -$5,000 in the next year. When
using the sum of the absolute values, the idea is that a business making +$5,000 in one year and -$5,000 in the next year is a business of absolute size $5,000. Hence, size absorbs part of the risk in this definition. Overall, regardless of the definition used, the results about the qualitative
comparison between business and labor income are similar to those in section 7.2.
. We use the average in order to smooth out some of the most extreme fluctuations in business income. We use the absolute value of the sum in order to capture the
idea that a business making +$15,000 in one year and -$5,000 in the next year is a business of size +$10,000. We use the sum of the absolute values to address the problem that the previous definition would encounter when the business makes +$5,000 in one year and -$5,000 in the next year. When
using the sum of the absolute values, the idea is that a business making +$5,000 in one year and -$5,000 in the next year is a business of absolute size $5,000. Hence, size absorbs part of the risk in this definition. Overall, regardless of the definition used, the results about the qualitative
comparison between business and labor income are similar to those in section 7.2.
Third, we address the concern that the bigger riskiness of business income is due to business income changes around zero. In other words, when business income changes from " small" positive to " small" negative values (or vice versa), this will register as a very large percent change, and
might unduly influence the analysis. In addition, the concern might be that small, in absolute value, business income observations may indicate a household that is not truly involved in business endeavors. To that end, we truncate income based on some (arbitrary) thresholds. For example, if a
business income observation is higher than zero but less than $5,000, we set it to $5,000, and if it is lower than zero but bigger than -$5,000, we set it to -$5,000. We have also tried thresholds ![]() ,
,
![]() ,
,
![]() , and
, and
![]() .31 In addition, we have experimented
with dropping entirely the observations in between the positive and the symmetric negative threshold. Regardless of treatment, the results remain qualitatively similar to those in section 7.2. Hence, the bigger riskiness of business income, compared to labor income, is not due to the influence of
income observations around zero or to the swing from small levels of profits to small levels of losses.
.31 In addition, we have experimented
with dropping entirely the observations in between the positive and the symmetric negative threshold. Regardless of treatment, the results remain qualitatively similar to those in section 7.2. Hence, the bigger riskiness of business income, compared to labor income, is not due to the influence of
income observations around zero or to the swing from small levels of profits to small levels of losses.
Fourth, we verify that our results about the comparison of the dispersion and the distribution of percent changes across business and labor income also hold when we weight the observations of percent changes by either the number of years each household is present in the panel or by each household's average total income.
Fifth, we also examine whether the dispersion of the distribution of percent changes is higher for business income when the horizon is longer. To that end, we construct three and five year percent changes, using the corresponding adaptation of (2). We find that the distribution of percent changes for business income is more dispersed than that for labor income, even when using more "long run" measures of income.
7.3 Time series standard deviations
In this section, we continue the comparison of risk by studying household-level time-series standard deviations for each type of income. Again, we use our benchmark "drop zeros" panels, i.e. the results are conditional on no exit from the business endeavor or from the labor market. Our results
turn out to be similar, regardless of whether we use levels of income or residuals from our first stage regression in (1). In what follows, we will focus on the case of income residuals. In particular, for each household ![]() , we construct the standard deviation of its residual business income over time, denoted by
, we construct the standard deviation of its residual business income over time, denoted by ![]() . We also calculate its average total income or average ATI
over time, denoted by
. We also calculate its average total income or average ATI
over time, denoted by
![]() . We then construct the ratio
. We then construct the ratio
![]() , which is like a coefficient of variation for each household. This coefficient essentially shows the exposure of total household income to the risk stemming from
the household's business endeavors over time. Finally, we calculate the cross sectional average of those coefficients of variation across households, either unweighted or weighted by the number of years each household is present in the sample,
, which is like a coefficient of variation for each household. This coefficient essentially shows the exposure of total household income to the risk stemming from
the household's business endeavors over time. Finally, we calculate the cross sectional average of those coefficients of variation across households, either unweighted or weighted by the number of years each household is present in the sample, ![]() . In particular, the weighted cross sectional average of household-level business income coefficients of variation is given by:
. In particular, the weighted cross sectional average of household-level business income coefficients of variation is given by:
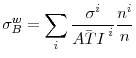 |
(3) |
where
We find that
![]() , whereas
, whereas
![]() , i.e. the cross sectional average of business income coefficients of variation is higher for business than for labor income. We note that the value of
, i.e. the cross sectional average of business income coefficients of variation is higher for business than for labor income. We note that the value of
![]() is the closest empirical analog to the theoretical concept of the variance of (uninsurable) idiosyncratic income risk from privately-held businesses that shows up in
calibrations of theoretical models in the macro and finance literature. Traditionally, researchers have used a number like
is the closest empirical analog to the theoretical concept of the variance of (uninsurable) idiosyncratic income risk from privately-held businesses that shows up in
calibrations of theoretical models in the macro and finance literature. Traditionally, researchers have used a number like ![]() , motivated by the analysis in Moskowitz and Vissing-Jorgensen
(2002), who, however, make inferences about the risk facing privately held businesses from either cross sectional heterogeneity among private business owners, or from extrapolations based on publicly-traded firms. Our number turns out to be very close to 50%, but it is in fact derived from a panel
of income from privately held businesses, and therefore appropriately captures risk, as opposed to heterogeneity.
, motivated by the analysis in Moskowitz and Vissing-Jorgensen
(2002), who, however, make inferences about the risk facing privately held businesses from either cross sectional heterogeneity among private business owners, or from extrapolations based on publicly-traded firms. Our number turns out to be very close to 50%, but it is in fact derived from a panel
of income from privately held businesses, and therefore appropriately captures risk, as opposed to heterogeneity.
7.3.1 Robustness tests
As already mentioned, the results are similar when we conduct the analysis using levels of income or when we do not weight the cross sectional household-level business income coefficients of variation in averaging. The results are also similar when we require households to be in the panel longer, say with over 8 years of non-zero business income.
7.4 Statistical models of income dynamics
In this section, we compare the risk of the business income to that of the labor income process using statistical models of income dynamics.
In our benchmark, we continue focusing on the case where we drop the zero observations of business (and labor) income, and therefore study the risk of the business endeavor conditional on no exit. Therefore, our benchmark considers the risk implied by all business spells for a given household over time, even if they are not continuous. By spell, we mean a continuous streak of non-zero business income. By continuous, we mean not interrupted by zeros. For example, we might observe a given household having non-zero business income for seven years, then having zeros for four years, then having non-zero business income for twelve years. This household then has two continuous business spells, one of duration seven and one of duration twelve. These spells are broken up by four years of zeros, which represent exit, namely a four year interval during which the household did not participate in the business endeavor. Our benchmark case drops the zeros, and focuses at the level of the household, in order to characterize the total risk the household faces over time from both its business spells, even though the spells are not continuous and even though they represent a " different" business. The idea here is that, for a given household and from a lifetime perspective, business risk does precisely capture the possibility that, say, a first restaurant may fail, at which point the household exits the business world and lets some time elapse, before it re-enters, with another restaurant that may (or may not) be more "successful". In other words, the risk inherent in business endeavors has naturally to do with the fact that a household possibly needs to try multiple times before succeeding. Of course, a household may never succeed, but the point is that business-minded households keep trying despite unsuccessful attempts, which also reveals that their risk preferences are different from those of other households.
However, although the notion of examining the risk stemming from all business spells makes intuitive sense from a household's lifetime perspective, and is the proper concept of risk associated with business endeavors, the (technical) caveat might be that statistical models of income dynamics have usually been employed to document the stochastic properties of continuous processes. Clearly, the data from our panel that drops the zero business income observations do not constitute a continuous process. To address this concern, we also perform two additional exercises. First, we keep the longest continuous business spell for each household, and we repeat the analysis in that sample. For instance, in the example above, we only keep the twelve year spell for that particular household. We refer to this panel as the "longest continuous histories" panel. This panel does not suffer from discontinuity issues. Additionally, our prior is that it will be characterized by lower business income risk, as it consists of the longest, and hence likely most successful, businesses. Second, we treat different business spells from the same household as separate observations, i.e. as coming from different households. In the example above, we treat the seven year spell and the twelve year spell from the same household as being observations from two different businesses. We refer to this panel as the "all continuous histories" panel. In this case, we are basically focusing the analysis at the business level, whereas our benchmark case is treating risk from a lifetime perspective at the household level. We expect this panel to exhibit an amount of business risk in between the highest risk implied by the benchmark or lifetime panel, and the lowest risk implied by the longest continuous histories panel. We will see that this intuition is verified in what follows.
7.4.1 Methodology for model estimation
Our model estimation methodology consists of three broad steps. First, we choose an appropriate transformation for the business income data, while at the same time also purging business and, more importantly, labor income from the predictable variation over the lifecycle that is due to observables. The first stage therefore yields residuals from a regression of transformed income on demographics. Second, we fit the residuals from the first stage into statistical models and we estimate the model-specific variance of business income. Third, we untransform the data in order to calculate the effect on the level of business income of, say, a positive one standard deviation model-estimated shock to income. As will become apparent in what follows, we have to revert back to levels in order to interpret the effect of the estimated shocks, because the appropriate transformation for business income is not unit invariant. We compare results across business and labor income, and we again demonstrate that business income entails higher risk than labor income.
We now turn to the first step of our model estimation methodology, namely the choice of an appropriate transformation for business income. In particular, the use of statistical models always requires imposing some structure on the data. For example, in the labor or earnings dynamics literature,
such structure is attained by excluding very low income observations and by logging the data to reduce the extreme skewness of the labor income distribution. The distribution of business income is also skewed, but business income cannot be transformed using logs, as it is very often negative. One
transformation that can address the issue of the negative income observations is the inverse hyperbolic sine (IHS).32 Letting ![]() denote income, the IHS transformation of the
denote income, the IHS transformation of the ![]() -observations is given by:
-observations is given by:
where
Hence, the IHS operates like a generalized Box-Cox transformation, both in terms of its location parameter, ![]() , and in terms of how that parameter is estimated. Here, we present the
intuition for the estimation of
, and in terms of how that parameter is estimated. Here, we present the
intuition for the estimation of ![]() , while the technical details are delegated to the appendix. The methodology is similar to that in the original Box and Cox paper. Pick any given
, while the technical details are delegated to the appendix. The methodology is similar to that in the original Box and Cox paper. Pick any given
![]() and transform business income,
and transform business income, ![]() , based on (4), to get transformed income,
, based on (4), to get transformed income,
![]() . Then, perform our standard first stage regression from (1) as follows:
. Then, perform our standard first stage regression from (1) as follows:
This is possible because, for a constant
We next turn to the second step of our model estimation methodology, namely to the choice of a statistical model for the residuals,
![]() , from the regression in (5). Consider the following very general model for
, from the regression in (5). Consider the following very general model for
![]() :
:
| (6) |
| (7) |
| (8) |
| (9) |
This very general model combines the following elements. First, a permanent part, consisting of an individual-specific, time-invariant component, ![]() , and a random-walk component,
, and a random-walk component,
![]() . These components are pre-multiplied by the year-specific factor loading,
. These components are pre-multiplied by the year-specific factor loading, ![]() , which allows the relative importance of the permanent part to vary over calendar year. Second, a transitory part,
, which allows the relative importance of the permanent part to vary over calendar year. Second, a transitory part, ![]() , specified as an AR(1) process. The
transitory innovations,
, specified as an AR(1) process. The
transitory innovations, ![]() , are multiplied by the year-specific factor loadings
, are multiplied by the year-specific factor loadings ![]() , which allow the variance of the innovations, and hence the relative importance of the transitory part, to vary by calendar year. The persistence of the transitory AR(1) component is given by parameter
, which allow the variance of the innovations, and hence the relative importance of the transitory part, to vary by calendar year. The persistence of the transitory AR(1) component is given by parameter ![]() . When
. When ![]() , the transitory part becomes essentially white noise (with time-varying variance).
, the transitory part becomes essentially white noise (with time-varying variance).
We estimate the model above, as well as simpler or restricted versions of it. The resulting models are very standard, and they also parsimoniously capture the main features of our business income data well. For example, the lifecycle variance profile in our business income data is slightly
concave. An AR(1) process with persistence ![]() implies a concave lifecycle variance profile, while a random walk process implies a linear lifecycle variance profile. A model with both a
random walk and an AR(1) component implies a concave variance profile. Below is the list of the models we estimate.
implies a concave lifecycle variance profile, while a random walk process implies a linear lifecycle variance profile. A model with both a
random walk and an AR(1) component implies a concave variance profile. Below is the list of the models we estimate.
(i) Fixed effect with AR(1) (![]() ):
):
![]()
(ii) Random walk (![]() ):
):
![]()
(iii) Fixed effect, random walk, AR(1) (
![]() ):
):
(iv) Fixed effect, random walk, white noise (
![]() ):
): ![]()
(v) Random walk with white noise (![]() ):
):
![]()
The model parameters, namely the persistence of the AR(1) process and the variances of the shocks, are then estimated using a minimum distance estimator that matches the model's theoretical variances and autocovariances to their empirical counterparts. In particular, each model above implies a
specific parametric form for each variance and autocovariance of residual income, for each calendar year ![]() and each lead
and each lead ![]() . These theoretical variances and autocovariances, denoted by
. These theoretical variances and autocovariances, denoted by ![]() , are functions of the model parameters, for
, are functions of the model parameters, for
![]() . Hence, we estimate the model parameters by minimizing the distance between the theoretical variances and autocovariances implied by the model, and their empirical
counterparts, which we compute from our panel data for
. Hence, we estimate the model parameters by minimizing the distance between the theoretical variances and autocovariances implied by the model, and their empirical
counterparts, which we compute from our panel data for
![]() and
and
![]() . Our minimum distance estimator uses a diagonal matrix as the weighting matrix, with weights equal to the inverse of the number of observations used to compute each empirical
statistical moment.34
. Our minimum distance estimator uses a diagonal matrix as the weighting matrix, with weights equal to the inverse of the number of observations used to compute each empirical
statistical moment.34
Finally, we move to the third step of our model methodology, namely calculating the effect of a one standard deviation shock, estimated from the model, on the levels of untransformed business and labor income. This step is necessary because of the properties of our IHS transformation, which
imply that we cannot directly interpret or compare the results of the model estimation across business and labor income. Specifically, the location parameter ![]() of the IHS will in general
be different for the business and the labor panels. In addition, the IHS transformation is not unit invariant, contrary to the log. Therefore, for a meaningful comparison, we need to untransform the data and revert back to levels. Then, we compare the effect of a one standard deviation shock,
estimated from each model, on the level of each type of income, for our benchmark case of a household with primary filer a 35 year old married male with two kids. The qualitative results are similar when we choose a different household as our measure of comparison. For example, for the case of
model (iii), we take a one standard deviation shock to income in year
of the IHS will in general
be different for the business and the labor panels. In addition, the IHS transformation is not unit invariant, contrary to the log. Therefore, for a meaningful comparison, we need to untransform the data and revert back to levels. Then, we compare the effect of a one standard deviation shock,
estimated from each model, on the level of each type of income, for our benchmark case of a household with primary filer a 35 year old married male with two kids. The qualitative results are similar when we choose a different household as our measure of comparison. For example, for the case of
model (iii), we take a one standard deviation shock to income in year ![]() ,
, ![]() ,
to be the sum of the shocks to the permanent and the transitory component, weighted by their respective factor loadings, i.e.
,
to be the sum of the shocks to the permanent and the transitory component, weighted by their respective factor loadings, i.e.
![]() . Then, we find the level of income for our benchmark average household without the shock and with, say, a positive
. Then, we find the level of income for our benchmark average household without the shock and with, say, a positive ![]() -shock.35 Next, for each year
-shock.35 Next, for each year ![]() , we calculate the percent change implied by these two income levels, using our formula (2). We then average across years, and we compare the resulting average percent changes for business and labor
income. We interpret a bigger percent change to the level of income resulting from a model-estimated shock to indicate higher income risk.
, we calculate the percent change implied by these two income levels, using our formula (2). We then average across years, and we compare the resulting average percent changes for business and labor
income. We interpret a bigger percent change to the level of income resulting from a model-estimated shock to indicate higher income risk.
7.4.2 Results
In this section, we present the results of our model estimation for our benchmark business and labor income panels, which drop zero income observations. This treatment then considers the lifetime risk a household faces from all business endeavors it is involved in over time.
From our first stage regression, the location parameter is estimated to be
![]() for business income and
for business income and
![]() for labor income. Next, table 7 shows the comparison of risk between business and labor income: It presents the implied percent change to the level of business income and to the
level of labor income, resulting from a positive one standard deviation shock estimated from each one of the models (i)-(v).
for labor income. Next, table 7 shows the comparison of risk between business and labor income: It presents the implied percent change to the level of business income and to the
level of labor income, resulting from a positive one standard deviation shock estimated from each one of the models (i)-(v).
For example, an estimated positive one standard deviation shock from the random walk model increases the level of business income of our benchmark average household by 62%, whereas it increases the level of labor income of that same household by 16%. The ratio of these percent changes is approximately 4, i.e. business income is about four times riskier than labor income. The table shows that, depending on the model, this ratio ranges between 4-6.5, so that business income is about 4 to 6 times riskier than labor income.
7.4.3 Robustness tests
To examine the robustness of our model-related results, we perform the following tests.
First, we examine whether the results are influenced by outliers, namely by large positive or negative (levels of) income observations. To that end, before we start our model analysis, we drop business income observations higher than +5 (or +2) business income standard deviations and lower than
-5 (or -2) business income standard deviations. Similarly, we also drop labor income observations higher than +5 (or +2) labor income standard deviations. We then conduct the rest of the analysis as detailed in section 7.4.1, including the calculation of the location parameter, ![]() , which will be different each time a sample changes. The results about the qualitative comparison between business and labor income remain unchanged, so that business income is still riskier than
labor income.
, which will be different each time a sample changes. The results about the qualitative comparison between business and labor income remain unchanged, so that business income is still riskier than
labor income.
Second, we examine whether the results are influenced by small, in absolute value, levels of income. The idea here is that small amounts of business income may be unduly affecting model estimation and/or they may indicate a household that is not truly involved in business endeavors. To that end,
before we start our model analysis, we drop business income observations between
![]() (or
(or
![]() or
or
![]() ), and labor income observations lower than
), and labor income observations lower than ![]() (or
(or ![]() or
or
![]() ). We also experiment with truncating income observations at the aforementioned thresholds. The resulting percent changes to the level of business income are now slightly lower
for each model (for example, 55% for the random walk model), compared to those reported in Table 7, consistent with the intuition that, by excluding observations around zero, we have excluded some of the really large variation that business income may take on when it switches from negative to
positive. Nonetheless, the results about the relative size of the percent changes between business and labor income continue to hold. This indicates that the higher riskiness of business income, compared to labor income, is not due to the effect of business income changes from small profits to
small losses (or vice versa). Another way of putting this is to say that our results are not due to people who occasionally, say, do some consulting and file a Schedule C, but are not really and truly involved in business endeavors.
). We also experiment with truncating income observations at the aforementioned thresholds. The resulting percent changes to the level of business income are now slightly lower
for each model (for example, 55% for the random walk model), compared to those reported in Table 7, consistent with the intuition that, by excluding observations around zero, we have excluded some of the really large variation that business income may take on when it switches from negative to
positive. Nonetheless, the results about the relative size of the percent changes between business and labor income continue to hold. This indicates that the higher riskiness of business income, compared to labor income, is not due to the effect of business income changes from small profits to
small losses (or vice versa). Another way of putting this is to say that our results are not due to people who occasionally, say, do some consulting and file a Schedule C, but are not really and truly involved in business endeavors.
Third, we examine whether our results are driven by the IHS transformation, by repeating the labor income analysis using the standard or well-known log treatment adopted in the literature of labor income dynamics. In particular, we drop labor income observations below a minimum threshold, we log the data, run our first stage regression, take the residuals, and feed them into our statistical models.36 For every model, the resulting percent changes to the level of labor income are very similar to those reported in Table 7, thereby demonstrating that the results of our methodology for the riskiness of labor income do not crucially depend on the IHS transformation.
Fourth, to address the concern that our statistical models are not appropriate for a discontinuous income process, such as our business income process that drops the zero observations, we also perform two additional exercises. In the first place, we keep the longest continuous (unbroken by zeros) business spell for each household, and we repeat the analysis in that sample. We refer to this panel as the "longest continuous histories" panel. This panel does not suffer from discontinuity issues. In the second place, we treat different business spells from the same household as coming from different households. We refer to this panel as the "all continuous histories" panel. In this case, we are basically focusing the analysis at the business level, whereas our benchmark case in section 7.4.2 is treating risk from a lifetime perspective at the household level. Table 8 presents the results for the various models across the three different sample selections: The first column repeats the results of Table 7 for our benchmark panel that drops the zeros and focuses on lifetime business income risk; the second column presents the results from the panel that keeps only the longest continuous business spell for each household; and the third column presents the results from the panel that keeps all continuous business spells, but treats each different spell from the same household as a different observation.
Consider, for example, the model with fixed effects and an AR(1) component. In the sample with only the longest continuous business spells, the resulting change to the level of business income from a positive one standard deviation model-estimated shock is 147%. This is lower than the change of 155% in the panel that focuses on the business level, which in turn is lower than the 158% in the benchmark panel that focuses on lifetime business risk. The same overall picture emerges, regardless of the model used. The following conclusions can therefore be drawn. First, the effect of the discontinuity in the business income process of the benchmark sample does not appear to be greatly influencing the analysis. Second, the qualitative results about the risk comparison between labor and business income are preserved even when restricting to the two versions of continuous histories, as the magnitudes in the second and third columns of Table 8 are comparable to those in the first column. Third, the results for the three business income samples make intuitive sense. In particular, regardless of model, business risk is lowest in the sample that restricts to the longest, and therefore likely most successful, business income spells; and it is highest in the benchmark sample that focuses on business risk from a lifetime perspective, and therefore takes into account all business endeavors entered into by a household over time.
8 Conclusions
Our paper is the first in the literature to document the properties of business income risk from privately held businesses in the US, using a long time dimension. Utilizing a new, large, and confidential panel of income tax returns for 1987-2009, we find that business income is much riskier than labor income, not only because of the probability of business exit, but also because of higher income fluctuations, conditional on no exit. We show that business income is less persistent, but is also has higher probabilities of extreme upward movement, compared to labor income. Furthermore, the distribution of percent changes for business income is more dispersed, and it indicates that business income faces substantially higher tail risks. Our results suggest that the high income households are more likely to bear both the big positive and the big negative business income risks. This evidence of risk heteroscedasticity indicates that business income risk could be responsible for the consumption and the investment spending behavior of the rich, for example during the recent recession.
This paper documents the stylized facts of business income risk, a necessary step in the examination of issues related to privately held businesses, given the lack of data with appropriate time dimension in the US. Subsequent work then studies a number of additional important issues. In particular, Debacker, Panousi, and Ramnath (2012a) focus on sole proprietors and construct imputed measures of assets, so as to study the properties of business returns. Furthermore, Debacker, Panousi, and Ramnath (2012b) examine whether participation in business endeavors pays, in the sense of resulting in higher lifetime income for the business households. They also look at the characteristics of the households who exit the labor market in order to establish a business. Panousi and Barnett (2012) focus on business income risk heteroskedasticity in the 2007-2009 period, using the most recent SCF panel. Using our data, a re-examination of the importance of entrepreneurial risk for portfolio choice and asset prices, along the lines of Heaton and Lucas (2000), would also be of interest.
References
-
Aït-Sahalia, Y., Parker, J. A., Yogo, M., 2005. Luxury goods and the equity premium. Journal of Finance 59, 2959-3004.
Angeletos, G.-M., 2007. Uninsured idiosyncratic investment risk and aggregate saving. Review of Economic Dynamics 10, 1-30.
Angeletos, G.-M., Calvet, L., 2006. Idiosyncratic production risk, growth and the business cycle. Journal of Monetary Economics 53, 1095-1115.
Angeletos, G.-M., Panousi, V., 2009. Financial integration, entrepreneurial risk and global dynamics. Journal of Economic Theory 146.
Angeletos, G.-M., Panousi, V., 2011. Revisiting the supply-side effects of government spending. Journal of Monetary Economics 56, 863-896.
Asker, J., Farre-Mensa, J., and Ljungqvist, A., 2012. Comparing the Investment Behavior of Public and Private Firms. Working paper.
Basaluzzo, G., 2006a. Entrepreneurship, Business Wealth, and Social Mobility. Working paper.
Basaluzzo, G., 2006b. Entrepreneurial Teams in Financially Constrained Economies. Working paper.
Boden, R., Nucci, A., 2004. Business dynamics among the smallest and newest of businesses: Preliminary analyses of longitudinally matched nonemployer and Business Register data. Paper presented at Annual Meetings, Eastern Economic Association. 19-24 February, Washington, D. C.
Brav, O., 2009. Access to capital, capital structure, and the funding of the firm. Journal of Finance 64, 263-208.
Benhabib, J., Zhou, S., 2008. Age, luck and inheritance. NBER Working Paper 14128.
Bitler, M., Moskowitz, T., Vissing-Jorgensen, A., 2005. Testing agency theory with entrepreneur effort and wealth. Journal of Finance 60, 539-576.
Andreoni, J., Erard, B., and J. Feinstein (1998), "Tax Compliance," Journal of Economic Literature 36:2, 818-860.
Brown, R.E., Mazur, M.J., 2003. IRS's comprehensive approach to compliance measurement. Internal Revenue Service.
Cagetti, M., De Nardi, M., 2006. Entrepreneurship, frictions, and wealth. Journal of Political Economy 114, 835-870.
Carroll, C.D., 2000. Portfolios of the rich. NBER Working Paper 7826.
Clotfelter, C.T., 1983. Tax evasion and tax rates: An analysis of individual returns. Review of Economics and Statistics 65, 363-373.
Castaneda, A., Diaz-Gimenez, J., Rios-Rull, J.-V., 2002. Accounting for the U.S. Earnings and Wealth Inequality. Journal of Political Economy.
Davis, S. J., Haltiwanger, J., 1999. Gross job flows. Handbook of Labor Economics, chapter 41, Ashenfelter, O. and Card, D. (eds.).
Davis, S. J., Haltiwanger, J., Jarmin, R. S., Miranda, J., 2006. Volatility and dispersion in business growth rates: Publicly traded versus privately held firms. NBER Working Paper 12354.
Davis, S. J., Haltiwanger, J., Jarmin, R. S., Krizan, C. J., Miranda, J., Nucci, A., Sandusky, K., 2009. Measuring the Dynamics of Young and Small Businesses Integrating the Employer and Nonemployer Universes. NBER Volume, Producer Dynamics: New Evidence from Micro Data.
DeBacker, J., Panousi, V., Ramnath, S, 2012. Sole proprietors and entrepreneurial returns to private businesses. Working paper.
De Nardi, M., Doctor, P., Krane, S. D., 2007. Evidence on entrepreneurs in the United States: Data from the 1989-2004 Survey of Consumer Finances. Economic Perspectives, Federal Reserve Bank of Chicago.
Feldman, N. E., Slemrod, J., 2005. Estimating tax noncompliance with evidence from unaudited tax returns. Discussion Paper 05-15, Monaster Center for Economic Research.
Hamilton, B.H., 2000. Does entrepreneurship pay? An empirical analysis of the returns of self-employment. Journal of Political Economy 108, 604-631.
Gao, H., Lemmon, M., and Li, K., 2010. A comparison of CEO pay in public and private U.S. firms, Working paper, University of British Columbia.
Haltiwanger, J., Jarmin, R.S., Miranda, J., 2009. Who Creates Jobs? Small vs. Large vs. Young. Working paper.
Haltiwanger, J., 2011. Job Creation and Firm Dynamics in the U.S. Working paper, University of Maryland.
Gentry, W. M., Hubbard, G., 2004. Entrepreneurship and household saving. Advances in Economic Analysis and Policy 4, 1053-1108.
Heaton, J., Lucas, D., 2000. Portfolio choice and asset prices: The importance of entrepreneurial risk. Journal of Finance 55, 1163-1198.
Holtz-Eakin, D., Rosen, H. S., Weathers, R., 2000. Horatio Alger Meets the Mobility Tables. NBER Working Paper No. 7619.
Hurst, E., Li, G., Pugsley, B., 2010. Are Household Surveys Like Tax Forms: Evidence from Income Underreporting of the Self Employed. NBER Working Paper No. 16527
Jarmin, R., Miranda, J. 2003. The longitudinal business database. Center for Economic Studies Working Paper 02-17.
Johns, A., Slemrod, J., 2008. The distribution of income tax noncompliance. Mimeo.
Klepper, S., Nagin, D., 1989. The anatomy of tax evasion. Journal of Law, Economics, and Organization 5, 1-24.
Kennickell, A. B., 2009. Ponds and Streams: Wealth and Income in the U.S., 1989 to 2007. Finance and Economics Discussion Series 2009-13, Board of Governors of the Federal Reserve System.
Knittel, M., Nelson, S., DeBacker, J., Kitchen, J., Pearce, J., Prisinzano, R., 2011. Methodology to Identify Small Businesses and Their Owners. OTA Technical Paper 4, August.
Malloy, C. J., Moskowitz, T. J., Vissing-Jorgensen, A., 2009. Long run stockholder consumption risk and asset returns. Journal of Finance 64, 2427-2479.
Michaely, R., Roberts, M. R., 2007. Corporate dividend policies: Lessons from private firms, Working paper, Cornell University.
Moskowitz, T. J., Vissing-Jorgensen, A., 2002. The Returns to Entrepreneurial Investment: A Private Equity Premium Puzzle?. American Economic Review 92, 745-778.
Moore, K., 2004. Comparing the earnings of employees and the self-employed, Federal Reserve Board.
Panousi, V., 2012. Capital taxation with entrepreneurial risk. Federal Reserve Board mimeo.
Panousi, V., Papanikolaou, D., 2011. Investment, idiosyncratic risk, and ownership. Journal of Finance, forthcoming.
Panousi, V., Reis, C., 2012. Optimal capital taxation with idiosyncratic investment risk. Working paper.
Panousi, V, Barnett, M., 2012. Heteroskedasticity of entrepreneurial risk and the great recession. Working paper.
Parker, J.A., Vissing-Jorgensen, A., 2009. Who bears aggregate fluctuations and how? American Economic Review, Papers and Proceedings 99, 399-405.
Polkovnichenko, V., 2003. Human capital and the private equity premium. Review of Economic Dynamics 6, 831-845.
Quadrini, V., 2000. Entrepreneurship, saving, and social mobility. Review of Economic Dynamics 3, 1-40.
Roussanov, N., 2010. Diversification and its discontents: Idiosyncratic entrepreneurial risk in the quest for social status. Journal of Finance 65, 1755-1788.
Saunders, A., Steffen, S. 2009. The costs of being private: Evidence from the loan market, Working paper, New York University.
Sheen, A., 2009. Do public and private firms behave differently? An examination of investment in the chemical industry. Working paper, UCLA.
Slemrod, J., 2007. Cheating ourselves: The economics of tax evasion. Journal of Economic Perspectives 21, 25-48.
Terajima, Y., 2006. Education and self-employment: changes in earnings and wealth inequality.
Wang, C., Wang, N., and Yang, J. (2011). Dynamics of entrepreneurship under incomplete markets. Working paper.
Zhu, S. (2009). Wealth distribution under idiosyncratic investment risk. Working paper.
Tables and Figures
Figure 1 shows the concentration of business income at the top of the adjusted total income (ATI) distribution. The data are from our annual cross sections, 1987-2009. The red line indicates households at the top 1% of the ATI distribution. The blue line indicates households at the top 5% of the ATI distribution. The purple line indicates households at the top 10% of the ATI distribution. Time in calendar years is on the horizontal axis. Business income held at the top, as a fraction of aggregate business income, is on the vertical axis. Figure 2 shows the concentration of labor income at the top of the adjusted total income (ATI) distribution. The data are from our annual cross sections, 1987-2009. The red line indicates households at the top 1% of the ATI distribution. The blue line indicates households at the top 5% of the ATI distribution. The purple line indicates households at the top 10% of the ATI distribution. Time in calendar years is on the horizontal axis. Labor income held at the top, as a fraction of aggregate labor income, is on the vertical axis.Table 1 presents the cross sectional distribution of business income for the year 2006. Business income is net income (profits or losses) received by a household from pass-through businesses, namely sole proprietorships, partnerships and S corporations. Business income is in real 2005 dollars. The third column shows the number of tax returns filed claiming some amount of business income from pass-through entities in the corresponding box of IRS Form 1040.
Table 2 presents descriptive statistics for our benchmark "drop zeros" business income panel. This panels keeps households who ever declared some business income during our sample period 1987-2009, for the years when they claim non-zero business income (i.e., the zero income observations have been dropped). The sample selection keeps households with primary filer aged 30-60 and drops households where the primary filer is a farmer (filing Schedule F). The mean, median and standard deviation are in real 2005 dollars.
Table 3 presents descriptive statistics for our benchmark labor income panel. This panels keeps households who ever declared some labor income (wages and salaries) during our sample period 1987-2009, for the years when they claim non-zero labor income (i.e., the zero income observations have been dropped). The sample selection keeps households with primary filer aged 30-60. The mean, median and standard deviation are in real 2005 dollars.
Table 4 presents the one year transition matrix for the business income distribution, conditional on no exit. Our benchmark "drop zeros" business income panel is used. Ages of primary filer are 30-60 and farmers have been dropped. Each year, we split the business income distribution (in real 2005 dollars) into deciles. The rows show the decile a household starts at in any given year and the columns show the decile the household reaches at the end of the transition period. The numbers in the table denote probabilities, and are calculated as the number of household-year observations for which there is a transition from decile x to decile y over the period, divided by the number of household-year observations of any transition over that same period. The calculations include households that are in the panel at both ends of the transition. Averaging over time, the bounds for the business income deciles are: lower than -6,000, [-6,000; -1,300], [-1,300; 0], [0; 1,000], [1,000; 4,000], [4,000; 8,000], [8,000; 13,000], [13,000; 24,000], [24,000; 51,000], higher than 51,000.
Table 5 presents the one year transition matrix for the labor income distribution, conditional on no exit from the labor market. Our benchmark labor income panel is used. Ages of primary filer are 30-60 and farmers have been dropped. Each year, we split the labor income distribution (in real 2005 dollars) into deciles. The rows show the decile a household starts at in any given year and the columns show the decile the household reaches at the end of the transition period. The numbers in the table denote probabilities, and are calculated as the number of household-year observations for which there is a transition from decile x to decile y over the period, divided by the number of household-year observations of any transition over that same period. The calculations include households that are in the panel at both ends of the transition. Averaging across time, the bounds for the labor income deciles are: [0; 10,000], [10,000; 18,000], [18,000; 25,000], [25,000; 33,000], [33,000; 41,000], [41,000; 50,000], [50,000; 61,000], [61,000; 77,000], [77,000; 103,000], higher than 103,000.
| 1.6 | 1.6 | 1.7 | 1.8 | 1.9 | 2.3 | 1.8 | 1.7 | 1.6 | 1.6 | 1.6 | 1.6 | 1.8 |
Table 6 presents the ratio of the percentiles of the distribution of one year percent changes for business income, divided by the corresponding percentiles of the distribution of one year percent changes for labor income. The panels used to construct percent changes in income for each household are our benchmark 1987-2009 panels, which drop zero income observations, restrict ages to 30-60, and exclude farmers. The one year percent changes are calculated from income residuals from the first stage regression in (1), see text for details. The calculations of percent changes use the formula (2). The distributions of percent changes are pooled across all sample years.

Figure 3 presents the (pooled) distribution of the size of the one year percent changes in income residuals, for business and for labor income. The panels used to construct percent changes in income for each household are our benchmark 1987-2009 panels, which drop zero income observations, restrict ages to 30-60, and exclude farmers. The one year percent changes are calculated from income residuals from the first stage regression in (1), see text for details. The calculations of percent changes use the formula (2). The blue bars indicate business income and the red bars indicate labor income. The horizontal axis shows the size of the percent change. All bins have a size of 10 percentage points, except the last bin on the right and the last bin on the left. The last bin on the right groups together all observations for which residual income increased by more than 100%. The last bin on the left groups together all observations for which residual income decreased by more than 100%. The vertical axis shows the fraction of all business or labor income observations of percent changes in each size-of-percent-change bin. |
 Figure 4 plots the Inverse Hyperbolic Sine (IHS), for a given location parameter, |
| Sample | Business income | Labor income |
| 158% | 28% | |
| 62% | 16% | |
|
|
219% | 37% |
|
|
324% |
49% |
| 361% | 58% |
Table 7 presents the percent changes to the levels of business and of labor income resulting from a positive one standard deviation model-estimated shock to each type of income. Model estimation uses our benchmark 1987-2009 business and labor income panels, which drop
zero income observations, restrict ages to 30-60, and exclude farmers. In the models, ![]() indicates fixed effects,
indicates fixed effects, ![]() indicates an AR(1) component,
indicates an AR(1) component, ![]() a random walk component, and
a random walk component, and ![]() a white noise component, see text for details. Our benchmark average household has a primary filer who is male, married, aged 35, and with two kids. For that household, the percent change in the level of income with and without the model-estimated shock is calculated using
(2).
a white noise component, see text for details. Our benchmark average household has a primary filer who is male, married, aged 35, and with two kids. For that household, the percent change in the level of income with and without the model-estimated shock is calculated using
(2).
| Sample | Benchmark | Longest continuous | All continuous |
| 158% | 147% | 155% | |
| 62% | 61% | 64% | |
|
|
219% | 205% | 211% |
|
|
324% | 275% | 284% |
| 361% | 338% | 354% |
Table 8 presents the implications of a positive one standard deviation model-estimated shock for the levels of business income, in three alternative business income panels. Column "benchmark" indicates our "drop zeros" business income panel. Column "Longest
continuous" keeps only the longest continuous (unbroken by zeros) business income spell for each household. Column "All continuous" keeps all continuous business spells from a household, but treats each one of them as a different observation, i.e. as coming from different households. All panels
are for the period 1987-2009, ages 30-60, and no farmers. In the models, ![]() indicates fixed effects,
indicates fixed effects, ![]() indicates an AR(1) component,
indicates an AR(1) component, ![]() a random walk component, and
a random walk component, and ![]() a white noise component. Our benchmark average household has a primary filer who is male, married, aged 35, and with two kids. For that household, the percent change in the level of income with and without the model-estimates shock is calculated using (2).
a white noise component. Our benchmark average household has a primary filer who is male, married, aged 35, and with two kids. For that household, the percent change in the level of income with and without the model-estimates shock is calculated using (2).
Appendix
Inverse Hyperbolic Sine (IHS) estimation. In order to estimate the location parameter, ![]() , for the Inverse Hyperbolic Sine (IHS), we assume that, for some
unknown
, for the Inverse Hyperbolic Sine (IHS), we assume that, for some
unknown ![]() , the transformed variables
, the transformed variables
![]() satisfy the full set of normal theory assumptions:
satisfy the full set of normal theory assumptions:
Then, the likelihood function with respect to the original observations,
where
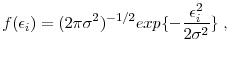 |
(12) |
Inspection of (11) indicates that, but for a constant (or, equivalently, for each given
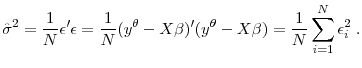 |
(14) |
Using this, we can re-write the likelihood in (11) as a function of
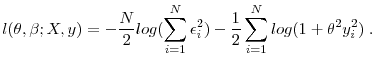 |
(15) |
In the concentrated log likelihood, the first term comes from the normal distribution and is the log sum of squared residuals from the linear model in (10). The second term comes from the Jacobian of the transformed observations in (13)b. We therefore find the maximum likelihood estimates as follows. First, for a given
Second, we search over all possible values of
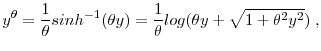
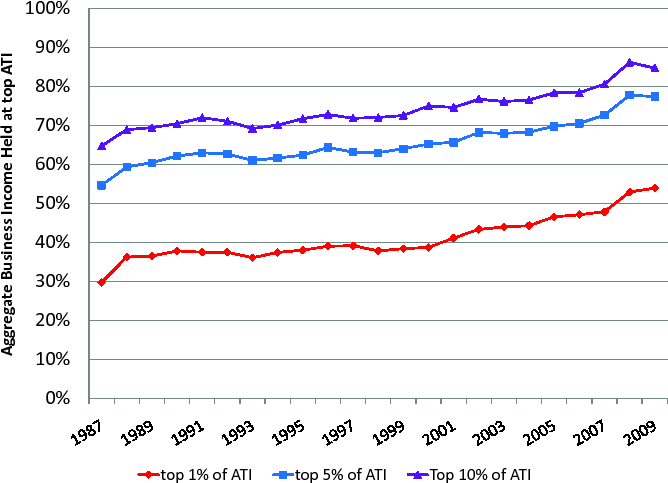
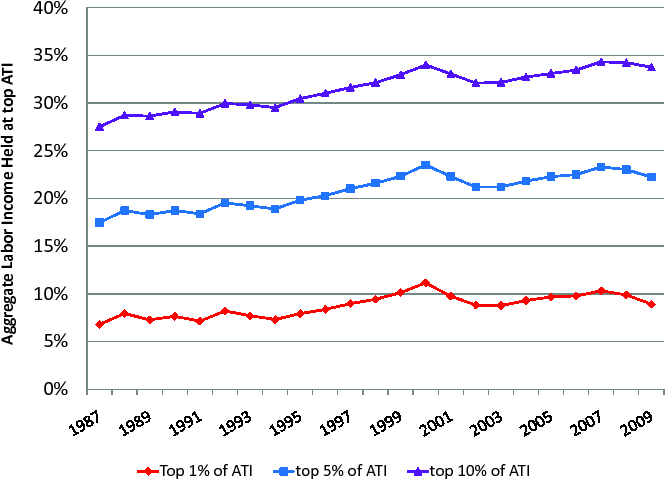

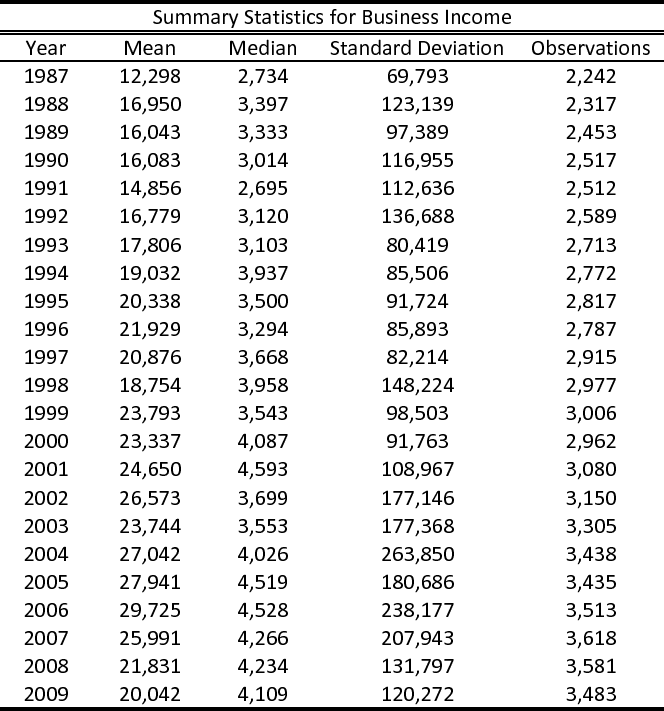
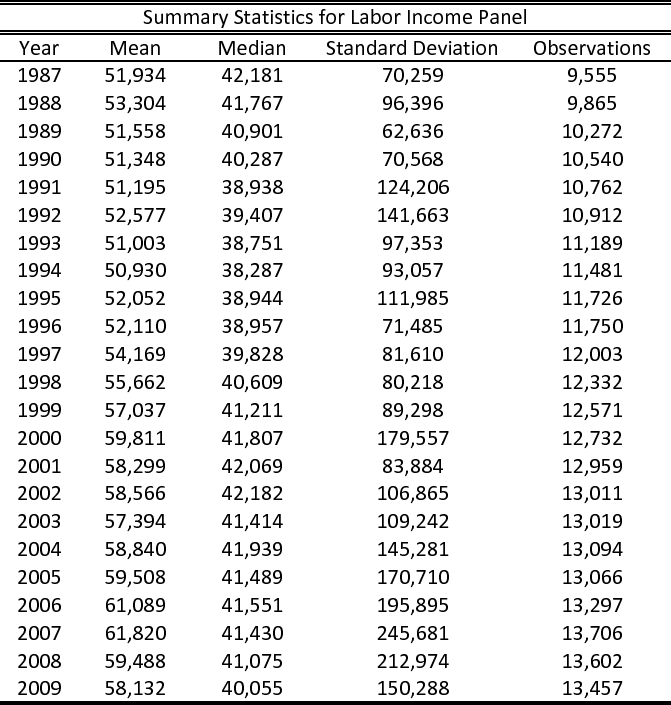
![Table 4: One Year Business Income Transition Matrix. This table presents the one year transition
matrix for the business income distribution, conditional on no
exit. Our benchmark \textquotedblleft drop
zeros\textquotedblright\ business income panel is used. Ages of
primary filer are 30-60 and farmers have been dropped. Each year,
we split the business income distribution (in real 2005 dollars)
into deciles. The rows show the decile a household starts at in
any given year and the columns show the decile the household
reaches at the end of the transition period. The numbers in the
table denote probabilities, and are calculated as the number of
household-year observations for which there is a transition from
decile x to decile y over the period, divided by the number of
household-year observations of any transition over that same
period. The calculations include households that are in the panel
at both ends of the transition. Averaging over time, the bounds
for the business income deciles are: lower than -6,000, [-6,000;
-1,300], [-1,300; 0], [0; 1,000], [1,000; 4,000], [4,000; 8,000],
[8,000; 13,000], [13,000; 24,000], [24,000; 51,000], higher than
51,000.](img90.gif)
![Table 5: One Year Labor Income Transition Matrix. This table presents the one year transition
matrix for the labor income distribution, conditional on no exit
from the labor market. Our benchmark labor income panel is used.
Ages of primary filer are 30-60 and farmers have been dropped.
Each year, we split the labor income distribution (in real 2005
dollars) into deciles. The rows show the decile a household starts
at in any given year and the columns show the decile the household
reaches at the end of the transition period. The numbers in the
table denote probabilities, and are calculated as the number of
household-year observations for which there is a transition from
decile x to decile y over the period, divided by the number of
household-year observations of any transition over that same
period. The calculations include households that are in the panel
at both ends of the transition. Averaging across time, the bounds
for the labor income deciles are: [0; 10,000], [10,000; 18,000],
[18,000; 25,000], [25,000; 33,000], [33,000; 41,000], [41,000;
50,000], [50,000; 61,000], [61,000; 77,000], [77,000; 103,000],
higher than 103,000.](img91.gif)