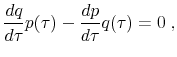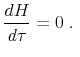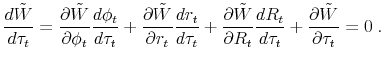Optimal Capital Taxation with Idiosyncratic Investment Risk
Keywords: Optimal capital taxation, idiosyncratic investment risk, general equilibrium, heterogeneous agents
Abstract:
1 Introduction
We study optimal capital taxation in a Ramsey framework and in an environment where agents face uninsurable idiosyncratic investment or capital-income risk. Such risk is empirically important for all investment decision makers, whether they are entrepreneurs and private business owners or managers of publicly traded firms. In this context, capital taxation raises an interesting trade-off: On the one hand, it comes at the usual cost, as it distorts agents' saving decisions. On the other hand, it has benefits, as it provides agents with partial insurance against idiosyncratic capital-income risk. Moreover, this insurance aspect of capital taxation may even lead to higher capital accumulation in general equilibrium, contrary to what happens in models of complete markets or uninsurable labor income risk. Therefore, a positive tax on capital income could be welfare improving, and more so than in other Ramsey environments.
Our modelling framework builds on Angeletos (2007), who develops a variant of the neoclassical growth model that allows for idiosyncratic investment risk, and studies the effects of such risk on macroeconomic aggregates. Agents own privately-held businesses that operate under constant returns to scale. These private businesses are subject to idiosyncratic risk that the agents cannot diversify away. However, agents are not exposed to labor-income risk, and they can also freely borrow and lend in a riskless bond. Abstracting from borrowing constraints, labor-income risk, and other market frictions, isolates the impact of the idiosyncratic investment risk, and preserves tractability of the model. There is a government, imposing a proportional tax on capital income, along with a non-contingent lump-sum tax or transfer. In a similar framework, Panousi (2012) performs comparative statics with respect to the capital income tax and finds that an increase in capital taxation may actually stimulate capital accumulation, due to a general equilibrium insurance aspect of the interest rate or safe rate adjustment.
We fully characterize the optimal taxation problem, where the social planner maximizes ex ante welfare, taking into account the entire transitional dynamics of the economy toward the steady state with the optimal tax. We prove that the ex ante optimal tax, evaluated at steady state, maximizes human wealth, namely the present discounted value of agents' future safe income, namely of income from wages or government transfers (or any other sources that are not subject to idiosyncratic risk). Furthermore, when the amount of idiosyncratic risk in the economy is higher than a minimum lower bound, the optimal tax is positive and it is precisely the tax that maximizes the economy-wide aggregates, such as the capital stock and output. By contrast, when the amount of risk is exogenously very low, then aggregate capital and output are falling with the tax at the optimum, and the social planner finds it optimal to increase social risk taking by subsidizing investment in capital.
As a simple and illustrative example, we provide the case of an ![]() economy. There, if the interest rate is endogenous, the optimal tax is always constant, even off steady state, it
maximizes the risk-adjusted growth rate of wealth (the difference between the risk-adjusted return to saving and the marginal propensity to consume), and it is equal to
economy. There, if the interest rate is endogenous, the optimal tax is always constant, even off steady state, it
maximizes the risk-adjusted growth rate of wealth (the difference between the risk-adjusted return to saving and the marginal propensity to consume), and it is equal to
![]() . Therefore, the optimal tax is positive when the mean return to the risky asset (capital),
. Therefore, the optimal tax is positive when the mean return to the risky asset (capital), ![]() , is lower than the variance of idiosyncratic capital-income risk,
, is lower than the variance of idiosyncratic capital-income risk, ![]() . If the interest rate is exogenous, then the optimal tax is actually always exactly equal to
zero.
. If the interest rate is exogenous, then the optimal tax is actually always exactly equal to
zero.
Our paper belongs in the optimal taxation literature in the Ramsey tradition, though it also allows for lump-sum transfers, and it shows that the rationale for positive capital income taxation in the long run does not necessarily extend to the case where markets are incomplete due to the presence of idiosyncratic capital income risk. However, regardless of whether the ex ante optimal tax is positive or negative, the planner's motivation for setting the optimal tax is always related to ensuring a sufficient amount of social risk taking. When the exogenous risk in the economy is sufficiently high, then the optimal capital tax is positive, so that the ensuing general equilibrium adjustment of the interest rate endogenously provides agents with the insurance they need to undertake risky capital investment, despite the fact that the tax tends to reduce the mean return to saving. When the exogenous risk in the economy is sufficiently low, then the optimal capital tax is negative, so that the capital subsidy encourages capital accumulation directly, by increasing the mean return to capital, despite the fact that the subsidy tends to reduce the interest rate and therefore wealth accumulation. This is because risk was low enough to begin with, and therefore the agents can tolerate the increase in the variance of risk resulting from the subsidy, both directly and indirectly through its general equilibrium effects.
2 Related Literature
We focus on an environment with idiosyncratic investment risk, because such risk is in fact empirically relevant for all investment decision makers, even in a financially developed country like the United States. First, Moskowitz and Vissing-Jorgensen (2002), among others, find that about 80 percent of all private equity in the US is owned by agents who are actively involved in the management of their own firm, and for whom such investment constitutes at least half of their total net worth. It seems plausible, then, that entrepreneurial risk must be even more prevalent in less developed economies. Second, Panousi and Papanikolaou (2012) show that the negative relationship between idiosyncratic risk and the investment of publicly-traded firms in the US is stronger in firms where the mangers hold a larger fraction of the firm's shares. Combined, these findings strengthen the empirical applicability of our model setup, because they demonstrate that a large fraction of total investment in the US is sensitive to idiosyncratic risk, essentially through the risk aversion of the agents making the investment decisions.
This paper relates to the macroeconomic literature on optimal taxation. Most of this literature has focused either on complete markets or on incomplete markets with labor-income risk. Starting with the Ramsey literature of exogenously given market structure and exogenous policy instruments, Chamley (1986), Judd (1985), and Atkeson, Chari and Kehoe (1999) establish the result of zero optimal capital taxation when markets are complete. Correia (1996) shows that, in the neoclassical model, if there are restrictions on the taxation of production factors, then the tax rate on capital income in steady state is different from zero. Aiyagari (1995) extends the complete-markets framework to include uninsurable labor-income risk and borrowing constraints, and finds that the optimal capital tax is positive in the long run.1 Chamley (2001) argues that it might be best to think of the reasoning behind Aiyagari's positive optimal capital tax result as related to the ex-ante insurance or ex-post redistribution aspect of the tax: the planner taxes agents with high income realizations, and subsidizes agents with low income realizations, thereby equalizing consumption across different types of agents. Our paper contributes to the literature on optimal taxation in the Ramsey tradition, though also allowing for lump-sum transfers, and shows that, when markets are incomplete due to the presence of uninsurable capital-income risk, then the optimal capital tax will be different from zero, and will be positive or negative depending on general equilibrium insurance considerations.
Moving to the Mirrlees literature of endogenous market incompleteness and endogenous policy instruments, Albanesi (2006) considers optimal taxation in a two-period model of entrepreneurial activity in a constrained-efficiency setting. Shourideh (2011) also studies the optimal taxation of entrepreneurial income. In his model, as in our paper, the intertemporal wedge determining the tax on wealth cannot be unambiguously signed. However, the incentive constraint seems to create a force towards a wealth subsidy, since increasing capital tends to loosen the incentive compatibility constraint in the future. In general, however, the extensive theoretical work on taxation originating from the Mirrlees tradition focuses on labor-income risk. This literature shows that, if insurance is limited due to the presence of asymmetric information, then it may be best to restrict free access to savings. This result has in turn been interpreted as a justification for capital taxation. Some additional examples include Diamond and Mirrlees (1978), Golosov, Kocherlakota, and Tsyvinski (2003), Albanesi and Sleet (2006), and Golosov, Troshkin, Tsyvinsky and Weinzierl (2010). Farhi and Werning (2010) study optimal nonlinear taxation of labor and capital in a political economy model with heterogeneous agents, where policies are chosen sequentially over time, without commitment, as the outcome of democratic elections. They find that credible policies show a concern for future inequality and that capital taxation emerges as an efficient redistributive tool for this purpose.
The overlapping-generations literature has often found support for positive optimal capital taxation. Conesa, Kitao and Krueger (2009) quantitatively characterize the optimal capital and labor income taxes in an overlapping generations model with idiosyncratic uninsurable income shocks and permanent productivity differences across households. They find that the optimal capital-income tax rate is significantly positive at 36 percent, mainly driven by the life-cycle structure of the model.2 Erosa and Gervais (2002), in an overlapping-generations economy where agents' productivity varies over time, find that positive capital taxes may be optimal when labor taxes cannot be conditioned on age. Garriga (2003), and Peterman (2011) also find similar results.
A strand of the public finance literature has examined the effects of capital taxation on risk taking, mostly in a partial equilibrium framework. Some examples include Domar and Musgrave (1944), Stiglitz (1969), Ahsan (1974), Sandmo (1977), and Kanbur (1981). These authors argued that, by effectively reducing the variance of capital income, the capital tax allowed for increased social risk taking, leading to an increase in investment in the risky asset (capital). Our results are of similar flavor, though reflecting general equilibrium considerations that this literature cannot capture, even in the case where the optimal tax turns out to be negative. As it turns out, a capital subsidy enhances risk taking in cases where the amount of exogenous risk in the economy was too low to begin with. Our paper is also related to Varian (1980), who assumes that differences in observed income are due to exogenous differences in luck. In a two-period model of endogenous saving, he finds that the optimal capital-income tax is positive, due to the trade-off it involves between the distortion in the saving decision and the provision of social insurance through redistribution.
Finally, Angeletos and Panousi (2009) use a model similar to the one in the present paper to examine the effects of government consumption on steady state aggregates, for the case where government spending is financed solely through lump-sum taxes.
3 The basic model
Time is continuous and indexed by
![]() . There is a continuum of infinitely lived households distributed uniformly over
. There is a continuum of infinitely lived households distributed uniformly over ![]() . Each household consists of a worker and an entrepreneur. The worker is endowed with one unit of labor, supplied inelastically in a competitive labor market. The entrepreneur owns and runs a privately-held firm. Each firm employs labor in the competitive labor market, but can
only use the capital stock invested by the particular household. Each firm is hit by idiosyncratic shocks, which the household can only partially diversify, as it cannot invest in other households' firms. However, each household can freely save or borrow in a riskless bond (up to a natural
borrowing constraint), which is in zero net supply. In terms of timing for the firm's problem, first capital is installed, then the idiosyncratic shock is realized, and lastly the labor choice is made. All uncertainty is purely idiosyncratic, and therefore aggregates are deterministic. Finally, the
government imposes proportional taxes on savings and labor income, and balances the budget by giving back to agents, in the form of lump-sum transfers, the proceeds of taxation minus any government spending. Throughout the paper, for any variable
. Each household consists of a worker and an entrepreneur. The worker is endowed with one unit of labor, supplied inelastically in a competitive labor market. The entrepreneur owns and runs a privately-held firm. Each firm employs labor in the competitive labor market, but can
only use the capital stock invested by the particular household. Each firm is hit by idiosyncratic shocks, which the household can only partially diversify, as it cannot invest in other households' firms. However, each household can freely save or borrow in a riskless bond (up to a natural
borrowing constraint), which is in zero net supply. In terms of timing for the firm's problem, first capital is installed, then the idiosyncratic shock is realized, and lastly the labor choice is made. All uncertainty is purely idiosyncratic, and therefore aggregates are deterministic. Finally, the
government imposes proportional taxes on savings and labor income, and balances the budget by giving back to agents, in the form of lump-sum transfers, the proceeds of taxation minus any government spending. Throughout the paper, for any variable ![]() , the notation
, the notation ![]() is used as short-hand notation for
is used as short-hand notation for ![]() , where
, where ![]() is time.
is time.
3.1 Households, firms, and idiosyncratic risk
Preferences are logarithmic over consumption, ![]() :
:
where
The financial wealth of a household ![]() , denoted by
, denoted by ![]() , is the sum of its
asset holdings in private capital,
, is the sum of its
asset holdings in private capital, ![]() , and in the riskless bond,
, and in the riskless bond, ![]() ,
so that
,
so that
![]() . The evolution of
. The evolution of ![]() is given by the household
budget:
is given by the household
budget:
where
Firm profits are subject to undiversified idiosyncratic risk:
Here,
3.2 Government
At each point in time the government taxes capital income and bond income at the rate ![]() . The government also does some government spending at the rate
. The government also does some government spending at the rate ![]() , where
, where ![]() does not enter any production or utility functions. The proceeds of taxation, minus any government
consumption, are then distributed back to the households in the form of non-contingent lump-sum transfers,
does not enter any production or utility functions. The proceeds of taxation, minus any government
consumption, are then distributed back to the households in the form of non-contingent lump-sum transfers, ![]() . The government budget constraint is therefore:
. The government budget constraint is therefore:
where
4 Equilibrium and steady state
This section characterizes the equilibrium of the economy. First, it solves for households' optimal plans, given the sequences of prices and policies. It then aggregates across households to derive the general equilibrium dynamics.
4.1 Individual behavior
Entrepreneurs choose employment after their capital stock has been installed and their idiosyncratic shock has been observed. Hence, since their production function, ![]() , exhibits constant
returns to scale, optimal firm employment and profits are linear in own capital:
, exhibits constant
returns to scale, optimal firm employment and profits are linear in own capital:
where
Next, define total effective wealth,
Total effective wealth is then the only state variable relevant for the household's optimization problem. The only constrained imposed is that consumption is non-negative, which implies non-negativity of total effective wealth, so that:
In other words, there is no ad hoc borrowing constraint, and agents can freely borrow and lend up to the natural borrowing limit. The evolution of total effective wealth is then described by:
The first term in
where the fraction of effective wealth invested in capital,
and the marginal propensity to consume,
The wealth evolution constraint, incorporating bond market clearing and individual optimization, is:
Using
where
where
4.2 General equilibrium
The initial position of the economy is given by the cross sectional distribution of
![]() across households. Households choose plans
across households. Households choose plans
![]() for
for
![]() , contingent on the history of their idiosyncratic shocks, and given the price sequence and the government policy, so as to maximize their lifetime utility. Idiosyncratic risk
washes out in the aggregate. An equilibrium is then defined as a deterministic sequence of prices
, contingent on the history of their idiosyncratic shocks, and given the price sequence and the government policy, so as to maximize their lifetime utility. Idiosyncratic risk
washes out in the aggregate. An equilibrium is then defined as a deterministic sequence of prices
![]() , policies
, policies
![]() , and macroeconomic variables
, and macroeconomic variables
![]() , along with a collection of individual contingent plans
, along with a collection of individual contingent plans
![]() for
for
![]() , such that the following conditions hold: (i) given the sequences of prices and policies, the plans are optimal for the households; (ii) the labor market clears,
, such that the following conditions hold: (i) given the sequences of prices and policies, the plans are optimal for the households; (ii) the labor market clears,
![]() , in all
, in all ![]() ; (iii) the bond market clears,
; (iii) the bond market clears,
![]() , in all
, in all ![]() ; (iv) the government budget constraint
; (iv) the government budget constraint
![]() is satisfied in all
is satisfied in all ![]() ; and (v) the
aggregates are consistent with individual behavior,
; and (v) the
aggregates are consistent with individual behavior,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , in all
, in all ![]() . Note that the aggregates do not depend on the
extend of wealth inequality, because individual policies are linear in wealth.
. Note that the aggregates do not depend on the
extend of wealth inequality, because individual policies are linear in wealth.
Define
![]() . From Proposition 4.1, the equilibrium ratio of capital to effective wealth and the equilibrium mean return to savings are identical
across agents and can be expressed as functions of the capital stock and risk-free rate:
. From Proposition 4.1, the equilibrium ratio of capital to effective wealth and the equilibrium mean return to savings are identical
across agents and can be expressed as functions of the capital stock and risk-free rate:
![]() and
and
![]() . Similarly, the wage is
. Similarly, the wage is
![]() . Using this, aggregating the policy rules across agents, and imposing bond market clearing, we arrive at the following characterization
of the general equilibrium.
. Using this, aggregating the policy rules across agents, and imposing bond market clearing, we arrive at the following characterization
of the general equilibrium.
From this point on, and for simplicity, we let ![]() without loss of generality.4 The aggregate resource constraint of the economy is then:
without loss of generality.4 The aggregate resource constraint of the economy is then:
4.3 Steady state
The steady state is the fixed point of the dynamic system described in Proposition
![]() . The following proposition characterizes the steady state.
. The following proposition characterizes the steady state.
where
Equation
![]() combines stationarity of wealth from
combines stationarity of wealth from
![]() with the definition of the mean return to saving,
with the definition of the mean return to saving,
![]() . Note from
. Note from
![]() that wealth stationarity requires
that wealth stationarity requires
![]() , namely that the mean return to saving is equal to the marginal propensity to consume. But since
, namely that the mean return to saving is equal to the marginal propensity to consume. But since
![]() , it follows that
, it follows that
![]() in steady state. This is a manifestation of the precautionary saving motive, with a rationale similar to that in Aiyagari (1994).5 Equation
in steady state. This is a manifestation of the precautionary saving motive, with a rationale similar to that in Aiyagari (1994).5 Equation
![]() follows from stationarity of human wealth in
follows from stationarity of human wealth in
![]() , bond market clearing in
, bond market clearing in
![]() , and the government budget constraint.
, and the government budget constraint.
Lastly, we note that, in this model, as shown in Angeletos (2007), steady state capital is below complete markets, if and only if the elasticity of intertemporal substitution is higher than the ratio
![]() , where
, where ![]() is the fraction of total effective wealth invested in
capital. Here, because the elasticity of intertemporal substitution is 1 with log preferences, and because
is the fraction of total effective wealth invested in
capital. Here, because the elasticity of intertemporal substitution is 1 with log preferences, and because ![]() , the steady state aggregates will always be below the corresponding ones in complete markets.
, the steady state aggregates will always be below the corresponding ones in complete markets.
5 The ex ante optimal tax
The optimal tax in our framework is the one maximizing ex ante welfare. In particular, assume that at time ![]() the economy rests at an arbitrary steady state, and that the social planner
is considering implementing an unexpected policy change at some future time
the economy rests at an arbitrary steady state, and that the social planner
is considering implementing an unexpected policy change at some future time ![]() . The question posed from an ex ante perspective is: What is the impact of that policy change on agents'
welfare at time
. The question posed from an ex ante perspective is: What is the impact of that policy change on agents'
welfare at time ![]() , taking into account the entire transitional dynamics of the economy toward the new steady state resulting from the policy change? The tax maximizing agents' utility at
time
, taking into account the entire transitional dynamics of the economy toward the new steady state resulting from the policy change? The tax maximizing agents' utility at
time ![]() is then the (ex ante) optimal tax. We will first characterize the planner's problem of maximizing ex ante welfare, and then we will evaluate the solution of the problem in steady
state.6
is then the (ex ante) optimal tax. We will first characterize the planner's problem of maximizing ex ante welfare, and then we will evaluate the solution of the problem in steady
state.6
5.1 The planner's problem
From Proposition 4.1, it follows that the value function for an agent with initial wealth ![]() at
at ![]() , given the tax sequence
, given the tax sequence
![]() , is the solution to the problem:
, is the solution to the problem:
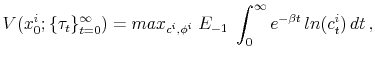 |
(20) |
where the maximands are the optimal policy functions described in Proposition 4.1.
The social planner's objective is to choose the tax sequence
![]() that maximizes ex ante expected utility, subject to the conditions for individual optimization and general equilibrium in section
that maximizes ex ante expected utility, subject to the conditions for individual optimization and general equilibrium in section
![]() . The planner's objective function,
. The planner's objective function, ![]() , is then weighted sum of agents' value functions,
, is then weighted sum of agents' value functions, ![]() , where the weights,
, where the weights,
![]() , depend on the initial wealth of each agent:
, depend on the initial wealth of each agent:
Without loss of generality, we will assume that at
subject to the following constraints:
Hence, at time
Therefore, the planner maximizes an objective consisting of two terms. The first captures the effect of the entire path of future prices and tax policies on effective wealth at time zero, ![]() . This is because effective wealth is the sum of asset holdings,
. This is because effective wealth is the sum of asset holdings,
![]() , which are historically given, and human wealth,
, which are historically given, and human wealth, ![]() , which is the
present discounted value of future wages and transfers (i.e. of future safe income), and therefore depends on the entire future path for the tax, the wage, the return to capital, and the interest rate. The second term in the planner's objective captures both the direct effects of the capital tax on
the mean return to saving and on the effective volatility of risk, as well as the indirect effects of the tax through the corresponding adjustment of the risky return,
, which is the
present discounted value of future wages and transfers (i.e. of future safe income), and therefore depends on the entire future path for the tax, the wage, the return to capital, and the interest rate. The second term in the planner's objective captures both the direct effects of the capital tax on
the mean return to saving and on the effective volatility of risk, as well as the indirect effects of the tax through the corresponding adjustment of the risky return, ![]() , the risk-free
rate,
, the risk-free
rate, ![]() , and portfolio allocation,
, and portfolio allocation, ![]() . Note that the term
. Note that the term
![]() in the planner's objective is actually the risk-adjusted return to saving,
in the planner's objective is actually the risk-adjusted return to saving,
![]() .
.
In other words, the planner has to weigh two considerations when choosing the optimal tax sequence. First, how the path of the taxes will affect the paths of wages and prices, thereby possibly maximizing time-zero wealth, ![]() , through
, through ![]() . Second, whether the path of the taxes will maximize the difference between the risk-adjusted return to saving,
. Second, whether the path of the taxes will maximize the difference between the risk-adjusted return to saving,
![]() , and the marginal propensity to consume,
, and the marginal propensity to consume, ![]() , i.e. the risk-adjusted
rate of growth of household consumption and wealth (see equation
, i.e. the risk-adjusted
rate of growth of household consumption and wealth (see equation
![]() ).
).
We can also see from
![]() that, if
that, if ![]() did not include human
wealth,
did not include human
wealth, ![]() , then
, then
![]() would be historically given and therefore not relevant for the planner's maximization problem. In turn, absence of human wealth means that there is only risky income in the
economy, as in an
would be historically given and therefore not relevant for the planner's maximization problem. In turn, absence of human wealth means that there is only risky income in the
economy, as in an ![]() version of our model. In that case, the planner chooses the path of taxes to maximize
version of our model. In that case, the planner chooses the path of taxes to maximize
![]() , which is exactly the difference between the risk-adjusted return to saving and the marginal propensity to consume, or the risk-adjusted growth rate of individual
consumption and wealth.
, which is exactly the difference between the risk-adjusted return to saving and the marginal propensity to consume, or the risk-adjusted growth rate of individual
consumption and wealth.
The next step is now to characterize each one of the derivatives in equation
![]() in turn. Simple differentiation of the objective function yields:
in turn. Simple differentiation of the objective function yields:
The calculation of the derivatives
![]() ,
,
![]() ,
,
![]() , and
, and
![]() is more complicated. Intuitively, these derivatives indicate the effect on the objective at time
is more complicated. Intuitively, these derivatives indicate the effect on the objective at time ![]() of a change in the functions
of a change in the functions ![]() ,
, ![]() , and
, and ![]() at time
at time ![]() , due to a tax change at that point in
time. Hence, the calculations use the definition of a functional derivative, with the Dirac delta function as the appropriate test function. In turn, the Dirac delta function allows for an impulse change in the functions at time
, due to a tax change at that point in
time. Hence, the calculations use the definition of a functional derivative, with the Dirac delta function as the appropriate test function. In turn, the Dirac delta function allows for an impulse change in the functions at time ![]() , due to a change in the tax at that time, while the functions remain unchanged at all other points in time. The outcome is:
, due to a change in the tax at that time, while the functions remain unchanged at all other points in time. The outcome is:
From
In order to calculate the derivative
![]() , note first that we can write
, note first that we can write ![]() as:
as:
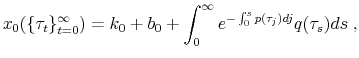 |
(34) |
where
are, respectively, the equilibrium after-tax interest rate and the equilibrium safe income from wages and transfers, both as a function of prices only. The latter is given by the sum of
where
This leaves us with the derivatives
![]() ,
,
![]() , and
, and
![]() . Unfortunately, we cannot explicitly characterize these derivatives along the transition. Therefore, in the next section, we will proceed to evaluate them in steady state.
. Unfortunately, we cannot explicitly characterize these derivatives along the transition. Therefore, in the next section, we will proceed to evaluate them in steady state.
5.2 Evaluating the ex ante optimal tax in steady state
In this section, we will evaluate the ex ante optimal policy in steady state.7 In steady state, and using the fact that
![]() ,
, ![]() , and
, and ![]() , the aggregate resource constraint
, the aggregate resource constraint
![]() yields:
yields:
Substituting this as well as portfolio allocation from
![\displaystyle (1-\tau)(1-\phi)(\frac{\alpha \beta}{\phi}-\phi \sigma^2 (1-\tau))-\beta[1-(1-\tau)\alpha]=0 \;.](img207.gif) |
Define the left-hand-side of this equation as:
![\displaystyle G(\phi, \tau) \equiv (1-\tau)(\frac{\alpha \beta}{\phi}-\phi \sigma^2 (1-\tau))(1-\phi)-\beta[1-(1-\tau)\alpha]](img208.gif) |
(41) |
From the implicity function theorem it follows that:
where
Hence,
At this point, note also that, since
![]() , it follows:
, it follows:
Therefore, when
We can show that
This completes the derivation of all the equations needed to evaluate the planner's first order condition
![]() in steady state. Plugging everything we have derived so far into
in steady state. Plugging everything we have derived so far into
![]() , imposing steady state, doing some algebra, and using the notation
, imposing steady state, doing some algebra, and using the notation ![]() to denote the derivative of a variable
to denote the derivative of a variable ![]() with respect to the tax in steady state, we get that the optimal tax in steady state solves:
with respect to the tax in steady state, we get that the optimal tax in steady state solves:
where the second term is zero as
where
In other words, conditions
If the optimal tax turns out to be positive, then it also maximizes aggregate capital, ![]() , and aggregate consumption,
, and aggregate consumption, ![]() , in addition to also maximizing human wealth,
, in addition to also maximizing human wealth, ![]() . This case is illustrated in Figure
. This case is illustrated in Figure
![]() . The top left panel plots the planner's first order condition
. The top left panel plots the planner's first order condition
![]() , evaluated at steady state, against the capital tax. The optimal tax is determined at the point where the first order condition curve intersects
the horizontal axis, which in this example occurs at
, evaluated at steady state, against the capital tax. The optimal tax is determined at the point where the first order condition curve intersects
the horizontal axis, which in this example occurs at ![]() . At that point,
. At that point,
![]() , as shown in the top right panel, which means that the share of wealth invested in risky capital is at a maximum. Furthermore, the bottom left and rights panels show that
aggregate capital,
, as shown in the top right panel, which means that the share of wealth invested in risky capital is at a maximum. Furthermore, the bottom left and rights panels show that
aggregate capital, ![]() , and human wealth,
, and human wealth, ![]() , also attain their maximum at the same
tax.
, also attain their maximum at the same
tax.
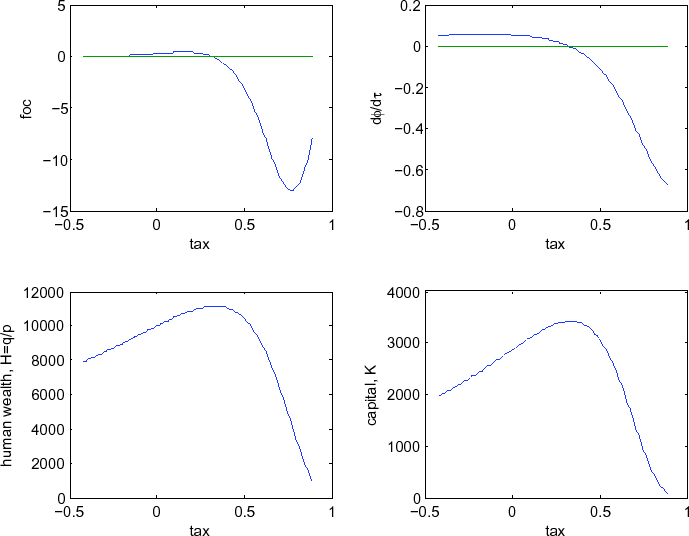
If the optimal tax is negative, then it will not maximize capital and, for example, capital may be falling at the optimum. This case is illustrated in Figure
![]() . The top left panel again plots the planner's first order condition
. The top left panel again plots the planner's first order condition
![]() , evaluated at steady state, and shows that the optimal tax is actually a subsidy at
, evaluated at steady state, and shows that the optimal tax is actually a subsidy at
![]() . The top right panel show that, at the optimal tax,
. The top right panel show that, at the optimal tax,
![]() , which means that the share of capital in wealth is falling at the optimum. The bottom left panel captures the fact that, at the optimum, human wealth is at a maximum, as
shown in Proposition
, which means that the share of capital in wealth is falling at the optimum. The bottom left panel captures the fact that, at the optimum, human wealth is at a maximum, as
shown in Proposition
![]() . The bottom right panel shows that, as is the case with
. The bottom right panel shows that, as is the case with ![]() , capital is also falling at the optimum. Note that this is a case where
, capital is also falling at the optimum. Note that this is a case where
![]() , whereas the rest of the parameters remain as in Figure
, whereas the rest of the parameters remain as in Figure
![]() . We could also obtain results of similar flavor if we set
. We could also obtain results of similar flavor if we set
![]() , while keeping the rest of the parameters as in Figure
, while keeping the rest of the parameters as in Figure
![]() . In other words, when risk in the economy is below a minimum lower bound, as captured either by low volatility of risk or low returns to the
risky asset in the production, then the planner finds it optimal to subsidize capital. This increases the effective variance of risk, but it also increases capital accumulation, as capital is a decreasing function of the tax. The agents can in fact undertake this increase in risk endogenously,
because the exogenous risk in the economy was too low to begin with.
. In other words, when risk in the economy is below a minimum lower bound, as captured either by low volatility of risk or low returns to the
risky asset in the production, then the planner finds it optimal to subsidize capital. This increases the effective variance of risk, but it also increases capital accumulation, as capital is a decreasing function of the tax. The agents can in fact undertake this increase in risk endogenously,
because the exogenous risk in the economy was too low to begin with.
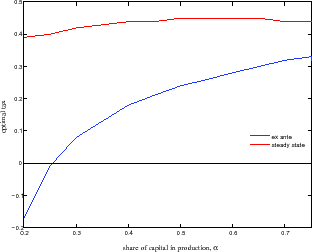
Hence, as already discussed, the optimal tax is always the one that maximizes the steady state value of human wealth, ![]() . However, at the optimum, capital and the rest of the aggregates
will either be at a maximum or they will be falling with the tax. Calibrations show that the latter will be the case when the variance of idiosyncratic risk,
. However, at the optimum, capital and the rest of the aggregates
will either be at a maximum or they will be falling with the tax. Calibrations show that the latter will be the case when the variance of idiosyncratic risk, ![]() is very low, see Figure
3, panel (b). This is a case where basically there is not enough risk taking in the economy. By subsidizing capital, the planner increases the effective variance of risk,
is very low, see Figure
3, panel (b). This is a case where basically there is not enough risk taking in the economy. By subsidizing capital, the planner increases the effective variance of risk,
![]() , and also levies a lump sum tax on agents, thereby reducing their human wealth. In addition, because capital is falling all the way with the tax, the subsidy increases
capital accumulation, which translates into endogenously higher risk taking in the economy. Agents are actually able to undertake this endogenous increase in risk, as the exogenous variance of risk,
, and also levies a lump sum tax on agents, thereby reducing their human wealth. In addition, because capital is falling all the way with the tax, the subsidy increases
capital accumulation, which translates into endogenously higher risk taking in the economy. Agents are actually able to undertake this endogenous increase in risk, as the exogenous variance of risk, ![]() , was very low to begin with.
, was very low to begin with.
5.3 A simple example: the AK model
The ![]() version of the present model is the one where there is no safe income in the economy, such as income from wages or government transfers. In this case, human wealth is zero,
version of the present model is the one where there is no safe income in the economy, such as income from wages or government transfers. In this case, human wealth is zero,
![]() . Hence, as already mentioned in section
. Hence, as already mentioned in section
![]() and indicated in Proposition
and indicated in Proposition
![]() , the planner then maximizes the difference between the risk-adjusted return to saving,
, the planner then maximizes the difference between the risk-adjusted return to saving,
![]() , and the marginal propensity to consume,
, and the marginal propensity to consume, ![]() , i.e. the risk-adjusted
rate of growth of consumption and wealth. In that case, the planner's first order condition becomes:
, i.e. the risk-adjusted
rate of growth of consumption and wealth. In that case, the planner's first order condition becomes:
Note that in the
 |
(53) |
Note that this is the case even off the steady state (we have not imposed any steady state restrictions here), and therefore the optimal tax in the
6 Conclusions
We study the optimal taxation of capital in a Ramsey setting of a general-equilibrium heterogeneous-agent economy with uninsurable idiosyncratic investment or capital-income risk. We prove that the ex ante optimal tax, evaluated at steady state, maximizes human wealth, namely the present discounted value of agents' income from sources that are not subject to capital risk. Furthermore, when the amount of idiosyncratic risk in the economy is higher than a minimum lower bound, the optimal tax is positive and it is precisely the tax that maximizes the economy-wide aggregates, such as the capital stock and output. By contrast, when the amount of risk is exogenously very low, the social planner finds it optimal to increase social risk taking by subsidizing investment in capital.
Our paper contributes to the optimal taxation literature in the Ramsey tradition, though also allowing for lump-sum transfers, and it shows that the rationale for positive capital income taxation in the long run does not necessarily extend to the case where markets are incomplete due to the presence of idiosyncratic capital income risk. However, regardless of whether the ex ante optimal tax is positive or negative, the planner's motivation for setting the optimal tax is always related to ensuring a sufficient amount of social risk taking. When the exogenous risk in the economy is sufficiently high, then the optimal capital tax is positive, so that the ensuing general equilibrium adjustment of the interest rate endogenously provides agents with the insurance they need to undertake risky capital investment, despite the fact that the tax tends to reduce the mean return to saving. When the exogenous risk in the economy is sufficiently low, then the optimal capital tax is negative, so that the capital subsidy encourages capital accumulation directly, by increasing the mean return to capital, despite the fact that the subsidy tends to reduce the interest rate and therefore wealth accumulation. This is because risk was low enough to begin with, and therefore the agents can tolerate the increase in the variance of risk resulting from the subsidy, both directly and indirectly through its general equilibrium effects. In both cases, the outcome of the optimal tax is therefore higher investment in the risky asset, higher capital accumulation, and a higher amount of social risk taking in the economy.
References
Ahsan, S.M., 1976. Taxation in a two-period temporal model of consumption and portfolio allocation. Journal of Public Economics 5, 337-352.
Aiyagari, S.R., 1994. Uninsured idiosyncratic risk and aggregate saving. Quarterly Journal of Economics 109, 659-684.
Aiyagari, S.R., 1995. Optimal capital income taxation with incomplete markets, borrowing constraints, and constant discounting. Journal of Political Economy 103, 1158-1175.
Albanesi, S., 2006. Optimal taxation of entrepreneurial capital with private information. NBER Working Paper 12419.
Albanesi, S., Sleet, C., 2006. Dynamic optimal taxation with private information. Review of Economic Studies 73, 1-30.
Angeletos, G.-M., 2007. Uninsured idiosyncratic investment risk and aggregate saving. Review of Economic Dynamics 10, 1-30.
Angeletos, G.-M., Panousi, V., 2009. Revisiting the supply-side effects of government spending. Journal of Monetary Economics 56, 137-153.
Atkeson, A., Chari, V.V., Kehoe, P.J., 1999. Taxing capital income: a bad idea. Quarterly Review, Federal Reserve Bank of Minneapolis, Summer issue, 3-17.
Chamley, C., 1986. Optimal taxation of capital income in general equilibrium with infinite lives. Econometrica 54, 607-622.
Chamley, C., 2001. Capital income taxation, wealth distribution and borrowing constraints. Journal of Public Economics 79, 55-69.
Conesa, C., Kitao, S., Krueger, D., 2009. Taxing capital? Not a bad idea after all! American Economic Review 99, 25-48.
Correia, I.H., 1996. Should capital income be taxed in the steady state? Journal of Public Economics 60, 147-151.
Davila, J., Hong, J. H., Krusell, P., Ríos-Rull, J.-V., 2007. Constrained efficiency in the neoclassical growth model with uninsurable idiosyncratic shocks. PIER Working Paper Archive, Penn Institute for Economic Research.
Diamond, P.A., Mirrlees, J.A., 1978. A model of social insurance with variable retirement. Journal of Public Economics 10, 295-336.
Domar, E.D., Musgrave, R.S., 1944. Proportional income taxation and risk-taking. Quarterly Journal of Economics 58, 388-422.
Erosa, A., Gervais, M., 2002. Optimal taxation in life-cycle economies. Journal of Economic Theory 105, 338-369.
Farhi, E., Werning, I., 2010. Insurance and taxation over the life cycle. Working paper.
Garriga, C., 2001. Optimal Fiscal Policy in Overlapping Generations Models, Universitat de Barcelona working paper.
Golosov, M., Kocherlakota, N., Tsyvinski, A., 2003. Optimal indirect and capital taxation. Review of Economic Studies 70, 569-587.
Golosov, M., Troshkin, M., Tsyvinski, A., Weinzierl, M., 2012. Preference heterogeneity and optimal commodity taxation. Working paper.
Judd, K.L., 1985. Redistributive taxation in a simple perfect foresight model. Journal of Public Economics 28, 59-83.
Kanbur, S.M., 1981. Risk taking and taxation. Journal of Public Economics 15, 163-184.
Moskowitz, T., Vissing-Jorgensen, A., 2002. The returns to entrepreneurial investment: A private equity premium puzzle? American Economic Review 92, 745-778.
Panousi, V., Papanikolaou, D., 2012. Investment, idiosyncratic risk, and ownership. Journal of Finance (forthcoming, June).
Panousi, V., 2012. Capital taxation with entrepreneurial risk. Federal Reserve Board mimeo.
Peterman, W.B., 2011. The effect of endogenous human capital accumulation on optimal taxation. Federal Reserve Board working paper.
Sandmo, A., 1977. Portfolio theory, asset demand and taxation: Comparative statics with many assets. Review of Economic Studies 44, 369-379.
Shourideh, A., 2011. Optimal taxation of capital income: A Mirrleesian approach to capital accumulation. Working paper.
Stiglitz, J.E., 1969. The effects of income, wealth, and capital gains taxation on risk-taking. Quarterly Journal of Economics 83, 263-283.
Varian, H.R., 1980. Redistributive taxation as social insurance. Journal of Public Economics 14, 49-68.
 |
 |
|
[Share of Capital]
Figure
[Volatility of Risk] 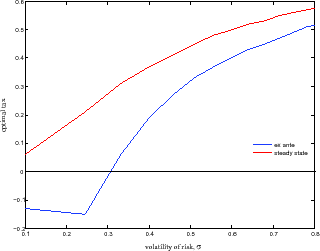
[Discount Factor] 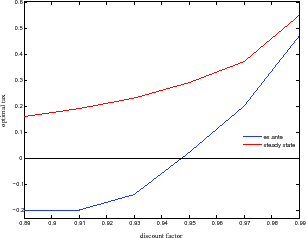 |
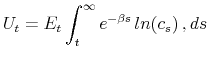
![\displaystyle 0=[\;\tau_t\,(\,F_{K_t}(\int_{i}k^i_t,1)-\delta\,)\,\int_{i}k^i_t-G_t-T_t\;]\;dt\,,](img38.gif)
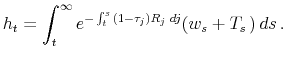
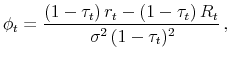
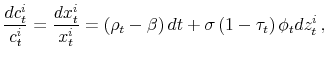
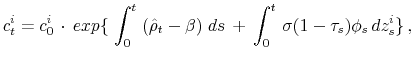
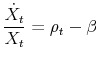
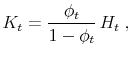
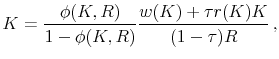
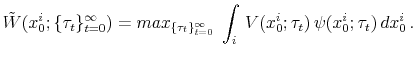
![\displaystyle \tilde{W}(x^i_0; \{\tau_t\}_{t=0}^{\infty}) = \int_{0}^{\infty} e^{-\beta t} \{ ln(\beta x^i_0) + \int_{0}^{t} [(1-\tau_s)r_s\phi_s+(1-\tau_s)R_s(1-\phi_s)-\beta-\frac{1}{2}\sigma^2 (1-\tau_s)^2 \phi_s^2] ds \} dt \;,](img136.gif)
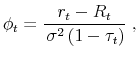
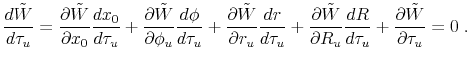
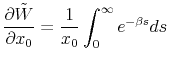
![\displaystyle \frac{\partial \tilde{W}}{\partial \phi_u}= [(1-\tau_u)r_u-(1-\tau_u)R_u-\sigma^2 (1-\tau_u)^2 \phi_u]\int_{u}^{\infty} e^{-\beta s} ds \;](img167.gif)
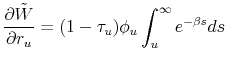
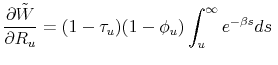
![\displaystyle \frac{\partial \tilde{W}}{\partial \tau_u}= [-r_u\phi_u-R_u(1-\phi_u)+\sigma^2(1-\tau_u)\phi_u^2] \int_{u}^{\infty} e^{-\beta s}ds \;.](img170.gif)
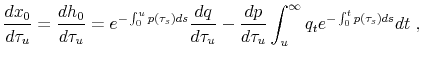
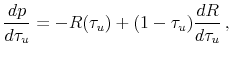
![\displaystyle \frac{dq}{d \tau_u}= \alpha^{1/(1-\alpha)} r(\tau_u)^{\alpha/(\alpha-1)}+ [(1-\alpha) \alpha^{\alpha/(1-\alpha)}+\tau_{u} \alpha^{1/(1-\alpha)}]\alpha (\alpha-1)^{-1}r(\tau_u)^{1/(\alpha-1)}\frac{d r}{d \tau_u} \;.](img196.gif)
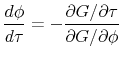
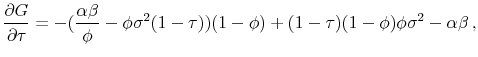
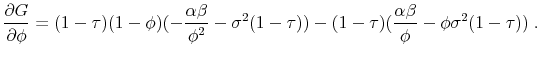
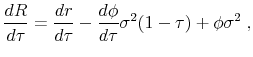
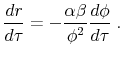


![\displaystyle \lim_{u \rightarrow \infty} \{ (q_{\tau}-p_{\tau}\frac{q}{p})+x_0[(1-\tau)\phi r_{\tau}+(1-\tau)(1-\phi)R_{\tau}-R]\frac{e^{-\beta u}}{e^{-pu}} \}=0](img236.gif)