
Financial Stress and Economic Dynamics: the transmission of crises*
Keywords: Nonlinearity, Markov switching, financial crises, monetary policy transmission
Abstract:
1 Introduction
The United States continues to struggle to crawl out from under the financial crisis of 2008-9 and the ensuing recession. By most accounts, the roots of the crisis were the bursting of the housing bubble and the associated collapse of the market for mortgage backed securities. The resulting turmoil spread across a number of asset classes and markets, enhancing counterparty risks, seizing up interbank funding markets, severely aggravating liquidity problems among banks, sharply widening risky spreads in capital markets, and leading ultimately to the collapse of major financial institutions. The macroeconomic implications were severe and long lived: As financial market developments fed real-side economic outcomes and vice versa, U.S. stock market wealth fell from its peak in 2007 by 50 percent, real estate wealth declined by an unprecedented 15 percent, while the unemployment rate doubled in less than two years.1 At the time, there were few if any macroeconomic models up to the task of explaining this outcome, even after the fact.
Financial factors have long been recognized as being important for understanding macroeconomic dynamics; for examples see Bernanke and Blinder (1988) and Kashyup, Stein and Wilcox (1993). And yet the inclusion of financial frictions within dynamic stochastic general equilibrium (DSGE) models has been a notably recent phenomenon. One reason why modeling financial frictions was neglected is that it is empirically challenging. As the survey articles by Kashyup and Stein (1994) and Hubbard (1998) make clear, it has been remarkably difficult to uncover significant effects of financial frictions in macroeconomic time-series data. Indeed, with the noteworthy exceptions of Carlstrom and Fuerst (1997) and Bernanke, Gertler and Gilchrist (BGG 1999), DSGE models with financial frictions have all sprung out of the experience of the recent financial crisis and subsequent recession. In this paper, we will argue that a reason why statistically significant and macroeconomically important linkages have been elusive is because the importance of financial factors tend to be episodic in nature. In "normal times," firms make investment decisions on the basis of whether a project's expected rate of return exceeds the after-tax user cost of capital, and then having made that decision, seek the financing that completes the deal that has already been decided. In such times, the financing decision is, in some sense, subordinate to all the real-side decisions the firm must undertake, at least with established firms in advanced countries where banking and financial systems are efficient; finance "doesn't matter." In other times, however, when the financial system is not operating normally, financing cannot be taken as given, even for some well-established firms. Financial frictions, stemming from information asymmetries and the associated moral hazard issues, become important as firms find that lending terms and standards tighten, rendering the interest rate a much less reliable metric of the cost of funds, broadly defined. During such times, which we will call stress events, the terms of credit and indeed its availability cannot be taken for granted; in such circumstances, credit can seem like it is the only thing that matters.
Our contention that there are stress events that are episodic in nature, together with the associated interdependency of the financial sector and the macroeconomy, leads us to examine the issue in a nonlinear, multivariate framework. In particular, we build on the work of Sims, Waggoner and Zha (SWZ 2008) by employing a richly parameterized Markov switching vector autoregression (MS-VAR) model, estimated with Bayesian methods.2 Our primary focus is on whether the economy behaves differently during periods of high stress, as the story sketched above suggests. Does the economy propagate shocks--transmit crises--differently during such periods? Thus we will investigate whether the VAR coefficients shift over time, and whether these shifts coincide with established events in U.S. economic and financial history. Mindful of the possibility that financial stress could arise from a rare event shock, we also explicitly allow for switching in the variances of shocks--or variance switching, for short. Besides being an important issue in its own right, allowing for variance switching is important to avoid biasing results toward the erroneous finding of coefficient switching. As in the literature on the sources of the great moderation, variance switching and coefficient switching are rivals in explaining the data.3 And just as authors have debated explaining whether it was "good luck," as represented by time variation in the variances of shocks, that explains the great moderation, or whether it was "good policy," as represented by shifts in policy rule coefficients, similar issues in econometrics and inference arise here.
In carrying out this research, we introduce a financial stress index that was formulated and used by the Federal Reserve Board staff during the crisis--on the fly, as it were--to analyze financial conditions and their macroeconomic consequences. Thus, a second contribution of this paper will be assessing the efficacy of this measure of financial stress for nowcasting the economic and financial environment.
Ours is not the first paper in this area, broadly defined. Since the onset of the crisis, DSGE models with financial frictions have sprung up, building on the canonical DSGE papers of BGG (1999), Christiano, Eichenbaum and Evans (2005) and Smets and Wouters (2007), including Iacoviello (2005), Gertler, Gilchrist and Natalucci (2007), Curdia and Woodford (2009) and Jermann and Quadrini (2012). These papers have added insight to thinking about financial frictions as a source of shock amplification, but in most instances, their depiction of model economies allows for a single time-invariant steady state; no role for instability, volatility dynamics or important nonlinear effects is considered. There are also Markov switching DSGE models, including Liu, Waggoner and Zha (2010). However, Liu et al. is focussed on the ordinary ups and downs of business cycles, rather than financial stress.4 The myriad ways in which financial stress manifests itself--widened spreads of risky bonds over Treasury bond rates, jumps in volatility, substantial increases in liquidity premiums in bond markets, shifts in the equity premium--together with the multiplicity of channels through which stress can operate, leads us to avoid the restrictions implied by a DSGE model, at least until the literature identifies the most important channels of effect. The MS-VAR model is particularly appropriate to model the abrupt, discrete changes in economic dynamics as observed during the recent crisis and as we will document below. Among the empirical models in the area, Lown and Morgan (2006) examine the interaction of real variables and the responses to the Fed's Senior Loan Officers' Opinion Survey in a quarterly time-invariant VAR. Among the very few Markov switching models that pay attention to financial stress that we are aware of is Davig and Hakkio (2010) who, like us, employ an index of financial stress; however, their model is much simpler than ours and omits any consideration of monetary policy or price determination. Kaufmann and Valderama (2007) look at switching in VAR models with credit and asset prices, but do not examine financial stress.5
To presage the results, taking a standard, time-invariant Gaussian VAR model as a benchmark, we find substantial evidence of nonlinearities or non-Gaussian shock processes--the linkage between financial stress and the macroeconomy is not well described by the simple linear benchmark. Second, variance switching alone is not sufficient to characterize departures from the benchmark model; unlike the business cycle characterization of SZ (2006), or the depiction of the drivers of the most recent recession described by Stock and Watson (2012), both of which explain the phenomena under study as arising from unusual sequences of shocks, we find that coefficient switching--and hence, nonlinear dynamics--is an important part of the mechanism linking financial stress and macroeconomic outcomes.6 Third, we find that the financial stress index we use is a useful tool that can aid in capturing periods of financial stress in quasi-real time. Fourth, our results suggest that conventional monetary policy is not particularly effective in times of high financial stress; a much more powerful tool is to induce a switch from a high-stress state back to "normal times." We argue that these results have meaningful implications for the construction of DSGE models. While linearized DSGE models may be useful for thinking about garden variety business fluctuations and how financial factors can amplify shocks, to the extent that one is interested in the sort of dynamics that underscored the 2008-9 financial crisis--which, after all, was the motivation for many or most of the models in this area--linearized DSGE models will not be up to the task. Rather, MS-DSGE models, such as F. Bianchi (2011), or fully articulated nonlinear models that are solved with global methods are better equipped for the job. Examples of the latter include Brunnermeir and Sannikov (2010). Mendoza (2010), He and Krishnamurthy (2012), and J. Bianchi (2011).7 On the empirical side, it also follows that inference regarding the relationship between financial stress and the macroeconomy that is gleaned from a constant-parameter model may be inappropriate.
The remainder of the paper proceeds as follows. In section 2, we discuss the history of financial stress in the United States. We also introduce our data and link these events to the data. The third section discusses our modeling framework and econometric strategy while the fourth presents our results. A fifth and final section sums up and concludes.
2.1 Some history
To casual observers, financial stress would seem like a recent phenomenon. But it has been more prevalent than one might think. Students of banking history know that there were banking crises in the U.S. in 1837, 1857, 1873, 1907 and 1933. It is only recently that crises have become rare. But the absence of full-blown crises does not mean that there has not been episodes of financial stress. Table 2.1 lays out some events over the last twenty years that have buffeted financial markets.
Table 2.1 Selected Financial Events Affecting the US Economy, 1986-2011
| Event description | Date(s) | |
| a | Savings & loan (S&L) crisis and its aftermath | 1986-1992 |
| b | Iraqi invation of Kuwait | August 2, 1990 |
| c | Mexican peso crisis | Dec. 1994-1995 |
| d | Asia crisis | July 1997-1999 |
| e | Decline and fall of Long-Term Capital Management (LTCM) | May-Sept. 1998 |
| f | Russian debt default | Aug. 1998 |
| g | Technology bubble bursts (NASDAQ descent) | Mar '00-Apr '01 |
| h | Enron scandal and bankruptcy | Oct.-Nov. 2001 |
| i | Argentine financial crisis | Dec. 2001-2002 |
| j | Bear Stearns halts redemptions from two of its funds | July 17, 2007 |
| k | Fed announces Term Auction Facility (TAF) | Dec. 12, 2007 |
| l | "Exigent circumstances" leads to TSLF and PDCF; Bear Stearns sold. | March 2008 |
| m | AIG announces imminent bankrupty, gets bailed out | Sept. 16, 2008 |
| n | Lehmann Brothers declares bankruptcy | Sept. 14, 2008 |
| o | Congress passes Troubled Asset Relief Program (TARP) | Oct. 3, 2008 |
| p | Term Asset-backed Securities Loan Facility (TALF) announced | Nov. 25, 2008 |
| q | Treasury department announces stress tests | Feb. 10, 2009 |
| r | US bank stress test results released | May 7, 2009 |
| s | Greek government admits deficit-to-GDP ratio of 12 percent | Oct 18, 2009 |
| t | First Eurozone-IMF rescue plan completed | May 2, 2010 |
| u | ECB offers massive loans to distressed banks | Dec. 21, 2012 |
There were financial crises long before troubles at hedge funds owned by Bear Stearns showed up in the spring of 2007. Many of these originated from outside the country, but not the S&L crisis wherein more than a thousand mostly small, regional financial institutions collapsed in the late 1980s and early 1990s. The S&L crisis has been cited as both a cause and a propagation mechanism of the 1991 recession and the subsequent "jobless recovery".
2.2 A Financial Stress Index
As the financial crisis began to take hold in 2007, the paucity of financial channels in the Board staff's macromodels became apparent. To augment the existing models, and to capture the higher frequency dynamics that no quarterly model could absorb in real time, a Financial Stress Index (FSI) for the United States was constructed. Built up from daily data, the earliest versions were used for more-or-less instantaneous assessment of developments as they unfolded.8 To be clear, our purpose here is not to construct the best, ex post, measure of financial stress; it seems likely that any such index would turn out to be optimal only for a particular episode in history. We are interested in this index in part because it was used by the Board's staff during the crisis; indeed, one of us was involved in its use during this period. Thus, one contribution of this paper will be our ability to assess whether the construction and use of this particular FSI was a helpful step for the Board's staff to have undertaken.
The index is focussed on capital market measures of stress, as opposed to banking measures. There are costs and benefits associated with this focus. As we noted in the introduction, financial stress manifests itself through both price and non-price channels, and in both capital markets and in
banking. A common source of data for (something like) stress in banking is the Senior Loan Officer Opinion Survey (SLOOS), also a product of the Federal Reserve.9 The merits of the SLOOS, are aptly demonstrated by Lown and Morgan (2008). However, for our purposes, the fact that it is a quarterly survey and only comes out a month or so after the survey is conducted represents a significant drawback, as does the short sample of the
SLOOS. There are capital-markets based measures of banking stress, such as the well-known TED spread, but these too have own problems.10 Finally, there are
other indexes of financial stress, including some constructed by the Federal Reserve Banks, that mostly use principal components analysis of fairly large numbers of series, including some we use, as well as banking related series, and the levels of interest rates which we prefer to avoid.11 They share some similarities to the one we use. However, none of these series goes back as far as ours and not all are available at daily frequency.12![]() 13
13
Table 2.2 below describes the constituent parts of the FSI. As can be seen, the index includes two variables that measure risky spreads on bonds (#1 and 2), two that capture liquidity premiums on bonds (#6 and 7),14 three variables that capture market volatility as measured from options prices (#4, 5 and 9) in bond and equity markets, a variable measuring the slope of the term structure at the short end (#3) and finally a measure of the equity premium (#8). Data availability limits the start date of the (monthly version of the) index to 1988:12; the last observation we use is 2011:12, leaving 277 observations.
Table 2.2 Components of the Federal Reserve Board staff's Financial Stress Index![]()
| # | Description | Source | Std.dev. |
| 1. | AA bond rate-Treasury spread, const. maturity | Merrill L. & Bloomberg | 66.3 |
| 2. | BBB bond rate-Treasury spread, const. maturity | Merrill L. & Bloomberg | 96.2 |
| 3. | Federal funds rate less 2-yr Treasury yield | FRB & Bloomberg | 0.70 |
| 4. | 10-year Treasury bond implied volatility | Bloomberg | 1.40 |
| 5. | Private long-term bond implied volatility | Bloomberg | 2.30 |
| 6. | 10-year Treasury on-the-run premium | Bloomberg | 9.43 |
| 7. | 2-year Treasury on-the-run premium | Bloomberg | 3.60 |
| 8. | S&P 500 earnings/price less 10-year Treasury | I/B/E/S & FRB | 2.01 |
| 9. | S&P 100 implied volatility (VIX) | Bloomberg | 8.53 |
The components of the FSI capture different aspects of risk and uncertainty in capital markets. Risk premiums, for example, reflect default risk whereas liquidity premia capture unwillingness to trade. The two concepts are likely to be associated but are not the same. Table 2.3 shows the correlation matrix for the series. In general, the components are correlated, of course, and sometimes quite strongly, but not so much that one would argue that a series is redundant.
Table 2.3 Correlation coefficients on components of Financial Stress Index![]()
| 1 | |||||||||
|
|
0.94 | 1 | |||||||
| 0.27 | 0.15 | 1 | |||||||
| 0.53 | 0.61 | -0.20 | 1 | ||||||
| 0.67 | 0.73 | -0.12 | 0.86 | 1 | |||||
| 0.69 | 0.75 | -0.04 | 0.56 | 0.57 | 1 | ||||
| 0.22 | 0.21 | 0.25 | 0.06 | 0.04 | 0.28 | 1 | |||
|
|
0.55 | 0.47 | 0.14 | 0.24 | 0.52 | 0.09 | -0.30 | 1 | |
| 0.76 | 0.77 | 0.25 | 0.55 | 0.64 | 0.67 | 0.32 | 0.20 | 1 |
Figure 2.1 shows the FSI at a monthly frequency. The first thing to notice about the index itself is that it does not look like a stationary process with Gaussian disturbances; rather, the index appears to have lengthy periods of low stress with modest fluctuations, together with shorter episodes of high and volatile stress. This impression is reinforced by our overlay of some of the key dates in US financial history discussed in the previous subsection. Clearly, the periods of what the unaided eye sees as high stress are associated with well-known events in financial history. At the same time, however, it must be said that the period beginning with the forced merger of Bear Stearns stands out as one of particularly high stress. In an appendix on robustness, we investigate perturbations to our measure of financial stress. On the other hand, it is not the case that every headline generating event manifests itself in high stress: the Peso crisis in 1994-95 generated much discussion, and a great deal of activity at the U.S. Treasury, and yet resulted in scarcely any movement in the FSI.
3.1 The model
Our investigation is concerned with uncovering nonlinear and possibly state-dependent relationships between financial stress--which appears, at least superficially, to have non-linear univariate dynamics--and key macroeconomic variables. The Markov-switching framework is ideal for our purposes for several reasons. First, and most obviously, it provides a formal framework to investigate the presence of nonlinearities. Moreover, it does so by allowing discrete shifts, which for the questions under study, is more appropriate than the alternative time-varying parameters framework since drifting parameters will be unable to pick up the flight-to-safety phenomena that often occurs in financial markets. Second, it can distinguish between variance switching as the source of time variation, and coefficient switching that alters the transmission of financial shocks to the real economy.
2.1: FRB Staff Financial Stress Index Regime switching in coefficients would suggest either that agents change their behavior during episodes of high financial stress, or that the environment they face is materially different; taken at face value, regime switching in shocks would suggest that financial crises are a matter of happenstance. And third, the MS-VAR framework allows us to investigate feedback and potential amplification effects between the real and the financial sector.The combination of high dimensionality of the model we have in mind combined with the relatively short sample of data with which we must work presents a challenge from an econometric point of view. Fortunately, recent advances in econometrics facilitate our investigation. In particular, we employ state-of-the-art Bayesian econometric tools for MS-VAR models, as developed by SWZ (2008). In this section, we lay out the basic model and discuss our methodology.
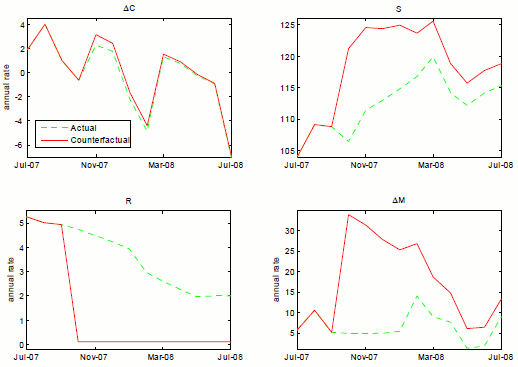
We consider (possibly) nonlinear vector stochastic processes of the following form:
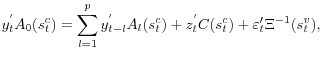 |
(3.1) |
where
| (3.2) |
Let
then the model can be written as
where ![]() is the sample size. Let us designate
is the sample size. Let us designate ![]()
![]() as the vector
as the vector ![]() stacked in the time dimension. We
assume that the structural disturbances are normal, conditional on the state:
stacked in the time dimension. We
assume that the structural disturbances are normal, conditional on the state:
The reduced-form system is then:
with
As can be seen in equations (3.5) through (3.7), the reduced form contains structural parameters and shocks that make distinguishing regime switching impossible, whereas it is possible in the structural form, equations (3.3). More important for our application, notice that switching in the coefficients,
In December 2008 the Federal Reserve reduced the federal funds rate to its effective lower bound where it stayed for the remainder of our sample ending in December 2011. In the context of a Markov switching model, the effective lower bound is handled in two ways. First, and most straightforwardly, the effective lower bound can be thought of as simply another regime which the model can pick out, if warranted. Specifically, once the effective lower bound is obtained, the perception, if applicable, that the funds rate can fall no further would be captured by switching in coefficients that would rule out shocks from equations other than the federal funds rate equation resulting in negative values of the funds rate, plus switching in shock variances such that negative shocks to the funds rate do not obtain.16Second, there could be a change in the relatiionship between the federal funds rate and the stock of money either directly because of the effective lower bound, or because of nonstardard monetary policy measures that take stand in for conventional monetary policy. Indeed, this is one reason why money growth is included in our model. Thus, the model can, in principle, pick out new states to capture the effective lower bound.
Finally, we will be interested in comparing our preferred MS-VAR model with a constant-parameter, constant-variance version, which imposes the restriction ![]() .
.
3.2 Model Estimation and Evaluation
We employ a blockwise optimization algorithm to estimate the posterior mode, as described in SWZ08 that improves over, for example, the MCEM method proposed by Chib (1996), which can be very time-consuming, particularly for large-dimensional systems. In a first step, parameters are divided into blocks and the resulting initial guesses for the parameters are used in a hill-climbing quasi-Newton optimization routine.
To evaluate our models, we use a number of criteria--not merely goodness of fit--as discussed below. Within the realm of fit, however, consistent with standard practice in the Bayesian literature, we compare the marginal data densities (MDDs) of candidate specifications. A number of alternative methods have been promoted for computing MDDs, beginning with the standard modified harmonic mean (MHM) calculation of Gelfand and Dey (1994). However, it has been established that the MHM computation is not likely to work well with models whose posterior distributions may be far from Gaussian as is the case with many Markov switching models. At least three alternatives have been proposed, that use weighting functions to approximate the unknown posterior distribution, including the bridge method of Meng and Wong (1996), a method suggested by Ulrich Müeller of Princeton University in an unpublished paper, and a method by Waggoner and Zha (2011), Appendix B. We used all three methods and came up with conflicting results. To address the issue, we carried out trials with artificial data created using a model like ours and found that the method of SWZ (2008) was the most reliable for our purposes.17 In the appendix, we offer a few remarks about computation.
4 Macro-financial Linkages and Financial Stress
We focus on five-variable MS-VARs identified using the well-known Choleski decomposition.18 In particular, let
![]() where
where ![]() is the monthly growth in personal consumption expenditures (PCE);
is the monthly growth in personal consumption expenditures (PCE); ![]() is CPI inflation, excluding food and energy prices (hereinafter, core
inflation);
is CPI inflation, excluding food and energy prices (hereinafter, core
inflation); ![]() is the nominal federal funds rate;
is the nominal federal funds rate; ![]() is growth in the nominal M2
monetary aggregate; and
is growth in the nominal M2
monetary aggregate; and ![]() represents the financial stress index. All variables are monthly (or monthly averages of daily rates, where applicable), seasonally adjusted, and expressed at annual
rates. The data run from 1988:12 to 2011:12.19
represents the financial stress index. All variables are monthly (or monthly averages of daily rates, where applicable), seasonally adjusted, and expressed at annual
rates. The data run from 1988:12 to 2011:12.19
We are interested primarily in three questions: first, whether there are periods of high financial stress, and if those periods are marked by different dynamics than more normal times; second, if there is evidence of regime switching, whether it is confined to variance switching, as SZ (2006) find, or whether differences in economic behavior, as captured by coefficient switching, better explain the data; and third, whether any regime switching is confined to specific equations--such as the stress equation alone, or the monetary policy response to stress--as opposed to applying to all equations.
Before proceeding to our results, we discuss briefly our criteria for model selection. Bayesian econometrics lends itself to model assessment on the basis of comparing the marginal data density (marginal likelihood) of alternative models.20 While we carry out comparisons of this nature, we use broader criteria for model selection. Among these criteria, we place some weight on the plausibility of the model, as captured by the state probabilities and the economic interpretation of their timing and duration in the light of past events. Finally, we also make reference to the ranking of posterior modes and log likelihoods of the model. Because the posterior mode of the model is proportional to the prior times the likelihood, if the ranking of posterior modes is seriously out of line with rankings of the marginal data densities (MDDs), it hints that the prior probabilities might be the dominant force behind the former ranking. Conversely, when the ranking of posterior modes and the ranking of MDDs coincide, it provides greater assurance of what the preferred model should be, at least insofar as statistical criteria are concerned. See the appendix for a review of priors.
4.1 Financial stress regimes: Is it just the shocks or do agents change behavior?
At this point, it is useful to introduce a bit of notation in order to facilitate the interpretation of the tables that follow. We designate
![]() to indicate the number of independent Markov states governing variance switching, and
to indicate the number of independent Markov states governing variance switching, and ![]() to indicate the number of states governing coefficient switching (that is, slope and intercept parameters). Also, when shifts in structural parameters are constrained to a particular equation(s), the
restriction is indicated by adding the letter of the variable,
to indicate the number of states governing coefficient switching (that is, slope and intercept parameters). Also, when shifts in structural parameters are constrained to a particular equation(s), the
restriction is indicated by adding the letter of the variable,
![]() , with
, with ![]() representing a null entry. So, for example, an MS-VAR
with two Markov states in the variances and two in coefficients with the latter restricted to the financial stress variable would be designated as
representing a null entry. So, for example, an MS-VAR
with two Markov states in the variances and two in coefficients with the latter restricted to the financial stress variable would be designated as ![]() .
.
Our presentation of results begins with Table 4.1, which focusses on models where switching is entertained in all equations but could be in either variance switching alone or in variances and coefficients. The first line of the table shows MDDs. The second line of the table is perhaps the most informative: it shows the difference in the MDD from that of the best fitting model in the same table. The remaining two lines are essentially reference items that show the posterior mode and log likelihood evaluated at the posterior mode for each model; taken together, these two lines allow the reader to see how much influence the prior is having on the rankings of posterior modes on the one hand and how much the MDD calculations are having on the ranking on the other.
There are a number of interesting observations that can be taken from Table 4.1. First, the garden-variety VAR model-that is, a model with constant coefficients and constant shock variances, the ![]() model, shown in column [1]-is not favored by the data: extensions of the model to add a second state in variances--column [2]--or in coefficients--column [4]--improves the fit, and substantially so. It follows from this that the transmission of stress in the US economy is
properly thought of as a nonlinear phenomenon, or a non-Gaussian one, or both.21 Second, while SZ (2006) argued in a different context that allowing for
switching in coefficients provides no incremental benefit in explaining the Great Moderation in post-war U.S. business cycles after allowing for switching in shock variances, and Stock and Watson (2012) advanced a similar argument as an explanation for the recent recession using a TVP factor model,
in this setting we can say with some assurance that allowing for coefficient switching is beneficial.22 The comparison of the
model, shown in column [1]-is not favored by the data: extensions of the model to add a second state in variances--column [2]--or in coefficients--column [4]--improves the fit, and substantially so. It follows from this that the transmission of stress in the US economy is
properly thought of as a nonlinear phenomenon, or a non-Gaussian one, or both.21 Second, while SZ (2006) argued in a different context that allowing for
switching in coefficients provides no incremental benefit in explaining the Great Moderation in post-war U.S. business cycles after allowing for switching in shock variances, and Stock and Watson (2012) advanced a similar argument as an explanation for the recent recession using a TVP factor model,
in this setting we can say with some assurance that allowing for coefficient switching is beneficial.22 The comparison of the ![]() model in column [2] with that of the
model in column [2] with that of the ![]() model in column [5] provides an example: the improvement in fit
from adding switching in coefficients is of the order of 60 in terms of MDDs, which is very large; by comparison, adding a third Markov state for variances, as in column [3], improves the fit only in small ways. Thus, the transmission of crises would appear to be not merely a non-Gaussian
phenomena, but a non-linear one as well. Third, of the models shown in the table, the model that is favored on purely goodness-of-fit criteria is the
model in column [5] provides an example: the improvement in fit
from adding switching in coefficients is of the order of 60 in terms of MDDs, which is very large; by comparison, adding a third Markov state for variances, as in column [3], improves the fit only in small ways. Thus, the transmission of crises would appear to be not merely a non-Gaussian
phenomena, but a non-linear one as well. Third, of the models shown in the table, the model that is favored on purely goodness-of-fit criteria is the ![]() model, shown in column [6].23 This model, with three states in the variances of shocks and two in the VAR coefficients, is obviously fairly elaborate, and indeed based solely on MDD
computations, an even more elaborate model, the
model, shown in column [6].23 This model, with three states in the variances of shocks and two in the VAR coefficients, is obviously fairly elaborate, and indeed based solely on MDD
computations, an even more elaborate model, the ![]() specification, not shown in the table, is better still. The improvement in fit over the
specification, not shown in the table, is better still. The improvement in fit over the ![]() model, however, is very small and, more important, the model's economic dynamics are difficult to interpret.24 Indeed, as we discuss below, the
model, however, is very small and, more important, the model's economic dynamics are difficult to interpret.24 Indeed, as we discuss below, the ![]() model favored on goodness-of-fit criterion in Table 4.1 is economically little different from the
model favored on goodness-of-fit criterion in Table 4.1 is economically little different from the ![]() model in column [5]. The economic dynamics of the two specifications are quite similar, a fact we will rely on to make more general points about economic dynamics later on.
model in column [5]. The economic dynamics of the two specifications are quite similar, a fact we will rely on to make more general points about economic dynamics later on.
Table 4.1 MS-VAR model results : general models
| [1] |
[2] |
[3] |
[4] |
[5] |
[6] |
|
| marginal data density | -2569.74 | -2438.38 | -2425.00 | -2464.70 | -2366.9 | -2349.09 |
| - difference from best fit | -220.65 | -89.29 | -75.91 | -115.61 | -17.81 | 0 |
| posterior density | -2286.86 | 2213.84 | -2113.55 | -2169.15 | -2076.22 | -2047.58 |
| log likelihood | -2418.13 | -2245.23 | -2235.85 | -2249.42 | -2152.98 | -2127.62 |
4.2 Whence switching: is it just in stress or everywhere?
This section compares the statistically preferred ![]() model from Table 4.1 against models of similar size but with coefficient switching restricted to certain equations. We have already
established the importance of switching for explaining the data. The idea here is to investigate whether, for example, the switching concerning financial phenomena is restricted to just financial factors or whether it is more general. It is conceivable, for example, that financial crises are
associated merely with different transmission of shocks originating from the financial sector but the policy response to this different financial market behavior is unchanged. Similarly, the real and price responses to changes in financial market regime could be no different than in "ordinary
times," just larger, in proportion to the shocks. Or it could be the case that changes in financial sector behavior is met by induced changes in monetary policy responses, but the real side of the economy responds normally.
model from Table 4.1 against models of similar size but with coefficient switching restricted to certain equations. We have already
established the importance of switching for explaining the data. The idea here is to investigate whether, for example, the switching concerning financial phenomena is restricted to just financial factors or whether it is more general. It is conceivable, for example, that financial crises are
associated merely with different transmission of shocks originating from the financial sector but the policy response to this different financial market behavior is unchanged. Similarly, the real and price responses to changes in financial market regime could be no different than in "ordinary
times," just larger, in proportion to the shocks. Or it could be the case that changes in financial sector behavior is met by induced changes in monetary policy responses, but the real side of the economy responds normally.
An assortment of restricted models are entertained; Table 4.2 focusses on the ones that are the most economically meaningful as well as those that boasted the best fit.25 We consider restrictions of coefficient switching in four combinations of equations: the stress equation, ![]() , arguably the most obvious restriction because as we
noted in the Introduction, it is financial stress that is so often left out of macro models in general and VARs in particular, due it its episodic importance; to stress and the real economy,
, arguably the most obvious restriction because as we
noted in the Introduction, it is financial stress that is so often left out of macro models in general and VARs in particular, due it its episodic importance; to stress and the real economy, ![]() , on the grounds that it is disparate response of the real economy to unusual developments in stress that motivates concern with the issue in the first place; and to stress and monetary policy,
, on the grounds that it is disparate response of the real economy to unusual developments in stress that motivates concern with the issue in the first place; and to stress and monetary policy, ![]() because, at least in principle, it is policy that should respond differently to disproportionate developments in stress. From the perspective of the monetary authority, a shift to a period of high financial stress is an exogenous event that puts the authority in a
quandary: does it stick to its policy rule because consistent monetary behavior is important for establishing a rational expectations equilibrium, or does it switch to a policy that is germane to the special conditions of the day? If the former is the case, switching will be observed in the
because, at least in principle, it is policy that should respond differently to disproportionate developments in stress. From the perspective of the monetary authority, a shift to a period of high financial stress is an exogenous event that puts the authority in a
quandary: does it stick to its policy rule because consistent monetary behavior is important for establishing a rational expectations equilibrium, or does it switch to a policy that is germane to the special conditions of the day? If the former is the case, switching will be observed in the
![]() equation but not in the policy equations; otherwise both sets of equations will exhibit switching. There is also the possibility that policy could switch seemingly on its own, perhaps owing
to "taking out insurance" against financial or other shocks that do not occur but are thought possible. Indeed it is conceivable that high financial stress is caused, in some sense, by switching in monetary policy.
equation but not in the policy equations; otherwise both sets of equations will exhibit switching. There is also the possibility that policy could switch seemingly on its own, perhaps owing
to "taking out insurance" against financial or other shocks that do not occur but are thought possible. Indeed it is conceivable that high financial stress is caused, in some sense, by switching in monetary policy.
Table 4.2 shows that the data favor switching in all equations, over the restricted specifications. Of the alternative specifications, only the ![]() specification comes even close to
the
specification comes even close to
the ![]() case, and even then, not all that close. Moreover, the log likelihood calculations shown in the last row of the table confirm this conclusion. This means that the dynamics of
monetary policy have differed in parts of recent monetary history, and these changes have coincided with changes in the behavior of other variables, most notably financial stress. Indeed, although this causality cannot be formally tested, it seems reasonable to assume that changes in the behavior
of financial stress induced concomitant changes in the operation of monetary policy. At the same time, however, the limits to what monetary policy can do are indicated by the fact that shifts in monetary policy induced by shifts in financial stress were insufficient to leave the behavior of the
real economy and inflation unchanged.
case, and even then, not all that close. Moreover, the log likelihood calculations shown in the last row of the table confirm this conclusion. This means that the dynamics of
monetary policy have differed in parts of recent monetary history, and these changes have coincided with changes in the behavior of other variables, most notably financial stress. Indeed, although this causality cannot be formally tested, it seems reasonable to assume that changes in the behavior
of financial stress induced concomitant changes in the operation of monetary policy. At the same time, however, the limits to what monetary policy can do are indicated by the fact that shifts in monetary policy induced by shifts in financial stress were insufficient to leave the behavior of the
real economy and inflation unchanged.
Table 4.2 MS-VAR model results : restricted models
| [1] |
[2] |
[3] |
[4] |
[5] |
|
| marginal data density | -2349.09 | -2438.13 | -2397.05 | -2370.43 | -2408.44 |
| - difference from best fit | 0 | -89.04 | -47.96 | -21.34 | -59.35 |
| posterior density | -2047.58 | -2115.80 | -2102.48 | -2055.10 | -2098.53 |
| log likelihood | -2127.62 | -2230.06 | -2225.16 | -2135.36 | -2170.16 |
4.3 The economic history of stress: state probabilities
Figure 4.1 below shows the (two-sided) estimated state probabilities for shock variances for the preferred ![]() specification. As can be seen, the high-stress variance state, shown in the
bottom panel, is not a common one, although there are periods other than the crisis of 2008-9 that are identified as high-stress variance states. The first cluster of high-stress variance states begins in December 2000 when the tech-stock boom was cresting and ends in September 2001. The second
cluster has a spike in February 2008, a month after major U.S. mortgage lenders and investment banks announced large fourth-quarter financial losses, and a second in September 2008, the month that Lehman Brothers declared bankruptcy.
specification. As can be seen, the high-stress variance state, shown in the
bottom panel, is not a common one, although there are periods other than the crisis of 2008-9 that are identified as high-stress variance states. The first cluster of high-stress variance states begins in December 2000 when the tech-stock boom was cresting and ends in September 2001. The second
cluster has a spike in February 2008, a month after major U.S. mortgage lenders and investment banks announced large fourth-quarter financial losses, and a second in September 2008, the month that Lehman Brothers declared bankruptcy.
We designate state 3, in the bottom panel, as the "high stress" state for shock variances because it was in effect during the financial crisis of 2008-9, although this identification is somewhat arbitrary. Table 4.3 shows why this is so. The table shows the diagonal of the variance-covariance
matrix of shocks as a function of regime. The salient point to be taken from the table is the absence of any dramatic difference in the variances of the forcing shocks across regimes. Of particular note is the last column of the table showing the variances of the stress shocks which indicates that
high-stress regimes are not associated with outsized shocks to stress. One might have thought that banking and capital market developments during financial crises would manifest themselves in stress shocks, but this seems not to be the case. Moreover, with the noteworthy exception that the variance
of ![]() shocks declines, and the variance of
shocks declines, and the variance of ![]() shocks rises, as one goes from
low-stress variance shocks to high, there is little pattern in shocks from state to state. Perhaps the most substantive difference in shocks across regimes is in the covariance terms, which are not shown in the table in order to avoid excessive clutter. In the low- and medium-stress variance
states, the covariance terms are small, never exceeding 0.14 in absolute value; in the high-stress variance state, however, the covariance of shocks between
shocks rises, as one goes from
low-stress variance shocks to high, there is little pattern in shocks from state to state. Perhaps the most substantive difference in shocks across regimes is in the covariance terms, which are not shown in the table in order to avoid excessive clutter. In the low- and medium-stress variance
states, the covariance terms are small, never exceeding 0.14 in absolute value; in the high-stress variance state, however, the covariance of shocks between ![]() and
and ![]() , and between
, and between ![]() and
and ![]() , are fairy large and negative at -0.63 and -0.46, respectively. Taken together these observations suggest that periods of financial stress and associated poor economic performance are not an outcome of particularly unusual shocks; rather it is the transmission
of shocks that explains the transmission of crises. This is particularly so if one defines "transmission of shocks" broadly to include the covariance, which seems reasonable as it is unlikely that the covariance of shocks during high-stress variance regimes is a matter of happenstance. Rather it
seems likely that this is due to emergent structural simultaneity during crises, although the model cannot explicitly identify it as such. Although the setting is quite different, this result stands in stark contrast to that of SZ (2006), who argue that for post-war U.S. business cycle switching,
it is variance switching that matters with little or no contribution attributable to switching in coefficients.
, are fairy large and negative at -0.63 and -0.46, respectively. Taken together these observations suggest that periods of financial stress and associated poor economic performance are not an outcome of particularly unusual shocks; rather it is the transmission
of shocks that explains the transmission of crises. This is particularly so if one defines "transmission of shocks" broadly to include the covariance, which seems reasonable as it is unlikely that the covariance of shocks during high-stress variance regimes is a matter of happenstance. Rather it
seems likely that this is due to emergent structural simultaneity during crises, although the model cannot explicitly identify it as such. Although the setting is quite different, this result stands in stark contrast to that of SZ (2006), who argue that for post-war U.S. business cycle switching,
it is variance switching that matters with little or no contribution attributable to switching in coefficients.
Table 4.3 Estimated variances of shocks by regime (![]() model)
model)
| variance regime | |||||
|
|
0.92 | 1.01 | 1.15 | 0.93 | 0.90 |
| 1.01 | 0.89 | 0.65 | 0.95 | 0.96 | |
|
|
0.88 | 1.11 | 0.57 | 1.04 | 0.93 |
Of greater interest is the probability of being in a high-stress coefficient state, because to be in such a state would suggest fundamental differences in economic behavior--differences in the transmission of crises--as opposed to just enhanced volatility. As shown in Figure 4.2, there have
been, according to the preferred ![]() specification, perhaps five periods of high stress in coefficients. The first is a cluster in the early part of the sample ending in July 1992, probably
associated with the first Persian Gulf war and associated developments in oil prices; the second, is in 1998 and corresponds with the Russian debt default and the collapse of Long-Term Capital Management; the third period, in November 2002 and July 2003, matches up well with the the aftermath of
the Argentine debt default, or perhaps the bankruptcy of Worldcom; the fourth, which begins in August 2007 and ends in April 2009 with the leaking of the results of U.S. bank stress tests, is the 2008-9 financial crisis and associated recession; and finally, there is a short-lived spike in June
2011 which lines up with some developments in the European sovereign debt crisis. Overall, there are two dates at which the economy was already in a high-stress coefficient state and the economy transitioned into the high-stress state for
shock variances: February 2008 and September 2008.27
specification, perhaps five periods of high stress in coefficients. The first is a cluster in the early part of the sample ending in July 1992, probably
associated with the first Persian Gulf war and associated developments in oil prices; the second, is in 1998 and corresponds with the Russian debt default and the collapse of Long-Term Capital Management; the third period, in November 2002 and July 2003, matches up well with the the aftermath of
the Argentine debt default, or perhaps the bankruptcy of Worldcom; the fourth, which begins in August 2007 and ends in April 2009 with the leaking of the results of U.S. bank stress tests, is the 2008-9 financial crisis and associated recession; and finally, there is a short-lived spike in June
2011 which lines up with some developments in the European sovereign debt crisis. Overall, there are two dates at which the economy was already in a high-stress coefficient state and the economy transitioned into the high-stress state for
shock variances: February 2008 and September 2008.27
These periods of high stress and their correspondence with known financial events notwithstanding, it is not the case that one need only observe that the FSI is elevated to conclude that one is in a high-stress coefficient state. There are periods, such as the early 1990s when high-stress coefficients are uncovered even though the FSI in Figure 2.1 is low. And there are also periods such as late in 2002 when the FSI is quite high, and yet the estimated coefficient state is low. It is the joint behavior of stress and the rest of the system that determines the Markov state.
Taking Figure 4.1 and 4.2 together helps us understand the great recession. From Figure 4.1 we see that the period from 2004 to 2006 was a lengthy one where shock variances were in a low stress state (the upper panel of the figure); Figure 4.2 shows that this was also a period in which the coefficient state was low stress as well. Figure 2.1 shows that this was also the period in which the FSI itself was at a very low level for an extended period; in addition, interest rates were very low. In response, it is commonly alleged that financial firms began "chasing yield:" increasing leverage in order to magnify returns; see, e.g., Geanakoplos (2010) among many other references. Back on Figure 4.1, the economy then transitions in late 2006--about the time that prices of existing homes at the national level began to fall--to the medium-stress variance state (the middle panel). The crisis begins in earnest when the economy transitions in August 2007 to the high-stress coefficient state and finally reaches full bore in September 2008 when the variance state also jumps to high stress (the lower panel of Figure 4.1). All this leads to a proposed definition of a stress event: when the shock variance state is either medium or high, and the coefficient state is high. As can be seen in Figure 4.3 below, this definition eliminates the periods of high-stress coefficients in the early 1990s at which time there was apparently insufficient turbulence to create much in the way of difficulties for the real economy (although there was, in fact, a mild recession and a slow, "jobless" recovery). Also omitted from this status is the September 11, 2001 attacks and the associated extraordinary provision of liquidity by the Federal Reserve that followed those attacks.28 This definition leaves in, however, a spike in 1998 associated with the Russian debt default and the LTCM failure, two spikes that might be associated with the Argentine debt default or the failure of Worldcom, the great recession and a very recent spike connected to the European sovereign debt crisis.
Table 4.4 shows the estimated transition probabilities taken from the posterior mode of the distribution for selected model specifications. By comparing the first and third lines of the table, we see that the introduction of a second state in coefficients to what would otherwise be the
![]() model changes the probabilities of the variance states quite dramatically. This finding illustrates the fact that switching in shock variances and switching in coefficients are rivals in
explaining the data; as SZ (2006) have emphasized, failing to account adequately for one will bias estimates of the other. The fact that the
model changes the probabilities of the variance states quite dramatically. This finding illustrates the fact that switching in shock variances and switching in coefficients are rivals in
explaining the data; as SZ (2006) have emphasized, failing to account adequately for one will bias estimates of the other. The fact that the ![]() model and the
model and the ![]() model are economically similar is demonstrated by the fact that the state probabilities that the two models have in common does not change markedly with the introduction of the third state in variances. In both
specifications, it is the case that the high-stress coefficient state is short-lived in duration, on average. The severity of the 2008-9 episode is therefore marked by two unusual phenomena by historical standards: the fact that the high-stress coefficient state lasted as long as it did, and the
fact that it was also associated with a period of high-stress shock variances.29 Figure 4.4 shows our estimates of stress events defined in this way. The
figure reveals that the early-sample periods of high-stress coefficients were not terribly consequential because they were not associated with shock-variance regimes that were conducive to widespread contagion.
model are economically similar is demonstrated by the fact that the state probabilities that the two models have in common does not change markedly with the introduction of the third state in variances. In both
specifications, it is the case that the high-stress coefficient state is short-lived in duration, on average. The severity of the 2008-9 episode is therefore marked by two unusual phenomena by historical standards: the fact that the high-stress coefficient state lasted as long as it did, and the
fact that it was also associated with a period of high-stress shock variances.29 Figure 4.4 shows our estimates of stress events defined in this way. The
figure reveals that the early-sample periods of high-stress coefficients were not terribly consequential because they were not associated with shock-variance regimes that were conducive to widespread contagion.
|
|
|
|
|
|
|
| 0.80 | 0.89 | 0.89 | - | - | |
| - | 0.92 | 0.95 | 0.76 | 0.95 | |
| 0.83 | 0.93 | 0.97 | 0.73 | 0.95 |
4.4 The FSI: why does it work?
Table 2.2 showed the composition of the FSI. As a test of robustness and an exploration of what channels one might wish to investigate in a structural model, we exclude, in the context of our preferred ![]() specification, each of six classes of components of the FSI. These are risky bond rate spreads (rows 1 and 2 of Table 2), the yield spread (row 3), implied bond rate volatilities (lines 4 and 5), on-the-run premiums (line 6 and 7), equity premium (line 8) and the VIX, that is,
the implied volatility of the S&P 500 price index (line 9).
specification, each of six classes of components of the FSI. These are risky bond rate spreads (rows 1 and 2 of Table 2), the yield spread (row 3), implied bond rate volatilities (lines 4 and 5), on-the-run premiums (line 6 and 7), equity premium (line 8) and the VIX, that is,
the implied volatility of the S&P 500 price index (line 9).
None of these subsets of the broader index produced results that were preferred to our base case. In several instances, however, the results were very similar. In particular, omitting the on-the-run premiums or the implied volatilities of bonds made only slight differences in either switching probabilities or model properties. Given that these variables measure market liquidity this finding suggests either that liquidity is not particularly important or is encompassed by other variables. By contrast, omitting the VIX or especially the risky spreads does make a material difference to the results. The latter observation is consistent with the findings of Adrian et al. (2012). Risky spreads measure default risk on corporate bonds, while the VIX measures market perceptions of the riskiness of expected returns on corporate equities. We conclude that explorations using structural models of nonlinearities in the interaction between financial markets and the macroeconomy might be profitably focused on endogenously generated perceptions of default.
4.5 Real-time properties
As we noted in the Introduction, the FSI was constructed and used by the Federal Reserve Board staff in real time during the financial crisis and recession. We have already demonstrated that the model shows switches to high-stress coefficient regimes in general, and stress events in particular, that coincide with well-known financial events in U.S. history. The usefulness of the index would be limited, however, if its performance in real time were substandard. Figure 4.4 examines this question, showing with the colored lines the (quasi-) real-time estimates of the state probabilities for the high-stress coefficient state; that is, the probability measured at each point in time based on information up to the current period..30 Two noteworthy conclusions may be drawn from this figure. First, the switches in coefficients indicated in ex post data, the black line, were revealed in the real-time estimates, the colored lines; that is, false negatives are negligible. Second, while there are hints of false positives-for example in 1996 and 2002-at no time did the real-time data adamantly call for a switch that was rescinded ex post.31 All in all, we would argue that the model does remarkably well in real time.
4.6 The transmission of financial stress
To illustrate some properties of the model and provide some historical perspective, we carry out two classes of simulations on the model. The first are counterfactual simulations, some designed to illustrate the unique features of our model in a compact and intuitive fashion, and others set around the 2008-9 financial crisis. The latter simulations provide a useful historical perspective on the model and the issues the model is meant to address. The second class of simulations is a conditional forecast initiated from the end of the sample period. These exercises provide very much the same information as do impulse responses, except more compactly, and in a more intuitively appealing context.
Markov switching aside, the unique aspect of our model is the financial stress index. To illustrate how financial stress affects the economy, we carry out two counterfactual simulations involving alternative paths for stress (![]() in the figures), one carried out during a period of low stress, the other from more strained conditions.
in the figures), one carried out during a period of low stress, the other from more strained conditions.
We begin with an autonomous increase in stress during a low-stress period in July 1989. Figure 4.5 shows the results. The noteworthy aspects are two-fold: first, the monetary response is slight, with the federal funds rate (![]() ) falling only marginally, relative to the data. The implications for real activity, as measured by growth in personal consumption expenditures (
) falling only marginally, relative to the data. The implications for real activity, as measured by growth in personal consumption expenditures (![]() )
in the upper-left panel are relatively small and short lived. Thus, this exercise ratifies our assertion, made in the Introduction, that financial stress has been underappreciated through much of economic history as an important factor in the transmission of business cycles because in normal
times--that is, through the bulk of history--stress has not been a major driver of events.
)
in the upper-left panel are relatively small and short lived. Thus, this exercise ratifies our assertion, made in the Introduction, that financial stress has been underappreciated through much of economic history as an important factor in the transmission of business cycles because in normal
times--that is, through the bulk of history--stress has not been a major driver of events.
Figure 4.5 :\ Counterfactual experiment where financial stress rises to 120 in July 1989, a normal-times period, 3v2c specification.

Figure 4.6 carries out a broadly similar exercise, this time from conditions of a stress event. Our period in history is August 1998, during the Russian debt default and associated collapse of LTCM.32 As the upper-right panel indicates, in the data ![]() climbed rapidly and substantially with the onset of the crisis. Our
counterfactual imagines that stress had instead remained at the level inherited from the previous month.
climbed rapidly and substantially with the onset of the crisis. Our
counterfactual imagines that stress had instead remained at the level inherited from the previous month.
The message of this counterfactual is found in the lower-left panel where we see a substantial reaction from monetary policy offsetting the expansionary implications of the lower level of stress. This response is in sharp contrast with the previous experiment, carried out in low-stress conditions (with the opposite sign). The implications for real activity end up being quite modest, which would have been well advised at the time since PCE growth was quite strong, on average, during this time. What this says is that monetary policy, when it has the capacity to do so, is well disposed to respond to increases in stress, holding constant the stress regime, when those increases are moderate and temporary, as was the case in 1998. Arguably, actions by the Federal Reserve to elicit an orderly reorganization of LTCM ensured that this stress event was brief, and monetary policy defined in terms of setting the federal funds rate was in a position to ease. The contrast with the 2008-9 financial crisis is fairly stark. The shock in the latter instance was larger, as shown in Figure 4.3 the stress event lasted longer, and conventional monetary policy was limited in its ability to respond.
Figure 4.6. Counterfactual experiment where financial stress is held at its August 1998 level, a high-stress coefficient state, 3v2c specification
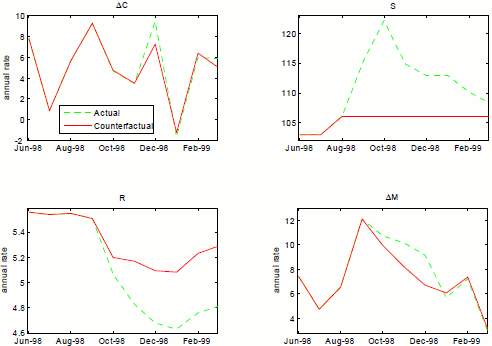
Let us now turn to the recent financial crisis and consider counterfactual changes in regime. Model estimates show, and Figure 4.3 confirms, that a stress event began in the second half of 2007. The economy had already switched to medium-variance shocks late in 2006--by itself not such a big deal but sometimes a precursor to worse things--followed by a persistent switch to high-stress coefficients in October 2007; then, in September 2008, the state switched to high-stress variances together with the already existing high-stress coefficients. This was, of course, a bad time for the U.S. economy, although it would not be until December 2008 that the NBER would certify that a recession had started in December 2007. In Figure 4.7 we pose the question, what would have happened, according to the model, if the state had remained in the low-stress coefficient state?
Figure 4.7 : Counterfactual experiment where state returnes to low-stress coefficient state in October 2007, 3v2c specification

To be clear, in this experiment, we allow all the shocks borne by the economy to remain in play; the only thing that is counterfactual here is the set of coefficients through which those shocks play out. The figure shows that financial stress itself (![]() ), would have been much lower than otherwise; this, in turn, would have obviated the need for very easy monetary policy, so that the federal funds rate (
), would have been much lower than otherwise; this, in turn, would have obviated the need for very easy monetary policy, so that the federal funds rate (![]() ) ends up about 2-1/2 percentage points higher than in history by mid-2008, and money growth would have been lower.33 Tighter
monetary policy notwithstanding, real consumption growth would have been notably better than what the historical experience delivered. Clearly, the implications for the economy of a persistent switch in the coefficient state--that is, a stress event--are substantial. (As might be expected, changes
in shock variances have a relatively modest effect on economic performance in a scenario of this nature, all else equal.).
) ends up about 2-1/2 percentage points higher than in history by mid-2008, and money growth would have been lower.33 Tighter
monetary policy notwithstanding, real consumption growth would have been notably better than what the historical experience delivered. Clearly, the implications for the economy of a persistent switch in the coefficient state--that is, a stress event--are substantial. (As might be expected, changes
in shock variances have a relatively modest effect on economic performance in a scenario of this nature, all else equal.).
Figure 4.8 considers a different counterfactual carried out over the same period beginning in October 2007. We suppose that the Federal Reserve could have foreseen the grave conditions that were to come and thus immediately reduced the federal funds rate to the effective lower bound of 0.12 percent.
Figure 4.8 : Counterfactual experiment where federal funds rate falls to 0.12 percent in October 2007, 3v2c specification
As can be seen from the bottom-left panel of the figure, this is a large intervention, which induces a very large increase in money growth, the bottom-right panel. The effect on real PCE growth is relatively small, however. The upper-right panel gives an indication of why this is so: financial stress rises substantially and persistently with the policy intervention. Evidently, in high-stress situations, agents regard conventional policy actions that would normally be beneficial as confirmation of incipient financial difficulties. The resulting higher levels of stress choke off the salutary effects of easy monetary policy. We emphasize that this result is germane to stress events: in low-stress states, a surprise reduction in the federal funds rate reduces financial stress rather than increasing it. We conclude that conventional monetary policy actions, in the absence of actions to alleviate the fundamental causes of the stress event, or actions to arrest increases in financial stress, will only be modestly helpful for economic performance. At one level, this should not be surprising: it is received wisdom in economics that would-be policy cures should be tailored to the ultimate causes of the problem as opposed to the symptoms that those causes engender.
Finally, we turn to our second class of experiments, a conditional forecast that illustrates the importance of initial conditions for economic outcomes. Figure 4.9 shows two forecast paths beginning immediately following the end of our sample in 2011:12, one (the red solid line) conditional on a high stress regimes in both coefficients and variances, the other (the blue dashed line) on a low stress in both coefficients and variances. All else is held constant, and unlike the figures immediately above, there are no shocks other than those in history that set out the initial conditions for the scenario.
As can be seen, PCE growth is much weaker in the high-stress world and this low growth is accompanied by elevated levels of financial stress, particularly in comparison with the low-stress world. Of significance is that the high-stress state is associated with higher price inflation than in the low-stress state, a finding that is consistent with an interpretation of a stress event as a negative supply shock that reduces real output and puts upward pressure on prices, all else equal. All else is not equal here: monetary policy, as measured by the federal funds rate (or the growth rate of M2, not shown) is easier in the high-stress world than otherwise; but with the interpretation of reduced potential output, this easy monetary policy is seen as something of a palliative that reduces the pain only modestly, and instead leads to upward pressure on prices. As we argued above, true recovery requires a shift to the low-stress state
5 Conclusions
This paper has considered the implications of financial stress for the macroeconomy in the United States using a richly specified Markov-switching vector autoregression model, estimated with state-of-the-art Bayesian methods, and exploiting a unique series for financial stress constructed and monitored by the staff of the Federal Reserve Board. Our objective was to uncover whether shifts in the state of the economy have been an important feature of the real-financial linkage in the U.S. economy, and if so, whether the transmission of financial stress differs in some states of the world than others. We also examined whether monetary policy in the high-stress state differs from what it is in low stress states. And we assessed whether the Board staff's Financial Stress Index is up to the task of providing real-time insight on financial stress and its relation to macroeconomic outcomes.
Our analysis shows substantial evidence that a single-regime model of the macroeconomy and financial stress is inadequate to capture the dynamics of the economy. Moreover, the data show that there have been periodic shifts in the dynamics of the economy as well as in stochastic shocks. We further find that these shifts are best described as having occurred in all of the model equations, rather than being restricted to subsets of equations. In particular, there is no evidence that the interest-rate reaction function has constant parameters. This finding implies that inference regarding the conduct of monetary policy that is gleaned from a constant-parameter Gaussian model may be inappropriate for periods when the policy is conditioned on movements in financial stress.
Quantitatively, we find that output reacts differently to financial shocks in times of high financial stress than in normal times, with macroeconomic dynamics being highly conditional on the financial stress regime: Stress is of negligible importance in "normal" times, but of critical importance when the economy is in a high-stress coefficient state. We also found that an important precursor to adverse economic events is a switch to what we call a stress event: a period in which the shock variance is at a relatively high-stress level and the coefficient state is also at a high-stress level. It is often the case that stress events occur when shock volatility begins to rise and is followed by the change in coefficient state. The fact that such switches in state can be reliably inferred in real time leads one toward optimism regarding the efficacy of nowcasting stress events. Lastly, we showed that the Federal Reserve Board staff's use of the financial stress index described in this paper appears to have been an efficacious choice.
The joint findings of the prevalence of Markov switching in model coefficients together with the observation that conventional monetary policy is not very powerful in high-stress coefficient states speaks to the issue of whether there are conflicts in central banks' mandates for price stability and maximum employment on the one hand, and financial stability on the other. The issue is whether there exists merely an assignment problem in which financial instruments need only be assigned to financial goals and monetary instruments to monetary goals, or whether there are times when monetary policy needs to be concerned with the goal of financial stability, regardless of financial stability instruments. Markov switching is exogenous in this paper, but our findings suggest that unless alternative mechanisms can be found to rule out switching to the high-stress coefficient state, it is possible that monetary policy might at times need to contribute to maintaining financial stability.
Lastly, we have noted that it is the components of the financial stress index that are associated with market perceptions of default risk that are instrumental in driving our results. This suggests that nonlinear structural models aimed at explaining the same sort of quantitative phenomena as this paper would be well advised to assign a prominent role to considerations of default risk.
6 Appendix
6.1 Priors
There are two sets of priors of relevance to our model, one on the reduced-form parameters of the VAR conditional on a state, ![]() , and the other on the transition matrix. The priors on the
reduced-form VAR are simply the standard Minnesota prior of Litterman (1986) on the lag decay dampening the influence of long lags. In other words, this prior shrinks the model towards a random walk. Furthermore, it seems reasonable that the importance of a variance decreases with lag length; and
that priors on exogenous and deterministic variables,
, and the other on the transition matrix. The priors on the
reduced-form VAR are simply the standard Minnesota prior of Litterman (1986) on the lag decay dampening the influence of long lags. In other words, this prior shrinks the model towards a random walk. Furthermore, it seems reasonable that the importance of a variance decreases with lag length; and
that priors on exogenous and deterministic variables, ![]() , be relatively uninformative. Let the relative tightness on the prior on the own lags, non-own lags, and exogenous or deterministic
variables be
, be relatively uninformative. Let the relative tightness on the prior on the own lags, non-own lags, and exogenous or deterministic
variables be ![]() through
through ![]() respectively. The prior variances of the
parameters are then specified as:
respectively. The prior variances of the
parameters are then specified as:
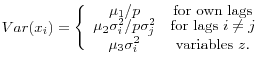 |
The priors that apply to switching are less straightforward. Even without restrictions of some sort,
![]() and
and
![]() could, in principle, be estimated straightforwardly, using the method of Chib (1996) for example, but as
could, in principle, be estimated straightforwardly, using the method of Chib (1996) for example, but as ![]() or
or ![]() grows, the curse of dimensionality quickly sets in. The problem is particularly acute in situations where one (or more) of the unobserved states
lasts for only a short proportion of the number of total observations, as may be the case for us. The matrix
grows, the curse of dimensionality quickly sets in. The problem is particularly acute in situations where one (or more) of the unobserved states
lasts for only a short proportion of the number of total observations, as may be the case for us. The matrix ![]() can be rewritten as
can be rewritten as
which means that a mean-zero prior can be placed on
The fact that the latent state, ![]() is discrete and that the transition probabilities of states must sum to unity lends itself toward the priors of the Dirichlet form. Dirichlet priors also
have the advantageous property of being conjugate. Letting
is discrete and that the transition probabilities of states must sum to unity lends itself toward the priors of the Dirichlet form. Dirichlet priors also
have the advantageous property of being conjugate. Letting
![]() be a hyperparameter indexing the expected duration of regime
be a hyperparameter indexing the expected duration of regime ![]() before
switching to regime
before
switching to regime ![]() , the prior on
, the prior on ![]() can be written:
can be written:
where
For our baseline specification, we use priors that are well-suited for a monthly model. In particular, we specify
![]() and Dirichlet priors of 5.6 for
both variances and coefficients. With the values of
and Dirichlet priors of 5.6 for
both variances and coefficients. With the values of ![]() we begin with what Sims and Zha (1998) and SWZ (2008) suggest for monthly data. The Dirichlet priors we use are looser than what
would be usually used for monthly data. They imply an 85 percent prior probability that the economy will, in the next period, continue in the same state as it is in the current period. This
strikes us a fairly low probability, consistent with the notion that shifts are associated with jumps in asset prices.
we begin with what Sims and Zha (1998) and SWZ (2008) suggest for monthly data. The Dirichlet priors we use are looser than what
would be usually used for monthly data. They imply an 85 percent prior probability that the economy will, in the next period, continue in the same state as it is in the current period. This
strikes us a fairly low probability, consistent with the notion that shifts are associated with jumps in asset prices.
6.2 Robustness of priors selection
In this section we consider a range of robustness checks, devoted mostly to the measure of stress used. In one set of cases, we examine how narrowing our stress index by excluding classes of variables affects the results. In the second set, we employ different priors. We note that because in all cases we are using alternative data, likelihood-based calculations are not comparable across models.
In broad terms, our preferred model is quite resilient to moderate changes in model priors. For example, if we alter the priors governing VAR coefficients that we used following SZ (2006) with alternatives, such as those that SZ (2006) recommend for a quarterly model, we get, once again, three periods of high-stress coefficients and many periods of switching in variances. Altering the Dirichlet prior such that higher persistence of regimes is somewhat favored returns what looks like the same results as we showed for our preferred model.
6.3 Computation
In our MCMC computations, we use 100,000 proposal draws and 500,000 posterior draws, net, retaining every tenth posterior draw in order to minmize correlation across draws. A Markov-switching Bayesian VAR can have a very non-Gaussian likelihood surface, with multiple peaks and ridge lines. To ensure that our solutions are robust, we explored the parameter space by doing random global perturbations first with relatively larger perturbations, and then, once the the neighborhood of the posterior mode is found, with smaller perurburbations. When those perturbations direct the algorithm to a different region, the process is continued until convergence is achieved. This can be thought of as randomizing over the initial conditions from which the block-wise computation of the posterior mode is done. Computation of a specification's posterior mode and the marginal data density takes a minimum of 7 hours in clock time and can take as long as 8 days, depending on the specifics of the run. Adding lags, imposing restrictions on switching on variances and restricting switching in equation coefficients is costly in terms of computing times.
Footnotes
The Cleveland Fed's CFSI uses daily data from credit, foreign exchange, equity and interbank markets and dates back to 1994. See also Oet et al. (2011).
The Kansas City Fed's index (KCFSI) is constructed using principal components of 11 monthly financial market variables. See Hakkio and Keeton (2009) for details. Return to Text
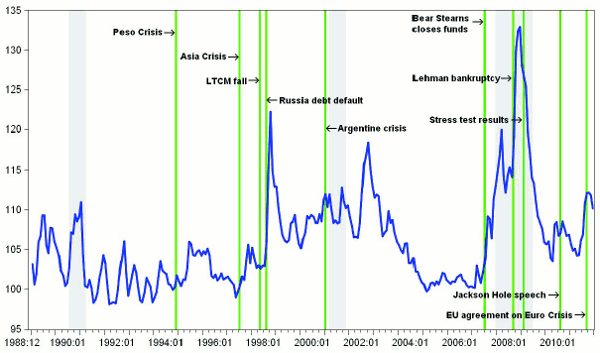

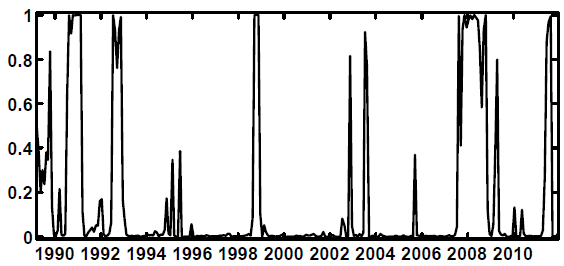
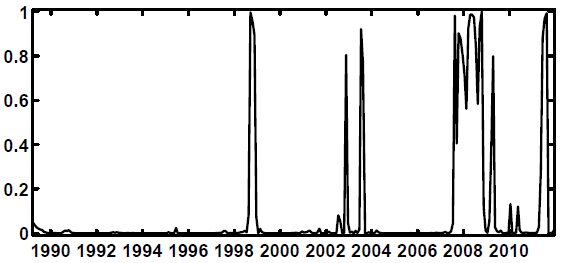
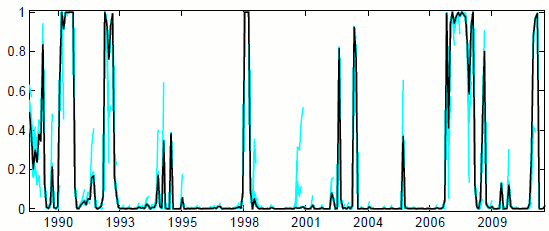
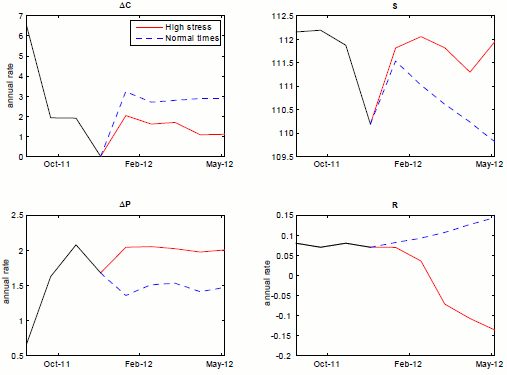
![\displaystyle p(P)=\underset{k\in H}{\Pi }\left[ \frac{\Gamma (\sum_{i\in H}\alpha _{ik})}{% \Pi _{i\in H}~\Gamma (\alpha _{ik})}\right] \times \underset{i\in H}{\Pi }% p_{ik})^{\alpha _{ik}-1}](img106.gif)