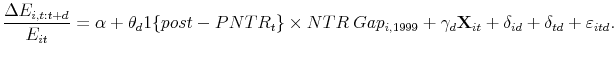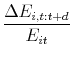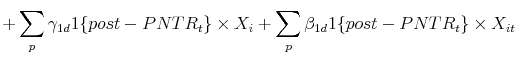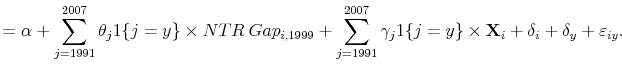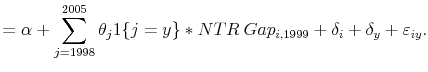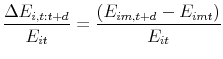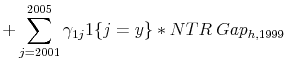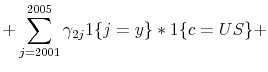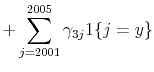Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2014-04 Screen Reader version ^♣

The Surprisingly Swift Decline of U.S. Manufacturing Employment*

Justin R. Pierce†

Board of Governors of the Federal Reserve System

Peter K. Schott‡

Yale School of Management & NBER

First Draft: November 2012

This Draft: November 2013

Abstract:

This paper finds a link between the sharp drop in U.S. manufacturing employment beginning in 2001 and a change in U.S. trade policy that eliminated potential tariff increases on Chinese imports. Industries where the threat of tariff hikes declines the most experience more severe employment losses along with larger increases in the value of imports from China and the number of firms engaged in China-U.S. trade. These results are robust to other potential explanations of the employment loss, and we show that the U.S. employment trends differ from those in the EU, where there was no change in policy.

1 Introduction

U.S. manufacturing employment fluctuated around 18 million workers between 1965 and 2000 before plunging 18 percent from March 2001 to March 2007. In this paper, we find a link between this sharp decline and the U.S. granting of Permanent Normal Trade Relations (PNTR) to China.

Conferral of PNTR was unique in that it did not change the actual import tariff rates the United States applied to Chinese goods over this period. U.S. imports from China had been subject to the relatively low NTR tariff rates reserved for WTO members since the 1980s. But for China, these low rates required annual renewals that were uncertain and politically contentious. Without renewal, U.S. import tariffs on Chinese goods would have jumped to the higher non-NTR tariff rates assigned to non-market economies and originally established under the Smoot-Hawley Tariff Act of 1930. PNTR - and the subsequent December 2001 accession of China to the WTO - eliminated the uncertainty associated with these annual renewals by permanently setting U.S. duties on Chinese imports to NTR levels.

Ending the possibility of sudden spikes in Chinese import tariffs likely strengthened import competition and suppressed U.S. employment growth. For example, the decline in uncertainty and expected tariffs associated with PNTR may have increased U.S. firms' incentives to incur the sunk costs associated with opening a plant in China or establishing a relationship with an existing Chinese supplier. Likewise, PNTR may have provided Chinese producers with greater incentives to invest in entering or expanding into the U.S. market, putting further price pressure on U.S. producers. PNTR also may have reduced U.S. manufacturing employment by inducing U.S. producers to invest in capital- or skill-intensive production technologies or less labor-intensive mixes of products that are more consistent with U.S. comparative advantage. Intuition for these responses comes in part from models of investment under uncertainty, where firms are more likely to undertake irreversible investments as the ambiguity surrounding their expected profit decreases.¹

The nature of the policy change provides a straightforward measure of its potential effect. We refer to this measure as the "NTR gap" and define it as the difference between NTR tariff rates (which average 4 percent across industries in 1999), and the non-NTR rates to which they would have risen if annual renewal had failed (which average 36 percent in 1999). NTR gaps exhibit substantial variation across industries: in 1999, their standard deviation is 15 percentage points.

Our difference-in-differences identification strategy exploits this variation in the NTR gap to test whether employment loss in manufacturing industries with higher NTR gaps (first difference) is larger after PNTR has been instituted, relative to employment changes in the pre-PNTR era (second difference). Because PNTR was granted near the 2001 business cycle peak, we compare employment growth after 2001 to employment changes after the previous peak, in 1990. One attractive feature of this approach is its ability to isolate the role of the change in policy. While industries with high and low gaps are not identical, comparing outcomes within industries across peaks isolates the differential impact of China's change in status. At the same time, comparison of employment changes across similar intervals of the business cycle helps control for manufacturing's inherent cyclicality.

Our estimates reveal a negative and statistically significant relationship between the change in U.S. policy and subsequent employment growth in manufacturing. This relationship is also economically significant: for an industry with the average NTR gap, the shift in U.S. policy reduces employment growth from 2001 to 2002 by an additional -3 to -4 percentage points compared with the same interval after the 1990 peak. Six years after the 2001 peak, the implied difference grows to -12 to -16 percentage points.

Transaction-level U.S. import data provide circumstantial evidence that these changes in employment are driven in part by offshoring. We find that U.S. imports of the goods most affected by the policy change increase substantially after 2001, and that this growth is driven by imports from China. Furthermore, we show that this jump in trade value is mediated by a relative expansion in the number of U.S. firms importing from China, the number of Chinese firms exporting to the United States, and the number of U.S.-China importer-exporter pairs. This relative growth along the extensive margin of U.S. and Chinese trading firms is consistent with greater policy-driven incentives to invest in new trade relationships, and shows that U.S. imports from China surge in the same industries that experience the largest reductions in employment.

As part of its accession to the WTO, China agreed to institute a number of policy changes which also might have influenced U.S. manufacturing employment, including a reduction in import tariffs, the phasing out of export licensing requirements and production subsidies, and the elimination of barriers to foreign investment. Using data from a variety of sources, including firm-level microdata from China's National Bureau of Statistics, we show that while these policies also are related to employment outcomes in the United States, their implied contribution is small relative to PNTR. We also find that our results are robust to other U.S. economic developments contemporaneous with PNTR, such as the bursting of the 1990s information technology bubble, the expiration of the global Multi-Fiber Arrangement governing Chinese textile and clothing export quotas, and declining union membership in the United States. Finally, we compare the U.S. experience to that of the European Union, which gave China the equivalent of PNTR in 1980. In contrast to the United States, we find no relationship between post-2001 manufacturing employment and the U.S. NTR gap in the EU.

We pursue several extensions of our baseline findings. First, we decompose industry employment growth along gross margins of adjustment and show that both elevated job destruction and suppressed job creation make sizable contributions to the overall implied impact of the change in U.S. policy. Second, we show that industries most affected by PNTR exhibit increases in skill intensity. Third, examining outcomes at the plant level, we find that the change in U.S. policy is associated with declining employment within continuing establishments as well as a higher probability of establishment death. Finally we investigate the extent to which PNTR's effects are transmitted via up- and downstream industries and find that exposure along both dimensions is associated with greater probability of plant death.

The paper proceeds as follows: Section 2 outlines our contribution to existing research; Sections 3 and 4 describe our data and empirical strategy; Sections 5 through 8 present our results; and Section 9 concludes. An online appendix provides additional empirical results.

2 Related Literature

This paper makes several contributions to a large body of research spanning international trade, labor and macroeconomics. First, we show that a substantial portion of the loss of U.S. manufacturing employment since 2001 is related to a discrete and easily identifiable change in policy - the U.S. conferral of PNTR on China.² While others, including most recently Autor, Dorn and Hanson (2012), have highlighted a negative relationship between low-wage country imports and U.S. employment, our research points to a specific policy change in the United States as the cause for the acceleration of Chinese imports, and relates it to a wide range of outcomes across both U.S. and Chinese producers.³ In particular, we show that the largest relative declines in employment in the years after 2001 are concentrated in industries that experienced the largest declines in uncertainty and expected tariffs as a result of PNTR, and that these industries also experience relatively large increases in Chinese import value, as well as the number of U.S. importers and Chinese exporters.⁴

Second, our examination of firms' reactions to the elimination of uncertainty over tariff rates rather than actual reductions in tariffs contributes to the literature analyzing investment under uncertainty (e.g. Dixit and Pyndick 1994; Bloom, Bond and Van Reenen (2007)), as well as its application to international trade. Our effort is closely related to the work of Handley (2012) and Handley and Limao (2012, 2013), who show that if uncertainty regarding either the timing or the magnitude of tariff changes in a destination market falls, exporting to that market rises as relatively low-productivity firms lose their incentive to wait and see how tariffs will change before absorbing the sunk costs associated with entry. Here, we demonstrate the strong and wide-ranging effects on both the exporting and importing country of perhaps the most significant change in import-tariff uncertainty since the turn of the century - the granting of PNTR to China.⁵ Our finding that PNTR is associated with increases in the number of U.S. importers, Chinese exporters and importer-exporter pairs is evidence that firms reacted to the policy change by making irreversible investments of the type discussed in these models. In addition, our examination of how plants subsequently adjust their capital and skill intensity in response to PNTR is related to Bloom, Draca and Van Reenen's (2012) research on trade-induced technical change.

Third, our analysis of employment changes along gross margins of adjustment provides evidence of a link between international trade and the joblessness of the 2001 recovery in manufacturing. Several papers, including Baily and Lawrence (2004) and Mankiw and Swagel (2006) have found that international trade plays a small role in this phenomenon. We expand on these analyses by considering the effect of PNTR on both job creation and job destruction, as well as its impact on upstream and downstream industries and find that trade is directly and indirectly associated with the large and long-lasting decline in U.S. manufacturing employment after 2001. Moreover, our finding that PNTR has a more profound effect on production workers than non-production workers relates to recent research by Jaimovich and Siu (2012), which shows that the increasing joblessness of both manufacturing and non-manufacturing recoveries in recent decades is driven by the disproportionate loss of jobs that perform routine tasks during recessions. Here, we show that PNTR magnifies these losses in manufacturing in the years following the 2001 peak.

Finally, our research contributes to a growing literature on supply-chain co-location by relating employment loss to exposure to PNTR via upstream and downstream industries. Baldwin and Venables (2012), for example, consider different forms of supply chains that emerge in response to the forces that encourage (e.g., transport costs) or discourage (e.g., variation in factor costs) co-location. A key implication of their model is that offshoring may jump discretely if a change in trade costs triggers a relatively large portion of a supply chain to move abroad. Relatedly, Ellison, Glaeser and Kerr (2010) show that proximity to input suppliers and final customers is the most important factor in the agglomeration patterns of U.S. manufacturing industries. In this paper, we use the "NTR gap" to identify employment loss associated with potential increased competition from China in an establishment's own industry. In addition, we calculate upstream and downstream NTR gaps using input-output tables to explore the extent to which PNTR's effects are transmitted via the supply chain.

3 Data

3.1 Measuring the Effect of PNTR: The NTR Gap

According to U.S. law, imports from non-market economies such as China are, in principal, subject to relatively high tariff rates originally set under the Smoot-Hawley Tariff Act of 1930. These rates, known as "non-NTR" or "column 2" tariffs are typically substantially larger than the "NTR" or "column 1" rates the U.S. offers fellow members of the World Trade Organization (WTO).

The U.S. Trade Act of 1974 allows the President to grant NTR tariff rates to non-market economies on a temporary basis subject to Congressional approval. U.S. Presidents began granting waivers to China in 1980. While these waivers kept the actual tariff rates applied to Chinese goods low, the need for annual approval by Congress created uncertainty about whether the low tariffs would continue, particularly after the Tiananmen Square incident in 1989. In fact, the U.S. House of Representatives attempted to revoke China's temporary NTR status every year from 1990 to 2001. While these votes succeeded in 1990, 1991 and 1992, China's status was not overturned because the U.S. Senate failed to act on the House's votes. From 1990 to 2001, the average House vote against NTR renewal was 38 percent.⁶

The U.S. Congress passed a bill granting permanent NTR status to China in October 2000, which became effective upon China's accession to the WTO in 2001. The change in China's PNTR status had two effects. First, it ended the uncertainty associated with annual renewals of U.S. NTR status, thereby eliminating any option value of waiting for U.S. or Chinese firms seeking to incur sunk costs associated with greater U.S.-China trade.⁷ Second, it led to a substantial reduction in expected U.S. import tariffs on Chinese goods.⁸

We measure the impact of PNTR on industry as the difference between the non-NTR and NTR tariff rates. We refer to this measure as the "NTR gap",and expect that industries with larger gaps are more likely to be affected by the change in U.S. policy.We measure the impact of PNTR on industry as the difference between the non-NTR and NTR tariff rates. We refer to this measure as the "NTR gap" and define it as follows:

$\displaystyle NTR\: Gap_{i}=Non\: NTR\: Rate_{i}-NTR\: Rate_{i}.$

(1)

We expect that industries with larger gaps are more likely to be affected by the change in U.S. policy. One attractive feature of this measure is its plausible exogeneity to employment growth after 2001. Eighty-nine percent of the variation in the NTR gap across industries arises from variation in non-NTR rates, set 70 years prior to passage of PNTR. This feature of non-NTR rates effectively rules out reverse causality that would arise if non-NTR rates could be set to protect industries with declining employment. Furthermore, to the extent that NTR tariffs were set to protect industries with declining employment prior to PNTR, these higher NTR rates would result in lower NTR gaps, biasing our results away from finding an effect of PNTR. Moreover, the main results of the paper are robust to calculation of the NTR gap using the NTR rate from 1989, which is unaffected by employment conditions in 2001.

We compute NTR gaps using tariff data provided by Feenstra, Romalis and Schott (2002), henceforth FRS. FRS report the ad valorem equivalent NTR and non-NTR tariff rates for each year from 1989 to 2001. Both types of tariffs are set at the eight-digit Harmonized System (HS) level, also referred to as "tariff lines." We compute industry-level NTR gaps using concordances provided by the U.S. Bureau of Economic Analysis (BEA); the gap for industry is the average NTR gap across the eight-digit HS tariff lines belonging to that industry.⁹

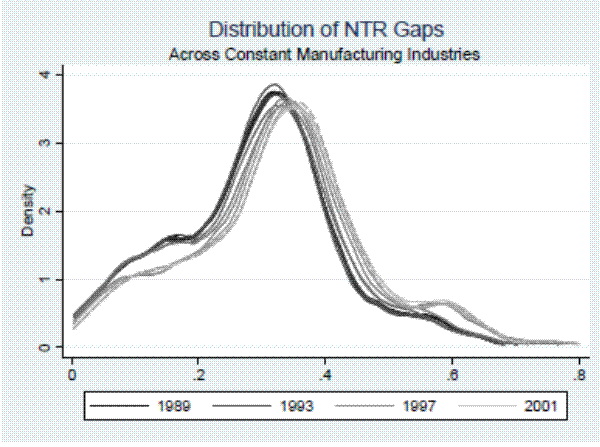
Figure A.1 of the online appendix plots the distribution of the NTR gap in each year across the constant set of manufacturing industries captured in our regressions, which is defined in the next section. As indicated in the figure, where lighter lines represent later years, the distributions are relatively stable across time. The largest change is a shift toward somewhat higher NTR gaps in the mid 1990s. There are two reasons for this shift. The first is that tariff reductions negotiated in the Uruguay Round are implemented beginning in 1997; by pushing down some NTR rates, these reductions raise their associated NTR gaps. The second cause for the shift in the distributions over time is technical: changes to the HS system in 1997, which included retiring some older HS codes and introducing some newer ones, changed the mix of underlying goods associated with certain HS codes and therefore their NTR and non-NTR rates.¹⁰ Though we use the NTR gaps for 1999 - the year before passage of PNTR in the United States - in our regression analysis below, we note that our results are robust to using the NTR gaps from any available year. Furthermore, in some of our specifications we explicitly control for changes in NTR rates over our sample period. In 1999, the average NTR gap across industries is 0.32 with a standard deviation of 0.15. The corresponding statistics are 0.04 and 0.05 for the NTR rate and 0.36 and 0.15 for the non-NTR rate.

Table 1 summarizes the relationships between the 1999 NTR gap and other industry-level variables using a series of bi-variate OLS regressions, where bold type indicates statistical significance at the 10 percent level. We discuss how these variables can be used to account for alternate explanations of the decline in U.S. manufacturing employment in Section 6. Their sources, as well as details associated with their construction, are summarized in Section C of the online appendix.

The industry attributes considered in Table 1 are: 1999 capital intensity; 1999 skill intensity; Nunn's (2007) measure of contract intensity, defined as the share of intermediate inputs requiring relationship-specific investments in 1997; changes in Chinese import tariffs from 1996 to 2005; changes in the Chinese production subsidies per total sales from 1999 to 2005; the share of Chinese firms eligible to export in 1999; an indicator for industries where Chinese textile and clothing export quotas were relaxed from 2001 to 2005; the share of U.S. workers belonging to a union in 1999; an indicator for industries containing advanced technology products; an indicator for industries in which U.S. firms filed countervailing duty (CVD) or anti-dumping (AD) claims against Chinese firms from 2001 to 2007; employment growth in the industry prior to PNTR, from 1997 to 2000; and the 1999 NTR and non-NTR rates in levels. For reference, the final two rows of the table report the mean and standard deviation of each of these covariates. We use those statistics to interpret the economic significance of some of our regression results in Section 6.

As indicated in the table, the 1999 NTR gap has negative and statistically significant relationships with capital intensity, union membership, and changes in Chinese production subsidies. It has positive and statistically significant associations with contract intensity, the share of Chinese firms eligible to export under Chinese licensing constraints, and the indicators for industries affected by quota relaxation and containing advanced technology. The share of variation in the NTR gap explained by each of these regressors is generally low, and does not exceed 0.21 (for capital intensity).

3.2 U.S. Manufacturing Employment

We track annual U.S. manufacturing employment using the U.S. Census Bureau's Longitudinal Business Database (LBD), assembled and updated annually by Jarmin and Miranda (2002). The LBD tracks the employment and major industry of virtually every establishment with employment in the non-farm private U.S. economy annually as of March 12.¹¹ In these data, "establishments" correspond to facilities in a given geographic location, such as a manufacturing plant or retail outlet, and their major industry is defined as the four-digit Standard Industrial Classification (SIC) or six-digit North American Industry Classification System (NAICS) category representing their largest share of shipments. Information from Census's Company Organization Survey is used to map establishments to "firms," and longitudinal identifiers in the LBD allow establishments and firms to be followed over time. With these identifiers, we can determine the births and deaths of establishments and firms and thereby decompose changes in industry employment along gross intensive and extensive margins of adjustment.

We augment the data in the LBD with detailed establishment-level characteristics from Census's quinquennial Census of Manufactures (CM), conducted in years ending in "2" and "7." For every manufacturing establishment, the CM provides more detailed employment data, including a breakdown of workers between production and non-production roles, production hours and the capital stock (book value). Nominal data are deflated using industry-level price indexes in the NBER-CES Manufacturing Industry Database from Becker, Gray and Marvakov (2013).

The long time horizon considered in this paper presents two complications to analyzing the evolution of manufacturing employment. The first complication is that the industry classification scheme used to track establishments' major industries' changes from the SIC to the NAICS in 1997. Moreover, some activities (e.g., parts of printing and publishing) are re-classified out of "manufacturing" in the SIC to NAICS transition. To account for these changes, we use the algorithm developed in Pierce and Schott (2012) to create "families" of four-digit SIC and six-digit NAICS codes that collect similar manufacturing activities within and across the SIC and NAICS industry classification systems.¹² We then drop from our analysis any families that contain SIC or NAICS industries that are not considered part of manufacturing during this period. The second complication associated with examining changes in manufacturing employment is that establishments may switch into or out of manufacturing over time. To prevent such changes from affecting our results, we drop all establishments whose major industry code changes between manufacturing and non-manufacturing over any particular time interval we examine. Neither of these drops has a material impact on the general trend of manufacturing employment over the past several decades.

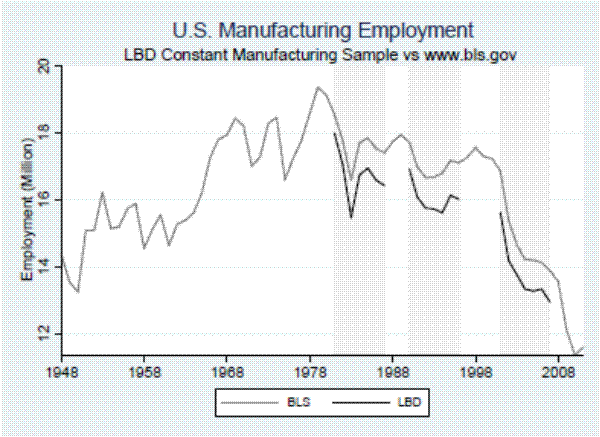
Figure A.2 of the online appendix displays annual employment in our "constant" manufacturing sample against the manufacturing employment series available publicly from the U.S. Bureau of Labor Statistics.¹³ As expected, given the procedure outlined above, the "constant" manufacturing sample accounts for less employment than the BLS series. Despite this level difference, the LBD exhibits a similarly stark drop in employment after 2001.¹⁴

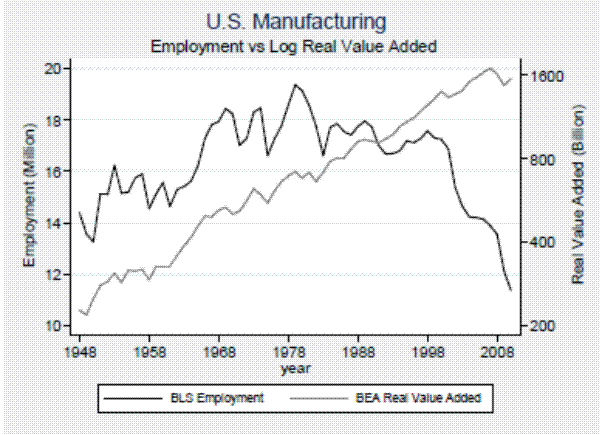
While the loss of U.S. manufacturing employment after 2001 is dramatic, we note that it is not accompanied by a similarly steep decline in value added. Indeed, as illustrated in Figure 1, real value added in U.S. manufacturing as measured by the BEA continues to increase after 2001, though at a slower rate (2.8 percent) compared with the average from 1948 to 2000 (3.7 percent).¹⁵

3.3 U.S. Imports

We use transaction-level U.S. import data from the Census Bureau's Longitudinal Foreign Trade Transaction Database (LFTTD) to investigate the relationship between PNTR and U.S. trade. As described in greater detail in Bernard, Jensen and Schott (2009), the LFTTD tracks all U.S. international trade transactions by U.S. firms from 1992 to 2008. For each import transaction we observe the ten-digit Harmonized System (HS) product traded, the U.S. dollar value and quantity shipped, the shipment date and the origin country. In addition, the data contain codes identifying both the U.S. importer and the ultimate foreign supplier of the imported product. These firm-level identifiers allow us to examine the behavior U.S. and Chinese firms engaged in this trade, including their entry and exit into trade.

4 Empirical Strategy

We estimate the effect of PNTR on U.S. manufacturing employment using an OLS difference-in-differences (DID) specification that examines whether employment losses in industries with higher NTR gaps (first difference) are larger after the imposition of PNTR than during a pre-PNTR period (second difference). As noted in Section 3.1, the fact that non-NTR rates were set during the 1930s renders the NTR gap plausibly exogenous to employment growth after 2001. Given the proximity of PNTR to the 2001 business cycle peak, we choose the years following the previous peak, in 1990, as the appropriate "pre-PNTR" period to control for fluctuations in employment associated with the business cycle.¹⁶

Our approach has the standard attributes of DID estimation. That is, while industry employment growth after PNTR may vary with industry characteristics as noted in Section 3.1, comparing outcomes within industries before and after PNTR eliminates biases associated with any time-invariant industry attributes. Likewise, the use of peak-year fixed effects controls for aggregate shocks that affect both sets of industries equally. Moreover, all specifications include industry capital intensity and skill intensity to account for two time-varying industry characteristics closely associated with U.S. comparative advantage.

Figure 2, based on publicly available employment data from the NBER-CES Manufacturing Industry Database, offers simple, initial support for our empirical approach. Breaking all U.S. six-digit NAICS manufacturing industries into two groups according to whether their NTR gaps in 1999 were above or below the median across all industries, the figure shows that employment evolves similarly from 1981 to 2001, consistent with the parallel trends assumption inherent in difference-in-differences analysis. After PNTR, the series diverge, with employment in high-gap industries falling more sharply than employment in low-gap industries.¹⁷

Figure 3 offers similar evidence with respect to U.S. imports. We divide all U.S. import products contained in publicly available U.S. import data from Schott (2008) by the median NTR gap in 1999, and then by country of origin, aggregating imports from all countries but China into a "rest-of-world" category. As indicated in the figure, U.S. imports from China increase dramatically in the post-PNTR period, with the largest gains recorded in products with high NTR gaps. This pattern is not present for U.S. imports from other trading partners.¹⁸

We provide more formal examinations of the validity of our DID approach in Section 7.1 below.

5 Baseline Results

In this section we report baseline results showing that employment losses and the growth of imports from China are larger in industries where the threat of tariff hikes declined the most.

5.1 PNTR and U.S. Manufacturing Employment (LBD)

We compare employment ( ) growth years after 2001 (the post-PNTR period) to employment growth years after the prior NBER peak, in 1990 (the pre-PNTR period), within industries with different NTR gaps. We estimate the following equation separately for intervals of increasing length, from to , to examine how the effect of PNTR evolves over time:

$\displaystyle \frac{\Delta E_{i,t:t+d}}{E_{it}}=\alpha+\theta_{d}1\{post-PNTR_{t}\}\times NTR\: Gap_{i,1999}+\gamma_{d}\mathbf{X}_{it}+\delta_{id}+\delta_{td}+\varepsilon_{itd}.$

(2)

The dependent variable is the cumulative percent change in industry

's employment between year $t=\{1990,2001\}$ and year

. The first variable on the right-hand-side of the equation is the DID term, an interaction of an indicator variable for the post-PNTR period with industries' NTR gaps in 1999. Recall that NTR gaps vary by industry but not by year

or elapsed years

. $\mathbf{X}_{it}$ is a vector of industry characteristics in year

; in our baseline specification, these are restricted to industry capital intensity and skill intensity. We measure capital intensity as the log of the ratio of real book value of capital to total employment, $ln(K/E_{it})$ and skill intensity as the log of the ratio of non-production workers to total employment, $ln(NP/E_{it})$ using data from the NBER-CES Manufacturing Industry Database, as these attributes are unavailable in the LBD. Industry and peak-year fixed effects are represented by $\delta_{id}$ and $\delta_{td}$ , respectively, and control for time-invariant differences between industries and common aggregate shocks.

Table 2 reports the results of estimating equation 2 using data from the LBD. Each column displays regression results for a different value of . Column 1, for example, compares employment growth from 2001 to 2002 to growth from 1990 to 1991. All estimates of $\theta_{d}$ are negative and statistically significant at the 10 percent level (noted with bold-faced type), indicating that employment declines are higher in industries with higher NTR gaps. Moreover, the absolute magnitudes of the coefficients rise with , from -0.104 for to -0.482 for , indicating that the effect of PNTR is persistent and increases over time. We report the implied impact of PNTR and its standard error in the last row of Table 2 by multiplying the estimated DID coefficients in the first row by the average NTR gap across industries (0.32, as noted in Section 3). These implied impacts are substantial, reducing the relative employment growth of the average industry by -3.4 percentage points (-0.104*0.32) after one year. This difference expands to -15.6 percentage points (-0.482*0.32) after six years.

Coefficients for capital and skill intensity are mostly positive and negative, respectively, indicating that higher capital intensity is associated with higher employment growth, while higher skill intensity is associated with lower employment growth. These coefficients, however, are generally statistically insignificant at conventional levels. For a sense of their economic significance, note that a one standard deviation increase in capital intensity (0.82, from the last row of Table 1) is associated with a 13.9 percentage point increase in relative employment growth six years after PNTR. A one standard deviation increase in skill intensity (0.40), on the other hand, corresponds to a decline in relative employment growth of -4 to -6 percentage points 2 to 3 years after PNTR.

5.2 PNTR and U.S. Imports (LFTTD)

PNTR may have affected U.S. employment growth by making U.S.-China trade more attractive and by raising U.S. firms' incentives to adopt labor-saving technologies. In this section we use firm-level U.S. import data from the LFTTD to investigate the relationship between PNTR and China-U.S. trade. As the LFTTD is unavailable prior to 1992, we amend our DID specification to compare outcomes across trading partners from 2001 to 2005 (the post-PNTR period) versus 1997 to 2001 (the pre-PNTR period), rather than across business cycle peaks:

$\displaystyle \Delta Z_{ch,t:t+4}$	$\displaystyle =\alpha+\theta1\{c=China\}\times1\{post-PNTR_{t}\}\times NTR\: Gap_{h,1999}$	(3)
	$\displaystyle +\gamma_{1}1\{post-PNTR_{t}\}+\gamma_{2}1\{post-PNTR_{t}\}\times NTR\: Gap_{h,1999}$
	$\displaystyle +\gamma_{3}1\{post-PNTR_{t}\}\times1\{c=China\}+\gamma_{4}1\{c=China\}\times NTR\: Gap_{h,1999}$
	$\displaystyle +\delta_{c}+\delta_{h}+\varepsilon_{ch}$

The left-hand side variable $\Delta Z_{ch,t:t+4}$ represents the change in one of several dimensions of U.S. import activity over the pre- or post-PNTR period, measured at the eight-digit HS product (

) by source country (

) level, and where $t=\{1997,2001\}$ .¹⁹ These dimensions are import value, the number of U.S. firms importing product

from country

, the number of country

firms exporting product

to the United States, and the number of importer-exporter pairs involved with U.S. imports of product

from country

. The first term on the right-hand side of equation 3 is a triple interaction of an indicator for the post-PNTR period, an indicator for China, and the 1999 NTR gap for product

. The coefficient $\theta$ captures the relative post-PNTR increase in import value (or number of firms, etc.) for products more affected by the policy change for China versus all other U.S. trading partners. The next four variables control for additional interactions needed to estimate the triple-difference coefficient $\theta$ . $\delta_{c}$ and $\delta_{h}$ represent country and product fixed effects that control for unobserved time-invariant country and product attributes.

As product-country trade data exhibit an abundance of zeros, we use the normalized growth rate introduced by Davis, Haltiwanger and Schuh (1996) for the dependent variable, $\Delta Z_{ch,t:t+4}=\left(Z_{ch,t+4}-t_{ch,t}\right)/\frac{1}{2}\left(Z_{ch,t+4}+Z_{ch,t}\right),$ which is bounded by 2 and -2 and equals those values for observations that start or end at zero, respectively.²⁰

Results are reported in Table 3. Coefficient estimates for the DID term are positive and statistically significant for all four dimensions of U.S. importing. Our estimates imply that a product with the average NTR gap (0.32) exhibits growth in import value from China between 2001 and 2005 that is 14 "normalized" percentage points higher than the growth in import value across all other U.S. trading partners relative to the pre-period. The relative growth rates for the numbers of U.S. importers, Chinese exporters and importer-exporter pairs are 12, 12 and 11 "normalized" percentage points, respectively.²¹

Together, the results in Tables 2 and 3 demonstrate that U.S. imports from China surge in precisely the set of goods where domestic employment loss is concentrated. This link provides indirect evidence that PNTR encouraged offshoring.²² Furthermore, the relative increase in U.S. and Chinese firms engaging in China-U.S. trade is consistent with models of investment (e.g., Handley 2012, Handley and Limao 2012, 2013), in which reductions in trade policy uncertainty increase firms' incentives to sink investment in new trade relationships.

6 Considering Alternate Explanations

Plausible alternate explanations for the sharp decline in U.S. manufacturing employment and concomitant increase in U.S. imports from China must explain two empirical facts. The first relates to timing: alternate explanations need to account for why the sharp decline in employment and surge in Chinese imports occur at the same time as PNTR and yet are unrelated to the policy change. The second fact is variation in outcomes across industries within manufacturing: alternate explanations must explain why the largest declines in employment and sharpest surges in imports occur in industries most exposed to PNTR via the NTR gap and yet are unrelated to the policy change.

In this section we consider a range of potential alternate explanations and assemble data to account for them empirically. We then generalize the empirical specification in equation 2 as follows:

$\displaystyle \frac{\Delta E_{i,t:t+d}}{E_{it}}$	$\displaystyle =\alpha+\theta_{d}1\{post-PNTR_{t}\}\times NTR\: Gap_{i,1999}$	(4)
	$\displaystyle +\sum_{p}\gamma_{1d}1\{post-PNTR_{t}\}\times X_{i}+\sum_{p}\beta_{1d}1\{post-PNTR_{t}\}\times X_{it}$
	$\displaystyle +\beta_{2d}X_{it}+\delta_{id}+\delta_{td}+\varepsilon_{itd}.$

The first interaction on the right-hand side of equation 4 is the same DID estimator employed in equation 2 above. The next two terms are interactions of a post-PNTR indicator with the time-invariant ( $X_{i}$ ) and time-varying ( $X_{it}$ ) industry attributes associated with the potential alternate explanations, which are discussed in detail in the remainder of this section. In cases where these attributes are time-varying, so that their coefficients can be identified separately from the industry fixed effects ( $\delta_{id}$ ), they are also included in levels (fourth term). The interactions of industry attributes with the post-PNTR indicator yield a highly flexible DID specification in that it not only controls for proxies of alternate explanations of our baseline results, but also allows for the relationship between these proxies and employment growth to differ between the pre- and post-PNTR periods.

Before continuing, we note that consideration of potential alternate explanations does not materially change the implied impact of PNTR on manufacturing employment growth. As indicated in the last row of Table 4, even with the flexible specification in equation 4 we continue to find a substantial effect of PNTR: relative employment growth from to years after the change in policy is -4.1 to -11.8 percent, compared with -3.4 to -15.6 percent in the last row of Table 2. The remainder of the section presents potential alternate explanations for our results, describes proxies for each of these candidate explanations and reports the relationship between those proxies and U.S. employment growth.

6.1 Changes in Chinese Policy

As part of its accession to the WTO, China agreed to ease formal and informal restrictions on foreign investment, reduce import barriers, and eliminate export licensing requirements and production subsidies (WTO 2001). China's entry into the WTO also eliminated quotas on certain apparel and textile exports that already had been relaxed for other developing economies (Brambilla et al. 2009). These WTO-related reforms, like PNTR, may have influenced both manufacturing employment in the United States and China-U.S. trade. We discuss each of these Chinese policy changes in turn.

Barriers to Investment: In joining the WTO, China agreed to treat foreign enterprises no less favorably than domestic firms. This reduction in barriers to investment may have reduced the fixed and variable costs associated with offshoring, providing U.S. firms with a greater incentive to relocate some or all of their production to China. As direct evidence of these reforms is unavailable, we examine whether U.S. employment losses are concentrated in industries most likely to benefit from changes in the institutional environment, i.e., industries in which contracting over inputs is more important. To account for this potential relationship, we add to our baseline regression an interaction of a post-PNTR dummy and Nunn's (2007) measure of industries' contract intensity, which rises with the share of intermediate inputs requiring relationship-specific investment. We expect a negative point estimate: assuming investment in China became easier after WTO accession, it should have the largest impact on U.S. employment in industries where contracting is more important. As indicated in Table 4, the relationship is statistically insignificant in all years.

Tariff Barriers: China reduced import tariffs on a number of products both before and after its accession to the WTO. Reductions in Chinese import tariffs might be expected to boost U.S. exports to China and thereby raise U.S. employment. On the other hand, by lowering the cost of foreign inputs and thereby making China a more attractive location for manufacturing, they may have had the opposite effect. Using Chinese tariff data from Brandt et al. (2010), we include an interaction of a post-PNTR dummy with the change in Chinese import tariffs from 1996 to 2005. As indicated in Table 4, we find a generally positive relationship that is statistically significant in years 4 and 5, suggesting the second explanation dominates. The coefficient estimates for those two years imply that a one standard deviation decline in Chinese tariff barriers (0.07, from Table 1) reduces relative employment growth in the United States five years after 2001 by about 2 percentage points.

Export Licensing: As discussed in detail in Bai et al. (2013), China agreed to phase out export licensing requirements by 2003. Because export licenses had formerly been more difficult to obtain in some industries than others, their removal may have led to a surge in Chinese exports and subsequent decline in U.S. manufacturing employment in the industries where licensing was most binding.²³ To account for this potential influence, we include in our regression an interaction of a post-PNTR indicator with the share of firms eligible for export licenses in 1999 from Bai et al. (2013). As indicated in Table 4, this coefficient is statistically insignificant in all years.

Production Subsidies: Some have argued that the rapid expansion of China's manufacturing sector was driven by subsidies, which may affect some industries more than others (Haley and Haley 2013). We follow Girma et al. (2009) and Aghion et al. (2012) and use firm-level data published by China's National Bureau of Statistics (NBS) to compute industry-level changes in the subsidy-per-sales ratio from 1999 to 2005, and interact this variable with an indicator for the post-PNTR period. Here, a negative relationship indicates rising subsidies are associated with falling employment. As indicated in Table 4, we find a negative but statistically insignificant relationship between this covariate and employment growth in all years.

Under the assumption that rising subsidies induce U.S. firms to file countervailing duty (CVD) claims against Chinese producers, we also use data from Bown (2012) to construct an indicator variable for industries in which either CVD or anti-dumping (AD) claims have been filed between 1990 and 1996 (pre-PNTR period) and 2001 through 2007 (post-PNTR period). We consider both CVD and AD filings because, under U.S. trade policy, CVD claims could not be filed against Chinese firms until 2006.²⁴

As indicated in Table 4, results for the interaction are negative and are statistically insignificant except for years 5 and 6 (when CVD filings were permitted). Together, the level and interaction coefficient estimates for these years imply that industries in which CVD or AD filings occur experience relative employment declines of approximately -4 percentage points.

Finally, some suspect China of subsidizing a reallocation of production towards products with higher levels of technology, which we measure using an indicator that picks out industries identified by the U.S. Census Bureau as containing products with "advanced technology." As indicated in the table, coefficient estimates for the interaction of this variable with the post-PNTR dummy are negative but statistically insignificant at conventional levels.

Textile and Clothing Quotas: During the Uruguay Round of trade negotiations, the United States, the EU and Canada agreed to eliminate quotas on developing country textile and clothing exports in four phases starting in 1995 (Brambilla et al. 2009). China was not eligible for these reductions until its accession to the WTO. We use data provided by Khandelwal et al. (2013) to identify industries where the majority of HS products experience relaxed quotas starting in 2001, and include an interaction of this variable with a post-PNTR dummy variable. As indicated in Table 4, we find a positive and generally statistically significant relationship between this interaction and job loss after PNTR. This coefficient reflects the fact (evident in Table A.4 below) that while job loss continued in these industries during the 2000s, losses were relatively greater in the 1990s, when MFA quotas began being phased out for developing countries other than China.

6.2 Shocks to U.S. Comparative Disadvantage Industries

As documented in Table 1, NTR gaps are negatively related to industry capital intensity, with that attribute explaining 21 percent of the variation in the NTR gap across industries. Assuming the U.S. has a comparative disadvantage vis a vis China in the production of labor-intensive goods, an alternate explanation of the results in Section 5 is a post-2001 decline in the U.S. competitiveness of labor-intensive industries for some reason unrelated to PNTR, e.g. a general movement towards offshoring perhaps encouraged by the 2001 recession, or a positive productivity shock in China.²⁵

While the baseline results presented in Section 5.1 already control for capital and skill intensity, interactions of these attributes with a post-PNTR dummy allow the relationship between factor intensity and employment growth to be different after 2001. As indicated in Table 4, for capital intensity we find that the interactions are negative and statistically significant in years 3 and 4, while the coefficient on the level is not statistically significant. Together, the interaction and level coefficient estimates for year 4, for example, imply that industries with capital intensity that is one standard deviation larger have employment growth that is 3.1 percentage points higher in the post-PNTR period.

For skill intensity, the coefficients for the level are negative and statistically significant in all years, while coefficients for the interactions are positive and statistically significant after year 2. Together, the interaction and level coefficient estimates across all years imply that industries with skill intensity that is one standard deviation larger have employment growth that is -1.4 (year 5) to -6.5 (year 3) percentage points lower in the post-PNTR period.

6.3 Union Resistance

Given the negative association between the NTR gap and union membership displayed in Table 1, an alternate explanation of our results might be that all manufacturing firms desired to reduce employment after 2001, but that unions impeded reductions in some industries. We account for this potential explanation by including the level of union membership in each peak year in our regressions. We also include an interaction of this variable with a post-PNTR dummy to determine if the relationship between union membership and employment growth changes after 2001.

As indicated in Table 4, we find a negative but generally statistically insignificant relationship between union membership and employment growth, but find that this relationship becomes less negative after PNTR. The level and interaction estimates for imply that a one standard deviation increase in union membership is associated with a reduction in employment growth five years after 2001 of -0.4 percentage points.

6.4 The IT Boom-Bust

The information technology (IT) sector experienced a well-known boom and bust around the time that PNTR was implemented. More generally, sectors that experience greater employment growth leading up to a peak may suffer greater declines after it, or may continue to grow at faster rates. We account for these potential explanations of our results in two ways. First, we include in our regression a variable measuring industries' employment growth in the three years before each peak, 1997 to 2000 and 1988 to 1990 for the post- and pre-PNTR periods, respectively, as well as interactions of this variable with a post-PNTR dummy. As indicated in Table 4, coefficients for the level are generally positive while coefficients for the interaction are generally negative. Together, the statistically significant coefficients for years 3, 4 and 5 indicate that industries with prior growth that is one standard deviation higher (0.12, from Table 1) are associated with relative changes in employment growth of 0.2, -1.2 and -2.0 percentage points.

The interaction of an indicator for advanced technology products and a post-PNTR dummy variable discussed in Section 6.1 also provides information about the behavior of the IT sector. As noted there, coefficient estimates are negative but statistically insignificant at conventional levels.

6.5 The U.S. NTR Rate

Some of the variation in post- versus pre-PNTR U.S. manufacturing employment growth may be driven by changes to U.S. NTR tariff rates over our sample period. To control for such changes, the results in Table 4 include a measure of the change in U.S. ad valorem equivalent NTR tariff rates from 1990 to 2001 interacted with an indicator for the post-PNTR period.²⁶ This interaction allows for the possibility that reductions in U.S. tariffs over that period had a differential impact on U.S. employment before and after the 2001 peak. Coefficient estimates for the effect of changes in the NTR rate are not statistically significant.

6.6 Non-PNTR-Induced Technical Change

Another explanation for our results is that they are driven by labor-saving technical changes, such as automation, which are spuriously correlated with the NTR gap. While technical change unrelated to PNTR is difficult to measure, several of the variables discussed above - including indicators for advanced technology products (ATP) and measures of industry skill and capital intensity - serve as useful proxies for where it might show up. Coefficient estimates for these variables, however, do not provide much evidence in favor of technical change that is independent of the change in U.S. trade policy.

Moreover, we show in the next section that there is no relationship between the U.S. NTR gap and the growth of manufacturing employment in the EU. If labor-saving technological innovations unrelated to PNTR were spuriously correlated with the U.S. NTR gap, their impact also should be manifest in other developed economies.²⁷

7 Robustness

In this section we examine the validity of our DID assumptions, consider an alternate DID specification, and compare manufacturing employment loss in the United States to that of the European Union, which was not subject to the policy change experienced in the United States.

7.1 Placebo DID Regressions

We consider two placebo regressions to assess the validity of our DID estimator. First, we estimate the relationship between employment growth and the NTR gap in the pre-PNTR and post-PNTR periods separately. As indicated in Table A.4 of the online appendix, we find no effect of the NTR gap on employment growth in the pre-PNTR period, but find that a higher NTR gap is associated with lower employment growth in the post-PNTR period.

Second, we apply the the same DID specification used above to an earlier period that did not contain the policy change. Specifically, we estimate equation 4 to examine the relationship between the NTR gap and employment growth after the two NBER peaks prior to PNTR, 1990 versus 1981. As shown in Table A.5 of the online appendix, the DID coefficient is statistically insignificant at conventional levels in this regression, providing further support for our empirical strategy.

7.2 An Alternate DID Specification

Next, we re-estimate the effect of PNTR using an alternate DID specification that makes use of annual employment data from 1990 to 2007:

$\displaystyle ln(E_{iy})$

$\displaystyle =\alpha+\sum_{j=1991}^{2007}\theta_{j}1\{j=y\}\times NTR\: Gap_{i,1999}+\sum_{j=1991}^{2007}\gamma_{j}1\{j=y\}\times\mathbf{X}_{i}+\delta_{i}+\delta_{y}+\varepsilon_{iy}.$

(5)

This specification regresses log industry employment in year

on interactions of the full set of year dummies and the NTR gap (the first summation term), interactions of year dummies and the industry characteristics discussed in Section 6 (second summation term), and both year and industry fixed effects.²⁸ In contrast with equation 2, this specification allows for a different relationship between the NTR gap and employment in each year of the sample period, as well as a different relationship between all of the additional industry characteristics and employment in each year.

Estimates of $\theta_{j}$ are reported in Table 5, where the results in the first column are from a regression that omits the interactions of year fixed effects with $\mathbf{X}_{i}$ while the results in the second column are from a regression that includes them. (Estimates of $\gamma_{j}$ are omitted from column 2 to conserve space, but are available upon request.)

Three aspects of the results stand out. First, estimates of $\theta_{j}$ are negative and statistically significant in the post-PNTR period, consistent with our earlier finding that PNTR is associated with lower manufacturing employment. Second, estimates of $\theta_{j}$ are not statistically significant in the pre-PNTR period, indicating that losses in the post-PNTR period are not part of a pre-existing trend. Third, the implied impact of PNTR on relative employment growth after six years (i.e, from 2001 and 2007 versus 1990 to 1996) is 15.3 percentage points in column 1 and 18.1 percentage points in column 2, versus 15.6 and 11.8 percentage points in the final rows of Tables 2 and 4, respectively.²⁹ This robust relationship between the NTR gap and manufacturing employment is particularly compelling given the highly flexible nature of equation 5.³⁰

7.3 A Comparison With the EU

In this section, we compare manufacturing employment growth in the United States to the European Union. In contrast to the United States, the European Union granted permanent most-favored-nation status to China in 1980 (Casarini 2006). China's accession to the WTO, therefore, had little effect on either actual or expected tariffs in the EU, and imports from China were not subject to the annual potential tariff increases present in the United States.³¹

We compare U.S. and EU outcomes using data on manufacturing employment at the four-digit International Standard Industrial Classification (ISIC) level available from UNIDO.³² As these data are available only for the years 1997 to 2005 (with 2003 missing for the United States), we make use of a DID specification similar to that described in the previous sub-section,

$\displaystyle ln(E_{iy})$

$\displaystyle =\alpha+\sum_{j=1998}^{2005}\theta_{j}1\{j=y\}*NTR\: Gap_{i,1999}+\delta_{i}+\delta_{y}+\varepsilon_{iy}.$

(6)

The variables associated with the summation represent interactions of the full set of year dummies with the NTR gap, while $\delta_{i}$ and $\delta_{y}$ are industry and year fixed effects, respectively. Table 6 reports the results of estimating this equation separately on EU versus U.S. employment. As shown in the first column of the table, the DID coefficients for the EU are statistically insignificant at conventional levels in all years. By contrast, results for the United States, in column 2, are consistent with those reported in Table 5: coefficients for interactions of the NTR gap with year dummies are both negative and statistically significant starting in 2001, after PNTR is enacted.³³

These results have two implications. First, they indicate that employment declines associated with the NTR gap in the United States do not appear to be correlated with an unobserved shock affecting manufacturing employment globally. For example, if the trends in U.S. employment were due to a technology shock in industries that happen to be high gap, or to a productivity shock in China, we would expect to see similar effects in the EU, another large developed economy. The lack of a relationship between the NTR gap and employment in the EU is further evidence against these explanations. Second, these results confirm the relationship between employment declines and the NTR gap in the United States using an entirely different dataset and industrial classification system for employment.

8 Additional Effects of PNTR

8.1 Job Creation versus Job Destruction

In this section we decompose the implied impact of PNTR on overall industry employment growth by the gross margins of job creation (JC) versus job destruction (JD). Job creation is the change in employment due to expansion at continuing plants, the birth of plants within continuing firms and the birth of new firms. Job destruction is the change in employment due to contraction at continuing plants, the death of plants within continuing firms and the death of existing firms.³⁴

Using equation 4, we estimate a separate regression for each gross margin $m=\{JC,JD\}$ and interval , where the dependent variable is the cumulative change in employment along the margin as a percent of initial industry employment,

$\displaystyle \frac{\Delta E_{i,t:t+d}}{E_{it}}=\frac{\left(E_{im,t+d}-E_{imt}\right)}{E_{it}}$

$\displaystyle .$

(7)

This variable is designed so that the sum of the changes across margins equals the overall change from equation 4, i.e., ${\textstyle \sum_{m}}\Delta E_{im,t:t+d}/E_{it}=\Delta E_{i,t:t+d}/E_{it}$ .

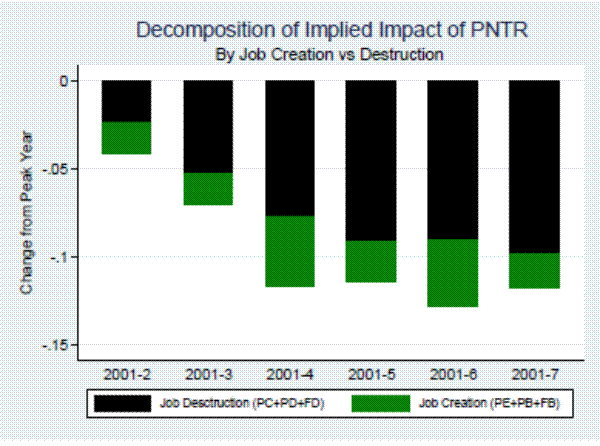
To conserve space, we summarize the results of these regressions in Figure 4, which displays the respective contributions of JC and JD to the overall implied impact of PNTR reported in the last row of Table 4. As can be seen in the figure, both margins are influential in overall employment loss, with elevated job destruction accounting for approximately three quarters of the overall cumulative relative decline between 2001 and 2007, and anemic job creation accounting for the remaining quarter.

These results suggest a role for trade policy in trends that have been associated with the joblessness of the 2001 recovery in manufacturing. Faberman (2012), for example, points out that the sluggishness of that recovery coincides with a decline in job creation rates and an increase in job destruction rates in the manufacturing sector starting in the late 1990s. Our results show that PNTR is associated with employment loss along each of these margins of adjustment.

8.2 Other Industry Outcomes

In this section we employ data from the CM to examine the effects of PNTR on a rich set of industry characteristics - including disaggregations of employment by type of worker, as well as capital and skill intensity - that are not reported in the LBD. The DID specification we use for this analysis takes the same general form as equation 2, but because the CM is conducted only in years ending in 2 and 7, the pre-PNTR period is defined as the decade around the 1990 peak, 1987 to 1997, while the post-PNTR period is defined as the decade around the 2001 peak, 1997 to 2007.

We begin by estimating the relationship between the NTR gap and several categories of employment. Results are reported in Table 7. The negative and statistically significant coefficient in the first column implies that PNTR reduced total employment growth by -19.5 percentage points from 1997 to 2007 versus the prior decade. Results in columns 2 and 3 reveal that the implied impact of PNTR is roughly twice as large for production workers (-23.4 percentage points) as for non-production workers (-11.2 percentage points). The estimates in column 4 indicate that PNTR also had a substantial (-18.7 percentage points) negative effect on the growth rate of production hours, confirming that the decline in employment can not be solely attributed to an increase in the number of hours worked per employee.

Next, we examine the association between PNTR and changes in the factor intensity of the production process. The results in column 5 show that capital declines less than overall employment (-15.3 versus -19.5 percentage points) and, as a result, column 6 reports an increase in capital intensity associated with PNTR, although the estimated effect is not statistically significant. In terms of the labor composition of production, the results in column 7 indicate that PNTR is associated with a statistically significant increase in skilled labor intensity.

These results on the relationship between PNTR and factor intensity complement recent research in international trade and macroeconomics in three ways. First, to the extent that non-production workers embody higher levels of human capital than production workers, they suggest increases in skill intensity consistent with those reported by Bloom, Draca and Van Reenen (2012) for the United Kingdom. Second, they are also in accord with research by Bernard et al. (2006), Khandelwal (2010) and Schott (2008) that shows that firms in high-wage countries like the United States alter their product mix towards goods more consistent with comparative advantage in response to competition from low-wage countries. Third, to the extent that production workers are more likely to engage in routine tasks, they relate to Jaimovich and Siu's (2012) finding that jobs focusing on such tasks were more likely to disappear following recessions.

8.3 Plant Outcomes

In this section, we examine the impact of PNTR on outcomes at the plant level. This analysis is useful for several reasons. First, it provides information on the extent to which the industry-level results estimated in the previous section can be attributed to changes within continuing plants, versus those arising from plant birth and death. Second, it allows us to investigate whether plant attributes moderate the estimated affects of PNTR.³⁵ Lastly, we can use information from the CM on the set of products produced by each plant to analyze the relationship between plant outcomes and a plant-specific measure of the NTR gap, which we calculate as the weighted-average NTR gap across all of the industries in which the plant is active.³⁶ We first estimate the relationship between these gaps and the log growth in outcomes ( ) among continuing plants:

$\displaystyle \Delta ln(O_{p,t:t+10})$	$\displaystyle =\alpha+\theta1\{Post-PNTR_{t}\}\times NTR\: Gap_{p,1999}$	(8)
	$\displaystyle +\mathbf{\gamma_{1}}1\{Post-PNTR_{t}\}\times\mathbf{X}_{pt}+\mathbf{\gamma_{2}}\mathbf{X}_{pt}+\delta_{t}+\delta_{p}+\varepsilon_{pt}$

As in the previous section, there are two observations for each plant (

) corresponding to growth ten years after $t=\{1987,1997\}$ . $\mathbf{X}_{pt}$ is a matrix of plant characteristics in year

that includes capital and skill intensity, age and total factor productivity (TFP).³⁷ As with our industry-level regressions, we allow the relationship between the dependent variables and plant attributes to vary across the pre- and post-PNTR periods. Regressions also include plant ( $\delta_{p}$ ) and period

( $\delta_{t}$ ) fixed effects to control for unobserved, time-invariant plant attributes and aggregate shocks that affect all plants equally.

The results reported in the first seven columns of Table 8 yield implied effects that are qualitatively similar to those found at the industry level (Table 7), though larger in absolute magnitude. The first column reveals that the implied impact of PNTR on continuing plants' relative employment growth is substantial, at -23.9 percentage points. Results in the next two columns show that PNTR again has roughly twice the impact on production workers (-30.7 percentage points; column 3) as non-production workers (-15.8 percentage points; column 2). Here, however, the implied impact on continuing plants' skill intensity (column 7), like capital intensity (column 6), is statistically insignificant at conventional levels. Finally, the results in column 4 indicate that the implied impact of PNTR on production hours (-27.0 percentage points) is roughly the same as on production employment, suggesting no substantial change in hours worked per employee. The similarity of the plant- and industry-level estimates have two implications. First, they indicate that the effects of PNTR are not due solely to plant birth and death. Second, they confirm a role for PNTR even when controlling for variation in plant attributes within industries.

To investigate the impact of PNTR on the extensive margin of plant death, we amend equation 8 by defining the dependent variable to be one if a plant exits between year and year , and zero otherwise. The relationship between PNTR and plant death is then estimated in a linear probability model, where the independent variables are identical to those in equation 8. Results are displayed in the final column of Table 8. We find that PNTR is associated with a higher probability of plant death, with plants in the average industry being 9.2 percent (0.288*0.32) more likely to die relative to the pre-period. These findings provide additional evidence of a link between PNTR and offshoring by demonstrating that higher NTR gaps are associated with greater probability of exit as well as greater declines in employment and larger increases in imports from China.

8.4 Input-Output Linkages

In this section, we explore whether the effects of PNTR are transmitted through input-output linkages by computing up- and downstream NTR gaps that reflect the exposure of each plant to PNTR via its supply chain. To the extent that lower-cost inputs benefit plants in downstream industries there may be a positive relationship between employment in plant and its upstream NTR gap. On the other hand, there may be a negative relationship between employment and the downstream gap if PNTR adversely affects plants' customers. Furthermore, if greater exposure to PNTR induces plant 's up- or downstream industries to relocate to China, it may increase the probability that plant also exits the United States, since proximity to the supply chain is an important determinant of the location of manufacturing activity (Ellison, Glaeser and Kerr 2010).

As we do not have information on the industries from which individual plants buy and to which they sell, we approximate plants' up- and downstream NTR gaps using industry-level information from U.S. input-output tables. We calculate the upstream NTR gap for a plant in six-digit NAICS industry ( $Upstream\: NTR\: Gap_{i}$ ) as the weighted average NTR gap across all six-digit NAICS industries used to produce , employing IO coefficients from the BEA's 1997 total requirements table as weights. However, given that plants often produce a range of goods within the same sector (Bernard et al. 2010), we set the weights for any six-digit NAICS input within 's three-digit NAICS root to zero. We compute industry 's downstream NTR Gap ( $Downstream\: NTR\: Gap_{i}$ ) analogously. Using the concordances referenced in Section 3, we then map these NAICS-based up- and downstream NTR gaps to the major industry of each plant.³⁸ These gaps are then incorporated into equation 8.

Before continuing, we note that our measures of supply chain linkages to PNTR have several weaknesses. First, the upstream and downstream gaps are based on industry-level IO relationships and therefore do not take into account the substantial heterogeneity across plants in the industries from which they source inputs and to which they sell outputs. In particular, some plants may produce inputs that other plants source from an upstream industry. Second, the own, upstream and downstream gaps are highly related, with correlations of 0.46 and 0.24 for own versus upstream and own versus downstream, respectively.³⁹ These high correlations likely reduce the precision of our estimates by inflating the associated standard errors. Finally, supply chains linkages need not be uni-directional (Baldwin and Venables 2012), since it is possible for plants in one industry to both purchase inputs from and sell outputs to plants in another industry. Given these caveats, results based on the up- and downstream NTR gaps should be interpreted with some caution.

We report results for continuing plants' total employment growth as well as plant death in Table 9. As indicated in the first column of the table, the coefficient estimate for a plant's own-industry NTR gap on employment growth continues to be negative and statistically significant, and of a similar magnitude to the estimate in Table 8 (-0.701 versus -0.748). The coefficients for plants' up- and downstream NTR gaps, however, are not statistically significant at conventional levels, suggesting little role for our measures of PNTR's supply chain effects in explaining employment growth at continuing plants. Summing the effects of the own, upstream and downstream NTR gaps, we find that PNTR lowered relative employment growth at continuing plants by -26.3 (-0.701*.32+-0.556*.11+0.200*.11) percentage points, slightly larger than the -23.9 percentage point effect attributed to the own-industry NTR gap alone in Table 8.

In contrast with the results for employment growth at continuing firms, however, we do find evidence of PNTR having effects via the supply chain when examining the probability of plant death. As shown in the second column of Table 9, a higher own-industry NTR gap continues to be associated with a higher probability of death, as in the last column of Table 8. Here, however, we find that the coefficient estimates for the up- and downstream NTR gaps are both positive and statistically significant, indicating that plants are more likely to die when industries either up or down their supply chain have greater exposure to PNTR. This increase in the probability of plant death due to up- and downstream exposure to PNTR may reflect pressure to exit and relocate if the policy change induces a large segment of the U.S. supply chain to move offshore, as argued in Baldwin and Venables (2012). Aggregating the effects of the own, upstream and downstream NTR gaps on the probability of plant death, we estimate that a plant in the average industry is 15.4 (0.149*0.32+0.570*0.11+0.393*0.11) percent more likely to die as a result of PNTR, versus 9.2 percent in the final column of Table 8.

9 Conclusion

This paper documents a strong relationship between the sharp decline in U.S. manufacturing employment beginning in 2001 and the United States' conferral of permanent normal trade relations on China, a policy that is notable for eliminating the possibility of future tariff increases rather than reducing the tariffs actually applied to Chinese goods.

We measure the effect of PNTR as the gap between the low NTR rates that were made permanent by PNTR and the higher non-NTR rates to which they would have risen if an annual renewal of NTR had failed. Using a difference-in-differences specification, we show that industries with higher NTR gaps experience larger employment declines, along with disproportionate increases in U.S. imports from China, the number of U.S. firms importing from China, the number of Chinese firms exporting to the United States, and the number of U.S.-China importer-exporter pairs. These results are robust to inclusion of variables proxying for a wide range of alternate explanations for the observed trends in employment and trade. Moreover, we demonstrate that the pattern of employment losses in the United States - which experienced the policy change - are not present in the European Union, which had granted China the equivalent of PNTR status in 1980.

Having established a strong link between the change in trade policy and U.S. employment outcomes, this research raises several important, but challenging questions. To what extent can PNTR explain the diverging trends of value-added and employment in the U.S. manufacturing sector? What impact did PNTR have on U.S. prices and consumption patterns? To what extent did U.S. firms change the composition of their output in response to PNTR, and how large were the associated transition costs? We hope to bring additional data to bear on these questions in future research.

References

[1] Aghion, Philippe, Mathias Dewatripont, Luosha Du, Ann Harrison and Patrick Legros., 2012. "Industrial Policy and Competition." NBER Working Paper 18048.

[2] Autor, David H., David Dorn and Gordon H. Hanson. 2012. "The China Syndrome: Local Labor Market Effects of Import Competition in the United States." American Economic Review. Forthcoming.

[3] Autor, David H., David Dorn, Gordon H. Hanson and Jae Song., 2013. "Trade Adjustment: Worker Level Evidence." NBER Working Paper 19226.

[4] Bai, Xue, Kala Krishna and Hong Ma., 2013. How You Export Matters: Export Mode, Learning and Productivity in China" Unpublished.

[5] Baily, Martin and Robert Z. Lawrence., 2004. "What Happened to the Great U.S. Jobs Machine? The Role of Trade and Electronic Offshoring." Brookings Papers on Economic Activity 2004(2): 211-270.

[6] Baldwin, Richard and Anthony J. Venables., 2012. "Relocating the Value Chain: Off-shoring and Agglomeration in the Global Economy." CEPR Discussion Paper 8163.

[7] Becker, Randy, Wayne B. Gray and Jordan Marvakov. 2013. "NBER-CES Manufacturing Industry Database." Available at www.nber.org/data/nberces5809.html.

[8] Bernard, Andrew B., J. Bradford Jensen, and Peter K. Schott., 2006. "Survival of the Best Fit: Exposure to Low-Wage Countries and the (Uneven) Growth of US Manufacturing Plants." Journal of International Economics 68(1): 219-237.

[9] Bernard, Andrew B., J. Bradford Jensen and Peter K. Schott., 2009. "Importers, Exporters and Multinationals: A Portrait of Firms in the U.S. that Trade Goods." In Timothy Dunne, J. Bradford Jensen and Mark J. Roberts, eds., Producer Dynamics: New Evidence from Micro Data. Chicago: University of Chicago Press.

[10] Bernard, Andrew, Stephen J. Redding and Peter K. Schott. 2010. "Multi-Product Firms and Product-Switching." American Economic Review 100: 70-97.

[11] Bertrand, Marianne, Esther Duflo and Sendhil Mullainathan. 2004. "How Much Should We Trust Differences-In-Differences Estimates?" The Quarterly Journal of Economics 119(1): 249-275.

[12] Bloom, Nick, Stephen Bond and John Van Reenen., 2007. "Uncertainty and Investment Dynamics." Review of Economic Studies 74(2007): 391-415.

[13] Bloom, Nick, Mirko Draca and John Van Reenen., 2012. "Trade Induced Technical Change: The Impact of Chinese Imports on Innovation, Diffusion and Productivity." NBER Working Paper 16717.

[14] Bown, Chad P., 2012. "Global Antidumping Database," available at http://econ.worldbank.org/ttbd/gad/.

[15] Brambilla, Irene, Amit K. Khandelwal and Peter K. Schott., 2009. "China's Experience Under the Multifiber Arrangement (MFA) and the Agreement on Textiles and Clothing (ATC)." In Robert Feenstra and Shang-Jin Wei, eds., China's Growing Roll in World Trade. Chicago: University of Chicago Press. Forthcoming.

[16] Brandt, Loren, Johannes Van Biesebroeck, Luhang Wang and Yifan Wang., 2012. "WTO Accession and Performance of Chinese Manufacturing Firms." CEPR Working Paper 9166.

[17] Casarini, Nicola., 2006. "The Evolution of the EU-China Relationship: From Constructive Engagement to Strategic Partnership." Occasional Paper Number 64, European Union Institute for Security Studies.

[18] Davis, Steven J., John C. Haltiwanger and Scott Schuh. 1996. Job Creation and Destruction. Cambridge: MIT Press.

[19] De Loecker, Jan, Pinelopi K. Goldberg, Amit K. Khandelwal and Nina Pavcnik., 2012. "Prices, Markups and Trade Reform." NBER Working Paper 17925.

[20] Dey, Matthew, Susan N. Houseman and Anne E. Polivka. 2012. "Manufacturers' Outsourcing to Staffing Services." Industrial & Labor Relations Review 65(3): 533-559.

[21] Dixit, A. K. and Robert S. Pindyck., 1994. Investment Under Uncertainty. Princeton: Princeton University Press.

[22] Dumbaugh, Kerry., 2001. "Voting on NTR for China Again in 2001, and Past Congressional Decisions." CRS Report for Congress RS20691.

[23] Ebenstein, Avraham, Margaret McMillan, Yaohui Zhao and Chanchuan Zhang., 2011. "Understanding the Role of China in the `Decline' of US Manufacturing." Unpublished.

[24] Ebenstein, Avraham, Ann Harrison and Margaret McMillan. 2013. "Why are American Workers Getting Poorer? China, Trade and Offshoring." Unpublished.

[25] Edwards, Lawrence and Robert Z. Lawrence., 2013.

Rising Tide: Is Growth in Emerging Economies Good for the United States? Washington, DC: Peterson Institute for International Economics.

[26] Ellison, Glenn, Edward Glaeser, and William R. Kerr. 2010. "What Causes Industry Agglomeration? Evidence from Coagglomeration Patterns." American Economic Review 100 (June, 2010 ): 1195-1213.

[27] European Commission., 2003. Overview of the Terms of China's Accession to WTO, 2. Brussels, Germany. Retrieved from http://trade.ec.europa.eu/doclib/docs/2003/october/tradoc_111955.pdf

[28] Faberman, R. Jason., 2012.

"Job Flows, Jobless Recoveries and the Great Moderation." Unpublished.

[29] Feenstra, Robert C., John Romalis and Peter K. Schott. 2002. "U.S. Imports, Exports and Tariff Data, 1989 -2001." NBER Working Paper 9387.

[30] Foster, Lucia S., John C. Haltiwanger and Chad Syverson. 2008. "Reallocation, Firm Turnover and Efficiency: Selection on Productivity or Profitability." American Economic Review 98: 394-425.

[31] Freeman, R., Katz, L., 1991. "Industrial Wage and Employment Determination in an Open Economy, in Immigration, Trade and Labor Market," edited by John M. Abowd and Richard B. Freeman. Chicago: University of Chicago Press.

[32] Girma, S., Gong, Y., Görg, H. and Yu, Z., 2009. "Can Production Subsidies Explain China's Export Performance? Evidence from Firm-level Data." The Scandinavian Journal of Economics 111: 863-891.

[33] Groizard, Jose L., Priya Ranjan and Jose Antonio Rodriguez-Lopez. 2012. "Input Trade Flows." Unpublished.

[34] Jaimovich, Nir and Henry Siu., 2012. "The Trend is the Cycle: Job Polarization and Jobless Recoveries." Unpublished.

[35] Jarmin, Ron and Javier Miranda., 2002. "The Longitudinal Business Database." Center for Economic Studies Discussion Paper 101647.

[36] Handley, Kyle., 2012. "Exporting Under Trade Policy Uncertainty: Theory and Evidence." Unpublished. [37] Handley, Kyle and Nuno Limao., 2012. "Trade and Investment under Policy Uncertainty: Theory and Firm Evidence." NBER Working Paper 17790.

[38] Handley, Kyle and Nuno Limao., 2013. "Policy uncertainty, Trade and Welfare: Evidence from the U.S. and China." NBER Working Paper 19376.

[39] Harrison, Ann and Margaret McMillan., 2011. "Offshoring Jobs? Multinationals and U.S. Manufacturing Employment." The Review of Economics and Statistics 93(3): 857-875.

[40] Holmes, Thomas J. and John J. Stevens., 2013. "An Alternative Theory of the Plant Size Distribution with an Application to Trade." Journal of Political Economy. Forthcoming.

[41] Houseman, Susan, Christopher Kurz, Paul Lengermann and Benjamin Mandel., 2011. Offshoring Bias in U.S. Manufacturing. Journal of Economic Perspectives 25: 111-132.

[42] Khandelwal, Amit., 2010. "The Long and Short (of) Quality Ladders." Review of Economic Studies 77(4), 1450-1476.

[43] Khandelwal, Amit K., Peter K. Schott and Shang-Jin Wei., 2012. "Trade Liberalization and Embedded Institutional Reform: Evidence from Chinese Exporters." American Economic Review. Forthcoming.

[44] Mankiw, N.G. and P. L. Swagel., 2006. "The Politics and Economics of Offshore Outsourcing." Journal of Monetary Economics 53(5): 1027-1056.

[45] Morisi, Teresa L., 2003. "Recent Changes in the National Current Employment Statistics Survey." Monthly Labor Review (June).

[46] Mion, Giordano and Like Zhu., 2013. "Import Competition From and Outsourcing to China: A Curse or a Blessing for Firms." Journal of International Economics 89(1): 202-215.

[47] Nunn, Nathan., 2007. "Relationship-Specificity, Incomplete Contracts and the Pattern of Trade." Quarterly Journal of Economics 122(2) 569-600.

[48] Pierce, Justin R., 2011. "Plant-Level Responses to Antidumping Duties: Evidence from U.S. Manufacturers." Journal of International Economics 85(2): 369-378.

[49] Pierce, Justin R. and Peter K. Schott., 2012. "Concording U.S. Harmonized System Codes Over Time." Journal of Official Statistics 28(1): 53-68.

[50] Revenga, A.L., 1992. "Exporting Jobs? The Impact of Import Competition on Employment and Wages in U.S. Manufacturing," Quarterly Journal of Economics 107(1): 255-284.

[51] Sachs, J.D., Shatz, H.J., 1994. "Trade and Jobs in U.S. Manufacturing," Brookings Papers on Economic Activity 1994(1): 1-69.

[52] Schott, Peter K., 2008. "The Relative Sophistication of Chinese Exports." Economic Policy 53: 5-49.

[53] U.S. Department of the Treasury., 2012.

Report to Congress on International Economic and Exchange Rate Policies. Available for download at www.treasury.gov/resource-center/international/exchange-rate-policies/Documents/Foreign Exchange Report May 2012.pdf.

[54] Utar, Hale and Luis B. Torres Ruiz., 2013. "International Competition and Industrial Evolution: Evidence form the Impact of Chinese Competition on Mexican Maquiladoras." Journal of Development Economics 105: 267-287.

[55] WTO., 2001.Report of the Working Party on the Accession of China. WTO Publication WT/MIN(01)/3. Available for download at www.wto.org.

Table 1: 1999 NTR Gap versus Other Industry Attributes

Dependent variable: 1999 NTR Gap	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions	Industry-level OLS regressions
ln(K/L)	-0.080													-0.060
ln(K/L): Robust standard errors	0.009													0.011
ln(S/L)		-0.019												-0.034
ln(S/L): Robust standard errors		0.019												0.022
Nunn Contract Intensity			0.176											-0.026
Nunn Contract Intensity: Robust standard errors			0.035											0.051
ΔChinese Import Tariffs (1996-05)				-0.045										0.036
ΔChinese Import Tariffs (1996-05): Robust standard errors				0.096										0.087
ΔChinese Subsidy (1999-05)					-10.760									-8.076
ΔChinese Subsidy (1999-05): Robust standard errors					4.909									4.004
Share of Chinese Firms Eligible to Export (1999)						0.330								0.254
Share of Chinese Firms Eligible to Export (1999): Robust standard errors						0.066								0.074
1{MFA Apparel}							0.235							0.177
1{MFA Apparel}: Robust standard errors							0.029							0.024
Union Membership (1999)								-0.606						-0.392
Union Membership (1999): Robust standard errors								0.082						0.095
1{Advanced Technology Products}									0.036					0.010
1{Advanced Technology Products}: Robust standard errors									0.014					0.018
1{Anti-Dumping Filings 2001-07}										0.002				0.031
1{Anti-Dumping Filings 2001-07}: Robust standard errors										0.019				0.019
Prior Growth (1997-2000)											-0.042			-0.008
Prior Growth (1997-2000): Robust standard errors											0.077			0.063
U.S. NTR Rate (1999)												0.083
U.S. NTR Rate (1999): Robust standard errors												0.222
U.S. Non-NTR Rate (1999)													0.889
U.S. Non-NTR Rate (1999): Robust standard errors													0.015
Industries	326	326	326	326	326	326	326	326	326	326	326	326	326	326
R-squared	0.21	0.00	0.07	0.00	0.02	0.09	0.11	0.13	0.01	0.00	0.00	0.00	0.90	0.39
Covariate Mean	4.61	-1.30	0.52	-0.15	-0.0002	0.50	0.04	0.14	0.15	0.16	-0.04	0.04	0.36
Covariate Std Dev	0.82	0.40	0.22	0.12	0.0016	0.13	0.20	0.09	0.36	0.36	0.12	0.05	0.15

Notes: Table reports the results of industry-level OLS regressions summarizing the relationship between the 1999 NTR gap and noted industry attributes. Coefficient for constant is suppressed. See text for a discussion of these attributes and their sources.

Table 2: PNTR and U.S. Manufacturing Employment (LBD)

	Percent Change in Industry Employment Years After NBER Peak (LBD): 1	Percent Change in Industry Employment Years After NBER Peak (LBD): 2	Percent Change in Industry Employment Years After NBER Peak (LBD): 3	Percent Change in Industry Employment Years After NBER Peak (LBD): 4	Percent Change in Industry Employment Years After NBER Peak (LBD): 5	Percent Change in Industry Employment Years After NBER Peak (LBD): 6
1{post-PNTR} x NTR Gap_i	-0.104	-0.187	-0.332	-0.387	-0.469	-0.482
1{post-PNTR} x NTR Gap_i: Robust standard errors	0.058	0.082	0.105	0.114	0.149	0.147
ln(K/L_it)	-0.058	-0.032	0.021	0.099	0.140	0.170
ln(K/L_it) : Robust standard errors	0.036	0.056	0.071	0.077	0.101	0.093
ln(S/L_it)	-0.048	-0.110	-0.140	-0.131	-0.087	-0.108
ln(S/L_it) : Robust standard errors	0.046	0.059	0.075	0.087	0.096	0.111
Observations	652	652	652	652	652	652
R2	0.67	0.70	0.70	0.70	0.66	0.66
Fixed Effects	it	it	it	it	it	it
Employment Weighted	Yes	Yes	Yes	Yes	Yes	Yes
Implied Impact of PNTR	-0.034	-0.060	-0.107	-0.125	-0.151	-0.156
Implied Impact of PNTR : Robust standard errors)	0.019	0.026	0.034	0.037	0.048	0.047

Notes: Each column displays the results of an OLS regression of the cumulative percent change in industry (i) employment on a difference-in-differences term and industry capital and skill intensity. There are two observations for each industry corresponding to growth up to six years after the 1990 and 2001 peaks indexed by t. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed. Final rows reports the implied impact of PNTR by multiplying the DID coefficients with the average NTR gap.

Table 3: PNTR and China-U.S. Trade

	Normalized Change 2001-2005 versus 1997-2001: Value	Normalized Change 2001-2005 versus 1997-2001: Number of U.S. Importers	Normalized Change 2001-2005 versus 1997-2001: Number of Chinese Exporters	Normalized Change 2001-2005 versus 1997-2001: Number of Importer-Exporer Pairs
1{post-PNTR} x 1{c=China} x NTR Gap_i	0.427	0.381	0.361	0.334
1{post-PNTR} x 1{c=China} x NTR Gap_i: robust standard errors	0.104	0.086	0.088	0.088
Observations	341239	341239	341239	341239
R2	0.06	0.07	0.07	0.07
Robust SE	Yes	Yes	Yes	Yes
Fixed Effects	h,c	h,c	h,c	h,c

Notes: Each column displays the results of an eight-digit HS (h) by importing-country (c) level OLS regression. Dependent variable is the normalized change (see text) in the noted variable for 1997 to 2001 versus 2001 to 2005. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant fixed effects and interactions between the China dummy the NTR Gap and the post dummy are suppressed.

Table 4: PNTR and U.S. Manufacturing Employment (LBD)

	Percent Change in industry Employment Years After NBER Peak (LBD): 1	Percent Change in industry Employment Years After NBER Peak (LBD): 2	Percent Change in industry Employment Years After NBER Peak (LBD): 3	Percent Change in industry Employment Years After NBER Peak (LBD): 4	Percent Change in industry Employment Years After NBER Peak (LBD): 5	Percent Change in industry Employment Years After NBER Peak (LBD): 6
1{post-PNTR} x NTR Gap_i	-0.128	-0.219	-0.362	-0.352	-0.395	-0.366
1{post-PNTR} x NTR Gap_i: Standard errors	0.076	0.121	0.152	0.158	0.196	0.185
1{post-PNTR} x Contract Intensity_i	0.051	0.006	-0.021	0.035	-0.019	-0.059
1{post-PNTR} x Contract Intensity_i: Robust standard errors	0.049	0.065	0.080	0.092	0.118	0.121
1{post-PNTR} x ΔChina Import Tariffs_i	-0.046	0.051	0.174	0.273	0.298	0.241
1{post-PNTR} x ΔChina Import Tariffs_i : Robust standard errors	0.065	0.093	0.112	0.124	0.159	0.172
1{post-PNTR} x ΔChina Licensing_i	0.033	0.015	0.006	-0.105	-0.039	-0.030
1{post-PNTR} x ΔChina Licensing_i : Robust standard errors	0.091	0.139	0.173	0.190	0.235	0.218
1{post-PNTR} x ΔChina Subsidies_i	-2.019	-3.227	-2.023	-4.158	-9.861	-4.904
1{post-PNTR} x ΔChina Subsidies_i : Robust standard errors	4.869	7.558	9.007	9.717	12.360	12.160
Anti-Dumping Filings_i	-0.015	-0.017	-0.023	0.016	0.048	0.052
Anti-Dumping Filings_i: Robust standard errors	0.014	0.021	0.025	0.027	0.037	0.042
1{post-PNTR} x Anti-Dumping Filings_i	-0.011	-0.016	-0.026	-0.049	-0.112	-0.113
1{post-PNTR} x Anti-Dumping Filings_i: Robust standard errors	0.018	0.027	0.032	0.034	0.047	0.056
1{post-PNTR} x 1{Advanced Tech_i}	-0.031	-0.044	-0.030	-0.021	-0.013	-0.045
1{post-PNTR} x 1{Advanced Tech_i} : Robust standard errors	0.024	0.033	0.038	0.041	0.051	0.052
1{post-PNTR} x 1{MFA Apparel}_i	-0.007	0.069	0.115	0.066	0.081	0.074
1{post-PNTR} x 1{MFA Apparel}_i: Robust standard errors	0.039	0.041	0.043	0.037	0.046	0.052
ln(K/L_it)	-0.038	-0.011	0.031	0.079	0.068	0.100
ln(K/L_it) : Robust standard errors	0.034	0.050	0.059	0.067	0.083	0.090
1{post-PNTR} x ln(K/L_it)	-0.005	-0.002	-0.031	-0.041	-0.034	-0.026
1{post-PNTR} x ln(K/L_it) : Robust standard errors	0.011	0.014	0.016	0.018	0.022	0.028
ln(S/L_it)	-0.073	-0.132	-0.226	-0.244	-0.175	-0.219
ln(S/L_it) :Robust standard errors	0.039	0.057	0.074	0.080	0.095	0.109
1{post-PNTR} x ln(S/L_it)	-0.013	0.015	0.064	0.092	0.141	0.166
1{post-PNTR} x ln(S/L_it) : Robust standard errors	0.023	0.026	0.033	0.037	0.048	0.054
Union Membership_it	-0.106	-0.139	-0.498	-0.397	-0.430	-0.515
Union Membership_it: Robust standard errors	0.165	0.204	0.248	0.275	0.362	0.419
1{post-PNTR} x Union Membership_it	0.012	-0.009	0.077	0.246	0.378	0.362
1{post-PNTR} x Union Membership_it: Robust standard errors	0.084	0.117	0.138	0.157	0.196	0.250
Prior Growth_it	0.112	0.092	0.290	0.354	0.429	0.279
Prior Growth_it: Robust standard errors	0.096	0.123	0.176	0.202	0.263	0.290
1{post-PNTR} x Prior Growth_it	-0.035	-0.023	-0.273	-0.450	-0.596	-0.598
1{post-PNTR} x Prior Growth_it: Robust standard errors	0.124	0.162	0.210	0.254	0.310	0.372
1{post-PNTR} x Δ NTR_i	-0.243	-0.240	0.126	0.199	-0.112	0.158
1{post-PNTR} x Δ NTR_i: Robust standard errors	0.280	0.449	0.479	0.507	0.602	0.643
Observations	652	652	652	652	652	652
R2	0.70	0.72	0.73	0.74	0.71	0.70
Fixed Effects	it	it	it	it	it	it
Employment Weighted	Yes	Yes	Yes	Yes	Yes	Yes
Implied Impact of PNTR	-0.041	-0.071	-0.117	-0.114	-0.128	-0.118
Implied Impact of PNTR: standard errors	0.025	0.039	0.049	0.051	0.063	0.060

Notes: Each column displays the results of an OLS regression of the cumulative percent change in industry (i) employment on a difference-in-differences term and various industry attributes. There are two observations for each industry corresponding to growth up to six years after the 1990 and 2001 peaks indexed by t. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed. Final rows reports the implied impact of PNTR by multiplying the DID coefficients with the average NTR gap.

Table 5: PNTR and U.S. Manufacturing Employment, Alternate Specification

	ln(Employment_iy)	ln(Employment_iy)
1{year=1991} x NTR Gap_i	-0.044	-0.008
1{year=1991} x NTR Gap_i: Robust standard errors	0.283	0.258
1{year=1992} x NTR Gap_i	-0.025	0.000
1{year=1992} x NTR Gap_i: Robust standard errors	0.274	0.241
1{year=1993} x NTR Gapi	0.005	0.073
1{year=1993} x NTR Gap_i: robust standard errors	0.254	0.226
1{year=1994} x NTR Gap_i	-0.012	0.089
1{year=1994} x NTR Gap_i: robust standard errors	0.236	0.212
1{year=1995} x NTR Gap_i	-0.012	0.065
1{year=1995} x NTR Gap_i: robust standard errors	0.227	0.204
1{year=1996} x NTR Gap_i	-0.040	0.077
1{year=1996} x NTR Gap_i: robust standard errors	0.216	0.199
1{year=1997} x NTR Gap_i	-0.072	0.032
1{year=1997} x NTR Gap_i: robust standard errors	0.209	0.195
1{year=1998} x NTR Gap_i	-0.103	0.011
1{year=1998} x NTR Gap_i: robust standard errors	0.204	0.193
1{year=1999} x NTR Gap_i	-0.214	-0.092
1{year=1999} x NTR Gap_i: robust standard errors	0.204	0.195
1{year=2000} x NTR Gap_i	-0.296	-0.117
1{year=2000} x NTR Gap_i: robust standard errors	0.212	0.201
1{year=2001} x NTR Gap_i	-0.397	-0.184
1{year=2001} x NTR Gap_i: robust standard errors	0.222	0.207
1{year=2002} x NTR Gap_i	-0.652	-0.392
1{year=2002} x NTR Gap_i: robust standard errors	0.234	0.207
1{year=2003} x NTR Gap_i	-0.749	-0.462
1{year=2003} x NTR Gap_i: robust standard errors	0.244	0.214
1{year=2004} x NTR Gap_i	-0.872	-0.556
1{year=2004} x NTR Gap_i: robust standard errors	0.251	0.224
1{year=2005} x NTR Gap_i	-0.890	-0.611
1{year=2005} x NTR Gap_i: robust standard errors	0.253	0.230
1{year=2006} x NTR Gap_i	-0.943	-0.655
1{year=2006} x NTR Gap_i: robust standard errors	0.265	0.245
1{year=2007} x NTR Gap_i	-1.044	-0.744
1{year=2007} x NTR Gap_i: robust standard errors	0.277	0.257
Observations	5868	5868
R2	0.98	0.98
Employment Weighted	Yes	Yes
Fixed Effects	i,y	i,y
Additonal Covariates	No	Yes

Notes: Each column displays the results of an industry-level OLS regression of the log of manufacturing employment on interactions of year fixed effects and the 1999 NTR gap. Results for year (t) and industry (i) fixed effects are suppressed. Regression in second column also includes as additional controls the NTR rate as well as interactions of year fixed effects with log capital intensity log skill intensity contract intensity the change in Chinese import tariffs the change in Chinese subsidies Chinese export restrictiveness prior to 2001 and dummies for MFA advanced technology and anti-dumping-filing industries. Regressions are weighted by industry employment in 1990. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level.

Table 6: PNTR and U.S. versus EU Manufacturing Employment

	ln(EU Employment_iy)	ln(US Employment_iy)
1{y=1998} x NTR Gap_i	-0.019	-0.079
1{y=1998} x NTR Gap_i: robust standard errors	-0.148	-0.285
1{y=1999} x NTR Gap_i	-0.010	-0.189
1{y=1999} x NTR Gap_i: robust standard errors	-0.120	-0.238
1{y=2000} x NTR Gap_i	0.007	-0.304
1{y=2000} x NTR Gap_i: robust standard errors	-0.112	-0.224
1{y=2001} x NTR Gap_i	0.032	-0.395
1{y=2001} x NTR Gap_i: robust standard errors	-0.112	-0.222
1{y=2002} x NTR Gap_i	0.015	-0.636
1{y=2002} x NTR Gap_i: robust standard errors	-0.115	-0.235
1{y=2003} x NTR Gap_i	0.041
1{y=2003} x NTR Gapi: robust standard errors	-0.128
1{y=2004} x NTR Gap_i	0.010	-1.057
1{y=2004} x NTR Gap_i: robust standard errors	-0.136	-0.296
1{y=2005} x NTR Gap_i	-0.042	-1.078
1{y=2005} x NTR Gap_i: robust standard errors	-0.144	-0.334
Observations	999	832
R2	0.99	0.99
Employment Weighted	Yes	Yes
Fixed Effects	i,t	i,t

Notes: Each column displays the results of an ISIC-industry (i) level OLS regression of the log of manufacturing employment on year (t) fixed effects industry fixed effects and interactions of year fixed effects with the 1999 U.S. NTR gap. Coefficient estimates for all but the latter are suppressed. Data are from the UNIDO INDSTAT4 database (see text) for 1997 to 2005. U.S. data for 1993 are missing from this dataset. Industries for which data are not available in all years for a particular country are dropped. Regressions are weighted by 1997 employment. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level.

Table 7: PNTR and U.S. Manufacturing Employment (CM)

	Percent Change Across CM Decades: Total Employment	Percent Change Across CM Decades: Non-Prod Workers	Percent Change Across CM Decades: Production Workers	Percent Change Across CM Decades: Production Hours	Percent Change Across CM Decades: Capital Stock	Percent Change Across CM Decades: Capital Intensity	Percent Change Across CM Decades: Skill Intensity
1{post-PNTR} x NTR Gap_i	-0.606	-0.346	-0.728	-0.582	-0.475	0.379	0.387
1{post-PNTR} x NTR Gap_i: robust standard errors	0.150	0.173	0.154	0.174	0.264	0.343	0.126
ln(K/L_it)	0.253	0.202	0.231	0.326	-0.447		-0.097
ln(K/L_it) : robust standard errors	0.091	0.093	0.096	0.130	0.202		0.041
ln(S/L_it)	0.061	-0.693	0.406	0.531	0.164	0.230
ln(S/L_it) : robust standard errors	0.176	0.201	0.184	0.201	0.379	0.481
Observations	652	652	652	652	652	652	652
R2	0.78	0.73	0.78	0.58	0.65	0.50	0.70
Fixed Effects	it	it	it	it	it	it	it
Employment Weighted	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Implied Impact of PNTR	-0.195	-0.112	-0.234	-0.187	-0.153	0.122	0.125
Implied Impact of PNTR: robust standard errors	0.048	0.056	0.050	0.056	0.085	0.111	0.041

Notes: Each column displays the results of an OLS regression of the cumulative percent change in an attribute for industry (i) on a difference-in-differences term and industry capital and skill intensity. There are two observations for each industry corresponding to growth ten years after 1987 and 1997 indexed by t. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed. Observations are weighted by period t employment. The final two rows report the implied impact of PNTR computed by multiplying the DID coefficients with the average NTR gap (0.32) and its standard error.

Table 8: PNTR and Plant Outcomes

	Log Change Across CM Decades (Continuing Plants Only): Total Employment	Log Change Across CM Decades (Continuing Plants Only): Non- Production Workers	Log Change Across CM Decades (Continuing Plants Only): Production Workers	Log Change Across CM Decades (Continuing Plants Only): Production Hours	Log Change Across CM Decades (Continuing Plants Only): Capital Stock	Log Change Across CM Decades (Continuing Plants Only): Capital Intensity	Log Change Across CM Decades (Continuing Plants Only): Skill Intensity	Plant Death
1{post-PNTR} x NTR Gap_pt	-0.748	-0.493	-0.959	-0.843	-0.785	-0.057	0.152	0.288
1{post-PNTR} x NTR Gap_pt: Robust standard errors	0.118	0.190	0.134	0.141	0.235	0.336	0.140	0.045
ln(K/L)_pt	0.093	0.134	0.080	0.076	-1.406		-0.017	0.033
ln(K/L)_pt: Robust standard errors	0.021	0.025	0.027	0.027	0.036		0.020	0.007
1{post-PNTR} x ln(K/L)_pt	0.030	-0.009	0.030	0.003	-0.205		-0.001	-0.048
1{post-PNTR} x ln(K/L)_pt: Robust standard errors	0.015	0.019	0.019	0.020	0.022		0.014	0.005
ln(S/L)_pt	-0.014	-1.236	0.412	0.336	-0.068	0.018		0.039
ln(S/L)_pt: Robust standard errors	0.028	0.040	0.043	0.046	0.045	0.062		0.012
1{post-PNTR} x ln(S/L)_pt	0.128	-0.139	0.218	0.229	0.206	-0.102		-0.031
1{post-PNTR} x ln(S/L)_pt: Robust standard errors	0.033	0.044	0.051	0.050	0.042	0.059		0.010
ln(Age)_pt	-0.069	-0.120	-0.054	-0.110	-0.088	0.127	-0.125	0.028
ln(Age)_pt: Robust standard errors	0.176	0.185	0.219	0.192	0.201	0.233	0.167	0.053
1{post-PNTR} x ln(Age)_pt	0.474	0.304	0.484	0.383	0.474	0.135	-0.370	-0.007
1{post-PNTR} x ln(Age)_pt: Robust standard errors	0.337	0.372	0.423	0.388	0.391	0.480	0.313	0.100
ln(TFP)_pt	-0.072	-0.080	-0.053	-0.052	-0.059	0.114	0.007	0.004
ln(TFP)_pt: Robust standard errors	0.021	0.026	0.022	0.024	0.023	0.038	0.020	0.005
1{post-PNTR} x ln(TFP)_pt	0.021	0.039	0.012	-0.003	0.023	-0.004	0.004	-0.006
1{post-PNTR} x ln(TFP)_pt: Robust standard errors	0.012	0.022	0.011	0.011	0.013	0.021	0.007	0.004
Observations	140735	140735	140735	140735	140735	140735	140735	272183
R2	0.76	0.80	0.75	0.73	0.84	0.51	0.58	0.79
Fixed Effects	pt	pt	pt	pt	pt	pt	pt	pt
Employment Weighted	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Implied Impact of PNTR	-0.239	-0.158	-0.307	-0.270	-0.251	-0.018	0.049	0.092
Implied Impact of PNTR: Robust standard errors	0.038	0.061	0.043	0.045	0.075	0.108	0.045	0.015

Notes: First eight columns are restricted to continuing establisments and display the results of an OLS regression of the log difference of the noted plant (p) attribute on the noted covariates (see text). Final column displays the results of an OLS regression of an indicator for plant death on the noted covariates. There are two observations for each plant corresponding to growth over the pre- (1987 to 1997) and post-PNTR (1997 to 2007) periods. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed. Final rows reports the implied impact of PNTR by multiplying the DID coefficients with the average NTR gap.

Table 9: PNTR and Supply Chain Linkages

	Across CM Decades: Employment Growth	Across CM Decades: Plant Death
1{post-PNTR} x NTR Gap_pt	-0.701	0.149
1{post-PNTR} x NTR Gap_pt: Robust standard errors	0.147	0.057
1{post-PNTR} x NTR Upstream Gap_pt	-0.556	0.570
1{post-PNTR} x NTR Upstream Gap_pt: Robust standard errors	0.353	0.183
1{post-PNTR} x NTR Downstream Gap_pt	0.200	0.393
1{post-PNTR} x NTR Downstream Gap_pt: Robust standard errors	0.226	0.091
ln(K/L)_pt	0.097	0.033
ln(K/L)_pt: Robust standard errors	0.021	0.008
1{post-PNTR} x ln(K/L)_pt	0.024	-0.048
1{post-PNTR} x ln(K/L)_pt: Robust standard errors	0.015	0.005
ln(S/L)_pt	-0.014	0.036
ln(S/L)_pt: Robust standard errors	0.028	0.012
1{post-PNTR} x ln(S/L)_pt	0.125	-0.026
1{post-PNTR} x ln(S/L)_pt: Robust standard errors	0.034	0.010
ln(Age)_pt	-0.071	0.024
ln(Age)_pt : Robust standard errors	0.177	0.053
1{post-PNTR} x ln(Age)_pt	0.466	-0.017
1{post-PNTR} x ln(Age)_pt: Robust standard errors	0.339	0.100
ln(TFP)_pt	-0.073	0.004
ln(TFP)_pt: Robust standard errors	0.022	0.005
1{post-PNTR} x ln(TFP)_pt	0.022	-0.006
1{post-PNTR} x ln(TFP)_pt: Robust standard errors	0.013	0.004
Observations	140735	272183
R2	0.76	0.79
Fixed Effects	p,t	p,t
Employment Weighted	Yes	Yes

Notes: Each column displays the results of a plant-level OLS regression. First column examines employment growth among continuing plants. Second column examines plant death. There are two observations for each plant corresponding to growth or survival over the pre- (1987 to 1997) and post-PNTR (1997 to 2007) periods. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed.

Figure 1: U.S. Manufacturing Employment versus Value Added

Notes: Figure compares annual manufacturing employment as of March according to the U.S. Bureau of Labor Statistics (series CEU3000000001) to real value added as measured by the Bureau of Economic Analysis.

Figure 2: U.S. Manufacturing Employment for High vs Low NTR Gap Industries (Public Data)

Notes: Figure displays the evolution of U.S. manufacturing employment as measured in the publicly available NBER-CES Manufacturing Industry Productivity Database. NAICS manufacturing industries are split into two groups depending on whether their NTR gap in 1999 is above or below the median across all manufacturing industries.

Figure 3: U.S. Imp orts by Origin and NTR Gap (Public Data).

Figure 4: Implied Impact of PNTR by Gross Margins

Notes: Figure decomposes the implied contribution of PNTR from the last row of Table 4 by job creation versus job destruction. Job creation is due to growth at continuing plants, plant births at continuing firms and firm birth. Job destruction is due to decline at continuing plants, plant death at continuing firms and firm death.

Online Appendix (For Online Publication)

This appendix contains more detailed explanations of how some of the data in the main text were computed, as well as additional empirical results referenced in the main text.

A Constructing NTR Gaps

Computation of the NTR gap for each NAICS industry takes four steps. First, NTR gaps are computed at the eight-digit HS level as the difference between the non-NTR and NTR import tariff rates described in the next section. Second, using the concordance developed by Pierce and Schott (2012b), we match all HS import codes used by the United States between 1989 and 2001 to a time-invariant set of eight-digit HS code families. This step ensures that NTR gaps from HS codes added or deleted over time are incorporated in all years for which we may want to compute an NTR gap. Without this step, NTR gaps might be available for a different number of NAICS industries across the years 1989 to 2001, if HS codes matched to certain NAICS industries appear in some years but not others. Third, we match these time consistent HS codes to NAICS industries using an HS-NAICS concordance from the U.S. Bureau of Economic Analysis (BEA).⁴⁰ Fourth, we compute the NTR gap for each NAICS industry as the average NTR gap across all time-consistent HS codes matched to that NAICS industry.

We calculate the upstream NTR gap for NAICS industry as the weighted average NTR gap across all industries used to produce , using the coefficients from the BEA's industry-by-industry total requirements input-output matrix as weights.⁴¹ Likewise, the downstream NTR gap for NAICS industry is the weighted average NTR gap of all industries supplied by industry , again using the total requirements table coefficients as weights. In computing both weighted averages, we set the IO weights to zero for up- and downstream industries within industry 's three-digit NAICS sector. We do this in recognition of the fact that U.S. manufacturing establishments often produce clusters of products within the same three-digit NAICS sector (Bernard et al. 2010).

B U.S. Trade Policy Towards China

B.1 Statutory U.S. Import Tariffs

As noted in the main text, we use the ad valorem equivalent NTR and non-NTR tariff rates from Feenstra, Romalis and Schott (2002) to compute the NTR gaps by industry and year. This section describes the distribution of NTR and non-NTR tariff rates by eight-digit HS tariff line and year.

Non-NTR tariff rates, which can contain ad valorem, specific and "other" components - exhibit little change from 1989 to 2001. Indeed, 92 percent of the 13,700 unique tariff lines that appear in the Feenstra et al. (2002) dataset exhibit no change in their underlying "ad valorem" component over the years for which they are used. Even fewer tariff lines - 55 and 2, respectively - exhibit changes to their "specific" or "other" components. Furthermore, we find that more than 95 percent of the changes to the "ad valorem" component of the non-NTR rates occur in 1997, indicating they likely are related to changes triggered by the revision of HS codes in that year. For further detail, Pierce and Schott (2012) provide a detailed discussion of these changes.

NTR tariff rates exhibit greater variation than non-NTR tariff rates. Of the 13,700 tariff lines used during the 1989 to 2001 period, 6,127, 1,164 and 11 exhibit variation in their underlying "ad valorem", "specific" and "other" components, respectively, during this period. These changes generally are implemented from 1995 to 1999, indicating they are related to the tariff reductions negotiated during the Uruguay Round of the GATT.

B.2 Annual Renewals of NTR Status

The U.S. House of Representatives voted to overturn the Presidential waiver on Chinese import tariffs every year from 1990 to 2001. Table A.1 records the share of votes against renewal during these years.

C Data Sources

This section describes the sources for the non-U.S.-Census data used in the main text.

Chinese Import Tariffs: Brandt et al. (2012) report Chinese import tariffs by eight-digit Chinese HS code for 1996 to 2005, though data for some HS codes are missing. We aggregate these tariffs up to the six-digit HS level and then from the six-digit HS level to U.S. NAICS codes using concordances developed by Pierce and Schott (2012a). For each U.S. industry-year, this aggregation is the simple average of the tariffs of the six-digit HS codes encompassed by the industry. We then calculate the change in Chinese import tariff rates over the maximum span for which tariffs are available - 1996 to 2005 - and refer to this variable as the change in Chinese import tariffs.
Chinese Production Subsidies: We use confidential data from the Annual Report of Industrial Enterprise Statistics compiled by China's National Bureau of Statistics (NBS), which reports the subsidies provided to responding firms. Following Girma et al. (2009) and Aghion et al. (2012), we use the variable "subsidy" in this dataset to compute subsidy per sales ratios for each four-digit China Industry Classification (CIC) and year. We then concord the CICs to ISIC and then U.S. SIC industries using concordances provided by Dean and Lovely (2010). The NBS data encompass a census of state-owned enterprises (SOEs) and a survey of all non-SOEs with annual sales above 5 million Renminbi (~$600,000). The version of the NBS dataset available to us from Khandelwal et al. (2013) spans the period 1998 to 2005.
Chinese Export Eligibility: Prior to their phasing out by 2003, export licenses were more difficult to obtain in some Chinese industries than others. Bai et al. (2013) use the features of this policy to determine the share of Chinese producers in each four-digit CIC industry that were eligible to export in 1999. We concord these shares to ISIC and then U.S. SIC industries using concordances provided by Dean and Lovely (2010) and the United Nations, available at http://unstats.un.org/unsd/cr/registry/regot.asp.
Quotas on Chinese Textile and Clothing Exports to the United States: We identify industries in which quotas on Chinese exports of textiles and clothing are relaxed from 2001 to 2007 using data reported by Khandelwal et al. (2013). These data list the HS codes for which quotas are relaxed. Here, we match these HS codes to industries using concordances developed by Pierce and Schott (2012a).
Industries' Contract Intensity: Nunn (2007) uses the 1997 U.S. input-output tables to develop a measure of the portion of industries' intermediate inputs that require relationship-specific investments. Industries with higher shares (e.g., automobiles) are assumed to be harder to contract over than industries with lower shares (e.g., poultry processing). These data are available from Nunn's website at http://scholar.harvard.edu/nunn/pages/data-0.
U.S. Union Membership: The website www.unionstats.com - assembled by Hirsch and Macpherson (2003) - publishes information on the share of workers that are members of a union by Current Population Survey (CPS) industry classification and year. We match CPS industries to SIC codes using the concordances posted at unionstats.com.
Advanced Technology Products (ATP): The U.S. Census Bureau identifies products - defined at the ten-digit HS level - that contain advanced technology in ten areas: biotech, life sciences, opto-electronics, IT, electronics, flexible manufacturing, advanced materials, aerospace, weapons and nuclear technology. We match these HS codes to NAICS industries using concordances developed by Pierce and Schott (2012a). The Census ATP classification can be downloaded from http://www.census.gov/foreign-trade/reference/codes/atp/.
U.S. Anti-dumping (AD) and Countervailing Duty (CVD) Filings: We identify industries that received AD and CVD protection using datasets assembled by Bown (2012), which list AD and CVD actions by HS code and year.⁴² We match these HS codes to industries using concordances developed by Pierce and Schott (2012a). The AD and CVD data are available online at http://data.worldbank.org/data-catalog/temporary-trade-barriers-database.

D Creating a "Constant Manufacturing" Sample

As noted in the main text, we use the algorithm developed in Pierce and Schott (2012b) to create a constant manufacturing sample over which employment changes can be analyzed. This algorithm creates "families" of four-digit SIC and six-digit NAICS codes that group related SIC and NAICS categories together over the 1977 to 1997 and 1997 to 2007 periods over which SIC and NAICS codes were used, respectively.

For example, if an SIC code splits into several NAICS codes between 1997 and 2002, the SIC code and its NAICS "children" would be grouped into the same family. If one of those NAICS codes later matches with an updated NAICS code whose family history includes a broader set of SIC, those subsequent NAICS and SIC codes join the original family.

Given this process, it is easy to see that some families can grow to be quite large. For this reason, we have created several concordances that limit the inclusion of children that do not account for some threshold level of their parents' activity. (Industry-to-industry concordances generally specify both paternity and the share of activity - in terms of output or employment - which they inherit.) These limits create a tradeoff. Higher thresholds generate a larger number of families with more closely related underlying SIC and NAICS codes. Lower thresholds lead to a smaller number of families, most of which are likely to include both manufacturing and non-manufacturing codes.

In all of the results contained in the main text, we use a threshold of 50 percent to create families.⁴³ This threshold works as follows. First, sort all children industries that match to parent industries in descending order according to their importance in value terms to parent industry . Keep all children matches until the cumulative share of value explainedexceeds 50 percent. In most cases, a single child accounts for the overwhelming majority of parent overall value.

E Chinese Exporters

In the main text, we use an identifier in the U.S. trade data to count the number of Chinese firms exporting to the United States. In this section, we use the transaction-level trade data from China's National Bureau of Statistics, provided by Khandelwal et al. (2013), to examine the relative growth of Chinese firms exporting to the U.S. market versus other markets. Given the short sample period - data are available from 2000 to 2005, we employ a variant of the DID specification used in Section 7:

$\displaystyle ln(N_{hcy})$	$\displaystyle =\alpha+\sum_{j=2001}^{2005}\theta_{j}1\{j=y\}1\{c=US\}NTR\: Gap_{h,1999}$	(A.1)
	$\displaystyle +\sum_{j=2001}^{2005}\gamma_{1j}1\{j=y\}*NTR\: Gap_{h,1999}$
	$\displaystyle +\sum_{j=2001}^{2005}\gamma_{2j}1\{j=y\}*1\{c=US\}+$
	$\displaystyle +\sum_{j=2001}^{2005}\gamma_{3j}1\{j=y\}$
	$\displaystyle +\gamma_{4}1\{c=US\}\times NTR\: Gap_{h,1999}$
	$\displaystyle +\delta_{c}+\delta_{h}+\varepsilon_{chy}.$

The left-hand side variable represents the log of the number of Chinese firms exporting six-digit HS product

to country

in year

. The first set of covariates on the right-hand side of the specification represent the DID terms of interest, i.e., interactions of the 1999 U.S. NTR gap, an indicator for exports to the United States and an indicator for the year. The remaining terms on the right-hand side of the equation are all possible interactions of these three covariates.

Results for $\theta_{j}$ are reported in Table A.2. As indicated in the table, coefficients are positive in all years and statistically significant at the ten percent level for 2002 to 2005. The coefficients for the 2002 and 2005 interactions indicate that the number of Chinese firms exporting to the U.S. was 9.7 and 35.2 percent larger, respectively, for an industry with the average NTR gap.⁴⁴

F Chinese Productivity Growth

We use the firm-level Chinese production data described in Section C of this online appendix to investigate the relationship between productivity growth in Chinese industries and the U.S. NTR gap. Following Khandelwal et al. (2013), we define the total factor productivity for firm as $\ln(TFP_{f})=\ln(va_{f})-\alpha_{f}\ln(w_{f})-(1-\alpha_{f})\ln(k_{f})$ , where $va_{f}$ , $w_{f}$ , and $k_{f}$ denote firm value added, wages and fixed assets (net of depreciation) and $\alpha_{f}$ is the firm's share of wages in total value added. Wages are defined as reported firm wages plus employee benefits (unemployment insurance, housing subsidies, pension and medical insurance), and capital is defined as reported capital stock at original purchase price less accumulated depreciation.⁴⁵ We aggregate these productivity measures to the industry level by taking weighted averages using firms' employment as weights. Next, we use concordances provided by Brandt et al. (2013) to match HS-level NTR gaps for the United State to the four-digit Chinese Industry Classification (CIC) codes used in the NBS data.

Table A.3 reports the results of industry-level OLS regressions of Chinese TFP on year fixed effects, industry fixed effects and interactions of year fixed effects and the U.S. NTR gap. Coefficient estimates for all but the interaction terms are suppressed. As indicated in the table, the association between TFP and the NTR gap is statistically insignificant at conventional levels in all years.

G U.S. and E.U. Employment Data from UNIDO

Our comparison of the relationship between the NTR gap and manufacturing employment in the United States and the European Union in Section 7.3 uses data from the United Nations Industrial Development Organization's (UNIDO) INDSTAT 4 database for 1997 to 2005.⁴⁶ This database contains information on a number of industry characteristics, including employment, at the four-digit International Standard Industrial Classification (ISIC) Revision 3 level. Manufacturing industries in the ISIC begin with two digit codes from 15 to 37. We exclude industries that begin with 22 from our definition of manufacturing as they include publishing, which was classified as manufacturing under the SIC, but not the NAICS. Our definition of the European Union is based on the current set of 28 EU members, available at europa.eu/about-eu/countries/member-countries. Because of instances of missing data, our sample includes only industry-country pairs for which data are present in every year. Lastly, we note that data for the U.S. are unavailable in 2003.

H U.S. Business Cycle Peaks

Figure A.3 compares economic activity around the 2001 and two prior NBER peaks. As illustrated in the figure, the 1981 recession stands out in terms of both GDP and Industrial Production Index (IP) declines. Peak to trough, IP falls 8.6 percent during the 1981 recession versus less than half that amount during the 1990 and 2001 recessions. Loss of manufacturing employment, by contrast, is far more severe following the 2001 recession than the 1981 and 1990 recessions.

Appendix References

Aghion, Philippe, Mathias Dewatripont, Luosha Du, Ann Harrison and Patrick Legros. 2012. "Industrial Policy and Competition." NBER Working Paper 18048.
Bai, Xue, Kala Krishna and Hong Ma. 2013. How You Export Matters: Export Mode, Learning and Productivity in China." Unpublished.
Becker, Randy, Wayne B. Gray and Jordan Marvakov. 2013. "NBER-CES Manufacturing Industry Database." Available at www.nber.org/data/nberces5809.html.
Bernard, Andrew, Stephen J. Redding and Peter K. Schott. 2010. "Multi-Product Firms and Product-Switching." American Economic Review 100: 70-97.
Brandt, Loren, Johannes Van Biesebroeck, Luhang Wang and Yifan Wang. 2012. "WTO Accession and Performance of Chinese Manufacturing Firms." CEPR Working Paper 9166.
Bown, Chad P. 2012. "Temporary Trade Barriers Database," available at
http://econ.worldbank.org/ttbd
Dean, Judith M. and Mary E. Lovely. 2010. ''Trade Growth, Production Fragmentation, and China's Environment.'' in China's Growing Role in World Trade. Ed. R. Feenstra and S. Wei. Chicago: NBER and University of Chicago Press.
European Commission (2003). Overview of the Terms of China's Accession to WTO, 2. Brussels, Germany. Retrieved from
http://trade.ec.europa.eu/doclib/docs/2003/october/tradoc_111955.pdf
Feenstra, Robert C., John Romalis and Peter K. Schott. 2002. "U.S. Imports, Exports and Tariff Data, 1989-2001." NBER Working Paper 9387.
Girma, S., Gong, Y., Görg, H. and Yu, Z. (2009). "Can Production Subsidies Explain China's Export Performance? Evidence from Firm-level Data." The Scandinavian Journal of Economics 111: 863-891.
Hirsch, Barry T. and David A. Macpherson. 2003. "Union Membership and Coverage Database for the Current Population Survey." Industrial and Labor Relations Review 56(2): 349-54.
Khandelwal, Amit K., Peter K. Schott and Shang-Jin Wei. 2012. "Trade Liberalization and Embedded Institutional Reform: Evidence from Chinese Exporters." American Economic Review. Forthcoming.
Nunn, Nathan. 2007. "Relationship-Specificity, Incomplete Contracts and the Pattern of Trade." Quarterly Journal of Economics 122(2) 569-600.
Pierce, Justin R. and Peter K. Schott. 2012a. "A Concordance Between Ten-Digit U.S. Harmonized System Codes and SIC/NAICS Product Classes and Industries," Journal of Economic and Social Measurement 37(1-2):61-96.
Pierce, Justin R. and Peter K. Schott. 2012b. "Concording U.S. Harmonized System Codes Over Time," Journal of Official Statistics 28: 53-68.

Appendix Tables and Figures

Table A.1: U.S. Votes to Overturn China's Temp orary NTR Status, 1990-2001

	House Votes for Continuation of China's NTR Status: Dissaprove	House Votes for Continuation of China's NTR Status: Approve	House Votes for Continuation of China's NTR Status: %Disapprove*
1990	247	174	57
1991	223	204	51
1992	258	135	59
1993	105	318	24
1994	75	356	17
1995*	321	107	26
1996	141	286	32
1997	173	259	40
1998	166	264	38
1999	170	260	39
2000	147	281	34
2001	169	259	39
Mean	183	242	38

Notes: The 1995 vote is for tabling the measure; therefore the "approve" vote is included in the average for disapprove in that year. Total possible votes are 435.

Table A.2: Chinese Firms Exporting to the United States

	ln(Chinese Exporters_hcy)
1{c=US} x 1{year=2001} x NTR Gap_h	0.083
1{c=US} x 1{year=2001} x NTR Gap_h: Robust standard errors	0.111
1{c=US} x 1{year=2002} x NTR Gap_h	0.288
1{c=US} x 1{year=2002} x NTR Gap_h: Robust standard errors	0.113
1{c=US} x 1{year=2003} x NTR Gap_h	0.416
1{c=US} x 1{year=2003} x NTR Gap_h: Robust standard errors	0.117
1{c=US} x 1{year=2004} x NTR Gap_h	0.503
1{c=US} x 1{year=2004} x NTR Gap_h: Robust standard errors	0.119
1{c=US} x 1{year=2005} x NTR Gap_h	0.933
1{c=US} x 1{year=2005} x NTR Gap_h: Robust standard errors	0.124
Observations	1327583
R2	0.60
Fixed Effects	HS6 Country
Additional Covariates	Yes

Notes: Table displays the results of a six-digit HS (h) by country (c) by year (t) OLS regression. Dependent variable is the log of the number of Chinese firms exporting a product to a country in a given year. Data are available for 2000 to 2005. Results for the interaction of an indicator for exports to the United States an indicator for the year and the 1999 U.S. NTR gap are reported in the table. Each regression also includes all combinations of these three covariates as well as HS and country fixed effects (see text for specification). Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level.

Table A.3: PNTR and Chinese Productivity Growth

	ln(TFPiy)
1{y=1999} x NTR Gap_i	0.205
1{y=1999} x NTR Gap_i: Robust standard errors	0.190
1{y=2000} x NTR Gap_i	0.164
1{y=2000} x NTR Gap_i: Robust standard errors	0.184
1{y=2001} x NTR Gap_i	0.176
1{y=2001} x NTR Gap_i: Robust standard errors	0.247
1{y=2002} x NTR Gap_i	-0.206
1{y=2002} x NTR Gap_i: Robust standard errors	0.251
1{y=2003} x NTR Gap_i	-0.127
1{y=2003} x NTR Gap_i: Robust standard errors	0.244
1{y=2004} x NTR Gap_i	-0.233
1{y=2004} x NTR Gap_i: Robust standard errors	0.192
1{y=2005} x NTR Gap_i	-0.193
1{y=2005} x NTR Gap_i: Robust standard errors	0.201
Observations	3379
R2	0.49
Fixed Effects	yi

Notes: Table displays the results of a four-digit CIC industry-level OLS regression of log TFP on year (y) fixed effects industry (i) fixed effects and interactions of year fixed effects and the 1999 U.S. NTR gap. Coefficient estimates for all but the interactions are suppressed. Robust standard errors are displayed below each coefficient. No coefficients are statistically significant at the 10 percent level.

Table A.4: PNTR and U.S. Manufacturing Employment, Pre- versus Post-Perio d

	Percent Change in Industry Employment Years After 1990 Peak: 1	Percent Change in Industry Employment Years After 1990 Peak: 2	Percent Change in Industry Employment Years After 1990 Peak: 3	Percent Change in Industry Employment Years After 1990 Peak: 4	Percent Change in Industry Employment Years After 1990 Peak: 5	Percent Change in Industry Employment Years After 1990 Peak: 6	Percent Change in Industry Employment Years After 2001 Peak: 1	Percent Change in Industry Employment Years After 2001 Peak: 2	Percent Change in Industry Employment Years After 2001 Peak: 3	Percent Change in Industry Employment Years After 2001 Peak: 4	Percent Change in Industry Employment Years After 2001 Peak: 5	Percent Change in Industry Employment Years After 2001 Peak: 6
NTR Gap_i	-0.043	-0.006	0.041	0.036	0.044	0.011	-0.119	-0.154	-0.232	-0.218	-0.235	-0.299
NTR Gap_i: Robust standard errors	0.040	0.060	0.085	0.090	0.108	0.125	0.049	0.065	0.090	0.094	0.108	0.109
Contract Intensity_i	-0.113	-0.107	-0.077	-0.086	-0.046	-0.041	-0.086	-0.136	-0.144	-0.092	-0.115	-0.170
Contract Intensity_i: Robust standard errors	0.030	0.043	0.055	0.060	0.072	0.084	0.032	0.043	0.062	0.063	0.075	0.072
Δ China Import Tariffs_i	0.000	0.000	0.000	0.000	0.000	0.000	-0.165	-0.233	-0.245	-0.137	-0.104	-0.103
Δ China Import Tariffs_i: Robust standard errors	0.000	0.000	0.000	0.000	0.000	0.000	0.056	0.074	0.095	0.098	0.114	0.123
Δ China Licensing_i	-0.016	-0.022	-0.027	-0.007	-0.045	-0.107	-0.061	-0.077	-0.063	-0.097	-0.062	-0.014
Δ China Licensing_i: Robust standard errors	0.045	0.104	0.150	0.147	0.153	0.169	0.071	0.094	0.125	0.135	0.156	0.144
Δ China Subsidies_i	-3.664	-3.454	-1.376	5.470	11.240	10.990	-2.154	-2.247	2.297	3.768	4.906	4.606
Δ China Subsidies_i: Robust standard errors	3.492	6.489	8.612	8.401	8.617	9.744	3.865	5.560	6.913	6.633	7.449	7.465
Anti-Dumping Filings_i	-0.005	0.009	0.019	0.036	0.060	0.054	-0.032	-0.028	-0.040	-0.037	-0.053	-0.047
Anti-Dumping Filings_i: Robust standard errors	0.008	0.015	0.022	0.027	0.035	0.039	0.015	0.017	0.023	0.023	0.027	0.026
1{Advanced Tech_i}	0.027	0.013	-0.000	-0.019	-0.026	-0.013	-0.007	-0.018	-0.006	-0.007	0.002	-0.019
1{Advanced Tech_i}: Robust standard erorrs	0.011	0.016	0.022	0.026	0.032	0.037	0.020	0.026	0.029	0.032	0.034	0.039
1{MFA Apparel}_i	0.014	-0.004	-0.044	-0.034	-0.070	-0.050	-0.015	0.034	0.020	-0.013	-0.022	-0.002
1{MFA Apparel}_i: Robust standard errors	0.028	0.024	0.030	0.044	0.055	0.060	0.023	0.040	0.042	0.044	0.047	0.070
ln(K/L_it)	-0.007	-0.010	-0.000	0.001	0.002	0.007	-0.005	-0.004	-0.024	-0.041	-0.048	-0.036
ln(K/L_it): Robust standard errors	0.008	0.010	0.013	0.015	0.019	0.022	0.010	0.014	0.015	0.017	0.017	0.021
ln(S/L_it)	0.025	-0.000	-0.037	-0.057	-0.073	-0.048	0.010	0.013	0.022	0.028	0.049	0.089
ln(S/L_it): Robust standard errors	0.012	0.016	0.021	0.026	0.031	0.039	0.017	0.021	0.028	0.030	0.036	0.037
Union Membership_i	-0.010	0.077	0.062	0.065	0.039	0.026	0.113	0.173	0.290	0.375	0.456	0.323
Union Membership_i: Robust standard errors	0.040	0.061	0.079	0.104	0.130	0.148	0.082	0.100	0.131	0.134	0.147	0.173
Prior Growth_i	0.116	0.165	0.381	0.593	0.778	0.895	0.014	0.103	0.198	0.234	0.279	0.265
Prior Growth_i: Robust standard errors	0.059	0.083	0.107	0.131	0.168	0.196	0.091	0.132	0.141	0.161	0.144	0.179
ΔNTR_i	0.144	0.230	0.001	0.047	0.050	-0.360	-0.105	0.009	0.246	0.432	0.239	-0.019
ΔNTR_i: Robust standard errors	0.170	0.301	0.406	0.456	0.509	0.569	0.287	0.413	0.488	0.531	0.557	0.633
Observations	326	326	326	326	326	326	326	326	326	326	326	326
R2	0.27	0.15	0.19	0.29	0.30	0.25	0.26	0.31	0.29	0.24	0.21	0.17
Fixed Effects	i	i	i	i	i	i	i	i	i	i	i	i
Employment Weighted	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes

Notes: Each column displays the results of an OLS regression of the cumulative percent change in industry (i) employment after 1990 on the noted covariates (see text). Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed.

Table A.5: PNTR and U.S. Manufacturing Employment, 1990 versus 1981

	Years After NBER Peak (LBD): 1	Years After NBER Peak (LBD): 2	Years After NBER Peak (LBD): 3	Years After NBER Peak (LBD): 4	Years After NBER Peak (LBD): 5	Years After NBER Peak (LBD): 6
1{t=1990} x NTR Gap_i	-0.072	-0.003	0.039	0.057	0.099	0.115
1{t=1990} x NTR Gap_i : robust standard errors	0.049	0.098	0.126	0.134	0.148	0.179
1{t=1990} x Contract Intensity_i	-0.108	-0.078	-0.198	-0.236	-0.192	-0.143
1{t=1990} x Contract Intensity_i: robust standard errors	0.037	0.058	0.084	0.087	0.093	0.106
1{t=1990} x ΔChina Import Tariffs_i	0.049	0.100	-0.122	-0.126	-0.011	0.060
1{t=1990} x ΔChina Import Tariffs_i : robust standard errors	0.064	0.119	0.180	0.180	0.168	0.177
1{t=1990} x ΔChina Licensing_i	0.065	0.041	-0.051	-0.039	-0.044	-0.114
1{t=1990} x ΔChina Licensing_i : robust standard errors	0.069	0.147	0.210	0.219	0.234	0.268
1{t=1990} x ΔChina Subsidies_i	-3.232	-2.971	-7.899	0.202	7.220	3.888
1{t=1990} x ΔChina Subsidies_i : robust standard errors	3.602	6.877	10.530	10.270	9.107	10.580
Anti-Dumping Filings_i	0.001	-0.044	-0.049	-0.069	-0.073	-0.078
Anti-Dumping Filings_i: robust standard errors	0.019	0.027	0.034	0.041	0.050	0.058
1{t=1990} x 1{Advanced Tech_i}	0.037	0.206	0.350	0.489	0.595	0.538
1{t=1990} x 1{Advanced Tech_i} : robust standard errors	0.052	0.085	0.119	0.143	0.174	0.183
1{t=1990} x 1{MFA Apparel}_i	0.022	0.026	-0.041	-0.076	-0.101	-0.042
1{t=1990} x 1{MFA Apparel}_i: robust standard errors	0.044	0.048	0.046	0.050	0.053	0.056
ln(K/L_it)	0.003	0.083	0.137	0.173	0.221	0.267
ln(K/L_it) : robust standard errors	0.027	0.036	0.050	0.059	0.065	0.070
1{t=1990} x ln(K/L_it)	-0.019	-0.041	-0.025	-0.078	-0.088	-0.067
1{t=1990} x ln(K/L_it) : robust standard errors	0.014	0.024	0.028	0.034	0.043	0.049
ln(S/L_it)	-0.034	0.129	0.140	0.095	0.027	0.086
ln(S/L_it) : robust standard errors	0.043	0.068	0.085	0.091	0.106	0.128
1{t=1990} x ln(S/L_it)	0.074	0.228	0.187	0.197	0.035	0.083
1{t=1990} x ln(S/L_it) : robust standard errors	0.059	0.098	0.130	0.138	0.149	0.181
1{t=1990} x Union Membership_it	0.017	0.045	0.027	0.033	0.043	0.037
1{t=1990} x Union Membership_it: robust standard errors	0.010	0.015	0.019	0.021	0.025	0.029
Union Membership_it	0.068	0.072	0.057	0.219	-0.145	-0.463
Union Membership_it: robust standard errors	0.125	0.201	0.283	0.318	0.338	0.392
Prior Growth_it	0.008	0.014	0.014	0.013	0.031	0.056
Prior Growth_it: robust standard errors	0.010	0.016	0.021	0.022	0.025	0.028
1{t=1990} x Prior Growth_it	0.083	0.269	0.352	0.334	0.408	0.542
1{t=1990} x Prior Growth_it: robust standard errors	0.099	0.169	0.201	0.269	0.334	0.363
1{t=1990} x ΔNTR_i	-0.246	-0.438	-0.561	-0.682	-0.595	-0.748
1{t=1990} x ΔNTR_i : robust standard errors	0.220	0.365	0.578	0.644	0.649	0.647
Observations	652	652	652	652	652	652
R2	0.72	0.75	0.70	0.73	0.74	0.74
Fixed Effects	i,t	i,t	i,t	i,t	i,t	i,t
Employment Weighted	Yes	Yes	Yes	Yes	Yes	Yes

Notes: Each column displays the results of an OLS regression of the cumulative percent change in industry (i) employment on a difference-in-differences term and various industry attributes. There are two observations for each industry corresponding to growth up to six years after the 1981 and 1990 peaks indexed by t. Robust standard errors are displayed below each coefficient. Coefficients in bold are statistically significant at the 10 percent level. Estimates for the constant and fixed effects are suppressed.

Figure A.1: Distribution of NTR Gaps Across Industries, 1989-2001

Notes: Figure displays the distribution of NTR gaps across constant manufacturing industries (see text) by year for 1989 to 2001. Darker lines are for earlier years. Dashed line is for 1999.

Figure A.2: U.S. Manufacturing Employment (LBD vs BLS)

Notes: Figure compares annual manufacturing emplyoment as of March according to the U.S. Bureau of Labor Statistics (series CEU300000001) and the authors' constant manufacturing sample, constructed from the Census Bureau's Longitudinal Business Database (see text). Shaded areas correspond to periods 1981 to 1987, 1990 to 1996 and 2001 to 2007.

Figure A.3: Real GDP and IP Around the 1981, 1990 and 2001 Peaks

Notes: Figure compares real GDP and the Industrial Production index from four quarters before to sixteen quarters after the noted official NBER peaks. GDP data are from the U.S. Bureau of Economics Analysis. IP data are from the Federal Reserve Board's G.17 release.

Footnotes

* Schott thanks the National Science Foundation (SES-0241474 and SES-0550190) for research support. We thank Lorenzo Caliendo,Teresa Fort, Kyle Handley, Gordon Hanson, Marc Muendler, Mina Kim and seminar participants at numerous institutions for helpful comments. We also thank Jonathan Ende and Rebecca Hammer for helpful research assistance. Any opinions and conclusions expressed herein are those of the authors and do not necessarily represent the views of the U.S. Census Bureau, the Board of Governors or its research staff. All results have been reviewed to ensure that no confidential information is disclosed. Return to Text

† 20th & C Streets NW, Washington, DC 20551, tel: (202) 452-2980, email: [email protected]. Return to Text

‡ 135 Prospect Street, New Haven, CT 06520, tel: (203) 436-4260, email: [email protected]. Return to Text

1. Dixit and Pindyck (1994) provide a general overview of investment under uncertainty. See Handley and Limao (2012) for one of the first applications to international trade. Return to Text

2. Early research on import competition by Freeman and Katz (1991) and Revenga (1992) documents a negative relationship between growth in U.S. manufacturing employment and either imports or changes in import prices at the industry level. Subsequent research focuses on the impact of imports from low-wage countries across industries (e.g., Sachs and Shatz 1994) and establishments (Bernard et al. 2006). More recent papers investigate the effect of China on manufacturing employment in a range of countries, including Belgium (Mion and Zhu 2013), the EU (Bloom et al. 2012), Mexico (Utar and Torres Ruiz 2013) and the United States (Ebenstein et al. 2011, Autor et al. 2012, and Autor et al. 2013). Return to Text

3. In focusing on the impact of a particular policy, this paper is closest to Bloom et al. (2012), who show that employment losses across EU apparel and textile manufacturers coincide with the removal of import quotas on Chinese exports of these goods, and to Utar and Torres Ruiz (2013), who find a reduction in employment at Mexican maquiladoras associated with China's accession to the World Trade Organization. Return to Text

4. Models of importing also provide insight into the potential impact of PNTR. Groizard, Ranjan and Rodriguez-Lopez (2012), for example, show that a decline in import tariffs raises the demand for foreign inputs and thereby reduces domestic employment. Return to Text

5. Handley and Limao (2013) examine the effect of the elimination of trade policy uncertainty associated with China's accession to the WTO using product-level international trade data but do not consider its effects on U.S. employment. Return to Text

6. Table A.1 of the online appendix summarizes the House and Senate votes by year. Both the House and Senate passed legislation placing human rights conditions on re-approval in 1991 and 1992, but they were vetoed by President Bush (Dumbaugh 2001). Heightened uncertainty continued through the 1990s, with substantial opposition in annual House votes and increasing legislative activity focused on China's human rights practices. From 1998 to 2001, the number of Representatives voting against renewed NTR status reached were 166, 170, 147 and 169 out of 435. Return to Text

7. While our discussion treats the October 2000 PNTR vote as the date of the policy change, there were several milestones in China-U.S. trade policy over a relatively short period, most notably the China-U.S. bilateral agreement governing China's eventual accession to the WTO in November 1999 and China's actual accession to the WTO in December 2001. Though each of these events likely contributed to the overall reduction in policy uncertainty, we are unable to identify their separate contributions given the annual frequency of our establishment-level employment data. Return to Text

8. To our knowledge, no other U.S. trade policy generates similar uncertainty with respect to China. For example, while the the Omnibus Trade and Competitiveness Act of 1988 requires the U.S. Treasury Secretary to provide semiannual reports indicating whether any major trading partner of the United States is manipulating its currency, such a designation only requires the Secretary to initiate negotiations to have the exchange rate adjusted "promptly" (Treasury 2012). Return to Text

9. Further detail on the construction of NTR gaps is provided in Section A of the online appendix. Return to Text

10. As discussed further in Section B of the online appendix, non-NTR tariffs for HS codes not subject to revision do not change. Return to Text

11. The LBD definition of employment includes both full- and part-time workers; in Section 8.3 we show that our main employment results are robust to examining production hours instead of employment. While the use of staffing services by manufacturing firms was increasing during the 2000s, Dey, Houseman and Polivka (2012) show that this trend does not account for the steep decline in manufacturing employment after 2001. Return to Text

12. Further detail on the creation of time-consistent industry codes is provided in Section D in the appendix. All references to "industry" in this paper refers to these families unless otherwise noted. Return to Text

13. Series CEU3000000001, available at www.bls.gov. As the BLS series is NAICS-based, manufacturing employment prior to 1997 excludes SIC industries that do not map into NAICS manufacturing industries. As noted above, our sample is SIC-NAICS-based, meaning that we also drop NAICS industries not classified as manufacturing under the SIC. For further detail on construction of the BLS series, see Morisi (2003). Return to Text

14. As indicated by the roughly sideways movement of manufacturing employment from mid-1960s through 2000, the share of manufacturing employment in total private employment was declining for some time prior to PNTR, a trend discussed in Edwards and Lawrence (2013). Return to Text

15. Houseman, Kurz, Lengermann and Mandel (2011) argue that gains in manufacturing value-added in the later years of Figure 1 may be overstated as purchases of low-cost foreign materials are not fully captured in input price indexes. The authors also note that two thirds of the overall growth in manufacturing value added between 1997 and 2007 occurred in the computer and electronics manufacturing industry, which accounted for roughly one tenth of overall manufacturing value added. Return to Text

16. We consider an alternate difference-in-differences specification in section 7.2 that is not tied to an explicit comparison of growth across business cycle peaks. Return to Text

17. Both series exhibit declining employment after PNTR as all industries are affected by the policy change, with larger effects expected in industries with higher NTR gaps. Return to Text

18. If anything, U.S. imports of high-NTR gap products from the rest of the world increase at a slower rate than those of low-gap products, potentially due to the shifting of production from other countries to China. Return to Text

19. As with SIC and NAICS industries, the eight-digit HS product codes are linked to time-invariant families using the concordance from Pierce and Schott (2012). Return to Text

20. We obtain qualitatively similar results when growth is measured as the log difference and the analysis is limited to trade flows that are present in both the beginning and end years. Return to Text

21. As reported in Section E of the online Appendix, we find similar growth in the number of Chinese firms exporting to the United States relative to other countries using transaction-level trade data from China. Return to Text

22. Our findings are in line with those of Harrison and McMillan (2011) who show that, in general, offshore employment in low wage countries is a substitute for domestic employment among U.S. manufacturers. Ebenstein, Harrison and McMillan (2013) find that offshoring and increased import competition are associated with wage declines for workers in exposed occupations. Return to Text

23. Khandelwal et al. (2013) show that the allocation of export licenses in the apparel industry restricted the exports of its most productive producers. Return to Text

24. Obviously, to the extent that employment losses are required to demonstrate "injury" in CVD and AD investigations, this variable could be subject to reverse causality. Return to Text

25. In fact, we show in Section F of the online appendix that China's TFP growth is uncorrelated with the NTR gap. Return to Text

26. Ad valorem equivalents of specific import tariffs are not available after 2001. Nonetheless, we note that most of the changes in NTR tariffs driven by the Uruguay round had been implemented by 2001, and that separate analysis of the ad valorem and specific tariffs in the U.S. tariff schedule indicates few changes to U.S. NTR tariffs between 2001 and 2007. Return to Text

27. In contrast, we do find evidence for trade-induced technical change that is associated with PNTR, as discussed in section 8.2 below. Return to Text

28. For industry attributes that are time-varying, e.g., capital intensity, $\mathbf{X}_{i}$ is defined as the level in the first year of the sample, 1990. Return to Text

29. Employment growth

years after 1990 or 2001 is computed in three steps. First, multiply the coefficient estimates in either column of Table 5 by 0.32, the average value of the NTR gap from Section 3. Second, exponentiate this product and subtract 1. Third, for growth

years after 2001, subtract the growth up to that year from the result in step 2. The estimated changes in employment from 1990 to 1996 are -1.3 (column 1) and 2.5 (column 2) percent. The corresponding growth rates for 2001 to 2007 are -16.6 and -15.6 percentage points. Return to Text

30. While this alternate DID specification is highly flexible, its long sample period renders it susceptible to biased standard errors associated with serial correlation (Bertrand, Duflo and Mullainathan 2003). For that reason, and because equation 2 is more amenable to decomposition by gross margins in Section 8.1, equation 2 remains as our preferred specification. Return to Text

31. China was a Generalized System of Preferences (GSP) beneficiary in the EU before and after its accession to the WTO. According to European Commission (2003), Chinese import tariffs under the EU GSP program did not change when it joined the WTO. The EU renews GSP every decade and conducts annual revisions to their rates. These changes are generally made on a product-by-product rather than country-by-country basis, suggesting that they are not biased towards China. Nevertheless, we note that the majority of the EU's GSP rate changes in recent years involve products in which Chinese exporters are active. Return to Text

32. See section G of the online appendix for additional information regarding the UNIDO data. Return to Text

33. The four-digit ISIC industries across which employment is reported are more aggregate than either the SIC and NAICS industries across which U.S. employment data is reported by the Census, accounting for some of the variation between the results for the United States in this and the preceding section. We aggregate NTR gaps to the six-digit HS level and then map them to the four-digit ISIC level using publicly available concordances from the World Bank, available at www.wits.worldbank.org/wits/product_concordance.html. Return to Text

34. A plant is coded as being born within an incumbent firm if it appears in the data for the first time during the noted interval and is associated with an already present firm identifier. A plant is classified as dying within a continuing firm if it is part of the firm at the beginning of the interval but is no longer present afterward. A firm is classified as being born during an interval if none of its plants are present in the LBD before that interval. A firm is classified as dying if all of its plants no longer appear in the data after the interval. Return to Text

35. Holmes and Stevens (2013), for example discuss how increased import competition from China can have heterogeneous effects among plants within an industry, with the biggest negative effect observed at large plants producing standardized goods, while small plants producing specialty goods are less affected. Return to Text

36. Bernard et al. (2010) provide a detailed discussion of these data. Return to Text

37. We measure TFP with an index number approach in which output is measured as the logarithm of deflated revenue and inputs - cost of materials, production employment, non-production employment and book value of capital - weighted by the average cost share for each input, at the industry level. While we deflate revenue with industry-level price deflators from Becker et al. (2013) to obtain our measure of output, we note that productivity measures constructed from revenue information may be biased due to establishment-level variation in prices. These prices reflect variation in demand shocks or markups, which can also be affected by changes in trade policy (Pierce 2011 and De Loecker, Goldberg, Khandelwal and Pavcnik 2012). For a detailed discussion of the properties of this TFP measure, as well as the limitations of revenue-based forms of productivity, see Foster, Haltiwanger and Syverson (2008). Return to Text

38. The mean and standard deviation of the upstream NTR gap is 0.11 and 0.04. For the downstream NTR gap, they are 0.11 and 0.08, respectively. Return to Text

39. The correlation between the up- and downstream NTR gaps is -0.03. Return to Text

40. The HS-industry concordance is contained in the file "HSConcord.txt" available at http://www.bea.gov/industry/zip/NDN0317.zip. Return to Text

41. The industry-by-industry total requirements table is contained in the file "ndn0310.zip" available at http://www.bea.gov/industry/zip/NDN0310.zip. Return to Text

42. The United States filed 165 anti-dumping cases against China between 1980 and 2012, of which 65 were filed between 1999 and 2007. U.S. firms were unable to file CVD cases against Chinese firms until 2006. The number of CVD cases in the years from 2006 to 2011 are 1, 7, 5, 10, 3, 4, and 2, respectively. We note that CVD investigations filed in 2006 and 2007 are in industries in which AD cases also were filed in those years. Return to Text

43. However, we note that the main results in the paper are qualitatively identical to those obtained when we define industries at the standard six-digit NAICS level, indicating that the results are not driven by our definition of industry families. Return to Text

44. These magnitudes are calculated by multiplying the coefficient estimates reported in Table A.2 by the average NTR gap, 0.323, exponentiating the product and then subtracting 1. Return to Text

45. This approach assumes revenue-based TFP reveals variation in physical efficiency, an assumption whose limitations are discussed in Section 8.3 of the main text. Return to Text

46. See www.unido.org/resources/statistics/statistical-databases/indstat4-2013-edition.html. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text