Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2014-06 Screen Reader version ^♣

The Credit Crunch and Fall in Employment during the Great Recession

Samuel Haltenhof

University of Michigan

Seung Jung Lee

Board of Governors of the Federal Reserve System

Viktors Stebunovs^*

Board of Governors of the Federal Reserve System

March 31, 2014

Forthcoming in the Journal of Economic Dynamics and Control

Abstract:

We study how a bank credit crunch--a dramatic worsening of firm and consumer access to bank credit, such as the one observed over the Great Recession--translates into job losses in U.S. manufacturing industries. To identify the impact of the recent credit crunch, we rely on differences in the degree of dependence on external finance and of tangibility of assets across manufacturing industries and in the sensitivity of these industries output to changes in the supply of consumer credit. We find that, for employment, household access to bank loans matters more than firm access to bank loans. In addition, we show that, over the recent financial crisis, tightening access to commercial and industrial loans and, in particular, consumer installment loans may have contributed significantly to the drop in employment in the manufacturing sector.

KEYWORDS: Bank credit, credit crunch, job losses, Great Recession, Senior Loan Officer Opinion Survey.

JEL CLASSIFICATION: G21, G28, G30, J20, L25.

1 Introduction

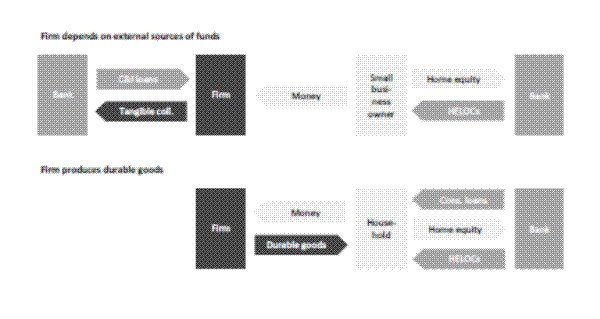
        This paper investigates how a bank credit crunch--a dramatic worsening of firm and consumer access to bank credit, such as the one observed over the Great Recession--translates into job losses in U.S. manufacturing industries. To establish the ideas, Figure 1 shows four separate channels through which access to bank credit may affect employment in the manufacturing sector: (1) the supply of commercial and industrial (C&I) loans directly to firms, (2) the availability of home equity loans or home equity lines of credit (HELOCs) to small business owners to prop up their businesses, (3) the supply of consumer installment loans to households, and (4) the availability of HELOCs to consumer-households. The paper examines these four channels using data for U.S. manufacturing industries and the Senior Loan Officer Opinion Survey (SLOOS) over the 1993-2011 period.

There are three reasons behind our choice to study the linkages between access to bank credit and U.S. manufacturing employment. First, by studying the real effects of changes in the supply of bank credit, we account for the possible substitution of funding sources at the firm and household levels. In fact, the key to identifying these economic effects is that bank loans are not perfectly substitutable with other types of external finance.¹ Second, over the past few decades, the manufacturing sector has had a relatively stable structure, and banks have continued to supply a significant share of C&I loans to the sector. In contrast, other industries, such as retail trade, have experienced a shift toward large multi-unit firms with access to national capital markets. This shift has likely weakened these non-manufacturing industries' reliance on local bank credit. Third, manufacturing industries' output--in particular, the output of industries that produce durable goods--is sensitive to changes in the supply of consumer credit. Indeed, most purchases of durable goods, such as cars or large appliances, tend to be financed. This feature allows us to judge the importance of consumer access to bank credit for U.S. manufacturing employment.

Our explained variables--growth in employment, number of establishments, and average establishment size--are from the Quarterly Census of Employment and Wages (QCEW). To our knowledge, this is a novel application of the QCEW data. One of the advantages of this data set is that it does not contain a structural break in the classification of industries due to the transition from the Standard Industrial Classification (SIC) to the North American Industry Classification System (NAICS) in the late 1990s. Hence, the data set covers two recessions, including the Great Recession, on a consistent basis. We focus on employment in manufacturing rather than output because employment at the industry-state level can be measured more precisely. While the U.S. Census makes industry-state level output data available, the data are noisy by the Census' own admission, and the data compilation approaches alternate between census and non-census years.

Our explanatory variables are from several sources. Based on bank-specific responses to questions in the SLOOS, changes in commercial banks' C&I lending standards and in their willingness to originate consumer installment loans proxy for changes in firm and household access to bank credit, respectively. Indeed, a sharp tightening of C&I lending standards is followed by a steep contraction in employment in the manufacturing sector, as shown in Figure 2. In addition, estimates of growth in home equity proxy for changes in the availability of home equity loans. We use the state- and national-level house price indices compiled by CoreLogic, state- and national-level mortgage debt per borrower taken from TransUnion's Trend Data, and the national level household balance sheet data from the Federal Reserve's Z.1 statistical release to construct proxies for growth in home equity.

Our identification approach takes advantage of differences in the presence of large banks across different U.S. states and is similar to that used in the literature.² We posit that, in accordance with the questions in the SLOOS, changes in major banks' C&I lending standards, apportioned to a particular state, are exogenous to developments in a given industry in a given state and at a given point in time. In other words, tightening (or easing) C&I lending standards does not target a particular industry in a given state. Indeed, the vast majority of the SLOOS respondents cite risk aversion or changes in the broad economic outlook as important reasons for changes in these lending standards. Variation in the geographical presence of large banks and in their timing of tightening (or easing) generates variation in changes in C&I lending standards. Similarly, changes in commercial banks' willingness to originate consumer installment loans and growth in households' home equity are understood to be exogenous to developments in a given industry in a given state and at a given point in time.

Our identification approach also relies on large mature firms' use of external finance and asset structure. As the literature suggests, cash flows and balance sheets of these firms covered by Compustat reflect deep technological parameters of the financially-unconstrained firms and, hence, captures their true demand for external funds and the ability to access them.³ We thus achieve identification by measuring the differential effect of a change in C&I lending standards on employment growth in manufacturing industries that depend relatively more on external finance and, at the same time, have relatively more pledgable assets (that is, industries most likely to be affected by changes in bank credit supply to firms) compared with other manufacturing industries. This setup also allows to control for bias due to omitted variables--for example, shocks that drive changes in both lending standards and manufacturing employment.

This definition of the treatment group builds on the setup that has been widely used in the literature to tease out a differential impact of credit supply changes on industries that depend on external finance, as in (Cetorelli and Strahan (2006) ). The novelty is that we take into account not only the need to borrow to finance physical capital investment (captured by the (Rajan and Zinglaes (1998) ) measure of dependence on external finance), but also the ability of manufacturing firms to access C&I loans by pledging tangible assets (captured by the (Braun, 2002) and (Claessens & Laeven, 2003) measure of asset tangibility). We interact these industry-specific indicators with SLOOS-based state-level changes in banks' C&I lending standards to isolate the effects of changes in the supply of local bank credit on employment growth in manufacturing. For the home equity channel that potentially affects employment growth at small businesses, we interact only our measure of dependence on external finance with estimates of growth in state-level home equity, a proxy for home equity availability.

The final piece to identification is quite intuitive and novel in the context of the paper. Consumption of durable goods is likely to be financed rather than paid for outright. Therefore, changes in consumer access to credit, though affecting consumption of both durable and nondurable goods, should affect the former to a larger extent.⁴ As the locations of production and consumption of durable goods may not be the same, we interact the indicator for industries producing durable goods with SLOOS-based national-level changes in banks' willingness to originate consumer installment loans to identify the effects of changes in the supply of consumer loans, and with estimates of national-level growth in home equity to identify the effects of changes in home equity availability to households.⁵

Several caveats to our list of identification assumptions exist. First, we apportion banks' changes in C&I lending standards according to whether these banks have deposit-taking branches in a given state. Close linkages between deposits taking and loan originating at the local level have been supported, to a certain extent, by the Community Reinvestment Act (CRA) of 1977.⁶ Still, potential borrowers in a given state may borrow from banks located in another state. For example, (Petersen & Rajan, 2002) show that banks were much more likely to lend over long geographic distances in the 1990s than they were in the 1970s. However, as banks began to operate branches across state lines, in particular with the passage of the Riegle-Neal Interstate Banking and Branching Efficiency Act of 1994, CRA compliance was again emphasized.⁷ In the banking literature, the deposit footprint has been used as a proxy for the loan footprint as well. For example, (Peek & Rosengren, 1995) use deposits as a proxy for loans.⁸ Second, following the literature, for example, (Cetorelli & Strahan, 2006), we associate dependence on external sources of finance in the Rajan-Zingales sense with dependence on bank loans. However, because C&I loans, unlike other sources of external finance, are predominantly collateralized, we also take into account borrowers' ability to pledge tangible collateral (as in (Braun, 2002) and (Claessens & Laeven, 2003)) so that we identify industries that most likely depend particularly on C&I loans. Indeed, as the Census' data suggests, the manufacturing industries that depend relatively more on external finance and have relatively more tangible assets have bank loans to total liabilities ratios that are 5 to 7 percentage points higher than those of other manufacturing industries.⁹ Third, we assume that banks' changes in C&I lending standards reported for all industries reflect changes in such standards for manufacturing industries. However, according to the FR Y-14 supervisory data covering bank holding companies with assets of more than $50 billion, the share of outstanding C&I loans to the manufacturing sector was 23 percent of the total as of the third quarter of 2012, a nontrivial share.

Our results show that changes in access to C&I and consumer installment loans, and changes in the availability of home equity loans notably affect manufacturing employment growth over the sample period.¹⁰ Specifically, we show that, for employment, household access to loans matters more than firm access to local loans, and that changes in access to bank credit affects employment growth mostly through changes in the size of firms rather than through changes in their numbers. The latter finding appears to be consistent with the literature. Small firms' entry decisions may depend less on the availability of bank credit and more on local economic conditions. Indeed, in our data, while the smallest establishments employ a relatively small fraction of employees in the manufacturing sector, these establishments are numerous and introduce noise into the aggregate series for the number of establishments. As for larger firms, consistent with the "hysteresis" behavior modeled in the literature, it may be that, following a tightening of access to credit (an unfavorable shock), the sunk cost aspect of the firm entry decision in the presence of fixed per-period costs results in these firms continuing to serve the market, but perhaps at a smaller scale that requires fewer employees.¹¹

Structural break tests support the notion that a significant portion of manufacturing employment losses over the Great Recession was the manifestation of an unusually large tightening in credit availability--a credit crunch--rather than a structural change in the linkages between access to bank credit and employment. Indeed, our back-of-the-envelope exercise shows that, over the crisis, dramatic tightening in access to both C&I and consumer installment loans may have contributed significantly to the drop in employment in the manufacturing sector. Considering only the differential effects, the drastic worsening of access to C&I and consumer installment loans between 2007 and 2009 suggests a 5.1 percent decline in employment, nearly a third of the actual drop of 17.4 percent. In addition, the decline in the availability of home equity loans suggests an extra 1.4 percent decline in employment.

The outline of the paper is as follows. After a short literature review in the second section, we describe our data sources and the ways we transformed the raw data in the third. The fourth section goes over our empirical strategy and econometric specification. The fifth section presents the estimation results. We then detail the economic significance of changes in access to bank credit by estimating employment losses in manufacturing industries attributable to tightening access to business and consumer loans over the Great Recession. We end with some concluding remarks and policy implications.

2 Literature

        Our identification assumption takes advantage of the differences in bank presence across U.S. states and is similar to that in (Peek & Rosengren, 2000), (Garmaise & Moskowitz, 2006), and (Lee & Stebunovs, 2012). For example, (Peek & Rosengren, 2000) use the Japanese banking crisis to test whether a loan supply shock to branches and agencies of Japanese banks affected construction activity in the U.S. commercial real estate market in California, New York, and Illinois. Similarly, (Garmaise & Moskowitz, 2006) study the effects of large bank mergers on changes in crime at the MSA level, arguing that such merger activity instruments for changes in bank competition at the local level. (Lee & Stebunovs, 2012) use a similar setup to study the effects of bank balance sheet pressures, manifested through bank capital ratios apportioned to a given state, on employment in different manufacturing industries in that state.

Our paper also contributes to the nascent literature that investigates the real effects of worsening access to bank credit over the Great Recession. In this literature strand, using employee-specific data, (Duygan-Bump et al., 2010) find that workers in small firms were more likely to become unemployed during the 2007-2009 financial crisis if they worked in industries with significant needs for external financing. From a more international perspective, (Bijlsma et al., 2010) find evidence that the credit crunch in 2008 and 2009 resulted in lower industrial growth in industries that are more dependent on external finance in OECD countries. In addition, (Bentolila et al., 2013) provide evidence that, in Spain, employment at firms funded by weak banks fell considerably more than employment at firms funded by healthier banks. From a reduced form perspective, (Fort et al., 2013) suggest that the collapse in house prices accounts for a significant part of the large decline in young/small firms during the Great Recession. However, because of their VAR approach, their "financing channel" reflects both the associated credit demand and supply factors, whereas we attempt to identify the economic impact of disruptions in the supply of bank credit.¹²

3 Description of the data

        We focus on manufacturing industries for a few reasons. First, U.S. manufacturing industries are often studied in the finance and banking literature--for example, as in (Cetorelli & Strahan, 2006) and (Kerr & Nanda, 2009). Second, in contrast to some other industries that have experienced a shift over time toward multi-unit firms, manufacturing industries have had relatively stable structures, and many manufacturing firms continue to rely on local bank loans.¹³ Third, because consumption of durable goods is predominantly financed, we can evaluate the importance of household access to consumer loans for manufacturing employment and contrast that with the importance of firm access to bank loans.

Our explained variables come from the QCEW. Explanatory variables are derived from the SLOOS, TransUnion's Trend Data, CoreLogic's house price data, the Federal Reserve's Z.1 statistical release, and other sources.

3.1 The Quarterly Census of Employment and Wages

        The QCEW program publishes quarterly employment and wages data by industry at the county, MSA, state, and national levels as reported by employers, accounting for 98 percent of U.S. jobs.¹⁴ The program's primary outlet is the tabulation of the employment and wages of establishments that report to the Unemployment Insurance (UI) programs. Employment covered by these UI programs represents about 99.7 percent of all wage and salary civilian employment in the country. The QCEW data are collected on an establishment basis. An establishment is an economic unit, such as a farm, mine, factory, or store, that produces goods or provides services. It is typically at a single physical location and engaged in one, or predominantly one, type of economic activity to which a single industrial classification may be applied.

Admittedly, if someone is interested in the number of firms rather than the number of establishments in a given industry, then there might be some measurement error in our dependent variable induced by the fact that large firms often operate multiple establishments. Nevertheless, the number of establishments from the QCEW is highly correlated with the economic quantity--the number of firms--for at least two reasons. First, according to the Bureau of Labor Statistics, most employers have only one establishment.¹⁵ Second, earlier research--for example, by (Black & Strahan, 2002)--has shown that the rate of creation of new businesses is correlated with the share of new establishments in a local economy.

The QCEW data are reported under a promise of confidentiality. The Bureau of Labor Statistics withholds the publication of data for any industry level when necessary to protect the identity of cooperating employers. In fact, at a low level of aggregation, many data points are not reported. However, totals at the industry level for the states and the country include the undisclosed data suppressed within the more detailed tables. We limit ourselves to studying growth in employment, the number of establishments, and the average establishment size (measured in employees) over the 1993-2011 period at the industry-state level.¹⁶

3.2 Dependence on external finance

        To examine how bank credit supply affects firms or small business owners, we first construct measures of dependence on external sources of finance for each of the 21 manufacturing industries in our sample. These measures are based on (Rajan and Zingales (1998) ) and are calculated as the fraction of total capital expenditures not financed by internal cash flows from operations.¹⁷ The measures are widely viewed as technologically determined industry characteristics that are innate to the manufacturing processes and exogenous from the perspective of individual firms. Each industry is classified as either relatively more dependent on external finance ( industry) or less dependent ( industry) based on whether its Rajan-Zingales measure lies above or below the median Rajan-Zingales measure for the 21 manufacturing industries. Although particular values of the Rajan-Zingales measures change over time, the relative ordering of the measures changes very little as we show in the appendix. The industries that our approach identifies as depending relatively more on external finance remain generally the same whether we use the 1980s data or more recent data.¹⁸ To sum up, as in (Cetorelli & Strahan, 2006), implicit in our identification strategy is the assumption that dependence on external finance is constant over time, or rather that the industry ordering is not altered substantially. Since we compute measures of dependence on external finance using mature firms, which are likely closer to industry steady state conditions, this assumption appears to be reasonable.

We associate dependence on external sources of finance in the Rajan-Zingales sense with dependence on bank credit.¹⁹ Although, in aggregate, U.S. firms' dependence on bank loans may be somewhat limited, the dependence is nevertheless larger for some firms (such as relatively small privately held firms) than for others (such as large publicly traded firms). For example, the Census' data suggest that, for firms with less than $25 million in total assets, the ratio of bank loans to total liabilities is more than 20 percent, while that for firms with more than $25 million in total assets is less than 10 percent.²⁰ Using a more direct measure to capture dependence on bank loans would subject our analysis to endogeneity concerns, as a given industry's low dependence on bank loans could simply indicate financing constraints. In this vein, (Cetorelli & Strahan, 2006) argue that the Rajan-Zingales measures computed for only mature firms provide a "powerful instrument for small firms' demand for bank credit," but a direct measure of bank credit dependence--based on bank loans to assets ratios of small businesses from the 1998 Survey of Small Business Finance (SSBF)--does not.²¹ Ultimately, as shown in (Colla et al., 2013), even larger firms may specialize in a certain debt type and may not be able to quickly substitute away from scarce bank loans; hence, they may be forced to downsize or shut down. In other words, if small and large firms alike were able to substitute away from scarce bank loans completely, we would not be able to identify any real effects of a tightening in credit supply using our regression models.

To sharpen our identification approach, we also consider firms' ability to pledge collateral in obtaining bank C&I loans. As suggested by the Survey of Terms of Bank Lending (the Federal Reserve's E.2 statistical release), C&I loans tend to be secured by collateral, such as equipment and machinery. To reflect this particular feature of C&I loans, we consider asset tangibility by industry. We reason that firms in manufacturing industries with a relatively larger share of tangible assets relative to total book-value assets should have the ability to access C&I loans because such collateral is easy to pledge and to evaluate. Following the guidelines in (Braun, 2002) and (Claessens & Laeven, 2003), we compute such tangibility ratios at the three-digit NAICS level using the data for large U.S.-based firms over the sample period. Again, we are not interested in the exact value of the asset tangibility metric for each industry as such. Similar to our dependence on the external finance measure, the asset tangibility measure shows little difference in relative ordering regardless of which time period is used.²² Therefore, based on whether the measure for a given industry is below or above the median, we sort industries into those with a smaller share of tangible assets ( industries) and those with a larger share of tangible assets ( industries).²³

Finally, we can define a treatment group: the industries that depend relatively more on external sources of funding in the (Rajan and Zingales (1998) ) sense and that have a relatively higher ability to pledge collateral to secure access to C&I loans in the sense of (Braun, 2002) and (Claessens & Laeven, 2003). For a given industry, the first part of the definition tells us the need to borrow, and the second part the ability to do so.²⁴ Indeed, as the Census' data suggests, the manufacturing industries that depend relatively more on external finance and have relatively more tangible assets have bank loans to total liabilities ratios that are 5 to 7 percentage points higher than those of other manufacturing industries.²⁵ In addition, to stay consistent with the literature, we consider the treatment group separately to gauge the effects of changes in home equity availability on employment growth at small businesses.

We define another treatment group by recognizing that the degree of consumer reliance on bank credit for consumption of durable goods is different than that of consumption of nondurable goods. Consumption of durable goods is more likely to be financed with consumer or home equity loans (rather than paid for outright) than consumption of nondurable goods. Hence, to a certain extent, the producers of durable goods are at the mercy of lenders to consumers. We follow the U.S. Census Bureau's breakdown of manufacturing industries into industries that produce durable goods ( industries) and those that do not ( industries).

Table 1 shows the breakdown of three-digit NAICS manufacturing industries into those that depend relatively more on external finance ( ), those that have relatively larger shares of tangible assets ( ), and those that produce durable goods ( ). Some industries do not have any of these characteristics, while others have one, two, or all three, which helps with our identification. In aggregate, manufacturing industries account for nearly 10 percent of non-farm employment and about 20 percent of the country's output.

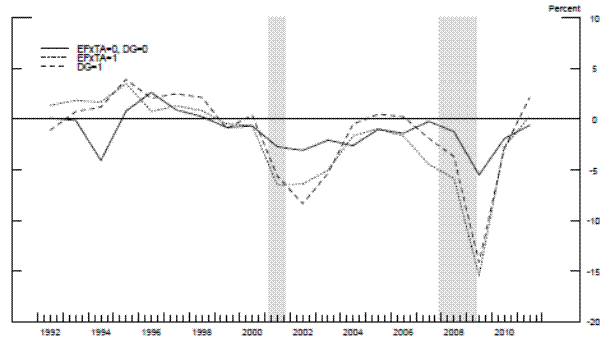
Having defined the control and treatment groups, we look into the growth in employment, number of establishments, and average establishment size (measured in employees) in each of the groups. Figures 3 to 5 plot these measures for the entire economy. The figures suggest that growth in employment and the growth in the average establishment size in the treatment group are more procyclical than those in the control group. However, for the growth in the number of establishments, the business cycle pattern for the treatment group relative to the control group is less clear.²⁶

3.3 Definitions of loan types and the Senior Loan Officer Opinion Survey

3.3.1 Definitions of loan types

        To identify how access to different types of bank loans affects employment in manufacturing industries, we focus on three types of loans: C&I loans, consumer installment loans, and HELOCs.²⁷ C&I loans include loans for commercial and industrial purposes to sole proprietorships, partnerships, corporations, and other businesses, whether secured or unsecured, and whether single payment or installment. C&I loans exclude the following: loans secured by real estate; loans to financial institutions; loans to finance agricultural production and other loans to farmers; loans to individuals for household, family, and other personal expenditures; and other miscellaneous loan categories. Typically, the interest rate for C&I loans is set as a spread over the prime rate or Libor and adjusts with movement in the benchmark rate over the loan term. Consumer installment loans are loans to individuals--for household, family, and other personal expenditures--that are not secured by real estate, such as auto loans. Typically, the interest rate for consumer installment loans is set as a spread over the prime rate or Libor and remains fixed over the loan term.

Available data sources suggest that banks provide a significant share of C&I loans to the manufacturing sector over our sample period. According to the Federal Reserve's G.27 statistical release, as of December 1982, about 28 percent of C&I loans outstanding at large commercial banks (with assets of more than $1 billion) were to the manufacturing sector. According to the FR Y-14 supervisory data covering bank holding companies with assets of more than $50 billion, as of the third quarter of 2012, the share of outstanding C&I loans to the manufacturing sector was 23 percent of the total.

In recent years, the popularity of HELOCs--revolving, open-ended lines of credit secured by residential properties--has overshadowed the use of non-collateralized consumer installment loans. HELOCs are typically secured by junior liens and are usually accessible by check or credit card. The rate on new home equity loans is often set as a spread to the prime rate or Libor. Lenders typically offer home equity loans up to 100 percent of the appraised property value, less the amount of any outstanding first mortgage liens.

3.3.2 The Senior Loan Officer Opinion Survey

        Changes in C&I lending standards and in the willingness to originate consumer installment loans are based on bank-specific responses to questions about changes in lending standards and terms from the Federal Reserve's SLOOS.²⁸ Papers such as (Bassett et al., 2014), (Gilchrist & Zakrajšek, 2012), and (Lown & Morgan, 2006) have studied aggregated responses of the survey results to examine how bank credit shocks affect or are associated with economy-wide real and financial variables.

The survey is usually conducted four times per year by the Federal Reserve Board, and up to 60 banks participate in each survey. The survey is voluntary; it typically includes the largest banks in each Federal Reserve district and is roughly nationally representative. All surveyed banks are considered relatively large: no bank in the survey has assets of less than $3 billion.

In the survey, banks are asked to report whether they have changed their credit standards over the past three months on six categories of core loans, including C&I loans. Both the series indicating changes in credit standards on C&I loans and the series capturing changes in banks' willingness to originate consumer loans are available from the May 1990 survey. (Questions regarding changes in standards on credit card loans and other consumer loans were added to the survey in February 1996 and May 1996, respectively, and were not used in the paper.) The SLOOS asks banks to report changes in their lending practices over the previous three months, and the survey is conducted so that it coincides with regular meetings of the Federal Open Market Committee. Hence, the January SLOOS refers to the period from October to December of the prior year.

We aggregate bank responses concerning changes in C&I lending standards to the state level in two steps. First, we map individual bank responses to indicator variables. Second, we sum these responses across banks for each U.S. state at an annual frequency. The following two paragraphs describe the two steps in detail.

The question about changes in C&I lending standards reads, "Over the past three months, how have your bank's credit standards for approving applications for C&I loans or credit lines--other than those to be used to finance mergers and acquisitions--to large and middle-market firms and to small firms changed?" Banks respond to that question using a categorical scale from 1 to 5: 1 = eased considerably, 2 = eased somewhat, 3 = remained about unchanged, 4 = tightened somewhat, and 5 = tightened considerably. We use the answers based on banks' responses with respect to small firms because the QCEW data is predominantly composed of small businesses and we attempt to capture how local bank credit supply affects firms.²⁹ In addition, though banks were extremely unlikely to characterize their changes in lending standards as having "eased considerably" or "tightened considerably," we use all five of the classifications available to survey respondents. Letting index the respondent banks and index time, we define an indicator variable as follows: if bank reported considerable easing of standards at time , if bank reported some easing, if bank reported no change in standards, if bank reported some tightening, and if bank reported considerable tightening.³⁰

We aggregate individual bank responses across banks for each U.S. state and convert those from quarterly to annual frequency. Using the indicator variables, we construct a composite of changes in lending standards for a particular state , weighted by total business loans (C&I loans plus commercial real estate loans) for each year , in part to strengthen the exogeneity assumption that banks with exposure to a broader economy affect industry-state employment growth dynamics. In other words, the largest of banks with branches in multiple states get weighted the most; this is desirable because a large fraction of small business loans are originated by the largest banks.³¹ More specifically, the tightening measure we use is calculated as follows: , where denotes a quarter of the year. Of the banks that participate in the SLOOS, we select only those that have deposit taking branches in state according to the Summary of Deposits. Hence, the total number of banks, , in a given state may be below 60 for a particular state. We limit the coverage to 32 states (including the District of Columbia) where the selected banks have a material cumulative share of deposits in every year of our sample.³² These filters ensure that our state-level tightening measure is, in fact, representative for a given state.

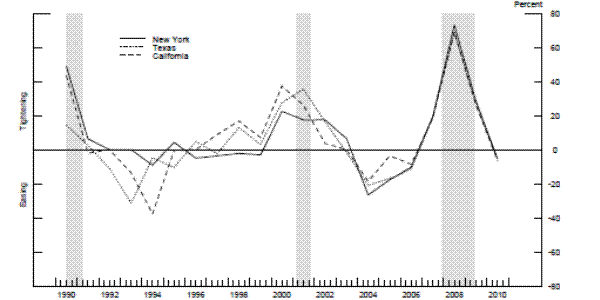
Figure 6 shows the weighted average tightening of C&I lending standards, --that is, the weighted average of individual bank's responses, --for three states: California, New York, and Texas. It shows a drastic tightening of C&I lending standards around the past three recessions as well as a notable loosening of the standards in the mid-2000s. Across the 32 states in our sample, we observe adequate cross-sectional variation in the measures of changes in C&I lending standards, which helps with identification.

Changes in banks' willingness to originate consumer installment loans proxy for the changes in standards on consumer loans. The question about changes in consumer installment loans reads, "Please indicate your bank's willingness to make consumer installment loans now as opposed to three months ago." Among available options, the respondents indicate whether they are more or less willing to originate these loans.³³ By analogy with the construction of , we construct a national composite measure of changes in willingness to make consumer installment loans, , weighted by total consumer loans (excluding residential real-estate loans) as the location of production and consumption of durable goods are usually not the same. Figure 7 plots the weighted average change in banks' willingness to originate consumer installment loans at the national level, .³⁴

3.4 Access to home equity lines of credit

        Because the SLOOS only recently began including questions about the availability of HELOCs, we rely on estimates of growth in (unencumbered) home equity to proxy for changes in the availability of HELOCs. To construct these estimates at the state level, we use house price data from CoreLogic and mortgage debt data from TransUnion's Trend Data.³⁵ Although these estimates are only available starting from 1993, there is notable heterogeneity across states in the timing and magnitude of house price changes to our advantage. Some areas experienced strong decreases in home values over the recent crisis, while other areas avoided the housing boom and experienced no significant house price depreciation. As for the estimates at the national level, we rely on CoreLogic for house price data and the Federal Reserve's Z.1 statistical release for mortgages, HELOCs, and home equity loans secured by junior liens.

We construct the proxy for changes in the availability of HELOCs as follows. We start with the premise of (Avery et al., 2011) that the difference between house prices and outstanding mortgage debt (as well as junior liens and HELOCs, if available) should approximate home equity. Since we cast our regression models in growth rates, we construct a proxy for the growth rate of home equity (using the inverse of the loan-to-value ratio) for a given state as: , where is the growth rate of home equity in state at time , is the growth rate of the house price index in state at time , and is the growth rate of mortgage debt in state at time .³⁶ Admittedly, this might be a noisy proxy for growth in home equity, but we believe it is the best available state-level measure. Similarly, we construct a proxy for the growth rate in home equity at the national level, denoted by . However, in this instance, because of the richness of the Federal Reserve's Z.1 statistical release, we can estimate unencumbered home equity a bit more precisely by accounting for outstanding HELOCs and junior liens.³⁷ The measures, and , appear to be satisfactory proxies for changes in the availability of HELOCs, that is, growth in unencumbered home equity appears to be reflective of changes in the bank credit supply of HELOCs. For example, in the past six years, the correlation between and an aggregate measure of tightening of credit standards for HELOCs based on the SLOOS responses was -0.77 on a quarterly basis.

We include into our regression models growth in aggregate household net worth ( ), constructed using the Federal Reserve's Z.1 statistical release, to control for household wealth-driven demand. The inclusion of growth in aggregate household net worth in the regression sharpens the interpretation of growth in home equity as a proxy for changes in access to home equity loans.

4 Variation, identification, and the empirical model

        The unit of observation for employment growth is at the NAICS three-digit manufacturing industry level in a given state and a given year. To ensure more robust identification, we could have worked with county- or MSA-level data, but at such a low level of aggregation, there would have been too many missing observations due to confidentiality and non-disclosure issues. In contrast, the QCEW industry data at the state level are available over a long period and include the undisclosed data suppressed within the detailed disaggregated tables. Hence, working with state-level data appears to strike a balance between exogeneity concerns and data quality. Although the QCEW is a quarterly frequency data set, we choose to work with its annual averages for a few reasons. We are interested neither in immediate responses of employment growth to changes in access to bank credit, which might later be reversed, nor in the seasonality of manufacturing employment growth and changes in credit provision.³⁸

We examine how changes in credit supply conditions for both firms and households affect growth in manufacturing employment. To isolate these effects and to control for omitted variable bias (for example, from technological changes that drive both changes in lending standards and employment), we exploit the variation in industries' dependence on external finance and the availability of tangible assets as well as the variation in households' dependence on consumer loans. Specifically, we examine whether changes in C&I lending standards, the ability of small business owners to extract home equity to prop their businesses, banks' willingness to originate consumer installment loans, and the ability of consumer-households to extract home equity matter for changes in employment in manufacturing industries.

Given a high degree of persistence in the explained variables over the sample period, as well as the nature of the measure of changes in C&I lending standards and in the willingness to originate consumer installment loans, we work with an empirical model cast in growth rates. This model is stationary and allows us to control for aggregate trends in levels and growth rates (because of included fixed effects). The growth rates of the explained variables are not persistent, with very low autoregressive coefficients; lagged dependent variables are therefore omitted from our regression models.

Our identification assumption is that changes in banks' lending standards, apportioned to a particular state, and growth in home equity are exogenous to developments in a given manufacturing industry in a given state and at a given point in time. In accordance with the questions in the SLOOS, we postulate that banks tighten C&I lending standards broadly across the country rather than targeting a particular state and/or a particular industry. Variation in the geographical presence of banks and in the timing of tightening generates variation in our explanatory variables.³⁹

Besides omitted variables, we control for aggregate credit, state, and national economic conditions. In addition to stand-alone SLOOS measures, growth in home equity, and growth in net worth, aggregate credit conditions are proxied by the change in the realized real interest rate calculated by the difference in the three-month Libor and the PCE inflation rate. As a proxy for national economic conditions, we include the growth rate of U.S. real GDP. With the exception of growth in real GDP and the change in the real interest rate, the controls for contemporaneous economic conditions, all other explanatory variables are lagged one year. To address the potential endogeneity of industry location choices and industry-state-specific trends, industry-state fixed effects are included.

Putting all the pieces together, the benchmark specification is:

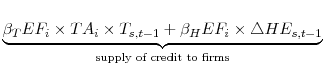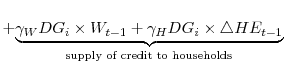where is the growth rate of employment (or the growth rate of the number of establishments or the growth rate of the average establishment size) in industry and state at time ; is the coefficient of the interaction term between the indicator for the dependence on external finance for industry , , asset tangibility, , and the weighted average tightening of standards for C&I loans in state at time , ; is the coefficient of the interaction term between the indicator for the dependence on external finance for industry , , and the growth rate of state-level home equity in state at time , ; is the coefficient of the interaction term between the indicator for durable goods industry , , and the weighted average change in banks' willingness to originate consumer installment loans, ; is the coefficient of the interaction term between the indicator for durable goods industry , , and the growth rate of national-level home equity at time , ; is the coefficient of the interaction term between the indicator for durable goods industry , , and the growth rate of aggregate household net worth at time , ; and are vectors of the coefficients of the lagged state and national conditions variables, captured by and , respectively, which include , , , , and ; is the vector of coefficients for contemporaneous economy-wide credit and economic conditions variables, --U.S. real GDP growth and the first difference of the Libor-based realized real interest rate; is the coefficient for the industry-state fixed effect, which captures any trends in employment growth in the manufacturing industry in state ; and, finally, is the error term robust to heteroskedasticity.⁴⁰

We compute errors clustered separately in several ways: clustering by , clustering by , and double clustering by and . The multiple clustered errors are calculated using the (Cameron et al., 2011) code.

The 32 states used in our regressions appear to be representative of the population of manufacturing industries in the entire country. We checked the data breakdown by employment, the number of establishments, and the average establishment size for two years, 2007 and 2010. The population measures are shown in Table 4 and the same measures for the 32 states in our sample are shown in Table 3. In percentage terms, the breakdown of employment and number of establishments in our sample is very similar to that in the population. In addition, the average establishment size in the sample is nearly identical to that in the population as our sample accounts for more than 80 percent of the total employment in the United States as of 2010.⁴¹

5 Results

5.1 Four channels of bank credit supply

        First, we determine whether each of the credit channels mentioned in Figure 1 exists separately from the others. For the effects of the supply of credit to firms, we find that a percentage point increase in the tightening of C&I lending standards ( ) in the prior year leads to a 0.04 percentage point decrease in employment growth in industries that depend relatively more on external finance and have a relatively higher ability to pledge tangible assets ( industries), as can be seen in the first column of Table 4. Next, a percentage point increase in the availability of home equity loans to small business owners ( ) in the prior year drives up employment growth in industries that depend relatively more on external fiance ( industries) by 0.06 percentage point, as shown in the second column. As for the effect of the supply of credit to households, we find that employment growth in industries that produce durable goods ( industries) increases by 0.06 percentage point with a percentage point increase in additional willingness to originate consumer installment loans ( ) in the prior year, as described in the third column. Finally, a percentage point increase in the availability of home equity credit ( ) for household-consumers in the prior year has a positive effect of nearly 0.11 percentage point on employment growth in the treatment industries, as stated in the fourth column. All of these coefficients are statistically significant at conventional levels.

Next, Tables 5 to 7 present empirical results with all four channels included simultaneously: Table 5 shows the results for growth in employment, Table 6 shows those for growth in the number of establishments (the extensive margin), and Table 7 shows those for growth in the average establishment size (the intensive margin). Given that the growth rate of employment is just a sum of the growth rates of the number of establishments and the average establishment size, the regression coefficients in the employment growth regression in Table 5 are nearly exact sums of the corresponding coefficients in Tables 6 and 7. Each of the these three tables shows the estimation results for models with industry-state fixed effects and various specifications of error clustering. In each table, in the first column, errors are clustered by industry-state; in the second, by year; and, in the third, double-clustered by industry-state and year.⁴²

As the first row in Table 5 shows, for the credit supply to firms, a percentage point increase in the tightening of C&I lending standards reduces the growth rate in employment in the treatment industries by 0.04 percentage point, a similar result to that in Table 4. Note that this result is statistically significant at conventional levels even in the regression with double-clustered errors. (The economic significance of this and other coefficients will be explored later in section 6.) The regression coefficient in the second row, capturing the impact of the ability of small business owners to extract home equity to finance their businesses, is positive, but no longer robustly statistically significant. As for the credit supply to households (shown in the third row), a percentage point increase in additional willingness to originate consumer installment loans boosts the growth rate of employment in the treatment industries by 0.06 percentage point. In addition, as seen in the fourth row, a percentage point increase in growth in home equity propels the growth rate in employment in the treatment industries by 0.15 percentage point. In contrast, growth in households' net worth--a proxy for other wealth-driven consumption of durable goods included as a demand side control--does not appear to have a robustly statistically significant impact on employment growth in the treatment industries. As for the other explanatory variables, all the estimated coefficients, with the exception of the coefficient for state-level home equity, are of the expected signs. However, only the coefficient to real GDP growth is estimated to be robustly statistically significant across all our error-clustering specifications.

Table 6 shows the regression results for growth in the number of establishments. For the credit supply to firms, the results show that the tightening of C&I lending standards does not have a statistically significant effect on the growth in the number of establishments in any of the specifications. Changes in the availability of HELOCS, on the other hand, appear to have a statistically significant effect on the growth in the number of establishments for industries depending relatively more on external finance. As for the credit supply to households, the results show that an increase in banks' willingness to originate consumer installment loans has a statistically significant effect on growth in the number of establishments only in the first specification, that is, in the model with the least strict error specification. Changes in the availability of HELOCs do not appear to have any statistically significant effect on the growth in the number of establishments for durable goods industries.

The lack of evidence that the supply of C&I loans has an effect on the number of establishments appears to be consistent with the literature. Small firms' entry decisions may depend less on the availability of bank credit and more on local economic conditions. Setting up a firm may not be that costly. For example, according to (Djankov et al., 2002), entrepreneurs' average cost of starting a firm (including the time to start up a firm) was 1.7 percent of per-capita income in the United States in 1999, or $520. In addition, layoffs by firms that are induced by stricter lending standards may spur some creation of firms (counted as establishments in our data), which may boost the number of establishments in times of distress. For example, (Aaronson et al., 2004) document the increase in the number of firms, which was accompanied by a fall in employment at the aggregate level. Indeed, in our data, while the smallest establishments employ a relatively small fraction of employees in the manufacturing sector, these establishments are numerous and introduce noise into the aggregate series for the number of establishments. As for larger firms, consistent with the "hysteresis" behavior modeled in other strands of the literature, it may be that, following a tightening of access to credit (an unfavorable shock), the sunk cost aspect of the firm entry decision in the presence of fixed per-period costs results in these firms continuing to serve the market, but perhaps at a smaller scale that require fewer employees, similar to (Alessandria & Choi, 2007).

Although analyzing employment growth separately at small and large firms would be desirable, our data do not have this categorization at the desired industry-state level. However, we can infer from another data set--the Census' County Business Patterns (CBP)-- that, for the entire country, changes in the number of establishments in the small establishment size classes do introduce noticeable noise to the aggregate number of establishments.⁴³ However, because these small establishments employ, in aggregate, a small number of workers, changes in employment at these establishments have a very limited impact on aggregate employment growth.

Table 7 shows the estimation results for the growth rate in the average establishment size. For the credit supply to firms, the results show that a percentage point increase in the tightening of credit standards leads to a 0.04 percentage point decrease in the growth rate of the average size of the establishments in the treatment groups. The results also show that an improvement in small business owners' access to HELOCs does not have a statistically robust impact on the average establishment size in any of the three specifications. As for the credit supply to households, the results show that a percentage point increase in additional willingness to originate consumer installment loans leads to a nearly 0.05 percentage point increase in the growth rate of the average establishment size in the treatment industries. In addition, a percentage point increase in the availability of home equity boosts the growth rate of the average establishment size by 0.15 percentage point. These results suggest that most of the industry-wide employment growth dynamics driven by changes in bank credit availability are explained by changes in average establishment size (the intensive margin) rather than by changes in the number of establishments (the extensive margin).

5.2 Breakdown of the 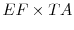channel

        To be consistent with the traditional approach, we check whether dependence on external finance or the availability of pledgable assets matter separately for employment growth in manufacturing industries. As Table 8 shows, it is the former that is statistically significant. However, we believe that it is correct to study the intersection of and industries for at least two reasons.⁴⁴ First, the C&I loan definition and many survey results suggest the importance of pledgable assets for firms' access to bank credit. Indeed, as the Census' data suggests, the manufacturing industries that depend relatively more on external finance and have relatively more tangible assets have bank loans to total liabilities ratios that are 5 to 7 percentage points higher than those of other manufacturing industries. Second, the joint consideration of and industries, as a comparison of Tables 5 and 8 reveals, strengthens the effects of tightening of C&I lending standards on employment growth in the treatment industries. Specifically, the coefficient on the term in the benchmark specification in Table 5 is almost twice as large as the coefficient on the changes in C&I credit standards interacted only with .

5.3 Structural breaks in the bank credit supply channels

        Next, we check whether our results are driven by the developments specific to the Great Recession. To do so, we estimate a regression model that allows a break in the coefficients on the measures of changes in access to C&I, consumer installment, and home equity loans after 2007. In the regression model in Table 9, the proxies for changes in access to various types of credit are interacted with both respective industry-type dummies and a crisis indicator ( ) that captures the period from 2007 to 2011. The estimation results suggest no statistically robust evidence of structural breaks in the relationship between changes in access to the four types of bank lending and employment growth across manufacturing industries. That said, there is some indication that, over the crisis, for growth in manufacturing employment, the channel that links changes in small business owners' access to home equity loans to employment gains may have become impaired, which is a reason we do not see this channel at work in our benchmark model. However, controlling for the crisis, this channel appears to be statistically significant as shown by the coefficients to without the interaction. In addition, in the first specification, changes in households' access to consumer installment and home equity loans may have become less important (the triple interaction terms and have negative coefficients). However, this result is not statistically significant in the other error-clustering specifications.

6 Potential effects of the credit crunch on employment

        We perform a back-of-the-envelope exercise to gauge the potential contribution of a dramatic worsening of the availability of C&I and consumer installment loans to the drop in employment in the manufacturing sector over the Great Recession. We only take into account the differential effect of tightening access to bank credit on employment growth in the treatment industries.⁴⁵ The differential effects of a percentage point tightening in C&I lending standards ( ) and additional willingness to originate consumer installment loans ( ) may be inferred from the coefficients estimated in Table 5, lines 1 and 3. The values of and are inferred from state-level data and national level data, respectively, similar to what is shown in Figures 6 and 7. Over the 2007-2009 period, ranged from 38 to 56 percent, on average, per year, across the 32 states, and was about negative 34 percent, on average, per year, at the national level.⁴⁶ As a benchmark, to judge the importance of the bank credit supply factors, we rely on actual declines in manufacturing employment. For the manufacturing sector in our 32-state sample, the pre- and post-crisis breakdowns in employment are shown in Table 3. Over the Great Recession, employment in the manufacturing sector declined about 17.4 percent, and the treatment groups ( and ) experienced notably larger declines in employment than the control groups ( and ).

Considering only the differential effects, keeping all other explanatory variables fixed and ignoring numerous fixed effects, we perform the back-of-the-envelope exercise as follows. For industry in state , let be employment in 2007 and be the change in employment over the 2007 to 2010 period. Then our back-of-the envelope exercise consists of two steps. The first is simply the following: 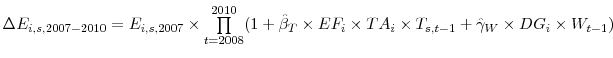, where and , which are estimated coefficients from Table 5. The second step is aggregation of industry-state specific across states and industries by industry type.

The back-of-the-envelope exercise shows that the dramatic tightening of access to both C&I and consumer installment loans may have contributed significantly to the drop in employment in the manufacturing sector. As the top panel in Table 10 shows, worsening access to C&I and consumer installment loans over the financial crisis suggests a 5.1 percent decline in employment, nearly a third of the actual drop of 17.4 percent. For the industries that depend relatively more on external sources of funding, have a larger share of tangible assets, and produce durable goods ( and ), the suggested impact on employment growth is the largest. For the industries that depend relatively more on external sources of funding, have a larger share of tangible assets, and produce nondurable goods ( and ), the impact on employment growth was the smallest. The bottom panel of Table 10 shows declines in employment in absolute terms. The exercise associates about a 588,000 decline in employment with the worsening in access to C&I and consumer installment loans, while the actual decline was about 2 million in the 32 states in our sample. Given the estimation results shown in Tables 6 and 7, the employment declines were likely driven primarily by a shrinkage in the establishment sizes rather than by a fall in the number of establishments.

For industries that produce durable goods, the regression results suggest that there is an additional channel at work--the availability of home equity loans to consumer-households. The proxy for the growth in home equity declined, on average, about 5.7 percent per year during the 2007-2009 period. Per similar calculations to those above, the reduction in the availability of home equity loans suggests an additional 1.4 percent decline in manufacturing employment.

The back-of-the-envelope exercise has several caveats. First, it is merely an illustration of the potential economic significance of the worsening availability of C&I and consumer installment loans to the fall in employment. It is not a formal in-sample forecasting exercise, as we do not take into account the potentially offsetting impact of other variables, such as lower real interest rates or certain fixed effects. Second, the s of, at most, 30 percent suggest that the estimated models leave a sizeable variation in employment growth at an industry-state level unexplained. Presumably, a large fraction of the unexplained variation is related to a fall in demand. In fact, (Mian & Sufi, 2012) point to a large negative demand shock, in part, attributable to household overindebtedness, underlying employment losses in the non-traded goods sector over the Great Recession. Third, we caution that any generalization of the back-of-the-envelope exercise to the entire economy is limited because we only consider job losses in manufacturing industries and do not account for displaced workers that may be absorbed by firms in other sectors. However, we believe that our findings are indicative of developments in other sectors reliant on bank credit as well.

7 Conclusion

        This paper investigates how a bank credit crunch--a dramatic worsening of firm and consumer access to bank credit, such as the one observed over the Great Recession--translates into job losses in in U.S. manufacturing industries. To isolate these effects, we exploit variation in changes in C&I lending standards, in changes in banks' willingness to originate consumer installment loans, and in growth in home equity. To control for omitted variable bias, we rely on differences in the degree of industries' dependence on external finance and in the sensitivity of these industries' output to changes in consumer credit. We show that changes in C&I lending standards, in willingness to originate consumer installment loans, and in the availability of home equity loans notably affect employment growth in manufacturing industries over the 1993-2011 period. In particular, the results highlight the adverse effects that disruptions in the supply of bank credit had on manufacturing employment growth over the Great Recession.

These results have a few implications for understanding the recovery in the economy and the labor market going forward. To some extent, the tightening of lending standards and the decrease in willingness to originate loans reflect commercial banks' efforts to deleverage. By changing the composition of their balance sheets from business and consumer loans toward U.S. Treasury securities, commercial banks may improve their standing with both bank regulators and investors. These adjustments may temporarily hold back employment growth in manufacturing industries, and, thus, contribute to persistently weak conditions in the labor market more generally. Moreover, the housing market may need to improve more substantially to have a more noticeable effect on manufacturing employment growth. In the longer term, the displaced workers in the industries affected the most may be absorbed by firms in other sectors of the economy.

When dealing with the unusually low levels of employment growth in manufacturing in an environment like the Great Recession, a policy prescription that follows from our back-of-the-envelope exercise is that household access to bank credit appears to matter more for manufacturing employment than firms' access to bank loans. This conclusion is consistent with some stylized facts about the U.S. economy. First, the share of consumption in the country's GDP, at about 70 percent, by far dominates the share of physical capital investment. Second, while households rely more on banks for credit, many large firms may have the ability to access capital markets directly. However, one should bear in mind that prolonged periods of underinvestment in physical capital may have implications on productivity growth and potential output in the long run.

Acknowledgments

We thank William Bassett, Thorsten Beck, Nicholas Bloom, Christopher Carroll, John Driscoll, Lucca Guerrieri, John Haltiwanger, and Jonathan Rose as well as seminar participants at the Federal Reserve Board for helpful comments and suggestions. In addition, we thank discussants Adonis Antoniades, Oscar Arce, Chiara Banti, Jin Cao, Enrique Martinez-Garcia, Anthony Murphy, Leonard Nakamura, Francisco Rodríguez-Fernández, and Pei Shao and participants at numerous conference and meetings for valuable comments and suggestions. We thank Shaily Patel for excellent research assistance. Viktors Stebunovs thanks the Office of Financial Stability Policy and Research for its hospitality.

Appendix A. Data Description and Robustness Checks

        In the appendix, we provide details on the Rajan-Zingales measures of dependence on external finance and the Braun-Claessens-Laeven measures of asset tangibility. We also discuss several robustness checks: two models estimated using the scale dependence and tangibility measures, rather then the industry-type dummies based on these measures; a model estimated using the ratios of bank loans to total assets computed for the 1998 Survey of Small Business Finance; and a model with industry-specific trends. Our final significant robustness check concerns the usage of different measures of the weighted average tightening of C&I lending standards and the weighted average change in banks' willingness to originate consumer installment loans. Finally, we touch upon briefly less significant robustness checks.

As in (Cetorelli & Strahan, 2006), implicit in our identification strategy is the assumption that dependence on external financial is constant over time, or rather that the industry ordering (in terms of dependence on external finance) is not altered substantially. Indeed, as Table A1 shows, the Rajan-Zingales measures for mature firms change somewhat over time, but the industry ordering remains relatively stable.⁴⁷ The first column shows these measure for different three-digit NAICS codes from the 1980s period used in (Rajan and Zingales (1998) ); the second column the measures based on the 1980-1997 period used in (Cetorelli & Strahan, 2006), and the third column the measures based on the 1990-2011 period used in our paper. Note that the columns show the measures that we calculated, even those for the periods used in (Rajan and Zingales (1998) ) and (Cetorelli & Strahan, 2006), to present the data on a more comparable basis. While (Rajan and Zingales (1998) ) relies on the ISIC and (Cetorelli & Strahan, 2006) on the SIC, all our calculations are based on NAICS. However, as the Census' information suggests, these classifications may not be directly comparable.⁴⁸ In the table, a measure in bold indicates whether the corresponding industry depends relatively more on external finance than others based on whether its measure is above or equal to the median Rajan-Zingales measures for the 21 industries in the sample. A comparison across the columns points to a remarkable stability in the industries that our approach identifies as relatively more dependent on external finance. For example, only one manufacturing industry (325 - Chemical Manufacturing) that is relatively more dependent on external finance in our sample period was not classified as such based on the 1980s period used in (Rajan and Zingales (1998) ).

In addition, implicit in our identification strategy is the assumption that industries asset tangibility is constant over time, or rather that the industry ordering is not altered substantially. Again, as Table A2 shows, asset tangibility measures change over time, but a comparison across the columns points to a remarkable stability in the industries that we identify as those with relatively more tangible assets. For example, only two industries (312 - Beverage and Tobacco Product Manufacturing and 314 - Textile Product Mills) that has relatively more more asset tangibility in our sample period were not so classified in the 1980s period used in (Rajan and Zingales (1998) ); whereas only one industry (312 - Beverage and Tobacco Product Manufacturing) that has relatively more asset tangibility in our sample period was classified differently in the 1980-1997 period used in (Cetorelli & Strahan, 2006). Such findings support our identification approach which relies on the ordering of the industries rather than on the usage of particular measures of dependence on external finance and availability of tangible assets that change over time. Our results are robust to using other periods in calculations of the Rajan-Zingales and Braun-Claessens-Laeven measures for construction of our and industry-type dummies. Moreover, our results hold if we identify our treatment industries as those in the top third of the joint distribution of the Rajan-Zingales and Braun-Claessens-Laeven measures.

For further robustness, albeit with significant shortcomings, we estimate two models with dependence on external finance and asset tangibility captured by scale Rajan-Zingales and Braun- Claessens-Laeven measures, rather then the industry-type dummies based on these measures. Recall that to identify the impact of tightening C&I credit standards ( ) on employment growth we define a treatment group comprising the industries that depend relatively more on external finance ( ) and have relatively more tangible assets ( ) than other industries. By analogy, when using scale Rajan-Zingales ( ) and Braun-Claessens-Laeven ( ) measures, the triple interaction term may be . Because both and may assume positive and negative values, it is difficult to interpret the regression coefficient for this new triple interaction term. (Note that such interpretation ambiguity is not an issue for some other papers because they interact the Rajan-Zingales measure with a categorical variable--for example, with the dummy indicating whether a state allows for interstate banking or not as in robustness checks in (Cetorelli & Strahan, 2006). Moreover, these papers tend to have less complex treatment groups, making the triple interaction terms unnecessary.) To circumvent this ambiguity, we map the Rajan-Zingales measures into a interval. (The mapping formula is as follows: , where and .) While this transformation fixes the issue with negative s, it does not address a possibility of an outlier driving the estimation results one way or another.⁴⁹ In contrast, our and approach is more resilient to such outliers. Finally, the difficulties with the interpretation of the coefficient and the identification approach still remain. In our benchmark model, the interaction term, , has a straightforward interpretation when it equals one. Specifically, these are the industries that depend relatively more on external finance and have relatively more tangible assets than other industries; this breakdown clearly identifies the industries that are potentially affected the most by changes in the availability of C&I loans. In contrast, the interaction term , a product of the transformed Rajan-Zingales measures and the Braun-Claessens-Laeven measures, is much less intuitive. In particular, this interaction term may be high if is high, or is high or both, and it is the combination of both high and high that should identify the treatment group, that is, the industries that have the need to seek C&I loans and have the ability to obtain them by pledging tangible assets. In short, the interaction term obscures identification. These arguments notwithstanding, the first two columns of Table A3 show the estimation results. The first column includes the double interaction terms and to our benchmark specification. Not surprisingly, these new additional double interaction terms appear to be collinear with the triple interaction term , as the results in the second column illustrate. In the model with only the triple interaction term included, its regression coefficient is negative and statistically significant. Again, the meaning of the value of the coefficient, however, is difficult to interpret.

As another robustness check, we re-estimate the benchmark model using the ratios of bank loans to total assets computed for the 1998 Survey of Small Business Finance to identify our treatment groups. The estimation results are shown in the third column of Table A3.⁵⁰ It appears that both easing access to C&I loans and easing of small business owners' access to HELOCs have a positive, statistically significant impact on growth in manufacturing employment. This finding appears to be broadly consistent with the literature that the smallest (youngest) firms rely more on funds supplied by the owners than on bank loans. We are cautions about promoting this finding because industries' sorting based on the ratios of bank loans to total assets likely introduces endogeneity into the estimation. In contrast to the Rajan-Zingales measures, that reflect deep technological parameters of the least financially-unconstrained firms, the ratios of bank loans to total assets are computed for undoubtedly financially constrained firms. And a low ratio may simply indicate firms' severe financial constraints.

As yet another robustness check, we re-estimate the benchmark model with separate time trends for each of the 21 manufacturing industries in the sample. Our results, shown in the fourth column in Table A3, are robust to accounting for these trends. However, we believe the inclusion of these regressors in the model is redundant, as only a few industries have statistically significant trends. We emphasize that our benchmark regressions are cast in growth rates, and this should take into account any trends in the level of employment across manufacturing industries. In addition, we have industry-state fixed effects that control for (a) the trend in growth rates that differ by state and industry and (b) industries' self-selected locations across the states.

Our final significant robustness check concerns the usage of different measures of the weighted average tightening of C&I lending standards and the weighted average change in banks' willingness to originate consumer installment loans. We noted in the main text that banks were extremely unlikely to characterize their changes in lending standards as having "eased considerably" or "tightened considerably," or to characterize their changes in willingness to originate consumer installment loans as "much more willing" or "much less willing." Indeed, over the past two decades, with the exception of 2008, no more than a handful out of usually close to 200 bank responses over the course of a year have reported such extreme responses as can be seen in Tables A4 and A5. Similarly, if we use a more simple method of categorizing the survey results, namely, when we define the indicator variable as follows: if bank reported considerable or some easing of standards at time , if bank reported no change in standards, and if bank reported some or considerable tightening (and similarly for responses to the changes in willingness to originate consumer installment loans), we get the results shown in Table A6 that are quantitatively similar to those in Table 5.

Finally, we conduct a few more robustness checks (not shown). Our results are robust to exclusion of the growth rate of real GDP, inclusion of state-level GDP, alternative home equity definitions, and inclusion of lagged dependent variables. Our results also hold when we exclude from the sample "bank-friendly" states, such as Delaware and South Dakota, or large states, such as California. We find some evidence that the trade credit channel--captured by the interaction of an indicator of dependence on trade credit and the three-month Libor--was operational, but it is not statistically robust.

References

Aaronson, D., E. R. Rissman, and D. G. Sullivan (2004): Assessing the Jobless Recovery, Federal Reserve Bank of Chicago Economic Perspectives, 28(2), 2-20.

Adrian, T., P. Colla, and H. S. Shin (2012): Which Financial Frictions? Parsing the Evidence from the Financial Crisis of 2007-9, NBER Working Paper No. 18335.

Alessandria, G., and H. Choi (2007): Do Sunk Costs of Exporting Matter for Net Export Dynamics?, Quarterly Journal of Economics, 122(1), 289-336.

Avery, R., K. P. Brevoort, and K. Samolyk (2011): Housing Cycles, Household Credit Performance, and Economic Activity, Working Paper.

Bassett, W. F., M. B. Chosak, J. C. Driscoll, and E. Zakrajsek (2014): Changes in Bank Lending Standards and the Macroeconomy, Journal of Monetary Economics, 62, 23-40.

Bentolila, S., M. Jansen, G. Jimenez, and S. Ruano (2013): When Credit Dries Up: Job Losses in the Great Recession, Working Paper.

Bijlsma, M., A. Dubovik, and B. Straathof (2010): How Large was the Credit Crunch in the OECD?, CPB Discussion Paper 232, CPB Netherlands Bureau for Economic Policy Analysis.

Black, S. E., and P. E. Strahan (2002): Entrepreneurship and Bank Credit Availability, Journal of Finance, 57(6), 2807-2833.

Braun, M. (2002):Financial Contractibility and Assets Hardness: Industrial Composition and Growth, Working Paper.

Braun, M., and B. Larrain (2006): Finance and the Business Cycle: International, Inter-Industry Evidence, Journal of Finance, 60(3), 1097-1128.

Cameron, A. C., J. B. Gelbach, and D. L. Miller (2011): Robust Inference With Multiway Clustering, Journal of Business and Economic Statistics, 29(2), 238-249.

Cetorelli, N., and P. E. Strahan (2006): Finance as a Barrier to Entry: Bank Competition and Industry Structure in Local U.S. Markets, Journal of Finance, 61(1), 437-461.

Claessens, S., and L. Laeven (2003):Financial Development, Property Rights, and Growth, Journal of Finance, 58(6), 2401-2436.

Colla, P., F. Ippolito, and K. Li (2013): Debt Specialization, Journal of Finance, 68(5), 2117-2141.

Davis, S. J., J. Haltiwanger, R. Jarmin, and J. Miranda (2006): Volatility and Dispersion in Business Growth Rates: Publicly Traded versus Privately Held Firm, NBER Working Paper No. 12354.

Djankov, S., R. L. Porta, F. Lopez-De-Silanes, and A. Shleifer (2002): The Regulation of Entry, Quarterly Journal of Economics, 117(1), 1-37.

Duchin, R., O. Ozbas, and B. A. Sensoy (2010): Costly External Finance, Corporate Investment, and the Subprime Mortgage Credit Crisis, Journal of Financial Economics, 97(3), 418-435.

Duygan-Bump, B., A. Levkov, and J. Montroiol-Garriga (2010): Financing Constraints and Unemployment: Evidence from the Great Recession,Quantitative Analysis Unit Series Paper QUA10-6, Federal Reserve Bank of Boston.

Fort, T. C., J. Haltiwanger, R. Jarmin, and J. Miranda (2013): How Firms Respond to Business Cycles: The Role of Firm Age and Firm Size, NBER Working Paper No. 19134.

Garmaise, M. J., and T. J. Moskowitz (2006): Bank Mergers and Crime: The Real and Social Effects of Credit Market Competition, Journal of Finance, 61(2), 495-539.

Gilchrist, S., and E. Zakrajsek (2012): Credit Spreads and Businss Cycle Fluctuations, American Economic Review, 102(4), 1692-1720.

Jarmin, R. S., S. D. Klimek, and J. Miranda (2009): The Role of Retail Chains: National, Regional and Industry Results, in Producer Dynamics: New Evidence from Micro Data, ed. by T. Dunne, J. B. Jensen, and M. J. Roberts, pp. 237-262. University of Chicago Press.

Kerr, W. R., and R. Nanda (2009): Democratizing Entry: Banking Deregulations, Financing Constraints, and Entrepreneurship, Journal of Financial Economics, 94(1), 124-149.

Lee, S. J., and V. Stebunovs (2012): Bank Capital Ratios and the Structure of Nonfinancial Industries, Finance and Economics Discussion Series 2012-53, Board of Governors of the Federal Reserve System (U.S.).

Lown, C. S., and D. P. Morgan (2006): The Credit Cycle and the Business Cycle: New Findings Using the Loan Officer Opinion Survey, Journal of Money, Credit, and Banking, 38(6), 1575-1597.

Mian, A. R., and A. Sufi (2012): What Explains High Unemployment? The Aggregate Demand Channel, NBER Working Paper No. 17830.

Peek, J., and E. S. Rosengren (1995): The Capital Crunch: Neither a Borrower nor a Lender Be, Journal of Money, Credit and Banking, 27(3), 625-638.

____(2000): Collateral Damage: Effects of the Japanese Bank Crisis on Real Activity in the United States, American Economic Review, 90(1), 30-45.

Peersman, G., and F. Smets (2005): The Inudstry Effects of Monetary Policy in the EURO Area, The Economic Journal, 115(4), 319-342.

Petersen, M. A., and R. G. Rajan (2002): Does Distance Still Matter? The 39. Information Revolution in Small Business Lending, Journal of Finance, 57(6), 2533-2570.

Rajan, R., and L. Zingales (1998): Financial Dependence and Growth, American Economic Review, 88(3), 559-586.

Thompson, S. (2011): Simple Formulas for Standard Errors that Cluster by Both Firm and Time, Journal of Financial Economics, 99, 1-10. 40

Figure 1: Four channels of bank credit supply

Figure 2: Changes in C&I lending standards for small firms and growth in employment in the U.S. manufacturing sector

Figure 2 Data

Source: Federal Reserve Board, Senior Loan Officer Opinions Survey on Bank Lending Practices. Note: Changes in C&I lending standards for small firms is calculated by the net percentage of respondent banks reporting tightening of standards on C&I loans to small firms, weighted by business loans. Shaded areas are NBER-defined recessions.

Figure 3: Growth in employment in manufacturing industries in the United States

Figure 3 Data

Note: EFxTA = 0 are manufacturing industries that either depend relatively less on external sources of funding or have relatively less ability to pledge collateral to secure access to C&I loans. DG = 0 are manufacturing industries that produce nondurable goods. EFxTA = 1 are manufacturing industries that depend relatively more on external sources of funding and have relatively more ability to pledge collateral to secure access to C&I loans. DG = 0 are manufacturing industries that do not produce durable goods. DG = 1 are manufacturing industries that produce durable goods. Shaded areas are NBER-defined recessions.

Figure 4: Growth in the number of establishments in manufacturing industries in the United States

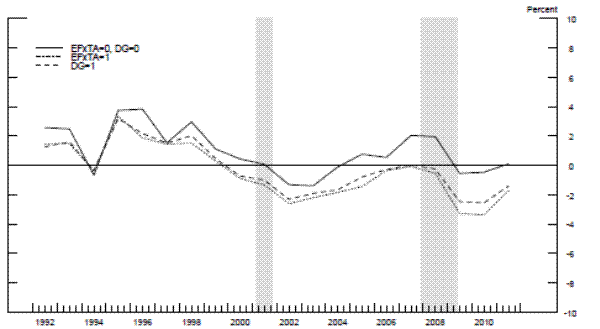Figure 4 Data

Note: EFxTA = 0 are manufacturing industries that either depend relatively less on external sources of funding or have relatively less ability to pledge collateral to secure access to C&I loans. DG = 0 are manufacturing industries that produce nondurable goods. EFxTA = 1 are manufacturing industries that depend relatively more on external sources of funding and have relatively more ability to pledge collateral to secure access to C&I loans. DG = 0 are manufacturing industries that do not produce durable goods. DG = 1 are manufacturing industries that produce durable goods. Shaded areas are NBER-defined recessions.

Figure 5: Growth in the average size of establishments in manufacturing industries in the United States

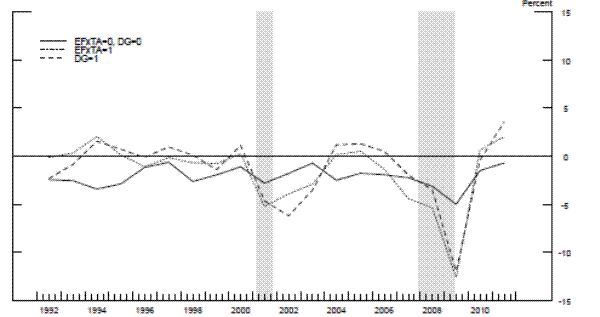Figure 5 Data

Note: EFxTA = 0 are manufacturing industries that either depend relatively less on external sources of funding or have relatively less ability to pledge collateral to secure access to C&I loans. DG = 0 are manufacturing industries that produce nondurable goods. EFxTA = 1 are manufacturing industries that depend relatively more on external sources of funding and have relatively more ability to pledge collateral to secure access to C&I loans. DG = 0 are manufacturing industries that do not produce durable goods. DG = 1 are manufacturing industries that produce durable goods. Shaded areas are NBER-defined recessions.

Figure 6: The weighted average tightening of C&I lending standards for small firms

Figure 6 Data

Source: Federal Reserve Board, Senior Loan Officer Opinions Survey on Bank Lending Practices.Note: Shaded areas are NBER-defined recessions.

Figure 7: The weighted average change in banks' willingness to originate consumer installment loans

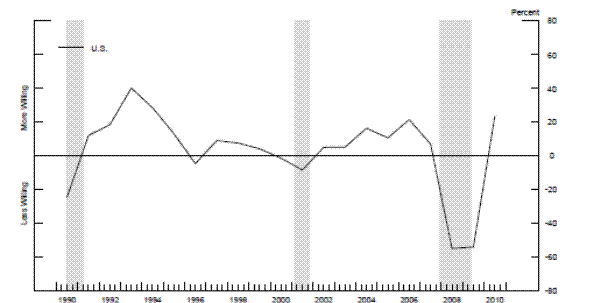Figure 7 Data

Source: Federal Reserve Board, Senior Loan Officer Opinions Survey on Bank Lending Practices. Note: Shaded areas are NBER-defined recessions.

Table 1: Characteristics of manufacturing industries

NAICS	Description				Empl. Share (Percent)	Output Share (Percent)
311	Food Manufacturing				1.2	2.8
312	Beverage and Tobacco Product Manufacturing				0.0	0.0
313	Textile Mills				0.2	0.2
314	Textile Product Mills				0.0	0.0
315	Apparel Manufacturing				0.2	0.1
316	Leather and Allied Product Manufacturing				0.0	0.0
321	Wood Product Manufacturing				0.4	0.4
322	Paper Manufacturing				0.3	0.7
323	Printing and Related Support Activities				0.4	0.4
324	Petroleum and Coal Products Manufacturing				0.1	2.3
325	Chemical Manufacturing				0.6	2.6
326	Plastics and Rubber Products Manufacturing				0.5	0.8
327	Nonmetallic Mineral Product Manufacturing				0.4	0.5
331	Primary Metal Manufacturing				0.3	1.0
332	Fabricated Metal Product Manufacturing				1.1	1.3
333	Machinery Manufacturing				0.8	1.3
334	Computer and Electronic Product Manufacturing				0.9	1.6
335	Electrical Equipment, Appliance, and Component				0.3	0.5
336	Transportation Equipment Manufacturing				1.2	2.9
337	Furniture and Related Product Manufacturing				0.4	0.3
339	Miscellaneous Manufacturing				0.5	0.6
31-33	Total Manufacturing				9.7	20.3

Source: BLS and BEA.
Note: Employment and output shares are relative to the entire economy as of 2007.

Table 2: Breakdown of employment in manufacturing industries: Employment in manufacturing in 2007 in the U.S.

			Row total
	3,514,947	1,537,086	5,052,033
	7,311,679	1,469,312	8,780,991
Column total	10,826,626	3,006,398	13,833,024

Note: are manufacturing industries that either depend relatively less on external sources of funding or have relatively less ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce nondurable goods. are manufacturing industries that depend relatively more on external sources of funding and have relatively more ability to pledge collateral to secure access to C&I loans. are manufacturing industries that do not produce durable goods. are manufacturing industries that produce durable goods.

Table 2: Breakdown of employment in manufacturing industries: Employment in manufacturing in 2010

			Row total
	3,193,000	1,254,642	4,447,642
	5,971,005	1,068,850	7,039,855
Column total	9,164,005	2,323,492	11,487,497

Note: are manufacturing industries that either depend relatively less on external sources of funding or have relatively less ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce nondurable goods. are manufacturing industries that depend relatively more on external sources of funding and have relatively more ability to pledge collateral to secure access to C&I loans. are manufacturing industries that do not produce durable goods. are manufacturing industries that produce durable goods.

Table 2: Breakdown of employment in manufacturing industries: Percentage change in employment in manufacturing

			Row total
	-9.2	-18.4	-12.0
	-18.3	-27.3	-19.8
Column total	-15.4	-22.7	-17.0

Note: are manufacturing industries that either depend relatively less on external sources of funding or have relatively less ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce nondurable goods. are manufacturing industries that depend relatively more on external sources of funding and have relatively more ability to pledge collateral to secure access to C&I loans. are manufacturing industries that do not produce durable goods. are manufacturing industries that produce durable goods.

Table 3: Breakdown of employment in manufacturing industries in our 32-state sample:Employment in manufacturing in 2007

			Row total
	2,866,375	1,300,945	4,167,320
	6,167,899	1,204,016	7,371,915
Column total	9,034,274	2,504,961	11,539,235

Note: are manufacturing industries that either do not depend on external sources of funding or do not have the ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce nondurable goods. are manufacturing industries that depend on external sources of funding and have the ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce durable goods.

Table 3: Breakdown of employment in manufacturing industries in our 32-state sample:Employment in manufacturing in 2010

			Row total
	2,577,517	1,052,484	3,630,001
	5,030,604	872,793	5,903,397
Column total	7,608,121	1,925,277	9,533,398

Note: are manufacturing industries that either do not depend on external sources of funding or do not have the ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce nondurable goods. are manufacturing industries that depend on external sources of funding and have the ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce durable goods.

Table 3: Breakdown of employment in manufacturing industries in our 32-state sample:Percentage change in employment in manufacturing

			Row total
	-10.1	-19.1	-12.9
	-18.4	-27.5	-19.9
Column total	-15.8	-23.1	-17.4

Note: are manufacturing industries that either do not depend on external sources of funding or do not have the ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce nondurable goods. are manufacturing industries that depend on external sources of funding and have the ability to pledge collateral to secure access to C&I loans. are manufacturing industries that produce durable goods.

Table 4: Separate channels of bank credit supply, regression results for growth in employment

	(1)	(2)	(3)	(4)
	-0.039***
: t-statistics	(-5.238)
		0.064**
: t-statistics		(2.144)
			0.057***
:t-statistics			(7.932)
				0.105***
: t-statistics				(3.456)
				0.049***
: t-statistics				(3.767)
	-0.016**	-0.029***	-0.030***	-0.026***
:t-statistics	(-2.325)	(-4.896)	(-4.999)	(-4.255)
	-0.043***	-0.075***	-0.043***	-0.049***
:t-statistics	(-2.668)	(-3.051)	(-2.662)	(-2.979)
	0.047***	0.047***	0.019***	0.050***
: t-statistics	(9.498)	(9.512)	(3.223)	(9.810)
	-0.009	-0.009	-0.009	-0.072***
:t-statistics	(-0.555)	(-0.538)	(-0.525)	(-2.826)
	0.048**	0.048**	0.048**	0.059***
:t-statistics	(2.382)	(2.382)	(2.365)	(2.793)
	0.877***	0.877***	0.876***	0.816***
:t-statistics	(10.638)	(10.639)	(10.625)	(9.497)
	-0.149***	-0.149***	-0.149***	-0.175***
:t-statistics	(-3.777)	(-3.772)	(-3.780)	(-4.334)
Num. of observations	10062	10062	10062	10062
Num. of clusters	559	559	559	559
R-sq. overall	0.28	0.28	0.29	0.28
Error clustering	I×S	I×S	I×S	I×S

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level. is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level. is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by . Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Table 5: Regression results for growth in employment

	(1)	(2)	(3)
	-0.041***	-0.041**	-0.042**
:t-statistics	(-6.155)	(-2.198)	(-1.974)
	0.036	0.036	0.040
:t-statistics	(1.270)	(1.677)	(1.227)
	0.064***	0.064**	0.064**
:t-statistics	(8.896)	(2.774)	(2.527)
	0.152***	0.152**	0.155**
:t-statistics	(4.854)	(2.379)	(2.138)
	0.034***	0.034	0.032
:t-statistics	(2.673)	(0.485)	(0.429)
	-0.014*	-0.014	-0.013
:t-statistics	(-1.949)	(-0.788)	(-0.663)
	-0.064***	-0.064	-0.066
:t-statistics	(-2.635)	(-1.570)	(-1.340)
	0.018***	0.018	0.018
:t-statistics	(2.901)	(0.816)	(0.742)
	-0.091***	-0.091	-0.092
:t-statistics	(-3.502)	(-1.350)	(-1.216)
	0.054***	0.054	0.054
:t-statistics	(2.600)	(0.558)	(0.505)
	0.834***	0.834**	0.837**
:t-statistics	(9.763)	(2.233)	(2.018)
	-0.167***	-0.167	-0.166
:t-statistics	(-4.118)	(-0.816)	(-0.721)
Num. of observations	10062	10062	10062
Num. of clusters	559	18	559×18
R-sq. overall	0.30	0.30	0.30
Error clustering	I×S	Y	I×S×Y

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level. is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level. is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by in column (1), by in column (2), and double-clustered by and in column (3). Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Table 6: Regression results for growth in the number of establishments

	(1)	(2)	(3)
	-0.005	-0.005	-0.005
: t-statistics	(-0.908)	(-0.688)	(-0.578)
	0.063***	0.063***	0.064***
:t-statistics	(3.074)	(3.293)	(2.626)
	0.013***	0.013	0.013
:t-statistics	(2.665)	(1.660)	(1.433)
	0.020	0.020	0.018
:t-statistics	(0.778)	(0.470)	(0.358)
	0.007	0.007	0.009
:t-statistics	(0.609)	(0.209)	(0.240)
	0.001	0.001	0.001
:t-statistics	(0.098)	(0.043)	(0.055)
	-0.041***	-0.041	-0.042
:t-statistics	(-2.613)	(-1.321)	(-1.190)
	0.018***	0.018	0.018
:t-statistics	(3.834)	(1.502)	(1.358)
	-0.058***	-0.058	-0.057
:t-statistics	(-2.697)	(-1.170)	(-1.043)
	-0.019	-0.019	-0.019
:t-statistics	(-1.258)	(-0.253)	(-0.221)
	0.304***	0.304	0.302
:t-statistics	(5.151)	(1.202)	(1.088)
	0.017	0.017	0.016
:t-statistics	(0.563)	(0.110)	(0.094)
Num. of observations	10062	10062	10062
Num. of clusters	559	18	599×18
R-sq. overall	0.16	0.16	0.16
Error clustering	I×S	Y	I×S×Y

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level. is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level. is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by in column (1), by in column (2), and double-clustered by and in column (3). Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Table 7: Regression results for growth in average establishment size

	(1)	(2)	(3)
	-0.038***	-0.038*	-0.038*
:t-statistics	(-5.701)	(-2.081)	(-1.913)
	-0.028	-0.028	-0.025
:t-statistics	(-1.084)	(-1.054)	(-0.748)
	0.053***	0.053**	0.053**
:t-statistics	(7.838)	(2.597)	(2.367)
	0.145***	0.145**	0.151**
:t-statistics	(3.858)	(2.634)	(2.347)
	0.024	0.024	0.020
:t-statistics	(1.626)	(0.489)	(0.382)
	-0.013*	-0.013	-0.013
:t-statistics	(-1.861)	(-0.882)	(-0.804)
	-0.022	-0.022	-0.023
:t-statistics	(-0.994)	(-0.585)	(-0.520)
	-0.001	-0.001	-0.001
:t-statistics	(-0.091)	(-0.034)	(-0.038)
	-0.046	-0.046	-0.048
:t-statistics	(-1.508)	(-0.940)	(-0.822)
	0.083***	0.083*	0.082*
:t-statistics	(3.867)	(1.954)	(1.746)
	0.528***	0.528*	0.533
:t-statistics	(6.326)	(1.782)	(1.636)
	-0.202***	-0.202	-0.199
:t-statistics	(-4.764)	(-1.530)	(-1.374)
Num. of observations	10062	10062	10062
Num. of clusters	559	18	559×18
R-sq. overall	0.16	0.16	0.16
Error clustering	I×S	Y	I×S×Y

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level. is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level. is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by in column (1), by in column (2), and double-clustered by and in column (3). Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Table 8: Separation of and channels for growth in employment

	(1)	(2)	(3)
	-0.022***	-0.022***	-0.024**
:t-statistics	(-2.886)	(-3.114)	(-2.248)
	-0.005	-0.005	-0.002
:t-statistics	(-0.585)	(-0.295)	(-0.133)
	0.041	0.041*	0.045
:t-statistics	(1.433)	(1.852)	(1.355)
	0.063***	0.063**	0.062**
:t-statistics	(8.192)	(2.553)	(2.338)
	0.152***	0.152**	0.155**
:t-statistics	(4.868)	(2.401)	(2.156)
	0.033**	0.033	0.031
:t-statistics	(2.561)	(0.474)	(0.413)
	-0.014*	-0.014	-0.015
:t-statistics	(-1.715)	(-0.727)	(-0.645)
	-0.067***	-0.067	-0.069
:t-statistics	(-2.732)	(-1.662)	(-1.406)
	0.019***	0.019	0.019
:t-statistics	(3.003)	(0.836)	(0.775)
	-0.090***	-0.090	-0.091
:t-statistics	(-3.495)	(-1.348)	(-1.210)
	0.055***	0.055	0.055
:t-statistics	(2.611)	(0.563)	(0.510)
	0.835***	0.835**	0.838**
:t-statistics	(9.746)	(2.244)	(2.028)
	-0.167***	-0.167	-0.165
:t-statistics	(-4.097)	(-0.813)	(-0.717)
Num. of observations	10062	10062	10062
Num. of clusters	559	18	559×18
R-sq. overall	0.30	0.30	0.30
Error clustering	I×S	Y	I×S×Y

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively mroe on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level. is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level. is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by in column (1), by in column (2), and double-clustered by and in column (3). Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Table 9: Structural breaks in bank credit supply channels for growth in employment

	(1)	(2)	(3)
	-0.043***	-0.043**	-0.044**
: t-statistics	(-4.830)	(-2.846)	(-2.520)
	-0.008	-0.008	-0.006
: t-statistics	(-0.642)	(-0.307)	(-0.215)
	0.080**	0.080**	0.085*
: t-statistics	(2.332)	(2.470)	(1.909)
	-0.100*	-0.100	-0.100
: t-statistics	(-1.912)	(-1.452)	(-1.102)
	0.105***	0.105**	0.104**
: t-statistics	(9.126)	(2.232)	(2.041)
	-0.058***	-0.058	-0.056
: t-statistics	(-4.330)	(-0.994)	(-0.883)
	0.177***	0.177	0.179
: t-statistics	(4.904)	(1.664)	(1.497)
	-0.070*	-0.070	-0.064
: t-statistics	(-1.955)	(-0.483)	(-0.412)
	0.033**	0.033	0.028
: t-statistics	(2.167)	(0.380)	(0.298)
	-0.003	-0.003	0.000
: t-statistics	(-0.106)	(-0.024)	(0.004)
	-0.013*	-0.013	-0.012
: t-statistics	(-1.708)	(-0.776)	(-0.658)
	-0.049*	-0.049	-0.052
: t-statistics	(-1.878)	(-1.498)	(-1.214)
	0.018***	0.018	0.018
: t-statistics	(2.640)	(0.765)	(0.696)
	-0.085***	-0.085	-0.087
: t-statistics	(-3.188)	(-1.304)	(-1.175)
	0.057**	0.057	0.057
: t-statistics	(2.566)	(0.602)	(0.546)
	0.847***	0.847**	0.853**
: t-statistics	(9.691)	(2.259)	(2.054)
	-0.179***	-0.179	-0.178
: t-statistics	(-3.806)	(-0.939)	(-0.826)
Num. of observations	10062	10062	10062
Num. of clusters	559	18	559×18
R-sq. overall	0.30	0.30	0.30
Error clustering	I×S	Y	I×S×Y

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level. is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level. is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by in column (1), by in column (2), and double-clustered by and in column (3). Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Table 10: Back-of-the envelope macro effects in growth rates: Implied percentage change in employment in manufacturing

			Row total
	0.0	-4.5	-1.4
	-6.5	-10.8	-7.2
Column total	-4.4	-7.6	-5.1

Table 10: Back-of-the envelope macro effects in growth rates: Implied changes in employment in manufacturing

			Row total
	0	-58,903	-58,903
	-398,988	-130,490	-529,478
Column total	-398,988	-189,394	-588,381

Table A1: Rajan-Zingales measures by industry

NAICS	Rajan and Zingales (1998):1980s	Cetorelli and Strahan (2006):1980-1997	Our sample:1990-2011
311	-0.55	0.01	-0.68
312	-1.29	-0.62	-0.55
313	-0.14	0.06	-0.15
314	-0.13	-0.13	0.05
315	-0.24	-0.14	-1.40
316	-0.67	-0.10	-2.61
321	0.24	0.43	-0.27
322	-0.04	0.19	-0.31
323	-0.37	0.07	-0.83
324	-0.01	0.25	-0.44
325	-0.41	0.14	2.54
326	-0.11	0.01	-0.43
327	-0.19	0.11	-0.40
331	0.09	0.27	-0.35
332	-0.43	0.07	-0.89
333	-0.33	-0.10	-0.80
334	-0.04	0.09	-0.32
335	-0.24	0.06	-0.40
336	-0.35	-0.10	-0.60
337	-0.32	0.19	-1.06
339	-0.18	-0.03	-0.51
Median	-0.24	0.06	-0.44

Note: Industries more dependent on external finance are in bold.

Table A2: Asset Tangibility by industry

NAICS	Rajan and Zingales (1998): 1980s	Cetorelli and Strahan (2006): 1980-1997	Our sample:1990-2011
311	0.37	0.38	0.32
312	0.23	0.23	0.30
313	0.36	0.37	0.40
314	0.27	0.30	0.36
315	0.17	0.16	0.13
316	0.17	0.14	0.10
321	0.30	0.32	0.41
322	0.50	0.49	0.46
323	0.32	0.34	0.29
324	0.57	0.61	0.55
325	0.30	0.26	0.13
326	0.35	0.35	0.34
327	0.48	0.41	0.40
331	0.41	0.43	0.37
332	0.29	0.30	0.26
333	0.25	0.22	0.17
334	0.23	0.18	0.12
335	0.26	0.24	0.19
336	0.28	0.28	0.22
337	0.30	0.30	0.25
339	0.23	0.21	0.15
Median	0.30	0.30	0.29

Note: Industries with more tangible assets are in bold.

Table A3: Regression results for growth in employment

	(1)	(2)	(3)	(4)
	0.066
:t-statistics	(1.036)
	0.119
:t-statistics	(0.601)
	-0.443	-0.146**
:t-statistics	(-1.038)	(-2.162)
	0.231**	0.207**
:t-statistics	(2.409)	(2.190)
			-0.013*	-0.030***
:t-statistics			(-1.808)	(-4.416)
			0.099***	0.019
:t-statistics			(3.407)	(0.674)
	0.067***	0.066***	0.066***	0.064***
:t-statistics	(8.899)	(8.641)	(8.849)	(7.768)
	0.151***	0.151***	0.149***	0.151***
:t-statistics	(4.840)	(4.840)	(4.794)	(4.539)
	0.036***	0.036***	0.037***	0.036***
:t-statistics	(2.804)	(2.761)	(2.846)	(2.744)
	-0.036	-0.010	-0.022***	-0.018**
:t-statistics	(-1.069)	(-0.949)	(-3.127)	(-2.580)
	-0.142***	-0.133***	-0.097***	-0.057**
:t-statistics	(-2.979)	(-2.794)	(-4.160)	(-2.352)
	0.017***	0.017***	0.017***	0.015**
:t-statistics	(2.699)	(2.746)	(2.749)	(2.080)
	-0.091***	-0.090***	-0.090***	-0.096***
:t-statistics	(-3.498)	(-3.490)	(-3.479)	(-3.393)
	0.055***	0.055***	0.055***	0.071***
:t-statistics	(2.618)	(2.626)	(2.646)	(3.110)
	0.832***	0.832***	0.829***	0.745***
:t-statistics	(9.728)	(9.736)	(9.722)	(6.865)
	-0.168***	-0.168***	-0.168***	-0.165***
:t-statistics	(-4.141)	(-4.139)	(-4.136)	(-4.051)
Num. of observations	10062	10062	10062	10062
Num. of clusters	559	559	559	559
R-sq. overall	0.29	0.29	0.29	0.31
Error clustering	I×S	I×S	I×S	I×S

Note: The dependent variable is growth in employment for a given industry in a given state. denotes the Rajan-Zingales measures of dependence on external finance scaled to the unit interval, the Braun-Claessens-Laeven measures of asset tangibility, a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. Column (1) and (2) use the raw Rajan-Zingales measures transformed to lie on a interval, column (3) uses an measure based on the bank loans to assets ratio based on the 1998 SSBF, and column (4) includes industry-specific time trends. All specifications include industry-state fixed effects. Standard errors are clustered by . t-statistics are reported below the coefficients. Industry-specific trend coefficients are not shown.

Table A4: Change in C&I lending standards for small firms

Year	Number of bank responses: Tightened considerably	Number of bank responses: Tightened somewhat	Number of bank responses: No change	Number of bank responses: Eased somewhat	Number of bank responses: Eased considerably
1993	0	2	207	22	0
1994	1	3	197	24	2
1995	0	9	206	11	2
1996	1	4	205	15	0
1997	1	7	199	12	0
1998	0	17	194	11	0
1999	0	16	200	4	0
2000	3	63	154	1	0
2001	0	84	140	0	0
2002	1	30	190	2	0
2003	0	16	194	14	0
2004	0	4	183	34	0
2005	0	1	193	26	1
2006	0	13	194	16	0
2007	2	27	181	2	0
2008	16	124	75	0	0
2009	4	48	162	1	0
2010	0	8	193	18	0
2011	0	3	185	16	0

Source: Federal Reserve Board, Senior Loan Officer Opinion Survey on Bank Lending Practices.

Table A5: Change in willingness to originate consumer installment loans

Year	Number of bank responses: Much more willing	Number of bank responses: Somewhat more willing	Number of bank responses: About unchanged	Number of bank responses: Somewhat less willing	Number of bank responses: Much less willing
1993	4	54	172	1	0
1994	1	51	170	1	0
1995	3	23	190	6	0
1996	3	9	170	20	0
1997	1	19	169	11	0
1998	1	19	182	2	1
1999	3	18	187	3	0
2000	0	5	204	8	0
2001	0	4	202	11	0
2002	3	11	201	5	0
2003	2	26	186	4	0
2004	3	27	181	3	0
2005	1	28	177	2	0
2006	0	16	197	2	0
2007	2	6	180	15	0
2008	0	4	136	57	9
2009	1	11	180	11	3
2010	1	41	169	1	0
2011	5	41	156	1	1

Source: Federal Reserve Board, Senior Loan Officer Opinion Survey on Bank Lending Practices.

Table A6: Regression results for growth in employment and alternative s and

	(1)	(2)	(3)
	-0.043***	-0.043*	-0.043*
: t-statistics	(-5.901)	(-2.054)	(-1.852)
	0.040	0.040*	0.044
:t-statistics	(1.411)	(1.879)	(1.352)
	0.059***	0.059**	0.059**
:t-statistics	(8.005)	(2.414)	(2.206)
	0.149***	0.149**	0.152**
:t-statistics	(4.790)	(2.438)	(2.175)
	0.033***	0.033	0.032
:t-statistics	(2.644)	(0.502)	(0.444)
	-0.015**	-0.015	-0.015
:t-statistics	(-1.968)	(-0.839)	(-0.712)
	-0.066***	-0.066	-0.068
: t-statistics	(-2.693)	(-1.618)	(-1.365)
	0.032***	0.032	0.031
:t-statistics	(4.474)	(1.235)	(1.115)
	-0.083***	-0.083	-0.084
: t-statistics	(-3.262)	(-1.309)	(-1.170)
	0.045**	0.045	0.045
: t-statistics	(2.149)	(0.483)	(0.433)
	0.821***	0.821**	0.823**
: t-statistics	(9.642)	(2.198)	(1.988)
	-0.188***	-0.188	-0.187
:t-statistics	(-4.526)	(-1.007)	(-0.888)
Num. of observations	10062	10062	10062
Num. of clusters	559	18	559×18
R-sq. overall	0.30	0.30	0.30
Error clustering	I×S	Y	I×S×Y

Note: The dependent variable is growth in employment for a given industry in a given state. denotes a dummy for industries that depend relatively more on external finance, a dummy for industries that have relatively more tangible assets, and a dummy for industries that produce durable goods. is the weighted average tightening of C&I lending standards for small firms at the state level, treating responses of tightening (easing) "considerably" equal to responses of tightening (easing) "somewhat". is growth in home equity at the state level. is the weighted average change in banks' willingness to originate consumer installment loans at the national level, treating responses of "much more (less) willing" equal to respones of "somewhat more (less) willing." is growth in home equity at the national level. is growth of net worth at the national level. is growth in real GDP, while is the change in the real interest rate. All specifications include industry-state fixed effects. Standard errors are clustered by in column (1), by in column (2), and double-clustered by and in column (3). Coefficients are reported with * if significant at the 10% level, ** at the 5% level, and *** at the 1% level. t-statistics are reported below the coefficients.

Footnotes

The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or the Federal Reserve System. All errors and omissions are our responsibility alone. An older version of this paper was circulated under the title "Bank Lending Channels during the Great Recession."

* Corresponding author. Tel.: +1 (202) 452-2936; fax: +1 (202) 872-4926. E-mail address: [email protected]. Return to Text

1. One might imagine that firms and households will substitute away from more limited bank credit to more easily available alternatives, perhaps mitigating the impact of cutbacks in the supply of bank credit on manufacturing employment growth. For example, while bank credit declined sharply, the bond market was quite robust over the financial crisis, at least in terms of issuance volumes, as shown in (Adrian et al., 2012). This example implies that, for large borrowers, the two sources of funds are at least somewhat substitutable. Return to Text

2. For example, (Peek & Rosengren, 2000) use the Japanese banking crisis to test whether a loan supply shock to branches and agencies of Japanese banks affected construction activity in the U.S. commercial real estate market in California, New York, and Illinois. Return to Text

3. As in (Rajan and Zingales (1998) ), (Cetorelli & Strahan, 2006), and many others. Return to Text

4. This breakdown of industries into those that produce durable goods and those that do not has been used in (Braun & Larrain, 2006) and (Peersman & Smets, 2005) in the context of financial frictions. Return to Text

5. However, the results using state-level changes in banks' willingness to originate consumer installment loans and growth in home equity are qualitatively similar. Return to Text

6. The CRA is intended to encourage depository institutions to help meet the credit needs of communities in which they operate, including low- and moderate-income neighborhoods and to small businesses, consistent with safe and sound operations. It was enacted by the Congress in 1977 (12 U.S.C. 2901) and is implemented by Regulation BB (12 CFR 228). The regulation was substantially revised in May 1995 and updated again in August 2005. A bank's CRA performance record is taken into account in considering an institution's application for deposit facilities. Return to Text

7. The Riegle-Neal Interstate Banking and Branching Efficiency Act amended the laws governing federally chartered banks, allowing these banks to set up branches freely across the country. Among other notable changes, with its "Prohibition against deposit production offices," the Act stipulated that a federally chartered bank wishing to expand must first undergo a review of its CRA compliance. Return to Text

8. (Peek & Rosengren, 1995) develop a model to demonstrate that, following a negative shock, banks that are capital constrained will reduce both deposits and loans, while unconstrained banks only reduce loans. In their analysis of difficulties in the New England banking sector in the early 1990s, they find a relationship between capital ratios and deposit growth, which they take as evidence that loan supply contracted. Return to Text

9. However, low bank loans to total liabilities ratios may indicate the existence of financing constraints. Return to Text

10. Although we do not consider a short-term credit supply channel, which includes trade credit or short-term bank loans, we believe that disruptions in the supply of loans of these types over the Great Recession possibly also had a significant impact on employment in manufacturing industries. Return to Text

11. For an example of the hysteresis effects in the international trade literature, see (Alessandria & Choi, 2007). Return to Text

12. In addition, other papers attribute a fall in firms' spending on physical capital investment over the Great Recession to disruptions in the supply of credit as in (Duchin et al., 2010). Return to Text

13. For example, (Jarmin et al., 2009) report that the share of U.S. retail activity accounted for by single-establishment firms fell from 60 percent in 1967 to just 39 percent in 1997. Return to Text

14. We draw on the Bureau of Labor Statistics' materials to write parts of this section. Return to Text

15. Indeed, the analysis of the U.S. Census Bureau's Longitudinal Business Database suggests that most U.S. firms have only one establishment. In 2000, there were about 4.7 million privately held firms and less than 7,400 publicly traded firms. While a typical publicly traded firm operates about 90 establishments, an average privately held firm operates only 1.16 establishments. For details, see (Davis et al., 2006). Return to Text

16. More precisely, average establishment size is calculated as the average number of employees per establishment. Return to Text

17. We calculated Rajan-Zingales measures for each manufacturing industry at the three-digit NAICS level using the Compustat data over the last two decades for mature domestic firms. Each measure is the median value of capital expenditures (CAPX) minus cash flows from operations divided by capital expenditures for firms in each of the 21 manufacturing industries. Cash flows are calculated by summing up the following items in Compustat: IBC, DPC, TXDC, ESUBC, SPPIV, and FOPO. Return to Text

18. (Rajan and Zingales (1998) ) use data from the 1980s, while (Cetorelli & Strahan, 2006) use data from the 1980-1997 period. See the appendix for specific values for the 21 manufacturing industries calculated for each time period. Return to Text

19. In the Rajan-Zingales context, whether gaps in financing of physical capital investment are met with bank or market funding is irrelevant. Moreover, for many large firms, the degree of dependence on bank loans cannot be reliably estimated using Compustat data. Return to Text

20. These are averages calculated using the Quarterly Finance Review data over the 2000-2007 period, that is, the recent pre-crisis period. Return to Text

21. Still, we re-estimate the benchmark model with control and treatment groups based on the 1998 SSBF data on bank loans; the estimation results are shown in the third column in Table A3 in the appendix. The results are robust to redefining industries depending relatively more on external finance in such a manner. Return to Text

22. See the appendix for details on the asset tangibility measures calculated for all 21 manufacturing industries for different time periods. Return to Text

23. We calculate the measures of asset tangibility based on firms of all ages, as done in the literature. Although the Rajan-Zingales measure is sensitive to whether we use only mature firms or all firms, the tangibility measure is not, implying that financially constrained firms may be more constrained in the total size of their balance sheet, but not necessarily in the composition of their assets. Return to Text

24. In the appendix, we also show the results for a model with continuous Rajan-Zingales measures, a specification with some shortcomings. In particular, because both the Rajan-Zingales measure and the measure of tightening C&I lending standards can have negative values, we have to map the Rajan-Zingales measures into an interval from zero to one. The interpretation of the corresponding regression coefficient is less clear. Return to Text

25. Averaging the Quarterly Finance Review data over the 2000-2007 period, that is, the recent pre-crisis period, the bank loans to total liabilities ratio for the manufacturing industries that depend relatively more on external finance and have relatively more tangible assets is 12.9 percent, and for other manufacturing industries just 7.6 percent. The Quarterly Finance Review follows its own industry classification that tends to mimic three- to four-digit NAICS industries. Return to Text

26. We discuss why this might be the case in section 5.1. Return to Text

27. More broadly speaking, firms may use business loans, which include both C&I and commercial real estate loans, to finance investment, while households may use general consumer loans, which include both consumer installment and credit card loans, to finance consumption. However, we focus on access to C&I loans because the data we have on changes in lending standards for commercial real estate loans from the SLOOS may be driven by changes in lending standards for construction and land development loans, which may be more relevant for employment growth dynamics in the construction industries as opposed to manufacturing. We also focus on access to consumer installment loans because of data limitations--the data regarding changes in lending standards on credit card loans and other consumer loans in the SLOOS are not available for the entire sample period. Return to Text

28. Individual bank survey responses are confidential. For more details, see (Bassett et al., 2014). Return to Text

29. However, changes in C&I lending standards for large and middle-market firms are highly correlated with those for small firms. Return to Text

30. Our results do not change if we ignore the "considerably" and "somewhat" distinction. See the appendix for results based on a more simple method of categorizing the survey results, namely, when we define the indicator variable as follows: if bank reported considerable or some easing of standards at time , if bank reported no change in standards, and if bank reported some or considerable tightening. Return to Text

31. According to regulatory Call Reports, as of the second quarter of 2013, about one-third of all loans with original amounts of under $1 million, a proxy for small business loans, were booked in the top five banks in terms of total assets. The data for loans with small original amounts begins in 2001. Return to Text

32. These 32 states, which include the three largest economies in the country, are Alabama, Arizona, California, Colorado, Connecticut, Delaware, the District of Columbia, Florida, Georgia, Illinois, Indiana, Kentucky, Maine, Massachusetts, Michigan, Minnesota, Missouri, Nevada, New Jersey, New Mexico, New York, North Carolina, Ohio, Oregon, Pennsylvania, Rhode Island, South Carolina, South Dakota, Tennessee, Texas, Virginia, and Washington. Only 7 bank-respondents, on average, have branches in only one of these 32 states. Among the survey respondents included in our sample, the top five banks (by total assets) had branches in more than 20 states in the beginning of the sample period and since 2004 have had branches in all the 32 states. Return to Text

33. More specifically, banks may indicate that their willingness to originate consumer installment loans is about unchanged or that they are much more, somewhat more, somewhat less, or much less willing to originate such loans. Return to Text

34. Note that credit cycles may vary by loan category in terms of both timing and magnitude. In addition, they may be quite different from macroeconomic business cycles. According to the Federal Reserve's H.8 statistical release, around the 2001 recession, C&I loans outstanding at commercial banks dropped, while consumer loans outstanding changed very little. In the aftermath of the recession, C&I loans outstanding stopped contracting only in the fourth quarter of 2004, well into the period of the economic expansion. In contrast, around the Great Recession, likely highlighting differences in the nature of the latest recessions, consumer loans outstanding were more negatively affected than C&I loans outstanding at banks. Return to Text

35. Trend Data is an aggregated consumer credit database that offers quarterly snapshots of randomly sampled consumers. Return to Text

36. Define the equity ratio as and, after taking logs and differentiating, obtain the expression in the text. Return to Text

37. Note that the correlation between the national measure computed using the Federal Reserve's data and the same measure constructed using the TransUnion, at 0.74, is sufficiently high. This indicates that our state-level measure is an adequate proxy for growth in unencumbered home equity. Return to Text

38. In a quarterly model, a set of lagged explanatory variables would weaken identification because of collinearity. Return to Text

39. Note that the SLOOS data suggest that tightening of C&I lending standards for large and small firms is highly correlated, and so many banks change their standards on C&I loans for borrowers of all sizes rather than targeting a size-specific subset of borrowers. Return to Text

40. The industry-state fixed effects should also control for self-selected locations across the states. Return to Text

41. We also checked whether balancing the panel introduced any selection biases by estimating the regression model on an unbalanced panel. The results are qualitatively similar. Return to Text

42. That is, the latter specification is robust to simultaneous correlation of residuals across industry-states and time. Double clustering is a valid exercise as the standard error estimates are accurate even in small samples, as (Thompson, 2011) argues. Return to Text

43. We do not use the CBP data set because its coverage on a NAICS basis is too short and its coverage by establishment size is not comprehensive at the industry-state level due to confidentiality concerns. In addition, the CBP data are as of the first quarter for each year, rather than on a year-average basis, so data seasonality might be a significant issue. Return to Text

44. However, it might be the case that the literature defines pledgable assets too narrowly. For example, accounts receivable often serve as collateral for C&I loans, a feature not modeled in this paper. Return to Text

45. Although we could have evaluated the effect on both the control and treatment groups based on the non-interacted explanatory variables, we believe that such calculations go against the spirit of identification and may reflect factors not directly related to credit supply, including demand-side factors. Return to Text

46. These percentages are cardinal numbers and have a specific interpretation, though the underlying data on whether a bank reports a "somewhat tightening of lending standards," for example, are subjective. (Bassett et al., 2014) and (Lown & Morgan, 2006) use similar logic in describing changes in credit standards and the impact of these changes on lending and economic output. Return to Text

47. (Rajan and Zingales (1998) ) define a mature firm as that covered by Compustat for 10 years or more, and we follow their convention. Return to Text

48. While the NAICS is relatively comparable to the ISIC, the SIC is not. The NAICS defines significantly more industries than the SIC, and assigns many of them to different industry groups than the SIC. For more details, see Development of NAICS, URL: https://www.census.gov/epcd/www/naicsdev.htm, last accessed on March 25, 2014. Return to Text

49. We choose this particular transformation on the insistence of an anonymous referee. Had we performed an alternative transformation of actual s, the regression coefficient would have been different and its statistical significance may have been higher or lower. Return to Text

50. We assigned three-digit NAICS codes to the ratios computed by (Cetorelli & Strahan, 2006) at a two-digit SIC level. This assignment is necessarily rough as the two classifications are not fully compatible even at a low level of aggregation. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Home | Economic Research and Data | Accessibility | Contact us
Last update: July 9, 2014