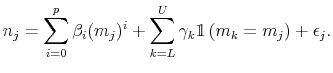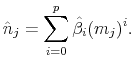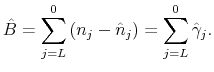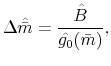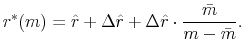THE INTEREST RATE ELASTICITY OF MORTGAGE DEMAND: EVIDENCE FROM BUNCHING AT THE CONFORMING LOAN LIMIT*
Abstract:
1 Introduction
Buyers face a bewildering array of financing options when purchasing a home. Should they pay cash, or take out a mortgage? If the latter, should it have a fixed rate or an adjustable rate? How large a down payment should they make? Given that housing makes up the lion's share of most owners' portfolios, these and related questions are fundamental to their financial well-being. Yet there is little research that credibly identifies how households respond to changes in the many parameters of this problem. In this paper, we focus on one element of the problem--the choice of how much debt to incur--in order to provide novel and credible estimates of the interest rate elasticity of mortgage demand.
The magnitude of this elasticity has important implications for policy-relevant questions in several areas of economics. For example, given that mortgages constitute the majority of total household debt, the elasticity plays a significant role in governing the degree to which monetary policy affects aggregate consumption and savings behavior (Hall,1988; Mishkin,1995;Browning and Lusardi ,1996). In public finance, the elasticity is also important for understanding the effect of the home mortgage interest deduction on both government tax revenue and household consumption (Poterba, 1984; Poterba and Sinai, 2008, 2011). Similarly, the elasticity also has implications for the effects of government intervention in the secondary mortgage market, where federal policy directly influences mortgage rates through the purchase activity of the government-sponsored enterprises (GSEs), Fannie Mae and Freddie Mac (Sherlund, 2008; Adelino et al., 2012; Kaufman, 2012). This final consideration has become particularly salient recently in light of the ongoing debate over the future of the GSEs in the wake of the 2007-2008 financial crisis.
Yet, despite these potentially important policy implications, there are relatively few empirical estimates of the extent to which individual loan sizes respond to changes in interest rates. This is due in large part to data limitations, which have led prior research in this area to focus on other aspects of mortgage choice or to rely on endogenous variation in interest rates (Follain and Dunsky, 1997; Gary-Bobo and Larribeau, 2004; Martins and Villanueva, 2006; Jappelli and Pistaferri, 2007) . The literature estimating interest rate elasticities of other smaller components of consumer credit--such as credit card, auto, and micro-finance debt--has been more fruitful, thanks to the availability of detailed microdata and variation in interest rates arising from either direct randomization or quasi-experimental policy changes (Gross and Souleles,2002;Alessie et al.,2005 ;Karlan and Zinman, 2008 ;Attanasio et al. ,2008). In the spirit of these studies, we estimate the interest rate elasticity of mortgage demand using microdata on over 2.7 million mortgages and an identification strategy leveraging "bunching" at nonlinearities in household budget constraints.
We identify the effect of interest rates on borrower behavior by exploiting a regulatory requirement imposed on the GSEs that generates exogenous variation in the relationship between loan size and interest rates. Specifically, the GSEs are only allowed to purchase loans for dollar amounts that fall below the conforming loan limit (CLL), a nominal cap set by their regulator each year. Because loans purchased by the GSEs are backed by an implicit government guarantee, interest rates on loans above this limit ("jumbo loans") are typically higher than rates on comparable loans below the limit. The difference in interest rates between jumbo and conforming loans creates a substantial "notch" in the intertemporal budget constraint of households deciding how much mortgage debt to incur. This notch induces some borrowers who would otherwise take out loans above the conforming limit to instead bunch right at the limit.
Recent papers in public finance have developed methods for estimating behavioral responses to nonlinear incentives in similar settings Saez ,2010; Chetty et al. , 2011 ;Kleven and Waseem,2013.1 We adapt these methods to the case of mortgage choice in the face of a notched interest rate schedule. Intuitively, the excess mass of households who bunch at exactly the conforming limit provides us with a measure of the behavioral response to the interest rate differential. We combine this estimate of bunching with estimates of the interest rate spread between jumbo and conforming loans to yield an estimate of the average interest rate (semi-)elasticity of mortgage demand.2 To the best of our knowledge, ours is the first application of these methods to the mortgage market, or to a consumer credit market of any kind.
Our preferred specifications indicate that the average size of a borrower's first mortgage declines by between 2 and 3 percent for each 1 percentage point rise in the mortgage rate. Because both the bunching estimates and the jumbo-conforming spread estimates vary depending on the assumptions used in estimation, we provide alternative estimates under a range of different scenarios. These estimates imply a decline of between 1.5 and 5 percent for a 1 percentage point increase in the mortgage rate. We also discuss heterogeneity in the responsiveness of different groups, as well as the implications of fixed adjustment costs and extensive margin responses--buyers dropping out of the market entirely--for the interpretation of our estimates and their external validity.
While the mortgage demand elasticity is of innate interest, its interpretation depends in part on the channels through which borrowers adjust their first mortgage balance. Our second main contribution is to provide suggestive evidence on this margin. Borrowers can reduce the initial balance of their first mortgage in at least three ways: First, they can make a larger down payment on the same house at the same price. Second, they can take out a second mortgage to cover the loan balance in excess of the conforming limit. Third, they can lower the price of the house they buy, either by negotiating with the seller or by choosing a less expensive house.
We show that about one-third of bunching borrowers take out second mortgages, which suggests that the reduction in total mortgage debt in response to a 1 percentage point rise in the first mortgage interest rate is between 1.5 and 2 percent. We also argue that the pattern of loan-to-value ratios (LTVs) around the limit suggests that the remaining two-thirds are putting up more cash rather than buying cheaper houses.
To gauge the economic magnitude of the effects we estimate, we apply them to recently proposed increases to the fee that the GSEs charge lenders to cover the costs associated with guaranteeing investor returns on their mortgage-backed securities. We estimate that the proposed fee increases would reduce the total volume of fixed-rate conforming mortgage originations by approximately one-fifth of one percent. When we apply our elasticity to similar increases in fees that have occurred in the recent past, we estimate an effect on the order of one-half of one percent.
The remainder of the paper is organized as follows. In section 2 we provide relevant institutional details on the GSEs and the conforming loan limit. Section 3 presents our conceptual framework. In sections 4 and 5 we discuss our data and empirical research design. We then present our main results in sections 6-8. Section 9 applies these results to changes in the GSE guarantee fees and section 10 concludes by discussing avenues for future research.
2 The GSEs and the Conforming Loan Limit
The two large government sponsored enterprises--the Federal National Mortgage Association (Fannie Mae) and the Federal Home Loan Mortgage Corporation (Freddie Mac)--were created to encourage mortgage lending. The GSEs purchase mortgages from lenders and either hold them in portfolio or package them into mortgage-backed securities (MBS), which are guaranteed by the GSEs and sold to investors in the secondary market. By purchasing mortgages, the GSEs free up lender capital, allowing the lenders to make additional loans, thus expanding the general availability of mortgage credit.
The GSEs play a large role and exert a substantial amount of influence in the mortgage market.3 However, they are only allowed to purchase loans which satisfy a specific set of criteria as outlined by their regulator. These criteria include requirements for loan documentation, debt-to-income ratios, leverage, and a nominal cap on the dollar amount of any purchased loan. Loans which meet these criteria and are therefore eligible to be purchased by the GSEs are referred to as "conforming loans." In this paper we are primarily interested in the cap on loan size, known as the "conforming limit". Mortgages exceeding this limit are not eligible for GSE purchase and are referred to as "jumbo loans".
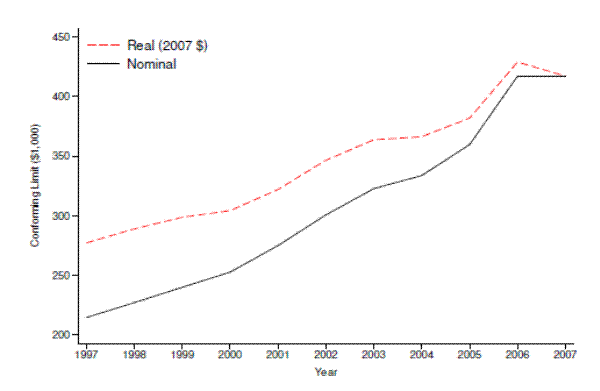
Figure 1 plots the conforming limit in nominal terms (the solid black line) and in real 2007 dollars (the dashed red line) for each year during our sample period. During this period, the GSEs were regulated by the Office of Federal Housing Enterprise Oversight (OFHEO), which set the limit each year based on changes in the national median house price. The limit was the same for all mortgages in a given year irrespective of local housing market conditions.4 Following the trend in national house prices, the nominal limit increased from around $215,000 in 1997 to its peak in 2006 and 2007 at approximately $420,000. In real terms, the limit also rose sharply over this period, especially during the house price boom of the mid-2000s.
Interest rates on loans above the conforming limit are typically higher than those on comparable loans below the limit for two reasons. First, because the debt underlying the MBS issued by the GSEs is backed by an implicit government guarantee, investors are willing to accept lower yields in exchange for that guarantee.5 Part of this savings is eventually passed on to borrowers in the form of lower interest rates on conforming loans.6 Second, the GSEs are also granted several special privileges that private securitizers are not. These include access to a line of credit at the U.S. Treasury, exemption from disclosure and registration requirements with the Securities and Exchange Commission (SEC), as well as exemptions from state and local income taxes.7 These advantages lower the cost of securitizing mortgages for the GSEs relative to private market securitizers, with some of the savings passed on to borrowers in the form of lower interest rates on loans below the conforming limit.
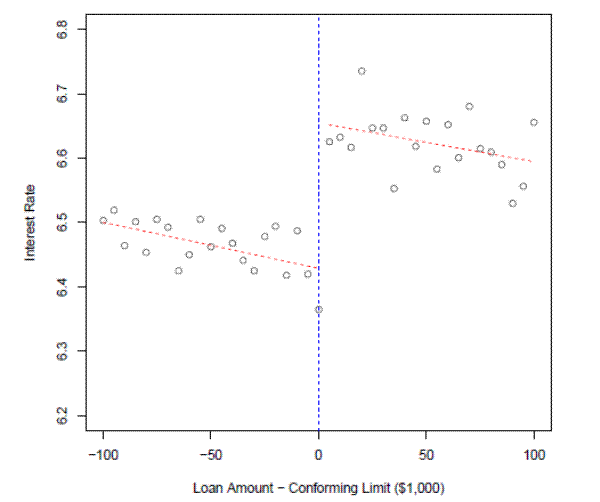
The difference in interest rates between loans above and below the conforming limit is called the jumbo-conforming spread. Even with good mortgage data, identifying the spread is challenging because borrowers are likely to sort themselves around it, leading to differences in borrower characteristics that may or may not be observable.8 Although we address these issues in detail below in section 5, some insight can still be gleaned from examining the raw data. For example, figure 2 plots the interest rate for all fixed-rate mortgages in our analysis sample that were originated in 2006 as a function of the difference between the loan amount and the conforming limit.9 Each dot is the average interest rate within a given $5,000 bin relative to the limit. The dashed red lines are the predicted values from a regression fit using the binned data, allowing for changes in the slope and intercept at the limit. There is a clear discontinuity precisely at the limit, with average interest rates on loans just above the limit being approximately 20 basis points higher than those on loans just below the limit. While 20 basis points may not reflect the "true" jumbo-conforming spread due to sorting around the limit, this figure is at least suggestive evidence of a sharp change in the cost of credit as loan size crosses the threshold.
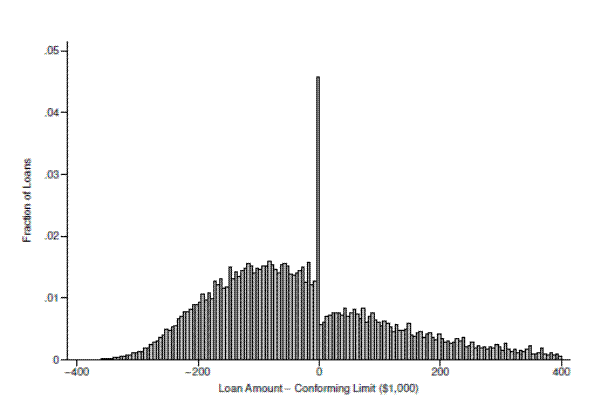
Regardless of the precise size of the jumbo-conforming spread, its existence introduces a nonlinearity in the budget constraint of an individual deciding how much mortgage debt to incur. This nonlinearity induces borrowers who would otherwise take out loans above the conforming limit to bunch at the limit, perhaps by putting up a larger down payment or taking out a second loan. The histogram in figure 3 confirms this, showing the fraction of all loans in our analysis sample which fall into any given $5,000 bin relative to the conforming limit in effect at the date of origination. Consistent with the notion that borrowers bunch at the conforming limit, the figure shows a sharp spike in the fraction of loans originated in the bin immediately below the limit, which is accompanied by a sizable region of missing mass immediately to the right of the limit. The intuition behind our empirical strategy is to combine reasonable estimates of the jumbo-conforming spread with a measure of the excess mass of individuals who bunch precisely at the conforming limit to back out estimates of the interest rate elasticity of demand for mortgage debt. The next section provides a conceptual framework that we use to formalize this intuition.
3 Theoretical Framework
We begin by considering a simple two-period model of household mortgage choice.10 Although highly stylized, this model highlights the most relevant features of our empirical environment and generates useful predictions for household behavior in the presence of a nonlinear mortgage interest rate schedule. The model is similar in spirit to those in the recent literature in public finance studying behavioral responses to nonlinear incentives in other contexts. For example, Saez (2010),Chetty et al. (2011), Chetty et al. (2013), and Gelber et al. (2013) study labor supply and earnings responses to kinked income tax and social security benefit schedules. Similar models have also been developed to study behavioral responses in applications somewhat more analogous to ours, where the budget constraint features a notch as opposed to a kink. Applications of this framework include fuel economy regulation (Sallee and Slemrod, 2010), retirement incentives (Manoli and Weber, 2011), income taxes (Kleven and Waseem, 2013) , and real estate transfer taxes (Best and Kleven, 2014; Kopczuk and Munroe, 2013). Ours is the first application to the mortgage market, or to a credit market of any kind.
3.1 Baseline Case: Linear Interest Rate Schedule
Households live for two periods. In our baseline model, we shut down housing choice by assuming that each household must purchase one unit of housing services in the first period at an exogenous per-unit price of ![]() .11 Households can finance their housing purchase with a mortgage,
.11 Households can finance their housing purchase with a mortgage, ![]() , which may not exceed the total value of the house. The baseline interest rate on the mortgage is given by
, which may not exceed the total value of the house. The baseline interest rate on the mortgage is given by ![]() and does not depend on
the mortgage amount. In the second period, housing is liquidated, the mortgage is paid off, and households consume all of their remaining wealth.
and does not depend on
the mortgage amount. In the second period, housing is liquidated, the mortgage is paid off, and households consume all of their remaining wealth.
The household's problem is to maximize lifetime utility by choosing consumption in each period, denoted by ![]() and
and ![]() .12 In general, the household solves:
.12 In general, the household solves:
where
subject now only to the borrowing constraint (4).
To proceed, we make several simplifying assumptions. First, we assume that household preferences are given by the constant elasticity function
![]() .13 Second,
heterogeneity in the model is driven by the discount factor, which is assumed to be distributed smoothly in the population according to the distribution function
.13 Second,
heterogeneity in the model is driven by the discount factor, which is assumed to be distributed smoothly in the population according to the distribution function ![]() and density
function
and density
function ![]() . For illustrative purposes, we assume that
. For illustrative purposes, we assume that ![]() and
and ![]() are constant across households; however, this assumption is not crucial and we discuss below how relaxing it affects the interpretation of our results. Finally, we assume that households end up at an
interior solution with a positive mortgage amount and a loan-to-value ratio of less that 100 percent--that is, constraint (4) does not bind.
are constant across households; however, this assumption is not crucial and we discuss below how relaxing it affects the interpretation of our results. Finally, we assume that households end up at an
interior solution with a positive mortgage amount and a loan-to-value ratio of less that 100 percent--that is, constraint (4) does not bind.
Under these assumptions, we can solve explicitly for mortgage demand, which is given by:
Because
3.2 Notched Interest Rate Schedule
We now consider the effect of introducing a notch in the baseline interest rate schedule at the conforming loan amount ![]() . Loans above this limit are subject to a higher interest
rate for reasons discussed in section 2, leading to the new schedule
. Loans above this limit are subject to a higher interest
rate for reasons discussed in section 2, leading to the new schedule
![]() . Here,
. Here, ![]() is the
difference in interest rates between jumbo and conforming loans and
is the
difference in interest rates between jumbo and conforming loans and
![]() is an indicator for jumbo loan status. Combining equations (2) and (3) yields the
lifetime budget constraint
is an indicator for jumbo loan status. Combining equations (2) and (3) yields the
lifetime budget constraint
where
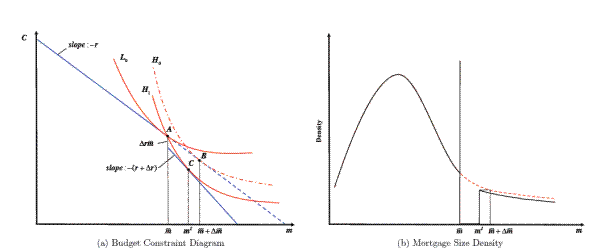
The notch in the budget constraint induces some households to bunch at the conforming loan limit. In figure 4a, household ![]() is the household with
the lowest baseline mortgage amount--the largest
is the household with
the lowest baseline mortgage amount--the largest ![]() --who locates at the conforming limit in the presence of a notch. This household is unaffected by the change in rates and takes out a
loan of size
--who locates at the conforming limit in the presence of a notch. This household is unaffected by the change in rates and takes out a
loan of size ![]() regardless of whether the notch exists. Household
regardless of whether the notch exists. Household ![]() is the
household with the highest pre-notch mortgage amount--the smallest
is the
household with the highest pre-notch mortgage amount--the smallest ![]() --that locates at the conforming limit when the notch exists. When faced with a linear interest rate schedule, this
household would choose a mortgage of size
--that locates at the conforming limit when the notch exists. When faced with a linear interest rate schedule, this
household would choose a mortgage of size
![]() . With the notch, however, the household is indifferent between locating at
. With the notch, however, the household is indifferent between locating at ![]() and the best interior point beyond the conforming limit,
and the best interior point beyond the conforming limit, ![]() . Any household with a baseline mortgage amount in the interval
. Any household with a baseline mortgage amount in the interval
![]() will bunch at the conforming loan amount,
will bunch at the conforming loan amount, ![]() . Furthermore, no household will choose to locate between
. Furthermore, no household will choose to locate between ![]() and
and ![]() in the notch scenario.
in the notch scenario.
This means that the density when a notch exists, ![]() , will be characterized by both a mass of households locating precisely at the conforming limit as well as a missing mass of
households immediately to the right of the limit. The effect of the notch on the mortgage size distribution is shown in the density diagram in figure 4b. The solid black line shows the density of loan amounts in the presence of the notch and the heavy dashed
red line to the right of the notch shows the counterfactual density that would exist in the absence of the conforming loan limit.
, will be characterized by both a mass of households locating precisely at the conforming limit as well as a missing mass of
households immediately to the right of the limit. The effect of the notch on the mortgage size distribution is shown in the density diagram in figure 4b. The solid black line shows the density of loan amounts in the presence of the notch and the heavy dashed
red line to the right of the notch shows the counterfactual density that would exist in the absence of the conforming loan limit.
Because households can be uniquely indexed by their position in the pre-notch mortgage size distribution, the number of households bunching at the conforming limit is given by:
where the approximation assumes that the counterfactual no-notch distribution is constant on the bunching interval
It is worth emphasizing that much of the structure in the model above is not needed for this result to hold. All we require is that households can be uniquely indexed by their choice of mortgage size in the pre-notch scenario and that the counterfactual distribution of mortgage sizes be smooth. Any model for which these conditions hold would generate equation (8).
3.3 Heterogeneous Intertemporal Elasticities and Incomes
The derivation of equation (8) was under the assumption that ![]() and
and ![]() were constant across households. In that case, it was possible to back out the exact change in mortgage amount for the marginal bunching individual. When intertemporal elasticities and incomes are allowed to vary across households, the amount of bunching instead identifies the
average response among the marginal bunching individuals associated with each intertemporal elasticity and income level. To see this, let the joint distribution of discount factors, intertemporal elasticities, and incomes be given by
were constant across households. In that case, it was possible to back out the exact change in mortgage amount for the marginal bunching individual. When intertemporal elasticities and incomes are allowed to vary across households, the amount of bunching instead identifies the
average response among the marginal bunching individuals associated with each intertemporal elasticity and income level. To see this, let the joint distribution of discount factors, intertemporal elasticities, and incomes be given by
![]() , where
, where
![]() and
and
![]() for some upper bounds,
for some upper bounds, ![]() and
and ![]() . For a fixed
. For a fixed ![]() pair, the bunching interval is determined in exactly the same
way as in the baseline model. Denote this interval
pair, the bunching interval is determined in exactly the same
way as in the baseline model. Denote this interval
![]() , where
, where
![]() is the behavioral response of the marginal bunching individual among those with intertemporal elasticity
is the behavioral response of the marginal bunching individual among those with intertemporal elasticity ![]() and income
and income ![]() . Further, let
. Further, let
![]() denote the joint distribution of mortgage sizes, intertemporal elasticities, and incomes in the pre-notch scenario and
denote the joint distribution of mortgage sizes, intertemporal elasticities, and incomes in the pre-notch scenario and
![]() the unconditional mortgage size distribution. The amount of bunching can then be expressed as
the unconditional mortgage size distribution. The amount of bunching can then be expressed as
In this case, estimates of bunching and the counterfactual mortgage size distribution near the conforming limit allow us to back out the average change in mortgage amounts due to the interest rate difference generated by the conforming loan limit.16
3.4 Endogenous Housing Choice
With the choice of housing fixed, as in the discussion above, borrowers can only respond to the presence of a notch by adjusting their mortgage balance. In other words, all households buy the same house at the same price as in the absence of a notch, but some households respond to the notch by
making a larger down payment or taking out a second mortgage. In reality, some households may instead choose to buy a lower quality home, leading to a lower level of ![]() .
.
Our model extends to cover endogenous housing choice, albeit at the cost of a closed-form solution. Consider again equation (5), the household's intertemporal optimization problem. Households can now choose the quantity of housing services to purchase (![]() ), and this quantity has a direct effect on first-period utility, so that
), and this quantity has a direct effect on first-period utility, so that
with
The optimal ![]() and
and ![]() must now satisfy two first-order conditions:
must now satisfy two first-order conditions:
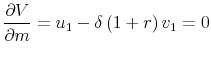 |
(11) |
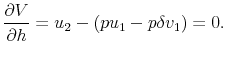 |
(12) |
Intuitively, the first condition captures the trade-off, using mortgage debt, between consumption today and consumption tomorrow. The second condition says that households trade off the cost of purchasing housing today, less the amount recovered tomorrow when it is sold, against its consumption value today.
While there are no obvious functional forms that allow us to derive equivalents to equation (6), the intuition remains the same. Under standard conditions, there are optimal ![]() and
and ![]() , both of which can shift in response to the notch in the interest rate schedule. Our bunching estimation will capture the shifts in
, both of which can shift in response to the notch in the interest rate schedule. Our bunching estimation will capture the shifts in ![]() , which could result in part from changes in housing consumption (
, which could result in part from changes in housing consumption (![]() ).
).
4 Data
To conduct our empirical analysis, we use data on loan sizes and interest rates that come from two main sources. The first is a proprietary data set of housing transactions from DataQuick (DQ), a private vendor which collects the universe of deed transfers and property assessment records from municipalities across the U.S. These data serve as our primary source of information on loan size. For descriptive purposes, we have also matched the DQ data to loan application information made available through the Home Mortgage Disclosure Act (HMDA), which provides us with a limited set of borrower demographics.17 The second data source consists of loan-level records collected by Lender Processing Services (LPS) and contains extensive information on interest rates, borrower characteristics, and loan terms, which we use to estimate the jumbo-conforming spread. A brief description of each data source and our sample selection procedures is given below.
4.1 DataQuick
Each record in the DQ data set represents a single transaction and contains information on the price, location, and physical characteristics of the house, as well as the loan amounts on up to three loans used to finance the purchase. We restrict the sample to include only transactions of single-family homes with positive first loan amounts that took place within metropolitan statistical areas (MSAs) in California between 1997 and 2007. We use data from California because that is where the information from DataQuick is most reliable, particularly for identifying when multiple loans were used to finance a purchase. In addition, because average house prices in California are higher than in other states, we expect that the differences between the typical transaction and one financed with a loan near the conforming limit will be less stark in California than in other parts of the country.
We limit our time frame to the period between 1997 and 2007 for several reasons. First, the LPS data that we use to estimate the jumbo-conforming spread are most comprehensive from the mid-1990s on. Second, we want to ensure that the conforming limit was being set in a consistent way across all years in the sample. Until 2007, a single conforming limit was set annually according to a formula and was imposed uniformly across all of the lower 48 states. However, after 2008, when the GSEs were taken into government conservatorship, the standards for determining the conforming limit were changed in several ways, including a provision which allows it to vary across different metropolitan areas.
Another reason we avoid using post-2007 data is that there were significant changes to the structure of the mortgage market during the financial crisis that could potentially confound our analysis. For example, the jumbo securitization market almost completely dried up during this period, which lead to a sharp reduction in the number of jumbo loans originated and a large rise in the jumbo-conforming spread (Fuster and Vickery, 2013). We limit our sample period to years before 2007 in order to avoid conflating the reduction in supply of jumbo loans during the housing bust with the demand-side response to the conforming limit that we are most interested in. Finally, we drop all loans originated from October through December, since banks may hold such loans in their portfolios until the conforming limit changes in January (Fuster and Vickery, 2013).18
These restrictions leave us with a primary estimation sample of approximately 2.7 million transactions representing 26 MSAs. Table 1 presents summary statistics for this sample as well as the sub-sample of transactions with first loan amounts within $50,000 of the conforming limit that was in place in the year of the transaction. All dollar amounts here and throughout the analysis are converted to real 2007 dollars.
In the full sample, shown in column 1, the mean first loan size is approximately $350,000 and the mean transaction price is $465,000. Column 3 shows the means from the restricted sample. Although the large sample size leads many of the differences between columns 1 and 3 to be statistically significant, they are qualitatively similar along all dimensions. Interestingly, because the restricted sample drops both high priced houses and low priced houses, the average transaction price and loan amount near the conforming limit are actually a bit lower than the averages for the entire sample. In many states with lower average house prices, there are relatively few loans made substantially above the limit, but in California such transactions are much more common.
4.2 LPS
The primary disadvantage of the DQ data set for studying mortgages is that it does not record interest rates and lacks important information on borrower characteristics, such as credit scores and debt-to-income ratios. Consequently, we turn to data from LPS to estimate the jumbo-conforming spread, as well as interest rates on second mortgages taken out at closing. The LPS data are at the loan level and run from 1997 to the present, covering approximately two-thirds of the residential mortgage market.19 The data contain extensive information on mortgage terms and borrower characteristics, as well as geographic identifiers down to the zip code level. We focus on first mortgage originations for home purchases and apply the same set of restrictions described above for the DQ data, in particular the limitations to California and the first nine months of each year between 1997 and 2007.
Table 2 presents summary statistics from the LPS data, for fixed-rate (FRM) and adjustable-rate (ARM) loans separately. Columns 1 and 3 report statistics for the full analysis sample, while columns 2 and 4 restrict the sample to loans within $50,000 of the conforming loan limit. In general, the restricted samples for each loan type are quite similar to the full sample, suggesting that loans near the limit are reasonably representative of the entire sample, at least along these dimensions.
5.1 Estimating the Behavioral Response to the Conforming Limit
In section 3, we showed that the behavioral response to the conforming loan limit can be derived from estimates of the amount of bunching and the counterfactual mass at the limit. To estimate these quantities we follow the approach taken by Kleven and Waseem (2013).
Since we are primarily interested in estimating the behavioral response in percentage terms, we first take logarithms of the loan amounts. We then center each loan in our data set at the (log) conforming limit in the year that the loan was originated. A value of zero thus represents a loan size
exactly equal to the conforming limit while all other values represent (approximate) percentage deviations from the conforming limit. We group these normalized loan amounts into bins centered at the values ![]() , with
, with
![]() , and count the number of loans in each bin,
, and count the number of loans in each bin, ![]() . To obtain estimates of bunching and the counterfactual loan size distribution we define a region around the conforming limit,
. To obtain estimates of bunching and the counterfactual loan size distribution we define a region around the conforming limit,
![]() , such that
, such that
![]() and fit the following regression to the count of loans in each bin
and fit the following regression to the count of loans in each bin
The first term on the right hand side is a
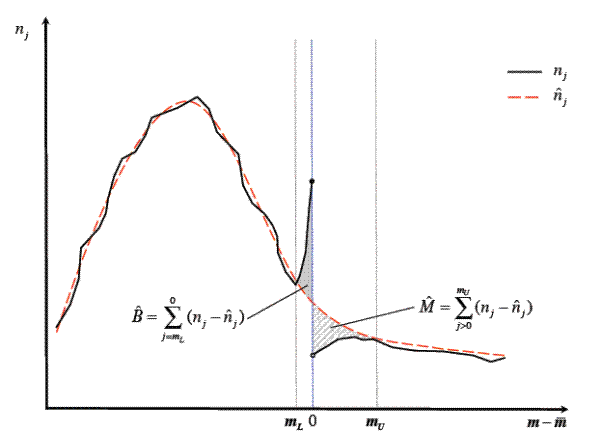
Bunching is then estimated as the difference between the observed and counterfactual bin counts in the excluded region at and to the left of the conforming loan limit,
This procedure is illustrated graphically in figure 5. The solid black line represents the empirical count of loans in each bin, the heavy dashed red line is the estimated counterfactual distribution, the solid shaded gray area is the bunching estimate, and the cross hatched shaded gray area is the amount of missing mass due to bunching,
The parameter of primary interest is
![]() , the empirical analogue of
, the empirical analogue of
![]() from equation (8). This parameter represents the average behavioral response of the marginal bunching individual measured as a percentage deviation
from the conforming limit. Following the theory, we calculate it as
from equation (8). This parameter represents the average behavioral response of the marginal bunching individual measured as a percentage deviation
from the conforming limit. Following the theory, we calculate it as
where
There are two key identifying assumptions necessary for equation (16) to provide a valid estimate of the behavioral response to the conforming limit. The first is that the counterfactual loan size distribution that would exist in the absence of the limit would be smooth. That is, any spike in the loan size distribution at the conforming limit can be solely attributed to the existence of the limit and not some other factor. We test for violations of this assumption below by examining how the distribution of loan sizes changes when the conforming limit moves from one year to another. The second assumption is that households can be uniquely indexed by their counterfactual choice of mortgage size in the absence of the limit--that is, there is a well-defined marginal buncher. While this assumption is fundamentally untestable, most reasonable models of mortgage choice would imply such a result.
In order to estimate the components of equation (16), there are several free parameters that we must choose: the bin width (
![]() ), the order of the polynomial (
), the order of the polynomial (![]() ), and the
location of the lower and upper limits of the excluded region (
), and the
location of the lower and upper limits of the excluded region (![]() and
and ![]() ).
Following Kleven and Waseem (2013), we choose the upper limit to minimize the difference between bunching (
).
Following Kleven and Waseem (2013), we choose the upper limit to minimize the difference between bunching (![]() ) and missing mass to the right of the notch in the excluded region (
) and missing mass to the right of the notch in the excluded region (![]() ). This is done using the following iterative procedure: First, initialize
). This is done using the following iterative procedure: First, initialize ![]() at a
small amount (
at a
small amount (![]() ) near the limit and estimate bunching (
) near the limit and estimate bunching (
![]() ), missing mass (
), missing mass (
![]() ), and the difference between the two, (
), and the difference between the two, (
![]() ). Next, increase
). Next, increase ![]() by a small amount to
by a small amount to ![]() and calculate the difference
and calculate the difference
![]() . We repeat this process until
. We repeat this process until
![]() , at which point we stop and take
, at which point we stop and take
![]() to be the upper limit of the excluded region.
to be the upper limit of the excluded region.
For the other three parameters, our preferred specification uses 1-percent bins, a 13th-degree polynomial, and sets ![]() . We prefer this specification because, among the parameter
configurations we considered, it yields the smallest difference between
. We prefer this specification because, among the parameter
configurations we considered, it yields the smallest difference between ![]() and
and ![]() in the sample that pools across all years and loan types. It is worth noting, however, that the estimated missing mass from the right of the limit need not be exactly equal to the number of bunched loans. In fact, the theory predicts that the two will likely differ.
in the sample that pools across all years and loan types. It is worth noting, however, that the estimated missing mass from the right of the limit need not be exactly equal to the number of bunched loans. In fact, the theory predicts that the two will likely differ.
As noted by Kleven and Waseem (2013), the procedure we use to estimate bunching ignores both extensive margin responses, and the leftward shift of the distribution outside of the excluded region generated by intensive responses among those who do not bunch. In response to the higher interest rate, some borrowers who
would have located to the right of the limit may instead choose not to purchase a home at all (extensive margin responses), and jumbo borrowers who are not induced to bunch will still presumably choose to borrow slightly less than they would at conforming rates (intensive margin responses). If
these types of responses have a large enough effect on the observed loan size distribution, then choosing parameters to minimize the difference between bunching and missing mass could lead to bias in the estimated behavioral response. To account for this, we explore robustness to various choices of
the underlying parameters, which often yield estimates of ![]() that are smaller than
that are smaller than ![]() , but, most importantly, give very similar estimates of
, but, most importantly, give very similar estimates of
![]() to our preferred specification.
to our preferred specification.
Finally, we calculate standard errors for all estimated parameters using a bootstrap procedure, as in Chetty et al. (2011). At each iteration (![]() ) of the bootstrap loop we draw with replacement from the
estimated errors,
) of the bootstrap loop we draw with replacement from the
estimated errors,
![]() , in equation (13) to generate a new set of bin counts,
, in equation (13) to generate a new set of bin counts, ![]() . We then re-estimate the amount of bunching using these new counts. Our estimate of the standard error for
. We then re-estimate the amount of bunching using these new counts. Our estimate of the standard error for
![]() is the standard deviation of the estimated
is the standard deviation of the estimated
![]() s. The same procedure produces standard errors for all the other bunching parameters that we report.
s. The same procedure produces standard errors for all the other bunching parameters that we report.
5.2 Estimating the Jumbo-Conforming Spread
Although our estimates of bunching provide a reliable measure of the behavioral response to the conforming loan limit, in order to convert that response into an elasticity we also need to estimate the magnitude of the change in rates that borrowers face. This exercise is complicated by the fact that there is a large class of borrowers who, as we demonstrate, bunch precisely at the conforming limit. These borrowers may have unobserved characteristics that are correlated with interest rates and that might bias an estimate of the jumbo-conforming spread based on a simple comparison of observed mortgage rates. However, this concern is not as grave as it may first appear. In particular, we are aided greatly by the fact that mortgage rates are typically determined based on a well defined set of borrower and loan characteristics that are all readily observable in the LPS data. To the extent that we are able to fully control for these characteristics, our estimates of the jumbo-conforming spread should be relatively close to the true interest rate differential facing the average borrower in our sample.
With this in mind, our main approach to estimating the jumbo-conforming spread follows that of Sherlund (2008), who exploits the sharp discontinuity at the conforming loan limit while also controlling semiparametrically for all other relevant determinants of interest rates. Of course, in a finite sample, it is not possible to control completely flexibly for all observed determinants of interest rates and there may be some unobserved characteristics which our controls are unable to capture. To account for this, we also estimate models which use the appraised value of the home as an instrumental variable (IV) for jumbo loan status, as described in detail below.
Unlike Sherlund (2008), who uses an analogue to local linear regression, we incorporate the semiparametrics in standard ordinary least squares regressions. We do this both to reduce the computational burden and to allow for a straightforward comparison with the IV estimates. In particular, we estimate variants of the following equation
where
If there are other unobserved determinants of interest rates which are also correlated with jumbo loan status, than estimates of ![]() based on equation (17)
will produce biased estimates of the true jumbo-conforming spread. To gauge the extent to which this may be affecting our results, we also estimate a version of equation (17) in which we instrument for jumbo loan status using a discontinuous function of the appraised value
of the home, following Kaufman (2012).21 Because mortgage contracts are frequently determined prior to the actual date of transaction, the official loan-to-value (LTV)
ratio used by the bank to determine whether a borrower qualifies for a loan is often set based on an independent appraisal value, not the actual transaction price. Moreover, since many homebuyers purchase a home with an LTV of exactly 80 percent, if a home appraisal comes in just over the
conforming loan limit divided by 0.8, then a buyer is substantially more likely to take out a jumbo loan. This suggests an approach in which we instrument for
based on equation (17)
will produce biased estimates of the true jumbo-conforming spread. To gauge the extent to which this may be affecting our results, we also estimate a version of equation (17) in which we instrument for jumbo loan status using a discontinuous function of the appraised value
of the home, following Kaufman (2012).21 Because mortgage contracts are frequently determined prior to the actual date of transaction, the official loan-to-value (LTV)
ratio used by the bank to determine whether a borrower qualifies for a loan is often set based on an independent appraisal value, not the actual transaction price. Moreover, since many homebuyers purchase a home with an LTV of exactly 80 percent, if a home appraisal comes in just over the
conforming loan limit divided by 0.8, then a buyer is substantially more likely to take out a jumbo loan. This suggests an approach in which we instrument for ![]() in equation (17) with whether an appraisal is above or below
in equation (17) with whether an appraisal is above or below
![]() . The key to this "appraisal limit" being a valid instrument is that, unlike their actual loan amount, borrowers likely have little control over the exact outcome of
their appraisal.
. The key to this "appraisal limit" being a valid instrument is that, unlike their actual loan amount, borrowers likely have little control over the exact outcome of
their appraisal.
This IV approach is not a panacea, however. As Kaufman (2012) notes, it identifies a local average treatment effect among borrowers who choose to increase their first mortgage balance in order to keep their LTV constant in response to a high appraisal. But in this paper, we are interested in estimating the average elasticity among the entire population of borrowers with counterfactual loan amounts above the limit. If there is heterogeneity in the jumbo-conforming spread, then those facing the lowest spread will be the most likely to take out a larger loan in response to a high appraisal. Consequently, it is likely that the IV estimates provide a lower bound on the average spread in the population. Given the clear difficulty of estimating the "true" jumbo-conforming spread in the full population of borrowers, our preferred approach is to estimate the spread using both techniques and present a range of plausible elasticities.
6 Bunching and Jumbo-Conforming Spread Estimates
The next three sections present our primary empirical results. We begin in this section by presenting graphical evidence documenting bunching at the conforming loan limit as well as formal estimates of bunching and the behavioral response to the jumbo-conforming spread. We then present a series of estimates of the magnitude of the jumbo-conforming spread which we combine with the bunching estimates in section 7 to calculate elasticities. In section 8, we conclude with a discussion on the ways in which borrowers appear to be adjusting their loan sizes.
6.1.1 Results for all Borrowers
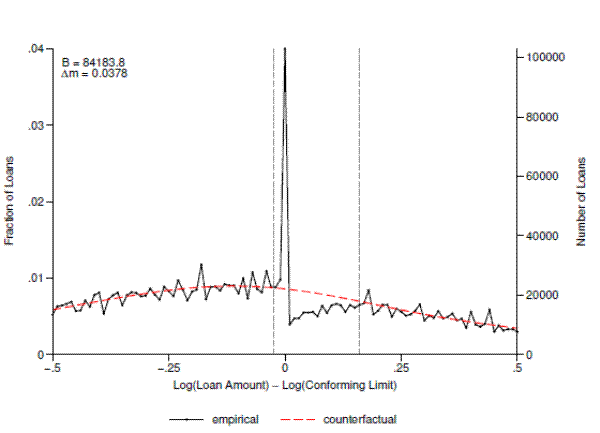
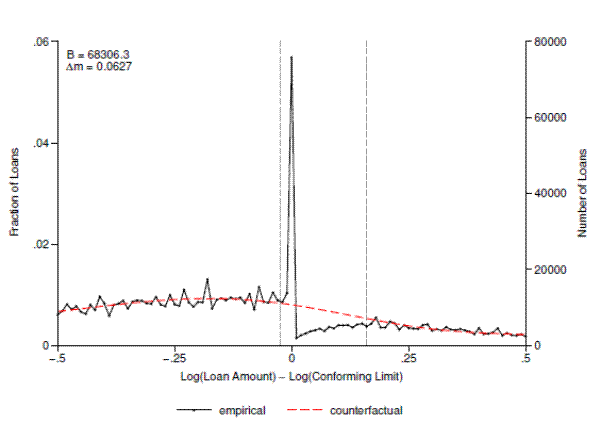
As a starting point for our empirical analysis, figure 6 plots both the observed (log) loan size distribution and the counterfactual distribution estimated from the bunching procedure using all available loans in the DQ sample. Although our estimation is carried out in the full sample, in this (and subsequent) figures we have narrowed our focus to the range of loans which fall within 50 percent of the conforming limit. The x-axis shows the difference between the log loan amount and the log conforming limit in the year the loan was originated, so that 0 is the limit itself and each bin represents roughly a 1 percent incremental deviation from the limit. The y-axis on the right indicates the number of loans in each bin, while the y-axis on the left indicates the fraction of all loans represented by that number.
The connected black line plots the histogram of (log) loan size, which exhibits a sharp peak precisely at the limit. This bin contains approximately 100,000 loans representing 4 percent of the entire sample, which is roughly four times as many loans as in the bin immediately to the left. The
black line also shows a clear deficit of loans to the right of the limit, with the first bin containing only about half as many loans as the bin immediately to the left of the limit. The heavy dashed red line shows the fitted polynomial that we take as our counterfactual loan size distribution. The
vertical dashed gray lines represent the lower (![]() ) and upper (
) and upper (![]() ) limits of
the excluded region, as defined in section 5.1.
) limits of
the excluded region, as defined in section 5.1.
The estimated number of loans bunching at the limit is reported in the figure and is calculated as the sum of the differences between the black and red lines in each bin in the excluded region at and to the left of the conforming limit. As the plot makes clear, bunching is remarkably sharp;
almost all of the approximately 84,000 "extra" loans in this region are in the bin that contains the limit itself. Our estimate of
![]() , the behavioral response to the conforming limit, is also reported in the figure. It implies that the average marginal bunching borrower reduces his loan balance by
roughly 3.8 percent.
, the behavioral response to the conforming limit, is also reported in the figure. It implies that the average marginal bunching borrower reduces his loan balance by
roughly 3.8 percent.
The first column of table 3 repeats these estimates along with their standard errors and several other parameters estimated during the bunching procedure. As another way of gauging the magnitude of the response, the third row of table 3 reports a measure of the "excess mass" at the conforming limit. We calculate this as the ratio of the number of loans bunching at the limit to the number of loans which would have been there in its absence. The estimate implies that there are roughly 3.78 times more loans at the conforming limit than would have otherwise been expected. All of these parameters are precisely estimated.
In the last row of table 3, we also report the upper limit of the excluded region used in estimation (![]() ). If there were no extensive margin responses
(borrowers leaving the market entirely) then this number would provide an estimate of the largest percent reduction in mortgage size among bunching individuals. That is, no individual with a counterfactual loan size more than
). If there were no extensive margin responses
(borrowers leaving the market entirely) then this number would provide an estimate of the largest percent reduction in mortgage size among bunching individuals. That is, no individual with a counterfactual loan size more than ![]() percent larger than the conforming limit would be induced to bunch. Given extensive margin responses, it is possible that our estimate of
percent larger than the conforming limit would be induced to bunch. Given extensive margin responses, it is possible that our estimate of ![]() differs
from the true cutoff value. Nonetheless, it provides a useful gauge of the magnitude of behavioral responses among those who reduce their mortgage sizes the most. The estimate implies an upper bound on behavioral responses of roughly 16 percent, meaning that nearly all of the borrowers bunching at
the conforming limit would have had mortgages that were less than 16 percent larger than the limit had it not existed.
differs
from the true cutoff value. Nonetheless, it provides a useful gauge of the magnitude of behavioral responses among those who reduce their mortgage sizes the most. The estimate implies an upper bound on behavioral responses of roughly 16 percent, meaning that nearly all of the borrowers bunching at
the conforming limit would have had mortgages that were less than 16 percent larger than the limit had it not existed.
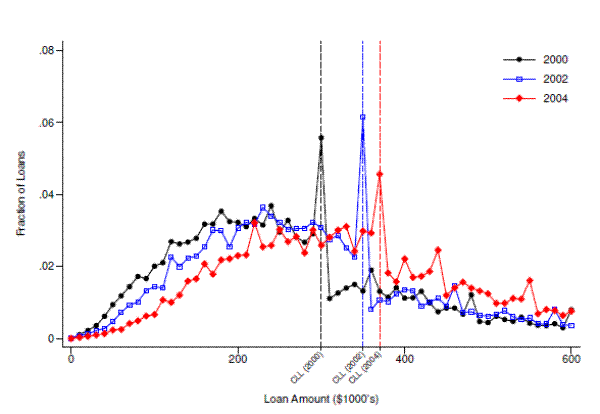
As noted above, one of the key assumptions necessary for bunching to identify behavioral responses is that the counterfactual loan size distribution be smooth. While there is no way to directly test this assumption, one way to evaluate its plausibility is to examine what happens to the empirical distribution of loan sizes as the conforming limit moves from one year to the next. If the conforming limit is the only thing causing bunching, then bunching should track the movement of the conforming limit, and the distribution should be smooth at previous and future conforming limits. Figure 7 plots the empirical loan size distribution separately for the years 2000, 2002, and 2004.22 At any given nominal loan amount, the distribution appears to be smooth except in the year for which that loan amount serves as the conforming limit. While not definitive, this result strongly supports the counterfactual smoothness assumption.
6.1.2 Fixed versus Adjustable Rate Mortgages
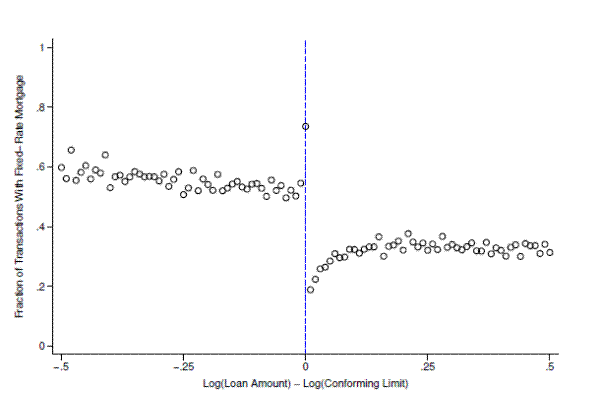
In addition to looking at the effect of the conforming limit on overall loan size, recent work by both Fuster and Vickery (2013) and Kaufman (2012) draws attention to several stylized facts that make it particularly interesting to investigate heterogeneity in the response by type of loan. In particular, these authors document a sizable and sharp decline in the share of fixed-rate mortgages (FRMs) relative to adjustable-rate mortgages (ARMs) precisely at the conforming limit. We replicate this stylized fact in figure 8 using our own sample of loans from DataQuick. Using the same 1 percent bins as before, this figure plots the share of loans that are FRMs as a function of loan size relative to the conforming limit. To the left of the limit, the FRM share declines gradually as the loan amount increases, reaching roughly 55 percent just below the limit. It then spikes to about 75 percent at the limit before falling to 20 percent immediately to the right. Beyond the conforming limit, the share then rises, eventually reaching a plateau of about 35 percent.
This drop in the FRM share is not a coincidence. Fixed-rate mortgages are generally estimated to have a larger jumbo-conforming spread relative to ARMs due to the fact that their returns are much more vulnerable to interest rate risk.23 Since the FRM share well to the right of the limit is substantially lower the FRM share to the left of the limit, a quick glance at figure 8 might suggest an extensive margin response. That is, in response to the higher jumbo spread for FRMs some borrowers may choose to substitute toward adjustable-rate mortgages.
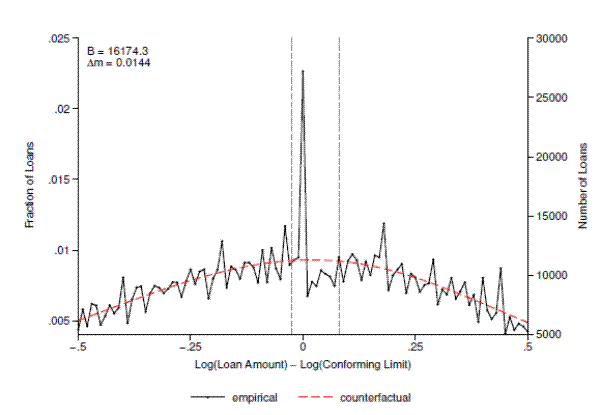
In contrast, we argue that the change in the FRM share at the conforming limit occurs because more FRM borrowers than ARM borrowers bunch at the limit, and not because individual borrowers are choosing ARMs over FRMs. To show this, we separately estimate bunching for both fixed-rate and adjustable-rate mortgages. If the drop in FRM share at the limit is driven primarily by borrowers substituting to ARMs, then we should expect to see both a downward shift in the observed distribution of FRMs relative to its counterfactual immediately to the right of the limit and a concomitant upward shift in the ARM distribution.
Figures 9 and 10 show the results from this exercise for fixed and adjustable-rate mortgages, respectively. As with the combined results, the standard errors and additional bunching parameters are also reported separately for each loan type in columns 2 and 3 of table 3. While figure 9 shows a substantial downward shift in the FRM distribution to the right of the limit, figure 10 shows no corresponding upward shift in the ARM distribution. In fact, much like in the figures for the FRM and combined samples, the ARM distribution features a region of missing mass immediately to the right of the limit. Moreover, in our preferred specification, the missing mass for each type of loan is roughly equal to the mass of that type of loan bunching at the limit. These results suggest, at least in aggregate, that the drop in the FRM share at the conforming limit is driven primarily by differential bunching within loan type rather than borrowers substituting from one type of mortgage to another.24 This is further reflected in the estimate of excess mass reported in table 3, which is roughly 4.4 times larger for FRMs than for ARMs.
While we do not believe that our results invalidate any of the conclusions drawn by Fuster and Vickery (2013) or Kaufman (2012), they do illuminate the fact that perhaps the most intuitive channel for the drop in the FRM share above the limit--substitution between FRMs and ARMs--is not the correct one. With this in mind, for the remainder of the paper we will present estimates for FRMs and ARMs separately.
6.1.3 Heterogeneity by Borrower Type
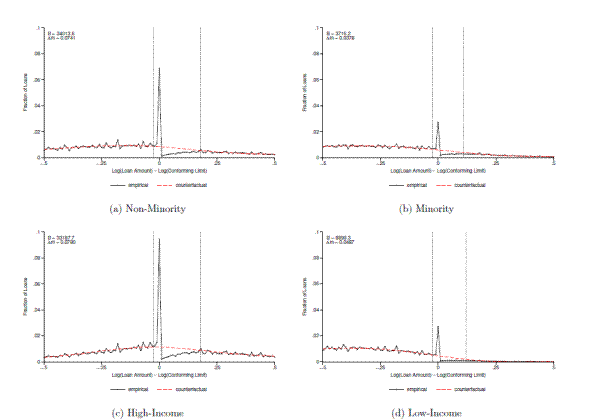
In addition to investigating bunching behavior by loan type, it is also interesting to examine whether bunching varies with the observable characteristics of borrowers. While the available information on borrower demographics is somewhat limited, we are able to provide several rough cuts of the data based on race and income using the subset of DQ transactions that we matched to HMDA loan applications. For this exercise we restrict attention to fixed-rate mortgages, where the sample sizes are largest. Using the race and ethnicity information in HMDA data, we define a loan as belonging to a "minority" borrower if the primary loan applicant reports his race as black or his ethnicity as Hispanic, and as belonging to a "non-minority" borrower otherwise. Similarly, we define a borrower as "low-income" if the income reported on the loan application was below the median income reported across all loans and "high-income" if the reported income is above the median.
Figure 11 shows results from estimating bunching separately in each of these four sub-samples. Panels (a) and (b) show results for non-minority and minority borrowers while panels (c) and (d) present the results for high-income and low-income borrowers, respectively. In each case there is substantial evidence of heterogeneous responses, with far less bunching among minority and low-income borrowers than among non-minority and high-income borrowers. For non-minority and high-income borrowers the estimated percentage reduction in loan size is roughly 7 to 8 percent, while for minority and low-income borrowers it is closer to 4 to 5 percent.25 Table 4 confirms the visual impressions given by figure 11, reporting the point estimates and standard errors for the bunching parameters we estimate. For each of the reported parameters, the standard errors are small enough to reject the null that bunching behavior is the same across the high-income and low-income samples, as well as across the non-minority and minority samples.
These differences could arise from at least three sources: heterogeneous preferences, heterogeneous costs of adjusting first mortgage balances, or borrower-level differences in the magnitude of the jumbo-conforming spread. While we cannot test for differences in the magnitude of the spread along these dimensions because the LPS data do not contain information on race or income, we do not find robust evidence of differences along other dimensions that are likely correlated with these characteristics, such as borrowers' credit scores. This finding suggests that one of the first two sources of heterogeneity are likely operative.
In the context of income taxes, Kleven and Waseem (2013) are able to distinguish between the role of preferences and adjustment costs using the fact that a notch can sometimes create a dominated region in which no wage earner, regardless of tax elasticity, would choose to locate in the absence of adjustment costs. By counting the number of wage earners observed in the dominated region they are able to back out an estimate of adjustment costs. Unfortunately, we cannot perform a similar exercise here because there is no such dominated region in our setting. In the terminology of Kleven and Waseem (2013), the jumbo-conforming spread creates a "downward notch" where, for any finite loan amount above the limit, there exists a first mortgage demand elasticity sufficiently close to zero such that some borrower would be willing to take out that loan. It is therefore not possible to estimate the magnitude of any differences in adjustment costs across these four groups.
While it seems more likely that these differences are driven by adjustment costs than by differences in underlying preferences for first mortgage debt, we leave a full analysis of this issue for future research. However, it is important to note that because we are not able to determine the magnitude of such adjustment costs, the elasticities we estimate below are necessarily "reduced form", in the sense that they incorporate the effect of adjustment costs and are not driven entirely by the intertemporal elasticity of substitution alone.
6.2 Jumbo-Conforming Spread
To convert the behavioral responses estimated from bunching into elasticities, we next need to obtain an estimate of the interest rate differential at the limit. Table 5 presents estimates of the jumbo-conforming spread, following the strategies discussed in section 5.2. We estimate the spread using OLS and IV, for fixed- and adjustable-rate mortgages separately, with four different specifications each. All of the specifications include controls for the distance to the conforming limit (linear, quadratic, and cubic terms) interacted with the jumbo loan indicator variable, as well as controls for the loan-to-value (LTV) ratio, debt-to-income (DTI) ratio, missing DTI ratio, FICO credit score, missing FICO score, whether the loan includes private mortgage insurance (PMI), and whether the loan has a prepayment penalty. They also include zip code by month fixed effects and fixed effects for standard loan lengths, such as 15, 30, and 40 years, as well as a linear term to capture the effects of nonstandard lengths. Analogous estimates of the spread, estimated in logs, are provided in table 6. These estimates are used in calculating the elasticities below, but we discuss the results in levels here because it is more intuitive to think of changes in interest rates in terms of basis or percentage points.
Across the columns of the table, the four specifications are: (1) a baseline, using all available data, with linear controls for the LTV and DTI ratios and the FICO score; (2) the same specification replacing the linear controls for LTV, DTI and FICO with more flexible cubic B-splines; (3) the same specification as in (2) but with a sample limited to loans within $50,000 of the conforming limit; and (4) the same specification in (2) but with a sample limited to loans within $10,000 of the limit.
For fixed-rate mortgages, applying least squares yields estimates of the jumbo-conforming spread that are tightly clustered around 17 to 18 basis points and precisely estimated, regardless of the specification. These estimates are similar to Sherlund's (2008) estimate of 22 basis points, despite our use of a simpler estimation technique and a different data set covering a smaller geographic area and a shorter time horizon.26
However, as discussed above, the OLS specifications do not control for borrower selection around the conforming limit. As we have just shown, a large fraction of borrowers who would otherwise get loans just above the limit instead choose to bunch at the limit to get conforming loans and reduce their rates. If these borrowers differ in any unobserved ways from those who do not reduce their rates, the estimates of the spread could be biased.
To address this potential selection issue, the row labeled "IV" presents estimates of the spread when we instrument for the jumbo indicator with an indicator for whether the appraised value of the house exceeds the "appraisal limit" (the conforming limit divided by 0.8). As would be expected, these estimates are somewhat less precise than the OLS results but are nonetheless still significant at conventional levels. The estimates run from 10 to 13 basis points and are uniformly smaller than the OLS results, possibly reflecting either borrower selection or the fact that the IV approach estimates a local average treatment effect among a population of borrowers who may face a lower spread.27 Reassuringly, these estimates are quite similar to (Kaufman's (2012) estimate of 10 basis points, using essentially the same technique but a different sample of loans.28
Our estimates of the jumbo-conforming spread for initial ARM rates, presented in the lower half of table 5, are considerably more noisy and merit further study. The OLS estimates are uniformly negative--that is, jumbo loans have lower rates than conforming loans--and the negative coefficient gets bigger as the sample becomes more focused on loans near the limit. It is quite unlikely that this is an accurate representation of pricing of ARMs above and below the conforming limit. Indeed, we saw in the previous section that a significant fraction of borrowers with ARM balances that would be just above the limit under the counterfactual instead choose to bunch at the limit, although the effect is smaller than in the FRM market. Some aspect of the loans must be leading those borrowers to prefer loans at the limit to loans above it. One possibility is that the negative coefficients result from selection. The "IV" row uses the same "appraisal limit" instrument as in the FRM results. Here we see coefficients that range from about zero, in the first two columns, to 7 and 4 basis points, in columns 3 and 4. The standard errors are too large to rule out a negative spread, although the point estimates are comparable to other estimates in the literature that are also close to zero.29
It is somewhat surprising that addressing borrower selection around the limit using the IV specification produces more positive coefficients in the ARM case and less positive coefficients in the FRM case. Given the observed bunching at the limit among ARM borrowers, it is also surprising to find no strong support for a positive jumbo-conforming spread among ARM loans. While we control for many relevant aspects of mortgage contracts, such as prepayment penalties and private mortgage insurance, it is possible that there are other unobserved factors that are more relevant for ARMs than for FRMs and which could be biasing these results. Consequently, the remaining discussion in this paper, including the calculation of elasticities, focuses on the results for FRMs.
7.1 Calculating Elasticities with a Notched Budget Constraint
As discussed above, the higher mortgage rate for loans above the conforming limit creates a "notch" in which the average price jumps discontinuously, rather than a "kink" in which the marginal price changes discontinuously but the average price is continuous. That is, borrowers must pay the higher interest rate on the entire balance of the loan, not just the balance in excess of the limit. As a result, it is not appropriate to calculate an elasticity using the change in the marginal price of the loan.
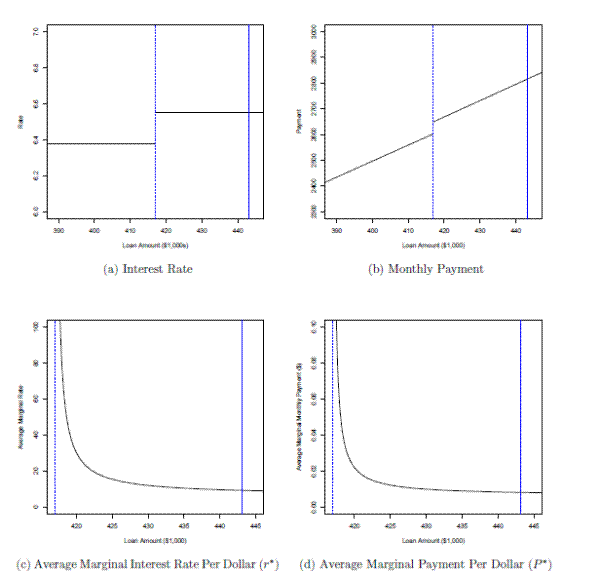
Figure 12 illustrates this point using numbers from 2006 as an example. Panel (a) shows the overall interest rate on a 30-year FRM given the size of the loan.30 The rate jumps at the conforming loan limit of $417,000--the dashed blue line--from 6.38 percent to 6.55 percent.31 Panel (b) shows the equivalent monthly mortgage payment, which jumps by about $45 at the limit.32
Although the marginal increase in payment per dollar of the loan--the slope of the line--is only slightly higher above the limit than below it, the discontinuity implies a much more substantial effect on incentives. To see this, let
![]() denote the monthly payment on a 30-year mortgage of amount
denote the monthly payment on a 30-year mortgage of amount ![]() at
fixed interest rate
at
fixed interest rate ![]() . Then the total increase in payment for a loan of size
. Then the total increase in payment for a loan of size ![]() relative to a loan at the conforming limit,
relative to a loan at the conforming limit, ![]() , is equal to
, is equal to
| (18) |
where
The marginal increase in payment per dollar of the loan, averaged over the distance from the limit to ![]() , is then
, is then
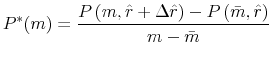 |
(19) |
Panel (d) of figure 12 plots
While the monthly payment is an intuitive metric, the correct theoretical price per dollar of the loan is the underlying interest rate. Define ![]() such that
such that
| (20) |
This
Equation (21) makes clear that
Panel (c) of figure 12 plots ![]() for our 2006 example. We calculate that
for our 2006 example. We calculate that ![]() for a loan $1,000 over the limit to be about 77 percent. This implies that, all else equal, borrowers in 2006 who took out a jumbo loan for $418,000 at
for a loan $1,000 over the limit to be about 77 percent. This implies that, all else equal, borrowers in 2006 who took out a jumbo loan for $418,000 at
![]() must have weakly preferred that loan to the combination of a conforming loan for $417,000 at
must have weakly preferred that loan to the combination of a conforming loan for $417,000 at
![]() and a second mortgage at
and a second mortgage at
![]() . Of course, second mortgages in 2006 were available at far lower interest rates, so the average borrower who wanted a $418,000 mortgage would have been much better off with the
conforming/second combination, ignoring any additional costs associated with the second mortgage.35
. Of course, second mortgages in 2006 were available at far lower interest rates, so the average borrower who wanted a $418,000 mortgage would have been much better off with the
conforming/second combination, ignoring any additional costs associated with the second mortgage.35
As the borrower's desired mortgage balance increases, however, ![]() declines. At our estimate of
declines. At our estimate of
![]() , which implies a loan size of $443,000, we calculate
, which implies a loan size of $443,000, we calculate ![]() to be 9.3 percent, which is about 2.9 percentage points above the conforming rate of 6.38 percent. By comparison, in a sample of matched first and second 30-year FRMs from 2006 in LPS, we find that the second mortgage has a rate about 2.4 percentage points higher than the
associated first mortgage.36
to be 9.3 percent, which is about 2.9 percentage points above the conforming rate of 6.38 percent. By comparison, in a sample of matched first and second 30-year FRMs from 2006 in LPS, we find that the second mortgage has a rate about 2.4 percentage points higher than the
associated first mortgage.36
Since
![]() is, on average, the loan amount in excess of the conforming limit at which borrowers are indifferent between taking out a jumbo loan and reducing their first mortgage
balance to the limit, the similarity of the implied
is, on average, the loan amount in excess of the conforming limit at which borrowers are indifferent between taking out a jumbo loan and reducing their first mortgage
balance to the limit, the similarity of the implied ![]() and the estimated conforming/second spread lends substantial credence to our bunching estimate. However, they need not be exactly
equal since taking out a second mortgage may entail additional unobserved costs that make the jumbo loan slightly more attractive. Indeed, there are some jumbo loans made only slightly above the limit, which can only be justified by having extremely low elasticities or facing substantial adjustment
costs.
and the estimated conforming/second spread lends substantial credence to our bunching estimate. However, they need not be exactly
equal since taking out a second mortgage may entail additional unobserved costs that make the jumbo loan slightly more attractive. Indeed, there are some jumbo loans made only slightly above the limit, which can only be justified by having extremely low elasticities or facing substantial adjustment
costs.
Given estimates of ![]() and
and ![]() , we can calculate the elasticities of
(first) mortgage demand implied by our estimate of
, we can calculate the elasticities of
(first) mortgage demand implied by our estimate of
![]() . Let
. Let
![]() be the (constant) marginal payment per dollar of the loan for loans made at the conforming interest rate
be the (constant) marginal payment per dollar of the loan for loans made at the conforming interest rate ![]() . Then we can define
. Then we can define
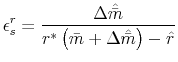 |
(22) |
and
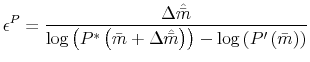 |
(23) |
as the semi-elasticity of mortgage demand with respect to the interest rate and the elasticity of mortgage demand with respect to the increase in payment, respectively. As before,
7.2 Estimated Elasticities of Mortgage Demand
The first two columns of table 7 report the semi-elasticities we calculate for a range of estimates of
![]() and the jumbo-conforming spread,
and the jumbo-conforming spread,
![]() . The semi-elasticities and associated standard errors, calculated using the delta method, are shown in the lower-right portion of the table. Each semi-elasticity is calculated
from the estimate of
. The semi-elasticities and associated standard errors, calculated using the delta method, are shown in the lower-right portion of the table. Each semi-elasticity is calculated
from the estimate of
![]() reported at the top of that column and the estimate of
reported at the top of that column and the estimate of
![]() at the beginning of that row.
at the beginning of that row.
Our preferred estimate of bunching for FRMs from table 3 (0.063) is shown in the middle row. The other two estimates (0.052 and 0.083) are the smallest and largest estimates of
![]() across a range of different options for the three parameters chosen ex ante: the bin width, the polynomial order, and the lower limit of the
excluded region.39 They provide reasonable bounds on the variation in the elasticity implied by these parameters. The jumbo-conforming spread estimates are
taken from column 3 of table 5 and correspond to the OLS (column 1) and IV (column 2) estimates, respectively.
across a range of different options for the three parameters chosen ex ante: the bin width, the polynomial order, and the lower limit of the
excluded region.39 They provide reasonable bounds on the variation in the elasticity implied by these parameters. The jumbo-conforming spread estimates are
taken from column 3 of table 5 and correspond to the OLS (column 1) and IV (column 2) estimates, respectively.
The estimated semi-elasticities range from about -0.015 to about -0.053, with our preferred estimates in the middle row at -0.022 and -0.31. The associated standard errors are relatively small, although those using the noisier IV estimate of the jumbo-conforming spread are larger than those using the OLS estimate. The semi-elasticities can be interpreted as the percentage change in the balance of a first mortgage demanded in response to a 1 basis point increase in the interest rate. As an example, our preferred estimates imply that an increase in the mortgage rate from 5 percent to 6 percent--100 basis points--would lead to a decline in first mortgage demand of 2 to 3 percent, which strikes us as a reasonably small but plausible estimate.
Columns 3 and 4 report the analogous elasticities with respect to the marginal monthly payment for the same set of estimates of
![]() and equivalent estimates of the jumbo-confirming spread in logs, taken from table 6. The preferred estimates in the middle row are
-0.27 using the OLS estimate of the spread and -0.35 using the IV estimate, indicating that a one percent increase in payment leads to about a third of a percent decline in mortgage demand.
and equivalent estimates of the jumbo-confirming spread in logs, taken from table 6. The preferred estimates in the middle row are
-0.27 using the OLS estimate of the spread and -0.35 using the IV estimate, indicating that a one percent increase in payment leads to about a third of a percent decline in mortgage demand.
8 How Do Borrowers Adjust?
Although the elasticities reported in table 7 are valid estimates of the amount by which borrowers reduce their first mortgage balance in response to the jumbo-conforming spread, they do not provide any information regarding the margins along which this adjustment occurs. In this section we present suggestive evidence that helps to distinguish between several methods that borrowers may be using to adjust their mortgage balance.
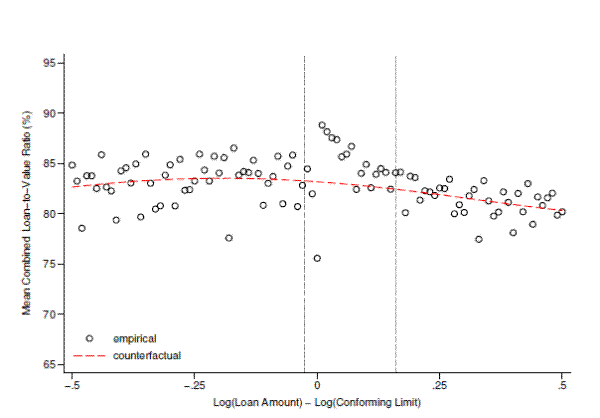
There are three primary channels through which a borrower can reduce the size of her first mortgage, each of which have different implications for the interpretation of our main results. First, a borrower could simply bring more cash to the table, making a larger down payment and taking out a smaller loan.40 Second, she could take out an additional mortgage for the amount of debt desired in excess of the conforming limit. Finally, she could spend less on housing, which (holding leverage constant) would lead her to take out a smaller mortgage.41 While borrowers likely use various combinations of these three strategies to lower their mortgage balances, if we consider the extreme cases in which only one of the three is used, we can provide a rough sense of the extent to which each may be contributing to the bunching behavior we observe.
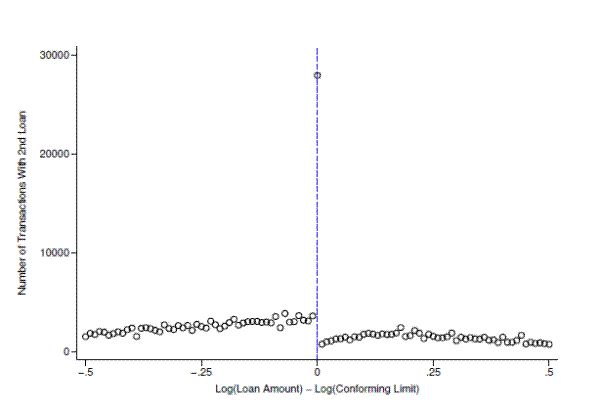
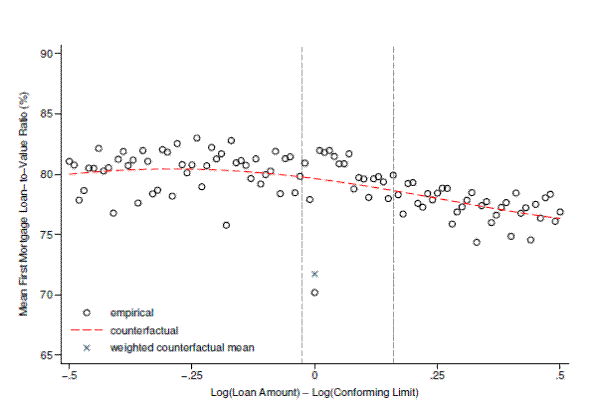
To measure the extent to which borrowers are using second mortgages to lower their first mortgage balance, figure 13 plots the number of transactions financed using second loans as a function of the associated first mortgage value relative to the conforming limit for all fixed-rate first mortgages in the DQ sample. Consistent with the notion that many of the bunching borrowers take out second mortgages, there is a sharp spike in the number of transactions which are financed with two loans precisely at the limit. The plot suggests that roughly 25,000 more second loans were taken out in the bin at the conforming limit relative to the bin just below it, which provides a reasonable counterfactual. Returning to table 3, we estimated that about 70,000 FRM borrowers bunched at the limit, suggesting that roughly 35 percent of FRM borrowers who bunch do so by taking out a second mortgage. These borrowers are presumably shifting debt from their first mortgage onto their second, holding combined LTV roughly constant while reducing their first-mortgage LTV.
The remaining 65 percent of "excess" borrowers must be either putting up more cash, or spending less on housing than they otherwise would. If they are spending less on housing while holding their leverage roughly constant, then both their first and combined LTVs should be little changed relative to the counterfactual in which the conforming limit does not exist.42 Therefore, if all of the bunching borrowers were either taking out second mortgages or buying cheaper houses, then we would expect the average combined LTV at the conforming limit to be about the same as in nearby bins. Figure 14, which plots the combined LTV against the first mortgage amount, makes clear that this (admittedly extreme) scenario is far from true. The combined LTV at the limit is about 75 percent, well below the 80 to 85 percent that would be predicted based on the red line, which is a polynomial fit using the data outside of the same excluded region that was used to estimate bunching in figure 9.43 Thus, a significant portion of the 65 percent of borrowers who bunch without a second mortgage must be doing so by putting up more cash as opposed to spending less on housing.
In the most extreme case, all of these borrowers are putting up more cash. Since both putting up more cash and taking out a second mortgage reduce a borrower's first-mortgage LTV while spending less on housing does not, we can gauge the plausibility of this extreme case by examining the relationship between first-mortgage LTV ratios and loan size near the limit. To do so, figure 15 plots the first-mortgage LTV against the first mortgage amount. This figure is analogous to figure 14 except for the blue "X", which is a first-mortgage LTV calculated under the assumption that none of the bunching borrowers adjust their housing expenditure.44 Somewhat surprisingly, the observed LTV at the limit is even lower than under the extreme scenario used to calculate the "X", in which no borrower adjusts her house price. Even allowing for some noise in the estimates, this comparison suggests that very few borrowers who bunch at the limit do so by buying cheaper houses. This LTV result is consistent with the results in Adelino et al,, who also document that borrowers who purchase homes using mortgages at the conforming limit have substantially lower first loan LTVs than those just above the limit.
Although these calculations suggest that there is no direct impact of the interest rate differential on house prices and the demand for housing itself, we do not necessarily want to draw that inference, for three reasons. First, the LTV calculations above are "back of the envelope" and there are several untested assumptions involved. Second, the interest rate differential at the limit is relatively small and may not be as informative about larger changes in rates over time. Finally, we think that another paper, Adelino et al. (2012), is likely to be better suited to studying the effects of rates on house prices. They estimate the elasticity of house prices to interest rates by following similar houses over time as they become more or less difficult to finance with a conforming loan at a constant LTV of 80 percent, essentially a difference-in-difference approach rather than the bunching approach we follow. This approach has advantages over ours for this particular question, especially because we cannot observe borrowers who drop out of the market entirely (the extensive margin).
Regardless of how they do so, the roughly two-thirds of borrowers who bunch at the conforming limit without the use of a second mortgage must be reducing their total mortgage debt. Unfortunately, we only know the average reduction in first loan size (
![]() ) among marginal bunching borrowers, so we cannot solve for the response of total mortgage debt. If, however, the fraction of marginal bunching individuals who take out a
second loan is the same as the fraction who do so in the population of all bunchers, then scaling down our elasticity estimates by a factor of one-third should provide a rough estimate of the effect of a change in rates on total mortgage debt. Specifically, multiplying our preferred first mortgage
semi-elasticity estimates of -0.022 and -0.031 by two thirds yields total debt semi-elasticities of about -0.015 and -0.021. That is, a one percentage point increase in rates should reduce total mortgage debt by between 1.5 and 2 percent.
) among marginal bunching borrowers, so we cannot solve for the response of total mortgage debt. If, however, the fraction of marginal bunching individuals who take out a
second loan is the same as the fraction who do so in the population of all bunchers, then scaling down our elasticity estimates by a factor of one-third should provide a rough estimate of the effect of a change in rates on total mortgage debt. Specifically, multiplying our preferred first mortgage
semi-elasticity estimates of -0.022 and -0.031 by two thirds yields total debt semi-elasticities of about -0.015 and -0.021. That is, a one percentage point increase in rates should reduce total mortgage debt by between 1.5 and 2 percent.
9 Policy Application: GSE Guarantee Fee Increases
As noted in the introduction, the magnitude of borrower responses to changes in mortgage interest rates has important implications in several domains of economic policy. In this section, we provide some basic calculations using our estimated mortgage demand elasticities to illustrate how these estimates could be used to gauge the potential effects of one recently proposed policy change.
In February 2012, the Federal Housing Finance Agency (FHFA) published its "Strategic Plan for Enterprise Conservatorships," outlining the steps that the agency plans to take to fulfill its legal obligations as conservator for the GSEs. As part of this plan, the FHFA established a goal of gradually reducing the dominant role that the GSEs currently play in the mortgage market. One of the primary proposed mechanisms for achieving this goal is a series of increases in the GSEs' guarantee fee (or "g-fee") up to the level that "one might expect to see if mortgage credit risk was borne solely by private capital" (FHFA, 2012).
The g-fee is the amount that Fannie Mae and Freddie Mac charge mortgage lenders in order to cover the costs associated with meeting credit obligations to investors in GSE mortgage-backed securities (MBS). It is typically collected in two components: an upfront fee assessed as a fraction of the balance of the loan at origination and a recurring annual fee equal to a fraction of the outstanding principal balance remaining at the end of each year. In 2012, g-fees from single-family mortgages generated roughly $12.5 billion in revenue for the GSEs, up 12% from the previous year (FHFA OIG, 2013). The fee has risen several times in recent years, both by Congressional mandate and as part of the first steps in implementing FHFA's strategic plan.
In December 2013 the FHFA announced plans to increase the recurring fee by an additional 10 basis points for all loans and to reduce the up-front fee by 25 basis points for loans originated in all but four states.45 The FHFA estimated that the combined effect of these increases and decreases would generate an overall average increase in the effective annual g-fee of roughly 11 basis points (FHFA, 2013).46 A report by the FHFA Inspector General noted that "Significant guarantee fee increases, under some scenarios, could result in higher mortgage borrowing costs and dampen both consumer demand for housing and private sector interest in mortgage credit risk."(FHFA OIG, 2013).47
Our estimates of the interest rate elasticity of mortgage demand can be used to gauge the potential magnitude of any reductions in mortgage borrowing resulting from the proposed g-fee increases. To carry out this calculation we make three simplifying assumptions. First, we assume that the full 11 basis point increase in the g-fee would be passed through to borrowers in the form of higher interest rates on conforming mortgages. Second, we assume that this increase in rates for conforming mortgages would not have any general equilibrium effects on interest rates for non-conforming loans. Finally, we assume that our estimates of the total mortgage demand (semi)-elasticity of 1.5 to 2 apply at all points of the mortgage size distribution, not just at the conforming limit. Under these assumptions, our estimates imply that the proposed increase in the g-fee would reduce the total dollar volume of fixed-rate conforming mortgage originations by roughly 0.17 to 0.22 percent relative to what it otherwise would have been.
Under the same set of assumptions, we can also provide an estimate of the cumulative effects of g-fee increases to date. Between 2006 and the first quarter of 2013, the g-fee rose from approximately 20 basis points to 50 basis points, with much of the rise occurring in two waves in 2012 (FHFA OIG, 2013). Multiplying the 30 basis point differential by our elasticity implies a reduction in the dollar volume of fixed-rate conforming mortgage originations of 0.45 to 0.60 percent. While our elasticity is well suited to examining the direct effects of these relatively small changes in fees, we emphasize that we cannot draw any inference on more general questions, such as how high the fees would need to rise to draw private capital back into this part of the MBS market.
10 Conclusion
In this paper, we use techniques for estimating behavioral responses from bunching at budget constraint nonlinearities in order to estimate the effects of the conforming loan limit on first mortgage demand. We combine these estimates with estimates of the jumbo-conforming spread to calculate the interest rate (semi-)elasticity of mortgage demand. Our estimates imply that size of a borrowers first mortgage falls by between 2 and 3 percent in response to a 1 percentage point increase in rates.
Accounting for the third of bunching borrowers who take out second mortgages suggests that total mortgage demand falls by between 1.5 and 2 percent in response to a 1 percentage point increase in the first mortgage interest rate. The remaining two-thirds of bunchers appear to be bringing more cash to the table rather than spending less on housing. Applying these elasticity estimates to recently proposed increases in GSE guarantee fees implies a reduction in fixed-rate conforming mortgage originations of approximately one-fifth of one percent. The implied cumulative effect of similar increases that have occurred over the past several years has been to reduce originations by approximately one-half of one percent.
We conclude by pointing to two potentially useful avenues for future research. First, our estimates are necessarily limited by their context. A large number of salient factors, especially the presence of adjustment costs and the availability of second mortgages, affect how borrowers respond to the limit and, in turn, our estimates of the demand elasticity. A better understanding of the importance of these factors for our estimates is required before they can be applied to more general policy questions. Second, the differential responses of minority versus non-minority and high-income versus low-income borrowers suggests that there could be heterogeneity in elasticities or adjustment costs along a wide range of characteristics. Understanding this heterogeneity may be as important as pinning down the overall average elasticity of demand.
References
Adelino, Manuel, Antoinette Schoar, and Felipe Severino, "Credit Supply and House Prices: Evidence From Mortgage Market Segmentation," February 2012. NBER Working Paper No. 17832.
Alessie, Rob, Stefan Hochguertel, and Guglielmo Weber, "Consumer Credit: Evidence from Italian Micro Data," Journal of the European Economic Association, 2005, 3 (1), 144-178.
Attanasio, Orazio P., Pinelopi Koujianou Goldberg, and Ekaterini Kyriazidou, "Credit Constraints in the Market for Consumer Durables: Evidence from Micro Data on Car Loans," International Economic Review, 2008, 49 (2), 401-436.
Best, Michael and Henrik J. Kleven, "Property Transaction Taxes and the Housing Market: Evidence from Notches and Housing Stimulus in the UK," September 2013. Working Paper.
Browning, Martin and Annamaria Lusardi, "Household Saving: Micro Theories and Micro Facts," Journal of Economic Literature, 1996, 34 (4), 1797-1855.
Brueckner, Jan K., "The Demand for Mortgage Debt: Some Basic Results," Journal of Housing Economics, 1994, 3, 251-262.
Chetty, Raj, John N. Friedman, and Emmanuel Saez, "Using Differences in Knowledge Across Neighborhoods to Uncover the Impact of the EITC on Earnings," 2013. Forthcoming, American Economic Review.
_,_ , Tore Olsen, and Luigi Pistaferri, "Adjustment Costs, Firm Responses, and Mico vs. Macro Labor Supply Elasticities: Evidence from Danish Tax Records," Quarterly Journal of Economics, 2011, 126 (749-804).
Congressional Budget Office, "Federal Subsidies and the Housing GSEs," 2001.
Federal Housing Finance Agency, "A Strategic Plan for Enterprise Conservatorships: The Next Chapter in a Story that Needs and Ending," February 2012.
_, "FHFA Takes Further Steps to Advance Conservatorship Strategic Plan by Announcing and Increase in Guarantee Fees," December 2013.
Federal Housing Finance Agency Office of Inspector General, "FHFA's Initiative to Reduce the Enterprises' Dominant Position in the Housing Finance System by Raising Gradually Their Gaurantee Fees," July 2013.
Follain, James R. and Robert M. Dunsky, "The Demand for Mortgage Debt and the Income Tax," Journal of Housing Research, 1997, 8 (2), 155-199.
Fuster, Andreas and James Vickery, "Securitization and the Fixed-Rate Mortgage," January 2013. Federal Reserve Bank of New York Staff Report No. 594.
Gary-Bobo, Robert J. and Sophie Larribeau, "A Structural Econometric Model of Price Discrimination in the French Lending Industry," International Journal of Industrial Organization, 2004, 22, 101-134.
Gelber, Alexander M., Damon Jones, and Daniel W. Sacks, "Earnings Adjustment Frictions: Evidence from the Social Security Earnings Test," September 2013. Working Paper.
Gross, David B. and Nicholas S. Souleles, "Do Liquidity Constraints and Interest Rates Matter for Consumer Behavior? Evidence from Credit Card Data," Quarterly Journal of Economics, 2002, 117 (1), 149-185.
Hall, Robert E., "Intertemporal Substitution in Consumption," Journal of Political Economy, 1988, 96 (2), 339-357.
Hendershott, Patric H. and James D. Shilling, "The Impact of the Agencies on Conventional Fixed-Rate Mortgage Yields," Journal of Real Estate Finance and Economics, 1989, 2 (101-115).
Jaffee, Dwight and John M. Quigley, "The Future of the Government Sponsored Enterprises: The Role for Government in the U.S. Mortgage Market," in Edward Glaeser and Todd Sinai, eds., Housing and the Financial Crisis, University of Chicago Press, 2012.
Jappelli, Tullio and Luigi Pistaferri, "Do People Respond to Tax Incentives? An Analysis of the Italian Reform to the Deductibility of Home Mortgage Interest," European Economic Review, 2007, 51, 247-271.
Karlan, Dean S. and Jonathan Zinman, "Credit Elasticities in Less-Developed Economies: Implications for Microfinance," American Economic Review, 2008, 98 (3), 1040-1068.
Kaufman, Alex, "The Influence of Fannie and Freddie on Mortgage Loan Terms," 2012. Federal Reserve Board Finance and Economics Discussion Series.
Kleven, Henrik J. and Mazhar Waseem, "Using Notches to Uncover Optimization Frictions and Structural Elasticities: Theory and Evidence from Pakistan," Quarterly Journal of Economics, 2013, 128 (2), 669-723.
Kopczuk, Wojciech and David J. Munroe, "Mansion Tax: The Effect of Transfer Taxes on Residential Real Estate Market," August 2013. Working Paper.
Manoli, Dayanand S. and Andrea Weber, "Nonparametric Evidence on the Effects of Financial Incentives on Retirement Decisions," August 2011. NBER Working Paper No. 17320.
Martins, Nuno C. and Ernesto Villanueva, "The Impact of Mortgage Interest-Rate Subsidies on Household Borrowing," Journal of Public Economics, 2006, 90 (8-9), 1601-1623.
Mishkin, Frederic S., "Symposium on the Monetary Transmission Mechanism," Journal of Economic Perspectives, 1995, 9 (4), 3-10.
Passmore, Wayne, Roger Sparks, and Jamie Ingpen, "GSEs, Mortgage Rates, and the Long-Run Effects of Mortgage Securitization," Journal of Real Estate Finance and Economics, 2002, 25 (2), 215-242.
_, Shane M. Sherlund, and Gillian Burgess, "The Effect of Housing Government Sponsored Enterprises on Mortgage Rates," Real Estate Economics, 2005, 33 (3), 427-463.
Poterba, James, "Tax Subsides to Owner-Occupied Housing: An Asset-Market Approach," Quarterly Journal of Economics, 1984, 99 (4), 729-752.
_and Todd Sinai, "Tax Expenditures for Owner-Occupied Housing: Deductions for Property Taxes and Mortgage Interest and the Exclusion of Imputed Rental Income," American Economic Review Papers and Proceedings, 2008, 98 (2), 84-89.
_ and_ , "Revenue Costs and Incentive Effects of the Mortgage Interest Deduction for Owner-Occupied Housing," National Tax Journal, 2011, 64, 531-564.
Saez, Emmanuel, "Do Taxpayers Bunch at Kink Points," American Economic Journal: Economic Policy, 2010, 2, 180-212.
Sallee, James M. and Joel Slemrod, "Car Notches: Strategic Automaker Responses to Fuel Economy Policy," December 2010. NBER Working Paper No. 16604.
Sherlund, Shane M., "The Jumbo-Conforming Spread: A Semiparametric Approach," 2008.
Federal Reserve Board Finance and Economics Discussion Series.
| Full Sample (1) Mean | Full Sample (2) SD | Within $50k of CLL (3) Mean | Within $50k of CLL (4) SD | |
| Transaction and Loan Characteristics: First Loan Amount ($1,000) | 349 | (229) | 342 | (55) |
| Transaction and Loan Characteristics: Transaction Price ($1,000) | 465 | (340) | 449 | (123) |
| Transaction and Loan Characteristics: Has Second Loan | 0.37 | (0.48) | 0.41 | (0.49) |
| Transaction and Loan Characteristics: First Loan ARM | 0.49 | (0.50) | 0.48 | (0.50) |
| Housing Characteristics: Square Footage | 1,764 | (4,614) | 1,787 | (2,979) |
| Housing Characteristics: Property Age (Years) | 29 | (25) | 29 | (24) |
| Housing Characteristics: Number of Bedrooms | 3.2 | (1.3) | 3.3 | (1.4) |
| Housing Characteristics: Number of Bathrooms | 2.1 | (1.0) | 2.2 | (0.9) |
| Borrower Characteristics: Applicant Income ($1,000) | 142 | (181) | 133 | (127) |
| Borrower Characteristics: White | 0.50 | (0.50) | 0.50 | (0.50) |
| Borrower Characteristics: Black | 0.03 | (0.18) | 0.03 | (0.17) |
| Borrower Characteristics: Hispanic | 0.21 | (0.41) | 0.19 | (0.39) |
| Observations | 2,739,775 | 2,739,775 | 637,369 | 637,369 |
| (1) Full Sample | (2) Within $50k of CLL | (3) Full Sample | (4) Within $50k of CLL | |
| Interest Rate (Initial for ARMs) | 6.69 | 6.70 | 5.05 | 5.04 |
| Interest Rate (Initial for ARMs): std. deviations | (0.91) | (0.90) | (2.13) | (2.09) |
| Jumbo | 0.17 | 0.14 | 0.50 | 0.39 |
| Jumbo : std. deviations | (0.38) | (0.35) | (0.50) | (0.49) |
| First Loan Amount ($1,000) | 278.03 | 322.55 | 452.13 | 376.95 |
| First Loan Amount ($1,000) : std. deviations | (174.40) | (56.81) | (283.42) | (47.29) |
| Appraisal Amount ($1,000) | 396.50 | 447.16 | 611.28 | 497.01 |
| Appraisal Amount ($1,000) : std. deviations | (281.31) | (156.74) | (438.51) | (105.31) |
| Loan-to-Value Ratio | 74.09 | 76.09 | 76.31 | 77.33 |
| Loan-to-Value Ratio : std. deviations | (16.35) | (13.63) | (10.07) | (9.17) |
| Debt-to-Income Ratio | 35.62 | 36.79 | 35.51 | 36.50 |
| Debt-to-Income Ratio : std. deviations | (12.47) | (11.96) | (11.96) | (11.46) |
| Missing DTI Ratio | 0.70 | 0.75 | 0.45 | 0.45 |
| Missing DTI Ratio : std. deviations | (0.46) | (0.44) | (0.50) | (0.50) |
| FICO Score | 731.18 | 731.70 | 719.70 | 717.97 |
| FICO Score : std. deviations | (51.81) | (49.98) | (52.82) | (52.52) |
| Missing FICO Score | 0.32 | 0.35 | 0.20 | 0.22 |
| Missing FICO Score : std. deviations | (0.47) | (0.48) | (0.40) | (0.41) |
| Term (Months) | 345.91 | 350.14 | 365.78 | 365.63 |
| Term (Months) : std. deviations | (52.58) | (46.44) | (30.73) | (28.83) |
| 30-Year | 0.90 | 0.93 | 0.93 | 0.94 |
| 30-Year : std. deviations | (0.30) | (0.26) | (0.25) | (0.23) |
| Observations | 1,062,164 | 264,654 | 947,565 | 224,475 |
| (1) Combined | (2) FRMs | (3) ARMs | |
| Bunched Loans ( |
84183.8 | 68306.3 | 16174.3 |
| Bunched Loans ( |
(2687.0) | (1561.6) | (1446.7) |
| Behavioral Response (
|
0.0378 | 0.0627 | 0.0144 |
| Behavioral Response (
|
(0.0018) | (0.0025) | (0.0014) |
| Excess Mass (
|
3.781 | 6.266 | 1.436 |
| Excess Mass (
|
(0.175) | (0.253) | (0.141) |
| Upper Limit ( |
0.160 | 0.160 | 0.080 |
| Upper Limit ( |
(0.028) | (0.021) | (0.012) |
| (1) High-Income | (2) Low-Income | (3) Non-Minority | (4) Minority | |
| Bunched Loans ( |
33187.7 | 8899.3 | 34013.6 | 3715.2 |
| Bunched Loans ( |
(548.4) | (464.6) | (736.5) | (150.3) |
| Behavioral Response (
|
0.0780 | 0.0487 | 0.0741 | 0.0378 |
| Behavioral Response (
|
(0.0028) | (0.0036) | (0.0033) | (0.0019) |
| Excess Mass (
|
7.801 | 4.868 | 7.406 | 3.777 |
| Excess Mass (
|
(0.276) | (0.362) | (0.328) | (0.196) |
| Upper Limit ( |
0.180 | 0.120 | 0.180 | 0.110 |
| Upper Limit ( |
(0.021) | (0.019) | (0.023) | (0.015) |
| (1) Baseline | (2) Splines | (3) Within $50k of CLL | (4) Within $10k of CLL | |
| Fixed-Rate Mortgages: OLS | 0.179 | 0.182 | 0.171 | 0.172 |
| Fixed-Rate Mortgages: OLS (std. errors) | (0.002) | (0.002) | (0.014) | (0.038) |
| Fixed-Rate Mortgages: IV | 0.107 | 0.121 | 0.118 | 0.126 |
| Fixed-Rate Mortgages: IV (std. errors) | (0.010) | (0.009) | (0.028) | (0.056) |
| Fixed-Rate Mortgages: Observations | 1,061,738 | 1,061,738 | 263,641 | 87,617 |
| Adjustable-Rate Mortgages: OLS | -0.076 | -0.090 | -0.299 | -0.362 |
| Adjustable-Rate Mortgages: OLS (std. errors) | (0.009) | (0.009) | (0.037) | (0.083) |
| Adjustable-Rate Mortgages: IV | -0.001 | 0.004 | 0.074 | 0.040 |
| Adjustable-Rate Mortgages: IV (std. errors) | (0.020) | (0.019) | (0.054) | (0.109) |
| Adjustable-Rate Mortgages: Observations | 692,233 | 692,233 | 157,779 | 39,542 |
| (1) Baseline | (2) Splines | (3) Within $50k of CLL | (4) Within $10k of CLL | |
| Fixed-Rate Mortgages: OLS | 0.026 | 0.027 | 0.023 | 0.025 |
| Fixed-Rate Mortgages: OLS (std. errors) | (0.000) | (0.000) | (0.002) | (0.006) |
| Fixed-Rate Mortgages: IV | 0.017 | 0.018 | 0.017 | 0.017 |
| Fixed-Rate Mortgages: IV (std. errors) | (0.002) | (0.001) | (0.005) | (0.010) |
| Fixed-Rate Mortgages: Observations | 1,061,738 | 1,061,738 | 263,641 | 87,617 |
| Adjustable-Rate Mortgages: OLS | -0.051 | -0.053 | -0.168 | -0.210 |
| Adjustable-Rate Mortgages: OLS (std. errors) | (0.003) | (0.003) | (0.015) | (0.034) |
| Adjustable-Rate Mortgages: IV | 0.005 | 0.009 | 0.014 | 0.002 |
| Adjustable-Rate Mortgages: IV (std. errors) | (0.008) | (0.008) | (0.022) | (0.045) |
| Observations | 686,970 | 686,970 | 156,403 | 39,198 |
| 0.171 | 0.118 | 0.023 | 0.017 | |
| (0.014) | (0.028) | (0.002) | (0.005) | |
| 0.052 | -0.015 | -0.022 | -0.188 | -0.246 |
| (0.003) | (0.002) | (0.005) | (0.022) | (0.064) |
| 0.063 | -0.022 | -0.031 | -0.267 | -0.351 |
| (0.003) | (0.002) | (0.008) | (0.028) | (0.091) |
| 0.083 | -0.037 | -0.053 | -0.445 | -0.589 |
| (0.004) | (0.004) | (0.013) | (0.051) | (0.156) |
Footnotes
 , where
, where 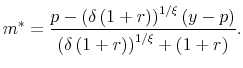
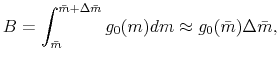
![\displaystyle B=\int_{\xi}\int_{y}\int_{\bar{m}}^{\bar{m}+\Delta\bar{m}_{\xi,y}}\bar{g}_{0}(m,\xi,y)dmdyd\xi\approx g_{0}(\bar{m})E\left[\Delta\bar{m}_{\xi,y}\right].](img66.gif)