
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 835, July 2005, revised January 2006 --- Screen Reader
Version*
SIGMA: A New Open Economy Model for Policy Analysis*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In this paper, we describe a new multi-country open economy SDGE model named "SIGMA" that we have developed as a quantitative tool for policy analysis. We compare SIGMA's implications to those of an estimated large-scale econometric policy model (the FRB/Global model) for an array of shocks that are often examined in policy simulations. We show that SIGMA's implications for the near-term responses of key variables are generally similar to those of FRB/Global. Nevertheless, some quantitative disparities between the two models remain due to certain restrictive aspects of SIGMA's optimization-based framework. We conclude by using long-term simulations to illustrate some areas of comparative advantage of our SDGE modeling framework.
Keywords: SDGE model, open economy macroeconomics
JEL classification: E32, F41
1 Introduction
In the wake of the Lucas critique and the early Real Business Cycle (RBC) literature, a wide gap emerged between the models examined in the academic literature and those utilized in policy analysis by most central banks. While central bank policy models retained a heavy emphasis on fitting short-run properties of the data, academic models increasingly heeded the methodological imperative of the RBC literature that required optimizing-agent foundations and model consistent expectations. But the focus of the latter on coherent theoretical underpinnings came at the expense of empirical realism.
In recent years, there has been a surge of interest in developing optimization-based models that are more suited to fitting the data. Consistent with this more empirical orientation, "state-of-the-art" Stochastic Dynamic General Equilibrium (SDGE) models have evolved to include a large array of nominal and real rigidities. Important work by Christiano, Eichenbaum, and Evans (2005) showed that their optimization-based model, which includes both sticky nominal wages and various types of adjustment costs in the expenditure components, is quite successful in accounting for the estimated effects of a monetary policy shock. Smets and Wouters (2003) demonstrated that the forecasting ability of a similar model appears comparable to that of an unconstrained Bayesian vector autoregression.
A salient motivation of this recent research has been to enhance the latitude of the SDGE models to contribute to policy analysis. In this vein, a number of central banks and other institutions such as the IMF are in the process of developing micro-founded models that can provide quantitative input into the policy process.1 But while recent empirical work validating certain features of the micro-founded models is encouraging, it remains an open question whether these models can yield plausible implications across the rather broad spectrum of shocks considered routinely in policy work.
In this paper, we address this question using a new multi-country open economy SDGE model (SIGMA) that we have developed for quantitative policy analysis. Our new model has its antecedents in the seminal open economy modeling framework of Obstfeld and Rogoff (1995). However, it includes many of the nominal and real frictions that have been identified as empirically important in the closed economy models of Christiano, Eichenbaum, and Evans (2005) and Smets and Wouters (2003), such as habit persistence in consumption and adjustment costs in investment. Moreover, it incorporates analogous frictions relevant in an open economy framework, including both local currency pricing (e.g., Betts and Devereux (1996) or Devereux and Engel (2002)) and costs of adjusting trade flows.
Our approach consists in comparing the implications of SIGMA with those of the FRB/Global model, a large-scale econometric model used extensively in policy analysis at the Federal Reserve Board.2 Our comparisons involve examining the impulse response functions to a number of shocks often considered in policy work. These include domestic monetary and fiscal shocks, a taste shock to home (U.S.) consumption demand, a shock to the risk premium in the uncovered interest parity equation, and alternative shocks to foreign demand. The large-scale models form an important benchmark for evaluating the new SDGE models both because they provide a reasonably accurate reduced-form characterization of the data, and because they embed the priors of policymakers who have applied these models to policy questions for several decades.3 While we do not exclude an eventual departure from the responses of the large-scale econometric models if the data provide sufficient grounds for doing so, it seems crucial that the new SDGE models not a priori rule out such responses due to arbitrary structural restrictions in the theoretical framework.
Our model comparisons indicate that the short-run responses of SIGMA are qualitatively similar to FRB/Global for a large array of macroeconomic variables, including output, prices, interest rates, real exchange rates, and the trade balance. We highlight two features of our framework that are instrumental in giving SIGMA greater flexibility to generate responses that are more closely aligned with FRB/Global quantitatively, including more persistent responses of both real and nominal variables. These features include "information frictions," which posit agents as having incomplete information about the persistence of shocks, and non-Ricardian households.
With information frictions, agents use the Kalman filter to estimate the nature of shocks affecting the economy, and to make projections. This simple learning mechanism typically implies gradual responses to underlying shocks that are similar to adaptive expectations models, while retaining the appealing property of model-consistent expectations. As emphasized by Erceg and Levin (2003), it implies that model dynamics may depend crucially on the credibility and transparency of policy changes.
Our model breaks Ricardian equivalence by assuming that some fraction of households simply consume their current after-tax disposable income.4 Accordingly, the short-run fiscal multiplier associated with temporary increases in government spending exceeds unity and the response of private consumption is positive. The inclusion of both non-Ricardian agents and of information frictions in our model can account for a highly persistent fiscal multiplier similar to that in FRB/Global.5
But our comparisons also reveal some noticeable quantitative disparities between the SIGMA and FRB/Global models. First, import prices adjust much more quickly and completely to exchange rate changes in SIGMA, with full exchange rate passthrough after a few quarters. Second, SIGMA tends to imply substantially greater volatility in the expenditure components of GDP than FRB/Global. Finally, SIGMA tends to imply smaller and less persistent spillover effects from foreign shocks to the domestic economy (though the disparity is small if the increase in foreign demand is investment-driven).
We argue that these differences are particularly significant insofar as they stem from features of our SDGE framework that appear robust to reasonable departures from our benchmark calibration; specifically, they reflect certain restrictive theoretical constraints that are likely to hold in a broad class of current open economy SDGE models. For instance, high exchange rate passthrough after a few quarters is likely to characterize any model in which the desired price markup is either fixed (as in SIGMA) or exhibits only modest variation. In turn, the large volatility in expenditure components is partly attributable to high passthrough, and to a marked sensitivity of private absorption to very persistent changes in real interest rates. Finally, insofar as SIGMA relies on trade linkages to account for spillover effects from foreign demand disturbances - a feature common to most open economy SDGE models - it may understate the importance of spillovers arising through other channels, including financial linkages.
Nothwithstanding some limitations, the SDGE framework possesses some key advantages over existing econometric models as a tool for policy analysis. The last section of our paper focuses on some of these advantages in the context of longer-term simulations of SIGMA, including simulations of cuts in distortionary tax rates, and of a productivity acceleration. One advantage of the SDGE framework is that it facilitates assessing how structural features of the economy affect its responses to shocks. For example, it is often of interest to consider how the effects of a tax cut depend on the elasticity of household labor supply, or on extent to which households are Ricardian in their consumption behavior. Such experiments are more difficult to design in typical large-scale econometric models in which there may exist no clear linkage between structural features and reduced form parameters. Another major advantage of the SDGE framework for policy questions is that it fully articulates the channels through which the economy returns to its balanced growth path following initial "imbalances." For instance, in the case of the productivity acceleration, we illustrate the economic forces that induce the trade balance to eventually move into surplus following an initial trade deficit, and discuss how different initial perceptions about the underlying shock influence adjustment dynamics.
The remainder of this paper is organized as follows. Section 2 presents our basic open economy model. The calibration is discussed in Section 3. Section 4 compares short-run impulse response functions in SIGMA and FRB/Global for an array of shocks frequently considered in policy analysis. Section 5 examines long-run simulations in SIGMA under alternative calibrations. Section 6 concludes and provides a discussion of directions for future research.
2 The Model
Our model consists of two countries that may differ in size, but are otherwise isomorphic.6 Hence, our exposition below focuses on the "home" country. Each country in effect produces a single domestic output good, although we adopt a standard monopolistically competitive framework to rationalize stickiness in the aggregate price level. While household utility depends on consumption of both the domestic output good and imported goods, it is convenient to assume that a competitive distribution sector purchases both inputs, and simply resells a final consumption good to households. Similarly, we assume that competitive distributors combine the domestic output good with imports to produce a final investment good.
To introduce non-Ricardian consumption behavior, we assume that there are two types of households. One type of households maximize welfare subject to an intertemporal budget constraint. These households own the entire capital stock, accumulate capital subject to adjustment costs, and exhibit habit persistence in their consumption decisions. They are also regarded as monopolistic competitors in the labor market to account for aggregate wage stickiness. The other set of households ("hand-to-mouth" households) simply consume their entire after-tax disposable income.
2.1 Firms and Price Setting
Production of Domestic Intermediate Goods. There is a continuum of differentiated intermediate goods (indexed by i ∈ [0, 1]) in the home country, each of which is produced by a single monopolistically competitive firm. As in Betts and Devereux (1996), intermediate goods firms charge different prices at home and abroad (i.e., they practice local currency pricing). In the home market, firm i faces a demand function that varies inversely with its output price PDt(i) and directly with aggregate demand at home YDt :
![$\displaystyle Y_{Dt}(i) =\left[ \frac{P_{Dt}(i) }{P_{Dt}}\right] ^{\frac{-\left( 1+\theta _{p}\right) }{\theta _{p}}}Y_{Dt},$](img9.gif)
|
(1) |
where φp > 0, and PDt is an aggregate price index defined below. Similarly, in the foreign market, firm i faces the demand function:
![$\displaystyle X_{t}(i) =\left[ \frac{P^{*}_{Mt}(i)}{P^{*}_{Mt}}\right] ^{\frac{-\left( 1+\theta _{p}\right) }{\theta _{p}}}M^{*}_{t},$](img13.gif)
|
(2) |
where ![]() denotes the foreign quantity
demanded of home good i,
denotes the foreign quantity
demanded of home good i,
![]() denotes the price that firm
i sets in the foreign market (denominated in
foreign currency),
denotes the price that firm
i sets in the foreign market (denominated in
foreign currency),
![]() is the foreign import price index,
and
is the foreign import price index,
and ![]() is aggregate foreign imports (we
use an asterisk to denote foreign variables).
is aggregate foreign imports (we
use an asterisk to denote foreign variables).
Each producer utilizes capital services Kt(i) and a labor index Lt(i) (defined below) to produce its respective output good. The production function is assumed to have a constant-elasticity of substitution (CES) form:
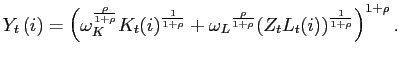
|
(3) |
The production function exhibits constant-returns-to-scale in both inputs, and technological progress Zt is given by:
| (4) |
where zt is a country-specific shock to the level of technology and gz, the deterministic rate of technological growth, is assumed to be the same in both countries. Firms face perfectly competitive factor markets for hiring capital and labor. Thus, each firm chooses Kt(i) and Lt(i), taking as given both the rental price of capital RKt and the aggregate wage index Wt (defined below). Firms can costlessly adjust either factor of production. Thus, the standard static first-order conditions for cost minimization imply that all firms have identical marginal cost per unit of output, MCt.
We assume that the home and foreign prices of the intermediate
goods are determined by Calvo-style staggered contracts (see
Calvo (1983)). In each period, a firm faces a constant
probability, ![]() , of being able to reoptimize its
price at home (
, of being able to reoptimize its
price at home (![]() ) and
) and
![]() probability of being able to
reoptimize its price abroad (
probability of being able to
reoptimize its price abroad (
![]() ). These probabilities are
assumed to be independent across firms, time, and countries. If a
firm is not allowed to optimize its prices, we follow
Christiano, Eichenbaum, and Evans (2005) and assume the firm must reset its home price
based on lagged aggregate inflation (i.e.,
). These probabilities are
assumed to be independent across firms, time, and countries. If a
firm is not allowed to optimize its prices, we follow
Christiano, Eichenbaum, and Evans (2005) and assume the firm must reset its home price
based on lagged aggregate inflation (i.e.,
![]() , where
, where
![]() ).7 In foreign
markets, if a firm cannot reoptimize its price, the price is
changed according to an analogous rule (i.e.,
).7 In foreign
markets, if a firm cannot reoptimize its price, the price is
changed according to an analogous rule (i.e.,
![]() , where
, where
![]() ). This
form of lagged indexation is a mechanism for introducing inflation
inertia into the key price-setting equations.
). This
form of lagged indexation is a mechanism for introducing inflation
inertia into the key price-setting equations.
When firm i is allowed to reoptimize its price in the domestic market in period t, the firm maximizes
![$\displaystyle \widetilde{\mathbb{E}}_{t}\sum_{j=0}^{\infty}\xi_p^{j}\psi _{t,t+j}\left[V_{Dt+j}P_{Dt}\left( i\right) Y_{Dt+j}\left( i\right) -MC_{t+j}Y_{Dt+j}\left( i\right) \right].$](img45.gif)
|
(5) |
The operator
![]() represents the
conditional expectation based on the information available to
agents at period t. The firm discounts profits
received at date t + j by the state-contingent discount
factor
represents the
conditional expectation based on the information available to
agents at period t. The firm discounts profits
received at date t + j by the state-contingent discount
factor
![]() ; for notational simplicity, we
have suppressed all of the state indices.8 Also,
; for notational simplicity, we
have suppressed all of the state indices.8 Also, ![]() is defined by
is defined by
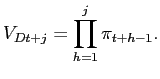 |
(6) |
The first-order condition for setting the contract price of good i in the home market is
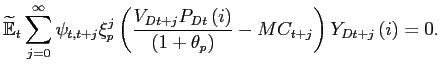
|
(7) |
Defining a similar profit functional to equation (5) for a firm's optimal choice of its contract price in the foreign market at date t, the associated first-order condition is:
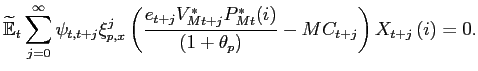
|
(8) |
In equation (8),
et is the price of a unit of foreign
currency in terms of the home currency (so that a rise in
et corresponds to a depreciation of the
home currency), and
![]() is defined as:
is defined as:
 |
(9) |
Production of the Domestic Output Index. Because households have identical Dixit-Stiglitz preferences, it is convenient to assume that a representative aggregator combines the differentiated intermediate products into a composite home-produced good YDt :
![$\displaystyle Y_{Dt}=\left[ \int_{0}^{1}Y_{Dt}\left( i\right) ^{\frac{1}{1+\theta _{p}}}di \right] ^{1+\theta _{p}}.$](img65.gif)
|
(10) |
The aggregator chooses the bundle of goods that minimizes the cost of producing YDt, taking the price PDt(i) of each intermediate good YDt(i) as given. The aggregator sells units of each sectoral output index at its unit cost PDt :
![$\displaystyle P_{Dt}=\left[ \int_{0}^{1}P_{Dt}\left( i\right) ^{\frac{-1\,\,}{\theta _{p}\, }}di\right] ^{-\theta _{p}} .$](img70.gif)
|
(11) |
We also assume a representative aggregator in the foreign economy who combines the differentiated home products Xt(i) into a single index for foreign imports:
![$\displaystyle M^{*}_{t}=\left[ \int_{0}^{1}X_{t}\left( i\right) ^{\frac{1}{1+\theta _{p}}}di \right] ^{1+\theta _{p}},$](img72.gif)
|
(12) |
and sells ![]() at price
at price
![]() :
:
![$\displaystyle P^{*}_{Mt}=\left[ \int_{0}^{1}P^{*}_{Mt}\left( i\right) ^{\frac{-1\,\,}{\theta _{p}\, }}di\right] ^{-\theta _{p}}.$](img75.gif)
|
(13) |
Production of Consumption and Investment Goods. Final consumption goods are produced by a representative "consumption good distributor." This firm combines purchases of domestically-produced goods with imported goods to produce a final consumption good (Ct ) according to a constant-returns-to-scale CES production function:
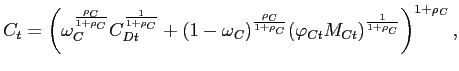
|
(14) |
where CDt denotes the consumption good
distributor's demand for the index of domestically-produced goods,
MCt denotes the distributor's demand for
the index of foreign-produced goods, and
![]() reflects costs of adjusting
consumption imports. The form of the production function mirrors
the preferences of households over consumption of
domestically-produced goods and imports. Accordingly, the
quasi-share parameter
reflects costs of adjusting
consumption imports. The form of the production function mirrors
the preferences of households over consumption of
domestically-produced goods and imports. Accordingly, the
quasi-share parameter
![]() may be interpreted as determining
household preferences for home relative to foreign goods, or
equivalently, the degree of home bias in household consumption
expenditure. Finally, the adjustment cost term
may be interpreted as determining
household preferences for home relative to foreign goods, or
equivalently, the degree of home bias in household consumption
expenditure. Finally, the adjustment cost term
![]() is assumed to take the
quadratic form:
is assumed to take the
quadratic form:
![$\displaystyle \varphi _{Ct}=\left[ 1-\frac{\varphi _{M_{C}}}{2}\left( \frac{\frac{M_{Ct}}{C_{Dt}}}{\frac{M_{Ct-1}}{C_{Dt-1}}}-1\right) ^{2}\right].$](img83.gif)
|
(15) |
This specification implies that it is costly to change the proportion of domestic and foreign goods in the aggregate consumption bundle, even though the level of imports may jump costlessly in response to changes in overall consumption demand. It aims to capture the intuitively-appealing notion that households may have limited ability in the short-run to vary the mix of domestic relative to foreign goods in producing consumption services, even if longer-run substitution possibilities are more favorable. From an empirical perspective, our specification is consistent with evidence which suggests that imports adjust slowly in response to relative price changes, but respond rapidly to changes in real activity, e.g., McDaniel and Balistreri (2003).
Given the presence of adjustment costs, the representative
consumption goods distributor chooses (a contingency plan for)
CDt and MCt to minimize
its discounted expected costs of producing the aggregate
consumption good:
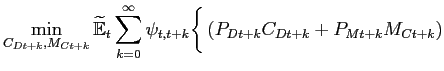
|
(16) |
![$\displaystyle \left.+P_{Ct+k}\left[ C_{t+k}-\left( \omega_{C}^{\frac{\rho_{C}}{1+\rho_{C}} }C_{Dt+k}^{\frac{1}{1+\rho_{C}}}+(1-\omega_{C})^{\frac{\rho_{C}}{1+\rho_{C}}}(\varphi _{Ct+k}M_{Ct+k})^{\frac{1}{1+\rho _{C}}}\right) ^{1+\rho _{C}} \right]\right\}. \notag$](img87.gif)
|
The distributor sells the final consumption good to households at a price PCt, which may be interpreted as the consumption price index (or equivalently, as the shadow cost of producing an additional unit of the consumption good).
We model the production of final investment goods in an analogous manner. Thus, the representative "investment goods distributor" produces a final investment good by combining its purchases of domestically-produced goods with purchases of foreign-produced goods according to a constant-returns-to-scale CES production function:
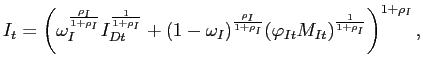
|
(17) |
where IDt denotes the investment goods
distributor's demand for the index of domestically-produced goods,
MIt denotes the distributor's demand for
the index of foreign goods, and
![]() reflects costs of adjusting
imports of investment goods. As in the case of consumption goods,
the quasi-share parameter
reflects costs of adjusting
imports of investment goods. As in the case of consumption goods,
the quasi-share parameter
![]() may be interpreted as determining
the degree of home bias in the production of final investment
goods. The adjustment cost
may be interpreted as determining
the degree of home bias in the production of final investment
goods. The adjustment cost
![]() takes a form that is analogous
to the adjustment cost specification for imported consumption
goods, so that:
takes a form that is analogous
to the adjustment cost specification for imported consumption
goods, so that:
![$\displaystyle \varphi _{It}=\left[ 1-\frac{\varphi _{M_{I}}}{2}\left( \frac{\frac{M_{It}}{ I_{Dt}}}{\frac{M_{It-1}}{I_{Dt-1}}}-1\right) ^{2}\right].$](img95.gif)
|
(18) |
Investment goods distributors solve an intertemporal cost minimization problem isomorphic to that of consumption goods distributors. Each distributor sells the final investment good to households at a price PIt , which may be interpreted as the investment price index. This price may differ from the price index of the consumption good PCt because of differences in import composition, even in the absence of the adjustment costs for consumption and investment imports.
2.2 Households and Wage Setting
We assume a continuum of monopolistically competitive households (indexed on the unit interval), each of which supplies a differentiated labor service to the intermediate goods-producing sector (the only producers demanding labor services in our framework). It is convenient to assume that a representative labor aggregator (or "employment agency") combines households' labor hours in the same proportions as firms would choose. Thus, the aggregator's demand for each household's labor is equal to the sum of firms' demands. The aggregate labor index Lt has the Dixit-Stiglitz form:
![$\displaystyle L_{t}=\left[ \int_{0}^{1}\left( \zeta_{t}N_{t}\left( h\right) \right) ^{\frac{ 1}{1+\theta _{w}}}dh\right] ^{1+\theta_{w}},$](img99.gif)
|
(19) |
where
![]() and
and ![]() is hours worked by a typical member of household h.
Also,
is hours worked by a typical member of household h.
Also,
![]() is the size of a household of
type h and evolves according to
is the size of a household of
type h and evolves according to
![]() (effectively,
(effectively,
![]() and
and ![]() determine
the size and growth rate of the population). The aggregator
minimizes the cost of producing a given amount of the aggregate
labor index, taking each household's wage rate
Wt(h) as given, and then
sells units of the labor index to the production sector at their
unit cost Wt :
determine
the size and growth rate of the population). The aggregator
minimizes the cost of producing a given amount of the aggregate
labor index, taking each household's wage rate
Wt(h) as given, and then
sells units of the labor index to the production sector at their
unit cost Wt :
![$\displaystyle W_{t}=\left[ \int_{0}^{1}W_{t}{}\left( h\right) ^{\frac{-1}{\theta _{w}}}dh \right] ^{-\theta _{w}}.$](img110.gif)
|
(20) |
It is natural to interpret Wt as the aggregate wage index. The aggregator's demand for the labor services of a typical member of household h is given by
![$\displaystyle N_{t}\left( h\right) =\left[ \frac{W_{t}\left( h\right) }{W_{t}}\right] ^{- \frac{1+\theta _{w}}{\theta _{w}}}L_{t}/\zeta_{t}.$](img113.gif)
|
(21) |
We assume that there are two types of households: households that make intertemporal consumption, labor supply, and capital accumulation decisions in a forward-looking manner by maximizing utility subject to an intertemporal budget constraint (FL households, for "forward-looking"); and the remainder that simply consume their after-tax disposable income (HM households, for "hand-to-mouth" households). The latter type receive no capital rental income or profits, and choose to set their wage to be the average wage of optimizing households. Given that households of each type grow at the same rate, the share of each type of household in the population is fixed. We denote the share of FL households by ς and the share of HM households by 1 - ς.
We consider first the problem faced by FL households. The utility functional for an optimizing representative member of household h is
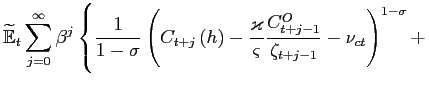
|
|
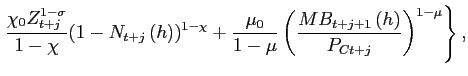
|
(22) |
where the discount factor β satisfies 0 < β < 1. As in Smets and Wouters (2003), we
allow for the possibility of external habits, where each household
member cares about its consumption relative to lagged aggregate
consumption per capita of optimizing agents,
![]() . The
period utility function depends on an each member's current leisure 1 -
Nt(h), his end-of-period
real money balances,
. The
period utility function depends on an each member's current leisure 1 -
Nt(h), his end-of-period
real money balances,
![]() , and
a preference shock,
, and
a preference shock, ![]() . We allow for
preferences over leisure to shift with the level of technology so
that the model is consistent with balanced growth, even if the
subutility function over consumption is not logarithmic.9
. We allow for
preferences over leisure to shift with the level of technology so
that the model is consistent with balanced growth, even if the
subutility function over consumption is not logarithmic.9
Household h faces a flow budget constraint in period t which states that its combined expenditure on goods and on the net accumulation of financial assets must equal its disposable income:
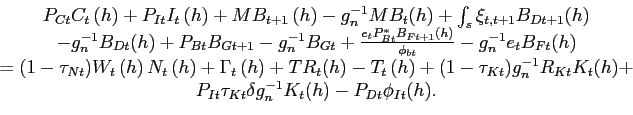
|
(23) |
The presence of the population growth parameter gn in the household's budget constraint reflects that equation (23) is expressed in per capita terms as well as the assumption that new household members are born without any initial holdings of bonds, capital, or money. Final consumption goods are purchased at a price PCt , and final investment goods at a price PIt . Investment in physical capital augments the per capita capital stock Kt+1 (h) according to a linear transition law of the form:
| (24) |
where δ is the depreciation rate of capital.
Financial asset accumulation of a typical member of FL household
h consists of increases in nominal money
holdings (
![]() and
the net acquisition of bonds. We assume that agents within a
country can engage in frictionless trading of a complete set of
contingent claims, while trade in international assets is
restricted to a non-state contingent nominal bond. The term
and
the net acquisition of bonds. We assume that agents within a
country can engage in frictionless trading of a complete set of
contingent claims, while trade in international assets is
restricted to a non-state contingent nominal bond. The term
![]() represents
each household member's net purchases of domestic government bonds,
while
represents
each household member's net purchases of domestic government bonds,
while
![]() are net
purchases of state-contingent domestic bonds. We denote
are net
purchases of state-contingent domestic bonds. We denote
![]() as the price of an asset that
will pay one unit of domestic currency in a particular state of
nature at date t + 1, while
as the price of an asset that
will pay one unit of domestic currency in a particular state of
nature at date t + 1, while
![]() represents the
quantity of such claims purchased by a typical member of household
h at time t. Thus, the gross
outlay on new state-contingent domestic claims is given by
integrating over all states at time t + 1, while
represents the
quantity of such claims purchased by a typical member of household
h at time t. Thus, the gross
outlay on new state-contingent domestic claims is given by
integrating over all states at time t + 1, while
![]() indicates the value
of the household's existing claims (on a per capita basis) given
the realized state of nature.
indicates the value
of the household's existing claims (on a per capita basis) given
the realized state of nature.
In equation (23),
![]() represents the quantity of a
non-state contingent bond purchased by a typical member of
household h at time t that pays
one unit of foreign currency in the subsequent period,
represents the quantity of a
non-state contingent bond purchased by a typical member of
household h at time t that pays
one unit of foreign currency in the subsequent period,
![]() is the foreign currency price
of the bond, and
is the foreign currency price
of the bond, and ![]() is the exchange rate expressed
in units of home currency per unit of foreign currency. We follow
Turnovsky (1985) and assume there is an intermediation cost
is the exchange rate expressed
in units of home currency per unit of foreign currency. We follow
Turnovsky (1985) and assume there is an intermediation cost
![]() paid by households in the home
country for purchases of foreign bonds, which ensures that net
foreign assets are stationary in the model.10 More
specifically, the intermediation costs depend on the ratio of
economy-wide holdings of net foreign assets to nominal GDP,
paid by households in the home
country for purchases of foreign bonds, which ensures that net
foreign assets are stationary in the model.10 More
specifically, the intermediation costs depend on the ratio of
economy-wide holdings of net foreign assets to nominal GDP,
![]() , and are given by:
, and are given by:
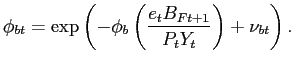
|
(25) |
In the above, ![]() is a mean-zero stochastic
process, which we interpret as a risk-premium shock or shock to the
uncovered interest-rate parity condition. Abstracting from this
shock, if the home economy has an overall net lender position
internationally, then a household will earn a lower return on any
holdings of foreign bonds. By contrast, if the economy has a net
debtor position, a household will pay a higher return on its
foreign liabilities.
is a mean-zero stochastic
process, which we interpret as a risk-premium shock or shock to the
uncovered interest-rate parity condition. Abstracting from this
shock, if the home economy has an overall net lender position
internationally, then a household will earn a lower return on any
holdings of foreign bonds. By contrast, if the economy has a net
debtor position, a household will pay a higher return on its
foreign liabilities.
Each member of FL household h earns after-tax
labor income,
![]() ,
where
,
where ![]() is a stochastic tax on labor
income. The household leases capital to firms at the after-tax
rental rate
is a stochastic tax on labor
income. The household leases capital to firms at the after-tax
rental rate
![]() , where
, where ![]() is a stochastic tax on capital income. The
household receives a depreciation writeoff of
is a stochastic tax on capital income. The
household receives a depreciation writeoff of
![]() per unit of capital.
Each member also receives an aliquot share
per unit of capital.
Each member also receives an aliquot share
![]() of the profits of
all firms and a lump-sum government transfer,
of the profits of
all firms and a lump-sum government transfer,
![]() and pays a lump-sum
tax
and pays a lump-sum
tax ![]() . Following Christiano, Eichenbaum, and Evans (2005), we
assume that it is costly to change the level of gross investment
from the previous period, so that the acceleration in the capital
stock is penalized:
. Following Christiano, Eichenbaum, and Evans (2005), we
assume that it is costly to change the level of gross investment
from the previous period, so that the acceleration in the capital
stock is penalized:
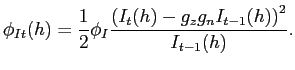
|
(26) |
In every period t, each member of FL household h maximizes the utility functional (22) with respect to its consumption, investment, (end-of-period) capital stock, money balances, holdings of contingent claims, and holdings of foreign bonds, subject to its labor demand function (21), budget constraint (23), and transition equation for capital (24). In doing so, a household takes as given prices, taxes and transfers, and aggregate quantities such as lagged aggregate consumption and the aggregate net foreign asset position.
Forward-looking (FL) households set nominal wages in staggered
contracts that are analogous to the price contracts described
above. In particular, with probability ![]() , each
member of a household is allowed to reoptimize its wage contract.
If a household is not allowed to optimize its wage rate, we assume
each household member resets its wage according to:
, each
member of a household is allowed to reoptimize its wage contract.
If a household is not allowed to optimize its wage rate, we assume
each household member resets its wage according to:
| (27) |
where
![]() and in steady state
and in steady state
![]() .11 Each member of
household h chooses the value of
.11 Each member of
household h chooses the value of ![]() to maximize its utility functional (22), yielding the
following first-order condition:
to maximize its utility functional (22), yielding the
following first-order condition:
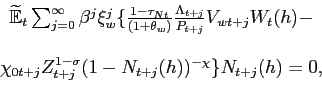
|
(28) |
where
![]() is the marginal value of a unit
of consumption, and
is the marginal value of a unit
of consumption, and ![]() is defined as:
is defined as:
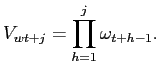 |
(29) |
Roughly speaking, equation (28) says that the household chooses its contract wage to equate the present discounted value of working an additional unit of time to the discounted marginal cost.
Finally, we consider the determination of consumption and labor supply of the hand-to-mouth (HM) households. A typical member of a HM household simply equates his nominal consumption spending to his current after-tax disposable income, which consists of labor income plus net lump-sum transfers from the government:
| (30) |
The HM households set their wage to be the average wage of the forward-looking households. Since HM households face the same labor demand schedule as the forward-looking households, each HM household works the same number of hours as the average for forward-looking households.
2.3 Monetary Policy
We assume that the central bank follows an interest rate reaction function similar in form to the historical rule estimated by Orphanides and Wieland (1998) over the Volcker-Greenspan period. Thus, the short-term nominal interest rate is adjusted so that the ex post real interest rate rises when inflation exceeds its constant target value, or when output growth rises above some target value. With some allowance for interest rate smoothing, monetary policy is described by the following interest rate reaction function:
| (31) |
In the above, ![]() is the annualized nominal interest
rate,
is the annualized nominal interest
rate,
![]() is the four-quarter inflation
rate of the GDP deflator (i.e.,
is the four-quarter inflation
rate of the GDP deflator (i.e.,
![]() ),
),
![]() and
and
![]() are the steady-state real
interest rate and the central bank's constant inflation target
(both expressed at annual rate). Also,
are the steady-state real
interest rate and the central bank's constant inflation target
(both expressed at annual rate). Also,
![]() is the four-quarter growth
rate of output, and
is the four-quarter growth
rate of output, and ![]() is its corresponding
steady state value.
is its corresponding
steady state value.
2.4 Fiscal Policy
Some of the domestically-produced good is purchased by the
government. Government purchases (Gt ) are
assumed to have no direct effect on the utility of a
household.12 We also assume that government
purchases as a fraction of output,
![]() , follow
an exogenous stochastic process.
, follow
an exogenous stochastic process.
The government can issue debt ![]() to finance
a deficit so that its budget constraint is given by:
to finance
a deficit so that its budget constraint is given by:
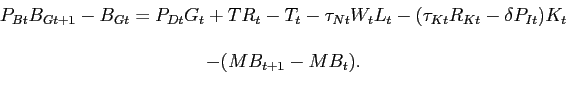
|
(32) |
In equation (32),
we have aggregated the capital stock, money and bond holdings, and
transfers and taxes over all households so that, for example,
![]() . As noted
above, labor and capital taxes are determined exogenously, while we
assume that real transfers as a fraction of domestic output,
. As noted
above, labor and capital taxes are determined exogenously, while we
assume that real transfers as a fraction of domestic output,
![]() , evolve
according to an exogenous stochastic process. Given that the
central bank uses the nominal interest rate as its policy
instrument, the level of seignorage revenues are determined by
nominal money demand.
, evolve
according to an exogenous stochastic process. Given that the
central bank uses the nominal interest rate as its policy
instrument, the level of seignorage revenues are determined by
nominal money demand.
Lump-sum taxes are adjusted in a manner that the government
satisfies an intertemporal solvency constraint, requiring that the
present discounted value of the government debt stock tends toward
zero in the long run. In particular, we assume that the real
lump-sum tax rate,
![]() , is
determined according to the following reaction function:
, is
determined according to the following reaction function:
| (33) |
where
![]() and
and
![]() is the government's target value for the
ratio of government debt to nominal output.13
is the government's target value for the
ratio of government debt to nominal output.13
2.5 Resource Constraint and Net Foreign Assets
The home economy's aggregate resource constraint can be written as:
| (34) |
and ![]() is the adjustment cost on
investment aggregated across all households. Total exports may be
allocated to either the consumption or the investment sector
abroad:
is the adjustment cost on
investment aggregated across all households. Total exports may be
allocated to either the consumption or the investment sector
abroad:
| (35) |
Finally, at the level of the individual firm:
| (36) |
The evolution of net foreign assets can be expressed as:

|
(37) |
This expression can be derived from the budget constraint of the FL
households after imposing the government budget constraint, the
consumption rule of the HM households, the definition of firm
profits, and the condition that domestic bonds (![]() ) are in zero net supply.14
) are in zero net supply.14
Finally, we assume that the structure of the foreign economy (the "rest of the world") is isomorphic to that of the home country.
2.6 Description of Shocks and the Optimal Filtering Problem
As discussed above, our model includes shocks to the level of
home productivity (![]() real government
spending (
real government
spending (![]() ), real transfers (
), real transfers (![]() , labor tax rate (
, labor tax rate (![]() ), capital
tax rate (
), capital
tax rate (![]() ), preferences (
), preferences (![]() ), and similar shocks to the foreign country (which
may be regarded as alternative sources of foreign demand shocks
from the perspective of the home country). In addition, it includes
a shock to the financial intermediation technology (
), and similar shocks to the foreign country (which
may be regarded as alternative sources of foreign demand shocks
from the perspective of the home country). In addition, it includes
a shock to the financial intermediation technology (![]() ), which can be interpreted as a risk premium
shock.
), which can be interpreted as a risk premium
shock.
We assume that the each shock in the model has two underlying
components with different levels of persistence. Agents observe the
shock, but they cannot observe the separate components. It is
helpful to illustrate the nature of the forecasting problem with
reference to a particular shock, since the treatment of the other
shocks is basically isomorphic. Thus, focusing on the case of the
productivity growth shock examined in Section 5 below, and
recalling from equation (4) that
productivity growth can be written as
![]() , our
approach attributes changes in
, our
approach attributes changes in ![]() to two separate
components:
to two separate
components:
| (38) |
The first component,
![]() , is a highly persistent shock
that shifts the "trend" level of productivity growth, and the
second,
, is a highly persistent shock
that shifts the "trend" level of productivity growth, and the
second,
![]() , is a transient shock to
productivity growth. The bivariate process determining the
evolution of each component may be represented as:
, is a transient shock to
productivity growth. The bivariate process determining the
evolution of each component may be represented as:
![\begin{displaymath}\begin{array}{c} \left[ \begin{array}{c} \Delta z_{Pt} \\ \Delta z_{Tt} \end{array} \right] =\left[ \begin{array}{cc} \rho _{p} & 0 \\ 0 & 0 \end{array} \right] \left[ \begin{array}{c} \Delta z_{Pt-1} \\ \Delta z_{Tt-1} \end{array} \right] +\left[ \begin{array}{c} \varepsilon _{Pt} \\ \varepsilon _{Tt} \end{array} \right], \end{array}\end{displaymath}](img217.gif)
|
(39) |
where the persistence parameter ![]() is assumed
to be slightly below unity, and the transient shock is assumed to
be i.i.d. in the case of this particular shock (for other
shocks, e.g., to government spending, we allow the transient
component to be somewhat persistent, though much less persistent
than the permanent shock). Thus, an innovation to the growth rate
of the transient component has a permanent effect on the level of
productivity, but no effect on the future growth rate. Moreover,
the innovations
is assumed
to be slightly below unity, and the transient shock is assumed to
be i.i.d. in the case of this particular shock (for other
shocks, e.g., to government spending, we allow the transient
component to be somewhat persistent, though much less persistent
than the permanent shock). Thus, an innovation to the growth rate
of the transient component has a permanent effect on the level of
productivity, but no effect on the future growth rate. Moreover,
the innovations
![]() and
and
![]() are mutually uncorrelated
with variances
are mutually uncorrelated
with variances ![]() and
and ![]() ,
respectively.
,
respectively.
Agents observe the current level of productivity in the economy,
and hence observe
![]() but cannot observe the growth
rate of the underlying components
but cannot observe the growth
rate of the underlying components
![]() and
and
![]() . Thus, agents solve a signal
extraction problem to forecast the future level of productivity.
Given that agents know the underlying parameters of the bivariate
process for productivity growth, the Kalman filter can be used to
obtain an optimal solution.
. Thus, agents solve a signal
extraction problem to forecast the future level of productivity.
Given that agents know the underlying parameters of the bivariate
process for productivity growth, the Kalman filter can be used to
obtain an optimal solution.
The expected level of productivity at a future date K periods
ahead depends only on the current level of productivity, and on the
expected growth rate of the permanent component:
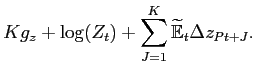
|
(40) |
The Kalman filtering algorithm implies that the expected growth rate of the permanent component is updated according to:
| (41) |
Thus, agents update their assessment of the persistent component of
the productivity growth process by the product of the forecast
error innovation and a constant coefficient. This coefficient,
which is proportional to the scalar Kalman gain parameter
kg is an increasing function of the
signal-to-noise ratio
![]() (the ratio of the
variances of the persistent and transitory components of the
productivity growth process).
(the ratio of the
variances of the persistent and transitory components of the
productivity growth process).
3 Solution Method and Calibration
Because the levels of technology and the population are non-stationary, real variables (including output and the expenditure components of GDP) are also non-stationary. Accordingly, prior to solving the model, we scale real variables in the home and foreign country by the common deterministic trends in technology and population size. Nominal variables are scaled to account both for growth in the corresponding real variable, and for the steady state inflation rate.
We solve the model by log-linearizing the equations (specified in terms of the transformed variables) around the steady state associated with common growth rates of technology and population in the two countries. To obtain the reduced-form solution of the model, we use the numerical algorithm of Anderson and Moore (1985), which provides an efficient implementation of the method proposed by Blanchard and Kahn (1980) (see also Anderson (1997)).15
3.1 Calibration of Parameters
The model is calibrated at a quarterly frequency. Structural
parameters are set at identical values for each of the two
countries, except for the parameters determining population size
(as discussed below). We assume that the discount factor β = 0.997 and the rate of technological
growth gz = 1.0037. These values are consistent
with a steady-state annualized real interest rate
![]() of about 3 percent.
of about 3 percent.
The utility functional parameter σ is set
equal to 2, while the parameter determining the degree of habit
persistence in consumption
![]() . We set χ = 10, implying a Frisch elasticity of labor supply of
1/5, which is considerably lower than if preferences were
logarithmic in leisure, but well within the range of most empirical
estimates. The utility parameter χ0 is set so
that employment comprises one-third of the household's time
endowment, while the parameter μ0 on the
subutility function for real balances is set at an arbitrarily low
value (although given the separable specification, variation in
real balances has no impact on other variables). We choose
ς = 0.5 so that 50 percent of
households are Ricardian FL agents.16
. We set χ = 10, implying a Frisch elasticity of labor supply of
1/5, which is considerably lower than if preferences were
logarithmic in leisure, but well within the range of most empirical
estimates. The utility parameter χ0 is set so
that employment comprises one-third of the household's time
endowment, while the parameter μ0 on the
subutility function for real balances is set at an arbitrarily low
value (although given the separable specification, variation in
real balances has no impact on other variables). We choose
ς = 0.5 so that 50 percent of
households are Ricardian FL agents.16
The depreciation rate of capital δ is set
at 0.025 (consistent with an annual depreciation rate of 10
percent). We fix the price and wage markup parameters so that
![]() =
=
![]() = 0.20, similar to the estimated
values obtained by Rotemberg and Woodford (1999) and Amato and Laubach (2003).17 We
set
= 0.20, similar to the estimated
values obtained by Rotemberg and Woodford (1999) and Amato and Laubach (2003).17 We
set ![]() and
and ![]() to be
consistent with four-quarter contracts (subject to full
indexation).18 The parameter
to be
consistent with four-quarter contracts (subject to full
indexation).18 The parameter ![]() is chosen to be consistent with two-quarter
contracts.19 We set the steady state inflation
rate π to yield an annual inflation rate of
four percent.
is chosen to be consistent with two-quarter
contracts.19 We set the steady state inflation
rate π to yield an annual inflation rate of
four percent.
The parameter ρ in the CES production function
of the intermediate goods producers is set to -2, implying an
elasticity of substitution between capital and labor of 1/2. Thus,
capital and labor are less substitutable than the unitary
elasticity case implied by the Cobb-Douglas specification. The
quasi-capital share parameter
![]() is chosen to imply a steady
state investment to output ratio of 20 percent. The private
consumption to output ratio is 70 percent, while government
consumption is 10 percent of steady state output. We set the cost
of adjusting investment parameter
is chosen to imply a steady
state investment to output ratio of 20 percent. The private
consumption to output ratio is 70 percent, while government
consumption is 10 percent of steady state output. We set the cost
of adjusting investment parameter
![]() , slightly below the value used
by Christiano, Eichenbaum, and Evans (2005).
, slightly below the value used
by Christiano, Eichenbaum, and Evans (2005).
The parameter
![]() is chosen to match the estimated
average share of imports in total U.S. consumption of about 9
percent (based on data from the U.S. Bureau of Economic Analysis);
while the parameter
is chosen to match the estimated
average share of imports in total U.S. consumption of about 9
percent (based on data from the U.S. Bureau of Economic Analysis);
while the parameter
![]() is chosen to match the average
share of imports in total U.S. investment of about 38 percent.
Given that trade is balanced in steady state, this parameterization
implies an import or export to GDP ratio for the home country (the
United States) of about 13 percent. We choose the initial
population levels
is chosen to match the average
share of imports in total U.S. investment of about 38 percent.
Given that trade is balanced in steady state, this parameterization
implies an import or export to GDP ratio for the home country (the
United States) of about 13 percent. We choose the initial
population levels ![]() and
and
![]() so that the home country
constitutes 25 percent of world output. This implies an import (or
export) share of output of the foreign country of about 3
percent.
so that the home country
constitutes 25 percent of world output. This implies an import (or
export) share of output of the foreign country of about 3
percent.
We assume that
![]() , consistent with a
long-run price elasticity of demand for imported consumption and
investment goods of 1.5. While this is higher than most empirical
estimates using macro data, we emphasize that the presence of
adjustment costs translates into a much lower relative price
sensitivity in the short to medium-term. In particular, we set the
adjustment cost parameters
, consistent with a
long-run price elasticity of demand for imported consumption and
investment goods of 1.5. While this is higher than most empirical
estimates using macro data, we emphasize that the presence of
adjustment costs translates into a much lower relative price
sensitivity in the short to medium-term. In particular, we set the
adjustment cost parameters
![]() =
=
![]() = 10, implying a
price-elasticity near unity after four quarters. We choose a small
value (0.001) for the financial intermediation cost
= 10, implying a
price-elasticity near unity after four quarters. We choose a small
value (0.001) for the financial intermediation cost ![]() , which is sufficient to ensure the model has a unique
steady state.
, which is sufficient to ensure the model has a unique
steady state.
We estimated the parameters of the monetary policy rule using U.S. data from 1983:1-2003:4.20 Our estimates imply γπ = 0.6, γy = 0.28, and γi = 0.8. For the tax rate reaction function, we choose ν0 = 1, ν1 = 0.1, ν2 = 0.001, and bG = 0. We set the steady state capital and labor tax rates equal to 0.3 and 0.2, respectively.
4 Comparisons of SIGMA and FRB/Global
We now turn to assessing the short-run properties of our SIGMA model, comparing the implications of SIGMA with those of FRB/Global for an array of shocks often considered in policy analysis. To facilitate comparison across models, we specify the monetary policy rule in FRB/Global to be the same as in the benchmark version of SIGMA.
4.1 Loosening of Monetary Policy
We begin by examining the effects of a transient innovation to the monetary policy rule in SIGMA, i.e., a rise in εit in equation (31). The shock is scaled to induce an initial decline in the short-term nominal interest rate of about 75 basis points. As shown in Figure 1, this policy shock raises output by slightly less than 0.2 percent after 2-3 quarters. The response of investment is roughly three times larger than the response of consumption, reflecting the higher interest-sensitivity of the former. The fall in domestic real interest rates drives a modest depreciation of the real exchange rate (a rise in the figure), which pushes up import prices (not shown). The combination of a positive output gap and higher import prices causes consumer price inflation to rise.
While the figure shows that the qualitative effects of the shock are similar in FRB/Global, the peak effects on real GDP and the expenditure components are noticeably larger in FRB/Global than in SIGMA. This primarily reflects that long-term real interest rates (which are determined by a small-scale vector autoregression in FRB/Global) drop much more sharply and persistently than in SIGMA (in which long-term real rates are effectively determined by the expectations hypothesis). Given this disparity in the long-term real interest rate responses, it is useful to control for differences in the simulation results that are attributable to alternative term structure equations. Accordingly, the dash-dotted line in the figure shows an alternative calibration of the shock in SIGMA that implies a response of the 5 year real interest rate that comes very close to matching that in FRB/Global (this calibration assumes that the persistence of the monetary policy error εit in the interest rate reaction function is 0.6 rather than zero as in our benchmark). In this case, the peak responses of GDP and the real expenditure components are very close across the two models; the notable difference is in the inflation response, which is much larger in SIGMA.
These results indicate that the responses of the two models to a monetary policy shock that has similar effects on long-term real interest rates is quite similar across the two models (at least for real variables). However, we caution that the similarity in responses appears sensitive to the persistence of the underlying shock. Thus, the results should not be interpreted more broadly as indicating that the interest-sensitivity of aggregate demand is similar across the two models, irrespective of persistence of the shock's effect on real interest rates. As we show below, SIGMA appears to exhibit a somewhat greater interest-elasticity to shocks that exert highly persistent effects on long-term real interest rates.21
4.2 Rise in Government Spending
Figure 2 shows the effects of an exogenous rise in the U.S. government spending share of GDP of one percentage point relative to baseline. The shock is highly persistent (ρg = 0.975), so that the government spending share remains about 0.6 percentage point above baseline after five years.
The rise in government spending induces an immediate expansion of output. The government spending multiplier exceeds unity in the impact period due to the sharp rise in consumption of the HM households (as implied by the dotted line, the impact multiplier would be below unity if all households were optimizers, reflecting a sharp immediate fall in aggregate consumption). However, rising real interest rates quickly crowd out private investment and the consumption of the interest-sensitive optimizing households, which is depressed further due to the negative wealth effect of higher government spending. In fact, the fall in consumption for the optimizing households is exacerbated by the presence of the HM households, as real interest rates rise even more than would occur if all households were optimizers. Thus, overall private consumption falls below baseline after only a few quarters, and most of the output expansion is reversed. The small but more persistent component of the output increase reflects a rise in labor supply that is induced by the negative wealth effect.
Figure 2 also shows impulse responses derived from the FRB/Global model for a similar-sized rise in government spending. Clearly, the output response is noticeably more persistent in FRB/Global, as output remains nearly 0.4 percent above baseline three years after the shock occurs. The greater persistence of the output response reflects that the crowding out of private investment and consumption spending occurs much more gradually. This partly reflects that negative wealth effects play a less prominent role in depressing consumption in FRB/Global. In addition, private absorption (especially investment) is considerably less sensitive to persistent changes in the long-term real interest rate in FRB/Global, especially in the short-run. Thus, while the responses in SIGMA and FRB/Global are similar qualitatively, the responses in the latter tend to exhibit noticeably greater persistence. The empirical vector autoregression evidence of Blanchard and Perotti (2002) also suggests that government spending shocks exert highly persistent effects on output and on the expenditure components that appear more consistent with the FRB/Global responses.
A plausible channel for inducing greater persistence in the impulse responses of the SIGMA model is to allow for imperfect information, as also shown in the figure (dash-dotted lines).22 Because agents initially perceive that the increase in government spending is temporary under imperfect information, there is a larger increase in GDP in this case than in the benchmark. Furthermore, the rise in GDP is more persistent, as agents only slowly update their beliefs about the persistence of the shock and are continually surprised by the higher-than-expected levels of government spending. Given both a less pronounced rise in real longer-term interest rates and a smaller negative wealth effect (since agents think the government spending rise will be temporary), there is much less crowding out of consumption and investment spending - with consumption even remaining above baseline for a sustained duration. Thus, the inclusion of both non-Ricardian agents and information frictions would seem to provide a tractable channel for increasing the flexibility of SDGE models to account for responses that are similar to large-scale policy models, and to encompass the range of responses derived from empirical vector autoregressions.
4.3 Rise in Home Consumption Demand
Figure 3 assesses the effects of a taste shock νct to equation (22) that raises the marginal utility of consumption. This shock may regarded as tantamount to the "autonomous shift in consumption demand" that is often considered in policy simulations. The shock is scaled so that it induces private consumption to rise by one percent above baseline at peak impact, and has a persistence of 0.975.
The taste shock exerts a highly persistent positive effect on real interest rates, accounting for the immediate rise in the 5 year real interest rate shown in the figure. As a result, the stimulative effects of the rise in consumption demand on output are partly offset by a contraction in investment demand, and by a reduction in real net exports. The latter occurs because higher real interest rates generate an appreciation of the real exchange rate. The exchange rate appreciation causes consumer price inflation to fall in the near-term, although higher demand pressures eventually push up domestic goods prices by enough to cause consumer prices to rise.
These effects are qualitatively similar in the case of an autonomous shock to consumption demand in FRB/Global, i.e., a shock to the statistical residual in the consumption equation that is scaled to have the same effect on consumption. But from a quantitative perspective, the output effects are considerably larger in FRB/Global, because there is less crowding out of investment and a smaller decline in real net exports in that model (not shown). The smaller investment decline in FRB/Global reflects that investment is less sensitive to the long-term real interest rate (noting that long rates rise by a roughly commensurate amount in each model). The smaller decline in real net exports in FRB/Global reflects several factors, including less passthrough of the exchange rate to import prices, modestly lower trade price elasticities, and somewhat smaller real appreciation.
As in the case of the government spending rise, allowing for imperfect information about the persistence of the taste shock allows SIGMA to imply a larger and more persistent output response that is very similar to that in FRB/Global. The more gradual rise in long-term interest rates reduces the magnitude of real exchange rate appreciation, leading to a smaller export decline.
4.4 Fall in Home Currency Risk Premium
Figure 4 shows the effects on the home country of a decline in the risk premium (νbt) on home currency-denominated assets. As in McCallum and Nelson (1999) and in Kollman (2001), in this simulation we shock the exogenous component of the risk premium in the uncovered interest parity condition implied by the log-linearized model. The shock is scaled so that it induces an initial real appreciation of 10 percent, and the persistence of the shock is ρb = 0.95.
This shock reduces the required real return on all home-currency denominated assets relative to the return on foreign assets. The lower required real return on home-currency assets occurs through a combination of persistently lower real interest rates, and through expected real currency depreciation. Thus, long-term real interest rates fall (not shown), and given that the shock has no long-run effect on the real exchange rate, the exchange rate is required to appreciate sharply in the impact period.
The appreciation of the real exchange rate depresses real exports, and raises imports - and thus exerts a contractionary effect on real GDP. However, private domestic absorption is stimulated by lower real interest rates and lower import prices. As a result, real GDP shows only a modest contraction in the near term, and actually rises above baseline after a few years as higher investment spending leads to progressive capital deepening. The combination of stronger domestic demand and real exchange rate appreciation induce a significant deterioration of the nominal trade balance exceeding 1-1/2 percentage points of GDP. Finally, PCE inflation shows a sizeable but transient drop due to declining import prices.
The qualitative effects in FRB/Global are very similar, with the exchange rate appreciation leading to an initial output decline, lower real interest rates, some decline in inflation, and a trade balance deterioration. But while the response of GDP is fairly similar across models, there is considerable quantitative disparity in the responses of the expenditure components: private absorption rises much more in SIGMA than in FRB/Global, and real net exports correspondingly exhibit a larger contraction (not shown, though suggested by the larger trade balance response). A key factor accounting for these differences is that the passthrough of exchange rate changes to import prices is effectively 100 percent after a couple of quarters in SIGMA, whereas it is only about 30 percent in FRB/Global. The higher passthrough directly accounts for the larger effects on real imports and exports in the former model, and contributes significantly to driving the sharper swings in PCE price inflation and private absorption. As noted in the discussion of the government spending shock, the substantial response of private absorption in SIGMA also reflects a highly elastic response to the persistent decline in long-term real interest rates (not shown).
SIGMA's implication of very high exchange rate passthrough to import prices seems at odds with empirical evidence for the United States that estimates long-run passthrough in the range of 20-30 percent.23Importantly, we emphasize that any model in which the desired markup is fixed (as in SIGMA) would appear unable to match the empirical pattern of import price response incorporated into FRB/Global, in which import prices react fairly quickly to exchange rate changes, but then adjust little subsequently. For example, the dash-dotted lines marked "sluggish import prices" use a calibration of SIGMA in which the mean duration of export prices is eight quarters (rather than two quarters as in the baseline). Even in this case of long-lived local currency pricing, exchange rate passthrough is nearly complete after two years, and there is much larger trade adjustment than in FRB/Global.
Given the central role of exchange rate passthrough in affecting the transmission of open economy shocks, we believe that it is of crucial importance to develop a theoretical framework that has the flexibility to account for the empirical features of passthrough evident in U.S. data. While some microfounded models can account for long-run passthrough that is below unity, including models with a distribution sector for retail goods as in Corsetti and Dedola (2003), and Corsetti, Dedola, and LEduc (2005), such models do not allow enough variation in desired markups to come close to matching the low level of passthrough in U.S. data.24 Without much variation in the desired markup, models such as SIGMA imply implausibly large expenditure-switching effects in response to exchange rate movements that may limit their usefulness in addressing some important policy questions. Moreover, such restrictions may lead to large biases in the estimates of structural parameters.
4.5 Alternative Foreign Demand Shocks
Figure 5 shows the effect on the home country of a rise in foreign investment demand. Specifically, investment in the foreign country increases due to a highly persistent decline in its capital income tax rate; but it is useful to interpret the shock more broadly as reflecting changes in the investment climate abroad that boost the perceived return to capital. The shock is scaled so that foreign output eventually rises by 1 percent relative to baseline.
This foreign investment demand shock operates through similar channels both in SIGMA and in FRB/Global, and has qualitatively similar effects in each. Thus, the rise in foreign demand stimulates home real net exports, both directly because of the rise in foreign absorption, and indirectly through a depreciation of the home country's real exchange rate (not shown). This raises home output, though the stimulative effect on GDP arising from higher net exports is partly offset by declining private absorption (as domestic interest rates rise). The rise in real net exports generates an improvement in the nominal trade balance, while consumer prices rise due to higher import prices and stronger activity.
From a quantitative perspective, the "spillover effects" of the foreign demand increase on the home country are broadly similar for the first two years following the shock across the two models. This suggests that SDGE models may account for substantial spillover effects through trade channels in response to certain types of shocks, although we caution that the fact that the shock affects foreign investment spending - which is heavily import-intensive - plays an important role in accounting for the relatively large effects. In addition, the spillover effects would decline if SIGMA incorporated lower exchange rate passthrough, since this would diminish the magnitude of the home country's export improvement. It is also evident that SIGMA implies much greater volatility in the expenditure components than FRB/Global. The trade balance exhibits a much larger improvement, and the components of private absorption fall much more sharply than in FRB/Global. As might be expected, the inclusion of imperfect information can markedly damp the volatility of the expenditure components in SIGMA by generating a smaller and more gradual response of long-term real interest rates, and by damping the impact on the real exchange rate.
Figure 6 illustrates that spillover effects on the home economy would be much smaller if the foreign output expansion were instead attributable to higher consumption spending. In particular, this alternative simulation assumes that foreign consumption demand rises due to a taste shock, with the shock again scaled so that foreign output peaks at 1 percent above baseline. Given that foreign investment is crowded out by the shock, the shock has much smaller effects on the home country's real exports, and induces only a small and transient rise in output in our benchmark calibration of SIGMA. While it is interesting economically that SIGMA implies that the source of the foreign demand shock may be quite important in determining its effects on the domestic economy (whereas the domestic output increase in FRB/Global is broadly similar across the foreign demand shocks), it is plausible that certain features of SIGMA may unduly restrict the ability of the model to generate substantial spillover effects. These include both the high interest sensitivity of private absorption to the long-term real interest rate, and the omission of other potentially important financial channels. Recent work by Gilchrist, Hairault, and Kempf (2002) suggests that a financial accelerator may serve to enhance the ability of open economy SDGE models to account for larger spillover effects.
5 Long-run simulations in SIGMA
We now examine our model's implications for several supply-side shocks. Each shock exerts a highly persistent effect on output, in part because capital accumulation is very gradual. In addition to illustrating the model's long-run implications for the path of adjustment to each of these shocks, our analysis highlights the endogenous channels through which this adjustment occurs.
5.1 Persistent Rise in Productivity Growth
Figure 7 shows the responses of key variables to a productivity growth rate shock under alternative assumptions about the information structure. The shock raises technology growth by 1 percentage point per year over the the first five years of the simulation horizon, and then decays slowly following an AR(1) process with an autocorrelation parameter of ρp = .975. The magnitude of the technology growth shock is similar to that experienced in the United States between 1996 and 2000; given the decay rate, it is consistent with agents projecting GDP growth 5 years-ahead to rise immediately by about 3/4 percentage point above baseline.
We begin by analyzing the effects of the shock under the assumption that agents have full information, and hence correctly ascertain that the shock will have highly persistent effects on the future growth rate of productivity (see the solid lines in the figure). Households project a much sharper rise in their future income than in the pre-shock baseline. This immediately stimulates consumption demand, and depresses the saving rate. The increase in the expected marginal product of capital induces investment to rise (after a short delay). The expansion of domestic demand leads to higher real interest rates, putting upward pressure on the real exchange rate (not shown), and inducing a prolonged deterioration of the trade balance.
A hallmark feature of microfounded models such as SIGMA is that they completely articulate the longer-term economic forces that operate to correct any "imbalances," including in trade, its components, and the real exchange rate. The imposition of intertemporal budget constraints (and a debt-elastic risk premium) play a key role in generating these endogenous adjustments. In the case of the productivity acceleration, several aspects of the adjustment process account for the eventual movement of the trade balance into surplus. First, there is a long-run depreciation of the real exchange rate due to an increase in the supply of U.S. goods, which stimulates exports and reduces imports. Second, while the saving rate declines initially, it eventually increases as current income converges towards permanent income. Finally, after peaking about 10 years after the initial shock, the investment rate declines as capital approaches its new long-run level.
While these simulation results are instructive in understanding the forces that bring about long-run adjustment, the assumption that agents immediately recognize a productivity acceleration as permanent may be somewhat implausible. For example, in the U.S. experience of the late 1990s, forecasts of long-term output growth (i.e., 5-10 years ahead) did not change noticeably until several years after the initial rise in productivity growth. This provides some empirical motivation for considering a "gradual learning" case in which agents do not immediately recognize that the productivity growth shock is highly persistent: given our calibration of the steady state Kalman gain parameter, they initially believe the shock is mainly transitory.25 In this case, agents project a much less pronounced rise in their income profile, so that consumption jumps much less than in the full information case; correspondingly, the figure shows that the consumption share of output remains nearly flat. Given reduced aggregate demand pressure relative to the full information case, real interest rates rise much less abruptly, which accounts for the somewhat larger rise in the investment share. While the trade deficit expands, the deterioration is also somewhat muted relative to the case of full information. This gradual adjustment of both domestic demand and external variables in response to the shock is more in line with the U.S. experience in the late 1990s, including with the relative constancy of the saving rate during that period.
5.2 Reduction in Labor Tax Rate
As another illustration of the forces that ensure long-run adjustment in the SIGMA model, Figure 8 shows the effects of a cut in the labor tax rate. The tax cut is scaled so that government's labor tax revenue would fall by one percentage point of GDP if pre-tax labor income and output were unaffected. The shock is assumed to be highly persistent, with the autoregressive parameter ρτN set to 0.975. This labor tax cut induces the fiscal deficit to rise initially by about 1 percent of GDP, and to decay slowly thereafter.26
The cut in labor taxes induces a sharp initial rise in output. The shock exerts a strong stimulative effect on aggregate demand in the short-run, as the HM households immediately expand their consumption in response to the increase in their after-tax income. The high level of persistence of aggregate consumption reflects that the consumption of the HM households remains high for an extended duration (given that the cut to labor taxes is very persistent, and lump-sum taxes adjust slowly). Output declines from its initial peak as higher real interest rates crowd out investment spending and the consumption of optimizing households. However, output remains persistently above its pre-shock even in the longer-term because the shock exerts substantial supply-side effects: lower tax rates induce households to work more by raising the cost of leisure, and the rise in labor supply in turn encourages capital accumulation.
A clear advantage of our framework is that it is well-suited to explore sensitivity to various structural characteristics determining consumption and labor supply behavior. In the context of assessing the effects of tax cuts, it is often of interest to policymakers to ascertain how results depend on the extent to which households are "Ricardian," or on their labor supply elasticity. We explore each of these alternatives in the figures. The dashed lines show the case in which all households are optimizers (rather than assuming 50 percent are optimizers as in the baseline). Because all households internalize the future tax increases necessary to satisfy the government intertemporal budget constraint, consumption shows a much smaller initial increase. In the longer-term, the responses are similar to the benchmark, though there is somewhat greater capital deepening in this case. The dash-dotted line shows the case of a much higher Frisch labor supply elasticity (equal to unity, rather than 0.2 in our baseline). The larger labor supply response induces a much higher level of capital accumulation; accordingly, the longer-run output and consumption rise is greatly accentuated relative to the benchmark calibration.
The implications for the real exchange rate and trade balance under the alternative calibrations are shown in the lower panels. In the benchmark, the sharp rise in the real interest rate induces an initial appreciation in the real exchange rate, which drives the trade balance to deteriorate by around 0.1 percentage point of GDP. In the longer-term, the supply-side effects dominate. Thus, the real exchange rate depreciates due to the higher supply of U.S. goods, while the trade balance shifts into surplus for the same reasons as in the case of the productivity acceleration. The trade balance exhibits a slightly larger deterioration in the calibration with a high labor supply elasticity (given the large stimulative effect on investment), while real exchange rates and trade show little reaction in the case in which all agents optimize.
5.3 Reduction in the Capital Tax Rate
Figure 9 shows the effects of a cut in the capital income tax rate that is scaled so that capital tax revenue would fall by one percentage point of GDP if pre-tax labor income and output were unaffected. The shock is assumed to be highly persistent, with the autoregressive parameter set to 0.95. The capital tax cut induces the fiscal deficit to rise initially by about 1 percent of GDP, and to decay slowly thereafter.
Given that the HM agents do not pay capital taxes, the capital tax rate reduction does not impart the same sort of short-run aggregate demand stimulus evident in the case of the labor tax cut. Accordingly, output increases slowly in line with the gradual rise in the capital stock. Higher real interest rates encourage somewhat greater saving by optimizing agents, even though the aggregate saving rate responds somewhat less due to the presence of the HM agents. The sharp rise in investment and high import-content of investment goods encourages a substantial rise in imports, and this pressure on the trade balance is reinforced by a short-run real exchange rate appreciation: as a result, the trade balance experiences a peak deterioration of roughly 1/4 percentage point of GDP. In the long run, real exchange rate depreciation, a fall in the investment rate, and some rise in the saving rate (in part due to higher taxes on HM agents) induce the trade balance to move into persistent surplus.
Figure 9 also shows that output and investment would exhibit larger responses to a capital tax cut if all agents were optimizers (dotted lines). This reflects that the larger response of domestic saving in the latter case reduces pressure on real interest rates. The output response would be markedly accentuated if all agents were optimizers and had a much higher Frisch elasticity of labor supply of unity (five times higher than in the baseline case; see the dash-dotted lines), since the larger labor supply response would encourage higher capital accumulation.
6 Conclusion
The recent surge in interest in developing SDGE models for policy analysis seems warranted. The SDGE framework possesses some key advantages over that of existing large-scale econometric models by providing a clear linkage between structural features of the economy and its responses to shocks. Moreover, it offers a theoretically consistent framework for analyzing both short- and long-run responses that is helpful in assessing how the economy returns to its balanced growth path following disturbances.
While estimation remains an important future research objective, we have argued that an essential prerequisite involves identifying theoretical constraints of the particular SDGE framework that may preclude fitting the data on key dimensions. In this vein, even though it is encouraging that SIGMA implies responses to policy shocks that are generally similar to FRB/Global, there are at least two salient differences that seem attributable to restrictive aspects of our framework: namely, SIGMA implies much larger responses of both trade flows and the domestic expenditure components in response to shocks, and smaller and more transient spillover effects in response to foreign disturbances. Importantly, SIGMA's implications along these dimensions are likely to characterize a broad class of current SDGE models that imply fixed (or nearly fixed) desired markups, and that adopt a fairly standard framework for modeling investment and consumption behavior.
Given the importance of the magnitude of expenditure-switching effects for a wide range of open economy questions, we believe that it will be important in future work to develop mechanisms that can account for much lower long-term passthrough than implied by our model. Moreover, it will also be desirable to incorporate features that can potentially account for larger responses to foreign disturbances, at least under some conditions. It seems plausible that allowing for sectoral attachments of factors of production or the inclusion of a financial accelerator may allow SDGE models greater flexibility on this dimension.
Finally, while comparisons with FRB/Global are useful in evaluating the flexibility of SIGMA to fit responses similar to that of a data-oriented econometric model, we intend to adopt an estimation strategy that would allow significant departures from the responses of FRB/Global if the data provide a strong enough rationale. In particular, FRB/Global responses could be helpful in setting priors over certain estimated parameters in SIGMA in the context of a Bayesian approach, though sizeable differences could emerge between the responses of the two models if the posterior distribution over the parameters diverged significantly from the prior.
References
Amato, J. D. and T. Laubach (2003). Estimation and Control of an Optimization-Based Model with Sticky Prices and Wages. Journal of Economic Dynamics and Control, 7, 1181-1215.
Anderson, G. (1997). A Reliable and Computationally Efficient Algorithm for Imposing the Saddle Point Property in Dynamic Models. Federal Reserve Board Occasional Staff's Studies 4.
Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247-52.
Bergin, P. R. and R. C. Feenstra (2001). Pricing-to-Market, Staggered Contracts, and Real Exchange Rate Persistence. Journal of International Economics 54, 333-59.
Betts, C. and M. B. Devereux (1996). The Exchange Rate in a Model of Pricing-to-Market. European Economic Review 40, 1007-21.
Blanchard, O. J. and C. M. Kahm (1980). The Solution of Linear Difference Models under Rational Expectations. Econometrica 48(5), 1305-1312.
Blanchard, O. J. and R. Perotti (2002). An Empirical Characterization of the Dynamic Effects of Changes in Government Spending and Taxes on Output. Quarterly Journal of Economics 117(4), 1329-68
Brayton, F., A. Levin, R. Tryon, and J. C. Williams (1997). The Evolution of Macro Models at the Federal Reserve Board. Federal Reserve Board, Finance and Economics Discussion Series, No. 1997-29.
Brayton, F. and P. Tinsley (1996). A Guide to FRB/US. Federal Reserve Board, Finance and Economics Discussion Series, No. 1996-42.
Calvo, G. A. (1983). Staggered Prices in a Utility-Maximizing Framework. Journal of Monetary Economics 12, 383-398.
Campa, J. and L. Goldberg (2004). Exchange Rate Pass-Through into Import Prices. CEPR Discussion Papers, No. 4391.
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. Journal of Political Economy 113(1), 1-45.
Corsetti, G. and L. Dedola (2003). Macroeconomics of International Price Discrimination. CEPR Discussion Papers, No. 3710.
Corsetti, G., L. Dedola, and S. Leduc (2005). DSGE Models of High Exchange Rate Volatility and Low Pass-Through. Federal Reserve Board, International Finance Discussion Papers, No. 845.
Devereux, M. B. and C. Engel (2002). Exchange Rate Pass-Through, Exchange Rate Volatility, and the Exchange Rate Disconnect. Journal of Monetary Economics 49, 913-40.
Elmendorf, D. W. and D. L. Reifschneider (2002). Short-Run Effects of Fiscal Policy with Forward-Looking Financial Markets. National Tax Journal 55(3), 357-387.
Erceg, C., L. Guerrieri, and C. Gust (2005). Expansionary Fiscal Shocks and the U.S. Trade Deficit. International Finance 8(3),, 363-97.
Erceg, C. J., D. W. Henderson, and A. T. Levin (2000). Optimal Monetary Policy with Staggered Wage and Price Contracts. Jouranl of Monetary Economics 46, 281-313.
Erceg, C. J. and A. T. Levin (2003). Imperfect Credibility and Inflation Persistence. Journal of Monetary Economics 50, 915-44.
Fatás, A. and I. Mihov (2001). The Effects of Fiscal Policy on Consumption and Employment. CEPR Discussion Papers, No. 2760.
Galí, J., D. López-Salido, and D. Vallés (2004). Rule-of-Thumb Consumers and the Design of Interest Rate Rules. Journal of Money, Credit, and Banking 36(4), 739-763.
Gilchrist, S., J.-O. Hairault, and H. Kemf (2002). Monetary Policy and the Financial Accelerator in a Monetary Union. Federal Reserve Board, International Finance Discussion Papers, No. 750.
Guerrieri, L. (2005). Oil Shocks and the Global Economy. Manuscript, Federal Reserve Board.
Gust, C. and N. Sheets (2006). The Adjustment of Global External Imbalances: Does Partial Exchange Rate Pass-Through to Trade Prices Matter? Federal Reserve Board, International Finance Discussion Papers, No. 850.
Harrison, R., K. Nikolov, M. Quinn, G. Ramsay, A. Scott, and R. Thomas (2005). The Bank of England Quarterly Model. London: Bank of England Publications.
Kiley, M. (2001). Business Investment in the Federal Reserve Board's U.S. Model (FRB/US): Specifications and Implications. Manuscript, Federal Reserve Board.
Kimball, M. S. (1995). The Quantitative Analytics of the Neomonetarist Model. Journal of Money, Credit, and Banking 27, 1241-77.
Kollman, R. (2001). The Exchange Rate in a Dynamic-Optimizing Business Cycle Model with Nominal Rigidities: A Quantitative Investigation. Journal of International Economics 55(2), 243-62.
Laxton, D. and P. Pesenti (2003). Monetary Policy Rules for Small, Open, Emerging Economies. Journal of Monetary Economics 50, 1109-1146.
Mankiw, N. G. (2000). The Savers-Spenders Theory of Fiscal Policy. NBER Working Paper, No. 7571
Marazzi, M., N. Sheets and R. Vigfusson (2005). Exchange Rate Pass-Through to U.S. Import Prices: Some New Evidence. Federal Reserve Board, International Finance Discussion Papers, No. 833.
McCallum, B. T. and E. Nelson (1999). Nominal Income Targeting in an Open-Economy Optimizing Model. Journal of Monetary Economics 43(3), 553-579.
McDaniel, C. and E. Balistreri (2003). A Review of Armington Trade Substitution Elasticities. Integration and Trade Journal 7(18), 161-73.
Obstfeld, M. and K. Rogoff (1995). Exchange Rate Dynamics Redux. Journal of Political Economy 103, 624-60.
Orphanides, A. and V. Wieland (1998). Price Stability and Monetary Policy Ineffectiveness when Nominal Interest Rates are Bounded at Zero. Federal Reserve Board, Finance and Economics Discussion Series, No. 98-35.
Rotemberg, J. J. and M. Woodford (1999). Interest Rate Rules in an Estimated Sticky Price Model, pp. 57-119. Chicago: University of Chicago Press.
Smets, F. and R. Wouters (2003). An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area. Journal of the European Economic Association 1(5), 1124-1175.
Turnovsky, S. J. (1985). Domestic and Foreign Disturbances in a Optimizing Model of Exchange-Rate Determination. Journal of International Money and Finance 4(1), 151-71.
Woodford, M. (2003). Interest and Prices. Princeton: Princeton University Press.
Yun, T. (1996). Nominal Price Rigidity, Money Supply Endogeneity, and Business Cycles. Journal of Monetary Economics 37, 345-370.
Figure 1: Monetary Policy Loosening
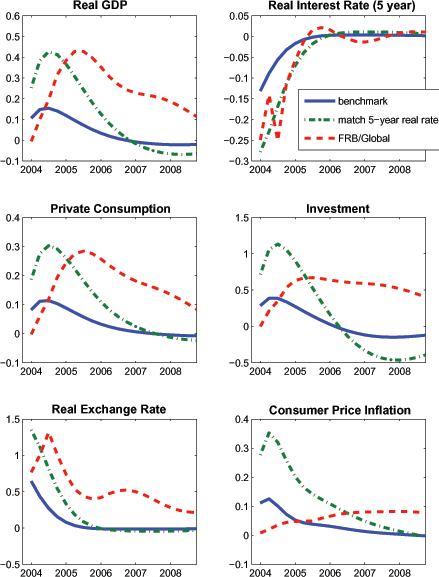
Figure 2: Rise in Government Spending
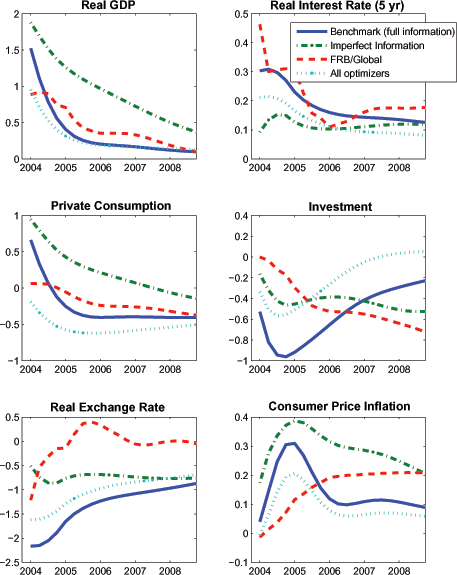
Figure 3: Rise in Home Consumption Demand
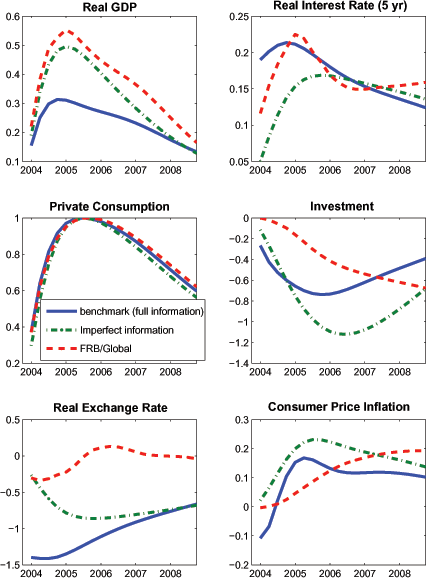
Figure 4: Fall in Home Currency Risk Premium
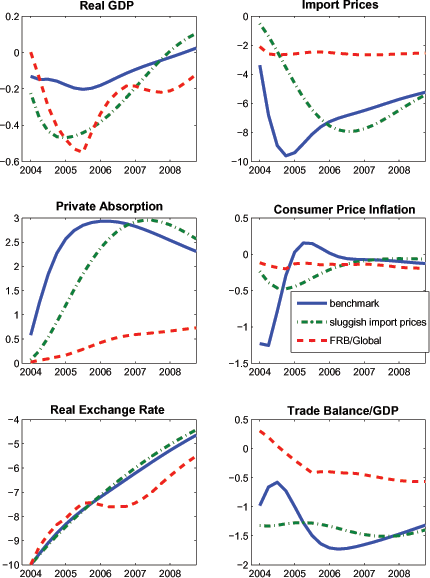
Figure 5: Rise in Foreign Investment Demand
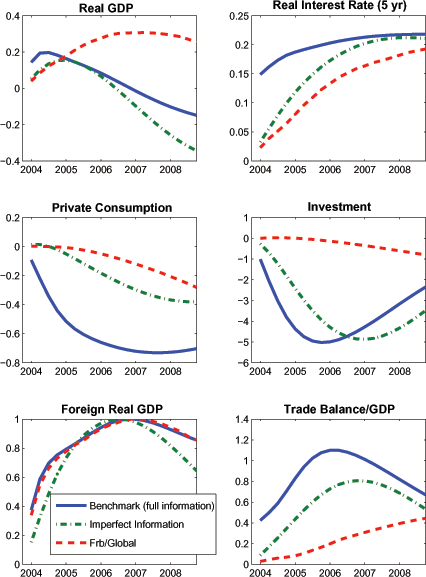
Figure 6: Rise in Foreign Consumption Demand
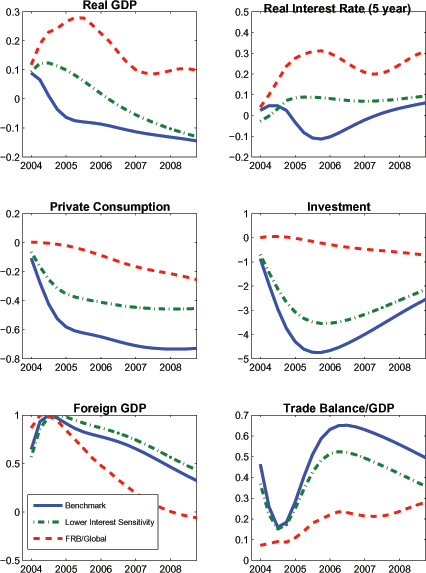
Figure 7: Rise in Home Productivity Growth Rate
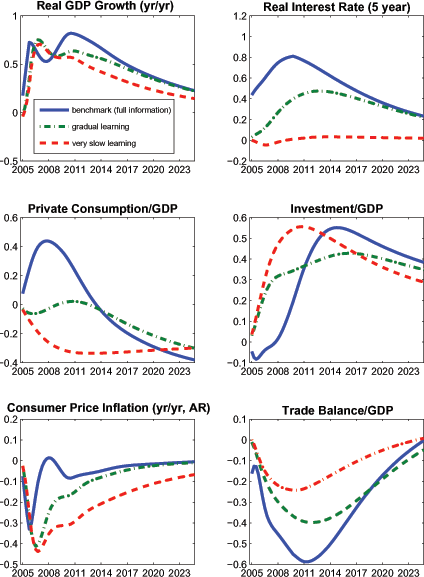
Figure 8: Fall in Home Labor Tax Rate
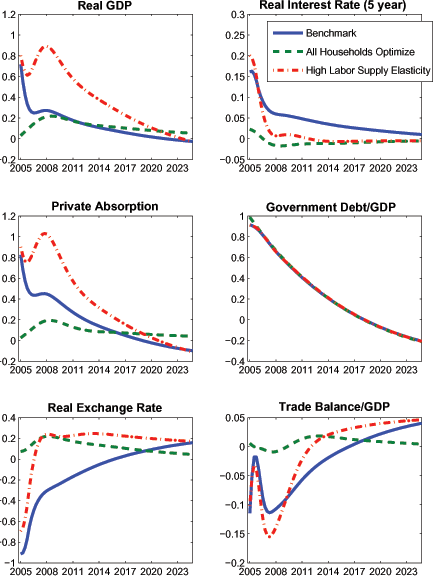
Figure 9: Fall In Home Capital Tax Rate
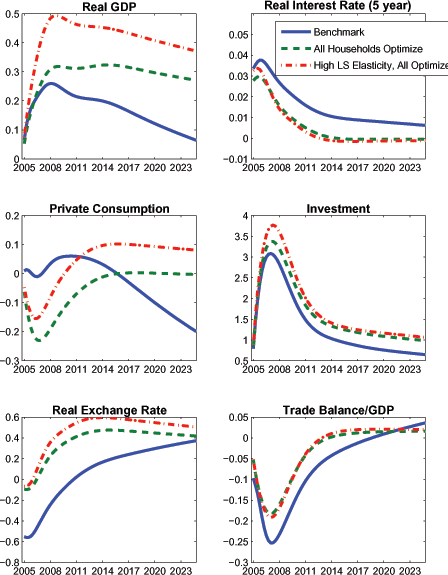
Footnotes
* We appreciate comments and suggestions from Tamim Bayoumi, Ralph Bryant, Pablo Burriel (discussant), Matthew Canzonieri, Lawrence Christiano, Behzad Diba, Martin Eichenbaum, Joe Gagnon, Jordi Galí, Fabio Ghironi, Dale Henderson, Ben Hunt, Steve Kamin, Doug Laxton, Andrew Levin, Stephen Murchison, Paolo Pesenti, Alessandro Rebucci, Trevor Reeve, Stephanie Schmitt-Grohe, Christopher Sims (discussant), Ralph Tryon, Martin Uribe, and participants in workshops at the Bank of Canada, Duke University, the Bank of Finland, the Federal Reserve Board, the Federal Reserve Bank of Dallas, Georgetown University, and the University of Montreal. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
** Corresponding Author: Telephone 202-452-2575, Fax 202-872-4926. Email addresses: [email protected], [email protected], and [email protected]. Return to text
1. The IMF's new SDGE model "GEM" is described by Laxton and Pesenti (2003). The Bank of England's new model "BEQM" is described by Harrison, Nikolov, Quinn, Ramsay, Scott, and Thomas (2005). Return to text
2. While the FRB/Global model essentially has neo-classical properties in the long-run, the behavioral equations are formulated to allow considerable flexibility in accounting for the short-run properties of the data. This model assumes that expectations are formed adaptively, i.e., expectations are derived from small-scale vector autoregressions. In our analysis, we focus on the implications for the U.S. block of the model, which consists of about 80 estimated behavioral equations and 300 identities; the foreign sector consists of 29 country blocks and roughly 4000 equations. Brayton, Levin, Tryon, and Williams (1997) provide a description of the model's basic structure. The U.S. block of the FRB/Global model, augmented with a small external sector, can also be run as an independent model (FRB/US) under either adaptive or rational expectations. See Brayton and Tinsley (1996) for an overview; Kiley (2001) describes the specification and estimation of the business investment sector; and Elmendorf and Reifschneider (2002) provide an application to fiscal policy. Return to text
3. We also provide some comparisons to estimates from Structural Vector Autoregressions (SVAR). However, comparisons with FRB/Global have the advantage that we can consider a larger set of shocks than typically analyzed in the SVAR literature. Moreover, estimates from the SVAR literature often show considerable divergence, making it difficult to gauge the appropriate benchmark. Return to text
4. Our approach is similar to that of Galí, López-Salido, and Vallés (2004) and Mankiw (2000). Return to text
5. The highly persistent fiscal multiplier and positive consumption response are in line with the empirical findings of Fatás and Mihov (2001) and of Blanchard and Perotti (2002). Return to text
6. For expositional purposes, we focus on a two country variant of SIGMA. However, in actual policy analysis we typically use a variant with seven country blocks that includes the United States, the euro area, Japan, Canada, Mexico, Developing Asia, and a rest-of-the-world sector. Moreover, the expanded model incorporates features designed to account for the effects of oil shocks, which include allowing oil to enter both the consumption bundle of households, and the production function of firms (see Guerrieri (2005). For the shocks that we analyze in this study, the effects on the home country (i.e., the United States) are quantitatively very similar in the two country model discussed below as in the larger policy model. Return to text
7. In alternative calibrations of SIGMA, we also consider the specification used by Yun (1996) and Erceg, Henderson, and Levin (2000) where PDt(i) = πPDt-1(i) so that VDt+j = πj in the profit functional defined below. For this alternative calibration, prices are updated according to PMt(i) = π*PDt-1(i) in foreign markets. Return to text
8. We define ξt,t+j to be the price in period t of a claim that pays one dollar if the specified state occurs in period t + j (see the household problem below); then the corresponding element of ψt,t+j equals ξt,t+j divided by the probability that the specified state will occur. Return to text
9. This statement is only strictly true in the absence of permanent country-specific technology shocks. In this case, a permanent increase in technology in the home country that does not occur abroad will be associated with a permanent deterioration in the home country's terms of trade that moves the home economy off its balanced growth path. Return to text
10. This intermediation cost is asymmetric, as foreign households do not face these costs; rather, they collect profits on the monopoly rents associated with these intermediation costs. Return to text
11. In alternative specifications, we also consider Wt(h) = ωWt-1(h). Return to text
12. The model's dynamics would be unchanged if we had assumed instead that government purchases entered separably in the utility function, although the welfare consequences would be different. Return to text
13. We found that the inclusion of the term (bGt+1 - bGt) was instrumental in yielding a determinate rational expectations equilibrium over a large region of the parameter space. Return to text
14. The derivation of the evolution of net foreign assets also requires that PCtCt = PDtCDt + PMtMCt and PItIt = PDtIDt + PMtMIt . Given that these conditions are satisfied even in the presence of adjustment costs for imports, the import adjustment cost terms do not appear in equation (37). Return to text
15. The steady state around which we linearize depends on the relative level of technology in each country, which we initialize to unity (so that per capita income in each country is identical in the steady state, though GDP may differ across countries due to population differences). We evaluated the robustness of our solution procedure by using a nonlinear Newton-Raphson algorithm that does not rely on linearization around an initial steady state, and found that the results were nearly identical to those reported. Return to text
16. Galí, López-Salido, and Vallés (2004) found in a New-Keynesian sticky price model with HM agents that the equilibrium becomes indeterminate when the share of HM agents is substantial. By contrast, our model produces a determinate rational expectations solution even for much higher values of the share of HM households than the 50 percent assumed in our baseline. Return to text
17. Rotemberg and Woodford (1997) found φp = 0.15, while Amato and Laubach (2003) obtained φp = 0.19 and φω = 0.13. Given our assumption that there is perfect capital mobility across firms within a country, the parameter φp only affects steady state relationships, and does not otherwise appear in the dynamic equations of the log-linearized model. Return to text
18. The inclusion of strategic complementarities along the lines suggested by Kimball (1995) and Woodford (2003) would allow our model to generate similar dynamic responses with shorter contract durations. Return to text
19. The rapid adjustment of import prices is consistent with the evidence Campa and Goldberg (2004) derived from a panel of OECD countries, nothwithstanding their finding that long-run passthrough is generally well below 100 percent for OECD countries. Return to text
20. We estimated the rule using instrumental variables with lags of inflation and output growth as instruments. Return to text
21. The results from our SIGMA model also appear broadly consistent with the implications of the empirical vector autoregression (VAR) literature that estimates responses to a monetary policy innovation. For example, the results of Christiano, Eichenbaum, and Evans (2005) indicate that a monetary policy innovation that reduces the nominal interest rate by about 75 basis points induces output to rise about 0.4 percent, which is very close to our model for the calibration in which the monetary policy error follows an AR(1) with a persistence parameter of 0.6. However, direct comparisons of the quantitative effects are somewhat difficult because model results are fairly sensitive to the form of the monetary policy rule, which differs from that imposed in the VAR. Return to text
22. The temporary shock follows an AR(1) with a persistence parameter of 0.5. The innovation variances imply a Kalman gain parameter on the permanent component of 0.07. We use a similar calibration for the home consumption taste shock and foreign investment demand shocks considered below. Return to text
23. The low long-run passthrough in FRB/Global is consistent with recent empirical estimates for the United States; see Marazzi, Sheets, and Vigfusson (2005). Return to text
24. For example, Corsett, Dedola, and Leduc (i2005) find that their inclusion of a distribution sector can account for a reduction in long-run passthrough from unity to around 0.9. Other frameworks, such as Bergin and Feenstra (2001) and Gust and Sheets (2006) incorporate strategic complementarities in price setting à la Kimball (1995) that allow for greater variation in desired markups. These appear to be promising avenues to reduce long-run passthrough. Return to text
25. The temporary shock in this case is iid, and the Kalman gain parameter on the permanent component is 0.10. Return to text
26. We provide a more detailed discussion of the effects on the trade deficit in Erceg, Guerrieri, and Gust (2005). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text