Constructive Data Mining: Modeling Argentine Broad Money Demand

Neil R. Ericsson and Steven B. Kamin^*

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper assesses the empirical merits of PcGets and Autometrics--two recent algorithms for computer-automated model selection--using them to improve upon Kamin and Ericsson's (1993) model of Argentine broad money demand. The selected model is an economically sensible and statistically satisfactory error correction model, in which cointegration between money, inflation, the interest rate, and exchange rate depreciation depends on the inclusion of a "ratchet" variable that captures irreversible effects of inflation. Short-run dynamics differ markedly from the long run. Algorithmically based model selection complements opportunities for the researcher to contribute value added in the empirical analysis.

Keywords: Argentina, autometrics, broad money, dynamic specification, cointegration, conditional models, currency substitution, dollarization, error correction, exogeneity, hyperinflation, irreversibility, model design, model selection, money demand, PcGets, ratchet effect

JEL classification: C52, E41

1 Introduction

We are delighted to contribute to this Festschrift in honor of David F. Hendry. As discussed in Ericsson (2004), David has contributed to numerous areas of econometrics and economics, including:

money demand,
error correction models and cointegration,
exogeneity,
model development and design,
econometric software,
economic policy,
consumers' expenditure,
Monte Carlo methodology,
the history of econometrics, and
the theory of economic forecasting.

We draw on David's contributions to the first six topics to assess and improve upon Kamin and Ericsson's (1993) model of Argentine broad money demand, focusing on model design and cointegration analysis. Recent developments by David and co-authors in computer-automated model selection help us obtain a more parsimonious, empirically constant, data-coherent, error correction model for broad money demand in Argentina. Cointegration between money, inflation, the interest rate, and exchange rate depreciation depends on the inclusion of a "ratchet" variable that captures irreversible effects of inflation.

To better understand money demand and currency substitution in a hyperinflationary economy, Kamin and Ericsson (1993) develop an empirical model of broad money (M3) in Argentina for monthly data over 1978-1993, a period including hyperinflation and a subsequent decline in inflation to a rate close to contemporary U.S. and European levels. Kamin and Ericsson's underlying economic theory is a standard money demand model, augmented by short-run nonlinear dynamics and a ratchet effect from inflation. Their empirical model clarifies the relative importance of factors determining money demand and currency holdings. Also, the structure of broad money demand in Argentina does not appear to have changed over the 1980s and 1990s. Rather, the fall in demand during the late 1980s and into the 1990s is explained by changes in the determinants of money demand itself.

That said, the analysis in Kamin and Ericsson (1993) has three notable shortcomings. First, their cointegration analysis excludes a trend, which may have affected inferences. Second, in their single equation modeling of Argentine money demand, Kamin and Ericsson augment the data from the cointegration analysis with an impulse dummy (for a known asset freeze from the Plan Bonex) and an asymmetric term in price acceleration. While both variables are stationary in principle, their exclusion from the cointegration analysis could have affected the results obtained. Third, an alternative single equation model might have been obtained if a different model search path had been followed.

Following the approach in Ericsson (2008, Chapters 9 and 10), the current paper addresses these issues, as follows. Cointegration is re-analyzed, including the impulse dummy, the asymmetric inflation term, and a trend. The cointegrating vector in this expanded framework is similar to the one obtained by Kamin and Ericsson (1993). Path dependence in model selection is examined by using two model selection algorithms: David Hendry and Hans-Martin Krolzig's (2001) PcGets, and Jurgen Doornik and David Hendry's (2007) Autometrics. Kamin and Ericsson's (1993) analysis is robust to multi-path searches by both algorithms; at the same time, Autometrics finds an even more parsimonious specification. The details of the model improvement highlight the strengths and the limitations of computer-automated model selection. Our approach thus illustrates new techniques, which shed light on existing results. And, re-examination of an existing dataset with new techniques is very much in the spirit of other work in this area, including Hendry and Mizon (1978), Engle and Hendry (1993), Doornik, Hendry, and Nielsen (1998), and Hendry (2006).

This paper is organized as follows. Section 2 briefly describes the economic theory and the data. Section 3 summarizes the cointegration analysis and error correction model for Argentine money demand in Kamin and Ericsson (1993). Section 4 re-analyzes the long-run properties of Argentine money demand on the expanded dataset. Section 5 then designs a single equation model of money demand, using the algorithms for computer-automated model selection in PcGets and Autometrics. Depending upon the modeling strategy, pre-search testing, choice of required regressors, and representation and choice of the initial general model, PcGets and Autometrics obtain several distinct--albeit similar--final models in their general-to-specific selection processes. Additional analysis of those models obtains a final specification that is similar to--but more parsimonious than--the one in Kamin and Ericsson (1993). That final specification appears well-specified with empirically constant coefficients; and its economic interpretation is straightforward. Section 6 concludes.

For expositional convenience, two conventions are adopted. First, "domestic" means Argentine. Second, Argentine currency is always denominated in pesos (the Argentine currency at the end of the sample) although historically other currencies were used.

2 Economic Theory and the Data

This section first discusses the theory of money demand (Section 2.1) and then considers the data themselves (Section 2.2).

3.1 Economic Theory

The standard theory of money demand posits:

$\begin{displaymath}\begin{array}[b]{lll} M^{d}/P & \;\;= & \;\;q(Y,\mathbf{R})\;, \end{array}\end{displaymath}$

(1)

where $M^{d}$ is nominal money demanded, is the price level, is a scale variable, and $\mathbf{R}$ (in bold) is a vector of returns on various assets. The function $q(\cdot,\cdot)$ is increasing in , decreasing in those elements of $\mathbf{R}$ associated with assets excluded from , and increasing in those elements of $\mathbf{R}$ for assets included in .

Three assets for Argentine residents are considered: broad money (M3), domestic goods, and dollars. Their nominal returns are denoted , $\Delta p$ , and $\Delta e$ , where is the exchange rate (domestic/foreign), variables in lowercase are in logarithms, and $\Delta$ is the difference operator. This choice of assets and returns seems reasonable. Relatively few peso instruments outside of M3 were held in significant quantities during most of the sample period. Also, the interest rate on dollar deposits was small and unvarying relative to $\Delta e$ , so it was excluded in calculating the return on dollar-denominated assets.

Empirical models below employ (1) in its standard log-linear form, with two modifications. First, the scale variable is omitted, as in Cagan's (1956) money demand model for hyperinflationary economies. ¹ Second, following Enzler, Johnson, and Paulus (1976), Simpson and Porter (1980), Piterman (1988), Melnick (1990), Ahumada (1992, and Uribe (1997) inter alia, the money demand equation includes a ratchet variable, which is the maximum inflation rate to date, denoted $\Delta p^{max}$ . Higher inflation rates may induce innovations to economize on the use of domestic money balances. Once inflation subsides, these innovations are unlikely to disappear immediately (if at all), leading to a long-lived negative effect of inflation on money demand. Hence, $\Delta p^{max}$ may proxy for financial innovation, be it a shift toward dollar usage or toward other forms of economizing on domestic money holdings.

With these two modifications, equation (1) has the following form:

$\begin{displaymath}\begin{array}[b]{lll} m-p & \;\;= & \;\;\gamma_{0}\;+\;\gamma_{1}R\;+\;\gamma_{2}\Delta p\;+\;\gamma_{3}\Delta e\;+\;\gamma_{4}\Delta p^{max}\;. \end{array}\end{displaymath}$

(2)

Anticipated signs of coefficients are $\gamma_{1}>0$ , $\gamma_{2} <0$ , $\gamma_{3}<0$ , and $\gamma_{4}\leq0$ . Broad money is composed primarily of interest-bearing deposits, so the interest rate should exert a positive effect on money demand. The coefficients on $\Delta p$ and $\Delta e$ should be negative: goods and dollars are alternatives to holding money. Because $\Delta p^{max}$ increases monotonically throughout the sample, a strictly negative $\gamma_{4}$ implies irreversible reductions in money demand due to historically higher rates of inflation.

If , $\Delta p$ , and $\Delta e$ enter equation (2) only as relative rates of return, then $\gamma_{2}+\gamma_{3}=-\gamma_{1}$ , and equation (2) can be rewritten as:

$\begin{displaymath}\begin{array}[b]{lll} m-p & \;\;= & \;\;\gamma_{0}\;-\;\gamma_{2}(R-\Delta p)\;-\;\gamma _{3}(R-\Delta e)\;+\;\gamma_{4}\Delta p^{max}\;. \end{array}\end{displaymath}$

(3)

Equation (3) links real money demand to two opportunity costs and the ratchet effect. This representation is particularly useful when interpreting empirical error correction models in the context of multiple markets influencing money demand.

2.2 The Data

This subsection describes the data available and considers some of their basic properties. The data are a broad measure of money (M3), as measured by all peso-denominated currency and domestic bank deposits (, millions of pesos); the domestic consumer price index (, 1968 = 1.00); the interest rate on domestic peso-denominated 30-day fixed-term bank deposits (, fraction at a monthly rate); and the free-market exchange rate (, in pesos per dollar). Also, is transformed to the variable $\max(0,\Delta$ $^{2}p)$ [denoted $\Delta$ $^{2}p^{pos}$ ] to measure the differential effect of positive (rather than negative) accelerations in prices, as in Ahumada (1992). The variable $\Delta$ $^{2}p^{pos}$ is interpretable as allowing asymmetric short-run effects of inflation, similar to $\Delta p^{max}$ allowing asymmetric long-run effects. All data are monthly and seasonally unadjusted, over January 1977-January 1993. Allowing for lags and transformations, estimation is over February 1978-January 1993 () unless otherwise noted. Two dummy variables are also used: , an impulse dummy for the beginning of the Plan Bonex (January 1990); and , the seasonal dummy. Kamin and Ericsson (1993, Appendix) provide further details on the data.

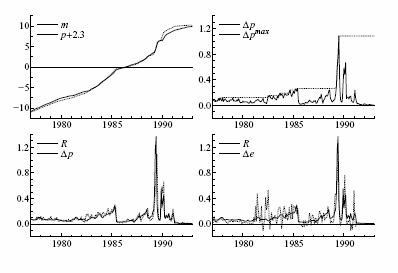
Figure 1a plots the logarithms of nominal money and prices ( and ), which are notable by spanning orders of magnitude. Sharp increases in both series are visible around 1985 and 1989. While is the variable of central interest in this study, its evolution is most easily understood in light of the various rates of return. Figure 1b plots the (monthly) inflation rate $\Delta p$ , along with the generated ratchet variable $\Delta p^{max}$ . Figure 1c plots $\Delta p$ and the interest rate , which move closely together, albeit with inflation being more volatile on a month-to-month basis. Figure 1d graphs and the depreciation in the nominal exchange rate $\Delta e$ , which also move closely together, with exchange rate depreciation being highly volatile. That said, real ex post monthly returns are commonly in excess of (plus-or-minus) two per cent, in large part owing to the high variability in the inflation rate.

Figure 1: The logarithms of nominal money and prices (m and p), inflation Δp and maximal inflation Δp^max, R and Δp, and R and Δe.

Data for Figure 1 immediately follows.

Data for Figure 1

Date	Panel 1a: m	Panel 1a: p+2.3$	Panel 1b: Δp	Panel 1b: Δp^max	Panel 1c: R	Panel 1c: Δp	Panel 1d: R	Panel 1d: Δe
1977-1	-10.857155	-10.961625	-	-	0.073000	-	0.073000	-
1977-2	-10.758755	-10.884239	0.077387	0.077387	0.074200	0.077387	0.074200	0.021706
1977-3	-10.665355	-10.812413	0.071826	0.077387	0.067500	0.071826	0.067500	0.122035
1977-4	-10.510381	-10.750043	0.062370	0.077387	0.064900	0.062370	0.064900	0.031535
1977-5	-10.362285	-10.686959	0.063084	0.077387	0.061800	0.063084	0.061800	0.051217
1977-6	-10.273848	-10.615349	0.071610	0.077387	0.062100	0.071610	0.062100	0.021707
1977-7	-10.183742	-10.544732	0.070618	0.077387	0.066500	0.070618	0.066500	0.052291
1977-8	-10.101167	-10.437101	0.107631	0.107631	0.073000	0.107631	0.073000	0.051739
1977-9	-10.035613	-10.358629	0.078472	0.107631	0.079800	0.078472	0.079800	0.079201
1977-10	-9.969053	-10.240148	0.118482	0.118482	0.092800	0.118482	0.092800	0.081071
1977-11	-9.892544	-10.151973	0.088175	0.118482	0.102100	0.088175	0.102100	0.087666
1977-12	-9.736444	-10.082810	0.069163	0.118482	0.103200	0.069163	0.103200	0.072623
1978-1	-9.648976	-9.957366	0.125444	0.125444	0.099300	0.125444	0.099300	0.059934
1978-2	-9.552247	-9.896122	0.061244	0.125444	0.080400	0.061244	0.080400	0.072993
1978-3	-9.484175	-9.805323	0.090800	0.125444	0.070000	0.090800	0.070000	0.058169
1978-4	-9.387805	-9.700686	0.104637	0.125444	0.066800	0.104637	0.066800	0.051728
1978-5	-9.295144	-9.617891	0.082795	0.125444	0.068700	0.082795	0.068700	0.036894
1978-6	-9.174142	-9.555416	0.062475	0.125444	0.071800	0.062475	0.071800	0.015402
1978-7	-9.092109	-9.491317	0.064098	0.125444	0.068800	0.064098	0.068800	0.012762
1978-8	-9.004701	-9.416266	0.075051	0.125444	0.067600	0.075051	0.067600	0.028552
1978-9	-8.941602	-9.353338	0.062929	0.125444	0.062400	0.062929	0.062400	0.044944
1978-10	-8.876114	-9.261066	0.092272	0.125444	0.064400	0.092272	0.064400	0.042898
1978-11	-8.795786	-9.176594	0.084472	0.125444	0.067300	0.084472	0.067300	0.050277
1978-12	-8.696307	-9.089823	0.086770	0.125444	0.070000	0.086770	0.070000	0.063505
1979-1	-8.606243	-8.969195	0.120628	0.125444	0.067800	0.120628	0.067800	0.026983
1979-2	-8.522809	-8.898115	0.071081	0.125444	0.063600	0.071081	0.063600	0.054739
1979-3	-8.442039	-8.822912	0.075202	0.125444	0.063600	0.075202	0.063600	0.043862
1979-4	-8.358780	-8.755501	0.067412	0.125444	0.064200	0.067412	0.064200	0.042590
1979-5	-8.267602	-8.688789	0.066712	0.125444	0.065000	0.066712	0.065000	0.047245
1979-6	-8.165586	-8.596120	0.092669	0.125444	0.066700	0.092669	0.066700	0.042813
1979-7	-8.082428	-8.526803	0.069317	0.125444	0.069800	0.069317	0.069800	0.040016
1979-8	-7.992849	-8.418576	0.108226	0.125444	0.073000	0.108226	0.073000	0.037462
1979-9	-7.908298	-8.352147	0.066429	0.125444	0.073800	0.066429	0.073800	0.035247
1979-10	-7.798524	-8.309923	0.042225	0.125444	0.071700	0.042225	0.071700	0.071391
1979-11	-7.719123	-8.259724	0.050198	0.125444	0.062100	0.050198	0.062100	0.045074
1979-12	-7.624806	-8.215239	0.044485	0.125444	0.059200	0.044485	0.059200	-0.011181
1980-1	-7.555929	-8.145804	0.069435	0.125444	0.057600	0.069435	0.057600	0.026769
1980-2	-7.493682	-8.093531	0.052273	0.125444	0.051700	0.052273	0.051700	0.028371
1980-3	-7.448851	-8.037352	0.056179	0.125444	0.048400	0.056179	0.048400	0.025772
1980-4	-7.423711	-7.977454	0.059898	0.125444	0.044700	0.059898	0.044700	0.021437
1980-5	-7.404086	-7.921217	0.056237	0.125444	0.045400	0.056237	0.045400	0.020672
1980-6	-7.339939	-7.865372	0.055845	0.125444	0.053400	0.055845	0.053400	0.019462
1980-7	-7.262675	-7.820649	0.044723	0.125444	0.060200	0.044723	0.060200	0.016708
1980-8	-7.200075	-7.786930	0.033719	0.125444	0.050000	0.033719	0.050000	0.014678
1980-9	-7.158090	-7.742520	0.044410	0.125444	0.043300	0.044410	0.043300	0.012905
1980-10	-7.118279	-7.669200	0.073320	0.125444	0.043100	0.073320	0.043100	0.010585
1980-11	-7.077157	-7.623486	0.045714	0.125444	0.046200	0.045714	0.046200	0.010012
1980-12	-6.999202	-7.586041	0.037446	0.125444	0.054300	0.037446	0.054300	0.010119
1981-1	-6.987589	-7.538262	0.047779	0.125444	0.056300	0.047779	0.056300	0.015168
1981-2	-6.976816	-7.497327	0.040934	0.125444	0.066300	0.040934	0.066300	0.108388
1981-3	-6.968674	-7.439160	0.058167	0.125444	0.081200	0.058167	0.081200	0.039644
1981-4	-6.902320	-7.363212	0.075949	0.125444	0.074800	0.075949	0.074800	0.280808
1981-5	-6.871076	-7.290576	0.072635	0.125444	0.080200	0.072635	0.080200	0.042066
1981-6	-6.797861	-7.200960	0.089616	0.125444	0.101500	0.089616	0.101500	0.474811
1981-7	-6.700253	-7.103440	0.097520	0.125444	0.108200	0.097520	0.108200	0.266651
1981-8	-6.621937	-7.027211	0.076228	0.125444	0.102700	0.076228	0.102700	0.127959
1981-9	-6.522663	-6.958166	0.069045	0.125444	0.083700	0.069045	0.083700	0.027101
1981-10	-6.452535	-6.901579	0.056587	0.125444	0.069500	0.056587	0.069500	0.065734
1981-11	-6.393071	-6.831991	0.069587	0.125444	0.073900	0.069587	0.073900	0.279507
1981-12	-6.278992	-6.747626	0.084365	0.125444	0.069400	0.084365	0.069400	-0.025449
1982-1	-6.220360	-6.634984	0.112643	0.125444	0.072600	0.112643	0.072600	-0.110983
1982-2	-6.153410	-6.583486	0.051498	0.125444	0.071300	0.051498	0.071300	0.009184
1982-3	-6.099371	-6.537398	0.046087	0.125444	0.068500	0.046087	0.068500	0.088953
1982-4	-6.034084	-6.496378	0.041020	0.125444	0.082000	0.041020	0.082000	0.420186
1982-5	-5.974305	-6.466232	0.030146	0.125444	0.074000	0.030146	0.074000	0.223469
1982-6	-5.926861	-6.390238	0.075994	0.125444	0.058600	0.075994	0.058600	0.280055
1982-7	-5.882427	-6.239592	0.150646	0.150646	0.051100	0.150646	0.051100	0.529450
1982-8	-5.875913	-6.102704	0.136888	0.150646	0.049800	0.136888	0.049800	0.134455
1982-9	-5.849319	-5.944955	0.157750	0.157750	0.069800	0.157750	0.069800	-0.078225
1982-10	-5.770586	-5.825489	0.119466	0.157750	0.069900	0.119466	0.069900	0.056761
1982-11	-5.683845	-5.718025	0.107464	0.157750	0.084800	0.107464	0.084800	0.178078
1982-12	-5.511313	-5.617094	0.100932	0.157750	0.084900	0.100932	0.084900	0.055395
1983-1	-5.348622	-5.468777	0.148317	0.157750	0.104900	0.148317	0.104900	0.065786
1983-2	-5.270488	-5.346381	0.122396	0.157750	0.099900	0.122396	0.099900	0.090393
1983-3	-5.184310	-5.239619	0.106762	0.157750	0.100000	0.106762	0.100000	0.137318
1983-4	-5.077400	-5.141867	0.097753	0.157750	0.100000	0.097753	0.100000	0.079840
1983-5	-4.956389	-5.055090	0.086777	0.157750	0.100000	0.086777	0.100000	0.001308
1983-6	-4.836573	-4.908198	0.146891	0.157750	0.089000	0.146891	0.089000	0.077235
1983-7	-4.735985	-4.790825	0.117373	0.157750	0.105000	0.117373	0.105000	0.232099
1983-8	-4.618722	-4.631741	0.159084	0.159084	0.116000	0.159084	0.116000	0.257112
1983-9	-4.495025	-4.438088	0.193652	0.193652	0.142000	0.193652	0.142000	0.268383
1983-10	-4.336541	-4.281312	0.156777	0.193652	0.145000	0.156777	0.145000	0.158403
1983-11	-4.152186	-4.105393	0.175918	0.193652	0.145000	0.175918	0.145000	-0.073155
1983-12	-3.888824	-3.942416	0.162977	0.193652	0.145000	0.162977	0.145000	0.037707
1984-1	-3.709658	-3.824530	0.117886	0.193652	0.115000	0.117886	0.115000	0.221229
1984-2	-3.558588	-3.667592	0.156938	0.193652	0.100000	0.156938	0.100000	0.275041
1984-3	-3.423682	-3.483124	0.184467	0.193652	0.100000	0.184467	0.100000	0.211368
1984-4	-3.298880	-3.313404	0.169721	0.193652	0.130000	0.169721	0.130000	0.087301
1984-5	-3.169924	-3.155722	0.157681	0.193652	0.130000	0.157681	0.130000	0.172524
1984-6	-2.996246	-2.990957	0.164766	0.193652	0.130000	0.164766	0.130000	0.065345
1984-7	-2.830250	-2.823051	0.167906	0.193652	0.155000	0.167906	0.155000	0.086602
1984-8	-2.661351	-2.617280	0.205770	0.205770	0.155000	0.205770	0.155000	0.262119
1984-9	-2.529654	-2.373963	0.243317	0.243317	0.155000	0.243317	0.155000	0.142697
1984-10	-2.410457	-2.197303	0.176660	0.243317	0.170000	0.176660	0.170000	0.076308
1984-11	-2.216226	-2.057763	0.139539	0.243317	0.170000	0.139539	0.170000	0.311530
1984-12	-2.026495	-1.878126	0.179637	0.243317	0.170000	0.179637	0.170000	0.079912
1985-1	-1.844120	-1.653950	0.224176	0.243317	0.175000	0.224176	0.175000	0.283278
1985-2	-1.672341	-1.466076	0.187874	0.243317	0.180000	0.187874	0.180000	0.279051
1985-3	-1.518627	-1.231011	0.235065	0.243317	0.200000	0.235065	0.200000	0.239069
1985-4	-1.280792	-0.972767	0.258244	0.258244	0.240000	0.258244	0.240000	0.269167
1985-5	-1.032818	-0.748694	0.224073	0.258244	0.300000	0.224073	0.300000	0.160410
1985-6	-0.765922	-0.482222	0.266472	0.266472	0.160000	0.266472	0.160000	0.253104
1985-7	-0.629167	-0.422124	0.060098	0.266472	0.035000	0.060098	0.035000	0.167337
1985-8	-0.560295	-0.391946	0.030178	0.266472	0.035000	0.030178	0.035000	0.009836
1985-9	-0.486941	-0.372189	0.019757	0.266472	0.035000	0.019757	0.035000	-0.013240
1985-10	-0.405698	-0.352912	0.019277	0.266472	0.031000	0.019277	0.031000	-0.016050
1985-11	-0.372643	-0.329503	0.023409	0.266472	0.031000	0.023409	0.031000	-0.029143
1985-12	-0.252200	-0.298290	0.031213	0.266472	0.031000	0.031213	0.031000	-0.048801
1986-1	-0.204695	-0.268444	0.029846	0.266472	0.031000	0.029846	0.031000	0.050383
1986-2	-0.146945	-0.251688	0.016757	0.266472	0.031000	0.016757	0.031000	-0.043814
1986-3	-0.112600	-0.206273	0.045415	0.266472	0.031000	0.045415	0.031000	0.054048
1986-4	-0.060502	-0.160015	0.046258	0.266472	0.031000	0.046258	0.031000	0.014350
1986-5	0.001138	-0.120536	0.039479	0.266472	0.031000	0.039479	0.031000	-0.023821
1986-6	0.067780	-0.076084	0.044451	0.266472	0.033000	0.044451	0.033000	-0.005586
1986-7	0.130938	-0.010650	0.065435	0.266472	0.035000	0.065435	0.035000	0.021883
1986-8	0.162822	0.073552	0.084201	0.266472	0.051000	0.084201	0.051000	0.171870
1986-9	0.209891	0.143366	0.069815	0.266472	0.045000	0.069815	0.045000	0.117772
1986-10	0.323973	0.202126	0.058759	0.266472	0.050000	0.058759	0.050000	-0.019841
1986-11	0.386451	0.253722	0.051597	0.266472	0.055000	0.051597	0.055000	0.119049
1986-12	0.521417	0.300035	0.046312	0.266472	0.055000	0.046312	0.055000	0.147807
1987-1	0.578201	0.372909	0.072874	0.266472	0.055000	0.072874	0.055000	0.090841
1987-2	0.609968	0.435909	0.063000	0.266472	0.060000	0.063000	0.060000	-0.000776
1987-3	0.682155	0.514714	0.078805	0.266472	0.030000	0.078805	0.030000	0.093407
1987-4	0.731072	0.547805	0.033092	0.266472	0.042000	0.033092	0.042000	0.081494
1987-5	0.794314	0.588707	0.040901	0.266472	0.047000	0.040901	0.047000	0.013330
1987-6	0.875165	0.665680	0.076974	0.266472	0.065000	0.076974	0.065000	0.004614
1987-7	0.956445	0.762078	0.096398	0.266472	0.075000	0.096398	0.075000	0.138354
1987-8	1.009318	0.890617	0.128539	0.266472	0.095000	0.128539	0.095000	0.204818
1987-9	1.098891	1.001141	0.110524	0.266472	0.110000	0.110524	0.110000	0.164973
1987-10	1.217278	1.179679	0.178538	0.266472	0.135000	0.178538	0.135000	0.136400
1987-11	1.326410	1.277429	0.097750	0.266472	0.089000	0.097750	0.089000	0.028094
1987-12	1.460809	1.310883	0.033454	0.266472	0.124000	0.033454	0.124000	0.116676
1988-1	1.534796	1.397910	0.087027	0.266472	0.132000	0.087027	0.132000	0.176399
1988-2	1.622239	1.497143	0.099232	0.266472	0.133000	0.099232	0.133000	0.057968
1988-3	1.770242	1.634633	0.137490	0.266472	0.156000	0.137490	0.156000	0.090983
1988-4	1.879811	1.793618	0.158984	0.266472	0.162000	0.158984	0.162000	0.090271
1988-5	2.016426	1.939633	0.146015	0.266472	0.173000	0.146015	0.173000	0.117629
1988-6	2.198877	2.104847	0.165215	0.266472	0.195000	0.165215	0.195000	0.273394
1988-7	2.379716	2.333106	0.228259	0.266472	0.227000	0.228259	0.227000	0.172848
1988-8	2.595137	2.577033	0.243927	0.266472	0.108000	0.243927	0.108000	0.147626
1988-9	2.748841	2.687613	0.110580	0.266472	0.091000	0.110580	0.091000	0.013891
1988-10	2.840920	2.773728	0.086115	0.266472	0.093000	0.086115	0.093000	0.043619
1988-11	2.966466	2.829298	0.055570	0.266472	0.102000	0.055570	0.102000	0.029556
1988-12	3.160743	2.895457	0.066159	0.266472	0.122000	0.066159	0.122000	0.021767
1989-1	3.329408	2.980918	0.085461	0.266472	0.121000	0.085461	0.121000	0.066074
1989-2	3.415708	3.072503	0.091586	0.266472	0.190000	0.091586	0.190000	0.401292
1989-3	3.538077	3.229550	0.157047	0.266472	0.216000	0.157047	0.216000	0.477542
1989-4	3.720073	3.517527	0.287976	0.287976	0.447000	0.287976	0.447000	0.461351
1989-5	4.078186	4.096765	0.579239	0.579239	1.154000	0.579239	1.154000	0.689090
1989-6	4.758953	4.859782	0.763017	0.763017	1.369000	0.763017	1.369000	1.143784
1989-7	5.474110	5.947093	1.087311	1.087311	0.339000	1.087311	0.339000	0.473116
1989-8	6.023763	6.268176	0.321083	1.087311	0.128000	0.321083	0.128000	0.033621
1989-9	6.250978	6.357611	0.089435	1.087311	0.074000	0.089435	0.074000	-0.023767
1989-10	6.420034	6.412053	0.054442	1.087311	0.061000	0.054442	0.061000	0.074776
1989-11	6.496225	6.475218	0.063164	1.087311	0.096000	0.063164	0.096000	0.229980
1989-12	6.546786	6.812210	0.336993	1.087311	0.553000	0.336993	0.553000	0.399647
1990-1	6.413787	7.395565	0.583354	1.087311	0.264000	0.583354	0.264000	0.243769
1990-2	6.698515	7.875335	0.479771	1.087311	0.361000	0.479771	0.361000	0.760012
1990-3	6.988321	8.545857	0.670521	1.087311	0.456000	0.670521	0.456000	0.309943
1990-4	7.417761	8.653568	0.107711	1.087311	0.116000	0.107711	0.116000	0.022064
1990-5	7.681653	8.781147	0.127579	1.087311	0.088000	0.127579	0.088000	0.000000
1990-6	7.882654	8.911279	0.130132	1.087311	0.140000	0.130132	0.140000	0.050644
1990-7	8.064762	9.014065	0.102786	1.087311	0.111000	0.102786	0.111000	0.033617
1990-8	8.155649	9.156759	0.142694	1.087311	0.098000	0.142694	0.098000	0.129045
1990-9	8.239013	9.302393	0.145635	1.087311	0.167000	0.145635	0.167000	-0.099192
1990-10	8.361124	9.376484	0.074091	1.087311	0.109000	0.074091	0.109000	-0.008054
1990-11	8.479201	9.436455	0.059971	1.087311	0.067000	0.059971	0.067000	-0.082366
1990-12	8.630933	9.482158	0.045702	1.087311	0.067000	0.045702	0.067000	0.085954
1991-1	8.709647	9.556325	0.074167	1.087311	0.135900	0.074167	0.135900	0.522751
1991-2	8.769492	9.795266	0.238941	1.087311	0.167900	0.238941	0.167900	0.057748
1991-3	8.869370	9.900007	0.104741	1.087311	0.115900	0.104741	0.115900	-0.036219
1991-4	8.990641	9.953648	0.053641	1.087311	0.014200	0.053641	0.014200	0.018529
1991-5	9.066966	9.981307	0.027659	1.087311	0.015500	0.027659	0.015500	0.010147
1991-6	9.125882	10.012066	0.030760	1.087311	0.017000	0.030760	0.017000	0.006541
1991-7	9.164841	10.037646	0.025580	1.087311	0.018000	0.025580	0.018000	-0.001506
1991-8	9.211370	10.050571	0.012925	1.087311	0.014000	0.012925	0.014000	0.000502
1991-9	9.255362	10.068411	0.017840	1.087311	0.011000	0.017840	0.011000	-0.005537
1991-10	9.306332	10.082314	0.013903	1.087311	0.011000	0.013903	0.011000	0.000000
1991-11	9.362787	10.086306	0.003992	1.087311	0.011000	0.003992	0.011000	0.000000
1991-12	9.451363	10.092288	0.005982	1.087311	0.013000	0.005982	0.013000	0.008044
1992-1	9.502009	10.121825	0.029537	1.087311	0.011000	0.029537	0.011000	-0.008044
1992-2	9.529100	10.143137	0.021312	1.087311	0.010000	0.021312	0.010000	0.000000
1992-3	9.545197	10.163915	0.020779	1.087311	0.009000	0.020779	0.009000	0.002017
1992-4	9.591533	10.176701	0.012785	1.087311	0.010000	0.012785	0.010000	-0.002017
1992-5	9.670212	10.183409	0.006708	1.087311	0.009000	0.006708	0.009000	0.000000
1992-6	9.740716	10.191219	0.007810	1.087311	0.008000	0.007810	0.008000	0.000000
1992-7	9.789311	10.208359	0.017140	1.087311	0.010000	0.017140	0.010000	0.000000
1992-8	9.820106	10.223214	0.014855	1.087311	0.009000	0.014855	0.009000	0.000000
1992-9	9.846282	10.233499	0.010285	1.087311	0.009000	0.010285	0.009000	0.000000
1992-10	9.858072	10.246079	0.012580	1.087311	0.009000	0.012580	0.009000	0.000000
1992-11	9.870603	10.250678	0.004599	1.087311	0.010000	0.004599	0.010000	0.000000
1992-12	9.900182	10.253511	0.002833	1.087311	0.011000	0.002833	0.011000	0.000000
1993-1	9.949273	10.261800	0.008289	1.087311	0.009000	0.008289	0.009000	-0.000505
1993-2	-	10.269078	0.007278	1.087311	0.010500	0.007278	0.010500	-
1993-3	-	-	-	1.087311	-	-	-	-
1993-4	-	-	-	1.087311	-	-	-	-
1993-5	-	-	-	1.087311	-	-	-	-
1993-6	-	-	-	1.087311	-	-	-	-
1993-7	-	-	-	1.087311	-	-	-	-
1993-8	-	-	-	1.087311	-	-	-	-
1993-9	-	-	-	1.087311	-	-	-	-
1993-10	-	-	-	1.087311	-	-	-	-
1993-11	-	-	-	1.087311	-	-	-	-
1993-12	-	-	-	1.087311	-	-	-	-

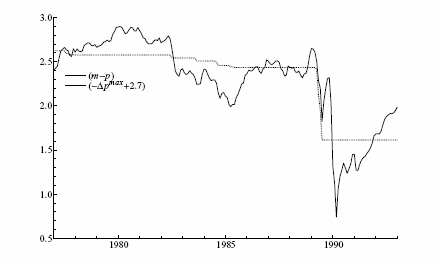
Figure 2: The logarithms of real money (m - p), and the negative of the maximal inflation rate (Δp^max), adjusted for means.

Data for Figure 2 immediately follows.

Data for Figure 2

Date	(m - p)	(-Δp^max + 2.7)
1977-1	2.4044708	-
1977-2	2.4254841	2.6226133
1977-3	2.4470578	2.6226133
1977-4	2.5396620	2.6226133
1977-5	2.6246740	2.6226133
1977-6	2.6415009	2.6226133
1977-7	2.6609896	2.6226133
1977-8	2.6359337	2.5923693
1977-9	2.6230167	2.5923693
1977-10	2.5710950	2.5815184
1977-11	2.5594291	2.5815184
1977-12	2.6463657	2.5815184
1978-1	2.6083901	2.5745561
1978-2	2.6438750	2.5745561
1978-3	2.6211474	2.5745561
1978-4	2.6128812	2.5745561
1978-5	2.6227467	2.5745561
1978-6	2.6812740	2.5745561
1978-7	2.6992086	2.5745561
1978-8	2.7115654	2.5745561
1978-9	2.7117352	2.5745561
1978-10	2.6849520	2.5745561
1978-11	2.6808076	2.5745561
1978-12	2.6935160	2.5745561
1979-1	2.6629523	2.5745561
1979-2	2.6753058	2.5745561
1979-3	2.6808731	2.5745561
1979-4	2.6967204	2.5745561
1979-5	2.7211864	2.5745561
1979-6	2.7305335	2.5745561
1979-7	2.7443747	2.5745561
1979-8	2.7257271	2.5745561
1979-9	2.7438499	2.5745561
1979-10	2.8113982	2.5745561
1979-11	2.8406013	2.5745561
1979-12	2.8904332	2.5745561
1980-1	2.8898747	2.5745561
1980-2	2.8998490	2.5745561
1980-3	2.8885010	2.5745561
1980-4	2.8537433	2.5745561
1980-5	2.8171301	2.5745561
1980-6	2.8254328	2.5745561
1980-7	2.8579744	2.5745561
1980-8	2.8868550	2.5745561
1980-9	2.8844296	2.5745561
1980-10	2.8509213	2.5745561
1980-11	2.8463295	2.5745561
1980-12	2.8868387	2.5745561
1981-1	2.8506729	2.5745561
1981-2	2.8205113	2.5745561
1981-3	2.7704866	2.5745561
1981-4	2.7608915	2.5745561
1981-5	2.7195002	2.5745561
1981-6	2.7030990	2.5745561
1981-7	2.7031864	2.5745561
1981-8	2.7052739	2.5745561
1981-9	2.7355030	2.5745561
1981-10	2.7490435	2.5745561
1981-11	2.7389203	2.5745561
1981-12	2.7686345	2.5745561
1982-1	2.7146243	2.5745561
1982-2	2.7300761	2.5745561
1982-3	2.7380279	2.5745561
1982-4	2.7622941	2.5745561
1982-5	2.7919270	2.5745561
1982-6	2.7633769	2.5745561
1982-7	2.6571650	2.5493543
1982-8	2.5267911	2.5493543
1982-9	2.3956354	2.5422503
1982-10	2.3549030	2.5422503
1982-11	2.3341807	2.5422503
1982-12	2.4057812	2.5422503
1983-1	2.4201552	2.5422503
1983-2	2.3758929	2.5422503
1983-3	2.3553089	2.5422503
1983-4	2.3644663	2.5422503
1983-5	2.3987012	2.5422503
1983-6	2.3716257	2.5422503
1983-7	2.3548398	2.5422503
1983-8	2.3130190	2.5409155
1983-9	2.2430633	2.5063478
1983-10	2.2447708	2.5063478
1983-11	2.2532078	2.5063478
1983-12	2.3535920	2.5063478
1984-1	2.4148719	2.5063478
1984-2	2.4090035	2.5063478
1984-3	2.3594421	2.5063478
1984-4	2.3145235	2.5063478
1984-5	2.2857986	2.5063478
1984-6	2.2947101	2.5063478
1984-7	2.2928006	2.5063478
1984-8	2.2559294	2.4942296
1984-9	2.1443092	2.4566829
1984-10	2.0868463	2.4566829
1984-11	2.1415376	2.4566829
1984-12	2.1516308	2.4566829
1985-1	2.1098295	2.4566829
1985-2	2.0937349	2.4566829
1985-3	2.0123842	2.4566829
1985-4	1.9919753	2.4417561
1985-5	2.0158762	2.4417561
1985-6	2.0162998	2.4335278
1985-7	2.0929571	2.4335278
1985-8	2.1316508	2.4335278
1985-9	2.1852480	2.4335278
1985-10	2.2472136	2.4335278
1985-11	2.2568599	2.4335278
1985-12	2.3460897	2.4335278
1986-1	2.3637493	2.4335278
1986-2	2.4047426	2.4335278
1986-3	2.3936728	2.4335278
1986-4	2.3995127	2.4335278
1986-5	2.4216740	2.4335278
1986-6	2.4438638	2.4335278
1986-7	2.4415871	2.4335278
1986-8	2.3892707	2.4335278
1986-9	2.3665251	2.4335278
1986-10	2.4218475	2.4335278
1986-11	2.4327286	2.4335278
1986-12	2.5213821	2.4335278
1987-1	2.5052922	2.4335278
1987-2	2.4740590	2.4335278
1987-3	2.4674419	2.4335278
1987-4	2.4832662	2.4335278
1987-5	2.5056079	2.4335278
1987-6	2.5094849	2.4335278
1987-7	2.4943674	2.4335278
1987-8	2.4187012	2.4335278
1987-9	2.3977493	2.4335278
1987-10	2.3375993	2.4335278
1987-11	2.3489815	2.4335278
1987-12	2.4499263	2.4335278
1988-1	2.4368860	2.4335278
1988-2	2.4250962	2.4335278
1988-3	2.4356083	2.4335278
1988-4	2.3861927	2.4335278
1988-5	2.3767931	2.4335278
1988-6	2.3940302	2.4335278
1988-7	2.3466101	2.4335278
1988-8	2.3181037	2.4335278
1988-9	2.3612281	2.4335278
1988-10	2.3671925	2.4335278
1988-11	2.4371680	2.4335278
1988-12	2.5652860	2.4335278
1989-1	2.6484900	2.4335278
1989-2	2.6432048	2.4335278
1989-3	2.6085265	2.4335278
1989-4	2.5025463	2.4120239
1989-5	2.2814211	2.1207613
1989-6	2.1991703	1.9369831
1989-7	1.8270167	1.6126887
1989-8	2.0555861	1.6126887
1989-9	2.1933668	1.6126887
1989-10	2.3079804	1.6126887
1989-11	2.3210075	1.6126887
1989-12	2.0345762	1.6126887
1990-1	1.3182223	1.6126887
1990-2	1.1231794	1.6126887
1990-3	0.7424642	1.6126887
1990-4	1.0641926	1.6126887
1990-5	1.2005059	1.6126887
1990-6	1.2713758	1.6126887
1990-7	1.3506973	1.6126887
1990-8	1.2988905	1.6126887
1990-9	1.2366191	1.6126887
1990-10	1.2846400	1.6126887
1990-11	1.3427452	1.6126887
1990-12	1.4487749	1.6126887
1991-1	1.4533218	1.6126887
1991-2	1.2742258	1.6126887
1991-3	1.2693630	1.6126887
1991-4	1.3369932	1.6126887
1991-5	1.3856598	1.6126887
1991-6	1.4138158	1.6126887
1991-7	1.4271944	1.6126887
1991-8	1.4607986	1.6126887
1991-9	1.4869504	1.6126887
1991-10	1.5240181	1.6126887
1991-11	1.5764808	1.6126887
1991-12	1.6590749	1.6126887
1992-1	1.6801847	1.6126887
1992-2	1.6859629	1.6126887
1992-3	1.6812817	1.6126887
1992-4	1.7148326	1.6126887
1992-5	1.7868029	1.6126887
1992-6	1.8494967	1.6126887
1992-7	1.8809513	1.6126887
1992-8	1.8968918	1.6126887
1992-9	1.9127827	1.6126887
1992-10	1.9119928	1.6126887
1992-11	1.9199251	1.6126887
1992-12	1.9466715	1.6126887
1993-1	1.9874732	1.6126887
1993-2	-	1.6126887
1993-3	-	1.6126887
1993-4	-	1.6126887
1993-5	-	1.6126887
1993-6	-	1.6126887
1993-7	-	1.6126887
1993-8	-	1.6126887
1993-9	-	1.6126887
1993-10	-	1.6126887
1993-11	-	1.6126887
1993-12	-	1.6126887

The overall behavior of inflation (and so of and $\Delta e$ ) can be characterized by periods of increasing inflation, followed by government "plans" to reign in inflation. The acceleration of prices during the early 1980s was sharply reversed in mid-1985 by the Plan Austral, which combined wage, price, and exchange rate freezes with some fiscal adjustment. Reductions in the fiscal deficit were not sufficient to eliminate inflationary pressures, which resumed in earnest by 1987. The August 1988 Plan Primavera ("Spring Plan") followed, and it aimed to limit the growth of prices and the official exchange rate to 4 percent per month. While inflation fell temporarily, the real exchange rate appreciated and the fiscal situation deteriorated. In February 1989, the Central Bank floated the exchange rate for financial transactions, which promptly depreciated sharply; and inflation rapidly increased to a record 197 percent per month in July 1989.

Under newly elected President Menem, the authorities announced a new program similar to the Plan Austral. Initially, inflation fell dramatically; but appreciation of the real exchange rate forced the Central Bank to float the commercial exchange rate, which quickly depreciated in value and spurred price inflation. In January 1990, the authorities attempted to restrain inflation by freezing most domestic peso-denominated bank time deposits and converting them to 10-year dollar-denominated bonds known as Bonex. The so-called Plan Bonex had little immediate effect upon inflation, but it did further reduce the Argentine public's faith in their financial system. By March 1990, when inflation reached 95.5 percent per month, broad money reached a record low of 3.1 percent of GDP .

Subsequently, inflation declined to single-digit levels due to a reduction in monetary emission made possible by concerted efforts to achieve fiscal adjustment. The fiscal deficit declined from over 20 percent of GDP in 1989 to about 3 percent in 1990 and 2 percent in 1991. In March 1991, the government announced the "Convertibility Program," which fixed the exchange rate against the dollar and required the Central Bank to hold international reserves equivalent to the monetary base. Subsequently, the inflation rate fell to under 1 percent per month.

Figure 2 graphs the log of real money () and the negative of the ratchet variable $\Delta p^{max}$ . Real money initially increases gradually, then falls abruptly by 20% in 1982. After continuing to fall through 1984, real money increases until the hyperinflation in 1989, when it plummets to approximately half its "pre-hyper" level. Even after very low inflation in subsequent years, real money did not return to its level of early 1989. Declines in real money are closely correlated with increases in the ratchet variable, although the stability of a relation between these variables may be an issue, noting the remaining large deviations between them.²

3 Previous Results

This section summarizes the model of Argentine money demand developed by Kamin and Ericsson (1993).

Kamin and Ericsson (1993) test for and find cointegration between real money, the interest rate, the inflation rate, exchange rate depreciation, and the ratchet variable; and the ratchet variable is key to finding cointegration. While the interest rate and the exchange rate do not appear to be weakly exogenous, there are only minor differences between system estimates of the cointegrating vector and the solved long-run coefficients from a conditional single-equation autoregressive distributed lag (ADL) model. So, Kamin and Ericsson (1993) model broad money as a single-equation conditional error correction model (ECM).

In their single equation modeling, Kamin and Ericsson (1993) start with a seventh-order ADL that has 63 coefficients and simplify it to a more restricted "intermediate" ADL with only 30 coefficients. Kamin and Ericsson (1993) then further simplify to obtain the following 16-coefficient model, which is their equation (6).

Δ	$\displaystyle \hspace*{-0.25in} \begin{array}[t]{l} \begin{array}[b]{lll} \widehat{\Delta(m-p)_{t}} & \;\;\;= & \;\;\;\ \begin{array}[t]{c} {0.264}\\ ({0.028})\\ {[0.035]} \end{array} \Delta(m-p)_{t-1}\;+\ \begin{array}[t]{c} {0.091}\\ ({0.031})\\ {[0.032]} \end{array} \Delta^{2}(m-p)_{t-5}\;\\ & \; & \\ & & \;-\ \begin{array}[t]{c} {0.740}\\ ({0.040})\\ {[0.041]} \end{array} \Delta^{2}p_{t}\;+\ \begin{array}[t]{c} {0.101}\\ ({0.040})\\ {[0.054]} \end{array} \Delta^{2}p_{t-5}\;-\ \begin{array}[t]{c} {0.594}\\ ({0.078})\\ {[0.089]} \end{array} \Delta^{2}p_{t}^{pos}\\ & & \\ & & \;+\ \begin{array}[t]{c} {0.059}\\ ({0.018})\\ {[0.021]} \end{array} \Delta\Delta_{6}p_{t}\;\;+\ \begin{array}[t]{c} {0.182}\\ ({0.022})\\ {[0.018]} \end{array} \Delta^{2}R_{t}\;+\ \begin{array}[t]{c} {0.536}\\ ({0.044})\\ {[0.045]} \end{array} (R-\Delta p)_{t-1}\\ & & \\ & & \ +\ \begin{array}[t]{c} {0.103}\\ ({0.022})\\ {[0.022]} \end{array} \;-\ \begin{array}[t]{c} {0.0337}\\ ({0.0078})\\ {[0.0080]} \end{array} (m-p)_{t-1}\;-\ \begin{array}[t]{c} {0.069}\\ ({0.017})\\ {[0.019]} \end{array} \Delta e_{t-1}\\ & & \\ & & \;-\ \begin{array}[t]{c} {0.028}\\ ({0.010})\\ {[0.010]} \end{array} \Delta p_{t-1}^{max}\;-\ \begin{array}[t]{c} {0.216}\\ ({0.038})\\ {[0.039]} \end{array} B_{t}\;+\ \begin{array}[t]{c} {0.179}\\ ({0.032})\\ {[0.020]} \end{array} B_{t-3}\\ & & \\ & & \;+\ \begin{array}[t]{c} 2{.45}\\ ({0.64})\\ {[0.43]} \end{array} S_{t-6}\ +\ \begin{array}[t]{c} 5{.09}\\ ({0.62})\\ {[0.74]} \end{array} S_{t-12} \end{array} \\ \; \end{array}$	(4)
	$\begin{displaymath} \begin{array}[t]{l} T=180\;\text{[1978(2)--1993(1)]}\;\;\;\;\;\text{R}^{2}=0.9489\;\;\;\;\;\hat {\sigma}=2.192\%\;\;\;\;\;dw=2.08\;\smallskip\ Inn_{1}:F(47,117)=1.47^{+}\;\;\;\;\;Inn_{2} :F(14,150)=1.46\;\;\;\;\;AR:F(7,157)=0.61\;\;\;\;\;\smallskip\ ARCH:F(7,150)=2.75^{\ast}\;\;\;\;\;Normality:\chi^{2} (2)=0.59\;\;\;\;\;RESET:F(1,163)=0.43\smallskip\ Hetero:F(26,137)=0.99\;\;\;\;Form:F(102,61)=0.71\;\;\;\;\;Chow:F(33,131)=0.76,\ \; \end{array}\smallskip\end{displaymath}$

where a circumflex $\hat{~}$ on the dependent variable denotes its fitted value, the subscript is the time index, $\Delta\Delta_{6}p_{t} =\Delta(p_{t}-p_{t-6})$ , R² is the squared multiple correlation coefficient, and $\hat{\sigma}$ is the estimated residual standard error. The long-run solution to equation (4) is: $\vspace*{-0.15in}$

$\begin{displaymath}\begin{array}[b]{lll} m-p & \;\;\;= & \;\;\ \begin{array}[t]{c} 3{.05} \end{array} \;+\; \begin{array}[t]{c} 15{.93} \end{array} (R-\Delta p)\;-\ \begin{array}[t]{c} 2{.04} \end{array} \Delta e\;-\ \begin{array}[t]{c} {0.84} \end{array} \Delta p^{max}\;. \end{array}\end{displaymath}$

(5)

Kamin and Ericsson (1993) show that equation (4) has a straightforward economic interpretation and is statistically satisfactory. Economically, the long-run coefficients in (5) satisfy sign restrictions that are consonant with a money demand function. The short-run variables and coefficients in (4) are also easily understood. Each short-run variable enters as a second difference (an acceleration), which is a natural transformation to stationarity for a potentially I(2) variable. The coefficient on $\Delta^{2}p_{t}$ is close to -1, implying that, in the short run, agents are in essence adjusting nominal (and not real) money.³ The lag lengths on $\Delta^{2}(m-p)_{t-5}$ , $\Delta^{2}p_{t-5}$ , and $\Delta\Delta_{6}p_{t}$ are consistent with agents' adjustments for seasonality in the data. The variable $\Delta\Delta_{6}p_{t}$ is also consistent with a natural data-based predictor of future (seasonal) inflation, extending the theoretical and empirical developments on such predictors in Flemming (1976), Hendry and Ericsson (1991), and Campos and Ericsson (1999). And, the coefficient on $\Delta^{2}p_{t}^{pos}$ is very negative and statistically significant, implying stronger reactions to rising inflation than to falling inflation.

The estimated money demand function also shed lights on the dollarization of the Argentine economy. Kamin and Ericsson (2003) reinterpret the ratchet effect in light of data measuring the extent of dollarization. Specifically, the reduction in peso money demand attributable to the ratchet effect is comparable in magnitude to the estimated stock of total dollar assets held domestically by Argentine residents, where those assets are estimated from U.S. Treasury data. This suggests that secular reductions in the demand for pesos reflect substitution into dollars rather than mere economizing on peso balances (or other forms of financial innovation). Thus, the ratchet may proxy for dollar holdings, which relaxes the draconian assumption of true irreversibility.

Statistically, Kamin and Ericsson (1993) show that equation (4) is parsimonious and empirically constant and satisfies a variety of diagnostic tests. Equation (4) and the regressions below report diagnostic statistics for testing against various alternative hypotheses: residual autocorrelation ( and ), skewness and excess kurtosis (), autoregressive conditional heteroscedasticity (), RESET (), heteroscedasticity ( and ), non-innovation errors relative to a more general model (), and predictive failure (, Chow's prediction interval statistic). The asymptotic null distribution is designated by $\chi^{2}(\cdot)$ or $F(\cdot,\cdot)$ , where the degrees of freedom fill the parentheses. Estimated standard errors are in parentheses $(\cdot)$ , below coefficient estimates; heteroscedasticity-consistent standard errors are in brackets $[\cdot]$ . See Doornik and Hendry (2007) for details and references.

In spite of the apparent robustness of equation (4), its design has shortcomings. The associated cointegration analysis excludes $\Delta^{2} p_{\;}^{pos}$ , a linear trend, and an impulse dummy for the Plan Bonex. And, equation (4) may depend on the path taken for model selection. The remainder of the current paper addresses these issues.

4 Integration and Cointegration

This section presents unit root tests for the variables of interest (Section 4.1). Then, Johansen's maximum likelihood procedure is applied to test for cointegration among real money, inflation, the interest rate, exchange rate depreciation, $\Delta$ $^{2}p^{pos}$ , the ratchet variable, and a linear trend (Section 4.2). Coefficient restrictions and the adjustment mechanism are examined in the Johansen framework.

4.1 Integration

Table 1 lists augmented Dickey-Fuller (ADF) statistics and related calculations for the data. In order to test whether a given series is I(0), I(1), I(2), or I(3), Table 1 calculates unit root tests for the original variables, for their changes, and for the changes of the changes. This permits testing the order of integration, albeit by testing adjacent orders of integration in a pairwise fashion. The largest estimated root ( $\hat{\rho}$ ) is listed adjacent to each ADF statistic: this root should be approximately unity if the null hypothesis is correct. The lag length of the reported ADF regression is based on minimizing the AIC, starting with a maximum of twelve lags.

Table 1: ADF statistics for testing a unit root in various time series

Variable^a,b	lag $\ell$	$t_{ADF(\ell)}$	$\;\hat{\rho}\;$	$\hat{\sigma}\;(\%)$	t-prob (%)	F-prob (%)	AIC
m	8	-2.81	0.988	5.318	2.1	52.1	-5.75
p	12	-2.95	0.984	7.741	17.8	--	-4.98
e	8	-3.07	0.970	12.63	0.1	43.7	-4.02
m - p	11	-3.08	0.934	6.912	2.9	47.1	-5.22
R	12	-2.06	0.821	9.208	8.2	--	-4.64
Δp^max	10	-1.74	0.983	2.631	5.7	62.9	-7.15
R - Δp	5	-4.64**	0.079	9.300	0.1	12.4	-4.65
R - Δe	1	-9.72**	0.069	10.65	1.4	24.2	-4.40
Δm	8	-2.28	0.849	5.431	15.8	48.6	-5.71
Δp	12	-2.45	0.810	7.905	8.1	--	-4.94
Δe	8	-2.76	0.703	12.96	13.7	84.6	-3.97
Δ(m - p)	7	-3.95*	0.380	7.118	14.0	67.5	-5.18
ΔR	11	-5.46**	-1.952	9.334	2.4	43.5	-4.61
Δ(Δp^max)	9	-4.27**	0.487	2.657	3.0	76.4	-7.14
Δ(R -Δp)	11	-6.16**	-5.268	9.670	1.1	81.7	-4.54
Δ(R -Δe)	12	-7.49**	-7.758	10.71	9.1	--	-4.33
Δ²m	6	-9.12**	-1.348	5.520	1.7	40.8	-5.69
Δ²p	10	-4.96**	-1.517	8.072	11.7	43.9	-4.91
Δ²e	6	-9.36**	-2.257	13.26	0.0	66.7	-3.94
Δ²(m - p)	9	-7.56**	-3.759	7.323	1.2	46.0	-5.11
Δ²R	12	-7.87**	-11.81	9.888	4.1	--	-4.49
Δ²(Δp^max)	10	-6.09**	-2.108	2.778	11.6	78.5	-7.04
Δ²(R - Δp)	11	-7.67**	-17.68	10.65	2.3	86.0	-4.35
Δ²(R - Δe)	12	-8.49**	-19.20	12.19	0.2	--	-4.07
Δ²p^pos	5	-3.17 $^{+}$	0.643	4.188	0.7	76.7	-6.24

Notes:
a. Twelfth-order ADF regressions were initially estimated, and the final lag length was selected to minimize the Akaike Information Criterion (AIC). The columns report the name of the variable examined, the selected lag length $\ell$ , the ADF statistic on the simplified regression ( $t_{ADF(\ell)}$ ), the estimated coefficient on the lagged level that is being tested for a unit value ( $\hat{\rho}$ ), the regression's residual standard error ( $\hat{\sigma}$ , in %), the tail probability of the t-statistic on the longest lag of the final regression (t-prob, in %), the tail probability of the F-statistic for the lags dropped (F-prob, in %), and the AIC.
b. All of the ADF regressions include an intercept, monthly dummies, and a linear trend. MacKinnon's (1991) approximate finite-sample critical values for the corresponding ADF statistics are -3.14 (10%), -3.44 (5%), and -4.01 (1%) for T = 177. In this table, and in the other results reported herein, rejection of the indicated null hypothesis is denoted by ⁺, *, and ** for the 10%, 5%, and 1% levels. Samples sizes are T = 179, T = 178, and T = 177 respectively for the three null hypotheses.

Nominal money, prices, and the exchange rate appear to be I(2). Real money, the nominal interest rate, inflation, and the inflation ratchet variable appear to be I(1). The ex post real interest rate and $R-\Delta e$ appear stationary.

4.2 Cointegration

Cointegration analysis helps clarify the long-run relationships between integrated variables. A brief review leads to the current analysis and places the latter in context.

Johansen's (1988, 1991) procedure is maximum likelihood for finite-order vector autoregressions (VARs) with variables that are integrated of order one [I(1)], and it is easily calculated for such systems. Various approaches exist for modeling possibly cointegrated I(2) variables. Johansen (1992b) proposes and implements a unified (vector autoregressive) system approach for the entire testing sequence going from I(2) to I(1) to I(0). His empirical application uses data on U.K. narrow money demand, which appear to have the same orders of integration as the Argentine series above. For the U.K. data, Johansen (1992b) tests for and finds that nominal money and prices (which are I(2)) cointegrate with a (+1 : -1) cointegrating vector to give real money, which is I(1). He then tests for and finds that real money, inflation, real income, and interest rates (all of which are I(1)) cointegrate. Because the I(2) Argentine variables and appear to cointegrate as the I(1) variable , the cointegration analysis here begins with the variables , $\Delta p$ , , $\Delta p^{max}$ , $\Delta e$ , $\Delta$ $^{2}p^{pos}$ , and a linear trend.

Empirically, the lag order of the VAR is not known a priori, so some testing of lag order may be fruitful in order to ensure reasonable power of the Johansen procedure. Given the number of variables, the number of observations, and the data's periodicity, the largest system considered is a seventh-order VAR of , $\Delta p$ , , $\Delta p^{max}$ , $\Delta e$ , and $\Delta$ $^{2}p^{pos}$ . In that VAR, the linear trend is restricted to lie in the cointegration space; and an intercept, seasonal dummies, and the Plan Bonex dummy (and three of its lags) enter freely. Empirically, the seventh lag may be statistically insignificant, but no further lag restrictions appear feasible, so inferences below are for the seventh-order VAR .

Table 2 reports the standard statistics, 95% critical values (c.v.'s), and estimates for Johansen's procedure applied to this seventh-order VAR . The maximal eigenvalue and trace eigenvalue statistics ( $\lambda_{max}$ and $\lambda_{trace}$ ) strongly reject the null of no cointegration in favor of at least one cointegrating relationship, and likely in favor of two cointegrating relationships. However, parallel statistics with a degrees-of-freedom adjustment ( $\lambda_{max}^{a}$ and $\lambda_{trace}^{a}$ ) suggest only one cointegrating relationship. Because the VAR for Table 2 uses a large number of degrees of freedom in estimation, inferences are based on the adjusted eigenvalue statistics.

Table 2: A cointegration analysis of the Argentine money demand data: Panel A: Rank r

Rank r	r = 0	r ≤ 1	r ≤ 2	r ≤ 3	r ≤ 4	r ≤ 5	r ≤ 6
Log-likelihood	2497.21	2528.69	2551.50	2563.38	2571.45	2576.82	2578.52
Eigenvalue λ_r	-	0.295	0.224	0.124	0.086	0.058	0.019

Table 2: A cointegration analysis of the Argentine money demand data: Panel B: Null hypothesis

Statistic	r = 0	r ≤ 1	r ≤ 2	r ≤ 3	r ≤ 4	r ≤ 5
λ_max	62.98**	45.61**	23.77	16.13	10.75	3.38
λ^a_max	48.28*	34.97	18.22	12.37	8.24	2.59
95% c.v.	43.97	37.52	31.46	25.54	18.96	12.25
λ_trace	162.6**	99.64**	54.03	30.26	14.13	3.38
λ^a_trace	124.7*	76.39	41.42	23.20	10.83	2.59
95% c.v.	114.9	87.31	62.99	42.44	25.32	12.25

Table 2: A cointegration analysis of the Argentine money demand data: Panel C: Eigenvectors β'

Variable	(m - p)	Δp	R	Δp^max	Δe	Δ²p^pos	trend
Row 1	1	10.89	-17.53	1.20	6.17	62.69	-0.0028
Row 2	0.08	1	-0.78	0.04	-0.30	0.50	0.0003
Row 3	-0.25	-2.40	1	-0.29	-0.49	4.66	-0.0002
Row 4	-0.61	-8.49	47.66	1	-17.90	-5.39	-0.0062
Row 5	-1.43	15.50	-18.97	-0.38	1	7.94	-0.0092
Row 6	-0.63	0.34	-2.35	-1.27	0.35	1	0.0058

Table 2: A cointegration analysis of the Argentine money demand data: Panel D: Adjustment Coefficients α

Variable	Column 1	Column 2	Column 3	Column 4	Column 5	Column 6
(m - p)	-0.020	0.265	0.083	0.002	0.010	0.010
Δp	0.015	-0.365	0.015	-0.002	-0.013	-0.002
R	0.034	0.085	-0.067	0.002	-0.020	0.015
Δp^max	0.016	-0.137	-0.005	0.002	-0.004	0.002
Δe	-0.048	0.877	0.093	0.011	-0.034	-0.012
Δ²p^pos	0.005	-0.344	-0.052	0.000	-0.009	0.001

Table 2: A cointegration analysis of the Argentine money demand data: Panel E: Weak exogeneity test statistics

Variable	(m - p)	Δp	R	Δp^max	Δe	Δ²p^pos
χ²(1)	6.57*	3.70⁺	9.89**	12.6**	4.58*	0.59

Table 2: A cointegration analysis of the Argentine money demand data: Panel F: Statistics for testing the significance of a given variable in β'x

Variable	(m - p)	Δp	R	Δp^max	Δe	Δ²p^pos	trend
χ²(1)	2.71⁺	2.79⁺	7.65**	3.89*	7.44**	16.7**	1.31

Table 2: A cointegration analysis of the Argentine money demand data: Panel G: Multivariate statistics for testing trend stationarity

Variable	(m - p)	Δp	R	Δp^max	Δe	Δ²p^pos
χ²(5)	48.4**	45.7**	43.7**	56.6**	30.6**	24.2**

Note: A box surrounds the first row of numbers in Panel C, and another box surrounds the first column of numbers in Panel D.

Table 2 also reports the standardized eigenvectors and adjustment coefficients, denoted $\beta^{\prime}$ and $\alpha$ in a common notation. The first row of $\beta^{\prime}$ is the estimated cointegrating vector, which can be written in the form of (2):

$\begin{displaymath}\begin{array}[b]{lll} m-p & \;\;\;= & \;\;\ \begin{array}[t]{c} \mathrm{intercept} \end{array} \;\;-{}{ \begin{array}[t]{c} {10.89}\\ \hspace*{0.08in}(3.72) \end{array} }\hspace*{-0.08in}\Delta p\;\;+{}{ \begin{array}[t]{c} {17.53}\\ \hspace*{0.08in}(4.48) \end{array} }\hspace*{-0.08in}R\;\;-{}{ \begin{array}[t]{c} {1.20}\\ (0.32) \end{array} }\hspace*{-0.08in}\Delta p^{max}\\ & \; & \\ & & -\;{ \begin{array}[t]{c} 6.17\\ (1.55) \end{array} }\hspace*{-0.08in}\Delta e\;\;-{}{ \begin{array}[t]{c} {62.69}\\ (10.68) \end{array} }\hspace*{-0.08in}\Delta^{2}p^{pos}\;\;+{}{ \begin{array}[t]{c} 0.0028\\ (0.0020) \end{array} }\hspace*{-0.08in}t. \end{array}\end{displaymath}$

(6)

All coefficients have their anticipated signs. Also, the trend appears to be statistically insignificant: $\chi^{2}(1)=1.31$ , where the asymptotic -value is in square brackets. And, the hypothesis of "relative rates of return" in (3) appears acceptable. Numerically, the sum of the coefficients on $\Delta p$ and $\Delta e$ (-17.06) is approximately equal to minus the coefficient on (17.53). Statistically, that restriction cannot be rejected: $\chi^{2}(1)=0.04$ [0.850]. Jointly, the restrictions on the trend and rates of return also appear acceptable: $\chi^{2}(2)=1.39$ [0.498].

Table 3 reports the estimated values of $\alpha$ and $\beta$ when estimated unrestrictedly, and when estimated with a zero coefficient on the trend imposed, with the hypothesis of "relative rates of return" imposed, and with both of those restrictions imposed. The similarity of coefficient estimates across the various restrictions points to the robustness of the results and is partial evidence in favor of those restrictions.

Table 3: Just-identified and over-identified estimates of β and α, with corresponding estimated standard errors, from a cointegration analysis of Argentine money demand.: Panel A: Variable corresponding to an element of β'

Estimate of β'	m - p	Δp	R	Δp^max	Δe	Δ²p^pos	trend
Just-identified	1	10.89 (3.72)	-17.53 (4.48)	1.20 (0.32)	6.17 (1.55)	62.69 (10.68)	-0.0028 (0.0020)
Zero coefficient on trend imposed	1	10.45 (2.71)	-14.49 (3.27)	0.92 (0.14)	3.51 (1.07)	45.28 (7.75)	0
Rates-of-return restriction imposed	1	10.64 (3.55)	-16.60 (3.87)	1.21 (0.27)	5.96 (1.46)	58.67 (8.14)	-0.0027 (0.0019)
Trend and rates-of-return restrictions imposed	1	10.19 (2.56)	-13.58 (2.76)	0.94 (0.12)	3.38 (1.01)	41.48 (5.51)	0

Estimate of α'	m - p	Δp	R	Δp^max	Δe	Δ²p^pos
Just-identified	-0.020 (0.007)	0.015 (0.007)	0.034 (0.012)	0.016 (0.004)	-0.048 (0.021)	0.005 (0.005)
Zero coefficient on trend imposed	-0.024 (0.010)	0.016 (0.009)	0.050 (0.016)	0.020 (0.005)	-0.051 (0.029)	0.003 (0.007)
Rates-of-return restriction imposed	-0.021 (0.008)	0.015 (0.007)	0.036 (0.012)	0.017 (0.004)	-0.050 (0.022)	0.005 (0.005)
Trend and rates-of-return restrictions imposed	-0.026 (0.011)	0.017 (0.010)	0.054 (0.017)	0.022 (0.006)	-0.054 (0.031)	0.004 (0.007)

Thus, the nominal interest rate and inflation enter the long-run money demand function as the ex post real rate, with a semi-elasticity of about eleven, which is about unity at annual rates. The nominal interest rate relative to the exchange-rate depreciation has about half that effect on money demand. Money demand is highly sensitive to the movement of inflation, both through $\Delta^{2}p^{pos}$ and through the ratchet variable $\Delta p^{max}$ . In particular, for each additional percent in the maximal monthly inflation rate over the relative past, the coefficient on $\Delta p^{max}$ implies approximately one percent lower money holdings.

Figure 3 plots key aspects of equation (6)--namely, the relationship between the variables , $\Delta p^{max}$ , and $(R-\Delta p)$ . Real money holdings fall as $\Delta p^{max}$ increases and as the return on money relative to goods $(R-\Delta p)$ declines.

Figure 3: The logarithm of real money (m - p), plotted against the maximal inflation rate (Δp^max) and the real interest rate (R - Δp)

Data for Figure 3 immediately follows.

Data for Figure 3

Date	(m - p)	Δp^max	R - Δp
1977-1	2.404471	-	-
1977-2	2.425484	0.077387	-0.003187
1977-3	2.447058	0.077387	-0.004326
1977-4	2.539662	0.077387	0.002530
1977-5	2.624674	0.077387	-0.001284
1977-6	2.641501	0.077387	-0.009510
1977-7	2.660990	0.077387	-0.004118
1977-8	2.635934	0.107631	-0.034631
1977-9	2.623017	0.107631	0.001328
1977-10	2.571095	0.118482	-0.025682
1977-11	2.559429	0.118482	0.013925
1977-12	2.646366	0.118482	0.034037
1978-1	2.608390	0.125444	-0.026144
1978-2	2.643875	0.125444	0.019156
1978-3	2.621147	0.125444	-0.020800
1978-4	2.612881	0.125444	-0.037837
1978-5	2.622747	0.125444	-0.014095
1978-6	2.681274	0.125444	0.009325
1978-7	2.699209	0.125444	0.004702
1978-8	2.711565	0.125444	-0.007451
1978-9	2.711735	0.125444	-0.000529
1978-10	2.684952	0.125444	-0.027872
1978-11	2.680808	0.125444	-0.017172
1978-12	2.693516	0.125444	-0.016770
1979-1	2.662952	0.125444	-0.052828
1979-2	2.675306	0.125444	-0.007481
1979-3	2.680873	0.125444	-0.011602
1979-4	2.696720	0.125444	-0.003212
1979-5	2.721186	0.125444	-0.001712
1979-6	2.730533	0.125444	-0.025969
1979-7	2.744375	0.125444	0.000483
1979-8	2.725727	0.125444	-0.035226
1979-9	2.743850	0.125444	0.007371
1979-10	2.811398	0.125444	0.029475
1979-11	2.840601	0.125444	0.011902
1979-12	2.890433	0.125444	0.014715
1980-1	2.889875	0.125444	-0.011835
1980-2	2.899849	0.125444	-0.000573
1980-3	2.888501	0.125444	-0.007779
1980-4	2.853743	0.125444	-0.015198
1980-5	2.817130	0.125444	-0.010837
1980-6	2.825433	0.125444	-0.002445
1980-7	2.857974	0.125444	0.015477
1980-8	2.886855	0.125444	0.016281
1980-9	2.884430	0.125444	-0.001110
1980-10	2.850921	0.125444	-0.030220
1980-11	2.846330	0.125444	0.000486
1980-12	2.886839	0.125444	0.016854
1981-1	2.850673	0.125444	0.008521
1981-2	2.820511	0.125444	0.025366
1981-3	2.770487	0.125444	0.023033
1981-4	2.760892	0.125444	-0.001149
1981-5	2.719500	0.125444	0.007565
1981-6	2.703099	0.125444	0.011884
1981-7	2.703186	0.125444	0.010680
1981-8	2.705274	0.125444	0.026472
1981-9	2.735503	0.125444	0.014655
1981-10	2.749043	0.125444	0.012913
1981-11	2.738920	0.125444	0.004313
1981-12	2.768634	0.125444	-0.014965
1982-1	2.714624	0.125444	-0.040043
1982-2	2.730076	0.125444	0.019802
1982-3	2.738028	0.125444	0.022413
1982-4	2.762294	0.125444	0.040980
1982-5	2.791927	0.125444	0.043854
1982-6	2.763377	0.125444	-0.017394
1982-7	2.657165	0.150646	-0.099546
1982-8	2.526791	0.150646	-0.087088
1982-9	2.395635	0.157750	-0.087950
1982-10	2.354903	0.157750	-0.049566
1982-11	2.334181	0.157750	-0.022664
1982-12	2.405781	0.157750	-0.016032
1983-1	2.420155	0.157750	-0.043417
1983-2	2.375893	0.157750	-0.022496
1983-3	2.355309	0.157750	-0.006762
1983-4	2.364466	0.157750	0.002247
1983-5	2.398701	0.157750	0.013223
1983-6	2.371626	0.157750	-0.057891
1983-7	2.354840	0.157750	-0.012373
1983-8	2.313019	0.159084	-0.043084
1983-9	2.243063	0.193652	-0.051652
1983-10	2.244771	0.193652	-0.011777
1983-11	2.253208	0.193652	-0.030918
1983-12	2.353592	0.193652	-0.017977
1984-1	2.414872	0.193652	-0.002886
1984-2	2.409003	0.193652	-0.056938
1984-3	2.359442	0.193652	-0.084467
1984-4	2.314524	0.193652	-0.039721
1984-5	2.285799	0.193652	-0.027681
1984-6	2.294710	0.193652	-0.034766
1984-7	2.292801	0.193652	-0.012906
1984-8	2.255929	0.205770	-0.050770
1984-9	2.144309	0.243317	-0.088317
1984-10	2.086846	0.243317	-0.006660
1984-11	2.141538	0.243317	0.030461
1984-12	2.151631	0.243317	-0.009637
1985-1	2.109829	0.243317	-0.049176
1985-2	2.093735	0.243317	-0.007874
1985-3	2.012384	0.243317	-0.035065
1985-4	1.991975	0.258244	-0.018244
1985-5	2.015876	0.258244	0.075927
1985-6	2.016300	0.266472	-0.106472
1985-7	2.092957	0.266472	-0.025098
1985-8	2.131651	0.266472	0.004822
1985-9	2.185248	0.266472	0.015243
1985-10	2.247214	0.266472	0.011723
1985-11	2.256860	0.266472	0.007591
1985-12	2.346090	0.266472	-0.000213
1986-1	2.363749	0.266472	0.001154
1986-2	2.404743	0.266472	0.014243
1986-3	2.393673	0.266472	-0.014415
1986-4	2.399513	0.266472	-0.015258
1986-5	2.421674	0.266472	-0.008479
1986-6	2.443864	0.266472	-0.011451
1986-7	2.441587	0.266472	-0.030435
1986-8	2.389271	0.266472	-0.033201
1986-9	2.366525	0.266472	-0.024815
1986-10	2.421847	0.266472	-0.008759
1986-11	2.432729	0.266472	0.003403
1986-12	2.521382	0.266472	0.008688
1987-1	2.505292	0.266472	-0.017874
1987-2	2.474059	0.266472	-0.003000
1987-3	2.467442	0.266472	-0.048805
1987-4	2.483266	0.266472	0.008908
1987-5	2.505608	0.266472	0.006099
1987-6	2.509485	0.266472	-0.011974
1987-7	2.494367	0.266472	-0.021398
1987-8	2.418701	0.266472	-0.033539
1987-9	2.397749	0.266472	-0.000524
1987-10	2.337599	0.266472	-0.043538
1987-11	2.348982	0.266472	-0.008750
1987-12	2.449926	0.266472	0.090546
1988-1	2.436886	0.266472	0.044973
1988-2	2.425096	0.266472	0.033768
1988-3	2.435608	0.266472	0.018510
1988-4	2.386193	0.266472	0.003016
1988-5	2.376793	0.266472	0.026985
1988-6	2.394030	0.266472	0.029785
1988-7	2.346610	0.266472	-0.001259
1988-8	2.318104	0.266472	-0.135927
1988-9	2.361228	0.266472	-0.019580
1988-10	2.367192	0.266472	0.006885
1988-11	2.437168	0.266472	0.046430
1988-12	2.565286	0.266472	0.055841
1989-1	2.648490	0.266472	0.035539
1989-2	2.643205	0.266472	0.098414
1989-3	2.608526	0.266472	0.058953
1989-4	2.502546	0.287976	0.159024
1989-5	2.281421	0.579239	0.574761
1989-6	2.199170	0.763017	0.605983
1989-7	1.827017	1.087311	-0.748311
1989-8	2.055586	1.087311	-0.193083
1989-9	2.193367	1.087311	-0.015435
1989-10	2.307980	1.087311	0.006558
1989-11	2.321008	1.087311	0.032836
1989-12	2.034576	1.087311	0.216007
1990-1	1.318222	1.087311	-0.319354
1990-2	1.123179	1.087311	-0.118771
1990-3	0.742464	1.087311	-0.214521
1990-4	1.064193	1.087311	0.008289
1990-5	1.200506	1.087311	-0.039579
1990-6	1.271376	1.087311	0.009868
1990-7	1.350697	1.087311	0.008214
1990-8	1.298890	1.087311	-0.044694
1990-9	1.236619	1.087311	0.021365
1990-10	1.284640	1.087311	0.034909
1990-11	1.342745	1.087311	0.007029
1990-12	1.448775	1.087311	0.021298
1991-1	1.453322	1.087311	0.061733
1991-2	1.274226	1.087311	-0.071041
1991-3	1.269363	1.087311	0.011159
1991-4	1.336993	1.087311	-0.039441
1991-5	1.385660	1.087311	-0.012159
1991-6	1.413816	1.087311	-0.013760
1991-7	1.427194	1.087311	-0.007580
1991-8	1.460799	1.087311	0.001075
1991-9	1.486950	1.087311	-0.006840
1991-10	1.524018	1.087311	-0.002903
1991-11	1.576481	1.087311	0.007008
1991-12	1.659075	1.087311	0.007018
1992-1	1.680185	1.087311	-0.018537
1992-2	1.685963	1.087311	-0.011312
1992-3	1.681282	1.087311	-0.011779
1992-4	1.714833	1.087311	-0.002785
1992-5	1.786803	1.087311	0.002292
1992-6	1.849497	1.087311	0.000190
1992-7	1.880951	1.087311	-0.007140
1992-8	1.896892	1.087311	-0.005855
1992-9	1.912783	1.087311	-0.001285
1992-10	1.911993	1.087311	-0.003580
1992-11	1.919925	1.087311	0.005401
1992-12	1.946672	1.087311	0.008167
1993-1	1.987473	1.087311	0.000711
1993-2	-	1.087311	0.003222
1993-3	-	1.087311	-
1993-4	-	1.087311	-
1993-5	-	1.087311	-
1993-6	-	1.087311	-
1993-7	-	1.087311	-
1993-8	-	1.087311	-
1993-9	-	1.087311	-
1993-10	-	1.087311	-
1993-11	-	1.087311	-
1993-12	-	1.087311	-

Returning to Table 2, the coefficients in the first column of $\alpha$ measure the feedback effects of the (lagged) disequilibrium in the cointegrating relation on the variables in the vector autoregression. Specifically, -0.020 is the estimated feedback coefficient for the money equation. The negative coefficient implies that lagged excess money induces smaller holdings of current money. The coefficient's numerical value implies slow adjustment to remaining disequilibrium. The estimated coefficient is numerically smaller than those for quarterly broad money demand (e.g., -0.26, -0.15, and -0.20 in Taylor (1986)) and monthly currency demand (e.g., -0.14 for Argentina in Ahumada (1992)). However, smaller adjustment coefficients are plausible with high-frequency data for a broad aggregate.

The third block from the bottom of Table 2 reports values of the statistic for testing weak exogeneity of a given variable for the cointegrating vector. Equivalently, the statistic tests whether or not the corresponding row of $\alpha$ is zero; see Johansen (1992a, 1992b). If the row of $\alpha$ is zero, disequilibrium in the cointegrating relationship does not feed back onto that variable. Surprisingly, inflation (including in its form $\Delta^{2}p^{pos}$ ) may be weakly exogenous. However, the interest rate, the exchange rate, and the ratchet variable are not weakly exogenous, justifying a systems approach to analyzing cointegration.

The penultimate block in Table 2 reports statistics for testing the significance of individual variables in the cointegrating vector. Each variable is significant, except the linear trend.

The final block in Table 2 reports values of a multivariate statistic for testing the trend stationarity of a given variable. Specifically, this statistic tests the restriction that the cointegrating vector contains all zeros except for a unity corresponding to the designated variable and an unrestricted coefficient on the trend, with the test being conditional on the presence of exactly one cointegrating vector; see Johansen (1995), p. 74]. For instance, the null hypothesis of trend-stationary real money implies that the cointegrating vector is (1 0 0 0 0 0 *)′, where "*" represents an unrestricted coefficient on the linear trend. Empirically, all of the stationarity tests reject with p-values less than 0.1%. By being multivariate, these statistics may have higher power than their univariate counterparts. Also, the null hypothesis is the stationarity of a given variable rather than the nonstationarity thereof, and stationarity may be a more appealing null hypothesis. That said, these rejections of stationarity are in line with the inability in Table 1 to reject the null hypothesis of a unit root in each of , $\Delta p$ , , $\Delta p^{max}$ , and $\Delta e$ .

Because , $\Delta p^{max}$ , and $\Delta e$ are not weakly exogenous for the cointegrating vector, inferences in a single equation for broad money could be hazardous if the cointegrating vector is estimated jointly with the equation's dynamics; see Hendry (1995). One solution is to model a subsystem. A second solution is to construct an error correction term from the system estimates and then develop a single equation ECM that uses that system-based error correction term. A third solution--adopted below--is to develop a single equation ECM from the single equation ADL, noting that the system estimate of the cointegrating relationship is numerically close to the ADL's long-run solution. See Hendry and Doornik (1994) and Juselius (1992) for paradigms of the first two approaches.

5 Computer-automated Model Selection

This section first describes the model selection algorithms in PcGets and Autometrics (Section 5.1) and then applies these algorithms to an ECM representation of an ADL for Argentine money demand (Section 5.2).

5.1 The Algorithms in PcGets and Autometrics

Hendry and Krolzig (2001) develop a computer program PcGets, which extends and improves upon Hoover and Perez's (1999) automated model-selection algorithm; see also Hendry and Krolzig (1999, 2003, 2005) and Krolzig and Hendry (2001). Doornik and Hendry (2007) implement a third-generation algorithm called Autometrics, which is part of PcGive version 12. PcGets and Autometrics utilize one-step and multi-step simplifications along multiple paths, diagnostic tests as additional checks on the simplified models, and encompassing tests to resolve multiple terminal models. Both analytical and Monte Carlo evidence show that the resulting model selection is relatively non-distortionary for Type I errors. At an intuitive level, PcGets and Autometrics function as a series of sieves that aim to retain parsimonious congruent models while discarding both noncongruent models and over-parameterized congruent models. This feature of the algorithms is eminently sensible, noting that the data generation process itself is congruent and is as parsimonious as feasible.

The remainder of the current subsection summarizes PcGets and Autometrics as automated model-selection algorithms, thereby providing the necessary background for interpreting their application in Section 5.2. For ease of reference, the algorithm in PcGets is divided into four "stages", denoted Stage 0, Stage 1, Stage 2, and Stage 3. For full details of PcGets's algorithm, see Hendry and Krolzig (2001), Appendix A1). Hendry and Krolzig (2003) describe the relationship of the general-to-specific approach to other modeling approaches in the literature, and Hoover and Perez (2004) extend the general-to-specific approach to cross-section regressions.

Stage 0: the general model and F pre-search tests. Stage 0 involves two parts: the estimation and evaluation of the general model, and some pre-search tests aimed at simplifying the general model before instigating formal multi-path searches.

First, the general model is estimated, and diagnostic statistics are calculated for it. If any of those diagnostic statistics is unsatisfactory, the modeler must decide what to do next--whether to "go back to the drawing board" and develop another general model, or whether to continue with the simplification procedure, perhaps ignoring the offending diagnostic statistic or statistics.

Second, PcGets attempts to drop various sets of potentially insignificant variables. PcGets does so by dropping all variables at a given lag, starting with the longest lag. PcGets also does so by ordering the variables by the magnitude of their t-ratios and either dropping a group of individually insignificant variables or (alternatively) retaining a group of individually statistically significant variables. In effect, an F pre-search test for a group of variables is a single test for multiple simplification paths, a characteristic that helps control the costs of search. If these tests result in a statistically satisfactory reduction of the general model, then that new model is the starting point for Stage 1. Otherwise, the general model itself is the starting point for Stage 1.

Stage 1: a multi-path encompassing search. Stage 1 tries to simplify the model from Stage 0 by searching along multiple paths, all the while ensuring that the diagnostic tests are not rejected. If all variables are individually statistically significant, then the initial model in Stage 1 is the final model. If some variables are statistically insignificant, then PcGets tries deleting those variables to obtain a simpler model. PcGets proceeds down a given simplification path only if the models along that path have satisfactory diagnostic statistics. If a simplification is rejected or if a diagnostic statistic fails, PcGets backtracks along that simplification path to the most recent previous acceptable model and then tries a different simplification path. A terminal model results if the model's diagnostic statistics are satisfactory and if no remaining regressors can be deleted.

If PcGets obtains only one terminal model, then that model is the final model, and PcGets proceeds to Stage 3. However, because PcGets pursues multiple simplification paths in Stage 1, PcGets may obtain multiple terminal models. To resolve such a situation, PcGets creates a union model from those terminal models and tests each terminal model against that union model. PcGets then creates a new union model, which nests all of the surviving terminal models; and that union model is passed on to Stage 2.

Stage 2: another multi-path encompassing search. Stage 2 in effect repeats Stage 1, applying the simplification procedures from Stage 1 to the union model obtained at the end of Stage 1. The resulting model is the final model. If Stage 2 obtains more than one terminal model after applying encompassing tests, then the final model is selected by using the Akaike, Schwarz, and Hannan-Quinn information criteria. See Akaike (1973, 1981), Schwarz (1978), and Hannan and Quinn (1979) for the design of these information criteria, and Atkinson (1981) for the relationships between them.

Stage 3: subsample evaluation. Stage 3 re-estimates the final model over two subsamples and reports the results. If a variable is statistically significant in the full sample and in both subsamples, then the inclusion of that variable in the final model is regarded as "100% reliable". If a variable is statistically insignificant in one or both subsamples or in the full sample, then its measure of reliability is reduced. A variable that is statistically insignificant in both subsamples and in the full sample is regarded as being "0% reliable". The modeler is left to decide what action, if any, to take in light of the degree of reliability assigned to each of the regressors.

PcGets thus has two components:

Estimation and diagnostic testing of the general unrestricted model (Stage 0); and

Selection of the final model by

(a) pre-search simplification of the general unrestricted model (Stage 0),
(b) multi-path (and possibly iterative) selection of the final model (Stages 1 and 2), and
(c) post-search evaluation of the final model (Stage 3).

This subsection's description of these four stages summarizes the algorithm in PcGets. Below, Section 5.2 summarizes the actual simplifications found by PcGets in practice, thereby providing additional insight into PcGets's algorithm.

PcGets requires the modeler to choose which tests are calculated and to specify the critical values for those tests. In PcGets, the modeler can choose the test statistics and their critical values directly, although doing so is tedious because of the number of statistics involved. To simplify matters, PcGets offers two options with pre-designated selections of test statistics and critical values. These two options are called "liberal" and "conservative" model selection strategies. The liberal strategy errs on the side of keeping some variables, even although they may not actually matter. The conservative strategy keeps only variables that are clearly significant statistically, erring in the direction of excluding some variables, even although those variables may matter. Which strategy is preferable depends in part on the data themselves and in part on the objectives of the modeling exercise, although (as below) the two approaches may generate similar or identical results.

The algorithm in PcGets is general-to-specifc, multi-path, iterative, and encompassing, with diagnostic tests providing additional assessments of statistical adequacy, and with options for pre-search simplification. The algorithm in Autometrics shares these characteristics with the algorithm in PcGets; hence, many of the remarks above about PcGets apply directly to Autometrics. However, Autometrics (unlike PcGets) uses a tree search method, with refinements on pre-search simplification and on the objective function. See Doornik and Hendry (2007) and Doornik (2008) for details.

5.2 Modeling of Argentine Money Demand Revisited

Using PcGets and Autometrics, the current subsection assesses the possible path dependence of equation (4). The initial general model is estimated; and the algorithms simplify that general model under each of the permutations implied by the list of choices below. While the algorithms do obtain multiple distinct final models, equation (4)--or simple variants of it--appears statistically sensible; and one variant obtained by Autometrics is even more parsimonious than (4). These results bolster the model design in Kamin and Ericsson (1993) and offer an improvement on it.

The multi-path searches in PcGets and Autometrics allow investigation of equation (4)'s robustness and examination of the empirical properties of the two algorithms themselves. In addition, four choices within the model selection process permit further insights. In PcGive, these choices concern the following.

Model strategy: either liberal ("L") or conservative ("C").

Pre-search testing (Stage 0): either switched on ("Yes") or off ("No").

The representation of the initial general ECM (three options): either the representation as tabulated, or either of two representations that explicitly nest equation (4). The latter two representations are distinguished by whether the variables from (4) are "free" or "fixed". Fixed variables are forced to always be included in regression, whereas free variables may be deleted by the algorithm.

The choice of the general model: either the unrestricted ADL, or the intermediate ADL described in Section 3.

For model strategy (choice #1), the options in Autometrics do not correspond precisely to PcGets's liberal and conservative strategies. Instead, Autometrics allows the user to select a "target size", which is meant to equal "the proportion of irrelevant variables that survives the [simplification] process" (Doornik, 2008). In the analysis below, Autometrics's target size is either 5% or 1%, which appear to approximate liberal and conservative strategies in PcGets. For pre-search testing (choice #2), the selected option in Autometrics is either pre-search for both variable reduction and lag reduction, or no pre-search for either--in order to match PcGets as closely as possible. The third choice above is identical for PcGets and Autometrics, as is the fourth choice.

For both PcGets and Autometrics, the third choice (the representation of the initial general ECM) can affect the final model selected. In simplifying the initial model, PcGets and Autometrics impose only "zero restrictions", i.e., the algorithms can set coefficients to be equal only to zero. Although a linear model is invariant to nonsingular linear transformations of its data, the coefficients of that model are not invariant to such transformations. For example, a model with regressors $x_{t}$ and $x_{t-1}$ is invariant to including the regressors $\Delta x_{t}$ and $x_{t-1}$ instead; but the deletion of $x_{t-1}$ results in two different simplifications, depending on the representation. See Campos and Ericsson (1999) for additional discussion.

Table 4 lists the estimates and standard errors for the ECM representation of the unrestricted seventh-order ADL model of , $\Delta p$ , , $\Delta p^{max}$ , $\Delta e$ , and $\Delta$ $^{2}p^{pos}$ . The standard diagnostic statistics do not reject. The implied coefficient on the error correction term appears to be highly significant statistically, with a t-ratio of -3.53. The intermediate ADL (in ECM representation) is Table 4, but re-estimated with the "boxed-in" coefficients in Table 4 set to zero. Kamin and Ericsson (1993) show that the estimated coefficients in this intermediate model are close to those in the unrestricted ECM in Table 4; and the intermediate ADL is a statistically acceptable reduction of Table 4, with $Inn:F(33,117)=1.42\;[0.091]$ . For ease of reference, the intermediate ADL is denoted Table 4*.

Table 4: An unrestricted error correction representation for real money conditional on inflation, the interest rate, and the change in the exchange rate: Panel A: Regression coefficients and estimated standard errors.

Variable^a,b,c	Lag j = 0	Lag j = 1	Lag j = 2	Lag j = 3	Lag j = 4	Lag j = 5	Lag j = 6	Lag j = 7
Δ(m - p)_t-j	-1 (-)	0.270 (0.088)	0.154 (0.093)	-0.019 (0.094)	0.029 (0.079)	0.204 (0.079)	-0.125 (0.072)	-
Δp_t-j	-0.768 (0.101)	0.177 (0.149)	-0.041 (0.140)	0.144 (0.136)	0.121 (0.117)	0.168 (0.119)	-0.275 (0.122)	-0.053 (0.079)
ΔR_t-j	0.222 (0.053)	0.031 (0.159)	0.172 (0.149)	0.140 (0.143)	-0.039 (0.128)	0.002 (0.096)	-0.131 (0.090)	-
$\Delta(\Delta p_{t-j}^{max})\rule[-0.28in]{0in}{0.45in}$	-0.223 (0.155)	-0.169 (0.184)	0.327 (0.281)	0.599 (0.297)	-0.104 (0.268)	-0.211 (0.264)	0.132 (0.317)	-
Δ $^{2}p_{t-j}^{pos}\rule[-0.28in]{0in}{0.45in}$	-0.406 (0.162)	-0.049 (0.154)	0.180 (0.161)	-0.114 (0.156)	-0.168 (0.133)	0.003 (0.137)	0.181 (0.130)	-0.017 (0.112)
Δe_t-j	-0.004 (0.020)	-0.040 (0.022)	-0.014 (0.023)	0.025 (0.022)	-0.040 (0.022)	0.011 (0.023)	0.032 (0.023)	-0.032 (0.022)
(m - p)_t-j	-	-0.053 (0.015)	-	-	-	-	-	-
R_t-j	-	0.441 (0.158)	-	-	-	-	-	-
$\Delta p_{t-j}^{max}\rule[-0.28in]{0in}{0.45in}$	-	-0.055 (0.019)	-	-	-	-	-	-
B_t-j	-0.353 (0.139)	0.178 (0.078)	0.058 (0.073)	0.286 (0.084)	-	-	-	-
S_t-j	0.160 (0.047)	-	-1.62 (1.20)	-0.08 (1.21)	0.41 (1.10)	-0.21 (1.16)	2.81 (1.02)	-
S_t-j-6	-	0.06 (0.97)	0.10 (1.03)	-0.55 (1.01)	0.86 (1.03)	0.20 (1.02)	4.35 (1.02)	-

Table 4: An unrestricted error correction representation for real money conditional on inflation, the interest rate, and the change in the exchange rate: Panel B: Regression statistics.

$\begin{displaymath} \begin{array}[t]{l} \;\vspace*{-0.05in}\ \begin{array}[c]{l} T=180\;[\text{1978(2)--1993(1)}]\;\;\;\;\;R^{2}=0.968\;\;\;\;\;\hat{\sigma }=2.058\%\smallskip \end{array}\ \begin{array}[c]{l} dw=2.02\;\;\;\;\;\text{\emph{AR}}:F(7,110)=0.67\;[0.695]\;\;\;\;\;LM_{p} :F(1,116)=0.08\;[0.773]^{d}\smallskip \end{array}\ \begin{array}[c]{l} \text{\emph{ARCH}}:F(7,103)=0.92\;[0.491]\;\;\;\;\;\text{\emph{Normality} }:\chi^{2}(2)=0.77\;[0.682]\smallskip \end{array}\ \begin{array}[c]{l} \text{\emph{Hetero}}:F(109,7)=0.08\;[1.000]\;\;\;\;\;\text{\emph{RESET} }:F(1,116)=1.89\;[0.171]\medskip \end{array}\end{array}\end{displaymath}$

Notes:
a. The dependent variable is Δ(m - p)_t. Even so, the equation is in levels, not in differences, noting the inclusion of the regressor (m - p)_t-1.
b. The variables {S_t-i} are the seasonal dummies, except that S₀ is the intercept. February is S_t-2, March is S_t-3, etc. For readability, the coefficients and estimated standard errors for the seasonal dummies have been multiplied by 100.
c. The 33 coefficients that are "boxed in" are set equal to zero in the partially restricted intermediate error correction representation denoted Table 4*.
d. The statistic LM_p is the Lagrange multiplier statistic for testing the imposed restriction of long-run price homogeneity.
e. A box surrounds the coefficients corresponding to variables dropped in Table 4*. Those variables are Δ(m - p)_t-j for j=2,3,4; Δp_t-j for j=2,3,4,7; ΔR_t-j for j=2,3,4,5,6; Δ(Δp_t-j^max) for j=0,1,2,3,4,5,6; Δ²p_t-j^pos for j=1,2,3,4,5,6,7; and Δe_t-j for j = 0,2,3,4,5,6,7.

Table 5 summarizes PcGets's model simplifications under the 24 different scenarios described above; Table 6 does likewise for Autometrics. In these tables, $k_{1}$ is the number of regressors in the general model for multi-path searches, $k_{f}$ is the number of coefficients in the final specific model for multi-path searches, the "number of paths" is the number of different simplification paths considered in a multi-path search, the "number of terminal models" is the number of distinct terminal specifications after a multi-path search, and $\hat{\sigma}$ is the residual standard error of the final specific model. If multi-path searches are iterated, the table lists values for each iteration, where appropriate. The "number of models estimated" is the total number of distinct models estimated in the multi-path search.

Table 5: Statistics on computer-automated model selection by PcGets of models for Argentine money demand, categorized according to model strategy, pre-search testing, representation of the general model, and choice of general model: Panel A: The general model is Table 4 or equivalent

Model Strategy	Pre-search?	Representation?	k₁	k_f	Number of paths	Number of terminal models	$\hat{\sigma}$ (%)
L	No	Table 4	63, 31	19	55, 7	13, 1	2.132
L	No	Nested	63, 31, 26	24	56, 18, 9	9, 3, 5	1.952
L	No	Fixed	63, 25	22	53, 10	6, 3	1.954
L	Yes	Table 4	26	21	10	3	2.078
L	Yes	Nested	28	23	11	3	1.989
L	Yes	Fixed	23	22	6	2	1.986
C	No	Table 4	63, 32, 31	23	61, 21, 20	10, 5, 4	2.015
C	No	Nested	63, 31	21	61, 22	9, 5	2.007
C	No	Fixed	63, 24	21	55, 9	6, 3	1.988
C	Yes	Table 4	21	21	1	1	2.139
C	Yes	Nested	22, 21	21	10, 8	2, 1	2.073
C	Yes	Fixed	24, 18	18	11, 3	1, 1	2.137

Model Strategy	Pre-search?	Representation?	k₁	k_f	Number of paths	Number of terminal models	$\hat{\sigma}$ (%)
L	No	Table 4*	30	20	18	1	2.149
L	No	Nested	30	18	20	1	2.137
L	No	Fixed	30	18	20	1	2.137
L	Yes	Table 4*	20	20	1	1	2.149
L	Yes	Nested	18	18	1	1	2.137
L	Yes	Fixed	18	18	1	1	2.137
C	No	Table 4*	30, 20	20	19, 3	1, 1	2.149
C	No	Nested	30, 18	18	22, 3	2, 1	2.137
C	No	Fixed	30, 18	18	22, 3	2, 1	2.137
C	Yes	4*	20, 20	20	3, 3	1, 1	2.149
C	Yes	Nested	18, 18	18	3, 3	1, 1	2.137
C	Yes	Fixed	18, 18	18	3, 3	1, 1	2.137

Table 6: Statistics on computer-automated model selection by Autometrics of models for Argentine money demand, categorized according to target size, pre-search testing, representation of the general model, and choice of general model: Panel A: The general model is Table 4 or equivalent

Target Size	Pre-search?	Representation?	k₁	k_f	Number of Models Estimated	Number of terminal models	$\hat{\sigma}$ (%)
5%	No	Table 4	63, 41	23	706	10, 17	1.997
5%	No	Nested	63, 36	21	378	8, 13	1.978
5%	No	Fixed	63, 31	20	306	6, 7	2.003
5%	Yes	Table 4	57, 37	22	470	6, 12	2.008
5%	Yes	Nested	50, 32	22	371	6, 7	1.972
5%	Yes	Fixed	45, 30	22	255	8, 8	1.986
1%	No	Table 4	63, 37	19	751	10, 20	2.095
1%	No	Nested	63, 29	21	501	8, 10	1.978
1%	No	Fixed	63, 22	18	497	2, 2	2.096
1%	Yes	Table 4	41, 35	20	677	10, 20	2.072
1%	Yes	Nested	39, 26	20	394	5, 5	2.014
1%	Yes	Fixed	30, 23	19	168	4, 4	2.078

Target Size	Pre-search?	Representation?	k₁	k_f	Number of Models Estimated	Number of terminal models	$\hat{\sigma}$ (%)
5%	No	Table 4*	30, 20	20	46	1, 1	2.149
5%	No	Nested	30, 18	18	65	1, 1	2.137
5%	No	Fixed	30, 18	18	65	1, 1	2.137
5%	Yes	Table 4*	25, 20	20	36	1, 1	2.149
5%	Yes	Nested	23, 18	18	40	1, 1	2.137
5%	Yes	Fixed	23, 18	18	43	1, 1	2.137
1%	No	Table 4*	30, 18	18	77	1, 1	2.211
1%	No	Nested	30, 14	14	139	1, 1	2.236
1%	No	Fixed	30, 16	16	2	1	2.192
1%	Yes	Table 4*	21, 20	20	30	1, 1	2.149
1%	Yes	Nested	19, 17	17	36	1, 1	2.168
1%	Yes	Fixed	19, 17	17	38	1, 1	2.168

Note: A box surrounds the eighth row of entries in the second panel.

Several features of the simplifications in Tables 5 and 6 are notable. First, pre-search testing typically reduces the number of paths that need to be searched in Stage 1, and often markedly so. As a consequence, pre-search testing frequently reduces the number of multiple terminal models and, in some instances, obtains the final model. Second, if the initial general model is the intermediate ECM (Table 4*, rather than the general ECM in Table 4), that choice is in effect a pre-search, albeit an informal one. That choice also typically obtains a single terminal model on the initial multi-path search. Third, a conservative strategy generally obtains a more parsimonious model than a liberal strategy, as expected. Fourth, Kamin and Ericsson's (1993) model results from a conservative-like strategy, as is apparent from examining the specifications of the final models in Tables 5 and 6. Fifth, the 1% and 5% target sizes in Autometrics appear closely comparable to the liberal and conservative strategies in PcGets. That said, in several instances, Autometrics dominates PcGets by obtaining a more parsimonious model with a better fit (in terms of $\hat{\sigma}$ ), whereas PcGets never dominates Autometrics in that sense. This outcome reflects differences in the algorithms' details. Finally, data transformations through the "nesting" approach permit a final representation that is more highly parsimonious than previously obtained; see the boxed-in result for Autometrics on Table 6.

The corresponding model, which improves on equation (4), is as follows.

Δ	$\displaystyle \hspace*{-0.25in} \begin{array}[t]{l} \begin{array}[b]{lll} \widehat{\Delta(m-p)_{t}} & \;\;\;= & \;\;\;\ \begin{array}[t]{c} {0.281}\\ ({0.025})\\ {[0.024]} \end{array} \Delta(m-p)_{t-1}\;-\ \begin{array}[t]{c} {0.759}\\ ({0.041})\\ {[0.040]} \end{array} \Delta^{2}p_{t}\;\\ & \; & \\ & & \;-\ \begin{array}[t]{c} {0.564}\\ ({0.078})\\ {[0.090]} \end{array} \Delta^{2}p_{t}^{pos}\;+\ \begin{array}[t]{c} {0.040}\\ ({0.017})\\ {[0.022]} \end{array} \Delta\Delta_{6}p_{t}\;\\ & & \\ & & \;+\ \begin{array}[t]{c} {0.180}\\ ({0.022})\\ {[0.019]} \end{array} \Delta^{2}R_{t}\;+\ \begin{array}[t]{c} {0.543}\\ ({0.044})\\ {[0.041]} \end{array} (R-\Delta p)_{t-1}\\ & & \\ & & \ +\ \begin{array}[t]{c} {0.093}\\ ({0.022})\\ {[0.025]} \end{array} \;-\ \begin{array}[t]{c} {0.0300}\\ ({0.0078})\\ {[0.0088]} \end{array} (m-p)_{t-1}\;-\ \begin{array}[t]{c} {0.060}\\ ({0.018})\\ {[0.019]} \end{array} \Delta e_{t-1}\\ & & \\ & & \;-\ \begin{array}[t]{c} {0.025}\\ ({0.010})\\ {[0.011]} \end{array} \Delta p_{t-1}^{max}\;-\ \begin{array}[t]{c} {0.253}\\ ({0.034})\\ {[0.030]} \end{array} B_{t}\;+\ \begin{array}[t]{c} {0.170}\\ ({0.032})\\ {[0.023]} \end{array} B_{t-3}\\ & & \\ & & \;+\ \begin{array}[t]{c} 1{.97}\\ ({0.62})\\ {[0.37]} \end{array} S_{t-6}\ +\ \begin{array}[t]{c} 4{.78}\\ ({0.62})\\ {[0.74]} \end{array} S_{t-12} \end{array} \\ \; \end{array}$	(7)
	$\begin{displaymath} \begin{array}[t]{l} T=180\;\text{[1978(2)--1993(1)]}\;\;\;\;\;\text{R}^{2}=0.9462\;\;\;\;\;\hat {\sigma}=2.236\%\;\;\;\;\;dw=2.10\;\smallskip\ Inn_{3}:F(49,117)=1.61^{\ast}\;\;\;\;\;Inn_{4}:F(16,150)=1.85^{\ast }\;\;\;\;\;AR:F(7,159)=1.65\;\;\;\;\;\smallskip\ ARCH:F(7,152)=2.73^{\ast}\;\;\;\;\;Normality:\chi^{2} (2)=0.44\;\;\;\;\;RESET:F(1,165)=1.60\smallskip\ Hetero:F(22,143)=1.08\;\;\;\;Form:F(75,90)=0.92\;\;\;\;\;Chow:F(33,133)=0.86\ \; \end{array}\bigskip\end{displaymath}$

The coefficients in equation (7) are little changed from the corresponding ones in equation (4), except that the coefficients for $\Delta^{2}(m-p)_{t-5}$ and $\Delta^{2}p_{t-5}$ are restricted to be zero. No tests reject at the 1% level (an implication of choices made in the algorithm's parameters), although some do at the 5% level. Equation (7) has virtually the same economic interpretation as equation (4), and it is more parsimonious than (4). PcGets and Autometrics thus verify the robustness of equation (4)'s specification, and Autometrics improves upon that specification.

6 Conclusions

Computer-automated model selection with the software packages PcGets and Autometrics demonstrates the robustness of Kamin and Ericsson's (1993) final error correction model and improves on it by using multi-path searches that would be tedious and prohibitively time-consuming with standard econometrics packages. Long-run money demand is driven by a negative ratchet effect from inflation, and by the opportunity cost of holding peso-denominated financial assets rather than Argentine goods or U.S. dollars. Short-run dynamics are consistent with an Ss-type inventory model that is interpretable as having either real or nominal short-run bounds.

Several general remarks are germane, and each suggests extensions to the current analysis. First, improvements to the model selection algorithms may and do obtain an improved model specification. Computer-automated model-selection algorithms are still in their youth--if not in their infancy--and considerable analytical, Monte Carlo, and empirical research is ongoing; see Hendry and Krolzig (1999, 2003, 2005), Krolzig and Hendry (2001), Hoover and Perez (2004), Doornik (2008), Hendry, Johansen, and Santos (2008), Hoover, Demiralp, and Perez (2008), Hoover, Johansen, and Juselius (2008), and Johansen and Nielsen (2008).

Second, insights by other researchers may improve the current model in a progressive research strategy. For example, Nielsen (2004), building on Hendry, von Ungern-Sternberg (1981), proposes an alternative measure of the opportunity cost of holding money that may better capture agents' behavior in a hyperinflationary environment. Preliminary tests for that alternative measure as an omitted variable in Table 4 do not reveal an improved specification, however. For instance, for a variable in levels, define $\nabla X_{t}$ as $(X_{t}-X_{t-1})/(X_{t-1})$ , which is 's percentage change, measured as a fraction. Omitted variables tests include $F(8,109)=1.23\;[0.290]$ for $\{\nabla P_{t-i};$ $i=0,\ldots,7\}$ , $F(24,93)=1.10\;[0.363]$ for $\{\nabla P_{t-i},\ \nabla P_{t-i}^{max} ,\ \Delta\nabla P_{t-i}^{pos};\ i=0,\ldots,7\}$ , and $F(32,85)=1.01\;[0.474]$ for $\{\nabla P_{t-i},$ $\nabla P_{t-i}^{max},$ $\Delta\nabla P_{t-i} ^{pos},$ $\nabla E_{t-i};\ i=0,\ldots,7\}$ . None of these tests reject at standard levels. Still, Table 4 is a relatively unrestricted model, so further investigation is merited, particularly because $\Delta p_{t}$ differs substantially from $\nabla P_{t}$ at high inflation rates and hence the interpretation of $\Delta p_{t}$ may be affected.

Third, Kongsted (2005) develops a procedure for testing the nominal-to-real transformation, which is only informally investigated herein for money by using the ADF statistics. Fourth, in the VAR, the variables $\Delta p^{max}$ and $\Delta$ $^{2}p^{pos}$ are transformations of $\Delta p$ , so further consideration of their joint distributional properties is desirable. Fifth, data observations after 1993 may be informative. Even so, mechanistic extensions of the existing data may not be sufficient, as when data definitions change, the array of available assets alters, and underlying economic conditions shift; see Ericsson, Hendry, and Prestwich (1998).

References

Ahumada, H. (1992) "A Dynamic Model of the Demand for Currency: Argentina 1977-1988", Journal of Policy Modeling, 14, 3, 335-361.

Akaike, H. (1973) "Information Theory and an Extension of the Maximum Likelihood Principle", in B. N. Petrov and F. Csáki (eds.) Second International Symposium on Information Theory, Akadémiai Kiadó, Budapest, 267-281.

Akaike, H. (1981) "Likelihood of a Model and Information Criteria", Journal of Econometrics, 16, 1, 3-14.

Atkinson, A. C. (1981) "Likelihood Ratios, Posterior Odds and Information Criteria", Journal of Econometrics, 16, 1, 15-20.

Baba, Y., D. F. Hendry, and R. M. Starr (1992) "The Demand for M1 in the U.S.A., 1960-1988", Review of Economic Studies, 59, 1, 25-61.

Beckerman, P. (1992) The Economics of High Inflation, St. Martin's Press, New York.

Cagan, P. (1956) "The Monetary Dynamics of Hyperinflation", Chapter 2 in M. Friedman (ed.) Studies in the Quantity Theory of Money, University of Chicago Press, Chicago, 23-117.

Campos, J., and N. R. Ericsson (1999) "Constructive Data Mining: Modeling Consumers' Expenditure in Venezuela", Econometrics Journal, 2, 2, 226-240.

Dominguez, K. M. E, and L. L. Tesar (2007) "International Borrowing and Macroeconomic Performance in Argentina", Chapter 7 in S. Edwards (ed.) Capital Controls and Capital Flows in Emerging Economies: Policies, Practices, and Consequences, University of Chicago, Chicago, 297-342 (with discussion).

Doornik, J. A. (2008) "Autometrics", in J. L. Castle and N. Shephard (eds.) The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry, Oxford University Press, Oxford, this volume.

Doornik, J. A., and D. F. Hendry (2007) PcGive 12, Timberlake Consultants Ltd, London (4 volumes).

Doornik, J. A., D. F. Hendry, and B. Nielsen (1998) "Inference in Cointegrating Models: UK M1 Revisited", Journal of Economic Surveys, 12, 5, 533-572.

Engle, R. F., and D. F. Hendry (1993) "Testing Super Exogeneity and Invariance in Regression Models", Journal of Econometrics, 56, 1/2, 119-139.

Enzler, J., L. Johnson, and J. Paulus (1976) "Some Problems of Money Demand", Brookings Papers on Economic Activity, 1976, 1, 261-280 (with discussion).

Ericsson, N. R. (2004) "The ET Interview: Professor David F. Hendry", Econometric Theory, 20, 4, 743-804.

Ericsson, N. R. (2008) Empirical Modeling of Economic Time Series, in preparation.

Ericsson, N. R., D. F. Hendry, and K. M. Prestwich (1998) "The Demand for Broad Money in the United Kingdom, 1878-1993", Scandinavian Journal of Economics, 100, 1, 289-324.

Flemming, J. S. (1976) Inflation, Oxford University Press, Oxford.

Hannan, E. J., and B. G. Quinn (1979) "The Determination of the Order of an Autoregression", Journal of the Royal Statistical Society, Series B, 41, 2, 190-195.

Helkie, W. L., and D. H. Howard (1994) "External Adjustment in Selected Developing Countries in the 1990s", Journal of Policy Modeling, 16, 4, 353-393.

Hendry, D. F. (1995) "On the Interactions of Unit Roots and Exogeneity", Econometric Reviews, 14, 4, 383-419.

Hendry, D. F. (2006) "Robustifying Forecasts from Equilibrium-correction Systems", Journal of Econometrics, 135, 1-2, 399-426.

Hendry, D. F., and J. A. Doornik (1994) "Modelling Linear Dynamic Econometric Systems", Scottish Journal of Political Economy, 41, 1, 1-33.

Hendry, D. F., and N. R. Ericsson (1991) "Modeling the Demand for Narrow Money in the United Kingdom and the United States", European Economic Review, 35, 4, 833-881 (with discussion).

Hendry, D. F., S. Johansen, and C. Santos (2008) "Automatic Selection of Indicators in a Fully Saturated Regression", Computational Statistics, 23, 2, 317-355, 337-339.

Hendry, D. F., and H.-M. Krolzig (1999) "Improving on 'Data Mining Reconsidered' by K. D. Hoover and S. J. Perez", Econometrics Journal, 2, 2, 202-219.

Hendry, D. F., and H.-M. Krolzig (2001) Automatic Econometric Model Selection Using PcGets 1.0, Timberlake Consultants Press, London.

Hendry, D. F., and H.-M. Krolzig (2003) "New Developments in Automatic General-to-Specific Modeling", Chapter 16 in B. P. Stigum (ed.) Econometrics and the Philosophy of Economics: Theory-Data Confrontations in Economics, Princeton University Press, Princeton, 379-419.

Hendry, D. F., and H.-M. Krolzig (2005) "The Properties of Automatic Gets Modelling", Economic Journal, 115, 502, C32-C61.

Hendry, D. F., and G. E. Mizon (1978) "Serial Correlation as a Convenient Simplification, Not a Nuisance: A Comment on a Study of the Demand for Money by the Bank of England", Economic Journal, 88, 351, 549-563.

Hendry, D. F., and T. von Ungern-Sternberg (1981) "Liquidity and Inflation Effects on Consumers' Expenditure", Chapter 9 in A. S. Deaton (ed.) Essays in the Theory and Measurement of Consumer Behaviour: In Honour of Sir Richard Stone, Cambridge University Press, Cambridge, 237-260.

Hoover, K. D., S. Demiralp, and S. J. Perez (2008) "Empirical Identification of the Vector Autoregression: The Causes and Effects of U.S. M2", in J. L. Castle and N. Shephard (eds.) The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry, Oxford University Press, Oxford, this volume.

Hoover, K. D., S. Johansen, and K. Juselius (2008) "Allowing the Data to Speak Freely: The Macroeconometrics of the Cointegrated Vector Autoregression", American Economic Review, 98, 2, 251-255.

Hoover, K. D., and S. J. Perez (1999) "Data Mining Reconsidered: Encompassing and the General-to-specific Approach to Specification Search", Econometrics Journal, 2, 2, 167-191 (with discussion).

Hoover, K. D., and S. J. Perez (2004) "Truth and Robustness in Cross-country Growth Regressions", Oxford Bulletin of Economics and Statistics, 66, 5, 765-798.

Howard, D. H (1987) "Exchange Rate Regimes and Macroeconomic Stabilization in a Developing Country", International Finance Discussion Paper No. 314, Board of Governors of the Federal Reserve System, Washington, D.C., November.

Johansen, S. (1988) "Statistical Analysis of Cointegration Vectors", Journal of Economic Dynamics and Control, 12, 2/3, 231-254.

Johansen, S. (1991) "Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models", Econometrica, 59, 6, 1551-1580.

Johansen, S. (1992a) "Cointegration in Partial Systems and the Efficiency of Single-equation Analysis", Journal of Econometrics, 52, 3, 389-402.

Johansen, S. (1992b) "Testing Weak Exogeneity and the Order of Cointegration in UK Money Demand Data", Journal of Policy Modeling, 14, 3, 313-334.

Johansen, S. (1995) Likelihood-based Inference in Cointegrated Vector Autoregressive Models, Oxford University Press, Oxford.

Johansen, S., and B. Nielsen (2008) "An Analysis of the Indicator Saturation Estimator as a Robust Regression Estimator", in J. L. Castle and N. Shephard (eds.) The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry, Oxford University Press, Oxford, this volume.

Juselius, K. (1992) "Domestic and Foreign Effects on Prices in an Open Economy: The Case of Denmark", Journal of Policy Modeling, 14, 4, 401-428.

Kamin, S. B. (1991) "Argentina's Experience with Parallel Exchange Markets: 1981-1990", International Finance Discussion Paper No. 407, Board of Governors of the Federal Reserve System, Washington, D.C., August.

Kamin, S. B., and N. R. Ericsson (1993) "Dollarization in Argentina", International Finance Discussion Paper No. 460, Board of Governors of the Federal Reserve System, Washington, D.C., November.

Kamin, S. B., and N. R. Ericsson (2003) "Dollarization in Post-hyperinflationary Argentina", Journal of International Money and Finance, 22, 2, 185-211.

Kiguel, M. A. (1991) "Inflation in Argentina: Stop and Go Since the Austral Plan", World Development, 19, 8, 969-986.

Kongsted, H. C. (2005) "Testing the Nominal-to-real Transformation", Journal of Econometrics, 124, 2, 205-225.

Krolzig, H.-M., and D. F. Hendry (2001) "Computer Automation of General-to-specific Model Selection Procedures", Journal of Economic Dynamics and Control, 25, 6-7, 831-866.

MacKinnon, J. G. (1991) "Critical Values for Cointegration Tests", Chapter 13 in R. F. Engle and C. W. J. Granger (eds.) Long-run Economic Relationships: Readings in Cointegration, Oxford University Press, Oxford, 267-276.

Manzetti, L. (1991) The International Monetary Fund and Economic Stabilization: The Argentine Case, Praeger, New York.

Melnick, R. (1990) "The Demand for Money in Argentina 1978-1987: Before and After the Austral Program", Journal of Business and Economic Statistics, 8, 4, 427-434.

Nielsen, B. (2004) "Money Demand in the Yugoslavian Hyperinflation 1991-1994", Economics Working Paper No. 2004-W31, Nuffield College, University of Oxford, Oxford, December.

Piterman, S. (1988) "The Irreversibility of the Relationship Between Inflation and Real Balances", Bank of Israel Economic Review, 60, January, 72-83.

Schwarz, G. (1978) "Estimating the Dimension of a Model", Annals of Statistics, 6, 2, 461-464.

Simpson, T. D., and R. D. Porter (1980) "Some Issues Involving the Definition and Interpretation of the Monetary Aggregates", in the Federal Reserve Bank of Boston (ed.) Controlling Monetary Aggregates III, Federal Reserve Bank of Boston, Boston, Conference Series No. 23, 161-234 (with discussion).

Taylor, M. P. (1986) "From the General to the Specific: The Demand for M2 in the Three European Countries", Empirical Economics, 11, 4, 243-261.

Uribe, M. (1997) "Hysteresis in a Simple Model of Currency Substitution", Journal of Monetary Economics, 40, 1, 185-202.

World Bank (1990) Argentina: Reforms for Price Stability and Growth, World Bank, Washington, D.C.

Footnotes

* Forthcoming in Jennifer L. Castle and Neil Shephard (eds.) The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry, Oxford University Press, Oxford, 2008. The authors are staff economists in the Division of International Finance, Board of Governors of the Federal Reserve System, Washinton D.C. 20551 U.S.A.; and they may be reached on the Internet at [email protected] and [email protected] respectivityl. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. The authors are grateful to Julia Campos, Jennifer Castle, Dale Henderson, David Hendry, Katarina Juselius, Jaime Marquez, Bent Nielsen, Anders Rahbek, Neil Shephard, and two referees for helpful comments. All numerical results were obtained using PcGiv Version 12.00, Autometrics Version 1.5, and PcGets Version 1.02; see Doornik and Hendry (2007), Doornik (2008), and Hendry and Krolzig (2001). Return to text

1. A preliminary investigation found little role for Y in the cointegration analysis or in error correction modeling. This is consistent with Ahumada's (1992) evidence on currency demand, and may be due to the relatively stationary nature of real GDP in Argentina over the sample period. Return to text

2. For further analytical and empirical discussion of the Argentine economy, see Howard (1987), the World Bank (1990), Kamin (1991), Kiguel (1991), Manzetti (1991), Beckerman (1992), Kamin and Ericsson (1993), and Helkie and Howard (1994). See Dominguez and Tesar (2007) for a history of the post-1990 period. Return to text

3. Hendry and Ericsson (1991, p. 853] and Baba, Hendry, and Starr (1992) find similar results for narrow money demand in the United Kingdom and the United States. Also, in keeping with this observation about Δ²p_t, Kamin and Ericsson (1993) simplify the restricted intermediate ADL to obtain an alternative ECM where that ECM has Δm_t as the dependent variable. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text