
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 965, January 2009 --- Screen Reader
Version*
Tax Smoothing in Frictional Labor Markets
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We re-examine the optimality of tax smoothing from the point of view of frictional labor markets. Our central result is that whether or not this cornerstone optimal fiscal policy prescription carries over to an environment with labor market frictions depends crucially on the cyclical nature of labor force participation. If the participation rate is exogenous at business-cycle frequencies--as is typically assumed in the literature--we show it is not optimal to smooth tax rates on labor income in the face of business-cycle shocks. However, if households do optimize at the participation margin, then tax-smoothing is optimal despite the presence of matching frictions. To understand these results, we develop a concept of general-equilibrium efficiency in search-based environments, which builds on existing (partial-equilibrium) search-efficiency conditions. Using this concept, we develop a notion of search-based labor-market wedges that allows us to trace the source of the sharply-contrasting fiscal policy prescriptions to the value of adjusting participation rates. Our results demonstrate that policy prescriptions can be very sensitive to the cyclical nature of labor-force participation in search-based environments.
Keywords: Labor market frictions, optimal taxation
JEL classification: E24, E50, E62, E63
1. Introduction
We have two main aims in this paper. The first is to re-examine a classic issue in the theory of fiscal policy -- the optimality of labor-income tax smoothing -- from the point of view of frictional labor markets. Since Barro's (1979) partial-equilibrium intuition, Lucas and Stokey's (1983) general-equilibrium analysis, and continuing through to today's quantitative DSGE models used to study optimal fiscal policy, the prescription that governments ought to hold labor tax rates virtually constant in the face of aggregate shocks is well-known to macroeconomists. We show that this cornerstone policy prescription and the intuition underlying it carry over to a general-equilibrium environment in which search and matching frictions exist in labor markets only if households optimally adjust their labor-force participation over the business cycle. In contrast, if the labor-force participation rate is exogenous at business cycle horizons, as is almost uniformly assumed in the recent vintages of DSGE labor-search models, then purposeful tax-rate volatility is optimal. The optimal degree of tax-rate variability in this case is one to two orders of magnitude larger than benchmark results in the Ramsey literature. Nevertheless, the degree of cyclical variability in the participation rate implied by our model in this case is well within empirical ranges. Our results demonstrate that a model's policy prescriptions can be very sensitive to its assumed cyclical nature of labor-force participation.
The second aim of our work is to provide a general notion of efficiency for use in search-based general-equilibrium macroeconomic models. As part of the recent surge in popularity in building DSGE models featuring search and matching frictions in labor markets, many studies have focused on the transmission channels of macroeconomic policy and the determination of optimal policy. Efficiency concerns lie at the heart of any model studying optimal policy. In light of this, a contribution of this paper is that we develop a general-equilibrium notion of efficiency for search-based models that not only clearly shows the conditions under which tax-smoothing is and is not optimal, but also may be helpful in casting light on results that are starting to emerge elsewhere in the literature.
In particular, we develop a precise notion of the marginal rate of transformation (MRT) between leisure (being outside the labor force) and output that takes into account search frictions and the long-lived nature of employment relationships that they endogenously generate. With this concept of MRT, we are able to characterize general-equilibrium efficiency in a search model using only the basic principle that MRTs should be equated to their associated marginal rates of substitution (MRS). This characterization of efficiency in turn allows us to define a novel type of labor wedge, which is explicitly search-based, between MRS and MRT. This view of wedges pinpoints the conditions under which smoothing of labor income tax rates is optimal even though labor markets are always frictional in our model. Our notion of efficiency has as a necessary, but not sufficient, component the well-known Hosios (1990) condition for (partial-equilibrium) search efficiency. Our definition of the MRT nests as a special case the RBC neoclassical-based notion of the MRT between leisure and output. Similarly, our notion of the search-based labor wedge nests as a special case the neoclassical notion of the labor wedge emphasized by Chari, Kehoe, and McGrattan (2007), Shimer (2008), and others. We view as virtues of our definitions of efficiency and wedges that they nest their counterparts in the widely-understood RBC model.
Our baseline search and matching environment is identical to the one that has come into widespread use in recent DSGE modeling efforts. The crucial feature for our analysis is that -- in keeping with nearly all of the existing literature -- it assumes the size of the labor force is exogenous. We quantitatively demonstrate the optimality of labor tax-rate volatility in this environment and trace the source of this volatility directly to the inability of the labor-force-participation rate to adjust to business-cycle shocks. The inability of the participation rate to adjust is reflected in cyclical variations in the shadow value of the fixed participation margin. Cyclical variations in this shadow value shift the search-based labor wedge that we identify. Time-variation in tax rates is then used to stabilize the overall labor wedge. In a calibrated version of this economy, the optimal degree of labor tax volatility is large: the standard deviation of the optimal tax rate is between 2 and 6 percent, depending on precise parameter values, around a mean of about 20 percent. For comparison, the Ramsey literature's conventional tax-smoothing result entails optimal tax-rate volatility near 0.1 percent or less -- for example, see the overview in Chari and Kehoe (1999). Thus, optimal labor tax rates are one to two orders of magnitude more volatile in the widely-used baseline search model than in simple neoclassical-based Ramsey environments.
On the other hand, if participation is endogenous over the business cycle, we show that, despite the presence of search frictions, the labor tax rate is the only aspect of the economy that creates a labor wedge. Even though the labor wedge we define is a generalization of the standard notion, the basic prescription that a Ramsey government should keep wedges nearly constant over time applies, which in this case calls for tax-rate smoothing. Thus, if participation adjusts, the analytical insights developed by Werning (2007) and Scott (2007) on the optimality of tax smoothing in a neoclassical labor market also seem to apply to frictional labor markets. More broadly, endogeneity of labor-force participation bridges the gap between a frictionless neoclassical environment and frictional environments (ala Pissarides (2000)) by allowing households a unilateral optimization margin with respect to some aspect of their labor-market outcomes. Such an optimization margin is at the core of any neoclassical-based macro model, but is absent in virtually all search-based macro models.
In our model, the optimization margin with respect to labor-market outcomes is the participation decision: optimal policy critically depends on whether or not labor-force participation fluctuates optimally at business cycle horizons. Most of the empirical evidence suggests very small fluctuations along the participation margin at business-cycle timeframes. Elsby, Michaels, and Solon (2008) and many others argue that because cyclical adjustment of participation is so small, assuming no cyclical fluctuations in participation is a useful approximation in order to focus on other labor-market transitions. Empirical arguments such as the latter are often used in theoretical work to justify modeling the size of the labor force as fixed over the business cycle. However, our results show that modeling small fluctuations in participation as zero fluctuations can lead to sharply contrasting policy prescriptions. In particular, in the version of our model featuring adjustment of participation rates, the equilibrium fluctuations along this margin indeed turn out to be very small: our model predicts that the participation rate varies by about half a percentage point around a mean of 66 percent. This range of variation is very much in line with what is observed in data. Thus, using the narrow range of observed participation rates as a basis for ignoring the participation margin altogether can matter quantitatively and qualitatively for some policy-relevant questions. It is not the narrow range of fluctuations in participation rates that matters for our results; rather, it is the fluctuations in associated shadow prices that matter. Veracierto (2008), while focused on a different range of issues, is another recent example demonstrating that predictions of modern labor-market models can be sensitive to the assumed cyclical nature of labor force participation.
To conduct our analysis, we formulate a DSGE labor-search model in a way that nests both the typical exogenous-labor-force specification as well as the endogenous labor-force specification. We nest these two frameworks by defining a shadow value of adjustment along the participation margin, and this shadow value appears in key equilibrium conditions of the model, including the search wedge described above. If participation always adjusts optimally, this shadow value is by construction zero; if participation does not adjust to shocks, this shadow value fluctuates over time, thus shifting equilibrium conditions. Because our formulation is easy to use, it can be applied to any DSGE search model in order to shed light on the economic forces at work.
Finally, we note that tax volatility in our model is not driven by any incompleteness of government debt markets, which is a well-understood point in Ramsey models since Aiyagari, Marcet, Marimon, and Sargent (2002). Thus, our only point of departure from a neoclassically-based complete-markets Ramsey setup, such as the textbook Chari and Kehoe (1999) presentation, is that we model labor trades as governed by primitive search and matching frictions. While search-based DSGE models have become commonplace in recent years, their ability to shed new insights on optimal fiscal policy has not yet been much explored.2 Our model features no capital accumulation, in order to highlight the dynamics of labor taxes. We see no reason why our basic intuition and results would not extend to the classic case of Ramsey taxation of both labor and capital income.
The rest of our work is organized as follows. Section 2 lays out the basic search model, in which we are able to capture in nested form both an environment that does feature and an environment that does not feature cyclical adjustment of labor-force participation. In Section 3, we develop our general-equilibrium concepts of MRT and efficiency. In Section 4, we show which features of the decentralized search economy create wedges in the efficiency condition we propose. Section 5 presents the Ramsey problem. Section 6 presents our main results. Section 7 concludes.
2. Model
As many other recent studies have done, we embed the baseline Pissarides (2000) textbook search model into a DSGE framework. The baseline Pissarides (2000) framework features no labor-force participation decision. Virtually all of the recent DSGE models adopting a search-theoretic foundation for labor markets have inherited this structure. We instead consider two variants of the environment facing households, one in which the number of individuals in the labor force (defined as individuals either working or actively seeking employment) is exogenous and one in which it is endogenous. Despite search and matching frictions, the latter setup renders our model close to DSGE models based on neoclassical labor markets, in which the key equilibrium margin is often the labor-force participation margin.3 Regardless of whether participation is endogenous or exogenous, however, transitions into employment are always subject to search and matching frictions in our model.
We present these two versions of our search model in a unified, nested way. Specifically, rather than construct essentially two different environments, we construct one very general framework that allows for an endogenous participation decision but that, by introducing one additional constraint, can also allow for exogenous participation. As described below, nesting the two environments in this way allows us to clearly isolate the incentives relevant for optimal policy. These incentives turn out to be captured by the shadow value of the constraint that allows us to move between the exogenous- and the endogenous-participation versions of our model.
We present in turn the choice problems of the representative firm, the representative household, the determination of wages, the actions of the government, and the definition of private-sector equilibrium.
2.1 Production
The production side of the economy features a representative firm that must open vacancies, which entail costs, in order to hire workers and produce. The representative firm is "large" in the sense that it operates many jobs and consequently has many individual workers attached to it through those jobs.
The firm requires only labor to produce its output. The firm
must engage in costly search for a worker to fill each of its job
openings. In each job ![]() that will produce output, the
worker and firm bargain over the pre-tax real wage
that will produce output, the
worker and firm bargain over the pre-tax real wage ![]() paid in that position. Output of any job
paid in that position. Output of any job ![]() is given by
is given by
![]() , which is subject to a common
technology realization
, which is subject to a common
technology realization ![]() .
.
Any two jobs ![]() and
and ![]() at the
firm are identical, so from here on we suppress the second
subscript and denote by
at the
firm are identical, so from here on we suppress the second
subscript and denote by ![]() the real wage in any job,
and so on. Total output of the firm thus depends on the technology
realization and the measure of matches
the real wage in any job,
and so on. Total output of the firm thus depends on the technology
realization and the measure of matches ![]() that
produce,
that
produce,
| (1) |
The total real wage bill of the firm is the sum of wages paid at
all of its positions,
![]() .
.
The firm begins period ![]() with employment stock
with employment stock
![]() . Its period-
. Its period-![]() productive employment stock,
productive employment stock, ![]() , depends on
its period-
, depends on
its period-![]() vacancy-posting choices as well as the
random matching process described below.4 With probability
vacancy-posting choices as well as the
random matching process described below.4 With probability
![]() , taken as given by the firm, a
vacancy will be filled by a worker. Labor-market tightness is
, taken as given by the firm, a
vacancy will be filled by a worker. Labor-market tightness is
![]() , where
, where ![]() denotes the number of individuals searching for jobs. Matching
probabilities for both firms and households depend only on
aggregate market tightness given the Cobb-Douglas matching function
assumed below.
denotes the number of individuals searching for jobs. Matching
probabilities for both firms and households depend only on
aggregate market tightness given the Cobb-Douglas matching function
assumed below.
Our baseline wage-determination mechanism is Nash bargaining, as described below. In the firm's profit maximization problem, the wage-setting protocol is taken as given.5 We employ Nash bargaining because it has become familiar in DSGE search models, and thus enhances comparability with existing studies. However, as we note below, our results are identical if we employ an alternative equilibrium concept, competitive search equilibrium, in which wages are determined in a decentralized fashion rather than through bilateral negotiations.
The firm thus chooses vacancies to post ![]() and
a current employment stock
and
a current employment stock ![]() to maximize
discounted profits starting at date
to maximize
discounted profits starting at date ![]() ,
,
![$\displaystyle E_{t} \sum_{t=0}^{\infty} \beta^{t} \left\{ \Xi_{t\vert} \left[ z_{t} n^{f}_{t} - w_{t} n^{f}_{t} - \gamma v_{t} \right] \right\} ,$](img23.gif)
|
(2) |
where ![]() is the period-0 value to the
representative household of period-
is the period-0 value to the
representative household of period-![]() goods, which
we assume the firm uses to discount profit flows because households
are the ultimate owners of firms.6 In period
goods, which
we assume the firm uses to discount profit flows because households
are the ultimate owners of firms.6 In period ![]() , the firm's problem is thus to choose
, the firm's problem is thus to choose ![]() and
and ![]() to maximize (2) subject to a
sequence of perceived laws of motion for its employment level,
to maximize (2) subject to a
sequence of perceived laws of motion for its employment level,
| (3) |
Firms incur the real cost ![]() for each
vacancy created, and job separation occurs with exogenous fixed
probability
for each
vacancy created, and job separation occurs with exogenous fixed
probability ![]() . Note the timing of events
embodied in the law of motion (3). Period
. Note the timing of events
embodied in the law of motion (3). Period
![]() begins with employment stock
begins with employment stock
![]() , some of whom separate from the
firm before period-
, some of whom separate from the
firm before period-![]() production occurs; the firm
posts vacancies and hires a flow of new employees
production occurs; the firm
posts vacancies and hires a flow of new employees
![]() , which depends on
both the firm's decisions and market conditions; the employment
stock
, which depends on
both the firm's decisions and market conditions; the employment
stock ![]() then engages in production.
then engages in production.
The firm's first-order conditions with respect to ![]() and
and ![]() yield a standard
job-creation condition
yield a standard
job-creation condition
![$\displaystyle \frac{\gamma}{k^{f}(\theta_{t})} = z_{t} - w_{t} + (1-\rho^{x}) E_{t} \left[ \Xi_{t+1\vert t} \frac{\gamma}{k^{f}(\theta_{t+1})} \right] ,$](img41.gif)
|
(4) |
where
![]() is the
household discount factor (again, technically, the real interest
rate) between period
is the
household discount factor (again, technically, the real interest
rate) between period ![]() and
and ![]() . The
job-creation condition states that at the optimal choice, the
vacancy-creation cost incurred by the firm is equated to the
discounted expected value of profits from a match. Profits from a
match take into account future marginal revenue product from the
match, the wage cost of the match, and the asset value of having a
pre-existing relationship with an employee in period
. The
job-creation condition states that at the optimal choice, the
vacancy-creation cost incurred by the firm is equated to the
discounted expected value of profits from a match. Profits from a
match take into account future marginal revenue product from the
match, the wage cost of the match, and the asset value of having a
pre-existing relationship with an employee in period ![]() . This condition is a free-entry condition in the creation
of vacancies and is a standard equilibrium condition in a labor
search and matching model.
. This condition is a free-entry condition in the creation
of vacancies and is a standard equilibrium condition in a labor
search and matching model.
2.2 Households
There is a representative household in the economy. Each household consists of a continuum of measure one of family members, and each individual family member is classified as either inside the labor force or outside the labor force. An individual family member that is outside the labor force enjoys leisure. An individual family member that is part of the labor force is engaged in one of two activities: working, or not working but actively searching for a job. The convenience of an "infinitely-large" household is that we can naturally suppose that each individual family member experiences the same level of consumption regardless of his personal labor-market status. This tractable way of modeling perfect consumption insurance in general-equilibrium search-theoretic models of labor markets has been common since Andolfatto (1996) and Merz (1995). We use the terms "individual" and "family member" interchangeably from here on. Given the basics of the environment, we also use the terms "leisure" and "outside the labor force" interchangeably from here on.
As noted above, we construct our model in a flexible way to
allow for two cases regarding labor-force participation. In the
first case, which corresponds to the benchmark Pissarides (2000)
model, the size of the labor force is exogenously fixed at the
measure
![]() , with
, with
![]() a parameter to be calibrated below.
With the labor-force participation rate fixed at
a parameter to be calibrated below.
With the labor-force participation rate fixed at ![]() , the fixed measure
, the fixed measure
![]() of family
members thus enjoy leisure in every period. For reasons that will
become clear immediately below, we label this version of our model
the pseudo-labor-force-participation model, or pseudo-LFP
model for short. In the second case, households each period
optimally choose the size of
of family
members thus enjoy leisure in every period. For reasons that will
become clear immediately below, we label this version of our model
the pseudo-labor-force-participation model, or pseudo-LFP
model for short. In the second case, households each period
optimally choose the size of
![]() ; the labor-force
participation rate is thus endogenous in every period
; the labor-force
participation rate is thus endogenous in every period ![]() . We label this version of the model the
labor-force-participation model (LFP model). As the
descriptions below show, with the exception of one constraint, the
household problem is identical in both the pseudo-LFP model and the
LFP model.
. We label this version of the model the
labor-force-participation model (LFP model). As the
descriptions below show, with the exception of one constraint, the
household problem is identical in both the pseudo-LFP model and the
LFP model.
2.2.1 Pseudo-LFP Model
Although the labor-force participation rate is fixed in the
baseline environment, we formulate the household problem as if
there were free choice over the participation rate, but impose
a constraint that ensures it is always ![]() . This
formulation motivates our label "pseudo" LFP model. Households are
fully aware of the constraint
. This
formulation motivates our label "pseudo" LFP model. Households are
fully aware of the constraint
![]() . The advantage of
this formulation of the problem is that the shadow value of this
constraint directly sheds light on the mechanism driving our
optimal-policy results and makes quite transparent comparisons with
the full LFP model described next.
. The advantage of
this formulation of the problem is that the shadow value of this
constraint directly sheds light on the mechanism driving our
optimal-policy results and makes quite transparent comparisons with
the full LFP model described next.
The representative household maximizes expected lifetime discounted utility
![$\displaystyle E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(c_{t}) + g(1-u^{h}_{t}-n^{h}_{t}) \right]$](img54.gif)
|
(5) |
subject to a sequence of flow budget constraints
| (6) |
a sequence of perceived laws of motion for the measure of family members that are employed,
| (7) |
and the exogenous restriction on the size of the labor force
| (8) |
The functions ![]() and
and ![]() are
standard strictly-increasing and strictly-concave subutility
functions over consumption and leisure, respectively.
are
standard strictly-increasing and strictly-concave subutility
functions over consumption and leisure, respectively.
A utility value of leisure is often what is meant when partial-equilibrium labor-search models refer casually to the "outside benefit of not working." Our model formalizes this idea in a way that is easily comparable to RBC-based models. This way of modeling (part of) the outside benefit of not working is identical to that in Shi and Wen (1999) and Domeij (2005). As emphasized by Blanchard and Gali (2008), the fact that, at the household level, the marginal rate of substitution between consumption and leisure is not an exogenous constant also distinguishes our model from partial-equilibrium search environments.
A second notion of the "outside benefit of not working" is
represented by ![]() , which is the flow of
unemployment benefits each unemployed individual (actively
searching for employment) receives. We assume the unemployment
benefit is time-invariant. Because our model explicitly depicts
three labor-market states, we can meaningfully distinguish
between unemployment benefits and the utility of leisure, which are
often referred to and modeled interchangeably in
partial-equilibrium environments and in even some
general-equilibrium search environments.
, which is the flow of
unemployment benefits each unemployed individual (actively
searching for employment) receives. We assume the unemployment
benefit is time-invariant. Because our model explicitly depicts
three labor-market states, we can meaningfully distinguish
between unemployment benefits and the utility of leisure, which are
often referred to and modeled interchangeably in
partial-equilibrium environments and in even some
general-equilibrium search environments.
The rest of the terms in the constraints are as follows. The
after-tax real wage rate each employed individual earns is
![]() . The household takes
as given the probability
. The household takes
as given the probability
![]() that one of its unemployed and
searching individuals will find employment. As with matching
probabilities for firms,
that one of its unemployed and
searching individuals will find employment. As with matching
probabilities for firms, ![]() depends only on
aggregate labor-market tightness given the assumption of a
Cobb-Douglas matching technology. Finally,
depends only on
aggregate labor-market tightness given the assumption of a
Cobb-Douglas matching technology. Finally, ![]() is
the household's holdings of a state-contingent one-period real
government bond at the end of period
is
the household's holdings of a state-contingent one-period real
government bond at the end of period ![]() , which has
gross state-contingent payoff
, which has
gross state-contingent payoff ![]() at the
beginning of period
at the
beginning of period ![]() . Important to note is that
the government is able to issue fully state-contingent debt; thus,
none of our optimal policy results will be driven by an inability
on the part of the government to use debt as a shock absorber.
Incompleteness of government debt markets can be an important
driver of results in Ramsey models -- see, for example, Aiyagari,
Marcet, Marimon, and Sargent (2002). Of course, because this is a
Ramsey-taxation model, there are no lump-sum taxes or transfers
between the government and the private sector.
. Important to note is that
the government is able to issue fully state-contingent debt; thus,
none of our optimal policy results will be driven by an inability
on the part of the government to use debt as a shock absorber.
Incompleteness of government debt markets can be an important
driver of results in Ramsey models -- see, for example, Aiyagari,
Marcet, Marimon, and Sargent (2002). Of course, because this is a
Ramsey-taxation model, there are no lump-sum taxes or transfers
between the government and the private sector.
Due to firms' sunk resource and time costs of finding employees,
firms earn positive flows of economic profits. These profits are
transferred to households at the end of each period in lump-sum
fashion: ![]() is the household's receipts of firms'
flow profits. We permit government taxation of households' receipts
of dividends at the fixed tax rate
is the household's receipts of firms'
flow profits. We permit government taxation of households' receipts
of dividends at the fixed tax rate ![]() . As is
well-understood in the Ramsey literature, flows of untaxed
dividends received by households in and of themselves affect
optimal-policy prescriptions.7 To make our results as comparable
as possible to baseline models that prescribe labor-tax-rate
smoothing, in which there are zero economic profits/dividends, our
main analysis is conducted assuming
. As is
well-understood in the Ramsey literature, flows of untaxed
dividends received by households in and of themselves affect
optimal-policy prescriptions.7 To make our results as comparable
as possible to baseline models that prescribe labor-tax-rate
smoothing, in which there are zero economic profits/dividends, our
main analysis is conducted assuming
![]() . The consequence of this
assumption is that any predictions made by our model regarding
optimal labor-income taxation cannot be due to incentives to tax
profits, either in the long-run or the short-run. In robustness
exercises presented in Appendix G, we consider the
opposite extreme of
. The consequence of this
assumption is that any predictions made by our model regarding
optimal labor-income taxation cannot be due to incentives to tax
profits, either in the long-run or the short-run. In robustness
exercises presented in Appendix G, we consider the
opposite extreme of
![]() and show that our main results
are unaffected.
and show that our main results
are unaffected.
The formal analysis of this problem is presented in Appendix A; here we simply describe intuitively the outcome of household optimization. One condition stemming from household optimization is a standard consumption-savings condition,
| (9) |
As usual, this condition defines the stochastic discount factor,
![]() , with which firms, in equilibrium, discount profit flows.
, with which firms, in equilibrium, discount profit flows.
More important for the analysis of the pseudo-LFP model is the household's pseudo-labor-force participation condition
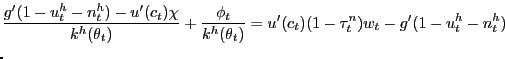 |
|
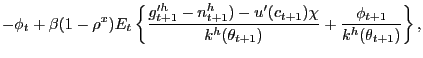 |
(10) |
which is derived in detail in Appendix A.
In (10),
![]() denotes the Lagrange multiplier
associated with the constraint (8). Suppose for a
moment that
denotes the Lagrange multiplier
associated with the constraint (8). Suppose for a
moment that
![]() ,
, ![]() ,
which means there is no exogenous restriction on the participation
rate. With
,
which means there is no exogenous restriction on the participation
rate. With
![]() , condition (10) has a
straightforward interpretation: at the optimum, the household each
period sends a measure
, condition (10) has a
straightforward interpretation: at the optimum, the household each
period sends a measure ![]() of family members to
search for jobs until the expected cost of search -- the
left-hand-side of (10) -- is equated
to the expected benefit of search -- the right-hand-side
of (10).
The expected cost of search is measured by the marginal utility of
leisure (each unit of search involves forgoing one unit of leisure)
net of the direct unemployment benefits obtained by searchers
(converted into appropriate units using the marginal utility of
wealth). The expected benefit of search involves the marginal
utility value of after-tax wage income and the marginal disutility
of work (the first two terms on the right-hand-side
of (10)),
along with the asset value to the household of having an additional
family member engaged in an ongoing employment relationship (the
term in expectations on the right-hand-side of (10)). This asset
value reflects the value to the household of sending one fewer
family member out to look for a job in the future.
of family members to
search for jobs until the expected cost of search -- the
left-hand-side of (10) -- is equated
to the expected benefit of search -- the right-hand-side
of (10).
The expected cost of search is measured by the marginal utility of
leisure (each unit of search involves forgoing one unit of leisure)
net of the direct unemployment benefits obtained by searchers
(converted into appropriate units using the marginal utility of
wealth). The expected benefit of search involves the marginal
utility value of after-tax wage income and the marginal disutility
of work (the first two terms on the right-hand-side
of (10)),
along with the asset value to the household of having an additional
family member engaged in an ongoing employment relationship (the
term in expectations on the right-hand-side of (10)). This asset
value reflects the value to the household of sending one fewer
family member out to look for a job in the future.
With
![]() , condition (10) naturally has
the interpretation of a free-entry condition into the labor force.
However, because in the pseudo-LFP model the size of the labor
force is fixed at
, condition (10) naturally has
the interpretation of a free-entry condition into the labor force.
However, because in the pseudo-LFP model the size of the labor
force is fixed at
![]() , the shadow value
, the shadow value ![]() is non-zero. The shadow value
is non-zero. The shadow value ![]() measures the value to the household of being able to
freely adjust its participation rate; as such, it can be
interpreted as the price of participation. In equilibrium, this
shadow price always adjusts so that condition (10) results in
no net entry into or exit from the labor force. Hence the
terminology pseudo labor-force participation condition to
refer to (10). The dynamics
of the shadow price
measures the value to the household of being able to
freely adjust its participation rate; as such, it can be
interpreted as the price of participation. In equilibrium, this
shadow price always adjusts so that condition (10) results in
no net entry into or exit from the labor force. Hence the
terminology pseudo labor-force participation condition to
refer to (10). The dynamics
of the shadow price ![]() are crucial in
driving the dynamics of the optimal labor-income tax rate in our
analysis below.
are crucial in
driving the dynamics of the optimal labor-income tax rate in our
analysis below.
We emphasize that in this version of the model, the
participation rate
![]() is indeed fixed at
is indeed fixed at
![]() every period. Hence, our pseudo-LFP
formulation delivers the same household decisions as if we had
taken the more standard approach of specifying the household
problem as one of choosing only
every period. Hence, our pseudo-LFP
formulation delivers the same household decisions as if we had
taken the more standard approach of specifying the household
problem as one of choosing only ![]() subject to the
budget constraint (6), completely
dropping constraints (7)
and (8),
setting
subject to the
budget constraint (6), completely
dropping constraints (7)
and (8),
setting ![]() , and setting, as is common in DSGE
search models,
, and setting, as is common in DSGE
search models,
![]()
![]() . It is not the underlying optimal
choices of the household that we change by specifying the model
this way, it is only the way we cast the household problem that is
different. The important gain our formulation brings to the
analysis is being able to measure the shadow value
. It is not the underlying optimal
choices of the household that we change by specifying the model
this way, it is only the way we cast the household problem that is
different. The important gain our formulation brings to the
analysis is being able to measure the shadow value ![]() .
.
2.2.2 LFP Model
If households were instead free to choose the labor-force participation rate, the household's decision problem would be exactly as just described, except of course constraint (8) would not bind household behavior. Household optimal choices would thus be characterized by the consumption-savings optimality condition (9) and the " true" labor-force participation condition,
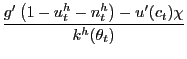
|
||
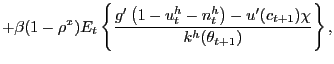
|
(11) |
which of course is simply condition (10) with
![]()
![]() .
.
Despite the search frictions and long-lived nature of employment
relationships, the labor-force participation
condition (11)
has the same interpretation as the labor-supply function in a
simple neoclassical labor market, as exists in standard Ramsey
models used to study the optimality of tax-smoothing. Indeed, we
can recover a neoclassical labor market by setting
![]() (all employment "relationships"
are one-period, spot, transactions), setting
(all employment "relationships"
are one-period, spot, transactions), setting ![]() (because there is no notion of "unemployment" hence
of "unemployment benefits" in a neoclassical market), and fixing
the probability of "finding a job" to
(because there is no notion of "unemployment" hence
of "unemployment benefits" in a neoclassical market), and fixing
the probability of "finding a job" to
![]() (because in a neoclassical
market there of course is no friction in "finding a job").
Imposing these assumptions and logic on (11), we obtain
(because in a neoclassical
market there of course is no friction in "finding a job").
Imposing these assumptions and logic on (11), we obtain
![]() ,
which defines the labor-supply function in a neoclassical
market.
,
which defines the labor-supply function in a neoclassical
market.
With matching frictions that create a meaningful separation of
the labor force into those individuals that are employed and those
individuals that are unemployed, condition (11) defines
transitions of individuals from outside the labor force (leisure,
in our model) into the pool of searching unemployed, from where the
aggregate matching process will pull some individuals into
employment. In the pseudo-LFP model, condition (10) plays the same
conceptual role, but, because the participation rate is exogenous,
what it pins down is the shadow price ![]() rather than the participation rate. We thus speak of (11)
and (10)
as labor-force participation functions, rather than labor-supply
functions.
rather than the participation rate. We thus speak of (11)
and (10)
as labor-force participation functions, rather than labor-supply
functions.
2.3 Wage Bargaining
Our baseline wage-determination mechanism is Nash bargaining. Specifically, we assume that wages of all workers, whether newly-hired or not, are set in period-by-period Nash negotiations. This assumption is common in search-based DSGE models, which is why we use it as our benchmark. A detailed derivation of the wage-bargaining problem is presented in Appendix B for the pseudo-LFP model and in Appendix C for the LFP model. In what follows, we simply present the bargaining outcomes. However, none of our results is sensitive to wages being determined in an explicitly bilateral fashion, as is the case with Nash bargaining. An alternative equilibrium concept for search models, due to Moen (1997), is a competitive search equilibrium. In competitive search equilibrium, wages are determined by decentralized forces and taken as given by all market participants. In Appendix H, we show that competitive search delivers exactly the same wage outcome as period-by-period Nash negotiations; hence its policy implications are identical.8
Assuming that
![]() is a worker's Nash bargaining
power and
is a worker's Nash bargaining
power and ![]() a firm's Nash bargaining power,
the Nash wage outcome in the pseudo-LFP model is given by
a firm's Nash bargaining power,
the Nash wage outcome in the pseudo-LFP model is given by
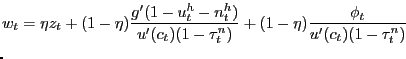 |
|
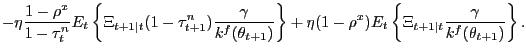 |
(12) |
The bargained wage is a convex combination of the maximum value to
a firm of entering into the marginal employment relationship and
the minimum value required for the household to send a family
member on the margin into a new employment relationship. The first
line of (12) shows that part
of the period-![]() wage payment is a convex combination
of the contemporaneous values to the firm and the household, given,
respectively, by the marginal product of a new employment match
wage payment is a convex combination
of the contemporaneous values to the firm and the household, given,
respectively, by the marginal product of a new employment match
![]() and the after-tax MRS between
consumption and participation. This after-tax MRS includes the
usual MRS
and the after-tax MRS between
consumption and participation. This after-tax MRS includes the
usual MRS
![]() but also a
second MRS-like term that reflects the price the household would be
willing to pay to be able to send additional members to search for
jobs. This value is reflected in the shadow price
but also a
second MRS-like term that reflects the price the household would be
willing to pay to be able to send additional members to search for
jobs. This value is reflected in the shadow price ![]() . The second line of (12) captures
the forward-looking, relationship, aspect of employment, whose
value is also capitalized in the period-
. The second line of (12) captures
the forward-looking, relationship, aspect of employment, whose
value is also capitalized in the period-![]() wage
payment. Apart from the fact that expectations of future (period
wage
payment. Apart from the fact that expectations of future (period
![]() ) tax rates appear in this
forward-looking term, this forward-looking aspect of wages is
standard in search models that use Nash bargaining.
) tax rates appear in this
forward-looking term, this forward-looking aspect of wages is
standard in search models that use Nash bargaining.
If instead participation rates adjust optimally over the business cycle, the Nash wage outcome is given by
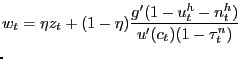 |
|
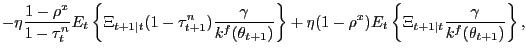 |
(13) |
which of course is simply (12) with
![]() . The wage rules (12)
and (13)
thus differ only in whether or not the shadow price of the
participation restriction affects the bargained wage.
. The wage rules (12)
and (13)
thus differ only in whether or not the shadow price of the
participation restriction affects the bargained wage.
Finally, note that if labor taxes were constant at
![]()
![]() , the wage outcome would be
, the wage outcome would be
![]() . In this case, the presence of the labor tax only changes firms'
effective bargaining power in a static manner:
. In this case, the presence of the labor tax only changes firms'
effective bargaining power in a static manner:
![]() causes
causes
![]() .
This kind of static bargaining wedge underpins the results in
Arseneau and Chugh (2006); in our model here, this purely static
effect would be unable to offset cyclical variations in the shadow
prices of the participation restriction.
.
This kind of static bargaining wedge underpins the results in
Arseneau and Chugh (2006); in our model here, this purely static
effect would be unable to offset cyclical variations in the shadow
prices of the participation restriction.
2.4 Government
The government finances an exogenous stream of spending
![]() by collecting labor income taxes,
dividend income taxes, and issuing real state-contingent debt. The
period-
by collecting labor income taxes,
dividend income taxes, and issuing real state-contingent debt. The
period-![]() government budget constraint is
government budget constraint is
| (14) |
As noted when we presented the problem of the representative household, the fact that the government is able to issue fully state-contingent real debt means that none of our results is driven by incompleteness of debt markets.
We include payment of unemployment benefits as a government
activity for two reasons. First, we think it empirically
descriptive to view the government as providing such insurance.
Second, from a technical standpoint, including
![]() in the government budget
constraint means that
in the government budget
constraint means that ![]() does not appear
in the economy-wide resource constraint (presented below). In DSGE
labor-search models, it is common to include unemployment benefits
in the household budget constraint but yet exclude them from the
economy-wide resource constraint -- see, for example, Krause and
Lubik (2007) or Faia (2008). In such models, the government budget
constraint is a residual object due to the presence of a lump-sum
tax. In contrast, we rule out lump-sum taxes in order to conduct
our Ramsey analysis and thus cannot treat the government's budget
as residual. A Ramsey problem requires specifying both the resource
constraint and either the government or household budget constraint
as equilibrium objects, and this requires us to take a more precise
stand on the source of unemployment benefits than usually taken in
the literature. To make our model setup as close as possible to
existing ones that study tax smoothing, we must assert that payment
of unemployment benefits is a transfer between the government and
households.
does not appear
in the economy-wide resource constraint (presented below). In DSGE
labor-search models, it is common to include unemployment benefits
in the household budget constraint but yet exclude them from the
economy-wide resource constraint -- see, for example, Krause and
Lubik (2007) or Faia (2008). In such models, the government budget
constraint is a residual object due to the presence of a lump-sum
tax. In contrast, we rule out lump-sum taxes in order to conduct
our Ramsey analysis and thus cannot treat the government's budget
as residual. A Ramsey problem requires specifying both the resource
constraint and either the government or household budget constraint
as equilibrium objects, and this requires us to take a more precise
stand on the source of unemployment benefits than usually taken in
the literature. To make our model setup as close as possible to
existing ones that study tax smoothing, we must assert that payment
of unemployment benefits is a transfer between the government and
households.
2.5 Matching Technology
In equilibrium,
![]() , so we now
refer to employment simply as
, so we now
refer to employment simply as ![]() . Matches
between unemployed individuals searching for jobs and firms
searching to fill vacancies are formed according to a
constant-returns matching technology,
. Matches
between unemployed individuals searching for jobs and firms
searching to fill vacancies are formed according to a
constant-returns matching technology,
![]() , where
, where ![]() is the number of searching individuals and
is the number of searching individuals and ![]() is the number of posted vacancies. A fraction
is the number of posted vacancies. A fraction
![]() of matches that produced in period
of matches that produced in period
![]() are exogenously destroyed before period
are exogenously destroyed before period
![]() . All newly-formed matches produce at least
once before possibly dissolving. The evolution of aggregate
employment is thus given by
. All newly-formed matches produce at least
once before possibly dissolving. The evolution of aggregate
employment is thus given by
| (15) |
2.6 Private-Sector Equilibrium
Whether considering the pseudo-LFP model or the LFP model, a
symmetric private-sector equilibrium is made up of endogenous
processes
![]() that satisfy the vacancy-posting condition (4), the
consumption-savings optimality condition (9), the
government budget constraint (14), the law of
motion for the aggregate stock of employment (15), and the
aggregate resource constraint of the economy
that satisfy the vacancy-posting condition (4), the
consumption-savings optimality condition (9), the
government budget constraint (14), the law of
motion for the aggregate stock of employment (15), and the
aggregate resource constraint of the economy
| (16) |
In (16), total
costs of posting vacancies
![]() are a resource cost for the
economy. As discussed above, unemployment benefits
are a resource cost for the
economy. As discussed above, unemployment benefits ![]() do not absorb any part of market output.
do not absorb any part of market output.
In the LFP model, the labor-force participation condition (11) and the period-by-period Nash wage outcome (13) complete the set of conditions characterizing equilibrium. In the pseudo-LFP model, the pseudo-LFP condition (10) and the Nash wage outcome (12) are instead part of the set of private-sector equilibrium conditions, as is the exogenous restriction on the total size of the labor force
| (17) |
In the pseudo-LFP model, the endogenous process of shadow prices
![]() is also added
to the list of endogenous equilibrium processes. Finally, in either
the pseudo-LFP model or the LFP model, the private sector takes as
given stochastic processes
is also added
to the list of endogenous equilibrium processes. Finally, in either
the pseudo-LFP model or the LFP model, the private sector takes as
given stochastic processes
![]() .
.
3. Search Efficiency in General Equilibrium
To understand the optimal tax results that emerge from the
Ramsey problem, it is useful to first present the conditions that
characterize the constrained-efficient allocation that would be
chosen by a Social Planner that is restricted by the matching
technology. Our focus is on developing a general-equilibrium
search-theoretic notion of efficiency along the consumption-leisure
margin. Although Hosios-efficiency is a necessary component of it,
the efficiency condition we present below is different from the
well-known Hosios (1990) condition, which, because it describes
outcomes only in the labor market, is a partial-equilibrium
efficiency condition. Our efficiency condition links outcomes
across markets. Furthermore, for our general-equilibrium notion of
efficiency, the unemployment benefit ![]() is
irrelevant because, as discussed in Section 2.4, we assume that
unemployment benefits do not appear in the economy-wide
resource frontier. As in a model with neoclassical markets,
efficiency only takes into consideration preferences and
technologies; in our model,
is
irrelevant because, as discussed in Section 2.4, we assume that
unemployment benefits do not appear in the economy-wide
resource frontier. As in a model with neoclassical markets,
efficiency only takes into consideration preferences and
technologies; in our model, ![]() is a feature of
neither preferences nor technology, but rather simply a transfer
between the government and households. We assume throughout this
discussion (and in the remainder of the paper) that the matching
technology of the economy is Cobb-Douglas,
is a feature of
neither preferences nor technology, but rather simply a transfer
between the government and households. We assume throughout this
discussion (and in the remainder of the paper) that the matching
technology of the economy is Cobb-Douglas,
![]() , with
, with
![]() .
.
The Social Planner's problem is described by
![$\displaystyle \max_{\{c_{t},n_{t},u_{t},v_{t}\}}E_{0}\sum_{t=0}^{\infty}\beta^{t}\left[ u(c_{t})+g(1-u_{t}-n_{t})\right]$](img146.gif)
|
(18) |
subject to the sequence of laws of motion for the employment
stock (15) and
resource constraints (16). We do not view
the Social Planner here as being restricted by the exogenous
participation limit
![]() : we think it most
natural and informative to consider a Social Planner that can
freely and efficiently allocate the total number of individuals in
the economy between the labor force and leisure. The full solution
of this problem appears in Appendix D; here, we focus
only on efficiency along the consumption-leisure margin, as
summarized by the following proposition.
: we think it most
natural and informative to consider a Social Planner that can
freely and efficiently allocate the total number of individuals in
the economy between the labor force and leisure. The full solution
of this problem appears in Appendix D; here, we focus
only on efficiency along the consumption-leisure margin, as
summarized by the following proposition.
Proposition 1. There exists a constrained-efficient (first-best) allocation in which efficiency along the consumption-leisure margin is characterized by
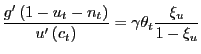
|
(19) |
The formal proof of this proposition is detailed in Appendix D. Here, we simply provide intuition by reconstructing condition (19) from the basic tenet that under consumption-leisure efficiency, the marginal rate of substitution (MRS) between consumption and leisure (outside the labor force) must equal the corresponding marginal rate of transformation (MRT). That the left-hand-side of (19) is the household's MRS between consumption and leisure (outside the labor force) is obvious. The right-hand-side of (19) must therefore have the interpretation of the MRT between consumption and leisure.
Rather than take (19) as prima facie
evidence that the right-hand-side must be the MRT, we can describe
the MRT conceptually from first principles as follows. Consider the
economy's resource frontier (16) and the
identity limiting the size of the population (household),
![]() , where
, where
![]() is the measure of individuals
outside the labor force and hence enjoying leisure. There are two
ways the economy can transform a unit of leisure in period
is the measure of individuals
outside the labor force and hence enjoying leisure. There are two
ways the economy can transform a unit of leisure in period
![]() into a unit of output, and hence
consumption, in period
into a unit of output, and hence
consumption, in period ![]() . We trace the MRT in these
two possible ways, and then connect them.
. We trace the MRT in these
two possible ways, and then connect them.
One way for the economy to achieve transformation of
![]() into output (and hence
into output (and hence
![]() ) is to first trade off one unit of
) is to first trade off one unit of
![]() for vacancy postings
for vacancy postings ![]() ; doing so yields
; doing so yields ![]() additional
vacancy postings, as (16) shows.9
This marginal addition to the flow of vacancy postings increases
the number of aggregate labor-market matches by
additional
vacancy postings, as (16) shows.9
This marginal addition to the flow of vacancy postings increases
the number of aggregate labor-market matches by
![]() .
Because labor-market matches are long-lived, this marginal
additional to the stock of period-
.
Because labor-market matches are long-lived, this marginal
additional to the stock of period-![]() employment
increases output by
employment
increases output by
![]() , which can be expressed compactly as
, which can be expressed compactly as
![$\displaystyle MRT^{l \rightarrow v} = \left[ z_{t} + (1-\rho^{x}) E_{t} \sum_{s=0}^{\infty} z_{t+1+s}\right] \frac{m_{vt}}{\gamma}.$](img165.gif)
|
(20) |
Alternatively, the economy can achieve transformation of
![]() into output by first trading off
one unit of
into output by first trading off
one unit of
![]() for one unit of
for one unit of ![]() , which follows simply from the restriction
, which follows simply from the restriction
![]() . This
marginal addition to the flow of searching unemployed individuals
increases the number of aggregate labor-market matches by
. This
marginal addition to the flow of searching unemployed individuals
increases the number of aggregate labor-market matches by
![]() . In
turn, because labor-market matches are long-lived, this marginal
additional to the stock of period-
. In
turn, because labor-market matches are long-lived, this marginal
additional to the stock of period-![]() employment
increases output by
employment
increases output by
![]() , which can be expressed compactly as
, which can be expressed compactly as
![$\displaystyle MRT^{l \rightarrow u} = \left[ z_{t} + (1-\rho^{x}) E_{t} \sum_{s=0}^{\infty} z_{t+1+s}\right] m_{ut}.$](img173.gif)
|
(21) |
For the economy to be on its production possibilities frontier,
the two ways of transforming leisure into output must be
equivalent. This is satisfied if
![]() . Because the matching
technology is Cobb-Douglas, we have
. Because the matching
technology is Cobb-Douglas, we have
![]() , where, as
mentioned above,
, where, as
mentioned above,
![]() is the elasticity of the
matching technology with respect to
is the elasticity of the
matching technology with respect to ![]() and,
recall,
and,
recall,
![]() . Using this
fact and the efficiency requirement that the two ways of
transforming leisure into output must be identical, we have
. Using this
fact and the efficiency requirement that the two ways of
transforming leisure into output must be identical, we have
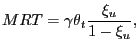
|
(22) |
which indeed is the right-hand-side of (19).
This conceptualization of the MRT between output (consumption)
and leisure (outside the labor force) is novel. It compactly
describes the two technologies -- the matching technology
![]() and the production
technology
and the production
technology
![]() -- that must operate for leisure
to be transformed into output and hence consumption. As
search-theoretic frameworks become increasingly popular in general
equilibrium models, it is useful to be able to describe
transformation frontiers and the MRTs implied by them in general
ways.10 Our notion of the MRT between
consumption and leisure encompasses that in a standard RBC model.
As noted above, one can recover a standard neoclassical labor
market by assuming vacancy-creation costs are zero (
-- that must operate for leisure
to be transformed into output and hence consumption. As
search-theoretic frameworks become increasingly popular in general
equilibrium models, it is useful to be able to describe
transformation frontiers and the MRTs implied by them in general
ways.10 Our notion of the MRT between
consumption and leisure encompasses that in a standard RBC model.
As noted above, one can recover a standard neoclassical labor
market by assuming vacancy-creation costs are zero (![]() ) (in which case, because they are costless, the
number of vacancies posted is infinite) and that all "employment
relationships" last only one period (
) (in which case, because they are costless, the
number of vacancies posted is infinite) and that all "employment
relationships" last only one period (
![]() ). With Cobb-Douglas matching and
an infinity of vacancy postings,
). With Cobb-Douglas matching and
an infinity of vacancy postings,
![]() and
and ![]() .
Imposing these assumptions and results in the preceding logic, we
obtain
.
Imposing these assumptions and results in the preceding logic, we
obtain
![]() , obviously identical to that in
a simple DSGE model featuring linear-in-labor production.
, obviously identical to that in
a simple DSGE model featuring linear-in-labor production.
For the purposes of our Ramsey analysis, we show in the next section how three particular features of our model's decentralized economy -- proportional labor taxation, the potential inability by households to freely choose the labor-force participation rate, and, of a bit less importance for our optimal-policy results, transfers of unemployment benefits from the government to households -- disrupt efficiency along the consumption-leisure margin.
4. Search-Based Labor Wedge
In any Ramsey problem, the basic tension is between raising revenue for the government via proportional taxation and creating wedges between MRS/MRT pairs. We prove the following in Appendix E:
Proposition 2. In the decentralized economy with Nash bargaining, proportional labor taxation, and unemployment benefits, the equilibrium consumption-leisure margin can be expressed as
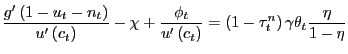
|
(23) |
Comparing (27) with the efficiency condition (19), it is clear that for the decentralized economy with Nash bargaining to achieve efficiency, four conditions must be satisfied:
- The decentralized economy must feature
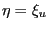 , which corresponds to the
Hosios (1990) condition for search efficiency;
, which corresponds to the
Hosios (1990) condition for search efficiency; - The transfer of unemployment benefits from the government to
households must be zero -- that is,
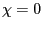 ;
; - Households must be able to optimally choose the labor-force
participation rate in every period, so that
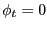
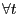 ;
; - Proportional labor income taxation must be zero -- that is,
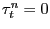
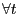 .
.
The first condition is the usual Hosios (1990) condition. The
standard Hosios efficiency condition is a partial-equilibrium
statement because it focuses only on the labor market and takes as
given outcomes in goods markets and intertemporal markets. Our
efficiency condition is a general-equilibrium one, linking outcomes
across markets. Thus, Hosios efficiency is a necessary, though not
sufficient, condition for our general-equilibrium notion of search
efficiency. Also required is zero-taxation of labor income and the
absence of any transfers of unemployment benefits between the
government and households, because unemployment benefits are not
part of the technology of the economy. In a Ramsey taxation
problem,
![]() of course cannot occur.11
Given this, most important for our results is that for efficiency,
households must be able to optimally choose the participation rate
of course cannot occur.11
Given this, most important for our results is that for efficiency,
households must be able to optimally choose the participation rate
![]() , which would render the shadow
value
, which would render the shadow
value
![]() . If
. If
![]() , as occurs in the pseudo-LFP
model because the participation rate is exogenous, efficiency is
disrupted.
, as occurs in the pseudo-LFP
model because the participation rate is exogenous, efficiency is
disrupted.
In all of our analysis, we assume the Hosios (1990) condition is
satisfied. Also, for simplicity, assume for a moment that
![]() .12 In this case, we can
express (27) as
.12 In this case, we can
express (27) as
![$\displaystyle \frac{g^{\prime}(1-u_{t}-n_{t})}{u^{\prime}(c_{t})} = \gamma\theta_{t} \frac{\xi_{u}}{1-\xi_{u}} \left[ (1-\tau^{n}_{t}) - \frac{\phi_{t}}{u^{\prime}(c_{t})} \frac{1-\xi_{u}}{\xi_{u}} \frac{1} {\gamma\theta_{t}} \right] .$](img202.gif)
|
(24) |
The term in square brackets is the equilibrium wedge between the
MRS between consumption and leisure and the MRT between consumption
and leisure, both which we defined in Section 3. Clearly, if
households can freely choose the labor-force participation rate
every period -- which implies the shadow value
![]()
![]() --
then the only wedge between MRS and MRT is the labor-income tax.
Although our model is not a neoclassical one, the basic
optimal-taxation principle of (nearly) equating deadweight losses
across (intertemporal) markets (which is the essence of the
widely-known dynamic tax-smoothing result) leads to the natural
conjecture that in this case tax-smoothing is optimal.
--
then the only wedge between MRS and MRT is the labor-income tax.
Although our model is not a neoclassical one, the basic
optimal-taxation principle of (nearly) equating deadweight losses
across (intertemporal) markets (which is the essence of the
widely-known dynamic tax-smoothing result) leads to the natural
conjecture that in this case tax-smoothing is optimal.
On the other hand, if households are restricted in their
labor-force participation, we would expect ![]() in general to be time-varying. In this case, fluctuations in the
second term in brackets would require offsetting fluctuations in
in general to be time-varying. In this case, fluctuations in the
second term in brackets would require offsetting fluctuations in
![]() in order to keep the
total deadweight loss (nearly) constant over time. As
in order to keep the
total deadweight loss (nearly) constant over time. As
![]() rises above zero, the above modifies
slightly to
rises above zero, the above modifies
slightly to
![$\displaystyle \frac{g^{\prime}(1-u_{t}-n_{t})}{u^{\prime}(c_{t})} = \gamma\theta_{t} \frac{\xi_{u}}{1-\xi_{u}} \left[ (1-\tau^{n}_{t}) - \left( \frac{\phi_{t}}{u^{\prime}(c_{t})} - \chi\right) \frac{1-\xi_{u}}{\xi_{u}} \frac{1}{\gamma\theta_{t}} \right] ,$](img208.gif)
|
(25) |
but all of the logic still applies.
The term
![$\displaystyle \left[ (1-\tau^{n}_{t}) - \left( \frac{\phi_{t}} {u^{\prime}(c_{t})} - \chi\right) \frac{1-\xi_{u}}{\xi_{u}}\frac{1} {\gamma\theta_{t}} \right]$](img209.gif)
|
(26) |
is thus a novel notion of a labor wedge. In particular, it is a more general notion of a labor wedge than that measured by Chari, Kehoe, and McGrattan (2007), Shimer (2008), Ohanian, Raffo, and Rogerson (2008), and others. Future empirical work may be able to exploit this way of formulating the labor wedge. Premised as it is on the idea that employment experiences are fundamentally long-lived economic phenomena, rather than spot transactions, it offers a new way to understand what Chari, Kehoe, and McGrattan (2007), Smets and Wouters (2007), Shimer (2008), and others have identified as perhaps the most important area in macroeconomics where much deeper empirical and theoretical understanding is required. We leave such empirical investigation to future work.
We mentioned above that our results are invariant to whether wages are determined through Nash bargaining (at the Hosios condition) or through competitive search. We prove the following in Appendix H:
Proposition 3. In the decentralized economy with competitive search, proportional labor taxation, and unemployment benefits, the equilibrium consumption-leisure margin can be expressed as
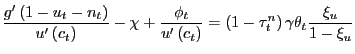
|
(27) |
Hence, under competitive search, the labor wedge is identical to that presented in (26). Using this notion of a labor wedge, we now turn to a quantitative assessment of our conjectures regarding the optimality of tax smoothing. Specifically, we conjecture that in the pseudo-LFP model, tax-smoothing will not be optimal, whereas in the LFP model tax-smoothing will be optimal. We first present the Ramsey problem and then present results.
5. Ramsey Problem
A standard approach in Ramsey models based on neoclassical markets is to capture in a single, present-value implementability constraint (PVIC) all equilibrium conditions of the economy apart from the resource frontier. The PVIC is the key constraint in any Ramsey problem because it governs the welfare loss of using non-lump-sum taxes to finance government expenditures.13 The PVIC is the household (equivalently, government) budget constraint expressed in intertemporal form with all prices and policies substituted out using equilibrium conditions. In relatively simple models, the PVIC encodes all the equilibrium conditions that must be respected by Ramsey allocations in addition to feasibility. In complicated environments that deviate substantially from neoclassical markets, however, such as Schmitt-Grohe and Uribe (2005), Chugh (2006), and Arseneau and Chugh (2008), it is not always possible to construct such a single constraint, meaning that, in principle, all of the equilibrium conditions must be imposed explicitly as constraints on the Ramsey problem.
Our model presents an environment in which it is instructive to construct a PVIC but nonetheless leave some equilibrium conditions as separate constraints on the Ramsey planner. As we show in Appendix F, we can construct a PVIC starting from the household flow budget constraint (6) and using the household optimality conditions (9) and (10). The PVIC for our model is given by
![$\displaystyle E_{0} \sum_{t=0}^{\infty} \beta^{t} \left\{ u^{\prime} (c_{t})c_{t} - \left[ g^{\prime}(1-u_{t}-n_{t}) + \phi_{t}\right] (n_{t} + u^{h}_{t}) - u^{\prime}(c_{t}) (1-\tau^{pr})d_{t} \right\} = A_{0},$](img211.gif)
|
(28) |
where the time-zero assets of the private-sector are given by
![$\displaystyle A_{0} \equiv u^{\prime}(c_{0}) R_{0} b_{-1} + (1-\rho^{x}) \left[ \frac{g^{\prime}_{0} - u^{\prime}_{0}\chi}{k^{h}(\theta_{0})} + \frac{\phi _{0}}{k^{h}(\theta_{0})} \right] n_{-1}.$](img212.gif)
|
(29) |
Several observations about this PVIC are in order. First, because
employment is a state variable, the household's "ownership" of the
initial stock of employment relationships, ![]() ,
is part of its time-zero assets, as shown in
,
is part of its time-zero assets, as shown in ![]() . Second, with free choice by households regarding
labor-force participation, we would have
. Second, with free choice by households regarding
labor-force participation, we would have
![]()
![]() .
Third, if labor markets were neoclassical, the sum
.
Third, if labor markets were neoclassical, the sum
![]() would be interpreted as total
labor in the economy, because a neoclassical environment of
course features no notion of unemployment. Fourth, as we mentioned
above, a spot, neoclassical labor market can be interpreted as
featuring
would be interpreted as total
labor in the economy, because a neoclassical environment of
course features no notion of unemployment. Fourth, as we mentioned
above, a spot, neoclassical labor market can be interpreted as
featuring
![]() because there is no long-lived
aspect to labor-market transactions. Fifth, with a constant-returns
production technology in a neoclassical environment,
because there is no long-lived
aspect to labor-market transactions. Fifth, with a constant-returns
production technology in a neoclassical environment, ![]()
![]() . Imposing the last four of
these conditions in our model collapses the PVIC (28), as well as the
initial assets
. Imposing the last four of
these conditions in our model collapses the PVIC (28), as well as the
initial assets ![]() , to that in a standard Ramsey
model based on neoclassical markets.14
, to that in a standard Ramsey
model based on neoclassical markets.14
However, unlike in a neoclassical model, the PVIC (28) does not capture all equilibrium conditions of the decentralized economy. In particular, Ramsey allocations must also respect the vacancy-posting condition (4), the Nash wage outcome ((13) for the LFP model or (12) for the pseudo-LFP model), the law of motion for the aggregate employment stock (15), and, for the pseudo-LFP model, the participation restriction (17). None of these restrictions is encoded in the PVIC (28).
The Ramsey problem is thus to choose state-contingent
processes
![]() to maximize (5) subject to the
PVIC (28), the
vacancy-posting condition (4), the Nash wage
outcome (either (13)
or (12)), the law of
motion for the aggregate employment stock (15), the aggregate
resource constraint (16), and, if the
pseudo-LFP environment is under consideration, the restriction on
the size of the labor force (17). If the LFP
environment is under consideration, the constraint (17) is dropped and
the process of shadow values
to maximize (5) subject to the
PVIC (28), the
vacancy-posting condition (4), the Nash wage
outcome (either (13)
or (12)), the law of
motion for the aggregate employment stock (15), the aggregate
resource constraint (16), and, if the
pseudo-LFP environment is under consideration, the restriction on
the size of the labor force (17). If the LFP
environment is under consideration, the constraint (17) is dropped and
the process of shadow values
![]() is trivially set to zero. For
computational convenience, we leave both the bargained real wage
and the labor tax rate as explicit Ramsey choice variables. We
instead could have inverted the Nash wage equation to eliminate one
of them; in any case, however, we would still be left with the
other as an explicit Ramsey choice variable.
is trivially set to zero. For
computational convenience, we leave both the bargained real wage
and the labor tax rate as explicit Ramsey choice variables. We
instead could have inverted the Nash wage equation to eliminate one
of them; in any case, however, we would still be left with the
other as an explicit Ramsey choice variable.
As is standard in Ramsey taxation problems, we assume full commitment. Thus, we emphasize that none of our results is driven by the use of a discretionary policy. Finally, throughout our analysis, we assume that the first-order conditions of the Ramsey problem are necessary and sufficient and that all allocations are interior.
6. Optimal Taxation
We characterize both the Ramsey steady state and dynamics numerically. Before presenting quantitative results, we describe our parameterization.
6.1 Parameterization and Solution Strategy
Parameters are set so that the long-run (deterministic) Ramsey steady state is identical in both the LFP model and the pseudo-LFP model, which allows us to cleanly focus just on the differential business-cycle responses of policy in the two cases. For utility, standard functional forms are used,
| (30) |
and
| (31) |
We set ![]() to deliver a unit elasticity of
labor-force participation. This value is a common compromise in
DSGE models because it lies between macro evidence that suggests a
very high elasticity of labor supply and micro evidence that
suggests a very low elasticity of labor supply. We emphasize,
however, that
to deliver a unit elasticity of
labor-force participation. This value is a common compromise in
DSGE models because it lies between macro evidence that suggests a
very high elasticity of labor supply and micro evidence that
suggests a very low elasticity of labor supply. We emphasize,
however, that ![]() measures the elasticity of
labor-force participation in our environment, not the elasticity of
labor supply per se, due to the search frictions. We nonetheless
set
measures the elasticity of
labor-force participation in our environment, not the elasticity of
labor supply per se, due to the search frictions. We nonetheless
set ![]() to achieve some comparability with
standard DSGE models that study optimal policy, but our qualitative
results are not driven by this choice.
to achieve some comparability with
standard DSGE models that study optimal policy, but our qualitative
results are not driven by this choice.
The average labor-force participation rate in the U.S. during
the period 1988-2007 was 66 percent, so we set
![]() as the measure of individuals
in the representative household that are in the labor force on
average. Thus, in the pseudo-LFP model, the participation rate by
construction is always 66 percent even as the economy is hit by
shocks. The parameter
as the measure of individuals
in the representative household that are in the labor force on
average. Thus, in the pseudo-LFP model, the participation rate by
construction is always 66 percent even as the economy is hit by
shocks. The parameter ![]() is then chosen so that
is then chosen so that
![]() in the Ramsey
steady-state of the LFP model. The resulting value is
in the Ramsey
steady-state of the LFP model. The resulting value is
![]() . Because this setting for
. Because this setting for
![]() makes
makes
![]() endogenously optimal in the LFP
model, it has the consequence that in the pseudo-LFP model, in
which we exogenously impose
endogenously optimal in the LFP
model, it has the consequence that in the pseudo-LFP model, in
which we exogenously impose
![]() , the multiplier
, the multiplier ![]() is exactly zero. It is thus this precise setting for
is exactly zero. It is thus this precise setting for
![]() that, in concert with the rest of the
calibration, makes the Ramsey steady-states identical in the two
cases.
that, in concert with the rest of the
calibration, makes the Ramsey steady-states identical in the two
cases.
Well-understood since Hagedorn and Manovskii (2008) is that the
(net-of-tax) social flow gain from employment is important for
dynamics in search models. In partial equilibrium search models,
the flow gain is governed by the difference between the marginal
output of a match and a typically-exogenous "outside benefit" that
is interchangeably referred to as "unemployment benefits," "the
value of leisure," and "the value of home production." Because the
basic Pissarides (2000) model, on which the analyses of Shimer
(2005), Hall (2005), and Hagedorn and Manovskii (2008) are based,
is partial equilibrium, a precise stand on the nature of the
outside benefit is unnecessary. In our general-equilibrium model,
we have well-defined notions of government-provided unemployment
benefits and the value of leisure.15 Measured in terms of
goods, the former is ![]() and the latter is
and the latter is
![]() , the MRS between
consumption and leisure. Of course, because we have three
groups of individuals -- the employed, the searching unemployed,
and those outside the labor force -- these outside benefits accrue
to different groups. The unemployment benefit
, the MRS between
consumption and leisure. Of course, because we have three
groups of individuals -- the employed, the searching unemployed,
and those outside the labor force -- these outside benefits accrue
to different groups. The unemployment benefit ![]() is received by a searching unemployed individual, while
the MRS
is received by a searching unemployed individual, while
the MRS
![]() is received by
an individual outside the labor force.
is received by
an individual outside the labor force.
We use as our baseline parameter setting ![]() ,
so that only individuals outside the labor force receive an outside
benefit. This setting makes our results comparable to RBC models in
which it is only the value of leisure -- being outside the labor
force -- that an individual obtains by not working. Given the rest
of our calibration, setting
,
so that only individuals outside the labor force receive an outside
benefit. This setting makes our results comparable to RBC models in
which it is only the value of leisure -- being outside the labor
force -- that an individual obtains by not working. Given the rest
of our calibration, setting ![]() delivers an
outside benefit of nearly 90 percent of the after-tax wage rate.
Specifically, in the Ramsey steady state (of either the pseudo-LFP
model or the LFP model), setting
delivers an
outside benefit of nearly 90 percent of the after-tax wage rate.
Specifically, in the Ramsey steady state (of either the pseudo-LFP
model or the LFP model), setting ![]() delivers
delivers
![]() ,
which is close to Hagedorn and Manovskii's (2008) preferred
calibration of the outside benefit. We also conduct experiments
setting
,
which is close to Hagedorn and Manovskii's (2008) preferred
calibration of the outside benefit. We also conduct experiments
setting ![]() at a positive value in the Ramsey
steady state such that
at a positive value in the Ramsey
steady state such that
![]() , the value
suggested by Shimer (2005). The important point is that because our
environment explicitly models both the value of leisure
and the value of government-provided unemployment benefits,
we can accommodate both the Shimer (2005) view and/or the Hagedorn
and Manovskii (2008) view. Our main results do not hinge on
adopting one or the other calibration.
, the value
suggested by Shimer (2005). The important point is that because our
environment explicitly models both the value of leisure
and the value of government-provided unemployment benefits,
we can accommodate both the Shimer (2005) view and/or the Hagedorn
and Manovskii (2008) view. Our main results do not hinge on
adopting one or the other calibration.
The rest of our calibration is relatively standard in this class
of models. We assume a quarterly subjective discount factor
![]() . The matching function is
Cobb-Douglas,
. The matching function is
Cobb-Douglas,
![]() , with
, with
![]() , in line with the evidence in
Blanchard and Diamond (1989), and
, in line with the evidence in
Blanchard and Diamond (1989), and ![]() chosen so
that the quarterly job-finding rate of a searching individual is 90
percent in the model with zero government-provided unemployment
benefits. The resulting value is
chosen so
that the quarterly job-finding rate of a searching individual is 90
percent in the model with zero government-provided unemployment
benefits. The resulting value is ![]() . Given our
Cobb-Douglas matching specification, this also directly fixes the
matching rate for an open vacancy at the same value,
. Given our
Cobb-Douglas matching specification, this also directly fixes the
matching rate for an open vacancy at the same value,
![]() . The fixed cost
. The fixed cost
![]() of opening a vacancy is set so that
posting costs absorb 5 percent of total output in the Ramsey steady
state with zero unemployment benefits; the resulting value is
of opening a vacancy is set so that
posting costs absorb 5 percent of total output in the Ramsey steady
state with zero unemployment benefits; the resulting value is
![]() .
.
We fix the Nash bargaining weight at
![]() so that it ostensibly satisfies
the well-known Hosios (1990) condition
so that it ostensibly satisfies
the well-known Hosios (1990) condition
![]() for partial-equilibrium search
efficiency. We use this as our main guidepost, although we point
out that because
for partial-equilibrium search
efficiency. We use this as our main guidepost, although we point
out that because
![]() in the Ramsey equilibrium,
the naive calibration
in the Ramsey equilibrium,
the naive calibration
![]() actually does not deliver
search efficiency. This point was discussed in
Section 4.
Rather, the proper setting must also take into account the
steady-state distortionary tax rate.16 Our main focus,
though, is not on steady-state inefficiencies, but rather on
cyclical policy responses.
actually does not deliver
search efficiency. This point was discussed in
Section 4.
Rather, the proper setting must also take into account the
steady-state distortionary tax rate.16 Our main focus,
though, is not on steady-state inefficiencies, but rather on
cyclical policy responses.
Finally, the exogenous productivity and government spending shocks follow AR(1) processes in logs,
| (32) |
| (33) |
where ![]() denotes the steady-state level of
government spending, which we calibrate in our baseline model with
a 40-percent replacement rate to constitute 19 percent of
steady-state output in the Ramsey allocation. The resulting value
is
denotes the steady-state level of
government spending, which we calibrate in our baseline model with
a 40-percent replacement rate to constitute 19 percent of
steady-state output in the Ramsey allocation. The resulting value
is
![]() , which we hold constant
across all experiments and all specifications of our model. The
innovations
, which we hold constant
across all experiments and all specifications of our model. The
innovations
![]() and
and
![]() are distributed
are distributed
![]() and
and
![]() ,
respectively, and are independent of each other. We choose
parameters
,
respectively, and are independent of each other. We choose
parameters
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , consistent with
the RBC literature and Chari and Kehoe (1999). Also regarding
policy, we assume that the steady-state government debt-to-GDP
ratio (at an annual frequency) is 0.4, in line with evidence for
the U.S. economy and with the calibrations of Schmitt-Grohe and
Uribe (2005), Chugh (2006), and Arseneau and Chugh (2008).
, consistent with
the RBC literature and Chari and Kehoe (1999). Also regarding
policy, we assume that the steady-state government debt-to-GDP
ratio (at an annual frequency) is 0.4, in line with evidence for
the U.S. economy and with the calibrations of Schmitt-Grohe and
Uribe (2005), Chugh (2006), and Arseneau and Chugh (2008).
We use a nonlinear numerical solution algorithm to compute the
Ramsey deterministic steady-state equilibrium. To study dynamics,
we perform a second-order approximation of the Ramsey first-order
conditions for time ![]() in levels around the
non-stochastic steady-state of these conditions. We conduct a
second-order approximation, rather than a more commonly-employed
first-order approximation, to guard against the computational
inaccuracies of Ramsey-optimal policies pointed out by Chari,
Kehoe, and Christiano (1995, p. 383) in a baseline neoclassical
model. They demonstrated that inaccuracies of first-order
approximations tend to be more severe for policy variables than for
Ramsey allocation variables. Because our main focus is on the
dynamics of optimal policy -- the labor tax rate -- we mitigate
this computational inaccuracy by approximating the Ramsey
equilibrium to second-order.17 Our numerical method is our own
implementation of the perturbation algorithm described by
Schmitt-Grohe and Uribe (2004).
in levels around the
non-stochastic steady-state of these conditions. We conduct a
second-order approximation, rather than a more commonly-employed
first-order approximation, to guard against the computational
inaccuracies of Ramsey-optimal policies pointed out by Chari,
Kehoe, and Christiano (1995, p. 383) in a baseline neoclassical
model. They demonstrated that inaccuracies of first-order
approximations tend to be more severe for policy variables than for
Ramsey allocation variables. Because our main focus is on the
dynamics of optimal policy -- the labor tax rate -- we mitigate
this computational inaccuracy by approximating the Ramsey
equilibrium to second-order.17 Our numerical method is our own
implementation of the perturbation algorithm described by
Schmitt-Grohe and Uribe (2004).
We use our second-order accurate decision rules to simulate time-paths of the Ramsey equilibrium in the face of TFP and government spending realizations, the shocks to which we draw according to the parameters of the laws of motion described above. As is common when focusing on asymptotic policy dynamics, we assume that the initial state of the economy is the asymptotic Ramsey steady state, thus adopting the timeless perspective. As we mentioned above, we assume throughout, as is also typical in the literature, that the first-order conditions of the Ramsey problem are necessary and sufficient and that Ramsey allocations are interior. We conduct 1000 simulations, each 200 periods long. For each simulation, we then compute first and second moments and report the medians of these moments across the 1000 simulations.
6.2 Main Results
The main results are presented in Table 1. Panel A presents summary statistics from simulations from the pseudo-LFP model, and panel B presents the same information for the LFP model. As discussed above, the two models are calibrated such that the long-run Ramsey equilibria are identical. This allows for sharp focus on the cyclical properties of optimal policy. Accordingly, the mean realizations for the simulated policy and allocation variables in the first column of Table 1 are identical in panels A and B, with differences only due to numerical differences in approximation.
As comparison of the first row of each panel of the table shows, the optimal labor-income tax rate is much more volatile -- over an order of magnitude more volatile -- in the pseudo-LFP model than in the LFP model. If there is no adjustment at the participation margin -- as is the case in the vast majority of the existing literature studying policy in DSGE labor search models -- the standard deviation of the optimal tax rate is near 2 percent. In contrast, if participation adjusts cyclically, the standard deviation of the tax rate is around 0.1 percent. This latter figure fits right into the benchmark results of Chari and Kehoe (1999), Werning (2007), and Scott (2007) regarding the optimal degree of variability in tax rates in neoclassical markets, even though our environment always features matching frictions. Thus, whether or not cyclical adjustment occurs along the participation margin can matter a great deal for optimal policy prescriptions.
The bottom two rows of the panel A of Table 1
quantify the cyclical fluctuations in the value of the binding
participation margin in the pseudo-LFP model: the next-to-last row
displays the dynamics of the multiplier ![]() itself, while the last row converts this into goods by deflating by
itself, while the last row converts this into goods by deflating by
![]() . It is the goods value of
the binding participation restriction, and in particular its
fluctuating nature, that has direct interpretation. Indeed, recall
from (12) that it is
. It is the goods value of
the binding participation restriction, and in particular its
fluctuating nature, that has direct interpretation. Indeed, recall
from (12) that it is
![]() that affects the
bargained wage and that enters the wedge condition (26).
that affects the
bargained wage and that enters the wedge condition (26).
The shadow value of the binding participation constraint clearly
fluctuates substantially. It is this variation in the shadow value
of participation that gives rise to a role for cyclical variation
in the labor tax rate. Referring back to the labor
wedge (26)
that we developed, any variation in
![]() is designed to offset
variations in the second term of (26), so that the
overall labor wedge is smoothed over time. At its core,
smoothing of labor wedges over time is what the basic Ramsey
prescription of tax-smoothing is designed to achieve.18In a
simple neoclassical model of fiscal policy, it is typically only
the labor tax that enters this wedge -- wedge-smoothing thus
implies tax smoothing in neoclassical Ramsey environments. Werning
(2007) and Scott (2007) recently shed new analytical insight on
this long-established result. In contrast, here, the binding
participation restriction endogenously causes shifts in the labor
wedge. To offset this time-variation in labor wedges, the Ramsey
government moves tax rates in offsetting ways. To see this last
point clearly, notice that the contemporaneous correlations between
is designed to offset
variations in the second term of (26), so that the
overall labor wedge is smoothed over time. At its core,
smoothing of labor wedges over time is what the basic Ramsey
prescription of tax-smoothing is designed to achieve.18In a
simple neoclassical model of fiscal policy, it is typically only
the labor tax that enters this wedge -- wedge-smoothing thus
implies tax smoothing in neoclassical Ramsey environments. Werning
(2007) and Scott (2007) recently shed new analytical insight on
this long-established result. In contrast, here, the binding
participation restriction endogenously causes shifts in the labor
wedge. To offset this time-variation in labor wedges, the Ramsey
government moves tax rates in offsetting ways. To see this last
point clearly, notice that the contemporaneous correlations between
![]() and GDP, the TFP realization,
and the government spending realization are all exactly
opposite to the contemporaneous correlations between
and GDP, the TFP realization,
and the government spending realization are all exactly
opposite to the contemporaneous correlations between
![]() and these
aggregates. For example, the correlation between the tax rate and
GDP is -0.193, while the correlation between the shadow value
and these
aggregates. For example, the correlation between the tax rate and
GDP is -0.193, while the correlation between the shadow value
![]() and GDP is
0.193.
and GDP is
0.193.
As further evidence that the variations in the labor tax rate
are designed to offset movements in the shadow value of the
participation constraint, Figure 1 displays the
response of the Ramsey policy to one-standard-deviation positive
impulses to government spending and TFP. The countercyclical nature
of the optimal tax rate to the shadow value is obvious; indeed, the
correlation between the two is virtually -1 in the face of either a
shock to government spending or to TFP. Corroborating this evidence
is that, in our simulated economies, the median contemporaneous
correlation between
![]() and
and
![]() was -0.998.
was -0.998.
The intuition behind the tax volatility result is simple. Suppose a shock hits the economy that, if there were no restriction on participation, would cause the participation rate to rise. Because of institutional or other restrictions, however, participation cannot respond, which causes the shadow value of the constraint to rise instead. This lowers the value of leisure relative to the value of participating in the formal labor market. From an efficiency standpoint, this misalignment of values is suboptimal. The Ramsey government can realign these values by raising the reward for work (the after-tax wage) by lowering the tax rate. In contrast, if there is no institutional impediment to adjusting participation, the shadow value is of course always zero and the optimality of tax-smoothing re-emerges.
We mentioned at the outset the conventional empirical view, as
recently described by Elsby, Michaels, and Solon (2008), that
cyclical variation in participation is "...miniscule relative to
the cyclical variation in unemployment" (Elsby et al). For our LFP
model, panel B of Table 1 shows that the participation rate fluctuates very little. Across
our simulations, the median standard deviation of ![]() is 0.0035 around a mean of 0.66. Thus, over the business
cycle and given that the optimal fiscal policy is in place,
two-thirds of the observations on the participation rate lie
between 65.65 percent and 66.35 percent under the optimal policy.
Although our model is not calibrated to match the observed cyclical
volatility of the labor-force participation rate, it matches
extremely well with the data. Shown in Figure 2 is quarterly
participation rates (as a fraction of the entire population) in the
U.S. between 1959:1 and 2006:2 along with its HP filter (smoothing
parameter 1600) trend. The standard deviation of the cyclical
component of the participation rate is 0.0032, very close to the
volatility implied by our model. Our results are thus not driven by
counterfactually large cyclical fluctuations in participation.
is 0.0035 around a mean of 0.66. Thus, over the business
cycle and given that the optimal fiscal policy is in place,
two-thirds of the observations on the participation rate lie
between 65.65 percent and 66.35 percent under the optimal policy.
Although our model is not calibrated to match the observed cyclical
volatility of the labor-force participation rate, it matches
extremely well with the data. Shown in Figure 2 is quarterly
participation rates (as a fraction of the entire population) in the
U.S. between 1959:1 and 2006:2 along with its HP filter (smoothing
parameter 1600) trend. The standard deviation of the cyclical
component of the participation rate is 0.0032, very close to the
volatility implied by our model. Our results are thus not driven by
counterfactually large cyclical fluctuations in participation.
Nevertheless, in our model, very small fluctuations in participation lead to a very different policy prescription than if there is literally zero adjustment at the participation margin. Our results thus offer a cautionary note for policy analysis in search-based models: on empirical grounds, modeling participation as completely exogenous over the cycle may seem justified. However, even very small equilibrium adjustments can qualitatively affect the policy insights a model delivers. Given the simple nested formulations of the seemingly very different models we have developed, it seems at least worthwhile to check sensitivity of results along this dimension.
As Table 1 shows and as we have been discussing, tax volatility arises in the environment in which the participation rate is inelastic. A natural conjecture is that if labor-supply were inelastic in a neoclassical labor market and, as in our model, labor were the only input to production, tax-rate volatility would be optimal there, as well. We agree with this conjecture. However, in that environment, the labor-income tax would be akin to a lump-sum tax because the equilibrium quantity of labor is inelastic, not simply households' supply of labor. Such an environment renders Ramsey analysis of "optimal taxation" moot because clearly there would be no distortions from any time-pattern of tax rates. In contrast, in a search and matching environment that acknowledges there are three labor-market states, not just two, even if participation is inelastic, the equilibrium quantity of labor is elastic and is governed by search and matching. Thus, while it is true that an RBC model with inelastic labor would deliver a policy prescription of tax-rate volatility, it would do so for somewhat trivial reasons.
Finally, Table 2 shows that the
main results remain intact if the government provides unemployment
benefits. For the experiments presented in Table 2, we choose, as
we described above, a ![]() so that in the
deterministic Ramsey steady state,
so that in the
deterministic Ramsey steady state,
![]() , which is
consistent with the calibration of Shimer (2005). All other
parameter settings are held constant at the values underlying the
results in Table 2. Because
unemployment benefits are government-financed, the mean labor tax
rate must rise in both the pseudo-LFP model and the LFP model; as
the table shows, the mean tax rate rises to about 25 percent,
compared to about 20 percent if there are zero unemployment
benefits as in Table 1.
Unlike the case with zero unemployment benefits, the
contemporaneous correlations between
, which is
consistent with the calibration of Shimer (2005). All other
parameter settings are held constant at the values underlying the
results in Table 2. Because
unemployment benefits are government-financed, the mean labor tax
rate must rise in both the pseudo-LFP model and the LFP model; as
the table shows, the mean tax rate rises to about 25 percent,
compared to about 20 percent if there are zero unemployment
benefits as in Table 1.
Unlike the case with zero unemployment benefits, the
contemporaneous correlations between
![]() and
and
![]() is not
exactly the mirror image of the correlations between
is not
exactly the mirror image of the correlations between
![]() and these
aggregates. Nonetheless, the correlation between
and these
aggregates. Nonetheless, the correlation between
![]() and
and
![]() is still highly
negative: averaging over our simulated economies, the median
contemporaneous correlation between them was -0.96. Hence, as the
wedge condition (26) shows,
is still highly
negative: averaging over our simulated economies, the median
contemporaneous correlation between them was -0.96. Hence, as the
wedge condition (26) shows,
![]() does open up a gap between the shadow
value and the tax rate, but it is still clearly fluctuations in the
shadow value that tax-rate volatility is designed to offset. And,
once again, if participation can adjust cyclically, the optimality
of tax-rate smoothing is restored, as the first row of panel B of Table 2 shows.
does open up a gap between the shadow
value and the tax rate, but it is still clearly fluctuations in the
shadow value that tax-rate volatility is designed to offset. And,
once again, if participation can adjust cyclically, the optimality
of tax-rate smoothing is restored, as the first row of panel B of Table 2 shows.
6.3 Efficiency Considerations and Tax Volatility
We have explained our results regarding optimal tax-rate dynamics in terms of the labor wedge defined by (26). To demonstrate that the lack of tax-smoothing in our pseudo-LFP model is indeed fundamentally driven by fluctuations in this wedge and not by some interactions between search frictions and the Ramsey financing problem itself, we can introduce a lump-sum tax into our environment. The presence of a lump-sum tax makes identically zero the Ramsey multiplier on the PVIC (28), which thus means that public-finance considerations are absent.19 Performing our experiments in the presence of lump-sum taxes therefore isolates the efficiency concerns underlying the dynamics of tax rates.
Figure 3 reports the
results of the same impulse experiments underlying
Figure 1,
except with a lump-sum tax assumed available. All parameters are
held constant at their benchmark values, and we assume ![]() for this demonstration. With lump-sum taxation
available, there is no reason to use labor-income taxation, hence
in the long-run
for this demonstration. With lump-sum taxation
available, there is no reason to use labor-income taxation, hence
in the long-run
![]() , as the upper row of
Figure 3 shows. Following
a shock to either government spending or TFP, however, the labor
tax rate deviates from zero. Although the effect is more dramatic
for a government spending impulse than for a TFP impulse,
comparison of Figure 3 with
Figure 1 shows that the patterns of responses are the same, and, in
particular, movements in the tax rate are designed to stabilize
movements in the overall wedge. Furthermore, in simulation
exercises we conducted with a lump-sum tax assumed available, we
found that the standard deviation of the labor-income tax rate was
2.27 percent, which is comparable to the 1.83 percentage point
standard deviation reported in the first row of Table 1 for the full Ramsey financing problem.
, as the upper row of
Figure 3 shows. Following
a shock to either government spending or TFP, however, the labor
tax rate deviates from zero. Although the effect is more dramatic
for a government spending impulse than for a TFP impulse,
comparison of Figure 3 with
Figure 1 shows that the patterns of responses are the same, and, in
particular, movements in the tax rate are designed to stabilize
movements in the overall wedge. Furthermore, in simulation
exercises we conducted with a lump-sum tax assumed available, we
found that the standard deviation of the labor-income tax rate was
2.27 percent, which is comparable to the 1.83 percentage point
standard deviation reported in the first row of Table 1 for the full Ramsey financing problem.
We conclude from these experiments that it is indeed movements in the search labor wedge (26) that tax-rate fluctuations are designed to mitigate when the labor-force participation rate is fixed over the business cycle. This cyclical efficiency concern is not blurred by consideration of the full Ramsey public-financing problem.
6.4 Alternative Policy Instruments
Finally, one may reasonably ask whether the presence of other
policy instruments might re-instate the optimality of tax-smoothing
even if participation is exogenous. Simply inspecting the
wedge (26),
it is clear that if the unemployment benefit ![]() were time-varying and always equal to
were time-varying and always equal to
![]() , the second part
of this wedge condition would drop out, leaving only the labor
income tax rate. Smoothing
, the second part
of this wedge condition would drop out, leaving only the labor
income tax rate. Smoothing
![]() then follows from standard
Ramsey principles.
then follows from standard
Ramsey principles.
Alternatively, suppose the government had access to a
time-varying proportional vacancy subsidy, which lowers for firms
the cost of searching workers. Denoting by
![]() the proportional
vacancy-posting subsidy rate, this subsidy would make the cost
faced by the firm for each vacancy created
the proportional
vacancy-posting subsidy rate, this subsidy would make the cost
faced by the firm for each vacancy created
![]() . It is
straightforward to show that in all equilibrium conditions (apart
from the aggregate resource constraint) where
. It is
straightforward to show that in all equilibrium conditions (apart
from the aggregate resource constraint) where ![]() appears,
appears,
![]() would instead appear.
In particular, the wedge presented in (26) would modify
to
would instead appear.
In particular, the wedge presented in (26) would modify
to
![$\displaystyle \left[ (1-\tau^{n}_{t}) - \left( \frac{\phi_{t}} {u^{\prime}(c_{t})} - \chi_{t} \right) \frac{1-\xi_{u}}{\xi_{u}}\frac{1}{ (1-\tau^{s}_{t})\gamma\theta_{t}} \right] ,$](img355.gif)
|
(34) |
in which we have also, based on the immediately preceding
discussion, also supposed that the unemployment benefit ![]() can be time-varying.
can be time-varying.
With all three instruments
![]() ,
, ![]() , and
, and
![]() appearing in the single
wedge (34),
there is an infinite number of potential decentralizations for any
given allocation. To achieve a given target for the overall wedge,
one decentralization involves fixing both
appearing in the single
wedge (34),
there is an infinite number of potential decentralizations for any
given allocation. To achieve a given target for the overall wedge,
one decentralization involves fixing both ![]() and
and
![]() at time-invariant rates and
allowing fluctuations in
at time-invariant rates and
allowing fluctuations in
![]() to do the job. This is the
decentralization we pursued in our main analysis. Another
decentralization is to keep
to do the job. This is the
decentralization we pursued in our main analysis. Another
decentralization is to keep
![]() constant ("tax-smoothing") and
allow some appropriate combination of fluctuations in
constant ("tax-smoothing") and
allow some appropriate combination of fluctuations in ![]() and
and
![]() to stabilize the overall
wedge.
to stabilize the overall
wedge.
If one were to prefer the latter way of "restoring the optimality of tax-smoothing," it must be driven by considerations outside the scope of the model. This is because, within the scope of our model, our baseline specification of policy instruments was already complete, in the sense understood in the literature on optimal taxation.20 When a tax system is complete, introducing additional policy instruments does not at all change the Ramsey allocation problem; instead, as in the example just described, all it does is create indeterminacies about which instruments should be used in which configurations to support the Ramsey allocation. The model does not provide any basis for preferring one decentralization over another, which is a well-understood point in Ramsey models of optimal taxation. Hence, loading redundant policy instruments onto the same, single, wedge (34) is an uninteresting way of restoring labor-tax-smoothing.
7. Conclusion
We have shown that the optimality of smoothing labor-income tax rates over time, a basic result in the theory of optimal fiscal policy, does not carry over to the most common DSGE specification of a search and matching model of labor markets. The crucial missing margin of adjustment in much of the existing work is household optimization with respect to labor-market outcomes. Such a margin is at the core of any standard macro model, but absent in a baseline search-based macro model. By formulating the standard exogenous-participation search model in way that makes it seem as if a participation margin does exist, we have shown that cyclical fluctuations in the shadow value associated with the participation restriction disrupt labor-market efficiency. Purposeful tax-rate volatility is then optimal because it offsets shifts in labor-market wedges. In contrast, if there is no impediment to adjusting participation at business-cycle frequencies, tax-smoothing is optimal despite the presence of search and matching frictions.
Clearly, more empirical resolution is needed about the cyclical
nature of labor-force participation. There are many types of
individuals for whom participation is difficult to adjust quickly:
a person engaged in child-rearing or education may not be able to
make himself available for work within the few quarters or few
years over which business-cycle shocks have their impact. On the
other hand, there are many types of individuals for whom
participation may be easy to adjust quickly: a person engaged in
short-term schooling or short-term (re-)training may be able to
(re-)join the labor force within weeks or months. With
participation endogenous, our quantitative results show that it may
nonetheless fluctuate very little, which in turn may lead one to
favor the exogeneity assumption on the basis of simplicity. But
optimal-policy prescriptions are dramatically different under an
exogenous-participation view than under an endogenous-participation
view even though equilibrium fluctuations in this margin may be
small. In the end, though, which view of cyclical fluctuations in
participation is more relevant is an open question. Our work raises
an important cautionary note for typical formulations of DSGE
labor-search models, especially as they are increasingly applied to
study policy questions.
To understand our optimal-policy results, we have developed a notion of general-equilibrium efficiency in search-based models. This view of efficiency encompasses the Hosios (1990) condition for search efficiency, but is especially intended for general-equilibrium analysis. As search-based quantitative general-equilibrium models become increasingly popular for studying policy questions, the general notion of efficiency developed here may be useful for gaining insights into existing and newly-emerging results. We have in mind in particular the growing body of policy analysis conducted in search-based New Keynesian monetary models.
A. Deriving the Pseudo-Labor-Force Participation Condition
The household optimization problem is to choose state-contingent
processes for
![]() ,
,
![]() ,
,
![]() , and
, and
![]() to maximize
to maximize
![$\displaystyle \max E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(c_{t}) + g(1-u^{h} _{t}-n^{h}_{t}) \right]$](img370.gif)
|
(35) |
subject to sequences of flow budget constraints
| (36) |
perceived laws of motion for the employment stock
| (37) |
and the restriction that the size of the labor force is fixed
| (38) |
Denote by
![]() ,
,
![]() , and
, and
![]() the sequences of Lagrange
multipliers on the sequences of these constraints, respectively.
The first-order conditions with respect to
the sequences of Lagrange
multipliers on the sequences of these constraints, respectively.
The first-order conditions with respect to ![]() ,
,
![]() ,
, ![]() and
and
![]() ; they are, respectively,
; they are, respectively,
| (39) |
| (40) |
| (41) |
and
| (42) |
Conditions (39) and (40) clearly yield a standard bond-Euler equation, which is expression (9) in the main text.
To obtain the pseudo-labor-force-participation (LFP) condition,
start with (41)
and (42).
Solving (41) for
![]() ,
,
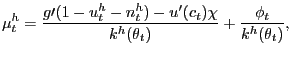
|
(43) |
in which we have used the result
![]() , which follows
from (39). Using this
expression and its period
, which follows
from (39). Using this
expression and its period ![]() analog
in (42), we have
analog
in (42), we have
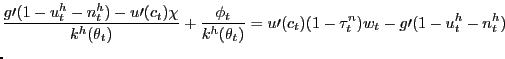 |
|
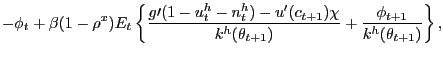 |
(44) |
which is the pseudo-LFP condition presented in condition (10) in the main text.
B. Nash Bargaining in Model with Pseudo-Labor-Force Participation Margin
Starting with the solution to the household problem obtained in
Appendix A, we next use the
envelope conditions of the household's optimization problem to
define the value equations relevant for the Nash bargaining
problem. Note that because we refrain from making the substitution
![]() , both
, both
![]() and
and
![]() are state variables in the
formulation of the household optimization problem offered in
Appendix A.
are state variables in the
formulation of the household optimization problem offered in
Appendix A.
Let
![]() denote
the value function associated with the solution to this problem.
The envelope conditions are thus
denote
the value function associated with the solution to this problem.
The envelope conditions are thus
![]() and
and
| (45) |
Recognizing the relationship at the optimal solution between
![]() and allocations defined
by (43), and
substituting
and allocations defined
by (43), and
substituting
![]() into (44), we can write
into (44), we can write
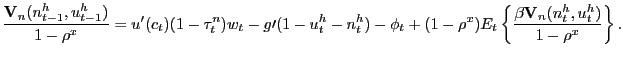
|
(46) |
To express things in terms of goods, recognize that
![]() at the
optimum and define
at the
optimum and define
![]() as
as
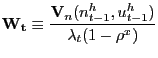
|
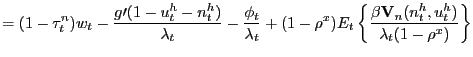
|
|
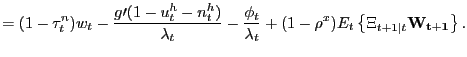
|
(47) |
In the second line, we have made use of the definition of the
one-period-ahead stochastic discount factor,
![]() . We have
. We have
![]() . From the point of view of the household, it is the surplus
. From the point of view of the household, it is the surplus
![]() over which it
is bargaining.
over which it
is bargaining.
On the firm side, we have the surplus to a firm of the marginal worker is
| (48) |
for use below, note that
![]() .
.
In generalized Nash bargaining, the parties choose ![]() to maximize
to maximize
| (49) |
The solution to this problem gives the time-![]() generalized Nash sharing rule,
generalized Nash sharing rule,
![]() .
.
Now proceed to derive an explicit expression for ![]() . Inserting the definition of
. Inserting the definition of
![]() into the Nash sharing
rule,
into the Nash sharing
rule,
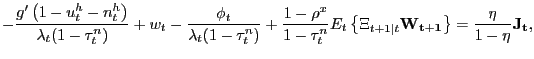
|
(50) |
and then using the time-![]() Nash sharing rule,
Nash sharing rule,
|
(51) |
Make the substitution
![]() , and
similarly for
, and
similarly for
![]() , which yields
, which yields
|
(52) |
Next, use the job-creation condition
![]() to substitute on the right-hand-side, which gives
to substitute on the right-hand-side, which gives
![$\displaystyle {\scriptsize -\frac{g^{\prime}\left( 1-u_{t}^{h}-n_{t}^{h}\right) } {\lambda_{t}(1-\tau_{t}^{n})}+w_{t}-\frac{\phi_{t}}{\lambda_{t}(1-\tau_{t} ^{n})}+\frac{1-\rho^{x}}{1-\tau_{t}^{n}}E_{t}\left\{ \Xi_{t+1\vert t}(1-\tau _{t+1}^{n})\frac{\eta}{1-\eta}\frac{\gamma}{k^{f}(\theta_{t+1})}\right\} =\frac{\eta}{1-\eta}\left[ z_{t}-w_{t}+(1-\rho^{x})E_{t}\left\{ \Xi _{t+1\vert t}\frac{\gamma}{k^{f}(\theta_{t+1})}\right\} \right] .}$](img423.gif)
|
(53) |
Grouping terms involving ![]() ,
,
![$\displaystyle \lefteqn{w_{t}\left[ 1+\frac{\eta}{1-\eta}\right] =\frac{\eta}{1-\eta} z_{t}+\frac{g\prime(1-u_{t}^{h}-n_{t}^{h})}{\lambda_{t}(1-\tau_{t}^{n})} +\frac{\phi_{t}}{\lambda_{t}(1-\tau_{t}^{n})}}$](img425.gif) |
|
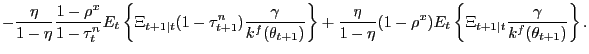 |
(54) |
Finally, multiplying by ![]() gives the wage
equation
gives the wage
equation
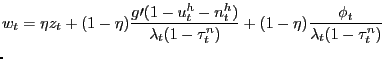 |
|
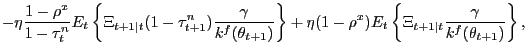 |
(55) |
which is expression (12) in the main text.
If tax rates never fluctuated, so that
![]() , the
last two terms would cancel, leaving
, the
last two terms would cancel, leaving
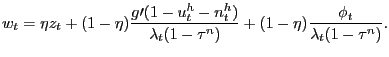
|
(56) |
The last term reflects the value to the household of not being able to resize the labor force, and this value is shared between firms and households via bargaining.
C. Nash Bargaining in Model with Labor-Force Participation Margin
With endogenous labor-force-participation and instantaneous hiring, the household problem is as described above, except the perceived law of motion is now
| (57) |
We again define the bargaining-relevant value equations using the
household-level envelope condition. Define
![]() as the value
function associated with the optimal plan that solves the household
problem. The envelope condition is thus
as the value
function associated with the optimal plan that solves the household
problem. The envelope condition is thus
![]() , where
, where
![]() is the Lagrange multiplier
associated with the time-
is the Lagrange multiplier
associated with the time-![]() perceived law of motion.
Next, use the household's optimality condition on
perceived law of motion.
Next, use the household's optimality condition on ![]() , which is
, which is
![]() , to express the envelope condition as
, to express the envelope condition as
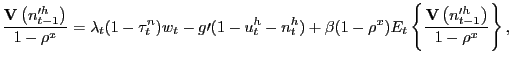
|
(58) |
in which we have normalized by
![]() due to the timing of events.
due to the timing of events.
To express things in units of goods, define
![]() as
as
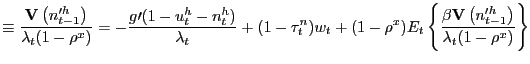
|
||
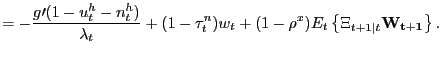
|
(59) |
As before, the second line makes use of the definition of the
one-period-ahead stochastic discount factor,
![]() .
.
On the firm side, we still have
| (60) |
and, for use below, note that
![]() .
.
As above, we have
![]() ; and, as above, the time-
; and, as above, the time-![]() generalized Nash sharing
rule is
generalized Nash sharing
rule is
![]() .
.
Now proceed to derive an explicit expression for ![]() . Inserting the definition of
. Inserting the definition of
![]() into the Nash sharing
rule,
into the Nash sharing
rule,
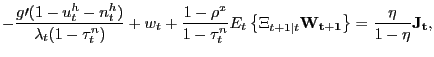
|
(61) |
and then using the time-![]() Nash sharing rule,
Nash sharing rule,
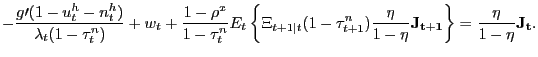
|
(62) |
Make the substitution
![]() , and
similarly for
, and
similarly for
![]() , which yields
, which yields
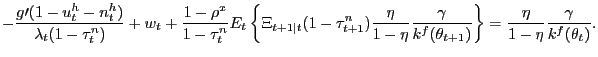
|
(63) |
Next, use the job-creation condition
![]() to substitute on the right-hand-side, which gives
to substitute on the right-hand-side, which gives
![$\displaystyle {\scriptsize -\frac{g\prime(1-u_{t}^{h}-n_{t}^{h})}{\lambda_{t}(1-\tau_{t} ^{n})}+w_{t}+\frac{1-\rho^{x}}{1-\tau_{t}^{n}}E_{t}\left\{ \Xi_{t+1\vert t} (1-\tau_{t+1}^{n})\frac{\eta}{1-\eta}\frac{\gamma}{k^{f}(\theta_{t+1} )}\right\} =\frac{\eta}{1-\eta}\left[ z_{t}-w_{t}+(1-\rho^{x})E_{t}\left\{ \Xi_{t+1\vert t}\frac{\gamma}{k^{f}(\theta_{t+1})}\right\} \right] .}$](img460.gif)
|
(64) |
Grouping terms involving ![]() ,
,
![$\displaystyle \lefteqn{w_{t}\left[ 1+\frac{\eta}{1-\eta}\right] =\frac{\eta}{1-\eta} z_{t}+\frac{g\prime(1-u_{t}^{h}-n_{t}^{h})}{\lambda_{t}(1-\tau_{t}^{n})} }$](img462.gif) |
|
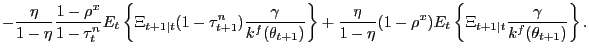 |
(65) |
Finally, multiplying by ![]() gives the wage
equation
gives the wage
equation
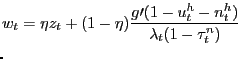 |
|
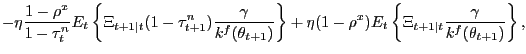 |
(66) |
which is expression (13) in the main
text. As in the case of model with a one-period delay before new
matches become productive, if
![]() , the
last two terms cancel with each other and the wage collapses to a
simple static split,
, the
last two terms cancel with each other and the wage collapses to a
simple static split,
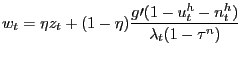
|
(67) |
D. Social Planner Problem
Here we prove the efficiency condition presented in
Proposition 1. A Social
Planner in our economy optimally allocates the measure one of
individuals in the representative household to leisure and the
labor force. Denote by
![]() the measure of individuals that
enjoy leisure in period
the measure of individuals that
enjoy leisure in period ![]() . That is,
. That is,
![]() is the measure of
individuals outside the labor force, neither working nor actively
in the pool of searching unemployed. Our main interest in the
social-planning problem is on developing a search-theoretic notion
of static efficiency between leisure (search) and consumption. To
emphasize static variables, and move the focus away from the
endogenously-evolving stock of employment
is the measure of
individuals outside the labor force, neither working nor actively
in the pool of searching unemployed. Our main interest in the
social-planning problem is on developing a search-theoretic notion
of static efficiency between leisure (search) and consumption. To
emphasize static variables, and move the focus away from the
endogenously-evolving stock of employment ![]() , we
cast the social planning problem as one of choosing
, we
cast the social planning problem as one of choosing ![]() and
and
![]() , rather than as one of choosing
, rather than as one of choosing
![]() . Of course, a choice of
. Of course, a choice of ![]() and
and
![]() implies a choice of
implies a choice of ![]() .
.
The social-planning problem is thus
![$\displaystyle \max E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(c_{t}) + g(\varrho_{t}) \right]$](img479.gif)
|
(68) |
subject to the sequence of resource constraints
| (69) |
and laws of motion for the employment stock
| (70) |
As noted above, because our focus is on the margin within a period
between ![]() and
and ![]() , we have
expressed
, we have
expressed ![]() in the constraints as
in the constraints as
![]() .
.
Denote by
![]() and
and
![]() the Lagrange multipliers on
these two constraints, respectively. The first-order conditions
with respect to
the Lagrange multipliers on
these two constraints, respectively. The first-order conditions
with respect to ![]() ,
, ![]() ,
,
![]() , and
, and
![]() are thus
are thus
| (71) |
| (72) |
| (73) |
and
| (74) |
Conditions (73) and (74) imply
| (75) |
Using (72), this can be expressed as
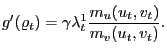
|
(76) |
Using (71), this can be expressed as
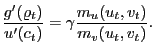
|
(77) |
Given a Cobb-Douglas matching technology
![]() , we have
that
, we have
that
![]() (where
(where
![]() ).
).
We thus can express static efficiency along the consumption-leisure margin as
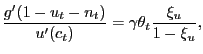
|
(78) |
in which we have re-inserted the identity
![]() .
Condition (78) characterizes
efficiency along the static consumption-leisure margin. The
left-hand-side is clearly the marginal rate of substitution (MRS)
for the household between consumption and leisure. Under the basic
tenet that efficiency occurs where MRS is equated to the associated
marginal rate of transformation (MRT), the right-hand-side
of (78)
is thus the MRT between consumption and leisure in a search-based
environment.
.
Condition (78) characterizes
efficiency along the static consumption-leisure margin. The
left-hand-side is clearly the marginal rate of substitution (MRS)
for the household between consumption and leisure. Under the basic
tenet that efficiency occurs where MRS is equated to the associated
marginal rate of transformation (MRT), the right-hand-side
of (78)
is thus the MRT between consumption and leisure in a search-based
environment.
E. General Equilibrium Consumption-Leisure Wedges
Here we prove Proposition 2. To derive the equilibrium margin between consumption and leisure and to see which features of the decentralized economy disrupt consumption-leisure efficiency, start with the pseudo-labor-force participation condition
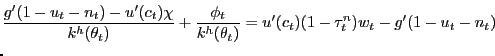 |
|
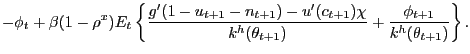 |
(79) |
and the job-creation condition
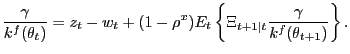
|
(80) |
Divide (79) by (80) to get
![$\displaystyle \lefteqn{ \frac{ k^{f}(\theta_{t}) \left[ \frac{ g'(1-u_{t}-n_{t}) - u'(c_{t}) \chi}{k^{h}(\theta_{t})} + \frac{\phi_{t}}{k^{h}(\theta_{t})} \right] } {\gamma} }$](img507.gif) |
|
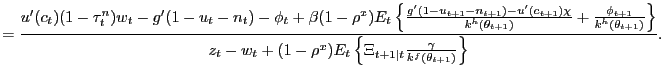 |
(81) |
Using the result that
![]() due to
the assumption of Cobb-Douglas matching, we can re-arrange the
left-hand-side as
due to
the assumption of Cobb-Douglas matching, we can re-arrange the
left-hand-side as
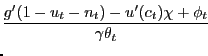 |
|
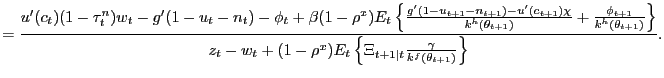 |
(82) |
Next, note from our work in Appendix B that
the numerator on the right-hand-side is
![]() , the surplus to the household (expressed in terms of utility) of
having the marginal member enter into an employment relationship.
Also note that the denominator on the right-hand-side of the
previous expression is
, the surplus to the household (expressed in terms of utility) of
having the marginal member enter into an employment relationship.
Also note that the denominator on the right-hand-side of the
previous expression is
![]() , the surplus to the firm of
entering into an employment relationship with one additional
worker.
, the surplus to the firm of
entering into an employment relationship with one additional
worker.
Thus, the last expression can be simplified to
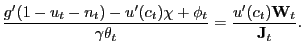
|
(83) |
Using in this expression the private economy's Nash-bargaining
outcome
![]() , we have
, we have
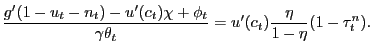
|
(84) |
Rearranging, we have that in the decentralized Nash-bargaining economy with taxes, unemployment benefits, and no ability for households to enter or exit the labor force,
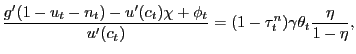
|
(85) |
in which, recall,
![]() is the Nash bargaining power of
households.
is the Nash bargaining power of
households.
Comparing (85) with the efficiency condition (78), it is clear that four things are needed in the decentralized economy in order for consumption-leisure efficiency to be achieved:
- The decentralized economy must feature
 , which corresponds to the
Hosios (1990) condition for search efficiency
, which corresponds to the
Hosios (1990) condition for search efficiency - The transfer of unemployment benefits from the government to
households must be zero -- that is,
- Households must be able to optimize with respect to the size of
the total labor force every period -- that is,
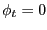
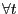
- Proportional labor income taxation must be zero -- that is,
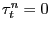
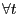
7. Derivation of Implementability Constraint
The derivation of the implementability constraint follows that laid out in Lucas and Stokey (1983) and Chari and Kehoe (1999). The derivation presented here nests that for the both the pseudo-LFP model and the LFP model -- obtaining the implementability constraint for the latter from the former requires setting the shadow value on the exogenous labor-force size restriction to zero, as has been discussed in the text.
From the pseudo-labor-force participation model, we will be able to use the household's (pseudo) perceived law of motion for employment,
| (86) |
the size restriction
| (87) |
and the pseudo-labor-force-participation condition
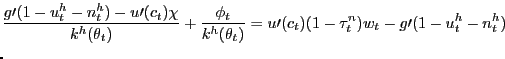 |
|
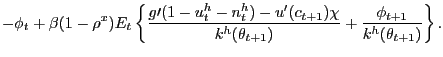 |
(88) |
Start with the household flow budget constraint in equilibrium
| (89) |
Multiply by
![]() and sum over
dates and states starting from
and sum over
dates and states starting from ![]() ,
,
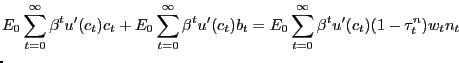 |
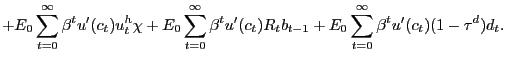 |
Use the household's Euler equation,
![]() , to substitute for
, to substitute for
![]() in the term on the
left-hand-side involving
in the term on the
left-hand-side involving ![]() ,
,
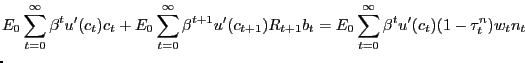 |
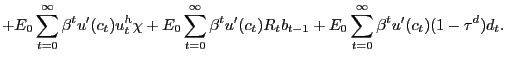 |
From here on, we suppress the ![]() operator to
conserve on notation.
operator to
conserve on notation.
Canceling terms in the second summation on the left-hand-side with the third summation on the right-hand-side leaves only the time-zero bond position,
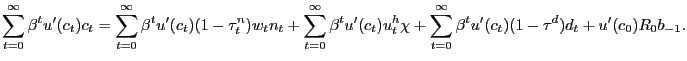
|
(90) |
Next, use (88) to substitute
for the sequence of terms
![]() in
the first summation on the right-hand-side, which gives
in
the first summation on the right-hand-side, which gives
![$\displaystyle \lefteqn{ \sum_{t=0}^{\infty}\beta^{t} u'(c_{t})c_{t} = \sum_{t=0}^{\infty }\beta^{t} \left[ \frac{g'_{t} - u'(c_{t}) \chi}{k^{h}(\theta_{t})} + \frac{\phi_{t}}{k^{h}(\theta_{t})}\right] n_{t} + \sum_{t=0}^{\infty} \beta^{t} \left[ g'_{t} + \phi_{t}\right] n_{t} }$](img542.gif) |
|
![$\displaystyle - (1-\rho^{x}) \sum_{t=0}^{\infty} \beta^{t+1} \left[ \frac{g^{\prime }_{t+1} - u^{\prime}(c_{t+1})\chi}{k^{h}(\theta_{t+1})} + \frac{\phi_{t+1} }{k^{h}(\theta_{t+1})} \right] n_{t} + \sum_{t=0}^{\infty}\beta^{t} u^{\prime}(c_{t}) u^{h}_{t} \chi+ \sum_{t=0}^{\infty}\beta^{t} u^{\prime }(c_{t}) (1-\tau^{d})d_{t} + u^{\prime}(c_{0}) R_{0} b_{-1}.$](img543.gif) |
(91) |
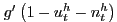 .
.
Next, use
![]() to
substitute for the sequence of
to
substitute for the sequence of ![]() terms that
appear in the first summation on the right-hand-side, which
gives
terms that
appear in the first summation on the right-hand-side, which
gives
![$\displaystyle \lefteqn{ \sum_{t=0}^{\infty}\beta^{t} u'(c_{t})c_{t} = (1-\rho^{x}) \sum_{t=0}^{\infty}\beta^{t} \left[ \frac{g'_{t} - u'(c_{t}) \chi} {k^{h}(\theta_{t})} + \frac{\phi_{t}}{k^{h}(\theta_{t})}\right] n_{t-1} }$](img548.gif) |
|
![$\displaystyle + \sum_{t=0}^{\infty}\beta^{t} \left[ \frac{g^{\prime}_{t} - u^{\prime }(c_{t}) \chi}{k^{h}(\theta_{t})} + \frac{\phi_{t}}{k^{h}(\theta_{t})}\right] k^{h}(\theta_{t}) u^{h}_{t} + \sum_{t=0}^{\infty}\beta^{t} \left[ g^{\prime }_{t} + \phi_{t}\right] n_{t}$](img549.gif) |
|
![$\displaystyle - (1-\rho^{x}) \sum_{t=0}^{\infty} \beta^{t+1} \left[ \frac{g^{\prime }_{t+1} - u^{\prime}(c_{t+1})\chi}{k^{h}(\theta_{t+1})} + \frac{\phi_{t+1} }{k^{h}(\theta_{t+1})} \right] n_{t} + \sum_{t=0}^{\infty}\beta^{t} u^{\prime}(c_{t}) u^{h}_{t} \chi+ \sum_{t=0}^{\infty}\beta^{t} u^{\prime }(c_{t}) (1-\tau^{d})d_{t} + u^{\prime}(c_{0}) R_{0} b_{-1}.$](img550.gif) |
(92) |
The first summation on the right-hand-side cancels with the fourth summation on the right-hand-side, leaving only the time-zero term:
![$\displaystyle \lefteqn{ \sum_{t=0}^{\infty}\beta^{t} u'(c_{t})c_{t} = \sum_{t=0}^{\infty }\beta^{t} \left[ \frac{g'_{t} - u'(c_{t}) \chi}{k^{h}(\theta_{t})} + \frac{\phi_{t}}{k^{h}(\theta_{t})}\right] k^{h}(\theta_{t}) u^{h}_{t} + \sum_{t=0}^{\infty}\beta^{t} \left[ g'_{t} + \phi_{t}\right] n_{t} }$](img551.gif) |
|
![$\displaystyle + \sum_{t=0}^{\infty}\beta^{t} u^{\prime}(c_{t}) u^{h}_{t} \chi+ \sum _{t=0}^{\infty}\beta^{t} u^{\prime}(c_{t}) (1-\tau^{d})d_{t} + u^{\prime }(c_{0}) R_{0} b_{-1} + (1-\rho^{x}) \left[ \frac{g^{\prime}_{0} - u^{\prime }(c_{0})\chi}{k^{h}(\theta_{0})} + \frac{\phi_{0}}{k^{h}(\theta_{0})} \right] n_{-1}.$](img552.gif) |
(93) |
Expanding and rearranging the first summation on the right-hand-side,
![$\displaystyle \lefteqn{ \sum_{t=0}^{\infty}\beta^{t} u'(c_{t})c_{t} = \sum_{t=0}^{\infty }\beta^{t} \left[ g'_{t} + \phi_{t} \right] u^{h}_{t} + \sum_{t=0}^{\infty }\beta^{t} \left[ g'_{t} + \phi_{t}\right] n_{t} - \sum_{t=0}^{\infty} \beta^{t} u'(c_{t}) u^{h}_{t} \chi}$](img553.gif) |
|
![$\displaystyle + \sum_{t=0}^{\infty}\beta^{t} u^{\prime}(c_{t}) u^{h}_{t} \chi+ \sum _{t=0}^{\infty}\beta^{t} u^{\prime}(c_{t}) (1-\tau^{d}) d_{t} + u^{\prime }(c_{0}) R_{0} b_{-1} + (1-\rho^{x}) \left[ \frac{g^{\prime}_{0} - u^{\prime }(c_{0})\chi}{k^{h}(\theta_{0})} + \frac{\phi_{0}}{k^{h}(\theta_{0})} \right] n_{-1}.$](img554.gif) |
(94) |
Finally, canceling the third and fourth summations on the
right-hand-side and re-introducing the conditional expectation
![]() , we have the present-value
implementability constraint
, we have the present-value
implementability constraint
![$\displaystyle E_{0} \sum_{t=0}^{\infty} \beta^{t} \left\{ u^{\prime}(c_{t})c_{t} - \left[ g^{\prime h}_{t}-n_{t}) + \phi_{t}\right] (n_{t}+u^{h}_{t}) - u^{\prime }(c_{t}) (1-\tau^{d}) d_{t} \right\} = A_{0},$](img556.gif)
|
(95) |
where
![$\displaystyle A_{0} \equiv u^{\prime}(c_{0}) R_{0} b_{-1} + (1-\rho^{x}) \left[ \frac{g^{\prime}_{0} - u^{\prime}(c_{0})\chi}{k^{h}(\theta_{0})} + \frac {\phi_{0}}{k^{h}(\theta_{0})} \right] n_{-1}.$](img557.gif)
|
(96) |
G. Zero Taxation of Dividend Income
We briefly explore the sensitivity of our results to the
assumption of zero dividend taxation. All the quantitative results
presented thus far have assumed 100-percent taxation of the
dividend income received by households. As we noted in
Section 2.2, it is
well-understood in Ramsey models that the unavailability of profit
taxes can affect policy prescriptions. This is because, following
production, profit flows (which is what households' dividend income
reflects) represent an inelastic source of revenue which the
government would like to tax heavily. A 100-percent profit/dividend
tax is thus trivially optimal, and this is the case on which we
have focused. To demonstrate the robustness of our main results to
the absence of a profit tax, we report in Table 3 simulation-based
results under the polar opposite assumption of zero dividend
taxation,
![]() . As comparison of the results in
Table 3 with those
reported in Table 1
shows, the cyclical properties of optimal policy in both the
pseudo-LFP model and the LFP model are virtually identical under
zero or full taxation of dividend income. Table 3 tabulates
results for the case of zero government-provided unemployment
benefits. For the case of positive government-provided unemployment
benefits, we find results very nearly the same as those reported in
Table 2; for brevity,
though, we do not report these results.
. As comparison of the results in
Table 3 with those
reported in Table 1
shows, the cyclical properties of optimal policy in both the
pseudo-LFP model and the LFP model are virtually identical under
zero or full taxation of dividend income. Table 3 tabulates
results for the case of zero government-provided unemployment
benefits. For the case of positive government-provided unemployment
benefits, we find results very nearly the same as those reported in
Table 2; for brevity,
though, we do not report these results.
H. Competitive Search Equilibrium
While Nash bargaining has become the standard wage-determination mechanism in DSGE search models, many other models of wage determination have been developed and usefully employed in the literature on labor-market theory. One particularly appealing alternative is competitive search equilibrium, which entails decentralized determination of wages which are taken as given by both firms and households in their optimal search behavior. From the point of view of standard DSGE macroeconomic models, this equilibrium concept is appealing because there are no bilateral negotiations whatsoever; wages are always determined in a market-clearing fashion. Because competitive search has not yet found its way to mainstream DSGE macro models, we show here how to implement a competitive search equilibrium. Our treatment adapts Moen's (1997) implementation for a full general-equilibrium environment. As we show, the condition characterizing equilibrium along the consumption-leisure (outside the labor force) margin that arises from competitive search is identical to that which arises under Nash bargaining under the Hosios (1990) parameterization for bargaining power. Because the Hosios parameterization is the case for which our main results are obtained, all of our optimal-policy results are thus identical under competitive search. Indeed, the derivations below can be viewed as extending the equivalence shown by Moen (1997) between competitive search equilibrium and Nash-Hosios bargaining.
To implement competitive search equilibrium, we must first
define payoff functions to search for both firms and households. In
a particular labor submarket ![]() , any firm
, any firm
![]() that pays the vacancy-posting cost
that pays the vacancy-posting cost
![]() has expected payoff of matching with
a worker
has expected payoff of matching with
a worker
![$\displaystyle k^{f}(\theta_{ijt}) \left[ z_{t} - w_{ijt} + (1-\rho^{x}) E_{t} \left\{ \Xi_{t+1\vert t} \frac{\gamma}{\theta_{it+1}} \right\} \right] .$](img587.gif)
|
(97) |
As in Moen (1997), the matching probability in period ![]() ,
,
![]() ), and the wage payment
in period
), and the wage payment
in period ![]() ,
, ![]() , are firm
, are firm
![]() -specific. The continuation value captured
by
-specific. The continuation value captured
by
![]() , however, is a
sub-market-specific value, reflecting the replacement value of a
given worker at sub-market
, however, is a
sub-market-specific value, reflecting the replacement value of a
given worker at sub-market ![]() prices (because
there are no match-specific idiosyncracies regarding employment in
our model).
prices (because
there are no match-specific idiosyncracies regarding employment in
our model).
For the representative household, payoff functions, defined in
terms of goods, for searching for (" applying to") a job at firm
![]() in labor submarket
in labor submarket ![]() are
given by
are
given by
![$\displaystyle k^{h}(\theta_{ijt})\left[ -\frac{g\prime(1-u_{t}^{h}-n_{t}^{h})}{\lambda_{t} }+(1-\tau_{t}^{n})w_{ijt}+(1-\rho^{x})E_{t}\left\{ \Xi_{t+1\vert t}\mathbf{W_{t+1} }\right\} \right]$](img597.gif)
|
(98) |
if match-formation at firm ![]() is successful,
which occurs with probability
is successful,
which occurs with probability
![]() , and
, and
| (99) |
if match-formation is unsuccessful, which occurs with probability
![]() . Note that these
payoffs are from the point of view of the household -- i.e., they
reflect the gain to the household of having one more household
member search for a job at firm
. Note that these
payoffs are from the point of view of the household -- i.e., they
reflect the gain to the household of having one more household
member search for a job at firm ![]() -- and are
straightforward generalizations of the payoff functions defined in
Appendix C. As derived in
Appendix C, there is zero
payoff to the household if search is unsuccessful.
-- and are
straightforward generalizations of the payoff functions defined in
Appendix C. As derived in
Appendix C, there is zero
payoff to the household if search is unsuccessful.
For the concept of competitive search equilibrium,
directed search, rather than random search, is a critical
component.21 The consequence of
optimally-directed job search at firm ![]() is thus
that
is thus
that
| (100) |
where ![]() is the expected payoff of searching for a
job at a firm different from
is the expected payoff of searching for a
job at a firm different from ![]() (at either a
different firm in labor submarket
(at either a
different firm in labor submarket ![]() or in another
labor submarket altogether) and hence is independent of firm
or in another
labor submarket altogether) and hence is independent of firm
![]() outcomes. In writing (100), we have
used
outcomes. In writing (100), we have
used
![]() from Appendix C. The
competitive-search wage
from Appendix C. The
competitive-search wage ![]() and tightness
and tightness
![]() are the solutions to
maximization of (97) subject
to (100).
are the solutions to
maximization of (97) subject
to (100).
Denoting by
![]() the multiplier on the
constraint, the first-order condition with respect to
the multiplier on the
constraint, the first-order condition with respect to ![]() yields
yields
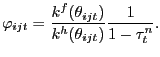
|
(101) |
Given constant-returns-to-scale matching, this reduces to
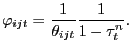
|
(102) |
Then, using this expression in the first-order condition with
respect to
![]() , we have
, we have
![$\displaystyle \frac{\partial k^{f}(\theta_{ijt})}{\partial\theta_{ijt}} \left[ z_{t} - w_{ijt} + (1-\rho^{x}) E_{t} \left\{ \Xi_{t+1\vert t} \frac{\gamma}{k^{f} (\theta_{it+1})} \right\} \right] = - \frac{1}{\theta_{ijt}} \frac{1} {1-\tau^{n}_{t}} \frac{\partial k^{h}(\theta_{ijt})}{\partial\theta_{ijt}} \mathbf{W_{ijt}}.$](img617.gif)
|
(103) |
We now restrict attention to equilibria that are symmetric
across firms in a given submarket and across submarkets, so we drop
![]() indexes. Given Cobb-Douglas matching
indexes. Given Cobb-Douglas matching
![]() , we have
, we have
![]() . Also, using the symmetric-equilibrium version of the
vacancy-creation condition, we can replace the term in brackets on
the left hand side of the previous expression with
. Also, using the symmetric-equilibrium version of the
vacancy-creation condition, we can replace the term in brackets on
the left hand side of the previous expression with
![]() ; making these
substitutions,
; making these
substitutions,
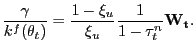
|
(104) |
Next, from optimal household labor-force-participation and the
definition of
![]() above, this can be written as
above, this can be written as
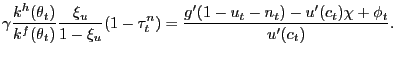
|
(105) |
Once again recognizing that
![]() because of constant-returns matching, we have that
period-
because of constant-returns matching, we have that
period-![]() equilibrium outcomes under competitive
search are described by
equilibrium outcomes under competitive
search are described by
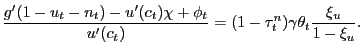
|
(106) |
Comparing this with the outcome in the decentralized bargaining
economy (under the Hosios parameterization
![]() ) presented in
condition (27) shows that they
are identical. Hence, the search-based labor wedge in the
competitive search economy is identical to the wedge in the
bargaining economy, which necessarily implies that optimal policy
in the competitive search economy is identical to that in the
bargaining economy.
) presented in
condition (27) shows that they
are identical. Hence, the search-based labor wedge in the
competitive search economy is identical to the wedge in the
bargaining economy, which necessarily implies that optimal policy
in the competitive search economy is identical to that in the
bargaining economy.
Table 1a. Ramsey Dynamics With Zero Government-Provided Unemployment Benefits - Panel A: Pseudo-Labor-Force Participation
| Variable | Mean | Std. Dev. | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|
| 0.2055 | 0.0183 | 0.9136 | -0.1818 | -0.1871 | 0.9804 | |
| 0.5940 | 0.0092 | 0.9047 | 1 | 0.9941 | -0.0407 | |
| 0.4078 | 0.0062 | 0.9196 | 0.7204 | 0.7257 | -0.6597 | |
| 0.5936 | 0.0006 | 0.9632 | 0.8024 | 0.7842 | 0.0257 | |
| 0.0661 | 0.0006 | 0.9631 | -0.8912 | -0.8760 | -0.0313 | |
| 0.6600 | 0 | |||||
| 0.8606 | 0.0143 | 0.9077 | 0.9885 | 0.9882 | -0.1052 | |
| 0.9974 | 0.0193 | 0.9046 | 0.9143 | 0.9022 | 0.0361 | |
| 0.0659 | 0.0007 | 0.8125 | 0.8920 | 0.8835 | 0.0399 | |
| -0.0040 | 0.0393 | 0.9142 | 0.1826 | 0.1880 | -0.9795 | |
| | -0.0013 | 0.0160 | 0.9142 | 0.1829 | 0.1884 | -0.9797 |
Table 1b. Ramsey Dynamics With Zero Government-Provided Unemployment Benefits - Panel B: Full-Labor-Force Participation
| Variable | Mean | Std. Dev. | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|
| 0.2041 | 0.0014 | 0.7638 | 0.1851 | -0.0063 | 0.6292 | |
| 0.5937 | 0.0092 | 0.9001 | 1 | 0.9383 | 0.2215 | |
| 0.4082 | 0.0048 | 0.8603 | 0.6091 | 0.8007 | -0.5246 | |
| 0.5932 | 0.0027 | 0.9456 | 0.2970 | 0.0329 | 0.8617 | |
| 0.0666 | 0.0016 | 0.7082 | -0.4540 | -0.5659 | 0.4761 | |
| 0.6599 | 0.0036 | 0.8985 | 0.0710 | -0.1932 | 0.9679 | |
| 0.8613 | 0.0142 | 0.8927 | 0.9179 | 0.9818 | -0.1039 | |
| 0.9823 | 0.0340 | 0.8874 | 0.7268 | 0.7495 | -0.1128 | |
| 0.0653 | 0.0014 | 0.6662 | 0.5938 | 0.5260 | 0.2773 | |
| 0 | 0 |
Table 2a. Ramsey Dynamics With Zero Government-Provided Unemployment Benefits 40 Percent After-Tax Wages - Panel A: Pseudo-Labor-Force Participation
| Variable | Mean | Std. Dev. | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|
| 0.2520 | 0.0601 | 0.9407 | -0.6559 | -0.4033 | 0.8162 | |
| 0.5735 | 0.0122 | 0.9291 | 1.0000 | 0.9403 | -0.3340 | |
| 0.4035 | 0.0066 | 0.9565 | 0.8961 | 0.7066 | -0.6701 | |
| 0.5730 | 0.0050 | 0.9629 | 0.7762 | 0.5548 | -0.6829 | |
| 0.0867 | 0.0050 | 0.9630 | -0.8323 | -0.6137 | 0.7472 | |
| 0.6600 | 0 | |||||
| 0.8871 | 0.0129 | 0.8127 | 0.5472 | 0.7297 | 0.4262 | |
| 0.5976 | 0.0716 | 0.8911 | 0.8267 | 0.6288 | -0.7599 | |
| 0.0512 | 0.0034 | 0.7888 | 0.7568 | 0.5924 | -0.7139 | |
| 0.0099 | 0.1829 | 0.9506 | 0.7083 | 0.4607 | -0.8525 | |
| | 0.0060 | 0.0738 | 0.9506 | 0.7084 | 0.4609 | -0.8522 |
Table 2b. Ramsey Dynamics With Zero Government-Provided Unemployment Benefits 40 Percent After-Tax Wages - Panel B: Full-Labor-Force Participation
| Variable | Mean | Std. Dev. | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|
| 0.2541 | 0.0086 | -0.6462 | 0.0713 | 0.2069 | -0.0611 | |
| 0.5735 | 0.0083 | 0.8730 | 1.0000 | 0.8802 | 0.3615 | |
| 0.4038 | 0.0046 | 0.8541 | 0.4923 | 0.8020 | -0.5670 | |
| 0.5731 | 0.0038 | 0.9407 | 0.1906 | -0.2192 | 0.8507 | |
| 0.0869 | 0.0027 | 0.1992 | -0.3445 | -0.5610 | 0.3649 | |
| 0.6600 | 0.0056 | 0.6609 | -0.0333 | -0.4295 | 0.7974 | |
| 0.8873 | 0.0166 | 0.4639 | 0.7856 | 0.8731 | -0.1212 | |
| 0.5953 | 0.0158 | 0.6522 | 0.7667 | 0.9061 | -0.0573 | |
| 0.0517 | 0.0010 | 0.3384 | 0.5158 | 0.3462 | 0.5285 | |
| 0 | 0 |
Table 3a. Ramsey
Dynamics With Zero Government-Provided Unemployment Benefits and
Zero Taxation of Dividend Income (
![]() ) - Panel A: Pseudo-Labor-Force Participation
) - Panel A: Pseudo-Labor-Force Participation
| Variable | Mean | Std. Dev. | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|
| 0.2176 | 0.0179 | 0.8324 | -0.2243 | -0.2263 | 0.9660 | |
| 0.5942 | 0.0092 | 0.9059 | 1.0000 | 0.9998 | -0.0496 | |
| 0.4080 | 0.0060 | 0.9133 | 0.7354 | 0.7358 | -0.6639 | |
| 0.5937 | 0.0006 | 0.9580 | 0.8623 | 0.8532 | -0.0363 | |
| 0.0659 | 0.0006 | 0.9580 | -0.9585 | -0.9527 | 0.0395 | |
| 0 | ||||||
| 0.8612 | 0.0150 | 0.7677 | 0.9647 | 0.9675 | -0.1142 | |
| 1.0007 | 0.0180 | 0.8824 | 0.9781 | 0.9756 | -0.0385 | |
| 0.0660 | 0.0006 | 0.7659 | 0.9454 | 0.9463 | -0.0349 | |
| -0.0245 | 0.0371 | 0.8580 | 0.2426 | 0.2442 | -0.9664 |
Table 3b. Ramsey
Dynamics With Zero Government-Provided Unemployment Benefits and
Zero Taxation of Dividend Income (
![]() ) - Panel B: Full Labor-Force Participation
) - Panel B: Full Labor-Force Participation
| Variable | Mean | Std. Dev. | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|
| 0.2194 | 0.0009 | 0.0392 | 0.6254 | 0.5896 | 0.1612 | |
| 0.5906 | 0.0089 | 0.9008 | 1.0000 | 0.9237 | 0.2848 | |
| 0.4049 | 0.0050 | 0.8766 | 0.5692 | 0.8141 | -0.5594 | |
| 0.5902 | 0.0032 | 0.9634 | 0.2444 | -0.0848 | 0.8942 | |
| 0.0655 | 0.0013 | 0.5554 | -0.3980 | -0.5849 | 0.5341 | |
| 0.6557 | 0.0040 | 0.8761 | 0.0750 | -0.2569 | 0.9679 | |
| 0.8611 | 0.0142 | 0.9096 | 0.9006 | 0.9957 | -0.1073 | |
| 1.0008 | 0.0189 | 0.8511 | 0.8724 | 0.9777 | -0.1541 | |
| 0.0656 | 0.0009 | 0.5621 | 0.6033 | 0.4653 | 0.5650 | |
| 0 | 0 |
Figure 1. Impulse Responses of Optimal Policy to One-Standard-Deviation Positive Shock to Govenment Spending (left panels) and TFP (right panels).
Figure 2. U.S. Labor Force Participation Rate 1951:Q1 - 2006:Q2.
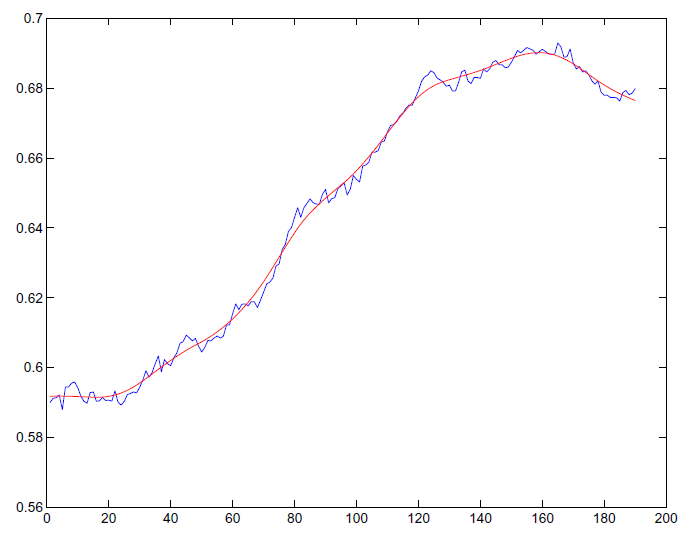
Blue line is actual participation rate, red line is HP filter trend (obtained with smoothing parameter 1600). The standard deviation of the cyclical component of the participation rate is 0.0032.
Figure 3. Impulse Responses of Optimal Policy to One-Standard-Deviation Positive Shock to Government Spending (left panels) and TFP (right panels) in Economy With Lump-sum Taxes
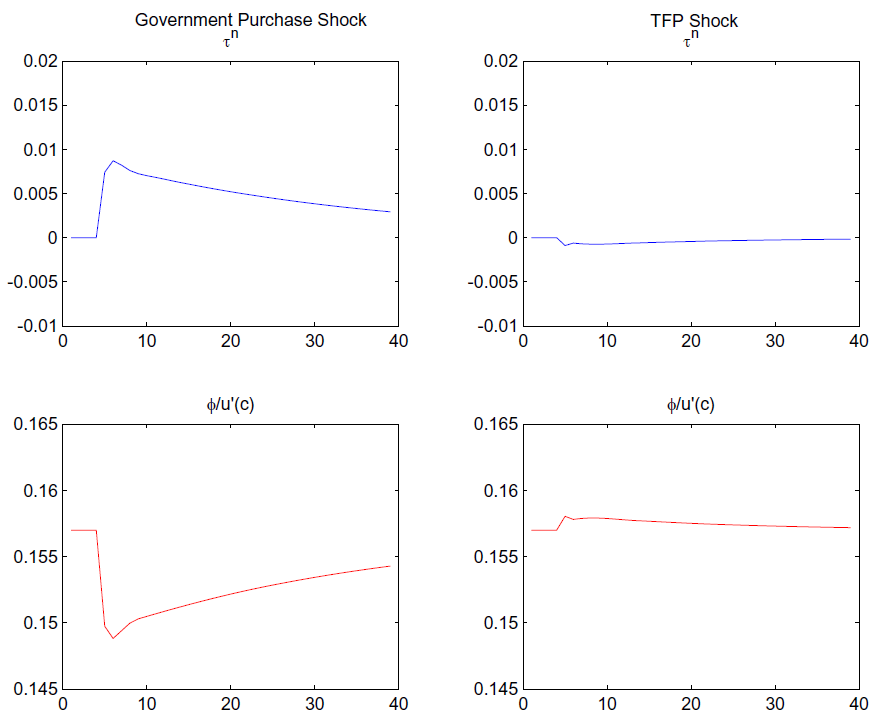
References
Aiyagari, S. Rao, Albert Marcet, Thomas J, Sargent, and Juha Seppala. 2002. "Optimal Taxation without State-Contingent Debt." Journal of Political Economy, Vol. 110, 1220-1254.
Andolfatto, David. 1996. "Business Cycles and Labor-Market Search." American Economic Review, Vol. 86, 112-132.
Arseneau, David M. and Sanjay K. Chugh. 2006. "Ramsey Meets Hosios: The Optimal Capital Tax and Labor Market Efficiency." International Finance Discussion Paper 870, Board of Governors of the Federal Reserve System.
Arseneau, David M. and Sanjay K. Chugh. 2008. "Optimal Fiscal and Monetary Policy with Costly Wage Bargaining." Journal of Monetary Economics. Vol. 55, 1401-1414.
Arseneau, David M., Sanjay K. Chugh, and Andre Kurmann. 2008. "Optimal Capital Taxation in an Economy with Capital Allocation Frictions." University of Maryland.
Aruoba, S. Boragan and Sanjay K. Chugh. 2008. "Money and Optimal Capital Taxation." University of Maryland.
Barro, Robert J. 1979. "On the Determination of the Public Debt." Journal of Political Economy, Vol. 87, 940-971.
Blanchard, Olivier and Peter Diamond. 1989. "The Beveridge Curve." Brookings Papers on Economic Activity, Vol. 1, 1-76.
Blanchard, Olivier and Jordi Gali. 2007. "Real Wage Rigidities and the New Keynesian Model." Journal of Money, Credit, and Banking, Vol. 39, 35-65.
Blanchard, Olivier and Jordi Gali. 2008. "A New Keynesian Model with Unemployment." MIT.
Boone, Jan and Lans Bovenberg. 2002. "Optimal Labor Taxation and Search." Journal of Public Economics, Vol. 85, 53-97.
Cahuc, Pierre, Francois Marque, and Etienne Wasmer. 2008. "Intrafirm Wage Bargaining in Matching Models: Macroeconomic Implications and Resolutions Methods with Multiple Labor Inputs." International Economic Review. Forthcoming.
Chari, V.V., Lawrence Christiano, and Patrick Kehoe. 1995. "Policy Analysis in Business Cycle Models." In Frontiers of Business Cycle Research. edited by Thomas F. Cooley. Princeton.
Chari V. V., and Patrick J. Kehoe. 1999. "Optimal Fiscal and Monetary Policy." In Handbook of Macroeconomics. edited by John B. Taylor and Michael Woodford, Vol. 1C. Elsevier.
Chari, V.V., Patrick J. Kehoe, and Ellen R. McGrattan. 2007. "Business Cycle Accounting." Econometrica, Vol. 75, 781-836.
Chugh, Sanjay K. 2006. "Optimal Fiscal and Monetary Policy with Sticky Wages and Sticky Prices." Review of Economic Dynamics, Vol. 9, 683-714.
Davis, Steven J, R. Jason Faberman, and John Haltiwanger. 2006. "The Flow Approach to Labor Markets: New Data Sources and Micro-Macro Links." Journal of Economic Perspectives, Vol. 20, 3-26.
Domeij, David. 2005. "Optimal Capital Taxation and Labor Market Search." Review of Economic Dynamics, Vol. 8, 623-650.
Elsby, Michael, Ryan Michaels, and Gary Solon. 2008. "The Ins and Outs of Cyclical Unemployment." American Economic Journals: Macroeconomics. Forthcoming.
Faia, Ester. 2008. "Optimal Monetary Policy Rules with Labor Market Frictions." Journal Economic Dynamics and Control, Vol. 32, 1357-1370.
Hagedorn, Marcus and Iourii Manovskii. 2008. "The Cyclical Behavior of Equilibrium Unemployment and Vacancies Revisited." American Economic Review, Vol. 98, 1692-1706.
Hosios, Arthur J. 1990. "On the Efficiency of Matching and Related Models of Search and Unemployment." Review of Economic Studies, Vol. 57, 279-298.
Jones, Larry E., Rodolfo E. Manuelli, and Peter E. Rossi. 1997. "On the Optimal Taxation of Capital Income." Journal of Economic Theory, Vol. 73, 93-117.
Krause, Michael U., David Lopez-Salido, and Thomas A. Lubik. 2007. "Inflation Dynamics with Search Frictions: A Structural Econometric Analysis." Federal Reserve Bank of Richmond.
Krause, Michael U. and Thomas A. Lubik. 2006. "Does Intra-Firm Bargaining Matter for Business Cycle Dynamics." Federal Reserve Bank of Richmond.
Krause, Michael U. and Thomas A. Lubik. 2007. "The (Ir)relevance of Real Wage Rigidity in the New Keynesian Model with Search Frictions." Journal of Monetary Economics, Vol. 54, 706-727.
Kydland, Finn E. and Edward C. Prescott. 1982. "Time to Build and Aggregate Fluctuations." Econometrica, Vol. 50, 1345-1370.
Ljungqvist, Lars and Thomas J. Sargent. 2004. Recursive Macroeconomic Theory. MIT Press.
Merz, Monika. 1995. "Search in the Labor Market and the Real Business Cycle." Journal of Monetary Economics, Vol. 36, 269-300.
Moen, Espen. 1997. "Competitive Search Equilibrium." Journal of Political Economy, Vol. 105, 385-411.
Ohanian, Lee E., Andrea Raffo, and Richard Rogerson. 2008. "Long-Term Changes in Labor Supply and Taxes: Evidence from OECD Countries, 1956-2004." Journal of Monetary Economics. Forthcoming.
Pissarides, Christopher A. 2000. Equilibrium Unemployment Theory. MIT Press.
Rogerson, Richard, Robert Shimer, and Randall Wright. 2005. "Search-Theoretic Models of the Labor Market: A Survey." Journal of Economic Literature, Vol. 43, 959-988.
Schmitt-Grohe, Stephanie and Martin Uribe. 2004. "Solving Dynamic General Equilibrium Models Using a Second-Order Approximation to the Policy Function." Journal of Economic Dynamics and Control, Vol. 28, 755-775.
Schmitt-Grohe, Stephanie and Martin Uribe. 2005. "Optimal Fiscal and Monetary Policy in a Medium-Scale Macroeconomic Model." NBER Macroeconomics Annual 2005.
Scott, Andrew. 2007. "Optimal Taxation and OECD Labor Taxes." Journal of Monetary Economics, Vol. 54, 924-944.
Shi, Shouyong and Quan Wen. 1999. "Labor Market Search and the Dynamic Effects of Taxes and Subsidies." Journal of Monetary Economics, Vol. 43, 457-495.
Shimer, Robert. 2005. The Cyclical Behavior of Equilibrium Unemployment and Vacancies. American Economic Review. 95. 25-49.
Shimer, Robert. 2008. "The Labor Wedge." American Economic Journals: Macroeconomics. Forthcoming.
Siu, Henry E. 2004. "Optimal Fiscal and Monetary Policy with Sticky Prices." Journal of Monetary Economics, Vol. 51, 576-607.
Smets, Frank and Rafael Wouters. 2007. "Shocks and Frictions in U.S. Business Cycles: A Bayesian DSGE Approach." American Economic Review, Vol. 97, 586-606.
Smith, Eric. 1999. "Search, Concave Production, and Optimal Firm Size." Review of Economic Dynamics, Vol. 2, 456-471.
Stiglitz, Joseph E. and P. Dasgupta. 1971. "Differential Taxation, Public Goods, and Economic Efficiency." Review of Economic Studies, Vol. 38, 151-174.
Veracierto, Marcelo. 2008. "On the Cyclical Behavior of Employment, Unemployment and Labor Force Participation." Journal of Monetary Economics, Vol. 55, 1143-1157.
Werning Ivan. 2007. "Optimal Fiscal Policy with Redistribution." Quarterly Journal of Economics, Vol. 122, 925-967.
Footnotes
1. We thank seminar participants at the University of Delaware, the University of Maryland, the Federal Reserve Board's International Finance Workshop, and the Federal Reserve Bank of Atlanta for comments, as well as conference participants at the 2008 European Central Bank International Research Forum on Monetary Policy. We also thank David Stockman, Andrea Raffo, John Haltiwanger, Eric Smith, Andrew Scott, and Harald Uhlig for helpful discussions. The views expressed here are solely those of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Earlier drafts of this paper circulated under the titles "Frictional Labor Markets, Bargaining Wedges, and Optimal Tax-Rate Volatility," and "Tax Smoothing May Not Be As Important As You Think." E-mail addresses: [email protected] and [email protected] Return to text
2. To our knowledge, the only work investigating aspects of optimal fiscal policy in labor-search dynamic general equilibrium models is Domeij (2005), Boone and Bovenberg (2002), and our own previous work, Arseneau and Chugh (2006, 2008). In none of these is the focus explicitly on tax smoothing. Return to text
3. Because an RBC model only considers two labor-market states, rather than all three, one can interchangeably refer to the relevant margin there as either a participation margin or, in the more commonly-used language, a labor-supply margin. Although the latter terminology has been the most commonly-used, the former characterization seems equally well-justified. For example, Kydland and Prescott (1982, p. 1350-1351) themselves refer to the time allocated to non-work as time allocated to non-market activities such as household production. Another example would be education. From the point of view of macroeconomic models, we think it seems natural to consider individuals engaged in non-market activities as outside the labor force. Return to text
4. Labor-market matching thus occurs within a period, which, given the quarterly calibration we will pursue, is empirically descriptive of U.S. labor-market flows -- see, for example, the evidence of Davis, Faberman, and Haltiwanger (2006). This so-called "instantaneous-hiring" view of labor-market flows has recently become widely used in this class of models, employed by, among others, Blanchard and Gali (2007, 2008) and Krause, Lopez-Salido, and Lubik (2007). Return to text
5. This assumption is without loss of generality in the standard Pissarides-type model because even if the firm believed it could opportunistically manipulate the wages it paid by under- or over-hiring, the fact that labor's marginal product is independent of total employment prevents such opportunistic manipulation of wage-bargaining sets. Thus, in the standard exogenous-productivity Pissarides model, holdup problems are in principle present, but there is no lever by which firms can strategically react to them. If firm output exhibited diminishing marginal product in its total employment level, then the firm would have an incentive to over-hire, and it would not be innocuous to assume that firms take wages as given when choosing how many vacancies to post. See, for example, Smith (1999), Cahuc, Marque, and Wasmer (2008), and Krause and Lubik (2006). Return to text
6. Technically, of course, it is the real
interest rate with which firms discount profits, and in equilibrium
the real interest rate between time zero and time ![]() is measured by
is measured by ![]() . Because there will be
no confusion using this equilibrium result "too early," we skip
this intermediate level of notation and structure. Return to text
. Because there will be
no confusion using this equilibrium result "too early," we skip
this intermediate level of notation and structure. Return to text
7. See, for example, Stiglitz and Dasgupta (1971), Jones, Manuelli, and Rossi (1997), Schmitt-Grohe and Uribe (2004), Siu (2004), and Arseneau, Chugh, and Kurmann (2008) for examples in various contexts of this type of taxation incentive. Return to text
8. This equivalence is a DSGE extension of the equivalence shown by Moen (1997) between competitive search outcomes and Nash bargaining under the well-known Hosios (1990) condition. As we discuss below, all of our analysis of the bargaining economy satisfies the Hosios (1990) condition. See also Rogerson, Shimer, and Wright (2005) for more on competitive search. Return to text
9. To see this, first note that
![]() Furthermore, because the first time a newly-formed match produces
output is in the period of match-creation, omitted from this
transformation is
Furthermore, because the first time a newly-formed match produces
output is in the period of match-creation, omitted from this
transformation is ![]() ;
; ![]() only results from a successful new match formed in
only results from a successful new match formed in
![]() . Return to
text
. Return to
text
10. In a general-equilibrium search-model of physical capital markets and in a search-theoretic model of monetary exchange, Arseneau, Chugh, and Kurmann (2008) and Aruoba and Chugh (2008), respectively, develop analogous search-based notions of intertemporal MRTs. Return to text
11. Unless the initial assets of the government were so large, either by assumption or via an effective initial lump-sum levy on existing assets, that it never needed to impose labor taxes. As usual in the Ramsey literature, we rule out these possibilities because they assume away the nature of the Ramsey problem. Return to text
12. Our numerical work is conducted
assuming two alternative values for ![]() :
:
![]() and a
and a ![]() such that
unemployment transfers represent 40 percent of after-tax wages,
which corresponds to Shimer's (2005) calibration. Return to text
such that
unemployment transfers represent 40 percent of after-tax wages,
which corresponds to Shimer's (2005) calibration. Return to text
13. See, for example, Ljungqvist and Sargent (2004, p. 494) for more discussion. Return to text
14. In particular, we would have
![]() , where
, where
![]() . This PVIC is
identical to that in Chari and Kehoe (1999) for an environment
without physical capital. Return to
text
. This PVIC is
identical to that in Chari and Kehoe (1999) for an environment
without physical capital. Return to
text
15. We of course have not modeled home production; it may be interesting to extend our model to allow this feature. Return to text
16. Setting a particular
![]() would restore
partial-equilibrium search efficiency, but this value of
would restore
partial-equilibrium search efficiency, but this value of
![]() is endogenous to the Ramsey policy.
There is little justification for endogenizing the Nash parameter
in this way, so we think this is an uninteresting very special
case. Return to text
is endogenous to the Ramsey policy.
There is little justification for endogenizing the Nash parameter
in this way, so we think this is an uninteresting very special
case. Return to text
17. However, the results using a first-order approximation were extremely similar to the ones reported here. Moreover, the deterministic steady state, which is the point around which we conduct the second-order approximation, turned out to not be very far from the stochastic steady state to which the equilibrium converged using the second-order accurate decision rules. Return to text
18. Indeed, tax-smoothing in simple Ramsey models is nothing more than an intertemporal application of the basic optimal-policy prescription to, under certain preference specifications, smooth tax rates across goods in a static setting. Return to text
19. See again Ljungqvist and Sargent (2004, p. 494) for more discussion on this. Return to text
20. As Chari and Kehoe (1999, p. 1679-1680) define it, an incomplete tax system is in place if, for at least one pair of goods in the economy, the government has no policy instrument that drives a wedge between its MRS and its MRT. If this is not the case, then the tax system is instead said to be complete. Return to text
21. See Rogerson, Shimer, and Wright (2005, p. 972-976) for more discussion. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text