
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1036, November 2011--- Screen Reader
Version*
Monetary regime switches and unstable objectives
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Monetary policy objectives and targets are not necessarily stable over time. The regime switching literature has typically analyzed and interpreted changes in policymakers' behavior through simple interest rate rules. This paper analyzes policy regime switches explicitly modeling policymakers' behavior and objectives. We show how current monetary policy is affected and should optimally respond to alternative regimes. We also show that changes in the parameters of simple rules do not necessarily correspond to changes in policymakers' preferences. In fact, capturing and interpreting regime changes in preferences through interest rate rules can lead to misleading results.
Keywords: Monetary policy, regime witches, unstable objectives.
JEL classification: E32, E42, E52
1 Introduction
The analysis of policy regime switches has been central to several economic problems. The debate on the existence and sources of the great moderation is a clear example.1 Regime switches have also been examined in the context of rational expectations determinacy (e.g. Davig and Leeper (2007), Farmer et al. (2009)) and DSGE estimation (e.g. Owyang and Ramey (2004), Davig and Doh (2008), Bianchi (2010)). Building on relatively standard New Keynesian models, this literature has typically modeled policymakers' behavior with time varying or Markov-switching simple instrument rules.
The extensive use of simple rules in both theoretical and empirical studies is justified by several reasons: their simplicity and potential for practical use, their fairly good performance when compared to the optimal policy, and their robustness across several model specifications.2 However, simple rules are reduced form representations of policymakers' behavior, and cannot be used to identify the structural sources of behavioral changes. Reduced form representations limit the differentiation between factors the central bank can and can not control. This limitation is relevant at the time of distinguishing between monetary regimes, and assessing the central bank's performance (e.g. "good policy" vs. "good luck").
In a rational expectations equilibrium - given the forward looking nature of economic agents and decisions - the possibility of future regime switches affects the economy immediately. Therefore, this possibility should also be internalized by the central bank, which can react with an appropriately chosen policy.3 In other words, following the Lucas (1976) critique, policymakers' behavior is not invariant to the presence of alternative regimes. For these reasons, we study the effects of regime switches when the central bank behavior is determined through an endogenous decision process.
A natural source of policy regime switches is a change in policymakers' preferences, in terms of the relative weight assigned to different objectives and the desired targets. Objectives and targets can change over time due to a variety of reasons. Policy objectives may change with appointments of governors and central bank staff, who may have different views from their predecessors. Also, even among academic economists there is scope for different opinions and evolving theories on the benefits of output vs. inflation stabilization, and what is, in practice, the exact output level that should be targeted.4
We first consider two regimes differing in the relative weight assigned to inflation stabilization. The optimal policy response shows that policymakers try to counteract the effects generated by alternative regimes. The possibility of a future dovish regime induces the hawkish regime to increase the inflation response to cost-push shocks, through an accommodation effect. At the same time, the hawkish regime tries to anchor inflation expectations by promising to be even more hawkish in the future. The immediate effect is a sharper output contraction, which is the opposite of what the dovish regime is aiming for. We also examine the optimal policy response when regime changes are delayed or regard other targets.
Characterizing policy through an endogenous process enables us to examine whether the switches in simple interest rate rules identified in the data are likely to stem from changes in policymaker's preferences. Imposing a structure on the policymakers' decision process amounts to imposing restrictions on the possible switches in the resulting policies.
We find that changes in simple rules parameters cannot be interpreted solely as changes in policymakers' preferences. Intuitively, changes in policymaker's preferences imply a movement along the policy frontier, where reducing the volatility of one variable implies increasing the volatility of another variable. Instead, switches in simple interest rate rules often imply movements of the frontier itself. In addition, using simple rules to capture changes in policymakers' objectives can lead to misleading results: the presence of regime switches can be wrongly rejected and indeterminacy can be wrongly detected. Altogether, our findings restrict the possible interpretations of what are the deep sources of the existing estimates of changes in policymakers' behavior and the associated normative implications.
Our paper is partially related to the literature on political economy and monetary policy (see e.g. Alesina et al. (1997)), but our goal is not to provide a partisan analysis of monetary policy. In fact, we shed light on the difficulty of the partisan empirical literature to match timely and systematically certain parties with effective changes in monetary policy - in our model a future dovish regime implies an increase in inflation even if the current regime remains hawkish.5 Our model is also related to the literature on robust control (e.g. Hansen and Sargent (2007)) and optimal monetary policy with noisy indicators (e.g. Aoki (2003)). However, our analysis focuses on the effects of evolving objectives, and assumes the structural relationships describing the economy and the exogenous shocks to be known and common knowledge.
The paper is organized as follows. Section 2 introduces the model. Section 3 presents the results on optimal policy. Section 4 analyzes the relationship with simple rules, and section 5 concludes. The appendix contains additional derivations.
2 The Model
We base our analysis on a simple monetary model. Inflation dynamics are described by a New Keynesian Phillips curve (NKPC). As it is well known, the NKPC is a reduced form approximation of the relationship between inflation and output in an economy with monopolistic competition and staggered price setting
| (1) |
where ![]() denotes price inflation and
denotes price inflation and
![]() measures the output-gap, i.e. the
difference between current output and the output level that would
prevail under flexible prices.6 The term
measures the output-gap, i.e. the
difference between current output and the output level that would
prevail under flexible prices.6 The term ![]() constitutes an exogenous cost-push shock, introducing a trade-off
between inflation and output stabilization and following the
process
constitutes an exogenous cost-push shock, introducing a trade-off
between inflation and output stabilization and following the
process
![]() , with
, with
![]() being an i.i.d.
disturbance.
being an i.i.d.
disturbance.
As it is standard in the optimal monetary policy literature, we assume that the central bank controls inflation and the output-gap directly. The monetary policy authority minimizes a weighted average of deviations of inflation and output-gap from their respective targets
![$\displaystyle U_t=\frac{1}{2}\left[ \pi_{t}^{2}+w(y_{t}-\widetilde{y})^{2}\right] .$](img7.gif)
|
(2) |
The parameter ![]() measures the relative importance of
output stabilization. The inflation target is normalized to zero,
while
measures the relative importance of
output stabilization. The inflation target is normalized to zero,
while
![]() represents the (exogenously
given) output-gap target. The target
represents the (exogenously
given) output-gap target. The target
![]() can be interpreted as the
difference between the efficient level of output and the output
that would prevail under flexible prices.
can be interpreted as the
difference between the efficient level of output and the output
that would prevail under flexible prices.
We model changes in the objective function in a straightforward
way that allows for analytical solutions. In any period, current
objectives can persist or change with probability ![]() and
and ![]() , respectively. We consider the objectives
of the central bank to be either dovish (
, respectively. We consider the objectives
of the central bank to be either dovish (![]() )
or hawkish (
)
or hawkish (![]() ). The term dovish regime
refers to a case where the output-gap target or the relative weight
to output stabilization are higher than in a hawkish regime, that
is
). The term dovish regime
refers to a case where the output-gap target or the relative weight
to output stabilization are higher than in a hawkish regime, that
is
![]() or
or
![]() .7
.7
We assume that the central bank can only make credible commitments about future policy while objectives remain unchanged. If objectives do change, a new policy will be set, and previous commitments will be disregarded. This assumption can be justified on the grounds that if objectives change, the central bank will adopt the best possible policy to fulfill its new objectives, and thus will disregard the plans made when priorities were different. Details on this type of policy formulation are available in Roberds (1987), Schaumburg and Tambalotti (2007), and Debortoli and Nunes (2010a).
In this context, it can be shown that under regime ![]() policy plans solve the following problem:
policy plans solve the following problem:
![$\displaystyle =\underset{\{\pi_{t},y_{t}\}_{t=0}^{\infty}}{\max}E_0\sum _{t=0}^{\infty}\left( \beta q\right) ^{t}\{-\frac{1}{2}\left[ \pi_{t} ^{2}+w^{i}\left( y_{t}-\tilde{y}^{i}\right) ^{2}\right] +\beta (1-q)V^{ij}(u_t)\}$](img19.gif) |
(3) | |
The objective function is given by an infinite sum discounted at
the rate ![]() , summarizing the events in which
objectives remain unchanged. Each term in the summation is composed
by two parts. The first part, in square brackets, is the period
loss function. The second part is the value function
, summarizing the events in which
objectives remain unchanged. Each term in the summation is composed
by two parts. The first part, in square brackets, is the period
loss function. The second part is the value function ![]() , summarizing the utility the central bank obtains if
next period objectives change.
, summarizing the utility the central bank obtains if
next period objectives change.
The central bank faces a sequence of constraints represented by
the NKPC, where in any period ![]() inflation
expectations are an average between two terms. The first term, with
weight
inflation
expectations are an average between two terms. The first term, with
weight ![]() , is the inflation that would prevail under
the current regime
, is the inflation that would prevail under
the current regime
![]() and upon which there is
commitment. The second term, with weight
and upon which there is
commitment. The second term, with weight ![]() , is
the inflation that would be implemented under the alternative
regime
, is
the inflation that would be implemented under the alternative
regime
![]() , which is taken as given
by the current central bank. As stated in the equilibrium
definition, such level of inflation is determined by solving a
symmetric problem to the one described above.
, which is taken as given
by the current central bank. As stated in the equilibrium
definition, such level of inflation is determined by solving a
symmetric problem to the one described above.
Definition 1 A
Markov Perfect Equilibrium with objective changes must satisfy the
following condition. For any ![]() and
and ![]() , given the sequence
, given the sequence
![]()
- The sequence
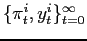 is
optimal.
is
optimal. - The value function
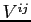 satisfies equation
satisfies equation
![$\displaystyle V^{ij}(u_0)\equiv E_{0}\sum_{t=0}^{\infty}\left( \beta q\right) ^{t}\left[ -\frac{1}{2}\left( (\pi_{t}^{j})^{2}+w^{i}(y_{t}^{j})^{2}\right) +\beta(1-q)V^{ii}(u_t)\right] $](img36.gif)
- The sequence
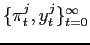 is
optimal, solving the symmetric problem of regime
is
optimal, solving the symmetric problem of regime 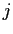 .
.
The first requirement imposes the optimality of the policy
functions given
![]() and
and
![]() . The second part defines the value
function
. The second part defines the value
function ![]() as the continuation value in case the
regime changes. The value function
as the continuation value in case the
regime changes. The value function ![]() takes
into account that regime
takes
into account that regime ![]() may become relevant again in
the future.8 The first two conditions in the
definition leave the sequence
may become relevant again in
the future.8 The first two conditions in the
definition leave the sequence
![]() and
the institutional setting of regime
and
the institutional setting of regime ![]() unspecified.
The third part of the definition states that regime
unspecified.
The third part of the definition states that regime ![]() solves a symmetric problem. We refer to Markov Perfect Equilibrium
because in a reoptimization period - the initial period in which
the regime changes - policy only depends on natural state
variables.9
solves a symmetric problem. We refer to Markov Perfect Equilibrium
because in a reoptimization period - the initial period in which
the regime changes - policy only depends on natural state
variables.9
3 The Effects of Unstable Objectives
3.1 Changes in the Relative Weight of Output
The baseline case for our analysis is one where regimes only
differ in the relative weight assigned to output stabilization, and
the output-gap target is set to
![]() .
Arranging the first order conditions of problem (3) yields
.
Arranging the first order conditions of problem (3) yields
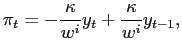 |
(4) |
where ![]() is equalized to zero. Equation
(4) can be
interpreted as a targeting rule, as e.g. in Giannoni and Woodford (2010). Since it does not depend on the
parameters of alternative regimes, it is robust to the presence
unstable objectives.10
is equalized to zero. Equation
(4) can be
interpreted as a targeting rule, as e.g. in Giannoni and Woodford (2010). Since it does not depend on the
parameters of alternative regimes, it is robust to the presence
unstable objectives.10
Nevertheless, objective instability changes the dynamics of the economy. Combining (1) and (4), the evolution of inflation and output is determined by:
![$\displaystyle \left[\begin{array}[c]{c} \pi_{t}\\ y_{t}\end{array}\right] = \left[\begin{array}[c]{cc} \frac{w^{i}}{\kappa}\left( 1-\psi_{y}^{i}\right) & \psi_{u}^{i}\\ \psi_{y}^{i} & -\frac{\kappa}{w^{i}}\psi_{u}^{i}\end{array}\right] \par \left[\begin{array}[c]{c}y_{t-1}\\ u_{t}\end{array}\right],$](img54.gif) |
(5) |
with
![]() ,
,
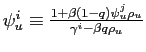 , and the term
, and the term
![$\displaystyle \gamma^{i}\equiv\frac{1}{2}\left[1+ \frac{\kappa^2}{w^{i}}+\beta q + \sqrt{(1+ \frac{\kappa^2}{w^{i}}+\beta q)^2 - 4\beta q}\right]>1$](img57.gif) |
(6) |
is increasing in ![]() and decreasing in
and decreasing in ![]() . The persistence of output
. The persistence of output ![]() is not
affected by the parameters of the alternative regime. Instead, the
inflation response to cost-push shocks
is not
affected by the parameters of the alternative regime. Instead, the
inflation response to cost-push shocks
![]() depends on
depends on
![]() . The more likely is the regime
switch (the lower is
. The more likely is the regime
switch (the lower is ![]() ) and the more persistent are
the cost-push shocks, the stronger are the spillovers between
alternative regimes.11 The difference in the initial
response then propagates over time through the state variable
) and the more persistent are
the cost-push shocks, the stronger are the spillovers between
alternative regimes.11 The difference in the initial
response then propagates over time through the state variable
![]() .
.
As a benchmark for our analysis, we first analyze the standard
case with full-commitment and stable objectives (of type
![]() ).12 In that case, and denoting the
corresponding variables with an upper bar, the dynamics are
described by equation (5),
where the relevant parameters are given by
).12 In that case, and denoting the
corresponding variables with an upper bar, the dynamics are
described by equation (5),
where the relevant parameters are given by
![]() ,
,
![]() , and
, and
![]() is the value taken by
equation (6)
when
is the value taken by
equation (6)
when ![]() .
.
With unstable objectives (![]() and
and
![]() ), and assuming regime
), and assuming regime
![]() solves a symmetric problem, it can be
easily shown that
solves a symmetric problem, it can be
easily shown that
![]() is given by
is given by
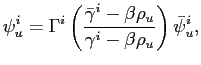
|
(7) |
where
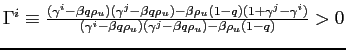 . In equation (7), the term in
parenthesis is always bigger than one, since
. In equation (7), the term in
parenthesis is always bigger than one, since
![]() .13
Instead, it holds that
.13
Instead, it holds that
![]() if and only if
if and only if
![]() (or equivalently
(or equivalently
![]() ).
).
For a hawkish regime with
![]() , being
, being
![]() , equation (7) univocally
implies
, equation (7) univocally
implies
![]() . This
means that instability of objectives forces the hawkish regime into
a stronger inflation hike and a sharper output contraction in
response to a positive cost-push shock, relative to the stable
objectives counterpart. In other words, the hawkish regime faces a
worse contemporaneous trade-off caused by the possibility of a
future change to a dovish regime.
. This
means that instability of objectives forces the hawkish regime into
a stronger inflation hike and a sharper output contraction in
response to a positive cost-push shock, relative to the stable
objectives counterpart. In other words, the hawkish regime faces a
worse contemporaneous trade-off caused by the possibility of a
future change to a dovish regime.
The results for a dovish regime are less clear cut, since in
that case
![]() . The relation between
. The relation between
![]() and
and
![]() depends on the exact
parameterization. If the hawkish regime assigns a sufficiently low
weight to output (i.e.
depends on the exact
parameterization. If the hawkish regime assigns a sufficiently low
weight to output (i.e. ![]() is close to 0),
objective instability may improve the trade-off faced by the dovish
regime. This feature differentiates the effects of unstable
objectives from those of limited commitment and stable objectives,
as in Schaumburg and Tambalotti (2007). Indeed, limited
commitment per se always worsens the trade-off in the
cost-push shock response.
is close to 0),
objective instability may improve the trade-off faced by the dovish
regime. This feature differentiates the effects of unstable
objectives from those of limited commitment and stable objectives,
as in Schaumburg and Tambalotti (2007). Indeed, limited
commitment per se always worsens the trade-off in the
cost-push shock response.
Dynamic Response
After the initial inflation surge in response to a positive cost-push shock, inflation is reduced in subsequent periods. The possibility of regime switches impacts expectations and consequently the optimal speed at which inflation is reduced. As shown in appendix A-1.1 the (absolute) inflation change, in comparison with the stable objective case is given by
![$\displaystyle \left\vert E_0 \pi_{1} - \pi_{0}\right\vert - \left\vert E_0\bar{\pi}_{1}- \bar{\pi}_{0}\right\vert = \left[ (2-\frac{1}{\gamma}-\rho_u)\Gamma\frac{\bar{\gamma}-\beta\rho_{u}}{\gamma-\beta\rho_{u}} - (2-\frac{1}{\bar{\gamma}}-\rho_u)\right]\bar{\psi}^{i}_{u}u_0,\\ $](img90.gif)
|
(8) |
where, for convenience, the ![]() superscripts have
been suppressed since all coefficients refer to the same regime.
For a hawkish regime, being
superscripts have
been suppressed since all coefficients refer to the same regime.
For a hawkish regime, being ![]() , a
sufficient condition for (8) to be
positive is
, a
sufficient condition for (8) to be
positive is
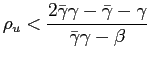
|
(9) |
Under standard calibrations of the relative weight of output
stabilization (![]() ) the latter condition is satisfied
even in the limiting case with
) the latter condition is satisfied
even in the limiting case with ![]() .14
This means that the hawkish regime reduces inflation more rapidly
under unstable objectives.15 The intuition for this result is the
following. The possibility that the dovish regime takes place next
period increases inflation expectations. Besides the optimal impact
response described in equation (7), the hawkish
regime promises to reduce inflation faster in the next period. This
promise anchors inflation expectations, dampening the negative
impact on current variables. The promise to lower inflation at a
faster speed is based on a time-inconsistent promise, and
constitutes a clear example of how an optimizing central bank
equates the distortions across time and states of nature.
.14
This means that the hawkish regime reduces inflation more rapidly
under unstable objectives.15 The intuition for this result is the
following. The possibility that the dovish regime takes place next
period increases inflation expectations. Besides the optimal impact
response described in equation (7), the hawkish
regime promises to reduce inflation faster in the next period. This
promise anchors inflation expectations, dampening the negative
impact on current variables. The promise to lower inflation at a
faster speed is based on a time-inconsistent promise, and
constitutes a clear example of how an optimizing central bank
equates the distortions across time and states of nature.
To provide a quantitative illustration of our results, we adopt
a quarterly calibration that is summarized in Table (1). The structural
parameters ![]() ,
, ![]() and
and
![]() follow the calibration of Gali (2008). We set
follow the calibration of Gali (2008). We set ![]() according to the
utility-based welfare criterion implied by those parameters. The
value assigned to
according to the
utility-based welfare criterion implied by those parameters. The
value assigned to ![]() implies that the
dovish regime assigns to output stabilization half of the weight
assigned to price stabilization. The persistence of policy
objectives is measured by the parameter
implies that the
dovish regime assigns to output stabilization half of the weight
assigned to price stabilization. The persistence of policy
objectives is measured by the parameter ![]() , which is
in the range of recent estimates of Markov-switching New Keynesian
models.16 The autocorrelation of the cost-push
shock is set to
, which is
in the range of recent estimates of Markov-switching New Keynesian
models.16 The autocorrelation of the cost-push
shock is set to ![]() . There is no widespread
consensus on the value of
. There is no widespread
consensus on the value of ![]() . Values found
in the literature range from the i.i.d. case considered in Rabanal and Rubio-Ramirez (2005)
. Values found
in the literature range from the i.i.d. case considered in Rabanal and Rubio-Ramirez (2005) ![]() found in Ireland (2004). As discussed earlier, the choice of
a low degree of persistence reduces the spillovers between
policymakers. Finally, the standard deviation of the cost-push
shock is set to .2% in line with Adam and Billi (2006), Davig and Doh (2008), and Bianchi (2010) in
similar small-scale New Keynesian models.17
found in Ireland (2004). As discussed earlier, the choice of
a low degree of persistence reduces the spillovers between
policymakers. Finally, the standard deviation of the cost-push
shock is set to .2% in line with Adam and Billi (2006), Davig and Doh (2008), and Bianchi (2010) in
similar small-scale New Keynesian models.17
Second moments and welfare are reported in Table (2). The upper and lower panels are conditional on the hawkish and dovish regime, respectively.
Table 1: Calibration
| Parameter | Value | Description |
|---|---|---|
| Structural: | 0.99 | Discount Factor |
| Structural: | 0.1275 | Slope of Phillips Curve |
| Structural: | 1.0 | Real rate elasticity of output |
| Policymakers: | 0.0213 | Weight on Output-gap Hawkish Regime |
| Policymakers: | 0.5 | Weight on Output-gap Dovish Regime |
| Policymakers: | .9 | Probability of a objectives remaining constant |
| Shocks: | 0.2 | Autocorrelation of cost-push shocks |
| Shocks: | 0.9 | Autocorrelation of real rate shocks |
| Shocks: | 0.2 | Std. dev. cost-push innovation |
| Shocks: | 0.2 | Std. dev. real rate innovation |
Moving from full-commitment to unstable objectives leads to an increase in the volatility of output and inflation both for the hawkish and the dovish regime.18 However, when objectives are unstable a switch from a dovish to a hawkish regime implies lower volatility of inflation but higher volatility of output.
3.2 Output-Gap Target Instability
In this section we consider two regimes that have different output-gap targets. This difference in targets can obviously be the consequence of disparate views on what kind of distortions and events should be accounted for by the central bank,
Table 2: Second Moments and Welfare
| Full Com. | Loose Com. | Unstable Objectives | |
|---|---|---|---|
| Hawkish: Output | 3.395 | 3.540 | 3.579 |
| Hawkish: Inflation | 0.519 | 0.535 | 0.540 |
| Hawkish: Av. Period Loss | 0.536 | 0.575 | 0.588 |
| Dovish: Output | 0.558 | 0.656 | 0.649 |
| Dovish: Inflation | 1.028 | 1.072 | 1.061 |
| Dovish: Av. Period Loss | 1.265 | 1.424 | 1.393 |
Note: The table reports the standard deviations of our variables (in relative terms of the std. dev. of the cost-push shock), as well as the implied welfare loss, conditional on being under the hawkish regime (upper panel) or the dovish regime (lower panel).
as has been quite evident in the recent crisis.19 In addition, another likely source of disagreement on the output-gap target lies in the measurement of the output level prevailing if prices would be flexible. Even if a consensus would exist that the output-gap target should be zero, as long as the flexible price output level is not perfectly observed and is subject to mismeasurement, substantial disagreement on the operative output-gap target can emerge. This issue is not a mere theoretical curiosity and is actually quite likely to occur in practice. Orphanides (2001, 2002) and several related papers showed that structural breaks in productivity can be hard to detect and do lead to dramatic different concepts regarding the output-gap target and the conduct of monetary policy. Chari et al. (2009) also discuss that the interpretation of shocks is not always straightforward which can lead to different views on the flexible price output level.20
We consider the dovish and hawkish regime to be characterized as
![]() and
and
![]() . For brevity of exposition we do
not consider the cost-push shock since such analysis was already
carried previously. The dynamics are characterized by the
system
. For brevity of exposition we do
not consider the cost-push shock since such analysis was already
carried previously. The dynamics are characterized by the
system
![$\displaystyle \left[\begin{array}[c]{c} \pi^{i}_{t}\\ y^{i}_{t}-\widetilde{y}^{i} \end{array}\right] = \left[\begin{array}[c]{cc} \frac{w}{\kappa}\left( 1-\psi_{y}\right) & \frac{1}{\gamma-\beta}\\ \psi_{y} & -\frac{\kappa}{w}\frac{1}{\gamma-\beta}\end{array}\right] \par \left[\begin{array}[c]{c}y^{i}_{t-1}-\widetilde{y}^{i}\\ \left((1-\Phi)\kappa\widetilde{y}^{i}+\Phi\kappa\frac{\widetilde{y}^{j} +\Phi\widetilde{y}^{i}}{(1+\Phi)}\right)\end{array}\right],$](img120.gif)
|
(10) |
where
![]() and
and
![]() .21 The dynamics
coincides with those described in section 3.1, for the
particular case of cost-push shocks with a unitary root
(
.21 The dynamics
coincides with those described in section 3.1, for the
particular case of cost-push shocks with a unitary root
(![]() ). The coefficient on the lagged
output-gap to target difference
). The coefficient on the lagged
output-gap to target difference
![]() remains unchanged.
In addition, the coefficient
remains unchanged.
In addition, the coefficient
![]() is equivalent to
is equivalent to
![]() , as given by equation (7), after imposing
, as given by equation (7), after imposing
![]() holding in the present
case, and setting
holding in the present
case, and setting ![]() . That coefficient
now multiplies a constant term which is increasing on the
output-gap targets of both regimes. Under the plausible assumption
of positive output-gap targets, that term is always positive.
. That coefficient
now multiplies a constant term which is increasing on the
output-gap targets of both regimes. Under the plausible assumption
of positive output-gap targets, that term is always positive.
Hence, as illustrated in Figure (1), the possibility of a dovish regime induces the hawk to increase inflation and reduce output on impact, and then reduce inflation faster in case objectives remain hawkish. For the dovish regime the effects of unstable objectives counteract the effects of limited commitment. For instance, limited commitment makes the output-gap to be lower. However, when objectives are unstable (and commitment is also limited) the presence of the hawk improves the response for the dovish regime.
These considerations show that our results of section 3.1 do not depend on the presence of cost-push shocks, since changes in output-gap targets affect the equations in a similar way.
Figure 1: Output-Gap Target Instability
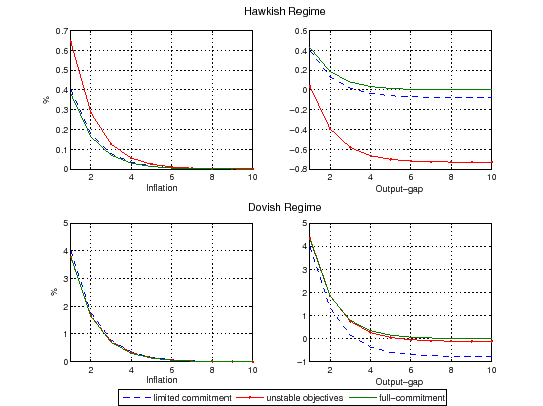
Note: The upper and lower panel plot the impulse response functions for the hawkish and dovish regime, respectively. The values reported are percentages and inflation is annualized.
In this regard, this model can be seen as endogenously incorporating shocks that create a wedge between inflation and the output-gap.22 However, there are three important differences between the effects we identify and the traditional cost-push shocks. First, the reduction in output and increase in inflation occurs in response to the anticipation of future dovish objectives, and not in response to a current change in objectives or a current shock.23 Second, the anticipation of objective changes creates permanent effects instead of transitory ones. Third, the magnitude of the shock is endogenous and can be influenced by the monetary authority. Indeed, as long as the Phillips curve is not purely forward looking, the current central bank can set inflation and strategically influence future decisions and distortions.
3.3 Delayed Regime Changes
It may not be entirely plausible to assume that a regime change
can occur in every period. In practice, objectives can only be
changed with some delay due to institutional aspects and policy
implementation lags. We investigate whether incorporating these
features alters or introduces additional interactions among policy
regimes. We assume that objectives remain unchanged with certainty
for ![]() periods. Only after
periods. Only after ![]() periods, current objectives can eventually change. In this setting,
the problem of the central bank can be written as:
periods, current objectives can eventually change. In this setting,
the problem of the central bank can be written as:
![$\displaystyle V^{i}=\max_{\{\pi_{t},y_{t}\}_{t=0}^{\infty}}E_{0}\sum_{m=0}^{\infty}\left( \beta^{T}q\right) ^{m}\left[ -\frac{1}{2}\sum_{t=0}^{T-1}\beta^{t}\left[ \pi_{m+t}^{2}+w^{i}(y_{m+t}-{\widetilde{y}}^{i})^{2}\right] +\beta ^{T}(1-q)V^{ij}\right]$](img133.gif) |
(11) |
| (12) | ||
| (13) | ||
| |
where ![]() indexes the sequence of regimes each
lasting for
indexes the sequence of regimes each
lasting for ![]() periods. In order to solve problem
(11), we first write
its recursive formulation. To do so we apply the technique of Marcet and Marimon (1998) and write the problem as a
saddle point functional equation that generalizes the usual Bellman
equation. The proof of that result requires considering each tenure
as one fictional big period, and then applying the results of Debortoli and Nunes (2010a) to address the probabilistic
switch at the end of each tenure. Proposition (1) in the appendix
proves this result in detail. As stated in Proposition (2) in the
appendix, the solution can be characterized as tenure invariant
functions of the Lagrange multipliers associated with constraints
(12) and
(13).24
periods. In order to solve problem
(11), we first write
its recursive formulation. To do so we apply the technique of Marcet and Marimon (1998) and write the problem as a
saddle point functional equation that generalizes the usual Bellman
equation. The proof of that result requires considering each tenure
as one fictional big period, and then applying the results of Debortoli and Nunes (2010a) to address the probabilistic
switch at the end of each tenure. Proposition (1) in the appendix
proves this result in detail. As stated in Proposition (2) in the
appendix, the solution can be characterized as tenure invariant
functions of the Lagrange multipliers associated with constraints
(12) and
(13).24
Figure (2) plots the
optimal policy functions with unstable objectives (continuous
line). The upper and lower panel correspond to the hawkish and
dovish regime with output-gap targets of 0.01 and 0.1,
respectively.25 Each regime implements the policy
functions shown in each period until the regime is changed. We
calibrate the model such that regimes can only change with
probability ![]() every
every ![]() periods
(signaled with continuous vertical lines). For comparison, Figure
(2) also plots the
policy functions that occur in a limited commitment setting without
regime changes (dashed line).
periods
(signaled with continuous vertical lines). For comparison, Figure
(2) also plots the
policy functions that occur in a limited commitment setting without
regime changes (dashed line).
The hawkish regime implements a low inflation level immediately after knowing that the dovish regime has dissipated and objectives will not change in the following four periods (periods 5, 9, 13 in the graph).26 Differently from the model where regime changes can occur in every period, the strengths of the accommodation and anchoring effects are not constant over time. These two effects explain why the hawk starts with low inflation and then increases it.
This model puts in evidence the interactions between the two regimes and the potential difficulties in identifying them trough simple processes - it is difficult to distinguish whether the accommodation effect is making a hawk to increase inflation, or if in fact the regime already became dovish. Our findings are qualitatively robust to two alternative specifications. First, we have solved the model with a hybrid Phillips curve. Second, we assumed that objectives may change but the central bank never reoptimizes and, therefore, makes state contingent promises regarding the objectives.27
Figure 2: Delayed Regime Changes
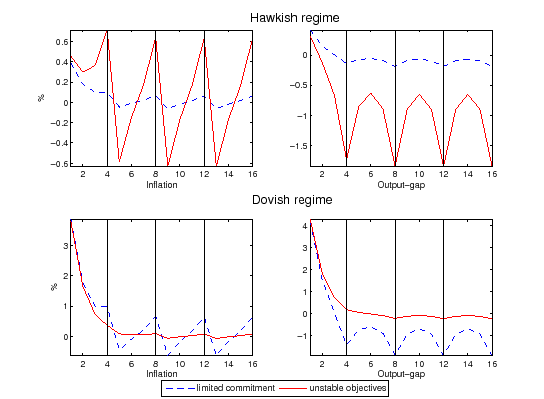
Note: This figure refers to the model where objectives can not change immediately. The upper two panels plot the policy functions (inflation and output-gap) of a hawkish regime, and the lower two panels refer to a dovish regime. Changes in objectives can only occur every four periods - periods marked with continuous vertical lines. The case with objective changes and limited commitment is plotted with a continuous line. The case of no objective changes and limited commitment is plotted with a dashed line. In all panels the horizontal axis refers to the number of periods elapsed after the last regime change or reoptimization. Values are in percentages and inflation is annualized. The policy functions are truncated at period 16 in the figure but not in the solution method.
4 Unstable Objectives and Switches in Interest-Rate Rules
The most common approach followed in the monetary policy literature is to model regime switches as exogenous changes in the parameters of an interest rate rule. Some empirical studies support the view that interest rate rule parameters have changed over time.28 Such changes are typically interpreted as a signal of switches between "good" and "bad" policies.
The goal of this section is to understand if there is a relationship between changes in the parameters of an interest rate rule (the common approach in the literature) and the changes in policy preferences modeled in the previous sections. We proceed in two different directions. First, we compare some qualitative implications of the two approaches. Second, we perform a Monte Carlo experiment, where we check if changes in policy objectives would be detected by estimating an interest rate rule with Markov-switching coefficients.
4.1 Qualitative Effects on Volatilities
Consider the interest rate rule
| (14) |
where the parameters
![]() and
and ![]() measure the response of the interest rate to changes in inflation
and output-gap, respectively.29 In order to show how this policy
rule affects the behavior of inflation and output, we need to
supplement the NKPC (1) with an IS
equation describing the demand-side of the economy
measure the response of the interest rate to changes in inflation
and output-gap, respectively.29 In order to show how this policy
rule affects the behavior of inflation and output, we need to
supplement the NKPC (1) with an IS
equation describing the demand-side of the economy
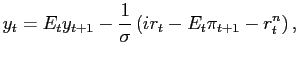
|
(15) |
where the term ![]() represents a real interest
rate shock, which may result either from demand or supply shocks,
and is assumed to follow an AR(1) process
represents a real interest
rate shock, which may result either from demand or supply shocks,
and is assumed to follow an AR(1) process
![]() . The
calibration of the real rate shock follows standard values
described in Table (1). For simplicity
and without loss of generality, we assume the innovation to the
real rate shock,
. The
calibration of the real rate shock follows standard values
described in Table (1). For simplicity
and without loss of generality, we assume the innovation to the
real rate shock, ![]() , and the innovation to the
cost-push shock,
, and the innovation to the
cost-push shock, ![]() , to be uncorrelated.30
, to be uncorrelated.30
The solution of the three-equation system (1), (14) and (15) is given by
![$\displaystyle \left[\begin{array}[c]{c} \pi_{t}\\ y_{t} \end{array}\right] = \left[\begin{array}[c]{cc} (\sigma(1-\rho_u)+\phi_y)\Lambda_u & \kappa \Lambda_r\\ -(\phi_\pi-\rho_u) \Lambda_u & (1-\beta\rho_r) \Lambda_r\end{array}\right] \par \left[\begin{array}[c]{c}u_t\\ r^n_t\end{array}\right] \equiv H \left[\begin{array}[c]{c}u_t\\ r^n_t\end{array}\right],$](img161.gif)
|
16) |
where
![]() and
and
![]() .
.
As opposed to optimal policy, here inflation and output also
respond to the real rate shock ![]() . The intensity
of the response to
. The intensity
of the response to ![]() depends on the
magnitude of
depends on the
magnitude of ![]() and
and ![]() through
the parameter
through
the parameter ![]() . In particular, since
. In particular, since
![]() and
and
![]() , an increase
in the policy parameters
, an increase
in the policy parameters ![]() or
or ![]() lead to a simultaneous reduction in the volatility of
both inflation and output, conditional on the shock
lead to a simultaneous reduction in the volatility of
both inflation and output, conditional on the shock ![]() . Unconditional volatilities may follow a similar
pattern, as long as the volatility of the real rate shocks is
sufficiently higher than the volatility of cost-push shocks, as it
seems more plausible from an empirical viewpoint.31 The
appendix shows that a change in the policy parameters
. Unconditional volatilities may follow a similar
pattern, as long as the volatility of the real rate shocks is
sufficiently higher than the volatility of cost-push shocks, as it
seems more plausible from an empirical viewpoint.31 The
appendix shows that a change in the policy parameters
![]() and
and ![]() drive
the volatilities of inflation and output-gap in the same direction,
as long as
drive
the volatilities of inflation and output-gap in the same direction,
as long as
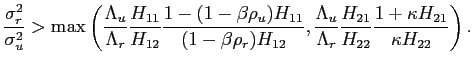
|
(17) |
This inequality is easily satisfied. According to our calibration, for the above condition to be violated the volatility of the innovations to cost-push shocks should be more than 10 times than that of real shocks.
We can then conclude that changes in simple rule parameters cannot always be interpreted as changes in policy objectives. Changes in simple rules may drive the volatility of output-gap and inflation in the same direction, while changes in policy objectives always drive those volatilities in opposite directions. This result is more general and applies to a broader set of models and policy rules. Intuitively, when the central bank behaves optimally, it stabilizes different objectives according to certain weights. A change in those weights is restricted to be a movement along a policy frontier. Such restrictions are not necessarily satisfied by changes in the parameters of a simple rule.32
For example, empirical studies have typically found that both the volatility of inflation and output were reduced after the Volcker disinflation period. This constitutes a shift of the policy frontier itself and cannot be interpreted as a reduction in the relative weight assigned to output stabilization. Instead, as shown in Table (2) a movement of the policy frontier can be associated with a change in the probability of regime switching (e.g. moving from the third to the first column), or a change in the perception of the alternative regime objectives. Both the explanations are not related to the preferences of the regime in power nor to factors fully under its control. It is then unclear to what extent changes in simple rule parameters can be interpreted as "good" or "bad" policies for which the current central bank is responsible.
Another implication concerns the central bank vulnerability to objective instability. Using a regime switching model with interest rate rules, Liu et al. (2009) find that "active'' regimes are more insulated from the spillovers generated by regime switches. Our findings show that this result does not hold when policymakers' differ in their relative preference for output stabilization and set policy optimally. If a regime is more insulated in terms of inflation volatility, it would necessarily suffer a higher exposure in terms of output volatility.
4.2 Are Unstable Objectives Detected by Markow-Switching Simple Rules?
In this section we examine whether changes in policy objectives could be identified in the data as changes in interest rate rule coefficients. We try to address this issue through a Monte Carlo exercise. We simulate our baseline model of section 3.1 for different realizations of the cost-push shock, the real rate shock, and the regime switching shock. We then use the resulting series to estimate the following (standard) Taylor-type interest rate rule
| (18) |
where
![]() is an unobservable residual,
assumed to be uncorrelated with the regressors.33 Equation
(18)
includes a lagged interest rate term because of empirical
plausibility and the endogenous persistence in the data generating
process. Following Hamilton (1989) and Kim and Nelson (1999), we estimate equation (18) by maximum
likelihood allowing for
is an unobservable residual,
assumed to be uncorrelated with the regressors.33 Equation
(18)
includes a lagged interest rate term because of empirical
plausibility and the endogenous persistence in the data generating
process. Following Hamilton (1989) and Kim and Nelson (1999), we estimate equation (18) by maximum
likelihood allowing for ![]() ,
, ![]() ,
, ![]() , and
, and
![]() to follow a two state
Markov-switching process.34
to follow a two state
Markov-switching process.34
Table (3) shows that, according to the Markov-switching criterion developed by Smith et al. (2006), the two-regime model is preferred to a single regime specification only in 13% of the cases. In addition, the algorithm identifies correctly the regime in place in a certain period only in 60% of the cases, a relatively small improvement over the 50% probability of being right without any information.
The mean estimates seem plausible. The coefficient on the lagged
interest rate is in accordance with empirical studies. The
coefficients ![]() and
and ![]() are
also plausible for the hawk.35 The two regimes differ in an
important dimension. While the policy rule followed by the hawkish
regime implies a determinate equilibrium (when combined with the
other equations of the model), the dovish regime implies an
indeterminate one. This result is consistent with many empirical
studies arguing that monetary policy became more hawkish leading to
equilibrium determinacy. But our results are due to a
misinterpretation of the source of regime switches rather than the
determinacy characteristics. Indeterminacy is not a feature of the
data generating process - both regimes follow an optimal policy
delivering a determinate solution.36
are
also plausible for the hawk.35 The two regimes differ in an
important dimension. While the policy rule followed by the hawkish
regime implies a determinate equilibrium (when combined with the
other equations of the model), the dovish regime implies an
indeterminate one. This result is consistent with many empirical
studies arguing that monetary policy became more hawkish leading to
equilibrium determinacy. But our results are due to a
misinterpretation of the source of regime switches rather than the
determinacy characteristics. Indeterminacy is not a feature of the
data generating process - both regimes follow an optimal policy
delivering a determinate solution.36
The results in Table (3) show the risks associated with estimating simple policy rules to draw conclusions about the underlying objectives of the central bank. The presence of regime switches may be wrongly rejected, the specific regime in power may be hard to identify, and the determinacy properties that each regime would imply may be erroneous.
We performed many alternative exercises to check the robustness
of our results, as reported in the last two columns of Table
(3).
In these exercises we constrained ![]() to
be constant across regimes, which simplifies the algorithm task to
identify switches in the interest rate response to inflation and
output-gap. Also, we increased the cost-push volatility to the
level of the real rate volatility, which we see as an upper bound.
As discussed in section 4.1,
such calibration allows the simple interest rate rule to better
capture the optimal policy data generating process. The performance
of the estimation algorithm improves, but the main conclusions
reached with the baseline calibration are still valid.
to
be constant across regimes, which simplifies the algorithm task to
identify switches in the interest rate response to inflation and
output-gap. Also, we increased the cost-push volatility to the
level of the real rate volatility, which we see as an upper bound.
As discussed in section 4.1,
such calibration allows the simple interest rate rule to better
capture the optimal policy data generating process. The performance
of the estimation algorithm improves, but the main conclusions
reached with the baseline calibration are still valid.
Finally, we checked the dependence of the results on the
presence of a strategic interaction between regimes. To do so, we
simulated the model imposing ![]() , thus shutting down the spillovers between the regimes.37
, thus shutting down the spillovers between the regimes.37
Table 3a: Markov-Switching Maximum Likelihood Estimation of a Simple Interest Rate Rule
| Baseline | |||
|---|---|---|---|
| % MSC(2) | .13 | .36 | .43 |
| % Right Regime | .60 | .72 | .77 |
Table 3b: Markov-Switching Maximum Likelihood Estimation of a Simple Interest Rate Rule - Means of Parameters Estimates
| Hawk | Dove | Hawk | Dove | Hawk | Dove | |
|---|---|---|---|---|---|---|
| .8577 (.0185) | .8452 (.0319) | .7526 (.0238) | .7526 (.0238) | .8417 (.0299) | .8417 (.0299) | |
| .2270 (.0635) | .1469 (.0792) | .7200 (.1066) | -.1124 (.0547) | 2.3285 (.2294) | -.2578 (.1232) | |
| -.1954 (.0154) | -.1780 (.0288) | -.1525 (.0193) | -.1703 (.0426) | -.0775 (.0428) | -.3482 (.1159) | |
| | .1396 (.040) | .1470 (.049) | .2007 (.1030) | .1980 (.0843) | .1664 (.0686) | .1841 (.0762) |
| .6191 (.0692) | .6525 (.0711) | .7685 (.1097) | .7287 (.0881) | .8413 (.0913) | .8400 (.0795) | |
| Determinacy | Yes | No | Yes | No | Yes | No |
Notes: The Markov-switching criterion was computed for the 2-state model (MSC(2)) and the alternative specification with constant parameter across regimes (MSC(1)). The second row displays the average fraction of periods the estimation correctly identifies the regime in power. For each parameter, the table presents the mean estimate over 1000 simulations, each of 200 observations. Standard errors are reported in parenthesis. The convergence to global maxima was checked using alternative initial conditions
The performance of the estimation algorithm improves significantly, since it detects the presence of regime switches in 43% of the cases, and the correct regime is identified in 77% of the periods. This result, however, does not undermine the main conclusions obtained above, but rather highlights why explicitly modeling the strategic interactions is important. Strategic interactions between different policy regimes would be present in any economy with endogenous state variables, like private capital or public debt. In those cases, estimating simple policy rules that ignores such interactions may lead to erroneous conclusions about the underlying monetary policy decision process.
5 Conclusions
Regime shifts in macroeconomic relationships in general and central bank behavior in particular have been identified in the data. We study the effects of unstable objectives as a potential source of regime changes, and characterize policy choices in a variety of models and specifications. The central bank is allowed to react to the possibility of future changes, a central feature of modern economics that simple interest rules can not easily capture in a regime shifting framework.
The paper illustrates some perils of using switches in simple rules for positive and normative analyses, and identifies the conditions under which such analyses are less prone to error. We show that changes in simple rules cannot be interpreted solely as changes in policy objectives, but are potentially related to factors not under the central bank's control. Similarly, it may be difficult to detect unstable objectives, the regime in place, and the determinacy conditions through changes in simple rules.
It can be argued that central banks do not behave optimally, and that changes in simple rules reflect the central banks' ability to approach optimal policy. Our intuitions do not require an optimal behavior, but the weaker requirements of the presence of spillovers among alternative regimes and that central banks recognize a trade-off between inflation and output stabilization.
Finally, it is not our claim that unstable objectives are the main source of regime switches. Other factors not considered in the paper may also play a role, like structural factors or the information available to central banks. In this respect, incorporating the monetary monetary decision process into more complete regime switching models would constitute a crucial step towards the identification and the interpretation of the sources of monetary regime switches.
References
Adam, K., Billi, R., 2006. Optimal monetary policy under commitment with a zero bound on nominal interest rates. Journal of Money, Credit and Banking 38 (7), 1877-1905.
Alesina, A., Roubini, N., Cohen, G., 1997. Political Cycles and the Macroeconomy. The MIT Press.
Aoki, K., 2003. On the optimal monetary policy response to noisy indicators. Journal of Monetary Economics 50, 501-523.
Ball, L., Mankiw, N. G., 2002. The nairu in theory and practice. Journal of Economic Perspectives 16 (4), 115-136.
Barro, R. J., Gordon, D. B., 1983. Rules, discretion and reputation in a model of monetary policy. Journal of Monetary Economics 12 (1), 101-121.
Beaudry, P., Portier, F., September 2006. Stock prices, news, and economic fluctuations. American Economic Review 96, 1293-1307.
Bianchi, F., 2010. Regime switches, agents' beliefs, and post-world war ii u.s. macroeconomic dynamics. Duke University. Manuscript.
Blanchard, O., Dell'Ariccia, G., Mauro, P., 2010. Rethinking macroeconomic policy. International Monetary Fund Staff Position Note.
Canova, F., Gambetti, L., 2009. Structural changes in the us economy: Is there a role for monetary policy? Journal of Economic Dynamics and Control 33 (2), 477-490.
Carboni, G., Ellison, M., 2009. The great inflation and the greenbook. Journal of Monetary Economics 56 (6), 831-841.
Chari, V., Kehoe, P., McGrattan, E., 2009. New keynesian models: Not yet useful for policy analysis. American Economic Journal: Macroeconomics 1 (1), 242-266.
Clarida, R., Gali, J., Gertler, M., 2000. Monetary policy rules and macroeconomic stability: Evidence and some theory. Quarterly Journal of Economics 115 (1), 147-180.
Cogley, T., Sargent, T. J., 02 2002. Evolving post-world war ii u.s. inflation dynamics. In: NBER Macroeconomics Annual 2001, Volume 16. NBER Chapters. National Bureau of Economic Research, Inc, pp. 331-388.
Davig, T., Doh, T., 2008. Monetary policy regime shifts and inflation persistence. Federal Reserve Bank of Kansas City. Research Working Paper.
Davig, T., Leeper, E., 2007. Generalizing the taylor principle. American Economic Review 97 (3), 607-635.
Debortoli, D., Nunes, R., 2010a. Fiscal policy under loose commitment. Journal of Economic Theory 145-3, 1005-1032.
Debortoli, D., Nunes, R., 2010b. The macroeconomic effect of external pressures on monetary policy. International Finance Discussion Papers N.944.
Dennis, R., 2004. Inferring policy objectives from economic outcomes. Oxford Bulletin of Economics and Statistics 66 (1), 735-764.
Dennis, R., 2006. The policy preferences of the us federal reserve. Journal of Applied Econometrics 21 (1), 55-77.
Farmer, R. E., Waggoner, D. F., Zha, T., 2009. Understanding markov-switching rational expectations models. Journal of Economic Theory 144 (5), 1849-1867.
Faust, J., Irons, J., 1999. Money, politics and the post-war busines cycle. Journal of Monetary Economics 43 (1), 61-89.
Gali, J., 2008. Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework. Princeton University Press.
Gali, J., Gertler, M., Lopez-Salido, D., 2007. Markups, gaps and the welfare costs of business fluctuations. Review of Economics and Statistics 89 (1), 44-59.
Giannoni, M., Woodford, M., 2010. Optimal target criteria for stabilization policy. NBER Working Paper 15757.
Greenspan, A., 1994. Statement to the u.s. house committee on the budget, june 22, 1994. Federal Reserve Bulletin 80 (8), 714-719.
Hamilton, J. D., 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57 (2), 357-84.
Hansen, L., Sargent, T., 2007. Robustness. Princeton University Press. Ireland, P. N., 2004. Technology shocks in the new keynesian model. The Review of Economics and Statistics 86 (4), 923-936.
Justiniano, A., Primiceri, G., 2008. Potential and natural output. Manuscript. Kim, C.-J., Nelson, C. R., 1999. State-Space Models with Regime-Switching: Classical and Gibbs-Sampling Approaches with Applications. The MIT Press, Cambridge Massachusets.
Liu, Z., Waggoner, D., Zha, T., 2009. Asymmetric expectation effects of regime shifts in monetary policy. Review of Economic Dynamics 12 (2), 284-303.
Lubik, T. A., Schorfheide, F., 2004. Testing for indeterminacy: An application to u.s. monetary policy. American Economic Review 94 (1), 190-217.
Lucas, R. J., 1976. Econometric policy evaluation: A critique. Carnegie-Rochester Conference Series on Public Policy 1 (1), 19-46.
Marcet, A., Marimon, R., 1998. Recursive contracts. Universitat Pompeu Fabra. Working Paper.
Orphanides, A., 2001. Monetary policy rules based on real-time data. The American Economic Review 91 (4), 964-985.
Orphanides, A., 2002. Monetary-policy rules and the great inflation. The American Economic Review 92 (2), 115-120.
Orphanides, A., 2006. The road to price stability. The American Economic Review 96 (2), 178-181.
Owyang, M. T., Ramey, G., 2004. Regime switching and monetary policy measurement. Journal of Monetary Economics 51 (8), 1577-1597.
Rabanal, P., Rubio-Ramirez, J. F., 2005. Comparing new keynesian models of the business cycle: A bayesian approach. Journal of Monetary Economics 52 (6), 1151-1166.
Roberds, W., 1987. Models of policy under stochastic replanning. International Economic Review 28 (3), 731-755.
Schaumburg, E., Tambalotti, A., 2007. An investigation of the gains from commitment in monetary policy. Journal of Monetary Economics 54 (2), 302-324.
Sims, C. A., Zha, T., 2006. Were there regime switches in u.s. monetary policy? American Economic Review 96 (1), 54-81.
Smets, F., Wouters, R., 2003. An estimated dynamic stochastic general equilibrium model of the euro area. Journal of the European Economic Association 1 (5), 1123-1175.
Smith, A., Naik, P. A., Tsai, C.-L., 2006. Markov-switching model selection using markov-switching model selection using kullback-leibler divergence. Journal of Econometrics 134, 553-577.
Stock, J., Watson, M., 2002. Has the Business Cycle Changed and Why? NBER Macroeconomics Annual, 159-218.
Woodford, M., 2003. Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton University Press.
Yun, T., 1996. Nominal price rigidity, money supply endogeneity and business cycles. Journal of Monetary Economics 37 (2), 345-370.
Zampolli, F., 2006. Optimal monetary policy in a regime-switching economy: The response to abrupt shifts in exchange rate dynamics. Journal of Economic Dynamics and Control 30 (9-10), 1527-1567.
Appendix
Changes in the Relative Weight of Output-Gap Stabilization
Here we consider a particular case of problem (3), where
![]() ,
,
![]() and
and ![]() .38 The first-order conditions of the
problem are given by
.38 The first-order conditions of the
problem are given by
| (A-1) | ||
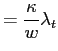 |
(A-2) | |
| (A-3) |
where
![]() is the Lagrange multiplier
associated with the NKPC and
is the Lagrange multiplier
associated with the NKPC and
![]() .39 Since the model is
linear-quadratic, we guess that expected inflation prevailing when
objectives change is given by a linear rule
.39 Since the model is
linear-quadratic, we guess that expected inflation prevailing when
objectives change is given by a linear rule
where ![]() is a coefficient to be determined.
Rearranging equations (A-1) - (A-3) the following
second-order difference equation is obtained:
is a coefficient to be determined.
Rearranging equations (A-1) - (A-3) the following
second-order difference equation is obtained:
![$\displaystyle \left[ \beta qL^{-2}-\left(1+\beta q+\frac{\kappa^{2}}{w}\right)L^{-1}+1\right] \lambda_{t-1}=\left[ 1+\beta\left( 1-q\right) \psi_{u} ^{j}\rho_{u}\right] u_{t},$](img212.gif)
|
(A-4) |
whose solution is given by
| (A-5) |
where
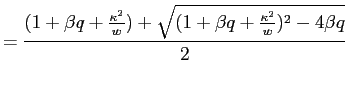
|
(A-6) | |
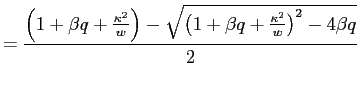
|
(A-7) |
Note that
![]() and
and
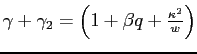 and
and
![]() . 40
Moreover,
. 40
Moreover,
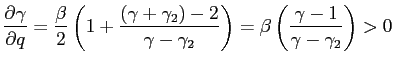
|
(A-8) |
and
![]() . The
unique stable solution to (A-5) is given by the
expression
. The
unique stable solution to (A-5) is given by the
expression
| (A-9) |
where
![]() and
and
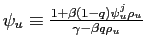 . Combining (A-9) with (A-1), using (A-2) to eliminate
the Lagrange multiplier, and imposing the initial condition
. Combining (A-9) with (A-1), using (A-2) to eliminate
the Lagrange multiplier, and imposing the initial condition
![]() , equation (5) in
the main text is obtained.
, equation (5) in
the main text is obtained.
In the limiting case where ![]() , equations
(A-2) and (A-3) remains
unaltered, while (A-1) takes the form
, equations
(A-2) and (A-3) remains
unaltered, while (A-1) takes the form
![]() . Solving for the
equilibrium, it holds
. Solving for the
equilibrium, it holds
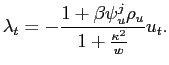
|
(A-10) |
The resulting law of motion is similar to (A-9). Indeed, the
coefficient multiplying ![]() is the same as
is the same as
![]() in (A-9) after imposing
the condition
in (A-9) after imposing
the condition ![]() . However, none of the variables
depend on
. However, none of the variables
depend on
![]() (or equivalently on
(or equivalently on
![]() ).
).
A-1.1 Slope of the Impulse Response Function
Given the above law of motion, it follows that in response to a cost-push shock
| (A-11) |
Following a positive cost-push shock, the (absolute) initial change in inflation is therefore given by:
| (A-12) |
An identical expression holds for the (standard) full-commitment and stable objectives case, whose corresponding variables are indicated with an upper bar. In comparison with that case, the slope of the impulse response function is then given by
![$\displaystyle = \left[ (2-\frac{1}{\gamma}-\rho_u)\Gamma\frac{\bar{\gamma}-\beta\rho_{u}}{\gamma-\beta\rho_{u}} - (2-\frac{1}{\bar{\gamma}}-\rho_u)\right]\bar{\psi}^{i}_{u}u_0,$](img244.gif)
|
which coincides with (8), and
where the second equality is obtained using equation (7) and the
definition of ![]() and
and
![]() . For that expression to be
positive, and setting
. For that expression to be
positive, and setting ![]() - the lowest
possible value taken by that parameter for a hawkish regime - it
must be that
- the lowest
possible value taken by that parameter for a hawkish regime - it
must be that
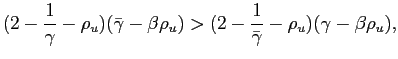
|
or equivalently,
The right hand side of (A-13) only depends on
the parameters ![]() ,
, ![]() and on the
ratio
and on the
ratio
![]() . Fixing
. Fixing ![]() and
and ![]() to the values described in
Table (1),
Figure (A-1) shows that
condition (A-13) is always
satisfied as long as
to the values described in
Table (1),
Figure (A-1) shows that
condition (A-13) is always
satisfied as long as ![]() and
and
![]() - a value well above the
available estimates.
- a value well above the
available estimates.
A-2 Unstable Output-Gap Targets
Consider that
![]() ,
,
![]() , and for simplicity that the
cost push-shock is not present then the FOCs of regime
, and for simplicity that the
cost push-shock is not present then the FOCs of regime ![]() are:
are:
| (A-14) | |
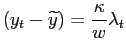
|
(A-15) |
| (A-16) |
Figure A-1
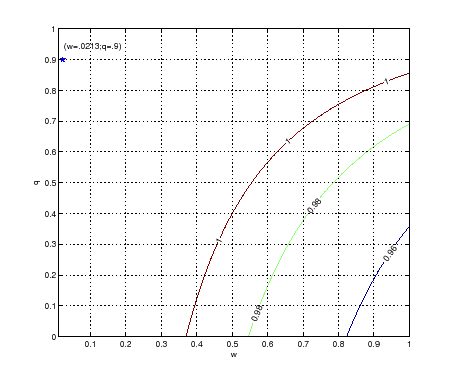
Note: For any value of
![]() , the regions above the corresponding
contour line indicate the values of
, the regions above the corresponding
contour line indicate the values of ![]() and
and
![]() satisfying condition (A-13). The dot on
the top-left corner indicates our baseline calibration for those
parameters. The parameters
satisfying condition (A-13). The dot on
the top-left corner indicates our baseline calibration for those
parameters. The parameters ![]() and
and
![]() are set to the values described in
Table (1).
are set to the values described in
Table (1).
Substituting (A14) and (A-15) into (A-16), and solving the resulting second-order difference equation, the following expression is obtained
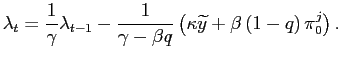
|
(A-17) |
where ![]() is defined as in equation (A-6). For
convenience, define
is defined as in equation (A-6). For
convenience, define
![]() , and notice that
, and notice that
![]() .
Assuming regime
.
Assuming regime ![]() is solving a symmetric problem,
equations (A-17) and (A-14), together with
the initial condition
is solving a symmetric problem,
equations (A-17) and (A-14), together with
the initial condition
![]() implies
implies
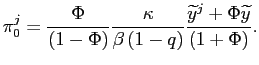
|
(A-18) |
Substituting the last expression into (A-17), and using the
fact that
![]() the
law of motion of the Lagrange multiplier is given by
the
law of motion of the Lagrange multiplier is given by
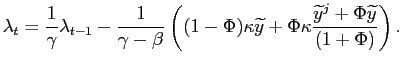
|
(A-19) |
Substituting this expression into (A-14) and (A-15), and imposing
the initial condition
![]() (or equivalently
(or equivalently
![]() ), the law of motion in
equation (10) in the text is
obtained. Notice that in the law of motion of the endogenous
variables
), the law of motion in
equation (10) in the text is
obtained. Notice that in the law of motion of the endogenous
variables ![]() and
and
![]() the coefficients
coincide with the case of the previous section in the limiting case
where
the coefficients
coincide with the case of the previous section in the limiting case
where ![]() , but are responding to different
variables. Indeed the previous term
, but are responding to different
variables. Indeed the previous term ![]() is now
replaced by a regime weighted output-gap measure.
is now
replaced by a regime weighted output-gap measure.
A-3 Delayed Regime Changes
For notational convenience only, we consider a purely forward looking Phillips curve and we abstract from the presence of uncertainty other than the one regarding the policy objective changes. Results in the presence of a hybrid Phillips curve are available in the working paper version (). The problem is
![$\displaystyle V^{i}=\max_{\{\pi_{t},y_{t}\}_{t=0}^{\infty}}E_{0}\sum_{m=0}^{\infty}\left( \beta^{T}q\right) ^{m}\left[ -\frac{1}{2}\sum_{t=0}^{T-1}\beta^{t}\left[ \pi_{m+t}^{2}+w^{i}(y_{m+t}-{\widetilde{y}}^{i})^{2}\right] +\beta ^{T}(1-q)V^{ij}\right]$](img285.gif)
|
(A-20) |
| (A-21) | ||
| (A-22) | ||
| |
Proposition 1 Being ![]() the vector of lagrange
multipliers associated with the constraints (A-21) and (A-22), problem
(A-20) can
be written as a saddle point functional equation (SPFE) as
follows:
the vector of lagrange
multipliers associated with the constraints (A-21) and (A-22), problem
(A-20) can
be written as a saddle point functional equation (SPFE) as
follows:
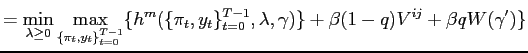
|
||
where
![$\displaystyle \equiv\sum_{t=0}^{T-1}\beta^{t}\left[ {\pi_{t}}^{2}+w^{i}(y_{t}-{\widetilde{y}})^{2}\right]$](img301.gif)
|
![$\displaystyle \equiv\left[ \begin{array}[c]{c} \pi_{0}-\kappa y_{0}-\beta\pi_{1}\\ \vdots\\ \pi_{T-2}-\kappa y_{T-2}-\beta\pi_{T-1}\\ \pi_{T-1}-\kappa y_{T-1}-\beta(1-q)\pi_{T}^{j} \end{array} \right]$](img303.gif)
|
||
![$\displaystyle \equiv\left[ \begin{array}[c]{c} 0\\ \vdots\\ 0\\ \pi_{0}^{i} \end{array} \right]$](img305.gif)
|
Proof. of Proposition 1. Define the
real valued function ![]() as follows:
as follows:
![$\displaystyle \equiv-\frac{1}{2}\sum_{t=0}^{T-1} \beta^{t}\left[ \pi_{t}^{2}+w^{i}(y_{t}-{\widetilde{y}}^{i})^{2}\right] +\beta^{T}(1-q)V^{ij}$](img309.gif)
|
Moreover,
![]() and
and
![]() are defined as in the second
part of the proposition. Problem (A-20) is therefore
equivalent to:
are defined as in the second
part of the proposition. Problem (A-20) is therefore
equivalent to:
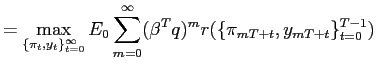
|
||
This formulation fits the definition of Program 1 in Marcet and Marimon (1998). We can therefore write the problem as a saddle point functional equation in the sense that there exists a unique function satisfying:
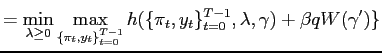
|
||
where
or in a more intuitive formulation define
![$\displaystyle \equiv\sum_{t=0}^{T-1}\beta^{t}\left[ {\pi_{t}}^{2}+w^{i}(y_{t}-{\widetilde{y}})^{2}\right]$](img325.gif)
|
and the saddle point functional equation is:
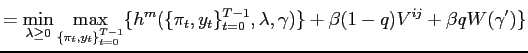
|
||
Proposition 2 For any type of policy objectives ![]() the
solution of problem (A-20) is a tenure
invariant function
the
solution of problem (A-20) is a tenure
invariant function
![]() , such that:
, such that:
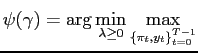
|
||
Proof. of Proposition 2. Using Proposition 1, this proof follows directly from the results of Marcet and Marimon (1998).
A-4 Simple Interest Rate Rules and Volatility
Consider a simple New-Keynesian economy characterized by a dynamic IS equation (15), a NKPC (1) and where monetary policy is conducted according to the simple interest rate rule (14). The solution of this model is given by
![$\displaystyle \left[\begin{array}[c]{c} \pi_{t}\\ y_{t} \end{array}\right] = \left[\begin{array}[c]{cc} (\sigma(1-\rho_u)+\phi_y)\Lambda_u & \kappa \Lambda_r\\ -(\phi_\pi-\rho_u) \Lambda_u & (1-\beta\rho_r) \Lambda_r\end{array}\right] \par \left[\begin{array}[c]{c}u_t\\ r^n_t\end{array}\right] \equiv H \left[\begin{array}[c]{c}u_t\\ r^n_t\end{array}\right]$](img338.gif)
|
(A-23) |
where
![]() and
and
![]() , corresponding to equation (16) in the main
text.41 We are assuming a standard
calibration with stationary shocks
, corresponding to equation (16) in the main
text.41 We are assuming a standard
calibration with stationary shocks
![]() ,
positive interest rate rule coefficients
,
positive interest rate rule coefficients
![]() , and a unique
rational expectations stationary equilibrium
, and a unique
rational expectations stationary equilibrium
![]() .
.
It is now possible to analyze how the responses of our variables to the different shocks, and the implied conditional volatilities, are affected by changes in policy parameters. It can be noticed that
![$\displaystyle =\left[ \begin{array}[c]{cc} -\kappa\Lambda_{u}H_{11}& -\kappa\Lambda_{r}H_{12}\\ -\Lambda_{u}(1+\kappa H_{21}) & -\kappa\Lambda_{r}H_{22} \end{array} \right]$](img345.gif)
|
(A-24) | |
![$\displaystyle =\left[ \begin{array}[c]{cc} \Lambda_{u}(1-(1-\beta\rho_{u})H_{11}) & -(1-\beta\rho_{r})\Lambda _{r}H_{12}\\ -(1-\beta\rho_{u})\Lambda_{u}H_{21} & -(1-\beta\rho_{r})\Lambda_{r}H_{22} \end{array} \right] .$](img347.gif)
|
(A-25) |
The following properties are then satisfied:
- In response to a cost-push shock (
 ):
):
- an increase in
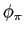 dampens the response of inflation
and magnifies the response of output,
dampens the response of inflation
and magnifies the response of output, - an increase in
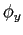 magnifies the
response of inflation and dampens the response of output.
magnifies the
response of inflation and dampens the response of output.
- an increase in
- In response to a real interest rate shock (
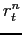 ), the response of both inflation and output is
dampened by increasing
), the response of both inflation and output is
dampened by increasing
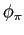 and
and 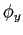 .
.
The composite effects on the unconditional volatilities of our
variables thus depend on the volatilities of the shocks
![]() ,
,
![]() as well as on their correlation
as well as on their correlation
![]() .
.
The (unconditional) volatility of inflation and output are given by
| (A-26) | ||
| (A-27) |
where
![]() ,
,
![]() and
and
![]() are, respectively, the variances
of the shocks
are, respectively, the variances
of the shocks ![]() ,
, ![]() and
their contemporaneous correlation.
and
their contemporaneous correlation.
Taking the derivatives of (A-26) and (A-27), and assuming
that the two shocks are uncorrelated (
![]() ), the following hold:
), the following hold:
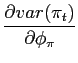
|
(A-28) | |
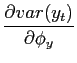 |
(A-29) |
In other words, regardless of the relative volatility of the
underlying shocks, the unconditional volatility of inflation is
decreasing in
![]() and the unconditional volatility
of output is decreasing in
and the unconditional volatility
of output is decreasing in ![]() .42
Moreover,
.42
Moreover,
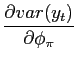
|
(A-30) | |
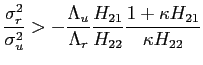
|
(A-31) |
and
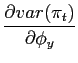
|
(A-32) | |
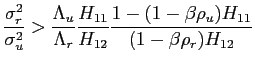
|
(A-33) |
We can then conclude that, as long as condition (17) holds, a change in policy parameters leads to the volatility of both inflation and output to move in the same direction.
A-5 Optimal Policy and Volatility
If objectives are stable and the central bank is behaving optimally
the implied paths of inflation and output are described by the
equations (5) and (6) for the case
where ![]() . The (unconditional) variances of
inflation and output are given by:
. The (unconditional) variances of
inflation and output are given by:
| (A-34) | ||
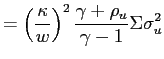
|
(A-35) |
with
![]() and
and
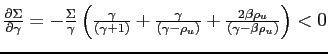 .
.
In this case a change in policy parameters is given by a change
in the relative weight of output stabilization (![]() ). Noticing that
). Noticing that
![]() ,
it follows that
,
it follows that
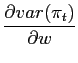 |
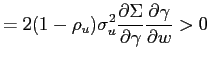
|
|
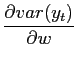 |
![$\displaystyle =\sigma_{u}^{2}\left[ 2\left( \frac{\kappa}{w}\right) ^{2}\left( -\frac{1}{w}\right) \frac{\gamma +\rho_{u}}{\gamma-1}\Sigma+\left( \frac{\kappa}{w}\right) ^{2}\frac {\partial{\gamma}}{\partial{w}}\left( \frac{\partial\Sigma}{\partial\gamma }\frac{\gamma+\rho_{u}}{\gamma-1}-\Sigma\frac{1+\rho_{u}}{(\gamma-1)^{2} }\right) \right]$](img396.gif)
|
|
![$\displaystyle =-\frac{var(y_{t})}{w}\left[ 2-\frac{(\gamma-\beta)(\gamma-1)}{\gamma ^{2}-\beta}\left( \frac{\gamma}{\gamma+1}+\frac{\gamma}{\gamma-\rho_{u} }+\frac{2\beta\rho_{u}}{\gamma-\beta\rho_{u}}+\frac{\gamma(1+\rho_{u} )}{(\gamma-1)(\gamma+\rho_{u})}\right) \right]$](img397.gif)
|
||
![$\displaystyle <-\frac{var(y_{t})}{w}\left[ 2-\frac{(\gamma-\beta)(\gamma-1)}{\gamma ^{2}-\beta}\left( 2\frac{\gamma^{2}-\beta}{(\gamma-\beta)(\gamma-1)}\right) \right] =0$](img398.gif)
|
where the last inequality follows from noticing that the term in
the round brackets is increasing in ![]() and
taking its limit as
and
taking its limit as
![]() . This clarifies that a
change in
. This clarifies that a
change in ![]() , as opposed to changes in simple rule
parameters, always drives the volatility of inflation and output in
opposite directions.
, as opposed to changes in simple rule
parameters, always drives the volatility of inflation and output in
opposite directions.
Footnotes
1. See for instance Cogley and Sargent (2002), Stock and Watson (2002), Sims and Zha (2006), Canova and Gambetti (2009) and the literature reviewed therein. Return to text
2. Dennis (2004, 2006) are two exceptions considering that monetary policy is set optimally in the estimation exercise. Return to text
3. For a recent paper on the importance of the policymaker's expectations see Carboni and Ellison (2009). Return to text
4. While there is some agreement that the output target should be the output level with flexible prices, there is much less agreement on how to measure such concept and which shocks affect it. The inflation target itself is also subject to debate, see for instance Blanchard et al. (2010). Return to text
5. Theoretical models in this literature did not contemplate this possibility. On the empirical side, Alesina et al. (1997) point out several empirical successes of political cycle models, whereas Faust and Irons (1999) conclude that partisan effects in US macroeconomic data are fragile, and that there is little evidence that the partisan effects on the economy operate through changes in monetary policy. Return to text
6. The theoretical framework underlying such relationship is described in Yun (1996), Woodford (2003) and Galí (2008). This specification of the NKPC holds in a neighborhood of a zero inflation steady state. Throughout our analysis, we abstract from the changes that may derive from having a different steady state level of inflation. Return to text
7. It is also plausible that different views coexist in central bank boards, in which case the current regime would correspond to the one holding decision power at a certain point in time. Orphanides (2006) states that "members of the FOMC hold diverse views, and consequently the views of the chairman do not necessarily reflect the consensus of the Committee". The appointment of a new Board member could therefore introduce a regime change. Return to text
8. ![]() and
and
![]() are value functions in the presence of
disagreement between successive policymakers, therefore unlike Debortoli and Nunes (2010a) one can not use an envelope
result. We have also examined the results with a hybrid NKPC, in
which case the value function derivative enters the first order
conditions. Return to text
are value functions in the presence of
disagreement between successive policymakers, therefore unlike Debortoli and Nunes (2010a) one can not use an envelope
result. We have also examined the results with a hybrid NKPC, in
which case the value function derivative enters the first order
conditions. Return to text
9. We are therefore not considering trigger strategies as in Barro and Gordon (1983). When a reoptimization does not occur, policies depend both on the natural state variables and past promises as in Marcet and Marimon (1998). Return to text
10. This holds conditionally on being in a
certain regime ![]() . When objectives switch to type
. When objectives switch to type
![]() , a new plan is made and the term on lagged
output is discarded. Return to
text
, a new plan is made and the term on lagged
output is discarded. Return to
text
11. Zampolli (2006) analyzes exchange rate regime switches and optimal policy in a model with backward looking expectations where these type of interactions are not present. In our forward-looking model such spillovers would be absent only in the very particular case of i.i.d. cost-push shocks and no endogenous state variables. Section 3.2 considers an alternative type of objective instability that turns out to be similar to a unit root in the cost-push shock process. Return to text
12. See for instance the examples in Woodford (2003, ch. 4) and Galí (2008, ch. 5). Return to text
13. This follows from the definition of
![]() together with the fact that
together with the fact that
![]() is increasing in
is increasing in ![]() . Return to text
. Return to text
14. Section A-1.1 in the
appendix explores more extreme calibrations. As long as the hawkish
regime weights inflation more than output (![]() ),
it suffices that
),
it suffices that
![]() , a value well above available
estimates. Return to text
, a value well above available
estimates. Return to text
15. Using a similar argument as above, the sign of (8) depends on the parametrization and cannot be univocally determined for the dovish regime. Return to text
16. See e.g. Davig and Doh (2008) and Bianchi (2010). Results
are amplified when considering more frequent switches or a central
bank with a dual mandate (![]() ). Return to text
). Return to text
17. The available estimates of medium and large scale DSGE models (e.g. Smets and Wouters (2003)) with multiple sources of fluctuations are not directly comparable with our reduced form shocks. The chosen values for the standard deviations of the shocks are only relevant for the Monte Carlo exercise of section 4 where we also consider alternative calibrations. Return to text
18. This result is due in part to a loss in credibility, as can be seen in the table comparing the volatilities with full and limited commitment. However, unstable objectives in comparison with limited commitment increase the volatilities for the hawk but reduce them for the dove. Accordingly, the hawk induces a positive welfare externality, whereas the dove introduces a negative externality with respect to the limited commitment case. Return to text
19. It is not clear that central banks have the credibility to disregard distortions that impair ignificantly economic activity. The Federal Reserve and ECB actions in the 2008-2010 crisis constitute examples where such issues are at the very least debatable. Return to text
20. Policymakers themselves seem to be aware of such issues; answering a question on "the so-called 'natural rate' of unemployment" Alan Greenspan on June 22, 1994 said "[w]hile the idea of a national 'threshold' at which short-term inflation rises or falls is statistically appealing, it is very difficult in practice to arrive at useful estimates that would identify such a natural rate." (see Greenspan (1994)). For a discussion see Ball and Mankiw (2002) and for recent attempts to estimate the efficient level of output see for example Gali et al. (2007) and Justiniano an Primiceri (2008). Return to text
21. The system is initialized at
![]() . Return to text
. Return to text
22. Since the micro-foundations of cost-push shocks are not well understood, we regard this result as a contribution in itself. Cost-push shocks have been modeled, for example, as exogenous variations in price and wage markups (see e.g. Woodford (2003) and Galí (2008)). Return to text
23. When objectives change and become dovish, both inflation and output expand. Therefore, it is the anticipation and not the realization of the shock that resembles the traditional (positive) cost-push shock. In this respect, our argument is similar to the important distinction between current shocks and news about future shocks (see e.g. Beaudry and Portier (2006)). Return to text
24. We are not claiming that the policy
functions are time-invariant, as they change in different periods
within a tenure. In order to solve our problem we have to find the
policy functions satisfying the equilibrium conditions (![]() policy functions per regime). As shown in equation
(13), the
policies of each regime interact and therefore we have to solve a
fixed point problem in such policy functions. In addition, the
implied value functions
policy functions per regime). As shown in equation
(13), the
policies of each regime interact and therefore we have to solve a
fixed point problem in such policy functions. In addition, the
implied value functions ![]() and
and ![]() also enter the problem and need to be solved for
endogenously. We also have to take into account the possibility of
default on past promises, an event that occurs whenever there is a
change in objectives. Return to
text
also enter the problem and need to be solved for
endogenously. We also have to take into account the possibility of
default on past promises, an event that occurs whenever there is a
change in objectives. Return to
text
25. Schaumburg and Tambalotti (2007) also consider an output-gap target of 0.1. Return to text
26. The first period of the hawkish regime (period 1) is fundamentally different from any initial period after being reconfirmed (periods 5, 9, 13 in the graph). Periods 5, 9, and 13 are characterized by low inflation that was promised in the previous period. Past promises are not binding in period 1 because each regime reoptimizes. Return to text
27. The corresponding derivations are omitted for brevity and available in the working paper version Debortoli and Nunes (2010b). Return to text
28. For instance Clarida et al. (2000) and Lubik and Schorfheide (2004) find regime switches whereas Sims and Zha (2006) do not. Return to text
29. We have explored numerically that the results obtained are robust to many alternative interest rate rules displaying forward and backward looking terms in inflation, output-gap and interest rate. Return to text
30. This assumption greatly simplifies our
algebra without affecting qualitatively the results. A non-zero
correlation between ![]() and
and ![]() arises when the flexible price equilibrium is not
attainable. For example, in a model with sticky prices and sticky
wages the term
arises when the flexible price equilibrium is not
attainable. For example, in a model with sticky prices and sticky
wages the term ![]() would be an endogenous variable,
which is a linear function of the shock
would be an endogenous variable,
which is a linear function of the shock ![]() . Return to text
. Return to text
31. See for instance Rabanal and Rubio-Ramirez (2005) and Adam and Billi (2006). Return to text
32. Our analysis focuses mainly on simple interest rate rules because these are usually employed in empirical studies. Giannoni and Woodford (2010) discuss targeting rules implementing the optimal policy with similar form to simple interest rate rules. In some cases, those rules can be invariant to objective instability. However, the targeting rule parameters depend on the preferences. If the implied cross restrictions on the parameters are ignored, similar issues arise. Return to text
33. The Monte Carlo exercise uses 1000 histories of 200 periods each, which is comparable to the number of quarters available using the actual data from 1960-2010. The exercise also assumes that the econometrician knows all the parameters except those of the simple rule. Removing that assumption gives less information to the econometrician and may imply that the misspecification problem biases the estimation of the other structural parameters. Examining such bias is interesting but goes beyond the scope of this paper. Return to text
34. We chose maximum likelihood estimation over Bayesian estimation methods because we need to estimate the model many times. Using Bayesian methods would increase the computation time dramatically and could bias the results of the Monte Carlo experiment by imposing restrictive priors. Return to text
35. The estimates in some studies should
be changed to
![]() for direct
comparability. Return to text
for direct
comparability. Return to text
36. In the work of Davig and Leeper (2007), considering the dove in isolation would deliver an indeterminate solution, but the presence of the hawk renders the solution determinate. Here the problem is of a different nature. Indeterminacy is detected even though the hawk and the dove always deliver a determinate equilibrium both in isolation and jointly. The calculation of determinacy conditions with regime switches and specially when the dynamic system has lagged variables is not clear and is subject to debate (see Davig and Leeper (2007) and Farmer et al. (2009) among others). Due to this reason, we have calculated the determinacy conditions ignoring the possibility of regime changes. Return to text
37. We are also not allowing for switches on the output-gap target, which would introduce a strategic interaction as shown in section 3.2. Return to text
38. For notational convenience, we
suppress the superscript ![]() , and indicate with the
superscript
, and indicate with the
superscript ![]() the variables related to the
alternative regime. Return to
text
the variables related to the
alternative regime. Return to
text
39. See Marcet and Marimon (1998). Return to text
40. The solution is always a real number
since
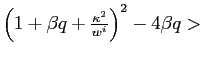
41. The associated derivations are standard, and available upon request. Return to text
42. This holds also in the more general
cases with a positive correlation between ![]() and
and
![]()
![]() . Return to text
. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text