The Federal Reserve Board eagle logo links to home page

The Cyclicality of Job-to-Job Transitions and Its Implications for Aggregate Productivity

Toshihiko Mukoyama**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper analyzes the job-to-job transitions of workers in the United States. I propose a new method of correcting the time-aggregation bias. The bias-corrected series from 1996 to 2011 reveals a procyclical pattern of job-to-job transition and a large decline since the beginning of the 2000s. I construct a model of on-the-job search and explore the implications of this phenomenon. The calibrated model shows that the decline in the reallocation of workers through job-to-job transitions has had a substantial effect on total factor productivity (TFP). From 2009 to 2011, the model accounts for about 0.5%-0.7% annual decline in TFP

Keywords: Job-to-job transition, time-aggregation bias, on-the-job search

JEL classification: E24, E32, J62


1  Introduction

From a macroeconomic perspective, job-to-job transition is an important part of the reallocation of productive resources. Job-to-job transition, defined as a worker moving across jobs without experiencing nonemployment, is very common in the U.S. economy--occurring on a magnitude comparable to the movement of workers from employment to unemployment. It contributes to an improvement in resource allocation because workers tend to be better suited to the new job when they move; in support of this view, microeconomic studies have documented substantial wage gain at the time of job switch.1 While early literature on frictional unemployment argues that unemployment contributes to such reallocation by giving opportunities to find new jobs, this view has been criticized by Tobin (1972), who points out that many job switches occur without any intervening unemployment period and that the majority of these switches end up being an improvement.

Despite their significance, the macroeconomic implications of job-to-job transitions are much less studied than the flows across labor market states (employed, unemployed, and not in the labor force).2 One of the reasons for this discrepancy is the measurement challenge: the study of job-to-job transition requires panel data recording the identity of a worker's employer, and in the past no such data, both nationally representative and of sufficiently high frequency, were available. However, significant data development has occurred in recent years, and this paper uses the information from one of these datasets. Job-to-job transition is the only component of the total hires and separations that does not involve a switch across labor market states, and understanding its behavior enhances our knowledge on the process of worker reallocation.

In addition to its quantitative significance, job-to-job transition is also conceptually interesting. It can be viewed as a part of "separations" by the employer who is losing the worker, but from the viewpoint of the new employer, it is a part of "new hires." These dual views of job-to-job transition pose a challenge for how to model it appropriately.

Earlier studies observed that job-to-job transition rates in the United States are procyclical. Barlevy (2002) argues that recessions can reduce aggregate productivity through the lack of reallocation that results from this procyclicality. He names this effect the "sullying effect of recessions" and contrasts it with commonly argued efficiency gains in recessions coming from increased destruction of unproductive job-worker matches (often called the "cleansing effect of recessions").

The aim of this paper is to quantify the effect of job-to-job transitions on aggregate productivity using recent U.S. data and a simple model of on-the-job search. One advantage of this paper over Barlevy's study is that I use higher-frequency data based on the monthly Current Population Survey (CPS) from the Bureau of Labor Statistics (BLS), while Barlevy relied on annual data mainly from Panel Study of Income Dynamics.3 It turns out that the job-to-job transition rate has dramatically declined since the beginning of the 2000s, and the recent data further clarify its effect on productivity. Also, my model is substantially simpler than Barlevy's, and thus the role of each assumption is more transparent.

This paper makes two contributions. The first is its methodological contribution to the measurement of the job-to-job transition rate. This paper uses the monthly observation of job switching in the CPS, tabulated by Fallick and Fleishman (2004). One problem with using monthly observations is that they give no information on workers' behavior between two data points. For example, a worker who reports being employed in two consecutive months for different employers may have experienced brief unemployment in between. Since such short-time unemployment is cyclical, ignoring that possibility may bias the measured cyclicality of the true job-to-job transition. This bias, called a "time-aggregation bias," is discussed extensively in the context of measuring the true transitions between employment and unemployment (and other labor market states).4 Nagypál (2008) attempted to address this issue for job-to-job transition. Her approach was to use another dataset, the Survey of Income and Program Participation (SIPP), which contains weekly information on labor market status. In contrast, my method is analogous to the ones developed for the analysis of transition across labor market states, such as the one employed in Shimer (2012). Two main advantages of my approach are that it is a continuous-time adjustment and that it can be implemented easily without relying on other data sources.5 An additional advantage is that the underlying assumptions on the stochastic process are similar to the commonly employed methods for the transitions across different labor market states.

My second contribution is to use the time-aggregation adjusted data to examine the implications for aggregate productivity. To this end, I extend the model developed by Shimer (2005a). It is a simple model that keeps track of the movement of (ex post) heterogeneous workers. The model can provide rich predictions on how job-to-job transition rates evolve in the economy based only on a few assumptions about worker behavior. In the calibrated version of the model, I find that productivity loss from the recent decline in job-to-job transition can account for a large part of the recent decline in total factor productivity (TFP). In the basic model, about a 0.7% annual decline of TFP over 2009-2011 is accounted for by the mechanism described in the model. In the model with the cleansing effect of recessions, that is, a relatively larger destruction of bad job-worker matches during recessions, the annual decline of model TFP over the same period is about 0.5%.6

The paper is organized as follows. Section 2 describes the data and the methodology for time-aggregation adjustment. Section 3 looks further into the past by using information from another dataset. Section 4 analyzes a model of on-the-job search and quantitatively examines the implications of job-to-job transition on aggregate productivity. Section 5 extends the model to incorporate the cleansing effect of recessions. Section 6 concludes.


2  Data and time-aggregation adjustment

The data I use come from Fallick and Fleishman (2004).7 They use the "dependent interviewing" feature of CPS since its 1994 redesign.8 CPS has some panel aspects (BLS interviews the same household for 4 months and then, after an interval of 8 months, interviews them for 4 more months), and since the redesign, the interviewers have asked some questions that refer back to previous months' answers (this process is called "dependent interviewing"). In particular, if a person is employed in one month and also employed in the previous month, the interviewer asks whether the person still works for the same employer as reported in the previous month. Fallick and Fleishman construct series of the number (and the rate) of workers who work for the same employer, as well as the flows across different labor market states. I use their tabulation for all flow rates in 1996-2011.9 Since their tabulated numbers are not seasonally adjusted, I first use the X12-ARIMA procedure to perform seasonal adjustment for all flow rates (both job change and labor market state change). The fraction of the workers who stayed at the same labor market status are calculated as one minus the sum of the fractions of workers who changed their labor market status.

2.1  Time-aggregation adjustment: Method

Before performing the time-aggregation adjustment on the job-to-job transition data, I make the time-aggregation adjustment for the flows across the labor market states. I assume that the switch from labor market state $ i$ to $ j$ follows a Poisson process within a month, with the Poisson probability $ \lambda_t^{ij}$ between times $ t$ and $ t+1$. Here, $ i$ and $ j$ are each one of three labor market states: (i) employment $ E$, (ii) unemployment $ U$, and (iii) not in the labor force $ N$. The aim of the adjustment is to recover $ \lambda_t^{ij}$ from the observed flow (the fraction of workers who are in state $ j$ at time $ t+1$ among the ones who are in state $ i$ at time $ t$), $ p_t^{ij}$. This part of the adjustment is identical to Shimer (2012), and I do not repeat it here. For completeness, I describe the details of this procedure in Appendix A. This adjustment is independent of job-to-job switching behavior of workers, and thus I can make this adjustment first and use the results as inputs of the analysis below.

My time-aggregation adjustment of job-to-job transition data is based on a similar assumption--I assume that the direct job-to-job switch follows a Poisson process with probability $ \lambda_t^{JS}$ ($ JS$ represents "job switch"). The goal is to recover $ \lambda_t^{JS}$ from the information of the observed job-switching flow (the ratio of workers who are working for a different employer at time $ t+1$ among the ones who were working at time $ t$), denoted by $ p_t^{JS}$, as well as the above information ( $ \lambda_t^{ij}$ and $ p_t^{ij}$ for $ i,j=E, U, N$).

One important factor that influences this adjustment is the frequency of "recalls"--the many instances in which workers who separate from an employer come back to the original employer after working for another employer or experiencing a spell of nonemployment. The degree (and the direction) of time-aggregation adjustment depends on how frequently a recall occurs. In the following, I first present a general method that encompasses different frequency of recalls and then implement the method for two extreme cases.

My method proceeds with three steps. First, consider the fraction (among the workers employed at time $ t$) of workers who have never experienced the job-switching shock or the labor market state-changing shock between $ t$ and $ t+\tau$, where $ \tau\in[0,1)$. Call it $ \chi_0^E(t,t+\tau)$. It satisfies the following differential equation:

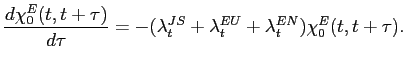
$\displaystyle \frac{d\chi^E_0(t,t+\tau)}{d\tau}=-(\lambda_t^{JS}+\lambda_t^{EU}+\lambda_t^{EN})\chi^E_0(t,t+\tau). $

With the boundary condition $ \chi^E_0(t,t)=1$, this equation can be solved as

$\displaystyle \chi^E_0(t,t+\tau)=\exp(-(\lambda_t^{JS}+\lambda_t^{EU}+\lambda_t^{EN})\tau).$ (1)

Second, consider the fraction (again, among the workers employed at time $ t$) of workers who (i) experienced a job-switching shock exactly once and (ii) have never changed their labor market state between time $ t$ and $ t+\tau$ to be $ \chi^E_1(t,t+\tau)$, where $ \tau\in[0,1)$. Call it $ \chi_1^E(t,t+\tau)$. It satisfies the following differential equation:

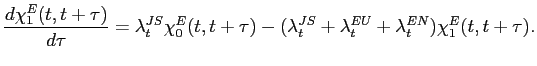
$\displaystyle \frac{d\chi^E_1(t,t+\tau)}{d\tau}=\lambda_t^{JS}\chi^E_0(t,t+\tau)-(\lambda_t^{JS}+\lambda_t^{EU}+\lambda_t^{EN})\chi^E_1(t,t+\tau). $

From the above solution for $ \chi^E_0(t,t+\tau)$ and the boundary condition $ \chi^E_1(t,t)=0$, the solution is

$\displaystyle \chi^E_1(t,t+\tau)=\tau \lambda_t^{JS}\exp(-(\lambda_t^{JS}+\lambda_t^{EU}+\lambda_t^{EN})\tau).$ (2)

Third, I make an assumption about recalls and use the above formulas to obtain the equation whose solution is $ \lambda_t^{JS}$. It is clear that, regardless of the existence of recalls, the workers who are in $ \chi^E_0(t,t+1)$ are not observed in $ p_t^{JS}$ (but are observed in $ p_t^{EE}$).10 It is also clear that, again regardless of the existence of recalls, the workers in $ \chi^E_1(t,t+1)$ are observed in $ p_t^{JS}$ (and also in $ p_t^{EE}$). The rest of the workers who are employed in both period $ t$ and $ t+1$, the workers in $ p_t^{EE}-\chi^E_0(t,t+1)-\chi^E_1(t,t+1)$, are in the "gray area." These workers include the ones who are hit by the job-switching shock more than twice within a month and the workers who are hit by the labor market state switching shock more than twice (and come back to employment) within a month. If there are no recalls, they would be working for a different employer at time $ t+1$ and therefore would be included in $ p_t^{JS}$. If there are recalls, some of them may be back at the original employer and, in that case, are not in $ p_t^{JS}$.

In general, therefore, the formula for the time-aggregation adjustment is the solution $ \lambda_t^{JS}$ to the equation

$\displaystyle p_t^{JS}=\chi^E_1(t,t+1)+(1-r_t)(p_t^{EE}-\chi^E_0(t,t+1)-\chi^E_1(t,t+1)),$ (3)

where $ \chi^E_0(t,t+1)$ and $ \chi^E_1(t,t+1)$ can be derived from (1) and (2). Note that $ r_t\in[0,1]$ is the ratio of recalled workers within "gray area" workers and that all variables in equation (3) are observable (or obtained earlier), except for $ \lambda_t^{JS}$.

Below I implement this time-aggregation adjustment method for two extreme cases.11 One is the case where there are no recalls: $ r_t=0$. The other is $ r_t=1$. The latter is the case where all workers who can possibly go back to the original employer actually go back. I call it the "perfect recall" case.

In the case of no recall, using (1) and (2) with $ \tau=1$, (3) can be rewritten as

$\displaystyle \lambda_t^{JS}=-\log(p_t^{EE}-p_t^{JS})-\lambda_t^{EU}-\lambda_t^{EN}.$ (4)

With the assumption of perfect recall, (3) boils down to $ \chi^E_1(t,t+1)=p_t^{JS}$. Thus, using (2) with $ \tau=1$, $ \lambda_t^{JS}$ is equal to the solution of

$\displaystyle \lambda_t^{JS}-\log(\lambda_t^{JS})=-\log(p_t^{JS})-\lambda_t^{EU}-\lambda_t^{EN}.$ (5)

Equations (4) and (5) are used to calculate $ \lambda_t^{JS}$ below.

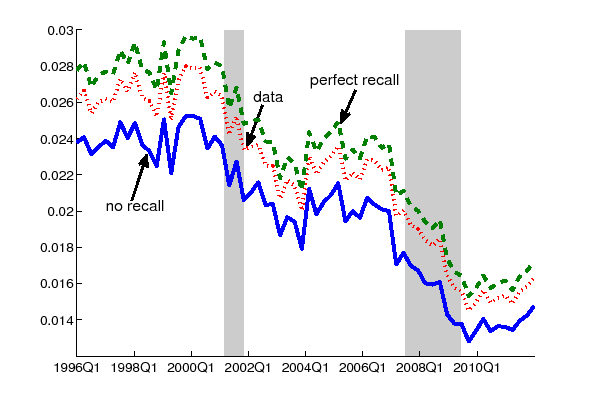
Figure 1: The probability of job-to-job transition with time-aggregation adjustment: (labeled as "data") and with different recall assumptions (labeled as "no recall" and "perfect recall")

Figure 1: Figure 1 plots three time series: the monthly job-to-job transition rate in the raw data and two time-aggregation adjusted series. One time-aggregation adjustment is made under the assumption of perfect recall and the other adjustment is made under the assumption of no recall. The y-axis runs from 0.012 to 0.03 and the x-axis runs from 1996Q1 to 2011Q4. All three series exhibit a procyclical pattern and a large decline since early 2000s.

2.2  Time-aggregation adjustment: Results

The probability of receiving a job switching shock at least once during one period is computed as

$\displaystyle \tilde p_t^{JS}=1-\exp(-\lambda_t^{JS}). $

Figure 1 plots $ p_t^{JS}$ (labeled as "data") and $ \tilde p_t^{JS}$ with the no recall assumption (labeled as "no recall") and the perfect recall assumption (labeled as "perfect recall"). The monthly $ p_t$ and $ \tilde p_t$ are somewhat noisy, and here I plot the quarterly average of the monthly results. All time series exhibit a procyclical pattern of job-switching behavior and a declining trend after the early 2000s. The decline in recent years is particularly dramatic: the job-switching probability in 2010-2011 is almost half of the probability in the late 1990s.

Regarding the time-aggregation adjustment, one can see that $ \tilde p_t^{JS}$ is smaller than $ p_t^{JS}$ in the no recall case, since the main correction that the adjustment accomplishes is the elimination of instances of within-period short-term unemployment that are contained in $ p_t^{JS}$. Note that $ \tilde p_t^{JS}$ in the perfect recall case is larger than $ p_t^{JS}$, since now all short-term unemployed are counted as "working for the same employer" in the data. Some workers experience the job-switching shock multiple times (or one job-switching shock and multiple labor market status-changing shocks) and end up at the original job by the assumption of perfect recall. These people are not counted in $ p_t^{JS}$ in the data but do experience job-switching shocks; thus the actual probability is adjusted upwards.12 In both cases, the time-aggregation adjustment is quantitatively small and does not significantly alter the cyclical properties of the job-switching shock. In particular, the assumption on recalls does not have a significant effect on the cyclical properties. The band between the no recall case and the perfect recall case is narrow, and the recent decline of $ \tilde p_t^{JS}$ is apparent regardless of how $ r_t$ changed over time.13

Figure 2: Unemployment-to-employment transition probability and employment-to-unemployment probability

Figure 2: Figure 2 plots two time series. The x-axis runs from 1996Q1 to 2011Q4. One is the job-finding probability in the data, and the y-axis corresponding to this series runs from 0.15 to 0.5. This series exhibit procyclicality. The other series is the separation probability in the data, and the y-axis corresponding to this series runs from 0.015 to 0.022. This series is countercyclical.

How should the recent dramatic decline be interpreted? A job-to-job transition has two "faces": it is a job finding (or a hiring from an employer's viewpoint) at the same time as it is a separation. Should it be interpreted as a job finding or a separation? Figure 2 plots the time series of $ \tilde p_t^{UE}$ and $ \tilde p_t^{EU}$, where, similar to $ \tilde p_t^{JS}$, $ \tilde p_t^{ij}$ is calculated as $ 1-\exp(-\lambda_t^{ij})$ ( $ i,j=E, U, N$). Clearly, the time series of $ \tilde p_t^{JS}$ looks more similar to $ \tilde p_t^{UE}$. Thus, it seems more reasonable to associate the job-switching behavior with the job-finding behavior. This observation is important in making the modeling choice later on.

Figure 3: The probability of job-to-job transition divided by the unemployment-to-employment transition probability

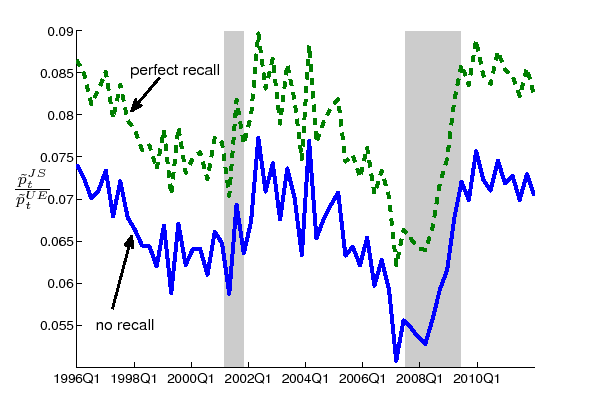
Figure 3: Figure 3 plots two time series. The x-axis runs from 1996Q1 to 2011Q4. Both represent the ratio of job-switching probability to the job-finding probability. One series is based on the job-switching probability with perfect recall assumption and the other series is based on the job-switching probability with perfect recall assumption. The y-axis runs from 0.05 to 0.09. Both series do not have a clear trend, but exhibit some cyclicality.

In order to see the similarities and discrepancies between job-switching and job-finding, I plot $ \tilde{p}_t^{JS}/\tilde{p}_t^{UE}$ in Figure 3.14 The first observation is that this ratio looks stationary: aside from cyclical movements, this ratio does not have an apparent trend. This finding is a stark contrast with Figure 1, which exhibits a clear downward trend. For example, at the recovery phase of the 2007-2008 recession, the level of $ \tilde{p}_t^{JS}$ is much lower compared to the previous recovery, but the level of $ \tilde{p}_t^{JS}/\tilde{p}_t^{UE}$ is almost the same as in the previous recovery. This finding indicates that common factors are influencing $ \tilde{p}_t^{UE}$ and $ \tilde{p}_t^{JS}$ with respect to the low level of both variables in recent years. Thus, if it is the case that the low job-finding probability of unemployed workers in recent years is the result of weak labor demand, it is likely that the same can be said for the job-to-job transitions.

The second observation about Figure 3 is that $ \tilde{p}_t^{JS}/\tilde{p}_t^{UE} $ has some cyclicality. It will be seen later on that the model can qualitatively replicate this pattern through the change in the composition of employed workers.


3  Looking further into the past

The main findings in Section 2 are that (i) job-to-job transition is procyclical and (ii) the job-to-job transition rate has declined significantly since the beginning of the 2000s. A natural question is how these facts compare to the behavior of the job-to-job transition rate in the past. The data in Section 2 can only go back to 1996, but this section uses another dataset to make this comparison.

Earlier studies, such as Blanchard and Diamond (1990) and Shimer (2005a) use the March supplement to the CPS to measure the annual job-to-job transition rate. Since 1976, the March CPS has asked workers the number of employers they worked for during the previous year. The workers are also asked the number of spells of job search. Using this information, Blanchard and Diamond (1990) construct three measures of the job-to-job finding rate, and Shimer (2005a) constructs three additional measures. Here I extend their analyses through 2011.

The information obtained from the March CPS is less ideal than the monthly information in Section 2 for the following three reasons: First, the survey is annual and thus less frequent than the typical frequency used in business cycle analysis. Second, there is a problem of "recall bias," since the survey relies on workers remembering their employment history over the previous year. Third, as will be mentioned below, some of the answers are "capped" by an upper bound. An obvious advantage of the March CPS is that it can go back until 1975 (the information from 1975 is in the 1976 survey), and the purpose of this section is to compare the information obtained from the March CPS to the results in Section 2 in order to obtain a historical perspective on the results obtained above.

I focus on Shimer's measures in this section and I discuss Blanchard and Diamond's measures in Appendix C. Shimer first computes $ \Theta_1\equiv \sum_{i=1}^3 n_i(i-1)$, where $ n_i$ is the number of workers who experienced $ i$ number of employers. He considers $ \Theta_1$ the "upper bound" of the total job-to-job transitions in the economy in the previous year, since the worker with $ i$ number of employers experienced the job-to-job transition $ i-1$ times at most. The value of $ i$ is capped at $ 3$ in the interview, and thus there still is a possibility that even this "upper bound" understates the total number of job-to-job transitions. To translate $ \Theta_1$ into the transition rate, it has to be divided by the number of employed workers in each year. Shimer approximates this figure by the total number of workers times the average fraction of weeks worked, which is equivalent to (total number of weeks worked)/52. He calls the result the "upper measure."

Shimer's second measure (the "lower measure") computes the same object as $ \Theta_1$ above, but only for the workers who reported working for 52 weeks. He considers this figure the "lower bound" of the total job-to-job transition since even the workers who did not work some part of the year may experience job-to-job transitions. Again, he divides this figure by (total number of weeks worked)/52 to obtain the transition rate.

His third measure (the "intermediate measure") uses an additional piece of information, which is the number of job search spells. He first computes $ \Theta_2\equiv \sum_{i=1}^3\sum_{j=0}^3 n_{ij}\max\{i-j-1,0\}$ instead of $ \Theta_1$. Here, $ i$ is the number of employers, $ j$ is the number of job search spells (which is also capped at 3), and $ n_{ij}$ is the number of workers who report $ i$ employers and $ j$ spells. Again, he divides $ \Theta_2$ by (total number of weeks worked)/52 to obtain the transition rate.

Figure 4 plots these three measures. Note that these measures are already "rates," so time-aggregation corrections are not necessary. For comparison, Figure 4 also plots the time series of $ \lambda_t^{JS}$ that is computed in Section 2 (with no recall, annual average), multiplied by $ 12$ so that it is adjusted from a monthly rate to an annual rate.

From 1996 to 2011, Shimer's measures from the March CPS are all lower than (the frequency-adjusted version of) $ \lambda_t^{JS}$ from Section 2. This difference is partly due to the caps in the March CPS measurement mentioned above. There is the additional issue of reporting error (recall bias). If the Poisson assumption does not hold in annual frequency, adjusting the frequency by multiplying by 12 may not be appropriate.

Figure 4: Annual job-to-job transition probabilities

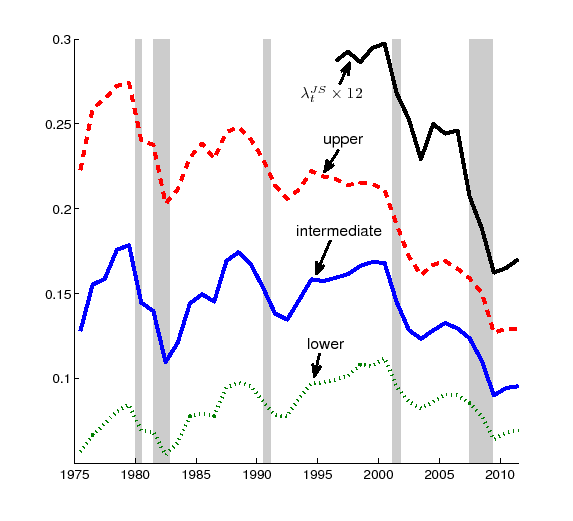
Figure 4: Figure 4 plots four series. The x-axis runs from 1975 to 2011. One is the annualized time-series of the job-switching probability that is calculated earlier in the paper from monthly CPS. The other three are calculated from the March CPS using the method of Shimer (2005a). The y-axis runs from 0.05 to 0.3. The level of each series is different, but all series exhibit procyclical pattern and a significant decline since early 2000s.

Despite the differences in level, however, the overall movement of the job-to-job transition rates over 1996-2011 is consistent across different measures. In particular, each series shows that the job-to-job transition rate is procyclical and that it exhibits a large decline from the beginning of the 2000s.

Looking back in time, the job-to-job transition rates were also procyclical in the 1980s and 1990s. Although different measures disagree in terms of levels, they all indicate that there was a large decline in the job-to-job transition rate in the early 1980s. They also provide some insight into the recent decline--the declines in each of the recent recessions (2001 and 2008-2009) were comparable to the past recessions, but the combined decline became unusually large because the recovery in the mid-2000s was very small.

One important conclusion from Figure 4 is that the amount of the total decline in job-to-job transition rates since the early 2000s is quite unusual, even compared to the historical standards from the 1970s. The next section analyzes how this decline has affected the macroeconomic performance of the U.S. economy.


4  Model

How does the procyclical job-to-job transition matter for macroeconomic performance? How about the persistent decline in the job-to-job transition rate in recent years? In order to assess the implications of the change in job-to-job transitions for aggregate productivity, I built a simple model and quantitatively evaluated it. The basic model is identical to the one used by Shimer (2005a), who analyzes an on-the-job search model in the tradition of Burdett (1978).15 It is a quantitative dynamic model of unemployment and job-to-job transition with a only few assumptions. This model focuses on the behavior of workers (employed workers in particular) and remains agnostic about employers' behavior. This agnosticism is an advantage rather than a shortcoming of the model, since I can directly use the measured probabilities that are calculated in the previous section without taking a stand on why these probabilities behave as observed. Since this model employs only a few assumptions, it is consistent with many models that have more structures.

4.1  Model setup

There are two background assumptions that I make throughout the following analysis. First, I only consider transitions between unemployment and employment, ignoring the "not in the labor force" status. This choice is mainly motivated by the simplicity of the analysis, but it is also based on the fact that our focus is the effect of labor market frictions (which are associated with unemployment) on resource allocation.16 To the extent that the job-to-job transition is about the match between a job and a worker, rather than the general (ex ante) productivity of workers, this omission should not have a large influence on my results.

The second background assumption is that the economy is in a steady state in the beginning of 1996 (with the parameter values that are measured in the first quarter of 1996). This assumption is made due to the lack of information, and I believe that it is reasonable, but it has to be kept in mind that the behavior of the model economy in the late 1990s is somewhat influenced by this assumption.

The model is in continuous time. At time $ s\in \mathbb{R}_+$, an unemployed worker finds a job with a Poisson rate $ f_s$. Each job-worker match is characterized by match quality, $ z$. The value of $ z$ stays constant over time during the lifetime of a particular match. I call a job with a higher value of $ z$ a "better job." Later I will be more specific about how I link the match quality to wage and productivity. On meeting, a new match draws a new $ z$ from a time-invariant distribution. I assume that $ z$ follows a uniform distribution on [0, 1]. As Shimer (2005a) argues, this assumption is without loss of generality (in my analysis, up to the point where I start measuring the aggregate productivity)--if the actual $ z$ follows a different distribution, one can consider the value of $ z$ on the uniform [0, 1] distribution to be its percentile at the actual distribution. An employed worker with match quality $ z$ loses a job and moves to unemployment at rate $ \ell_s(z)$. There is also on-the-job search: employed workers find an alternative job at rate $ f^e_s$.

The behavioral assumptions of the unemployed and the employed workers are the following:

  1. An employed worker accepts a job that is better than the current one.
  2. An unemployed worker accepts any job offer.

The first is relatively uncontroversial and holds in most of the existing models with on-the-job search. The idea here is that a job with a high match quality provides a better wage. (Later I will assume that a better job is also associated with higher productivity.) One implicit assumption here is that the mobility cost does not exist. If there is a substantial mobility cost, it is possible that the worker will decide not to move even if the newly offered job provides a better wage. It is unlikely, however, that this assumption is very important in our measurement--one can interpret the match quality of the new job as the "net benefit" after taking the mobility cost into account, or interpret $ f^e_s$ as the job offers that do not involve a very high mobility cost. The second assumption can be somewhat more controversial, given that unemployed workers' reservation wage may change over the business cycle.17 From the viewpoint of the measurement of the impact of procyclical job-to-job transition on productivity, a procyclical reservation wage would worsen the productivity during the recession, thus deepening the deterioration of productivity in recessions.18

In the basic model, an additional assumption is that all separations are exogenous, that is, $ \ell_s(z)$ is independent of $ z$. This assumption rules out the cleansing effect, and it is not necessarily suited for our purpose of contrasting the productivity loss from less job-to-job transition in recessions versus the productivity gain from the cleansing effect in recessions. Later I extend the model to make $ \ell_s(z)$ dependent on $ z$ in order to see to what extent incorporating the cleansing effect would change our conclusion.

Let $ E_s$ be the number of employed workers and $ U_s$ be the number of unemployed workers, where $ E_s+U_s=1$. Under the assumptions above, $ E_t$ satisfies the following differential equation:

$\displaystyle \frac{d E_s}{ds} = f_sU_s-\ell_sE_s.$ (6)

The quality distribution of active jobs is characterized by the density function $ g_s(z)$. That is, $ G_s(z)\equiv\int_0^z g_s(z')dz'$ is the number of employed workers with match quality below $ z$ at time $ s$. Note that $ g_s(z)$ satisfies the differential equation

$\displaystyle \frac{d(g_s(z) E_s)}{ds}=f_s U_s-\ell_s g_s(z)E_s-f^e_s(1-z)g_s(z)E_s+f^e_sG_s(z) E_s.$ (7)

The left-hand side is the change of the mass of employed workers who are employed at match quality $ z$. The first term in the right-hand side is the entry of workers with match quality $ z$ from unemployment. The second term is the exit by separation. The third term is the outflow from quality $ z$ due to job-to-job transition ( $ f^e_s(1-z)$ is the probability that they receive a job offer better than $ z$). The last term is the inflow from lower qualities into quality $ z$ due to job-to-job transition.

4.2  Calibration and computation

I solve the model numerically, with the assumption that in the beginning of 1996 the economy is in the steady state of (6) and (7), that is, $ dE_s/ds=0$ and $ dg_s(z)/ds=0$ for all $ z$. The inputs required are $ f_s$, $ f^e_s$, and $ \ell_s$. I assume that $ f_{t+\tau}=\lambda_t^{UE}$ and $ s_{t+\tau}=\lambda_t^{EU}$, where $ t=0,1,...$ (each month in the data) and $ \tau\in[0,1)$. Shimer (2005a) assumes that $ f^e_s$ is proportional to $ f_s$, and this seems reasonable given that we observed that the job-to-job transition rate looks similar to the job-finding rate of unemployed workers. Thus $ f^e_s=af_s$, where a constant $ a$ is set so that the steady-state job-to-job transition rate in the model (with the initial January 1996 values of $ \lambda_t^{EU}$ and $ \lambda_t^{UE}$) is identical to the January 1996 value of $ \lambda_t^{JS}$.19 This procedure leads us to set $ a$ equal to 0.247. It is not necessarily clear which value of $ a$ is a reasonable one--for example, Tobin (1972) criticizes the "frictional unemployment" models that do not include on-the-job search and argues that there is not much reason to rule out that $ a=1$.20 I will return to this point later on.

The computation of the model is based on discretization. I put 1000 grids on $ z$ and 10 grids on $ s$ (that is, one period is divided into 10 subperiods).

4.3  Results

Note that I have only used the initial value of $ \lambda_t^{JS}$ as the calibration target. Thus one way of assessing whether the model reflects the reality well is to compare the model-generated job-to-job transition rate to the job-to-job transition patterns in the data. In the model, the instantaneous job-switching probability can be computed as

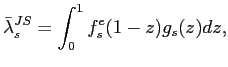
$\displaystyle \bar\lambda_s^{JS}= \int_0^1f^e_s(1-z)g_s(z)dz, $

and monthly job-to-job transition probability can be calculated as $ \bar p_t^{JS}=1-\exp(-\int_0^1\bar\lambda_{t+\tau}^{JS}d\tau)$.

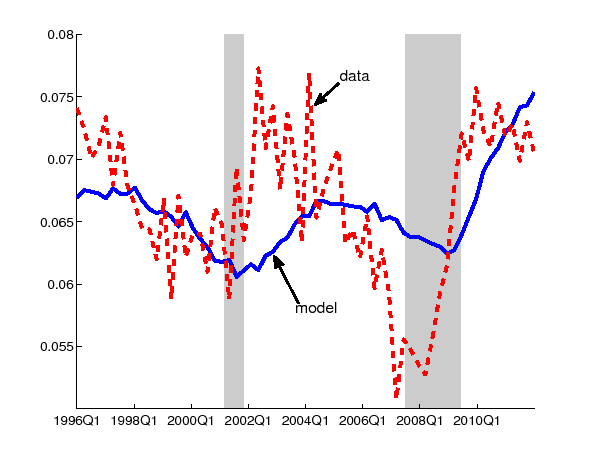
Figure 5 compares the job-to-job transition probability per month (average for each quarter) generated from the model to $ \tilde p_t^{JS}$ calculated from the data in the previous section (under the assumption of no recall--see Figure 1). The two time series match very well. To examine the difference between data and model more closely, Figure 6 plots the same probability ratio as Figure 3 for model and data (the data are the no recall case). The two series move in the same direction qualitatively. In particular, the model captures the property of the data that this ratio goes up in the beginning of the recovery and falls later on. This behavior is driven by the movement of the distribution of match quality over time. Because $ f^e_s$ falls during the recession, the distribution of match quality worsens during the recession (more and more workers are "mismatch employed"). When the recovery starts and $ f_s^e$ starts to go up, the job-to-job transition rate goes up faster than $ f_s^e$ does (and therefore faster than $ f_s$ does) because workers with a bad match are more willing to move, and at that point, there are more of them than at the average time. As the recovery continues, these workers with bad matches are "cleared up," and the distribution of the match quality improves. This improvement slows down the job-to-job transition rate. The job-to-job transition rate is high relative to the job-finding probability of unemployed workers in 2011 because the 2008-2009 recession was long and significantly deteriorated the distribution of match quality. Quantitatively, the mechanism of this basic model does not generate as much swing in this ratio as the data do.

Figure 5: Job-to-job transition probability per month, model and data

Figure 5: Figure 5 compares the job-to-job transition probability per month in the model and in the data. The x-axis runs from 1996Q1 to 2011Q4 and the y-axis runs from 0.01 to 0.028. The data series is identical to the adjusted series with no recall assumption in Figure 1. These two series look very similar.

Figure 6: The probability of job-to-job transition divided by the unemployment to employment transition probability, model and data

Figure 6: Figure 6 compares the ratio of job-switching probability to the job-finding probability in the model and the data. The x-axis runs from 1996Q1 to 2011Q4 and the y-axis runs from 0.05 to 0.08. The data series is identical to the adjusted series with no recall assumption in Figure 3. The model series is smoother than the data series, but qualitatively the two series tend to move in the same direction.

Next, I analyze the implications of the movement of the job-to-job transition probability on aggregate productivity. In order to analyze the aggregate productivity, I need to (i) specify the wage-offer distribution (rather than using a normalized uniform distribution) and (ii) link the wage to the productivity. Denote the wage of worker $ i$ working at employer $ j$ as $ w_{ij}$ and the worker's productivity as $ y_{ij}$. I assume that both consist of two parts: the worker-specific factor and the match-specific factor.21 Let

$\displaystyle \log(w_{ij})=\alpha_i+\varepsilon_{ij},$ (8)

where $ \alpha_i$ is the worker-specific factor and $ \varepsilon_{ij}$ is the match-specific factor, and

$\displaystyle \log(y_{ij})=\gamma_i+\eta\varepsilon_{ij}, $

where $ \gamma_i$ is the worker-specific factor and $ \eta>0$ is the inverse of the elasticity of wage with respect to productivity.22 When the match-specific productivity increases by 1%, the wage increases by $ 1/\eta$%. From the balanced-growth perspective, $ \eta=1$ is the most reasonable value in the long run. As is argued in Shimer (2005b) and Hornstein et al. (2007), in a typical Diamond-Mortensen-Pissarides model, $ 1/\eta$ is close to 1. Wage rigidity makes the value of $ \eta$ larger. Below we will consider the case with $ \eta=1$.

I assume that $ \alpha_i$ and $ \varepsilon_{ij}$ are independent, and also that $ \gamma_i$ and $ \varepsilon_{ij}$ are independent. (I allow $ \alpha_i$ and $ \gamma_i$ to be correlated--I do not need to make any further assumption about these two in the current context.) With these independence assumptions, given that different workers do not interact with each other (and $ f_s$, $ f_s^e$, and $ \ell_s$ are independent of $ \alpha_i$ and $ \gamma_i$), I will be able to omit $ \alpha_i$ and $ \gamma_i$ from the model and focus on $ \varepsilon_{ij}$. The reasoning is as follows. First, since $ \alpha_i$ does not change for a given worker, the worker's decision to switch jobs only depends on $ \varepsilon_{ij}$. Second, $ \gamma_i$ is irrelevant for the worker's decision. Thus, an economy where $ \log(w_{ij})$ is determined by (8) and an economy where $ \log(w_{ij})=\varepsilon_{ij}$ (or its monotonic transformation) would behave identically in terms of worker behavior. I will later use the average wage gain on switching a job for calibrating the dispersion of the wage-offer distribution. The log change of the wage from job $ j$ to job $ j'$ is $ \log(w_{ij})-\log(w_{ij'})=\varepsilon_{ij}-\varepsilon_{ij'}$, and it is also independent of $ \alpha_i$.

The aggregate productivity is measured as

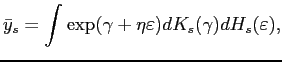
$\displaystyle \bar y_s=\int \exp(\gamma +\eta\varepsilon)dK_s(\gamma)dH_s(\varepsilon), $

where $ K_s(\gamma)$ is the distribution function of $ \gamma$ and $ H_s(\varepsilon)$ is the distribution function of $ \varepsilon$. From the independence assumption (and the fact that the behavior of a worker is independent of $ \gamma$), the distributions of $ \gamma$ and $ \varepsilon$ are independent across employed workers. Thus when the average productivity is compared to its initial time $ s_0$ (that is, January 1996) level,

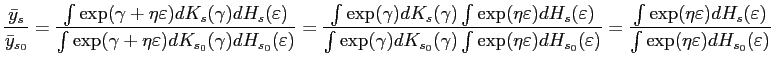
$\displaystyle \frac{\bar y_s}{\bar y_{s_0}}=\frac{\int \exp(\gamma +\eta\varepsilon)dK_s(\gamma)dH_s(\varepsilon)}{\int \exp(\gamma +\eta\varepsilon)dK_{s_0}(\gamma)dH_{s_0}(\varepsilon)}=\frac{\int \exp(\gamma)dK_s(\gamma)\int\exp(\eta\varepsilon)dH_s(\varepsilon)}{\int \exp(\gamma)dK_{s_0}(\gamma)\int\exp(\eta\varepsilon)dH_{s_0}(\varepsilon)}=\frac{\int\exp(\eta\varepsilon)dH_{s}(\varepsilon)}{\int\exp(\eta\varepsilon)dH_{s_0}(\varepsilon)} $

holds, and this ratio is independent of $ \alpha$ and $ \gamma$. The second equality is from the independence of $ \gamma$ and $ \varepsilon$. The third equality holds because the distribution of $ \gamma$ among employed workers is identical over time because of the independence assumption and the fact that the behavior of a worker is independent of $ \gamma$.

I choose the distribution of $ \varepsilon$ in offered wages so that the steady-state distribution of $ H_s(\varepsilon)$ at $ s=s_0$ (with all parameter values at $ s_0$) follows a normal distribution with mean 0 and variance $ \sigma^2$. (Thus the wage conditional on $ \alpha_i$ follows a lognormal distribution.) I set the value of $ \sigma$ so that the average wage gain on switching a job in the model (in the initial steady state) matches the data. Given other parameters, a higher $ \sigma$ increases the wage dispersion and the average gain from switching a job. Here I follow Topel and Ward's (1992) estimate of the average wage gain from switching a job being about 12% and use it as the target.23

The resulting value of $ \sigma$ is 0.13.24 This value implies that the wage ratio of the 90th percentile to the 50th percentile (and also of the 50th percentile to the 10th percentile) is 1.18, which is much smaller than measured wage dispersion. Autor, Katz, and Kearney's (2008) measure of the "residual wage inequality" (the wage inequality after controlling for observable worker characteristics) gives this ratio at about 1.5 to 1.8 (from their Figure 8). Lemieux's (2006) result is somewhat smaller, but it implies a log standard deviation of the residual wage of 0.41 to 0.44 (from his Figure 1). Not all residual wage inequality is the result of the heterogeneity in match quality, and therefore it is reasonable that my $ \sigma$ is smaller than the estimates from the residual wage inequality. If I assume a higher value of $ \sigma$, the effect of the change in job-to-job transition rate on aggregate productivity would be stronger.

Figure 7: Average match quality from the model (relative to 1996:Q1 level) and the utilization-adjusted TFP (deviation from the trend) in the data

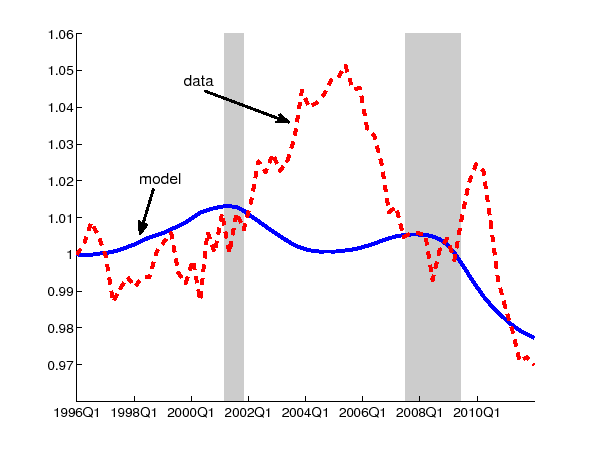
Figure 7: Figure 7 compares the average match quality from the model and the de-trended utilization-adjusted TFP level. Both are constructed so that the initial level in the graph is 1. The x-axis runs from 1996Q1 to 2011Q4 and the y-axis runs from 0.96 to 1.06. Both series exhibits an increase before 2000 and after 2008, but the model series stays low during mid-2000s while the data series exhibits a significant increase.

Figure 7 presents the results. The solid line plots $ \bar y_s/\bar y_{s_0}$. The dotted line is the de-trended utilization-adjusted TFP level (normalizing the 1996:Q1 level as 1) calculated from Fernald's (2012) dataset.25 The trend is assumed as constant 0.25% quarterly growth. Note that the model is not meant to explain all of the movements in TFP. There are factors other than reallocations that change TFP--each job-worker match can become more productive over time, for example. In Figure 7, reallocations due to job-to-job transitions do not contribute much to the increase in TFP in the early 2000s, while they account for a large part of the TFP decline in the recent few years. From the start of 2009, the model accounts for about a 0.7% annual decline in the TFP.


5  The role of the cleansing effect

This section extends the model to incorporate the idea of the cleansing effect of recessions. The basic structure of the model remains the same, but here I make the separation rate $ \ell_s$ dependent on $ z$ (and denote it as $ \ell_s(z)$). In particular, I will assume that $ \ell_s(z)$ is decreasing in $ z$--a job with low match quality is destroyed more frequently. In the following, I consider two different specifications of $ \ell_s(z)$.

5.1  Weak cleansing

The first specification is

$\displaystyle \ell_s(z)=\ell_s(1)[1+(\zeta-1) (1-z)], $

where $ \zeta\geq 1$ is a parameter. This equation implies that $ \ell_s(0)=\zeta \ell_s(1)$ for all $ s$. The value of $ \ell_{t+\tau}(1)$ at each $ t=0,1,...$ and $ \tau\in[0,1)$ is set so that the separation rate at each instant is consistent with the data:

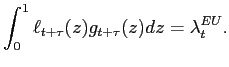
$\displaystyle \int_0^1 \ell_{t+\tau}(z)g_{t+\tau}(z)dz=\lambda_t^{EU}.$ (9)

The special case with $ \zeta=1$ is the model in Section 4. The case with $ \zeta>1$ exhibits a cleansing effect in the sense that when $ \lambda_t^{EU}$ increases, $ s_{t+\tau}(z)$ increases for all $ z$ but increases more for a smaller $ z$. That is, for a different time $ t+\tau$ and $ t'+\tau'$ ( $ t,t'=0,1,...$ and $ \tau,\tau'\in[0,1)$),

$\displaystyle \ell_{t'+\tau'}(z)-\ell_{t+\tau}(z)=(\ell_{t'+\tau'}(1)-\ell_{t+\tau}(1))[1+\zeta(1-z)]. $

Thus when $ \ell_{t'+\tau'}(1)>\ell_{t+\tau}(1)$, $ \ell_{t'+\tau'}(z)-\ell_{t+\tau}(z)$ is decreasing in $ z$. I call this specification "weak cleansing." It is called "weak" since the ratio of separation rates $ \ell_{t'+\tau'}(z)/\ell_{t+\tau}(z)$ is independent of $ z$.

In this section and the following, I focus on the case of $ \eta=1$. Note that the other parameters have to be adjusted with the change of $ \ell_s(z)$. The dispersion of the log-wage offer distribution, $ \sigma$, has to be adjusted so that the average wage gain on job change is still 12%. The efficiency of on-the-job search compared to off-the-job search, $ a$, has to adjust so that the job-to-job transition rate at the initial time (January 1996) is consistent between the data and the steady state of the model. In general, both $ \sigma$ and $ a$ have to increase with $ \zeta$. These adjustments have to be made because more cleansing implies that the steady-state distribution of match quality is better for a given set of parameter values, and therefore there is less room for improvement for an already employed worker.

Figure 8: Average match quality from the model (relative to 1996:Q1 level) without cleansing effect ($ \zeta=1$), with $ \zeta=25$, and $ \zeta=75$

Figure 8: Figure 8 compares the average match quality series in Figure 7 with the series under the assumption of =25 and =75. They move similarly, although the ones with =25 and =75 exhibit smaller ups and downs. The x-axis runs from 1996Q1 to 2011Q4 and the y-axis runs from 0.97 to 1.015.

Since a good estimate of $ \zeta$ is not available, I compare several cases with different values of $ \zeta$, ranging from $ \zeta=1$ (no cleansing effect) to an extremely large value of $ \zeta$. Figure 8 compares three cases: $ \zeta=1$, $ \zeta=25$, and $ \zeta=75$. The $ \zeta=1$ case is analyzed in the previous section. The case with $ \zeta=25$ is already quite extreme--it implies that $ \ell_s(0)$ is 25 times larger than $ \ell_s(1)$. In this case, $ \sigma$ is adjusted to 0.16 and $ a$ is adjusted to 0.63. The case with $ \zeta=75$ requires $ \sigma=0.18$ and $ a=1.00$. The value of $ a=1.00$ means that an employed worker receives job offers with the same frequency as an unemployed worker. Tobin (1972) argues that there is no evidence that an employed worker is less efficient in job finding than an unemployed worker; thus $ a=1.00$ is a useful benchmark from this perspective.

Comparing different time paths of the average match quality in Figure 8, it can be seen that the existence of the cleansing effect dampens its fluctuations. Because of the cleansing effect, the average match quality increases over a large part of the 2007-2008 recession in the cases of $ \zeta=25$ and $ \zeta=75$. The drop of average match quality from the peak in recent years (2008:Q4 for $ \zeta=25$ and 2009:Q1 for $ \zeta=75$) to the end of 2011 is still sizable in both cases: 1.7% for $ \zeta=25$ and 1.4% for $ \zeta=75$. The existence of the cleansing effect does not overturn the detrimental effect of reduced reallocation. In particular, even with these extreme specifications, the model accounts for about a 0.5% annual decline in TFP.

5.2  Strong cleansing

The second formulation I consider is

$\displaystyle \ell_s(z)=\ell_{s_0}(1)[1+(\tilde\zeta_s-1) (1-z)],$ (10)

where $ s_0$ is the initial time (January 1996). When $ s=s_0$, $ \tilde\zeta_s$ is set equal to the value of a parameter $ \xi$. Equation (10) means that $ \ell_s(1)$ is always constant at the value of $ \ell_{s_0}(1)$ and that $ \ell_s(0)=\tilde\zeta_s \ell_s(1)$ for all $ s$. When $ s= s_0$, the value of $ \ell_{s_0}(1)$ is set so that (9) is satisfied at the steady state of the model with $ t=s_0$ (that is, January 1996) parameters. When $ s\neq s_0$, $ \tilde\zeta_s$ is adjusted so that (9) is satisfied for each particular $ s$ (with $ s=t+\tau$). Therefore, other things equal, $ \tilde\zeta_{t+\tau}$ is high when $ \lambda_t^{EU}$ is high for $ t=0,1,...$ and $ \tau\in[0,1)$. I call this case "strong cleansing" because not only is the difference of the separation rates $ \ell_{t'+\tau'}(z)-\ell_{t+\tau}(z)=\ell_{s_0}(1)(\tilde\zeta_{t'+\tau'}-\tilde\zeta_{t+\tau}) (1-z)$ decreasing in $ z$ when $ \lambda_{t'}^{EU}>\lambda_{t}^{EU}$, but also the ratio $ \ell_{t'+\tau'}(z)/\ell_{t+\tau}(z)=[1+(\tilde\zeta_{t'+\tau'}-1) (1-z)]/[1+(\tilde\zeta_{t+\tau}-1) (1-z)]$ is also decreasing in $ z$ in that case (where $ t,t'=0,1,....$ and $ \tau,\tau'\in[0,1)$).

Figure 9: Average match quality from the model (relative to 1996:Q1 level) without cleansing effect and $ \xi=75$.

Figure 9: Figure 9 compares the average match quality series in Figure 7 with the series under the assumption of =25. They move similarly, although the series with =75 exhibits smaller ups and downs. The x-axis runs from 1996Q1 to 2011Q4 and the y-axis runs from 0.97 to 1.015.

Figure 9 compares the no cleansing case with the case with $ \xi=75$. In the initial steady state, the $ \xi=75$ case is identical to the $ \zeta=75$ case in the previous section, so the parameters of $ \sigma=0.18$ and $ a=1.00$ are the same as in that case. It can be seen that, similar to the previous section, the existence of the cleansing effect dampens the fluctuations of the average match quality and also tends to raise the match quality during the recessions. In the $ \xi=75$ case, the drop from the recent peak (2009:Q1) to the end of 2011 is 1.6%--still a sizable amount. Similar to the previous section, the model accounts for about a 0.5% annual decline of TFP. The main takeaway from this section is that the main conclusion of Section 4, that a sizable decline of TFP in recent years is accounted for by the decline in the job-to-job transition, is robust to the inclusion of an extreme amount of the cleansing effect.


6  Conclusion

This paper analyzes the job-to-job transition behavior of workers. The paper has two contributions. First, it develops a simple method of time-aggregation correction for the data. Second, using a simple model, it evaluates the effect of the recent movement of job-to-job transition rates on aggregate productivity.

My time-aggregation adjustment method is simple and uses a similar set of assumptions to the existing adjustment methods for other labor market flows. The adjusted time series reveals that the behavior of the job-to-job transition is procyclical and has been declining since the early 2000s. My method can accommodate recalls--the existence of recalls alters the outcome of the adjustment, but it does not overturn the cyclicality and the recent declining trend.

The model is based on a few simple assumptions about worker behavior. The decline of job-to-job transitions reduces the reallocation of workers to better matches and therefore is detrimental to aggregate productivity. The calibrated version of the model reveals that the change in job-to-job transition rates significantly affects aggregate productivity. From 2009 to 2011, the model TFP declined about 0.7% annually.

My model can accommodate the cleansing effect of recessions, that is, that more bad matches are destroyed during recessions compared to good matches, improving aggregate productivity. It turns out that even under extreme assumptions about the cleansing effect, the model accounts for a large decline in productivity in recent years--from 2009 to 2011, the model TFP declined about 0.5% annually.

This paper focuses on the consequences rather than the causes of the change in job-to-job transition rates. A natural question is why the job-to-job transition rate behaves in the observed manner. To answer this question, one has to analyze the incentives of the employers in hiring workers from the employment pool as well as from the nonemployment pool. This important future research topic is beyond the scope of this paper.


Appendix


A  Three-state time-aggregation adjustment

The following method is identical to the one developed by Shimer (2012). Let $ \lambda_t^{ij}\geq 0$ denote the Poisson arrival probability of a shock that moves a worker from state $ i$ to state $ j$ ($ i\neq j$), where $ i,j\in \{E,U,N\}$, which applies during the time interval $ [t,t+1)$. For example, denoting the number of workers in state $ i$ at time $ t+\tau\in[t,t+1)$ as $ \chi^i(t+\tau)$,

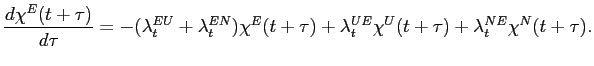
$\displaystyle \frac{d \chi^E (t+\tau)}{d\tau}= -(\lambda_t^{EU}+\lambda_t^{EN})\chi^E(t+\tau)+\lambda_t^{UE}\chi^U(t+\tau)+\lambda_t^{NE}\chi^N(t+\tau). $

Let $ \lambda^{ii}_t\equiv -\sum_{i\neq j} \lambda_t^{ij}$. Then, the above equation becomes

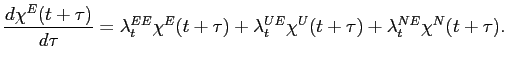
$\displaystyle \frac{d \chi^E (t+\tau)}{d\tau}= \lambda_t^{EE}\chi^E(t+\tau)+\lambda_t^{UE}\chi^U(t+\tau)+\lambda_t^{NE}\chi^N(t+\tau). $

With a discrete-time approximation, denoting $ \Delta$ as a small time interval,

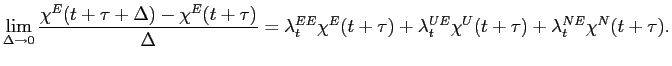
$\displaystyle \lim_{\Delta\rightarrow 0}\frac{\chi^E(t+\tau+\Delta)-\chi^E(t+\tau)}{\Delta}=\lambda_t^{EE}\chi^E(t+\tau)+\lambda_t^{UE}\chi^U(t+\tau)+\lambda_t^{NE}\chi^N(t+\tau). $

Let

\begin{displaymath} \chi(t+\tau)\equiv\left( \begin{array}{c} \chi^E(t+\tau)\ \chi^U(t+\tau)\ \chi^N(t+\tau) \end{array}\right) \end{displaymath}

and

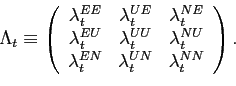
\begin{displaymath} \Lambda_t\equiv\left( \begin{array}{c c c} \lambda_t^{EE} & \lambda_t^{UE} & \lambda_t^{NE}\ \lambda_t^{EU} & \lambda_t^{UU} & \lambda_t^{NU}\ \lambda_t^{EN} & \lambda_t^{UN} & \lambda_t^{NN} \end{array}\right). \end{displaymath}

Note that each column sums to 0. The transition equation can be written in matrix form:

$\displaystyle \lim_{\Delta\rightarrow 0}\frac{\chi(t+\tau+\Delta)-\chi(t+\tau)}{\Delta}=\Lambda_t \chi(t+\tau).$ (11)

Since $ \lambda$'s are not directly observed, $ \Lambda$ is recovered from the observed Markov transitions in discrete time. Let $ p_t^{ij}$ be the probability of a worker moving from state $ i$ to $ j$ (where $ i,j\in\{E,U,N\}$) between periods $ t$ and $ t+1$. Inmatrix form,

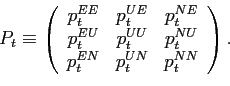
\begin{displaymath} P_t\equiv \left( \begin{array}{c c c} p_t^{EE} & p_t^{UE} & p_t^{NE}\ p_t^{EU} & p_t^{UU} & p_t^{NU}\ p_t^{EN} & p_t^{UN} & p_t^{NN} \end{array}\right). \end{displaymath}

Note that each column sums to 1. The matrix $ P_t$ can be recovered from the CPS data (with the assumption that all workers are subject to the same shock probabilities). In terms of the populations,

$\displaystyle \chi(t+1)=P_t\chi(t) $

holds.

If we divide one period into a sequence of ($ 1/\Delta$ numbers of) subperiods whose length is $ \Delta$ each, the transition probability during each subperiod can be defined as $ P_{t,\Delta}$, which satisfies

$\displaystyle P_t={P_{t,\Delta}}^{1/\Delta}.$ (12)

Also, for $ \tau=0,\Delta, 2\Delta,...$,

$\displaystyle \chi(t+\tau+\Delta)=P_{t,\Delta}\chi(t+\tau) $

holds. Thus, once a $ P_{t,\Delta}$ that satisfies (12) is found,

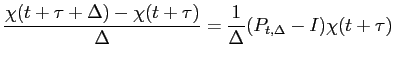
$\displaystyle \frac{\chi(t+\tau+\Delta)-\chi(t+\tau)}{\Delta}=\frac{1}{\Delta}(P_{t,\Delta}-I)\chi(t+\tau) $

(where $ I$ is the identity matrix) can be calculated, and from (11), $ \Lambda_t$ can be recovered by

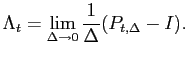
$\displaystyle \Lambda_t=\lim_{\Delta\rightarrow 0} \frac{1}{\Delta}(P_{t,\Delta}-I). $

In order to calculate the right-hand side of the equation, suppose first that $ P_t$ can be diagonalized as

$\displaystyle P_t=V_tD_t{V_t}^{-1}, $

where is the diagonal matrix (and suppose that all elements of $ D_t$ are real and distinct) of $ P_t$'s eigenvalues an$ D_t$d $ V_t$ consists of corresponding eigenvectors. Then the matrix $ P_{t,\Delta}$, calculated by

$\displaystyle P_{t,\Delta}=V_t{D_t^\Delta}{V_t}^{-1}, $

where $ D_t^\Delta$ is a diagonal matrix whose elements are the corresponding elements of $ D_t$ raised to the $ \Delta$th power) satisfies (). Therefore (since $ I=V_tI{V_t}^{-1}$ for any $ V_t$),

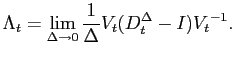
$\displaystyle \Lambda_t=\lim_{\Delta\rightarrow 0}\frac{1}{\Delta}V_t(D_t^\Delta-I){V_t}^{-1}. $

And since $ \lim_{\Delta\rightarrow 0} (d^\Delta-1)/\Delta=\log d$,

$\displaystyle \Lambda_t=V_t\tilde D_t{V_t}^{-1}, $

where $ \tilde D_t$ is a diagonal matrix whose diagonal elements are the natural log of corresponding elements of $ D_t$.


B  An alternative value of 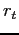$ r_t$ in time-aggregation adjustment

In a recent paper, Fujita and Moscarini (2013) measure the frequency of recalls using the SIPP data. The average value of the recall probability in their data is about 37% (the average value of their Table 3, third row). Here, I use $ r_t=0.37$ to the method developed in Section 2.1.26 In particular, I solve the equation (3) using (1) and (2) for $ \lambda_t^{JS}$ under the assumption of $ r_t=0.37$. The values of $ p_t^{JS}$ and $ p_t^{EE}$ directly come from the data, and $ \lambda_t^{EU}$ and $ \lambda_t^{EN}$ are calculated using the method of Appendix A.

Figure 10: The probability of job-to-job transition with time-aggregation adjustment: $ p_t^{JS}$ (labeled as "data") and $ \tilde p_t^{JS}$ with $ r_t=0.37$

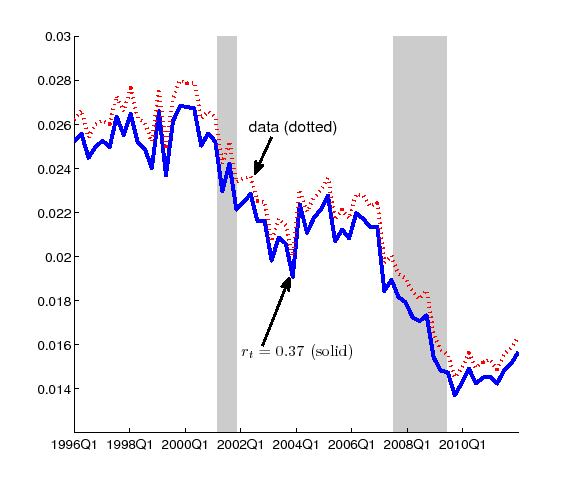
Figure 10: Figure 10 plots the data series from Figure 1 with the time-aggregation adjusted series with the assumption of r_t=0.37. The y-axis runs from 0.012 to 0.03 and the x-axis runs from 1996Q1 to 2011Q4. The time-aggregation adjusted series is slightly smaller, but both series look very similar.

Figure 10 corresponds to Figure 1 in the main text. The time-aggregation adjustment moves the job-switching probability down, but the magnitude of adjustment is small and the cyclicality of the adjusted series is very similar to that of the original data.


C  Job-to-job transition rates following Blanchard and Diamond (1990)

Blanchard and Diamond (1990) construct the time series of job-to-job transition rates using the information from the March CPS. They characterize individuals with three numbers: $ x$, $ y$, and $ z$. They set $ x$ equal to 1 if the individual was not in the labor force at any point during the year, and 0 otherwise. Their $ y$ runs from 0 to 3 and stands for the number of employers (here, 3 is actually 3 or more since the number is capped). Their $ z$ also runs from 0 to 3, and it stands for stretches of unemployment (again, it is capped at 3; also note that $ z$ is unknown for a worker who did not work during the year and was not in the labor force at least once). Let $ X_{xyz}$ be the fraction of individuals in each category.

Blanchard and Diamond then calculate the "upper bound" measure, the intermediate ("best guess") measure, and the "lower bound" measure by

   upper$\displaystyle =\sum_{z=0}^3 X_{02z}+2\sum_{z=0}^3 X_{03z}+\sum_{z=0}^3 X_{12z}+2\sum_{z=0}^3 X_{13z}, $
   intermediate$\displaystyle =X_{020}+0.5X_{021}+2X_{030}+1.5X_{031}+0.5X_{120}+1.5X_{130}+X_{131}, $

and

   lower$\displaystyle =X_{020}+2X_{030}+X_{031}+X_{130}. $

Figure 11: Annual job-to-job transition probabilities

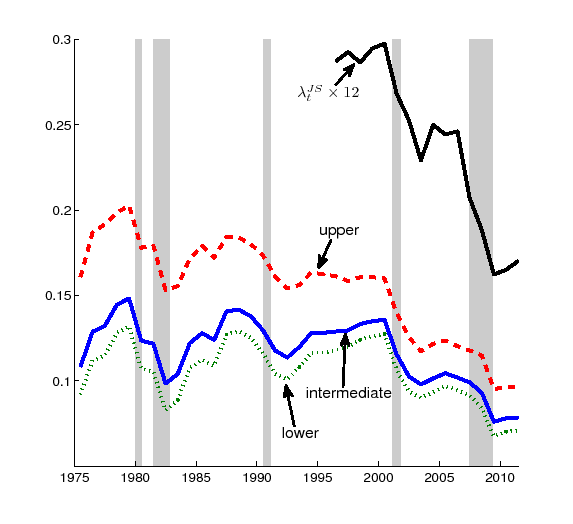
Figure 11: Figure 11 repeats the same plot as Figure 4, but instead of Shimer’s (2005a) method, it follows Blanchard and Diamond’s (1990) method. Again, there are four series: one is from the monthly CPS and three are from March CPS. The x-axis runs from 1975 to 2011 and the y-axis runs from 0.05 to 0.3. The level of each series is different, but all series exhibit procyclical pattern and a significant decline since early 2000s.
 

Figure 11 plots these three series, along with $ \lambda_t^{JS}\times 12$ from Section 2 (with no recall, annual average). The overall properties are similar to Shimer's (1995a) measures, and the discussions in Section 3 also apply here.


References

Autor, David H.; Lawrence F. Katz; and Melissa S. Kearney (2008). "Trends in U.S. Wage Inequality: Revising the Revisionists," Review of Economics and Statistics 90, 300-323.

Barlevy, Gadi (2002). "The Sullying Effect of Recessions," Review of Economic Studies 69, 65-96.

Blanchard, Olivier J. and Peter Diamond (1990). "The Cyclical Behavior of the Gross Flows of U.S. Workers," Brookings Papers on Economic Activity 2, 85-155.

Blanchard, Olivier and Jordi Galí (2010). "Labor Markets and Monetary Policy: A New Keynesian Model with Unemployment," American Economic Journal: Macroeconomics 2, 1-30.

Burdett, Kenneth (1978). "A Theory of Employee Search and Quits," American Economic Review 68, 212-220.

Elsby, Michael W. L.; Ryan Michaels; and Gary Solon (2009). "The Ins and Outs of Cyclical Unemployment," American Economic Journal: Macroeconomics 1, 84-110.

Fallick, Bruce and Charles A. Fleischman (2004). "Employer-to-Employer Flows in the U.S. Labor Market: The Complete Picture of Gross Worker Flows," FEDS Working Papers 2004-34, Federal Reserve Board.

Fallick, Bruce; John Haltiwanger; and Erika McEntarfer (2012). "Job-to-Job Flows and the Consequences of Job Separations," FEDS Working Paper 2012-73.

Fernald, John (2012). "A Quarterly, Utilization-Adjusted Series on Total Factor Productivity," Federal Reserve Bank of San Francisco Working Paper 2012-19.

Fujita, Shigeru and Giuseppe Moscarini (2013). "Recall and Unemployment," mimeo. Federal Reserve Bank of Philadelphia and Yale University.

Hagedorn, Marcus and Iourii Manovskii (2010). "Search Frictions and Wage Dispersion," mimeo. University of Zurich and University of Pennsylvania.

Hall, Robert E. and Andreas Müller (2012). "Viewing Job-Seekers' Reservation Wages and Acceptance Decisions through the Lens of Search Theory," mimeo. Stanford University and Columbia Business School.

Hornstein, Andreas; Per Krusell; Giovanni L. Violante (2005). "Unemployment and Vacancy Fluctuations in the Matching Model: Inspecting the Mechanism," Federal Reserve Bank of Richmond Economic Quarterly 19-50.

Hyatt, Henry and Erika McEntarfer (2012). "Job-to-Job Flows and the Business Cycle," CES Discussion Paper 12-04.

Krueger, Alan B. and Andreas Mueller (2011). "Job Search, Emotional Well-Being, and Job Finding in a Period of Mass Unemployment: Evidence from High-Frequency Longitudinal Data," Brookings Papers on Economic Activity, Spring, 1-70.

Krusell, Per; Toshihiko Mukoyama, Richard Rogerson, and Aysegül Sahin (2012). "Is Labor Supply Important for Business Cycles?" NBER WP 17779.

Lazear, Edward P. and James R. Spletzer (2012). "Hiring, Churn and the Business Cycle," NBER WP 17910.

Lemieux, Thomas (2006). "Increased Residual Wage Inequality: Composition Effects, Noisy Data, or Rising Demand for Skill?" American Economic Review 96, 461-498.

Moscarini, Giuseppe and Kaj Thomsson (2007). "Occupational and Job Mobility in the U.S.," Scandinavian Journal of Economics 109, 807-836.

Nagypál, Éva (2008). "Worker Reallocation over the Business Cycle: The Importance of Employer-to-Employer Transition," mimeo. Northwestern University.

Nunn, Ryan (2012). "Match Quality with Unpriced Amenities," mimeo. University of Michigan.

Postel-Vinay, Fabien and Jean-Marc Robin (2002). "Equilibrium Wage Dispersion with Worker and Employer Heterogeneity," Econometrica 70, 2295-2350.

Shimer, Robert (2005a). "The Cyclicality of Hires, Separations, and Job-to-Job Transitions," Federal Reserve Bank of St. Louis Review 87, 493-507.

Shimer, Robert (2005b). "The Cyclical Behavior of Equilibrium Unemployment and Vacancies," American Economic Review 95, 25-49.

Shimer, Robert (2012). "Reassessing the Ins and Outs of Unemployment," Review of Economic Dynamics 15, 127-148.

Tobin, James (1972). "Inflation and Unemployment," American Economic Review 62, 1-18.

Topel, Robert H. and Michael P. Ward (1992). "Job Mobility and the Careers of Young Men," Quarterly Journal of Economics 107, 439-479.


Footnotes

**  Federal Reserve Board and University of Virginia, e-mail: toshihiko.mukoyama@frb.gov. I thank Tomaz Cajner, Bruce Fallick, David Ratner, Aysegul Sahin, and Jim Spletzer for comments and John Weber for excellent research assistance. The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1.  See, for example, Topel and Ward (1992). Return to text

2.  See, for example, Shimer (2012) for an empirical study of the cyclicality of flows across labor market states. Krusell et al. (2012) analyzes a theoretical model of flows across labor market states. Return to text

3.  Barlevy also identifies the job-to-job transition rate with quit rates, rather than measuring it directly. Nagypál (2008) argues that job-to-job transitions follow both layoffs and quits, although their share among quits is higher. In her analysis of the Survey of Income and Program Participation (SIPP) dataset, which contains weekly information on labor market status, 55% of the layoffs are followed by a job-to-job transition. Return to text

4.  See, for example, Shimer (2012). Return to text

5.  Note that a recent paper by Elsby, Michaels, and Solon (2009) discusses some caveats on using a continuous-time adjustment. I will discuss one of these caveats below. Return to text

6.  Lazear and Spletzer (2012) documents that the replacement hire (they use the term "churn") is procyclical using the Job Openings and Labor Turnover Survey. Churn and job-to-job transitions are both a part of the gross worker flow, but they are conceptually distinct. An economy can have a large amount of churn without any job-to-job transitions and an economy can have many job-to-job transitions with no churn. (They are not unrelated--in an economy without any job flows, a job-to-job transition necessarily creates churn.) In their Figure 1, the churn is procyclical but does not have a declining trend from early 2000s, unlike the job-to-job transition rate. In measuring "the cost of reduced churn" in recent years, they use the wage gain from job-to-job transition measured in Fallick, Haltiwanger, and McEntarfer (2012), which does not necessarily correspond to the gain from churn. (In order to measure the gain from churn, they need a productivity gain from replacing a worker in a given position.) The analysis of this paper has a more direct link between the model and the data. Return to text

7.  They update their tabulation at http://www.federalreserve.gov/econresdata/researchdata/feds200434.html.  Return to text

8.  Other studies that use this feature include Moscarini and Thomsson (2007) and Nagypál (2008). Return to text

9.  The data on the flows across the labor market states are also publicly available from the BLS. Here I use Fallick and Fleishman's numbers for consistency. The flow numbers from both sources are very similar, other than that Fallick and Fleishman's data appears somewhat noisier. Since some values in 1995 surveys are missing in Fallick and Fleishman's dataset, I start from 1996 rather than 1994. Return to text

10.  One of the caveats from Elsby, Michaels, and Solon (2009) regarding the continuous-time adjustment is that the CPS asks about the labor market states of a worker in the reference week, rather than in a particular day. The current method can overcome this problem by using, for example, $ \chi^E_0(t,t+3/4)$ instead of $ \chi^E_0(t,t+1)$. I follow a more conventional approach here, using $ \chi^E_0(t,t+1)$. Return to text

11.  It is clear from the above argument that once can recursively compute the fraction of workers who were hit by the job switching shocks $ i$ times and the labor market switching shocks $ j$ times between time $ t$ and $ t+\tau$, where $ i,j=0,1,...$; $ t=0,1,...$; and $ \tau\in[0,1)$. This computation would allow a more elaborate adjustment if necessary. Indeed, this type of logic can be used for time-aggregation adjustments for other types of shocks, as long as the underlying process can reasonably be assumed as Poisson. Return to text

12.  Nagypál (2008) reports the job-to-job flow rate constructed from the weekly data of SIPP. She reports that the time-aggregation adjustment from using the weekly SIPP compared to the monthly CPS makes the probability of job-switching smaller by 7.2% on average. With my no recall adjustment, the probability is 10.3% lower than the original data. With the perfect recall adjustment, the probability is 5.7% higher than the original probability. Given that my adjustment obtains instantaneous probabilities rather than weekly transitions, Nagypál's adjustment amount would be smaller than my result even if the underlying stochastic process is the same. Consequently, from this comparison, it seems more likely that the reality is closer to the no recall case than the perfect recall case. Return to text

13.  Appendix B considers another value of $ r_t$ ($ r_t=0.37$), based on Fujita and Moscarini (2013). This also yields a similar outcome. Return to text

14.  It would look very similar if I instead plotted $ \lambda_t^{JS}/\lambda_t^{UE}$. Return to text

15.  This type of model is often called a "job ladder model." Return to text

16.  Krusell et al. (2012) built a model that incorporates all three labor market states (but abstracts from the job-to-job transitions) and conclude that the frictions are essential in accounting for the behavior of unemployment, while the labor supply behavior (which shows up as the decision to participate in the labor market) is heavily influenced by the change in "attractiveness of working," the average level of wages. Another conclusion of their study is that (ex ante) heterogeneity of workers is essential in accounting for the behavior of labor force participation flows, and thus the model becomes substantially more complex if I intend to incorporate this margin. Return to text

17.  Existing data are too limited to directly estimate the cyclicality of the reservation wages in the U.S. economy. Krueger and Mueller's (2011) recent survey is only for 2009 and 2010 and therefore cannot be used for estimating the cyclicality of reservation wages.  Return to text

18.  Since we will "back out" the wage-offer distribution using the model, our outcome should not be affected as long as the reservation wages are not cyclical. Return to text

19.  Another possible modeling strategy for $ f^e_s$ would be to make $ a$ vary over time so that the job-to-job transition rate of the model matches exactly with the data. I experimented with this strategy, and the results are very similar to the ones reported here. Return to text

20.  Hall and Müller (2012) argue that their model with $ a=1$ generates a reasonable fit to the wage distribution in Krueger and Mueller's (2011) data. Return to text

21.  In this paper, I do not have to distinguish between the employer-specific factor and the match-specific factor, since it makes no difference to the worker's behavior. Return to text

22.  In the search and matching literature, this type of relationship between wage and productivity is often assumed as a way of parameterizing the real wage rigidity. For example, Blanchard and Galí (2010) assume this form of wage-setting rule. Return to text

23.  Topel and Ward's (1992) samples are young men below 34 years old. Fallick, Haltiwanger, and McEntarfer's (2012) samples include 25- to 55-year-old male and female workers, and their number is comparable (median 10% earnings gain for a worker who switched jobs within a quarter). Hyatt and McEntarfer's (2012) Figure 5 reports that median earnings gains ranged from 6% to 11%. Some authors point out that negative wage changes are often observed at the time of a job-to-job transition (e.g. Postel-Vinay and Robin (2002) and Nunn (2012)) while the job ladder model cannot generate a negative wage change. Explicitly dealing with these cases by incorporating other elements such as measurement errors, wage growth, and non-wage job characteristics is beyond the scope of this paper. The current calibration strategy implies that an omission of negative wage changes is always accompanied by an omission of above-average positive wage changes, since the mean wage change has to match the data. To the extent that these two offset, the main results below are not going to be significantly affected by taking the negative wage changes into account. Return to text

24.  The corresponding standard deviation of the (log) wage-offer distribution is 0.12. Hall and Müller (2012) estimate this value to be 0.075. Their estimate is based on Krueger and Mueller's (2011) survey data of unemployed workers' reservation wages and the assumption that the reservation wage is proportional to the worker's productivity. My steady-state variance of the log match quality, $ 0.13^2=0.0169$, is very similar to Hagedorn and Manovskii's (2010) estimate of the variance of the log match quality, 0.016. Return to text

25.  The data is downloadable from http://www.frbsf.org/csip/tfp.php. Return to text

26.  The time-series variation of the recall probability is small in Fujita and Moscarini (2013). It moves between 32% and 42%. Return to text


This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: February 12, 2014