
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1090, November 2013 --- Screen Reader
Version*
Interest Rate Swaps and Corporate Default*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper studies firms' usage of interest rate swaps to manage risk in a model economy driven by aggregate productivity shocks, inflation shocks, and counter-cyclical idiosyncratic productivity risk. Consistent with empirical evidence, firms in the model are fixed-rate payers, and swap positions are negatively correlated with the term spread. In the model, swaps affect firms' investment decisions and debt pricing very moderately, and the availability of swaps generates only small economic gains for the typical firm.
Keywords: Interest Rate swaps, corporate default, risk management, swap position, debt pricing
JEL classification: E44, G1
1 Introduction
Interest rate swaps are derivative contracts through which two parties exchange fixed and floating rate coupon payments. Such swaps were first used in the early 1980s. By now they are among the most popular derivative contracts. As shown in Figure 1, the notional amount of outstanding interest rate swaps denominated in dollars, for non-financial institutions, is about 10 trillion dollars. In surveys of derivative usage, a sizable fraction of the larger firms in the US typically indicate that they are using interest rate swaps, and that swaps are their favorite derivative contract for managing interest rate risk.1
Several empirical and theoretical studies have examined why firms use swaps, and how firm characteristics affect the use of swaps. However, to the best of our knowledge, there are no quantitative models of swap choice, and little is known about the impact of the use of interest rate swaps on corporate default rates, borrowing decisions, real production decisions, and the economy more generally.
In this paper, we develop a model of firms' production and financing decisions with firms that are subject to aggregate and idiosyncratic productivity risk, as well as interest rate risk and inflation risk. The objective is to examine the optimal swap choice and the impact of the use of interest rate swaps on the pricing of corporate debt. This is done in an equilibrium setting, by considering production and financing decisions as well as default in a consistent way. As a first take on these issues, we consider a relatively simple business cycle model that, in addition to an interest rate swap, includes only the most standard ingredients. In particular, we abstract from explicit agency problems and behavioral issues that have been related to swap usage in some theoretical studies and in some non-structural empirical studies in the literature.
A well documented stylized fact of U.S. firms' interest rate swap usage is that nonfinancial firms overall tend to be fixed rate payers. Typically, a firm with floating rate debt can enter a swap contract to convert the variable payments into payments known in advance. For instance, Li and Mao (2003) find that in their sample of U.S. non-financial firms that use swaps 44% are fixed payers, 20% are floating payers, 18% are both, and for 18 this information isn't available. These proportions are in line with Saunders' (1999) findings that were derived from different data. This is also consistent with Chernenko and Faulkender (2011), and with the survey of Bondnar et al (2011). In a fully specified model, where swap payouts are correlated with a number of economic risk factors, firms' do not necessarily choose to be fixed rate payers. Our analysis can help us better understand under what conditions this is the case, and what the key determinants of firms' swap choices are.
Another characteristic that has attracted attention is that firms seem to be using interest rate swaps for timing the market. That is, when the yield curve is steep, firms use swaps to pay a floating rate on their debt, that-at least in the short run-is relatively low; and, when the yield curve is flat (or inverted), firms use swaps to lock in the relatively attractive fixed (long-term) rate. Figure 2, based on swap usage data from Chernenko and Faulkender (2011), shows a strong negative correlation between the aggregate net fixed swap position and the spread between 10-year and 6 month government yields. The contemporaneous correlation is -0.42, and with annual growth rates -0.21; if the swap is lagged by one year, these correlations are -0.56 and -0.57, respectively. While it is tempting to explain this type of behavior as firms being myopic, it is important to know under what assumptions this negative correlation can emerge with fully rational agents with no explicit conflicts of interest.
We find that our model can explain these stylized facts about swap usage. In the benchmark version of our model, firms are fixed-rate payers and swap positions are negatively correlated with the yield spread. Counter-cyclical idiosyncratic productivity risk turns out to be a key contributor to firms being fixed-rate payers. Without counter-cyclical idiosyncratic productivity risk, firms in our model would typically choose to be floating rate payers to hedge the risk of deflation on their nominal debt. We also find that in the model swaps affect firms' investment decisions and debt pricing very moderately, and the availability of swaps generates only small economic gains for the typical firm.
Our analysis is related to a number of theoretical studies that have considered the motivations for using interest rate swaps, or derivative contracts more generally. Smith and Stulz (1985) present a number of reasons why value-maximizing firms use derivative contracts for hedging. As in their analysis, our model focuses on bankruptcy costs as a motive for risk management. Wall (1989) links swap usage to some classic agency problems associated with long-term debt. For instance, Myers (1977) pointed out that long term debt can lead to under-investment, because creditors share the benefit of new investments through a reduced probability of bankruptcy. Barnea, Haugen and Senbet (1980) suggested that long term debt encourages risk shifting behavior, that is, the adoption of high risk projects after debt has been issued. Both of these agency problems can be addressed by issuing short term debt instead. Wall (1989) argues that swaps are useful in this context, because they allow firms to hedge the interest rate risk associated with short term borrowing. Titman (1992), building on ideas of Flannery (1986), suggests that short term debt allows firms with positive private information to lower the expected cost of borrowing. Interest swaps allow firms to hedge the interest rate risk associated with short term borrowing. While not modelling any of these agency problems explicitly, in our model, firms are limited to short term debt as a simple way of representing an inherent advantage for short term debt.
Our analysis is also related to some recent studies that consider equilibrium models with defaultable debt, such as Gomes and Schmid (2010), or Bhamra, Kuehn and Strebulaev (2008). As in these studies we model firm default explicitly. In addition to the defaultable debt considered in these studies, our model also allows firms to trade derivative contracts. More recently, Begenau, Piazzesi, and Schneider (2012) estimate banks' exposures to interest rate risk including swap positions.
Section 1 presents the model. Section 2 presents a simplified model that admits a closed form solution that we can use to better understand our main model. Section 3 contains the quantitative analysis, and Section 4 concludes.
2 Model
A key ingredient of our model are firms with long-term projects that are financed with short-term debt. This market incompleteness highlights the role played by interest rate swaps as a tool to manage risks associated with interest rates, inflation and productivity. We consider a general equilibrium model where asset prices are endogenously determined. Given the huge size of the aggregate value of the outstanding swap contracts, it seems a priori reasonable to examine the impact of swaps on the aggregate economy. Another advantage of the general equilibrium analysis is that we do not need to exogenously parameterize a process for the state prices and its relation to aggregate productivity, as in a partial equilibrium analysis. Of course, this comes at the cost of possible misspecification. To minimize the effects of misspecificiation, our quantitative analysis seeks to match as closely as possible important empirical properties.
For the reminder of this section, we first describe firms and their decisions, and then close the model with investors and consumers.
2.1 Firms with Long-Term Projects
The focus of our analysis is on firms with projects that have a longer maturity than the available debt financing. It is in this case that an interest rate swap is potentially useful. In this subsection, we describe their technology and available financial instruments, and we characterize optimal financing and production decisions.
2.1.1 Technology
A firm's life extends over three periods, 0, 1 and 2. Production requires
an initial capital input
![]() in period 0, and
total output is given by the (concave) production function
in period 0, and
total output is given by the (concave) production function
![]() in period
2. The logarithm of the productivity level
in period
2. The logarithm of the productivity level
![]() is determined by
aggregate and idiosyncratic shocks that are realized in period 1
and 2. We label the aggregate productivity shock by
is determined by
aggregate and idiosyncratic shocks that are realized in period 1
and 2. We label the aggregate productivity shock by
![]() ,
and assume it follows a Markov chain, and the idiosyncratic shock
by
,
and assume it follows a Markov chain, and the idiosyncratic shock
by
![]() . The
idiosyncratic shock is independently drawn from a continuous
distribution
. The
idiosyncratic shock is independently drawn from a continuous
distribution
![]() , conditional on
, conditional on
![]() , with the expectation of
, with the expectation of
![]() equal to 1.
Productivity depends on the history of aggregate and idiosyncratic
shocks such that
equal to 1.
Productivity depends on the history of aggregate and idiosyncratic
shocks such that
![]() and
and
![]() are the aggregate
productivity shocks in period 1 and 2, respectively. The
idiosyncratic shocks
are the aggregate
productivity shocks in period 1 and 2, respectively. The
idiosyncratic shocks
![]() and
and
![]() are assumed to be known in
period 1 and 2, respectively.
are assumed to be known in
period 1 and 2, respectively.
In each time period, a continuum of measure one of new firms
enter the market. Firms are ex-ante identical, but differ ex-post
due to the realization of the idiosyncratic shocks ![]() .
Therefore, in each period, there are three vintages of firms active
in production. There is a first group of identical firms that are
investing in new projects. In the second group, firms have active
projects in place, and their first period productivity shocks are
revealed. In the third group, the second period shocks are
revealed, production is completed, and firms exit.
.
Therefore, in each period, there are three vintages of firms active
in production. There is a first group of identical firms that are
investing in new projects. In the second group, firms have active
projects in place, and their first period productivity shocks are
revealed. In the third group, the second period shocks are
revealed, production is completed, and firms exit.
2.1.2 Financial Contracts
A firm can borrow from investors in the form of one-period
nominal debt. A firm initially borrows
![]() to finance its
investment.
to finance its
investment. ![]() is the (gross) interest rate on
the first period debt, where the superscript
is the (gross) interest rate on
the first period debt, where the superscript ![]() stands for corporate debt, which is subject to default. After one
period, the aggregate shock
stands for corporate debt, which is subject to default. After one
period, the aggregate shock
![]() and the idiosyncratic shock
and the idiosyncratic shock
![]() are realized. At this point, the
firm needs to roll over its debt because the project has not
produced any output yet. That is, the firm needs to borrow
are realized. At this point, the
firm needs to roll over its debt because the project has not
produced any output yet. That is, the firm needs to borrow
![]() for another period. No additional
investment in the project is needed. If the firm can roll over the
debt, the new interest rate is
for another period. No additional
investment in the project is needed. If the firm can roll over the
debt, the new interest rate is ![]() . Because
the first period idiosyncratic shock
. Because
the first period idiosyncratic shock
![]() is realized, and firms at this
stage are heterogeneous, the second period debt interest rates
is realized, and firms at this
stage are heterogeneous, the second period debt interest rates
![]() depends on the firm specific
realization of
depends on the firm specific
realization of
![]() . At the end of the project's
second stage, the firm gets output from the project, repays the
second period debt, and pays out profits.
. At the end of the project's
second stage, the firm gets output from the project, repays the
second period debt, and pays out profits.
Default on the debt is a possibility. In the second period, the firm defaults if its output is insufficient to repay the second period debt. In the first period, the firm defaults, if it cannot roll over its initial debt. The firm cannot roll over its debt, if the firm's assets are valued less than its debt.
In addition to one-period debt, firms have access to an interest
rate swap that is chosen in period 0. According to a swap contract,
one party agrees to pay a fixed coupon with a gross rate
![]() to the other party in period 1 and
period 2;
to the other party in period 1 and
period 2; ![]() is called the swap rate. In
exchange, payments that are indexed to the one-period risk free
rates
is called the swap rate. In
exchange, payments that are indexed to the one-period risk free
rates ![]() and
and ![]() are received in
period 1 and 2, respectively; this is the floating rate. We assume
that the swap rate
are received in
period 1 and 2, respectively; this is the floating rate. We assume
that the swap rate ![]() is determined so that
the present value of the contract (abstracting from default costs)
is zero under the pricing measure used in the economy.
is determined so that
the present value of the contract (abstracting from default costs)
is zero under the pricing measure used in the economy.
The amount of the swap is denoted by ![]() , which is
measured as a fraction of first-period debt
, which is
measured as a fraction of first-period debt ![]() . Due
to the firm's default risk on the interest rate swap, the firm also
needs to pay a default spread in each period. In particular, we
assume that in period 1, the firm needs to pay
. Due
to the firm's default risk on the interest rate swap, the firm also
needs to pay a default spread in each period. In particular, we
assume that in period 1, the firm needs to pay
and in period 2
where
![]() and
and
![]() denote the default
spreads, and
denote the default
spreads, and
![]() is the vector of next period's
realized aggregate state variables which include productivity
is the vector of next period's
realized aggregate state variables which include productivity
![]() and inflation (to be defined
below). To save on notation, for now, our notation does not
explicitly acknowledge the dependence on endogenous state
variables, which will be described later. We assume that
and inflation (to be defined
below). To save on notation, for now, our notation does not
explicitly acknowledge the dependence on endogenous state
variables, which will be described later. We assume that
![]() is
determined in period 1, and that it represents at that time the
fair market value of the losses expected for period 2. Similarly,
is
determined in period 1, and that it represents at that time the
fair market value of the losses expected for period 2. Similarly,
![]() is determined at
time 0 and represents the compensation for possible losses due to
default that might have occurred at time 1. We assume absolute
priority for the swap, that is, the swap will first get fully paid
before lenders get anything.2 We assume that the firms' swap
counterparties will always fully honor their commitments.
is determined at
time 0 and represents the compensation for possible losses due to
default that might have occurred at time 1. We assume absolute
priority for the swap, that is, the swap will first get fully paid
before lenders get anything.2 We assume that the firms' swap
counterparties will always fully honor their commitments.
Clearly, at the time the swap contract is signed, the future
one-period interest rate ![]() is not known; it will be
known at time 1. Therefore, swap payouts are a function of the
future one-period interest rate
is not known; it will be
known at time 1. Therefore, swap payouts are a function of the
future one-period interest rate ![]() . Because future
interest rates are correlated with a number of risks the firm is
exposed to, swaps allow the firm to manage these risks.3
. Because future
interest rates are correlated with a number of risks the firm is
exposed to, swaps allow the firm to manage these risks.3
2.1.3 Firms' Problem
An individual firm takes as given the interest rate schedule for corporate debt, the schedule for the swap spreads, as well as the risk-free interest rates that determine the swap payouts. In period 0, a new firm chooses the amount of investment (equivalently debt), and the amount of the swap to maximize its expected value under the owners' pricing measure.
In addition to exogenous aggregate and idiosyncratic
productivity shocks, the firms and investors are subject to shocks
in the rate of inflation, ![]() . Inflation is
assumed to follow a Markov chain. To keep the model as simple as
possible, the inflation process is assumed to be exogenous.
However, money is not neutral in this economy, because inflation
matters for default, and thus, firms take it into account when
making investment and financing decisions. For compactness the
aggregate shock is denoted by
. Inflation is
assumed to follow a Markov chain. To keep the model as simple as
possible, the inflation process is assumed to be exogenous.
However, money is not neutral in this economy, because inflation
matters for default, and thus, firms take it into account when
making investment and financing decisions. For compactness the
aggregate shock is denoted by
![]() .4
.4
We denote the joint distribution of
![]() conditional on the aggregate shocks
conditional on the aggregate shocks ![]() as
as
![]() ,
,
with transition matrix
![]() , and
the corresponding pricing measure is denoted by
, and
the corresponding pricing measure is denoted by
| (1) |
where
![]() is the (real) stochastic
discount factor;
is the (real) stochastic
discount factor;
![]() also depends on the
endogenous state variables to be defined later. This representation
expresses the fact that idiosyncratic risk does not require a risk
premium.
also depends on the
endogenous state variables to be defined later. This representation
expresses the fact that idiosyncratic risk does not require a risk
premium.
In period 2, conditional on the firm not having defaulted on its obligations before, default occurs if output is not sufficient to cover the firm's financial obligations. In this case, the counterparties for the swap and the debt obtain the available output according to the established priority rules. We assume that the counterparties do not incur any additional cost for default in period 2. This assumption helps making the problem more tractable numerically. Due to this assumption, the value of the firm at time 1 is not affected by the possibility of default at time 2. This is because the default spreads on the swap and on the one-period debt determined in period 1 are such as to exactly compensate the investors for expected default losses in period 2. Without a cost of default, the firm values the ability to default as being equal to the default spread determined by the investors. Of course, this result also depends crucially on the assumption that the firm values profits with the same stochastic discount factor as the investors. This is a version of Modigliani-Miller's theorem; see Appendix A for details.
Under the made assumptions, in period 1 the (equity) value of the firm is given by
![$\displaystyle \int F\left( b^{l},\varepsilon ^{\prime \prime }\right) dP_{X^{\prime \prime },z^{\prime \prime }\vert X^{\prime }}^{\ast }-\frac{b^{l}}{\pi ^{\prime }} \left\{ R_{1}^{c}\left( b^{l},s\right) +s\left[ R_{S}+ss\left( b^{l},s\right) -R_{1}+\frac{R_{S}-R_{2}\left( X^{\prime }\right) }{ R_{2}\left( X^{\prime }\right) }\right] \right\} .$](img55.gif)
|
(2) |
The present value of the firm's operational revenues is given by
![]() , and
, and ![]() is
is ![]() deflated by the
price level, that is, the debt (and the capital stock) in units of
the numeraire good.5 Interest due on debt is represented by
deflated by the
price level, that is, the debt (and the capital stock) in units of
the numeraire good.5 Interest due on debt is represented by
![]() . The term in
square brackets displays the per unit value of the swap including
the payments due in period 1. Given our assumption that default in
period 2 is not subject to a deadweight cost, and that a fairly
valued default spread is added to the swap payment, the present
value of the swap payment due in period 2,
. The term in
square brackets displays the per unit value of the swap including
the payments due in period 1. Given our assumption that default in
period 2 is not subject to a deadweight cost, and that a fairly
valued default spread is added to the swap payment, the present
value of the swap payment due in period 2,
![]() , can be obtained by discounting at the risk free rate,
, can be obtained by discounting at the risk free rate,
![]() . As is clear
in the equation above, realized inflation
. As is clear
in the equation above, realized inflation
![]() affects the real value of the
debt and the swap.
affects the real value of the
debt and the swap.
If the value of the firm at time 1 is positive, then the
one-period debt due
![]() is rolled
over. We can assume that the payment received, or due, from the
swap
is rolled
over. We can assume that the payment received, or due, from the
swap
![]() is used to decrease/increase the debt, although the exact timing
of the settlement of the swap is unimportant here.
is used to decrease/increase the debt, although the exact timing
of the settlement of the swap is unimportant here.
If the firm value given in equation 2 is negative, the
firm is in default at time 1. In particular, the firm will be
unable to find new investors to roll over its existing debt because
the value of the remaining assets is below the value of the
existing debt. We assume that this will generate a default cost
modelled as a reduction in the output available for the creditors
to
![]() with
with
![]() . In default, we assume that the
swap is honored fully before debt holders get paid. This is
intended to capture that quite often swaps involve some form of
collateral and can thus be thought as representing a more senior
claim than debt. Counterparties are given shares in the remaining
firm assets. Specifically, if
. In default, we assume that the
swap is honored fully before debt holders get paid. This is
intended to capture that quite often swaps involve some form of
collateral and can thus be thought as representing a more senior
claim than debt. Counterparties are given shares in the remaining
firm assets. Specifically, if
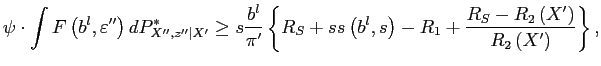
|
(3) |
swap counterparties get fully paid, and the reminder is distributed to the debt holders. In case the swap has a positive value for the firm, that is, the RHS of Equation (3) is negative, debt holders, as the new owners, take over as creditors from the firm. If
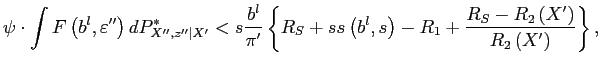
|
(4) |
then the swap counterparties get all the remaining assets from the
firm, that is, they get
![]() , the debt holders get nothing. Depending on the realization of the
idiosyncratic shock
, the debt holders get nothing. Depending on the realization of the
idiosyncratic shock
![]() we have either one of the three
outcomes. Typically, for values of
we have either one of the three
outcomes. Typically, for values of
![]() above a given threshold there is
no default. Below that threshold, default reduces the debt holders'
claim. And for very low values of
above a given threshold there is
no default. Below that threshold, default reduces the debt holders'
claim. And for very low values of
![]() , swap counterparties do not get
fully paid (assuming they are owed anything). The aggregate shock
realization
, swap counterparties do not get
fully paid (assuming they are owed anything). The aggregate shock
realization
![]() and the endogenous state
variables affect these cutoff levels.
and the endogenous state
variables affect these cutoff levels.
We can now state the firm's objective as maximizing the expected
value as of period 0 of its expected value as of period 1 over the
no-default set for
![]() denoted by
denoted by
![]() ,
,
![$\displaystyle \max_{b^{l},s}\int_{ND_{1}\left( b^{l},s\right) }\left\{ \begin{array}{c} \int F\left( b^{l},\varepsilon ^{\prime \prime }\right) dP_{{\small X} ^{\prime \prime }{\small ,z}^{\prime \prime }{\small \vert X}^{\prime }}^{\ast } \\ \\ -\frac{b^{l}}{\pi ^{\prime }}\left( R_{1}^{c}\left( b^{l},s\right) +s\cdot \left[ R_{S}+ss\left( b^{l},s\right) -R_{1}+\frac{R_{S}-R_{2}\left( X^{\prime }\right) }{R_{2}\left( X^{\prime }\right) }\right] \right) \end{array} \right\} dP_{{\small X}^{\prime }{\small ,z}^{\prime }{\small \vert X}}^{\ast }.$](img78.gif)
|
In our model, as a function of the firms' decisions, creditors
and counterparties are compensated for default losses through
additional payments in the no-default states. In order to solve for
the firms' problem, we need to derive the default spreads built
into the corporate interest rate
![]() and the
default spread for the swap in the first period
and the
default spread for the swap in the first period
![]() . To solve for
optimal decisions, we can aggregate the default spread into a total
default spread
. To solve for
optimal decisions, we can aggregate the default spread into a total
default spread
By no-arbitrage, for a given choice
![]() , the default spread
, the default spread
![]() is given by
is given by
where ![]() is the stochastic discount factor
introduced in eq. (1). We assume that
bond investors and swap counterparties use the same pricing measure
as the firms' equity holders. Substituting in the creditors'
default loss and rearranging yields
is the stochastic discount factor
introduced in eq. (1). We assume that
bond investors and swap counterparties use the same pricing measure
as the firms' equity holders. Substituting in the creditors'
default loss and rearranging yields
![$\displaystyle ts\left( b^{l},s\right) =\frac{\int_{{\small D}_{1}\left( X^{\prime }\right) }\left\{ \frac{R_{1}}{\pi ^{\prime }}+\frac{s}{\pi ^{\prime }}\left[ R_{S}-R_{1}+\frac{R_{S}-R_{2}\left( X^{\prime }\right) }{R_{2}\left( X^{\prime }\right) }\right] -\left( \psi /b^{l}\right) \int F\left( b^{l},\varepsilon ^{\prime \prime }\right) dP_{X^{\prime \prime },z^{\prime \prime }\vert X^{\prime }}^{\ast }\right\} dP_{{\small X}^{\prime }{\small ,z} ^{\prime }{\small \vert X}}^{\ast }}{\int_{{\small ND}_{1}\left( X^{\prime }\right) }\frac{1}{\pi ^{\prime }}dP_{{\small X}^{\prime }{\small ,z} ^{\prime }{\small \vert X}}^{\ast }}.$](img86.gif)
|
The numerator represents the value lost at default relative to default free contracts, the denominator is the risk-adjusted no-default probability.
Once the model is solved, including ![]() it is
straightforward to compute the default spread for debt and the swap
separately, following the seniority rule outlined above. Similarly,
default spreads for period 2 can be computed after the model is
solved.
it is
straightforward to compute the default spread for debt and the swap
separately, following the seniority rule outlined above. Similarly,
default spreads for period 2 can be computed after the model is
solved.
Using default spreads defined in this way, after some algebra, the firm's objective can be rewritten as
![$\displaystyle \max_{b^{l},s}\left\{ \begin{array}{c} \int \left[ \int F\left( b^{l},\varepsilon ^{\prime \prime }\right) dP_{X^{\prime \prime },z^{\prime \prime }\vert X^{\prime }}^{\ast }\right] dP_{X^{\prime },z^{\prime }\vert X}^{\ast }-b^{l} \\ -\int_{D_{1}\left( b^{l},s\right) }\left[ \int \left( 1-\psi \right) F\left( b^{l},\varepsilon ^{\prime \prime }\right) dP_{X^{\prime \prime },z^{\prime \prime }\vert X^{\prime }}^{\ast }\right] dP_{X^{\prime },z^{\prime }\vert X}^{\ast } \end{array} \right\} ,$](img88.gif)
|
(5) |
where
![]() stands for the
default set. This representation makes it clear that the firm value
is given by the following three components
stands for the
default set. This representation makes it clear that the firm value
is given by the following three components
| PV(output) |
where PV(.) stands for present value. This decomposition shows that
the swap only affects the firm value through the default cost. This
implies that without default cost, that is, if ![]() the swap choice is indeterminate. This is because the
swap then simply represents a contract that has a zero market
value. With default costs
the swap choice is indeterminate. This is because the
swap then simply represents a contract that has a zero market
value. With default costs ![]() the firm
optimally chooses the swap to reduce default costs. This property
is related to the analysis of Smith and Stulz (1985). While
inflation does not seem to appear in Equation (5), inflation
the firm
optimally chooses the swap to reduce default costs. This property
is related to the analysis of Smith and Stulz (1985). While
inflation does not seem to appear in Equation (5), inflation
![]() does enter through its effect
on the default set
does enter through its effect
on the default set
![]() , as shown in
Equations (3)
and (4).
, as shown in
Equations (3)
and (4).
2.2 Firms with Short-Term Projects
In addition to firms with long-term projects that require two periods to produce output, there are firms with short-term projects that produce output in one period. At a conceptual level, the short-term firms add very little to our analysis. They are however needed to produce reasonable quantitative implications. In particular, our model without these firms would typically produce strongly oscillating movements in short-term interest rates. This is due to the fact that the consumers'/investors' desire to smooth consumption between two adjacent periods will have to be frustrated with such interest rate movements because there would be no technology to transfer resources from one period to the one immediately next. This problem is reminiscent of the oscillating interest rates in models with time-to-build in investment (see for instance, Rouwenhorst (1991) or Kuehn (2009)). With short-term firms, the economy has the ability to physically transfer resources from one period to the next, and this essentially eliminates oscillating interest rates. We keep this sector as simple as possible.
Firms invest ![]() at time 0, and produce output
one period later according to a production function
at time 0, and produce output
one period later according to a production function
that depends on aggregate and idiosyncratic productivity
![]() and
and
![]() . Capital is financed with
one-period defaultable debt. For computational simplicity, we
assume no default cost. Given our presentation of the long-term
firms problem, the short-term firms' problem is straightforward and
thus omitted from the presentation.
. Capital is financed with
one-period defaultable debt. For computational simplicity, we
assume no default cost. Given our presentation of the long-term
firms problem, the short-term firms' problem is straightforward and
thus omitted from the presentation.
2.3 Consumers/Investors and Equilibrium
We assume a continuum of measure one of identical, infinitely-lived, consumers/investors. We can thus focus on a representative whose goal is to maximize lifetime utility given by
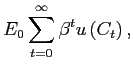
|
with ![]() the time discount factor,
the time discount factor, ![]() consumption in period
consumption in period ![]() , and
, and
![]() a concave momentary
utility. In every period, the consumers earn profits from owning
firms, receive interest, and make or receive payments associated
with swaps. To save on notation, we do not write out the budget
constraint.
a concave momentary
utility. In every period, the consumers earn profits from owning
firms, receive interest, and make or receive payments associated
with swaps. To save on notation, we do not write out the budget
constraint.
We assume that consumers/investors take all prices as given and choose consumption and investment strategies for debt and swaps to maximize lifetime utility. In equilibrium, bond markets and swap markets clear, and the economy-wide resource constraint holds. The later is given by
where ![]() and
and ![]() are aggregate
output and investment in the two sectors. As is clear from the
resource constraint, it is assumed that default costs are not
deadweight costs at the level of the economy. Given that we
typically think of default costs as due to legal costs or asset
fire sales, losses to firms and investors correspond to gains for
lawyers and vulture investors.
are aggregate
output and investment in the two sectors. As is clear from the
resource constraint, it is assumed that default costs are not
deadweight costs at the level of the economy. Given that we
typically think of default costs as due to legal costs or asset
fire sales, losses to firms and investors correspond to gains for
lawyers and vulture investors.
In this model, the asset pricing measure is given by
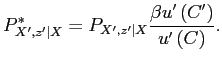
|
2.4 Functional Forms and Aggregate State Variables
We use the standard utility function
![]() ,
with risk aversion coefficient
,
with risk aversion coefficient ![]() . The
production function for long-term and short-term firms is
represented by
. The
production function for long-term and short-term firms is
represented by
with ![]() .
. ![]() is a
scale parameter. Parameter values can potentially be different for
the long-term and short-term firms. In particular, we set
is a
scale parameter. Parameter values can potentially be different for
the long-term and short-term firms. In particular, we set
![]() for the long-term sector as a
normalization,
for the long-term sector as a
normalization, ![]() then determines the relative
size of the short-term sector. The fact that
then determines the relative
size of the short-term sector. The fact that
![]() is also multiplied
by the productivity shock
is also multiplied
by the productivity shock
![]() is somewhat
nonstandard, and effectively introduces stochastic depreciation.
This specification reduces the number of state variables, and thus
improves numerical tractability.
is somewhat
nonstandard, and effectively introduces stochastic depreciation.
This specification reduces the number of state variables, and thus
improves numerical tractability.
Included in the aggregate state vector
![]() are the current aggregate
shocks
are the current aggregate
shocks
![]() plus two variables
that summarize the amount of resources in the economy that are at
different stages of production. In particular, this includes
plus two variables
that summarize the amount of resources in the economy that are at
different stages of production. In particular, this includes
![]() the amount of debt/capital chosen
by long-term firms that were started in the previous period, as
well as
the amount of debt/capital chosen
by long-term firms that were started in the previous period, as
well as
![]() which summarizes the accumulated aggregate resources due to
long-term firms started two periods ago and the short-term firms
started in the previous period.
which summarizes the accumulated aggregate resources due to
long-term firms started two periods ago and the short-term firms
started in the previous period.
The model is solved numerically by guessing policy functions for
![]() and
and
![]() . Based on
these, aggregate consumption and the state-prices can be computed
for future periods 1 and 2. Then, the firms' problems are solved,
including default cost schedules. The policy functions
. Based on
these, aggregate consumption and the state-prices can be computed
for future periods 1 and 2. Then, the firms' problems are solved,
including default cost schedules. The policy functions
![]() and
and
![]() are
updated until convergence.
are
updated until convergence.
3 Simplified Model of Swap Choice
To help understand model mechanisms, this section describes a simplified model that focuses on the swap choice only, and that admits a closed-form solution.
Under a set of simplifying assumptions, the firms' problem for choosing the swap is equivalent to minimizing the variance of the total position at time 1 that is given in equation 2. Most important is the assumption that default losses are not state contingent. While the assumptions needed are not exactly satisfied in our main model, the simple model here illustrates some key quantitative channels. See Appendix B for an explicit derivation that spells out all the required assumptions.
Consider the problem of a firm choosing the fraction of debt
that is swapped ![]() so as to minimize the variance of
the value of equity at time 1,
so as to minimize the variance of
the value of equity at time 1,
![$\displaystyle \min_{s}var\left( E_{1}\left[ m_{1,2}F^{\prime \prime }\right] -\frac{b}{\pi ^{\prime }}\left[ R_{1}+ts+s\left( R^{S}-R_{1}+\frac{R^{S}-R_{2}}{R_{2}} \right) \right] \right) ,$](img128.gif)
|
where
![]() represents the
expected value of output conditional on productivity realized at
time 1. Slightly rewriting yields
represents the
expected value of output conditional on productivity realized at
time 1. Slightly rewriting yields
![$\displaystyle \min_{s}var\left( E_{1}\left[ \mathbf{m}_{1,2}F\vert\mathbf{A}^{\prime }\right] - \frac{b\left[ R_{1}+ts\right] }{\mathbf{\pi }^{\prime }}-s\frac{b}{\mathbf{ \pi }^{\prime }}\left[ \left( R^{S}-R_{1}+\frac{R^{S}}{\mathbf{R}_{2}} -1\right) \right] \right)$](img130.gif)
|
(6) |
with the stochastic terms in bold
![]() . In the same order, these are: the stochastic discount factor,
productivity realized at time 1, inflation realized at time 1, and
the one-period interest at time 1. The first two terms in the
variance in equation (6) represent the
firm's exposure to risk, that is, the initial position that is
subject to interest rate, productivity, and inflation risk. The
third (and last) term represents the effect of the swap. Minimizing
the variance of the hedged position is typically the way finance
practitioners' text books present the choice of an optimal hedge;
see, for instance, Hull (2000).
. In the same order, these are: the stochastic discount factor,
productivity realized at time 1, inflation realized at time 1, and
the one-period interest at time 1. The first two terms in the
variance in equation (6) represent the
firm's exposure to risk, that is, the initial position that is
subject to interest rate, productivity, and inflation risk. The
third (and last) term represents the effect of the swap. Minimizing
the variance of the hedged position is typically the way finance
practitioners' text books present the choice of an optimal hedge;
see, for instance, Hull (2000).
Linearizing the terms in the variance gives
![$\displaystyle \frac{F}{R_{2}/\pi ^{\prime \prime }}\left( \hat{A}^{\prime }-\hat{R}_{2}+E \widehat{\pi ^{\prime \prime }}\right) +\left( \frac{b\left[ R_{1}+ts\right] }{\pi ^{\prime }}\right) \widehat{\pi ^{\prime }}+s\left( \frac{b}{\pi ^{\prime }}\frac{R^{S}}{R_{2}}\right) \hat{R}_{2}$](img132.gif)
|
(7) |
where
![]() . Note that
. Note that
![]() , that is, the (log-linearized) nominal interest rate equals the
real interest rate plus expected inflation. Also note that realized
inflation doesn't multiply the swap because the expected value as
of time 0 of
, that is, the (log-linearized) nominal interest rate equals the
real interest rate plus expected inflation. Also note that realized
inflation doesn't multiply the swap because the expected value as
of time 0 of
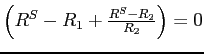 , and
this is the point of linearization. Thus, to a first-order
approximation, the swap doesn't create any exposure to realized
inflation.
, and
this is the point of linearization. Thus, to a first-order
approximation, the swap doesn't create any exposure to realized
inflation.
Taking first-order conditions with respect to ![]() and rearranging terms gives the optimal level of the swap as
and rearranging terms gives the optimal level of the swap as
![$\displaystyle s^{\ast }=\left( \frac{\frac{F}{R_{2}/\pi ^{\prime \prime }}}{\frac{b}{\pi ^{\prime }}\frac{R^{S}}{R_{2}}}\right) \left[ \underset{\text{Real interest rate risk}}{\underbrace{\beta ^{\hat{R}_{2}-E\widehat{\pi ^{\prime \prime }}} }}-\underset{\text{Productivity risk}}{\underbrace{\beta ^{\widehat{ A^{\prime }}}}}\right] -\left( \frac{R_{1}+ts}{R^{S}/R_{2}}\right) \underset{ \text{Inflation risk}}{\underbrace{\beta ^{\widehat{\pi ^{\prime }}}}},$](img137.gif)
|
(8) |
where
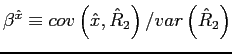 , the coefficient in a regression of the nominal interest rate on
, the coefficient in a regression of the nominal interest rate on
![]() .6
.6
These interest rate betas measure the contribution to the optimal hedge due to each of the three sources of risk.
- The first term in brackets represents the hedge against real
interest rate risk for the firm's assets that comes from the (real)
stochastic discount factor. The more volatile the real interest
rate relative to the nominal interest rate, the more risk there is,
and the larger is the swap position. Unless expected inflation is
very volatile, this term will be positive. If expected inflation is
non-stochastic
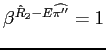 .
. - The second term in brackets,
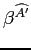 , represents
the hedge against productivity risk. Given that output and nominal
interest rates are typically negatively correlated (empirically, at
least, over the long run), this term contributes positively to the
swap position.
, represents
the hedge against productivity risk. Given that output and nominal
interest rates are typically negatively correlated (empirically, at
least, over the long run), this term contributes positively to the
swap position. - The third term represents the hedge against inflation (or
deflation) risk associated with the nominal debt. Typically,
realized inflation is positively correlated with nominal interest
rates, thus we expect the overall contribution of this term to the
swap position to be negative. Intuitively, inflation risk on the
nominal debt is hedged by getting a swap that requires the firm to
pay the floating rate. For instance, when realized inflation is
low, there is a capital loss due to the increase in the real value
of the debt, and this can be compensated by lower floating rate
payments on the swap. Thus, this term contributes negatively to the
swap position
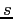 (which we have defined as a swap that
requires the firm to pay fixed and receive floating).
(which we have defined as a swap that
requires the firm to pay fixed and receive floating).
The two terms in round brackets capture the exposures due to
firm assets and debt divided by the sensitivity of the swap to
changes in interest rates. Both of these terms are positive. To a
first approximation
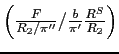 equals the total value of the firm divided by debt, that is, the
inverse of the leverage ratio. In the aggregate, we would expect
this term to be slightly larger than 2, while
equals the total value of the firm divided by debt, that is, the
inverse of the leverage ratio. In the aggregate, we would expect
this term to be slightly larger than 2, while
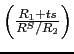 is slightly larger than 1. Thus, the first two hedging motives are
magnified compared to inflation risk.
is slightly larger than 1. Thus, the first two hedging motives are
magnified compared to inflation risk.
Finally, we can see that persistent expected inflation,
everything else equal, scales up the swap position. If the swap
position is positive, higher (persistent) inflation requires a
bigger swap position. To see this, assume
![]() , and
, and
![]() , which holds to a
first-order approximation, and
, which holds to a
first-order approximation, and
![]() ,
then
,
then
![$\displaystyle s=\pi \left\{ \left( \frac{\frac{F}{R_{2}^{r}}}{b\frac{R^{S,r}}{R_{2}^{r}}} \right) \left[ \beta ^{\hat{R}_{2}-E\widehat{\pi ^{\prime \prime }}}-\beta ^{ \widehat{A^{\prime }}}\right] -\left( \frac{R_{1}^{r}+t^{r}s}{ R^{S,r}/R_{2}^{r}}\right) \beta ^{\widehat{\pi ^{\prime }}}\right\} .$](img153.gif)
|
Intuitively, inflation contributes to shrinking the real size of the swap position over time given that the notional is in nominal terms. The optimal hedge counters this effect by scaling up the position. We will return to this model when discussing the implications of the fully specified model.
4 Quantitative Analysis
In this section the model is parameterized and quantitative properties are examined.
4.1 Parameterization
Parameter values are chosen according to two types of criteria. A first set of parameters are given values based on direct evidence on the parameters or to keep the model simple. A second set of parameters values are chosen so that selected moments of endogenous model quantities match empirical counterparts.
Table 1 shows the first set of parameter values.
Table 1: Parameter Values
| Parameter | Value | |
|---|---|---|
| Depreciation (annual) | δ | 0.1 |
| Risk aversion | γ | 15 |
| Capital curvature | α | 0.5 |
| Short term sector size | Zd | 0.75 |
The depreciation rate ![]() at 0.1 annually is a
standard value. We assume a model period of five years. Based on
this, the depreciation rates in the model are
at 0.1 annually is a
standard value. We assume a model period of five years. Based on
this, the depreciation rates in the model are
![]() with
with
![]() equal to 5 or
10 for short-term and long-term firms,
respectively.
equal to 5 or
10 for short-term and long-term firms,
respectively. ![]() is set to 0.75 to
have the short term sector roughly produce half of the economy's
output, the other half being produced by the long-term sector. The
capital curvature parameter
is set to 0.75 to
have the short term sector roughly produce half of the economy's
output, the other half being produced by the long-term sector. The
capital curvature parameter ![]() is set to
0.5. Plant level estimates of this parameter
from Cooper and Haltiwanger (2006) and Cooper and Ejarque (2003)
are around 0.6-0.7, the typical values used in
business cycle studies for aggregate production functions are
around 0.3-0.4. We set risk aversion to 15, as a
way of generating nonnegligeable risk premiums. Alternatively, we
could introduce a richer utility specification as typically used in
asset pricing studies. Given the computational cost, and given that
the focus of the paper is not on the ability to match the overall
size of risk premiums, we prefer this more parsimonious
approach.
is set to
0.5. Plant level estimates of this parameter
from Cooper and Haltiwanger (2006) and Cooper and Ejarque (2003)
are around 0.6-0.7, the typical values used in
business cycle studies for aggregate production functions are
around 0.3-0.4. We set risk aversion to 15, as a
way of generating nonnegligeable risk premiums. Alternatively, we
could introduce a richer utility specification as typically used in
asset pricing studies. Given the computational cost, and given that
the focus of the paper is not on the ability to match the overall
size of risk premiums, we prefer this more parsimonious
approach.
Table 2 presents a list of parameters with values chosen so that
the model closely replicates empirical counterparts. Model
statistics are based on a very long simulated sample. The joint
process for aggregate productivity, ![]() , and
inflation,
, and
inflation, ![]() , is built from two two-state Markov
chains. For both, the diagonal elements are set to determine the
serial correlation coefficients. In the combined four-state Markov
process, elements that are associated with relatively high (or low)
realizations for both, productivity and inflation, are increased by
, is built from two two-state Markov
chains. For both, the diagonal elements are set to determine the
serial correlation coefficients. In the combined four-state Markov
process, elements that are associated with relatively high (or low)
realizations for both, productivity and inflation, are increased by
![]() , the others are decreased by
, the others are decreased by
![]() . This is a convenient way to introduce
non-zero correlation between productivity and inflation. For
instance, as is easy to see, if both productivity and inflation are
IID, then
. This is a convenient way to introduce
non-zero correlation between productivity and inflation. For
instance, as is easy to see, if both productivity and inflation are
IID, then ![]() equals the correlation coefficient
between productivity and inflation. Given that inflation is
exogenous, it is easy to perfectly match mean, standard deviation
and first-order serial correlation of the data.
equals the correlation coefficient
between productivity and inflation. Given that inflation is
exogenous, it is easy to perfectly match mean, standard deviation
and first-order serial correlation of the data.
All other target moments are endogenous, and the simulated model
comes very close to matching the calibration targets. The empirical
counterparts for consumption and output are based on constructing
aggregates for 5 year periods, the interest rate is taken to be a
five year rate. Logarithms are taken of consumption, output,
interest rates and inflation. The Appendix contains a more detailed
description of how empirical counterparts are constructed.
Following Bloom et al (2009), idiosyncratic productivity risk
varies countercyclically with aggregate productivity, so that with
low aggregate productivity it is
![]() and with high aggregate
productivity
and with high aggregate
productivity
![]() . The level of
. The level of
![]() is set to match default rates in
the data, and the variation,
is set to match default rates in
the data, and the variation, ![]() , is in the
range of the empirical evidence presented in Bloom et al (2009). In
particular, they report the % increase of various dispersion
measures in recessions relative to expansions to be between
0.23 and 0.67; our model
target is set to 0.5. The correlation between
inflation and productivity,
, is in the
range of the empirical evidence presented in Bloom et al (2009). In
particular, they report the % increase of various dispersion
measures in recessions relative to expansions to be between
0.23 and 0.67; our model
target is set to 0.5. The correlation between
inflation and productivity,
![]() , is set so that
the model is reasonably close to the data for the correlations of
output growth with both inflation and the nominal interest rate.
The model cannot exactly match both of these correlations. As we
show below, this parameter matters mainly for the correlation of
the swap and the term spread.
, is set so that
the model is reasonably close to the data for the correlations of
output growth with both inflation and the nominal interest rate.
The model cannot exactly match both of these correlations. As we
show below, this parameter matters mainly for the correlation of
the swap and the term spread.
Table 2: Parameters Set to Match Moments
| Parameter | Target Statistic | Data | Model |
|---|---|---|---|
| β: 0.78 | E(r) | 0.302 | 0.314 |
| ψ: 0.5 | E(Recovery rate) | 0.40 | 0.43 |
| σz 0.37 | E(Default rate) | 0.0709 | 0.0722 |
| Δ, in σz + Δ: 0.075 | Dispersion (Rec.)/Disp(Exp.) -1 | 0.23 - 0.67 | 0.5 |
| Std(A): 0.0625 | Std (Δc) | 0.032 | 0.035 |
| ρ(A): 0 | ρ(Δc) | -0.06 | -0.03 |
| E(π): 0.184 | E(π) | 0.184 | 0.184 |
| Std(π): 0.11 | Std(π) | 0.11 | 0.11 |
| ρ(π): 0.45 | ρ(π) | 0.45 | 0.45 |
| corr(π, A): -0.3 | Corr(π, Δy) | -0.2 | -0.23 |
| corr(π, A): -0.3 | Corr(r, Δy) | -0.31 | -0.22 |
4.2 Model Implications for Swaps
Two facts about firms' swap usage emerge from empirical studies: swap positions are positive (firms are net fixed payers), and swap positions commove negatively with the term spread, so that firms increase net fixed rate obligations when long-term interest rates are relatively low. As shown in Table 3, the model's benchmark calibration can produce these two properties, with the expected swap level at 0.33 and the correlation between the swap and the term spread at -0.75. As is clear from Table 3, the model's ability to produce these facts hinges critically on the types of risks included in the model.
To better understand the determinants of the level and the cyclical behavior of the swap, it is useful to consider the solution of the simplified model, which we reproduce here for convenience
![$\displaystyle s^{\ast }=\left( \frac{\frac{F}{R_{2}/\pi ^{\prime \prime }}}{\frac{b}{\pi ^{\prime }}\frac{R^{S}}{R_{2}}}\right) \left[ \underset{\text{Real interest rate risk}}{\underbrace{\beta ^{\hat{R}_{2}-E\widehat{\pi ^{\prime \prime }}} }}-\underset{\text{Productivity risk}}{\underbrace{\beta ^{\widehat{ A^{\prime }}}}}\right] -\left( \frac{R_{1}+ts}{R^{S}/R_{2}}\right) \underset{ \text{Inflation risk}}{\underbrace{\beta ^{\widehat{\pi ^{\prime }}}}}.$](img182.gif)
|
(9) |
4.2.1 Swap Level
We compare different model versions, starting with version A in
Table 3 that has only aggregate productivity shocks. Idiosyncratic
productivity shocks with constant variance are included in versions
A, B and C; the benchmark version features idiosyncratic
productivity shocks with countercyclical variance. For case A, the
level of the swap is positive and large, with an expected value of 5.98. The high level is easy to understand
with the solution of the simplified model in equation (9). Indeed, as
shown in Table 3, the real interest rate beta,
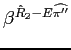 , is
equal to one, because there is no expected inflation risk.
Productivity risk also makes a large positive contribution.
Interest rates and productivity are negatively related, and
(conditional) interest rate volatility is low, thus the large value
for
, is
equal to one, because there is no expected inflation risk.
Productivity risk also makes a large positive contribution.
Interest rates and productivity are negatively related, and
(conditional) interest rate volatility is low, thus the large value
for
![]() . The
inflation beta,
. The
inflation beta,
![]() , is
obviously equal to zero in this case. Note, Table 3 reports the
average of the conditional betas, computed from the model solution,
as it is the conditional relation that determines the swap choice.
Also, betas are computed under the risk neutral probabilities (that
is, physical probabilities are scaled by the stochastic discount
factor), as this is what firms care about (not the physical
probabilities).
, is
obviously equal to zero in this case. Note, Table 3 reports the
average of the conditional betas, computed from the model solution,
as it is the conditional relation that determines the swap choice.
Also, betas are computed under the risk neutral probabilities (that
is, physical probabilities are scaled by the stochastic discount
factor), as this is what firms care about (not the physical
probabilities).
Column B in Table 3 displays the case with productivity and inflation shocks, assuming that the two are uncorrelated. Unlike the case A with only productivity risk, this case produces a negative swap position, with an expected value of -1.96. Clearly, inflation risk has a first-order impact on swap choice. As shown in Table 3, the change in the betas drives the strongly lower, and now negative, swap position. Most importantly, the inflation beta makes a large negative contribution. This is because realized inflation and expected inflation (and thus interest rates) are positively correlated. With interest rates now being driven to a large extent by expected inflation (see the conditional interest rate volatility), the real interest rate beta and the productivity beta are now making a considerably weaker contribution.
Table 3: Model Implications: Swap Choice Depending on Risks in the Model
| Statistic | (A): σA | (B): σA,σI | (C): σA,σI,σA,I | (D): σA,σI,σA,I,Δ |
|---|---|---|---|---|
| E(swap) | 5.98 | -1.96 | -1.37 | 0.32 |
| Corr(swap, term spread) | 0.24 | 0.95 | -0.92 | -0.76 |
| Std(swap) | 0.05 | 0.16 | 0.13 | 0.12 |
| Corr(swap, interest rate) | -0.27 | -0.81 | 0.43 | 0.96 |
| Corr(swap, inflation) | - | -0.94 | 0.94 | 0.72 |
| Std(r) | 0.0626 | 0.0791 | 0.0872 | 0.0873 |
| E(StdQ(r/t-1)) | 0.0180 | 0.0476 | 0.0528 | 0.0528 |
| Std(StdQ(r/t-1)) | 0.0012 | 0.0004 | 0.0030 | 0.0030 |
| 1 | 0.14 | 0.23 | 0.23 | |
| 3.08 | 0.44 | 0.63 | 0.63 | |
| 0 | -1.91 | -1.73 | -1.73 |
(σA, aggregate productivity shocks, σI, ination shocks, σA, I negatively correlated productivity and inflation, Δ time-varying idiosyncratic productity)
Case C introduces negative correlation between exogenous aggregate productivity and inflation. Relative to case B with uncorrelated productivity and inflation, this has a modest effect on the level of the swap. Among the betas, the contribution of the productivity beta changes the most. This is now larger, because with negatively correlated productivity and inflation, the negative correlation between productivity and the interest rate is stronger.
The Benchmark case shown in Table 3, in addition to the shocks in case C, also features idiosyncratic productivity shocks with countercyclical variance. As shown in Table 3, this has a big effect on the level, making it positive, with a mean of 0.32. While the simplified model doesn't explicitly include time-varying idiosyncratic risk, the model nevertheless suggests how this can increase the level of the swap. With idiosyncratic risk higher when productivity is lower, idiosyncratic productivity risk amplifies aggregate productivity risk, and this amplification can be seen as requiring an increase in the swap position for hedging against aggregate productivity risk.
Overall, time-varying idiosyncratic productivity risk is a necessary ingredient to generate positive swap positions and to overturn the strong negative effect from inflation risk.
4.2.2 Swap Fluctuations
Table 3 presents correlations of the swap with the term spread, and several other moments that characterize the fluctuations of the swap. Inflation shocks again play a crucial role. First, inflation shocks make the swap more volatile, as seen in case B. Second, when inflation is negatively correlated with productivity as in case C, the swap moves negatively with the term spread, as does its empirical counterpart. Cyclical properties are only moderately affected when adding idiosyncratic productivity risk in the benchmark case.
As shown in Table 3, in case B, the introduction of inflation
shocks substantially increases the volatility of the swap compared
to A, and this produces a strong positive correlation between the
swap and the term spread. Figure 3 illustrates how fluctuations in
the swap are related to the components of the swap choice from the
simple model presented in equation (9). The upper row
shows fluctuations due to each of the three sources of risk. The
lower panels show the corresponding betas. For instance, "total
productivity risk" refers to the effect of fluctuations in
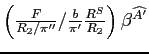 on the approximate swap from the simple model. In this case, only
this term is allowed to change, while the other terms in equation
(9) are held
constant at their average level. The figure displays a random
sample of 100 periods. To produce this figure, the swap of the
simple model is scaled to match the mean and standard deviation of
the swap from the full model, because the level of the swap in the
simple model does not match exactly the level in the full
model.
on the approximate swap from the simple model. In this case, only
this term is allowed to change, while the other terms in equation
(9) are held
constant at their average level. The figure displays a random
sample of 100 periods. To produce this figure, the swap of the
simple model is scaled to match the mean and standard deviation of
the swap from the full model, because the level of the swap in the
simple model does not match exactly the level in the full
model.
In the third panel on the top row of Figure 3 we can see that
total inflation risk,
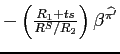 , closely tracks the movements of the swap. Given that the
inflation beta does not track the swap that closely, it is the
"exposure" term
, closely tracks the movements of the swap. Given that the
inflation beta does not track the swap that closely, it is the
"exposure" term
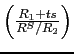 that makes an important contribution to the variation in the swap.
As is clear, this term is strongly positively correlated with the
current one-period rate,
that makes an important contribution to the variation in the swap.
As is clear, this term is strongly positively correlated with the
current one-period rate, ![]() , and because of the
negative sign, this produces the negative correlation of
, and because of the
negative sign, this produces the negative correlation of
![]() of the swap and the current interest
rate, shown in Table 3. Given that the term spread
of the swap and the current interest
rate, shown in Table 3. Given that the term spread
![]() moves
negatively with the short rate
moves
negatively with the short rate ![]() , this explains
the positive correlation between the swap and the term spread in
case B.
, this explains
the positive correlation between the swap and the term spread in
case B.
As shown in Table 3, introducing a negative correlation between
productivity and inflation (going from case B to C) dramatically
changes the cyclical behavior of the swap. The correlation between
the swap and the term spread is now negative, at -0.92. Figure 4 provides some indication about why the
correlation of the swap and the term spread changes so much.
Indeed, total inflation risk now plays a minor role, but the betas,
and the productivity beta in particular, are dominant drivers. The
movement in the inflation beta mostly offsets the movement in the
"exposure" term
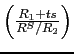 , this is why
inflation risk now makes a marginal contribution to the
time-variation. Clearly, from the movements in the betas we can see
that there is some heteroscedasticity in the model. Table 3 shows
that the standard deviation of the short rate,
, this is why
inflation risk now makes a marginal contribution to the
time-variation. Clearly, from the movements in the betas we can see
that there is some heteroscedasticity in the model. Table 3 shows
that the standard deviation of the short rate, ![]() , under the risk free measure, is about 8 times larger
with correlated inflation than with uncorrelated inflation. While
quantitatively small in itself, this effect has a significant
impact on the cyclical fluctuations of the swap.
, under the risk free measure, is about 8 times larger
with correlated inflation than with uncorrelated inflation. While
quantitatively small in itself, this effect has a significant
impact on the cyclical fluctuations of the swap.
The main results highlighted here are not very sensitive to
changes in most of the calibrated parameter values. As suggested by
the discussion in the preceding paragraph, one parameter that can
have some impact on some of the results is the correlation between
inflation and productivity. For the benchmark calibration this is
set to
![]() , as shown in
Table 3. With this value, the model correlation of output growth
and inflation
, as shown in
Table 3. With this value, the model correlation of output growth
and inflation
![]() is -0.23, in the data this is -0.2, and the model
correlation of output growth and the nominal interest rates is -0.22, in the data this is -0.31. Setting
is -0.23, in the data this is -0.2, and the model
correlation of output growth and the nominal interest rates is -0.22, in the data this is -0.31. Setting
![]() to either -0.25 or -0.4, so that the
model either exactly matches
to either -0.25 or -0.4, so that the
model either exactly matches
![]() or
or
![]() respecetively, makes the
correlation of the swap with the term spread to be either
respecetively, makes the
correlation of the swap with the term spread to be either
![]() or
or ![]() respectively,
in the benchmark case it is -0.76. In sum, while
varying the value of
respectively,
in the benchmark case it is -0.76. In sum, while
varying the value of
![]() can have a
significant quantitative impact, within the range of reasonable
values our main conclusions remain unchanged.
can have a
significant quantitative impact, within the range of reasonable
values our main conclusions remain unchanged.
4.2.3 Other Model Implications
Table 4 presents a set of model implications and their empirical counterparts that demonstrate that the model captures reasonably well a number of additional facts it was not calibrated to. Importantly, the model roughly matches the interest rate volatility and the volatility of output. The model falls somewhat short on the investment volatility. However, the empirical volatility of investment is particularly high due to the selected sample period that the includes the Great Depression.
Table 4: Model Implications
| Statistic | Data | Model |
|---|---|---|
| Std(r) | 0.114 | 0.087 |
| Std(Δy) | 0.097 | 0.071 |
| Std(Δinv) | 0.231 | 0.153 |
| Std(default rate) | 0.037 | 0.066 |
| Std(recovery rate) | 0.047 | 0.021 |
4.3 Consequences and Value of Swap Usage
So far we have focused on the optimal swap choice, we consider now how the availability of interest rate swaps changes other equilibrium outcomes in the model, and how much value is created by firms' access to interest rate swaps. For this purpose, we introduce a swap transaction cost that is proportional to the swap position. In period 1, with a swap, the firm now needs to pay
with
![]() , and in period 2
, and in period 2
The transaction cost ![]() adds to the bid-ask
spread of the swap. If the firm is a fixed rate payer,
adds to the bid-ask
spread of the swap. If the firm is a fixed rate payer, ![]() , then
, then ![]() is added to the fixed
rate that is paid by the firm and received by the swap
counterparty, and vice versa with
is added to the fixed
rate that is paid by the firm and received by the swap
counterparty, and vice versa with ![]() .
Empirically, firms pay for swaps through a bid-ask spread of this
type. So far, the swap default spreads
.
Empirically, firms pay for swaps through a bid-ask spread of this
type. So far, the swap default spreads
![]() and
and
![]() allowed for some
bid-ask spread. However, given the vanishingly small default
probabilities on the swap in the cases considered, the spread has
been essentially zero. Clearly, making
allowed for some
bid-ask spread. However, given the vanishingly small default
probabilities on the swap in the cases considered, the spread has
been essentially zero. Clearly, making ![]() large
enough will lead firms to stop using interest rate swaps. The
sensitivity of the swap choice to
large
enough will lead firms to stop using interest rate swaps. The
sensitivity of the swap choice to ![]() is
also informative about the value created by the swap.
is
also informative about the value created by the swap.
Consider first the issue how swap usage affects firm behavior
and debt pricing. For this we can compare column 2 and column 4, in
Table 5. Both consider the benchmark calibration with all the risks
included. Column 2 is the benchmark case with no transaction cost
(and is the same case as reported in Table 3). Column 4 has a
transaction cost of 10 basis points,
![]() , and with this level of cost
firms stop using swaps. No real quantities are included in Table 5,
as there are no significant real differences in the two cases in
the model. There are some differences in default behavior and the
debt risk premiums, though these are also relatively minor. As
shown in equation (5), the swap
choice is driven by the objective to minimize default costs. Table
5 shows that despite this objective default rates are not
necessarily lower when firms have access to swaps. But, default
becomes slightly less frequent in states with low aggregate
productivity-for which state prices are relatively high-and
defaults become more common in high productivity state that have
lower state prices. The outcome of this shift of defaults can be
seen in the default spread and the debt risk premium, both are
moderately reduced by the presence of the swap.7
, and with this level of cost
firms stop using swaps. No real quantities are included in Table 5,
as there are no significant real differences in the two cases in
the model. There are some differences in default behavior and the
debt risk premiums, though these are also relatively minor. As
shown in equation (5), the swap
choice is driven by the objective to minimize default costs. Table
5 shows that despite this objective default rates are not
necessarily lower when firms have access to swaps. But, default
becomes slightly less frequent in states with low aggregate
productivity-for which state prices are relatively high-and
defaults become more common in high productivity state that have
lower state prices. The outcome of this shift of defaults can be
seen in the default spread and the debt risk premium, both are
moderately reduced by the presence of the swap.7
To further illustrate the effects of swaps on default and debt
pricing, consider the case with only productivity shocks, displayed
in the last two columns of Table 5. Without the swap, that is the
case where
![]() , the default rate is 7.86% with low aggregate productivity and 3.10% with high productivity. Allowing for the swap without
costs equalizes average default rates conditioned on low and high
productivity. In this model version, there are is only one type of
aggregate risk, the productivity shock, and conditionally,
productivity and interest rates are perfectly (negatively)
correlated. Therefore, the swap is very effective in managing
default risk induced by aggregate shocks.
, the default rate is 7.86% with low aggregate productivity and 3.10% with high productivity. Allowing for the swap without
costs equalizes average default rates conditioned on low and high
productivity. In this model version, there are is only one type of
aggregate risk, the productivity shock, and conditionally,
productivity and interest rates are perfectly (negatively)
correlated. Therefore, the swap is very effective in managing
default risk induced by aggregate shocks.
Table 5: Model Implications as Function of Swap Transaction Cost, η
| Statistic | (2) Benchmark η = 0 | (3) Benchmark η = 0.0025 | (4) Benchmark η = 0.001 | (5) Productivity shocks only η = 0 | (6) Productivity shocks only η = 0.001 |
|---|---|---|---|---|---|
| E(swap) | 0.32 | 0.06 | 0 | 5.98 | 0 |
| Corr(swap, term spread) | -0.76 | -0.76 | - | 0.24 | - |
| E(default rate) | 0.0722 | 0.0719 | 0.0718 | 0.0624 | 0.0548 |
| E(default rate/Alow) | 0.1274 | 0.1285 | 0.1288 | 0.0624 | 0.0786 |
| E(default rate/Ahigh) | 0.0169 | 0.0152 | 0.0147 | 0.0623 | 0.0310 |
| Default spread, E ln Rc/R1 | 0.0607 | 0.0608 | 0.0608 | 0.0362 | 0.0384 |
| Debt risk premium | 0.0177 | 0.0180 | 0.0180 | -0.002 | 0.007 |
Based on the fact that with a transaction cost of 10 basis
points, firms stop using swaps, this can be taken as the upper
bound of the value (per period) created by the swap. It is probably
uncontroversial that this is a rather small number. It might be
interesting then to compare this to the empirical level of costs
for interest rate swaps. According to current Reuter's quotes,
bid-ask spreads for 10-year interest rate swaps in USD are about 1
basis point (at an annualized basis). That is, from the end-users'
perspective, the cost of a swap is about 1/2 of a basis point on an
annualized basis, and 2.5 basis point for a 5-year period.
Introducing such a transaction spread into the model leads firms to
substantially reduce swap usage. As shown in Table 5, with a 2.5
basis points cost, swap usage is reduced to an average of 0.06
compared to 0.33 in the case with ![]() . There
is no change on the correlation of the swap and the term spread.
The conclusion from this analysis is that swaps do not create a lot
of value for the typical firms in this model. But, because swaps
are cheap, it nevertheless makes sense to use them. The simplifying
assumption that all firms are initially identical seems to be one
reason why swaps do not create a lot of value in our model. To the
extent that some firms have relatively high probabilities of
default, they would attach a higher value to the insurance provided
by the swap.
. There
is no change on the correlation of the swap and the term spread.
The conclusion from this analysis is that swaps do not create a lot
of value for the typical firms in this model. But, because swaps
are cheap, it nevertheless makes sense to use them. The simplifying
assumption that all firms are initially identical seems to be one
reason why swaps do not create a lot of value in our model. To the
extent that some firms have relatively high probabilities of
default, they would attach a higher value to the insurance provided
by the swap.
5 Conclusion
We have built a simple equilibrium model to study swap usage. Based on available empirical evidence, the focus is on whether this model can produce positive positions for endusers of swaps that require fixed rate payments, and a negative co-movement between swaps and term spreads. The calibrated model with uncertainty about aggregate productivity and inflation, and with countercyclical idiosyncratic productivity shocks, can produce these two properties. Specifically, firms optimally reduce the share of debt that is swapped into fixed when long term rates are high relative to short rates. In the model, all firms behave rationally, and there are no explicit agency conflicts between managers and shareholders. Considering the impact of swap usage, we find that swaps have essentially no effect on firms' real investment behavior. The firms' objective to use swaps to minimize default costs does not result in a reduction of the overall default frequency. However, firms end up with moderately decreased default rates in recessions-for which stochastic discount factors are high-and with moderately increased default rates in expansions-when stochastic discount factors are low. Thus, the cost of debt financing is somewhat reduced by the swap. Overall, we find only small economic gains from swap usage.
Given that the conclusions of the analysis depend on the modelling assumptions, one can speculate about how general these findings are. The model was designed to be as simple as possible and to only include first-order macroeconomic risks. Additional risks and richer processes have the potential to change some of the conclusions about the level and cyclical behavior of interest rate swaps. For swaps to have a larger economic impact, more fundamental changes in the model are needed. In typical macroeconomic models, risk does not have first-order effects on production choices, therefore, our conclusions on this dimension are likely to be robust for a large class of models.
References
Barnea, Amir, Robert A. Haugen,and Lemma W. Senbet, 1980, A Rationale for Debt Maturity Structure and Call Provisions in the Agency Theory Framework, Journal of Finance, Vol. 35, No. 5, December, pp. 1223-43.
Bhamra, Harjoat, Lars-Alexander Kuehn and Ilya Strebulaev, 2008, The Levered Equity Risk Premium and Credit Spreads: A Unified Framework, forthcoming, Review of Financial Studies.
Begenau, Juliane, Monika Piazzesi, and Martin Schneider, 2012, Banks' risk exposures. Unpublished manuscript.
Bloom, Nicholas, Max Floetotto and Nir Jaimovich, 2009, Really Uncertain Business Cycles, unpublished manuscript.
Bodnar, Gordon M, John Graham, Campbell R. Harvey., and Richard C. Marston, 2011, Managing Risk Management, unpublished manuscript.
Chernenko, Sergey, and Michael Faulkender, 2011, The Two Sides of Derivatives Usage: Hedging and Speculating with Interest Rate Swaps, Journal of Financial and Quantitative Analysis, December.
Cooper, Russell, and Joao Ejarque, 2003, Financial frictions and investment: Requiem in Q, Review of Economic Dynamics 6, 710-728.
Cooper, Russell and John Haltiwanger, 2006, On the nature of capital adjustment costs, Review of Economic Studies 73 (3) : 611 - 633
Flannery, Mark J., 1986, Asymmetric Information and Risky Debt Maturity Choice, Journal of Finance, vol. 41(1), pages 19-37.
Gomes, Joao, and Lukas Schmid, 2010, Equilibrium Credit Spreads and the Macroeconomy, unpublished manuscript.
Hull, John C., 2000, Options, Futures & Other Derivatives, Prentice Hall.
Kuehn, Lars-Alexander, 2009, Disentangling Investment Returns and Stock Returns: The Importance of Time-to-Build, unpublished manuscript, Carnegie Mellon University.
Li, Haitao and Connie X. Mao, 2003, Corporate Use of Interest Rate Swaps: Theory and Evidence, Journal of Banking and Finance, Volume 27, Issue 8, August, Pages 1511-1538.
Marshall, John Francis and Kenneth R.Kapner, 1993, Understanding Swaps, John Wiley & Sons.
Moody's Investors Service, 2006, Default and Recovery Rates of Corporate Bond Issuers, 1920-2005.
Myers, Stewart, 1977, Determinants of Corporate Borrowing, Journal of Financial Economics, Volume 5, Issue 2, November, Pages 147-175
Rouwenhorst, K. Geert, 1991, Time to Build and Aggregate Fluctuations: A Reconsideration, Journal of Monetary Economics, vol. 27(2), April, pages 241-254.
Smith, Clifford, W, and Rene M, Stulz, 1985, The Determinants of Firms' Hedging Policies, Journal of Financial and Quantitative Analysis, Vol. 20, no. 4, December, pp. 391-405.
Saunder, Kent T., 1999, The Interest Rate Swap: Theory and Evidence, Journal of Corporate Finance, Volume 5, Issue 1, March, Pages 55-78.
Titman, Sheridan, 1992, Interest Rate Swaps and Corporate Financing Choices, Journal of Finance, September, Volume 47, Issue 4, pp. 1503-1516.
Wall, Larry D., 1989, Interest Rate Swaps in an Agency Theoretic Model with Uncertain Interest Rates, Journal of Banking & Finance, Volume 13, Issue 2, May, Pages 261-270.
A Default Spread and Deadweight Cost
This section shows how default spreads are determined, and how deadweight costs introduce a wedge between the spread determined by the investor and the valuation of the option to default for the firm. This section is added for completeness, the derived results are standard.
Securities are priced by the investors (the market) through the
stochastic discount factor ![]() so that the price
of the security
so that the price
of the security ![]() is given by
is given by
where Payout is the state contingent payment to be received by the owner.
Consider a defaultable version of this security and consider
splitting the set of possible states into two: no-default states
and default states. In a no-default state the security pays the
promised Payout and in a default state the security pays
![]() Payout
Payout
![]() . Clearly, this security
will have a lower price than the non-defaultable claim. To justify
the same price as the non-defaultable security, the defaultable
security needs to offer a default spread
. Clearly, this security
will have a lower price than the non-defaultable claim. To justify
the same price as the non-defaultable security, the defaultable
security needs to offer a default spread ![]() which we take to be a constant, so that in no-default states the
security pays Payout
which we take to be a constant, so that in no-default states the
security pays Payout
![]() while in default
states it pays
while in default
states it pays
![]() . The default spread
is found as the solution to
. The default spread
is found as the solution to
where
![]() denotes the partial
expectation over the set
denotes the partial
expectation over the set ![]() . This implies
. This implies
which implies
![$\displaystyle \rho =\frac{\widetilde{E}_{D}\left( M\cdot \left[ \text{\textit{Payout-}} \gamma \left( s\right) \right] \right) }{\widetilde{E}_{ND}\left[ M\right] }.$](img254.gif)
|
(10) |
Thus, there is an easy way to keep the price of the defaultable
security identical to the non-defaultable one. It involves adding a
default spread that equals the value of the loss given default
![]() scaled by the value of the no-default states.
scaled by the value of the no-default states.
From the firm's ( the borrower's) perspective, the default
spread is the price that is paid for the option to default in some
states. It is easy to see that if there are no deadweight costs for
default, then a borrower that uses the same ![]() values
this option to default also as
values
this option to default also as ![]() . However, with
a deadweight cost this is no longer the case, and the borrower's
value of the default option will be lower than
. However, with
a deadweight cost this is no longer the case, and the borrower's
value of the default option will be lower than ![]() , because the borrower effectively pays the deadweight
cost.
, because the borrower effectively pays the deadweight
cost.
Assuming as in the main text that
![]() , with
, with
![]() capturing the deadweight cost,
that is, while at default the borrower pays
capturing the deadweight cost,
that is, while at default the borrower pays
![]() the lender gets only a
fraction
the lender gets only a
fraction ![]() of it. In this case, the value
that the borrower attaches to the option to default is given by
of it. In this case, the value
that the borrower attaches to the option to default is given by
![$\displaystyle \rho ^{Bor}=\frac{\widetilde{E}_{D}\left[ M\cdot \left( 1-g\left( s\right) \right) \right] }{\widetilde{E}_{ND}\left[ M\right] }<\frac{\widetilde{E}_{D} \left[ M\cdot \left( 1-\psi g\left( s\right) \right) \right] }{\widetilde{E} _{ND}\left[ M\right] }=\rho ,$](img263.gif)
|
that is, it is smaller than the spread actually paid. The wedge between the cost and the value of the option to default for the borrower is given by
![$\displaystyle \rho ^{Bor}-\rho =\frac{\widetilde{E}_{D}\left[ M\cdot \left( g\left( s\right) \right) \right] }{\widetilde{E}_{ND}\left[ M\right] }\left( 1-\psi \right) .$](img264.gif)
|
Clearly, this wedge is larger, the smaller the recovery parameter
![]() , the more likely default is, and the
more expensive default states are. Without deadweight costs,
, the more likely default is, and the
more expensive default states are. Without deadweight costs,
![]() , there is no wedge.
, there is no wedge.
B Simplified Model
This appendix derives the simplified model of swap choice presented in the main text. As shown in Eq. (5), for a given amount of debt, the swap is chosen to minimize the expected value of default costs. For the simplified model, it is assumed that default losses are constant across states of nature, which is approximately true if the loss imposed on default is relatively large. The objective is then to minimize the probability of default (under the risk-neutral distribution), which for convenience we rewrite as
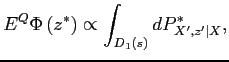
|
where ![]() is the expectation under the
risk-neutral distribution,
is the expectation under the
risk-neutral distribution, ![]() the cutoff
level for default of the idiosyncratic shock,
the cutoff
level for default of the idiosyncratic shock,
![]() , and
, and
![]() the cdf of
the cdf of
![]() .
.
To solve
![]() ,
the first-order necessary condition is
,
the first-order necessary condition is
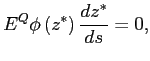
|
with
![]() the pdf.
the pdf.
The linear approximation of the equity value given in Eq.
![]() can be written as
can be written as
![$\displaystyle E_{q}+\frac{F}{R_{2}/\pi ^{\prime \prime }}\left( \hat{z}^{\prime }+\hat{A} ^{\prime }-\hat{R}_{2}+E\widehat{\pi ^{\prime \prime }}\right) +\left( \frac{ b\left[ R_{1}+ts\right] }{\pi ^{\prime }}\right) \widehat{\pi ^{\prime }} +s\left( \frac{b}{\pi ^{\prime }}\frac{R^{S}}{R_{2}}\right) \hat{R}_{2}$](img278.gif)
|
where variables with `^' are the random variables, and
![]() , and
, and ![]() the level of the equity value around which we
approximate.
the level of the equity value around which we
approximate.
The cutoff value for
![]() ,
, ![]() , is implicitly defined by setting this to 0, so
that
, is implicitly defined by setting this to 0, so
that
![$\displaystyle -\frac{\left( \frac{b\left[ R_{1}+ts\right] }{\pi ^{\prime }} \right) }{\frac{F}{R_{2}/\pi ^{\prime \prime }}}\widehat{\pi ^{\prime }}-s \frac{\left( \frac{b}{\pi ^{\prime }}\frac{R^{S}}{R_{2}}\right) }{\frac{F}{ R_{2}/\pi ^{\prime \prime }}}\hat{R}_{2}-E_{q}-\hat{A}^{\prime }+\left( \hat{ R}_{2}+E\widehat{\pi ^{\prime \prime }}\right)$](img285.gif)
|
||
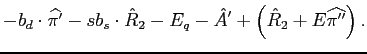
|
The first-order condition can then be rewritten as
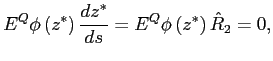
|
implying
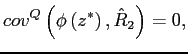
|
because to a first-order approximation
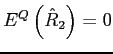 .
.
Consider a first-order approximation of the pdf, so that we can
write
![]() .
The first-order condition can be then solved for
.
The first-order condition can be then solved for ![]()
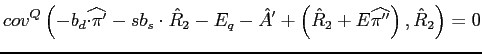
|
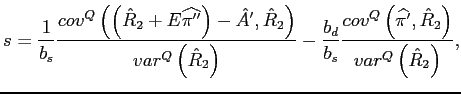
|
which corresponds to Eq. (8) in the main text.
C Data
Consumption, output and investment are from NIPA. A model period being 5 years, annual data, 1930-2006, is summed over 5-year periods. Interest rates are 5-year Treasury constant maturity rate rates, 1953-2007, from Board of Governors of the Federal Reserve System, averaged over 5-year periods. Inflation is the CIP-U, 1930-2009, averaged over 5-year periods. Default and recovery rates are from Moody's (2006) for all issuers. Default rates cover 1920-2005 for the average of 5-year cumulative default rates, 1970-2005 for the standard deviation. Recovery rates cover 1982-2005.
D Definition of Default Risk Premium
We can think of corporate default spreads as being determined by two components. First, the investor is compensated for the possibility of receiving less than the promised debt payment. Second, there is a risk premium due to the covariance between the realized return and the implied stochastic discount factor. This section is added for completeness, the derived results are standard.
Define the realized return on a corporate bond as
![]() , where
, where
![]() is the recovery rate. The
spread can be decomposed as follows
is the recovery rate. The
spread can be decomposed as follows
![$\displaystyle \ln \left( R^{c}/R_{1}\right) =\underset{\text{Risk premium}}{\underbrace{ \ln \left[ R^{c}/R_{1}\frac{1}{E\left( \gamma \right) }\right] }}+\underset{ \text{Expected default loss}}{\underbrace{\ln 1/E\left( \gamma \right) }}.$](img298.gif)
|
The second term on the right hand side is the expected default loss, and the first term, the residual, is called the risk premium. To link this first term explicitly to the risk premium, consider the no-arbitrage relationship
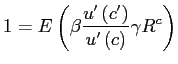
|
that implies
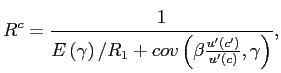
|
with the covariance term capturing the risk premium. As is easily
seen, if
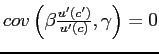 , then
, then
![]() ,
which explicitly justifies our labelling of the residual term as
the risk premium in the first equation of this section.
Alternatively, by definition,
,
which explicitly justifies our labelling of the residual term as
the risk premium in the first equation of this section.
Alternatively, by definition,
![]() ,
where
,
where ![]() is the expectation under risk-neutral
probabilities. Thus, the risk premium equals
is the expectation under risk-neutral
probabilities. Thus, the risk premium equals
![]() .
.
Figure 1: US Dollar Interest Rate Swaps by Non-Financial Institutions (Notional Amounts in trn USD, Source BIS)
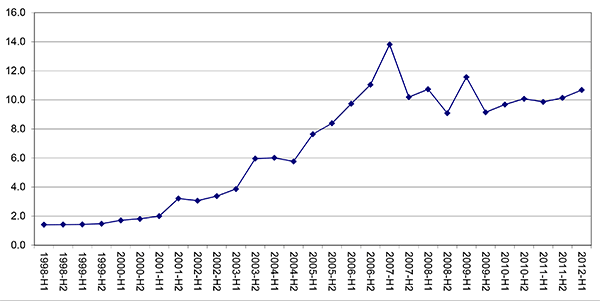
Figure 2: US Corporate Swap Usage Compared to Yield Spread (Swap % of Total Debt, Source Chernenko and Faulkender (2011))
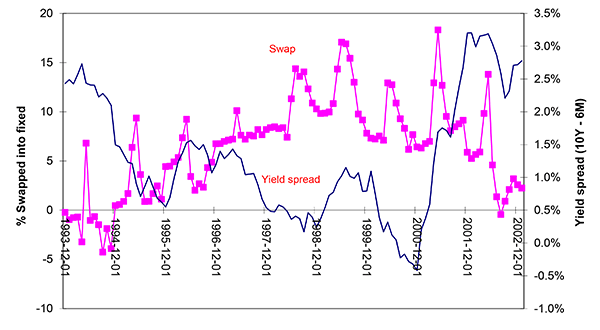
Figure 3: Drivers of Swap Fluctuations with Inflation Risk (Case B)
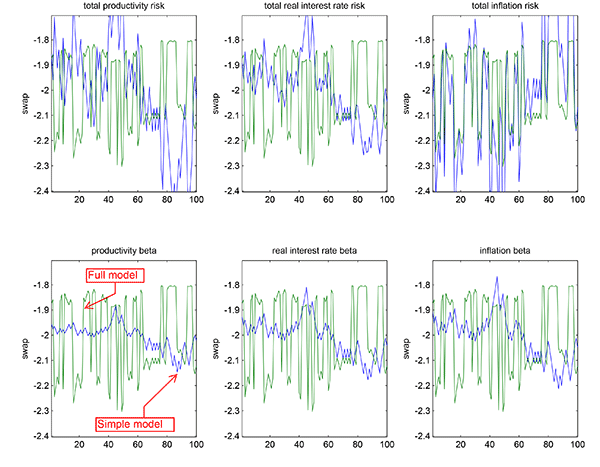
Figure 4: Drivers of Swap Fluctuations with Inflation and Productivity Correlated (Case C)
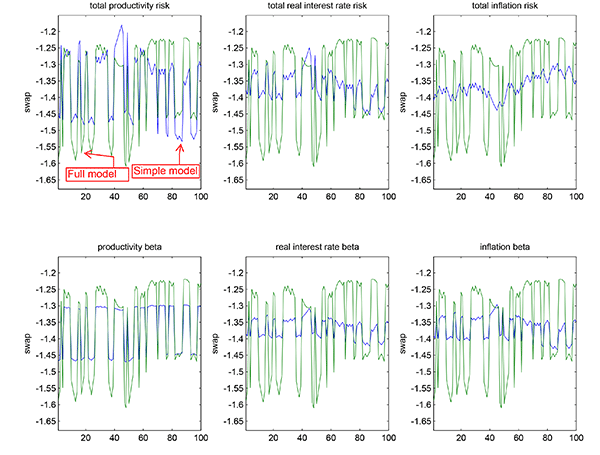
Footnotes
* We are grateful for comments from seminar participants at Columbia University, NYU, Ohio State, Rochester, CKGSB, the Federal Reserve Board, Johns Hopkins University, the 2013 Minnesota Macro-Asset Pricing Conference, as well as from Adrien Verdelhan, Suresh Sundaresan, and Xiaoji Lin. We thank Michael Faulkender for sharing his data. Yue acknowledges the financial support from European Central Bank Lamfalussy Research Fellowship. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. See Marshall and Kapner (1993) for historical and institutational background, and Bodnar et al. (2011) for current derivative usage. Return to text
2. To the extent that default risk is priced in interest rate swaps, it is typically build into the fixed rate. Thus, our assumption of a variable default premium deviates somewhat from the most immediate specification. We make this assumption for numerical tractability, as becomes clear below. Given that defaults on swaps are extremely rare in the model, this assumption does not affect any of our results. Return to text
3. Typically, fixed-for-floating interest rates swaps have maturities of several years, and coupon exchanges take place at quarterly, bi-annual or annual frequencies. We choose a two-period swap contract as the most tractable specification that captures the swap's risk management properties. Return to text
4. Assuming an exogenous inflation process is not necessarily that restrictive. In particular, inflation will be allowed to be correlated with aggregate productivity. Return to text
5. There is some abuse of notation for
the sake of brievity, the pricing schedules, such as
![]() , are
henceforth denoted as function of the debt in real terms
, are
henceforth denoted as function of the debt in real terms
![]() . Return to
text
. Return to
text
6. For instance, for
![]() , with random
variables
, with random
variables ![]() and
and ![]() , setting the derivative with respect to
, setting the derivative with respect to ![]() to 0 yields
to 0 yields
![]() . Return to text
. Return to text
7. See the Appendix for a formal definition of the debt risk premium. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text