
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1106, June 2014 --- Screen Reader
Version*
The Decline of Drudgery and The Paradox of Hard Work1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We develop a theory that focuses on the general equilibrium and long-run macroeconomic consequences of trends in job utility. Given secular increases in job utility, work hours per capita can remain approximately constant over time even if the income effect of higher wages on labor supply exceeds the substitution effect. In addition, secular improvements in job utility can be substantial relative to welfare gains from ordinary technological progress. These two implications are connected by an equation flowing from optimal hours choices: improvements in job utility that have a significant effect on labor supply tend to have large welfare effects.
Keywords: Labor supply, work hours, drudgery, income effect, substitution effect, job utility
JEL classification: E24, J22, O40
1 Introduction
In his 1930 essay, "Economic Possibilities for Our Grandchildren," Keynes predicted that a large increase in leisure would take place over the following century, but robust signs of such a leisure boom have failed to materialize. As shown in Figure (1), for a large set of OECD countries, from 1956 through 2009 aggregate (real) consumption per working-age population (ages 15-64) rose by 100% and more, while work hours per working-age population have been dramatically flat in comparison.4
It is not unreasonable to think, as Keynes did, that the extent to which consumption has increased, along with long-run growth in real wages, should have led to a prominent trend decline in work hours driven by the income effect overtaking the substitution effect. Indeed, there is good reason to think that income effects are substantial (see, for instance, Kimball and Shapiro 2008). Why are people still working so hard? And, what are the welfare effects of this paradox of hard work?
Figure 1: Work Hours Per Population (Left) and Private Consumption per Population (Right)
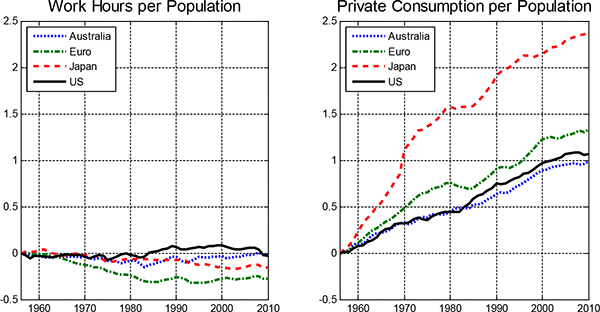
In principle there are four alternative, but not mutually exclusive, explanations through which the paradox of hard work can be rationalized (detailed just below). Of the set of explanations for the paradox of hard work, in this paper we focus on job utility. Economists have long understood that cross-sectional differences in job utility at a particular time give rise to compensating differentials. We develop a theory that focuses on a less-studied topic: understanding the long-run macroeconomic consequences of trends in job utility.
The four rationalizations of the paradox of hard work are as follows.
- Assuming that the elasticity of intertemporal substitution is large. However, empirical evidence suggests the contrary. Hall (1988) finds this elasticity to be approximately zero, Basu and Kimball (2002) find that plausible values are less than 0.7, and Kimball, Sahm, and Shapiro (2011) find a value of approximately 0.08.5
- An increasing ratio of effective marginal wages to consumption. This could be the result, for instance, of a reduction in the progressivity of the tax system, an intensification of competition for promotions within firms, and increasing educational debts.6
- Anything that keeps the marginal utility of consumption high. This could be, for example, because of habit formation, whether internal and external ("keeping up with the Joneses"), and from the introduction of new goods.7
- Anything that serves to keep the marginal disutility of work low. This can be, for instance, the result of technological progress in household production, non-separability between consumption and leisure (King, Plosser, and Rebelo (1988), Basu and Kimball (2002)), and jobs getting nicer.8
We propose an intertemporal framework for thinking about the causes and effects of secular increases in job utility, that is, of jobs getting nicer. Some of the questions that our framework provides answers to are the following.
- How do (on-the-job) effort, amenities, job-enjoyment technology, and labor-augmenting technology interact?
- What are the key determinants of long-run labor supply given job utility?
- How does job utility matter for firms' optimization problems and firms' ongoing ability to operate, attract workers, and establish job parameters given long-run changes in labor-augmenting technology and job-enjoyment technology?
- What are the long-run welfare effects of changes in job utility?
In turn, the answers to these questions lead to two contributions to the macro and labor economics literatures. First, we show that secular improvements in job utility--the decline of drudgery--can induce work hours to remain approximately constant over time even if the income effect of higher wages on labor supply exceeds the substitution effect of higher wages. Therefore, the paradox of hard work is not necessarily evidence that the elasticity of intertemporal substitution is large, that preferences are strongly non-separable, or that preferences have some other feature such as habit formation. Second, we show that secular improvements in job utility can be very substantial in comparison to the welfare gains from ordinary (say, labor-augmenting) technological progress. These two implications are connected by an equation: improvements in job utility that have a significant effect on labor supply tend to have large welfare effects.
This paper proceeds as follows. Section 2 relates our work to the static theory of compensating differentials. Section 3 provides a general overview of our framework. Then, Section 4 discusses the variables we focus on and how our formulation maps into the real world. Sections 5 and 6 focus, respectively, on the optimization problems of individuals and firms. Section 7 deals with the economy's general equilibrium. Then, Section 8 addresses the welfare consequence of changes in job utility. Finally, section 9 concludes.
2 The Static Theory of Compensating Differentials
The natural point of reference for our analysis is the theory of compensating differentials, spelled out originally in the first ten chapters of Book I of "The Wealth of Nations" (Smith, 1776). A standard modern reference on compensating differentials is Rosen (1986).
2.1 Worker and Firm Choices
The solid line in the left panel of Figure 2 is a
wage/job-utility frontier: jobs offering lower job utility will, in
principle, compensate by offering higher real wages (in the figure
![]() is the real wage and
is the real wage and ![]() is job utility). Thus, all else equal, individuals face a trade-off
between these two variables. Conditional on individual preferences,
a particular worker optimizes by choosing a feasible point on the
(solid) frontier in the
is job utility). Thus, all else equal, individuals face a trade-off
between these two variables. Conditional on individual preferences,
a particular worker optimizes by choosing a feasible point on the
(solid) frontier in the ![]() plane.
plane.
The solid line in the right panel of Figure 2 is a
job-utility/output frontier: in order to improve job utility firms
must divert part of their resources away from the production of
output (![]() ). Given its idiosyncratic costs of job
utility in terms of output, a particular firm optimizes by choosing
a feasible point on the (solid) frontier in the
). Given its idiosyncratic costs of job
utility in terms of output, a particular firm optimizes by choosing
a feasible point on the (solid) frontier in the
![]() plane.
plane.
Figure 2. Theory of Compensating Differentials. Left
panel: real wage (![]() ) / job utility (
) / job utility (![]() ) frontier faced by workers. Right panel: job utility /
output (
) frontier faced by workers. Right panel: job utility /
output (![]() ) frontier faced by firms.
) frontier faced by firms.
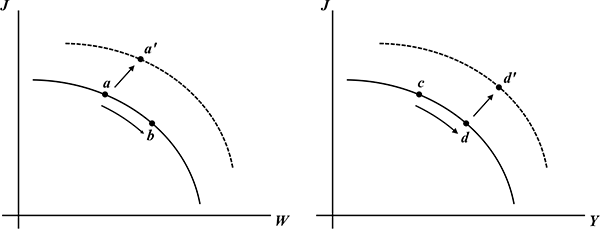
2.2 Movements Along the Frontiers
Suppose higher output and higher real wages came from movements
along the solid frontiers (![]() to
to
![]() in the left panel and
in the left panel and ![]() to
to ![]() in the right panel). As argued in Kimball
and Shapiro (2008), income effects on labor supply are substantial.
So, the higher real wage implied by moving from point
in the right panel). As argued in Kimball
and Shapiro (2008), income effects on labor supply are substantial.
So, the higher real wage implied by moving from point ![]() to point
to point ![]() would tend to reduce work hours. In
addition, if work hours are increasing in job utility, then lower
job utility implied by moving from point
would tend to reduce work hours. In
addition, if work hours are increasing in job utility, then lower
job utility implied by moving from point ![]() to point
to point
![]() also puts downward pressure on work
hours.
also puts downward pressure on work
hours.
2.3 Movements of the Frontiers
However, the frontiers themselves can shift (the dashed lines in
Figure 2). As the economy's choice set expands, optimal choices can
entail moving to points such as
![]() and
and
![]() , in which case job utility,
output, and real wages all rise, and increases in job utility
emerge as potentially offsetting to income effects.
, in which case job utility,
output, and real wages all rise, and increases in job utility
emerge as potentially offsetting to income effects.
The theory we develop in this paper focuses attention on understanding the dynamic general equilibrium implications and endogenous foundations of such intertemporal changes in the economy's choice set. This understanding is complementary to the long-standing static, partial equilibrium microeconomic framework of compensating differentials.
3 The Social Planner's Perspective
There are no distortions in our model so the planning version of the economy is equivalent to a decentralized economy with perfect competition. Both perspectives are valuable, and we begin with the social planning perspective.
Consider individuals who obtain utility from consumption and non-work time. A standard assumption is that any time devoted to work always subtracts from utility. Our alternative assumption is that process benefits and process costs of work--what we call "job utility" --matter as well.
The problem that an idealized social planner would face helps summarize our overall framework. The social planner's problem involves choosing consumption, capital, work hours devoted to particular jobs, effort demands by a particular job (per hour of work), and amenities provided by a particular job in order to maximize a household's lifetime utility given firms' production structures and other standard constraints.
3.1 Baseline Assumptions
We consider a small open economy in which agents can freely
borrow and lend at the exogenously determined real interest rate
![]() (equal to
(equal to ![]() , the rate
at which all economic agents discount the future). Capital is
freely mobile across firms and boarders. We assume that all
benefits and costs to firms and workers other than the utility from
leisure and consumption are proportional to work hours. These
assumptions jointly guarantee that there will never be any
disagreement between workers and firms about job parameters other
than the wage. Furthermore, given fully mobile capital and the
exogenous world interest rate, we can focus on steady state
analysis since the absence of state variables implies that changes
between steady states occur instantaneously. The model is cast in
continuous time (we omit time indexes in order to avoid notational
clutter).
, the rate
at which all economic agents discount the future). Capital is
freely mobile across firms and boarders. We assume that all
benefits and costs to firms and workers other than the utility from
leisure and consumption are proportional to work hours. These
assumptions jointly guarantee that there will never be any
disagreement between workers and firms about job parameters other
than the wage. Furthermore, given fully mobile capital and the
exogenous world interest rate, we can focus on steady state
analysis since the absence of state variables implies that changes
between steady states occur instantaneously. The model is cast in
continuous time (we omit time indexes in order to avoid notational
clutter).
3.2 Individuals and Firms
The economy is inhabited by ![]() ,...,
,...,![]() firms all of which are producers of the same final good and
a continuum of individuals whose mass is normalized to one.
Households each have only one individual, so we will use the terms
household and worker interchangeably.
firms all of which are producers of the same final good and
a continuum of individuals whose mass is normalized to one.
Households each have only one individual, so we will use the terms
household and worker interchangeably.
Utility depends on consumption, the division of time into work time and non-work time, and job utility per hour of work. Job utility depends on effort, amenities, and job-enjoyment technology (we elaborate on all of these further below).
Firms produce output using capital and effective labor input (the product of hours, effort and labor-augmenting technology), and can vary in their real wage and job utility offerings.
3.3 Planning Problem
Table 1 below lays out our notation. In that notation, the planning problem is:
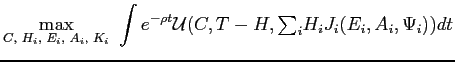
For any variable ![]() ,
, ![]() refers to its
change over time.
refers to its
change over time.
Table 1: Variables adn Parameters
| Variable/Parameter | Description |
|---|---|
| Variable: U | Instantaneous utility |
| Variable: J | Job utility function |
| Variable: t | Denotes time |
| Variable: C | Total consumption of final output |
| Variable: H | Total work hours |
| Variable: Hi | Work hours devoted to ith firm |
| Variable: Ei | ith firm effort demands |
| Variable: Ai | ith firm amenities provision |
| Variable: Yi | ith firm final output |
| Variable: Ki | ith firm capital use |
| Variable: Zi | ith firm labor-augmenting technology |
| Parameter: ρ | Discount rate |
| Parameter: T | Time endowment |
| Parameter: Ψi | Job-enjoyment technology |
| Parameter: Π | Non-labor, non-interest income |
| Parameter: δ | Depreciation rate |
4 From Planning Problem to Real World
Our objective is to deal with many real world features of jobs without adding too much to the complexity of our model. So, we have a broad interpretation of consumption, work hours, effort, amenities, and job utility that allows each to address multiple dimensions of the real world. For example, job-enjoyment technology is meant to capture both innovations in the nature of work proper and innovations in the nature of the work environment.
4.1 Consumption and Work Hours
4.1.1 Consumption
Consumption, ![]() , is meant to capture all the
richness of how resources other than time affect life outside of
working hours. For instance, a broad notion of consumption
necessarily accounts for fringe benefits.
, is meant to capture all the
richness of how resources other than time affect life outside of
working hours. For instance, a broad notion of consumption
necessarily accounts for fringe benefits.
4.1.2 Work Hours
Work hours, ![]() , is meant to capture every way in
which a person's job interferes with the quantity and enjoyment of
non-work time and home production. For example, if an individual is
unable to stop thinking about work issues while at home and this
interferes with other activities at home, then that can be
considered an effective reduction in leisure and hence an increase
in
, is meant to capture every way in
which a person's job interferes with the quantity and enjoyment of
non-work time and home production. For example, if an individual is
unable to stop thinking about work issues while at home and this
interferes with other activities at home, then that can be
considered an effective reduction in leisure and hence an increase
in ![]() . Also, consider time spent away from home
due to work-related travel. Travel may boost the utility of
non-work time if it provides pleasant and interesting experiences.
However, work-related travel can also hamper the enjoyment of
non-work time because of being away from friends and family. In
either case, an adjustment to
. Also, consider time spent away from home
due to work-related travel. Travel may boost the utility of
non-work time if it provides pleasant and interesting experiences.
However, work-related travel can also hamper the enjoyment of
non-work time because of being away from friends and family. In
either case, an adjustment to ![]() may be
warranted.
may be
warranted.
4.2 Job Utility
4.2.1 Effort
Effort, ![]() , is meant to capture all aspects of a
job that generate proportionate changes in effective productive
input from labor. Effort has many dimensions. For example, the
intensity of a worker's concentration on a task while at his or her
work station, the amount of time spent at the water cooler or in
other forms of on-the-job leisure, own time spent cleaning and
beautifying the work place, time spent in office parties or morale
building exercises during work hours, and amount of time spent
pursuing worker interests that have some productivity to the firm
but would not be the boss's first priority, are all dimensions of
effort.
, is meant to capture all aspects of a
job that generate proportionate changes in effective productive
input from labor. Effort has many dimensions. For example, the
intensity of a worker's concentration on a task while at his or her
work station, the amount of time spent at the water cooler or in
other forms of on-the-job leisure, own time spent cleaning and
beautifying the work place, time spent in office parties or morale
building exercises during work hours, and amount of time spent
pursuing worker interests that have some productivity to the firm
but would not be the boss's first priority, are all dimensions of
effort.
4.2.2 Amenities
Amenities, ![]() , are job characteristics whose cost to
the firm is in terms of goods. The real-world characterization of
amenities is just as rich as the characterization of effort. For
instance, amenities include the number of parking spots, the
quality of air conditioning, and the quality and capacity relative
to the number of employees of the office gym.9
, are job characteristics whose cost to
the firm is in terms of goods. The real-world characterization of
amenities is just as rich as the characterization of effort. For
instance, amenities include the number of parking spots, the
quality of air conditioning, and the quality and capacity relative
to the number of employees of the office gym.9
4.2.3 Job-Enjoyment Technology
Job-enjoyment technology affects the mapping of effort and amenities into overall job utility. Therefore, changes in this technological component can be interpreted as capturing innovations in the nature of work proper, or innovations related to the work environment.
Innovations in the Nature of Work Proper Innovations in the nature of work proper come in many forms. For example, working in groups, establishing clear guidelines about what is expected from the worker, allowing workers to have greater discretion in the way projects are carried out, developing creative ways to give workers feedback on their performance (including constructive criticism techniques rather than, say, yelling at the worker about what he or she is doing wrong), improving the organizational structure of the firm in terms of who does what, how they do it and when they do it, and allowing individuals greater flexibility in determining the time during which work is carried out all count historically as innovations in the nature of work proper.
Innovations in the Nature of the External Work Environment Innovations related to the external work environment come in many forms as well. In particular, think of the advent of air conditioning, the distribution, design, and allocation of physical work space (such as cubicalization or open office environments), the provision of on-site childcare, exercise, and laundry facilities, and the institution of measures to reduce the incidence of sexual harassment.
4.2.4 Interpretation of the Job Utility Function
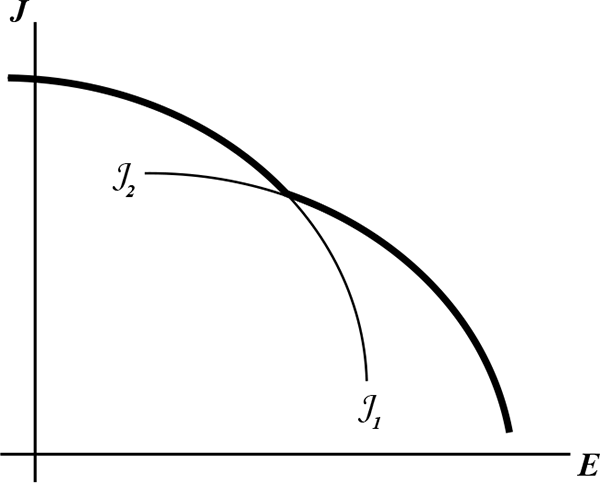
The job utility function ![]() itself is the
optimum over many possible ways of doing things. For example,
consider two production techniques, as shown in Figure 3 in
itself is the
optimum over many possible ways of doing things. For example,
consider two production techniques, as shown in Figure 3 in
![]() space. Production
technique 1, yielding
space. Production
technique 1, yielding
![]() , results in relatively
higher job utility at lower levels of effort, while production
technique 2, yielding
, results in relatively
higher job utility at lower levels of effort, while production
technique 2, yielding
![]() , results in relatively
higher job utility at higher levels of effort. Then,
, results in relatively
higher job utility at higher levels of effort. Then, ![]() is the upper envelope (bold) of these two techniques.
The analytical framework that we develop is robust to such
non-concavities in job-utility functions.
is the upper envelope (bold) of these two techniques.
The analytical framework that we develop is robust to such
non-concavities in job-utility functions.
Figure 3: The Job-Utility Function, ![]() , as the Upper Envelope of the Two Different Production
Techniques
, as the Upper Envelope of the Two Different Production
Techniques
![]() and
and
![]()
4.2.5 Reducing the Number of Dimensions for the Arguments of Job Utility
The function
![]() maps
maps
![]() ,
,
![]() , and
, and ![]() into the hourly utility associated with being at work.
into the hourly utility associated with being at work.
![]() is a vector describing all
dimensions of what the average hour of work is like that affects
productivity (aspects of effort, including the fraction of time
spent in each different activity at work).
is a vector describing all
dimensions of what the average hour of work is like that affects
productivity (aspects of effort, including the fraction of time
spent in each different activity at work).
![]() is the amenities counterpart
to this. Recall that
is the amenities counterpart
to this. Recall that ![]() is job-utility
technology.
is job-utility
technology.
![]() and
and
![]() are determined optimally by
firms.
are determined optimally by
firms.
The reduced form job utility function comes from maximizing over these vectors, subject to keeping effort-related productivity and the cost of amenities the same, that is,
s.t.
where
![]() is a vector of real
amenity prices. So, the number
is a vector of real
amenity prices. So, the number ![]() --hourly effort
per worker--gives effective productive input from an hour of labor
before multiplication by labor-augmenting technology, while the
number
--hourly effort
per worker--gives effective productive input from an hour of labor
before multiplication by labor-augmenting technology, while the
number ![]() summarizes the expenditure on amenities
per hour of work.10
summarizes the expenditure on amenities
per hour of work.10
We allow for ![]() to be either positive or
negative and we allow for the possibility that job utility is
increasing in effort at relatively small levels of effort, but we
assume it must be decreasing in effort at relatively high levels of
effort if only because physical and mental exhaustion eventually
push
to be either positive or
negative and we allow for the possibility that job utility is
increasing in effort at relatively small levels of effort, but we
assume it must be decreasing in effort at relatively high levels of
effort if only because physical and mental exhaustion eventually
push ![]() toward
toward ![]() (otherwise there would be no upper limit to feasible
(otherwise there would be no upper limit to feasible ![]() ).11 We also assume that
).11 We also assume that
![]() and
and
![]() .
.
5 The Household
5.1 Optimization
We now focus on the decentralized version of the representative worker's optimization problem. We show that this problem can be broken into three optimization subproblems that jointly answer the following question: Once job utility is accounted for, what are the key determinants of labor supply?
5.1.1 Main Problem
Given financial wealth ![]() and job
opportunities, the worker chooses consumption
and job
opportunities, the worker chooses consumption ![]() ,
total work hours
,
total work hours ![]() , work hours devoted to each job
, work hours devoted to each job
![]() , to maximize utility
, to maximize utility
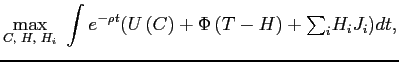
s.t.
| (1) |
and
Overall flow utility comes from consumption utility ![]() , utility from off-the-job leisure
, utility from off-the-job leisure ![]() ,
,
![]() is the real wage offered by the
is the real wage offered by the
![]() th job, which the worker takes as given. We
assume that
th job, which the worker takes as given. We
assume that
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . The choice of job
is represented simply as the choice of whether to devote strictly
positive work hours to any one job in particular. Here, we assume
that utility is additively separable between consumption
. The choice of job
is represented simply as the choice of whether to devote strictly
positive work hours to any one job in particular. Here, we assume
that utility is additively separable between consumption
![]() and all the dimensions of labor. (A
companion paper relaxes that assumption, and yields broadly similar
results as those we obtain in the present paper).
and all the dimensions of labor. (A
companion paper relaxes that assumption, and yields broadly similar
results as those we obtain in the present paper).
5.1.2 Optimization Subproblems
The current-value Hamiltonian associated with the worker's problem is
This maximization problem can be broken down into four optimization subproblems:
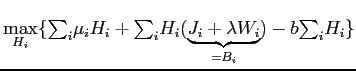 .
. |
Above, ![]() is the costate variable giving the
marginal value of real wealth; the Euler equation is
is the costate variable giving the
marginal value of real wealth; the Euler equation is
![]() .
. ![]() is the multiplier on the work-hours constraint.
is the multiplier on the work-hours constraint. ![]() is the multiplier on the nonnegativity constraint for
hours at each possible job.12 Finally,
is the multiplier on the nonnegativity constraint for
hours at each possible job.12 Finally, ![]() denotes
the marginal hourly net job benefits associated with a job
of type
denotes
the marginal hourly net job benefits associated with a job
of type ![]() . The four optimization subproblems nested
within maximization of the current-value Hamiltonian are:(1) the
consumption decision; (2) job choice; (3) the decision about work
hours for each job; and (4) the overall hours decision.
. The four optimization subproblems nested
within maximization of the current-value Hamiltonian are:(1) the
consumption decision; (2) job choice; (3) the decision about work
hours for each job; and (4) the overall hours decision.
In the additively separable case here we normalize ![]() and
and ![]() so that
so that
![]() .13
Given this normalization,
.13
Given this normalization, ![]() means
that a worker would be willing to spend at least some time on a job
even if unpaid, should that be the only job available. On the other
hand,
means
that a worker would be willing to spend at least some time on a job
even if unpaid, should that be the only job available. On the other
hand, ![]() means that a worker would never
do such a job unless paid.
means that a worker would never
do such a job unless paid.
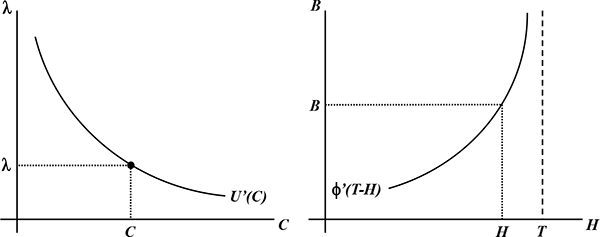
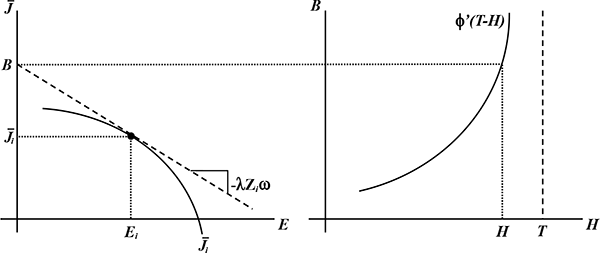
Choice of Consumption As shown in the left panel of Figure 4, the solution to the
first optimization sub-problem,
![]() , is to choose consumption to satisfy the first order condition
, is to choose consumption to satisfy the first order condition
![]() .
.
Figure 4: Household Solution to Choice of Consumption,
![]() , and Total Work Hours,
, and Total Work Hours, ![]()
Choice of Jobs and Hours at Each
Job Job choice involves surveying all possible job types and
choosing the job or jobs with the highest ![]() . At
an optimum
. At
an optimum
![]()
![]() . It follows that if total work hours are spread across
more than one job type it must be the case that each job with
positive hours for the individual is offering the same level of
(hourly marginal net) job benefits--although they need not be
offering the same combination of real wage and job utility.
Formally, the level of hourly net job benefits for all jobs with
strictly positive hours is
. It follows that if total work hours are spread across
more than one job type it must be the case that each job with
positive hours for the individual is offering the same level of
(hourly marginal net) job benefits--although they need not be
offering the same combination of real wage and job utility.
Formally, the level of hourly net job benefits for all jobs with
strictly positive hours is
![]() . We elaborate on
the fraction of time devoted to each job later.
. We elaborate on
the fraction of time devoted to each job later.
Choice of Overall Work Hours Combining the job choice with the choice of work hours at each
job, optimization requires ![]() if
if
![]() and
and
![]() when
when ![]() . This implies that
. This implies that ![]() : the
marginal benefit of overall work hours is equal to the marginal
benefit of hours at the job with the highest job benefits.
Therefore, total work hours should be chosen to satisfy
: the
marginal benefit of overall work hours is equal to the marginal
benefit of hours at the job with the highest job benefits.
Therefore, total work hours should be chosen to satisfy
![]() . In words, at the optimal
level of work hours, the marginal utility from off-the-job leisure
is equal to job benefits
. In words, at the optimal
level of work hours, the marginal utility from off-the-job leisure
is equal to job benefits ![]() of the most attractive job.
Thus, the right panel of Figure 4 shows the determination of the
optimal choice of
of the most attractive job.
Thus, the right panel of Figure 4 shows the determination of the
optimal choice of ![]() . Note that the
labor-hours supply function is
. Note that the
labor-hours supply function is
![]() , and the equivalent to a
market clearing price for work hours is job benefits
, and the equivalent to a
market clearing price for work hours is job benefits ![]() . (We postpone discussion of the determination of the
general equilibrium value of
. (We postpone discussion of the determination of the
general equilibrium value of ![]() to Section
7.).
to Section
7.).
5.2 Implications
Three questions follow immediately. First, how do long-run changes in work hours depend on job utility? Second, assuming there is more than one viable employment opportunity available (that is, assuming more than one firm is able to offer the highest job benefits), how does the worker decide to allocate work hours between jobs? Third, how do short-run changes in work hours depend on job utility?
5.2.1 Implications for Long-Run Labor Supply
Kimball and Shapiro (2008) argue that income effects on labor supply are likely to be substantial. They then look at what that would imply for the Frisch (marginal value of wealth held constant )labor supply elasticity if income and substitution effects on labor supply cancel out. But, our framework allows for work hours to remain relatively constant even if the income effect dominates the substitution effect. Consider the effects when consumption and real wages rise.
Recall that
![]() , and that as shown in
the right panel of Figure 4, work hours are increasing in
, and that as shown in
the right panel of Figure 4, work hours are increasing in
![]() . If the income effect dominates the
substitution effect, then
. If the income effect dominates the
substitution effect, then
![]() is decreasing (
is decreasing (![]() is growing, but
is growing, but ![]() is declining
in line with increases in consumption), which. All else equal that
makes
is declining
in line with increases in consumption), which. All else equal that
makes ![]() --and therefore work hours--decrease as
well.
--and therefore work hours--decrease as
well.
But if job utility, ![]() , is rising
sufficiently, then the income effect can be counterbalanced by the
increase in
, is rising
sufficiently, then the income effect can be counterbalanced by the
increase in ![]() along with the increase in
along with the increase in
![]() that blunts the fall of
that blunts the fall of
![]() in
in
![]() .
.
There is another surprising implication. Even if
![]() because the income
effect overwhelms the substitution effect (that is, because
because the income
effect overwhelms the substitution effect (that is, because
![]() more quickly than
more quickly than
![]() ), work hours will tend to some
constant
), work hours will tend to some
constant ![]() as long as job utility
as long as job utility
![]() tends to some constant
tends to some constant
![]() . That is, even
if people face quickly declining marginal utility for additional
consumption, a positive asymptote for work hours can exist if there
are jobs people enjoy as much as the marginal non-work activity
they would otherwise fill out their days with.
. That is, even
if people face quickly declining marginal utility for additional
consumption, a positive asymptote for work hours can exist if there
are jobs people enjoy as much as the marginal non-work activity
they would otherwise fill out their days with.
5.2.2 Implications for Job Choices
If two jobs have both the same wages and the same job utility,
the division of time between them can only be pinned down by
general equilibrium forces. But, when two jobs have the same net
job benefits but different combinations of wages and job utility,
the endogenous determination of ![]() can lead to
a determinate interior optimum based on worker optimization alone.
Suppose
can lead to
a determinate interior optimum based on worker optimization alone.
Suppose
![]() with
with
![]() and
and
![]() . That is, job 1 is higher
paid than but job 2 is more pleasant. Let
. That is, job 1 is higher
paid than but job 2 is more pleasant. Let ![]() be
the fraction of total work hours that the worker devotes to working
for firm
be
the fraction of total work hours that the worker devotes to working
for firm ![]() . At an interior optimum for a worker
. At an interior optimum for a worker
so
![]() .Given the labor-hours
supply function, the optimal level of work hours satisfies
.Given the labor-hours
supply function, the optimal level of work hours satisfies
![]() .
Substituting into the worker's budget constraint implies that
.
Substituting into the worker's budget constraint implies that
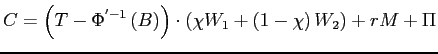 ,
,which after rearrangement yields
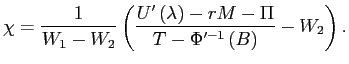
It follows that for any given marginal value of wealth and job
benefits, higher exogenous wealth is associated with greater work
hours being devoted to jobs with higher job utility and lower
wages. Alternatively, at any given set of wages and equilibrium job
benefits, the higher ![]() is the more work
hours are devoted to jobs with the highest wages.
is the more work
hours are devoted to jobs with the highest wages.
Also, note that in the event that more than two jobs have the
same net job benefits, any but the extreme of these set of jobs-the
one with the highest wage and lowest job utility and the one with
the lowest wage and highest job utility-is equivalent from the
worker's perspective to a convex combination of time devoted to the
extreme jobs. So, in the absence of fixed costs of going to work
the analysis for ![]() jobs is essentially the same
as for two jobs. (If there are fixed small costs per job, the
worker might slightly prefer an in-between job and would never
choose three jobs).
jobs is essentially the same
as for two jobs. (If there are fixed small costs per job, the
worker might slightly prefer an in-between job and would never
choose three jobs).
5.2.3 Implications for Short-Run Labor Supply
At any given level of job benefits ![]() , having a
more pleasant, lower-paying job will result in a lower (Frisch)
labor supply elasticity. To see this, rewrite
, having a
more pleasant, lower-paying job will result in a lower (Frisch)
labor supply elasticity. To see this, rewrite
![]() as
as
![]() ,
where
,
where
![]() is the
fraction of the wage that is a compensating differential. Defining
the elasticity of work hours with respect to
is the
fraction of the wage that is a compensating differential. Defining
the elasticity of work hours with respect to ![]() by
by
![]() , then
, then
![]() so that holding
everything constant except wages
so that holding
everything constant except wages
![]() . So, with
. So, with
![]() and
and ![]() held
constant,
held
constant,
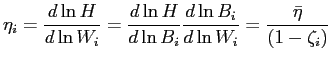
is the Frisch elasticity of labor supply. Thus, the higher job utility is, the lower is labor supply elasticity with respect to temporary changes in the real wage.
The results about multiple jobs in Section 5.2.2 suggested that as
economies become richer, workers are likely to switch to jobs with
higher job utility. Therefore, if
![]() as determined by the curvature of
as determined by the curvature of
![]() stays relatively constant as an economy
gets richer, the volatility of work hours will fall relative to the
volatility of temporary changes in the real wage.
Cross-sectionally, and more speculatively, workers employed in jobs
that they "hate" should have a higher Frisch labor supply
elasticity if the relevant curvature of
stays relatively constant as an economy
gets richer, the volatility of work hours will fall relative to the
volatility of temporary changes in the real wage.
Cross-sectionally, and more speculatively, workers employed in jobs
that they "hate" should have a higher Frisch labor supply
elasticity if the relevant curvature of ![]() is
similar across workers in these different jobs.
is
similar across workers in these different jobs.
6 Firms
In the decentralized version of the optimization problem for firms, the firms are price takers in the product market. Each firm's production function takes as inputs capital and effective labor input (the product of hours, effort, and labor-augmenting technology). The firm rents capital at an exogenous rental rate (determined by the international real interest rate). The hourly cost of labor is captured by the inclusive wage: the sum of the real wage and the hourly cost of amenities. The solution to the firm's cost minimization problem implies that its cost function can be stated as a function of the rental rate of capital and the effective wage: the ratio of the inclusive wage to effective labor productivity (the product of effort and labor-augmenting technology). Minimization of the effective wage is the focus of the firm's optimization subproblems.
6.1 Cost Minimization
Consider a representative providing a job with job-enjoyment
technology ![]() . The firm's production function
is
. The firm's production function
is
![]() ,
where capital's share
,
where capital's share
![]() and other
variables are as defined earlier. Let
and other
variables are as defined earlier. Let ![]() denote the
rental rate of capital, which is exogenous to the firm. (There are
no adjustment costs, so
denote the
rental rate of capital, which is exogenous to the firm. (There are
no adjustment costs, so
![]() ).
).
For any output level
![]() a firm's cost minimization
problem involves choosing capital
a firm's cost minimization
problem involves choosing capital ![]() , and
total work hours
, and
total work hours ![]() , to minimize total cost
, to minimize total cost
![]() subject to
subject to
![]() .
.
![]() is the inclusive
wage:
is the inclusive
wage:
That is, in payment for their labor, workers receive the real wage
![]() (which includes fringe benefits), and
as indirect payment--through job utility--amenities
(which includes fringe benefits), and
as indirect payment--through job utility--amenities ![]() .
.
The solution to the firm's costs minimization problem is
standard. The firm's total cost is a function of the desired level
of output, ![]() , the rental rate of capital,
, the rental rate of capital,
![]() , and the effective wage,
, and the effective wage,
![]() . The effective wage
. The effective wage
![]() is equal to the inclusive wage
per labor effectiveness:
is equal to the inclusive wage
per labor effectiveness:
![]() . Thus,
the firm's cost function is
. Thus,
the firm's cost function is
| (2) |
6.2 Optimization Subproblems for Firms
The rental rate of capital is exogenous, but the effective wage is a function of the real wage, effort, and amenities, all of which are choice variables: How should the firm analyze its decision? First, unless the firm is going to shut down, the firm must choose the effective wage so that the firm offers are at least as high as equilibrium job benefits. Then, two nested subproblems follow. The first subproblem involves the choice of amenities. Then, given the optimal choice of amenities, the firm faces a decision about the real wage and effort. The solution to both of these nested subproblems can be summarized in terms of tangency conditions.
6.2.1 The Central Optimization Subproblem: Minimizing the Effective Wage
Given equation (2) , any operating firm should minimize its effective wage subject to its constraints:
s.t.
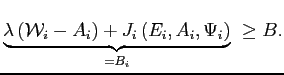
In solving this optimization subproblem firms take the marginal
value of wealth ![]() , the rental rate of capital
, the rental rate of capital
![]() , and equilibrium job benefits
, and equilibrium job benefits ![]() , as given. However, both the real wage
, as given. However, both the real wage ![]() , and amenities
, and amenities ![]() , are choice
variables. We will assume additive separability in job utility
between effort and amenities:
, are choice
variables. We will assume additive separability in job utility
between effort and amenities:
| (3) |
where
![]() captures innovations in the
nature of work proper and
captures innovations in the
nature of work proper and
![]() captures innovations in the
nature of the work environment. We will write
captures innovations in the
nature of the work environment. We will write
![]() .
.
6.2.2 First Nested Subproblem: Choice of Amenities
By the definitions of the inclusive and effective wages
so
![]() . Substituting this last equation into the firm's problem of
meeting the market level of
. Substituting this last equation into the firm's problem of
meeting the market level of ![]() so it can attract
workers (which must bind at the optimal solution) it follows that
so it can attract
workers (which must bind at the optimal solution) it follows that
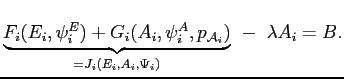
This implies the nested subproblem:
Thus, the choice of amenities should satisfy the tangency condition
![]() . This
optimality condition is shown graphically in
. This
optimality condition is shown graphically in
![]() space in the left panel
of Figure 5.
space in the left panel
of Figure 5.
Figure 5: Solution to a Representative Firm's Optimization Subproblems
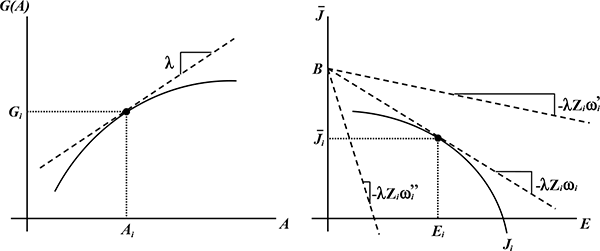
It is helpful to define
the individual surplus received from the firm's optimal choice of
amenities. Note that
![]() by the envelope theorem.
Thus, the lower the marginal value of wealth (intuitively, the
richer a worker is), the greater the surplus from amenities.
by the envelope theorem.
Thus, the lower the marginal value of wealth (intuitively, the
richer a worker is), the greater the surplus from amenities.
6.2.3 Second Nested Subproblem: Choice of Effort
Given the optimal choice of amenities, the firm's problem of minimizing the effective wage reduces to a second nested subproblem:
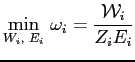
s.t.
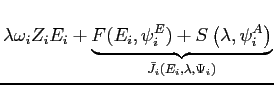 |
(4) |
where
![]() is the net job utility function
(net of the costs of amenity provision measured in utils).
Rearranging,
is the net job utility function
(net of the costs of amenity provision measured in utils).
Rearranging,
| (5) |
and the objective is to find a feasible value of
![]() corresponding to the lowest
corresponding to the lowest
![]() . In
. In
![]() space the left-hand
side of equation
(5) traces out all effort and job-utility combinations that are
consistent with any given effective wage: the firm's isocost lines
shown as downward sloping lines in the right panel of Figure 5. In
that same panel the job utility function is shown as a concave
curve. The firm's objective is to find the tangency that yields an
isocost line with the intercept at
space the left-hand
side of equation
(5) traces out all effort and job-utility combinations that are
consistent with any given effective wage: the firm's isocost lines
shown as downward sloping lines in the right panel of Figure 5. In
that same panel the job utility function is shown as a concave
curve. The firm's objective is to find the tangency that yields an
isocost line with the intercept at ![]() and minimum
downward (absolute value) slope that touches the job utility curve.
and minimum
downward (absolute value) slope that touches the job utility curve.
In other words, given ![]() , the solution to the firm's
optimization subproblem is implicitly captured by the isocost line
that has the flattest (algebraically greatest) feasible slope.
Feasibility is determined by the firm's net job utility function,
which captures all net job utility and effort combinations that a
firm is able to offer. As seen in the right panel of Figure 5,
, the solution to the firm's
optimization subproblem is implicitly captured by the isocost line
that has the flattest (algebraically greatest) feasible slope.
Feasibility is determined by the firm's net job utility function,
which captures all net job utility and effort combinations that a
firm is able to offer. As seen in the right panel of Figure 5,
![]() and
and
![]() is the firm's optimal effective
wage: it can do better than
is the firm's optimal effective
wage: it can do better than
![]() , and although
, and although
![]() is preferred to
is preferred to
![]() , the former is not feasible given
the firm's net job utility function.
, the former is not feasible given
the firm's net job utility function.
Given ![]() and
and
![]() , once
the optimal
, once
the optimal ![]() and
and
![]() are pinned down, it is
straightforward to back out the optimal
are pinned down, it is
straightforward to back out the optimal ![]() using
the definition of the effective wage and the value of
using
the definition of the effective wage and the value of ![]() given the definition of net job utility.
given the definition of net job utility.
6.2.4 Why Effort is Unpleasant at the Optimum
Despite the fact that job utility can be increasing in effort for some part of the range, the tangency condition shown in the right panel of Figure 5 implies that effort will be unpleasant at the optimum. Indeed, at the optimum:
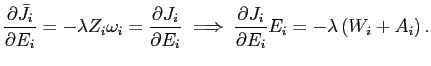
Then, ![]() and
and ![]() imply that for positive wages (and nonnegative amenities), at the
optimal choice of effort
imply that for positive wages (and nonnegative amenities), at the
optimal choice of effort
![]() . That is,
the optimal choice of effort occurs where job utility is decreasing
in effort.
. That is,
the optimal choice of effort occurs where job utility is decreasing
in effort.
In other words, since effort is productive it would make no sense to limit effort when additional effort is also pleasant. Effort should be increased until additional effort is painful enough that it counterbalances the extra productivity.
7 Equilibrium
The next question is: How are equilibrium job benefits and the marginal value of wealth determined?
7.1 Job Benefits
From any firm's point of view the firm-specific effective wage,
![]() , must equal the prevailing market
value of
, must equal the prevailing market
value of ![]() for the firm to have positive output.
Perfect competition in the product market implies that, in
equilibrium, each firm's marginal cost is equal to the price of
final output--which is normalized to 1. Given the cost function in
equation
for the firm to have positive output.
Perfect competition in the product market implies that, in
equilibrium, each firm's marginal cost is equal to the price of
final output--which is normalized to 1. Given the cost function in
equation
![]() that means firms with positive output must have
that means firms with positive output must have
which implies
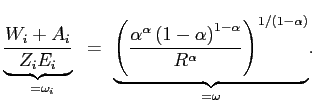
Figure 6 extends the intuition from Figure 5 to this case in
which, as far as a representative firm is concerned, the slope of
an isocost line
![]() is exogenously
determined. Because cost minimization must hold, optimality
continues to require being at a point of tangency between the net
job utility function and an isocost line. Amenities
is exogenously
determined. Because cost minimization must hold, optimality
continues to require being at a point of tangency between the net
job utility function and an isocost line. Amenities ![]() are determined as earlier.
are determined as earlier.
Given the values of ![]() ,
, ![]() , and
, and ![]() , the firm faces, the left
panel of Figure 6 shows optimal effort requirements,
, the firm faces, the left
panel of Figure 6 shows optimal effort requirements, ![]() , and net job utility,
, and net job utility,
![]() . These determine the optimal
real wage
. These determine the optimal
real wage
![]() , and job
utility
, and job
utility ![]() .
.
Figure 6: Determination of Total Work Hours Under Perfect Competition
The intersection of the firm's isocost line with the horizontal
axis now determines equilibrium job benefits ![]() .
Given this equilibrium level of
.
Given this equilibrium level of ![]() , the right panel
of Figure 6 shows the determination of total work hours,
, the right panel
of Figure 6 shows the determination of total work hours,
![]() . This logic can be expressed by the
functions
. This logic can be expressed by the
functions
![]() and
and
![]() . Note
that the firm that is able to offer the highest job benefits is the
firm that implicitly sets the economy's equilibrium level of job
benefits.
. Note
that the firm that is able to offer the highest job benefits is the
firm that implicitly sets the economy's equilibrium level of job
benefits.
7.2 The Marginal Value of Wealth
7.2.1 The Labor Earnings Functions
In general equilibrium, our open-economy framework has
![]() , and
, and
![]() , where
, where
![]() is the fraction of total work hours
that the individual devotes to firm
is the fraction of total work hours
that the individual devotes to firm ![]() . (Thus,
. (Thus,
![]() .).
Let
.).
Let
![]() denote the wage averaged across jobs. Given the individual's
first-order condition for consumption, a labor-earnings demand
function (
denote the wage averaged across jobs. Given the individual's
first-order condition for consumption, a labor-earnings demand
function (![]() ) can be defined as follows:
) can be defined as follows:
| (6) |
Since
![]() , a
labor-earnings supply function (
, a
labor-earnings supply function (![]() ) can be
defined in this way:
) can be
defined in this way:
| (7) |
where once again we have made use of the definition of the average wage.
7.2.2 Graphing Labor-Earnings Demand and Labor-Earnings Supply
Labor-Earnings Demand
![]() is decreasing
in
is decreasing
in ![]() . Therefore, equation
. Therefore, equation
![]() implies
a negative relationship between
implies
a negative relationship between ![]() and
labor-earnings demand as measured by
and
labor-earnings demand as measured by
![]() . Thus, in
. Thus, in
![]() space the
labor-earnings demand function is downward sloping.
space the
labor-earnings demand function is downward sloping.
Labor-Earnings Supply For labor-earnings supply consider first the case in which only
clones of firm ![]() exist. Then,
exist. Then, ![]() is given by
is given by
Showing that in
![]() space labor-earnings
supply is downward sloping requires answering the following three
questions.
space labor-earnings
supply is downward sloping requires answering the following three
questions.
(a) What does a change in ![]() imply for amenities? Suppose that the marginal value of
wealth
imply for amenities? Suppose that the marginal value of
wealth ![]() rises to
rises to
![]() . Then, as shown in the
left panel of Figure 7, amenities decrease. This means that the
surplus from amenities received by individuals,
. Then, as shown in the
left panel of Figure 7, amenities decrease. This means that the
surplus from amenities received by individuals,
![]() ,
declines, which--as shown in the right panel of Figure 7--induces a
downward shift in the net job utility function in
,
declines, which--as shown in the right panel of Figure 7--induces a
downward shift in the net job utility function in
![]() space.
space.
Figure 7: Derivation of Labor-Earnings Supply Curve
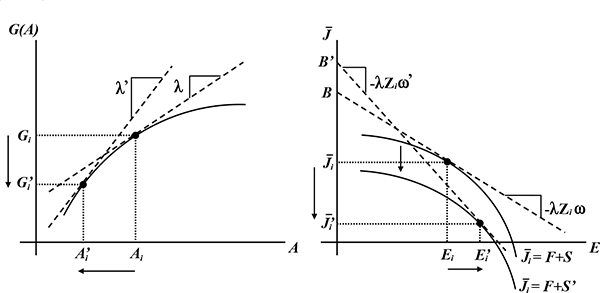
(b) What does a change in ![]() imply for the isocost lines? The right panel of Figure 7
shows that higher
imply for the isocost lines? The right panel of Figure 7
shows that higher
![]() implies a steeper isocost
line, which in turn leads to a decline in net job utility and a
rise in effort. Also, although the change can seem ambiguous, job
benefits rise to
implies a steeper isocost
line, which in turn leads to a decline in net job utility and a
rise in effort. Also, although the change can seem ambiguous, job
benefits rise to
![]() , which leads to higher work
hours.14
, which leads to higher work
hours.14
![]() means that the
means that the ![]() in
in
![]() goes up.
goes up.
(c) How do real wages factor in? If all firms are
identical
![]() is trivially equal to
is trivially equal to ![]() . The analysis behind Figure 7 showed that the result of
higher marginal value of wealth includes lower amenities,
. The analysis behind Figure 7 showed that the result of
higher marginal value of wealth includes lower amenities,
![]() , and higher effort,
, and higher effort, ![]() .
. ![]() is unchanged, and since
is unchanged, and since
![]()
Taken together, the answers to these three questions imply that
labor-earnings is increasing in ![]() so that
so that
![]() is upward sloping in
is upward sloping in
![]() space.
space.
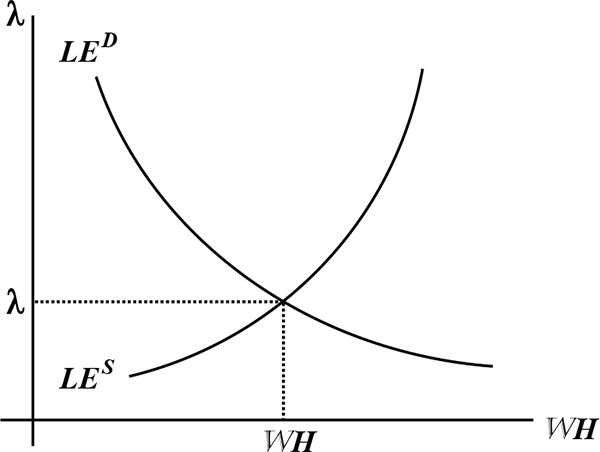
Determination of the Marginal Value of Wealth Figure 8 shows ![]() and
and ![]() , and the determination of equilibrium
, and the determination of equilibrium ![]() and labor earnings
and labor earnings
![]() when all firms are
identical.
when all firms are
identical.
Figure 8: Equilibrium Labor Earnings and the Marginal Value of Wealth Using Labor-Earnings Supply and Demand
What about the determination of the marginal value of wealth and
labor earnings when firms with a range of wage/effort combinations
are operational? For simplicity, consider the case of two types of
firms indexed by ![]() , which, as noted in Section
5.2.2, can be thought
of as the relevant extremes.
, which, as noted in Section
5.2.2, can be thought
of as the relevant extremes.
Suppose these two types of firms have job utility functions
given by
![]() and
and
![]() as depicted in Figure
3. Then, what is relevant is the upper envelope of these job
utility functions. For a sufficiently low marginal value of real
wealth, say
as depicted in Figure
3. Then, what is relevant is the upper envelope of these job
utility functions. For a sufficiently low marginal value of real
wealth, say
![]() , firm 1 is able to offer
the highest marginal net job benefits and type 2 firms do not
operate. For a higher marginal value of real wealth, say,
, firm 1 is able to offer
the highest marginal net job benefits and type 2 firms do not
operate. For a higher marginal value of real wealth, say,
![]() both type 1 and type 2 firms are able to offer the same marginal
net job benefits and workers allocate hours across firms according
to the logic in Section 5.2.2. Finally for even higher
marginal values of real wealth such as, say,
both type 1 and type 2 firms are able to offer the same marginal
net job benefits and workers allocate hours across firms according
to the logic in Section 5.2.2. Finally for even higher
marginal values of real wealth such as, say,
![]() type
2 firms are able to offer the highest marginal net job benefits,
and type 1 firms are unable to operate.
type
2 firms are able to offer the highest marginal net job benefits,
and type 1 firms are unable to operate.
Market equilibrium can be shown in the labor-earnings supply and
demand diagram. ![]() is a simple extension what we
derived above. In particular, labor-earnings demand is described by
is a simple extension what we
derived above. In particular, labor-earnings demand is described by
where ![]() is the fraction of total work hours
devoted to firms of type 1. The appropriate version of
labor-earnings supply is slightly different than that considered
earlier. For sufficiently low values of
is the fraction of total work hours
devoted to firms of type 1. The appropriate version of
labor-earnings supply is slightly different than that considered
earlier. For sufficiently low values of ![]() only
firms of type 1 operate and the associated real wages, marginal net
job benefits, and work hours are relatively low. Therefore, in
terms of labor-earnings supply, low values of
only
firms of type 1 operate and the associated real wages, marginal net
job benefits, and work hours are relatively low. Therefore, in
terms of labor-earnings supply, low values of ![]() are associated with low labor earnings.
are associated with low labor earnings.
At the critical value
![]() noted above both
types of firms are operational. Figure 9 shows an equilibrium in
which both types of firms are operational. Wages, marginal net job
benefits, and hours are higher than under
noted above both
types of firms are operational. Figure 9 shows an equilibrium in
which both types of firms are operational. Wages, marginal net job
benefits, and hours are higher than under
![]() -and therefore so are labor
earnings. However at
-and therefore so are labor
earnings. However at
![]() any level of labor
earnings within a certain range is an equilibrium, implying a
perfectly elastic portion of the labor-earnings supply curve. In
this region, an increase in non-labor income that shifts
any level of labor
earnings within a certain range is an equilibrium, implying a
perfectly elastic portion of the labor-earnings supply curve. In
this region, an increase in non-labor income that shifts
![]() out leads to allocations of more
hours toward the more pleasant job without changing
out leads to allocations of more
hours toward the more pleasant job without changing ![]() .
.
Finally, for higher values of ![]() only firms
of type 2 are operational. This is associated with higher wages,
marginal net job benefits, and hours. Thus, in terms of
labor-earnings supply high values of
only firms
of type 2 are operational. This is associated with higher wages,
marginal net job benefits, and hours. Thus, in terms of
labor-earnings supply high values of ![]() are
associated with high values of labor earnings.
are
associated with high values of labor earnings.
Figure 9: Labor Earnings Supply and Demand With Two Firms
7.3 Implications
Our framework allows us to address several interesting questions. For instance: How does a firm's overall technology matter for its competitiveness? What are the effects of changes in technology (whether changes in labor-augmenting technology or job-enjoyment technology) on labor earnings and the marginal value of wealth? Which changes in technology are consistent with higher real wages and trendless labor hours if the income effect outweighs the substitution effect?
In the Appendix, we show the following. First, within our framework, differences in job-enjoyment technology between firms can counterbalance differences in labor-augmenting technology, and vice versa. In particular, a firm falling behind in labor-augmenting technological progress can keep up its ability to attract workers even with lower wages if its job enjoyability technology advances sufficiently. Second, within our framework, a permanent increase in labor augmenting technology, a permanent positive innovation in the nature of work proper, or a permanent positive innovation in the nature of the work environment can each lead simultaneously to higher labor earnings, a lower marginal value of real wealth, and trendless or nearly trendless work hours.
In essence, then, anything that "regular" technology can do, job enjoyability technology can do as well. To the extent that higher job utility matters for competitiveness, it is even plausible that firms might set what would otherwise be above-optimal effort requirements in order to induce workers themselves to think of ways to increase job utility. This amounts to a low cost form of research and development in job enjoyment technology.
8 Welfare
We argue above that and upward trend in job utility make it possible for work hours to remain approximately constant over time even if the income effect of higher real wages on labor supply exceeds the substitution effect of higher real wages. The question that immediately follows is: What are the welfare effects of such changes? In this section, we elaborate on the relationship between job utility and welfare, suggest ways in which theoretical relationships can be operationalized and give a numerical example for the potential welfare gains associated with secular changes in job utility. Under straightforward though far from certain assumptions, given constant work hours, an observed increase in consumption of 1% might be associated with an increase in welfare of 2%. In this case, at least half of these welfare gains are coming from increases in job utility.
8.1 Measuring Welfare
In our framework, changes in welfare induced by changes in
exogenous parameters are well assessed via comparative steady-state
analysis. In steady state, given ![]() , an
individual's problem is equivalent to the static optimization
problem
, an
individual's problem is equivalent to the static optimization
problem
s.t
and
Given the multipliers ![]() and
and ![]() ,
let
,
let
Recall that the optimal choice of ![]() yields
two cases:
yields
two cases: ![]() and
and
![]() , or
, or ![]() and
and
![]() . Therefore,
. Therefore,
![]() , where,
, where, ![]() denotes the
economy's level of equilibrium marginal net job benefits.
denotes the
economy's level of equilibrium marginal net job benefits.
Using the envelope theorem,
| (8) |
Above, each of the three terms on the right-hand side highlight
distinct ways in which the economy's opportunity set becomes
larger. Changes in welfare from changes in job utility are captured
by the first term; changes in welfare from higher wages are
reflected in the second term; and changes in welfare from changes
in exogenous wealth appear in the last term. The first term
![]() can be interpreted as the portion of the change in the maximized
value of utility that answers the question of how much the worker
would have to be paid per year in order to be willing to go back to
working in yesterday's conditions.
can be interpreted as the portion of the change in the maximized
value of utility that answers the question of how much the worker
would have to be paid per year in order to be willing to go back to
working in yesterday's conditions.
8.2 Toward Pinning Down the Implied Increase in Welfare
To better understand the implications of the envelope theorem as laid out in equation (8) note that the second term on the right-hand side is the change in wages for narrowly defined job categories (for which, empirically, it should be possible to obtain a direct measure) and satisfies
Therefore, to gauge this component of welfare, we need to adjust
the change in overall labor earnings by subtracting not only extra
earnings from people working longer hours overall, but also extra
earnings coming from people switching towards jobs that are more
highly paid and have lower job utility. If ![]() is moving down, then the overall trend should involve compositional
shifts towards jobs with higher job utility and relatively lower
pay than other available jobs. This means that the increase in
labor earnings will tend to understate the true increase in welfare
(leaving aside changes in overall hours, which obviously need to be
adjusted for).
is moving down, then the overall trend should involve compositional
shifts towards jobs with higher job utility and relatively lower
pay than other available jobs. This means that the increase in
labor earnings will tend to understate the true increase in welfare
(leaving aside changes in overall hours, which obviously need to be
adjusted for).
In terms of understanding the remaining terms for the change in welfare, note that
which implies
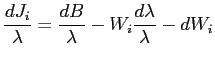 .
.Thus, pinning down the first term in the right-hand side of equation (8) calls for looking at labor hours, consumption, and hourly wages. Substituting into equation (8) and rearranging yields
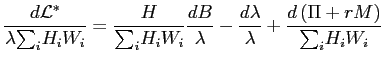 . . |
(9) |
The last term on the right-hand side-the value of extra non-labor income-is easy to understand. Hence, we will focus on getting measures for the first two terms on the right-hand side of equation (9).
Define
![]() . (That is,
. (That is,
![]() is the elasticity of intertemporal
substitution.). Then
is the elasticity of intertemporal
substitution.). Then
![]() . Moreover, as
discussed earlier, for any job
. Moreover, as
discussed earlier, for any job ![]() the Frisch
elasticity of labor supply
the Frisch
elasticity of labor supply ![]() and the
fraction
and the
fraction ![]() of the wage that is a compensating
differential,
of the wage that is a compensating
differential,
![]() , where
, where
![]() , it follows that
, it follows that
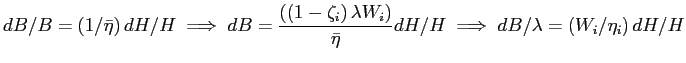 . . |
(10) |
Substituting the appropriate expressions into equation (9) and simplifying yields
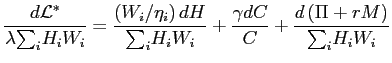 . . |
(11) |
The intuition for equation (11) is
that in the additively separable case ![]() tells
how many times bigger the income effect is than the substitution
effect. If hours are relatively constant despite increasing wages,
then there must be substantial increases in job utility to
counteract the income effects associated with increases in
consumption. On the other hand, if hours
tells
how many times bigger the income effect is than the substitution
effect. If hours are relatively constant despite increasing wages,
then there must be substantial increases in job utility to
counteract the income effects associated with increases in
consumption. On the other hand, if hours ![]() move in
the direction indicated by the income effect it gives less hint of
improvements in job utility. (If
move in
the direction indicated by the income effect it gives less hint of
improvements in job utility. (If ![]() , income and
substitution effects cancel, but increases in consumption still
have the usual effect on welfare.).
, income and
substitution effects cancel, but increases in consumption still
have the usual effect on welfare.).
8.3 Calibrating 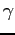 from Job Choices
from Job Choices
In addition to evidence from the effects of interest rates on
the path of consumption, in principle evidence about ![]() can be found from workers' job choices. Consider an
individual working two jobs satisfying
can be found from workers' job choices. Consider an
individual working two jobs satisfying
![]() . Then,
. Then,
![]() ,
meaning that
,
meaning that
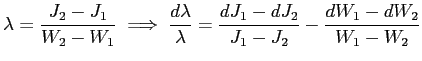 .
.For any individual with
![]() , for example,
, for example,
![]() , then
, then
and using
![]() it follows
that
it follows
that
8.4 Illustrating the Calculation of Welfare Gains
The short-run elasticity of intertemporal substitution has been
suggested by Hall (1988) to be approximately zero, and by Kimball,
Sahm, and Shapiro (2011) to be 0.08. However, there are reasons to
think the long-run elasticity of intertemporal substitution should
be higher than its short-run counterpart. This includes taking
account of full adjustment, new goods, habit formation, and "keeping up with the Joneses." In the context of our analysis, it
is the long-run elasticity of intertemporal substitution that
should be used. Suppose the long-run elasticity of intertemporal
substitution is 0.5, in which case ![]() .
Using this value for
.
Using this value for ![]() along with equation
along with equation
![]() implies that for
implies that for ![]() ,
, ![]() , and
, and
![]() , a 1% increase in consumption would be
associated with a welfare increase of at least 2%.
, a 1% increase in consumption would be
associated with a welfare increase of at least 2%.
A natural question that follows is what fraction of welfare
gains are attributable to higher job utility. To see this, note
that dividing equation
(8) by
![]() and
combining it with equation
(11) yields
and
combining it with equation
(11) yields
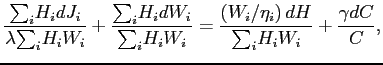
or
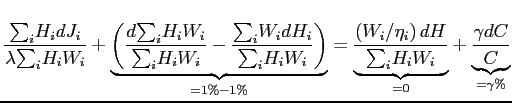 , , |
(12) |
where the second term on the left-hand side reflects switching from
relatively higher paid jobs to relatively lower paid jobs. If there
were no changes in job utility or hours then a 1% increase in consumption is just a 1% increase in consumption. But, if consumption increases 1%, ![]() ,
, ![]() endogenously despite the income effect exceeding the substitution
effect, then this equation implies an increase in welfare
equivalent to the direct effect of a 2% increase
in consumption. So, the difference, 1%, must be
due to improvements in job utility from the two terms on the left
of equation (12).
endogenously despite the income effect exceeding the substitution
effect, then this equation implies an increase in welfare
equivalent to the direct effect of a 2% increase
in consumption. So, the difference, 1%, must be
due to improvements in job utility from the two terms on the left
of equation (12).
9 Conclusions
The paradox of hard work is this: for decades, work hours per capita among adults have remained roughly trendless, despite strong trends in macroeconomic variables, such as real consumption and real wages. In principle, the paradox of hard work can be rationalized in several different ways. Of these alternatives, we focus on the general equilibrium effects of secular changes that make work more pleasant. Economists have long understood that cross-sectional differences in job utility at a particular time give rise to compensating differentials. In this paper, we develop a theory that focuses on the less-studied long-run macroeconomic consequences of trends in job utility.
Our theory allows for the interaction of work hours (which stands in for all aspects of the job that interfere with leisure and home production) and effort (which stands in for all aspects of a job whose cost is in terms of proportionate changes in effective productive input from labor). We also consider the role of amenities (which we define to be job characteristics whose cost is in terms of goods) and the role of secular increases in job utility (that is, secular declines in drudgery, which can stem from changes in standard notions of technology, such as labor-augmenting technology, and also from changes in job-enjoyment technology). General equilibrium can be analyzed through two new theoretical objects: labor-earnings supply and labor-earnings demand.
Two main implications emerge. First, secular improvements in job utility imply that work hours can remain approximately constant over time even if the income effect of higher wages on labor supply exceeds the substitution effect of higher wages. Second, secular improvements in job utility can themselves be a substantial component of the welfare gains from technological progress. These two implications are connected by an equation flowing from optimal hours choices: improvements in job utility that have a significant effect on labor supply tend to have large welfare effects.
Bibliography
Abel, Andrew B. 1990. "Asset Prices Under Habit Formation and Catching Up With the Joneses." American Economic Review, 80(2): 38-42.
Alesina, Alberto F., Edward L. Glaeser and Bruce Sacerdote. 2006. "Work and Leisure in the U.S. and Europe: Why So Different?" In NBER Macroeconomics Annual 2005, Volume 20, edited by Mark Gertler and Kenneth Rogoff. MIT Press.
Altonji, Joseph G. 1982. "The Intertemporal Substitution Model of Labour Market Fluctuations: An Empirical Analysis." Review of Economic Studies, 49 (5): 783-824.
Barsky, Robert B., F. Thomas Juster, Miles S. Kimball, and Matthew D. Shapiro. 1997. "Preference Parameters and Behavioral Heterogeneity: An Experimental Approach in the Health and Retirement Study." Quarterly Journal of Economics 112(2): 537-579.
Basu, Susanto, and Miles S. Kimball. 2002. "Long-Run Labor Supply and the Elasticity of Intertemporal Substitution for Consumption." Boston College and University of Michigan: unpublished manuscript.
Blundell, Richard, Pierre-Andre Chiappori, Thierry Magnac and Costas Meghir. 2001. "Collective Labor Supply: Heterogeneity and Nonparticipation." Institute for Fiscal Studies, London Working Paper 01/19.
Blundell, Richard and Thomas MaCurdy. 1999. "Labor Supply: A Review of Alternative Approaches." In Orley Ashenfelter and David Card, eds. Handbook of Labor Economics Vol. 3A. Amsterdam: North-Holland.
Blundell, Richard, Costas Meghir and Pedro Neves. 1993. "Labor Supply and Intertemporal Substitution." Journal of Econometrics 59: 197-160.
Coulibaly, Brahima. 2006. "Changes in Job Quality and Trends in Labor Hours." International Finance Discussion Papers 882. Washington: Board of Governors of the Federal Reserve System.
Epstein, Brendan and Ryan Nunn. 2013. "Taxation, Match Quality, and Social Welfare." International Finance Discussion Papers 1079. Washington: Board of Governors of the Federal Reserve System.
Epstein, Brendan and Shanthi P. Ramnath. 2014. "Taxes and Long-Run Changes in OECD Work Hours Revisited." Board of Governors of the Federal Reserve System and United States Treasury Department: unpublished manuscript.
Faggio, Giulia and Stephen Nickell. 2007. "Patterns of Work Across the OECD." The Economic Journal, 117 (521): F416-F440.
Fang, Lei and Cara McDaniel. 2011. "Trends in Home Hours in the U.S. and Europe." Unpublished manuscript available at www.caramcdaniel.com
Francis, Neville and Valerie Ramey. 2009. "A Century of Work and Leisure." American Economic Journal: Macroeconomics, 1 (2): 189-224.
Fuhrer, Jeffrey C. 2000. "Habit Formation in Consumption and its Implications for Monetary Policy Models." American Economic Review, 90 (3): 367-390.
Guner, Nezih, Remzi Kaygusuz and Gustavo Ventura. 2012. "Taxation and Household Labor Supply." Review of Economic Studies, 79 (3): 1113-1149.
Hall, Robert E. 1988. "Intertemporal Substitution in Consumption." The Journal of Political Economy, 96: 339-357.
Hansen, Gary D. 1985. "Indivisible Labor and the Business Cycle." Journal of Monetary Economics, 16 (3): 309-327.
Heston, Alan, Robert Summers and Bettina Aten. Penn World Table, Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania.
Keynes, John Maynard. 1930. "Economic Possibilities for Our Grandchildren." Printed in Vol. IX of The Collected Writings of JM Keynes, 1973. London: Macmillan for The Royal Economic Society.
Kimball, Miles S., Claudia Sahm and Matthew D. Shapiro. 2011. "Measuring Time Preference and the Elasticity of Intertemporal Substitution Using Web Surveys." Board of Governors of the Federal Reserve System and University of Michigan: unpublished manuscript.
Kimball, Miles S., and Matthew D. Shapiro. 2008. "Labor Supply: Are the Income Effects Both Large or Both Small?" NBER Working Paper No. 14208.
King, Robert G., Charles I. Plosser, and Sergio R. Rebelo. 1988. "Production, Growth and Business Cycles: I. The Basic Neoclassical Model." Journal of Monetary Economics 21: 195-232.
Krusell, Per, Toshihiko Mukoyama, Richard Rogerson and Aysegul Sahin. 2008. "Aggregate Implications of Indivisible Labor, Incomplete Markets, and Labor Market Frictions." Journal of Monetary Economics, 55 (5): 961-979.
Ljungqvist, Lars and Thomas J. Sargent. 2007. "Do Taxes Explain European Employment? Indivisible Labor, Human Capital, Lotteries, and Personal Savings." In NBER Macroeconomics Annual 2006, Volume 21, edited by D. Acemoglu, K. Rogoff, and M. Woodford, 181-246. The MIT Press.
Luttmer, Erzo F.P. 2005. "Neighbors as Negatives: Relative Earnings and Well-Being." The Quarterly Journal of Economics, 120 (3): 963-1002.
MaCurdy, Thomas E. 1981. "An Empirical Model of Labor Supply in a Life-Cycle Setting." Journal of Political Economy, 89: 1059-1085.
Mankiw, Gregory N., Julio J. Rotemberg and Lawrence H. Summers. 1985. "Intertemporal Substitution in Macroeconomics." The Quarterly Journal of Economics, 100 (1): 225-251.
McDaniel, Cara. 2011. "Forces Shaping Hours Worked in the OECD, 1960-2004." American Economic Journal: Macroeconomics, 3 (4): 27-52.
Mulligan, Casey B. 1998. "Substitution Over Time: Another Look at Life-Cycle Labor Supply." In Ben S. Bernanke and Julio Rotemberg, eds. NBER Macroeconomics Annual 1998. Cambridge: MIT Press.
Mulligan, Casey B. 2001. "Aggregate Implications of Indivisible Labor." NBER Working Paper No. 8159.
Ohanian, Lee, Andrea Raffo and Richard Rogerson. 2008. "Long-Term Changes in Labor Supply and Taxes: Evidence from OECD Countries, 1956-2004." Journal of Monetary Economics, 55 (8): 1353-1362.
Patterson, Kerry D. and Bahram Pesaran. 1992. "The Intertemporal Elasticity of Substitution in Consumption in the United States and the United Kingdom." The Review of Economics and Statistics, 74 (4): 573-584.
Prescott, Edward C. 2004. "Why do Americans Work so Much More than Europeans?" NBER Working Paper No. 10316.
Prescott, Edward C., Richard Rogerson and Johanna Wallenius. 2009. "Lifetime Aggregate Labor Supply with Endogenous Workweek Length." Review of Economic Dynamics, 12 (1): 23-36.
Prescott, Edward C. and Johanna Wallenius. 2011. "Aggregate Labor Supply." Staff Report 457, Federal Reserve Bank of Minneapolis.
Rayo, Luis, and Gary S. Becker. 2007. "Habits, Peers, and Happiness: An Evolutionary Perspective." American Economic Review, 97 (2): 487-491.
Rogerson, Richard. 1988. "Indivisible Labor, Lotteries, and Equilibrium." Journal of Monetary Economics, 21 (1): 3-16.
Rogerson, Richard. 2006. "Understanding Differences in Hours Worked." Review of Economic Dynamics, 9 (3): 365-409.
Rogerson, Richard. 2007. "Taxation and Market Work: Is Scandinavia an outlier?" Economic Theory, 32 (1): 59-85.
Rogerson, Richard. 2009. "Market Work, Home Work and Taxes: A Cross-Country Analysis." Review of International Economics, 17 (3): 588-601.
Rosen, Sherwin. "The Theory of Equalizing Differences." 1986. Handbook of Labor Economics, 1: 641-692.
Shimer, Robert. 2009. "Convergence in Macroeconomics: The Labor Wedge." American Economic Journal: Macroeconomics. 1 (1): 280-297.
Smith, Adam. 1776. "An Inquiry Into the Nature and Causes of The Wealth of Nations." Chicago: University of Chicago Press, 1976. Edwin Cannan, Ed.
Struck, Clemens C. 2013. "Habit Persistence and the Long-Run Labor Supply." Trinity College, Dublin: unpublished manuscript.
Vissing-Jorgensen, Annette. 2002. "Limited Asset Market Participation and the Elasticity of Intertemporal Substitution" Journal of Political Economy, 110 (4): 825-853.
Yogo, Motohiro. 2004. "Estimating the Elasticity of Intertemporal Substitution When Instruments are Weak." The Review of Economics and Statistics, 86 (3): 797-810.
A Details for the Labor-Earnings Supply Derivation
Firms maximize net job benefits given the constraints they face. In particular,
The envelope theorem implies that when ![]() changes
changes
whenever ![]() . Since this is true for all jobs,
the maximum
. Since this is true for all jobs,
the maximum ![]() over all
over all ![]() must
also increase.
must
also increase.
The fact that
![]() highlights an interesting
role for amenities. Consider a decline in the marginal value of
wealth. In the absence of amenities, in
highlights an interesting
role for amenities. Consider a decline in the marginal value of
wealth. In the absence of amenities, in
![]() space the job
utility function would remain fixed while isocost curves became
less steep and job benefits declined. Yet, once amenities are
considered, a lower marginal value of wealth shifts the net job
utility function shifts up in
space the job
utility function would remain fixed while isocost curves became
less steep and job benefits declined. Yet, once amenities are
considered, a lower marginal value of wealth shifts the net job
utility function shifts up in
![]() space. Because of
the logic of the envelope theorem job benefits must still decline,
but not as much as they would in the absence of amenities. Thus,
endogenous provision of amenities blunts the effect of lower
space. Because of
the logic of the envelope theorem job benefits must still decline,
but not as much as they would in the absence of amenities. Thus,
endogenous provision of amenities blunts the effect of lower
![]() . In other words, changes in
amenities serve as endogenous buffers to income effects on labor
supply.
. In other words, changes in
amenities serve as endogenous buffers to income effects on labor
supply.
B The Role of Technology
B.1 Competitiveness
Across firms, differences in job-enjoyment technology can
counterbalance differences in labor-augmenting technology, and vice
versa. To see this, consider firms 1 and 2 as shown in Figure A1,
where
![]() ,
,
![]() , and firms differ in their
net job utility curves. As depicted, although firm 1 has lower
labor-augmenting technology, given its higher job-enjoyment
technology it is the one that would implicitly set the economy's
equilibrium level of job benefits (recall that, all else equal,
higher
, and firms differ in their
net job utility curves. As depicted, although firm 1 has lower
labor-augmenting technology, given its higher job-enjoyment
technology it is the one that would implicitly set the economy's
equilibrium level of job benefits (recall that, all else equal,
higher ![]() shifts the job utility curve up).
Because workers take jobs with the highest
shifts the job utility curve up).
Because workers take jobs with the highest ![]() , firm 2
is unable to attract workers--and therefore must shut down.
, firm 2
is unable to attract workers--and therefore must shut down.
For a higher value of ![]() (which would shift
(which would shift
![]() sufficiently high up) or a
higher
sufficiently high up) or a
higher ![]() (which would make firm 2's isocost
lines sufficiently steep) firm 2 could offer the exact same level
of job benefits as firm 1--in which case both firms would be able
to operate--or even higher job benefits--in which case firm 2 would
be the one to implicitly establish economy-wide equilibrium
(which would make firm 2's isocost
lines sufficiently steep) firm 2 could offer the exact same level
of job benefits as firm 1--in which case both firms would be able
to operate--or even higher job benefits--in which case firm 2 would
be the one to implicitly establish economy-wide equilibrium
![]() , and firm 1 would be unable to attract
workers.
, and firm 1 would be unable to attract
workers.
Figure A1: A Difference in Job Utility Overwhelming a Difference in Labor-Augmenting Technology
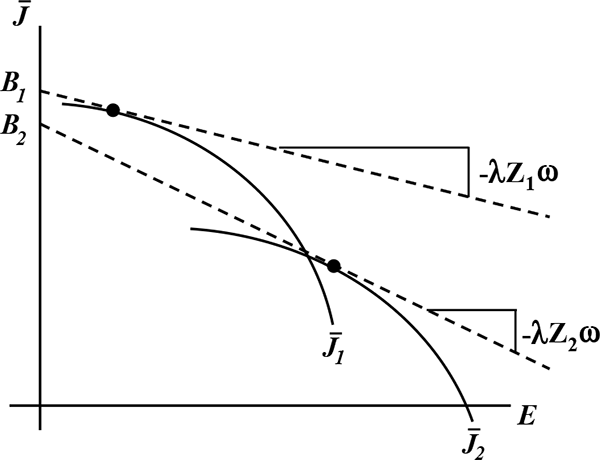
B.2 Labor Earnings and the Marginal Value of Wealth
For the sake of intuition, throughout the remainder of this
section we make four simplifying assumptions. 1) We revert to
assuming that there is only one firm and therefore avoid
![]() indexes. 2) For the effects of changes in
the nature of work proper,
indexes. 2) For the effects of changes in
the nature of work proper, ![]() , three
possibilities emerge depending on whether
, three
possibilities emerge depending on whether
![]() ,
,
![]() , or
, or
![]() .
.
![]() means
that changes in
means
that changes in ![]() do not affect how onerous
extra effort is.
do not affect how onerous
extra effort is.
![]() means
that higher
means
that higher ![]() makes extra effort more
onerous.
makes extra effort more
onerous.
![]() means
that higher
means
that higher ![]() makes increases in effort less
onerous. We focus on
makes increases in effort less
onerous. We focus on
![]() since
it is the most intuitively appealing possibility. 3) Base on
another bit of intuition, we only consider cases in which
since
it is the most intuitively appealing possibility. 3) Base on
another bit of intuition, we only consider cases in which
![]() . 4) We
continue to assume the additively separable case
. 4) We
continue to assume the additively separable case ![]() . Relaxing these assumption leads to interesting
analysis but not quite interesting enough to include here.
. Relaxing these assumption leads to interesting
analysis but not quite interesting enough to include here.
B.2.1 The Effect of a Rise in  on
on  and
and
Suppose labor-augmenting technology increases from ![]() to
to
![]() . The left panel of Figure A2
shows that, all else equal, higher
. The left panel of Figure A2
shows that, all else equal, higher ![]() leads to
higher job benefits (meaning higher work hours) and higher effort,
which leads to higher real wages because the effective wage is
constant. These changes jointly imply higher
leads to
higher job benefits (meaning higher work hours) and higher effort,
which leads to higher real wages because the effective wage is
constant. These changes jointly imply higher
![]() . Now, consider the implications
of higher
. Now, consider the implications
of higher
![]() .
. ![]() shifts
out because at any given
shifts
out because at any given ![]() higher
higher ![]() is consistent with higher labor earnings. This outward
shift in
is consistent with higher labor earnings. This outward
shift in ![]() implies a decrease in equilibrium
implies a decrease in equilibrium
![]() and an increase in equilibrium
and an increase in equilibrium
![]() (the lower
(the lower ![]() induces changes exactly opposite to those in the left
panel of Figure 8 in the main text).
induces changes exactly opposite to those in the left
panel of Figure 8 in the main text).
Figure A2: Effects of Increase in Labor-Augmenting Technology and Effects of Positive Innovation in the Nature of Work Proper
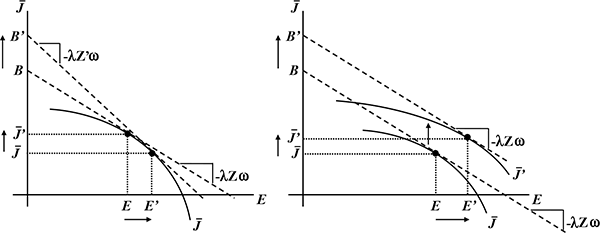
B.2.2 Effect of a Rise in  on
on  and
and
Consider an increase in ![]() to
to
![]() (that is, a
positive innovation in the nature of work proper). Start from the
right panel of Figure A2, where
(that is, a
positive innovation in the nature of work proper). Start from the
right panel of Figure A2, where
![]() is
assumed: all else equal, higher
is
assumed: all else equal, higher ![]() is
consistent with higher job benefits (meaning higher work hours) and
higher effort (meaning--because the effective wage is an exogenous
constant-- higher real wages). If
is
consistent with higher job benefits (meaning higher work hours) and
higher effort (meaning--because the effective wage is an exogenous
constant-- higher real wages). If
![]() the new
the new
![]() effort remains unchanged but job
benefits rise. In either case, labor earnings rise. All other
changes are then analogous to those in Section B.2.1.
effort remains unchanged but job
benefits rise. In either case, labor earnings rise. All other
changes are then analogous to those in Section B.2.1.
B.2.3 Effect of a Rise in 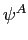 on
on 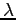 and
and
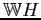
If
![]() and
and
![]() rises (that is, a positive
innovation in the nature of the work environment occurs), the
optimal level of amenities rises as shown in the left panel of
Figure A3. This induces an upward shift in the net job utility
function akin to that shown in the right panel of Figure 8 in the
main text, but without any accompanying change in the slope of
isocost lines. Therefore, effort remains fixed. Because the
effective wage is an exogenously determined constant, all else
equal, higher amenities imply that real wages must decline. So,
although job benefits are higher, the net effect on labor earnings,
rises (that is, a positive
innovation in the nature of the work environment occurs), the
optimal level of amenities rises as shown in the left panel of
Figure A3. This induces an upward shift in the net job utility
function akin to that shown in the right panel of Figure 8 in the
main text, but without any accompanying change in the slope of
isocost lines. Therefore, effort remains fixed. Because the
effective wage is an exogenously determined constant, all else
equal, higher amenities imply that real wages must decline. So,
although job benefits are higher, the net effect on labor earnings,
![]() , is ambiguous. If instead
, is ambiguous. If instead
![]() and
and
![]() rises, as shown in the right panel
of Figure A3 the level of amenities remains fixed, but the surplus
from amenities rises. This induces an upward shift in the net job
utility function, which is consistent with effort remaining fixed
and job benefits rising. Because the effective wage must remain
constant, real wages rise, and all other change are analogous to
those in Section B.2.1.
rises, as shown in the right panel
of Figure A3 the level of amenities remains fixed, but the surplus
from amenities rises. This induces an upward shift in the net job
utility function, which is consistent with effort remaining fixed
and job benefits rising. Because the effective wage must remain
constant, real wages rise, and all other change are analogous to
those in Section B.2.1.
Figure A3: Effect of Positive Innovation in the Nature of the Work Environment
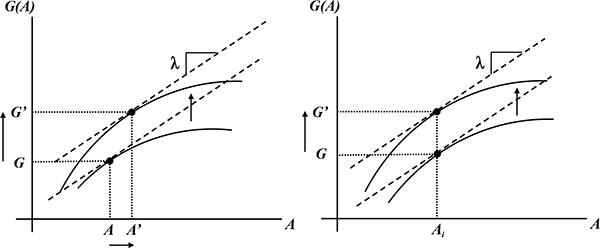
B.3 Real Wages and Trendless Work Hours
B.3.1 Unaltered Slope of Net Job Utility
Consider an initial equilibrium such as point ![]() in the left panel of Figure A4, which corresponds to an isocost
line with slope
in the left panel of Figure A4, which corresponds to an isocost
line with slope
![]() . Then, if labor-augmenting
technology rises, or there is a positive innovation in the nature
of work proper and
. Then, if labor-augmenting
technology rises, or there is a positive innovation in the nature
of work proper and
![]() , or there
is a positive innovation in the nature of the work environment and
, or there
is a positive innovation in the nature of the work environment and
![]() , as shown
in Section B.2 labor
earnings rise and the marginal value of wealth decreases. And, at
lower
, as shown
in Section B.2 labor
earnings rise and the marginal value of wealth decreases. And, at
lower ![]() amenities are optimally higher, and
the surplus from amenities is also higher--which is consistent with
an upward shift in the net job utility function (with no change in
its slope) and less steep isocost lines. If there is no change in
labor hours, then the new equilibrium must be at a point such as
amenities are optimally higher, and
the surplus from amenities is also higher--which is consistent with
an upward shift in the net job utility function (with no change in
its slope) and less steep isocost lines. If there is no change in
labor hours, then the new equilibrium must be at a point such as
![]() ' in the left panel of Figure A4. There,
effort is lower but the effective wage
' in the left panel of Figure A4. There,
effort is lower but the effective wage
![]() is unchanged.15
is unchanged.15
Figure A4: Impact of Technological Changes
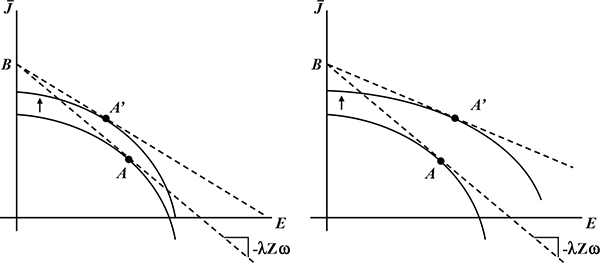
Increase in Labor-Augmenting Technology In the case in which ![]() rises, because effort
declines and amenities rise, the real wage can only be higher after
the increase in labor-augmenting technology if the product
rises, because effort
declines and amenities rise, the real wage can only be higher after
the increase in labor-augmenting technology if the product
![]() is higher and proportionally greater than
the increase in amenities. In mathematical terms, because the
effective wage must remain constant, then a rise in
is higher and proportionally greater than
the increase in amenities. In mathematical terms, because the
effective wage must remain constant, then a rise in ![]() triggers a rise in real wages only if
triggers a rise in real wages only if
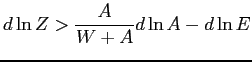 .
.Increase in Labor-Augmenting Technology In such case, because after the rise in ![]() real wages
are higher and so is job utility, then work hours remain constant
as a result of the rise in job utility countervailing the income
effect's outweighing of the substitution effect. So, an increase in
labor-augmenting technology can indeed be consistent with higher
real wages and trendless labor hours (and higher effective labor
productivity).
real wages
are higher and so is job utility, then work hours remain constant
as a result of the rise in job utility countervailing the income
effect's outweighing of the substitution effect. So, an increase in
labor-augmenting technology can indeed be consistent with higher
real wages and trendless labor hours (and higher effective labor
productivity).
Positive Innovations in Job-Enjoyment Technology If labor-augmenting technology rises, or there is a positive
innovation in the nature of work proper and
![]() , or there
is a positive innovation in the nature of the work environment and
, or there
is a positive innovation in the nature of the work environment and
![]() , then,
again, at point
, then,
again, at point ![]() ' effort is lower. Because
amenities are higher and the effective wage must remain constant,
then given that the product
' effort is lower. Because
amenities are higher and the effective wage must remain constant,
then given that the product ![]() is lower real
wages must decline. And this decline must exactly satisfy
is lower real
wages must decline. And this decline must exactly satisfy
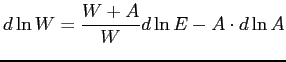 .
.So, all else equal, neither a positive innovation in the nature of
work proper with
![]() nor a
positive innovation in the nature of the work environment with
nor a
positive innovation in the nature of the work environment with
![]() are
consistent with both trendless work hours and higher real wages.
are
consistent with both trendless work hours and higher real wages.
B.3.2 Altered Slope of Net Job Utility
Consider an initial equilibrium such as point ![]() in t
in t![]() he right panel of Figure A5, which corresponds to an isocost
line with slope
. Then, given a positive
innovation in the nature of work proper with
he right panel of Figure A5, which corresponds to an isocost
line with slope
. Then, given a positive
innovation in the nature of work proper with
![]() , as
shown in Section B.2.2 labor
earnings rise and the marginal value of real wealth decreases. And,
at lower
, as
shown in Section B.2.2 labor
earnings rise and the marginal value of real wealth decreases. And,
at lower ![]() amenities are optimally higher, and
the surplus from amenities is also higher--which is consistent with
an upward shift in the net job utility function (with change in
slope as implied by
amenities are optimally higher, and
the surplus from amenities is also higher--which is consistent with
an upward shift in the net job utility function (with change in
slope as implied by
![]() ) and
less steep isocost lines. If there is no change in labor hours but
the income effect outweighs the substitution effect, then the new
equilibrium must be at a point such as
) and
less steep isocost lines. If there is no change in labor hours but
the income effect outweighs the substitution effect, then the new
equilibrium must be at a point such as ![]() ' in the left
panel of Figure A4--job utility must be higher. At point
' in the left
panel of Figure A4--job utility must be higher. At point
![]() effort is higher but the
effective wage
effort is higher but the
effective wage
![]() must remain unchanged. Because amenities are also higher, real
wages are higher only if
must remain unchanged. Because amenities are also higher, real
wages are higher only if
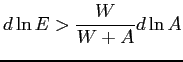 .
.So, when positive innovations in the nature of work proper make
effort less taxing, a rise in ![]() can indeed
be consistent with higher real wages and trendless labor hours (and
higher effective labor productivity).
can indeed
be consistent with higher real wages and trendless labor hours (and
higher effective labor productivity).
B.3.3 Technological Equivalence
Comparison of the left and right panels of Figure A4 along with results from Sections B.3.1 and B.3.2 imply that, in principle, the impact of an increase in labor-augmenting technology can be exactly equal to the impact of a positive innovation in the nature of work proper.
Footnotes
1. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. The authors are thankful, without implicating, for comments received by seminar participants at the University of Michigan and also during visits to the Board of Governors of the Federal Reserve System, Brown University, the Federal Reserve Bank of Atlanta, the Federal Reserve Bank of Philadelphia, the Federal Reserve Bank of Richmond, and McMaster University. Return to text
2. Board of Governors of the Federal Reserve System (e-mail: [email protected]). Return to text
3. Professor, University of Michigan, and NBER ([email protected]). Return to text
4. See Prescott (2004), Alesina, Glaeser, and Sacerdote (2006), Rogerson (2006, 2007, and 2009), Faggio and Nickell (2007), Ljungqvist and Sargent (2007), Ohanian, Raffo, and Rogerson (2008), Shimer (2009), Fang and McDaniel (2011), McDaniel (2011), Guner, Kaygusuz and Ventura (2012), and Epstein and Ramnath (2014) for complementary work related to cross-country differences in hours worked per population. Return to text
5. See also, for example, Altonji (1982), Card (1994), Patterson and Pesaran (1992), Fuhrer (2000), Vissing-Jorgensen (2002), and Yogo (2002). Return to text
6. For additional discussion, see, for instance, Shapiro and Kimball (2008). Return to text
7. See, for instance, Abel (1990), Fuhrer (2000), Luttmer (2005), Rayo and Becker (2007), and Struck (2013). Return to text
8. It follows that our research is broadly related to many literatures. These literatures include, but are not limited to, work by MaCurdy (1981), Altonji (1982 and 1986), Hansen (1985), Mankiw, Rotemberg and Summers (1985), Rogerson (1988), Blundell, Meghir, and Neves (1993), Mulligan (1998), Blundell and MaCurdy (1999), Blundell, Chiappori, Magnac, and Meghir (2001), Mulligan (2001), Coulibaly (2006), Krusell, Mukoyama, Rogerson, and Sahin (2008), Francis and Ramey (2009), Prescott, Rogerson, and Wallenius (2009), and Prescott and Wallenius (2011). Return to text
9. See Epstein and Nunn (2013) for a treatment of amenities in an environment with search frictions. Return to text
10. The relative price of amenities can
simply be thought of as being part of the overall technological
component ![]() . Indeed, think of production of
firm
. Indeed, think of production of
firm ![]() s
s ![]() th ammenity as
th ammenity as
where
![]() is technology and
is technology and ![]() is the amount of the firm's total output,
is the amount of the firm's total output,
![]() , devoted to producing the amenity.
Then, the firm's total expenditure on amenity
, devoted to producing the amenity.
Then, the firm's total expenditure on amenity ![]() is
is
![]() and we
define
and we
define
![]() . Thus, for
instance, an increase in technology
. Thus, for
instance, an increase in technology
![]() decreases the relative price
of the
decreases the relative price
of the ![]() th amenity. Except when the real prices of
amenities are visible in markets it might be impossible to
distinguish between an improvement in job-enjoyment technology and
a fall in the price of an amenity. Return to text
th amenity. Except when the real prices of
amenities are visible in markets it might be impossible to
distinguish between an improvement in job-enjoyment technology and
a fall in the price of an amenity. Return to text
11. We consider this to be the more intuitive case, although our results are unaltered by assuming that job utility is always decreasing in effort. Return to text
12. The worker's problem would be dramatically different if it were possible to devote negative work hours to unpleasant, badly paid jobs. Return to text
13. Consider
![]() with
with
![]() , where
, where
![]() is a constant. Define
is a constant. Define
![]() and
and
![]() . Then,
. Then,
![]() , and
, and
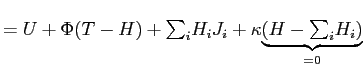 . . |
14. See the appendix for additional details. Return to text
15. Note that
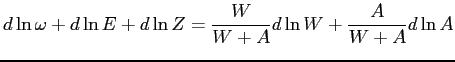
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text