FEDS Notes
September 20, 2024
Financial Conditions and Risks to the Economic Outlook
Andrea Ajello, Giovanni Favara, Gregory Marchal, Balint Szoke1
Financial conditions have swung considerably over the past two and half years. They moved from very accommodative levels in late 2021 to providing a significant drag on economic activity in 2022 and 2023. Since early this year, they eased moderately amid monetary policy communications signaling that the federal funds rate had likely reached its peak for this monetary policy tightening cycle.
In light of these significant swings in financial conditions, and the lags through which they affect economic activity, a question of interest is how risks to the economic outlook implied by financial conditions have evolved over the recent tightening cycle. Are risks to the medium-term outlook for GDP growth, employment growth, and inflation less pronounced today than they were at the beginning of the tightening cycle or at the end of 2023 when financial conditions reached their tightening peaked? Are current financial conditions tight relative to their historical distribution, and what do they signal for recession risks over the year ahead?
In this note, we tackle these questions with the help of a statistical model that maps financial conditions to the year-ahead distribution of GDP growth. We use this model to identify, at each point in time, levels of financial conditions that predict GDP growth distributions that are consistent with either recessionary or non-recessionary outcomes. The analysis suggests that financial conditions currently stand near the top of the range of values that are compatible with the empirical distribution of GDP growth observed in the United States in periods of economic expansion.
We extend our analysis to understand how the evolution of financial conditions over the last few years have affected risks to the outlook for the Fed's dual mandate. The analysis suggests that at the beginning of the tightening cycle, financial conditions were associated with conditional distributions of employment growth that featured very little downside risk, while the predictive distribution of inflation was skewed toward higher inflation outcomes. In recent months, downside risks to employment growth are estimated to be lower than those predicted at the end of 2023, when financial conditions peaked. Meanwhile the conditional distribution of inflation has shifted uniformly to the left, with the modal forecast centered approximately around 2 percent.
Measuring financial conditions
We gauge financial conditions by means of the Financial Conditions Impulse on Growth (FCI-G). This index aggregates the information content of seven key financial variables using weights implied by the FRB/US model.2 One appealing feature of the FCI-G is that it accounts for the lags through which changes in financial variables affect future economic activity. Another feature of this index is that it provides a gauge of the extent to which changes in financial variables pose headwinds or tailwinds to year-ahead GDP growth (see Ajello et al. (2023), for a more in-depth discussion of the FCI-G).
A monthly version of the FCI-G is plotted in Figure 1, with higher (lower) values of the index denoting tighter (easier) financial conditions, measured in percentage points of headwinds (tailwinds) to GDP growth over the following year. As shown in the left panel, financial conditions typically tighten during recessions (the grey bars) and monetary policy tightening cycles (the dashed bars), and they generally ease in expansions and during periods of monetary policy easing. The historical average level of the FCI-G (the grey dot-dashed line) points to modest tailwinds, stemming from the positive average growth rate of stock and house prices over the index history, and it is compatible with the positive average growth rate of the U.S. economy.
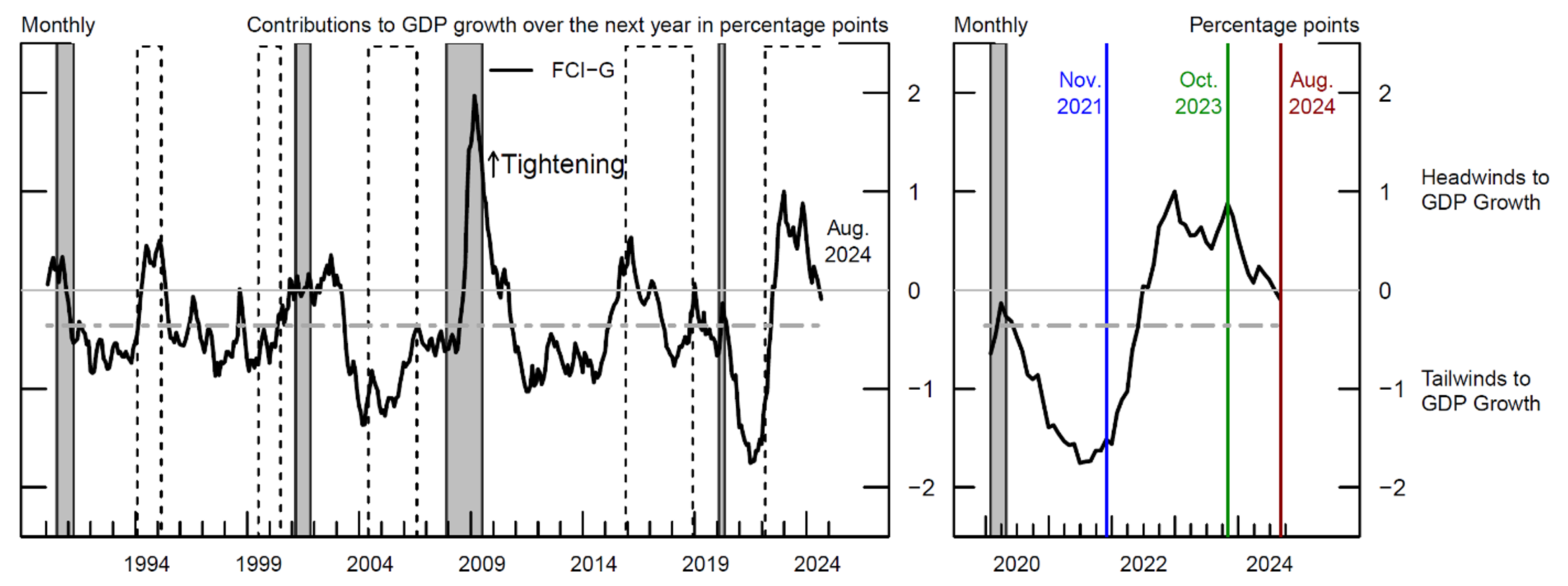
Note: The figure shows the FCI-G. Positive (negative) values of the index denote headwinds (tailwinds) to GDP growth over the next year. The FCI-G value for August 2024 is estimated using data available as of August 30, 2024. Grey-shaded areas denote periods of recession as dated by the National Bureau of Economic Research: July 1990-March 1991, March 2001-November 2001, December 2007-June 2009, and February 2020-April 2020. The dashed bars represent monetary policy tightening cycles: February 1994-March 1995, July 1999-July 2000, June 2004-August 2006, December 2015-July 2018, and March 2022-present. Tightening cycles are defined to start on the month of the first federal funds rate increase and end after the last rate hike. The grey dot-dashed line displays the average value of the index computed since January 1990.
Source: Haver Analytics; Decennial Census of Population and Housing; CoreLogic; Authors' calculations.
The right panel of Figure 1, which zooms on the last four years of data, suggests that financial conditions have fluctuated considerably and went from being a tailwind to year-ahead growth to representing a notable headwind, reaching a tightening peak in late 2023 and easing moderately since then. In this note we assess how risks to the economic outlook predicted by financial conditions have changed over the full course of the recent financial conditions cycle.
To tackle this question, we use a statistical model to predict the full distribution of future real GDP growth as a function of financial conditions, accounting for nonlinearities and asymmetries in the relationship. We then compare the statistical "distance" between the GDP growth distribution implied by our model and the historical GDP growth distribution of the U.S. economy in non-recession periods. This comparison allows us to identify levels of financial conditions that are either tighter or looser than those consistent with the historical non-recessionary growth distribution.
Our model takes the whole distribution of GDP growth—not just the mean—as its building block. This approach enables us to assess financial conditions based on their effects to the risks to GDP growth. Our goal, however, is not to predict recessions but rather to evaluate the implications of financial conditions for the medium-term growth outlook.
Statistical Model
Our statistical model is inspired by the empirical literature documenting that financial variables have predictive power for future economic activity (see e.g., Faust, Gilchrist, Wright and Zakrajsek, 2012) and that measures of financial conditions and stress are significant determinants of risks to the growth outlook (Adrian, Boyarchenko, Giannone, 2019).3
We start the analysis by assuming that the conditional distribution of GDP growth $$h$$-periods ahead, $$ y_{t,^{\circ}t+h} $$ follows a skewed $$t$$−distribution (Azzalini and Capitanio, 2003), with time-varying location ($$ \mu $$), scale ($$ \sigma $$), and shape ($$ \alpha $$ ) parameters, and a fixed degree of freedom, $$ \nu $$:
$$$$ y_{t,\ t+h} \text{~ skewed} - t(\mu_{t}, \sigma_{t}, \alpha_{t}, \nu) $$$$
Four parameters ($$ \mu \text{,} \sigma \text{,} \alpha \text{,} \nu $$ ) determine the conditional mean, variance, skewness, and kurtosis of the distribution.
To predict the future distribution of GDP growth as a function of current financial conditions, we assume that the time-varying parameters $$ (\mu_{t} \text{,} \sigma_{t} \text{,} \alpha_{t} )$$ are linear functions of current financial conditions:
$$$$ \mu_{t} = \varphi_{\mu} + \beta_{\mu} FCI_{t} \\ $$$$
$$$$ log \sigma_{t} = \varphi_{\sigma} + \beta_{\sigma} FCI_{t} \\ $$$$
$$$$ \alpha_{t} = \varphi_{\alpha} + \beta+{\alpha} FCI_{t} $$$$
where $$FCI_{t}$$ represents the FCI-G. We model the logarithm (instead of the level) of $$σ$$ to guarantee that the distribution has positive variance.4
We set the forecast horizon h to one year and estimate model parameters on expanding samples—that is, we obtain a maximum likelihood estimate of ($$ \varphi_{\mu} \text{,} \varphi_{\sigma} \text{,} \varphi_{\alpha} \text{,} \beta_{\mu} \text{,} \beta_{\sigma}\text{,} \beta_{\alpha} \text{,} \nu $$) over a first sample period that starts in 1979:Q1 and ends in 1989:Q4, and progressively update the parameter estimates expanding the sample window, adding quarterly observations through 2024:Q2. This procedure allows us to avoid lookback bias and to capture the time-varying nature of the relationship between financial conditions and the predictive distribution of GDP growth, employment growth, and core PCE inflation.
Financial conditions and GDP growth distributions
The left panel of Figure 2 plots three conditional GDP growth distributions implied by our model, conditioned on monthly values of the FCI-G.5 The blue line is the one-year-ahead GDP growth distribution predicted by the November 2021 level of FCI-G, the green line is the year-ahead GDP growth distribution predicted by the October 2023 peak of our gauge of financial conditions, and the red line is the year-ahead GDP growth distribution predicted by the most recent reading of the FCI-G as of August 2024.6 The chart shows that since late 2021, the one-year-ahead conditional distribution of GDP growth has shifted to the left and become skewed toward lower outcomes. However, since late 2023, downside risks to the growth outlook have decreased notably.
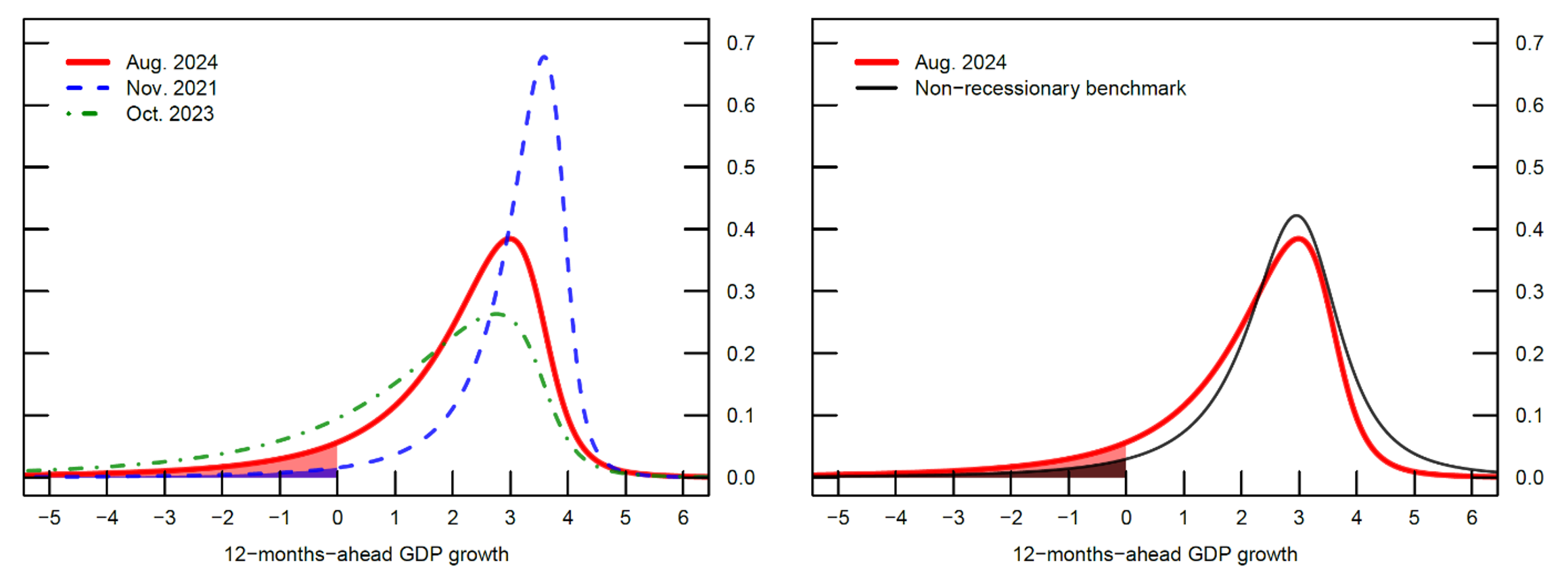
Note: This model assumes that moments (mean, variance, and skewness) of the distribution of one-year-ahead GDP growth (in annualized percentage points) depend linearly on the FCI-G. The red line in both the left and right panels show the June 2024 distribution. In the left panel, the dashed blue line shows the November 2021 distribution, and the dot-dashed green line shows the October 2023 distribution. In the right panel, the thin black line shows the non-recessionary benchmark.
Source: Authors' calculations.
To gauge the economic significance of the most recent shift, the right panel of Figure 2 compares the August 2024 conditional distribution with a "non-recessionary benchmark" that is defined as the empirical GDP growth distribution for the U.S. economy since 1979, excluding NBER-dated recessions (the black line). The choice to exclude past U.S. recessions is also motivated by the desire to minimize the influence on the distribution of GDP growth of sharp turning points associated with the transition between periods of high and low economic activity.
As shown in the right panel, the conditional distribution of one-year-ahead GDP growth implied by the August 2024 level of the FCI-G is skewed to the left of the non-recessionary benchmark distribution: median growth is 0.4 percentage points lower and downside risk to growth—defined as the probability of negative average GDP growth over the next year (shaded regions)—is approximately twice as large than under the non-recessionary distribution.
Growth-consistent range of financial conditions
Are the recent shifts in the predictive distribution of GDP growth unusual by historical standards? One way to address this question is to compare the statistical similarity between the predicted distribution implied by current financial conditions (the red line in the right panel of figure 2) to the distribution of GDP growth in non-recessionary periods (the black line). To determine whether the two distributions are close, we use a likelihood ratio test (described in the Appendix). For a given confidence level, this test compares the statistical distance between the two distributions. The higher the confidence level, the further apart the two distributions must be for the test to confidently conclude that they are different.
The test allows us to identify a range of financial conditions consistent with non-recessionary growth whenever the conditional and non-recessionary GDP growth distributions are statistically close to each other. Naturally, a real-time estimate of the growth-consistent range is affected by the estimated model parameters and the non-recessionary GDP growth distribution, both of which are influenced by the available data. Consistently with our parametric model estimates, we construct the time series of the range recursively, meaning that the range in any period $$t$$ is computed testing the distance of the model-implied predictive distribution of year-ahead GDP growth and the non-recessionary growth benchmark distribution computed from data from January 1979 until period $$t$$.
As a result of the time-varying estimates of the model parameters and of the benchmark non-recessionary growth distribution, the growth-consistent range varies over time. Moreover, the width of the range can vary with the desired confidence level that the predicted and the empirical distributions are not equivalent, with lower confidence levels being associated with a narrower range of financial conditions that is compatible with non-recessionary GDP growth.
Figure 3 plots the FCI-G (black solid line) and the range of financial conditions (the shaded green bands) that are consistent with non-recessionary GDP growth, assuming either a 90 percent (dark green) or a 95 percent confidence level (light green).7 When the FCI-G is above (below) the green band, financial conditions are considered to be tighter (looser) than levels that would predict a GDP growth distribution that is compatible with its historical non-recessionary counterpart.
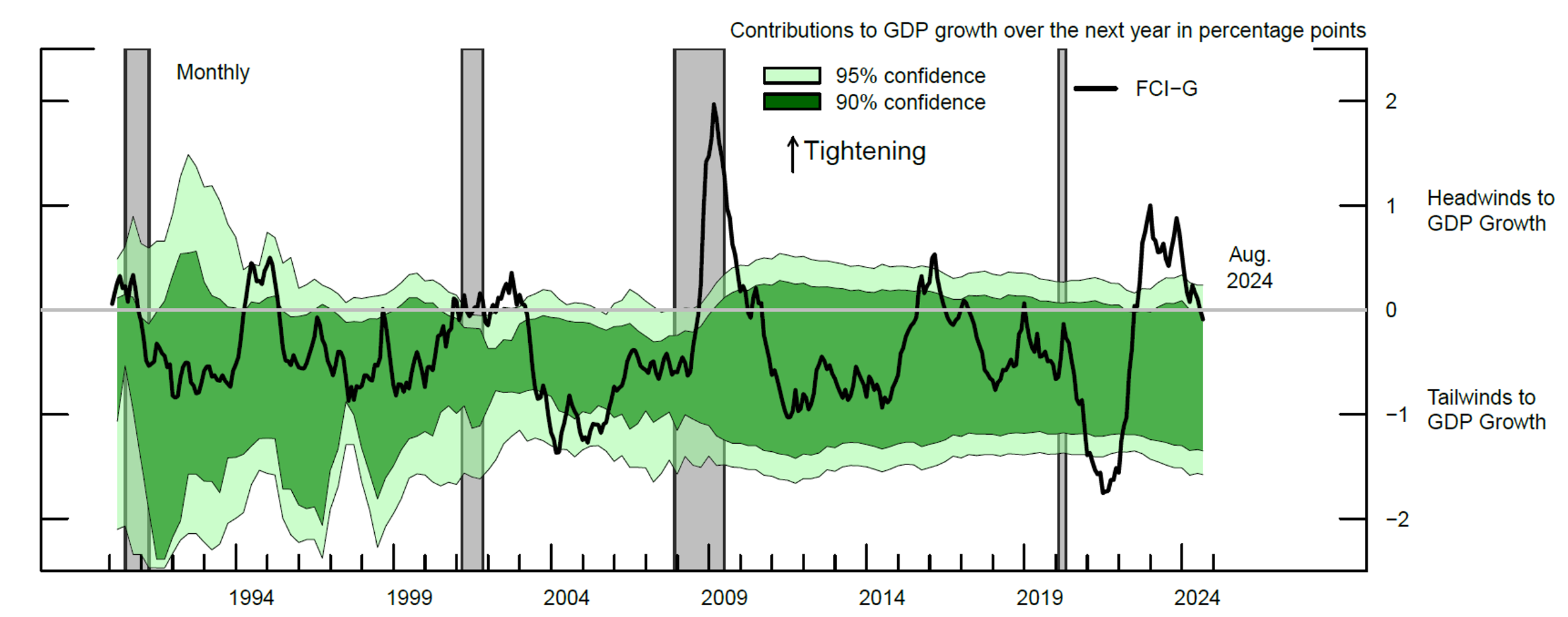
Note: The green shaded region represents the four-quarter (backward) moving average of the range of financial conditions consistent with sustained growth, assuming either a 90 percent (dark green) or a 95 percent confidence level (light green). Grey-shaded areas denote periods of recession as dated by the National Bureau of Economic Research: July 1990-March 1991, March 2001-November 2001, December 2007-June 2009, and February 2020-April 2020.
Source: Haver Analytics; Decennial Census of Population and Housing; CoreLogic; Authors' calculations.
As shown in Figure 3, the FCI-G has fluctuated within the estimated range of growth-consistent financial conditions for most of the past 25 years. However, there have been a few periods when the FCI-G has moved outside this range. For example, financial conditions were relatively loose in 2004—just before the Fed began to steadily raise the federal funds rate during the 2004-2005 tightening cycle—and in 2020 and 2021 when the Fed provided unprecedented policy support to the economy in response to the Covid-19 pandemic. Conversely, financial conditions have been relatively tight during or before the onset of three of the past four recessions, at the end of the 1994 monetary policy tightening cycle, and during a few periods of significant financial markets stress, such as those associated with the stock market downturn of 2002 and in late 2015.
Focusing on the last three years of data, financial conditions have tightened notably from relatively loose levels in late 2021, with readings up to late 2023 pointing to notable headwinds for economic growth over the coming year, while the most recent readings suggest that financial conditions have fallen back within the range that is compatible with non-recessionary growth.
Implications for Inflation and Employment
What are the key implications of this assessment for the inflation and employment outlook, were financial conditions to remain at the current level, and how do they compare to the conditions that the U.S. economy faced at the October 2023 peak of the FCI-G?
Translating one-year-ahead GDP growth distributions into inflation and employment growth predictions is a challenging task, as it requires a structural model and non-trivial assumptions about the relationship between these variables. Historically, economic downturns have not always been accompanied by lower inflation. For instance, during the Great Inflation and stagflation of the mid-1970s and early 1980s, the U.S. economy experienced high inflation and high unemployment. Conversely, during the dot-com bubble recession and the Great Recession, inflation remained relatively stable, despite sharp contractions in economic activity.
In light of these non-trivial relationships and lacking a fully-fledged structural model of risks to inflation, employment, and GDP growth, we take a much simpler approach. We use the same univariate statistical model described above to predict the one-year-ahead distribution of inflation and employment growth as a function of current financial conditions.8
Figure 4 displays the predictive distributions of one-year-ahead core PCE inflation (left) and one-year-ahead growth in total nonfarm employment (right). The red lines show the one-year-ahead predicted distributions as of August 2024, while the blue dashed lines show the corresponding distributions in November 2021, and the green dot-dashed lines show the corresponding distributions in October 2023. For comparison, the black solid lines represent the empirical distributions of inflation and employment growth since 1979, excluding NBER-dated recessions.
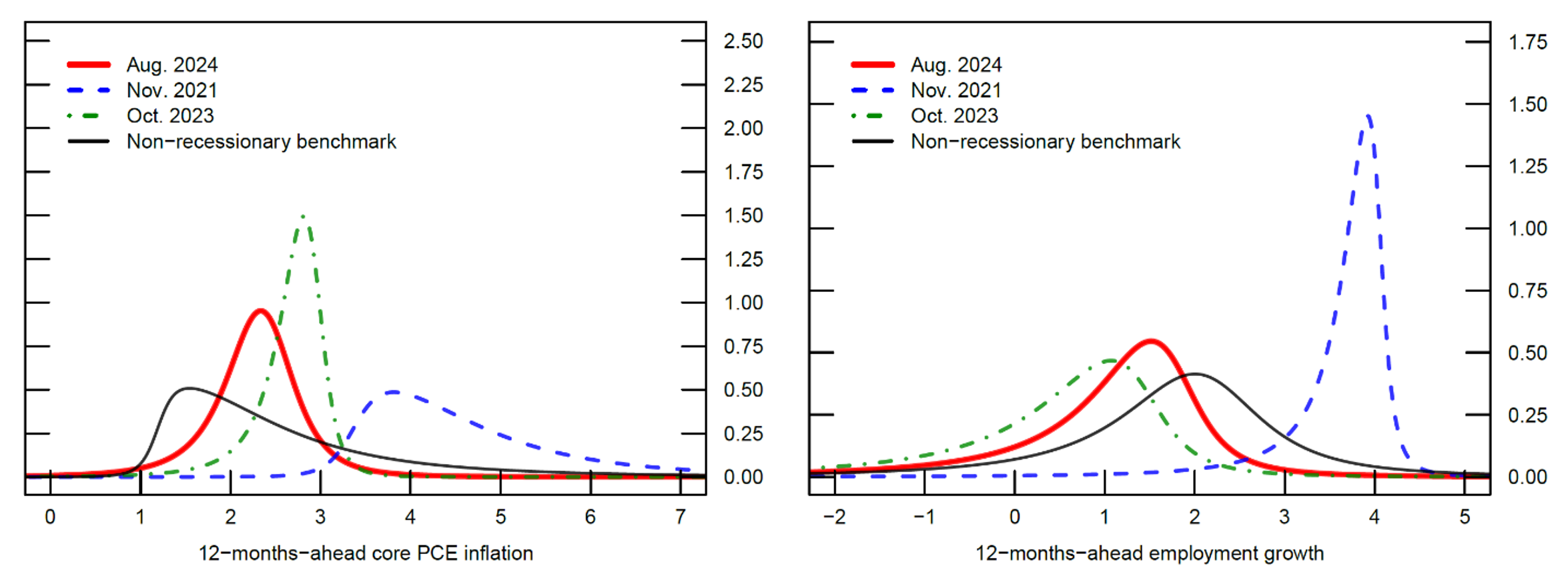
Note: This model assumes that moments (mean, variance, and skewness) of the distributions of one-year-ahead core PCE inflation (left, in annualized percentage points) and one-year-ahead employment growth (right, in annualized percentage points) depend linearly on the FCI-G and on their most recent realization. In both the left and right panels, the thick red lines show the August 2024 distributions, the dashed blue lines show the November 2021 distributions, the dot-dashed green lines show the October 2023 distributions, and the thin black lines show the non-recessionary benchmarks.
Source: Authors' calculations.
As financial conditions have tightened considerably over the past two years, the one-year-ahead distribution for inflation has become less skewed toward higher inflation outcomes, compared to the conditional distribution implied by the November 2021 readings of the FCI-G. Our model suggested that there were sizable upside risks to inflation in October 2023 that have since subsided. The most recent predicted distribution still indicates substantial risks that core PCE inflation will print between 2 and 3 percent next year.
The distribution of one-year-ahead employment growth has shifted to the left relative to the November 2021 distribution and become more dispersed. In addition, the probability of a decrease in employment over the next year as measured in October 2023 was notably higher than the level suggested by the non-recessionary historical benchmark and has since moderated in response to easing financial conditions.
References
Ajello, A., Cavallo, M., Favara, G., Peterman, W. B., Schindler J., and Sinha, N. R. (2023). A New Index to Measure U.S. Financial Conditions. FEDS Notes. https://doi.org/10.17016/2380-7172.3281.
Adrian, T., Boyarchenko, N. and Giannone, D. (2019). Vulnerable Growth. American Economic Review, 109 (4), 1263–1289.
Azzalini, A. and Capitanio, A. (2003). Distributions Generated by Perturbation of Symmetry with Emphasis on a Multivariate Skew $$t$$-distribution. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 65, 367–389.
Faust, J., Gilchrist S., Wright, J., and Zakrajšek E. (2013) Credit Spreads as Predictors of Real-Time Economic Activity: A Bayesian Model-Averaging Approach. The Review of Economics and Statistics, 95 (5), 1501-1519.
Plagborg-Møller, M., Reichlin L., Ricco, G., and Hasenzagl, T. (2020). When is Growth at Tisk? Brookings Papers on Economic Activity, Spring, 167-229.
Appendix – Test of equality of distributions
Detection Error Probability: Let $$ L_{A} $$ and $$ L_{B} $$ be the probability density functions of model A and B, respectively, and let $$ d_{n} $$ denote a random sample of size n. To assess the goodness of fit of the two competing distributions, we use a likelihood ratio test which selects
distribution $$A$$ if $$ ln \frac{L_{A}(d_{n})}{L_{B}(d_{n})} \geq 0 $$ and distribution $$B$$ if $$ ln \frac{L_{A}(d_{n})}{L_{B}(d_{n})}< 0.$$
Let $$ p_{A}^{n} $$ denote the probability that this likelihood ratio test selects distribution B when in fact $$ d_{n} $$ is generated by distribution A. Similarly, let $$ p_{B}^{n} $$ denote the probability that the test selects distribution A when $$ d_{n} $$ is generated by distribution B. Detection error probability is then:
$$$$ p_{AB}^{n} = \frac{1}{2}(p_{A}^{n} + p_{B}^{n}). $$$$
It is highest, $$ p_{A,B}^{n} = 0.5 $$, when distributions A and B are equivalent, in which case the test cannot do better than a coin flip. In contrast, low values of $$ p_{A,B}^{n} $$ indicate that the two distributions are relatively far from each other in the sense that it is relatively easy to tell them apart. Alternatively, the distance between distributions can be measured by the complement probability, expressing a required level of confidence that the test's conclusion is correct. The higher our required level of confidence the farther two distributions must be away from each other so that the test can confidently tell them apart.
Implementation: Drawing random samples from skewed $$t$$−distributions is relatively straightforward. As a result, we can use standard Monte Carlo techniques to approximate the detection error probability $$ p_{A,B}^{n} $$ corresponding to any two distributions. We are particularly interested in the distance of the fixed non-recessionary benchmark distribution (model A)—the empirical distribution of U.S. GDP growth since 1979 excluding recessions—from the conditional GDP growth distributions predicted by a given level of the FCI-G (model B). As the notation suggests, an important aspect of the detection error probability is the sample size $$n$$. Intuitively, the larger the sample size the easier it is to tell any two distributions apart irrespective of the chosen level of confidence. A potential choice of $$n$$ is the sample size that we use to estimate the non-recessionary benchmark distribution (model A). However, the likelihood ratio test assumes that the sample $$ d_{n} $$ is drawn independently, while it is well-known that the GDP growth series exhibits notable persistence. To control for this persistence, we set $$n$$ equal to the effective sample size (ESS) of the GDP growth series.9 This measure estimates the sample size of an independent sample with information content that is comparable to our autocorrelated sample.
Data Appendix
1. FCI-G,
Monthly series available from Federal Reserve Board at:
https://www.federalreserve.gov/econres/notes/feds-notes/a-new-index-to-measure-us-financial-conditions-20230630.html
2. GDP,
Quarterly series available from:
Federal Reserve Economic Data (FRED): Real GDP (GDPC1:
https://fred.stlouisfed.org/series/GDPC1).
3. Non-farm Payroll Employment,
Monthly series available from:
Federal Reserve Economic Data (FRED): Non-Farm Payroll Employment (PAYEMS: https://fred.stlouisfed.org/series/PAYEMS).
4. Core PCE Inflation,
Monthly series available from:
Federal Reserve Economic Data (FRED): Core PCE Inflation (PCEPILFE: https://fred.stlouisfed.org/series/PCEPILFE).
1. We thank Rochelle Edge, David Lopez-Salido, Francesca Loria, Michael Palumbo for comments on earlier versions of this work. The views expressed in this note are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of anyone else associated with the Federal Reserve System. Return to text
2. The financial variables are the federal funds rate, the 10-year Treasury yield, the 30-year fixed mortgage rate, the triple-B corporate bond yield, equity prices, house prices, and the nominal broad dollar index. The FRB/US model is a large-scale dynamic general equilibrium macroeconomic model of the U.S. economy that is designed to fit the U.S. data well. In this model the seven financial variables affect agents' behavior through standard channels, like the cost of capital, wealth channel or term of trade effect. Return to text
3. The traditional argument is that financial variables are inherently forward looking and should therefore embed information about investors' expectations of future economic outcomes. Return to text
4. Plagborg-Møller, Reichlin, Ricco and Hasenzagl (2020) describe this model as a parametric version of the two-step quantile regression approach developed by Adrian, Boyarchenko and Giannone (2019). Return to text
5. We are interested in the relationship between the FCI-G—available at monthly frequency—and the distribution of GDP growth. As GDP data is available at quarterly frequency, we first estimate the seven model parameters on quarterly data for GDP growth and the FCI-G. In a second step, we extend the quarterly model estimates of the predictive distribution of year-ahead GDP growth to the monthly observations of the FCI-G for each added quarter of data. Return to text
6. The statistical model is estimated using detrended series. The distributions in Figure 2 are recentered around the 2024Q2 trend value estimate for GDP growth—standing at approximately 2.4 percentage points. According to the historical GDP growth distribution, the U.S. economy—outside of recession years—has grown, relative to trend, between -10 and 11 percent—the mean growth is 0.32 percentage point, and the standard deviation is 1.85 percentage point. Return to text
7. Due to the relatively small sample size in the early part of our sample, there is substantial fluctuation in the estimated model parameters (and the range itself) during the 1990s. To avoid putting too much emphasis on these movements, Figure 3 shows the one-year (backward) moving average of the range. This adjustment does not affect our assessment of financial conditions post 2000. Return to text
8. For core PCE inflation, at each point in time t we predict the distribution of year-ahead non-detrended inflation, whose location, scale, and shape parameter are linear functions of the FCI-G and of the most recent realization of core PCE inflation for the twelve-month period ending in time $$t$$. For symmetry, we use a similar autoregressive structure for the model of the predictive distribution of employment growth. Since core PCE inflation and employment growth are available at monthly frequency, we estimate predicted distributions at a monthly frequency. Return to text
9. To estimate the sample autocorrelation necessary to compute the ESS, we use Geyer's initial monotone sequence criterion as is standard in the statistics literature. Naturally, the ESS depends on the sample at hand, so it must be re-estimated every time new data become available. We find the estimated ESS ranging from n=10 (1990:Q1) to n=43 (2024:Q1). Return to text
Ajello, Andrea, Giovanni Favara, Gregory Marchal, and Balint Szoke (2024). "Financial Conditions and Risks to the Economic Outlook," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, September 20, 2024, https://doi.org/10.17016/2380-7172.3599.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.