FEDS Notes
September 03, 2024
The Treasury Tantrum of 2023
Anthony M. Diercks and Dev Asnani*
Executive Summary
This FEDS note investigates the rise and fall of the 10-year Treasury yield during the second half of 2023, offering a detailed decomposition of the yield changes into expectations and term premiums through various models and surveys. This decomposition is important because it could have different implications for the response of monetary policy. Our analysis suggests that the rise in yields was primarily driven by an increase in term premiums, fueled by the combination of quantitative tightening, greater Treasury issuance, and heightened uncertainty about the economic outlook. However, survey-based measures likely overstated the rise in term premiums due to their delayed response to economic developments, a sluggishness for which we provide formal evidence. We find that as yields declined, expectations likely played a relatively larger role amid a series of lower than expected data prints. Additionally, we identify a useful rule of thumb that emerges when averaging across the models: a rise in the slope (10-year minus 2-year) corresponds nearly one-to-one with a rise in term premiums, while changes in the 2-year yield seem to be evenly split between expectations and term premiums.
Introduction
In the second half of last year, the 10-year Treasury yield skyrocketed from below 4 percent to above 5 percent, and then back down to 3.9 percent (Figure 1).1 On the way up, market commentary cited several key drivers for the rapid increase, including strong employment and inflation data, unexpectedly high Treasury issuance, and FOMC communications indicating that rates may need to be higher for longer. Conversely, on the way down, softer-than-expected data releases reportedly contributed to the rapid decline. In this FEDS note, our aim is to show how models and surveys can be utilized to interpret these historically unusual movements (as illustrated by the histogram in Figure 2).2 We also propose a novel simple rule-of-thumb for decomposing yield changes into term premiums and expectations, which we preview below:
Δ10y Term Premium≈1.0∗Δ(10y−2y Yield)+0.5∗Δ(2y Yield)
Δ10y Expectations≈0.0∗Δ(10y−2y Yield)+0.5∗Δ(2y Yield)
![Figure 1. [INSERT FIGURE TITLE HERE]. See accessible link for data.](/econres/notes/feds-notes/fig1-3500.png)
Note: The Ten-Year Treasury yield corresponds to the on-the-run coupon yield, spaced at 5-minute intervals from 8:00 a.m. to 4:00 p.m. on business days.
Source: Bloomberg.
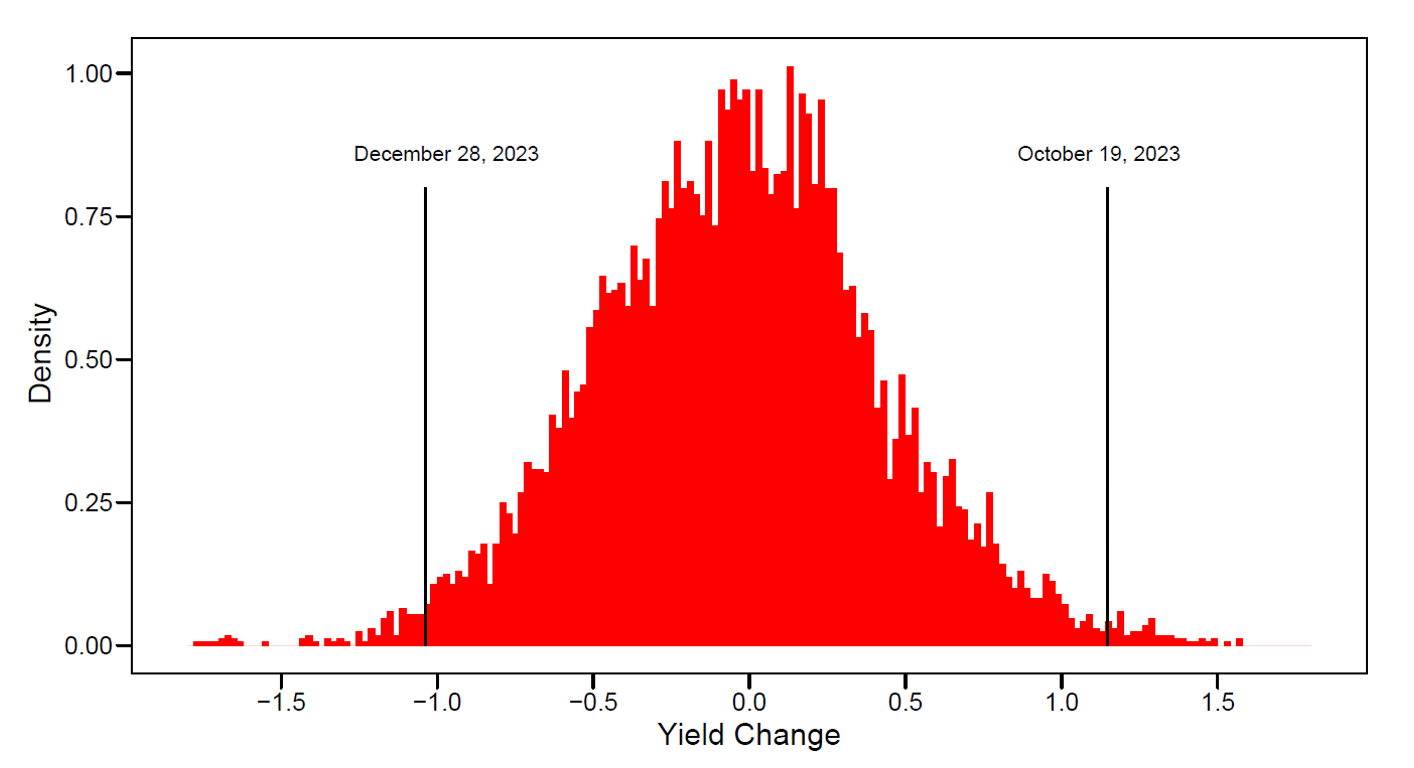
Note: The Ten-Year Treasury yield corresponds to the on-the-run coupon yield at the end of the day, based on H15 data. The interval 2.5 months reflects overlapping changes with daily data for every day since 1990 and was chosen to be consistent with the window from the July FOMC to the peak reached on October 19, 2023.
Source: Board of Governors of the Federal Reserve System, Selected Interest Rates - Business Daily, https://www.federalreserve.gov/releases/h15/
Importance of Decomposing Yields
Longer-term Treasury yields can be decomposed into two components: the expected average federal funds rate and the term premium that compensates investors for bearing interest rate risk. This can be important because policy makers could choose to respond differently depending on the decomposition.
…If increase reflects expectations. For instance, if the 10-year yield increase was strictly due to a rise in expectations, it could suggest investors believe monetary policy will be more restrictive well into the future with higher short-term rates. If monetary policy did not meet these expectations of higher short-term rates, it could generate a series of expansionary shocks to the economy, as short-term rates end up being lower than investors expected. This could potentially lead to higher inflation, which may not be preferable if inflation is already above target.
…If increase reflects term premiums. In contrast, if the increase in the 10-year yield was strictly due to higher term premiums, this could introduce additional tightness on financial conditions, without any expectation for monetary policy to increase short-term rates (expectations remain steady). All else equal, more restrictive financial conditions due to higher term premiums would reduce economic activity and inflation. This cooling effect on the economy could reduce the extent to which short-term rates need to rise to bring down inflation.3
Hence, the decomposition of yield changes into expectations and term premiums is important: a rise due to term premiums could require a relatively lower path of short-term rates to stabilize inflation, while a rise due to expectations could argue for a relatively higher path of short-term rates, all else equal.
Term structure models
Term structure models and surveys can be used to estimate term premiums. To put it simply, term structure models are designed to generate an estimate of the expected average short rate over various horizons. The models tend to achieve this based on how well historical elements of the yield curve (i.e. level, slope, curvature) predicted future yields. Alternatively, models may also use the past relationship between interest rates and survey forecasts. The difference between observed yields and these model-generated expectations is the model-based term premium. Another approach to this decomposition is just to use survey-based measures of the expected federal funds rate path and subtract this from yields to estimate the term premium. This approach, which is model-free, may be less reliant on historical dynamics and may better handle structural shifts in the data, as survey respondents may be less constrained when constructing their forecasts.
The term structure models that we will cover can be split into two groups:
(1) Models that rely strictly on historical dynamics of yields
- Adrian, Crump and Moench (2013, ACM)
- Christensen and Rudebusch (2012, CR)
(2) Models that also incorporate information from surveys
- Kim and Wright (2005, KW)
- Simple linear regression of Blue Chip surveys onto the level, slope, and curvature of the yield curve.4
…Different sample periods imply different long-run levels. Table 1 compares the decomposition of the peak 10-year yield reached on Oct 19, 2023 across models. The first column shows the starting point for the estimation period. For the models that rely exclusively on yields for their estimation, such as ACM and CR, the choice of the sample can play a significant role in determining the level to which the model believes the federal funds rate will converge to over the next several years. This level tends to correspond to the mean of the short rate over the full sample, which is why the choice of the sample time period matters (see Kiley (2024) for similar discussion on the importance of the sample period). For example, the ACM model (shown in blue in Figure 3, left panel) implies a substantially higher expected rate component than the CR model. This is because the ACM model's sample period dates back to 1961, a period over which the short rate has been much higher, on average. In contrast, the sample for the CR model (shown in red) starts in 1987, a period in which the average short rate has been much lower. Consistent with the differences in the historical average rate over the two samples, Table 1 shows the 5 to 10 year expected rate was higher for the ACM model and lower for the CR model when the 10-year yield hit its peak on October 19, 2023.5 Consequently, the expected average rate over the next ten years was also higher for the ACM model and as a result, ACM's model-based term premium was relatively lower (fifth column).
Table 1: Model Details and Levels at Peak Ten-Year Yield
Peak Ten-Year Yield (October 19, 2023)
Make Full Screen| Sample Start | Surveys | Expected Rate 5 to 10 years ahead | Expected Avg. Rate for next 10 years | 10-year Term Premium | |
|---|---|---|---|---|---|
| ACM | 1961 | No | 4.34 | 4.59 | 0.46 |
| CR | 1987 | No | 3.18 | 3.69 | 1.37 |
| KW | 1987 | Yes | 4.48 | 4.61 | 0.39 |
| Lin. Regress. | 1991 | Yes | 4.20 | 4.34 | 0.72 |
| Blue Chip (Oct. 10) | -- | -- | 2.65 | 3.06 | 2.00 |
| SEP (Sept. 20) | -- | -- | 2.50 | 3.17 | 1.89 |
Note: In the table, ACM corresponds to the model of Adrian, Crump, and Moench (2013), CR corresponds to Christensen and Rudebusch (2012), KW is Kim and Wright (2005), "Lin. Regress" is the estimates from the regression of the Blue Chip Survey on the level, slope, and curvature of the yield curve. The values in this table are for zero-coupon yields. Blue Chip corresponds to the Blue Chip Economic Indicators survey. The SEP typically only provides projections for year-end federal funds rate for three years in addition to a long-run projection. We use some interpolation to combine these projections to form a 10-year average and subtract this from the 10-year yield to generate the term premium.
Source: Wolters Kluwer, Blue Chip.
Figure 3. Expected Average Rate for Next 10 Years and Model and Survey-Implied 10-Year Term Premiums
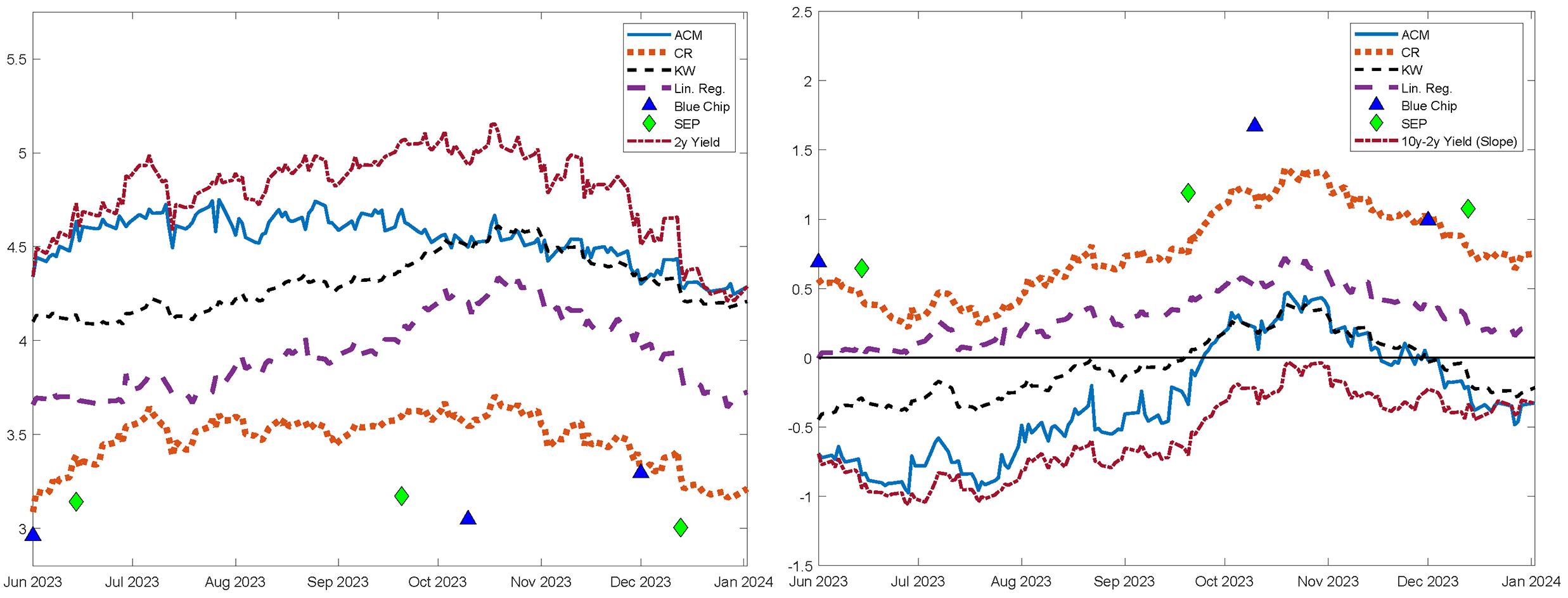
Note: The SEP typically only provides projections for year-end federal funds rate for three years in addition to a long-run projection. We use some interpolation to combine these projections to form an estimated 10-year average, which we then subtract from the 10-year yield to construct the term premium.
Source: Wolters Kluwer, Blue Chip.
…Survey-based models are less sensitive to sample period. In contrast, for the models that incorporate surveys such as KW and the simple linear regression, there is less reliance on the mean of the yields over the sample period as these models take independent signal directly from the longer horizon survey-based expectations (as opposed to a strict reversion or iteration forward of the short rate to a longer-run mean). For example, the simple linear regression model's estimates are computed independently for each horizon. While this approach may violate no-arbitrage restrictions, Duffee (2011) shows this assumption makes little difference.
Interestingly, all of the models imply higher expected rates and lower term premiums than the Blue Chip survey would suggest (as can also be seen in Figure 3). In contrast, the Blue Chip survey is not far from the implied rates coming from the Summary of Economic Projections. This divergence between the models and the actual survey will be discussed in greater detail below.
Understanding the decomposition of the changes in yields in the most recent period
While Table 1 focused on levels, Table 2 shows the change in expectations and term premiums for each of the models along with the Blue Chip Survey from July 26, 2023 through October 19, 2023 (when the 10-year yield peaked). Both of the yields-only models appeared to attribute a greater share of the rise in yields to term premiums. In contrast, the survey-based models attributed relatively more to a rise in expectations.
Table 2: Changes in Term Premiums and Expectations and Regression Coefficients
| Chg in Term Prem from July to Peak | Chg in Exp. Rates from July to Peak | TP Coeff. on slope | Exp. Rate Coeff. on slope | TP Coeff. on 2-Year Yield | Exp. Rate Coeff. on 2-Year Yield | |
|---|---|---|---|---|---|---|
| ACM | 1.16 | 0.01 | 1.30 | -0.30 | 0.47 | 0.53 |
| CR | 1.03 | 0.14 | 0.97 | 0.03 | 0.42 | 0.58 |
| KW | 0.69 | 0.44 | 0.70 | 0.29 | 0.39 | 0.60 |
| Lin. Reg. | 0.64 | 0.53 | 0.52 | 0.48 | 0.40 | 0.60 |
| Blue Chip | 1.08 | 0.09 | -- | -- | -- | -- |
Note: In the table, ACM corresponds to the model of Adrian, Crump, and Moench (2013), CR corresponds to Christensen and Rudebusch (2012), KW is Kim and Wright (2005), "Lin. Regress" is the estimates from the regression of the Blue Chip Survey on the level, slope, and curvature of the yield curve. Blue Chip corresponds to the Blue Chip Financial Forecasts (June) and Blue Chip Economic Indicators (October) survey.
Source: Wolters Kluwer, Blue Chip.
To get a better understanding of why the models resulted in different decompositions, we can run regressions of the model-based expected rates and term premiums on components of the yield curve over the full historical sample. The components of the yield curve that we focus on are the 2-year Treasury yield, which is frequently associated with monetary policy expectations, and the 10-year minus 2-year Treasury yield spread (the "slope"), which is often associated with term premiums.6
…The increase in slope was a key driver of term premiums. Over this period, the 2-year yield rose by about 30 basis points, while the slope increased by about 85 basis points, as the 10-year yield rose considerably more than the 2-year yield. As shown in table 2, for the yields-only models of ACM and CR, the coefficient of the slope on the term premium is very high (1.30 and 0.97), while the effect of the slope on expected rates is close to zero or even negative. In contrast, the survey-based models (KW and Lin. Reg.) attribute less of the slope movements to term premiums and more to expectations.
Interestingly, the KW model, which puts weight on historical yields and surveys, seems to be at the midpoint of the slope coefficients of the CR model (yields only, 0.97) and linear regression model (surveys only, 0.52). In addition, the coefficient of 0.52 for the linear regression model suggests survey respondents attribute about half-and-half to expectations and term premiums when they observe a rise in the slope, all else equal. In terms of the 2-year yield's effects, these tend to be more associated with expectations, as shown by the relatively higher coefficients (column 6). This is intuitive as movements in the 2-year yield tend to be more related to expectations than term premiums.
…Why is the slope strongly associated with term premiums? The results of the yields-only models imply that in the historical data, if the 10-year yield goes up, while the 2-year yield is little changed, the short rate does not tend to perfectly follow the slope higher, as shown by the fourth column in Table 2. In other words, a steepening of the yield curve has often been associated with higher subsequent excess returns of long-term bonds over short-term bonds.
In contrast, for the survey-based models, survey respondents have in the past tended to raise their forecasts when they see the slope rise because they usually take that as a signal that the federal funds rate will be increasing. Therefore, the term premium coefficient on the slope for the KW model is much smaller compared to the yields-only models and greater weight is placed on surveys.
…Potential simple rule-of-thumb for decomposing yield changes. To simplify matters when considering how to interpret changes in the 10-year yield, we propose taking an average of the coefficients for our regressions onto the slope and the 2-year yield. In particular, with coefficients of 1.30, 0.97, and 0.7 when regressing the term premium onto the slope, the average of these coefficients is around 1.7 Thus, all else equal, a rise in the slope (10-year minus 2-year yield) seems to correspond one-to-one with a rise in the term premium based on the average implications of the three models. Likewise, for changes in yields that move the 2-year yield and 10-year yield by a similar amount, the regressions suggest attributing about half-and-half to term premiums and expectations.8
Δ10y Term Premium≈1.0∗Δ(10y−2y Yield)+0.5∗Δ(2y Yield)
Δ10y Expectations≈0.0∗Δ(10y−2y Yield)+0.5∗Δ(2y Yield)
The survey-based models' expectations vs actual surveys
Over this time period, the survey-based models' expectations rose considerably, while the Blue Chip Financial Forecast consensus expected average rate over the next ten years only went up 9 basis points, suggesting nearly all of the rise in the 10-year yield was due to increased term premiums.
…Why the divergence? This departure from the typical past relationship between survey expectations and the slope of the yield curve could have indicated that survey respondents were placing unusually high weight on factors that affect the term premium required to hold long-term bonds, such as greater interest rate risk and the outlook for Treasury supply. It seemed plausible that the increased Treasury issuance, amid quantitative tightening, amid increased uncertainty, and amid changing hedging properties of bonds were all interacting in a way to amplify their potential effects on term premiums.
That said, an alternative view was that the surveys tend to be inertial and respond more slowly to news than market prices (Gurkaynak and Wright, 2012). From this perspective, surveys at the time could have been understating the true increase in financial market investors' expected rates and surveys would eventually rise more to catch up with the market.
Did investors expect the rise in the 10-year yield to persist?
…The surveys suggested rise was expected to be temporary. Projections of the 10-year yield were also provided in the October Blue Chip and October Wall Street Journal survey. Both surveys implied that the 10-year yield was expected to fall below 4 percent by the end of 2024 and stabilize at about 3.5% over the longer-run. We can also use projections of the short-term interest rate from these surveys to compute an implied projection for the 10-year term premium (measured as the difference between the 10-year yield minus the 10-year average expected rate). The surveys imply that the 10-year term premium was expected to fall from just below 2 percent then to between 1.0% and 1.2% in 2024 and stabilize at around 0.8% over the longer run.
For historical perspective, the "Taper Tantrum" in 2013 was another period in which term premiums rose dramatically. In the year that followed, nearly all of the increase in term premiums unwound. However, that subsequent decline was a period of growing global growth concerns, so may not have only reflected a reversal of an outsized move.9
Developments after the 10-year yield peaked in late October
After the 10-year yield peaked on October 19, 2023, it declined by over 100 basis points by the end of 2023, on net. This decline happened amid a series of lower than expected data prints including the October and November CPI, November PCE, an unexpected moderation in planned longer-dated Treasury issuance, and some reportedly less restrictive than expected Federal Reserve communications.
Table 3 shows the decompositions for the rise and fall in rates. Notably, three out of the four models put greater weight on expectations for the decline than they did for the rise in yields. This is consistent with the 2-year yield declining by 90 basis points, while the slope declined 25 basis points. Recall that for the corresponding rise in yields, the 2-year increased only 30 basis points, while the slope rose 85 basis points.
Table 3: Changes Across Models for Rise and Fall
| Chg in Term Prem from July to Peak | Chg in Exp. Rates from July to Peak | Chg in Term Prem from Peak to Year-end | Chg in Exp. Rates from Peak to Year-end | |
|---|---|---|---|---|
| ACM | 1.16 | 0.01 | -0.80 | -0.34 |
| CR | 1.03 | 0.14 | -0.63 | -0.52 |
| KW | 0.69 | 0.44 | -0.64 | -0.42 |
| Lin. Reg. | 0.64 | 0.53 | -0.51 | -0.63 |
| Blue Chip | 1.08 | 0.09 | -1.39 | 0.25 |
Note: In the table, ACM corresponds to the model of Adrian, Crump, and Moench (2012), CR corresponds to Christensen and Rudebusch (2012), KW is Kim and Wright (2007), "Lin. Regress" is the estimates from the regression of the Blue Chip Survey on the level, slope, and curvature of the yield curve. Blue Chip corresponds to the Blue Chip Financial Forecasts (June, December) and Blue Chip Economic Indicators (October) survey. The peak refers to the date that the 10-year yield peaked on October 19, 2023.
Source: Wolters Kluwer, Blue Chip.
Another long-range Blue Chip survey was conducted after October. Surprisingly, between the October Blue Chip Economic Indicators and the December Blue Chip Financial Forecasts, expectations for the average rate over the next ten years rose another 24 basis points, whereas it had only increased about 9 basis points from June to October. This is surprising because over this shorter time period, the 10-year yield actually declined 80 basis points, amid less restrictive than expected Federal Reserve communications and the notably lower than expected October CPI. Expectations rising amid these developments are difficult to rationalize unless there is sluggishness or inertia in surveys.10
…Sluggishness in surveys. The example above of the delayed response in surveys suggests that we might be able to predict future changes in the survey expectations based on changes in yields. To more formally test this, we run a regression of changes in the survey expectations onto lagged changes in the 10 year yield and find a statistically significant relationship for the first three lags. This evidence suggests that survey respondents may be responding to financial markets with a delay. In contrast, changes in the 10-year Treasury yield are not predictable and neither are the expected rates from the linear regression model.
Table 4: Sluggishness in Surveys
| Chg. in Survey 10-year average Expected Rate | Chg. in 10-year Treasury Yield | Chg. in 10-year Expected Rates from Lin. Regress. Model | |
|---|---|---|---|
| Constant | 0.00 | -0.02 | -0.01 |
| [0.02] | [-0.59] | [-0.37] | |
| Chg. in 10-year yield (t-1) | 0.185*** | 0.052 | 0.06 |
| [3.97] | [0.57] | [1.24] | |
| Chg. in 10-year yield (t-2) | 0.085* | -0.076 | -0.004 |
| [1.87] | [-0.84] | [-0.07] | |
| Chg. in 10-year yield (t-3) | 0.090* | 0.006 | 0.011 |
| [1.93] | [0.07] | [0.22] | |
| Chg. in 10-year yield (t-4) | 0.051 | -0.076 | -0.035 |
| [1.10] | [-0.81] | [-0.71] | |
| R2 | 0.17 | 0.01 | 0.02 |
Note: These time series are irregularly spaced, as the Blue Chip surveys come out in April, June, October, and December of each year. Interpolating between those points at a monthly frequency would generate similar results.
Source: Wolters Kluwer, Blue Chip; Board of Governors of the Federal Reserve System, Selected Interest Rates - Business Daily, https://www.federalreserve.gov/releases/h15/
What happened to the 10-year yields during previous hiking cycles?
One could look at previous hiking cycles to get additional historical perspective. Figure 4 plots the cumulative change in the 10-year yield across the 1994, 1999, 2004, 2015, and current 2022 hiking cycle. The current cycle (solid green line) appears most similar to the 1994 episode, as the increase in the 10-year yield was steepest for these episodes. Interestingly, the 1994 episode is the one hiking cycle which did not end in a recession.
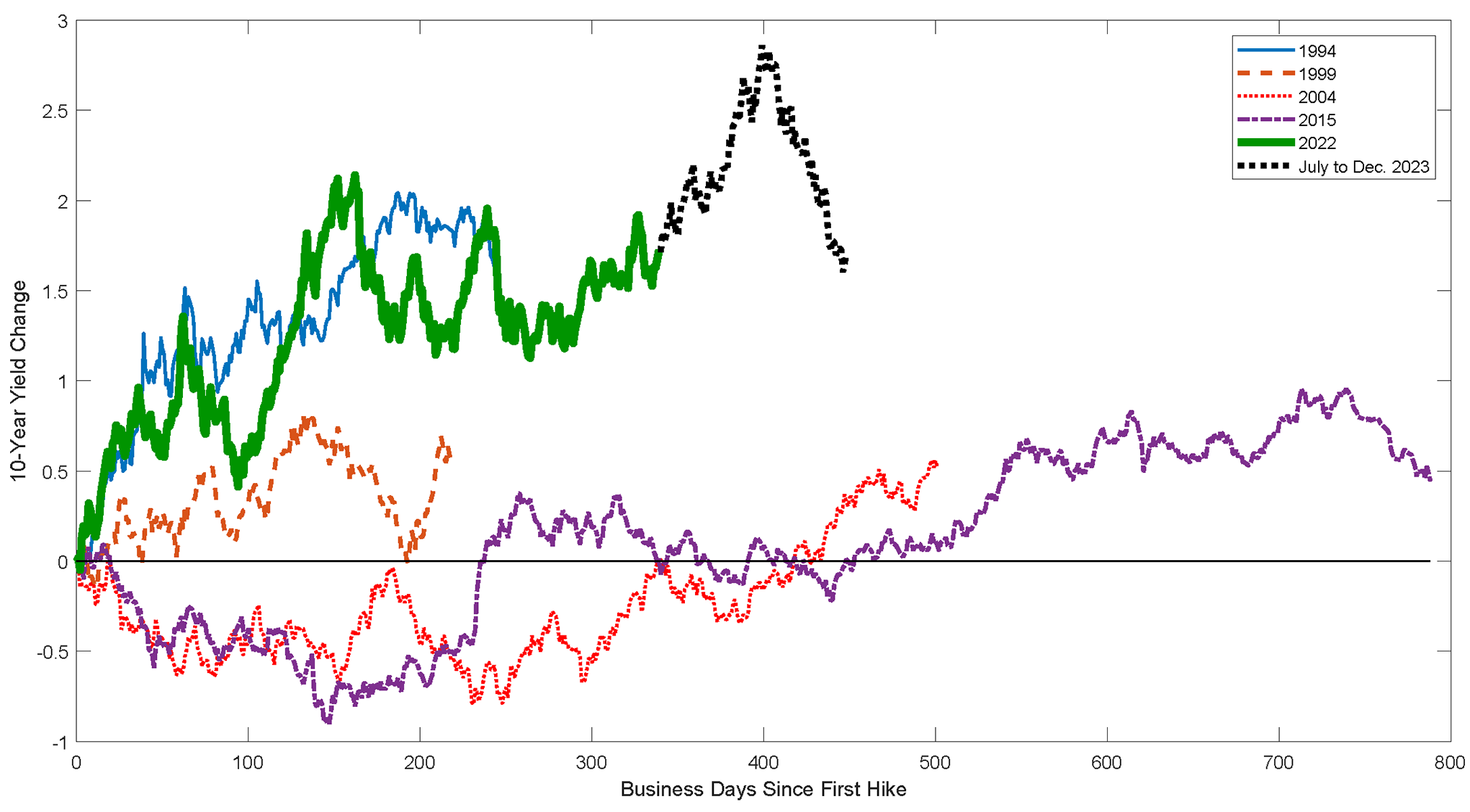
Note: Plotted is the cumulative change in the 10-year yield, starting with the first hike in each cycle and ending with the last hike. The dashed black portion for 2022 corresponds to July 26, 2023 to December 29, 2023 and corresponds to what is plotted in Figure 1.
Source: Board of Governors of the Federal Reserve System, Selected Interest Rates - Business Daily, https://www.federalreserve.gov/releases/h15/.
Conclusion
Overall, there are several takeaways from this analysis. First, the decomposition of yields into expectations and risk premiums is important because it could have different implications for the response of monetary policy. Second, we can shed light on term structure models by focusing on how the 2-year Treasury yield and slope of the term structure (10-year minus 2-year) are related to the model-implied term premiums and expectations. Intuitively, we show that the slope plays an important role for term premiums and the 2-year yield is important for expectations. On that note, we propose a simple rule-of-thumb, in which rises in the slope (10y-2y yield) correspond to a one-to-one rise in term premiums, while a rise in the 2-year yield attributes about half to term premiums and half to expectations. In addition, with respect to the levels of term premiums, we observe that the choice of sample period (for which the long-run mean is computed) can play an important role, especially for yields-only models.
Third, term premiums likely rose with the increase in yields due to the combination of quantitative tightening with increased Treasury issuance amid increased uncertainty about the economic outlook. That said, the Blue Chip survey-based term premium likely overstated the rise in the term premium, as expectations from the survey did not rise until well after yields started coming back down. We provided additional evidence for this inertia by showing that changes in the survey could be predicted based on past yield changes.
Fourth, professional forecasters (along with historical precedent based on the taper tantrum in 2013) correctly predicted that much of the original rise in term premiums would not persist. Finally, this rate hiking cycle appears to most closely resemble the 1994 episode, which is the one recent hiking cycle that did not end in a recession.
Appendix: The Real vs Inflation Compensation Decomposition
An alternative way we can decompose the movements in the 10-year yield is to consider how much of the moves were due to changes in inflation compensation versus changes in real yields. Conducting this exercise can help us determine whether the increased risks are more associated with real and/or inflation factors.
Table 5 shows that most of the moves can be attributed to real yields and thus real risk premiums. This is consistent with investors' focus over this time period on Treasury issuance and quantitative tightening, in addition to the potential changing hedging properties of bonds and interest rate uncertainty more broadly. With little change in inflation expectations over the next ten years, the moves in inflation compensation most likely reflected changing inflation risk premiums, but these were small compared to the real side.
Table 5: Real versus Inflation Compensation Changes for Each Period
| Level after last hike (July 26) | Chg from July to Peak (Oct. 19) | Chg from Peak to Year-end | Year-end level | |
|---|---|---|---|---|
| 10-Yr Nominal Treasury Yield | 3.88 | 1.17 | -1.13 | 3.92 |
| 10-Yr TIPS-based Real Yield | 1.62 | 0.93 | -0.75 | 1.80 |
| 10-Yr Inflation Compensation | 2.26 | 0.24 | -0.38 | 2.12 |
Note: In the table, the inflation compensation in this table is constructed as the difference between the nominal Treasury yield and the corresponding TIPS-based real yield.
Source: Bloomberg.
References
Adrian, T., Crump, R. K., Mills, B., & Moench, E. (2014). Treasury term premia: 1961-present (No. 20140512). Federal Reserve Bank of New York.
Adrian, Tobias, Richard K. Crump, and Emanuel Moench. "Pricing the term structure with linear regressions." Journal of Financial Economics 110.1 (2013): 110-138.
Aronovich, Alex, and Andrew C. Meldrum. High-Frequency Estimates of the Natural Real Rate and Inflation Expectations. No. 2021-034. Board of Governors of the Federal Reserve System (US), 2021.
Christensen, Jens HE, and Glenn D. Rudebusch. "The response of interest rates to US and UK quantitative easing." The Economic Journal 122.564 (2012): F385-F414.
Diercks, Anthony M., and Haitham Jendoubi. "Expectations of financial market participants." Handbook of Economic Expectations. Academic Press, 2023. 385-410.
Diercks, Anthony, and Isfar Munir. "Conflicting Signals: Implications of Divergence in Surveys and Market-Based Measures of Policy Expectations." (2020).
Diercks, Anthony M., Hiroatsu Tanaka, and Paul Cordova. "Asymmetric monetary policy expectations." Available at SSRN 3930267 (2022).
Duffee, Gregory R. Forecasting with the term structure: The role of no-arbitrage restrictions. No. 576. Working paper, 2011.
Engstrom, Eric C., and Steven A. Sharpe. "The near-term forward yield spread as a leading indicator: A less distorted mirror." Financial Analysts Journal 75.4 (2019): 37-49.
Estrella, Arturo, and Frederic S. Mishkin. "Predicting US recessions: Financial variables as leading indicators." Review of Economics and Statistics 80.1 (1998): 45-61.
Kim, Don H., and Jonathan H. Wright. "An arbitrage-free three-factor term structure model and the recent behavior of long-term yields and distant-horizon forward rates." Finance and Economics Discussion Series 2005-33 (2005).
Gürkaynak, Refet S., Brian Sack, and Jonathan H. Wright. "The US Treasury yield curve: 1961 to the present." Journal of Monetary Economics 54.8 (2007): 2291-2304.
Gürkaynak, Refet S., and Jonathan H. Wright. "Macroeconomics and the term structure." Journal of Economic Literature 50.2 (2012): 331-367.
Harikrishnan, Nira, Benjamin Silk, and Emre Yoldas (2023). "U.S. Interest Rates and Emerging Market Currencies: Taking Stock 10 Years After the Taper Tantrum," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, October 04. 2023,
Harvey, Campbell R. "The real term structure and consumption growth." Journal of financial Economics 22.2 (1988): 305-333.Kiley, Michael T. "Why Have Long-term Treasury Yields Fallen Since the 1980s? Expected Short Rates and Term Premiums in (Quasi-) Real Time." Finance and Economics Discussion Series 2024-54 (2024).
Li, Canlin, Andrew Meldrum, and Marius Rodriguez. Robustness of Long-Maturity Term Premium Estimates. No. 2017-04-03. Board of Governors of the Federal Reserve System (US), 2017.
* We thank Sarena Goodman, Don Kim, Edith Liu, Andrew Meldrum, David Miller, and Marius Rodriguez for helpful conversations and feedback. The analysis and conclusions set forth are those of the authors and do not indicate concurrence by the Board of Governors of the Federal Reserve System. Any errors or omissions are the responsibility of the authors. Return to text
1. The rapid rise from late July to October was close to 115 basis points, which was above the 99th percentile of moves over periods of the same length since 1990. Yields plummeted back to levels below 4% within the next two months, marking a similarly historic decline. Return to text
2. For previous discussions on term premiums and comparisons across models, see Li, Meldrum, and Rodriguez (2017) and Adrian, Crump, Mills, and Moench (2014). Return to text
3. A similar view was conveyed in a speech by FRB Dallas President Lorie Logan on October 9, 2023: https://www.dallasfed.org/news/speeches/logan/2023/lkl231009 Return to text
4. Aronovich and Meldrum (2022) also look into linear regressions using Blue Chip regressions. Return to text
5. These levels are subject to somewhat large confidence intervals. Return to text
6. In practice, yield curve factors typically reflect the first three principal components of the yield curve. Results are similar if these factors are used instead. We exclude the curvature factor because it has limited effect over this time period. Return to text
7. We focus on the ACM, CR, and the KW models because these are based on work originating from the Federal Reserve System. Return to text
8. Although the regression of the term premium and expectations is conducted on the 2-year yield, because the regression also includes the 10y-2y slope, the interpretation of the 2y coefficient provides the implied effect if the 10y-2y slope is unchanged, or if the 10y yield moves by the same amount as the 2y yield. Return to text
9. See Harikrishnan, Silk, and Yoldas (2023) for a discussion of the global growth concerns. Return to text
10. Diercks and Munir (2020) document that surveys' forecasts underperform markets and model-based measures at shorter horizons and maturities. Surveys may also be more inertial due to their modal nature, see Diercks, Tanaka, and Cordova (2022). For further discussion on issues associated with surveys, see Diercks and Jendoubi (2023). Return to text
Diercks, Anthony M., and Dev Asnani (2024). "The Treasury Tantrum of 2023," FEDS Notes. Washington: Board of Governors of the Federal Reserve System, September 03, 2024, https://doi.org/10.17016/2380-7172.3500.
Disclaimer: FEDS Notes are articles in which Board staff offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than FEDS Working Papers and IFDP papers.