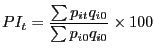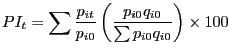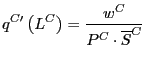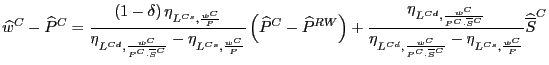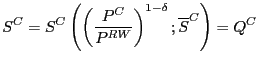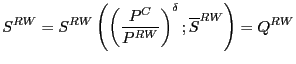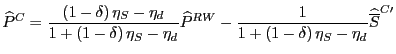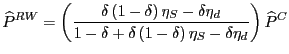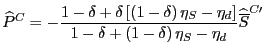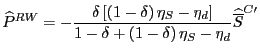Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 791, January 2004--Screen Reader Version*
Is China "Exporting Deflation"?
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In the past few years, observers increasingly have pointed to China as a source of downward pressure on global prices. This paper evaluates the theoretical and empirical evidence bearing on the question of whether China's buoyant export growth has led to significant changes in the inflation performance of its trading partners. This evidence suggests that the impact of Chinese exports on global prices has been, while non-negligible, fairly modest. On a priori grounds, our theoretical analysis suggests that China's economy is still too small relative to the world economy to have much effect on global inflation-a back-of-the-envelope calculation puts that effect at about 1/3 percentage point in recent years. In terms of the empirical evidence, we identify a statistically significant effect of U.S. imports from China on U.S. import prices, but given the size of this effect and the relatively low share of imports in U.S. GDP, the ultimate impact on the U.S. consumer prices has likely been quite small. Moreover, imports from China had little apparent effect on U.S. producer prices. Finally, using a multi-country database of trade transactions, we estimate that since 1993, Chinese exports lowered annual import inflation in a large set of economies by 1/4 percentage point or less on average, similar to the prediction of our theoretical model.
Keywords: China, exports, deflation, prices
*The authors are Deputy Associate Director, Economist, and Economist, respectively, in the International Finance Division of the Federal Reserve Board. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any person associated with the Federal Reserve System. We would like to thank David Howard, Carolyn Evans, Jon Faust, Caroline Freund, Jane Haltmaier, Bill Helkie, Karen Johnson, Deb Lindner, Catherine Mann, Jaime Marquez, Michael Prell, Trevor Reeve, John Rogers, Nathan Sheets, Beth Anne Wilson, and participants in the International Finance Workshop for helpful comments and advice. James Chavez and Craig Evers provided able research assistance. Correspondence should be addressed to: Steven B. Kamin ([email protected]), Mario Marazzi ([email protected]), or John W. Schindler ([email protected]), Board of Governors of the Federal Reserve System, Washington DC 20551, USA. Return to text
I. Introduction and Summary
In the past few years, as the issue of deflation has grown in prominence, observers increasingly have pointed to China as a source of downward pressures on global prices.1 Such concerns have been prompted by several factors. First, as indicated in Chart 1, Chinese exports have continued to grow strongly in recent years, even as world trade decelerated with the global economic slowdown, leading to increases in China's share of world markets. Second, China has run sustained current account surpluses, contributing to a substantial accumulation of international reserves and leading observers to assert that China is adding more to world supply than it is to world demand. Third, notwithstanding vigorous economic growth, consumer prices in China had been roughly flat or declining for several years (although they have picked up in recent months) ; with China's exchange rate fixed to the dollar, this has supported the view that Chinese export prices, measured in dollars, must have been declining as well. Finally, but perhaps most importantly, while China exports an increasingly wide range of products, it has made especially deep inroads into particular sectors-toys, sporting goods, apparel, and consumer electronics, among others. In consequence, considerable anecdotal evidence has emerged of competition from Chinese exports leading to downward price pressure and lost market share on the part of producers outside of China.
The view that China's export surge has contributed importantly to declines in global inflation, and adds to the risk of global deflation, is not universally shared.2 Critics of this view argue that it is unlikely that China could have a pronounced deflationary effect on the global economy. First, as large as China's economy is in dollar terms, and as rapidly as it has grown, it still accounts for only about 5 percent of global exports and GDP (Table 1); therefore, it seems unlikely that it could restrain global activity and prices much by itself.3 Second, China's record of very high export growth is by no means exceptional in East Asia; as shown in Chart 2, Hong Kong and Korea also posted very high export growth in the 1980s and 1990s, but no one at the time suggested that they contributed to global deflation. Third, China's rapid export growth has been associated with equally rapid import growth; thus China is contributing to global demand as well as supply. In fact, concerns have been raised that Chinese imports are boosting global commodity prices.4 Finally, while relatively large at $35 billion, China's current account surplus in 2002 was unexceptional as a share of Chinese GDP (2.9 percent, Table 2) and minuscule as a share of global GDP (0.1 percent).
So far, neither side of the debate over China's impact on global inflation, and, more generally, the global economy, has prevailed. This, in part, reflects a lack of clarity in the discussion as to whether and how, in principle, China could ``export deflation''. Commentators rarely spell out their assumptions regarding the channels through which Chinese export growth might affect global inflation, the extent to which Chinese goods compete with goods produced in other countries, or the likely responses of monetary policies outside of China to deflationary effects of Chinese exports. To clarify these issues, this paper develops a simple analytical framework to help think about the impact on global consumer prices of a step-up in Chinese productivity and exports.
Perhaps more important than any theoretical ambiguities, however, the continued debate over the impact of China on global inflation trends reflects the paucity of empirical evidence bearing directly on this issue. We are not aware of any research that has measured the impact of Chinese export performance on foreign (i.e., non-Chinese) prices at an aggregate (i.e., national as opposed to sectoral) level.5
To address this gap in our knowledge, this paper utilizes such data as are available to assess the impact of China's exports on the prices (mainly import prices) of its trading partners. We utilize two main sources of data on import prices. The relatively more reliable data are U.S. import prices, dis-aggregated by end-use category. These data are not available on a bilateral basis, so we cannot directly identify the effect of changes in Chinese export prices on U.S. import prices. However, we do have data on the share of imports in each category purchased from China. Therefore, to gain a sense of the impact of Chinese exports on U.S. import prices, we can assess whether those sectors experiencing the largest increase in the share of purchases from China are also those experiencing the greatest declines in import prices.
The data on U.S. import prices are considered relatively reliable, since they are adjusted for differences in quality. For most countries, however, such data are not available. Therefore, we also draw on a set of export and import unit values that are available for a large number of countries, drawn from the International Trade by Commodity Statistics (ITCS) database of the OECD. Because unit values are not adjusted for differences in quality, they are considered less reliable than actual price estimates, but they should at least be indicative of movements in trade prices. Moreover, these unit values are available on a bilateral basis, and hence provide the only direct reading available on the prices paid for Chinese exports by its trading partners. Using these data, we analyze changes in import unit values in 26 countries for which sufficient data are available and gauge the extent to which these changes could be attributed to differences in the behavior of Chinese export prices relative to the export prices of other countries.
Our basic conclusions are as follows. First, the different approaches we've taken to assess the impact of Chinese exports on global prices all concur that this impact is likely to have been, while non-negligible, fairly modest. To summarize the results of our approaches: (1) Our theoretical model suggests, plausibly enough, that the effect of higher Chinese productivity-one possible source of Chinese export growth-on the CPIs of its trading partners should be proportional to China's share in global output; with that share equal to only about 5 percent, a back-of-the-envelope calculation would predict Chinese productivity growth to have reduced global inflation on the order of only 0.3 percentage point annually in recent years. (2) We identified a statistically significant impact across sectors of the share of U.S. imports from China on U.S. import prices, suggesting that the roughly half percentage point average annual rise in China's share of U.S. imports since 1993 has lowered overall U.S. import price inflation by about 0.8 percentage point per year; given the relatively low share of imports in U.S. GDP, however, the ultimate impact on the U.S. consumer prices has likely been quite small. (3) Using the OECD ITCS database, we estimate that Chinese exports lowered average annual import unit-value inflation in a large set of economies since 1993 by about 1/10 to 1/4 percentage point, in the neighborhood of the prediction of our theoretical model, and by 1 percentage point in the United States. Moreover, we should note that all of these approaches gauge only the effects of higher Chinese exports on the prices of its trading partners; to the extent that rising Chinese imports have bolstered aggregate demand among China's trading partners, this should offset to some extent the disinflationary effect of China's exports.
Second, China's exports have likely restrained the import prices of its trading partners through various means: (1) replacement of more expensive imports from other countries with cheaper goods from China, (2) greater declines in Chinese prices compared with those of imports from other countries; and (3) the effect of competition from China in lowering the prices of imports from other countries. Our decomposition of changes in import unit value based on the ITCS data suggested channels (1) and (2) were both important. Although our decomposition of the ITCS data does not shed much light on channel (3), our regression analysis does not point to this effect as having been very large, at least for U.S. import prices.
Finally, our analysis suggests that, at least in the United States, the downward pressure on import prices stemming from Chinese imports has had little discernable impact on domestic producer prices. Specifically, we identified no statistically significant correlation between the share of U.S. imports in a particular sector coming from China and the rate of PPI inflation in that sector. Although producer prices exclude the prices of imports, this is surprising, given numerous accounts of Chinese competition reducing price margins for domestic producers. We offer three ways of rationalizing our result: Chinese goods may in general not be very substitutable with U.S. goods; the share of Chinese goods in many U.S. markets may not be large enough to allow a discernable effect on pricing; and increases in the share of U.S. imports coming from China may merely be offsetting reductions in shares from other countries, as export platforms in other of our trading partners move to China.
Before proceeding, several additional points should be emphasized. First, it is generally understood that in the long run, inflation is determined primarily by monetary policy. However, this does not preclude Chinese exports restraining inflation in its trading partners over some shorter interval, until that disinflationary effect is recognized and steps are taken to offset it. Second, our research does not attempt to gauge the effects of Chinese exports on other aspects of economic performance besides inflation, e.g., output or employment. Most economists believe that greater trade leads to higher incomes and prosperity in the long run, even if there are adjustment costs for some segments of the economy in the short run, but such effects lie beyond the scope of this paper.
The plan of the paper is as follows. Section II describes our theoretical analysis of the impact of Chinese export growth on global prices. Section III focuses on the impact of imports from China on U.S. import prices, while Section IV focuses on their impact on U.S. producer prices. Section V addresses the role of Chinese exports on the behavior of import unit values for a wide range of countries.
II. A Simple Analytical Framework
Discussions of China's possible impact on global inflation trends frequently are muddied by a lack of clarity in various respects. First, some observers downplay the possibility that Chinese exports could induce global deflation. Aggregate prices, they argue, are in the final analysis influenced by monetary policy, and any downward pressures on prices induced by a surge in Chinese exports could be reversed by policy loosening on the part of the world's monetary authorities.6 This argument, however, may overstate the control by central banks over national inflation rates in the short- and medium-term, and thereby oversimplifies the monetary policy decision. In practice, it may take time for deflationary pressures to become apparent and elicit a policy response, and it will also take time for changes in monetary policy to counteract those pressures.
A second area of confusion concerns which Chinese prices are likely to affect the prices of China's trading partners. The fact that the Chinese CPI was falling while its exchange rate against the dollar remained fixed could be taken to mean that China's export prices must have been falling and China was thus exporting its deflation abroad, and analysts frequently are unclear on this point. Yet, the dollar prices of much of China's exports are likely set in global markets, and trends in those prices could well differ from trends in Chinese consumer prices.
Finally, discussions of the impact of Chinese exports on global prices often fail to specify the channels through which this impact may occur. On the supply side, cheaper imports from China might push down CPIs and/or producer prices without adversely affecting domestic activity and profits. On the demand side, lower Chinese prices could reduce the market share of domestic producers and thus depress domestic wages and producer prices.
To help clarify our thinking about the impact of Chinese exports on global price trends, we borrow from standard textbook analyses of international trade to fill in some of the conceptual gaps described above. We develop a very simple framework that incorporates an explicit, albeit rudimentary, monetary policy assumption. Our model focuses on how the prices of two goods-those of China and of the rest of the world-are set by global supplies and demands. And, finally, it incorporates both supply-side and demand-side channels through which increases in Chinese production can lead to lower global consumer price inflation.
Observers have suggested several complementary explanations for the on-going boom in Chinese exports, including productivity growth stemming from market-oriented reforms, heavy direct foreign investment into China, the advantage of low wages, and a highly competitive exchange rate. We do not attempt to distinguish among these explanations here. Rather, we assume an exogenous increase in Chinese productivity and focus on the effect of resultant higher exports on prices in the rest of the world.
II.1 Initial Assumptions
To develop the simplest possible framework, we assume a world comprised of two countries: China (C) and the rest of the world (RW). Each country produces a single distinct good, which is consumed in both countries and the price of which is determined by global supply and demand. There is a single global currency-this is not that unrealistic an assumption, given that China's exchange rate is fixed against the currency of its most prominent trading partner, the United States. However, capital controls allow the money supply in each country to be determined exclusively by that country's monetary authority.
Demand for goods
The velocity of money in each country is assumed to be fixed and equal to unity, so that nominal expenditures in each country are equal to that country's (exogenous) money supply:
E![]() = M
= M![]() (1)
(1)
E![]() = M
= M![]() (2)
(2)
E![]() : nominal
expenditures in country i (C, RW)
: nominal
expenditures in country i (C, RW)
M![]() : nominal money
supply in country i (C, RW)
: nominal money
supply in country i (C, RW)
For algebraic convenience later on, we assume that the shares of expenditures devoted to Chinese goods and rest-of-world goods are identical in China and in the rest of the world:
P![]() D
D
![]() E
E
![]() M
M![]() (3)
(3)
P![]() D
D
![]() E
E
![]() M
M![]() (4)
(4)
P![]() D
D
![]() E
E
![]() M
M![]() (5)
(5)
P![]() D
D
![]() E
E
![]() M
M![]() (6)
(6)
P![]() : price of good
produced by country i (C, RW)
: price of good
produced by country i (C, RW)
Dj![]() : demand by
country j (C, RW) for the good of country i (C,RW)
: demand by
country j (C, RW) for the good of country i (C,RW)
![]() share of
expenditures spent on goods from China
share of
expenditures spent on goods from China
The share factor ![]() is assumed to depend on the relative price of Chinese and
rest-of-world goods:
is assumed to depend on the relative price of Chinese and
rest-of-world goods:
![]() (P
(P![]() /P
/P![]() ,
, ![]() `(
`(
![]() 0
(7)
0
(7)
Supply of goods
The supply of each country's good S is assumed to depend on two factors: an exogenous productivity parameter S* (reflecting technology, capital, and other endowments) and the relative price of the two goods:
S![]() = S
= S![]() ( (P
( (P![]() /P
/P
![]() ; S
; S![]() (8)
(8)
![]() S
S![]() /
/![]() (P
(P![]() /P
/P
![]() 0,
0, ![]() S
S![]() /
/![]() S
S![]() 0
0
S![]() = S
= S![]() ( (P
( (P![]() /P
/P
![]() ; S
; S
![]() (9)
(9)
![]() S
S![]() /
/![]() (P
(P![]() /P
/P
![]() 0 ,
0 ,
![]() S
S![]() /
/![]() S
S
![]() 0
0
These functions are derived in Appendix A. The rationale for the productivity parameter is obvious: increases in productivity, all else equal, raise the supply of the good.
The rationale for the relative price term is slightly more
complicated. We assume competitive full-employment labor markets in
both countries, with labor supplies that are positively related to
real consumption wages. In the rest of the world, for example,
higher Chinese prices raise the RW cost of living, induce upward
pressure on RW wages, and thus, in the absence of adjustment of the
RW product price, would lower the supply of RW goods, S![]() . The higher the share of
consumption devoted to Chinese goods
. The higher the share of
consumption devoted to Chinese goods ![]() , the greater this effect will be. Analogous
considerations hold for the supply of Chinese goods S
, the greater this effect will be. Analogous
considerations hold for the supply of Chinese goods S![]() .
.
Goods market equilibrium
Equilibrium in the goods market entails the supplies of both Chinese goods and rest-of-world goods equaling their respective demands:
P![]() S
S![]() = P
= P![]() D
D![]() + P
+ P![]() D
D
![]() M
M
![]() M
M
![]() M
M![]() M
M![]() (10)
(10)
P![]() S
S![]() = P
= P![]() D
D
![]() +
P
+
P![]() D
D
![]() M
M
![]() M
M![]() =
=
![]() (M
(M![]() +
M
+
M![]() (11)
(11)
This is a system of two equations in two unknowns -
P![]() and P
and P![]() - and hence for given Chinese and
rest-of-world money supplies, this yields determinate outcomes for
the two goods prices.
- and hence for given Chinese and
rest-of-world money supplies, this yields determinate outcomes for
the two goods prices.
II.2 Effect of an increase in Chinese productivity
Impact on the global price level
We now consider the impact of a positive, exogenous shocks to
Chinese productivity S![]() * on the prices of both goods, assuming domestic
money supplies are left unchanged. This is accomplished by totally
(log-) differentiating equations (10) and (11) and solving for
reduced forms of the rate of change of P
* on the prices of both goods, assuming domestic
money supplies are left unchanged. This is accomplished by totally
(log-) differentiating equations (10) and (11) and solving for
reduced forms of the rate of change of P![]() and P
and P![]() as functions of the rate of
change of S
as functions of the rate of
change of S![]() *.
*.
Skipping many laborious derivations, which are sketched out in Appendix B, we first consider the global consumer price index P, which depends on the prices of both types of goods in the model. Because the shares of expenditures devoted to Chinese goods and rest-of-world goods are identical for consumers in China and in the rest of the world, the consumer price index is identical as well:
P = ![]() P
P
![]() P
P
![]() (12)
(12)
Our first key result is quite straightforward:
%![]() P = -
P = -
![]() (%
(%![]() S
S![]() *) (13)
*) (13)
Equation (13) shows that the response of global consumer prices
to an increase in Chinese productivity (where %![]() denotes percentage change) is
equal to the increase in Chinese productivity itself, %
denotes percentage change) is
equal to the increase in Chinese productivity itself, %![]() S
S![]() *, multiplied by (1) the elasticity of Chinese
supply with respect to productivity,
*, multiplied by (1) the elasticity of Chinese
supply with respect to productivity,
![]() , and
(2) the share of Chinese goods in total expenditures
, and
(2) the share of Chinese goods in total expenditures ![]() . The simplicity of this result
should not be surprising: with the global money supply-and hence
total nominal expenditures-held constant, any increase in Chinese
production will have to lower global prices by the same proportion
as global production rises.
. The simplicity of this result
should not be surprising: with the global money supply-and hence
total nominal expenditures-held constant, any increase in Chinese
production will have to lower global prices by the same proportion
as global production rises.
Simple as it is, however, this result provides a more formal
rationale for the view that, given its small size in the global
economy, increases in Chinese production are unlikely, by
themselves, to induce substantial declines in global prices. Assume
the Chinese share in global consumption is roughly similar to its
share in global production, so ![]() = .05; the elasticity of Chinese supply with
respect to Chinese productivity growth is equal to unity; and labor
productivity growth in China is running at 6 percent annually
(although estimates of productivity growth are generally quite
uncertain). Equation (13) then implies that Chinese productivity
growth has been lowering global consumer price inflation by 0.3
percentage point per year, a non-negligible amount, but certainly
not enough to raise concerns about global deflation.
= .05; the elasticity of Chinese supply with
respect to Chinese productivity growth is equal to unity; and labor
productivity growth in China is running at 6 percent annually
(although estimates of productivity growth are generally quite
uncertain). Equation (13) then implies that Chinese productivity
growth has been lowering global consumer price inflation by 0.3
percentage point per year, a non-negligible amount, but certainly
not enough to raise concerns about global deflation.
It has been suggested that the impact of China on global prices might be greater than that implied by its share in global production, if China can produce goods more cheaply than its foreign competitors at the margin. That is, even if China's share in output currently is small, the threat of being able to supply more goods and at lower prices may suffice to restrain the prices of goods produced outside China. However, this threat is likely to be credible only if China has enormous amounts of excess capacity, so that it can indeed raise its production and market share sufficiently to lower global prices as shown in equation (13). China may indeed have extensive amounts of underutilized low cost labor, and certain sectors are currently believed to be running below full capacity. Nevertheless, it is far from clear that China could further boost production by a significant share of global GDP in the very near term.
Finally, we would underscore the dependence of the result in equation (13) on the assumption that money supplies remain constant. Clearly, any disinflationary effect of China on its trading partners can be offset through looser monetary policy on the part of the latter's central banks. Alternatively, a loosening of Chinese monetary policy, by increasing demand for both Chinese goods and imports from the rest of the world, would also moderate the disinflationary effect of higher productivity growth.
Impact on prices of Chinese and rest-of-world goods
Less straightforward than the impact of a Chinese productivity increase on aggregate global prices are its separate impacts on the prices of Chinese and rest-of-world goods:
%![]() P
P
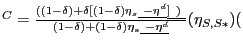 %
%![]() S
S![]() *)
(14)
*)
(14)
%![]() P
P
![]() %
%![]() S
S![]() *)
(15)
*)
(15)
![]() : elasticity
of the share
: elasticity
of the share ![]() with
respect to relative prices P
with
respect to relative prices P![]() /P
/P![]()
![]() : elasticity
of Chinese supply with respect to relative prices P
: elasticity
of Chinese supply with respect to relative prices P![]() /P
/P![]()
(also, the negative of the elasticity of rest-of-world supply with respect
to relative prices P![]() /P
/P![]()
Daunting as they may appear, equations (14) and (15) help illuminate the channels through which higher Chinese productivity lowers global prices, as shown in equation (13).
In the first channel, higher Chinese productivity, by reducing
the prices of Chinese goods, directly lowers CPIs in China and
elsewhere. Consider a case in which supply curves in China and the
rest of the world are unresponsive to relative prices, so
![]() = 0, and in
which the expenditure share
= 0, and in
which the expenditure share ![]() is unresponsive to relative prices as well, so
is unresponsive to relative prices as well, so
![]() = 0; the
latter case corresponds to that of unit price elasticities of
demand for Chinese and rest-of-world goods, so movements in their
prices elicit exactly offsetting changes in their demanded
quantities. In that case, equations (14) and (15) can be
re-written:
= 0; the
latter case corresponds to that of unit price elasticities of
demand for Chinese and rest-of-world goods, so movements in their
prices elicit exactly offsetting changes in their demanded
quantities. In that case, equations (14) and (15) can be
re-written:
%![]() P
P
![]() (%
(%
![]() S
S![]() *) =
*) =
![]() (%
(%![]() S
S![]() *)
(14a)
*)
(14a)
%![]() P
P
![]() (
(
![]() (%
(%![]() S
S![]() *) =
0 (15a)
*) =
0 (15a)
In this extreme case, both the supply and demand for goods produced outside China are unaffected by the rise in Chinese production, so that the price of rest-of-world goods remains unchanged. In consequence, the prices of Chinese goods fall by the exact extent that production rises, and the fall in global prices indicated in equation (13) results entirely from the decline in the price of Chinese goods in the CPI.
In a second channel, lower Chinese prices reduce global prices
by lowering production costs in the rest of the world. Consider a
slightly less restrictive case than above in which supplies of
goods are allowed to respond to relative prices ![]() 0) but the expenditure
shares remain invariant (
0) but the expenditure
shares remain invariant (![]() = 0):
= 0):
%![]() P
P
![]() (
(
![]() %
%![]() S
S![]() *)
(14b)
*)
(14b)
%![]() P
P
![]() (
(
![]() %
%![]() S
S![]() *)
(15b)
*)
(15b)
As equations (14b) and (15b) make clear, once supply effects are introduced, the increase in Chinese productivity leads to a smaller decline in the prices of Chinese goods (compared with equation 14a) but some decline (as opposed to no decline) in the price of goods produced outside China. However, this latter decline does not involve any disruption of activity on the part of non-Chinese producers. The fall in their prices occurs as lower Chinese prices reduce the cost of living abroad-this leads to a lower nominal wage (albeit not a lower real wage, measured against overall consumer prices) and allows non-Chinese producers to sell more of their goods at lower prices.
In the final channel, lower Chinese prices lower the prices of
rest-of-world goods by diverting demand from them. Consider a case
in which supplies do not respond to relative prices (![]() = 0) but the share of
expenditures devoted to Chinese and non-Chinese goods is allowed to
respond to relative prices (
= 0) but the share of
expenditures devoted to Chinese and non-Chinese goods is allowed to
respond to relative prices (
![]() 0):
0):
%![]() P
P
![]() %
%![]() S
S![]() *)
(14c)
*)
(14c)
%![]() P
P
![]() %
%![]() S
S![]() *)
(15c)
*)
(15c)
Consider, first, the case where a lower ratio of
Chinese/non-Chinese prices raises the share of expenditures devoted
to Chinese goods: ![]()
![]() 0. This
corresponds to a case where the price elasticity of demand for
Chinese goods exceeds one, as might prevail if Chinese and
non-Chinese goods are highly substitutable with each other. In this
instance, the price of non-Chinese goods unambiguously declines,
albeit not as much as the price of Chinese goods. This decline in
non-Chinese goods prices exclusively reflects competition from
Chinese goods for market share, and corresponds to the scenario in
which higher Chinese production detracts from production activity
overseas.
0. This
corresponds to a case where the price elasticity of demand for
Chinese goods exceeds one, as might prevail if Chinese and
non-Chinese goods are highly substitutable with each other. In this
instance, the price of non-Chinese goods unambiguously declines,
albeit not as much as the price of Chinese goods. This decline in
non-Chinese goods prices exclusively reflects competition from
Chinese goods for market share, and corresponds to the scenario in
which higher Chinese production detracts from production activity
overseas.
Yet, this is not the only scenario that is possible. If Chinese
and non-Chinese goods are not very substitutable and the price
elasticity of demand for Chinese goods is accordingly fairly
inelastic, reductions in Chinese prices will cause declines in the
share of expenditures devoted to Chinese goods, consistent with
![]() 0. Under
these circumstances, as indicated in equation (15c), the prices of
rest-of-world goods could actually rise in response to lower
Chinese prices. This occurs because a reduced share of expenditures
on Chinese goods corresponds to a higher share devoted to
non-Chinese goods-the higher demand drives up the prices of the
latter category.7
0. Under
these circumstances, as indicated in equation (15c), the prices of
rest-of-world goods could actually rise in response to lower
Chinese prices. This occurs because a reduced share of expenditures
on Chinese goods corresponds to a higher share devoted to
non-Chinese goods-the higher demand drives up the prices of the
latter category.7
Summing up
The model highlights three channels through which Chinese productivity growth and lower export prices would lower foreign (non-Chinese) consumer prices: (1) direct effects on foreign (non-Chinese) CPIs stemming from lower costs of import goods; (2) indirect effects working through lower foreign production costs, as the lower CPIs mentioned above depress nominal wages;8 and (3) effects on the demand for and price of foreign products resulting from lower Chinese export prices. Only the third channel leads to loss of markets, profits, and activity on the part of foreign producers, and whether or not this actually takes place is ambiguous a priori: if the demand for Chinese exports is highly elastic, lower Chinese prices will reduce the share of income spent on foreign products; however, if the demand for Chinese exports is highly inelastic, lower Chinese prices might merely reduce expenditures on imports from China and raise expenditures on domestic goods. Identifying the elasticity of demand for Chinese goods would therefore represent a high priority for further research.
III. Analysis of U.S. Import Prices
The simple framework described above does not distinguish between consumer prices, output prices, and import prices. In practice, however, such distinctions are likely to be important. In this section, we assess whether the expansion of China's exports has led to a significant reduction in U.S. import prices.
Chart 3 presents data on the inflation rates (percent changes in year-average price levels) for the U.S. Consumer Price Index (CPI), the CPI for goods, and the U.S. Import Price Index; the upper panel compares inflation rates for all items, whereas the bottom panel removes the effect of oil prices. The chart makes clear that U.S. import price inflation has generally stayed well below consumer price inflation. Import price inflation also indicates some downward tendency over the 1990s. This makes it a prima facie candidate to help explain the decline in CPI inflation, although one would not want to push that hypothesis too strongly in the absence of further investigation.9 To what extent the declining tendency in U.S. import inflation is attributable to China is difficult to say, as import prices are not available by country of origin, but only for broad regional aggregates. Chart 4 depicts U.S. import inflation by region of origin; China is included in ``other countries'', accounting for about 16 percent of U.S. imports from these countries over the past decade. The chart does not present strong evidence that China has been pushing down U.S. import prices. In most years, prices of imports from the ``other countries'' are not falling discernibly faster than those of imports from other regions. The panels in Chart 5 present similar data, but divided into non-manufactured and manufactured categories. For manufactured goods, prices of goods imported from the ``other countries'' region do appear to have been particularly weak, especially since 1998, although it is difficult to say how much of this owes to China's export performance.
III.1 Empirical Strategy
If we had data on import prices and import volumes by country of origin, it would be relatively straightforward to compute the contribution of imports from China to changes in aggregate U.S. import prices. As noted above, such data are not available. However, we do have data on the prices of imports, aggregated across all countries of origin, but dis-aggregated by end-use sector, e.g., sporting goods, apparel, consumer electronics. Additionally, data are available on the share of nominal imports accounted for by imports from China, also broken down by end-use sector. In principle, if Chinese export prices are lower than those of other countries and/or falling more rapidly, then those types of goods with particularly high or rising shares of imports from China should be experiencing particularly low rates of price inflation. This, in turn, should result in negative correlations, across end-use sectors, between import price inflation, on the one hand, and the level and/or change in shares of imports purchased from China, on the other.
To test this hypothesis, we estimate the following equation:
%![]() P
P
![]() Share
Share
![]() Share
Share
![]() (16)
(16)
P![]() : price of US
imports in sector i in year t
: price of US
imports in sector i in year t
Share
![]() : share of
U.S. imports in sector i coming from
: share of
U.S. imports in sector i coming from
region j (j = C, RW) in year t
Equation (16) represents a cross-sectional regression equation,
to be estimated across end-use import sectors i. For each
observation, the rate of import price inflation in sector i, over a
particular period from t-n to t, is matched against the change in
the share of that type of import accounted for by China,
![]() Share
Share
![]() , and the
initial level of the Chinese share, Share
, and the
initial level of the Chinese share, Share
![]() .
.
We would stress that equation (16) is not a structural behavioral equation, as the coefficients on the share variables likely reflect a mixture of channels through which Chinese exports may affect U.S. import prices. First, these coefficients likely reflect the direct arithmetic effect of these shares on the average price of imports. If Chinese goods are cheaper than those imported from other countries, then the larger the increase in the Chinese share (and thus the more that cheap Chinese goods are substituted for expensive goods from other countries), the more will the average price of U.S. imports decline. And if prices of imports from China are falling more rapidly (or rising more slowly) than those of imports from other countries, than the higher China's share in U.S. imports, the greater the restraint on average U.S. import prices.10
Second, the coefficients on the share variables will likely reflect these variables' correlation with other measures of Chinese export performance that affect U.S. import prices. In sectors where prices of imported Chinese goods are especially low or falling especially fast, for example, this will directly restrain average U.S. import prices for those goods. In such sectors, moreover, Chinese competition will likely induce downward pressure on the prices of goods imported from other countries, thus restraining U.S. import prices indirectly as well. Because those sectors are likely to be ones where the share of Chinese goods in U.S. imports is high and/or rising, however, this correlation will likely cause the coefficients on the share and/or change-in-share variables to become more negative, compared with what their arithmetic effect on U.S. import prices alone would dictate.11 12
Thus, the estimation results for (16) should be interpreted as
summarizing associations in the data between shares of Chinese
imports and U.S. import prices rather than estimates of a
structural equation. Even those associations, however, could be
spurious and misleading if competitive conditions (due to
globalization or changes in market structure) in a given sector
both reduced prices and induced manufacturers to source their
products from a low-wage country, say China. In this case, both
%![]() P
P![]() and
and ![]() Share
Share
![]() would be
correlated with a third variable-competitive conditions-and this
could lead the coefficient on
would be
correlated with a third variable-competitive conditions-and this
could lead the coefficient on ![]() Share
Share
![]() to be more
negative than would be implied by the actual effect of Chinese
exports alone on U.S. import prices. To address this concern, we
add lagged import price inflation as an explanatory variable, as
indicated in equation (17); this controls for other factors -
globalization, market structure, etc. - that tend to lower
inflation in a particular sector, so that the coefficient on
to be more
negative than would be implied by the actual effect of Chinese
exports alone on U.S. import prices. To address this concern, we
add lagged import price inflation as an explanatory variable, as
indicated in equation (17); this controls for other factors -
globalization, market structure, etc. - that tend to lower
inflation in a particular sector, so that the coefficient on
![]() Share
Share
![]() represents
the genuine impact of additional imports from China on import
prices in that sector.
represents
the genuine impact of additional imports from China on import
prices in that sector.
%![]() P
P
![]() Share
Share
![]() Share
Share
![]() %
%![]() P
P![]() (17)
(17)
Finally, it is possible that declines in Chinese export prices could have induced sufficient declines in the prices of other countries' exports so that the latter's shares in U.S. imports remained unchanged. Thus, in principle, China could have depressed U.S. import prices without any change in the China-share variables, causing equation (17) to underestimate the impact of Chinese exports on U.S. import prices. In practice, however, this scenario, while perhaps applicable to homogenous commodities such as oil, would appear unlikely to apply to the differentiated manufactures that China tends to export.
III.2 Data
The data used in our analysis are based on the five-digit end-use13 sectoral classification scheme for U.S. imports during the 1993-2002 period. For each sector, U.S. import price levels are collected from the International Price Program of the Bureau of Labor Statistics (BLS). However, price data are not available for all five-digit end-use sectors. Currently, the BLS publishes only 93 import price series for five-digit end-use sectors out of a total of nearly 140 sectors. Moreover, the price series have different start dates and as a result many sectors had to be dropped.14 In the end, we were left with 74 sectors. These 74 sectors accounted for over three quarters of the value of all U.S. merchandise imports during the 1993-2002 period. Chart 6 illustrates the year-average inflation rate in the overall U.S. import price index published by the BLS and compares it with the rate of change of the U.S. import price index we constructed from the 74 available sectors-by and large, the two inflation rates track each other reasonably closely.
To calculate the import shares, for each sector, annual U.S. import values are drawn from data collected on a Census basis by the Department of Commerce. Chinese import shares for each sector are then calculated by dividing the U.S. import value from China (in year t and sector i) by the overall U.S. import value (in year t and sector i).
Table 3 and Chart 7 display some sample statistics of the data; a comprehensive tabulation of the data is presented in Appendix C. During the 1993-2002 period, average annual import inflation for most sectors was close to zero-in the -1 percent to +1 percent range. However, extremely negative inflation rates in high-tech sectors (where hedonic pricing is employed) bring the equally-weighted mean over all sectors into the deflationary range.
At the same time, most of the sectors experienced an increase in the share of U.S. imports coming from China during the 1993-2002 period. The increases were particularly pronounced in consumer goods sectors, such as home entertainment equipment, toys and furniture, but increases occurred in many other sectors as well.
III.3 Econometric Results
Chart 8 presents scatterplots of sectoral rates of import price inflation against sectoral increases in China's import share (the top panel) and against initial levels of China's import share (the bottom panel). Regression lines indicating the bivariate relationship between the variables are also shown. The scatterplots provide some, albeit not especially strong, evidence of a negative correlation between sectoral import inflation rates and the level and changes in China's import share.
The first column of Table 4 indicates the results of regressing average annual import inflation during 1993-2002, by sector, on both the average annual change in China's import share over that period and the initial level of that share. The coefficient on the change in share is negative, as expected, and is significantly different from 0. Contrary to expectations, the coefficient on the initial level of the share is positive, albeit insignificantly different from zero.
The second column of Table 4 presents similar estimates to those in the first column, but includes a lagged dependent variable to serve as a control variable for the effects of competition and/or market structure, as described above. (Owing to data limitations, the import inflation variable on the left-hand-side is now measured only from 1997 to 2002, and the time periods over which the right-hand-side variables are measured have been adjusted accordingly.) However, the coefficient on lagged inflation is essentially zero, suggesting it is unlikely to be acting as a control variable in the manner described in Section III.1.
To look into this further, we examined the relationship between sectoral inflation rates in the 1993-97 and 1997-2002 periods. As shown in the scatterplot in Chart 9, there is generally a positive relationship between inflation rates in the two periods, but this is obscured by several outliers. In particular, prices of green coffee-which barely figure in imports from China-rose by 21 percent in the 1993-97 period and then fell by 22 percent in the 1997-2002 period.
Returning to Table 4, the third column indicates the results of estimating the same regression as in column (2), but with the observation for coffee imports removed. The coefficient on lagged inflation now becomes positive and highly significant, while that on changes in China's import share remains negative and significant. At -0.79, the coefficient indicates that a one percentage point rise in the Chinese import share of a given sector during 1997-2002 was associated, on impact, with 0.79 percentage point lower annual import inflation in that sector. Surprisingly, the coefficient on the initial level of China's import share remains positive, but is not significantly different from zero.
These results would suggest that imports from China have indeed depressed U.S. import price inflation to some extent.15 The estimated long-run impact of higher Chinese import shares on U.S. import inflation, based on equation (3), is about -1.3 (calculated as: -.791/[1 - .384]). Considering that the share of imports from China in total U.S. imports grew by an average rate of about 0.6 percentage point annually over the past decade, this coefficient suggests, as a back-of-the-envelope estimate, that imports from China might have depressed overall U.S. import inflation by about 0.8 percentage point annually. This represents a far from negligible impact on U.S. import prices, and moreover, prices in many sectors were likely affected to a considerably greater degree.16 Even so, with merchandise imports accounting for only about 11 percent of U.S. GDP and merchandise imports of consumer goods accounting for less than 10 percent of U.S. consumption, the direct effect of imports from China on U.S. consumer price inflation in recent years would likely have been quite small, on the order of 0.1 percentage point or less.17
IV. Analysis of U.S. Producer Prices
While direct effects of Chinese imports on U.S. consumer prices were likely quite small, the analytical framework described in section II describes two other channels through which Chinese imports could affect U.S. prices. One channel operates through the demand side, with Chinese imports competing for market share with U.S. products, thereby lowering the demand for and prices of U.S. products. A second channel is through the supply side; lower Chinese import prices could lower the cost of living and thus restrain nominal wages and production costs, more likely, they could reduce the costs of imported intermediate inputs-an effect not explicitly incorporated into the theoretical model described in Section II.18
As one means of gauging the extent to which Chinese imports have affected U.S. producer prices, we perform an analysis similar to that which we applied to U.S. import prices: we examine the correlation between movements in the producer price index (PPI) for selected categories of goods and in the shares of Chinese imports in total U.S. imports of the same goods category. Specifically, we estimate regressions similar to equation (17) above:
%![]() PP
PP
![]() Share
Share
![]() Share
Share
![]() %
%![]() PP
PP
![]() (18)
(18)
Here, PP![]() refers
to the level of producer prices in sector i at time t. The
motivation for equation (18) is similar to that described in
section III above. Lagged PPI inflation serves as a control to
ensure that the estimated coefficients on the share variables do
not reflect their correlation with other, omitted variables that
might be affecting producer price inflation.
refers
to the level of producer prices in sector i at time t. The
motivation for equation (18) is similar to that described in
section III above. Lagged PPI inflation serves as a control to
ensure that the estimated coefficients on the share variables do
not reflect their correlation with other, omitted variables that
might be affecting producer price inflation.
IV.1 Data and Initial Econometric Results
Unlike the U.S. import prices and import shares analyzed in Section III, the BLS producer price index (PPI) is not available, disaggregated by end-use sector. However, both the PPI and imports shares are available, disaggregated on the basis of the 4-digit Standard Industrial Classification (SIC) system, revision 1987; import data come from the U.S. International Trade Commission. Because these data are available on a more disaggregate basis than under the end-use classification system, we have been able to compute changes in import shares and corresponding PPI inflation for 388 sectors (accounting for over 80 percent of U.S. merchandise imports), compared with only 74 sectors under the less-disaggregated end-use system. Moreover, as manufacturing and non-manufacturing sectors are broken out in the SIC system, this allows us to focus on China's impact on producer prices within the manufacturing sector alone.
Chart 10 presents scatterplots of both changes and levels of Chinese imports shares, by SIC sector, against rates of PPI inflation. These scatterplots indicate little correlation between Chinese import shares and PPI prices.
The lack of correlation between Chinese import shares and PPI inflation is confirmed by the regression estimates shown in Table 5. Regardless of whether or not lagged inflation is included as an explanatory variable, and whether the analysis is performed on all sectors or only
those identified in the SIC system as manufacturing sectors, the estimated coefficients on the share and change-in-share variables are very small and not significantly different from zero.19
The lack of correlation between Chinese import shares and U.S. PPI inflation is surprising, considering that, as described in Section III, we estimated a statistically significant correlation between Chinese import shares and U.S. import prices. It is possible that producer prices are most sensitive to import prices (and hence Chinese import shares) in sectors for which imports account for a large fraction of the domestic market; because the regressions shown in Table 5 do not control for the share of total imports in the domestic market, they may be failing to identify the effect of China's share of those imports. To address this concern, we augmented our equation (18) with a measure of import penetration, IPR:20
![]() PP
PP
![]() Share
Share
![]() Share
Share
![]() %
%![]() PP
PP
![]() Share
Share
![]() )(IPR
)(IPR
![]() (Share
(Share
![]() (IPR
(IPR
![]() (19)
(19)
IPR![]() : import
penetration ratio for sector i = (imports
: import
penetration ratio for sector i = (imports![]() /(domestic shipments
/(domestic shipments![]() + imports
+ imports![]() - exports
- exports![]()
In the second line of equation (19), the Chinese share and change-in-share variables are interacted with initial levels of the import penetration ratio for that sector. The import penetration ratio represents the share of total imports of a good in the domestic market-shipments of domestic producers plus imports less exports-for that good. Thus, Chinese import shares are weighted by the prominence of imports in the domestic market.21
Data for domestic shipments on a basis comparable to that for
producer prices and Chinese import shares are available, from the
U.S. Census Bureau, for 38 3-digit SIC sectors-covering roughly 40
percent of both U.S. merchandise imports and manufacturing
shipments-over a time span ending in 2000. The first column of
Table 6 presents our re-estimation of equation (18) using the
3-digit SIC data. The results, which indicate no effect of Chinese
import shares on producer prices, are similar to those (Table 5,
column 4) based on the 4-digit SIC data. The second column of Table
6 presents estimation results for equation (19); the Initial Share
and Initial Share*IPR variables were dropped because their
coefficients were positive and insignificant. Even so, the
remaining ![]() Share
variable is still insignificant, while the
Share
variable is still insignificant, while the ![]() Share*IPR variable is only
significantly different from zero at the 15 level. Moreover, even
if the latter variable was significant, its coefficient estimate,
taking into account that the average value of the IPR was only
about 20 percent in 1995, implies that the roughly 0.6 percentage
point annual rise in the share of Chinese imports in total imports
during the past decade or so led to only 3/10 percentage point less
producer price inflation.
Share*IPR variable is only
significantly different from zero at the 15 level. Moreover, even
if the latter variable was significant, its coefficient estimate,
taking into account that the average value of the IPR was only
about 20 percent in 1995, implies that the roughly 0.6 percentage
point annual rise in the share of Chinese imports in total imports
during the past decade or so led to only 3/10 percentage point less
producer price inflation.
In column 3 of Table 6, we have deleted the insignificant
![]() Share
Share![]() variable and added the Initial
IPR variable by itself; the motivation is to capture effects of
total imports on producer prices, as distinct from effects related
primarily to Chinese import shares. Addition of the IPR variable,
while not significant itself, substantially reduces the size and
significance of the coefficient on the
variable and added the Initial
IPR variable by itself; the motivation is to capture effects of
total imports on producer prices, as distinct from effects related
primarily to Chinese import shares. Addition of the IPR variable,
while not significant itself, substantially reduces the size and
significance of the coefficient on the ![]() Share
Share![]() IPR variable. When the latter
variable is dropped from the equation (column 4), the IPR term
becomes borderline significant. With the IPR term averaging about
20 percent, its coefficient implies that overall import penetration
lowered producer price inflation by 8/10 percentage point annually.
This is a sizeable effect.22 However,
with Chinese imports comprising only about 4 percent of total
imports in this sample in 1995, this implies that, through their
contribution to total import penetration, Chinese imports
apparently depressed producer price inflation by a negligible
extent.
IPR variable. When the latter
variable is dropped from the equation (column 4), the IPR term
becomes borderline significant. With the IPR term averaging about
20 percent, its coefficient implies that overall import penetration
lowered producer price inflation by 8/10 percentage point annually.
This is a sizeable effect.22 However,
with Chinese imports comprising only about 4 percent of total
imports in this sample in 1995, this implies that, through their
contribution to total import penetration, Chinese imports
apparently depressed producer price inflation by a negligible
extent.
IV.3 Conclusion and Conjectures
Our empirical work suggests that even though the rising share of Chinese goods in U.S. imports has restrained import prices somewhat, it has had little effect on U.S. producer prices. This is surprising, given assertions that competition from China is depressing prices and reducing profit margins.23 We offer several explanations for our seemingly contradictory findings.
First, products imported from China may not generally compete with U.S. products. As discussed in Section II.2, above, if U.S. and Chinese goods are not very substitutable with each other, lower Chinese prices may have little impact on U.S. producer prices.24 Of course, even if most U.S. products do not compete with Chinese goods, there would likely be at least a limited range of U.S. products that are indeed exposed to Chinese competition, and firms in these sectors could certainly experience adverse effects.25
Second, even if many Chinese products are broadly substitutable with U.S. products, Chinese imports may represent a small enough share of the U.S. market in most sectors such that their impact on prices is limited. Although Chinese imports have grown to about 11 percent of total U.S. merchandise imports, they still represent only about 1 percent of U.S. GDP. This is consistent with our data for 38 3-digit SIC categories described above: with an average import penetration ratio of 20 percent and an average China share in imports of 4 percent, this implies an average share of Chinese imports in the domestic market of a little less than 1 percent. Of course, there would likely be some U.S. producers who were indeed affected by competition from Chinese products, even if U.S. producer prices more generally were not.
Finally, increases in the shares of Chinese goods in U.S. imports in a sector may overstate the extent to which overall imports in that sector have risen. As indicated in Chart 11, increases in China's share in several major end-use categories-consumer goods, capital goods-have been associated with declines in the overall Asian share of U.S. imports in those categories. This may have been the result of China out-competing its neighbors for market share. In a related development, non-China Asian economies have shifted from exporting directly to the United States to exporting to China; China then further processes these goods and re-exports them to the United States.26 Under these circumstances, increases in imports from China may not reflect increases in the overall supply of imported goods and hence may be less likely to compete with and lower the prices of U.S.-produced goods.
V. Analysis of International Import Unit Values
In this section, we attempt to go beyond the data for the United States alone and gauge the impact of Chinese exports on the import prices of a broad group of countries. As noted in the introduction, sectorally disaggregated import prices are not available on a consistent basis for many countries. However the OECD's International Trade by Commodity Statistics (ITCS) database contains disaggregated export and import unit values on a consistent basis.
Unit values are merely the value of imports or exports, divided by a measure of their quantity (e.g., number of units, kilograms, etc.). Because these measures of quantity are not adjusted for differences in quality or other characteristics, unit values are considered less reliable than actual price surveys. However, for most types of goods these data should be at least indicative of movements in trade prices. Moreover, the data are available at a high degree of disaggregation, making it more likely that unit values will be computed for comparable goods, and hence that they will be accurate.
We use the ITCS database to compute the contribution of Chinese exports to trends in import unit values among the 26 countries in the database for which sufficient data are available. Unlike in our analysis of U.S. import prices, where data on import shares were available by trading partner but data on import prices were not, the ITCS database makes available, for each sector and disaggregated by trading partner, data on both shares of imports and on import unit values. Therefore, for each sector in a given country, we can separate import inflation into the part attributable to China and that attributable to the country's other trading partners. This calculation is then aggregated across sectors to compute China's effect on a country's overall import inflation.
V.1 Data
The ITCS database is a subset of the United Nations COMTRADE database, and it contains data from 33 economies (the OECD plus China, Taiwan, and Hong Kong) at a highly disaggregated level. For each economy we pulled data for 1993 and 2001 on the value and quantity of their imports from the world and from China for each of roughly 2500, 5-digit, SITC Rev. 3 commodity categories.27 (We picked up only two years of data, owing to data storage and handling constraints; even only two years implies on the order of 2 million observations.) Using these data, we calculated, for each economy, imports from China and imports from the rest of the world in each category, and then calculated the corresponding unit values.
These sectoral unit values were then used to construct overall import unit value indices for each country for 1993 and 2001. To do this we calculated a Laspeyres index for each country, the formula for which is:
where
The resulting indices are shown in Table 7, alongside similarly constructed import unit value indices from the IMF's International Financial Statistics. While the correlation between these two measures of unit values-the correlation coefficient is .43-is not perfect, they generally capture similar broad trends.31 This is further seen in Chart 12, where the calculated Laspeyres indices are shown against the IFS indices in a scatterplot. The points, while not tightly bunched around the 45-degree line, are generally close to it.
V.2 Impact of Chinese Exports on Trading-Partner Import Unit Values
For each country, we first computed the contribution of Chinese exports to the rate of growth of import unit values over 1993 - 2001 in each of roughly 2,500 sectors, depending upon the country. We employed a decomposition equivalent to that shown in footnote [11] and reproduced below, for convenience:32
%![]() P
P![]() = %
= %![]() P
P![]() (P
(P![]() /P
/P![]() (21)
(21)
+ ![]() Share
Share![]() [(P
[(P![]() - P
- P
![]() /P
/P![]() ]
]
The first term in (21) represents the contribution of a country's other trading partners to import unit-value inflation in sector i, while the second two terms represent the impact of China on unit-value inflation. By construction, China is considered to have no impact on import inflation if its export unit values are the same as those of a country's other trading partners (the second term) and if its export unit values rise at the same rate as the other trading partners (the third term).
Equation (2) below indicates that a Laspeyres index for import unit values can be expressed as an average of sectoral ratios of current- to initial-period unit values, weighted by initial-period shares of that sector in total nominal imports.
We therefore compute the contribution of Chinese exports to the growth of a country's overall unit value index as their contribution to each import sector's unit value growth, weighted by that sector's initial share in import expenditures.
Table 8a presents our decompositions of the average annual growth of import unit values during 1993 - 2001 for the 26 countries in the ITCS database for which sufficient data were available.33 The first column shows the overall inflation rate in each country's calculated import unit value index. The second column represents the import inflation attributable to the country's other trading partners, corresponding to the first term in equation (21) above. The third column represents the total contribution of Chinese exports to the country's import inflation-this includes both the contribution resulting from increases in China's share in imports (the second term in equation 21) and that resulting from different growth rate of Chinese and non-Chinese unit values (the third term in equation 21).
Table 8a indicates that, from country to country, the contribution of imports from China to import inflation has varied considerably. Not surprisingly, this contribution is highest for economies with whom China has the strongest trading links: Japan, Korea, and the United States. Even for these economies, however, the estimated disinflationary impact of China has been relatively moderate: Chinese imports are calculated to have depressed average annual import unit-value inflation by about 1 percentage point below what it otherwise would have been. On average for all of the countries in the sample, the contribution of China to import deflation has been much smaller: from 1/10 (median) to 1/4 (mean) percentage point. Hence, our calculations provide little support for the view that China has exerted strong deflationary pressures on global trade prices.
V.3 Further decomposition of the China effect
Now we take this analysis a step further by breaking the China effect down into the two components shown in equation (21). Recall that the second and third terms of (21) collectively represent as the China effect. The second term in (21) could be referred to as the China share effect, or the effect that China has had on import unit values by virtue of its increasing import share (as cheaper Chinese goods replace more expensive goods imported from other countries). The third term could be referred to as a China price effect, resulting from the unit values of Chinese goods growing at a different rate than those of goods imported from other countries.
In Table 8a, our calculations of the China price and China share effect are shown in columns four and five. Across countries, neither components appears to dominate the overall China effect. The price effect is generally negative, with Japan, Korea, and the United States-China's largest trading partners-having especially large negative values. The share effect is more consistently negative and a bit more evenly distributed across countries. Thus China's influence on global import inflation apparently is working both through the change in its export unit values and the change in its share of other countries' imports.34
The remaining columns of Table 8a indicate that China's import share increased for every country except Portugal and Sweden. The countries for whom the increase was largest-Australia, Japan, Korea, and the United States-are those for whom the overall China effect was largest.
V.4 Comparison of decomposition analysis with regression results
One final consideration is that our decomposition analysis only identifies the direct effect of Chinese exports on the average import unit values paid by its trading partners. It does not capture any effects that Chinese exports might have in competing with and lowering the prices of the exports of other countries. How much our estimated contributions of China to import price inflation, shown on Table 8a, may be understated is difficult to say.
It is worth noting, however, that our estimate of China's contribution to the United States' import price inflation, in Section III, is not subject to this problem: the estimated coefficients on the China shares would capture both direct effects of Chinese exports and indirect effects working through the export prices of other countries. Even so, the estimated effect, based on the regression analysis of Section III, of China on U.S. import inflation-about -0.8 percentage point annually-is actually somewhat smaller than the effect on U.S. inflation measured using the ITCS data-about 1 percentage point. This suggests that the downward bias resulting from the omission of third-country competition effects may not be too great.
As a check on the robustness of our regression results from Section III, which were based on U.S. BLS data, we re-estimated equation (17) using the data on import inflation and China trade shares for the United States contained in the ITCS database. Table 9 displays the results of
this regression.35 The results are broadly similar to those for the regressions based on U.S. BLS data, shown in Table 4: a negative and significant coefficient on the change in China shares (albeit the magnitude of the coefficient is smaller) and a positive and insignificant coefficient on the level of the China share. Multiplying the average annual change in the China share between 1993 and 2001 (0.6 percentage points) by its coefficient, this implies a reduction in overall U.S. import inflation of 0.1 percentage points annually. This is smaller than both the -0.8 percentage point impact derived from the regression in Section III and the -1 percentage point estimate from the decomposition exercise in Section V.2, although still in the same general ballpark. These results reinforce our assessment that the effect of Chinese competition in lowering the prices of goods imported from other countries probably has not been very large.
References
Anderson, Jonathan (2002), "Five Great Myths About China and the World," GS Global Economics Website, www.gs.com.
Becker, Elizabeth and Edmund L. Andrews (2003), "Currency of China is Emerging as Tough Business Issue," New York Times, August 25.
Campa, Jose and Linda S. Goldberg (1997), "The Evolving External Orientation of Manufacturing: A Profile of Four Countries," FRBNY Economic Policy Review, July.
Chan-Lau Jorge A. and Stephen Tokarick (1999), "Why Has Inflation in the United States Remained So Low? Reassessing the Importance of Labor Costs and the Price of Imports," International Monetary Fund Working Paper 99/149, November.
Clark, H., Higgin, M., and K. Yi (2003), `The Chinese Juggernaut: How Has it Affected the World Economy?' presentation at Federal Reserve Bank of New York, March 17.
Cox, W. Micheal, and Jahyeong Koo (2003), ``China: Awakening Giant,'' Federal Reserve Bank of Dallas, Southwest Economy, September/October.
Day, Phillip (2003), "China's Trade Lifts Neighbors," The Wall Street Journal, August 18.
Economic Analytical Unit (2003), ``China's Industrial Rise: East Asia's Challenge,'' Department of Foreign Affairs and Trade, Australian Government.
Fels, Joachim (2003), "The China Syndrome," Morgan Stanley Global Economic Forum, February 8.
Gamber, Edward N. and Juann H. Hung (2001), "Has the Rise in Globalization Reduced U.S. Inflation in the 1990s?" Economic Inquiry, Vol. 39, No. 1, 58-73.
Hanke, Steve H. (2003), "John Snow is Wrong about China Exporting Deflation," Cato Institute Daily Commentary, www.cato.org., October 3.
Hogan, Vincent (1998), "Explaining the Recent Behavior of Inflation and Unemployment in the United States," International Monetary Fund Working Paper 98/145, September.
Hu, Angang (2003), "Is China the Root Cause of Global Deflation?" China and the World Economy, No. 3, November.
Ihrig, Jane and Jaime Marquez (2003), "An Empirical Analysis of Inflation in OECD Countries" Board of Governors of the Federal Reserve System, International Finance Discussion Paper No. 765, May.
International Monetary Fund (2003), "Deflation: Determinants, Risks, and Policy Options - Findings of an Interdepartmental Task Force", Washington, D.C., April.
Jenkins, Paul (2003), "Canada and the Global Economy: Trends in Asia and Elsewhere," speech to Association of Professional Economists of British Columbia, Victoria, British Columbia, April 3,
Kilman, Scott (2003), ``U.S. Crop Prices Soar As China Fuels Demand,''The Wall Street Journal, November 13.
Kynge, James and Dan Roberts (2003), "Cut-throat Competitors," Financial Times, FT.com, February 4.
Kuroda, Haruhiko and Masahiro Kawai (2002), ``Time for a Switch to Global Reflation,''Financial Times, FT.com, December 1.
Lardy, Nicholas (2003), ``United States-China Ties: Reassessing the Economic Relationship,'' Testimony before the House Committee on International Relations, October 21.
Larhart, Justin (2003), "The China Syndrome," CNNmoney, money.cnn.com, May 30.
Leggett, Karby and Peter Wonacott (2002), ``Surge in Exports From China Gives a Jolt to Global Industry,''The Wall Street Journal, October 10.
Morrison, Kevin and Christopher Swann (2003), ``Raw Material Prices Fuel New Inflation Fears,''Financial Times, October 27.
Noland, Marcus and Adam Posen (2002), ``The Scapegoats for Japanese Deflation,''Financial Times, December 5.
Revenga, Ana L. (1992), ``Exporting Jobs? The Impact of Import Competition on Employment and Wages in U.S. Manufacturing,'' Quarterly Journal of Economics, Vol. 107, No. 1, 255-284.
Roach, Stephen (2002a), "The China Factor," Morgan Stanley Global Economic Forum, October 14.
Roach, Stephen (2002b), "Stop Bashing China," Morgan Stanley Global Economic Forum, December 13.
Swagel, Phillip (1995), "Import Prices and the Competing Goods Effect," Board of Governors of the Federal Reserve System, International Finance Discussion Paper No. 508, April.
Taylor, John B. (2003), "China's Exchange Rate Regime and its Effects on the U.S. Economy," Testimony before the House Committee on Financial Services, October 1.
Testa, William (2003), "Midwest Manufacturing and Trade with China," Federal Reserve Bank of Chicago, Chicago Fed Letter, November.
Tootell, Geoffrey M.B. (1998), "Globalization and U.S. Inflation," Federal Reserve Bank of Boston, New England Economic Review, July/August.
U.S. International Trade Commission (2003), ``Shifts in U.S. Merchandise Trade 2002,''Washington, D.C., July.
Valleta, Rob (2003), "Is Our IT Manufacturing Edge Drifting Overseas?" Federal Reserve Bank of San Francisco Economic Letter, October 10.
Wolf, Martin (2003), ``The world must learn to live with a wide-awake China,'' Financial Times, November 12.
World Bank (2002), "China is Becoming the World's Manufacturing Powerhouse," Transition Newsletter.
Yam, Denise (2002), "China: Exporting More Deflation," Morgan Stanley Global Economic Forum, September 16.
Young, Jeffrey (2003), ``China: Part of Japan's Solution, Not Problem,'' NikkoSalomonSmithBarney,Japan: Issues and Prospects, February 20.
Table 1: China's Share of Global GDP and Exports
Chinese export data are on a balance of payments basis. Sources: IMF World Economic Outlook 2003 (Global data and Chinese GDP) and CEIC (Chinese exports).| Year | GDP | Exports |
|---|---|---|
| 1990 | 1.7 | 1.2 |
| 1995 | 2.4 | 2.0 |
| 2002 | 3.9 | 4.2 |
Table 2: 2002 Current Account Balance
| Rank | Country | Current Account Balance
($ Billions) |
Current Account Balance
(Percent of GDP) |
|---|---|---|---|
| 1 | Japan | 112 | 2.8 |
| 2 | Germany | 50 | 2.5 |
| 3 | China | 35 | 2.9 |
| 4 | Russia | 33 | 9.7 |
| 5 | Switzerland | 32 | 11.9 |
| 6 | Norway | 26 | 14.6 |
| 7 | France | 26 | 1.8 |
| 8 | Taiwan | 26 | 1.9 |
| 9 | Singapore | 19 | 21.0 |
| 10 | Hong Kong | 17 | 10.7 |
Sources: IMF World Economic Outlook 2003, Haver, and CEIC.
Table 3: Sample Statistics: 1993 - 2002
| Variable | # of obs. | Unweighted Mean | Std. Dev. | Min | Max | Weighted Mean*** | Total US**** |
|---|---|---|---|---|---|---|---|
| Annualized import inflation* | 74 | -0.29% | 0.03 | -17.43% | 5.88% | -1.68% | -0.06% |
| Annualized change in China's import share** | 74 | 0.67% | 0.01 | -0.37% | 3.87% | 0.68% | 0.59% |
*Compounded annual growth of year-average price level from 1993 to 2002.
** Difference between 2002 and 1993 import shares, divided by 9.
*** Weighted by share of each sector in total imports for 74-sector sample.
**** Includes sectors not covered in the 74-sector sample.
Table 4: Dependent Variable: Annual U.S. import price inflation
variable |
1993-2002
(1) |
1997-2002
(2) |
1997-2002
(excluding gr. coffee) (3) |
|---|---|---|---|
| constant | 0.002
(0.004) |
-0.010
(0.006) |
-0.012
(0.004)*** |
|
|
-0.874
(0.422)** |
-1.097
(0.555)** |
-0.791
(0.384)** |
| Initial Share | 0.031
(0.046) |
0.060
(0.047) |
0.040
(0.033) |
| Lagged Inflation | -0.016
(0.108) |
0.384
(0.087)** |
|
| Adjusted R |
0.036 | 0.014 | 0.275 |
| # of observations | 74 | 74 | 73 |
Standard errors in parenthesis. *, ** and *** indicate significance at the 10, 5 and 1 percent levels respectively.
Table 5: Dependent Variable: Annual U.S. producer price inflation by 4-digit SIC sector
variable |
1993-2001 All sectors (1) |
1993-2001 Manufacturing (2) |
1997-2001 All sectors (3) |
1997-2001 Manufacturing (4 ) |
||||
|---|---|---|---|---|---|---|---|---|
| constant | 0.014
(0.001)*** |
0.014
(0.001)*** |
0.002
(0.002) |
0.001
(0.002) |
||||
|
|
-0.030
(0.078) |
-0.030
(0.091) |
0.015
(0.079) |
-0.033
(0.104) |
||||
| Initial Share | -0.008
(0.009) |
-0.008
(0.009) |
0.008
(0.010) |
0.008
(0.010) |
||||
| Lagged Inflation | 0.146
(0.056)*** |
0.223
(0.056)*** |
||||||
| Adj. R |
-0.002 | -0.002 | 0.011 | 0.033 | ||||
| Number of obs. | 388 | 374 | 388 | 374 | ||||
Standard errors in parenthesis. *, ** and *** indicate significance at the 10, 5 and 1 percent levels respectively.
Table 6: Dependent Variable: Annual U.S. producer price inflation (1995-2000) by 3-digit SIC sector
| variable | (1) | (2) | (3) | (4) | |
|---|---|---|---|---|---|
| constant | -0.003
(0.004) |
-0.000
(0.004) |
0.003
(0.005) |
0.003
(0.005) |
|
| Lagged Inflation | 0.407
(0.166)*** |
0.308
(0.167)* |
0.290
(0.165)* |
0.297
(0.161)* |
|
|
|
-0.058
(0.196) |
0.115
(0.199) |
|||
| Initial Share | 0.010
(0.043) |
||||
| Initial IPR | -0.024
(0.020) |
-0.028
(0.016)* |
|||
|
|
-1.661
(1.126) |
-0.409
(1.230) |
|||
| Adj. R |
0.081 | 0.135 | 0.160 | 0.181 | |
| Number of obs. | 38 | 38 | 38 | 38 |
Standard errors in parenthesis. *, ** and *** indicate significance at the 10, 5 and 1 percent levels respectively.
Table 7: Comparison of Calculated Import Unit Values with IMF International Financial Statistics (1993=100)
Country |
2001 Kamin-Marazzi-Schindler |
2001 IFS |
2001 KMS/IFS |
||
|---|---|---|---|---|---|
| Australia | 91.6 | 88.9 | 1.03 | ||
| Austria | 81.9 | ||||
| Belgium | 94.0 | 101.0 | 0.93 | ||
| Canada | 104.7 | 97.3 | 1.08 | ||
| Denmark | 95.5 | ||||
| Finland | 101.7 | 90.5 | 1.12 | ||
| France | 88.8 | 73.4 | 1.21 | ||
| Germany | 86.1 | 84.9 | 1.01 | ||
| Greece | 87.7 | 88.4 | 0.99 | ||
| Hungary | 97.0 | 92.1 | 1.05 | ||
| Iceland | 94.2 | ||||
| Ireland | 105.4 | 96.3 | 1.09 | ||
| Italy | 86.2 | 96.7 | 0.89 | ||
| Japan | 94.0 | 91.7 | 1.03 | ||
| Korea* | 90.5 | 84.9 | 1.07 | ||
| Netherlands | 84.4 | 90.8 | 0.93 | ||
| New Zealand | 99.5 | 90.7 | 1.10 | ||
| Norway | 94.6 | 83.6 | 1.13 | ||
| Poland* | 98.9 | 90.6 | 1.03 | ||
| Portugal | 90.1 | ||||
| Spain | 86.7 | 86.2 | 1.01 | ||
| Sweden** | 91.0 | 102.1 | 0.89 | ||
| Switzerland | 88.4 | 86.9 | 1.02 | ||
| Turkey | 96.8 | ||||
| United Kingdom | 94.7 | 94.4 | 1.00 | ||
| United States | 103.5 | 101.9 | 1.02 | ||
Data are taken from IFS Yearbook, 2002 and IFS November 2003. * Data start in 1994; 1994=100 for our calculation and for IFS ** Data end in 2000.
Table 8a: Decomposition of Import Unit Value Inflation - All categories (Annual Average Percent Change)*
| Country | Total | ROW
Effect |
China
Effect |
China Price Effect | China Share Effect | China Share 1993 | China Share 2001 | Change in Share (ppt) |
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Australia | -1.05 | -0.65 | -0.40 | -0.09 | -0.31 | 6.6 | 12.3 | 5.8 |
| Austria | -2.26 | -2.28 | 0.01 | 0.06 | -0.05 | 1.7 | 2.1 | 0.4 |
| Belgium | -0.75 | -0.48 | -0.29 | -0.19 | -0.10 | 1.8 | 2.7 | 0.9 |
| Canada | 0.59 | 0.79 | -0.20 | -0.24 | 0.05 | 2.5 | 4.5 | 2.1 |
| Denmark | -0.56 | -0.31 | -0.24 | -0.18 | -0.06 | 2.1 | 3.2 | 1.1 |
| Finland | 0.21 | 0.35 | -0.14 | -0.04 | -0.10 | 2.1 | 3.1 | 1.0 |
| France | -1.40 | -1.36 | -0.04 | 0.04 | -0.08 | 2.6 | 4.1 | 1.5 |
| Germany | -1.74 | -1.56 | -0.16 | -0.01 | -0.16 | 3.5 | 4.8 | 1.3 |
| Greece | -1.54 | -1.66 | 0.13 | 0.04 | 0.09 | 1.4 | 4.5 | 3.1 |
| Hungary | -0.38 | -0.30 | -0.08 | 0.03 | -0.10 | 0.5 | 3.0 | 2.5 |
| Iceland | -0.73 | -0.60 | -0.13 | 0.00 | -0.13 | 1.1 | 3.8 | 2.8 |
| Ireland | 0.68 | 0.71 | -0.04 | -0.01 | -0.03 | 1.3 | 2.3 | 1.0 |
| Italy | -1.73 | -1.66 | -0.06 | 0.00 | -0.06 | 2.4 | 3.7 | 1.4 |
| Japan | -0.75 | 0.44 | -1.19 | -0.71 | -0.48 | 10.3 | 20.6 | 10.3 |
| Korea** | -1.36 | -0.37 | -0.99 | -0.90 | -0.10 | 6.6 | 12.9 | 6.3 |
| Netherlands | -1.95 | -1.59 | -0.36 | -0.11 | -0.26 | 1.9 | 5.3 | 3.4 |
| New Zealand | -0.06 | 0.30 | -0.36 | -0.03 | -0.33 | 4.5 | 8.8 | 4.3 |
| Norway | -0.68 | -0.58 | -0.10 | -0.01 | -0.09 | 1.5 | 3.1 | 1.6 |
| Poland** | -0.16 | 0.13 | -0.29 | -0.24 | -0.04 | 1.3 | 3.1 | 1.8 |
| Portugal | -1.24 | -1.19 | -0.06 | -0.06 | 0.00 | 1.1 | 1.1 | 0.0 |
| Spain | -1.66 | -1.34 | -0.33 | -0.18 | -0.15 | 2.5 | 4.0 | 1.5 |
| Sweden*** | -1.29 | -1.31 | 0.03 | 0.01 | 0.01 | 2.2 | 1.8 | -0.4 |
| Switzerland | -1.45 | -1.35 | -0.10 | 0.01 | -0.11 | 1.2 | 1.8 | 0.6 |
| Turkey | -0.40 | -0.29 | -0.11 | -0.01 | -0.10 | 0.8 | 2.7 | 1.8 |
| U.K. | -0.66 | -0.66 | 0.00 | 0.03 | -0.03 | 3.0 | 3.7 | 0.7 |
| United States | 0.44 | 1.48 | -1.03 | -0.53 | -0.50 | 9.2 | 14.3 | 5.1 |
| Average | -0.84 | -0.59 | -0.25 | -0.13 | -0.12 | 2.9 | 5.3 | 2.4 |
| Median | -0.75 | -0.59 | -0.13 | -0.02 | -0.10 | 2.1 | 3.7 | 1.6 |
| * A
simple average of the total change is taken for columns (1) - (7)
to maintain additivity.
** Data start in 1994. *** Data end in 2000. |
||||||||
| Table
8b - Decomposition of Import Unit Value Inflation
Categories where China's share is positive in 1993 and 2001 (Annual Average Percent Change)* |
||||||||
| Country | Total | ROW
Effect |
China
Effect |
China Price Effect | China Share Effect | China Share 1993 | China Share 2001 | Change in Share (ppt) |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Australia | -1.43 | -0.84 | -0.59 | -0.14 | -0.45 | 9.7 | 17.1 | 7.4 |
| Austria | -2.73 | -2.75 | 0.03 | 0.13 | -0.10 | 3.3 | 4.0 | 0.7 |
| Belgium | -0.96 | -0.35 | -0.61 | -0.45 | -0.16 | 4.2 | 5.7 | 1.5 |
| Canada | 0.20 | 0.89 | -0.69 | -0.51 | -0.18 | 5.1 | 9.6 | 4.5 |
| Denmark | 0.05 | 0.59 | -0.54 | -0.43 | -0.13 | 4.5 | 6.6 | 2.0 |
| Finland | -0.46 | -0.14 | -0.33 | -0.09 | -0.23 | 5.5 | 7.3 | 1.8 |
| France | -1.68 | -1.61 | -0.06 | 0.05 | -0.11 | 4.5 | 7.2 | 2.7 |
| Germany | -1.96 | -1.74 | -0.23 | -0.01 | -0.23 | 4.9 | 6.5 | 1.6 |
| Greece | -2.98 | -3.00 | 0.03 | 0.13 | -0.10 | 5.0 | 10.6 | 5.7 |
| Hungary | -0.06 | 0.20 | -0.26 | 0.14 | -0.40 | 2.7 | 4.4 | 1.6 |
| Iceland | -1.03 | -0.83 | -0.20 | 0.01 | -0.21 | 3.1 | 7.1 | 4.0 |
| Ireland | 0.43 | 0.50 | -0.08 | -0.03 | -0.05 | 3.7 | 5.7 | 2.1 |
| Italy | -1.96 | -1.86 | -0.11 | 0.01 | -0.11 | 4.7 | 6.9 | 2.1 |
| Japan | -0.61 | 0.88 | -1.49 | -0.95 | -0.54 | 13.7 | 25.1 | 11.5 |
| Korea** | -1.06 | 0.54 | -1.60 | -1.33 | -0.27 | 9.7 | 17.9 | 8.2 |
| Netherlands | -2.28 | -1.58 | -0.71 | -0.23 | -0.49 | 3.8 | 9.2 | 5.4 |
| New Zealand | -0.81 | -0.13 | -0.69 | -0.06 | -0.63 | 10.1 | 19.0 | 8.9 |
| Norway | -1.08 | -0.85 | -0.23 | -0.03 | -0.19 | 3.6 | 6.7 | 3.1 |
| Poland** | 1.74 | 3.20 | -1.46 | -1.54 | 0.09 | 7.7 | 13.9 | 6.2 |
| Portugal | -1.45 | -1.28 | -0.18 | -0.20 | 0.04 | 3.5 | 3.0 | -0.5 |
| Spain | -2.14 | -1.50 | -0.65 | -0.36 | -0.29 | 4.9 | 7.7 | 2.8 |
| Sweden*** | -1.97 | -2.06 | 0.09 | 0.06 | 0.04 | 5.5 | 4.6 | -0.9 |
| Switzerland | -1.78 | -1.60 | -0.18 | 0.03 | -0.20 | 2.4 | 3.5 | 1.1 |
| Turkey | -0.69 | -0.35 | -0.34 | -0.03 | -0.31 | 3.0 | 7.1 | 4.1 |
| U.K. | -1.23 | -1.26 | 0.04 | 0.05 | 0.00 | 4.8 | 5.7 | 0.9 |
| United States | 0.29 | 1.54 | -1.26 | -0.66 | -0.60 | 11.6 | 17.8 | 6.3 |
| Average | -1.06 | -0.59 | -0.47 | -0.25 | -0.22 | 5.6 | 9.2 | 3.6 |
| Median | -1.07 | -0.83 | -0.29 | -0.04 | -0.19 | 4.8 | 7.1 | 2.8 |
| * A
simple average of the total change is taken for columns (1) - (7)
to maintain additivity.
** Data start in 1994. *** Data end in 2000. |
||||||||
Table 9: U.S. cross-sectional regressions using ITCS database (1993-2001)
| variable | Dependent Variable %
|
|---|---|
| constant | 0.005
(0.001)*** |
|
|
-0.211
(0.064)*** |
| Initial share | 0.006
(0.007) |
| Adj.
R |
0.006 |
| Number of obs. | 1566 |
Subscript i indicates a 5-digit SITC sector.
Appendix A: Derivation of Supply Curves
Suppose there are identical production functions in China (C) and the rest of the world (RW), which depend on labor inputs, with capital and technology fixed and incorporated intoIn China, producers solve the following problem:
which defines an implicit labor demand function:
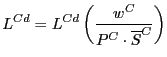
Next, we assume labor supply depends on the real consumption wage:
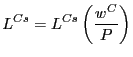
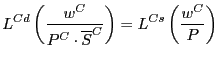
![$\displaystyle \frac{dL^{Cd}}{d\left( \frac{w^{C}}{P^{C}\cdot\overline{S}^{C}}\r...
...^{C}}
{P}\right) }\left[ \frac{1}{P}dw^{C}-w^{C}\left( P\right) ^{-2}dP\right]
$](imgx21.gif)
![$\displaystyle \frac{dL^{Cd}}{d\left( \frac{w^{C}}{P^{C}\cdot\overline{S}^{C}}\r...
...{C}}{P}\right) }\frac{w^{C}}{P}\left[
\frac{dw^{C}}{w^{C}}-\frac{dP}{P}\right]
$](imgx24.gif)
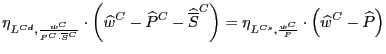
Because
This function has the usual properties of supply functions:
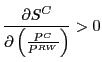 and
and 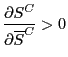
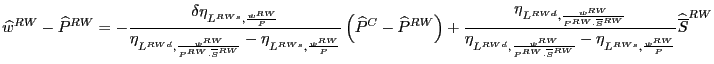
which also has the usual properties of supply functions:
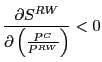 and
and 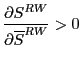
Appendix B: Response of Prices to Chinese Supply Shock
Assume a supply shock in China
![]() Recall the
goods market clearing condition in China:
Recall the
goods market clearing condition in China:
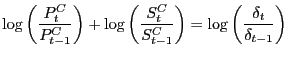
Totally differentiating equation 3,
![$\displaystyle dS^{C}=S_{1}^{C}\left[ \left( \frac{1}{P^{RW}}\right) ^{1-\delta}...
...ft( P^{RW}\right) ^{\delta
-2}dP^{RW}\right] +S_{2}^{C}\cdot d\overline{S}^{C}
$](imgx57.gif)
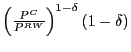 out of the first term on the RHS and dividing by
out of the first term on the RHS and dividing by 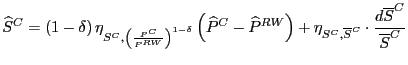
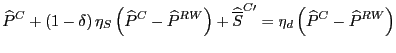
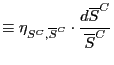 |
||
Solving for
Similarly, in the rest of the world, the goods market equilibrium is given by:
Totally differentiating equation 4, assuming no supply shock to the rest of the world, factoring out
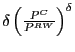 of the RHS, dividing by
of the RHS, dividing by 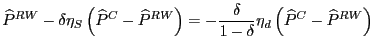
Solving for
Next, we solve for Chinese inflation by plugging equation 8 into equation 6:
Then, we can use this expression to solve for rest of the world inflation in equation 8:
Finally, we solve for the global CPI:
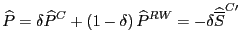
Appendix C: Import Price Inflation and China Import Shares by End-use Category
| Annual U.S. import inflation (1993-2002) | China's share in U.S. imports 1993 | China's share in U.S. imports 2002 | ||
|---|---|---|---|---|
| Green coffee | -5.2% | 0.0% | 0.1% | |
| Meat, products and poultry | -1.5% | 0.3% | 0.9% | |
| Fruit and fruit preparations, including frozen juices | 0.7% | 0.7% | 3.2% | |
| Vegetables and preparations | 0.6% | 4.5% | 3.3% | |
| Wine and related products | 1.1% | 0.4% | 0.1% | |
| Fish and shellfish | 0.2% | 5.1% | 8.6% | |
| Whiskey and other alcoholic beverages | 1.6% | 0.1% | 0.1% | |
| Crude petroleum | 4.8% | 0.6% | 0.2% | |
| Fuel oil | 4.2% | 0.0% | 0.0% | |
| Other petroleum products | 2.9% | 0.2% | 1.0% | |
| Liquified petroleum gasses | 3.2% | 0.0% | 0.0% | |
| Gas - natural | 3.1% | 0.0% | 0.0% | |
| Paper-base stocks - pulpwood and woodpulp | 1.3% | 0.0% | 0.0% | |
| Newsprint | 0.5% | 0.0% | 0.0% | |
| Paper and paper products, nec | 1.6% | 0.5% | 2.2% | |
| Farming materials, including farm animals and animals for breeding | -1.0% | 3.4% | 1.8% | |
| Other agricultural materials for industry | 1.1% | 5.5% | 8.3% | |
| Cotton, fibers, yarn, and fabric | -1.0% | 11.6% | 9.5% | |
| Plastic materials | -0.6% | 0.5% | 1.2% | |
| Fertilizers, pesticides, and insecticides | -0.1% | 0.2% | 2.2% | |
| Industrial inorganic chemicals | -0.1% | 4.2% | 12.1% | |
| Industrial organic chemicals | 0.8% | 1.5% | 4.3% | |
| Other chemicals (coloring agents, photographic chemicals, inks, and paint) | -0.3% | 1.3% | 3.3% | |
| Lumber and wood in the rough | 0.4% | 0.0% | 0.0% | |
| Steelmaking and ferroalloying materials | -0.9% | 2.2% | 2.6% | |
| Iron and steel mill products - semifinished | 0.5% | 0.2% | 1.6% | |
| Bauxite and aluminum | 3.1% | 0.4% | 0.7% | |
| Copper | 0.0% | 0.0% | 0.1% | |
| Nickel | 1.1% | 0.0% | 0.0% | |
| Zinc | -2.9% | 0.1% | 3.2% | |
| Nonmonetary gold | -2.0% | 0.0% | 0.0% | |
| Other precious metals | 5.9% | 0.0% | 1.0% | |
| Iron and steel products, ex advanced manufacturing | -1.0% | 1.4% | 6.5% | |
| Iron and steel manufactures - advanced | -0.8% | 4.5% | 14.5% | |
| Finished metal shapes and advanced manufactures | 0.2% | 4.4% | 11.5% | |
| Blank audio and visual tapes and other media | -6.0% | 11.4% | 11.4% | |
| Other finished nonmetals (boxes, belting, glass, abrasives, etc) | 0.6% | 7.7% | 11.6% | |
| Generators, transformers, and accessories | -0.2% | 5.4% | 10.7% | |
| Electric equipment and parts, nec | -0.7% | 4.3% | 14.1% | |
| Excavating, paving and construction machinery | 2.1% | 0.3% | 1.7% | |
| Industrial engines, pumps, compressors and generators | 0.0% | 1.1% | 5.6% | |
| Machine tools, metal working, molding and rolling-mill machinery | 0.8% | 1.1% | 2.7% | |
| Textile, sewing, and leather-working machinery | -0.4% | 0.5% | 2.8% | |
| Woodworking, glass-working, and plastic- and rubber-molding machinery | 0.1% | 0.6% | 6.6% | |
| Pulp and paper machinery, bookbinding, printing and packaging machinery | -0.2% | 0.2% | 1.4% | |
| Measuring, testing and control instruments | 0.2% | 1.8% | 4.2% | |
| Other industrial machinery | 0.3% | 1.6% | 5.2% | |
| Photo- and service-industry machinery and trade tools | -0.4% | 6.7% | 20.8% | |
| Agricultural machinery and equipment | 0.8% | 0.5% | 3.6% | |
| Computers (where data are based on 1995-2002) | -17.4% | 2.1% | 9.9% | |
| Computer accessories, peripherals and parts | -9.2% | 2.1% | 22.3% | |
| Semiconductors and related devices | -5.6% | 0.1% | 2.8% | |
| Telecommunications equipment | -2.6% | 6.2% | 12.2% | |
| Other office and business machines | -0.8% | 4.2% | 28.3% | |
| Other scientific, hospital, and medical equipment | -0.6% | 1.4% | 6.4% | |
| Passengers cars, new and used | 1.3% | 0.0% | 0.0% | |
| Apparel and household goods - cotton | 0.1% | 9.8% | 7.8% | |
| Apparel and household goods - wool | 0.7% | 7.4% | 8.4% | |
| Apparel and household goods - other textiles | 0.3% | 28.7% | 25.3% | |
| Nontextile apparel and household goods | 0.2% | 39.0% | 63.3% | |
| Footwear of leather, rubber and other materials | 0.2% | 41.1% | 64.1% | |
| Medicinal, dental, and pharmaceutical preparations, including vitamins | 0.3% | 1.9% | 0.8% | |
| Books, magazines, and other printed matter | 1.4% | 2.7% | 16.3% | |
| Toiletries and cosmetics | 0.1% | 2.8% | 8.7% | |
| Other products (notions, writing and art supplies, tobacco products, etc) | -0.8% | 17.7% | 25.3% | |
| Furniture, household items, and baskets | -0.6% | 9.9% | 39.4% | |
| Glassware, porcelain, and chinaware | 0.5% | 13.3% | 38.0% | |
| Cookware, cutlery, house and garden wares, and tools | -0.4% | 18.7% | 49.9% | |
| Household and kitchen appliances | -0.8% | 15.2% | 35.3% | |
| Other household goods (clocks, portable typewriters, etc) | -0.9% | 29.3% | 38.6% | |
| Toys, shooting, and sporting goods, bicycles, ex apparel | -0.8% | 34.7% | 64.0% | |
| Television receivers, video receivers, and other video equipment | -3.3% | 2.9% | 18.5% | |
| Radios, phonographs, tape decks, and other stereo equipment | -1.1% | 19.4% | 54.2% | |
| Jewelery (watches, rings, etc) | 0.2% | 3.3% | 9.9% | |
Chart 1
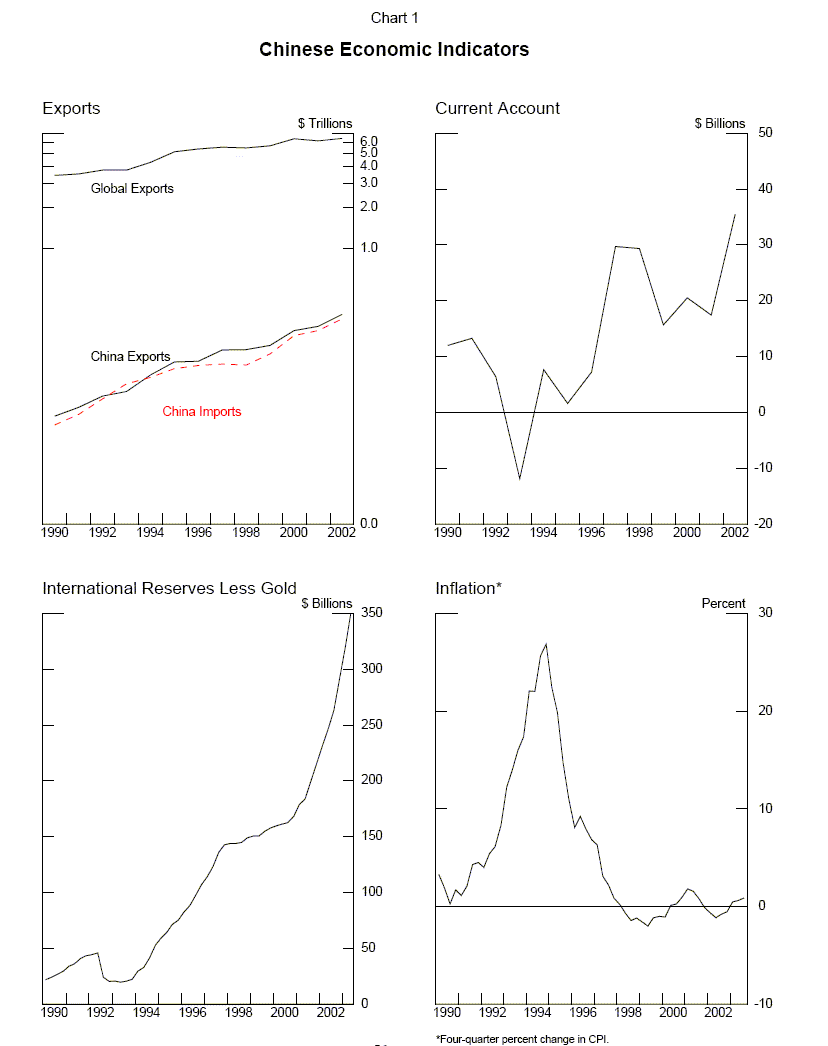
Chart 1 (top left panel -- $ trillions)
| Year | China's Imports | China's Exports | Global Exports |
|---|---|---|---|
| 1990 | 0.05 | 0.06 | 3.33 |
| 1991 | 0.06 | 0.07 | 3.42 |
| 1992 | 0.08 | 0.08 | 3.64 |
| 1993 | 0.1 | 0.09 | 3.64 |
| 1994 | 0.12 | 0.12 | 4.14 |
| 1995 | 0.13 | 0.15 | 4.95 |
| 1996 | 0.14 | 0.15 | 5.17 |
| 1997 | 0.14 | 0.18 | 5.54 |
| 1998 | 0.14 | 0.18 | 5.45 |
| 1999 | 0.17 | 0.2 | 5.65 |
| 2000 | 0.22 | 0.25 | 6.38 |
| 2001 | 0.24 | 0.27 | 6.13 |
| 2002 | 0.29 | 0.32 | 6.43 |
Chart 1 (top right panel -- $ Billions)
| China's Current Account |
|---|
| 12 |
| 13.27 |
| 6.4 |
| -11.9 |
| 7.66 |
| 1.62 |
| 7.24 |
| 29.72 |
| 29.32 |
| 21.11 |
| 20.52 |
| 17.41 |
| 35.42 |
Chart 1 bottom left panel ($ Billions)
| International Reserves less Gold | |
| 1990q1 | 22.27 |
| 1990q2 | 24.37 |
| 1990q3 | 26.84 |
| 1990q4 | 29.59 |
| 1991q1 | 34.09 |
| 1991q2 | 36.14 |
| 1991q3 | 40.92 |
| 1991q4 | 43.67 |
| 1992q1 | 44.46 |
| 1992q2 | 46.12 |
| 1992q3 | 24.3 |
| 1992q4 | 20.62 |
| 1993q1 | 20.97 |
| 1993q2 | 20.06 |
| 1993q3 | 20.85 |
| 1993q4 | 22.39 |
| 1994q1 | 29.83 |
| 1994q2 | 33.1 |
| 1994q3 | 41.24 |
| 1994q4 | 52.91 |
| 1995q1 | 59.35 |
| 1995q2 | 64.23 |
| 1995q3 | 71.43 |
| 1995q4 | 75.38 |
| 1996q1 | 82.7 |
| 1996q2 | 88.61 |
| 1996q3 | 97.36 |
| 1996q4 | 107.04 |
| 1997q1 | 113.96 |
| 1997q2 | 122.83 |
| 1997q3 | 136.02 |
| 1997q4 | 142.76 |
| 1998q1 | 143.98 |
| 1998q2 | 143.96 |
| 1998q3 | 145.02 |
| 1998q4 | 149.19 |
| 1999q1 | 150.5 |
| 1999q2 | 150.57 |
| 1999q3 | 154.73 |
| 1999q4 | 157.73 |
| 2000q1 | 159.77 |
| 2000q2 | 161.29 |
| 2000q3 | 162.59 |
| 2000q4 | 168.28 |
| 2001q1 | 178.89 |
| 2001q2 | 183.86 |
| 2001q3 | 199.28 |
| 2001q4 | 215.61 |
| 2002q1 | 230.87 |
| 2002q2 | 246.75 |
| 2002q3 | 262.96 |
| 2002q4 | 291.13 |
| 2003q1 | 320.87 |
| 2003q2 | 351.36 |
Chart 1 (bottom right panel -- 4-quarter percent change)
| Quarter | Consumer Price Inflation |
|---|---|
| 1990q1 | 3.28 |
| 1990q2 | 1.92 |
| 1990q3 | 0.27 |
| 1990q4 | 1.71 |
| 1991q1 | 1.12 |
| 1991q2 | 2.12 |
| 1991q3 | 4.3 |
| 1991q4 | 4.47 |
| 1992q1 | 5.29 |
| 1992q2 | 5.42 |
| 1992q3 | 6.15 |
| 1992q4 | 8.41 |
| 1993q1 | 10.91 |
| 1993q2 | 13.98 |
| 1993q3 | 15.97 |
| 1993q4 | 17.34 |
| 1994q1 | 22.06 |
| 1994q2 | 22.01 |
| 1994q3 | 25.62 |
| 1994q4 | 26.82 |
| 1995q1 | 22.48 |
| 1995q2 | 19.83 |
| 1995q3 | 14.78 |
| 1995q4 | 11.11 |
| 1996q1 | 9.36 |
| 1996q2 | 9.26 |
| 1996q3 | 7.94 |
| 1996q4 | 6.83 |
| 1997q1 | 5.07 |
| 1997q2 | 3.09 |
| 1997q3 | 2.17 |
| 1997q4 | 0.82 |
| 1998q1 | 0.19 |
| 1998q2 | -0.65 |
| 1998q3 | -1.39 |
| 1998q4 | -1.2 |
| 1999q1 | -1.54 |
| 1999q2 | -1.94 |
| 1999q3 | -1.08 |
| 1999q4 | -1.03 |
| 2000q1 | 0.16 |
| 2000q2 | 0.1 |
| 2000q3 | 0.2 |
| 2000q4 | 0.96 |
| 2001q1 | 0.59 |
| 2001q2 | 1.58 |
| 2001q3 | 0.81 |
| 2001q4 | -0.1 |
| 2002q1 | -0.64 |
| 2002q2 | -1.11 |
| 2002q3 | -0.79 |
| 2002q4 | -0.52 |
| 2003q1 | 0.59 |
| 2003q2 | 0.6 |
Chart 2
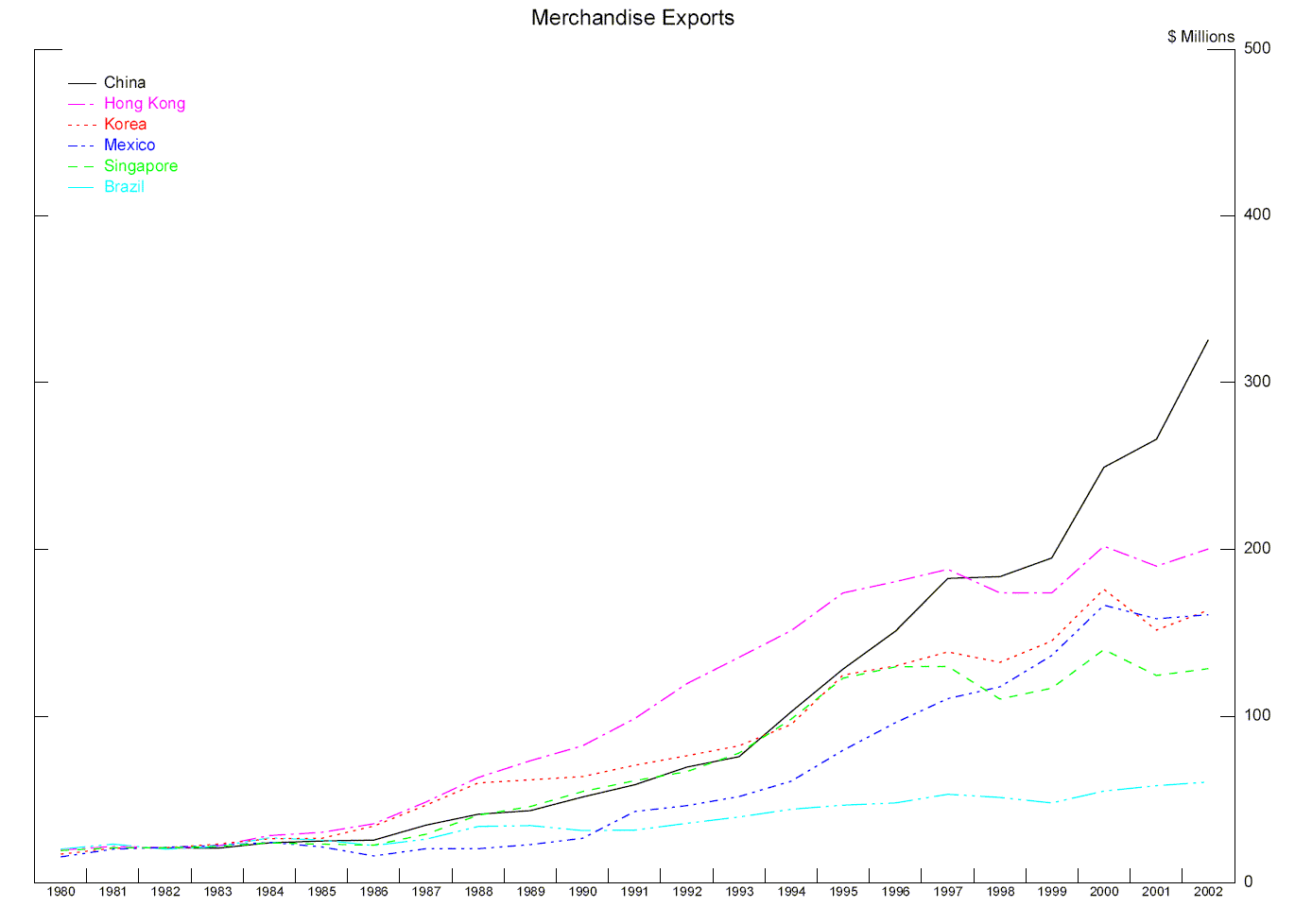
Chart 2 (Merchandise Exports -- $ Billions)
| Year | Hong Kong | Korea | Mexico | Singapore | China | Brazil |
|---|---|---|---|---|---|---|
| 1980 | 19.75 | 17.25 | 15.51 | 19.43 | 20.13 | |
| 1981 | 21.83 | 20.75 | 20.1 | 21.09 | 22.01 | 23.28 |
| 1982 | 21.01 | 20.93 | 21.23 | 21.02 | 21.87 | 20.17 |
| 1983 | 21.97 | 23.27 | 22.31 | 21.89 | 22.18 | 21.9 |
| 1984 | 28.32 | 26.49 | 24.2 | 24.09 | 24.83 | 27 |
| 1985 | 30.18 | 26.63 | 21.66 | 23.19 | 27.33 | 25.63 |
| 1986 | 35.44 | 34.13 | 16.16 | 22.73 | 31.15 | 22.35 |
| 1987 | 48.48 | 46.56 | 20.49 | 29.16 | 39.54 | 26.21 |
| 1988 | 63.16 | 59.97 | 20.55 | 40.73 | 47.54 | 33.77 |
| 1989 | 73.13 | 61.83 | 22.84 | 45.69 | 51.63 | 34.38 |
| 1990 | 82.16 | 63.66 | 26.84 | 54.88 | 60.92 | 31.41 |
| 1991 | 98.58 | 70.55 | 42.69 | 61.35 | 70.29 | 31.62 |
| 1992 | 119.52 | 76.21 | 46.2 | 66.6 | 84.94 | 35.79 |
| 1993 | 135.25 | 82.1 | 51.89 | 77.92 | 91.74 | 39.63 |
| 1994 | 151.39 | 94.98 | 60.88 | 98.31 | 121.01 | 44.1 |
| 1995 | 173.76 | 124.93 | 79.54 | 129.56 | 148.78 | 46.51 |
| 1996 | 180.74 | 130.04 | 96 | 137.5 | 151.05 | 47.85 |
| 1997 | 188.05 | 138.73 | 110.43 | 138.72 | 182.79 | 53.19 |
| 1998 | 174 | 132.25 | 117.54 | 117.72 | 183.71 | 51.14 |
| 1999 | 174.03 | 145.38 | 136.36 | 124.47 | 194.93 | 48.01 |
| 2000 | 202.05 | 176.22 | 166.12 | 149.23 | 249.2 | 55.09 |
| 2001 | 190.08 | 151.48 | 158.78 | 133.74 | 266.1 | 58.22 |
| 2002 | 200.3 | 163.41 | 161.05 | 137.75 | 325.6 | 60.36 |
Chart 3
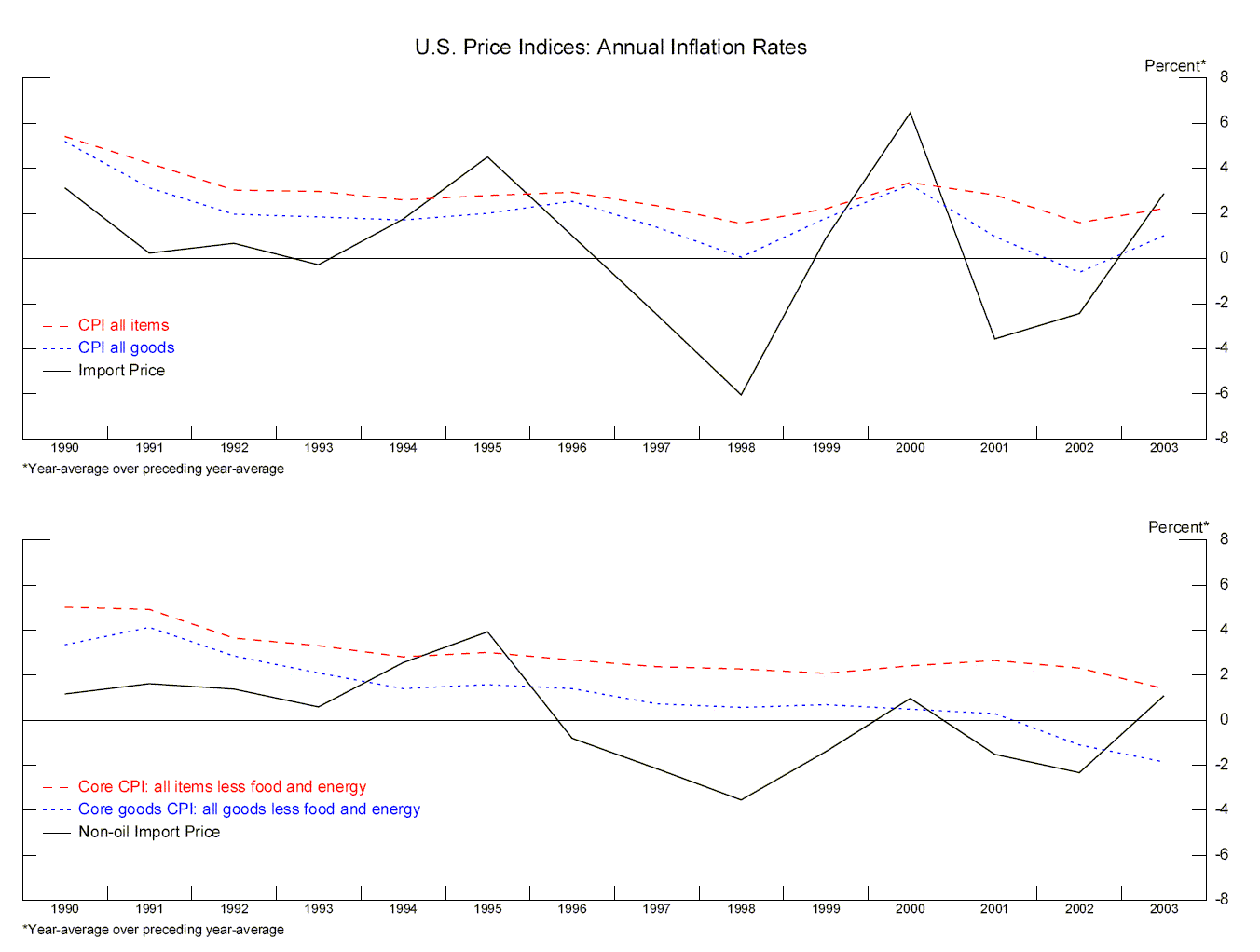
Chart 3 : U.S. Price Indices: Annual Inflation Rates (Year-average over preceding year-average)
| Year | Import price | CPI - all items | CPI - all goods | Non-oil Import price | Core CPI - all items less food and energy | Core Goods CPI - all goods less food and energy |
|---|---|---|---|---|---|---|
| 1990 | 3.14 | 5.41 | 5.2 | 1.17 | 5.03 | 3.38 |
| 1991 | 0.24 | 4.22 | 3.13 | 1.62 | 4.92 | 4.15 |
| 1992 | 0.67 | 3.04 | 1.97 | 1.38 | 3.66 | 2.87 |
| 1993 | -0.27 | 2.98 | 1.86 | 0.6 | 3.32 | 2.09 |
| 1994 | 1.74 | 2.6 | 1.71 | 2.56 | 2.82 | 1.42 |
| 1995 | 4.5 | 2.8 | 2 | 3.94 | 3.01 | 1.57 |
| 1996 | 1.01 | 2.93 | 2.53 | -0.79 | 2.68 | 1.41 |
| 1997 | -2.47 | 2.34 | 1.39 | -2.14 | 2.39 | 0.77 |
| 1998 | -6.03 | 1.55 | 0.06 | -3.54 | 2.29 | 0.56 |
| 1999 | 0.89 | 2.2 | 1.78 | -1.39 | 2.07 | 0.68 |
| 2000 | 6.47 | 3.36 | 3.28 | 0.98 | 2.43 | 0.5 |
| 2001 | -3.56 | 2.83 | 0.98 | -1.51 | 2.66 | 0.3 |
| 2002 | -2.43 | 1.57 | -0.61 | -2.33 | 2.32 | -1.09 |
| 2003 | 2.93 | 2.28 | 0.96 | 1.11 | 1.46 | -1.98 |
Chart 4
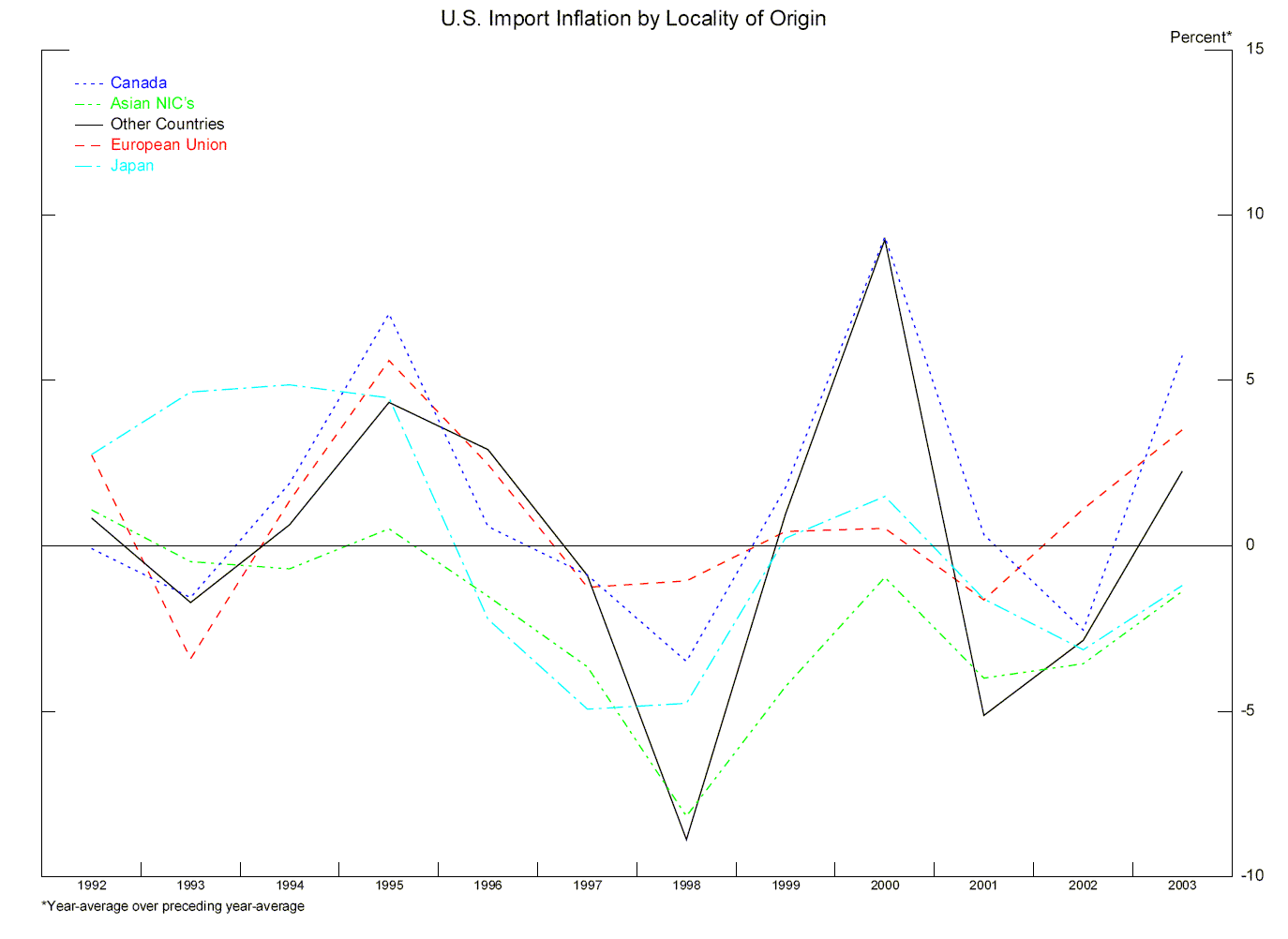
Chart 4: U.S. Import Price Inflation by Locality of Origin (Year-average over preceding year-average)
| European Union | Other countries | Canada | Japan | Asian NICs | |
|---|---|---|---|---|---|
| 1992 | 2.74 | 0.84 | -0.08 | 2.75 | 1.08 |
| 1993 | -3.41 | -1.72 | -1.57 | 4.65 | -0.48 |
| 1994 | 1.36 | 0.64 | 1.88 | 4.86 | -0.7 |
| 1995 | 5.6 | 4.33 | 7.01 | 4.47 | 0.52 |
| 1996 | 2.46 | 2.91 | 0.58 | -2.22 | -1.53 |
| 1997 | -1.25 | -0.89 | -0.89 | -4.93 | -3.65 |
| 1998 | -1.06 | -8.88 | -3.49 | -4.76 | -8.17 |
| 1999 | 0.44 | 0.95 | 1.75 | 0.23 | -4.26 |
| 2000 | 0.53 | 9.26 | 9.34 | 1.5 | -0.96 |
| 2001 | -1.63 | -5.13 | 0.33 | -1.61 | -4 |
| 2002 | 1.11 | -2.85 | -2.54 | -3.14 | -3.56 |
| 2003 | 3.53 | 2.27 | 5.85 | -1.15 | -1.37 |
Chart 5
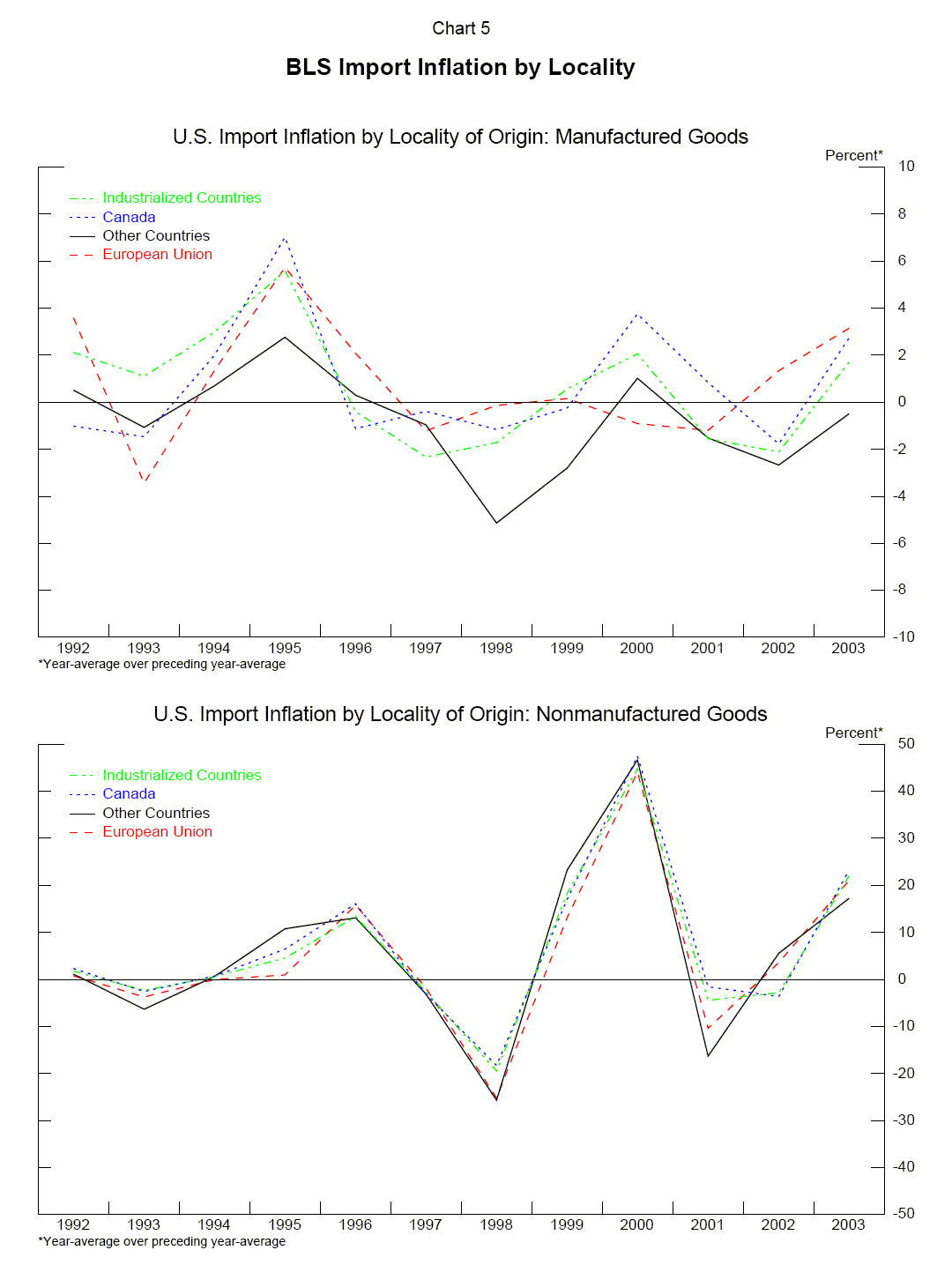
Chart 5: (top panel) BLS Import Inflation by Locality (Year-average over preceding year-average)
| Year | U.S. Import Inflation by Locality of Origin: Manufactured Goods Europe |
U.S. Import Inflation by Locality of Origin: Manufactured Goods Industrialized Countries |
U.S. Import Inflation by Locality of Origin: Manufactured Goods Other countries |
U.S. Import Inflation by Locality of Origin: Manufactured Goods Canada |
|---|---|---|---|---|
| 1992 | 3.58 | 2.11 | 0.5 | -1.01 |
| 1993 | -3.44 | 1.11 | -1.07 | -1.46 |
| 1994 | 1.34 | 2.98 | 0.69 | 1.99 |
| 1995 | 5.74 | 5.58 | 2.76 | 7.01 |
| 1996 | 2.08 | -0.41 | 0.3 | -1.13 |
| 1997 | -1.21 | -2.33 | -0.97 | -0.38 |
| 1998 | -0.13 | -1.71 | -5.14 | -1.16 |
| 1999 | 0.15 | 0.57 | -2.81 | -0.25 |
| 2000 | -0.91 | 2.07 | 1.01 | 3.75 |
| 2001 | -1.2 | -1.55 | -1.53 | 0.84 |
| 2002 | 1.34 | -2.12 | -2.67 | -1.78 |
| 2003 | 3.14 | 1.73 | -0.52 | 2.75 |
Year |
U.S. Import Inflation by Locality of Origin: Non-Manufactured Goods Europe |
U.S. Import Inflation by Locality of Origin: Non-Manufactured Goods Industrialized Countries |
U.S. Import Inflation by Locality of Origin: Non-Manufactured Goods Other Countries |
U.S. Import Inflation by Locality of Origin: Non-Manufactured Goods Canada |
|---|---|---|---|---|
| 1992 | 0.77 | 1.75 | 1.11 | 2.28 |
| 1993 | -3.71 | -2.37 | -6.34 | -2.55 |
| 1994 | -0.04 | 0.62 | 0.62 | 0.65 |
| 1995 | 0.92 | 4.6 | 10.79 | 6.42 |
| 1996 | 15.8 | 13.35 | 13.09 | 16.12 |
| 1997 | -1.85 | -2.61 | -3.06 | -3.1 |
| 1998 | -25.26 | -19.52 | -25.66 | -18.3 |
| 1999 | 13.21 | 18.35 | 23.28 | 17.09 |
| 2000 | 44.09 | 44.77 | 46.69 | 47.46 |
| 2001 | -10.39 | -4.41 | -16.33 | -1.55 |
| 2002 | 3.61 | -2.79 | 5.58 | -3.65 |
| 2003 | 21.66 | 22.36 | 17.44 | 23.62 |
Chart 6
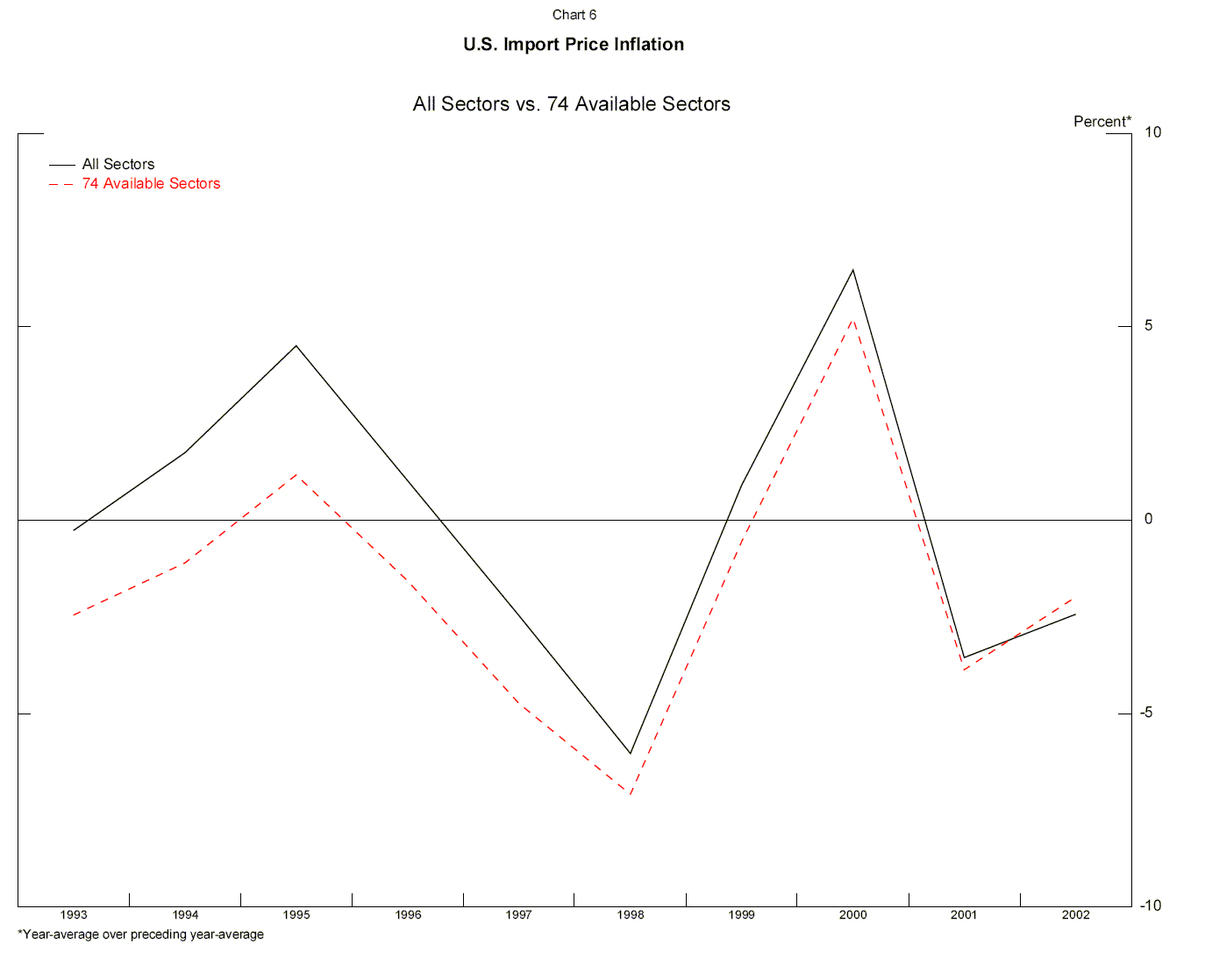
Chart 6: U.S. Import Price Inflation (Year-average over preceding year-average)
| Year | All sectors | Available 74 sectors |
|---|---|---|
| 1993 | -0.27 | -2.45 |
| 1994 | 1.74 | -1.11 |
| 1995 | 4.5 | 1.16 |
| 1996 | 1.01 | -1.58 |
| 1997 | -2.47 | -4.74 |
| 1998 | -6.03 | -7.1 |
| 1999 | 0.89 | -0.57 |
| 2000 | 6.47 | 5.21 |
| 2001 | -3.56 | -3.87 |
| 2002 | -2.43 | -1.99 |
Chart 7
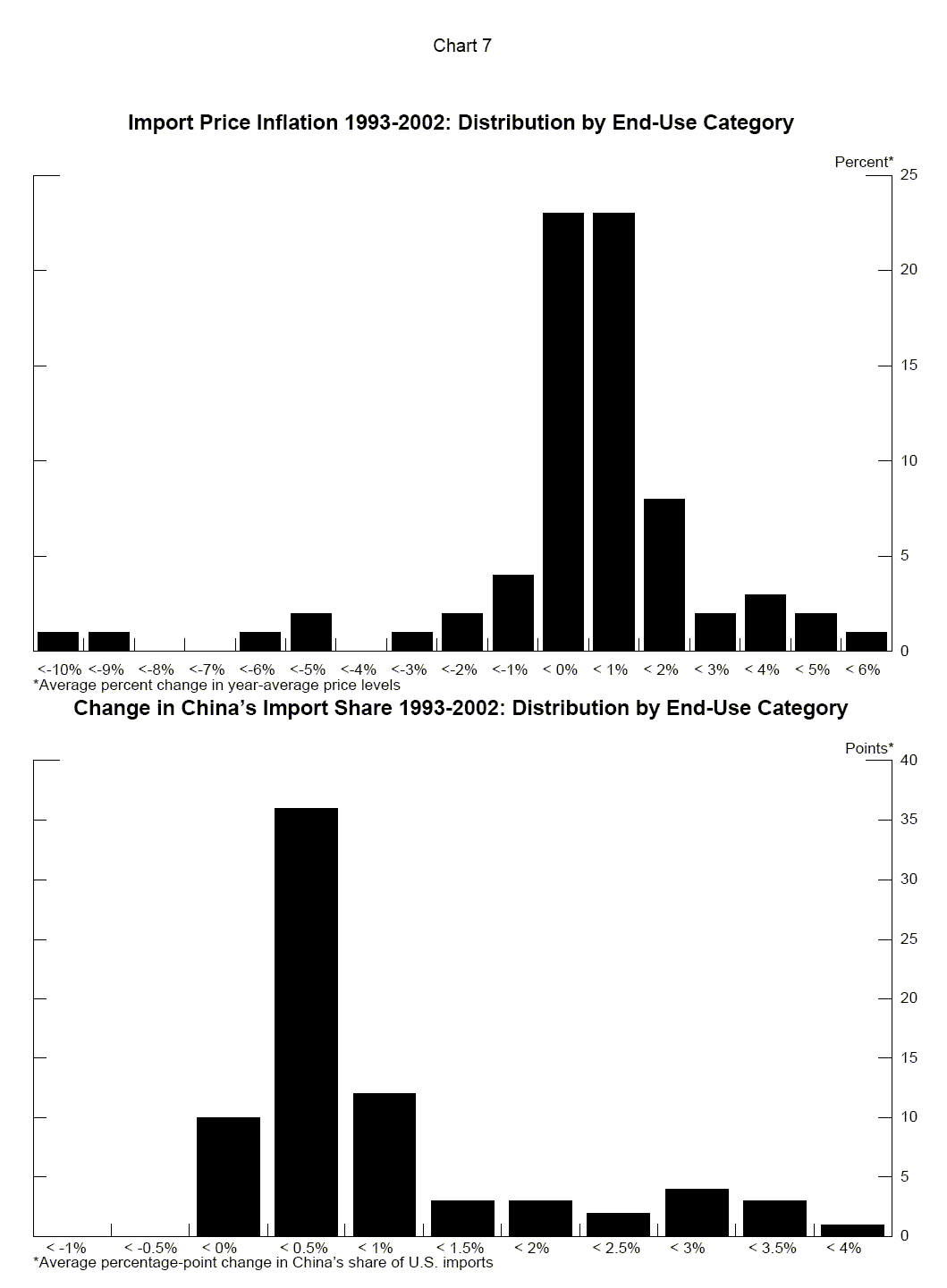
Chart 7: Import Price Inflation 1993-2002: Distribution by End-Use Category (Average percent change in year-average price levels)
| 1 | |
| 1 | |
| 0 | |
| 0 | |
| 1 | |
| 2 | |
| 0 | |
| 1 | |
| 2 | |
| 4 | |
| 23 | |
| 23 | |
| 8 | |
| 2 | |
| 3 | |
| 2 | |
| 1 | |
| Change in China's Import Share 1993-2002: Distribution by End-Use Category (Average percentage-point change in China's share of U.S. imports) | |
| 0 | |
| 0 | |
| 10 | |
| 36 | |
| 12 | |
| 3 | |
| 3 | |
| 2 | |
| 4 | |
| 3 | |
| 1 |
Chart 8
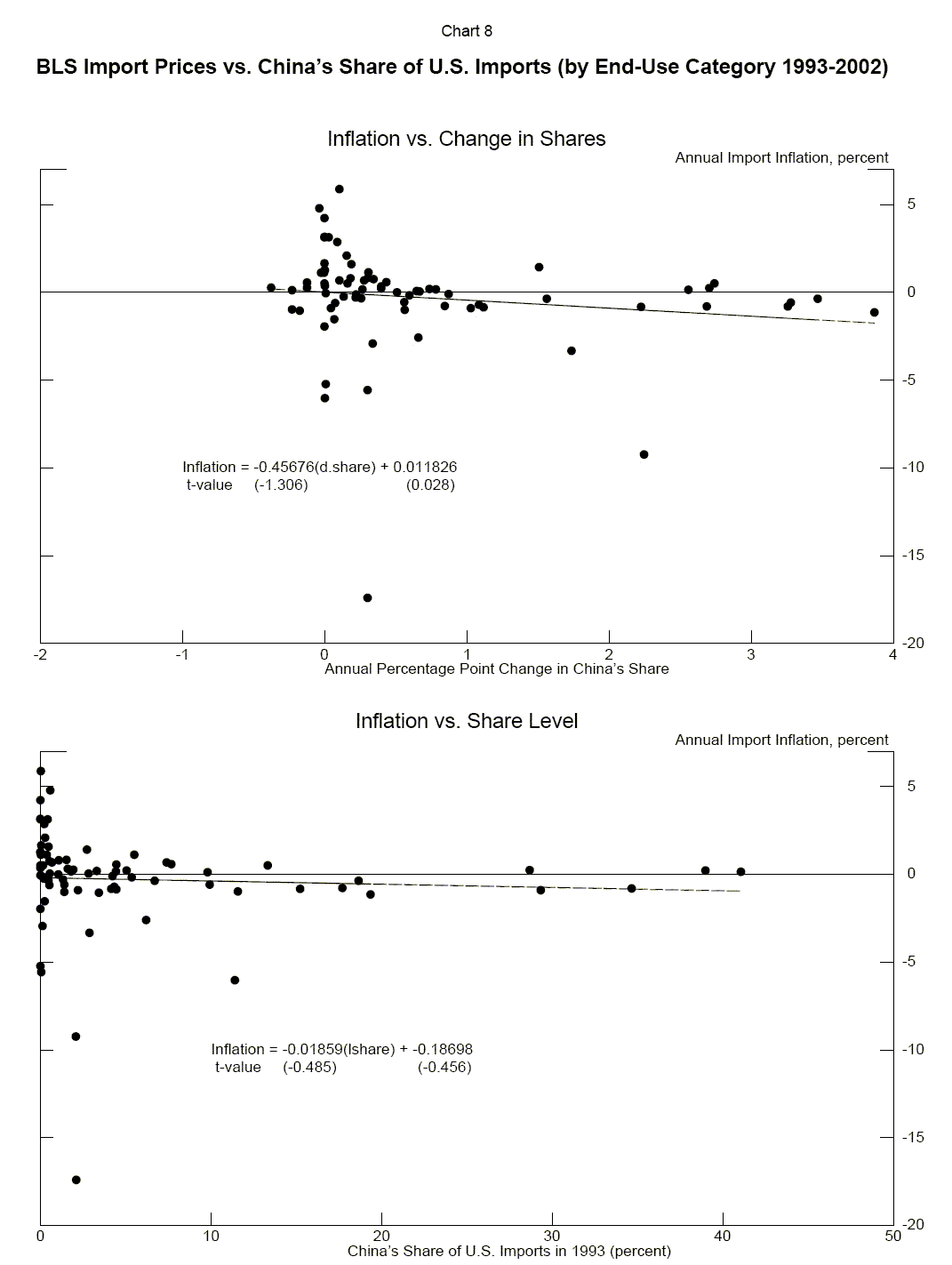
Chart 8: (top panel) BLS Import Prices vs. China's Share of U.S. Imports (by End-Use Category 1993-2002) Inflation vs. Change in Shares
| Annual Import Inflation | Annual Percentage Point Change in China's Share |
|---|---|
| -17.41 | 1.11 |
| 2.16 | 0.01 |
| -2.93 | 0.34 |
| -1.88 | 0.07 |
| 0.68 | 0.28 |
| 0.56 | -0.12 |
| 1.11 | -0.03 |
| 0.21 | 0.4 |
| 1.65 | 0 |
| 4.8 | -0.04 |
| 4.23 | 0 |
| 2.88 | 0.09 |
| 3.16 | 0 |
| 3.13 | 0 |
| 1.26 | 0 |
| 0.51 | 0 |
| 1.59 | 0.19 |
| -1.05 | -0.18 |
| 1.13 | 0.31 |
| -1.3 | -0.23 |
| -0.61 | 0.08 |
| -0.13 | 0.22 |
| -0.1 | 0.87 |
| 0.83 | 0.31 |
| -0.29 | 0.22 |
| 0.36 | 0 |
| -0.91 | 0.05 |
| 0.52 | 0.16 |
| 3.14 | 0.03 |
| -0.04 | 0.01 |
| 1.11 | 0 |
| -1.96 | 0 |
| 5.88 | 0.11 |
| -0.99 | 0.56 |
| -0.84 | 1.12 |
| 0.16 | 0.78 |
| -6.03 | 0 |
| 0.59 | 0.43 |
| -0.16 | 0.6 |
| -0.71 | 1.09 |
| 2.09 | 0.16 |
| -0.01 | 0.51 |
| 0.8 | 0.18 |
| -0.35 | 0.26 |
| 0.05 | 0.67 |
| -0.24 | 0.14 |
| 0.18 | 0.27 |
| 0.33 | 0.4 |
| -0.36 | 1.56 |
| 0.75 | 0.35 |
| -9.24 | 2.25 |
| -5.56 | 0.3 |
| -2.59 | 0.66 |
| -0.82 | 2.69 |
| -0.57 | 0.56 |
| 1.26 | 0 |
| 0.12 | -0.23 |
| 0.67 | 0.1 |
| 0.26 | -0.37 |
| 0.23 | 2.71 |
| 0.16 | 2.56 |
| 0.27 | -0.12 |
| 1.42 | 1.51 |
| 0.06 | 0.65 |
| -0.78 | 0.84 |
| -0.58 | 3.28 |
| 0.51 | 2.74 |
| -0.37 | 3.47 |
| -0.82 | 2.23 |
| -0.9 | 1.03 |
| -0.8 | 3.26 |
| -3.33 | 1.74 |
| -1.13 | 3.87 |
| 0.19 | 0.74 |
| Resulting regression estimation: | |
| Inflation = -0.45676 * (d.share) + 0.011826 | |
| t-value (-1.306) (0.028) |
| Annual Import Inflation | China's Share of U.S. Imports in 1993 (percent) |
|---|---|
| -17.41 | 2.12 |
| 2.16 | 0 |
| -2.93 | 0.14 |
| -1.88 | 0.27 |
| 0.68 | 0.69 |
| 0.56 | 4.45 |
| 1.11 | 0.37 |
| 0.21 | 5.06 |
| 1.65 | 0.07 |
| 4.8 | 0.58 |
| 4.23 | 0 |
| 2.88 | 0.24 |
| 3.16 | 0 |
| 3.13 | 0 |
| 1.26 | 0 |
| 0.51 | 0 |
| 1.59 | 0.48 |
| -1.05 | 3.43 |
| 1.13 | 5.51 |
| -1.3 | 11.59 |
| -0.61 | 0.54 |
| -0.13 | 0.17 |
| -0.1 | 4.25 |
| 0.83 | 1.54 |
| -0.29 | 1.35 |
| 0.36 | 0 |
| -0.91 | 2.2 |
| 0.52 | 0.17 |
| 3.14 | 0.44 |
| -0.04 | 0 |
| 1.11 | 0.05 |
| -1.96 | 0 |
| 5.88 | 0.04 |
| -0.99 | 1.42 |
| -0.84 | 4.47 |
| 0.16 | 4.43 |
| -6.03 | 11.42 |
| 0.59 | 7.68 |
| -0.16 | 5.36 |
| -0.71 | 4.35 |
| 2.09 | 0.28 |
| -0.01 | 1.05 |
| 0.8 | 1.08 |
| -0.35 | 0.5 |
| 0.05 | 0.57 |
| -0.24 | 0.2 |
| 0.18 | 1.81 |
| 0.33 | 1.6 |
| -0.36 | 6.71 |
| 0.75 | 0.54 |
| -9.24 | 2.1 |
| -5.56 | 0.07 |
| -2.59 | 6.22 |
| -0.82 | 4.16 |
| -0.57 | 1.41 |
| 1.26 | 0 |
| 0.12 | 9.82 |
| 0.67 | 7.42 |
| 0.26 | 28.69 |
| 0.23 | 38.98 |
| 0.16 | 41.06 |
| 0.27 | 1.94 |
| 1.42 | 2.74 |
| 0.06 | 2.84 |
| -0.78 | 17.71 |
| -0.58 | 9.93 |
| 0.51 | 13.33 |
| -0.37 | 18.66 |
| -0.82 | 15.24 |
| -0.9 | 29.35 |
| -0.8 | 34.65 |
| -3.33 | 2.89 |
| -1.13 | 19.37 |
| 0.19 | 3.31 |
| Resulting regression estimation: | |
| Inflation = -0.01859 * (lshare) + -0.18698 | |
| t-value (-0.485) (-0.456) |
Chart 9
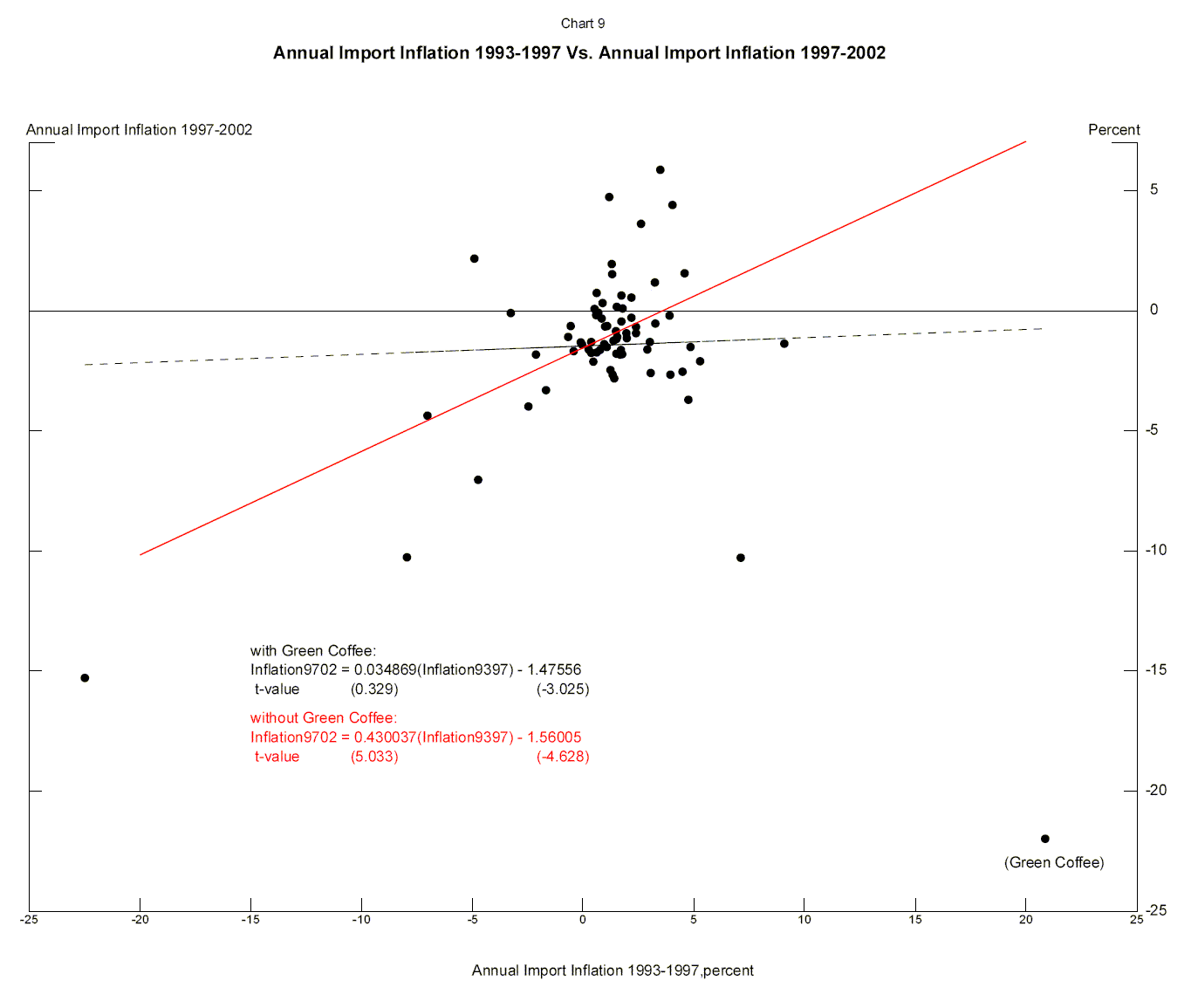
Chart 9: Annual Import Inflation 1993-1997 Vs. Annual Import Inflation 1997-2002
| Annual Import Inflation 1997-2002 | Annual Import Inflation 1993-1997 | Annual Import Inflation 1993-1997 | Annual Import Inflation 1993-1997 |
|---|---|---|---|
| -15.29 | -22.48 | Resulting regression estimation: | |
| -21.98 | 20.87 | Green Coffee | with Green Coffee: |
| -10.28 | 7.12 | Inflation9702 = 0.034869 * (Inflation9397) - 1.47556 | |
| -0.12 | -3.26 | t-value (0.329) (-3.025) | |
| -0.68 | 2.39 | ||
| 0.3 | 0.88 | without Green Coffee: | |
| 0.61 | 1.74 | Inflation9702 = 0.430037 * (Inflation9397) - 1.56005 | |
| -2.68 | 3.94 | t-value (5.033) (-4.628) | |
| 1.94 | 1.29 | ||
| 5.85 | 3.5 | ||
| 4.39 | 4.03 | ||
| 1.54 | 4.58 | ||
| 3.59 | 2.61 | ||
| 4.71 | 1.18 | ||
| -1.52 | 4.85 | ||
| -2.55 | 4.48 | ||
| -0.22 | 3.9 | ||
| 2.15 | -4.91 | ||
| -0.55 | 3.26 | ||
| -2.83 | 1.42 | ||
| -0.65 | -0.55 | ||
| -2.61 | 3.05 | ||
| -1.26 | 1.38 | ||
| 0.08 | 1.78 | ||
| -1.83 | 1.67 | ||
| -1.63 | 2.9 | ||
| -2.67 | 1.34 | ||
| -0.95 | 2.38 | ||
| -1.39 | 9.09 | ||
| -3.72 | 4.75 | ||
| -2.11 | 5.29 | ||
| -1.83 | -2.12 | ||
| 8.91 | 2.22 | ||
| -2.13 | 0.46 | ||
| -2.47 | 1.24 | ||
| -0.18 | 0.59 | ||
| -7.05 | -4.73 | ||
| -1.31 | 3.01 | ||
| -1.65 | 1.72 | ||
| -1.75 | 0.61 | ||
| 1.17 | 3.25 | ||
| -1.19 | 1.5 | ||
| -0.3 | 2.19 | ||
| -1.81 | 1.5 | ||
| -1.11 | 1.53 | ||
| -1.82 | 1.78 | ||
| -0.86 | 1.49 | ||
| -0.95 | 1.95 | ||
| -1.39 | 0.95 | ||
| 0.14 | 1.52 | ||
| -10.27 | -7.94 | ||
| -4.38 | -7.03 | ||
| -3.31 | -1.67 | ||
| -1.42 | -0.05 | ||
| -1.31 | 0.36 | ||
| 0.53 | 2.19 | ||
| -0.65 | 1.1 | ||
| 0.73 | 0.61 | ||
| -0.09 | 0.69 | ||
| -1.15 | 1.98 | ||
| -0.2 | 0.6 | ||
| 0.07 | 0.52 | ||
| 1.51 | 1.31 | ||
| -0.67 | 0.99 | ||
| -1.33 | -0.1 | ||
| -1.65 | 0.77 | ||
| -0.47 | 1.73 | ||
| -1.51 | 1.08 | ||
| -1.77 | 0.38 | ||
| -1.1 | -0.66 | ||
| -1.63 | 0.25 | ||
| -4 | -2.48 | ||
| -1.7 | -0.42 | ||
| -0.34 | 0.8 |
Chart 10
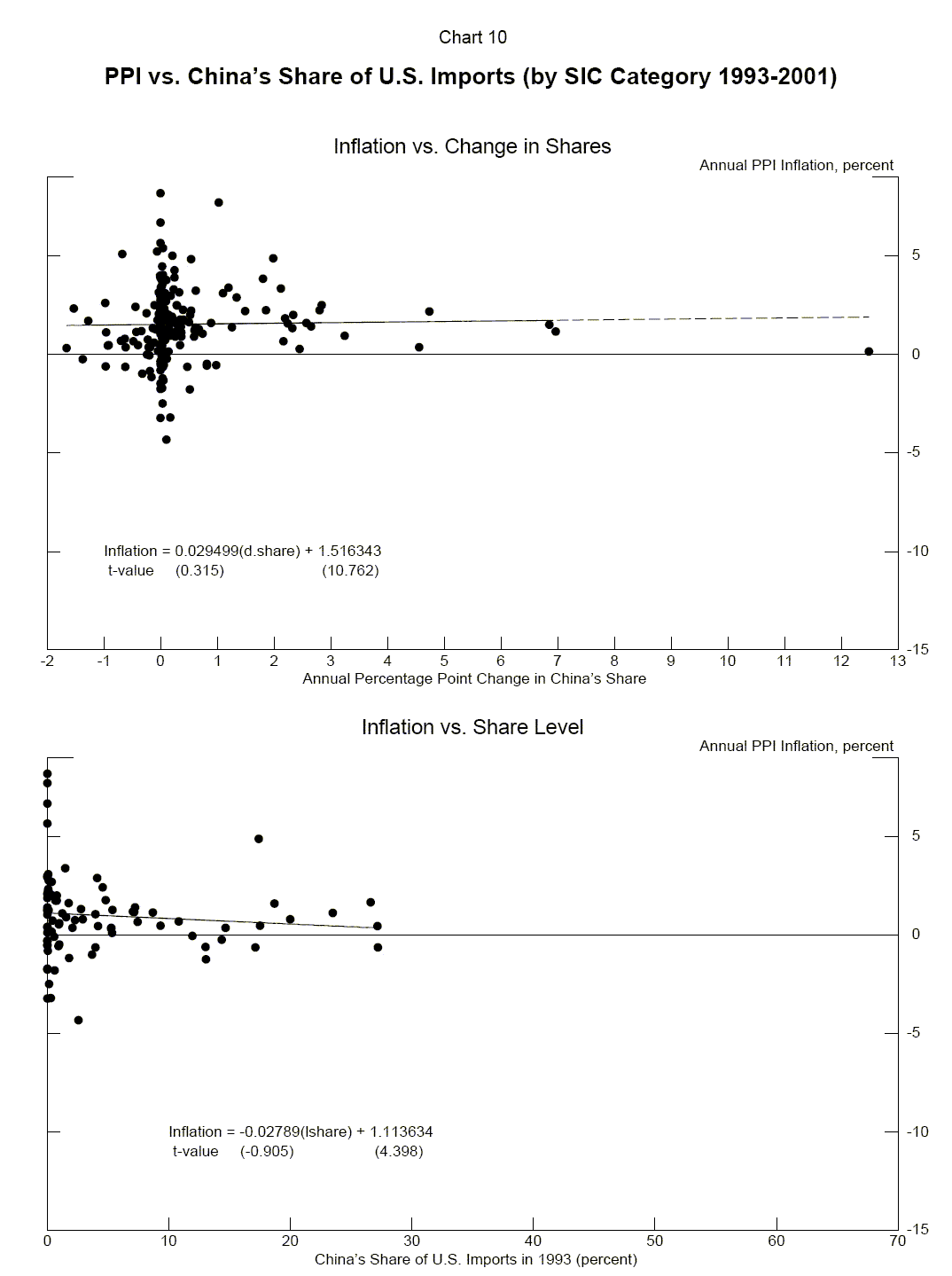
Chart 10: PPI vs. China's Share of U.S. Imports (by SIC Category 1993-2001)
| Top-panel: Inflation vs. Change in Shares | Top-panel: Inflation vs. Change in Shares | Bottom-panel: Inflation vs. Share Level | Bottom-panel: Inflation vs. Share Level |
|---|---|---|---|
| Annual PPI Inflation | Annual Percentage Point Change in China's Share | Annual PPI Inflation | China's Share of U.S. Imports in 1993 (percent) |
| 1.87 | 0 | 1.87 | 0 |
| 0.41 | 0 | 0.41 | 0 |
| 1.03 | 0 | 1.03 | 0 |
| -3.23 | 0 | -3.23 | 0 |
| -4.33 | 0.11 | -4.33 | 2.57 |
| 0.13 | 12.49 | 0.13 | 0 |
| 3.38 | 1.2 | 3.38 | 1.49 |
| 3.09 | 0.08 | 3.09 | 0.09 |
| 2.23 | 2.8 | 2.23 | 0.09 |
| 0.76 | -0.23 | 0.76 | 2.28 |
| 1.32 | -0.13 | 1.32 | 2.8 |
| -0.52 | 0.06 | -0.52 | 0.02 |
| -1.23 | 0.04 | -1.23 | 13.08 |
| 1.99 | 0.14 | 1.99 | 0.78 |
| 0.72 | 0.08 | 0.72 | 0.45 |
| 0.37 | -0.21 | 0.37 | 5.28 |
| 8.18 | 0 | 8.18 | 0 |
| 2.09 | 0 | 2.09 | 0 |
| 2.01 | 0.03 | 2.01 | 0.04 |
| 2.93 | 0 | 2.93 | 0 |
| 3.01 | 0 | 3.01 | 0 |
| 2.12 | 0 | 2.12 | 0.12 |
| 1.39 | 0.36 | 1.39 | 7.22 |
| 0.47 | 0.35 | 0.47 | 9.34 |
| 0.8 | 0.03 | 0.8 | 2.93 |
| 0.9 | 0.26 | 0.9 | 1.55 |
| -0.3 | 0.01 | -0.3 | 0.03 |
| -0.28 | 0.02 | -0.28 | 0.02 |
| -1.72 | 0.03 | -1.72 | 0.03 |
| 1.25 | -0.01 | 1.25 | 0.11 |
| -0.1 | 0.03 | -0.1 | 0.59 |
| 1.24 | 0.1 | 1.24 | 0 |
| -0.48 | 0.82 | -0.48 | 1 |
| 2.7 | 0.1 | 2.7 | 0.38 |
| -0.8 | 0 | -0.8 | 0.05 |
| 1.61 | 0.27 | 1.61 | 1.75 |
| 2.42 | -0.44 | 2.42 | 4.57 |
| 0.32 | 0.02 | 0.32 | 5.25 |
| -1.76 | 0 | -1.76 | 0 |
| -3.2 | 0.17 | -3.2 | 0.31 |
| -2.5 | 0.04 | -2.5 | 0.17 |
| -1.79 | 0.52 | -1.79 | 0.61 |
| 0.61 | -0.11 | 0.61 | 0.99 |
| 1.75 | -0.06 | 1.75 | 0.7 |
| 1.29 | 0 | 1.29 | 0 |
| 2.11 | 0 | 2.11 | 0.05 |
| 2.24 | 0 | 2.24 | 0.1 |
| 2.1 | 0.09 | 2.1 | 0.16 |
| 1.74 | -0.04 | 1.74 | 0.8 |
| -0.56 | 0.98 | -0.56 | 0.92 |
| 2.75 | 0 | 2.75 | 0.11 |
| 2.33 | 0.07 | 2.33 | 0.1 |
| 1.39 | 0 | 1.39 | 0 |
| 0.09 | 0.1 | 0.09 | 5.34 |
| 1.26 | -0.09 | 1.26 | 5.38 |
| 7.7 | 1.03 | 7.7 | 0.02 |
| 6.68 | 0 | 6.68 | 0 |
| 5.65 | 0 | 5.65 | 0 |
| 0.41 | 0 | 0.41 | 0 |
| -0.06 | -0.2 | -0.06 | 11.94 |
| -0.64 | 0.47 | -0.64 | 3.98 |
| 0.36 | -0.18 | 0.36 | 2.08 |
| 1.1 | 0.37 | 1.1 | 1.23 |
| 0.54 | 0.01 | 0.54 | 0.95 |
| -1.16 | -0.16 | -1.16 | 1.82 |
| 0.46 | -0.4 | 0.46 | 4.17 |
| 1.12 | -0.96 | 1.12 | 23.48 |
| -0.99 | -0.33 | -0.99 | 3.69 |
| 1.77 | 0.34 | 1.77 | 4.82 |
| 2.02 | 0.06 | 2.02 | 0.35 |
| -0.51 | 0 | -0.51 | 0 |
| 0.16 | -0.04 | 0.16 | 0.36 |
| 2.89 | 1.34 | 2.89 | 4.11 |
| 1.19 | -0.34 | 1.19 | 7.04 |
| 1.14 | -0.43 | 1.14 | 8.71 |
| -0.62 | -0.97 | -0.62 | 13.05 |
| -0.24 | -1.37 | -0.24 | 14.36 |
| 1.06 | 0.74 | 1.06 | 3.97 |
| 0.69 | -0.7 | 0.69 | 10.83 |
| 0.8 | -0.63 | 0.8 | 20.01 |
| 0.45 | -0.93 | 0.45 | 27.17 |
| -0.64 | -0.62 | -0.64 | 27.21 |
| -0.63 | 0.05 | -0.63 | 17.12 |
| 0.65 | -0.48 | 0.65 | 7.44 |
| 0.35 | -0.62 | 0.35 | 14.7 |
| 1.16 | 0.18 | 1.16 | 7.17 |
| 1.66 | 0.03 | 1.66 | 26.63 |
| 0.46 | -0.92 | 0.46 | 17.52 |
| 4.88 | 1.98 | 4.88 | 17.4 |
| 1.6 | 0.89 | 1.6 | 18.71 |
| 1.69 | -1.27 | ||
| 0.66 | 2.17 | ||
| 0.36 | 4.56 | ||
| 1.42 | 2.65 | ||
| 2.33 | -1.53 | ||
| 0.32 | -1.66 | ||
| 2.61 | -0.98 | ||
| 5.09 | -0.68 | ||
| 1.15 | 0.66 | ||
| 1.66 | 0.31 | ||
| 0.94 | 3.25 | ||
| -1.32 | 0.05 | ||
| -1.49 | 0 | ||
| 1.92 | 0.2 | ||
| 1.39 | 0 | ||
| 1.29 | 0.67 | ||
| 2.49 | -0.1 | ||
| 1.64 | 0.5 | ||
| -0.85 | -0.19 | ||
| 0.91 | 0.37 | ||
| 1.2 | 0 | ||
| 2.98 | 0.18 | ||
| 3.18 | 0 | ||
| 3.77 | 0.02 | ||
| 1.72 | 0.01 | ||
| -0.36 | 0 | ||
| 2.23 | 1.86 | ||
| 1.16 | 6.97 | ||
| 1.33 | 2.33 | ||
| 1.45 | -0.01 | ||
| 1.51 | 6.85 | ||
| 1.59 | 2.57 | ||
| 2.17 | 4.74 | ||
| 1.56 | 2.24 | ||
| 1.89 | 0.01 | ||
| 2.19 | 0.04 | ||
| 3.87 | 0 | ||
| 3.34 | 2.12 | ||
| 4.83 | 0.54 | ||
| 3.99 | -0.01 | ||
| 3.1 | 1.1 | ||
| 1.23 | 0.3 | ||
| 2.2 | 1.49 | ||
| 2.49 | 0.28 | ||
| 1.82 | 2.2 | ||
| 0.44 | 0.03 | ||
| 2.43 | 0 | ||
| 3.14 | 0.33 | ||
| 1.73 | 0.1 | ||
| 4.46 | 0.03 | ||
| 3.44 | 0.02 | ||
| 3.83 | 1.81 | ||
| 3.9 | 0.25 | ||
| 1.99 | 0.52 | ||
| 5.21 | -0.06 | ||
| 3.29 | 0.23 | ||
| 1.99 | 2.34 | ||
| -0.1 | 0.02 | ||
| 5.39 | 0.04 | ||
| 2.25 | 0.4 | ||
| 1.23 | 0.6 | ||
| 2.47 | 0.29 | ||
| 2.4 | -0.01 | ||
| 1.37 | 1.26 | ||
| 0.13 | 0.14 | ||
| 2.09 | -0.25 | ||
| 3.4 | 0 | ||
| 2.16 | -0.01 | ||
| 3.14 | -0.03 | ||
| 0.98 | 0.1 | ||
| 1.45 | 0.16 | ||
| 2.05 | -0.03 | ||
| 0.91 | 0.59 | ||
| 2.6 | 0.04 | ||
| 3.23 | 0.62 | ||
| -0.23 | 0.11 | ||
| 5 | 0.21 | ||
| 4.27 | 0.25 | ||
| 3.6 | 0.04 | ||
| 1.04 | 0.2 | ||
| 2.21 | 0.54 | ||
| -0.01 | -0.24 | ||
| 0.93 | 0.16 | ||
| 4.01 | 0.01 | ||
| 1.76 | 0.4 | ||
| 4.02 | 0.05 | ||
| 3.77 | 0.1 | ||
| 1.45 | 0 | ||
| 2.5 | 2.84 | ||
| -0.56 | 0.81 | ||
| 0.27 | 2.45 | ||
| 1.83 | 0.21 | ||
| 1.52 | 0.29 | ||
| 1.34 | 0.61 |
Chart 11
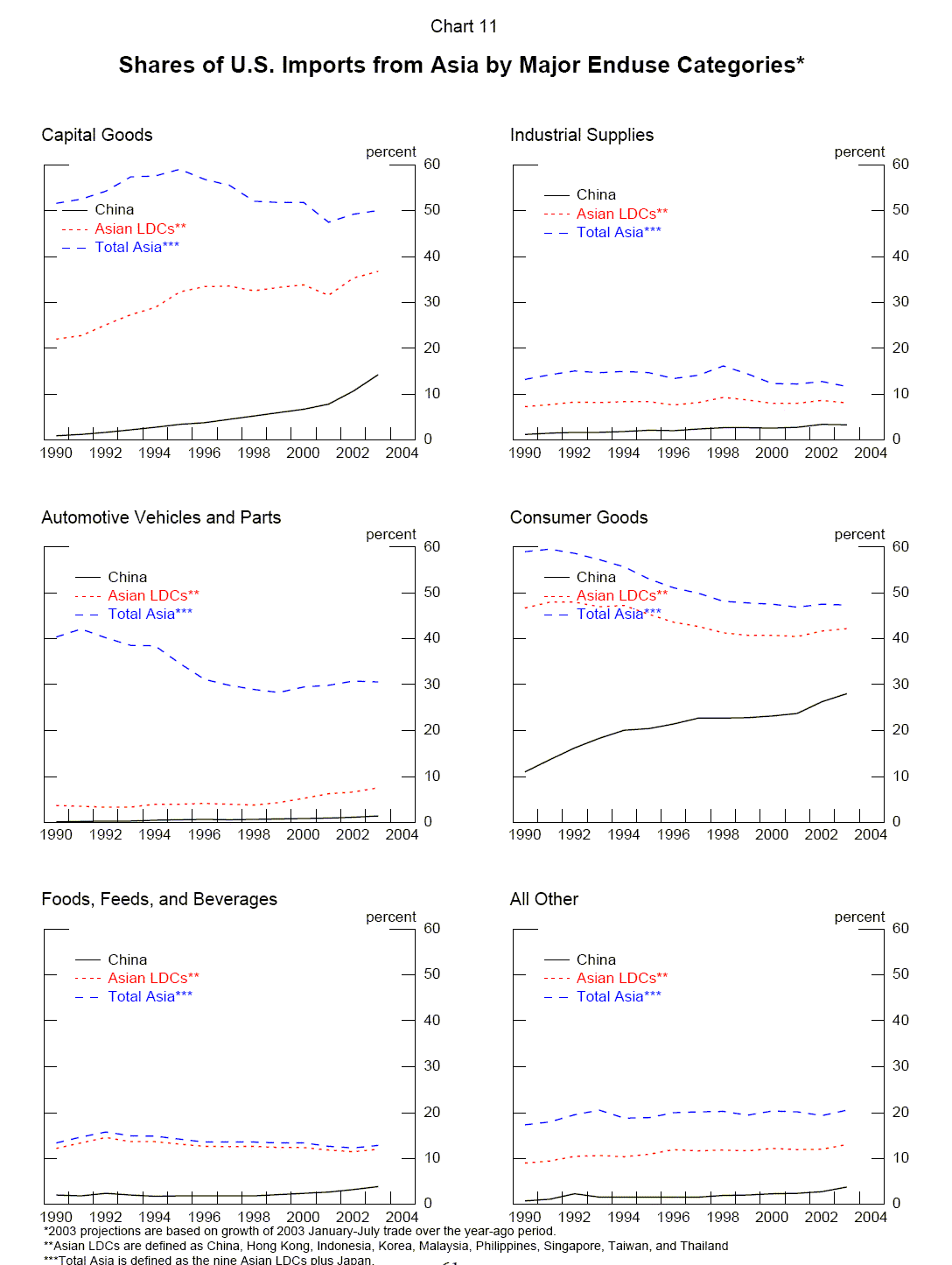
Chart 11: Shares of U.S. Imports from Asia by Major Enduse Categories*
| Top-left panel: Capital Goods | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| China | 0.94 | 1.26 | 1.7 | 2.21 | 2.8 | 3.42 | 3.8 | 4.52 | 5.21 | 6 | 6.71 | 7.79 | 10.66 | 11.75 |
| Asian LDCs ** | 21.94 | 22.66 | 25.03 | 27.24 | 28.82 | 32.29 | 33.46 | 33.48 | 32.5 | 33.3 | 33.84 | 31.53 | 35.31 | 35.9 |
| Total Asia *** | 51.56 | 52.48 | 54.23 | 57.3 | 57.57 | 59.03 | 56.81 | 55.54 | 52.02 | 51.75 | 51.76 | 47.47 | 49.18 | 49.35 |
| Top-right panel: Industrial Supplies | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| China | 1.26 | 1.51 | 1.71 | 1.71 | 1.89 | 2.12 | 2.09 | 2.42 | 2.73 | 2.69 | 2.55 | 2.76 | 3.39 | 3.56 |
| Asian LDCs ** | 7.29 | 7.71 | 8.27 | 8.2 | 8.32 | 8.34 | 7.59 | 8.07 | 9.19 | 8.77 | 7.96 | 8.03 | 8.66 | 8.49 |
| Total Asia *** | 13.22 | 14.21 | 15.05 | 14.68 | 14.96 | 14.73 | 13.38 | 14.03 | 16.04 | 14.4 | 12.32 | 12.22 | 12.73 | 12.13 |
| Middle-left panel: Automotive Vehicles and Parts | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| China | 0.09 | 0.16 | 0.24 | 0.28 | 0.44 | 0.51 | 0.58 | 0.57 | 0.64 | 0.67 | 0.8 | 0.89 | 1.08 | 1.49 |
| Asian LDCs ** | 3.62 | 3.47 | 3.29 | 3.3 | 3.95 | 3.91 | 4.12 | 3.94 | 3.75 | 4.26 | 5.2 | 6.23 | 6.6 | 6.87 |
| Total Asia *** | 40.35 | 42.12 | 40.17 | 38.51 | 38.35 | 34.54 | 31.02 | 29.8 | 28.83 | 28.28 | 29.48 | 29.86 | 30.78 | 31.8 |
| Middle-right panel: Consumer Goods | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| China | 11.01 | 13.64 | 16.17 | 18.34 | 19.99 | 20.34 | 21.32 | 22.6 | 22.68 | 22.77 | 23.18 | 23.71 | 26.23 | 29.75 |
| Asian LDCs ** | 46.74 | 48.01 | 48.01 | 47 | 47.22 | 45.23 | 43.52 | 42.68 | 41.36 | 40.75 | 40.71 | 40.42 | 41.64 | 43.85 |
| Total Asia *** | 58.96 | 59.52 | 58.59 | 57.21 | 55.71 | 52.96 | 51.04 | 49.91 | 48.2 | 47.81 | 47.55 | 46.85 | 47.47 | 49.39 |
| Bottom-left panel: Foods, Feeds and Beverages | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| China | 2.08 | 1.81 | 2.35 | 2.06 | 1.76 | 1.87 | 1.85 | 1.85 | 1.86 | 2.15 | 2.4 | 2.64 | 3.23 | 3.41 |
| Asian LDCs ** | 12.15 | 13.33 | 14.51 | 13.6 | 13.61 | 13.08 | 12.63 | 12.51 | 12.6 | 12.39 | 12.39 | 11.83 | 11.5 | 11.83 |
| Total Asia *** | 13.39 | 14.62 | 15.78 | 14.91 | 14.86 | 14.17 | 13.6 | 13.58 | 13.58 | 13.37 | 13.35 | 12.66 | 12.32 | 12.66 |
| Bottom-right panel: All Other Goods | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| China | 0.77 | 1.1 | 2.27 | 1.6 | 1.54 | 1.58 | 1.54 | 1.58 | 1.97 | 2.08 | 2.29 | 2.45 | 2.81 | 3.15 |
| Asian LDCs ** | 8.95 | 9.42 | 10.42 | 10.6 | 10.37 | 10.89 | 11.89 | 11.62 | 11.88 | 11.67 | 12.16 | 11.97 | 11.98 | 12 |
| Total Asia *** | 17.33 | 17.95 | 19.51 | 20.55 | 18.82 | 18.93 | 20.03 | 20.13 | 20.24 | 19.45 | 20.35 | 20.17 | 19.36 | 19.24 |
* 2003 projections are based on growth of 2003 January-July trade over the year-ago period.
**Asian LDCs are defined as China, Hong Kong, Indonesia, Korea, Malaysia, Philippines, Singapore, Taiwan, and Thailand.
***Total Asia is defined
as the nine Asian LDCs plus Japan.
Chart 12
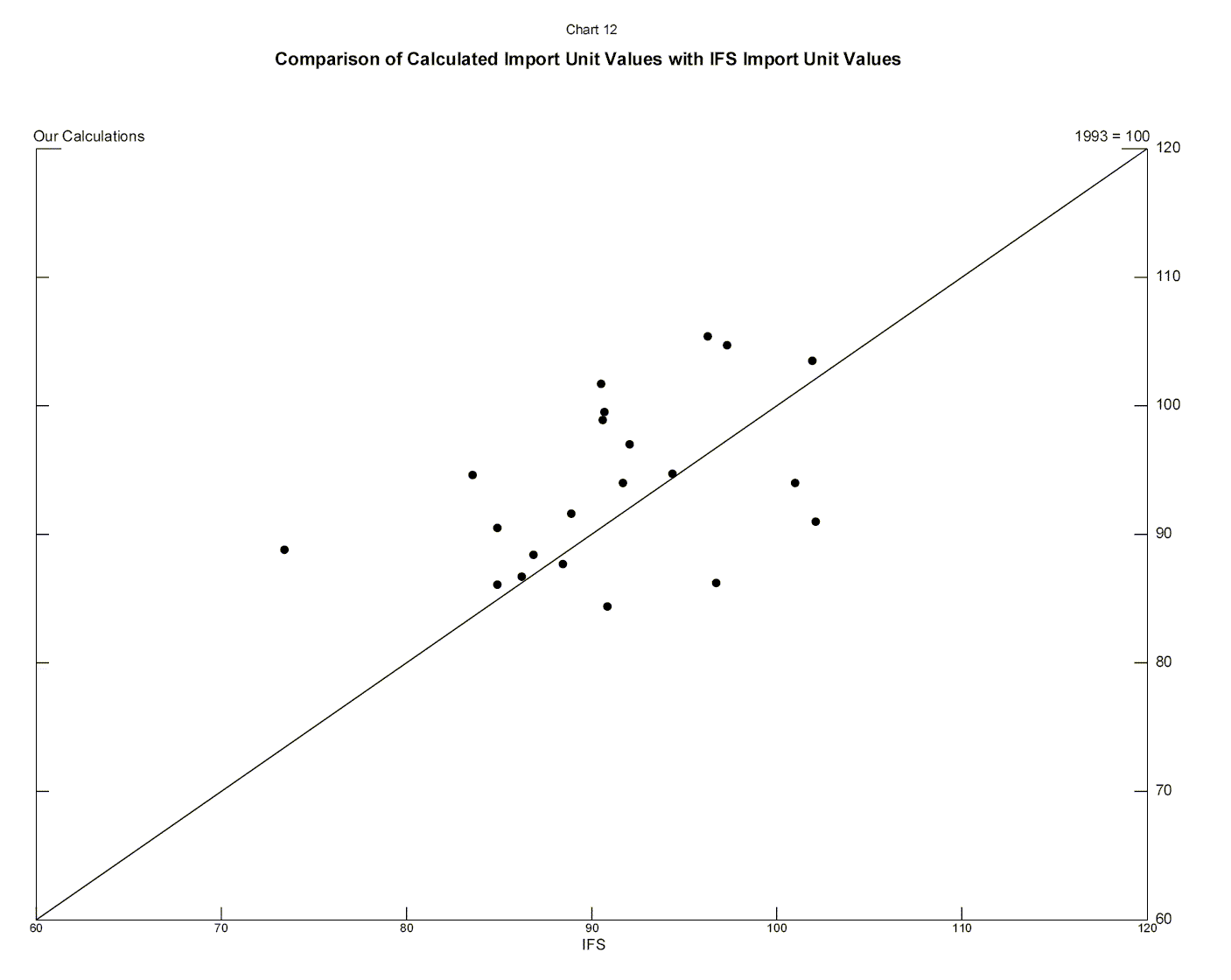
Chart 12: Comparison of Calculated Import Unit Values with IFS Import Unit Values -- See table 7.
Footnotes
1. Roach (2002a) refered to Asia as ``an exporter of deflation to the rest of the world. And China is leading the way.'' See also Kuroda and Kawai (2002), World Bank (2002), Yam (2002), Leggett and Wonacott (2002), Becker and Andrews (2003), Kynge and Roberts (2003), and Lahart (2003), among others. Return to text
2. See, among others, Anderson (2002), Noland and Posen (2002), Clark, Higgins, and Yi (2003), Fels (2003), Hanke (2003), Hu (2003), and Jenkins (2003). Return to text
3. Roach (2002b), among others, cites the low share of imports from China in U.S. GDP as a reason why these imports are unlikely to impact the general price level. Return to text
4. See, among other, Morrison and Swann (2003) and Kilman (2003). Return to text
5. While some research (IMF, 2003) has looked into the impact of China's CPI inflation on foreign inflation, it is generally understood that it is Chinese exports and export prices that are most likely to be influencing foreign prices. Anderson (2002) provides a broad-ranging and insightful analysis of China's impact on foreign activity and prices, but does not provide estimates of aggregate effects. Young (2003) takes a general look at China's impact on prices in Japan, but does not come up with estimates of the effect. Return to text
6. See Fels (2003) and Jenkins (2003). Return to text
7. Various analysts have noted that macroeconomic activity in China's trading partners could benefit from improved terms of trade against China, particularly in sectors that do not compete much with imports from China; see Fels (2003), Jenkins (2003), Testa (2003), Wolf (2003), EAU (2003), and IMF (2003). Return to text
8. A variant on this channel would be a reduction in non-labor production costs, such as might arise if imported intermediate goods from China were cheaper than those produced domestically or imported from other countries. Return to text
9. There is no consensus on the role of import prices in the decline in U.S. inflation during the 1990s. See, among others, Hogan (1998), Tootell (1998), Chan-Lau and Tokarick (1999), Gamber and Hung (2001), and Ihrig and Marquez (2003). Return to text
10. More formally, we express the
import price in end-use sector i, P![]() , as a weighted average of the prices of imports
from China, P
, as a weighted average of the prices of imports
from China, P![]() , and
from the rest of the world (excluding the United States)
P
, and
from the rest of the world (excluding the United States)
P![]() ; the weights
are shares of U.S. imports from China and the rest of the
world.
; the weights
are shares of U.S. imports from China and the rest of the
world.
P![]() = Share
= Share![]() P
P![]() + Share
+ Share![]() P
P![]() = Share
= Share![]() P
P![]() + (1- Share
+ (1- Share![]() P
P![]()
Totally differentiating and expressing in percent changes:
%![]() P
P![]() = %
= %![]() P
P![]() (P
(P![]() /P
/P![]()
+ ![]() Share
Share![]() [(P
[(P![]() - P
- P
![]() /P
/P![]() ]
]
+ Share![]() [%
[%![]() P
P![]() (P
(P![]() /P
/P![]() - %
- %![]() P
P![]() (P
(P![]() /P
/P![]() ] Return to
text
] Return to
text
11. These considerations imply that
in addition to the direct, arithmetic linkages between import
inflation %![]() P
P![]() and
the share variables
and
the share variables ![]() Share
Share![]() and Share
and Share![]() described in footnote 11, the share variables
may affect import inflation indirectly via their effect on prices
of goods imported from other countries, %
described in footnote 11, the share variables
may affect import inflation indirectly via their effect on prices
of goods imported from other countries, %![]() P
P![]() . Return to
text
. Return to
text
12. An offsetting factor, however, is that in cases where Chinese prices are falling more rapidly than those of other exporters, this will by itself depress China's share in the value of U.S. imports. Quantity shares would thus be more useful here than value shares; unfortunately, data on U.S. bilateral trade volumes are not available. Return to text
13. For the sake of robustness, the SITC classification scheme was also employed. The results obtained were essentially identical. Return to text
14. One notable exception was in computer trade (i.e. sector 21300). Despite a lapse in the price data in 1994, we decided the computer sector was too important to drop from our regressions. As a result, we have decided to treat the computer sector (both import shares and prices) as starting in 1995 in all of our import price regressions. All variables used are on an annualized basis. Thus, this problem will not affect our results too much, as long as the relationship between computer prices and imports did not change much between the 1993-1995 and 1995-2002 periods. Return to text
15. Because many Chinese exports to the United States are exported first to Hong Kong and then re-exported to the United States, it is likely that measured Chinese exports, by themselves, under-estimate total Chinese exports to the United States. Therefore, we also estimated the regressions shown in Table 4 using the combined share of Chinese and Hong Kong exports to the United States as the explanatory variable. However, the regressions results remained essentially unchanged. Return to text
16. Declines in import prices likely weighed on consumer prices of goods where imports figured prominently; however, the CPI and import prices are disaggregated on very different bases, so it is difficult to compare sectoral movements in consumer and import prices. Return to text
17. Estimates of the short-term coefficient on import price inflation in Phillips curve equations for the U.S. economy range from 0 (or insignificant) to somewhat over 0.1, with several in the range of 0.04 - 0.07. See Hogan (1998), Tootell (1998), Chan-Lau and Tokarick (1998), Gamber and Hung (2001), and Ihrig and Marquez (2003). Return to text
18. Testa (2003) notes that "imports can consist of intermediate components that become embodied in domestic production of a final good. To the extent that such components are most cheaply sourced overseas, they may keep domestic production competitive for the final good in the domestic market ..." Campa and Goldberg (1997) calculate that imported inputs accounted for about 8 percent of the value of U.S. manufacturing production in 1995. Return to text
19. The use of the combined China + Hong Kong share of U.S. imports instead of China alone did not alter these results significantly. Return to text
20. This analysis follows closely on that described in Gamber and Hung (2001). Return to text
21. Our specification is based on the premise that the greater the share of total imports in the domestic market for a good, the greater will be the impact of import prices on domestic producer prices of that good; with the share of Chinese imports in total imports having been shown, in Section III, to affect overall import prices, we thus interact it with the IPR as shown in equation (19). An alternative approach would be to estimate the impact on producer prices of the penetration of imports from China alone in domestic markets; however, in separate regressions (not shown) we found that neither this share-(imports from China)/(domestic shipments + imports - exports)-nor its rate of change was significant in equations for sectoral producer price inflation. Return to text
22. Prior findings on the effects of overall imports and import prices on producer prices have been mixed. Gamber and Hung (2001) find significant and sizeable effects of import prices on producer prices, whereas Swagel (1995) generally does not. Revenga (1992) finds significant effects of import prices on wage rates. Return to text
23. See Leggett and Wonacott (2002) and Becker and Andrews (2003). Return to text
24. Anderson (2002) argues that China's deflationary effect on foreign producer prices is limited to the labor-intensive light manufacturing in which China has the greatest comparative advantage; even in this area, he adds, the impact on foreign prices has been relatively small. Focusing on high-tech products, Valletta (2003) notes "at this time, China's IT sector focuses primarily on assembly of less-advanced products at low cost, which does not threaten the U.S. dominance in leading-edge technology and innovative products." Return to text
25. Testa (2003) notes that notwithstanding its low share in the total U.S. market, "China has become a dominant player in individual product categories, especially those that are very labor intensive. In particular, our estimates suggest a Chinese market share for the U.S. of over one-half for certain categories of dolls and stuffed toys, fur and leather apparel, and women's handbags." Cox and Koo (2003) also document China's prominence in selected import categories. Return to text
26. See, among others, Anderson (2002), Lardy (2003), Taylor (2003), Day (2003), and U.S. International Trade Commission (2003). Return to text
27. The number of categories reported varies from country to country, as does the date range. Thus, results for some countries do not cover the same date range, and other countries had to be dropped due to insufficient data. Return to text
28. The indices are largely robust to the thresholds chosen so long as the upper and lower thresholds are moved symmetrically and until there arise extreme values, where the inclusion or exclusion of a single observation can make a large difference in the overall value of the index. The upper threshold eliminated on the order of 200 categories per country and the lower threshold about 230, though both numbers varied considerably across countries. Return to text
29. We believe that such large changes are most likely reflective of errors in the data rather than actual large price swings, and because some of the those observations had a large influence on the calculation of the China effect, it was necessary to find an objective way of deleting them. We intentionally erred on the side of eliminating too many rather than too few observations to ensure that whatever remained was predominantly error free. Return to text
30. In addition to calculating price indices using Laspayres indices, we recalculated the indices using Paasche indices. The results were broadly similar after accounting for the known downward bias in Paasche indices. Return to text
31. The reasons our calculations might not agree with the numbers reported in IFS include: (1) some countries report import price indices in IFS as opposed to import unit value indices, (2) the method used to calculated the indices used in IFS vary from country to country and include Laspeyres, Paasche, and Fischer formulas, and (3) some countries may have changed the way they calculate the indices over time. Return to text
32. In practice, we sometimes used a variant of this equation to decompose the growth rates of import unit values between time t-n (1993) and t (2001):
%![]() P
P![]() = %
= %![]() P
P![]() (P
(P![]() /P
/P![]()
+ Share
![]() [(P
[(P
![]() - P
- P
![]() /P
/P![]() ]
]
- Share
![]() [(P
[(P
![]() - P
- P
![]() /P
/P![]() ]]
]]
Unlike equation (21), this formulation permits us to calculate
China's contribution to import unit value growth when it has not
exported anything in the first period, and hence %![]() P
P![]() is undefined. Return to text
is undefined. Return to text
33. All of the annual averages were calculated by dividing the overall effect found for the period by the length of the sample (eight years in most cases, but seven years for Korea, Poland, and Sweden). The mathematically correct formula involves raising the growth in unit values to the 1/8th power, but this simple average maintains the additivity of the results, and hence the ability to break down the overall effect and the China effect into their components. Using the mathematically correct way of calculating the average would make them slightly smaller. Return to text
34. Calculation of the China price effect and China share effect is slightly more complicated when China's share is zero in either 1993 or 2001. In those cases, the China price effect is zero, because no unit-value change can be calculated. If China's share is positive in either period, however, the China share effect can be calculated using the following formula:
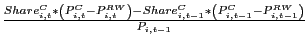 ,
,
which comes from the derivation of (21) and was mentioned earlier in footnote 33. In addition to the calculations shown in Table 8a, we redid the analysis using only those categories of goods for which China's share was positive in both 1993 and 2001, thus obviating the need to use this alternate formula to calculate the China share effect. The results from that analysis were broadly similar and are shown in Table 8b. Return to text
35. We have not included a lagged dependent variable, as the 1997 data we pulled for this purpose resulted in a negative and improbably precise coefficient on this term. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.