An Example Calling the MATLAB Implementation of AIM
This model is from Jeffrey C. Fuhrer's June 2000 AER Paper "Habit Formation in Consumption and Its Implications for Monetary Policy". The paper argues that the inclusion of habit formation in the consumer's utility function improves the short-run dynamic behavior of the model. The data on real consumption spending exhibit a hump-shaped response to monetary shocks. Habit formation allows the model to match the delayed response of real spending to shocks. In addition, the more gradual response in real spending implies a more gradual response of inflation to policy shocks.
The consumption function is derived from the utility function
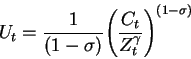
where Z is the habit-formation reference consumption level, defined as
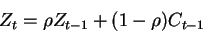
The Habit Formation Model
The Euler equation is expressed as:
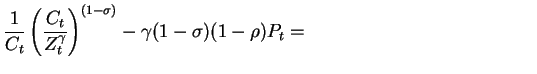
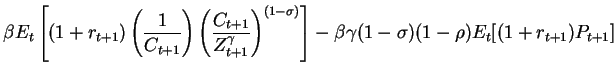
where
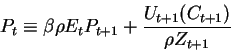
The Linear System to Estimate
The approximate log-linear consumption function:
![c sub(t) minus y sub(t) equals E sub(t) times the summation from j equals 1 to infinity of the quantity mu to the j times [ delta y sub(t+j) plus a_star sub(1) times the quantity p sub(t+j+1) minus p sub(t+j) plus a_star sub(2) times the quantity z sub(t+j+1) minus z sub(t+j) minus delta times r sub(t+j+1) ]](https://www.federalreserve.gov/econresdata/ama/images/img5.gif)
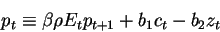
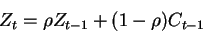
The ex-ante real interest rate is defined as discounted weighted average of future short-term real interest rates:
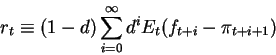
Using the Anderson Moore Algorithm
The AIM routine requires three input files:
- A model file in MDLEZ syntax.
- A parameter file.
- A script to execute AIM.
Model Representation in MDLEZ
AIM requires an equation for each variable in the system. Some could be simple AR(1), VAR equations, or behavioral equations with or without restrictions. AIM will solve the complete system simultaneously for the saddle point solution. Also note, that the infinite lead equations have to be transformed to first order conditions.
Here is what the MODELEZ file for our example looks like.
Below we will explain each line of the file.
MODEL > habitrot
ENDOG >
cnsndt
c_
yddt
rff
pdotcpix
rreal
z
P
pvdy
pvdP
pvdz
one
EQUATION > cnsndt
EQ > cnsndt - yddt = c0*one + (1-lambda)*pvdy + (1-lambda)*((gam*(1-sig)*(1-rho))/sig)*pvdP +
(1-lambda)*(((1-sig)*gam)/sig)*pvdz - (1-lambda)*(delt/sig)*rreal + c_
EQUATION > c_
EQ > c_ = acc*LAG(c_,1)
EQUATION > yddt
EQ > yddt =
0.42308 * LAG(cnsndt ,1)
-0.22215 * LAG(cnsndt ,2)
+0.71526 * LAG(cnsndt ,3)
-0.52802 * LAG(cnsndt ,4)
+0.61076 * LAG(yddt ,1)
+0.14172 * LAG(yddt ,2)
-0.042076 * LAG(yddt ,3)
-0.11279 * LAG(yddt ,4)
+0.10946 * LAG(rff ,1)
-0.26679 * LAG(rff ,2)
+0.22829 * LAG(rff ,3)
-0.031833 * LAG(rff ,4)
-0.17172 * LAG(pdotcpix,1)
+0.11959 * LAG(pdotcpix,2)
+0.012267 * LAG(pdotcpix,3)
-0.024734 * LAG(pdotcpix,4)
+0.00011277 * one
EQUATION > rff
EQ > rff =
0.46672 * LAG(cnsndt ,1)
-1.06382 * LAG(cnsndt ,2)
+1.34250 * LAG(cnsndt ,3)
-0.46436 * LAG(cnsndt ,4)
+0.11369 * LAG(yddt ,1)
+0.02255 * LAG(yddt ,2)
-0.16794 * LAG(yddt ,3)
-0.16131 * LAG(yddt ,4)
+1.10657 * LAG(rff ,1)
-0.51594 * LAG(rff ,2)
+0.35818 * LAG(rff ,3)
-0.02744 * LAG(rff ,4)
+0.26021 * LAG(pdotcpix,1)
-0.08949 * LAG(pdotcpix,2)
+0.09837 * LAG(pdotcpix,3)
-0.17087 * LAG(pdotcpix,4)
+0.00141 * one
EQUATION > pdotcpix
EQ > pdotcpix =
0.56316 * LAG(cnsndt ,1)
-0.70552 * LAG(cnsndt ,2)
-0.03313 * LAG(cnsndt ,3)
+0.23292 * LAG(cnsndt ,4)
+0.08268 * LAG(yddt ,1)
+0.24697 * LAG(yddt ,2)
-0.15223 * LAG(yddt ,3)
-0.08512 * LAG(yddt ,4)
+0.16054 * LAG(rff ,1)
-0.21888 * LAG(rff ,2)
-0.01572 * LAG(rff ,3)
+0.04213 * LAG(rff ,4)
+0.68637 * LAG(pdotcpix,1)
+0.07805 * LAG(pdotcpix,2)
+0.34762 * LAG(pdotcpix,3)
-0.14149 * LAG(pdotcpix,4)
+0.00348 * one
EQUATION > rreal
EQ > rff - LEAD(pdotcpix,1) = rreal - 40.0*(LEAD(rreal,1) - rreal)
EQUATION > z
EQ > z = rhoz*LAG(z,1) + (1-rhoz)*LAG(cnsndt,1)
EQUATION > P
EQ > P = bet*rhoz*LEAD(P,1) + (((rho-sig)/(1-sig))*cnsndt - ((gam*(1-sig)-1)*(1-sig))*z)
EQUATION > pvdy
EQ > pvdy = rho*LEAD(pvdy,1) + (LEAD(yddt,1) - yddt)
EQUATION > pvdP
EQ > pvdP = rho*LEAD(pvdP,1) + (LEAD(P,1) - P)
EQUATION > pvdz
EQ > pvdz = rho*LEAD(pvdz,1) + (LEAD(z,1) - z)
EQUATION > one
EQ > one = LAG(one,1)
END
The MDLEZ syntax of the linear model:
- MODEL>
- The name of the model.
- ENDOG>
- The names of the endogenous variables. In the AIM formulation, models must completely describe the long-run behavior of the system. Thus all variables are endogenous. "Exogenous variables must have, at least, a trivial forecasting equation.
- EQUATION>
- The name of the equation.
- EQ>
- The model equation definition.
The parameter file for our example called habitmodparams.m:
% New parameter estimates c0 = 0.11490; lambda = 0.25882; gam = 0.79706; sig = 6.11251; rho = 0.99578; delt = 28.48666; acc = 0.88879; rhoz = 0.00147; bet = 0.99900; % Like values: 2366.38
The following script, which we call runhabitmod.m, executes AIM for the habit model:
dirnam='./'; % directory of this example parnam='habitmodparams'; modnam='habitmod'; [cof, scof, cofb, param_, eqname_,... endog_, eqtype_, vtype_, neq, nlag, nlead, rts, lgrts,aimcode]=... SPSolve(dirnam, modnam, parnam);
Sample run of the habit model:
Change the directory to the directory where the script resides:
In our example:
The script to run aim is: runhabitmod.m
The model file name is: habitmod
The parameter file name is: habitmodparams.m
mqmx3(174)% cd ~/yourPathTo/examples/habitmod
Call matlab and run the script
msulx1(127)% matlab -nodesktop
< M A T L A B >
Copyright 1984-2005 The MathWorks, Inc.
Version 7.0.4.352 (R14) Service Pack 2
January 29, 2005
To get started, type one of these: helpwin, helpdesk, or demo.
For product information, visit www.mathworks.com.
>> addpath('~/sp_solve')
addpath('~/sp_solve')
>> runhabitmod
runhabitmod
SPSolve version:($Name: $,$Revision: 1.4 $)
ans =
found Aim on system classpath
initializing parsers
Aim Java Parser Version 1.03: Reading from file ./habitmod...
Aim Java Parser Version 1.03: No syntactic errors found.
Checking for errors......
No semantic errors found.
chose modelez parser
>>
Displaying the results:
In the output below:
"cof" is the structural coefficients matrix (neqs by neqs*(nlag+nlead+1))
"cofb" is the reduced form coefficients matrix (neqs by neqs * nlag)
"scof" is the observable structure matrix (neqs by neqs*(nlag+1))
"rts" returns the eigenvector
"aimerr(aimcode)" returns a diagnostic message about the model
where: "neq" = number of equations
"nlag" =number of lags
"nlead" =number of leads
cof =
Columns 1 through 7
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0.5280 0 0.1128 0.0318 0.0247 0 0
0.4644 0 0.1613 0.0274 0.1709 0 0
-0.2329 0 0.0851 -0.0421 0.1415 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 8 through 14
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 -0.7153 0
0 0 0 0 0 -1.3425 0
0 0 0 0 0 0.0331 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 15 through 21
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0.0421 -0.2283 -0.0123 0 0 0 0
0.1679 -0.3582 -0.0984 0 0 0 0
0.1522 0.0157 -0.3476 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 22 through 28
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0.2221 0 -0.1417 0.2668
0 0 0 1.0638 0 -0.0226 0.5159
0 0 0 0.7055 0 -0.2470 0.2189
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 29 through 35
0 0 0 0 0 0 0
0 0 0 0 0 0 0
-0.1196 0 0 0 0 0 0
0.0895 0 0 0 0 0 0
-0.0780 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 36 through 42
0 0 0 0 0 0 0
0 0 -0.8888 0 0 0 0
0 -0.4231 0 -0.6108 -0.1095 0.1717 0
0 -0.4667 0 -0.1137 -1.1066 -0.2602 0
0 -0.5632 0 -0.0827 -0.1605 -0.6864 0
0 0 0 0 0 0 0
0 -0.9985 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 43 through 49
0 0 0 0 0 0 1.0000
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
-0.0015 0 0 0 0 0 0
0 0 0 0 0 0 -1.0008
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 -1.0000 0
Columns 50 through 56
-1.0000 -1.0000 0 0 3.4542 0 0
1.0000 0 0 0 0 0 0
0 1.0000 0 0 0 0 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 0 0
0 0 1.0000 0 -41.0000 0 0
0 0 0 0 0 1.0000 0
0 0 0 0 0 25.9459 1.0000
0 1.0000 0 0 0 0 0
0 0 0 0 0 0 1.0000
0 0 0 0 0 1.0000 0
0 0 0 0 0 0 0
Columns 57 through 63
-0.7412 0.0021 0.4941 -0.1149 0 0 0
0 0 0 0 0 0 0
0 0 0 -0.0001 0 0 0
0 0 0 -0.0014 0 0 0
0 0 0 -0.0035 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
1.0000 0 0 0 0 0 -1.0000
0 1.0000 0 0 0 0 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 0 0
Columns 64 through 70
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 -1.0000 40.0000 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 -0.0015 0 0
0 0 0 0 0 -0.9958 0
0 0 0 0 -1.0000 0 -0.9958
0 0 0 -1.0000 0 0 0
0 0 0 0 0 0 0
Columns 71 through 72
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
-0.9958 0
0 0
> cofb
cofb
cofb =
Columns 1 through 7
0.0275 0 0.0205 0.0038 0.0510 0 0
0 0 0 0 0 0 0
-0.5280 0 -0.1128 -0.0318 -0.0247 0 0
-0.4644 0 -0.1613 -0.0274 -0.1709 0 0
0.2329 0 -0.0851 0.0421 -0.1415 0 0
-0.0487 0 -0.0144 -0.0036 -0.0164 0 0
0 0 0 0 0 0 0
0.0266 0 0.0198 0.0037 0.0493 0 0
0.5215 0 0.1143 0.0309 0.0283 0 0
0.0236 0 -0.0818 0.0108 -0.1525 0 0
-0.0020 0 0.0025 -0.0006 0.0041 0 0
0 0 0 0 0 0 0
Columns 8 through 14
0 0 0 0 0 -0.1501 0
0 0 0 0 0 0 0
0 0 0 0 0 0.7153 0
0 0 0 0 0 1.3425 0
0 0 0 0 0 -0.0331 0
0 0 0 0 0 0.0964 0
0 0 0 0 0 0 0
0 0 0 0 0 -0.1450 0
0 0 0 0 0 -0.7249 0
0 0 0 0 0 0.4363 0
0 0 0 0 0 -0.0116 0
0 0 0 0 0 0 0
Columns 15 through 21
0.0803 -0.0570 0.0332 0 0 0 0
0 0 0 0 0 0 0
-0.0421 0.2283 0.0123 0 0 0 0
-0.1679 0.3582 0.0984 0 0 0 0
-0.1522 -0.0157 0.3476 0 0 0 0
-0.0262 0.0337 -0.0091 0 0 0 0
0 0 0 0 0 0 0
0.0775 -0.0550 0.0320 0 0 0 0
0.0468 -0.2292 -0.0156 0 0 0 0
-0.2465 0.1273 0.0285 0 0 0 0
0.0068 -0.0029 -0.0024 0 0 0 0
0 0 0 0 0 0 0
Columns 22 through 28
0 0 0 0.0076 0 0.1320 -0.0010
0 0 0 0 0 0 0
0 0 0 -0.2221 0 0.1417 -0.2668
0 0 0 -1.0638 0 0.0226 -0.5159
0 0 0 -0.7055 0 0.2470 -0.2189
0 0 0 -0.0178 0 -0.0276 -0.0193
0 0 0 0 0 0 0
0 0 0 0.0076 0 0.1273 -0.0009
0 0 0 0.2326 0 -0.1401 0.2714
0 0 0 -0.2488 0 -0.2211 -0.1108
0 0 0 0.0097 0 0.0037 0.0045
0 0 0 0 0 0 0
Columns 29 through 35
0.1409 0 0 0 0 0 0
0 0 0 0 0 0 0
0.1196 0 0 0 0 0 0
-0.0895 0 0 0 0 0 0
0.0780 0 0 0 0 0 0
-0.0321 0 0 0 0 0 0
0 0 0 0 0 0 0
0.1359 0 0 0 0 0 0
-0.1221 0 0 0 0 0 0
-0.0970 0 0 0 0 0 0
-0.0016 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 36 through 42
0 0.4096 0.5316 0.2817 -0.3703 -0.0072 0
0 0 0.8888 0 0 0 0
0 0.4231 0 0.6108 0.1095 -0.1717 0
0 0.4667 0 0.1137 1.1066 0.2602 0
0 0.5632 0 0.0827 0.1605 0.6864 0
0 0.0410 0.1052 -0.0349 0.1152 -0.0125 0
0 0.9985 0 0 0 0 0
0 -25.5133 0.5128 0.2718 -0.3573 -0.0069 0
0 -0.4211 0.0173 -0.6039 -0.1157 0.1539 0
0 25.5232 -0.9480 -0.4163 0.6149 0.4201 0
0 -0.9990 0.0173 0.0057 -0.0103 -0.0165 0
0 0 0 0 0 0 0
Columns 43 through 48
0.0006 0 0 0 0 0.0247
0 0 0 0 0 0
0 0 0 0 0 0.0001
0 0 0 0 0 0.0014
0 0 0 0 0 0.0035
0.0000 0 0 0 0 0.0266
0.0015 0 0 0 0 0
-0.0376 0 0 0 0 0.0239
0.0000 0 0 0 0 0.0050
0.0375 0 0 0 0 -0.1522
-0.0015 0 0 0 0 0.0051
0 0 0 0 0 1.0000
> scof
scof
scof =
Columns 1 through 7
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0.5280 0 0.1128 0.0318 0.0247 0 0
0.4644 0 0.1613 0.0274 0.1709 0 0
-0.2329 0 0.0851 -0.0421 0.1415 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 8 through 14
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 -0.7153 0
0 0 0 0 0 -1.3425 0
0 0 0 0 0 0.0331 0
0 0 0 0 0 -2.1792 0
0 0 0 0 0 0 0
0 0 0 0 0 -0.0000 0
0 0 0 0 0 0.0087 0
0 0 0 0 0 -0.0500 0
0 0 0 0 0 0.0020 0
0 0 0 0 0 0 0
Columns 15 through 21
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0.0421 -0.2283 -0.0123 0 0 0 0
0.1679 -0.3582 -0.0984 0 0 0 0
0.1522 0.0157 -0.3476 0 0 0 0
-0.4892 -0.1867 -0.5132 0 0 0 0
0 0 0 0 0 0 0
-0.0000 -0.0000 -0.0001 0 0 0 0
-0.0010 0.0010 -0.0034 0 0 0 0
0.0617 -0.0145 0.1026 0 0 0 0
-0.0025 0.0006 -0.0041 0 0 0 0
0 0 0 0 0 0 0
Columns 22 through 28
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0.2221 0 -0.1417 0.2668
0 0 0 1.0638 0 -0.0226 0.5159
0 0 0 0.7055 0 -0.2470 0.2189
0 0 0 3.8889 0 -0.8960 1.3656
0 0 0 0 0 0 0
0 0 0 0.0002 0 -0.0001 0.0001
0 0 0 0.0066 0 -0.0045 -0.0001
0 0 0 -0.2894 0 0.1680 -0.0718
0 0 0 0.0116 0 -0.0067 0.0029
0 0 0 0 0 0 0
Columns 29 through 35
0 0 0 0 0 0 0
0 0 0 0 0 0 0
-0.1196 0 0 0 0 0 0
0.0895 0 0 0 0 0 0
-0.0780 0 0 0 0 0 0
-0.7108 0 0 0 0 0 0
0 0 0 0 0 0 0
-0.0000 0 0 0 0 0 0
0.0032 0 0 0 0 0 0
-0.0604 0 0 0 0 0 0
0.0024 0 0 0 0 0 0
0 0 0 0 0 0 0
Columns 36 through 42
0 0 0 0 0 0 0
0 0 -0.8888 0 0 0 0
0 -0.4231 0 -0.6108 -0.1095 0.1717 0
0 -0.4667 0 -0.1137 -1.1066 -0.2602 0
0 -0.5632 0 -0.0827 -0.1605 -0.6864 0
0 -0.0078 0 -1.3527 -0.5530 -1.3616 0
0 -0.9985 0 0 0 0 0
0 -0.0000 0 -0.0002 0.0000 -0.0002 0
0 -0.0095 0 -0.0022 -0.0034 0.0020 0
0 0.2401 0 0.0928 0.1112 -0.0393 0
0 -0.0096 0 -0.0037 -0.0045 0.0016 0
0 0 0 0 0 0 0
Columns 43 through 49
0 0 0 0 0 0 1.0000
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 1.0785
-0.0015 0 0 0 0 0 0
0 0 0 0 0 0 -0.9634
0 0 0 0 0 0 -0.0037
0 0 0 0 0 0 0.0977
0 0 0 0 0 0 -0.0037
0 0 0 0 0 -1.0000 0
Columns 50 through 56
-1.0000 -1.0000 0 0 3.4542 0 0
1.0000 0 0 0 0 0 0
0 1.0000 0 0 0 0 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 0 0
4.2089 -1.4786 5.4462 -1.1865 -41.0000 0.0006 0
0 0 0 0 0 1.0000 0
-0.0008 -0.0004 0.0005 0.0000 0 25.9459 1.0000
-0.0172 0.9906 0.0057 0.0185 0 -0.0000 0
0.4312 0.1428 -0.2550 -0.4115 0 0.0002 1.0000
-0.0173 -0.0057 0.0102 0.0165 0 1.0000 0
0 0 0 0 0 0 0
Columns 57 through 60
-0.7412 0.0021 0.4941 -0.1149
0 0 0 0
0 0 0 -0.0001
0 0 0 -0.0014
0 0 0 -0.0035
0 0 0 1.0596
0 0 0 0
0 0 0 -0.0000
1.0000 0 0 -0.0051
0 1.0000 0 0.1277
0 0 1.0000 -0.0051
0 0 0 1.0000
> rts
rts
rts =
1.0e+02 *
6.7958
0.0112
0.0100 + 0.0000i
0.0100 - 0.0000i
0.0100
0.0100
0.0092 + 0.0009i
0.0092 - 0.0009i
0.0089
0.0071
0.0059 + 0.0027i
0.0059 - 0.0027i
-0.0013 + 0.0062i
-0.0013 - 0.0062i
-0.0029 + 0.0051i
-0.0029 - 0.0051i
-0.0023 + 0.0028i
-0.0023 - 0.0028i
0.0020 + 0.0016i
0.0020 - 0.0016i
-0.0000 + 0.0000i
-0.0000 - 0.0000i
0.0000 + 0.0000i
0.0000 - 0.0000i
> aimerr(aimcode)
aimerr(aimcode)
ans =
Aim: unique solution.
>
References
1 Gary Anderson. A reliable and computationally efficient algorithm for imposing the saddle point property in dynamic models. Unpublished Manuscript, Board of Governors of the Federal Reserve System, 1997.
2 Gary Anderson and George Moore. A linear algebraic procedure for solving linear perfect foresight models. Economics Letters, 17, 1985.
3 Michael W. Berry. Large scale sparse singular value computations. University of Tennessee, Department of Computer Science, 1996.
4 Olivier Jean Blanchard and C. Kahn. The solution of linear difference models under rational expectations. Econometrica, 48, 1980.
5 Gene H. Golub and Charles F. van Loan. Matrix Computations. Johns Hopkins, 1989.
6 E. V. Krishnamurthy. Parallel Processing: Principles and Practice. Addison-Wesley, 1989.
7 David G. Luenberger. Time-invariant descriptor systems. Automatica, 14:473-480, 1978.
8 Ben Noble. Applied Linear Algebra. Prentice-Hall, Inc., 1969.
9 J. Taylor. Conditions for unique solutions in stochastic macroeconomic models with rational expectations. Econometrica, 45:1377-1385, |SEP| 77.
10 C. H. Whiteman. Linear Rational Expectations Models: A User's Guide. University of Minnesota, 1983.