1. Home
  2. Economic Research
  3. Other Research
  4. Anderson-Moore Algorithm (AMA)
  5. Code Implemeting AMA

Anderson-Moore Algorithm (AMA)

AMA Code

Problem Statement

Characterize the dynamics of xt where

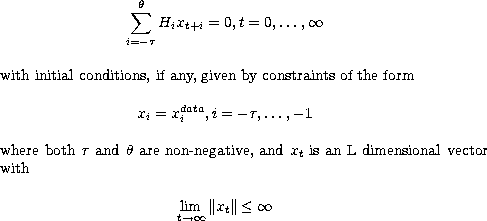
The summation (from i=-tau to theta) of H(subscript i) times x(subscript t + i) equals 0 , where t equals 0, 1, 2, ..., infinitywith initial conditions, if any, given by constraints of the form x(subscript i) equals x(subscript i; superscript data), where i equals -tau , ... , -1where both tau and theta are non-negative, and x(subscript t) is an L dimensional vectorwith the limit (as t approaches infinity) of the norm of x(subscript t) is less than or equal to infinity

Anderson-Moore Algorithm Output Matrices

Q - Asymptotic Linear Constraints Matrix such that

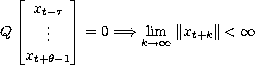
Q times the column vector containing x(subscript t - tau) ... x(subscript t + theta -1) = 0 This leads to the inequality: the limit (as k goes to infinity) of the norm of x(subscript t + k) is less than infinity

for all xt satisfying the linear homogeneous system.

B - Autoregressive Representation Matrix

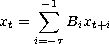
xt = the summation (from i=-tau to -1) of B(subscript i)*x(subscript t + i)

satisfies the linear homogeneous system and lim kas k goes to infinity ||xt+k|| < infinty .


S - Observable Structure Matrix
determine the existence and uniqueness of an observable structure matrix, S such that

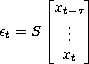
epsilon(subscript t) equals S times the column vector with elements x(subscript t - tau) to x(subscript t)

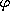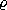phi, rho - Stochastic Transition Matrices

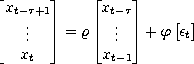
the column vector containing elements x(subscript t-tau+1) through x(subscript t) equals rho times the column vector with elements x(subscript t - tau) to x(subscript t-1) plus phi times epsilon(subscript t)

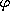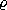The SPSolve routine computes cof(for H), cofb(for B), scof(for S), dTrans(for phi), and bTrans(for rho).

 

Back to Top
Last Update: March 17, 2017